Алгоритм форни для вычисления значений ошибок

From Wikipedia, the free encyclopedia

In coding theory, the Forney algorithm (or Forney’s algorithm) calculates the error values at known error locations. It is used as one of the steps in decoding BCH codes and Reed–Solomon codes (a subclass of BCH codes). George David Forney Jr. developed the algorithm.[1]

Procedure[edit]

Need to introduce terminology and the setup…

Code words look like polynomials. By design, the generator polynomial has consecutive roots αc, αc+1, …, αc+d−2.

Syndromes

Error location polynomial[2]

{displaystyle Lambda (x)=prod _{i=1}^{nu }(1-x,X_{i})=1+sum _{i=1}^{nu }lambda _{i},x^{i}}

The zeros of Λ(x) are X1−1, …, Xν−1. The zeros are the reciprocals of the error locations {displaystyle X_{j}=alpha ^{i_{j}}}.

Once the error locations are known, the next step is to determine the error values at those locations. The error values are then used to correct the received values at those locations to recover the original codeword.

In the more general case, the error weights ej can be determined by solving the linear system

{displaystyle s_{0}=e_{1}alpha ^{(c+0),i_{1}}+e_{2}alpha ^{(c+0),i_{2}}+cdots ,}
{displaystyle s_{1}=e_{1}alpha ^{(c+1),i_{1}}+e_{2}alpha ^{(c+1),i_{2}}+cdots ,}
{displaystyle cdots ,}

However, there is a more efficient method known as the Forney algorithm, which is based on Lagrange interpolation. First calculate the error evaluator polynomial[3]

{displaystyle Omega (x)=S(x),Lambda (x){pmod {x^{2t}}},}

Where S(x) is the partial syndrome polynomial:[4]

{displaystyle S(x)=s_{0}x^{0}+s_{1}x^{1}+s_{2}x^{2}+cdots +s_{2t-1}x^{2t-1}.}

Then evaluate the error values:[3]

{displaystyle e_{j}=-{frac {X_{j}^{1-c},Omega (X_{j}^{-1})}{Lambda '(X_{j}^{-1})}},}

The value c is often called the «first consecutive root» or «fcr». Some codes select c = 1, so the expression simplifies to:

{displaystyle e_{j}=-{frac {Omega (X_{j}^{-1})}{Lambda '(X_{j}^{-1})}}}

Formal derivative[edit]

Λ'(x) is the formal derivative of the error locator polynomial Λ(x):[3]

{displaystyle Lambda '(x)=sum _{i=1}^{nu }i,cdot ,lambda _{i},x^{i-1}}

In the above expression, note that i is an integer, and λi would be an element of the finite field. The operator · represents ordinary multiplication (repeated addition in the finite field) which is the same as the finite field’s multiplication operator, i.e.

{displaystyle ilambda =(1+ldots +1)lambda =lambda +ldots +lambda .}

For instance, in characteristic 2, {displaystyle ilambda =0,lambda } according as i is even or odd.

Derivation[edit]

Lagrange interpolation

Gill (n.d., pp. 52–54) gives a derivation of the Forney algorithm.

Erasures[edit]

Define the erasure locator polynomial

{displaystyle Gamma (x)=prod (1-x,alpha ^{j_{i}})}

Where the erasure locations are given by ji. Apply the procedure described above, substituting Γ for Λ.

If both errors and erasures are present, use the error-and-erasure locator polynomial

{displaystyle Psi (x)=Lambda (x),Gamma (x)}

See also[edit]

  • BCH code
  • Reed–Solomon error correction

References[edit]

  1. ^ Forney 1965
  2. ^ Gill n.d., p. 24
  3. ^ a b c Gill n.d., p. 47
  4. ^ Gill (n.d., p. 48)
  • Forney, G. (October 1965), «On Decoding BCH Codes», IEEE Transactions on Information Theory, 11 (4): 549–557, doi:10.1109/TIT.1965.1053825, ISSN 0018-9448
  • Gill, John (n.d.), EE387 Notes #7, Handout #28 (PDF), Stanford University, pp. 42–45, archived from the original (PDF) on June 30, 2014, retrieved April 21, 2010
  • W. Wesley Peterson’s book
Источник

Важной задачей кодологии при обработке информационных потоков кодированных сообщений в каналах систем связи и компьютерных является разделение потоков и селектирование их по заданным признакам. Выделенный поток расчленяется на отдельные сообщения и для каждого из них выполняется углубленный анализ с целью установления кода и его характеристик с последующим декодированием и доступом к семантике сообщения.

Так, например, для определенного Рида-Соломона кода (РС-кода) необходимо установить:

  • длину n кодового слова (блока);
  • количество k информационных и N-k проверочных символов;
  • неприводимый многочлен р(х), задающий конечное поле GF(2r);
  • примитивный элемент α конечного поля;
  • порождающий многочлен g(x);
  • параметр j кода;
  • используемое перемежение;
  • последовательность передачи кодовых слов или символов в канал и еще некоторые другие.

Здесь в работе рассматривается несколько другая частная задача — моделирование собственно РС-кода, являющаяся центральной основной частью названной выше задачи анализа кода.

Описание РС-кода и его характеристик

Для удобства и лучшего уяснения сущности устройства РС-кода и процесса кодирования вначале приведем основные понятия и термины (элементы) кода.

Рида – Соломона коды (РС-код) можно интерпретировать как недвоичные коды БЧХ (Боуза – Чоудхури – Хоквингема), значения кодовых символов которых взяты из поля GF(2r), т. е. r информационных символов отображаются отдельным элементом поля. Коды Рида – Соломона – это линейные недвоичные систематические циклические коды, символы которых представляют собой r-битовые последовательности, где r – целое положительное число, большее 1.

Коды Рида – Соломона (n, k) определены на r-битовых символах при всех n и k, для которых:
0 < k < n < 2r + 2, где
k – число информационных символов, подлежащих кодированию,
n – число кодовых символов в кодируемом блоке.

Для большинства (n, k)-кодов Рида – Соломона; (n, k) = (2r–1, 2r–1–2∙t), где
t – количество ошибочных символов, которые может исправить код, а
n–k = 2t – число контрольных символов.

Код Рида – Соломона обладает наибольшим минимальным расстоянием (числом символов, которыми отличаются последовательности), возможным для линейного кода. Для кодов Рида – Соломона минимальное расстояние определяется следующим образом: dmin = n–k +1.

Определение. РС-кодом над полем GF(q=рm), с длиной блока n = qm-1, исправляющим t ошибок, является множество всех кодовых слов u(n) над GF(q), для которых 2t последовательных компонентов спектра с номерами $m_0,m_0 +1,...,m_0+2t-1$ равны 0.

Тот факт, что 2t последовательных степеней α — корни порождающего многочлена g(x) или что спектр содержит 2t последовательных нулевых компонентов, является важным свойством кода, позволяющим исправлять t ошибок.

Информационный многочлен Q. Задает текст сообщения, которое делится на блоки (слова) постоянной длины и оцифровывается. Это то, что подлежит передаче в системе связи.
Порождающий многочлен g(x) РС-кода — многочлен, который преобразует информационные многочлены (сообщения) в кодовые слова путем перемножения Q·g(x)= С =u(n) над GF(q).

Проверочный многочлен h(x) позволяет устанавливать наличие искаженных символов в слове.
Синдромный многочлен S(z). Многочлен, содержащий компоненты соответствующие ошибочным позициям. Вычисляется для каждого принятого декодером слова.
Многочлен ошибок E. Многочлен с длиной равной кодовому слову, с нулевыми значениями во всех позициях, кроме тех, что содержат искажения символов кодового слова.

Многочлен локаторов ошибок Λ(z) обеспечивает нахождение корней, указывающих позиции ошибок в словах, принятых приемной стороной канала связи (декодером). Корни его могут быть найдены методом проб и ошибок, т.е. путем подстановки по очереди всех элементов поля, пока Λ(z) не станет равным нулю.
Многочлен значений ошибок Ω(z)≡Λ(z)·S(z) (modz2t) сравним по модулю z2t с произведением многочлена локаторов ошибок на синдромный многочлен.

Неприводимый многочлен поля р(x). Конечные поля существуют не при любом числе элементов, а только в случае, если число элементов является простым числом р или степенью q=рm простого числа. В первом случае поле называется простым (его элементы-вычеты чисел по модулю простого числа р), во втором-расширением соответствующего простого поля (его q элементов-многочленов степени m-1 и менее — это вычеты многочленов по модулю неприводимого над простым полем многочлена р(x) степени m)

Примитивный многочлен. Если корнем неприводимого многочлена поля является примитивный элемент α, то р(x) называют неприводимым примитивным многочленом.

В ходе изложения действий с РС-кодом нам потребуется неоднократно обращение к полю Галуа, поэтому сразу здесь поместим рабочую таблицу с элементами этого поля при разных представлениях элементов (десятичным числом, двоичным вектором, многочленом, степенью примитивного элемента).

Таблица П — Характеристики элементов конечного поля расширения GF(24), неприводимый многочлен p(x) = x4+x+1, примитивный элемент α =0010= 210

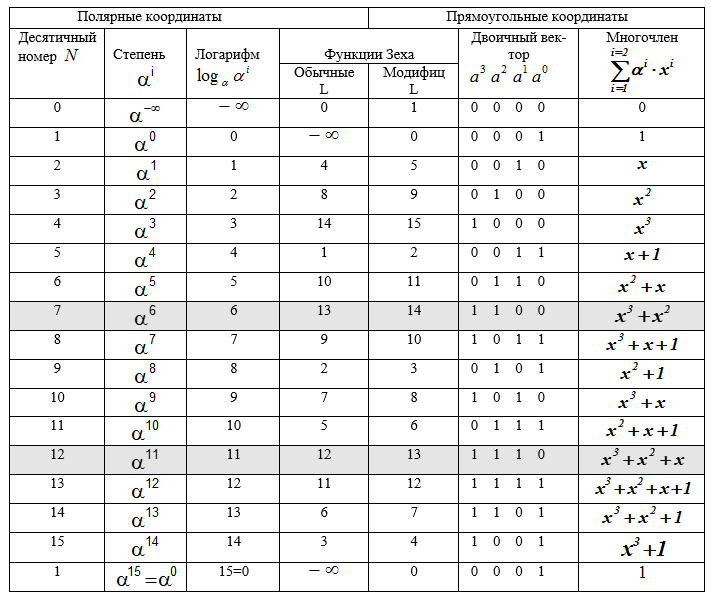
Пример 1. Над конечным полем GF(24), задан неприводимый многочлен поля p(x) = x4 + x + 1, примитивный элемент α =2, и задан (n, k)- код Рида-Соломона (РС-код). Кодовое расстояние этого кода равно d = n — k + 1 = 7. Такой код может исправлять до трёх ошибок в блоке (кодовом слове) сообщения.

Порождающий многочлен g(z) кода имеет степень m =n-k = 15-9 = 6 (его корнями являются 6 элементов поля GF(24) в десятичном представлении, а именно элементы 2, 3, 4, 5, 6, 7) и определяется соотношением, т.е. многочленом от z с коэффициентами (элементами) из GF(24) в десятичном представлении при i = 1(1)6. В рассматриваемом РС-коде 29 = 512 кодовых слов.

Кодирование сообщений РС-кодом

В таблице П эти корни имеют и степенное представление $α^1=2, α^2=3,...,α^6=7$.

Здесь z- абстрактная переменная, а α -примитивный элемент поля, через его степени выражены все (16) элементы поля. Многочленное представление элементов поля использует переменную х.
Вычисление порождающего многочлена g(x)=А·В РС-кода выполним частями (по три скобки):

Векторное представление (через коэффициенты g(z) элементами поля в десятичном представлении) порождающего многочлена имеет вид

g(z) = G<7>= (1, 11, 15, 5, 7, 10, 7).

После формирования порождающего многочлена РС-кода, ориентированного на обнаружение и исправление ошибок, задается сообщение. Сообщение представляется в цифровом виде (например, ASCII- кодом), от которого переходят к многочленному или векторному представлению.

Информационный вектор (слово сообщения) имеет k — компонентов из (n, k). В примере k = 9, вектор получается 9-компонентный, все компоненты – это элементы поля GF(24) в десятичном представлении Q<9> = (11, 13, 9, 6, 7, 15, 14, 12, 10).

Из этого вектора формируется кодовое слово u<15> — вектор с 15 компонентами. Кодовые слова, как и сами коды, бывают систематическими и несистематическими. Несистематическое кодовое слово получают умножением информационного вектора Q на вектор, соответствующий порождающему многочлену

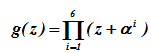
После преобразований получаем несистематическое кодовое слово (вектор) в виде
Q·g = <11, 15, 3, 9, 6, 14, 7, 5, 12, 15, 14, 3, 3, 7, 1>.

При систематическом кодировании сообщение (информационный вектор) представляют многочленом Q(z) в форме Q(z)=q(z)·g(z) + R(z), где степень degR(z)<m = 6. После этого к вектору Q справа приписывается остаток R (всё в десятичном виде). Это делается так.

Многочлен Q сдвигают в сторону старших разрядов на величину m = n — k, что достигается путём умножения Q(z) на Zn — k (в примере Zn — k = Z 6) и выполняют после сдвига деление Q(z)·Zn — k на g(z). В результате находят остаток от деления R(z). Все операции выполняют над полем GF(24)

(11, 13, 9, 6, 7, 15, 14, 12, 10, 0, 0, 0, 0, 0, 0) =
=(1, 11, 15, 5, 7, 10, 7)·(11, 15, 9, 10,12,10,10,10, 3) + (1, 2, 3, 7, 13, 9) = G·S + R.

Остаток при делении многочленов вычисляется обычным способом (уголком см.здесь Пример 6). Деление выполняется по образцу: Пусть Q = 26, g(z) = 7 тогда 26 = 7·3 +R(z), R(z)=26 -7·3 =26-21 = 5. Вычисление остатка R(z) от деления многочленов. Приписываем к вектору Q справа остаток R.

Получаем u<15> — кодовое слово в систематическом виде. Этот вид явно содержит информационное сообщение в k старших разрядах кодового слова

u<15> = (11,13,9,6,7,15,14,12,10; 1, 2, 3, 7, 13, 9)

Разряды вектора нумеруются справа налево от 0(1)14. Шесть младших разрядов справа являются проверочными.

Декодирование кодов Рида-Соломона

После получения блока декодер обрабатывает каждый блок (кодовое слово) и исправляет ошибки, которые возникли во время передачи или хранения. Декодер делит полученный многочлен на порождающий многочлен кода РС. Если остаток равен нулю, то ошибок не обнаружено, в противном случае — имеют место ошибки.

Типичный РС-декодер выполняет пять этапов в цикле декодирования, а именно:

  1. Вычисление синдромного многочлена (его коэффициентов ), обнаруживаются ошибки.
  2. Решается ключевое уравнение Падэ — вычисление значений ошибок и их позиций соответствующих местоположений.
  3. Реализуется процедура Ченя — нахождение корней многочлена локатора ошибок.
  4. Используется алгоритм Форни для вычисления значения ошибки.
  5. Вносятся корректирующие поправки в искаженные кодовые слова;

Завершается цикл извлечением сообщения из кодовых слов (снятие кода).

Вычисление синдрома.

Генерация синдрома из принятого кодового слова является первым этапом процесса
декодирования. Здесь вычисляются синдромы и определяется, есть ли ошибки в полученном кодовом слове или нет

Декодирование кодовых слов РС – кода может быть организовано разными способами. К классическим способам относится декодирование с привлечением алгоритмов, работающих во временной или в частотной области, которые используют вычисление синдрома, либо не используют. Не углубляясь в теорию этого вопроса, остановим свой выбор на декодировании с вычислением синдромов кодовых слов во временной области.

Обнаружение искажений

Синдромный $S = (S_v,S_{v+1},...,S_{m+v-1})$, где $v∊{0, 1}$ вектор последовательно определяется для каждого из полученных декодером на его входе кодовых слов. При нулевых значениях компонентов вектора синдрома $Sj = 0, j=v,v+1,...,m + v - 1$, декодер считает, что в принятом слове ошибки нет. Если же хотя бы для одного $j≥1,Sj≠0$, то декодер делает вывод о наличии ошибок в кодовом векторе и приступает к их выявлению, что является 1-м шагом работы декодера.

Вычисление синдромного многочлена
Умножение на приемной стороне кодового слова С на проверочную матрицу Н может давать в результате два исхода:

  • синдромный вектор S=0, что соответствует отсутствию ошибок в векторе C;
  • синдромный вектор S≠0, что означает наличие ошибок (одной или более) в компонентах вектора C.

Интерес представляет второй случай.

Кодовый вектор с ошибками представлен в виде C(E) =C + E, E– вектор ошибок. Тогда $(C +E)H^t = CH^t + EH^t = 0 + EH^t = S$

Компоненты Sj синдрома определяются либо соотношением суммирования
для n = q-1 и j = 1(1)m = n-k, либо схемой Горнера:

$S_j = C_0 +α^j(C_1 +α^j(C_2 +...+α^j(C_{n-2} +α^jC_{n-1})...))$

Пример 2. Пусть вектор ошибок имеет вид Е =<0 0 0 0 12 0 0 0 0 0 0 8 0 0 0>. Он искажает в кодовом векторе символы на 3-й и 10-й позициях. Значения ошибок соответственно 8 и 12 — эти значения также являются элементами поля GF(24) и заданы в десятичном (табл. П) представлении. В векторе Е нумерация позиций от младших справа налево, начиная с 0(1)14.

Сформируем теперь кодовый вектор с двумя ошибками в 3-ем разряде и в 10-ом со значениями 8 и 12 соответственно. Это осуществляется суммированием в поле GF(24) по правилам арифметики этого поля. Суммирование элементов поля с нулем не изменяет их значения. Ненулевые значения (элементы поля) суммируются после преобразования их к многочленному представлению, как обычно суммируются многочлены, но коэффициенты при неизвестной приводятся по mod 2.

После получения результата суммирования они вновь преобразуются к десятичному представлению, пройдя предварительно через степенное представление

Ниже показано вычисление искажённых ошибками значений в 10 и 3 позициях кодового слова:

$(7+12) →α^6+α^11 =x^3 +x^2 +x^3 +x^2 +x^1 =α^1 = 2,$
$(3 + 8) →α^2+ α^7 =x^2 +x^3 +x^1 + 1 =α^{12}=13.$

Декодер вычисления выполняет по общей формуле для компонентов Sj, j=1(1)m. Здесь (в модели) используем соотношение $S=EH^t$, так как E задаём (моделируем) в программе сами, то ненулевые слагаемые получаются только при i = 3 и i = 10.

Специально ниже покажем вычисления по этой формуле в развернутом виде.

Проверочная матрица РС – кода

Как только сформулирован порождающий многочлен кода, появляется возможность построения проверочной матрицы для кодовых слов, а также определение количества исправляемых ошибок (см.здесь, декодер ). Построим вспомогательную матрицу [7×15], из которой могут быть получены две разные проверочные матрицы: первые шесть строк – одна и последние шесть строк – другая.

Сама матрица формируется специальным образом. Первые две строки очевидны, третья строка и все последующие получены вычитанием из предыдущей (второй) строки отрезка чисел натурального ряда 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 по mod 15. При возникновении нулевого значения оно заменяется числом 15, отрицательные вычеты преобразуются в положительные.

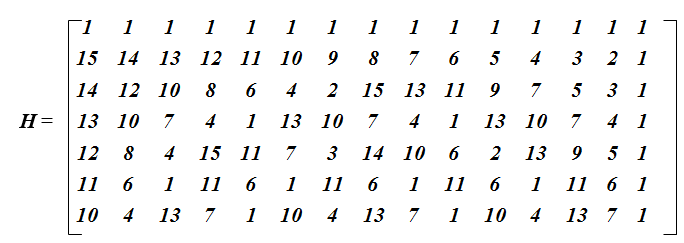
Каждая матрица соответствует своему порождающему многочлену для систематического и несистематического кодирования.

Определение коэффициентов синдромного многочлена

Далее будем определять коэффициенты синдромного многочлена при j=1(1)6.
Относительно кодового слова с длиной $n<q=p^r$, поступающего на вход декодера мы допускаем, что оно искажено ошибками.

Относительно вектора ошибок для его выявления необходимо знать следующее:

Как вычисляется и используется далее синдромный вектор (многочлен) S? Его роль при декодировании кодовых слов очень значительна. Покажем это с иллюстрацией на числовом примере.

Пример 3. (Вычисление компонентов синдромного вектора $S_{<6>}$ )

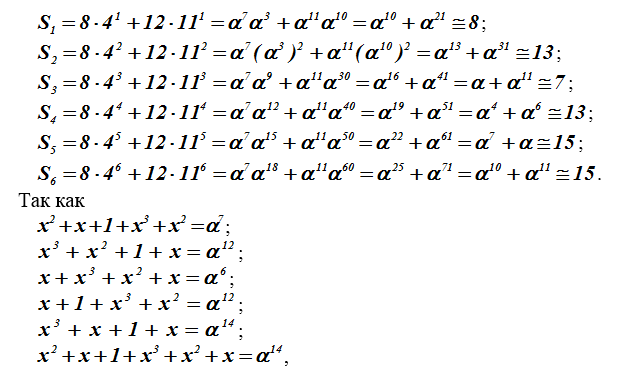
то в итоге имеем $S_{<6>}=(S_1,S_2,S_3,S_4,S_5,S_6)$ =<8,13,7,13,15,15>

Для дальнейшего рассмотрения введем новые понятия. Величину $x_i = α^{ℓ_i}$будем называть локатором ошибок, здесь искаженный символ кодового слова на позиции $ℓ_i$, α – примитивный элемент поля GF(24).

Множество локаторов ошибок конкретного кодового слова рассматривается далее как коэффициенты многочлена локаторов ошибок σ(z), корнями $z_i$ которого являются значения $x_i ^{-1}$, обратные локаторам.

При этом выражения $(1-zx_i)=0 $обращаются в нуль.

$σ(z) = (1-zx_1)(1-zx_2)...(1-zx_v) =σ_vz^v +σ_{v-1}z^{v-1} +...+σ_1z +σ_0$
всегда свободный член уравнения всегда свободный член уравнения $σ_0 =1$.
Степень многочлена локаторов ошибок равна v – количеству ошибок и не превышает величины $v≤v_{max}=0.5m$.

Все искаженные символы находятся на разных позициях слова, следовательно, среди локаторов $x_i = α^i$, не может быть повторяющихся элементов поля, а многочлен σ(z)=0 не имеет кратных корней.

Величины ошибок для удобства записи переобозначим символом $Y_i = e_i$. Для коэффициентов синдромного многочлена ранее рассматривались нелинейные уравнения. В нашем случае v=1 начало отсчета компонентов синдрома.

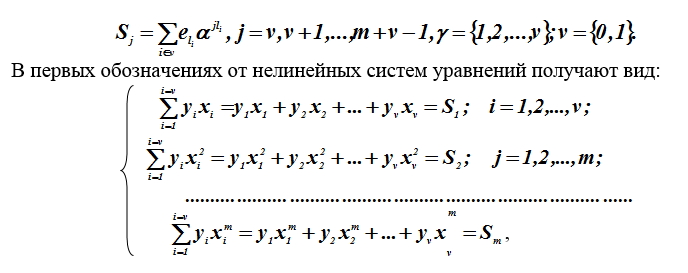
где $y_i,x_i$ — неизвестные величины, а $S_j$ — известные, вычисляемые на первом этапе декодирования, параметры (компоненты синдромного вектора).

Методы решения подобных систем нелинейных уравнений неизвестны, но решения отыскивают, используя ухищрения (обходные пути). Выполняется переход к Ганкелевой (теплицевой) системе линейных уравнений относительно коэффициентов $σ_i$ многочлена локаторов.

Преобразование к системе линейных уравнений

В уравнение $σ_i$ многочлена локаторов ошибок подставляется значение его корней $z =x_i^{-1}$. При этом многочлен обращается в нуль. Образуется тождество, обе части которого умножаем на $y_ix_i^{j+v}$, получаем:

$y_i(σ_vx_i^{j}+σ_{v-1}x_i^{j+1}+...+σ_1x_i^{j+v-1}+x_i^{j+v})=0,1≤i≤v, 1≤j≤v$.

Таких равенств получаем $v×v =v^2$

Суммируем эти равенства по всем $ i, 1≤i≤v$, при которых эти равенства выполняются. Так как многочлен σ(z) имеет v корней $x_i^{-1}$, раскроем скобки и перенесем коэффициенты $σ_i$ за знак суммы:

В этом равенстве согласно системе нелинейных уравнений, приведенной
ранее, каждая сумма равна одному из компонентов вектора синдрома. Отсюда заключает, что относительно коэффициентов $σ_v, σ_{v-1},...,σ_1$ можно выписать систему уже линейных уравнений.

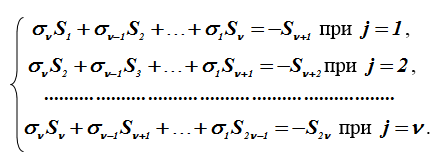
Знаки «–» при вычислениях над двоичным полем опускаются, так как со-ответствуют «+». Полученная система линейных уравнений является ганкелевой и ей соответствует матрица с размерами $v×(v+1)$ бит.

Эта матрица не вырождена, если число ошибок в кодовом слове C(E) строго равно $v , v ≤0.5(n-k)$, т.е. способность помехоустойчивости данного кода не нарушилась.

Решение системы линейных уравнений

Полученная система линейных уравнений в качестве неизвестных содержит коэффициенты $σ_i =1(1)t$ многочлена локаторов ошибок для кодового слова C(E). Известными считаются вычисленные ранее компоненты синдромного вектора $S_j, j=1(1)m$. Здесь t – количество ошибок в слове, m – количество проверочных позиций в слове.

Существуют разные методы решения сформированной системы.

Отметим, что матрица (ганкелева) не вырождена для размерностей, ограниченных количеством допустимым в отдельном слове (меньшем 0.5m) ошибок. При этом система уравнений однозначно разрешается, а задача может быть сведена просто к обращению ганкелевой матрицы. Желательно было бы снять ограничение на размерность матриц, т.е. над бесконечным полем.

Над бесконечными полями известны методы решения ганкелевой системы линейных уравнений:

  • итеративный метод Тренча – Берлекэмпа — Месси (ТБМ-метод); (1)
  • прямой детерминированный Питерсона — Горенштейна — Цирлера; (ПГЦ — метод); (2)
  • метод Сугиямы, использующий алгоритм Евклида для нахождения НОД (С-метод).(3)

Не рассматривая других методов, остановим свой выбор на ТБМ-методе. Мотивировка выбора следующая.

Метод (ПГЦ) прост и хорош, но для малого количества исправляемых ошибок, С-метод сложен для реализации на ЭВМ и ограниченно опубликован (освещен) в источниках, хотя С-метод как и ТБМ-метод по известному многочлену синдромов S(z) обеспечивает решение уравнения Падэ над полем Галуа. Это уравнение сформировано для многочлена локаторов ошибок σ(z) и многочлена ω(z), в теории кодирования называется ключевым уравнением Падэ:

$S(z)σ(z) = ω(z)(mod z^m)$.

Решением ключевого уравнения является совокупность $x_i^{-1}$ корней многочлена σ(z), и соответственно локаторов $x_i =α^{ℓ_i}$, т.е. позиции ошибок. Значения (величины) ошибок $e_i$ определяются из формулы Форни в виде

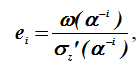
где $σ_z^{'}(α^{-i})$ и $ ω(α^{-i})$ — значения многочленов σ(z) и ω(z) в точке $z =α^{-i}$, обратной корню многочлена σ(z);
i — позиция ошибки;$σ_z^{'}(z)$ — формальная производная многочлена σ(z) по z;

Формальная производная многочлена в конечном поле

Имеются различия и сходство для производной по переменной в поле вещественных чисел и формальной производной в конечном поле. Рассмотрим многочлен

$a_i$ – это элементы поля, i = 1(1)n

Элементы поля. Задан код над вещественным полем GF(24). Производная по z имеет вид:

В бесконечном вещественном поле операции умножить на n и суммировать n раз совпадают. Для конечных полей производная определяется иначе.

Производная по аналогии определяется соотношением:

где ((i)) = 1+1+…+1, (i) раз, суммируемых по правилам конечного поля: знак + обозначает операцию «суммировать столько-то раз», т.е. элемент $a_2z$ повторить 2 раза, элемент $a_3z^2$ повторить 3 раза, элемент $a_nz^{n-1}$ повторить n раз.

Ясно, что эта операция не совпадает с операции умножения в конечном поле. В частности, в полях GF(2r) сумма четного числа одинаковых слагаемых берется по mod2 и обнуляется, а нечетного – равна самому слагаемому без изменений. Следовательно, в поле GF(2r) производная получает вид

вторая и старшие четные производные в этом поле равны нулю.

Из алгебры известно, если многочлен имеет кратные корни (кратность р ), то производная многочлена будет иметь этот же корень, но с кратностью р-1. Если р = 1, то f(z) и f ‘(z) не имеет общего корня. Следовательно, если многочлен и его производная имеют общий делитель, то существует кратный корень. Все корни производной f ‘(z) эти корни кратные в f(z).

Метод решения ключевого уравнения

ТМБ (Тренча-Берлекэмпа-Месси) — метод решения ключевого уравнения. Итеративный алгоритм обеспечивает определение многочленов σ(z) и ω(z), и решение уравнения Падэ (ключевого).

Исходные данные: коэффициенты многочлена $S_1,S_2,...,S_n$ степени n-1.
Цель. Определение в явном (аналитическом) виде многочленов σ(z) и ω(z).

В алгоритме используются обозначения: j — номер шага, $v_j$ — степень многочлена, $σ_j(z) =σ_{ji}z^i +σ_{ji-1}z^{i-1}+...+σ_{j1}z+σ_{j0}$ — разложение многочлена по степеням $z, k_j, L_j, θ_j(z)$ и $ Ω_j(z)$ — промежуточные переменные и функции на j-м шаге алгоритма;

Начальные условия необходимо задавать, так как здесь используется рекурсия.

Начальные условия:

Пример 4. Выполнение итеративного алгоритма для вектора
S=(8,13,7,13,15,15). Определяются многочлены $σ(z) =σ_n(z)$ и $ω(z) = ω_n(z)$.

Таблица 2 – Расчет многочленов локаторов ошибок

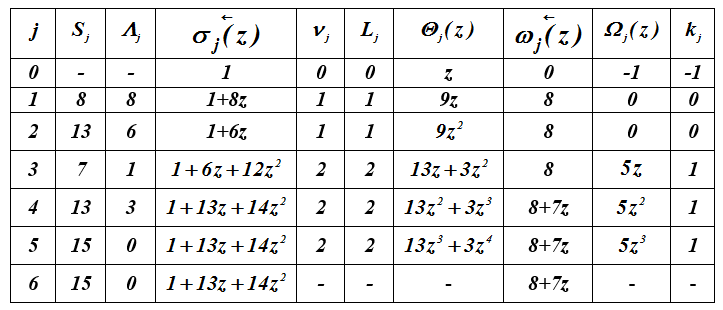
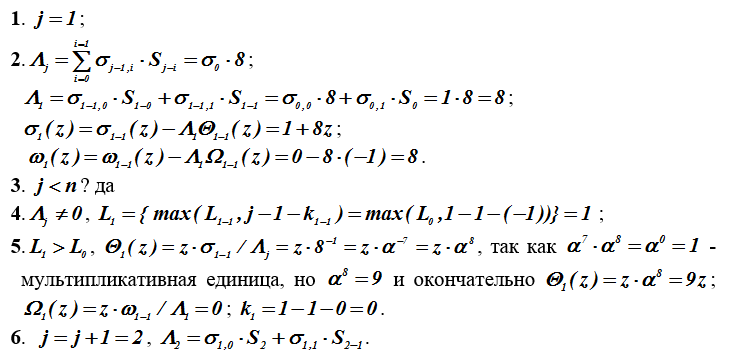
Итак $σ_j^←(z)=14z^2+13z+1$, $ω_j^←(z)$=7z+8.

Многочлен локаторов ошибок σ(z) над полем GF(24) с неприводимым многочленом p(x) = x4 + x + 1 имеет корни

$z_1 = α^{-i_1} = 13 = 4^{-1}$ и $z_2 =α^{-i_2} = 6 = 11^{-1}$, в этом легко убедиться непосредственной проверкой, т.е. $i_1= 3, i_2 =10, 13 = α^{12}, 1 =α^{12}α^{3}$ и $α^{12} =α^{-3}=>13=4^{-1}$. Подстановка корней в
$σ(z=13)=14(13)^2+13·13+1=α^{13}(α^{12})^2+(α^{12})^2+α^0= α^{37}+α^{24} +α^{0}$=
=$α^{7}+α^{9}+α^0 =x^3+x+1=0(mod2)$;
$σ(z = 6)=14(6)^2+13·6+1 = α^{13}(α^{5})^2+(α^{5})^2+α^{0}$=
=$α^{8}+α^{2} +α^{0} = x^2 +1+x^2 +1 = 0(mod2)$.

Взяв формальную производную от σ(z), получаем σ_2(z) =2·14+13 =13, так как 14z берется в сумме 2 раза и по mod 2 обращается в нуль.

С использованием формулы Форни найдем выражения для расчета величин ошибок $e_i$.

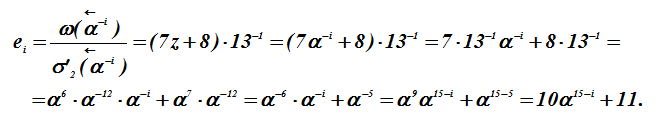
Подстановкой значений i = 3 и i = 10 позиций в последнее выражение
находим

$е_3 = 10α^{15-3}+11 =α^{6}+α^{10}$= =$x^3+x^2+x^2+x+1=x^3+x+1=α^{7}=>8$;
$е_{10} = 10α^{15-10}+11 =α^{9}α^{5}+α^{10}=α^{14}+α^{10}$= =$x^3+x^2+x=α^{11}=>12$.

Архитектура построения программного комплекса

Для построения программного комплекса предлагается использовать следующее архитектурное решение. Программный комплекс реализуется в виде приложения с графическим интерфейсом пользователя.

Исходными данными для программного комплекса является цифровой поток информации, выгруженной с помощью дампа из файла. Для удобства анализа и наглядности работы комплекса предполагается использование .txt файлов.

Загруженный цифровой поток представляется в виде массивов данных, в ходе работы комплекса над которыми применяются различные вычислительные действия.

На каждом этапе работы комплекса предоставляется возможность наглядного представления промежуточных результатов работы.

Результаты работы программного комплекса представляются в виде числовых данных, отображающихся в таблицах.

Сохранение промежуточных и окончательных результатов анализа производится в файлы.

Схема функционирования программного комплекса

Работа с комплекса начинается с загрузки цифрового потока с помощью дампа из файла. После загрузки пользователю предоставляется возможность визуального представления двоичного содержимого файла и его текстового содержимого.

В рамках данного интерфейса должны реализовываться следующие функциональные задачи:

  • Загрузка исходного сообщения;
  • Преобразование сообщения в дамп;
  • Кодирование сообщения;
  • Моделирование перехваченного сообщения
  • Построение спектров полученных кодовых слов с целью анализа их визуального представления;
  • Вывод на экран параметров кода.

Описание работы программного комплекса

При запуске исполняемого файла программы на экране появляется окно представленное на рисунке 2, в котором отображён основной интерфейс программы.

На вход программы подается файл, который нужно передать по каналу связи. Для его передачи по реальным каналам связи требуется кодирование – добавление к нему проверочных символов, необходимых для однозначного декодирования слова на источнике-получателе. Для начала работы комплекса необходимо с помощью кнопки “Загрузить файл” выбрать нужный текстовый файл. Его содержимое будет отображено в нижнем поле главного окна программы.

Двоичное представление сообщения будет представлено в соответствующем поле, двоичное представление информационных слов – в поле “Двоичное представление информационных слов”.

Число бит исходного сообщения и общее число слов в нем отображаются в полях “Количество бит в передаваемом сообщении” и “Количество слов в передаваемом сообщении”.

Сформированные информационные и кодовые слова отображаются в таблицах в правой части основного окна программы.

Окно программы с промежуточными результатами представлено на рисунке 3.

Рисунок 3 – Промежуточное представление результатов работы программного комплекса

Рисунок 4. Результаты загрузки файла сообщения

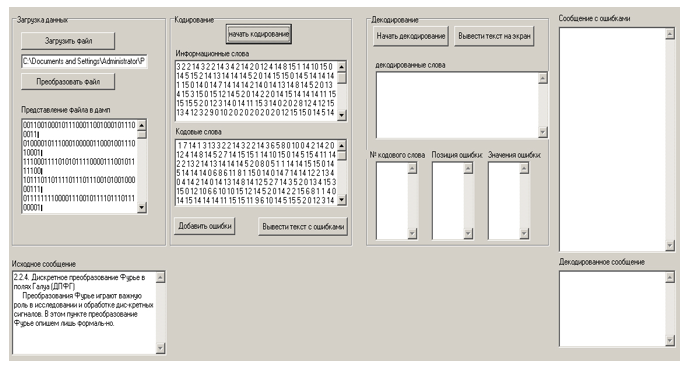
Рисунок 5. Результаты кодирования файла

Рисунок 6. Вывод сообщения с внесенными в него ошибками.

Рисунок 7. Вывод результатов декодирования и сообщения с внесенными в него ошибками


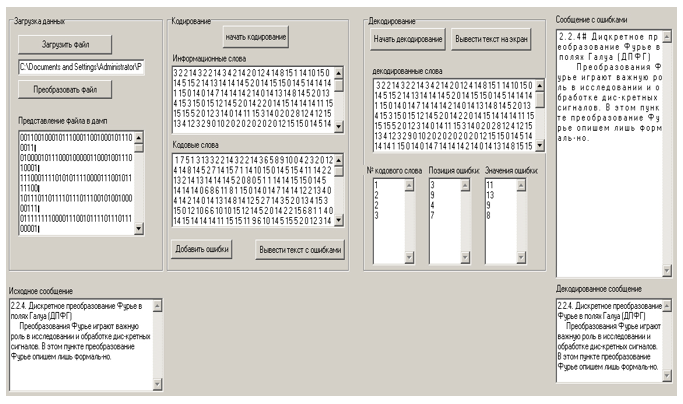
Рисунок 8. Вывод декодированного сообщения.

Заключение

АНБ США является главным оператором глобальной системы перехвата «Эшелон». «Эшелон» располагает разветвлённой инфраструктурой, включающей в себя станции наземного слежения, расположенные по всему миру. Отслеживаются практически все мировые информационные потоки.

Исследование возможностей получения доступа к семантике кодированных информационных сообщений в настоящее время активной информационной борьбы как в области технологий, так и в политике — стало очередным вызовом и одной из актуальных и востребованных задач современности.

В подавляющем большинстве кодов кодирование и декодирование сообщений (информации) реализуется на строгой математической основе конечных расширенных полей Галуа. Работа с элементами таких полей отличается от общепринятых в арифметике и требует при использовании вычислительных средств написания специальных процедур манипулирования с элементами полей.
Предлагаемая вниманию читателей работа слегка приоткрывает завесу тайны над подобной деятельностью на уровне фирм, компаний и государств в целом.

Список используемой литературы

  1. Блейхут Р. Теория и практика кодов, контролирующих ошибки. – М.: Мир, 1986. – 576 с.
  2. Мак-Вильямс Ф. Дж, Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. – М.: Связь, 1979. – 744 с.
  3. Берлекэмп Э. Алгебраическая теория кодирования. – М.: Мир, 1971. – 478 с.
  4. Габидулин Э.М., Афанасьев В.Б. Кодирование в радиоэлектронике. – М.: Радио и связь, 1986. – 176 с., ил.
  5. Вернер М. Основы кодирования. Учебник для ВУЗов. – М.: Техносфера, 2004. – 288 с.
  6. Трифонов П.В. Адаптивное кодирование в многочастотных системах. Диссертация на соискание ученой степени кандидата технических наук. – СПб: Санкт-Петербургский государственный политехнический университет, 2005. – 147 с.
  7. Фомичев С. М., Абилов А.В. Обзор математических моделей каналов связи и их применение в телекоммуникационных системах. – Ижевск: Ижевский государственный технический университет, 2001. – 60 с.
  8. Касами Т., Токура Н., Ивадари Е., Инагаки Я. Теория кодирования. – М.: Мир, 1978. – 576 с.
  9. Муттер В. М. Основы помехоустойчивой телепередачи информации. – Л.: Энергоатомиздат. Ленинградское отделение, 1990. – 288 с.
  10. Ваулин А. Е., Смирнов С.И. «Моделирование помехозащищенного канала передачи сообщения в системе связи»/Сборник алгоритмов и программ типовых задач. Вып.26. под редакцией ктн доц. И.А. Кудряшова –. СПб.: ВКА им А.Ф. Можайского, 2007. – стр. 121-130.
  11. Карпушев С.И Конспект лекций по алгебре (часть 2. Абстрактная алгебра). – ВИКУ им. А. Ф. Можайского, 2002. – 97 с.
  12. Зайцев И. Е. Методика определения параметров помехоустойчивого каскадного кодирования. – Л.: ВИКИ, 1987 – 120 с.
Источник

From Wikipedia, the free encyclopedia

In coding theory, the Forney algorithm (or Forney’s algorithm) calculates the error values at known error locations. It is used as one of the steps in decoding BCH codes and Reed–Solomon codes (a subclass of BCH codes). George David Forney Jr. developed the algorithm.[1]

Procedure[edit]

Need to introduce terminology and the setup…

Code words look like polynomials. By design, the generator polynomial has consecutive roots αc, αc+1, …, αc+d−2.

Syndromes

Error location polynomial[2]

{displaystyle Lambda (x)=prod _{i=1}^{nu }(1-x,X_{i})=1+sum _{i=1}^{nu }lambda _{i},x^{i}}

The zeros of Λ(x) are X1−1, …, Xν−1. The zeros are the reciprocals of the error locations {displaystyle X_{j}=alpha ^{i_{j}}}.

Once the error locations are known, the next step is to determine the error values at those locations. The error values are then used to correct the received values at those locations to recover the original codeword.

In the more general case, the error weights ej can be determined by solving the linear system

{displaystyle s_{0}=e_{1}alpha ^{(c+0),i_{1}}+e_{2}alpha ^{(c+0),i_{2}}+cdots ,}
{displaystyle s_{1}=e_{1}alpha ^{(c+1),i_{1}}+e_{2}alpha ^{(c+1),i_{2}}+cdots ,}
{displaystyle cdots ,}

However, there is a more efficient method known as the Forney algorithm, which is based on Lagrange interpolation. First calculate the error evaluator polynomial[3]

{displaystyle Omega (x)=S(x),Lambda (x){pmod {x^{2t}}},}

Where S(x) is the partial syndrome polynomial:[4]

{displaystyle S(x)=s_{0}x^{0}+s_{1}x^{1}+s_{2}x^{2}+cdots +s_{2t-1}x^{2t-1}.}

Then evaluate the error values:[3]

{displaystyle e_{j}=-{frac {X_{j}^{1-c},Omega (X_{j}^{-1})}{Lambda'(X_{j}^{-1})}},}

The value c is often called the «first consecutive root» or «fcr». Some codes select c = 1, so the expression simplifies to:

{displaystyle e_{j}=-{frac {Omega (X_{j}^{-1})}{Lambda'(X_{j}^{-1})}}}

Formal derivative[edit]

Λ'(x) is the formal derivative of the error locator polynomial Λ(x):[3]

{displaystyle Lambda'(x)=sum _{i=1}^{nu }i,cdot ,lambda _{i},x^{i-1}}

In the above expression, note that i is an integer, and λi would be an element of the finite field. The operator · represents ordinary multiplication (repeated addition in the finite field) and not the finite field’s multiplication operator.

Derivation[edit]

Lagrange interpolation

Gill (n.d., pp. 52–54) gives a derivation of the Forney algorithm.

Erasures[edit]

Define the erasure locator polynomial

{displaystyle Gamma (x)=prod (1-x,alpha ^{j_{i}})}

Where the erasure locations are given by ji. Apply the procedure described above, substituting Γ for Λ.

If both errors and erasures are present, use the error-and-erasure locator polynomial

{displaystyle Psi (x)=Lambda (x),Gamma (x)}

See also[edit]

  • BCH code
  • Reed–Solomon error correction

References[edit]

  1. ^ Forney 1965
  2. ^ Gill n.d., p. 24
  3. ^ a b c Gill n.d., p. 47
  4. ^ Gill (n.d., p. 48)
  • Forney, G. (October 1965), «On Decoding BCH Codes», IEEE Transactions on Information Theory, 11 (4): 549–557, doi:10.1109/TIT.1965.1053825, ISSN 0018-9448
  • Gill, John (n.d.), EE387 Notes #7, Handout #28 (PDF), Stanford University, pp. 42–45, archived from the original (PDF) on June 30, 2014, retrieved April 21, 2010
  • W. Wesley Peterson’s book

From Wikipedia, the free encyclopedia

In coding theory, the Forney algorithm (or Forney’s algorithm) calculates the error values at known error locations. It is used as one of the steps in decoding BCH codes and Reed–Solomon codes (a subclass of BCH codes). George David Forney Jr. developed the algorithm.[1]

Procedure[edit]

Need to introduce terminology and the setup…

Code words look like polynomials. By design, the generator polynomial has consecutive roots αc, αc+1, …, αc+d−2.

Syndromes

Error location polynomial[2]

{displaystyle Lambda (x)=prod _{i=1}^{nu }(1-x,X_{i})=1+sum _{i=1}^{nu }lambda _{i},x^{i}}

The zeros of Λ(x) are X1−1, …, Xν−1. The zeros are the reciprocals of the error locations {displaystyle X_{j}=alpha ^{i_{j}}}.

Once the error locations are known, the next step is to determine the error values at those locations. The error values are then used to correct the received values at those locations to recover the original codeword.

In the more general case, the error weights ej can be determined by solving the linear system

{displaystyle s_{0}=e_{1}alpha ^{(c+0),i_{1}}+e_{2}alpha ^{(c+0),i_{2}}+cdots ,}
{displaystyle s_{1}=e_{1}alpha ^{(c+1),i_{1}}+e_{2}alpha ^{(c+1),i_{2}}+cdots ,}
{displaystyle cdots ,}

However, there is a more efficient method known as the Forney algorithm, which is based on Lagrange interpolation. First calculate the error evaluator polynomial[3]

{displaystyle Omega (x)=S(x),Lambda (x){pmod {x^{2t}}},}

Where S(x) is the partial syndrome polynomial:[4]

{displaystyle S(x)=s_{0}x^{0}+s_{1}x^{1}+s_{2}x^{2}+cdots +s_{2t-1}x^{2t-1}.}

Then evaluate the error values:[3]

{displaystyle e_{j}=-{frac {X_{j}^{1-c},Omega (X_{j}^{-1})}{Lambda'(X_{j}^{-1})}},}

The value c is often called the «first consecutive root» or «fcr». Some codes select c = 1, so the expression simplifies to:

{displaystyle e_{j}=-{frac {Omega (X_{j}^{-1})}{Lambda'(X_{j}^{-1})}}}

Formal derivative[edit]

Λ'(x) is the formal derivative of the error locator polynomial Λ(x):[3]

{displaystyle Lambda'(x)=sum _{i=1}^{nu }i,cdot ,lambda _{i},x^{i-1}}

In the above expression, note that i is an integer, and λi would be an element of the finite field. The operator · represents ordinary multiplication (repeated addition in the finite field) and not the finite field’s multiplication operator.

Derivation[edit]

Lagrange interpolation

Gill (n.d., pp. 52–54) gives a derivation of the Forney algorithm.

Erasures[edit]

Define the erasure locator polynomial

{displaystyle Gamma (x)=prod (1-x,alpha ^{j_{i}})}

Where the erasure locations are given by ji. Apply the procedure described above, substituting Γ for Λ.

If both errors and erasures are present, use the error-and-erasure locator polynomial

{displaystyle Psi (x)=Lambda (x),Gamma (x)}

See also[edit]

  • BCH code
  • Reed–Solomon error correction

References[edit]

  1. ^ Forney 1965
  2. ^ Gill n.d., p. 24
  3. ^ a b c Gill n.d., p. 47
  4. ^ Gill (n.d., p. 48)
  • Forney, G. (October 1965), «On Decoding BCH Codes», IEEE Transactions on Information Theory, 11 (4): 549–557, doi:10.1109/TIT.1965.1053825, ISSN 0018-9448
  • Gill, John (n.d.), EE387 Notes #7, Handout #28 (PDF), Stanford University, pp. 42–45, archived from the original (PDF) on June 30, 2014, retrieved April 21, 2010
  • W. Wesley Peterson’s book

В теория кодирования, то Алгоритм Форни (или же Алгоритм Форни) вычисляет значения ошибок в известных местах ошибок. Он используется как один из этапов декодирования Коды BCH и Коды Рида – Соломона (подкласс кодов BCH). Джордж Дэвид Форни мл. разработал алгоритм.[1]

Процедура

Необходимо ввести терминологию и настройку …

Кодовые слова выглядят как полиномы. По замыслу порождающий полином имеет последовательные корни αc, αc+1, …, αc+d−2.

Синдромы

Многочлен определения места ошибки[2]

{ displaystyle Lambda (x) = prod _ {i = 1} ^ { nu} (1-x , X_ {i}) = 1+ sum _ {i = 1} ^ { nu} лямбда _ {i} , x ^ {i}}

Нули Λ (Икс) находятся Икс1−1, …, Иксν−1. Нули — это обратные значения местоположений ошибок. { displaystyle X_ {j} = alpha ^ {i_ {j}}}.

После того, как места возникновения ошибок известны, следующим шагом будет определение значений ошибок в этих местах. Затем значения ошибок используются для исправления полученных значений в этих местах для восстановления исходного кодового слова.

В более общем случае веса ошибок еj можно определить, решив линейную систему

{ displaystyle s_ {0} = e_ {1} alpha ^ {(c + 0) , i_ {1}} + e_ {2} alpha ^ {(c + 0) , i_ {2}} + cdots ,}
{ displaystyle s_ {1} = e_ {1} alpha ^ {(c + 1) , i_ {1}} + e_ {2} alpha ^ {(c + 1) , i_ {2}} + cdots ,}
{ Displaystyle cdots ,}

Однако существует более эффективный метод, известный как алгоритм Форни, который основан на Интерполяция Лагранжа. Сначала вычислите полином оценщика ошибок[3]

{ Displaystyle Omega (x) = S (x) , Lambda (x) { pmod {x ^ {2t}}} ,}

Где S(Икс) — полином частичного синдрома:[4]

{ Displaystyle S (x) = s_ {0} x ^ {0} + s_ {1} x ^ {1} + s_ {2} x ^ {2} + cdots + s_ {2t-1} x ^ { 2т-1}.}

Затем оцените значения ошибок:[3]

{ displaystyle e_ {j} = - { frac {X_ {j} ^ {1-c} , Omega (X_ {j} ^ {- 1})} { Lambda'(X_ {j} ^ { -1})}} ,}

Значение c часто называют «первым последовательным корнем» или «fcr». Некоторые коды выбирают c = 1, поэтому выражение упрощается до:

{ displaystyle e_ {j} = - { frac { Omega (X_ {j} ^ {- 1})} { Lambda'(X_ {j} ^ {- 1})}}}

Формальная производная

Λ ‘(Икс) это формальная производная полинома локатора ошибок Λ (Икс):[3]

{ displaystyle Lambda'(x) = sum _ {i = 1} ^ { nu} i , cdot , lambda _ {i} , x ^ {i-1}}

В приведенном выше выражении обратите внимание, что я — целое число, а λя был бы элементом конечного поля. Оператор · представляет собой обычное умножение (повторное сложение в конечном поле), а не оператор умножения конечного поля.

Вывод

Интерполяция Лагранжа

Гилл (без даты., pp. 52–54) дает вывод алгоритма Форни.

Стирания

Определите полином локатора стирания

{ displaystyle Gamma (x) = prod (1-x , alpha ^ {j_ {i}})}

Где места стирания указаны jя. Примените процедуру, описанную выше, заменив Λ Γ.

Если присутствуют и ошибки, и стирания, используйте полином локатора ошибок и стирания

{ Displaystyle пси (х) = лямбда (х) , гамма (х)}

Смотрите также

  • Код BCH
  • Исправление ошибок Рида – Соломона

Рекомендации

  1. ^ Форни 1965
  2. ^ Гилл н.д., п. 24
  3. ^ а б c Гилл н.д., п. 47
  4. ^ Гилл (без даты., п. 48)
  • Форни, Г. (Октябрь 1965 г.), «О декодировании кодов BCH», IEEE Transactions по теории информации, 11 (4): 549–557, Дои:10.1109 / TIT.1965.1053825, ISSN  0018-9448
  • Джилл, Джон (нет данных), EE387 Заметки № 7, Раздаточный материал № 28 (PDF), Стэнфордский университет, стр. 42–45, заархивировано оригинал (PDF) 30 июня 2014 г., получено 21 апреля, 2010
  • В. Уэсли Петерсон книга

внешняя ссылка

Макеты страниц

Уяснение работы декодера Пнтерсоиа-Горенстейна-Цирлера — лучший путь к пониманию процесса декодирования кодов БЧХ. Но при построении декодера приходится жертвовать концептуальной ясностью во имя вычислительной эффективности. Опи

санный в § 7.2 декодер Питерсона-Горенстейна-Цирлера предполагает обращение двух матриц размера Хотя обращение матрицы в конечном поле не приводит к ошибкам округления, вычислительная работа, особенно для больших значений может оказаться чрезмерно большой. В то же время обращения обеих матриц можно избежать. Обращение первой матрицы, необходимое для вычисления многочлена локаторов сшибок, можно обойти, используя алгоритм Берлекэмпа-Месси. Обращение второй матрицы, необходимое для вычисления значений ошибок, можно обойти, воспользовавшись процедурой, носящей название алгоритма Форнн. Этот параграф начнется с описания алгоритма Форни, а затем будет продолжено рассмотрение алгоритма Берлекэмпа-Месси.

Для описания алгоритма Форни нам понадобится многочлен локаторов ошибок

имеющий корни

Определим синдромный многочлен

и многочлен значений ошибок

Многочлен значений ошибок будет иногда использоваться в дальнейших рассуждениях. Его связь с локаторами и значениями ошибок устанавливается следующей теоремой.

Теорема 7.5.1. Многочлен значений ошибок можно записать в следующем виде:

Доказательство. Из определения сомножителей, входящих в равенство для получаем

Выражение в квадратных скобках является разложением для Таким образом,

Последнее выражение, взятое по модулю совпадает с выражением, которое требуется доказать. Тем самым теорема доказана.

Теперь все готово для того, чтобы выписать выражение для значений ошибок, которое намного проще аналотнчного выражения, использующего обращение матрицы.

Теорема 7.5.2 (алгоритм Форни). Значения ошибок получаются из равенства

Доказательство. Используя равенство из утверждения теоремы 7.5.1 при получим

откуда вытекает первая часть теоремы.

С другой стороны, производная многочлена равна

и таким образом,

откуда сразу следует утверждение теоремы.

Алгоритм Форни обладает существенным преимуществом перед обращением матрицы, но использует деление. В гл. 9 будет предложено другое решение, не использующее деление.

Теперь вернемся к вычислению многочлена локаторов ошибок, использующему алгоритм Берлекэмпа-Месси теоремы 7.4.1. Предложенный Месси вариант решения этой задачи показан на рис. 7.4, а. По заданным находится вектор минимальной длины, удовлетворяющий уравнениям

Это означает, что требуется по заданным 21 компонентам вектора из свертки вычислить вектор А, если априори известно,

Рис. 7.4. Генерации спектра ошибок, а — вариант Месси; б — вариант Берлекэмпа.

что Удовлетворяющий этому равенству вектор определяет коэффициенты многочлена локаторов ошибок

где являются локаторами ошибок. Многочлен значений ошибок не вычисляется с помощью этого алгоритма, но получается позже из и согласно определению

Вариант Берлекэмна решения этой задачи показан на рис. 7.4.6, из которого видно, что многочлену значений ошибок отводится центральная роль. Такой вариант предполагает поиск векторов компоненты которых рапиы нулю при К. и удовлетворяют 11 уравнениям

где при . Заметим, что пробегает значений. Решение задачи чается двумя многочленами: многочленом локаторов ошибок и многочленом значений ошибок.

Два описанных выше варианта эквивалентны. В дальнейшем будет рассмотрен варнант, предложенный Мессн При

необходимости алгоритм Берлекэмпа-Месси можно преобразовать в форму Берлекэмпа, производя итерации непосредственно для многочленов

На рис. 7.5 приведена блок-схема алгоритма Берлекэмпа— Месси. Как было показано, этот алгоритм позволяет вычислять многочлен локаторов ошибок исходя из заданных компонент

Рис. 7.5. (см. скан) Алгоритм Берлекэмпа-Месси,

синдрома Если в коде отлично от 1, то определим Эти компоненты синдрома участвуют в вычислениях точно так же, как и прежние компоненты. Сам алгоритм при этом не претерпевает никаких изменений, и дело сводится лишь к соответствующему изменению индексов внутренних переменных в алгоритме.

Этот алгоритм и его обоснование будут понятнее, если во всех деталях проследить работу алгоритма по схеме на рис. 7.5 для конкретных примеров. В табл. 7.3 приведены необходимые вычисления для -кода Рида-Соломона, исправляющего тройные ошибки. В достоверности приведенных вычислений можно убедиться, проделав шесть итераций по изображенной на рис. 7.5 схеме. Табл. 7.4 содержит анвлогичные вычисления для исправляющего тройные ошибки -кода БЧХ.

Внутренняя логика работы алгоритма Берлекэмпа-Месси может показаться несколько загадочной. Возможно, ответы на

Таблица 7.3 (см. скан) Алгоритм Берлекэмпа-Месси для -кода Рида-Соломона, исправляющего тройные ошибки

Таблица 7.4 (см. скан) Алгоритм Берлекэмпа-Месси для -кода БЧХ, исправляющего тройные ошибки

возникшие вопросы помогут найти следующие соображения. На некоторых итерациях, скажем на итерации, наравне с выбранным по алгоритму Берлекэмпа-Месси регистром с линейной обратной связью могут существовать другие регистры минимальной длины с линейной обратной связью, генерирующие требуемые символы. Все эти регистры будут генерировать одну и ту же требуемую последовательность компонент синдрома; в то же время последующие компоненты, не входящие в итерацию, у них будут различны. Каждый раз, когда это возможно, на следующей итерации выбирается регистр сдвига с линейной обратной связью с прежней длиной, генерирующий следующую требуемую компоненту синдрома; если такого регистра не оказывается, то длину регистра приходится увеличивать. Однако при решении вопроса о необходимости увеличения длины регистра никак не учитывается значение следующей компоненты синдрома (проверяется лишь выполнение соотношения

Рис. 7.6. Схема аппаратурной реализации алгоритма Берлекэмпа-Месси. Замечания Требуется 21 итераций из тактов каждая. Все данные передаются параллельными битами.

Таким образом, на -шаге имеется по меньшей мере столько же возможных вариантов регистра сдвига, сколько значений может принимать

Описанный алгоритм может быть реализован в виде программы для универсальных или специализированных ЭВМ, предназначенных для вычислений в полях Галуа. Если требуется очень большая скорость декодирования, то можно воспользоваться специальным жестким исполнением декодера, возможно включающим регистры сдвига.

Схема аппаратурной реализации построенного на регистрах сдвига устройства приведена на рис. 7.6. Три регистра, изображенные на рисунке, используются для хранения значений коэффициентов многочленов длина каждого регистра должнабыть не меньше той, которая необходима для хранения соответствующего многочлена наибольшей степени, а иногда выбирается немного большей. Если регистры содержат многочлены со степенями меньше максимальных, то

ошибок, такой декодер выдаст правильное выражение для многочлена локаторов ошибок. В случае когда произойдет более ошибок, декодирование будет неудачным и получится либо многочлен, не удовлетворяющий условиям, которым должен удовлетворять многочлен локаторов ошибок, либо допустимый, но неправильный многочлен. В первом случае декодер может обнаружить ошибку и пометить сообщение как не поддающееся декодированию. Решение об обнаружении неисправляемой конфигурации ошибок принимается тогда, когда выполняется хотя бы одно из двух условий:

1) число различных лежащих в корней отлично от

2) значения ошибок не лежат в поле символов кода.

При декодировании сначала осуществляется проверка многочлена локаторов ошибок. Если он удовлетворяет требуемым условиям, то декодер приступает к вычислению многочлена значений ошибок. Может случиться, что значения ошибок не будут лежать в поле символов кодовых слов, если последнее меньше поля локаторов ошибок. Такой символ не может быть внесен каналом, и, следовательно, его наличие указывает на то, что вектор ошибок содержит более искаженных позиций.

В § 9.6 будут рассмотрены способы декодирования кодов БЧХ с исправлением некоторых конфигураций более чем ошибок; здесь же мы обсудим противоположный случай, когда число исправляемых ошибок ограничивается конструктивным расстоянием. На практике такое декодирование используется для значительного уменьшения вероятности ошибки декодирования, платой за которое является увеличение вероятности отказа от декодирования

Для уменьшения вероятности неправильного декодирования число исправляемых декодером ошибок можно ограничить числом таким, что будет строго меньше (при четном это выполняется всегда). В этом случае декодер всегда будет обнаруживать неисправляемую конфигурацию ошибок при условии, что число действительно случившихся ошибок удовлетворяет неравенству

поскольку для перехода кодового слова в неправильную сферу декодирования должно произойти не менее ошибок.

В таком декодере хорошо применять алгоритм Берлекэмпа-Месси. Для вычисления необходимо сделать 21 итераций по алгоритму Берлекэмпа — Месси. Остальные итераций, требуются для проверки равенства нулю невязок Если хотя бы при одной из этих дополнительных

итераций не равняется нулю, то принятое слово объявляется словом, в котором произошло более ошибок.

Правомерность описанной процедуры доказывается следующей теоремой.

Теорема 7.5.3. Пусть произошло не более ошибок и заданы при Пусть, далее, регистр сдвига с линейной обратной связью, генерирующий последовательность и

причем равняются нулю при Тогда произошло не более ошибок и будет являться правильным многочленом локаторов ошибок.

Доказательство. В условии теоремы заданы компоненты синдрома для Если бы имелись еще компонент синдрома то можно было бы исправлять ошибок, т. е. любую конфигурацию предполагаемых ошибок. Вообразим на минуту, что эти дополнительные компоненты сообщены нам добрым волшебником или переданы по неведомому добавочному каналу. Тогда, используя алгоритм Берлекэмпа-Месси, можно найти многочлен локаторов ошибок, степень которого равна числу ошибок. Но при итерации и по предположению равняется нулю при Поэтому значение не будет меняться до итерации с номером и, следовательно, но правилу изменения

а это противоречит предположению о том, что произошло не более ошибок.

1

Оглавление

  • ОТ РЕДАКТОРА ПЕРЕВОДА
  • ПРЕДИСЛОВИЕ
  • ГЛАВА 1. ВВЕДЕНИЕ
  • 1.1. ДИСКРЕТНЫЙ КАНАЛ, СВЯЗИ
  • 1.2. ИСТОРИЯ КОДИРОВАНИЯ, КОНТРОЛИРУЮЩЕГО ОШИБКИ
  • 1.3. ПРИЛОЖЕНИЯ
  • 1.4. ОСНОВНЫЕ ПОНЯТИЯ
  • 1.5. ПРОСТЕЙШИЕ КОДЫ
  • ГЛАВА 2. ВВЕДЕНИЕ В АЛГЕБРУ
  • 2.1. 2-ПОЛЕ И 6-10-ПОЛЕ
  • 2.2. ГРУППЫ
  • 2.3. КОЛЬЦА
  • 2.4. ПОЛЯ
  • 2.5. ВЕКТОРНЫЕ ПРОСТРАНСТВА
  • 2.6. ЛИНЕЙНАЯ АЛГЕБРА
  • ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
  • 3.1. СТРУКТУРА ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
  • 3.2. МАТРИЧНОЕ ОПИСАНИЕ ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
  • 3.3. СТАНДАРТНОЕ РАСПОЛОЖЕНИЕ
  • 3.4. КОДЫ ХЭММИНГА
  • 3.5. СОВЕРШЕННЫЕ И КВАЗИСОВЕРШЕННЫЕ КОДЫ
  • 3.6. ПРОСТЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНОГО КОДА
  • 3.7. КОДЫ РИДА—МАЛЛЕРА
  • ГЛАВА 4. АРИФМЕТИКА ПОЛЕЙ ГАЛУА
  • 4.2. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
  • 4.3. КОЛЬЦА МНОГОЧЛЕНОВ
  • 4.4. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦАХ МНОГОЧЛЕНОВ
  • 4.5. ПРИМИТИВНЫЕ ЭЛЕМЕНТЫ
  • 4.6. СТРУКТУРА КОНЕЧНОГО ПОЛЯ
  • ГЛАВА 5. ЦИКЛИЧЕСКИЕ КОДЫ
  • 5.2. ПОЛИНОМИАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
  • 5.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ И СОПРЯЖЕНИЯ
  • 5.4. МАТРИЧНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
  • 5.5. КОДЫ ХЭММИНГА КАК ЦИКЛИЧЕСКИЕ КОДЫ
  • 5.6. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ
  • 5.7. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ПАКЕТЫ ОШИБОК
  • 5.8. ДВОИЧНЫЙ КОД ГОЛЕЯ
  • 5.9. КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
  • ГЛАВА 6. СХЕМНАЯ РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКОГО КОДИРОВАНИЯ
  • 6.1. ЛОГИЧЕСКИЕ ЦЕПИ ДЛЯ АРИФМЕТИКИ КОНЕЧНОГО ПОЛЯ
  • 6.2. ЦИФРОВЫЕ ФИЛЬТРЫ
  • 6.3. КОДЕРЫ И ДЕКОДЕРЫ НА РЕГИСТРАХ СДВИГА
  • 6.4. ДЕКОДЕР МЕГГИТТА
  • 6.5. ВЫЛАВЛИВАНИЕ ОШИБОК
  • 6.6. УКОРОЧЕННЫЕ ЦИКЛИЧЕСКИЕ КОДЫ
  • 6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ. КОДА ГОЛЕЯ
  • ГЛАВА 7. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
  • 7.2. ДЕКОДЕР ПИТЕРСОНА ГОРЕНСТЕЙНА—ЦИРЛЕРА
  • 7.3. КОДЫ РИДА СОЛОМОНА
  • 7.4. СИНТЕЗ АВТОРЕГРЕССИОННЫХ ФИЛЬТРОВ
  • 7.5. БЫСТРОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
  • 7.6. ДЕКОДИРОВАНИЕ ДВОИЧНЫХ КОДОВ БЧХ
  • 7.7. ДЕКОДИРОВАНИЕ С ПОМОЩЬЮ АЛГОРИТМА ЕВКЛИДА
  • 7.8. КАСКАДНЫЕ (ГНЕЗДОВЫЕ) КОДЫ
  • 7.9. КОДЫ ЮСТЕСЕНА
  • ГЛАВА 8. КОДЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
  • 8.2. ОГРАНИЧЕНИЯ СОПРЯЖЕННОСТИ И ИДЕМПОТЕНТЫ
  • 8.3. СПЕКТРАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
  • 8.4. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
  • 8.5. РАСШИРЕННЫЕ КОДЫ БЧХ
  • 8.6. АЛЬТЕРНАНТНЫЕ КОДЫ
  • 8.7. ХАРАКТЕРИСТИКИ АЛЬТЕРНАНТНЫХ КОДОВ
  • 8.8. КОДЫ ГОППЫ
  • 8.9. КОДЫ ПРЕПАРАТЫ
  • ГЛАВА 9. АЛГОРИТМЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
  • 9.2. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК
  • 9.3. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ РИДА—СОЛОМОНА
  • 9.4. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ БЧХ
  • 9.5. ДЕКОДИРОВАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ
  • 9.6. ДЕКОДИРОВАНИЕ ЗА ГРАНИЦЕЙ БЧХ
  • 9.7. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
  • 9.8. ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЙ В КОНЕЧНЫХ ПОЛЯХ
  • ГЛАВА 10. МНОГОМЕРНЫЕ СПЕКТРАЛЬНЫЕ МЕТОДЫ
  • 10.1. КОДЫ-ПРОИЗВЕДЕНИЯ
  • 10.2. КИТАЙСКИЕ ТЕОРЕМЫ ОБ ОСТАТКАХ
  • 10.3. ДЕКОДИРОВАНИЕ КОДА-ПРОИЗВЕДЕНИЯ
  • 10.4. МНОГОМЕРНЫЕ СПЕКТРЫ
  • 10.5. БЫСТРЫЕ КОДЫ БЧХ
  • 10.6. ДЕКОДИРОВАНИЕ МНОГОМЕРНЫХ КОДОВ
  • 10.7. ДЛИННЫЕ КОДЫ НАД МАЛЫМИ ПОЛЯМИ
  • ГЛАВА 11. БЫСТРЫЕ АЛГОРИТМЫ
  • 11.1. ЛИНЕЙНАЯ СВЕРТКА И ЦИКЛИЧЕСКАЯ СВЕРТКА
  • 11.2. БЫСТРЫЕ АЛГОРИТМЫ СВЕРТКИ
  • 11.3. БЫСТРЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
  • 11.4. АЛГОРИТМЫ АГАРВАЛА—КУЛИ ВЫЧИСЛЕНИЯ СВЕРТОК
  • 11.5. АЛГОРИТМ ВИНОГРАДА БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
  • 11.6. УСКОРЕННЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
  • 11.7. РЕКУРРЕНТНЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
  • 11.8. УСКОРЕННОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
  • 11.9. СВЕРТКА В СУРРОГАТНЫХ ПОЛЯХ
  • ГЛАВА 12. СВЕРТОЧНЫЕ КОДЫ
  • 12.2. ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ С ПОМОЩЬЮ МНОГОЧЛЕНОВ
  • 12.3. ИСПРАВЛЕНИЕ ОШИБОК И ПОНЯТИЯ РАССТОЯНИЯ
  • 12.4. МАТРИЧНОЕ ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ
  • 12.5. НЕКОТОРЫЕ ПРОСТЫЕ СВЕРТОЧНЫЕ КОДЫ
  • 12.6. АЛГОРИТМЫ СИНДРОМНОГО ДЕКОДИРОВАНИЯ
  • 12.7. ОБЕРТОЧНЫЕ КОДЫ ДЛЯ ИСПРАВЛЕНИЯ ПАКЕТОВ ОШИБОК
  • 12.8. АЛГОРИТМ ДЕКОДИРОВАНИЯ ВИТЕРБИ
  • 12.9. АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ
  • ГЛАВА 13. КОДЫ И АЛГОРИТМЫ ДЛЯ ДЕКОДИРОВАНИЯ МАЖОРИТАРНЫМ МЕТОДОМ
  • 13.1. ДЕКОДИРОВАНИЕ МАЖОРИТАРНЫМ МЕТОДОМ
  • 13.2. СХЕМЫ МАЖОРИТАРНОГО ДЕКОДИРОВАНИЯ
  • 13.3. АФФИННЫЕ ПЕРЕСТАНОВКИ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ
  • 13.4. ЦИКЛИЧЕСКИЕ КОДЫ, ОСНОВАННЫЕ НА ПЕРЕСТАНОВКАХ
  • 13.5. СВЕРТОЧНЫЕ КОДЫ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
  • 13.6. ОБОБЩЕННЫЕ КОДЫ РИДА—МАЛЛЕРА
  • 13.7. ЕВКЛИДОВО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
  • 13.8. ПРОЕКТИВНО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
  • ГЛАВА 14. КОМПОЗИЦИЯ И ХАРАКТЕРИСТИКИ КОНТРОЛИРУЮЩИХ ОШИБКИ КОДОВ
  • 14.2. ВЕРОЯТНОСТИ ОШИБОЧНОГО ДЕКОДИРОВАНИЯ И НЕУДАЧНОГО ДЕКОДИРОВАНИЯ
  • 14.3. РАСПРЕДЕЛЕНИЕ ВЕСОВ СВЕРТОЧНЫХ КОДОВ
  • 14.4. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ БЛОКОВЫХ КОДОВ
  • 14.5. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ
  • ГЛАВА 15. ЭФФЕКТИВНАЯ ПЕРЕДАЧА СИГНАЛОВ ПО ЗАШУМЛЕННЫМ КАНАЛАМ
  • 15.1. ОГРАНИЧЕННЫЙ ПО ПОЛОСЕ ГАУССОВСКИЙ КАНАЛ
  • 15.2. ЭНЕРГИЯ НА БИТ И ЧАСТОТА ОШИБОК НА БИТ
  • 15.3. МЯГКОЕ ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
  • 15.4. МЯГКОЕ ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ
  • 15.5. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
  • ЛИТЕРАТУРА

Граница Синглтона

Пусть (C) – код над алфавитом мощности (q) с длиной кодового слова (n) и минимальным кодовым расстоянием (d.) Тогда, если построить на его основе код (C^*), просто удалив первые (d-1) символов из каждого кодового слова, новый код останется однозначным, и следовательно (abs{C^*} = abs{C}.)

Длина кодового слова в (C^*) равна (n — (d-1) = n-d+1,) и его мощность не может превышать (abs{C} = abs{C^*} le q^{n-d+1}.)

Соотношение (abs{C} le q^{n-d+1}) называется границей Синглтона.

БЧХ-коды

Коды Боуза-Чоудхури-Хоквингема (БЧХ)
класс помехоустойчивых кодов, являющийся подмножеством циклических кодов. БЧХ-коды задаются над полем (GF(p^k)), где (p) – простое число.

Основным интересным свойством БЧХ-кодов является возможность конструировать коды с заведомо известным минимальным кодовым расстоянием.

Конструкция порождающего многочлена примитивного БЧХ-кода

Как и любой циклический код, БЧХ-код задаётся порождающим многочленом, и допускает “простое” либо систематическое построение кодовых слов.

Порождающий многочлен БЧХ-кода задаётся следующим образом. Выбирается желаемое минимальное кодовое расстояние (d). Выбирается длина кодового слова (n = q^m — 1) (такой код называется примитивным). Пусть (α) – примитивный элемент поля (GF(q^m)). Пусть (m_i(x)) – минимальный многочлен с коэффициентами в (GF(q)) для (α^i), т.е. многочлен с минимальной степенью, имеющий корнем (α^i). Тогда порождающий многочлен БЧХ-кода может быть построен как [g(x) = lcm(m_1(x),ldots,m_{d-1}(x)).]

Конструкция порождающего многочлена обобщённого БЧХ-кода

Обобщённый БЧХ-код отличается от примитивного тем, что вместо примитивного элемента (α), выбирается корень (n)-той степени из (1). Длина кодового слова (n = mathrm{ord}(α),) т.е. порядок (α).

Выбирается (GF(q),) где (q) – целая степень простого числа. Выбираются целые (m, n, d, c,) такие, что (2 le d le n,) (gcd(n,q)=1,) (m) – мультипликативный порядок (q) по модулю (n). Пусть (α) – корень (n)-той степени из (1) в (GF(q^m)), и пусть (m_i(x)) – минимальный многочлен над (GF(q)) для (α^i). Порождающий многочлен тогда [g(x) = lcm(m_с(x),ldots,m_{с+d-2}(x)),] где (c) – некоторое целое, (cge 0.)

Кодирование БЧХ-кодом

Абсолютно аналогично кодированию любым другим циклическим кодом. Пусть (c(x)) – многочлен, соответствующий кодовому слову, (g(x)) – порождающий многочлен и (m(x)) соответствует сообщению. Тогда, либо [c(x) = g(x) m(x),] либо [c(x) = m(x)x^r — r(x),] где (r(x) = m(x) x^r pmod {g(x)},) а (r) – число проверочных символов.

Декодирование БЧХ-кодов

Декодирование БЧХ-кода использует оптимизированный метод декодирования по синдрому. Существуют различные алгоритмы нахождения вектора ошибки на основе синдрома, но большинство работает по следующему принципу:

  1. Вычисляются синдромы (s_j)
  2. Из синдрома определяется число ошибок (t) и вычисляется многочлен локатора ошибок (Λ(x))
  3. Вычисляются корни (Λ(x)), которые дают местонахождение ошибок (x_i)
  4. Вычисляются значения ошибок (y_i)
  5. Ошибки исправляются.

Вычисление синдромов

Полученный вектор (r(x)) вычисляется в нулях порождающего многочлена: (α^c,ldots,α^{c+d-2}). Понятно, что если кодовое слово передано без ошибок, оно делится на (g(x)), и все синдромы будут равны нулю. В противном случае, какие-то из синдромов не будут равны нулю, и какие именно – содержит информацию о положении ошибок.

Вычисление (Λ(x))

Если синдромы не равны (0,) то вектор ошибки имеет вид [e(x) = e_1x^{i_1} + e_2x^{i_2} + ldots + e_tx^{i_t}]

Тогда находится многочлен [Λ(x) = prod_{j=1}^{t} paren{xα^{i_j} — 1},] такой, что (t) минимально, и (e(x)) соответствует найденным синдромам.

Корнями этого многочлена являются (x = α^{-i_j},) что позволяет вычислить (i_j) (отсюда название “локатор ошибок”).

Существует три популярных алгоритма для нахождения (Λ(x)):

  1. Алгоритм Питерсона-Горнстейна-Цирлера

    Достаточно неэффективный и по сути сводится к прямому поиску.

  2. Алгоритм Берлекэмпа-Мэсси

    Достаточно эффективен, но сравнительно сложен, поэтому чаще используется в программной реализации.

  3. Евклидов алгоритм (алгоритм Сугиямы)

    Основан на расширенном алгоритме Евклида, существуют крайне эффективные аппаратные реализации.

Нахождение значений ошибок

Если известны места, в которых произошли ошибки, то нахождение значений ошибок сводится к решению системы линейных уравнений

[s_j = e_1 α^{(j+с) i_1} + e_2 α^{(j+с) i_2} + ldots]

Для решения этой системы уравнений можно использовать любой стандартный метод, но существует более эффективный алгоритм, известный как алгоритм Форни.

Алгоритм Форни

Алгоритм Форни основан на применении интерполяции Лагранжа, но в конечном итоге эта деталь не слишком нас интересует.

Смысл в том, чтобы найти многочлен [Ω(x) = s(x)Λ(x) pmod {x^{d-1}},] называемый вычислителем ошибок, где [s(x) = sum_{i=0}^{d-2} x^i s_i,] и вычислить значения ошибок прямо как [e_j = — frac{X_j^{1-c}Ω(X_j^{-1})}{Λ'(X_j^{-1})},] где (X_j^{-1}) – корни (Λ(x),) а (Λ'(x)) – так называемая формальная производная, [Λ'(x) = sum_{i=1}^{t} i λ_i x^{i-1}]

Алгоритм Сугиямы

Многочлен синдромов (s(x),) локатор ошибок (Λ(x)) и вычислитель ошибок (Ω(x)) удовлетворяют соотношению [Λ(x)s(x) = q(x)x^{d-1} + Ω(x),] эквивалентно [Ω(x) = Λ(x)s(x) — q(x)x^{d-1},]

Расширенный алгоритм Евклида может найти последовательность многочленов, [r_i(x) = a_i(x) s(x) + b_i(x) x^{d-1},] причём степень (r_i) убывает с увеличением (i). Тогда, как только степень (r_i(x)) меньше ((d-1)/2,) т.е. количеству ошибок, которые код может исправить, имеем [a_i(x) = Λ(x),] [b_i(x) = -q(x),] [r_i(x) = Ω(x).]

Коды Рида-Соломона

Исторически, коды Рида-Соломона не являлись БЧХ-кодами, однако наиболее популярная (в силу эффективности) модификация кодов Рида-Соломона представляет собой ни что иное как БЧХ-код с (m=1). Обычно, под кодами Рида-Соломона понимается именно эта модификация.

Коды Рида-Соломона являются оптимальными в смысле границы Синглтона (что прямо следует из свойств циклических кодов).

Наибольшее распространение получили коды Рида-Соломона:

  • В записи на оптические носители информации
  • В высокоскоростной связи
  • В мобильной связи
  • В космической связи (со спутниками, зондами и т.п.)
  • В штрих- и QR-кодах

По построению, код Рида-Соломона не может быть двоичным. Действительно, длина кода (n) не больше, чем степень примитивного элемента, а для двоичного кода, (n = 1,) и такой код был бы бесполезен.

Преимущество кодов РС в том, что ошибки редко случаются в одном бите: обычно они возникают в нескольких битах подряд. Поскольку код РС работает над алфавитом большей размерности, он более эффективно справляется с сериями битовых ошибок, чем двоичные коды.

В качестве размера поля обычно выбирается степень двойки. Крайне распространён вариант (GF(2^8),) т.е. кода, построенного над октетами (байтами) – что кстати сказать упрощает работу с таким кодом.

Форни-алгоритм

В теории кодирования algorithm Форни (или algorithm Форни) вычисляет значения ошибок в известных местоположениях ошибок. он используется как один из шагов в декодировании кодов BCH и кодов Рида-Соломона (подкласс кодов BCH). Джордж Дэвид Форни-младший разработал algorithm.

Процедура

Нужно представить терминологию и установку…

Кодовые слова выглядят как многочлены. По замыслу образующий многочлен имеет последовательные корни & alpha; c, & alpha; c + 1,…, & alpha; c + d & minus; 2.

Синдромы

Полином расположения ошибок

Нули & Lambda; (x) — X1 & minus; 1,…, X & nu; & minus; 1. Нули — это значения rechyprocals для мест возникновения ошибок.

Как только местоположения ошибок известны, следующим шагом является определение значений ошибок в этих местоположениях. Затем значения ошибок используются для коррекции полученных значений в этих местоположениях для восстановления исходного кодового слова.

В более общем случае ошибки могут быть определены путем решения линейной системы

Однако существует более эффективный метод, известный как algorithm Форни, который основан на интерполяции Лагранжа. Сначала вычислите полином генератора ошибок

Где — полином парциального синдрома:

Затем значения ошибок:

Значение часто называют «первый освящённый корень» или «fcr». Некоторые коды выбираются, поэтому выражение :

Формальный вативный

& Lambda; (x) — формальный параметр полинома локатора ошибок & Lambda; (x):

В приведенном выше выражении обратите внимание, что i является целым числом, и & lambda; i будет элементом конечного поля. Оператор & ot; представляет собой ординарную лицензию (повторяющееся сложение в конечном поле), а не оператор лицензии конечного поля.

Ивация

Интерполяция Лагрейнджа

даёт прилив форнеевского альгоритма.

Стирания

Определение полинома локатора стирания

Где места стирания даны по ji. Примените описанную выше процедуру, sub uting & Gamma; для & Lambda;.

Если присутствуют и ошибки, и стирание, используйте полином локатора ошибок и стирания

См. также

  • Код BCH
  • Ошибка Рида-Соломона
  • Книга Юли Петерсона

Внешние связи

Способы
кодирования и декодирования РС-кодов
достаточно хорошо разработаны в
теоретическом и реализационном плане.
Их основу составляют процедуры исправления
стираний, ошибок и совместного исправления
ошибок и стираний. Рассмотрим процедуры,
нашедшие применение в отечественной
технике передачи данных.

Рассмотрим
процедуру декодирования с исправлением
ошибок, известную [ 4 ] как алгоритм Форни.

Пусть
в приемник аппаратуры передачи данных
(АПД) поступила кодовая комбинация
РС-кода

C(x)=f(x)+e(x),

где
f(x)
– переданная передатчиком (АПД) кодовая
комбинация, в которой в процессе передачи
по каналу связи произошло v
ошибок , отображаемых многочленом e(x)
степени .
Каждый ненулевой компонент e(x)
описывается парой элементов: Yi –
величина ошибок и Xi
– номер позиции ошибки (локатор ошибки).
Yi,
Xi
– элементы GF(q),
и элемент Xi=αi,αi
Є GF(q).

Для описания ошибок
используются:

1. Многочлен локаторов ошибок:

имеющий
корни Xi–1,
i
= 1, …,v
взаимные к локаторам ошибок, т. е.
Xi–1∙αi
= 1.

2.Синдромный многочлен

–многочлен
бесконечной степени, для которого
известны только
2t
коэффициентов
для поступившей комбинации РС-кода.

Здесь – элемент синдрома, αj
– корень порождающего многочлена
РС-кода. Значения Sj e(αj)
задаются проверками:

Sj=C(αj)=f(αj)+e(αj)=e(αj),

где
m0jm0+2t–1
при m0=1.

3. Многочлен значений ошибок

Ω(x)S(x)Λ(x)
(modx2t),
(*)

Равенство
(*) определяет множество из (2t–υ)
уравнений и называетсяключевым
уравнением, так как оно представляется
«ключом» решения задачи декодирования.

Это
становится понятным, если учесть, что
степень Ω(x)
не превышает υ–1 и поэтому справедливо:

,
(**),

где
.

Из
(**) можно получить υ уравнений для υ
неизвестных коэффициентов Λk.
Эти уравнения являются линейными. Они
могут быть решены обычными методами
либо с помощью итерационных процедур.
После нахождения многочлена Λ(x)
ключевое уравнение позволяет найти
неизвестные компоненты вектора e(x)
и по ним выходной вектор декодера:
f(x)=C(x)+e(x).

Простейшим
путем нахождения корней многочлена
Λ(x)
является метод проб и ошибок, известный
как процедура
Ченя. Эта
процедура состоит в последовательном
вычислении Λ(αj)
для каждого j
и проверки полученных значений на ноль.
Если величина Λ(α–k)
равна нулю, то αk
является
взаимным к корню многочлена локаторов
ошибок и k-й
элемент кодовой комбинации содержит
ошибку. Наиболее простым способом
вычисления значения Λ(x)
в точке β является схема
Горнера:

.

Для
вычисления Λ(β)
по схеме Горнера требуется только υ
умножений и υ сложений, где υ – степень
Λ(x).

После
определения локаторов ошибок с помощью
ключевого уравнения находим значения
ошибок. Для этого, используя значения
сомножителей, входящих в равенство для
Ω(x),
перепишем ключевое уравнение следующим
образом:

Сворачивая
выражение в квадратных скобках, получаем
окончательно

Приводя
это выражение по модулю x2t
, получаем

.

Вычислим многочлен
значений ошибок на позиции l:.

,

Откуда

.

Найдем производную
от многочлена локаторов ошибок Λ(x):

.

Для l-й
позиции получаем:

.

С учетом последнего
выражения Ylзначение ошибки на позицииlпринимает вид

.

Рассмотренный
способ декодирования позволяет найти
значение ошибок по известным многочленам
локаторов и значений ошибок. Он известен
в литературе [ 4 ] как алгоритм Форни.
Указанные многочлены вычисляются в
результате решения ключевого уравнения.
Более подробно декодирование кодов
Рида-Соломона рассматривается в разделе
7.2.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

В теории кодирования , то Форни алгоритм (или алгоритм Форней в ) вычисляет значение ошибок в известных местах ошибок. Он используется в качестве одного из этапов декодирования БЧХ кодов и кодов Рида-Соломона (подкласс кодов БЧХ). Джордж Дэвид Форни-младший разработал алгоритм.

Процедура

Необходимо ввести терминологию и настройку …

Кодовые слова выглядят как полиномы. По замыслу порождающий полином имеет последовательные корни α c , α c +1 , …, α c + d −2 .

Синдромы

Многочлен определения места ошибки

{ displaystyle Lambda (x) = prod _ {i = 1} ^ { nu} (1-x , X_ {i}) = 1+ sum _ {i = 1} ^ { nu} лямбда _ {i} , x ^ {i}}

Нули Λ ( x ) — это X 1 −1 , …, X ν −1 . Нули — это обратные значения местоположений ошибок .
{ displaystyle X_ {j} = alpha ^ {i_ {j}}}

После того, как места возникновения ошибок известны, следующим шагом будет определение значений ошибок в этих местах. Затем значения ошибок используются для исправления полученных значений в этих местах для восстановления исходного кодового слова.

В более общем случае веса ошибок e j могут быть определены путем решения линейной системы

{ displaystyle s_ {0} = e_ {1} alpha ^ {(c + 0) , i_ {1}} + e_ {2} alpha ^ {(c + 0) , i_ {2}} + cdots ,}
{ Displaystyle s_ {1} = e_ {1} alpha ^ {(c + 1) , i_ {1}} + e_ {2} alpha ^ {(c + 1) , i_ {2}} + cdots ,}
{ Displaystyle cdots ,}

Однако существует более эффективный метод, известный как алгоритм Форни, который основан на интерполяции Лагранжа . Сначала вычислите полином оценщика ошибок

{ Displaystyle Omega (x) = S (x) , Lambda (x) { pmod {x ^ {2t}}} ,}

Где S ( x ) — полином частичного синдрома:

{ Displaystyle S (x) = s_ {0} x ^ {0} + s_ {1} x ^ {1} + s_ {2} x ^ {2} + cdots + s_ {2t-1} x ^ { 2т-1}.}

Затем оцените значения ошибок:

{ displaystyle e_ {j} = - { frac {X_ {j} ^ {1-c} , Omega (X_ {j} ^ {- 1})} { Lambda '(X_ {j} ^ { -1})}} ,}

Значение c часто называют «первым последовательным корнем» или «fcr». Некоторые коды выбирают c = 1 , поэтому выражение упрощается до:

{ displaystyle e_ {j} = - { frac { Omega (X_ {j} ^ {- 1})} { Lambda '(X_ {j} ^ {- 1})}}}

Формальная производная

Λ ‘( x ) — формальная производная полинома локатора ошибок Λ ( x ):

{ displaystyle Lambda '(x) = sum _ {i = 1} ^ { nu} i , cdot , lambda _ {i} , x ^ {i-1}}

В приведенном выше выражении обратите внимание, что i — целое число, а λ i — элемент конечного поля. Оператор · представляет собой обычное умножение (повторное сложение в конечном поле), а не оператор умножения конечного поля.

Вывод

Интерполяция Лагранжа

Гилл (nd , стр. 52–54) дает вывод алгоритма Форни.

Стирания

Определите полином локатора стирания

{ displaystyle Gamma (x) = prod (1-x , alpha ^ {j_ {i}})}

Где места стирания указаны j i . Примените описанную выше процедуру, заменив Λ Γ.

Если присутствуют и ошибки, и стирания, используйте полином локатора ошибок и стирания

{ Displaystyle пси (х) = лямбда (х) , гамма (х)}

Смотрите также

  • Код BCH
  • Исправление ошибок Рида – Соломона

Ссылки

  • Форни, Г. (октябрь 1965), «О кодах декодирования БЧХ», IEEE Transactions по теории информации , 11 (4): 549-557, DOI : 10,1109 / TIT.1965.1053825 , ISSN  0018-9448
  • Джилл, Джон (nd), EE387 Notes # 7, раздаточный материал # 28 (PDF) , Stanford University, стр. 42–45, заархивировано из оригинала (PDF) 30 июня 2014 г. , получено 21 апреля 2010 г.
  • Книга У. Уэсли Петерсона

внешние ссылки

Источник

Рассмотрим примеры
применения рассмотренных алгоритмов
для декодирования с исправлением ошибок
кодами Рида-Соломона.

Пример
7.7. Пусть над полем
GF(23)
с элементами 000,
α=1=100,
α1=010,
α2=001,

α3=110,
α4=011,
α5=111,
α6=101
построен код
Рида-Соломона (7,3) с dmin=5,
способный
исправлять 2-х кратные ошибки. Корнями
порождающего многочлена
являются следующие элементы GF(23):
α1=010,
α2=110,α3=110,α4=011..
Порождающий
многочлен кода имеет вид;

g(x)=(x+α)(x+α2)(x+α3)(x+α4)=α3+α1x+α0x2+α3x3+x4

Предположим,
что по каналу связи была передана
комбинация (0000000),а
на вход декодера поступила комбинация.
f(x)=а2х3+а5х4.
Схема
вычисления синдрома определила компоненты
синдромного многочлена:

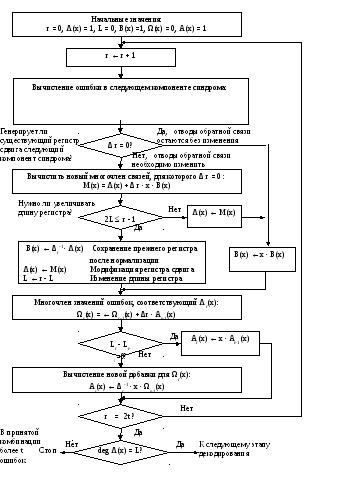
Рис.7.1.Алгоритм
Берлекемпа-Месси

S1=f(x=α)=α5+α2=α3

S2=f(x=α2)=α1+α6=α5

S3=f(x=α3)=α4+α3=α6

S4=f(x=α4)=α0+α0=0

При
вычислении значений элементов Si,
показатели степеней элементов поля
приводятся
по mod
7, т.к. для GF(23)
а0=а7=1.
Итак,
для принятой комбинации
синдромный многочлен имеет вид:
S(x)=α3+α5x+α6x2.

Определим
для принятой комбинации многочлен
локаторов ошибок Λ(х).

1.Алгоритм
Питерсона.
Матричное
уравнение для нахождения компонентов
Λ(х)
по
S(х)
имеет вид:

.

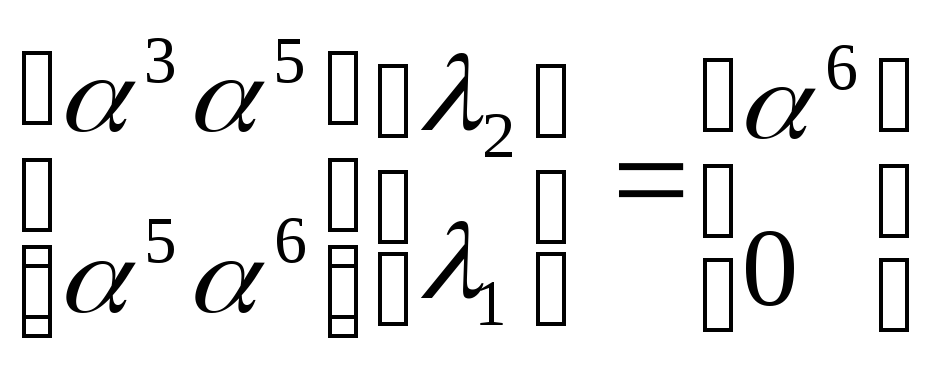В
предложении, что произошло максимальное
число исправляемых кодом ошибок
t=2
воспользуемся
теоремой Крамера
[5] для решения системы линейных
уравнений, представленных в матричной
форме Ах=С,
в
случае, когда
det
А существует
и отличен от нуля, В этом случае система
имеет одно определенное решение , и
каждое из неизвестных выражается частным
двух определителей, причем в знаменателе
стоит определитель |А|, а в числителе,
определитель
который из него получается заменой
коэффициентов при определяемом
неизвестном соответствующими свободными
членами:
.

Применяя
теорему Крамера для нахождения λi
получаем:

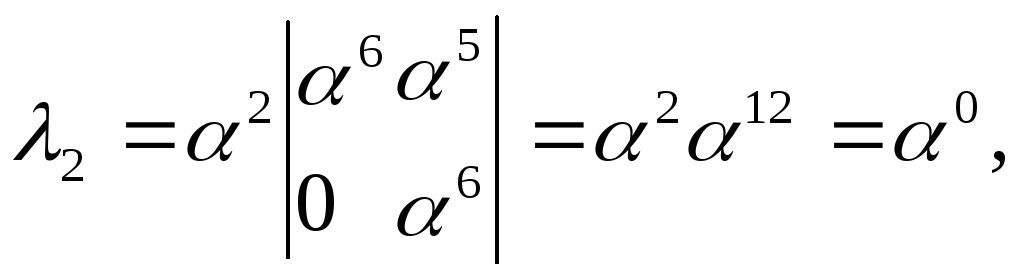
Таким образом,
многочлен локаторов ошибок имеет вид:

Λ(x)=1+α6x+α0x2.

Корнями
многочлена Λ{х)
являются элементы GF(23):
α3
и α4,
т.е. локаторы ошибок

Это дает возможность
представить многочлен локаторов ошибок
и виде;

Λ(х)=(1+α3х)(1+α4х)

Алгоритм
Питерсона позволяет найти также и
значения ошибок. Для этого выразим
компоненты синдромного многочлена S1
и S2
через
локаторы ошибок Xl,
и значения ошибок Yl:

S1=Y1X1
+ Y2X2

S2=Y1X12
+ Y2X2

Представим
эти уравнения в матричной форме:


или

Решим
это уравнение тем же способом, каким
были найдены λ1
λ2
.Вычислим
определитель:

.

Теперь
находим:

=α(α4+α2)=α5+α3=α2
,

=α(α+α2)=α2+α3=α5.

Полученные
значения Y1
и
Y2
соответствуют
коэффициентам многочлена ошибок.

2.Алгоритм
Евклида

Поиск
значений Λi(x)
в Ωi(x),
удовлетворяющих приведенным выше
критериям, представим в виде таблицы.

i

-1

0

1

Λi(x)

0

1

α+х+αx2=α(1+α6x+x2)

Ωi(x)

х4

S(x)

α
4+α
4х=α(α3+α3х)

qi(x)

___

___

[х4
/S(x)]=α+x+αx2

Из
приведенной таблицы видно, что найденное
значение Λ(х)=α(1+
α6x+x2)
отличается от Λ
(х), подученного по алгоритму Питерсона,
постоянным сомножителем α.
Понятно, что корни этих многочленов
совпадают, т,е, постоянный сомножитель
не влияет на определение локаторов
ошибок.

3,
Алгоритм Берлекемпа-Месси.
Вычисление Λ(х)
и Ω(x) в соответствии с доработанным
алгоритмом Берлекемпа-Месси представим
ввиде следующей таблицы:

r

S
r

Δr

M(x)

B(x)

Λ(x)

L

Ω(x)

A(x)

0

1

1

0

0

1

1

α3

α3

1+α3x

α4

1+α3x

1

α3

0

2

α5

α

1+α2x

a4x

1+α2x

1

α3

0

3

α6

α2

1+α2x+α6x

α5+x

1+α2x+a6x2

2

α3

αx

4

0

α2

1+α6x+x2

α5x+x2

1+α6x+x2

2

α3+
α3x

αx

Найденному
значению Λ(х)=1+α6x+x2
соответствует регистр сдвига с обратными
связями,
определенными видом Λ(х), длины L=2,
способный генерировать все компоненты
синдромного многочлена по двум младшим.
Этот регистр имеет вид:

В
исходном состоянии в ячейках памяти
регистра записаны компоненты синдрома
S1=α3
и
S2=α5.
По первому такту S1=α3
поступает
на выход, а в ячейках остаются S2=α5
и
S3=α6.
По второму такту S2=α5
поступает на выход, а в ячейках остаются
S3=α6
и S4=0,
которые за два следующих такта поступают
на выход.

4.
Алгоритм Форни.

Для
вычисления значений ошибок необходимо
знание Λ(х) и его корней, а также
должен быть известен многочлен Ω(x).
Непосредственным
вычислением
находим: ■

Ω(x)=S(x)Λ(x)(modx2t)=(α3+α5x+а6х2)(1+α6x+x2)(modx4)=α3+α3х.
Расчетные
значения Λ(х)
и Ω(x)
полностью
совпадают с полученными по алгоритму
Берлекемпа-Месси и отличаются постоянным
сомножителем при вычислении
по алгоритму Евклида.

Для
нахождения значений ошибок по алгоритму
Форни найдем Λ′(х)=а6.
Подставляя
в Ω(х)
вместо
x
значения корней Λ(x)
получаем:

Итак,
вычисленное значение многочлена ошибок
е(х)= α2x3+α5x4
полностью
совпадает с принятой комбинацией f(х)
и, следовательно, по каналу
связи передавалась комбинация (0000000).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

  • Алгоритм проверки уголовного дела на ошибки следователей
  • Алгоритм проверки орфографических ошибок
  • Алгоритм обучения нейронной сети методом обратного распространения ошибки
  • Алгоритм обратного распространения ошибки это
  • Алгоритм обратного распространения ошибки хабр