Алгоритм обратного распространения ошибки для многослойного персептрона

Время на прочтение
5 мин

Количество просмотров 82K

В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.

Обучение сверточной нейронной сети

На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.

Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.

Алгоритм обратного распространения ошибки

Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.

Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.

Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:

Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:

Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:

Выход каждого нейрона j является значением активационной функции

, которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.

Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:

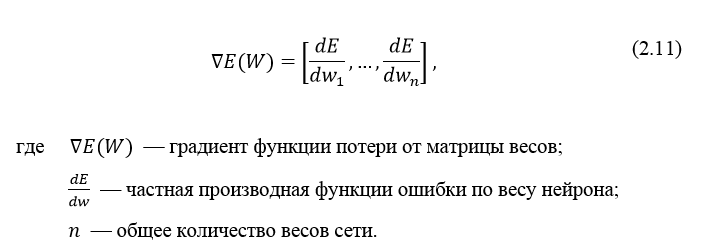
Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:

Ошибка нейрона обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.

Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:

Алгоритм распространения ошибки сводится к следующим этапам:

• прямое распространение сигнала по сети, вычисления состояния нейронов;
• вычисление значения ошибки δ для выходного слоя;
• обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
• обновление весов сети на вычисленную ранее δ ошибки.

Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:

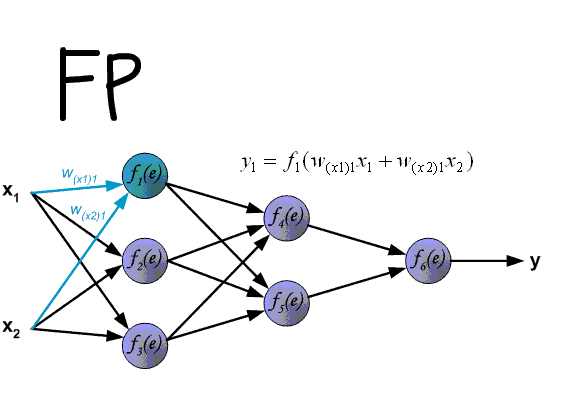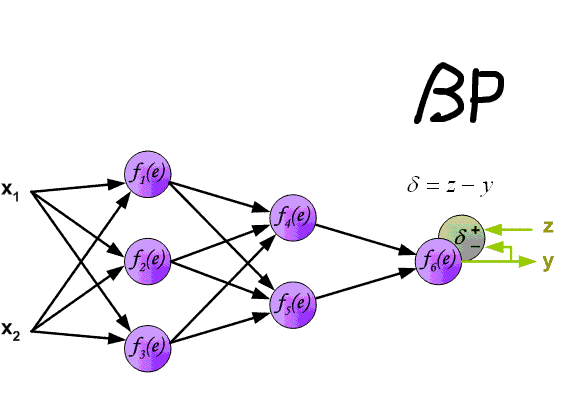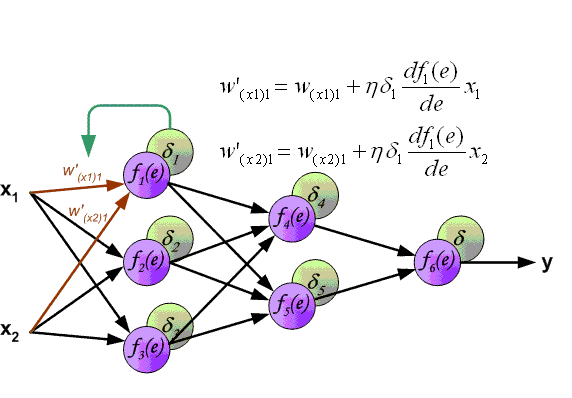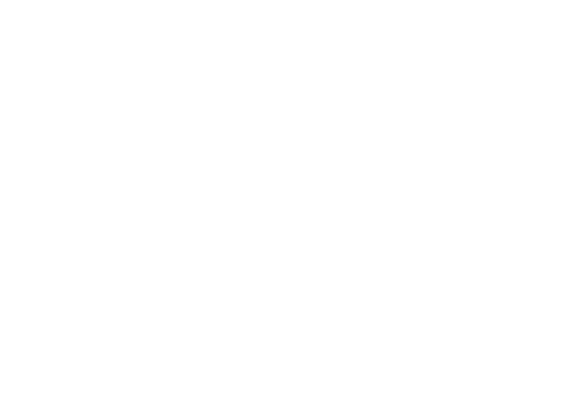
До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.

Расчет ошибки на подвыборочном слое

Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.

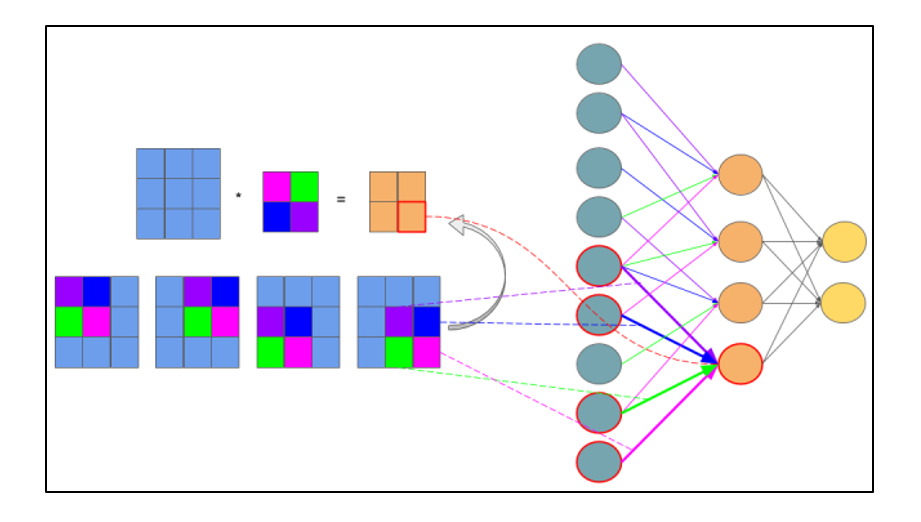
Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка

Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.

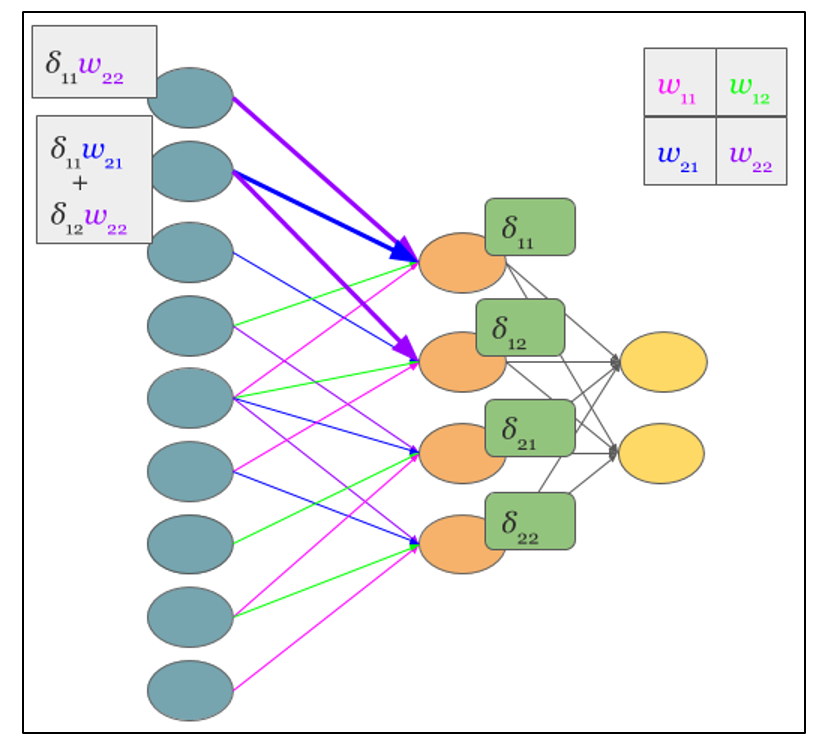
Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра

Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.

Рисунок 2.10 — Результат операции обратной свертки

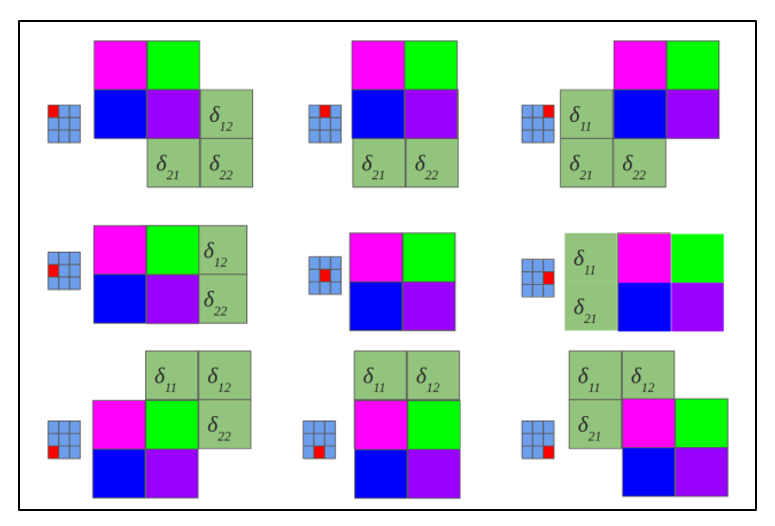
Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту

Расчет ошибки на сверточном слое

Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.

Заключение

Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.

Источники

Алгоритм обратного распространения ошибки для сверточной нейронной сети

Обратное распространение ошибки в сверточных слоях
раз и два

Обратное распространение ошибки в персептроне

Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ

Введение

• В последнее время, с ростом популярности этих двух методов появилось много библиотек на Matlab, R, Python, C ++ и т.д., которые получают на вход обучающий набор и автоматически создают соответствующую нейронную сеть для вашей задачи.

• Однако при использовании готовых библиотек бывает сложно понять, что именно происходит и как мы получаем оптимизированную сеть. А ведь знание основ решения важно для дальнейшего развития этих методов. Итак, в данной статье мы создадим очень простую структуру для алгоритма нейронной сети.

• Мы постараемся понять, как работает базовый тип нейронной сети — перцептрон с одним нейроном и многослойный перцептрон — замечательный алгоритм, который отвечает за обучение сети (градиентный спуск и обратное распространение). Эти сетевые модели будут основой для более сложных моделей, существующих на сегодняшний день.

Краткий обзор истории

• Первая нейронная сеть была задумана Уорренном Маккалоком и Уолтером Питтсом в 1943 году. Они написали великолепную статью о том, как должны работать нейроны, а затем построили модель на основе своих идей — создали простую нейронную сеть с электрическими цепями.

• Исследования в области искусственного интеллекта быстро развивались, и в 1980 году Кунихико Фукусима разработал первую настоящую многослойную нейронную сеть.

• Первоначальной целью нейронной сети было создание компьютерной системы, способной решать проблемы подобно тому, как это делает человеческий мозг. Однако, со временем исследователи сменили фокус и начали использовать нейронные сети для решения особенных задач. С тех пор нейронные сети выполняют самые разнообразные задачи, включая компьютерное зрение, распознавание голоса, машинный перевод, фильтрацию социальных сетей, настольные игры или видеоигры, медицинскую диагностику, прогноз погоды, прогнозирование временных рядов, распознавание (изображения, текста, голоса) и др.

Компьютерная модель нейрона: перцептрон

Перцептрон

Перцептрон вдохновлен идеей обработки информации единственной нервной клетки, называемой нейроном. Нейрон принимает на вход сигналы через свои дендриты, которые передают электрический сигнал телу клетки. Точно так же перцептрон получает входные сигналы из примеров обучающих данных, которые предварительно взвесили и объединили в линейное уравнение, называемое активацией.

• z = sum(weight_i * x_i) + bias

Где weight — это вес сети, X — это входное значение, i — индекс веса или входные данные, а смещение — это специальный вес, который не имеет множитель в виде входного значения (можем считать, что входные данные всегда равны 1.0).

Затем активация преобразуется в выходное (прогнозируемое) значение с помощью передаточной функции (функция активации).

• y = 1.0 если z >= 0.0, иначе 0.0

Таким образом, перцептрон представляет собой алгоритм классификации проблем с двумя классами (двоичный классификатор), где для разделения двух классов может использоваться линейное уравнение.

Это тесно связано с линейной регрессией и логистической регрессией, которые осуществляют прогнозы аналогичным образом (например, взвешенная сумма входов).

Алгоритм перцептрона — простейший вид искусственной нейронной сети. Это модель одного нейрона, которая может использоваться в задачах классификации двух классов и обеспечивает основу для дальнейшего развития гораздо более крупных сетей.

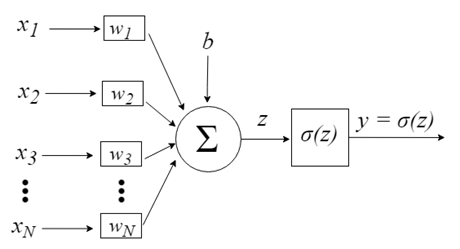
Входы нейронов представлены вектором x = [x1, x2, x3,…, xN], который может соответствовать, к примеру, ряду торговых цен актива, значениям технических индикаторов, числовой последовательности в пикселях изображения. Когда они попадают к нейрону, они умножаются на соответствующие синаптические веса, которые являются элементами вектора w = [w1, w2, w3, …, wN], и таким образом генерируют значение z, обычно называемое потенциалом активации, согласно выражению:

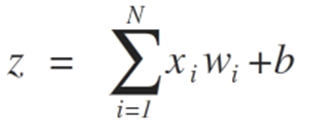
b обеспечивает более высокую степень свободы и не зависит от входа в это выражение, что обычно соответствует нейрону смещения (склонности). Затем z-значение проходит через функцию активации σ, которая отвечает за ограничение этого значения определенным интервалом (например, 0 — 1), что дает окончательное выходное значение и значение нейрона. Некоторые используемые триггерные функции: шаг, сигмоид, гиперболический тангенс, softmax и ReLU («rectified linear unit»).

Чтобы проиллюстрировать процесс, направленный на достижение предела разделимости классов, ниже мы показываем две ситуации, которые демонстрируют их сближение к стабилизации с учетом только двух входов {x1 и x2}

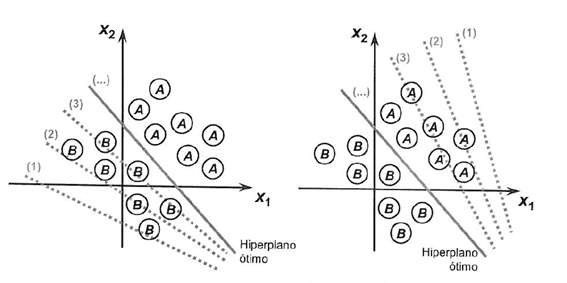
Веса алгоритма перцептрона следует оценивать на основе данных обучения с использованием стохастического градиентного спуска.

Стохастический градиент

Градиентный спуск — это процесс минимизации функции в направлении градиента функции стоимости.

Это подразумевает знание формулы стоимости, а также производной, чтобы с определенной точки мы могли узнать наклон и могли двигаться в этом направлении, например, вниз по направлению к минимальному значению.

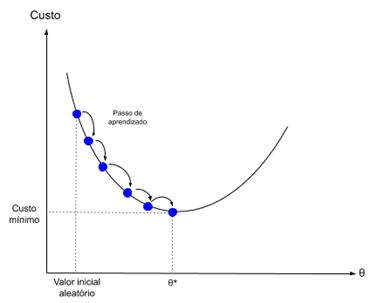
В машинном обучении мы можем использовать метод, который оценивает и обновляет веса для каждой итерации, называемый стохастическим градиентным спуском, чтобы минимизировать ошибку модели в наших обучающих данных.

Принцип работы этого алгоритма оптимизации заключается в том, что каждый обучающий экземпляр показывается модели по одному. Модель делает прогноз для обучающего экземпляра, вычисляет ошибку и обновляет модель, чтобы уменьшить ошибку для следующего прогноза.

Эту процедуру можно использовать для поиска набора весов в модели, который дает наименьшую ошибку для модели в обучающих данных.

Для алгоритма перцептрона на каждой итерации веса w обновляются с использованием уравнения:

• w = w + learning_rate * (expected — predicted) * x

Где w оптимизируется, learning_rate — это скорость обучения, которую мы должны установить (например, 0.1), (expected — predicted) — ошибка прогнозирования для модели в обучающих данных, относящихся к весу, а x — входное значение.

Для стохастического градиентного спуска требуются два параметра:

• Коэффициент обучения: используется для ограничения размера корректировки веса при каждом его обновлении.
• Эпохи — сколько раз обучающие данные должны выполняться при обновлении веса.

Они вместе с обучающими данными будут аргументами для функции.

Нам нужно выполнить 3 цикла в функции:

1. Цикл для каждой эпохи.

2. Цикл для каждой строки в обучающих данных для эпохи.

3. Цикл для каждого веса, который обновляется для одной строке в одной эпохи.

Веса обновляются в зависимости от ошибки, допущенной моделью. Ошибка рассчитывается как разница между фактическим значением и прогнозом, сделанным с помощью весов.

Для каждого входного атрибута есть свой вес, и они постоянно обновляются, например:

• w(t+1)= w(t) + learning_rate * (expected(t) — predicted(t)) * x(t)

Смещение обновляется аналогичным образом, только без входа, поскольку оно не связано с конкретным входным значением:

• bias(t+1) = bias(t) + learning_rate * (expected(t) — predicted(t)).

Применение модели нейрона:

Теперь перейдем к практическому применению.

Этот урок разделен на 2 части:

1. Делаем прогнозы

2. Оптимизация веса сети

Эти шаги обеспечат основу для реализации и применения алгоритма перцептрона к другим задачам классификации.

Нам нужно определить количество столбцов в нашем наборе X, для этого мы определяем константу

#define nINPUT 3

---

В MQL5 многомерный массив может быть статическим или динамическим только для первого измерения, а поскольку все остальные измерения будут статическими, при объявлении массива необходимо указать размер.

1. Делаем прогнозы

Первый шаг — разработать функцию, которая может делать прогнозы.

Это будет необходимо как при оценке значений весов кандидатов при стохастическом градиентном спуске, так и после завершения модели. Прогнозы надо делать и на тестовых данных, и на новых.

Ниже приведена функция predict, которая прогнозирует выходное значение для строки исходя от определенного набора весов.

Первый вес всегда является смещением, поскольку он автономен и не работает с конкретным входным значением.

template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }

Перенос нейронов:

Как только нейрон активирован, нам нужно передать активацию, чтобы увидеть, каковы на самом деле выходные данные нейрона.

double activation(const double activation) 
  {
   return activation>=0.0?1.0:0.0;
  }

Мы получаем в качестве аргумента в функции прогнозирования входной набор X, массив с весами (W) и строку, для которой прогнозируется входной набор X.

Мы можем придумать небольшой набор данных, чтобы проверить нашу функцию прогнозирования.

Мы также можем использовать заранее подготовленные веса, чтобы делать прогнозы для этого набора данных.

double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};

После того, как мы собрали все это вместе, мы можем протестировать нашу функцию прогнозирования ниже.

#define nINPUT 3



void OnStart()
  {

   random.seed(42);
   double dataset[][nINPUT] = {     
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }


template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }



double activation(const double activation) 
  {
   return activation>=0.0?1.0:0.0;
  }

Есть два входных значения (X1 и X2) и три коэффициента веса (bias, w1 и w2). Уравнение активации, которое мы моделируем для данной проблемы, выглядит так:

activation = (w1 * X1) + (w2 * X2) + b

Или с конкретными значениями веса, мы вручную выбираем как:

activation = (0.206 * X1) + (-0.234 * X2) + -0.1

После завершения работы функции мы получаем прогнозы, которые соответствуют ожидаемым выходным значениям y.

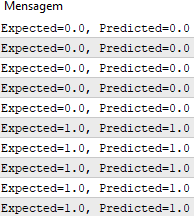
Теперь можем реализовать стохастический градиентный спуск для оптимизации значений веса.

2. Оптимизируем веса сети

Веса для наших обучающих данных можно оценить, используя стохастический градиентный спуск, как было сказано ранее.

Ниже приведена функция train_weights(), которая вычисляет значения веса для набора обучающих данных с использованием стохастического градиентного спуска.

В MQL5 мы не можем получить возврат из этого массива с данными обученных весов, потому что, в отличие от переменных, массивы могут быть переданы в функцию только по ссылке. Это означает, что функция не создает собственный экземпляр массива, а вместо этого работает напрямую с переданным ей массивом. Таким образом, все изменения, осуществляемые в этом массиве внутри функции влияют на исходный массив.

template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   for(int i=0; i<ArrayRange(X, 1); i++)
     {
      weights[i]=random.random();
     }
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

На каждой эпохе мы отслеживаем сумму квадратичной ошибки (положительное значение), чтобы отслеживать уменьшение ошибки. Это позволяет наблюдать как алгоритм минимизирует ошибку на каждой эпохе.

Давайте протестируем нашу функцию с одним и тем же набором данных, представленным выше.

#define nINPUT 3



void OnStart()
  {

   random.seed(42);
   double dataset[][nINPUT] = {     
                               {2.7810836,2.550537003,0},
                               {1.465489372,2.362125076,0},
                               {3.396561688,4.400293529,0},
                               {1.38807019,1.850220317,0},
                               {3.06407232,3.005305973,0},
                               {7.627531214,2.759262235,1},
                               {5.332441248,2.088626775,1},
                               {6.922596716,1.77106367,1},
                               {8.675418651,-0.242068655,1},
                               {7.673756466,3.508563011,1}
                              };
   double weights[];
   train_weights(weights, dataset);
   ArrayPrint(weights, 20);
   for(int row=0; row<ArrayRange(dataset, 0); row++)
     {
      double predict = predict(dataset, weights, row);
      printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict);
     }
  }


template <typename Array>
double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0)
  {
   double z = weights[0];
   for(int i=0; i<ArrayRange(X, 1)-1; i++)
     {
      z+=weights[i+1]*X[row][i];
     }
   return activation(z);
  }



double activation(const double activation) 
  {
   return activation>=0.0?1.0:0.0;
  }



template <typename Array>
void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5)
  {
   ArrayResize(weights, ArrayRange(X, 1));
   ArrayInitialize(weights, 0);
     
   for(int epoch=0; epoch<n_epoch; epoch++)
     {
      double sum_error = 0.0;
      for(int row=0; row<ArrayRange(X, 0); row++)
        {
         double y = predict(X, weights, row);
         double error = X[row][nINPUT-1] - y;
         sum_error += pow(error, 2);
         weights[0] = weights[0] + l_rate * error;

         for(int i=0; i<ArrayRange(X, 1)-1; i++)
           {
            weights[i+1] = weights[i+1] + l_rate * error * X[row][i];
           }
        }
      printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error);
     }
  }

Мы используем скорость обучения 0,1 и обучаем модель только для 5 эпох или 5 показов весов для всего набора обучающих данных.

При выполнении примера для каждой эпохи печатается сообщение с суммой квадратичной ошибки для этой эпохи и окончательным набором весов.

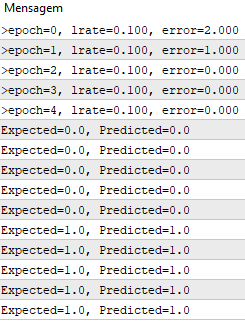
Мы видим, как быстро алгоритм выучивает проблему.

Этот тест можно найти в файле PerceptronScript.mq5.

Многослойный перцептрон

• Объединеняем нейроны в слои

   С одним нейроном мало что можно сделать, но мы можем объединить их в многоуровневую структуру, каждый с разным количеством нейронов, и сформировать нейронную сеть, называемую многослойным перцептроном («multi layer perceptron, MLP»). Вектор входных значений X проходит через начальный слой, выходные значения которого связаны со входами следующего уровня, и так далее, пока сеть не предоставит выходные значения последнего слоя в качестве результата. Сеть может быть организована в несколько слоев, что делает ее глубокой и способной выучить все более сложные отношения.

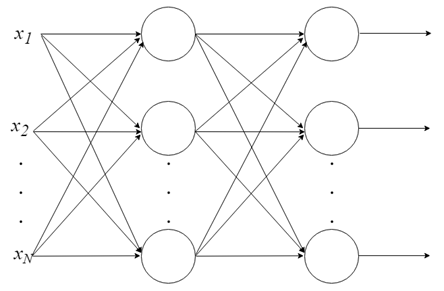
Обучение MLP

   Для того, чтобы такая сеть работала, ее нужно обучать. Это как учить ребенка читать. Обучение MLP происходит в контексте машинного обучения с учителем, но как это работает?

Обучение с учителем:

• Нам дается набор отмеченных данных, для которых мы уже знаем какой именно является нашим правильным выходом, и он должен быть аналогичен набору, имея представление о том, что существует связь между входом и выходом.
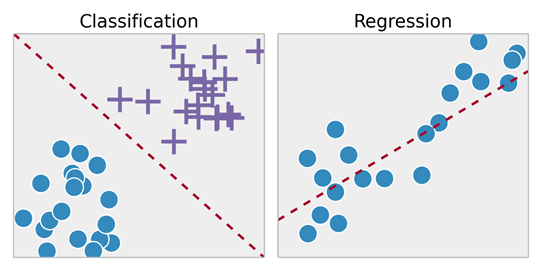
• Задачи обучения с учителем подразделяются на задачи «регрессии» и «классификации». В задачах регрессии мы пытаемся предсказать результаты на непрерывном выходе, что означает, что мы пытаемся сопоставить входные переменные с некоторой непрерывной функцией. В задачах классификации мы стараемся предсказать результаты на дискретном выходе. Другими словами, мы пытаемся сопоставить входные переменные по разным категориям.

Пример 1:

• Учитывая набор данных о размерах домов на рынке недвижимости, попробуйте спрогнозировать их цену. Цена в зависимости от размера — это непрерывный результат, так что это проблема регрессии.
• Мы могли бы также превратить этот пример в задачу классификации, чтобы прогнозировать о том, «продастся ли дом дороже или дешевле, чем запрашиваемая цена». Здесь мы рассортируем дома по цене на две разные категории.

Обратное распространение

Обратное распространение, без сомнений, является самым важным алгоритмом в истории нейронных сетей — без (эффективного) обратного распространения, было бы невозможно обучить сети глубокого обучения так, как мы это делаем сегодня. Обратное распространение можно считать краеугольным камнем современных нейронных сетей и глубокого обучения.

Разве мы не учимся на ошибках?

Идея алгоритма обратного распространения ошибки состоит в том, чтобы на основе расчетной ошибки, полученной на выходном слое нейронной сети, пересчитать значение весов вектора W последнего слоя нейронов. Затем мы переходим к предыдущему слою и так далее, от конца к началу, то есть, он состоит из обновления всех весов W слоев, от последнего до достижения входного слоя сети путем обратного распространения ошибки, полученной сетью. Другими словами, ошибка вычисляется между тем, что предсказала сеть, и тем, что она была на самом деле (фактический 1, предсказанный 0; у нас есть ошибка!), поэтому мы пересчитываем значения всех весов, начиная с последнего слоя и переходя к первому, всегда обращая внимание на уменьшение этой ошибки.

Алгоритм обратного распространения ошибки состоит из двух этапов:

1. Прямой проход («forward pass»), при котором наши входы проходят через сеть и получают прогнозы выхода (этот шаг также известен как фаза распространения).

2. Обратный проход («backward pass»), при котором мы вычисляем градиент функции потерь на последнем слое (то есть слое прогнозирования) сети и используем этот градиент для рекурсивного применения цепного правила («chain rule») для обновления весов в нашей сети (также известного как стадия обновления веса или обратное распространение)

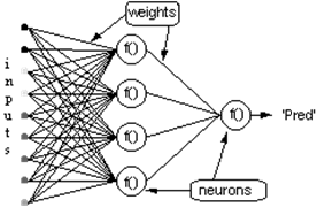
Рассмотрим сеть выше со слоем скрытых нейронов и выходным нейроном. Когда входной вектор распространяется по сети, для текущего набора весов существует выходной Pred(y). Цель обучения с учителем — настроить веса так, чтобы уменьшить разницу между Pred(y) сети и требуемым выходным Req(y). Для этого требуется алгоритм, который уменьшает абсолютную ошибку, что аналогично уменьшению квадратичной ошибки, где:

(1)

Сетевая ошибка = Pred — Req

      = E

Алгоритм должен регулировать веса, чтобы минимизировать E². Обратное распространение — это алгоритм, который выполняет минимизацию градиентного спуска E². Чтобы минимизировать E², необходимо рассчитать его чувствительность к каждому весу. Другими словами, нам нужно знать, какое влияние будет иметь изменение каждого веса на E². Если нам будет известно, веса можно будет отрегулировать в направлении, уменьшающем абсолютную ошибку. Последующее описание правила обратного распространения основано на такой диаграмме:

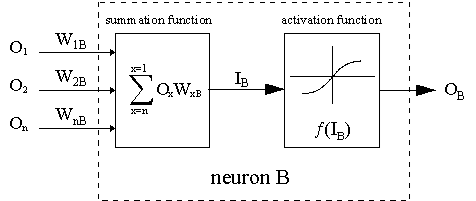
Пунктирная линия представляет нейрон B, который может быть скрытым или выходным нейроном. Выходы n нейронов (O 1 … O n) на предыдущем слое являются взодами для нейрона B. Если нейрон B находится в скрытом слое, он просто является входным вектором. Эти выходы умножаются на соответствующие веса (W1B … WnB), где WnB — вес, соединяющий нейрон n и нейрону B. Функция суммы складывает все эти произведения для получения входных данных, IB, который обрабатывается функцией триггера f(.) нейрона B. f (IB) это выход OB нейрона B. Рассмотрим пример. Назовем нейрон 1 нейроном A и рассмотрим вес WAB между двумя нейронами. Подход, используемый для изменения веса, определяется правилом дельты:

(2)

где — параметр скорости обучения, который определяет скорость обучения, а

является чувствительностью ошибки E² к весу WAB и определяет направление поиска в пространстве весов для нового веса WAB (новый), как изображено на рисунке ниже.

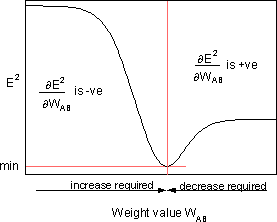
Чтобы минимизировать E², правило дельты обеспечивает необходимое направление изменения веса.

Ключевой концепцией приведенного выше уравнения является вычисление выражения ∂E² /∂WAB,  которое состоит в вычислении частных производных функции ошибок E² по отношению к каждому весу вектора W.

Дифференцирование сложной функции:

(3)

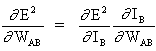
и

(4)

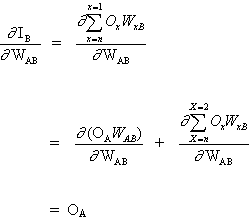
поскольку остальные входы нейрона B не зависят от веса WAB. Таким образом, исходя из уравнений (3) и (4), уравнение (2) становится

(5)

и изменение веса WAB зависит от чувствительности квадрата ошибки E² на входе IB, единицы B и входного сигнала OА.

Возможны две ситуации:

1. B — выходной нейрон;

2. B — скрытый нейрон.

Рассмотриваем первый случай:

Поскольку B является выходным нейроном, изменение квадрата ошибки из-за настроки WAB просто является изменением квадрата ошибки выходного сигнала B.

(6)

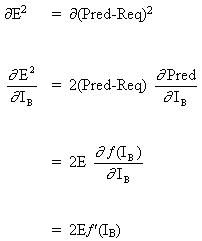
объединяя уравнение (5) и уравнение (6), получаем

(7)

Правило изменения весов, когда нейрон B является выходным нейроном, если выходная функция активации, f (.), является логистической функцией:

(8)

Дифференцируем уравнение (8) по аргументу x:

(9)

Но,

(10)

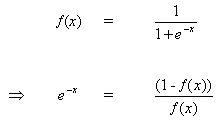
при вставке (10) в (9) получаем:

(11)

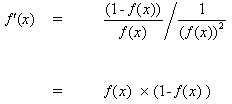
таким же образом для функции tanh

или для линейной функции (identity)

Так мы получаем:

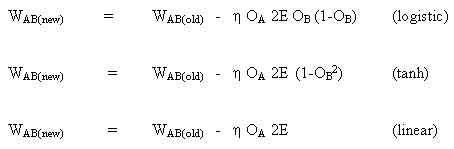
Рассматривая второй случай:

B это скрытый нейрон

(12)

где O представляет выходной нейрон

(13)

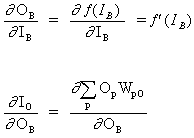
где p это индекс, который охватывает все нейроны, включая нейрон B, который обеспечивает входные сигналы для выходного нейрона. Расширяем правую часть уравнения (13),

(14)

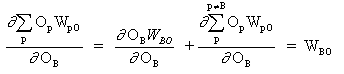
поскольку веса других нейронов WpO (p! = B) не имеют зависимости от OB.

При вставке (13) и (13) в (12):

(15)

Следовательно, теперь это выражается как функция от , вычисляемая, как описано в уравнении (6).

Полное правило изменения веса WAB между нейроном A, который посылает сигнал нейрону B, является таким:

(16)

где

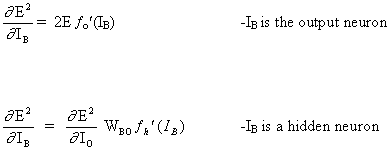
где fo (.) и fh (.) это скрытые функции активации и выхода соответственно.

Пример

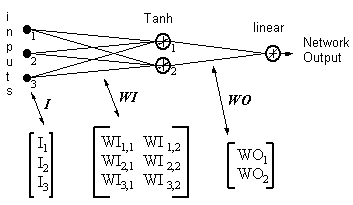
Выход из сети = [tanh(I ^T .WI)] . WO

HID = [Tanh(I ^T.WI)] ^T— выходы скрытых нейронов

ERROR = (выход из сети — нужный выход)

LR = коеффициент обучения

Обновления веса становятся

нейроном с линейным выходом

(17)

WO = WO — ( LR x ERROR x HID )

скрытым нейроном

(18)

WI = WI — { LR x [ERROR x WO x (1- HID ²)] . I ^T } ^T

Уравнения 17 и 18 показывают, что изменение веса — это входной сигнал, умноженный на локальный градиент. Это обеспечивает направление, величина которого также зависит от величины ошибки. Если берем направление без величины, все изменения будут одинакового размера, и это будет зависеть от темпа обучения. Вышеуказанный алгоритм является упрощенной версией, так как имеется только один выходной нейрон. В исходном алгоритме допускается более одного выхода, а уменьшение градиента минимизирует общую квадратную ошибку всех выходов. Есть много алгоритмов, которые произошли от исходного алгоритма для увеличения скорости обучения. Они кратко изложены в:

« Back Propagation family album» — Technical report C/TR96-05, Department of Computing, Macquarie University, NSW, Australia».

Обратное распространение — это элегантный и умелый алгоритм. Современные модели глубокого обучения, такие как сверточные нейронные сети, хотя и более совершенные, чем MLP, показали себя намного лучше в таких задачах, как классификация изображений и используют обратное распространение в качестве метода обучения, а также так называемые рекуррентные нейронные сети в условиях естественной языковой обработки, которые также используют этот алгоритм. Самое невероятное, что таким моделям удается находить ненаблюдаемые и непонятные закономерности для нас, людей, что удивляет и позволяет нам считать, что скоро мы получим помощь глубокого обучения для решения многих основных проблем, с которыми сталкивается человечество.

Применение модели MLP

Этот урок разделен на 5 частей:

1.       Инициализация сети.

2.       Прямое распространение (FeedForward).

3.       Обратное распространение.

4.       Обучение сети.

5.       Прогноз.

Для нашей разработки мы реализуем применение на чистом MQL. Нам уже известно, что существуют библиотеки на других языках, которые уже являются гораздо более сложными, и настоятельно рекомендуется использовать их из практических соображений и соображений производительности, но, как уже было сказано в начале, важно понимать внутреннее устройство таких библиотек, чтобы иметь больший контроль над всем процессом. Мы также не использовали ООП в нашем тесте, поскольку это всего лишь алгоритм для иллюстрации предыдущих уравнений, в нем нет необходимости. Однако в реальных случаях гораздо практичнее использовать ООП, поскольку оно обеспечивает масштабируемость проекта.

1. Инициализация сети

У каждого нейрона есть набор весов, которые необходимо поддерживать. Вес для каждого входного соединения и дополнительный вес для смещения.

Рекомендуем инициализировать веса сети для небольших случайных чисел. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1. Для этого мы создали функцию для генерации случайных чисел.

double random(void)
  {
   return ((double)rand())/(double)SHORT_MAX;
  }

Ниже представлена ​​функция под названием initialize_network(), которая создает веса нашей нейронной сети.

void forward_propagate(void)
  {


   int i = 0;
   for(i = 0; i<numHidden; i++)
     {
      hiddenVal[i] = 0.0;
      for(int j = 0; j<numInputs; j++)
        {
         hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]);
        }
      hiddenVal[i] = tanh(hiddenVal[i]);
     }


   outPred = 0.0;
   for(i = 0; i<numHidden; i++)
     {
      outPred += hiddenVal[i] * weightsHO[i];
     }

   errThisPat = outPred - y[patNum];
  }

3. Обратное распространение

Алгоритм обратного распространения назван в честь способа обучения весов

Ошибка вычисляется между ожидаемыми выходами и выходными сигналами сети прямого распространения. Затем эти ошибки передаются обратно по сети от выходного слоя к скрытому слою, перекладывая ответственность за ошибку и обновляя веса по мере их поступления.

Математика ошибки обратного распространения была объяснена выше.

void backward_propagate_error(void)
  {

   for(int k = 0; k<numHidden; k++)
     {
      double weightChange = LR_HO * errThisPat * hiddenVal[k];
      weightsHO[k] -= weightChange;
      
      regularisationWeights(weightsHO[k]);
     }

   for(int i = 0; i<numHidden; i++)
     {
      for(int k = 0; k<numInputs; k++)
        {
         double x = 1 - pow(hiddenVal[i],2);
         x = x * weightsHO[i] * errThisPat * LR_IH;
         x = x * X[patNum][k];
         double weightChange = x;
         weightsIH[k][i] -= weightChange;
        }
     }
  }

метод regularizationWeights был создан только для регуляризации весов в диапазоне от -5 до 5.

void regularisationWeights(double &weight)
  {
   weight<-5?weight=-5:weight>5?weight=5:weight=weight;
  }

4. Обучение сети

Сеть обучается методом стохастического градиентного спуска.

Это включает в себя несколько итераций, раскрывающих набор обучающих данных в сети, и для каждой строки данных прямое распространение входных данных, обратное распространение ошибки и обновление весов сети.

//# Train a network for a fixed number of epochs
void train(void)
  {
   for(int j = 0; j <= numEpochs; j++)
     {
      for(int i = 0; i<numPatterns; i++)
        {
         
         patNum = rand()%numPatterns;
         
         
         forward_propagate();
         backward_propagate_error();
        }
      
      
      calcOverallError();
      printf("epoch = %d RMS Error = %f",j,RMSerror);
     }
  }

5. Прогноз

Делать прогнозы с помощью обученной нейронной сети довольно просто.

Мы уже видели, как распространить паттерн входа для получения выходных данных. Это все, что нам нужно сделать, чтобы осуществить прогноз. Мы можем использовать выходные значения напрямую как вероятность принадлежности паттерна к каждому выходному классу.

void predict(void)
  {
   for(int i = 0; i<numPatterns; i++)
     {
      patNum = i;
      forward_propagate();
      printf("real = %d predict = %f",y[patNum],outPred);
     }
  }

Полный пример можно найти в файле MLP_Script.mq5.

Заключение

Мы занимались вычислениями, задействованными в процессе развития нейрона перцептрона, а также сети нейронов перцептрона, называемой «multi layer perceptron, MLP». В данном процессе мы поняли, как осуществляется обучение этого типа сетей с использованием обратного распространения ошибки и градиентного спуска.

Многослойные перцептроны

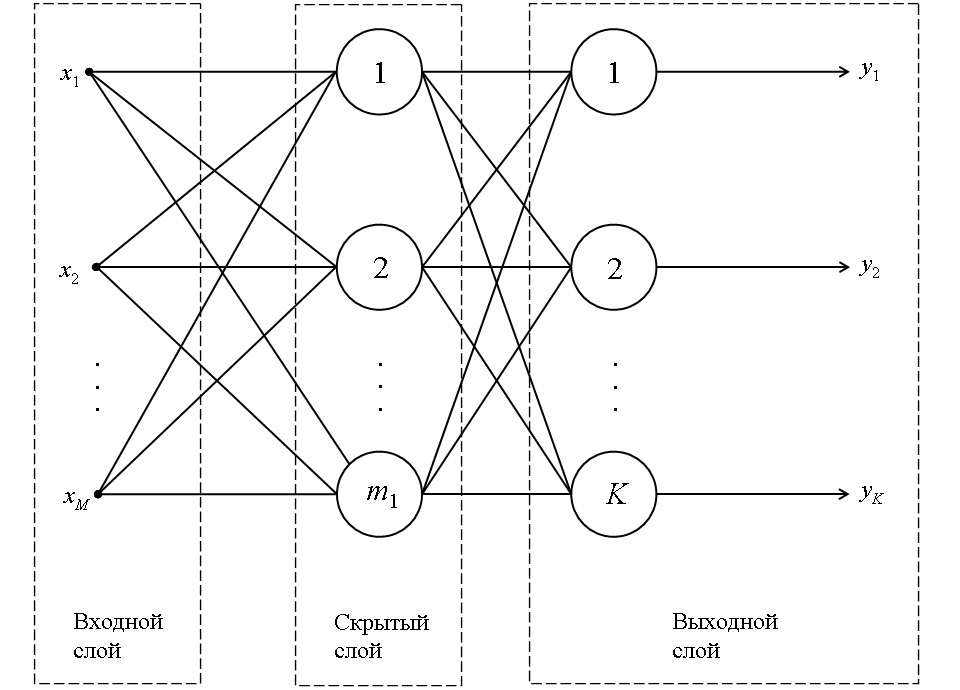
Многослойные перцептроны эффективны при решении тех же самых задач, что и однослойные перцептроны, но обладают значительно большей вычислительной способностью в сравнении с однослойными перцептронами. Благодаря этой своей способности они могут гораздо точнее описывать многомерные зависимости с большой степенью нелинейности и высоким уровнем перекрестного и группового влияния входных переменных на выходные.

Пример двухслойного перцептрона с M входами и K выходами был ранее приведен на рис. 1. При необходимости использования сетей более сложной структуры добавляются новые скрытые слои или наращивается количество нейронов в скрытых слоях.

Рис. 1. Схема двухслойной искусственной нейронной сети

Количество весовых коэффициентов, настраиваемых в процессе обучения многослойного перцептрона с L скрытыми слоями по m_l нейронов в каждом, рассчитывается следующим образом:

.

Для каждого нейрона сети помимо синаптических связей с элементами входного вектора настраивается связь с фиктивным единичным входом (коэффициент смещения).

Для большинства задач, решаемых с помощью многослойных перцептронов, выбор структуры нейронной сети должен осуществляться на основе следующего правила («Правила 2–5»): количество настраиваемых в процессе обучения весовых коэффициентов должно быть в 2–5 раз меньше, чем количество примеров обучающей выборки. Если это соотношение меньше 2, сеть теряет способность к обобщению обучающей информации, а при достижении 1 и меньше просто запоминает ответы для каждого обучающего примера. Если же количество обучающих примеров слишком велико для выбранной структуры сети, нейросетевая модель во многих случаях просто усредняет выходные значения для различных комбинаций входных векторов, теряя способность к корректному отклику в отдельных частных случаях и повышая величину максимальной выборочной ошибки.

Кроме того, при выборе структуры многослойного перцептрона следует задавать количество нейронов в скрытом слое, предшествующем выходному слою, не меньшим, чем количество самих выходов.

Метод Уидроу–Хоффа, рассмотренный в предыдущей главе, не может быть использован для настройки весовых коэффициентов многослойных перцептронов, поскольку он позволяет сделать прямую коррекцию по величине ошибки только для нейронов выходного слоя, тогда как синаптические коэффициенты скрытых нейронов также требуют изменения.

Задача обучения многослойных перцептронов может быть сформулирована как оптимизационная, в которой целевой функцией (критерием оптимизации) является общая ошибка, рассчитанная по обучающей выборке. Соответственно, и решать данную задачу можно как любую задачу многомерной оптимизации с использованием методов детерминированного, градиентного или стохастического поиска.

Наиболее распространенный метод обучения многослойного перцептрона – метод обратного распространения ошибки. Суть данного метода заключается в том, что сигнал ошибки каждого выходного значения, рассчитанный на текущем такте обучения, распространяется по слоям в обратном направлении (от выходного к первому) с учетом тех же весовых коэффициентов, которые использовались при прямом прохождении входных сигналов по нейронной сети и расчете выходных значений.

Алгоритм метода обратного распространения ошибки включает следующие этапы.

1. Весовые коэффициенты многослойного перцептрона выбранной структуры инициализируются небольшими по абсолютной величине (не более M^–1(L + 1)^–1) случайными значениями, где L – количество скрытых слоев.

2. На входы нейронной сети подается входной вектор одного из примеров обучающей выборки. Производится прямое распространение сигналов по сети с расчетом значений выходных переменных

3. Для каждого рассчитанного значения выходной переменной по соотношению 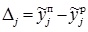 вычисляется погрешность по сравнению со значениями элементов выходного вектора взятого обучающего примера .

4. По полученным погрешностям рассчитываются невязки нейронов выходного слоя с учетом производных соответствующих активационных функций:

                                        (1)

Если активационная функция имеет вид сигмоиды или функции Гаусса, следует воспользоваться соотношениями для аналитического расчета ее производной.

5. В обратной последовательности (от последнего скрытого слоя к первому) рассчитываются невязки нейронов остальных слоев с учетом связывающих слои синаптических связей:

.                                 (2)

6. Для всех слоев нейронов, кроме первого, пересчитываются значения весовых коэффициентов по следующим соотношениям:

                                        (3)

                                     (4)

где ν – коэффициент скорости обучения.

Для первого скрытого слоя нейронов коррекция весовых коэффициентов происходит не по выходам предыдущего слоя, а по нормализованным значениям входных переменных нейронной сети:

                                        (5)

Для расчета коэффициентов смещения нейронов первого скрытого слоя, как и для всех других слоев, используется соотношение (3).

7. Цикл повторяется с шага 2 до выполнения одного или нескольких условий окончания:

– исчерпано заданное предельное количество эпох обучения;

– достигнут удовлетворительный уровень ошибки по всей обучающей выборке;

– не происходит уменьшения ошибки обучающей выборки на протяжении заданного предельного количества эпох обучения;

– исчерпано заданное предельное физическое время обучения.

На протяжении одной эпохи обучения последовательно или в случайном порядке предъявляются все примеры обучающей выборки, причем каждый пример должен быть предъявлен однократно.

Коэффициент скорости обучения задается положительной константой или переменной величиной (0 < v <= 1), постепенно уменьшающейся в процессе обучения нейронной сети.

Одна из особенностей метода обратного распространения ошибки заключается в том, что средние абсолютные значения невязок уменьшаются от последнего слоя нейронов к первому на порядки. Следствием этого становится практически незначительная величина изменения весовых коэффициентов первых скрытых слоев и, соответственно, требуется очень большое количество эпох обучения для значимой коррекции весов. Для устранения данного недостатка в многослойных перцептронах с более чем одним скрытым слоем можно использовать коэффициент скорости обучения, увеличивающийся от последнего скрытого слоя к первому в пределах одной эпохи обучения, в том числе, значения v_l > 1./p>

Ошибки работы всей нейронной сети по обучающей и тестовой выборкам могут быть рассчитаны по соотношениям из предыдущей статьи.

Метод обратного распространения ошибки базовый для обучения многослойных перцептронов, но не единственно возможный. С одной стороны, поскольку задача обучения любых перцептронов, по сути своей, оптимизационная, с этой целью могут использоваться практически любые методы оптимизации многомерных функций. С другой стороны, оптимизируемая функция ошибки (соотношение 3) не просто многомерная, а в большинстве случаев имеет очень высокую размерность в несколько десятков или даже сотен переменных – синаптических коэффициентов, и, к тому же, может обладать очень сложным рельефом поверхности, что делает невозможным использование на практике большинства традиционных методов. В этой связи реальной заменой методов градиентного поиска, адаптированных для обучения нейронных сетей (например, метода обратного распространения ошибки или метода Левенберга–Марквардта), могут быть лишь эволюционные или многоагентные методы (генетические алгоритмы, искусственные иммунные системы и другие), относящиеся к группе методов стохастического поиска. Зачастую такие методы могут быть даже более полезны, поскольку позволяют на любой эпохе обучения оперировать значениями переменных из всей области их определения, а не останавливаются в локальных оптимумах функции ошибки как методы градиентного поиска.

Если сравнивать архитектуры многослойных и однослойных перцептронов, можно выделить несколько ее отличительных особенностей:

– для одного и того же состава входных и выходных переменных в качестве нейросетевой модели могут быть использованы многослойные перцептроны различной структуры (с различным количеством скрытых слоев и нейронов в них), тогда как при использовании однослойных перцептронов возможен лишь один вариант структуры сети;

– многослойные перцептроны позволяют получить более корректное математическое описание многосвязных функциональных зависимостей с ярко выраженной нелинейностью;

– для обучения многослойных перцептронов требуется выбор более сложного алгоритма, чем для обучения однослойных перцептронов;

– обучение многослойных перцептронов занимает большее время и требует больший объем вычислительных ресурсов компьютера.

Рассмотрим пример решения задачи классификации образов с использованием двухслойного перцептрона. Пусть дана выборка данных (табл. 1), включающая 48 примеров. Используем первые 40 примеров для обучения перцептрона, а остальные 8 (выделены курсивом) – для тестирования обученной нейронной сети.

Таблица 1

Исходная выборка данных для обучения и практического
использования двухслойного перцептрона

№	x1	x2	x3	x4	x5	x6	y3	y4
1	–0,12	0,42	0,52	0,17	–0,64	–1,89	0	1
2	0,97	0,66	0,47	0,37	0,39	0,51	1	0
3	–2,60	–1,08	–0,24	–0,10	–0,65	–1,90	0	1
4	–1,45	–0,61	–0,41	–0,86	–1,96	–3,70	0	1
5	0,55	0,97	1,11	0,97	0,55	–0,15	0	1
6	0,54	0,53	0,57	0,64	0,75	0,90	1	0
7	0,93	0,93	1,11	1,47	2,00	2,72	1	0
8	–4,07	–2,36	–1,46	–1,36	–2,06	–3,56	0	1
9	3,66	2,25	1,73	2,08	3,31	5,42	1	0
10	4,87	2,25	0,29	–1,02	–1,67	–1,67	1	0
11	0,82	0,79	0,76	0,75	0,74	0,75	1	0
12	4,29	2,19	0,62	–0,41	–0,91	–0,88	1	0
13	–1,06	0,91	1,89	1,86	0,83	–1,20	0	1
14	–1,11	–0,49	–0,46	–1,03	–2,20	–3,97	0	1
15	0,71	–0,31	–0,85	–0,92	–0,51	0,37	1	0
16	–0,93	–0,63	–0,43	–0,35	–0,36	–0,48	0	1
17	–4,78	–2,71	–1,26	–0,46	–0,29	–0,75	0	1
18	–0,42	–0,41	–1,16	–2,67	–4,94	–7,97	0	1

№	x1	x2	x3	x4	x5	x6	y3	y4
19	3,25	2,21	1,60	1,42	1,67	2,35	1	0
20	–2,07	–1,40	–0,95	–0,72	–0,71	–0,92	0	1
21	4,35	1,59	–0,26	–1,20	–1,22	–0,32	1	0
22	0,68	0,13	0,04	0,42	1,27	2,58	1	0
23	–1,63	–1,58	–2,42	–4,16	–6,79	–10,31	0	1
24	0,97	0,42	0,07	–0,09	–0,05	0,18	1	0
25	–0,38	–0,47	–0,12	0,65	1,85	3,48	1	0
26	–2,19	–1,51	–1,44	–2,00	–3,16	–4,95	0	1
27	–1,16	–1,12	–1,16	–1,29	–1,49	–1,77	0	1
28	–0,80	–0,31	0,02	0,19	0,20	0,05	0	1
29	–1,97	–0,74	–0,04	0,13	–0,22	–1,10	0	1
30	1,67	1,86	1,74	1,31	0,58	–0,46	0	1
31	7,55	4,56	2,35	0,93	0,30	0,46	1	0
32	–0,79	–0,70	–0,69	–0,77	–0,93	–1,17	0	1
33	4,14	1,60	–0,24	–1,38	–1,83	–1,58	1	0
34	–0,91	–1,69	–1,64	–0,75	0,97	3,52	1	0
35	–4,79	–2,04	–0,08	1,09	1,48	1,07	0	1
36	–3,02	–2,26	–1,75	–1,51	–1,51	–1,77	0	1
37	4,36	2,67	1,82	1,82	2,66	4,35	1	0
38	2,23	1,91	2,14	2,92	4,25	6,13	1	0
39	2,47	0,50	–0,56	–0,70	0,06	1,73	1	0
40	0,36	–0,39	–0,59	–0,25	0,63	2,05	1	0
41	–2,04	–0,29	0,53	0,42	–0,61	–2,57	0	1
42	0,00	0,16	–0,13	–0,88	–2,09	–3,76	0	1
43	–2,75	–1,95	–1,40	–1,08	–0,99	–1,15	0	1
44	0,64	0,17	–0,03	0,04	0,37	0,97	1	0
45	–0,78	–1,06	–0,87	–0,22	0,89	2,48	1	0
46	–0,90	–1,00	–0,98	–0,82	–0,54	–0,13	1	0
47	0,33	1,14	1,60	1,71	1,46	0,86	0	1
48	2,20	1,84	1,98	2,62	3,75	5,37	1	0
Мин. зн.	–4,79	–2,71	–2,42	–4,16	–6,79	–10,31	0	0
Макс. зн.	7,55	4,56	2,35	2,92	4,25	6,13	1	1

Требуется разработать нейросетевую модель на основе двухслойного перцептрона, позволяющую классифицировать тип оптимума некоторой функции (минимум или максимум) по последовательно взятым 6 значениям этой функции на произвольном интервале в произвольных точках.

Соответственно, рассматриваемая нейронная сеть должна иметь 6 входных переменных, кодирующих входную последовательность значений функции, и 2 выходные переменные, позволяющие идентифицировать класс оптимума (y₃ – минимум, y₄ – максимум): единица указывает на принадлежность классу, 0 – на ее отсутствие. При использовании «Правила 2–5» двухслойный перцептрон с указанным количеством входов и выходов, обучающийся на 40 примерах, может содержать один или два скрытых нейрона. Рассмотрим процедуру обучения нейронной сети с двумя нейронами в скрытом слое (рис. 2).

Рис. 2. Структура двухслойного перцептрона для решения задачи
классификации типа оптимального значения

Выполним линейную нормализацию входных и выходных данных исходной выборки в пределах [0, 1] с использованием соотношения 3 статьи «Способы нормализации переменных». Нормализованные значения, используемые далее для обучения и тестирования двухслойного перцептрона, представлены в табл. 2. Курсивом, как и раньше, выделены тестовые примеры.

Рис. 3. Примеры функций активации типа гистерезиса

Выходные значения в обучающей выборке имеют бинарную форму, поэтому в качестве активационной функции выходных нейронов может выступать как функция единичного скачка (рис. 3, а, б), так и сигмоидная логистическая функция (рис. 3, д) с достаточно большой величиной параметра α, приближающей ее к скачкообразной форме, как показано на рисунке из статьи «Способы нормализации переменных».

Таблица 2

Нормализованная исходная выборка данных для обучения
и практического использования двухслойного перцептрона

№
1	0,378	0,431	0,616	0,612	0,557	0,512	0	1
2	0,467	0,464	0,606	0,640	0,650	0,658	1	0
3	0,177	0,224	0,457	0,573	0,556	0,512	0	1
4	0,271	0,289	0,421	0,466	0,438	0,402	0	1
5	0,433	0,506	0,740	0,725	0,665	0,618	0	1
6	0,432	0,446	0,627	0,678	0,683	0,682	1	0
7	0,464	0,501	0,740	0,795	0,796	0,793	1	0
8	0,058	0,048	0,201	0,395	0,428	0,411	0	1
9	0,685	0,682	0,870	0,881	0,915	0,957	1	0
10	0,783	0,682	0,568	0,444	0,464	0,526	1	0
11	0,455	0,481	0,667	0,694	0,682	0,673	1	0
12	0,736	0,674	0,637	0,530	0,533	0,574	1	0
13	0,302	0,498	0,904	0,850	0,690	0,554	0	1
14	0,298	0,305	0,411	0,442	0,416	0,386	0	1
15	0,446	0,330	0,329	0,458	0,569	0,650	1	0
16	0,313	0,286	0,417	0,538	0,582	0,598	0	1
17	0,001	0,000	0,243	0,523	0,589	0,582	0	1
18	0,354	0,316	0,264	0,210	0,168	0,142	0	1
19	0,652	0,677	0,843	0,788	0,766	0,770	1	0
20	0,220	0,180	0,308	0,486	0,551	0,571	0	1
21	0,741	0,591	0,453	0,418	0,505	0,608	1	0
22	0,443	0,391	0,516	0,647	0,730	0,784	1	0
23	0,256	0,155	0,000	0,000	0,000	0,000	0	1
24	0,467	0,431	0,522	0,575	0,611	0,638	1	0
25	0,357	0,308	0,482	0,679	0,783	0,839	1	0
26	0,211	0,165	0,205	0,305	0,329	0,326	0	1
27	0,294	0,219	0,264	0,405	0,480	0,519	0	1
28	0,323	0,330	0,512	0,614	0,633	0,630	0	1
29	0,229	0,271	0,499	0,606	0,595	0,560	0	1
30	0,524	0,629	0,872	0,773	0,668	0,599	0	1
31	1,000	1,000	1,000	0,719	0,642	0,655	1	0
32	0,324	0,276	0,363	0,479	0,531	0,556	0	1
33	0,724	0,593	0,457	0,393	0,449	0,531	1	0
34	0,314	0,140	0,164	0,482	0,703	0,841	1	0
35	0,000	0,092	0,491	0,742	0,749	0,692	0	1
36	0,143	0,062	0,140	0,374	0,478	0,519	0	1
37	0,741	0,740	0,889	0,845	0,856	0,892	1	0
38	0,569	0,635	0,956	1,000	1,000	1,000	1	0
39	0,588	0,442	0,390	0,489	0,620	0,732	1	0

40	0,417	0,319	0,384	0,552	0,672	0,752	1	0
41	0,223	0,333	0,618	0,647	0,560	0,471	0	1
42	0,388	0,395	0,480	0,463	0,426	0,398	0	1
43	0,165	0,105	0,214	0,435	0,525	0,557	0	1
44	0,440	0,396	0,501	0,593	0,649	0,686	1	0
45	0,325	0,227	0,325	0,556	0,696	0,778	1	0
46	0,315	0,235	0,302	0,472	0,566	0,619	1	0
47	0,415	0,530	0,843	0,829	0,747	0,679	0	1
48	0,566	0,626	0,922	0,958	0,955	0,954	1	0

Для обучения двухслойного перцептрона выберем метод обратного распространения ошибки, требующий дифференцируемость активационных функций для всей области определения. Следовательно, остановим выбор активационной функции для всех нейронов, включая скрытый, на сигмоидной логистической функции с α = 2,0, а получаемый аналоговый результат расчета по нейронной сети будем округлять для корректного решения задачи классификации. Коэффициент скорости обучения примем равным 0,5.

В соответствии с алгоритмом метода обратного распространения ошибки зададимся следующими начальными значениями весовых коэффициентов:w₀₁ = 0,03, w₁₁ = –0,08, w₂₁ = –0,06 w₃₁ = 0,02, w₄₁ = 0,02, w₅₁ = –0,08, w₆₁ = –0,07, w₀₂ = 0,02, w₁₂ = –0,05, w₂₂ = –0,01, w₃₂ = 0,05, w₄₂ = –0,04, w₅₂ = –0,01, w₆₂ = 0,01, w₀₃ = 0,04, w₁₃ = 0,01, w₂₃ = 0,04, w₀₄ = 0,07, w₁₄ = 0,02, w₂₄ = 0,01.

Предъявим сети элементы нормализованного входного вектора первого обучающего примера из табл. 2. Расчет состояний и выходных значений нейронов производится с использованием выражений  и . В результате получим: s₁ = –0,082, s₂ = –0,0027, 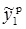 = 0,459,  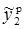= 0,501,s₃ = 0,065, s₄ = 0,084,  = 0,532,  = 0,542.

С использованием выражения (8.1) получим погрешности выходных значений: Δ₃ = –0,532, Δ₄ = 0,458.

Зная выходы всех нейронов, вычислим производные активационной функции в точках, соответствующих состояниям каждого нейрона по соотношению :  y’₁= 0,497, y’₂ = 0,500, y’₃ = 0,498, y’₄ = 0,496.

По погрешностям и производным активационной функции нейронов выходного слоя рассчитаем их невязки по соотношению (1): δ₃ = –0,265, δ₄ = 0,227, а с учетом этих значений по соотношению (2) – невязки скрытых нейронов: δ₁ = 0,0009, δ₂ = –0,0042.

Зная все невязки, выполним коррекцию весовых коэффициентов выходных нейронов по соотношениям (3) и (4) и скрытых нейронов по соотношениям (3) и (5). Новые значения весов записаны в первой строке данных в табл. 3.

В целом, в табл. 3 показано изменение весовых коэффициентов в ходе их коррекции при последовательном предъявлении 24 обучающих примеров первой эпохи обучения. В последней строке показаны значения весовых коэффициентов по окончании 100-й эпохи обучения.

Для обученной нейронной сети проведено тестирование на обучающей и тестовой выборках. Из 40 примеров обучающей выборки правильно оказались распознаны 38 примеров, что соответствует 95 % случаев верной классификации. Ошибки классификации выявлены для примеров №№ 6 и 11. Анализ входных векторов этих примеров показывает, что оптимальное значение в них выражено крайне слабо (отличается на 0,01 от одной из соседних точек) и находится близко к левой или правой границам. Учитывая эти особенности примеров с ошибками, а также ограниченный объем использованной выборки и простоту структуры двухслойного перцептрона, следует признать полученный результат тестирования очень хорошим.

Для тестовой выборки получены правильные результаты классификации в 7 случаях из 8 (табл. 4), что составляет 87,5 %.

Таблица 4

Результаты классификации тестовых примеров

№ примера					Корректность классификации
41	0	1	0	1	+
42	0	1	0	1	+
43	0	1	0	1	+
44	1	0	1	0	+
45	1	0	1	0	+
46	1	0	0	1	–
47	0	1	0	1	+
48	1	0	1	0	+

Единственная ошибка для примера № 46 не может объясняться теми же причинами, что для ошибок обучающей выборки. В данном случае очевидная причина – отсутствие примеров с близким характером и диапазоном изменения значений входных переменных в обучающей выборке. Будь обучающая выборка более объемной, этой ошибки, скорее всего, удалось бы избежать.

---

Если у вас есть статья, заметка или обзор, которыми вы хотите поделиться с аудиторией нашего сайта, присылайте информацию на: neuronus.com@yandex.ru.

Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.

Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.

Общее описание алгоритма обратного распространения ошибки

К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:

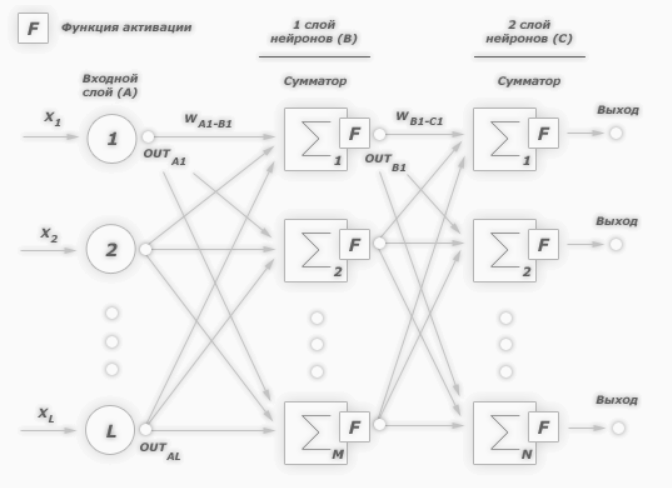
В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:

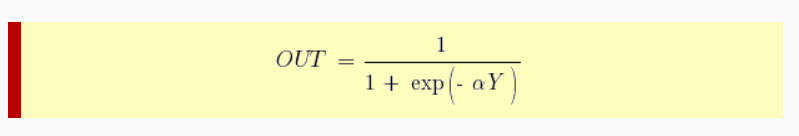
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.

Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.

Цель обучения сети

Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.

Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.

При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.

Пошаговая реализация метода обратного распространения ошибки

Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.

Виды обучения сети по методу обратного распространения

Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).

Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.

Преимущества и недостатки метода

К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.

Значение метода обратного распространения

Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.

Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».

распространения
ошибки.

Строгие математические
доказательства М. Минского и С. Пайперта
были неуязвимы. Всеобщий энтузиазм
сменился не менее всеобщим пессимизмом.
Правительство США прекратило финансирование
нейропроектов, и персептроны были
преданы забвению, длившемуся более 20
лет.

Тем не менее, работы
в области нейросетевых и нейрокомпьютерных
технологий продолжались отдельными
наиболее настойчивыми исследователями.
Многие понимали, что надо усложнять
структуру персептронов, т. е. продолжать
приближать компьютерную модель к
оригиналу — человеческому мозгу.
Оказалось, что проблему «Исключающее
ИЛИ» можно решить с помощью двухслойного
персептрона, изображенного на рис.3.26.

Рис.3.26. Двухслойный
персептрон, реализующий функцию

«Исключающее ИЛИ»

Работа этого
персептрона происходит по следующему
алгоритму.

Нейрон № 1: S₁=0,5х₁
+ (-0,5)х₂;
y₁=
1, если S₁θ;
y₁=
0, если S₁<θ.

Нейрон № 2: S₂
=(-0,5)x₁
+0,5x₂;
у₂
= 1, если S₂θ;
у₂
= 0, если S₂
<θ.

Нейрон
№ 3: S₃=lx_l+lx₂;
y₃
= 1, если
S₃
θ;
y₃=
0, если
S₃
<θ.

С помощью этих
формул легко проверить таблицу истинности
персептрона, составленную при задании
порога θ= 0,5 (табл.3.9).

Таблица
3.9

Таблица
истинности двухслойного персептрона
(см. рис.3.26)

x1	x2	S1	S2	y1	y2	S3	y3	y
0	0	0	0	0	0	0	0	0
0	1	-0,5	0,5	0	1	1	1	1
1	0	0,5	-0,5	1	0	1	1	1
1	1	0	0	0	0	0	0	0

Советским ученым
С.О. Мкртчяном был разработан специальный
математический аппарат, позволяющий
без обучения строить многослойные
персептроны, моделирующие любые булевы
функции.

Многие исследователи
понимали, что объединение нейронов в
нейронные сети расширяет класс задач,
решаемых персептроном, но не представляли,
как такие сети обучать. Простые и изящные
правила Хебба и их обобщение —
дельта-правило — годились только для
корректировки синаптических весов
нейронов выходного слоя, тогда как
вопрос о настройке параметров внутренних
нейронных слоев оставался открытым.

Эффективный
алгоритм обучения многослойных
персептронов, открывший путь для их
широкого практического применения,
стал известен только в 1986 г., благодаря
работе Румельхарта, Хилтона и Вильямса.
Интересно, что данный фундаментальный
алгоритм, называемый алгоритмом
обратного распространения ошибки
(back propagation), был предложен на один год
ранее в работах Паркера и Ле-Кана,
изданных независимо одна от другой.
Более того, еще в 1974 г. этот простой и
изящный алгоритм обратного распространения
ошибки был защищен Вербосом в его
докторской диссертации. Однако тогда
он остался незамеченным и только спустя
более десяти лет был «переоткрыт» заново
и получил всеобщее признание и применение.

Рассмотрим идею
алгоритма обратного распространения
ошибки, попытавшись обобщить дельта-правило
для случая обучения двухслойного
персептрона, имеющего N
входов, I
выходов и скрытый слой из J
нейронов (рис.3.27). Алгоритм корректировки
синаптических весов нейронов выходного
слоя оставим таким же, как для однослойного
персептрона, заменив x_j
на у_j.

w_ij(t+1)
= w_ij(t)
+ Δw_ij;
(3.11)

Δw_ij=ηδ_iy_j;
(3.12)

(3.13)

Рис.
3.27. Двухслойный персептрон с N
входами, I
выходами и скрытым слоем из J
нейронов

Синаптические
веса нейронов скрытого слоя попытаемся
корректировать с помощью тех же самых
формул, в которых индекс i
заменим на j, а индекс j — на n:

(3.14)

(3.15)

Понятно, что в
последнем выражении в качестве у_n
следует использовать х_n.
Однако неясным здесь остается вопрос
о вычислении нейронной ошибки (d_j
— y_j),
которая для скрытого слоя неизвестна.
Идея авторов рассматриваемого алгоритма
состояла в том, чтобы в качестве этой
ошибки использовать суммарные ошибки
с выходного слоя, помноженные на силы
соответствующих синаптических связей,
т.е.
(3.16)

Итак, для скрытого
слоя окончательно имеем:
(3.17)

(3.18)

Используя эту
идею, несложно расписать алгоритм
обратного распространения ошибки для
обучения персептрона, имеющего
произвольное число скрытых слоев. Однако
прежде внесем еще одно изменение в
модель нейрона. К сумме, которую вычисляет
нейрон, полезно добавить некоторое
число, называемое порогом, или смещением:

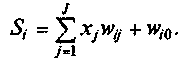(3.19)

Смещение w_i0
задается так же, как и синаптические
веса w_ij,
т.е. датчиком случайных чисел. Ввод
смещения в формулу преобразования
нейрона можно интерпретировать как
добавление еще одного входного сигнала
x₀,
который всегда равен единице. Поэтому,
чтобы не усложнять выкладки, сумму
(3.19) представим в более компактном виде
(приняв x₀=
1):

(3.20)

Алгоритм обратного
распространения ошибки
распишем для многослойного персептрона,
имеющего входной слой k=
0, несколько скрытых слоев k=1,2,…,К-1
и выходной слой k=K
(рис.3.28). Нейроны входного слоя
математических преобразований не
выполняют, а лишь передают входные
сигналы нейронам первого слоя.

Рис.3.28.
Многослойный персептрон (MLP —
MultiLayerPerseptron)

Будем полагать,
что каждый k-й
слой содержит H_k
нейронов. Таким образом, персептрон
имеет N =H₀
входов и М= H_К
выходов. В алгоритме будем использовать
следующие обозначения: i
— порядковый номер нейрона k-го слоя; j
— порядковый номер нейрона (k-1)-го
слоя; l
— порядковый номер нейрона (k+1)-го
слоя.

Шаг 1. Инициализация
синаптических весов и смещений.

В циклах по
k=1,2,…,К;
i=1,2,…,H_k;
j =1,2,…,Н_k-1
синаптическим весам и смещениям w_ij^(k)
датчиком случайных чи­сел присваиваются
малые величины, например, из интервала
от -1 до 1.

Шаг 2. Представление
из обучающей выборки очередного входного
вектора X_q=(х₁,х₂,…,x_N)_q
и соответствующего ему желаемого
выходного вектора D_q=(d₁,d₂,
…,d_M)_q,
где q — номер примера в обучающей выборке.

Шаг 3. Прямой проход.

В циклах по
k=1,2,…,К;
i=1,2,…,Н_k
вычисляются выходные сигналы i-го
нейрона в k-м
слое

(3.21)

где y_j⁽⁰⁾
=x_j,
x₀=1,
y_j^(k-1)
= 1 и выходные сигналы персептрона
y_i=y_i^(K).

Шаг 4. Обратный
проход.

В циклах по k=
К,К-1,…,1; i=1,2,…,H_k;j=1,2,
…,H_k-1
вычисляются синаптические веса на новой
эпохе

(3.22)

где

(3.23)

причем для выходного
слоя k=
К согласно (3.13)

а для всех других
случаев согласно (3.18)

(3.24)

Шаг 5. Повторение
шагов 2 — 4 необходимое число раз.

Входные векторы
обучающих примеров Х_q
и D_q
на втором шаге алгоритма обычно
представляются последовательно от
первого до последнего, т.е. q=1,2,…,Q, где
Q — общее число примеров. Например, в
случае распознавания букв русского
алфавита Q=33. После того как для каждого
обучающего примера будут скорректированы
весовые коэффициенты персептрона, т.е.
шаги 2-4 будут повторены 33 раза, на пятом
шаге алгоритма вычисляется среднеквадратичная
ошибка, усредненная по всем обучающим
примерам:

(3.25)

Помимо
среднеквадратичной ошибки может быть
также оценена максимальная разность
между желаемым и фактическим выходами
персептрона:

(3.26)

Итерационный
процесс заканчивается после того, как
погрешность ε, вычисляемая по формулам
(3.25) или (3.26), достигнет заданной величины,
либо при достижении предельного числа
эпох обучения. В результате персептрон
обучится выполнять нужное отображение
любого входного вектора Х_q
на выходной вектор Yq,
отличающийся от желаемого вектора D_q
на некоторую малую величину.

Теперь представим
себе, что на входное табло фотоэлементов
попала карточка с какой-либо буквой,
выполненной другим шрифтом. Фотоэлементы
сформируют входной вектор X,
не совпадающий ни с одним из векторов
из использованной обучающей выборки.
Если шрифт, которым выполнена входная
буква не слишком отличается от шрифта
обучающей выборки, а персептрон хорошо
спроектирован и обучен, то он вычислит
вектор Y,
в котором выход нейрона, соответствующего
представленной на вход букве, будет
иметь максимальное значение. Таким
образом, персептрон, несмотря на помехи
и искажения входного образа, выдаст
правильное заключение о его принадлежности
к тому или иному классу. Свойство
персептрона правильно реагировать на
входные образы, которых не было в
обучающей выборке, называется свойством
обобщения.

Соседние файлы в папке ОСИИ учебное пособие

• #
• #
• #
• #