Время на прочтение
19 мин
Количество просмотров 285K
Тема нейронных сетей была уже ни раз освещена на хабре, однако сегодня я бы хотел познакомить читателей с алгоритмом обучения многослойной нейронной сети методом обратного распространения ошибки и привести реализацию данного метода.
Сразу хочу оговориться, что не являюсь экспертом в области нейронных сетей, поэтому жду от читателей конструктивной критики, замечаний и дополнений.
Теоретическая часть
Данный материал предполагает знакомство с основами нейронных сетей, однако я считаю возможным ввести читателя в курс темы без излишних мытарств по теории нейронных сетей. Итак, для тех, кто впервые слышит словосочетание «нейронная сеть», предлагаю воспринимать нейронную сеть в качестве взвешенного направленного графа, узлы ( нейроны ) которого расположены слоями. Кроме того, узел одного слоя имеет связи со всеми узлами предыдущего слоя. В нашем случае у такого графа будут иметься входной и выходной слои, узлы которых выполняют роль входов и
выходов соответственно. Каждый узел ( нейрон ) обладает активационной функцией — функцией, ответственной за вычисление сигнала на выходе узла ( нейрона ). Также существует понятие смещения, представляющего из себя узел, на выходе которого всегда появляется единица. В данной статье мы будем рассматривать процесс обучения нейронной сети, предполагающий наличие «учителя», то есть процесс обучения, при котором обучение происходит путем предоставления сети последовательности обучающих примеров с правильными откликами.
Как и в случае с большинством нейронных сетей, наша цель состоит в обучении сети таким образом, чтобы достичь баланса между способностью сети давать верный отклик на входные данные, использовавшиеся в процессе обучения ( запоминания ), и способностью выдавать правильные результаты в ответ на входные данные, схожие, но неидентичные тем, что были использованы при обучении ( принцип обобщения). Обучение сети методом обратного распространения ошибки включает в себя три этапа: подачу на вход данных, с последующим распространением данных в направлении выходов, вычисление и обратное распространение соответствующей ошибки и корректировку весов. После обучения предполагается лишь подача на вход сети данных и распространение их в направлении выходов. При этом, если обучение сети может являться довольно длительным процессом, то непосредственное вычисление результатов обученной сетью происходит очень быстро. Кроме того, существуют многочисленные вариации метода обратного распространения ошибки, разработанные с целью увеличения скорости протекания
процесса обучения.
Также стоит отметить, что однослойная нейронная сеть существенно ограничена в том, обучению каким шаблонам входных данных она подлежит, в то время, как многослойная сеть ( с одним или более скрытым слоем ) не имеет такого недостатка. Далее будет дано описание стандартной нейронной сети с обратным распространением ошибки.
Архитектура
На рисунке 1 показана многослойная нейронная сеть с одним слоем скрытых нейронов ( элементы Z ).
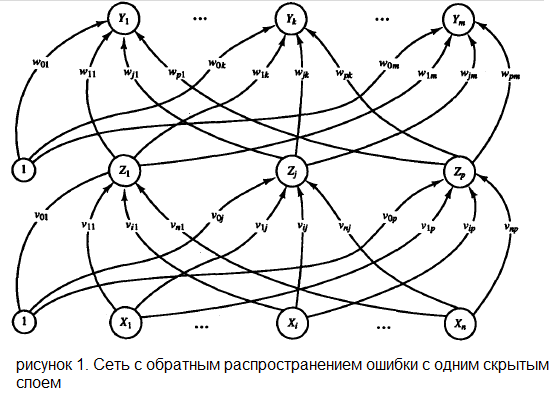
Нейроны, представляющие собой выходы сети ( обозначены  ), и скрытые нейроны могут иметь смещение( как показано на изображении ). Смещение, соответствующий выходу
), и скрытые нейроны могут иметь смещение( как показано на изображении ). Смещение, соответствующий выходу  обозначен
обозначен , скрытому элементу
, скрытому элементу  —
— 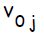 . Эти смещения служат в качестве весов на связях, исходящих от нейронов, на выходе которых всегда появляется 1 ( на рисунке 1 они показаны, но обычно явно не отображаются, подразумеваясь). Кроме того, на рисунке 1 стрелками показано перемещение информации в ходе фазы распространения данных от входов к выходам. В процессе обучения сигналы распространяются в обратном направлении.
. Эти смещения служат в качестве весов на связях, исходящих от нейронов, на выходе которых всегда появляется 1 ( на рисунке 1 они показаны, но обычно явно не отображаются, подразумеваясь). Кроме того, на рисунке 1 стрелками показано перемещение информации в ходе фазы распространения данных от входов к выходам. В процессе обучения сигналы распространяются в обратном направлении.
Описание алгоритма
Алгоритм, представленный далее, применим к нейронной сети с одним скрытым слоем, что является допустимой и адекватной ситуацией для большинства приложений. Как уже было сказано ранее, обучение сети включает в себя три стадии: подача на входы сети обучающих данных, обратное распространение ошибки и корректировка весов. В ходе первого этапа каждый входной нейрон  получает сигнал и широковещательно транслирует его каждому из скрытых нейронов
получает сигнал и широковещательно транслирует его каждому из скрытых нейронов  . Каждый скрытый нейрон затем вычисляет результат его активационной функции ( сетевой функции ) и рассылает свой сигнал
. Каждый скрытый нейрон затем вычисляет результат его активационной функции ( сетевой функции ) и рассылает свой сигнал  всем выходным нейронам. Каждый выходной нейрон
всем выходным нейронам. Каждый выходной нейрон  , в свою очередь, вычисляет результат своей активационной функции
, в свою очередь, вычисляет результат своей активационной функции  , который представляет собой ничто иное, как выходной сигнал данного нейрона для соответствующих входных данных. В процессе обучения, каждый нейрон на выходе сети сравнивает вычисленное значение
, который представляет собой ничто иное, как выходной сигнал данного нейрона для соответствующих входных данных. В процессе обучения, каждый нейрон на выходе сети сравнивает вычисленное значение  с предоставленным учителем
с предоставленным учителем  ( целевым значением ), определяя соответствующее значение ошибки для данного входного шаблона. На основании этой ошибки вычисляется
( целевым значением ), определяя соответствующее значение ошибки для данного входного шаблона. На основании этой ошибки вычисляется  .
.  используется при распространении ошибки от
используется при распространении ошибки от  до всех элементов сети предыдущего слоя ( скрытых нейронов, связанных с
до всех элементов сети предыдущего слоя ( скрытых нейронов, связанных с  ), а также позже при изменении весов связей между выходными нейронами и скрытыми. Аналогичным образом вычисляется
), а также позже при изменении весов связей между выходными нейронами и скрытыми. Аналогичным образом вычисляется 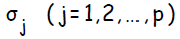 для каждого скрытого нейрона
для каждого скрытого нейрона  . Несмотря на то, что распространять ошибку до входного слоя необходимости нет,
. Несмотря на то, что распространять ошибку до входного слоя необходимости нет, 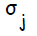 используется для изменения весов связей между нейронами скрытого слоя и входными нейронами. После того как все
используется для изменения весов связей между нейронами скрытого слоя и входными нейронами. После того как все 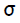 были определены, происходит одновременная корректировка весов всех связей.
были определены, происходит одновременная корректировка весов всех связей.
Обозначения:
В алгоритме обучения сети используются следующие обозначения:
 Входной вектор обучающих данных
Входной вектор обучающих данных 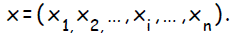
 Вектор целевых выходных значений, предоставляемых учителем
Вектор целевых выходных значений, предоставляемых учителем
 Составляющая корректировки весов связей
Составляющая корректировки весов связей 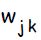 , соответствующая ошибке выходного нейрона
, соответствующая ошибке выходного нейрона  ; также, информация об ошибке нейрона
; также, информация об ошибке нейрона  , которая распространяется тем нейронам скрытого слоя, которые связаны с
, которая распространяется тем нейронам скрытого слоя, которые связаны с  .
.
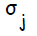 Составляющая корректировки весов связей
Составляющая корректировки весов связей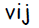 , соответствующая распространяемой от выходного слоя к скрытому нейрону
, соответствующая распространяемой от выходного слоя к скрытому нейрону  информации об ошибке.
информации об ошибке.
 Скорость обучения.
Скорость обучения.
 Нейрон на входе с индексом i. Для входных нейронов входной и выходной сигналы одинаковы —
Нейрон на входе с индексом i. Для входных нейронов входной и выходной сигналы одинаковы —  .
.
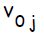 Смещение скрытого нейрона j.
Смещение скрытого нейрона j.
 Скрытый нейрон j; Суммарное значение подаваемое на вход скрытого элемента
Скрытый нейрон j; Суммарное значение подаваемое на вход скрытого элемента  обозначается
обозначается 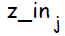 :
: 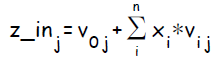
Сигнал на выходе ( результат применения к
( результат применения к 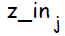 активационной функции ) обозначается
активационной функции ) обозначается  :
: 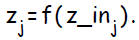
 Смещение нейрона на выходе.
Смещение нейрона на выходе.
 Нейрон на выходе под индексом k; Суммарное значение подаваемое на вход выходного элемента
Нейрон на выходе под индексом k; Суммарное значение подаваемое на вход выходного элемента  обозначается
обозначается 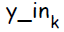 :
:  . Сигнал на выходе
. Сигнал на выходе  ( результат применения к
( результат применения к 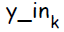 активационной функции ) обозначается
активационной функции ) обозначается  :
:
Функция активации
Функция активация в алгоритме обратного распространения ошибки должна обладать несколькими важными характеристиками: непрерывностью, дифференцируемостью и являться монотонно неубывающей. Более того, ради эффективности вычислений, желательно, чтобы ее производная легко находилась. Зачастую, активационная функция также является функцией с насыщением. Одной из наиболее часто используемых активационных функций является бинарная сигмоидальная функция с областью значений в ( 0, 1 ) и определенная как:


Другой широко распространенной активационной функцией является биполярный сигмоид с областью значений ( -1, 1 ) и определенный как:
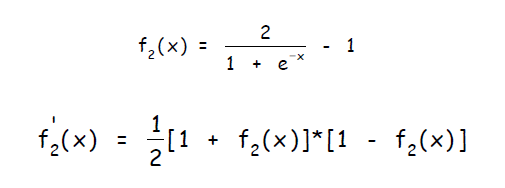
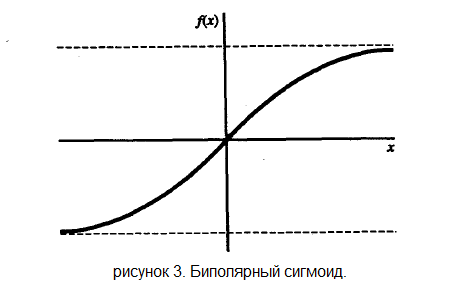
Алгоритм обучения
Алгоритм обучения выглядит следующим образом:
Шаг 0.
Инициализация весов ( веса всех связей инициализируются случайными небольшими значениями ).
Шаг 1.
До тех пор пока условие прекращения работы алгоритма неверно, выполняются шаги 2 — 9.
Шаг 2.
Для каждой пары { данные, целевое значение } выполняются шаги 3 — 8.
Распространение данных от входов к выходам:
Шаг 3.
Каждый входной нейрон 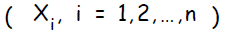 отправляет полученный сигнал
отправляет полученный сигнал  всем нейронам в следующем слое ( скрытом ).
всем нейронам в следующем слое ( скрытом ).
Шаг 4.
Каждый скрытый нейрон  суммирует взвешенные входящие сигналы:
суммирует взвешенные входящие сигналы: 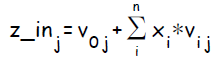 и применяет активационную функцию:
и применяет активационную функцию: 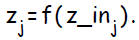 После чего посылает результат всем элементам следующего слоя ( выходного ).
После чего посылает результат всем элементам следующего слоя ( выходного ).
Шаг 5.
Каждый выходной нейрон  суммирует взвешенные входящие сигналы:
суммирует взвешенные входящие сигналы:  и применяет активационную функцию, вычисляя выходной сигнал:
и применяет активационную функцию, вычисляя выходной сигнал: 
Обратное распространение ошибки:
Шаг 6.
Каждый выходной нейрон  получает целевое значение — то выходное значение, которое является правильным для данного входного сигнала, и вычисляет ошибку:
получает целевое значение — то выходное значение, которое является правильным для данного входного сигнала, и вычисляет ошибку:  , так же вычисляет величину, на которую изменится вес связи
, так же вычисляет величину, на которую изменится вес связи 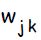 :
:  . Помимо этого, вычисляет величину корректировки смещения:
. Помимо этого, вычисляет величину корректировки смещения:  и посылает
и посылает  нейронам в предыдущем слое.
нейронам в предыдущем слое.
Шаг 7.
Каждый скрытый нейрон  суммирует входящие ошибки ( от нейронов в последующем слое )
суммирует входящие ошибки ( от нейронов в последующем слое )  и вычисляет величину ошибки, умножая полученное значение на производную активационной функции:
и вычисляет величину ошибки, умножая полученное значение на производную активационной функции: 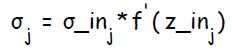 , так же вычисляет величину, на которую изменится вес связи
, так же вычисляет величину, на которую изменится вес связи 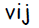 :
:  . Помимо этого, вычисляет величину корректировки смещения:
. Помимо этого, вычисляет величину корректировки смещения: 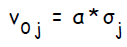
Шаг 8. Изменение весов.
Каждый выходной нейрон  изменяет веса своих связей с элементом смещения и скрытыми нейронами:
изменяет веса своих связей с элементом смещения и скрытыми нейронами: 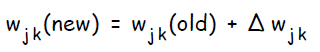
Каждый скрытый нейрон  изменяет веса своих связей с элементом смещения и выходными нейронами:
изменяет веса своих связей с элементом смещения и выходными нейронами: 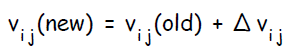
Шаг 9.
Проверка условия прекращения работы алгоритма.
Условием прекращения работы алгоритма может быть как достижение суммарной квадратичной ошибкой результата на выходе сети предустановленного заранее минимума в ходе процесса обучения, так и выполнения определенного количества итераций алгоритма. В основе алгоритма лежит метод под названием градиентный спуск. В зависимости от знака, градиент функции ( в данном случае значение функции — это ошибка, а параметры — это веса связей в сети ) дает направление, в котором значения функции возрастают (или убывают) наиболее стремительно.
Выбор первоначальных весов и смещения
Случайная инициализация. Выбор начальных весов окажет влияние на то, сумеет ли сеть достичь глобального ( или только локального) минимума ошибки, и насколько быстро этот процесс будет происходить. Изменение весов между двумя нейронами связано с производной активационной функции нейрона из последующего слоя и активационной функции нейрона слоя предыдущего. В связи с этим, важно избегать выбора таких начальных весов, которые обнулят активационную функцию или ее производную. Также начальные веса не должны быть слишком большими ( или входные сигнал для каждого скрытого или выходного нейрона скорее всего попадут в регион очень малых значений сигмоида ( регион насыщения ) ). С другой стороны, если начальные веса будут слишком маленькими, то входной сигнал на скрытые или выходные нейроны будет близок к нулю, что также приведет к очень низкой скорости обучения. Стандартная процедура инициализации весов состоит в присвоении им случайных значений в интервале ( -0,5; 0,5). Значения могут быть как положительными, так и отрицательными, так как конечные веса, получающиеся после обучения сети, могут быть обоих знаков. Инициализация Nguyen – Widrow. Представленная далее простая модификация стандартной процедуру инициализации способствует более быстрому обучению: Веса связей скрытых и выходных нейронов, а также смещение выходного слоя инициализируются также, как и в стандартной процедуре — случайными значениями из интервала ( -0,5; 0,5).
Введем обозначения:
 количество входных нейронов
количество входных нейронов
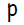 количество скрытых нейронов
количество скрытых нейронов
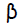 фактор масштабирования:
фактор масштабирования:
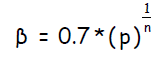
Процедура состоит из следующих простых шагов:
Для каждого скрытого нейрона  :
:
инициализировать его вектор весов ( связей с входными нейронами ):
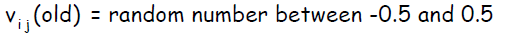
вычислить 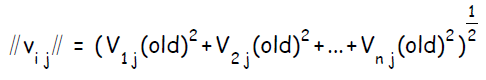
переинициализировать веса: 
задать значение смещения: 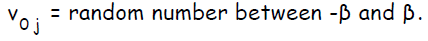
Практическая часть
Начну с реализации концепции нейрона. Было решено представить нейроны входного слоя базовым классом, а скрытые и выходные как декораторы базового класса. Кроме того, нейрон хранит в себе информацию об исходящих и входящих связях, а также каждый нейрон композиционно имеет в своем составе активационную функцию.
Интерфейс нейрона
/**
* Neuron base class.
* Represents a basic element of neural network, node in the net's graph.
* There are several possibilities for creation an object of type Neuron, different constructors suites for
* different situations.
*/
template <typename T>
class Neuron
{
public:
/**
* A default Neuron constructor.
* - Description: Creates a Neuron; general purposes.
* - Purpose: Creates a Neuron, linked to nothing, with a Linear network function.
* - Prerequisites: None.
*/
Neuron( ) : mNetFunc( new Linear ), mSumOfCharges( 0.0 ) { };
/**
* A Neuron constructor based on NetworkFunction.
* - Description: Creates a Neuron; mostly designed to create an output kind of neurons.
* @param inNetFunc - a network function which is producing neuron's output signal;
* - Purpose: Creates a Neuron, linked to nothing, with a specific network function.
* - Prerequisites: The existence of NetworkFunction object.
*/
Neuron( NetworkFunction * inNetFunc ) : mNetFunc( inNetFunc ), mSumOfCharges( 0.0 ){ };
Neuron( std::vector<NeuralLink<T > *>& inLinksToNeurons, NetworkFunction * inNetFunc ) :
mNetFunc( inNetFunc ),
mLinksToNeurons(inLinksToNeurons),
mSumOfCharges(0.0){ };
/**
* A Neuron constructor based on layer of Neurons.
* - Description: Creates a Neuron; mostly designed to create an input and hidden kinds of neurons.
* @param inNeuronsLinkTo - a vector of pointers to Neurons which is representing a layer;
* @param inNetFunc - a network function which is producing neuron's output signal;
* - Purpose: Creates a Neuron, linked to every Neuron in provided layer.
* - Prerequisites: The existence of std::vector<Neuron *> and NetworkFunction.
*/
Neuron( std::vector<Neuron *>& inNeuronsLinkTo, NetworkFunction * inNetFunc );
virtual ~Neuron( );
virtual std::vector<NeuralLink<T > *>& GetLinksToNeurons( ){ return mLinksToNeurons; };
virtual NeuralLink<T> * at( const int& inIndexOfNeuralLink ) { return mLinksToNeurons[ inIndexOfNeuralLink ]; };
virtual void SetLinkToNeuron( NeuralLink<T> * inNeuralLink ){ mLinksToNeurons.push_back( inNeuralLink ); };
virtual void Input( double inInputData ){ mSumOfCharges += inInputData; };
virtual double Fire( );
virtual int GetNumOfLinks( ) { return mLinksToNeurons.size( ); };
virtual double GetSumOfCharges( );
virtual void ResetSumOfCharges( ){ mSumOfCharges = 0.0; };
virtual double Process( ) { return mNetFunc->Process( mSumOfCharges ); };
virtual double Process( double inArg ){ return mNetFunc->Process( inArg ); };
virtual double Derivative( ){ return mNetFunc->Derivative( mSumOfCharges ); };
virtual void SetInputLink( NeuralLink<T> * inLink ){ mInputLinks.push_back( inLink ); };
virtual std::vector<NeuralLink<T > *>& GetInputLink( ){ return mInputLinks; };
virtual double PerformTrainingProcess( double inTarget );
virtual void PerformWeightsUpdating( );
virtual void ShowNeuronState( );
protected:
NetworkFunction * mNetFunc;
std::vector<NeuralLink<T > *> mInputLinks;
std::vector<NeuralLink<T > *> mLinksToNeurons;
double mSumOfCharges;
};
template <typename T>
class OutputLayerNeuronDecorator : public Neuron<T>
{
public:
OutputLayerNeuronDecorator( Neuron<T> * inNeuron ){ mOutputCharge = 0; mNeuron = inNeuron; };
virtual ~OutputLayerNeuronDecorator( );
virtual std::vector<NeuralLink<T > *>& GetLinksToNeurons( ){ return mNeuron->GetLinksToNeurons( ) ;};
virtual NeuralLink<T> * at( const int& inIndexOfNeuralLink ){ return ( mNeuron->at( inIndexOfNeuralLink ) ) ;};
virtual void SetLinkToNeuron( NeuralLink<T> * inNeuralLink ){ mNeuron->SetLinkToNeuron( inNeuralLink ); };
virtual double GetSumOfCharges( ) { return mNeuron->GetSumOfCharges( ); };
virtual void ResetSumOfCharges( ){ mNeuron->ResetSumOfCharges( ); };
virtual void Input( double inInputData ){ mNeuron->Input( inInputData ); };
virtual double Fire( );
virtual int GetNumOfLinks( ) { return mNeuron->GetNumOfLinks( ); };
virtual double Process( ) { return mNeuron->Process( ); };
virtual double Process( double inArg ){ return mNeuron->Process( inArg ); };
virtual double Derivative( ) { return mNeuron->Derivative( ); };
virtual void SetInputLink( NeuralLink<T> * inLink ){ mNeuron->SetInputLink( inLink ); };
virtual std::vector<NeuralLink<T > *>& GetInputLink( ) { return mNeuron->GetInputLink( ); };
virtual double PerformTrainingProcess( double inTarget );
virtual void PerformWeightsUpdating( );
virtual void ShowNeuronState( ) { mNeuron->ShowNeuronState( ); };
protected:
double mOutputCharge;
Neuron<T> * mNeuron;
};
template <typename T>
class HiddenLayerNeuronDecorator : public Neuron<T>
{
public:
HiddenLayerNeuronDecorator( Neuron<T> * inNeuron ) { mNeuron = inNeuron; };
virtual ~HiddenLayerNeuronDecorator( );
virtual std::vector<NeuralLink<T > *>& GetLinksToNeurons( ){ return mNeuron->GetLinksToNeurons( ); };
virtual void SetLinkToNeuron( NeuralLink<T> * inNeuralLink ){ mNeuron->SetLinkToNeuron( inNeuralLink ); };
virtual double GetSumOfCharges( ){ return mNeuron->GetSumOfCharges( ) ;};
virtual void ResetSumOfCharges( ){mNeuron->ResetSumOfCharges( ); };
virtual void Input( double inInputData ){ mNeuron->Input( inInputData ); };
virtual double Fire( );
virtual int GetNumOfLinks( ){ return mNeuron->GetNumOfLinks( ); };
virtual NeuralLink<T> * ( const int& inIndexOfNeuralLink ){ return ( mNeuron->at( inIndexOfNeuralLink) ); };
virtual double Process( ){ return mNeuron->Process( ); };
virtual double Process( double inArg ){ return mNeuron->Process( inArg ); };
virtual double Derivative( ){ return mNeuron->Derivative( ); };
virtual void SetInputLink( NeuralLink<T> * inLink ){ mNeuron->SetInputLink( inLink ); };
virtual std::vector<NeuralLink<T > *>& GetInputLink( ){ return mNeuron->GetInputLink( ); };
virtual double PerformTrainingProcess( double inTarget );
virtual void PerformWeightsUpdating( );
virtual void ShowNeuronState( ){ mNeuron->ShowNeuronState( ); };
protected:
Neuron<T> * mNeuron;
};
Интерфейс нейронных связей представлен ниже, каждая связь хранит вес и указатель на нейрон:
Интерфейс нейронной связи
template <typename T>
class Neuron;
template <typename T>
class NeuralLink
{
public:
NeuralLink( ) : mWeightToNeuron( 0.0 ),
mNeuronLinkedTo( 0 ),
mWeightCorrectionTerm( 0 ),
mErrorInformationTerm( 0 ),
mLastTranslatedSignal( 0 ){ };
NeuralLink( Neuron<T> * inNeuronLinkedTo, double inWeightToNeuron = 0.0 ) :
mWeightToNeuron( inWeightToNeuron ),
mNeuronLinkedTo( inNeuronLinkedTo ),
mWeightCorrectionTerm( 0 ),
mErrorInformationTerm( 0 ),
mLastTranslatedSignal( 0 ){ };
void SetWeight( const double& inWeight ){ mWeightToNeuron = inWeight; };
const double& GetWeight( ){ return mWeightToNeuron; };
void SetNeuronLinkedTo( Neuron<T> * inNeuronLinkedTo ){ mNeuronLinkedTo = inNeuronLinkedTo; };
Neuron<T> * GetNeuronLinkedTo( ){ return mNeuronLinkedTo; };
void SetWeightCorrectionTerm( double inWeightCorrectionTerm ){ mWeightCorrectionTerm = inWeightCorrectionTerm; };
double GetWeightCorrectionTerm( ){ return mWeightCorrectionTerm; };
void UpdateWeight( ){ mWeightToNeuron = mWeightToNeuron + mWeightCorrectionTerm; };
double GetErrorInFormationTerm( ){ return mErrorInformationTerm; };
void SetErrorInFormationTerm( double inEITerm ){ mErrorInformationTerm = inEITerm; };
void SetLastTranslatedSignal( double inLastTranslatedSignal ){ mLastTranslatedSignal = inLastTranslatedSignal; };
double GetLastTranslatedSignal( ){ return mLastTranslatedSignal; };
protected:
double mWeightToNeuron;
Neuron<T> * mNeuronLinkedTo;
double mWeightCorrectionTerm;
double mErrorInformationTerm;
double mLastTranslatedSignal;
};
Каждая активационная функция наследует от абстрактного класса, реализуя саму функцию и производную:
Интерфейс активационной функции
class NetworkFunction {
public:
NetworkFunction(){};
virtual ~NetworkFunction(){};
virtual double Process( double inParam ) = 0;
virtual double Derivative( double inParam ) = 0;
};
class Linear : public NetworkFunction {
public:
Linear(){};
virtual ~Linear(){};
virtual double Process( double inParam ){ return inParam; };
virtual double Derivative( double inParam ){ return 0; };
};
class Sigmoid : public NetworkFunction {
public:
Sigmoid(){};
virtual ~Sigmoid(){};
virtual double Process( double inParam ){ return ( 1 / ( 1 + exp( -inParam ) ) ); };
virtual double Derivative( double inParam ){ return ( this->Process(inParam)*(1 - this->Process(inParam)) );};
};
class BipolarSigmoid : public NetworkFunction {
public:
BipolarSigmoid(){};
virtual ~BipolarSigmoid(){};
virtual double Process( double inParam ){ return ( 2 / ( 1 + exp( -inParam ) ) - 1 ) ;};
virtual double Derivative( double inParam ){ return ( 0.5 * ( 1 + this->Process( inParam ) ) * ( 1 - this->Process( inParam ) ) ); };
};
За производство нейронов ответственна нейронная фабрика:
Интерфейс нейронной фабрики
template <typename T>
class NeuronFactory
{
public:
NeuronFactory(){};
virtual ~NeuronFactory(){};
virtual Neuron<T> * CreateInputNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ) = 0;
virtual Neuron<T> * CreateOutputNeuron( NetworkFunction * inNetFunc ) = 0;
virtual Neuron<T> * CreateHiddenNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ) = 0;
};
template <typename T>
class PerceptronNeuronFactory : public NeuronFactory<T>
{
public:
PerceptronNeuronFactory(){};
virtual ~PerceptronNeuronFactory(){};
virtual Neuron<T> * CreateInputNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ){ return new Neuron<T>( inNeuronsLinkTo, inNetFunc ); };
virtual Neuron<T> * CreateOutputNeuron( NetworkFunction * inNetFunc ){ return new OutputLayerNeuronDecorator<T>( new Neuron<T>( inNetFunc ) ); };
virtual Neuron<T> * CreateHiddenNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ){ return new HiddenLayerNeuronDecorator<T>( new Neuron<T>( inNeuronsLinkTo, inNetFunc ) ); };
};
Сама нейронная сеть хранит указатели на нейроны, организованные
слоями ( вообще, указатели на нейроны хранятся в векторах, которые
нужно заменить на объекты-слои ), включает в себя абстрактную
фабрику нейронов, а также алгоритм обучения сети.
Интерфейс нейронной сети
template <typename T>
class TrainAlgorithm;
/**
* Neural network class.
* An object of that type represents a neural network of several types:
* - Single layer perceptron;
* - Multiple layers perceptron.
*
* There are several training algorithms available as well:
* - Perceptron;
* - Backpropagation.
*
* How to use this class:
* To be able to use neural network , you have to create an instance of that class, specifying
* a number of input neurons, output neurons, number of hidden layers and amount of neurons in hidden layers.
* You can also specify a type of neural network, by passing a string with a name of neural network, otherwise
* MultiLayerPerceptron will be used. ( A training algorithm can be changed via public calls);
*
* Once the neural network was created, all u have to do is to set the biggest MSE required to achieve during
* the training phase ( or u can skip this step, then mMinMSE will be set to 0.01 ),
* train the network by providing a training data with target results.
* Afterwards u can obtain the net response by feeding the net with data;
*
*/
template <typename T>
class NeuralNetwork
{
public:
/**
* A Neural Network constructor.
* - Description: A template constructor. T is a data type, all the nodes will operate with. Create a neural network by providing it with:
* @param inInputs - an integer argument - number of input neurons of newly created neural network;
* @param inOutputs- an integer argument - number of output neurons of newly created neural network;
* @param inNumOfHiddenLayers - an integer argument - number of hidden layers of newly created neural network, default is 0;
* @param inNumOfNeuronsInHiddenLayers - an integer argument - number of neurons in hidden layers of newly created neural network ( note that every hidden layer has the same amount of neurons), default is 0;
* @param inTypeOfNeuralNetwork - a const char * argument - a type of neural network, we are going to create. The values may be:
* <UL>
* <LI>MultiLayerPerceptron;</LI>
* <LI>Default is MultiLayerPerceptron.</LI>
* </UL>
* - Purpose: Creates a neural network for solving some interesting problems.
* - Prerequisites: The template parameter has to be picked based on your input data.
*
*/
NeuralNetwork( const int& inInputs,
const int& inOutputs,
const int& inNumOfHiddenLayers = 0,
const int& inNumOfNeuronsInHiddenLayers = 0,
const char * inTypeOfNeuralNetwork = "MultiLayerPerceptron"
);
~NeuralNetwork( );
/**
* Public method Train.
* - Description: Method for training the network.
* - Purpose: Trains a network, so the weights on the links adjusted in the way to be able to solve problem.
* - Prerequisites:
* @param inData - a vector of vectors with data to train with;
* @param inTarget - a vector of vectors with target data;
* - the number of data samples and target samples has to be equal;
* - the data and targets has to be in the appropriate order u want the network to learn.
*/
bool Train( const std::vector<std::vector<T > >& inData,
const std::vector<std::vector<T > >& inTarget );
/**
* Public method GetNetResponse.
* - Description: Method for actually get response from net by feeding it with data.
* - Purpose: By calling this method u make the network evaluate the response for u.
* - Prerequisites:
* @param inData - a vector data to feed with.
*/
std::vector<int> GetNetResponse( const std::vector<T>& inData );
/**
* Public method SetAlgorithm.
* - Description: Setter for algorithm of training the net.
* - Purpose: Can be used for dynamic change of training algorithm.
* - Prerequisites:
* @param inTrainingAlgorithm - an existence of already created object of type TrainAlgorithm.
*/
void SetAlgorithm( TrainAlgorithm<T> * inTrainingAlgorithm ) { mTrainingAlgoritm = inTrainingAlgorithm; };
/**
* Public method SetNeuronFactory.
* - Description: Setter for the factory, which is making neurons for the net.
* - Purpose: Can be used for dynamic change of neuron factory.
* - Prerequisites:
* @param inNeuronFactory - an existence of already created object of type NeuronFactory.
*/
void SetNeuronFactory( NeuronFactory<T> * inNeuronFactory ) { mNeuronFactory = inNeuronFactory; };
/**
* Public method ShowNetworkState.
* - Description: Prints current state to the standard output: weight of every link.
* - Purpose: Can be used for monitoring the weights change during training of the net.
* - Prerequisites: None.
*/
void ShowNetworkState( );
/**
* Public method GetMinMSE.
* - Description: Returns the biggest MSE required to achieve during the training phase.
* - Purpose: Can be used for getting the biggest MSE required to achieve during the training phase.
* - Prerequisites: None.
*/
const double& GetMinMSE( ){ return mMinMSE; };
/**
* Public method SetMinMSE.
* - Description: Setter for the biggest MSE required to achieve during the training phase.
* - Purpose: Can be used for setting the biggest MSE required to achieve during the training phase.
* - Prerequisites:
* @param inMinMse - double value, the biggest MSE required to achieve during the training phase.
*/
void SetMinMSE( const double& inMinMse ){ mMinMSE = inMinMse; };
/**
* Friend class.
*/
friend class Hebb<T>;
/**
* Friend class.
*/
friend class Backpropagation<T>;
protected:
/**
* Protected method GetLayer.
* - Description: Getter for the layer by index of that layer.
* - Purpose: Can be used by inner implementation for getting access to neural network's layers.
* - Prerequisites:
* @param inInd - an integer index of layer.
*/
std::vector<Neuron<T > *>& GetLayer( const int& inInd ){ return mLayers[inInd]; };
/**
* Protected method size.
* - Description: Returns the number of layers in the network.
* - Purpose: Can be used by inner implementation for getting number of layers in the network.
* - Prerequisites: None.
*/
unsigned int size( ){ return mLayers.size( ); };
/**
* Protected method GetNumOfOutputs.
* - Description: Returns the number of units in the output layer.
* - Purpose: Can be used by inner implementation for getting number of units in the output layer.
* - Prerequisites: None.
*/
std::vector<Neuron<T > *>& GetOutputLayer( ){ return mLayers[mLayers.size( )-1]; };
/**
* Protected method GetInputLayer.
* - Description: Returns the input layer.
* - Purpose: Can be used by inner implementation for getting the input layer.
* - Prerequisites: None.
*/
std::vector<Neuron<T > *>& GetInputLayer( ){ return mLayers[0]; };
/**
* Protected method GetBiasLayer.
* - Description: Returns the vector of Biases.
* - Purpose: Can be used by inner implementation for getting vector of Biases.
* - Prerequisites: None.
*/
std::vector<Neuron<T > *>& GetBiasLayer( ) { return mBiasLayer; };
/**
* Protected method UpdateWeights.
* - Description: Updates the weights of every link between the neurons.
* - Purpose: Can be used by inner implementation for updating the weights of links between the neurons.
* - Prerequisites: None, but only makes sense, when its called during the training phase.
*/
void UpdateWeights( );
/**
* Protected method ResetCharges.
* - Description: Resets the neuron's data received during iteration of net training.
* - Purpose: Can be used by inner implementation for reset the neuron's data between iterations.
* - Prerequisites: None, but only makes sense, when its called during the training phase.
*/
void ResetCharges( );
/**
* Protected method AddMSE.
* - Description: Changes MSE during the training phase.
* - Purpose: Can be used by inner implementation for changing MSE during the training phase.
* - Prerequisites:
* @param inInd - a double amount of MSE to be add.
*/
void AddMSE( double inPortion ){ mMeanSquaredError += inPortion; };
/**
* Protected method GetMSE.
* - Description: Getter for MSE value.
* - Purpose: Can be used by inner implementation for getting access to the MSE value.
* - Prerequisites: None.
*/
double GetMSE( ){ return mMeanSquaredError; };
/**
* Protected method ResetMSE.
* - Description: Resets MSE value.
* - Purpose: Can be used by inner implementation for resetting MSE value.
* - Prerequisites: None.
*/
void ResetMSE( ) { mMeanSquaredError = 0; };
NeuronFactory<T> * mNeuronFactory; /*!< Member, which is responsible for creating neurons @see SetNeuronFactory */
TrainAlgorithm<T> * mTrainingAlgoritm; /*!< Member, which is responsible for the way the network will trained @see SetAlgorithm */
std::vector<std::vector<Neuron<T > *> > mLayers; /*!< Inner representation of neural networks */
std::vector<Neuron<T > *> mBiasLayer; /*!< Container for biases */
unsigned int mInputs, mOutputs, mHidden; /*!< Number of inputs, outputs and hidden units */
double mMeanSquaredError; /*!< Mean Squared Error which is changing every iteration of the training*/
double mMinMSE; /*!< The biggest Mean Squared Error required for training to stop*/
};
И, наконец, сам интерфейс класса, ответственного за обучение сети:
Интерфейс алгоритма обучения
template <typename T>
class NeuralNetwork;
template <typename T>
class TrainAlgorithm
{
public:
virtual ~TrainAlgorithm(){};
virtual double Train(const std::vector<T>& inData, const std::vector<T>& inTarget) = 0;
virtual void WeightsInitialization() = 0;
protected:
};
template <typename T>
class Hebb : public TrainAlgorithm<T>
{
public:
Hebb(NeuralNetwork<T> * inNeuralNetwork) : mNeuralNetwork(inNeuralNetwork){};
virtual ~Hebb(){};
virtual double Train(const std::vector<T>& inData, const std::vector<T>& inTarget);
virtual void WeightsInitialization();
protected:
NeuralNetwork<T> * mNeuralNetwork;
};
template <typename T>
class Backpropagation : public TrainAlgorithm<T>
{
public:
Backpropagation(NeuralNetwork<T> * inNeuralNetwork);
virtual ~Backpropagation(){};
virtual double Train(const std::vector<T>& inData, const std::vector<T>& inTarget);
virtual void WeightsInitialization();
protected:
void NguyenWidrowWeightsInitialization();
void CommonInitialization();
NeuralNetwork<T> * mNeuralNetwork;
};
Весь код доступен на github: Sovietmade/NeuralNetworks
В качестве заключения, хотелось бы отметить, что тема нейронных сетей на данный момент не разработана полностью, вновь и вновь мы видим на страницах хабра упоминания о новых достижениях ученых в области нейронных сетей, новых удивительных разработках. С моей стороны,
эта статья была первым шагом освоения интереснейшей технологии, и я надеюсь для кого — то она окажется небесполезной.
Использованная литература:
Алгоритм обучения нейронной сети был взят из изумительной книги:
Laurene V. Fausett “Fundamentals of Neural Networks: Architectures, Algorithms And Applications”.
Знакомимся с методом обратного распространения ошибки
Время на прочтение
6 мин
Количество просмотров 46K
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!

Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.

Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.

Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:

Для l = 3:

W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.

Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.

b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.

Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:

Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:

Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:

И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:

(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:

Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.

Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:

(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:

(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:

«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
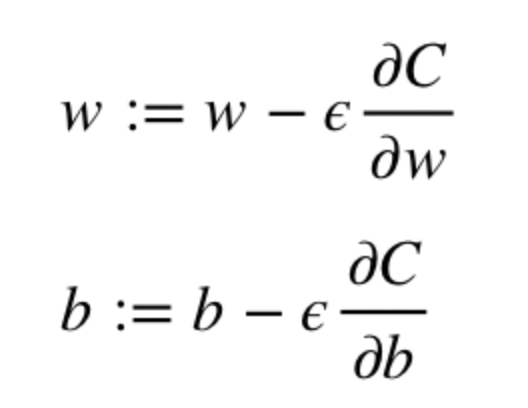
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:

Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z3)2 и (a3)2:

Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
Время на прочтение
5 мин
Количество просмотров 82K
В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.
Обучение сверточной нейронной сети
На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.
Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.
Алгоритм обратного распространения ошибки
Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.
Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.
Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:

Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:

Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:

Выход каждого нейрона j является значением активационной функции
 , которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:
, которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.

Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:
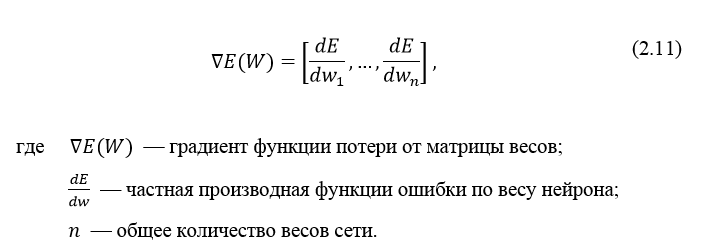
Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:

Ошибка нейрона  обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.
обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.
Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:

Алгоритм распространения ошибки сводится к следующим этапам:
- прямое распространение сигнала по сети, вычисления состояния нейронов;
- вычисление значения ошибки δ для выходного слоя;
- обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
- обновление весов сети на вычисленную ранее δ ошибки.
Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:
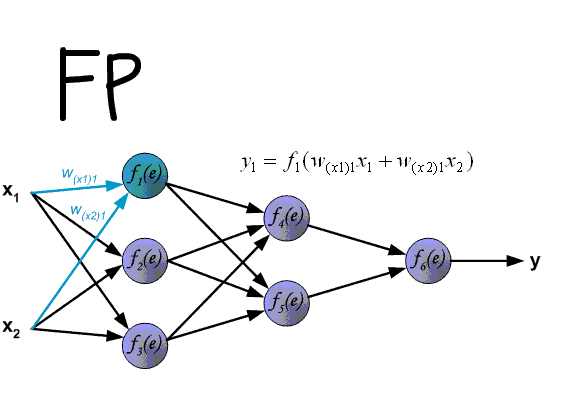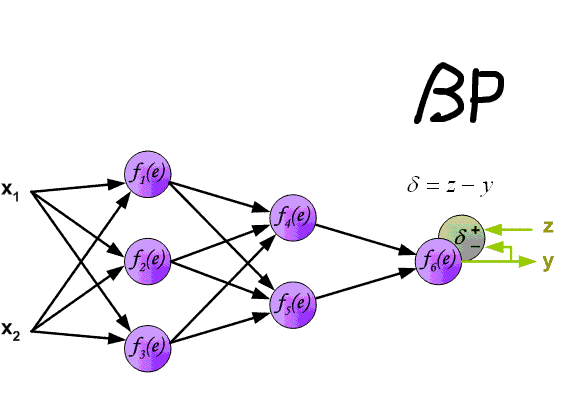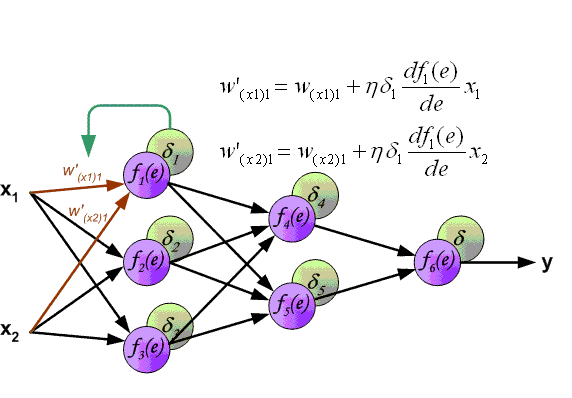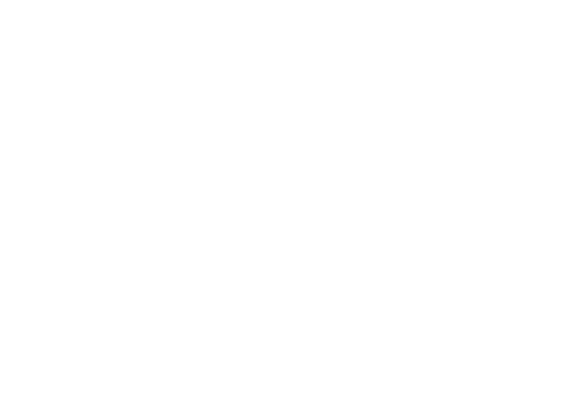
До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.
Расчет ошибки на подвыборочном слое
Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.
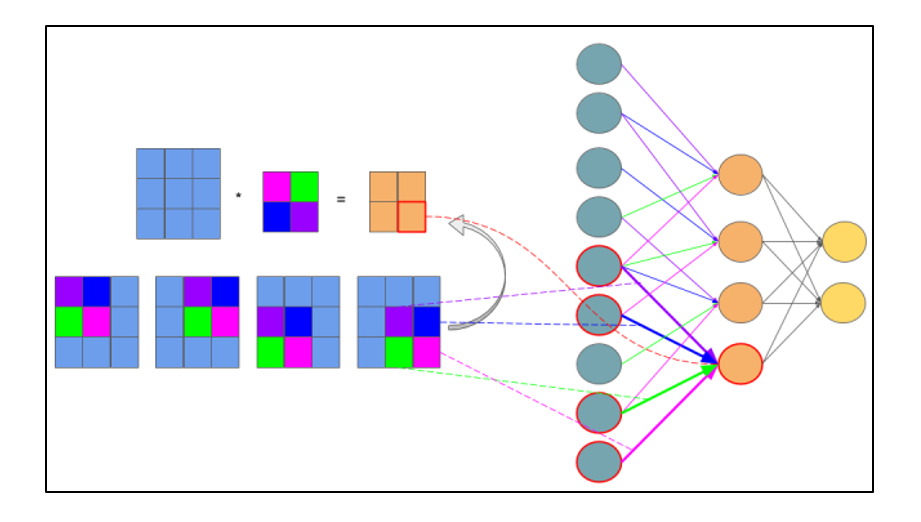
Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.
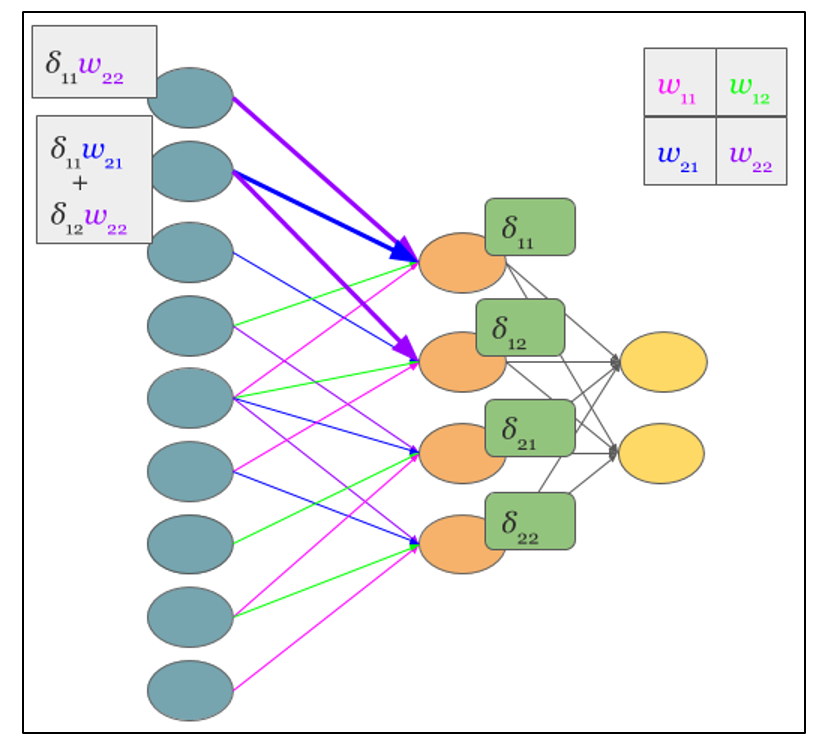
Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.

Рисунок 2.10 — Результат операции обратной свертки
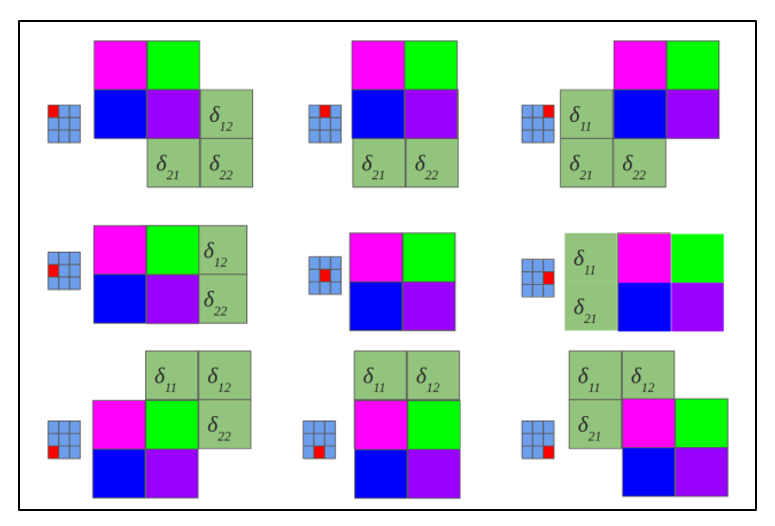
Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту
Расчет ошибки на сверточном слое
Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.
Заключение
Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.
Источники
Алгоритм обратного распространения ошибки для сверточной нейронной сети
Обратное распространение ошибки в сверточных слоях
раз и два
Обратное распространение ошибки в персептроне
Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ
Время на прочтение
9 мин
Количество просмотров 6.4K
Поскольку я столкнулся с существенными затруднениями в поисках объяснения механизма обратного распространения ошибки, которое мне понравилось бы, я решил написать собственный пост об обратном распространении ошибки реализовав алгоритм Word2Vec. Моя цель, — объяснить сущность алгоритма, используя простую, но нетривиальную нейросеть. Кроме того, word2vec стал настолько популярным в NLP сообществе, что будет полезно сосредоточиться на нем.
Данный пост связан с другим, более практическим постом который рекомендую прочитать, в нем рассматривается непосредственная реализация word2vec на языке python. В данном же посте мы сосредоточимся в основном на теоретической части.
Начнем с вещей которые необходимы для настоящего понимания обратного распространения. Помимо понятий из машинного обучения, таких как, функция потерь и градиентный спуск, пригодятся еще два компонента из математики:
- линейная алгебра (в частности матричное умножение)
- правило цепочки дифференцирования функций от многих переменных
Если вам знакомы эти понятия, то дальнейшие рассуждения окажутся простыми. Если же вы еще не освоили их, то все равно сможете понять основы обратного распространения.
Сперва я хочу дать определение понятию обратного распространения, если смысл будет недостаточно понятен, он будет раскрыт подробнее в следующих пунктах.
1. Что такое алгоритм обратного распространения
В рамках нейронной сети, единственными параметрами участвующими в обучении сети, то есть минимизации функции потерь, являются веса (здесь имею в виду веса в широком смысле, относя к ним и смещения). Веса изменяются на каждой итерации, пока мы не приблизимся к минимуму функции потерь.
В таком контексте, обратное распространение — это эффективный алгоритм нахождения оптимальных весов нейронной сети, то есть тех, которые оптимизируют функцию потерь.
Стандартный способ нахождения этих весов, применение алгоритма градиентного спуска, который подразумевает нахождение частных производных функции потерь по всем весам.
Для тривиальных задач в которых всего две переменных, легко представить как работает градиентный спуск, если вы посмотрите на рисунок, то увидите трехмерный график функции потерь, как функции весов w1 и w2.

Рисунок 1. Визуальное объяснение алгоритма градиентного спуска.
Вначале мы не знаем оптимальные значения, то есть не знаем какие значения w1 и w2 минимизируют функцию потерь.
Допустим, мы начинаем с красной точки. Если мы знаем как изменяется функция потерь при изменении весов, то есть если мы знаем производные и
, то мы можем сдвинуть красную точку ближе к минимуму функции потерь, которая представлена на графике синей точкой. Шаг сдвига определяется параметром
, который обычно называется параметром обучения.
2. Word2Vec
Задача алгоритма word2vec, найти эмбеддинги слов в заданном текстовом корпусе, другими словами, это методика поиска представлений слов в низкой размерности. Как следствие, когда мы говорим о word2vec, мы обычно говорим о приложениях NLP.
Например, модель word2vec обученная со скрытым слоем размерности [N, 3], где N -количество слов в словаре, даст трехмерные эмбеддинги слов. Это значит что, например, слово ‘квартира’, будет представлено трехмерным вектором действительных чисел, который будет близок (воспринимайте это как Евклидову метрику), к представлению аналогичного слова, такого как ‘дом’. Другими словами, word2vec это техника отображения слов в числа.
В контексте word2vec используются две основные модели: мешок слов (CBOW) и скипграммы (skip-gram). Сначала мы рассмотрим простейшую модель, CBOW, с окном из одного слова, затем перейдем к окну из нескольких слов и наконец рассмотрим модель skip-gram.
По мере продвижения я покажу несколько небольших примеров с текстом состоящим всего из нескольких слов. Однако имейте в виду, что обычно woed2vec тренируется с миллиардами слов.
3. Простая модель CBOW
В CBOW модели задача состоит в поиске слова по его контексту. В простейшем случае когда контекст слова представлен одним словом, нейронная сеть будет выглядеть так:

Рисунок 2. Топология модели Continuous Bag-of-Words модели с контекстом из одного слова
Один входной слой, один скрытый слой и выходной слой, функция активации скрытого слоя
a = 1 (identity function, или функция линейной активации, хотя последнее неправильно).
В качестве функции активации выходного слоя используется Softmax.
Входной слой представлен one hot encoding вектором, длина которого совпадает с размером массива слов, все элементы данного вектора равны нулю, кроме элементов, индексы которых совпадают с индексами слов из контекста, по данным индексам значения вектора равны 1.
Пример: словарь [‘мама’, ‘мыла’, ‘раму’, ‘маша’, ‘ела’, ‘кашу’]
OneHot(‘маша’) = [0, 0, 0, 1, 0, 0]
OneHot([‘мама’, ‘маша’]) = [1, 0, 0, 1, 0, 0]
OneHot([‘мама’, ‘ела’, ‘кашу’]) = [1, 0, 0, 0, 1, 1]
Перейдем к весам, весовые коэффициенты между входным и скрытым слоем представлены матрицей W размера , матрица между скрытым и выходным слоем
размером
, где V — размер словаря, N — размер эмбеддинг вектора (то есть, те вектора которые и пытается найти word2vec)
Выходной вектор y сравниваем с ожидаемым вектором t, чем они ближе, тем выше эффективность нейронной сети, и, соответственно, меньше функция потерь.
Если на текущем этапе что то звучит непонятно, то пример ниже должен прояснить ситуацию.
Пример
Предположим, мы хотим обучить word2vec следующим текстом:
«I like playing football»
Мы решаем обучить модель CBOW с одним контекстным словом как на рисунке (2) выше.
Учитывая текст который у нас есть, наш словарь будет состоять из 4 слов, соответственно V=4, также установим что скрытый слой будет иметь два нейрона, то есть N=2, наша нейросеть будет выглядеть так:

Со словарём:
Далее мы определяем как выбирать ‘целевое’ и ‘контекстное’ слово, и мы можем построить наши обучающие примеры двигаясь окном по тексту. Например:

Тогда обучающие примеры будут выглядеть так:
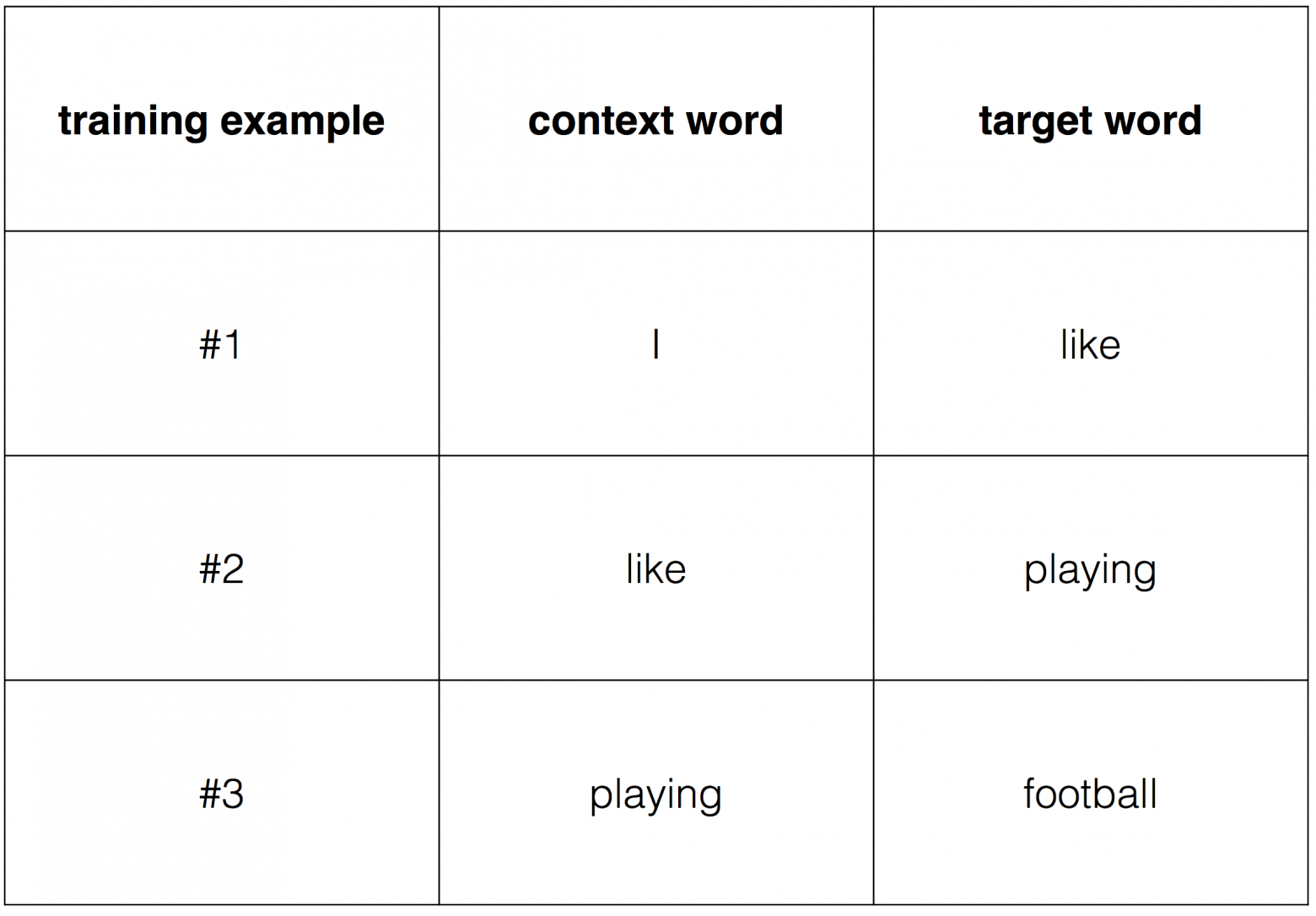
Чтобы передать эти данные в алгоритм понадобится преобразовать их в числа, для чего используем one-hot encoding.

На данный момент, мы хотим обучить нашу модель, находя веса, которые минимизируют функцию потерь. Это соответствует нахождению весов, которые с учетом вектора контекста могут с высокой точностью предсказать, что является соответствующим целевым словом.
3.1 Функция потерь (Loss function)
Исходя из топологии на рисунке 1, давайте запишем как посчитать значения скрытого и выходного слоев, при входе x:
где, h — сумма на скрытом слое, u — сумма на выходном слое, y — выход сети.
Теперь, предположим, мы обучаем модель по паре целевое слово, контекстное слово (wt, wc). Целевое слово представляет собой идеальное предсказание нейронной сети, в виде onehot encoding вектора.
Функция потерь должна будет оценить выходной слой, относительно onehot вектора wt (целевого слова).
Поскольку значения softmax можно интерпретировать как условные вероятности целевого слова, то учитывая контекстное слово функцию потерь можно записать в следующем виде:
, где j* — ожидаемая позиция правильно предсказанного слова.
Добавление функции логарифма является стандартным подходом. Из данного выражения мы получаем уравнение (1):
Функция потерь максимизирует вероятность предсказания правильного слова исходя из заданного контекста.
Пример
Вернемся к предыдущему примеру предложения «I like play football», предположим мы обучаем модель по первой записи обучающих данных, с контекстным словом «I» и целевым словом «like», в идеале веса сети должны быть такими, чтобы при вводе — что соответствует слову «I», результат работы был близок к
, что соответствует слову «like».
Стандартный подход к инициализации весов word2vec, использование нормального распределения. Примем начальное состояние весов матрицы W размером
И начальное состояние весов матрицы размером
Для обучающих данных «I like» мы получаем:
Затем
И наконец
На этом этапе функция потерь будет отрицательным логарифмом второго элемента , или
Также, мы могли бы рассчитать ее при помощи уравнения (1):
Теперь, прежде чем перейти к следующему обучающему примеру «like play», мы должны изменить веса нейросети, как это сделать расскажет следующий пункт про обратное распространение.
3.2 Алгоритм обратного распространения для модели CBOW
Теперь, имея в наличии функцию потерь, мы хотим найти веса W и W` которые ее минимизируют. В терминах машинного обучения, мы хотим чтобы модель обучилась.
В первом разделе мы уже обсудили что в мире нейронный сетей эта проблема решается использованием градиентного спуска. На рисунке (1) показано как применить этот метод и обновить матрицы весов W и W`. Нам нужно найти производные и
Я считаю что самый простой способ понять как это сделать, это записать соотношения между функцией потерь и матрицами весов. Глядя на уравнение (1) ясно что функция потерь зависит от весов W и W`, через переменную u=[u1, …., uV], или
Получить производные можно из правила цепочки для функций многих переменных:
и
И это большая часть алгоритма обратного распространения, на данный момент нам просто нужно определить уравнения (2) и (3) для нашего случая.
Начнем с уравнения (2), обратите внимание что вес Wij, относится к матрице W, и соединяет нейрон i в скрытом слое с нейроном j в выходном слое, и соответственно оказывает влияние только на выход uj (соответственно и на yj).
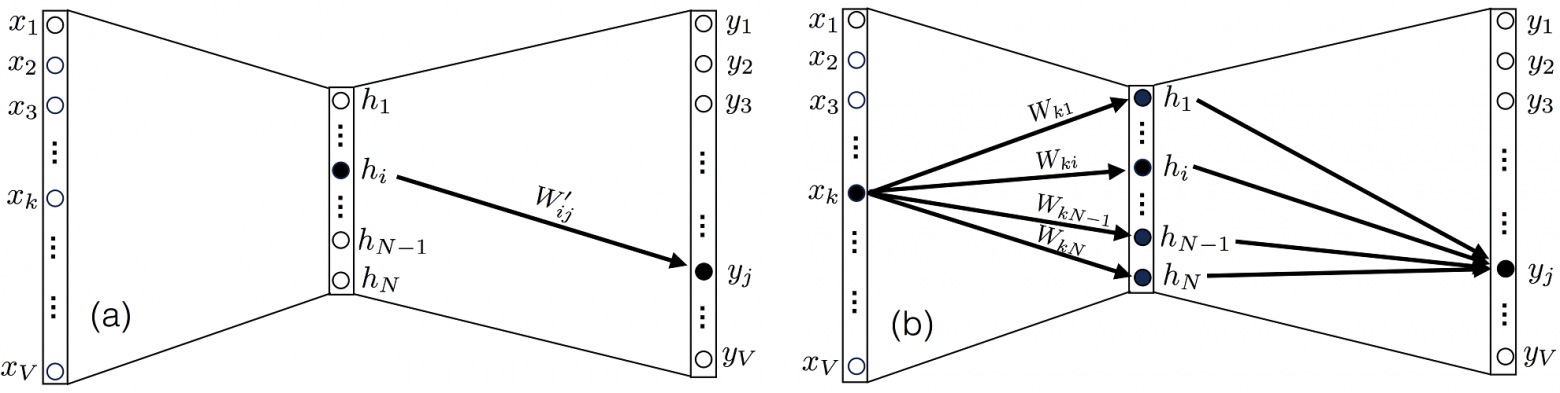
Рисунок 3. (a) Выходной узел зависит от общего узла
скрытого слоя только через элемент
матрицы
. (b) Но кроме того, этот же выходной узел зависит от общего входного узла
через N элементов
матрицы W.
Следовательно, среди всех производных , только одна, где k=j, будет отличаться от 0.
Уравнение (4):
Давайте посчитаем , уравнение (5):
, где — дельта Кронекера, функция двух целых переменных, которая равна 1, если они равны, и 0 в противном случае.
В уравнении (5) мы ввели вектор e размерности N (размер словаря), который мы используем чтобы снизить сложность обозначений, этот вектор представляет собой разницу между полученным и ожидаемым результатом, то есть это вектор ошибок предсказания.
Для второго члена правой части уравнения (4) мы получим уравнения (6):
После подставновки уравнений (5) и (6) в уравнение (4) мы получим уравнение (7):
Мы можем найти выполнить аналогичное упражнение для поиска производной , однако на этот раз отметим что после задания входа Xk, выход yj нейрона j зависит от всех элементов матрицы W соединенных со входом, как видно на рисунке 3(b). Поэтому мы должны оценивать все элементы в сумме. Прежде чем перейти к оценке
, полезно перезаписать выражение для элемента uk из вектора u как:
Из этого уравнения легко вывести , поскольку единственный выживший член производной будет с индексами l=i и m=j, или же в виде уравнения (8):
Наконец применив уравнения (5) и (8) мы получим результат, уравнение (9):
Векторизация
Мы можем упростить запись уравнений. (7) и (9) используя векторную нотацию. Сделав это мы получим для уравнения (7)
Где символ ⊗ обозначает векторное произведение.
Для уравнения (9) мы получим:
3.3 Градиентный спуск на основе полученных выше результатов
Теперь, когда у нас есть уравнения (7) и (9), у нас есть все необходимое для реализации одной итерации обучения нейросети на базе алгоритма обратного распространения ошибки, применяя градиентный спуск. Каждая итерация должна немного приближать к минимуму функцию потерь. После задания скорости обучения , мы можем обновить наши веса следующим образом:
3.4 Итерация алгоритма
Все описанное выше является всего лишь одним маленьким шагов всего процесса оптимизации. В частности, до этого момента мы обучали нашу нейросеть всего на одном тренировочном примере. Чтобы завершить первый проход, мы должны применить все обучающие примеры. Сделав это, мы пройдем одну эпоху обучения. После чего нам нужно будет повторять цикл обучения, пройдя достаточное количество эпох, пока изменения функции потерь не станут незначительными, после чего можно будет остановиться и считать нейросеть обученной.
4. Алгоритм обратного распространения для контекста из нескольких слов в модели CBOW
Мы уже знаем как работает алгоритм обратного распространения для модели CBOW с одним словом на входе. Теперь увеличим сложность и добавим в контекст несколько слов. Рисунок (4) показывает как выглядит нейросеть теперь. Вход теперь представляет собой серию OneHot Encoded векторов слов входящих в контекст. Количество слов в контексте является параметром который мы можем задавать при инициализации word2vec. Скрытый слой получает усреднение из всех контекстных слов.

Рисунок 4. Топология модели CBOW с контекстом из нескольких слов
Уравнения модели CBOW с несколькими контекстными словами являются обобщением уравнений модели CBOW с одним контекстным словом.
Обратите внимание, что для удобства мы ввели определение ‘усредненный’ входной вектор
Как и прежде, чтобы применить алгоритм обратного распространения нам нужно выписать функцию потерь и выписать ее зависимости. Функция потерь выглядит также как и раньше:
Снова выпишем уравнения по правилу цепочки, аналогично предыдущим:
и
Производные функции потерь по весам такие же как для модели CBOW с одним словом на входе, с единственным отличием, что мы заменим входной вектор из одного слова на усредненный вектор из слов контекста. Выведем эти уравнения начиная с производной по
Теперь запишем производную по :
Подведя итог имеем следующее:
и
Векторизация
Перепишем уравнения (17) и (18) в записи для векторов.
Уравнение (17) примет вид:
Для уравнения (18):
Еще раз, обратите внимание что уравнения идентичны уравнениям в модели CBOW для контекста из одного слова.
Оператор ⊗ обозначает векторное произведение.
5. Алгоритм обратного распространения для модели Skip-gram
Данная модель по сути обратна модели CBOW, на вход подается центральное слово, на выходе предсказывается его контекст. Полученная нейросеть выглядит следующим образом:

Рисунок 5.Топология Skip-gram модели.
Уравнения skip-gram модели следующие:
Обратите внимание что выходные вектора (как и вектор ) идентичны,
. Функция потерь выглядит следующим образом:
Для модели skip-gram функция потерь зависит от переменных
через:
Соответственно правило цепочки выглядит так:
и
Посчитаем , получим:
Аналогично модели CBOW получаем:
Производная по самая сложная, но выполнимая:
Подведя итог, для модели skip-gram мы имеем:
и
Векторизация
Векторизованная версия уравнения (21):
Уравнение (22):
6. Что дальше
Мы подробно рассмотрели как работает алгоритм обратного распространения в случае word2vec. Однако рассмотренная реализация неэффективна для больших текстовых корпусов. В оригинальной статье [2] применяются некоторые трюки для преодоления этих проблем (иерархический softmax, negative sampling), однако я не буду на них останавливаться подробно. Вы можете найти подробное описание по ссылке [1].
Несмотря на вычислительную неэффективность реализации описанной здесь, она содержит всё необходимое для обучения нейронных сетей word2vec.
Следующим шагом будет реализация этих уравнений на вашем любимом языке программирования. Если вам нравится Python, я уже реализовал эти уравнения в моем следующем посте.
Надеюсь увидеть вас там!
Дополнительные ссылки
[1] X. Rong, word2vec Parameter Learning Explained, arXiv:1411.2738 (2014).
[2] T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space, arXiv:1301.3781 (2013).
В прошлой главе мы видели, как нейросети могут самостоятельно обучаться весам и смещениям с использованием алгоритма градиентного спуска. Однако в нашем объяснении имелся пробел: мы не обсуждали подсчёт градиента функции стоимости. А это приличный пробел! В этой главе я расскажу быстрый алгоритм для вычисления подобных градиентов, известный, как обратное распространение.
Впервые алгоритм обратного распространения придумали в 1970-х, но его важность не была до конца осознана вплоть до знаменитой работы 1986 года, которую написали Дэвид Румельхарт, Джоффри Хинтон и Рональд Уильямс. В работе описано несколько нейросетей, в которых обратное распространение работает гораздо быстрее, чем в более ранних подходах к обучению, из-за чего с тех пор можно было использовать нейросеть для решения ранее неразрешимых проблем. Сегодня алгоритм обратного распространения – рабочая лошадка обучения нейросети.
Эта глава содержит больше математики, чем все остальные в книге. Если вам не особенно по нраву математика, у вас может возникнуть искушение пропустить эту главу и просто относиться к обратному распространению, как к чёрному ящику, подробности работы которого вы готовы игнорировать. Зачем тратить время на их изучение?
Причина, конечно, в понимании. В основе обратного распространения лежит выражение частной производной ∂C / ∂w функции стоимости C по весу w (или смещению b) сети. Выражение показывает, насколько быстро меняется стоимость при изменении весов и смещений. И хотя это выражение довольно сложное, у него есть своя красота, ведь у каждого его элемента есть естественная и интуитивная интерпретация. Поэтому обратное распространение – не просто быстрый алгоритм для обучения. Он даёт нам подробное понимание того, как изменение весов и смещений меняет всё поведение сети. А это стоит того, чтобы изучить подробности.
Учитывая всё это, если вы хотите просто пролистать эту главу или перепрыгнуть к следующей, ничего страшного. Я написал остальную книгу так, чтобы она была понятной, даже если считать обратное распространение чёрным ящиком. Конечно, позднее в книге будут моменты, с которых я делаю отсылки к результатам этой главы. Но в тот момент вам должны быть понятны основные заключения, даже если вы не отслеживали все рассуждения.
Для разогрева: быстрый матричный подход вычисления выходных данных нейросети
Перед обсуждением обратного распространения, давайте разогреемся быстрым матричным алгоритмом для вычисления выходных данных нейросети. Мы вообще-то уже встречались с этим алгоритмом к концу предыдущей главы, но я описал его быстро, поэтому его стоит заново рассмотреть подробнее. В частности, это будет хороший способ приспособиться к записи, используемой в обратном распространении, но в знакомом контексте.
Начнём с записи, позволяющей нам недвусмысленно обозначать веса в сети. Мы будем использовать wljk для обозначения веса связи нейрона №k в слое №(l-1) с нейроном №j в слое №l. Так, к примеру, на диаграмме ниже показан вес связи четвёртого нейрона второго слоя со вторым нейроном третьего слоя:
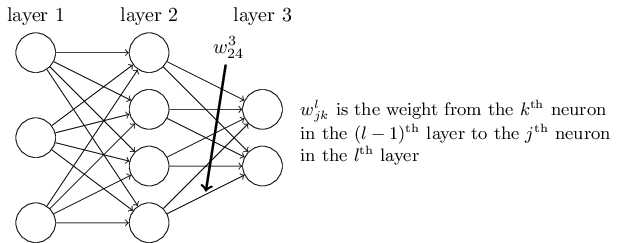
Сначала такая запись кажется неуклюжей, и требует некоторых усилий на привыкание. Однако вскоре она покажется вам простой и естественной. Одна её особенность – порядок индексов j и k. Вы могли бы решить, что разумнее было бы использовать j для обозначения входного нейрона, а k – для выходного, а не наоборот, как у нас. Причину такой особенности я объясню ниже.
Сходные обозначения мы будем использовать для смещений и активаций сети. В частности, blj будет обозначать смещение нейрона №j в слое №l. alj будет обозначать активацию нейрона №j в слое №l. На следующей диаграмме показаны примеры использования этой записи:

С такой записью активация alj нейрона №j в слое №l связана с активацией в слое №(l-1) следующим уравнением (сравните с уравнением (4) и его обсуждением в прошлой главе):
где сумма идёт по всем нейронам k в слое (l-1). Чтобы перезаписать это выражение в матричном виде, мы определим матрицу весов wl для каждого слоя l. Элементы матрицы весов – это просто веса, соединённые со слоем №l, то есть, элемент в строке №j и столбце №k будет wljk. Сходным образом для каждого слоя l мы определяем вектор смещения bl. Вы, наверное, догадались, как это работает – компонентами вектора смещения будут просто значения blj, по одному компоненту для каждого нейрона в слое №l. И, наконец, мы определим вектор активации al, компонентами которого будут активации alj.
Последним ингредиентом, необходимым для того, чтобы перезаписать (23), будет матричная форма векторизации функции σ. С векторизацией мы вскользь столкнулись в прошлой главе – идея в том, что мы хотим применить функцию σ к каждому элементу вектора v. Мы используем очевидную запись σ(v) для обозначения поэлементного применения функции. То есть, компонентами σ(v) будут просто σ(v)j = σ(vj). Для примера, если у нас есть функция f(x) = x2, то векторизованная форма f даёт нам
то есть, векторизованная f просто возводит в квадрат каждый элемент вектора.
Учитывая все эти формы записи, уравнение (23) можно переписать в красивой и компактной векторизованной форме:
Такое выражение позволяет нам более глобально взглянуть на связь активаций одного слоя с активациями предыдущего: мы просто применяем матрицу весов к активациям, добавляем вектор смещения и потом применяем сигмоиду. Кстати, именно эта запись и требует использования записи wljk. Если бы мы использовали индекс j для обозначения входного нейрона, а k для выходного, нам пришлось бы заменить матрицу весов в уравнении (25) на транспонированную. Это небольшое, но раздражающее изменение, и мы бы потеряли простоту заявления (и размышления) о «применении матрицы весов к активациям». Такой глобальный подход проще и лаконичнее (и использует меньше индексов!), чем понейронный. Это просто способ избежать индексного ада, не теряя точности обозначения происходящего. Также это выражение полезно на практике, поскольку большинство матричных библиотек предлагают быстрые способы перемножения матриц, сложения векторов и векторизации. Код в прошлой главе непосредственно пользовался этим выражением для вычисления поведения сети.
Используя уравнение (25) для вычисления al, мы вычисляем промежуточное значение zl ≡ wlal−1+bl. Эта величина оказывается достаточно полезной для именования: мы называем zl взвешенным входом нейронов слоя №l. Позднее мы активно будем использовать этот взвешенный вход. Уравнение (25) иногда записывают через взвешенный вход, как al = σ(zl). Стоит также отметить, что у zl есть компоненты , то есть, zlj — это всего лишь взвешенный вход функции активации нейрона j в слое l.
Два необходимых предположения по поводу функции стоимости
Цель обратного распространения – вычислить частные производные ∂C/∂w и ∂C/∂b функции стоимости C для каждого веса w и смещения b сети. Чтобы обратное распространение сработало, нам необходимо сделать два главных предположения по поводу формы функции стоимости. Однако перед этим полезно будет представлять себе пример функции стоимости. Мы используем квадратичную функцию из прошлой главы (уравнение (6)). В записи из предыдущего раздела она будет иметь вид
где: n – общее количество обучающих примеров; сумма идёт по всем примерам x; y=y(x) – необходимые выходные данные; L обозначает количество слоёв в сети; aL = aL (x) – вектор выхода активаций сети, когда на входе x.
Ладно, так какие нам нужны предположения касательно функции стоимости С, чтобы применять обратное распространение? Первое – функцию стоимости можно записать как среднее C = 1/n ∑x Cx функций стоимости Cx для отдельных обучающих примеров x. Это выполняется в случае квадратичной функции стоимости, где стоимость одного обучающего примера Cx = 1/2 ||y − aL||2. Это предположение будет верным и для всех остальных функций стоимости, которые встретятся нам в книге.
Это предположение нужно нам потому, что на самом деле обратное распространение позволяет нам вычислять частные производные ∂C/∂w и ∂C/∂b, усредняя по обучающим примерам. Приняв это предположение, мы предположим, что обучающий пример x фиксирован, и перестанем указывать индекс x, записывая стоимость Cx как C. Потом мы вернём x, но пока что лучше его просто подразумевать.
Второе предположение касательно функции стоимости – её можно записать как функцию выхода нейросети:
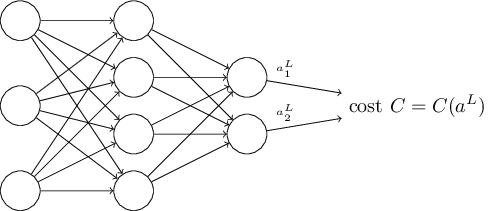
К примеру, квадратичная функция стоимости удовлетворяет этому требованию, поскольку квадратичную стоимость одного обучающего примера x можно записать, как
что и будет функцией выходных активаций. Конечно, эта функция стоимости также зависит от желаемого выхода y, и вы можете удивиться, почему мы не рассматриваем C как функцию ещё и от y. Однако вспомним, что входной обучающий пример x фиксирован, поэтому выход y тоже фиксирован. В частности, его мы не можем изменить, меняя веса и смещения, то есть, это не то, что выучивает нейросеть. Поэтому имеет смысл считать C функцией от только выходных активаций aL, а y – просто параметром, помогающим её определять.
Произведение Адамара s⊙t
Алгоритм обратного распространения основан на обычных операциях линейной алгебры – сложении векторов, умножении вектора на матрицу, и т.д. Однако одна из операций используется менее часто. Допустим, s и t – два вектора одной размерности. Тогда через s⊙t мы обозначим поэлементное перемножение двух векторов. Тогда компоненты s⊙t будут просто (s⊙t)j = sjtj. Например:
Такое поэлементное произведение иногда называют произведением Адамара или произведением Шура. Мы будем называть его произведением Адамара. Хорошие библиотеки для работы с матрицами обычно имеют быструю реализацию произведения Адамара, и это бывает удобно при реализации обратного распространения.
Четыре фундаментальных уравнения в основе обратного распространения
Обратное распространение связано с пониманием того, как изменение весов и смещений сети меняет функцию стоимости. По сути, это означает подсчёт частных производных ∂C/∂wljk и ∂C/∂blj. Но для их вычисления сначала мы вычисляем промежуточное значение δlj, которую мы называем ошибкой в нейроне №j в слое №l. Обратное распространение даст нам процедуру для вычисления ошибки δlj, а потом свяжет δlj с ∂C/∂wljk и ∂C/∂blj.
Чтобы понять, как определяется ошибка, представьте, что в нашей нейросети завёлся демон:

Он сидит на нейроне №j в слое №l. При поступлении входных данных демон нарушает работу нейрона. Он добавляет небольшое изменение Δzlj к взвешенному входу нейрона, и вместо того, чтобы выдавать σ(zlj), нейрон выдаст σ(zlj + Δzlj). Это изменение распространится и через следующие слои сети, что в итоге изменит общую стоимость на (∂C/∂zlj) * Δzlj.
Но наш демон хороший, и он пытается помочь вам улучшить стоимость, то есть, найти Δzlj, уменьшающее стоимость. Допустим, значение ∂C/∂zlj велико (положительное или отрицательное). Тогда демон может серьёзно уменьшить стоимость, выбрав Δzlj со знаком, противоположным ∂C/∂zlj. А если же ∂C/∂zlj близко к нулю, тогда демон не может сильно улучшить стоимость, меняя взвешенный вход zlj. Так что, с точки зрения демона, нейрон уже близок к оптимуму (это, конечно, верно только для малых Δzlj. Допустим, таковы ограничения действий демона). Поэтому в эвристическом смысле ∂C/∂zlj является мерой ошибки нейрона.
Под мотивацией от этой истории определим ошибку δlj нейрона j в слое l, как
По обычному нашему соглашению мы используем δl для обозначения вектора ошибок, связанного со слоем l. Обратное распространение даст нам способ подсчитать δl для любого слоя, а потом соотнести эти ошибки с теми величинами, которые нас реально интересуют, ∂C/∂wljk и ∂C/∂blj.
Вас может интересовать, почему демон меняет взвешенный вход zlj. Ведь было бы естественнее представить, что демон изменяет выходную активацию alj, чтобы мы использовали ∂C/∂alj в качестве меры ошибки. На самом деле, если сделать так, то всё получается очень похожим на то, что мы будем обсуждать дальше. Однако в этом случае представление обратного распространения будет алгебраически чуть более сложным. Поэтому мы остановимся на варианте δlj = ∂C/∂zlj в качестве меры ошибки.
В задачах классификации термин «ошибка» иногда означает количество неправильных классификаций. К примеру, если нейросеть правильно классифицирует 96,0% цифр, то ошибка будет равна 4,0%. Очевидно, это совсем не то, что мы имеем в виду под векторами δ. Но на практике обычно можно без труда понять, какое значение имеется в виду.
План атаки: обратное распространение основано на четырёх фундаментальных уравнениях. Совместно они дают нам способ вычислить как ошибку δl, так и градиент функции стоимости. Я привожу их ниже. Не нужно ожидать их мгновенного освоения. Вы будете разочарованы. Уравнения обратного распространения настолько глубоки, что для хорошего их понимания требуется ощутимое время и терпение, и постепенное углубление в вопрос. Хорошие новости в том, что это терпение окупится сторицей. Поэтому в данном разделе наши рассуждения только начинаются, помогая вам идти по пути глубокого понимания уравнений.
Вот схема того, как мы будем углубляться в эти уравнения позже: я дам их краткое доказательство, помогающее объяснить, почему они верны; мы перепишем их в алгоритмической форме в виде псевдокода, и увидим, как реализовать его в реальном коде на python; в последней части главы мы выработаем интуитивное представление о значении уравнений обратного распространения, и о том, как их можно найти с нуля. Мы будем периодически возвращаться к четырём фундаментальным уравнениям, и чем глубже вы будете их понимать, тем более комфортными, и возможно, красивыми и естественными они будут вам казаться.
Уравнение ошибки выходного слоя, δL: компоненты δL считаются, как
Очень естественное выражение. Первый член справа, ∂C / ∂aLj, измеряет, насколько быстро стоимость меняется как функция выходной активации №j. Если, к примеру, C не особенно зависит от конкретного выходного нейрона j, тогда δLj будет малым, как и ожидается. Второй член справа, σ'(zLj), измеряет, насколько быстро функция активации σ меняется в zLj.
Заметьте, что всё в (BP1) легко подсчитать. В частности, мы вычисляем zLj при подсчёте поведения сети, и на вычисление σ'(zLj) уйдёт незначительно больше ресурсов. Конечно, точная форма ∂C / ∂aLj зависит от формы функции стоимость. Однако, если функция стоимости известна, то не должно быть проблем с вычислением ∂C / ∂aLj. К примеру, если мы используем квадратичную функцию стоимости, тогда C = 1/2 ∑j (yj − aLj)2, поэтому ∂C / ∂aLj = (aLj − yj), что легко подсчитать.
Уравнение (BP1) – это покомпонентное выражение δL. Оно совершенно нормальное, но не записано в матричной форме, которая нужна нам для обратного распространения. Однако, его легко переписать в матричной форме, как
Здесь ∇a C определяется, как вектор, чьими компонентами будут частные производные ∂C / ∂aLj. Его можно представлять, как выражение скорости изменения C по отношению к выходным активациям. Легко видеть, что уравнения (BP1a) и (BP1) эквивалентны, поэтому далее мы будем использовать (BP1) для отсылки к любому из них. К примеру, в случае с квадратичной стоимостью, у нас будет ∇a C = (aL — y), поэтому полной матричной формой (BP1) будет
Всё в этом выражении имеет удобную векторную форму, и его легко вычислить при помощи такой библиотеки, как, например, Numpy.
Выражение ошибки δl через ошибку в следующем слое, δl+1: в частности,
где (wl+1)T — транспонирование весовой матрицы wl+1 для слоя №(l+1). Уравнение кажется сложным, но каждый его элемент легко интерпретировать. Допустим, мы знаем ошибку δl+1 для слоя (l+1). Транспонирование весовой матрицы, (wl+1)T, можно представить себе, как перемещение ошибки назад по сети, что даёт нам некую меру ошибки на выходе слоя №l. Затем мы считаем произведение Адамара ⊙σ'(zl). Это продвигает ошибку назад через функцию активации в слое l, давая нам значение ошибки δl во взвешенном входе для слоя l.
Комбинируя (BP2) с (BP1), мы можем подсчитать ошибку δl для любого слоя сети. Мы начинаем с использования (BP1) для подсчёта δL, затем применяем уравнение (BP2) для подсчёта δL-1, затем снова для подсчёта δL-2, и так далее, до упора по сети в обратную сторону.
Уравнение скорости изменения стоимости по отношению к любому смещению в сети: в частности:
То есть, ошибка δlj точно равна скорости изменения ∂C / ∂blj. Это превосходно, поскольку (BP1) и (BP2) уже рассказали нам, как подсчитывать δlj. Мы можем перезаписать (BP3) короче, как
где δ оценивается для того же нейрона, что и смещение b.
Уравнение для скорости изменения стоимости по отношению к любому весу в сети: в частности:
Отсюда мы узнаём, как подсчитать частную производную ∂C/∂wljk через значения δl и al-1, способ расчёта которых нам уже известен. Это уравнение можно переписать в менее загруженной индексами форме:
где ain — активация нейронного входа для веса w, а δout — ошибка нейронного выхода от веса w. Если подробнее посмотреть на вес w и два соединённых им нейрона, то можно будет нарисовать это так:
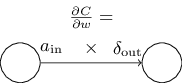
Приятное следствие уравнения (32) в том, что когда активация ain мала, ain ≈ 0, член градиента ∂C/∂w тоже стремится к нулю. В таком случае мы говорим, что вес обучается медленно, то есть, не сильно меняется во время градиентного спуска. Иначе говоря, одним из следствий (BP4) будет то, что весовой выход нейронов с низкой активацией обучается медленно.
Из (BP1)-(BP4) можно почерпнуть и другие идеи. Начнём с выходного слоя. Рассмотрим член σ'(zLj) в (BP1). Вспомним из графика сигмоиды из прошлой главы, что она становится плоской, когда σ(zLj) приближается к 0 или 1. В данных случаях σ'(zLj) ≈ 0. Поэтому вес в последнем слое будет обучаться медленно, если активация выходного нейрона мала (≈ 0) или велика (≈ 1). В таком случае обычно говорят, что выходной нейрон насыщен, и в итоге вес перестал обучаться (или обучается медленно). Те же замечания справедливы и для смещений выходного нейрона.
Сходные идеи можно получить и касательно более ранних слоёв. В частности, рассмотрим член σ'(zl) в (BP2). Это значит, что δlj, скорее всего, будет малой при приближении нейрона к насыщению. А это, в свою очередь, означает, что любые веса на входе насыщенного нейрона будут обучаться медленно (правда, это не сработает, если у wl+1Tδl+1 будут достаточно большие элементы, компенсирующие небольшое значение σ'(zLj)).
Подытожим: мы узнали, что вес будет обучаться медленно, если либо активация входного нейрона мала, либо выходной нейрон насыщен, то есть его активация мала или велика.
В этом нет ничего особенно удивительного. И всё же, эти наблюдения помогают улучшить наше представление о том, что происходит при обучении сети. Более того, мы можем подойти к этим рассуждениям с обратной стороны. Четыре фундаментальных уравнения справедливы для любой функции активации, а не только для стандартной сигмоиды (поскольку, как мы увидим далее, в доказательствах не используются свойства сигмоиды). Поэтому эти уравнения можно использовать для разработки функций активации с определёнными нужными свойствами обучения. Для примера, допустим, мы выбрали функцию активации σ, непохожую на сигмоиду, такую, что σ’ всегда положительна и не приближается к нулю. Это предотвратить замедление обучения, происходящее при насыщении обычных сигмоидных нейронов. Позднее в книге мы увидим примеры, где функция активации меняется подобным образом. Учитывая уравнения (BP1)-(BP4), мы можем объяснить, зачем нужны такие модификации, и как они могут повлиять на ситуацию.

Итог: уравнения обратного распространения
Задачи
- Альтернативная запись уравнений обратного распространения. Я записал уравнения обратного распространения с использованием произведения Адамара. Это может сбить с толку людей, не привыкших к этому произведению. Есть и другой подход, на основе обычного перемножения матриц, который может оказаться поучительным для некоторых читателей. Покажите, что (BP1) можно переписать, как
где Σ'(zL) – квадратная матрица, у которой по диагонали расположены значения σ'(zLj), а другие элементы равны 0. Учтите, что эта матрица взаимодействует с ∇a C через обычное перемножение матриц.
Покажите, что (BP2) можно переписать, как
Комбинируя предыдущие задачи, покажите, что:
Для читателей, привычных к матричному перемножению, это уравнение будет легче понять, чем (BP1) и (BP2). Я концентрируюсь на (BP1) и (BP2) потому, что этот подход оказывается быстрее реализовать численно. [здесь Σ — это не сумма (∑), а заглавная σ (сигма) / прим. перев.]
Доказательство четырёх фундаментальных уравнений (необязательный раздел)
Теперь докажем четыре фундаментальных уравнения (BP1)-(BP4). Все они являются следствиями цепного правила (правила дифференцирования сложной функции) из анализа функций многих переменных. Если вы хорошо знакомы с цепным правилом, настоятельно рекомендую попробовать посчитать производные самостоятельно перед тем, как продолжить чтение.
Начнём с уравнения (BP1), которое даёт нам выражение для выходной ошибки δL. Чтобы доказать его, вспомним, что, по определению:
Применяя цепное правило, перепишем частные производные через частные производные по выходным активациям:
где суммирование идёт по всем нейронам k в выходном слое. Конечно, выходная активация aLk нейрона №k зависит только от взвешенного входа zLj для нейрона №j, когда k=j. Поэтому ∂aLk / ∂zLj исчезает, когда k ≠ j. В итоге мы упрощаем предыдущее уравнение до
Вспомнив, что aLj = σ(zLj), мы можем переписать второй член справа, как σ'(zLj), и уравнение превращается в
то есть, в (BP1) в покомпонентном виде.
Затем докажем (BP2), дающее уравнение для ошибки δl через ошибку в следующем слое δl+1. Для этого нам надо переписать δlj = ∂C / ∂zlj через δl+1k = ∂C / ∂zl+1k. Это можно сделать при помощи цепного правила:
где в последней строчке мы поменяли местами два члена справа, и подставили определение δl+1k. Чтобы вычислить первый член на последней строчке, отметим, что
Продифференцировав, получим
Подставив это в (42), получим
То есть, (BP2) в покомпонентной записи.
Остаётся доказать (BP3) и (BP4). Они тоже следуют из цепного правила, примерно таким же методом, как и два предыдущих. Оставлю их вам в качестве упражнения.
Упражнение
- Докажите (BP3) и (BP4).
Вот и всё доказательство четырёх фундаментальных уравнений обратного распространения. Оно может показаться сложным. Но на самом деле это просто результат аккуратного применения цепного правила. Говоря менее лаконично, обратное распространение можно представить себе, как способ подсчёта градиента функции стоимости через систематическое применение цепного правила из анализа функций многих переменных. И это реально всё, что представляет собой обратное распространение – остальное просто детали.
Алгоритм обратного распространения
Уравнения обратного распространения дают нам метод подсчёта градиента функции стоимости. Давайте запишем это явно в виде алгоритма:
- Вход x: назначить соответствующую активацию a1 для входного слоя.
- Прямое распространение: для каждого l = 2,3,…,L вычислить zl = wlal−1+bl и al = σ(zl).
- Выходная ошибка δL: вычислить вектор δL = ∇a C ⊙ σ'(zL).
- Обратное распространение ошибки: для каждого l = L−1,L−2,…,2 вычислить δl = ((wl+1)Tδl+1) ⊙ σ'(zl).
- Выход: градиент функции стоимости задаётся
и
.
Посмотрев на алгоритм, вы поймёте, почему он называется обратное распространение. Мы вычисляем векторы ошибки δl задом наперёд, начиная с последнего слоя. Может показаться странным, что мы идём по сети назад. Но если подумать о доказательстве обратного распространения, то обратное движение является следствием того, что стоимость – это функция выхода сети. Чтобы понять, как меняется стоимость в зависимости от ранних весов и смещений, нам нужно раз за разом применять цепное правило, идя назад через слои, чтобы получить полезные выражения.
Упражнения
- Обратное распространение с одним изменённым нейроном. Допустим, мы изменили один нейрон в сети с прямым распространением так, чтобы его выход был f(∑j wjxj+b), где f – некая функция, не похожая на сигмоиду. Как нам поменять алгоритм обратного распространения в данном случае?
- Обратное распространение с линейными нейронами. Допустим, мы заменим обычную нелинейную сигмоиду на σ(z) = z по всей сети. Перепишите алгоритм обратного распространения для данного случая.
Как я уже пояснял ранее, алгоритм обратного распространения вычисляет градиент функции стоимости для одного обучающего примера, C = Cx. На практике часто комбинируют обратное распространение с алгоритмом обучения, например, со стохастическим градиентным спуском, когда мы подсчитываем градиент для многих обучающих примеров. В частности, при заданном мини-пакете m обучающих примеров, следующий алгоритм применяет градиентный спуск на основе этого мини-пакета:
- Вход: набор обучающих примеров.
- Для каждого обучающего примера x назначить соответствующую входную активацию ax,1 и выполнить следующие шаги:
- Прямое распространение для каждого l=2,3,…,L вычислить zx,l = wlax,l−1+bl и ax,l = σ(zx,l).
- Выходная ошибка δx,L: вычислить вектор δx,L = ∇a Cx ⋅ σ'(zx,L).
- Обратное распространение ошибки: для каждого l=L−1,L−2,…,2 вычислить δx,l = ((wl+1)Tδx,l+1) ⋅ σ'(zx,l).
- Градиентный спуск: для каждого l=L,L−1,…,2 обновить веса согласно правилу
, и смещения согласно правилу
.
Конечно, для реализации стохастического градиентного спуска на практике также понадобится внешний цикл, генерирующий мини-пакеты обучающих примеров, и внешний цикл, проходящий по нескольким эпохам обучения. Для простоты я их опустил.
Код для обратного распространения
Поняв абстрактную сторону обратного распространения, теперь мы можем понять код, использованный в предыдущей главе, реализующий обратное распространение. Вспомним из той главы, что код содержался в методах update_mini_batch и backprop класс Network. Код этих методов – прямой перевод описанного выше алгоритма. В частности, метод update_mini_batch обновляет веса и смещения сети, подсчитывая градиент для текущего mini_batch обучающих примеров:
class Network(object):
...
def update_mini_batch(self, mini_batch, eta):
"""Обновить веса и смещения сети, применяя градиентный спуск с использованием обратного распространения к одному мини-пакету. mini_batch – это список кортежей (x, y), а eta – скорость обучения."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]Большую часть работы делают строки delta_nabla_b, delta_nabla_w = self.backprop(x, y), использующие метод backprop для подсчёта частных производных ∂Cx/∂blj и ∂Cx/∂wljk. Метод backprop почти повторяет алгоритм предыдущего раздела. Есть одно небольшое отличие – мы используем немного другой подход к индексированию слоёв. Это сделано для того, чтобы воспользоваться особенностью python, отрицательными индексами массива, позволяющими отсчитывать элементы назад, с конца. l[-3] будет третьим элементом с конца массива l. Код backprop приведён ниже, вместе со вспомогательными функциями, используемыми для подсчёта сигмоиды, её производной и производной функции стоимости. С ними код получается законченным и понятным. Если что-то неясно, обратитесь к первому описанию кода с полным листингом.
class Network(object):
...
def backprop(self, x, y):
"""Вернуть кортеж ``(nabla_b, nabla_w)``, представляющий градиент для функции стоимости C_x. ``nabla_b`` и ``nabla_w`` - послойные списки массивов numpy, похожие на ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# прямой проход
activation = x
activations = [x] # список для послойного хранения активаций
zs = [] # список для послойного хранения z-векторов
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# обратный проход
delta = self.cost_derivative(activations[-1], y) *
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
"""Переменная l в цикле ниже используется не так, как описано во второй главе книги. l = 1 означает последний слой нейронов, l = 2 – предпоследний, и так далее. Мы пользуемся преимуществом того, что в python можно использовать отрицательные индексы в массивах."""
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
...
def cost_derivative(self, output_activations, y):
"""Вернуть вектор частных производных (чп C_x / чп a) для выходных активаций."""
return (output_activations-y)
def sigmoid(z):
"""Сигмоида."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Производная сигмоиды."""
return sigmoid(z)*(1-sigmoid(z))Задача
- Полностью основанный на матрицах подход к обратному распространению на мини-пакете. Наша реализация стохастического градиентного спуска использует цикл по обучающим примерам из мини-пакета. Алгоритм обратного распространения можно поменять так, чтобы он вычислял градиенты для всех обучающих примерах мини-пакета одновременно. Вместо того, чтобы начинать с одного вектора x, мы можем начать с матрицы X=[x1x2…xm], чьими столбцами будут векторы мини-пакета. Прямое распространение идёт через произведение весовых матриц, добавление подходящей матрицы для смещений и повсеместного применения сигмоиды. Обратное распространение идёт по той же схеме. Напишите псевдокод для такого подхода для алгоритма обратного распространения. Измените network.py так, чтобы он использовал этот матричный подход. Преимуществом такого подхода будет использование всех преимуществ современных библиотек для линейной алгебры. В итоге он может работать быстрее цикла по мини-пакеты (к примеру, на моём компьютере программа ускоряется примерно в 2 раза на задачах классификации MNIST). На практике все серьёзные библиотеки для обратного распространения используют такой полноматричный подход или какой-то его вариант.
В каком смысле обратное распространение является быстрым алгоритмом?
В каком смысле обратное распространение является быстрым алгоритмом? Для ответа на этот вопрос рассмотрим ещё один подход к вычислению градиента. Представьте себе ранние дни исследований нейросетей. Возможно, это 1950-е или 1960-е годы, и вы – первый человек в мире, придумавший использовать для обучения градиентный спуск! Но чтобы это сработало, вам нужно подсчитать градиент функции стоимости. Вы вспоминаете алгебру и решаете посмотреть, можно ли использовать цепное правило для вычисления градиента. Немного поигравшись, вы видите, что алгебра кажется сложной, и вы разочаровываетесь. Вы пытаетесь найти другой подход. Вы решаете считать стоимость функцией только весов C=C(w) (к смещениям вернёмся чуть позже). Вы нумеруете веса w1, w2,… и хотите вычислить ∂C/∂wj для веса wj. Очевидный способ – использовать приближение
Где ε > 0 – небольшое положительное число, а ej — единичный вектор направления j. Иначе говоря, мы можем приблизительно оценить ∂C/∂wj, вычислив стоимость C для двух немного различных значений wj, а потом применить уравнение (46). Та же идея позволит нам подсчитать частные производные ∂C/∂b по смещениям.
Подход выглядит многообещающим. Концептуально простой, легко реализуемый, использует только несколько строк кода. Он выглядит гораздо более многообещающим, чем идея использования цепного правила для подсчёта градиента!
К сожалении, хотя такой подход выглядит многообещающим, при его реализации в коде оказывается, что работает он крайне медленно. Чтобы понять, почему, представьте, что у нас в сети миллион весов. Тогда для каждого веса wj нам нужно вычислить C(w + εej), чтобы подсчитать ∂C/∂wj. А это значит, что для вычисления градиента нам нужно вычислить функцию стоимости миллион раз, что потребует миллион прямых проходов по сети (на каждый обучающий пример). А ещё нам надо подсчитать C(w), так что получается миллион и один проход по сети.
Хитрость обратного распространения в том, что она позволяет нам одновременно вычислять все частные производные ∂C/∂wj, используя только один прямой проход по сети, за которым следует один обратный проход. Грубо говоря, вычислительная стоимость обратного прохода примерно такая же, как у прямого.
Поэтому общая стоимость обратного распространения примерно такая же, как у двух прямых проходов по сети. Сравните это с миллионом и одним прямым проходом, необходимым для реализации метода (46)! Так что, хотя обратное распространение внешне выглядит более сложным подходом, в реальности он куда как более быстрый.
Впервые это ускорение сполна оценили в 1986, и это резко расширило диапазон задач, решаемых с помощью нейросетей. В свою очередь, это привело к увеличению количества людей, использующих нейросети. Конечно, обратное распространение – не панацея. Даже в конце 1980-х люди уже натолкнулись на её ограничения, особенно при попытках использовать обратное распространение для обучения глубоких нейросетей, то есть сетей со множеством скрытых слоёв. Позже мы увидим, как современные компьютеры и новые хитрые идеи позволяют использовать обратное распространение для обучения таких глубоких нейросетей.
Обратное распространение: в общем и целом
Как я уже объяснил, обратное распространение являет нам две загадки. Первая, что на самом деле делает алгоритм? Мы выработали схему обратного распространения ошибки от выходных данных. Можно ли углубиться дальше, получить более интуитивное представление о происходящем во время всех этих перемножений векторов и матриц? Вторая загадка – как вообще кто-то мог обнаружить обратное распространение? Одно дело, следовать шагам алгоритма или доказательству его работы. Но это не значит, что вы так хорошо поняли задачу, что могли изобрести этот алгоритм. Есть ли разумная цепочка рассуждений, способная привести нас к открытию алгоритма обратного распространения? В этом разделе я освещу обе загадки.
Чтобы улучшить понимание работы алгоритма, представим, что мы провели небольшое изменение Δwljk некоего веса wljk:
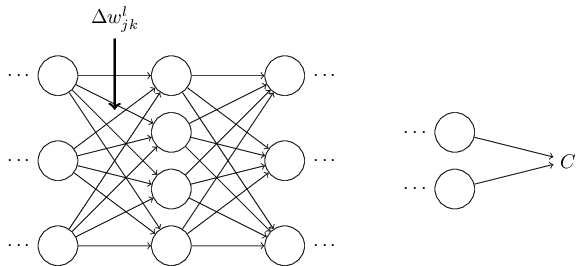
Это изменение веса приведёт к изменению выходной активации соответствующего нейрона:
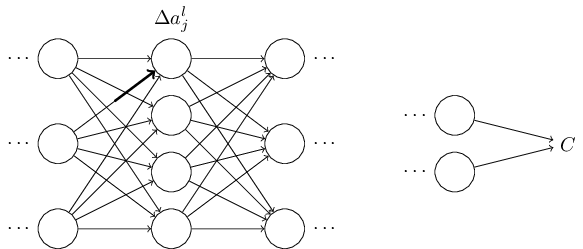
Это приведёт к изменению всех активаций следующего слоя:

Эти изменения приведут к изменениям следующего слоя, и так далее, вплоть до последнего, а потом к изменениям функции стоимости:

Изменение ΔC связано с изменением Δwljk уравнением
Из этого следует, что вероятным подходом к вычислению ∂C/∂wljk будет тщательное отслеживание распространения небольшого изменения wljk, приводящего к небольшому изменению в C. Если мы сможем это сделать, тщательно выражая по пути всё в величинах, которые легко вычислить, то мы сможем вычислить и ∂C/∂wljk.
Давайте попробуем. Изменение Δwljk вызывает небольшое изменение Δalj в активации нейрона j в слое l. Это изменение задаётся
Изменение активации Δalj приводит к изменениям во всех активациях следующего слоя, (l+1). Мы сконцентрируемся только на одной из этих изменённых активаций, допустим, al+1q,
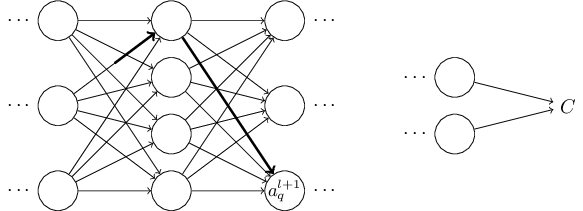
Это приведёт к следующим изменениям:
Подставляя уравнение (48), получаем:
Конечно, изменение Δal+1q изменит и активации в следующем слое. Мы даже можем представить путь по всей сети от wljk до C, где каждое изменение активации приводит к изменению следующей активации, и, наконец, к изменению стоимости на выходе. Если путь проходит через активации alj, al+1q,…,aL−1n, aLm, тогда итоговое выражение будет
То есть, мы выбираем член вида ∂a/∂a для каждого следуюшего проходимого нами нейрона, а также для члена ∂C / ∂aLm в конце. Это представление изменений в C из-за изменений в активациях по данному конкретному пути сквозь сеть. Конечно, существует много путей, по которым изменение в wljk может пройти и повлиять на стоимость, а мы рассматривали только один из них. Чтобы подсчитать общее изменение C разумно предположить, что мы должны просуммировать все возможные пути от веса до конечной стоимости:
где мы просуммировали все возможные выборы для промежуточных нейронов по пути. Сравнивая это с (47), мы видим, что:
Уравнение (53) выглядит сложно. Однако у него есть приятная интуитивная интерпретация. Мы подсчитываем изменение C по отношению к весам сети. Оно говорит нам, что каждое ребро между двумя нейронами сети связано с фактором отношения, являющимся только лишь частной производной активации одного нейрона по отношению к активации другого нейрона. У ребра от первого веса до первого нейрона фактор отношения равен ∂alj / ∂wljk. Коэффициент отношения для пути – это просто произведение коэффициентов по всему пути. А общий коэффициент изменения ∂C / ∂wljk является суммой коэффициентов по всем путям от начального веса до конечной стоимости. Эта процедура показана далее, для одного пути:
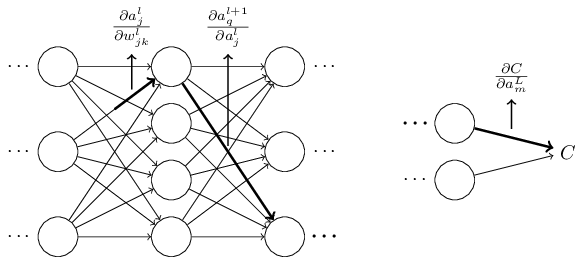
Пока что мы давали эвристический аргумент, способ представить происходящее при изменении весов сети. Позвольте мне обрисовать дальнейший вариант мышления на эту тему для развития данного аргумента. Во-первых, можно вывести точные выражение для всех отдельных частных производных в уравнении (53). Это легко сделать с использованием несложной алгебры. После этого можно попробовать понять, как записать все суммы по индексам в виде произведений матриц. Это оказывается утомительной задачей, требующей терпения, но не чем-то экстраординарным. После всего этого и максимального упрощения вы увидите, что получился ровно тот же самый алгоритм обратного распространения! Поэтому алгоритм обратного распространения можно представлять себе, как способ вычисления суммы коэффициентов по всем путям. Или, если переформулировать, алгоритм обратного распространения – хитроумный способ отслеживания небольших изменений весов (и смещений), когда они распространяются по сети, достигают выхода и влияют на стоимость.
Здесь я не буду делать всего этого. Это дело малопривлекательное, требующее тщательной проработки деталей. Если вы готовы к такому, вам может понравиться этим заниматься. Если нет, то надеюсь, что подобные размышления дадут вам некоторые идеи по поводу целей обратного распространения.
Что насчёт другой загадки – как вообще можно было открыть обратное распространение? На самом деле, если вы последуете по обрисованному мною пути, вы получите доказательство обратного распространения. К несчастью, доказательство будет длиннее и сложнее чем то, что я описал ранее. Так как же было открыто то короткое (но ещё более загадочное) доказательство? Если записать все детали длинного доказательства, вам сразу бросятся в глаза несколько очевидных упрощений. Вы применяете упрощения, получаете более простое доказательство, записываете его. А затем вам опять на глаза попадаются несколько очевидных упрощений. И вы повторяете процесс. После нескольких повторений получится то доказательство, что мы видели ранее – короткое, но немного непонятное, поскольку из него удалены все путеводные вехи! Я, конечно, предлагаю вам поверить мне на слово, однако никакой загадки происхождения приведённого доказательства на самом деле нет. Просто много тяжёлой работы по упрощению доказательства, описанного мною в этом разделе.
Однако в этом процессе есть один хитроумный трюк. В уравнении (53) промежуточные переменные – это активации, типа al+1q. Хитрость в том, чтобы перейти к использованию взвешенных входов, типа zl+1q, в качестве промежуточных переменных. Если не пользоваться этим, и продолжать использовать активации, полученное доказательство будет немногим более сложным, чем данное ранее в этой главе.
