Время на прочтение
14 мин
Количество просмотров 83K
Привет. Я хочу продолжить тему реализации методов машинного обучения на c#, и в этой статье я расскажу про алгоритм обратного распространения ошибки для обучения нейронной сети прямого распространения, а также приведу его реализацию на языке C#. Особенность данной реализации в том, что реализация алгоритма абстрагирована от реализаций целевой функции (той, которую нейросеть пытается минимизировать) и функции активации нейронов. В итоге получится некий конструктор, с помощью которого можно поиграться с различными параметрами сети и алгоритма обучения, посмотреть и сравнить результат. Предполагается, что вы уже знакомы с тем, что такое искусственная нейросеть (если нет, то настоятельно рекомендую для начала изучить википедию или одну из подобных статей). Интересно? Лезем под кат.
Обозначения
Для начала рассмотрим обозначения, которые я буду использовать в статье, а за одно вспомним основные понятия, я не буду приводить картинок с нейронами и слоями, этого всего полно в википедии и здесь, на хабре. Итак, сразу в бой, индуцированное локальное поле нейрона (или просто сумматор) выглядит следующим образом:
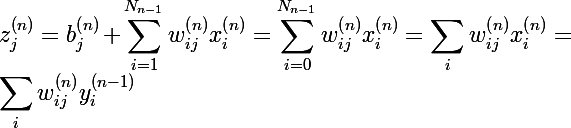
Функция активации нейрона, или передаточная функция от значения сумматора:
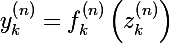
- у каждого нейрона сети может быть своя функция активации
- для всех слоев кроме первого, входным вектором будет являться выходной вектор предыдущего слоя, так что
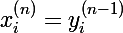
От нейрона перейдем к самой сети. Нейросеть — это модель, она обладает параметрами, и задача алгоритма обучения заключается в подборе таких параметров сети, чтобы минимизоровать значение функции ошибки. Функцию ошибки будем обозначать через E. Параметрами модели являются веса нейронов: 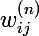 — вес j-ого нейрона слоя n, который берет свое начало в i-ом нейроне слоя (n — 1).
— вес j-ого нейрона слоя n, который берет свое начало в i-ом нейроне слоя (n — 1).
Греческой эта 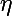 обозначим гиперпараметр алгоритма обучения — скорость обучения.
обозначим гиперпараметр алгоритма обучения — скорость обучения.
Изменение веса обозначим через дельта:

- направление градиента показывает нам в сторону роста значения функции, но нам для минимизации необходимо двигаться в обратном направлении
Таким образом, новый вес нейрона выглядит следующим образом: 
Стоит упомянуть, что к изменению веса еще можно (или, скорее, нужно) добавить регуляризацию. Функция регуляризации R — это функция от параметров модели, в нашем случае это веса нейронов. Таким образом, новая функция ошибки выглядит как E + R, а формула изменения веса преобразуется в следующую:
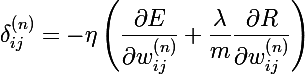
- лямбда — гиперпараметр обучения, коэффициент регуляризации (похож на скорость обучения)
- m — размер обучающей выборки
Вообще говоря, реализацию регуляризации тоже можно абстрагировать от алгоритма обучения, но я пока этого делать не буду, поскольку текущая реализация алгоритма обучения и так не самая быстрая, поскольку в противному случае на каждой эпохе обучения (прогон всех обучающих примеров) придется в одном цикле считать аккумулированную ошибку, а в другом — регуляризацию.Еще одна причина заключается в том, что существует не так много видов регуляризации (я, например, знаю только L1 и L2), которые применяются при обучении нейросетей. В данной реализации я буду использовать L2 норму, и она будет неотъемлемой частью алгоритма обучения.
Алгоритм обратного распространения ошибки
Для начала остановимся на режимах обучения. Изменять веса можно несколькими способами:
- либо после каждого обучающего примера (обучение в реальном режиме времени, online обучение, batchSize = 1)
- либо накопить изменения для всей обучающей выборки, а затем изменить все веса (full-batch, batchSize = trainingSet.Length)
- либо после прогона некоторого количества обучающих примеров (mini-batch, batchSize = any_number < trainingSet.Length)
Рассмотрим ситуацию с онлайн-обучением, так будет проще. Итак, на вход сети пришел импульс 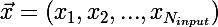 , сеть выдала отклик
, сеть выдала отклик 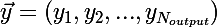 , хотя правильной реакцией на x, является
, хотя правильной реакцией на x, является 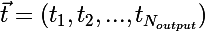 .
.
Рассмотрим частную производную функции ошибки E:
Дальнейшее рассуждение разделяется на две ветки: для последнего слоя и для остальных слоев.
Выходной слой
Для выходного слоя все просто, для коррекции ошибки нам достаточно вычислить производную целевой функции по одному из весов и вычислить значение дельты. Учтем, что целевая функция полностью зависит только от выходного значения нейрона, или значения функции активации, а сама функция активации зависит только от сумматора
Тут видно, что для вычисления ошибки выходного слоя нужно вычислить значение частных производных в точках, независимо от того, какая у нас целевая функция или же функция активации нейрона.
Любой скрытый слой
Но если слой не выходной, то нам нужно аккумулировать значения ошибок всех последующих слоев.
PS: я заметил, что в верхних индексах забыл ставить скобки, чтобы обозначить, что это не степень, а индекс слоя; учтите это, пока степеней нигде не было.
Что же мы имеем:
- вычисление производной некой функции активации — это как раз то что нужно
- вычисление частной производной целевой функции по значению сумматора следующего слоя; тут тоже все просто, мы ведь находимся не на последнем слое, и вычисление изменений весов ведем от последнего к первому, так что это значение уже вычислено на предыдущем шаге
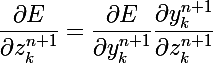
- в случае, если следующий слой последний, то мы вычислим это значение для текущего слоя, и таким образом распространим решение на всю сеть
Реализация
Функция ошибки
С формулами покончили, давайте перейдем к реализации, и начнем с понятия функции ошибки. У меня это представлено в виде метрики (по сути, это так и есть). Метод CalculatePartialDerivaitveByV2Index вычисляет значение частной производной функции для входных векторов по индексу переменное из v2.
public interface IMetrics<T>
{
double Calculate(T[] v1, T[] v2);
/// <summary>
/// Calculate value of partial derivative by v2[v2Index]
/// </summary>
T CalculatePartialDerivaitveByV2Index(T[] v1, T[] v2, int v2Index);
}
Таким образом, мы можем вычислить значение частной производной функции ошибки для последнего слоя по реальному выходу сети 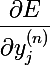 .
.
Для примера давайте напишем несколько реализаций.
Минимизация половины квадрата Евклидова расстояния
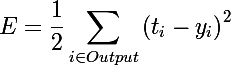
А производная будет выглядеть следующим образом:

internal class HalfSquaredEuclidianDistance : IMetrics<T>
{
public override double Calculate(double[] v1, double[] v2)
{
double d = 0;
for (int i = 0; i < v1.Length; i++)
{
d += (v1[i] - v2[i]) * (v1[i] - v2[i]);
}
return 0.5 * d;
}
public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index)
{
return v2[v2Index] - v1[v2Index];
}
}
Минимизация логарифмического правдоподобия

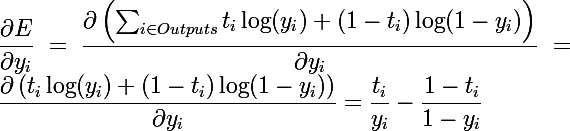
internal class Loglikelihood : IMetrics<double>
{
public override double Calculate(double[] v1, double[] v2)
{
double d = 0;
for (int i = 0; i < v1.Length; i++)
{
d += v1[i]*Math.Log(v2[i]) + (1 - v1[i])*Math.Log(1 - v2[i]);
}
return -d;
}
public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index)
{
return -(v1[v2Index]/v2[v2Index] - (1 - v1[v2Index])/(1 - v2[v2Index]));
}
}
Здесь главное не забыть, что логарифмическое правдоподобие вычисляется со знаком минус в начале, и производная тоже будет с минусом. Я не заостряю внимания на проверках или избегания случаев деления на ноль, или логарифма от нуля.
Функция активации нейрона
Аналогичным способом опишем функцию активации нейрона.
public interface IFunction
{
double Compute(double x);
double ComputeFirstDerivative(double x);
}
И примеры.
Сигмоид
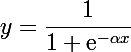

internal class SigmoidFunction : IFunction
{
private double _alpha = 1;
internal SigmoidFunction(double alpha)
{
_alpha = alpha;
}
public double Compute(double x)
{
double r = (1 / (1 + Math.Exp(-1 * _alpha * x)));
//return r == 1f ? 0.9999999f : r;
return r;
}
public double ComputeFirstDerivative(double x)
{
return _alpha * this.Compute(x) * (1 - this.Compute(x));
}
}
Гиперболический тангенс
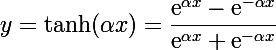
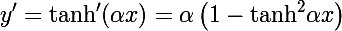
internal class HyperbolicTangensFunction : IFunction
{
private double _alpha = 1;
internal HyperbolicTangensFunction(double alpha)
{
_alpha = alpha;
}
public double Compute(double x)
{
return (Math.Tanh(_alpha * x));
}
public double ComputeFirstDerivative(double x)
{
double t = Math.Tanh(_alpha*x);
return _alpha*(1 - t*t);
}
}
Нейрон, слой и сеть
В данном разделе рассмотрим представление основных элементов сети, реализацию их я приводить не буду, т.к. она очевидно. Алгоритм будет приведен для полносвязной «слоеной» сети, так что и реализацию сети нужно будет делать соответствующую.
Итак, нейрон выглядит следующим образом.
public interface INeuron
{
/// <summary>
/// Weights of the neuron
/// </summary>
double[] Weights { get; }
/// <summary>
/// Offset/bias of neuron (default is 0)
/// </summary>
double Bias { get; set; }
/// <summary>
/// Compute NET of the neuron by input vector
/// </summary>
/// <param name="inputVector">Input vector (must be the same dimension as was set in SetDimension)</param>
/// <returns>NET of neuron</returns>
double NET(double[] inputVector);
/// <summary>
/// Compute state of neuron
/// </summary>
/// <param name="inputVector">Input vector (must be the same dimension as was set in SetDimension)</param>
/// <returns>State of neuron</returns>
double Activate(double[] inputVector);
/// <summary>
/// Last calculated state in Activate
/// </summary>
double LastState { get; set; }
/// <summary>
/// Last calculated NET in NET
/// </summary>
double LastNET { get; set; }
IList<INeuron> Childs { get; }
IList<INeuron> Parents { get; }
IFunction ActivationFunction { get; set; }
double dEdz { get; set; }
}
Т.к. мы рассматриваем полносвязную «слоеную» сеть, то Childs и Parents можно не имплементировать, но если делать общий алгоритм, то придется. Рассмотрим поля, которые особо важны для алгоритма обучения:
- LastNET — сумматор нейрона, тут хранится последнее вычисленное значение
- LastState — выход нейрона, тут хранится последнее вычисленное значение
- dEdz — это то самое dE/dz нейрона, что упоминается выше, и вычисляется в зависимости от того на каком слое находится текущий нейрон; частная производная функции ошибки по сумматору нейрона
Слой сети выглядит проще:
public interface ILayer
{
/// <summary>
/// Compute output of the layer
/// </summary>
/// <param name="inputVector">Input vector</param>
/// <returns>Output vector</returns>
double[] Compute(double[] inputVector);
/// <summary>
/// Get last output of the layer
/// </summary>
double[] LastOutput { get; }
/// <summary>
/// Get neurons of the layer
/// </summary>
INeuron[] Neurons { get; }
/// <summary>
/// Get input dimension of neurons
/// </summary>
int InputDimension { get; }
}
И представление сети:
public interface INeuralNetwork
{
/// <summary>
/// Compute output vector by input vector
/// </summary>
/// <param name="inputVector">Input vector (double[])</param>
/// <returns>Output vector (double[])</returns>
double[] ComputeOutput(double[] inputVector);
Stream Save();
/// <summary>
/// Train network with given inputs and outputs
/// </summary>
/// <param name="inputs">Set of input vectors</param>
/// <param name="outputs">Set if output vectors</param>
void Train(IList<DataItem<double>> data);
}
Но мы рассматриваем многослойную нейросеть, так что будет использоваться особое представление:
public interface IMultilayerNeuralNetwork : INeuralNetwork
{
/// <summary>
/// Get array of layers of network
/// </summary>
ILayer[] Layers { get; }
}
Алгоритм обучения
Алгоритм обучения будет реализован через паттерн стратегия:
public interface ILearningStrategy<T>
{
/// <summary>
/// Train neural network
/// </summary>
/// <param name="network">Neural network for training</param>
/// <param name="inputs">Set of input vectors</param>
/// <param name="outputs">Set of output vectors</param>
void Train(T network, IList<DataItem<double>> data);
}
Для более наглядного понимания приведу типичную функцию Train любой нейросети в контексте данной реализации:
public void Train(IList<DataItem<double>> data)
{
_learningStrategy.Train(this, data);
}
Формат входных данных
Я использую следующий формат входных данных:
public class DataItem<T>
{
private T[] _input = null;
private T[] _output = null;
public DataItem()
{
}
public DataItem(T[] input, T[] output)
{
_input = input;
_output = output;
}
public T[] Input
{
get { return _input; }
set { _input = value; }
}
public T[] Output
{
get { return _output; }
set { _output = value; }
}
}
Как видно из кода в предыдущих частях, нейросеть работает с
DataItem.Параметры алгоритма обучения
Данным классом описываются параметры алгоритма обучения, я думаю названия полей говорят сами за себя (и комментарии), так что не буду дублировать текстом:
public class LearningAlgorithmConfig
{
public double LearningRate { get; set; }
/// <summary>
/// Size of the butch. -1 means fullbutch size.
/// </summary>
public int BatchSize { get; set; }
public double RegularizationFactor { get; set; }
public int MaxEpoches { get; set; }
/// <summary>
/// If cumulative error for all training examples is less then MinError, then algorithm stops
/// </summary>
public double MinError { get; set; }
/// <summary>
/// If cumulative error change for all training examples is less then MinErrorChange, then algorithm stops
/// </summary>
public double MinErrorChange { get; set; }
/// <summary>
/// Function to minimize
/// </summary>
public IMetrics<double> ErrorFunction { get; set; }
}
Алгоритм
Ну и наконец, показав весь контекст, можно перейти к собственно реализации алгоритма обучения нейросети
internal class BackpropagationFCNLearningAlgorithm : ILearningStrategy, функция public void Train(IMultilayerNeuralNetwork network, IList<DataItem> data).
Для начала подготавливаем некоторые переменные (общие для всех эпох обучения) для работы алгоритма:
if (_config.BatchSize < 1 || _config.BatchSize > data.Count)
{
_config.BatchSize = data.Count;
}
double currentError = Single.MaxValue;
double lastError = 0;
int epochNumber = 0;
Logger.Instance.Log("Start learning...");
Затем запустится основной цикл работы алгоритма, в котором происходит прямой и обратный прогон всего массива данных, один прогон называется эпохой:
do
{
//...
} while (epochNumber < _config.MaxEpoches &&
currentError > _config.MinError &&
Math.Abs(currentError - lastError) > _config.MinErrorChange);
Заходим в цикл, и перед тем как пройтись по всем примерам, инициализируем вспомогательные переменные важные только для текущей эпохи. В случае, если batch не полный, то перемешиваем данные.
lastError = currentError;
DateTime dtStart = DateTime.Now;
//preparation for epoche
int[] trainingIndices = new int[data.Count];
for (int i = 0; i < data.Count; i++)
{
trainingIndices[i] = i;
}
if (_config.BatchSize > 0)
{
trainingIndices = Shuffle(trainingIndices);
}
Далее наступает процесс обработки данных, в зависимости от размера пачки, и изменение весов, это выглядит так:
//process data set
int currentIndex = 0;
do
{
#region initialize accumulated error for batch, for weights and biases
double[][][] nablaWeights = new double[network.Layers.Length][][];
double[][] nablaBiases = new double[network.Layers.Length][];
for (int i = 0; i < network.Layers.Length; i++)
{
nablaBiases[i] = new double[network.Layers[i].Neurons.Length];
nablaWeights[i] = new double[network.Layers[i].Neurons.Length][];
for (int j = 0; j < network.Layers[i].Neurons.Length; j++)
{
nablaBiases[i][j] = 0;
nablaWeights[i][j] = new double[network.Layers[i].Neurons[j].Weights.Length];
for (int k = 0; k < network.Layers[i].Neurons[j].Weights.Length; k++)
{
nablaWeights[i][j][k] = 0;
}
}
}
#endregion
//process one batch
for (int inBatchIndex = currentIndex; inBatchIndex < currentIndex + _config.BatchSize && inBatchIndex < data.Count; inBatchIndex++)
{
//forward pass
double[] realOutput = network.ComputeOutput(data[trainingIndices[inBatchIndex]].Input);
//backward pass, error propagation
//last layer
//.......................................ОБРАБОТКА ПОСЛЕДНЕГО СЛОЯ
//hidden layers
//.......................................ОБРАБОТКА СКРЫТЫХ СЛОЕВ
}
//update weights and bias
for (int layerIndex = 0; layerIndex < network.Layers.Length; layerIndex++)
{
for (int neuronIndex = 0; neuronIndex < network.Layers[layerIndex].Neurons.Length; neuronIndex++)
{
network.Layers[layerIndex].Neurons[neuronIndex].Bias -= nablaBiases[layerIndex][neuronIndex];
for (int weightIndex = 0; weightIndex < network.Layers[layerIndex].Neurons[neuronIndex].Weights.Length; weightIndex++)
{
network.Layers[layerIndex].Neurons[neuronIndex].Weights[weightIndex] -=
nablaWeights[layerIndex][neuronIndex][weightIndex];
}
}
}
currentIndex += _config.BatchSize;
} while (currentIndex < data.Count);
Рассмотрим обработку последнего слоя:
- инициализировали "наблЫ", там мы храним аккумулированное значение градиента для пачки входных данных (при онлайн обучении, там окажется просто градиент по одному примеру)
- пробегаемся по всем нейронам последнего слоя
- вычисляем dE/dz
- а затем вычисляем значение градиента для весов и смещения
//last layer
for (int j = 0; j < network.Layers[network.Layers.Length - 1].Neurons.Length; j++)
{
network.Layers[network.Layers.Length - 1].Neurons[j].dEdz =
_config.ErrorFunction.CalculatePartialDerivaitveByV2Index(data[inBatchIndex].Output,
realOutput, j) *
network.Layers[network.Layers.Length - 1].Neurons[j].ActivationFunction.
ComputeFirstDerivative(network.Layers[network.Layers.Length - 1].Neurons[j].LastNET);
nablaBiases[network.Layers.Length - 1][j] += _config.LearningRate *
network.Layers[network.Layers.Length - 1].Neurons[j].dEdz;
for (int i = 0; i < network.Layers[network.Layers.Length - 1].Neurons[j].Weights.Length; i++)
{
nablaWeights[network.Layers.Length - 1][j][i] +=
_config.LearningRate*(network.Layers[network.Layers.Length - 1].Neurons[j].dEdz*
(network.Layers.Length > 1 ?
network.Layers[network.Layers.Length - 1 - 1].Neurons[i].LastState :
data[inBatchIndex].Input[i])
+
_config.RegularizationFactor *
network.Layers[network.Layers.Length - 1].Neurons[j].Weights[i]
/ data.Count);
}
}
Очень похоже на последний слой выглядит обработка всех скрытых слоев сети:
- пробегаемся по всем скрытым слоям
- инициализировали "наблЫ", там мы храним аккумулированное значение градиента для пачки входных данных (при онлайн обучении, там окажется просто градиент по одному примеру)
- пробегаемся по всем нейронам последнего слоя
- вычисляем dE/dz, но уже для этого мы используем значения вычисленные, на слое старше текущего
- а затем вычисляем значение градиента для весов и смещения
//hidden layers
for (int hiddenLayerIndex = network.Layers.Length - 2; hiddenLayerIndex >= 0; hiddenLayerIndex--)
{
for (int j = 0; j < network.Layers[hiddenLayerIndex].Neurons.Length; j++)
{
network.Layers[hiddenLayerIndex].Neurons[j].dEdz = 0;
for (int k = 0; k < network.Layers[hiddenLayerIndex + 1].Neurons.Length; k++)
{
network.Layers[hiddenLayerIndex].Neurons[j].dEdz +=
network.Layers[hiddenLayerIndex + 1].Neurons[k].Weights[j]*
network.Layers[hiddenLayerIndex + 1].Neurons[k].dEdz;
}
network.Layers[hiddenLayerIndex].Neurons[j].dEdz *=
network.Layers[hiddenLayerIndex].Neurons[j].ActivationFunction.
ComputeFirstDerivative(
network.Layers[hiddenLayerIndex].Neurons[j].LastNET
);
nablaBiases[hiddenLayerIndex][j] += _config.LearningRate*
network.Layers[hiddenLayerIndex].Neurons[j].dEdz;
for (int i = 0; i < network.Layers[hiddenLayerIndex].Neurons[j].Weights.Length; i++)
{
nablaWeights[hiddenLayerIndex][j][i] += _config.LearningRate * (
network.Layers[hiddenLayerIndex].Neurons[j].dEdz *
(hiddenLayerIndex > 0 ? network.Layers[hiddenLayerIndex - 1].Neurons[i].LastState : data[inBatchIndex].Input[i])
+
_config.RegularizationFactor * network.Layers[hiddenLayerIndex].Neurons[j].Weights[i] / data.Count
);
}
}
}
Тут основной код заканчивается, и остается сделать пару штрихов в виде вычисления средней ошибки сети на массиве данных (с учетом регуляризации), и логирование:
//recalculating error on all data
//real error
currentError = 0;
for (int i = 0; i < data.Count; i++)
{
double[] realOutput = network.ComputeOutput(data[i].Input);
currentError += _config.ErrorFunction.Calculate(data[i].Output, realOutput);
}
currentError *= 1d/data.Count;
//regularization term
if (Math.Abs(_config.RegularizationFactor - 0d) > Double.Epsilon)
{
double reg = 0;
for (int layerIndex = 0; layerIndex < network.Layers.Length; layerIndex++)
{
for (int neuronIndex = 0; neuronIndex < network.Layers[layerIndex].Neurons.Length; neuronIndex++)
{
for (int weightIndex = 0; weightIndex < network.Layers[layerIndex].Neurons[neuronIndex].Weights.Length; weightIndex++)
{
reg += network.Layers[layerIndex].Neurons[neuronIndex].Weights[weightIndex] *
network.Layers[layerIndex].Neurons[neuronIndex].Weights[weightIndex];
}
}
}
currentError += _config.RegularizationFactor * reg / (2 * data.Count);
}
epochNumber++;
Logger.Instance.Log("Eposh #" + epochNumber.ToString() +
" finished; current error is " + currentError.ToString() +
"; it takes: " +
(DateTime.Now - dtStart).Duration().ToString());
Этот блок находится прямиком перед выходом из основного цикла, продублирую код для наглядности:
} while (epochNumber < _config.MaxEpoches &&
currentError > _config.MinError &&
Math.Abs(currentError - lastError) > _config.MinErrorChange);
Итог
Собственно все. От себя хочу вот что добавить, данный текст я привел примерно в том виде, в каком я его хотел бы видеть, когда первый раз читал про алгоритм обратного распространения. Обычно в литературе авторы заранее говорят что будет использоваться такая то функция ошибки и активации нейрона. И в процессе вывода формул с частными производными они вставляют эти производные в вывод, и в итоге получается примерно так же, как, например, в википедии, где рассматривается алгоритм для минимизации квадрата Евклидова расстояния.
Вот формула для последнего слоя:
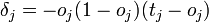
и для остальных:
 .
.
Конечно, если вы очень умны, то вам не составит труда понять что тут от какого дифференциала, но я смог понять это только когда взял в руки ручку и бумагу, и написал весь вывод. Потом то же самое сделал для другой функции ошибки и только потом обобщил и осознал -)
Время на прочтение
8 мин
Количество просмотров 515K
О чём статья
Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Дайте код!
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
l1 = 1/(1+np.exp(-(np.dot(X,syn0))))
l2 = 1/(1+np.exp(-(np.dot(l1,syn1))))
l2_delta = (y - l2)*(l2*(1-l2))
l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))
syn1 += l1.T.dot(l2_delta)
syn0 += X.T.dot(l1_delta)
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
import numpy as np
# Сигмоида
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
# набор входных данных
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
# выходные данные
y = np.array([[0,0,1,1]]).T
# сделаем случайные числа более определёнными
np.random.seed(1)
# инициализируем веса случайным образом со средним 0
syn0 = 2*np.random.random((3,1)) - 1
for iter in xrange(10000):
# прямое распространение
l0 = X
l1 = nonlin(np.dot(l0,syn0))
# насколько мы ошиблись?
l1_error = y - l1
# перемножим это с наклоном сигмоиды
# на основе значений в l1
l1_delta = l1_error * nonlin(l1,True) # !!!
# обновим веса
syn0 += np.dot(l0.T,l1_delta) # !!!
print "Выходные данные после тренировки:"
print l1
Выходные данные после тренировки:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
«*» — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
«-» – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена !!!)
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена !!!)
Разберём код по строчкам
import numpy as np
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
def nonlin(x,deriv=False):
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
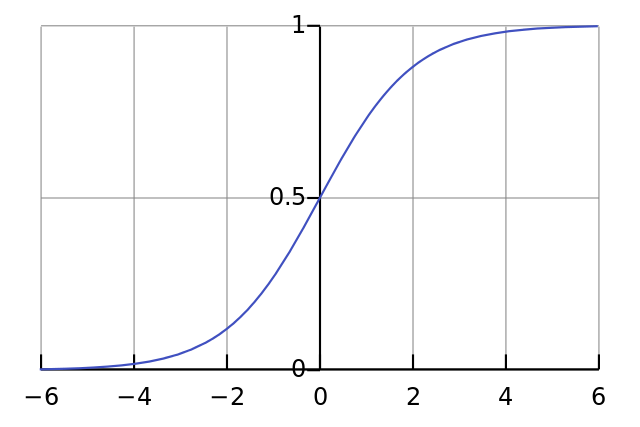
if(deriv==True):
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
X = np.array([ [0,0,1], …
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
y = np.array([[0,0,1,1]]).T
Инициализирует выходные данные. «.T» – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
np.random.seed(1)
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
syn0 = 2*np.random.random((3,1)) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.
for iter in xrange(10000):
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
l0 = X
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
l1 = nonlin(np.dot(l0,syn0))
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
(4 x 3) dot (3 x 1) = (4 x 1)
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.
Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.
l1_error = y - l1
Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.
l1_delta = l1_error * nonlin(l1,True)
А вот и секретный ингредиент. Эту строку нужно разбирать по частям.
Первая часть: производная
nonlin(l1,True)
l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.
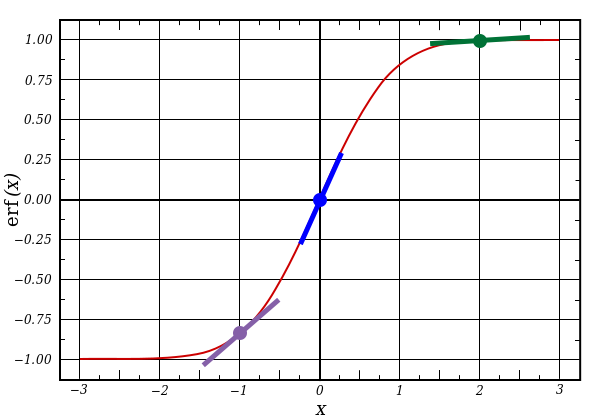
Полное выражение: производная, взвешенная по ошибкам
l1_delta = l1_error * nonlin(l1,True)
Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.
Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.
syn0 += np.dot(l0.T,l1_delta)
Мы готовы к обновлению сети. Рассмотрим один тренировочный пример. В нём мы будем обновлять веса. Обновим крайний левый вес (9.5)
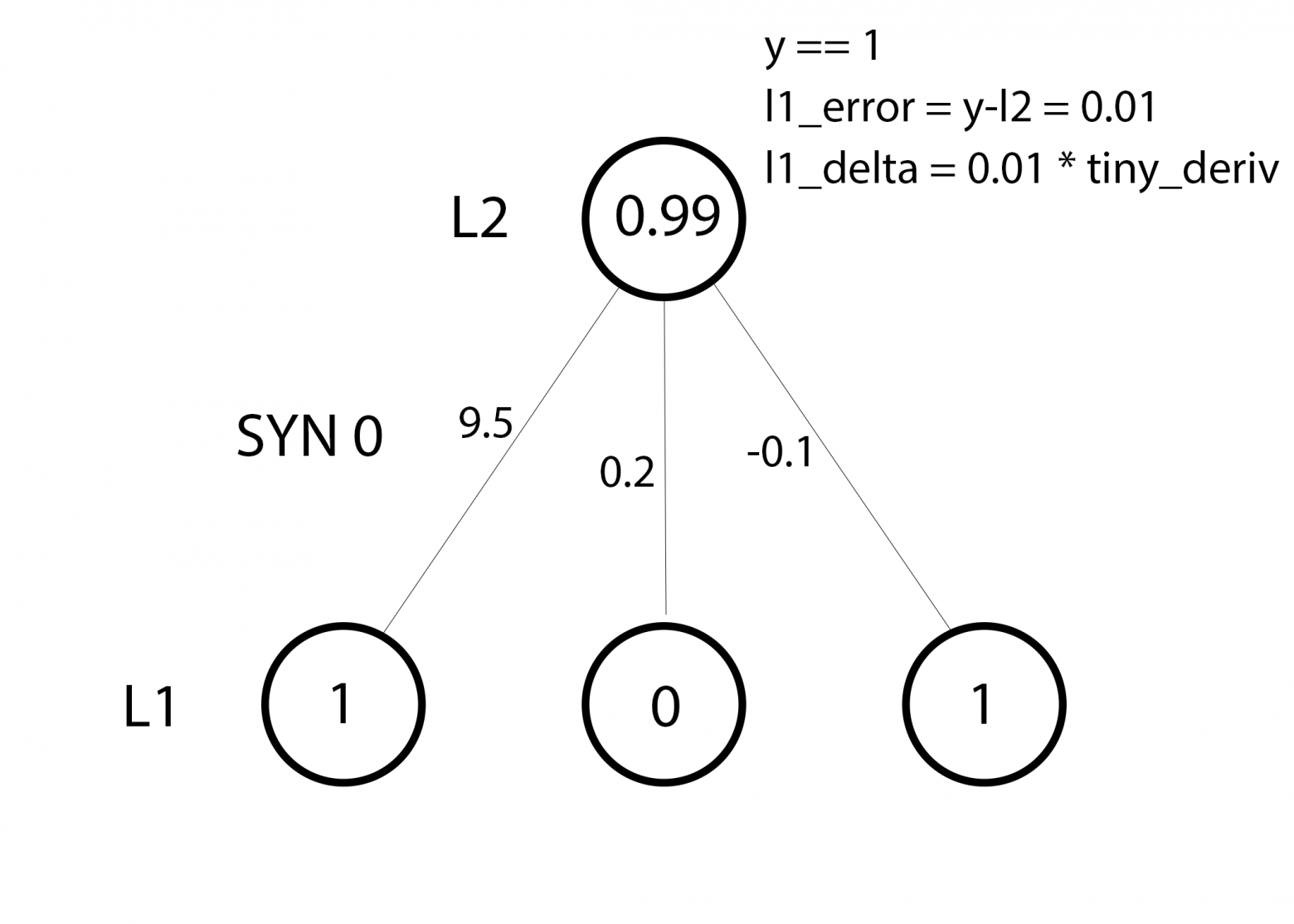
weight_update = input_value * l1_delta
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.
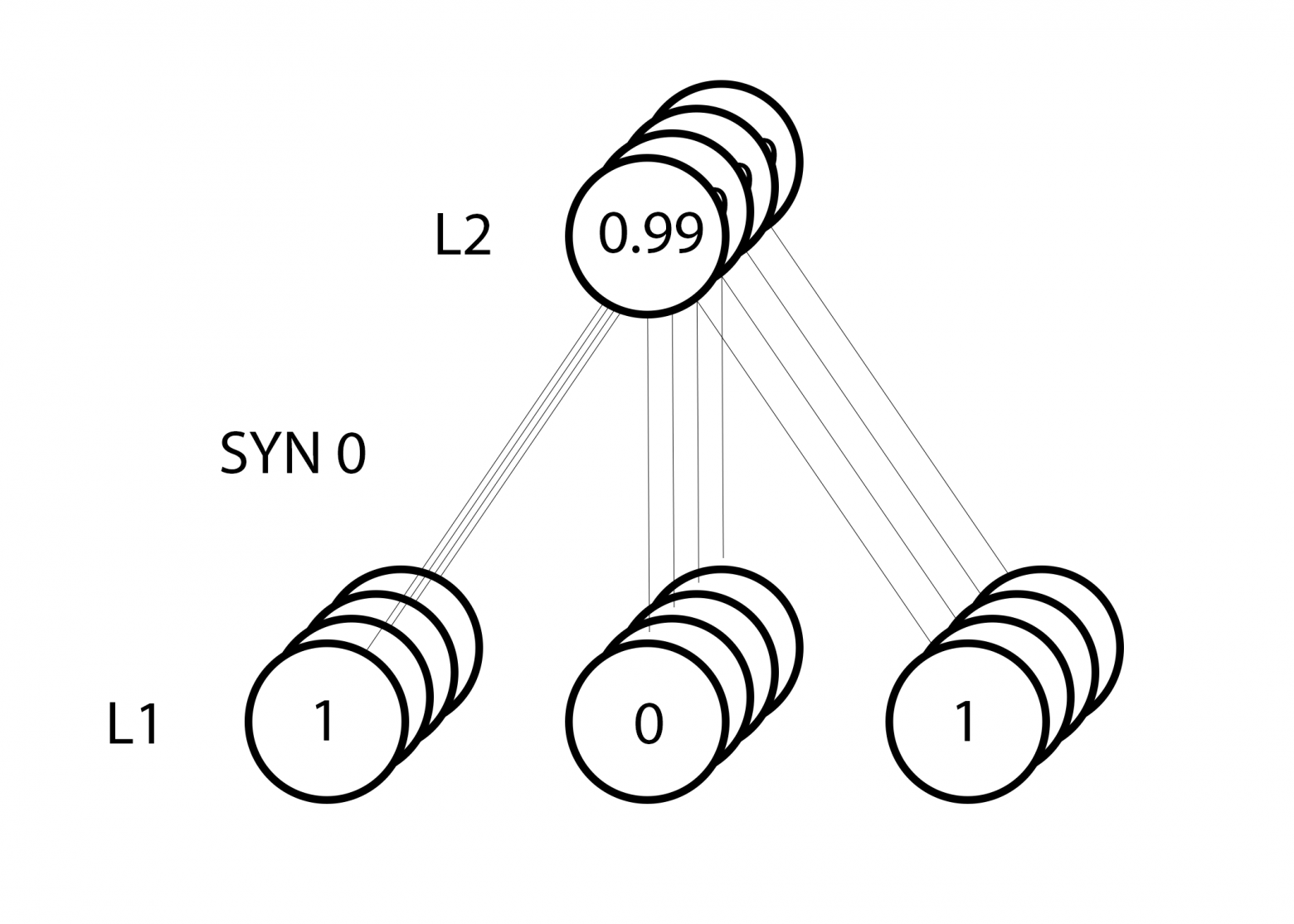
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.
Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.
Часть 2: задачка посложнее
Вход Выход
0 0 1 0
0 1 1 1
1 0 1 1
1 1 1 0
Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.
Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).
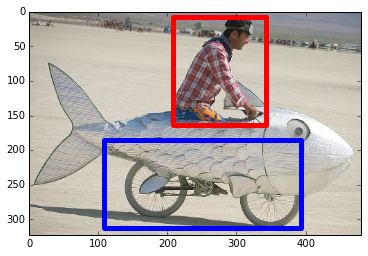

Стратегия
Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.
Вход (l0) Скрытые веса (l1) Выход (l2)
0 0 1 0.1 0.2 0.5 0.2 0
0 1 1 0.2 0.6 0.7 0.1 1
1 0 1 0.3 0.2 0.3 0.9 1
1 1 1 0.2 0.1 0.3 0.8 0
Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.
Нейросеть в три слоя
import numpy as np
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0],
[1],
[1],
[0]])
np.random.seed(1)
# случайно инициализируем веса, в среднем - 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
# проходим вперёд по слоям 0, 1 и 2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# как сильно мы ошиблись относительно нужной величины?
l2_error = y - l2
if (j% 10000) == 0:
print "Error:" + str(np.mean(np.abs(l2_error)))
# в какую сторону нужно двигаться?
# если мы были уверены в предсказании, то сильно менять его не надо
l2_delta = l2_error*nonlin(l2,deriv=True)
# как сильно значения l1 влияют на ошибки в l2?
l1_error = l2_delta.dot(syn1.T)
# в каком направлении нужно двигаться, чтобы прийти к l1?
# если мы были уверены в предсказании, то сильно менять его не надо
l1_delta = l1_error * nonlin(l1,deriv=True)
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
l1_error = l2_delta.dot(syn1.T)
Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Статья публикуется в переводе, автор оригинального текста Victor Zhou.
***
Термин «нейронные сети» сейчас можно услышать из каждого утюга, и многие верят, будто это что-то очень сложное. На самом деле нейронные сети совсем не такие сложные, как может показаться! Мы разберемся, как они работают, реализовав одну сеть с нуля на Python.
Эта статья предназначена для полных новичков, не имеющих никакого опыта в машинном обучении. Поехали!
1. Составные элементы: нейроны
Прежде всего нам придется обсудить нейроны, базовые элементы нейронной сети. Нейрон принимает несколько входов, выполняет над ними кое-какие математические операции, а потом выдает один выход. Вот как выглядит нейрон с двумя входами:
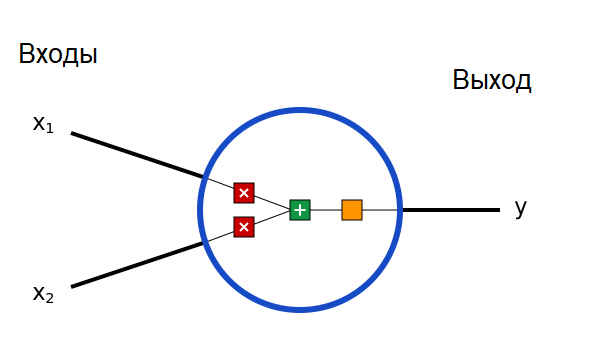
Внутри нейрона происходят три операции. Сначала значения входов умножаются на веса:
Затем взвешенные входы складываются, и к ним прибавляется значение порога b:
Наконец, полученная сумма проходит через функцию активации:
Функция активации преобразует неограниченные значения входов в выход, имеющий ясную и предсказуемую форму. Одна из часто используемых функций активации – сигмоида:
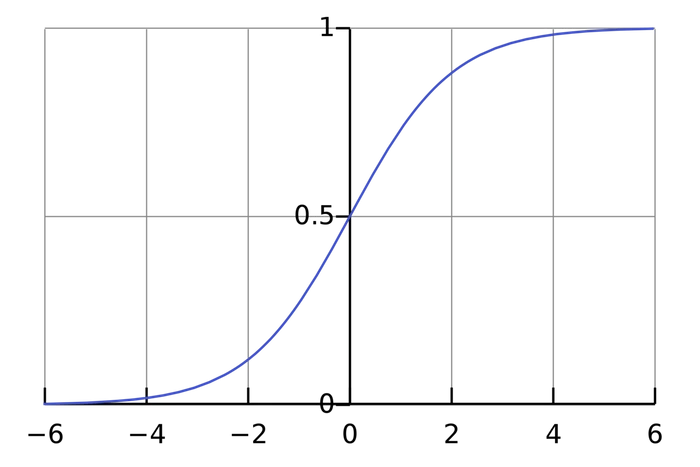
Сигмоида выдает результаты в интервале (0, 1). Можно представить, что она «упаковывает» интервал от минус бесконечности до плюс бесконечности в (0, 1): большие отрицательные числа превращаются в числа, близкие к 0, а большие положительные – к 1.
Простой пример
Допустим, наш двухвходовой нейрон использует сигмоидную функцию активации и имеет следующие параметры:
w=[0, 1] – это всего лишь запись w1=0, w2=1 в векторном виде. Теперь зададим нашему нейрону входные данные: x=[2, 3]. Мы используем скалярное произведение векторов, чтобы записать формулу в сжатом виде:
Наш нейрон выдал 0.999 при входах x=[2, 3]. Вот и все! Процесс передачи значений входов дальше, чтобы получить выход, называется прямой связью (feed forward).
Пишем код для нейрона
Настало время написать свой нейрон! Мы используем NumPy, популярную и мощную расчетную библиотеку для Python, которая поможет нам с вычислениями:
import numpy as np
def sigmoid(x):
# Наша функция активации: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
class Neuron:
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
# Умножаем входы на веса, прибавляем порог, затем используем функцию активации
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4 # b = 4
n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994
Узнаете эти числа? Это тот самый пример, который мы только что рассчитали! И мы получили тот же результат – 0.999.
2. Собираем нейронную сеть из нейронов
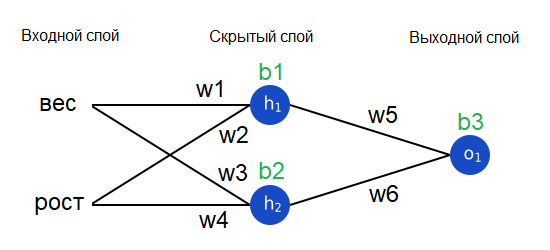
Нейронная сеть – это всего лишь несколько нейронов, соединенных вместе. Вот как может выглядеть простая нейронная сеть:
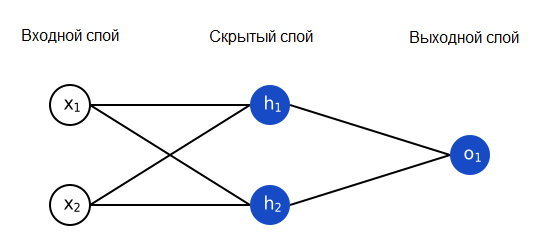
У этой сети два входа, скрытый слой с двумя нейронами (h1 и h2) и выходной слой с одним нейроном (o1). Обратите внимание, что входы для o1 – это выходы из h1 и h2. Именно это создает из нейронов сеть.
Замечание
Скрытый слой – это любой слой между входным (первым) слоем сети и выходным (последним). Скрытых слоев может быть много!
Пример: прямая связь
Давайте используем сеть, изображенную выше, и будем считать, что все нейроны имеют одинаковые веса w=[0, 1], одинаковые пороговые значения b=0, и одинаковую функцию активации – сигмоиду. Пусть h1, h2 и o1 обозначают выходные значения соответствующих нейронов.
Что получится, если мы подадим на вход x=[2, 3]?
Если подать на вход нашей нейронной сети x=[2, 3], на выходе получится 0.7216. Достаточно просто, не правда ли?
Нейронная сеть может иметь любое количество слоев, и в этих слоях может быть любое количество нейронов. Основная идея остается той же: передавайте входные данные по нейронам сети, пока не получите выходные значения. Для простоты мы будем использовать сеть, показанную выше, до конца статьи.
Пишем код нейронной сети
Давайте реализуем прямую связь для нашей нейронной сети. Напомним, как она выглядит:
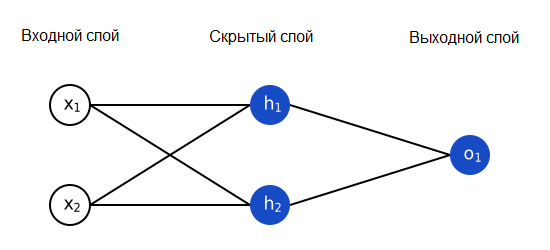
import numpy as np
# ... вставьте сюда код из предыдущего раздела
class OurNeuralNetwork:
'''
Нейронная сеть с:
- 2 входами
- скрытым слоем с 2 нейронами (h1, h2)
- выходным слоем с 1 нейроном (o1)
Все нейроны имеют одинаковые веса и пороги:
- w = [0, 1]
- b = 0
'''
def __init__(self):
weights = np.array([0, 1])
bias = 0
# Используем класс Neuron из предыдущего раздела
self.h1 = Neuron(weights, bias)
self.h2 = Neuron(weights, bias)
self.o1 = Neuron(weights, bias)
def feedforward(self, x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
# Входы для o1 - это выходы h1 и h2
out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421
Мы снова получили 0.7216! Похоже, наша сеть работает.
3. Обучаем нейронную сеть (часть 1)
Допустим, у нас есть следующие измерения:
| Имя | Вес (в фунтах) | Рост (в дюймах) | Пол |
| Алиса | 133 (54.4 кг) | 65 (165,1 см) | Ж |
| Боб | 160 (65,44 кг) | 72 (183 см) | М |
| Чарли | 152 (62.2 кг) | 70 (178 см) | М |
| Диана | 120 (49 кг) | 60 (152 см) | Ж |
Давайте обучим нашу нейронную сеть предсказывать пол человека по его росту и весу.
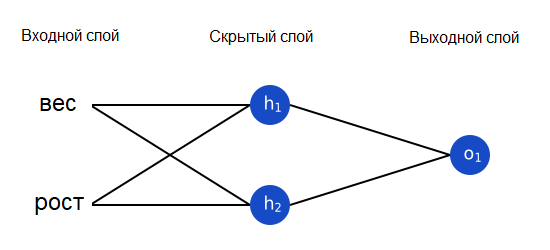
Мы будем представлять мужской пол как 0, женский – как 1, а также сдвинем данные, чтобы их было проще использовать:
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
| Боб | 25 | 6 | 0 |
| Чарли | 17 | 4 | 0 |
| Диана | -15 | -6 | 1 |
Замечание
Я выбрал величину сдвигов (135 и 66), чтобы числа выглядели попроще. Обычно сдвигают на среднее значение.
Потери
Прежде чем обучать нашу нейронную сеть, нам нужно как-то измерить, насколько «хорошо» она работает, чтобы она смогла работать «лучше». Это измерение и есть потери (loss).
Мы используем для расчета потерь среднюю квадратичную ошибку (mean squared error, MSE):
Давайте рассмотрим все используемые переменные:
- n – это количество измерений, в нашем случае 4 (Алиса, Боб, Чарли и Диана).
- y представляет предсказываемое значение, Пол.
- ytrue – истинное значение переменной («правильный ответ»). Например, для Алисы ytrue будет равна 1 (женский пол).
- ypred – предсказанное значение переменной. Это то, что выдаст наша нейронная сеть.
(ytrue-ypred)2 называется квадратичной ошибкой. Наша функция потерь просто берет среднее значение всех квадратичных ошибок – поэтому она и называется средней квадратичной ошибкой. Чем лучшими будут наши предсказания, тем меньшими будут наши потери!
Лучшие предсказания = меньшие потери.
Обучение нейронной сети = минимизация ее потерь.
Пример расчета потерь
Предположим, что наша сеть всегда возвращает 0 – иными словами, она уверена, что все люди мужчины. Насколько велики будут наши потери?
| Имя | ytrue | ypred | (ytrue-ypred)2 |
| Алиса | 1 | 0 | 1 |
| Боб | 0 | 0 | 0 |
| Чарли | 0 | 0 | 0 |
| Диана | 1 | 0 | 1 |
Пишем функцию средней квадратичной ошибки
Вот небольшой кусок кода, который рассчитает наши потери. Если вы не понимаете, почему он работает, прочитайте в руководстве NumPy про операции с массивами.
import numpy as np
def mse_loss(y_true, y_pred):
# y_true и y_pred - массивы numpy одинаковой длины.
return ((y_true - y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5
Отлично. Идем дальше!
4. Обучаем нейронную сеть (часть 2)
Теперь у нас есть четкая цель: минимизировать потери нейронной сети. Мы знаем, что можем изменять веса и пороги нейронов, чтобы изменить ее предсказания, но как нам делать это таким образом, чтобы минимизировать потери?
Внимание: математика!
Этот раздел использует частные производные по нескольким переменным. Если вы плохо знакомы с дифференциальным исчислением, можете просто пропускать математические формулы.
Для простоты давайте представим, что в нашем наборе данных только одна Алиса.
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
Тогда средняя квадратичная ошибка будет квадратичной ошибкой только для Алисы:
Другой метод – это рассматривать функцию потерь как функцию от весов и порогов. Давайте отметим все веса и пороги нашей нейронной сети:
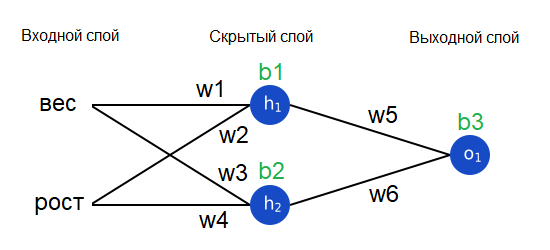
Теперь мы можем записать функцию потерь как функцию от нескольких переменных:
Предположим, мы хотим отрегулировать w1. Как изменится значение потери L при изменении w1? На этот вопрос может ответить частная производная dL/dw1. Как мы ее рассчитаем?
Не падайте духом!
Здесь математика становится более сложной. Возьмите бумагу и ручку, чтобы не отставать – это поможет вам понять, что происходит.
Прежде всего, давайте перепишем эту частную производную через dypred/dw1, воспользовавшись цепным правилом:
Мы можем рассчитать dL/dypred, поскольку мы уже выяснили выше, что L=(1-ypred)2:
Теперь давайте решим, что делать с dypred/dw1. Обозначая выходы нейронов, как прежде, h1, h2 и o1, получаем:
Вспомните, что f() – это наша функция активации, сигмоида. Поскольку w1 влияет только на h1 (но не на h2), мы можем снова использовать цепное правило и записать:
Мы можем сделать то же самое для dh1/dw1, снова применяя цепное правило:
В этой формуле x1 – это вес, а x2 – рост. Вот уже второй раз мы встречаем f'(x) – производную сигмоидной функции! Давайте вычислим ее:
Мы используем эту красивую форму для f'(x) позже. На этом мы закончили! Мы сумели разложить dL/dw1 на несколько частей, которые мы можем рассчитать:
Такой метод расчета частных производных «от конца к началу» называется методом обратного распространения (backpropagation).
Уффф. Здесь было очень много символов, так что не страшно, если вы пока не все понимаете. Давайте покажем, как это работает, на практическом примере!
Пример. Считаем частную производную
Мы по-прежнему считаем, что наш набор данных состоит из одной Алисы:
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
Давайте инициализируем все веса как 1, а все пороги как 0. Если мы выполним прямой проход по нейронной сети, то получим:
Наша сеть выдает ypred=0.524, что находится примерно на полпути между Мужским полом (0) и Женским (1). Давайте рассчитаем dL/dw1:
Напоминаем:
Ранее мы получили формулу для производной сигмоиды f'(x)=f(x)(1-f(x))
Вот и все! Результат говорит нам, что при увеличении w1, функция ошибки чуть-чуть повышается.
Обучение: стохастический градиентный спуск
Теперь у нас есть все нужные инструменты для обучения нейронной сети! Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (stochastic gradient descent), который определит, как мы будем изменять наши веса и пороги для минимизации потерь. Фактически, он заключается в следующей формуле обновления:
Скорость обучения определяет, как быстро наша сеть учится. Все, что мы делаем – это вычитаем eta*dL/dw1 из w1:
- Если dL/dw1 положительна, w1 уменьшится, что уменьшит L.
- Если dL/dw1 отрицательна, w1 увеличится, что также уменьшит L.
Если мы сделаем то же самое для каждого веса и порога в сети, потери будут постепенно уменьшаться, и наша сеть будет выдавать более точные результаты.
Процесс обучения сети будет выглядеть примерно так:
- Выбираем одно наблюдение из набора данных. Именно то, что мы работаем только с одним наблюдением, делает наш градиентный спуск стохастическим.
- Считаем все частные производные функции потерь по всем весам и порогам (dL/dw1, dL/dw2 и т.д.)
- Используем формулу обновления, чтобы обновить значения каждого веса и порога.
- Снова переходим к шагу 1.
Пишем код всей нейронной сети
Наконец настало время реализовать всю нейронную сеть.
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
| Боб | 25 | 6 | 0 |
| Чарли | 17 | 4 | 0 |
| Диана | -15 | -6 |
import numpy as np
def sigmoid(x):
# Сигмоидная функция активации: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Производная сигмоиды: f'(x) = f(x) * (1 - f(x))
fx = sigmoid(x)
return fx * (1 - fx)
def mse_loss(y_true, y_pred):
# y_true и y_pred - массивы numpy одинаковой длины.
return ((y_true - y_pred) ** 2).mean()
class OurNeuralNetwork:
'''
Нейронная сеть с:
- 2 входами
- скрытым слоем с 2 нейронами (h1, h2)
- выходной слой с 1 нейроном (o1)
*** DISCLAIMER ***:
Следующий код простой и обучающий, но НЕ оптимальный.
Код реальных нейронных сетей совсем на него не похож. НЕ копируйте его!
Изучайте и запускайте его, чтобы понять, как работает эта нейронная сеть.
'''
def __init__(self):
# Веса
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# Пороги
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self, x):
# x is a numpy array with 2 elements.
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
'''
- data - массив numpy (n x 2) numpy, n = к-во наблюдений в наборе.
- all_y_trues - массив numpy с n элементами.
Элементы all_y_trues соответствуют наблюдениям в data.
'''
learn_rate = 0.1
epochs = 1000 # сколько раз пройти по всему набору данных
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# --- Прямой проход (эти значения нам понадобятся позже)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# --- Считаем частные производные.
# --- Имена: d_L_d_w1 = "частная производная L по w1"
d_L_d_ypred = -2 * (y_true - y_pred)
# Нейрон o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Нейрон h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Нейрон h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# --- Обновляем веса и пороги
# Нейрон h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Нейрон h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# Нейрон o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# --- Считаем полные потери в конце каждой эпохи
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f" % (epoch, loss))
# Определим набор данных
data = np.array([
[-2, -1], # Алиса
[25, 6], # Боб
[17, 4], # Чарли
[-15, -6], # Диана
])
all_y_trues = np.array([
1, # Алиса
0, # Боб
0, # Чарли
1, # Диана
])
# Обучаем нашу нейронную сеть!
network = OurNeuralNetwork()
network.train(data, all_y_trues)
По мере обучения сети ее потери постепенно уменьшаются:
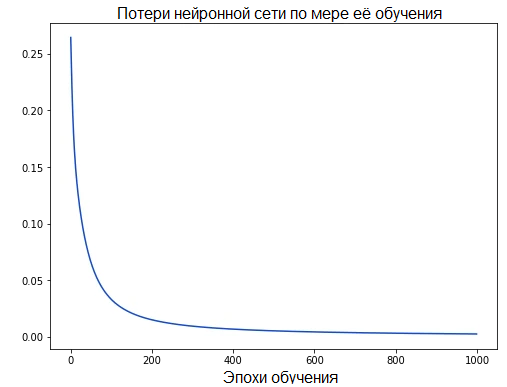
Теперь мы можем использовать нашу сеть для предсказания пола:
# Делаем пару предсказаний
emily = np.array([-7, -3]) # 128 фунтов (52.35 кг), 63 дюйма (160 см)
frank = np.array([20, 2]) # 155 pounds (63.4 кг), 68 inches (173 см)
print("Эмили: %.3f" % network.feedforward(emily)) # 0.951 - Ж
print("Фрэнк: %.3f" % network.feedforward(frank)) # 0.039 - М
Что теперь?
Вы сделали это! Давайте перечислим все, что мы с вами сделали:
- Определили нейроны, составные элементы нейронных сетей.
- Использовали сигмоидную функцию активации для наших нейронов.
- Увидели, что нейронные сети – это всего лишь несколько нейронов, соединенных друг с другом.
- Создали набор данных, в котором Вес и Рост были входными данными (или признаками), а Пол – выходным (или меткой).
- Узнали о функции потерь и средней квадратичной ошибке (MSE).
- Поняли, что обучение нейронной сети – это всего лишь минимизация ее потерь.
- Использовали метод обратного распространения (backpropagation) для расчета частных производных.
- Использовали стохастический градиентный спуск (SGD) для обучения нашей сети.
Перед вами – множество путей, на которых вас ждет масса нового и интересного:
- Экспериментируйте с большими и лучшими нейронными сетями, используя подходящие библиотеки вроде Tensorflow, Keras и PyTorch.
- Создайте свою первую нейронную сеть с помощью Keras.
- Прочитайте остальные статьи из серии «Нейронные сети с нуля».
- Исследуйте другие функции активации, кроме сигмоиды, например, Softmax.
- Исследуйте другие оптимизаторы, кроме стохастического градиентного спуска.
Спасибо за внимание!
***
На Python создают прикладные приложения, пишут тесты и бэкенд веб-приложений, автоматизируют задачи в системном администрировании, его используют в нейронных сетях и анализе больших данных. Язык можно изучить самостоятельно, но на это придется потратить немало времени. Если вы хотите быстро понять основы программирования на Python, обратите внимание на онлайн-курс «Библиотеки программиста». За 30 уроков (15 теоретических и 15 практических занятий) под руководством практикующих экспертов вы не только изучите основы синтаксиса, но и освоите две интегрированные среды разработки (PyCharm и Jupyter Notebook), работу со словарями, парсинг веб-страниц, создание ботов для Telegram и Instagram, тестирование кода и даже анализ данных. Чтобы процесс обучения стал более интересным и комфортным, студенты получат от нас обратную связь. Кураторы и преподаватели курса ответят на все вопросы по теме лекций и практических занятий.
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
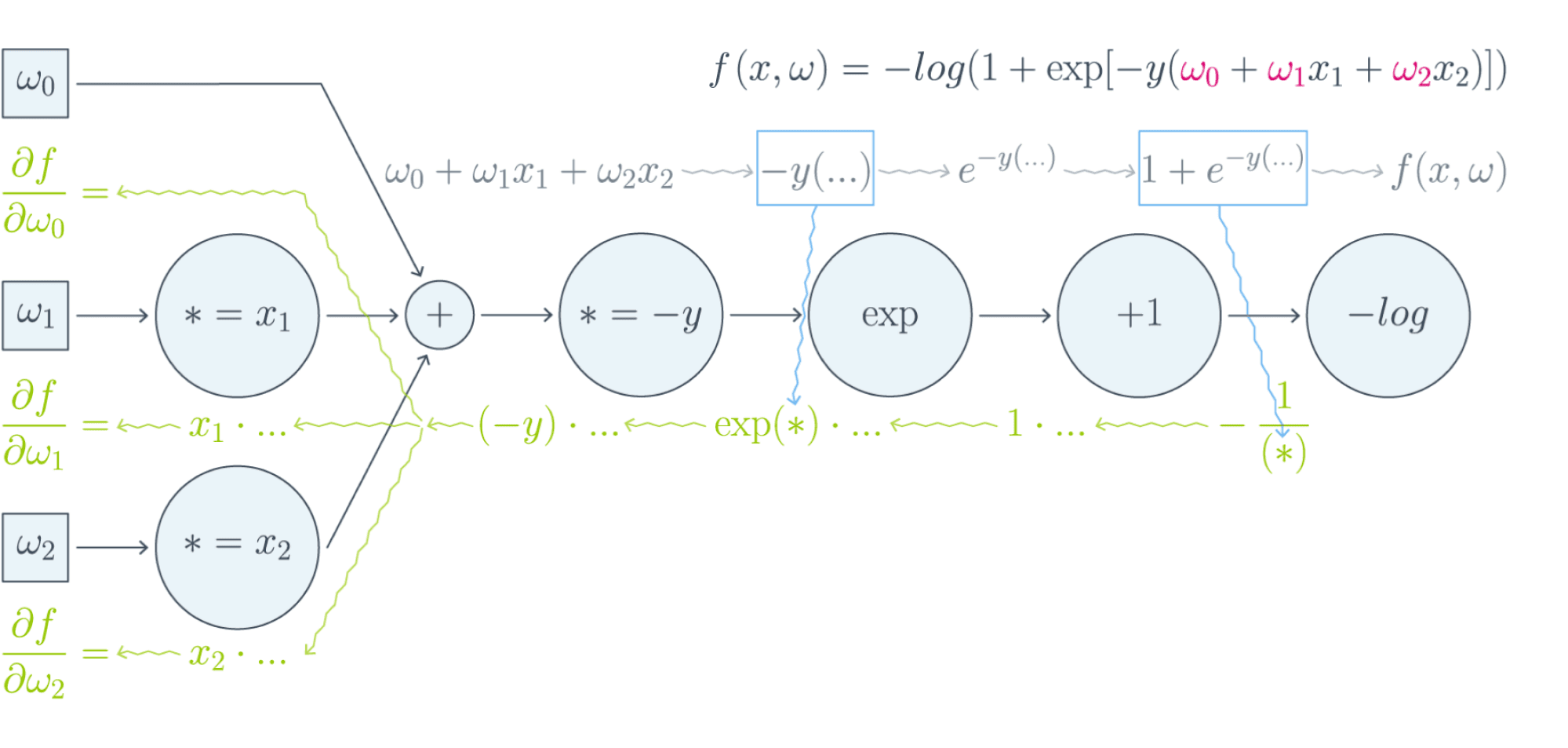
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
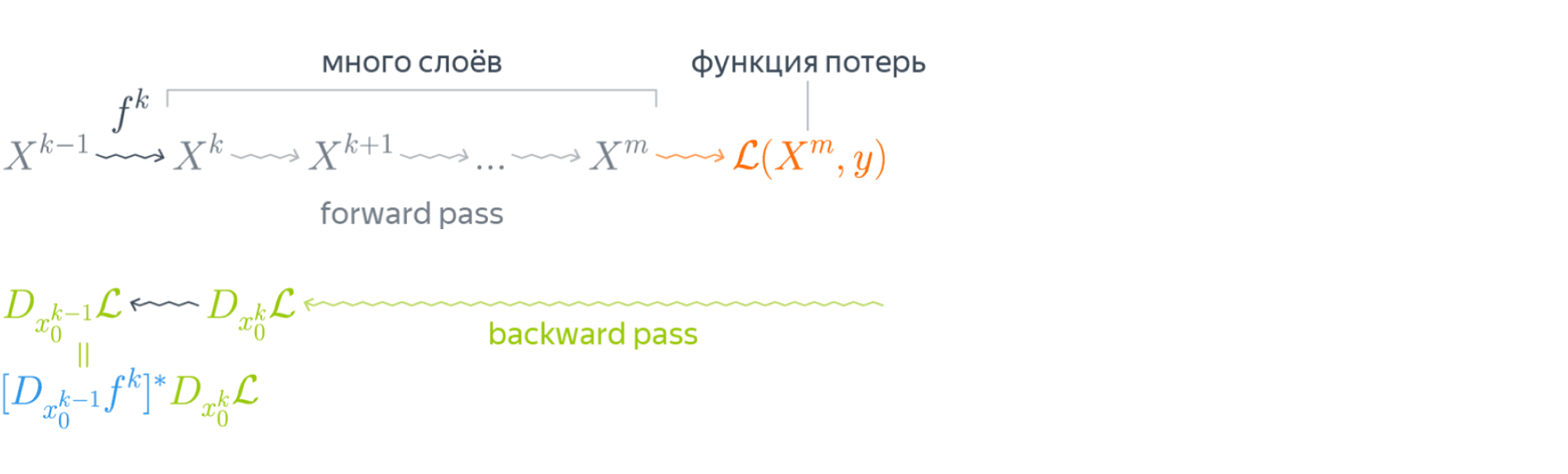
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
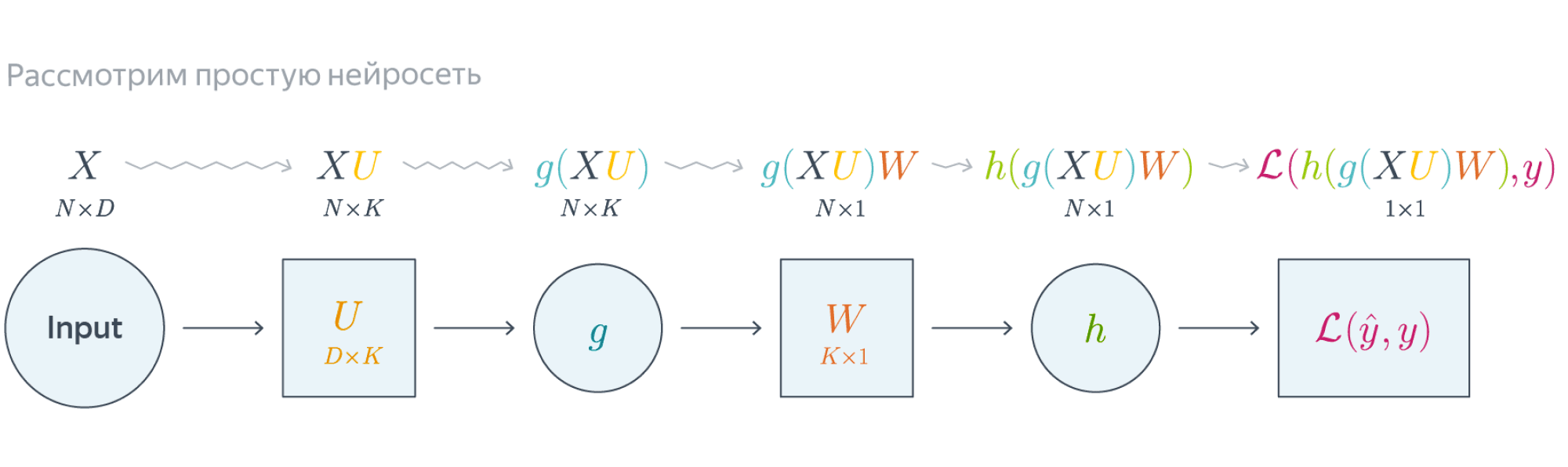 Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?
Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
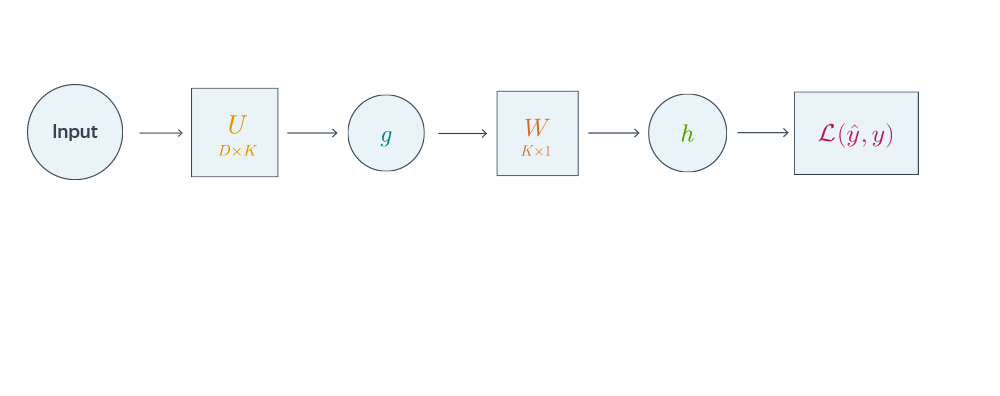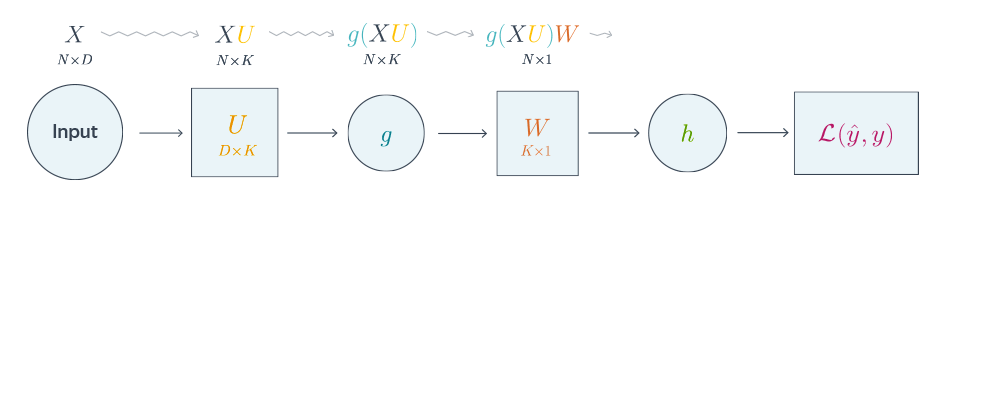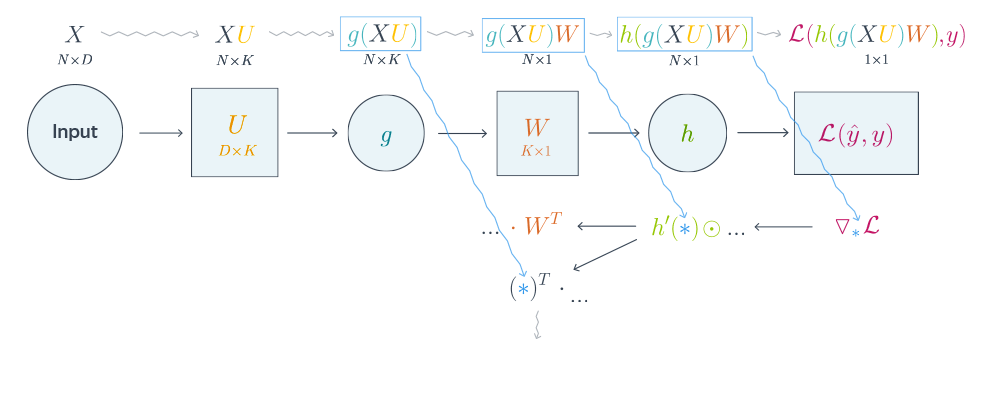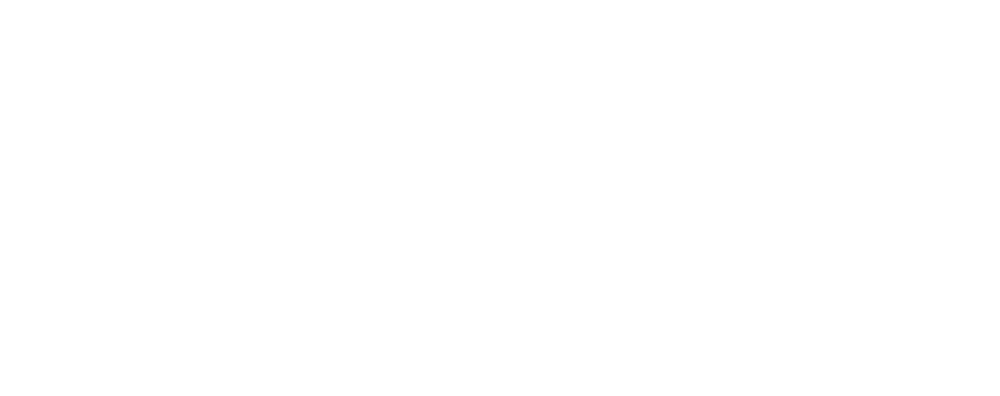
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Перевод
Ссылка на автора
Алгоритм обратного распространения — это классическая искусственная нейронная сеть с прямой связью.
Эта техника до сих пор используется для тренировки большого глубокое обучение сетей.
В этом руководстве вы узнаете, как реализовать алгоритм обратного распространения с нуля с помощью Python.
После завершения этого урока вы узнаете:
- Как переадресовать входные данные для вычисления выходных данных.
- Как распространять ошибки и обучать сеть.
- Как применить алгоритм обратного распространения к реальной задаче прогнозного моделирования.
Давайте начнем.
- Обновление ноябрь 2016: Исправлена ошибка в функции activ (). Спасибо Алекс!
- Обновление январь / 2017: Изменено вычисление fold_size в cross_validation_split (), чтобы оно всегда было целым числом. Исправляет проблемы с Python 3.
- Обновление январь / 2017: Обновлена небольшая ошибка в update_weights (). Спасибо, Томаш!
- Обновление апрель / 2018: Добавлена прямая ссылка на набор данных CSV.
- Обновление Авг / 2018: Протестировано и обновлено для работы с Python 3.6.

Описание
В этом разделе дается краткое введение в алгоритм обратного распространения и набор данных семян пшеницы, которые мы будем использовать в этом руководстве.
Алгоритм обратного распространения
Алгоритм обратного распространения — это контролируемый метод обучения для многослойных сетей прямой связи из области искусственных нейронных сетей.
Прямые нейронные сети вдохновлены обработкой информации одной или нескольких нейронных клеток, называемых нейронами. Нейрон принимает входные сигналы через свои дендриты, которые передают электрический сигнал в тело клетки. Аксон передает сигнал в синапсы, которые являются связями аксона клетки с дендритами другой клетки.
Принцип обратного распространения заключается в моделировании заданной функции путем изменения внутренних весовых коэффициентов входных сигналов для получения ожидаемого выходного сигнала. Система обучается с использованием метода контролируемого обучения, где ошибка между выходными данными системы и известным ожидаемым выходным значением представляется системе и используется для изменения ее внутреннего состояния.
Технически алгоритм обратного распространения — это метод обучения весов в многослойной нейронной сети с прямой связью. Как таковой, он требует, чтобы сетевая структура была определена из одного или нескольких уровней, где один уровень полностью связан со следующим уровнем. Стандартная сетевая структура — это один входной слой, один скрытый слой и один выходной слой.
Обратное распространение можно использовать как для задач классификации, так и для задач регрессии, но в этом руководстве мы сосредоточимся на классификации.
В задачах классификации наилучшие результаты достигаются, когда сеть имеет один нейрон в выходном слое для каждого значения класса. Например, проблема 2-классовой или двоичной классификации со значениями классов A и B. Эти ожидаемые результаты должны быть преобразованы в двоичные векторы с одним столбцом для каждого значения класса. Например, [1, 0] и [0, 1] для A и B соответственно. Это называется горячим кодированием.
Набор данных семян пшеницы
Набор данных семян включает в себя прогнозирование видов с учетом измерений семян из разных сортов пшеницы.
Есть 201 записей и 7 числовых входных переменных. Это проблема классификации с 3 выходными классами. Шкала для каждого числового входного значения варьируется, поэтому может потребоваться некоторая нормализация данных для использования с алгоритмами, которые взвешивают входные данные, такие как алгоритм обратного распространения.
Ниже приведен образец первых 5 строк набора данных.
15.26,14.84,0.871,5.763,3.312,2.221,5.22,1
14.88,14.57,0.8811,5.554,3.333,1.018,4.956,1
14.29,14.09,0.905,5.291,3.337,2.699,4.825,1
13.84,13.94,0.8955,5.324,3.379,2.259,4.805,1
16.14,14.99,0.9034,5.658,3.562,1.355,5.175,1При использовании алгоритма нулевого правила, который прогнозирует наиболее распространенное значение класса, базовая точность задачи составляет 28,095%.
Вы можете узнать больше и загрузить набор данных семян из UCI Хранилище Машинного Обучения,
Загрузите набор данных seed и поместите его в текущий рабочий каталог с именем файлаseeds_dataset.csv,
Набор данных представлен в формате табуляции, поэтому его необходимо преобразовать в CSV с помощью текстового редактора или программы для работы с электронными таблицами.
Обновите, загрузите набор данных в формате CSV напрямую:
- Скачать набор данных семян пшеницы
Руководство
Этот урок разбит на 6 частей:
- Инициализировать сеть.
- Вперед Распространять.
- Ошибка обратного распространения.
- Сеть поездов.
- Предсказать.
- Пример набора данных семян.
Эти шаги обеспечат основу, необходимую для реализации алгоритма обратного распространения с нуля и применения его к собственным задачам прогнозного моделирования.
1. Инициализировать сеть
Давайте начнем с чего-то простого, создания новой сети, готовой к обучению.
Каждый нейрон имеет набор весов, которые необходимо поддерживать. Один вес для каждого входного соединения и дополнительный вес для смещения. Нам нужно будет хранить дополнительные свойства для нейрона во время обучения, поэтому мы будем использовать словарь для представления каждого нейрона и сохранять свойства по именам, таким как ‘веса‘Для весов.
Сеть организована в слои. Входной слой на самом деле просто строка из нашего набора обучающих данных Первый настоящий слой — это скрытый слой. Затем следует выходной слой, который имеет один нейрон для каждого значения класса.
Мы организуем слои как массивы словарей и будем рассматривать всю сеть как массив слоев.
Хорошей практикой является инициализация весов сети небольшими случайными числами. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1.
Ниже приведена функция с именемinitialize_network ()это создает новую нейронную сеть, готовую к обучению. Он принимает три параметра: количество входов, количество нейронов в скрытом слое и количество выходов.
Вы можете видеть, что для скрытого слоя мы создаемn_hiddenнейроны и каждый нейрон в скрытом слое имеетn_inputs + 1веса, один для каждого входного столбца в наборе данных и дополнительный для смещения.
Вы также можете видеть, что выходной слой, который подключается к скрытому слою, имеетn_outputsнейроны, каждый сn_hidden + 1веса. Это означает, что каждый нейрон в выходном слое соединяется (имеет вес) с каждым нейроном в скрытом слое.
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return networkДавайте проверим эту функцию. Ниже приведен полный пример, который создает небольшую сеть.
from random import seed
from random import random
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
seed(1)
network = initialize_network(2, 1, 2)
for layer in network:
print(layer)Запустив пример, вы можете увидеть, что код распечатывает каждый слой по одному. Вы можете видеть, что скрытый слой имеет один нейрон с 2 входными весами плюс смещение. Выходной слой имеет 2 нейрона, каждый с 1 весом плюс смещение.
[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}]
[{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]Теперь, когда мы знаем, как создать и инициализировать сеть, давайте посмотрим, как мы можем использовать ее для вычисления результата.
2. Вперед Распространение
Мы можем вычислить выход из нейронной сети, распространяя входной сигнал через каждый уровень, пока выходной уровень не выведет свои значения.
Мы называем это продвижением вперед.
Это метод, который нам понадобится для генерации прогнозов во время обучения, который необходимо будет исправить, и это метод, который нам понадобится после обучения сети для прогнозирования новых данных.
Мы можем разбить распространение вперед на три части:
- Активация нейронов.
- Передача нейронов.
- Вперед Распространение.
2.1. Активация нейронов
Первым шагом является вычисление активации одного нейрона с учетом входных данных.
Входными данными может быть строка из нашего обучающего набора данных, как в случае со скрытым слоем. Это также могут быть выходы от каждого нейрона в скрытом слое, в случае выходного слоя.
Активация нейрона рассчитывается как взвешенная сумма входов. Очень похоже на линейную регрессию.
activation = sum(weight_i * input_i) + biasкудавесвес сети,входявляется входом,яэто индекс веса или ввода исмещениеэто специальный вес, который не имеет входных данных для умножения (или вы можете думать, что входные данные всегда равны 1,0).
Ниже приведена реализация этого в функции с именемактивировать (), Вы можете видеть, что функция предполагает, что смещение является последним весом в списке весов. Это помогает здесь и позже сделать код легче для чтения.
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activationТеперь давайте посмотрим, как использовать активацию нейронов.
2.2. Нейрон Трансфер
Как только нейрон активирован, нам нужно перенести активацию, чтобы увидеть, что на самом деле представляет собой выход нейрона.
Различные передаточные функции могут быть использованы. Традиционно использовать функция активации сигмовидной кишки, но вы также можете использовать танх (тангенс гиперболический) функция для передачи выходов. Совсем недавно передаточная функция выпрямителя был популярен в крупных сетях глубокого обучения.
Функция активации сигмоида выглядит как S-образная форма, ее также называют логистической функцией. Он может принимать любое входное значение и производить число от 0 до 1 на S-кривой. Это также функция, из которой мы можем легко рассчитать производную (наклон), которая понадобится нам позже при ошибке обратного распространения.
Мы можем передать функцию активации с помощью функции сигмоида следующим образом:
output = 1 / (1 + e^(-activation))кудаеявляется основанием натуральных логарифмов (Номер Эйлера).
Ниже приведена функция с именемперечислить()который реализует сигмовидное уравнение.
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))Теперь, когда у нас есть кусочки, давайте посмотрим, как они используются.
2,3. Прямое распространение
Вперед, распространение входных данных просто.
Мы работаем через каждый слой нашей сети, вычисляя выходы для каждого нейрона. Все выходы из одного слоя становятся входами для нейронов на следующем слое.
Ниже приведена функция с именемforward_propagate ()это реализует прямое распространение для ряда данных из нашего набора данных с нашей нейронной сетью.
Вы можете видеть, что выходное значение нейрона хранится в нейроне с именем ‘выход«. Вы также можете увидеть, что мы собираем выходные данные для слоя в массиве с именемnew_inputsэто становится массивомвходныеи используется в качестве входных данных для следующего слоя.
Функция возвращает выходные данные из последнего слоя, также называемого выходным слоем.
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputsДавайте соединим все эти части и протестируем прямое распространение нашей сети.
Мы определяем нашу сеть, встроенную одним скрытым нейроном, который ожидает 2 входных значения, и выходной слой с двумя нейронами.
from math import exp
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# test forward propagation
network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
[{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]]
row = [1, 0, None]
output = forward_propagate(network, row)
print(output)Выполнение примера распространяет входной шаблон [1, 0] и выдает выходное значение, которое печатается. Поскольку выходной слой имеет два нейрона, мы получаем список из двух чисел в качестве вывода.
Фактические выходные значения на данный момент просто бессмыслица, но затем мы начнем изучать, как сделать веса в нейронах более полезными.
[0.6629970129852887, 0.7253160725279748]3. Ошибка обратного распространения
Алгоритм обратного распространения назван по способу обучения весов.
Ошибка рассчитывается между ожидаемыми выходами и выходами, передаваемыми по сети. Эти ошибки затем распространяются в обратном направлении через сеть от выходного уровня к скрытому слою, назначая вину за ошибку и обновляя веса по мере их появления.
Математика для ошибки обратного распространения коренится в исчислении, но мы останемся на высоком уровне в этом разделе и сосредоточимся на том, что рассчитывается и как, а не почему расчеты принимают эту конкретную форму.
Эта часть разбита на две части.
- Передача Производная.
- Ошибка обратного распространения.
3.1. Производная передача
Учитывая выходное значение от нейрона, нам нужно вычислить его наклон.
Мы используем передаточную функцию сигмоида, производную которой можно рассчитать следующим образом:
derivative = output * (1.0 - output)Ниже приведена функция с именемtransfer_derivative ()который реализует это уравнение.
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)Теперь посмотрим, как это можно использовать.
3.2. Ошибка обратного распространения
Первым шагом является вычисление ошибки для каждого выходного нейрона, это даст нам наш сигнал ошибки (вход) для распространения в обратном направлении по сети.
Ошибка для данного нейрона может быть рассчитана следующим образом:
error = (expected - output) * transfer_derivative(output)кудаожидаемыйявляется ожидаемым выходным значением для нейрона,выходэто выходное значение для нейрона иtransfer_derivative ()вычисляет наклон выходного значения нейрона, как показано выше.
Этот расчет ошибки используется для нейронов в выходном слое. Ожидаемое значение — это само значение класса. В скрытом слое все немного сложнее.
Сигнал ошибки для нейрона в скрытом слое рассчитывается как взвешенная ошибка каждого нейрона в выходном слое. Подумайте об ошибке, связанной с перемещением весов выходного слоя к нейронам в скрытом слое.
Обратно распространяющийся сигнал ошибки накапливается и затем используется для определения ошибки для нейрона в скрытом слое следующим образом:
error = (weight_k * error_j) * transfer_derivative(output)кудаerror_jэто сигнал ошибки отJй нейрон в выходном слое,weight_kэто вес, который соединяетКТретий нейрон к текущему нейрону и выход — это выход для текущего нейрона.
Ниже приведена функция с именемbackward_propagate_error ()который реализует эту процедуру.
Вы можете видеть, что сигнал ошибки, рассчитанный для каждого нейрона, хранится с именем «delta». Вы можете видеть, что слои сети перебираются в обратном порядке, начиная с выхода и работая в обратном направлении. Это гарантирует, что нейроны в выходном слое сначала рассчитывают значения «дельта», которые нейроны в скрытом слое могут использовать в последующей итерации. Я выбрал имя «дельта», чтобы отразить изменение, которое ошибка вносит в нейрон (например, дельта веса).
Вы можете видеть, что сигнал ошибки для нейронов в скрытом слое накапливается от нейронов в выходном слое, где скрыт номер нейронаJтакже индекс веса нейрона в выходном слоенейрон [грузики ‘] [J],
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])Давайте соберем все части вместе и посмотрим, как это работает.
Мы определяем фиксированную нейронную сеть с выходными значениями и распространяем ожидаемый выходной шаблон. Полный пример приведен ниже.
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# test backpropagation of error
network = [[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
[{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095]}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763]}]]
expected = [0, 1]
backward_propagate_error(network, expected)
for layer in network:
print(layer)При выполнении примера печатается сеть после обратного распространения ошибки. Вы можете видеть, что значения ошибок рассчитываются и сохраняются в нейронах для выходного слоя и скрытого слоя.
[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614], 'delta': -0.0005348048046610517}]
[{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095], 'delta': -0.14619064683582808}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763], 'delta': 0.0771723774346327}]Теперь давайте использовать обратное распространение ошибки для обучения сети.
4. Сеть поездов
Сеть обучается с использованием стохастического градиентного спуска.
Это включает в себя несколько итераций представления обучающего набора данных в сеть и для каждой строки данных, передавая входные данные, распространяя ошибку в обратном направлении и обновляя веса сети.
Эта часть разбита на две части:
- Обновление весов.
- Сеть поездов.
4.1. Обновление весов
Как только ошибки рассчитаны для каждого нейрона в сети с помощью метода обратного распространения, описанного выше, их можно использовать для обновления весов.
Веса сети обновляются следующим образом:
weight = weight + learning_rate * error * inputкудавесзаданный вес,learning_rateэто параметр, который вы должны указать,ошибкаошибка, рассчитанная по процедуре обратного распространения для нейрона ивходэто входное значение, вызвавшее ошибку
Та же процедура может использоваться для обновления веса смещения, за исключением того, что нет входного термина или входное значение является фиксированным значением 1,0.
Скорость обучения определяет, насколько изменить вес, чтобы исправить ошибку. Например, значение 0,1 обновит вес на 10% от суммы, которую он мог бы обновить. Предпочтительными являются малые скорости обучения, которые вызывают более медленное обучение в течение большого количества итераций обучения. Это увеличивает вероятность того, что сеть найдет хороший набор весов на всех уровнях, а не самый быстрый набор весов, которые минимизируют ошибку (так называемая преждевременная сходимость).
Ниже приведена функция с именемupdate_weights ()который обновляет весовые коэффициенты для сети с учетом входной строки данных, скорости обучения и предполагает, что прямое и обратное распространение уже выполнено.
Помните, что вход для выходного слоя представляет собой набор выходов из скрытого слоя.
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']Теперь мы знаем, как обновить вес сети, давайте посмотрим, как мы можем сделать это многократно.
4.2. Сеть поездов
Как уже упоминалось, сеть обновляется с использованием стохастического градиентного спуска.
Это включает в себя первый цикл для фиксированного числа эпох и в каждой эпохе обновление сети для каждой строки в наборе обучающих данных.
Поскольку обновления производятся для каждого шаблона обучения, этот тип обучения называется онлайн-обучением. Если ошибки были накоплены за период до обновления весов, это называется периодическим обучением или пакетным градиентным спуском.
Ниже приведена функция, которая реализует обучение уже инициализированной нейронной сети с заданным набором обучающих данных, скоростью обучения, фиксированным числом эпох и ожидаемым количеством выходных значений.
Ожидаемое количество выходных значений используется для преобразования значений класса в обучающих данных в одно горячее кодирование. Это двоичный вектор с одним столбцом для каждого значения класса, чтобы соответствовать выходу сети. Это необходимо для расчета ошибки для выходного слоя.
Вы также можете видеть, что ошибка квадрата суммы между ожидаемым выходом и выходом сети накапливается каждую эпоху и печатается. Это полезно для отслеживания того, насколько сеть изучает и совершенствует каждую эпоху.
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
sum_error = 0
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))Теперь у нас есть все для обучения сети. Мы можем собрать пример, который включает в себя все, что мы видели до сих пор, включая инициализацию сети и обучение сети на небольшом наборе данных.
Ниже приведен небольшой надуманный набор данных, который мы можем использовать для тестирования нашей нейронной сети.
X1 X2 Y
2.7810836 2.550537003 0
1.465489372 2.362125076 0
3.396561688 4.400293529 0
1.38807019 1.850220317 0
3.06407232 3.005305973 0
7.627531214 2.759262235 1
5.332441248 2.088626775 1
6.922596716 1.77106367 1
8.675418651 -0.242068655 1
7.673756466 3.508563011 1Ниже приведен полный пример. Мы будем использовать 2 нейрона в скрытом слое. Это проблема двоичной классификации (2 класса), поэтому в выходном слое будет два нейрона. Сеть будет обучаться в течение 20 эпох со скоростью обучения 0,5, что является высоким показателем, потому что мы готовим так мало итераций.
from math import exp
from random import seed
from random import random
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
sum_error = 0
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))
# Test training backprop algorithm
seed(1)
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
n_inputs = len(dataset[0]) - 1
n_outputs = len(set([row[-1] for row in dataset]))
network = initialize_network(n_inputs, 2, n_outputs)
train_network(network, dataset, 0.5, 20, n_outputs)
for layer in network:
print(layer)При запуске примера сначала выводится ошибка квадрата суммы в каждую эпоху обучения. Мы можем видеть тенденцию уменьшения этой ошибки с каждой эпохой.
После обучения распечатывается сеть с отображением изученных весов. Также все еще в сети находятся выходные и дельта-значения, которые можно игнорировать. Мы могли бы обновить нашу функцию обучения, чтобы удалить эти данные, если мы хотим.
>epoch=0, lrate=0.500, error=6.350
>epoch=1, lrate=0.500, error=5.531
>epoch=2, lrate=0.500, error=5.221
>epoch=3, lrate=0.500, error=4.951
>epoch=4, lrate=0.500, error=4.519
>epoch=5, lrate=0.500, error=4.173
>epoch=6, lrate=0.500, error=3.835
>epoch=7, lrate=0.500, error=3.506
>epoch=8, lrate=0.500, error=3.192
>epoch=9, lrate=0.500, error=2.898
>epoch=10, lrate=0.500, error=2.626
>epoch=11, lrate=0.500, error=2.377
>epoch=12, lrate=0.500, error=2.153
>epoch=13, lrate=0.500, error=1.953
>epoch=14, lrate=0.500, error=1.774
>epoch=15, lrate=0.500, error=1.614
>epoch=16, lrate=0.500, error=1.472
>epoch=17, lrate=0.500, error=1.346
>epoch=18, lrate=0.500, error=1.233
>epoch=19, lrate=0.500, error=1.132
[{'weights': [-1.4688375095432327, 1.850887325439514, 1.0858178629550297], 'output': 0.029980305604426185, 'delta': -0.0059546604162323625}, {'weights': [0.37711098142462157, -0.0625909894552989, 0.2765123702642716], 'output': 0.9456229000211323, 'delta': 0.0026279652850863837}]
[{'weights': [2.515394649397849, -0.3391927502445985, -0.9671565426390275], 'output': 0.23648794202357587, 'delta': -0.04270059278364587}, {'weights': [-2.5584149848484263, 1.0036422106209202, 0.42383086467582715], 'output': 0.7790535202438367, 'delta': 0.03803132596437354}]Как только сеть обучена, мы должны использовать ее для прогнозирования.
5. Предсказать
Делать прогнозы с помощью обученной нейронной сети достаточно просто.
Мы уже видели, как распространять входной шаблон для получения выходного сигнала. Это все, что нам нужно сделать, чтобы сделать прогноз. Мы можем непосредственно использовать выходные значения как вероятность того, что шаблон принадлежит каждому выходному классу.
Возможно, было бы более полезно превратить этот вывод в четкое предсказание класса. Мы можем сделать это, выбрав значение класса с большей вероятностью. Это также называется функция arg max,
Ниже приведена функция с именемпредсказать, ()который реализует эту процедуру. Возвращает индекс в выходных данных сети, который имеет наибольшую вероятность. Предполагается, что значения класса были преобразованы в целые числа, начиная с 0.
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))Мы можем соединить это с нашим кодом выше для входного распространения и с нашим небольшим надуманным набором данных, чтобы проверить предсказания с уже обученной сетью. Пример жестко кодирует сеть, обученную на предыдущем шаге.
Полный пример приведен ниже.
from math import exp
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))
# Test making predictions with the network
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
network = [[{'weights': [-1.482313569067226, 1.8308790073202204, 1.078381922048799]}, {'weights': [0.23244990332399884, 0.3621998343835864, 0.40289821191094327]}],
[{'weights': [2.5001872433501404, 0.7887233511355132, -1.1026649757805829]}, {'weights': [-2.429350576245497, 0.8357651039198697, 1.0699217181280656]}]]
for row in dataset:
prediction = predict(network, row)
print('Expected=%d, Got=%d' % (row[-1], prediction))При выполнении примера выводится ожидаемый результат для каждой записи в наборе обучающих данных, за которым следует четкое предсказание, сделанное сетью.
Это показывает, что сеть достигает 100% точности в этом небольшом наборе данных.
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1Теперь мы готовы применить наш алгоритм обратного распространения к реальному набору данных.
6. Набор данных семян пшеницы
В этом разделе применяется алгоритм обратного распространения к набору данных семян пшеницы.
Первым шагом является загрузка набора данных и преобразование загруженных данных в числа, которые мы можем использовать в нашей нейронной сети. Для этого мы будем использовать вспомогательную функциюload_csv ()загрузить файл,str_column_to_float ()преобразовать строковые числа в числа с плавающей запятой иstr_column_to_int ()преобразовать столбец класса в целочисленные значения.
Входные значения различаются по масштабу и должны быть нормализованы в диапазоне от 0 до 1. Обычно рекомендуется нормализовать входные значения в диапазоне выбранной передаточной функции, в данном случае сигмоидальной функции, которая выводит значения в диапазоне от 0 до 1. .dataset_minmax ()а такжеnormalize_dataset ()вспомогательные функции были использованы для нормализации входных значений.
Мы оценим алгоритм с использованием k-кратной перекрестной проверки с 5-кратным увеличением. Это означает, что 201/5 = 40,2 или 40 записей будут в каждом сгибе. Мы будем использовать вспомогательные функцииevaluate_algorithm ()оценить алгоритм с перекрестной проверкой иaccuracy_metric ()рассчитать точность прогнозов.
Новая функция с именемback_propagation ()был разработан для управления приложением алгоритма Backpropagation, сначала инициализируя сеть, обучая ее на наборе обучающих данных, а затем используя обученную сеть, чтобы делать прогнозы на тестовом наборе данных.
Полный пример приведен ниже.
# Backprop on the Seeds Dataset
from random import seed
from random import randrange
from random import random
from csv import reader
from math import exp
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
stats = [[min(column), max(column)] for column in zip(*dataset)]
return stats
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)-1):
row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for i in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(expected[j] - neuron['output'])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] += l_rate * neuron['delta']
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))
# Backpropagation Algorithm With Stochastic Gradient Descent
def back_propagation(train, test, l_rate, n_epoch, n_hidden):
n_inputs = len(train[0]) - 1
n_outputs = len(set([row[-1] for row in train]))
network = initialize_network(n_inputs, n_hidden, n_outputs)
train_network(network, train, l_rate, n_epoch, n_outputs)
predictions = list()
for row in test:
prediction = predict(network, row)
predictions.append(prediction)
return(predictions)
# Test Backprop on Seeds dataset
seed(1)
# load and prepare data
filename = 'seeds_dataset.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# normalize input variables
minmax = dataset_minmax(dataset)
normalize_dataset(dataset, minmax)
# evaluate algorithm
n_folds = 5
l_rate = 0.3
n_epoch = 500
n_hidden = 5
scores = evaluate_algorithm(dataset, back_propagation, n_folds, l_rate, n_epoch, n_hidden)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))Была построена сеть с 5 нейронами в скрытом слое и 3 нейронами в выходном слое. Сеть была подготовлена для 500 эпох с темпом обучения 0,3. Эти параметры были найдены с небольшой пробой и ошибкой, но вы можете сделать это намного лучше.
При выполнении примера выводится средняя точность классификации для каждого сгиба, а также средняя производительность по всем сгибам.
Вы можете видеть, что обратное распространение и выбранная конфигурация достигли средней точности классификации около 93%, что значительно лучше, чем алгоритм нулевого правила, который немного лучше, чем точность 28%.
Scores: [92.85714285714286, 92.85714285714286, 97.61904761904762, 92.85714285714286, 90.47619047619048]
Mean Accuracy: 93.333%расширения
В этом разделе перечислены расширения к учебнику, которые вы можете изучить.
- Параметры алгоритма настройки, Попробуйте большие или меньшие сети, обученные дольше или короче. Посмотрите, сможете ли вы улучшить производительность набора данных seed.
- Дополнительные методы, Поэкспериментируйте с различными методами инициализации веса (такими как небольшие случайные числа) и различными передаточными функциями (такими как tanh).
- Больше слоев, Добавьте поддержку для большего количества скрытых слоев, обученных так же, как один скрытый слой, используемый в этом руководстве.
- регрессия, Измените сеть так, чтобы в выходном слое был только один нейрон, и чтобы было предсказано реальное значение. Выберите регрессионный набор данных для практики. Линейная передаточная функция может использоваться для нейронов в выходном слое, или выходные значения выбранного набора данных могут быть масштабированы до значений между 0 и 1.
- Пакетный градиентный спуск, Измените процедуру обучения с онлайн на пакетный градиентный спуск и обновляйте веса только в конце каждой эпохи.
Вы пробовали какие-либо из этих расширений?
Поделитесь своим опытом в комментариях ниже.
Обзор
В этом руководстве вы узнали, как реализовать алгоритм обратного распространения с нуля.
В частности, вы узнали:
- Как переслать распространение входа для расчета выхода сети.
- Как обратно распространять ошибки и обновлять вес сети.
- Как применить алгоритм обратного распространения к реальному набору данных.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

