Время на прочтение
8 мин
Количество просмотров 515K
О чём статья
Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Дайте код!
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
l1 = 1/(1+np.exp(-(np.dot(X,syn0))))
l2 = 1/(1+np.exp(-(np.dot(l1,syn1))))
l2_delta = (y - l2)*(l2*(1-l2))
l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))
syn1 += l1.T.dot(l2_delta)
syn0 += X.T.dot(l1_delta)
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
import numpy as np
# Сигмоида
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
# набор входных данных
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
# выходные данные
y = np.array([[0,0,1,1]]).T
# сделаем случайные числа более определёнными
np.random.seed(1)
# инициализируем веса случайным образом со средним 0
syn0 = 2*np.random.random((3,1)) - 1
for iter in xrange(10000):
# прямое распространение
l0 = X
l1 = nonlin(np.dot(l0,syn0))
# насколько мы ошиблись?
l1_error = y - l1
# перемножим это с наклоном сигмоиды
# на основе значений в l1
l1_delta = l1_error * nonlin(l1,True) # !!!
# обновим веса
syn0 += np.dot(l0.T,l1_delta) # !!!
print "Выходные данные после тренировки:"
print l1
Выходные данные после тренировки:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
«*» — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
«-» – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена !!!)
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена !!!)
Разберём код по строчкам
import numpy as np
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
def nonlin(x,deriv=False):
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
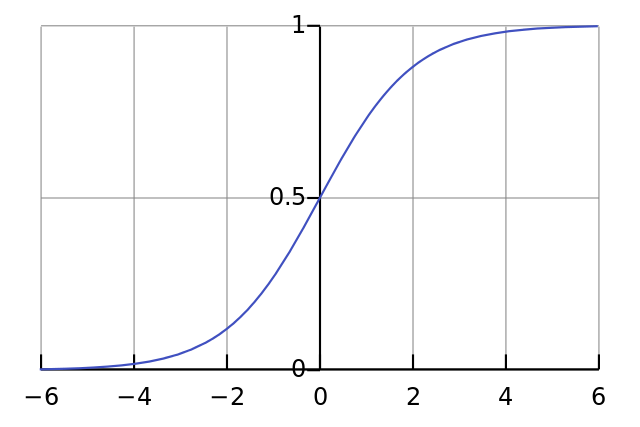
if(deriv==True):
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
X = np.array([ [0,0,1], …
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
y = np.array([[0,0,1,1]]).T
Инициализирует выходные данные. «.T» – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
np.random.seed(1)
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
syn0 = 2*np.random.random((3,1)) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.
for iter in xrange(10000):
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
l0 = X
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
l1 = nonlin(np.dot(l0,syn0))
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
(4 x 3) dot (3 x 1) = (4 x 1)
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.
Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.
l1_error = y - l1
Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.
l1_delta = l1_error * nonlin(l1,True)
А вот и секретный ингредиент. Эту строку нужно разбирать по частям.
Первая часть: производная
nonlin(l1,True)
l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.
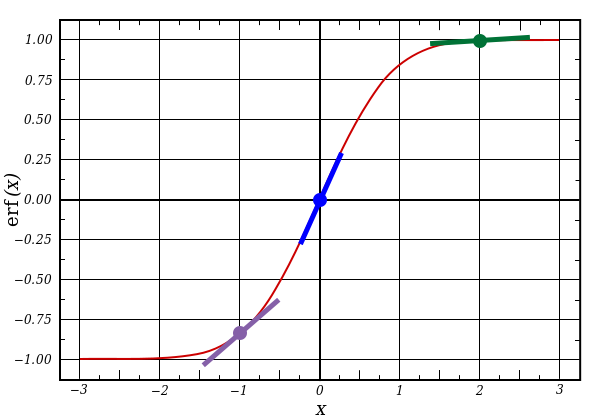
Полное выражение: производная, взвешенная по ошибкам
l1_delta = l1_error * nonlin(l1,True)
Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.
Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.
syn0 += np.dot(l0.T,l1_delta)
Мы готовы к обновлению сети. Рассмотрим один тренировочный пример. В нём мы будем обновлять веса. Обновим крайний левый вес (9.5)
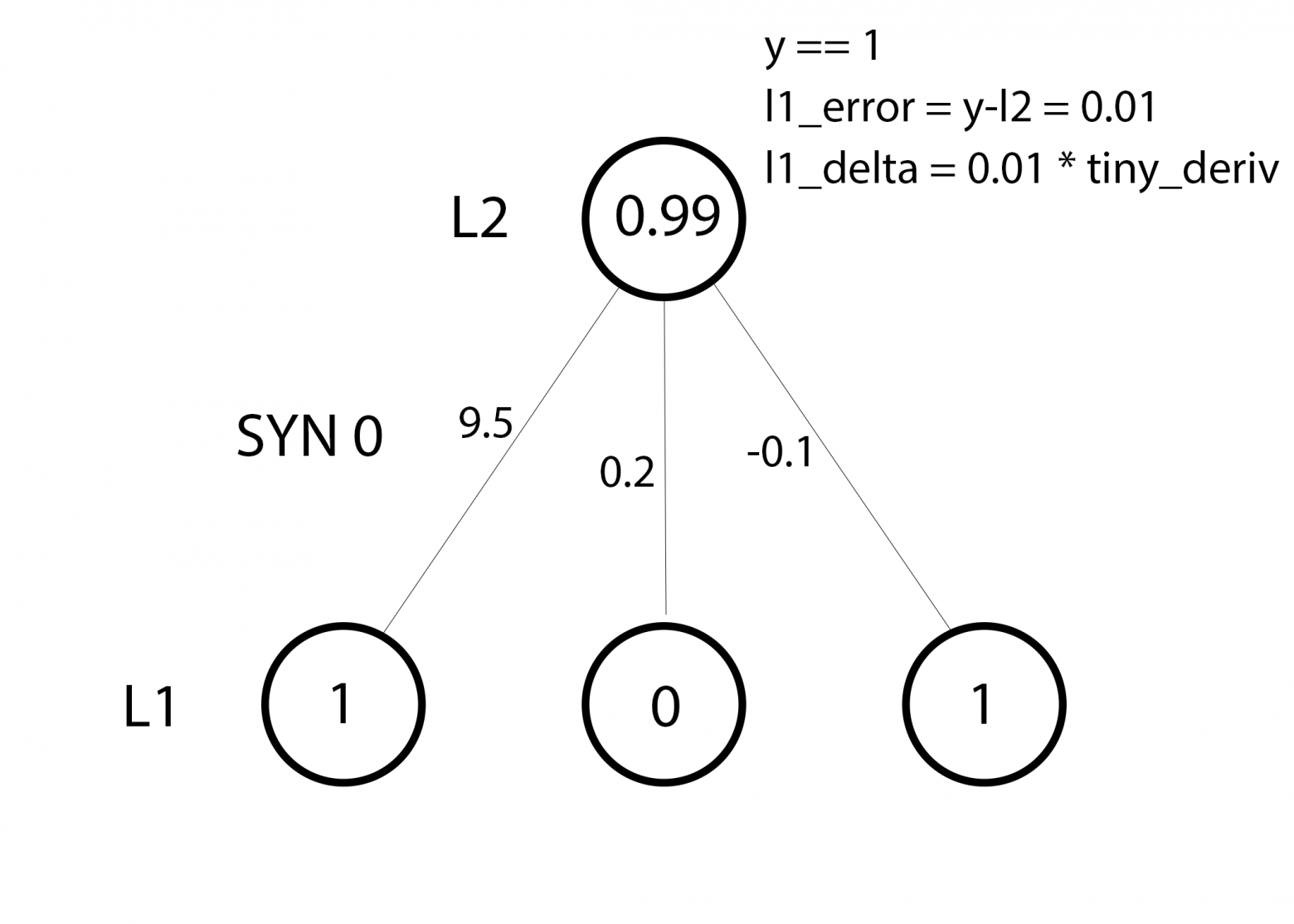
weight_update = input_value * l1_delta
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.
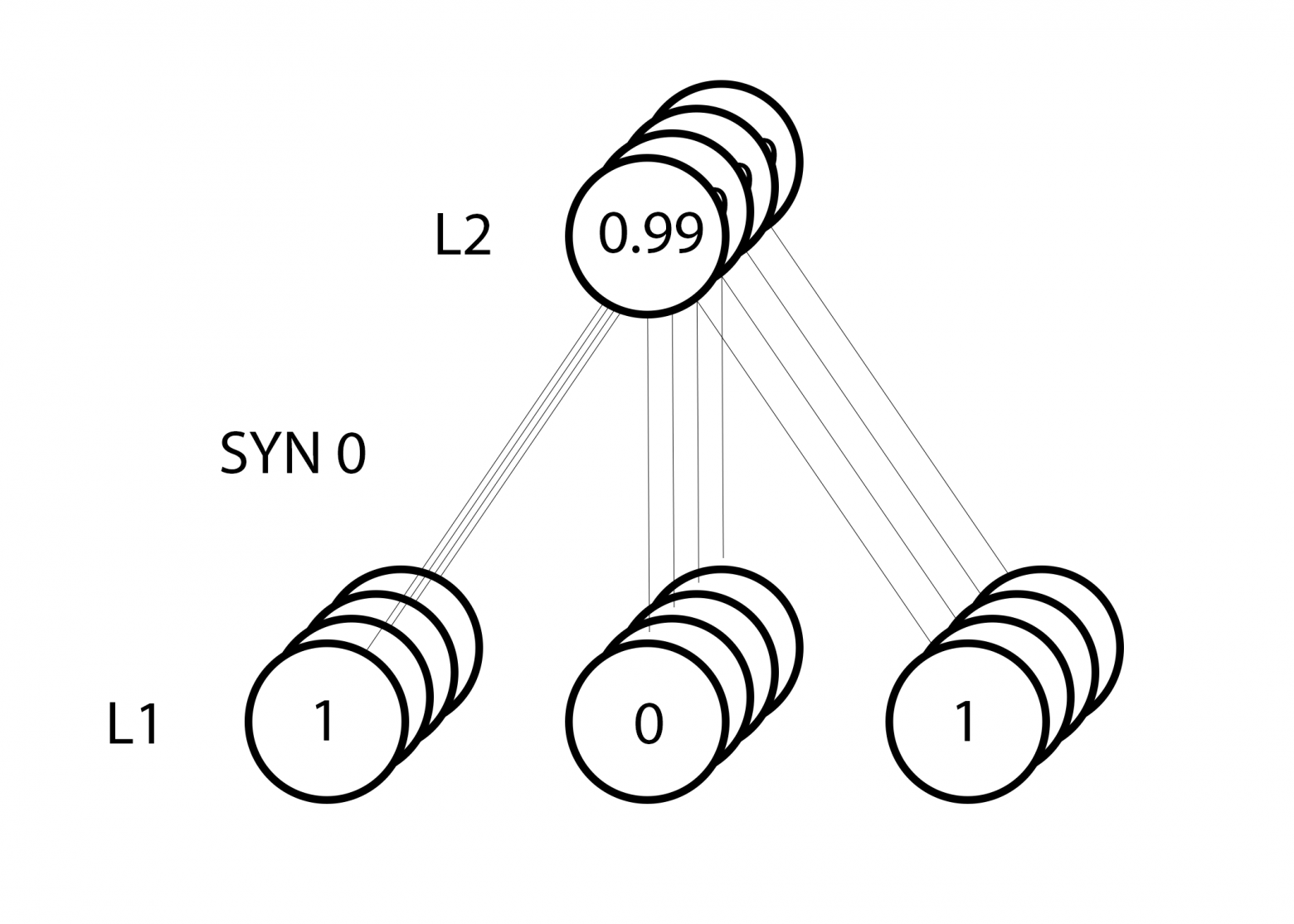
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.
Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.
Часть 2: задачка посложнее
Вход Выход
0 0 1 0
0 1 1 1
1 0 1 1
1 1 1 0
Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.
Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).
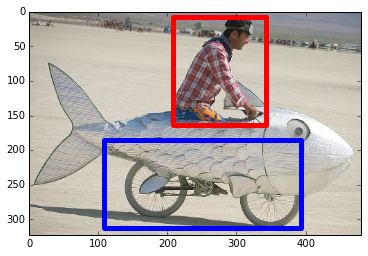

Стратегия
Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.
Вход (l0) Скрытые веса (l1) Выход (l2)
0 0 1 0.1 0.2 0.5 0.2 0
0 1 1 0.2 0.6 0.7 0.1 1
1 0 1 0.3 0.2 0.3 0.9 1
1 1 1 0.2 0.1 0.3 0.8 0
Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.
Нейросеть в три слоя
import numpy as np
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0],
[1],
[1],
[0]])
np.random.seed(1)
# случайно инициализируем веса, в среднем - 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
# проходим вперёд по слоям 0, 1 и 2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# как сильно мы ошиблись относительно нужной величины?
l2_error = y - l2
if (j% 10000) == 0:
print "Error:" + str(np.mean(np.abs(l2_error)))
# в какую сторону нужно двигаться?
# если мы были уверены в предсказании, то сильно менять его не надо
l2_delta = l2_error*nonlin(l2,deriv=True)
# как сильно значения l1 влияют на ошибки в l2?
l1_error = l2_delta.dot(syn1.T)
# в каком направлении нужно двигаться, чтобы прийти к l1?
# если мы были уверены в предсказании, то сильно менять его не надо
l1_delta = l1_error * nonlin(l1,deriv=True)
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
l1_error = l2_delta.dot(syn1.T)
Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Статья публикуется в переводе, автор оригинального текста Victor Zhou.
***
Термин «нейронные сети» сейчас можно услышать из каждого утюга, и многие верят, будто это что-то очень сложное. На самом деле нейронные сети совсем не такие сложные, как может показаться! Мы разберемся, как они работают, реализовав одну сеть с нуля на Python.
Эта статья предназначена для полных новичков, не имеющих никакого опыта в машинном обучении. Поехали!
1. Составные элементы: нейроны
Прежде всего нам придется обсудить нейроны, базовые элементы нейронной сети. Нейрон принимает несколько входов, выполняет над ними кое-какие математические операции, а потом выдает один выход. Вот как выглядит нейрон с двумя входами:
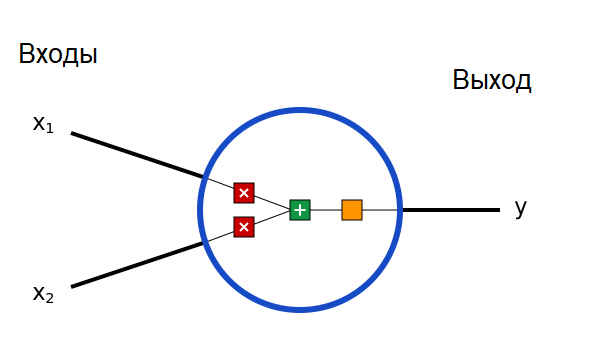
Внутри нейрона происходят три операции. Сначала значения входов умножаются на веса:
Затем взвешенные входы складываются, и к ним прибавляется значение порога b:
Наконец, полученная сумма проходит через функцию активации:
Функция активации преобразует неограниченные значения входов в выход, имеющий ясную и предсказуемую форму. Одна из часто используемых функций активации – сигмоида:
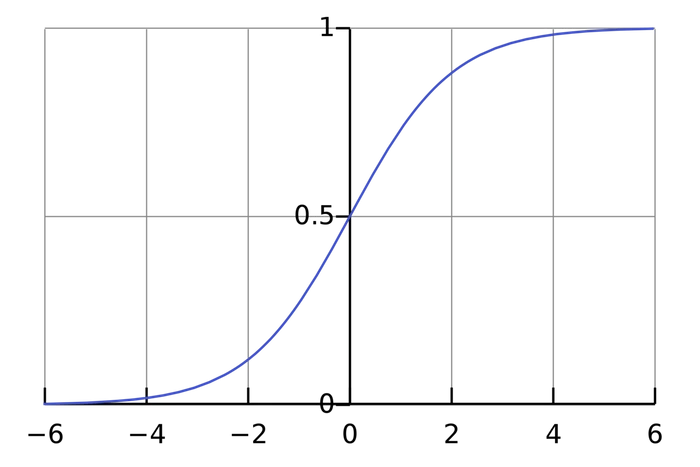
Сигмоида выдает результаты в интервале (0, 1). Можно представить, что она «упаковывает» интервал от минус бесконечности до плюс бесконечности в (0, 1): большие отрицательные числа превращаются в числа, близкие к 0, а большие положительные – к 1.
Простой пример
Допустим, наш двухвходовой нейрон использует сигмоидную функцию активации и имеет следующие параметры:
w=[0, 1] – это всего лишь запись w1=0, w2=1 в векторном виде. Теперь зададим нашему нейрону входные данные: x=[2, 3]. Мы используем скалярное произведение векторов, чтобы записать формулу в сжатом виде:
Наш нейрон выдал 0.999 при входах x=[2, 3]. Вот и все! Процесс передачи значений входов дальше, чтобы получить выход, называется прямой связью (feed forward).
Пишем код для нейрона
Настало время написать свой нейрон! Мы используем NumPy, популярную и мощную расчетную библиотеку для Python, которая поможет нам с вычислениями:
import numpy as np
def sigmoid(x):
# Наша функция активации: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
class Neuron:
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
# Умножаем входы на веса, прибавляем порог, затем используем функцию активации
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4 # b = 4
n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994
Узнаете эти числа? Это тот самый пример, который мы только что рассчитали! И мы получили тот же результат – 0.999.
2. Собираем нейронную сеть из нейронов
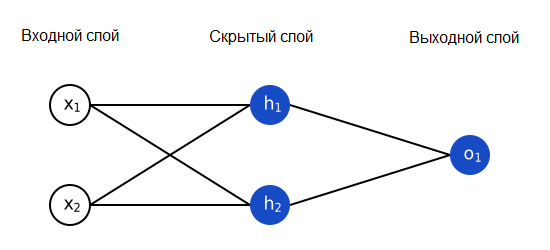
Нейронная сеть – это всего лишь несколько нейронов, соединенных вместе. Вот как может выглядеть простая нейронная сеть:
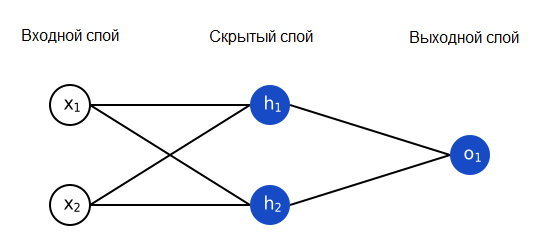
У этой сети два входа, скрытый слой с двумя нейронами (h1 и h2) и выходной слой с одним нейроном (o1). Обратите внимание, что входы для o1 – это выходы из h1 и h2. Именно это создает из нейронов сеть.
Замечание
Скрытый слой – это любой слой между входным (первым) слоем сети и выходным (последним). Скрытых слоев может быть много!
Пример: прямая связь
Давайте используем сеть, изображенную выше, и будем считать, что все нейроны имеют одинаковые веса w=[0, 1], одинаковые пороговые значения b=0, и одинаковую функцию активации – сигмоиду. Пусть h1, h2 и o1 обозначают выходные значения соответствующих нейронов.
Что получится, если мы подадим на вход x=[2, 3]?
Если подать на вход нашей нейронной сети x=[2, 3], на выходе получится 0.7216. Достаточно просто, не правда ли?
Нейронная сеть может иметь любое количество слоев, и в этих слоях может быть любое количество нейронов. Основная идея остается той же: передавайте входные данные по нейронам сети, пока не получите выходные значения. Для простоты мы будем использовать сеть, показанную выше, до конца статьи.
Пишем код нейронной сети
Давайте реализуем прямую связь для нашей нейронной сети. Напомним, как она выглядит:
import numpy as np
# ... вставьте сюда код из предыдущего раздела
class OurNeuralNetwork:
'''
Нейронная сеть с:
- 2 входами
- скрытым слоем с 2 нейронами (h1, h2)
- выходным слоем с 1 нейроном (o1)
Все нейроны имеют одинаковые веса и пороги:
- w = [0, 1]
- b = 0
'''
def __init__(self):
weights = np.array([0, 1])
bias = 0
# Используем класс Neuron из предыдущего раздела
self.h1 = Neuron(weights, bias)
self.h2 = Neuron(weights, bias)
self.o1 = Neuron(weights, bias)
def feedforward(self, x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
# Входы для o1 - это выходы h1 и h2
out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421
Мы снова получили 0.7216! Похоже, наша сеть работает.
3. Обучаем нейронную сеть (часть 1)
Допустим, у нас есть следующие измерения:
| Имя | Вес (в фунтах) | Рост (в дюймах) | Пол |
| Алиса | 133 (54.4 кг) | 65 (165,1 см) | Ж |
| Боб | 160 (65,44 кг) | 72 (183 см) | М |
| Чарли | 152 (62.2 кг) | 70 (178 см) | М |
| Диана | 120 (49 кг) | 60 (152 см) | Ж |
Давайте обучим нашу нейронную сеть предсказывать пол человека по его росту и весу.
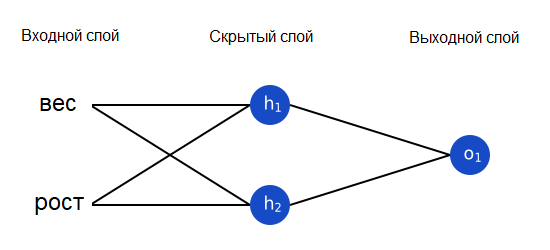
Мы будем представлять мужской пол как 0, женский – как 1, а также сдвинем данные, чтобы их было проще использовать:
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
| Боб | 25 | 6 | 0 |
| Чарли | 17 | 4 | 0 |
| Диана | -15 | -6 | 1 |
Замечание
Я выбрал величину сдвигов (135 и 66), чтобы числа выглядели попроще. Обычно сдвигают на среднее значение.
Потери
Прежде чем обучать нашу нейронную сеть, нам нужно как-то измерить, насколько «хорошо» она работает, чтобы она смогла работать «лучше». Это измерение и есть потери (loss).
Мы используем для расчета потерь среднюю квадратичную ошибку (mean squared error, MSE):
Давайте рассмотрим все используемые переменные:
- n – это количество измерений, в нашем случае 4 (Алиса, Боб, Чарли и Диана).
- y представляет предсказываемое значение, Пол.
- ytrue – истинное значение переменной («правильный ответ»). Например, для Алисы ytrue будет равна 1 (женский пол).
- ypred – предсказанное значение переменной. Это то, что выдаст наша нейронная сеть.
(ytrue-ypred)2 называется квадратичной ошибкой. Наша функция потерь просто берет среднее значение всех квадратичных ошибок – поэтому она и называется средней квадратичной ошибкой. Чем лучшими будут наши предсказания, тем меньшими будут наши потери!
Лучшие предсказания = меньшие потери.
Обучение нейронной сети = минимизация ее потерь.
Пример расчета потерь
Предположим, что наша сеть всегда возвращает 0 – иными словами, она уверена, что все люди мужчины. Насколько велики будут наши потери?
| Имя | ytrue | ypred | (ytrue-ypred)2 |
| Алиса | 1 | 0 | 1 |
| Боб | 0 | 0 | 0 |
| Чарли | 0 | 0 | 0 |
| Диана | 1 | 0 | 1 |
Пишем функцию средней квадратичной ошибки
Вот небольшой кусок кода, который рассчитает наши потери. Если вы не понимаете, почему он работает, прочитайте в руководстве NumPy про операции с массивами.
import numpy as np
def mse_loss(y_true, y_pred):
# y_true и y_pred - массивы numpy одинаковой длины.
return ((y_true - y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5
Отлично. Идем дальше!
4. Обучаем нейронную сеть (часть 2)
Теперь у нас есть четкая цель: минимизировать потери нейронной сети. Мы знаем, что можем изменять веса и пороги нейронов, чтобы изменить ее предсказания, но как нам делать это таким образом, чтобы минимизировать потери?
Внимание: математика!
Этот раздел использует частные производные по нескольким переменным. Если вы плохо знакомы с дифференциальным исчислением, можете просто пропускать математические формулы.
Для простоты давайте представим, что в нашем наборе данных только одна Алиса.
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
Тогда средняя квадратичная ошибка будет квадратичной ошибкой только для Алисы:
Другой метод – это рассматривать функцию потерь как функцию от весов и порогов. Давайте отметим все веса и пороги нашей нейронной сети:
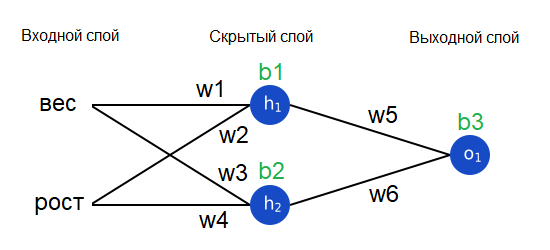
Теперь мы можем записать функцию потерь как функцию от нескольких переменных:
Предположим, мы хотим отрегулировать w1. Как изменится значение потери L при изменении w1? На этот вопрос может ответить частная производная dL/dw1. Как мы ее рассчитаем?
Не падайте духом!
Здесь математика становится более сложной. Возьмите бумагу и ручку, чтобы не отставать – это поможет вам понять, что происходит.
Прежде всего, давайте перепишем эту частную производную через dypred/dw1, воспользовавшись цепным правилом:
Мы можем рассчитать dL/dypred, поскольку мы уже выяснили выше, что L=(1-ypred)2:
Теперь давайте решим, что делать с dypred/dw1. Обозначая выходы нейронов, как прежде, h1, h2 и o1, получаем:
Вспомните, что f() – это наша функция активации, сигмоида. Поскольку w1 влияет только на h1 (но не на h2), мы можем снова использовать цепное правило и записать:
Мы можем сделать то же самое для dh1/dw1, снова применяя цепное правило:
В этой формуле x1 – это вес, а x2 – рост. Вот уже второй раз мы встречаем f'(x) – производную сигмоидной функции! Давайте вычислим ее:
Мы используем эту красивую форму для f'(x) позже. На этом мы закончили! Мы сумели разложить dL/dw1 на несколько частей, которые мы можем рассчитать:
Такой метод расчета частных производных «от конца к началу» называется методом обратного распространения (backpropagation).
Уффф. Здесь было очень много символов, так что не страшно, если вы пока не все понимаете. Давайте покажем, как это работает, на практическом примере!
Пример. Считаем частную производную
Мы по-прежнему считаем, что наш набор данных состоит из одной Алисы:
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
Давайте инициализируем все веса как 1, а все пороги как 0. Если мы выполним прямой проход по нейронной сети, то получим:
Наша сеть выдает ypred=0.524, что находится примерно на полпути между Мужским полом (0) и Женским (1). Давайте рассчитаем dL/dw1:
Напоминаем:
Ранее мы получили формулу для производной сигмоиды f'(x)=f(x)(1-f(x))
Вот и все! Результат говорит нам, что при увеличении w1, функция ошибки чуть-чуть повышается.
Обучение: стохастический градиентный спуск
Теперь у нас есть все нужные инструменты для обучения нейронной сети! Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (stochastic gradient descent), который определит, как мы будем изменять наши веса и пороги для минимизации потерь. Фактически, он заключается в следующей формуле обновления:
Скорость обучения определяет, как быстро наша сеть учится. Все, что мы делаем – это вычитаем eta*dL/dw1 из w1:
- Если dL/dw1 положительна, w1 уменьшится, что уменьшит L.
- Если dL/dw1 отрицательна, w1 увеличится, что также уменьшит L.
Если мы сделаем то же самое для каждого веса и порога в сети, потери будут постепенно уменьшаться, и наша сеть будет выдавать более точные результаты.
Процесс обучения сети будет выглядеть примерно так:
- Выбираем одно наблюдение из набора данных. Именно то, что мы работаем только с одним наблюдением, делает наш градиентный спуск стохастическим.
- Считаем все частные производные функции потерь по всем весам и порогам (dL/dw1, dL/dw2 и т.д.)
- Используем формулу обновления, чтобы обновить значения каждого веса и порога.
- Снова переходим к шагу 1.
Пишем код всей нейронной сети
Наконец настало время реализовать всю нейронную сеть.
| Имя | Вес (минус 135) | Рост (минус 66) | Пол |
| Алиса | -2 | -1 | 1 |
| Боб | 25 | 6 | 0 |
| Чарли | 17 | 4 | 0 |
| Диана | -15 | -6 |
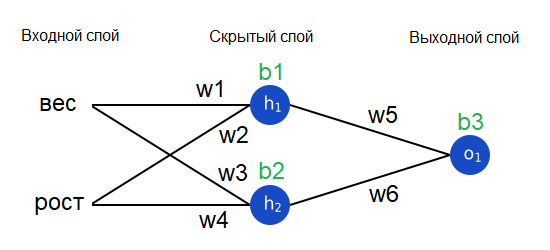
import numpy as np
def sigmoid(x):
# Сигмоидная функция активации: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Производная сигмоиды: f'(x) = f(x) * (1 - f(x))
fx = sigmoid(x)
return fx * (1 - fx)
def mse_loss(y_true, y_pred):
# y_true и y_pred - массивы numpy одинаковой длины.
return ((y_true - y_pred) ** 2).mean()
class OurNeuralNetwork:
'''
Нейронная сеть с:
- 2 входами
- скрытым слоем с 2 нейронами (h1, h2)
- выходной слой с 1 нейроном (o1)
*** DISCLAIMER ***:
Следующий код простой и обучающий, но НЕ оптимальный.
Код реальных нейронных сетей совсем на него не похож. НЕ копируйте его!
Изучайте и запускайте его, чтобы понять, как работает эта нейронная сеть.
'''
def __init__(self):
# Веса
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# Пороги
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self, x):
# x is a numpy array with 2 elements.
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
'''
- data - массив numpy (n x 2) numpy, n = к-во наблюдений в наборе.
- all_y_trues - массив numpy с n элементами.
Элементы all_y_trues соответствуют наблюдениям в data.
'''
learn_rate = 0.1
epochs = 1000 # сколько раз пройти по всему набору данных
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# --- Прямой проход (эти значения нам понадобятся позже)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# --- Считаем частные производные.
# --- Имена: d_L_d_w1 = "частная производная L по w1"
d_L_d_ypred = -2 * (y_true - y_pred)
# Нейрон o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Нейрон h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Нейрон h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# --- Обновляем веса и пороги
# Нейрон h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Нейрон h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# Нейрон o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# --- Считаем полные потери в конце каждой эпохи
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f" % (epoch, loss))
# Определим набор данных
data = np.array([
[-2, -1], # Алиса
[25, 6], # Боб
[17, 4], # Чарли
[-15, -6], # Диана
])
all_y_trues = np.array([
1, # Алиса
0, # Боб
0, # Чарли
1, # Диана
])
# Обучаем нашу нейронную сеть!
network = OurNeuralNetwork()
network.train(data, all_y_trues)
По мере обучения сети ее потери постепенно уменьшаются:
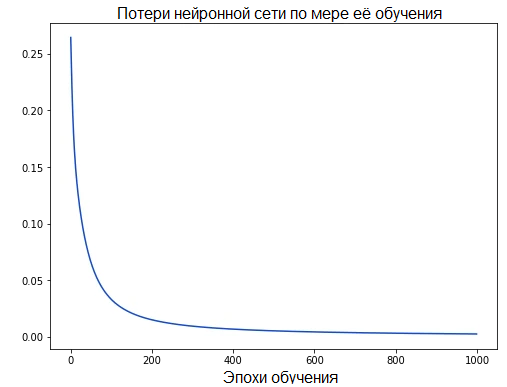
Теперь мы можем использовать нашу сеть для предсказания пола:
# Делаем пару предсказаний
emily = np.array([-7, -3]) # 128 фунтов (52.35 кг), 63 дюйма (160 см)
frank = np.array([20, 2]) # 155 pounds (63.4 кг), 68 inches (173 см)
print("Эмили: %.3f" % network.feedforward(emily)) # 0.951 - Ж
print("Фрэнк: %.3f" % network.feedforward(frank)) # 0.039 - М
Что теперь?
Вы сделали это! Давайте перечислим все, что мы с вами сделали:
- Определили нейроны, составные элементы нейронных сетей.
- Использовали сигмоидную функцию активации для наших нейронов.
- Увидели, что нейронные сети – это всего лишь несколько нейронов, соединенных друг с другом.
- Создали набор данных, в котором Вес и Рост были входными данными (или признаками), а Пол – выходным (или меткой).
- Узнали о функции потерь и средней квадратичной ошибке (MSE).
- Поняли, что обучение нейронной сети – это всего лишь минимизация ее потерь.
- Использовали метод обратного распространения (backpropagation) для расчета частных производных.
- Использовали стохастический градиентный спуск (SGD) для обучения нашей сети.
Перед вами – множество путей, на которых вас ждет масса нового и интересного:
- Экспериментируйте с большими и лучшими нейронными сетями, используя подходящие библиотеки вроде Tensorflow, Keras и PyTorch.
- Создайте свою первую нейронную сеть с помощью Keras.
- Прочитайте остальные статьи из серии «Нейронные сети с нуля».
- Исследуйте другие функции активации, кроме сигмоиды, например, Softmax.
- Исследуйте другие оптимизаторы, кроме стохастического градиентного спуска.
Спасибо за внимание!
***
На Python создают прикладные приложения, пишут тесты и бэкенд веб-приложений, автоматизируют задачи в системном администрировании, его используют в нейронных сетях и анализе больших данных. Язык можно изучить самостоятельно, но на это придется потратить немало времени. Если вы хотите быстро понять основы программирования на Python, обратите внимание на онлайн-курс «Библиотеки программиста». За 30 уроков (15 теоретических и 15 практических занятий) под руководством практикующих экспертов вы не только изучите основы синтаксиса, но и освоите две интегрированные среды разработки (PyCharm и Jupyter Notebook), работу со словарями, парсинг веб-страниц, создание ботов для Telegram и Instagram, тестирование кода и даже анализ данных. Чтобы процесс обучения стал более интересным и комфортным, студенты получат от нас обратную связь. Кураторы и преподаватели курса ответят на все вопросы по теме лекций и практических занятий.
Практическая работа №1: Реализация метода обратного распространения ошибки для двухслойной полностью связанной нейронной сети
Задача
Требуется вывести расчетные формулы и спроектировать программную реализацию метода обратного распространения ошибки для двухслойной полносвязной нейронной сети. Обучение и тестирование сети происходит на наборе данных MNIST, функция активации скрытого слоя – relu, функция активации выходного слоя – softmax, функция ошибки – кросс-энтропия.
Математическая модель
Модель нейрона описывается следующими уравнениями:
где – входной сигнал,
– синаптический вес сигнала
,
– функция активации,
– смещение
Прямой ход
Для получения предсказания сети, производится прямой ход: для каждого нейрона последовательно, от начальных слоёв к конечным, вычисляется линейная активация входных сигналов, к ней применяется функция активации, после чего этот сигнал передаётся на следующий слой. В случае данной архитектуры:
где – выход скрытого слоя,
– функция активации скрытого слоя (relu),
– вход сети,
– выход сети,
– функция активации выходного слоя (softmax),
Метод обратного распространения ошибки
Метод обратного распространения ошибки определяет стратегию выбора весов сети 𝑤 с использованием градиентных методов оптимизации.
Схема обратного распространения ошибки состоит из следующих этапов:
-
Прямой проход по нейронной сети. На данном этапе вычисляются значения выходных сигналов каждого слоя, а так же производные их функций активации.
-
Вычисление значений целевой функции и её производной.
Целевая функция – кросс-энтропия, вычисляется как
где
– ожидаемый выход (метки)
Производную целевой функции по весам можно вывести следующим образом:
По весам второго слоя:
из условия
получаем
По весам первого слоя
-
Обратный проход нейронной сети и корректировка весов
-
Повторение этапов 1-3 до выполнения условия останова
Описание программной реализации
Network.py
Содержит реализацию нейронной сети
Класс NN содержит данные и методы для работы с сетью
Поля класса NN:
_input_size – размер входного слоя
_hidden_size – размер скрытого слоя
_output_size – размер выходного слоя
_w1, _b1 – массивы для хранения весов и смещений первого слоя
_w2, _b2 – массивы для хранения весов и смещений второго слоя
Методы класса NN:
_forward(input) – прямой проход сети. Возвращает выходной сигнал первого и второго слоя
_calculate_dE(input, label, output1, output2) – вычисление градиента функции ошибки. Возвращает градиент функции по весам и биасам первого и второго слоёв
_backprop(learning_rate, size, dEb1, dEb2) – корректировка весов сети при помощи посчитанных градиентов
init_weights() – инициализация весов нормальным распределением с дисперсией 1/10
fit(input, label, validate_data = None, batch_size = 100, learning_rate = 0.1, epochs = 100) – пакетное обучение сети на epochs эпохах, скоростью обучения learning_rate, размером пакета batch_size. Выводит точность и значение целевой функции на каждой эпохе
predict(input) – получение предсказания сети
utils.py:
Содержит вспомогательные функции.
relu(X) – функция relu
reluD(X) – производная функции relu
calcilate_E(predict, label) – подсчёт функции ошибки на основании предсказания сети и верной разметки
calculate_acc(prediction ,label) – посчёт точности на основании предсказания сети и верной разметки
main.py
Обучает сеть из класса NN на MNIST с параметрами из аргументов запуска. Измеряет время обучения.
Аргументы:
-
—hidden – количество нейронов в скрытом слое
-
—epochs – количество эпох обучения
-
—lr – скорость обучения
-
—batch – размер пакета
Как вызывать:
python main.py --hidden 30 --epochs 20 --lr 0,1 --batch 100
(в примере указаны параметры по умолчанию)
Эксперименты
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9729 train error: 0.0913
validate accuracy: 0.9613 validate error: 0.1238
Time: 28.309726 seconds
Размер скрытого слоя: 10, эпох: 20, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9469 train error: 0.1805
validate accuracy: 0.9404 validate error: 0.2013
Time: 18.23942 seconds
Размер скрытого слоя: 10, эпох: 20, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9874 train error: 0.0467
validate accuracy: 0.9721 validate error: 0.0878
Time: 58.233283 seconds
Размер скрытого слоя: 30, эпох: 50, скорость обучения: 0,1, размер пакета: 100
train accuracy: 0.9875 train error: 0.0418
validate accuracy: 0.9678 validate error: 0.1216
Time: 70.004101 seconds
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,5, размер пакета: 100
train accuracy: 0.9766 train error: 0.0732
validate accuracy: 0.9622 validate error: 0.1614
Time: 26.213141 seconds
Размер скрытого слоя: 30, эпох: 30, скорость обучения: 0,05, размер пакета: 100
train accuracy: 0.971 train error: 0.0998
validate accuracy: 0.9625 validate error: 0.1225
Time: 40.577051 seconds
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,1, размер пакета: 10
train accuracy: 0.9724 train error: 0.0928
validate accuracy: 0.9533 validate error: 0.2423
Time: 65.179444 seconds
Размер скрытого слоя: 30, эпох: 20, скорость обучения: 0,1, размер пакета: 1000
train accuracy: 0.9268 train error: 0.2588
validate accuracy: 0.9264 validate error: 0.2576
Time: 25.455479 seconds
На предыдущих
занятиях мы с вами рассматривали НС с выбранными весами, либо устанавливали их,
исходя из определенных математических соображений. Это можно сделать, когда
сеть относительно небольшая. Но при увеличении числа нейронов и связей, ручной
подбор становится попросту невозможным и возникает задача нахождения весовых
коэффициентов связей НС. Этот процесс и называют обучением нейронной сети.
Один из
распространенных подходов к обучению заключается в последовательном
предъявлении НС векторов наблюдений и последующей корректировки весовых
коэффициентов так, чтобы выходное значение совпадало с требуемым:
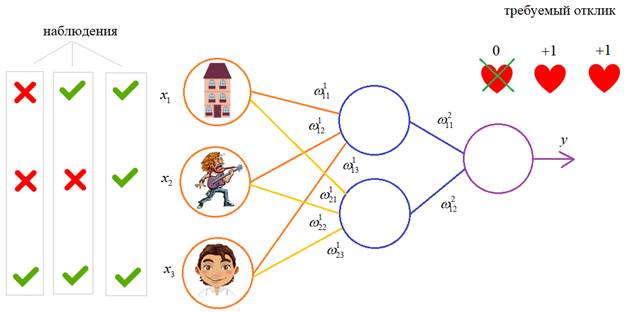
Это называется обучение
с учителем, так как для каждого вектора мы знаем нужный ответ и именно его
требуем от нашей НС.
Теперь, главный
вопрос: как построить алгоритм, который бы наилучшим образом находил весовые
коэффициенты. Наилучший – это значит, максимально быстро и с максимально
близкими выходными значениями для требуемых откликов. В общем случае эта задача
не решена. Нет универсального алгоритма обучения. Поэтому, лучшее, что мы можем
сделать – это выбрать тот алгоритм, который хорошо себя зарекомендовал в
прошлом. Основной «рабочей лошадкой» здесь является алгоритм back propagation (обратного
распространения ошибки), который, в свою очередь, базируется на алгоритме градиентного
спуска.
Сначала, я думал
рассказать о нем со всеми математическими выкладками, но потом решил этого не
делать, а просто показать принцип работы и рассмотреть реализацию конкретного
примера на Python.
Чтобы все лучше
понять, предположим, что у нас имеется вот такая полносвязная НС прямого
распространения с весами связей, выбранными произвольным образом в диапазоне от
[-0.5; 0,5]. Здесь верхний индекс показывает принадлежность к тому или иному слою
сети. Также, каждый нейрон имеет некоторую активационную функцию ![]() :
:
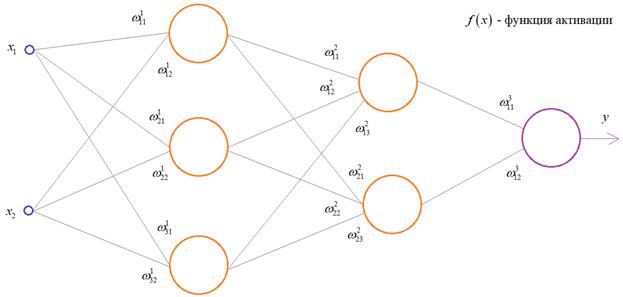
На первом шаге
делается прямой проход по сети. Мы пропускаем вектор наблюдения ![]() через
через
эту сеть, и запоминаем все выходные значения нейронов скрытых слоев:
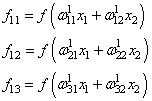
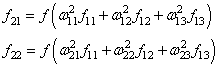
и последнее
выходное значение y:
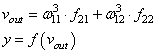
Далее, мы знаем
требуемый отклик d для текущего вектора ![]() ,
,
значит для него можно вычислить ошибку работы НС. Она будет равна:
![]()
На данный момент
все должно быть понятно. Мы на первом занятии подробно рассматривали процесс
распространения сигнала по НС. И вы это уже хорошо себе представляете. А вот
дальше начинается самое главное – корректировка весов. Для этого делается
обратный проход по НС: от последнего слоя – к первому.
Итак, у нас есть
ошибка e и некая функция
активации нейронов ![]() .
.
Первое, что нам нужно – это вычислить локальный градиент для выходного нейрона.
Это делается по формуле:
![]()
Этот момент
требует пояснения. Смотрите, ранее используемая пороговая функция:
![]()
нам уже не
подходит, т.к. она не дифференцируема на всем диапазоне значений x. Вместо этого
для сетей с небольшим числом слоев, часто применяют или гиперболический
тангенс:
![]()
или логистическую
функцию:
![]()
Фактически, они
отличаются только тем, что первая дает выходной интервал [-1; 1], а вторая – [0;
1]. И мы уже берем ту, которая нас больше устраивает в данной конкретной
ситуации. Например, выберем логистическую функцию.
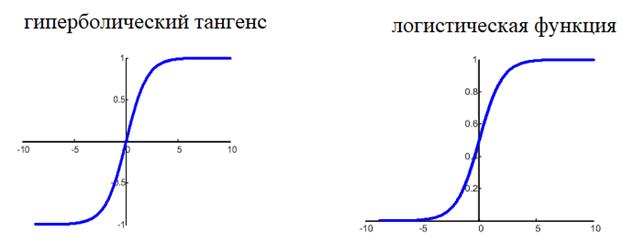
Ее производная
функции по аргументу x дает очень простое выражение:
![]()
Именно его мы и
запишем в нашу формулу вычисления локального градиента:
![]()
Но, так как
![]()
то локальный
градиент последнего нейрона, равен:
![]()
Отлично, это
сделали. Теперь у нас есть все, чтобы выполнить коррекцию весов. Начнем со
связи ![]() ,
,
формула будет такой:
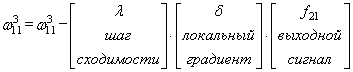
Для второй связи
все то же самое, только входной сигнал берется от второго нейрона:
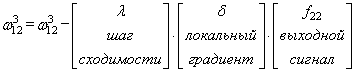
Здесь у вас
может возникнуть вопрос: что такое параметр λ и где его брать? Он
подбирается самостоятельно, вручную самим разработчиком. В самом простом случае
можно попробовать следующие значения:
![]()
(Мы подробно о
нем говорили на занятии по алгоритму градиентного спуска):
Итак, мы с вами
скорректировали связи последнего слоя. Если вам все это понятно, значит, вы уже
практически поняли весь алгоритм обучения, потому что дальше действуем подобным
образом. Переходим к нейрону следующего с конца слоя и для его входящих связей
повторим ту же саму процедуру. Но для этого, нужно знать значение его
локального градиента. Определяется он просто. Локальный градиент последнего
нейрона взвешивается весами входящих в него связей. Полученные значения на
каждом нейроне умножаются на производную функции активации, взятую в точках
входной суммы:
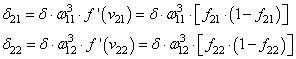
А дальше
действуем по такой же самой схеме, корректируем входные связи по той же
формуле:
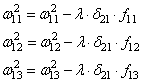
И для второго
нейрона:
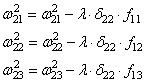
Осталось
скорректировать веса первого слоя. Снова вычисляем локальные градиенты для
нейронов первого слоя, но так как каждый из них имеет два выхода, то сначала
вычисляем сумму от каждого выхода:
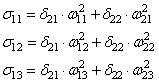
А затем,
значения локальных градиентов на нейронах первого скрытого слоя:
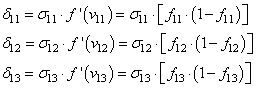
Ну и осталось
выполнить коррекцию весов первого слоя все по той же формуле:
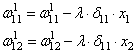
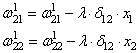
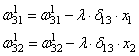
В результате, мы
выполнили одну итерацию алгоритма обучения НС. На следующей итерации мы должны
взять другой входной вектор из нашего обучающего множества. Лучше всего это
сделать случайным образом, чтобы не формировались возможные ложные
закономерности в последовательности данных при обучении НС. Повторяя много раз
этот процесс, весовые связи будут все точнее описывать обучающую выборку.
Отлично, процесс
обучения в целом мы рассмотрели. Но какой критерий качества минимизировался
алгоритмом градиентного спуска? В действительности, мы стремились получить
минимум суммы квадратов ошибок для обучающей выборки:
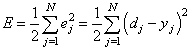
То есть, с
помощью алгоритма градиентного спуска веса корректируются так, чтобы
минимизировать этот критерий качества работы НС. Позже мы еще увидим, что на
практике используется не только такой, но и другие критерии.
Вот так, в целом
выглядит идея работы алгоритма обучения по методу обратного распространения
ошибки. Давайте теперь в качестве примера обучим следующую НС:
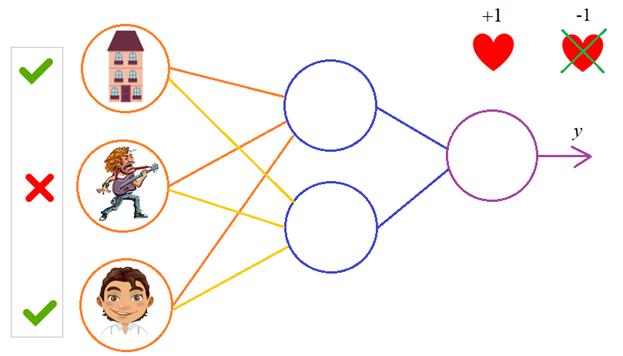
В качестве
обучающего множества выберем все возможные варианты (здесь 1 – это да, -1 – это
нет):
|
Вектор |
Требуемый |
|
[-1, -1, -1] |
-1 |
|
[-1, -1, |
1 |
|
[-1, 1, -1] |
-1 |
|
[-1, 1, 1] |
1 |
|
[1, -1, -1] |
-1 |
|
[1, -1, 1] |
1 |
|
[1, 1, -1] |
-1 |
|
[1, 1, 1] |
-1 |
На каждой
итерации работы алгоритма, мы будем подавать случайно выбранный вектор и
корректировать веса, чтобы приблизиться к значению требуемого отклика.
В качестве
активационной функции выберем гиперболический тангенс:
![]()
со значением
производной:
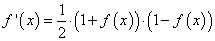
Программа на Python будет такой:
lesson 3. Back propagation.py
Ну, конечно, это
довольно простой, примитивный пример, частный случай, когда мы можем обучить НС
так, чтобы она вообще не выдавала никаких ошибок. Часто, в задачах обучения встречаются
варианты, когда мы этого сделать не можем и, конечно, какой-то процент ошибок
всегда остается. И наша задача сделать так, чтобы этих ошибок было как можно
меньше. Но более подробно как происходит обучение, какие нюансы существуют, как
создавать обучающую выборку, как ее проверять и так далее, мы об этом подробнее
будем говорить уже на следующем занятии.
Видео по теме
Background
Backpropagation is a common method for training a neural network. There is no shortage of papers online that attempt to explain how backpropagation works, but few that include an example with actual numbers. This post is my attempt to explain how it works with a concrete example that folks can compare their own calculations to in order to ensure they understand backpropagation correctly.
Backpropagation in Python
You can play around with a Python script that I wrote that implements the backpropagation algorithm in this Github repo.
Backpropagation Visualization
For an interactive visualization showing a neural network as it learns, check out my Neural Network visualization.
Additional Resources
If you find this tutorial useful and want to continue learning about neural networks, machine learning, and deep learning, I highly recommend checking out Adrian Rosebrock’s new book, Deep Learning for Computer Vision with Python. I really enjoyed the book and will have a full review up soon.
Overview
For this tutorial, we’re going to use a neural network with two inputs, two hidden neurons, two output neurons. Additionally, the hidden and output neurons will include a bias.
Here’s the basic structure:

In order to have some numbers to work with, here are the initial weights, the biases, and training inputs/outputs:
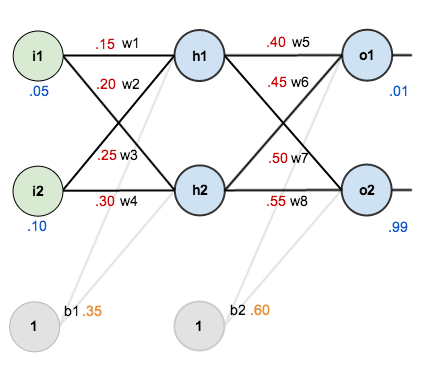
The goal of backpropagation is to optimize the weights so that the neural network can learn how to correctly map arbitrary inputs to outputs.
For the rest of this tutorial we’re going to work with a single training set: given inputs 0.05 and 0.10, we want the neural network to output 0.01 and 0.99.
The Forward Pass
To begin, lets see what the neural network currently predicts given the weights and biases above and inputs of 0.05 and 0.10. To do this we’ll feed those inputs forward though the network.
We figure out the total net input to each hidden layer neuron, squash the total net input using an activation function (here we use the logistic function), then repeat the process with the output layer neurons.
Total net input is also referred to as just net input by some sources.
Here’s how we calculate the total net input for :
We then squash it using the logistic function to get the output of :
Carrying out the same process for we get:
We repeat this process for the output layer neurons, using the output from the hidden layer neurons as inputs.
Here’s the output for :
And carrying out the same process for we get:
Calculating the Total Error
We can now calculate the error for each output neuron using the squared error function and sum them to get the total error:
Some sources refer to the target as the ideal and the output as the actual.
The is included so that exponent is cancelled when we differentiate later on. The result is eventually multiplied by a learning rate anyway so it doesn’t matter that we introduce a constant here [1].
For example, the target output for is 0.01 but the neural network output 0.75136507, therefore its error is:
Repeating this process for (remembering that the target is 0.99) we get:
The total error for the neural network is the sum of these errors:
The Backwards Pass
Our goal with backpropagation is to update each of the weights in the network so that they cause the actual output to be closer the target output, thereby minimizing the error for each output neuron and the network as a whole.
Output Layer
Consider . We want to know how much a change in
affects the total error, aka
.
is read as “the partial derivative of
with respect to
“. You can also say “the gradient with respect to
“.
By applying the chain rule we know that:
Visually, here’s what we’re doing:

We need to figure out each piece in this equation.
First, how much does the total error change with respect to the output?
is sometimes expressed as
When we take the partial derivative of the total error with respect to , the quantity
becomes zero because
does not affect it which means we’re taking the derivative of a constant which is zero.
Next, how much does the output of change with respect to its total net input?
The partial derivative of the logistic function is the output multiplied by 1 minus the output:
Finally, how much does the total net input of change with respect to
?
Putting it all together:
You’ll often see this calculation combined in the form of the delta rule:
Alternatively, we have and
which can be written as
, aka
(the Greek letter delta) aka the node delta. We can use this to rewrite the calculation above:
Therefore:
Some sources extract the negative sign from so it would be written as:
To decrease the error, we then subtract this value from the current weight (optionally multiplied by some learning rate, eta, which we’ll set to 0.5):
We can repeat this process to get the new weights ,
, and
:
We perform the actual updates in the neural network after we have the new weights leading into the hidden layer neurons (ie, we use the original weights, not the updated weights, when we continue the backpropagation algorithm below).
Hidden Layer
Next, we’ll continue the backwards pass by calculating new values for ,
,
, and
.
Big picture, here’s what we need to figure out:
Visually:
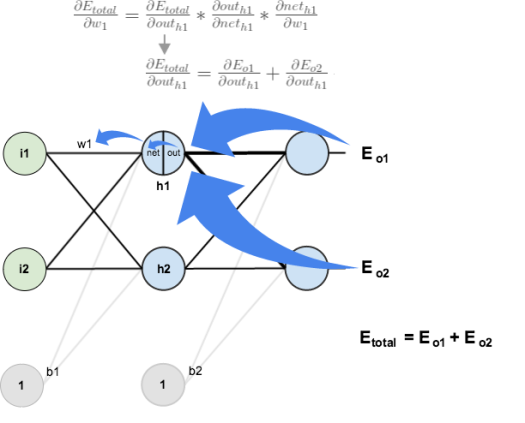
We’re going to use a similar process as we did for the output layer, but slightly different to account for the fact that the output of each hidden layer neuron contributes to the output (and therefore error) of multiple output neurons. We know that affects both
and
therefore the
needs to take into consideration its effect on the both output neurons:
Starting with :
We can calculate using values we calculated earlier:
And is equal to
:
Plugging them in:
Following the same process for , we get:
Therefore:
Now that we have , we need to figure out
and then
for each weight:
We calculate the partial derivative of the total net input to with respect to
the same as we did for the output neuron:
Putting it all together:
You might also see this written as:
We can now update :
Repeating this for ,
, and
Finally, we’ve updated all of our weights! When we fed forward the 0.05 and 0.1 inputs originally, the error on the network was 0.298371109. After this first round of backpropagation, the total error is now down to 0.291027924. It might not seem like much, but after repeating this process 10,000 times, for example, the error plummets to 0.0000351085. At this point, when we feed forward 0.05 and 0.1, the two outputs neurons generate 0.015912196 (vs 0.01 target) and 0.984065734 (vs 0.99 target).
If you’ve made it this far and found any errors in any of the above or can think of any ways to make it clearer for future readers, don’t hesitate to drop me a note. Thanks!
And while I have you…
In addition to dabbling in data science, I run Preceden timeline maker, the best timeline maker software on the web. If you ever need to create a high level timeline or roadmap to get organized or align your team, Preceden is a great option.
