Знакомимся с методом обратного распространения ошибки
Время на прочтение
6 мин
Количество просмотров 46K
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!

Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
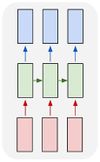
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.

Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.

Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:

Для l = 3:

W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.

Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.

b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.

Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:

Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:

Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:

И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:

(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:

Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.

Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:

(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:

(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:

«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
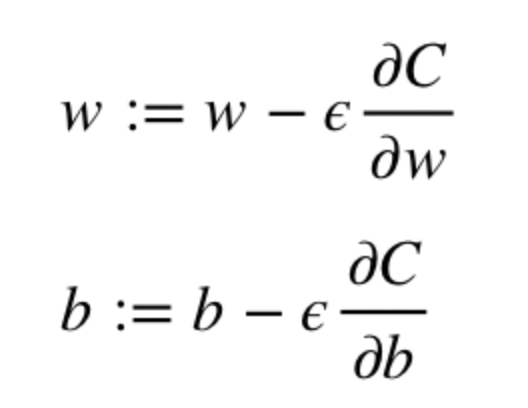
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:

Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z3)2 и (a3)2:

Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
Рекуррентная нейронная сеть (англ. recurrent neural network, RNN) — вид нейронных сетей, где связи между элементами образуют направленную последовательность.
Содержание
- 1 Описание
- 2 Области и примеры применения
- 3 Виды RNN
- 3.1 Один к одному
- 3.2 Один ко многим
- 3.3 Многие к одному
- 3.4 Многие ко многим
- 4 Архитектуры
- 4.1 Полностью рекуррентная сеть
- 4.2 Рекурсивная сеть
- 4.3 Нейронная сеть Хопфилда
- 4.4 Двунаправленная ассоциативная память (BAM)
- 4.5 Сеть Элмана
- 4.6 Сеть Джордана
- 4.7 Эхо-сети
- 4.8 Нейронный компрессор истории
- 4.9 Сети долго-краткосрочной памяти
- 4.10 Управляемые рекуррентные блоки
- 4.11 Двунаправленные рекуррентные сети
- 4.12 Seq-2-seq сети
- 5 Пример кода
- 5.1 Пример кода на Python с использованием библиотеки Keras.[9]
- 5.2 Пример на языке Java
- 6 См. также
- 7 Примечания
Описание
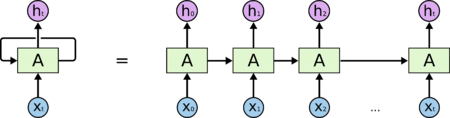
Рисунок 1. RNN и ее развернутое представление [1]
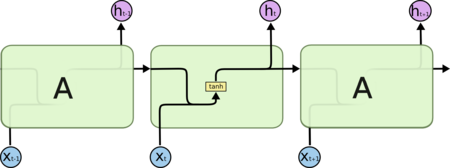
Рисунок 2. Схема слоя рекуррентной сети [2]
Рекуррентные нейронные сети — сети с циклами, которые хорошо подходят для обработки последовательностей (рис. 1).
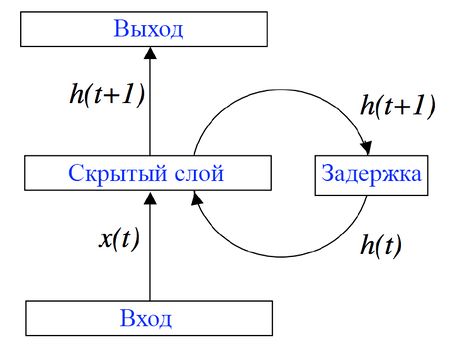
Рисунок 3. RNN с задержкой на скрытом слое
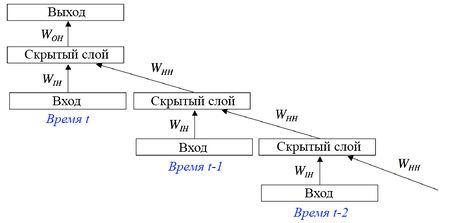
Обучение RNN аналогично обучению обычной нейронной сети. Мы также используем алгоритм обратного распространения ошибки (англ. Backpropagation), но с небольшим изменением. Поскольку одни и те же параметры используются на всех временных этапах в сети, градиент на каждом выходе зависит не только от расчетов текущего шага, но и от предыдущих временных шагов (рис. 4). Например, чтобы вычислить градиент для четвертого элемента последовательности, нам нужно было бы «распространить ошибку» на 3 шага и суммировать градиенты. Этот алгоритм называется «алгоритмом обратного распространения ошибки сквозь время» (англ. Backpropagation Through Time, BPTT).[3][4]
Алгоритм обратного распространения ошибки сквозь время:
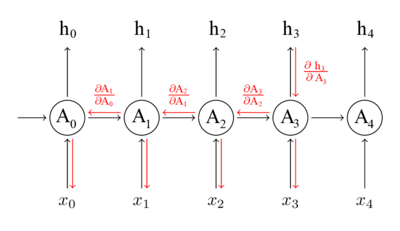
Области и примеры применения
Используются, когда важно соблюдать последовательность, когда важен порядок поступающих объектов.
- Обработка текста на естественном языке:
- Анализ текста;
- Автоматический перевод;
- Обработка аудио:
- Автоматическое распознавание речи;
- Обработка видео:
- Прогнозирование следующего кадра на основе предыдущих;
- Распознавание эмоций;
- Обработка изображений:
- Прогнозирование следующего пикселя на основе окружения;
- Генерация описания изображений.
Виды RNN
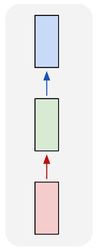
Один к одному
|
|
Архитектура по сути является обычной нейронной сетью. |
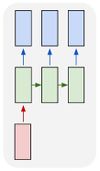
Один ко многим
|
|
Один вход ко многим выходам может применяться, например, для генерации аудиозаписи. На вход подаем жанр музыки, который хотим получить, на выходе получаем последовательность аудиозаписи. |
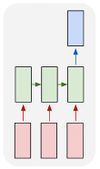
Многие к одному
|
|
Много входов и один выход может применяться, если мы хотим оценить тональность рецензии. На вход подаем слова рецензии, на выходе получаем оценку ее тональности: позитивная рецензия или негативная. |
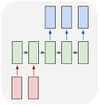
Многие ко многим
|
|
Данную архитектуру можно использовать для перевода текста с одного языка на другой. |
|
|
Такой вариант подойдет для определения для классификации каждого слова в предложении в зависимости от контекста. |
Архитектуры
Полностью рекуррентная сеть
Это базовая архитектура, разработанная в 1980-х. Сеть строится из узлов, каждый из которых соединён со всеми другими узлами. У каждого нейрона порог активации меняется со временем и является вещественным числом. Каждое соединение имеет переменный вещественный вес. Узлы разделяются на входные, выходные и скрытые.
Рекурсивная сеть
Рекурсивные нейронные сети (англ. Recurrent neural networks) представляют собой более общий случай рекуррентных сетей, когда сигнал в сети проходит через структуру в виде дерева (обычно бинарные деревья). Те же самые матрицы весов используются рекурсивно по всему графу в соответствии с его топологией.
Нейронная сеть Хопфилда
Тип рекуррентной сети, когда все соединения симметричны. Изобретена Джоном Хопфилдом в 1982 году и гарантируется, что динамика такой сети сходится к одному из положений равновесия.
Двунаправленная ассоциативная память (BAM)
Вариацией сети Хопфилда является двунаправленная ассоциативная память (BAM). BAM имеет два слоя, каждый из которых может выступать в качестве входного, находить (вспоминать) ассоциацию и генерировать результат для другого слоя.
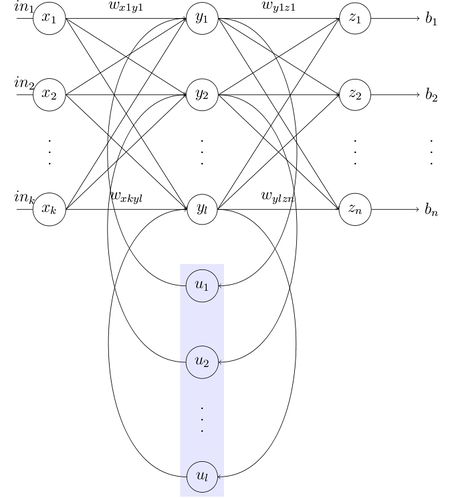
Сеть Элмана
Нейронная сеть Элмана состоит из трёх слоев: , , . Дополнительно к сети добавлен набор «контекстных блоков»: (рис. 5). Средний (скрытый) слой соединён с контекстными блоками с фиксированным весом, равным единице. С каждым шагом времени на вход поступает информация, которая проходит прямой ход к выходному слою в соответствии с правилами обучения. Фиксированные обратные связи сохраняют предыдущие значения скрытого слоя в контекстных блоках (до того как скрытый слой поменяет значение в процессе обучения). Таким способом сеть сохраняет своё состояние, что может использоваться в предсказании последовательностей, выходя за пределы мощности многослойного перцептрона.
,
,
Обозначения переменных и функций:
- : вектор входного слоя;
- : вектор скрытого слоя;
- : вектор выходного слоя;
- : матрица и вектор параметров;
- : функция активации.
Сеть Джордана
Нейронная сеть Джордана подобна сети Элмана, но контекстные блоки связаны не со скрытым слоем, а с выходным слоем. Контекстные блоки таким образом сохраняют своё состояние. Они обладают рекуррентной связью с собой.
,
,
Эхо-сети
Эхо-сеть (англ. Echo State Network, ESN) характеризуется одним скрытым слоем (который называется резервуаром) со случайными редкими связями между нейронами. При этом связи внутри резервуара фиксированы, но связи с выходным слоем подлежат обучению. Состояние резервуара (state) вычисляется через предыдущие состояния резервуара, а также предыдущие состояния входного и выходного сигналов. Так как эхо-сети обладают только одним скрытым слоем, они обладают достаточно низкой вычислительной сложностью.
Нейронный компрессор истории
Нейронный компрессор исторических данных — это блок, позволяющий в сжатом виде хранить существенные исторические особенности процесса, который является своего рода стеком рекуррентной нейронной сети, формируемым в процессе самообучения.
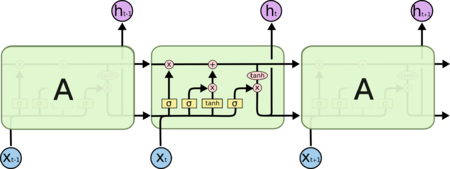
Рисунок 6. Схема слоев рекуррентной сети долго-краткосрочной памяти [5]
Сети долго-краткосрочной памяти
Сеть долго-краткосрочной памяти (англ. Long short-term memory, LSTM) является самой популярной архитектурой рекуррентной нейронной сети на текущий момент, такая архитектура способна запоминать данные на долгое время (рис. 6).[6]
Управляемые рекуррентные блоки
Управляемые рекуррентные блоки (англ. Gated Recurrent Units, GRU) — обладает меньшим количеством параметров, чем у LSTM, и в ней отсутствует выходное управление. При этом производительность в моделях речевого сигнала или полифонической музыки оказалась сопоставимой с LSTM.
Двунаправленные рекуррентные сети
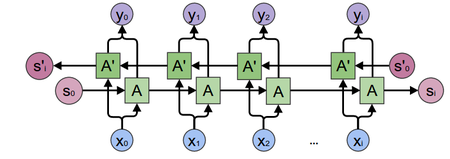
Рисунок 7. Двунаправленная рекуррентная сеть [7]
Двунаправленная рекуррентная сеть (англ. Bidirectional Recurrent Neural Network, biRNN) представляет собой две однонаправленные рекуррентные сети, одна из которых обрабатывает входную последовательность в прямом порядке, а другая — в обратном (рис. 7). Таким образом, для каждого элемента входной последовательности считается два вектора скрытых состояний, на основе которых вычисляется выход сети. Благодаря данной архитектуре сети доступна информация о контексте как из прошлого, так и из будущего, что решает проблему однонаправленных рекуррентных сетей. Для обучения biRNN используются те же алгоритмы, что и для RNN.
,
,
,
где , , , , , — матрицы весов, , , , — байесы, , , — функции активаций, и — выходы однонаправленных рекуррентных сетей, — их конкатенированный вектор, а — выход сети на шаге .
Seq-2-seq сети
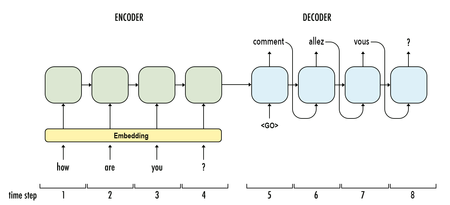
Рисунок 8. Seq-2-seq сеть [8]
Seq-2-seq (Sequence to sequence, Seq2seq) сеть является базовой архитектурой many-to-many RNN и используется для трансляции одной последовательности в другую (рис. 8). Она состоит из двух рекуррентных сетей: кодировщика и декодировщика. Кодировщик вычисляет вектор, кодирующий входную последовательность. Далее данный вектор передается декодировщику, который в свою очередь по полученному скрытому представлению восстанавливает целевую последовательность. При этом каждый посчитанный выход используется для обновления скрытого представления.
Пример кода
Пример кода на Python с использованием библиотеки Keras.[9]
# Импорты import numpy as np from keras.preprocessing import sequence from keras.models import Sequential from keras.layers import Dense, Activation, Embedding from keras.layers import LSTM from keras.datasets import imdb # Устанавливаем seed для обеспечения повторяемости результатов np.random.seed(42) # Указываем количество слов из частотного словаря, которое будет использоваться (отсортированы по частоте использования) max_features = 5000 # Загружаем данные (датасет IMDB содержит 25000 рецензий на фильмы с правильным ответом для обучения и 25000 рецензий на фильмы с правильным ответом для тестирования) (X_train, y_train), (X_test, y_test) = imdb.load_data(nb_words = max_features) # Устанавливаем максимальную длину рецензий в словах, чтобы они все были одной длины maxlen = 80 # Заполняем короткие рецензии пробелами, а длинные обрезаем X_train = sequence.pad_sequences(X_train, maxlen = maxlen) X_test = sequence.pad_sequences(X_test, maxlen = maxlen) # Создаем модель последовательной сети model = Sequential() # Добавляем слой для векторного представления слов (5000 слов, каждое представлено вектором из 32 чисел, отключаем входной сигнал с вероятностью 20% для предотвращения переобучения) model.add(Embedding(max_features, 32, dropout = 0.2)) # Добавляем слой долго-краткосрочной памяти (100 элементов для долговременного хранения информации, отключаем входной сигнал с вероятностью 20%, отключаем рекуррентный сигнал с вероятностью 20%) model.add(LSTM(100, dropout_W = 0.2, dropout_U = 0.2)) # Добавляем полносвязный слой из 1 элемента для классификации, в качестве функции активации будем использовать сигмоидальную функцию model.add(Dense(1, activation = 'sigmoid')) # Компилируем модель нейронной сети model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy']) # Обучаем нейронную сеть (данные для обучения, ответы к данным для обучения, количество рецензий после анализа которого будут изменены веса, число эпох обучения, тестовые данные, показывать progress bar или нет) model.fit(X_train, y_train, batch_size = 64, nb_epoch = 7, validation_data = (X_test, y_test), verbose = 1) # Проверяем качество обучения на тестовых данных (если есть данные, которые не участвовали в обучении, лучше использовать их, но в нашем случае таковых нет) scores = model.evaluate(X_test, y_test, batch_size = 64) print('Точность на тестовых данных: %.2f%%' % (scores[1] * 100))
Пример на языке Java
Пример простой рекуррентной нейронной сети, способной генерировать заданную строку по первому символу, с применением библиотеки deeplearning4j.
См. также
- Сверточные нейронные сети
- Нейронные сети, перцептрон
- Рекурсивные нейронные сети
Примечания
- ↑ Understanding LSTM Networks
- ↑ Understanding LSTM Networks
- ↑ Backpropagation Through Time
- ↑ Backpropagation Through Time
- ↑ Understanding LSTM Networks
- ↑ Sepp Hochreiter, Jurgen Schmidhuber. Long short-term memory (1997). Neural Computation.
- ↑ Understanding Bidirectional RNN in PyTorch
- ↑ Implementation of seq2seq model
- ↑ Keras RNN
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
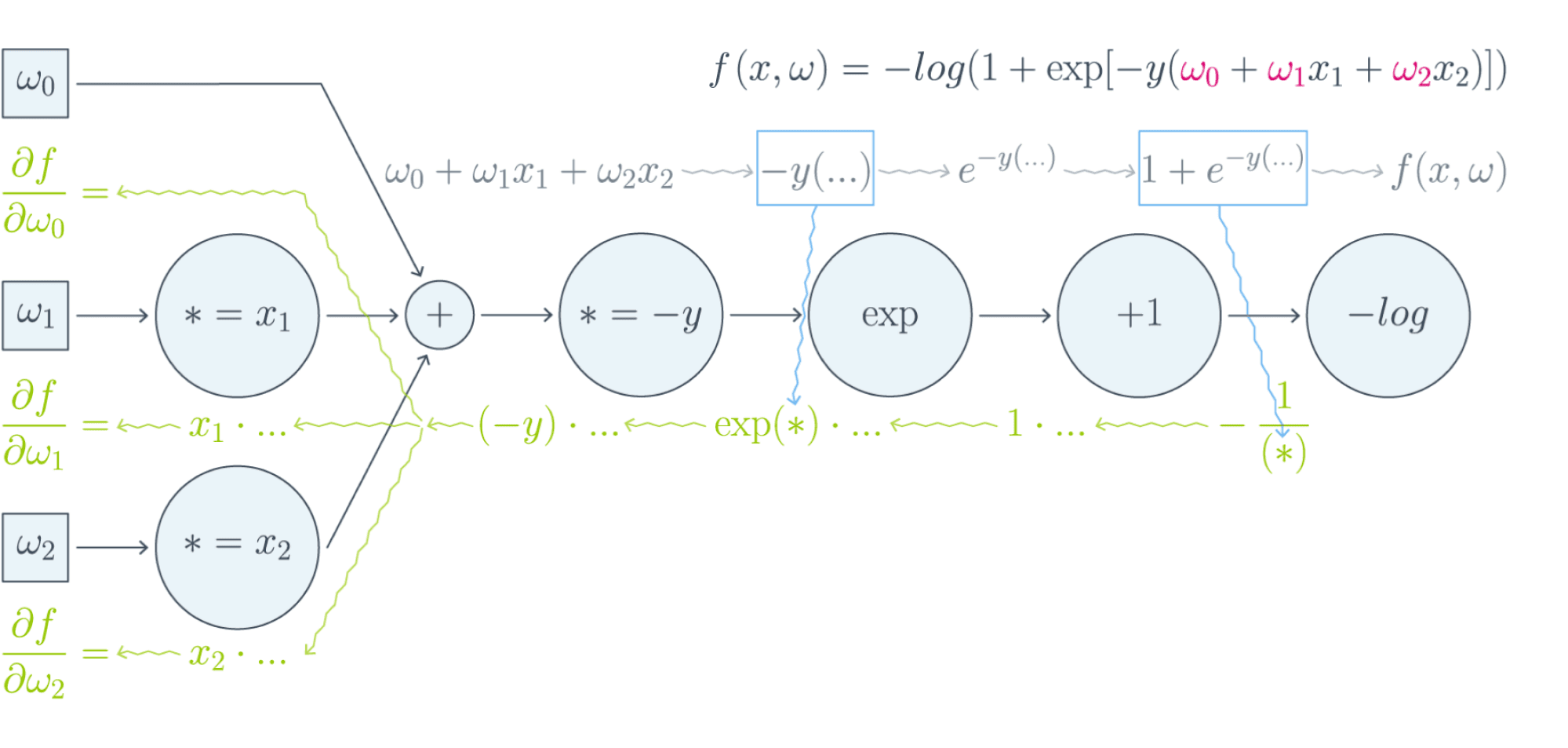
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
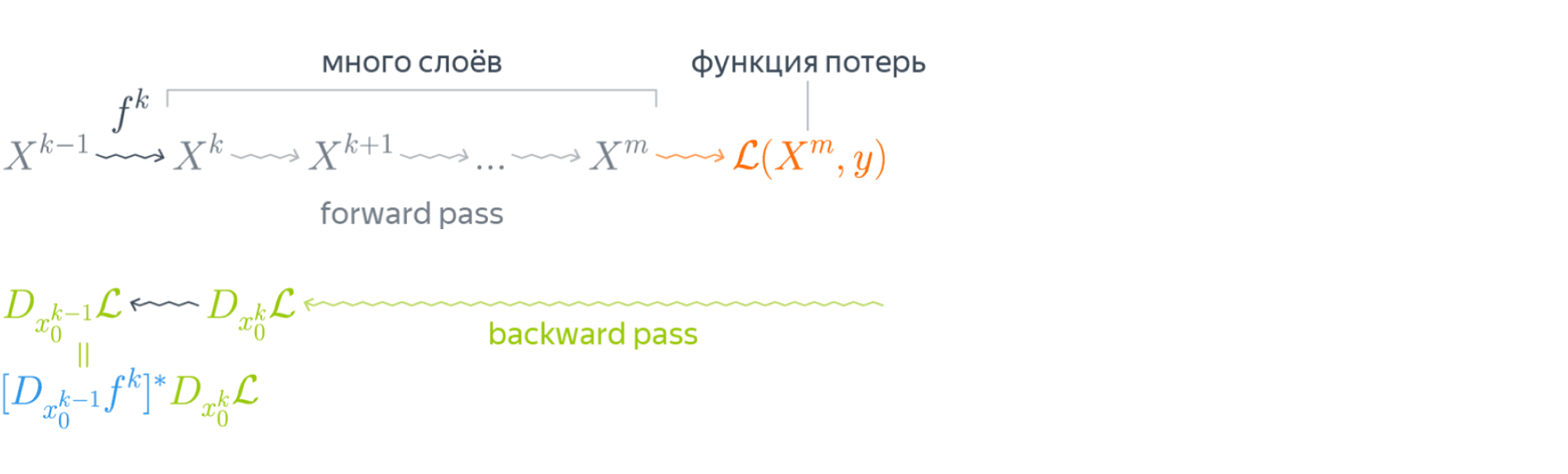
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
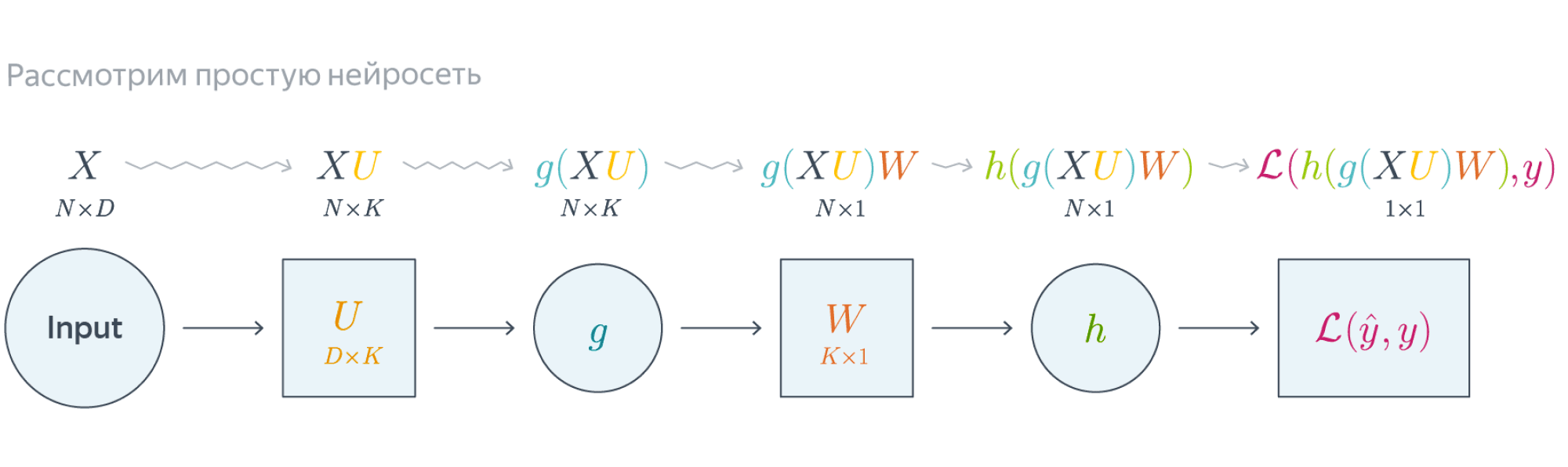 Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?
Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
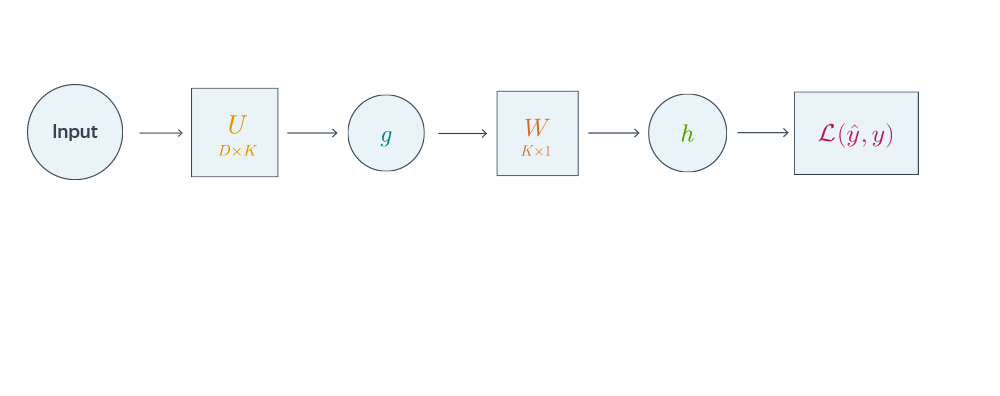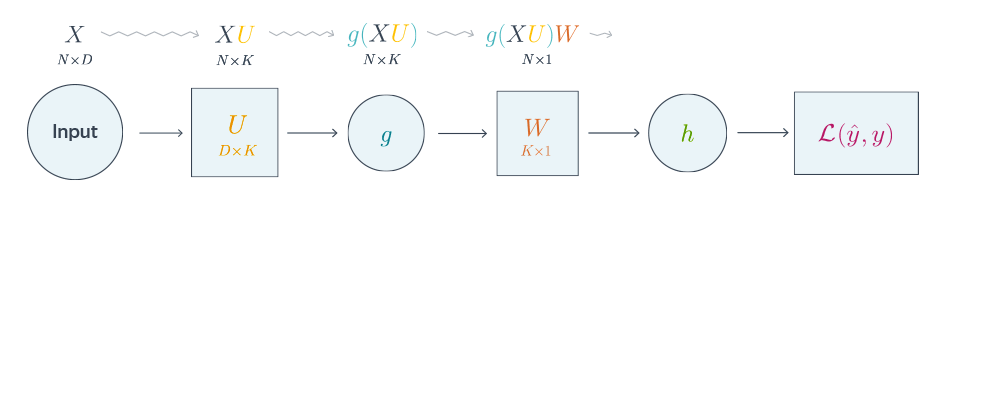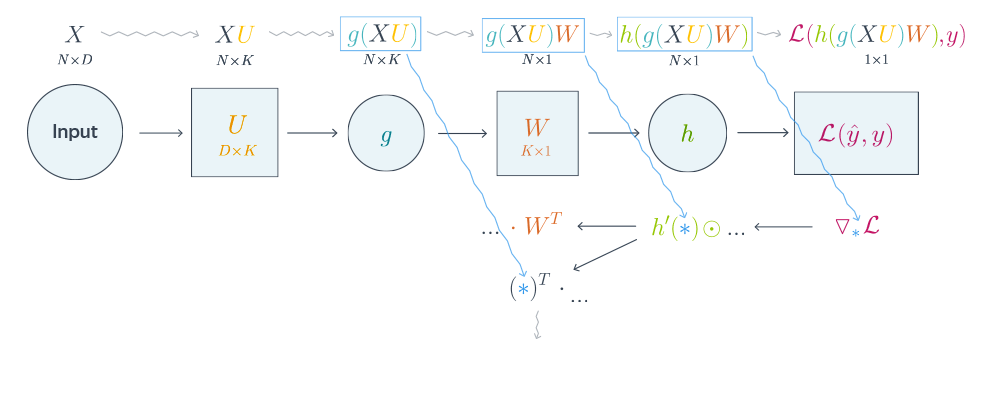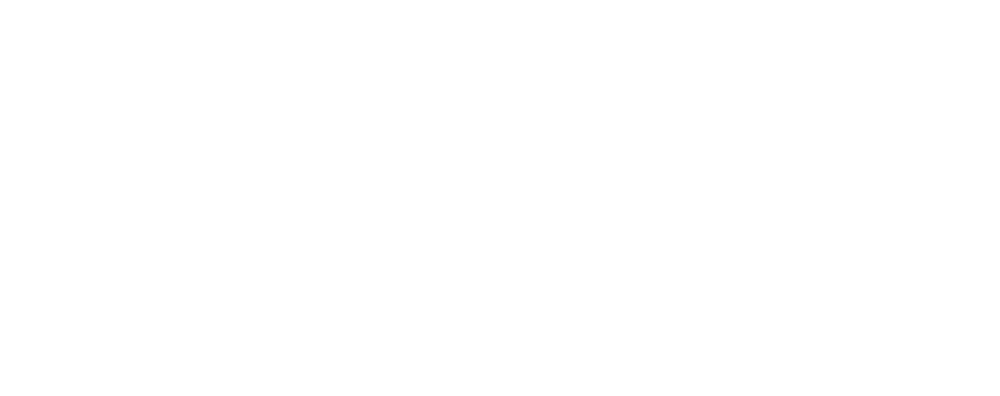
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Привет, Вы узнаете про обратное распространение во времени, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
обратное распространение во времени, bptt, bpts, обратное распространение через структуру
, настоятельно рекомендую прочитать все из категории Машинное обучение.
обратное распространение во времени (BPTT) — это метод на основе градиента для обучения определенных типов рекуррентных нейронных сетей . Его можно использовать для обучения сетей Эльмана . Алгоритм был независимо разработан многочисленными исследователями.
Данные обучения для рекуррентной нейронной сети представляют собой упорядоченную последовательность пары ввода-вывода,
. Для скрытого состояния необходимо указать начальное значение
. Обычно для этой цели используется вектор всех нулей.

BPTT разворачивает повторяющуюся нейронную сеть во времени.
BPTT начинается с развертывания повторяющейся нейронной сети во времени. Развернутая сеть содержитвходы и выходы, но все копии сети имеют одни и те же параметры. Затем алгоритм обратного распространения ошибки используется для нахождения градиента стоимости по всем параметрам сети.
Рассмотрим пример нейронной сети, содержащей повторяющийся слой.и слой с прямой связью
. Есть разные способы определения стоимости обучения, но общая стоимость всегда является средней стоимостью каждого временного шага. Стоимость каждого временного шага можно рассчитать отдельно. На рисунке выше показано, как стоимость во времени
можно вычислить, развернув повторяющийся слой
для трех временных шагов и добавление слоя прямой связи
. Каждый экземпляр
в развернутой сети имеет те же параметры . Об этом говорит сайт https://intellect.icu . Таким образом, вес обновляется в каждом случае (
) суммируются.
Псевдокод BPTT
Псевдокод для усеченной версии BPTT, где обучающие данные содержат пары ввода-вывода, но сеть развернута на
временные шаги:
Преимущества BPTT
BPTT имеет тенденцию быть значительно быстрее для обучения повторяющихся нейронных сетей, чем универсальные методы оптимизации, такие как эволюционная оптимизация.
Недостатки BPTT
BPTT испытывает трудности с локальным оптимумом. Для рекуррентных нейронных сетей локальные оптимумы представляют собой гораздо более серьезную проблему, чем для нейронных сетей с прямой связью. Периодическая обратная связь в таких сетях имеет тенденцию создавать хаотические отклики на поверхности ошибки, что приводит к частому возникновению локальных оптимумов и в плохих местах на поверхности ошибки.
обратное распространение через структуру (BPTS)
Рисунок 1: Стандартный LRAAM (A) и BPTS архитектура (B).
Обратное распространение через структуру (BPTS) — это основанный на градиенте метод обучения рекурсивных нейронных сетей (надмножество рекуррентных нейронных сетей ), который подробно описан в статье 1996 года, написанной Кристофом Голлером и Андреасом Кюхлером. Представление структур в виде DAG-файлов. Давайте сначала подробнее рассмотрим способ кодирования структур с помощью Labeling Recursive Auto-Associative Memory (LRAAM) . Все виды рекурсивных символьных структур данных, к которым мы стремимся, могут быть отображены на маркированные направленные ациклические графы (НАГ) DAG, Мы не рассматриваем здесь циклические структуры.. Чтобы вычислить представление графа, сначала необходимо вычислить представления всех подграфов. На этапе обучения LRAAM для каждого узла одна фаза прямого распространения активаций и одна фаза обратного распространения (каждый через три уровня сети) ошибок за эпоху нужно. Выбор НАГ-представления для структур, которые позволяют представлять различные вхождения (под) структуры в обучающем наборе только как один узел может привести к значительному (даже экспоненциальное) снижение сложности стандартного LRAAM. Этот аргумент справедлив и для нашей архитектуры (см. раздел 3). Вместо того, чтобы выбирать древовидное представление, поэтому мы предпочитаем НАГ-подобное представление для наших терминов, как показано на Рис 2.
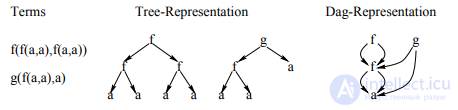
Рисунок 2: Дерево и DAG-представление набора терминов.
2 BPTS для деревьев
Для простоты мы сначала ограничимся древовидными структурами. в прямой фазе кодировщика (рис. 1, B) используется для вычисления представления для
дано дерево так же, как и в равнине LRAAM. Это делается путем рекурсивной передачи предыдущие вычисленные представления прямых поддеревьев на входном уровне кодировщика.
Этот процесс кодирования запускается на листьях дерева и генерирует представление для дерева, которое затем передается на следующий уровень, давая результат классификации на выходе Блока. Следующая метафора помогает нам объяснить обратную фазу. Представьте себе кодировщик
виртуально развернут (с скопированными весами) согласно древовидной структуре (см. рисунок 3).
Теперь ошибка, переданная от классификатора к скрытому слою, распространяется через развернутую сеть кодировщика.

Рисунок 3: Кодирующая сеть, развернутая структурой f (X; g (a; Y)).
Это развертывание по структуре аналогично развертыванию повторяющейся сети во времени (BPTT). побудило нас ввести термин обратное распространение через структуру (BPTS). Давайте сначала рассмотрим случай, когда для каждого появления (под) термина один выделенный узел в обучающей выборке зарезервирован (древовидное представление). Аргументируя аналогично BPTT [Wer90] мы видим, что вычисляется точный градиент. Представьте себе, что каждая копия
части кодировщика имеет собственный набор весов. Тогда по правильности обычного обратного распространения, вычисляется точный градиент. Если весовые матрицы разных копий идентифицированы, ясно, что нам просто нужно просуммировать компоненты, поступающие из разных копий, чтобы получить
точный градиент. Точная формулировка приведена ниже:
Для каждого (под) дерева 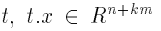 является входным вектором кодировщика
является входным вектором кодировщика 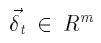 вектор дельт (ошибок) для представления t, и Q
вектор дельт (ошибок) для представления t, и Q
(t: x; t’) проекция t: x на t поддерево t’
. Пусть далее W — матрица кодировщика, f ‘ производная передаточной функции и  умножение двух векторов на компоненты.
умножение двух векторов на компоненты.
Δ W рассчитывается как сумма по всем (под) деревьям (1).  для каждого поддерева t’ рассчитывается путем распространения
для каждого поддерева t’ рассчитывается путем распространения 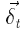 одного определенного родительского узла t из t` обратно по (2):
одного определенного родительского узла t из t` обратно по (2):

Для каждого (под) дерева в обучающем наборе для одной эпохи требуется ровно одно прямое и одно
обратная фаза через энкодер. Тренировочная выборка статическая (без движущейся мишени).
3 BPTS для направленных ациклических графов DAG
Однако, если мы используем DAG-представление и представляем (под) структуру t только как один узел независимо от количества его вхождений, то могут быть разные 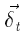 в (1) и (2) для каждого вхождения t. Мы называем эту ситуацию — дельта-конфликтом. Предположим, что (под) структуры ti и tj идентичны. Конечно, это означает, что соответствующие подструктуры внутри ti и tj тоже идентичны. Это явно дает нам ti: x = tj: x, но у нас может быть
в (1) и (2) для каждого вхождения t. Мы называем эту ситуацию — дельта-конфликтом. Предположим, что (под) структуры ti и tj идентичны. Конечно, это означает, что соответствующие подструктуры внутри ti и tj тоже идентичны. Это явно дает нам ti: x = tj: x, но у нас может быть 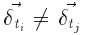
Для вычисления Δ W нам понадобится только сумма 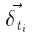 и
и 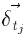
. Об этом свидетельствуют следующее преобразование (1), которое выполняется из-за линейности умножения матриц:

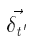 с соответствующих детьми t` из ti и tj можно вычислить более эффективно, распространяю сумму
с соответствующих детьми t` из ti и tj можно вычислить более эффективно, распространяю сумму  и
и  обратно в (2). Аналогичное преобразование (линейность
обратно в (2). Аналогичное преобразование (линейность 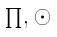 и матричное умножение) для (2) показывает это.
и матричное умножение) для (2) показывает это.
Суммируя все различия, возникающие в каждом случае (под) структуры, получаем правильное (с самым крутым градиентом) решение дельта-конуса ict и позволяет очень эффективно реализовать BPTS для DAG. Нам просто нужно организовать узлы обучающего набора в топологическом порядке.
Прямая фаза начинается с листовых узлов и продолжается в обратном порядке, гарантируя, что представления для идентичных подструктур должны быть вычислены только один раз. Обратная фаза следует топологическому порядку, начиная с корневых узлов.
Таким образом, δ всех вхождений узла суммируются перед обработкой этого узла.. Опять же для каждого узла в обучающем наборе для одной эпохи требуется ровно одна прямая и одна обратная фаза через кодировщик.
2.4.4 Онлайн в сравнении с пакетным режимом
Подобно стандартному распространению ошибки , BPTS можно использовать в пакетном или онлайн-режиме. BPTS-партия обновляет веса после того, как был представлен весь обучающий набор. Путем оптимизации методы, обсуждаемые в Разделе 3 (-суммирование и DAG-представление), каждый узел
нужно обрабатывать только один раз за эпоху. Это не относится к онлайн-режиму, потому что веса обновляются сразу после представления одной структуры и, следовательно, подструктуры должны обрабатываться для каждого случая отдельно.
Вау!! 😲 Ты еще не читал? Это зря!
- обучение с учителем , метод коррекции ошибки , метод обратного распространения ошибки ,
- анализ алгоритма обратного распространения ошибки нейронной сети ,
Надеюсь, эта статья про обратное распространение во времени, была вам полезна,счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое обратное распространение во времени, bptt, bpts, обратное распространение через структуру
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Машинное обучение
Рекуррентные нейронные сети: типы, обучение, примеры и применение
Рекуррентные нейронные сети (Recurrent Neural Networks, RNNs) — популярные модели, используемые в обработке естественного языка (NLP). Во-первых, они оценивают произвольные предложения на основе того, насколько часто они встречались в текстах. Это дает нам меру грамматической и семантической корректности. Такие модели используются в машинном переводе. Во-вторых, языковые модели генерируют новый текст. Обучение модели на поэмах Шекспира позволит генерировать новый текст, похожий на Шекспира.
Что такое рекуррентные нейронные сети?
Идея RNN заключается в последовательном использовании информации. В традиционных нейронных сетях подразумевается, что все входы и выходы независимы. Но для многих задач это не подходит. Если вы хотите предсказать следующее слово в предложении, лучше учитывать предшествующие ему слова. RNN называются рекуррентными, потому что они выполняют одну и ту же задачу для каждого элемента последовательности, причем выход зависит от предыдущих вычислений. Еще одна интерпретация RNN: это сети, у которых есть «память», которая учитывает предшествующую информацию. Теоретически RNN могут использовать информацию в произвольно длинных последовательностях, но на практике они ограничены лишь несколькими шагами (подробнее об этом позже).

Рекуррентная нейронная сеть и ее развертка (unfolding)
На диаграмме выше показано, что RNN разворачивается в полную сеть. Разверткой мы просто выписываем сеть для полной последовательности. Например, если последовательность представляет собой предложение из 5 слов, развертка будет состоять из 5 слоев, по слою на каждое слово. Формулы, задающие вычисления в RNN следующие:
- x_t — вход на временном шаге t. Например x_1 может быть вектором с одним горячим состоянием (one-hot vector), соответствующим второму слову предложения.
- s_t — это скрытое состояние на шаге t. Это «память» сети. s_t зависит, как функция, от предыдущих состояний и текущего входа x_t: s_t=f(Ux_t+Ws_{t-1}). Функция f обычно нелинейная, например tanh или ReLU . s_{-1}, которое требуется для вычисление первого скрытого состояния, обычно инициализируется нулем (нулевым вектором).
- o_t — выход на шаге t. Например, если мы хотим предсказать слово в предложении, выход может быть вектором вероятностей в нашем словаре. o_t = softmax(Vs_t)
Несколько заметок:
- Можно интерпретировать s_t как память сети. s_t содержит информацию о том, что произошло на предыдущих шагах времени. Выход o_t вычисляется исключительно на основе «памяти» s_t. На практике все немного сложнее: s_t не может содержать информацию слишком большого количества предшествующих шагов;
- В отличие от традиционной глубокой нейронной сети , которая использует разные параметры на каждом слое, RNN имеет одинаковые (U, V, W) на всех этапах. Это отражает тот факт, что мы выполняем одну и ту же задачу на каждом шаге, используя только разные входы. Это значительно уменьшает общее количество параметров, которые нам нужно подобрать;
- Диаграмма выше имеет выходы на каждом шаге, но, в зависимости от задачи, они могут не понадобиться. Например при определении эмоциональной окраски предложения, целесообразно заботиться только о конечном результате, а не о окраске после каждого слова. Аналогично, нам может не потребоваться ввод данных на каждом шаге. Основной особенностью RNN является скрытое состояние, которое содержит некоторую информацию о последовательности.
Где используют рекуррентные нейросети?
Рекуррентные нейронные сети продемонстрировали большой успех во многих задачах NLP. На этом этапе нужно упомянуть, что наиболее часто используемым типом RNN являются LSTM, которые намного лучше захватывают (хранят) долгосрочные зависимости, чем RNN. Но не волнуйтесь, LSTM — это, по сути, то же самое, что и RNN, которые мы разберем в этом уроке, у них просто есть другой способ вычисления скрытого состояния. Более подробно мы рассмотрим LSTM в другом посте. Вот некоторые примеры приложений RNN в NLP (без ссылок на исчерпывающий список).
Языковое моделирование и генерация текстов
Учитывая последовательность слов, мы хотим предсказать вероятность каждого слова (в словаре). Языковые модели позволяют нам измерить вероятность выбора, что является важным вкладом в машинный перевод (поскольку предложения с большой вероятностью правильны). Побочным эффектом такой способности является возможность генерировать новые тексты путем выбора из выходных вероятностей. Мы можем генерировать и другие вещи , в зависимости от того, что из себя представляют наши данные. В языковом моделировании наш вход обычно представляет последовательность слов (например, закодированных как вектор с одним горячим состоянием (one-hot)), а выход — последовательность предсказанных слов. При обучении нейронной сети , мы подаем на вход следующему слою предыдущий выход o_t=x_{t+1}, поскольку хотим, чтобы результат на шаге t был следующим словом.
Исследования по языковому моделированию и генерации текста:
- Word2Vec: как работать с векторными представлениями слов
- NLP Architect от Intel: open source библиотека моделей обработки естественного языка
Машинный перевод
Машинный перевод похож на языковое моделирование, поскольку вектор входных параметров представляет собой последовательность слов на исходном языке (например, на немецком). Мы хотим получить последовательность слов на целевом языке (например, на английском). Ключевое различие заключается в том, что мы получим эту последовательность только после того, как увидим все входные параметры, поскольку первое слово переводимого предложения может потребовать информации всей последовательности вводимых слов.

RNN для машинного перевода
Распознавание речи
По входной последовательности акустических сигналов от звуковой волны, мы можем предсказать последовательность фонетических сегментов вместе со своими вероятностями.
Генерация описания изображений
Вместе со сверточными нейронными сетями RNN использовались как часть модели генерации описаний неразмеченных изображений. Удивительно, насколько хорошо они работают. Комбинированная модель совмещает сгенерированные слова с признаками, найденными на изображениях.

Глубокие визуально-семантические совмещения для генерации описания изображений. Источник: http://cs.stanford.edu/people/karpathy/deepimagesent/
Обучение RNN
Обучение RNN аналогично обучению обычной нейронной сети. Мы также используем алгоритм обратного распространения ошибки (backpropagation), но с небольшим изменением. Поскольку одни и те же параметры используются на всех временных этапах в сети, градиент на каждом выходе зависит не только от расчетов текущего шага, но и от предыдущих временных шагов. Например, чтобы вычислить градиент при t = 4, нам нужно было бы «распространить ошибку» на 3 шага и суммировать градиенты. Этот алгоритм называется «алгоритмом обратного распространения ошибки сквозь время» (Backpropagation Through Time, BPTT). Если вы не видите в этом смысла, не беспокойтесь, у нас еще будет статья со всеми кровавыми подробностями. На данный момент просто помните о том, что рекуррентные нейронные сети, прошедшие обучение с BPTT, испытывают трудности с изучением долгосрочных зависимостей (например, зависимость между шагами, которые находятся далеко друг от друга) из-за затухания/взрывания градиента. Чтобы обойти эти проблемы, существует определенный механизм, были разработаны специальные архитектуры PNN (например LSTM).
Модификации RNN
На протяжении многих лет исследователи разрабатывали более сложные типы RNN, чтобы справиться с некоторыми из недостатков классической модели. Мы рассмотрим их более подробно в другой статье позже, но я хочу, чтобы этот раздел послужил кратким обзором, чтобы познакомить вас с классификацией моделей.
Двунаправленные рекуррентные нейронные сети (Bidirectional RNNs) основаны на той идее, что выход в момент времени t может зависеть не только от предыдущих элементов в последовательности, но и от будущих. Например, если вы хотите предсказать недостающее слово в последовательности, учитывая как в левый, так и в правый контекст. Двунаправленные рекуррентные нейронные сети довольно просты. Это всего лишь два RNN, уложенных друг на друга. Затем выход вычисляется на основе скрытого состояния обоих RNN.

Глубинные рекуррентные нейронные сети похожи на двунаправленные RNN, только теперь у нас есть несколько уровней на каждый шаг времени. На практике это даст более высокий потенциал, но нам также потребуется много данных для обучения.
Сети LSTM довольно популярны в наши дни, мы кратко говорили о них выше. LSTM не имеют принципиально отличающейся архитектуры от RNN, но они используют другую функцию для вычисления скрытого состояния. Память в LSTM называется ячейками, и вы можете рассматривать их как черные ящики, которые принимают в качестве входных данных предыдущее состояние h_ {t-1} и текущий входной параметр x_t. Внутри, эти ячейки, решают, какую память сохранить и какую стереть. Затем они объединяют предыдущее состояние, текущую память и входной параметр. Оказывается, эти типы единиц очень эффективны в захвате (хранении) долгосрочных зависимостей.
RNN