Министерство
сельского хозяйства РФ
Федеральное
государственное бюджетное образовательное
учреждение
высшего профессионального образования
«Пермская
государственная сельскохозяйственная
академия
имени
академика Д.Н.Прянишникова»
Кафедра финансов,
кредита и экономического анализа
|
Выполнила: студентка По Группа Гонцова Проверил: |
Пермь 2014
Содержание
-
Ошибки
аппроксимации и ее определение………………………………….3 -
Аналитический
способ выравнивания временного ряда
и используемые при этом
функции……………………………………………………………..4 -
Практическая
часть…………………………………………………………..11-
Задание
1………………………………………………………………11 -
Задание
2……………………………………………….………………19
-
Список
использованной литературы…………………………………………..25
-
Ошибки аппроксимации и ее определение.
Средняя ошибка
аппроксимации
– это среднее отклонение расчетных
данных от фактических. Она определяется
в процентах по модулю.
Фактические
значения результативного признака
отличаются от теоретических. Чем меньше
это отличие, тем ближе теоретические
значения подходят к эмпирическим данным,
это лучшее качество модели. Величина
отклонений фактических и расчетных
значений результативного признака по
каждому наблюдению представляет собой
ошибку аппроксимации. Их число
соответствует объему совокупности. В
отдельных случаях ошибка апроксимации
может оказаться равной нулю. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям.
Поскольку может
быть как величиной положительной, так
и отрицательной, то ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю. Отклонения можно
рассматривать как абсолютную ошибку
аппроксимации, и как относительную
ошибку аппроксимации. Чтоб иметь общее
суждение о качестве модели из относительных
отклонений по каждому наблюдению,
определяют среднюю ошибку аппроксимации
как среднюю арифметическую простую.
Среднюю ошибку
аппроксимации рассчитают по формуле:
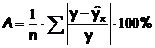
Возможно и иное
определение средней ошибки аппроксимации:
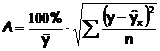
Если А£10-12%, то
можно говорить о хорошем качестве
модели.
-
Аналитический способ выравнивания временного ряда и используемые при этом функции.
Более
совершенным приемом выявления основной
тенденции развития в рядах динамики
является аналитическое выравнивание.
При изучении общей тенденции методом
аналитического выравнивания исходят
из того, что изменения уровней ряда
динамики могут быть с той или иной
степенью точности приближения выражены
определенными математическими функциями.
Вид уравнения определяется характером
динамики развития конкретного явления.
На практике по имеющемуся временному
ряду задают вид и находят параметры
функции y=f(t), а затем анализируют поведение
отклонений от тенденции. Чаще всего при
выравнивании используются следующие
зависимости: линейная, параболическая
и экспоненциальная. Во многих случаях
моделирование рядов динамики с помощью
полиномов или экспоненциальной функции
не дает удовлетворительных результатов,
так как в рядах динамики содержатся
заметные периодические колебания вокруг
общей тенденции. В таких случаях следует
использовать гармонический анализ
(гармоники ряда Фурье). Применение,
именно, этого метода предпочтительно,
поскольку он определяет закон, по
которому можно достаточно точно
спрогнозировать значения уровней ряда.
![]()
Целью же аналитического
выравнивания динамического ряда является
определение аналитической или графической
зависимости y=f(t). Функцию y=f(t) выбирают
таким образом, чтобы она давала
содержательное объяснение изучаемого
процесса. Это могут быть различные
функции.
Системы уравнений
вида y=f(t) для оценки параметров полиномов
по МНК
(кликабельно)
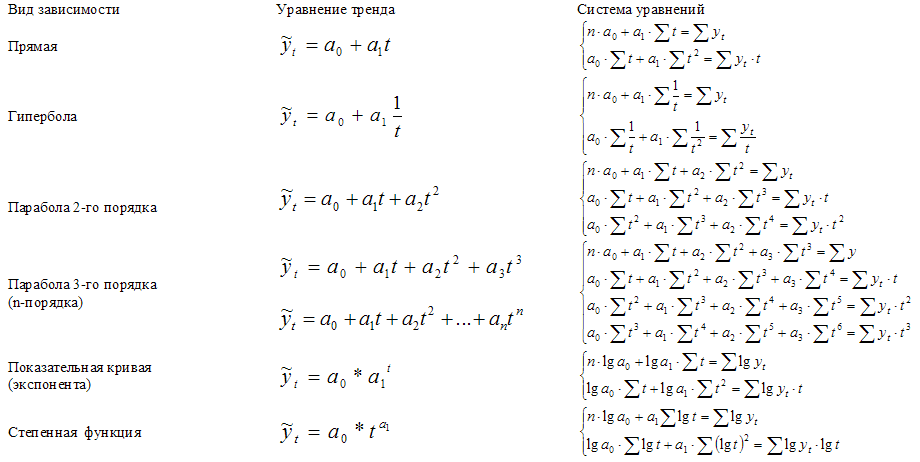
Графическое
представление полиномов n-порядка
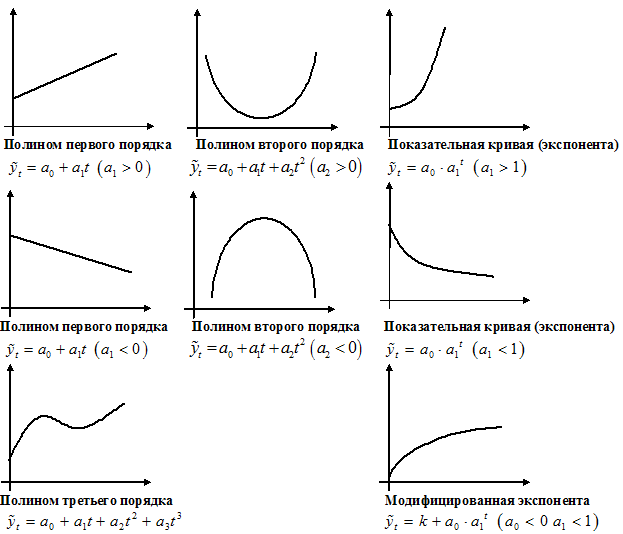
1.
Если изменение уровней ряда характеризуется
равномерным увеличением (уменьшением)
уровней, когда абсолютные цепные приросты
близки по величине, тенденцию развития
характеризует уравнение прямой линии.
2.
Если в результате анализа типа тенденции
динамики установлена криволинейная
зависимость, примерно с постоянным
ускорением, то форма тенденции выражается
уравнением параболы второго порядка.
3.
Если рост уровней ряда динамики происходит
в геометрической прогрессии, т.е. цепные
коэффициенты роста более или менее
постоянны, выравнивание ряда динамики
ведется по показательной функции.
После
выбора вида уравнения необходимо
определить параметры уравнения. Самый
распространенный способ определения
параметров уравнения — это метод
наименьших квадратов, в котором в
качестве решения принимается точка
минимума суммы квадратов отклонений
между теоретическими (выравненными по
выбранному уравнению) и эмпирическими
уровнями.
Выравнивание
по прямой (определение линии тренда)
имеет выражение: yt=a0+a1t
t—условное
обозначение времени;
а
0 и a1—параметры искомой прямой.
Параметры
прямой находятся из решения системы
уравнений:
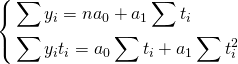
Система уравнений
упрощается, если значения t подобрать
так, чтобы их сумма равнялась Σt = 0, т. е.
начало отсчета времени перенести в
середину рассматриваемого периода.
Если до переноса точки отсчета t = 1, 2, 3,
4…, то после переноса:
если число уровней
ряда нечетное t = -4 -3 -2 -1 0 +1 +2 +3 +4
если
число уровней ряда четное t = -7 -5 -3
-1 +1 +3 +5 +7
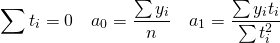
Таким образом, ∑t
в нечетной степени всегда будет равна
нулю.
Аналогично находятся
параметры параболы 2-го порядка из
решения системы уравнений:
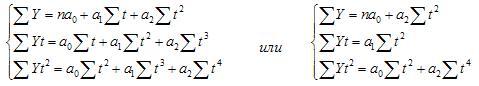
Выравнивание
по среднему абсолютному приросту или
среднему коэффициенту роста:

Δ-средний абсолютный
прирост;
К-средний коэффициент
роста;
У0-начальный уровень
ряда;
Уn-конечный уровень
ряда;
t-порядковый номер
уровня, начиная с нуля.
Построив
уравнение регрессии, проводят оценку
его надежности. Значимость выбранного
уравнения регрессии, параметров уравнения
и коэффициента корреляции следует
оценить, применив критические методы
оценки:
F-критерий Фишера,
t–критерий Стьюдента, при этом, расчетные
значения критериев сравниваются с
табличными (критическими) при заданном
уровне значимости и числе степеней
свободы. Fфакт > Fтеор — уравнение
регрессии адекватно.
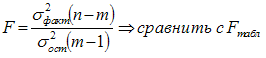
n — число наблюдений
(уровней ряда), m — число параметров
уравнения (модели) регрессии.
Проверка
адекватности уравнения регрессии (
качества модели в целом) осуществляется
с помощью средней ошибки аппроксимации,
величина которой не должна превышать
10-12% (рекомендовано).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Одной из задач, возникающих при анализе рядов
динамики, является установление закономерности изменения уровней изучаемого
показателя во времени. В некоторых случаях эта закономерность, общая тенденция
развития объекта вполне ясно отображается уровнями динамического ряда. Но часто
приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают
самые различные изменения (то возрастают, то убывают) и можно говорить лишь об
общей тенденции развития явления, либо о тенденции к росту, либо к снижению. В
этих случаях для определения основной тенденции развития явления, достаточно
устойчивой на протяжении данного периода, используют особые приемы обработки
рядов динамики.
Уровни ряда динамики формируются под совокупным
влиянием множества длительно и кратковременно действующих факторов и в том
числе различного рода случайных обстоятельств.
Выявление основной закономерности изменения уровней
ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных
воздействий. Выявление основной тенденции развития (тренда) называется в
статистике также выравниванием временного ряда, а методы выявления основной
тенденции — методами выравнивания. Выравнивание позволяет характеризовать
особенность изменения во времени данного динамического ряда в наиболее общем
виде как функцию времени, предполагая, что через время можно выразить влияние
всех основных факторов.
Приемы сглаживания динамических рядов (укрупнение
интервала и метод скользящей средней) могут рассматриваться как важное
вспомогательное средство, облегчающее применение других методов и, в частности,
более строгих методов выявления тенденции. Для того чтобы представить
количественную модель, выражающую общую тенденцию изменений уровней
динамического ряда во времени, используется аналитическое выравнивание ряда
динамики.
В этом случае фактические уровни заменяются
уровнями, вычисленными на основе определенной кривой.
Предполагается, что она отражает общую тенденцию изменения во времени
изучаемого показателя.
При аналитическом выравнивании ряда динамики
закономерно изменяющийся уровень изучаемого показателя оценивается как функция
времени
,
Где
—
уровни динамического ряда, вычисленные по соответствующему аналитическому
уравнению на момент времени t.
При выборе формы уравнения следует исходить и из
объема имеющейся информации. Чем больше параметров содержит уравнение тренда,
тем больше должно быть наблюдений при одной и той же степени надежности
оценивания. Выбор формы кривой может осуществляться: и на основе принятого
критерия, в качестве которого может служить сумма квадратов отклонений
фактических значений от значений, рассчитанных по уравнению тренда. Из
совокупности кривых выбирается та, которой соответствует минимальное значение
критерия. Рассмотрим аналитическое выравнивание ряда динамики
по прямой, т.е. аналитическое уравнение вида:
где
-порядковый номер
периодов или моментов времени.
Параметры
и
прямой рассчитываются
по методу наименьших квадратов (МНК).
Система нормальных уравнений в данном
случае имеет вид:
Поиск параметров уравнения можно упростить, если
отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда
динамики была равна нулю
.
При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отчета времени
(этому периоду или моменту времени придается нулевое значение). Даты времени,
стоящие выше этого уровня, обозначаются натуральными числами со знаками минус,
а ниже -натуральными числами со знаками плюс.
При условии
получим:
Правильность расчета уровней выравниваемого ряда
динамики может быть проверена следующим образом: сумма значений эмпирического
ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е.
Аналитическое уравнение представляет собой математическую
модель развития явления и дает выражение статистической закономерности,
проявляющейся в рядах динамики. Следует помнить, что прием аналитического
выравнивания содержит в себе ряд условностей, связанных
прежде всего с тем, что уровни, характеризующие тот или иной динамический ряд,
рассматриваются как функция времени. В действительности же развитие явлений
обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие
факторы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает
как внешнее выражение этих факторов, как их суммарное действие; оказывающее
влияние на изменение уровня в отдельно взятые промежутки или моменты времени.
Выявить основную тенденцию развития явления методом наименьших квадратов можно
лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на
всем рассматриваемом промежутке времени одинаково, что их количественное и
качественное изменение происходит под действием одного и того же комплекса основных
факторов, определяющих движение данного ряда динамики.
Модели, учитывающие общие закономерности изменения
экономического явления в изучаемый интервал времени и изменения во времени
влияния комплекса факторов, называют многофакторными динамическими моделями.
Выделим особенности моделей аналитического
выравнивания уровней динамического ряда, накладывающие ограничения на их
использование. Во-первых, динамические ряды, к которым применяется
аппроксимация, должны быть достаточно длинными. Во-вторых, применение
аппроксимации наиболее целесообразно в случае медленно и плавно меняющегося
уровня. В-третьих, аппроксимация как метод моделирования практически не
адаптируется к изменяющимся условиям формирования уровней ряда; при появлении
новых данных построение модели должно быть проведено заново. В-четвертых, при
использовании для расчета параметров уравнения метода наименьших квадратов
(МНК) считается, что значимость информации в пределах отрезка аппроксимации
одинакова независимо от давности полученных данных, в то время как более
поздние данные имеют большую ценность.
Помимо этого, динамические ряды экономических
показателей часто имеют небольшую длину и подвержены значительным колебаниям,
которые аппроксимация предвидеть не может.
Задача
В таблице приведены готовые данные о
трудоемкости производства:
| Год | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| Трудоемкость производства, человек-часов |
8 | 8.4 | 7.6 | 7 | 7.3 | 6.6 | 5.9 | 5 | 5.2 |
-
Провести аналитическое выравнивание ряда динамики по прямой.
Построить точечный и интервальный
прогноз на 2018 год.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Решение
1) Произведем аналитическое выравнивание ряда по прямой.
Составим расчетную таблицу:
Расчетная вспомогательная таблица 1
| Годы | ||||
| 2009 | -4 | 8 | 16 | -32 |
| 2010 | -3 | 8,4 | 9 | -25,2 |
| 2011 | -2 | 7,6 | 4 | -15,2 |
| 2012 | -1 | 7 | 1 | -7 |
| 2013 | 0 | 7,3 | 0 | 0,0 |
| 2014 | 1 | 6,6 | 1 | 6,6 |
| 2015 | 2 | 5,9 | 4 | 11,8 |
| 2016 | 3 | 5 | 9 | 15 |
| 2017 | 4 | 5,2 | 16 | 20,8 |
| Итого | 0 | 61,0 | 60 | -25,2 |
Коэффициенты уравнения линейного тренда найдем по формулам:
Уравнение линейного тренда имеет вид:
2) Составим расчетную таблицу:
Расчетная вспомогательная таблица 2
| Годы |
Теоретические значения |
|||
| 2009 | -4 | 8 | 8,48 | 0,2304 |
| 2010 | -3 | 8,4 | 8,06 | 0,1156 |
| 2011 | -2 | 7,6 | 7,64 | 0,0016 |
| 2012 | -1 | 7 | 7,22 | 0,0484 |
| 2013 | 0 | 7,3 | 6,8 | 0,25 |
| 2014 | 1 | 6,6 | 6,38 | 0,0484 |
| 2015 | 2 | 5,9 | 5,96 | 0,0036 |
| 2016 | 3 | 5 | 5,54 | 0,2916 |
| 2017 | 4 | 5,2 | 5,12 | 0,0064 |
| Итого | — | — | — | 0,996 |
Среднеквадратическая ошибка:
Точечный прогноз на 2018 год (t=5):
Ошибка
прогноза составит:
По таблице критерия Стьюдента,
для доверительной вероятности
(уровня значимости
) находим:
Вывод к задаче
Таким образом
тренд для трудоемкости производства выражается линейным уравнением
.
Согласно прогнозу, в 2018 году трудоемкость производства с вероятностью 0,95
будет лежать в пределах от 3,6 до 5,8 человеко-часов.
Динамические ряды — краткое руководство по анализу изменений явлений во времени
Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.
Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.
Целью анализа динамических рядов является:
- выявление закономерности изменения изучаемого явления во времени;
- прогнозирование (экстраполирование) полученных данных на последующие
годы.
Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).
Типы динамических рядов:
- В зависимости от вида уровня ряда:
а) простые (уровень ряда выражен абсолютными числами);
б) сложные (уровень ряда выражен обобщающими коэффициентами).
- В зависимости от способа формирования временного интервала:
а) моментные (данные собираются на определенный момент времени);
б) интервальные (данные собираются за определенный период времени).
- В зависимости от выраженности изменений явления во времени (определяется по коэффициенту корреляции между временем и изучаемым явлением).
а) с выраженной тенденцией (r =0,7 — 1,0);
б) с неустойчивой тенденцией (r =0,3 — 0,69);
в) с отсутствием тенденции ( r = 0 — 0,29).
Основное требование, предъявляемое к анализируемым динамическим рядам, заключается в сопоставимости их уровней. Для оценки сопоставимости проводят предварительный анализ полученных данных по следующим критериям:
- единство территории, на которой проводился сбор данных;
- единая методология учета данных;
- единые временные интервалы, в течение которых проводилась регистрация
данных.
Методика анализа динамических рядов
Методика аналитики предусматривает выполнение последовательных действий:
- Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.
- Оценить наличие и силу корреляции изучаемого явления от времени.
- Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа — разделить эти компоненты и выявить основную закономерность изменения явления во времени. Для выявления и описания тренда динамический ряд подвергают обработке — выравниванию.
Способы выравнивания динамических рядов
Чтобы произвести выравнивание динамических рядов потребуются следующие действия:
- Укрупнение временных интервалов (периодов), в течение которых изучается явление.
- Сглаживание ряда методом скользящей средней.
- Аналитический способ.
При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:
а) линейная зависимость:![]()
б) экспоненциальная зависимость:![]()
в) показательная зависимость:![]()
г) параболическая зависимость:![]()
и др.
где a0, a1, а2 — параметры уравнения;
у – теоретический уровень;
t – временной интервал.
В качестве примера возьмем линейную зависимость и проведем выравнивание, используя для нахождения параметров уравнения а0 ,а1 способ наименьших квадратов. Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:
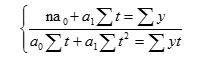
где у — уровни фактического ряда;
n — количество уровней;
t — порядковый номер временного периода.
Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда. При нечетном ряде середина обозначается через 0, а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины (например: -5,-4,-3,-2,-1, 0,+1.+2,+3,->:4,+5). При четном ряде две средние временные точки обозначаются через +1 и -1, а остальные ранги присваиваются через две единицы (например: -5,-3,-1,+1,+3,+5).
При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:
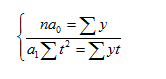
Отсюда находим параметры уравнения:
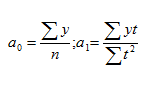
Подставляя в уравнение у = а0 + а1t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.
При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обусловлено как случайными колебаниями, так и неправильно подобранным аппроксимирующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.
Оценка точности аппроксимации возможна с помощью нахождения
Для получения точной оценки необходимо найти такие величины:
а) коэффициент вариации:

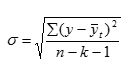
где у- фактический уровень ряда;
yt — теоретический уровень ряда;
k- число параметров уравнения;
n- число уровней ряда.
Аппроксимация считается точной при Cv не более 15%.
б) коэффициент расхождения Тейла:
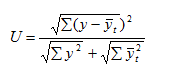
где у — фактический уровень ряда;
yt — теоретический уровень ряда.
Аппроксимация считается точной при U не более 5%
После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факторов и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.
Вычисление основных показателей динамического ряда
Алгоритм вычислений ведущих параметров динамических рядов:
Условные обозначения:
yi- текущий уровень (сравниваемый);
уi-1— базисный уровень (с каким сравнивают);
t- период времени, в течение которого уровень предполагается неизменным.
1.Абсолютный прирост (убыль) :
![]()
2.Темп роста (убыли):
![]()
3.Темп прироста (относительная скорость), темп убыли :
![]()
4.Средний темп прироста (убыли):
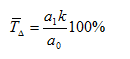
где а0; а1 — параметры уравнения;
k = 1 при нечетном ряде;
k = 2 при четном ряде.
5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.
Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
Более совершенным приемом выявления основной тенденции развития в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления. На практике по имеющемуся временному ряду задают вид и находят параметры функции y=f(t), а затем анализируют поведение отклонений от тенденции. Чаще всего при выравнивании используются следующие зависимости: линейная, параболическая и экспоненциальная. Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции. В таких случаях следует использовать гармонический анализ (гармоники ряда Фурье). Применение, именно, этого метода предпочтительно, поскольку он определяет закон, по которому можно достаточно точно спрогнозировать значения уровней ряда.
![]()
Целью же аналитического выравнивания динамического ряда является определение аналитической или графической зависимости y=f(t). Функцию y=f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. Это могут быть различные функции.
Системы уравнений вида y=f(t) для оценки параметров полиномов по МНК
(кликабельно)

Графическое представление полиномов n-порядка

1. Если изменение уровней ряда характеризуется равномерным увеличением (уменьшением) уровней, когда абсолютные цепные приросты близки по величине, тенденцию развития характеризует уравнение прямой линии.
2. Если в результате анализа типа тенденции динамики установлена криволинейная зависимость, примерно с постоянным ускорением, то форма тенденции выражается уравнением параболы второго порядка.
3. Если рост уровней ряда динамики происходит в геометрической прогрессии, т.е. цепные коэффициенты роста более или менее постоянны, выравнивание ряда динамики ведется по показательной функции.
После выбора вида уравнения необходимо определить параметры уравнения. Самый распространенный способ определения параметров уравнения — это метод наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими (выравненными по выбранному уравнению) и эмпирическими уровнями.
Выравнивание по прямой (определение линии тренда) имеет выражение: yt=a0+a1t
- t—условное обозначение времени;
- а0 и a1—параметры искомой прямой.
Параметры прямой находятся из решения системы уравнений:
![Rendered by QuickLaTeX.com [left{ begin{gathered} sum {{y_i} = n{a_0} + {a_1}sum {{t_i}} } hfill sum {{y_i}{t_i} = {a_0}sum {{t_i} + {a_1}sum {t_i^2} } } hfill end{gathered} right.]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-8eefa365ccc5999df86b01ec72109949_l3.png)
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась Σt = 0, т. е. начало отсчета времени перенести в середину рассматриваемого периода. Если до переноса точки отсчета t = 1, 2, 3, 4…, то после переноса:
- если число уровней ряда нечетное t = -4 -3 -2 -1 0 +1 +2 +3 +4
- если число уровней ряда четное t = -7 -5 -3 -1 +1 +3 +5 +7
![]()
Таким образом, ∑t в нечетной степени всегда будет равна нулю.
Аналогично находятся параметры параболы 2-го порядка из решения системы уравнений:

Выравнивание по среднему абсолютному приросту или среднему коэффициенту роста:
![]()
- Δ-средний абсолютный прирост;
- К-средний коэффициент роста;
- У0-начальный уровень ряда;
- Уn-конечный уровень ряда;
- t-порядковый номер уровня, начиная с нуля.
Построив уравнение регрессии, проводят оценку его надежности. Значимость выбранного уравнения регрессии, параметров уравнения и коэффициента корреляции следует оценить, применив критические методы оценки:
F-критерий Фишера, t–критерий Стьюдента, при этом, расчетные значения критериев сравниваются с табличными (критическими) при заданном уровне значимости и числе степеней свободы. Fфакт > Fтеор – уравнение регрессии адекватно.

n — число наблюдений (уровней ряда), m — число параметров уравнения (модели) регрессии.
Проверка адекватности уравнения регрессии ( качества модели в целом) осуществляется с помощью средней ошибки аппроксимации, величина которой не должна превышать 10-12% (рекомендовано).

Рассмотрим на примере аналитическое выравнивание ряда динамики по прямой с переносом точки отсчета в середину ряда:
|
Годы |
Объем валовой продукции |
Условное обозн. года |
Расчетные значения |
Выровненный ряд |
|
|
Yi |
t |
t2 |
Y*t |
Ỹ=209,06+3,91t |
|
|
1990 |
187,8 |
-5 |
25 |
-939,00 |
189,51 |
|
1991 |
185,7 |
-4 |
16 |
-742,94 |
193,42 |
|
1992 |
195,8 |
-3 |
9 |
-587,29 |
197,33 |
|
1993 |
207,9 |
-2 |
4 |
-415,80 |
201,24 |
|
1994 |
208,3 |
-1 |
1 |
-208,32 |
205,15 |
|
1995 |
208,6 |
0 |
0 |
0,00 |
209,06 |
|
1996 |
219,7 |
1 |
1 |
219,70 |
212,97 |
|
1997 |
218,5 |
2 |
4 |
437,00 |
216,88 |
|
1998 |
222,2 |
3 |
9 |
666,60 |
220,79 |
|
1999 |
225,1 |
4 |
16 |
900,40 |
224,7 |
|
2000 |
220,0 |
5 |
25 |
1100,00 |
228,61 |
|
Итого |
2299,62 |
0 |
110 |
430,35 |
2299,62 |
|
ΣYi |
Σt |
Σt2 |
ΣY*t |
ΣỸ |
Решение системы линейных уравнений:
![]()
Σt в нечетной степени всегда равна нулю, поэтому система уравнений упрощается и принимает следующий вид:
![]()
![]()
![]()
Сумма уровней выровненного ряда должна равняться сумме уровней исходного ряда, что, в свою очередь, подтверждает правильность расчетов. Выровненный ряд динамики по прямой вида (линейный тренд): Ỹ=209,06+3,91t

Смотри аналитическое выравнивание на примере:
- п.V: Сезонная корректировка временного ряда
- Аналитическое выравнивание себестоимости зерновых культур
Министерство
сельского хозяйства РФ
Федеральное
государственное бюджетное образовательное
учреждение
высшего профессионального образования
«Пермская
государственная сельскохозяйственная
академия
имени
академика Д.Н.Прянишникова»
Кафедра финансов,
кредита и экономического анализа
|
Выполнила: студентка По Группа Гонцова Проверил: |
Пермь 2014
Содержание
-
Ошибки
аппроксимации и ее определение………………………………….3 -
Аналитический
способ выравнивания временного ряда
и используемые при этом
функции……………………………………………………………..4 -
Практическая
часть…………………………………………………………..11-
Задание
1………………………………………………………………11 -
Задание
2……………………………………………….………………19
-
Список
использованной литературы…………………………………………..25
-
Ошибки аппроксимации и ее определение.
Средняя ошибка
аппроксимации
– это среднее отклонение расчетных
данных от фактических. Она определяется
в процентах по модулю.
Фактические
значения результативного признака
отличаются от теоретических. Чем меньше
это отличие, тем ближе теоретические
значения подходят к эмпирическим данным,
это лучшее качество модели. Величина
отклонений фактических и расчетных
значений результативного признака по
каждому наблюдению представляет собой
ошибку аппроксимации. Их число
соответствует объему совокупности. В
отдельных случаях ошибка апроксимации
может оказаться равной нулю. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям.
Поскольку может
быть как величиной положительной, так
и отрицательной, то ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю. Отклонения можно
рассматривать как абсолютную ошибку
аппроксимации, и как относительную
ошибку аппроксимации. Чтоб иметь общее
суждение о качестве модели из относительных
отклонений по каждому наблюдению,
определяют среднюю ошибку аппроксимации
как среднюю арифметическую простую.
Среднюю ошибку
аппроксимации рассчитают по формуле:
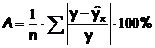
Возможно и иное
определение средней ошибки аппроксимации:
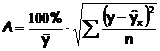
Если А£10-12%, то
можно говорить о хорошем качестве
модели.
-
Аналитический способ выравнивания временного ряда и используемые при этом функции.
Более
совершенным приемом выявления основной
тенденции развития в рядах динамики
является аналитическое выравнивание.
При изучении общей тенденции методом
аналитического выравнивания исходят
из того, что изменения уровней ряда
динамики могут быть с той или иной
степенью точности приближения выражены
определенными математическими функциями.
Вид уравнения определяется характером
динамики развития конкретного явления.
На практике по имеющемуся временному
ряду задают вид и находят параметры
функции y=f(t), а затем анализируют поведение
отклонений от тенденции. Чаще всего при
выравнивании используются следующие
зависимости: линейная, параболическая
и экспоненциальная. Во многих случаях
моделирование рядов динамики с помощью
полиномов или экспоненциальной функции
не дает удовлетворительных результатов,
так как в рядах динамики содержатся
заметные периодические колебания вокруг
общей тенденции. В таких случаях следует
использовать гармонический анализ
(гармоники ряда Фурье). Применение,
именно, этого метода предпочтительно,
поскольку он определяет закон, по
которому можно достаточно точно
спрогнозировать значения уровней ряда.
![]()
Целью же аналитического
выравнивания динамического ряда является
определение аналитической или графической
зависимости y=f(t). Функцию y=f(t) выбирают
таким образом, чтобы она давала
содержательное объяснение изучаемого
процесса. Это могут быть различные
функции.
Системы уравнений
вида y=f(t) для оценки параметров полиномов
по МНК
(кликабельно)
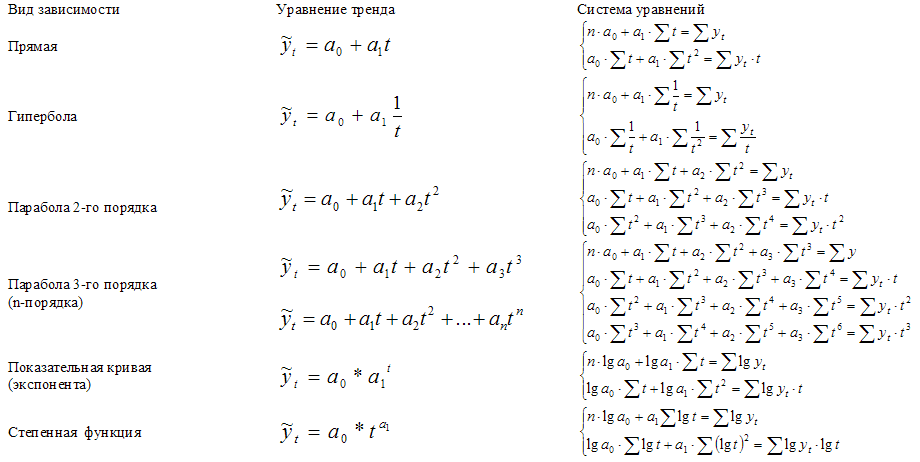
Графическое
представление полиномов n-порядка

1.
Если изменение уровней ряда характеризуется
равномерным увеличением (уменьшением)
уровней, когда абсолютные цепные приросты
близки по величине, тенденцию развития
характеризует уравнение прямой линии.
2.
Если в результате анализа типа тенденции
динамики установлена криволинейная
зависимость, примерно с постоянным
ускорением, то форма тенденции выражается
уравнением параболы второго порядка.
3.
Если рост уровней ряда динамики происходит
в геометрической прогрессии, т.е. цепные
коэффициенты роста более или менее
постоянны, выравнивание ряда динамики
ведется по показательной функции.
После
выбора вида уравнения необходимо
определить параметры уравнения. Самый
распространенный способ определения
параметров уравнения — это метод
наименьших квадратов, в котором в
качестве решения принимается точка
минимума суммы квадратов отклонений
между теоретическими (выравненными по
выбранному уравнению) и эмпирическими
уровнями.
Выравнивание
по прямой (определение линии тренда)
имеет выражение: yt=a0+a1t
t—условное
обозначение времени;
а
0 и a1—параметры искомой прямой.
Параметры
прямой находятся из решения системы
уравнений:
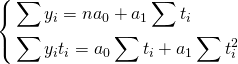
Система уравнений
упрощается, если значения t подобрать
так, чтобы их сумма равнялась Σt = 0, т. е.
начало отсчета времени перенести в
середину рассматриваемого периода.
Если до переноса точки отсчета t = 1, 2, 3,
4…, то после переноса:
если число уровней
ряда нечетное t = -4 -3 -2 -1 0 +1 +2 +3 +4
если
число уровней ряда четное t = -7 -5 -3
-1 +1 +3 +5 +7
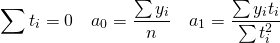
Таким образом, ∑t
в нечетной степени всегда будет равна
нулю.
Аналогично находятся
параметры параболы 2-го порядка из
решения системы уравнений:
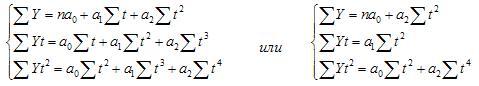
Выравнивание
по среднему абсолютному приросту или
среднему коэффициенту роста:

Δ-средний абсолютный
прирост;
К-средний коэффициент
роста;
У0-начальный уровень
ряда;
Уn-конечный уровень
ряда;
t-порядковый номер
уровня, начиная с нуля.
Построив
уравнение регрессии, проводят оценку
его надежности. Значимость выбранного
уравнения регрессии, параметров уравнения
и коэффициента корреляции следует
оценить, применив критические методы
оценки:
F-критерий Фишера,
t–критерий Стьюдента, при этом, расчетные
значения критериев сравниваются с
табличными (критическими) при заданном
уровне значимости и числе степеней
свободы. Fфакт > Fтеор — уравнение
регрессии адекватно.
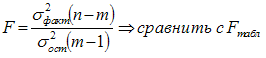
n — число наблюдений
(уровней ряда), m — число параметров
уравнения (модели) регрессии.
Проверка
адекватности уравнения регрессии (
качества модели в целом) осуществляется
с помощью средней ошибки аппроксимации,
величина которой не должна превышать
10-12% (рекомендовано).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Одной из задач, возникающих при анализе рядов
динамики, является установление закономерности изменения уровней изучаемого
показателя во времени. В некоторых случаях эта закономерность, общая тенденция
развития объекта вполне ясно отображается уровнями динамического ряда. Но часто
приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают
самые различные изменения (то возрастают, то убывают) и можно говорить лишь об
общей тенденции развития явления, либо о тенденции к росту, либо к снижению. В
этих случаях для определения основной тенденции развития явления, достаточно
устойчивой на протяжении данного периода, используют особые приемы обработки
рядов динамики.
Уровни ряда динамики формируются под совокупным
влиянием множества длительно и кратковременно действующих факторов и в том
числе различного рода случайных обстоятельств.
Выявление основной закономерности изменения уровней
ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных
воздействий. Выявление основной тенденции развития (тренда) называется в
статистике также выравниванием временного ряда, а методы выявления основной
тенденции — методами выравнивания. Выравнивание позволяет характеризовать
особенность изменения во времени данного динамического ряда в наиболее общем
виде как функцию времени, предполагая, что через время можно выразить влияние
всех основных факторов.
Приемы сглаживания динамических рядов (укрупнение
интервала и метод скользящей средней) могут рассматриваться как важное
вспомогательное средство, облегчающее применение других методов и, в частности,
более строгих методов выявления тенденции. Для того чтобы представить
количественную модель, выражающую общую тенденцию изменений уровней
динамического ряда во времени, используется аналитическое выравнивание ряда
динамики.
В этом случае фактические уровни заменяются
уровнями, вычисленными на основе определенной кривой.
Предполагается, что она отражает общую тенденцию изменения во времени
изучаемого показателя.
При аналитическом выравнивании ряда динамики
закономерно изменяющийся уровень изучаемого показателя оценивается как функция
времени
,
Где
—
уровни динамического ряда, вычисленные по соответствующему аналитическому
уравнению на момент времени t.
При выборе формы уравнения следует исходить и из
объема имеющейся информации. Чем больше параметров содержит уравнение тренда,
тем больше должно быть наблюдений при одной и той же степени надежности
оценивания. Выбор формы кривой может осуществляться: и на основе принятого
критерия, в качестве которого может служить сумма квадратов отклонений
фактических значений от значений, рассчитанных по уравнению тренда. Из
совокупности кривых выбирается та, которой соответствует минимальное значение
критерия. Рассмотрим аналитическое выравнивание ряда динамики
по прямой, т.е. аналитическое уравнение вида:
где
-порядковый номер
периодов или моментов времени.
Параметры
и
прямой рассчитываются
по методу наименьших квадратов (МНК).
Система нормальных уравнений в данном
случае имеет вид:
Поиск параметров уравнения можно упростить, если
отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда
динамики была равна нулю
.
При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отчета времени
(этому периоду или моменту времени придается нулевое значение). Даты времени,
стоящие выше этого уровня, обозначаются натуральными числами со знаками минус,
а ниже -натуральными числами со знаками плюс.
При условии
получим:
Правильность расчета уровней выравниваемого ряда
динамики может быть проверена следующим образом: сумма значений эмпирического
ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е.
Аналитическое уравнение представляет собой математическую
модель развития явления и дает выражение статистической закономерности,
проявляющейся в рядах динамики. Следует помнить, что прием аналитического
выравнивания содержит в себе ряд условностей, связанных
прежде всего с тем, что уровни, характеризующие тот или иной динамический ряд,
рассматриваются как функция времени. В действительности же развитие явлений
обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие
факторы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает
как внешнее выражение этих факторов, как их суммарное действие; оказывающее
влияние на изменение уровня в отдельно взятые промежутки или моменты времени.
Выявить основную тенденцию развития явления методом наименьших квадратов можно
лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на
всем рассматриваемом промежутке времени одинаково, что их количественное и
качественное изменение происходит под действием одного и того же комплекса основных
факторов, определяющих движение данного ряда динамики.
Модели, учитывающие общие закономерности изменения
экономического явления в изучаемый интервал времени и изменения во времени
влияния комплекса факторов, называют многофакторными динамическими моделями.
Выделим особенности моделей аналитического
выравнивания уровней динамического ряда, накладывающие ограничения на их
использование. Во-первых, динамические ряды, к которым применяется
аппроксимация, должны быть достаточно длинными. Во-вторых, применение
аппроксимации наиболее целесообразно в случае медленно и плавно меняющегося
уровня. В-третьих, аппроксимация как метод моделирования практически не
адаптируется к изменяющимся условиям формирования уровней ряда; при появлении
новых данных построение модели должно быть проведено заново. В-четвертых, при
использовании для расчета параметров уравнения метода наименьших квадратов
(МНК) считается, что значимость информации в пределах отрезка аппроксимации
одинакова независимо от давности полученных данных, в то время как более
поздние данные имеют большую ценность.
Помимо этого, динамические ряды экономических
показателей часто имеют небольшую длину и подвержены значительным колебаниям,
которые аппроксимация предвидеть не может.
Задача
В таблице приведены готовые данные о
трудоемкости производства:
| Год | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|
Трудоемкость производства, человек-часов |
8 | 8.4 | 7.6 | 7 | 7.3 | 6.6 | 5.9 | 5 | 5.2 |
-
Провести аналитическое выравнивание ряда динамики по прямой.
Построить точечный и интервальный
прогноз на 2018 год.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
1) Произведем аналитическое выравнивание ряда по прямой.
Составим расчетную таблицу:
Расчетная вспомогательная таблица 1
| Годы |
|
|
|
|
| 2009 | -4 | 8 | 16 | -32 |
| 2010 | -3 | 8,4 | 9 | -25,2 |
| 2011 | -2 | 7,6 | 4 | -15,2 |
| 2012 | -1 | 7 | 1 | -7 |
| 2013 | 0 | 7,3 | 0 | 0,0 |
| 2014 | 1 | 6,6 | 1 | 6,6 |
| 2015 | 2 | 5,9 | 4 | 11,8 |
| 2016 | 3 | 5 | 9 | 15 |
| 2017 | 4 | 5,2 | 16 | 20,8 |
| Итого | 0 | 61,0 | 60 | -25,2 |
Коэффициенты уравнения линейного тренда найдем по формулам:
Уравнение линейного тренда имеет вид:
2) Составим расчетную таблицу:
Расчетная вспомогательная таблица 2
| Годы |
|
|
Теоретические значения |
|
| 2009 | -4 | 8 | 8,48 | 0,2304 |
| 2010 | -3 | 8,4 | 8,06 | 0,1156 |
| 2011 | -2 | 7,6 | 7,64 | 0,0016 |
| 2012 | -1 | 7 | 7,22 | 0,0484 |
| 2013 | 0 | 7,3 | 6,8 | 0,25 |
| 2014 | 1 | 6,6 | 6,38 | 0,0484 |
| 2015 | 2 | 5,9 | 5,96 | 0,0036 |
| 2016 | 3 | 5 | 5,54 | 0,2916 |
| 2017 | 4 | 5,2 | 5,12 | 0,0064 |
| Итого | — | — | — | 0,996 |
Среднеквадратическая ошибка:
Точечный прогноз на 2018 год (t=5):
Ошибка
прогноза составит:
По таблице критерия Стьюдента,
для доверительной вероятности
(уровня значимости
) находим:
Вывод к задаче
Таким образом
тренд для трудоемкости производства выражается линейным уравнением
.
Согласно прогнозу, в 2018 году трудоемкость производства с вероятностью 0,95
будет лежать в пределах от 3,6 до 5,8 человеко-часов.
Находим параметры уравнения методом наименьших квадратов
|
t |
y |
t 2 |
y 2 |
t•y |
y(t) |
(y-y cp) 2 |
(y-y(t))2 |
(t-t p) 2 |
(y-y(t)) : y |
|
1 |
223.97 |
1 |
50162.56 |
223.97 |
231.54 |
365.65 |
57.27 |
4 |
0.0338 |
|
2 |
219.44 |
4 |
48153.91 |
438.88 |
218.19 |
212.93 |
1.56 |
1 |
0.0057 |
|
3 |
214.87 |
9 |
46169.12 |
644.61 |
204.85 |
100.44 |
100.44 |
0 |
0.0466 |
|
4 |
197.99 |
16 |
39200.04 |
791.96 |
191.5 |
47.03 |
42.08 |
1 |
0.0328 |
|
5 |
167.97 |
25 |
28213.92 |
839.85 |
178.16 |
1359.99 |
103.8 |
4 |
0.0607 |
|
15 |
1024.24 |
55 |
211899.55 |
2939.27 |
1024.24 |
2086.04 |
305.15 |
10 |
0.18 |
Система уравнений МНК:
a0 n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
Для наших данных система уравнений имеет вид:
5a0 + 15a1 = 1024.24
15a0 + 55a1 = 2939.27
Из первого уравнения выражаем а0 и подставляем во второе уравнение, в результате получаем:
a0 = -13.35, a1 = 244.88
Уравнение тренда:
y = -13.35 t + 244.88
Эмпирические коэффициенты тренда a0 и a1 (b) являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. Коэффициент тренда a1(b) =-13.35 показывает среднее изменение результативного показателя с изменением периода времени t на единицу его измерения (год). В данном примере с увеличением t (времени) на 1 год, y (себестоимость) уменьшится в среднем на ( -13.35).

Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
![]()
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения:
![Rendered by QuickLaTeX.com [bar t = frac{{sumlimits_{i = 1}^n {{t_i}} }}{n} = frac{{15}}{5} = 3]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-b42bae07f971d4d747f7b56aec7b031b_l3.png)
![Rendered by QuickLaTeX.com [bar y = frac{{sumlimits_{i = 1}^n {{y_i}} }}{n} = frac{{1024.24}}{5} = 204.85]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-45a741af091236a904ad626780ff4ef9_l3.png)
![Rendered by QuickLaTeX.com [overline {ty} = frac{{sumlimits_{i = 1}^n {{t_i}{y_i}} }}{n} = frac{{2939.27}}{5} = 587.85]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-a8856bd9ea6104275919143ed4c37c06_l3.png)
Дисперсия:
![]()
![]()
Среднеквадратическое отклонение:
![]()
![]()
Коэффициент эластичности.
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.

Коэффициент эластичности меньше 1. Следовательно, при изменении t на 1%,Y изменится менее чем на 1%. Другими словами — влияние t на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерения тесноты зависимости между анализируемыми показателями (факторами). Изменяется в пределах [0;1].

В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1]. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
Полученная величина свидетельствует о том, что изменение временного периода t существенно влияет на y.
Коэффициент детерминации.
 т.е. в 85.37% случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая.
т.е. в 85.37% случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая.
Анализ точности определения оценок параметров уравнения тренда.
m = 1 — количество влияющих факторов в модели тренда

По таблице Стьюдента находим tтабл
tтабл (n-m-1; α/2) = (3;0.025) = 3.182
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 1
(244.88 -13.35*1 — 3.182*40.59; 244.88 -13.35*1 — 3.182*40.59)
(190.94; 272.13)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.

где L — период упреждения; уn+L — точечный прогноз по модели на (n + L)-й момент времени; n — количество наблюдений во временном ряду; Sy — стандартная ошибка прогнозируемого показателя; tα — табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
Проверка гипотез относительно коэффициентов линейного уравнения тренда.
Критерий Стьюдента. t-статистика.

Доверительный интервал для коэффициентов уравнения тренда. Определим доверительные интервалы коэффициентов тренда, которые с надежностью 95% будут следующими:
(b — tнабл Sb; b + tнабл Sb)
(-13.35 — 3.182•3.19; -13.35 + 3.182•3.19)
(-23.4933; -3.1967)
(a — t набл Sa; a + t набл Sa)
(244.88 — 3.182•10.58; 244.88 + 3.182•10.58)
(211.2249; 278.5411)
Критерий Фишера. F-статистика.

Fтабл. = 10.1 (a =0.05; df1=1 df2=3)
где m — количество факторов в уравнении тренда (m=1).
Поскольку Fрасч. > Fтабл., то коэффициент детерминации (и в целом уравнение тренда) статистически значим.
Проверка на наличие автокорреляции остатков.
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения εi с моментами их получения i. При этом, по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения εi (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости, скорее всего, будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости εi от εi-1
2. Коэффициент автокорреляции остатков:
![]()
Если коэффициент автокорреляции rei < 0.5, то есть основания утверждать, что автокорреляция отсутствует.
3. Критерий Дарбина-Уотсона.
Этот критерий является наиболее известным для обнаружения автокорреляции.
При статистическом анализе уравнения регрессии на начальном этапе часто проверяют выполнимость одной предпосылки: условия статистической независимости отклонений между собой. При этом проверяется некоррелированность соседних величин ei
|
y |
y(x) |
ei = y-y(x) |
e2 |
(ei — ei-1)2 |
|
223.97 |
231.54 |
-7.57 |
57.27 |
0 |
|
219.44 |
218.19 |
1.25 |
1.56 |
77.7 |
|
214.87 |
204.85 |
10.02 |
100.44 |
77 |
|
197.99 |
191.5 |
6.49 |
42.08 |
12.5 |
|
167.97 |
178.16 |
-10.19 |
103.8 |
278.06 |
|
305.15 |
445.26 |
Для анализа коррелированности отклонений используют статистику Дарбина-Уотсона:

Критические значения d1 и d2 определяются на основе таблиц Распределения Дарбина-Уотсона для требуемого уровня значимости α, числа наблюдений n = 5 и количества объясняющих переменных m=1.
Автокорреляция отсутствует, если выполняется следующее условие:
d1 < DW и d2 < DW < 4 — d2
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Поскольку 1.5 > 1.46 < 2.5, то автокорреляция остатков присутствует.
Для более надежного вывода целесообразно обращаться к табличным значениям.
По таблице Дарбина-Уотсона для n=5 и k=1 (уровень значимости 5%) находим: d1 = 1.08; d2 = 1.36.
Поскольку 1.08 < 1.46 и 1.36 < 1.46 < 4 — 1.36, то автокорреляция остатков отсутствует.
Проверка наличия гетероскедастичности.
1) Методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X, а по оси ординат либо отклонения ei, либо их квадраты ei2 Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии гетероскедастичности.
2) При помощи теста ранговой корреляции Спирмена.
Коэффициент ранговой корреляции Спирмена.
Присвоим ранги признаку ei и фактору X. Найдем сумму разности квадратов d2. По формуле вычислим коэффициент ранговой корреляции Спирмена:

|
X |
ei |
ранг X, dx |
ранг ei, dy |
(dx — dy)2 |
|
1 |
7.57 |
1 |
4 |
9 |
|
2 |
-1.25 |
2 |
3 |
1 |
|
3 |
-10.02 |
3 |
1 |
4 |
|
4 |
-6.49 |
4 |
2 |
4 |
|
5 |
10.19 |
5 |
5 |
0 |
|
18 |
Связь между признаком ei и фактором X слабая и прямая.
Оценка коэффициента ранговой корреляции Спирмена. Значимость коэффициента ранговой корреляции Спирмена:

По таблице Стьюдента находим tтабл:
tтабл (n-m-1; α/2) = (3; 0.05/2) = 3.182
Поскольку tнабл. < tтабл., то принимаем гипотезу о равенстве р=0 коэффициента ранговой корреляции. Другими словами, коэффициент ранговой корреляции статистически — не значим.
Интервальная оценка для коэффициента корреляции (доверительный интервал).

Доверительный интервал для коэффициента ранговой корреляции:
r (-1.3088; 1.5088)
Проверим нулевую гипотезу H0: гетероскедастичность отсутсвует. Поскольку 3.182 > 0.17, то гипотеза об отсутствии гетероскедастичности принимается.
Динамические ряды — краткое руководство по анализу изменений явлений во времени
Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.
Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.
Целью анализа динамических рядов является:
- выявление закономерности изменения изучаемого явления во времени;
- прогнозирование (экстраполирование) полученных данных на последующие
годы.
Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).
Типы динамических рядов:
- В зависимости от вида уровня ряда:
а) простые (уровень ряда выражен абсолютными числами);
б) сложные (уровень ряда выражен обобщающими коэффициентами).
- В зависимости от способа формирования временного интервала:
а) моментные (данные собираются на определенный момент времени);
б) интервальные (данные собираются за определенный период времени).
- В зависимости от выраженности изменений явления во времени (определяется по коэффициенту корреляции между временем и изучаемым явлением).
а) с выраженной тенденцией (r =0,7 — 1,0);
б) с неустойчивой тенденцией (r =0,3 — 0,69);
в) с отсутствием тенденции ( r = 0 — 0,29).
Основное требование, предъявляемое к анализируемым динамическим рядам, заключается в сопоставимости их уровней. Для оценки сопоставимости проводят предварительный анализ полученных данных по следующим критериям:
- единство территории, на которой проводился сбор данных;
- единая методология учета данных;
- единые временные интервалы, в течение которых проводилась регистрация
данных.
Методика анализа динамических рядов
Методика аналитики предусматривает выполнение последовательных действий:
- Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.
- Оценить наличие и силу корреляции изучаемого явления от времени.
- Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа — разделить эти компоненты и выявить основную закономерность изменения явления во времени. Для выявления и описания тренда динамический ряд подвергают обработке — выравниванию.
Способы выравнивания динамических рядов
Чтобы произвести выравнивание динамических рядов потребуются следующие действия:
- Укрупнение временных интервалов (периодов), в течение которых изучается явление.
- Сглаживание ряда методом скользящей средней.
- Аналитический способ.
При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:
а) линейная зависимость:![]()
б) экспоненциальная зависимость:![]()
в) показательная зависимость:![]()
г) параболическая зависимость:![]()
и др.
где a0, a1, а2 — параметры уравнения;
у – теоретический уровень;
t – временной интервал.
В качестве примера возьмем линейную зависимость и проведем выравнивание, используя для нахождения параметров уравнения а0 ,а1 способ наименьших квадратов. Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:
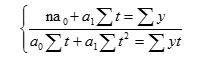
где у — уровни фактического ряда;
n — количество уровней;
t — порядковый номер временного периода.
Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда. При нечетном ряде середина обозначается через 0, а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины (например: -5,-4,-3,-2,-1, 0,+1.+2,+3,->:4,+5). При четном ряде две средние временные точки обозначаются через +1 и -1, а остальные ранги присваиваются через две единицы (например: -5,-3,-1,+1,+3,+5).
При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:
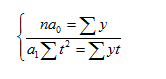
Отсюда находим параметры уравнения:
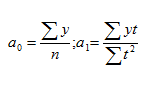
Подставляя в уравнение у = а0 + а1t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.
При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обусловлено как случайными колебаниями, так и неправильно подобранным аппроксимирующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.
Оценка точности аппроксимации возможна с помощью нахождения
Для получения точной оценки необходимо найти такие величины:
а) коэффициент вариации:

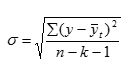
где у- фактический уровень ряда;
yt — теоретический уровень ряда;
k- число параметров уравнения;
n- число уровней ряда.
Аппроксимация считается точной при Cv не более 15%.
б) коэффициент расхождения Тейла:
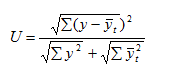
где у — фактический уровень ряда;
yt — теоретический уровень ряда.
Аппроксимация считается точной при U не более 5%
После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факторов и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.
Вычисление основных показателей динамического ряда
Алгоритм вычислений ведущих параметров динамических рядов:
Условные обозначения:
yi- текущий уровень (сравниваемый);
уi-1— базисный уровень (с каким сравнивают);
t- период времени, в течение которого уровень предполагается неизменным.
1.Абсолютный прирост (убыль) :
![]()
2.Темп роста (убыли):
![]()
3.Темп прироста (относительная скорость), темп убыли :
![]()
4.Средний темп прироста (убыли):
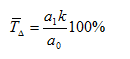
где а0; а1 — параметры уравнения;
k = 1 при нечетном ряде;
k = 2 при четном ряде.
5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.
Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
