Бит четности позволяет обнаружить сколько ошибок

From Wikipedia, the free encyclopedia

7 bits of data (count of 1-bits) 8 bits including parity
even odd
0000000 0 00000000 00000001
1010001 3 10100011 10100010
1101001 4 11010010 11010011
1111111 7 11111111 11111110

A parity bit, or check bit, is a bit added to a string of binary code. Parity bits are a simple form of error detecting code. Parity bits are generally applied to the smallest units of a communication protocol, typically 8-bit octets (bytes), although they can also be applied separately to an entire message string of bits.

The parity bit ensures that the total number of 1-bits in the string is even or odd.[1] Accordingly, there are two variants of parity bits: even parity bit and odd parity bit. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1s in the whole set (including the parity bit) an even number. If the count of 1s in a given set of bits is already even, the parity bit’s value is 0. In the case of odd parity, the coding is reversed. For a given set of bits, if the count of bits with a value of 1 is even, the parity bit value is set to 1 making the total count of 1s in the whole set (including the parity bit) an odd number. If the count of bits with a value of 1 is odd, the count is already odd so the parity bit’s value is 0. Even parity is a special case of a cyclic redundancy check (CRC), where the 1-bit CRC is generated by the polynomial x+1.

Parity[edit]

In mathematics parity can refer to the evenness or oddness of an integer, which, when written in its binary form, can be determined just by examining only its least significant bit.

In information technology parity refers to the evenness or oddness, given any set of binary digits, of the number of those bits with value one. Because parity is determined by the state of every one of the bits, this property of parity—being dependent upon all the bits and changing its value from even to odd parity if any one bit changes—allows for its use in error detection and correction schemes.

In telecommunications the parity referred to by some protocols is for error-detection. The transmission medium is preset, at both end points, to agree on either odd parity or even parity. For each string of bits ready to transmit (data packet) the sender calculates its parity bit, zero or one, to make it conform to the agreed parity, even or odd. The receiver of that packet first checks that the parity of the packet as a whole is in accordance with the preset agreement, then, if there was a parity error in that packet, requests a re-transmission of that packet.

In computer science the parity stripe or parity disk in a RAID provides error-correction. Parity bits are written at the rate of one parity bit per n bits, where n is the number of disks in the array. When a read error occurs, each bit in the error region is recalculated from its set of n bits. In this way, using one parity bit creates «redundancy» for a region from the size of one bit to the size of one disk. See § Redundant Array of Independent Disks below.

In electronics, transcoding data with parity can be very efficient, as XOR gates output what is equivalent to a check bit that creates an even parity, and XOR logic design easily scales to any number of inputs. XOR and AND structures comprise the bulk of most integrated circuitry.

Error detection[edit]

If an odd number of bits (including the parity bit) are transmitted incorrectly, the parity bit will be incorrect, thus indicating that a parity error occurred in the transmission. The parity bit is only suitable for detecting errors; it cannot correct any errors, as there is no way to determine which particular bit is corrupted. The data must be discarded entirely, and re-transmitted from scratch. On a noisy transmission medium, successful transmission can therefore take a long time, or even never occur. However, parity has the advantage that it uses only a single bit and requires only a number of XOR gates to generate. See Hamming code for an example of an error-correcting code.

Parity bit checking is used occasionally for transmitting ASCII characters, which have 7 bits, leaving the 8th bit as a parity bit.

For example, the parity bit can be computed as follows. Assume Alice and Bob are communicating and Alice wants to send Bob the simple 4-bit message 1001.

Type of bit parity Successful transmission scenario
Even parity

Alice wants to transmit: 1001 and 1011

Alice computes parity bit value:
1+0+0+1 (mod 2) = 0

1+0+1+1 (mod 2) = 1

Alice adds parity bit and sends:
10010 and 10111

Bob receives: 10010 and 10111

Bob computes parity:
1+0+0+1+0 (mod 2) = 0

1+0+1+1+1 (mod 2) = 0

Bob reports correct transmission after observing expected even result.

Odd parity

Alice wants to transmit: 1001 and 1011

Alice computes parity bit value:

1+0+0+1 (+ 1 mod 2) = 1

1+0+1+1 (+ 1 mod 2) = 0

Alice adds parity bit and sends:
10011 and 10110

Bob receives: 10011 and 10110

Bob computes overall parity:
1+0+0+1+1 (mod 2) = 1

1+0+1+1+0 (mod 2) = 1

Bob reports correct transmission after observing expected odd result.

This mechanism enables the detection of single bit errors, because if one bit gets flipped due to line noise, there will be an incorrect number of ones in the received data. In the two examples above, Bob’s calculated parity value matches the parity bit in its received value, indicating there are no single bit errors. Consider the following example with a transmission error in the second bit using XOR:

Type of bit parity error Failed transmission scenario
Even parity

Error in the second bit

Alice wants to transmit: 1001

Alice computes parity bit value: 1^0^0^1 = 0

Alice adds parity bit and sends: 10010

…TRANSMISSION ERROR…

Bob receives: 11010

Bob computes overall parity: 1^1^0^1^0 = 1

Bob reports incorrect transmission after observing unexpected odd result.

Even parity

Error in the parity bit

Alice wants to transmit: 1001

Alice computes even parity value: 1^0^0^1 = 0

Alice sends: 10010

…TRANSMISSION ERROR…

Bob receives: 10011

Bob computes overall parity: 1^0^0^1^1 = 1

Bob reports incorrect transmission after observing unexpected odd result.

There is a limitation to parity schemes. A parity bit is only guaranteed to detect an odd number of bit errors. If an even number of bits have errors, the parity bit records the correct number of ones, even though the data is corrupt. (See also Error detection and correction.) Consider the same example as before with an even number of corrupted bits:

Type of bit parity error Failed transmission scenario
Even parity

Two corrupted bits

Alice wants to transmit: 1001

Alice computes even parity value: 1^0^0^1 = 0

Alice sends: 10010

…TRANSMISSION ERROR…

Bob receives: 11011

Bob computes overall parity: 1^1^0^1^1 = 0

Bob reports correct transmission though actually incorrect.

Bob observes even parity, as expected, thereby failing to catch the two bit errors.

Usage[edit]

Because of its simplicity, parity is used in many hardware applications where an operation can be repeated in case of difficulty, or where simply detecting the error is helpful. For example, the SCSI and PCI buses use parity to detect transmission errors, and many microprocessor instruction caches include parity protection. Because the I-cache data is just a copy of main memory, it can be disregarded and re-fetched if it is found to be corrupted.

In serial data transmission, a common format is 7 data bits, an even parity bit, and one or two stop bits. This format accommodates all the 7-bit ASCII characters in an 8-bit byte. Other formats are possible; 8 bits of data plus a parity bit can convey all 8-bit byte values.

In serial communication contexts, parity is usually generated and checked by interface hardware (e.g., a UART) and, on reception, the result made available to a processor such as the CPU (and so too, for instance, the operating system) via a status bit in a hardware register in the interface hardware. Recovery from the error is usually done by retransmitting the data, the details of which are usually handled by software (e.g., the operating system I/O routines).

When the total number of transmitted bits, including the parity bit, is even, odd parity has the advantage that the all-zeros and all-ones patterns are both detected as errors. If the total number of bits is odd, only one of the patterns is detected as an error, and the choice can be made based on which is expected to be the more common error.

RAID array[edit]

Parity data is used by RAID arrays (redundant array of independent/inexpensive disks) to achieve redundancy. If a drive in the array fails, remaining data on the other drives can be combined with the parity data (using the Boolean XOR function) to reconstruct the missing data.

For example, suppose two drives in a three-drive RAID 5 array contained the following data:

Drive 1: 01101101
Drive 2: 11010100

To calculate parity data for the two drives, an XOR is performed on their data:

01101101
  XOR     11010100
10111001

The resulting parity data, 10111001, is then stored on Drive 3.

Should any of the three drives fail, the contents of the failed drive can be reconstructed on a replacement drive by subjecting the data from the remaining drives to the same XOR operation. If Drive 2 were to fail, its data could be rebuilt using the XOR results of the contents of the two remaining drives, Drive 1 and Drive 3:

Drive 1: 01101101
Drive 3: 10111001

as follows:

10111001
  XOR     01101101
11010100

The result of that XOR calculation yields Drive 2’s contents. 11010100 is then stored on Drive 2, fully repairing the array.

XOR logic is also equivalent to even parity (because a XOR b XOR c XOR … may be treated as XOR(a,b,c,…) which is an n-ary operator which is true if and only if an odd number of arguments are true). So the same XOR concept above applies similarly to larger RAID arrays with parity, using any number of disks. In the case of a RAID 3 array of 12 drives, 11 drives participate in the XOR calculation shown above and yield a value that is then stored on the dedicated parity drive.

Extensions and variations on the parity bit mechanism «double,» «dual,» or «diagonal» parity, are used in RAID-DP.

History[edit]

A parity track was present on the first magnetic tape data storage in 1951. Parity in this form, applied across multiple parallel signals, is known as a transverse redundancy check. This can be combined with parity computed over multiple bits sent on a single signal, a longitudinal redundancy check. In a parallel bus, there is one longitudinal redundancy check bit per parallel signal.

Parity was also used on at least some paper-tape (punched tape) data entry systems (which preceded magnetic tape systems). On the systems sold by British company ICL (formerly ICT) the 1-inch-wide (25 mm) paper tape had 8 hole positions running across it, with the 8th being for parity. 7 positions were used for the data, e.g., 7-bit ASCII. The 8th position had a hole punched in it depending on the number of data holes punched.

See also[edit]

  • BIP-8
  • Parity function
  • Single-event upset
  • 8-N-1
  • Check digit

References[edit]

  1. ^ Ziemer, RodgerE.; Tranter, William H. (17 March 2014). Principles of communication : systems, modulation, and noise (Seventh ed.). Hoboken, New Jersey. ISBN 9781118078914. OCLC 856647730.

External links[edit]

  • Different methods of generating the parity bit, among other bit operations

From Wikipedia, the free encyclopedia

7 bits of data (count of 1-bits) 8 bits including parity
even odd
0000000 0 00000000 00000001
1010001 3 10100011 10100010
1101001 4 11010010 11010011
1111111 7 11111111 11111110

A parity bit, or check bit, is a bit added to a string of binary code. Parity bits are a simple form of error detecting code. Parity bits are generally applied to the smallest units of a communication protocol, typically 8-bit octets (bytes), although they can also be applied separately to an entire message string of bits.

The parity bit ensures that the total number of 1-bits in the string is even or odd.[1] Accordingly, there are two variants of parity bits: even parity bit and odd parity bit. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1s in the whole set (including the parity bit) an even number. If the count of 1s in a given set of bits is already even, the parity bit’s value is 0. In the case of odd parity, the coding is reversed. For a given set of bits, if the count of bits with a value of 1 is even, the parity bit value is set to 1 making the total count of 1s in the whole set (including the parity bit) an odd number. If the count of bits with a value of 1 is odd, the count is already odd so the parity bit’s value is 0. Even parity is a special case of a cyclic redundancy check (CRC), where the 1-bit CRC is generated by the polynomial x+1.

Parity[edit]

In mathematics parity can refer to the evenness or oddness of an integer, which, when written in its binary form, can be determined just by examining only its least significant bit.

In information technology parity refers to the evenness or oddness, given any set of binary digits, of the number of those bits with value one. Because parity is determined by the state of every one of the bits, this property of parity—being dependent upon all the bits and changing its value from even to odd parity if any one bit changes—allows for its use in error detection and correction schemes.

In telecommunications the parity referred to by some protocols is for error-detection. The transmission medium is preset, at both end points, to agree on either odd parity or even parity. For each string of bits ready to transmit (data packet) the sender calculates its parity bit, zero or one, to make it conform to the agreed parity, even or odd. The receiver of that packet first checks that the parity of the packet as a whole is in accordance with the preset agreement, then, if there was a parity error in that packet, requests a re-transmission of that packet.

In computer science the parity stripe or parity disk in a RAID provides error-correction. Parity bits are written at the rate of one parity bit per n bits, where n is the number of disks in the array. When a read error occurs, each bit in the error region is recalculated from its set of n bits. In this way, using one parity bit creates «redundancy» for a region from the size of one bit to the size of one disk. See § Redundant Array of Independent Disks below.

In electronics, transcoding data with parity can be very efficient, as XOR gates output what is equivalent to a check bit that creates an even parity, and XOR logic design easily scales to any number of inputs. XOR and AND structures comprise the bulk of most integrated circuitry.

Error detection[edit]

If an odd number of bits (including the parity bit) are transmitted incorrectly, the parity bit will be incorrect, thus indicating that a parity error occurred in the transmission. The parity bit is only suitable for detecting errors; it cannot correct any errors, as there is no way to determine which particular bit is corrupted. The data must be discarded entirely, and re-transmitted from scratch. On a noisy transmission medium, successful transmission can therefore take a long time, or even never occur. However, parity has the advantage that it uses only a single bit and requires only a number of XOR gates to generate. See Hamming code for an example of an error-correcting code.

Parity bit checking is used occasionally for transmitting ASCII characters, which have 7 bits, leaving the 8th bit as a parity bit.

For example, the parity bit can be computed as follows. Assume Alice and Bob are communicating and Alice wants to send Bob the simple 4-bit message 1001.

Type of bit parity Successful transmission scenario
Even parity

Alice wants to transmit: 1001 and 1011

Alice computes parity bit value:
1+0+0+1 (mod 2) = 0

1+0+1+1 (mod 2) = 1

Alice adds parity bit and sends:
10010 and 10111

Bob receives: 10010 and 10111

Bob computes parity:
1+0+0+1+0 (mod 2) = 0

1+0+1+1+1 (mod 2) = 0

Bob reports correct transmission after observing expected even result.

Odd parity

Alice wants to transmit: 1001 and 1011

Alice computes parity bit value:

1+0+0+1 (+ 1 mod 2) = 1

1+0+1+1 (+ 1 mod 2) = 0

Alice adds parity bit and sends:
10011 and 10110

Bob receives: 10011 and 10110

Bob computes overall parity:
1+0+0+1+1 (mod 2) = 1

1+0+1+1+0 (mod 2) = 1

Bob reports correct transmission after observing expected odd result.

This mechanism enables the detection of single bit errors, because if one bit gets flipped due to line noise, there will be an incorrect number of ones in the received data. In the two examples above, Bob’s calculated parity value matches the parity bit in its received value, indicating there are no single bit errors. Consider the following example with a transmission error in the second bit using XOR:

Type of bit parity error Failed transmission scenario
Even parity

Error in the second bit

Alice wants to transmit: 1001

Alice computes parity bit value: 1^0^0^1 = 0

Alice adds parity bit and sends: 10010

…TRANSMISSION ERROR…

Bob receives: 11010

Bob computes overall parity: 1^1^0^1^0 = 1

Bob reports incorrect transmission after observing unexpected odd result.

Even parity

Error in the parity bit

Alice wants to transmit: 1001

Alice computes even parity value: 1^0^0^1 = 0

Alice sends: 10010

…TRANSMISSION ERROR…

Bob receives: 10011

Bob computes overall parity: 1^0^0^1^1 = 1

Bob reports incorrect transmission after observing unexpected odd result.

There is a limitation to parity schemes. A parity bit is only guaranteed to detect an odd number of bit errors. If an even number of bits have errors, the parity bit records the correct number of ones, even though the data is corrupt. (See also Error detection and correction.) Consider the same example as before with an even number of corrupted bits:

Type of bit parity error Failed transmission scenario
Even parity

Two corrupted bits

Alice wants to transmit: 1001

Alice computes even parity value: 1^0^0^1 = 0

Alice sends: 10010

…TRANSMISSION ERROR…

Bob receives: 11011

Bob computes overall parity: 1^1^0^1^1 = 0

Bob reports correct transmission though actually incorrect.

Bob observes even parity, as expected, thereby failing to catch the two bit errors.

Usage[edit]

Because of its simplicity, parity is used in many hardware applications where an operation can be repeated in case of difficulty, or where simply detecting the error is helpful. For example, the SCSI and PCI buses use parity to detect transmission errors, and many microprocessor instruction caches include parity protection. Because the I-cache data is just a copy of main memory, it can be disregarded and re-fetched if it is found to be corrupted.

In serial data transmission, a common format is 7 data bits, an even parity bit, and one or two stop bits. This format accommodates all the 7-bit ASCII characters in an 8-bit byte. Other formats are possible; 8 bits of data plus a parity bit can convey all 8-bit byte values.

In serial communication contexts, parity is usually generated and checked by interface hardware (e.g., a UART) and, on reception, the result made available to a processor such as the CPU (and so too, for instance, the operating system) via a status bit in a hardware register in the interface hardware. Recovery from the error is usually done by retransmitting the data, the details of which are usually handled by software (e.g., the operating system I/O routines).

When the total number of transmitted bits, including the parity bit, is even, odd parity has the advantage that the all-zeros and all-ones patterns are both detected as errors. If the total number of bits is odd, only one of the patterns is detected as an error, and the choice can be made based on which is expected to be the more common error.

RAID array[edit]

Parity data is used by RAID arrays (redundant array of independent/inexpensive disks) to achieve redundancy. If a drive in the array fails, remaining data on the other drives can be combined with the parity data (using the Boolean XOR function) to reconstruct the missing data.

For example, suppose two drives in a three-drive RAID 5 array contained the following data:

Drive 1: 01101101
Drive 2: 11010100

To calculate parity data for the two drives, an XOR is performed on their data:

01101101
  XOR     11010100
10111001

The resulting parity data, 10111001, is then stored on Drive 3.

Should any of the three drives fail, the contents of the failed drive can be reconstructed on a replacement drive by subjecting the data from the remaining drives to the same XOR operation. If Drive 2 were to fail, its data could be rebuilt using the XOR results of the contents of the two remaining drives, Drive 1 and Drive 3:

Drive 1: 01101101
Drive 3: 10111001

as follows:

10111001
  XOR     01101101
11010100

The result of that XOR calculation yields Drive 2’s contents. 11010100 is then stored on Drive 2, fully repairing the array.

XOR logic is also equivalent to even parity (because a XOR b XOR c XOR … may be treated as XOR(a,b,c,…) which is an n-ary operator which is true if and only if an odd number of arguments are true). So the same XOR concept above applies similarly to larger RAID arrays with parity, using any number of disks. In the case of a RAID 3 array of 12 drives, 11 drives participate in the XOR calculation shown above and yield a value that is then stored on the dedicated parity drive.

Extensions and variations on the parity bit mechanism «double,» «dual,» or «diagonal» parity, are used in RAID-DP.

History[edit]

A parity track was present on the first magnetic tape data storage in 1951. Parity in this form, applied across multiple parallel signals, is known as a transverse redundancy check. This can be combined with parity computed over multiple bits sent on a single signal, a longitudinal redundancy check. In a parallel bus, there is one longitudinal redundancy check bit per parallel signal.

Parity was also used on at least some paper-tape (punched tape) data entry systems (which preceded magnetic tape systems). On the systems sold by British company ICL (formerly ICT) the 1-inch-wide (25 mm) paper tape had 8 hole positions running across it, with the 8th being for parity. 7 positions were used for the data, e.g., 7-bit ASCII. The 8th position had a hole punched in it depending on the number of data holes punched.

See also[edit]

  • BIP-8
  • Parity function
  • Single-event upset
  • 8-N-1
  • Check digit

References[edit]

  1. ^ Ziemer, RodgerE.; Tranter, William H. (17 March 2014). Principles of communication : systems, modulation, and noise (Seventh ed.). Hoboken, New Jersey. ISBN 9781118078914. OCLC 856647730.

External links[edit]

  • Different methods of generating the parity bit, among other bit operations

Бит четности является параметром со значением 0 или 1 , который используется в способе обнаружения ошибок передачи , в которой 0 или 1 добавляется к каждой группе 7-8 битов (байт). Цель состоит в том, чтобы каждый байт всегда имел нечетное общее количество «1» или четное общее количество «1» в соответствии с установленной четностью.

Четность — это метод обнаружения ошибок, используемый в асинхронной связи. Он используется для проверки целостности каждого байта в передаваемом потоке. Например, если установлена ​​нечетная четность, любой байт, полученный из передачи с общим числом «1», который является четным, должен содержать ошибку.

Источник: pixabay.com

Используются два типа проверки на четность: проверка на четность, при которой бит четности 1 добавляется, если в предыдущем байте имеется нечетное общее количество битов «1», и проверка на четность, когда выполняется обратное. С помощью этого метода вы сможете узнать только то, что произошла ошибка, но вы не узнаете, где произошла ошибка.

Для чего нужен бит четности?

При отправке цифровых данных может быть ошибка между переданным кодом и полученным кодом. Существует множество источников ошибок в виде различных типов шума, таких как электромагнитный шум или тепловой шум.

Следовательно, необходимо реализовать некоторый метод, чтобы проверить, ошибочны ли полученные коды или байты.

Однако как получатель может узнать, ошибочен ли полученный код? Получатель не может узнать код до его получения.

Например, предположим, что отправитель передает код 01100110, но после прохождения через зашумленную линию получатель получает код 00100110. Получатель не будет знать, что он получил код с ошибкой во втором бите.

Получатель не может знать, что сообщение содержит ошибку в первом бите, потому что это будет означать, что получатель уже знает сообщение от передатчика до передачи.

Контроль ошибок

Проблема, с которой приемник может проверить наличие ошибки, может быть решена с помощью кодирования с контролем ошибок.

Основная идея кодирования с контролем ошибок заключается в добавлении дополнительного бита в информацию, которая должна быть отправлена, чтобы ошибка обнаруживалась и исправлялась. Есть много кодировок обработки ошибок. Самый простой — это бит четности.

Бит четности добавляется к каждому передаваемому байту. Этот бит используется для проверки того, что информация была доставлена ​​точно.

Бит четности для каждого байта устанавливается так, чтобы все байты имели нечетное число или четное число битов «1».

пример

Предположим, что два диска обмениваются данными с проверкой четности, которая является наиболее распространенной формой проверки четности.

В зависимости от единицы передачи он отправляет байты и сначала подсчитывает количество битов «1» в каждой группе из семи битов (байтах). Если количество битов «1» четное, установите бит четности в 0. Если количество битов «1» нечетное, установите бит четности в 1. Таким образом, каждый байт будет иметь четное количество битов «1».

Приемник проверяет каждый байт, чтобы убедиться, что он имеет четное количество битов «1». Если в байте обнаружено нечетное количество битов «1», приемник будет знать, что во время передачи произошла ошибка.

Ранее и получатель, и отправитель должны были договориться об использовании проверки четности и о том, должна ли четность быть нечетной или четной. Если обе стороны не настроены с одинаковым чувством паритета, связь будет невозможна.

Обнаружение ошибок

Проверка четности — самый простой метод обнаружения ошибок связи.

Однако, хотя он может обнаруживать множество ошибок, он не является безошибочным, поскольку он не способен обнаруживать компоновку, когда четное количество битов в одном и том же байте изменяется из-за электрического шума.

Проверка четности используется не только при обмене данными, но и для тестирования запоминающих устройств. Например, многие персональные компьютеры выполняют проверку на четность всякий раз, когда байт данных считывается из памяти.

Как это работает?

Предположим, у вас есть 7-битные коды данных и дополнительный бит, который является битом четности, добавлен для формирования 8-битного кода данных. Можно использовать два метода: четность и нечетность.

В качестве образца можно взять метод четности. Вы поступили бы наоборот, если бы выбрали метод нечетной четности.

Метод четной четности

Этот метод указывает, что добавляемый бит четности должен быть таким, чтобы общая сумма «1» в окончательном коде была четной. Например:

Следовательно, для первого 7-битного кода: 0010010 с четным количеством «1» (2) переданный 8-битный код будет: 00100100 с четным количеством «1» (2).

Для 7-битного кода 1110110 с нечетным количеством «1» (5) переданный 8-битный код будет 11101101 с четным количеством «1» (6).

После того, как получатель получит 8 битов, он проверит количество «1» в полученном коде, если количество «1» четное, это означает, что ошибки нет, если количество нечетное, это означает, что ошибка.

Когда вычисленная четность полученного байта не совпадает со значением принятого бита четности, считается, что произошла ошибка четности, и обычно байт отбрасывается.

В случае ошибки приемник предупредит передатчик, чтобы он отправил код еще раз.

Не безошибочный

Однако у этих методов контроля четности есть недостаток: если код 1110110 преобразуется шумом линии в 11111001, вызывая 2-битную ошибку, то этот метод не может обнаружить, что ошибка произошла.

Четность хороша при обнаружении ошибок и всегда обнаруживает любое нечетное количество ошибок в полученном байте. Однако при четном количестве ошибок средство проверки четности не сможет найти ошибку.

Ссылки

  1. Ванги Бил (2019). Проверка четности. Webopedia. Взято с: webopedia.com.
  2. Группа исследований электроники (2019). Четность символов. Взято с: erg.abdn.ac.uk.
  3. Словарь (2019) .. Бит паритета. Взято с сайта vocabulary.com.
  4. Ангмс (2013). Самый простой код контроля ошибок — Parity Bit. Взято с сайта angms.science.
  5. Кристенсон, (2011). Определение бита четности. Techterms. Взято с: techterms.com.

Перейти к контенту

Информатика-11-класс-Поляков

§ 2. Передача данных ГДЗ по Информатике 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю.

7. Что такое бит чётности? В каких случаях с помощью бита чётности можно обнаружить ошибку, а в каких — нельзя?

Ответ

Бит чётности (англ. Parity bit) — контрольный бит в вычислительной технике и сетях передачи данных, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе). В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.

В длинной цепочке применение бита чётности позволяет обнаруживать нечётное число ошибок (1, 3, 5, …), а ошибки в чётном количестве разрядов остаются незамеченными. Контроль с помощью бита чётности применяется для небольших блоков данных (чаще всего — для каждого отдельного байта) и хорошо работает тогда, когда отдельные ошибки при передаче независимы одна от другой и встречаются редко.

Если при передаче неверно передан только один из битов, количество единиц в сообщении стало нечётным, это и служит признаком ошибки при передаче. Однако исправить ошибку нельзя, потому что непонятно, в каком именно разряде она случилась. Если же изменилось два бита, чётность не меняется, и такая ошибка не обнаруживается.

эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален.
Найдите источники: «Бит четности»  – Новости  · газеты  · книги  · ученый  · JSTOR (Январь 2013) (Узнайте, как и когда удалить этот шаблон сообщения)
7 бит данных (количество 1 бит) 8 бит, включая четность
даже странный
0000000 0 00000000 00000001
1010001 3 10100011 10100010
1101001 4 11010010 11010011
1111111 7 11111111 11111110

А бит четности, или же проверить бит, это кусочек добавлен к строке бинарный код. Биты четности используются как простейшая форма код обнаружения ошибок. Биты четности обычно применяются к самым маленьким блокам протокола связи, обычно 8-битным. октеты (байты), хотя они также могут применяться отдельно ко всей цепочке битов сообщения.

Бит четности гарантирует, что общее количество единиц в строке равно четным или нечетным.[1] Соответственно, есть два варианта битов четности: бит четности и бит нечетной четности. В случае четности для данного набора битов подсчитываются вхождения битов, значение которых равно 1. Если этот счетчик нечетный, значение бита четности устанавливается в 1, в результате чего общее количество вхождений единиц во всем наборе (включая бит четности) становится четным. Если счетчик единиц в данном наборе битов уже является четным, значение бита четности равно 0. В случае нечетной четности кодирование меняется на противоположное. Для данного набора битов, если количество битов со значением 1 является четным, значение бита четности устанавливается в 1, что делает общее количество единиц во всем наборе (включая бит четности) нечетным числом. Если количество битов со значением 1 нечетное, счет уже нечетный, поэтому значение бита четности равно 0. Четность — это частный случай циклическая проверка избыточности (CRC), где 1-битный CRC генерируется многочлен Икс+1.

Если бит присутствует в точке, иначе выделенной для бита четности, но не используется для проверки четности, он может называться маркировать бит четности если бит четности всегда равен 1, или бит четности пространства если бит всегда равен 0. В таких случаях, когда значение бита постоянно, его можно назвать придерживаться бит четности хотя его функция не имеет ничего общего с четностью.[2] Функция таких битов зависит от конструкции системы, но примеры функций для таких битов включают в себя управление синхронизацией или идентификацию пакета как имеющего значение данных или адреса.[3] Если его фактическое значение бита не имеет отношения к его функции, бит составляет срок безразличия.[4]

Паритет

В математике паритет относится к четности или нечетности целого числа, которое для двоичное число определяется только младший бит. В телекоммуникациях и вычислительной технике четность относится к четности или нечетности числа битов со значением один в заданном наборе битов и, таким образом, определяется значением всех битов. Его можно рассчитать через XOR сумма битов, дающая 0 для четности и 1 для нечетной четности. Это свойство зависимости от всех битов и изменения значения при изменении любого одного бита позволяет использовать его в обнаружение ошибок схемы.

Обнаружение ошибок

Если нечетное количество бит (включая бит четности) переданный неправильно, бит четности будет неправильным, что указывает на то, что ошибка четности произошло в передаче. Бит четности подходит только для обнаружения ошибок; это не может правильный любые ошибки, так как невозможно определить, какой именно бит поврежден. Данные должны быть полностью отброшены, и ретранслировать с нуля. Следовательно, в шумной среде передачи успешная передача может занять много времени или даже не произойти. Однако у четности есть то преимущество, что она использует только один бит и требует только нескольких Ворота XOR генерировать. Видеть Код Хэмминга для примера кода исправления ошибок.

Проверка битов на четность иногда используется для передачи ASCII символы, которые имеют 7 бит, оставляя 8-й бит как бит четности.

Например, бит четности можно вычислить следующим образом. Предполагать Алиса и Боб общаются, и Алиса хочет отправить Бобу простое 4-битное сообщение 1001.

Тип битовой четности Сценарий успешной передачи
Четный паритет

Алиса хочет передать: 1001

Алиса вычисляет значение бита четности: 1 + 0 + 0 + 1 (mod 2) = 0

Алиса добавляет бит четности и отправляет: 10010

Боб получает: 10010

Боб вычисляет четность: 1 + 0 + 0 + 1 + 0 (mod 2) = 0

Боб сообщает о правильной передаче после получения ожидаемого равномерного результата.
Нечетная четность

Алиса хочет передать: 1001

Алиса вычисляет значение бита четности: 1 + 0 + 0 + 1 (mod 2) = 0

Алиса добавляет бит четности и отправляет: 10011

Боб получает: 10011

Боб вычисляет общую четность: 1 + 0 + 0 + 1 + 1 (mod 2) = 1

Боб сообщает о правильной передаче после наблюдения ожидаемого нечетного результата.

Этот механизм позволяет обнаруживать одиночные битовые ошибки, потому что, если один бит перевернут из-за шума линии, в полученных данных будет неправильное количество единиц. В двух приведенных выше примерах вычисленное Бобом значение четности совпадает с битом четности в полученном значении, что указывает на отсутствие одиночных битовых ошибок. Рассмотрим следующий пример с ошибкой передачи во втором бите с использованием XOR:

Тип битовой ошибки четности Сценарий неудачной передачи
Четный паритет

Ошибка во втором бите

Алиса хочет передать: 1001

Алиса вычисляет значение бита четности: 1 ^ 0 ^ 0 ^ 1 = 0

Алиса добавляет бит четности и отправляет: 10010

… ОШИБКА ПЕРЕДАЧИ …

Боб получает: 11010

Боб вычисляет общую четность: 1 ^ 1 ^ 0 ^ 1 ^ 0 = 1

Боб сообщает о неправильной передаче после получения неожиданного нечетного результата.
Четный паритет

Ошибка в бите четности

Алиса хочет передать: 1001

Алиса вычисляет значение четности: 1 ^ 0 ^ 0 ^ 1 = 0

Алиса отправляет: 10010

… ОШИБКА ПЕРЕДАЧИ …

Боб получает: 10011

Боб вычисляет общую четность: 1 ^ 0 ^ 0 ^ 1 ^ 1 = 1

Боб сообщает о неправильной передаче после получения неожиданного нечетного результата.

Есть ограничение на схемы четности. Бит четности гарантированно обнаруживает нечетное количество битовых ошибок. Если четное количество битов содержит ошибки, бит четности записывает правильное количество единиц, даже если данные повреждены. (Смотрите также обнаружение и исправление ошибок.) Рассмотрим тот же пример, что и раньше, с четным числом поврежденных битов:

Тип битовой ошибки четности Сценарий неудачной передачи
Четный паритет

Два поврежденных бита

Алиса хочет передать: 1001

Алиса вычисляет значение четности: 1 ^ 0 ^ 0 ^ 1 = 0

Алиса отправляет: 10010

… ОШИБКА ПЕРЕДАЧИ …

Боб получает: 11011

Боб вычисляет общую четность: 1 ^ 1 ^ 0 ^ 1 ^ 1 = 0

Боб сообщает о правильной передаче, хотя на самом деле неверной.

Боб, как и ожидалось, наблюдает четность, тем самым не обнаруживая двух битовых ошибок.

Применение

Из-за своей простоты четность используется во многих аппаратное обеспечение приложения, в которых операция может быть повторена в случае затруднения, или где полезно простое обнаружение ошибки. Например, SCSI и Шины PCI использовать четность для обнаружения ошибок передачи, и многие микропроцессор инструкция тайники включить защиту четности. Поскольку I-cache данные — это просто копия основная память, его можно проигнорировать и повторно загрузить, если обнаружится, что он поврежден.

В серийный передача данных, общий формат — 7 бит данных, бит четности и один или два стоповые биты. Этот формат поддерживает все 7-битные ASCII символы в 8-битном байте. Возможны другие форматы; 8 бит данных плюс бит четности могут передавать все 8-битные байтовые значения.

В контексте последовательной связи четность обычно генерируется и проверяется аппаратным обеспечением интерфейса (например, UART ) и, при приеме, результат предоставляется процессор такие как ЦП (и то же самое, например, Операционная система ) через бит состояния в регистр оборудования в интерфейс аппаратное обеспечение. Восстановление после ошибки обычно осуществляется путем повторной передачи данных, детали которой обычно обрабатываются программным обеспечением (например, процедурами ввода-вывода операционной системы).

Когда общее количество переданных битов, включая бит четности, является четным, нечетная четность имеет то преимущество, что обе комбинации из нулей и все единицы обнаруживаются как ошибки. Если общее количество битов нечетное, только один из шаблонов обнаруживается как ошибка, и выбор может быть сделан на основе того, какая, как ожидается, будет более распространенной ошибкой.

Избыточный массив независимых дисков

Данные о четности используются некоторыми избыточный массив независимых дисков (RAID) уровни для достижения избыточность. Если диск в массиве выходит из строя, оставшиеся данные на других дисках можно объединить с данными четности (с помощью логического XOR функция), чтобы восстановить недостающие данные.

Например, предположим, что два диска в трех RAID 5 массив содержал следующие данные:

Привод 1: 01101101
Привод 2: 11010100

Чтобы вычислить данные о четности для двух дисков, над их данными выполняется XOR:

         01101101
XOR 11010100
_____________
        10111001

Полученные данные о четности, 10111001, затем сохраняется на Диске 3.

Если какой-либо из трех дисков выйдет из строя, содержимое неисправного диска может быть восстановлено на заменяющем диске, подвергнув данные с оставшихся дисков той же операции XOR. Если диск 2 выйдет из строя, его данные можно будет восстановить, используя результаты XOR содержимого двух оставшихся дисков, диска 1 и диска 3:

Привод 1: 01101101
Привод 3: 10111001

следующим образом:

         10111001
XOR 01101101
_____________
        11010100

Результат этого вычисления XOR дает содержимое диска 2. 11010100 затем сохраняется на Диске 2, полностью восстанавливая массив. Та же самая концепция XOR применима аналогично к большим массивам с использованием любого количества дисков. В случае массива RAID 3 из 12 дисков 11 дисков участвуют в вычислении XOR, показанном выше, и выдают значение, которое затем сохраняется на выделенном диске четности.

Расширения и вариации механизма битов четности «двойная», «двойная» или «диагональная» четность используются в RAID-DP.

История

«Трек паритета» присутствовал на первом хранение данных на магнитной ленте в 1951 г. Четность в этой форме, применяемая к нескольким параллельным сигналам, известна как поперечный контроль избыточности. Это можно комбинировать с проверкой четности, вычисляемой по нескольким битам, отправляемым в одном сигнале, проверка продольного дублирования. В параллельной шине на каждый параллельный сигнал приходится один бит проверки продольным избыточным кодом.

Четность также использовалась хоть на какой-то бумажной ленте (перфолента ) системы ввода данных (предшествовавшие системам на магнитной ленте). В системах, продаваемых британской компанией ICL (ранее ICT), бумажная лента шириной 1 дюйм (25 мм) имела 8 отверстий, проходящих через нее, причем 8-е было для проверки четности. Для данных использовалось 7 позиций, например, 7-битный ASCII. В 8-й позиции было пробито отверстие в зависимости от количества пробитых отверстий для данных.

Смотрите также

  • БИП-8
  • Функция четности
  • Одно событие расстроено
  • 8-Н-1
  • Контрольная цифра

Рекомендации

  1. ^ Ziemer, RodgerE .; Трантер, Уильям Х. Принципы связи: системы, модуляция и шум (Седьмое изд.). Хобокен, Нью-Джерси. ISBN  9781118078914. OCLC  856647730.
  2. ^ «В чем разница между использованием четности меток или пробелов и без четности».[ненадежный источник? ]
  3. ^ «Какова цель Stick Parity?».
  4. ^ «Последовательная связь», Сб-дайджест, получено 2020-03-23

внешняя ссылка

  • Различные методы генерации бита четности среди других битовых операций

Вертикальная проверка избыточности также известна как проверка четности. В этом методе к каждому блоку данных добавляется избыточный бит, также называемый битом четности. Этот метод включает в себя четность и нечетность. Четность означает, что общее количество единиц в данных должно быть четным, а нечетная четность означает, что общее количество единиц в данных должно быть нечетным.

Пример —
Если источник хочет передать блок данных 1100111 с использованием четности по назначению. Источник должен будет пройти через генератор четности.

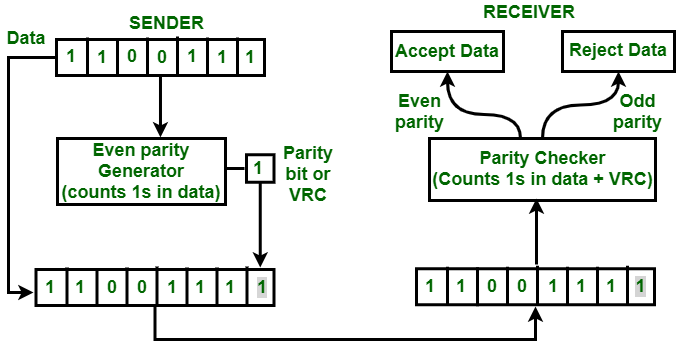
Четный паритет VRC

Генератор четности подсчитает количество единиц в единице данных и добавит бит четности. В приведенном выше примере количество единиц в блоке данных равно 5, генератор четности добавляет бит четности 1 к этому блоку данных, делая общее количество единиц равным 6, что ясно из рисунка выше.

Затем данные вместе с битом четности передаются по сети. В этом случае будет передано 11001111. В пункте назначения эти данные передаются в средство проверки четности в пункте назначения. Количество единиц в данных подсчитывается средством проверки четности.

Если количество единиц считается нечетным, например 5 или 7, то пункт назначения узнает, что в данных есть некоторая ошибка. Затем получатель отклоняет такой ошибочный блок данных.

Преимущества :

  • VRC может обнаруживать все одиночные битовые ошибки.
  • Он также может обнаруживать пакетные ошибки, но только в тех случаях, когда количество измененных битов нечетное, то есть 1, 3, 5, 7, ……. И т. Д.

Недостатки:
Основным недостатком использования этого метода для обнаружения ошибок является то, что он не может обнаружить пакетную ошибку, если количество измененных битов четное, то есть 2, 4, 6, 8, ……. И т. Д.

Пример —
Если исходные данные — 1100111. После добавления VRC, единица данных, которая будет передана, будет 11001111. Предположим, что на пути 2 бита равны 0 10 1 1111. Когда эти данные достигнут пункта назначения, средство проверки четности подсчитает количество единиц в данных и получается четное, т.е. 8. Таким образом, в данном случае паритет не меняется, он остается четным. Пункт назначения предполагает, что в данных нет ошибки, даже если данные ошибочны.

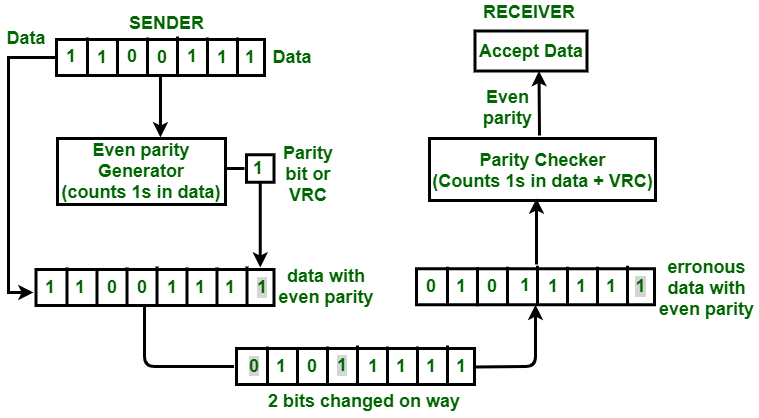
Получатель принимает ошибочные данные с измененным количеством битов

РЕКОМЕНДУЕМЫЕ СТАТЬИ

В статье рассмотрены основные методы защиты данных от ошибок при передаче по каналу с сильным шумом. Приведены примеры использования.

При передаче данных в условиях высокого внешнего шума возникают ошибки, даже если используются качественные компоненты и датчики. Источники шума разнообразны. Это может быть электромагнитное излучение от оборудования и двигателей, помехи от передачи по радиоканалу или электросети 50–60 Гц и т.д. В статье рассмотрено влияние шума на цифровые данные при передаче сигнала от датчика или АЦП в микроконтроллер (МК).
Для обнаружения ошибок, вызванных шумом, используются четыре основных метода:
– добавление бита четности;
– вычисление контрольной суммы;
– многократная передача;
– циклический контроль избыточности (CRC).
Рассмотрим достоинства и недостатки каждого подхода на примере интерфейсной схемы AFE LMP90100, в которой корректность принимаемых данных оценивается по CRC.
Микросхема LMP90100, разработанная Texas Instruments, обеспечивает высокоточный интерфейс для датчика с 24-разрядным АЦП. При использовании в промышленной среде, где помехи очень сильные, рекомендуется располагать LMP90100 близко к датчику, чтобы обеспечить целостность поступающего с него аналогового сигнала. Между LMP90100 и МК могут создаваться длинные линии связи. В этом случае вероятность того, что внешний шум исказит исходные данные, увеличивается.
Внешние помехи могут провоцировать появление ошибок в любой части передаваемых данных. Например, при передаче 10000000b (0x80) по зашумленному каналу МК может принять значение 00000000b (0x00), либо 100000001b (0x81). Второй случай не так опасен, как первый, когда данные значительно отличаются от истинных.
Предположим, что микросхема LMP90100 считывает данные с термопары и пересылает их в МК. Изменение в любом из разрядов МК интерпретирует как изменение температуры и предпринимает ответные действия. Однако необходимо проверить, не вызвано ли изменение данных помехами.

Бит четности

Перед передачей данных подсчитывается количество единиц в байте, затем добавляется девятый разряд, называемый битом четности. Существует два типа битов четности: четный и нечетный. Если используется четный бит, то дополнительный девятый бит подбирается так, чтобы общее количество единиц в байте было четным. В таблице 1 приведены примеры использования двух типов битов четности. В первой строке в байте данных содержатся 4 единицы, поэтому четный бит четности принимает значение 0, нечетный — 1.

Таблица 1. Добавление бита четности

Исходные данные

Четный бит

Нечетный бит

10010101

0 10010101

1 10010101

11100000

1 11100000

0 11100000

10101101

1 10101101

0 10101101

Использование битов четности является самым простым методом защиты от шума. Он добавляет мало служебной информации, всего один бит на байт данных. В то же время по биту четности можно выявить только единичные ошибки. Случаи, когда сразу два разряда меняют свои значения, будут пропущены.

Контрольная сумма

Метод контрольной суммы применяется к большому объему данных (больше 1 байта). Для вычисления контрольной суммы (КС) необходимо сложить данные и отбросить разряды переполнения. Далее к полученной сумме причисляется дополнение, которое передается вместо исходных данных. Получив данные, приемник складывает их с КС и отбрасывает бит переполнения.
Если в результате получается нулевой байт, принятые данные верны. В противном случае они содержат ошибку, тогда приемник выставляет запрос на повторную передачу. Этот метод также просто реализовать, хотя он характеризуется большей избыточностью, чем добавление бита четности.
КС не позволяет выявить случаи, когда биты данных меняются местами, или если добавляются или теряются нулевые байты. В таблице 2 показан принцип вычисления контрольной суммы. Видно, что при появлении ошибки сложение принятых данных с контрольной суммой не дает в результате ноль.

Таблица 2. Метод контрольной суммы

Корректные данные

Данные с ошибками

Перестановка байтов

Удаление нулевого бита

Данные

10101010

10101010

10101010

10101010

00000000

00000000

00000000

10001000

10001000

00001000

10001001

10001001

10001001

10001001

10001000

Сумма

10111011

00111011

10111011

10111011

Контрольная сумма

01000101

01000101

01000101

01000101

Итог

00000000

10000000

00000000

00000000

Многократная передача

Наиболее надежный способ избежать ошибок — сравнивать все переданные данные. Это можно сделать двумя способами: либо приемник возвращает полученные данные в передатчик, либо передатчик пересылает данные несколько раз.
В первом случае переданные и принятые данные сравниваются в передатчике. Если они не совпадают, констатируется возникновение ошибки, и передача повторяется. Во втором случае данные сравниваются в приемнике. Если они не совпадают, запрашивается повторная передача.
Многократная передача — самый надежный способ предотвращения приема ошибочных данных, однако он слишком нерационален при обмене большим объемом данных.

Циклический контроль избыточности

Данный метод (CRC) похож на предыдущий. Сначала вычисляется контрольная сумма, которая передается вместе с информационными данными. Приемник проводит те же вычисления с принятыми данными и сравнивает свой результат с принятой КС. Если они совпадают, данные с высокой степенью вероятности приняты корректно. Данный метод имеет простую схемотехническую реализацию, поэтому широко применяется. При необходимости можно отключить передачу CRC.
Рассмотрим пример. Пусть данные каждой выборки LMP90100 передаются по последовательной шине в условиях сильного шума кусками по 24 бита. Контрольная сумма должна содержать 8-разрядов. Для вычисления CRC используется генератор полиномов. Полином должен быть на один бит длиннее, чем CRC. Для LMP90100 используется многочлен восьмого
порядка: x8 + x5 + x4 + 1. Использование многочлена первого порядка (x + 1) эквивалентно добавлению бита четности. Порядок многочлена обычно не превышает 64. Для USB используется полином пятого порядка: x5 + x2 + 1. Для Bluetooth многочлен еще большего порядка: x16 + x12 + x5 + 1, для Ethernet — 32-го порядка.
Для вычисления СRC полином представляется в двоичной форме. В нашем случае полином выглядит следующим образом: 100110001 (коэффициент при x8 равен 1, при x7 равен 0 и т.д.). Передаваемые данные сдвигаются влево на столько разрядов, сколько их в CRC, освободившиеся разряды справа заполняются нулями. Пусть исходные данные имеют вид: 0101 0101 1000 1001 0100 1011. Сдвигаем их на 8 бит, получаем 0101 0101 1000 1001 0100 1011 0000 0000. Для наглядности принцип формирования CRC показан на рисунке 1. Под измененными данными пишется полином в двоичной форме. Старшая единица полинома помещается под первой слева единицей данных. Выполняется сложение по модулю 2. Нули слева отбрасываются. Затем снова под первой единицей остатка располагается полином и выполняется сложение по модулю 2. Процедура повторяется до тех пор, пока левая единица остатка не займет восьмой или младше разряд.

32

31

30

29

28

27

26

25

24

23

22

21

20

19

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

↓ Добавленные нули

0

1

0

1

0

1

0

1

1

0

0

0

1

0

0

1

0

1

0

0

1

0

1

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

← Полином

0

0

0

1

1

0

0

1

1

1

0

0

1

0

0

1

0

1

0

0

1

0

1

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

1

0

1

0

1

1

0

1

1

0

0

1

0

1

0

0

1

0

1

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

0

1

1

0

1

0

1

0

0

0

1

0

1

0

0

1

0

1

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

1

0

0

1

1

0

0

1

1

0

1

0

0

1

0

1

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

0

0

0

0

0

0

1

0

0

1

0

0

1

0

1

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

0

0

0

1

0

1

0

0

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

0

0

1

1

1

1

0

0

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

1

1

0

1

1

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

0

1

0

0

1

1

0

0

0

0

0

1

0

0

1

1

0

0

0

1

CRC →

0

0

0

0

1

1

1

0

Рис. 1. Вычисление CRC

Полученная контрольная сумма СRC передается вместе с данными. Здесь есть тонкость. Для нулевых данных 0x000000 CRC равна 0x00, т.е. передатчик будет передавать нулевой сигнал 0x00000000 (три байта данных и CRC). Чтобы избежать недоразумений, особенно в случае многократной передачи, вместо CRC передается дополнение к ней. Тогда передаваемое значение будет равно 0x000000FF.
Данные АЦП в LMP90100 хранятся в регистрах 0x1A, 0x1B и 0x1C. Дополнение CRC сохраняется в регистрах 0x1D, чтобы МК считал полное значение. В МК выполняются те же операции с данными, что и в LMP90100. Контрольные суммы сравниваются. При несовпадении запрашивается повторная передача.

Заключение

Целостность передаваемых данных имеет большое значение. В условиях высокого шума она может быть нарушена, поэтому необходимо применять противодействующие меры. Мы рассмотрели, как проводится циклический контроль избыточности в интерфейсе датчика LMP90100.

Литература

1. Stout М. Ensuring data integrity in a noisy world//www.eetimes.com.

Мы знаем, что биты 0 и 1 соответствуют двум разным диапазонам аналоговых напряжений. Таким образом, во время передачи двоичных данных из одной системы в другую, шум также может быть добавлен. Из-за этого могут быть ошибки в полученных данных в другой системе.

Это означает, что бит 0 может измениться на 1 или бит 1 может измениться на 0. Мы не можем избежать помех от шума. Но мы можем сначала получить исходные данные, обнаружив, присутствуют ли какие-либо ошибки, а затем исправив эти ошибки. Для этой цели мы можем использовать следующие коды.

  • Коды обнаружения ошибок
  • Коды исправления ошибок

Коды обнаружения ошибок – используются для обнаружения ошибок, присутствующих в принятых данных (битовом потоке). Эти коды содержат некоторые биты, которые включены (добавлены) в исходный поток битов. Эти коды обнаруживают ошибку, если она произошла во время передачи исходных данных (потока битов). Пример – код четности, код Хэмминга.

Коды исправления ошибок – используются для исправления ошибок, присутствующих в полученных данных (битовом потоке), чтобы мы получили исходные данные. Коды исправления ошибок также используют аналогичную стратегию кодов обнаружения ошибок. Пример – код Хэмминга.

Поэтому, чтобы обнаружить и исправить ошибки, дополнительные биты добавляются к битам данных во время передачи.

Код паритета

Легко включить (добавить) один бит четности либо слева от MSB, либо справа от LSB исходного битового потока. Существует два типа кодов четности, а именно четный код четности и нечетный код четности, в зависимости от типа выбранной четности.

Четный код

Значение четного бита должно быть равно нулю, если в двоичном коде присутствует четное количество единиц. В противном случае он должен быть один. Таким образом, четное число единиц присутствует в четном коде четности . Четный код четности содержит биты данных и четный бит четности.

В следующей таблице приведены коды четности, соответствующие каждому 3-битному двоичному коду. Здесь бит четности включен справа от LSB двоичного кода.

Бинарный код Четный бит Четный код
000 0 0000
001 1 0011
010 1 0101
011 0 0110
100 1 1001
101 0 1010
110 0 1100
111 1 1111

Здесь число битов, присутствующих в четных кодах четности, равно 4. Таким образом, возможное четное число единиц в этих четных кодах четности равно 0, 2 и 4.

  • Если другая система получает один из этих четных кодов четности, то в полученных данных нет ошибки. Биты, отличные от четного бита, совпадают с битами двоичного кода.

  • Если другая система получит коды, отличные от четных, то в полученных данных возникнет ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.

Если другая система получает один из этих четных кодов четности, то в полученных данных нет ошибки. Биты, отличные от четного бита, совпадают с битами двоичного кода.

Если другая система получит коды, отличные от четных, то в полученных данных возникнет ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.

Поэтому четный бит четности полезен только для обнаружения ошибки в принятом коде четности. Но недостаточно исправить ошибку.

Код нечетного паритета

Значение нечетного бита четности должно быть нулевым, если в двоичном коде присутствует нечетное число единиц. В противном случае, он должен быть один. Так что нечетное количество единиц присутствует в нечетном коде четности . Нечетный код четности содержит биты данных и нечетный бит четности.

В следующей таблице показаны нечетные коды четности, соответствующие каждому 3-битному двоичному коду. Здесь нечетный бит четности включен справа от LSB двоичного кода.

Бинарный код Нечетный бит четности Код нечетного паритета
000 1 0001
001 0 0010
010 0 0100
011 1 0111
100 0 1000
101 1 1011
110 1 1101
111 0 1110

Здесь число битов, присутствующих в нечетных кодах четности, равно 4. Таким образом, возможное нечетное число единиц в этих нечетных кодах четности равно 1 и 3.

  • Если другая система получает один из этих нечетных кодов четности, то в полученных данных нет ошибки. Биты, отличные от нечетного бита четности, совпадают с битами двоичного кода.

  • Если другая система получает не четные коды четности, то в полученных данных есть ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.

Если другая система получает один из этих нечетных кодов четности, то в полученных данных нет ошибки. Биты, отличные от нечетного бита четности, совпадают с битами двоичного кода.

Если другая система получает не четные коды четности, то в полученных данных есть ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.

Следовательно, нечетный бит четности полезен только для обнаружения ошибки в принятом коде четности. Но недостаточно исправить ошибку.

Код Хэмминга

Код Хэмминга полезен как для обнаружения, так и для исправления ошибок, присутствующих в полученных данных. Этот код использует несколько битов четности, и мы должны поместить эти биты четности в позиции степеней 2.

Минимальное значение «k», для которого следующее соотношение является правильным (действительным), является не чем иным, как требуемым количеством битов четности.

2k geqn+k+1

Куда,

«n» – количество бит в двоичном коде (информация)

‘k’ – количество бит четности

Следовательно, количество битов в коде Хэмминга равно n + k.

Пусть код Хэмминга равен bn+kbn+k−1.....b3b2b1 и битам четности pk,pk−1,....p1. Мы можем поместить биты четности ‘k’ только в степени 2 позиции. В оставшихся битовых позициях мы можем разместить n бит двоичного кода.

Исходя из требований, мы можем использовать четную или нечетную четность при формировании кода Хемминга. Но тот же метод контроля четности следует использовать для того, чтобы определить, присутствует ли какая-либо ошибка в полученных данных.

Выполните эту процедуру для поиска битов четности .

  • Найдите значение p 1 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .

  • Найдите значение p 2 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .

  • Найдите значение p 3 , основанное на количестве единиц, присутствующих в позициях битов b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .

  • Аналогично найдите другие значения битов четности.

Найдите значение p 1 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .

Найдите значение p 2 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .

Найдите значение p 3 , основанное на количестве единиц, присутствующих в позициях битов b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .

Аналогично найдите другие значения битов четности.

Выполните эту процедуру для поиска контрольных битов .

  • Найдите значение c 1 , основанное на количестве единиц, присутствующих в битовых позициях b 1 , b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .

  • Найдите значение c 2 , основанное на количестве единиц, присутствующих в позициях битов b 2 , b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .

  • Найдите значение c 3 , основанное на количестве единиц, присутствующих в позициях битов b 4 , b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .

  • Аналогично найдите другие значения контрольных битов.

Найдите значение c 1 , основанное на количестве единиц, присутствующих в битовых позициях b 1 , b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .

Найдите значение c 2 , основанное на количестве единиц, присутствующих в позициях битов b 2 , b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .

Найдите значение c 3 , основанное на количестве единиц, присутствующих в позициях битов b 4 , b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .

Аналогично найдите другие значения контрольных битов.

Десятичный эквивалент контрольных битов в полученных данных дает значение позиции бита, где присутствует ошибка. Просто добавьте значение, присутствующее в этой позиции бита. Поэтому мы получим оригинальный двоичный код после удаления битов четности.

Пример 1

Найдем код Хемминга для двоичного кода: d 4 d 3 d 2 d 1 = 1000. Рассмотрим четные биты четности.

Количество битов в данном двоичном коде равно n = 4.

Мы можем найти необходимое количество бит четности, используя следующее математическое соотношение.

2k geqn+k+1

Подставим n = 4 в вышеприведенном математическом соотношении.

 Rightarrow2k geq4+k+1

 Rightarrow2k geq5+k

Минимальное значение k, удовлетворяющее указанному выше соотношению, равно 3. Следовательно, нам требуется 3 бита четности p 1 , p 2 и p 3 . Следовательно, количество битов в коде Хэмминга будет равно 7, поскольку в двоичном коде 4 бита и 3 бита четности. Мы должны поместить биты четности и биты двоичного кода в код Хэмминга, как показано ниже.

7-битный код Хэмминга : b7b6b5b4b3b2b1=d4d3d2p3D1р−2bp1

Подставляя биты двоичного кода, код Хэмминга будет b7b6b5b4b3b2b1=100p3Op2p1. Теперь давайте найдем биты четности.

p1=b7 oplusb5 oplusb3=1 oplus0 oplus0=1

p2=b7 oplusb6 oplusb3=1 oplus0 oplus0=1

p3=b7 oplusb6 oplusb5=1 oplus0 oplus0=1

Подставляя эти биты четности, код Хэмминга будет иметь значение b7b6b5b4b3b2b1=1001011.

Пример 2

В приведенном выше примере мы получили код Хэмминга в виде b7b6b5b4b3b2b1=1001011. Теперь давайте найдем позицию ошибки, когда полученный код равен b7b6b5b4b3b2b1=1001111.

Теперь давайте найдем контрольные биты.

c1=b7 oplusb5 oplusb3 oplusb1=1 oplus0 oplus1 oplus1=1

c2=b7 oplusb6 oplusb3 oplusb2=1 oplus0 oplus1 oplus1=1

c3=b7 oplusb6 oplusb5 oplusb4=1 oplus0 oplus0 oplus1=0

Десятичное значение контрольных битов дает позицию ошибки в полученном коде Хэмминга.

c3c2c1= left(011 right)2= left(3 right)10

Следовательно, ошибка присутствует в третьем бите (b 3 ) кода Хэмминга. Просто добавьте значение, присутствующее в этом бите, и удалите биты четности, чтобы получить исходный двоичный код.

Бит четности, также известный как контрольный бит, является единственным битом, который может быть добавлен к двоичной строке. Он имеет значение 1 или 0, чтобы сделать общее число 1- битов четным («четная четность») или нечетным («нечетная четность»).

Цель бита четности — предоставить простой способ проверки на наличие ошибок позже. Когда данные хранятся или передаются в электронном виде, нередки случаи, когда биты «переворачиваются» — меняются с 1 на 0 или наоборот. Проверка четности может помочь обнаружить некоторые из этих ошибок. Например, чтобы проверить двоичную последовательность, которая имеет четную четность, можно подсчитать общее количество единиц. Если число единиц не является четным, вероятно, произошла ошибка.

Недостатком этого типа проверки ошибок является то, что он может обнаруживать только нечетное количество ошибок в последовательности. Если четное количество бит перевернуто, проверка на четность не поймает его.

Пример проверки на четность

  1. Данные 10101 получают четный бит четности 1, что приводит к битовой последовательности 101011 .
  2. Эти данные передаются на другой компьютер. При передаче данные повреждены, и компьютер получает неверные данные 100011 .
  3. Принимающий компьютер вычисляет соотношение: 1 + 0 + 0 + 0 + 1 + 1 = 3 . Затем он выполняет 3 по модулю 2 (остаток от 3 делится на 2), ожидая результата 0, который будет указывать, что число является четным.
  4. Вместо этого он получает результат 3 по модулю 2 = 1, указывающий, что число нечетное. Поскольку он ищет числа с четной четностью, он просит исходный компьютер снова отправить данные.
  5. На этот раз данные поступают без ошибок: 101011 . Принимающий компьютер вычисляет 1 + 0 + 1 + 0 + 1 + 1 = 4 .
  6. 4 по модулю 2 = 0, что указывает на четность. Бит четности удаляется с конца последовательности, и данные 10101 принимаются.

Проверить биты, Условия аппаратного обеспечения, Отметить четность, Проверка четности, Пространственная четность

Источник

Error Detection Codes : The binary information is transferred from one location to another location through some communication medium. The external noise can change bits from 1 to 0 or 0 to 1.This changes in values changes the meaning of actual message and is called error. For efficient data transfer, there should be an error detection and correction codes. An error detection code is a binary code that detects digital errors during transmission. To detect error in the received message, we add some extra bits to the actual data. 

Without addition of redundant bits, it is not possible to detect errors in the received message. There are 3 ways in which we can detect errors in the received message : 

1. Parity Bit 

2. CheckSum

3. Cyclic Redundancy Check (CRC)

We’ll be understanding the parity bit method in this article in depth :-

Parity Bit Method : A parity bit is an extra bit included in binary message to make total number of 1’s either odd or even. Parity word denotes number of 1’s in a binary string. There are two parity system – even and odd parity checks.

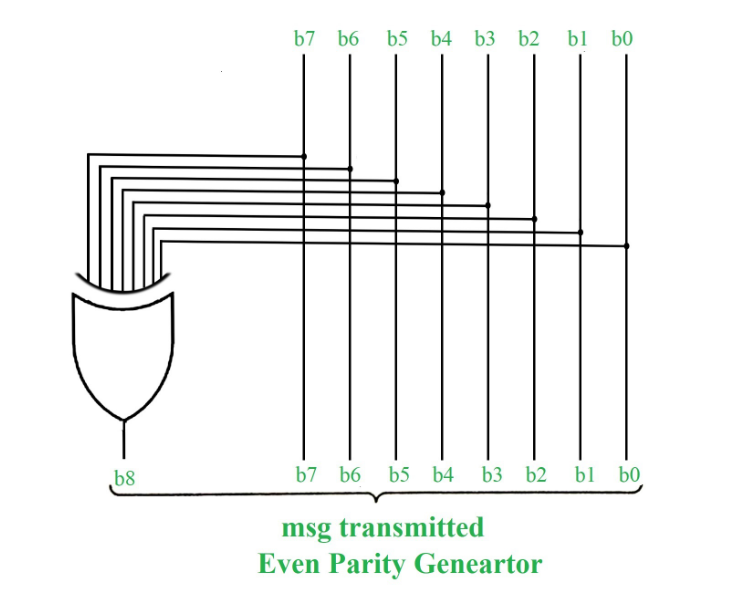
1. Even Parity Check: Total number of 1’s in the given data bit should be even. So if the total number of 1’s in the data bit is odd then a single 1 will be appended to make total number of 1’s even else 0 will be appended(if total number of 1’s  are already even). Hence, if any error occurs, the parity check circuit will detect it at the receiver’s end. Let’s understand this with example, see the below diagram : 

Even Parity Check (fig – 1.1)

In the above image, as we can see the data bits are ‘1011000’ and since this is even parity check that we’re talking about, 1 will be appended as the parity bit (highlighted in red) to make total count of 1’s even in the data sent. So here, our parity bit is 1. If the total count of 1 in the given data bits were already even, then 0 would’ve been appended.

 

2. Odd Parity Check: In odd parity system, if the total number of 1’s in the given binary string (or data bits) are even then 1 is appended to make the total count of 1’s as odd else 0 is appended. The receiver knows that whether sender is an odd parity generator or even parity generator. Suppose if sender is an odd parity generator then there must be an odd number of 1’s in received binary string. If an error occurs to a single bit that is either bit is changed to 1 to 0 or 0 to 1, received binary bit will have an even number of 1’s which will indicate an error. 

Take reference from fig(1.1) and rather than appending the 1 as parity bit, append 0 because total number of 1’s are already odd.  

 

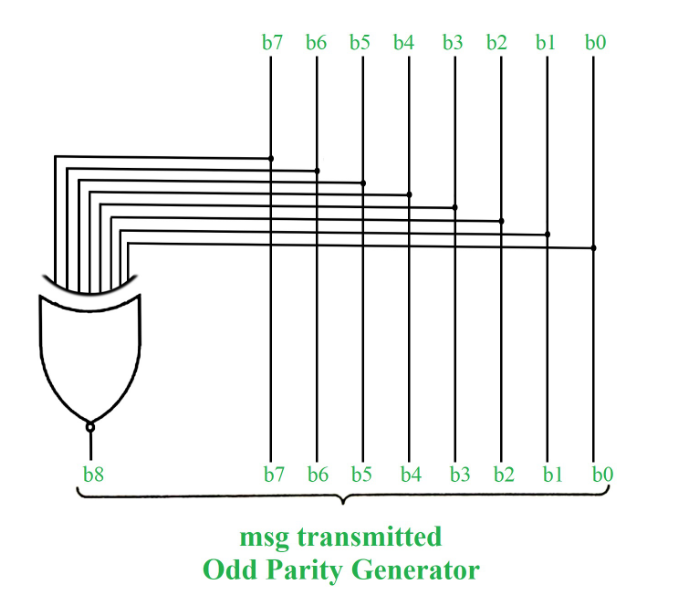
Some more examples :-

Message (XYZ) P(Odd) P(Even)
000 1 0
001 0 1
010 0 1
011 1 0
100 0 1
101 1 0
110 1 0
111 0 1

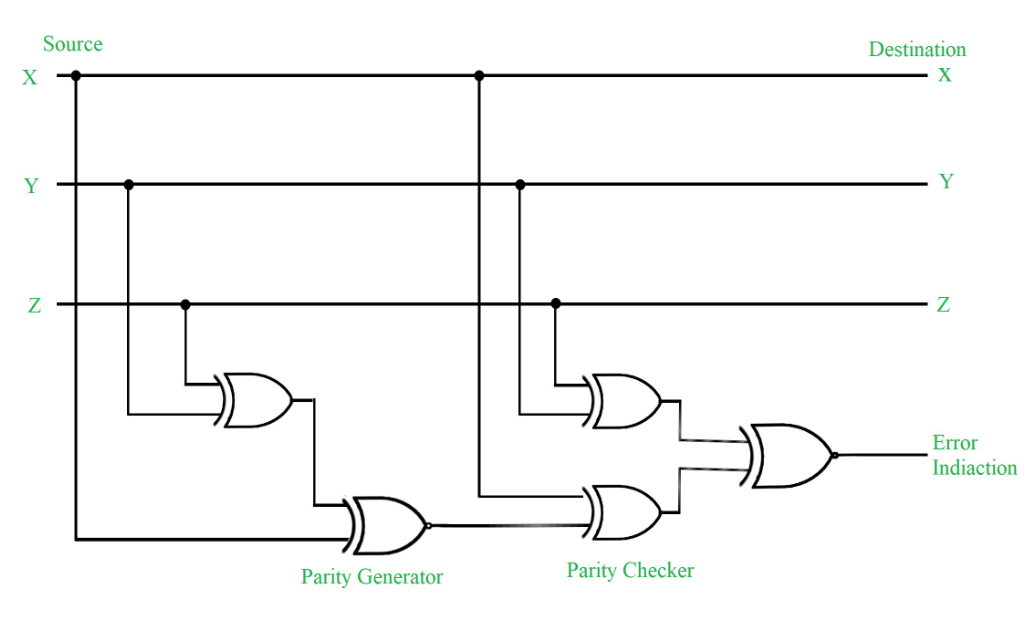Figure – Error Detection with Odd Parity Bit

Limitations : 

1. The limitation of this method is that only error in a single bit would be identified and we also cannot determine the exact location of error in the data bit.

2. If the number of bits in even parity check increase or decrease (data changed) but remained to be even then it won’t be able to detect error as the number of bits are still even and same goes for odd parity check.

See the below image for more details : 

Can’t detect error (Even Parity Check)

In the above example, the the data bits has been changed but as we can see the total count of 1’s remain to be even, the error can’t be detected even though the message’s meaning has been changed. You can visualize the same for odd parity check the number of 1’s will remain odd, even if the data bits have been changed and the odd parity check won’t be able to detect error.

Points to Remember :

  • In 1’s complement of signed number +0 and -0 has two different representation.
  • The range of signed magnitude representation of an 8-bit number in which 1-bit is used as a signed bit as follows -27 to +27.
  • Floating point number is said to be normalized if most significant digit of mantissa is one. For example, 6-bit binary number 001101 is normalized because of two leading 0’s.
  • Booth algorithm that uses two n bit numbers for multiplication gives results in 2n bits.
  • The booth algorithm uses 2’s complement representation of numbers and work for both positive and negative numbers.
  • If k-bits are used to represent exponent then bits number = (2k-1) and range of exponent = – (2k-1 -1) to (2k-1).

Last Updated :
12 May, 2023

Like Article

Save Article

Источник

Перейти к контенту

Информатика 11 класс Поляков Углубленный ГДЗ § 2. Передача данных

§ 2. Передача данных ГДЗ по Информатике 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю.

7. Что такое бит чётности? В каких случаях с помощью бита чётности можно обнаружить ошибку, а в каких — нельзя?

Ответ

Бит чётности (англ. Parity bit) — контрольный бит в вычислительной технике и сетях передачи данных, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе). В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.

В длинной цепочке применение бита чётности позволяет обнаруживать нечётное число ошибок (1, 3, 5, …), а ошибки в чётном количестве разрядов остаются незамеченными. Контроль с помощью бита чётности применяется для небольших блоков данных (чаще всего — для каждого отдельного байта) и хорошо работает тогда, когда отдельные ошибки при передаче независимы одна от другой и встречаются редко.

Если при передаче неверно передан только один из битов, количество единиц в сообщении стало нечётным, это и служит признаком ошибки при передаче. Однако исправить ошибку нельзя, потому что непонятно, в каком именно разряде она случилась. Если же изменилось два бита, чётность не меняется, и такая ошибка не обнаруживается.

Источник

Бит четности является параметром со значением 0 или 1 , который используется в способе обнаружения ошибок передачи , в которой 0 или 1 добавляется к каждой группе 7-8 битов (байт). Цель состоит в том, чтобы каждый байт всегда имел нечетное общее количество «1» или четное общее количество «1» в соответствии с установленной четностью.

Четность — это метод обнаружения ошибок, используемый в асинхронной связи. Он используется для проверки целостности каждого байта в передаваемом потоке. Например, если установлена ​​нечетная четность, любой байт, полученный из передачи с общим числом «1», который является четным, должен содержать ошибку.

Источник: pixabay.com

Используются два типа проверки на четность: проверка на четность, при которой бит четности 1 добавляется, если в предыдущем байте имеется нечетное общее количество битов «1», и проверка на четность, когда выполняется обратное. С помощью этого метода вы сможете узнать только то, что произошла ошибка, но вы не узнаете, где произошла ошибка.

Для чего нужен бит четности?

При отправке цифровых данных может быть ошибка между переданным кодом и полученным кодом. Существует множество источников ошибок в виде различных типов шума, таких как электромагнитный шум или тепловой шум.

Следовательно, необходимо реализовать некоторый метод, чтобы проверить, ошибочны ли полученные коды или байты.

Однако как получатель может узнать, ошибочен ли полученный код? Получатель не может узнать код до его получения.

Например, предположим, что отправитель передает код 01100110, но после прохождения через зашумленную линию получатель получает код 00100110. Получатель не будет знать, что он получил код с ошибкой во втором бите.

Получатель не может знать, что сообщение содержит ошибку в первом бите, потому что это будет означать, что получатель уже знает сообщение от передатчика до передачи.

Контроль ошибок

Проблема, с которой приемник может проверить наличие ошибки, может быть решена с помощью кодирования с контролем ошибок.

Основная идея кодирования с контролем ошибок заключается в добавлении дополнительного бита в информацию, которая должна быть отправлена, чтобы ошибка обнаруживалась и исправлялась. Есть много кодировок обработки ошибок. Самый простой — это бит четности.

Бит четности добавляется к каждому передаваемому байту. Этот бит используется для проверки того, что информация была доставлена ​​точно.

Бит четности для каждого байта устанавливается так, чтобы все байты имели нечетное число или четное число битов «1».

пример

Предположим, что два диска обмениваются данными с проверкой четности, которая является наиболее распространенной формой проверки четности.

В зависимости от единицы передачи он отправляет байты и сначала подсчитывает количество битов «1» в каждой группе из семи битов (байтах). Если количество битов «1» четное, установите бит четности в 0. Если количество битов «1» нечетное, установите бит четности в 1. Таким образом, каждый байт будет иметь четное количество битов «1».

Приемник проверяет каждый байт, чтобы убедиться, что он имеет четное количество битов «1». Если в байте обнаружено нечетное количество битов «1», приемник будет знать, что во время передачи произошла ошибка.

Ранее и получатель, и отправитель должны были договориться об использовании проверки четности и о том, должна ли четность быть нечетной или четной. Если обе стороны не настроены с одинаковым чувством паритета, связь будет невозможна.

Обнаружение ошибок

Проверка четности — самый простой метод обнаружения ошибок связи.

Однако, хотя он может обнаруживать множество ошибок, он не является безошибочным, поскольку он не способен обнаруживать компоновку, когда четное количество битов в одном и том же байте изменяется из-за электрического шума.

Проверка четности используется не только при обмене данными, но и для тестирования запоминающих устройств. Например, многие персональные компьютеры выполняют проверку на четность всякий раз, когда байт данных считывается из памяти.

Как это работает?

Предположим, у вас есть 7-битные коды данных и дополнительный бит, который является битом четности, добавлен для формирования 8-битного кода данных. Можно использовать два метода: четность и нечетность.

В качестве образца можно взять метод четности. Вы поступили бы наоборот, если бы выбрали метод нечетной четности.

Метод четной четности

Этот метод указывает, что добавляемый бит четности должен быть таким, чтобы общая сумма «1» в окончательном коде была четной. Например:

Следовательно, для первого 7-битного кода: 0010010 с четным количеством «1» (2) переданный 8-битный код будет: 00100100 с четным количеством «1» (2).

Для 7-битного кода 1110110 с нечетным количеством «1» (5) переданный 8-битный код будет 11101101 с четным количеством «1» (6).

После того, как получатель получит 8 битов, он проверит количество «1» в полученном коде, если количество «1» четное, это означает, что ошибки нет, если количество нечетное, это означает, что ошибка.

Когда вычисленная четность полученного байта не совпадает со значением принятого бита четности, считается, что произошла ошибка четности, и обычно байт отбрасывается.

В случае ошибки приемник предупредит передатчик, чтобы он отправил код еще раз.

Не безошибочный

Однако у этих методов контроля четности есть недостаток: если код 1110110 преобразуется шумом линии в 11111001, вызывая 2-битную ошибку, то этот метод не может обнаружить, что ошибка произошла.

Четность хороша при обнаружении ошибок и всегда обнаруживает любое нечетное количество ошибок в полученном байте. Однако при четном количестве ошибок средство проверки четности не сможет найти ошибку.

Ссылки

  1. Ванги Бил (2019). Проверка четности. Webopedia. Взято с: webopedia.com.
  2. Группа исследований электроники (2019). Четность символов. Взято с: erg.abdn.ac.uk.
  3. Словарь (2019) .. Бит паритета. Взято с сайта vocabulary.com.
  4. Ангмс (2013). Самый простой код контроля ошибок — Parity Bit. Взято с сайта angms.science.
  5. Кристенсон, (2011). Определение бита четности. Techterms. Взято с: techterms.com.
Источник

ЕГЭ – 2021, задание 5, часть 2. Элементы теории алгоритмов: бит четности и др.

При решении заданий 5 ЕГЭ-2021, часть 2 рассматриваются несколько типов задач на алгоритмизацию. При этом нужно учесть,, что алгоритм — это четкий порядок действий, подлежащих выполнению, то есть при решении задач на алгоритмизацию следует внимательно читать условие задачи и точно, аккуратно и без спешки (в этом залог быстрого и точного решения задачи!) выполнять описанные в нем действия.

При этом обратим внимание, что одни и те же действия в разных задачах могут описываться разными условиями, например:

— «складываются все цифры двоичной записи числа» или «считается количество единиц в двоичной записи числа»: поскольку сумма цифр двоичной записи числа равна количеству единиц в двоичном числе, то при решении задач быстрее и проще посчитать количество единиц в записи и получить результат для данного условия;

— «остаток от деления суммы (количества единиц) на два», «бит чётности», «четное число или нет» — в результате проверки всех этих условий проверяется остаток от деления числа на 2: по умолчанию это ноль для четного числа и единица — для нечетного. Но в условии задач этот результат может меняться, поэтому следует точно выполнять действия, заданные в алгоритме!

Следует также внимательно смотреть, какое из чисел – N или R – следует искать в данной задаче.

Пример 1 (ДЕМО – 2021)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

  1. Строится двоичная запись числа N.

  2. К этой записи дописываются справа ещё два разряда по следующему правилу:

  1. складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

  2. над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.

Решение:

Так как в задании указан результат работы алгоритма, то выполняем действия строго по алгоритму, но в обратную сторону:

  1. Переведем в двоичную систему первое число, удовлетворяющее условию задачи (наименьшее число R, которое больше числа 77) — число 78:

78 = 26 + 23 + 22 + 21 = 10011102

  1. Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма

N = 100112 и цифры 10, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 1 – верно, так как количество единиц в числе N равно трем;

  2. 0 – верно, так как теперь в полученном результате уже 4 единицы.

Так как условия выполнения алгоритма совпадают с полученным результатом, то искомое число N = 100112 и будет искомым. Переводим его в десятичную систему счисления и получаем ответ:

N = 100112 = 20 + 21 + 02 + 03 + 24 = 1 + 2 + 16 = 19.

Примечание: для быстрого и точного перевода числа из двоичной системы в десятичную я записываю степени с конца, чтобы не делать лишних действий и не допускать возможных ошибок.

Ответ: 19

Пример 2 (1426)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

  1. Строится двоичная запись числа N.

  2. К этой записи дописываются справа ещё два разряда по следующему правилу:

  1. в конец числа (справа) дописывается 1, если число единиц в двоичной записи числа чётно, и 0, если число единиц в двоичной записи числа нечётно;

  2. к этой записи справа дописывается остаток от деления количества единиц на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает 31 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

Решение:

Так как в задании указан результат работы алгоритма, то выполняем действия строго по алгоритму, но в обратную сторону:

  1. Переведем в двоичную систему первое число, удовлетворяющее условию задачи (наименьшее число R, которое больше числа 31) — число 32:

32 = 25 = 1000002

  1. Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 10002 и цифры 00, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 0 – верно, так как количество единиц в числе N нечетно;

  2. 0 – неверно, так как остаток от деления количества единиц на 2 равен 1.

Так как условия выполнения алгоритма НЕ совпадают с полученным результатом, то берем следующее возможное число искомое число R = 33 и проверяем его.

1. Переведем число 33 в двоичную систему счисления: 33 = 25 = 1000012

2. Для проверки, может ли данное число R быть результатом работы алгоритма,

отделяем от него справа две последние цифры (которые являются результатом

выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 10002

и цифры 01, которые получены в результате двух следующих шагов выполнения

алгоритма:

  1. 0 – верно, так как количество единиц в числе N нечетно;

  2. 1 – верно, так как результат от деления количества единиц на 2 равен 1.

Так как условия выполнения алгоритма совпадают с полученным результатом, то искомое число N = 110002 и будет искомым. Переводим его в десятичную систему счисления и получаем ответ:

N = 1100112 = 20 + 21 + 02 + 03 + 24 = 1 + 2 + 16 = 19.

Ответ: 33

Пример 3 (1431)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

  1. Строится двоичная запись числа N.

  2. К этой записи дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если нечётное.

  3. К полученному результату дописывается ещё один бит чётности.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 96. В ответе это число запишите в десятичной системе.

Решение 1 – короткое:

Так как в задании указан результат работы алгоритма, то выполняем действия строго по алгоритму, но в обратную сторону:

Переведем в двоичную систему первое число, удовлетворяющее условию задачи (наименьшее число R, которое больше числа 96) — число 97:

97 = 26 + 25 + 20 = 11000012

Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и получаем, что для числа N = 110002 последними цифрами должны быть 00, но тогда число R = 11000002 = 96 не удовлетворяет условию задачи.

Числа с двумя последними цифрами 01 (97 = 11000012), 10 (98 = 11000102) и 11 (99=11000112) также не подходят. Это значит, что нужно увеличивать само число N, тогда получаем N = 110012 и в результате работы алгоритма получим R = 11001102 = 102.

Тогда искомое число N = 110012 = 25

Ответ: 25

Решение 2 – длинное (обычное):

Так как в задании указан результат работы алгоритма, то выполняем действия строго по алгоритму, но в обратную сторону:

  1. Переведем в двоичную систему первое число, удовлетворяющее условию задачи (наименьшее число R, которое больше числа 96) — число 97:

97 = 26 + 25 + 20 = 11000012

Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 110002 и цифры 01, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 0 – верно, так как количество единиц в числе N четно;

  2. 1 –неверно, так как количество единиц в числе N четно.

Так как условия выполнения алгоритма НЕ совпадают с полученным результатом, то берем следующее возможное число R = 98 и проверяем его.

  1. Переведем в двоичную систему число 98:

98 = 26 + 25 + 21 = 11000102

Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 110002 и цифры 10, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 1 – неверно, так как количество единиц в числе N четно;

  2. 0 – неверно, так как количество единиц в числе N нечетно.

Так как условия выполнения алгоритма опять НЕ совпадают с полученным результатом, то берем следующее возможное число R = 99 и проверяем его.

  1. Переведем в двоичную систему число 99:

  1. = 26 + 25 + 21 + 20 = 11000112

Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 110002 и цифры 11, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 1 – неверно, так как количество единиц в числе N четно

  2. 1–верно, так как количество единиц в числе N нечетно.

Так как условия выполнения алгоритма опять НЕ совпадают с полученным результатом, то берем следующее возможное число R = 100 и проверяем его.

  1. Переведем в двоичную систему число100:

  1. = 26 + 25 + 22 = 11001002

Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 110012 и цифры 00, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 0 – неверно, так как количество единиц в числе N нечетно

  2. 0 – неверно, так как количество единиц в числе N нечетно.

Так как условия выполнения алгоритма опять НЕ совпадают с полученным результатом, то берем следующее возможное число R = 101 и проверяем его.

  1. Переведем в двоичную систему число 101:

  1. = 26 + 25 + 22 + 20 = 11001012

Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 110012 и цифры 01, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 0 – неверно, так как количество единиц в числе N нечетно

  2. 1 – верно, так как количество единиц в числе N нечетно.

Так как условия выполнения алгоритма опять НЕ совпадают с полученным результатом, то берем следующее возможное число R = 102 и проверяем его.

  1. Переведем в двоичную систему число 102:

  1. = 26 + 25 + 22 + 21 = 11001102

Для проверки, может ли данное число R быть результатом работы алгоритма, отделяем от него справа две последние цифры (которые являются результатом выполнения алгоритма) и проверяем исходное число до работы алгоритма N = 110012 и цифры 10, которые получены в результате двух следующих шагов выполнения алгоритма:

  1. 1 – верно, так как количество единиц в числе N нечетно

  2. 0 – верно, так как количество единиц в числе N четно.

Так как оба условия выполнения алгоритма совпадают с полученным результатом, то искомое число N = 100112 и будет искомым. Переводим его в десятичную систему счисления и получаем ответ:

N = 110012 = 20 + 01 + 02 + 23 + 24 = 1 + 8 + 16 = 25.

Ответ: 25

Пример 4 (4796)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) Складываются все цифры двоичной записи числа. Если сумма четная, то в конец числа (справа) дописывается 1, а если нечетная, то дописывается 0. Например, запись числа 10 преобразуется в запись 100;
3) К полученному результату применяется еще раз пункт 2 этого алгоритма.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите количество чисел R, которые могут быть получены в результате работы этого алгоритма, и лежат в диапазоне 16 ≤ R ≤ 32.

Решение:

Так как в задании указан результат работы алгоритма, то выполняем действия строго по алгоритму, но в обратную сторону.

Переведем в двоичную систему первое число, удовлетворяющее условию задачи границы диапазона возможных чисел R:

Rmin = 24 = 100002

Rmax = 25 = 1000002

Соответственно получаем Nmin = 22 = 1002 и Nmax = 23 = 10002.

Далее берем все возможные числа N внутри данного диапазона (возможны только три варианта – 101, 110 и 111) и проверяем результат работы алгоритма над ними:

при N = 1012 возможно только одно R = 101102 = 22

при N = 1102 возможно только одно R = 110102 = 26

при N = 1112 возможно только одно R = 111002 = 28

Тогда всего получаем 5 подходящих чисел.

Ответ: 5

Пример 5 (4846).

Автомат обрабатывает натуральное число N
1) Строится восьмибитная двоичная запись числа N–1.
2) Инвертируются разряды исходного числа (0 заменяется на 1, 1 на 0).
3) Полученное число переводится в десятичную систему счисления.
Для какого числа N результат работы алгоритма равен 113?

Решение:

Переводим число 113 в двоичную систему счисления и получаем

N — 1 = 26 + 25 + 24 + 20 = 11100012

Дополняем его до восьми бит и инвертируем:

N — 1 = 011100012 = 100011102 = 21 + 22 + 23+ 27 = 142, тогда N = 142 + 1= 143.

Ответ: 143

Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Содержание:

  • Объяснение 5 задания
    • Исполнитель для возведения в квадрат, деления, умножения и сложения
    • Проверка числовой последовательности на соответствие алгоритму
  • Разбор 5 задания
    • Решение задания про алгоритм, который строит число R
    • Решение заданий для темы Проверка числовой последовательности (Автомат)

5-е задание: «Анализ алгоритмов и исполнители»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

  
Проверяемые элементы содержания: Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд

До ЕГЭ 2021 года — это было задание № 6 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Как и в других заданиях базового уровня сложности, источником ошибок служит недостаточная внимательность и отсутствие или поверхностность самостоятельной проверки полученного ответа»

ФГБНУ «Федеральный институт педагогических измерений»

Проверка числовой последовательности на соответствие алгоритму

  • для выполнения некоторых заданий необходимо повторить тему системы счисления;
  • максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
  • для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:
    • например: 
 310 = 112 
после добавления бита четности: 110
----
 410 = 1002 
после добавления бита четности: 1001
  • добавление к двоичной записи числа нуль справа увеличивает число в 2 раза:
    • например:
1112 - это 710
добавим 0 справа:
11102 - это 1410

Теперь будем рассматривать конкретные типовые экзаменационные варианты по информатике с объяснением их решения.

Разбор 5 задания

Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:

Решение задания про алгоритм, который строит число R

5_11:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

  1. Строится двоичная запись числа 4N.
  2. К этой записи дописываются справа еще два разряда по следующему правилу:
    • складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
    • над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

    Полученная таким образом запись является двоичной записью искомого числа R.

    Укажите такое наименьшее число N, для которого результат работы алгоритма больше 129. В ответе это число запишите в десятичной системе счисления.

  
Типовые задания для тренировки

✍ Решение:

    ✎ Решение аналитическим способом:

  • Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
  • Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(130). Получим: 
    • 13010 = 100000102
  • Это двоичное число получилось из исходного двоичного, после того как дважды был добавлен остаток от деления суммы цифр на 2. Т.е.: 
    • в обратном порядке:
было 1000001 -> стало 10000010 
еще раз то же самое: 
было 100000 -> стало 1000001
  • Значит, необходимое нам двоичное число — это 100000.
  • Переведем 100000 в 10-ю систему. Для этого можно воспользоваться калькулятором, либо использовать интерпретатор Питона: int('100000',2).
    • 1000002 = 3210
  • Так как по условию у нас 4*N, то 32 делим на 4 — > 8.

    • ✎ Решение с использованием программирования:

    PascalAbc.Net:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

    uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := 4*n_;
    var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost)
    ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost;
    if n > 129 then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

    Python:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

    n_ = 1
while True:
    n = 4*n_
    r = str(bin(n))
    r = r[2:]
    for i in range(2):
        if r.count('1') % 2 == 0:
            r+='0'
        else:
            r+='1'
 
    n = int(r, base=2)
    if n > 129:
        print(n_)
        break
    n_+=1

Результат: 8

Для более детального разбора предлагаем посмотреть видео теоретического решения данного 5 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_12: Демоверсия ЕГЭ 2018 информатика:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

  1. Строится двоичная запись числа N.
  2. К этой записи дописываются справа ещё два разряда по следующему правилу:
  3. складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
  4. над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

    5. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

    Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

  • Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
  • Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
  • Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(84). Получим:
    • 84 = 1010100
  • В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так как оно нечетное. А мы имеем 0. Соответственно, это оно не подходит.
  • Возьмем следующее четное число — 86. Переведем его в двоичную систему счисления:
    • 86 = 1010110
  • В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так и есть: 101011. А затем добавляется 0: 1010110. Соответственно, оно подходит.

Результат: 86

Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:

📹 Видеорешение на RuTube здесь -> аналитическое решение

5_18:

Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3. Шаг 2 повторяется ещё два раза.
4. Результат переводится в десятичную систему счисления.

При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?

Типовые задания для тренировки

✍ Решение:

    ✎ Решение с использованием программирования:

    PascalAbc.Net:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

    uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
    for var i := 1 to 3 do 
    begin
      if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем
        if n mod 2 = 0 then // если четное, то в конце 0
          n := 2 * n  // добавляем разряд = 0
        else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
      else if bin(n).CountOf('1') > bin(n).CountOf('0') then
        n := 2 * n
      else
        n := 2 * n + 1
    end;
    if (n_ > 65) and (n mod 4 = 0) then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

    Python:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

    n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(3):
        if r.count('1') == r.count('0'):
            r+=r[-1] 
        elif r.count('1')>r.count('0'):
            r+='0'
        else:
            r+='1'
    n = int(r, base=2)
    if n_ > 65 and n % 4 == 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 79

5_19:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Число N переводим в двоичную запись.
2) Инвертируем все биты числа кроме первого.
3) Переводим в десятичную запись.
4) Складываем результат с исходным числом N.
Полученное число является искомым числом R.

Укажите наименьшее нечетное число N, для которого результат работы данного алгоритма больше 99. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

    ✎ Решение с использованием программирования:

    PascalAbc.Net:

    Python:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

    n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(1,len(r)):
        if r[i]== '0':
            r=r[:i]+'1'+r[i+1:] 
        else:
            r=r[:i]+'0'+r[i+1:] 
    n = int(r, base=2)
    n+=n_
    if n > 99 and n_ % 2 != 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 65

5_13:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
— если N делится нацело на 4, в конец числа (справа) дописывается сначала ноль, а затем еще один ноль;
— если N при делении на 4 дает в остатке 1, то в конец числа (справа) дописывается сначала ноль, а затем единица;
— если N при делении на 4 дает в остатке 2, то в конец числа (справа) дописывается сначала один, а затем ноль;
— если N при делении на 4 дает в остатке 3, в конец числа (справа) дописывается сначала один, а затем еще одна единица.

Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.

  
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.

Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе это число запишите

в десятичной системе счисления

.

  
Типовые задания для тренировки

✍ Решение:

  • Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые < 100 — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(99). Получим:
    • 99 = 11000112
  • По алгоритму это число получилось путем добавления справа двух разрядов, значение которых зависит от исходного N:
    • 1100011
  N
  • Т.е. в конце были добавлены две единицы — по алгоритму это значит, что исходное N должно в остатке при делении на 4 давать 3. Переведем найденное N в десятичную систему. Можно использовать калькулятор либо консоль пайтон: int('11000',2)
    • 11000 = 2410
  • 24 делится на 4 нацело, т.е. в конце по алгоритму должны были добавиться два разряда — 00. У нас же в конце 11. Т.е. число 99 не подходит. Проверим следующее — 98.
    • 98 = 11000102  : 10 в конце добавлено алгоритмом
N = 110002 = 2410
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 10 
98 - не подходит

97 = 11000012 : 01 в конце добавлено алгоритмом
N = 110002 = 2410
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 01 
97 - не подходит

96 = 11000002 : 00 в конце добавлено алгоритмом
N = 110002 = 2410
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, у нас 00 - верно!
96 - подходит!

Результат: 96

Предлагаем посмотреть видео теоретического решения:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_14:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.

  
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.

Типовые задания для тренировки  

✍ Решение:

    ✎ Решение аналитическим способом:

  • В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона: bin(114))
    • 114 = 11100102
  • Проанализируем, как могло бы получиться двоичное число 114 (R) по алгоритму:

    • 2. В полученное числе N = 1110 дублируется последняя цифра и получается 11100.
    3. Поскольку число единиц (3) — нечетное, то справа добавляется 1: 111001.
    4. Т.к. в полученном наборе цифр четное число единиц, то добавляем 0: 1110010

  • Поскольку из числа N = 1110 по алгоритму могла получиться только такая последовательность цифр (1110010), то для получения минимального R, но большего чем R = 114, увеличим в N = 1110 самый младший разряд на единицу и рассмотрим работу алгоритма с полученным числом:
    • 1. N = 1110 + 1 = 1111

Работа по алгоритму:
2. 11111 - дублирование последней цифры.
3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное)
4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.
  • Ответ нужно получить в десятичной системе счисления (для перевода можно воспользоваться интерпретатором Питона: int('1111110',2)):
    • min R = 11111102 = 12610

    ✎ Решение с использованием программирования:

    PascalAbc.Net:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

    uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
          // дублирвание последней цифры
    if n mod 2 = 0 then // если четное, то в конце 0
      n := 2 * n  // добавляем разряд = 0
    else 
      n := 2 * n + 1; // иначе добавляем разряд = 1
    for var i := 1 to 2 do
    begin
      if bin(n).CountOf('1') mod 2 = 0 then
        n := 2 * n  // добавляем разряд = 0
     else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
    end;
    if n > 114 then
    begin
      println(n);
      break
    end;
    n_ += 1;
  end;
end.

    Python:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

    n_ = 1
while True:
    n = n_
    r  = str(bin(n)) # строковое значение
    r = r[2:] # убираем 0b
    r=r+r[-1]
    for i in range (2):
        if r.count('1') % 2 == 0:
            r = r+'0'
        else:
            r = r+'1'
    r = int(r,base = 2) # в 10-ю с.с.
    if r > 114:
        print(r)
        break
    n_+= 1

Результат: 126

5_17: Досрочный вариант 1 ЕГЭ по информатике 2020, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
  — если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы.

Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

  
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.

Укажите минимальное число N, для которого результат работы алгоритма будет больше 134. В ответе это число запишите в десятичной системе счисления.

Ответ: 33

  
Видео -> теоретическое решение 
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_16:

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:

1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.

  
Какое число нужно ввести в автомат, чтобы в результате получилось 45?

✍ Решение:

  • Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:
    • 45 = 001011012
  • Пронумеруем биты слева направо, начиная с единицы. Рассмотрим каждый бит отдельно, начиная с левого бита под номером 1.
  • 1. Так как биты в уменьшаемом и вычитаемом должны быть различны, то единица в результате может получится только 1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:
    •    .
_  1 _ _ _ _ _ _ _    N инвертируемое
=  0 _ _ _ _ _ _ _    N исходное
   0 0 1 0 1 1 0 1  = 45   результат
  • 2. 1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:
    •    . .
_  1 0 _ _ _ _ _ _ 
=  0 1 _ _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат
  • 3. 1 - 0 не может быть, так как у следующего слева нуля мы заняли.
    Значит 0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:
    •    . .
_  1 0 0 _ _ _ _ _ 
=  0 1 1 _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат
  • 4. 0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.
    •    . .   .
_  1 0 0 1 _ _ _ _ 
=  0 1 1 0 _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат
  • 5. 1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:
    •    . .   .
_  1 0 0 1 0 _ _ _ 
=  0 1 1 0 1 _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат
  • 6. 0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:
    •    . .   .
_  1 0 0 1 0 1 _ _ 
=  0 1 1 0 1 0 _ _ 
   0 0 1 0 1 1 0 1  = 45   результат
  • 7. 0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:
    •    . .   .     .
_  1 0 0 1 0 1 1 _ 
=  0 1 1 0 1 0 0 _ 
   0 0 1 0 1 1 0 1  = 45   результат
  • 8. Чтобы получить 1, имеем 0 - 1:
    •    . .   .     .
_  1 0 0 1 0 1 1 0 
=  0 1 1 0 1 0 0 1
   0 0 1 0 1 1 0 1  = 45   результат
  • Полученное число (вычитаемое) и есть искомое N. Переведем его в 10-ю с.с.:
    • 01101001 = 10510

Ответ: 105

Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

Решение заданий для темы Проверка числовой последовательности (Автомат)

5_7:

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

  1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
  2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.

Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

✍ Решение:

Результат: 2949

Процесс теоретического решения данного 5 задания представлен в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_8:

Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:

  • Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
  • Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).

    • Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.

✍ Решение:

  • Число 2512 можно разбить на 2, 5, 12
  • Начнем с 12. Необходимо получить наибольшее число, поэтому разобьем на слагаемые с наибольшей цифрой — 9:
    • 12=9+3
  • То есть первые две цифры:
    •  93**
  • В число 2 тройка не входит, значит забираем тройку из 5. Остается 2. А, значит, из состава 2 остается 0.
  • Получим число: 9320.

    • Результат: 9320

    Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь -> теоретическое решение

    5_9:

    Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам:

    1. Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
    2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).

      3. Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.

    Какие из предложенных чисел могут быть результатом работы автомата?
    Перечислите в алфавитном порядке буквы, соответствующие этим числам, без пробелов и знаков препинания.

    Варианты:
    A) 127
    B) C6
    C) BA
    D) E3
    E) D1

    ✍ Решение:

    Проанализируем все варианты:

  • Вариант А. 127 не подходит, так как число 12 в шестнадцатеричной системе записывается как С.
  • Вариант В. С6 разбиваем на 12 и 6. Число может быть результатом работы автомата. Исходные числа, например, 35 и 37
  • Вариант С. BA разбиваем на 11 и 10. Число может быть результатом работы автомата. Исходные числа, например, 55 и 56
  • Вариант D. E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.
  • Вариант E. D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.

    • Результат: BC

    Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь -> теоретическое решение

    5_10: Задание 5 ГВЭ 11 класс 2018 год ФИПИ

    Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 7 (если в числе есть цифра больше 7, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.

    1. Вычисляются два шестнадцатеричных числа: сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
    2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).

    Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.

    Определите, какое из предложенных чисел может быть результатом работы автомата.

    Варианты:
    1) AD
    2) 64
    3) CF
    4) 811

    ✍ Решение:

    Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь -> теоретическое решение

    5_15:

    Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам:
    1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 7.
    2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 2.
    3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.

    Пример. Исходное число: 55. Остаток от деления на 7 равен 6; остаток от деления на 2 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 610.

      
    Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?

    Типовые задания для тренировки

    ✍ Решение:

    • Обозначим каждую цифру числа Y согласно заданию:
      • Y =    3       1       2
       x mod 7    x mod 2    x mod 5
    • Сделаем выводы:

      • 1. x mod 2 = 1 => значит, X — нечетное число
      2. x mod 5 = 2 => значит, X — либо ?2, либо ?7.
      3. раз x — нечетное, то из пред. пункта получаем x = ?7
      4. x mod 7 = 3 => переберем все варианты:

      97 - не подходит, 
87 - подходит (87 / 7 = 12, остаток = 3)
77 - не подходит,
67 - не подходит,
57 - не подходит,
47 - не подходит,
37 - не подходит,
27 - не подходит,
17 - подходит (17 / 7 = 2, остаток = 3)

    Результат: 2

    Перейти к контенту

    Информатика 11 класс Поляков Углубленный ГДЗ § 2. Передача данных

    § 2. Передача данных ГДЗ по Информатике 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю.

    7. Что такое бит чётности? В каких случаях с помощью бита чётности можно обнаружить ошибку, а в каких — нельзя?

    Ответ

    Бит чётности (англ. Parity bit) — контрольный бит в вычислительной технике и сетях передачи данных, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе). В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.

    В длинной цепочке применение бита чётности позволяет обнаруживать нечётное число ошибок (1, 3, 5, …), а ошибки в чётном количестве разрядов остаются незамеченными. Контроль с помощью бита чётности применяется для небольших блоков данных (чаще всего — для каждого отдельного байта) и хорошо работает тогда, когда отдельные ошибки при передаче независимы одна от другой и встречаются редко.

    Если при передаче неверно передан только один из битов, количество единиц в сообщении стало нечётным, это и служит признаком ошибки при передаче. Однако исправить ошибку нельзя, потому что непонятно, в каком именно разряде она случилась. Если же изменилось два бита, чётность не меняется, и такая ошибка не обнаруживается.

    Тема 5.

    Простейшие исполнители и алгоритмы

    Вспоминай формулы по каждой теме

    Решай новые задачи каждый день

    Вдумчиво разбирай решения

    ШКОЛКОВО.

    Готовиться с нами — ЛЕГКО!

    Подтемы раздела

    простейшие исполнители и алгоритмы

    5.01Двоичная запись числа

    5.02Бит чётности

    5.03Работа с цифрами числа

    5.04Нестандартные задачи

    Решаем задачи

    Автомат обрабатывает натуральное число N по следующему алгоритму:

    1. Строится двоичная запись числа N .

    2. Складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления
    полученной суммы на 2 .

    3. Предыдущий пункт повторяется для записи с добавленной цифрой.

    4. Результат переводится в десятичную систему и выводится на экран.

    Пример. Дано число N = 13 . Алгоритм работает следующим образом:

    1. Двоичная запись числа N : 1101 .

    2. Сумма цифр двоичной записи 3 , остаток от деления на 2 равен 1 , новая запись 11011 .

    3. Сумма цифр полученной записи 4 , остаток от деления на 2 равен 0 , новая запись 110110 .

    4. На экран выводится число 54 .

    Какое наименьшее число, большее вашего балла на ЕГЭ (100 ), может появится на экране в результате работы
    автомата?

    Показать ответ и решение

    for i in range(1000000):
    s = bin(i)[2::]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    if int(s, 2) > 100:
        print(int(s, 2))
        break

    Аналитическое решение:

    Имеется число N . Все числа в двоичной записи складываются и добавляется остаток от деления на 2 этой суммы, то
    есть цифра 0 или 1, значит если сумма чётна, то дописываем 0, иначе 1. Если мы дописали единичку, то количество единиц
    увеличится на 1, а значит, что после этого сумма будет чётна, и уже в следующем пункте мы допишем нолик. Если мы
    дописали ноль, то сумма числа не меняется, а значит в следующем пункте мы также допишем нолик. Значит число в 2 СС
    заканчивается на 00 или 10.

    Нам необходимо найти число, большее, чем 100, которое в 2 СС заканчивается на 00 или 10. Будем перебирать с
    минимального.

    Подойдет ли число 10110 = 11001012 ? Нет, оно кончается на 01.

    Подойдет ли число 10210 = 11001102 ? Да, так как оно заканчивается на 10. Значит это и есть наш ответ.

    Показать ответ и решение

    for i in range(1000000):
    s = bin(i)[2:]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    if int(s, 2) > 1024:
        print(int(s, 2))
        break

    Показать ответ и решение

    for n in range(1, 1000):
    r = bin(n)[2:]
    r += r[-1]
    if bin(n)[2:].count(’1’) % 2 == 0:
        r += ’0’
    else:
        r += ’1’
    if r.count(’1’) % 2 == 0:
        r += ’0’
    else:
        r += ’1’
    if int(r, 2) > 120:
        print(n)
        break

    Показать ответ и решение

    Решение программой:

    for i in range(1, 1000000):
    s = bin(i)[2::]
    s += ’1’
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    # второй if не нужен, потому что всегда будет дописываться 0
    # подумайте почему)
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    if int(s, 2) > 212:
        print(int(s, 2))
        break

    Аналитическое решение:

    Каким бы не было число, на втором шаге к нему всегда дописывается единица, так что давайте называть это число
    «изначальным».

    Если изначальное число N имеет чётное количество единиц, то после добавления нуля количество единиц не
    изменится, а потому на следующем шаге также добавится ноль. Итого к числу допишут два нуля.

    Если изначально число N имеет нечётное количество единиц, то после добавления единицы количество единиц
    увеличится на 1 , что означает, что количество единиц станет чётным числом, а значит на следующем шаге уже будут
    добавлять ноль. Итого к числу допишут единицу и ноль.

    Значит мы будем проверять только числа, которые кончаются на 100 или 110 .

    Могло ли получиться число 213 ? Нет, в двоичной СС оно выглядит как 110101012 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 214 ? В двоичной СС оно выглядит как 11010110 2 . Так что вполне возможно. Если
    откинем последние три цифры, то у нас останется число 110102 , добавим к нему единицу и получим число 1101012 , у
    него чётное число единиц, а значит после работы алгоритма к нему дописали бы два нуля, но мы откинули 110 , а значит
    это не то число, которое нам нужно.

    Могло ли получиться число 215 ? Нет, в двоичной СС оно выглядит как 110101112 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 216 ? Нет, в двоичной СС оно выглядит как 110110002 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 217 ? Нет, в двоичной СС оно выглядит как 110110012 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 218 ? Нет, в двоичной СС оно выглядит как 110110102 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 219 ? Нет, в двоичной СС оно выглядит как 110110112 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 220 ? В двоичной СС оно выглядит как 110111002 . Так что вполне возможно. Если
    откинем последние три цифры, то у нас останется число 110112 , добавим к нему единицу и получим число 1101112 , у
    него нечётное число единиц, а значит после работы алгоритма к нему дописали бы единицу и ноль, но мы откинули 100 , а
    значит это не то число, которое нам нужно.

    Могло ли получиться число 221 ? Нет, в двоичной СС оно выглядит как 110111012 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 222 ? В двоичной СС оно выглядит как 110111102 . Так что вполне возможно. Если
    откинем последние три цифры, то у нас останется число 110112 , добавим к нему единицу и получим число 1101112 , у
    него нечётное число единиц, а значит после работы алгоритма к нему дописали бы единицу и ноль, а мы откинули как раз
    110 , значит 222 – это интересующее нас число.

    Показать ответ и решение

    for i in range(10000):

         s = bin(i)[2::]

         if i % 2 == 0:

             s += ’11’

         else:

             s += ’00’

         x = int(s, 2) — len(bin(i)[2::])  # Длина в 2-сс числа N

         if x == 126:

             print(i)

    На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим
    образом:

    1)Строится двоичная запись числа N.

    2)К этой записи дописываются справа ещё два разряда по следующему правилу:

    а)Дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если
    нечётное;

    б)К полученному результату дописывается ещё один бит чётности

    Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной
    записью искомого числа R.

    Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем
    78. В ответе это число запишите в десятичной системе.

    Показать ответ и решение

    for i in range(1, 1000):
    s = bin(i)[2::]
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    if int(s, 2) > 78:
        print(i)
        break

    Аналитическое решение:

    Если изначальное число N имеет чётное количество единиц, то после добавления нуля количество единиц не
    изменится, а потому на следующем шаге также добавится ноль. Итого к числу допишут два нуля.

    Если изначально число N имеет нечётное количество единиц, то после добавления единицы количество единиц
    увеличится на 1, что означает, что количество единиц станет чётным числом, а значит на следующем шаге уже будут
    добавлять ноль. Итого к числу допишут единицу и ноль.

    Значит мы будем проверять только числа, которые кончаются на 00 или 10 .

    Могло ли получиться число 79 ? Нет, в двоичной СС оно выглядит как 10011112 , а значит получиться после
    алгоритма не могло.

    Могло ли получиться число 80? В двоичной СС оно выглядит как 10100002 . Так что вполне возможно. Если откинем
    последние две цифры, то у нас останется число 101002 , у него чётное число единиц, а значит после работы алгоритма к
    нему дописали бы два нуля, но это как раз те самые цифры, которые мы откинули, значит 101002 = 2010 и есть искомое
    число.

    На вход алгоритма подаётся натуральное число N . Алгоритм строит по нему новое число R следующим
    образом.

    1) Строится двоичная запись числа N

    2) К этой записи дописываются разряды по следующему правилу:

    а) если число чётное, то к двоичной записи числа в конце дописывается 11

    б) если число нечётное, то к двоичной записи числа в конце дописывается 01

    Полученная таким образом запись является двоичной записью искомого числа R . Укажите наибольшее число R
    меньшее 128 , которое может получиться после обработки этого алгоритма. В ответе запишите это число в десятичной
    записи.

    Показать ответ и решение

    ans = 0
for i in range(1, 1000):
    s = bin(i)[2:]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    if int(s, 2) < 77 and int(s, 2) > ans:
        ans = int(s, 2)
print(ans)

    На вход алгоритма подаётся натуральное число N . Алгоритм строит по нему новое число R следующим
    образом.

    1) Строится двоичная запись числа N

    2) К этой записи дописываются разряды по следующему правилу:

    а) если число чётное, то к двоичной записи числа в конце дописывается 11

    б) если число нечётное, то к двоичной записи числа в конце дописывается 01

    Полученная таким образом запись является двоичной записью искомого числа R . Укажите наибольшее число R ,
    меньшее 128 , которое может получиться после обработки этого алгоритма. В ответе запишите это число в десятичной
    записи.

    Показать ответ и решение

    for i in range(1, 100000):
    s = bin(i)[2:]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    r = int(s, 2)
    if r > 103:
        print(r)
        break

    Показать ответ и решение

    for n in range(1, 10000):
    r = bin(n)[2:]
    r = r + str(r.count(’1’) % 2)
    r = r + str(r.count(’1’) % 2)
    r = int(r, 2)
    if r > 150:
        print(r)
        break

    На вход алгоритма подаётся натуральное число N . Алгоритм строит по нему новое число R следующим
    образом.

    1. Строится двоичная запись числа N .

    2. К этой записи дописывается единица.

    3. Затем справа дописывается бит чётности: 0 , если в двоичном коде полученного числа чётное число единиц, и 1 ,
    если нечётное.

    4. К полученному результату дописывается ещё один бит чётности.

    Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N ) является двоичной
    записью искомого числа R . Какое минимальное число R , большее 168 , может быть получено в результате работы
    автомата?

    Показать ответ и решение

    for i in range(100000):
    n = i
    s = bin(n)[2:]
    s = s + ’1’
    s = s + str(s.count(’1’) % 2)
    s = s + str(s.count(’1’) % 2)
    r = int(s, 2)
    if r > 168:
        print(r)
        break

    Аналитическое решение:

    Имеется число N . В любом случае к нему дописывается единица, поэтому будем рассуждать, будто бы число и было
    таким(с дописанной единицей) изначально. Если количество единиц чётно, то и сумма цифр числа чётна, а значит к числу
    допишется ноль. Если же количество единиц нечётно, то и сумма цифр числа нечётна, а значит к числу допишется
    единица. Если мы дописали единичку, то количество единиц увеличится на 1, а значит, что после этого сумма
    будет чётна, и уже в следующем пункте мы допишем нолик. Если мы дописали ноль, то сумма числа не
    меняется, а значит в следующем пункте мы также допишем нолик. Значит число в 2 СС заканчивается на
    100 или 110 (учли, что мы изначально при любых обстоятельствах дописываем единицу, а потом 00 или
    10).

    Нам необходимо найти число, большее, чем 168, которое в 2 СС заканчивается на 100 или 110. Будем перебирать с
    минимального.

    Подойдет ли число 169 = 10101001 10 2 ? Нет, оно кончается на 001.

    Подойдет ли число 17010 = 101010102 ? Нет, оно кончается на 010.

    Подойдет ли число 17110 = 101010112 ? Нет, оно кончается на 011.

    Подойдет ли число 17210 = 101011002 ? Да, так как оно заканчивается на 100. Значит это и есть наш
    ответ.

    Показать ответ и решение

    Аналитическое решение:
    Заметим, что если число единиц в двоичной записи нечётное, то в первый раз допишется единица, а затем число единиц
    станет чётным, и во второй раз мы допишем ноль. Если же число единиц в двоичной записи чётное, то в первый раз мы
    допишем ноль, затем количество единиц не изменится, и мы снова допишем ноль. Таким образом, в любом случае
    последняя цифра числа — ноль. Напишем программу:

    for i in range(1, 100):
    s = bin(i)[2::]
    a = 0
    for j in range(len(s)):
        a += int(s[j])
    if a % 2 == 0:
        s += ’00’
    else:
        s += ’10’
    if int(s, 2) > 43:
        print(int(s, 2))
        break

    From Wikipedia, the free encyclopedia

    7 bits of data (count of 1-bits) 8 bits including parity
    even odd
    0000000 0 00000000 00000001
    1010001 3 10100011 10100010
    1101001 4 11010010 11010011
    1111111 7 11111111 11111110

    A parity bit, or check bit, is a bit added to a string of binary code. Parity bits are a simple form of error detecting code. Parity bits are generally applied to the smallest units of a communication protocol, typically 8-bit octets (bytes), although they can also be applied separately to an entire message string of bits.

    The parity bit ensures that the total number of 1-bits in the string is even or odd.[1] Accordingly, there are two variants of parity bits: even parity bit and odd parity bit. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1s in the whole set (including the parity bit) an even number. If the count of 1s in a given set of bits is already even, the parity bit’s value is 0. In the case of odd parity, the coding is reversed. For a given set of bits, if the count of bits with a value of 1 is even, the parity bit value is set to 1 making the total count of 1s in the whole set (including the parity bit) an odd number. If the count of bits with a value of 1 is odd, the count is already odd so the parity bit’s value is 0. Even parity is a special case of a cyclic redundancy check (CRC), where the 1-bit CRC is generated by the polynomial x+1.

    Parity[edit]

    In mathematics parity can refer to the evenness or oddness of an integer, which, when written in its binary form, can be determined just by examining only its least significant bit.

    In information technology parity refers to the evenness or oddness, given any set of binary digits, of the number of those bits with value one. Because parity is determined by the state of every one of the bits, this property of parity—being dependent upon all the bits and changing its value from even to odd parity if any one bit changes—allows for its use in error detection and correction schemes.

    In telecommunications the parity referred to by some protocols is for error-detection. The transmission medium is preset, at both end points, to agree on either odd parity or even parity. For each string of bits ready to transmit (data packet) the sender calculates its parity bit, zero or one, to make it conform to the agreed parity, even or odd. The receiver of that packet first checks that the parity of the packet as a whole is in accordance with the preset agreement, then, if there was a parity error in that packet, requests a re-transmission of that packet.

    In computer science the parity stripe or parity disk in a RAID provides error-correction. Parity bits are written at the rate of one parity bit per n bits, where n is the number of disks in the array. When a read error occurs, each bit in the error region is recalculated from its set of n bits. In this way, using one parity bit creates «redundancy» for a region from the size of one bit to the size of one disk. See § Redundant Array of Independent Disks below.

    In electronics, transcoding data with parity can be very efficient, as XOR gates output what is equivalent to a check bit that creates an even parity, and XOR logic design easily scales to any number of inputs. XOR and AND structures comprise the bulk of most integrated circuitry.

    Error detection[edit]

    If an odd number of bits (including the parity bit) are transmitted incorrectly, the parity bit will be incorrect, thus indicating that a parity error occurred in the transmission. The parity bit is only suitable for detecting errors; it cannot correct any errors, as there is no way to determine which particular bit is corrupted. The data must be discarded entirely, and re-transmitted from scratch. On a noisy transmission medium, successful transmission can therefore take a long time, or even never occur. However, parity has the advantage that it uses only a single bit and requires only a number of XOR gates to generate. See Hamming code for an example of an error-correcting code.

    Parity bit checking is used occasionally for transmitting ASCII characters, which have 7 bits, leaving the 8th bit as a parity bit.

    For example, the parity bit can be computed as follows. Assume Alice and Bob are communicating and Alice wants to send Bob the simple 4-bit message 1001.

    Type of bit parity Successful transmission scenario
    Even parity

    Alice wants to transmit: 1001 and 1011

    Alice computes parity bit value:
    1+0+0+1 (mod 2) = 0

    1+0+1+1 (mod 2) = 1

    Alice adds parity bit and sends:
    10010 and 10111

    Bob receives: 10010 and 10111

    Bob computes parity:
    1+0+0+1+0 (mod 2) = 0

    1+0+1+1+1 (mod 2) = 0

    Bob reports correct transmission after observing expected even result.

    Odd parity

    Alice wants to transmit: 1001 and 1011

    Alice computes parity bit value:

    1+0+0+1 (+ 1 mod 2) = 1

    1+0+1+1 (+ 1 mod 2) = 0

    Alice adds parity bit and sends:
    10011 and 10110

    Bob receives: 10011 and 10110

    Bob computes overall parity:
    1+0+0+1+1 (mod 2) = 1

    1+0+1+1+0 (mod 2) = 1

    Bob reports correct transmission after observing expected odd result.

    This mechanism enables the detection of single bit errors, because if one bit gets flipped due to line noise, there will be an incorrect number of ones in the received data. In the two examples above, Bob’s calculated parity value matches the parity bit in its received value, indicating there are no single bit errors. Consider the following example with a transmission error in the second bit using XOR:

    Type of bit parity error Failed transmission scenario
    Even parity

    Error in the second bit

    		Alice wants to transmit: 1001

    Alice computes parity bit value: 1^0^0^1 = 0

    Alice adds parity bit and sends: 10010

    …TRANSMISSION ERROR…

    Bob receives: 11010

    Bob computes overall parity: 1^1^0^1^0 = 1

    Bob reports incorrect transmission after observing unexpected odd result.

    Even parity

    Error in the parity bit

    		Alice wants to transmit: 1001

    Alice computes even parity value: 1^0^0^1 = 0

    Alice sends: 10010

    …TRANSMISSION ERROR…

    Bob receives: 10011

    Bob computes overall parity: 1^0^0^1^1 = 1

    Bob reports incorrect transmission after observing unexpected odd result.

    There is a limitation to parity schemes. A parity bit is only guaranteed to detect an odd number of bit errors. If an even number of bits have errors, the parity bit records the correct number of ones, even though the data is corrupt. (See also Error detection and correction.) Consider the same example as before with an even number of corrupted bits:

    Type of bit parity error Failed transmission scenario
    Even parity

    Two corrupted bits

    		Alice wants to transmit: 1001

    Alice computes even parity value: 1^0^0^1 = 0

    Alice sends: 10010

    …TRANSMISSION ERROR…

    Bob receives: 11011

    Bob computes overall parity: 1^1^0^1^1 = 0

    Bob reports correct transmission though actually incorrect.

    Bob observes even parity, as expected, thereby failing to catch the two bit errors.

    Usage[edit]

    Because of its simplicity, parity is used in many hardware applications where an operation can be repeated in case of difficulty, or where simply detecting the error is helpful. For example, the SCSI and PCI buses use parity to detect transmission errors, and many microprocessor instruction caches include parity protection. Because the I-cache data is just a copy of main memory, it can be disregarded and re-fetched if it is found to be corrupted.

    In serial data transmission, a common format is 7 data bits, an even parity bit, and one or two stop bits. This format accommodates all the 7-bit ASCII characters in an 8-bit byte. Other formats are possible; 8 bits of data plus a parity bit can convey all 8-bit byte values.

    In serial communication contexts, parity is usually generated and checked by interface hardware (e.g., a UART) and, on reception, the result made available to a processor such as the CPU (and so too, for instance, the operating system) via a status bit in a hardware register in the interface hardware. Recovery from the error is usually done by retransmitting the data, the details of which are usually handled by software (e.g., the operating system I/O routines).

    When the total number of transmitted bits, including the parity bit, is even, odd parity has the advantage that the all-zeros and all-ones patterns are both detected as errors. If the total number of bits is odd, only one of the patterns is detected as an error, and the choice can be made based on which is expected to be the more common error.

    RAID array[edit]

    Parity data is used by RAID arrays (redundant array of independent/inexpensive disks) to achieve redundancy. If a drive in the array fails, remaining data on the other drives can be combined with the parity data (using the Boolean XOR function) to reconstruct the missing data.

    For example, suppose two drives in a three-drive RAID 5 array contained the following data:

    Drive 1: 01101101
    Drive 2: 11010100

    To calculate parity data for the two drives, an XOR is performed on their data:

    01101101
      XOR     11010100
    10111001

    The resulting parity data, 10111001, is then stored on Drive 3.

    Should any of the three drives fail, the contents of the failed drive can be reconstructed on a replacement drive by subjecting the data from the remaining drives to the same XOR operation. If Drive 2 were to fail, its data could be rebuilt using the XOR results of the contents of the two remaining drives, Drive 1 and Drive 3:

    Drive 1: 01101101
    Drive 3: 10111001

    as follows:

    10111001
      XOR     01101101
    11010100

    The result of that XOR calculation yields Drive 2’s contents. 11010100 is then stored on Drive 2, fully repairing the array.

    XOR logic is also equivalent to even parity (because a XOR b XOR c XOR … may be treated as XOR(a,b,c,…) which is an n-ary operator which is true if and only if an odd number of arguments are true). So the same XOR concept above applies similarly to larger RAID arrays with parity, using any number of disks. In the case of a RAID 3 array of 12 drives, 11 drives participate in the XOR calculation shown above and yield a value that is then stored on the dedicated parity drive.

    Extensions and variations on the parity bit mechanism «double,» «dual,» or «diagonal» parity, are used in RAID-DP.

    History[edit]

    A parity track was present on the first magnetic tape data storage in 1951. Parity in this form, applied across multiple parallel signals, is known as a transverse redundancy check. This can be combined with parity computed over multiple bits sent on a single signal, a longitudinal redundancy check. In a parallel bus, there is one longitudinal redundancy check bit per parallel signal.

    Parity was also used on at least some paper-tape (punched tape) data entry systems (which preceded magnetic tape systems). On the systems sold by British company ICL (formerly ICT) the 1-inch-wide (25 mm) paper tape had 8 hole positions running across it, with the 8th being for parity. 7 positions were used for the data, e.g., 7-bit ASCII. The 8th position had a hole punched in it depending on the number of data holes punched.

    See also[edit]

    • BIP-8
    • Parity function
    • Single-event upset
    • 8-N-1
    • Check digit

    References[edit]

    1. ^ Ziemer, RodgerE.; Tranter, William H. (17 March 2014). Principles of communication : systems, modulation, and noise (Seventh ed.). Hoboken, New Jersey. ISBN 9781118078914. OCLC 856647730.

    External links[edit]

    • Different methods of generating the parity bit, among other bit operations

    From Wikipedia, the free encyclopedia

    7 bits of data (count of 1-bits) 8 bits including parity
    even odd
    0000000 0 00000000 00000001
    1010001 3 10100011 10100010
    1101001 4 11010010 11010011
    1111111 7 11111111 11111110

    A parity bit, or check bit, is a bit added to a string of binary code. Parity bits are a simple form of error detecting code. Parity bits are generally applied to the smallest units of a communication protocol, typically 8-bit octets (bytes), although they can also be applied separately to an entire message string of bits.

    The parity bit ensures that the total number of 1-bits in the string is even or odd.[1] Accordingly, there are two variants of parity bits: even parity bit and odd parity bit. In the case of even parity, for a given set of bits, the bits whose value is 1 are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1s in the whole set (including the parity bit) an even number. If the count of 1s in a given set of bits is already even, the parity bit’s value is 0. In the case of odd parity, the coding is reversed. For a given set of bits, if the count of bits with a value of 1 is even, the parity bit value is set to 1 making the total count of 1s in the whole set (including the parity bit) an odd number. If the count of bits with a value of 1 is odd, the count is already odd so the parity bit’s value is 0. Even parity is a special case of a cyclic redundancy check (CRC), where the 1-bit CRC is generated by the polynomial x+1.

    Parity[edit]

    In mathematics parity can refer to the evenness or oddness of an integer, which, when written in its binary form, can be determined just by examining only its least significant bit.

    In information technology parity refers to the evenness or oddness, given any set of binary digits, of the number of those bits with value one. Because parity is determined by the state of every one of the bits, this property of parity—being dependent upon all the bits and changing its value from even to odd parity if any one bit changes—allows for its use in error detection and correction schemes.

    In telecommunications the parity referred to by some protocols is for error-detection. The transmission medium is preset, at both end points, to agree on either odd parity or even parity. For each string of bits ready to transmit (data packet) the sender calculates its parity bit, zero or one, to make it conform to the agreed parity, even or odd. The receiver of that packet first checks that the parity of the packet as a whole is in accordance with the preset agreement, then, if there was a parity error in that packet, requests a re-transmission of that packet.

    In computer science the parity stripe or parity disk in a RAID provides error-correction. Parity bits are written at the rate of one parity bit per n bits, where n is the number of disks in the array. When a read error occurs, each bit in the error region is recalculated from its set of n bits. In this way, using one parity bit creates «redundancy» for a region from the size of one bit to the size of one disk. See § Redundant Array of Independent Disks below.

    In electronics, transcoding data with parity can be very efficient, as XOR gates output what is equivalent to a check bit that creates an even parity, and XOR logic design easily scales to any number of inputs. XOR and AND structures comprise the bulk of most integrated circuitry.

    Error detection[edit]

    If an odd number of bits (including the parity bit) are transmitted incorrectly, the parity bit will be incorrect, thus indicating that a parity error occurred in the transmission. The parity bit is only suitable for detecting errors; it cannot correct any errors, as there is no way to determine which particular bit is corrupted. The data must be discarded entirely, and re-transmitted from scratch. On a noisy transmission medium, successful transmission can therefore take a long time, or even never occur. However, parity has the advantage that it uses only a single bit and requires only a number of XOR gates to generate. See Hamming code for an example of an error-correcting code.

    Parity bit checking is used occasionally for transmitting ASCII characters, which have 7 bits, leaving the 8th bit as a parity bit.

    For example, the parity bit can be computed as follows. Assume Alice and Bob are communicating and Alice wants to send Bob the simple 4-bit message 1001.

    Type of bit parity Successful transmission scenario
    Even parity

    Alice wants to transmit: 1001 and 1011

    Alice computes parity bit value:
    1+0+0+1 (mod 2) = 0

    1+0+1+1 (mod 2) = 1

    Alice adds parity bit and sends:
    10010 and 10111

    Bob receives: 10010 and 10111

    Bob computes parity:
    1+0+0+1+0 (mod 2) = 0

    1+0+1+1+1 (mod 2) = 0

    Bob reports correct transmission after observing expected even result.

    Odd parity

    Alice wants to transmit: 1001 and 1011

    Alice computes parity bit value:

    1+0+0+1 (+ 1 mod 2) = 1

    1+0+1+1 (+ 1 mod 2) = 0

    Alice adds parity bit and sends:
    10011 and 10110

    Bob receives: 10011 and 10110

    Bob computes overall parity:
    1+0+0+1+1 (mod 2) = 1

    1+0+1+1+0 (mod 2) = 1

    Bob reports correct transmission after observing expected odd result.

    This mechanism enables the detection of single bit errors, because if one bit gets flipped due to line noise, there will be an incorrect number of ones in the received data. In the two examples above, Bob’s calculated parity value matches the parity bit in its received value, indicating there are no single bit errors. Consider the following example with a transmission error in the second bit using XOR:

    Type of bit parity error Failed transmission scenario
    Even parity

    Error in the second bit

    		Alice wants to transmit: 1001

    Alice computes parity bit value: 1^0^0^1 = 0

    Alice adds parity bit and sends: 10010

    …TRANSMISSION ERROR…

    Bob receives: 11010

    Bob computes overall parity: 1^1^0^1^0 = 1

    Bob reports incorrect transmission after observing unexpected odd result.

    Even parity

    Error in the parity bit

    		Alice wants to transmit: 1001

    Alice computes even parity value: 1^0^0^1 = 0

    Alice sends: 10010

    …TRANSMISSION ERROR…

    Bob receives: 10011

    Bob computes overall parity: 1^0^0^1^1 = 1

    Bob reports incorrect transmission after observing unexpected odd result.

    There is a limitation to parity schemes. A parity bit is only guaranteed to detect an odd number of bit errors. If an even number of bits have errors, the parity bit records the correct number of ones, even though the data is corrupt. (See also Error detection and correction.) Consider the same example as before with an even number of corrupted bits:

    Type of bit parity error Failed transmission scenario
    Even parity

    Two corrupted bits

    		Alice wants to transmit: 1001

    Alice computes even parity value: 1^0^0^1 = 0

    Alice sends: 10010

    …TRANSMISSION ERROR…

    Bob receives: 11011

    Bob computes overall parity: 1^1^0^1^1 = 0

    Bob reports correct transmission though actually incorrect.

    Bob observes even parity, as expected, thereby failing to catch the two bit errors.

    Usage[edit]

    Because of its simplicity, parity is used in many hardware applications where an operation can be repeated in case of difficulty, or where simply detecting the error is helpful. For example, the SCSI and PCI buses use parity to detect transmission errors, and many microprocessor instruction caches include parity protection. Because the I-cache data is just a copy of main memory, it can be disregarded and re-fetched if it is found to be corrupted.

    In serial data transmission, a common format is 7 data bits, an even parity bit, and one or two stop bits. This format accommodates all the 7-bit ASCII characters in an 8-bit byte. Other formats are possible; 8 bits of data plus a parity bit can convey all 8-bit byte values.

    In serial communication contexts, parity is usually generated and checked by interface hardware (e.g., a UART) and, on reception, the result made available to a processor such as the CPU (and so too, for instance, the operating system) via a status bit in a hardware register in the interface hardware. Recovery from the error is usually done by retransmitting the data, the details of which are usually handled by software (e.g., the operating system I/O routines).

    When the total number of transmitted bits, including the parity bit, is even, odd parity has the advantage that the all-zeros and all-ones patterns are both detected as errors. If the total number of bits is odd, only one of the patterns is detected as an error, and the choice can be made based on which is expected to be the more common error.

    RAID array[edit]

    Parity data is used by RAID arrays (redundant array of independent/inexpensive disks) to achieve redundancy. If a drive in the array fails, remaining data on the other drives can be combined with the parity data (using the Boolean XOR function) to reconstruct the missing data.

    For example, suppose two drives in a three-drive RAID 5 array contained the following data:

    Drive 1: 01101101
    Drive 2: 11010100

    To calculate parity data for the two drives, an XOR is performed on their data:

    01101101
      XOR     11010100
    10111001

    The resulting parity data, 10111001, is then stored on Drive 3.

    Should any of the three drives fail, the contents of the failed drive can be reconstructed on a replacement drive by subjecting the data from the remaining drives to the same XOR operation. If Drive 2 were to fail, its data could be rebuilt using the XOR results of the contents of the two remaining drives, Drive 1 and Drive 3:

    Drive 1: 01101101
    Drive 3: 10111001

    as follows:

    10111001
      XOR     01101101
    11010100

    The result of that XOR calculation yields Drive 2’s contents. 11010100 is then stored on Drive 2, fully repairing the array.

    XOR logic is also equivalent to even parity (because a XOR b XOR c XOR … may be treated as XOR(a,b,c,…) which is an n-ary operator which is true if and only if an odd number of arguments are true). So the same XOR concept above applies similarly to larger RAID arrays with parity, using any number of disks. In the case of a RAID 3 array of 12 drives, 11 drives participate in the XOR calculation shown above and yield a value that is then stored on the dedicated parity drive.

    Extensions and variations on the parity bit mechanism «double,» «dual,» or «diagonal» parity, are used in RAID-DP.

    History[edit]

    A parity track was present on the first magnetic tape data storage in 1951. Parity in this form, applied across multiple parallel signals, is known as a transverse redundancy check. This can be combined with parity computed over multiple bits sent on a single signal, a longitudinal redundancy check. In a parallel bus, there is one longitudinal redundancy check bit per parallel signal.

    Parity was also used on at least some paper-tape (punched tape) data entry systems (which preceded magnetic tape systems). On the systems sold by British company ICL (formerly ICT) the 1-inch-wide (25 mm) paper tape had 8 hole positions running across it, with the 8th being for parity. 7 positions were used for the data, e.g., 7-bit ASCII. The 8th position had a hole punched in it depending on the number of data holes punched.

    See also[edit]

    • BIP-8
    • Parity function
    • Single-event upset
    • 8-N-1
    • Check digit

    References[edit]

    1. ^ Ziemer, RodgerE.; Tranter, William H. (17 March 2014). Principles of communication : systems, modulation, and noise (Seventh ed.). Hoboken, New Jersey. ISBN 9781118078914. OCLC 856647730.

    External links[edit]

    • Different methods of generating the parity bit, among other bit operations

    Бит четности

    Бит четности

    В вычислительной технике и сетях передачи данных би́том чётности называют контрольный бит, принимающий значения ‘0’ или ‘1’ и служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе).

    Содержание

    • 1 Примеры
    • 2 Применение
    • 3 Полиномы CRC и бит чётности
    • 4 См. также
    • 5 Литература

    Примеры

    Бит чётности или контрольный разряд формируется при выполнении операции «Исключаюшее-ИЛИ» поразрядно. Рассмотрим схему, использующую девятибитные кодовые слова, состоящие из восьми бит данных, за которыми следует бит чётности.

    • Число 10111101 содержит 6 ‘1’ битов. Бит чётности будет 0, получаем кодовое слово 101111010.
    • Число 01110011 содержит 5 ‘1’ битов. Бит чётности будет 1, получаем кодовое слово 011100111.
    • Число 00000000 не содержит ‘1’ битов. Бит чётности будет 0, получаем кодовое слово 000000000.

    Пустой или несуществующий поток битов также имеет ноль единичных битов, поэтому бит чётности будет 0.

    Применение

    В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные UART). Признак ошибки становится доступен процессору (и ОС) через статусный регистр оборудования. Восстановление ошибок обычно производится повторной передачей данных, подробности которого обрабатываются программным обеспечением (например, функциями ввода/вывода операционной системы)

    Полиномы CRC и бит чётности

    Контроль по чётности фактически является специальным случаем проверки избыточности циклической суммы с полиномом x+1.

    См. также

    • Бит
    • Чётность используется для восстановления данных в
    • код Хемминга — следующий шаг после бита чётности

    Литература

    • Генри С. Уоррен, мл. Глава 5. Подсчет битов // Алгоритмические трюки для программистов = Hacker’s Delight. — М.: «Вильямс», 2007. — С. 288. — ISBN 0-201-91465-4

    Wikimedia Foundation.
    2010.

    Полезное

    Смотреть что такое «Бит четности» в других словарях:

    • бит четности — Дополнительный бит, добавляемый в группу для того, чтобы общее число единиц в группе было четным или нечетным (в зависимости от протокола).  [http://www.lexikon.ru/dict/net/index.html] Тематики сети вычислительные EN parity Bit …   Справочник технического переводчика

    • бит четности — lyginumo bitas statusas T sritis automatika atitikmenys: angl. parity bit; parity check bit vok. Paritätsbit, n; Paritätskontrollbit, n rus. бит четности, m; контрольный двоичный разряд четности, m; проверочный двоичный разряд четности, m pranc.… …   Automatikos terminų žodynas

    • бит четности (шины) — Линия (сигнал), по которой передается бит четности соответствующей шины системы, если в ней используется четность. [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ. Москва 1993] Тематики информационные технологии в… …   Справочник технического переводчика

    • бит контроля на четность — бит четности контрольный бит Контрольный бит, добавляемый к данным для контроля их верности таким образом, чтобы сумма двоичных единиц, составляющих данное, включая и единицу контрольного бита, всегда была четной (либо всегда нечетной). [Домарев… …   Справочник технического переводчика

    • контрольный двоичный разряд четности — lyginumo bitas statusas T sritis automatika atitikmenys: angl. parity bit; parity check bit vok. Paritätsbit, n; Paritätskontrollbit, n rus. бит четности, m; контрольный двоичный разряд четности, m; проверочный двоичный разряд четности, m pranc.… …   Automatikos terminų žodynas

    • проверочный двоичный разряд четности — lyginumo bitas statusas T sritis automatika atitikmenys: angl. parity bit; parity check bit vok. Paritätsbit, n; Paritätskontrollbit, n rus. бит четности, m; контрольный двоичный разряд четности, m; проверочный двоичный разряд четности, m pranc.… …   Automatikos terminų žodynas

    • двоичный разряд четности — бит проверки на четность разряд контроля четности — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы бит проверки на четностьразряд контроля четности …   Справочник технического переводчика

    • Контроль четности — В вычислительной технике и сетях передачи данных битом чётности называют контрольный бит, принимающий значения 0 или 1 и служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе). Содержание 1 Примеры 2… …   Википедия

    • генератор битов четности — генератор паритета Логическая схема, выполненная в виде сумматора по модулю 2, который генерирует “ложный” проверочный бит, добавляемый к исходным данным. Используется в системах, в которых протоколом предусматривается процедура проверки четности …   Справочник технического переводчика

    • Виганд (интерфейс) — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете …   Википедия

    Источник

  • Бит визион ошибка 400
  • Биссектрисой угла называется прямая делящая угол пополам логическая ошибка
  • Бисмарк только дураки учатся на своих ошибках
  • Бирюса морозильная камера ошибка
  • Бипилаб смад коды ошибок