Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
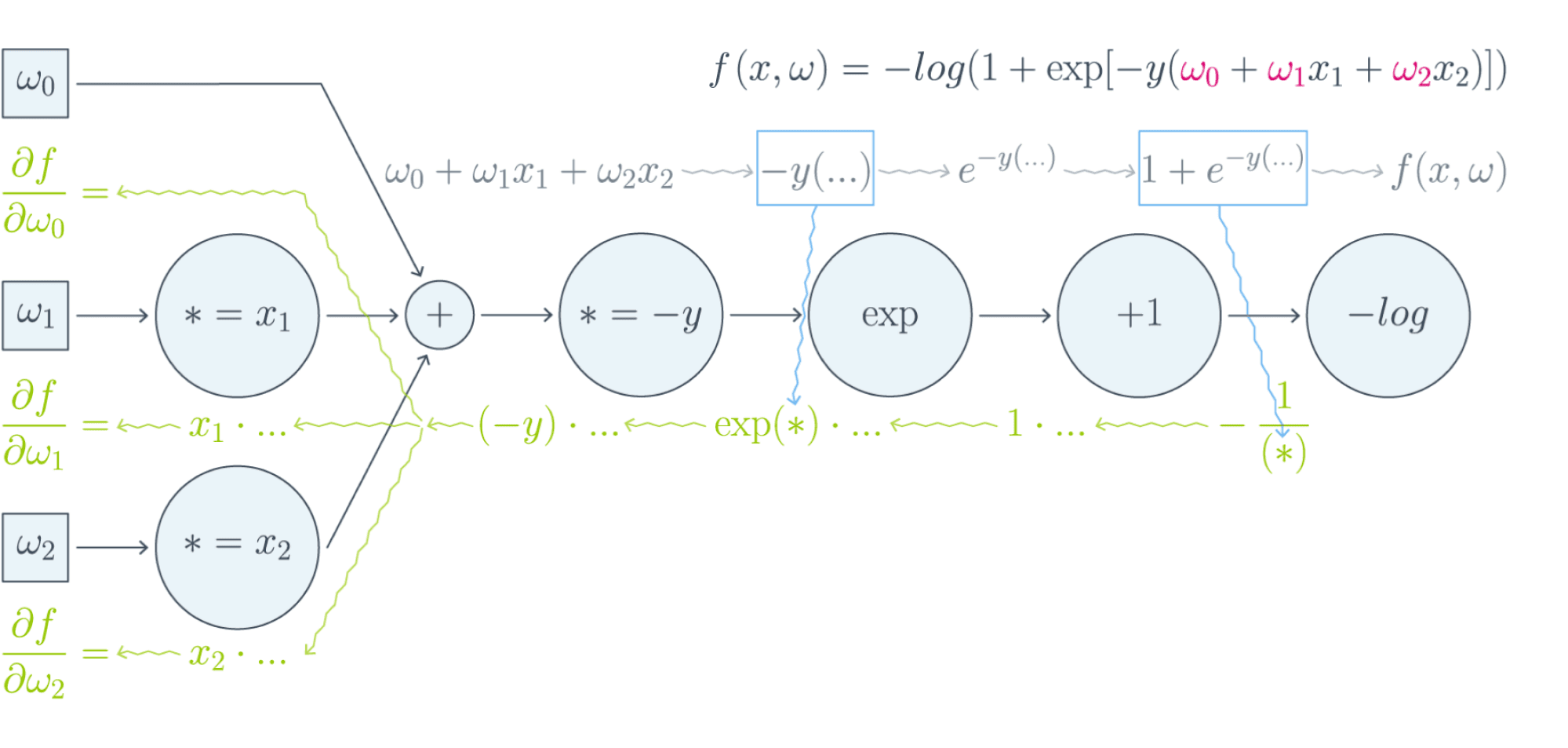
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
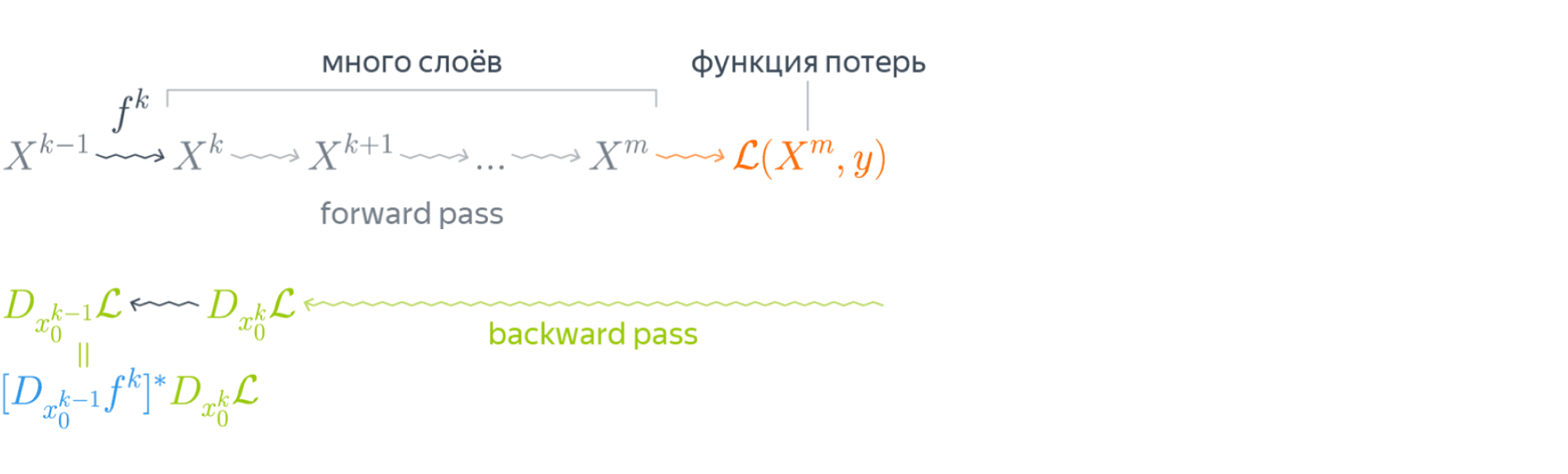
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1
vdots
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)
vdots
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$begin{multline*}
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =[0.1cm]
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
end{multline*},$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$begin{multline*}
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
end{multline*}$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$ begin{multline*}
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
end{multline*} $$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
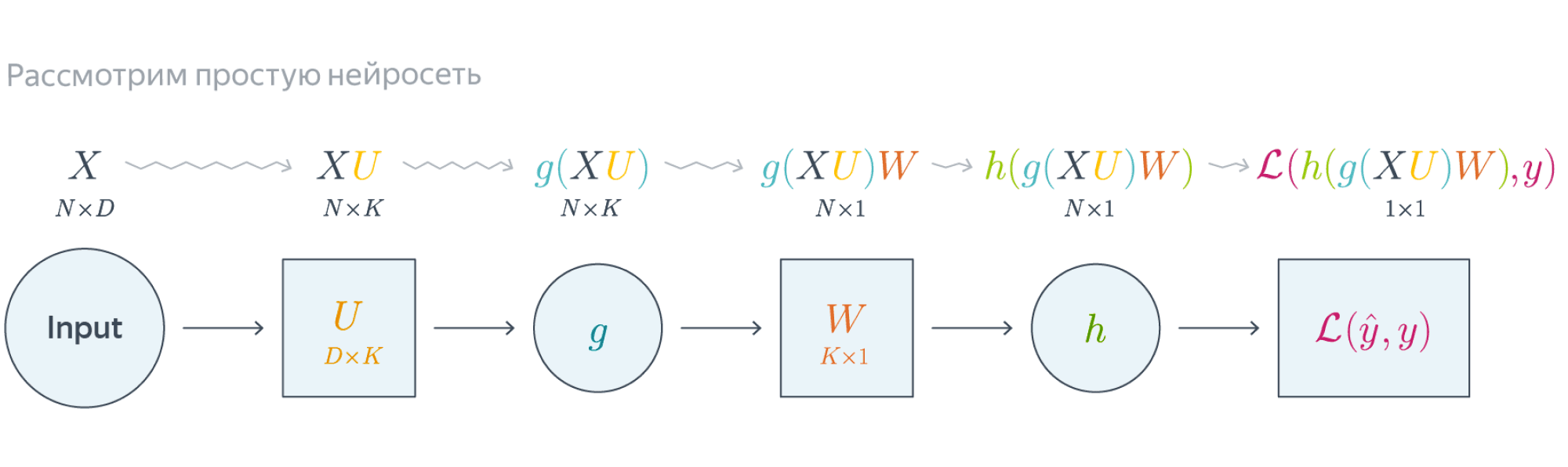 Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?
Обучаемые параметры – матрицы $U$ и $W$. Как найти градиенты по ним в точке $U_0, W_0$?
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
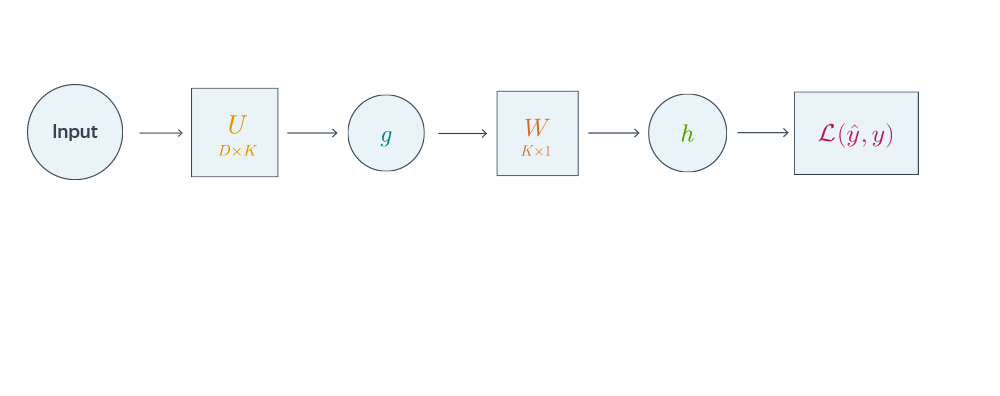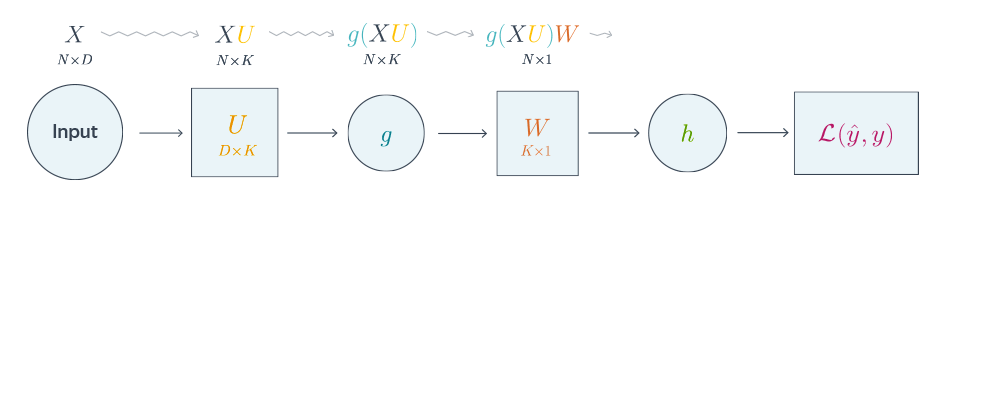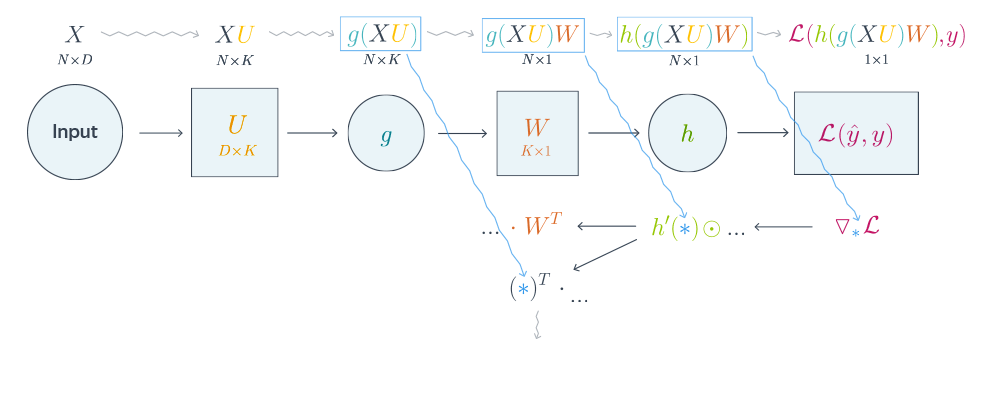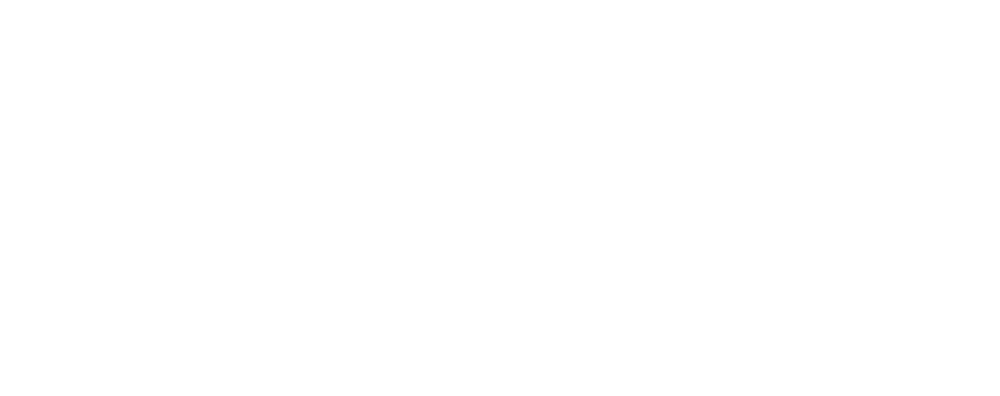
Backpropagation для двуслойной нейронной сети
Если вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$)Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
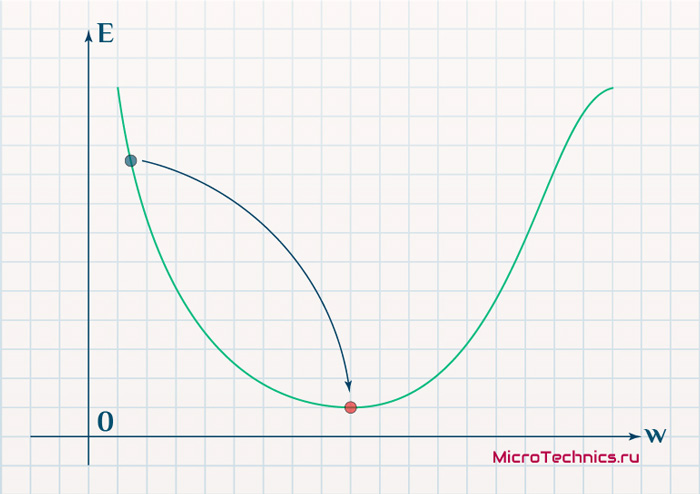
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
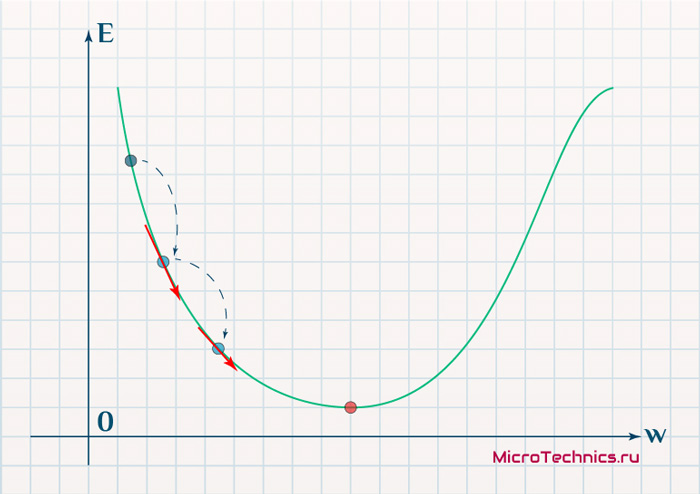
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
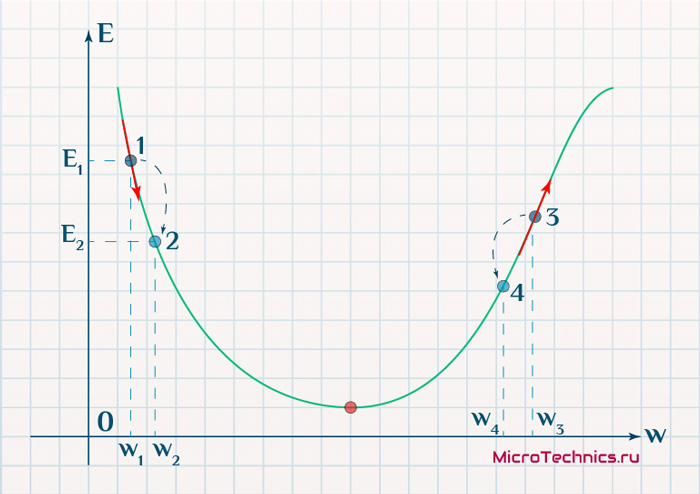
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
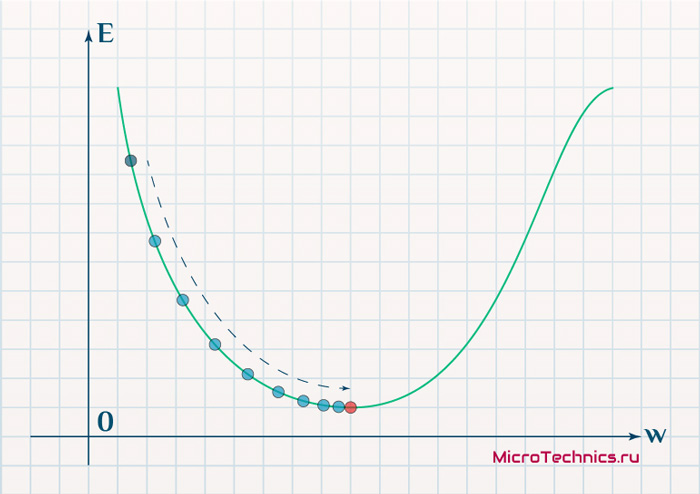
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
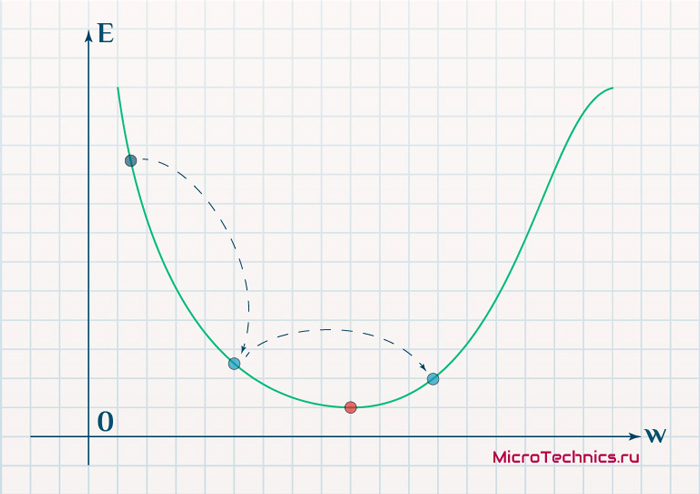
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
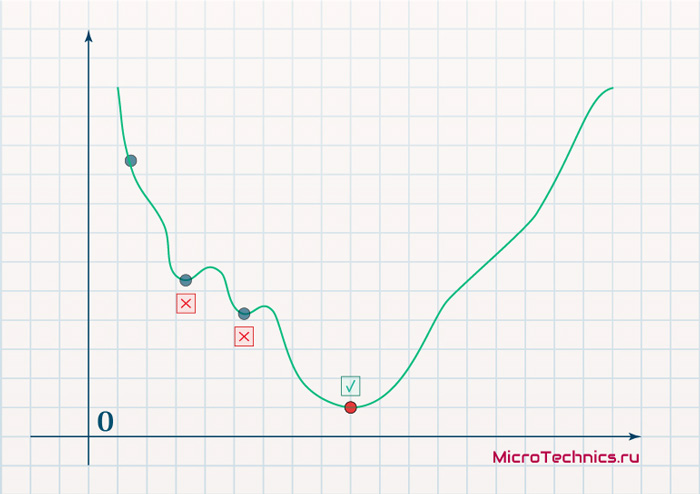
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
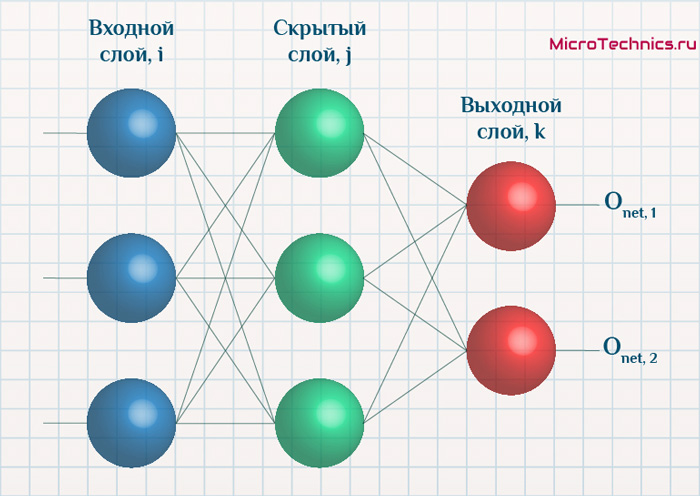
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
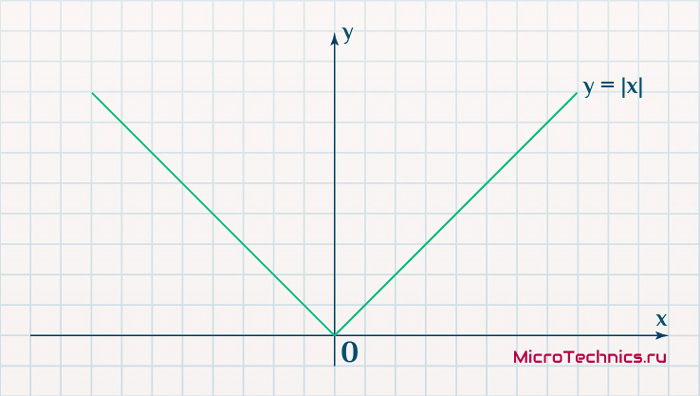
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
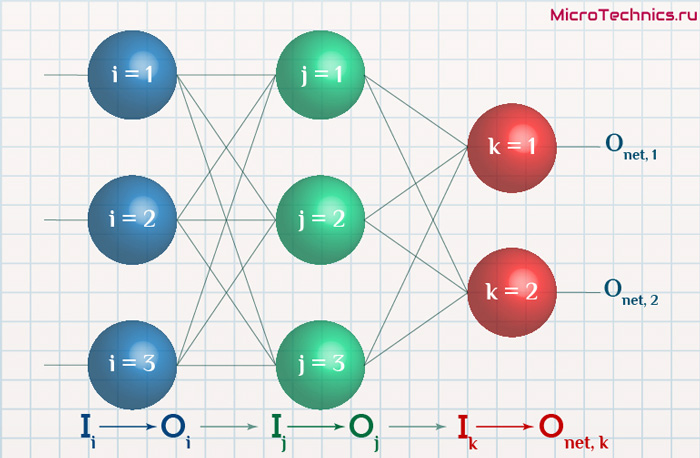
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
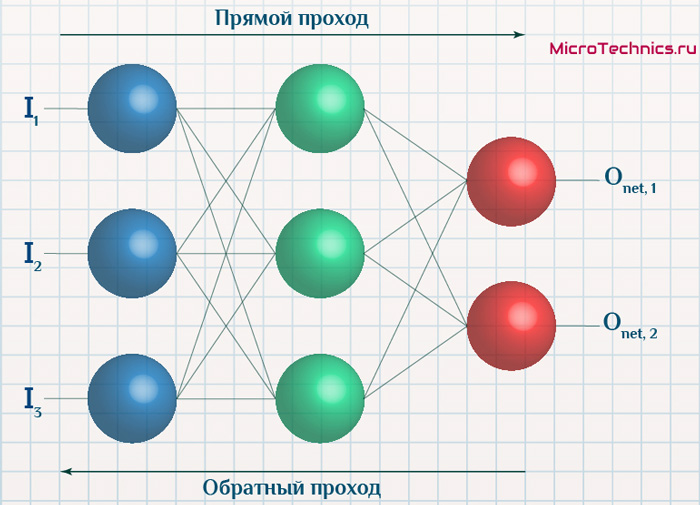
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
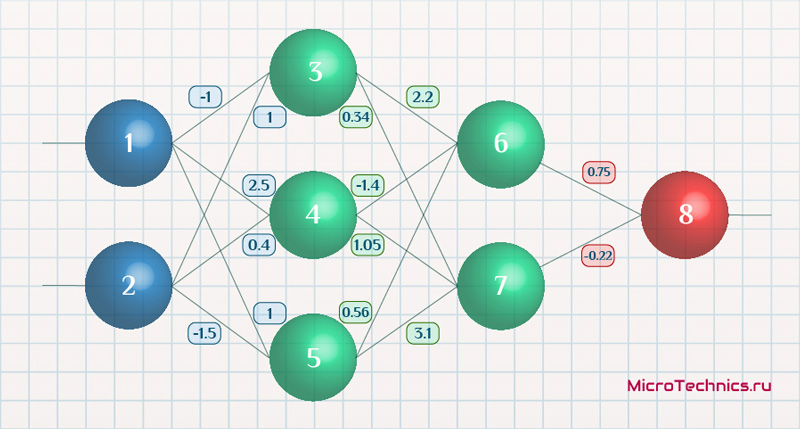
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 O_4 = 0.86 O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288
O_6 = f(I_6) = 0.54
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965
w_{68 medspace new} = 0.75+ 0.014 = 0.764
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998
w_{15 medspace new} = 1 + 0.00018 = 1.00018
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
на кривой, построенной на проверочном подмножестве. Однако на практике оказалось, что после прохождения этой точки сеть обучалась только посторонним шумам, содержащимся в обучающей выборке. Поэтому было принято решение об использовании точки минимума кривой тестирования в качестве критерия останова сеанса обучения. Когда ошибки на подмножествах оценивания и проверки не одинаково стремились к нулю(что характерно для данных не содержвщих шума), емкости сети оказывалось не достаточно для точного функционирования модели. В этом случае минимизировалась интегрированная квадратичная ошибка, что (приблизительно) эквивалентно минимизации обычной глобальной среднеквадратической ошибки при равномерном распределении входного сигнала.
Для повышения эффективности обучения ИНС использовалось комбинирование последовательного и пакетного режимов обучения. В рамках последовательного режима обучения корректировка весов проводилась после подачи каждого примера. Для примера рассмотрим эпоху, состоящую из N обучающих примеров, упорядоченных следующим образом: ((x1),d(1)),.., (x(N),d(N)). Сети предъявлялся первый пример(x(l),d(l)) этой эпохи, после чего выполнялись описанные выше прямые и обратные вычисления. В результате проводилась корректировка синаптических весов и уровней порогов в сети. После этого сети предъявлялась вторая пара (x(2),d(2)) в эпохе, повторялись прямой и обратный проходы, приводящие к поледующей коррекции синаптических весов и уровня порога. Этот процесс повторялся, пока сеть не завершала обработку последнего примера (пары) данной эпохи — (x(N), d(N)). В пакетном режиме обучения корректировка весов проводилась после подачи в сеть всех примеров обучения (всей эпохи). Для каждой эпохи функция стоимости определялась как среднеквадратическая ошибка, представленная в составной форме
|
1 |
N |
||||
|
Eav |
(n) = |
ååe 2j (n) , |
(3.37) |
||
|
2N n=1 jÎC |
где сигнал ошибки ej (n) соответствует нейрону j для примера обучения n. Ошибка ej (n) равна разности между dj(n) и уj(n) для j-гo элемента вектора желаемых откликов d(n) и соответствующего выходного нейрона сети. В выражении (3.36) внутреннее суммирование по j выполняется по всем нейронам выходного слоя сети, в то время как внешнее суммирование поп выполняется по всем образам данной эпохи. При заданном параметре скорости обученияh
корректировка, применяемая к синаптическому весу w ji связывающему нейроны i и j, определялась следующим дельта-правилом
|
¶E |
av |
h |
N |
¶e j |
(n) |
|||
|
Dw ji (n) = —h |
= — |
åe j (n) |
. |
(3.38) |
||||
|
¶w ji |
N n =1 |
¶w ji |
Согласно (3.38) в пакетном режиме корректировка веса Dwji (n) выполняется только после прохождения по сети всего множества примеров.
121
Процесс комбинирования данных режимов обучения состоял в следующем. В случае наличия избыточных данных использовался последовательный режим обучения. Его применение позволяло использовать меньший объем внутреннего хранилища для каждой синаптической связи. Более того, путем предъявления обучающих примеров в случайном порядке(в процессе последовательной корректировки весов) достигался стохастический поиск в пространстве весов. Это, в свою очередь, сокращало до минимума возможность остановки алгоритма в точках локальных минимумов. Во всех остальных случаях использовался пакетный режим обучения. Он обеспечивал более точную оценку вектора градиента при «обедненных» данных и позволял распараллелить вычисления.
Для обоснования критерия прекращения(останова) обучения рассматривались уникальные свойства локального и глобального минимумов поверхности ошибок. Обозначим символом w вектор весов, обеспечивающий минимум, будь то локальный или глобальный. Необходимым условием минимума является достижение вектора градиента g(w) (т.е. вектора частных производных первого порядка) для поверхности ошибок в точке нулевых значений. На практике это означает, что алгоритм обратного распространения ошибок сошелся, если евклидова норма вектора градиента достигла достаточно малых значений. Недостатком этого критерия сходимости является то, что для сходимости обучения может потребоваться довольно много времени. Кроме того, необходимо постоянно вычислять вектор градиентаg(w). Другим уникальным свойством минимума является то, что функция стоимости (или мера ошибки) Eav (w) в точке w = w* стабилизируется. Отсюда можно вывести еще один критерий сходимости. Критерием сходимости алгоритма обратного распространения ошибок является достаточно малая абсолютная интенсивность изменений среднеквадратической ошибки в течение эпохи. Практические результаты показали, что интенсивность изменения среднеквадратической ошибки можно считать достаточно малой, если она лежит в пределах от0,1-1 % за эпоху. В процессе функ-
ционирования алгоритма обратного распространения ошибок использовался еще один критерий сходимости. После каждой итерации обучения сеть тестировалась на эффективность обобщения. Процесс обучения останавливался, когда эффективность обобщения становилась удовлетворительной или когда оказывалось, что пик эффективности уже пройден.
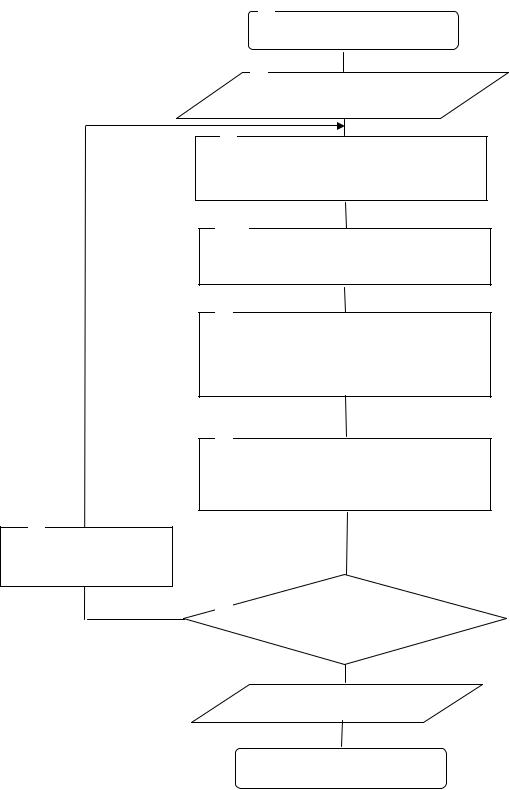
Блок-схема алгоритма обратного распространения ошибок представлена на рис. 3.13. Блоки 1,10 используются для пуска и остановки алгоритма обратного
распространения ошибок.
В блоке 2 реализован ввод исходных данных, таких как:
— элементы обучающей выборки (как правило, они должны быть нормализованы);
— значения весов (начальные значения весов могут быть случайными или детерминированными);
— вектор выходных значений сигналов.
122
1
Начало
2
Ввод исходных данных
3
Определение
выходного
сигнала
4
Определение функционала квадратичной ошибки
5
Определение производных сигналов ошибок обратного распространения
6
Фиксация знака производной
8
Генерация приращений весов
|
нения знака произ- |
|||
|
водной |
|||
|
Да |
|||
|
9 |
|||
|
Вывод результатов |
|||
|
10 |
Конец |
||
Рис. 3.13. Блок-схема алгоритма обратного распространения ошибок
123
Блок 3 обеспечивает расчет выходного сигнала.
В блоке 4 рассчитывается значение среднеквадратичной ошибки.
Блок 5 реализует определение производных сложной функции (сигнала и функции активации).
В блоке 6 фиксируется значение производной.
Блок 7 обеспечивает проверку изменения знака производной. Если он не изменился, то управление передается в блок 9. В противном случае управление передается в блок 8.
Блок 9 вывод результатов. В качестве результатов выступает набор весовых коэффициентов при которых достигается значение минимума функции ошибки.
Ниже приведен фрагмент программного кода, реализующий алгоритм обратного распространения ошибок:
procedure TNSet.MTeach; var
i, //слой
j, //нейрон k:Integer; // вход xsum:Double;
begin
//формирование массива ошибок // расчет фактических ошибок нейронов выходного слоя
for j:=1 to fConfig[LayerCount-1] do Osh[LayerCount-1,j]:=(outputm[LayerCount-1,j]-
inputm[LayerCount,j])*Posh[LayerCount-1,j]; //расчет суммарной ошибки
xsum:=0;
for j:=1 to fConfig[LayerCount-1] do xsum:=xsum+Osh[LayerCount-1,j]; Sosh:=xsum/fConfig[LayerCount-1];
//расчет фактических ошибок нейронов скрытых слоев приращений весов и новых весов
//начинаем от предпоследнего (последний скрытый) до 1-го for i:=LayerCount-2 downto 1 do
for j:=1 to fConfig[i] do begin
xsum:=0;
for k:=0 to fConfig[i+1] do xsum:=xsum+Osh[i+1,j]*w[i,j,k];
Osh[i,j]:=xsum*Posh[i,j];
//Osh[i,j]:=xsum*outputm[i,j]*(1-outputm[i,j]);
//находим приращение веса и новое значение веса
124
for k:=0 to fConfig[i+1] do begin
//WT[i,j,k]:=-Osh[i+1,j]*fMiu*outputm[i,j]; WT[i,j,k]:=-Osh[i+1,j]*fTS*outputm[i,j]+fMiu*WT[i,j,k];
w[i,j,k]:=w[i,j,k]+WT[i,j,k];
end;
end;
end;
Вкачестве альтернативного метода обучения ИНС использован«Алгоритм имитации отжига», который реализует одноименный алгоритм в интересах оптимизации поиска глобального экстремума целевой функции. Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Предложенный Н. Метрополисом в 1953 г.
[55]и доработанный многочисленными последователями, он в настоящее время считается одним из немногих алгоритмов, позволяющих оперативно находить глобальный минимум функции нескольких переменных. Метод имитаций отжига основан на идее, заимствованной из статической механики. Он отражает поведение материального тела при отвердевании с применением процедуры отжига. Для получения качественного материала из расплава при отвердевании его температура должна уменьшаться постепенно, вплоть до момента полной кристаллизации. Если процесс остывания протекает слишком быстро, образуются значительные нерегулярности структуры материала, которые вызывают внутренние напряжения. В результате общее энергетическое состояние тела, зависящее от его внутренней напряженности, остается на гораздо более высоком уровне, чем при медленном охлаждении. Быстрая фиксация энергетического состояния тела на уровне выше нормального аналогична сходимости оптимизационного алгоритма к точке локального минимума. Энергия состояния тела соответствует целевой функции, а абсолютный минимум этой энергии – глобальному минимуму. В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация тела сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на ка- кое-то время возрастать (в частности, при подогреве тела для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного
повышения энергетического уровня возможен выход из ловушек локальных минимумов, которые возникают при реализации процесса. Только понижение температуры тела до абсолютного нуля делает невозможным какое-либо самостоятельное повышение его энергетического уровня. В этом случае любые внутренние изменения ведут только к уменьшению общей энергии тела.
Вреальных процессах кристаллизации твердых тел температура понижается ступенчатым образом. На каждом уровне она какое-то время поддерживается постоянной, что необходимо для обеспечения термического равновесия. На протяжении всего периода, когда температура остается выше абсолютного
125
нуля, она может как понижаться, так и повышаться. За счет удержания температуры процесса поблизости от значения, соответствующего непрерывно снижающемуся уровню термического равновесия, удаётся обходить ловушки локальных минимумов, что при достижении нулевой температуры позволяет получить и минимальный энергетический уровень [173].
Блок-схема алгоритма имитации отжига, который использовался для обучения многослойного персептрона приведен на рис. 3.14.
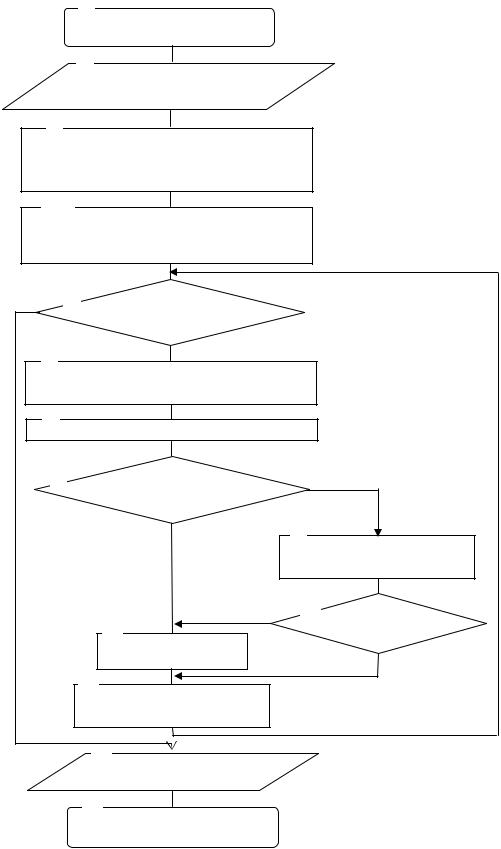
Блоки 1, 14 используются для пуска и остановки алгоритма.
Вблоке 2 реализован ввод исходных данных, таких как: значения входных параметров и соответствующего им отклика ИНС из обучающей или тестирующей выборок либо реальных данных.
Блок 3 обеспечивает генерацию начальных значений весов нейронных связей и температуры Tmax.
Вблоке 4 рассчитывается значение энергии в соответствии с соотноше-
нием E=(Y1 —Y1¢)2 +(Y2 —Y2¢)2 +(Y3 —Y3¢)2 +…+(Yn —Yn¢)2 .
Вблоке 5 реализована проверка условия наличия положительной температуры тела. Если данное условие выполнено, то управление передается в блок 6, в противном случае вычислительный процесс завершается и управление передается в блок 13.
Блок 6 обеспечивает генерацию значений приращений весов w’.
Вблоке 7 рассчитывается обновленное значение энергии E’.
Блок 8 предназначен для проверки условия превышения предыдущего значения энергии над текущим значением. Если данное условие выполняется, то управление передается в блок 11, в противном случае управление передается в блок 9.
В Блоке 9 реализована генерация случайных чисел в диапазоне от 0 до 1. Блок 10 предназначен для проверки условияexp(- D 2/T2)>R. Если данное
условие выполняется, то управление передается в блок11. В противном случае управление передается в блок 12.
Вблоке 11 весам присваиваются новые значения. Блок 12 обеспечивает снижение температуры.
Вблоке 13 осуществляется вывод полученных результатов– оптимальных значений весов ИНС.
Вданном алгоритме обучения реализован стохастически управляемый метод повторных рестартов. Для оценки его эффективности был проведен сравнительный анализ функционирования данного алгоритма, генетического алгоритма и алгоритма прямого перебора.
На рис. 3.15 приведена экранная форма интерфейса пользователя при исследовании данных алгоритмов обучения ИНС.
Окно имеет блочную структуру. В верхней части окна располагаются блоки заданий параметров трех алгоритмов обучения(генетического, имитации отжига и прямого перебора). Кроме того, в каждом блоке имеется окно, в котором отображается время выполнения соответствующего алгоритма обучения, а также кнопка его запуска – «Старт».
126
|
1 |
|||||
|
Начало |
|||||
|
2 |
|||||
|
Ввод исходных данных |
|||||
|
3 |
|||||
|
Генерация значений весов и началь- |
|||||
|
ной температуры T= Tmax |
|||||
|
4 |
|||||
|
Определение значения энергии: |
|||||
|
E=(Y1-Y1’)2+…+(Yn-Yn’)2 |
|||||
|
Нет |
5 |
T>0 |
|||
|
6 |
Да |
||||
|
Генерация значений |
|||||
|
приращений весов D w’ |
|||||
|
7 |
Расчет Е’ |
||||
|
8 |
Е’<Е |
Нет |
|||
|
Да |
9 |
||||
|
Генерация случайных чисел |
|||||
|
R в диапазоне [0;1]’ |
|||||
|
Да |
Да |
10 |
exp(- D 2/T2)>R |
||
|
11 |
|||||
|
Принять w=w’ |
Нет |
||||
|
12 |
|||||
|
Уменьшение температуры |
|||||
|
T=rT |
|||||
|
7 |
|||||
|
13 |
|||||
|
Вывод результатов |
14
Конец
Рис. 3.14. Блок-схема алгоритма имитации отжига
127
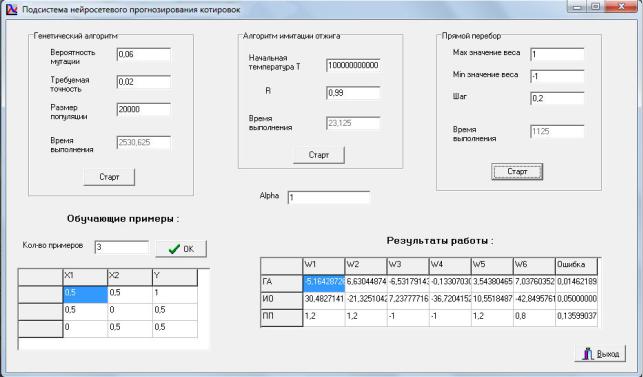
Рис. 3.15. Экранная форма интерфейса исследования алгоритмов обучения ИНС
В нижней левой части экранной формы находится компонент задания обучающих примеров. В нижней правой части экранной формы находится таблица, в которой отображаются значения весов нейронных связей и ошибки соответствующих ИНС. В центре экранной формы имеется окно задания параметра α. Данный параметр определяет крутизну функции активации. При
a ®¥ функция вырождается в пороговую.
При a ® 0 функция активации становится линейной функцией с пороговым значением — 0,5. При a ® 1 данная функция является плавной сигмоидальной функцией (вариант, представляющий интерес в данной работе).
В табл.3.3 и 3.4 приведены экспериментальные значения основных параметров функционирования (времени работы и значения ошибок) для трех алгоритмов обучения.
В таблице 3.3 приведены результаты работы двух алгоритмов обучения, при постоянных исходных данных. В таблице 3.4 представлены результаты функционирования алгоритма прямого перебора для 5 вариантов исходных данных:
1.Max значение веса – 1, Min значение веса – -1, Шаг – 0,2;
2.Max значение веса – 1, Min значение веса – -1, Шаг – 0,1;
3.Max значение веса – 2, Min значение веса – -2, Шаг – 0,2;
4.Max значение веса – 2, Min значение веса – -2, Шаг – 0,1;
5.Max значение веса – 3, Min значение веса – -3, Шаг – 0,2.
128
Таблица 3.3 Результаты работы генетического алгоритма и алгоритма имитации отжига
|
Критерии |
Генетический алгоритм |
|||||||||||||||||
|
Время рабо- |
||||||||||||||||||
|
ты (мсек) |
1324 |
1184 |
5471 |
2334 |
1091 |
1177 |
2330 |
1111 |
2354 |
1123 |
||||||||
|
Ошибка |
0,016 |
0,014 |
0,019 |
0,019 |
0,014 |
0,018 |
0,01 |
0,007 |
0,01 |
0,012 |
||||||||
|
Алгоритм имитации отжига |
||||||||||||||||||
|
Время рабо- |
||||||||||||||||||
|
ты (мсек) |
23 |
22 |
21 |
22 |
23 |
23 |
28 |
26 |
25 |
21 |
||||||||
|
Ошибка |
0,05 |
0,09 |
0,07 |
0,07 |
0,05 |
0,09 |
0,08 |
0,05 |
0,05 |
0,08 |
||||||||
|
Результаты работы алгоритма прямого перебора |
Таблица 3.4 |
|||||||||||||||||
|
Критерии |
Прямой перебор |
|||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
||||||||||||||
|
Время работы |
||||||||||||||||||
|
(мсек) |
1157 |
42960 |
39760 |
1673589 |
303858 |
|||||||||||||
|
Ошибка |
0,13 |
0,14 |
0,095 |
0,099 |
0,071 |
Анализ полученных результатов показывает, что алгоритм имитации отжига является наиболее оперативным, но не самым точным из рассматриваемых методов обучения. Более высокую точность показал генетический алгоритм, но он затрачивает намного больше времени на работу чем алгоритм имитации отжига. Теоретически алгоритм прямого перебора является самым точным методом поиска глобального минимума функции. Однако на практике, по причине недостаточной аппаратной мощности ПК, оказалось невозможным получить значение глобального минимума за приемлемое время.
Модуль «Генетический алгоритм» реализует случайный поиск экстремума функции для нескольких аргументов. Он представляет собой симбиоз переборного и градиентного методов. Его основу составляет естественный отборглавный механизм эволюции [25, 29, 57]. В нем реализуются генетические коды индивидуумов – ДНК (дезоксирибонуклеиновая кислота), приспособленность индивидуумов, хромосомы, скрещивание, мутации и др. Детальное описание генетического алгоритма приведено в разделе 2.5.
Большое значение для обучения ИНС имеет ее архитектура. Рассмотрим последовательность процесса обучения сети в плоскости поиска ее оптимальной архитектуры. Обучение ведется путем минимизации целевой функцииE(w), определяемой только на обучающем подмножестве L. При этом значение целевой функции определяется как
|
p |
|
|
E(w) = åE( yk (w),dk ) , |
(3.39) |
|
k =1 |
где р — количество обучающих пар(хk, dk), yk — вектор реакции сети на возбуждение хk.
129
Минимизация функции (3.39) обеспечивает достаточное соответствие выходных сигналов сети ожидаемым значениям из обучающих выборок.
Цель обучения состоит в таком подборе архитектуры и параметров сети, которые обеспечат минимальную погрешность распознавания тестового подмножества данных, не участвовавших в обучении. Эту погрешность будем называть погрешностью обобщения EG(w). Co статистической точки зрения погрешность обобщения зависит от уровня погрешности обученияEL(w) и от доверительного интервала e . Она характеризуется неравенством:
|
EG (w) =£ EL |
(w) + e( |
p |
, EL ) . |
(3.40) |
|
h |
Установлено [177], что значение e функционально зависит от уровня погрешности обучения EL(w) и от отношения количества обучающих выборок р к фактическому значению h параметра, называемого мерой ВапникаЧервоненкиса (МВЧ) и обозначаемого VCd. Данная мера отражает уровень сложности нейронной сети и тесно связана с количеством содержащихся в ней весов. Значение e уменьшается по мере возрастания отношения количества обучающих выборок к уровню сложности сети. Значение МВЧ функционально зависит от количества синаптических весов, связывающих нейроны между собой. Чем больше количество различных весов, тем больше сложность сети и соответственно значение меры VCd. Верхняя и нижняя границы МВЧ определяются в соответствии с неравенством:
|
é K ù |
|||||
|
2ê |
úN £ VCd |
£ 2N w (1 + lg Nn ) , |
(3.41) |
||
|
2 |
|||||
|
ë |
û |
где [ ] — целая часть числа, N — размерность входного вектора, К-количество нейронов скрытого слоя, Nw — общее количество весов сети, a Nn —общее количество нейронов сети.
Из выражения (3.41) следует, что нижняя граница диапазона приблизительно равна количеству весов, связывающих входной и скрытый слои, тогда как верхняя граница превышает двукратное суммарное количество всех весов сети. В связи с невозможностью точного определения меры VCd в качестве ее приближенного значения используется общее количество весов нейронной сети [174].
Таким образом, на погрешность обобщения оказывает влияние отношение числа обучающих выборок к количеству весов сети. Небольшой объем обучающего подмножества при фиксированном количестве весов вызывает хорошую адаптацию сети к его элементам, однако не усиливает способности к обобщению, так как в процессе обучения наблюдается относительное превышение числа подбираемых параметров(весов) над количеством пар фактических и ожидаемых выходных сигналов сети. Эти параметры адаптируются с чрезмерной (а вследствие превышения числа параметров над объемом обучающего множества — и неконтролируемой) точностью к значениям конкретных выборок, а не к диапазонам, которые эти выборки должны представлять. Фактически задача аппроксимации подменяется в этом случае задачей приближен-
130
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Содержание
- 1 Обучение как задача оптимизации
- 2 Дифференцирование для однослойной сети
- 2.1 Находим производную ошибки
- 3 Алгоритм
- 4 Недостатки алгоритма
- 4.1 Паралич сети
- 4.2 Локальные минимумы
- 5 Примечания
- 6 См. также
- 7 Источники информации
Обучение как задача оптимизации
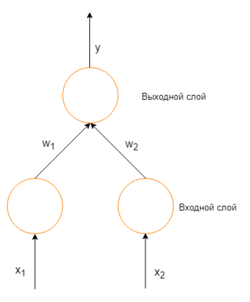
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:
- где ошибка.
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
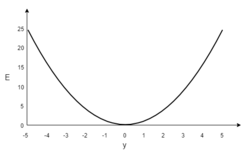
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.
Дифференцирование для однослойной сети
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:
- где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.
Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона , его выходное значение определено как
Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.
Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
у нее удобная производная:
Находим производную ошибки
Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:
Только одно слагаемое в зависит от , так что
Если нейрон в первом слое после входного, то — это просто .
Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и
Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.
Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,
и взять полную производную по , то получим рекурсивное выражение для производной:
Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.
Если собрать все месте:
и
Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:
Алгоритм
- — скорость обучения
- — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
- — обучающее множество
- — количество повторений
- — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
- — количество слоев в сети
- — множество нейронов в слое i
- — множество нейронов в выходном слое
fun BackPropagation:
init
repeat :
for = to :
=
for :
=
for = to :
for :
=
for :
=
=
return
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
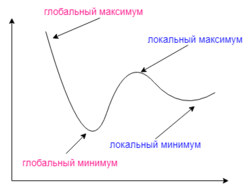
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Примечания
- Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- Neural Nets
- Understanding backpropagation
См. также
- Нейронные сети, перцептрон
- Стохастический градиентный спуск
- Настройка глубокой сети
- Практики реализации нейронных сетей
Источники информации
- https://en.wikipedia.org/wiki/Backpropagation
- https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
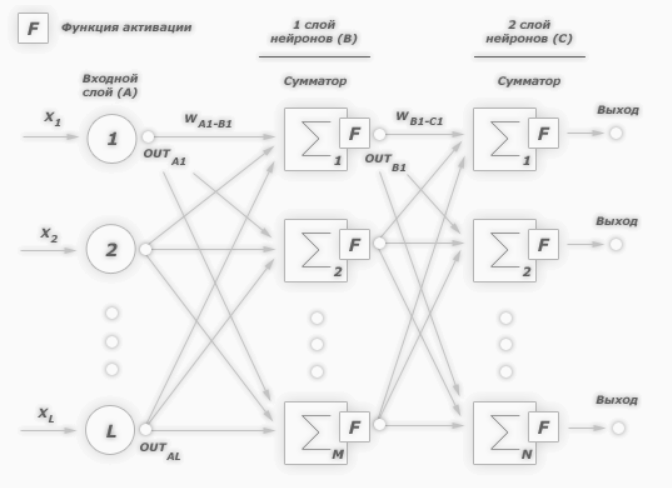

В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
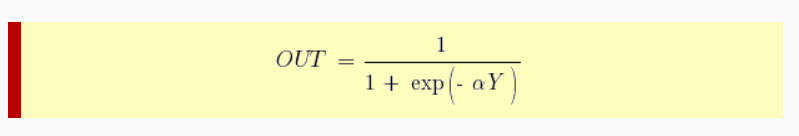
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».
Машинное обучение, Искусственный интеллект, Natural Language Processing
Рекомендация: подборка платных и бесплатных курсов PR-менеджеров — https://katalog-kursov.ru/
Поскольку я столкнулся с существенными затруднениями в поисках объяснения механизма обратного распространения ошибки, которое мне понравилось бы, я решил написать собственный пост об обратном распространении ошибки реализовав алгоритм Word2Vec. Моя цель, — объяснить сущность алгоритма, используя простую, но нетривиальную нейросеть. Кроме того, word2vec стал настолько популярным в NLP сообществе, что будет полезно сосредоточиться на нем.
Данный пост связан с другим, более практическим постом который рекомендую прочитать, в нем рассматривается непосредственная реализация word2vec на языке python. В данном же посте мы сосредоточимся в основном на теоретической части.
Начнем с вещей которые необходимы для настоящего понимания обратного распространения. Помимо понятий из машинного обучения, таких как, функция потерь и градиентный спуск, пригодятся еще два компонента из математики:
- линейная алгебра (в частности матричное умножение)
- правило цепочки дифференцирования функций от многих переменных
Если вам знакомы эти понятия, то дальнейшие рассуждения окажутся простыми. Если же вы еще не освоили их, то все равно сможете понять основы обратного распространения.
Сперва я хочу дать определение понятию обратного распространения, если смысл будет недостаточно понятен, он будет раскрыт подробнее в следующих пунктах.
1. Что такое алгоритм обратного распространения
В рамках нейронной сети, единственными параметрами участвующими в обучении сети, то есть минимизации функции потерь, являются веса (здесь имею в виду веса в широком смысле, относя к ним и смещения). Веса изменяются на каждой итерации, пока мы не приблизимся к минимуму функции потерь.
В таком контексте, обратное распространение — это эффективный алгоритм нахождения оптимальных весов нейронной сети, то есть тех, которые оптимизируют функцию потерь.
Стандартный способ нахождения этих весов, применение алгоритма градиентного спуска, который подразумевает нахождение частных производных функции потерь по всем весам.
Для тривиальных задач в которых всего две переменных, легко представить как работает градиентный спуск, если вы посмотрите на рисунок, то увидите трехмерный график функции потерь, как функции весов w1 и w2.

Рисунок 1. Визуальное объяснение алгоритма градиентного спуска.
Вначале мы не знаем оптимальные значения, то есть не знаем какие значения w1 и w2 минимизируют функцию потерь.
Допустим, мы начинаем с красной точки. Если мы знаем как изменяется функция потерь при изменении весов, то есть если мы знаем производные и
, то мы можем сдвинуть красную точку ближе к минимуму функции потерь, которая представлена на графике синей точкой. Шаг сдвига определяется параметром
, который обычно называется параметром обучения.
2. Word2Vec
Задача алгоритма word2vec, найти эмбеддинги слов в заданном текстовом корпусе, другими словами, это методика поиска представлений слов в низкой размерности. Как следствие, когда мы говорим о word2vec, мы обычно говорим о приложениях NLP.
Например, модель word2vec обученная со скрытым слоем размерности [N, 3], где N -количество слов в словаре, даст трехмерные эмбеддинги слов. Это значит что, например, слово ‘квартира’, будет представлено трехмерным вектором действительных чисел, который будет близок (воспринимайте это как Евклидову метрику), к представлению аналогичного слова, такого как ‘дом’. Другими словами, word2vec это техника отображения слов в числа.
В контексте word2vec используются две основные модели: мешок слов (CBOW) и скипграммы (skip-gram). Сначала мы рассмотрим простейшую модель, CBOW, с окном из одного слова, затем перейдем к окну из нескольких слов и наконец рассмотрим модель skip-gram.
По мере продвижения я покажу несколько небольших примеров с текстом состоящим всего из нескольких слов. Однако имейте в виду, что обычно woed2vec тренируется с миллиардами слов.
3. Простая модель CBOW
В CBOW модели задача состоит в поиске слова по его контексту. В простейшем случае когда контекст слова представлен одним словом, нейронная сеть будет выглядеть так:
Рисунок 2. Топология модели Continuous Bag-of-Words модели с контекстом из одного слова
Один входной слой, один скрытый слой и выходной слой, функция активации скрытого слоя
a = 1 (identity function, или функция линейной активации, хотя последнее неправильно).
В качестве функции активации выходного слоя используется Softmax.
Входной слой представлен one hot encoding вектором, длина которого совпадает с размером массива слов, все элементы данного вектора равны нулю, кроме элементов, индексы которых совпадают с индексами слов из контекста, по данным индексам значения вектора равны 1.
Пример: словарь [‘мама’, ‘мыла’, ‘раму’, ‘маша’, ‘ела’, ‘кашу’]
OneHot(‘маша’) = [0, 0, 0, 1, 0, 0]
OneHot([‘мама’, ‘маша’]) = [1, 0, 0, 1, 0, 0]
OneHot([‘мама’, ‘ела’, ‘кашу’]) = [1, 0, 0, 0, 1, 1]
Перейдем к весам, весовые коэффициенты между входным и скрытым слоем представлены матрицей W размера , матрица между скрытым и выходным слоем
размером
, где V — размер словаря, N — размер эмбеддинг вектора (то есть, те вектора которые и пытается найти word2vec)
Выходной вектор y сравниваем с ожидаемым вектором t, чем они ближе, тем выше эффективность нейронной сети, и, соответственно, меньше функция потерь.
Если на текущем этапе что то звучит непонятно, то пример ниже должен прояснить ситуацию.
Пример
Предположим, мы хотим обучить word2vec следующим текстом:
«I like playing football»
Мы решаем обучить модель CBOW с одним контекстным словом как на рисунке (2) выше.
Учитывая текст который у нас есть, наш словарь будет состоять из 4 слов, соответственно V=4, также установим что скрытый слой будет иметь два нейрона, то есть N=2, наша нейросеть будет выглядеть так:
Со словарём:
Далее мы определяем как выбирать ‘целевое’ и ‘контекстное’ слово, и мы можем построить наши обучающие примеры двигаясь окном по тексту. Например:

Тогда обучающие примеры будут выглядеть так:
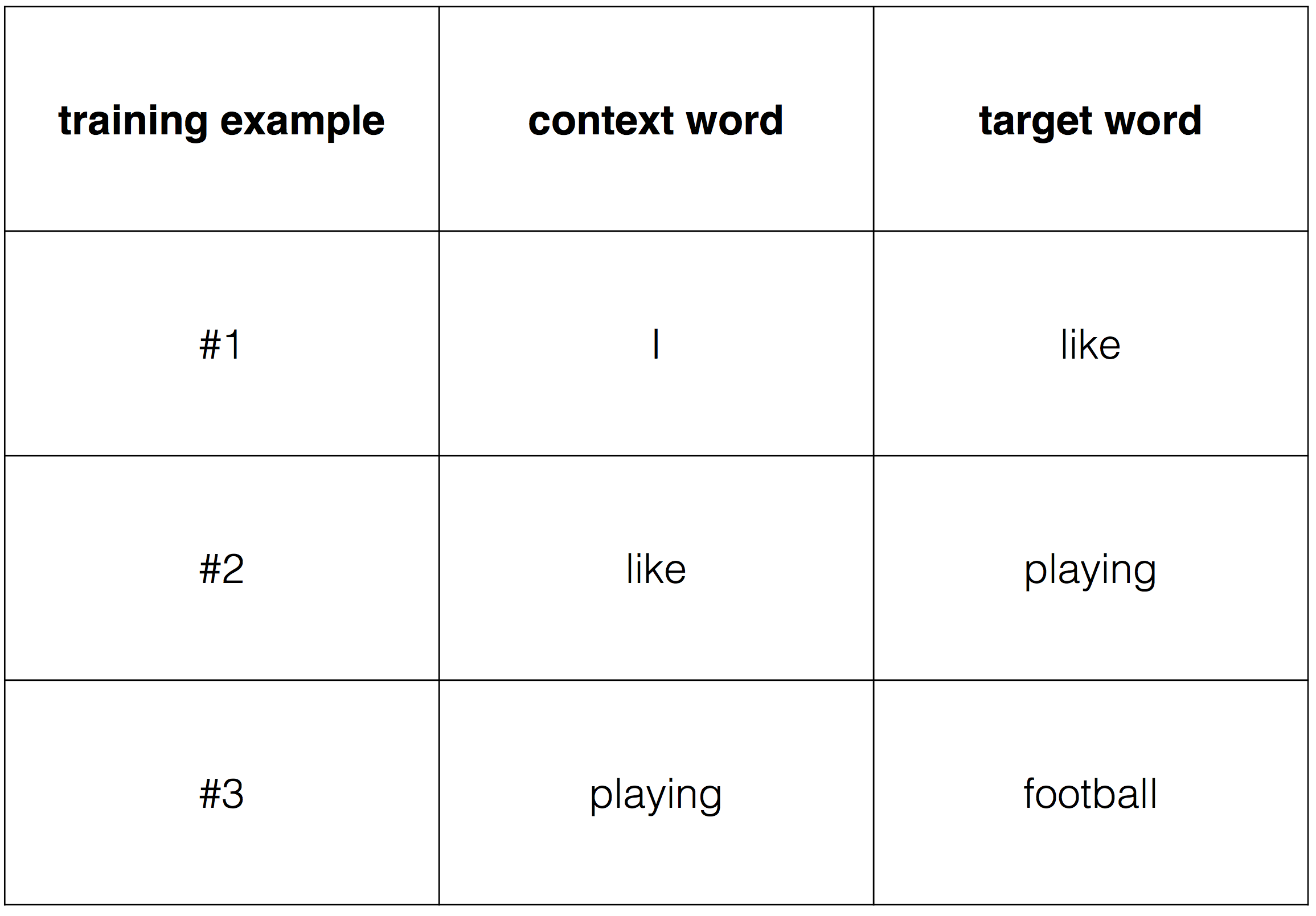
Чтобы передать эти данные в алгоритм понадобится преобразовать их в числа, для чего используем one-hot encoding.
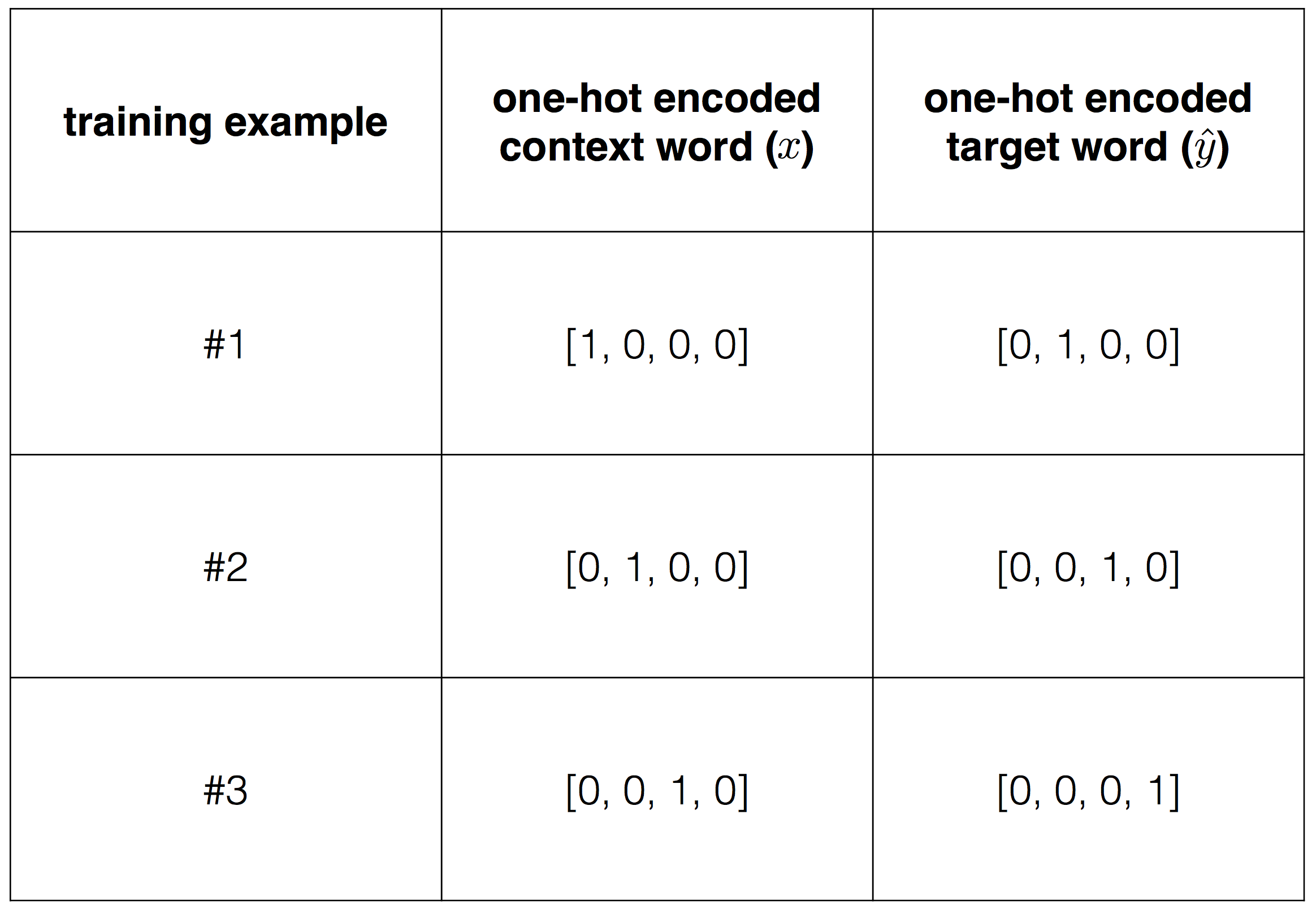
На данный момент, мы хотим обучить нашу модель, находя веса, которые минимизируют функцию потерь. Это соответствует нахождению весов, которые с учетом вектора контекста могут с высокой точностью предсказать, что является соответствующим целевым словом.
3.1 Функция потерь (Loss function)
Исходя из топологии на рисунке 1, давайте запишем как посчитать значения скрытого и выходного слоев, при входе x:
где, h — сумма на скрытом слое, u — сумма на выходном слое, y — выход сети.
Теперь, предположим, мы обучаем модель по паре целевое слово, контекстное слово (wt, wc). Целевое слово представляет собой идеальное предсказание нейронной сети, в виде onehot encoding вектора.
Функция потерь должна будет оценить выходной слой, относительно onehot вектора wt (целевого слова).
Поскольку значения softmax можно интерпретировать как условные вероятности целевого слова, то учитывая контекстное слово функцию потерь можно записать в следующем виде:
$$display$$begin{equation*} mathcal{L} = -log mathbb{P}(w_t|w_c)=-log y_{j^*} =-log[mathbb{S}textrm{oftmax}(u_{j^*})]=-logleft(frac{exp{u_{j^*}}}{sum_i exp{u_i}}right), end{equation*}$$display$$
, где j* — ожидаемая позиция правильно предсказанного слова.
Добавление функции логарифма является стандартным подходом. Из данного выражения мы получаем уравнение (1):
$$display$$begin{equation} bbox[lightblue,5px,border:2px solid red]{ mathcal{L} = -u_{j^*} + log sum_i exp{(u_i)}. } label{eq:loss} end{equation} >(1)$$display$$
Функция потерь максимизирует вероятность предсказания правильного слова исходя из заданного контекста.
Пример
Вернемся к предыдущему примеру предложения «I like play football», предположим мы обучаем модель по первой записи обучающих данных, с контекстным словом «I» и целевым словом «like», в идеале веса сети должны быть такими, чтобы при вводе — что соответствует слову «I», результат работы был близок к
, что соответствует слову «like».
Стандартный подход к инициализации весов word2vec, использование нормального распределения. Примем начальное состояние весов матрицы W размером
И начальное состояние весов матрицы размером
Для обучающих данных «I like» мы получаем:
Затем
И наконец
На этом этапе функция потерь будет отрицательным логарифмом второго элемента , или
Также, мы могли бы рассчитать ее при помощи уравнения (1):
Теперь, прежде чем перейти к следующему обучающему примеру «like play», мы должны изменить веса нейросети, как это сделать расскажет следующий пункт про обратное распространение.
3.2 Алгоритм обратного распространения для модели CBOW
Теперь, имея в наличии функцию потерь, мы хотим найти веса W и W` которые ее минимизируют. В терминах машинного обучения, мы хотим чтобы модель обучилась.
В первом разделе мы уже обсудили что в мире нейронный сетей эта проблема решается использованием градиентного спуска. На рисунке (1) показано как применить этот метод и обновить матрицы весов W и W`. Нам нужно найти производные и
Я считаю что самый простой способ понять как это сделать, это записать соотношения между функцией потерь и матрицами весов. Глядя на уравнение (1) ясно что функция потерь зависит от весов W и W`, через переменную u=[u1, …., uV], или
$$display$$begin{equation*} mathcal{L} = mathcal{L}(mathbf{u}(W,W’))=mathcal{L}(u_1(W,W’), u_2(W,W’),dots, u_V(W,W’)) . end{equation*}$$display$$
Получить производные можно из правила цепочки для функций многих переменных:
$$display$$begin{equation} frac{partialmathcal{L}}{partial W’_{ij}} = sum_{k=1}^Vfrac{partialmathcal{L}}{partial u_k}frac{partial u_k}{partial W’_{ij}} label{eq:dLdWp} end{equation} >(2)$$display$$
и
$$display$$begin{equation} frac{partialmathcal{L}}{partial W_{ij}} = sum_{k=1}^Vfrac{partialmathcal{L}}{partial u_k}frac{partial u_k}{partial W_{ij}} . label{eq:dLdW} end{equation} >(3)$$display$$
И это большая часть алгоритма обратного распространения, на данный момент нам просто нужно определить уравнения (2) и (3) для нашего случая.
Начнем с уравнения (2), обратите внимание что вес Wij, относится к матрице W, и соединяет нейрон i в скрытом слое с нейроном j в выходном слое, и соответственно оказывает влияние только на выход uj (соответственно и на yj).
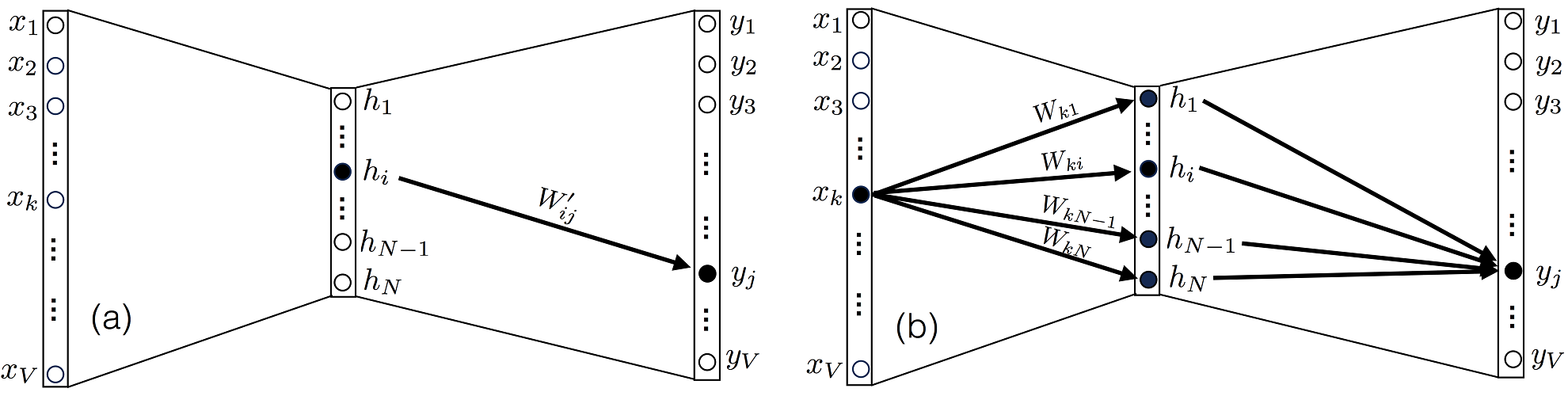
Рисунок 3. (a) Выходной узел зависит от общего узла
скрытого слоя только через элемент
матрицы
. (b) Но кроме того, этот же выходной узел зависит от общего входного узла
через N элементов
матрицы W.
Следовательно, среди всех производных , только одна, где k=j, будет отличаться от 0.
Уравнение (4):
$$display$$begin{equation} frac{partialmathcal{L}}{partial W’_{ij}} = frac{partialmathcal{L}}{partial u_j}frac{partial u_j} {partial W’_{ij}} label{eq:derivative#1} end{equation} >(4)$$display$$
Давайте посчитаем , уравнение (5):
$$display$$begin{equation} frac{partialmathcal{L}}{partial u_j} = -delta_{jj^*} + y_j := e_j label{eq:term#1} end{equation} >(5)$$display$$
, где — дельта Кронекера, функция двух целых переменных, которая равна 1, если они равны, и 0 в противном случае.
В уравнении (5) мы ввели вектор e размерности N (размер словаря), который мы используем чтобы снизить сложность обозначений, этот вектор представляет собой разницу между полученным и ожидаемым результатом, то есть это вектор ошибок предсказания.
Для второго члена правой части уравнения (4) мы получим уравнения (6):
$$display$$begin{equation} frac{partial u_j}{partial W’_{ij}} = sum_{k=1}^V W_{ik}x_k label{eq:term#2} end{equation} >(6)$$display$$
После подставновки уравнений (5) и (6) в уравнение (4) мы получим уравнение (7):
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W’_{ij}} = (-delta_{jj^*} + y_j) left(sum_{k=1}^V W_{ki}x_kright) } label{eq:backprop1} end{equation} >(7)$$display$$
Мы можем найти выполнить аналогичное упражнение для поиска производной , однако на этот раз отметим что после задания входа Xk, выход yj нейрона j зависит от всех элементов матрицы W соединенных со входом, как видно на рисунке 3(b). Поэтому мы должны оценивать все элементы в сумме. Прежде чем перейти к оценке
, полезно перезаписать выражение для элемента uk из вектора u как:
$$display$$begin{equation*} u_k = sum_{m=1}^Nsum_{l=1}^VW’_{mk}W_{lm}x_l . end{equation*}$$display$$
Из этого уравнения легко вывести , поскольку единственный выживший член производной будет с индексами l=i и m=j, или же в виде уравнения (8):
$$display$$begin{equation} frac{partial u_k}{partial W_{ij}} = W’_{jk}x_i . label{eq:term#3} end{equation} >(8)$$display$$
Наконец применив уравнения (5) и (8) мы получим результат, уравнение (9):
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partial mathcal{L}}{partial W_{ij}} = sum_{k=1}^V (-delta_{kk^*}+y_k)W’_{jk}x_i } label{eq:backprop2} end{equation} >(9)$$display$$
Векторизация
Мы можем упростить запись уравнений. (7) и (9) используя векторную нотацию. Сделав это мы получим для уравнения (7)
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W’} = (W^Ttextbf{x}) otimes textbf{e} } end{equation} >(10)$$display$$
Где символ ? обозначает векторное произведение.
Для уравнения (9) мы получим:
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partial mathcal{L}}{partial W} = textbf{x}otimes(W’textbf{e}) } end{equation} >(11)$$display$$
3.3 Градиентный спуск на основе полученных выше результатов
Теперь, когда у нас есть уравнения (7) и (9), у нас есть все необходимое для реализации одной итерации обучения нейросети на базе алгоритма обратного распространения ошибки, применяя градиентный спуск. Каждая итерация должна немного приближать к минимуму функцию потерь. После задания скорости обучения , мы можем обновить наши веса следующим образом:
3.4 Итерация алгоритма
Все описанное выше является всего лишь одним маленьким шагов всего процесса оптимизации. В частности, до этого момента мы обучали нашу нейросеть всего на одном тренировочном примере. Чтобы завершить первый проход, мы должны применить все обучающие примеры. Сделав это, мы пройдем одну эпоху обучения. После чего нам нужно будет повторять цикл обучения, пройдя достаточное количество эпох, пока изменения функции потерь не станут незначительными, после чего можно будет остановиться и считать нейросеть обученной.
4. Алгоритм обратного распространения для контекста из нескольких слов в модели CBOW
Мы уже знаем как работает алгоритм обратного распространения для модели CBOW с одним словом на входе. Теперь увеличим сложность и добавим в контекст несколько слов. Рисунок (4) показывает как выглядит нейросеть теперь. Вход теперь представляет собой серию OneHot Encoded векторов слов входящих в контекст. Количество слов в контексте является параметром который мы можем задавать при инициализации word2vec. Скрытый слой получает усреднение из всех контекстных слов.

Рисунок 4. Топология модели CBOW с контекстом из нескольких слов
Уравнения модели CBOW с несколькими контекстными словами являются обобщением уравнений модели CBOW с одним контекстным словом.
Обратите внимание, что для удобства мы ввели определение ‘усредненный’ входной вектор
Как и прежде, чтобы применить алгоритм обратного распространения нам нужно выписать функцию потерь и выписать ее зависимости. Функция потерь выглядит также как и раньше:
$$display$$begin{equation} mathcal{L} = -logmathbb{P}(w_o|w_{c,1},w_{c,2},dots,w_{c,C})=-u_{j^*} + log sum_i exp{(u_i)}. end{equation} >(12)$$display$$
Снова выпишем уравнения по правилу цепочки, аналогично предыдущим:
$$display$$begin{equation} frac{partialmathcal{L}}{partial W’_{ij}} = sum_{k=1}^Vfrac{partialmathcal{L}}{partial u_k}frac{partial u_k}{partial W’_{ij}} end{equation} >(13)$$display$$
и
$$display$$begin{equation} frac{partialmathcal{L}}{partial W_{ij}} = sum_{k=1}^Vfrac{partialmathcal{L}}{partial u_k}frac{partial u_k}{partial W_{ij}} . end{equation} >(14)$$display$$
Производные функции потерь по весам такие же как для модели CBOW с одним словом на входе, с единственным отличием, что мы заменим входной вектор из одного слова на усредненный вектор из слов контекста. Выведем эти уравнения начиная с производной по
$inline$begin{equation} frac{partialmathcal{L}}{partial W’_{ij}} = sum_{k=1}^Vfrac{partialmathcal{L}}{partial u_k}frac{partial u_k}{partial W’_{ij}} = frac{partialmathcal{L}}{partial u_j}frac{partial u_j}{partial W’_{ij}} = (-delta_{jj^*} + y_j) left(sum_{k=1}^V W_{ki}overline{x}_kright) end{equation} > (15)$inline$
Теперь запишем производную по :
$$display$$begin{equation} frac{partialmathcal{L}}{partial W_{ij}} = sum_{k=1}^Vfrac{partialmathcal{L}}{partial u_k}frac{partial}{partial W_{ij}}left(frac{1}{C}sum_{m=1}^Nsum_{l=1}^V W’_{mk}sum_{c=1}^C W_{lm}x_l^{(c)}right)=frac{1}{C}sum_{k=1}^Vsum_{c=1}^C(-delta_{kk^*} + y_k)W’_{jk}x_i^{(c)} . end{equation} >(16)$$display$$
Подведя итог имеем следующее:
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W’_{ij}} = (-delta_{jj^*} + y_j) left(sum_{k=1}^V W_{ki}overline{x}_kright) } label{eq:backprop1_multi} end{equation} >(17)$$display$$
и
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W_{ij}} = sum_{k=1}^V(-delta_{kk^*} + y_k)W’_{jk}overline{x}_i . } label{eq:backprop2_multi} end{equation} > (18)$$display$$
Векторизация
Перепишем уравнения (17) и (18) в записи для векторов.
Уравнение (17) примет вид:
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W’} = (W^Toverline{textbf{x}}) otimes textbf{e} } end{equation} >(19)$$display$$
Для уравнения (18):
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partial mathcal{L}}{partial W} =overline{textbf{x}}otimes(W’textbf{e}) } end{equation} >(20)$$display$$
Еще раз, обратите внимание что уравнения идентичны уравнениям в модели CBOW для контекста из одного слова.
Оператор ? обозначает векторное произведение.
5. Алгоритм обратного распространения для модели Skip-gram
Данная модель по сути обратна модели CBOW, на вход подается центральное слово, на выходе предсказывается его контекст. Полученная нейросеть выглядит следующим образом:
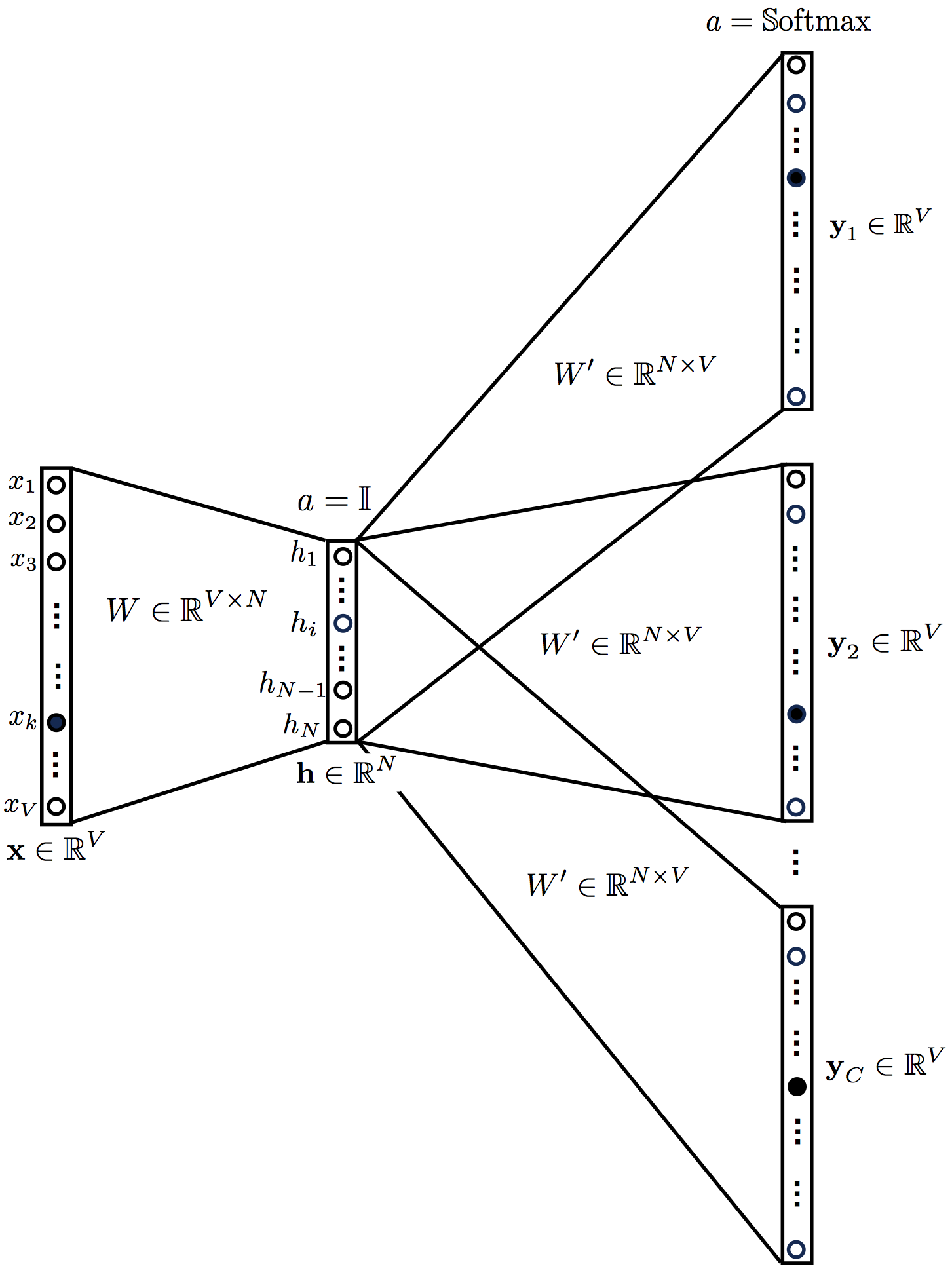
Рисунок 5.Топология Skip-gram модели.
Уравнения skip-gram модели следующие:
Обратите внимание что выходные вектора (как и вектор ) идентичны,
. Функция потерь выглядит следующим образом:
Для модели skip-gram функция потерь зависит от переменных
через:
$$display$$begin{equation*} mathcal{L} = mathcal{L}(mathbf{u_1}(W,W’), mathbf{u_2}(W,W’), dots, mathbf{u_C}(W,W’))=mathcal{L}(u_{1,1}(W,W’), u_{1,2}(W,W’), dots, u_{C,V}(W,W’)) end{equation*}$$display$$
Соответственно правило цепочки выглядит так:
$$display$$begin{equation*} frac{partialmathcal{L}}{partial W’_{ij}} = sum_{k=1}^Vsum_{c=1}^Cfrac{partialmathcal{L}}{partial u_{c,k}}frac{partial u_{c,k}}{partial W’_{ij}} end{equation*}$$display$$
и
$$display$$begin{equation*} frac{partialmathcal{L}}{partial W_{ij}} = sum_{k=1}^Vsum_{c=1}^Cfrac{partialmathcal{L}}{partial u_{c,k}}frac{partial u_{c,k}}{partial W_{ij}} . end{equation*}$$display$$
Посчитаем , получим:
$$display$$begin{equation*} frac{partialmathcal{L}}{partial u_{c,j}} = -delta_{jj_c^*} + y_{c,j} := e_{c,j} end{equation*}$$display$$
Аналогично модели CBOW получаем:
$$display$$begin{equation*} frac{partialmathcal{L}}{partial W’_{ij}} = sum_{k=1}^Vsum_{c=1}^Cfrac{partialmathcal{L}}{partial u_{c,k}}frac{partial u_{c,k}}{partial W’_{ij}} = sum_{c=1}^Cfrac{partialmathcal{L}}{partial u_{c,j}}frac{partial u_{c,j}}{partial W’_{ij}} = sum_{c=1}^C(-delta_{jj_c^*} + y_{c,j}) left(sum_{k=1}^V W_{ki}x_kright) end{equation*}$$display$$
Производная по самая сложная, но выполнимая:
$$display$$begin{equation*} frac{partialmathcal{L}}{partial W_{ij}} = sum_{k=1}^Vsum_{c=1}^Cfrac{partialmathcal{L}}{partial u_{c,k}}frac{partial}{partial W_{ij}}left(sum_{m=1}^Nsum_{l=1}^V W’_{mk} W_{lm}x_lright)=sum_{k=1}^Vsum_{c=1}^C (-delta_{kk_c^*} + y_{c,k})W’_{jk}x_i . end{equation*}$$display$$
Подведя итог, для модели skip-gram мы имеем:
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W’_{ij}} = sum_{c=1}^C(-delta_{jj_c^*} + y_{c,j}) left(sum_{k=1}^V W_{ki}x_kright) } label{eq:backprop1_skip} end{equation} >(21)$$display$$
и
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W_{ij}} = sum_{k=1}^Vsum_{c=1}^C (-delta_{kk_c^*} + y_{c,k})W’_{jk}x_i . } label{eq:backprop2_skip} end{equation} >(22)$$display$$
Векторизация
Векторизованная версия уравнения (21):
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partialmathcal{L}}{partial W’} = (W^Ttextbf{x}) otimes sum_{c=1}^Ctextbf{e}_c } end{equation} >(23)$$display$$
Уравнение (22):
$$display$$begin{equation} bbox[white,5px,border:2px dotted red]{ frac{partial mathcal{L}}{partial W} = textbf{x}otimesleft(W’sum_{c=1}^Ctextbf{e}_cright) } end{equation} >(24)$$display$$
6. Что дальше
Мы подробно рассмотрели как работает алгоритм обратного распространения в случае word2vec. Однако рассмотренная реализация неэффективна для больших текстовых корпусов. В оригинальной статье [2] применяются некоторые трюки для преодоления этих проблем (иерархический softmax, negative sampling), однако я не буду на них останавливаться подробно. Вы можете найти подробное описание по ссылке [1].
Несмотря на вычислительную неэффективность реализации описанной здесь, она содержит всё необходимое для обучения нейронных сетей word2vec.
Следующим шагом будет реализация этих уравнений на вашем любимом языке программирования. Если вам нравится Python, я уже реализовал эти уравнения в моем следующем посте.
Надеюсь увидеть вас там!
Дополнительные ссылки
[1] X. Rong, word2vec Parameter Learning Explained, arXiv:1411.2738 (2014).
[2] T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space, arXiv:1301.3781 (2013).
Привет, Вы узнаете про анализ алгоритма обратного распространения ошибки нейронной сети , Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
анализ алгоритма обратного распространения ошибки нейронной сети , настоятельно рекомендую прочитать все из категории Computational Neuroscience (вычислительная нейронаука) Теория и приложения искусственных нейронных сетей.
В статье изложены основы нейронной сети, а также проведен анализ функционирования алгоритма обратного распространения ошибки.
На сегодняшний день, нейронная сеть является одним из способов интеллектуального анализа данных. Интеллектуальный анализ данных позволяет решить такие проблемы, как: классификация и кластеризация, прогнозирования, распознавание образов, сжатия данных и ассоциативная память, диагностика заболеваний и т. д.
Нейронные сети — это одно из направлений исследований в области искусственного интеллекта, основанное на попытках воспроизвести нервную систему человека. А именно, способность нейронной сети обучаться и исправлять ошибки, что должно позволить смоделировать, хотя и достаточно грубо, работу человеческого мозга [1].
Нейронная сеть — это математическая модель человеческого мозга, состоящая из многих простых вычислительных элементов (нейронов) рисунок 1, работающих параллельно, функция которых определяется структурой сети, а вычисления производятся в самих элементах. Считается, что способность мозга к обработке информации в основном обусловлена функционированием сетей, состоящих из таких нейронов [1; 2].
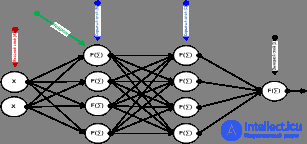
Рисунок 1. Многослойная нейронная сеть
Рассмотрим нейронную сеть стандартной архитектуры (рисунок 1), которая обычно имеет несколько слоев: А — рецепторный слой, на который подаются входные данные; B,C — скрытые слои, нейроны которых интерпретируют полученную информацию; D — выходной слой, предоставляющий реакцию нейронной сети.
Каждый слой сети состоит из нейронов. Нейрон — это основной элемент вычисления, нейронной сети. На рисунке 2 показана его структура.
В состав нейрона входит умножители, сумматоры и нелинейный преобразователь. Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи – веса синапсов.
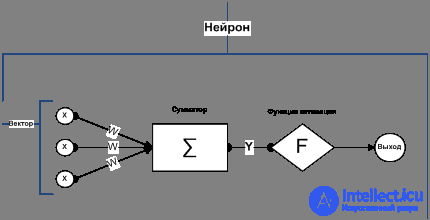
Рисунок. 2. Структура искусственного нейрона
Сумматор выполняет сложение сигналов, поступающих по синоптическим связям от других нейронов или внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента — выход сумматора. Это функция называется «функцией активации» или «передаточной функцией» нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента.
Математическая модель нейрона описывает соотношениями
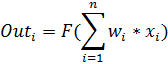
где — 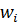 вес синапса
вес синапса  ; s— результат суммирования; xi — компонент входного вектора
; s— результат суммирования; xi — компонент входного вектора  ;
;
y — выходной сигнал нейрона; n — число входов нейрона; F— функция активации;
Главная задача в процессе разработки нейронной сети, является этап обучения, т. е . Об этом говорит сайт https://intellect.icu . корректировки весов сети, для минимизации ошибки на выходе нейронной сети.
Стандартная нейронная сеть прямого распространения приведена на рисунке 3, также известна как многослойный персептрон(MLP). Обратите внимание, что узлы входного уровня отличаются от узлов в других слоях, это означает, что никакая обработка не происходит в этих узлах, они служат только в качестве входов сети.
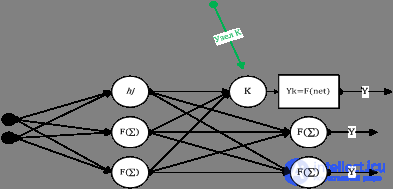
Рисунок 3. Стандартная сеть с прямым распространением
Каждый узел вычисляет взвешенную сумму его входов, и использует его как входные данные функции преобразования 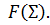
В классическом многослойном персептроне, функция преобразования — сигмоид.
Сигмоида — это гладкая монотонная нелинейная S — образная функция, которая часто применяется для «сглаживания» значений некоторой величины.
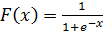 (1)
(1)
Рассмотрим узел k в скрытом слое. Его выход yk представляет 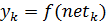 где f , функция активации (сигмоида), являются взвешенной суммой выходов узлов входного слоя A
где f , функция активации (сигмоида), являются взвешенной суммой выходов узлов входного слоя A
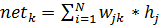 (2)
(2)
аналогично, выход каждого узла в каждом слое.
Для удобства, мы можем рассмотреть входы сети, как входной вектор X , где 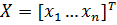 . Аналогично, выход для сети можно рассматривать как вектор выхода ,Y где
. Аналогично, выход для сети можно рассматривать как вектор выхода ,Y где  . Учебный набор для сети можно представить рядом пар K входных xi векторов и желаемых векторов выхода :
. Учебный набор для сети можно представить рядом пар K входных xi векторов и желаемых векторов выхода :  .
.
Каждый раз, когда входной вектор от учебного набора  применен к сети, сеть производит фактический выход
применен к сети, сеть производит фактический выход 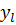 . Мы можем таким образом определить квадратичную ошибку для этого входного вектора, суммируя квадратичные ошибки в каждом узле выхода [3; 4]:
. Мы можем таким образом определить квадратичную ошибку для этого входного вектора, суммируя квадратичные ошибки в каждом узле выхода [3; 4]: 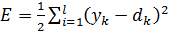 . (3)
. (3)
Главная задача, как уже было сказано в обучение нейронной сети, это минимизировать квадратичную ошибку E. Мы можем также определить полную квадратичную ошибку , суммирую все пары входа — выхода в учебном наборе:
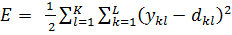 (4)
(4)
Для минимизации квадратичной ошибки, будем использовать алгоритм градиентного спуска. Определим какое направление является «скоростным спуском» на поверхности ошибок и изменим каждый вес так, чтобы мы двигались в этом направление. Математически это означает, что каждый вес будет изменен на небольшое значение в направлении уменьшения :
 (5)
(5)
Здесь  — вес во время t и
— вес во время t и  — обновленный вес. Уравнение 5 называется обобщенным дельта — правилом. Чтобы выполнить градиентный спуск, нужно найти частную производную каждого веса.
— обновленный вес. Уравнение 5 называется обобщенным дельта — правилом. Чтобы выполнить градиентный спуск, нужно найти частную производную каждого веса.
Для корректировки весов, между скрытым и выходным слоем, нужно найти частную производную, для каждого узла выходного слоя.
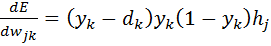 (6)
(6)
Таким образом, была найдена частная производная ошибки E по весам 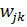 и можем использовать этот результат в уравнение 5, чтобы выполнить градиентный спуск для всех весов между скрытым и выходным слоями.
и можем использовать этот результат в уравнение 5, чтобы выполнить градиентный спуск для всех весов между скрытым и выходным слоями.
Теперь рассмотрим веса, между входным слоем и скрытым слоем.
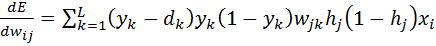 (7)
(7)
Была получена частная производная ошибки E по весу на основе известных величин (многие из которых мы уже вычислили при получении 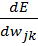 ).
).
Рассмотрим алгоритм обратного распространения ошибки в виде блок-схемы (рисунок 4).

Рисунок 4. Алгоритм обучения нейронной сети прямого распространения
Принцип функционирования алгоритма обратного распространения ошибки, заключается в использование метода градиентного спуска и корректировки весов, для минимизации ошибки нейронной сети.
В процессе разработки нейронной сети, одним из основных этапов является обучения нейронной сети. В данной статье был проведен анализ алгоритма обратного распространения ошибки, которая использует метод градиентного спуска, для корректировки весов.
Список литературы:
1. Рассел С., Норвиг П. Искусственный интеллект. Современный подход. — М.: Изд-во «Вильямс», 2006. — 1408 с.
2. Хайкин С. Нейронные сети: полный курс. — М.: Изд-во «Вильямс», 2006. — 1104 с.
3. Алгоритм обратного распространения ошибки. — [Электронный ресурс] — Режим доступа. — URL:http://www.aiportal.ru/articles/neural-networks/back-propagation.
4. Алгоритм обратного распространения ошибки. — [Электронный ресурс] — Режим доступа. — URL:http://masters.donntu.edu.ua/2006/kita/kornev/library/l10.htm.
На этом все! Теперь вы знаете все про анализ алгоритма обратного распространения ошибки нейронной сети , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое анализ алгоритма обратного распространения ошибки нейронной сети
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Computational Neuroscience (вычислительная нейронаука) Теория и приложения искусственных нейронных сетей
Время на прочтение
5 мин
Количество просмотров 82K
В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.
Обучение сверточной нейронной сети
На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.
Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.
Алгоритм обратного распространения ошибки
Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.
Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.
Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:

Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:

Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:

Выход каждого нейрона j является значением активационной функции
 , которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:
, которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.

Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:
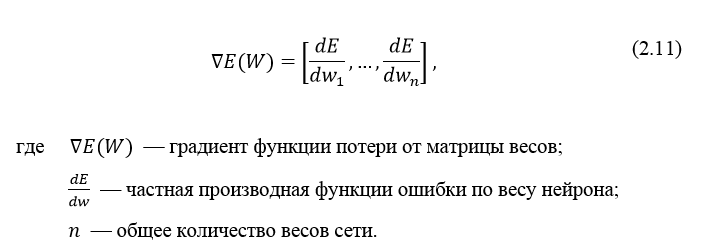
Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:

Ошибка нейрона  обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.
обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.
Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:

Алгоритм распространения ошибки сводится к следующим этапам:
- прямое распространение сигнала по сети, вычисления состояния нейронов;
- вычисление значения ошибки δ для выходного слоя;
- обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
- обновление весов сети на вычисленную ранее δ ошибки.
Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:
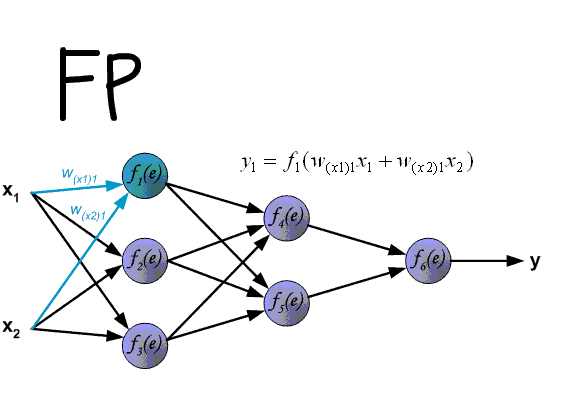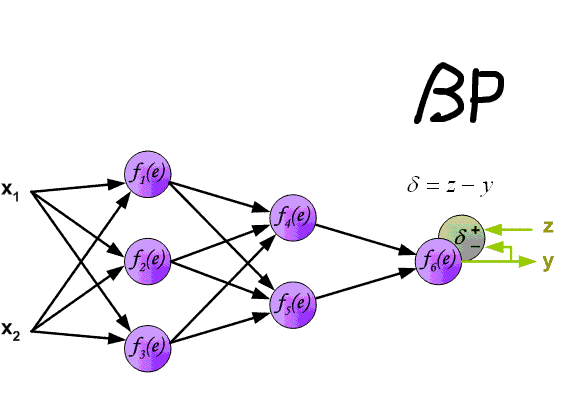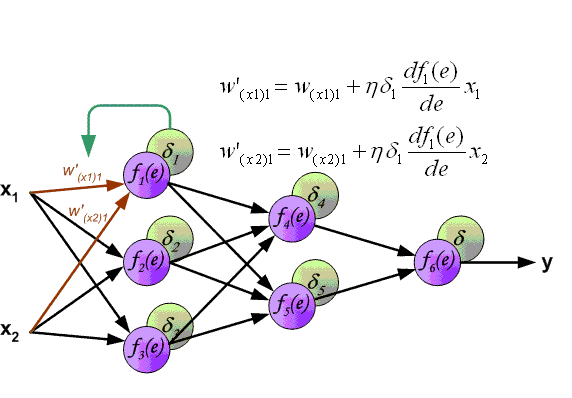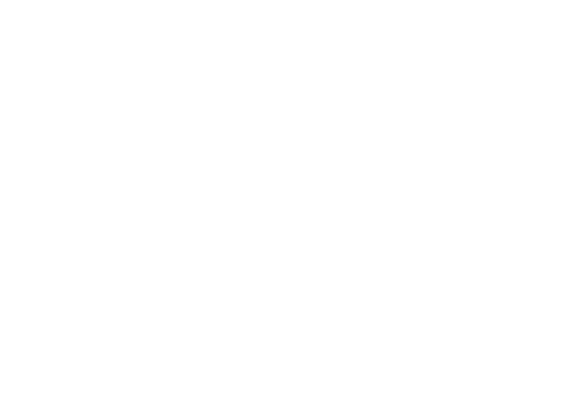
До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.
Расчет ошибки на подвыборочном слое
Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.
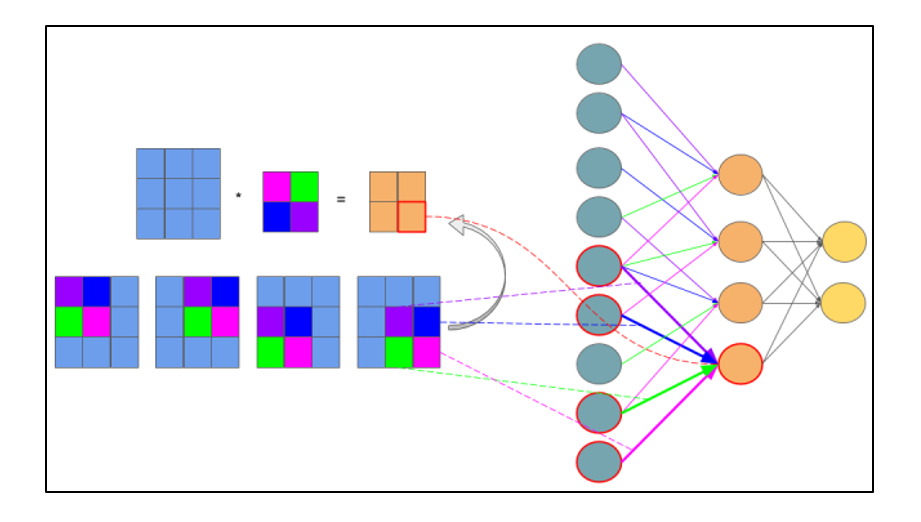
Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.
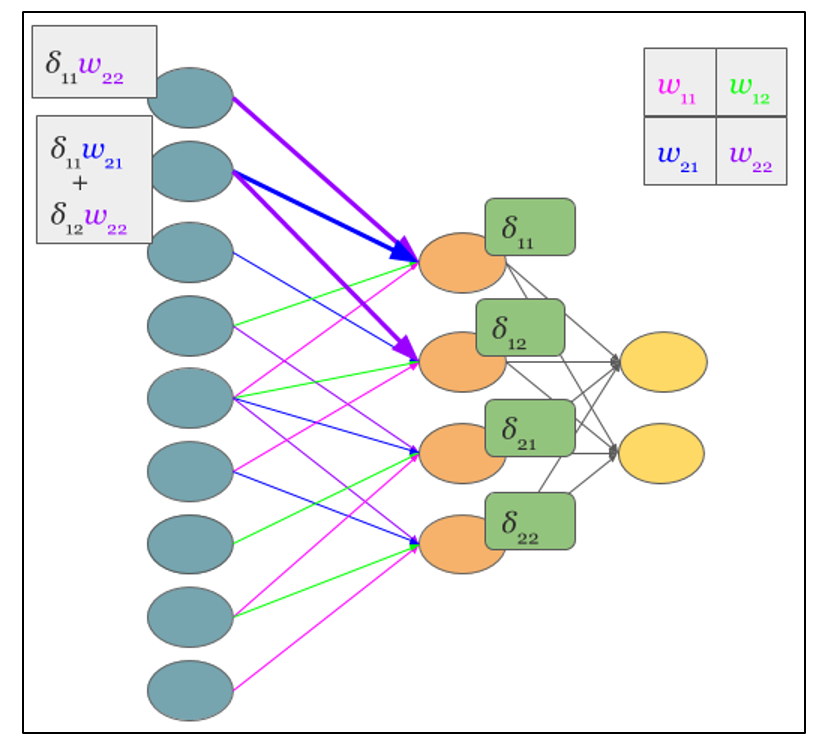
Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.

Рисунок 2.10 — Результат операции обратной свертки
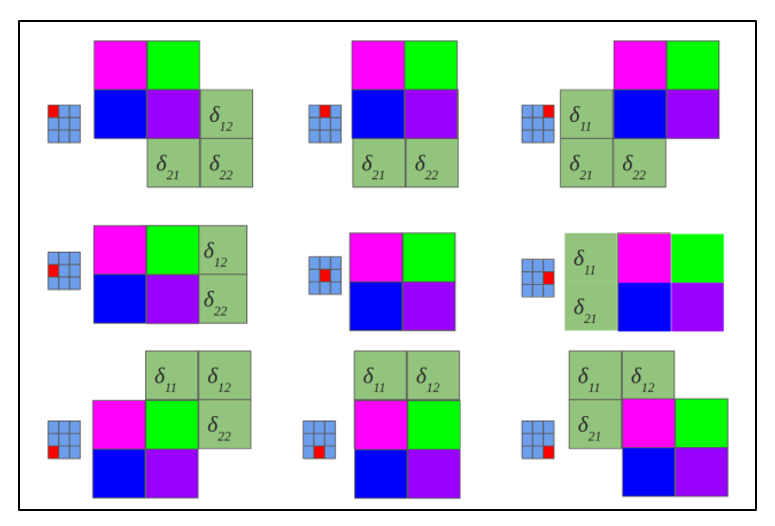
Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту
Расчет ошибки на сверточном слое
Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.
Заключение
Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.
Источники
Алгоритм обратного распространения ошибки для сверточной нейронной сети
Обратное распространение ошибки в сверточных слоях
раз и два
Обратное распространение ошибки в персептроне
Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ
на кривой, построенной на проверочном подмножестве. Однако на практике оказалось, что после прохождения этой точки сеть обучалась только посторонним шумам, содержащимся в обучающей выборке. Поэтому было принято решение об использовании точки минимума кривой тестирования в качестве критерия останова сеанса обучения. Когда ошибки на подмножествах оценивания и проверки не одинаково стремились к нулю(что характерно для данных не содержвщих шума), емкости сети оказывалось не достаточно для точного функционирования модели. В этом случае минимизировалась интегрированная квадратичная ошибка, что (приблизительно) эквивалентно минимизации обычной глобальной среднеквадратической ошибки при равномерном распределении входного сигнала.
Для повышения эффективности обучения ИНС использовалось комбинирование последовательного и пакетного режимов обучения. В рамках последовательного режима обучения корректировка весов проводилась после подачи каждого примера. Для примера рассмотрим эпоху, состоящую из N обучающих примеров, упорядоченных следующим образом: ((x1),d(1)),.., (x(N),d(N)). Сети предъявлялся первый пример(x(l),d(l)) этой эпохи, после чего выполнялись описанные выше прямые и обратные вычисления. В результате проводилась корректировка синаптических весов и уровней порогов в сети. После этого сети предъявлялась вторая пара (x(2),d(2)) в эпохе, повторялись прямой и обратный проходы, приводящие к поледующей коррекции синаптических весов и уровня порога. Этот процесс повторялся, пока сеть не завершала обработку последнего примера (пары) данной эпохи — (x(N), d(N)). В пакетном режиме обучения корректировка весов проводилась после подачи в сеть всех примеров обучения (всей эпохи). Для каждой эпохи функция стоимости определялась как среднеквадратическая ошибка, представленная в составной форме
|
1 |
N |
||||
|
Eav |
(n) = |
ååe 2j (n) , |
(3.37) |
||
|
2N n=1 jÎC |
где сигнал ошибки ej (n) соответствует нейрону j для примера обучения n. Ошибка ej (n) равна разности между dj(n) и уj(n) для j-гo элемента вектора желаемых откликов d(n) и соответствующего выходного нейрона сети. В выражении (3.36) внутреннее суммирование по j выполняется по всем нейронам выходного слоя сети, в то время как внешнее суммирование поп выполняется по всем образам данной эпохи. При заданном параметре скорости обученияh
корректировка, применяемая к синаптическому весу w ji связывающему нейроны i и j, определялась следующим дельта-правилом
|
¶E |
av |
h |
N |
¶e j |
(n) |
|||
|
Dw ji (n) = —h |
= — |
åe j (n) |
. |
(3.38) |
||||
|
¶w ji |
N n =1 |
¶w ji |
Согласно (3.38) в пакетном режиме корректировка веса Dwji (n) выполняется только после прохождения по сети всего множества примеров.
121
Процесс комбинирования данных режимов обучения состоял в следующем. В случае наличия избыточных данных использовался последовательный режим обучения. Его применение позволяло использовать меньший объем внутреннего хранилища для каждой синаптической связи. Более того, путем предъявления обучающих примеров в случайном порядке(в процессе последовательной корректировки весов) достигался стохастический поиск в пространстве весов. Это, в свою очередь, сокращало до минимума возможность остановки алгоритма в точках локальных минимумов. Во всех остальных случаях использовался пакетный режим обучения. Он обеспечивал более точную оценку вектора градиента при «обедненных» данных и позволял распараллелить вычисления.
Для обоснования критерия прекращения(останова) обучения рассматривались уникальные свойства локального и глобального минимумов поверхности ошибок. Обозначим символом w вектор весов, обеспечивающий минимум, будь то локальный или глобальный. Необходимым условием минимума является достижение вектора градиента g(w) (т.е. вектора частных производных первого порядка) для поверхности ошибок в точке нулевых значений. На практике это означает, что алгоритм обратного распространения ошибок сошелся, если евклидова норма вектора градиента достигла достаточно малых значений. Недостатком этого критерия сходимости является то, что для сходимости обучения может потребоваться довольно много времени. Кроме того, необходимо постоянно вычислять вектор градиентаg(w). Другим уникальным свойством минимума является то, что функция стоимости (или мера ошибки) Eav (w) в точке w = w* стабилизируется. Отсюда можно вывести еще один критерий сходимости. Критерием сходимости алгоритма обратного распространения ошибок является достаточно малая абсолютная интенсивность изменений среднеквадратической ошибки в течение эпохи. Практические результаты показали, что интенсивность изменения среднеквадратической ошибки можно считать достаточно малой, если она лежит в пределах от0,1-1 % за эпоху. В процессе функ-
ционирования алгоритма обратного распространения ошибок использовался еще один критерий сходимости. После каждой итерации обучения сеть тестировалась на эффективность обобщения. Процесс обучения останавливался, когда эффективность обобщения становилась удовлетворительной или когда оказывалось, что пик эффективности уже пройден.
Блок-схема алгоритма обратного распространения ошибок представлена на рис. 3.13. Блоки 1,10 используются для пуска и остановки алгоритма обратного
распространения ошибок.
В блоке 2 реализован ввод исходных данных, таких как:
— элементы обучающей выборки (как правило, они должны быть нормализованы);
— значения весов (начальные значения весов могут быть случайными или детерминированными);
— вектор выходных значений сигналов.
122

1
Начало
2
Ввод исходных данных
3
Определение
выходного
сигнала
4
Определение функционала квадратичной ошибки
5
Определение производных сигналов ошибок обратного распространения
6
Фиксация знака производной
8
Генерация приращений весов
|
нения знака произ- |
|||
|
водной |
|||
|
Да |
|||
|
9 |
|||
|
Вывод результатов |
|||
|
10 |
Конец |
||
Рис. 3.13. Блок-схема алгоритма обратного распространения ошибок
123
Блок 3 обеспечивает расчет выходного сигнала.
В блоке 4 рассчитывается значение среднеквадратичной ошибки.
Блок 5 реализует определение производных сложной функции (сигнала и функции активации).
В блоке 6 фиксируется значение производной.
Блок 7 обеспечивает проверку изменения знака производной. Если он не изменился, то управление передается в блок 9. В противном случае управление передается в блок 8.
Блок 9 вывод результатов. В качестве результатов выступает набор весовых коэффициентов при которых достигается значение минимума функции ошибки.
Ниже приведен фрагмент программного кода, реализующий алгоритм обратного распространения ошибок:
procedure TNSet.MTeach; var
i, //слой
j, //нейрон k:Integer; // вход xsum:Double;
begin
//формирование массива ошибок // расчет фактических ошибок нейронов выходного слоя
for j:=1 to fConfig[LayerCount-1] do Osh[LayerCount-1,j]:=(outputm[LayerCount-1,j]-
inputm[LayerCount,j])*Posh[LayerCount-1,j]; //расчет суммарной ошибки
xsum:=0;
for j:=1 to fConfig[LayerCount-1] do xsum:=xsum+Osh[LayerCount-1,j]; Sosh:=xsum/fConfig[LayerCount-1];
//расчет фактических ошибок нейронов скрытых слоев приращений весов и новых весов
//начинаем от предпоследнего (последний скрытый) до 1-го for i:=LayerCount-2 downto 1 do
for j:=1 to fConfig[i] do begin
xsum:=0;
for k:=0 to fConfig[i+1] do xsum:=xsum+Osh[i+1,j]*w[i,j,k];
Osh[i,j]:=xsum*Posh[i,j];
//Osh[i,j]:=xsum*outputm[i,j]*(1-outputm[i,j]);
//находим приращение веса и новое значение веса
124
for k:=0 to fConfig[i+1] do begin
//WT[i,j,k]:=-Osh[i+1,j]*fMiu*outputm[i,j]; WT[i,j,k]:=-Osh[i+1,j]*fTS*outputm[i,j]+fMiu*WT[i,j,k];
w[i,j,k]:=w[i,j,k]+WT[i,j,k];
end;
end;
end;
Вкачестве альтернативного метода обучения ИНС использован«Алгоритм имитации отжига», который реализует одноименный алгоритм в интересах оптимизации поиска глобального экстремума целевой функции. Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Предложенный Н. Метрополисом в 1953 г.
[55]и доработанный многочисленными последователями, он в настоящее время считается одним из немногих алгоритмов, позволяющих оперативно находить глобальный минимум функции нескольких переменных. Метод имитаций отжига основан на идее, заимствованной из статической механики. Он отражает поведение материального тела при отвердевании с применением процедуры отжига. Для получения качественного материала из расплава при отвердевании его температура должна уменьшаться постепенно, вплоть до момента полной кристаллизации. Если процесс остывания протекает слишком быстро, образуются значительные нерегулярности структуры материала, которые вызывают внутренние напряжения. В результате общее энергетическое состояние тела, зависящее от его внутренней напряженности, остается на гораздо более высоком уровне, чем при медленном охлаждении. Быстрая фиксация энергетического состояния тела на уровне выше нормального аналогична сходимости оптимизационного алгоритма к точке локального минимума. Энергия состояния тела соответствует целевой функции, а абсолютный минимум этой энергии – глобальному минимуму. В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация тела сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на ка- кое-то время возрастать (в частности, при подогреве тела для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного
повышения энергетического уровня возможен выход из ловушек локальных минимумов, которые возникают при реализации процесса. Только понижение температуры тела до абсолютного нуля делает невозможным какое-либо самостоятельное повышение его энергетического уровня. В этом случае любые внутренние изменения ведут только к уменьшению общей энергии тела.
Вреальных процессах кристаллизации твердых тел температура понижается ступенчатым образом. На каждом уровне она какое-то время поддерживается постоянной, что необходимо для обеспечения термического равновесия. На протяжении всего периода, когда температура остается выше абсолютного
125
нуля, она может как понижаться, так и повышаться. За счет удержания температуры процесса поблизости от значения, соответствующего непрерывно снижающемуся уровню термического равновесия, удаётся обходить ловушки локальных минимумов, что при достижении нулевой температуры позволяет получить и минимальный энергетический уровень [173].
Блок-схема алгоритма имитации отжига, который использовался для обучения многослойного персептрона приведен на рис. 3.14.
Блоки 1, 14 используются для пуска и остановки алгоритма.
Вблоке 2 реализован ввод исходных данных, таких как: значения входных параметров и соответствующего им отклика ИНС из обучающей или тестирующей выборок либо реальных данных.
Блок 3 обеспечивает генерацию начальных значений весов нейронных связей и температуры Tmax.
Вблоке 4 рассчитывается значение энергии в соответствии с соотноше-
нием E=(Y1 —Y1¢)2 +(Y2 —Y2¢)2 +(Y3 —Y3¢)2 +…+(Yn —Yn¢)2 .
Вблоке 5 реализована проверка условия наличия положительной температуры тела. Если данное условие выполнено, то управление передается в блок 6, в противном случае вычислительный процесс завершается и управление передается в блок 13.
Блок 6 обеспечивает генерацию значений приращений весов w’.
Вблоке 7 рассчитывается обновленное значение энергии E’.
Блок 8 предназначен для проверки условия превышения предыдущего значения энергии над текущим значением. Если данное условие выполняется, то управление передается в блок 11, в противном случае управление передается в блок 9.
В Блоке 9 реализована генерация случайных чисел в диапазоне от 0 до 1. Блок 10 предназначен для проверки условияexp(- D 2/T2)>R. Если данное
условие выполняется, то управление передается в блок11. В противном случае управление передается в блок 12.
Вблоке 11 весам присваиваются новые значения. Блок 12 обеспечивает снижение температуры.
Вблоке 13 осуществляется вывод полученных результатов– оптимальных значений весов ИНС.
Вданном алгоритме обучения реализован стохастически управляемый метод повторных рестартов. Для оценки его эффективности был проведен сравнительный анализ функционирования данного алгоритма, генетического алгоритма и алгоритма прямого перебора.
На рис. 3.15 приведена экранная форма интерфейса пользователя при исследовании данных алгоритмов обучения ИНС.
Окно имеет блочную структуру. В верхней части окна располагаются блоки заданий параметров трех алгоритмов обучения(генетического, имитации отжига и прямого перебора). Кроме того, в каждом блоке имеется окно, в котором отображается время выполнения соответствующего алгоритма обучения, а также кнопка его запуска – «Старт».
126

|
1 |
|||||
|
Начало |
|||||
|
2 |
|||||
|
Ввод исходных данных |
|||||
|
3 |
|||||
|
Генерация значений весов и началь- |
|||||
|
ной температуры T= Tmax |
|||||
|
4 |
|||||
|
Определение значения энергии: |
|||||
|
E=(Y1-Y1’)2+…+(Yn-Yn’)2 |
|||||
|
Нет |
5 |
T>0 |
|||
|
6 |
Да |
||||
|
Генерация значений |
|||||
|
приращений весов D w’ |
|||||
|
7 |
Расчет Е’ |
||||
|
8 |
Е’<Е |
Нет |
|||
|
Да |
9 |
||||
|
Генерация случайных чисел |
|||||
|
R в диапазоне [0;1]’ |
|||||
|
Да |
Да |
10 |
exp(- D 2/T2)>R |
||
|
11 |
|||||
|
Принять w=w’ |
Нет |
||||
|
12 |
|||||
|
Уменьшение температуры |
|||||
|
T=rT |
|||||
|
7 |
|||||
|
13 |
|||||
|
Вывод результатов |
14
Конец
Рис. 3.14. Блок-схема алгоритма имитации отжига
127

Рис. 3.15. Экранная форма интерфейса исследования алгоритмов обучения ИНС
В нижней левой части экранной формы находится компонент задания обучающих примеров. В нижней правой части экранной формы находится таблица, в которой отображаются значения весов нейронных связей и ошибки соответствующих ИНС. В центре экранной формы имеется окно задания параметра α. Данный параметр определяет крутизну функции активации. При
a ®¥ функция вырождается в пороговую.
При a ® 0 функция активации становится линейной функцией с пороговым значением — 0,5. При a ® 1 данная функция является плавной сигмоидальной функцией (вариант, представляющий интерес в данной работе).
В табл.3.3 и 3.4 приведены экспериментальные значения основных параметров функционирования (времени работы и значения ошибок) для трех алгоритмов обучения.
В таблице 3.3 приведены результаты работы двух алгоритмов обучения, при постоянных исходных данных. В таблице 3.4 представлены результаты функционирования алгоритма прямого перебора для 5 вариантов исходных данных:
1.Max значение веса – 1, Min значение веса – -1, Шаг – 0,2;
2.Max значение веса – 1, Min значение веса – -1, Шаг – 0,1;
3.Max значение веса – 2, Min значение веса – -2, Шаг – 0,2;
4.Max значение веса – 2, Min значение веса – -2, Шаг – 0,1;
5.Max значение веса – 3, Min значение веса – -3, Шаг – 0,2.
128
Таблица 3.3 Результаты работы генетического алгоритма и алгоритма имитации отжига
|
Критерии |
Генетический алгоритм |
|||||||||||||||||
|
Время рабо- |
||||||||||||||||||
|
ты (мсек) |
1324 |
1184 |
5471 |
2334 |
1091 |
1177 |
2330 |
1111 |
2354 |
1123 |
||||||||
|
Ошибка |
0,016 |
0,014 |
0,019 |
0,019 |
0,014 |
0,018 |
0,01 |
0,007 |
0,01 |
0,012 |
||||||||
|
Алгоритм имитации отжига |
||||||||||||||||||
|
Время рабо- |
||||||||||||||||||
|
ты (мсек) |
23 |
22 |
21 |
22 |
23 |
23 |
28 |
26 |
25 |
21 |
||||||||
|
Ошибка |
0,05 |
0,09 |
0,07 |
0,07 |
0,05 |
0,09 |
0,08 |
0,05 |
0,05 |
0,08 |
||||||||
|
Результаты работы алгоритма прямого перебора |
Таблица 3.4 |
|||||||||||||||||
|
Критерии |
Прямой перебор |
|||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
||||||||||||||
|
Время работы |
||||||||||||||||||
|
(мсек) |
1157 |
42960 |
39760 |
1673589 |
303858 |
|||||||||||||
|
Ошибка |
0,13 |
0,14 |
0,095 |
0,099 |
0,071 |
Анализ полученных результатов показывает, что алгоритм имитации отжига является наиболее оперативным, но не самым точным из рассматриваемых методов обучения. Более высокую точность показал генетический алгоритм, но он затрачивает намного больше времени на работу чем алгоритм имитации отжига. Теоретически алгоритм прямого перебора является самым точным методом поиска глобального минимума функции. Однако на практике, по причине недостаточной аппаратной мощности ПК, оказалось невозможным получить значение глобального минимума за приемлемое время.
Модуль «Генетический алгоритм» реализует случайный поиск экстремума функции для нескольких аргументов. Он представляет собой симбиоз переборного и градиентного методов. Его основу составляет естественный отборглавный механизм эволюции [25, 29, 57]. В нем реализуются генетические коды индивидуумов – ДНК (дезоксирибонуклеиновая кислота), приспособленность индивидуумов, хромосомы, скрещивание, мутации и др. Детальное описание генетического алгоритма приведено в разделе 2.5.
Большое значение для обучения ИНС имеет ее архитектура. Рассмотрим последовательность процесса обучения сети в плоскости поиска ее оптимальной архитектуры. Обучение ведется путем минимизации целевой функцииE(w), определяемой только на обучающем подмножестве L. При этом значение целевой функции определяется как
|
p |
|
|
E(w) = åE( yk (w),dk ) , |
(3.39) |
|
k =1 |
где р — количество обучающих пар(хk, dk), yk — вектор реакции сети на возбуждение хk.
129
Минимизация функции (3.39) обеспечивает достаточное соответствие выходных сигналов сети ожидаемым значениям из обучающих выборок.
Цель обучения состоит в таком подборе архитектуры и параметров сети, которые обеспечат минимальную погрешность распознавания тестового подмножества данных, не участвовавших в обучении. Эту погрешность будем называть погрешностью обобщения EG(w). Co статистической точки зрения погрешность обобщения зависит от уровня погрешности обученияEL(w) и от доверительного интервала e . Она характеризуется неравенством:
|
EG (w) =£ EL |
(w) + e( |
p |
, EL ) . |
(3.40) |
|
h |
Установлено [177], что значение e функционально зависит от уровня погрешности обучения EL(w) и от отношения количества обучающих выборок р к фактическому значению h параметра, называемого мерой ВапникаЧервоненкиса (МВЧ) и обозначаемого VCd. Данная мера отражает уровень сложности нейронной сети и тесно связана с количеством содержащихся в ней весов. Значение e уменьшается по мере возрастания отношения количества обучающих выборок к уровню сложности сети. Значение МВЧ функционально зависит от количества синаптических весов, связывающих нейроны между собой. Чем больше количество различных весов, тем больше сложность сети и соответственно значение меры VCd. Верхняя и нижняя границы МВЧ определяются в соответствии с неравенством:
|
é K ù |
|||||
|
2ê |
úN £ VCd |
£ 2N w (1 + lg Nn ) , |
(3.41) |
||
|
2 |
|||||
|
ë |
û |
где [ ] — целая часть числа, N — размерность входного вектора, К-количество нейронов скрытого слоя, Nw — общее количество весов сети, a Nn —общее количество нейронов сети.
Из выражения (3.41) следует, что нижняя граница диапазона приблизительно равна количеству весов, связывающих входной и скрытый слои, тогда как верхняя граница превышает двукратное суммарное количество всех весов сети. В связи с невозможностью точного определения меры VCd в качестве ее приближенного значения используется общее количество весов нейронной сети [174].
Таким образом, на погрешность обобщения оказывает влияние отношение числа обучающих выборок к количеству весов сети. Небольшой объем обучающего подмножества при фиксированном количестве весов вызывает хорошую адаптацию сети к его элементам, однако не усиливает способности к обобщению, так как в процессе обучения наблюдается относительное превышение числа подбираемых параметров(весов) над количеством пар фактических и ожидаемых выходных сигналов сети. Эти параметры адаптируются с чрезмерной (а вследствие превышения числа параметров над объемом обучающего множества — и неконтролируемой) точностью к значениям конкретных выборок, а не к диапазонам, которые эти выборки должны представлять. Фактически задача аппроксимации подменяется в этом случае задачей приближен-
130
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:

Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:

Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:

Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:

Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:

Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:

Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:

Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:

Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:

Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:

Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:

Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
