
9.1.Суть и причины автокорреляции
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений εi от значений отклонений во всех других наблюдениях (см. параграф 5.1). Отсутствие зависимости гарантирует отсутствие коррелированности между любыми отклонениями (σ(εi, εj) = cov(εi, εj) = 0 при i ≠ j) и, в частности, между соседними отклонениями (σ(εi−1, εi) = 0), i = 2, 3, …, n.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные данные). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов. При использовании перекрестных данных наличие автокорреляции (пространственной корреляции) крайне редко. В силу этого в дальнейших выкладках вместо символа i порядкового номера наблюдения будем использовать символ t, отражающий момент наблюдения. Объем выборки при этом будем обозначать символом T вместо n. В экономических задачах значительно чаще встречается так называемая
положительная автокорреляция (σ(εt−1, εt) > 0), нежели отрицательная автокорреляция (σ(εt−1, εt) < 0).
Чаще всего положительная автокорреляция вызывается направленным постоянным воздействием некоторых не учтенных в модели факторов. Суть автокорреляции поясним следующим примером. Пусть исследуется спрос Y на прохладительные напитки от дохода Х по ежемесячным данным. Трендовая зависимость, отражающая увеличение спроса с ростом дохода, может быть представлена линейной функцией Y= β0 + β1X, изображенной на рис. 9.1.
Лето
Зима
Зима
 X
X
Рис. 9.1
227

Однако фактические точки наблюдений обычно будут превышать трендовую линию в летние периоды и будут ниже ее в зимние.
Аналогичная картина может иметь место в макроэкономическом анализе с учетом циклов деловой активности.
Отрицательная автокорреляция фактически означает, что за положительным отклонением имеет место отрицательное и наоборот. Возможная схема рассеивания точек в этом случае представлена на
рис. 9.2.
Y 
 X Рис. 9.2
X Рис. 9.2
Такая ситуация может иметь место, например, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима − лето).
Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных.
Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции.
Проиллюстрируем это следующим примером. Анализируется зависимость предельных издержек МС от объема выпуска Q. Если для ее описания вместо реальной квадратичной модели MC = β0 + β1Q + + β2Q2 + ε выбрать линейную модель MC = β0 + β1Q + ε, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции.
228

MC = β0 + β1Q
Q
Рис. 9.3
Инерция. Многие экономические показатели (например, инфляция, безработица, ВНП и т. п.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Действительно, экономический подъем приводит к росту занятости, сокращению инфляции, увеличению ВНП и т. д. Этот рост продолжается до тех пор, пока изменение конъюнктуры рынка и ряда экономических характеристик не приведет к замедлению роста, затем остановке и движению вспять рассматриваемых показателей. В любом случае эта трансформация происходит не мгновенно, а обладает определенной инертностью.
Эффект паутины. Во многих сферах экономики экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом). Например, предложение сельскохозяйственной продукции реагирует на изменение цены с запаздыванием (равным периоду созревания урожая). Большая цена сельскохозяйственной продукции в прошлом году вызовет (скорее всего) ее перепроизводство в текущем году, а следовательно, цена на нее снизится и т. д. В этой ситуации нельзя предполагать случайность отклонений друг от друга.
Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его подынтервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что, в свою очередь, может послужить причиной автокорреляции.
229
9.2. Последствия автокорреляции
Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяются следующие.
1.Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок
(BLUE-оценок).
2.Дисперсии оценок являются смещенными. Зачастую дисперсии, вычисляемые по стандартным формулам, являются заниженными, что приводит к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться.
|
3. Оценка дисперсии регрессии S |
2 |
= ∑ |
e2t |
является смещенной |
|
n − m −1 |
оценкой истинного значения σ2 , во многих случаях занижая его.
4. В силу вышесказанного выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.
9.3.Обнаружение автокорреляции
Всилу неизвестности значений параметров уравнения регрессии
неизвестными будут также и истинные значения отклонений εt. Поэтому выводы об их независимости осуществляются на основе оце-
нок еt, полученных из эмпирического уравнения регрессии. Рассмотрим возможные методы определения автокорреляции.
9.3.1. Графический метод
Существует несколько вариантов графического определения автокорреляции. Один из них, увязывающий отклонения еt с моментами t их получения (их порядковыми номерами i), приведен на рис. 9.4. Это так называемые последовательно-временные графики. В этом случае по оси абсцисс обычно откладываются либо момент получения статистических данных, либо порядковый номер наблюдения, а по оси ординат отклонения εt (либо оценки отклонений еt).
Естественно предположить, что на рис. 9.4, а − г имеются определенные связи между отклонениями, т. е. автокорреляция имеет ме-
230
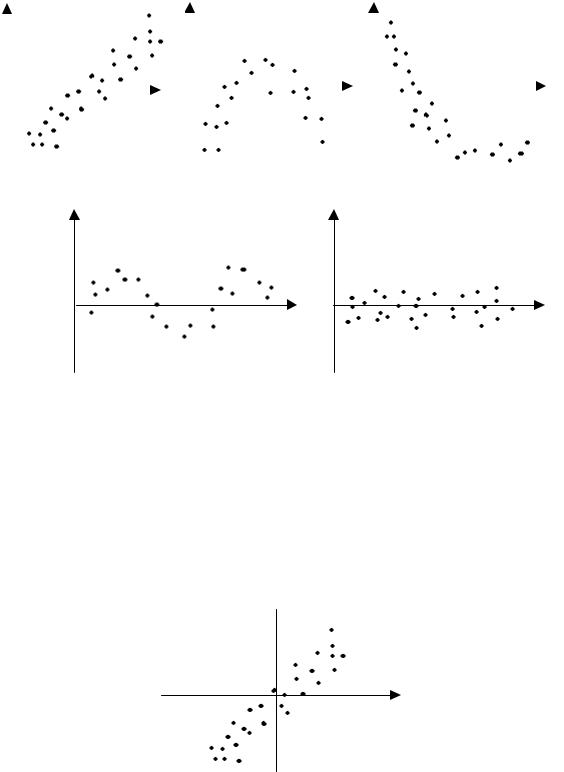
сто. Отсутствие зависимости на рис. 9.4, д, скорее всего, свидетельствует об отсутствии автокорреляции.
|
t(i) |
t(i) |
||||||
|
t(i) |
|||||||
|
а |
б |
в |
|||||
|
εt, et |
εt, et |
Рис. 9.4
Например, на рис. 9.4, б отклонения вначале в основном отрицательные, затем положительные, потом снова отрицательные. Это свидетельствует о наличии между отклонениями определенной зависимости. Более того, можно утверждать, что в этом случае имеет место положительная автокорреляция остатков. Она становится весьма наглядной, если график 9.4, б дополнить графиком зависимости еt от еt−1 , который в этом случае ориентировочно будет выглядеть так.
еt 
еt−1
Рис. 9.5
231
Подавляющее большинство точек на этом графике расположено в I и III четвертях декартовой системы координат, подтверждая положительную зависимость между соседними отклонениями.
Следует сказать, что в современных эконометрических пакетах аналитическое выражение регрессии дополняется графическим представлением результатов. На график реальных колебаний зависимой переменной накладывается график колебаний переменной по уравнению регрессии. Сопоставив эти два графика, можно выдвинуть гипотезу о наличии автокорреляции остатков. Если эти графики пересекаются редко, то можно предположить наличие положительной автокорреляции остатков.
9.3.2. Метод рядов
Этот метод достаточно прост: последовательно определяются знаки отклонений et. Например,
(− − − − −)(+ + + + + + +)(− − −)(+ + + +)(−), т. е. 5 “−“, 7 “+”, 3 “−”, 4 “+”, 1 “−” при 20 наблюдениях.
Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.
Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция. Для более детального анализа предлагается следующая процедура. Пусть
n − объем выборки;
n1 − общее количество знаков “+” при n наблюдениях (количество положительных отклонений et);
n2 − общее количество знаков “−” при n наблюдениях (количество отрицательных отклонений et);
k − количество рядов.
При достаточно большом количестве наблюдений (n1 > 10, n2 > 10) и отсутствии автокорреляции СВ k имеет асимптотически нормальное распределение с
|
M(k) = |
2n1n2 |
+ 1; |
D(k) = |
2n1n2 (2n1n2 − n1 − n2 ) |
. |
|
n1 + n2 |
(n1 + n2 )2 (n1 + n2 − 1) |
Тогда, если M(k) − uα/2 D(k) < k < M(k) + uα/2 D(k), то гипотеза об от-
сутствии автокорреляции не отклоняется.
232
При небольшом числе наблюдений (n1 < 20, n2 < 20) Свед и Эйзенхарт разработали таблицы критических значений количества рядов при n наблюдениях (приложение 7). Суть таблиц в следующем.
На пересечении строки n1 и столбца n2 определяются нижнее k1 и верхнее k2 значения при уровне значимости α = 0.05.
Если k1 < k < k2 , то говорят об отсутствии автокорреляции.
Если k ≤ k1, то говорят о положительной автокорреляции остат-
ков.
Если k ≥ k2 , то говорят об отрицательной автокорреляция остат-
ков.
В нашем примере n = 20, n1 = 11, n2 = 9, k = 5. По таблицам (приложение 7) определяем k1 = 6, k2 = 16. Поскольку k = 5 < 6 = k1 , то принимается предположение о наличии положительной автокорреляции при уровне значимости α = 0.05.
9.3.3. Критерий Дарбина–Уотсона
Наиболее известным критерием обнаружения автокорреляции первого порядка является критерий Дарбина–Уотсона. Статистика DW Дарбина–Уотсона приводится во всех эконометрических пакетах как важнейшая характеристика качества регрессионной модели. Метод определения автокорреляции на основе статистики DW подробно рассмотрен в параграфе 6.7. Суть его состоит в вычислении статистики DW Дарбина–Уотсона и на основе ее величины − осуществлении выводов об автокорреляции.
|
T |
− et −1)2 |
|||
|
∑( et |
||||
|
DW = |
t=2 |
. |
(9.1) |
|
|
T |
||||
|
∑e2t |
||||
|
t=1 |
Согласно формуле (6.46) статистика Дарбина–Уотсона тесно связана с выборочным коэффициентом корреляции retet−1 :
|
DW ≈ 2(1 − ret et−1 ). |
(9.2) |
Таким образом, 0 ≤ DW ≤ 4 и его значения могут указать на наличие либо отсутствие автокорреляции. Действительно, если ret et−1 ≈ 0
|
(автокорреляция отсутствует), то DW ≈ 2. Если |
ret et−1 ≈ 1 (положи- |
|
тельная автокорреляция), то DW ≈ 0. Если ret et−1 |
≈ −1 (отрицательная |
|
автокорреляция), то DW ≈ 4. |
|
|
233 |
Для более точного определения, какое значение DW свидетельствует об отсутствии автокорреляции, а какое об ее наличии, была построена таблица критических точек распределения Дарбина–Уотсона. По ней для заданного уровня значимости α, числа наблюдений n и количества объясняющих переменных m определяются два значения: dl − нижняя граница и du − верхняя граница.
Общая схема критерия Дарбина–Уотсона будет следующей:
1. По построенному эмпирическому уравнению регрессии
yt = b0 + b1xt1 + … + bm xtm определяются значения отклонений еt = уt − yt для каждого наблюдения t, t = 1, 2, …, T.
2.По формуле (9.1) рассчитывается статистика DW.
3.По таблице критических точек Дарбина–Уотсона определяются
два числа dl и du и осуществляют выводы по следующей схеме: 0 ≤ DW < dl − существует положительная автокорреляция,
dl ≤ DW < du − вывод о наличии автокорреляции не определен, du ≤ DW < 4 − du − автокорреляция отсутствует,
4 − du ≤ DW < 4 − dl − вывод о наличии автокорреляции не определен, 4 − dl ≤ DW ≤ 4 − существует отрицательная автокорреляция.
Отметим, что при использовании критерия Дарбина–Уотсона необходимо учитывать следующие ограничения.
1.Критерий DW применяется лишь для тех моделей, которые содержат свободный член.
2.Предполагается, что случайные отклонения εt определяются по следующей итерационной схеме εt = ρεt−1 + vt, называемой авторегрессионной схемой первого порядка AR(1). Здесь vt − случайный член.
3.Статистические данные должны иметь одинаковую периодичность (т. е. не должно быть пропусков в наблюдениях).
4.Критерий Дарбина–Уотсона не применим для регрессионных моделей, содержащих в составе объясняющих переменных зависимую переменную с временным лагом в один период, т. е. для так назы-
ваемых авторегрессионных моделей вида:
|
yt = β0 + β1xt1 + … + βmxtm + γYt−1 + εt. |
(9.3) |
Причину четвертого ограничения поясним следующим примером. Пусть уравнение регрессии имеет вид:
|
yt = β0 + β1xt + γyt−1 + εt . |
(9.4) |
234

Пусть случайное отклонение εt подвержено воздействию авторегрессии первого порядка:
Тогда уравнение регрессии (9.4) можно представить в следующем виде:
|
yt = β0 + β1xt + γyt−1 +ρεt−1 + vt. |
(9.6) |
Но yt−1 зависит от εt−1, т. к. если (9.4) верно для t, то оно верно и для t − 1. Следовательно, имеется систематическая связь между одной из объясняющих переменных и одним из компонентов случайного члена. То есть не выполняется одна из основных предпосылок МНК (предпосылка 40) − объясняющие переменные не должны быть случайными (т. е. не иметь случайной составляющей). Значение любой объясняющей переменной должно быть экзогенным, полностью определенным. В противном случае оценки будут смещенными даже при больших объемах выборок.
Для авторегрессионных моделей разработаны специальные тесты обнаружения автокорреляции, в частности h-статистика Дарбина, которая определяется по формуле
|
) |
n |
||
|
h = с |
1− nD(g) |
, |
(9.7) |
где с − оценка ρ автокорреляции первого порядка (9.5), D(g) − выбо-
рочная дисперсия коэффициента при лаговой переменной yt−1 , n − число наблюдений.
При большом объеме выборки n и справедливости нулевой гипотезы H0: ρ = 0 статистика h имеет стандартизированное нормальное распределение (h N(0, 1)). Поэтому по заданному уровню значимости α определяется критическая точка uα/2 из условия Ф(uα/2) = (1 − α) / 2 и сравнивается h с uα/2. Если h > uα/2 , то нулевая гипотеза об отсутствии автокорреляции должна быть отклонена. В противном случае она не отклоняется.
Отметим, что обычно значение с рассчитывается по формуле
с = 1 − 0.5 DW, а D(g) равна квадрату стандартной ошибки Sg оценки g
коэффициента γ. Поэтому h легко вычисляется на основе данных оцененной регрессии.
Основная проблема с использованием этого теста заключается в невозможности вычисления h при n D(g) > 1.
235
9.4. Методы устранения автокорреляции
Основной причиной наличия случайного члена в модели являются несовершенные знания о причинах и взаимосвязях, определяющих то или иное значение зависимой переменной. Поэтому свойства случайных отклонений, в том числе и автокорреляция, в первую очередь зависят от выбора формулы зависимости и состава объясняющих переменных. Так как автокорреляция чаще всего вызывается неправильной спецификацией модели, то для ее устранения необходимо, прежде всего, попытаться скорректировать саму модель. Возможно, автокорреляция вызвана отсутствием в модели некоторой важной объясняющей переменной. Необходимо попытаться определить данный фактор и учесть его в уравнении регрессии (см. пример из параграфа 6.7). Также можно попробовать изменить формулу зависимости (например, линейную на лог-линейную, линейную на гиперболическую и т. д.). Однако если все разумные процедуры изменения спецификации модели, на ваш взгляд, исчерпаны, а автокорреляция имеет место, то можно предположить, что она обусловлена какими-то внутренними свойствами ряда {et}. В этом случае можно воспользоваться авторегрессионным преобразованием. В линейной регрессионной модели либо в моделях, сводящихся к линейной, наиболее целесообразным и про-
стым преобразованием является авторегрессионная схема первого по-
рядка AR(1).
Для простоты изложения AR(1) рассмотрим модель парной линейной регрессии
|
Y = β0 + β1X + ε. |
(9.8) |
|
Тогда наблюдениям t и (t−1) соответствуют формулы |
|
|
yt = β0 + β1xt + εt , |
(9.9) |
|
yt−1 = β0 + β1xt−1 + εt−1. |
(9.10) |
Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка (9.5):
εt = ρεt−1 + υt,
где υt , t = 2, 3, … , T − случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент ρ известен.
Вычтем из (9.9) соотношение (9.10), умноженное на ρ:
|
yt − ρyt−1 = β0(1 − ρ) + β1(xt − ρxt−1) + (εt − ρεt−1). |
(9.11) |
236

Положив yt* = yt − ρyt−1, xt* = xt − ρxt−1, β0* = β0(1 − ρ) и с учетом
(9.5), получим:
|
yt* = β0* + β1xt* + υt. |
(9.12) |
Так как по предположению коэффициент ρ известен, то очевидно, yt*, xt*, υt вычисляются достаточно просто. В силу того, что случайные отклонения υt удовлетворяют предпосылкам МНК, то оценки β0* и β1 будут обладать свойствами наилучших линейных несмещенных оценок.
Однако способ вычисления yt*, xt* приводит к потере первого наблюдения (если мы не обладаем предшествующим ему наблюдением). Число степеней свободы уменьшится на единицу, что при больших выборках не так существенно, но при малых выборках может привести к потере эффективности. Эта проблема обычно преодолевается с помощью поправки Прайса–Винстена:
x1 = 1− с2 x1,
(9.13)
y1 =  1− с2 y1.
1− с2 y1.
Отметим, что авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т. е. использовано для уравнения множественной регрессии.
Авторегрессионное преобразование первого порядка AR(1) может быть обобщено на преобразования более высоких порядков
AR(2), AR(3) и т. д.:
εt = ρ1εt−1 + ρ2 εt−2 + υt ,
(9.14)
εt = ρ1εt−1 + ρ2 εt−2 + ρ3 εt−3 + υt.
Однако на практике значение коэффициента ρ обычно неизвестно и его необходимо оценивать. Существует несколько методов оценивания. Приведем наиболее употребляемые.
9.4.1. Определение ρ на основе статистики Дарбина–Уотсона
Напомним, что статистика Дарбина–Уотсона тесно связана с коэффициентом корреляции между соседними отклонениями через соотношение (9.2):
DW ≈ 2(1 − ret et−1 ).
Тогда в качестве оценки коэффициента ρ может быть взят коэффициент r = ret et−1 . Из (9.2) имеем:
237
r ≈ 1 −
Этот метод оценивания весьма блюдений. В этом случае оценка r точной.
DW2 . (9.15)
неплох при большом числе напараметра ρ будет достаточно
9.4.2. Метод Кохрана–Оркатта
Другим возможным методом оценивания ρ является итеративный процесс, называемый методом Кохрана–Оркатта. Опишем данный метод на примере парной регрессии (9.8):
Y = β0 + β1X + ε
и авторегрессионной схемы (9.5) первого порядка AR(1)
εt = ρ εt−1 + υt .
1.Оценивается по МНК регрессия (9.8) и для нее определяются оцен-
ки et отклонений εt, t = 1, 2, …, n.
2.Используя схему AR(1), оценивается регрессионная зависимость
|
et = с et−1 + υt, |
(9.16) |
|
где с − оценка коэффициента ρ. |
|
|
3. На основе данной оценки строится уравнение: |
|
|
(yt − сyt −1) = б(1− с) + в(x t − сxt −1) + (еt − сеt −1) , |
(9.17) |
с помощью которого оцениваются коэффициенты α и β (в этом случае значение с известно).
4.Значения β0 = б(1 − с) и β1 = β подставляются в (9.8). Вновь вычисляются оценки et отклонений и процесс возвращается к этапу 2.
Чередование этапов осуществляется до тех пор, пока не будет достигнута требуемая точность. То есть пока разность между предыдущей и последующей оценками ρ не станет меньше любого наперед заданного числа.
9.4.3. Метод Хилдрета–Лу
По данному методу регрессия (9.11) оценивается для каждого возможного значения ρ из интервала [−1, 1] с любым шагом (например, 0.001; 0.01 и т. д.). Величина с , дающая наименьшую стандарт-
ную ошибку регрессии, принимается в качестве оценки коэффициента
238
ρ. И значения β0* и β1 оцениваются из уравнения регрессии (9.11) именно с данным значением с .
Этот итерационный метод широко используется в эконометрических пакетах.
9.4.4.Метод первых разностей
Вслучае, когда есть основания считать, что автокорреляция отклонений очень велика, можно использовать метод первых разностей.
Для временных рядов характерна положительная автокорреляция
остатков. Поэтому при высокой автокорреляции полагают ρ = 1, и, следовательно, уравнение (9.11) принимает вид:
yt − yt−1 = β1( xt − xt−1) + ( εt − εt−1 )
|
или |
(9.18) |
|
|
yt − yt−1 = β1( xt − xt−1) + υt. |
||
|
Обозначив ∆yt = yt − yt−1 , |
∆xt = xt − xt−1 , |
из (9.18) получим |
|
∆yt |
= β1∆xt + υt. |
(9.19) |
Из уравнения (9.19) по МНК оценивается коэффициент β1. Заметим, что коэффициент β0 в данном случае не определяется непосредственно. Однако из МНК известно, что β0 = y − в1x .
В случае ρ = −1, сложив (9.9) и (9.10) с учетом (9.5), можно получить следующее уравнение регрессии:
yt + yt−1 = 2β0 + β1( xt + xt−1) + υt
|
или |
(9.20) |
|||||
|
yt + yt−1 |
= в0 |
+ в1 |
xt + xt−1 |
+ хt . |
||
|
2 |
2 |
|||||
Однако метод первых разностей предполагает уж слишком сильное упрощение (ρ = ± 1). Поэтому более предпочтительными являются приведенные выше итерационные методы.
Итак, подведем итог. В силу ряда причин (ошибок спецификации, инерционности рассматриваемых зависимостей и др.) в регрессионных моделях может иметь место корреляционная зависимость между соседними случайными отклонениями. Это нарушает одну из фундаментальных предпосылок МНК. Вследствие этого оценки, полученные на основе МНК, перестают быть эффективными. Это делает ненадежными выводы по значимости коэффициентов регрессии и по качеству самого уравнения. Поэтому достаточно важным является умение определить наличие автокорреляции и устранить это нежелатель-
239
ное явление. Существует несколько методов определения автокорреляции, среди которых были выделены графический, метод рядов, критерий Дарбина–Уотсона.
При установлении автокорреляции необходимо в первую очередь проанализировать правильность спецификации модели. Если после ряда возможных усовершенствований регрессии (уточнения состава объясняющих переменных либо изменения формы зависимости) автокорреляция по-прежнему имеет место, то, возможно, это связано с внутренними свойствами ряда отклонений {εt}. В этом случае возможны определенные преобразования, устраняющие автокорреляцию. Среди них выделяется авторегрессионная схема первого порядка AR(1), которая, в принципе, может быть обобщена в AR(k), k = 2, 3, …
Для применения указанных схем необходимо оценить коэффициент корреляции между отклонениями. Это может быть сделано различными методами: на основе статистики Дарбина–Уотсона, Кохрана–Ор- катта, Хилдрета–Лу и др. В случае наличия среди объясняющих переменных лаговой зависимой переменной наличие автокорреляции устанавливается с помощью h-статистики Дарбина. А для ее устранения в этом случае предпочтителен метод Хилдрета–Лу.
Вопросы для самопроверки
1.Что такое автокорреляция?
2.Назовите основные причины автокорреляции.
3.Что может вызвать отрицательную автокорреляцию?
4.Какая предпосылка МНК нарушается при автокорреляции?
5.Каковы последствия автокорреляции?
6.Перечислите основные методы обнаружения автокорреляции.
7.Опишите схему использования статистики DW Дарбина–Уотсона.
8.Перечислите ограничения использования статистики DW Дарбина–Уотсона.
9.Какая статистика используется для обнаружения автокорреляции в авторегрессионных моделях?
10.Опишите авторегрессионную схему первого порядка AR(1).
11.В чем смысл поправки Прайса–Винстена?
12.Опишите способы определения коэффициента автокорреляции ρ в авторегрессионной схеме первого порядка AR(1).
13.Будут ли верными или ложными следующие утверждения. Ответы поясните.
а) Автокорреляция характерна в основном для временных рядов.
б) При наличии автокорреляции оценки, полученные по МНК, являются смещенными.
240
в) Статистика DW Дарбина–Уотсона не используется в авторегрессионных моделях.
г) Статистика DW Дарбина–Уотсона лежит в пределах от 0 до 4.
д) Для использования статистики DW статистические данные должны иметь одинаковую периодичность.
е) Авторегрессионная схема первого порядка AR(1) устраняет автокорреляцию только в случае, когда коэффициент автокорреляции ρ = 1.
ж) При наличии автокорреляции значение коэффициента детерминации R2 будет всегда существенно ниже единицы.
з) Автокорреляция всегда является следствием неправильной спецификации модели.
Упражнения и задачи
1.Пусть при 50 наблюдениях и трех объясняющих переменных статистика DW принимает следующие значения:
а) 0.91; б) 1.37; в) 2.34; г) 3.01; д) 3.72.
Не заглядывая в таблицу критических точек Дарбина–Уотсона, выскажите мнение о наличии автокорреляции. Проверьте свои выводы по таблице.
2.По таблице критических точек Дарбина–Уотсона для α = 0.05 и α = 0.01 определите значения статистики DW, дающие основание отклонить гипотезу о наличии автокорреляции при объеме выборки n и числе объясняющих пере-
|
менных m: а) n = 20, m = 1; |
б) n = 25, m = 2; в) n = 50, m = 1; |
|
г) n = 50, m = 4; |
д) n = 100, m = 2. |
Сравните полученные результаты, сделайте выводы.
3.Используя таблицу Сведа и Эйзенхарта (приложение 7), определите наличие автокорреляции по методу рядов (n − объем выборки, n1 − общее количество
знаков “+”, n2 − общее количество знаков “−”, k − количество рядов).
|
а) |
n |
n1 |
n2 |
k |
|
20 |
12 |
8 |
3 |
|
|
б) |
30 |
16 |
16 |
21 |
|
в) |
25 |
16 |
9 |
4 |
|
г) |
15 |
8 |
7 |
5 |
4.По статистическим данным за 20 лет построено уравнение регрессии между ценой бензина и объемом продаж бензина, для которого DW = 0.71.
а) Будет ли в данном случае иметь место автокорреляция остатков? Если да, то она положительная или отрицательная?
б) Что могло послужить причиной автокорреляции?
в) Какой критерий вы использовали для определения наличия автокорреляции?
г) Какими будут ваши рекомендации по совершенствованию модели?
5.По квартальным данным за 9 лет анализируют зависимость между экспортом (EX) и импортом (IM). Имеются следующие статистические данные:
241
|
EX |
12.47 |
12.65 |
12.89 |
12.97 |
13.00 |
13.31 |
13.25 |
12.65 14.49 |
14.47 |
14.74 |
14.62 |
||||
|
IM |
11.07 |
11.50 |
12.01 |
12.28 |
13.16 |
13.43 |
13.28 |
13.50 |
15.32 |
15.62 |
17.44 |
16.14 |
|||
|
EX |
17.60 |
17.70 |
16.60 |
15.26 |
19.49 |
19.08 |
18.69 |
18.65 |
19.33 |
19.11 |
18.62 |
18.40 |
|||
|
IM |
16.13 |
16.08 |
16.55 |
15.00 |
18.72 |
17.80 |
16.64 |
17.39 |
18.70 |
18.02 |
17.46 |
16.96 |
|||
|
EX |
16.15 |
16.58 |
17.60 |
18.48 |
15.36 |
15.25 |
15.61 |
15.93 |
14.38 |
14.30 |
14.75 |
15.58 |
|||
|
IM |
15.06 |
16.01 |
16.63 |
17.86 |
14.56 |
15.64 |
16.45 |
17.42 |
14.30 |
14.59 |
14.66 |
14.95 |
|||
а) Постройте уравнение регрессии текущего импорта на текущий экспорт. б) Проверьте качество построенной модели на основе t-статистик и коэффи-
циента детерминации R2.
в) Вычислите значение статистики DW Дарбина–Уотсона и на ее основе проанализируйте наличие автокорреляции.
г) На основе полученных результатов будет ли отклоняться гипотеза о положительной зависимости между объемами экспорта и импорта.
д) По этим же статистическим данным постройте регрессию приращения
импорта (∆IM = IMt − IMt−1) на приращение экспорта (∆EX = EXt − EXt−1). е) Каково значение статистики DW для построенного уравнения и какой вывод из этого следует.
ж) Прокомментируйте полученные результаты.
6.По квартальным данным за 35 лет построено уравнение регрессии:
|
ln(DI)t = |
6.32 + 0.0084 t; |
|
(S) = |
(3.54) (0.017) R2 = 0.9931 DW = 0.173, |
где DI − располагаемый доход, t − время. В скобках указаны стандартные ошибки.
а) Сделайте выводы о качестве построенной модели.
б) Можно ли на основе построенной модели сделать заключение о возрастании располагаемого дохода на рассматриваемом временном интервале.
в) Какими могут быть предложения по совершенствованию модели?
г) Будет ли в данном случае рациональным, с точки зрения смягчения проблемы автокорреляции, переход от абсолютных значений рассматриваемых параметров к их приростам по аналогии с предыдущей задачей?
7.По тридцати годовым данным по МНК построено уравнение регрессии:
|
− 0.81 lnxt3 |
|||||
|
lnyt = |
5.12 + 0.31 lnxt1 + 0.52 lnxt2 |
2 = 0.62 DW = 0.49, |
|||
|
(S) |
(2.1) (0.18) |
(0.21) |
(0.29) |
||
|
R |
где yt − число банкротств; xt1 − уровень безработицы; xt2 − краткосрочная процентная ставка; xt3 − объем новых заказов в момент времени t.
а) Оцените качество построенной модели.
б) Проинтерпретируйте оцененный коэффициент для lnx3t.
в) Какая нулевая гипотеза проверяется на базе статистики DW? Проверьте данную гипотезу при уровне значимости α = 0.01.
242
г) Оказывает ли существенное влияние на число банкротств краткосрочная процентная ставка?
д) Можно ли оценить коэффициент корреляции между случайными отклонениями?
8.Осуществляется анализ средних годовых расходов (Y) студентов на развлечения. По статистическим данным за 32 года по МНК построено следующее
уравнение регрессии:
)
yt = 41.2 + 0.254 xt + 0.539yt−1
|
(S) |
(0.107) (0.133) |
R2 = 0.783 DW = 1.86, |
Х − располагаемый доход студента после уплаты за обучение и общежитие.
а) Оцените качество построенной модели.
б) Постройте 95%-ный доверительный интервал для коэффициента при Х. в) Насколько вырастут расходы на развлечения при росте располагаемого дохода на единицу.
г) Проверьте гипотезу об отсутствии автокорреляции остатков при альтернативной гипотезе о положительной автокорреляции с уровнем значимости
α = 0.01.
9.Приведены статистические данные за 25 лет по темпам прироста заработной платы Y%, производительности труда Х1%, а также уровню инфляции Х2%.
Оцените по МНК уравнение регрессии Y = β0 + β1X1 + β2X2 + ε.
Оцените качество построенного уравнения, проведя при этом проверку наличия гетероскедастичности и автокорреляции.
|
Год |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
||
|
X1 |
3.5 |
2.8 |
6.3 |
4.5 |
3.1 |
1.5 |
7.6 |
6.7 |
4.2 |
2.7 |
4.5 |
3.5 |
5.0 |
||
|
X2 |
4.5 |
3.0 |
3.1 |
3.8 |
3.8 |
1.1 |
2.3 |
3.6 |
7.5 |
8.0 |
3.9 |
4.7 |
6.1 |
||
|
Y |
9.0 |
6.0 |
8.9 |
9.0 |
7.1 |
3.2 |
6.5 |
9.1 |
14.6 |
11.9 |
9.2 |
8.8 |
12.0 |
||
|
Год |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|||
|
X1 |
2.3 |
2.8 |
1.5 |
6.0 |
2.9 |
2.8 |
2.6 |
1.5 |
0.9 |
0.6 |
0.7 |
3.1 |
|||
|
X2 |
6.9 |
3.5 |
7.1 |
3.1 |
3.7 |
3.9 |
4.0 |
4.8 |
4.8 |
4.2 |
4.9 |
3.2 |
|||
|
Y |
12.5 |
6.7 |
8.5 |
5.9 |
6.8 |
5.6 |
4.8 |
4.5 |
6.7 |
5.5 |
4.0 |
3.3 |
10.Анализируется зависимость между инфляцией (INF) и безработицей (U). Используются статистические данные за 25 лет:
|
INF |
3.07 |
0.70 |
4.08 |
2.20 |
2.38 |
0.90 |
1.10 |
5.12 |
0.93 |
2.54 |
1.55 |
3.45 |
1.09 |
||||||
|
U |
3.69 |
9.10 |
3.92 |
6.50 |
4.63 |
8.50 |
9.55 |
3.71 |
5.80 |
3.60 |
6.53 |
4.32 |
9.20 |
||||||
|
INF |
2.15 |
5.14 |
1.72 |
0.74 |
4.16 |
0.93 |
1.79 |
1.24 |
1.12 |
1.28 |
7.36 |
5.30 |
|||||||
|
U |
5.75 |
3.65 |
7.30 |
9.65 |
3.65 |
9.80 |
6.28 |
7.80 |
8.75 |
7.22 |
3.60 |
3.65 |
В качестве модели рекомендуется воспользоваться следующим уравнением:
243
ln INFt = β0 + β1lnUt + εt.
а) По МНК оцените коэффициенты β0 и β1.
б) Постройте 95 %-ный доверительный интервал для коэффициента β1. в) Оцените качество построенного уравнения.
г) Вычислите статистику DW Дарбина–Уотсона и на ее основе определите наличие автокорреляции.
д) Проверьте наличие автокорреляции с помощью метода рядов.
е) Сделайте вывод о качестве интервальной оценки для коэффициента β1. ж) Переоцените модель, используя для этого авторегрессионную схему первого порядка AR(1).
з) Постройте новый 95 %-ный доверительный интервал для коэффициента β1. Сравните его с предыдущим интервалом.
и) Прокомментируйте результаты.
11. По 30-годовым наблюдениям строится функция инвестиций: it = β0 + β1yt + β2rt + εt,
где it − объем инвестиций в году t; yt − ВНП в году t; rt − процентная ставка в году t.
|
Y |
8.58 |
10.45 |
8.35 |
10.65 |
9.7 |
12.0 |
13.45 |
14.2 |
14.45 |
13.85 |
|||
|
R |
18.12 |
11.05 |
9.0 |
17.0 |
16.25 |
13.8 |
19.95 |
18.74 |
13.8 |
9.55 |
|||
|
I |
11.55 |
13.25 |
10.9 |
10.45 |
15.1 |
17.5 |
17.77 |
16.1 |
10.59 |
10.65 |
|||
|
Y |
16.55 |
18.0 |
18.4 |
20.4 |
21.0 |
23.75 |
25.75 |
24.2 |
25.2 |
26.2 |
|||
|
R |
19.3 |
15.2 |
12.4 |
16.5 |
5.95 |
17.5 |
16.43 |
7.4 |
15.45 |
19.15 |
|||
|
I |
9.32 |
11.0 |
15.05 |
15.1 |
22.7 |
21.95 |
23.1 |
25.65 |
26.15 |
25.55 |
|||
|
Y |
28.6 |
30.6 |
31.32 |
26.0 |
26.85 |
32.1 |
32.95 |
33.3 |
33.85 |
35.6 |
|||
|
R |
5.45 |
9.52 |
7.95 |
7.45 |
19.9 |
8.65 |
21.35 |
11.11 |
15.82 |
21.67 |
|||
|
I |
28.1 |
24.2 |
32.3 |
21.5 |
22.95 |
30.45 |
24.6 |
32.5 |
31.2 |
29.5 |
а) Оцените по МНК коэффициенты искомого уравнения регрессии.
б) Оцените статистическую значимость коэффициентов и общее качество уравнения регрессии.
в) Используя статистику DW Дарбина–Уотсона, оцените наличие автокорреляции остатков для построенного уравнения.
г) При наличии автокорреляции переоцените уравнение регрессии, используя для этого авторегрессионную схему первого порядка AR(1).
д) Спрогнозируйте объем инвестиций на следующий год, если прогнозируемые значения ВНП и процентной ставки составят соответственно yt+1 = 37 и
rt+1 = 15.
е) Постройте 95 %-ный доверительный интервал для среднего значения прогноза.
244
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
[c.178]
Очевидно, что несостоятельность оценки (8.20) тем больше, чем сильнее автокорреляция ошибок е. На практике, однако, часто выполняется условие р у. В этом случае предел оценки наименьших квадратов будет близок к истинному значению параметра, хотя и не равен ему.
[c.202]
Автокорреляция ошибок в моделях со стохастическими регрессорами
[c.212]
При справедливости гипотезы р = 0 распределение статистики h при увеличении объема выборки стремится к нормальному с математическим ожиданием, равным нулю, и дисперсией, равной единице. Таким образом, гипотеза об отсутствии автокорреляции ошибок отвергается, если наблюдаемое значение статистики h окажется больше, чем критическое значение стандартного нормального распределения.
[c.214]
Подставляя эти значения в (8.56), получаем Л = 2,64. Так как это значение больше критического /70,о5 = 1,96, определяемого для нормального закона, гипотеза об отсутствии автокорреляции ошибок отвергается, имеет место авторегрессия ошибок первого порядка (еще раз заметим, что для рассматриваемой модели этот вывод был априорно очевиден).
[c.214]
В моделях временных рядов неверная спецификация может служить причиной автокорреляции ошибок регрессии.
[c.252]
Учебник содержит систематическое изложение основ эконометрики и написан на основе лекций, которые авторы в течение ряда лет читали в Российской экономической школе и Высшей школе экономики. Подробно изучаются линейные регрессионные модели (метод наименьших квадратов, проверка гипотез, гетероскедастичность, автокорреляция ошибок, спецификация модели). Отдельные главы посвящены системам одновременных уравнении, методу максимального правдоподобия в моделях регрессии, моделям с дискретными и ограниченными зависимыми переменными.
[c.2]
Итак, предыдущие аргументы показывают, что уравнение с авторегрессионными членами может быть оценено при помощи МНК. Существенными тут являются два условия. 1) Устойчивость. Для уравнения (11.11) это означает /3 < 1, лучше, если значения параметров будут отстоять на некоторое расстояние от границы критической области. 2) Отсутствует автокорреляция ошибок et.
[c.269]
Авторегрессионная модель при наличии автокорреляции ошибок
[c.270]
Усложним модель (11.11), добавив в нее автокорреляцию ошибок [c.270]
Таким образом, МНК-оценка коэффициентов регрессии оказывается несостоятельной в моделях с авторегрессионными членами и автокорреляцией ошибок. Можно показать, что оценка р, полученная из остатков МНК, также не является состоятельной [c.270]
Из предыдущего следует, что, перед тем как оценивать модель с авторегрессионными членами, необходимо проверить наличие автокорреляции ошибок.
[c.271]
Тест па автокорреляцию ошибок
[c.271]
Заметим, что полученное уравнение совпадает с моделью геометрических лагов (11.8) и может быть преобразовано к виду (11.9), который является частным случаем модели (11.23), если в последнем положить / з = 0 и ввести автокорреляцию ошибок.
[c.274]
Гетероскедастичность и автокорреляция ошибок
[c.85]
Оно лежит в интервале от 0 до 4, в случае отсутствия автокорреляции ошибок приблизительно равно 2, при положительной автокорреляции смещается в меньшую сторону, при отрицательной — в большую сторону.
[c.29]
Доказать, что в случае автокорреляции ошибок 1-го порядка матрица ковариации ошибок по наблюдениям и матрица авторегрессионного преобразования имеют указанную форму.
[c.31]
Отсутствие автокорреляции ошибок, т. е. значения ошибок различных наблюдений независимы друг от друга.
[c.13]
Недостатки метода наименьших квадратов (МНК). Использование процедуры оценки, основанной на методе наименьших квадратов, предполагает обязательное удовлетворение целого ряда предпосылок, невыполнение которых может привести к значительным ошибкам 1. Случайные ошибки имеют нулевую среднюю, конечные дисперсии и ковариации 2. Каждое измерение случайной ошибки характеризуется нулевым средним, не зависящим от значений наблюдаемых переменных 3. Дисперсии каждой случайной ошибки одинаковы, их величины независимы от значений наблюдаемых переменных (гомоскедастичность) 4. Отсутствие автокорреляции ошибок, т. е. значения ошибок различных наблюдений независимы друг от друга 5. Нормальность. Случайные ошибки имеют нормальное распределение 6. Значения эндогенной переменной х свободны от ошибок измерения и имеют конечные средние значения и дисперсии.
[c.68]
Таким образом, коррелированность регрессоров и ошибок регрессии оказывается значительно более неприятным обстоятельством, чем, например, гетероскедастичность или автокорреляция. Неадекватными оказываются не только результаты тестирования гипотез, но и сами оценочные значения параметров.
[c.194]
Обратим внимание на то, что хотя с помощью обратного преобразования Койка устранена коррелированность регрессо-ров с ошибками, но автокорреляция ошибок приобретает сложную структуру, и устранение ее может оказаться практически невозможным. Так что хотя получаемые таким образом оценки оказываются состоятельными, они обладают всеми теми недостатками, о которых подробно говорилось в гл.7.
[c.204]
Можно показать, что в этом случае значение статистики Дарбина—Уотсона будет часто попадать в область принятия гипотезы об отсутствии автокорреляции и в том случае, если на самом деле эта гипотеза неверна. Это обстоятельство и делает тест Дарбина—Уотсона неприменимым и обусловливает необходимость других инструментов для обнаружения автокорреляции ошибок регрессии в моделях со стохастическими регрессорами.
[c.213]
В модели с распределенными лагами ADL (0,1) (заметим, что все рассматриваемые нами модели относились именно к этому типу) для выявления автокорреляции ошибок можно применять Н-тест Дарбина. Рассмотрим модель
[c.213]
Существенно отличающееся от двух значение статистики d Дарбина—Уотсона указывает на то, что имеется положительная автокорреляция ошибок регрессии. Одна из возможностей — попробовать идентифицировать ряд остатков как ряд модели ARMA(p, q). При этом самая простая модель AR(l) оказывается вполне адекватной [c.253]
Как видно, значение статистики d Дарбина— Уотсона очень близко к двум, так что в новой модели проблема автокорреляции ошибок регрессии отсутствует. Отсюда следует, что ее причина была в неверной спецификации модели. Стоит также обратить внимание, что коэффициент регрессии при xt уменьшился вдвое — на товары роскоши, подобные дорогому отдыху, расходы рассредоточиваются по нескольким ближайшим годам.
[c.254]
Условие E( t s) = 0, t s указывает на некоррелированность ошибок для разных наблюдений. Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда это условие не выполняется, говорят об автокорреляции ошибок (serial orrelation).
[c.40]
Для простейшего случая автокорреляции ошибок, когда E(etet+i) = р 0, типичный вид данных представлен на рис. 2.За (р>0) и рис. 2.36 (р<0).
[c.40]
Переменная ж является экзогенной, yt-i коррелирована с xt i, поэтому xt i можно взять в качестве инструмента для yt-i- Оценка, полученная по методу инструментальных переменных, будет состоятельной. Однако вследствие автокорреляции ошибок оценки дисперсий оценок коэффициентов не будут состоятельными.
[c.271]
Если порядок процесса AR(p) заранее неизвестен, то рекомендуется включать возможно большее количество лагов, чтобы устранить возможную автокорреляцию ошибок. Дело в том, что в ADF тесте предполагается, что ошибки являются белым шумом и критические значения, указанные в таблице 11.1, справедливы только при этом условии. Однако включение чрезмерного количества лагов снижает мощность теста. Чтобы определить количество лагов, которое надо включить в уравнение, можно использовать критерии выбора порядка ARMA модели, описанные ниже, или статистическую значимость дополнительной лаговой переменной. Заметим, что тест Дики-Фуллера включен во все современные эконометрйческие пакеты.
[c.281]
В изучении корреляции признаков, не связанных согласованным изменением во времени, каждый признак изменяется под влиянием многих причин, принимаемых за случайные. В рядах динамики к ним прибавляется изменение во времпш каждого ряда. Это изменение приводит к так называемой автокорреляции — влиянию изменений уровней предыдущих рядов на последующие. Поэтому корреляция между уровнями динамических рядов правильно показывает тесноту связи между явлениями, отражаемыми в рядах динамики, лишь в том случае, если в каждом из них отсутствует автокорреляция. Кроме того, автокорреляция приводит к искажению величины среднеквадратических ошибок коэффициентов регрессии, что затрудняет построение доверительных интервалов для коэффициентов регрессии, а также проверки их значимости.
[c.70]
Cochrane-Orcutt assumes that the autocorrelation in your error term is due to the error term following an AR process. If this is your assumption, then just complete the estimation with the additional second-stage regression (with intercept) of $y_{t} — y_{t-1}rho$ against $x_{t} — x_{t-1}rho$ , where $rho$ is the estimated coefficient in the AR of residuals (i.e. first-order autocorr in residuals of the first regression). For more info look here . This source is exhaustive enough.
However notice that the assumption of AR structure on residuals of the first regression may be very restrictive and maybe not the case of your data. So for a more general idea of how to solve the problem, you should likely use a ARIMAX model, where the regression allows for a more general ARIMA Error term (if error terms are linearly autocorrelated) or a regression with Garch Error term (if their squares are autocorrelated). For the first look here and here for the second look here. If you find it useful for clarifications also see this.
Clearly this will give you more flexibility in the choice of the assumed structure of dependencies between residuals. You should choose between the 3 (or more) alternatives by following the typical model specification rules: in this case, you have to choose the residual structure that most closely resembles the actual distribution of your first-stage regression residuals (i.e., to be more precise and statistically correct, the one that best removes the dependencies in the standardized innovations in your final MLE model if you use ARIMAX or GARCH regression).
Cochrane-Orcutt assumes that the autocorrelation in your error term is due to the error term following an AR process. If this is your assumption, then just complete the estimation with the additional second-stage regression (with intercept) of $y_{t} — y_{t-1}rho$ against $x_{t} — x_{t-1}rho$ , where $rho$ is the estimated coefficient in the AR of residuals (i.e. first-order autocorr in residuals of the first regression). For more info look here . This source is exhaustive enough.
However notice that the assumption of AR structure on residuals of the first regression may be very restrictive and maybe not the case of your data. So for a more general idea of how to solve the problem, you should likely use a ARIMAX model, where the regression allows for a more general ARIMA Error term (if error terms are linearly autocorrelated) or a regression with Garch Error term (if their squares are autocorrelated). For the first look here and here for the second look here. If you find it useful for clarifications also see this.
Clearly this will give you more flexibility in the choice of the assumed structure of dependencies between residuals. You should choose between the 3 (or more) alternatives by following the typical model specification rules: in this case, you have to choose the residual structure that most closely resembles the actual distribution of your first-stage regression residuals (i.e., to be more precise and statistically correct, the one that best removes the dependencies in the standardized innovations in your final MLE model if you use ARIMAX or GARCH regression).
Если
матрица
ковариаций
ошибок
не
является
диагональной,
то
говорят
об
ав-
токорреляции
ошибок.
Обычно
при
этом
предполагают,
что
наблюдения
однород-
ны
по
дисперсии,
и
их
последовательность
имеет
определенный
смысл
и
жестко
фиксирована.
Как
правило,
такая
ситуация
имеет
место,
если
наблюдения
про-
водятся
в
последовательные
моменты
времени.
В
этом
случае
можно
говорить
о
зависимостях
ошибок
по
наблюдениям,
отстоящим
друг
от
друга
на
1,
2,
3
и
т.д.
момента
времени.
Обычно
рассматривается
частный
случай
автокорреляции,
когда
коэффициенты
ковариации
ошибок
зависят
только
от
расстояния
во
времени
меж-
ду
наблюдениями;
тогда
возникает
матрица
ковариаций,
в
которой
все
элементы
каждой
диагонали
(не
только
главной)
одинаковы1.
Поскольку
действие
причин,
обуславливающих
возникновение
ошибок,
доста-
точно
устойчиво
во
времени,
автокорреляции
ошибок,
как
правило,
положительны.
Это
ведет
к
тому,
что
значения
остаточной
дисперсии,
полученные
по
стандартным
(«штатным»)
формулам,
оказываются
ниже
их
действительных
значений.
Что,
как
отмечалось
и
в
предыдущем
пункте,
чревато
ошибочными
выводами
о
качестве
получаемых
моделей.
Это
утверждение
иллюстрируется
рисунком
8.4
(n
=
1).
На
этом
рисунке:
a
—
линия
истинной
регрессии.
Если
в
первый
момент
времени
истинная
ошибка
отрицательна,
то
в
силу
положительной
автокорреляции
ошибок
все
облако
наблю-
дений
сместится
вниз,
и
линия
оцененной
регрессии
займет
положение
b.
Если
в
первый
момент
времени
истинная
ошибка
положительна,
то
по
тем
же
причи-
нам
линия
оцененной
регрессии
сместится
вверх
и
займет
положение
c.
Поскольку
![]()
1
В
теории
временных
рядов
это
называется
слабой
стационарностью.
x c
a
b
время
Рис.
8.4

266 Глава
8.
Нарушение
гипотез
основной
линейной
модели
ошибки
случайны
и
в
первый
момент
времени
они
примерно
с
равной
вероятно-
стью
могут
оказаться
положительными
или
отрицательными,
то
становится
ясно,
насколько
увеличивается
разброс
оценок
регрессии
вокруг
истинных
по
сравнению
с
ситуацией
без
(положительной)
автокорреляции
ошибок.
Типичный
случай
автокорреляции
ошибок,
рассматриваемый
в
классической
эконометрии,
—
это
линейная
авторегрессия
ошибок
первого
порядка
AR(1):
εi
=
ρεi−1
+
ηi,
где
η
—
остатки,
удовлетворяющие
обычным
гипотезам;
ρ
—
коэффициент
авторегрессии
первого
порядка.
Коэффициент
ρ
вляется
также
коэффициентом
автокорреляции
(первого
по-
рядка).
Действительно,
по
определению,
коэффициент
авторегрессии
равен
(как
МНК-
оценка):
cov(εi
,
εi−1)
ρ
= var(ε
,
i−1)
но,
в
силу
гомоскедастичности,
var(εi−1)
=
,var(εi)var(εi−1)
и,
следовательно,![]()
ρ,
также
по
определению,
является
коэффициентом
автокорреляции.
Если
ρ
=
0,
то
εi
=
ηi
и
получаем
«штатную»
ситуацию.
Таким
образом,
проверку
того,
что
автокорреляция
отсутствует,
можно
проводить
как
проверку
нулевой
гипотезы
H0:
ρ
=
0
для
процесса
авторегрессии
1-го
порядка
в
ошибках.
Для
проверки
этой
гипотезы
можно
использовать
критерий
Дарбина—
Уотсона
или
DW—критерий.
Проверяется
нулевая
гипотеза
о
том,
что
автокорре-
ляция
ошибок
первого
порядка
отсутствует.
(При
автокорреляции
второго
и
более
высоких
порядков
его
мощность
может
быть
мала,
и
применение
данного
критерия
становится
ненадежным.)
Пусть
была
оценена
модель
регрессии
и
найдены
остатки
ei,
i
=
1,
.
.
.
,
N
.
Значение
статистики
Дарбина—Уотсона
(отношения
фон
Неймана),
или
DW-ста-
тистики,
рассчитывается
следующим
образом:
N
2
(ei
−
ei−1)
dc
=
i=2![]()
N
e
2
i
. (8.3)
i=1
Оно
лежит
в
интервале
от
0
до
4,
в
случае
отсутствия
автокорреляции
ошибок
приблизительно
равно
2,
при
положительной
автокорреляции
смещается
в
мень-
8.3.
Автокорреляция
ошибок 267

0 2
dL dU
4-dU
4
4-dL
Рис.
8.5
шую
сторону,
при
отрицательной
—
в
большую
сторону.
Эти
факты
подтвержда-
ются
тем,
что
при
больших
N
справедливо
следующее
соотношение:
dc
≈
2(1
−
r), (8.4)
где
r
—
оценка
коэффициента
авторегрессии.
Минимального
значения
величина
dc
достигает,
если
коэффициент
авторегрессии
равен
+1.
В
этом
случае
ei
=
e,
i
=
1,
.
.
.
,
N
,
и
dc
=
0.
Если
коэффициент
авторегрессии
равен
−1
и
ei
=
(−1)ie,
i
=
1,
.
.
.
,
N
,
то
величина
dc
достигает
значения
4
N
−
1![]()
N
(можно
достичь
и
более
высокого
значения
подбором
остатков),
которое
с
ростом
N
стремится
к
4.
Формула
(8.4)
следует
непосредственно
из
(8.3)
после
элементарных
преобразований:
N N
e
2
i
ei−1ei
N
e
2
i−1
dc
=
i=2
−
2
i=2 +
i=2 ,
N
e
2
i
i=1
N
e
2
i
i=1
N
e
2
i
i=1
поскольку
первое
и
третье
слагаемые
при
больших
N
близки
к
единице,
а
второе
слагаемое
является
оценкой
коэффициента
автокорреляции
(умноженной
на
−2).
Известно
распределение
величины
d,
если
ρ
=
0
(это
распределение
близко
к
нормальному),
но
параметры
этого
распределения
зависят
не
только
от
N
и
n,
как
для
t—
и
F
-статистик
при
нулевых
гипотезах.
Положение
«колокола»
функции
плотности
распределения
этой
величины
зависит
от
характера
Z
.
Тем
не
менее,
Дарбин
и
Уотсон
показали,
что
это
положение
имеет
две
крайние
позиции
(рис.
8.5).
Поэтому
существует
по
два
значения
для
каждого
(двустороннего)
квантиля,
соответствующего
определенным
N
и
n:
его
нижняя
dL
и
верхняя
dU
границы.
Нулевая
гипотеза
H0:
ρ
=
0
принимается,
если
dU
™
dc
™
4
−
dU
;
она
отвергается
в
пользу
гипотезы
о
положительной
автокорреляции,
если
dc
<
dL
,
и
в
пользу
268
Глава
8.
Нарушение
гипотез
основной
линейной
модели
гипотезы
об
отрицательной
автокорреляции,
если
dc
>
4
−
dL
.
Если
dL
™
dc
<
dU
или
4−dU
<
dc
™
4−dL
,
вопрос
остается
открытым
(это
—
зона
неопределенности
DW-критерия).
Пусть
нулевая
гипотеза
отвергнута.
Тогда
необходимо
дать
оценку
матрицы
Ω.
Оценка
r
параметра
авторегрессии
ρ
может
определяться
из
приближенного
равенства,
следующего
из
(8.4):
dc
r
≈
1
−
2
,![]()
или
рассчитываться
непосредственно
из
регрессии
e
на
него
самого
со
сдвигом
на
одно
наблюдение
с
принятием
«круговой»
гипотезы,
которая
заключается
в
том,
что
eN
+1
=
e1.
Оценкой
матрицы
Ω
является
2
1 r r
··· r
N
−1
r 1 r ··· rN
−2
1
r
2
1
−
r2
r 1 ··· r
−
N
3
,
.
..
...
...
.
.
.
..
.
rN
−1 rN
−2 rN
−3 ··· 1
а
матрица
D
преобразований
в
пространстве
наблюдений
равна
√
1
−
r2 0 0 ··· 0
−r 1 0 ··· 0
0 −r 1 ··· 0
.
.
...
.
.
. ..
...
.
.
.
0 0 0 ··· 1
Для
преобразования
в
пространстве
наблюдений,
называемом
в
данном
слу-
чае
авторегрессионным,
используют
обычно
указанную
матрицу
без
1-й
строки,
что
ведет
к
сокращению
количества
наблюдений
на
одно.
В
результате
такого
пре-
образования
из
каждого
наблюдения,
начиная
со
2-го,
вычитается
предыдущее,
умноженное
на
r,
теоретическими
остатками
становятся
η
,
которые,
по
предпо-
ложению,
удовлетворяют
гипотезе
g4.
8.3.
Автокорреляция
ошибок 269
После
этого
преобразования
снова
оцениваются
параметры
регрессии.
Если
новое
значение
DW-статистики
неудовлетворительно,
то
можно
провести
следую-
щее
авторегрессионное
преобразование.
Обобщает
процедуру
последовательных
авторегрессионных
преобразований
метод
Кочрена—Оркатта,
который
заключается
в
следующем.
Для
одновременной
оценки
r,
a
и
b
используется
критерий
ОМНК
(в
обозна-
чениях
исходной
формы
уравнения
регрессии):
1
N
i
− i−1
− i
− i−1 − −
((x rx ) (z rz )a (1 r)b)2

→
min,
N
i=2
где
zi
—
n-вектор-строка
значений
независимых
факторов
в
i-м
наблюдении
(i-строка
матрицы
Z
).
Поскольку
производные
функционала
по
искомым
величинам
нелинейны
от-
носительно
них,
применяется
итеративная
процедура,
на
каждом
шаге
которой
сначала
оцениваются
a
и
b
при
фиксированном
значении
r
предыдущего
шага
(на
первом
шаге
обычно
r
=
0),
а
затем
—
r
при
полученных
значениях
a
и
b.
Процесс,
как
правило,
сходится.
Как
и
в
случае
гетероскедастичности,
можно
не
использовать
модифицированные
методы
оценивания
(тем
более,
что
точный
вид
автокорреляции
может
быть
неиз-
вестен),
а
использовать
обычный
МНК
и
скорректировать
оценку
ковариационной
матрицы
параметров.
Наиболее
часто
используемая
оценка
Ньюи—Уэста
(устой-
чивая
к
гетероскедастичности
и
автокорреляции)
имеет
следующий
вид:
(ZrZ)−1
Q
(ZrZ)−1
,
где
N L N
Q
=
e2
+
λk
eiei
k
(z
zr
+
zi
k
zr),
i
i=1
k=1
i=k+1
− i
i−k −
i
а
λk
—
понижающие
коэффициенты,
которые
Ньюи
и
Уэст
предложили
рассчи-
k .
При
k
>
L
понижающие
коэффициенты
тывать
по
формуле
λk
=
1
−
L
+1
![]()
становятся
равными
нулю,
т.е.
более
дальние
корреляции
не
учитываются
Обоснование
этой
оценки
достаточно
сложно2.
Заметим
только,
что
если
заменить
попарные
произведения
остатков
соответствующими
ковариациями
и
убрать
пони-
жающие
коэффициенты,
то
получится
формула
ковариационной
матрицы
оценок
МНК.
Приведенная
оценка
зависит
от
выбора
параметра
отсечения
L.
В
настоящее
вре-
мя
не
существует
простых
теоретически
обоснованных
методов
для
такого
выбора.
На
практике
можно
ориентироваться
на
грубое
правило
L
=
.
4
T
100
2/9
.
.
![]()
2
Оно
связано
с
оценкой
спектральной
плотности
для
многомерного
временного
ряда.
270 Глава
8.
Нарушение
гипотез
основной
линейной
модели
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Cochrane-Orcutt assumes that the autocorrelation in your error term is due to the error term following an AR process. If this is your assumption, then just complete the estimation with the additional second-stage regression (with intercept) of $y_{t} — y_{t-1}rho$ against $x_{t} — x_{t-1}rho$ , where $rho$ is the estimated coefficient in the AR of residuals (i.e. first-order autocorr in residuals of the first regression). For more info look here . This source is exhaustive enough.
However notice that the assumption of AR structure on residuals of the first regression may be very restrictive and maybe not the case of your data. So for a more general idea of how to solve the problem, you should likely use a ARIMAX model, where the regression allows for a more general ARIMA Error term (if error terms are linearly autocorrelated) or a regression with Garch Error term (if their squares are autocorrelated). For the first look here and here for the second look here. If you find it useful for clarifications also see this.
Clearly this will give you more flexibility in the choice of the assumed structure of dependencies between residuals. You should choose between the 3 (or more) alternatives by following the typical model specification rules: in this case, you have to choose the residual structure that most closely resembles the actual distribution of your first-stage regression residuals (i.e., to be more precise and statistically correct, the one that best removes the dependencies in the standardized innovations in your final MLE model if you use ARIMAX or GARCH regression).
Очевидно, что несостоятельность оценки (8.20) тем больше, чем сильнее автокорреляция ошибок е. На практике, однако, часто выполняется условие р у. В этом случае предел оценки наименьших квадратов будет близок к истинному значению параметра, хотя и не равен ему. [c.202]
Автокорреляция ошибок в моделях со стохастическими регрессорами [c.212]
При справедливости гипотезы р = 0 распределение статистики h при увеличении объема выборки стремится к нормальному с математическим ожиданием, равным нулю, и дисперсией, равной единице. Таким образом, гипотеза об отсутствии автокорреляции ошибок отвергается, если наблюдаемое значение статистики h окажется больше, чем критическое значение стандартного нормального распределения. [c.214]
Подставляя эти значения в (8.56), получаем Л = 2,64. Так как это значение больше критического /70,о5 = 1,96, определяемого для нормального закона, гипотеза об отсутствии автокорреляции ошибок отвергается, имеет место авторегрессия ошибок первого порядка (еще раз заметим, что для рассматриваемой модели этот вывод был априорно очевиден). [c.214]
В моделях временных рядов неверная спецификация может служить причиной автокорреляции ошибок регрессии. [c.252]
Учебник содержит систематическое изложение основ эконометрики и написан на основе лекций, которые авторы в течение ряда лет читали в Российской экономической школе и Высшей школе экономики. Подробно изучаются линейные регрессионные модели (метод наименьших квадратов, проверка гипотез, гетероскедастичность, автокорреляция ошибок, спецификация модели). Отдельные главы посвящены системам одновременных уравнении, методу максимального правдоподобия в моделях регрессии, моделям с дискретными и ограниченными зависимыми переменными. [c.2]
Итак, предыдущие аргументы показывают, что уравнение с авторегрессионными членами может быть оценено при помощи МНК. Существенными тут являются два условия. 1) Устойчивость. Для уравнения (11.11) это означает /3 < 1, лучше, если значения параметров будут отстоять на некоторое расстояние от границы критической области. 2) Отсутствует автокорреляция ошибок et. [c.269]
Авторегрессионная модель при наличии автокорреляции ошибок [c.270]
Усложним модель (11.11), добавив в нее автокорреляцию ошибок [c.270]
Таким образом, МНК-оценка коэффициентов регрессии оказывается несостоятельной в моделях с авторегрессионными членами и автокорреляцией ошибок. Можно показать, что оценка р, полученная из остатков МНК, также не является состоятельной [c.270]
Из предыдущего следует, что, перед тем как оценивать модель с авторегрессионными членами, необходимо проверить наличие автокорреляции ошибок. [c.271]
Тест па автокорреляцию ошибок [c.271]
Заметим, что полученное уравнение совпадает с моделью геометрических лагов (11.8) и может быть преобразовано к виду (11.9), который является частным случаем модели (11.23), если в последнем положить / з = 0 и ввести автокорреляцию ошибок. [c.274]
Гетероскедастичность и автокорреляция ошибок [c.85]
Оно лежит в интервале от 0 до 4, в случае отсутствия автокорреляции ошибок приблизительно равно 2, при положительной автокорреляции смещается в меньшую сторону, при отрицательной — в большую сторону. [c.29]
Доказать, что в случае автокорреляции ошибок 1-го порядка матрица ковариации ошибок по наблюдениям и матрица авторегрессионного преобразования имеют указанную форму. [c.31]
Отсутствие автокорреляции ошибок, т. е. значения ошибок различных наблюдений независимы друг от друга. [c.13]
Недостатки метода наименьших квадратов (МНК). Использование процедуры оценки, основанной на методе наименьших квадратов, предполагает обязательное удовлетворение целого ряда предпосылок, невыполнение которых может привести к значительным ошибкам 1. Случайные ошибки имеют нулевую среднюю, конечные дисперсии и ковариации 2. Каждое измерение случайной ошибки характеризуется нулевым средним, не зависящим от значений наблюдаемых переменных 3. Дисперсии каждой случайной ошибки одинаковы, их величины независимы от значений наблюдаемых переменных (гомоскедастичность) 4. Отсутствие автокорреляции ошибок, т. е. значения ошибок различных наблюдений независимы друг от друга 5. Нормальность. Случайные ошибки имеют нормальное распределение 6. Значения эндогенной переменной х свободны от ошибок измерения и имеют конечные средние значения и дисперсии. [c.68]
Таким образом, коррелированность регрессоров и ошибок регрессии оказывается значительно более неприятным обстоятельством, чем, например, гетероскедастичность или автокорреляция. Неадекватными оказываются не только результаты тестирования гипотез, но и сами оценочные значения параметров. [c.194]
Обратим внимание на то, что хотя с помощью обратного преобразования Койка устранена коррелированность регрессо-ров с ошибками, но автокорреляция ошибок приобретает сложную структуру, и устранение ее может оказаться практически невозможным. Так что хотя получаемые таким образом оценки оказываются состоятельными, они обладают всеми теми недостатками, о которых подробно говорилось в гл.7. [c.204]
Можно показать, что в этом случае значение статистики Дарбина—Уотсона будет часто попадать в область принятия гипотезы об отсутствии автокорреляции и в том случае, если на самом деле эта гипотеза неверна. Это обстоятельство и делает тест Дарбина—Уотсона неприменимым и обусловливает необходимость других инструментов для обнаружения автокорреляции ошибок регрессии в моделях со стохастическими регрессорами. [c.213]
В модели с распределенными лагами ADL (0,1) (заметим, что все рассматриваемые нами модели относились именно к этому типу) для выявления автокорреляции ошибок можно применять Н-тест Дарбина. Рассмотрим модель [c.213]
Существенно отличающееся от двух значение статистики d Дарбина—Уотсона указывает на то, что имеется положительная автокорреляция ошибок регрессии. Одна из возможностей — попробовать идентифицировать ряд остатков как ряд модели ARMA(p, q). При этом самая простая модель AR(l) оказывается вполне адекватной [c.253]
Как видно, значение статистики d Дарбина— Уотсона очень близко к двум, так что в новой модели проблема автокорреляции ошибок регрессии отсутствует. Отсюда следует, что ее причина была в неверной спецификации модели. Стоит также обратить внимание, что коэффициент регрессии при xt уменьшился вдвое — на товары роскоши, подобные дорогому отдыху, расходы рассредоточиваются по нескольким ближайшим годам. [c.254]
Условие E( t s) = 0, t s указывает на некоррелированность ошибок для разных наблюдений. Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда это условие не выполняется, говорят об автокорреляции ошибок (serial orrelation). [c.40]
Для простейшего случая автокорреляции ошибок, когда E(etet+i) = р 0, типичный вид данных представлен на рис. 2.За (р>0) и рис. 2.36 (р<0). [c.40]
Переменная ж является экзогенной, yt-i коррелирована с xt i, поэтому xt i можно взять в качестве инструмента для yt-i- Оценка, полученная по методу инструментальных переменных, будет состоятельной. Однако вследствие автокорреляции ошибок оценки дисперсий оценок коэффициентов не будут состоятельными. [c.271]
Если порядок процесса AR(p) заранее неизвестен, то рекомендуется включать возможно большее количество лагов, чтобы устранить возможную автокорреляцию ошибок. Дело в том, что в ADF тесте предполагается, что ошибки являются белым шумом и критические значения, указанные в таблице 11.1, справедливы только при этом условии. Однако включение чрезмерного количества лагов снижает мощность теста. Чтобы определить количество лагов, которое надо включить в уравнение, можно использовать критерии выбора порядка ARMA модели, описанные ниже, или статистическую значимость дополнительной лаговой переменной. Заметим, что тест Дики-Фуллера включен во все современные эконометрйческие пакеты. [c.281]
В изучении корреляции признаков, не связанных согласованным изменением во времени, каждый признак изменяется под влиянием многих причин, принимаемых за случайные. В рядах динамики к ним прибавляется изменение во времпш каждого ряда. Это изменение приводит к так называемой автокорреляции — влиянию изменений уровней предыдущих рядов на последующие. Поэтому корреляция между уровнями динамических рядов правильно показывает тесноту связи между явлениями, отражаемыми в рядах динамики, лишь в том случае, если в каждом из них отсутствует автокорреляция. Кроме того, автокорреляция приводит к искажению величины среднеквадратических ошибок коэффициентов регрессии, что затрудняет построение доверительных интервалов для коэффициентов регрессии, а также проверки их значимости. [c.70]
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.
Для оценки качества модели регрессии используются специальные показатели.
Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:
G(y) – среднеквадратическое отклонение зависимой переменной.
Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии
Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах отминусеиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.
2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.
Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.
Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:
σ2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
δ2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:
1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:
Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.
2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:
Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;
характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;
где h– это количество параметров, входящих в модель регрессии.
Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.
Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:
Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.
13 .
Свойства дисперсии определяются свойствами МО. Напомним, дисперсия является центральным моментом второго порядка:
Дисперсия любой случайной величины независимо от вида распределения, которому она подчиняется обладает следующими свойствами.
1.ДИСПЕРСИЯ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ РАВНО НУЛЮ.
Пусть а — неслучайная величина. Тогда D(a)=M[(a-M(a))2]=M[0]=0.
2. ДИСПЕРСИЯ СУММЫ НЕСЛУЧАЙНОЙ И СЛУЧАЙНОЙ ВЕЛИЧИН РАВНА ДИСПЕРСИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ (ДИСПЕРСИЯ ИНВАРИАНТНА СДВИГУ).
Пусть а — неслучайная величина. Тогда D(a+x)=M[(a+x-M(a+x))2]= M[(x-M(x))2]=D(x).
3.ДИСПЕРСИЯ ПРОИЗВЕДЕНИЯ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ НА СЛУЧАЙНУЮ РАВНА ПРОИЗВЕДЕНИЮ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НА КВАДРАТ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ.
Пусть а — неслучайная величина. Тогда D(a*x)=M[(a*x-M(a*x))2]=M[(a*(x-M(x))2]=
4. ДИСПЕРСИЯ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН РАВНА СУММЕ ДИСПЕРСИЙ ЭТИХ ВЕЛИЧИН И УДВОЕННОЙ КОВАРИАЦИИ ЭТИХ ВЕЛИЧИН.
Пусть x и у — случайные величины. Тогда D(x+y)=M[((x+y)-M(x+y))2]= =M[((x-Mx)+(y-My))2]=M[(x-Mx)2+(y-My)2+2*(x-Mx)*(y-My)]=M[(x-Mx)2]+ +M[(y-My)]+2*M[(x-Mx)*(y-My)]=D(x)+D(y)+2*COV(x,y).
Величина COV(x,y)=M[(x-Mx)*(y-My)] называется ковариацией и обладает свойством: ДЛЯ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КОВАРИАЦИЯ ВСЕГДА РАВНА НУЛЮ. Отсюда, следует: ДИСПЕРСИЯ СУММЫ ДВУХ НЕЗАВИСИМЫХ (И ТОЛЬКО НЕЗАВИСИМЫХ) СЛУЧАЙНЫХ ВЕЛИЧИН РАВНА СУММЕ ДИСПЕРСИЙ ЭТИХ ВЕЛИЧИН.
Для оценки параметров нелинейных моделей используются два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. Второй подход обычно применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных. Таким образом, функции, которые показывают изменение одной переменной от другой в процентах или в несколько раз являются функциями, отражающими эластичность.
10.
Применение обычного метода наименьших квадратов при нарушении условия гомоскедастичности приводит к следующим отрицательным последствиям:
1. оценки неизвестных коэффициентов β неэффективны, то есть существуют другие оценки, которые являются несмещенными и имеют меньшую дисперсию.
2. стандартные ошибки коэффициентов регрессии будут занижены, а, следовательно, t -статистики – завышены, и будет получено неправильное представление о точности уравнения регрессии.
Рассмотрим метод оценивания при нарушении условия гомоскедастичности, матрица имеет вид β= (ХТ Ω-1 Х)-1 ХТ Ω-1у
Расчёт неизвестных коэффициентов регрессии по данной формуле называют обобщённым методом наименьших квадратов (ОМНК).
Теорема Айткена: при нарушении предположения гомоскедастичности оценки, полученные обобщенным методом наименьших квадратов, являются несмещенными и наиболее эффективными (имеющими наименьшую вариацию). На практике матрица Ω практически никогда не известна. Поэтому часто пытаются каким-либо методом оценить оценки матрицы Ω и использовать их для оценивания. Этот метод носит название доступного обобщенного метода наименьших квадратов.
Показать все связанные файлы Подборка по базе: 1. Лекция Особенности макетирования и верстки длинных документов, Медицинская статистика Лекция проф.Виноградова К.А.(1).pptx, 6 лекция Отбасы.ppt, 9-10 Лекция дуниетану.ppt, такт 5 лекция.doc, Тест к лекциям.doc, 3 лекция. куиз.docx, 3 лекция.pptx, антибиотики лекция.docx, ТПЭФМ_Практическое занятие 1_между лекциями 11 и 12.doc
2.1 Оценка общего качества уравнения регрессии
Для анализа общего качества полученного уравнения регрессии на количественном уровне используют коэффициент детерминации . Он рассчитывается по формуле:
.
В числителе вычитаемой из единицы дроби стоит сумма квадратов отклонений (СКО) выборочных значений зависимой переменной от теоретических, найденных с помощью уравнения регрессии . В знаменателе – СКО наблюдений зависимой переменной от среднего значения.
Коэффициент детерминации характеризует долю вариации (разброса) зависимой переменной, объяснённой с помощью данного уравнения.
Замечание. В случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента линейной корреляции.
Более точным является значение коэффициента детерминации с поправкой на число степеней свободы.
Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы:
– дисперсия, характеризующая общий разброс;
– остаточная дисперсия, где m – число независимых (объясняющих) переменных, в случае парной регрессии m =1 и формула имеет вид: .
Учитывая приведённые выше обозначения, формула коэффициента детерминации с поправкой на число степеней свободы будет иметь вид:
.
Значения коэффициента изменяются от 0 до +1 (в редких случаях значение может быть и отрицательным числом).
Близость коэффициента детерминации к +1 свидетельствует о том, что существует статистически значимая линейная связь между переменными, а уравнение имеет хорошее качество.
Близость к 0 говорит о том, что просто горизонтальная прямая является лучшей по сравнению с найденной регрессионной прямой.
Самостоятельную важность коэффициент детерминации приобретает только в случае множественной регрессии.
2.2 Оценка существенности параметров линейной регрессии и всего уравнения в целом
После того, как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включённых в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Проверка значимости производится на основе дисперсионного анализа.
Согласно идее дисперсионного анализа, общая сумма квадратов отклонений (СКО) y от среднего значения раскладывается на две части – объясненную и необъясненную:
или, соответственно:
Здесь возможны два крайних случая: когда общая СКО в точности равна остаточной и когда общая СКО равна факторной.
В первом случае фактор х не оказывает влияния на результат, вся дисперсия y обусловлена воздействием прочих факторов, линия регрессии параллельна оси Ох и уравнение должно иметь вид .
Во втором случае прочие факторы не влияют на результат, y связан с x функционально, и остаточная СКО равна нулю.
Однако на практике в правой части присутствуют оба слагаемых. Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации y приходится на объясненную вариацию. Если объясненная СКО будет больше остаточной СКО, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат y. Это равносильно тому, что коэффициент детерминации будет приближаться к единице.
Число степеней свободы (df-degrees of freedom) – это число независимо варьируемых значений признака.
Для общей СКО требуется (n-1) независимых отклонений,
Факторная СКО имеет одну степень свободы, и
Таким образом, можем записать:
Из этого баланса определяем, что = n–2.
Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы: — общая дисперсия, — факторная, — остаточная.
Анализ статистической значимости коэффициентов линейной регрессии
Хотя теоретические значения коэффициентов уравнения линейной зависимости предполагаются постоянными величинами, оценки а и b этих коэффициентов, получаемые в ходе построения уравнения по данным случайной выборки, являются случайными величинами. Если ошибки регрессии имеют нормальное распределение, то оценки коэффициентов также распределены нормально и могут характеризоваться своими средними значениями и дисперсией. Поэтому анализ коэффициентов начинается с расчёта этих характеристик.
Дисперсии коэффициентов рассчитываются по формулам:
Дисперсия коэффициента регрессии :
,
где – остаточная дисперсия на одну степень свободы.
Дисперсия параметра :
Отсюда стандартная ошибка коэффициента регрессии определяется по формуле:
,
Стандартная ошибка параметра определяется по формуле:
.
Далее рассчитываются t – статистики:
,
Они служат для проверки нулевых гипотез о том, что истинное значение коэффициента регрессии b или свободного члена a равно нулю: .
Альтернативная гипотеза имеет вид: .
t – статистики имеют t – распределение Стьюдента с степенями свободы. По таблицам распределения Стьюдента при определённом уровне значимости α и степенях свободы находят критическое значение .
Если , то нулевая гипотеза должна быть отклонена, коэффициенты считаются статистически значимыми.
Если , то нулевая гипотеза не может быть отклонена. (В случае, если коэффициент b статистически незначим, уравнение должно иметь вид , и это означает, что связь между признаками отсутствует. В случае, если коэффициент а статистически незначим, рекомендуется оценить новое уравнение в виде ).
Интервальные оценки коэффициентов линейного уравнения регрессии:
Доверительный интервал для а: .
Доверительный интервал для b:
Это означает, что с заданной надёжностью (где — уровень значимости) истинные значения а, b находятся в указанных интервалах.
Коэффициент регрессии имеет четкую экономическую интерпретацию, поэтому доверительные границы интервала не должны содержать противоречивых результатов, например, Они не должны включать нуль.
Анализ статистической значимости уравнения в целом.
Распределение Фишера в регрессионном анализе
Оценка значимости уравнения регрессии в целом дается с помощью F- критерия Фишера. При этом выдвигается нулевая гипотеза о том, что все коэффициенты регрессии, за исключением свободного члена а, равны нулю и, следовательно, фактор х не оказывает влияния на результат y ( или ).
Величина F – критерия связана с коэффициентом детерминации. В случае множественной регрессии:
,
где m – число независимых переменных.
В случае парной регрессии формула F – статистики принимает вид:
.
При нахождении табличного значения F- критерия задается уровень значимости (обычно 0,05 или 0,01) и две степени свободы: – в случае множественной регрессии, – для парной регрессии.
Если , то отклоняется и делается вывод о существенности статистической связи между y и x.
Если , то вероятность уравнение регрессии считается статистически незначимым, не отклоняется.
Замечание. В парной линейной регрессии . Кроме того, , поэтому . Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
Распределение Фишера может быть использовано не только для проверки гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии, но и гипотезы о равенстве нулю части этих коэффициентов. Это важно при развитии линейной регрессионной модели, так как позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных, или же, наоборот, включения их в это число.
Пусть, например, вначале была оценена множественная линейная регрессия по п наблюдениям с т объясняющими переменными, и коэффициент детерминации равен , затем последние k переменных исключены из числа объясняющих, и по тем же данным оценено уравнение , для которого коэффициент детерминации равен (, т.к. каждая дополнительная переменная объясняет часть , пусть небольшую, вариации зависимой переменной).
Для того, чтобы проверить гипотезу об одновременном равенстве нулю всех коэффициентов при исключённых переменных, рассчитывается величина
,
имеющая распределение Фишера с степенями свободы.
По таблицам распределения Фишера, при заданном уровне значимости, находят . И если , то нулевая гипотеза отвергается. В таком случае исключать все k переменных из уравнения некорректно.
Аналогичные рассуждения могут быть проведены и по поводу обоснованности включения в уравнение регрессии одной или нескольких k новых объясняющих переменных.
В этом случае рассчитывается F – статистика
,
имеющая распределение . И если она превышает критический уровень, то включение новых переменных объясняет существенную часть необъяснённой ранее дисперсии зависимой переменной (т.е. включение новых объясняющих переменных оправдано).
Замечания. 1. Включать новые переменные целесообразно по одной.
2. Для расчёта F – статистики при рассмотрении вопроса о включении объясняющих переменных в уравнение желательно рассматривать коэффициент детерминации с поправкой на число степеней свободы.
F – статистика Фишера используется также для проверки гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений.
Пусть имеются 2 выборки, содержащие, соответственно, наблюдений. Для каждой из этих выборок оценено уравнение регрессии вида . Пусть СКО от линии регрессии (т.е. ) равны для них, соответственно, .
Проверяется нулевая гипотеза : о том, что все соответствующие коэффициенты этих уравнений равны друг другу, т.е. уравнение регрессии для этих выборок одно и то же.
Пусть оценено уравнение регрессии того же вида сразу для всех наблюдений, и СКО .
Тогда рассчитывается F – статистика по формуле:
Она имеет распределение Фишера с степенями свободы. F – статистика будет близкой к нулю, если уравнение для обеих выборок одинаково, т.к. в этом случае . Т.е. если , то нулевая гипотеза принимается.
Если же , то нулевая гипотеза отвергается, и единое уравнение регрессии построить нельзя.
2.3 Проверка предпосылок, лежащих в основе МНК
Следующим этапом оценивания качества уравнения является проверка выполнения предпосылок, лежащих в основе метода расчёта параметров МНК.
Предпосылками МНК являются:
1. случайный характер ошибок регрессии;
2. нулевая средняя величина ошибок регрессии, не зависящая от значения объясняющих переменных;
3. независимость распределения ошибок для различных наблюдений; в случае оценки уравнения на временных рядах – отсутствие автокорреляции ошибок;
4. постоянство дисперсии ошибок, её независимость от значений объясняющих переменных – гомоскедастичность (если эта предпосылка не выполняется, то имеет место гетероскедастичность ошибок);
5. нормальность распределения ошибок регрессии.
Для проверки выполнения каждой из предпосылок применения МНК имеются специальные тесты. Реализация многих из этих тестов предполагает значительный объём исходных данных.
Если распределение случайных ошибок не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
Проверка первой предпосылки МНК
Прежде всего, проверяется случайный характер остатков – первая предпосылка МНК. С этой целью стоится график зависимости остатков от теоретических значений результативного признака (рис. 1). Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и МНК оправдан, теоретические значения хорошо аппроксимируют фактические значения .
Рис. 1. Зависимость случайных остатков от теоретических значений .
Возможны следующие случаи, если зависит от то:
Рис. 2. Зависимость случайных остатков от теоретических значений .
В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами.
Проверка второй предпосылки МНК
Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что (или ). Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
Вместе с тем, несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от независимости случайных остатков и величин , что также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью наряду с изложенным графиком зависимости остатков от теоретических значений результативного признака строится график зависимости случайных остатков от факторов, включенных в регрессию (рис. 3).
Рис. .3. Зависимость величины остатков от величины фактора .
Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений . Если же график показывает наличие зависимости и , то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора . Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от , например . Скопление точек в определенных участках значений фактора говорит о наличии систематической погрешности модели.
Замечание. Предпосылка о нормальном распределении остатков (пятая предпосылка) позволяет проводить проверку параметров регрессии и корреляции с помощью — и -критериев. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении пятой предпосылки МНК.
Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок.
Автокорреляция ошибок. Статистика Дарбина-Уотсона
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Отсутствие зависимости гарантирует отсутствие коррелированности между любыми отклонениями, т.е. и, в частности, между соседними отклонениями .
Автокорреляция (последовательная корреляция) остатков определяется как корреляция между соседними значениями случайных отклонений во времени (временные ряды) или в пространстве (перекрестные данные). Она обычно встречается во временных рядах и очень редко – в пространственных данных.
Возможны следующие случаи:
Эти случаи могут свидетельствовать о возможности улучшить уравнение путём оценивания новой нелинейной формулы или включения новой объясняющей переменной.
В экономических задачах значительно чаще встречается положительная автокорреляция, чем отрицательная автокорреляция.
Если же характер отклонений случаен, то можно предположить, что в половине случаев знаки соседних отклонений совпадают, а в половине – различны.
Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.
- Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.
- В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени .
От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках.
Для обнаружения автокорреляции используют либо графический метод. Либо статистические тесты.
Графический метод заключается в построении графика зависимости ошибок от времени (в случае временных рядов) или от объясняющих переменных и визуальном определении наличия или отсутствия автокорреляции. Наиболее известный критерий обнаружения автокорреляции первого порядка – критерий Дарбина-Уотсона. Статистика DW Дарбина-Уотсона приводится во всех специальных компьютерных программах как одна из важнейших характеристик качества регрессионной модели. Сначала по построенному эмпирическому уравнению регрессии определяются значения отклонений . А затем рассчитывается статистика Дарбина-Уотсона по формуле:
.
Статистика DW изменяется от 0 до 4. DW=0 соответствует положительной автокорреляции, при отрицательной автокорреляции DW=4. Когда автокорреляция отсутствует, коэффициент автокорреляции равен нулю, и статистика DW = 2. Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотезы и состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона (- нижняя граница признания положительной автокорреляции) и (-верхняя граница признания отсутствия положительной автокорреляции) для заданного числа наблюдений , числа независимых переменных модели и уровня значимости . По этим значениям числовой промежуток разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью осуществляется следующим образом:
– положительная автокорреляция, принимается ;
– зона неопределенности;
– автокорреляция отсутствует;
– зона неопределенности;
– отрицательная автокорреляция, принимается .
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу .
Можно показать, что статистика DW тесно связана с коэффициентом автокорреляции первого порядка:
Связь выражается формулой:
.
Значения r изменяются от –1 (в случае отрицательной автокорреляции) до +1 (в случае положительной автокорреляции). Близость r к нулю свидетельствует об отсутствии автокорреляции.
При отсутствии таблиц критических значений DW можно использовать следующее «грубое» правило: при достаточном числе наблюдений (12-15), при 1-3 объясняющих переменных, если , то отклонения от линии регрессии можно считать взаимно независимыми.
Либо применить к данным уменьшающее автокорреляцию преобразование (например автокорреляционное преобразование или метод скользящих средних).
Существует несколько ограничений на применение критерия Дарбина-Уотсона.
- Критерий DW применяется лишь для тех моделей, которые содержат свободный член.
- Предполагается, что случайные отклонения определяются по итерационной схеме
,
называемой авторегрессионной схемой первого порядка AR(1). Здесь – случайный член.
- Статистические данные должны иметь одинаковую периодичность (не должно быть пропусков в наблюдениях).
- Критерий Дарбина – Уотсона не применим к авторегрессионным моделям, которые содержат в числе факторов также зависимую переменную с временным лагом (запаздыванием) в один период.
Для авторегрессионных моделей предлагается h – статистика Дарбина
,
где – оценка коэффициента автокорреляции первого порядка, D(c) – выборочная дисперсия коэффициента при лаговой переменной yt-1, n – число наблюдений.
Обычно значение рассчитывается по формуле , а D(c) равна квадрату стандартной ошибки Sc оценки коэффициента с.
Методы устранения автокорреляции. Авторегрессионное преобразование
В случае наличия автокорреляции остатков полученная формула регрессии обычно считается неудовлетворительной. Автокорреляция ошибок первого порядка говорит о неверной спецификации модели. Поэтому следует попытаться скорректировать саму модель. Посмотрев на график ошибок, можно поискать другую (нелинейную) формулу зависимости, включить неучтённые до этого факторы, уточнить период проведения расчётов или разбить его на части.
Если все эти способы не помогают и автокорреляция вызвана какими–то внутренними свойствами ряда i>, можно воспользоваться преобразованием, которое называется авторегрессионной схемой первого порядка AR(1). (Авторегрессией это преобазование называется потому, что значение ошибки определяется значением той же самой величины, но с запаздыванием. Т.к. максимальное запаздывание равно 1, то это авторегрессия первого порядка).
Формула AR(1) имеет вид:
.
Где -коэффициент автокорреляции первого порядка ошибок регрессии.
Рассмотрим AR(1) на примере парной регрессии:
.
Тогда соседним наблюдениям соответствует формула:
(1),
(2).
Умножим (2) на и вычтем из (1):
.
Сделаем замены переменных
получим с учетом
:
(6).
Это преобразование называется авторегрессионным (преобразованием Бокса-Дженкинса).
Поскольку случайные отклонения удовлетворяют предпосылкам МНК, оценки а * и b будут обладать свойствами наилучших линейных несмещенных оценок. По преобразованным значениям всех переменных с помощью обычного МНК вычисляются оценки параметров а* и b, которые затем можно использовать в регрессии.
Т.о. если остатки по исходному уравнению регрессии автокоррелированы, то для оценки параметров уравнения используют следующие преобразования:
1) Преобразовать исходные переменные у и х к виду (3), (4).
2) Обычным МНК для уравнения (6) определить оценки а * и b.
3) Рассчитать параметр а исходного уравнения из соотношения (4).
4) Записать исходное уравнение (1) с параметрами а и b (где а — из п.3, а b берётся непосредственно из уравнения (6)).
Авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т.е. использовано для уравнения множественной регрессии.
Для преобразования AR(1) важно оценить коэффициент автокорреляции ρ. Это делается несколькими способами. Самое простое – оценить ρ на основе статистики DW:
,
где r берется в качестве оценки ρ. Этот метод хорошо работает при большом числе наблюдений.
В случае, когда есть основания считать, что положительная автокорреляция отклонений очень велика (), можно использовать метод первых разностей (метод исключения тенденции), уравнение принимает вид
.
Из уравнения по МНК оценивается коэффициент b. Параметр а здесь не определяется непосредственно, однако из МНК известно, что .
В случае полной отрицательной автокорреляции отклонений ()
,
получаем уравнение регрессии:
или .
Вычисляются средние за 2 периода, а затем по ним рассчитывают а и b. Данная модель называется моделью регрессии по скользящим средним.
Проверка гомоскедастичности дисперсии ошибок
В соответствии с четвёртой предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора остатки имеют одинаковую дисперсию . Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность.
В качестве примера реальной гетероскедастичности можно привести то, что люди с большим доходом не только тратят в среднем больше, чем люди с меньшим доходом, но и разброс в их потреблении также больше, поскольку они имеют больше простора для распределения дохода.
Наличие гетероскедастичности можно наглядно видеть из поля корреляции (- графический метод обнаружения гетероскедастичности).
Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков от теоретических значений результативного признака .
Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- и гетероскедастичности.
При нарушении гомоскедастичности имеем неравенства: , где — постоянная дисперсия ошибки при соблюдении предпосылки. Т.е. можно записать, что дисперсия ошибки при наблюдении пропорциональна постоянной дисперсии: .
— коэффициент пропорциональности. Он меняется при переходе от одного значения фактора к другому.
Задача состоит в том, чтобы определить величину и внести поправку в исходные переменные. При этом используют обобщённый МНК, который эквивалентен обычному МНК, применённому к преобразованным данным.
Чтобы убедиться в обоснованности использования обобщённого МНК проводят эмпирическое подтверждение наличия гетероскедастичности.
При малом объёме выборки, что наиболее характерно для эмпирических исследований, для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта (в 1965 г. они рассмотрели модель парной линейной регрессии, в которой дисперсия ошибок пропорциональна квадрату фактора). Пусть рассматривается модель, в которой дисперсия пропорциональна квадрату фактора: , . А также остатки имеют нормальное распределение и отсутствует автокорреляция остатков.
Параметрический тест (критерий) Гольдфельда – Квандта:
1. Все n наблюдений в выборке упорядочиваются по величине x.
2. Вся упорядоченная выборка разбивается на три подвыборки (объёмом k, С, k.)
.
Исключаются из рассмотрения С центральных наблюдений. (По рекомендациям специалистов, объём исключаемых данных С должен быть примерно равен четверти общего объёма выборки n, в частности, при n =20, С=4; при n =30, С = 8; при n =60, С=16).
3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для последней подвыборки (k последних наблюдений).
4. Определяются остаточные суммы квадратов для первой и второй групп. Если предположение о пропорциональности дисперсий отклонений значениям x верно, то .
5. Выдвигается нулевая гипотеза которая предполагает отсутствие гетероскедастичности.
Для проверки этой гипотезы рассчитывается отношение
,
которое имеет распределение Фишера с степеней свободы (здесь m – число объясняющих переменных).
Если , то гипотеза об отсутствии гетероскедастичности отклоняется при уровне значимости α.
Этот же тест может быть использован и при предположении об обратной пропорциональности между дисперсией и значениями объясняющей переменной . В этом случае статистика Фишера принимает вид:
.
При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений . Обобщенный метод наименьших квадратов (ОМНК)
При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов заменять обобщенным методом наименьших квадратов (ОМНК).
Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Остановимся на использовании ОМНК для корректировки гетероскедастичности. Рассмотрим ОМНК для корректировки гетероскедастичности. Будем предполагать, что среднее значение остаточных величин равно нулю , а дисперсия пропорциональна величине .
,
где – дисперсия ошибки при конкретном -м значении фактора; – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; – коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.
При этом предполагается, что неизвестна, а в отношении величин выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
В общем виде для уравнения модель примет вид:
.
В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе -го наблюдения, на . Тогда дисперсия остатков будет величиной постоянной, т. е. .
Иными словами, от регрессии по мы перейдем к регрессии на новых переменных: и . Уравнение регрессии примет вид:
,
а исходные данные для данного уравнения будут иметь вид:
,.
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные и взяты с весами .
Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений вида
.
Соответственно получим следующую систему нормальных уравнений:
,
Т.е. коэффициент регрессии при использовании обобщенного МНК с целью корректировки гетероскедастичности представляет собой взвешенную величину по отношению к обычному МНК с весом .
Если преобразованные переменные и взять в отклонениях от средних уровней, то коэффициент регрессии можно определить как
.
При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии определяется по формуле:.
Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии.
Для применения ОМНК необходимо знать фактические значения дисперсий отклонений . На практике такие значения известны крайне редко. Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях . В эконометрических исследованиях чаще всего предполагается, что дисперсии отклонений пропорциональны или значениям xi, или значениям , т.е или .
Если предположить, что дисперсии пропорциональны значениям фактора x, т.е. , тогда уравнение парной регрессии преобразуется делением его левой и правой частей на :
.
Здесь для случайных отклонений выполняется условие гомоскедастичности. Следовательно, для регрессии применим обычный МНК. Следует отметить, что новая регрессия не имеет свободного члена, но зависит от двух факторов. Оценив для неё по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии.
Если предположить, что дисперсии , то соответствующим преобразованием будет деление уравнения парной регрессии на xi:
или, если переобозначить остатки как :
.
Здесь для отклонений vi также выполняется условие гомоскедастичности.
В полученной регрессии по сравнению с исходным уравнением параметры поменялись ролями: свободный член а стал коэффициентом, а коэффициент b – свободным членом. Применяя обычный МНК в преобразованных переменных
,
получим оценки параметров, после чего возвращаемся к исходному уравнению.
Пример. Рассматривая зависимость сбережений от дохода , по первоначальным данным было получено уравнение регрессии
.
Применяя обобщенный МНК к данной модели в предположении, что ошибки пропорциональны доходу, было получено уравнение для преобразованных данных:
.
Коэффициент регрессии первого уравнения сравнивают со свободным членом второго уравнения, т.е. 0,1178 и 0,1026 – оценки параметра зависимости сбережений от дохода.
В случае множественной регрессии ,
Если предположить (т.е. дисперсия ошибок пропорциональна квадрату первой объясняющей переменной), то в этом случае обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения:
.
Следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.
Пример. Пусть – издержки производства, – объем продукции, – основные производственные фонды, – численность работников, тогда уравнение
является моделью издержек производства с объемными факторами. Предполагая, что пропорциональна квадрату численности работников , мы получим в качестве результативного признака затраты на одного работника , а в качестве факторов следующие показатели: производительность труда и фондовооруженность труда . Соответственно трансформированная модель примет вид
,
где параметры , , численно не совпадают с аналогичными параметрами предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фовдовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда.
Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату объема продукции, , можно перейти к уравнению регрессии вида
.
В нем новые переменные: – затраты на единицу (или на 1 руб. продукции), – фондоемкость продукции, – трудоемкость продукции.
В заключение следует отметить, что обнаружении гетероскедастичности и её корректировка являются весьма серьёзной и трудоёмкой проблемой. В случае применения обобщённого (взвешенного) МНК необходима определённая информация или обоснованные предположения о величинах .
Интерпретация уравнения регрессии
Интерпретация уравнения регрессии
- Интерпретация регрессионных уравнений Существует два этапа интерпретации уравнения регрессии. Первый этап Уточнить, потому что уравнения интерпретируются устно Тот, кто не является статистиком. Во вторых это Нет необходимости решать, делать это или больше. Тщательное исследование зависимости. Оба этапа очень важны.
- На втором этапе мы рассмотрим несколько поз А пока давайте обратим основное внимание на первый этап. Это объясняет Определяется регрессионной моделью функции спроса, то есть регрессией между расами Потребители переходят на еду (у) и располагаемый личный доход (х) Данные Отображается в графическом формате (рисунок 2.7). Предположим, что истинная модель описывается y = a + $ x + u, (2,41) И регрессионная оценка £ = 55,3 + 0,093 *. (2,42)
Данные приведены в таблице. Б.1 в США за период с 1959 по 1983 год. Людмила Фирмаль
Полученные результаты можно интерпретировать следующим образом: коэффициент в х (коэффициент градиента) Единица у увеличивается на 0,093 единицы. х и у оба измеряются в мил Миллиарды долларов по фиксированной цене. Поэтому склон Если выручка увеличится на 1 миллиард долларов, 64 Питательные вещества увеличились на 93 миллиона долларов.
Это значит Из реальных долларовых доходов 9,3 цента тратятся на еду. Как насчет констант уравнения? Формально она Если x = 0, указывает уровень прогнозирования ^. Это ясно имеет смысл. Иногда нет. Если х = 0 достаточно далеко от значения выборки х, В этом случае буквальная интерпретация может привести к неверным результатам.
Даже если Линия регрессии является очень точным представлением наблюдаемого значения выборки. Нет гарантии, что то же самое произойдет с экстраполяцией влево или вправо. в 150 грамм 100 грамм 50 Стоимость пища 200 400 600 800 —100 • ”0 120—0 X доходов Рисунок 2.7. Зависимость расходов на питание от дохода (США, 1959-1983).
В рассматриваемом случае путем экстраполяции на вертикальную ось Если доход равен нулю, стоимость еды Сделал бы 55,3 миллиарда долларов. Такое толкование может быть правдоподобным в отношении Лица, которые могут тратить накопления пищи Кредиты или заемные средства. Тем не менее, это не имеет смысла, если По отношению ко всему.
В этом случае константа сделает единственное Функция: может определить положение линии регрессии на графике Поддельный. Примеры констант с ясным значением приведены в упражнении. Институт 2.1. При интерпретации уравнений регрессии очень важно помнить три Вещь. Во-первых, a является только оценкой a, а a b является оценкой (3. Интерпретация на самом деле просто оценка.
Во-вторых Уравнение регрессии отражает только общую тенденцию выборки. В то же время Индивидуальные наблюдения подвержены случайности. третий В этих случаях точность интерпретации зависит от точности спецификации уравнения. По сути, мы построили довольно простую зависимость от функции спроса Мы вернемся к этому в следующем разделе и уточнить.
- Определяя как определения, так и статистические методы, используемые при измерении Коэффициент уравнения. В то же время читателям рекомендуется начать с Упражнение 2.4, определить путем проведения параллельных экспериментов Функция спроса на другие товары приведена в таблице. B.1. После оценки регрессии возникают следующие вопросы:
Есть ли способ определить точность оценки? Это очень важно Рост будет обсуждаться в следующем разделе. Сначала рассмотрим дальше Подробно объясните роль остаточного члена и его влияние на оценки a и p. Интерпретация уравнений линейной регрессии.
Представьте себе простой способ интерпретации линейных коэффициентов. Людмила Фирмаль
Уравнение регрессии у = а + бх Если есть простая естественная единичная переменная Измерение. Сначала увеличим х на 1 единицу ( Единица переменной х) увеличивается у в б (единица переменной у). Второй этап Проверка того, что собой представляет хна на самом деле, Замените слово «единица измерения» на фактическое количество.
Третий этап Проверка возможности более простого выражения результата Это может быть не очень удобно. В примере В этом разделе указана единица измерения для х и у Потому что миллиарды долларов были потрачены, Замечательное упрощение. Константа а дает предсказанное значение у (единица ^). х = 0 Это может иметь или не иметь смысла в зависимости от значения Конкретная ситуация. Упражнение 1 2.1.
Регрессия стоимости продуктов питания (на основе того же Данные, для которых уже описана функция спроса, описанная в тексте) Меню определено как f = 1 в 1959 году, t = 2 в 1960 году и т. Д. Нини: у = 95,3 + 2,53 /. Интерпретация в Сравнение результатов оценки регрессии с аналогом Аналогичные результаты для модели регрессии функции спроса Пожалуйста, смотрите текст.
В этом случае постоянная Есть простая интерпретация. 2.2. Регрессивная зависимость от одноразовой зависимости стоимости жилья 1 Упражнение 2.4 особенно важно в том смысле, что оно запускает серию регрессий для развлечения. Общий спрос. Это оценивается читателем на протяжении всей книги.
Если это упражнение Если это делается группой студентов, учитель должен дать студентам задания Товарные. Более подробная информация о доступных данных доступна в Приложении B.go Личный доход в соответствии с таблицей. B.1, оба количества Можно оформить миллиарды долларов с 1959 по 1983 В следующем формате: j> = -27,6 + 0,178х.
Регрессивная зависимость и определение стоимости жилья с течением времени То же самое, что и упражнение 2.1, можно выразить как: f = 48,9 + 4,84 г. Вот экономическая интерпретация этих регрессий. У них разные предложения Описание тех же данных в переменной y. Сколько они Вы можете согласиться? 2,3.
Создайте уравнение регрессии между p и e из данных упражнения 1.3, сначала используйте все 12 наблюдений, затем исключите наблюдения 1. Дает экономическую интерпретацию для Японии. 2,4. В таблице. B.1 — потребительские расходы США располагаемый личный доход за период 1959-1983 гг. Назовите один продукт — не еду, а не домашнюю Пропустите регрессию между y и x. х — располагаемый личный доход, использующий Данные за 25 лет.
Интерпретация коэффициентов регрессии 2.5. Таким образом, регрессия между характеристиками продукта и временем Мы сделаем это в упражнении 2.1. Правильная интерпретация и сравнение У нее есть интерпретация регрессии, полученная в упражнении 2.4. 2.6. Два человека строят один и тот же набор временных тенденций 25 наблюдений за переменной y с использованием модели: у = а + р / + и
Где t — время (принимает значения непрерывно от 1 до 25), а -case Член чаепития. Получите первое уравнение: j> = 6,70 + 1,79 /. Вторая по ошибке оценивает регрессию между / и у и этим уравнением По мнению: t = -0,25 + 0,44 >>. Из этого уравнения он получает: у = 0,57 + 2,27 /. Объясните это уравнение и несоответствие между уравнениями, Получено первым исследователем. 2,7.
Как изменяется регрессионный балл в упражнении 2.1 Фактическая дата (1959-1983) используется как / вместо числа из 1 до 25? 2,8. Исследователи, 1 Не начинайте сначала вычислять коэффициент регрессии. Заполнены большинство арифметических расчетов в упражнении 1.3. 2 Учителя являются учениками, если это групповое занятие.
Удар, чтобы дать задачу оценки регрессии различных видов товаров в дополнение к еде жилья.люги, основанные на данных АМЕ (у) и общем располагаемом личном доходе (х) Риканская экономика (обе измеряются в миллиардах долларов) Фиксированная цена) с использованием данных и модели временных рядов за год: y = a + px + u. 1.
Исследователь выполняет регрессионный анализ, чтобы получить уравнение. Используйте обычный метод наименьших квадратов. Если предположить, что Обе ценности могут быть значительно недооценены внутренней системой Личные счета за желание людей не платить налоги Правительство, исследователи принимают два альтернативных улучшения Недооцененная оценка. 2.
Исследователи добавляют $ 90 млрд к показателю каждый год >> и Показатель х 200 миллиардов долларов. 3. Исследователь увеличивает x и y на 10% Каждый год. Оценить влияние корректировок (2) и (3) на результаты рег. ressii. 2.9. Исследователи имеют общие годовые данные временных рядов.
Заработная плата (W), валовой доход (P) и валовой доход (Y) Для страны сроком на n лет. По определению Y = W + T1. Получите регулярное уравнение, используя метод наименьших квадратов Рссии: fr = a0 + aiY; ft = Z> 0 + bxY. Указывает, что коэффициент регрессии автоматически удовлетворяет Следующее уравнение: но х + * я = 1; * o + K = 0. Интуитивно объясните, почему так должно быть. 2.10.
Исследователи не имеют нестохастической части истинной модели у пропорционально х. y = $ x + u. Исходя из исходного принципа, выведите формулу b, оценка МНК б. В этом случае (2.31) указывает, что это можно записать следующим образом. S = bj] + b2J, xj -2 £ Xx,. > 7 Для этого b = 2, xiyi / Zxf. 2,11. Выведите оценку наименьших квадратов модели из первого предположения. у = а + у. 68 То есть у это просто сумма констант Случайные участники с нами. Сначала переопределите 5, а затем дифференцируйте Цитирование.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://topuch.ru/lekciya-po-ekonometrike/index2.html
http://lfirmal.com/interpretaciya-uravneniya-regressii/
