Matlab обратное распространение ошибки

---

Подборка по базе: Технологии современного производства 3Д моделирование.docx, Лабораторная работа 4. Классы сетей..docx, 1. Архитектура систем и сетей телекоммуникаций.docx, Курсовая работа — 3D моделирование.docx, ПЗ Моделирование экономических процессов.docx, Построение многоуровневых коммутируемых сетей.docx, Построение объединённых масштабируемых сетей.pdf, Основы построения объединенных сетей по технологиям CISCO — тест, Влияние социальных сетей на человека.docx, Принципы организации IP сетей.docx

---

ПРИМЕР 1 Создание и обучение нейронной сети с по­мощью алгоритма обратного распространения ошибки
Зададим с помощью графика исходную функцию:
% входы НС

P = [0 1 2 3 4 5 6 7 8];

% желаемые реакции НС

T = [0 0.44 0.88 0.11 -0.66 -0.95 -0.45 0.18 0.92];

% изображение аппроксимируемой функции

plot(P, T, ‘o‘);
Используем функцию newff,чтобы создать двухслойную сеть прямого распространения. Пусть сеть имеет входы с интервалом значений от 0 до 8, первый слой с 10 нелинейными сигмоидальными, второй – с одним линейным нейронами. Используем для обучения алгоритм обратного распространения ошибки (backpropagation) Левенберга – Марквардта (

рис. 6).
% создание двухслойной НС прямого распространения с интервалом

% значений входов от 0 до 8, причем первый слой содержит

% 10 нелинейных сигмоид, а второй — один линейный нейрон.

% Для обучения используется алгоритм обратного распространения

% ошибки (backpropagation).

net = newff([0 8], [10 1], {‘tansig’ ‘purelin’},’trainlm’);

% имитация работы необученной НС

yl = sim (net, P);

% изображение результатов работы необученной НС

plot(P, T, ‘o‘, P, yl, ‘x‘) ;

% Обучим сеть на 100 эпохах с целевой ошибкой 0.01:

% установка количества проходов

net.trainParam.epochs = 50;

% установка целевого значения ошибки

net.trainParam.goal = 0.01;

% обучениеНС (рис. 6)

net = train(net, P, T) ;

% имитация работы обученной НС

y2 = sim(net, P);

% изображение результатов работы НС (рис. 7)

plot(P, T, ‘o’, P, yl, ‘x’, P, y2, ‘+’);

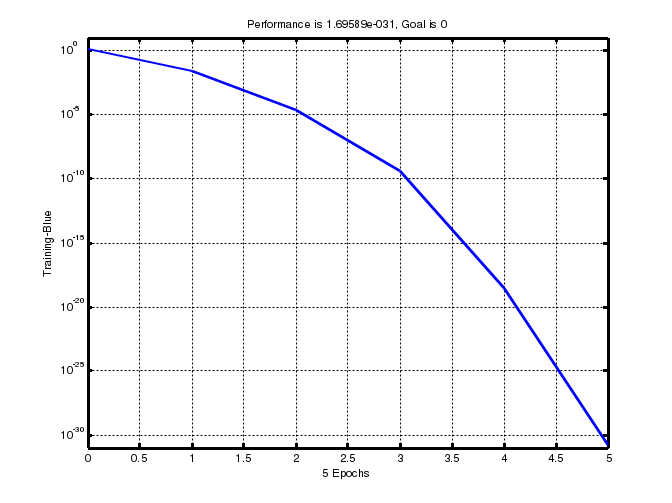
Рис. 6. График обучения двухслойного персептрона
Для исследования работы алгоритма обратного распространения ошибки воспользуемся примером, встроенным в Matlab toolbox, набрав команду demo.

В появившемся диалоговом окне необходимо последовательно выбирать пункты меню: Toolboxes->Neural Network->Other Demos->Other Neural Network Design textbook demos->Table of Contents->10-13->Backpropagation Calculation.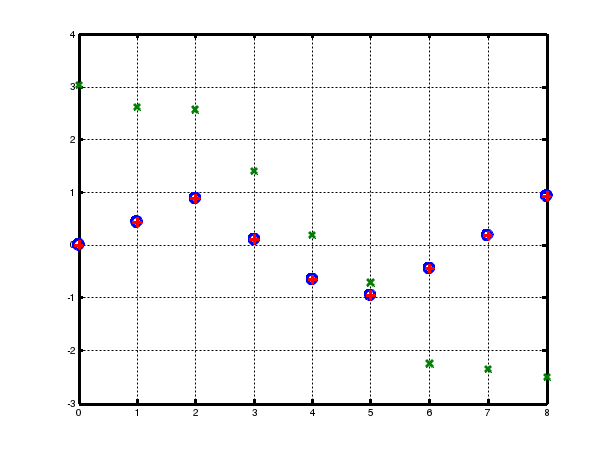

Рис. 7. Результат аппроксимации векторов двухслойным персептроном
В примере используется двухслойный персептрон с двумя нелинейными нейронами в первом слое и одним во втором. Действие алгоритма обратного распространения ошибки разбито на следующие шаги: назначение входа и желаемого вы­хода, прямой проход входного сигнала до выхода, обратное распространение ошибки, изменение весов. Переменные, по­зволяющие проследить работу алгоритма обратного распро­странения ошибки, обозначены следующим образом:

Р –входной сигнал;

W₁(i) –вектор весов первого слоя, W₁(1) –вес связи, пе­редающий входной сигнал на первый нейрон, a W₁(2) – на второй;

W₂(i) –вектор весов второго слоя, W₂(1) –вес связи, пе­редающий входной сигнал с первого нейрона во второй слой, a W₂(2) –со второго;

B₁(i) –вектор пороговых значений (bias) нейронов пер­вого слоя, i = 1, 2;

В₂– пороговое значение (bias) нейрона второго слоя;

N₁(i) – вектор выходов первого слоя, i = 1, 2;

N₂– выход второго слоя;

A₁(i) – вектор выходных сигналов первого слоя после вы­полнения функции активации (сигмоиды), i = 1, 2;

А₂– выход второго слоя после выполнения функции ак­тивации (линейной);

lr – коэффициент обучаемости.

Пусть входной сигнал Р = 1,0, а желаемый выход .

Результаты выполнения этапов алгоритма представлены в табл. 1.
Таблица 1
Результаты поэтапного выполнения алгоритма обратного распространения ошибки

Этап	Прямое распрост­ранение входного сигнала	Обратное распрост­ранение ошибки	Изменение весов
A1(1), A1(2)	Logsig(W1P+B1) = = [0,321, 0,368]	Не выполняется	Не выполняется
А2	purelin(W1P+В1)= = 0,446	То же	То же
е	t — A2 = 1,261	»	»
N1(1), N1(2)	Не выполняется		»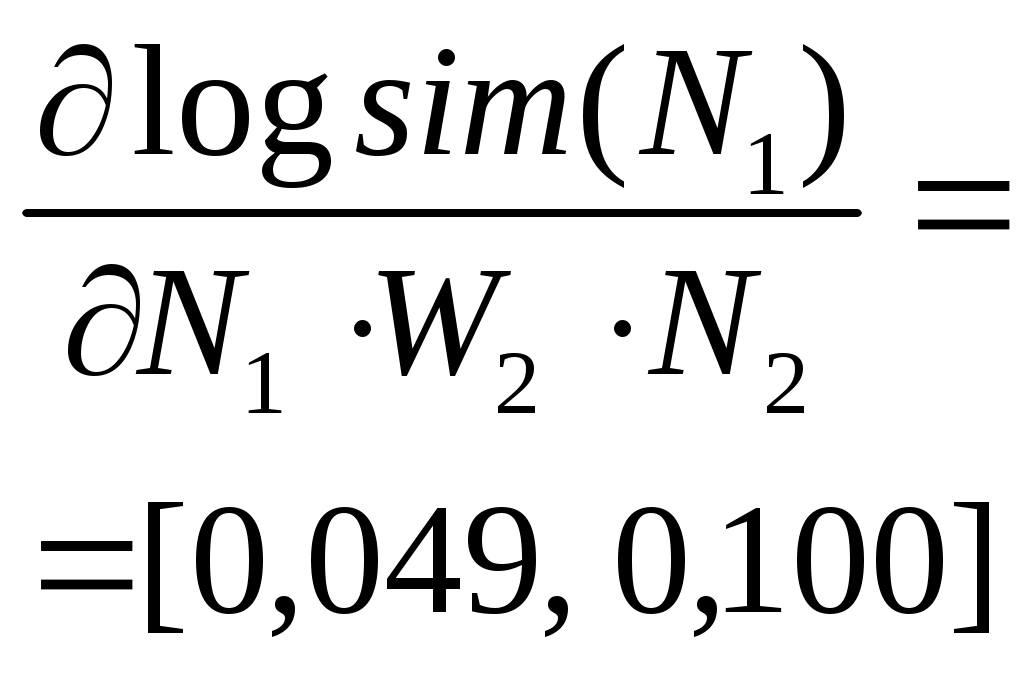
N2	То же		»
W1(1) W1(2)	»	Не выполняется
B1(1), B1(2)	»	То же
B2	»	»
W2(2)	»	»

4 КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каким алгоритмом обучают многослойные НС?

1. Из каких основных этапов состоит алгоритм обратного распространения ошибки?

1. Почему алгоритм обратного распространения ошибки от­носится к классу алгоритмов градиентного спуска?
2. Как влияет функция принадлежности на правило измене­ния весов в обратном алгоритме распространения ошибки?
3. Какая функция в среде MATLAB создает НС прямого распространения?
4. Какие функции активации могут быть назначены для нейронов НС прямого распространения?

Лабораторная работа № 3

ИЗУЧЕНИЕ РАДИАЛЬНЫХ БАЗИСНЫХ, ВЕРОЯТНОСТНЫХ НЕЙРОННЫХ СЕТЕЙ, СЕТЕЙ РЕГРЕССИИ
1 ЦЕЛЬ РАБОТЫ

Изучить модель вычислений радиаль­ного базисного нейрона, структуру и функции сетей регрес­сии, вероятностных нейронных сетей.
2 СВЕДЕНИЯ ИЗ ТЕОРИИ

2.1 Радиально-базисные сети. Сети регрессии. Вероятностные НС
Рассмотрим радиальный базисный нейрон с R входами. Струк­тура нейрона представлена на

рис. 8. Радиальный базисный нейрон (РБН) вычисляет расстояние между векторами входов X ивектором весов W,затем умножает его на фиксированный порог b. Функция активации РБН, полученная в среде MATLAB, представлена на рис. 10. Ра­диальная базисная функция имеет максимум, равный 1, когда ее входы нулевые. Следовательно, радиальный базисный ней­рон действует как детектор, который получает на выходе 1, когда вход X идентичен его вектору весов W. Фиксированный порог b даст возможность управлять чувствительностью ней­рона. Например, если нейрон имеет порог 0,1, то выход равен 0,5 для любого входного вектора X, находящегося на вектор­ном расстоянии 8,326 (8,326/b) от W.

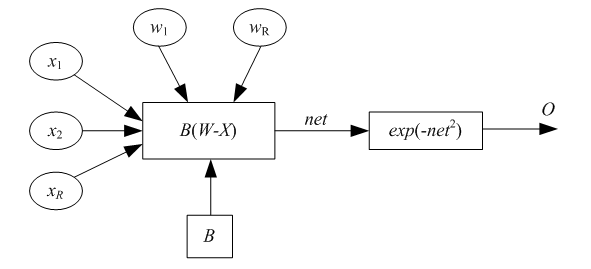
Рис. 8. Радиальный базисный нейрон
Радиальная базисная нейронная сеть (РБНС) состоит из двух слоев: скрытого радиального базисного слоя из S¹нейронов и выходного линейного слоя из S²нейронов. Элементы первого слоя РБНС вычисляют расстояния между входным вектором и векторами весов первого слоя, сформированных из строк матрицы W ^2,1. Вектор порогов В и расстояния поэлементно умножаются. Выход первого слоя можно выразить формулой

где A¹ – выход первого слоя; функция radbas – радиально-базисная функция; W – матрица весов первого слоя сети; X – входной вектор; В – вектор порогов первого слоя.

Согласно формуле радиальные базисные нейроны с век­тором весов, близким к X, сгенерируют значения, близкие к 1. Если нейрон имеет выход 1, то это значение весами второго слоя будет передано на его линейные нейроны. Фактически радиальный базисный нейрон с выходом 1превращает выхо­ды всех остальных нейронов в нули. Тем не менее, типичным является случай, когда несколько нейронов дают на выходах значимый результат, хотя и с разной степенью.

Радиальные базисные нейронные сети обучаются в три этапа. Опишем этапы обучения.

Первый этап – выделение центров (весов). Центры, представленные в РБН-слое, оптимизируются первыми с помощью обучения без учителя. Центры могут быть выделены разными алгоритмами, в частности обучением Кохонена. Ал­горитмы должны разместить центры, отражая кластеризацию исходных данных.

Второй этап – назначение отклонений. Отклонения могут быть назначены различными алгоритмами, например алгоритмом «ближайшего соседа».

Третий этап – линейная оптимизация. Можно ис­пользовать методы обучения по дельта-правилу, обратному распространению ошибки.

Нейронные сети регрессии (НСР) имеют такой же, как и РБНС, первый слой, но второй слой строится специальным образом. Для аппроксимации функций часто используются обобщенные сети регрессии (generalized regression neuron net­works). Второй слой, как и в случае РБНС, выполняет поэле­ментное произведение строки W_1,2и вектора выхода первого слоя a¹. Он имеет столько нейронов, сколько существует целевых пар <входной вектор/целевой вектор>. Матрица весов W – это на­бор целевых строк. Целевое значение – это значение аппрок­симируемой функции в обучающей выборке. Предположим, имеется один входной вектор х_i,который сгенерирует на выходе первого слоя выход, близкий к 1. В результате выход второго слоя будет близок к t_iодному из значений аппроксимируемой функции, использованной при формировании второго слоя.

Сети регрессии иногда называют Байесовскими вероятно­стными сетями регрессии, или обобщенными НС регрессии. Некоторые реализации сетей регрессии имеют четыре слоя: входной, выходной, слои радиальных центров, элементов рег­рессии. Радиальный слой представляет собой центры-класте­ры известных обучающих данных и содержит такое же коли­чество элементов, как обучающая выборка; РБН обучаются алгоритмом кластеризации. Слой регрессии имеет только на один элемент больше, чем выходной слой, и содержит линей­ные элементы одного из двух типов. Элемент первого типа вычисляет условную вероятность каждого выходного атрибу­та, элемент второго типа вычисляет плотность вероятности. Выходной слой выполняет специальные функции деления. Каждый элемент делит выходы, ассоциированные первым ти­пом, с помощью элементов второго типа.

Байесовские вероятностные НС используются только для проблем классификации. Они содержат четыре слоя: вход­ной, выходной, слой РБН и элементов линейной классифи­кации. Слои могут содержать квадратную матрицу потерь, включение которой возможно, только если третий и четвер­тый слои состоят из одинакового числа элементов. Радиаль­ные базисные нейроны в таких сетях используются для хра­нения образцов, взятых из обучающей выборки, которая бе­рется полностью. Следовательно, первый скрытый слой содержит такое же количество элементов, что и обучающая выборка. Так как элементы слоя классификации связаны с выходом каждого класса, можно оценить вероятность принадлежности последнему. Если используется матрица потерь, то цена решения минимальна. Такие сети обычно быстро тре­нируются, но медленно вычисляют из-за большого размера.

Вероятностные нейронные сети (ВНС, probabilistic neuron networks) используются для решения проблемы классифика­ции. Первым слоем в архитектуре ВНС является слой радиальных базисных нейронов, который вычисляет расстояние и век­тор индикаторов принадлежности другим входным векторам, используемым при обучении. Второй слой суммирует эти зна­чения для каждого класса входов и формирует выходы сети, как вектор вероятностей. Далее специальная функция активации (compete) определяет максимум вероятностей на выходе второ­го слоя и устанавливает данный выход в 1, а остальные выходы в 0. Матрица весов первого слоя W^1,1 установлена в соответ­ствии с обучающими парами. Блок расчета расстояний полу­чает вектор, элементы которого показывают, насколько близок входной вектор к векторам обучающего множества. Элементы вектора умножаются на вектор порогов и преобразуются ра­диальной базисной функцией. Входной вектор, близкий к не­которому образцу, устанавливается в 1 в выходном векторе первого слоя. Если входной вектор близок к нескольким образцам отдельного класса, то несколько элементов выходного вектора первого слоя будут иметь значения, близкие к 1.

Веса второго слоя W^1,1устанавливаются по матрице T целевых векторов, каждый вектор которой включает значение 1 в строке, связанной с определенным классом входов, и нули в остальных позициях. Произведения Т a¹ суммируют эле­менты выходного вектора первого слоя а¹ для каждого из K классов. Затем функция активации второго слоя (compete) ус­тановит значение 1 в позицию, соответствующую большему элементу выходного вектора, и 0 во все остальные. Следова­тельно, сеть классифицирует входные векторы, назначая вхо­ду единственный класс на основе максимальной вероятности принадлежности.

2.2 Описание основных функций
Функция newrb создает радиальную базисную сеть и имеет следующий синтаксис:
net = newrb(P, Т, goal, spread).
Радиальные базисные сети используют для аппроксимации функций. Функция newrb конструирует скрытый (первый) слой из радиальных базисных нейронов и использует значение средней квадратичной ошибки (goal). Функция newrb(P, Т, goal, spread) имеет следующие аргументы: Р – матрица Q входных векторов размерности R на Q; Т – матрица Q векторов целевых классов S на Q; goal –средняя квадратичная ошибка, по умолчанию 0,0; spread – разброс радиальной ба­зисной функции, по умолчанию 1,0. Функция создает и возвращает в качестве объекта радиальную базисную сеть. Большое значение разброса приводит к большей гладкости аппроксимации. Слишком большой разброс требует много нейронов, для того чтобы подстроиться под быстро изменяющуюся функцию, слишком малый – для достижения гладкости аппроксимации. Подобрать значение разброса можно с помощью многократных вызовов функции newrb. Создадим в среде MATLABрадиальную базисную сеть:
net = newrbe(P, T, spread).

Метод обратного распространения ошибки

Термин
«обратное распространение» относится
к процессу, с помощью которого могут
быть вычислены производные функционала
ошибки по параметрам сети. Этот процесс
может использоваться в сочетании с
различными стратегиями оптимизации.
Существует много вариантов и самого
алгоритма обратного распространения.
Обратимся к одному из них.

Рассмотрим выражение для градиента
критерия качества по весовым коэффициентам
для выходного слоя M:

(3.9)

где
–
число нейронов в слое;–k-й элемент вектора выхода слояM
для элемента выборки с номеромq.

Правило функционирования слоя M:

(3.10)

Из уравнения (3.8) следует

(3.11)

После подстановки (3.11) в (3.9) имеем:

Если обозначить

(3.12)

то получим

(3.13)

Перейдем к выводу соотношений для
настройки весов
слояM–1

(3.14)

где

Для слоев M–2,M–3,
…,1 вычисление частных производных
критерияJпо элементам
матриц весовых коэффициентов выполняется
аналогично. В итоге получаем следующую
общую формулу:

(3.15)

где r– номер слоя

На рис. 3.6 представлена схема вычислений,
соответствующая выражению (3.15).

Рис. 3.6

На этой схеме символом * обозначена
операция поэлементного умножения
векторов, а символом ** – умножение
вектора наa^T;
символ, обозначающий номер элемента
выборки, для краткости опущен.

Характеристика методов обучения

Методы,
используемые при обучении нейронных
сетей, во многом аналогичны методам
определения экстремума функции нескольких
переменных. В свою очередь, последние
делятся на 3 категории – методы нулевого,
первого и второго порядка.

В методах нулевого порядкадля
нахождения экстремума используется
только информация о значениях функции
в заданных точках.

В методах первого порядкаиспользуетсяградиент функционала ошибкипо
настраиваемым параметрам

(3.16)

где
– вектор параметров;– параметр скорости обучения;–
градиент функционала, соответствующие
итерации с номеромk.

Вектор в направлении, противоположном
градиенту, указывает направление
кратчайшего спуска по поверхности
функционала ошибки. Если реализуется
движение в этом направлении, то ошибка
будет уменьшаться. Последовательность
таких шагов в конце концов приведет к
значениям настраиваемых параметров,
обеспечивающим минимум функционала.
Определенную трудность здесь вызывает
выбор параметра скорости обучения
.
При большом значении параметрасходимость будет быстрой, но существует
опасность пропустить решение или уйти
в неправильном направлении. Классическим
примером является ситуация, когда
алгоритм очень медленно продвигается
по узкому оврагу с крутыми склонами,
перепрыгивая с одного на другой. Напротив,
при малом шаге, вероятно, будет выбрано
верное направление, однако при этом
потребуется очень много итераций. В
зависимости от принятого алгоритма
параметр скорости обучения может быть
постоянным или переменным. Правильный
выбор этого параметра зависит от
конкретной задачи и обычно осуществляется
опытным путем; в случае переменного
параметра его значение уменьшается по
мере приближения к минимуму функционала.

В алгоритмах сопряженного градиента[12] поиск минимума выполняется вдоль

сопряженных направлений, что
обеспечивает обычно более быструю
сходимость, чем
при наискорейшем
спуске. Все алгоритмы сопряженных
градиентов на первой итерации начинают
движение в направлении антиградиента

(3.17)

Тогда
направление следующего движения
определяется так, чтобы оно было сопряжено

с предыдущим.
Соответствующее выражение для нового
направления движения является комбинацией
нового направления наискорейшего спуска
и предыдущего направления:

(3.18)

Здесь
– направление движения,–
градиент функционала ошибки,– коэффициент соответствуют итерации
с номеромk. Когда направление спуска
определено,
то новое значение вектора
настраиваемых параметроввычисляется по формуле

. (3.19)

Методы второго порядка требуют
знания вторых производных функционала
ошибки.
К методам второго порядка
относится метод Ньютона. Основной шаг
метода Ньютона определяется по формуле

, (3.20)

где
– вектор значений параметров наk-й
итерации; H– матрица вторых частных
производных целевой функции, или матрица
Гессе;– вектор градиента наk-й итерации.
Во многих случаях метод Ньютона сходится
быстрее, чем методы сопряженного
градиента, но требует больших затрат
из-за вычисления гессиана. Для того
чтобы избежать вычисления матрицы
Гессе, предлагаются различные способы
ее замены приближенными выражениями,
что порождает так называемыеквазиньютоновыалгоритмы(алгоритм метода секущих
плоскостей OSS [1], алгоритм LM Левенберга
– Марквардта [17]).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Нейронная сеть

Искусственные нейронные сети связаны регулируемыми весами соединения многих нейронов, они обладают характеристиками крупномасштабной параллельной обработки, распределенного хранения информации и хорошими способностями к самоорганизации и самообучению.

---

• BP нейронная сеть
  Нейронная сеть BP — это многоуровневая сеть с прямой связью, обученная по алгоритму обратного распространения ошибок, которая является одной из наиболее широко используемых моделей нейронных сетей. Сеть BP может изучать и хранить большое количество отношений отображения режимов ввода-вывода, не раскрывая математических уравнений, заранее описывающих такие отношения отображения.

  Модель нейрона

  В этой модели нейрон получает входные сигналы от n других нейронов. Эти входные сигналы передаются через взвешенные соединения. Общее входное значение, полученное нейроном, будет сравниваться с пороговым значением нейрона, а затем Обработано функцией активации, чтобы произвести выход нейрона.
  

  Общие функции активации

  Вид функции активации
  

  Нейронная сеть

  Нейронная сеть связана многими такими нейронами в определенной иерархической структуре.

  Перцептроны и многослойные сети

  Персептрон состоит из двух слоев нейронов
  
  Веса и пороги могут быть получены с помощью обучения. Пороги могут рассматриваться как узлы с фиксированным вводом -1, так что изучение весов и порогов может быть объединено с изучением весов.
  
  Преимущества и недостатки персептрона: перцептрон имеет только нейроны выходного слоя для обработки функции активации, только один слой функциональных нейронов, ограниченную способность к обучению и не может решить проблему нелинейной отделимости. Но это применимо к линейно разделимым моделям.
  Многослойная нейронная сеть с прямой связью — это более общая структура нейронной сети, в которой нет соединений на одном уровне или межуровневых соединений между нейронами.

  Алгоритм обратного распространения ошибок

  Алгоритм обратного распространения ошибок называется алгоритмом BP, а весовые коэффициенты обновляются в примечаниях.
  Стандартный алгоритм BP предназначен только для одной выборки за раз, и параметры часто обновляются. Обновление параметров может быть смещено для разных выборок. Следовательно, для одновременного достижения минимальной ошибки часто требуется несколько итераций. Алгоритм накопленного BP направлен на минимизацию совокупной ошибки, а параметры обновляются только после считывания всего обучающего набора.
  Количество скрытых нейронов обычно устанавливается методом проб и ошибок.

  Глобальный минимум и локальный минимум

  Метод градиентного спуска — наш обычно используемый метод оптимизации: он быстрее всего идет по методу отрицательного градиента, но если градиент текущей точки равен нулю, он достиг локального минимума, но нельзя гарантировать, что это глобальный минимум. Обычно мы используем следующий метод, чтобы выпрыгнуть из локального минимума, чтобы на шаг приблизиться к глобальному минимуму.
  

  Другие распространенные нейронные сети

  Другими распространенными нейронными сетями являются сети RBF и сети ART, см. «Машинное обучение» Zhou Zhihua P108

  BP Network Toolbox

  Решение проблем с использованием сети BP можно разделить на следующие модули
  1) Ввод данных
  2) Нормализация данных
  3) Сетевое обучение
  4) Имитация исходных данных
  5) Сравните исходные данные с известным образцом
  6) Имитация новых данных
  Ниже приведен пример
  Использование набора инструментов

% clc
% Необработанных данных 
 % Людей (единица измерения: 10000 человек)
sqrs=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 ...
       41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
 % Автомобили (Единица: 10000)
sqjdcs=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6...
        2.7 2.85 2.95 3.1];
 % Площадь шоссе (единица измерения: 10000 квадратных километров)
sqglmj=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 ... 
         0.56 0.59 0.59 0.67 0.69 0.79];
 % Пассажирские перевозки по шоссе (единица измерения: 10000 человек)
glkyl=[5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 ...
        22598 25107 33442 36836 40548 42927 43462];
 % Объем автомобильных перевозок (единица измерения: 10000 тонн)
glhyl=[1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 ...
        13320 16762 18673 20724 20803 21804];
 p = [sqrs; sqjdcs; sqglmj];% входной матрицы данных
 t = [glkyl; glhyl];% целевой матрицы данных
 % Используйте функцию premnmx для нормализации данных
 [pn, minp, maxp, tn, mint, maxt] = premnmx (p, t);% нормализует входную матрицу p и выходную матрицу t
dx=[-1,1;-1,1;-1,1];% Минимальное значение после нормализации1, Максимум1
 Обучение сети% BP
net=newff(dx,[3,7,2],{'tansig','tansig','purelin'},'traingdx');% Постройте модель и тренируйте ее с градиентным спуском.
net.trainParam.show=1000;               %1000Результаты цикла показывают один раз
net.trainParam.Lr=0.05;% Скорость обучения0.05
net.trainParam.epochs=50000;% Максимальный тренировочный цикл50000второстепенный
net.trainParam.goal=0.65*10^(-3);% Среднеквадратичная ошибка
 net = train (net, pn, tn);% Начать обучение, где pn, tn - входные и выходные выборки соответственно
 % Использование необработанных данных для моделирования сети BP
 an = sim (net, pn);% используют обученную модель для симуляции
 a = postmnmx (an, mint, maxt);% восстанавливает данные моделирования до первоначального порядка;
 % В этом примере используются обучающие данные для тестирования из-за ограниченного размера выборки, и, как правило, их необходимо проверять на свежих данных
x=1990:2009;
newk=a(1,:);
newh=a(2,:);
figure (2);
subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+')% Составление сравнительной схемы пассажирских перевозок по автомагистралям;
legend(«Сеть вывода пассажиропотока»,«Фактический пассажиропоток»);
xlabel(«Год»);ylabel(«Пассажирские перевозки / 10000 человек»);
subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+')% Нарисуйте сравнительный график объема автомобильных перевозок;
legend(«Сеть исходящих грузов»,«Фактический объем перевозки»);
xlabel(«Год»);ylabel(«Объем груза / 10 000 тонн»);
 % Использовать обученную сеть для прогнозирования
 % При использовании обученной сети для прогнозирования новых данных pnew, они также должны обрабатываться соответствующим образом:
pnew=[73.39 75.55
      3.9635 4.0975
      0.9880 1.0268];           %2010Год и2011Соответствующие данные за год;
 pnewn = tramnmx (pnew, minp, maxp);% используют параметры нормализации исходных входных данных для нормализации новых данных;
 anewn = sim (net, pnewn);% используют нормализованные данные для моделирования;
 anew = postmnmx (anewn, mint, maxt)% восстанавливает данные моделирования до первоначального порядка;

Исходный код

% clc% очистить экран
% clear all;% clear memory для ускорения вычислений
% закрыть все;% закрыть все текущие изображения фигур
Применение% MATLAB в математическом моделировании P121
SamNum=20;                  % Количество входных отсчетов составляет 20
TestSamNum=20;              % Размер тестовой выборки также составляет 20
ForcastSamNum=2;            % Прогнозируемого размера выборки составляет 2
HiddenUnitNum=8;            % Количество скрытых узлов в среднем слое равно 8, что на один больше, чем в программе панели инструментов.
InDim=3;                    % Размер сетевого входа равен 3
OutDim=2;                   % Выходной размер сети равен 2

% Необработанных данных 
% Людей (единица измерения: 10000 человек)
sqrs=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 ...
       41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
% Автомобили (Единица: 10000)
sqjdcs=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6...
        2.7 2.85 2.95 3.1];
% Площадь шоссе (единица измерения: 10000 квадратных километров)
sqglmj=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 ... 
         0.56 0.59 0.59 0.67 0.69 0.79];
% Пассажирские перевозки по шоссе (единица измерения: 10000 человек)
glkyl=[5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 ...
        22598 25107 33442 36836 40548 42927 43462];
% Объем автомобильных перевозок (единица измерения: 10000 тонн)
glhyl=[1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 ...
        13320 16762 18673 20724 20803 21804];
p=[sqrs;sqjdcs;sqglmj];  % Матрицы входных данных
t=[glkyl;glhyl];           % Целевая матрица данных
[SamIn,minp,maxp,tn,mint,maxt]=premnmx(p,t); % Исходная выборка пары (вход и выход) инициализации

rand('state',sum(100*clock))   % Генерация случайного числа на основе системного тактового сигнала         
NoiseVar=0.01;                    % Интенсивность шума составляет 0,01 (целью добавления шума является предотвращение перегрузки сети)
Noise=NoiseVar*randn(2,SamNum);   % Произведенного шума
SamOut=tn + Noise;                   % Добавить шум к выходным выборкам

TestSamIn=SamIn;                           % Входная выборка здесь такая же, как тестовая выборка, потому что размер выборки слишком мал
TestSamOut=SamOut;                         % Также возьмите тот же выходной образец, что и тестовый образец.

MaxEpochs=50000;                              % Максимальное время тренировки составляет 50000
lr=0.035;                                       % Коэффициент обучения составляет 0,035
E0=0.65*10^(-3);                              % Целевая ошибка 0,65 * 10 ^ (-3)
W1=0.5*rand(HiddenUnitNum,InDim)-0.1;   % Инициализация веса между входным слоем и скрытым слоем
B1=0.5*rand(HiddenUnitNum,1)-0.1;       % Инициализировать порог между входным слоем и скрытым слоем
W2=0.5*rand(OutDim,HiddenUnitNum)-0.1; % Инициализировать вес между выходным слоем и скрытым слоем              
B2=0.5*rand(OutDim,1)-0.1;                % Инициализировать порог между выходным слоем и скрытым слоем

ErrHistory=[];                              % Предварительно занимает память для промежуточных переменных
for i=1:MaxEpochs

    HiddenOut=logsig(W1*SamIn+repmat(B1,1,SamNum)); % Скрытый сетевой выход
    NetworkOut=W2*HiddenOut+repmat(B2,1,SamNum);    % Выходного уровня сетевого выхода
    Error=SamOut-NetworkOut;                       Разница в% между фактическим выходом и выходом сети
    SSE=sumsqr(Error)                               Функция% энергии (сумма квадратов ошибок)

    ErrHistory=[ErrHistory SSE];

    if SSE<E0,break, end      % Если требование ошибки достигнуто, цикл обучения пропускается

    % Следующие шесть строк являются основными программами сети BP
    % Они являются динамическими корректировками для каждого шага веса (порога) на основе принципа отрицательного градиентного спуска энергетической функции.
    Delta2=Error;
    Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);    

    dW2=Delta2*HiddenOut';
    dB2=Delta2*ones(SamNum,1);

    dW1=Delta1*SamIn';
    dB1=Delta1*ones(SamNum,1);
    % Исправьте вес и порог между выходным слоем и скрытым слоем
    W2=W2+lr*dW2;
    B2=B2+lr*dB2;
    % Исправить вес и порог между входным слоем и скрытым слоем
    W1=W1+lr*dW1;
    B1=B1+lr*dB1;
end

HiddenOut=logsig(W1*SamIn+repmat(B1,1,TestSamNum)); % Скрытый слой выводит конечный результат
NetworkOut=W2*HiddenOut+repmat(B2,1,TestSamNum);    % Выходной слой выходной конечный результат
a=postmnmx(NetworkOut,mint,maxt);               % Восстановление результата сетевого уровня вывода
x=1990:2009;                                        % Шкала времени
newk=a(1,:);                                        % Выходной пассажиропоток сети
newh=a(2,:);                                        % Выходной сети
figure ;
subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+')    % Рисует сравнительную диаграмму пассажирских перевозок по шоссе;
legend(«Сеть вывода пассажиропотока»,«Фактический пассажиропоток»);
xlabel(«Год»);ylabel(«Пассажирские перевозки / 10000 человек»);
subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+')     % Нарисуйте сравнительную диаграмму объема автомобильных перевозок;
legend(«Сеть исходящих грузов»,«Фактический объем перевозки»);
xlabel(«Год»);ylabel(«Объем груза / 10 000 тонн»);

% Делать прогнозы, используя обученную сеть
% При использовании обученной сети для прогнозирования новых данных, они также должны обрабатываться соответствующим образом.
pnew=[73.39 75.55
      3.9635 4.0975
      0.9880 1.0268];                     % Соответствующие данные за 2010 и 2011 годы;
pnewn=tramnmx(pnew,minp,maxp);         % Используйте параметры нормализации исходных входных данных для нормализации новых данных;
HiddenOut=logsig(W1*pnewn+repmat(B1,1,ForcastSamNum)); % Результатов прогнозирования скрытого слоя
anewn=W2*HiddenOut+repmat(B2,1,ForcastSamNum);           % Выходного уровня выходного прогнозирования результата

% Восстановление данных, предсказанных сетью, до первоначального порядка;
anew=postmnmx(anewn,mint,maxt)