Pdop при спутниковых измерениях характеризует ошибки - Ремонт и установка крупной бытовой техники

Что такое показатели точности позиционирования в ГНСС?

Параметр Dop используется в сфере систем глобального позиционирования для описания геометрического положения небесных тел относительно принимаемого аппарата.Если спутники будут находиться в непосредственной близости друг к другу, то это означает, что геометрия расположения данных спутников является “слабой”, то есть величина dop будет больше среднего.Данный факт действует и наоборот, то есть если спутники расположены относительно друг друга далеко, то можно судить о том, что геометрия расположения данных спутников является “сильной”, это означает что величина dop будет меньше среднего. Позиционирование спутников, это не единственная область применения данного понятия, этот комплекс работает и в иных системах местности, принимающий в себя иные географические пункты.

Влияние условий снижающие точность:

траектория спутников;

под действием атмосферы;

присутствие предметов преград, заграждающие необходимую секцию в небосводе;

понижение безошибочности наблюдается в последствии отражения радиоволны.

Характеристики:

HDOP — показатель качества пространственной засечки в горизонтальной поверхности,

VDOP — показатель качества пространственной засечки в вертикальной поверхности,

PDOP — показатель качества пространственной засечки по месторасположению,

TDOP — показатель качества пространственной засечки по времени,

GDOP — суммарный геометрический показатель точности позиционирования по местоположению и времени.

Данные характеристики являются функциями ковариационной матрицы, которые состоят из частей глобальной системы координат и локальной системы координат. С помощью математики выявляют по местоположению работающих спутников (навигационный сигнал, то есть источник излучения). Много GPS приборов принимающий сигналы способны отобразить в данный момент времени положение абсолютно каждого небесного спутника («созвездие спутников») вместе с величиной DOP. Однако получим это: PDOP 2=HDOP 2+VDOP 2 и GDOP 2=PDOP 2+TDOP 2. Требуется знать, то что описано сверху действует не только для GPS комплексов, но и, к примеру, для систем электронного сопротивления, при выявлении положения источников излучения противника, такие системы постановки помех или простейшие комплексов радиосвязи.

Величина DOP:

Меньше либо равна единицы, абсолютная безошибочность (рекомендовано использовать там, где требуется максимальная точность);

1-4, превосходная точность (такая точность нужна в аппаратуре с высокой чувствительностью и программах);

5-7, нормальная точность (с помощью этих данных можно сделать выводы о результатах, но не стоит на них сильно рассчитывать. Выявленные данные могут быть применены в вычислениях);

7-8, точность ниже среднего (Данные могут применяться в дальнейших расчетах, но нужно со временем повысить безошибочность, к примеру, производить отсчеты на просторной площадке);

8-19, посредственная точность (Полученные значения нельзя воспринимать всерьез, их можно использовать для приближенного определения местоположения);

24-51, ужасная точность (Выходная точность очень низкая. Такие результаты не следует даже рассматривать их нужно сразу отбросить).

Многие приборы, которые принимают сигнал GPS могут выявлять число зафиксированных спутников, также и расположение спутников в небосводе. Данные возможности позволяют сделать вывод исполнителю, возникают ли проблемы со связью с каким либо спутником, неопределенность в значениях при передвижении всего лишь на 2-3 метра в сторону. Фирма производящие большое количество оборудования, делают выводы о безошибочности выявленных значений, которые на прямую зависит от большого количество разных условий. Чтобы узнать качества геометрического положения спутников за частую используются данные DOP.

В зависимости от того, какие условия нужно использовать для вычисления данных DOP, возможны самые различные варианты, вот основные:

GDOP- полная точность; 3D-координаты и время

PDOP- точность положения; 3D-координаты

TDOP- Точность временная; время

HDOP- горизонтальная точность; 2D-координаты

VDOP- вертикальная точность; высота

Размещено: 22.03.2017

Источник

From Wikipedia, the free encyclopedia

Dilution of precision (DOP), or geometric dilution of precision (GDOP), is a term used in satellite navigation and geomatics engineering to specify the error propagation as a mathematical effect of navigation satellite geometry on positional measurement precision.

Understanding the geometric dilution of precision (GDOP) with a simple example. In A someone has measured the distance to two landmarks, and plotted their point as the intersection of two circles with the measured radius. In B the measurement has some error bounds, and their true location will lie anywhere in the green area. In C the measurement error is the same, but the error on their position has grown considerably due to the arrangement of the landmarks.

Navigation satellites with poor geometry for geometric dilution of precision (GDOP).

Navigation satellites with good geometry for geometric dilution of precision (GDOP).

Introduction[edit]

The concept of dilution of precision (DOP) originated with users of the Loran-C navigation system.^[1] The idea of geometric DOP is to state how errors in the measurement will affect the final state estimation. This can be defined as:^[2]

${displaystyle operatorname {GDOP} ={frac {Delta ({text{output location}})}{Delta ({text{measured data}})}}}$

Conceptually you can geometrically imagine errors on a measurement resulting in the ${displaystyle Delta ({text{measured data}})}$ term changing. Ideally small changes in the measured data will not result in large changes in output location. The opposite of this ideal is the situation where the solution is very sensitive to measurement errors. The interpretation of this formula is shown in the figure to the right, showing two possible scenarios with acceptable and poor GDOP.

More recently, the term has come into much wider usage with the development and adoption of GPS. Neglecting ionospheric ^[3] and tropospheric^[4] effects, the signal from navigation satellites has a fixed precision. Therefore, the relative satellite-receiver geometry plays a major role in determining the precision of estimated positions and times. Due to the relative geometry of any given satellite to a receiver, the precision in the pseudorange of the satellite translates to a corresponding component in each of the four dimensions of position measured by the receiver (i.e., $x$ , $y$ , $z$ , and $t$ ). The precision of multiple satellites in view of a receiver combine according to the relative position of the satellites to determine the level of precision in each dimension of the receiver measurement. When visible navigation satellites are close together in the sky, the geometry is said to be weak and the DOP value is high; when far apart, the geometry is strong and the DOP value is low. Consider two overlapping rings, or annuli, of different centres. If they overlap at right angles, the greatest extent of the overlap is much smaller than if they overlap in near parallel. Thus a low DOP value represents a better positional precision due to the wider angular separation between the satellites used to calculate a unit’s position. Other factors that can increase the effective DOP are obstructions such as nearby mountains or buildings.

DOP can be expressed as a number of separate measurements:

HDOP: Horizontal dilution of precision
VDOP: Vertical dilution of precision
PDOP: Position (3D) dilution of precision
TDOP: Time dilution of precision
GDOP: Geometric dilution of precision

These values follow mathematically from the positions of the usable satellites. Signal receivers allow the display of these positions (skyplot) as well as the DOP values.

The term can also be applied to other location systems that employ several geographical spaced sites. It can occur in electronic-counter-counter-measures (electronic warfare) when computing the location of enemy emitters (radar jammers and radio communications devices). Using such an interferometry technique can provide certain geometric layout where there are degrees of freedom that cannot be accounted for due to inadequate configurations.

The effect of geometry of the satellites on position error is called geometric dilution of precision (GDOP) and it is roughly interpreted as ratio of position error to the range error. Imagine that a square pyramid is formed by lines joining four satellites with the receiver at the tip of the pyramid. The larger the volume of the pyramid, the better (lower) the value of GDOP; the smaller its volume, the worse (higher) the value of GDOP will be. Similarly, the greater the number of satellites, the better the value of GDOP.

Interpretation[edit]

DOP value	Rating^[5]	Description
<1	Ideal	Highest possible confidence level to be used for applications demanding the highest possible precision at all times.
1–2	Excellent	At this confidence level, positional measurements are considered accurate enough to meet all but the most sensitive applications.
2–5	Good	Represents a level that marks the minimum appropriate for making accurate decisions. Positional measurements could be used to make reliable in-route navigation suggestions to the user.
5–10	Moderate	Positional measurements could be used for calculations, but the fix quality could still be improved. A more open view of the sky is recommended.
10–20	Fair	Represents a low confidence level. Positional measurements should be discarded or used only to indicate a very rough estimate of the current location.
>20	Poor	At this level, measurements should be discarded.

The DOP factors are functions of the diagonal elements of the covariance matrix of the parameters, expressed either in a global or a local geodetic frame.

Computation[edit]

As a first step in computing DOP, consider the unit vectors from the receiver to satellite i:

${displaystyle {begin{aligned}&left({frac {x_{i}-x}{R_{i}}},{frac {y_{i}-y}{R_{i}}},{frac {z_{i}-z}{R_{i}}}right),&R_{i}&={sqrt {(x_{i}-x)^{2}+(y_{i}-y)^{2}+(z_{i}-z)^{2}}}end{aligned}}}$

where $x, y, z$ denote the position of the receiver and $x_{i},y_{i},z_{i}$ denote the position of satellite i. Formulate the matrix, A, which (for 4 pseudorange measurement residual equations) is:

${displaystyle A={begin{bmatrix}{frac {x_{1}-x}{R_{1}}}&{frac {y_{1}-y}{R_{1}}}&{frac {z_{1}-z}{R_{1}}}&1\{frac {x_{2}-x}{R_{2}}}&{frac {y_{2}-y}{R_{2}}}&{frac {z_{2}-z}{R_{2}}}&1\{frac {x_{3}-x}{R_{3}}}&{frac {y_{3}-y}{R_{3}}}&{frac {z_{3}-z}{R_{3}}}&1\{frac {x_{4}-x}{R_{4}}}&{frac {y_{4}-y}{R_{4}}}&{frac {z_{4}-z}{R_{4}}}&1end{bmatrix}}}$

The first three elements of each row of A are the components of a unit vector from the receiver to the indicated satellite. The last element of each row refers to the partial derivative of pseudorange w.r.t. receiver’s clock bias.
Formulate the matrix, Q, as the covariance matrix resulting from the least-squares normal matrix:

${displaystyle Q=left(A^{mathsf {T}}Aright)^{-1}}$

In general:

${displaystyle Q=left(J_{mathsf {x}}^{mathsf {T}}left(J_{d}C_{d}J_{d}^{mathsf {T}}right)^{-1}J_{x}right)^{-1}}$

where ${displaystyle J_{x}}$ is the Jacobian of the sensor measurement residual equations ${displaystyle f_{i}left({underline {x}},{underline {d}}right)=0}$ , with respect to the unknowns, ${underline {x}}$ ; ${displaystyle J_{d}}$ is the Jacobian of the sensor measurement residual equations with respect to the measured quantities ${displaystyle {underline {d}}}$ , and $C_{d}$ is the correlation matrix for noise in the measured quantities.

For the preceding case of 4 range measurement residual equations: ${displaystyle {underline {x}}=(x,y,z,tau )^{mathsf {T}}}$ , ${displaystyle {underline {d}}=left(tau _{1},tau _{2},tau _{3},tau _{4}right)^{mathsf {T}}}$ , ${displaystyle tau =ct}$ , ${displaystyle tau _{i}=ct_{i}}$ , ${displaystyle R_{i}=|tau _{i}-tau |={sqrt {(tau _{i}-tau )^{2}}}}$ , ${displaystyle f_{i}left({underline {x}},{underline {d}}right)={sqrt {(x_{i}-x)^{2}+(y_{i}-y)^{2}+(z_{i}-z)^{2}}}-{sqrt {(tau _{i}-tau )^{2}}}}$ , ${displaystyle J_{x}=A}$ , ${displaystyle J_{d}=-I}$ and the measurement noises for the different ${displaystyle tau _{i}}$ have been assumed to be independent which makes ${displaystyle C_{d}=I}$ .

This formula for Q arises from applying best linear unbiased estimation to a linearized version of the sensor measurement residual equations about the current solution ${displaystyle Delta {underline {x}}=-Q*left(J_{x}^{mathsf {T}}left(J_{d}C_{d}J_{d}^{mathsf {T}}right)^{-1}fright)}$ , except in the case of B.L.U.E. $C_{d}$ is a noise covariance matrix rather than the noise correlation matrix used in DOP, and the reason DOP makes this substitution is to obtain a relative error. When $C_{d}$ is a noise covariance matrix, $Q$ is an estimate of the matrix of covariance of noise in the unknowns due to the noise in the measured quantities. It is the estimate obtained by the first-order second moment (F.O.S.M.) uncertainty quantification technique which was state of the art in the 1980s. In order for the F.O.S.M. theory to be strictly applicable, either the input noise distributions need to be Gaussian or the measurement noise standard deviations need to be small relative to rate of change in the output near the solution. In this context, the second criteria is typically the one that is satisfied.

This (i.e. for the 4 time of arrival/range measurement residual equations) computation is in accordance with [6] where the weighting matrix,
${displaystyle P=left(J_{d}C_{d}J_{d}^{mathsf {T}}right)^{-1}}$ happens to simplify down to the identity matrix.

Note that P only simplifies down to the identity matrix because all the sensor measurement residual equations are time of arrival (pseudo range) equations. In other cases, for example when trying to locate someone broadcasting on an international distress frequency, $P$ would not simplify down to the identity matrix and in that case there would be a «frequency DOP» or FDOP component either in addition to or in place of the TDOP component. (Regarding «in place of the TDOP component»: Since the clocks on the legacy International Cospas-Sarsat Programme LEO satellites are much less accurate than GPS clocks, discarding their time measurements would actually increase the geolocation solution accuracy.)

The elements of $Q$ are designated as:

${displaystyle Q={begin{bmatrix}sigma _{x}^{2}&sigma _{xy}&sigma _{xz}&sigma _{xt}\sigma _{xy}&sigma _{y}^{2}&sigma _{yz}&sigma _{yt}\sigma _{xz}&sigma _{yz}&sigma _{z}^{2}&sigma _{zt}\sigma _{xt}&sigma _{yt}&sigma _{zt}&sigma _{t}^{2}end{bmatrix}}}$

PDOP, TDOP, and GDOP are given by:^[6]

${displaystyle {begin{aligned}operatorname {PDOP} &={sqrt {sigma _{x}^{2}+sigma _{y}^{2}+sigma _{z}^{2}}}\operatorname {TDOP} &={sqrt {sigma _{t}^{2}}}\operatorname {GDOP} &={sqrt {operatorname {PDOP} ^{2}+operatorname {TDOP} ^{2}}}\end{aligned}}}$

Notice GDOP is the square root of the trace of the $Q$ matrix.

The horizontal and vertical dilution of precision,

${displaystyle {begin{aligned}operatorname {HDOP} &={sqrt {sigma _{n}^{2}+sigma _{e}^{2}}}\operatorname {VDOP} &={sqrt {sigma _{u}^{2}}}end{aligned}}}$ ,

are both dependent on the coordinate system used. To correspond to the local horizon plane and the local vertical in either a north, east, up coordinate system.

EDOP^2   x      x      x
 x     NDOP^2   x      x
 x       x    VDOP^2   x
 x       x      x    TDOP^2

derived DOPs:

${displaystyle {begin{aligned}operatorname {GDOP} &={sqrt {operatorname {EDOP} ^{2}+operatorname {NDOP} ^{2}+operatorname {VDOP} ^{2}+operatorname {TDOP} ^{2}}}\operatorname {HDOP} &={sqrt {operatorname {EDOP} ^{2}+operatorname {NDOP} ^{2}}}\operatorname {PDOP} &={sqrt {operatorname {EDOP} ^{2}+operatorname {NDOP} ^{2}+operatorname {VDOP} ^{2}}}end{aligned}}}$

References[edit]

^
Richard B. Langley (May 1999). «Dilution of Precision» (PDF). GPS World. Archived (PDF) from the original on 2011-10-04. Retrieved 2011-10-12.
^
Dudek, Gregory; Jenkin, Michael (2000). Computational Principles of Mobile Robotics. Cambridge University Press. ISBN 0-521-56876-5.
^ Paul Kintner, Cornell University; Todd Humphreys; University of Texas-Austin; Joanna Hinks; Cornell University (July–August 2009). «GNSS and Ionospheric Scintillation: How to Survive the Next Solar Maximum». Inside GNSS. Archived from the original on 2011-11-06. Retrieved 2011-10-12.
^ «GPS errors (Trimble tutorial)». Archived from the original on 2016-03-07. Retrieved 2016-02-08.
^ Isik, Oguz Kagan; Hong, Juhyeon; Petrunin, Ivan; Tsourdos, Antonios (25 August 2020). «Integrity Analysis for GPS-Based Navigation of UAVs in Urban Environment». Robotics. 9 (3): 66. doi:10.3390/robotics9030066.
^ Section 1.4.9 of Principles of Satellite Positioning.

Further reading[edit]

DOP Factors
manually calculating GDOP
HDOP AND GPS HORIZONTAL POSITION ERRORS

Article on DOP and Trimble’s program: Determining Local GPS Satellite Geometry Effects On Position Accuracy.
Notes & GIF image on manually calculating GDOP: Geographer’s Craft
GPS Errors & Estimating Your Receiver’s Accuracy: Sam Wormley’s GPS Accuracy Web Page
GPS Accuracy, Errors & Precision: Radio-Electronics.com Archived 2014-02-22 at the Wayback Machine

Источник

no-translate-detected_318-51485 Ниже приведу краткий набор теоретических знаний, которые помогут при работе с GPS оборудованием.

О том что такое GPS, про всякие там спутники, частоты и т.д. – почитаете в интернете.

Мы будем заниматься конкретными вещами, необходимыми для успешной съемки.

Виды GPS-оборудования

Навигатор туристический. Это все, что встроено в телефоны, навигаторы Garmin и прочие туристические приблуды. Реальная точность таких приборов 5-30 метров. Подходят для поиска дороги, пунктов и т.д. Топографическую съемку такими приборами делать нельзя, но можно использовать для сбора ГИС-данных, где точность 5-30 м допустима
Одночастотные (L1) GPS – это приборы, которые работают только по первой базовой частоте. С них начиналась эра GPS-приемников. По факту – работают медленне, чем другие приборы. Подходят только для измерений по созданию геодезической основы. Работают ими методом «статика». В изысканиях могут использоваться, чтобы привязать наши заложенные репера к пунктам геодезической основы.
Двухчастотные (L1+L2) – более совершенные приборы. Используются для того же, что и приборы на L1, но работают быстрее и более точные.
Двухчастотные с поддержкой RTK – на сегодняшний день одни из самых современных приборов. Позволяют кроме привязки реперов полноценно проводить топографическую съемку местности.

Что влияет на качество сигнала GPS?

Понижают качество измерений следующие факторы:

Наличие препятствий вокруг приемника (строений, деревьев).

Каждый приемник обычно показывает количество спутников, сигнал от которых он принимает. В теории для работы приемника достаочно 4 общих спутника (общих для базы и ровера). На практике при числе спутников:

Число спутников	Действия
меньше 6	Нельзя проводить измерения. Надо дождаться повышения кол-ва спутников или поменять позицию
6-8	Можно начинать работать, но время измерений желательно увеличить
9 и более	Нормальное кол-во

Так что GPS могут хуже работать в лесу, между домами, которые закрывают горизонт прибору и т.д. Также если вы устанавливаете GPS на пункте триангуляции, где сохранилась металлическая пирамида – увеличте время стояния. Металл над антенной GPS тоже плохо влияет на измерения.

Объекты создающие активные помехи

Объекты, которые формируют вокруг себя электромагнитное поле – негативно влияют на прием сигналов GPS. К таким объектам относятся линии электропередач, активные радары аэропортов и военных объектов, промышленное электронное мощное оборудование.

То есть лучше избегать ставить GPS под линиями электропередач.

Геометрический фактор PDOP

PDOP – это коэффициент, который показывает «насколько хорошо GPS сейчас работается»

Это основной параметр, который отображается во многих GPS приборах

Значения PDOP:

1-3 Хорошее качество можно работать

3-7 Удовлетворительное качество, но лучше увеличить время сеанса на 50%

7 и более Плохое качество. Измерения могут не обработаться.

Режимы работы GPS

«Статика» (Static)

Метод статических определений.

Наиболее точный из всех методов. Позволяет получить милиметровую точность.

Используется для передачи координат от извесных пунктов к определяемым пунктам. Минимальный комплект приемников: 2 штуки. Один из приемников называют «база», второй «ровер». Базовый приемник устанавливается над пунктом с известными координатами. Замеряется его высота над точкой и он включается. Затем второй приемник (ровер) устанавливается на объекте над точкой, координаты которой мы хотим узнать. Приемники работают некоторое время. После измерений ровер переставляют на другие определяемые точки и повторяют наблюдения. Потом данные обрабатывают на компьютере и получают координаты определяемых точек. При этом измерения можно вводить в «сеть». Например провести насколько сеансов в разное время с разных пунктов, разными приемниками – свести их в единую сеть на компютере, обсчитать и уравнять.

Цепочка информации будет выглядеть так:

Координаты исходного пункта
Сеанс наблюдений (GPS база + ровер)
Обработка на компьютере
Координаты определяемых пунктов

Тут критически важно знать, что время измерений – это время в течении которого работают оба приемника (совместно). Именно совместная работа приемников с наличием общих спутников потом позволит получить координаты точек. От одной базы может работать множество роверов.

Пример временной записи:

В этом примере всего процесс занял у нас 2 часа (12-14), но полезное время совместных измерений было только 30 минут (12:30 – 13:30).

Надо указать, что расстояние между базой и ровером для приемников L1 не должно превышать 20км, а для приемников L2 – до 50 км. Измерения при базисе больше 50 км для приборов L2 проводить можно, но они обрабатываются в специальных программах.

Ограничение по расстоянию связано с кривизной земли и наличием общих спутников во время сеанса наблюдений. Однако стоит сказать, что когда я работал в аэрофотосъемке — мы используя специальные программы и приборы типа L2 обрабатывали базисы в 200-300 км. То есть это возможно, но требует дополнительных знаний.

Расчет времени работы в статике:

Каждая модель GPS приемника имеет обычно свои указания по расчету времени работы. Ниже приведу «примерное» время работы исходя из своего опыта.

Основные параметры влияющие на время сеанса: количество спутников, расстояние между приемниками и PDOP. Обычно достаточно знать расстояние между приемниками для планирования сеанса.

Расчет времени работы в статике приборами L1:

Расстояние	Время сеанса
0-5км	20 мин (лучше 30 мин)
5-10	1 час
10-20	2 часа
20-…	3 часа

Расчет времени работы в статике приборами L2:

Общая формула 10 мин. + 0,5минут на км

Пример: Расстояние бзиса 20 км = 10мин+0,5*20мин = 20мин

2й вариант (более точный)

Кол-во спутников Формула

10 10мин+2мин/км

8 10мин+5мин/км

6 10мин+10мин/км

То есть основное правило:

— Если все хорошо и до пункта менее 10 км – стоим 30 минут

— Если что-то не так – стоим 1..2..3 часа

Режим «Стой-Иди» (Stop&Go)

Режим очень похож на статику с той лишь разницей, что ровер стоит над каждой точкой около 3-х минут и перемещается далее. В приемниках L1 такой режим позволял проводить съемку открытых пространств. С появление RTK режима – теперь практически не используется.

Основные моменты:

Расстояние база ровер – менее 20 км

Время стояния ровером на точке – 3мин

Применяется для топосъемки открытых площадок приемниками L1

Режим RTK (Кинематика в реальном времени)

Основной современный режим съемки GPS оборудованием для проведения топографических съемок.

Надо сказать, что не смотря на наличие такого режима привязку временных реперов и других точных пунктов надо делать в режиме «статика».

Основная идея:

База стоИт над точками с известными координатами и через канал связи передает некие «поправки» роверу. Ровер их принимает и выдает координаты своего местоположения с высокой точностью.

Точность = примерно 1см + 0,5 * Дальность,км

Пример:

При удалении от базы на 20км получим точность ровера

1см + 0,5 * 20км = 11см

Это без учета всех остальных поправок

На практике получаем точность 0,5-5 см.

Каналы передачи данных

Существует насколько каналов по которым база может передавать поправки роверу:

GSM

Поправки передаются через мобильную связь. Для этого в базе и в ровере должны быть вставлены SIM-карточки мобильных операторов с услугой «CSD» (услуга факсимильной передачи данных)

На момент января 2018 г. для оператора МТС эта услуга стоит 1мин=2руб, кроме того теперь для МТС эта услуга называется «пакетная передача данных» и она выдается только юридическим лицам.

Для работы канала нужно мобильное покрытие территории и денюжка на карточках.

iRTK

Поправки передаются через мобильную сеть с выходом в интернет.

Условия для работы как и для GSM канала, но нужны уже просто любые SIM-карты с доступом в интернет и сервер для поддержки и обработки данных.

В среднем база потребляет 1,5мБ в час трафика

То есть при ежедневной работе по 8 часов за 30 дней понадобиться 360мб

При работе по 6 часов за 20 дней — 180мб

NTRIP Работа от базовой станции (БС)

В этом методе в качестве базы используются «базовые станции» сторонних организаций, установленные обычно в городах и «вещающие» свои координаты в эфир. Услуги платные и для работы понадобятся данные доступа к БС. При таком методе для работы вам понадобится только один ровер с контроллером. Очень удобно. Приехали на место, достали GPS, подключились к базовой станции и можно снимать.

Рекомендуемое удаление от БС – до 50км, хотя по факту нормально работали и на удалении 70-90км (точность падала до 2см). При этом базовые станции позволяют работать от них как в режиме RTK (NTRIP), так и в режиме «Статика» с последующей обработкой данных.

Радиомодем

Канал данных, при котором поправки передаются по радио. Бывают встроенные модемы, которые встроены в GPS (мощность до 2-6Вт) и обеспечивают связь на удалении до 1-2х километров от базы. Бывают также модемы внешние (мощностью около 20-35-60Вт), которые подключаются к GPS и обеспечат покрытие до 20-25км. Покрытие сильно зависит от типа местности, наличия строений, леса и т.д.

Надо сказать, что например в Москве и Питере работать по радио на территории города запрещено. Все там работают от базовых станций через мобильную сеть. Также могут быть проблемы при работе на территории аэропортов и военных объектов. Предварительно уточняйте можно ли работать на объекте в радиорежиме. В малонаселенных районах – этот канал передачи поправок основной.

Понятие «Фиксированное решение»

При работе в режиме RTK возникает следующая цепочка передачи информации

Момент, когда ровер успешно принимает поправки от базы и уверенно рассчитывает свои координаты – называется «Фиксированное решение» или в простонародье «Фикса».

Любой контроллер GPS этот момент всегда отображает.

Соответственно правило:

— Есть «фикса» — можно работать и снимать

— Нет «фиксы» — надо ее дождаться, снимать нельзя

Основные моменты когда фикса слетает:

— не работает канал передачи (закончились деньги на СИМ-карточке, далеко отошли от базы, базу спиздили, нет покрытия, сигнал поправок не доходит из-за препятствий)

— Ровер сверху перекрывает какое-то препятствие (крыша строения, трубы, арки, переходы)

— Неверные настройки канал передачи между базой и ровером

Каллибровка района работ

Существует такое понятие, как каллибровка района работ.

В чем суть.

Допустим, что вы приехали на новый объект. У вас есть координаты пунктов на район, но нет параметров перехода от системы WGS-84 (в которой работают приемники) к Системе координат, которая используется на объекте. Для того, чтобы связать WGS-84 и местную систему – используется каллибровка по пунктам. В самом простом случае каллибровка выглядит так:

Последовательно объезжаете известные пункты и какое-то время отстаиваете на них в режиме статики. При этом есть два варианта. 1 – Вы будете саму каллибровку проводить на компьютере после сбора всех данных. 2 – Калибровка может проводиться непосредственно в контроллере (тогда всю работу можно сделать и одним приемником).
После того, как будут отстояны все пункты с известными координатами (их желательно иметь 5-6 штук – данные обрабатываются и рассчитываются параметры перехода между системами координат на весь район, который ограничен отстаиваемыми пунктами.

Калибровку необходимо всегда проводить в новом для вас районе работ, или если вы не уверены в достоверности исходных пунктов. При рассчете станут известны «ошибки» на каждом из пунктов. Таким образом можно будет «вычислить плохие пункты» и исключить их из работы. Каллибровка – процесс ответственный, поэтому перед началом работ надо четко представлять последовательность действий.

В принципе это основные моменты о которых надо знать при работе с GPS-приемниками. Однако надо помнить, что самообразование – залог профессионализма 🙂

Источник

Концепция художника о спутнике GPS Block II-F на орбите

Анализ ошибок для Глобальная система позиционирования важна для понимания того, как работает GPS, и для понимания величины ожидаемых ошибок. GPS вносит поправки на ошибки часов, приемника и другие эффекты, но остаются остаточные ошибки, которые не исправляются. Положение приемника GPS вычисляется на основе данных, полученных со спутников. Ошибки влияния от геометрического снижения точности и показателей, перечисленных в таблице ниже.

Содержание

1 Обзор
2 Измерение времени прихода сигнала
3 Атмосферные эффекты
4 Многолучевые эффекты
5 Эфемериды и ошибки часов
6 Геометрическое снижение точности вычислений (GDOP)
- 6.1 Вычисление геометрического снижения точности
- 6.2 Вывод расчетов геометрического снижения точности
7 Выборочная доступность
8 Антиспуфинг
9 Относительность
- 9.1 Специальная и общая теория относительности
- 9.2 Расчет замедления времени
- 9.3 Искажение Саньяка
10 Естественные источники помех
11 Искусственные источники помех
12 См.
13 Примечания
14 Ссылки
15 Внешние ссылки

Обзор

Источники ошибок эквивалентного диапазона пользователя (UERE)

Источник	Эффект (м)
Поступление сигнал C / A	± 3
Сигнал приход P (Y)	± 0,3
Ионосферные эффекты	± 5
Погрешности эфемерид	± 2,5
Ошибки спутниковых часов	± 2
Многолучевое искажение	± 1
Troposp Герические эффекты	± 0, 5
3 σ R { Displaystyle 3 sigma _ {R}} $3 sigma_R$ C / A	± 6,7
3 σ R { Displaystyle 3 sigma _ {R}} $3 sigma_R$ P (Y)	± 6.0

Диаграмма геометрических погрешностей, показывающая типичное соотношение положения приемника, пересечение сфер, и истинное положение приемника с точки зрения ошибок, PDOP и числовых ошибок

Ошибки эквивалентного диапазона пользователя (UERE) показаны в таблице. Существует также числовая ошибка с точной величиной σ n u m { displaystyle sigma _ {num}} $sigma_ {num}$ около 1 метра. Стандартные отклонения σ R { displaystyle sigma _ {R}} $sigma_R$ для грубого / сбора данных (C / A) и точных кодов также показаны в таблице. Эти стандартные функции вычисляются путем извлечения квадратного корня из суммы квадратов отдельных компонентов (т. Е. RSS для корня из суммы квадратов). Чтобы получить стандартное отклонение оценки местоположения приемника, эти ошибки необходимо умножить на соответствующие члены с понижением точности, а затем объединить RSS с числовой ошибкой. Ошибки электроники — это один из нескольких факторов, снижающих точность перечисленных в таблице выше. Вместе взятые автономные гражданские GPS определения горизонтального положения обычно используют точность примерно до 15 метров (50 футов). Эти эффекты также снижают точность более точного кода P (Y). Определение местоположения гражданского GPS при хорошем обзоре неба составляет около 5 метров (16 футов) по горизонтали.

Термин «ошибка эквивалентного диапазона пользователя» (UERE) относится к компоненту на расстоянии от приемника до спутника. Эти ошибки UER представляют собой ошибки как ±, что они представляют собой несмещенными или нулевыми средними средними. Поэтому эти ошибки UERE используются при вычислении стандартных отклонений. Стандартное отклонение ошибки в положении приемника, σ rc { displaystyle sigma _ {rc}} $sigma_ {rc}$ , вычисляется путем умножения PDOP (снижение точности положения) на σ R { displaystyle sigma _ {R}} $sigma_R$ , стандартное отклонение диапазона, эквивалентного пользователю. σ R { displaystyle sigma _ {R}} $sigma_R$ вычисляется путем извлечения квадратного корня из суммы стандартных отклонений отдельных компонентов.

PDOP вычисляется как функция положения приемника и спутника. Подробное описание того, как рассчитать PDOP, приведено в разделе Геометрическое снижение точности вычислений (GDOP).

σ R { displaystyle sigma _ {R}} $sigma_R$ для C / Код задается следующим образом :

3 σ R = 3 2 + 5 2 + 2,5 2 + 2 2 + 1 2 + 0,5 2 m = 6,7 m { displaystyle 3 sigma _ {R} = { sqrt { 3 ^ {2} + 5 ^ {2} + 2.5 ^ {2} + 2 ^ {2} + 1 ^ {2} + 0.5 ^ {2}}} , mathrm {m} , = , 6.7 , mathrm {m}} $3 sigma_R = sqrt {3 ^ 2 + 5 ^ 2 + 2.5 ^ 2 + 2 ^ 2 + 1 ^ 2 + 0.5 ^ 2} , mathrm {m} , = , 6.7 , mathrm {m}$

Стандартное отклонение ошибки в расчетном положении приемника σ rc { displaystyle sigma _ {rc}} $sigma_ {rc}$ , снова для кода C / A дается выражение:

σ rc = PDOP 2 × σ R 2 + σ число 2 = PDOP 2 × 2,2 2 + 1 2 м { displaystyle sigma _ {rc} = { sqrt {PDOP ^ {2} times sigma _ {R} ^ {2} + sigma _ {num} ^ {2}}} = { sqrt {PDOP ^ {2} times 2.2 ^ {2} + 1 ^ {2}}} , mathrm {m} $sigma_ {rc} = sqrt {PDOP ^ 2 times sigma_R ^ 2 + sigma_ { число} ^ 2} = sqrt {PDOP ^ 2 times 2.2 ^ 2 + 1 ^ 2} , mathrm {m}$

Диаграмма ошибок слева показывает положение положения приемника, истинного положения приемника и пересечения четырех поверхностей.

Измерение времени прихода сигнала

Для определения местоположения, вычисляемого приемником GPS, требуется текущее время, местоположение спутника и измеренная задержка принятого сигнала. Точность определения местоположения в первую очередь зависит от местоположения спутника и задержки сигнала.

Чтобы измерить задержку, приемник сравнивает битовую последовательность, полученную от спутника, с версией, созданной внутри. Сравнивая передний и задний фронты битовых переходов, современная электроника может измерять смещение сигнала с точностью до одного процента от ширины битового импульса, 0,01 × 300, 000, 000 м / с (1,023 × 10 6 / с). { displaystyle { frac {0,01 times 300000000 м / с} {(1.023 times 10 ^ {6} / mathrm {s})}}} ${ displaystyle { frac {0,01 times 300 000 000 м / с} {(1,023 times 10 ^ {6} / mathrm {s})}}}$ , или примерно 10 наносекунд для C / Код. Сигналы GPS распространяются со скоростью скорости света, что составляет ошибку около 3 метров.

Этот компонент точности положения может быть улучшен в 10 раз, используя сигнал P (Y) с более высокой чиповой скоростью. Предполагаемая тот же самый процент точности ширины битового импульса, высокочастотный сигнал P (Y) дает точность (0,01 × 300, 000, 000 м / с) (10,23 × 10 6 / с) { displaystyle { frac {(0,01 times 300000000 mathrm {m / s})} {(10.23 times 10 ^ {6} / mathrm {s})}}} $frac {(0,01 times 300 000 000 mathrm {м / с})} {(10,23 times 10 ^ 6 / mathrm {s})}$ или около 30 сантиметров.

Атмосферные эффекты

Несогласованность атмосферных условий влияет на скорость сигналов GPS, когда они проходят через атмосферу Земли, особенно ионосферу. Исправление этих ошибок является серьезной проблемой для повышения точности определения местоположения GPS. Эти эффекты минимальны, когда спутник находится прямо над головой, когда спутник находится прямо над головой, и сильнее для спутников, спутников к горизонту, благодаря пути через атмосферу длиннее (см. воздушная масса ). Как только приблизительное местоположение приемника известно, можно использовать математическую модель для оценки и компенсации этих ошибок.

Ионосферная задержка микроволнового сигнала зависит от его частоты. Он возникает из ионизированной атмосферы (см. Содержание электронов ). Это явление известно как дисперсия и может быть вычислено на основе измерений задержек для двух или более полос частот, что позволяет использовать задержки на других частотах. Некоторые военные и дорогие гражданские приемники исследовательского класса атмосферную дисперсию на различных задержек на частотах L1 и L2 и применяют более точную поправку. Это может быть сделано в гражданских приемниках без дешифрования P (Y), передаваемого по L2 путем использования несущей вместо модулированного кода. Чтобы облегчить это на более дешевых приемниках, новый гражданский кодовый сигнал на L2, названный L2C, был добавлен к спутникам Block IIR-M, которые впервые были запущены в 2005 году. Он позволяет прямое сравнение сигналов L1 и L2 с использованием кодированных сигнал вместо несущей.

Воздействие ионосферы обычно изменяется медленно и может быть усреднено по времени. Эти значения для географической области можно легко вычислить, сравнив положение, измеренное с помощью GPS, с местом расположения. Эта поправка также действительна для других приемников в том же месте. Некоторые системы отправляют эту информацию по радио или другим каналам, чтобы приемники, работающие только на L1, могли вносить ионосферные поправки. Ионосферные данные передаются через спутник в спутниковых системах расширения (SBAS), таких как Wide Area Augmentation System (WAAS) (доступна в Северной Америке и на Гавайях), EGNOS (Европа и Азия), Многофункциональная спутниковая система дополнения (MSAS) (Япония) и GPS Aided Geo Augmented Navigation (GAGAN) (Индия), которая передает данные на GPS с использованием Специальная псевдослучайной шумовой псевовой последовательности (PRN), поэтому требуются только один приемник и антенна.

Влажность вызывает переменную задержку, приводящую к ошибкам, аналогичным ионосферной задержке, но вызывающим в тропосфере. Этот эффект более локализован, чем ионосферные эффекты, изменяется быстрее и не зависит от частоты. Эти характеристики делают измерение и компенсацию выбросов более сложными, чем ионосферные эффекты.

Атмосферное давление также может задержку приема сигналов из-за присутствия сухих газов в тропосфере (78% N2, 21% O2, 0,9% Ar…). Его влияние меняется в зависимости от местной температуры и атмосферного давления, вполне предсказуемым образом с использованием идеальных газов.

Эффекты многолучевого распространения

На сигналы GPS также может влиять многолучевость проблемы, при которых радиосигналы отражаются от окружающей местности; здания, стены каньона, твердый грунт и т. д. Эти задержанные сигналы ошибки измерения, которые различны для каждого типа сигнала GPS из-за его зависимости от длины волны.

Разнообразие методов, в первую очередь узкое расстояние между корреляторами, были разработаны для уменьшения ошибок, связанных с многолучевым распространением. При многолучевом распространении с большой задержкой приемник сам может распознать попутный сигнал и отбросить его. Для решения проблемы многолучевого распространения с более короткой задержкой сигнала, отражающегося от земли, местные антенны (например, кольцевая антенна ) для уменьшения мощности сигнала, принимаемой антенной. Отражения с короткой задержкой труднее отфильтровать, потому что они мешают истинному сигналу, вызывая эффекты, почти неотличимые от обычных атмосферных атмосферных явлений.

Эффекты многолучевого распространения менее серьезны для движущихся транспортных средств. Когда антенна GPS сходится, ложные решения с использованием отраженных сигналов быстро не идут, и только прямые сигналы приводят к стабильным решениям.

Ошибки эфемерид и часов

Хотя данные эфемерид передаются каждые 30 секунд, сама информация может быть старше двух часов. Изменчивость давления солнечной радиации влияет на точность GPS из-за влияния на ошибки эфемерид. Если требуется быстрое время для первого исправления (TTFF), можно загрузить действительные эфемериды в приемник, и в дополнение к установке времени определения местоположения может быть получено чем за десять секунд. Такие эфемеридные данные можно связать в Интернете, чтобы их можно было загрузить в мобильное устройство GPS. См. Также Assisted GPS.

Атомные часы спутников испытывают шум и ошибки дрейфа часов. В навигационном сообщении исправления этих ошибок и точности плохих часов. Однако они основаны на наблюдениях и могут указывать на текущее состояние часов.

Эти проблемы, как правило, очень маленькие, но могут составлять несколько метров (десятков футов) неточности.

Для очень точного позиционирования (например, в геодезии ) эти эффекты могут быть устранены с помощью дифференциальной GPS : одновременного использования двух или более приемников в нескольких точках съемки. В 1990-х годах, когда были разработаны некоторые методы квазидифференциальной системы GPS, использовались некоторые приемники, которые использовались только один приемник, но повторно использовались точки измерения. В Венском техническом университете метод получил название qGPS, и было разработано программное обеспечение для постобработки.

Геометрическое снижение точности вычислений (GDOP)

Вычисление геометрического снижения точности

Концепция геометрического снижения точности было введено в раздел, источники ошибок и анализ. Были предоставлены расчеты, чтобы показать, как использовался PDOP и как он влиял на стандартное отклонение ошибки местоположения приемника.

Когда видимые спутники GPS расположены близко друг к другу в небе (т. Е. С небольшим угловым разделением), значения DOP высокие; когда они далеко друг от друга, значения DOP низкие. Предусмотрено, что предоставлены предоставленные близко друг к другу спутники, которые находятся на большом расстоянии друг от друга. Низкие значения DOP обеспечивает лучшую точность позиционирования GPS из-за более широкого углового разнесения между спутниками, используемыми для расчета положения приемника GPS. HDOP, VDOP, PDOP и TDOP — это соответственно по горизонтали, вертикали, позиции (3-D) и временного снижения точности.

Рис. 3.1 Снижение точности данных Navstar GPS от береговой охраны США обеспечивает представление о том, как геометрия влияет на точность.

Теперь мы беремся за задачу, как вычислить снижение точности термины. В качестве первого шага в вычислении DOP рассмотрим единый вектор от приемника к спутнику я с компонентами (xi — x) R i { displaystyle { frac {(x_ {i} -x)} {R_ {i}}} } $frac {(x_i- x)} {R_i}$ , (yi — y) R i { displaystyle { frac {(y_ {i} -y)} {R_ {i}}}} $frac {(y_i-y)} {R_i}$ и (zi — z) R i { displaystyle { frac {(z_ {i} -z)} {R_ {i}}}} $frac {(z_i-z)} { R_i}$ где расстояние от приемника до спутника, R i { displaystyle R_ { i}} $R_i$ , определяется по формуле:

R i = (xi — x) 2 + (yi — y) 2 + (zi — z) 2 { displaystyle R_ {i} , = , { sqrt {(x_ {i} -x) ^ {2} + (y_ {i} -y) ^ {2} + (z_ {i} -z) ^ {2}}}} $R_i , = , sqrt {(x_i- x) ^ 2 + (y_i-y) ^ 2 + (z_i-z) ^ 2}$

где x, y, { displaystyle x, y,} $x, y,$ и z { displaystyle z} $z$ обозначают положение получатель и xi, yi, { displaystyle x_ {i}, y_ {i},} $x_i, y_i,$ и zi { displaystyle z_ {i}} $z_i$ обозначают положение спутника i. Эти компоненты x, y и z могут быть компонентами системы координат север, восток, вниз, юг, восток, вверх или в другой удобной системе. Сформулируйте матрицу A как:

A = [(x 1 — x) R 1 (y 1 — y) R 1 (z 1 — z) R 1 1 (x 2 — x) R 2 (y 2 — y) К 2 (z 2 — z) R 2 1 (x 3 — x) R 3 (y 3 — y) R 3 (z 3 — z) R 3 1 (x 4 — x) R 4 (y 4 — y).) R 4 (z 4 — z) R 4 1] { displaystyle A = { begin {bmatrix} { frac {(x_ {1} -x)} {R_ {1}}} { frac {( y_ {1} -y)} {R_ {1}}} { frac {(z_ {1} -z)} {R_ {1}}} 1 \ { frac {(x_ {2} — x)} {R_ {2}}} { frac {(y_ {2} -y)} {R_ {2}}} и { frac {(z_ {2} -z)} {R_ {2} }} 1 \ { frac {(x_ {3} -x)} {R_ {3}}} { frac {(y_ {3} -y)} {R_ {3}}} и { frac {(z_ {3} -z)} {R_ {3}}} 1 \ { frac {(x_ {4} -x)} {R_ {4}}} { frac {(y_ { 4} — y)} {R_ {4}}} { frac {(z_ {4} -z)} {R_ {4}}} 1 end {bmatrix}}} ${ displaystyle A = { begin {bmatrix} { frac {(x_ {1} -x)} {R_ { 1}}} { frac {(y_ {1} -y)} {R_ {1}}} { frac {(z_ {1} -z)} {R_ {1}}} 1 \ { frac {(x_ {2} -x)} {R_ {2}}} { frac {(y_ {2} -y)} {R_ {2}}} и { frac {(z_ {2} -z)} {R_ {2}}} 1 \ { frac {(x_ {3} -x)} {R_ {3}}} { frac {(y_ {3} -y)} {R_ {3}}} { frac {(z_ {3} -z)} {R_ {3}}} 1 \ { frac {(x_ {4} -x)} {R_ {4}}} { frac {(y_ {4} -y)} {R_ {4}}} { frac {(z_ {4} -z)} {R_ {4}}} 1 end {bmatrix}}}$

Первые три элемента каждого A — компоненты единичного вектора от приемника до спутника. Элементами в четвертом столбце являются c, где c обозначает скорость света. Сформулируйте матрицу Q в виде

Q = (ATA) — 1 { displaystyle Q = left (A ^ {T} A right) ^ {- 1}} $Q = left (A ^ TA right) ^ {- 1}$

Это вычисление выполняется в соответствии с главой 11 Глобальной системы позиционирования Паркинсона и Спилкера, где весовая матрица P установлена равной единичной матрице. Элементы матрицы Q обозначаются как:

Q = [dx 2 dxy 2 dxz 2 dxt 2 dxy 2 dy 2 dyz 2 dyt 2 dxz 2 dyz 2 dz 2 dzt 2 dxt 2 dyt 2 dzt 2 dt 2] { displaystyle Q = { begin {bmatrix} d_ {x} ^ {2} d_ {xy} ^ {2} d_ {xz} ^ {2} d_ {xt} ^ {2} \ d_ {xy} ^ {2 } d_ {y} ^ {2} d_ {yz} ^ {2} d_ {yt} ^ {2} \ d_ {xz} ^ {2} d_ {yz} ^ {2} d_ { z} ^ {2} d_ {zt} ^ {2} \ d_ {xt} ^ {2} d_ {yt} ^ {2} d_ {zt} ^ {2} d_ {t} ^ { 2} end {bmatrix}}} ${ displaystyle Q = { begin {bmatrix} d_ {x} ^ {2} d_ {xy} ^ {2} d_ {xz} ^ {2} d_ {xt} ^ {2} \ d_ {xy} ^ {2} d_ {y} ^ {2} d_ {yz} ^ {2} d_ {yt} ^ {2} \ d_ { xz} ^ {2} d_ {yz} ^ {2} d_ {z} ^ {2} d_ {zt} ^ {2} \ d_ {xt} ^ {2} d_ {yt} ^ {2} d_ { zt} ^ {2} d_ {t} ^ {2} end {bmatrix}}}$

Греческая буква σ { displaystyle sigma} $sigma$ используется довольно часто там, где мы использовали d. Однако элементы Q-матрицы не отличаются дисперсии и ковариации, поскольку они определены в вероятности и статистике. Вместо этого они являются геометрическими терминами. Таким образом, d as для снижения точности используется. PDOP, TDOP и GDOP задаются как

P D O P = d x 2 + d y 2 + d z 2 T D O P = d t 2 = | д т | GDOP = PDOP 2 + TDOP 2 { displaystyle { begin {align} PDOP = { sqrt {d_ {x} ^ {2} + d_ {y} ^ {2} + d_ {z} ^ {2}} } \ TDOP = { sqrt {d_ {t} ^ {2}}} = | d_ {t} | \ GDOP = { sqrt {PDOP ^ {2} + TDOP ^ {2}}} end {выровнено}} $begin {align} PDOP = sqrt { d_x ^ 2 + d_y ^ 2 + d_z ^ 2} \ TDOP = sqrt {d_ {t} ^ 2} = | d_ {t} | \ GDOP = sqrt {PDOP ^ 2 + TDOP ^ 2} end {align}$

в соответствии с «Разделом 1.4.9 ПРИНЦИПОВ РАЗМЕЩЕНИЯ СПУТНИКОВ».

Горизонтальное снижение точности, HDOP = dx 2 + dy 2 { displaystyle HDOP = { sqrt {d_ {x} ^ {2} + d_ {y} ^ {2}}}} $HDOP = sqrt {d_x ^ 2 + d_y ^ 2}$ , и вертикальное снижение точности, VDOP = dz 2 = | d z | { displaystyle VDOP = { sqrt {d_ {z} ^ {2}}} = | d_ {z} |} $VDOP = sqrt {d_ {z} ^ 2} = | d_z |$ , оба зависят от используемой системы координат. Чтобы вертикальной плоскости горизонта и местной, x, y и z должны обозначать позиции в системе координат север, восток, вниз или юг, восток, вверх.

Вывод для сравнения геометрического снижения точности

Уравнения для геометрического снижения точности были в предыдущем разделе. В этом разделе описывается вывод этих соотношений. Используемый здесь метод аналогичен методу, использованному в «Глобальная система позиционирования (предварительный просмотр) Паркинсона и Спайкера»

Рассмотрим вектор ошибки положения, e { displaystyle mathbf {e}} $mathbf {e}$ , определяемый как вектор от пересечения четырех поверхностей, псевдодальностям, до истинного положения приемника. e = exx ^ + eyy ^ + ezz ^ { displaystyle mathbf {e} = e_ {x} { hat {x}} + e_ {y} { hat {y}} + e_ {z} { hat {z}}} $mathbf {e} = e_x hat {x} + e_y hat {y} + e_z hat {z}$ где жирным шрифтом обозначен вектор, а x ^ { displaystyle { hat {x}}} ${ hat {x}}$ , y ^ { displaystyle { hat {y }}} ${ hat {y}}$ и z ^ { displaystyle { hat {z}}} ${ hat {z}}$ обозначают единичные вдоль осей x, y и z соответственно. Пусть e t { displaystyle e_ {t}} $e_t$ обозначает ошибку времени, истинное время минус время, указанное приемником. Предположим, что среднее значение трех компонентов e { displaystyle mathbf {e}} $mathbf {e}$ и et { displaystyle e_ {t}} $e_t$ равно нуль.

A [exeyezet] = [(x 1 — x) R 1 (y 1 — y) R 1 (z 1 — z) R 1 1 (x 2 — x) R 2 (y 2 — y) R 2 (z 2 — z) R 2 1 (x 3 — x) R 3 (y 3 — y) R 3 (z 3 — z) R 3 1 (x 4 — x) R 4 (y 4 — y) R 4 (z 4 — z) R 4 1] [exeyezet] = [e 1 e 2 e 3 e 4] (1) { displaystyle A { begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} \ e_ {t} end {bmatrix}} = { begin {bmatrix} { frac {(x_ {1} -x)} {R_ {1}}} { frac {(y_ { 1} -y)} {R_ {1}}} { frac {(z_ {1} -z)} {R_ {1}}} 1 \ { frac {(x_ {2} -x)} {R_ {2}}} { frac {(y_ {2} -y)} {R_ {2}}} и { frac {(z_ {2} -z)} {R_ {2}}} 1 \ { frac {(x_ {3} -x)} {R_ {3}}} { frac {(y_ {3} -y)} {R_ {3}}} { frac {(z_ {3} -z)} {R_ {3}}} 1 \ { frac {(x_ {4} -x)} {R_ {4}}} { frac {(y_ {4} -y) } {R_ {4}}} { frac {(z_ {4} -z)} {R_ {4}}} 1 end {bmatrix}} { begin {bmatrix} e_ {x} \ e_ { y} \ e_ {z} \ e_ {t} end {bmatrix}} = { begin {bmatrix} e_ {1} \ e_ {2} \ e_ {3} \ e_ {4} конец {bmatrix}} (1)} ${ displaystyle A { begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} \ e_ {t} end {bmatrix}} = { begin {bmatrix} { frac {(x_ {1} -x)} {R_ {1}}} { frac {(y_ {1} -y) } {R_ {1}}} { frac {(z_ {1} -z)} {R_ {1}}} 1 \ { frac {(x_ {2} -x)} {R_ {2} }} { frac {(y_ {2} -y)} {R_ {2}}} { frac {(z_ {2} -z)} {R_ {2}}} 1 \ { frac {(x_ {3} -x)} {R_ {3}}} и { frac {(y_ {3} -y)} {R_ {3}}} и { frac {(z_ {3} -z)} {R_ {3}}} 1 \ { frac {(x_ {4} -x)} {R_ {4}}} { frac {(y_ {4} -y)} {R_ {4 }}} { frac {(z_ {4} -z)} {R_ {4}}} 1 end {bmatrix}} { begin {bmatrix} e_ {x} \ e_ {y} \ e _ {z} \ e_ {t} end {bmatrix}} = { begin {bmatrix} e_ {1} \ e_ {2} \ e_ {3} \ e_ {4} end {bmatrix} } (1)}$

где е 1 { displaystyle e_ {1}} $e_ {1}$ , e 2 { displaystyle e_ {2}} $e_ {2}$ , e 3 { displaystyle e_ { 3}} $e_ { 3}$ и e 4 { displaystyle e_ {4}} $e_4$ являются ошибки в псевдодальностях с 1 по 4 соответственно. Это уравнение происходит от линеаризации уравнения Ньютона-Рафсона, связывающего псевдодальности сположением приемника, положениями спутников и ошибками часов приемника. Умножение обеих сторон на A — 1 { displaystyle A ^ {- 1}} $A ^ {- 1 }$ дает

[exeyezet] = A — 1 [e 1 e 2 e 3 e 4] (2) { Displaystyle { begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} \ e_ {t} end {bmatrix}} = A ^ {- 1} { begin {bmatrix} e_ {1} \ e_ {2} \ e_ {3} \ e_ {4} end {bmatrix}} (2)} ${ displaystyle { begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} \ e_ {t} end {bmatrix}} = A ^ {- 1} { begin {bmatrix} e_ {1} \ e_ {2} \ e_ {3} \ e_ {4} end {bmatrix}} (2)}$ .

Перемещение сторон:

[exeyezet] = [e 1 e 2 e 3 e 4] (A — 1) T (3) { displaystyle { begin {bmatrix} e_ {x} e_ {y} e_ {z} e_ {t} end {bmatrix}} = { begin {bmatrix} e_ {1} e_ {2} e_ {3} e_ {4} end {bmatrix}} left (A ^ {- 1} right) ^ {T} ( 3)} ${ displaystyle { begin {bmatrix} e_ {x} e_ {y} e_ {z} e_ {t} end {bmatrix}} = { begin {bmatrix} e_ {1} e_ {2} e_ {3} e_ {4} end {bmatrix}} left (A ^ {- 1} right) ^ {T} (3)}$ .

После умножения матриц с обеих сторон уравнения (2) на соответствующие матрицы в уравнении (3) accept

[exeyezet] [exeyezet] = A — 1 [e 1 e 2 e 3 e 4] [e 1 е 2 е 3 е 4] (A — 1) T (4) { displaystyle { begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} \ e_ {t} end {bmatrix}} { begin {bmatrix} e_ {x} e_ {y} e_ {z} e_ {t} end {bmatrix}} = A ^ {- 1} { begin {bmatrix} e_ { 1} e_ {2} \ e_ {3} \ e_ {4} end {bmatrix}} { begin {bmatrix} e_ {1} e_ {2} e_ {3} e_ {4} end {bma trix}} left (A ^ { — 1} right) ^ {T} (4)} ${ displaystyle { begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} e_ {t} end {bmatrix}} { begin {bmatrix } e_ {x} e_ {y} e_ {z} e_ {t} end {bmatrix}} = A ^ {- 1} { begin {bmatrix} e_ {1} \ e_ {2} \ e_ { 3} \ e_ {4} end {bmatrix}} { begin {bmatrix} e_ {1} e_ {2} e_ {3} e_ {4} end {bmatrix}} left (A ^ {- 1 } right) ^ {T} (4)}$ .

Взяв ожидаемое значение с обеих сторон и взяв неслучайные матрицы за пределами оператора ожидания, E, получаем результат:

E ([exeyezet] [exeyezet]) Знак равно A — 1 E ([e 1 e 2 e 3 e 4] [e 1 e 2 e 3 e 4]) (A — 1) T (5) { Displaystyle E left ({ begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} \ e_ {t} end {bmatrix}} { begin {bmatrix} e_ {x} e_ {y} e_ {z} e_ { t} end {bmatrix}} right) = A ^ {- 1} E left ({ begin {bmatrix} e_ {1} \ e_ {2} \ e_ {3} \ e_ {4} end {bmatrix}} { begin {bmatrix} e_ {1} e_ {2} e_ {3} e_ {4} end {bmatrix}} right) left (A ^ {- 1} справа) ^ {T} (5)} ${ displaystyle E left ({ begin {bmatrix} e_ {x} \ e_ {y} \ e_ {z} e_ {t} end {bmatrix}} { begin {bmatrix} e_ {x} e_ {y} e_ {z} e_ {t} end {bmatrix}} right) = A ^ {- 1} E left ({ be gin {bmatrix} e_ {1} \ e_ {2} \ e_ {3} \ e_ {4} end {bmatrix}} { begin {bmatrix} e_ {1} e_ {2} e_ {3} e_ {4} end {bmatrix}} right) left (A ^ {- 1} right) ^ {T} (5)}$

Предполагая, что ошибки псевдодальности некоррелированы и имеют одинаковую дисперсию, ковариационная матрица справа может быть выражена как скаляр, умноженный на единичную матрицу. Таким образом,

[σ x 2 σ xy 2 σ xz 2 σ xt 2 σ xy 2 σ y 2 σ yz 2 σ yt 2 σ xz 2 σ yz 2 σ z 2 σ zt 2 σ xt 2 σ yt 2 σ zt 2 σ T 2] знак равно σ р 2 A — 1 (A — 1) T знак равно σ R 2 (ATA) — 1 (6) { displaystyle { begin {bmatrix} sigma _ {x} ^ { 2} sigma _ {xy} ^ {2} sigma _ {xz} ^ {2} sigma _ {xt} ^ {2} \ sigma _ {xy} ^ {2} sigma _ {y} ^ {2} sigma _ {yz} ^ {2} sigma _ {yt} ^ {2} \ sigma _ {xz} ^ {2} sigma _ {yz} ^ {2} sigma _ {z} ^ {2} sigma _ {zt} ^ {2} \ sigma _ {xt} ^ {2} sigma _ {yt} ^ {2} sigma _ {zt} ^ {2} sigma _ {t} ^ {2} end {bmatrix}} = sigma _ {R} ^ {2} A ^ {- 1} left (A ^ { — 1} справа) ^ {T} = sigma _ {R} ^ {2} left (A ^ {T} A right) ^ {- 1} (6)} ${ displaystyle { begin {bmatrix} sigma _ {x} ^ {2} sigma _ {xy} ^ {2} сигма _ {xz} ^ {2} sigma _ {xt} ^ {2} \ sigma _ {xy} ^ {2} sigma _ {y} ^ {2} sigma _ {yz} ^ {2} sigma _ {yt} ^ {2} \ sigma _ {xz} ^ {2} sigma _ {yz} ^ {2} sigma _ {z} ^ {2} sigma _ {zt} ^ {2} \ sigma _ {xt} ^ {2} sigma _ {yt} ^ {2} sigma _ {zt} ^ {2} sigma _ {t } ^ {2} end {bmatrix}} = sigma _ {R} ^ {2} A ^ {- 1} left (A ^ {- 1} right) ^ {T} = sigma _ { R} ^ {2} left (A ^ {T} A right) ^ {- 1} (6)}$

начиная с A — 1 (A — 1) T (ATA) = I { displaystyle A ^ {- 1} left (A ^ {- 1} right) ^ {T} left (A ^ {T} A right) = I} $A ^ {- 1} left (A ^ {- 1} right) ^ T left (A ^ TA right) = I$

Примечание: (A — 1) T = (AT) — 1, { displaystyle left (A ^ {- 1} right) ^ {T} = left (A ^ {T} right) ^ {- 1},} $left (A ^ {- 1} right) ^ T = left (A ^ {T} right) ^ {- 1},$ , поскольку I = (AA — 1) T = (A — 1) TAT { displaystyle I = left (AA ^ {- 1} right) ^ {T} = left (A ^ {- 1} right) ^ {T} A ^ {T}} $I = left (AA ^ {- 1 } right) ^ T = left (A ^ {- 1} right) ^ TA ^ T$

Замена на (ATA) — 1 = Q { dis playstyle left (A ^ {T} A right) ^ {- 1} = Q} $left (A ^ TA right) ^ {- 1} = Q$ следует

[σ x 2 σ xy 2 σ xz 2 σ xt 2 σ xy 2 σ y 2 σ yz 2 σ yt 2 σ xz 2 σ yz 2 σ z 2 σ zt 2 σ xt 2 σ yt 2 σ zt 2 σ t 2] = σ R 2 [dx 2 dxy 2 dxz 2 dxt 2 dxy 2 dy 2 dyz 2 dyt 2 dxz 2 dyz 2 dz 2 dzt 2 dxt 2 dyt 2 dzt 2 dt 2] (7) { displaystyle { begin {bmatrix} sigma _ {x} ^ {2} sigma _ {xy} ^ {2} sigma _ {xz} ^ {2} sigma _ {xt} ^ {2} \ sigma _ {xy} ^ {2} sigma _ {y} ^ {2} сигма _ {yz} ^ {2} sigma _ {yt} ^ {2} \ sigma _ {xz} ^ {2} sigma _ {yz} ^ {2} sigma _ {z} ^ {2} сигма _ {zt} ^ {2} \ sigma _ {xt} ^ {2} sigma _ {yt} ^ {2} sigma _ {zt} ^ {2} sigma _ {t} ^ {2} end {bmatrix}} = sigma _ {R} ^ {2} { begin {bmatrix} d_ {x} ^ {2} d_ {xy} ^ {2} d_ {xz} ^ {2} d_ {x t} ^ {2} \ d_ {xy} ^ {2} d_ {y} ^ {2} d_ {yz} ^ {2} d_ {yt} ^ {2} d_ {xz} ^ {2} d_ {yz} ^ {2} d_ {z} ^ {2} d_ {zt} ^ {2} \ d_ {xt} ^ {2} d_ {yt} ^ {2} d_ {zt} ^ {2} d_ {t} ^ {2} end {bmatrix}} (7)} $begin {bmatrix} sigma_x ^ 2 sigma_ {xy} ^ 2 sigma_ {xz} ^ 2 sigma_ {xt} ^ 2 \ sigma_ {xy} ^ 2 sigma_ {y} ^ 2 sigma_ {yz} ^ 2 sigma_ {yt} ^ 2 \ sigma_ {xz} ^ 2 sigma_ {yz} ^ 2 sigma_ {z} ^ 2 sigma_ {zt} ^ 2 \ sigma_ {xt} ^ 2 sigma_ {yt} ^ 2 sigma_ {zt} ^ 2 sigma_ {t} ^ 2 end {bmatrix} = sigma_R ^ 2 begin {bmatrix} d_x ^ 2 d_ {xy} ^ 2 d_ {xz} ^ 2 d_ {xt} ^ 2 \ d_ {xy} ^ 2 d_ {y} ^ 2 d_ {yz} ^ 2 d_ {yt} ^ 2 \ d_ {xz} ^ 2 d_ {yz} ^ 2 d_ {z} ^ 2 d_ {zt} ^ 2 \ d_ {xt} ^ 2 d_ {yt} ^ 2 d_ {zt} ^ 2 d_ {t} ^ 2 end {bmatrix} (7)$

Из уравнения (7) следует, что отклонения положения приемника и времени

σ rc 2 знак равно σ Икс 2 + σ Y 2 + σ Z 2 знак равно σ р 2 (dx 2 + dy 2 + dz 2) = PDOP 2 σ R 2 { Displaystyle sigma _ {rc} ^ {2} = sigma _ {x} ^ {2} + sigma _ {y} ^ {2} + sigma _ {z} ^ {2} = sigma _ {R} ^ {2} left (d_ {x} ^ { 2} + d_ {y} ^ {2} + d_ {z} ^ {2} right) = PDOP ^ {2} sigma _ {R} ^ {2}} $sigma_ {rc} ^ 2 = sigma_x ^ 2 + sigma_y ^ 2 + sigma_z ^ 2 = sigma_R ^ 2 left ( d_x ^ 2 + d_y ^ 2 + d_z ^ 2 right) = PDOP ^ 2 sigma_R ^ 2$ и

σ T 2 знак равно σ р 2 dt 2 знак равно TDOP 2 σ р 2 { Displaystyle sigma _ {t} ^ {2} = sigma _ {R} ^ {2} d_ {t} ^ {2} = TDOP ^ {2} sigma _ {R} ^ {2}} $sigma_t ^ 2 = sigma_R ^ 2 d_t ^ 2 = TDOP ^ 2 sigma_R ^ 2$

Остальные члены дисперсии ошибки положения и времени след просто.

Выборочная доступность

В GPS включена функция выборочной доступности (SA), которая первимеренные изменяющиеся во времени ошибки до 100 метров (328 футов) к общедоступным навигационным сигналом. Это было сделано с целью запретить противнику использовать гражданские приемники GPS для наведения высокоточного оружия.

Ошибки SA на самом деле являются псевдослучайными, генерируемыми криптографическим алгоритмом из секретного начального ключа, доступного только авторизованным пользователям (вооруженным силам США, их союзникам и некоторым другим пользователям, в основном правительственным) специальный военный GPS-приемник. Простого владения приемником недостаточно; ему по-прежнему нужен строго контролируемый ежедневный ключ.

Перед отключением 2 мая 2000 г. типичные ошибки SA составляли около 50 м (164 футов) по горизонтали и около 100 м (328 футов) по вертикали. SA влияет на каждый приемник. GPS в данной области, фиксированная станция с определением местоположения. Это называется дифференциальным GPS или DGPS. DGPS также исправляет несколько других важных источников ошибок GPS, в частности, ионосферную задержку, поэтому он широко распространяет, даже несмотря на то, что SA отключена. Неэффективность SA перед широко доступным DGPS была обычным аргументом в пользу отключения SA, и это было наконец сделано по приказу президента Клинтона в 2000 году.

Услуги ДГПС широко доступны из коммерческих и государственных источников. К последним войскам WAAS и США. Береговая охрана сеть морских навигационных маяков LF. Точность поправок зависит от расстояния между пользователем и приемником DGPS. По мере увеличения расстояния на двух участках не будут коррелировать, что приведет к менее точным дифференциальным поправкам.

Во время войны в Персидском заливе 1990–91 годов нехватка военных единиц GPS вынудила многих солдат и их семьи покупать легкодоступные гражданские единицы. Использовать такое решение для использования GPS.

В 1990-х годах FAA начало создания давления на военных, чтобы они навсегда отключили SA. Это позволяет бы FAA ежегодно экономить миллионы долларов на обслуживании их собственных радионавигационных систем. Количество добавленных ошибок было «обнулено» в полночь 1 мая 2000 г. после объявления президента США Билла Клинтона, разрешающего доступ к безошибочному сигналу L1. Согласно диреке, вызванная ошибка SA была изменена, чтобы не добавить ошибки к общедным сигналам (код C / A). Указ Клинтона требовал, чтобы SA была обнулена к 2006 году; это произошло в 2000 году, когда американские военные разработали новую систему, которая позволяет блокировать GPS (и другие навигационные услуги) враждебным силам в специфическом кризисе.

19 сентября 2007 года Министерство обороны США объявило, что будущие спутники GPS III не будут поддерживать SA, что в конечном итоге сделало бы постоянную.

Антиспуфинг

Остается еще одно ограничение на GPS, антиспуфинг. Это зашифровывает P-код, так что он не может быть имитирован передатчиком, отправляющим ложную информацию. Немногие гражданские приемники когда-либо использовали P-код, и точность, достигаемая с помощью общедоступного кода C / A, было намного лучше, чем ожидалось изначально (особенно с DGPS ). Настолько, что политика защиты от подделки практически не влияет на большинство гражданских пользователей. Отключение функции защиты от подделки в первую очередь услуг по геодезистам и некоторым ученым, которым требуется самое быстрое положение для экспериментов, таких как отслеживание движения тектонических плит.

Относ

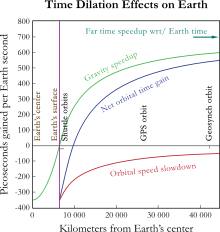Спутниковые часы замедляются из-за своей орбитальной скорости, но ускоряются из-за расстояния от гравитационного колодца Земли.

Существует ряд источников ошибок из-за релятивизма эффекты, которые сделают систему бесполезной, если ее не исправить. Три релятивистских эффекта — это замедление времени, гравитационный сдвиг частоты и эффекты эксцентриситета. Примеры включают релятивистское замедление времени из-за скорости спутника примерно 1 часть из 10, гравитационное замедление времени, из-за которого спутник движется примерно на 5 частей из 10 быстрее, чем земные часы, и эффект Саньяка из-за вращения относительно приемников на Земле. Эти темы рассматриваются ниже по очереди.

Специальная и общая теория относительности

Согласно теории относительности, из-за их постоянного движения и высоты относительно центрированной Земли, невращающейся ориентированной инерциальной системы отсчета на часы влияет их скорость. Специальная теория относительности предсказывает, что частота атомных часов, движущихся с орбитальной скоростью GPS, будет замедляться в , чем стационарные наземные часы, в v 2 2 c 2 ≈ 10-10 { displaystyle { frac {v ^ {2}} {2c ^ {2}}} приблизительно 10 ^ {- 10}} $frac {v ^ {2}} {2c ^ {2}} приблизительно 10 ^ {-10}$ , или приведет к задержке около 7 мкс / день, когда орбитальная скорость равна v = 4 км / с, а c = скорость света. Этот эффект замедления времени был измерен и подтвержден с помощью GPS.

Влияние сдвига частоты гравитации на GPS из-за общей теории относительности заключается в том, что часы расположены ближе к массивному объекту, будут медленнее, чем часы на более удаленном расстоянии. Применительно к GPS приемники находятся намного ближе к Земле, чем спутники, в результате чего часы GPS работают быстрее в 5 × 10 раз, или примерно на 45,9 мкс / день. Этот сдвиг частоты гравитации заметен.

При объединении замедления времени и гравитационного сдвига частоты расхождение составляет около 38 микросекунд в день, то есть разница в 4 465 частей на 10. Без исправления ошибок в позиции накапливаются примерно 11,4 км / день. Эта начальная ошибка псевдодальности исправляется в процессе решения навигационных уравнений. Вдобавок эллиптические, а не идеально круглые орбиты вызывают изменение во времени замедления времени и гравитационного сдвига частоты. Этот эффект эксцентриситета увеличивает или уменьшение разницы в тактовой частоте между спутником GPS и приемником в зависимости от высоты спутника.

Для компенсации несоответствия стандарту частоты на борту каждого спутника перед запуском идет сдвиг скорости, что делает его немного медленнее, чем желаемая частота на Земле; в частности, на 10,22999999543 МГц вместо 10,23 МГц. GPS-система автоматизированных часов на борту спутниковой связи. GPS точно настроена. Размещение атомных часов на искусственных спутниках для проверки общей теории Эйнштейна было предложено Фридвардтом Винтербергом в 1955 году.

Расчет количества замедления времени

Для расчета количества ежедневного замедления времени с помощью спутников GPS Земли нам нужно отдельно определить, обусловленные специальные теорией относительности (скорость) и общей теорией относительности (гравитация), и сложить их вместе.

Величина, обусловленная скоростью, будет определяться с помощью преобразования Лоренца. Это будет:

1 γ = 1 — v 2 c 2 { displaystyle { frac {1} { gamma}} = { sqrt {1 — { frac {v ^ {2}} {c ^ {2}}}}}} $frac {1} { gamma} = sqrt {1- frac {v ^ 2} {c ^ 2}}$

Для малых значений v / c при использовании биномиального разложения это приближается к:

1 γ ≈ 1 — v 2 2 c 2 { displaystyle { frac {1} { gamma}} приблизительно 1 — { frac {v ^ {2}} {2c ^ {2}}}} $frac {1} { gamma} приблизительно 1- frac {v ^ 2} {2 c ^ 2}$

Спутники GPS движутся со скоростью 3874 м / с относительно центра Земли. Таким образом, мы определяем:

1 γ ≈ 1 — 3874 2 2 (2,998 × 10

2 ≈ 1 — 8,349 × 10 — 11 { displaystyle { frac {1} { gamma}} приблизительно 1 — { frac {3874 ^ {2}} {2 left (2,998 times 10 ^ {8} right) ^ {2}}} приблизительно 1-8,349 times 10 ^ {- 11}} $frac {1} { gamma} приблизительно 1- frac {3874 ^ 2} { 2 влево (2,998 раз 10 ^ 8 вправо) ^ 2} примерно 1-8,349 раз 10 ^ {- 11}$

Эта разница ниже 1 из 8,349 × 10 представляет собой долю, на которую часы спутников движутся медленнее, чем часы Земли. Затем оно умножается на количество наносекунд в день:

— 8,349 × 10 — 11 × 60 × 60 × 24 × 10 9 ≈ — 7214 нс { displaystyle -8,349 times 10 ^ {- 11} times 60 times 60 times 24 times 10 ^ {9} приблизительно -7214 { text {ns}}} $-8.349 times 10 ^ {- 11} раз 60 раз 60 раз 24 раз 10 ^ 9 приблизительно -7214 текст {ns}$

То есть часы спутников теряют 7214 наносекунд в день из-за специальной теории относительности эффекты.

Обратите внимание, что эта скорость 3874 м / с измеряется относительно центра Земли, а не ее поверхности, где находятся приемники GPS (и пользователи). Это потому, что эквипотенциал Земли делает чистое замедление времени равным по всей ее геодезической поверхности. То есть комбинация специальных и общих эффектов делает чистое замедление времени на экваторе равным таковому у полюсов, которые, в свою очередь, находятся в покое относительно центра.. Таким образом, мы будем использовать центр в качестве опорной точки, чтобы представлять всю поверхность

Количество дилатации под действием силы тяжести будет определяться с помощью гравитационное замедление времени уравнение:

1 γ = 1 — 2 GM rc 2 { displaystyle { frac {1} { gamma}} = { sqrt {1 — { frac {2GM} {rc ^ {2}}}}}} $frac {1} { gamma} = sqrt {1- frac {2G M} {rc ^ 2}}$

Для малых значений M / r, используя биномиальное расширение, это приближается к:

1 γ ≈ 1 — GM rc 2 { displaystyle { frac {1} { gamma}} приблизительно 1 — { frac {GM } {rc ^ {2}}}} $frac {1} { gamma } приблизительно 1- frac {GM} {rc ^ 2}$

Нас снова интересует только дробь меньше 1 и разница между Землей и спутниками. Чтобы определить эту разницу, мы берем:

Δ (1 γ) ≈ GM земля R земля c 2 — GM земля R gps c 2 { displaystyle Delta left ({ frac {1} { gamma}} right) приблизительно { frac {GM _ { text {earth}}} {R _ { text {earth}} c ^ {2}}} — { frac {GM _ { text {earth}}} {R _ { текст {gps}} c ^ {2}}}} $Delta left ( frac {1} { gamma} right) приблизительно frac {G M _ { text {earth}}} {R _ { text {earth}} c ^ 2} - frac {G M _ { text {earth}}} {R_ { text {gps}} c ^ 2}$

Земля имеет радиус 6 357 км (на полюсах), что составляет R земля = 6 357 000 м, а высота спутников составляет 20 184 км. их радиус орбиты R gps = 26 541 000 м. Подставляя их в вышеприведенное уравнение, с M земля = 5,974 × 10, G = 6,674 × 10 и c = 2,998 × 10 (все в единицах SI ), получаем:

Δ (1 γ) ≈ 5,307 × 10–10 { displaystyle Delta left ({ frac {1} { gamma}} right) приблизительно 5,307 times 10 ^ {- 10}} $Delta left ( frac {1} { gamma} right) приблизительно 5,307 times 10 ^ {- 10}$

Это представляет собой долю, на которую часы спутников движутся быстрее, чем часы Земли. Затем оно умножается на количество наносекунд в день:

5,307 × 10 — 10 × 60 × 60 × 24 × 10 9 ≈ 45850 нс { displaystyle 5.307 times 10 ^ {- 10} times 60 times 60 times 24 times 10 ^ {9} приблизительно 45850 { text {ns}}} $5,307 times 10 ^ {- 10} times 60 times 60 times 24 times 10 ^ 9 приблизительно 45850 text {ns}$

То есть часы спутников ускоряются на 45 850 наносекунд в день из-за эффектов общей теории относительности. Эти эффекты суммируются, чтобы получить (округлено до 10 нс):

45850 — 7210 = 38640 нс

Следовательно, часы спутников ускоряются примерно на 38 640 наносекунд в день или 38,6 мкс в день в сумме за счет эффектов относительности.

Чтобы компенсировать это усиление, частота часов GPS должна быть уменьшена на дробную часть:

5,307 × 10 — 8,349 × 10 = 4,472 × 10

Эта дробь вычитается из 1 и умноженное на предварительно настроенную тактовую частоту 10,23 МГц:

(1 — 4,472 × 10) × 10,23 = 10,22999999543

То есть нам нужно замедлить тактовую частоту с 10,23 МГц до 10,22999999543 МГц, чтобы свести на нет эффекты относительности.

Искажение Саньяка

Обработка данных GPS-наблюдений также должна компенсировать эффект Саньяка. Шкала времени GPS определяется в инерциальной системе, но наблюдения обрабатываются в системе с центром на Земле , фиксированной на Земле (вращение в одном направлении), в системе, в которой согласовность не определена однозначно. Таким образом, для преобразования системы инерциальной системы в ECEF используется преобразование координат. Полученная поправка времени прохождения сигнала имеет противоположные алгебраические знаки для спутникового в Восточном и Западном небесных полушариях. Игнорирование этого эффекта приведет к ошибке восток-запад порядка сотен наносекунд или десятков метров в позиции.

Естественные источники помех

Сигналы GPS на наземных приемниках имеют тенденцию быть слабыми, естественными радиосигналами или рассеяние сигналов. GPS может снизить чувствительность приемника, получение и отслеживание спутниковых сигналов трудным или невозможным.

Космическая погода плохо работает двумя способами: прямые помехи из-за всплесков шума солнечного радио в той же полосе частот или рассеяние радиосигналы GPS в ионосферных неоднородностях, называемых сцинтилляциями. Обе формы деградации следуют 11-летнему солнечному циклу и достигают максимума при максимуме солнечного пятен, хотя могут произойти в любое время. Солнечные радиовсплески связаны с солнечными вспышками и выбросами корональной массы (CME), и их влияние может повлиять на прием на половину Земли, обращенной к Солнцу. Сцинтилляция чаще всего в тропических широтах, где это ночное явление возникает. Это происходит реже в высоких или средних широтах, где магнитные бури приводить к сцинтилляциям. Помимо мерцания, магнитные бури могут создавать сильные ионосферные градиенты, снижающие точность систем SBAS.

Искусственные источники помех

В автомобильных GPS-приемниках металлические элементы на лобовых стеклах, например, в дефростерах, или пленках для тонировки автомобильных стекол может действовать как клетка Фарадея, ухудшающаяся качество приема сигнала внутри автомобиля.

Искусственные EMI (электромагнитные помехи) также могут нарушать или заглушать сигналы GPS. В одном случае невозможно было принять сигналы GPS для всей гавани Мосс-Лендинг, Калифорния из-за непреднамеренных помех, вызванных неисправностью предварительных усилителей телевизионной антенны. Также возможно преднамеренное заклинивание. Как правило, более сильные сигналы могут создавать помехи для приемников GPS, когда они находятся в пределах радиосвязи или в пределах прямого видимости. В 2002 году подробное описание того, как построить глушитель GPS L1 C / A ближнего действия, было опубликовано в онлайн-журнале Phrack.

The U.S. Правительство считает, что такие глушители времени использовались во время войны в Афганистане, а военные США заявляют, что уничтожили глушителей GPS во время войны в Ираке, в том числе один, который был уничтожен с бомбой с GPS-наведением. Глушитель GPS относительно легко определяет его местонахождение, делает его привлекательной целью для противорадиационных ракет. 7 и 8 июня 2007 г. Министерство обороны Великобритании провело испытания системы глушения в западной части Великобритании.

В некоторых странах разрешено использование ретрансляторов GPS для приема сигналов GPS в помещениях и в темных местах; в то время как в других странах это запрещено, поскольку ретранслируемые сигналы могут вызывать многолучевые помехи для других приемников GPS, которые получают данные как от спутников GPS, так и от ретранслятора. В Великобритании Ofcom теперь разрешает использование повторителей GPS / GNSS в рамках режима «облегченного лицензирования».

Из-за возможности возникновения как естественного, так и искусственного шума, продолжают развиваться многочисленные методы устранения помех. Первое — не полагаться на GPS как на единственный источник. По словам Джона Рули, «пилоты IFR должны иметь запасной план на случай сбоя GPS». Автономный мониторинг целостности приемника (RAIM) — это функция, включенная в некоторые приемники, предназначенная для предупреждать пользователя при обнаружении заедания или другой проблемы. С 2004 года военные США также развернули свой модуль выборочной доступности / защиты от спуфинга (SAASM) в составе усовершенствованного GPS-приемника обороны (DAGR). В демонстрационных видеороликах было показано, что DAGR обнаруживает помехи и сохраняет свою блокировку на зашифрованных сигналах GPS во время помех, из-за которых гражданские приемники теряют захват.

См. Также

Примечания

Ссылки

Grewal, Mohinder S.; Вайль, Лоуренс Рэндольф; Эндрюс, Ангус П. (2001). Глобальные системы позиционирования, инерциальная навигация и интеграция. Джон Уайли и сыновья. ISBN 978-0-47135-032-3.
Паркинсон; Спилкер (1996). Глобальная система позиционирования. Американский институт аэронавтики и астрономии. ISBN 978-1-56347-106-3.
Уэбб, Стивен (2004). Из этого мира: сталкивающиеся вселенные, браны, струны и другие дикие идеи современной физики. Springer. ISBN 0-387-02930-3. Проверено 16 августа 2013 г.

Внешние ссылки

GPS.gov — веб-сайтом общего образования, созданным правительством США
Стандарт производительности GPS SPS — официальная спецификация стандартной службы определения местоположения (версия 2008 года).
Стандарт производительности GPS SPS — официальная спецификация стандартной службы определения местоположения (версия 2001 года).

Источник

Что такое показатели точности позиционирования в ГНСС?

Introduction[edit]

Interpretation[edit]

Computation[edit]

See also[edit]

References[edit]

Further reading[edit]

Виды GPS-оборудования

Что влияет на качество сигнала GPS?

Геометрический фактор PDOP

Режимы работы GPS

«Статика» (Static)

Режим «Стой-Иди» (Stop&Go)

Режим RTK (Кинематика в реальном времени)

Каналы передачи данных

Понятие «Фиксированное решение»

Содержание

Обзор

Измерение времени прихода сигнала

Атмосферные эффекты

Эффекты многолучевого распространения

Ошибки эфемерид и часов

Геометрическое снижение точности вычислений (GDOP)

Вычисление геометрического снижения точности

Вывод для сравнения геометрического снижения точности

Выборочная доступность

Антиспуфинг

Относ

Специальная и общая теория относительности

Расчет количества замедления времени

Искажение Саньяка

Естественные источники помех

Искусственные источники помех

См. Также

Примечания

Ссылки

Внешние ссылки