Перейти к контенту

§ 2. Передача данных ГДЗ по Информатике 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю.
12. Как исправляется ошибка при использовании помехоустойчивого кода?
Ответ
Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи.
8.4.1 Принципы обнаружения и исправления ошибок
В реальных условиях
прием двоичных символов всегда происходит
с ошибками, когда вместо символа 1
принимается символ 0 и наоборот. Ошибки
могут возникать из-за помех, действующих
в канале связи (особенно помех импульсного
характера), изменения за время передачи
характеристик канала (например,
замирания), снижения уровня передачи,
нестабильности амплитудно- и фазочастотных
характеристик канала и т. п.
Общепринятым
критерием оценки качества передачи в
дискретных каналах является нормированная
на знак или символ допустимая вероятность
ошибки для данного вида сообщений. Так,
допустимая вероятность ошибки при
телеграфной связи может составлять
![]()
(на знак), а при передаче данных — не
более
![]()
(на символ). Для обеспечения таких
значений вероятностей одного улучшения
только качественных показателей канала
связи может оказаться недостаточным.
Поэтому, основной мерой является
применение специальных методов повышения
качества приема передаваемой информации.
Эти методы можно разбить на две группы.
К первой группе
относятся методы увеличения
помехоустойчивости приема единичных
элементов (символов) дискретной
информации, связанные с выбором уровня
сигнала, отношения сигнал/помеха
(энергетические характеристики), ширины
полосы канала, методов приема и т. д.
Ко второй группе
относятся методы обнаружения и исправления
ошибок, основанные на искусственном
введении избыточности в передаваемое
сообщение. Наиболее эффективно
избыточность используется при применении
помехоустойчивых (корректирующих)
кодов.
При передаче данных
осуществляется объединение отдельных
единичных элементов в кодовые комбинации,
по которым определяется принятое
сообщение. У обычного (не помехоустойчивого)
кода для каждой кодовой комбинации во
всей совокупности есть другая комбинация,
отличающаяся от первой лишь одним
разрядом. При искажении одного из
разрядов кодовая комбинация превратится
в другую и поэтому принятое сообщение
будет выдано с ошибкой.
Помехоустойчивое,
или избыточное
кодирование
применяется для обнаружения и (или)
исправления ошибок, возникающих при
передаче по дискретному каналу.
Отличительное свойство помехоустойчивого
кодирования состоит в том, что избыточность
источника, образованного выходом кодера,
больше, чем избыточность источника на
входе кодера. Помехоустойчивое кодирование
используется в различных системах
связи, при хранении и передаче данных
в сетях ЭВМ, в бытовой и профессиональной
аудио- и видеотехнике, основанной на
цифровой записи.
При использовании
помехоустойчивого кода передаются в
канал не все кодовые комбинации, которые
можно сформировать из имеющегося числа
разрядов, а лишь обладающие определенным
свойством, и называемые разрешенными.
Другие неиспользованные комбинации
называются запрещенными.
Введение дополнительных отличных
признаков в переданные комбинации
позволяет существенно повысить
правильность приема. Помехоустойчивые
коды подразделяются на коды, которые
обнаруживают
ошибки, и
коды, которые исправляют
ошибки.
Для двоичного кода
все множество кодовых комбинаций равно
N=2n
. При
использовании кодов,
обнаруживающих ошибки,
все множество n-разрядных
комбинаций разбивается на два
непересекающихся подмножества. Одно
подмножество называется разрешенной,
а другое запрещенной
(рис 8.7 а). Эти подмножества известны,
как на передающей, так и на приемной
сторонах. Если в результате искажений
передаваемых кодов комбинация перейдет
в подмножество запрещенных комбинаций,
то ошибка будет обнаружена. Такие коды
позволяют только определить наличие
ошибок, но не указывающие номер искаженных
разрядов.

Передаются только
разрешенные кодовые комбинации, которые
имеют определенное свойство. Если
принятая кодовая комбинация относится
к разрешенным, то считается, что ошибки
нет.
При необходимости
исправления некоторых возникающих
искажений
поступают следующим образом. Все
множество кодовых комбинаций N
разбивают на N0<N
непересекающихся подмножеств. Каждое
из этих подмножеств, приписывается к
одной из N0
разрешенных комбинаций (рис 8.7 б). В
каждом подмножестве существует одна
разрешенная комбинация. Если принятая
комбинация Аj
входит в подмножество N0j
(AjNoj),
то принимается решение, что передана
комбинация Aj.
То есть, если принятая кодовая комбинация
осталась в том же подмножестве, что и
передаваемая, то прием будет без ошибки.
Если кодовая комбинация в результате
искажений переходит в другое подмножество,
то прием будет с ошибкой.
Коды, которые не
только обнаруживают ошибку, но и указывают
номер искаженной позиции, называются
кодами с
исправлением ошибок.
Как было сказано
выше, при использовании помехоустойчивого
кода в канале связи передаются только
разрешенные кодовые комбинации. Если
бы не было помех, то для передачи этих
кодовых комбинаций потребовалось бы
меньшее число разрядов m:
![]()
(8.17)
Таким образом,
обнаружение и исправление возникающих
в каналах связи ошибок достигается за
счет введения в передаваемые кодовые
комбинации избыточных разрядов.
Рассмотрим
возможность обнаружения и исправления
ошибок на простейшем примере. Предположим,
что информация передается одноразрядным
двоичным кодом. То есть передается
информация 0 или 1. Число возможных
кодовых комбинаций
![]() ,
,
где
![]() ,
,![]() .
.
В каждой кодовой
комбинации добавим еще один разряд:
![]() .
.
Число кодовых
комбинаций
![]() .
.
Эти комбинации
составляют множество, состоящее из:
00, 01, 10, 11.
Это множество
разделим на два подмножества разрешенных
и запрещенных комбинаций. К числу
разрешенных отнесем те комбинации, у
которых сумма единиц или нулей всегда
четная – это комбинации:
00 и 11.
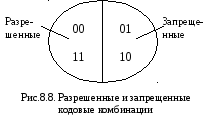
При таком выделении
разрешенных комбинаций любая одиночная
(или нечетная) ошибка будет изменять
число единиц на нечетное. Принятая
кодовая комбинация в этом случае
переходит в подмножество запрещенных
и ошибка будет обнаружена (рис. 8.8).
Е сли
сли
в кодовую комбинацию ввести количество
дополнительных разрядов, то можно не
только обнаруживать, но и исправлять
ошибки. Если разрешенные комбинации
определить таким образом, что любые из
них отличаются друг от друга не менее
чем тремя разрядами, то одиночная ошибка
может быть исправлена. Возможность
исправления одиночной ошибки в этом
случае связана с тем, что ошибочная
комбинация будет отличаться от истинной
только одним разрядом и останется в
области, относящейся к передаваемой
разрешенной комбинации.
Рис. 8.9. Геометрическая
модель помехоустойчивого кода
Рассмотрим сказанное
на геометрической модели трехразрядного
двоичного кода при помощи которого
можно получить 23=8
комбинаций. А именно: 000, 001, 010, 011, 100, 101,
110, 111. Каждую новую комбинацию можно
представить точкой в трехмерном
пространстве (рис. 8.9).
Для исправления
одиночной ошибки разобьем все множества
комбинации 110 и 001. Эти комбинации
отличаются друг от друга тремя разрядами.
Любая одиночная ошибка оставляет кодовую
комбинацию в области, относящейся к
передаваемой комбинации. Так, при
искажении одного разряда в комбинации
001 она превратится в 000, или в 100, или в
101. Все эти комбинации находятся в той
же области, что и комбинация 001.
Рассмотренные
примеры показывают, что для обнаружения
одиночных ошибок кодовые комбинации
должны различаться не менее чем двумя
разрядами. Для исправления одиночной
ошибки кодовые комбинации должны
различаться не менее чем тремя разрядами.
Это различие
именуют кодовым
(Хэмминговым) расстоянием.
Под кодовым
расстоянием
понимают
минимальное
число позиций, на которых символы данной
кодовой комбинации отличаются от
символов другой кодовой комбинации.
Например, для показанных на рисунке
8.10, кодовое расстояние d
равно 3.

Рис. 8.10. Кодовое
расстояние между двумя кодовыми
комбинациями
Поэтому можно
сказать, что возможности по обнаружению
или исправлению ошибок определяются
числом позиций, на которых отличаются
разрешенные кодовые комбинации, то есть
кодовым расстоянием.
Кодовое расстояние
между i-й
и j-й
кодовыми комбинациями
![]() определяется по формуле
определяется по формуле
![]() ,
,
(8.18)
где
![]() — значение символов
— значение символов![]() -й
-й
позиции j-й и i-й
кодовых комбинаций, знакозначает суммирование по модулю 2
(правила сложения по модулю 2: (1+1=0;
1+0=0+1=1; 0+0=0).
Соседние файлы в папке Пособие ТЕЗ_рус12
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Принципы помехоустойчивого кодирования
Помехоустойчивым (корректирующим) кодированием называется кодирование при котором осуществляется обнаружение либо обнаружение и исправление ошибок в принятых кодовых комбинациях.
Возможность помехоустойчивого кодирования осуществляется на основании теоремы, сформулированной Шенноном, согласно ей:
если производительность источника (Hи’(A)) меньше пропускной способности канала связи (Ск), то существует по крайней мере одна процедура кодирования и декодирования при которой вероятность ошибочного декодирования сколь угодно мала, если же производительность источника больше пропускной способности канала, то такой процедуры не существует.
Основным принципом помехоустойчивого кодирования является использование избыточных кодов, причем если для кодирования сообщения используется простой код, то в него специально вводят избыточность. Необходимость избыточности объясняется тем, что в простых кодах все кодовые комбинации являются разрешенными, поэтому при ошибке в любом из разрядов приведет к появлению другой разрешенной комбинации, и обнаружить ошибку будет не возможно. В избыточных кодах для передачи сообщений используется лишь часть кодовых комбинаций (разрешенные комбинации). Прием запрещенной кодовой комбинации означает ошибку. Причем, в процессе приема закодированного сообщения возможны три случая (рисунок 3).
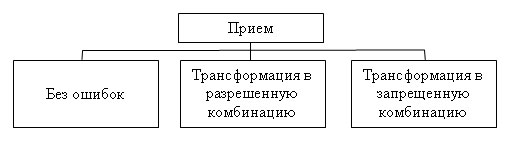
Рисунок 3 — Случаи приема закодированного сообщения
Прием сообщения без ошибок является оптимальным, но возможен только если канал связи идеальный. В этом случае помехоустойчивое декодирование не нужно.
В реальном канале из-за воздействия помех происходят ошибки в принимаемых кодовых комбинациях. Если принимаемая кодовая комбинация в результате воздействия помех перешла (трансформировалась) из одной разрешенной комбинации в другую, то определить ошибку не возможно, даже при использовании помехоустойчивого кодирования.
Если же передаваемая разрешенная кодовая комбинация, в результате воздействия помех, трансформируется в запрещенную комбинация, то в этом случае существует возможность обнаружить ошибку и исправить ее.
Помехоустойчивое кодирование может осуществляться двумя способами: с обнаружением ошибок либо с исправлением ошибок. Возможность кода обнаруживать или исправлять ошибки определяется кодовым расстоянием.
Если осуществляется кодирование с обнаружением ошибок, то кодовое расстояние должно быть хотя бы на единицу больше чем кратность обнаруживаемых ошибок, т. е.
d0? qо ош + 1.
Если данное условие не выполняется, то одни из ошибок обнаруживаются, а другие нет.
Если осуществляется кодирование с исправлением ошибок, то кодовое расстояние должно быть хотя бы на единицу больше удвоенного значения кратности исправляемых ошибок, т. е.
d0? 2qи ош + 1.
Если данное условие не выполняется, то одни из ошибок исправляются, а другие нет.
Следует отметить, что если код способен исправить одну ошибку (qи ош = 1), что соответствует кодовому расстоянию 3 (d0 = 1?2+1 = 3), то обнаружить он может две ошибки, т. к.
qо ош = d0 – 1 = 2.
Декодирование помехоустойчивых кодов
Декодирование — это процесс перехода от вторичного отображения сообщения к первичному алфавиту.
Декодирование помехоустойчивых кодов может осуществляться тремя способами: сравнения, синдромным и мажоритарным.
Способ сравнения основан на том, что, принятая кодовая комбинация сравнивается со всеми разрешенными комбинациями, которые заранее известны на приеме. Если принятая комбинация не совпадает ни с одной из разрешенных, выносится решение о принятии запрещенной комбинации. Недостатком данного способа является громоздкость и необходимость большого времени для декодирования в случае применения многоразрядных кодов. Данный способ используется в кодах с обнаружением ошибок.
Синдромный способ основан на вычислении определенным образом контрольного числа — синдрома ошибки (С). Если синдром ошибки равен нулю, то кодовая комбинация принята верно, если синдром не равен нулю, то комбинация принята не верно. Данный способ может быть использован в кодах с исправлением ошибок, в этом случае синдром указывает не только на наличие ошибки в кодовой комбинации, но и на место положение этой ошибки в кодовой комбинации. Для двоичного кода знание местоположения ошибки достаточно для ее исправления. Это объясняется тем, что любой символ кодовой комбинации может принимать всего два значения и если символ ошибочный, то его необходимо инвертировать. Следовательно, синдрома ошибки достаточно для исправления ошибок, если d0? 2qи ош + 1.
Мажоритарное декодирование основано на том, что каждый информационный символ кодовой комбинации определяется нескольким линейными выражениями через другие символы кодовой комбинации. Если принята комбинация без ошибок, то все соотношения остаются и все выражения дают одинаковые результаты (единицу или ноль). При ошибке в одном из разрядов эти соотношения нарушаются, в результате чего одни линейные выражения равны нулю, а другие единице. Решение о принятом символе определяется по большинству: если в результате вычислений выражений больше нулей, то принимается решение о принятии нуля, если больше единиц, то принимается решение о приеме единицы. Если, при декодировании, результаты вычисления выражений дают одинаковое число единиц и нулей, то при определении принятого символа приоритет имеет принятый символ, значение которого в данный момент определяется.
Классификация корректирующих кодов
Классификация корректирующих кодов представлена схемой (рисунок 4)
Блочные — это коды, в которых передаваемое сообщение разбивается на блоки и каждому блоку соответствует своя кодовая комбинация (например, в телеграфии каждой букве соответствует своя кодовая комбинация).
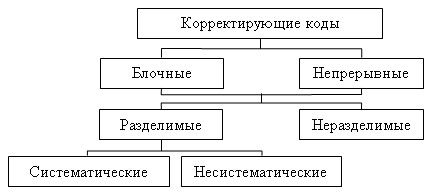
Рисунок 4 — Классификация корректирующих кодов
Непрерывные — коды, в которых сообщение не разбивается на блоки, а проверочные символы располагаются между информационными.
Неразделимые — это коды, в кодовых комбинациях которых нельзя выделить проверочные разряды.
Разделимые — это коды, в кодовых комбинациях которых можно указать положение проверочных разрядов, т. е. кодовые комбинации можно разделить на информационную и проверочную части.
Систематические (линейные) — это коды, в которых проверочные символы определяются как линейные комбинации информационных символов, в таких кодах суммирование по модулю два двух разрешенных кодовых комбинаций также дает разрешенную комбинацию. В несистематических кодах эти условия не выполняются.
Код с постоянным весом
Данный код относится к классу блочных не разделимых кодов. В нем все разрешенные кодовые комбинации имеют одинаковый вес. Примером кода с постоянным весом является Международный телеграфный код МТК-3. В этом коде все разрешенные кодовые комбинации имеют вес равный трем, разрядность же комбинаций n=7. Таким образом, из 128 комбинаций (N0 = 27 = 128) разрешенными являются Nа = 35 (именно столько комбинаций из всех имеют W=3). При декодировании кодовых комбинаций осуществляется вычисление веса кодовой комбинации и если W?3, то выносится решение об ошибке. Например, из принятых комбинаций 0110010, 1010010, 1000111 ошибочной является третья, т. к. W=4. Данный код способен обнаруживать все ошибки нечетной кратности и часть ошибок четной кратности. Не обнаруживаются только ошибки смещения, при которых вес комбинации не изменяется, например, передавалась комбинация 1001001, а принята 1010001 (вес комбинации не изменился W=3). Код МТК-3 способен только обнаруживать ошибки и не способен их исправлять. При обнаружении ошибки кодовая комбинация не используется для дальнейшей обработки, а на передающую сторону отправляется запрос о повторной передаче данной комбинации. Поэтому данный код используется в системах передачи информации с обратной связью.
Код с четным числом единиц
Данный код относится к классу блочных, разделимых, систематических кодов. В нем все разрешенные кодовые комбинации имеют четное число единиц. Это достигается введением в кодовую комбинацию одного проверочного символа, который равен единице если количество единиц в информационной комбинации нечетное и нулю ? если четное. Например:
При декодировании осуществляется поразрядное суммирование по модулю два всех элементов принятой кодовой комбинации и если результат равен единице, то принята комбинация с ошибкой, если результат равен нулю принята разрешенная комбинация. Например:
101101 = 1 + 0 + 1 + 1 + 0 + 1 = 0 — разрешенная комбинация
101111 = 1 + 0 + 1 + 1 + 1 + 1 = 1 — запрещенная комбинация.
Данный код способен обнаруживать как однократные ошибки, так и любые ошибки нечетной кратности, но не способен их исправлять. Данный код также используется в системах передачи информации с обратной связью.
Код Хэмминга
Код Хэмминга относится к классу блочных, разделимых, систематических кодов. Кодовое расстояние данного кода d0=3 или d0=4.
Блочные систематические коды характеризуются разрядностью кодовой комбинации n и количеством информационных разрядов в этой комбинации k остальные разряды являются проверочными (r):
r = n — k.
Данные коды обозначаются как (n,k).
Рассмотрим код Хэмминга (7,4). В данном коде каждая комбинация имеет 7 разрядов, из которых 4 являются информационными,
При кодировании формируется кодовая комбинация вида:
а1 а2 а3 а4 b1 b2 b
где аi — информационные символы;
bi — проверочные символы.
В данном коде проверочные элементы bi находятся через линейные комбинации информационных символов ai, причем, для каждого проверочного символа определяется свое правило. Для определения правил запишем таблицу синдромов кода (С) (таблица 3), в которой записываются все возможные синдромы, причем, синдромы имеющие в своем составе одну единицу соответствуют ошибкам в проверочных символах:
- синдром 100 соответствует ошибке в проверочном символе b1;
- синдром 010 соответствует ошибке в проверочном символе b2;
- синдром 001 соответствует ошибке в проверочном символе b3.
Синдромы с числом единиц больше 2 соответствуют ошибкам в информационных символах. Синдромы для различных элементов кодовой комбинации аi и bi должны быть различными.
Таблица 3 — Синдромы кода Хэмминга (7;4)
| Число | Элементы синдрома | Элементы кодовой | ||
| синдрома | С1 | С2 | С3 | комбинации |
| 1 | 0 | 0 | 1 | b3 |
| 2 | 0 | 1 | 0 | b2 |
| 3 | 0 | 1 | 1 | a1 |
| 4 | 1 | 0 | 0 | b1 |
| 5 | 1 | 0 | 1 | a2 |
| 6 | 1 | 1 | 0 | a3 |
| 7 | 1 | 1 | 1 | a4 |
Определим правило формирования элемента b3. Как следует из таблицы, ошибке в данном символе соответствует единица в младшем разряде синдрома С4. Поэтому, из таблицы, необходимо отобрать те элементы аi у которых, при возникновении ошибки, появляется единица в младшем разряде. Наличие единиц в младшем разряде, кроме b3,соответствует элементам a1, a2 и a4. Просуммировав эти информационные элементы получим правило формирования проверочного символа:
b3 = a1 + a2 + a4
Аналогично определяем правила для b2 и b1:
b2 = a1 + a3 + a4
b1 = a2 + a3 + a4
Пример 3, необходимо сформировать кодовую комбинацию кода Хэмминга (7,4) соответствующую информационным символам 1101.
В соответствии с проверочной матрицей определяем bi:
b1 = 1 + 0 + 1 = 0; b2 = 1 + 0 + 1=1; b3 = 1 + 1 + 1 = 1.
Добавляем проверочные символы к информационным и получаем кодовую комбинацию:
Biр = 1101001.
![]()
В теории циклических кодов все преобразования кодовых комбинаций производятся в виде математических операций над полиномами (степенными функциями). Поэтому двоичные комбинации преобразуют в полиномы согласно выражения:
Аi(х) = аn-1xn-1 + аn-2xn-2 +…+ а0x0
где an-1, … коэффициенты полинома принимающие значения 0 или 1. Например, комбинации 1001011 соответствует полином
Аi(х) = 1?x6 + 0?x5 + 0?x4 + 1?x3 + 0?x2 + 1?x+1?x0 ? x6 + x3 + x+1.
При формировании кодовых комбинаций над полиномами производят операции сложения, вычитания, умножения и деления. Операции умножения и деления производят по арифметическим правилам, сложение заменяется суммированием по модулю два, а вычитание заменяется суммированием.
Разрешенные кодовые комбинации циклических кодов обладают тем свойством, что все они делятся без остатка на образующий или порождающий полином G(х). Порождающий полином вычисляется с применением ЭВМ. В приложении приведена таблица синдромов.
Этапы формирования разрешенной кодовой комбинации разделимого циклического кода Biр(х).
1. Информационная кодовая комбинация Ai преобразуется из двоичной формы в полиномиальную (Ai(x)).
2. Полином Ai(x) умножается на хr,
Ai(x)?xr
где r количество проверочных разрядов:
r = n — k.
3. Вычисляется остаток от деления R(x) полученного произведения на порождающий полином:
R(x) = Ai(x)?xr/G(x).
4. Остаток от деления (проверочные разряды) прибавляется к информационным разрядам:
Biр(x) = Ai(x)?xr + R(x).
5. Кодовая комбинация Bip(x) преобразуется из полиномиальной формы в двоичную (Bip).
Пример 4. Необходимо сформировать кодовую комбинацию циклического кода (7,4) с порождающим полиномом G(x)=х3+х+1, соответствующую информационной комбинации 0110.
1. Преобразуем комбинацию в полиномиальную форму:
Ai = 0110 ? х2 + х = Ai(x).
2. Находим количество проверочных символов и умножаем полученный полином на xr:
r = n – k = 7 – 4 =3
Ai(x)?xr = (х2 + х)? x3 = х5 + х4
3. Определяем остаток от деления Ai(x)?xr на порождающий полином, деление осуществляется до тех пор пока наивысшая степень делимого не станет меньше наивысшей степени делителя:
R(x) = Ai(x)?xr/G(x)
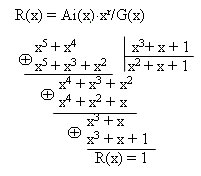
4. Прибавляем остаток от деления к информационным разрядам и переводим в двоичную систему счисления:
Biр(x) = Ai(x)?xr+ R(x) = х5 + х4 + 1? 0110001.
5. Преобразуем кодовую комбинацию из полиномиальной формы в двоичную:
Biр(x) = х5 + х4 + 1 ? 0110001 = Biр
Как видно из комбинации четыре старших разряда соответствуют информационной комбинации, а три младших — проверочные.
Формирование разрешенной кодовой комбинации неразделимого циклического кода.
Формирование данных комбинаций осуществляется умножением информационной комбинации на порождающий полином:
Biр(x) = Ai(x)?G(x).
Причем умножение можно производить в двоичной форме.
Пример 5, необходимо сформировать кодовую комбинацию неразделимого циклического кода используя данные примера 2, т. е. G(x) = х3+х+1, Ai(x) = 0110, код (7,4).
1. Переводим комбинацию из двоичной формы в полиномиальную:
Ai = 0110? х2+х = Ai(x)
2. Осуществляем деление Ai(x)?G(x)
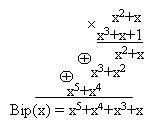
3. Переводим кодовую комбинацию из полиномиальной форы в двоичную:
Bip(x) = х5+х4+х3+х ? 0111010 = Bip
В этой комбинации невозможно выделить информационную и проверочную части.
Матричное представление систематических кодов
Систематические коды, рассмотренные выше (код Хэмминга и разделимый циклический код) удобно представить в виде матриц. Рассмотрим, как это осуществляется.
Поскольку систематические коды обладают тем свойством, что сумма двух разрешенных комбинаций по модулю два дают также разрешенную комбинацию, то для формирования комбинаций таких кодов используют производящую матрицу Gn,k. С помощью производящей матрицы можно получить любую кодовую комбинацию кода путем суммирования по модулю два строк матрицы в различных комбинациях. Для получения данной матрицы в нее заносятся исходные комбинации, которые полностью определяют систематический код. Исходные комбинации определяются исходя из условий:
1) все исходные комбинации должны быть различны;
2) нулевая комбинация не должна входить в число исходных комбинаций;
3) каждая исходная комбинация должна иметь вес не менее кодового расстояния, т. е. W?d0;
4) между любыми двумя исходными комбинациями расстояние Хэмминга должно быть не меньше кодового расстояния, т. е. dij?d0.
Производящая матрица имеет вид:
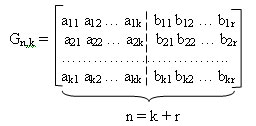
Производящая подматрица имеет k строк и n столбцов. Она образована двумя подматрицами: информационной (включает элементы аij) и проверочной (включает элементы bij). Информационная матрица имеет размеры k?k, а проверочная — r?k.
В качестве информационной подматрицы удобно брать единичную матрицу Ekk:
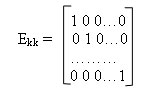
Проверочная подматрица Gr,k строится путем подбора различных r-разрядных комбинаций, удовлетворяющих следующим правилам:
1) в каждой строке подматрицы количество единиц должно быть не менее d0-1;
2) сумма по модулю два двух любых строк должна иметь не менее d0-2 единицы;
Полученная таким образом подматрица Gr,k приписывается справа к подматрице Ekk, в результате чего получается производящая матрица Gn,k. Затем, используя производящую матрицу, можно получить любую комбинацию кода путем суммирования двух и более строк по модулю два в различных комбинациях.
Пример 6. Необходимо построить производящую матрицу кода Хэмминга способного исправлять 1 ошибку и имеющего n=7. Закодировать с помощью полученной матрицы комбинацию Ai=1101.
Определяем кодовое расстояние:
d0=2qи ош+1= 2?1+1=3.
Для кодов с d0=3 количество проверочных разрядов определяется по формуле:
r=log2(n+1)= log28=3.
Определяем разрядность информационной части:
k = n — r = 7 — 4 =3.
Запишем все возможные комбинации проверочной подматрицы: 000, 001, 010, 011, 100, 101, 110, 111. Выберем из этих комбинаций те, что удовлетворяют правилам:
1) в каждой строке не менее d0-1, этому условию соответствуют комбинации 011, 101, 110, 111;
2) сумма двух любых комбинаций по модулю два содержит единиц не менее d0-2:
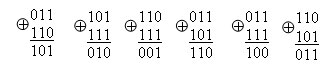
3) записываем проверочную подматрицу:
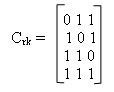
4) приписываем полученную подматрицу к единичной и получаем производящую матрицу:
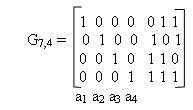
Если произвести определение d0 для исходных комбинаций полученной матрицы (определив расстояние Хэмминга для всех пар комбинаций), то оно окажется равным 3.
Для кодирования заданной комбинации Ai, необходимо просуммировать те строки матрицы G, которые в информационной части имеют единицу на том месте, на котором они находятся в комбинации Аi. Для заданной комбинации 1101 единичными разрядами являются а1, а2, а4. В матрице G единицы на этих местах имеют строки: первая, вторая и четвертая. Просуммировав их получаем разрешенную комбинацию заданного кода.
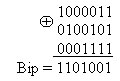
Сравнивая полученную кодовую комбинацию Bip с комбинацией полученной примере 3, для которой также использована комбинация Ai=1101, видим что они одинаковы.
Для кода Хэмминга выше были определены правила формирования проверочных символов bk:

Эти правила можно отобразить в виде проверочной матрицы Нn,k. Она состоит из n столбцов (соответствует разрядности кодовой комбинации) и r столбцов (соответствует количеству проверочных разрядов кодовой комбинации). В правой части матрицы указываются синдромы, соответствующие ошибкам в проверочных символах, в левой части записываются элементы информационной части комбинации, причем, те элементы, которые участвуют в образовании определенного элемента bi равны единицы, а те которые не участвуют — нулю.
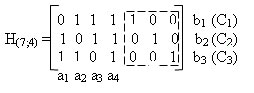
В данном случае обведенные пунктиром проверочные элементы образуют единичную матрицу. Проверочная матрица позволяет определить ошибочный разряд, поскольку каждый столбец данной матрицы представляет собой синдром соответствующего символа. При этом строки матрицы будут соответствовать разрядам синдрома Ck. Например, согласно приведенной проверочной матрице, синдром соответствующий ошибку в разряде а1 имеет вид 011, в разряде а2 — 101, в разряде а3 — 110, в разряде а4 — 111, в разряде b1 — 100, в разряде b2 — 010, в разряде b3 — 001. Также с помощью проверочной матрицы легко определить проверочные и символы и сформировать кодовую комбинацию. Например, необходимо сформировать кодовую комбинацию кода Хэмминга (7,4) соответствующую информационным символам 1101.
В соответствии с проверочной матрицей определяем bi:
b1 = 1 + 0 + 1 = 0; b2 = 1 + 0 + 1=0; b3 = 1 + 1 + 1 = 1.
Добавляем проверочные символы к информационным и получаем кодовую комбинацию:
Biр = 1101001.
Также проверочную матрицу можно построить и другим способом. Для этого сначала строится единичная матрица Еr. К которой слева приписывается подматрица Dk,r. Каждая строка этой подматрицы соответствует столбцу проверочных разрядов подматрицы Сr,k производящей матрицы Gn,k.
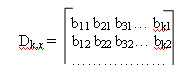
Такое преобразование строк матрицы в столбцы называется транспонированием.
В результате получаем
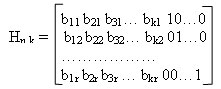
Декодирование циклических кодов
При декодировании таких кодов (разделимых и неразделимых) используется Синдромный способ. Вычисление синдрома осуществляется в три этапа:
1. принятая комбинация Bip’ преобразуется их двоичной формы в полиномиальную (Bip(x));
2. осуществляется деление Bip(x) на порождающий полином G(x) в результате чего определяется синдром ошибки C(x) (остаток от деления);
3. синдром ошибки преобразуется из полиномиальной формы в двоичную;
4. По проверочной матрице или таблице синдромов определяется ошибочный разряд;
5. Ошибочный разряд в Bip’(x) инвертируется;
6. Исправленная комбинация преобразуется из полиномиальной формы в двоичную Bip.
делением принятой кодовой комбинации Biр’(x) на порождающий полином G(x), который заранее известен на приеме. Остаток от деления и является синдромом ошибки С(х).
Мажоритарное декодирование циклических кодов
Мажоритарное декодирование может применятся только для декодирования систематических кодов (кода Хэмминга, циклического разделимого кода). Рассмотрим мажоритарное декодирование на примере циклического кода.
Контроль ошибок — комплекс методов обнаружения и исправления ошибок в данных (b) при их записи и воспроизведении или передаче по линиям связи.
Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом (b) , канальном (b) , транспортном (b) уровнях сетевой модели OSI (b) ) в связи с тем, что в процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Различные области применения контроля ошибок диктуют различные требования к используемым стратегиям и кодам.
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи[⇨] повреждённых блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- упреждающая коррекция ошибок добавляет к передаваемой информации такие дополнительные данные, которые позволяют исправить ошибки без дополнительного запроса.
В контроле ошибок, как правило, используется помехоустойчивое кодирование (b) — кодирование данных при записи или передаче и декодирование (b) при считывании или получении при помощи корректирующих кодов (b) , которые и позволяют обнаружить и, возможно, исправить ошибки в данных. Алгоритмы помехоустойчивого кодирования в различных приложениях могут быть реализованы как программно, так и аппаратно.
Современное развитие корректирующих кодов (b) приписывают Ричарду Хэммингу (b) с 1947 года (b) [1]. Описание кода Хэмминга (b) появилось в статье Клода Шеннона (b) «Математическая теория связи (b) »[2] и было обобщено Марселем Голеем (b) [3].
Стратегии исправления ошибок
Упреждающая коррекция ошибок
Упреждающая коррекция ошибок (также прямая коррекция ошибок, англ. (b) Forward Error Correction, FEC) — техника помехоустойчивого кодирования и декодирования (b) , позволяющая исправлять ошибки методом упреждения. Применяется для исправления сбоев и ошибок при передаче данных путём передачи избыточной служебной информации, на основе которой может быть восстановлено первоначальное содержание. На практике широко используется в сетях передачи данных (b) , телекоммуникационных технологиях. Коды, обеспечивающие прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, которые только обнаруживают ошибки.
Например, в спутниковом телевидении (b) при передаче цифрового сигнала с FEC 7/8 передаётся восемь бит информации: 7 бит полезной информации и 1 контрольный бит[4]; в DVB-S (b) используется всего 5 видов: 1/2, 2/3, 3/4 (наиболее популярен), 5/6 и 7/8. При прочих равных условиях, можно утверждать, что чем ниже значение FEC, тем меньше пакетов допустимо потерять, и, следовательно, выше требуемое качество сигнала.
Техника прямой коррекции ошибок широко применяется в различных устройствах хранения данных — жёстких дисках, флеш-памяти, оперативной памяти. В частности, в серверных приложениях применяется ECC-память (b) — оперативная память, способная распознавать и исправлять спонтанно возникшие ошибки.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (b) (англ. (b) Automatic Repeat Request, ARQ) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Идея запроса ARQ с остановками (англ. (b) stop-and-wait ARQ) заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем, как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного (b) канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Для метода непрерывного запроса ARQ с возвратом (continuous ARQ with pullback) необходим полнодуплексный (b) канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть передается ошибочный блок и все последующие).
При использовании метода непрерывного запроса ARQ с выборочным повторении (continuous ARQ with selective repeat) осуществляется передача только ошибочно принятых блоков данных.
Сетевое кодирование
Раздел теории информации (b) , изучающий вопрос оптимизации передачи данных по сети с использованием техник изменения пакетов данных на промежуточных узлах называют сетевым кодированием (b) . Для объяснения принципов сетевого кодирования используют пример сети «бабочка», предложенной в первой работе по сетевому кодированию «Network information flow»[5]. В отличие от статического сетевого кодирования, когда получателю известны все манипуляции, производимые с пакетом, также рассматривается вопрос о случайном сетевом кодировании, когда данная информация неизвестна. Авторство первых работ по данной тематике принадлежит Кёттеру, Кшишангу и Силве[6]. Также данный подход называют сетевым кодированием со случайными коэффициентами — когда коэффициенты, под которыми начальные пакеты, передаваемые источником, войдут в результирующие пакеты, принимаемые получателем, с неизвестными коэффициентами, которые могут зависеть от текущей структуры сети и даже от случайных решений, принимаемых на промежуточных узлах. Для неслучайного сетевого кодирования можно использовать стандартные способы защиты от помех и искажений, используемых для простой передачи информации по сети.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум (b) на входе демодулятора, таким образом, при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Примечания
- ↑ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, с. vii, ISBN 0-88385-023-0
- ↑ Shannon, C.E. (1948), A Mathematical Theory of Communication, Bell System Technical Journal (p. 418) Т. 27 (3): 379–423, PMID 9230594, DOI 10.1002/j.1538-7305.1948.tb01338.x
- ↑ Golay, Marcel J. E. (1949), Notes on Digital Coding, Proc.I.R.E. (I.E.E.E.) (p. 657) Т. 37
- ↑ Understanding Digital Television: An Introduction to Dvb Systems With … — Lars-Ingemar Lundström — Google Книги. Дата обращения: 19 мая 2020. Архивировано 11 ноября 2021 года.
- ↑ Ahlswede, R.; Ning Cai; Li, S.-Y.R.; Yeung, R.W., «Network information flow», Information Theory, IEEE Transactions on, vol.46, no.4, pp.1204-1216, Jul 2000
- ↑ Статьи:
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding// IEEE International Symposium on Information Theory. Proc.ISIT-07.-2007.- P. 791—795.
- Silva D., Kschischang F.R. Using rank-metric codes for error correction in random network coding // IEEE International Symposium on Information Theory. Proc. ISIT-07. — 2007.
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding // IEEE Transactions on Information Theory. — 2008- V. IT-54, N.8. — P. 3579-3591.
- Silva D., Kschischang F.R., Koetter R. A Rank-Metric Approach to Error Control in Random Network Coding // IEEE Transactions on Information Theory.- 2008- V. IT-54, N. 9.- P.3951-3967.
Литература
| Имеется викиучебник (b) по теме «Помехоустойчивое кодирование» |
- Блейхут Р. (b) Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир (b) , 1986. — 576 с.
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Морелос-Сарагоса Р. (b) Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева (b) . — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
- Clark, George C., Jr., and J. Bibb Cain. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981. ISBN 0-306-40615-2.
- Lin, Shu, and Daniel J. Costello, Jr. «Error Control Coding: Fundamentals and Applications». Englewood Cliffs, N.J.: Prentice-Hall, 1983. ISBN 0-13-283796-X.
- Mackenzie, Dana. «Communication speed nears terminal velocity». New Scientist 187.2507 (9 июля (b) 2005 (b) ): 38-41. ISSN 0262-4079.
- Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Englewood Cliffs, N.J.: Prentice-Hall, 1995. ISBN 0-13-200809-2.
- Wilson, Stephen G. Digital Modulation and Coding, Englewood Cliffs, N.J.: Prentice-Hall, 1996. ISBN 0-13-210071-1.
Ссылки
- Charles Wang, Dean Sklar, and Diana Johnson. Forward Error-Correction Coding. The Aerospace Corporation. — Volume 3, Number 1 (Winter 2001/2002). Дата обращения: 24 мая 2009. Архивировано из оригинала 20 февраля 2005 года. (англ.)
- Charles Wang, Dean Sklar, and Diana Johnson. How Forward Error-Correcting Codes Work (недоступная ссылка — история). The Aerospace Corporation. Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
- Morelos-Zaragoza, Robert The Error Correcting Codes (ECC) Page (недоступная ссылка — история) (2004). Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
Помехоустойчивые коды — КОД Хэмминга простыми словами
Помехоустойчивое кодирование. Коды Хэмминга
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т. к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С, D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, Скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т. д.
Второй параметр, Кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, Кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
По используемому алфавиту:
Блочные коды делятся на
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Помехоустойчивое кодирование. Коды Хэмминга
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т. к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С, D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, Скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т. д.
Второй параметр, Кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, Кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
По используемому алфавиту:
Блочные коды делятся на
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Ошибки программирования
Ошибки, которые обнаруживает компилятор, называют Синтаксическими ошибками или Ошибками компиляции. Синтаксические ошибки являются результатом ошибок в конструкции кода, таких как неправильное написание ключевого слова, пропуск необходимого знака пунктуации или использование открывающей фигурной скобки без соответствующей закрывающей фигурной скобки. Эти ошибки обычно легко обнаружить, поскольку компилятор говорит вам, где они находятся и что стало их причиной. Пример программы с синтаксической ошибкой:
Попытка компиляции приведённого кода:
Будет сообщено о четырёх ошибках, но в действительности программа содержит две ошибки:
Поскольку одна ошибка часто будет приводить к показу множества ошибок компиляции в разных строках, хорошей практикой является исправление ошибок начиная с верхней строки и постепенно двигаясь вниз. Исправление ошибок, которые ранее возникли в программе, может также исправить дополнительные ошибки, которые произошли позже.
Совет: если вы не знаете, как исправить ошибку, внимательно сравните вашу программу, символ за символом с похожими примерами в тексте. На начальном этапе обучения вы, вероятно, будете проводить много времени исправляя ошибки синтаксиса. Скоро вы будете знакомы с синтаксисом Java и сможете быстро исправлять синтаксические ошибки.
2. Ошибки во время выполнения
Ошибки во время выполнения – это ошибки, которые приводят к ненормальному обрывы работы программы. Они возникают во время работы программы, если среда обнаруживает операцию, которую невозможно выполнить. Обычно Ошибки ввода становятся причинами ошибок во время выполнения. Ошибки ввода возникают, когда программа ожидает от пользователя ввода значения, но пользователь вводит величину, которую программа не может обработать. Например, программа ожидает получение числа, но вместо этого пользователь вводит строку, это приводит к ошибкам в программе, связанным с типами данных.
Другой пример ошибок во время выполнения – это деление на ноль. Это происходит, когда в целочисленном деление делитель равен нулю. Пример программы, которая вызовет ошибку во время выполнения:
3. Логические ошибки
Логические ошибки происходят, когда программа неправильно выполняет то, для чего она была создана. Ошибки этого рода возникают по многим различным причинам. Допустим, вы написали программу, которая конвертирует 35 градусов Цельсия в градусы Фаренгейта следующим образом:
Вы получите 67 градусов по Фаренгейту, что является неверным. Должно быть 95.0. В Java целочисленное деление показывает только часть – дробная часть отсекается, по этой причине в Java 9 / 5 это 1. Для получения правильного результата, нужно использовать 9.0 / 5, что даст результат 1.8.
Обычно ошибки синтаксиса легко обнаружить и легко исправить, поскольку компилятор даёт указания откуда пришла ошибка и что не так. Ошибки во время выполнения не трудны для поиска, поскольку причина и место для этих ошибок также показывается в консоли во время прерывания программы. Поиск логических ошибок, в свою очередь, очень сложный. В последующих главах вы обучитесь техникам трассировки программ и поиска логических ошибок.
4. Распространённые ошибки
Пропуск закрывающей фигурной скобки, пропуск точки с запятой, пропуск кавычки для строки и неправильное написание имён – всё это самые распространённые ошибки для новых программистов.
Частые ошибки 1: Пропущенные фигурные скобки
Фигурные скобки используются для обозначения в программе блоков. Каждой открывающей фигурной скобке должна соответствовать закрывающая фигурная скобка. Распространённая ошибка – это пропуск закрывающей фигурной скобки. Чтобы избежать эту ошибки, печатайте закрывающую фигурную скобку всякий раз, когда печатаете открывающую фигурную скобку как показано в следующем примере:
Если вы используете IDE такую как NetBeans и Eclipse, то IDE автоматически вставит закрывающую фигурную скобку каждой введённой вами открывающей фигурной скобки.
Частые ошибки 2: Пропуск точки с запятой
Каждая инструкция заканчивается ограничителем инструкции (;). Часто новые программисты забывают поместить ограничитель инструкции для последней инструкции в блоке как это показано в следующем примере:
Частые ошибки 3: Пропуск кавычки
Строки должны помещаться в кавычки. Часто начинающие программисты забывают поместить кавычку в конце строки как показано в следующем примере:
Если вы используете IDE, такую как NetBeans и Eclipse, то IDE автоматически вставит закрывающую кавычку каждый раз, когда вы ввели открывающую кавычку.
Частые ошибки 4: Неправильное написание имён
Java чувствительная к регистру. Неправильное написание имён – частая ошибка для новых программистов. Например, пишут слово Main как Main, а вместо String пишут String. Пример:
Источники:
Https://zvondozvon. ru/radiosvyaz/kody-hemminga
Https://kodyoshibok01.ru/pomexoustojchivoe-kodirovanie-kody-xemminga-6/
8.4.1 Принципы обнаружения и исправления ошибок
В реальных условиях
прием двоичных символов всегда происходит
с ошибками, когда вместо символа 1
принимается символ 0 и наоборот. Ошибки
могут возникать из-за помех, действующих
в канале связи (особенно помех импульсного
характера), изменения за время передачи
характеристик канала (например,
замирания), снижения уровня передачи,
нестабильности амплитудно- и фазочастотных
характеристик канала и т. п.
Общепринятым
критерием оценки качества передачи в
дискретных каналах является нормированная
на знак или символ допустимая вероятность
ошибки для данного вида сообщений. Так,
допустимая вероятность ошибки при
телеграфной связи может составлять
![]()
(на знак), а при передаче данных — не
более
![]()
(на символ). Для обеспечения таких
значений вероятностей одного улучшения
только качественных показателей канала
связи может оказаться недостаточным.
Поэтому, основной мерой является
применение специальных методов повышения
качества приема передаваемой информации.
Эти методы можно разбить на две группы.
К первой группе
относятся методы увеличения
помехоустойчивости приема единичных
элементов (символов) дискретной
информации, связанные с выбором уровня
сигнала, отношения сигнал/помеха
(энергетические характеристики), ширины
полосы канала, методов приема и т. д.
Ко второй группе
относятся методы обнаружения и исправления
ошибок, основанные на искусственном
введении избыточности в передаваемое
сообщение. Наиболее эффективно
избыточность используется при применении
помехоустойчивых (корректирующих)
кодов.
При передаче данных
осуществляется объединение отдельных
единичных элементов в кодовые комбинации,
по которым определяется принятое
сообщение. У обычного (не помехоустойчивого)
кода для каждой кодовой комбинации во
всей совокупности есть другая комбинация,
отличающаяся от первой лишь одним
разрядом. При искажении одного из
разрядов кодовая комбинация превратится
в другую и поэтому принятое сообщение
будет выдано с ошибкой.
Помехоустойчивое,
или избыточное
кодирование
применяется для обнаружения и (или)
исправления ошибок, возникающих при
передаче по дискретному каналу.
Отличительное свойство помехоустойчивого
кодирования состоит в том, что избыточность
источника, образованного выходом кодера,
больше, чем избыточность источника на
входе кодера. Помехоустойчивое кодирование
используется в различных системах
связи, при хранении и передаче данных
в сетях ЭВМ, в бытовой и профессиональной
аудио- и видеотехнике, основанной на
цифровой записи.
При использовании
помехоустойчивого кода передаются в
канал не все кодовые комбинации, которые
можно сформировать из имеющегося числа
разрядов, а лишь обладающие определенным
свойством, и называемые разрешенными.
Другие неиспользованные комбинации
называются запрещенными.
Введение дополнительных отличных
признаков в переданные комбинации
позволяет существенно повысить
правильность приема. Помехоустойчивые
коды подразделяются на коды, которые
обнаруживают
ошибки, и
коды, которые исправляют
ошибки.
Для двоичного кода
все множество кодовых комбинаций равно
N=2n
. При
использовании кодов,
обнаруживающих ошибки,
все множество n-разрядных
комбинаций разбивается на два
непересекающихся подмножества. Одно
подмножество называется разрешенной,
а другое запрещенной
(рис 8.7 а). Эти подмножества известны,
как на передающей, так и на приемной
сторонах. Если в результате искажений
передаваемых кодов комбинация перейдет
в подмножество запрещенных комбинаций,
то ошибка будет обнаружена. Такие коды
позволяют только определить наличие
ошибок, но не указывающие номер искаженных
разрядов.

Передаются только
разрешенные кодовые комбинации, которые
имеют определенное свойство. Если
принятая кодовая комбинация относится
к разрешенным, то считается, что ошибки
нет.
При необходимости
исправления некоторых возникающих
искажений
поступают следующим образом. Все
множество кодовых комбинаций N
разбивают на N0<N
непересекающихся подмножеств. Каждое
из этих подмножеств, приписывается к
одной из N0
разрешенных комбинаций (рис 8.7 б). В
каждом подмножестве существует одна
разрешенная комбинация. Если принятая
комбинация Аj
входит в подмножество N0j
(AjNoj),
то принимается решение, что передана
комбинация Aj.
То есть, если принятая кодовая комбинация
осталась в том же подмножестве, что и
передаваемая, то прием будет без ошибки.
Если кодовая комбинация в результате
искажений переходит в другое подмножество,
то прием будет с ошибкой.
Коды, которые не
только обнаруживают ошибку, но и указывают
номер искаженной позиции, называются
кодами с
исправлением ошибок.
Как было сказано
выше, при использовании помехоустойчивого
кода в канале связи передаются только
разрешенные кодовые комбинации. Если
бы не было помех, то для передачи этих
кодовых комбинаций потребовалось бы
меньшее число разрядов m:
![]()
(8.17)
Таким образом,
обнаружение и исправление возникающих
в каналах связи ошибок достигается за
счет введения в передаваемые кодовые
комбинации избыточных разрядов.
Рассмотрим
возможность обнаружения и исправления
ошибок на простейшем примере. Предположим,
что информация передается одноразрядным
двоичным кодом. То есть передается
информация 0 или 1. Число возможных
кодовых комбинаций
![]() ,
,
где
![]() ,
,![]() .
.
В каждой кодовой
комбинации добавим еще один разряд:
![]() .
.
Число кодовых
комбинаций
![]() .
.
Эти комбинации
составляют множество, состоящее из:
00, 01, 10, 11.
Это множество
разделим на два подмножества разрешенных
и запрещенных комбинаций. К числу
разрешенных отнесем те комбинации, у
которых сумма единиц или нулей всегда
четная – это комбинации:
00 и 11.
При таком выделении
разрешенных комбинаций любая одиночная
(или нечетная) ошибка будет изменять
число единиц на нечетное. Принятая
кодовая комбинация в этом случае
переходит в подмножество запрещенных
и ошибка будет обнаружена (рис. 8.8).

Е сли
сли
в кодовую комбинацию ввести количество
дополнительных разрядов, то можно не
только обнаруживать, но и исправлять
ошибки. Если разрешенные комбинации
определить таким образом, что любые из
них отличаются друг от друга не менее
чем тремя разрядами, то одиночная ошибка
может быть исправлена. Возможность
исправления одиночной ошибки в этом
случае связана с тем, что ошибочная
комбинация будет отличаться от истинной
только одним разрядом и останется в
области, относящейся к передаваемой
разрешенной комбинации.
Рис. 8.9. Геометрическая
модель помехоустойчивого кода
Рассмотрим сказанное
на геометрической модели трехразрядного
двоичного кода при помощи которого
можно получить 23=8
комбинаций. А именно: 000, 001, 010, 011, 100, 101,
110, 111. Каждую новую комбинацию можно
представить точкой в трехмерном
пространстве (рис. 8.9).
Для исправления
одиночной ошибки разобьем все множества
комбинации 110 и 001. Эти комбинации
отличаются друг от друга тремя разрядами.
Любая одиночная ошибка оставляет кодовую
комбинацию в области, относящейся к
передаваемой комбинации. Так, при
искажении одного разряда в комбинации
001 она превратится в 000, или в 100, или в
101. Все эти комбинации находятся в той
же области, что и комбинация 001.
Рассмотренные
примеры показывают, что для обнаружения
одиночных ошибок кодовые комбинации
должны различаться не менее чем двумя
разрядами. Для исправления одиночной
ошибки кодовые комбинации должны
различаться не менее чем тремя разрядами.
Это различие
именуют кодовым
(Хэмминговым) расстоянием.
Под кодовым
расстоянием
понимают
минимальное
число позиций, на которых символы данной
кодовой комбинации отличаются от
символов другой кодовой комбинации.
Например, для показанных на рисунке
8.10, кодовое расстояние d
равно 3.

Рис. 8.10. Кодовое
расстояние между двумя кодовыми
комбинациями
Поэтому можно
сказать, что возможности по обнаружению
или исправлению ошибок определяются
числом позиций, на которых отличаются
разрешенные кодовые комбинации, то есть
кодовым расстоянием.
Кодовое расстояние
между i-й
и j-й
кодовыми комбинациями
![]() определяется по формуле
определяется по формуле
![]() ,
,
(8.18)
где
![]() — значение символов
— значение символов![]() -й
-й
позиции j-й и i-й
кодовых комбинаций, знакозначает суммирование по модулю 2
(правила сложения по модулю 2: (1+1=0;
1+0=0+1=1; 0+0=0).
Соседние файлы в папке Пособие ТЕЗ_рус12
- #
- #
- #
- #
- #
- #
- #
- #
- #
Корректирующие коды «на пальцах»
Время на прочтение
11 мин
Количество просмотров 63K
 Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.
Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.
Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
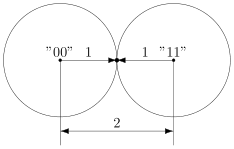
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
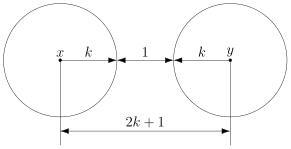
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
