Функция ошибок
| Аргумент функции ошибок erf(x) |
| Функция ошибок |
| Дополнительная функция ошибок |
Функция ошибок, она же функция Лапласа, он же интеграл вероятности — все это одна и та же сущность, которая выражается функцией
и используется в статистике и теории вероятностей.
Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.
Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией
Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую 

В приницпе это все, что можно сказать о ней.
Калькулятор высчитывает результат как в вещественном так и комплексном поле.
Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.
Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.
Несколько примеров:
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
Some authors define 

This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit.
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[3] The error function complement was also discussed by Glaisher in a separate publication in the same year.[4]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
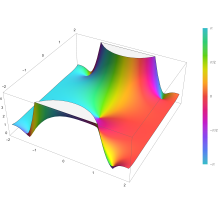
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
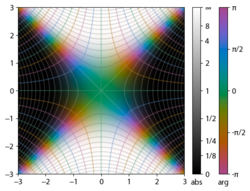
Integrand exp(−z2)

erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[5]
The defining integral cannot be evaluated in closed form in terms of elementary functions (see Liouville’s theorem), but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[6]
Bürmann series[edit]
An expansion,[7] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[8]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]

Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series[9]
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[10]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder is
which follows easily by induction, writing
and integrating by parts.
The asymptotic behavior of the remainder term, in Landau notation, is
as x → ∞. This can be found by
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[11]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[12] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[13][14]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[15]
- The above have been generalized to sums of N exponentials[16] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[17] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[18] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[19]
- A single-term lower bound is[20]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[21][22]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[23]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[24]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
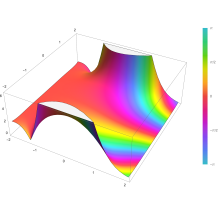
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[25] (which can be used instead of erfc to avoid arithmetic underflow[25][26]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[27]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[28]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as

Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[25]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
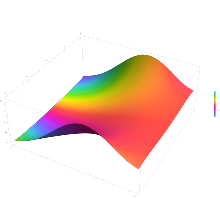
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]

Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[29]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In POSIX-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[30]
- The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[31]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
- Standard score
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. p. 341. ISBN 978-0-521-58807-2.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Dominici, Diego (2006). «Asymptotic analysis of the derivatives of the inverse error function». arXiv:math/0607230.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ «math.h — mathematical declarations». opengroup.org. 2018. Retrieved 21 April 2023.
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
 График функции
График функции
В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. { displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, { displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), { displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 { displaystyle f (x) = left ({ frac {c } { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p { displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). { displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) — operatorname {erf} (p { sqrt {c}}) right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ { displaystyle sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] { displaystyle X sim operatorname {Norm} [ mu, sigma]}![X sim operatorname {Norm} [ му, sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) { Displaystyle Pr [X Leq L] = { frac {1} {2 }} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k { displaystyle mu -L geq sigma { sqrt { ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B { displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ { displaystyle k to infty}
Свойства
Графики на комплексной плоскости  Интегрируем exp (-z)
Интегрируем exp (-z)  erf (z)
erf (z)
Свойство erf (- z) = — erf (z) { displaystyle operatorname {erf} (-z) = — operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ { displaystyle operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}}
где z ¯ { displaystyle { overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) { displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z — { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} — { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} — cdots right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К { Displaystyle OperatorName { erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) { displaystyle { frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) { displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. { displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. { displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. { displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. { displaystyle z operatorname {erfi} (z) — { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … { Displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}
где H { displaystyle { mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x { displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). { displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 — { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) — { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} — { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} — { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} — cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 { displaystyle c_ {1} = { frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). { displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} — { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}
Обратные функции
 Обратная функция
Обратная функция
Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z { displaystyle operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, { displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. { displaystyle c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200}}, ldots right }.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). { displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12} } z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). { displaystyle operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, { Displaystyle OperatorName {erfi} ^ {- 1} (г) = сумма _ {к = 0} ^ { infty} { гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1 + sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} ( -1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N { displaystyle N in mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N-1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) { displaystyle R_ {N} ( x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}
при x → ∞. { displaystyle x to infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, { Displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ { 1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ { displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. { displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+) dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R { displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b } { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- сходится для Re (z 2)>0. { displaystyle operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- zn ¯ { displaystyle z ^ { bar {n}}}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, { displaystyle {A, B } = {1.98,1.135 },}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 { displaystyle 1,2 times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {displaystyle operatorname {erf} (x)={begin{cases}1-tau xgeq 0\tau -1x<0end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) { displaystyle { begin {align} tau = t cdot exp left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} вправо. \ left. qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} right) end {align}}}
и
- t = 1 1 + 0,5 | х |. { displaystyle t = { frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc { displaystyle mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), { displaystyle { begin {выровнено} OperatorName {erfc} (x) = 1- operatorname {erf} (x) \ [5p t] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}
, который также определяет erfcx { displaystyle mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. { displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc { displaystyle mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. { displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} — { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), { displaystyle { begin {align} operatorname {erfi} (x) = — i operatorname {erf} (ix) \ [ 5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) { displaystyle operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). { displaystyle w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) { displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). { displaystyle { begin {align} operatorname {erf} (x) = 2 Phi left (x { sqrt {2}} right) -1 \ operatorname {erfc} (x) = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). { displaystyle Q (x) = { frac {1} {2}} — { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}
Обратное значение из Φ { displaystyle Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). { displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = — { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). { displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, — x ^ {2} right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). { displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}
sgn (x) { displaystyle operatorname {sgn} (x)}
Обобщенные функции ошибок
 График обобщенных функций ошибок E n (x):. серая кривая: E 1 (x) = (1 — e) /
График обобщенных функций ошибок E n (x):. серая кривая: E 1 (x) = (1 — e) /
π { displaystyle scriptstyle { sqrt { pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. { displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π { displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. { displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) — Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). { displaystyle operatorname {erf} (x) = 1 — { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] { displaystyle { begin {align } operatorname {i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operat orname {ierfc} (z) = { frac { 1} { sqrt { pi}}} e ^ {- z ^ {2}} — z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) { displaystyle 2n operatorname {i ^ {n} erfc} (z) = operatorname {i ^ { n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), { displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ { j}} {2 ^ {nj} j! Gamma left (1 + { frac {nj} {2}} right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! { displaystyle i ^ {2m} operatorname {erfc} (-z) = — i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. { displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
Внешние ссылки

В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая erf , является сложной функцией комплексной переменной, определяемой как:
Этот интеграл представляет собой специальную ( неэлементарную ) сигмовидную функцию, которая часто встречается в уравнениях вероятности , статистики и дифференциальных уравнений в частных производных . Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, то значение функции также является действительным.
В статистике для неотрицательных значений x функция ошибок имеет следующую интерпретацию: для случайной величины Y, которая нормально распределена со средним значением 0 и стандартным отклонением
1/√ 2, erf x — вероятность того, что Y попадает в диапазон [- x , x ] .
Две тесно связанные функции — это дополнительная функция ошибок ( erfc ), определяемая как
и функция мнимой ошибки ( erfi ), определяемая как
где i — мнимая единица .
Имя
Название «функция ошибок» и ее сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности и, в частности, теорией ошибок ». Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок, плотность которых определяется как
( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, тогда erf (а/σ √ 2) — вероятность того, что ошибка единичного измерения находится между — a и + a для положительного a . Это полезно, например, при определении частоты ошибок по битам в цифровой системе связи.
Ошибки и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные условия задаются ступенчатой функцией Хевисайда .
Функция ошибок и ее приближения могут использоваться для оценки результатов, которые имеют высокую или низкую вероятность. Дана случайная величина X ~ Norm [ μ , σ ] (нормальное распределение со средним μ и стандартным отклонением σ ) и константа L < μ :
где A и B — некоторые числовые константы. Если L достаточно далеко от среднего, а именно μ — L ≥ σ √ ln k , то:
поэтому вероятность стремится к 0 при k → ∞ .
Вероятность того, что X находится в интервале [ L a , L b ], может быть получена как
Характеристики

Интегрируем exp (- z 2 )

erf z
Свойство erf (- z ) = −erf z означает, что функция ошибок является нечетной функцией . Это напрямую связано с тем, что подынтегральное выражение e — t 2 является четной функцией (интегрирование четной функции дает нечетную функцию и наоборот).
Для любого комплексного числа z :
где г представляет собой комплексно сопряженное из г .
Подынтегральное выражение f = exp (- z 2 ) и f = erf z показано на комплексной плоскости z на рисунках справа с раскраской области .
Функция ошибок при + ∞ равна 1 (см. Интеграл Гаусса ). На действительной оси erf z стремится к единице при z → + ∞ и −1 при z → −∞ . На мнимой оси он стремится к ± i ∞ .
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x > 1 ».
Определяющий интеграл не может быть вычислен в замкнутой форме в терминах элементарных функций , но, раскладывая подынтегральное выражение e — z 2 в его ряд Маклорена и интегрируя член за членом, можно получить ряд Маклорена функции ошибок как:
которое выполняется для любого комплексного числа z . Члены знаменателя — это последовательность (последовательность A007680 в OEIS ) в OEIS .
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
потому что — (2 к — 1) z 2/к (2 к + 1)выражает множитель для превращения k- го члена в ( k + 1) -й член (считая z первым членом).
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
которое выполняется для любого комплексного числа z .
Производная и интеграл
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразная функции ошибки, получаемый путем интегрирования по частям , является
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
где H — полиномы Эрмита физиков .
Серия Bürmann
Разложение, которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с помощью теоремы Ганса Генриха Бюрмана :
где sgn — знаковая функция . Сохраняя только первые два коэффициента и выбирая c 1 =31 год/200и c 2 = —341/8000, полученное приближение показывает свою наибольшую относительную ошибку при x = ± 1,3796 , где она меньше 0,0036127:
Обратные функции

Для комплексного числа z не существует уникального комплексного числа w, удовлетворяющего erf w = z , поэтому истинная обратная функция будет многозначной. Однако для −1 < x <1 существует уникальное действительное число, обозначенное erf −1 x, удовлетворяющее
Функция обратной ошибки обычно определяется с помощью области (-1,1) , и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить на диск | z | <1 комплексной плоскости, используя ряд Маклорена
где c 0 = 1 и
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
(После отмены дроби числителя / знаменателя представляют собой записи OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены члены числителя приведены в записи OEIS : A002067 .) Значение функции ошибок при ± ∞ равно ± 1 .
Для | z | <1 , имеем erf (erf −1 z ) = z .
Обратная дополнительная функция ошибок определяются как
Для действительного x существует уникальное действительное число erfi −1 x, удовлетворяющее erfi (erfi −1 x ) = x . Функция обратной мнимой ошибки определяется как erfi −1 x .
Для любого вещественного х , метод Ньютона может быть использован для вычисления ЕрФИ -1 х , а для -1 ≤ х ≤ 1 , следующие сходится ряд Маклорена:
где c k определено, как указано выше.
Асимптотическое разложение
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших действительных x :
где (2 n — 1) !! — двойной факториал числа (2 n — 1) , который является произведением всех нечетных чисел до (2 n — 1) . Этот ряд расходится для любого конечного x , и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 выполняется
где остаток в обозначениях Ландау равен
при x → ∞ .
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
и интеграция по частям.
Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Непрерывное расширение фракции
Цепная дробь расширение дополнительной функции ошибок является:
Интеграл функции ошибок с функцией плотности Гаусса
которая, по-видимому, связана с Нг и Геллером, формула 13 в разделе 4.3 с заменой переменных.
Факторный ряд
Обратный факторный ряд :
сходится при Re ( z 2 )> 0 . Здесь
z n обозначает возрастающий факториал , а s ( n , k ) обозначает число Стирлинга первого рода со знаком . Также существует представление бесконечной суммой, содержащее двойной факториал :
Численные приближения
Приближение с элементарными функциями
- Абрамовиц и Стегун дают несколько приближений с различной точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности это:
(максимальная ошибка: 5 × 10 −4 )
где a 1 = 0,278393 , a 2 = 0,230389 , a 3 = 0,000972 , a 4 = 0,078108
(максимальная ошибка: 2,5 × 10 −5 )
где p = 0,47047 , a 1 = 0,3480242 , a 2 = −0,0958798 , a 3 = 0,7478556
(максимальная ошибка: 3 × 10 −7 )
где a 1 = 0,0705230784 , a 2 = 0,0422820123 , a 3 = 0,0092705272 , a 4 = 0,0001520143 , a 5 = 0,0002765672 , a 6 = 0,0000430638
(максимальная ошибка: 1,5 × 10 −7 )
где p = 0,3275911 , a 1 = 0,254829592 , a 2 = −0,284496736 , a 3 = 1,421413741 , a 4 = −1,453152027 , a 5 = 1,061405429.
Все эти приближения верны для x ≥ 0 . Чтобы использовать эти приближения для отрицательного x , используйте тот факт, что erf x — нечетная функция, поэтому erf x = −erf (- x ) .
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок даются формулами
- Вышеупомянутое было обобщено до сумм из N экспонент с возрастающей точностью в терминах N, так что erfc x может быть точно аппроксимирован или ограничен величиной 2 Q̃ ( √ 2 x ) , где
В частности, существует систематическая методология решения числовых коэффициентов {( a n , b n )}N
n = 1которые дают минимаксное приближение или оценку для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ) , Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0 . Коэффициенты {( a n , b n )}N
n = 1для многих вариаций экспоненциальных приближений и границ до N = 25 были выпущены в открытый доступ в виде исчерпывающего набора данных. - Точная аппроксимация дополнительной функции ошибок для x ∈ [0, ∞) дана Karagiannidis & Lioumpas (2007), которые показали для соответствующего выбора параметров { A , B }, что
Они определили { A , B } = {1.98,1.135} , что дает хорошее приближение для всех x ≥ 0 . Также доступны альтернативные коэффициенты для настройки точности для конкретного приложения или преобразования выражения в жесткую границу.
- Одноканальная нижняя граница
где параметр β может быть выбран так, чтобы минимизировать ошибку на желаемом интервале аппроксимации.
-
- Другое приближение дает Сергей Виницкий, используя свои «глобальные приближения Паде»:
куда
Это сделано так, чтобы быть очень точным в окрестности 0 и в окрестности бесконечности, а относительная ошибка меньше 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:
- Приближение с максимальной погрешностью 1,2 × 10 −7 для любого действительного аргумента:
с участием
а также
Таблица значений
| Икс | erf x | 1 — эрф х |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022 564 575 | 0,977 435 425 |
| 0,04 | 0,045 111 106 | 0,954 888 894 |
| 0,06 | 0,067 621 594 | 0,932 378 406 |
| 0,08 | 0,090 078 126 | 0,909 921 874 |
| 0,1 | 0,112 462 916 | 0,887 537 084 |
| 0,2 | 0,222 702 589 | 0,777 297 411 |
| 0,3 | 0,328 626 759 | 0,671 373 241 |
| 0,4 | 0,428 392 355 | 0,571 607 645 |
| 0,5 | 0,520 499 878 | 0,479 500 122 |
| 0,6 | 0,603 856 091 | 0,396 143 909 |
| 0,7 | 0,677 801 194 | 0,322 198 806 |
| 0,8 | 0,742 100 965 | 0,257 899 035 |
| 0,9 | 0,796 908 212 | 0,203 091 788 |
| 1 | 0,842 700 793 | 0,157 299 207 |
| 1.1 | 0,880 205 070 | 0,119 794 930 |
| 1.2 | 0,910 313 978 | 0,089 686 022 |
| 1.3 | 0,934 007 945 | 0,065 992 055 |
| 1.4 | 0,952 285 120 | 0,047 714 880 |
| 1.5 | 0,966 105 146 | 0,033 894 854 |
| 1.6 | 0,976 348 383 | 0,023 651 617 |
| 1,7 | 0,983 790 459 | 0,016 209 541 |
| 1,8 | 0,989 090 502 | 0,010 909 498 |
| 1.9 | 0,992 790 429 | 0,007 209 571 |
| 2 | 0,995 322 265 | 0,004 677 735 |
| 2.1 | 0,997 020 533 | 0,002 979 467 |
| 2.2 | 0,998 137 154 | 0,001 862 846 |
| 2.3 | 0,998 856 823 | 0,001 143 177 |
| 2,4 | 0,999 311 486 | 0,000 688 514 |
| 2,5 | 0,999 593 048 | 0,000 406 952 |
| 3 | 0,999 977 910 | 0,000 022 090 |
| 3.5 | 0,999 999 257 | 0,000 000 743 |
Дополнительная функция ошибок
Дополнительная функция ошибок , обозначаемая ERFC , определяется как
который также определяет erfcx , масштабированную дополнительную функцию ошибок (которую можно использовать вместо erfc, чтобы избежать арифметического переполнения ). Другая форма erfc x для x ≥ 0 известна как формула Крейга в честь ее первооткрывателя:
Это выражение действительно только для положительных значений x , но его можно использовать вместе с erfc x = 2 — erfc (- x ) для получения erfc ( x ) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом:
Функция мнимой ошибки
Функция мнимой ошибки , обозначаемая erfi , определяется как
где D ( x ) — функция Доусона (которую можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «мнимая функция ошибок», erfi x реально, когда x реально.
Когда функция ошибок оценивается для произвольных комплексных аргументов z , результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
Кумулятивная функция распределения
Функция ошибок по существу идентична стандартной нормальной кумулятивной функции распределения , обозначаемой Φ , также называемой нормой ( x ) в некоторых языках программного обеспечения, поскольку они различаются только масштабированием и преобразованием. Действительно,
или переставил для erf и erfc :
Следовательно, функция ошибок также тесно связана с Q-функцией , которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
Обратное из Ф называется нормальной функции квантиль , или пробит функции и могут быть выражены в терминах функции обратной ошибки как
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Он имеет простое выражение в терминах интеграла Френеля .
С точки зрения регуляризованном гамма — функции P и неполной гамма — функции ,
sgn x — знаковая функция .
Обобщенные функции ошибок

График обобщенных функций ошибок E n ( x ) :
серая кривая: E 1 ( x ) =1 — е — х/√ π
красная кривая: E 2 ( x ) = erf ( x )
зеленая кривая: E 3 ( x )
синяя кривая: E 4 ( x )
золотая кривая: E 5 ( x ) .
Некоторые авторы обсуждают более общие функции:
Известные случаи:
- E 0 ( x ) — прямая линия, проходящая через начало координат: E 0 ( x ) =Икс/е √ π
- E 2 ( x ) — функция ошибок, erf x .
После деления на п ! , все E n для нечетных n похожи (но не идентичны) друг на друга. Точно так же E n для четного n выглядят похожими (но не идентичными) друг на друга после простого деления на n ! . Все обобщенные функции ошибок для n > 0 выглядят одинаково на положительной стороне графика x .
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
а также
Реализации
Как реальная функция реального аргумента
- В Posix -совместимый операционных систем, заголовок math.h возвестят и математическая библиотека libm должна обеспечивать функции
erfиerfc( двойной точности ), а также их одинарной точности и повышенной точности аналоговerff,erflиerfcf,erfcl. - GNU Scientific Library предоставляет
erf,erfc,log(erf), и масштабируемые функции ошибок.
Как сложная функция сложного аргумента
-
libcerf , цифровая библиотека C для сложных функций ошибок, обеспечивает комплексные функции
cerf,cerfc,cerfcxи реальные функцииerfi,erfcxпримерно с 13-14 точностью цифр, на основе функции Фаддеева , как реализовано в MIT Фаддеевого пакете
Смотрите также
- Гауссовский интеграл по всей действительной прямой
- Функция Гаусса , производная
- Функция Доусона , перенормированная функция мнимой ошибки
- Интеграл Гудвина – Стэтона
По вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения , масштабированная и сдвинутая форма функции ошибок
- Пробит , обратная или квантильная функция нормального CDF
- Q-функция , хвостовая вероятность нормального распределения
использованная литература
дальнейшее чтение
- Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964]. «Глава 7» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN. 978-0-486-61272-0. LCCN 64-60036 . Руководство по ремонту 0167642 . LCCN 65-12253 .
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок» , Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля» , в Olver, Frank WJ ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник по математическим функциям NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
внешние ссылки
- MathWorld — Эрф
- Таблица интегралов функций ошибок
Время на прочтение
22 мин
Количество просмотров 70K

Пост содержит перевод статьи «Error Handling in Node.js», которую подготовили сотрудники компании Joyent. Статья была опубликована 28 марта 2014 года на сайте компании. Dave Pacheco поясняет, что статья призвана устранить неурядицу среди разработчиков, касаемо лучших практик работы с ошибками в Node.js, а так же ответить на вопросы, которые часто возникают у начинающих разработчиков.
Обработка ошибок в Node.js
По мере освоения Node.js можно достаточно долго писать программы, не уделяя при этом должного внимания корректной обработке ошибок. Однако, разработка серьёзных проектов на Node.js требует осознанного подхода к этой проблеме.
У начинающих разработчиков часто возникают следующие вопросы:
- Можно ли использовать
throw, что бы вернуть ошибку из функции или следует вызывать callback-функцию передав объект ошибки в качестве аргумента? В каких случаях необходимо генерировать событие'error'у объекта класса EventEmitter? - Нужно ли производить проверку аргументов переданных функции? Что, если в функцию переданы некорректные аргументы? Нужно ли в таком случае генерировать исключение или вызывать callback-функцию, передавая ей ошибку?
- Возможно ли программно различать ошибки по типу, что бы приложение могло соответствующим образом обрабатывать ошибки согласно их типу (например, «Bad Request» или «Service Unavailable»)?
- Как функция может наиболее информативно «сообщить» программе о возникновении ошибки, чтобы та могла корректно её обработать?
- Нужно ли обрабатывать ошибки вызванные «багами» в программе?
Данная статья состоит из семи частей:
- Введение. О том, что читатель должен знать перед ознакомлением со статьей.
- Программные ошибки и ошибки программиста. Ознакомление с типами ошибок.
- Шаблоны написания функций. Основополагающие принципы написания функций, реализующих корректную работу с ошибками.
- Правила написания функций. Перечень указаний которым следует придерживаться при написании функций.
- Пример. Пример написания функции.
- Резюме. Краткое представление основных положений рассмотренных в статье.
- Приложение. Общепринятые имена полей объектов ошибок.
1. Введение
Предполагается, что читатель:
- знаком с термином «исключение» в JavaScript, Java, Python, C++, или другом подобном языке и понимает принцип работы конструкции
try/catch; - знаком с разработкой на Node.js и освоил принципы асинхронного программирования.
Читатель должен понимать, почему в представленном ниже коде не работает перехват исключений, несмотря на наличие конструкции try/catch.1
function myFunc(callback)
{
/*
* Пример некорректного перехвата исключений
*/
try {
doSomeAsyncOperation(function (err) {
if (err) {
throw (err);
}
});
} catch (ex) {
callback(ex);
}
}
Читателю следует знать, что в Node.js существует 3 основных способа, которыми функция может вернуть ошибку:
- Бросание ошибки
throw(генерирование исключения). - Вызов callback-функции с объектом ошибки в качестве первого аргумента.
- Генерирование события
'error'у объекта класса EventEmitter.
Предполагается, что читатель не знаком с доменами в Node.js.
Читатель должен понимать разницу между ошибкой и исключением в JavaScript. Ошибка — это любой объект класса Error. Ошибка может быть создана конструктором класса и возвращена из функции либо брошена с помощью инструкции ThrowStatement. Когда объект ошибки брошен, возникает исключение. Далее приведён пример бросания ошибки (генерирование исключения):2
throw new Error('произошла ошибка');
Пример, где ошибка передаётся в callback-функцию:
callback(new Error('произошла ошибка'));
Второй вариант чаще встречается в Node.js, из-за асинхронности большинства выполняемых операций. Как правило, первый вариант используется лишь при десериализации данных (например, JSON.parse), при этом брошенное исключение перехватывается с помощью конструкции try/catch. Это отличает Node.js от Java или C++ и других языков, где приходится чаще работать с исключениями.
2. Программные ошибки и ошибки программиста
Ошибки можно условно разделить на два типа:3
- Программные ошибки представляют собой конфликты, возникающие в ходе нормального функционирования программы. Они не являются «багами». Обычно, они не связаны напрямую с программой: системные ошибки (например, переполнение памяти), ошибки конфигураций (например, неверно указан адрес удалённого сервера), ошибки интернет-соединения или ошибки возникшие на удалённом сервере.
Примеры программных ошибок:- пользователь ввёл некорректные данные,
- истекло время ожидания ответа на запрос (request timeout),
- сервер ответил на запрос ошибкой с кодом 500,
- разрыв соединения,
- израсходована выделенная память.
- Ошибки программиста — это дефекты кода, приводящие к некорректной работе программы. Ошибки данного типа не могут быть правильно обработаны, так как сам факт их наличия говорит о некорректности написанного кода. Ошибки этого типа возможно устранить изменив код программы. К ошибкам программиста можно отнести:
- попытку обратиться к какому-либо полю у значения
undefined, - вызов асинхронной функции без callback-функции,
- вызов функции с некорректными аргументами.
- попытку обратиться к какому-либо полю у значения
Разработчики используют термин «ошибка» для обоих типов ошибок, несмотря на их принципиальные различия. «Файл не найден» — программная ошибка, её возникновение может означать, что программе требуется создать искомый файл. Таким образом, возникновение этой ошибки не является некорректным поведением программы. Ошибки программиста, напротив, не предполагались разработчиком. Возможно, разработчик ошибся в имени переменной или неправильно описал проверку данных, введённых пользователем. Данный тип ошибок не поддается обработке.
Возможны случаи, когда по одной и той же причине возникают как программная ошибка, так и ошибка программиста. Предположим, HTTP-сервер производит попытку считать какое-либо поле у значения undefined, что является ошибкой программиста. В результате, сервер выходит из строя. Клиент, при этом, в качестве ответа на свой запрос получает ошибку ECONNRESET, обычно описываемую Node.js как: «socket hang-up». Для клиента, это программная ошибка и корректно написанная программа-клиент соответствующим образом обработает ошибку и продолжит работу.
Отсутствие обработчика программной ошибки является ошибкой программиста. Предположим, что программа-клиент, устанавливая соединение с сервером, сталкивается с ECONNREFUSED ошибкой, в результате, объект соединения генерирует событие 'error', но для данного события не зарегистрирована ни одна функция-обработчик, по этой причине программа выходит из строя. В данном случае, ошибка соединения является программной ошибкой, однако, отсутствие обработчика для события ‘error’ объекта соединения — ошибка программиста.
Важно понимать различия между ошибками программиста и программными ошибками. Поэтому, прежде чем продолжать чтение статьи, убедитесь, что вы разобрались в этих понятиях.
Обработка программных ошибок
Обработка программных ошибок, так же как и вопросы безопасности или производительности приложения, не относится к тому типу задач, которые могут быть решены внедрением какого-либо модуля — невозможно в одном месте исходного кода решить все проблемы связанные с обработкой ошибок. Для решения задачи обработки ошибок требуется децентрализованный подход. Для всех участков программы, где возможно возникновение ошибки (обращение к файловой системе, соединение с удалённым сервером, создание дочернего процесса и т.д.) необходимо предписать соответствующие сценарии обработки для каждого возможного типа ошибки. Значит, необходимо не только выделить проблемные участки, но и понять каких типов ошибки могут в них возникнуть.
В некоторых случаях приходится передавать объект ошибки из функции, в которой она возникла, через callback-функцию на уровень выше, а из него еще выше, таким образом ошибка «всплывает» до тех пор, пока не достигнет логического уровня приложения, который ответственен за обработку данного типа ошибок. На ответственном уровне программа может принять решение: запустить ли проблемную операцию повторно, сообщить ли об ошибке пользователю или записать информацию об ошибке в лог-файл и пр. Не следует всегда полагаться на эту схему и передавать ошибки более высоким уровням иерархии, так как callback-функции на высоких уровнях ничего не знают о том, в каком контексте возникла переданная им ошибка. В результате, может возникнуть ситуация, когда на выбранном логическом уровне будет сложно описать логику обработки, соответствующую возникшей ошибке.
Выделим возможные сценарии обработки ошибок:
- Устранение ошибки. Иногда, возникшую ошибку можно устранить. Предположим, возникла ошибка ENOENT, при попытке записать информацию в лог-файл. Это может означать, что программа запущена впервые и лог-файл еще не создан. В таком случае, обработчик может устранить ошибку, создав искомый файл. Приведём более интересный пример: программе необходимо постоянно поддерживать соединение с определённым севером (например, с базой данных), но в ходе работы возник разрыв соединения. В этом случае обработчик ошибки может произвести переподключение к базе данных.
- Информирование пользователя и прекращение обработки запроса. Если нельзя решить возникшую проблему, проще всего прервать работу текущей операции, и сообщить пользователю об ошибке. Данный сценарий применим в случаях, когда известно, что причина, по которой возникла ошибка, не исчезнет с течением времени. К примеру, если ошибка возникла при попытке десериализации JSON-данных, переданных клиентом, то нет смысла повторять попытку с этими же данными.
- Повторение операции. В случае ошибок связанных с работой по сети может помочь повторный запуск операции. Предположим, программа в ответ на запрос к удалённому сервису получила в ответе ошибку 503 (Service Unavailable error), в таком случае, возможно, стоит повторить запрос спустя несколько секунд. Важно определить конечное число повторов, а так же, с какой периодичностью должны выполняться попытки. Но не следует всегда полагаться на данный сценарий. Предположим, пользователь выполнил запрос к некоторому сервису, которому для обработки запроса потребовалось обратиться к вашей программе, а ваша программа, в свою очередь, осуществляет запрос к еще одному сервису, который ответил ошибкой 503. В этом случае, лучшим решением будет не выполнять повторных попыток, а незамедлительно дать возможность обработать ошибку исходному сервису, с которым работает пользователь. Если каждый сервис, участвующий в цепочке запросов, будет производить повторные попытки, то пользователь будет ожидать ответ на свой запрос дольше чем, если бы их выполнял только исходный сервис.
- Прекращение работы программы. Если произошла непредвиденная ситуация, появление которой невозможно при нормальном функционировании программы, следует записать информацию об ошибке в соответствующий лог-файл и прекратить работу. Данный сценарий может быть использован, если ваша программа израсходовала доступную память (однако, если ваша программа получила ошибку ENOMEM от дочернего процесса, то ошибку можно обработать и не прекращать работу программы). Так же, данный сценарий можно применить если у вашей программы нет прав доступа к необходимым для работы файлам.
- Запись ошибки в лог-файл и продолжение работы. В некоторых случаях нет необходимости прекращать работу программы даже если возникшая ошибка неустранима. В пример можно привести ситуацию, когда ваша программа периодически обращается к группе удалённых сервисов через систему DNS, и один из сервисов «выпал» из DNS. В данной ситуации программа может продолжить работу с оставшимися сервисами. Но, тем не менее, необходимо записать об ошибке в лог-файл. (Для любого правила всегда есть исключения, если ошибка возникает тысячу раз в секунду, и вы не можете ничего с ней поделать, то не нужно каждый раз выполнять запись в лог, однако, стоит периодически производить логирвоание.)
Обработка ошибок программиста
Не существует правильного способа обрабатывать ошибки программиста. По определению, если возникла такая ошибка, то код программы некорректен. Устранить проблему можно лишь исправив код.
Есть программисты считающие, что в некоторых случаях можно восстанавливать программу после произошедшей ошибки таким образом, что текущая операция прерывается, но программа, тем не менее, продолжает работать и обрабатывать другие запросы. Так поступать не рекомендуется. Принимая во внимание то, что ошибка программиста вводит программу в нестабильное состояние, можете ли вы быть уверены в том, что возникшая ошибка не нарушит работу других запросов? Если запросы работают с одними и теми же сущностями (например, сервер, сокет, соединения с базой данных и т.д.), остаётся лишь надеется, что последующие запросы будут правильно обработаны.
Рассмотрим REST-сервис (реализованный, например, с помощью модуля restify). Предположим, что один из обработчиков запросов бросил исключение RefferenceError из-за того, что программист сделал опечатку в имени переменной. Если немедленно не прекратить работу сервиса, может возникнуть ряд проблем, которые бывает сложно отследить:
- Если какая-то сущность в результате опечатки оказалась равна
nullилиundefined, то последующие запросы, обратившись к ней, так же, бросят исключения и не будут обработаны. - Если функция, которая бросила исключение, работала с базой данных, может произойти утечка соединия. Каждый раз, когда подобная ошибка будет повторяться, число соединений, используя которые сервис может работать с базой данных, будет уменьшаться.
- Более сложная ситуация может произойти, если в качестве базы данных используется postgres, и соединение осталось незакрытым в ходе выполнения транзакции. В этом случае, «повисшая» транзакция не даст очищать старые версии записей, которые для неё видны. Транзакция может оставаться открытой неделями. Размер, который таблица занимает в памяти, будет расти без ограничений, что приведёт к тому, что обработка последующих запросов будет замедляться.4 Конечно, данный пример достаточно специфичен и касается лишь postgres, однако, он отлично иллюстрирует, что опасно продолжать работу программы, которая пребывает в нестабильном состоянии.
- Соединение к удалённому сервису может остаться с незакрытой сессией, вследствие чего, следующий запрос может быть обработан от лица не того пользователя.
- Может остаться незакрытым сокет. По умолчанию Node.js закроет неактивный сокет через две минуты, но это поведение может быть переопределено, и если ошибка будет повторяться, то в итоге число возможных сокетов будет исчерпано. Если вы оставите конфигурации по умолчанию, отследить и исправить проблему будет тяжело, так как ошибка о неактивном сокете возникает с задержкой в две минуты.
- Может возникнуть утечка памяти, которая приведёт к её переполнению и выходу программы из строя. Или еще хуже — утечка может усложнить процесс сборки мусора, из-за чего начнет страдать производительность программы. Обнаружить причину проблемы в таком случае будет особенно затруднительно.
Учитывая вышеперечисленное, в таких ситуациях лучшим решением будет прервать работу программы. Вы можете перезапускать свою программу, после того как она была прервана — такой подход позволит автоматически восстанавливать стабильную работу вашего сервиса после возникающих ошибок.
Единственный, но существенный, недостаток этого подхода заключается в том, что будут отключены все пользователи работавшие с сервисом в момент перезапуска. Имейте ввиду следующее:
- Сбои вызванные ошибкой программиста вводят приложение в нестабильное состояние. Нужно стремиться к тому, чтобы таких ошибок не возникало, их устранение имеет наивысший приоритет.
- После перезапуска запросы могут как выполняться корректно, так и снова привести к ошибке. Может случиться так, что запросы обрабатываются некорректно, но отследить проблему сложно.
- В хорошо спроектированной системе, независимо от того вызвана ли ошибка проблемой с интернет-соединением или ошибка произошла в Node.js, программа-клиент должна уметь обрабатывать ошибки сервера (переподключаться, выполнять повторные запросы).
Если перезапуск программы происходит очень часто, то следует отлаживать код и устранять ошибки. Лучшим способом для отладки будет сохранение и анализ снимка ядра. Данный подход работает как в GNU/Linux-системах, так и в illumos-системах, и позволяет просмотреть не только последовательность функций, которые привели к ошибке, но и переданные им аргументы, а так же состояние других объектов, видимых через замыкания.
3. Шаблоны написания функций
Во-первых стоит отметить, что очень важно подробно документировать свои функции. Необходимо описывать, что возвращает функция, какие аргументы принимает и какие ошибки могут возникнуть в процессе выполнения функции. Если не определить типы возможных ошибок и не сформулировать, что они означают, то вы не сможете правильно написать обработчик.
Throw, callback или EventEmitter?
Существует три основных способа вернуть ошибку из функции:
throwвозвращает ошибку синхронно. Это значит, что исключение возникнет в том же контексте, в котором функция была вызвана. Если используется try/catch, то исключение будет поймано. В противном случае — программа выйдет из строя (если, конечно, исключение не отловит домен или обработчик события'uncaughtException'глобального объекта process, такой вариант будет рассмотрен далее).- Вызов callback-функции с объектом ошибки в качестве первого аргумента является наиболее часто используемым способом вернуть ошибку из асинхронной функции. Общепринятым шаблоном вызова callback-функции является вызов вида
callback(err, results), где только один из аргументов может принимать значения отличные отnull. - В более сложных случаях функция может генерировать событие
'error'объекта класса EventEmitter, тогда ошибка будет обработана, если зарегистрирован обработчик для события'error'. Данный вариант используется если:- производится комплексная операция, которая возвращает несколько результатов или ошибок. Примером может быть извлечение записей из базы данных. Функция возвращает объект класса EventEmitter и вызывает событие
'row'— при извлечении каждой записи,"end"— когда все записи извлечены и'error'— если возникает ошибка. - объект представляет собой сложный автомат, производящий множество асинхронных операций. В пример можно привести сокет, вызывающий события
'connect','end','timeout','drain'и'close'. При возникновении ошибки, объект будет генерировать событие'error'. Используя данный подход важно понимать, в каких ситуациях может возникать ошибка, могут ли при этом возникать и другие события и в каком порядке они возникают.
- производится комплексная операция, которая возвращает несколько результатов или ошибок. Примером может быть извлечение записей из базы данных. Функция возвращает объект класса EventEmitter и вызывает событие
Использование callback-функций и генерирование событий относятся к асинхронным способам возврата ошибок. Если производится асинхронная операция, то реализуется один из этих способов, но никогда не используются сразу оба.
Итак, когда же использовать throw, а когда использовать callback-функции или события? Это зависит от двух факторов:
- типа ошибки (ошибка программиста или программная ошибка),
- типа функции в которой возникла ошибка (асинхронная или синхронная).
Программные ошибки характерны в большей мере для асинхронных функций. Асинхронные функции принимают в качестве аргумента callback-функцию, при возникновении ошибки она вызвается с объектом ошибки в качестве аргумента. Такой подход отлично себя зарекомендовал и широко применяется. В качестве примера можно ознакомиться с Node.js модулем fs. Событийный подход так же используется, но уже в более сложных случаях.
Программные ошибки в синхронных функциях могут возникать, как правило, если функция работает с данными, введёнными пользователем (например JSON.parse). В таких функциях при возникновении ошибки бросается исключение, реже – объект ошибки возвращается оператором return.
Если в функции хотя бы одна из возможных ошибок асинхронна, то все возможные ошибки должны возвращаться из функции используя асинхронный подход. Даже если ошибка возникла в том же контексте, в котором была вызвана функция, объект ошибки следует вернуть асинхронно.
Есть важное правило: для возврата ошибок в одной и той же функции может быть реализован либо синхронный, либо асинхронный подход, но никогда и тот и другой вместе. Тогда, чтобы принимать у функции ошибку, нужно будет использовать либо callback-функцию (или функцию-обработчик события 'error'), либо конструкцию try/catch, но никогда и то и другое. В документации к функции следует указывать, какой из способов к ней применим.
Проверка входных аргументов как правило позволяет, предупредить многие ошибки, которые совершают программисты. Часто случается, что при вызове асинхронной функции, ей забывают передать callback-функцию, в результате, чтобы понять где возникает ошибка, разработчику приходится, как минимум, просмотреть стек вызванных функций. Поэтому, если функция асинхронна, то в первую очередь, важно проверять передана ли callback-функция. Если не передана, то необходимо генерировать исключение. Кроме того, в начале функции следует проверять типы переданных ей аргументов, и так же генерировать исключение, если если они некорректны.
Напомним, что ошибки программиста не являются частью нормального процесса работы программы. Они не должны отлавливаться и обрабатываться. Поэтому данные рекомендации о немедленном бросании исключений при ошибках программиста не противоречат сформулированному выше правилу о том, что одна и та же функция не должна реализовывать как синхронный так и асинхронный подход для возврата ошибок.
Рассмотренные рекомендации представлены в таблице:
| Пример функции | Тип функции | Ошибка | Тип ошибки | Как возвращать | Как обрабатывать |
fs.stat |
асинхронная | файл не найден | программная | callback | функция-обработчик |
JSON.parse |
синхронная | ошибка ввода | программная | throw |
try/catch |
fs.stat |
асинхронная | отсутствует обязательный аргумент | ошибка программиста | throw |
не обрабатывается (прекращение работы) |
В первой записи представлен наиболее часто встречаемый пример — асинхронная функция. Во второй строке – пример для синхронной функции, такой вариант встречается реже. В третей строке — ошибка программиста, желательно, чтобы подобные случаи имели место лишь в процессе разработки программы.
Ошибка ввода: ошибка программиста или программная ошибка?
Как различать ошибки программиста от программных ошибок? Вам решать, какие данные переданные функции являются корректными, а какие – нет. Если в функцию переданы аргументы не отвечающие поставленным вами требованиям, то это ошибка программиста. Если же аргументы корректны, но функция в данный момент не может с ними работать, то это программная ошибка.
Вам предстоит решать с какой строгостью производить проверку аргументов. Представим некую функцию connect, котороя принимает IP-адрес и callback-функцию в качестве аргументов. Предположим, что был произведён вызов этой функции с аргументом отличающимся по формату от IP-адреса, например: «bob». Рассмотрим что может произойти в таком случае:
- Если вы строго производите проверку, соответствует ли формат введённой строки формату IPv4 адреса, то ваша функция бросит исключение на этапе проверки аргументов. Такой сценарий является наиболее приемлимым.
- Если же вы проверяете лишь тип аргументов, то возникнет асинхронная ошибка о том, что невозможно подключиться к IP-адресу «bob».
Оба варианта удовлетворяют рассмотренным рекомендациям и вам решать насколько строго производить проверку. Функция Date.parse, например, принимает аргументы различных форматов, но на то есть причины. Всё же, для большинства функций рекомендуется строго проверять переданные аргументы. Чем более расплывчаты критерии проверки аргументов, тем более затруднительным становится процесс отладки кода. Как правило, чем строже проверка – тем лучше. И даже если в будущих версиях программы вы вдруг смягчите критерии проверки внутри какой-то функции, то вы не рискуете сломать ваш код.
Если переданное значение не удовлетворяет требованиям (например, undefined или строка имеет неверный формат), то функция должна сообщать о том, что переданное значение некорректно и прекращать работу программы. Прекращая работу программы, сообщив о некорректных аргументах, вы упрощаете процесс отладки кода себе и другим программистам.
Домены и process.on(‘uncaughtException’)
Программные ошибки всегда могут быть отловлены по определённому механизму: через try/catch, в callback-функции или обработчиком события 'error'. Домены и событие глобального объекта process 'uncaughtException' часто используются для перестраховки от непредвиденных ошибок, которые мог допустить программист. Учитывая рассмотренные выше положения, данный подход настоятельно не рекомендуется.
4. Правила написания функций
При написании функций придерживайтесь следующих правил:
- Пишите подробную документацию
Это самое важное правило. Документация к функции должна содержать информацию:- о том с какими аргументами работает функция;
- о том каких типов должны быть аргументы;
- о любых дополнительных ограничениях, которые накладываются на вид аргументов (пример: IP-адрес должен иметь корректный формат).
Если какое-то из установленных правил не выполняется, то функция должа немедленно бросать исключение.
Так же следует документировать:- какие программные ошибки могут возникнуть в ходе выполнения функции (включая имена ошибок),
- как обрабатывать возможные ошибки (отлавливать через
try/catchили использовать асинхронные подходы), - описание результата выполнения функции.
- Используйте объекты класса Error (или подклассов) для всех ошибок.
Все ваши ошибки должны быть объектами класса Error или классов, которые являются его наследниками. Используйте поляnameиmessage, полеstackтак же должно корректно работать. - Расширяйте объект ошибки полями, которые описывают подробности ошибки.
Если в функцию был передан некорректный аргумент, задайте в объекте ошибки поля propertyName и propertyValue. Для ошибок подключения к удалённому серверу расширяйте объект ошибки полем remoteIp, чтобы указать к какому адресу не удалось подключиться. При возникновении системной ошибки включайте в объект ошибки полеsyscall, поясняющее, какой системный вызов не был обработан, так же включите полеerrno, содержащее информацию о типе системной ошибки. В приложении к статье описаны рекомендуемые имена полей.Ошибка обязательно должна содержать корректные поля:
name: используется обработчиками для дифференциации ошибок по типу.message: текст описывающий возникшую проблему. Текст должен быть коротким, но достаточно ёмким, что бы можно было понять суть проблемы.stack: никогда не изменяйте объект стэка вызовов. V8 производит построение этого объекта только тогда, когда к нему производится обращение и процесс построения достаточно ресурсоёмкий, обращение к этому полю существенно снижает производительность программы.
Ошибка должна содержать достаточно информации, чтобы обработчик мог на её основе сформировать своё сообщение об ошибке, не используя при этом поле message исходной ошибки. Возможно обработчику потребуется формировать ошибку из нескольких, чтобы выводить их в форме таблицы конечному пользователю.
- Если ошибка возвращается с низкого уровня вложенности функций, то следует оборачивать её.
В начале статьи упоминалось, что возможна ситуация, когда приходится возвращать ошибку из функции, в которой она возникла через callback-функцию на уровень выше, а затем еще выше, до тех пор пока она не достигнет логического уровня приложения, который ответственен за обработку данного типа ошибок. В таких случаях рекомендуется производить обёртку ошибки по мере её «всплытия». Обёрткой функции называется расширение исходного объекта ошибки информацией о логическом уровне через который она была передана. Модуль verror позволяет реализовать такой механизм.
Рассмотрим некую функциюfetchConfig, извлекающую настройки из удалённой базы данных. ВызовfetchConfigвыполняется при старте работы сервиса. Алгоритм работы функции описан ниже.1. Извлечение настроек 1.1 Соединение с базой данных 1.1.1 Получение адреса через систему DNS 1.1.2 Создание TCP соединения с сервером базы данных 1.1.3 Аутентификация на сервере базы данных 1.2. Выполнение запроса к базе данных 1.3. Обработка результата запроса 1.4. Настройка сервиса 2. Запуск работы сервисаПредположим, что в пункте 1.1.2 возникла ошибка. Если передавать ошибку в контекст из которого была вызвана функция
fetchConfigне оборачивая её, то сообщение об ошибке будет иметь вид:myserver: Error: connect ECONNREFUSEDПользы от такого сообщения мало.
Далее представлено сообщение о той же ошибке, но с применением обёртки:myserver: failed to start up: failed to load configuration: failed to connect to database server: failed to connect to 127.0.0.1 port 1234: connect ECONNREFUSEDЕсли не выполнять обёртку на некоторых уровнях, то можно получить более лаконичное сообщение:
myserver: failed to load configuration: connection refused from database at 127.0.0.1 port 1234.Однако, как правило, избыток информации — лучше чем дефицит.
Есть несколько нюансов о которых нужно знать, если вы решили оборачивать свои ошибки:
- Старайтесь не изменять поля начального обьекта ошибки, обработчику может потребоваться информация об исходной ошибке.
- Поле
nameошибки при обёртке можно изменять, чтобы оно больше соответствовало контексту. Однако, нет необходимости это делать, если у объекта ошибки есть иные поля, по которым обработчик может распознать её тип. - Поле
messageпри обёртке тоже может быть изменено, но не следует при этом менять message исходного объекта. Не производите никаких действий с полемstack, как уже упоминалось выше, V8 формирует объектstack, только при обращении к нему и это достаточно ресурсоёмкий процесс, который может привести к существенному снижению производительности вашей программы.
В Joyent мы используем модуль verror для обёртки ошибок, так как он имеет минималистичный синтаксис. На момент написания статьи в модуле не реализованы некоторые из рассмотренных рекомендаций, однако он будет дорабатываться.
5. Пример
Рассмотрим в качестве примера функцию, которая создаёт TCP соединение по указанному IPv4 адресу.
/*
* Функция создаёт TCP соединение по указанному IPv4 адресу. Аргументы:
*
* ip4addr строка адреса формата IPv4;
*
* tcpPort натуральное число, TCP порт;
*
* timeout натуральное число, время в миллисекундах, в течение которого
* необходимо ждать ответа от удалённого сервера;
*
* callback функция вызываемая после завершения операции,
* если операция завершилась успешно, происходит
* вызов вида callback(null, socket), где socket это
* объект класса net.Socket, если возникла ошибка,
* выполняется вызов вида callback(err).
*
* В функции могут возникнуть ошибки следующих типов:
*
* SystemError Для "connection refused", "host unreachable" и других
* ошибок, возвращаемых системным вызовом connect(2). Для
* данного типа ошибок поле errno объекта err будет содержать
* соответствующее ошибке символьное представление.
*
* TimeoutError Данный тип ошибок возникает при истечении
* времени ожидания timeout.
*
* Все возвращаемые объекты ошибок имеют поля "remoteIp" и "remotePort".
* После возникновении ошибки, сокеты, которые были открыты функцией, будут закрыты.
*/
function connect(ip4addr, tcpPort, timeout, callback)
{
assert.equal(typeof (ip4addr), 'string',
"аргумент 'ip4addr' должен быть строкового типа");
assert.ok(net.isIPv4(ip4addr),
"аргумент 'ip4addr' должен содержать IPv4 адрес");
assert.equal(typeof (tcpPort), 'number',
"аргумент 'tcpPort' должен быть числового типа");
assert.ok(!isNaN(tcpPort) && tcpPort > 0 && tcpPort < 65536,
"аргумент 'tcpPort' должен быть натуральным числом в диапазоне от 1 до 65535");
assert.equal(typeof (timeout), 'number',
"аргумент 'timeout' должен быть числового типа");
assert.ok(!isNaN(timeout) && timeout > 0,
"аргумент 'timeout' должен быть натуральным числом");
assert.equal(typeof (callback), 'function');
/* код функции */
}
Этот пример достаточно примитивен, но он иллюстрирует многие из рассмотренных рекомендаций:
- Аргументы, их типы, и предъявляемые к ним требования подробно документированы.
- Функция проверяет переданные ей аргументы и бросает исключение, если аргументы не удовлетворяют критериям.
- Документированы типы возможных ошибок, а так же поля, которые они содержат.
- Указан способ, которым функция возвращает ошибки.
- Возвращаемые ошибки имеют поля «remoteIp» и «remotePort», что позволит обработчику на основе этой информации формировать сообщение ошибки.
- Документировано состояние соединений после возникновения ошибки: «после возникновении ошибки, сокеты которые были открыты функцией, будут закрыты».
Может показаться, что в представленном примере проделано много лишней работы, однако, десять минут потраченные на опиание документации могут сэкономить несколько часов вам или другим разработчикам.
6. Резюме
- Различайте ошибки программиста и программные ошибки.
- Програмные ошибки могут и должны обрабатываться, тогда как ошибки программиста не могут быть корректно обработаны. Не следует продолжать работу программы в случае возникновения ошибок программиста, так как дальнейшее поведение программы непредсказуемо.
- Для возврата ошибок в функции может быть реализован синхронный подход (например,
throw) или асинхронный подход (callback-функция или событие), но нельзя реализовывать оба подхода в одной функции. Тогда, при использовании функции, чтобы обрабатывать возникающие в ней ошибки, нужно будет применять либо callback-функции, либо конструкцию try/catch, но никогда и то и другое. - При написании функций подробно документируйте аргументы, их типы, предъявляемые к ним требования, а так же типы возможных ошибок и то, как функция возвращает ошибки (синхронно, используя
throw, или асинхронно, используя callback-функцию или событийный подход). - Возвращаемая ошибка должна быть объектом класса Error или класса-наследника. Расширяйте объект ошибки новыми полями, чтобы включить в объект необходимую информацию об ошибке. По возможности используйте общепринятые имена полей, представленные в приложении.
7. Приложение: общепринятые имена полей ошибок
Настоятельно рекомендуется для расширения объектов ошибок использовать приведённые в таблице имена полей. Представленные имена используются в стандартных модулях Node.js, следует пользоваться ими в обработчиках ошибок, а так же при формировании сообщений об ошибках.
| Имя поля объекта ошибки | Значение поля |
localHostname |
локальное DNS-имя (например, то, по которому принимаются соединения) |
localIp |
локальный IP-адрес (например, тот, по которому принимаются соединения) |
localPort |
локальный TCP порт (например, тот, по которому принимаются соединения) |
remoteHostname |
DNS-имя удалённого сервера (например, сервера, с которым устанавливается соединение) |
remoteIp |
IP-адрес удалённого сервера (например, сервера, с которым устанавливается соединение) |
remotePort |
порт удалённого сервера (например, сервера, с которым устанавливается соединение) |
path |
путь к файлу, директории иди сокет межпроцессного взаимодействия (IPC-сокет) (например, путь к файлу, который необходимо считать) |
srcpath |
путь используемый в качестве источника (например, для копирования фала) |
dstpath |
путь назначения (например, для копирования фала) |
hostname |
DNS имя (например, то, которое используется для попытки получить IP-адрес) |
ip |
IP-адрес (например, тот, для которого производится попытка получить DNS-имя) |
propertyName |
имя свойста объекта или имя аргумента (например, в ошибке, возникшей при проверке аргументов переданных в функцию) |
propertyValue |
значение поля объекта (например, в ошибке, возникшей при проверке аргументов переданных в функцию) |
syscall |
имя невыполненного системного вызова |
errno |
символьное представление errno (например, "ENOENT") |
1 Начинающие разработчики часто допускают подобную ошибку. В данном примере try/catch и вызов функции бросающей исключение выполнятся в разных контекстах из-за асинхронности функции doSomeAsyncOperation, поэтому исключение не будет поймано.
2 В JavaScript throw может работать со значениями и других типов, но рекомендуется использовать именно объекты класса Error. Если в ThrowStatement использовать другие значения, то будет невозможно получить стэк вызовов, который привел к ошибке, что усложнит отладку кода.
3 Данные понятия возникли задолго до появления Node.js. В Java аналогом можно считать проверяемые и непроверяемые исключения. В C для работы с ошибками программиста предусмотрены утверждения.
4 Приведённый пример может показаться слишком предметным, это потому, что он не вымышлен, мы действительно сталкивались с этой проблемой, это было неприятно.


}{{sqrt%20%20pi%20}}})






![{displaystyle {begin{aligned}Pr[Xleq L]&={frac {1}{2}}+{frac {1}{2}}operatorname {erf} {frac {L-mu }{{sqrt {2}}sigma }}\&approx Aexp left(-Bleft({frac {L-mu }{sigma }}right)^{2}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{displaystyle Pr[Xleq L]leq Aexp(-Bln {k})={frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)
![{displaystyle {begin{aligned}Pr[L_{a}leq Xleq L_{b}]&=int _{L_{a}}^{L_{b}}{frac {1}{{sqrt {2pi }}sigma }}exp left(-{frac {(x-mu )^{2}}{2sigma ^{2}}}right),mathrm {d} x\&={frac {1}{2}}left(operatorname {erf} {frac {L_{b}-mu }{{sqrt {2}}sigma }}-operatorname {erf} {frac {L_{a}-mu }{{sqrt {2}}sigma }}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)

![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z-{frac {z^{3}}{3}}+{frac {z^{5}}{10}}-{frac {z^{7}}{42}}+{frac {z^{9}}{216}}-cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }left(zprod _{k=1}^{n}{frac {-(2k-1)z^{2}}{k(2k+1)}}right)\[6pt]&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z}{2n+1}}prod _{k=1}^{n}{frac {-z^{2}}{k}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{displaystyle {begin{aligned}operatorname {erfi} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z+{frac {z^{3}}{3}}+{frac {z^{5}}{10}}+{frac {z^{7}}{42}}+{frac {z^{9}}{216}}+cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{displaystyle {begin{aligned}operatorname {erf} x&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left(1-{frac {1}{12}}left(1-e^{-x^{2}}right)-{frac {7}{480}}left(1-e^{-x^{2}}right)^{2}-{frac {5}{896}}left(1-e^{-x^{2}}right)^{3}-{frac {787}{276480}}left(1-e^{-x^{2}}right)^{4}-cdots right)\[10pt]&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left({frac {sqrt {pi }}{2}}+sum _{k=1}^{infty }c_{k}e^{-kx^{2}}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)







![{displaystyle {begin{aligned}operatorname {erfc} x&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}left(1+sum _{n=1}^{infty }(-1)^{n}{frac {1cdot 3cdot 5cdots (2n-1)}{left(2x^{2}right)^{n}}}right)\[6pt]&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}sum _{n=0}^{infty }(-1)^{n}{frac {(2n-1)!!}{left(2x^{2}right)^{n}}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)
























![{displaystyle {begin{aligned}operatorname {erfc} x&=1-operatorname {erf} x\[5pt]&={frac {2}{sqrt {pi }}}int _{x}^{infty }e^{-t^{2}},mathrm {d} t\[5pt]&=e^{-x^{2}}operatorname {erfcx} x,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)


![{displaystyle {begin{aligned}operatorname {erfi} x&=-ioperatorname {erf} ix\[5pt]&={frac {2}{sqrt {pi }}}int _{0}^{x}e^{t^{2}},mathrm {d} t\[5pt]&={frac {2}{sqrt {pi }}}e^{x^{2}}D(x),end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)

![{displaystyle {begin{aligned}Phi (x)&={frac {1}{sqrt {2pi }}}int _{-infty }^{x}e^{tfrac {-t^{2}}{2}},mathrm {d} t\[6pt]&={frac {1}{2}}left(1+operatorname {erf} {frac {x}{sqrt {2}}}right)\[6pt]&={frac {1}{2}}operatorname {erfc} left(-{frac {x}{sqrt {2}}}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{displaystyle {begin{aligned}operatorname {erf} (x)&=2Phi left(x{sqrt {2}}right)-1\[6pt]operatorname {erfc} (x)&=2Phi left(-x{sqrt {2}}right)\&=2left(1-Phi left(x{sqrt {2}}right)right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)







![{displaystyle {begin{aligned}operatorname {i} ^{n}!operatorname {erfc} z&=int _{z}^{infty }operatorname {i} ^{n-1}!operatorname {erfc} zeta ,mathrm {d} zeta \[6pt]operatorname {i} ^{0}!operatorname {erfc} z&=operatorname {erfc} z\operatorname {i} ^{1}!operatorname {erfc} z&=operatorname {ierfc} z={frac {1}{sqrt {pi }}}e^{-z^{2}}-zoperatorname {erfc} z\operatorname {i} ^{2}!operatorname {erfc} z&={tfrac {1}{4}}left(operatorname {erfc} z-2zoperatorname {ierfc} zright)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7b953efaa4d730a5479bd61a2c378c8f761dc)








![{ displaystyle Pr [X leq L ] = { frac {1} {2}} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma }} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72302c46832449e128a4d4e1adb28b514131270)









![{ displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left (1 - { frac {1} {12}} left (1 -e ^ {- x ^ {2}} right) - { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} - { frac {5} {896}} left (1-e ^ {- x ^ {2}} right) ^ {3} - { frac {787} {276480}} left (1-e ^ {- x ^ {2 }} right) ^ {4} - cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1 -e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24ddba05e595a553fee25644a3542188281bd844)







![{ displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1+ sum _ {n = 1} ^ { infty} (-1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ { n}}} right] = { frac {e ^ {-x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc8c3aefff3ba787b080c5186dd3aec8ec76ef9)





![{ displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b} { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, му, sigma in mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b6adc2c661b24b44dc1e3d7e16be70023daacd8)











![{ displaystyle { begin {align} operatorname {erfc} (x) = 1- operatorname {erf} (x) \ [5pt ] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8808e6f3ad9aab23f14d55db707a39388d256788)


![{ displaystyle { begin {align} operatorname {erfi} (x) = - i operatorname {erf} (ix) \ [5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2 }} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4480a8ec17e274a7ad6b8ef25cc76234d48c0433)
![{ displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x } e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x } { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} справа)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19dc7206f8b3b571e81153816c478abd91a679e)








![{ displaystyle { begin {align} operatorname { i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operatorname {ierfc} (z) = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac { 1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b57abb0a01139b31a14f5a8d651e4aa2e5f4f2)





![{ displaystyle { begin {align} Pr [L_ {a} leq X leq L_ {b}] & = int _ {L_ {a}} ^ {L_ {b}} { frac {1} {{ sqrt {2 pi}} sigma}} exp left (- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}} right) , dx \ & = { frac {1} {2}} left ( operatorname {erf} { frac {L_ {b} - mu} {{ sqrt {2}} sigma}} - operatorname {erf} { frac {L_ {a} - mu} {{ sqrt {2}} sigma}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b3e43d593e389ed348ff56374118ab644fcec8)



![{ displaystyle { begin {align} operatorname {erfc} x & = 1- operatorname {erf} x \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] & = e ^ {- x ^ {2}} operatorname {erfcx} x, end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/582ae24086ba008f0466a71991c48c405c8248ad)


![{ displaystyle { begin {align} operatorname {erfi} x & = - i operatorname {erf} ix \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { 0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] & = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (х), конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937f1aaa2801d245f8056cad15f727ccee0ba1a7)
![{ displaystyle { begin {align} Phi (x) & = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac { -t ^ {2}} {2}} , dt \ [6pt] & = { frac {1} {2}} left (1+ operatorname {erf} { frac {x} { sqrt {2}}} right) \ [6pt] & = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right ) конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c70647a7aa4dea3272cb7d90888444e1928c401)
![{ displaystyle { begin {align} operatorname {i} ^ {n} ! operatorname {erfc} z & = int _ {z} ^ { infty} operatorname {i} ^ {n-1} ! operatorname {erfc} zeta , d zeta \ [6pt] operatorname {i} ^ {0} ! operatorname {erfc} z & = operatorname {erfc} z \ operatorname {i} ^ {1} ! Operatorname {erfc} z & = operatorname {ierfc} z = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc } z \ operatorname {i} ^ {2} ! operatorname {erfc} z & = { tfrac {1} {4}} left ( operatorname {erfc} z-2z operatorname {ierfc} z вправо) \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d9046debe25c6cb2fa3709a961ac6a9715a37f)