Как найти коэффициент кратности ошибки

Оценка корректирующей способности блокового (n, k) кода

Кодовое (хемминговое) расстояние  — число несовпадающих разрядов двух кодовых комбинаций.

Минимальное кодовое расстояние (d) — минимальное расстояние, взятое по всем парам разрешенных кодовых комбинаций.

Кратность ошибки (r) —  число искаженных символов кодовой комбинации.

Вес кодовой комбинации — число единиц в двоичной кодовой комбинации.

Вектор ошибки — двоичный код, содержащий 1 в искаженных и 0 в остальных разрядах.

Доля обнаруживаемых ошибок  2^k(2ⁿ-2^k)/(2^k2ⁿ) = 1 — 2^k—n

Число кодовых комбинаций: любых 2ⁿ , разрешенных 2^к, запрещенных  2ⁿ — 2^k .

Число вариантов передачи кода  2^к 2ⁿ. Ошибка обнаруживается, если при передаче разрешенной комбинации получена запрещенная комбинация. Число таких вариантов 2^k(2ⁿ-2^k).

Рекомендуемые материалы

Доля исправляемых ошибок среди обнаруживаемых 2^k(2^n—k-1)/2^k(2ⁿ-2^k)=2^—k. Запрещенную кодовую комбинацию заменяют ближайшей разрешенной комбинацией. Ближайшими к разрешенной комбинации являются 2^n-k-1 запрещенных кодовых комбинаций. Ошибка будет исправлена, если принятая запрещенная комбинация окажется «ближайшей» к  переданной разрешенной комбинации. Число таких случаев  2^k(2^n-k-1).

Установим связь кодового расстояния d и кратности обнаруживаемых и исправляемых ошибок. Все возможные кодовые комбинации можно представить точками или векторами в многомерном пространстве.   Точки подмножества запрещенных комбинаций, соответствующих разрешенной комбинации, можно считать расположенными на сферах радиусов 1, 2, и т.д., равных кодовому расстоянию до разрешенной комбинации. Как видно из рисунка, где кодовое расстояние      d =6, можно обнаружить ошибки кратности r =5 и исправить ошибки кратности s =2. В общем случае должны выполняться условия:

Вместе с этой лекцией читают «3.6 Точечные случайные процессы. Формула Ито для считающих процессов. Компенсаторы».

d ³ r + 1   для обнаружения ошибки кратности r,

d ³ 2s + 1 для исправления  ошибки кратности s,

d ³ r + s + 1 (r ³ s) для обнаружения и одновременного исправления ошибок кратности  r и s.

Для исправления ошибки контрольная кодовая комбинация должна указывать место ошибки. Следовательно, число различных контрольных кодовых комбинаций должно быть не менее количества различных ошибок.. Число ошибок кратности r равно числу сочетаний С_n^r .   При  s = 1 (исправление ошибки кратности 1) должно выполняться условие 2^n—k-1 > C_n¹  = n, при  s = 2 — условие  2^n—k-1 > C_n¹+ C_n², в общем случае – условие

Эта оценка Хемминга определяет минимальную избыточность, необходимую для исправления ошибок. Коды с минимальной избыточностью, для которых неравенство превращается в равенство, называются совершенными.

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется. 

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

• запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
• прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу. 

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность. 

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию. 

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка. 

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный. 

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

• где n – количество символов закодированного сообщения (результата кодирования);
•   m – количество проверочных символов, добавляемых при кодировании;
•   k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов,  Рида-Соломона (15, 11) и т.д. 

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит. 

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1 

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1. 

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности. 

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется. 

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные. 

Рассчитаем скорость кода для: 

• 1 1 0 0 0 1 0 0 | 1 

Здесь R=8/9=0,88

• И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде. 

Классификация помехоустойчивых кодов

• Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
• Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности. 

По используемому алфавиту:

• Двоичные. Оперируют битами.
• Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды. 

Блочные коды делятся на

• Систематические  — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных. 
• Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных. 

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе. 

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.  

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную. 

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности. 

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость. 

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k. 

• n — количество символов на входе. 
• k — количество символов на выходе. 
• t — кратность исправляемых ошибок. 
• Отношение k/n — скорость кода. 
• G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности. 

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость. 

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель. 

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи. 

Компромисс:

1. Достоверность vs полоса пропускания.
2. Мощность vs полоса пропускания.
3. Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения. 

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам. 

Ошибка выборки
— это объективно
возникающее расхождение между
характеристиками выборки и генеральной
совокупности. Она зависит от ряда
факторов: степени вариации изучаемого
признака, численности выборки, метода
отбора единиц в выборочную совокупность,
принятого уровня достоверности результата
исследования.

Определение
ошибки выборочной средней.

При случайном
повторном отборе средняя
ошибка
выборочной средней рассчитывается по
формуле:

,

где
— средняя ошибка выборочной средней;

—дисперсия выборочной
совокупности;

n — численность
выборки.

При бесповторном
отборе она рассчитывается по формуле:

,

где N — численность
генеральной совокупности.

Определение
ошибки выборочной доли.

При повторном
отборе средняя ошибка выборочной доли
рассчитывается по формуле:

,

где
— выборочная доля единиц, обладающих
изучаемым признаком;

—число единиц,
обладающих изучаемым признаком;

—численность
выборки.

При бесповторном
способе отбора средняя ошибка выборочной
доли определяется по формулам:

.

Предельная ошибка
выборки

связана со средней ошибкой выборки
отношением:

.

При этом t как
коэффициент кратности средней ошибки
выборки зависит от значения вероятности
Р, с которой гарантируется величина
предельной ошибки выборки.

Предельная ошибка
выборки при бесповторном отборе
определяется по следующим формулам:

,

.

Предельная ошибка
выборки при повторном отборе определяется
по формуле:

,

.

1.6.3. Малая выборка

При контроле
качества товаров в экономических
исследованиях эксперимент может
проводиться на основе малой выборки.

Под малой
выборкой
понимается несплошное статистическое
обследование, при котором выборочная
совокупность образуется из сравнительно
небольшого числа единиц генеральной
совокупности. Объем малой выборки обычно
не превышает 30 единиц и может доходить
до 4 — 5 единиц.

Средняя ошибка
малой выборки
вычисляется по формуле:

,

где
— дисперсия малой выборки.

При определении
дисперсии
число степеней свободы равно n-1:

.

Предельная ошибка
малой выборки
определяется по формуле

При этом значение
коэффициента доверия t зависит не только
от заданной доверительной вероятности,
но и от численности единиц выборки n.
Для отдельных значений t и n доверительная
вероятность малой выборки определяется
по специальным таблицам Стьюдента
(Табл. 6.1.), в которых даны распределения
стандартизированных отклонений:

.

Таблица 6.1

n	t
	0,5	1,0	1,5	2,0	3,0
4	0,347	0,609	0,769	0,861	0,942
6	0,362	0,637	0,806	0,898	0,970
8	0,368	0,649	0,823	0,914	0,980
10	0,371	0,657	0,832	0,923	0,985
15	0,376	0,666	0,846	0,936	0,992
20	0,377	0,670	0,850	0,940	0,993

Поскольку при
проведении малой выборки в качестве
доверительной вероятности практически
принимается значение 0,59 или 0,99, то для
определения предельной ошибки малой
выборки
используются следующие показания
распределения Стьюдента (Табл. 6.2.)

Таблица 6.2

n
	0,95	0,99
4	3,183	5,841
5	2,777	4,604
6	2,571	4,032
7	2,447	3,707
8	2,364	3,500
9	2,307	3,356
10	2,263	3,250
15	2,119	2,921
20	2,078	2,832

Пример.

При контрольной
проверке качества поставленной в
торговлю колбасы получены данные о
содержании поваренной соли в пробах.
По данным выборочного обследования
нужно установить с вероятностью 0,95
предел, в котором находится средний
процент содержания поваренной соли в
данной партии товара.

Составляем расчётную
таблицу и по её итогам определяем среднюю
пробу малой выборки.

Таблица 6.3

Пробы
4,3	0,2	0,04
4,2	0,1	0,01
3,8	0,3	0,09
4,3	0,2	0,04
3,7	— 0,4	0,16
3,9	— 0,2	0,04
4,5	0,4	0,16
4,4	0,3	0,09
4,0	— 0,1	0,01
3,9	— 0,2	0,04
41,0	—	0,68

Определяем дисперсию
малой выборки:

Определяем среднюю
ошибку малой выборки:

Исходя из численности
выборки (n=10) и заданной вероятности
=0,95,
устанавливается по распределению
Стьюдента (см. Табл. 6.2.) значение
коэффициента доверия t=2,263.

Предельная ошибка
малой выборки составит:

Следовательно, с
вероятностью 0,95 можно утверждать, что
во всей партии колбасы содержание
поваренной соли находится в пределах:

,
т.е. от 4,1% — 0,2%=3,9%

до 4,1%+0,2%=4,3%.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Все помехоустойчивые коды делятся на блоковые и непрерывные (их называют также цепные или рекуррентные). При блоковом коди­ровании данные передаются отдельными блоками (словами, кодовыми комбинациями). При этом поступающие в кодер символы, разбиваются на блоки по k информационных символов. В кодере этот блок информационных символов преобразует­ся в блок из кодовых символов, где п называется дли­ной кода. Добавленные при кодировании r = n – k символов являются проверочными. Такой блоковый код принято обозначать как (n, k) – код. Величину R = k / n называют скоростью кода, а величину, обратную скорости, R_и = n / k называют избыточностью кода.

Проверочные символы являются избыточными, они необходимы для обнаружения и (или) исправления ошибок, возникших при передаче. Существуют безызбыточные (примитивные) коды. У этих кодов проверочных символов нет (n = k), поэтому у них самая высокая скорость кода R = 1, но они не способны обнаруживать ошибки.

Ошибки при передаче кодового слова возникают потому, что некоторые из переданных символов могут быть приняты неверно. Принцип обнаружения ошибок заключается в следующем. Если блоковый (n, k) – код имеет основание (количество символов в используемом алфавите) q, то возможно Q = qⁿ различных кодовых слов. Для передачи же используются только Q_р = q^k кодовых слов, которые называются разрешенными. Остальные Q_з = Q – Q_р слов априорно для передачи не используются и называются запрещенными.

В дальнейшем будут рассматриваться только двоичные коды, у которых алфавит состоит из двух символов 0 и 1, т. е. с основанием q = 2.

В памяти кодера и декодера хранится таблица разрешенных слов. Работа кодера заключается в выборе разрешенного кодового слова, соответствующего поступившему информационному слову. Приходящее в декодер кодовое слово сравнивается с таблицей разрешенных слов и, если происходит совпадение, то потребитель получает информационное слово, соответствующее данному разрешенному слову. Если же совпадение не наступает, то слово считается запрещенным, а потребитель получает сообщение об ошибке. Однако если совокупность ошибок превратит одно разрешенное слово в другое разрешенное, то возникшие ошибки не могут быть обнаружены.

Пример 1. Требуется передача сообщения о наступлении одного из четырех возможных событий A, B, C, D. Эти события представлены информационными словами 00, 01, 10, 11 соответственно. При передаче этих слов безызбыточным кодом все возможные комбинации являются разрешенными. Поэтому достаточно искажения хотя бы одного символа, чтобы сообщение было принято неверно. Так, если передавалось сообщение A в виде кодового слова 00, а принято было слово 01, то декодер, найдя в таблице такое разрешенное слово, вынесет решение о приеме сообщения B.

Если к вышеперечисленным информационным словам добавить по одному избыточному символу, поставив в соответствие разрешенные слова 000, 011, 101, 110, то искажение одного символа в переданном слове можно обнаружить. Так, если передавалось сообщение A в виде кодового слова 000, а принято было слово 001, то декодер, не найдя в таблице такого разрешенного слова, объявит принятое слово запрещенным и сообщит об обнаружении ошибки в слове. Однако если было принято слово 011, то декодер вынесет решение о приеме сообщения B.

Для сравнения слов необходимо задать метрику, т. е. способ измерения расстояний между кодовыми словами. Извест­но несколько способов выбора метрики, из которых наиболее распространенным является метрика Хэмминга. Расстоянием Хэмминга меж­ду двумя кодовыми словами называется количество несовпадающих символов в этих словах. Важнейшей характеристикой блочного кода является кодовое расстояние – d, оно равно наименьшему расстоянию из всех возможных для данного кода.

Пример 2. Для передачи используются три разрешенных слова 000, 100, 111. Расстояние между первым и вторым словами равно 1, между вторым и третьим словами – 2, а между первым и вторым – 3. Кодовое расстояние для данного кода d = 1.

Очевидно, что у безызбыточного кода d = 1, так как между любой парой его слов расстояние равно единице. Этот код не позволяет обнаруживать ошибки. Приведенный в примере 1 избыточный код (он называется кодом с проверкой на четность) имеет d = 2. Он позволяет гарантировано обнаружить однократную ошибку.

Кратностью ошибки называется количество неправильно принятых символов в кодовом слове. Если искажения символов возникают независимо друг от друга, то ошибки меньшей кратности более вероятны, чем ошибки большей кратности. Следовательно, прежде всего требуется вести борьбу с ошибками малой кратности.

Можно заметить, что максимальная кратность гарантировано обнаруживаемой ошибки t_о = d – 1. Действительно, при возникновении необнаруженной ошибки одно разрешенное слово должно превратиться в другое разрешенное слово. А для этого надо, чтобы кратность возникшей ошибки была не менее d, поскольку все разрешенные слова по определению кодового расстояния различаются не менее, чем на d символов. Если же принятое кодовое слово хотя бы на один символ отличается от разрешенных кодовых слов, то будет зафиксировано появление ошибки.

При декодировании вместо обнаружения ошибок возможно их исправление. Так, если было принято запрещенное кодовое слово, то можно не отбрасывать его, а найти наиболее похожее разрешенное слово и объявить его принятым. Таким образом, возникшие при передаче ошибки считаются исправленными, и потребитель получает не сообщение об ошибке, а очередное информационное слово. При декодировании с исправлением ошибок решение принимается по минимуму расстояния Хэмминга, т. е. переданным считается то разрешенное кодовое слово, которое отличается от принятого слова наименьшим количеством несовпадающих символов.

Пример 3. Для передачи используется два разрешенных кодовых слова 000 и 111. Было принято слово 001, на беглый взгляд оно больше похоже на 000, чем на 111. Действительно, слово 001 от первого разрешенного слова отличается на один символ, а от второго на два. Так как однократная ошибка вероятнее двукратной, то скорее всего было передано первое слово и в нем исказился один символ. Декодер принимает решение по минимуму расстояния Хэмминга и объявляет принятым разрешенное слово 000.

В
рассмотренном примере код имеет d = 3, он позволяет гарантировано исправлять однократную ошибку. Можно заметить, что максимальная кратность гарантировано исправляемой ошибки :

где [x] –целая часть числа x.

Существует так называемый прием со стиранием. Это частный случай приема с мягким решением. Его особенность состоит в том, что решающее устройство имеет область неопределенности, в которую попадают все сигналы, не превысившие установленный порог. Решающее устройство выдает при этом специальный символ, заменяющий неуверенно принятый сигнал. Этот символ оказывается, таким образом, «стертым». Так, при передаче двоичным кодом на выходе решающего устройства появляется один из трех символов: 0, 1 и символ стирания Х.

Восстановить стертые знаки часто оказывается легче, чем исправить ошибочные. Это обусловлено тем, что местонахождение стертых знаков известно, так как оно обозначено символом стирания Х, тогда как местоположение ошибок неизвестно, и каждый из знаков 0 или 1 может быть как верным, так и неверным.

Для сохранения различимости кодовых комбинаций при стирании не более s знаков кодовое расстояние d должно удовлетворять условию:

Для того, чтобы код мог одновременно исправлять t ошибок и восстанавливать s стертых символов кодовое расстояние должно быть:

Преимущество кодов со стираниями очевидно: например, при d = 3 такой код может как и обычный исправить одиночную ошибку, но может восстановить два стертых символа.

Описанный выше метод кодирования и декодирования, основанный на запоминании таблицы разрешенных слов, называется универсальным, поскольку годится для всех блочных кодов. Однако этот метод практически не применяется из-за сложности реализации и низкого быстродействия. Если длина информационного слова достаточно велика, то требуется большой объем памяти для хранения всех разрешенных слов. Кроме того, сравнение принятого слова со всей таблицей может продолжаться очень долго, что недопустимо при работе в режиме реального времени. Поэтому созданы другие методы кодирования и декодирования блочных кодов, в которых используется не поиск разрешенных слов, а математические операции над информационными и проверочными символами.

Чаще всего применяются систематические коды. Систематическим называется такой блочный код, у которого информационные и проверочные символы расположены на одних и тех же позициях во всех кодовых словах

В примере 1 был рассмотрен избыточный код с проверкой на четность. При его кодировании к информационному слову добавляется один проверочный символ так, чтобы количество единиц в кодовом слове было четным. При декодировании проверяется выполнение этого условия. Если количество единиц в принятом слове нечетно, то слово является запрещенным. Таким образом, можно обойтись без запоминания таблицы разрешенных слов.

Если в кодере используются лишь линейные операции над поступающими информационными символами, то код называется линейным. Принцип кодирования и декодирования линейного кода заключается в системе линейных уравнений, в которую входят информационные и проверочные символы. Для каждого кода эта система своя. Рассмотрим её на примере кода (7, 4), имеющего d = 3.

a₁  а₂  а₃  а₅ = 0

а₂  а₃  а₄  а₆ = 0

а₁  а₂  а₄  а₇ = 0

где  — знак сложения по модулю 2, символы а₁, а₂, а₃, а₄ являются информационными, а символы а₅, а₆, а₇ – проверочными. При кодировании проверочные символы вычисляются из информационных так, чтобы они удовлетворяли системе уравнений. При декодировании символы принятого слова подставляются в систему уравнений и вычисляется её правая часть. Эта правая часть представляет собой вектор, который называется исправляющим вектором или синдромом. Анализ синдрома позволяет исправлять ошибки. Каждому возможному синдрому соответствует номер искаженного символа.

Синдром	Номер искаженного символа
000	Ошибок не обнаружено
101	1
111	2
110	3
011	4

Проверочные символы вычисляются с помощью про­изводящей (порождающей) матрицы. Производящая матрица G – это таблица, у которой k строк и n столбцов, в которой записаны k ли­нейно независимых разрешенных комбинаций данного кода. По ней можно построить все остальные разрешенные кодовые комбинации, складывая поразрядно по модулю 2 строки производящей матрицы во всех возможных сочетаниях. В памяти кодера достаточно иметь производящую матрицу. С помощью набора сумматоров можно получить любую разрешенную кодовую комбинацию.

Производящую матрицу принято представлять в каноническом виде. Для рассматриваемого кода она будет:

Где левая часть матрицы — единичная матрица, соответствующая информационным символам, а правая часть матрицы соответствует проверочным символам. Схема кодирования строится на основе производящей матрицы. Кодер состоит из k-элементного регистра для информационного слова и n – k сумматоров по модулю 2. Элементы правой части производящей матрицы p_ij отвечают за вычисление проверочных символов. Они показывают связь i-ой ячейки регистра с j-м сумматором. Если p_ij = 1, то связь есть, если p_ij = 0 , то связи нет.

Д
ля декодирования требуется проверочная матрица H, содержащая n – k строк и n столбцов. В каждой строке этой матрицы единицы находятся в тех разрядах, которые входят в соответствующее проверочное уравнение. Для рассмотренного кода Хэмминга (7, 4) проверочная матрица будет иметь вид:

Существует особый класс блочных линейных кодов – циклические коды. Они отличаются тем, что всякая циклическая перестановка символов разрешенного кодового слова приводит также к разрешенному слову. Все кодовые комбинации можно получить циклическим сдвигом одного слова. Поэтому важным достоинством циклических кодов является то, что операции кодировании и декодирования легко реа­лизуются на сдвигающих регистрах.

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется. 

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

• запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
• прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу. 

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность. 

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию. 

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка. 

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный. 

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

• где n – количество символов закодированного сообщения (результата кодирования);
•   m – количество проверочных символов, добавляемых при кодировании;
•   k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов,  Рида-Соломона (15, 11) и т.д. 

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит. 

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1 

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1. 

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности. 

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется. 

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные. 

Рассчитаем скорость кода для: 

• 1 1 0 0 0 1 0 0 | 1 

Здесь R=8/9=0,88

• И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде. 

Классификация помехоустойчивых кодов

• Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
• Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности. 

По используемому алфавиту:

• Двоичные. Оперируют битами.
• Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды. 

Блочные коды делятся на

• Систематические  — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных. 
• Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных. 

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе. 

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.  

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную. 

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности. 

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость. 

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k. 

• n — количество символов на входе. 
• k — количество символов на выходе. 
• t — кратность исправляемых ошибок. 
• Отношение k/n — скорость кода. 
• G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности. 

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость. 

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель. 

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи. 

Компромисс:

1. Достоверность vs полоса пропускания.
2. Мощность vs полоса пропускания.
3. Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения. 

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам. 

7.1. Классификация корректирующих кодов

7.2. Принципы помехоустойчивого кодирования

7.3. Систематические коды

7.4. Код с четным числом единиц. Инверсионный код

7.5. Коды Хэмминга

7.6. Циклические коды

7.7. Коды с постоянным весом

7.8. Непрерывные коды

7.1. Классификация корректирующих кодов

В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать или обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим, кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны также коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.

Для того чтобы «од обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.

Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.

В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов [12]. На рис. 7.1 показана схема, поясняющая классификацию, проведенную по способам построения корректирующих кодов.

Все известные в настоящее время коды могут быть разделены

на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

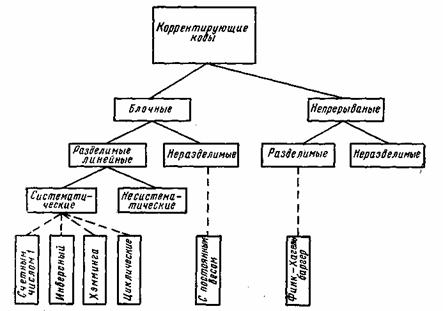
Рис. 7.1. Классификация корректирующих кодов

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат ‘исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.

В свою очередь, линейные коды могут быть |разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими. Вертикальными прямоугольниками на схеме рис. 7.1 представлены некоторые конкретные коды, описанные в последующих параграфах.

7.2. Принципы помехоустойчивого кодирования

В теории помехоустойчивого кодирования важным является  вопрос об использовании  избыточности для корректирования возникающих при  передаче ошибок. Здесь   удобно   рассмотреть блочные моды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Напомним, что для равномерных кодов, которые в дальнейшем только и будут изучаться, число возможных комбинаций равно M=2ⁿ, где п — значность кода. В обычном некорректирующем коде без избыточности, например в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М0и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число сообщений источника М0. Однако в.этом случае лишь М0комбинаций из общего числа  используется для передачи  информации.  Эти  комбинации называются разрешенными, а остальные М—М0комбинаций носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.

Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние d между двумя комбинациями  и  определяется количеством единиц в сумме этих комбинаций по модулю два. Например,

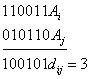
Для любого кода d. Минимальное расстояние между разрешенными комбинациями ,в данном коде называется кодовым расстоянием d.

Расстояние между комбинациями  и  условно обозначено на рис. 7.2а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. B общем случае некоторая пара разрешенных комбинаций  и , разделенных кодовым расстоянием d, изображается на прямой рис. 7.2б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация  преобразовалась в другую разрешенную комбинацию , должно исказиться d символов.

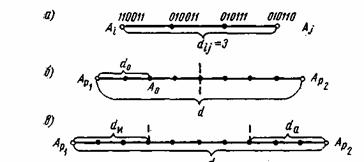
Рис. 7.2.  Геометрическое представление разрешенных и запрещенных кодовых комбинаций

При искажении меньшего числа символов комбинация  перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации,

                                                                                                              (7.1)

Если g>d, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация ib этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d=2.

Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g символов в n-значной комбинации будет равна:

                                                                                                         (7.2)

где — вероятность искажения одного символа. Так как обычно <<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация  (см.рис.7.2б), тогда принимается решение, что была передана комбинация . Это .правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального числа ошибок. Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который ib наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности

                                                                                                             (7.3)

Минимальное значение d, при котором еще возможно исправление любых одиночных ошибок, равно 3.

Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 7.2в ошибки кратности  исправляются, а ошибки, кратность которых лежит в пределах только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах , то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А вместо Aили наоборот.

Существуют двоичные системы связи, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще так называемый символ стирания . Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов  оказалось равным gc, причем

                                                                                                            (7.4)

а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов  необходимо перебрать всевозможные сочетания из gc символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок , то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из gc символов совместно с правильно принятыми символами образуют запрещенные комбинации и только одно- сочетание стертых символов даст разрешенную комбинацию, которую и следует считать как правильно восстановленную.

Если , то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.

Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или .восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие «оды обычно используются для корректирования ошибок малой кратности.

Корректирующая способность кода возрастает с увеличением d. При фиксированном числе разрешенных комбинаций Мувеличение d возможно лишь за счет роста количества запрещенных комбинаций:

                                                                                                  (7.5)

что, в свою очередь, требует избыточного числа символов r=n—k, где k — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить ее по аналогии с (6.12) как

                                                                                          (7.6)

При независимых ошибках вероятность определенного сочетания g ошибочных символов в n-значной кодовой комбинации выражается ф-лой ((7.2), а количество всевозможных сочетаний g ошибочных символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний

Отсюда полная вероятность ошибки кратности g, учитывающая все сочетания ошибочных символов, равняется:

                                                                                              (7.7)

Используя (7.7), можно записать формулы, определяющие вероятность отсутствия ошибок в кодовой комбинации, т. е. вероятность правильного приема

и вероятность правильного корректирования ошибок

Здесь суммирование ‘Производится по всем значениям кратности ошибок g, которые обнаруживаются и исправляются. Таким образом, вероятность некорректируемых ошибок равна:

                                                  (7.8)

Анализ ф-лы (7.8) показывает, что при малой величине Р0и сравнительно небольших значениях п наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.

Вероятность Р, избыточность  и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.

Общая задача, которая ставится при создании кода, заключается, в достижении наименьших значений Р и . Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.

В соответствии с общим принципом корректирования ошибок, основанным на использовании разрешенных и запрещенных комбинаций, необходимо сравнивать принятую комбинацию со всеми комбинациями данного кода. В результате М сопоставлений и принимается решение о переданной комбинации. Этот способ декодирования логически является наиболее простым, однако он требует сложных устройств, так как в них должны запоминаться все М комбинаций кода. Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодовых символов извлечь из них всю информацию о корректируемых ошибках. Изучению таких кодов и посвящены последующие разделы.

7.3. Систематические коды

Изучение конкретных способов помехоустойчивого кодирования начнем с систематических кодов, которые в соответствии с классификацией (рис. 7.1) относятся к блочным разделимым кодам, т. е. к кодам, где операции кодирования осуществляются независимо в пределах каждой комбинации, состоящей из информационных и контрольных символов.

Остановимся кратко на общих принципах построения систематических кодов. Если обозначить информационные символы буквами с, а контрольные — буквами е, то любую кодовую комбинацию, содержащую k информационных и r контрольных символов, можно представить последовательностью:, где с и е в двоичном коде принимают значения 0 или 1.

Процесс кодирования на передающем конце сводится к образованию контрольных символов, которые выражаются в виде линейной функции информационных символов:

                                                                       (7.9)

Здесь  — коэффициенты, равные 0 или 1, а  и  — знаки суммирования по модулю два. Значения  выбираются по определенным правилам, установленным для данного вида кода. Иными словами, символы е представляют собой суммы по модулю два информационных символов в различных сочетаниях. Процедура декодирования принятых комбинаций может осуществляться различными» методами. Один из них, так называемый метод контрольных чисел, состоит в следующем. Из информационных символов принятой кодовой комбинации  образуется по правилу (7.9) вторая группа контрольных символов

Затем производится сравнение обеих групп контрольных символов путем их суммирования по модулю два:

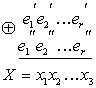                                                                                                (7.10)

Полученное число X называется контрольным числом или синдромом. С его помощью можно обнаружить или исправить часть ошибок. Если ошибки в принятой комбинации отсутствуют, то все суммы, а следовательно, и контрольное число X будут равны .нулю. При появлении ошибок некоторые значения х могут оказаться равным 1. В этом случае , что и позволяет обнаружить ошибки. Таким образом, контрольное число Х определяется путем r проверок на четность.

Для исправления ошибок знание одного факта их возникновения является недостаточным. Необходимо указать номер ошибочно принятых символов. С этой целью каждому сочетанию исправляемых ошибок в комбинации присваивается одно из контрольных чисел, что позволяет по известному контрольному числу определить место положения ошибок и исправить их.

Контрольное число X записывается в двоичной системе, поэтому общее количество различных контрольных чисел, отличающихся от нуля, равно. Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно . В этом случае должно выполняться условие

                                                                                                        (7.11)

Формула (7.11) позволяет при заданном количестве информационных символов k определить необходимое число контрольных символов r, с помощью которых исправляются все одиночные ошибки.

7.4. Код с чётным числом единиц. Инверсионный код

Рассмотрим некоторые простейшие систематические коды, применяемые только для обнаружения ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит, помимо информационных символов, один контрольный символ, выбираемый равным 0 или 1 так, чтобы сумма единиц в комбинации всегда была четной. Примером могут служить пятизначные комбинации кода Бодо, к которым добавляется шестой контрольный символ: 10101,1 и 01100,0. Правило вычисления контрольного символа можно выразить на

основании (7.9) в следующей форме: . Отсюда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю (— суммирование по модулю):

                                                                                                       (7.12)

Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем, случае ошибок нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы (7.12), поэтому такие ошибки не обнаруживаются. На основании ,(7.8) вероятность необнаруженной ошибки равна:

К достоинствам кода следует отнести простоту кодирующих и декодирующих устройств, а также малую .избыточность , однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.

Значительно лучшими корректирующими способностями обладает инверсный код, который также применяется только для обнаружения ошибок. С принципом построения такого кода удобно ознакомиться на примере двух комбинаций: 11000, 11000 и 01101, 10010. В каждой комбинации символы до запятой являются информационными, а последующие — контрольными.   Если   количество единиц в информационных символах четное, т. е. сумма этих

символов

                                                                                                                 (7.13)

равна нулю, то контрольные символы представляют собой простое повторение информационных. В противном случае, когда число единиц нечетное и сумма (7.13) равна 1, контрольные символы получаются из информационных посредством инвертирования, т. е. путем замены всех 0 на 1, а 1 на 0. Математическая форма записи образования контрольных символов имеет вид . При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е. , то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда c‘=1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность: . Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.

Анализ показывает, что при  наименьшая кратность необнаруживаемой ошибки g=4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100, 10100, а принята 10111, 10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения  равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением

Для g>4 вероятность необнаруженных ошибок еще меньше. Поэтому при достаточно малых вероятностях ошибочных символов ро можно полагать, что полная вероятность необнаруженных ошибок

Инверсный код обладает высокой обнаруживающей способностью, однако она достигается ценой сравнительно большой избыточности, которая, как нетрудно определить, составляет величину =0,5.

7.5. Коды Хэмминга

К этому типу кодов обычно относят систематические коды с расстоянием d=3, которые позволяют исправить все одиночные ошибки (7.3).

Рассмотрим построение семизначного кода Хэмминга, каждая комбинация которого содержит четыре  информационных и триконтрольных символа. Такой код, условно обозначаемый (7.4), удовлетворяет неравенству (7.11)    и   имеет   избыточность

Если информационные символы с занимают в комбинация первые четыре места, то последующие три контрольных символа образуются по общему правилу (7.9) как суммы:

                                                                              (7.14)

Декодирование осуществляется путем трех проверок на четность (7.10):

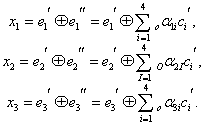                                                                                  (7.15)

Так как х равно 0 или 1, то всего может быть восемь контрольных чисел Х=х1х2х3: 000, 100, 010, 001, 011, 101, 110 и 111. Первое из них имеет место в случае правильного приема, а остальные семь появляются при наличии искажений и должны использоваться для определения местоположения одиночной ошибки в семизначной комбинации. Выясним, каким образом устанавливается взаимосвязь между контрольными числами я искаженными символами. Если искажен один из контрольных символов:  или , то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах.

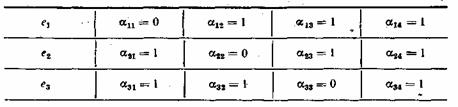
Таблица 7.1

Порядок присвоения контрольных чисел ошибочным информационным символам может устанавливаться любой, например, как показано в табл. 7.1. Нетрудно показать, что этому распределению контрольных чисел соответствуют коэффициенты , приведенные в табл. 7.2.

Таблица 7.2

Если подставить коэффициенты  в выражение (7.15), то получим:

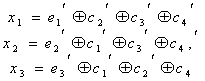                                                                                  (7.16)

При искажении одного из информационных символов становятся равными единице те суммы х, в которые входит этот символ. Легко проверить, что получающееся в этом случае контрольное число согласуется с табл. 7.1.Нетрудно заметить, что первые четыре контрольные числа табл. 7.1 совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов . Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1 определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 1 на 0. B качестве примера рассмотрим передачу комбинации, в которой информационными символами являются , Используя ф-лу (7.14) и табл. 7.2, вычислим контрольные символы:

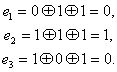
Передаваемая комбинация при этом будет . Предположим, что принята комбинация — 1001, 010 (искажен символ ). Подставляя соответствующие значения в (7.16), получим:

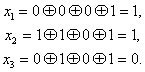
Вычисленное таким образом контрольное число  110 позволяет согласно табл. 7.1 исправить ошибку в символе.

Здесь был рассмотрен простейший способ построения и декодирования кодовых комбинаций, в которых первые места отводились информационным символам, а соответствие между контрольными числами и ошибками определялось таблице. Вместе с тем существует более изящный метод отыскания одиночных ошибок, предложенный впервые самим Хэммингом. При этом методе код строится так, что контрольное число в двоичной системе счисления сразу указывает номер искаженного символа. Правда, в этом случае контрольные символы необходимо располагать среди информационных, что усложняет процесс кодирования. Для кода (7.4) символы в комбинации должны размещаться в следующем порядке: , а контрольное число вычисляться по формулам:

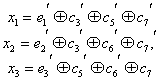                                                                                         (7.17)

Так, если произошла ошибка в информационном символе с’5 то контрольное  число , что соответствует  числу 5 в двоичной системе.

В заключение отметим, что в коде (7.4) при появлении многократных ошибок контрольное число также может отличаться от нуля. Однако декодирование в этом случае будет проведено неправильно, так как оно рассчитано на исправление лишь одиночных ошибок.

7.6. Циклические коды

Важное место среди систематических кодов занимают циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации  дает другую комбинацию  также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например, .

Комбинации циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты которых равны 0 или 1. Примером этому может служить следующая запись:

Помимо цикличности, кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени , где k—значность первичного кода без избыточности, а п-значность циклического кода

Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода A*(z) ,на порождающий полином G(z):

A(z)=A*(z)G(z).

Умножение производится по модулю zⁿ и в данном случае сводится к умножению по обычным правилам с приведением подобных членов по модулю два.

В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: деления A(z) на G(z).

Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа г нулей, что эквивалентно повышению полинома A*(z) на ,г разрядов, т. е. умножению его на гг. Затем произведение z^rA*(z) делится на порождающий полином. B общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда

Вычисленный остаток К(г) я используется для образования комбинации циклического кода в виде суммы

A(z)=z^rA*(z)@R(z).

Так как сложение и вычитание по модулю два дают один и тот же результат, то нетрудно заметить, что A(z) = Q(z)G(z), т. е. полученная комбинация удовлетворяет требованию делимости на порождающий полином. Степень полинома R{z) не превышает r—1, поэтому он замещает нули в комбинации zA*(z).

Для примера рассмотрим циклический код c n = 7, k=4, r=3 и G(z)=z³-z+1=1011. Необходимо закодировать комбинацию A*(z)=z*+1 = 1001. Тогда zA*(z)=z+z= 1001000. Для определения остатка делим z³A*(z) на G(z):

Окончательно получаем

В А(z) высшие четыре разряда занимают информационные символы, а остальные при — контрольные.

Контрольные символы в циклическом коде могут быть вычислены по общим ф-лам (7.9), однако здесь определение коэффициентов  затрудняется необходимостью выполнять требования делимости А(z) на порождающий полином G(z).

Процедура декодирования принятых комбинаций также основана на использовании полиномов G(z). Если ошибок в процессе передачи не было, то деление принятой комбинации A(z) на G(z) дает целое число. При наличии корректируемых ошибок в результате деления образуется остаток, который и позволяет обнаружить или исправить ошибки.

Кодирующие и декодирующие устройства циклических кодов в большинстве случаев обладают сравнительной простотой, что следует считать одним из основных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где действуют импульсные и сосредоточенные помехи или наблюдаются замирания сигнала.

В теории кодирования весом кодовых комбинаций принято называть .количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.

Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код обнаруживает все ошибки нечетной краткости и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей. Можно показать, что вероятность необнаруженной ошибки для кода 3/4 равна:

 при                                                                                (7.18)

В этом коде из общего числа комбинаций М = 2⁷=128 разрешенными являются лишь , поэтому в соответствии с (7.6) коэффициент избыточности

Код 3/4 находит применение при частотной манипуляции в каналах с селективными замираниями, где вероятность ошибок смещения невелика.

7.8. Непрерывные коды

Из непрерывных кодов, исправляющих ошибки, наиболее известны коды Финка—Хагельбаргера, в которых контрольные символы образуются путем линейной операции над двумя или более информационными символами. Принцип построения этих кодов рассмотрим на примере простейшего цепного кода. Контрольные символы в цепном коде формируются путем суммирования двух информационных символов, расположенных один относительно другого на определенном расстоянии:

;                                                                             (7.19)

Расстояние между информационными символами l=k—i определяет основные свойства кода и называется шагом сложения. Число контрольных символов при таком способе кодирования равно числу информационных символов, поэтому избыточность кода =0,5. Процесс образования последовательности контрольных символов показан на рис.7. символы разметаются  между информационными символами с задержкой на два шага сложения.

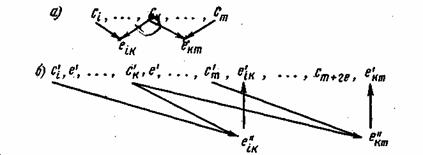
Рис. 7.3. Образование и размещение контрольных символов в цепном коде Финка—Хагельбаргера

При декодировании из принятых информационных символов по тому же правилу (7.19) формируется вспомогательная последовательность контрольных символов е», которая сравнивается с принятой последовательностью контрольных символов е’ (рис. 7.36). Если произошла ошибка в информационном символе, например, c‘k, то это вызовет искажения сразу двух символов e«k и e«km, что и обнаружится в результате их сравнения с  и e‘km. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с’Ошибка в принятом контрольном символе, например, e‘k приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление  такой ошибки не требуется.

Важное преимущество непрерывных кодов состоит в их способности исправлять не только одиночные ошибки, но я группы (пакеты) ошибок. Если задержка контрольных символов выбрана равной 2l, то можно показать, что максимальная длина исправляемого пакета ошибок также равна 2l при интервале между пакетами не менее 6l+1. Таким образом, возможность исправления длинных пакетов связана с увеличением шага сложения, а следовательно, и с усложнением кодирующих и декодирующих устройств.

Вопросы для повторения

1. Как могут быть  классифицированы  корректирующие коды?

2. Каким образом исправляются ошибки в кодах, которые только их обнаруживают?

3. В чем состоят основные принципы корректирования ошибок?

4. Дайте определение кодового расстояния.

5. При каких условиях код может обнаруживать или исправлять ошибки?

6. Как используется корректирующий код в системах со стиранием?

7. Какие характеристики определяют корректирующие способности кода?

8. Как осуществляется построение кодовых комбинаций в систематических кодах?

9. На чем  основан  принцип  корректирования  ошибок  с использованием  контрольного числа?

10. Объясните метод построения кода с четным числом единиц.

11. Как осуществляется процедура кодирования в семизначном коде Хэмминга?

12. Почему семизначный код 3/4 не обнаруживает ошибки смещения?

13. Каким образом производится непрерывное кодирование?

14. От чего зависит длина пакета исправляемых ошибок в коде Финка—Хагельбаргера?

7.1. Классификация корректирующих кодов

7.2. Принципы помехоустойчивого кодирования

7.3. Систематические коды

7.4. Код с четным числом единиц. Инверсионный код

7.5. Коды Хэмминга

7.6. Циклические коды

7.7. Коды с постоянным весом

7.8. Непрерывные коды

7.1. Классификация корректирующих кодов

В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать или обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим, кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны также коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.

Для того чтобы «од обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.

Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.

В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов [12]. На рис. 7.1 показана схема, поясняющая классификацию, проведенную по способам построения корректирующих кодов.

Все известные в настоящее время коды могут быть разделены

на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

Рис. 7.1. Классификация корректирующих кодов

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат ‘исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.

В свою очередь, линейные коды могут быть |разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими. Вертикальными прямоугольниками на схеме рис. 7.1 представлены некоторые конкретные коды, описанные в последующих параграфах.

7.2. Принципы помехоустойчивого кодирования

В теории помехоустойчивого кодирования важным является  вопрос об использовании  избыточности для корректирования возникающих при  передаче ошибок. Здесь   удобно   рассмотреть блочные моды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Напомним, что для равномерных кодов, которые в дальнейшем только и будут изучаться, число возможных комбинаций равно M=2ⁿ, где п — значность кода. В обычном некорректирующем коде без избыточности, например в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М0и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число сообщений источника М0. Однако в.этом случае лишь М0комбинаций из общего числа  используется для передачи  информации.  Эти  комбинации называются разрешенными, а остальные М—М0комбинаций носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.

Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние d между двумя комбинациями  и  определяется количеством единиц в сумме этих комбинаций по модулю два. Например,

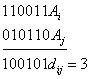
Для любого кода d. Минимальное расстояние между разрешенными комбинациями ,в данном коде называется кодовым расстоянием d.

Расстояние между комбинациями  и  условно обозначено на рис. 7.2а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. B общем случае некоторая пара разрешенных комбинаций  и , разделенных кодовым расстоянием d, изображается на прямой рис. 7.2б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация  преобразовалась в другую разрешенную комбинацию , должно исказиться d символов.

Рис. 7.2.  Геометрическое представление разрешенных и запрещенных кодовых комбинаций

При искажении меньшего числа символов комбинация  перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации,

                                                                                                              (7.1)

Если g>d, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация ib этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d=2.

Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g символов в n-значной комбинации будет равна:

                                                                                                         (7.2)

где — вероятность искажения одного символа. Так как обычно <<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация  (см.рис.7.2б), тогда принимается решение, что была передана комбинация . Это .правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального числа ошибок. Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который ib наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности

                                                                                                             (7.3)

Минимальное значение d, при котором еще возможно исправление любых одиночных ошибок, равно 3.

Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 7.2в ошибки кратности  исправляются, а ошибки, кратность которых лежит в пределах только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах , то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А вместо Aили наоборот.

Существуют двоичные системы связи, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще так называемый символ стирания . Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов  оказалось равным gc, причем

                                                                                                            (7.4)

а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов  необходимо перебрать всевозможные сочетания из gc символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок , то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из gc символов совместно с правильно принятыми символами образуют запрещенные комбинации и только одно- сочетание стертых символов даст разрешенную комбинацию, которую и следует считать как правильно восстановленную.

Если , то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.

Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или .восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие «оды обычно используются для корректирования ошибок малой кратности.

Корректирующая способность кода возрастает с увеличением d. При фиксированном числе разрешенных комбинаций Мувеличение d возможно лишь за счет роста количества запрещенных комбинаций:

                                                                                                  (7.5)

что, в свою очередь, требует избыточного числа символов r=n—k, где k — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить ее по аналогии с (6.12) как

                                                                                          (7.6)

При независимых ошибках вероятность определенного сочетания g ошибочных символов в n-значной кодовой комбинации выражается ф-лой ((7.2), а количество всевозможных сочетаний g ошибочных символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний

Отсюда полная вероятность ошибки кратности g, учитывающая все сочетания ошибочных символов, равняется:

                                                                                              (7.7)

Используя (7.7), можно записать формулы, определяющие вероятность отсутствия ошибок в кодовой комбинации, т. е. вероятность правильного приема

и вероятность правильного корректирования ошибок

Здесь суммирование ‘Производится по всем значениям кратности ошибок g, которые обнаруживаются и исправляются. Таким образом, вероятность некорректируемых ошибок равна:

                                                  (7.8)

Анализ ф-лы (7.8) показывает, что при малой величине Р0и сравнительно небольших значениях п наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.

Вероятность Р, избыточность  и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.

Общая задача, которая ставится при создании кода, заключается, в достижении наименьших значений Р и . Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.

В соответствии с общим принципом корректирования ошибок, основанным на использовании разрешенных и запрещенных комбинаций, необходимо сравнивать принятую комбинацию со всеми комбинациями данного кода. В результате М сопоставлений и принимается решение о переданной комбинации. Этот способ декодирования логически является наиболее простым, однако он требует сложных устройств, так как в них должны запоминаться все М комбинаций кода. Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодовых символов извлечь из них всю информацию о корректируемых ошибках. Изучению таких кодов и посвящены последующие разделы.

7.3. Систематические коды

Изучение конкретных способов помехоустойчивого кодирования начнем с систематических кодов, которые в соответствии с классификацией (рис. 7.1) относятся к блочным разделимым кодам, т. е. к кодам, где операции кодирования осуществляются независимо в пределах каждой комбинации, состоящей из информационных и контрольных символов.

Остановимся кратко на общих принципах построения систематических кодов. Если обозначить информационные символы буквами с, а контрольные — буквами е, то любую кодовую комбинацию, содержащую k информационных и r контрольных символов, можно представить последовательностью:, где с и е в двоичном коде принимают значения 0 или 1.

Процесс кодирования на передающем конце сводится к образованию контрольных символов, которые выражаются в виде линейной функции информационных символов:

                                                                       (7.9)

Здесь  — коэффициенты, равные 0 или 1, а  и  — знаки суммирования по модулю два. Значения  выбираются по определенным правилам, установленным для данного вида кода. Иными словами, символы е представляют собой суммы по модулю два информационных символов в различных сочетаниях. Процедура декодирования принятых комбинаций может осуществляться различными» методами. Один из них, так называемый метод контрольных чисел, состоит в следующем. Из информационных символов принятой кодовой комбинации  образуется по правилу (7.9) вторая группа контрольных символов

Затем производится сравнение обеих групп контрольных символов путем их суммирования по модулю два:

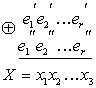                                                                                                (7.10)

Полученное число X называется контрольным числом или синдромом. С его помощью можно обнаружить или исправить часть ошибок. Если ошибки в принятой комбинации отсутствуют, то все суммы, а следовательно, и контрольное число X будут равны .нулю. При появлении ошибок некоторые значения х могут оказаться равным 1. В этом случае , что и позволяет обнаружить ошибки. Таким образом, контрольное число Х определяется путем r проверок на четность.

Для исправления ошибок знание одного факта их возникновения является недостаточным. Необходимо указать номер ошибочно принятых символов. С этой целью каждому сочетанию исправляемых ошибок в комбинации присваивается одно из контрольных чисел, что позволяет по известному контрольному числу определить место положения ошибок и исправить их.

Контрольное число X записывается в двоичной системе, поэтому общее количество различных контрольных чисел, отличающихся от нуля, равно. Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно . В этом случае должно выполняться условие

                                                                                                        (7.11)

Формула (7.11) позволяет при заданном количестве информационных символов k определить необходимое число контрольных символов r, с помощью которых исправляются все одиночные ошибки.

7.4. Код с чётным числом единиц. Инверсионный код

Рассмотрим некоторые простейшие систематические коды, применяемые только для обнаружения ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит, помимо информационных символов, один контрольный символ, выбираемый равным 0 или 1 так, чтобы сумма единиц в комбинации всегда была четной. Примером могут служить пятизначные комбинации кода Бодо, к которым добавляется шестой контрольный символ: 10101,1 и 01100,0. Правило вычисления контрольного символа можно выразить на

основании (7.9) в следующей форме: . Отсюда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю (— суммирование по модулю):

                                                                                                       (7.12)

Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем, случае ошибок нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы (7.12), поэтому такие ошибки не обнаруживаются. На основании ,(7.8) вероятность необнаруженной ошибки равна:

К достоинствам кода следует отнести простоту кодирующих и декодирующих устройств, а также малую .избыточность , однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.

Значительно лучшими корректирующими способностями обладает инверсный код, который также применяется только для обнаружения ошибок. С принципом построения такого кода удобно ознакомиться на примере двух комбинаций: 11000, 11000 и 01101, 10010. В каждой комбинации символы до запятой являются информационными, а последующие — контрольными.   Если   количество единиц в информационных символах четное, т. е. сумма этих

символов

                                                                                                                 (7.13)

равна нулю, то контрольные символы представляют собой простое повторение информационных. В противном случае, когда число единиц нечетное и сумма (7.13) равна 1, контрольные символы получаются из информационных посредством инвертирования, т. е. путем замены всех 0 на 1, а 1 на 0. Математическая форма записи образования контрольных символов имеет вид . При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е. , то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда c‘=1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность: . Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.

Анализ показывает, что при  наименьшая кратность необнаруживаемой ошибки g=4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100, 10100, а принята 10111, 10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения  равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением

Для g>4 вероятность необнаруженных ошибок еще меньше. Поэтому при достаточно малых вероятностях ошибочных символов ро можно полагать, что полная вероятность необнаруженных ошибок

Инверсный код обладает высокой обнаруживающей способностью, однако она достигается ценой сравнительно большой избыточности, которая, как нетрудно определить, составляет величину =0,5.

7.5. Коды Хэмминга

К этому типу кодов обычно относят систематические коды с расстоянием d=3, которые позволяют исправить все одиночные ошибки (7.3).

Рассмотрим построение семизначного кода Хэмминга, каждая комбинация которого содержит четыре  информационных и триконтрольных символа. Такой код, условно обозначаемый (7.4), удовлетворяет неравенству (7.11)    и   имеет   избыточность

Если информационные символы с занимают в комбинация первые четыре места, то последующие три контрольных символа образуются по общему правилу (7.9) как суммы:

                                                                              (7.14)

Декодирование осуществляется путем трех проверок на четность (7.10):

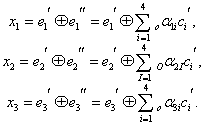                                                                                  (7.15)

Так как х равно 0 или 1, то всего может быть восемь контрольных чисел Х=х1х2х3: 000, 100, 010, 001, 011, 101, 110 и 111. Первое из них имеет место в случае правильного приема, а остальные семь появляются при наличии искажений и должны использоваться для определения местоположения одиночной ошибки в семизначной комбинации. Выясним, каким образом устанавливается взаимосвязь между контрольными числами я искаженными символами. Если искажен один из контрольных символов:  или , то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах.

Таблица 7.1

Порядок присвоения контрольных чисел ошибочным информационным символам может устанавливаться любой, например, как показано в табл. 7.1. Нетрудно показать, что этому распределению контрольных чисел соответствуют коэффициенты , приведенные в табл. 7.2.

Таблица 7.2

Если подставить коэффициенты  в выражение (7.15), то получим:

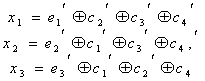                                                                                  (7.16)

При искажении одного из информационных символов становятся равными единице те суммы х, в которые входит этот символ. Легко проверить, что получающееся в этом случае контрольное число согласуется с табл. 7.1.Нетрудно заметить, что первые четыре контрольные числа табл. 7.1 совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов . Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1 определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 1 на 0. B качестве примера рассмотрим передачу комбинации, в которой информационными символами являются , Используя ф-лу (7.14) и табл. 7.2, вычислим контрольные символы:

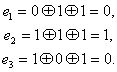
Передаваемая комбинация при этом будет . Предположим, что принята комбинация — 1001, 010 (искажен символ ). Подставляя соответствующие значения в (7.16), получим:

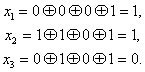
Вычисленное таким образом контрольное число  110 позволяет согласно табл. 7.1 исправить ошибку в символе.

Здесь был рассмотрен простейший способ построения и декодирования кодовых комбинаций, в которых первые места отводились информационным символам, а соответствие между контрольными числами и ошибками определялось таблице. Вместе с тем существует более изящный метод отыскания одиночных ошибок, предложенный впервые самим Хэммингом. При этом методе код строится так, что контрольное число в двоичной системе счисления сразу указывает номер искаженного символа. Правда, в этом случае контрольные символы необходимо располагать среди информационных, что усложняет процесс кодирования. Для кода (7.4) символы в комбинации должны размещаться в следующем порядке: , а контрольное число вычисляться по формулам:

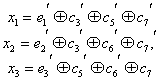                                                                                         (7.17)

Так, если произошла ошибка в информационном символе с’5 то контрольное  число , что соответствует  числу 5 в двоичной системе.

В заключение отметим, что в коде (7.4) при появлении многократных ошибок контрольное число также может отличаться от нуля. Однако декодирование в этом случае будет проведено неправильно, так как оно рассчитано на исправление лишь одиночных ошибок.

7.6. Циклические коды

Важное место среди систематических кодов занимают циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации  дает другую комбинацию  также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например, .

Комбинации циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты которых равны 0 или 1. Примером этому может служить следующая запись:

Помимо цикличности, кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени , где k—значность первичного кода без избыточности, а п-значность циклического кода

Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода A*(z) ,на порождающий полином G(z):

A(z)=A*(z)G(z).

Умножение производится по модулю zⁿ и в данном случае сводится к умножению по обычным правилам с приведением подобных членов по модулю два.

В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: деления A(z) на G(z).

Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа г нулей, что эквивалентно повышению полинома A*(z) на ,г разрядов, т. е. умножению его на гг. Затем произведение z^rA*(z) делится на порождающий полином. B общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда

Вычисленный остаток К(г) я используется для образования комбинации циклического кода в виде суммы

A(z)=z^rA*(z)@R(z).

Так как сложение и вычитание по модулю два дают один и тот же результат, то нетрудно заметить, что A(z) = Q(z)G(z), т. е. полученная комбинация удовлетворяет требованию делимости на порождающий полином. Степень полинома R{z) не превышает r—1, поэтому он замещает нули в комбинации zA*(z).

Для примера рассмотрим циклический код c n = 7, k=4, r=3 и G(z)=z³-z+1=1011. Необходимо закодировать комбинацию A*(z)=z*+1 = 1001. Тогда zA*(z)=z+z= 1001000. Для определения остатка делим z³A*(z) на G(z):

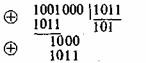
Окончательно получаем

В А(z) высшие четыре разряда занимают информационные символы, а остальные при — контрольные.

Контрольные символы в циклическом коде могут быть вычислены по общим ф-лам (7.9), однако здесь определение коэффициентов  затрудняется необходимостью выполнять требования делимости А(z) на порождающий полином G(z).

Процедура декодирования принятых комбинаций также основана на использовании полиномов G(z). Если ошибок в процессе передачи не было, то деление принятой комбинации A(z) на G(z) дает целое число. При наличии корректируемых ошибок в результате деления образуется остаток, который и позволяет обнаружить или исправить ошибки.

Кодирующие и декодирующие устройства циклических кодов в большинстве случаев обладают сравнительной простотой, что следует считать одним из основных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где действуют импульсные и сосредоточенные помехи или наблюдаются замирания сигнала.

В теории кодирования весом кодовых комбинаций принято называть .количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.

Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код обнаруживает все ошибки нечетной краткости и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей. Можно показать, что вероятность необнаруженной ошибки для кода 3/4 равна:

 при                                                                                (7.18)

В этом коде из общего числа комбинаций М = 2⁷=128 разрешенными являются лишь , поэтому в соответствии с (7.6) коэффициент избыточности

Код 3/4 находит применение при частотной манипуляции в каналах с селективными замираниями, где вероятность ошибок смещения невелика.

7.8. Непрерывные коды

Из непрерывных кодов, исправляющих ошибки, наиболее известны коды Финка—Хагельбаргера, в которых контрольные символы образуются путем линейной операции над двумя или более информационными символами. Принцип построения этих кодов рассмотрим на примере простейшего цепного кода. Контрольные символы в цепном коде формируются путем суммирования двух информационных символов, расположенных один относительно другого на определенном расстоянии:

;                                                                             (7.19)

Расстояние между информационными символами l=k—i определяет основные свойства кода и называется шагом сложения. Число контрольных символов при таком способе кодирования равно числу информационных символов, поэтому избыточность кода =0,5. Процесс образования последовательности контрольных символов показан на рис.7. символы разметаются  между информационными символами с задержкой на два шага сложения.

Рис. 7.3. Образование и размещение контрольных символов в цепном коде Финка—Хагельбаргера

При декодировании из принятых информационных символов по тому же правилу (7.19) формируется вспомогательная последовательность контрольных символов е», которая сравнивается с принятой последовательностью контрольных символов е’ (рис. 7.36). Если произошла ошибка в информационном символе, например, c‘k, то это вызовет искажения сразу двух символов e«k и e«km, что и обнаружится в результате их сравнения с  и e‘km. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с’Ошибка в принятом контрольном символе, например, e‘k приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление  такой ошибки не требуется.

Важное преимущество непрерывных кодов состоит в их способности исправлять не только одиночные ошибки, но я группы (пакеты) ошибок. Если задержка контрольных символов выбрана равной 2l, то можно показать, что максимальная длина исправляемого пакета ошибок также равна 2l при интервале между пакетами не менее 6l+1. Таким образом, возможность исправления длинных пакетов связана с увеличением шага сложения, а следовательно, и с усложнением кодирующих и декодирующих устройств.

Вопросы для повторения

1. Как могут быть  классифицированы  корректирующие коды?

2. Каким образом исправляются ошибки в кодах, которые только их обнаруживают?

3. В чем состоят основные принципы корректирования ошибок?

4. Дайте определение кодового расстояния.

5. При каких условиях код может обнаруживать или исправлять ошибки?

6. Как используется корректирующий код в системах со стиранием?

7. Какие характеристики определяют корректирующие способности кода?

8. Как осуществляется построение кодовых комбинаций в систематических кодах?

9. На чем  основан  принцип  корректирования  ошибок  с использованием  контрольного числа?

10. Объясните метод построения кода с четным числом единиц.

11. Как осуществляется процедура кодирования в семизначном коде Хэмминга?

12. Почему семизначный код 3/4 не обнаруживает ошибки смещения?

13. Каким образом производится непрерывное кодирование?

14. От чего зависит длина пакета исправляемых ошибок в коде Финка—Хагельбаргера?