Пусть — булевое множество. Рассмотрим и расстояние Хемминга . Пусть — разделяемый код постоянной длины. Обозначим .
Содержание
- 1 Коды, обнаруживающие и исправляющие ошибки
- 2 Булев шар
- 3 Определение и устранение ошибок в общем случае
- 4 Граница Хэмминга, граница Гильберта
- 5 См. также
Коды, обнаруживающие и исправляющие ошибки
| Определение: |
| Код обнаруживает ошибок, если . |
| Определение: |
| Код исправляет ошибок, если . |
| Утверждение: |
|
Код, исправляющий ошибок, обнаруживает ошибок. |
Булев шар
| Определение: |
| Булев шар — подмножество вида . называется его центром, — радиусом. Булев шар с центром и радиусом обознчается . |
| Определение: |
| Обьёмом шара в называется величина . Обьём шара радиуса в обозначается . |
| Утверждение: |
|
Обьём шара не зависит от его центра. |
|
Заметим, что шар всегда можно получить из другого шара с помощью «параллельного переноса» на вектор (здесь обозначает побитовый ), т.е. . |
Можно сформулировать свойство кодов, исправляющих ошибок, в терминах булевых шаров.
| Лемма: |
|
Пусть — код, исправляющий ошибок. |
| Доказательство: |
|
Т.к код исправляет ошибок, по определению . Допустим, такие, что и , т.е существует , такой что и . Тогда по неравенству треугольника . Это противоречит тому, что . |
Определение и устранение ошибок в общем случае
Пусть — исходный алфавит, — кодирование,
— расстояние Хэмминга между двумя кодами.
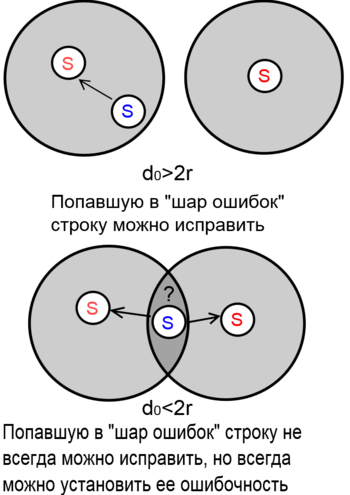
Код, может исправлять и обнаруживать ошибок. Действительно, при любом натуральном количестве допустимых ошибок любоое кодовое слово образует вокруг себя проколотый шар таких строк , что . Если этот шар не содержит других кодов (что выполняется при ) , то можно утверждать, что если в него попадает строка, то она ошибочна. Если шары всех кодов не пересекаются (что выполняется при ), то попавшую в шар строку можно считать ошибочной и исправить на центр шара — строку .
Граница Хэмминга, граница Гильберта
| Теорема (Граница Хэмминга): |
|
Пусть — код для -символьного алфавита, исправляющий ошибок. |
| Доказательство: |
|
Это прямое следствие предыдущей леммы. Их суммарный обьём равен , и он не может превосходить общее число возможных веткоров . |
Граница Хэмминга даёт верхнюю оценку на скорость передачи сообщений в канале с ошибками.
Прологарифмировав неравенство, получим .
Здесь это плотность кодирования, количество информации в одном символе алфавита на размер кода.
Таким образом, при кодировании с защитой от ошибок падает скорость передачи.
Аналогично составляется оценка в другую сторону.
| Теорема (Граница Гильберта): |
|
Если выполнено неравенство , то существует код для -символьного алфавита , исправляющий ошибок. |
Примером кода для случая является код Хэмминга.
См. также
- Избыточное кодирование, код Хэмминга
Процедура
декодирования циклического кода с
обнаружением ошибок, по аналогии с
процессом кодирования основана на
использовании свойства делимости без
остатка кодового многочлена Р(x)
циклического (n,m)-кода
на порождающий многочлен g(x).
Поэтому алгоритм декодирования включает
в себя деление принятого кодового слова,
описываемого многочленом F(x)
на g(x),
вычисление и анализ остатка R(x).
Если R(x)=0,
то принятое кодовое слово считается
неискаженным. Если R(x)0,
то принятое кодовое слово стирается и
формируется сигнал «ошибка».
2 Способы декодирования с исправлением ошибок
Декодирование
заключается в определении номера
искаженного разряда и его автоматического
исправления. А также отделения
информационных разрядов от контрольных.
Рассмотрим три
методики декодирования
Определение
искаженного разряда с помощью матрицы
ошибок.
Матрица одиночных
ошибок имеет вид
![]() ,
,
где
![]() —
—
единичная матрица;![]() — прямоугольная проверочная матрица.
— прямоугольная проверочная матрица.
Строки матрицы
![]() определяются из выражений
определяются из выражений
![]() — остаток от деления
— остаток от деления
![]() на образующий полином
на образующий полином![]() ,
,
где
![]() — значениеi-той
— значениеi-той
строки матрицы
![]() ;
;
i
— номер строки матрицы
![]() .
.
Пример. Матрица
![]() для (7,4)-кода на основе порождающего
для (7,4)-кода на основе порождающего
многочлена![]() имеет вид
имеет вид
 .
.
Единичная матрица
размерности 7х7
 .
.
Рассчитаем
проверочную матрицу
![]() .
.
При
![]()
![]() .
.
Определим остаток
от деления
![]() на образующий полином
на образующий полином![]() .
.
![]() .
.
При
![]()
![]() .
.
Определим остаток
от деления
![]() на образующий полином
на образующий полином![]() .
.
![]() .
.
При
![]()
![]() .
.
Определим остаток
от деления
![]() на образующий полином
на образующий полином![]() .
.
![]() 111.
111.
При
![]()
![]() .
.
![]() 101.
101.
При
![]()
![]() .
.
![]() 100.
100.
При
![]()
![]() .
.
![]() 010.
010.
При
![]()
![]() .
.
![]() 001.
001.
Тогда матрица
ошибок

Для определения
искаженного разряда необходимо определить
остаток от деления принятой кодовой
комбинации
![]() на порождающий многочлен
на порождающий многочлен![]() .
.
Пример
![]()
Внесем искажения
в четвертый разряд
![]()
Находим остаток
|
1 |
|
|
1 |
|
|
1 1 1 1 |
|
|
|
|
|
0 0 1 0 0 0 |
|
|
|
|
|
1 0 1 |
— |
Н аходим
аходим
строку в матрице ошибок с полученным
остатком (синдромом) 1 0 1
Искаженный разряд
– это разряд в данной строке, в которой
стоит «1».
Искаженный разряд
исправляем посредством сложения строки
в матрице ошибок с полученной комбинацией
 .
.
Сообщение исправлено.
Метод
дополнительного деления первоначального
остатка на образующий многочлен
Метод дополнительного
деления основывается на предыдущем
методе т.к. каждый такт дополнительного
деления (приписывания нуля справа)
соответствует переходу от данной строки
матрицы ошибок (строка с первоначальным
остатком) к строке следующей вверх
матрицы.
Дополнительное
деление продолжается до получения
остатка с «1» в первом разряде и нулями
в остальных разрядах, потому что этот
остаток равен остатку последней строки
матрицы ошибок. Отсчет искаженного
разряда производится от старшего разряда
сообщения, по количеству тактов
дополнительного деления. Такой отсчет
соответствует возвратному движению в
матрице ошибок.
Пример.
![]()
Внесем искажения
в четвертый разряд
![]()
Находим остаток
|
1 |
|
|
1 |
|
|
1 1 1 1 |
|
|
|
|
|
0 0 1 0 0 0 |
|
|
|
|
|
1 0 1 |
— |
Д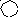 ополниетльное
ополниетльное
деление
|
|
Дополнительное |
|
1 |
|
|
|
Дополнительное |
|
1 |
|
|
|
Дополнительное |
|
1 |
|
|
0 |
— |
Понадобилось 4
такта дополнителоного деления. Тогда
 .
.
Четвертый такт
указывает номер искаженного разряда,
который исправляем.
Метод циклических
сдвигов
Метод циклических
сдвигов заключается в следующем:
-
Находится
остаток от деления
 на
на .
.
Если остаток равен нулю, то ошибок нет. -
Если
остаток отличен от нуля, определяется
вес остатка
 и выполнения условия
и выполнения условия ,
,
где —
—
количество исправляемых ошибок.
Если условие
выполняется, то производится суммирование
по модулю 2 полученного остатка с
комбинацией, из которой он получен.
Затем производятся сдвиги вправо столько
раз сколько было сделано сдвигов влево
В результате получаем исправленной
сообщение.
-
Если
вес остатка больше кратности исправляемых
разрядов, то производится сдвиг влево
полученной комбинации, т.е. умножение
кодовой комбинации на
 .
.
И снова находится остаток от деления
и переход к п.2.
Пример.
![]() ,
,
![]() .
.
Внесем искажения
в четвертый разряд
![]() .
.
Находим остаток
1 0 1.
Вес остатка
![]() .
.
1-й циклический
сдвиг
![]()
Находим остаток
|
0 |
|
|
1 |
|
|
0 |
|
|
1 |
|
|
1 |
— |
Вес остатка
![]() .
.
2-й циклический
сдвиг
![]()
Находим остаток
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
0 |
— |
Вес остатка
![]() .
.
3-й циклический
сдвиг
![]()
Находим остаток
|
0 |
|
|
1 |
|
|
0 |
|
|
1 |
|
|
0 |
|
|
1 |
|
|
0 |
— |
Вес остатка
![]() .
.
4-й циклический
сдвиг
![]()
Находим остаток
|
1 0 0 1 0 1 0 |
|
|
|
|
|
0 1 0 0 0 |
|
|
|
|
|
0 1 0 1 1 |
|
|
1 1 0 1 |
|
|
0 1 1 0 0 |
|
|
1 1 0 1 |
|
|
0 0 0 01 |
— |
Вес остатка
![]() .
.
Вес равен «1»
поэтому циклические сдвиги закончились.
Теперь необходимо остаток сложить с
той комбинацией, с которой мы его получили
|
1 0 0 1 0 1 0 |
|
|
|
1 0 0 1 0 1 1 |
Затем производятся
сдвиги вправо столько раз, сколько было
сделано сдвигов влево
1 0 0 1 0 1 1
1-й сдвиг
1 1 0 0 1 0 1
2-й сдвиг
1 1 1 0 0 1 0
3-й сдвиг
0 1 1 1 0 0 1
4-й сдвиг
1 0 1 1 1 0 0
Сообщение исправлено
![]() .
.
Свойства
циклических кодов по обнаружению ошибок
Свойства циклических
кодов полностью определяются выбранным
порождающим (образующим) многочленом
![]() .
.
I. Если порождающий
многочлен
![]() содержит более одного члена, то циклический
содержит более одного члена, то циклический
код обнаруживает все одиночные ошибки.
При представлении циклического кода
многочленами одиночная ошибка описывается
одночленом![]() ,
,
где![]() — указывает номер искаженного разряда
— указывает номер искаженного разряда![]() .
.
Поскольку одночлен не делится на
многочлен без остатка, то ошибка будет
обнаружена.
2. Циклический код
с порождающим многочленом
![]() обнаруживает все нечетные ошибки.
обнаруживает все нечетные ошибки.
Используя правила построения проверочной
матрицы для![]() ,
,
получим![]() .
.
При такой проверочной матрице остаток
определяется суммой по модулю 2 всех
элементов принятой кодовой комбинации
(проверка на четность). Поэтому все
искажения на нечетном количестве позиций
будут обнаружены.
3. Циклический код
обнаруживает все одиночные и двукратные
ошибки, если разрядность кода
![]() не больше длины цикла
не больше длины цикла![]() используемого порождающего многочлена,
используемого порождающего многочлена,
т.е.![]() .
.
Под длиной цикла многочлена понимают
минимальный показатель степени двучлена![]() ,
,
при котором этот двучлен делится без
остатка на образующий многочлен![]() .
.
4. Циклический код
с многочленом
![]() степени
степени![]() обнаруживает все групповые ошибки
обнаруживает все групповые ошибки
длительностью в![]() разрядов и менее. Любая групповая ошибка
разрядов и менее. Любая групповая ошибка
в![]() разрядов описывается многочленом
разрядов описывается многочленом
степени![]() ,
,
т.е.![]() .
.
Многочлен же степени![]() на многочлен степени
на многочлен степени![]() не делится и, таким образом, ошибка
не делится и, таким образом, ошибка
обнаруживается.
5. Циклический код
с порождающим многочленом
![]() степени
степени![]() не обнаруживает
не обнаруживает![]() часть ошибок
часть ошибок![]() -й
-й
кратности.
6. Циклический код
с порождающим многочленом
![]() степени
степени![]() не обнаруживает
не обнаруживает![]() часть ошибок более
часть ошибок более![]() -й
-й
кратности.
Анализируя
перечисленные свойства циклического
кода, можно увидеть, что способности
кода по обнаружению и исправлению ошибок
полностью определяются выбранным
образующим многочленом
![]() .
.
При обнаружении
ошибок стандартные многочлены имеют
вид:
![]() ,
,![]() при длине кодовой комбинации
при длине кодовой комбинации![]() ,
,
или
![]() ,
,![]() при длине кодовой комбинации
при длине кодовой комбинации![]() ;
;
![]() ,
,
![]() при длине кодовой комбинации
при длине кодовой комбинации![]() .
.
Разработан ряд
методик по выбору порождающего многочлена
![]() .
.
В литературе коды называют по фамилиям
ученых, предложивших ту или иную методику.
Так получили свое название коды
Боуза-Чоудхури-Хоквингема (БЧХ), коды
Рида-Соломона, коды Файра и др.
Укороченные
циклические коды
Циклические коды
предполагают равенство разрядности
формируемой кодовой комбинации длине
цикла порождающего
многочлена, т.е.
![]() .
.
Однако, это требование на практике
трудно выполнимо, поскольку разрядность
комбинаций, выдаваемых источником
информации, зачастую отличается от
целесообразной, в результате чего![]() .
.
В этих случаях циклический код
преобразуют
и используют так называемый укороченный
циклический код, который получается из
циклического путем исключения в нем
определенного числа разрядов.
При этом число
столбцов проверочной матрицы
![]() уменьшается на величину, равную числу
уменьшается на величину, равную числу
исключаемых информационных разрядов,
причем исключаются столбцы с наивысшими
номерами. Свойства кода по обнаружению
ошибок при этом не изменяются.
Принципы построения
кодирующих и декодирующих устройств
циклических кодов
Кодирующие и
декодирующие устройства циклических
кодов строятся на основе регистров с
обратными связями. Такие регистры иногда
называют многотактными линейными
переключающими схемами. При кодировании
и декодировании циклических кодов
получаемый остаток содержит число
разрядов, равное показателю степени
порождающего многочлена
![]() .
.
Поэтому регистр с обратными связями
(ОС) должен содержать![]() ячеек памяти. Как ранее указывалось,
ячеек памяти. Как ранее указывалось,
столбцы проверочной матрицы![]() являются остатками от деления одночлена
являются остатками от деления одночлена![]() на
на![]() .
.
Разделить же![]() при помощи регистра с ОС это значит
при помощи регистра с ОС это значит
осуществить сдвиг записанной в этот
регистр „1″ на![]() тактов после ввода ее в первую ячейку.
тактов после ввода ее в первую ячейку.
Таким образом, при каждом сдвиге
записанной в регистр „1” должен
получаться остаток, соответствующий
делению![]() на
на![]() .
.
Следовательно, содержание регистра при
каждом тактовом сдвиге должно
соответствовать содержанию столбца
проверочной матрицы.
В качестве примера
на рис. 8.15 показаны схема регистра с ОС
для порождающего многочлена
![]() и состояние ячеек этого регистра при
и состояние ячеек этого регистра при
сдвиге «1» записанных в первую ячейку
(табл. 8.19). На конкретном примере покажем,
что данный регистр производит операцию
деления.
Пусть требуется
закодировать кодовую комбинацию вида
1 1 0 1, многочлен которой имеет вид
![]() .
.
Разделим многочлен
![]() и отметим остатки, полученные перед
и отметим остатки, полученные перед
каждым следующим тактом деления:
|
х |
х |
||||
|
|
х |
||||
|
x5+ |
|||||
|
|
x5+ |
||||
|
x4 |
|||||
|
|
x4 |
||||
|
х3+ |
|||||
|
|
х |
||||
|
1 |
— |
|
|||
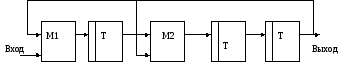
Рис. 8.15. Схема
регистра с ОС для порождающего многочлена
![]() .
.
Табл. 8.19. К пояснению
процесса кодирования

Деление сводится
к последовательному сложению по модулю
2 делителя со старшими разрядами делимого
или полученного остатка. Регистр с
обратными связями производит аналогичные
операции. Определим содержание регистра
перед каждым тактом деления и сравним
их с остатками, полученными путем
обычного деяния.
Процесс деления
в регистре производится только при
поступлении «1» в цепь обратной
связи. Поэтому содержание регистра, при
котором «1» находится в последней
ячейке, будет являться остатком перед
следующим тактом деления. В табл. 8.19
показано содержание ячеек регистра по
тактам. Сравнение остатков, полученных
как при обычном делении, так и при делении
с помощью регистра, показывает, что они
полностью совпадают.
Регистры с обратными
связями в соответствии с выбранным
порождающим многочленом строятся по
следующим правилам:
1. Число ячеек
регистра выбирают равным степени
порождающего многочлена
![]() .
.
2. Количество
сумматоров по модулю 2 берется на единицу
меньше числа ненулевых членов порождающего
многочлена.
3. Входы всех ячеек
регистра обозначают
![]() .
.
Выход последней ячейки обозначается![]() , а вход первой —
, а вход первой —![]() .
.

Рис 8.16. Схема
регистра с ОС для порождающего многочлена
![]() с обозначением
с обозначением![]() .
.
4. Сумматоры по
модулю 2 устанавливаются на входе тех
ячеек, для которых в формуле порождающего
многочлена
![]() имеет ненулевое значение. Например, для
имеет ненулевое значение. Например, для![]() (рис. 8.16) сумматоры устанавливаются на
(рис. 8.16) сумматоры устанавливаются на
входах ячеек 1 и 2 триггеров.
5. Выход последней
ячейки соединяется со входами сумматоров.
6. Выходы предыдущих
ячеек соединяются со входами последующих
через сумматоры или без них, в зависимости
от того, установлены они между ячейками
или нет.

Рис.26.2
Кодирующее устройство
Структурная схема
кодирующего устройства при порождающем
многочлене
![]() показана на рис.8.17. В регистре с обратными
показана на рис.8.17. В регистре с обратными
связями передаваемая кодовая комбинация
делится на исходный многочлен. При
помощи линии задержки передаваемая
комбинация смещается на![]() разрядов (в данном случае
разрядов (в данном случае![]() =4),
=4),
что равносильно умножению многочлена,
отображающего передаваемую кодовую
комбинацию, на![]() .
.
Устройство
функционирует следующим образом.
Передаваемая кодовая комбинация
последовательно подается на вход
регистра и линии задержки. Ключ
![]() находится в положений «1» ключ
находится в положений «1» ключ![]() — в положении «Включено»
— в положении «Включено»
(рис.8.18).

После того как
последний импульс с выхода линии задержки
передан в линию связи, ключ
![]() .
.
переключается в положение ,, 2″![]() — в положение „Выключено» и содержимое
— в положение „Выключено» и содержимое
регистра (остаток от деления) передается
в линию связи (рис.8.19).

Приведенная схема
кодирующего устройства обладает одним
существенным недостатком. Кодированное
сообщение задерживается на число тактов,
равное числу ячеек регистра. Устранить
такой недостаток можно при использовании
кодирующего.устройства без линии
задержки. В качестве примера на рис.8.20
изображена структурная схема такого
устройства с
![]() .
.

Регистры с обратными
связями для таких кодирующих устройств
строятся по правилам, указанным ранее.
Однако один из сумматоров устанавливается
не на входе первой ячейки памяти, а на
выходе последней ячейки.
Декодирующие
устройства также строятся на основе
использования регистров с обратными
связями. На рис.8.21 приведена структурная
схема декодирующего устройства,
предназначенного для обнаружения
ошибок. После приема кодовой комбинации
в регистре с обратными связями образуется
остаток
![]() .
.
Если этот остаток равен 0, то сигнал
запрета на выдачу принятой кодовой
комбинации потребителю не выдается.

При использовании
циклических кодов в качестве кодов с
исправлением ошибок схема декодирующего
устройства усложняется.
Кратко рассмотрим
методику построения таких декодирующих
устройств для наиболее простого метода
исправления ошибок -последовательного.
Этот метод основан
на следующем свойстве. Если возникшая
в кодовой комбинации ошибка исправляема,
то после введения принятой кодовой
комбинации в регистр с ОС можно
восстановить вектор ошибок. После
поразрядного сложения этого вектора с
вектором, отображающим принятую кодовую
комбинацию, ошибка исправляется.
Структурная схема такого декодирующего
устройства приведена на рис.8.22.
Принятая кодовая
комбинация поразрядно поступает в
регистр со сдвигом и в регистр с ОС.
Затем принятая комбинация последовательным
кодом через сумматор по модулю 2 (М2)
выдается потребителю. В то время, когда
искаженный разряд будет на выходе
регистра со сдвигом, при исправляемых
кодом ошибках содержание регистра с ОС
будет вполне определенным. Селектор
выделяет эту известную кодовую комбинацию
и выдает на сумматор по модулю 2 импульс
для исправления искаженного разряда.
Одновременно в регистр с ОС записывается
кодовая комбинация, при помощи которой
устраняется влияние исправленного
разряда на содержание этого регистра.
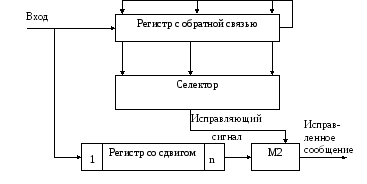
Рис 8.22. Декодирующее
устройство с исправлением ошибок
Вероятности
ошибочного декодирования циклических
кодов
Вектором ошибки
называется двоичная последовательность
длины
![]() ,
,
в которой единицы стоят на позициях
символов принятых с ошибкой. Отсюда
вероятность не обнаружения ошибки
заданным кодом равна вероятности
появления в заданном дискретном канале
векторов ошибок, совпадающих с кодовыми
словами
Относительно
просто эти вероятности могут быть
рассчитаны для двоичного симметричного
канала без памяти. В таком канале каждый
двоичный символ с некоторой фиксированной
вероятностью
![]() принимается правильно и с вероятностью
принимается правильно и с вероятностью![]() изменяется помехой на обратный.
изменяется помехой на обратный.
Передача/прием каждого символа полагается
событием независимым (канал без памяти).
Если по такому
каналу передается кодовое слово длины
![]() ,
,
то вероятность
![]() того, что не произойдет ни одной ошибки,
того, что не произойдет ни одной ошибки,
равна![]() .
.
Вероятность
![]()
того, что
будет одна ошибка в заданном символе,
равна
![]() .
.
Вероятность того,
что слово на выходе канала будет
отличаться от переданного слова в
заданных
![]() разрядах, т.е. вектор ошибок содержит
разрядах, т.е. вектор ошибок содержит![]() единиц, равна
единиц, равна
![]() .
.
Вероятность того,
что слово на выходе канала будет
отличаться от переданного слова в
любых
![]() разрядах, равна
разрядах, равна
![]() ,
,
где
![]()
—
число сочетаний из
![]()
по
![]() .
.
Предположим, что
некоторый линейный код (5,3) содержит
одно нулевое слово (как всякий линейный
код), два слова, вес которых равен 2,
четыре слова — весом 3, одно слово —
весом 4 (всего
![]() слов).
слов).
Вероятность
необнаруживаемой этим кодом ошибки
равна вероятности появления в ДСК
векторов ошибок, совпадающих с кодовыми
словами, т.е.:
![]()
В режиме исправления
ошибок декодер вычисляет остаток
![]()
от деления
принятой последовательности
![]()
на
![]() .
.
Этот остаток
называют синдромом.
Принятый
полином
![]()
представляет
собой сумму по модулю 2 переданного
слова
![]()
и вектора
ошибок
![]() :
:
![]() .
.
Тогда синдром
![]() ,
,
так как по
определению циклического кода
![]() .
.
Некоторому синдрому![]()
может быть
поставлен в соответствие определенный
вектор ошибок
![]() .
.
Тогда
переданное слово
![]() находят, складывая
находят, складывая![]() .
.
Однако один и тот
же синдром может соответствовать
![]()
различным
векторам ошибок. Предположим, синдром
![]() соответствует вектору ошибок
соответствует вектору ошибок![]() .
.
Но и все векторы ошибок, равные сумме![]() ,
,
где![]() — любое кодовое слово, будут давать тот
— любое кодовое слово, будут давать тот
же синдром. Поэтому, поставив в соответствие
синдрому![]() вектор ошибок
вектор ошибок![]() ,
,
мы будем
осуществлять правильное декодирование
в случае, когда действительно вектор
ошибок равен
![]() ,
,
во всех остальных![]() случаях декодирование будет ошибочным.
случаях декодирование будет ошибочным.
Для уменьшения
вероятности ошибки декодирования из
всех возможных векторов ошибок, дающих
один и тот же синдром, следует выбирать
в качестве исправляемого наиболее
вероятный в заданном канале.
Например, для
двоичного симметричного канала, в
котором вероятность
![]()
ошибочного
приема двоичного символа существенно
меньше вероятности
![]()
правильного
приема, вероятность появления векторов
ошибок уменьшается с увеличением их
веса
![]() .
.
В этом случае следует исправлять в
первую очередь вектор ошибок меньшего
веса.
Если кодом могут
быть исправлены только все векторы
ошибок веса
![]() и меньше, то любой вектор ошибки веса
и меньше, то любой вектор ошибки веса
от![]() доп будет
доп будет
приводить к ошибочному декодированию.
Вероятность
ошибочного декодирования будет равна
вероятности
![]()
появления
векторов ошибок веса
![]() и больше в заданном канале. Для ДСК эта
и больше в заданном канале. Для ДСК эта
вероятность будет равна
![]()
Общее число
различных векторов ошибок, которые
может исправлять циклический код,
равно числу ненулевых синдромов
![]() .
.
Соседние файлы в папке Пособие ТЕЗ_рус12
- #
- #
- #
- #
- #
- #
- #
- #
- #
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
6.5.2. Минимальное расстояние для линейного кода
6.5.3. Обнаружение и исправление ошибок
6.5.3.1. Распределение весовых коэффициентов кодовых слов
6.5.3.2.Одновременное обнаружение и исправление ошибок
6.5.4. Визуализация пространства 6-кортежей
6.5.5. Коррекция со стиранием ошибок
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
Конечно же, понятно, что правильно декодировать можно не все ошибочные комбинации. Возможности кода для исправления ошибок в первую очередь определяются его структурой. Весовой коэффициент Хэмминга (Hamming weight) w(U) кодового слова U определяется как число ненулевых элементов в U. Для двоичного вектора это эквивалентно числу единиц в векторе. Например, если U=100101101, то w(U) = 5. Расстояние Хэмминга (Hamming distance) между двумя кодовыми словами U и V, обозначаемое как d(U, V), определяется как количество элементов, которыми они отличаются.
U=100101101
V=011110100
d(U,V)=6
Согласно свойствам сложения по модулю 2, можно отметить, что сумма двух двоичных векторов является другим двоичным вектором, двоичные единицы которого расположены на тех позициях, которыми эти векторы отличаются.
U + V=111011001
Таким образом, можно видеть, что расстояние Хэмминга между двумя векторами равно весовому коэффициенту Хэмминга их суммы, т.е. d(U, V) = w(U + V). Также видно, что весовой коэффициент Хэмминга кодового слова равен его расстоянию Хэмминга до нулевого вектора.
6.5.2. Минимальное расстояние для линейного кода
Рассмотрим множество расстояний между всеми парами кодовых слой в пространстве Vn. Наименьший элемент этого множества называется минимальным расстоянием кода и обозначается dmin. Как вы думаете, почему нас интересует именно минимальное расстояние, а не максимальное? Минимальное расстояние подобно наиболее слабому звену в цепи, оно дает нам меру минимальных возможностей кода и, следовательно, характеризует его мощность.
Как обсуждалось ранее, сумма двух произвольных кодовых слов дает другой элемент пространства кодовых слов. Это свойство линейных кодов формулируется просто: если U и V — кодовые слова, то и W = U + V тоже должно быть кодовым словом. Следовательно, расстояние между двумя кодовыми словами равно весовому коэффициенту третьего кодового слова, т.е. d(U, V) = w(U + V) = w(W). Таким образом, минимальное расстояние линейного кода можно определить, не прибегая к изучению расстояний между всеми комбинациями пар кодовых слов. Нам нужно лишь определить вес каждого кодового слова (за исключением нулевого вектора) в подпространстве; минимальный вес соответствует минимальному расстоянию dmin. Иными словами, dmin соответствует наименьшему из множества расстояний между нулевым кодовым словом и всеми остальными кодовыми словами.
6.5.3. Обнаружение и исправление ошибок
Задача декодера после приема вектора r заключается в оценке переданного кодового слова Ui. Оптимальная стратегия декодирования может быть выражена в терминах алгоритма максимального правдоподобия (см. приложение Б); считается, что передано было слово Ui, если
![]() (6.41)
(6.41)
Поскольку для двоичного симметричного канала (binary symmetric channel — BSC) правдоподобие Ui относительно r обратно пропорционально расстоянию между r и U, можно сказать, что передано было слово Ui, если
![]() (6.42)
(6.42)
Другими словами, декодер определяет расстояние между r и всеми возможными переданными кодовыми словами Uj, после чего выбирает наиболее правдоподобное Uj, для которого
![]() (6.43)
(6.43)
где М = 2k — это размер множества кодовых слов. Если минимум не один, выбор между минимальными расстояниями является произвольным. Наше обсуждение метрики расстояний будет продолжено в главе 7.
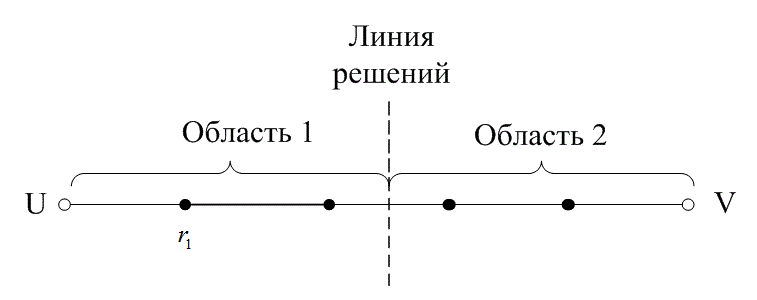
На рис. 6.13 расстояние между двумя кодовыми словами U и V показано как расстояние Хэмминга. Каждая черная точка обозначает искаженное кодовое слово. На рис. 6.13, а проиллюстрирован прием вектора r1 находящегося на расстоянии 1 от кодового слова U и на расстоянии 4 от кодового слова V. Декодер с коррекцией ошибок, следуя стратегии максимального правдоподобия, выберет при принятом векторе r1 кодовое слово U. Если r1 получился в результате появления одного ошибочного бита в переданном векторе кода U, декодер успешно исправит ошибку. Но если же это произошло в результате 4-битовой ошибки в векторе кода V, декодирование будет ошибочным. Точно так же, как показано на рис. 6.13, б, двойная ошибка при передаче U может привести к тому, что в качестве переданного вектора будет ошибочно определен вектор r2, находящийся на расстоянии 2 от вектора U и на расстоянии 3 от вектора кода V. На рис. 6.13 показана ситуация, когда в качестве переданного вектора ошибочно определен вектор r3, который находится на расстоянии 3 от вектора кода U и на расстоянии 2 от вектора V. Из рис. 6.13 видно, что если задача состоит только в обнаружении ошибок, а не в их исправлении, то можно определить искаженный вектор — изображенный черной точкой и представляющий одно-, двух-, трех- и четырехбитовую ошибку. В то же время пять ошибок при передаче могут привести к приему кодового слова V, когда в действительности было передано кодовое слово U; такую ошибку невозможно будет обнаружить.
Из рис. 6.13 можно видеть, что способность кода к обнаружению и исправлению ошибок связана с минимальным расстоянием между кодовыми словами. Линия решения на рисунке служит той же цели, что и в процессе демодуляции, — для разграничения областей решения.
а)
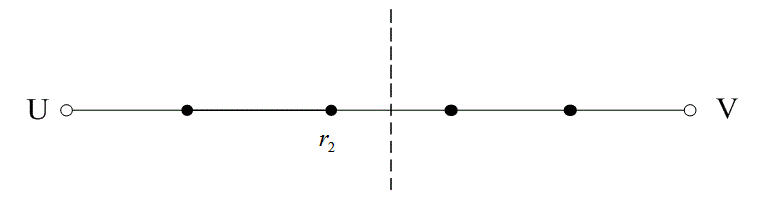
б)
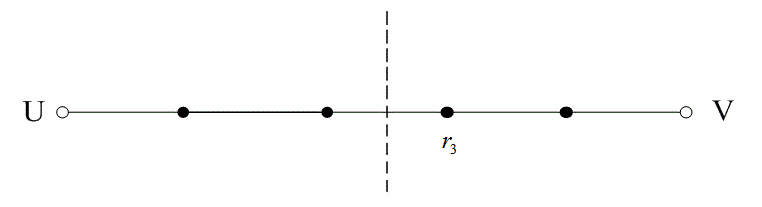
в)
Рис. 6.13. Возможности определения и исправления ошибок: а) принятый вектор r1; б) принятый вектор r2; в) принятый вектор r3
В примере, приведенном на рис. 6.13, критерий принятия решения может быть следующим: выбрать U, если r попадает в область 1, и выбрать V, если r попадает в область 2. Выше показывалось, что такой код (при dmin = 5) может исправить две ошибки. Вообще, способность кода к исправлению ошибок t определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово, и записывается следующим образом [4].
![]() (6.44)
(6.44)
Здесь ![]() означает наибольшее целое, не превышающее х. Часто код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, также может исправлять символы, содержащие t +1 ошибочных бит. Это можно увидеть на рис. 6.11. В этом случае dmin = 3, поэтому из уравнения (6.44) можно видеть, что исправимы все ошибочные комбинации из t = 1 бит. Также исправима одна ошибочная комбинация, содержащая / +1 (т.е. 2) ошибочных бит. Вообще, линейный код (n, k), способный исправлять все символы, содержащие t ошибочных бит, может исправить всего 2n—k ошибочных комбинаций. Если блочный код с возможностью исправления символов, имеющих ошибки в t бит, применяется для исправления ошибок в двоичном симметричном канале с вероятностью перехода р, то вероятность ошибки сообщения Рм(вероятность того, что декодер совершит неправильное декодирование и п-битовый блок содержит ошибку) можно оценить сверху, используя уравнение (6.18).
означает наибольшее целое, не превышающее х. Часто код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, также может исправлять символы, содержащие t +1 ошибочных бит. Это можно увидеть на рис. 6.11. В этом случае dmin = 3, поэтому из уравнения (6.44) можно видеть, что исправимы все ошибочные комбинации из t = 1 бит. Также исправима одна ошибочная комбинация, содержащая / +1 (т.е. 2) ошибочных бит. Вообще, линейный код (n, k), способный исправлять все символы, содержащие t ошибочных бит, может исправить всего 2n—k ошибочных комбинаций. Если блочный код с возможностью исправления символов, имеющих ошибки в t бит, применяется для исправления ошибок в двоичном симметричном канале с вероятностью перехода р, то вероятность ошибки сообщения Рм(вероятность того, что декодер совершит неправильное декодирование и п-битовый блок содержит ошибку) можно оценить сверху, используя уравнение (6.18).
![]() (6.45)
(6.45)
Оценка переходит в равенство, если декодер исправляет все ошибочные комбинации, содержащие до t ошибочных бит включительно, но не комбинации с числом ошибочных бит, большим t. Такие декодеры называются декодерами с ограниченным расстоянием. Вероятность ошибки в декодированном бите РB зависит от конкретного кода и декодера. Приближенно ее можно выразить следующим образом [5].
![]() (6.46)
(6.46)
В блочном коде, прежде чем исправлять ошибки, необходимо их обнаружить. (Или же код может использоваться только для определения наличия ошибок.) Из рис. 6.13 видно, что любой полученный вектор, который изображается черной точкой (искаженное кодовое слово), можно определить как ошибку. Следовательно, возможность определения наличия ошибки дается следующим выражением.
![]() (6.47)
(6.47)
Блочный код с минимальным расстоянием dmin гарантирует обнаружение всех ошибочных комбинаций, содержащих dmin — 1 или меньшее число ошибочных бит. Такой код также способен обнаружить и большую ошибочную комбинацию, содержащую dmin или более ошибок. Фактически код (n, k) может обнаружить 2n – 2k ошибочных комбинаций длины п. Объясняется это следующим образом. Всего в пространстве 2n n-кортежей существует 2n -1 возможных ненулевых ошибочных комбинаций. Даже правильное кодовое слово — это потенциальная ошибочная комбинация. Поэтому всего существует 2k -1 ошибочных комбинаций, которые идентичны 2k -1 ненулевым кодовым словам. При появлении любая из этих 2k — 1 ошибочных комбинаций изменяет передаваемое кодовое слово Uj на другое кодовое слово Uj. Таким образом, принимается кодовое слово Uj и его синдром равен нулю. Декодер принимает Uj за переданное кодовое слово, и поэтому декодирование дает неверный результат. Следовательно, существует 2k -1 необнаружимых ошибочных комбинаций. Если ошибочная комбинация не совпадает с одним из 2k кодовых слов, проверка вектора r с помощью синдромов дает ненулевой синдром и ошибка успешно обнаруживается. Отсюда следует, что существует ровно 2n-2k выявляемых ошибочных комбинаций. При больших n, когда 2k<<2n, необнаружимой будет только незначительная часть ошибочных комбинаций.
6.5.3.1. Распределение весовых коэффициентов кодовых слов
Пусть Aj — количество кодовых слов с весовым коэффициентом j в линейном коде (п, k). Числа A0,A1,…,An называются распределением весовых коэффициентов этого кода. Если код применяется только для обнаружения ошибок в двоичном симметричном канале, то вероятность того, что декодер не сможет определить ошибку, можно рассчитать, исходя из распределения весовых коэффициентов кода [5].
![]() (6.48)
(6.48)
где р — вероятность перехода в двоичном симметричном канале. Если минимальное расстояние кода равно dmin значения от А1 до ![]() , равны нулю.
, равны нулю.
Пример 6.5. Вероятность необнаруженной ошибки в коде
Пусть код (6,3), введенный в разделе 6.4.3, используется только для обнаружения наличия ошибок. Рассчитайте вероятность необнаруженной ошибки, если применяется двоичный симметричный канал, а вероятность перехода равна 10-2.
Решение
Распределение весовых коэффициентов этого кода выглядит следующим образом: A0=1, А1= А2 = 0, A3 = 4, A5 = 0, A6 = 0. Следовательно, используя уравнение (6.48), можно записать следующее.
![]()
Для р = 10-2 вероятность необнаруженной ошибки будет равна 3,9 х 10-6.
6.5.3.2. Одновременное обнаружение и исправление ошибок
Возможностями исправления ошибок с максимальным гарантированным (t), где t определяется уравнением (6.44), можно пожертвовать в пользу определения класса ошибок. Код можно использовать для одновременного исправления α и обнаружения β ошибок, причем ![]() , а минимальное расстояние кода дается следующим выражением [4].
, а минимальное расстояние кода дается следующим выражением [4].
![]() (6.49)
(6.49)
При появлении t или меньшего числа ошибок код способен обнаруживать и исправлять их. Если ошибок больше t, но меньше е+1, где е определяется уравнением (6.47), код может определять наличие ошибок, но исправить может только некоторые из них. Например, используя код с dmin = 7. можно выполнить обнаружение и исправление со следующими значениями α и β.
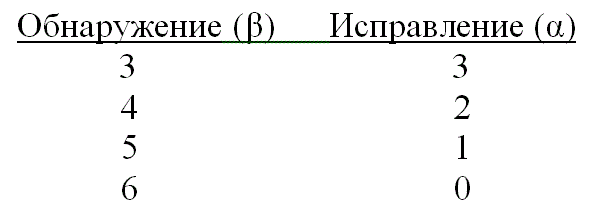
Заметим, что исправление ошибки подразумевает ее предварительное обнаружение. В приведенном выше примере (с тремя ошибками) все ошибки можно обнаружить и исправить. Если имеется пять ошибок, их можно обнаружить, но исправить можно только одну из них.
6.5.4. Визуализация пространства 6-кортежей
На рис. 6.14 визуально представлено восемь кодовых слов, фигурирующих в примере из раздела 6.4.3. Кодовые слова образованы посредством линейных комбинаций из трех независимых 6-кортежей, приведенных в уравнении (6.26); сами кодовые слова образуют трехмерное подпространство. На рисунке показано, что такое подпространство полностью занято восемью кодовыми словами (большие черные круги); координаты подпространства умышленно выбраны неортогональными. На рис. 6.14 предпринята попытка изобразить все пространство, содержащее шестьдесят четыре 6-кортежей, хотя точно нарисовать или составить такую модель невозможно. Каждое кодовое слово окружают сферические слои или оболочки. Радиус внутренних непересекающихся слоев — это расстояние Хэмминга, равное 1; радиус внешнего слоя — это расстояние Хэмминга, равное 2. Большие расстояния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая ошибочная комбинация, которая также поддается исправлению. Всего существует ![]() разных двухбитовых ошибочных комбинаций, которыми может быть искажено любое кодовое слово, но исправить можно только одну из них (в нашем примере это ошибочная комбинация 010001). Остальные четырнадцать двухбитовых ошибочных комбинаций описываются векторами, которые нельзя однозначно сопоставить с каким-либо одним кодовым словом; эти не поддающиеся исправлению ошибочные комбинации дают векторы, которые эквивалентны искаженным векторам двух или большего числа кодовых слов. На рисунке все (56) исправимые кодовые слова с одно- и двухбитовыми искажениями показаны маленькими черными кругами. Искаженные кодовые слова, не поддающиеся исправлению, представлены маленькими прозрачными кругами.
разных двухбитовых ошибочных комбинаций, которыми может быть искажено любое кодовое слово, но исправить можно только одну из них (в нашем примере это ошибочная комбинация 010001). Остальные четырнадцать двухбитовых ошибочных комбинаций описываются векторами, которые нельзя однозначно сопоставить с каким-либо одним кодовым словом; эти не поддающиеся исправлению ошибочные комбинации дают векторы, которые эквивалентны искаженным векторам двух или большего числа кодовых слов. На рисунке все (56) исправимые кодовые слова с одно- и двухбитовыми искажениями показаны маленькими черными кругами. Искаженные кодовые слова, не поддающиеся исправлению, представлены маленькими прозрачными кругами.
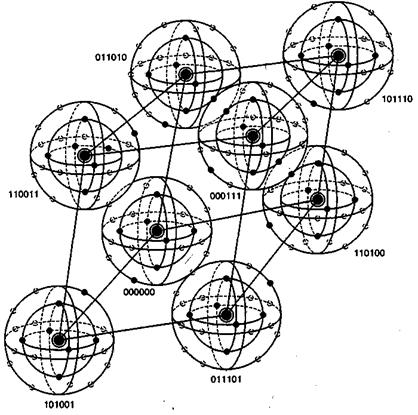
Рис, 6.14. Пример восьми кодовых слов в пространстве 6-кортежей
При представлении свойств класса кодов, известных как совершенные коды (perfect code), рис. 6.14 весьма полезен. Код, исправляющий ошибки в t битах, называется совершенным, если нормальная матрица содержит все ошибочные комбинации из t или меньшего числа ошибок и не содержит иных образующих элементов классов смежности (отсутствует возможность исправления остаточных ошибок). В контексте рис. 6.14 совершенный код с коррекцией ошибок в t битах — это такой код, который (при использовании обнаружения по принципу максимального правдоподобия) может исправить все искаженные кодовые слова, находящиеся на расстоянии Хэмминга t (или ближе) от исходного кодового слова, и не способен исправить ни одну из ошибок, находящихся на расстоянии, превышающем t.
Кроме того, рис. 6.14 способствует пониманию основной цели поиска хороших кодов. Предпочтительным является пространство, максимально заполненное кодовыми словами (эффективное использование введенной избыточности), а также желательно, чтобы кодовые слова были по возможности максимально удалены друг от друга. Очевидно, что эти цели противоречивы.
6.5.5. Коррекция со стиранием ошибок
Приемник можно сконструировать так, чтобы он объявлял символ стертым, если последний принят неоднозначно либо обнаружено наличие помех или кратковременных сбоев. Размер входного алфавита такого канала равен Q, а выходного —Q + 1; лишний выходной символ называется меткой стирания (erasure flag), или просто стиранием (erasure). Если демодулятор допускает символьную ошибку, то для ее исправления необходимы два параметра, определяющие ее расположение и правильное значение символа. В случае двоичных символов эти требования упрощаются — нам необходимо только расположение ошибки. В то же время, если демодулятор объявляет символ стертым (при этом правильное значение символа неизвестно), расположение этого символа известно, поэтому декодирование стертого кодового слова может оказаться проще исправления ошибки. Код защиты от ошибок можно использовать для исправления стертых символов или одновременного исправления ошибок и стертых символов. Если минимальное расстояние кода равно dmin, любая комбинация из ρ или меньшего числа стертых символов может быть исправлена при следующем условии [6].
![]() (6.50)
(6.50)
Предположим, что ошибки появляются вне позиций стирания. Преимущество исправления посредством стираний качественно можно выразить так: если минимальное расстояние кода равно dmin, согласно уравнению (6.50), можно восстановить dmin-1 стирание. Поскольку число ошибок, которые можно исправить без стирания информации, не превышает (dmin-1)/2, то преимущество исправления ошибок посредством стираний очевидно. Далее, любую комбинацию из α ошибок и γ стираний можно исправить одновременно, если, как показано в работе [6],
![]() (6.51)
(6.51)
Одновременное исправление ошибок и стираний можно осуществить следующим образом. Сначала позиции из у стираний замещаются нулями, и получаемое кодовое слово декодируется обычным образом. Затем позиции из у стираний замещаются единицами, и декодирование повторяется для этого варианта кодового слова. После обработки обоих кодовых слов (одно с подставленными нулями, другое — с подставленными единицами) выбирается то из них, которое соответствует наименьшему числу ошибок, исправленных вне позиций стирания. Если удовлетворяется неравенство (6.51), то описанный метод всегда дает верное декодирование.
Пример 6.6. Коррекция со стиранием ошибок
Рассмотрим набор кодовых слов, представленный в разделе 6.4.3.
000000 110100 011010 101110 101001 011101 110011 000111
Пусть передано кодовое слово 110011, в котором два крайних слева разряда приемник объявил стертыми. Проверьте, что поврежденную последовательность хx0011 можно исправить.
Решение
Поскольку ![]() , код может исправить
, код может исправить ![]() = 2 стирания. В этом легко убедиться из рис. 6.11 или приведенного выше перечня кодовых слов, сравнивая 4 крайних правых разряда xx00l1 с каждым из допустимых кодовых слов. Действительно переданное кодовое слово — это ближайшее (с точки зрения расстояния Хэмминга) к искаженной последовательности.
= 2 стирания. В этом легко убедиться из рис. 6.11 или приведенного выше перечня кодовых слов, сравнивая 4 крайних правых разряда xx00l1 с каждым из допустимых кодовых слов. Действительно переданное кодовое слово — это ближайшее (с точки зрения расстояния Хэмминга) к искаженной последовательности.

To clean up transmission errors introduced by Earth’s atmosphere (left), Goddard scientists applied Reed–Solomon error correction (right), which is commonly used in CDs and DVDs. Typical errors include missing pixels (white) and false signals (black). The white stripe indicates a brief period when transmission was interrupted.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Definitions[edit]
Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.
Error correction is the detection of errors and reconstruction of the original, error-free data.
History[edit]
In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.[5]
The modern development of error correction codes is credited to Richard Hamming in 1947.[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication[7] and was quickly generalized by Marcel J. E. Golay.[8]
Introduction[edit]
All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.
If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Types of error correction[edit]
There are three major types of error correction.[9]
Automatic repeat request[edit]
Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.
Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.
Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.
ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.[10]
For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.
Forward error correction[edit]
Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.[13]
Error-correcting codes are usually distinguished between convolutional codes and block codes:
- Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
- Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.
Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.
The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.
Hybrid schemes[edit]
Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:[10]
- Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
- Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.
The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.
Error detection schemes[edit]
Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).
Minimum distance coding[edit]
A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.
Repetition codes[edit]
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.
A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.[14][15]
Parity bit[edit]
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.
Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.
There are also other bit-grouping techniques.
Checksum[edit]
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy check[edit]
A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.
A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.
The parity bit can be seen as a special-case 1-bit CRC.
Cryptographic hash function[edit]
The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.
Error correction code[edit]
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.
Applications[edit]
Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.
Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.
Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.
Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.
Reliability and inspection engineering also make use of the theory of error-correcting codes.[16]
Internet[edit]
In a typical TCP/IP stack, error control is performed at multiple levels:
- Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
- The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
- The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
- UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
- TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.
Deep-space telecommunications[edit]
The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.
The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.
The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.
The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.
Satellite broadcasting[edit]
The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.
Data storage[edit]
Error detection and correction codes are often used to improve the reliability of data storage media.[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.
Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.
Error-correcting memory[edit]
Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.
Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.[22]
In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.[23][24][25] A few systems[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.
See also[edit]
- Berger code
- Burst error-correcting code
- ECC memory, a type of computer data storage
- Link adaptation
- List of algorithms § Error detection and correction
- List of hash functions
References[edit]
- ^ a b «Masorah». Jewish Encyclopedia.
- ^ Pratico, Gary D.; Pelt, Miles V. Van (2009). Basics of Biblical Hebrew Grammar: Second Edition. Zondervan. ISBN 978-0-310-55882-8.
- ^ Mounce, William D. (2007). Greek for the Rest of Us: Using Greek Tools Without Mastering Biblical Languages. Zondervan. p. 289. ISBN 978-0-310-28289-1.
- ^ Mishneh Torah, Tefillin, Mezuzah, and Sefer Torah, 1:2. Example English translation: Eliyahu Touger. The Rambam’s Mishneh Torah. Moznaim Publishing Corporation.
- ^ Brian M. Fagan (5 December 1996). «Dead Sea Scrolls». The Oxford Companion to Archaeology. Oxford University Press. ISBN 0195076184.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, p. vii, ISBN 0-88385-023-0
- ^ Shannon, C.E. (1948), «A Mathematical Theory of Communication», Bell System Technical Journal, 27 (3): 379–423, doi:10.1002/j.1538-7305.1948.tb01338.x, hdl:10338.dmlcz/101429, PMID 9230594
- ^ Golay, Marcel J. E. (1949), «Notes on Digital Coding», Proc.I.R.E. (I.E.E.E.), 37: 657
- ^ Gupta, Vikas; Verma, Chanderkant (November 2012). «Error Detection and Correction: An Introduction». International Journal of Advanced Research in Computer Science and Software Engineering. 2 (11). S2CID 17499858.
- ^ a b A. J. McAuley, Reliable Broadband Communication Using a Burst Erasure Correcting Code, ACM SIGCOMM, 1990.
- ^ Shah, Pradeep M.; Vyavahare, Prakash D.; Jain, Anjana (September 2015). «Modern error correcting codes for 4G and beyond: Turbo codes and LDPC codes». 2015 Radio and Antenna Days of the Indian Ocean (RADIO): 1–2. doi:10.1109/RADIO.2015.7323369. ISBN 978-9-9903-7339-4. S2CID 28885076. Retrieved 22 May 2022.
- ^ «IEEE SA — IEEE 802.11ac-2013». IEEE Standards Association.
- ^ «Transition to Advanced Format 4K Sector Hard Drives | Seagate US». Seagate.com. Retrieved 22 May 2022.
- ^ Frank van Gerwen. «Numbers (and other mysterious) stations». Archived from the original on 12 July 2017. Retrieved 12 March 2012.
- ^ Gary Cutlack (25 August 2010). «Mysterious Russian ‘Numbers Station’ Changes Broadcast After 20 Years». Gizmodo. Retrieved 12 March 2012.
- ^ Ben-Gal I.; Herer Y.; Raz T. (2003). «Self-correcting inspection procedure under inspection errors» (PDF). IIE Transactions. IIE Transactions on Quality and Reliability, 34(6), pp. 529-540. Archived from the original (PDF) on 2013-10-13. Retrieved 2014-01-10.
- ^ K. Andrews et al., The Development of Turbo and LDPC Codes for Deep-Space Applications, Proceedings of the IEEE, Vol. 95, No. 11, Nov. 2007.
- ^ Huffman, William Cary; Pless, Vera S. (2003). Fundamentals of Error-Correcting Codes. Cambridge University Press. ISBN 978-0-521-78280-7.
- ^ Kurtas, Erozan M.; Vasic, Bane (2018-10-03). Advanced Error Control Techniques for Data Storage Systems. CRC Press. ISBN 978-1-4200-3649-7.[permanent dead link]
- ^ Scott A. Moulton. «My Hard Drive Died». Archived from the original on 2008-02-02.
- ^ Qiao, Zhi; Fu, Song; Chen, Hsing-Bung; Settlemyer, Bradley (2019). «Building Reliable High-Performance Storage Systems: An Empirical and Analytical Study». 2019 IEEE International Conference on Cluster Computing (CLUSTER): 1–10. doi:10.1109/CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite». Tsinghua Space Center, Tsinghua University, Beijing. Archived from the original on 2011-10-02. Retrieved 2009-02-16.
- ^ Jeff Layton. «Error Detection and Correction». Linux Magazine. Retrieved 2014-08-12.
- ^ «EDAC Project». bluesmoke.sourceforge.net. Retrieved 2014-08-12.
- ^ «Documentation/edac.txt». Linux kernel documentation. kernel.org. 2014-06-16. Archived from the original on 2009-09-05. Retrieved 2014-08-12.
Further reading[edit]
- Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
- SoftECC: A System for Software Memory Integrity Checking
- A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
- Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing
External links[edit]
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
- ECC Page — implementations of popular ECC encoding and decoding routines

To clean up transmission errors introduced by Earth’s atmosphere (left), Goddard scientists applied Reed–Solomon error correction (right), which is commonly used in CDs and DVDs. Typical errors include missing pixels (white) and false signals (black). The white stripe indicates a brief period when transmission was interrupted.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
Definitions[edit]
Error detection is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver.
Error correction is the detection of errors and reconstruction of the original, error-free data.
History[edit]
In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever written in stichs, the copyists, in order to estimate the amount of work, had to count the letters.[1] This also helped ensure accuracy in the transmission of the text with the production of subsequent copies.[2][3] Between the 7th and 10th centuries CE a group of Jewish scribes formalized and expanded this to create the Numerical Masorah to ensure accurate reproduction of the sacred text. It included counts of the number of words in a line, section, book and groups of books, noting the middle stich of a book, word use statistics, and commentary.[1] Standards became such that a deviation in even a single letter in a Torah scroll was considered unacceptable.[4] The effectiveness of their error correction method was verified by the accuracy of copying through the centuries demonstrated by discovery of the Dead Sea Scrolls in 1947–1956, dating from c.150 BCE-75 CE.[5]
The modern development of error correction codes is credited to Richard Hamming in 1947.[6] A description of Hamming’s code appeared in Claude Shannon’s A Mathematical Theory of Communication[7] and was quickly generalized by Marcel J. E. Golay.[8]
Introduction[edit]
All error-detection and correction schemes add some redundancy (i.e., some extra data) to a message, which receivers can use to check consistency of the delivered message, and to recover data that has been determined to be corrupted. Error-detection and correction schemes can be either systematic or non-systematic. In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its output with the received check bits; if the values do not match, an error has occurred at some point during the transmission. In a system that uses a non-systematic code, the original message is transformed into an encoded message carrying the same information and that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the communication channel. Common channel models include memoryless models where errors occur randomly and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently, error-detecting and correcting codes can be generally distinguished between random-error-detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of random errors and burst errors.
If the channel characteristics cannot be determined, or are highly variable, an error-detection scheme may be combined with a system for retransmissions of erroneous data. This is known as automatic repeat request (ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Types of error correction[edit]
There are three major types of error correction.[9]
Automatic repeat request[edit]
Automatic repeat request (ARQ) is an error control method for data transmission that makes use of error-detection codes, acknowledgment and/or negative acknowledgment messages, and timeouts to achieve reliable data transmission. An acknowledgment is a message sent by the receiver to indicate that it has correctly received a data frame.
Usually, when the transmitter does not receive the acknowledgment before the timeout occurs (i.e., within a reasonable amount of time after sending the data frame), it retransmits the frame until it is either correctly received or the error persists beyond a predetermined number of retransmissions.
Three types of ARQ protocols are Stop-and-wait ARQ, Go-Back-N ARQ, and Selective Repeat ARQ.
ARQ is appropriate if the communication channel has varying or unknown capacity, such as is the case on the Internet. However, ARQ requires the availability of a back channel, results in possibly increased latency due to retransmissions, and requires the maintenance of buffers and timers for retransmissions, which in the case of network congestion can put a strain on the server and overall network capacity.[10]
For example, ARQ is used on shortwave radio data links in the form of ARQ-E, or combined with multiplexing as ARQ-M.
Forward error correction[edit]
Forward error correction (FEC) is a process of adding redundant data such as an error-correcting code (ECC) to a message so that it can be recovered by a receiver even when a number of errors (up to the capability of the code being used) are introduced, either during the process of transmission or on storage. Since the receiver does not have to ask the sender for retransmission of the data, a backchannel is not required in forward error correction. Error-correcting codes are used in lower-layer communication such as cellular network, high-speed fiber-optic communication and Wi-Fi,[11][12] as well as for reliable storage in media such as flash memory, hard disk and RAM.[13]
Error-correcting codes are usually distinguished between convolutional codes and block codes:
- Convolutional codes are processed on a bit-by-bit basis. They are particularly suitable for implementation in hardware, and the Viterbi decoder allows optimal decoding.
- Block codes are processed on a block-by-block basis. Early examples of block codes are repetition codes, Hamming codes and multidimensional parity-check codes. They were followed by a number of efficient codes, Reed–Solomon codes being the most notable due to their current widespread use. Turbo codes and low-density parity-check codes (LDPC) are relatively new constructions that can provide almost optimal efficiency.
Shannon’s theorem is an important theorem in forward error correction, and describes the maximum information rate at which reliable communication is possible over a channel that has a certain error probability or signal-to-noise ratio (SNR). This strict upper limit is expressed in terms of the channel capacity. More specifically, the theorem says that there exist codes such that with increasing encoding length the probability of error on a discrete memoryless channel can be made arbitrarily small, provided that the code rate is smaller than the channel capacity. The code rate is defined as the fraction k/n of k source symbols and n encoded symbols.
The actual maximum code rate allowed depends on the error-correcting code used, and may be lower. This is because Shannon’s proof was only of existential nature, and did not show how to construct codes which are both optimal and have efficient encoding and decoding algorithms.
Hybrid schemes[edit]
Hybrid ARQ is a combination of ARQ and forward error correction. There are two basic approaches:[10]
- Messages are always transmitted with FEC parity data (and error-detection redundancy). A receiver decodes a message using the parity information, and requests retransmission using ARQ only if the parity data was not sufficient for successful decoding (identified through a failed integrity check).
- Messages are transmitted without parity data (only with error-detection information). If a receiver detects an error, it requests FEC information from the transmitter using ARQ, and uses it to reconstruct the original message.
The latter approach is particularly attractive on an erasure channel when using a rateless erasure code.
Error detection schemes[edit]
Error detection is most commonly realized using a suitable hash function (or specifically, a checksum, cyclic redundancy check or other algorithm). A hash function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by recomputing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic redundancy check’s performance in detecting burst errors).
Minimum distance coding[edit]
A random-error-correcting code based on minimum distance coding can provide a strict guarantee on the number of detectable errors, but it may not protect against a preimage attack.
Repetition codes[edit]
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free communication. Given a stream of data to be transmitted, the data are divided into blocks of bits. Each block is transmitted some predetermined number of times. For example, to send the bit pattern «1011», the four-bit block can be repeated three times, thus producing «1011 1011 1011». If this twelve-bit pattern was received as «1010 1011 1011» – where the first block is unlike the other two – an error has occurred.
A repetition code is very inefficient, and can be susceptible to problems if the error occurs in exactly the same place for each group (e.g., «1010 1010 1010» in the previous example would be detected as correct). The advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of numbers stations.[14][15]
Parity bit[edit]
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the parity bit appear correct even though the data is erroneous.
Parity bits added to each «word» sent are called transverse redundancy checks, while those added at the end of a stream of «words» are called longitudinal redundancy checks. For example, if each of a series of m-bit «words» has a parity bit added, showing whether there were an odd or even number of ones in that word, any word with a single error in it will be detected. It will not be known where in the word the error is, however. If, in addition, after each stream of n words a parity sum is sent, each bit of which shows whether there were an odd or even number of ones at that bit-position sent in the most recent group, the exact position of the error can be determined and the error corrected. This method is only guaranteed to be effective, however, if there are no more than 1 error in every group of n words. With more error correction bits, more errors can be detected and in some cases corrected.
There are also other bit-grouping techniques.
Checksum[edit]
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g., byte values). The sum may be negated by means of a ones’-complement operation prior to transmission to detect unintentional all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum schemes, such as the Damm algorithm, the Luhn algorithm, and the Verhoeff algorithm, are specifically designed to detect errors commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy check[edit]
A cyclic redundancy check (CRC) is a non-secure hash function designed to detect accidental changes to digital data in computer networks. It is not suitable for detecting maliciously introduced errors. It is characterized by specification of a generator polynomial, which is used as the divisor in a polynomial long division over a finite field, taking the input data as the dividend. The remainder becomes the result.
A CRC has properties that make it well suited for detecting burst errors. CRCs are particularly easy to implement in hardware and are therefore commonly used in computer networks and storage devices such as hard disk drives.
The parity bit can be seen as a special-case 1-bit CRC.
Cryptographic hash function[edit]
The output of a cryptographic hash function, also known as a message digest, can provide strong assurances about data integrity, whether changes of the data are accidental (e.g., due to transmission errors) or maliciously introduced. Any modification to the data will likely be detected through a mismatching hash value. Furthermore, given some hash value, it is typically infeasible to find some input data (other than the one given) that will yield the same hash value. If an attacker can change not only the message but also the hash value, then a keyed hash or message authentication code (MAC) can be used for additional security. Without knowing the key, it is not possible for the attacker to easily or conveniently calculate the correct keyed hash value for a modified message.
Error correction code[edit]
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can detect up to d − 1 errors in a code word. Using minimum-distance-based error-correcting codes for error detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d = 2 are degenerate cases of error-correcting codes, and can be used to detect single errors. The parity bit is an example of a single-error-detecting code.
Applications[edit]
Applications that require low latency (such as telephone conversations) cannot use automatic repeat request (ARQ); they must use forward error correction (FEC). By the time an ARQ system discovers an error and re-transmits it, the re-sent data will arrive too late to be usable.
Applications where the transmitter immediately forgets the information as soon as it is sent (such as most television cameras) cannot use ARQ; they must use FEC because when an error occurs, the original data is no longer available.
Applications that use ARQ must have a return channel; applications having no return channel cannot use ARQ.
Applications that require extremely low error rates (such as digital money transfers) must use ARQ due to the possibility of uncorrectable errors with FEC.
Reliability and inspection engineering also make use of the theory of error-correcting codes.[16]
Internet[edit]
In a typical TCP/IP stack, error control is performed at multiple levels:
- Each Ethernet frame uses CRC-32 error detection. Frames with detected errors are discarded by the receiver hardware.
- The IPv4 header contains a checksum protecting the contents of the header. Packets with incorrect checksums are dropped within the network or at the receiver.
- The checksum was omitted from the IPv6 header in order to minimize processing costs in network routing and because current link layer technology is assumed to provide sufficient error detection (see also RFC 3819).
- UDP has an optional checksum covering the payload and addressing information in the UDP and IP headers. Packets with incorrect checksums are discarded by the network stack. The checksum is optional under IPv4, and required under IPv6. When omitted, it is assumed the data-link layer provides the desired level of error protection.
- TCP provides a checksum for protecting the payload and addressing information in the TCP and IP headers. Packets with incorrect checksums are discarded by the network stack, and eventually get retransmitted using ARQ, either explicitly (such as through three-way handshake) or implicitly due to a timeout.
Deep-space telecommunications[edit]
The development of error-correction codes was tightly coupled with the history of deep-space missions due to the extreme dilution of signal power over interplanetary distances, and the limited power availability aboard space probes. Whereas early missions sent their data uncoded, starting in 1968, digital error correction was implemented in the form of (sub-optimally decoded) convolutional codes and Reed–Muller codes.[17] The Reed–Muller code was well suited to the noise the spacecraft was subject to (approximately matching a bell curve), and was implemented for the Mariner spacecraft and used on missions between 1969 and 1977.
The Voyager 1 and Voyager 2 missions, which started in 1977, were designed to deliver color imaging and scientific information from Jupiter and Saturn.[18] This resulted in increased coding requirements, and thus, the spacecraft were supported by (optimally Viterbi-decoded) convolutional codes that could be concatenated with an outer Golay (24,12,8) code. The Voyager 2 craft additionally supported an implementation of a Reed–Solomon code. The concatenated Reed–Solomon–Viterbi (RSV) code allowed for very powerful error correction, and enabled the spacecraft’s extended journey to Uranus and Neptune. After ECC system upgrades in 1989, both crafts used V2 RSV coding.
The Consultative Committee for Space Data Systems currently recommends usage of error correction codes with performance similar to the Voyager 2 RSV code as a minimum. Concatenated codes are increasingly falling out of favor with space missions, and are replaced by more powerful codes such as Turbo codes or LDPC codes.
The different kinds of deep space and orbital missions that are conducted suggest that trying to find a one-size-fits-all error correction system will be an ongoing problem. For missions close to Earth, the nature of the noise in the communication channel is different from that which a spacecraft on an interplanetary mission experiences. Additionally, as a spacecraft increases its distance from Earth, the problem of correcting for noise becomes more difficult.
Satellite broadcasting[edit]
The demand for satellite transponder bandwidth continues to grow, fueled by the desire to deliver television (including new channels and high-definition television) and IP data. Transponder availability and bandwidth constraints have limited this growth. Transponder capacity is determined by the selected modulation scheme and the proportion of capacity consumed by FEC.
Data storage[edit]
Error detection and correction codes are often used to improve the reliability of data storage media.[19] A parity track capable of detecting single-bit errors was present on the first magnetic tape data storage in 1951. The optimal rectangular code used in group coded recording tapes not only detects but also corrects single-bit errors. Some file formats, particularly archive formats, include a checksum (most often CRC32) to detect corruption and truncation and can employ redundancy or parity files to recover portions of corrupted data. Reed-Solomon codes are used in compact discs to correct errors caused by scratches.
Modern hard drives use Reed–Solomon codes to detect and correct minor errors in sector reads, and to recover corrupted data from failing sectors and store that data in the spare sectors.[20] RAID systems use a variety of error correction techniques to recover data when a hard drive completely fails. Filesystems such as ZFS or Btrfs, as well as some RAID implementations, support data scrubbing and resilvering, which allows bad blocks to be detected and (hopefully) recovered before they are used.[21] The recovered data may be re-written to exactly the same physical location, to spare blocks elsewhere on the same piece of hardware, or the data may be rewritten onto replacement hardware.
Error-correcting memory[edit]
Dynamic random-access memory (DRAM) may provide stronger protection against soft errors by relying on error-correcting codes. Such error-correcting memory, known as ECC or EDAC-protected memory, is particularly desirable for mission-critical applications, such as scientific computing, financial, medical, etc. as well as extraterrestrial applications due to the increased radiation in space.
Error-correcting memory controllers traditionally use Hamming codes, although some use triple modular redundancy. Interleaving allows distributing the effect of a single cosmic ray potentially upsetting multiple physically neighboring bits across multiple words by associating neighboring bits to different words. As long as a single-event upset (SEU) does not exceed the error threshold (e.g., a single error) in any particular word between accesses, it can be corrected (e.g., by a single-bit error-correcting code), and the illusion of an error-free memory system may be maintained.[22]
In addition to hardware providing features required for ECC memory to operate, operating systems usually contain related reporting facilities that are used to provide notifications when soft errors are transparently recovered. One example is the Linux kernel’s EDAC subsystem (previously known as Bluesmoke), which collects the data from error-checking-enabled components inside a computer system; besides collecting and reporting back the events related to ECC memory, it also supports other checksumming errors, including those detected on the PCI bus.[23][24][25] A few systems[specify] also support memory scrubbing to catch and correct errors early before they become unrecoverable.
See also[edit]
- Berger code
- Burst error-correcting code
- ECC memory, a type of computer data storage
- Link adaptation
- List of algorithms § Error detection and correction
- List of hash functions
References[edit]
- ^ a b «Masorah». Jewish Encyclopedia.
- ^ Pratico, Gary D.; Pelt, Miles V. Van (2009). Basics of Biblical Hebrew Grammar: Second Edition. Zondervan. ISBN 978-0-310-55882-8.
- ^ Mounce, William D. (2007). Greek for the Rest of Us: Using Greek Tools Without Mastering Biblical Languages. Zondervan. p. 289. ISBN 978-0-310-28289-1.
- ^ Mishneh Torah, Tefillin, Mezuzah, and Sefer Torah, 1:2. Example English translation: Eliyahu Touger. The Rambam’s Mishneh Torah. Moznaim Publishing Corporation.
- ^ Brian M. Fagan (5 December 1996). «Dead Sea Scrolls». The Oxford Companion to Archaeology. Oxford University Press. ISBN 0195076184.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, p. vii, ISBN 0-88385-023-0
- ^ Shannon, C.E. (1948), «A Mathematical Theory of Communication», Bell System Technical Journal, 27 (3): 379–423, doi:10.1002/j.1538-7305.1948.tb01338.x, hdl:10338.dmlcz/101429, PMID 9230594
- ^ Golay, Marcel J. E. (1949), «Notes on Digital Coding», Proc.I.R.E. (I.E.E.E.), 37: 657
- ^ Gupta, Vikas; Verma, Chanderkant (November 2012). «Error Detection and Correction: An Introduction». International Journal of Advanced Research in Computer Science and Software Engineering. 2 (11). S2CID 17499858.
- ^ a b A. J. McAuley, Reliable Broadband Communication Using a Burst Erasure Correcting Code, ACM SIGCOMM, 1990.
- ^ Shah, Pradeep M.; Vyavahare, Prakash D.; Jain, Anjana (September 2015). «Modern error correcting codes for 4G and beyond: Turbo codes and LDPC codes». 2015 Radio and Antenna Days of the Indian Ocean (RADIO): 1–2. doi:10.1109/RADIO.2015.7323369. ISBN 978-9-9903-7339-4. S2CID 28885076. Retrieved 22 May 2022.
- ^ «IEEE SA — IEEE 802.11ac-2013». IEEE Standards Association.
- ^ «Transition to Advanced Format 4K Sector Hard Drives | Seagate US». Seagate.com. Retrieved 22 May 2022.
- ^ Frank van Gerwen. «Numbers (and other mysterious) stations». Archived from the original on 12 July 2017. Retrieved 12 March 2012.
- ^ Gary Cutlack (25 August 2010). «Mysterious Russian ‘Numbers Station’ Changes Broadcast After 20 Years». Gizmodo. Retrieved 12 March 2012.
- ^ Ben-Gal I.; Herer Y.; Raz T. (2003). «Self-correcting inspection procedure under inspection errors» (PDF). IIE Transactions. IIE Transactions on Quality and Reliability, 34(6), pp. 529-540. Archived from the original (PDF) on 2013-10-13. Retrieved 2014-01-10.
- ^ K. Andrews et al., The Development of Turbo and LDPC Codes for Deep-Space Applications, Proceedings of the IEEE, Vol. 95, No. 11, Nov. 2007.
- ^ Huffman, William Cary; Pless, Vera S. (2003). Fundamentals of Error-Correcting Codes. Cambridge University Press. ISBN 978-0-521-78280-7.
- ^ Kurtas, Erozan M.; Vasic, Bane (2018-10-03). Advanced Error Control Techniques for Data Storage Systems. CRC Press. ISBN 978-1-4200-3649-7.[permanent dead link]
- ^ Scott A. Moulton. «My Hard Drive Died». Archived from the original on 2008-02-02.
- ^ Qiao, Zhi; Fu, Song; Chen, Hsing-Bung; Settlemyer, Bradley (2019). «Building Reliable High-Performance Storage Systems: An Empirical and Analytical Study». 2019 IEEE International Conference on Cluster Computing (CLUSTER): 1–10. doi:10.1109/CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite». Tsinghua Space Center, Tsinghua University, Beijing. Archived from the original on 2011-10-02. Retrieved 2009-02-16.
- ^ Jeff Layton. «Error Detection and Correction». Linux Magazine. Retrieved 2014-08-12.
- ^ «EDAC Project». bluesmoke.sourceforge.net. Retrieved 2014-08-12.
- ^ «Documentation/edac.txt». Linux kernel documentation. kernel.org. 2014-06-16. Archived from the original on 2009-09-05. Retrieved 2014-08-12.
Further reading[edit]
- Shu Lin; Daniel J. Costello, Jr. (1983). Error Control Coding: Fundamentals and Applications. Prentice Hall. ISBN 0-13-283796-X.
- SoftECC: A System for Software Memory Integrity Checking
- A Tunable, Software-based DRAM Error Detection and Correction Library for HPC
- Detection and Correction of Silent Data Corruption for Large-Scale High-Performance Computing
External links[edit]
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, contains chapters on elementary error-correcting codes; on the theoretical limits of error-correction; and on the latest state-of-the-art error-correcting codes, including low-density parity-check codes, turbo codes, and fountain codes.
- ECC Page — implementations of popular ECC encoding and decoding routines
Аннотация: Контроль по четности, CRC, алгоритм Хэмминга. Введение в коды Рида-Соломона: принципы, архитектура и реализация. Метод коррекции ошибок FEC (Forward Error Correction).
Каналы передачи данных ненадежны (шумы, наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных ( М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок ( BER – Bit Error Rate) равна р = 10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p)8 = 7,9 х 10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p)8. Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p)9 – 9p(1 – p)8 = 3,6 x 10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как
для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
В Ethernet вычисление CRC производится аппаратно. На
рис.
4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x2 + x3 + x5 + x7. В этой схеме входной код приходит слева.
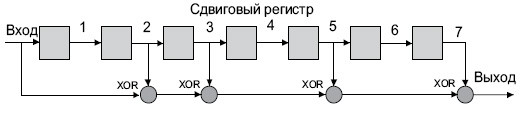
Рис.
4.1.
Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r — степень образующего полинома.
Таблица
4.1.
| CRC -12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC -16 | x16 + x15 + x2 + 1 |
| CRC -CCITT | x16 + x12 + x5 + 1 |
4.1. Алгоритмы коррекции ошибок
Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещеных процесса: обнаружение ошибки и определение места (идентификации сообщения и позиции в сообщении). После решения этих двух задач исправление тривиально — надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7), используемыми при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7 + 4 = 11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние Хэмминга 4):
00000000
11110000
00001111
11111111
При получении кода 00000111 нетрудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга.
Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7). Таблица 4.2.
Таблица
4.2.
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | * | 0 | 0 | 1 | * | 1 | * | * |
Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XoR (исключающее ИЛИ) над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 05= | 0101 |
| 03= | 0011 |
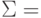 |
1110 |
Таким образом, приемник получит код
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Просуммируем снова коды позиций ненулевых битов и получим нуль;
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 08= | 1000 |
| 05= | 0101 |
| 04= | 0100 |
| 03= | 0011 |
| 02= | 0010 |
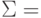 |
0000 |
Ну а теперь рассмотрим два случая ошибок в одном из битов посылки, например в бите 7 (1 вместо 0) и в бите 5 (0 вместо 1). Просуммируем коды позиций ненулевых битов еще раз:
В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме. Понятно, что если ошибка произойдет при передаче более чем одного бита, код Хэмминга при данной избыточности окажется бесполезен.
В общем случае код имеет N = M + C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М = 4, а N = 7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:
С1 = М1 + М2 + М4 С2 = М1 + М3 + М4 С3 = М2 + М3 + М4
Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):
С11 = С1 + М4 + М2 + М1 С12 = С2 + М4 + М3 + М1 С13 = С3 + М4 + М3 + М2
Результат вычисления интерпретируется следующим образом:
Таблица
4.4.
| C11 | C12 | C13 | Значение |
|---|---|---|---|
| 1 | 2 | 4 | Позиция бит |
| 0 | 0 | 0 | Ошибок нет |
| 0 | 0 | 1 | Бит С3 неверен |
| 0 | 1 | 0 | Бит С2 неверен |
| 0 | 1 | 1 | Бит M3 неверен |
| 1 | 0 | 0 | Бит С1 неверен |
| 1 | 0 | 1 | Бит M2 неверен |
| 1 | 1 | 0 | Бит M1 неверен |
| 1 | 1 | 1 | Бит M4 неверен |
Описанная схема легко переносится на любое число n и М.
Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N — число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга ) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более qm.
В теории кодирования существуют следующие оценки максимального числа N n -разрядных кодов с расстоянием D.
| d=1 | n=2n |
| d=2 | n=2n-1 |
| d=3 | N 2n/(1 + n) |
| d = 2q + 1 | (для кода Хэмминга это неравенство превращается в равенство) |
В случае кода Хэмминга первые k разрядов используются в качестве информационных, причем
K = n – log(n + 1), откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.
Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-hocquenghem). Эти коды имеют широкий выбор длин и возможностей исправления ошибок.
Одной из старейших схем коррекции ошибок является двух-и трехмерная позиционная схема (
рис.
4.2). Для каждого байта вычисляется бит четности (бит <Ч>, направление Х). Для каждого столбца также вычисляется бит четности (направление Y. Производится вычисление битов четности для комбинаций битов с координатами (X,Y) (направление Z, слои с 1 до N ). Если при транспортировке будет искажен один бит, он может быть найден и исправлен по неверным битам четности X и Y. Если же произошло две ошибки в одной из плоскостей, битов четности данной плоскости недостаточно. Здесь поможет плоскость битов четности N+1.
Таким образом, на 512 передаваемых байтов данных пересылается около 200 бит четности.
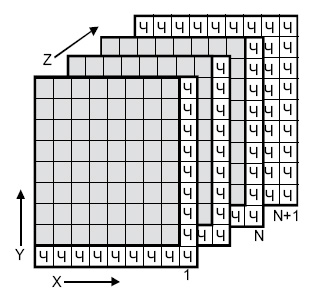
Рис.
4.2.
Позиционная схема коррекции ошибок
Корректирующие коды «на пальцах»
Время на прочтение
11 мин
Количество просмотров 63K
 Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.
Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.
Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
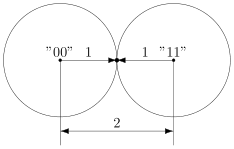
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
Методы, обеспечивающие надежную доставку цифровых данных по ненадежным каналам связи  Устранение ошибок передачи, вызванных атмосферой Земли ( слева), ученые Годдарда применили исправление ошибок Рида – Соломона (справа), которое обычно используется в компакт-дисках и DVD. Типичные ошибки включают отсутствие пикселей (белые) и ложные сигналы (черные). Белая полоса указывает на короткий период, когда передача была приостановлена.
Устранение ошибок передачи, вызванных атмосферой Земли ( слева), ученые Годдарда применили исправление ошибок Рида – Соломона (справа), которое обычно используется в компакт-дисках и DVD. Типичные ошибки включают отсутствие пикселей (белые) и ложные сигналы (черные). Белая полоса указывает на короткий период, когда передача была приостановлена.
В теории информации и теории кодирования с приложениями в информатике и телекоммуникациях, обнаружение и исправление ошибок или контроль ошибок — это методы, которые обеспечивают надежную доставку цифровых данных по ненадежным каналам связи. Многие каналы связи подвержены канальному шуму, и поэтому во время передачи от источника к приемнику могут возникать ошибки. Методы обнаружения ошибок позволяют обнаруживать такие ошибки, а исправление ошибок во многих случаях позволяет восстановить исходные данные.
Содержание
- 1 Определения
- 2 История
- 3 Введение
- 4 Типы исправления ошибок
- 4.1 Автоматический повторный запрос (ARQ)
- 4.2 Прямое исправление ошибок
- 4.3 Гибридные схемы
- 5 Схемы обнаружения ошибок
- 5.1 Кодирование на минимальном расстоянии
- 5.2 Коды повторения
- 5.3 Бит четности
- 5.4 Контрольная сумма
- 5.5 Циклическая проверка избыточности
- 5.6 Криптографическая хеш-функция
- 5.7 Ошибка код исправления
- 6 Приложения
- 6.1 Интернет
- 6.2 Связь в дальнем космосе
- 6.3 Спутниковое вещание
- 6.4 Хранение данных
- 6.5 Память с исправлением ошибок
- 7 См. также
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Определения
Обнаружение ошибок — это обнаружение ошибок, вызванных шумом или другими помехами во время передачи от передатчика к приемнику. Исправление ошибок — это обнаружение ошибок и восстановление исходных безошибочных данных.
История
Современная разработка кодов исправления ошибок приписывается Ричарду Хэммингу в 1947 году. Описание кода Хэмминга появилось в Математической теории коммуникации Клода Шеннона и было быстро обобщено Марселем Дж. Э. Голэем.
Введение
Все схемы обнаружения и исправления ошибок добавляют некоторые избыточность (т. е. некоторые дополнительные данные) сообщения, которые получатели могут использовать для проверки согласованности доставленного сообщения и для восстановления данных, которые были определены как поврежденные. Схемы обнаружения и исправления ошибок могут быть систематическими или несистематическими. В систематической схеме передатчик отправляет исходные данные и присоединяет фиксированное количество контрольных битов (или данных четности), которые выводятся из битов данных некоторым детерминированным алгоритмом. Если требуется только обнаружение ошибок, приемник может просто применить тот же алгоритм к полученным битам данных и сравнить свой вывод с полученными контрольными битами; если значения не совпадают, в какой-то момент во время передачи произошла ошибка. В системе, которая использует несистематический код, исходное сообщение преобразуется в закодированное сообщение, несущее ту же информацию и имеющее по крайней мере такое же количество битов, как и исходное сообщение.
Хорошие характеристики контроля ошибок требуют, чтобы схема была выбрана на основе характеристик канала связи. Распространенные модели каналов включают в себя модели без памяти, в которых ошибки возникают случайно и с определенной вероятностью, и динамические модели, в которых ошибки возникают в основном в пакетах . Следовательно, коды обнаружения и исправления ошибок можно в целом различать между обнаружением / исправлением случайных ошибок и обнаружением / исправлением пакетов ошибок. Некоторые коды также могут подходить для сочетания случайных ошибок и пакетных ошибок.
Если характеристики канала не могут быть определены или сильно изменяются, схема обнаружения ошибок может быть объединена с системой для повторных передач ошибочных данных. Это известно как автоматический запрос на повторение (ARQ) и наиболее широко используется в Интернете. Альтернативный подход для контроля ошибок — это гибридный автоматический запрос на повторение (HARQ), который представляет собой комбинацию ARQ и кодирования с исправлением ошибок.
Типы исправления ошибок
Существует три основных типа исправления ошибок.
Автоматический повторный запрос (ARQ)
Автоматический повторный запрос (ARQ) — это метод контроля ошибок для передачи данных, который использует коды обнаружения ошибок, сообщения подтверждения и / или отрицательного подтверждения и тайм-ауты для обеспечения надежной передачи данных. Подтверждение — это сообщение, отправленное получателем, чтобы указать, что он правильно получил кадр данных.
Обычно, когда передатчик не получает подтверждения до истечения тайм-аута (т. Е. В течение разумного периода времени после отправки фрейм данных), он повторно передает фрейм до тех пор, пока он либо не будет правильно принят, либо пока ошибка не останется сверх заранее определенного количества повторных передач.
Три типа протоколов ARQ: Stop-and-wait ARQ, Go-Back-N ARQ и Selective Repeat ARQ.
ARQ is подходит, если канал связи имеет переменную или неизвестную пропускную способность, например, в случае с Интернетом. Однако ARQ требует наличия обратного канала, что приводит к возможному увеличению задержки из-за повторных передач и требует обслуживания буферов и таймеров для повторных передач, что в случае перегрузка сети может вызвать нагрузку на сервер и общую пропускную способность сети.
Например, ARQ используется на коротковолновых радиоканалах в форме ARQ-E, или в сочетании с мультиплексированием как ARQ-M.
Прямое исправление ошибок
Прямое исправление ошибок (FEC) — это процесс добавления избыточных данных, таких как исправление ошибок code (ECC) в сообщение, чтобы оно могло быть восстановлено получателем, даже если в процессе передачи или при хранении был внесен ряд ошибок (в зависимости от возможностей используемого кода). Так как получатель не должен запрашивать у отправителя повторную передачу данных, обратный канал не требуется при прямом исправлении ошибок, и поэтому он подходит для симплексной связи, например вещание. Коды с исправлением ошибок часто используются в нижнем уровне связи, а также для надежного хранения на таких носителях, как CD, DVD, жесткие диски и RAM.
Коды с исправлением ошибок обычно различают между сверточными кодами и блочными кодами. :
- Сверточные коды обрабатываются побитно. Они особенно подходят для аппаратной реализации, а декодер Витерби обеспечивает оптимальное декодирование.
- Блочные коды обрабатываются на поблочной основе. Ранними примерами блочных кодов являются коды повторения, коды Хэмминга и многомерные коды контроля четности. За ними последовал ряд эффективных кодов, из которых коды Рида – Соломона являются наиболее известными из-за их широкого распространения в настоящее время. Турбокоды и коды с низкой плотностью проверки четности (LDPC) — это относительно новые конструкции, которые могут обеспечить почти оптимальную эффективность.
Теорема Шеннона — важная теорема при прямом исправлении ошибок и описывает максимальную информационную скорость, на которой возможна надежная связь по каналу, имеющему определенную вероятность ошибки или отношение сигнал / шум (SNR). Этот строгий верхний предел выражается в единицах пропускной способности канала . Более конкретно, в теореме говорится, что существуют такие коды, что с увеличением длины кодирования вероятность ошибки на дискретном канале без памяти может быть сделана сколь угодно малой при условии, что кодовая скорость меньше чем емкость канала. Кодовая скорость определяется как доля k / n из k исходных символов и n кодированных символов.
Фактическая максимальная разрешенная кодовая скорость зависит от используемого кода исправления ошибок и может быть ниже. Это связано с тем, что доказательство Шеннона носило только экзистенциальный характер и не показало, как создавать коды, которые одновременно являются оптимальными и имеют эффективные алгоритмы кодирования и декодирования.
Гибридные схемы
Гибридный ARQ — это комбинация ARQ и прямого исправления ошибок. Существует два основных подхода:
- Сообщения всегда передаются с данными четности FEC (и избыточностью для обнаружения ошибок). Получатель декодирует сообщение, используя информацию о четности, и запрашивает повторную передачу с использованием ARQ только в том случае, если данных четности было недостаточно для успешного декодирования (идентифицировано посредством неудачной проверки целостности).
- Сообщения передаются без данных четности (только с информация об обнаружении ошибок). Если приемник обнаруживает ошибку, он запрашивает информацию FEC от передатчика с помощью ARQ и использует ее для восстановления исходного сообщения.
Последний подход особенно привлекателен для канала стирания при использовании код бесскоростного стирания.
.
Схемы обнаружения ошибок
Обнаружение ошибок чаще всего реализуется с использованием подходящей хэш-функции (или, в частности, контрольной суммы, циклической проверка избыточности или другой алгоритм). Хеш-функция добавляет к сообщению тег фиксированной длины, который позволяет получателям проверять доставленное сообщение, повторно вычисляя тег и сравнивая его с предоставленным.
Существует огромное количество различных конструкций хеш-функций. Однако некоторые из них имеют особенно широкое распространение из-за их простоты или их пригодности для обнаружения определенных видов ошибок (например, производительности циклического контроля избыточности при обнаружении пакетных ошибок ).
Кодирование с минимальным расстоянием
Код с исправлением случайных ошибок на основе кодирования с минимальным расстоянием может обеспечить строгую гарантию количества обнаруживаемых ошибок, но может не защитить против атаки прообразом.
Коды повторения
A код повторения — это схема кодирования, которая повторяет биты по каналу для достижения безошибочной связи. Учитывая поток данных, которые необходимо передать, данные делятся на блоки битов. Каждый блок передается определенное количество раз. Например, чтобы отправить битовую комбинацию «1011», четырехбитовый блок можно повторить три раза, таким образом получая «1011 1011 1011». Если этот двенадцатибитовый шаблон был получен как «1010 1011 1011» — где первый блок не похож на два других, — произошла ошибка.
Код повторения очень неэффективен и может быть подвержен проблемам, если ошибка возникает в одном и том же месте для каждой группы (например, «1010 1010 1010» в предыдущем примере будет определено как правильное). Преимущество кодов повторения состоит в том, что они чрезвычайно просты и фактически используются в некоторых передачах номеров станций.
Бит четности
Бит четности — это бит, который добавляется к группе исходные биты, чтобы гарантировать, что количество установленных битов (т. е. битов со значением 1) в результате будет четным или нечетным. Это очень простая схема, которую можно использовать для обнаружения одного или любого другого нечетного числа (т. Е. Трех, пяти и т. Д.) Ошибок в выводе. Четное количество перевернутых битов сделает бит четности правильным, даже если данные ошибочны.
Расширениями и вариантами механизма битов четности являются проверки с продольным избыточным кодом, проверки с поперечным избыточным кодом и аналогичные методы группирования битов.
Контрольная сумма
Контрольная сумма сообщения — это модульная арифметическая сумма кодовых слов сообщения фиксированной длины слова (например, байтовых значений). Сумма может быть инвертирована посредством операции дополнения до единиц перед передачей для обнаружения непреднамеренных сообщений с нулевым значением.
Схемы контрольных сумм включают биты четности, контрольные цифры и проверки продольным избыточным кодом. Некоторые схемы контрольных сумм, такие как алгоритм Дамма, алгоритм Луна и алгоритм Верхоффа, специально разработаны для обнаружения ошибок, обычно вносимых людьми при записи или запоминание идентификационных номеров.
Проверка циклическим избыточным кодом
Проверка циклическим избыточным кодом (CRC) — это незащищенная хэш-функция, предназначенная для обнаружения случайных изменений цифровых данных в компьютерных сетях. Он не подходит для обнаружения злонамеренно внесенных ошибок. Он характеризуется указанием порождающего полинома, который используется в качестве делителя в полиномиальном делении над конечным полем, принимая входные данные в качестве дивиденд. остаток становится результатом.
CRC имеет свойства, которые делают его хорошо подходящим для обнаружения пакетных ошибок. CRC особенно легко реализовать на оборудовании и поэтому обычно используются в компьютерных сетях и устройствах хранения, таких как жесткие диски.
. Бит четности может рассматриваться как 1-битный частный случай. CRC.
Криптографическая хеш-функция
Выходные данные криптографической хеш-функции, также известные как дайджест сообщения, могут обеспечить надежную гарантию целостности данных, независимо от того, происходят ли изменения данных случайно (например, из-за ошибок передачи) или злонамеренно. Любая модификация данных, скорее всего, будет обнаружена по несоответствию хеш-значения. Кроме того, с учетом некоторого хэш-значения, как правило, невозможно найти некоторые входные данные (кроме заданных), которые дадут такое же хеш-значение. Если злоумышленник может изменить не только сообщение, но и значение хеш-функции, то для дополнительной безопасности можно использовать хэш-код с ключом или код аутентификации сообщения (MAC). Не зная ключа, злоумышленник не может легко или удобно вычислить правильное ключевое значение хеш-функции для измененного сообщения.
Код исправления ошибок
Для обнаружения ошибок можно использовать любой код исправления ошибок. Код с минимальным расстоянием Хэмминга, d, может обнаруживать до d — 1 ошибок в кодовом слове. Использование кодов с коррекцией ошибок на основе минимального расстояния для обнаружения ошибок может быть подходящим, если требуется строгое ограничение на минимальное количество обнаруживаемых ошибок.
Коды с минимальным расстоянием Хэмминга d = 2 являются вырожденными случаями кодов с исправлением ошибок и могут использоваться для обнаружения одиночных ошибок. Бит четности является примером кода обнаружения одиночной ошибки.
Приложения
Приложения, которым требуется низкая задержка (например, телефонные разговоры), не могут использовать автоматический запрос на повторение (ARQ); они должны использовать прямое исправление ошибок (FEC). К тому времени, когда система ARQ обнаружит ошибку и повторно передаст ее, повторно отправленные данные прибудут слишком поздно, чтобы их можно было использовать.
Приложения, в которых передатчик сразу же забывает информацию, как только она отправляется (например, большинство телекамер), не могут использовать ARQ; они должны использовать FEC, потому что при возникновении ошибки исходные данные больше не доступны.
Приложения, использующие ARQ, должны иметь канал возврата ; приложения, не имеющие обратного канала, не могут использовать ARQ.
Приложения, требующие чрезвычайно низкого уровня ошибок (например, цифровые денежные переводы), должны использовать ARQ из-за возможности неисправимых ошибок с помощью FEC.
Надежность и инженерная проверка также используют теорию кодов исправления ошибок.
Интернет
В типичном стеке TCP / IP ошибка управление осуществляется на нескольких уровнях:
- Каждый кадр Ethernet использует CRC-32 обнаружение ошибок. Фреймы с обнаруженными ошибками отбрасываются оборудованием приемника.
- Заголовок IPv4 содержит контрольную сумму , защищающую содержимое заголовка. Пакеты с неверными контрольными суммами отбрасываются в сети или на приемнике.
- Контрольная сумма не указана в заголовке IPv6, чтобы минимизировать затраты на обработку в сетевой маршрутизации и поскольку предполагается, что текущая технология канального уровня обеспечивает достаточное обнаружение ошибок (см. также RFC 3819 ).
- UDP, имеет дополнительную контрольную сумму, покрывающую полезную нагрузку и информацию об адресации в заголовки UDP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком . Контрольная сумма не является обязательной для IPv4 и требуется для IPv6. Если не указано, предполагается, что уровень канала передачи данных обеспечивает желаемый уровень защиты от ошибок.
- TCP обеспечивает контрольную сумму для защиты полезной нагрузки и адресной информации в заголовках TCP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком и в конечном итоге повторно передаются с использованием ARQ либо явно (например, как через тройное подтверждение ) или неявно из-за тайм-аута .
Телекоммуникации в дальнем космосе
Разработка кодов исправления ошибок была тесно связана с историей полетов в дальний космос из-за сильного ослабления мощности сигнала на межпланетных расстояниях и ограниченной мощности на борту космических зондов. В то время как ранние миссии отправляли свои данные в незашифрованном виде, начиная с 1968 года, цифровая коррекция ошибок была реализована в форме (субоптимально декодированных) сверточных кодов и кодов Рида – Маллера. Код Рида-Мюллера хорошо подходил к шуму, которому подвергался космический корабль (примерно соответствуя кривой ), и был реализован для космического корабля Mariner и использовался в миссиях между 1969 и 1977 годами.
Миссии «Вояджер-1 » и «Вояджер-2 «, начатые в 1977 году, были разработаны для доставки цветных изображений и научной информации с Юпитера и Сатурна. Это привело к повышенным требованиям к кодированию, и, таким образом, космический аппарат поддерживался (оптимально Витерби-декодированный ) сверточными кодами, которые могли быть сцеплены с внешним Голеем (24,12,  код. Корабль «Вояджер-2» дополнительно поддерживал реализацию кода Рида-Соломона. Конкатенированный код Рида – Соломона – Витерби (RSV) позволил произвести очень мощную коррекцию ошибок и позволил космическому кораблю совершить длительное путешествие к Урану и Нептуну. После модернизации системы ECC в 1989 году оба корабля использовали кодирование V2 RSV.
код. Корабль «Вояджер-2» дополнительно поддерживал реализацию кода Рида-Соломона. Конкатенированный код Рида – Соломона – Витерби (RSV) позволил произвести очень мощную коррекцию ошибок и позволил космическому кораблю совершить длительное путешествие к Урану и Нептуну. После модернизации системы ECC в 1989 году оба корабля использовали кодирование V2 RSV.
Консультативный комитет по космическим информационным системам в настоящее время рекомендует использовать коды исправления ошибок, как минимум, аналогичные RSV-коду Voyager 2. Составные коды все больше теряют популярность в космических миссиях и заменяются более мощными кодами, такими как Турбо-коды или LDPC-коды.
Различные виды выполняемых космических и орбитальных миссий. предполагают, что попытки найти универсальную систему исправления ошибок будут постоянной проблемой. Для полетов вблизи Земли характер шума в канале связи отличается от того, который испытывает космический корабль в межпланетной миссии. Кроме того, по мере того как космический корабль удаляется от Земли, проблема коррекции шума становится все более сложной.
Спутниковое вещание
Спрос на пропускную способность спутникового транспондера продолжает расти, чему способствует желание предоставлять телевидение (включая новые каналы и телевидение высокой четкости ) и данные IP. Доступность транспондеров и ограничения полосы пропускания ограничили этот рост. Емкость транспондера определяется выбранной схемой модуляции и долей мощности, потребляемой FEC.
Хранение данных
Коды обнаружения и исправления ошибок часто используются для повышения надежности носителей данных. «Дорожка четности» присутствовала на первом устройстве хранения данных на магнитной ленте в 1951 году. «Оптимальный прямоугольный код», используемый в записи с групповым кодированием, не только обнаруживает, но и корректирует однобитовые записи. ошибки. Некоторые форматы файлов, особенно архивные форматы, включают контрольную сумму (чаще всего CRC32 ) для обнаружения повреждений и усечения и могут использовать избыточность и / или четность files для восстановления поврежденных данных. Коды Рида-Соломона используются в компакт-дисках для исправления ошибок, вызванных царапинами.
Современные жесткие диски используют коды CRC для обнаружения и коды Рида – Соломона для исправления незначительных ошибок при чтении секторов, а также для восстановления данных из секторов, которые «испортились», и сохранения этих данных в резервных секторах. Системы RAID используют различные методы исправления ошибок для исправления ошибок, когда жесткий диск полностью выходит из строя. Файловые системы, такие как ZFS или Btrfs, а также некоторые реализации RAID, поддерживают очистку данных и восстановление обновлений, что позволяет удалять поврежденные блоки. обнаружены и (надеюсь) восстановлены, прежде чем они будут использованы. Восстановленные данные могут быть перезаписаны точно в том же физическом месте, чтобы освободить блоки в другом месте на том же оборудовании, или данные могут быть перезаписаны на заменяющее оборудование.
Память с исправлением ошибок
Память DRAM может обеспечить более надежную защиту от программных ошибок, полагаясь на коды исправления ошибок. Такая память с исправлением ошибок, известная как память с защитой ECC или EDAC, особенно желательна для критически важных приложений, таких как научные вычисления, финансы, медицина и т. Д., А также для приложений дальнего космоса из-за повышенное излучение в космосе.
Контроллеры памяти с исправлением ошибок традиционно используют коды Хэмминга, хотя некоторые используют тройную модульную избыточность.
Чередование позволяет распределить эффект одного космического луча, потенциально нарушающего множество физически соседние биты в нескольких словах путем связывания соседних битов с разными словами. До тех пор, пока нарушение единичного события (SEU) не превышает пороговое значение ошибки (например, одиночная ошибка) в любом конкретном слове между доступами, оно может быть исправлено (например, путем исправления однобитовой ошибки code), и может сохраняться иллюзия безошибочной системы памяти.
Помимо оборудования, обеспечивающего функции, необходимые для работы памяти ECC, операционные системы обычно содержат соответствующие средства отчетности, которые используются для предоставления уведомлений при прозрачном восстановлении программных ошибок. Увеличение количества программных ошибок может указывать на то, что модуль DIMM нуждается в замене, и такая обратная связь не была бы легко доступна без соответствующих возможностей отчетности. Одним из примеров является подсистема EDAC ядра Linux (ранее известная как Bluesmoke), которая собирает данные из компонентов компьютерной системы, поддерживающих проверку ошибок; Помимо сбора и отправки отчетов о событиях, связанных с памятью ECC, он также поддерживает другие ошибки контрольного суммирования, в том числе обнаруженные на шине PCI.
Некоторые системы также поддерживают очистку памяти.
См. также
Ссылки
Дополнительная литература
- Шу Линь; Дэниел Дж. Костелло младший (1983). Кодирование с контролем ошибок: основы и приложения. Прентис Холл. ISBN 0-13-283796-X.
Внешние ссылки
Пусть — булевое множество. Рассмотрим и расстояние Хемминга . Пусть — разделяемый код постоянной длины. Обозначим .
Содержание
- 1 Коды, обнаруживающие и исправляющие ошибки
- 2 Булев шар
- 3 Определение и устранение ошибок в общем случае
- 4 Граница Хэмминга, граница Гильберта
- 5 См. также
Коды, обнаруживающие и исправляющие ошибки
| Определение: |
| Код обнаруживает ошибок, если . |
| Определение: |
| Код исправляет ошибок, если . |
| Утверждение: |
|
Код, исправляющий ошибок, обнаруживает ошибок. |
Булев шар
| Определение: |
| Булев шар — подмножество вида . называется его центром, — радиусом. Булев шар с центром и радиусом обознчается . |
| Определение: |
| Обьёмом шара в называется величина . Обьём шара радиуса в обозначается . |
| Утверждение: |
|
Обьём шара не зависит от его центра. |
|
Заметим, что шар всегда можно получить из другого шара с помощью «параллельного переноса» на вектор (здесь обозначает побитовый ), т.е. . |
Можно сформулировать свойство кодов, исправляющих ошибок, в терминах булевых шаров.
| Лемма: |
|
Пусть — код, исправляющий ошибок. |
| Доказательство: |
|
Т.к код исправляет ошибок, по определению . Допустим, такие, что и , т.е существует , такой что и . Тогда по неравенству треугольника . Это противоречит тому, что . |
Определение и устранение ошибок в общем случае
Пусть — исходный алфавит, — кодирование,
— расстояние Хэмминга между двумя кодами.
Код, может исправлять и обнаруживать ошибок. Действительно, при любом натуральном количестве допустимых ошибок любоое кодовое слово образует вокруг себя проколотый шар таких строк , что . Если этот шар не содержит других кодов (что выполняется при ) , то можно утверждать, что если в него попадает строка, то она ошибочна. Если шары всех кодов не пересекаются (что выполняется при ), то попавшую в шар строку можно считать ошибочной и исправить на центр шара — строку .

Граница Хэмминга, граница Гильберта
| Теорема (Граница Хэмминга): |
|
Пусть — код для -символьного алфавита, исправляющий ошибок. |
| Доказательство: |
|
Это прямое следствие предыдущей леммы. Их суммарный обьём равен , и он не может превосходить общее число возможных веткоров . |
Граница Хэмминга даёт верхнюю оценку на скорость передачи сообщений в канале с ошибками.
Прологарифмировав неравенство, получим .
Здесь это плотность кодирования, количество информации в одном символе алфавита на размер кода.
Таким образом, при кодировании с защитой от ошибок падает скорость передачи.
Аналогично составляется оценка в другую сторону.
| Теорема (Граница Гильберта): |
|
Если выполнено неравенство , то существует код для -символьного алфавита , исправляющий ошибок. |
Примером кода для случая является код Хэмминга.
См. также
- Избыточное кодирование, код Хэмминга
Пример
. Предположим, в канале связи под действием
помех произошло искажение и вместо
0100101 было принято 01001(1)1.
Решение:
Для обнаружения ошибки производят уже
знакомые нам проверки на четность.
Первая
проверка:
сумма П1+П3+П5+П7
= 0+0+1+1 четна.
В младший разряд номера ошибочной
позиции запишем 0.
Вторая
проверка:
сумма П2+П3+П6+П7
= 1+0+1+1 нечетна.
Во второй разряд номера ошибочной
позиции запишем 1
Третья
проверка:
сумма П4+П5+П6+П7
= 0+1+1+1 нечетна.
В третий разряд номера ошибочной позиции
запишем 1. Номер ошибочной позиции 110=
6. Следовательно,
символ шестой позиции следует изменить
на обратный, и получим правильную кодовую
комбинацию.
Код, исправляющий
одиночную и обнаруживающий двойную
ошибки
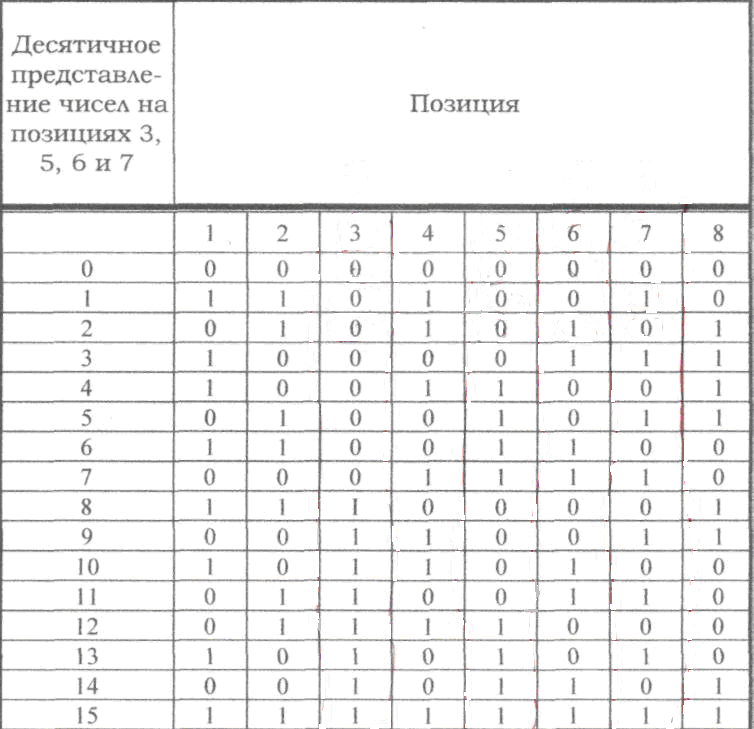
Если по изложенным
выше правилам строить корректирующий
код с обнаружением и исправлением
одиночной ошибки для равномерного
двоичного кода, то первые 16 кодовых
комбинаций будут иметь вид, показанный
в таблице. Такой код может быть использован
для построения кода с исправлением
одиночной ошибки и обнаружением двойной.
Для
этого, кроме указанных выше проверок
по контрольным позициям, следует провести
еще одну проверку на четность для всей
строки в целом. Чтобы осуществить такую
проверку, следует к каждой строке кода
добавить контрольные символы, записанные
в дополнительной колонке (таблица,
колонка 8). Тогда в случае одной ошибки
проверки по позициям укажут номер
ошибочной позиции, а проверка на четность
— на наличие ошибки. Если проверки позиций
укажут на наличие ошибки, а проверка на
четность не фиксирует ее, значит в
кодовой комбинации две ошибки.
Лекция 8
8.1 Двоичные циклические коды
Вышеприведенная
процедура построения линейного кода
матричным методом имеет ряд недостатков.
Она неоднозначна (МДР можно задать
различным образом) и неудобна
в реализации в виде технических устройств.
Этих недостатков лишены
линейные корректирующие коды, принадлежащие
к классу циклических.
Циклическими
называют
линейные (n,k)-коды,
обладающие
следующим свойством:
для любого кодового слова:
![]()
существует другое
кодовое слово:
![]()
полученное
циклическим сдвигом элементов исходного
кодового слова ||КС||
вправо
или влево, которое также принадлежит
этому коду.
Для
описания циклических кодов используют
полиномы с фиктивной переменной
X.
Например,
пусть кодовое слово ||КС||
=
||011010||.
Его
можно описать полиномом
![]()
Таким
образом, разряды кодового слова в
описывающем его полиноме используются
в качестве коэффициентов при степенях
фиктивной переменной
X.
Наибольшая
степень фиктивной переменной X
в
слагаемом с ненулевым
коэффициентом называется степенью
полинома. В вышеприведенном примере
получился полином 4-й степени.
Теперь
действия над кодовыми словами сводятся
к действиям над полиномами.
Вместо алгебры матриц здесь используется
алгебра полиномов.
Рассмотрим
алгебраические действия над полиномами,
используемые в теории
циклических кодов. Суммирование
полиномов разберем на примере
С(Х)=А(Х)+В(Х).
Пусть
||A||
= ||011010||,
||В|| =
||110111|.
Тогда
![]()
![]()
![]()
—————————————————————
![]()
Таким
образом, при суммировании коэффициентов
при X
в одинаковой степени
результат берется по модулю 2. При таком
правиле вычитание эквивалентно
суммированию.
Умножение
выполняется как обычно, но с использованием
суммирования
по модулю 2.
Рассмотрим
умножение на примере умножения полинома
(X3+X1+X0)
на
полином X1+X0
X3
+ 0*X2+X1+X0
*
X1+X0
—————————————————
X3+
0*X2+X1+Х0
X4+0*Х3+
X2+Х1
____________________________________
Х4+
X3+
X2+0*X1+X0
Операция
— обратная умножению -деление. Деление
полиномов выполняется как обычно, за
исключением того, что вычитание
выполняется по модулю 2. Вспомним, что
вычитание по модулю 2 эквивалентно
сложению по модулю 2
Пример
деления полинома X6+X4+X3
на полином
X3+X2+1
X6+0*X5+X4
+ X3+0*X2+0*X1+0
| X3+X2+1
X6+X5+0*X4+X3 результат== |X3+X2
————————————
X5
+X4
+ 0*X3+0*X2
X5
+X4
+ 0*X3+
X2
—————————————-
остаток==
X2
=
100
Циклический
сдвиг влево на одну позицию коэффициентов
полинома степени n-1
получается
путем его умножения на X
с
последующим вычитанием из
результата полинома Xn+1,
если его порядок >
п.
Проверим это на
примере.
Пусть требуется
выполнить циклический сдвиг влево на
одну позицию
коэффициентов
полинома
C(X)=X5+Х3+X2+1
→ (101101)
В результате должен
получиться полином
C1(X)=X4+Х3+X1+1
→ (011011)
Это легко
доказывается:
C1(X)=C(X)*X-(X6+1)=(X6+Х4+X3+X)+(
X6+1)=X4+Х3+X1+1
В
основе циклического кода лежит образующий
полином r-го
порядка
(напомним, что r—
число дополнительных разрядов). Будем
обозначать
его gr(X).
Образование
кодовых слов (кодирование) КС
выполняется
путем умножения
информационного полинома с коэффициентами,
являющимися информационной
последовательностью
И(Х)
порядка
i<k
на
образующий полином gr(X)
КСr+k(Х)=gr(X)+ИСk(Х).
Принятое кодовое
слово может отличаться от переданного
искаженными разрядами в результате
воздействия помех.
ПКС(Х)=КС(Х)+ВО(Х).
где
ВО(Х)
— полином
вектора ошибки, а суммирование, как
обычно, ведется
по модулю 2.
Декодирование,
как и раньше начинается с нахождения
опознавателя,
в данном случае в виде полинома ОП(Х).
Этот
полином вычисляется как
остаток от деления полинома принятого
кодового слова ПКС(Х)
на
образующий
полином g(Х):
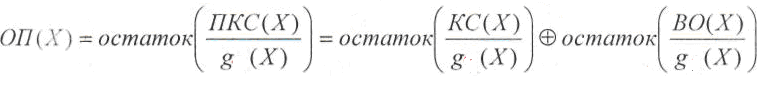
Первое
слагаемое остатка не имеет, т.к. кодовое
слово было образовано путем умножения
полинома информационной последовательности
на
образующий полином. Следовательно, и в
данном случае опознаватель
полностью зависит от вектора ошибки.
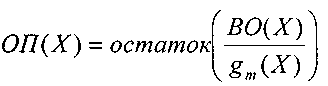
Образующий
полином выбирается таким, чтобы при
данном r
как
можно
большее число отношений ВО(Х)/g(Х)
давало
различные остатки.
Такому
требованию отвечают так называемые
неприводимые
полиномы,
которые
не делятся без остатка ни на один полином
степени r
и ниже, а
делятся только сами на себя и на 1.
Приведенная
здесь процедура образования кодового
слова неудобна тем,
что такой код получается несистематическим,
т.е. таким, в кодовых словах
которого нельзя выделить информационные
и дополнительные разряды.
Этот недостаток
был устранен следующим образом.
Способ
кодирования, приводящий к получению
систематического линейного циклического
кода, состоит в приписывании к
информационной
последовательности И
дополнительных разрядов ДР.
Эти
дополнительные разряды предлагается
находить по следующей формуле:
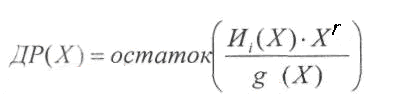
Порядок
полинома ДР(Х)
гарантировано
меньше r
(поскольку
это остаток).
Приписывание
дополнительных разрядов к информационной
последовательности,
используя алгебру полиномов, можно
описать формулой:
![]()
Одним
из свойств циклических линейных кодов
является то, что результат
деления любого разрешенного кодового
слова КС
на
образующий полином также, является
разрешенным кодовым словом.
Покажем,
что получаемые по вышеприведенному
алгоритму кодовые
слова являются кодовыми словами
циклического линейного кода. Для
этого нужно убедиться в том, что
произвольное разрешенное кодовое
слово делится на образующий полином
g(X)
без остатка:
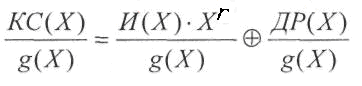
Рассмотрим первое
слагаемое:
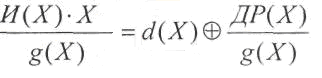
где
d(Х)
— целая
часть результата деления.
Подставим полученную
сумму на место первого слагаемого:
![]() Суммирование
Суммирование
последних двух слагаемых дает нулевой
результат (напомним,
что суммирование выполняется по модулю
2).
Значит
![]() —
—
целая часть деления. Остатка нет. Это
означает,
что описанный выше способ кодирования
соответствует циклическому
коду.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

 1 0 1 0
1 0 1 0 
 1 1 1 0
1 1 1 0
 0 0 1 1 0 0
0 0 1 1 0 0