Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
![]()
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
![]() измеряемой
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
![]()
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
![]()
(14)
Отношения
![]()
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
![]()
к среднему арифметическому значению
![]()
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
![]()
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
![]()
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
![]()
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
![]()
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
![]()
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
![]() :
:
![]() ,
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
![]() ,
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
![]()
(15)

(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
![]()
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
![]()
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:

(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
![]() —
—
среднее квадратичное отклонение;
![]() —
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).

Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
![]()
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
![]()
теоретически была определена в 1860 году
английским физиком Максвеллом

. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
![]()
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
![]() —
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:

(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.

Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n

-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
![]()
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
![]() (или
(или
высотой
![]()
– плотностью относительной частоты
![]() ).
).
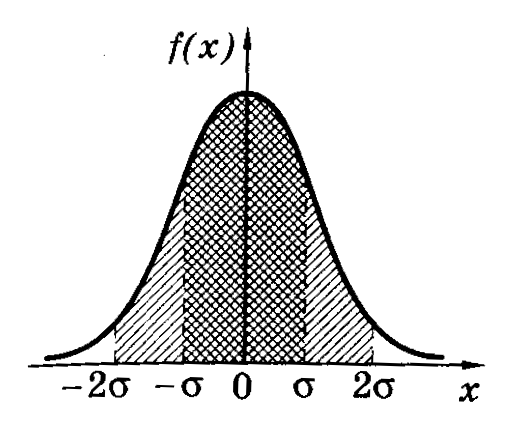
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
![]()
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:

(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
![]()
(25)
Где
![]()
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:

(26)
Загрузить PDF
Загрузить PDF
Абсолютная ошибка – это разность между измеренным значением и фактическим значением.[1]
Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.[2]
Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.
-

1
Запишите формулу для вычисления абсолютной ошибки. Формула:
, где
– абсолютная ошибка (разность между измеренным и фактическим значениями),
– измеренное значение,
– фактическое значение.[3]
-

2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
-

3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
-

4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[4]
Так вы вычислите абсолютную ошибку.- В нашем примере:
, то есть абсолютная ошибка измерения равна 1 м.
Реклама
- В нашем примере:
-

1
Запишите формулу для вычисления относительной ошибки. Формула:
, где
– относительная ошибка (отношение абсолютной ошибки к фактическому значению),
– измеренное значение,
– фактическое значение.[5]
-

2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
-

3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо
.
- Например, если фактическое значение равно 105 м, формула запишется так:
.
- Например, если фактическое значение равно 105 м, формула запишется так:
-

4
Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
-

5
Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете
, то есть измеренное значение.
-

6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[6]
Так вы вычислите абсолютную ошибку.- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
. Таким образом, абсолютная ошибка равна 2,1 м.
Реклама
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
-

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
-

2
-

3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.[9]
Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[10]
Так вы вычислите абсолютную ошибку.- Например, если измеренная длина поля равна
м, то есть абсолютная ошибка равна 0,5 м.
Реклама
- Например, если измеренная длина поля равна
Советы
- Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.
Реклама
Об этой статье
Эту страницу просматривали 25 861 раз.
Была ли эта статья полезной?
-
Полная погрешность прямых измерений
При измерениях
может быть несколько источников
погрешностей, поэтому важным является
вопрос о правилах нахождения суммарной
погрешности измерения по известным
значениям погрешностей составляющих
ее частей. В теории вероятностей
показывается, что если погрешность
измерений вызвана несколькими независимыми
друг от друга случайными причинами, то
полная абсолютная погрешность Δх
измеряемой величины определяется путем
суммирования квадратов складываемых
погрешностей по формуле
![]()
, (6)
где ∆хсл
– случайная погрешность (2) прямых
измерений, ∆хпр
– приборная погрешность.
Полная относительная
погрешность измерения
![]()
, (7)
где εсл,
εпр
– случайная и приборная относительные
погрешности.
При выполнении
расчетов для всех составляющих полной
погрешности выбирается одинаковое
значение доверительной вероятности.
Такая же вероятность будет и для полной
абсолютной погрешности Δх.
Из простых расчетов по формуле (7) следует,
что если какая-либо из складываемых
погрешностей в три и более раза меньше
другой, то ее вклад в полную погрешность
оказывается незначительным и такой
погрешностью можно пренебречь.
Иногда при
многократных измерениях получается
одно и то же значение измеряемой
физической величины. В этом случае
случайная погрешность не превышает
наименьшего значения, которое может
быть измерено данным прибором, а именно
– цены деления прибора, т.е. полная
погрешность целиком определяется
допустимой приборной погрешностью.
При обработке
результатов прямых измерений предлагается
следующий порядок операций.
-
Вычисляется
среднее арифметическое значение из n
результатов измерений
![]()
.
-
Определяются
случайные отклонения
![]()
.
-
Предварительно
определив по табл. 1 коэффициент Стьюдента
для числа измерений n
и доверительной вероятности Р = 0,95,
рассчитывается случайная погрешность
![]()
.
-
Определяется
приборная погрешность
![]()
.
-
Находится полная
абсолютная погрешность результата
измерений
![]()
.
-
Оценивается
относительная погрешность результата
измерений
![]()
.
7. Записывается
окончательный результат в виде:
![]()
,
![]()
.
Поскольку значения
физических величин, полученные в
результате измерений и обработки
результатов измерений, имеют погрешности,
они являются приближенными числами.
Перед окончательной записью результата
полученные при расчете числа следует
округлить, т. е. уменьшить количество
их значащих цифр. Так как найденные
значения погрешностей также являются
числами приближенными, то в соответствии
с точностью методов обработки результатов
измерений абсолютная погрешность
определяется не более чем до двух первых
значащих цифр. При простейших методах
обработки в вычисленной абсолютной
погрешности вторая цифра, как правило,
неверна. Поэтому абсолютную погрешность
округляют до одной значащей цифры.
Например, ΔL
= 0,467569 мм ≈ 0,5 мм;
ΔR
= 7,679 Ом ≈ 8 Ом.
Исключением из
этого правила являются погрешности,
первая цифра в значении которых единица.
Тогда во избежание грубой ошибки при
округлении в абсолютной погрешности
следует оставить две значащие цифры, а
в относительной – одну. Например, ΔL
= 0,167569 мм ≈ 0,17 мм; ΔR =
1,3791 Ом ≈ 1,4 Ом.
Знание погрешности
измерений позволяет правильно записать
окончательный ответ, оставив в нем
только верные и одну или две сомнительные
цифры. Последняя цифра результата и
последняя значащая цифра его абсолютной
погрешности должны принадлежать к
одному и тому же десятичному разряду.
Окончательный
результат измерений записывается вместе
с погрешностью и доверительной
вероятностью и должен иметь, например,
следующий вид:
L
= (1,12 ± 0,17) мм,
Р = 0,95
при округлении
погрешности до двух цифр, и
L
= (1,12 ± 0,04) мм, Р
= 0,95
при округлении
погрешности до одной значащей цифры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Абсолютная погрешность
- Причины возникновения погрешности измерения
- Систематическая и случайная погрешности
- Определение абсолютной погрешности
- Алгоритм оценки абсолютной погрешности в серии прямых измерений
- Значащие цифры и правила округления результатов измерений
- Примеры
Причины возникновения погрешности измерения
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.
Виды погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
$$ Delta x = |x_{изм}-x_{ист} | $$
Например:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
$m_i,г$
98,4
99,2
98,1
100,3
98,5
$Delta m_i, г$
1,6
0,8
1,9
0,3
1,5
Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $
Для оценки границы абсолютной погрешности на практике используются статистические методы.
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.
Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:
$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$
Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:
$$ Delta x_i = |x_i-a| $$
Шаг 4. Находим среднее арифметическое абсолютных погрешностей:
$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$
Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.
Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:
$$ h = max {d; Delta x_{cp} } $$
Шаг 7. Округляем и записываем результаты измерений в виде:
$$ a-h le x le a+h или x = a pm h $$
Значащие цифры и правила округления результатов измерений
Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Например:
0,00501 — три значащие цифры 5,0 и 1.
5,01 — три значащие цифры.
5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.
Внимание!
Правила округления.
Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).
Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.
Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:
$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$
Примеры
Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?
По условию $11,55 le t le 11,63$. Получаем систему уравнений:
$$ {left{ begin{array}{c} a-h = 11,55 \ a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 \ 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 \ h = 0,04end{array} right.} $$
$$ t = 11,59 pm 0,04 ℃ $$
Ответ: 0,04 ℃
Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.
$x_i$
15,3
16,4
15,3
15,8
15,7
16,2
15,9
Находим среднее арифметическое:
$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$
Находим абсолютные погрешности:
$$ Delta x_i = |x_i-a| $$
$ Delta x_i$
0,5
0,6
0,5
0
0,1
0,4
0,1
Находим среднее арифметическое:
$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$
Выбираем большую величину:
$$ h = max {d; Delta x_{ср} } = max {0,1; 0,31} = 0,31 $$
Округляем по правилам округления по избытку: $h approx ↑0,4$.
Получаем: x = 15, $8 pm 0,4$
Границы: $15,4 le x le 16,2$
Ответ: $15,4 le x le 16,2$
Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.
Более точное значение определяет более узкий интервал для x. По условию:
$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 \ 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 \ 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 \ 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$
Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:
$$ 5,3 le a le 5,9 $$
Ответ: $ 5,3 le a le 5,9 $
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
