Перевод
Ссылка на автора
Введение
В этом посте мы рассмотрим несколько случаев, когда алгоритм KMC работает неэффективно или может давать неинтуитивные результаты. В частности, мы рассмотрим следующие сценарии:
- Наше предположение о количестве (реальных) кластеров неверно.
- Особенность пространства очень размерна.
- Кластеры бывают странной или неправильной формы.
Все эти условия могут привести к проблемам с K-Means, так что давайте посмотрим.
Неверное количество кластеров
Чтобы сделать это проще, давайте определим вспомогательную функциюcompare, который создаст и решит проблему кластеризации для нас, а затем сравнит результаты.
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs, make_circles, make_moons
from mpl_toolkits.mplot3d import Axes3Dimport numpy as np
import pandas as pd
import itertoolsdef compare(N_features, C_centers, K_clusters, dims=[0, 1],*args):
data, targets = make_blobs(
n_samples=n_samples if 'n_samples' in args else 400,
n_features=N_features,
centers=C_centers,
cluster_std=cluster_std if 'cluster_std' in args else 0.5,
shuffle=True,
random_state=random_state if 'random_state' in args else 0)FEATS = ['x' + str(x) for x in range(N_features)]
X = pd.DataFrame(data, columns=FEATS)
X['cluster'] =
KMeans(n_clusters=K_clusters, random_state=0).fit_predict(X)fig, axs = plt.subplots(1, 2, figsize=(12, 4))
axs[0].scatter(data[:, dims[0]], data[:, dims[1]],
c='white', marker='o', edgecolor='black', s=20)
axs[0].set_xlabel('x{} [a.u.]'.format(dims[0]))
axs[0].set_ylabel('x{} [a.u.]'.format(dims[1]))
axs[0].set_title('Original dataset')
axs[1].set_xlabel('x{} [a.u.]'.format(dims[0]))
axs[1].set_ylabel('x{} [a.u.]'.format(dims[1]))
axs[1].set_title('Applying clustering')colors = itertools.cycle(['r', 'g', 'b', 'm', 'c', 'y'])
for k in range(K_clusters):
x = X[X['cluster'] == k][FEATS].to_numpy()
axs[1].scatter(
x[:, dims[0]],
x[:, dims[1]],
color=next(colors),
edgecolor='k',
alpha=0.5
)
plt.show()
Слишком мало кластеров

compare(2, 4, 3)).Несмотря на наличие отдельных кластеров в данных, мы недооценили их количество. Как следствие, некоторые непересекающиеся группы данных вынуждены вписываться в один более крупный кластер.
Слишком много кластеров

compare(2, 2, 4)).В отличие от последней ситуации, попытка обернуть данные в слишком много кластеров создает искусственные границы внутри реальных кластеров данных.
Высокие (er) размерные данные
Набор данных не должен быть настолько высоким в размерности, прежде чем мы начнем видеть проблемы. Хотя визуализация и, следовательно, некоторый анализ многомерных данных уже сложны (ругаясь сейчас…), поскольку KMC часто используется для понимания данных, это не помогает быть представленным с неоднозначностями.
Чтобы объяснить это, давайте сгенерируем трехмерный набор данных с четко различимыми кластерами.
fig = plt.figure(figsize=(14, 8))
ax = fig.add_subplot(111, projection='3d')data, targets = make_blobs(
n_samples=400,
n_features=3,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)ax.scatter(data[:, 0], data[:, 1],
zs=data[:, 2], zdir='z', s=25, c='black', depthshade=True)
ax.set_xlabel('x0 [a.u.]')
ax.set_ylabel('x1 [a.u.]')
ax.set_zlabel('x2 [a.u.]')
ax.set_title('Original distribution.')
plt.grid()
plt.show()

Хотя существует множество способов проецировать этот 3D-набор данных на 2D, существует три основных ортогональных подпространства:
Глядя наx2 : x0проекция, набор данных выглядит так, как если бы он имел только два кластера. Нижний правый «суперкластер» на самом деле представляет собой две отдельные группы, и даже если мы предполагаем,Кправильно(К = 3)Это выглядит как очевидная ошибка, несмотря на то, что кластеры очень локализованы.

compare(2, 2, 4, dims=[0, 2])).Чтобы быть уверенным, мы должны взглянуть на оставшиеся проекции, чтобы увидеть проблему, буквально, с разных сторон.

compare(2, 2, 4, dims=[1, 2])).
compare(2, 2, 4, dims=[0, 1])).Это имеет больше смысла!
С другой стороны, у нас было невероятное преимущество. Во-первых, с тремя измерениями мы смогли построить весь набор данных. Во-вторых, кластеры, которые существуют в наборе данных, были очень четкими, поэтому их легко обнаружить. Наконец, с трехмерным набором данных мы столкнулись только с тремя стандартными 2D-проекциями.
СлучайN, N> 3особенности, мы быне сможет построить весь набор данныхи число 2D проекций будет масштабироваться квадратично сN:
не говоря уже о том, что набор данных может иметь кластеры странной формы или нелокализованные, что является нашей следующей задачей.
Нерегулярные наборы данных
До сих пор мы упоминали о проблемах, которые «на нашей стороне». Мы посмотрели на очень «хорошо себя ведущий» набор данных и обсудили проблемы в области аналитики. Однако что делать, если набор данных не соответствует нашему решению или нашемуРешение проблемы не подходит?Это как раз тот случай, когда распределение данных происходит в странных или неправильных формах.
Если мы представим только этот график, мы можем обмануть себя, полагая, что в данных есть только два кластера. Однако при составлении графика остальных прогнозов мы быстро узнаем, что это не так.
fig, axs = plt.subplots(1, 3, figsize=(14, 4))# unequal variance
X, y = make_blobs(n_samples=1400,
cluster_std=[1.0, 2.5, 0.2],
random_state=2)
y_pred = KMeans(n_clusters=3, random_state=2).fit_predict(X)
colors = [['r', 'g', 'b'][c] for c in y_pred]axs[0].scatter(X[:, 0], X[:, 1],
color=colors, edgecolor='k', alpha=0.5)
axs[0].set_title("Unequal Variance")# anisotropically distributed data
X, y = make_blobs(n_samples=1400, random_state=156)
transformation = [
[0.60834549, -0.63667341],
[-0.40887718, 0.85253229]
]
X = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=0).fit_predict(X)
colors = [['r', 'g', 'b'][c] for c in y_pred]axs[1].scatter(X[:, 0], X[:, 1],
color=colors, edgecolor='k', alpha=0.5)
axs[1].set_title("Anisotropicly Distributed Blobs")# irregular shaped data
X, y = make_moons(n_samples=1400, shuffle=True,
noise=0.1, random_state=120)
y_pred = KMeans(n_clusters=2, random_state=0).fit_predict(X)
colors = [['r', 'g', 'b'][c] for c in y_pred]axs[2].scatter(X[:, 0], X[:, 1],
color=colors, edgecolor='k', alpha=0.5)
axs[2].set_title("Irregular Shaped Data")plt.show()

На левом графике показаны данные, чье распределение по Гауссу не имеет одинакового стандартного отклонения. Средний график представляетанизотропныйданные, означающие данные, которые вытянуты вдоль определенной оси. Наконец, правый график показывает данные, которые полностью негауссовы, несмотря на то, что они организованы в чистые кластеры.
В любом случае нерегулярность делает алгоритм KMC неэффективным. Поскольку алгоритм обрабатывает каждую точку данных одинаково и полностью независимо от других точек, алгоритмне в состоянии обнаружить любую возможную непрерывность или локальные изменения в кластере, То, что он делает, просто берет те же самые метрики и применяет это к каждой точке. В результате алгоритм KMC может производить странную или нелогичную кластеризацию в данных, даже если мы предполагаемКправильно и особенностиNне так много.
Выводы
В этом посте мы обсудили три основные причины, по которым алгоритм K-Means Clustering дает нам неправильные ответы.
- Во-первых, как количество кластеровКнужно решить априори, есть большая вероятность, что мы догадаемся
- Во-вторых, кластеризация в пространстве более высокого измерения становится громоздкой с аналитической точки зрения, и в этом случае KMC предоставит нам идеи, которые могут вводить в заблуждение.
- Наконец, для любых данных неправильной формы, KMC, скорее всего, искусственные кластеры, которые не соответствуют здравому смыслу.
Зная эти три ошибки, KMC остается полезным инструментом, особенно при проверке данных или создании меток.
Первоначально опубликовано на https://zerowithdot.com ,
Проблема оценки качества в задаче кластеризации трудноразрешима, как минимум, по двум причинам:
- Теорема невозможности Клейнберга — не существует оптимального алгоритма кластеризации.
- Многие алгоритмы кластеризации не способны определить настоящее количество кластеров в данных. Чаще всего количество кластеров подается на вход алгоритма и подбирается несколькими запусками алгоритма.
Содержание
- 1 Методы оценки качества кластеризации
- 2 Внешние меры оценки качества
- 2.1 Обозначения
- 2.2 Индекс Rand
- 2.3 Индекс Adjusted Rand
- 2.4 Индекс Жаккара (англ. Jaccard Index)
- 2.5 Индекс Фоулкса – Мэллова (англ. Fowlkes-Mallows Index)
- 2.6 Hubert Г statistic
- 2.7 Индекс Phi
- 2.8 Minkowski Score
- 2.9 Индекс Гудмэна-Крускала (англ. Goodman-Kruskal Index)
- 2.10 Entropy
- 2.11 Purity
- 2.12 F-мера
- 2.13 Variation of Information
- 3 Внутренние меры оценки качества
- 3.1 Компактность кластеров (англ. Cluster Cohesion)
- 3.2 Отделимость кластеров (англ. Cluster Separation)
- 3.3 Индекс Данна (англ. Dunn Index)
- 3.4 Обобщенный Индекс Данна (gD31, gD41, gD51, gD33, gD43, gD53)
- 3.5 Индекс S_Dbw
- 3.6 Силуэт (англ. Silhouette)
- 3.7 Индекс Calinski–Harabasz
- 3.8 Индекс C
- 3.9 Индекс Дэвиcа-Болдуина (англ. Davies–Bouldin Index)
- 3.10 Score function
- 3.11 Индекс Gamma
- 3.12 Индекс COP
- 3.13 Индекс CS
- 3.14 Индекс Sym
- 3.15 Индексы SymDB, SymD, Sym33
- 3.16 Negentropy increment
- 3.17 Индекс SV
- 3.18 Индекс OS
- 4 Сравнение
- 5 См. также
- 6 Источники информации
- 7 Примечания
Методы оценки качества кластеризации
Метод оценки качества кластеризации — инструментарий для количественной оценки результатов кластеризации.
Принято выделять две группы методов оценки качества кластеризации:
- Внешние (англ. External) меры основаны на сравнении результата кластеризации с априори известным разделением на классы.
- Внутренние (англ. Internal) меры отображают качество кластеризации только по информации в данных.
Внешние меры оценки качества
Данные меры используют дополнительные знания о кластеризуемом множестве: распределение по кластерам, количество кластеров и т.д.
Обозначения
Дано множество из элементов, разделение на классы , и полученное разделение на кластеры , совпадения между и могут быть отражены в таблице сопряженности , где каждое обозначает число объектов, входящих как в , так и в : .
Пусть .
Также рассмотрим пары из элементов кластеризуемого множества . Подсчитаем количество пар, в которых:
- Элементы принадлежат одному кластеру и одному классу —
- Элементы принадлежат одному кластеру, но разным классам —
- Элементы принадлежат разным кластерам, но одному классу —
- Элементы принадлежат разным кластерам и разным классам —
Индекс Rand
Индекс Rand оценивает, насколько много из тех пар элементов, которые находились в одном классе, и тех пар элементов, которые находились в разных классах, сохранили это состояние после кластеризации алгоритмом.
Имеет область определения от 0 до 1, где 1 — полное совпадение кластеров с заданными классами, а 0 — отсутствие совпадений.
Индекс Adjusted Rand
где — значения из таблицы сопряженности.
В отличие от обычного индекса Rand, индекс Adjusted Rand может принимать отрицательные значения, если .
Индекс Жаккара (англ. Jaccard Index)
Индекс Жаккара похож на Индекс Rand, только не учитывает пары элементов находящиеся в разные классах и разных кластерах ().
Имеет область определения от 0 до 1, где 1 — полное совпадение кластеров с заданными классами, а 0 — отсутствие совпадений.
Индекс Фоулкса – Мэллова (англ. Fowlkes-Mallows Index)
Индекс Фоулкса – Мэллова используется для определения сходства между двумя кластерами.
Более высокое значение индекса означает большее сходство между кластерами. Этот индекс также хорошо работает на зашумленных данных.
Hubert Г statistic
Данная мера отражает среднее расстояние между объектами разных кластеров:
где , — матрица близости, а
Можно заметить, что два объекта влияют на , только если они находятся в разных кластерах.
Чем больше значение меры — тем лучше.
Индекс Phi
Классическая мера корреляции между двумя переменными:
Minkowski Score
Индекс Гудмэна-Крускала (англ. Goodman-Kruskal Index)
Entropy
Энтропия измеряет «чистоту» меток классов:
Стоит отметить, что если все кластера состоят из объектов одного класса, то энтропия равна 0.
Purity
Чистота ставит в соответствие кластеру самый многочисленный в этом кластере класс.
Чистота находится в интервале [0, 1], причём значение = 1 отвечает оптимальной кластеризации.
F-мера
F-мера представляет собой гармоническое среднее между точностью (precision) и полнотой (recall).
Variation of Information
Данная мера измеряет количество информации, потерянной и полученной при переходе из одного кластера в другой.
Внутренние меры оценки качества
Данные меры оценивают качество структуры кластеров опираясь только непосредственно на нее, не используя внешней информации.
Компактность кластеров (англ. Cluster Cohesion)
Идея данного метода в том, что чем ближе друг к другу находятся объекты внутри кластеров, тем лучше разделение.
Таким образом, необходимо минимизировать внутриклассовое расстояние, например, сумму квадратов отклонений:
- , где — количество кластеров.
Отделимость кластеров (англ. Cluster Separation)
В данном случае идея противоположная — чем дальше друг от друга находятся объекты разных кластеров, тем лучше.
Поэтому здесь стоит задача максимизации суммы квадратов отклонений:
- , где — количество кластеров.
Индекс Данна (англ. Dunn Index)
Индекс Данна имеет множество вариаций, оригинальная версия выглядит следующим образом:
- ,
где:
- — межкластерное расстояние (оценка разделения), ,
- — диаметр кластера (оценка сплоченности), .
Обобщенный Индекс Данна (gD31, gD41, gD51, gD33, gD43, gD53)
Все эти вариации являются комбинациями 3 вариантов вычисления оценки разделения и оценки компактности
Оценки разделения:
- ,
- ,
- .
Оценки компактности:
- ,
- .
Обобщенный индекс Данна, как и обычный, должен возрастать вместе с улучшением качества кластеризации.
Индекс S_Dbw
Основан на вычислении Евклидовой нормы
и стандартных отклонений
- ,
- .
Сам индекс определяется формулой:
- .
Здесь
- ,
- ,
- , если и в ином случае.
Должен снижаться с улучшением кластеризации.
Силуэт (англ. Silhouette)
Значение силуэта показывает, насколько объект похож на свой кластер по сравнению с другими кластерами.
Оценка для всей кластерной структуры:
- ,
где:
- — среднее расстояние от до других объектов из кластера (компактность),
- — среднее расстояние от до объектов из другого кластера (отделимость).
Можно заметить, что
- .
Чем ближе данная оценка к 1, тем лучше.
Есть также упрощенная вариация силуэта: и вычисляются через центры кластеров.
Индекс Calinski–Harabasz
Компактность основана на расстоянии от точек кластера до их центроидов, а разделимость — на расстоянии от центроид кластеров до глобального центроида. Должен возрастать.
Индекс C
Индекс C представляет собой нормализованную оценку компактности:
- ,
где:
- ,
- — сумма минимальных (максимальных) расстояний между парами всех объектов во всем датасете.
Индекс Дэвиcа-Болдуина (англ. Davies–Bouldin Index)
Это, возможно, одна из самых используемых мер оценки качества кластеризации.
Она вычисляет компактность как расстояние от объектов кластера до их центроидов, а отделимость — как расстояние между центроидами.
- ,
где:
Существует еще одна вариация данной меры, которая была предложена автором вместе с основной версией:
C-индекс и индекс Дэвиcа-Болдуина должны минимизироваться для роста кластеризации.
Score function
Индекс, основанный на суммировании. Здесь оценка компактности выражается в дистанции от точек кластера до его центроида, а оценка разделимости — в дистанции от центроидов кластеров до глобального центроида.
- ,
где:
- ,
Чтобы функция оценки была эффективной, она должна максимизировать bcd, минимизировать wcd и быть ограниченной. Чем больше данный индекс, тем выше качество.
Индекс Gamma
где:
- — число пар таких, что (1) и принадлежат разным кластерам, и (2) ,
- .
Индекс COP
В данной мере компактность вычисляется как расстояние от точек кластера до его центроиды, а разделимость основана на расстоянии до самого отдаленного соседа.
- .
Индекс CS
Был предложен в области сжатия изображений, но может быть успешно адаптирован для любого другого окружения. Он оценивает компактность по диаметру кластера, а отделимость — как дистанцию между ближайшими элементами двух кластеров.
- .
Чем меньше значение данного индекса, тем выше качество кластеризации.
Индекс Sym
- .
Здесь — дистанция симметрии для точки из кластера .
Чем выше данное значение, тем лучше.
Индексы SymDB, SymD, Sym33
Модифицируют оценку компактности для индексов Дэвиса-Боулдина, Данна и gD33 соответственно.
SymDB вычисляется аналогично DB с изменением вычисления на:
- .
Данная оценка должна уменьшаться для улучшения качества кластеризации.
В SymD переопределена функция :
- .
в Sym33 аналогично SymD переопределена :
- .
Последние две оценки должны расти для улучшения качества кластеризации.
Negentropy increment
В отличие от подавляющего большинства других оценок, не основывается на сравнении компактности и разделимости. Определяется следующим образом:
- .
Здесь , — определитель ковариационной матрицы кластера , — определитель ковариационной матрицы всего датасета.
Данная оценка должна уменьшаться пропорционально росту качества кластеризации.
Индекс SV
Одна из самых новых из рассматриваемых в данном разделе оценок. Измеряет разделимость по дистанции между ближайшими точка кластеров, а компактность — по расстоянию от пограничных точек кластера до его центроида.
- .
Данная оценка должна увеличиваться.
Индекс OS
Отличается от предыдущей оценки усложненным способом вычисления оценки разделимости.
- .
Где
- .
при , и в ином случае.
Функции и определены следующим образом:
- .
- .
Данная оценка, как и предыдущая, должна возрастать.
Сравнение
Не существует лучшего метода оценки качества кластеризации. Однако, в рамках исследования[1] была предпринята попытка сравнить существующие меры на различных данных. Полученные результаты показали, что на искусственных датасетах наилучшим образом себя проявили индексы , и . На реальных датасетах лучше всех показал себя .
В Таблице 1 приведены оценки сложности мер качества кластеризации ( — число объектов в рассматриваемом наборе данных):
Таблица 1 — Оценка сложности для 19 мер качества кластеризации.
Из всех рассмотренных мер, меры , , и наиболее полно соответствуют когнитивному представлению асессоров о качестве кластеризации[2].
См. также
- Кластеризация
- Оценка качества в задачах классификации и регрессии[на 28.01.19 не создан]
Источники информации
- Wikipedia — Category:Clustering criteria
- Сивоголовко Е. В. Методы оценки качества четкой кластеризации
- Cluster Validation
- Halkidi, M., Batistakis, Y., Vazirgiannis, M., 2001. On clustering validation techniques. Journal of intelligent information systems, 17(2-3), pp.107-145.
- Pal, N.R., Biswas, J., 1997. Cluster validation using graph theoretic concepts. Pattern Recognition, 30(6), pp.847-857.
Примечания
- ↑ An extensive comparative study of cluster validity indices
- ↑ Towards cluster validity index evaluation and selection
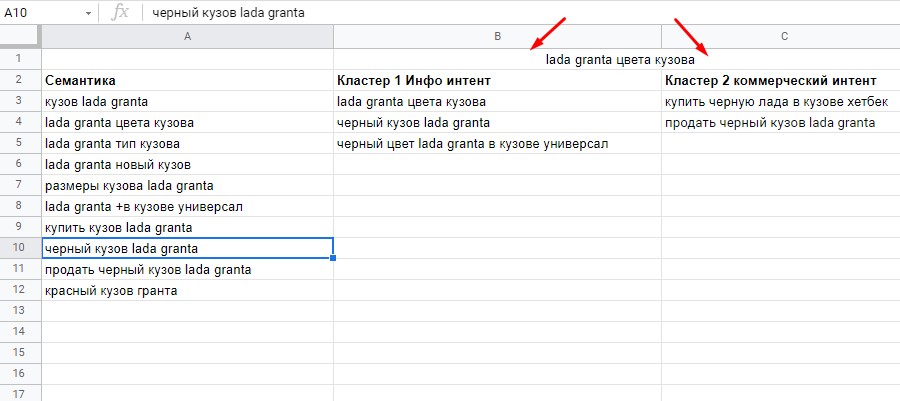
Кластеризация запросов (группировка) — это разделение семантического ядра на небольшие логические группы (кластеры),
которые можно продвигать на одной странице.
Кластеризация семантического ядра — главный источник головной боли и нервного тика при работе с семантикой у
начинающих оптимизаторов и предпринимателей, самостоятельно продвигающих свой сайт.
Сегодня мы разберем:
- Что скрывается за страшным словом «кластеризация».
- Какой поисковый интент у «поискового интента».
- Как выйти победителем при первой в своей жизни кластеризации.
А главное, как выбрать удобный способ кластеризации запросов без ущерба для точности сортировки и кошелька
оптимизатора.
Если вы не путаете «SEO» и «СЕО», но еще не знаете про разницу между Soft и Hard группировкой, то попали по адресу.
Погнали!
Определяем поисковый интент
Итак, семантическое ядро вы уже
составили. После сбора семантики и очистки ядра от нецелевых вхождений можно приступать к кластеризации.
Первый этап сортировки поисковых запросов начинается с определения интента.
Поисковый интент — это цель, намерение пользователя, которое вкладывается в запрос при поиске.
Поисковый интент используется Google и «Яндексом» для формирования релевантной выдачи, когда сайты сортируются в
поиске с учетом смысловой содержательности поискового запроса и намерения пользователя. Интент может быть
коммерческим, когда намерение пользователя — найти товар или заказать услуги, или информационным, где основная цель —
узнать информацию о продукте.
Для корректного ранжирования на посадочной странице все ключевые слова должны принадлежать одному интенту. При этом,
в зависимости от сезонности и спроса на товары, поисковый запрос может приобретать в разное время коммерческий или
информационный интент.
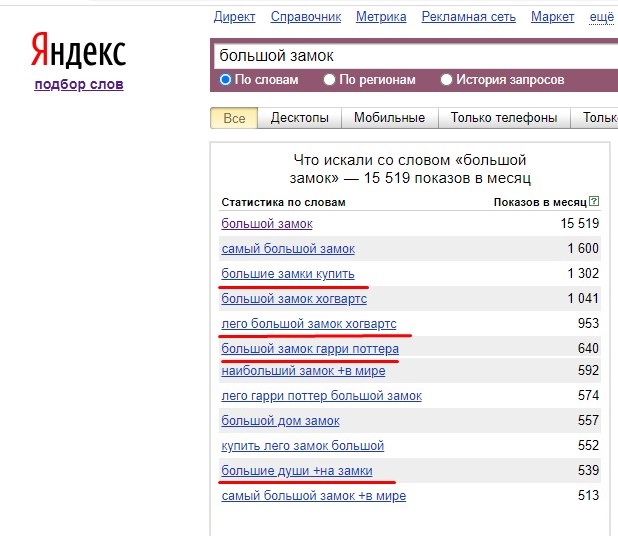
Сортировать ключевые слова в зависимости от интента можно по фактору коммерческости — показателя, определяющего уровень преобладания продающего намерения над информационным при поиске. Поисковые запросы с высоким уровнем коммерческости следует размещать на коммерческих страницах, с низким — в информационных, при смешанном показателе придется искать баланс.
Разберем тонкости проверки на примере условно-бесплатного Arsenkin Tools Commerce. Сервис позволяет бесплатно проверять до 100 ключевых слов в день, также можно приобрести подписку за 549 рублей на 1 месяц и проверять до 2 500 запросов. Для проверки достаточно вставить семантическое ядро, выбрать регион и запустить анализ.
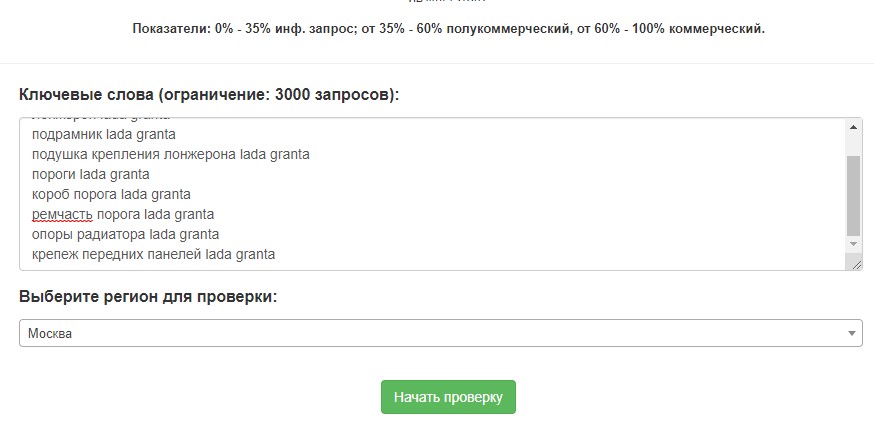
Результаты анализа выводятся в формате таблицы с отображением процента коммерческости.
Коммерческость поискового запроса — это доминирование коммерческого интента у пользователя, вводящего запрос в браузерной строке.
Запросы с коммерческостью менее 35 % имеют информационный интент и подходят для публикации в блоге, FAQ или гайдах, от 60 % — в каталоге товаров и коммерческих страницах. Поисковые запросы с коммерческостью в 35–60 % имеют смешанный интент — использовать их требуется аккуратно, иначе есть риск размыть релевантность страницы.
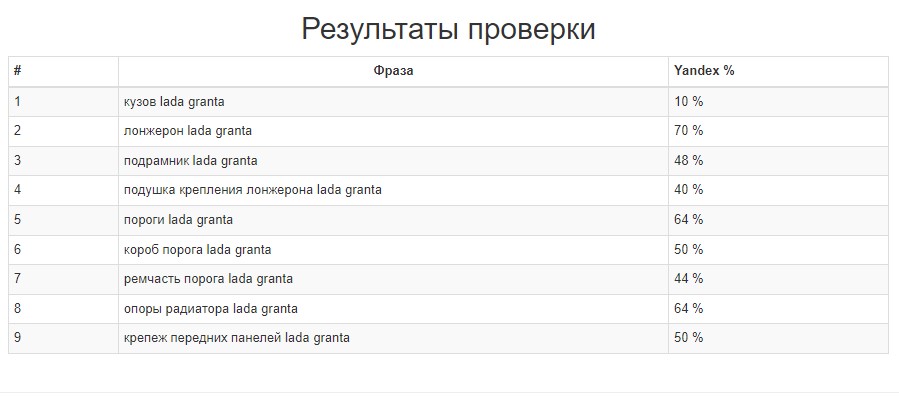
Для сортировки результаты копируем в таблицу Excel или «Google Таблицы», после чего выделяем столбец с процентным показателем комммерческости и сортируем.
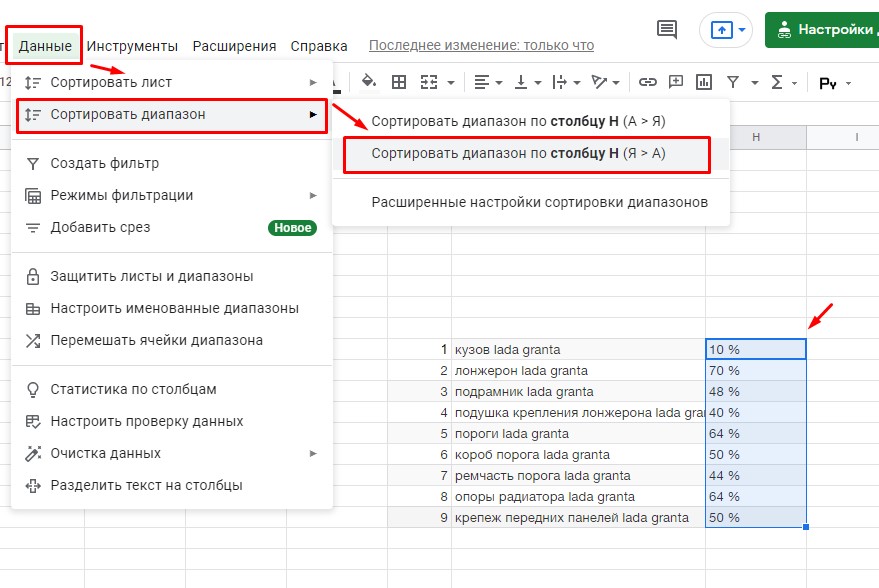
Таким образом таблица отсортируется. Вверху будут поисковые запросы с информационным интентом, а в нижней части — с коммерческим.
Выбираем подходящий метод кластеризации
Методика кластеризации поисковых запросов подбирается с учетом объема собранной семантики и количества страниц на сайте. Чаще всего применяется комбинированный метод, где используется несколько вариантов кластеризации, что позволяет добиться наиболее точного результата. Мы же разберем каждый метод по отдельности.
Логическая кластеризация
Точечный инструмент для группировки небольших семантических ядер. Кластеризация ключевых слов проводится вручную: оптимизатор определяет цель поиска и смысловую релевантность для каждого поискового запроса. Муторно, но действенно.
Точность и качество логической группировки зависит от объема семантического ядра. Чем больше требуется отсортировать поисковых запросов, тем выше риск допустить ошибки: сбиться с логики кластеризации, пропустить слова или неправильно определить интент.
Кластеризация по семантической схожести
Для кластеризации семантического ядра используются сложные формулы и обучаемые нейросети. Смысл группировки сводится к объединению в кластеры семантически близких поисковых запросов. При этом ключевые слова могут не иметь лексикографического сходства, но всегда похожи по семантике.
Пример. Группа в семантическом ядре формируется, если у всех поисковых запросов есть пересечение с ключевым словом. Например, “lada check engine”, “купить коврики lada”, и ”как почистить коврики lada” попадут в одну группу, при этом 2 последних поисковых запроса сформируют еще один отдельный кластер.
Проводить кластеризацию по семантической схожести для молодого сайта нет смысла: такая задача поручается нейросетям при наличии большого семантического ядра. При этом такая группировка не учитывает коммерческость, ведь после кластеризации придется еще сортировать ключи в зависимости от поискового интента.
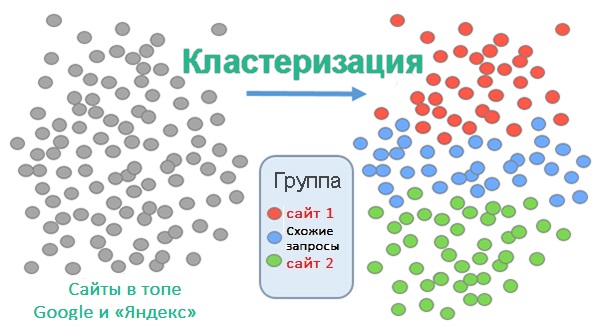
Кластеризация по топам
Наиболее правильный и популярный способ группировки семантики. Смысл кластеризации заключается в объединении поисковых запросов в кластеры согласно семантической базе сайтов, находящихся в топе выдачи «Яндекс» и Google.
Из популярных программ для кластеризации стоит выделить KeyClusterer, AllSubmitter, а также Key Collector. В отличие от онлайн-сервисов с оплатой по подписке, десктопное ПО приобретается единоразово по лицензии, а скорость кластеризации зависит от производительности компьютера.
Логика метода заключается в поиске пересечений ключевых слов на страницах сайтов, находящихся в топе поисковых систем. Обычно проводится кластеризация по топ-3 или топ-10, реже учитываются список из 50 сайтов в рейтинге.
Для увеличения точности группировки перед кластеризацией задается порог пересечений: ключевые слова объединяются в кластер только если будут найдены, например, на сразу двух, пяти или десяти сайтах.
| Логическая группировка | Кластеризация по топам | Группировка по семантической схожести | |
| Кому подойдет | Молодым сайтам, визиткам и лендингам | Многостраничным ресурсам и e-commerce | Маркетплейсам, онлайн-библиотекам |
| Когда подойдет | При небольшом семантическом ядре | Для работы с ядром среднестатистического сайта | Для группировки крупных семантических ядер |
| Преимущества | Точный результат, возможность учесть несколько переменных при кластеризации | Быстрый и недорогой способ обработать большое семантическое ядро | Возможность сегментировать большие массивы неструктурированных данных |
| Недостатки | Сложность группировки и высокий риск ошибок при долгой сортировке | Часто требуется повторная ручная кластеризация, чтобы сделать лучше, чем у конкурентов | Сложность реализации и необходимость повторной обработки семантики |
| Можно ли выполнить начинающему оптимизатору | Да, вручную | Да, через сервисы или софт | Нет, нужен сложный и дорогой софт |
На практике лучше совмещать несколько методов кластеризации. Например, группировать объемное ядро по топам, а сложные ключи со смешанным интентом сортировать вручную.
Подбираем алгоритм кластеризации семантического ядра по топам
Для корректной кластеризации даже для небольшого сайта рекомендуется сначала провести группировку семантики по топам поисковой выдачи и лишь затем сегментировать спорные ключевые слова вручную. Кластеризация на основании анализа поисковой выдачи может проводиться тремя способами-уровнями: Soft, Middle, Hard. Рассмотрим каждый из них.
Soft-кластеризация
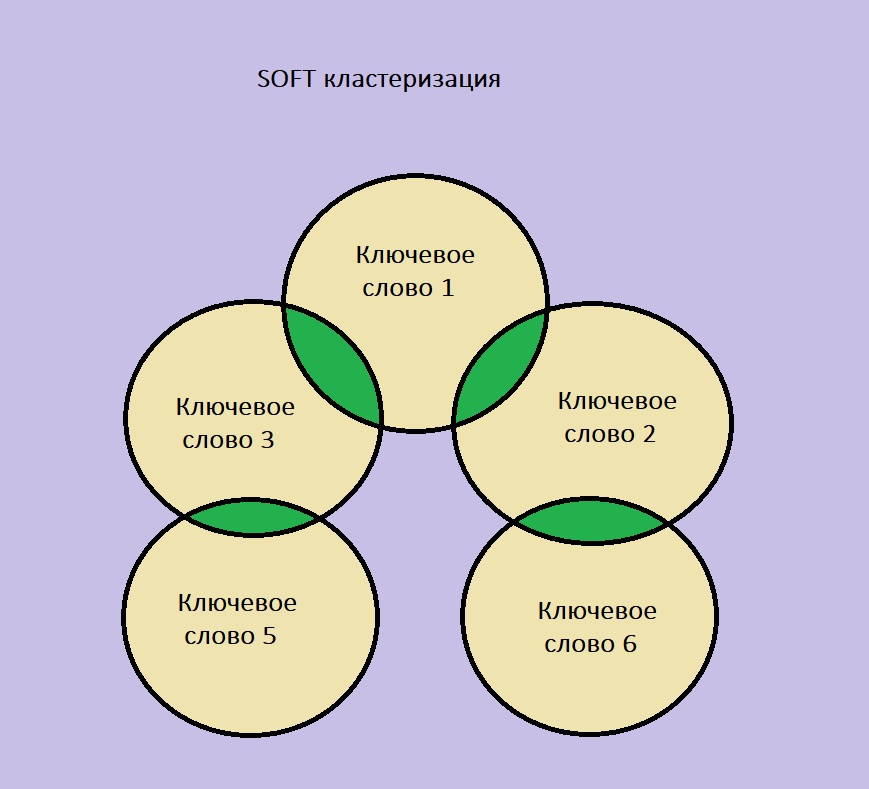
При мягкой кластеризации все поисковые запросы сравниваются с основным, тематико-задающим ключом, имеющим, как правило, наибольшую частотность. В кластер добавляются все ключевые слова, привязанные к URL в поисковой выдаче, которые пересекаются с главным поисковым запросом. Ключевое слово попадает в кластер семантического ядра, если количество одинаковых URL выше выбранного порога кластеризации. При этом второстепенные ключевые слова могут даже не пересечься между собой, из-за чего в кластер добавляется много поисковых запросов, но страдает точность группировки.
Метод предназначен для молодых проектов или неконкурентных тематик, где точность сортировки ключевых слов не столь важна.
Soft-кластеризация подойдет небольшим информационным сайтам или интернет-магазинам с маленьким ассортиментом товаров.
Soft-кластеризация может использоваться для сегментирования семантического ядра сайтов-визиток.
Hard-кластеризация
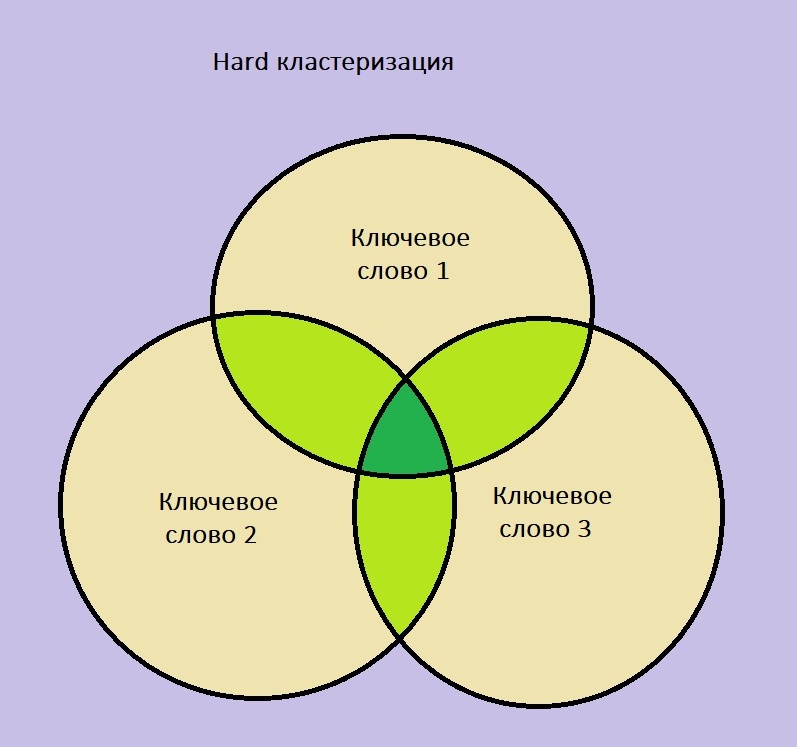
Это жесткий, но точный метод сегментации ключевых слов в семантическом ядре, который подходит для высококонкурентных и сложных тематик. При таком подходе отсеивается много поисковых запросов, однако удается создать кластер с максимально релевантными ключевыми словами к тематике посадочной страницы.
При Hard-кластеризации кластер создается только в случае пересечения всех ключевых фраз среди URL-адресов, входящих в топ-10 поисковой выдачи. Помимо пересечения главного ключевого слова также проводится сравнение вспомогательных поисковых запросов: кластер образуется только при выполнении обоих этих условий.
Порог кластеризации определяет число совпадений не только главного поискового запроса, но и всех входящих в кластер запросов. При этом чем выше порог кластеризации, тем меньше ключевых слов попадает в кластер семантического ядра.
Middle-кластеризация
Middle-кластеризация — компромисс между слабой точностью Soft-метода и жесткостью к отбору Hard-группировки. Выбирается главный тематико-задающий поисковый запрос, к которому привязываются остальные ключевые слова, прошедшие порог кластеризации по количеству URL в выдаче Google или «Яндекс». При этом кластеризатор сравнивает все зависимые с главным запросом ключевые слова друг с другом.
Так поисковые запросы связываются между собой внутри кластера семантического ядра, но могут отличаться в разных парах проверяемых URL. У всех ключевых слов в кластере нет задачи пройти пересечение по URL-адресам в топе, сопутствующие поисковые запросы попадают в группу вместе с тематикозадающим запросом.
Middle-кластеризация подходит для информационных ресурсов с большим семантическим ядром или интернет-магазинам в слабоконкурентных нишах. Такой подход обеспечивает большую точность, чем при Soft-кластеризации, и не позволяет отсеивать большинство ключевых слов, как при Hard-группировке.
Сервисы и приложения для кластеризации семантического ядра
Для кластеризации семантики по анализу поисковых топов можно использовать десктопное ПО или онлайн-сервисы. Различие — в скорости, функциональности и цене. Рассмотрим, какой вариант кластеризации предпочтительнее исходя из задач оптимизатора.
Программы для кластеризации семантики
Desktop-программы предлагают большую функциональность, чем онлайн-сервисы, что позволяет тонко выбрать параметры группировки поисковых запросов или настроить интерфейс софта. У офлайн-программ для кластеризации есть ряд преимуществ и недостатков:
| Плюсы | Минусы |
| Можно гибко настроить параметры кластеризации и редактировать семантическое ядро внутри программы | Кластеризация выполняется на компьютере пользователя: для работы с большим семантическим ядром требуется стабильный интернет и производительное железо |
| Возможность полностью автоматизировать работу с семантикой. Например, в Key Collector ядро можно спарсить, очистить и сразу кластеризовать | Все функциональные программы для кластеризации платные. Цена наиболее популярного Key Collector — 2 200 рублей |
| Desktop-программы поддерживают больше форматов для импорта и экспорта, а также позволяют создать шаблон с настройками для дальнейшей работы с семантикой | Интерфейс desktop-программ сложнее, чем у онлайн-сервисов. Для удобной работы требуется пройти обучение и посмотреть гайды |
Наиболее популярным софтом для кластеризации считаются AllSubmitter, KeyClusterer и Key Collector.
Пример кластеризации запросов в Key Collector
Рассмотрим пример группировки семантического ядра на основе анализа поисковой выдаче на примере Key Collector — пожалуй, обязательного инструмента для SEO-специалистов.
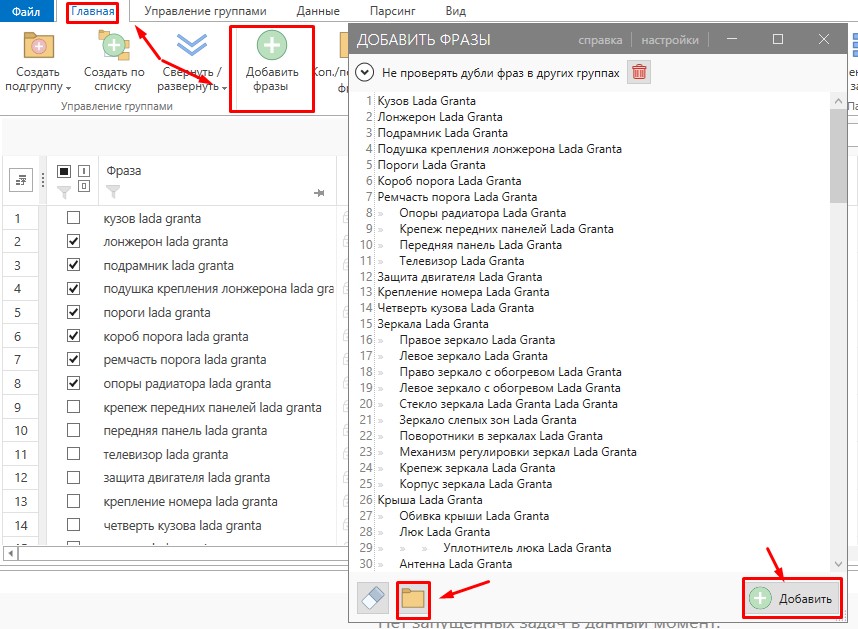
Прежде чем приступить к кластеризации, в программу требуется загрузить все семантическое ядро. Если данные собирались в Key Collector, нужно открыть сохраненный файл программы, если со сторонней программы — нужен импорт. Для импорта файлом или добавления вручную скопированных поисковых запросов переходим в раздел «Главная», где выбираем «Добавить фразы». Далее вставляем скопированную семантику или указываем адрес к файлу на компьютере:
Для группировки важно собрать по всем фразам частотность — это можно сделать здесь же в программе
Отмечаем галочкой все поисковые запросы и переходим в раздел «Данные», где нажимаем «Анализ групп». Теперь выбираем параметр «По поисковой выдаче (улучшенная)», отмечаем поисковые системы и количество URL в выдаче для анализа. Далее нужно выбрать силу SERP для кластеризации — для семантики, где преобладают двух- или трехсловные поисковые запросы, будет достаточно порога в 3 пересечения.
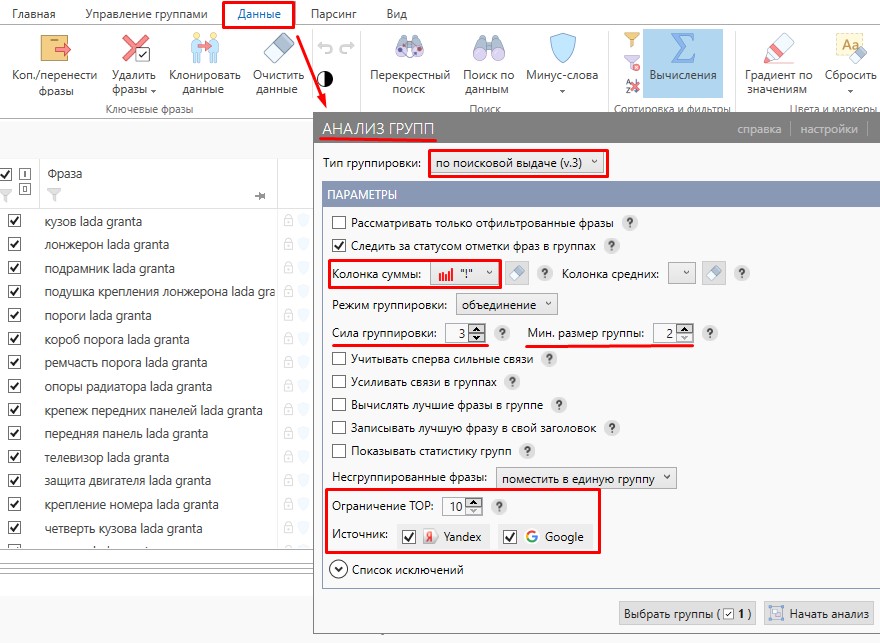
На скриншоте показан пример Soft-кластеризации методом «объединения» запросов. Для проведения Hard-кластеризации режим группировки в настройках нужно заменить на «пересечение». При обновлении семантического ядра процедуру кластеризации придется повторить.
Онлайн-сервисы для кластеризации
Более простой подход к кластеризации производится с помощью онлайн-сервисов. Это позволяет обработать семантику быстрее и не требует обучения, как для профильного софта. Здесь также есть свои преимущества и недостатки:
| Плюсы | Минусы |
| Кластеризация проходит в максимально удобном формате — в пару кликов | Сервисы не позволяют обрабатывать большие семантические ядра |
| Оптимизатору не требуется вникать в технические нюансы. Интерфейс крайне дружественен пользователям | У онлайн-сервисов много ограничений: по количеству проверок, числу ключевых слов в ядре |
| Для разовых или нерегулярных работ онлайн-сервисы — наиболее удобный инструмент для кластеризации | В долгосрочной перспективе приобретение профильного ПО оказывается выгоднее и практичнее |
Наиболее популярные сервисы для кластеризации — Coolakov, Semantist и SeoQuick.
Пример онлайн кластеризации запросов в SeoQuick
Для примера рассмотрим SeoQuick — это наиболее доступный и функциональный сервис. Он позволяет сделать за день 4 кластеризации с семантическим ядром до 5 000 ключевых слов.
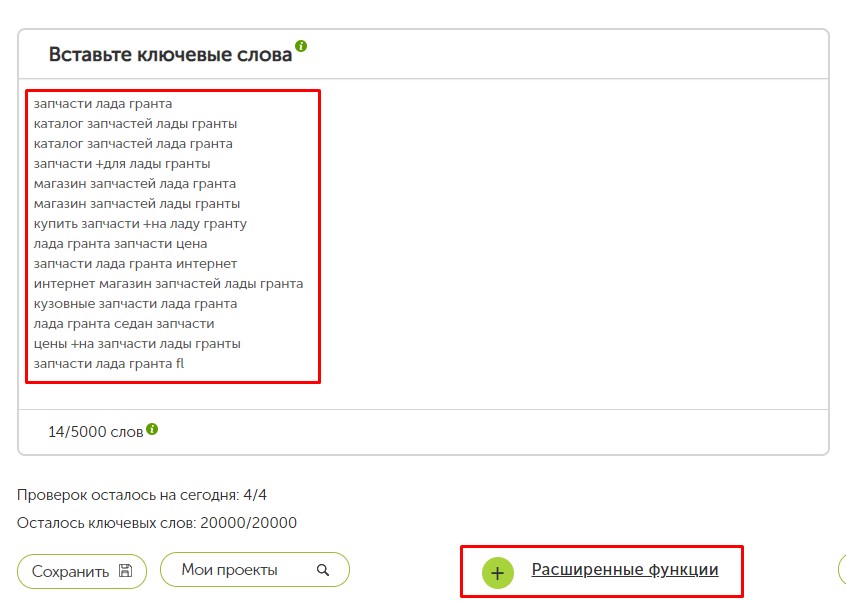
Затем открываем «Расширенные функции». Также можно импортировать файлы txt, xls, xlsx, csv.
В дополнительных настройках можно задать список стоп-слов, обязательных поисковых запросов или приказать учитывать словосочетания как одно цельное ключевое слово.
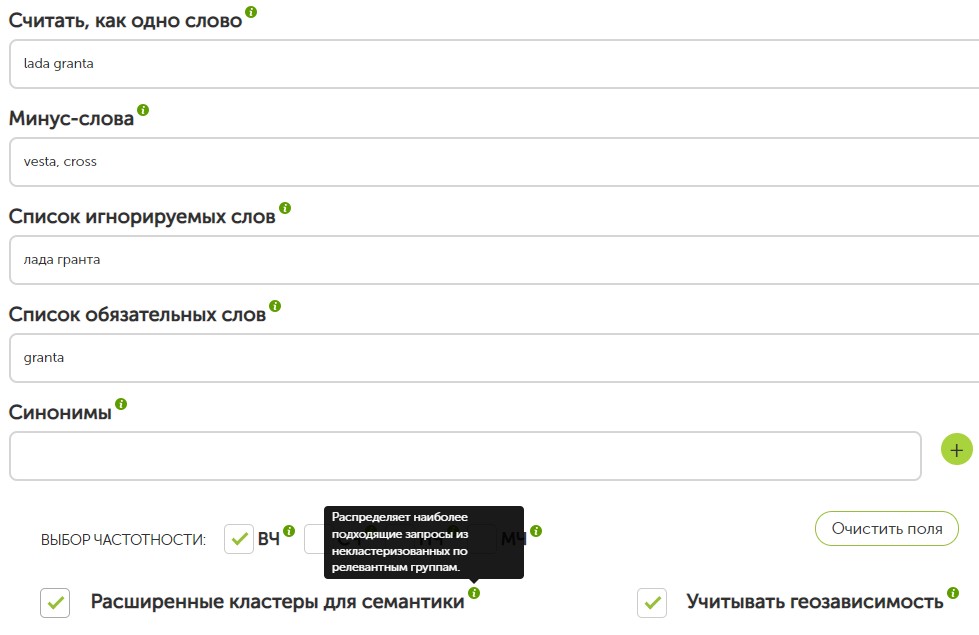
Разбираем основные ошибки при кластеризации семантического ядра
Кластеризация считается самым сложным этапом при работе с семантическим ядром, на котором часто возникают ошибки. Рассмотрим топ популярных ошибок и дадим рекомендации по их упреждению.
| Распространенная проблема | Почему данная ошибка так популярна | Как не допустить ошибки при кластеризации |
| Запрос с разным интентом в одном семантическом кластере | Отсутствие четкого понимания интента и отказ от сегментирования ключевых слов по коммерческости | Обязательно сортировать семантику по коммерческости при кластеризации |
| Несоответствие ключевых слов тематике посадочной страницы | Нарушена логика группировки при ручной кластеризации или сегментирование объемного ядра Soft-кластеризатором | Провести чистку семантики, увеличить точность кластеризации, выбрав Middle- или Hard-метод сортировки. Отсортировать проблемные кластеры вручную после кластеризации |
| Слишком много ключевых слов в одном кластере | Попытка структурировать большое семантическое ядро Soft-кластеризацией | Повысить точность кластеризации для объемной семантики поможет middle или hard группировка |
| Ошибки в ключевых словах | Ручная кластеризация или неправильный перенос собранных ключевых слов после сбора семантики | Предупредить ошибки в ключевых словах помогает автоматический парсинг и экспорт собранной семантики в кластеризатор. Для удаления уже имеющихся ошибок перед кластеризацией нужно провести чистку ядра |
| Много дублей, мусорных вхождений и запросов с нулевой частотностью | Запуск кластеризации сразу после парсинга семантики, без чистки ядра | Провести чистку семантического ядра перед кластеризацией |
Кластеризация — обязательный этап поисковой оптимизации после расширения структуры сайта и обновления семантического ядра. Посмотрите, как это работает на практике, на примере кейса для Rusplitka.ru.
Грамотная кластеризация специалистов агентства Kokoc Group позволила сегментировать семантику после крупного обновления товарного ассортимента, помогла улучшить ранжирование сайта в поиске и увеличить количество уникальных визитов.
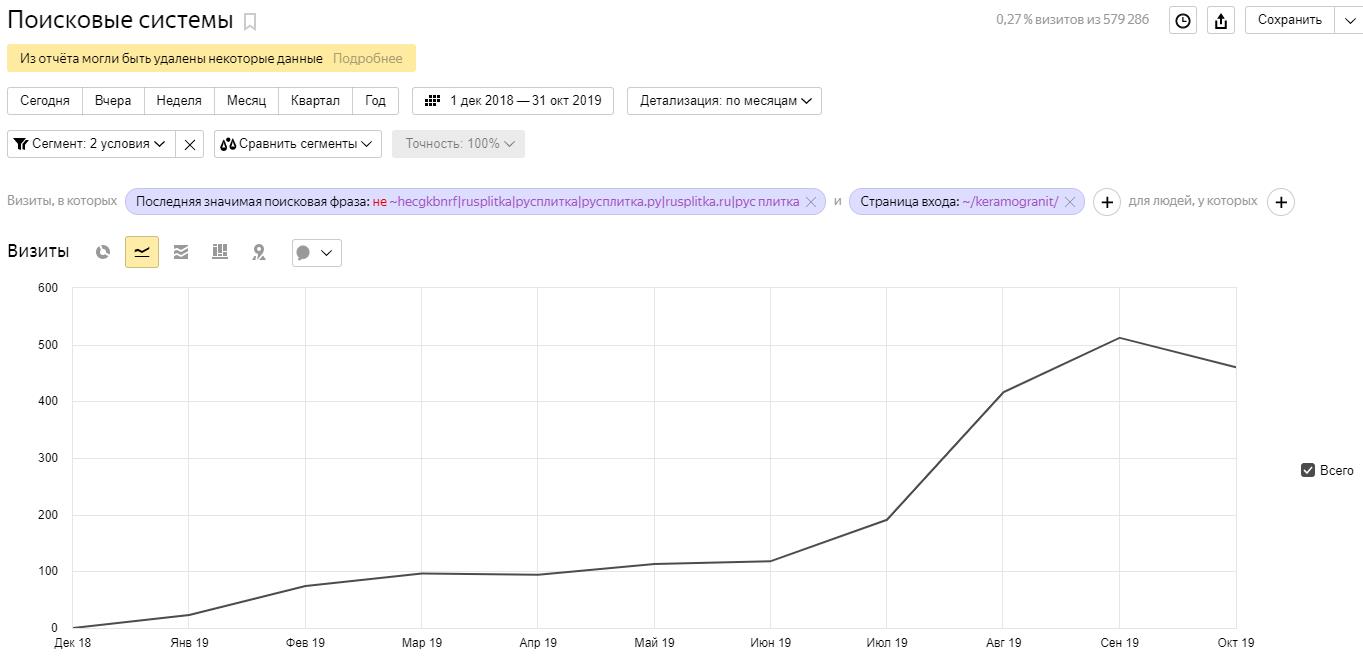
Это дало бонус при ранжировании и положительно повлияло на поведенческие факторы.
Если вам требуется помощь с кластеризацией большого семантического ядра или комплексное SEO-продвижение сайта, обращайтесь к специалистам Kokoc Group.
Кластеризация неразмеченных данных можно выполнить с помощью модуля sklearn.cluster.
Каждый алгоритм кластеризации имеет два варианта: класс, реализующий fit метод изучения кластеров на данных поезда, и функция, которая, учитывая данные поезда, возвращает массив целочисленных меток, соответствующих различным кластерам. Для класса метки над обучающими данными можно найти в labels_ атрибуте.
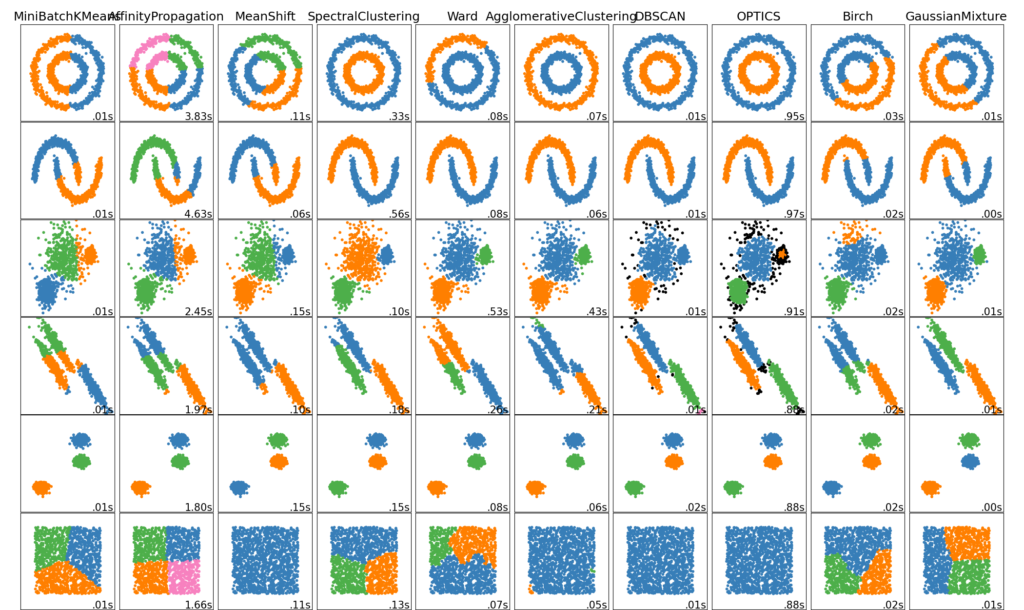
2.3.1. Обзор методов кластеризации
| Название метода | Параметры | Масштабируемость | Использование | Геометрия (используемая метрика) |
|---|---|---|---|---|
| К-средник | число кластеров | Очень большое значение n симплов среднее n_clusters вместе с Мини батчи K-средних | Универсальный, любой размер кластеров, плоская геометрия, не слишком много кластеров | Дистанция между точками |
| Афинное распространение | дамфинг, предпочтение выборки | Не масштабируется с помощью n_clusters | Много кластеров, не равномерный размер кластера, неплоская геометрия | Дистанция графа (например граф ближайших соседей) |
| Средний сдвиг | пропускная способность | Не масштабируется с помощью n_clusters | Много кластеров, не равномерный размер кластера, неплоская геометрия | Дистанция между точками |
| Спектральная кластеризация | число кластеров | Средняя n симплов маленькое n_clasters | Мало кластеров, или размер кластера, неплоская геометрия | Дистанция графа (например граф ближайших соседей) |
| Иерархическая кластеризация | чилсо кластеров или порог расстояния | Большое n симплов и n_clasters | Мало кластеров, возможно ограничене связей | Дистанция между точками |
| Агломеративная кластеризация | число кластеров, порог дистанции, тип связи, дистанция | Большое n симплов и n_clasters | Мало кластеров, возможно ограничене связей и не Евклидовое расстояние | Любая попарная дистанция |
| DBSCAN | размер окрестности | Очень большое n симплов и среднее n_clasters | не плоская геометрия, неравномерный размер кластеров | Дистанция между ближайшими точками |
| OPTICS | Минимальное количество элементов в кластере | Очень большое n симплов и большое n_clasters | не плоская геометрия, неравномерный размер кластеров, переменная плотность кластеров | Дистанция между точками |
| Гауссовская Смешаянная модель | много параметров | не масштабируемо | плоская геометрия, подходит для оценки плотности | Расстояния до центров Махаланобиса |
| Birch | факторы ветвления, порог, не обязательный глобальный кластер | Большое n симплов и n_clasters | Большой объем данных, удаление выбросов, сокращение данных | Евклидовое расстояние между точками |
Неплоская геометрия кластеризации полезно когда кластеры имеют специфичную форму, то есть многообразие и стандартное евклидовое расстояние в качестве метрики не подходят. Это случай возникает в двух верхних строках рисунка.
Гауссовская Смешаянная модель полезна для кластеризации описанные в другой статье документации, посвященная смешанным моделям. Метод K-средних можно расматривать как частный случай Гауссовской смешанной модели с равной ковариации для каждого компонента.
Методы трансдуктивной кластеризации (в отличие отметодов индуктивной кластеризации) не предназначены для применения к новым, невидимым данным.
2.3.2. K-средних
Эти KMeans данные алгоритмы кластеров пытаются отдельными образцы в п групп одинаковой дисперсии, сводя к минимуму критерия , известный как инерция или внутри-кластера сумм квадратов (см ниже). Этот алгоритм требует указания количества кластеров. Он хорошо масштабируется для большого количества образцов и используется в широком диапазоне областей применения во многих различных областях.
Алгоритм k-средних делит набор $N$ образцы $X$ в $K$ непересекающиеся кластеры $C$, каждый из которых описывается средним $mu_j$ образцов в кластере. Средние значения обычно называют «центроидами» кластера; обратите внимание, что это, как правило, не баллы из $X$, хотя они живут в одном пространстве.
Алгоритм K-средних нацелен на выбор центроидов, которые минимизируют инерцию или критерий суммы квадратов внутри кластера : $$sum_{i=0}^{n}min_{mu_j in C}(||x_i — mu_j||^2)$$
Инерцию можно определить как меру того, насколько кластеры внутренне связаны. Он страдает различными недостатками:
- Инерция предполагает, что кластеры выпуклые и изотропные, что не всегда так. Он плохо реагирует на удлиненные кластеры или коллекторы неправильной формы.
- Инерция — это не нормализованная метрика: мы просто знаем, что более низкие значения лучше, а ноль — оптимально. Но в очень многомерных пространствах евклидовы расстояния имеют тенденцию становиться раздутыми (это пример так называемого «проклятия размерности»). Выполнение алгоритма уменьшения размерности, такого как анализ главных компонентов (PCA) перед кластеризацией k-средних, может облегчить эту проблему и ускорить вычисления.
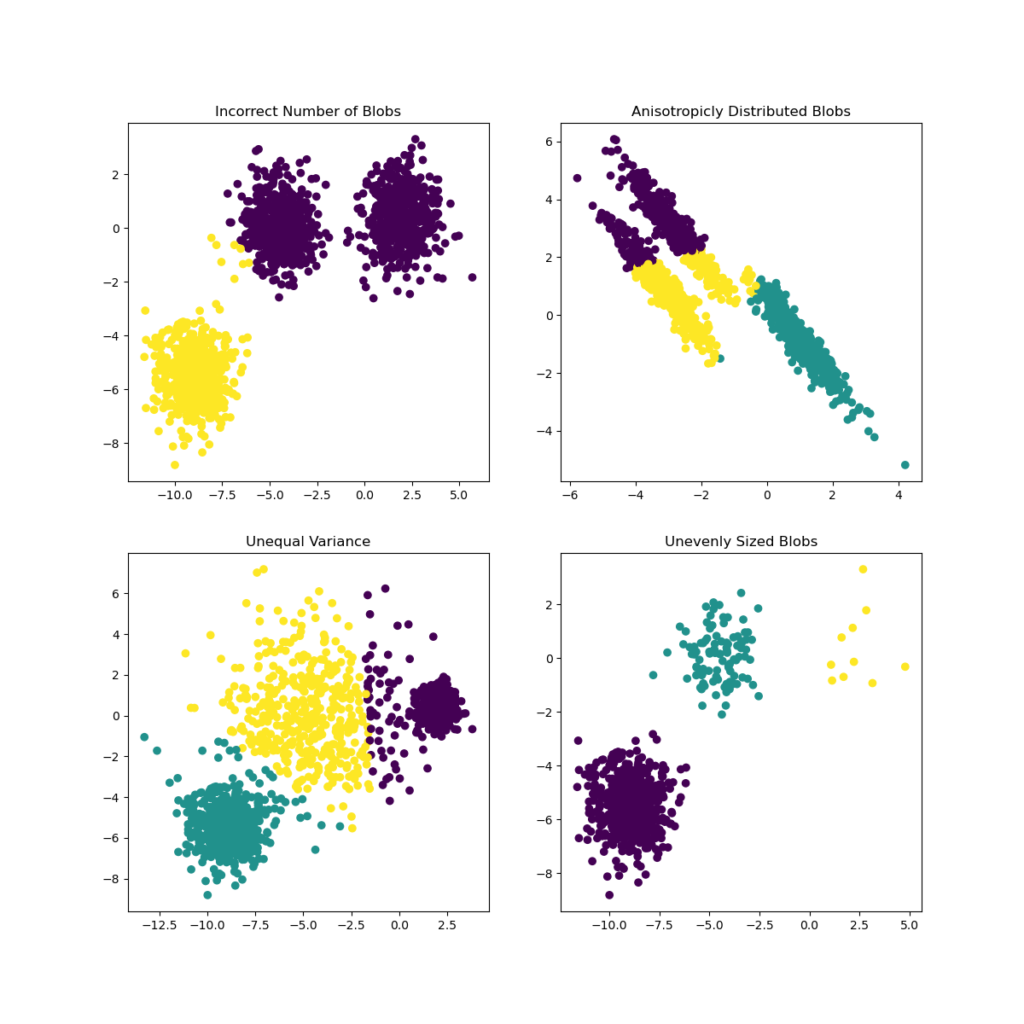
K-средних часто называют алгоритмом Ллойда. В общих чертах алгоритм состоит из трех шагов. На первом этапе выбираются начальные центроиды, а самый простой метод — выбрать $k$ образцы из набора данных $X$. После инициализации K-средних состоит из цикла между двумя другими шагами. Первый шаг присваивает каждой выборке ближайший центроид. На втором этапе создаются новые центроиды, взяв среднее значение всех выборок, назначенных каждому предыдущему центроиду. Вычисляется разница между старым и новым центроидами, и алгоритм повторяет эти последние два шага, пока это значение не станет меньше порогового значения. Другими словами, это повторяется до тех пор, пока центроиды не переместятся значительно.
K-средних эквивалентно алгоритму максимизации ожидания с маленькой, все равной диагональной ковариационной матрицей.
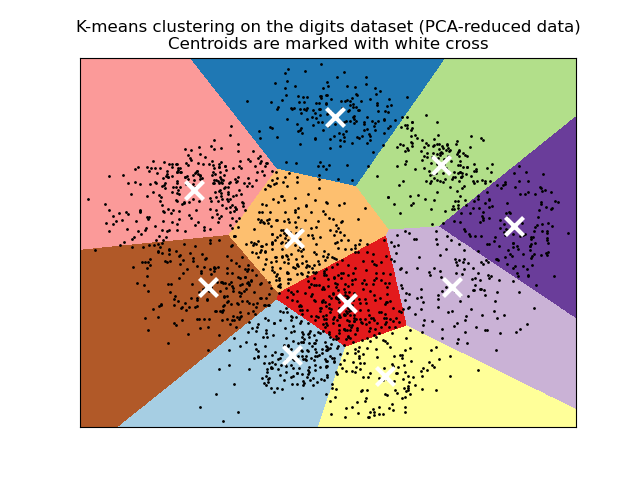
Алгоритм также можно понять через концепцию диаграмм Вороного. Сначала рассчитывается диаграмма Вороного точек с использованием текущих центроидов. Каждый сегмент на диаграмме Вороного становится отдельным кластером. Во-вторых, центроиды обновляются до среднего значения каждого сегмента. Затем алгоритм повторяет это до тех пор, пока не будет выполнен критерий остановки. Обычно алгоритм останавливается, когда относительное уменьшение целевой функции между итерациями меньше заданного значения допуска. В этой реализации дело обстоит иначе: итерация останавливается, когда центроиды перемещаются меньше допуска.
По прошествии достаточного времени K-средние всегда будут сходиться, однако это может быть локальным минимумом. Это сильно зависит от инициализации центроидов. В результате вычисление часто выполняется несколько раз с разными инициализациями центроидов. Одним из способов решения этой проблемы является схема инициализации k-means++, которая была реализована в scikit-learn (используйте init='k-means++'параметр). Это инициализирует центроиды (как правило) удаленными друг от друга, что, вероятно, приводит к лучшим результатам, чем случайная инициализация, как показано в справочнике.
K-means++ также может вызываться независимо для выбора начальных значений для других алгоритмов кластеризации, sklearn.cluster.kmeans_plusplus подробности и примеры использования см. В разделе .
Алгоритм поддерживает выборочные веса, которые могут быть заданы параметром sample_weight. Это позволяет присвоить некоторым выборкам больший вес при вычислении центров кластеров и значений инерции. Например, присвоение веса 2 выборке эквивалентно добавлению дубликата этой выборки в набор данных $X$.
Метод K-средних может использоваться для векторного квантования. Это достигается с помощью метода преобразования обученной модели KMeans.
2.3.2.1. Низкоуровневый параллелизм
KMeans преимущества параллелизма на основе OpenMP через Cython. Небольшие порции данных (256 выборок) обрабатываются параллельно, что, кроме того, снижает объем памяти. Дополнительные сведения о том, как контролировать количество потоков, см. В наших заметках о параллелизме .
Примеры:
- Демонстрация предположений k-средних : демонстрация того, когда k-средних работает интуитивно, а когда нет
- Демонстрация кластеризации K-средних на данных рукописных цифр : Кластеризация рукописных цифр
Рекомендации:
- «K-means ++: преимущества тщательного посева» Артур, Дэвид и Сергей Васильвицкий, Труды восемнадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам , Общество промышленной и прикладной математики (2007)
2.3.2.2. Мини-партия K-средних
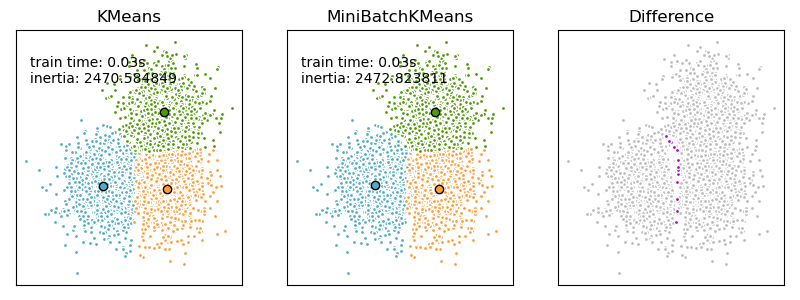
Это MiniBatchKMeans вариант KMeans алгоритма, который использует мини-пакеты для сокращения времени вычислений, но при этом пытается оптимизировать ту же целевую функцию. Мини-пакеты — это подмножества входных данных, которые выбираются случайным образом на каждой итерации обучения. Эти мини-пакеты резко сокращают объем вычислений, необходимых для схождения к локальному решению. В отличие от других алгоритмов, которые сокращают время сходимости k-средних, мини-пакетные k-средние дают результаты, которые, как правило, лишь немного хуже, чем стандартный алгоритм.
Алгоритм повторяется между двумя основными шагами, аналогично обычным k-средним. На первом этапе $b$ образцы выбираются случайным образом из набора данных, чтобы сформировать мини-пакет. Затем они присваиваются ближайшему центроиду. На втором этапе обновляются центроиды. В отличие от k-средних, это делается для каждой выборки. Для каждой выборки в мини-пакете назначенный центроид обновляется путем взятия среднего потокового значения выборки и всех предыдущих выборок, назначенных этому центроиду. Это приводит к снижению скорости изменения центроида с течением времени. Эти шаги выполняются до тех пор, пока не будет достигнута сходимость или заранее определенное количество итераций.
MiniBatchKMeans сходится быстрее, чем KMeans, но качество результатов снижается. На практике эта разница в качестве может быть довольно небольшой, как показано в примере и цитированной ссылке.
Примеры:
- Сравнение алгоритмов кластеризации K-средних и MiniBatchKMeans : сравнение KMeans и MiniBatchKMeans
- Кластеризация текстовых документов с использованием k-средних : кластеризация документов с использованием разреженных MiniBatchKMeans
- Онлайн обучение словаря частей лиц
2.3.3. Распространения близости (Affinity Propagation)
AffinityPropagation создает кластеры, отправляя сообщения между парами образцов до схождения. Затем набор данных описывается с использованием небольшого количества образцов, которые определяются как наиболее репрезентативные для других образцов. Сообщения, отправляемые между парами, представляют пригодность одного образца быть образцом другого, который обновляется в ответ на значения из других пар. Это обновление происходит итеративно до сходимости, после чего выбираются окончательные образцы и, следовательно, дается окончательная кластеризация.
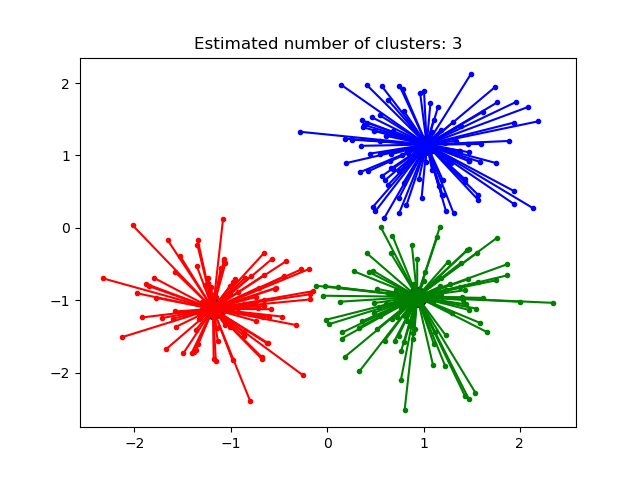
Метод Распространения близости может быть интересным, поскольку он выбирает количество кластеров на основе предоставленных данных. Для этой цели двумя важными параметрами являются предпочтение , которое контролирует, сколько экземпляров используется, и коэффициент демпфирования, который снижает ответственность и сообщения о доступности, чтобы избежать числовых колебаний при обновлении этих сообщений.
Главный недостаток метода Распространения близости — его сложность. Алгоритм имеет временную сложность порядка $O(N^2 T)$, где $N$ количество образцов и $T$ — количество итераций до сходимости. Далее, сложность памяти порядка $O(N^2)$ если используется плотная матрица подобия, но может быть сокращена, если используется разреженная матрица подобия. Это делает метод Распространения близости наиболее подходящим для наборов данных малого и среднего размера.
Примеры:
- Демонстрация алгоритма кластеризации распространения близости: метода Распространения близости на синтетических наборах данных 2D с 3 классами.
- Визуализация структуры фондового рынка Финансовые временные ряды метода Распространения близости для поиска групп компаний
Описание алгоритма: сообщения, отправляемые между точками, относятся к одной из двух категорий. Во-первых, это ответственность $r(i,k)$, которое является накопленным свидетельством того, что образец $k$ должен быть образцом для образца $i$. Второе — доступность $a(i,k)$ что является накопленным свидетельством того, что образец $i$ следует выбрать образец $k$ быть его образцом, и учитывает значения для всех других образцов, которые $k$ должен быть образцом. Таким образом, образцы выбираются по образцам, если они (1) достаточно похожи на многие образцы и (2) выбираются многими образцами, чтобы быть репрезентативными.
Более формально ответственность за образец $k$ быть образцом образца i дан кем-то: $$r(i, k) leftarrow s(i, k) — max [ a(i, k’) + s(i, k’) forall k’ neq k ]$$
Где $s(i,k)$ сходство между образцами $i$ а также $k$. Наличие образца $k$ быть образцом образца $i$ дан кем-то: $$a(i, k) leftarrow min [0, r(k, k) + sum_{i’~s.t.~i’ notin {i, k}}{r(i’, k)}]$$
Начнем с того, что все значения для $r$ и $a$ aустановлены в ноль, и расчет каждой итерации повторяется до сходимости. Как обсуждалось выше, чтобы избежать числовых колебаний при обновлении сообщений, коэффициент демпфирования $lambda$ вводится в итерационный процесс: $$r_{t+1}(i, k) = lambdacdot r_{t}(i, k) + (1-lambda)cdot r_{t+1}(i, k)$$ $$a_{t+1}(i, k) = lambdacdot a_{t}(i, k) + (1-lambda)cdot a_{t+1}(i, k)$$
где $t$ указывает время итерации.
2.3.4. Средний сдвиг
MeanShift кластеризация направлена на обнаружение капель в образцах с плавной плотностью. Это алгоритм на основе центроидов, который работает, обновляя кандидатов в центроиды, чтобы они были средними точками в данном регионе. Затем эти кандидаты фильтруются на этапе постобработки, чтобы исключить почти дубликаты и сформировать окончательный набор центроидов.
Учитывая центроид кандидата $x_i$ для итерации $t$, кандидат обновляется в соответствии со следующим уравнением: $$x_i^{t+1} = m(x_i^t)$$
Где $N(x_i)$ это соседство образцов на заданном расстоянии вокруг $x_i$ а также $m$ — вектор среднего сдвига, который вычисляется для каждого центроида, который указывает на область максимального увеличения плотности точек. Это вычисляется с использованием следующего уравнения, эффективно обновляющего центроид до среднего значения выборок в его окрестности: $$m(x_i) = frac{sum_{x_j in N(x_i)}K(x_j — x_i)x_j}{sum_{x_j in N(x_i)}K(x_j — x_i)}$$
Алгоритм автоматически устанавливает количество кластеров, вместо того, чтобы полагаться на параметр bandwidth, который определяет размер области для поиска. Этот параметр можно установить вручную, но можно оценить с помощью предоставленной estimate_bandwidth функции, которая вызывается, если полоса пропускания не задана.
Алгоритм не отличается высокой масштабируемостью, так как он требует многократного поиска ближайшего соседа во время выполнения алгоритма. Алгоритм гарантированно сходится, однако алгоритм прекратит итерацию, когда изменение центроидов будет небольшим.
Маркировка нового образца выполняется путем нахождения ближайшего центроида для данного образца.
Примеры:
- Демонстрация алгоритма кластеризации среднего сдвига: кластеризация среднего сдвига на синтетических наборах данных 2D с 3 классами.
Рекомендации:
- «Средний сдвиг: надежный подход к анализу пространства признаков». Д. Команичиу и П. Меер, IEEE Transactions on Pattern Analysis and Machine Intelligence (2002)
2.3.5. Спектральная кластеризация
SpectralClustering выполняет низкоразмерное встраивание матрицы аффинности между выборками с последующей кластеризацией, например, с помощью K-средних, компонентов собственных векторов в низкоразмерном пространстве. Это особенно эффективно с точки зрения вычислений, если матрица аффинности является разреженной, а amgрешатель используется для проблемы собственных значений (обратите внимание, amg что решающая программа требует, чтобы был установлен модуль pyamg ).
Текущая версия SpectralClustering требует, чтобы количество кластеров было указано заранее. Это хорошо работает для небольшого количества кластеров, но не рекомендуется для многих кластеров.
Для двух кластеров SpectralClustering решает выпуклую релаксацию проблемы нормализованных разрезов на графе подобия: разрезание графа пополам так, чтобы вес разрезаемых рёбер был мал по сравнению с весами рёбер внутри каждого кластера. Этот критерий особенно интересен при работе с изображениями, где вершинами графа являются пиксели, а веса ребер графа подобия вычисляются с использованием функции градиента изображения.
Предупреждение:
Преобразование расстояния в хорошее сходство
Обратите внимание, что если значения вашей матрицы подобия плохо распределены, например, с отрицательными значениями или с матрицей расстояний, а не с подобием, спектральная проблема будет сингулярной, а проблема неразрешима. В этом случае рекомендуется применить преобразование к элементам матрицы. Например, в случае матрицы расстояний со знаком обычно применяется тепловое ядро:
similarity = np.exp(-beta * distance / distance.std()) См. Примеры такого приложения.
Примеры:
- Спектральная кластеризация для сегментации изображения : сегментирование объектов на шумном фоне с использованием спектральной кластеризации.
- Сегментирование изображения греческих монет по регионам : спектральная кластеризация для разделения изображения монет по регионам.
2.3.5.1. Различные стратегии присвоения меток
Могут использоваться различные стратегии присвоения меток, соответствующие assign_labels параметру SpectralClustering. "kmeans" стратегия может соответствовать более тонким деталям, но может быть нестабильной. В частности, если вы не контролируете random_state, он может не воспроизводиться от запуска к запуску, так как это зависит от случайной инициализации. Альтернативная "discretize" стратегия воспроизводима на 100%, но имеет тенденцию создавать участки довольно ровной и геометрической формы.
2.3.5.2. Графики спектральной кластеризации
Спектральная кластеризация также может использоваться для разбиения графов через их спектральные вложения. В этом случае матрица аффинности является матрицей смежности графа, а SpectralClustering инициализируется с помощью affinity='precomputed':
>>> from sklearn.cluster import SpectralClustering >>> sc = SpectralClustering(3, affinity='precomputed', n_init=100, ... assign_labels='discretize') >>> sc.fit_predict(adjacency_matrix)
Рекомендации:
- «Учебное пособие по спектральной кластеризации» Ульрике фон Люксбург, 2007 г.
- «Нормализованные разрезы и сегментация изображения» Джианбо Ши, Джитендра Малик, 2000 г.
- «Случайный взгляд на спектральную сегментацию» Марина Мейла, Цзяньбо Ши, 2001
- «О спектральной кластеризации: анализ и алгоритм» Эндрю Й. Нг, Майкл И. Джордан, Яир Вайс, 2001 г.
- «Предварительно обусловленная спектральная кластеризация для задачи потокового графа стохастического разбиения блоков» Давид Жужунашвили, Андрей Князев
2.3.6. Иерархическая кластеризация
Иерархическая кластеризация — это общее семейство алгоритмов кластеризации, которые создают вложенные кластеры путем их последовательного слияния или разделения. Эта иерархия кластеров представлена в виде дерева (или дендрограммы). Корень дерева — это уникальный кластер, который собирает все образцы, а листья — это кластеры только с одним образцом. См. Страницу в Википедии для получения более подробной информации.
В AgglomerativeClustering объекте выполняет иерархическую кластеризацию с использованием подхода снизу вверх: каждый начинает наблюдения в своем собственном кластере, и кластеры последовательно объединены вместе. Критерии связывания определяют метрику, используемую для стратегии слияния:
- Ward минимизирует сумму квадратов разностей во всех кластерах. Это подход с минимизацией дисперсии, и в этом смысле он аналогичен целевой функции k-средних, но решается с помощью агломеративного иерархического подхода.
- Максимальное (Maximum) или полное связывание (complete linkage) сводит к минимуму максимальное расстояние между наблюдениями пар кластеров.
- Среднее связывание (Average linkage) минимизирует среднее расстояние между всеми наблюдениями пар кластеров.
- Одиночная связь (Single linkage) минимизирует расстояние между ближайшими наблюдениями пар кластеров.
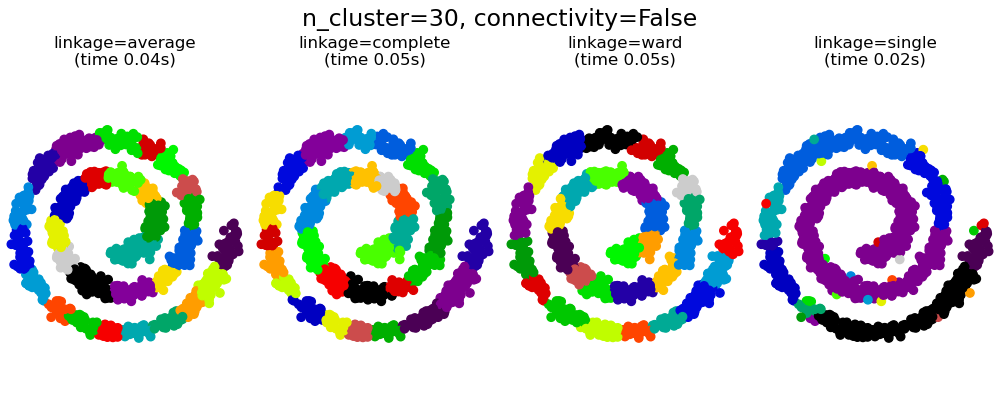
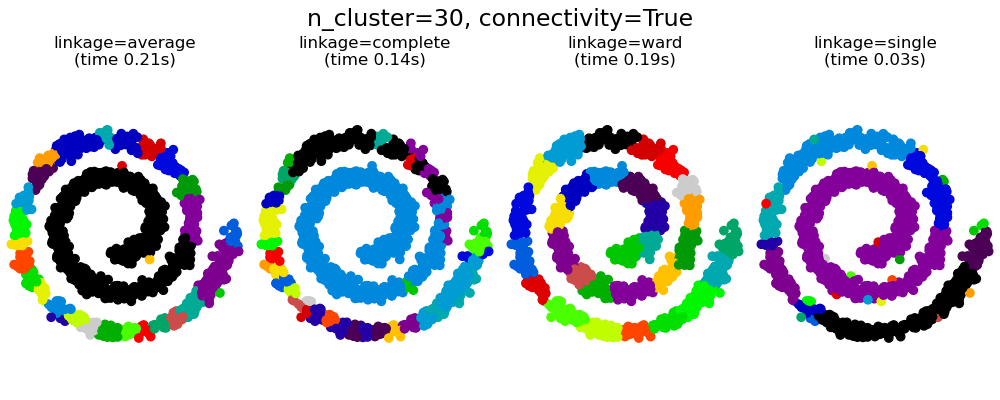
AgglomerativeClustering может также масштабироваться до большого количества выборок, когда он используется вместе с матрицей связности, но требует больших вычислительных затрат, когда между выборками не добавляются ограничения связности: он рассматривает на каждом шаге все возможные слияния.
2.3.6.1. Различные типы связи: Ward, полный, средний и одиночный связь
AgglomerativeClustering поддерживает стратегии Ward, одиночного, среднего и полного связывания.
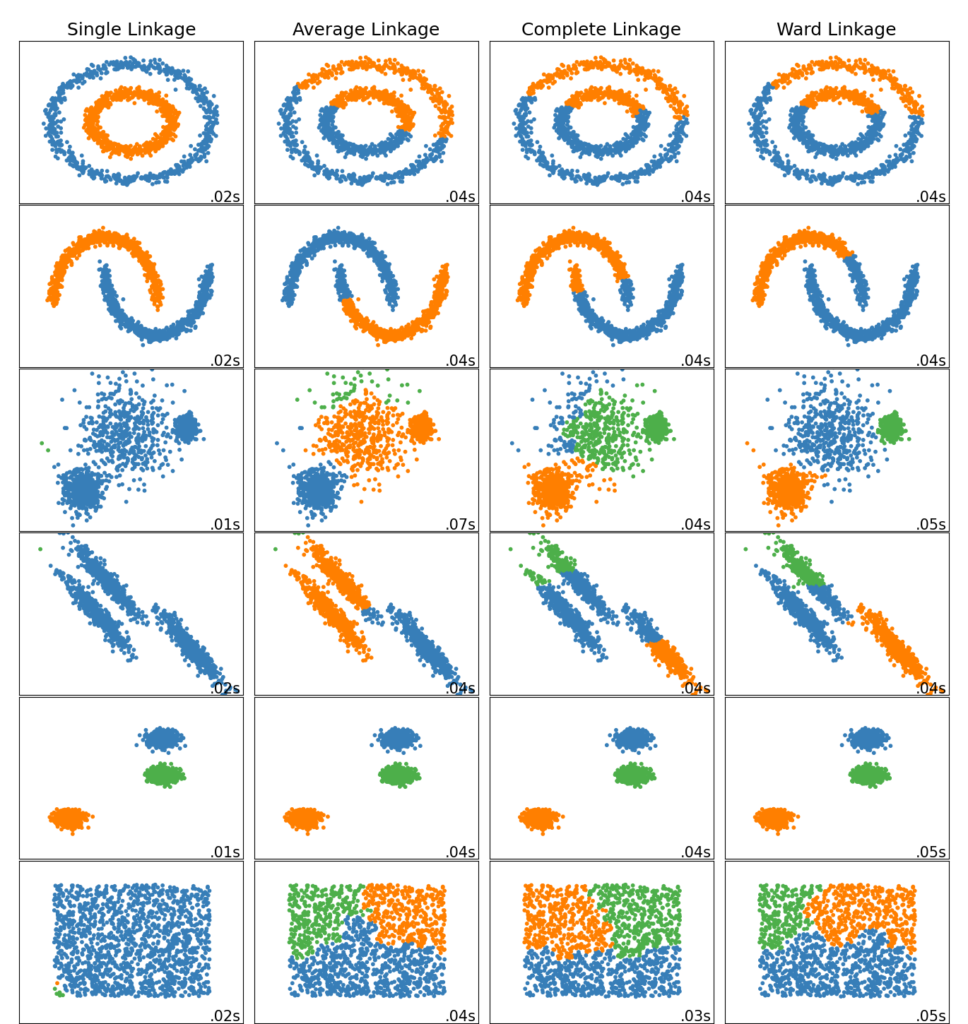
Агломеративный кластер ведет себя по принципу «богатый становится богатее», что приводит к неравномерному размеру кластера. В этом отношении одинарная связь — худшая стратегия, и Ward дает самые обычные размеры. Однако сродство (или расстояние, используемое при кластеризации) нельзя изменять с помощью Уорда, поэтому для неевклидовых показателей хорошей альтернативой является среднее связывание. Одиночная связь, хотя и не устойчива к зашумленным данным, может быть вычислена очень эффективно и поэтому может быть полезна для обеспечения иерархической кластеризации больших наборов данных. Одиночная связь также может хорошо работать с неглобулярными данными.
Примеры:
- Различная агломеративная кластеризация по двумерному встраиванию цифр : изучение различных стратегий связывания в реальном наборе данных.
2.3.6.2. Визуализация кластерной иерархии
Можно визуализировать дерево, представляющее иерархическое слияние кластеров, в виде дендрограммы. Визуальный осмотр часто может быть полезен для понимания структуры данных, особенно в случае небольших размеров выборки.
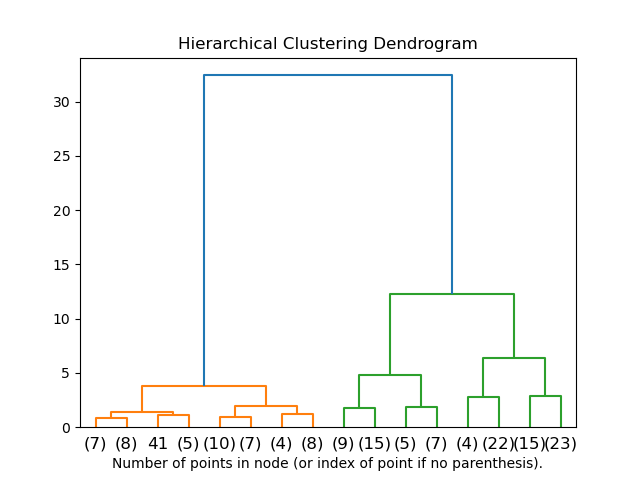
2.3.6.3. Добавление ограничений связи
Интересным аспектом AgglomerativeClustering является то, что к этому алгоритму могут быть добавлены ограничения связности (только соседние кластеры могут быть объединены вместе) через матрицу связности, которая определяет для каждой выборки соседние выборки, следующие заданной структуре данных. Например, в приведенном ниже примере швейцарского рулона ограничения связности запрещают объединение точек, которые не являются смежными на швейцарском рулоне, и, таким образом, избегают образования кластеров, которые проходят через перекрывающиеся складки рулона.
Эти ограничения полезны для наложения определенной локальной структуры, но они также ускоряют алгоритм, особенно когда количество выборок велико.
Ограничения связности накладываются через матрицу связности: scipy разреженную матрицу, которая имеет элементы только на пересечении строки и столбца с индексами набора данных, которые должны быть связаны. Эта матрица может быть построена из априорной информации: например, вы можете захотеть сгруппировать веб-страницы, объединяя только страницы со ссылкой, указывающей одну на другую. Это также можно узнать из данных, например, используя sklearn.neighbors.kneighbors_graph для ограничения слияния до ближайших соседей, как в этом примере , или с помощью, sklearn.feature_extraction.image.grid_to_graphчтобы разрешить слияние только соседних пикселей на изображении, как в примере с монетой.
Примеры:
- Демонстрация структурированной иерархической кластеризации Варда на изображении монет : Кластеризация Варда для разделения изображения монет на регионы.
- Иерархическая кластеризация: структурированная и неструктурированная палата : пример алгоритма Уорда в швейцарской системе, сравнение структурированных подходов и неструктурированных подходов.
- Агломерация признаков против одномерного выбора: пример уменьшения размерности с агломерацией признаков на основе иерархической кластеризации Уорда.
- Агломеративная кластеризация со структурой и без нее
Предупреждение Ограничения по подключению с одиночным, средним и полным подключением
Ограничения связности и одиночная, полная или средняя связь могут усилить аспект агломеративной кластеризации «богатый становится еще богаче», особенно если они построены на sklearn.neighbors.kneighbors_graph. В пределе небольшого числа кластеров они имеют тенденцию давать несколько макроскопически занятых кластеров и почти пустые. (см. обсуждение в разделе «Агломеративная кластеризация со структурой и без нее» ). Одиночная связь — самый хрупкий вариант связи в этом вопросе.


2.3.6.4. Варьируя метрику
Одиночная, средняя и полная связь может использоваться с различными расстояниями (или сходствами), в частности евклидовым расстоянием ( l2 ), манхэттенским расстоянием (или Cityblock, или l1 ), косинусным расстоянием или любой предварительно вычисленной матрицей аффинности.
- Расстояние l1 часто хорошо для разреженных функций или разреженного шума: то есть многие из функций равны нулю, как при интеллектуальном анализе текста с использованием вхождений редких слов.
- косинусное расстояние интересно тем, что оно инвариантно к глобальному масштабированию сигнала.
Рекомендации по выбору метрики — использовать метрику, которая максимизирует расстояние между выборками в разных классах и минимизирует его внутри каждого класса.
2.3.7. DBSCAN
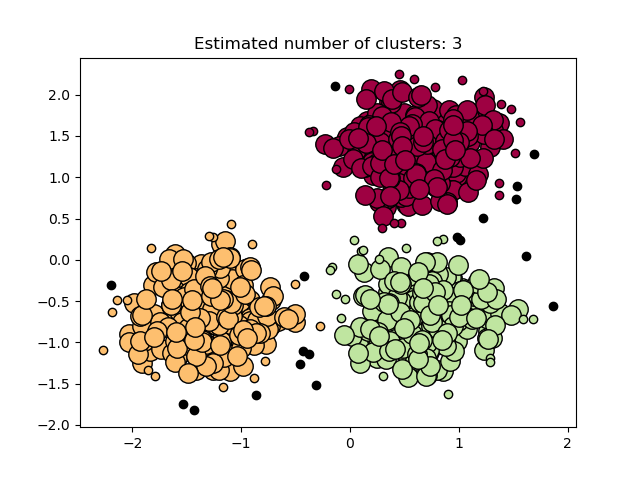
Алгоритм DBSCAN рассматривает кластеры , как участки высокой плотности , разделенных районах с низкой плотностью. Из-за этого довольно общего представления кластеры, обнаруженные с помощью DBSCAN, могут иметь любую форму, в отличие от k-средних, которое предполагает, что кластеры имеют выпуклую форму. Центральным компонентом DBSCAN является концепция образцов керна , то есть образцов, находящихся в областях с высокой плотностью. Таким образом, кластер представляет собой набор образцов керна, каждый из которых находится близко друг к другу (измеряется с помощью некоторой меры расстояния), и набор образцов, не относящихся к керну, которые близки к образцу керна (но сами не являются образцами керна). В алгоритме есть два параметра, min_samples и eps, которые формально определяют, что мы имеем в виду, когда говорим «плотный» . Выше min_samples или ниже eps указывают на более высокую плотность, необходимую для формирования кластера.
Более формально мы определяем образец керна как образец в наборе данных, так что существуют min_samples другие образцы на расстоянии eps, которые определены как соседи образца керна. Это говорит нам о том, что основной образец находится в плотной области векторного пространства. Кластер — это набор образцов керна, который можно построить путем рекурсивного взятия образца керна, поиска всех его соседей, которые являются образцами керна, поиска всех их соседей, которые являются образцами керна, и т. Кластер также имеет набор неосновных выборок, которые представляют собой выборки, которые являются соседями керновой выборки в кластере, но сами не являются основными выборками. Интуитивно эти образцы находятся на периферии кластера.
Любой образец керна по определению является частью кластера. Любая выборка, не являющаяся образцом керна и находящаяся по крайней мере eps на расстоянии от любой выборки керна, считается алгоритмом выбросом.
Хотя параметр в min_samples первую очередь контролирует устойчивость алгоритма к шуму (на зашумленных и больших наборах данных может быть желательно увеличить этот параметр), параметр epsимеет решающее значение для правильного выбора для набора данных и функции расстояния и обычно не может быть оставлен на значение по умолчанию. Он контролирует локальное окружение точек. Если выбран слишком маленький размер, большая часть данных вообще не будет кластеризована (и помечена как -1 для «шума»). Если выбран слишком большой, близкие кластеры будут объединены в один кластер, и в конечном итоге весь набор данных будет возвращен как единый кластер. Некоторые эвристики для выбора этого параметра обсуждались в литературе, например, на основе перегиба на графике расстояний до ближайших соседей (как обсуждается в ссылках ниже).
На рисунке ниже цвет указывает на принадлежность к кластеру, а большие кружки обозначают образцы керна, найденные алгоритмом. Меньшие кружки — это неосновные образцы, которые все еще являются частью кластера. Более того, выбросы обозначены ниже черными точками.
Выполнение
Алгоритм DBSCAN является детерминированным, всегда генерируя одни и те же кластеры, когда им предоставляются одни и те же данные в одном порядке. Однако результаты могут отличаться, если данные предоставляются в другом порядке. Во-первых, даже если основные образцы всегда будут назначаться одним и тем же кластерам, метки этих кластеров будут зависеть от порядка, в котором эти образцы встречаются в данных. Во-вторых, что более важно, кластеры, которым назначены неосновные выборки, могут различаться в зависимости от порядка данных. Это может произойти, если образец неосновного керна находится на расстоянии меньше, чем epsдва образца керна в разных кластерах. Согласно треугольному неравенству эти два образца керна должны быть дальше, чемepsдруг от друга, иначе они были бы в одном кластере. Неосновная выборка назначается тому кластеру, который сгенерирован первым при передаче данных, поэтому результаты будут зависеть от порядка данных.
Текущая реализация использует шаровые деревья и kd-деревья для определения окрестности точек, что позволяет избежать вычисления полной матрицы расстояний (как это было сделано в версиях scikit-learn до 0.14). Сохранена возможность использования пользовательских метрик; подробности см NearestNeighbors.
Потребление памяти для больших размеров выборки
Эта реализация по умолчанию неэффективна с точки зрения памяти, поскольку она строит полную матрицу попарного сходства в случае, когда нельзя использовать kd-деревья или шаровые деревья (например, с разреженными матрицами). Эта матрица будет потреблять $n^2$ плавает. Вот несколько способов обойти это:
- Используйте кластеризацию OPTICS вместе с
extract_dbscanметодом. Кластеризация OPTICS также вычисляет полную попарную матрицу, но сохраняет в памяти только одну строку (сложность памяти n). - График окрестностей с разреженным радиусом (где предполагается, что отсутствующие записи находятся вне eps) можно предварительно вычислить эффективным с точки зрения памяти способом, и dbscan можно обработать с помощью
metric='precomputed'. Смотритеsklearn.neighbors.NearestNeighbors.radius_neighbors_graph. - Набор данных можно сжать, удалив точные дубликаты, если они встречаются в ваших данных, или используя BIRCH. Тогда у вас будет относительно небольшое количество представителей для большого количества точек. Затем вы можете
sample_weightуказать при установке DBSCAN.
Рекомендации:
- «Алгоритм на основе плотности для обнаружения кластеров в больших пространственных базах данных с шумом» Эстер, М., Х. П. Кригель, Дж. Сандер и X. Сюй, в материалах 2-й Международной конференции по открытию знаний и интеллектуальному анализу данных, Портленд, штат Орегон , AAAI Press, стр. 226–231. 1996 г.
- «Новый взгляд на DBSCAN: почему и как вы должны (по-прежнему) использовать DBSCAN. Шуберт, Э., Сандер, Дж., Эстер, М., Кригель, HP, и Сюй, X. (2017). В транзакциях ACM в системах баз данных (TODS), 42 (3), 19.
2.3.8. ОПТИКА
В OPTICS акции алгоритма много общих с DBSCAN алгоритмом, и можно рассматривать как обобщение DBSCAN, что расслабляет epsтребование от одного значения до диапазона значений. Ключевое различие между DBSCAN и OPTICS заключается в том, что алгоритм OPTICS строит граф достижимости , который назначает каждой выборке reachability_ расстояние и точку в ordering_ атрибуте кластера ; эти два атрибута назначаются при подборе модели и используются для определения принадлежности к кластеру. Если OPTICS запускается со значением по умолчанию inf, установленным для max_eps, то извлечение кластера в стиле DBSCAN может выполняться повторно за линейное время для любого заданного eps значения с использованием этого cluster_optics_dbscan метода. Параметр max_eps более низкое значение приведет к сокращению времени выполнения, и его можно рассматривать как максимальный радиус окрестности от каждой точки для поиска других потенциальных достижимых точек.
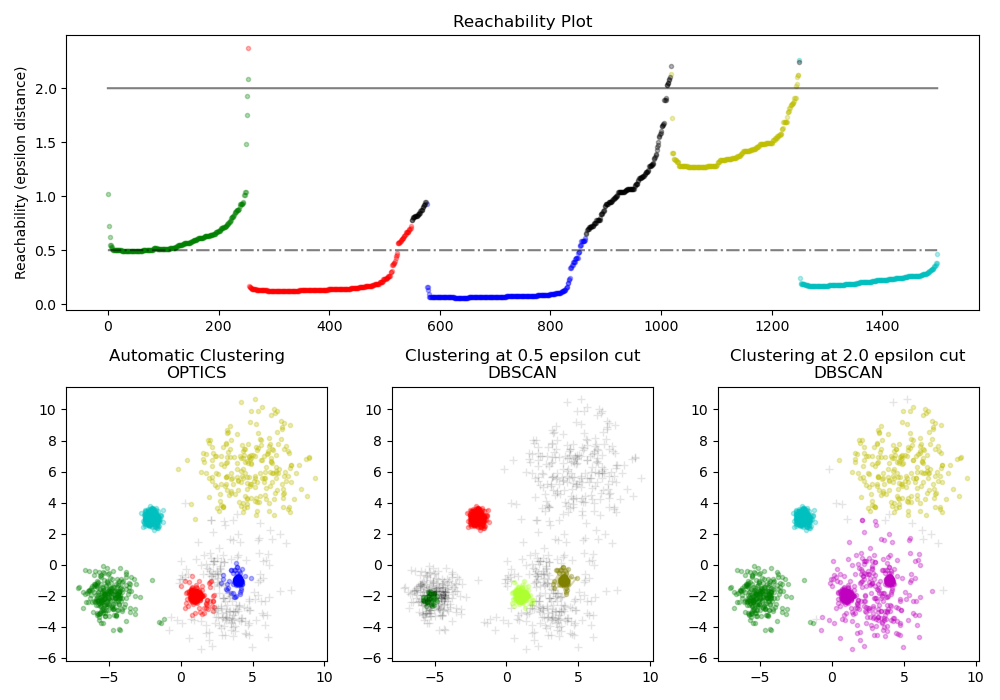
Расстояния достижимости, генерируемые OPTICS, позволяют извлекать кластеры с переменной плотностью в пределах одного набора данных. Как показано на приведенном выше графике, объединение расстояний достижимости и набора данных ordering_ дает график достижимости , где плотность точек представлена на оси Y, а точки упорядочены таким образом, что соседние точки являются смежными. «Вырезание» графика достижимости по одному значению дает результаты, подобные DBSCAN; все точки над «вырезом» классифицируются как шум, и каждый раз, когда есть перерыв при чтении слева направо, означает новый кластер. При извлечении кластеров по умолчанию с помощью OPTICS анализируются крутые уклоны на графике, чтобы найти кластеры, и пользователь может определить, что считается крутым уклоном, используя параметр xi. Существуют также другие возможности для анализа на самом графике, такие как создание иерархических представлений данных с помощью дендрограмм графика достижимости, а иерархия кластеров, обнаруженных алгоритмом, может быть доступна через cluster_hierarchy_ параметр. Приведенный выше график имеет цветовую кодировку, поэтому цвета кластеров в плоском пространстве соответствуют кластерам линейных сегментов на графике достижимости. Обратите внимание, что синий и красный кластеры находятся рядом на графике достижимости и могут быть иерархически представлены как дочерние элементы более крупного родительского кластера.
Сравнение с DBSCAN
Результаты cluster_optics_dbscan метода OPTICS и DBSCAN очень похожи, но не всегда идентичны; в частности, маркировка периферийных и шумовых точек. Отчасти это связано с тем, что первые образцы каждой плотной области, обработанной OPTICS, имеют большое значение достижимости, будучи близкими к другим точкам в своей области, и поэтому иногда будут помечены как шум, а не периферия. Это влияет на соседние точки, когда они рассматриваются как кандидаты на то, чтобы их пометить как периферию или как шум.
Обратите внимание, что для любого отдельного значения eps DBSCAN будет иметь более короткое время выполнения, чем OPTICS; однако для повторных запусков с разными eps значениями один запуск OPTICS может потребовать меньше совокупного времени выполнения, чем DBSCAN. Также важно отметить , что выход ОПТИКА» близок к DBSCAN, только если epsи max_eps близки.
Вычислительная сложность
Деревья пространственной индексации используются, чтобы избежать вычисления полной матрицы расстояний и обеспечить эффективное использование памяти для больших наборов выборок. С помощью metric ключевого слова можно указать различные метрики расстояния .
Для больших наборов данных аналогичные (но не идентичные) результаты можно получить с помощью HDBSCAN. Реализация HDBSCAN является многопоточной и имеет лучшую алгоритмическую сложность во время выполнения, чем OPTICS, за счет худшего масштабирования памяти. Для очень больших наборов данных, которые исчерпывают системную память с помощью HDBSCAN, OPTICS будет поддерживатьn (в отличие от $n^2$) масштабирование памяти; тем не менее, max_eps для получения решения в разумные сроки, вероятно, потребуется настройка параметра.
Рекомендации:
- «ОПТИКА: точки упорядочивания для определения структуры кластеризации». Анкерст, Михаэль, Маркус М. Бройниг, Ханс-Петер Кригель и Йорг Зандер. В ACM Sigmod Record, vol. 28, вып. 2. С. 49-60. ACM, 1999.
2.3.9. BIRCH (сбалансированное итеративное сокращение и кластеризация с использованием иерархий — balanced iterative reducing and clustering using hierarchies)
Для Birch заданных данных он строит дерево, называемое деревом функций кластеризации (CFT). Данные по существу сжимаются с потерями до набора узлов Clustering Feature (CF Nodes). Узлы CF имеют ряд подкластеров, называемых подкластерами функций кластеризации (подкластеры CF), и эти подкластеры CF, расположенные в нетерминальных узлах CF, могут иметь узлы CF в качестве дочерних.
Подкластеры CF содержат необходимую информацию для кластеризации, что избавляет от необходимости хранить все входные данные в памяти. Эта информация включает:
- Количество образцов в подкластере.
- Линейная сумма — n-мерный вектор, содержащий сумму всех выборок.
- Squared Sum — сумма квадратов нормы L2 всех выборок.
- Центроиды — чтобы избежать пересчета линейной суммы / n_samples.
- Квадратная норма центроидов.
Алгоритм BIRCH имеет два параметра: порог и коэффициент ветвления. Фактор ветвления ограничивает количество подкластеров в узле, а порог ограничивает расстояние между входящей выборкой и существующими подкластерами.
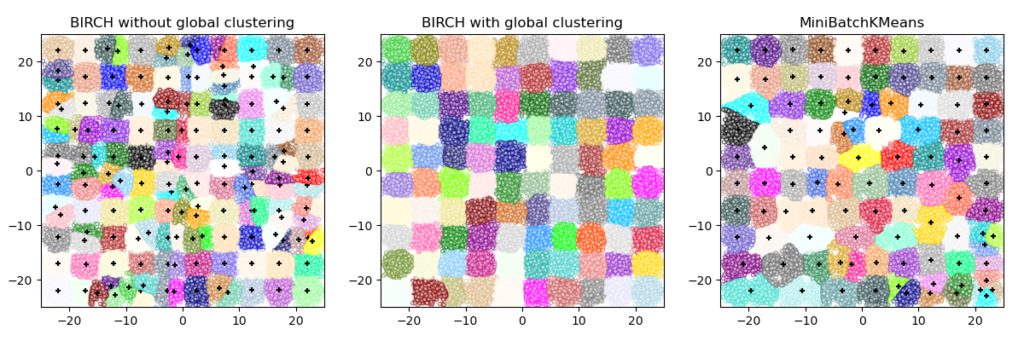
Этот алгоритм можно рассматривать как экземпляр или метод сокращения данных, поскольку он сокращает входные данные до набора подкластеров, которые получаются непосредственно из конечных точек CFT. Эти сокращенные данные могут быть дополнительно обработаны путем подачи их в глобальный кластеризатор. Этот глобальный кластеризатор может быть установлен с помощью n_clusters. Если n_clusters установлено значение None, подкластеры из листьев считываются напрямую, в противном случае шаг глобальной кластеризации помечает эти подкластеры в глобальные кластеры (метки), а выборки сопоставляются с глобальной меткой ближайшего подкластера.
Описание алгоритма:
- Новый образец вставляется в корень дерева CF, который является узлом CF. Затем он объединяется с подкластером корня, который имеет наименьший радиус после объединения, ограниченный пороговыми условиями и условиями фактора ветвления. Если у подкластера есть дочерний узел, то это повторяется до тех пор, пока он не достигнет листа. После нахождения ближайшего подкластера в листе свойства этого подкластера и родительских подкластеров рекурсивно обновляются.
- Если радиус подкластера, полученного путем слияния новой выборки и ближайшего подкластера, больше квадрата порога, и если количество подкластеров больше, чем коэффициент ветвления, то для этой новой выборки временно выделяется пространство. Берутся два самых дальних подкластера, и подкластеры делятся на две группы на основе расстояния между этими подкластерами.
- Если у этого разбитого узла есть родительский подкластер и есть место для нового подкластера, то родительский подкластер разбивается на два. Если места нет, то этот узел снова делится на две части, и процесс продолжается рекурсивно, пока не достигнет корня.
BIRCH или MiniBatchKMeans?
- BIRCH не очень хорошо масштабируется для данных большого размера. Как правило, если
n_featuresоно больше двадцати, лучше использовать MiniBatchKMeans. - Если количество экземпляров данных необходимо уменьшить или если требуется большое количество подкластеров в качестве этапа предварительной обработки или иным образом, BIRCH более полезен, чем MiniBatchKMeans.
Как использовать partial_fit?
Чтобы избежать вычисления глобальной кластеризации, при каждом обращении partial_fit пользователя рекомендуется
- Установить
n_clusters=Noneизначально - Обучите все данные несколькими вызовами partial_fit.
- Установите
n_clustersнеобходимое значение с помощьюbrc.set_params(n_clusters=n_clusters. - Вызов,
partial_fitнаконец, без аргументов, т.е.brc.partial_fit()который выполняет глобальную кластеризацию.
Рекомендации:
- Тиан Чжан, Рагху Рамакришнан, Марон Ливни БЕРЕЗА: эффективный метод кластеризации данных для больших баз данных. https://www.cs.sfu.ca/CourseCentral/459/han/papers/zhang96.pdf
- Роберто Пердиши JBirch — Java-реализация алгоритма кластеризации BIRCH https://code.google.com/archive/p/jbirch
2.3.10. Оценка эффективности кластеризации
Оценка производительности алгоритма кластеризации не так тривиальна, как подсчет количества ошибок или точности и отзыва контролируемого алгоритма классификации. В частности, любая метрика оценки должна учитывать не абсолютные значения меток кластера, а, скорее, если эта кластеризация определяет разделения данных, аналогичные некоторому основному набору истинных классов или удовлетворяющему некоторому предположению, так что члены, принадлежащие к одному классу, более похожи чем члены разных классов в соответствии с некоторой метрикой сходства.
2.3.10.1. Индекс Rand
Учитывая знания о назначениях базовых классов истинности labels_true и назначениях нашим алгоритмом кластеризации одних и тех же выборок labels_pred, (скорректированный или нескорректированный) индекс Рэнда — это функция, которая измеряет сходство двух назначений, игнорируя перестановки:
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2] >>> metrics.rand_score(labels_true, labels_pred) 0.66...
Индекс Rand не гарантирует получение значения, близкого к 0,0 при случайной маркировке. Скорректированный индекс Rand вносит поправку на случайность и дает такую основу.
>>> metrics.adjusted_rand_score(labels_true, labels_pred) 0.24...
Как и в случае со всеми метриками кластеризации, можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить ту же оценку:
>>> labels_pred = [1, 1, 0, 0, 3, 3] >>> metrics.rand_score(labels_true, labels_pred) 0.66... >>> metrics.adjusted_rand_score(labels_true, labels_pred) 0.24...
Более того, оба rand_score adjusted_rand_score они симметричны : замена аргумента не меняет оценок. Таким образом, их можно использовать в качестве критериев консенсуса:
>>> metrics.rand_score(labels_pred, labels_true) 0.66... >>> metrics.adjusted_rand_score(labels_pred, labels_true) 0.24...
Идеальная маркировка оценивается в 1,0:
>>> labels_pred = labels_true[:] >>> metrics.rand_score(labels_true, labels_pred) 1.0 >>> metrics.adjusted_rand_score(labels_true, labels_pred) 1.0
Плохо согласованные ярлыки (например, независимые ярлыки) имеют более низкие оценки, а для скорректированного индекса Rand оценка будет отрицательной или близкой к нулю. Однако для нескорректированного индекса Rand оценка, хотя и ниже, не обязательно будет близка к нулю:
>>> labels_true = [0, 0, 0, 0, 0, 0, 1, 1] >>> labels_pred = [0, 1, 2, 3, 4, 5, 5, 6] >>> metrics.rand_score(labels_true, labels_pred) 0.39... >>> metrics.adjusted_rand_score(labels_true, labels_pred) -0.07...
2.3.10.1.1. Преимущества
- Интерпретируемость : нескорректированный индекс Рэнда пропорционален количеству пар выборок, метки которых одинаковы в обоих
labels_predи /labels_trueили различаются в обоих. - Случайные (единообразные) присвоения меток имеют скорректированный балл индекса Rand, близкий к 0,0 для любого значения
n_clustersиn_samples(что не относится, например, к нескорректированному индексу Rand или V-мере). - Ограниченный диапазон : более низкие значения указывают на разные маркировки, аналогичные кластеры имеют высокий (скорректированный или нескорректированный) индекс Rand, 1,0 — это оценка идеального соответствия. Диапазон оценок составляет [0, 1] для нескорректированного индекса Rand и [-1, 1] для скорректированного индекса Rand.
- Не делается никаких предположений о структуре кластера: (скорректированный или нескорректированный) индекс Rand может использоваться для сравнения всех видов алгоритмов кластеризации и может использоваться для сравнения алгоритмов кластеризации, таких как k-средних, который предполагает изотропные формы капли с результатами спектрального анализа. алгоритмы кластеризации, которые могут найти кластер со «сложенными» формами.
2.3.10.1.2. Недостатки
- Вопреки инерции, (скорректированный или нескорректированный) индекс Рэнда требует знания основных классов истинности, что почти никогда не доступно на практике или требует ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения). Однако (скорректированный или нескорректированный) индекс Rand также может быть полезен в чисто неконтролируемой настройке в качестве строительного блока для консенсусного индекса, который может использоваться для выбора модели кластеризации (TODO).
- Нескорректированный индекс Rand часто близко к 1,0 , даже если самим кластеризациям существенно различаются. Это можно понять, интерпретируя индекс Рэнда как точность маркировки пар элементов, полученную в результате кластеризации: на практике часто существует большинство пар элементов, которым присваивается
differentметка пары как при прогнозируемой, так и при базовой кластеризации истинности, что приводит к высокой доля парных меток, которые согласны, что впоследствии приводит к высокой оценке.
Примеры:
- Поправка на случайность при оценке производительности кластеризации : анализ влияния размера набора данных на значение показателей кластеризации для случайных назначений.
2.3.10.1.3. Математическая постановка
Если C — это наземное присвоение класса истинности, а K — кластеризация, давайте определим $a$ и $b$ в виде:
- $a$, количество пар элементов, которые находятся в одном наборе в C и в одном наборе в K
- $b$, количество пар элементов, которые находятся в разных наборах в C и в разных наборах в K
Затем нескорректированный индекс Рэнда рассчитывается следующим образом: $$text{RI} = frac{a + b}{C_2^{n_{samples}}}$$
где $C_2^{n_{samples}}$ — общее количество возможных пар в наборе данных. Не имеет значения, выполняется ли расчет для упорядоченных пар или неупорядоченных пар, если расчет выполняется последовательно.
Однако индекс Rand не гарантирует, что случайные присвоения меток получат значение, близкое к нулю (особенно, если количество кластеров имеет тот же порядок величины, что и количество выборок).
Чтобы противостоять этому эффекту, мы можем дисконтировать ожидаемый RI. $E[text{RI}]$ случайных маркировок путем определения скорректированного индекса Rand следующим образом: $$text{ARI} = frac{text{RI} — E[text{RI}]}{max(text{RI}) — E[text{RI}]}$$
Рекомендации
- Сравнение разделов Л. Хуберт и П. Араби, Журнал классификации 1985 г.
- Свойства скорректированного индекса Рэнда Хьюберта- Араби Д. Стейнли, Психологические методы, 2004 г.
- Запись в Википедии для индекса Rand
- Запись в Википедии о скорректированном индексе Рэнда
2.3.10.2. Оценки на основе взаимной информации
Учитывая знания о назначениях базовых классов истинности labels_true и назначениях нашим алгоритмом кластеризации одних и тех же выборок labels_pred, взаимная информация — это функция, которая измеряет согласованность двух назначений, игнорируя перестановки. Доступны две различные нормализованные версии этой меры: нормализованная взаимная информация (NMI) и скорректированная взаимная информация (AMI) . NMI часто используется в литературе, в то время как AMI был предложен совсем недавно и нормируется на случайность :
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) 0.22504...
Можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить тот же результат:
>>> labels_pred = [1, 1, 0, 0, 3, 3] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) 0.22504...
Все, mutual_info_score, adjusted_mutual_info_scoreи normalized_mutual_info_scoreявляется симметричным: замена аргумента не меняет рейтинг. Таким образом, их можно использовать в качестве меры консенсуса :
>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true) 0.22504...
Идеальная маркировка оценивается в 1,0:
>>> labels_pred = labels_true[:] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) 1.0 >>> metrics.normalized_mutual_info_score(labels_true, labels_pred) 1.0
Это неверно mutual_info_score, поэтому судить о них труднее:
>>> metrics.mutual_info_score(labels_true, labels_pred) 0.69...
Плохие (например, независимые маркировки) имеют отрицательные оценки:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1] >>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2] >>> metrics.adjusted_mutual_info_score(labels_true, labels_pred) -0.10526...
2.3.10.2.1. Преимущества
- Случайные (унифицированные) присвоения меток имеют оценку AMI, близкую к 0,0 для любого значения
n_clustersиn_samples(что не относится, например, к необработанной взаимной информации или V-мере). - Верхняя граница 1 : значения, близкие к нулю, указывают на два назначения меток, которые в значительной степени независимы, а значения, близкие к единице, указывают на значительное согласие. Кроме того, AMI, равный ровно 1, указывает, что два присвоения меток равны (с перестановкой или без нее).
2.3.10.2.2. Недостатки
- Вопреки инерции, меры на основе MI требуют знания основных классов истинности, хотя на практике они почти никогда не доступны или требуют ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения).
Однако показатели на основе MI также могут быть полезны в чисто неконтролируемой настройке в качестве строительного блока для согласованного индекса, который можно использовать для выбора модели кластеризации
- NMI и MI не подвергаются случайной корректировке.
Примеры:
- Поправка на случайность при оценке производительности кластеризации: анализ влияния размера набора данных на значение показателей кластеризации для случайных назначений. Этот пример также включает скорректированный индекс ранда.
2.3.10.2.3. Математическая постановка
Предположим, что два присвоения метки (одних и тех же N объектов), $U$ а также $V$. Их энтропия — это величина неопределенности для набора разбиений, определяемая следующим образом:
$$H(U) = — sum_{i=1}^{|U|}P(i)log(P(i))$$
где $P(i) = |U_i| / N$ вероятность того, что объект выбран наугад из $U$ попадает в класс $U_i$. Аналогично дляV:
$$H(V) = — sum_{j=1}^{|V|}P'(j)log(P'(j))$$
С участием $P'(j) = |V_j| / N$. Взаимная информация (MI) между $U$ и $V$ рассчитывается по:
$$text{MI}(U, V) = sum_{i=1}^{|U|}sum_{j=1}^{|V|}P(i, j)logleft(frac{P(i,j)}{P(i)P'(j)}right)$$
где $P(i, j) = |U_i cap V_j| / N$ вероятность того, что случайно выбранный объект попадает в оба класса $U_i$ а также $V_j$.
Это также может быть выражено в формулировке множества элементов:
$$text{MI}(U, V) = sum_{i=1}^{|U|} sum_{j=1}^{|V|} frac{|U_i cap V_j|}{N}logleft(frac{N|U_i cap V_j|}{|U_i||V_j|}right)$$
Нормализованная взаимная информация определяется как
$$text{NMI}(U, V) = frac{text{MI}(U, V)}{text{mean}(H(U), H(V))}$$
Это значение взаимной информации, а также нормализованного варианта не скорректировано на случайность и будет иметь тенденцию к увеличению по мере увеличения количества различных меток (кластеров), независимо от фактического количества «взаимной информации» между назначениями меток.
Ожидаемое значение для взаимной информации можно рассчитать с помощью следующего уравнения [VEB2009] . В этом уравнении $a_i = |U_i|$ (количество элементов в $U_i$) а также $b_j = |V_j|$ (количество элементов в $V_j$).
$$E[text{MI}(U,V)]=sum_{i=1}^{|U|} sum_{j=1}^{|V|} sum_{n_{ij}=(a_i+b_j-N)^+ }^{min(a_i, b_j)} frac{n_{ij}}{N}log left( frac{ N.n_{ij}}{a_i b_j}right) frac{a_i!b_j!(N-a_i)!(N-b_j)!}{N!n_{ij}!(a_i-n_{ij})!(b_j-n_{ij})! (N-a_i-b_j+n_{ij})!}$$
Используя ожидаемое значение, скорректированная взаимная информация может быть затем рассчитана с использованием формы, аналогичной форме скорректированного индекса Rand:
$$text{AMI} = frac{text{MI} — E[text{MI}]}{text{mean}(H(U), H(V)) — E[text{MI}]}$$
Для нормализованной взаимной информации и скорректированной взаимной информации нормализующее значение обычно представляет собой некоторое обобщенное среднее энтропий каждой кластеризации. Существуют различные обобщенные средства, и не существует твердых правил предпочтения одного по сравнению с другим. Решение в основном принимается отдельно для каждого поля; например, при обнаружении сообществ чаще всего используется среднее арифметическое. Каждый метод нормализации обеспечивает «качественно похожее поведение» [YAT2016] . В нашей реализации это контролируется average_methodпараметром.
Vinh et al. (2010) назвали варианты NMI и AMI методом их усреднения [VEB2010] . Их средние «sqrt» и «sum» являются средними геометрическими и арифметическими; мы используем эти более общие имена.
2.3.10.3. Однородность, полнота и V-мера
Зная о назначении основных классов истинности выборкам, можно определить некоторую интуитивно понятную метрику, используя условный энтропийный анализ.
В частности, Розенберг и Хиршберг (2007) определяют следующие две желательные цели для любого кластерного задания:
- однородность : каждый кластер содержит только членов одного класса.
- полнота : все члены данного класса относятся к одному кластеру.
Мы можем превратить эти концепции в партитуры homogeneity_score и completeness_score. Оба ограничены снизу 0,0 и выше 1,0 (чем выше, тем лучше):
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2] >>> metrics.homogeneity_score(labels_true, labels_pred) 0.66... >>> metrics.completeness_score(labels_true, labels_pred) 0.42...
Их гармоническое среднее значение, называемое V-мерой , вычисляется по формуле v_measure_score:
>>> metrics.v_measure_score(labels_true, labels_pred) 0.51...
Формула этой функции выглядит следующим образом:
$$v = frac{(1 + beta) times text{homogeneity} times text{completeness}}{(beta times text{homogeneity} + text{completeness})}$$
beta по умолчанию используется значение 1.0, но для использования значения менее 1 для бета-версии:
>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6) 0.54...
больший вес будет приписан однородности, а использование значения больше 1:
>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8) 0.48...
больший вес будет приписан полноте.
V-мера фактически эквивалентна описанной выше взаимной информации (NMI), при этом функция агрегирования является средним арифметическим [B2011] .
Однородность, полнота и V-мера могут быть вычислены сразу, используя homogeneity_completeness_v_measure следующее:
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred) (0.66..., 0.42..., 0.51...)
Следующее назначение кластеризации немного лучше, поскольку оно однородное, но не полное:
>>> labels_pred = [0, 0, 0, 1, 2, 2] >>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred) (1.0, 0.68..., 0.81...)
Примечание:
v_measure_score является симметричным : его можно использовать для оценки соответствия двух независимых присвоений одному и тому же набору данных.
Это не относится к completeness_score и homogeneity_score: оба связаны отношениями:
homogeneity_score(a, b) == completeness_score(b, a)
2.3.10.3.1. Преимущества
- Ограниченные баллы : 0,0 — это настолько плохо, насколько это возможно, 1,0 — идеальный балл.
- Интуитивная интерпретация: кластеризацию с плохой V-мерой можно качественно проанализировать с точки зрения однородности и полноты, чтобы лучше понять, какие «ошибки» допускаются при задании.
- Не делается никаких предположений о структуре кластера : может использоваться для сравнения алгоритмов кластеризации, таких как k-среднее, которое предполагает изотропные формы капли, с результатами алгоритмов спектральной кластеризации, которые могут находить кластер со «сложенными» формами.
2.3.10.3.2. Недостатки
- Ранее введенные метрики не нормализованы в отношении случайной маркировки : это означает, что в зависимости от количества выборок, кластеров и основных классов истинности полностью случайная маркировка не всегда будет давать одинаковые значения для однородности, полноты и, следовательно, v-меры.
В частности, случайная маркировка не даст нулевых оценок, особенно когда количество кластеров велико. Эту проблему можно спокойно игнорировать, если количество выборок больше тысячи, а количество кластеров меньше 10. Для меньших размеров выборки или большего количества кластеров безопаснее использовать скорректированный индекс, такой как Скорректированный индекс ранда (ARI) .
- Эти метрики требуют знания основных классов истинности, хотя почти никогда не доступны на практике или требуют ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения).
Примеры:
- Поправка на случайность при оценке производительности кластеризации : анализ влияния размера набора данных на значение показателей кластеризации для случайных назначений.
2.3.10.3.3. Математическая постановка
Оценки однородности и полноты формально даются по формуле:
$$h = 1 — frac{H(C|K)}{H(C)}$$
$$c = 1 — frac{H(K|C)}{H(K)}$$
где $H(C|K)$ является условной энтропией классов с учетом кластерных назначений и определяется выражением:
$$H(C|K) = — sum_{c=1}^{|C|} sum_{k=1}^{|K|} frac{n_{c,k}}{n} cdot logleft(frac{n_{c,k}}{n_k}right)$$
а также $H(C)$ — энтропия классов и определяется выражением:
$$H(C) = — sum_{c=1}^{|C|} frac{n_c}{n} cdot logleft(frac{n_c}{n}right)$$
с участием n общее количество образцов, $n_c$ а также $n_k$ количество образцов, соответственно принадлежащих к классу c и кластер $k$, и наконец $n_{c, k}$ количество образцов из класса c назначен кластеру k.
Условная энтропия кластеров данного класса $H(C|K)$ и энтропия кластеров $H(K)$ определены симметричным образом.
Розенберг и Хиршберг далее определяют V-меру как гармоническое среднее однородности и полноты:
$$v = 2 cdot frac{h cdot c}{h + c}$$
2.3.10.4. Результаты Фаулкса-Мэллоуса
Индекс Фаулкса-Мэллоуса ( sklearn.metrics.fowlkes_mallows_score) может использоваться, когда известны наземные присвоения классов истинности выборкам. FMI по шкале Fowlkes-Mallows определяется как среднее геометрическое для попарной точности и отзыва:
$$text{FMI} = frac{text{TP}}{sqrt{(text{TP} + text{FP}) (text{TP} + text{FN})}}$$
Где TP— количество истинных положительных результатов (True Positive) (т.е. количество пар точек, принадлежащих одним и тем же кластерам как в истинных, так и в предсказанных метках), FP— это количество ложных положительных результатов (False Positive) (то есть количество пар точек, принадлежащих к одинаковые кластеры в истинных метках, а не в предсказанных метках) и FN является количеством ложно-отрицательных (False Negative) (т. е. количеством пар точек, принадлежащих одним и тем же кластерам в предсказанных метках, а не в истинных метках).
Оценка варьируется от 0 до 1. Высокое значение указывает на хорошее сходство между двумя кластерами.
>>> from sklearn import metrics >>> labels_true = [0, 0, 0, 1, 1, 1] >>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 0.47140...
Можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить тот же результат:
>>> labels_pred = [1, 1, 0, 0, 3, 3] >>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 0.47140...
Идеальная маркировка оценивается в 1,0:
>>> labels_pred = labels_true[:] >>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 1.0
Плохие (например, независимые маркировки) имеют нулевые баллы:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1] >>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2] >>> metrics.fowlkes_mallows_score(labels_true, labels_pred) 0.0
2.3.10.4.1. Преимущества
- Случайное (единообразное) присвоение меток имеет оценку FMI, близкую к 0,0 для любого значения
n_clustersиn_samples(что не относится, например, к необработанной взаимной информации или V-мере). - Верхний предел — 1 : значения, близкие к нулю, указывают на два назначения меток, которые в значительной степени независимы, а значения, близкие к единице, указывают на значительное согласие. Кроме того, значения ровно 0 указывают на чисто независимые присвоения меток, а FMI ровно 1 указывает, что два назначения меток равны (с перестановкой или без нее).
- Не делается никаких предположений о структуре кластера : может использоваться для сравнения алгоритмов кластеризации, таких как k-среднее, которое предполагает изотропные формы капли, с результатами алгоритмов спектральной кластеризации, которые могут находить кластер со «сложенными» формами.
2.3.10.4.2. Недостатки
- Вопреки инерции, меры, основанные на FMI, требуют знания основных классов истинности, хотя почти никогда не доступны на практике или требуют ручного назначения аннотаторами-людьми (как в условиях контролируемого обучения).
Рекомендации
- EB Fowkles и CL Mallows, 1983. «Метод сравнения двух иерархических кластеров». Журнал Американской статистической ассоциации. http://wildfire.stat.ucla.edu/pdflibrary/fowlkes.pdf
- Запись в Википедии об Индексе Фаулкса-Маллоуза
2.3.10.5. Коэффициент силуэта
Если наземные метки достоверности неизвестны, оценка должна выполняться с использованием самой модели. Коэффициент силуэта ( sklearn.metrics.silhouette_score) является примером такой оценки, где более высокий показатель коэффициента силуэта относится к модели с лучше определенными кластерами. Коэффициент силуэта определяется для каждого образца и состоит из двух баллов:
- a : Среднее расстояние между образцом и всеми другими точками того же класса.
- b : Среднее расстояние между образцом и всеми другими точками в следующем ближайшем кластере .
Тогда коэффициент силуэта s для одного образца определяется как:
$$s = frac{b — a}{max(a, b)}$$
Коэффициент силуэта для набора образцов дается как среднее значение коэффициента силуэта для каждого образца.
>>> from sklearn import metrics >>> from sklearn.metrics import pairwise_distances >>> from sklearn import datasets >>> X, y = datasets.load_iris(return_X_y=True)
При обычном использовании коэффициент силуэта применяется к результатам кластерного анализа.
>>> import numpy as np >>> from sklearn.cluster import KMeans >>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X) >>> labels = kmeans_model.labels_ >>> metrics.silhouette_score(X, labels, metric='euclidean') 0.55...
Рекомендации
- Питер Дж. Руссеу (1987). «Силуэты: графическое средство для интерпретации и проверки кластерного анализа». Вычислительная и прикладная математика 20: 53–65. DOI: 10.1016 / 0377-0427 (87) 90125-7 .
2.3.10.5.1. Преимущества
- Оценка ограничена от -1 за неправильную кластеризацию до +1 за высокоплотную кластеризацию. Баллы около нуля указывают на перекрывающиеся кластеры.
- Оценка выше, когда кластеры плотные и хорошо разделенные, что относится к стандартной концепции кластера.
2.3.10.5.2. Недостатки
- Коэффициент силуэта обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, подобные тем, которые получены с помощью DBSCAN.
Примеры:
- Выбор количества кластеров с анализом силуэта в кластеризации KMeans : в этом примере анализ силуэта используется для выбора оптимального значения для n_clusters.
2.3.10.6. Индекс Калински-Харабаса
Если наземные метки достоверности неизвестны, индекс Калински-Харабаса ( sklearn.metrics.calinski_harabasz_score) — также известный как критерий отношения дисперсии — можно использовать для оценки модели, где более высокий балл Калински-Харабаса относится к модели с более определенными кластерами.
Индекс представляет собой отношение суммы дисперсии между кластерами и дисперсии внутри кластера для всех кластеров (где дисперсия определяется как сумма квадратов расстояний):
>>> from sklearn import metrics >>> from sklearn.metrics import pairwise_distances >>> from sklearn import datasets >>> X, y = datasets.load_iris(return_X_y=True)
При обычном использовании индекс Калински-Харабаса применяется к результатам кластерного анализа:
>>> import numpy as np >>> from sklearn.cluster import KMeans >>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X) >>> labels = kmeans_model.labels_ >>> metrics.calinski_harabasz_score(X, labels) 561.62...
2.3.10.6.1. Преимущества
- Оценка выше, когда кластеры плотные и хорошо разделенные, что относится к стандартной концепции кластера.
- Счет быстро подсчитывается.
2.3.10.6.2. Недостатки
- Индекс Калински-Харабаса обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, подобные тем, которые получены с помощью DBSCAN.
2.3.10.6.3. Математическая постановка
Для набора данных $E$ размера $n_E$ который был сгруппирован в $k$ кластеры, оценка Калински-Харабаса $s$ определяется как отношение средней дисперсии между кластерами и дисперсии внутри кластера:
$$s = frac{mathrm{tr}(B_k)}{mathrm{tr}(W_k)} times frac{n_E — k}{k — 1}$$
где $tr(B_k)$ является следом межгрупповой дисперсионной матрицы и $tr(W_k)$ является следом матрицы дисперсии внутри кластера, определяемой следующим образом:
$$W_k = sum_{q=1}^k sum_{x in C_q} (x — c_q) (x — c_q)^T$$
$$B_k = sum_{q=1}^k n_q (c_q — c_E) (c_q — c_E)^T$$
с участием $C_q$ набор точек в кластере $q$, $c_q$ центр кластера $q$, $c_E$ центр $E$, а также $n_q$ количество точек в кластере $q$.
Рекомендации
- Калински Т. и Харабаш Дж. (1974). «Дендритный метод кластерного анализа» . Коммуникации в теории статистики и методах 3: 1-27. DOI: 10.1080 / 03610927408827101 .
2.3.10.7. Индекс Дэвиса-Болдина
Если наземные метки истинности неизвестны, для оценки модели можно использовать индекс Дэвиса-Болдина (sklearn.metrics.davies_bouldin_score), где более низкий индекс Дэвиса-Болдина относится к модели с лучшим разделением между кластерами.
Этот индекс означает среднее «сходство» между кластерами, где сходство — это мера, которая сравнивает расстояние между кластерами с размером самих кластеров.
Ноль — это наименьший возможный результат. Значения, близкие к нулю, указывают на лучшее разделение.
При обычном использовании индекс Дэвиса-Болдина применяется к результатам кластерного анализа следующим образом:
>>> from sklearn import datasets >>> iris = datasets.load_iris() >>> X = iris.data >>> from sklearn.cluster import KMeans >>> from sklearn.metrics import davies_bouldin_score >>> kmeans = KMeans(n_clusters=3, random_state=1).fit(X) >>> labels = kmeans.labels_ >>> davies_bouldin_score(X, labels) 0.6619...
2.3.10.7.1. Преимущества
- Вычисление Дэвиса-Боулдина проще, чем оценка Силуэта.
- В индексе вычисляются только количества и характеристики, присущие набору данных.
2.3.10.7.2. Недостатки
- Индекс Дэвиса-Боулдинга обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, подобные тем, которые получены из DBSCAN.
- Использование центроидного расстояния ограничивает метрику расстояния евклидовым пространством.
2.3.10.7.3. Математическая постановка
Индекс определяется как среднее сходство между каждым кластером. $C_i$ для $i=1, …, k$ и его самый похожий $C_j$. В контексте этого индекса сходство определяется как мера $R_{ij}$ что торгуется:
- $s_i$, среднее расстояние между каждой точкой кластера $i$ и центроид этого кластера — также известный как диаметр кластера.
- $d_{ij}$, расстояние между центрами скоплений $i$ а также $j$.
Простой выбор для построения $R_{ij}$ так что он неотрицателен и симметричен:
$$R_{ij} = frac{s_i + s_j}{d_{ij}}$$
Тогда индекс Дэвиса-Болдина определяется как:
$$DB = frac{1}{k} sum_{i=1}^k max_{i neq j} R_{ij}$$
Рекомендации
- Дэвис, Дэвид Л .; Боулдин, Дональд В. (1979). «Мера разделения кластеров» IEEE-транзакции по анализу шаблонов и машинному интеллекту. ПАМИ-1 (2): 224-227. DOI: 10.1109 / TPAMI.1979.4766909 .
- Халкиди, Мария; Батистакис, Яннис; Вазиргианнис, Михалис (2001). «О методах кластеризации валидации» Журнал интеллектуальных информационных систем, 17 (2-3), 107-145. DOI: 10,1023 / А: 1012801612483 .
- Запись в Википедии для индекса Дэвиса-Болдина .
2.3.10.8. Матрица непредвиденных обстоятельств
Матрица непредвиденных обстоятельств ( sklearn.metrics.cluster.contingency_matrix) сообщает мощность пересечения для каждой истинной / прогнозируемой пары кластеров. Матрица непредвиденных обстоятельств обеспечивает достаточную статистику для всех метрик кластеризации, где выборки независимы и одинаково распределены, и нет необходимости учитывать некоторые экземпляры, которые не были кластеризованы.
Вот пример:
>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
[0, 1, 2]])
Первая строка выходного массива указывает, что есть три образца, истинный кластер которых равен «a». Из них два находятся в предсказанном кластере 0, один — в 1 и ни один — в 2. И вторая строка указывает, что есть три выборки, истинный кластер которых равен «b». Из них ни один не находится в прогнозируемом кластере 0, один — в 1, а два — в 2.
Матрица неточностей для классификации является квадратной матрицей непредвиденной где порядок строк и столбцов соответствует списку классов.
2.3.10.8.1. Преимущества
- Позволяет изучить распространение каждого истинного кластера по прогнозируемым кластерам и наоборот.
- Вычисленная таблица непредвиденных обстоятельств обычно используется при вычислении статистики сходства (как и другие, перечисленные в этом документе) между двумя кластерами.
2.3.10.8.2. Недостатки
- Матрицу непредвиденных обстоятельств легко интерпретировать для небольшого количества кластеров, но становится очень трудно интерпретировать для большого количества кластеров.
- Он не дает ни одной метрики для использования в качестве цели для оптимизации кластеризации.
2.3.10.9. Матрица неточности пар
Матрица смешения пар ( sklearn.metrics.cluster.pair_confusion_matrix) представляет собой матрицу подобия 2×2
$$begin{split}C = left[begin{matrix}
C_{00} & C_{01}
C_{10} & C_{11}
end{matrix}right]end{split}$$
между двумя кластерами, вычисленными путем рассмотрения всех пар выборок и подсчета пар, которые назначены в один и тот же или в разные кластеры в рамках истинной и прогнозируемой кластеризации.
В нем есть следующие записи:
$C_{00}$: количество пар с обеими кластерами, в которых образцы не сгруппированы вместе
$C_{10}$: количество пар с истинной кластеризацией меток, в которых образцы сгруппированы вместе, но в другой кластеризации образцы не сгруппированы вместе
$C_{01}$: количество пар с истинной кластеризацией меток, в которых образцы не сгруппированы вместе, а другая кластеризация содержит образцы, сгруппированные вместе
$C_{11}$: количество пар с обеими кластерами, имеющими образцы, сгруппированные вместе
Если рассматривать пару образцов, сгруппированных вместе как положительную пару, то, как и в бинарной классификации, количество истинных отрицательных значений равно $C_{00}$, ложноотрицательные $C_{10}$, истинные положительные стороны $C_{11}$ а ложные срабатывания $C_{01}$.
Идеально совпадающие метки имеют все ненулевые записи на диагонали независимо от фактических значений меток:
>>> from sklearn.metrics.cluster import pair_confusion_matrix
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 1])
array([[8, 0],
[0, 4]])
>>> pair_confusion_matrix([0, 0, 1, 1], [1, 1, 0, 0])
array([[8, 0],
[0, 4]])
Метки, которые назначают все члены классов одним и тем же кластерам, являются полными, но не всегда могут быть чистыми, следовательно, наказываются и имеют некоторые недиагональные ненулевые записи:
>>> pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])
array([[8, 2],
[0, 2]])
Матрица не симметрична:
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 2])
array([[8, 0],
[2, 2]])
Если члены классов полностью разделены по разным кластерам, назначение полностью неполное, следовательно, матрица имеет все нулевые диагональные элементы:
>>> pair_confusion_matrix([0, 0, 0, 0], [0, 1, 2, 3])
array([[ 0, 0],
[12, 0]])
Рекомендации
- Л. Хьюберт и П. Араби, Сравнение разделов, журнал классификации 1985 < https://link.springer.com/article/10.1007%2FBF01908075 > _
Ни один опытный SEO-специалист не работает с сайтом без сбора семантического ядра. В идеале это делают еще во время планирования сайта, а уже потом обдумывают и структуру, и контент, и продвижение. Но чтобы список релевантных поисковых запросов и ключевых слов превратился в смысловую основу сайта, их нужно объединить в тематические кластеры по смыслу. Расскажем о кластеризации семантического ядра подробнее.
Определение кластеризации
Под кластеризацией ядра понимается деление имеющегося множества ключей на кластеры (группы по смыслу). Каждому кластеру должен соответствовать индивидуальный лендинг на сайте.
Если ключи грамотно сгруппированы, это сказывается на ранжировании в поисковой выдаче. Каждый лендинг создается осмысленно,а каждому из кластеров соответствует интересный конечному пользователю контент. Страницы, созданные под конкретные запросы, легко выходят в топ поисковой выдачи, что снижает расходы на продвижение сайта.
Один и тот же кластер объединяет разные ключевые слова, по которым потенциальные клиенты ищут примерно одно и то же. Это могут быть как синонимы, так и просто запросы, близкие по смыслу (к примеру, пользователи, ищущие «магазин обуви» и «обувь», на самом деле ищут, где эту обувь можно купить).
Ключи из одного и того же кластера, как правило, распределяются по одному лендингу, причем основной ключ идет в начале.
Читайте также: «Как составить семантическое ядро»
Поисковый интент
Начальный этап сортировки поисковых запросов — это определение поискового интента (намерения пользователя при поиске информации). Интент используется поисковыми системами для выдачи сайтов и веб-страниц, близких по смыслу тому, что ищет пользователь.
Интент бывает информационным (с целью информирования о чем-либо) или коммерческим (с целью покупки товаров и услуг). Один и тот же запрос может приобретать информационный или коммерческий интент в зависимости от спроса, его сезонности, доступности товара и других факторов.
Поисковый запрос с различным целями поиска: информационным и коммерческим
Сортировать ключи по интенту можно в том числе по фактору присутствия коммерческой составляющей: наиболее «коммерческие» запросы стоит соотносить с коммерческими лендингами, наименее — с информационными.
Распространенная ошибка — совмещение ключей с разным интентом в пределах одной страницы. Чаще всего, когда человек ищет информацию о каком-то объекте или уточняет детали, он не собирается ничего купить. К примеру, если пользователь интересуется, как починить компьютер, он вряд ли принял решение о покупке нового, а если ищет советы стилиста, заказывать одежду он если и будет, то позже. Совмещение фраз с коммерческим и информационным интентом ведет к снижению релевантности веб-страницы, повышению нецелевого трафика и процента отказов.
Александр Шестаков, руководитель направления ссылочных продуктов Links.Sape:
«Кластеризовать семантическое ядро можно различными способами. В числе основных: методы отбора по поисковому интенту, непосредственно по семантике и по соответствию топ-10 поисковой выдачи.
Семантика — самое широкое понятие, разделяющее все запросы на две объемные группы: коммерческие и информационные. Эти категории всегда продвигают на разных страницах сайта, не смешивая их.
Интент категоризирует запросы более узко, обозначая схожие намерения у разных групп пользователей. Размещать получившиеся кластеры можно на одних страницах, внимательно анализируя значения слов и поведенческие факторы.
При анализе топ-10 поисковой выдачи SEO-специалист ищет запросы, по которым в выдаче обнаруживаются общие результаты, и формирует кластеры исходя из таких пересечений. При этом строгость отбора может варьироваться: оптимизатор может ограничиться тем, чтобы каждый запрос пересекался только с 1-2 другими из того же кластера, а может оставить в кластере только те, которые пересекаются со всеми остальными одновременно. Чем выше требования к количеству пересечений, тем больше времени займет анализ. Скорее всего, кластер запросов в этом случае получится меньшего размера, но он будет более релевантным».
Методы кластеризации запросов
Существует несколько вариантов кластеризации поисковых запросов: как правило, они применяются в сочетании друг с другом. Перечислим и объясним основные методы.
Логическое разбиение
Это точечный инструмент ядер для небольших семантических, предполагающий ручную работу SEO-специалиста, который самостоятельно определяет релевантность каждого запроса по смыслу. Это кропотливая, но довольно действенная схема.
Читайте также: «SEO-продвижение интернет-магазина для начинающих»
По семантической схожести
Этот метод кластеризации осуществляется при помощи искусственного интеллекта, способного объединять поисковые запросы в кластеры по близости семантики, причем лексикографическое сходство ключей не является обязательным критерием.
Для недавно созданного сайта кластеризация по семантической схожести не работает: для нее нужно большое семантическое ядро. Ну и при автоматической кластеризации не учитывается коммерческая составляющая запросов, потому сортировать ключи по интенту придется вручную.
Группировка по топам
Кластеризация запросов по топам считается наиболее точным и действенным методом. В его основе лежит объединение в кластеры согласно базе сайтов из топа поисковой выдачи Google и Яндекс. Для кластеризации по топам используются специальные программы, о которых мы расскажем чуть позже. Проводить ее можно тремя методами.
Soft
В основе так называемого мягкого метода кластеризации находится высокочастотный ключ, являющийся своего рода связующим звеном с остальными ключами в группе, которые вообще могут не пересекаться друг с другом по URL. Достоинство этого метода заключается в большом объеме данных, но точность группировки при этом оставляет желать лучшего. Для информационных сайтов и небольших интернет-магазинов такой метод вполне подходит для увеличения трафика, но вот с целевыми запросами уже могут быть проблемы.
Hard
Жесткий метод кластеризации основан на наличии общего набора страниц в поисковой выдаче по всем входящим в группу ключам. Ключ не включается в кластер, если он находится за порогом пересечения с остальными: к примеру, если у вас есть порог в 3 URL, то каждый запрос должен совпадать с остальными фразами трижды. При таком пороге пересечений точность результатов достигает целых 90%, но объем кластера выходит значительно меньше, чем при мягком методе. Подобная методика идеально подходит для высококонкурентных ниш, в которых необходима высокая релевантность лендингов выбранным ключам: большинство интернет-магазинов вполне соответствует этому требованию.
Moderate или Middle
Этот метод представляет собой нечто среднее между двумя перечисленными выше. В отдельной группе каждый запрос должен быть связан с другими. Кластер же напоминает некое облако взаимосвязанных фраз без жестких требований по порогу пересечения, и коэффициенты пересечений адресов в топе у соседних ключей могут отличаться друг от друга.
Анна Юдачева. Индивидуальный предприниматель (ведет два производственных проекта и один по транспортным перевозкам; работает с маркетплейсами):
«Составление семантического ядра – первое с чего начинается работа над проектом. На первоначальном этапе должны быть выделены профильные направления деятельности организации. Это должны быть отдельные самостоятельные блоки, которые состоят из высокочастотных запросов.
Приведу пример кластеризации по контекстной рекламе для
завода по производству строительного материала – керамзита. Важными блоками будут такие разделы как «Керамзит», «Керамзитобетонные блоки», «Керамзитобетон» и др. Далее необходимо проработать каждый раздел на среднечастотные и низкочастотные запросы, из которых потом будет проводиться кластеризация по рекламным блокам. Остановимся на разделе «Керамзит», на этом этапе должно быть хорошее погружение в деятельность компании. Важно понимать, какие виды продукции выпускает завод, варианты фасовки, каким транспортным средством перевозят (водный, автомобильный, ж/д) и многое другое. Изучив эту информацию, маркетолог приступает к формированию среднечастотных и низкочастотных запросов, например «керамзит купить», «керамзит 10 20 мм», «керамзит в мешках », «сухая засыпка», «керамзит с доставкой» и т.д.
На следующем этапе необходимо проанализировать, с какими соседними городами или странами сотрудничает предприятие. Таким образом, первый кластер СЯ по выделенной теме может быть поделен по странам или по городам, куда отправляют груз. Соответственно, подобранные запросы будут повторяться в каждом блоке контекстной рекламы, но различаться по геолокации и цене запроса.
Второй способ кластеризации: «по определяющему слову» выделенных запросов для продвижения, например «купить», «заказать», «цена», «фракции». То есть в каждом блоке будут запросы с указанными вхождениями. При такой работе очень важно отминусовать запросы из соседних блоков, чтобы не было дублей ключевиков и не составлять самим себе конкуренцию и удорожать запрос. Например, в группе объявлений «купить», необходимо прописать минус-слова «цена», «в мешках», т.е. показывая рекламу по ключевому слову «купить керамзит» за счет минус-слов мы не будем дублировать запрос «купить керамзит в мешках», который будет показываться в кластере «в мешках».
И последний кластер, который хотела бы выделить — это деление рекламы на блоки по продукции, т.е. в разделе «керамзит» будут кластеры исключительно по видам продукции «керамзит 0 5 мм», «керамзит 5 10 мм», «керамзит 10 20 мм».
Отмечу, что выбор кластера должен быть сформирован от задач, которые стоят перед маркетологом. Если нужно продать любую фракцию керамзита фасованного именно в мешки, то это одна работа, а если нужно продать определенную фракцию любой фасовки, то деление на блоки будет другим».
Способы кластеризации ядра
Группировать ключи можно двумя основными способами — вручную либо автоматически.
Ручная кластеризация
Ручной способ применяется в основном при логическом разбиении. Но так как при этом методе возможны ошибки, готовые кластеры надо перепроверять: на группировку и перепроверки ядра, состоящего из 100 ключевиков, требуется полноценный рабочий день.
Ограничиться только ручной кластеризацией возможно лишь для небольших сайтов, где не нужно гнаться за высокой точностью. Однако грамотный специалист, владеющий конкретной тематикой, может сделать кластеры вручную так, что результат будет релевантен требованиям целевой аудитории. Вести статистику в таком случае целесообразно в Excel, LibreOffice Calc, Google Spreadsheets или аналогичных программах.
Автоматическая кластеризация
Большинство популярных онлайн-сервисов для кластеризации семантического ядра основано на топе поисковой выдачи. Более точные настройки уже зависят от конкретного сервиса: вручную задаются порог совпадений, поисковая система и регион. Стоимость кластеризации зависит от объема семантического ядра.
А теперь кратко расскажем об основных используемых программах для автоматической кластеризации.
Key Collector
Это платная профессиональная программа с бессрочной лицензией для работы с семантическим ядром. Делить запросы на группы можно по тегам групп, по поисковой выдаче и конкурентам в ней, отдельным словам или составу фраз.
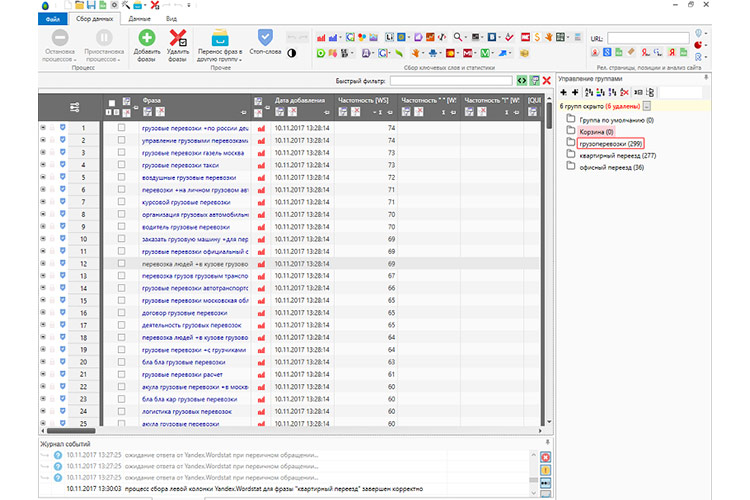
Программа Key Collector
KeyAssort
У этой программы существуют две версии : бесплатная демо-версия и платная полная. С ее помощью возможна кластеризация поисковых запросов, формирование структуры сайта на основе результатов и отчета по лидерам топа поисковой выдачи.
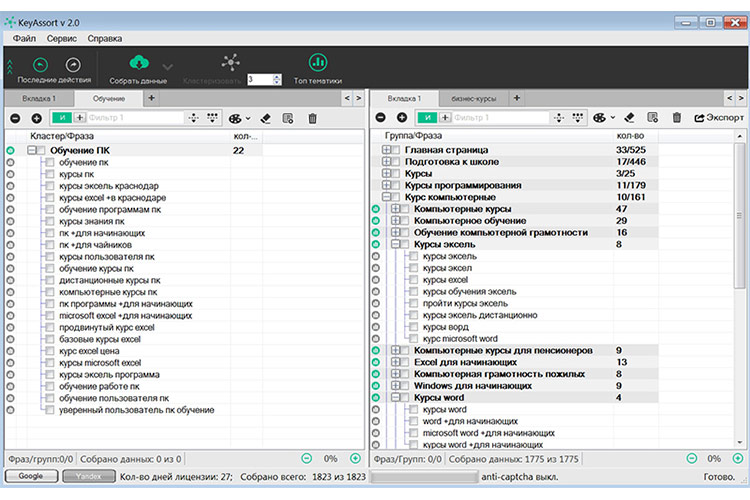
Программа KeyAssort
Key Clustered
Это бесплатное программное решение для кластеризации, работающее с семантическим ядром любого объема с результатом в виде таблицы Excel. Пользователь может выбрать вручную хард- или софт-метод, задать число позиций топа и порог пересечений, а на выходе получить не только кластеры, но и список основных конкурентов для сайта.
Программа Key Clustered
Владислав Сувернев, интернет-маркетолог, эксперт в области продвижения в интернете:
«Я для себя выделяю три способа кластеризации семантического ядра:
— Ручной. Сколько бы сервисов не придумало человечество, старые добрые глаза и руки специалиста они на 100% в этом вопросе не заменят. Я люблю заниматься кластеризацией семантики в обычной Гугл-таблице или Экселе. Но если ядро получилось на несколько тысяч запросов, кластеризовать его полностью вручную будет та еще задачка.
— Автоматический. Полная противоположность первому — здесь мы все отдаем на откуп сервисам типа Key Collector, Key Assort или Keys.so. Пользуюсь этим методом редко, только если сроки сильно горят и заказчик готов пожертвовать качеством ради скорости выполнения этой задачи. Обычно за такими сервисами все равно нужно подчищать руками, здесь на помощь как раз приходит третий метод.
— Комбинированный. Стараюсь пользоваться им как можно чаще, если не всегда. При этом методе первоначальную работу отдаю сервисам, которые перечислил выше, а затем руками подчищаю за ними. Такой метод позволяет сделать работу быстрее, чем ручной и качественнее, чем полностью автоматический.
Важно понимать, зачем вы делаете кластеризацию СЯ. Например, для рекламы в Яндекс Директ семантическое ядро разделяют на группы для того, чтобы не получить статус «Мало показов» и создать для каждой группы максимально релевантные запросам объявления. В таком случае нужно помнить, что есть техническое ограничение для кампаний в Директе — не больше 1000 групп на кампанию.
Если брать этот пример, то можно назвать «эффективной кластеризацией» ту, которая привела к появлению кампании без статуса «Мало показов» и в нужно лимите — до 1000 групп».
Дмитрий Матвеев. Предприниматель, генеральный директор компании «Мой Автопрокат»:
«Автоматизация процессов это, безусловно, полезно и правильно, но доверять всю работу программным алгоритмам нельзя, поэтому рекомендую использовать комбинированный способ. Первичная кластеризация производится с помощью онлайн-сервиса, а в дальнейшем дорабатывается вручную, т.к. ТОП выдачи поисковых машин в некоторых случаях не соответствует интенту (потребности пользователя), особенно для узкоспециализированных и низкоконкурентных ключевых фраз.
Для небольшого семантического ядра по низкоконкурентным запросам, как правило, отрабатывает Soft-метод кластеризации, при котором не производится дополнительная проверка совпадений URL по каждой ключевой фразе. Для ресурсов, которые имеют сложную структуру, продвигаются по высокочастотным запросам, дополнительная «шлифовка» кластеров с помощью Hard метода будет не лишней.
Мы протестировали несколько сервисов, начиная с Coolakov, который позволяет бесплатно кластеризовать до 500 ключевых фраз и не всегда группирует достаточно точно. Также были испытаны SerpStat, Топвизор, KeyAssort, Just Magic. В итоге выбор остановлен на Rush Analytics. Обладает точным алгоритмом и удобным интерфейсом. Единственным минусом можно считать глубину анализа – сервис работает по ТОП-10 выдачи поисковых систем».
Параметры, влияющие на эффективность кластеризации
На эффективность кластеризации влияет несколько важных параметров:
1. Качество и объем запросов по каждому кластеру и вхождение туда нужных ключевых слов и фраз.
2. Релевантность контента лендинга соответствующему кластеру и удовлетворенность пользователя качеством этого контента.
3. Совместимость различных запросов на одной и той же странице и отсутствие ключей с различным между собой интентом.
Ни одна программа для автоматической кластеризации не работает идеально точно и безошибочно. Но улучшить качество работы софта можно при грамотной подготовке семантического ядра и последующей ручной проверке получившихся кластеров.
Автоматическая кластеризация помогает значительно увеличить скорость работы с большими массивами данных, обработать которые вручную практически невозможно. Программа выполняет за несколько минут объем, на который у человека может уйти несколько месяцев работы, но ручная проверка результатов все равно необходима. Человеческий интеллект превосходит искусственный при работе с семантическими нюансами слов и фраз, отгадывании интента и корректность полученных групп, потому автоматическая работа всегда должна сочетаться с ручной.
Дмитрий Матвеев. Предприниматель, генеральный директор компании «Мой Автопрокат»:
«Всегда в первую очередь нужно отталкиваться от потребностей пользователя и брать интент за основу кластеризации. Набор важных технических параметров при формировании кластеров необходимо определять по конкретному типу ресурса, сфере деятельности, индивидуальным особенностям проекта. Для объемного семантического ядра в высококонкурентной сфере очень важно учитывать порог кластеризации, т.е. сколько одинаковых URL у разных запросов. Чем выше значение, тем точнее кластера, но увеличивается их количество и уменьшается размер, что может потребовать больших усилий и затрат по созданию новых страниц (что не всегда целесообразно). Также для некоторых проектов важно учитывать глубину анализа выдачи. Большая часть сервисов «пробивает» ТОП-10, однако некоторые позволяют анализировать ТОП-30 или даже ТОП-50. Благодаря этому можно снизить погрешности алгоритмов».
Частые ошибки, возникающие при кластеризации
Даже при качественно собранном семантическом ядре ошибки кластеризации могут негативно сказаться на поведенческих факторах ранжировании сайта. Среди наиболее распространенных ошибок стоит отметить разный интент запросов на одной и той же странице, отсутствие синонимов в семантическом ядре, несоответствие ключевых слов тематике лендинга, неполное ядро, содержащее только высоко- и среднечастотные запросы, обилие «мусора» (посторонних ключей, ошибок, опечаток, дублей, специальных символов). Все эти нюансы необходимо тщательно отслеживать.
Читайте также: «Как провести SEO-аудит сайта»
Кластеризация — незаменимый этап при подготовке семантики, от которого зависит разработка структуры сайта. Если же у вас уже есть готовый сайт, который вы намерены развивать и предлагать, то семантику необходимо периодически уточнять и группировать ключевые слова: без этого оптимизация невозможна.
Топ поисковой выдачи Google и Яндекс постоянно меняется, потому семантическое ядро не собирается раз и навсегда. Поэтому обновление семантики, обновление устаревших ключей и совершенствование контента сайта — это постоянная и кропотливая работа. Делать это стоит, используя специальные программы и проверяя результаты их работы вручную: так вы добьетесь оптимальной скорости процесса без потерь для качества.
Создать аккаунт на AdvantShop
На платформе вы сможете быстро создать интернет-магазин, лендинг или автоворонку.
Воспользоваться консультацией специалиста
Ответим на любые ваши вопросы и поможем выйти на маркетплейсы.
Связаться
Перевод
Ссылка на автора
Введение
В этом посте мы рассмотрим несколько случаев, когда алгоритм KMC работает неэффективно или может давать неинтуитивные результаты. В частности, мы рассмотрим следующие сценарии:
- Наше предположение о количестве (реальных) кластеров неверно.
- Особенность пространства очень размерна.
- Кластеры бывают странной или неправильной формы.
Все эти условия могут привести к проблемам с K-Means, так что давайте посмотрим.
Неверное количество кластеров
Чтобы сделать это проще, давайте определим вспомогательную функциюcompare, который создаст и решит проблему кластеризации для нас, а затем сравнит результаты.
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs, make_circles, make_moons
from mpl_toolkits.mplot3d import Axes3Dimport numpy as np
import pandas as pd
import itertoolsdef compare(N_features, C_centers, K_clusters, dims=[0, 1],*args):
data, targets = make_blobs(
n_samples=n_samples if 'n_samples' in args else 400,
n_features=N_features,
centers=C_centers,
cluster_std=cluster_std if 'cluster_std' in args else 0.5,
shuffle=True,
random_state=random_state if 'random_state' in args else 0)FEATS = ['x' + str(x) for x in range(N_features)]
X = pd.DataFrame(data, columns=FEATS)
X['cluster'] =
KMeans(n_clusters=K_clusters, random_state=0).fit_predict(X)fig, axs = plt.subplots(1, 2, figsize=(12, 4))
axs[0].scatter(data[:, dims[0]], data[:, dims[1]],
c='white', marker='o', edgecolor='black', s=20)
axs[0].set_xlabel('x{} [a.u.]'.format(dims[0]))
axs[0].set_ylabel('x{} [a.u.]'.format(dims[1]))
axs[0].set_title('Original dataset')
axs[1].set_xlabel('x{} [a.u.]'.format(dims[0]))
axs[1].set_ylabel('x{} [a.u.]'.format(dims[1]))
axs[1].set_title('Applying clustering')colors = itertools.cycle(['r', 'g', 'b', 'm', 'c', 'y'])
for k in range(K_clusters):
x = X[X['cluster'] == k][FEATS].to_numpy()
axs[1].scatter(
x[:, dims[0]],
x[:, dims[1]],
color=next(colors),
edgecolor='k',
alpha=0.5
)
plt.show()
Слишком мало кластеров

compare(2, 4, 3)).
Несмотря на наличие отдельных кластеров в данных, мы недооценили их количество. Как следствие, некоторые непересекающиеся группы данных вынуждены вписываться в один более крупный кластер.
Слишком много кластеров

compare(2, 2, 4)).
В отличие от последней ситуации, попытка обернуть данные в слишком много кластеров создает искусственные границы внутри реальных кластеров данных.
Высокие (er) размерные данные
Набор данных не должен быть настолько высоким в размерности, прежде чем мы начнем видеть проблемы. Хотя визуализация и, следовательно, некоторый анализ многомерных данных уже сложны (ругаясь сейчас…), поскольку KMC часто используется для понимания данных, это не помогает быть представленным с неоднозначностями.
Чтобы объяснить это, давайте сгенерируем трехмерный набор данных с четко различимыми кластерами.
fig = plt.figure(figsize=(14, 8))
ax = fig.add_subplot(111, projection='3d')data, targets = make_blobs(
n_samples=400,
n_features=3,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)ax.scatter(data[:, 0], data[:, 1],
zs=data[:, 2], zdir='z', s=25, c='black', depthshade=True)
ax.set_xlabel('x0 [a.u.]')
ax.set_ylabel('x1 [a.u.]')
ax.set_zlabel('x2 [a.u.]')
ax.set_title('Original distribution.')
plt.grid()
plt.show()

Хотя существует множество способов проецировать этот 3D-набор данных на 2D, существует три основных ортогональных подпространства:
Глядя наx2 : x0проекция, набор данных выглядит так, как если бы он имел только два кластера. Нижний правый «суперкластер» на самом деле представляет собой две отдельные группы, и даже если мы предполагаем,Кправильно(К = 3)Это выглядит как очевидная ошибка, несмотря на то, что кластеры очень локализованы.

compare(2, 2, 4, dims=[0, 2])).
Чтобы быть уверенным, мы должны взглянуть на оставшиеся проекции, чтобы увидеть проблему, буквально, с разных сторон.

compare(2, 2, 4, dims=[1, 2])).
compare(2, 2, 4, dims=[0, 1])).
Это имеет больше смысла!
С другой стороны, у нас было невероятное преимущество. Во-первых, с тремя измерениями мы смогли построить весь набор данных. Во-вторых, кластеры, которые существуют в наборе данных, были очень четкими, поэтому их легко обнаружить. Наконец, с трехмерным набором данных мы столкнулись только с тремя стандартными 2D-проекциями.
СлучайN, N> 3особенности, мы быне сможет построить весь набор данныхи число 2D проекций будет масштабироваться квадратично сN:
не говоря уже о том, что набор данных может иметь кластеры странной формы или нелокализованные, что является нашей следующей задачей.
Нерегулярные наборы данных
До сих пор мы упоминали о проблемах, которые «на нашей стороне». Мы посмотрели на очень «хорошо себя ведущий» набор данных и обсудили проблемы в области аналитики. Однако что делать, если набор данных не соответствует нашему решению или нашемуРешение проблемы не подходит?Это как раз тот случай, когда распределение данных происходит в странных или неправильных формах.
Если мы представим только этот график, мы можем обмануть себя, полагая, что в данных есть только два кластера. Однако при составлении графика остальных прогнозов мы быстро узнаем, что это не так.
fig, axs = plt.subplots(1, 3, figsize=(14, 4))# unequal variance
X, y = make_blobs(n_samples=1400,
cluster_std=[1.0, 2.5, 0.2],
random_state=2)
y_pred = KMeans(n_clusters=3, random_state=2).fit_predict(X)
colors = [['r', 'g', 'b'][c] for c in y_pred]axs[0].scatter(X[:, 0], X[:, 1],
color=colors, edgecolor='k', alpha=0.5)
axs[0].set_title("Unequal Variance")# anisotropically distributed data
X, y = make_blobs(n_samples=1400, random_state=156)
transformation = [
[0.60834549, -0.63667341],
[-0.40887718, 0.85253229]
]
X = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=0).fit_predict(X)
colors = [['r', 'g', 'b'][c] for c in y_pred]axs[1].scatter(X[:, 0], X[:, 1],
color=colors, edgecolor='k', alpha=0.5)
axs[1].set_title("Anisotropicly Distributed Blobs")# irregular shaped data
X, y = make_moons(n_samples=1400, shuffle=True,
noise=0.1, random_state=120)
y_pred = KMeans(n_clusters=2, random_state=0).fit_predict(X)
colors = [['r', 'g', 'b'][c] for c in y_pred]axs[2].scatter(X[:, 0], X[:, 1],
color=colors, edgecolor='k', alpha=0.5)
axs[2].set_title("Irregular Shaped Data")plt.show()

На левом графике показаны данные, чье распределение по Гауссу не имеет одинакового стандартного отклонения. Средний график представляетанизотропныйданные, означающие данные, которые вытянуты вдоль определенной оси. Наконец, правый график показывает данные, которые полностью негауссовы, несмотря на то, что они организованы в чистые кластеры.
В любом случае нерегулярность делает алгоритм KMC неэффективным. Поскольку алгоритм обрабатывает каждую точку данных одинаково и полностью независимо от других точек, алгоритмне в состоянии обнаружить любую возможную непрерывность или локальные изменения в кластере, То, что он делает, просто берет те же самые метрики и применяет это к каждой точке. В результате алгоритм KMC может производить странную или нелогичную кластеризацию в данных, даже если мы предполагаемКправильно и особенностиNне так много.
Выводы
В этом посте мы обсудили три основные причины, по которым алгоритм K-Means Clustering дает нам неправильные ответы.
- Во-первых, как количество кластеровКнужно решить априори, есть большая вероятность, что мы догадаемся
- Во-вторых, кластеризация в пространстве более высокого измерения становится громоздкой с аналитической точки зрения, и в этом случае KMC предоставит нам идеи, которые могут вводить в заблуждение.
- Наконец, для любых данных неправильной формы, KMC, скорее всего, искусственные кластеры, которые не соответствуют здравому смыслу.
Зная эти три ошибки, KMC остается полезным инструментом, особенно при проверке данных или создании меток.
Первоначально опубликовано на https://zerowithdot.com ,
From Wikipedia, the free encyclopedia
Clustered standard errors (or Liang-Zeger standard errors)[1] are measurements that estimate the standard error of a regression parameter in settings where observations may be subdivided into smaller-sized groups («clusters») and where the sampling and/or treatment assignment is correlated within each group.[2][3] Clustered standard errors are widely used in a variety of applied econometric settings, including difference-in-differences[4] or experiments.[5]
Analogous to how Huber-White standard errors are consistent in the presence of heteroscedasticity and Newey–West standard errors are consistent in the presence of accurately-modeled autocorrelation, clustered standard errors are consistent in the presence of cluster-based sampling or treatment assignment. Clustered standard errors are often justified by possible correlation in modeling residuals within each cluster; while recent work suggests that this is not the precise justification behind clustering,[6] it may be pedagogically useful.
Intuitive motivation[edit]
Clustered standard errors are often useful when treatment is assigned at the level of a cluster instead of at the individual level. For example, suppose that an educational researcher wants to discover whether a new teaching technique improves student test scores. She therefore assigns teachers in «treated» classrooms to try this new technique, while leaving «control» classrooms unaffected. When analyzing her results, she may want to keep the data at the student level (for example, to control for student-level observable characteristics). However, when estimating the standard error or confidence interval of her statistical model, she realizes that classical or even heteroscedasticity-robust standard errors are inappropriate because student test scores within each class are not independently distributed. Instead, students in classes with better teachers have especially high test scores (regardless of whether they receive the experimental treatment) while students in classes with worse teachers have especially low test scores. The researcher can cluster her standard errors at the level of a classroom to account for this aspect of her experiment.[7]
While this example is very specific, similar issues arise in a wide variety of settings. For example, in many panel data settings (such as difference-in-differences) clustering often offers a simple and effective way to account for non-independence between periods within each unit (sometimes referred to as «autocorrelation in residuals»).[4] Another common and logically distinct justification for clustering arises when a full population cannot be randomly sampled, and so instead clusters are sampled and then units are randomized within cluster. In this case, clustered standard errors account for the uncertainty driven by the fact that the researcher does not observe large parts of the population of interest.[8]
Mathematical motivation[edit]
A useful mathematical illustration comes from the case of one-way clustering in an ordinary least squares (OLS) model. Consider a simple model with N observations that are subdivided in C clusters. Let 







As is standard with OLS models, we minimize the sum of squared residuals 

From there, we can derive the classic «sandwich» estimator:
Denoting 
While one can develop a plug-in estimator by defining 







Clustered standard errors assume that 




By constructing plug-in matrices 


Further reading[edit]
- Alberto Abadie, Susan Athey, Guido W Imbens, and Jeffrey M Wooldridge. 2022. «When Should You Adjust Standard Errors for Clustering?» Quarterly Journal of Economics.
References[edit]
- ^ Liang, Kung-Yee; Zeger, Scott L. (1986-04-01). «Longitudinal data analysis using generalized linear models». Biometrika. 73 (1): 13–22. doi:10.1093/biomet/73.1.13. ISSN 0006-3444.
- ^ Cameron, A. Colin; Miller, Douglas L. (2015-03-31). «A Practitioner’s Guide to Cluster-Robust Inference». Journal of Human Resources. 50 (2): 317–372. doi:10.3368/jhr.50.2.317. ISSN 0022-166X. S2CID 1296789.
- ^ «ARE 212». Fiona Burlig. Retrieved 2020-07-05.
- ^ a b Bertrand, Marianne; Duflo, Esther; Mullainathan, Sendhil (2004-02-01). «How Much Should We Trust Differences-In-Differences Estimates?». The Quarterly Journal of Economics. 119 (1): 249–275. doi:10.1162/003355304772839588. hdl:1721.1/63690. ISSN 0033-5533. S2CID 470667.
- ^ Yixin Tang (2019-09-11). «Analyzing Switchback Experiments by Cluster Robust Standard Error to prevent false positive results». DoorDash Engineering Blog. Retrieved 2020-07-05.
- ^ Abadie, Alberto; Athey, Susan; Imbens, Guido; Wooldridge, Jeffrey (2017-10-24). «When Should You Adjust Standard Errors for Clustering?». arXiv:1710.02926 [math.ST].
- ^ «CLUSTERED STANDARD ERRORS». Economic Theory Blog. 2016. Archived from the original on 2016-11-06. Retrieved 28 September 2021.
- ^ «When should you cluster standard errors? New wisdom from the econometrics oracle». blogs.worldbank.org. Retrieved 2020-07-05.
In many scenarios, data are structured in groups or clusters, e.g. pupils within classes (within schools), survey respondents within countries or, for longitudinal surveys, survey answers per subject. Simply ignoring this structure will likely lead to spuriously low standard errors, i.e. a misleadingly precise estimate of our coefficients. This in turn leads to overly-narrow confidence intervals, overly-low p-values and possibly wrong conclusions.
Clustered standard errors are a common way to deal with this problem. Unlike Stata, R doesn’t have built-in functionality to estimate clustered standard errors. There are several packages though that add this functionality and this article will introduce three of them, explaining how they can be used and what their advantages and disadvantages are. Before that, I will outline the theory behind (clustered) standard errors for linear regression. The last section is used for a performance comparison between the three presented packages. If you’re already familiar with the concept of clustered standard errors, you may skip to the hands-on part right away.
Data
We’ll work with the dataset nlswork that’s included in Stata, so we can easily compare the results with Stata. The data comes from the US National Longitudinal Survey (NLS) and contains information about more than 4,000 young working women. As for this example, we’re interested in the relationship between wage (here as log-scaled GNP-adjusted wage) as dependent variable (DV) ln_wage and survey participant’s current age, job tenure in years and union membership as independent variables. It’s a longitudinal survey, so subjects were asked repeatedly between 1968 and 1988 and each subject is identified by an unique idcode.
The example data is used for illustrative purposes only and we skip many things that we’d normally do, such as investigating descriptive statistics and exploratory plots. To keep the data size limited, we’ll only work with a subset of the data (only subjects with IDs 1 to 100) and we also simply dismiss any observations that contain missing values.
library(webuse)
library(dplyr)
nlswork_orig <- webuse('nlswork')
nlswork <- filter(nlswork_orig, idcode <= 100) %>%
select(idcode, year, ln_wage, age, tenure, union) %>%
filter(complete.cases(.)) %>%
mutate(union = as.integer(union),
idcode = as.factor(idcode))
str(nlswork)
tibble [386 × 6] (S3: tbl_df/tbl/data.frame)
$ idcode : Factor w/ 82 levels "1","2","3","4",..: 1 1 1 1 1 1 1 2 2 2 …
$ year : num [1:386] 72 77 80 83 85 87 88 71 77 78 …
$ ln_wage: num [1:386] 1.59 1.78 2.55 2.42 2.61 …
$ age : num [1:386] 20 25 28 31 33 35 37 19 25 26 …
$ tenure : num [1:386] 0.917 1.5 1.833 0.667 1.917 …
$ union : int [1:386] 1 0 1 1 1 1 1 0 1 1 …
Let’s have a look at the first few observations. They contain data from subject #1, who was surveyed several times between 1972 and 1988, and a few observations from subject #2.
idcode year ln_wage age tenure union 1 72 1.59 20 0.917 1 1 77 1.78 25 1.5 0 1 80 2.55 28 1.83 1 1 83 2.42 31 0.667 1 1 85 2.61 33 1.92 1 1 87 2.54 35 3.92 1 1 88 2.46 37 5.33 1 2 71 1.36 19 0.25 0 2 77 1.73 25 2.67 1 2 78 1.69 26 3.67 1
A summary of all but the idcode variable gives the following:
year ln_wage age tenure union Min. :70.00 Min. :0.4733 Min. :18.0 Min. : 0.000 Min. :0.0000 1st Qu.:73.00 1st Qu.:1.6131 1st Qu.:25.0 1st Qu.: 1.167 1st Qu.:0.0000 Median :80.00 Median :1.9559 Median :31.0 Median : 2.417 Median :0.0000 Mean :79.61 Mean :1.9453 Mean :30.8 Mean : 3.636 Mean :0.2591 3rd Qu.:85.00 3rd Qu.:2.2349 3rd Qu.:36.0 3rd Qu.: 4.958 3rd Qu.:1.0000 Max. :88.00 Max. :3.5791 Max. :45.0 Max. :19.000 Max. :1.0000
We have 82 subjects in our subset and the number of times each subject was surveyed ranges from only once to twelve times:
summary(as.integer(table(nlswork$idcode))) Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 2.000 4.000 4.707 7.000 12.000
In more than one quarter of the observations, the subject answered to be currently member of a trade union.
The following shows the distribution of the DV in our data. It is roughly normally distributed with mean 1.95 and standard deviation (SD) 0.45.

We can calculate the mean and SD of the DV separately for each subject. A histogram of these subject-specific means reveals more variability:
y_mean_sd_cl <- sapply(levels(nlswork$idcode), function(idcode) {
y_cl <- nlswork$ln_wage[nlswork$idcode == idcode]
c(mean(y_cl), sd(y_cl))
})
hist(y_mean_sd_cl[1,], breaks = 20,
main = 'Histogram of DV means per subject', xlab = NA)

We can compare the SD of the subject-specific means with the mean of the SDs calculated from each subjects’ repeated measures.
c(sd(y_mean_sd_cl[1,]), mean(y_mean_sd_cl[2,], na.rm = TRUE)) [1] 0.4038449 0.2221142
The SD between the subject-specific means is almost twice as large as the mean of the SD from each subjects’ values. This shows that there’s much more variability between each subject than within each subject’s repeated measures regarding the DV.
Fixed-effects model, not adjusting for clustered observations
Our data contains repeated measures for each subject, so we have panel data in which each subject forms a group or cluster. We can use a fixed-effects (FE) model to account for unobserved subject-specific characteristics. We do so by including the subject’s idcode in our model formula. It’s important to note that idcode is of type factor (we applied idcode = as.factor(idcode) when we prepared the data) so that for each factor level (i.e. each subject) an FE coefficient will be estimated that represents the subject-specific mean of our DV. 1
Let’s specify and fit such a model using lm. We include job tenure, union membership and an interaction between both (the latter mainly for illustrative purposes later when we estimate marginal effects). We also control for age and add idcode as FE variable.
m1 <- lm(ln_wage ~ age + tenure + union + tenure:union + idcode,
data = nlswork)
summary(m1)
Call:
lm(formula = ln_wage ~ age + tenure + union + tenure:union +
idcode, data = nlswork)
Residuals:
Min 1Q Median 3Q Max
-0.96463 -0.09405 0.00000 0.11460 1.23525
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.882e+00 1.314e-01 14.325 < 2e-16 ***
age 5.631e-03 3.110e-03 1.811 0.071193 .
tenure 2.076e-02 6.964e-03 2.980 0.003115 **
union 1.746e-01 6.065e-02 2.879 0.004272 **
idcode2 -6.174e-01 1.285e-01 -4.803 2.47e-06 ***
idcode3 -5.625e-01 1.329e-01 -4.234 3.05e-05 ***
[...]
We’re not really interested in the subject-specific means (the FE coefficients), so let’s filter them out and only show our coefficients of interest:
m1coeffs_std <- data.frame(summary(m1)$coefficients)
coi_indices <- which(!startsWith(row.names(m1coeffs_std), 'idcode'))
m1coeffs_std[coi_indices,]
Estimate Std..Error t.value Pr...t..
(Intercept) 1.882478232 0.131411504 14.325064 8.022367e-36
age 0.005630809 0.003109803 1.810664 7.119315e-02
tenure 0.020756426 0.006964417 2.980353 3.114742e-03
union 0.174619394 0.060646038 2.879321 4.272027e-03
tenure:union 0.014974113 0.009548509 1.568215 1.178851e-01
Unsurprisingly, job tenure and especially union membership are positively associated with wage. The coefficient of the interaction term shows that with union membership the job tenure effect is even a bit higher, though not significantly.
In the next two sections we’ll see how standard errors for our estimates are usually computed and how this fits into a framework called “sandwich estimators.” Using this framework, we’ll see how the standard error calculations can be adjusted for clustered data.
In ordinary least squares (OLS) regression, we assume that the regression model errors are independent. This is not the case here: Each subject may be surveyed several times so within each subject’s repeated measures, the errors will be correlated. Although that is not a problem for our regression estimates (they are still unbiased [Roberts 2013]), it is a problem for for the precision of our estimates — the precision will typically be overestimated, i.e. the standard errors (SEs) will be lower than they should be [Cameron and Miller 2013]. The intuition behind this regarding our example is that within our clusters we usually have lower variance since the answers come from the same subject and are correlated. This lowers our estimates’ SEs.
We can deal with this using clustered standard errors with subjects representing our clusters. But before we do this, let’s first have a closer look on how “classic” OLS estimates’ SEs are actually computed.
In matrix notation, a linear model has the form
![]()
This model has ![]() parameters (including the intercept parameter
parameters (including the intercept parameter ![]() ) expressed as
) expressed as ![]() parameter vector
parameter vector ![]() . The parameters will be estimated from
. The parameters will be estimated from ![]() observations in our data. The DV is
observations in our data. The DV is ![]() (an
(an ![]() vector), the independent variables form an
vector), the independent variables form an ![]() matrix
matrix ![]() . Finally, the error term
. Finally, the error term ![]() is an
is an ![]() vector that captures everything that influences
vector that captures everything that influences ![]() but cannot be explained by
but cannot be explained by ![]() . In classic OLS, we assume that
. In classic OLS, we assume that ![]() has a mean of zero and a variance of
has a mean of zero and a variance of ![]() .
.
By minimizing ![]() an estimation for our parameters,
an estimation for our parameters, ![]() , can be found as
, can be found as ![]() . The estimated variance
. The estimated variance ![]() for these parameters is then
for these parameters is then
(1) ![]()
where ![]() is the estimated variance of the error or residual variance. This is calculated as
is the estimated variance of the error or residual variance. This is calculated as
![]()
with ![]() being the residuals. The numerator is also called the residual sum of squares and the denominator is the degrees of freedom.
being the residuals. The numerator is also called the residual sum of squares and the denominator is the degrees of freedom.
You can see for example in Sheather 2009 for how the formulas for ![]() and
and ![]() are derived or watch this video for a clear step-by-step derivation.
are derived or watch this video for a clear step-by-step derivation.
We now have all the pieces together to replicate the standard errors from model m1 with our own calculations. To translate these formulae to R, we use model.matrix to get the design matrix ![]() ,
, residuals for the residual vector ![]() ,
, nobs for the number of observations ![]() ,
, ncol(X) for the number or parameters, solve to calculate the inverse of ![]() and
and diag to extract the diagonal of a square matrix.
X <- model.matrix(m1) u <- residuals(m1) n <- nobs(m1) p <- ncol(X) sigma2 <- sum(u^2) / (n - p) # solve (X^T X) A = I, where I is identity matrix -> A is (X^T X)^-1 crossXinv <- solve(t(X) %*% X, diag(p)) m1se <- sqrt(diag(sigma2 * crossXinv)) m1se [1] 0.131411504 0.003109803 0.006964417 0.060646038 0.128532897 ...
Let’s check if this is equal to the standard errors calculated by lm (using near because of minor deviations due to floating point number imprecision):
all(near(m1se, m1coeffs_std$Std..Error)) [1] TRUE
We extracted our parameter estimates’ variance ![]() from the diagonal of the (variance-)covariance or vcov matrix and R has the
from the diagonal of the (variance-)covariance or vcov matrix and R has the vcov function to calculate it from a fitted model. It’s exactly what we computed before using eq. 1:
all(near(sigma2 * crossXinv, vcov(m1))) [1] TRUE
Clustered standard errors
Classic OLS SEs can be generalized so that some assumptions, namely that the regression model errors are independent, can be relaxed. The foundation for this is the sandwich estimator 2
(2) ![]()
Let’s first understand how the above equation relates to eq. 1, the classic OLS parameter variance: One assumption of classic OLS is constant variance (or homoscedasticity) in the errors across the full spectrum of our DV. This implicates that ![]() is a diagonal matrix with identical
is a diagonal matrix with identical ![]() elements, i.e.
elements, i.e. ![]() . Plugging this into eq. 2 gives eq. 1 which shows that the classic OLS parameter variance is a specialized form of the sandwich estimator. 3
. Plugging this into eq. 2 gives eq. 1 which shows that the classic OLS parameter variance is a specialized form of the sandwich estimator. 3
When we want to obtain clustered SEs, we need to consider that ![]() in the “meat” part of eq. 2 is not a diagonal matrix with identical
in the “meat” part of eq. 2 is not a diagonal matrix with identical ![]() elements anymore, hence this can’t be simplified to eq. 1. Instead, we can assume that
elements anymore, hence this can’t be simplified to eq. 1. Instead, we can assume that ![]() is block-diagonal with the clusters forming the blocks. This means we assume that the variance in the errors is constant only within clusters and so we first calculate
is block-diagonal with the clusters forming the blocks. This means we assume that the variance in the errors is constant only within clusters and so we first calculate ![]() per cluster
per cluster ![]() and then sum the
and then sum the ![]() . Cameron and Miller 2013 (p. 11) show how
. Cameron and Miller 2013 (p. 11) show how ![]() is calculated in detail and also which finite-sample correction factor is applied. From this article we get the equation
is calculated in detail and also which finite-sample correction factor is applied. From this article we get the equation
(3) 
where ![]() is the number of clusters. It’s interesting to see how the residuals are added up per cluster and then averaged. As Cameron and Miller 2013 (p. 13) notes, this implicates an important limitation: With a low number of clusters, this averaging is imprecise.
is the number of clusters. It’s interesting to see how the residuals are added up per cluster and then averaged. As Cameron and Miller 2013 (p. 13) notes, this implicates an important limitation: With a low number of clusters, this averaging is imprecise.
Let’s translate this formula to R. We already have ![]() as
as u (the residuals) and the design matrix X. We can generate a list of matrices ![]() , sum them and multiply the correction factor:
, sum them and multiply the correction factor:
omegaj <- lapply(levels(nlswork$idcode), function(idcode) {
j <- nlswork$idcode == idcode
# drop = FALSE: don't drop dimensions when we have only one obs.
X_j <- X[j, , drop = FALSE]
# tcrossprod is outer product x * x^T
t(X_j) %*% tcrossprod(u[j]) %*% X_j
})
n_cl <- length(levels(nlswork$idcode)) # num. clusters
# correction factor * sum of omega_j
omega <- (n-1) / (n-p) * (n_cl / (n_cl-1)) * Reduce('+', omegaj)
# sandwich formula; extract diagonal and take square root to get SEs
m1clse <- sqrt(diag(crossXinv %*% omega %*% crossXinv))
m1clse
[1] 0.157611390 0.006339777 0.011149190 0.101970509 0.020561516 ...
We will later check that this matches the estimates calculated with R packages that implement clustered SE estimation. For now, let’s compare the classic OLS SEs with the clustered SEs:
m1coeffs_with_clse <- cbind(m1coeffs_std, ClustSE = m1clse)
m1coeffs_with_clse[coi_indices, c(1, 2, 5)]
Estimate Std..Error ClustSE
(Intercept) 1.882478232 0.131411504 0.157611390
age 0.005630809 0.003109803 0.006339777
tenure 0.020756426 0.006964417 0.011149190
union 0.174619394 0.060646038 0.101970509
tenure:union 0.014974113 0.009548509 0.009646023
We can see that, as expected, the clustered SEs are all a bit higher than the classic OLS SEs.
The above calculations were used to show what’s happening “under the hood” and also how the formulas used for these calculations are motivated. However, doing these calculations “by hand” is error-prone and slow. It’s better to use well trusted packages for daily work and so next we’ll have a look at some of these packages and how they can be used. Still, it’s helpful to understand some background and the limitations for this approach. See Cameron and Miller 2013 for a much more thorough guide (though only with examples in Stata) that also considers topics like which variable(s) to use for clustering, what to do when dealing with a low number of clusters or how to implement multi-way clustering.
Option 1: sandwich and lmtest
The sandwich package implements several methods for robust covariance estimators, including clustered SEs. Details are explained in Zeileis et al. 2020. The accompanying lmtest package provides functions for coefficient tests that take into account the calculated robust covariance estimates.
As explained initially, the parameter estimates from our model are fine despite the clustered structure of our data. But the SEs are likely biased downward and need to be corrected. This is why we can resume to work with our initially estimated model m1 from lm. There’s no need to refit it and sandwich works with lm model objects (and also some other types of models such as some glm models). We only have to adjust how we test our coefficient estimates in the following way:
- We need to use
coeftestfrom the lmtest package; - we need to pass it our model and either a function to calculate the covariance matrix or an already estimated covariance matrix to the
vcovparameter; - we need to specify a cluster variable in the
clusterparameter.
The sandwich package provides several functions for estimating robust covariance matrices. We need vcovCL for clustered covariance estimation and will pass this function as vcov parameter. Furthermore, we cluster by subject ID, so the cluster variable is idcode.
library(sandwich)
library(lmtest)
m1coeffs_cl <- coeftest(m1, vcov = vcovCL, cluster = ~idcode)
m1coeffs_cl[coi_indices,]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.882478232 0.157611390 11.9437956 3.667970e-27
age 0.005630809 0.006339777 0.8881715 3.751601e-01
tenure 0.020756426 0.011149190 1.8616981 6.362342e-02
union 0.174619394 0.101970509 1.7124500 8.784708e-02
tenure:union 0.014974113 0.009646023 1.5523613 1.216301e-01
The calculated SE values seem familiar and they are indeed equal to what we calculated before as m1clse “by hand”:
all(near(m1clse, m1coeffs_cl[,2])) [1] TRUE
The lmtest package provides several functions for common post-estimation tasks, for example coefci to calculate confidence intervals (CIs). If we use these, we need to make sure to specify the same type of covariance estimation, again by passing the appropriate vcov and cluster parameters:
(m1cis <- coefci(m1, parm = coi_indices, vcov = vcovCL,
cluster = ~idcode))
2.5 % 97.5 %
(Intercept) 1.572314302 2.19264216
age -0.006845258 0.01810688
tenure -0.001184099 0.04269695
union -0.026048678 0.37528746
tenure:union -0.004008324 0.03395655
This is really important, as otherwise the classic (non-clustered) covariance estimation is applied by default. This, due to lower SEs, leads to narrower CIs:
coefci(m1, parm = coi_indices)
2.5 % 97.5 %
(Intercept) 1.6238731375 2.14108333
age -0.0004889822 0.01175060
tenure 0.0070511278 0.03446172
union 0.0552738733 0.29396491
tenure:union -0.0038164264 0.03376465
Here, the tenure and union CIs suddenly don’t include zero any more!
Instead of passing vcovCL as function to the vcov parameter, it’s more convenient and computationally more efficient to calculate the covariance matrix only once using vcovCL and then passing this matrix to functions like coeftest and coefci instead:
cl_vcov_mat <- vcovCL(m1, cluster = ~idcode)
Now we pass this matrix for the vcov parameter. We don’t need to specify the cluster parameter anymore, since this information was only needed in the previous step.
m1coeffs_cl2 <- coeftest(m1, vcov = cl_vcov_mat) all(near(m1coeffs_cl[,2], m1coeffs_cl2[,2])) # same SEs? [1] TRUE m1cis2 <- coefci(m1, parm = coi_indices, vcov = cl_vcov_mat) all(near(m1cis, m1cis2)) # same CIs? [1] TRUE
Another example would be to calculate marginal effects, for example with the margins package. Again, to arrive at clustered SEs we will need to pass the proper covariance matrix via the vcov parameter. We do this for the marginal effect of tenure at the two levels of union:
library(margins)
margins(m1, vcov = cl_vcov_mat, variables = 'tenure',
at = list(union = 0:1)) %>%
summary()
factor union AME SE z p lower upper
tenure 0.0000 0.0208 0.0111 1.8617 0.0626 -0.0011 0.0426
tenure 1.0000 0.0357 0.0083 4.3089 0.0000 0.0195 0.0520
Otherwise classic SEs are estimated, which are smaller:
margins(m1, variables = 'tenure', at = list(union = 0:1)) %>% summary() factor union AME SE z p lower upper tenure 0.0000 0.0208 0.0070 2.9804 0.0029 0.0071 0.0344 tenure 1.0000 0.0357 0.0081 4.3846 0.0000 0.0198 0.0517
As you can see, the combination of lm and the packages sandwich and lmtest are all you need for estimating clustered SEs and inference. However, you really need to be careful to include the covariance matrix at all steps of your calculations.
Option 2: lm.cluster from miceadds
There’s also lm.cluster from the package miceadds 4, which may be a bit more convenient to use. Internally, it basically does the same that we’ve done before by employing sandwich’s vcovCL (see source code parts here and there for example).
Instead of using lm, we fit the model with lm.cluster and specify a cluster variable (this time as string, not as formula). The model summary then contains the clustered SEs:
library(miceadds)
m2 <- lm.cluster(ln_wage ~ age + tenure + union + tenure:union + idcode,
cluster = 'idcode',
data = nlswork)
m2coeffs <- data.frame(summary(m2))
m2coeffs[!startsWith(row.names(m2coeffs), 'idcode'),]
Estimate Std..Error t.value Pr...t..
(Intercept) 1.882478232 0.157611390 11.9437956 6.995639e-33
age 0.005630809 0.006339777 0.8881715 3.744485e-01
tenure 0.020756426 0.011149190 1.8616981 6.264565e-02
union 0.174619394 0.101970509 1.7124500 8.681378e-02
tenure:union 0.014974113 0.009646023 1.5523613 1.205758e-01
An object m that is returned from lm.cluster is a list that contains the lm object as m$lmres and the covariance matrix as m$vcov. Again, these objects need to be “dragged along” if we want to do further computations. For margins, we also need to pass the data again via data = nlswork:
margins(m2$lm_res, vcov = m2$vcov, variables = 'tenure',
at = list(union = 0:1), data = nlswork) %>%
summary()
factor union AME SE z p lower upper
tenure 0.0000 0.0208 0.0111 1.8617 0.0626 -0.0011 0.0426
tenure 1.0000 0.0357 0.0083 4.3089 0.0000 0.0195 0.0520
The result is consistent with our former computations. The advantage over the “lm + sandwich + lmtest” approach is that you can do clustered SE estimation and inference in one go. For further calculations you still need to be careful to supply the covariance matrix from m$vcov.
Option 3: lm_robust from estimatr
Another option is to use lm_robust from the estimatr package which is part of the DeclareDesign framework [Blair et al. 2019]. Like lm.cluster, it’s more convenient to use, but it doesn’t rely on sandwich and lmtest in the background and instead comes with an own implementation for model fitting and covariance estimation. This implementation is supposed to be faster than the other approaches and we’ll check that for our example later.
But first, let’s fit a model with clustered SEs using lm_robust. We use the same formula as with lm or lm.cluster, but also specify the clusters parameter: 5
library(estimatr)
m3 <- lm_robust(ln_wage ~ age + tenure + union + tenure:union + idcode,
clusters = idcode,
data = nlswork)
summary(m3)
Call:
lm_robust(formula = ln_wage ~ age + tenure + union + tenure:union +
idcode, data = nlswork, clusters = idcode)
Standard error type: CR2
Coefficients:
Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper DF
(Intercept) 1.882e+00 0.141424 13.310872 8.596e-14 1.5930761 2.171880 28.642
age 5.631e-03 0.005726 0.983442 3.342e-01 -0.0061215 0.017383 26.790
tenure 2.076e-02 0.010089 2.057345 5.771e-02 -0.0007714 0.042284 14.812
union 1.746e-01 0.093790 1.861817 7.735e-02 -0.0209918 0.370231 20.049
idcode2 -6.174e-01 0.019094 -32.334722 2.810e-07 -0.6656871 -0.569086 5.283
idcode3 -5.625e-01 0.078607 -7.156034 9.687e-07 -0.7273116 -0.397718 18.550
Unlike lm, lm_robust allows to specify fixed effects in a separate fixed_effects formula parameter which, according to the documentation, should speed up computation for many types of SEs. Furthermore, this cleans up the summary output since there are no more FE coefficients:
m3fe <- lm_robust(ln_wage ~ age + tenure + union + tenure:union,
clusters = idcode,
fixed_effects = ~idcode,
data = nlswork)
summary(m3fe)
Call:
lm_robust(formula = ln_wage ~ age + tenure + union + tenure:union,
data = nlswork, clusters = idcode, fixed_effects = ~idcode)
Standard error type: CR2
Coefficients:
Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper DF
age 0.005631 0.005726 0.9834 0.33419 -0.0061215 0.01738 26.790
tenure 0.020756 0.010089 2.0573 0.05771 -0.0007714 0.04228 14.812
union 0.174619 0.093790 1.8618 0.07735 -0.0209918 0.37023 20.049
tenure:union 0.014974 0.009043 1.6558 0.14062 -0.0062982 0.03625 7.187
Multiple R-squared: 0.7554 , Adjusted R-squared: 0.6861
[...]
When we compare the results from lm_robust with lm, we can see that the point estimates are the same. The lm_robust SEs are, as expected, higher than the “classic” SEs from lm. However, the lm_robust SEs are also a bit smaller than those calculated from sandwich::vcovCL:
m3fe_df <- tidy(m3fe) %>% rename(est.lm_robust = estimate,
se.lm_robust = std.error)
m3fe_df$se.sandwich <- m1coeffs_cl[coi_indices,2][2:5]
m3fe_df$est.classic <- m1coeffs_std[coi_indices,1][2:5]
m3fe_df$se.classic <- m1coeffs_std[coi_indices,2][2:5]
m3fe_df[c('term', 'est.classic', 'est.lm_robust', 'se.classic',
'se.lm_robust', 'se.sandwich')]
term est.classic est.lm_robust se.classic se.lm_robust se.sandwich
age 0.005630809 0.005630809 0.003109803 0.005725617 0.006339777
tenure 0.020756426 0.020756426 0.006964417 0.010088940 0.011149190
union 0.174619394 0.174619394 0.060646038 0.093789776 0.101970509
tenure:union 0.014974113 0.014974113 0.009548509 0.009043429 0.009646023
This is because lm_robust by default uses a different cluster-robust variance estimator “to correct hypotheses tests for small samples and work with commonly specified fixed effects and weights” as explained in the Getting started vignette. Details can be found in the Mathematical notes for estimatr.
As with the lm and lm.cluster results, we can also estimate marginal effects with a lm_robust result object. However, this doesn’t seem to work when you specify FEs via fixed_effects parameter as done for m3fe:
margins(m3fe, variables = 'tenure', at = list(union = 0:1)) %>% summary() Error in predict.lm_robust(model, newdata = data, type = type, se.fit = TRUE, : Can't set `se.fit` == TRUE with `fixed_effects`
With m3 (where FEs were directly specified in the model formula), marginal effects estimation works and we don’t even need to pass a separate vcov matrix, since this information already comes with the lm_robust result object m3. 6
margins(m3, variables = 'tenure', at = list(union = 0:1)) %>% summary() factor union AME SE z p lower upper tenure 0.0000 0.0208 0.0101 2.0573 0.0397 0.0010 0.0405 tenure 1.0000 0.0357 0.0077 4.6174 0.0000 0.0206 0.0509
As already said, lm_robust uses a different variance estimator than sandwich’s vcovCL and Stata. However, by setting se_type to 'stata' we can replicate these “Stata Clustered SEs”:
m3stata <- lm_robust(ln_wage ~ age + tenure + union + tenure:union + idcode,
clusters = idcode,
se_type = 'stata',
data = nlswork)
m3stata_se <- tidy(m3stata) %>% pull(std.error)
all(near(m3stata_se, m1clse)) # same SEs?
[1] TRUE
In summary, lm_robust is as convenient to use as lm or lm.cluster, but offers similar flexibility as sandwich for estimating clustered SEs. A big advantage is that you don’t need to care about supplying the right covariance matrix to further post-estimation functions like margins. The proper covariance matrix is directy attached to the fitted lm_robust object (and can be accessed via model$vcov or vcov(model) if you need to). Is parameter estimation also faster with lm_robust?
Performance comparison
We’ll make a rather superficial performance comparison only using the nlswork dataset and microbenchmark. We will compare the following implementations for estimating model coefficients and clustered SEs:
lmandvcovCLfrom sandwichlm.clusterlm_robustwith default SEs (se_type = 'CR2')lm_robustwith Stata SEs (se_type = 'stata')lm_robustwithfixed_effectsparameter and Stata SEs (fixed_effects = idcode, se_type = 'stata')
For a fair comparison, we don’t calculate CIs (which lm_robust by default does). These are the results for 100 test runs:

As expected, lm/sandwich and lm.cluster have similar run times. lm_robust is faster for all three configurations (3. to 5.) and is especially fast when estimating Stata SEs (4. and 5.). With our example data, specifying fixed_effects (5.) doesn’t seem to speed up the calculations.
Conclusion
We’ve seen that it’s important to account for clusters in data when estimating model parameters, since ignoring this fact will likely result in overestimated precision which in turn can lead to wrong inference. R provides many ways to estimate clustered SEs. The packages sandwich and lmtest come with a rich set of tools for this task (and also for other types of robust SEs) and work with lm and other kinds of models. lm.cluster from the miceadds package provides a more convenient wrapper around sandwich and lmtest. However, users should be careful to not forget passing along the separate cluster robust covariance matrix for post-estimation tasks. This is something users don’t need to care for when using lm_robust from the estimatr package, since the covariance matrix is not separate from the fitted model object. Another advantage is that lm_robust seems to be faster than the other options.
The source code for this article can be found on GitHub.
References
Blair, Graeme, Jasper Cooper, Alexander Coppock, and Macartan Humphreys. 2019. “Declaring and Diagnosing Research Designs.” American Political Science Review 113 (3): 838–59.
Cameron, A Colin, and Douglas L Miller. 2013. “A Practitioner’s Guide to Cluster-Robust Inference.”
Roberts, Molly. 2013. “Robust and Clustered Standard Errors.”
Sheather, Simon. 2009. A Modern Approach to Regression with R. Springer Texts in Statistics. New York: Springer-Verlag.
Zeileis, Achim, Susanne Köll, and Nathaniel Graham. 2020. “Various Versatile Variances: An Object-Oriented Implementation of Clustered Covariances in R.” Journal of Statistical Software 95 (1).
-
It is not always necessary to use an FE model and you can very well estimate robust SEs from clustered data also without FEs. ↩
-
This is called sandwich estimator because of the structure of the formula: Between two slices of bread
 there is the meat
there is the meat  . ↩
. ↩ -
Plugging in
 in eq. 2 gives
in eq. 2 gives ![Rendered by QuickLaTeX.com hat V[hatbeta] = hatsigma^2 (X^TX)^{-1} X^T X (X^TX)^{-1}](https://i1.wp.com/datascience.blog.wzb.eu/wp-content/ql-cache/quicklatex.com-de2306774e3cb75941f8982fd0fa65be_l3.png?resize=269%2C22&ssl=1) which reduces to eq. 1. because
which reduces to eq. 1. because  ↩
↩ -
Once again a strange package name. Unlike sandwich this package name is not derived from a formula, but simply stands for additional functionality for imputation with the mice package — and just happens to include clustered SE estimation. ↩
-
Note that this time we have to use the “bare” unquoted variable name — not a formula, not a string. Every package has a different policy! ↩
-
The standard
vcovfunction will return the correct (cluster robust) covariance matrix for a fittedlm_robustmodel, whereas it will return the “classic” covariance matrix for a fittedlmmodel. ↩
Кластеризация — это такая магическая штука: она превращает большой объём неструктурированных данных в потенциально обозримый набор кластеров, анализ которых позволяет делать выводы о содержании этих данных.
Приложений у методов кластеризации огромное количество. Например, мы кластеризуем поисковые запросы для того, чтобы повышать обобщающую способность алгоритмов ранжирования: любая статистика, вычисленная по группе похожих запросов, надёжнее той же статистики, вычисленной для одного отдельного запроса. Кластеризация позволяет повышать качество на запросах с редко встречающимися формулировками. Другой понятный пример — Яндекс.Новости, которые автоматически формируют сюжеты из новостных сообщений.
В далёком 2013 году мне повезло поучаствовать в разработке очень сложного алгоритма кластеризации. Требовалось с очень высоким качеством кластеризовать сотни тысяч объектов и делать это быстро: за десятки секунд на одной машине. Первым делом нужно было построить систему оценки качества, и в этой статье я расскажу именно о ней.

Когда речь заходит об оценке качества, начинать нужно, конечно же, с метрик.
Алгоритм кластеризации можно и нужно оценивать с позиции сервиса, частью которого этот алгоритм является: рост качества кластеризации должен приводить к росту числа пользователей, конверсий, возвращаемости и так далее, так что классическое А/Б-тестирование вполне уместно. Вместе с тем любой большой системе нужны метрики, специфичные для каждого из её компонентов. Кластеризация — не исключение.
1. Метрики и их свойства
Обычно задано образцовое разбиение на кластеры и разбиение, построенное алгоритмически. Метрика качества должна оценить степень соответствия между ними.
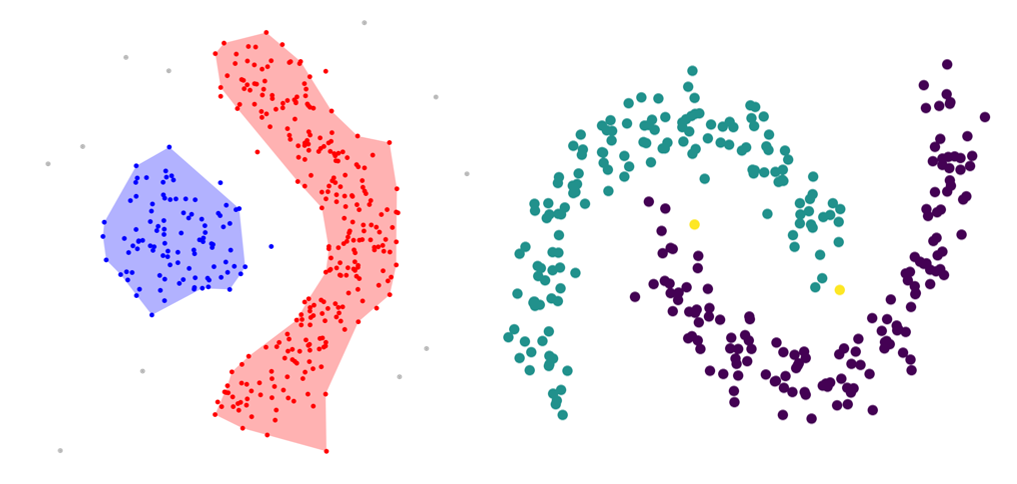
Обсуждение метрик стоит предварить обсуждением принципов, которым эти метрики должны удовлетворять. В статье Amigo et. al, 2009. A comparison of Extrinsic Clustering Evaluation Metrics based on Formal Constraints очень подробно разбирается ряд принципов, их корректность и то, как различные классы метрик удовлетворяют этим принципам.
1.1. Cluster Homogeneity, однородность кластеров

Значение метрики качества должно уменьшаться при объединении в один кластер двух эталонных.
1.2. Cluster Completeness, полнота кластеров

Это свойство, двойственное свойству однородности. Значение метрики качества должно уменьшаться при разделении эталонного кластера на части.
1.3. Rag Bag

Пусть есть два кластера: чистый, содержащий элементы из одного эталонного кластера, и шумный («лоскутный»), где собраны элементы из большого числа различных эталонных кластеров. Тогда значение метрики качества должно быть выше у той версии кластеризации, которая помещает новый нерелевантный обоим кластерам элемент в шумный кластер, по сравнению с версией, которая помещает этот элемент в чистый кластер.
Это свойство может показаться очень естественным, но обязательно нужно принимать во внимание специфику приложения. Скажем, в Яндекс.Новостях большие «лоскутные» кластеры очень вредны: их невозможно адекватно проаннотировать, а благодаря своему размеру и разнообразию источников они могут ранжироваться очень высоко.
1.4. Size vs Quantity

Значительное ухудшение кластеризации большого числа небольших кластеров должно обходиться дороже небольшого ухудшения кластеризации в крупном кластере.
2. Метрики качества кластеризации
Теперь обсудим несколько важных классов метрик качества кластеризации.
Будем считать заданным конечное множество объектов . Множеством кластеров будем называть всякую совокупность его непересекающихся непустых подмножеств. Таким образом,
— множество кластеров, если
При этом множество кластеров не обязательно является покрытием множества объектов: допускается неполная кластеризация. Впрочем, иногда удобно считать каждый некластеризованный элемент тривиальным одноэлементным кластером.
Будем считать, что определены два множества кластеров: эталонное и построенное алгоритмом
. Через
и
будем обозначать, соответственно, эталонный и алгоритмический кластеры, которым принадлежит объект
.
2.1. Метрики, основанные на подсчёте пар (классификационные)
В этом подходе задача кластеризации сводится к бинарной классификации на множестве пар объектов. Пара объектов считается относящейся к положительному классу тогда и только тогда, когда оба объекта относятся к одному и тому же эталонному кластеру. Предсказание считается положительным тогда и только тогда, когда эти объекты относятся к одному и тому же алгоритмическому кластеру.
Иллюстрация ниже поясняет это определение. Восемь объектов разбиты на три эталонных кластера размеров 3 («жёлтый»), 3 («фиолетовый») и 2 («синий»). Эти же объекты кластеризованы алгоритмом так: «синий» кластер собран абсолютно верно, а вот один из «фиолетовых» объектов ошибочно отнесён в кластер к «жёлтым».

Тогда здесь суммарно пар объектов, из них:
— положительных;
— отрицательных.
Построенная алгоритмом матрица содержит шесть лишних положительных элементов за счёт создания связей между «жёлтыми» объектами и одним из «фиолетовых» объектов, а также теряет четыре элемента из-за потери связей между «фиолетовыми» элементами.
В терминах качества бинарной классификации получается, что:
— пар определены как положительные и при этом являются положительными;
— пар определены как положительные, но ими не являются;
— пар определены как отрицательные и при этом являются отрицательными;
— пары определены как отрицательные, но ими не являются.
Теперь можно вычислить точность, полноту и любые другие метрики:
В процессе вычислений можно учитывать тот факт, что матрица симметрична: это вносит изменения в получаемые значения.
Описанный способ интуитивно очень понятен и прост в реализации. Другая его замечательная особенность в том, что получение оценок не требует построения эталонного разбиения на кластеры: достаточно разметить репрезентативное множество пар объектов.
Главный недостаток pairwise-метрик — квадратичная зависимость числа порождаемых пар от размера кластера. Из-за этого значение pairwise-метрик может быть обусловлено качеством кластеризации буквально нескольких самых крупных кластеров.
2.2. Метрики, основанные на сопоставлении множеств
Для определения метрик этого класса вначале вводятся метрики точности и полноты соответствия между кластером и эталоном:
Пример ниже содержит два эталонных кластера: «жёлтый» (y) и «фиолетовый» (v). Единственный алгоритмический кластер содержит 25 жёлтых точек и 10 фиолетовых. Точность соответствия этого кластера жёлтому кластеру составляет 25/35, а фиолетовому — 10/35. Вне кластера находятся ещё пять жёлтых и две фиолетовых точки. Значит, всего имеется 30 жёлтых и 12 фиолетовых точек, поэтому полнота соответствия жёлтому кластеру равна 25/30, фиолетовому — 10/12.
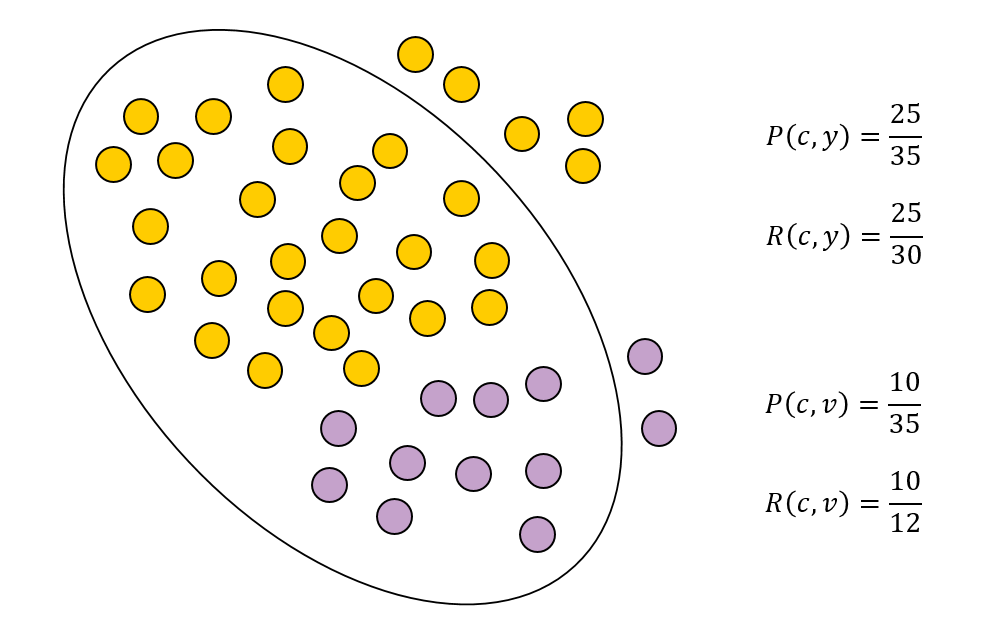
Физический смысл введённых величин прост: точность равна вероятности выбрать элемент эталонного кластера при выборе случайного элемента из алгоритмического кластера, полнота равна вероятности выбрать элемент алгоритмического кластера при выборе случайного элемента из эталонного кластера. Показатели двойственны:
Далее можно определить и F-меру:
Теперь необходимо определить интегральный показатель. Самый известный способ определить его через показатели отдельных соответствий приводит к метрике «чистоты» кластеров, Purity:
Вводится и двойственная метрика, в которой суммирование и нормировка производятся по эталонным кластерам:
Высокое значение означает, что для кластера найдётся хорошо соответствующий ему эталон. Высокое значение
— что для эталона найдётся хорошо соответствующий ему алгоритмический кластер. Значит ли это, что близость обеих метрик к единице гарантирует очень хорошее качество кластеризации? К сожалению, нет. Рассмотрим следующий пример:

Для примера можно взять ,
,
,
. Кластер
полностью находится внутри
, поэтому:
Отсюда можно вычислить метрики точности для соответствий:
Из этого уже ясно, что показатели Purity и InversePurity высоки для каждого из алгоритмических и эталонных кластеров соответственно. Аккуратное вычисление даёт:
Обе величины близки к единице, хотя для кластера в действительности нет ни одного хорошего представителя из числа алгоритмических кластеров. Метрики не заметили этого, т. к. при подсчёте Purity кластеру
соответствовал кластер
, а при подсчёте InversePurity — кластер
. При вычислении двух различных показателей в качестве оптимальных были выбраны различные соответствия!
Отчасти с этой проблемой помогает справиться F-мера:
Использование такого показателя может быть оправданным в некоторых ситуациях, но стоит иметь в виду, что один и тот же кластер может сопоставиться сразу нескольким эталонам. Кроме того, кластеризация элементов из кластеров, не сопоставленных ни одному из эталонов, не оказывает влияния на значение метрики.
2.3. BCubed-метрики
Этот класс метрик предлагает взглянуть на кластеризацию с точки зрения одного отдельного элемента. Предположим, пользователь изучает конкретный документ внутри новостного сюжета. Какова доля документов этого сюжета, относящихся к той же теме, что и изучаемый документ? А какую долю документы по этой теме в сюжете составляют от числа всех документов по теме?
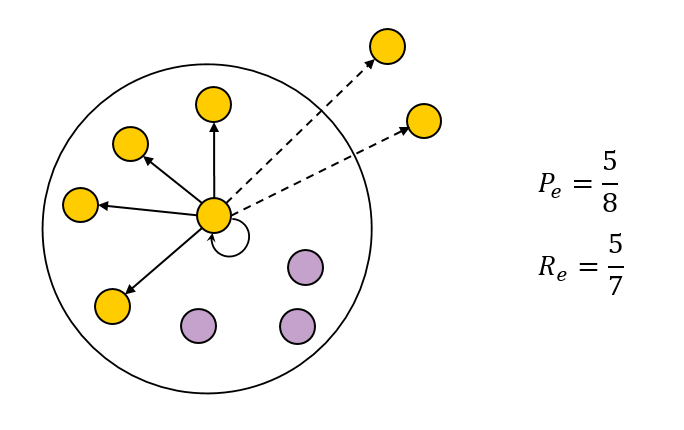
Вполне законные вопросы, и ответ на них приводит к BCubed-метрикам точности и полноты. Они определены для конкретного объекта:
Интегральные показатели определяются усреднением по элементам:
BCubed Precision удовлетворяет свойствам Cluster Homogeneity и Rag Bag, а BCubed Recall — свойствам Cluster Completeness и Size vs Quantity. Сводный показатель — F-мера — удовлетворяет всем четырём свойствам:
3. Метрики эталонных кластеров
В некоторых приложениях полезно оценивать не только интегральные показатели качества, но и качество кластеризации отдельных эталонных кластеров. Поэтому в нашей системе оценки качества все метрики определялись для эталонных кластеров, которые затем агрегировались путём усреднения.
Рассмотрим, как это работает, на следующем примере. Пусть множество объектов состоит из девяти элементов, образующих два эталонных кластера
и
(«зелёный» и «жёлтый» соответственно).
Алгоритмические кластеры не повторяют эталонные в точности: ,
.

3.1. BCubed
Введём BCubed-метрики для отдельных эталонных кластеров:
Для рассмотренного примера получим следующие значения метрики точности кластеризации отдельных элементов:
Отсюда метрики точности эталонных кластеров:
Аналогично для полноты:
Средневзвешенные по всем эталонным кластерам значения BCP и BCR будут такими:
Именно эти характеристики мы и использовали при оценке качества кластеризации.
3.2. Expected Cluster Completeness
Разложение качества кластеризации на характеристики точности и полноты бывает очень полезным для анализа и дальнейшего совершенствования алгоритма. Для принятия решений о том, какой из алгоритмов лучше, требуется, впрочем, выработать один-единственный показатель.
Стандартный способ — F-мера — подходит лишь в ограниченном смысле. Это действительно один показатель, но является ли его значение подходящим для принятия решений? Вовсе не факт.
В конечном счёте требование к алгоритму заключается в том, чтобы каждому эталонному кластеру сопоставить некоторый уникальный алгоритмический кластер, который служил бы для эталона «представителем». Алгоритмический кластер может представлять только один эталонный кластер. При этом из всех сопоставлений важно лишь одно — самое удачное. Такой ход рассуждений является естественным для многих приложений: например, при анализе поисковых запросов судить о содержании кластера проще всего по тексту типичного представителя, то есть единственного запроса.
Сопоставление — функция из множества алгоритмических кластеров в множество эталонных кластеров:
Тогда для конкретного эталона и сопоставления можно вычислить характеристику полноты (cluster completeness):
Среднее значение полноты:
Теперь возникает вопрос — как именно построить сопоставление, то есть функцию . В действительности никакой конкретный алгоритм не будет работать хорошо: незначительные изменения в кластеризации могут существенно повлиять на сопоставление и сильно изменить значение метрики.
Поэтому придётся ввести на множестве всех возможных сопоставлений вероятностную меру и затем вычислить математическое ожидание. Пусть вероятность того, что , равна
Теперь вероятность выбора функции определяется через произведение вероятностей выбора всех её значений:
Теперь можно вычислить ожидаемое покрытие для эталонного кластера:
Интегральный показатель можно определить так:
Либо эквивалентно:
Опишу и другой способ понять эту метрику. Пусть с эталоном пересекаются кластеры
,
, …,
, пронумерованные в порядке невозрастания размера пересечения:
Кластер выбирается в соответствие эталону
с вероятностью
При этом покрытие будет равно
Поскольку это максимально возможное покрытие, которое может обеспечить один из кластеров, то выбранные для других кластеров сопоставления не играют роли. Так что в этом случае покрытие окажется равным .
Если же для кластера выбрано другое сопоставление, то с вероятностью
эталону
будет сопоставлен кластер
. Тогда покрытие окажется равным
. Это рассуждение можно продолжить, и в конце концов мы получим, что математическое ожидание покрытия равняется
Код для вычисления метрики ECC для конкретного эталонного кластера получается очень простым. Вектор sortedMatchings состоит из всех кластеров, которые пересекаются с эталоном, он отсортирован по неубыванию полноты. Точность и полноту каждого соответствия эталону можно вычислить при помощи методов Precision() и Recall() соответственно. Тогда:
double ExpectedClusterCompleteness(const TMatchings& sortedMatchings) {
double expectedClusterCompleteness = 0.;
double probability = 1.;
for (const TMatching& matching : sortedMatchings) {
expectedClusterCompleteness += matching.Recall() * matching.Precision() * probability;
probability *= 1. - matching.Precision();
}
return expectedClusterCompleteness;
}Интересно, что в этой метрике агрегирующей функцией для точности и полноты в итоге оказалась не -мера, а простое произведение!
Вычислим теперь ECC для эталонных кластеров, с которых начался пункт 3. Максимальное покрытие эталону обеспечивает кластер
, а эталону
—
. Поэтому:
Интегральное значение вычисляется как среднее значение по всем эталонам, поэтому:
4. Реализация
Метрики, описанные в пункте 3, реализованы на C++ и выложены под лицензией MIT на GitHub. Реализация компилируется и запускается как на Linux, так и на Windows.
Программу легко собрать:
git clone https://github.com/yandex/cluster_metrics/ .
cmake .
cmake --build .После этого её можно запустить для того же примера, что разбирался в пункте 3. Расчёты из статьи совпадают с показаниями программы!
./cluster_metrics samples/sample_markup.tsv samples/sample_clusters.tsv
ECC 0.61250 (0.61250)
BCP 0.65125 (0.65125)
BCR 0.65250 (0.65250)
BCF1 0.65187 (0.65187)В скобках указываются значения метрик для «оптимистичного» сценария, когда все неразмеченные элементы в действительности относятся к тем эталонам, с которыми пересекаются содержащие их кластеры. На практике это даже слишком оптимистичная оценка, так как каждый объект может относиться только к одной конкретной теме, но не ко всем сразу. Тем не менее, эта оценка полезна для случаев, когда алгоритм уж очень сильно меняет множество кластеризованных элементов. Если значение метрики существенно меньше оптимистичной оценки — стоит расширить разметку.
5. Как понять, что метрики работают
После того, как метрики придуманы, нужно аккуратно убедиться в том, что они действительно позволяют принимать правильные решения.
Мы построили систему экспертного сравнения алгоритмов кластеризации. Всякий раз, как алгоритм претерпевал существенные изменения, асессоры размечали изменения. Интерфейс, если изображать схематично, выглядел так:
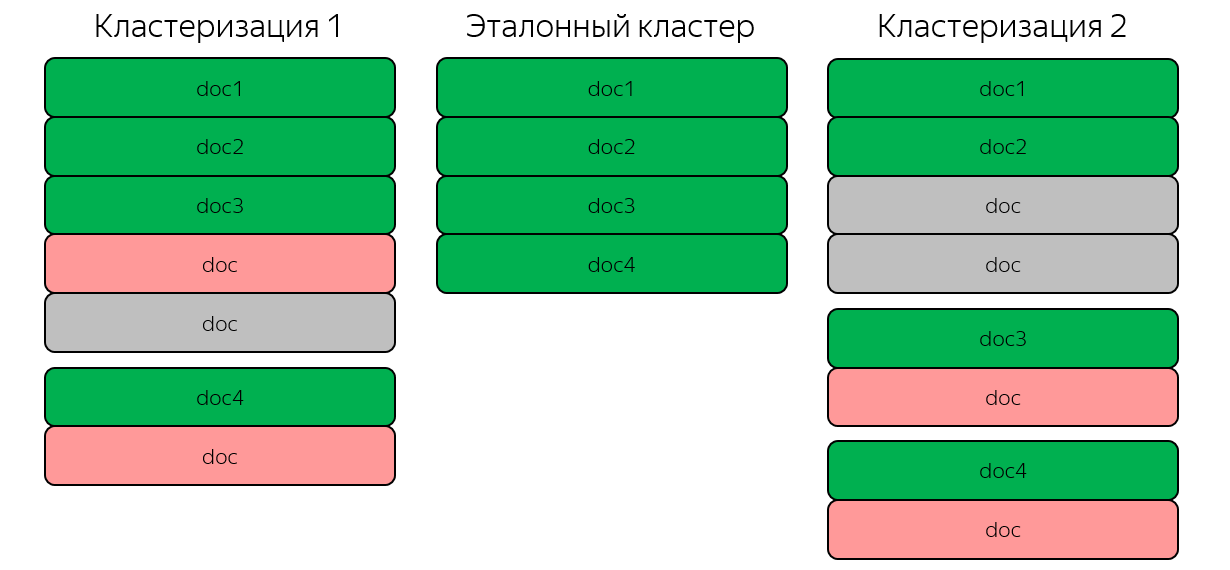
В центре экрана находился эталонный кластер: были перечислены все документы, отнесённые к нему в процессе разметки. С двух сторон от него отображались кластеры, построенные двумя соревнующимися алгоритмами, имеющие непустое пересечение с эталоном. Стороны для алгоритмов выбирались случайным образом, чтобы асессор не знал, с какой стороны находится старый алгоритм, а с какой — новый. Порядок кластеров для каждого алгоритма определялся сортировкой по произведению точности на полноту соответствия — совсем как в метрике ECC!
Зелёным помечались документы, относящиеся к выбранному эталонному кластеру, красным — относящиеся к другому эталонному кластеру. Серым обозначались неразмеченные документы.
Асессор смотрел на этот экран, изучал документы, при необходимости определял правильные эталонные кластеры для неразмеченных документов и в конце концов принимал решение о том, какой из алгоритмов сработал лучше. После разметки нескольких сотен эталонных кластеров можно было получить статистически значимый вывод о превосходстве того или иного алгоритма.
Такую процедуру мы использовали в течение нескольких месяцев, пока не обнаружили, что асессоры всегда выбирают тот алгоритм, для которого выше значение метрики ECC! Если показатели ECC различались хотя бы сколько-то существенно, асессоры всегда выбирали тот же вариант, что и метрика, это происходило буквально в 100% случаев. Поэтому со временем мы отказались от процедуры ручной приёмки и принимали решения просто по метрикам.
Интересно рассказать, что свойства метрик кластеризации из пункта 1 также исследовались на соответствие интуитивным представлениям о качестве кластеризации. В уже цитировавшейся статье описывается следующий эксперимент: для каждого правила формулировался пример — эталонное разбиение некоторого множества объектов и два альтернативных способа кластеризовать эти же объекты.
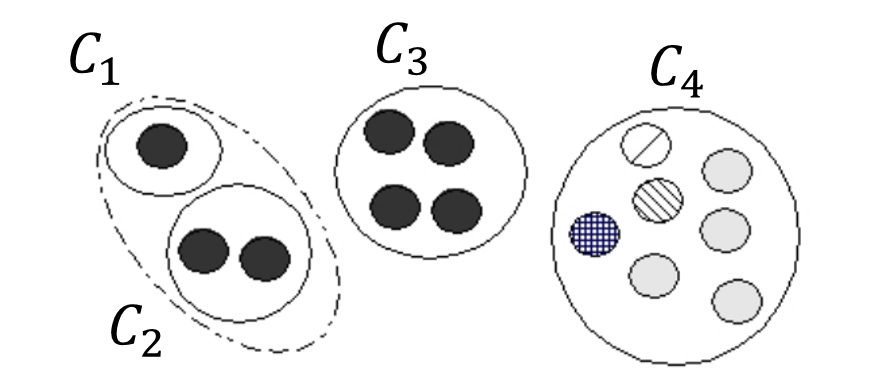
Пример сравнения двух разбиений на кластеры для свойства Cluster Completeness
Далее сорок асессоров выносили вердикты о том, какой из двух способов лучше, и их ответы сравнивались с вердиктами правил. Оказалось, что с каждым из правил Cluster Homogeneity, Cluster Completeness, Rag Bag не согласился только один из сорока асессоров, а свойству Size vs Quantity не противоречил никто.
Это очень интересное исследование, хотя оно и обладает очевидными недостатками: пример для каждого правила был только один, а восприятие качества кластеризации, очевидно, сильно связано с геометрической интерпретацией.
Уверенности в метриках, описанных в пункте 3, намного больше, так как мы исследовали их на многих сотнях или даже тысячах примеров.
Закончить, однако, хочу предостережением: в каждой новой задаче применимость тех или иных метрик нужно изучать заново. Мне лишь остаётся надеяться, что статья поможет всем, кто будет заниматься этой нелёгкой работой в будущем.







