From Wikipedia, the free encyclopedia
«Invalid proof» redirects here. For any type of invalid proof besides mathematics, see Fallacy.
«0 = 1» redirects here. For the algebraic structure where this equality holds, see Null ring.
In mathematics, certain kinds of mistaken proof are often exhibited, and sometimes collected, as illustrations of a concept called mathematical fallacy. There is a distinction between a simple mistake and a mathematical fallacy in a proof, in that a mistake in a proof leads to an invalid proof while in the best-known examples of mathematical fallacies there is some element of concealment or deception in the presentation of the proof.
For example, the reason why validity fails may be attributed to a division by zero that is hidden by algebraic notation. There is a certain quality of the mathematical fallacy: as typically presented, it leads not only to an absurd result, but does so in a crafty or clever way.[1] Therefore, these fallacies, for pedagogic reasons, usually take the form of spurious proofs of obvious contradictions. Although the proofs are flawed, the errors, usually by design, are comparatively subtle, or designed to show that certain steps are conditional, and are not applicable in the cases that are the exceptions to the rules.
The traditional way of presenting a mathematical fallacy is to give an invalid step of deduction mixed in with valid steps, so that the meaning of fallacy is here slightly different from the logical fallacy. The latter usually applies to a form of argument that does not comply with the valid inference rules of logic, whereas the problematic mathematical step is typically a correct rule applied with a tacit wrong assumption. Beyond pedagogy, the resolution of a fallacy can lead to deeper insights into a subject (e.g., the introduction of Pasch’s axiom of Euclidean geometry,[2] the five colour theorem of graph theory). Pseudaria, an ancient lost book of false proofs, is attributed to Euclid.[3]
Mathematical fallacies exist in many branches of mathematics. In elementary algebra, typical examples may involve a step where division by zero is performed, where a root is incorrectly extracted or, more generally, where different values of a multiple valued function are equated. Well-known fallacies also exist in elementary Euclidean geometry and calculus.[4][5]
Howlers[edit]
Anomalous cancellation in calculus
Examples exist of mathematically correct results derived by incorrect lines of reasoning. Such an argument, however true the conclusion appears to be, is mathematically invalid and is commonly known as a howler. The following is an example of a howler involving anomalous cancellation:
Here, although the conclusion 16/64 = 1/4 is correct, there is a fallacious, invalid cancellation in the middle step.[note 1] Another classical example of a howler is proving the Cayley–Hamilton theorem by simply substituting the scalar variables of the characteristic polynomial by the matrix.
Bogus proofs, calculations, or derivations constructed to produce a correct result in spite of incorrect logic or operations were termed «howlers» by Maxwell.[2] Outside the field of mathematics the term howler has various meanings, generally less specific.
Division by zero[edit]
The division-by-zero fallacy has many variants. The following example uses a disguised division by zero to «prove» that 2 = 1, but can be modified to prove that any number equals any other number.
- Let a and b be equal, nonzero quantities
- Multiply by a
- Subtract b2
- Factor both sides: the left factors as a difference of squares, the right is factored by extracting b from both terms
- Divide out (a − b)
- Use the fact that a = b
- Combine like terms on the left
- Divide by the non-zero b
- Q.E.D.[6]
The fallacy is in line 5: the progression from line 4 to line 5 involves division by a − b, which is zero since a = b. Since division by zero is undefined, the argument is invalid.
Analysis[edit]
Mathematical analysis as the mathematical study of change and limits can lead to mathematical fallacies — if the properties of integrals and differentials are ignored. For instance, a naive use of integration by parts can be used to give a false proof that 0 = 1.[7] Letting u = 1/log x and dv = dx/x, we may write:
after which the antiderivatives may be cancelled yielding 0 = 1. The problem is that antiderivatives are only defined up to a constant and shifting them by 1 or indeed any number is allowed. The error really comes to light when we introduce arbitrary integration limits a and b.
Since the difference between two values of a constant function vanishes, the same definite integral appears on both sides of the equation.
Multivalued functions[edit]
Many functions do not have a unique inverse. For instance, while squaring a number gives a unique value, there are two possible square roots of a positive number. The square root is multivalued. One value can be chosen by convention as the principal value; in the case of the square root the non-negative value is the principal value, but there is no guarantee that the square root given as the principal value of the square of a number will be equal to the original number (e.g. the principal square root of the square of −2 is 2). This remains true for nth roots.
Positive and negative roots[edit]
Care must be taken when taking the square root of both sides of an equality. Failing to do so results in a «proof» of[8] 5 = 4.
Proof:
- Start from
- Write this as
- Rewrite as
- Add 81/4 on both sides:
- These are perfect squares:
- Take the square root of both sides:
- Add 9/2 on both sides:
- Q.E.D.
The fallacy is in the second to last line, where the square root of both sides is taken: a2 = b2 only implies a = b if a and b have the same sign, which is not the case here. In this case, it implies that a = –b, so the equation should read
which, by adding 9/2 on both sides, correctly reduces to 5 = 5.
Another example illustrating the danger of taking the square root of both sides of an equation involves the following fundamental identity[9]
which holds as a consequence of the Pythagorean theorem. Then, by taking a square root,
Evaluating this when x = π , we get that
or
which is incorrect.
The error in each of these examples fundamentally lies in the fact that any equation of the form
where 
and it is essential to check which of these solutions is relevant to the problem at hand.[10] In the above fallacy, the square root that allowed the second equation to be deduced from the first is valid only when cos x is positive. In particular, when x is set to π, the second equation is rendered invalid.
Square roots of negative numbers[edit]
Invalid proofs utilizing powers and roots are often of the following kind:
The fallacy is that the rule 


Alternatively, imaginary roots are obfuscated in the following:
The error here lies in the third equality, as the rule 
Complex exponents[edit]
When a number is raised to a complex power, the result is not uniquely defined (see Exponentiation § Failure of power and logarithm identities). If this property is not recognized, then errors such as the following can result:
The error here is that the rule of multiplying exponents as when going to the third line does not apply unmodified with complex exponents, even if when putting both sides to the power i only the principal value is chosen. When treated as multivalued functions, both sides produce the same set of values, being {e2πn | n ∈ ℤ}.
Geometry[edit]
Many mathematical fallacies in geometry arise from using an additive equality involving oriented quantities (such as adding vectors along a given line or adding oriented angles in the plane) to a valid identity, but which fixes only the absolute value of (one of) these quantities. This quantity is then incorporated into the equation with the wrong orientation, so as to produce an absurd conclusion. This wrong orientation is usually suggested implicitly by supplying an imprecise diagram of the situation, where relative positions of points or lines are chosen in a way that is actually impossible under the hypotheses of the argument, but non-obviously so.
In general, such a fallacy is easy to expose by drawing a precise picture of the situation, in which some relative positions will be different from those in the provided diagram. In order to avoid such fallacies, a correct geometric argument using addition or subtraction of distances or angles should always prove that quantities are being incorporated with their correct orientation.
Fallacy of the isosceles triangle[edit]

The fallacy of the isosceles triangle, from (Maxwell 1959, Chapter II, § 1), purports to show that every triangle is isosceles, meaning that two sides of the triangle are congruent. This fallacy was known to Lewis Carroll and may have been discovered by him. It was published in 1899.[12][13]
Given a triangle △ABC, prove that AB = AC:
- Draw a line bisecting ∠A.
- Draw the perpendicular bisector of segment BC, which bisects BC at a point D.
- Let these two lines meet at a point O.
- Draw line OR perpendicular to AB, line OQ perpendicular to AC.
- Draw lines OB and OC.
- By AAS, △RAO ≅ △QAO (∠ORA = ∠OQA = 90°; ∠RAO = ∠QAO; AO = AO (common side)).
- By RHS,[note 2] △ROB ≅ △QOC (∠BRO = ∠CQO = 90°; BO = OC (hypotenuse); RO = OQ (leg)).
- Thus, AR = AQ, RB = QC, and AB = AR + RB = AQ + QC = AC.
Q.E.D.
As a corollary, one can show that all triangles are equilateral, by showing that AB = BC and AC = BC in the same way.
The error in the proof is the assumption in the diagram that the point O is inside the triangle. In fact, O always lies on the circumcircle of the △ABC (except for isosceles and equilateral triangles where AO and OD coincide). Furthermore, it can be shown that, if AB is longer than AC, then R will lie within AB, while Q will lie outside of AC, and vice versa (in fact, any diagram drawn with sufficiently accurate instruments will verify the above two facts). Because of this, AB is still AR + RB, but AC is actually AQ − QC; and thus the lengths are not necessarily the same.
Proof by induction[edit]
There exist several fallacious proofs by induction in which one of the components, basis case or inductive step, is incorrect. Intuitively, proofs by induction work by arguing that if a statement is true in one case, it is true in the next case, and hence by repeatedly applying this, it can be shown to be true for all cases. The following «proof» shows that all horses are the same colour.[14][note 3]
- Let us say that any group of N horses is all of the same colour.
- If we remove a horse from the group, we have a group of N − 1 horses of the same colour. If we add another horse, we have another group of N horses. By our previous assumption, all the horses are of the same colour in this new group, since it is a group of N horses.
- Thus we have constructed two groups of N horses all of the same colour, with N − 1 horses in common. Since these two groups have some horses in common, the two groups must be of the same colour as each other.
- Therefore, combining all the horses used, we have a group of N + 1 horses of the same colour.
- Thus if any N horses are all the same colour, any N + 1 horses are the same colour.
- This is clearly true for N = 1 (i.e., one horse is a group where all the horses are the same colour). Thus, by induction, N horses are the same colour for any positive integer N, and so all horses are the same colour.
The fallacy in this proof arises in line 3. For N = 1, the two groups of horses have N − 1 = 0 horses in common, and thus are not necessarily the same colour as each other, so the group of N + 1 = 2 horses is not necessarily all of the same colour. The implication «every N horses are of the same colour, then N + 1 horses are of the same colour» works for any N > 1, but fails to be true when N = 1. The basis case is correct, but the induction step has a fundamental flaw.
See also[edit]
- Anomalous cancellation – Kind of arithmetic error
- Division by zero – Class of mathematical expression
- List of incomplete proofs
- Mathematical coincidence – Coincidence in mathematics
- Paradox – Statement that apparently contradicts itself
- Proof by intimidation – Marking an argument as obvious or trivial
Notes[edit]
- ^ The same fallacy also applies to the following:
- ^ Hypotenuse–leg congruence
- ^ George Pólya’s original «proof» was that any n girls have the same colour eyes.
References[edit]
- ^ Maxwell 1959, p. 9
- ^ a b Maxwell 1959
- ^ Heath & Heiberg 1908, Chapter II, §I
- ^ Barbeau, Ed (1991). «Fallacies, Flaws, and Flimflam» (PDF). The College Mathematics Journal. 22 (5). ISSN 0746-8342.
- ^ «soft question – Best Fake Proofs? (A M.SE April Fools Day collection)». Mathematics Stack Exchange. Retrieved 2019-10-24.
- ^ Heuser, Harro (1989), Lehrbuch der Analysis – Teil 1 (6th ed.), Teubner, p. 51, ISBN 978-3-8351-0131-9
- ^ Barbeau, Ed (1990), «Fallacies, Flaws and Flimflam #19: Dolt’s Theorem», The College Mathematics Journal, 21 (3): 216–218, doi:10.1080/07468342.1990.11973308
- ^ Frohlichstein, Jack (1967). Mathematical Fun, Games and Puzzles (illustrated ed.). Courier Corporation. p. 207. ISBN 0-486-20789-7. Extract of page 207
- ^ Maxwell 1959, Chapter VI, §I.1
- ^ Maxwell 1959, Chapter VI, §II
- ^ Nahin, Paul J. (2010). An Imaginary Tale: The Story of «i«. Princeton University Press. p. 12. ISBN 978-1-4008-3029-9. Extract of page 12
- ^ S.D.Collingwood, ed. (1899), The Lewis Carroll Picture Book, Collins, pp. 190–191
- ^ Robin Wilson (2008), Lewis Carroll in Numberland, Penguin Books, pp. 169–170, ISBN 978-0-14-101610-8
- ^ Pólya, George (1954). Induction and Analogy in Mathematics. Mathematics and plausible reasoning. Vol. 1. Princeton. p. 120.
- Barbeau, Edward J. (2000), Mathematical fallacies, flaws, and flimflam, MAA Spectrum, Mathematical Association of America, ISBN 978-0-88385-529-4, MR 1725831.
- Bunch, Bryan (1997), Mathematical fallacies and paradoxes, New York: Dover Publications, ISBN 978-0-486-29664-7, MR 1461270.
- Heath, Sir Thomas Little; Heiberg, Johan Ludvig (1908), The thirteen books of Euclid’s Elements, Volume 1, The University Press.
- Maxwell, E. A. (1959), Fallacies in mathematics, Cambridge University Press, ISBN 0-521-05700-0, MR 0099907.
External links[edit]
- Invalid proofs at Cut-the-knot (including literature references)
- Classic fallacies with some discussion
- More invalid proofs from AhaJokes.com
- Math jokes including an invalid proof
From Wikipedia, the free encyclopedia
«Invalid proof» redirects here. For any type of invalid proof besides mathematics, see Fallacy.
«0 = 1» redirects here. For the algebraic structure where this equality holds, see Null ring.
In mathematics, certain kinds of mistaken proof are often exhibited, and sometimes collected, as illustrations of a concept called mathematical fallacy. There is a distinction between a simple mistake and a mathematical fallacy in a proof, in that a mistake in a proof leads to an invalid proof while in the best-known examples of mathematical fallacies there is some element of concealment or deception in the presentation of the proof.
For example, the reason why validity fails may be attributed to a division by zero that is hidden by algebraic notation. There is a certain quality of the mathematical fallacy: as typically presented, it leads not only to an absurd result, but does so in a crafty or clever way.[1] Therefore, these fallacies, for pedagogic reasons, usually take the form of spurious proofs of obvious contradictions. Although the proofs are flawed, the errors, usually by design, are comparatively subtle, or designed to show that certain steps are conditional, and are not applicable in the cases that are the exceptions to the rules.
The traditional way of presenting a mathematical fallacy is to give an invalid step of deduction mixed in with valid steps, so that the meaning of fallacy is here slightly different from the logical fallacy. The latter usually applies to a form of argument that does not comply with the valid inference rules of logic, whereas the problematic mathematical step is typically a correct rule applied with a tacit wrong assumption. Beyond pedagogy, the resolution of a fallacy can lead to deeper insights into a subject (e.g., the introduction of Pasch’s axiom of Euclidean geometry,[2] the five colour theorem of graph theory). Pseudaria, an ancient lost book of false proofs, is attributed to Euclid.[3]
Mathematical fallacies exist in many branches of mathematics. In elementary algebra, typical examples may involve a step where division by zero is performed, where a root is incorrectly extracted or, more generally, where different values of a multiple valued function are equated. Well-known fallacies also exist in elementary Euclidean geometry and calculus.[4][5]
Howlers[edit]
Anomalous cancellation in calculus
Examples exist of mathematically correct results derived by incorrect lines of reasoning. Such an argument, however true the conclusion appears to be, is mathematically invalid and is commonly known as a howler. The following is an example of a howler involving anomalous cancellation:
Here, although the conclusion 16/64 = 1/4 is correct, there is a fallacious, invalid cancellation in the middle step.[note 1] Another classical example of a howler is proving the Cayley–Hamilton theorem by simply substituting the scalar variables of the characteristic polynomial by the matrix.
Bogus proofs, calculations, or derivations constructed to produce a correct result in spite of incorrect logic or operations were termed «howlers» by Maxwell.[2] Outside the field of mathematics the term howler has various meanings, generally less specific.
Division by zero[edit]
The division-by-zero fallacy has many variants. The following example uses a disguised division by zero to «prove» that 2 = 1, but can be modified to prove that any number equals any other number.
- Let a and b be equal, nonzero quantities
- Multiply by a
- Subtract b2
- Factor both sides: the left factors as a difference of squares, the right is factored by extracting b from both terms
- Divide out (a − b)
- Use the fact that a = b
- Combine like terms on the left
- Divide by the non-zero b
- Q.E.D.[6]
The fallacy is in line 5: the progression from line 4 to line 5 involves division by a − b, which is zero since a = b. Since division by zero is undefined, the argument is invalid.
Analysis[edit]
Mathematical analysis as the mathematical study of change and limits can lead to mathematical fallacies — if the properties of integrals and differentials are ignored. For instance, a naive use of integration by parts can be used to give a false proof that 0 = 1.[7] Letting u = 1/log x and dv = dx/x, we may write:
after which the antiderivatives may be cancelled yielding 0 = 1. The problem is that antiderivatives are only defined up to a constant and shifting them by 1 or indeed any number is allowed. The error really comes to light when we introduce arbitrary integration limits a and b.
Since the difference between two values of a constant function vanishes, the same definite integral appears on both sides of the equation.
Multivalued functions[edit]
Many functions do not have a unique inverse. For instance, while squaring a number gives a unique value, there are two possible square roots of a positive number. The square root is multivalued. One value can be chosen by convention as the principal value; in the case of the square root the non-negative value is the principal value, but there is no guarantee that the square root given as the principal value of the square of a number will be equal to the original number (e.g. the principal square root of the square of −2 is 2). This remains true for nth roots.
Positive and negative roots[edit]
Care must be taken when taking the square root of both sides of an equality. Failing to do so results in a «proof» of[8] 5 = 4.
Proof:
- Start from
- Write this as
- Rewrite as
- Add 81/4 on both sides:
- These are perfect squares:
- Take the square root of both sides:
- Add 9/2 on both sides:
- Q.E.D.
The fallacy is in the second to last line, where the square root of both sides is taken: a2 = b2 only implies a = b if a and b have the same sign, which is not the case here. In this case, it implies that a = –b, so the equation should read
which, by adding 9/2 on both sides, correctly reduces to 5 = 5.
Another example illustrating the danger of taking the square root of both sides of an equation involves the following fundamental identity[9]
which holds as a consequence of the Pythagorean theorem. Then, by taking a square root,
Evaluating this when x = π , we get that
or
which is incorrect.
The error in each of these examples fundamentally lies in the fact that any equation of the form
where 
and it is essential to check which of these solutions is relevant to the problem at hand.[10] In the above fallacy, the square root that allowed the second equation to be deduced from the first is valid only when cos x is positive. In particular, when x is set to π, the second equation is rendered invalid.
Square roots of negative numbers[edit]
Invalid proofs utilizing powers and roots are often of the following kind:
The fallacy is that the rule 


Alternatively, imaginary roots are obfuscated in the following:
The error here lies in the third equality, as the rule 
Complex exponents[edit]
When a number is raised to a complex power, the result is not uniquely defined (see Exponentiation § Failure of power and logarithm identities). If this property is not recognized, then errors such as the following can result:
The error here is that the rule of multiplying exponents as when going to the third line does not apply unmodified with complex exponents, even if when putting both sides to the power i only the principal value is chosen. When treated as multivalued functions, both sides produce the same set of values, being {e2πn | n ∈ ℤ}.
Geometry[edit]
Many mathematical fallacies in geometry arise from using an additive equality involving oriented quantities (such as adding vectors along a given line or adding oriented angles in the plane) to a valid identity, but which fixes only the absolute value of (one of) these quantities. This quantity is then incorporated into the equation with the wrong orientation, so as to produce an absurd conclusion. This wrong orientation is usually suggested implicitly by supplying an imprecise diagram of the situation, where relative positions of points or lines are chosen in a way that is actually impossible under the hypotheses of the argument, but non-obviously so.
In general, such a fallacy is easy to expose by drawing a precise picture of the situation, in which some relative positions will be different from those in the provided diagram. In order to avoid such fallacies, a correct geometric argument using addition or subtraction of distances or angles should always prove that quantities are being incorporated with their correct orientation.
Fallacy of the isosceles triangle[edit]

The fallacy of the isosceles triangle, from (Maxwell 1959, Chapter II, § 1), purports to show that every triangle is isosceles, meaning that two sides of the triangle are congruent. This fallacy was known to Lewis Carroll and may have been discovered by him. It was published in 1899.[12][13]
Given a triangle △ABC, prove that AB = AC:
- Draw a line bisecting ∠A.
- Draw the perpendicular bisector of segment BC, which bisects BC at a point D.
- Let these two lines meet at a point O.
- Draw line OR perpendicular to AB, line OQ perpendicular to AC.
- Draw lines OB and OC.
- By AAS, △RAO ≅ △QAO (∠ORA = ∠OQA = 90°; ∠RAO = ∠QAO; AO = AO (common side)).
- By RHS,[note 2] △ROB ≅ △QOC (∠BRO = ∠CQO = 90°; BO = OC (hypotenuse); RO = OQ (leg)).
- Thus, AR = AQ, RB = QC, and AB = AR + RB = AQ + QC = AC.
Q.E.D.
As a corollary, one can show that all triangles are equilateral, by showing that AB = BC and AC = BC in the same way.
The error in the proof is the assumption in the diagram that the point O is inside the triangle. In fact, O always lies on the circumcircle of the △ABC (except for isosceles and equilateral triangles where AO and OD coincide). Furthermore, it can be shown that, if AB is longer than AC, then R will lie within AB, while Q will lie outside of AC, and vice versa (in fact, any diagram drawn with sufficiently accurate instruments will verify the above two facts). Because of this, AB is still AR + RB, but AC is actually AQ − QC; and thus the lengths are not necessarily the same.
Proof by induction[edit]
There exist several fallacious proofs by induction in which one of the components, basis case or inductive step, is incorrect. Intuitively, proofs by induction work by arguing that if a statement is true in one case, it is true in the next case, and hence by repeatedly applying this, it can be shown to be true for all cases. The following «proof» shows that all horses are the same colour.[14][note 3]
- Let us say that any group of N horses is all of the same colour.
- If we remove a horse from the group, we have a group of N − 1 horses of the same colour. If we add another horse, we have another group of N horses. By our previous assumption, all the horses are of the same colour in this new group, since it is a group of N horses.
- Thus we have constructed two groups of N horses all of the same colour, with N − 1 horses in common. Since these two groups have some horses in common, the two groups must be of the same colour as each other.
- Therefore, combining all the horses used, we have a group of N + 1 horses of the same colour.
- Thus if any N horses are all the same colour, any N + 1 horses are the same colour.
- This is clearly true for N = 1 (i.e. one horse is a group where all the horses are the same colour). Thus, by induction, N horses are the same colour for any positive integer N. i.e. all horses are the same colour.
The fallacy in this proof arises in line 3. For N = 1, the two groups of horses have N − 1 = 0 horses in common, and thus are not necessarily the same colour as each other, so the group of N + 1 = 2 horses is not necessarily all of the same colour. The implication «every N horses are of the same colour, then N + 1 horses are of the same colour» works for any N > 1, but fails to be true when N = 1. The basis case is correct, but the induction step has a fundamental flaw.
See also[edit]
- Anomalous cancellation – Kind of arithmetic error
- Division by zero – Class of mathematical expression
- List of incomplete proofs
- Mathematical coincidence – Coincidence in mathematics
- Paradox – Statement that apparently contradicts itself
- Proof by intimidation – Marking an argument as obvious or trivial
Notes[edit]
- ^ The same fallacy also applies to the following:
- ^ Hypotenuse–leg congruence
- ^ George Pólya’s original «proof» was that any n girls have the same colour eyes.
References[edit]
- ^ Maxwell 1959, p. 9
- ^ a b Maxwell 1959
- ^ Heath & Heiberg 1908, Chapter II, §I
- ^ Barbeau, Ed (1991). «Fallacies, Flaws, and Flimflam» (PDF). The College Mathematics Journal. 22 (5). ISSN 0746-8342.
- ^ «soft question – Best Fake Proofs? (A M.SE April Fools Day collection)». Mathematics Stack Exchange. Retrieved 2019-10-24.
- ^ Heuser, Harro (1989), Lehrbuch der Analysis – Teil 1 (6th ed.), Teubner, p. 51, ISBN 978-3-8351-0131-9
- ^ Barbeau, Ed (1990), «Fallacies, Flaws and Flimflam #19: Dolt’s Theorem», The College Mathematics Journal, 21 (3): 216–218, doi:10.1080/07468342.1990.11973308
- ^ Frohlichstein, Jack (1967). Mathematical Fun, Games and Puzzles (illustrated ed.). Courier Corporation. p. 207. ISBN 0-486-20789-7. Extract of page 207
- ^ Maxwell 1959, Chapter VI, §I.1
- ^ Maxwell 1959, Chapter VI, §II
- ^ Nahin, Paul J. (2010). An Imaginary Tale: The Story of «i«. Princeton University Press. p. 12. ISBN 978-1-4008-3029-9. Extract of page 12
- ^ S.D.Collingwood, ed. (1899), The Lewis Carroll Picture Book, Collins, pp. 190–191
- ^ Robin Wilson (2008), Lewis Carroll in Numberland, Penguin Books, pp. 169–170, ISBN 978-0-14-101610-8
- ^ Pólya, George (1954). Induction and Analogy in Mathematics. Mathematics and plausible reasoning. Vol. 1. Princeton. p. 120.
- Barbeau, Edward J. (2000), Mathematical fallacies, flaws, and flimflam, MAA Spectrum, Mathematical Association of America, ISBN 978-0-88385-529-4, MR 1725831.
- Bunch, Bryan (1997), Mathematical fallacies and paradoxes, New York: Dover Publications, ISBN 978-0-486-29664-7, MR 1461270.
- Heath, Sir Thomas Little; Heiberg, Johan Ludvig (1908), The thirteen books of Euclid’s Elements, Volume 1, The University Press.
- Maxwell, E. A. (1959), Fallacies in mathematics, Cambridge University Press, ISBN 0-521-05700-0, MR 0099907.
External links[edit]
- Invalid proofs at Cut-the-knot (including literature references)
- Classic fallacies with some discussion
- More invalid proofs from AhaJokes.com
- Math jokes including an invalid proof
From Wikipedia, the free encyclopedia
«Invalid proof» redirects here. For any type of invalid proof besides mathematics, see Fallacy.
«0 = 1» redirects here. For the algebraic structure where this equality holds, see Null ring.
In mathematics, certain kinds of mistaken proof are often exhibited, and sometimes collected, as illustrations of a concept called mathematical fallacy. There is a distinction between a simple mistake and a mathematical fallacy in a proof, in that a mistake in a proof leads to an invalid proof while in the best-known examples of mathematical fallacies there is some element of concealment or deception in the presentation of the proof.
For example, the reason why validity fails may be attributed to a division by zero that is hidden by algebraic notation. There is a certain quality of the mathematical fallacy: as typically presented, it leads not only to an absurd result, but does so in a crafty or clever way.[1] Therefore, these fallacies, for pedagogic reasons, usually take the form of spurious proofs of obvious contradictions. Although the proofs are flawed, the errors, usually by design, are comparatively subtle, or designed to show that certain steps are conditional, and are not applicable in the cases that are the exceptions to the rules.
The traditional way of presenting a mathematical fallacy is to give an invalid step of deduction mixed in with valid steps, so that the meaning of fallacy is here slightly different from the logical fallacy. The latter usually applies to a form of argument that does not comply with the valid inference rules of logic, whereas the problematic mathematical step is typically a correct rule applied with a tacit wrong assumption. Beyond pedagogy, the resolution of a fallacy can lead to deeper insights into a subject (e.g., the introduction of Pasch’s axiom of Euclidean geometry,[2] the five colour theorem of graph theory). Pseudaria, an ancient lost book of false proofs, is attributed to Euclid.[3]
Mathematical fallacies exist in many branches of mathematics. In elementary algebra, typical examples may involve a step where division by zero is performed, where a root is incorrectly extracted or, more generally, where different values of a multiple valued function are equated. Well-known fallacies also exist in elementary Euclidean geometry and calculus.[4][5]
Howlers[edit]
Anomalous cancellation in calculus
Examples exist of mathematically correct results derived by incorrect lines of reasoning. Such an argument, however true the conclusion appears to be, is mathematically invalid and is commonly known as a howler. The following is an example of a howler involving anomalous cancellation:
Here, although the conclusion 16/64 = 1/4 is correct, there is a fallacious, invalid cancellation in the middle step.[note 1] Another classical example of a howler is proving the Cayley–Hamilton theorem by simply substituting the scalar variables of the characteristic polynomial by the matrix.
Bogus proofs, calculations, or derivations constructed to produce a correct result in spite of incorrect logic or operations were termed «howlers» by Maxwell.[2] Outside the field of mathematics the term howler has various meanings, generally less specific.
Division by zero[edit]
The division-by-zero fallacy has many variants. The following example uses a disguised division by zero to «prove» that 2 = 1, but can be modified to prove that any number equals any other number.
- Let a and b be equal, nonzero quantities
- Multiply by a
- Subtract b2
- Factor both sides: the left factors as a difference of squares, the right is factored by extracting b from both terms
- Divide out (a − b)
- Use the fact that a = b
- Combine like terms on the left
- Divide by the non-zero b
- Q.E.D.[6]
The fallacy is in line 5: the progression from line 4 to line 5 involves division by a − b, which is zero since a = b. Since division by zero is undefined, the argument is invalid.
Analysis[edit]
Mathematical analysis as the mathematical study of change and limits can lead to mathematical fallacies — if the properties of integrals and differentials are ignored. For instance, a naive use of integration by parts can be used to give a false proof that 0 = 1.[7] Letting u = 1/log x and dv = dx/x, we may write:
after which the antiderivatives may be cancelled yielding 0 = 1. The problem is that antiderivatives are only defined up to a constant and shifting them by 1 or indeed any number is allowed. The error really comes to light when we introduce arbitrary integration limits a and b.
Since the difference between two values of a constant function vanishes, the same definite integral appears on both sides of the equation.
Multivalued functions[edit]
Many functions do not have a unique inverse. For instance, while squaring a number gives a unique value, there are two possible square roots of a positive number. The square root is multivalued. One value can be chosen by convention as the principal value; in the case of the square root the non-negative value is the principal value, but there is no guarantee that the square root given as the principal value of the square of a number will be equal to the original number (e.g. the principal square root of the square of −2 is 2). This remains true for nth roots.
Positive and negative roots[edit]
Care must be taken when taking the square root of both sides of an equality. Failing to do so results in a «proof» of[8] 5 = 4.
Proof:
- Start from
- Write this as
- Rewrite as
- Add 81/4 on both sides:
- These are perfect squares:
- Take the square root of both sides:
- Add 9/2 on both sides:
- Q.E.D.
The fallacy is in the second to last line, where the square root of both sides is taken: a2 = b2 only implies a = b if a and b have the same sign, which is not the case here. In this case, it implies that a = –b, so the equation should read
which, by adding 9/2 on both sides, correctly reduces to 5 = 5.
Another example illustrating the danger of taking the square root of both sides of an equation involves the following fundamental identity[9]
which holds as a consequence of the Pythagorean theorem. Then, by taking a square root,
Evaluating this when x = π , we get that
or
which is incorrect.
The error in each of these examples fundamentally lies in the fact that any equation of the form
where 
and it is essential to check which of these solutions is relevant to the problem at hand.[10] In the above fallacy, the square root that allowed the second equation to be deduced from the first is valid only when cos x is positive. In particular, when x is set to π, the second equation is rendered invalid.
Square roots of negative numbers[edit]
Invalid proofs utilizing powers and roots are often of the following kind:
The fallacy is that the rule 


Alternatively, imaginary roots are obfuscated in the following:
The error here lies in the third equality, as the rule 
Complex exponents[edit]
When a number is raised to a complex power, the result is not uniquely defined (see Exponentiation § Failure of power and logarithm identities). If this property is not recognized, then errors such as the following can result:
The error here is that the rule of multiplying exponents as when going to the third line does not apply unmodified with complex exponents, even if when putting both sides to the power i only the principal value is chosen. When treated as multivalued functions, both sides produce the same set of values, being {e2πn | n ∈ ℤ}.
Geometry[edit]
Many mathematical fallacies in geometry arise from using an additive equality involving oriented quantities (such as adding vectors along a given line or adding oriented angles in the plane) to a valid identity, but which fixes only the absolute value of (one of) these quantities. This quantity is then incorporated into the equation with the wrong orientation, so as to produce an absurd conclusion. This wrong orientation is usually suggested implicitly by supplying an imprecise diagram of the situation, where relative positions of points or lines are chosen in a way that is actually impossible under the hypotheses of the argument, but non-obviously so.
In general, such a fallacy is easy to expose by drawing a precise picture of the situation, in which some relative positions will be different from those in the provided diagram. In order to avoid such fallacies, a correct geometric argument using addition or subtraction of distances or angles should always prove that quantities are being incorporated with their correct orientation.
Fallacy of the isosceles triangle[edit]

The fallacy of the isosceles triangle, from (Maxwell 1959, Chapter II, § 1), purports to show that every triangle is isosceles, meaning that two sides of the triangle are congruent. This fallacy was known to Lewis Carroll and may have been discovered by him. It was published in 1899.[12][13]
Given a triangle △ABC, prove that AB = AC:
- Draw a line bisecting ∠A.
- Draw the perpendicular bisector of segment BC, which bisects BC at a point D.
- Let these two lines meet at a point O.
- Draw line OR perpendicular to AB, line OQ perpendicular to AC.
- Draw lines OB and OC.
- By AAS, △RAO ≅ △QAO (∠ORA = ∠OQA = 90°; ∠RAO = ∠QAO; AO = AO (common side)).
- By RHS,[note 2] △ROB ≅ △QOC (∠BRO = ∠CQO = 90°; BO = OC (hypotenuse); RO = OQ (leg)).
- Thus, AR = AQ, RB = QC, and AB = AR + RB = AQ + QC = AC.
Q.E.D.
As a corollary, one can show that all triangles are equilateral, by showing that AB = BC and AC = BC in the same way.
The error in the proof is the assumption in the diagram that the point O is inside the triangle. In fact, O always lies on the circumcircle of the △ABC (except for isosceles and equilateral triangles where AO and OD coincide). Furthermore, it can be shown that, if AB is longer than AC, then R will lie within AB, while Q will lie outside of AC, and vice versa (in fact, any diagram drawn with sufficiently accurate instruments will verify the above two facts). Because of this, AB is still AR + RB, but AC is actually AQ − QC; and thus the lengths are not necessarily the same.
Proof by induction[edit]
There exist several fallacious proofs by induction in which one of the components, basis case or inductive step, is incorrect. Intuitively, proofs by induction work by arguing that if a statement is true in one case, it is true in the next case, and hence by repeatedly applying this, it can be shown to be true for all cases. The following «proof» shows that all horses are the same colour.[14][note 3]
- Let us say that any group of N horses is all of the same colour.
- If we remove a horse from the group, we have a group of N − 1 horses of the same colour. If we add another horse, we have another group of N horses. By our previous assumption, all the horses are of the same colour in this new group, since it is a group of N horses.
- Thus we have constructed two groups of N horses all of the same colour, with N − 1 horses in common. Since these two groups have some horses in common, the two groups must be of the same colour as each other.
- Therefore, combining all the horses used, we have a group of N + 1 horses of the same colour.
- Thus if any N horses are all the same colour, any N + 1 horses are the same colour.
- This is clearly true for N = 1 (i.e. one horse is a group where all the horses are the same colour). Thus, by induction, N horses are the same colour for any positive integer N. i.e. all horses are the same colour.
The fallacy in this proof arises in line 3. For N = 1, the two groups of horses have N − 1 = 0 horses in common, and thus are not necessarily the same colour as each other, so the group of N + 1 = 2 horses is not necessarily all of the same colour. The implication «every N horses are of the same colour, then N + 1 horses are of the same colour» works for any N > 1, but fails to be true when N = 1. The basis case is correct, but the induction step has a fundamental flaw.
See also[edit]
- Anomalous cancellation – Kind of arithmetic error
- Division by zero – Class of mathematical expression
- List of incomplete proofs
- Mathematical coincidence – Coincidence in mathematics
- Paradox – Statement that apparently contradicts itself
- Proof by intimidation – Marking an argument as obvious or trivial
Notes[edit]
- ^ The same fallacy also applies to the following:
- ^ Hypotenuse–leg congruence
- ^ George Pólya’s original «proof» was that any n girls have the same colour eyes.
References[edit]
- ^ Maxwell 1959, p. 9
- ^ a b Maxwell 1959
- ^ Heath & Heiberg 1908, Chapter II, §I
- ^ Barbeau, Ed (1991). «Fallacies, Flaws, and Flimflam» (PDF). The College Mathematics Journal. 22 (5). ISSN 0746-8342.
- ^ «soft question – Best Fake Proofs? (A M.SE April Fools Day collection)». Mathematics Stack Exchange. Retrieved 2019-10-24.
- ^ Heuser, Harro (1989), Lehrbuch der Analysis – Teil 1 (6th ed.), Teubner, p. 51, ISBN 978-3-8351-0131-9
- ^ Barbeau, Ed (1990), «Fallacies, Flaws and Flimflam #19: Dolt’s Theorem», The College Mathematics Journal, 21 (3): 216–218, doi:10.1080/07468342.1990.11973308
- ^ Frohlichstein, Jack (1967). Mathematical Fun, Games and Puzzles (illustrated ed.). Courier Corporation. p. 207. ISBN 0-486-20789-7. Extract of page 207
- ^ Maxwell 1959, Chapter VI, §I.1
- ^ Maxwell 1959, Chapter VI, §II
- ^ Nahin, Paul J. (2010). An Imaginary Tale: The Story of «i«. Princeton University Press. p. 12. ISBN 978-1-4008-3029-9. Extract of page 12
- ^ S.D.Collingwood, ed. (1899), The Lewis Carroll Picture Book, Collins, pp. 190–191
- ^ Robin Wilson (2008), Lewis Carroll in Numberland, Penguin Books, pp. 169–170, ISBN 978-0-14-101610-8
- ^ Pólya, George (1954). Induction and Analogy in Mathematics. Mathematics and plausible reasoning. Vol. 1. Princeton. p. 120.
- Barbeau, Edward J. (2000), Mathematical fallacies, flaws, and flimflam, MAA Spectrum, Mathematical Association of America, ISBN 978-0-88385-529-4, MR 1725831.
- Bunch, Bryan (1997), Mathematical fallacies and paradoxes, New York: Dover Publications, ISBN 978-0-486-29664-7, MR 1461270.
- Heath, Sir Thomas Little; Heiberg, Johan Ludvig (1908), The thirteen books of Euclid’s Elements, Volume 1, The University Press.
- Maxwell, E. A. (1959), Fallacies in mathematics, Cambridge University Press, ISBN 0-521-05700-0, MR 0099907.
External links[edit]
- Invalid proofs at Cut-the-knot (including literature references)
- Classic fallacies with some discussion
- More invalid proofs from AhaJokes.com
- Math jokes including an invalid proof
Муниципальное казённое общеобразовательное учреждение
«Мармыжанская средняя общеобразовательная школа»
Советского района Курской области
Проектно-исследовательская работа
«К чему приводят
математические ошибки»
Выполнила:
Помогаева Виктория,
ученица 9 класса
Руководитель:
Гладилина Елена Петровна,
учитель математики
п. им. Ленина
2021 г.
Содержание
- Введение……………………………………………………………………3
- План работы над проектом………………………………………………..5
- Основная часть……………………………………………………………..6
- Математические ошибки на ТВ……………………………………….6
- Математические ошибки при использовании разных единиц измерения ………………………………………………………………7
- Математические ошибки при программировании…………………..10
- Математические ошибки в реальной жизни…………………………12
- Заключение………………………………………………………………..14
- Использованная литература………………………………………………15
-
Введение
«В математических вопросах нельзя
пренебрегать даже самыми мелкими
ошибками».
И. Ньютон.
Мы постоянно слышим от учителя на уроках математики: «Будьте внимательными, не делайте ошибок», и все делаем эти ошибки. Чаще всего просто в вычислениях. Думаем, что если бы мы пользовались на уроках математики и на экзаменах калькуляторами, то этих ошибок бы не было. Для нас, учеников, эти ошибки могут привести к неудовлетворительной оценке на уроке или, самое страшное, на экзамене. Во взрослой жизни все уже производят расчеты с помощью калькуляторов или ЭВМ. Неужели и там бывают математические ошибки? Почему они возникают и к каким последствиям могут привести?
Гипотеза: математическая ошибка может привести как к курьёзным ситуациям, так и к серьёзным проблемам (авариям, катастрофам, разрушениям)
Актуальность проекта:
Актуальность данной проблемы имеет как личный аспект, так и масштабный характер (ошибиться может каждый). Но к чему может привести математическая ошибка – это ключевой вопрос, в котором и хотелось разобраться. Ведь математика касается всех сфер нашей жизни, как частной, так и в масштабе государства.
Цель проекта: собрать и оформить информацию о последствиях математической ошибки; показать значимость математической ошибки.
Задачи проекта:
- найти примеры ошибок, которые приводили к курьёзным ситуациям;
- найти ответ на вопрос: были ли случаи, когда математические ошибки, повлекли за собой серьёзные проблемы: катастрофы, аварии, разрушения.
- найти ответ на вопрос: как может нам навредить математическая неграмотность.
- Поделиться информацией с одноклассниками
- План работы над проектом
- Наблюдения, сопоставления по теме проекта
- Нахождение информации о математических ошибках на телевидении
- Нахождение информации о математических ошибках, приведших к катастрофам, авариям. Попытаться их классифицировать.
- Поиск информации о математических ошибках в жизненных ситуациях
- Создание презентации к проекту
- Оформление проекта, защита проекта
- Показ одноклассникам презентации
- Основная часть
Изучая математику, мы уже можем заметить какие-то ошибки у взрослых. Например, многие путают понятия «число» и «цифра». Даже в средствах массовой информации говорят: «получилась солидная цифра», «цифра сто двадцать пять», «а теперь сопоставим полученные многозначные цифры», «сложив полученные цифры, получим…». Но ведь в математике цифр всего 10, а чисел — бесконечное множество и только с числами можно
проводить различные математические действия. Лишь, упоминая официальные показатели, например статистические данные, допускается говорить слово «цифра».
Часто мы слышим от взрослых, что когда температура воздуха изменилась с -100С до -200С, то «она стала больше». Но ведь -10 больше, чем -20. Поэтому грамотнее говорить, что температура понизилась.
Но все это всего лишь показывает математическую неграмотность человека и не может привести к какой-либо трагедии.
Введя запрос в Интернете «математические ошибки» я нашла много интересного. С этой информацией я и хочу поделиться.
- Математические ошибки на ТВ
- «Сериал «Звездный путь» Военный суд, 1967 г. Керк говорит, что компьютер может усилить звук в число раз, равное «единице в сороковой степени», а это равно единице». [1]
- Математическая ошибка Юрия Дудя о кратчайшем расстоянии между двумя объектами на Земле. Расстояние определяется не по параллели, а по диаметральному сечению.
- В комедийном фильме 1965 года «Операция „ы“ и другие приключения Шурика» Леонида Гайдая герой Михаила Пуговкина — прораб СМУ, рассказывая о достижениях в строительстве, говорит: «Если поставить этажи один на другой, то мы получим здание в два раза выше, чем всемирно известная Эйфелева башня или втрое выше, чем знаменитый Нотр-Дам де Пари».[1]
На самом деле, высота Эйфелевой башни 325 м (325*2=650), а Нотр-Дам де Пари — 35 м (35*3=105). - Кадр из американской программы новостей. Всего проголосовало 193% избирателей.
- 4 декабря 2011 года в России прошли выборы. Тогда на ТВ появилась такая интересная информация: «В Воронежской области насчитали 128,96% голосов. Однако, в Ростовской области и того больше — 146,47%. Свердловская область — 115,35%».
Такие ошибки часто называют «киноляпы» или «курьёзные ошибки». Замечают их не все, и они не приводят к какой-либо трагедии.
А теперь рассмотрим более серьезные ошибки в истории человечества.
Ошибки при использовании разных единиц измерения
Почти каждая страна в мире использует метрическую систему мер, Кроме Соединённых Штатов. Обычно это не особо большая проблема. Но на протяжении всей истории было несколько случаев, когда использование разных систем измерения величин приводило к катастрофическим результатам.
а) Потопление военного корабля «Ваза»
«10 августа 1628 года Швеция запустила новый, хорошо вооружённый и большой военный корабль «Ваза». Судно едва проплыло 20 минут, когда затонуло менее чем в миле от берега. Тридцать человек погибли в результате потопления. Корабль был позже найден в 20-м веке и сейчас хранится в Музее Вазы.
Историки измерили весь корабль и обнаружили, что его строители использовали две разные единицы измерения. Одной был шведский фут, а другой – амстердамский фут. Шведский фут составляет 30,48 см, в то время как амстердамский – 27,94 см.
Разница между обеими единицами измерения привела к тому, что одна сторона оказалась тяжелее другой. Вот почему корабль наклонился в сторону и быстро затонул после того, как по нему ударили два порыва ветра. Историки добавляют, что влияние ветра было усугублено тем фактом, что верх корабля был тяжелее его дна». [3]
б) В самолёте Air Canada закончилось топливо (1983 год)
«В июле 1983 года самолёт Boeing 767 Air Canada, летевший из Оттавы в Эдмонтон с 69 пассажирами и членами экипажа, вынужден был совершить аварийную посадку после того, как закончился запас топлива на высоте 12500 м. Двигатели внезапно потеряли мощность, и самолёт начал снижаться к земле.
Авария была связана с ошибкой преобразования. Air Canada использовала британскую систему мер, но перешла на метрическую, которую уже использовал этот Boeing 767. Наземные экипажи Air Canada использовали британскую систему при заправке самолёта. Они измеряли топливо в фунтах вместо килограммов.
Один килограмм равен 2,2 фунта. Это означало, что у самолёта было всего около половины количества топлива, необходимого для завершения полёта.
К счастью, 69 пассажиров на борту отделались незначительными травмами». [2]
в) Крушение орбитального аппарата Mars Climate Orbiter
«Mars Climate Orbiter был совместным проектом компании Lockheed Martin и NASA / JPL стоимостью 125 миллионов долларов. Проект получил неловкое завершение, когда орбитальный аппарат, скорее всего, потерпел крушение на Марсе из-за простой ошибки преобразования в 1999 году. Lockheed Martin использовал британскую систему мер при программировании программного обеспечения, но НАСА использовало метрическую систему.
Инженеры НАСА обнаружили бы ошибку, если бы обратили внимание. Однако они этого не сделали. Никто не понимал, что что-то не так во время девятимесячного путешествия Mars Climate Orbiter на Марс. Ошибка стала очевидной только тогда, когда НАСА потеряло связь с орбитальным аппаратом.
В ответ на инцидент Джон Логсдон из Института космической политики Университета имени Джорджа Вашингтона сказал, что всё это было «глупо». Джон Пайк из Федерации американских учёных добавил: «Было неловко потерять космический корабль из-за такой простой математической ошибки». [2]
г) Крушение американских горок в Токио (2003 год)
«В декабре 2003 года в токийском Диснейленде один из автомобилей аттракциона «Космическая гора» внезапно сошел с рельсов из-за сломанной оси. Почему сломалась ось? Согласно официальному отчёту, выпущенному в январе 2004 года, ось была не того размера, потому что существовала путаница в метрической и английской системах мер.
К счастью, никто из людей, не пострадал». [2]
д) Если вы думаете, что в нашей стране таких ошибок быть не может, то ошибаетесь. Вот, что рассказывает очевидец: «Привезли, значит, нам на завод какие-то нестандартные ж/д цистерны под концентрированную серную кислоту. …на них указана ёмкость — но, правда, в галлонах. Ну, мы ж не дураки: в инете полно калькуляторов по переводу единиц измерения! Пересчитываем в кубометры, задаём автомату указание, сколько наливать, ждём, когда отключится… А вот кислота начинает литься через край! Срочно вырубаем, но пролив уже есть, что, мягко говоря, неприятно. Последствия пролива устранили, стали разбираться, и выяснилось, что галлоны разные бывают! Судя по всему, мы посчитали объём цистерны в классических английских галлонах, а есть ещё и американские, которые меньше, и в которых эта самая ёмкость была указана на цистернах». [4]
(Американский галлон равен 3,785411784 литра. Британский галлон — 4,5461 литра)
3) Математические ошибки при программировании
Огромные суммы денег и оборудование стоимостью в миллионы долларов были потеряны просто потому, что кто-то допустил небольшую математическую ошибку. Компьютеры также допускают подобные ошибки, но в них можно винить людей, так как именно они занимались программированием.
а) «25 февраля 1991 года иракская ракета «Скад» нанесла удар по базе армии США в Даране, Саудовская Аравия, убив 28 солдат и ранив ещё 100. Катастрофа была неожиданной, если учесть, что база была защищена системой ПВО «Патриот». Расследования показали, что система не пыталась перехватить «Скад».
Ошибка была связана с программным обеспечением, питающим часы системы. Часы записывали время в десятых секундах (одна десятая секунды), но сохраняли эти данные в виде целого числа. Для этого они преобразовывали время в 24-битное число с плавающей точкой. Однако округление времени при их преобразовании привело к постепенному увеличению погрешности в работе системы. В результате система не смогла перехватить ракеты после 20 часов непрерывного использования.
Во время атаки рассматриваемая ракетная батарея «Патриот» проработала 100 часов. Разница во времени была такова, что она искала не в той части неба входящую ракету и поэтому не нашла цели. Армия США была проинформирована об этой проблеме с программным обеспечением и выпустила обновление 16 февраля. Обновление достигло базы в Дхаране 26 февраля, на следующий день после атаки». [4]
б) Испанская программа подводных лодок S-80
В 2003 году Испания запустила программу подводных лодок S-80 на сумму 2,7 миллиарда долларов для строительства чётырех дизель-электрических подводных лодок для ВМС Испании. Испания почти завершила строительство одной из них в 2013 году, когда обнаружила, что лодка на 70 тонн тяжелее, чем должна была быть. Испанский флот боялся, что подводная лодка никогда не всплывёт, если уйдёт под воду.
Подводная лодка оказалась тяжёлой после того, как кто-то поставил десятичную точку в неправильном месте во время вычислений. Никто не обнаружил ошибку, пока первая субмарина не была закончена, а остальные три уже строились. Позже Испания подписала контракт на 14 миллионов долларов с Electric Boat из Гротона, штат Коннектикут, чтобы те помогли им снизить вес 2200-тонной подводной лодки.
в) Взрыв ракеты Ariane 5
4 июня 1996 года ракета Ariane 5 Европейского космического агентства взорвалась через 37 секунд после взлёта. На борту космического корабля находились четыре спутника. Ракета и спутники стоили 370 миллионов долларов. Авария была связана с целочисленной ошибкой переполнения в программном обеспечении, используемом для запуска ракеты.
Целочисленное переполнение – это математическая ошибка, которая возникает, когда числа, сгенерированные системой, превышают объём памяти этой системы. Ariane 5 работала на 16-битном программном обеспечении, способном хранить числа до 32767. Ракете удалось создать числа намного больше этого.
Европейское космическое агентство использовало то же программное обеспечение, что и в ракетах Ariane 4. У них были проблемы с Ariane 5, потому что она была быстрее, чем Ariane 4. Чем быстрее, тем больше числа. Программное обеспечение не может обрабатывать большие показания, из-за чего ракета становится негодной. Наземный контроль приказал самоуничтожиться.
г) Разрушение ракеты — носителя «Протон-М» в 2010 году.
РИА новости сообщает: «К неудачному запуску трех спутников системы ГЛОНАСС могла привести математическая ошибка в программе, заложенной в бортовой комплекс ракеты — носителя. Сейчас ее эксперты занимаются выяснением всех обстоятельств аварии. По некоторым данным, ракета-носитель «Протон-М» после запуска отклонилась от заданной траектории на восемь градусов. Дмитрий Медведев поручил найти виновных в утрате спутников и проверить расходование средств на выполнение программы создания отечественной навигационной группировки». [5]
Все приведённые выше примеры заставляют задуматься над тем, что фактов, когда математическая ошибка ведет к серьёзным авариям, катастрофам, разрушениям значительно больше, чем можно было себе представить.
4)Математические ошибки в реальной жизни
Но, не все мы станем программистами, инженерами и т. д. Но математические ошибки в любой сфере деятельности могут причинить вред тебе самому и тем, кто тебя окружает. Есть люди, которые преднамеренно пользуются нашей математической неграмотностью. Я приведу лишь несколько примеров.
Вот некоторые уловки маркетологов в магазинах и супермаркетах:
1) «Снижение стоимости продукта всего на копейки, рубль может существенно увеличивать продажи. Все дело в том, что даже мизерное снижение стоимости товара дает нам чувство экономии. Для многих покупателей покупка продукта по 999 руб. воспринимается заметно выгодней, чем по цене в 1000 рублей. Этот эффект называют «эффектом левой цифры».
Благодаря подобной уловке маркетологи заставляют клиентов воспринимать только крайние левые числа. Например, психологически многие клиенты, купившие товар по цене 999 руб., воспринимают покупку по цене 900 рублей.
Примечательно, что эта ситуация для цен типа 549 и 550 рублей не производит такой же эффект, хотя разница в ценах составляет тот же 1 рубль. Но в этом примере в обоих сценариях психологически люди считают, что приобретают товар за 500 руб.
Именно поэтому разница между этими ценами не создает восприятия сбережения. Но почему так происходит? Все дело в том, что наш мозг обычно обращает внимание только на первую цифру. На уроках математики мы учимся округлять, делать прикидки, и если будем делать это автоматически, то не попадемся на эту уловку». [6]
2) Вес продукта
«Замечали такое, что ваш любимый товар внезапно становился дешевле? Например, молоко, сливочное масло, сок, майонез и т. д. Нередко маркетологи идут на хитрую уловку: снижают стоимость товара, уменьшая при этом вес. Поэтому, в следующий раз, когда вы захотите, не глядя бросить в корзину самый дешёвый товар, внимательно изучите его этикетку. Возможно, он несколько легче своих аналогов, а его цена дешевле лишь на 1 рубль». [6]
3)Микрокредиты
«Тема микрозаймов сейчас более чем актуальна в России. Это подтверждают цифры. Только по предварительным данным, за 2019 год 11 млн российских граждан взяли в долг больше 200 млрд руб. С каждым годом эти цифры увеличиваются примерно на четверть. Около 40 % клиентов МФО в России – это люди в возрасте 25–36 лет, другими словами, трудоспособное население.
Рассчитать, какой процент переплаты будет начислен, также очень просто. Если ставка равна 1 % в день, а заем берется на 15 дней, то переплата составит 15 %. За 20 дней переплата возрастет до 20 %, за 30 дней – до 30 % и т. д.» [7]
Прежде чем брать кредит, подумайте, сможете ли вы его погасить вовремя, и стоит ли столько процентов переплачивать.
- Заключение.
Вывод: Мною был собран и оформлен материал о последствиях математической ошибки. Продемонстрирована значимость математической ошибки. Нашла своё подтверждение гипотеза: математическая ошибка может привести не только к курьёзным ситуациям, но и к серьёзным проблемам. Последствия даже маленьких математических ошибок могут быть непредсказуемыми.
В нашем мире от математики зависит больше, чем когда-либо в истории, и поэтому цена ошибок, намного выше.
Человеческий фактор – самая главная причина различных катастроф. И обидно бывает, когда огромный труд многих людей губится из-за «незначительных» ошибок в расчетах, а то и вовсе из-за глупости тех, кто эти расчеты делал.
Поэтому, хочется сказать: «Ребята, уделяйте достаточно внимания изучению математики за школьной партой!» Дело в том, что когда мы станем взрослыми, то даже одна очень маленькая ошибка может стоить жизни многим людям.
Список литературы
Источники, представленные в Internet:
- http://hijos.ru/2011/11/06/matematicheskie-kinolyapy/
- https://m.fishki.net/3118774-10-dorogostojawih-matematicheskih-oshibok/gallery-7117630-photo.html
- https://ru.wikipedia.org/wiki/Ваза_(корабль)
- https://pikabu.ru/story/10_prostyikh_no_dorogostoyashchikh_matematicheskikh_oshibok_v_istorii_6912640
- РИА Новости (RIA.RU).
- https://basetop.ru/samyie-hitryie-marketingovyie-ulovki-dlya-povyisheniya-prodazh/
- https://iklife.ru/finansy/zajmy/chto-takoe-mikrozajm-prostymi-slovami.html
«Недействительное доказательство» перенаправляется сюда. По поводу любого типа недействительных доказательств, кроме математических, см. Заблуждение.
В математика, некоторые виды ошибочных доказательств часто выставляются, а иногда и собираются в качестве иллюстраций концепции, называемой математическая ошибка. Есть различие между простым ошибка и математическая ошибка в доказательстве, когда ошибка в доказательстве приводит к недействительному доказательству, в то время как в наиболее известных примерах математических ошибок присутствует некоторый элемент утаивания или обмана в представлении доказательства.[1]
Например, причину, по которой не действует достоверность, можно отнести к деление на ноль что скрыто алгебраической записью. Есть определенное качество математической ошибки: в том виде, в котором ее обычно представляют, она приводит не только к абсурдному результату, но и делает это хитрым или хитрым способом.[2] Поэтому эти заблуждения по педагогическим причинам обычно принимают форму ложных доказательства очевидного противоречия. Хотя доказательства ошибочны, ошибки, как правило, преднамеренные, являются сравнительно малозаметными или предназначены для демонстрации того, что определенные шаги являются условными и неприменимы в случаях, которые являются исключениями из правил.
Традиционный способ представления математической ошибки состоит в том, чтобы дать неверный шаг вывода, смешанный с действительными шагами, так что значение заблуждение здесь немного отличается от логическая ошибка. Последнее обычно применяется к форме аргументации, которая не соответствует действующим правилам логического вывода, тогда как проблемный математический шаг обычно является правильным правилом, применяемым с неявным неправильным предположением. Помимо педагогики, разрешение ошибки может привести к более глубокому пониманию предмета (например, введение Аксиома Паша из Евклидова геометрия[3], то теорема пяти цветов из теория графов ). Псевдария, древняя утерянная книга ложных доказательств, приписывается Евклид.[4]
Математические ошибки существуют во многих областях математики. В элементарная алгебра, типичные примеры могут включать этап, на котором деление на ноль выполняется, где корень неправильно извлекается или, в более общем смысле, где разные значения многозначная функция приравниваются. Известные заблуждения существуют также в элементарной евклидовой геометрии и исчисление.[5][6]
Ревуны
Аномальный
отмена
в исчислении
Существуют примеры математически правильных результатов, полученных в результате неправильных рассуждений. Такой аргумент, каким бы верным он ни казался, математически неверен. инвалид и широко известен как ревун.[1] Ниже приводится пример ревуна, включающего аномальная отмена:
Здесь хотя вывод 16/64 = 1/4 правильно, на среднем этапе происходит ошибочная, недействительная отмена.[примечание 1] Другой классический пример ревуна — доказательство теоремы Кэли – Гамильтона простой заменой скалярных переменных характеристического полинома матрицей.
Поддельные доказательства, вычисления или выводы, построенные для получения правильного результата, несмотря на неправильную логику или операции, Максвелл назвал «воплями».[7] За пределами области математики термин ревун имеет различные значения, как правило, менее конкретные.
Деление на ноль
В ошибка деления на ноль есть много вариантов. В следующем примере используется замаскированное деление на ноль, чтобы «доказать», что 2 = 1, но его можно изменить, чтобы доказать, что любое число равно любому другому числу.
- Позволять а и б равны, ненулевые величины
- Умножить на а
- Вычесть б2
- Фактор обе стороны: левые факторы как разница квадратов, право факторизуется путем извлечения б с обоих условий
- Разделить (а − б)
- Наблюдая за этим а = б
- Объедините похожие термины слева
- Разделить на ненулевое б
- Q.E.D.[8]
Ошибка в строке 5: переход от строки 4 к строке 5 включает деление на а − б, который равен нулю, поскольку а = б. С деление на ноль не определено, аргумент недопустим.
Анализ
Математический анализ как математическое исследование изменений и пределы может привести к математическим ошибкам — если свойства интегралы и дифференциалы игнорируются. Например, наивное использование интеграция по частям может использоваться для ложного доказательства того, что 0 = 1.[9] Сдача ты = 1/бревно Икс и dv = dx/Икс, мы можем написать:
после чего первообразные могут быть отменены, давая 0 = 1. Проблема в том, что первообразные определены только вплоть до а постоянный и смещение их на 1 или любое другое число разрешено. Ошибка действительно обнаруживается, когда мы вводим произвольные пределы интегрирования а и б.
Поскольку разница между двумя значениями постоянной функции равна нулю, по обе стороны уравнения появляется один и тот же определенный интеграл.
Многозначные функции
Многие функции не имеют уникального обратный. Например, возведение числа в квадрат дает уникальное значение, но есть два возможных квадратные корни положительного числа. Квадратный корень многозначный. По соглашению можно выбрать одно значение в качестве основная стоимость; в случае квадратного корня неотрицательное значение является главным значением, но нет гарантии, что квадратный корень, заданный как главное значение квадрата числа, будет равен исходному числу (например, главный квадратный корень квадрата −2 равно 2). Это остается верным для энные корни.
Положительные и отрицательные корни
Следует соблюдать осторожность при приеме квадратный корень обеих сторон равенство. Невыполнение этого требования приводит к «доказательству»[10] 5 = 4.
Доказательство:
- Начать с
- Напишите это как
- Перепишите как
- Добавлять 81/4 с обеих сторон:
- Это идеальные квадраты:
- Извлеките квадратный корень из обеих частей:
- Добавлять 9/2 с обеих сторон:
- Q.E.D.
Ошибка заключается в предпоследней строке, где извлекается квадратный корень из обеих частей: а2 = б2 только подразумевает а = б если а и б имеют такой же знак, чего здесь нет. В этом случае это означает, что а = –б, поэтому уравнение должно выглядеть так:
который, добавив 9/2 с обеих сторон правильно уменьшается до 5 = 5.
Другой пример, иллюстрирующий опасность извлечения квадратного корня из обеих частей уравнения, включает следующее фундаментальное тождество[11]
которое выполняется как следствие теорема Пифагора. Затем, извлекая квадратный корень,
так что
Но оценивая это, когда Икс = π мы получаем это
или же
что неверно.
Ошибка в каждом из этих примеров в основном заключается в том, что любое уравнение вида
куда 
и важно проверить, какое из этих решений имеет отношение к рассматриваемой проблеме.[12] В указанном выше заблуждении квадратный корень, который позволил вывести второе уравнение из первого, действителен только тогда, когда cosИкс положительный. В частности, когда Икс установлен на π, второе уравнение становится недействительным.
Квадратные корни отрицательных чисел
Недействительные доказательства, использующие силы и корни, часто бывают следующего вида:
Ошибка в том, что правило 


В качестве альтернативы мнимые корни запутываются в следующем:
Ошибка здесь заключается в последнем равенстве, где мы игнорируем другие корни четвертой степени из 1,[заметка 2] которые равны −1, я и —я (куда я это мнимая единица ). Поскольку мы возводили нашу фигуру в квадрат, а затем пустили корни, мы не всегда можем предположить, что все корни будут правильными. Итак, правильные корни четвертой степени я и —я, которые представляют собой мнимые числа, которые возводятся в квадрат до -1.
Комплексные показатели
Когда число возводится в комплексную степень, результат не определяется однозначно (см. Несостоятельность тождеств силы и логарифма ). Если это свойство не распознается, могут возникнуть следующие ошибки:
Ошибка здесь в том, что правило умножения показателей степени, как при переходе к третьей строке, не применяется без изменений со сложными показателями, даже если при установке обеих сторон в степень я выбирается только главное значение. Когда рассматривается как многозначные функции, обе стороны производят одинаковый набор значений, будучи {е2πп | п ∈ ℤ}.
Геометрия
Многие математические ошибки в геометрия возникают из-за использования аддитивного равенства, включающего ориентированные величины (например, добавление векторов вдоль заданной линии или добавление ориентированных углов в плоскости) к действительной идентичности, но которое фиксирует только абсолютное значение (одной из) этих величин. Затем эта величина включается в уравнение с неправильной ориентацией, чтобы сделать абсурдный вывод. Эта неправильная ориентация обычно подразумевается путем предоставления неточной схемы ситуации, в которой относительное положение точек или линий выбирается таким образом, который фактически невозможен в соответствии с гипотезами аргумента, но неочевидно.
В общем, такое заблуждение легко выявить, нарисовав точную картину ситуации, в которой некоторые относительные положения будут отличаться от тех, что указаны на представленной диаграмме. Чтобы избежать таких заблуждений, правильный геометрический аргумент с использованием сложения или вычитания расстояний или углов должен всегда доказывать, что величины включаются с их правильной ориентацией.
Ошибка равнобедренного треугольника

Ошибочность равнобедренного треугольника из (Максвелл 1959, Глава II, § 1), имеет целью показать, что каждый треугольник является равнобедренный, что означает, что две стороны треугольника равны конгруэнтный. Это заблуждение было приписано Льюис Кэрролл.[14]
Для треугольника △ ABC докажите, что AB = AC:
- Нарисуйте линию деление пополам ∠А.
- Нарисуйте серединный перпендикуляр к отрезку BC, который делит BC пополам в точке D.
- Пусть эти две прямые пересекаются в точке O.
- Проведите линию OR перпендикулярно AB, линию OQ перпендикулярно AC.
- Нарисуйте линии OB и OC.
- К ААС, △ RAO ≅ △ QAO (∠ORA = ∠OQA = 90 °; ∠RAO = ∠QAO; AO = AO (общая сторона)).
- К RHS,[заметка 3] △ ROB ≅ △ QOC (∠BRO = ∠CQO = 90 °; BO = OC (гипотенуза); RO = OQ (нога)).
- Таким образом, AR = AQ, RB = QC и AB = AR + RB = AQ + QC = AC.
Q.E.D.
Как следствие, можно показать, что все треугольники равносторонние, показав, что AB = BC и AC = BC таким же образом.
Ошибка доказательства состоит в предположении на диаграмме, что точка O внутри треугольник. Фактически, O всегда лежит в описанной окружности треугольника ABC (за исключением равнобедренных и равносторонних треугольников, в которых AO и OD совпадают). Кроме того, можно показать, что если AB длиннее, чем AC, то R будет лежать в AB, а Q будет лежать за пределами переменного тока, и наоборот (фактически, любая диаграмма, нарисованная с помощью достаточно точных инструментов, подтвердит два вышеуказанных факта). Из-за этого AB по-прежнему AR + RB, но AC на самом деле AQ — QC; и, следовательно, длины не обязательно одинаковы.
Доказательство по индукции.
Существует несколько ошибочных доказательства по индукции в котором один из компонентов, базисный случай или индуктивный шаг, неверен. Интуитивно, индукционные доказательства работают, утверждая, что если утверждение истинно в одном случае, оно истинно в следующем, и, следовательно, многократно применяя это утверждение, можно показать, что оно истинно для всех случаев. Следующее «доказательство» показывает, что все лошади одного цвета.[15][примечание 4]
- Скажем, что любая группа N лошади все одного цвета.
- Если мы удалим лошадь из группы, у нас будет группа N — 1 лошадь такого же цвета. Если мы добавим еще одну лошадь, у нас будет еще одна группа N лошади. По нашему предыдущему предположению, все лошади в этой новой группе одного цвета, поскольку это группа N лошади.
- Таким образом, мы построили две группы N лошади все одного цвета, с N — 1 общая лошадь. Поскольку у этих двух групп есть несколько общих лошадей, они должны быть одного цвета.
- Следовательно, объединив всех используемых лошадей, мы получим группу N + 1 лошадь одного цвета.
- Таким образом, если N лошади все одного цвета, любые N + 1 лошади одного цвета.
- Это явно верно для N = 1 (т.е. одна лошадь — это группа, в которой все лошади одного цвета). Таким образом, по индукции N лошади одного цвета для любого положительного целого числа N. т.е. все лошади одного цвета.
Ошибка в этом доказательстве возникает в строке 3. Ибо N = 1, две группы лошадей имеют N — 1 = 0 общих лошадей и, следовательно, не обязательно одного цвета, поэтому группа N + 1 = 2 лошади не обязательно одного цвета. Значение «каждый N лошади одного цвета, то N + 1 лошадь одного цвета «работает на любые N > 1, но это не так, когда N = 1. Базовый случай правильный, но индукционный шаг имеет фундаментальный недостаток. Если бы нам дополнительно дали тот факт, что любые две лошади одного цвета, то мы могли бы правильно произвести индукцию из базового случая N = 2.
Смотрите также
- Аномальная отмена — арифметическая ошибка
- Деление на ноль — Результат, полученный как действительное число при делении на ноль
- Список неполных доказательств — Статья со списком Википедии
- Математическое совпадение — совпадение по математике
- Парадокс — Заявление, которое явно противоречит самому себе
- Доказательство запугиванием — Метод убедить кого-то, используя жаргон или заявляя, что он понятен
Примечания
Рекомендации
- ^ а б «Окончательный глоссарий высшего математического жаргона — математическая ошибка». Математическое хранилище. 2019-08-01. Получено 2019-10-24.
- ^ Максвелл 1959, п. 9
- ^ Максвелл 1959
- ^ Хит и Хелберг 1908, Глава II, §I
- ^ Барбо, Эд (1991). «Заблуждения, недостатки и вздор» (PDF). Математический журнал колледжа. 22 (5). ISSN 0746-8342.
- ^ «Мягкий вопрос — Лучшие фальшивые доказательства? (Коллекция, посвященная Дню дураков от M.SE)». Обмен стеками математики. Получено 2019-10-24.
- ^ Максвелл 1959
- ^ Хойзер, Харро (1989), Lehrbuch der Analysis — часть 1 (6-е изд.), Teubner, p. 51, ISBN 978-3-8351-0131-9
- ^ Барбо, Эд (1990), «Заблуждения, недостатки и вздор № 19: Теорема Долта», Математический журнал колледжа, 21 (3): 216–218
- ^ Frohlichstein, Джек (1967). Математические развлечения, игры и головоломки (иллюстрированный ред.). Курьерская корпорация. п. 207. ISBN 0-486-20789-7. Отрывок страницы 207
- ^ Максвелл 1959, Глава VI, §I.1
- ^ Максвелл 1959, Глава VI, §II
- ^ Нахин, Пол Дж. (2010). Воображаемая сказка: История «я«. Издательство Принстонского университета. п. 12. ISBN 978-1-4008-3029-9. Выдержка страницы 12
- ^ Робин Уилсон (2008), Льюис Кэрролл в Numberland, Penguin Books, стр. 169–170, ISBN 978-0-14-101610-8
- ^ Полиа, Джордж (1954). Индукция и аналогия в математике. Математика и правдоподобные рассуждения. 1. Принстон. п. 120.
- Барбо, Эдвард Дж. (2000), Математические заблуждения, недостатки и вздор, МАА Спектр, Математическая ассоциация Америки, ISBN 978-0-88385-529-4, МИСТЕР 1725831.
- Связка, Брайан (1997), Математические заблуждения и парадоксы, Нью-Йорк: Dover Publications, ISBN 978-0-486-29664-7, МИСТЕР 1461270.
- Хит, сэр Томас Литтл; Хейберг, Йохан Людвиг (1908), Тринадцать книг Евклида Элементов, Том 1, Университетское издательство.
- Максвелл, Э. (1959), Заблуждения в математике, Издательство Кембриджского университета, ISBN 0-521-05700-0, МИСТЕР 0099907.
внешняя ссылка
- Недействительные доказательства в Разрезать узел (включая литературные ссылки)
- Классические заблуждения с некоторым обсуждением
- Больше недействительных доказательств с AhaJokes.com
- Математические анекдоты с недействительным доказательством
Муниципальное казенное общеобразовательное учреждение
«Средняя общеобразовательная школа №1» г. Поворино
Тема проекта:
«Анализ математических ошибок, приведших к катастрофам»
Проект по математике
ученицы 9б класса
Федосовой Валерии
Научный руководитель. учитель:
Карташова С. А.
Предмет математика
г. Поворино
2020-2021 учебный год
Содержание…………………………………………………………………….2
Введение……………………………………………………………………….3
Глава I Основная
часть………………………………………………………..4
§ 1. Анкетирование………………………..………..…………………………….4
§ 2. Десять
простых, но дорогостоящих математических ошибок в истории…………………………….….…………………………..……………5
§ 3. Математические ошибки,
которые привели к значительным катастрофам……………………………………………………………………11
Заключение…………………………………………………………………………16
Список использованных источников и литературы ………………………….17
Введение
В математических
вопросах
нельзя
пренебрегать даже
самыми мелкими
ошибками.
И. Ньютон
Мне хотелось бы сказать
вначале: «Дети! Учите математику! Потому что когда вы станете взрослыми, одна
маленькая ошибка может стоить жизни многим людям». Не верите? В своем проекте я
попытаюсь это доказать.
Гипотеза: математическая
ошибка может привести как к курьёзным ситуациям, так и к серьёзным проблемам
(авариям, катастрофам, разрушениям).
Тема моей работы: «Анализ Математических
ошибок, приведших к катастрофам».
Цель: собрать
информацию о последствиях математической ошибки; показать значимость
математической ошибки.
Задачи:
• исследовать типичные
ошибки одноклассников;
• провести анкетирование
среди одноклассников на тему «К чему может привести математическая ошибка?»;
• найти примеры ошибок,
которые приводили к курьёзным ситуациям;
•найти в Интернете ответ
на вопрос: были ли случаи, когда математические ошибки, повлекли за собой
серьёзные проблемы: катастрофы, аварии, разрушения.
Методы
исследования:
• изучение источников:
литературы, энциклопедий, сайтов в Интернете;
• наблюдения,
сопоставления;
• анализ и классификация
ошибок в работах учащихся 9 класса;
• отбор и классификация
материала.
Глава
I Основная часть.
Человечество
ошибается — и делает это отнюдь не редко. Когда дело касается крупных строений
или сложной техники, даже малейший огрех может привести к катастрофе.
Расплачивается же за это жизнью не сам конструктор, а доверившиеся его работе
люди. В истории бывали случаи, когда чудовищные катастрофы возникали
вследствие, казалось бы, небольших ошибок или чьей-то непредусмотрительности.
Иногда в этих катастрофах оказывались виноваты конкретные люди, отвечавшие за
безопасность и допустившие небрежность, иногда несчастье происходило в результате
череды маловероятных совпадений.
Минимальная
ошибка в расчетах может обернуться катастрофой, если речь идет о точных науках.
Здесь нет места словам «примерно» и «приблизительно». Одна
маленькая ошибка может стоить жизни многим людям.
Если вы считаете,
что это пустые слова, то я приведу реальные истории, которые подтверждают нашу
тревогу.
1. Анкетирование
Я провела
анкетирование среди одноклассников. В нем приняли участие 43 ученика
(Приложения №1 и №2). Обучающимся 9-х классов было предложено ответить на
следующие вопросы:
1.
Как часто
на уроках математики вы допускаете ошибки?
2.
Задумывались
ли вы о последствиях математической ошибки?
3.
Знакомы
ли вам примеры, когда математическая ошибка привела к катастрофе?
4.
Подумайте
и запишите, к чему может привести математическая ошибка?
5.
Хотели бы
вы познакомиться с курьёзными случаями математических ошибок?
На вопрос «Как
часто на уроках математики вы допускаете ошибки?» ответили «часто» и «почти
всегда» — 37 человек. На вопрос «Задумывались ли вы о последствиях математической
ошибки?» ответили «нет» — 39 человек. На вопрос «Знакомы ли вам примеры, когда
математическая ошибка привела к катастрофе?» ответили «нет» — 39 человек. На
вопрос «Хотели бы вы познакомиться с курьёзными случаями математических
ошибок?» ответили положительно – 41 человек. Анкетирование показало, что
школьники не задумываются о последствиях математической ошибки.
Наблюдения на
уроках математики и анализ ошибок в тетрадях одноклассников показал, что
ошибками могут стать неправильные расчёты, неправильное применение определений,
аксиом, теорем, незнание формул, правил. Ряд ошибок одноклассники допускают
из-за неразборчивого почерка, неаккуратно выполненного чертежа, по невнимательности.
Некоторые ошибки носят курьёзный характер.
Начну с простого.
2. Десять простых, но дорогостоящих
математических ошибок в истории.
Многие ненавидят
математику, хотя мир работает на математике. Огромные суммы денег и
оборудование стоимостью в миллионы долларов были потеряны просто потому, что
кто-то допустил небольшую математическую ошибку. Компьютеры также допускают
подобные ошибки, но в них можно винить людей, так как именно они занимались
программированием.
Чтобы было ясно,
некоторые бедствия были вызваны ошибками, связанными со сложной математикой,
которая, возможно, проще, чем, кажется. Тем не менее, здесь, в основном,
смехотворно простые ошибки, которые даже ученик начальной школы не мог бы
допустить.
2. 10. Атака ракет типа
«Скад» в войне в Персидском заливе
25 февраля 1991
года иракская ракета «Скад» нанесла удар по базе армии США в Даране, Саудовской
Аравии, убив 28 солдат и ранив ещё 100. Катастрофа была неожиданной, если
учесть, что база была защищена системой ПВО «Патриот». Расследования показали,
что система не пыталась перехватить «Скад».
Ошибка была
связана с программным обеспечением, питающим часы системы. Часы записывали
время в десятых секундах (одна десятая секунды), но сохраняли эти данные в виде
целого числа. Для этого они преобразовывали время в 24-битное число с плавающей
точкой. Однако округление времени при их преобразовании привело к постепенному
увеличению погрешности в работе системы. В результате система не смогла
перехватить ракеты после 20 часов непрерывного использования.
Во время атаки
рассматриваемая ракетная батарея «Патриот» проработала 100 часов. Разница во
времени была такова, что она искала не в той части неба входящую ракету и
поэтому не нашла цели.
Армия США была
проинформирована об этой проблеме с программным обеспечением и выпустила
обновление 16 февраля. Обновление достигло базы в Дхаране 26 февраля, на
следующий день после атаки.
2.9. Испанская программа
подводных лодок S-80
В 2003 году
Испания запустила программу подводных лодок S-80 на сумму 2,7 миллиарда
долларов для строительства четырёх дизель-электрических подводных лодок для ВМС
Испании. Испания почти завершила строительство одной из них в 2013 году, когда
обнаружила, что лодка на 70 тонн тяжелее, чем должна была быть. Испанский флот
боялся, что подводная лодка никогда не всплывёт, если уйдёт под воду.
Подводная лодка
оказалась тяжёлой после того, как кто-то поставил десятичную точку в
неправильном месте во время вычислений. Никто не обнаружил ошибку, пока первая
субмарина не была закончена, а остальные три уже строились. Позже Испания
подписала контракт на 14 миллионов долларов с Electric Boat из Гротона, штат
Коннектикут, чтобы те помогли им снизить вес 2200-тонной подводной лодки.
2.8. Рейс 143Air Canada
В июле 1983 года
самолёт Boeing 767 Air Canada, летевший из Оттавы в Эдмонтон с 69 пассажирами и
членами экипажа, вынужден был совершить аварийную посадку после того, как
закончился запас топлива на высоте 12500 м. Двигатели внезапно потеряли
мощность, и самолёт начал снижаться к земле. Он пролетел 100 километров до
посадки в Гимли, Манитоба.
Он приземлился на
ипподроме, который изначально был взлётно-посадочной полосой. К счастью, никто
не погиб. Однако два человека получили лёгкие травмы, а носовая часть была
разрушена. Эта посадка принесла Рейсу 143 прозвище «Планёр Гимли».
Авария была
связана с ошибкой преобразования. Air Canada использовала британскую систему
мер, но перешла на метрическую, которую уже использовал этот Boeing 767.
Наземные экипажи Air Canada использовали британскую систему при заправке
самолёта. Они измеряли топливо в фунтах вместо килограммов.
Один килограмм равен
2,2 фунта. Это означало, что у самолёта было всего около половины количества
топлива, необходимого для завершения полёта. Пилоты не заметили расхождений,
потому что датчик топлива не работал. Наземные экипажи использовали капельные
палочки для измерения топлива во время заполнения резервуаров.
Интересно, что
наземные экипажи ошиблись дважды. Первый раз в Монреале, а второй – в Оттаве.
Самолёт совершил перелёт из Монреаля в Оттаву без происшествий, но буквально
столкнулся с проблемами, когда летел из Оттавы в Эдмонтон.
2.7.Потопление «Вазы»
10 августа 1628
года Швеция запустила новый, хорошо вооружённый и большой военный корабль:
«Ваза». Судно едва проплыло 20 минут, когда затонуло менее чем в миле от
берега. Тридцать человек погибли в результате потопления. Корабль был позже
найден в 20-м веке и сейчас хранится в Музее Вазы.
Историки измерили
весь корабль и обнаружили, что его строители использовали две разные единицы
измерения. Одной был шведский фут, а другой – амстердамский фут. Шведский фут
составляет 30,48 см, в то время как амстердамский – 27,94 см.
Разница между
обеими единицами измерения привела к тому, что одна сторона оказалась тяжелее
другой. Вот почему корабль наклонился в сторону и быстро затонул после того,
как по нему ударили два порыва ветра. Историки добавляют, что влияние ветра
было усугублено тем фактом, что верх корабля был тяжелее его дна.
2.6. Крушение Mars Climate
Orbiter.
Mars Climate
Orbiter был совместным проектом компании Lockheed Martin и NASA / JPL
стоимостью 125 миллионов долларов. Проект получил неловкое завершение, когда
орбитальный аппарат, скорее всего, потерпел крушение на Марсе из-за простой
ошибки преобразования в 1999 году. Lockheed Martin использовал британскую
систему мер при программировании программного обеспечения, но НАСА использовало
метрическую систему.
Инженеры НАСА
обнаружили бы ошибку, если бы обратили внимание. Однако они этого не сделали.
Никто не понимал, что что-то не так во время девятимесячного путешествия Mars Climate
Orbiter на Марс. Ошибка стала очевидной только тогда, когда НАСА потеряло связь
с орбитальным аппаратом.
В ответ на
инцидент Джон Логсдон из Института космической политики Университета имени
Джорджа Вашингтона сказал, что всё это было «глупо». Джон Пайк из Федерации
американских учёных добавил: «Было неловко потерять космический корабль из-за
такой простой математической ошибки».
2.5.Взрыв ракеты Ariane 5
4 июня 1996 года
ракета Ariane 5 Европейского космического агентства взорвалась через 37 секунд
после взлёта. На борту космического корабля находились четыре спутника. Ракета
и спутники стоили 370 миллионов долларов. Авария была связана с целочисленной
ошибкой переполнения в программном обеспечении, используемом для запуска
ракеты.
Целочисленное переполнение
– это математическая ошибка, которая возникает, когда числа, сгенерированные
системой, превышают объём памяти этой системы. Ariane 5 работала на 16-битном
программном обеспечении, способном хранить числа до 32767. Ракете удалось
создать числа намного больше этого.
Европейское
космическое агентство использовало то же программное обеспечение, что и в
ракетах Ariane 4. У них были проблемы с Ariane 5, потому что она была быстрее,
чем Ariane 4. Чем быстрее, тем больше числа. Программное обеспечение не может
обрабатывать большие показания, из-за чего ракета становится негодной. Наземный
контроль приказал самоуничтожиться.
2.4. Выплата дивидендов и
выкуп акций Банка Америки
Федеральная
резервная система регулярно заставляет банки проходить стресс-тесты. Стресс-тест
– это анализ финансового состояния банка в условиях стимулированной негативной
экономической ситуации. Стресс-тесты необходимы, чтобы определить, достаточно
ли силён банк, чтобы преодолеть страшную рецессию или финансовый кризис.
В 2014 году Банк
Америки показал, что впервые после финансового кризиса 2008 года он прошёл
стресс-тест Федеральной резервной системы. Банк добавил, что собирается
выплатить дивиденды своим акционерам и выкупить акции на 4 миллиарда долларов.
Позже банк отозвал заявление и обнаружил, что допустил некоторые ошибки.
Банк Америки не
прошёл стресс-тест. Он только думал, что сделал это, потому что допустил ошибку
в определении стоимости некоторых облигаций, принадлежащих его дочерней
компании, Merrill Lynch. Акционеры были недовольны, и акции банка упали на 9
миллиардов долларов (пять процентов от общей стоимости) в тот же день, когда
была обнаружена ошибка.
2.3. Проблема моста в
Лауфенбурге
Некоторое время
назад Германия и Швейцария договорились построить мост через Рейн между своими
городами по обе стороны, оба под названием Лауфенбург. В соответствии с
соглашением, каждая страна должна была начать строительство со своей стороны
реки и встретиться посередине. Мост близился к завершению в 2003 году, когда
обе страны поняли, что одна половина моста была на 54 сантиметра выше, чем
другая.
Ошибка возникла
из-за того, что каждая страна по-своему определила термин «уровень моря».
Большинство стран используют разные методы определения уровня моря, учитывая,
что он не везде одинаков. Германия для его определения использует Северное
море, а Швейцария предпочитает Средиземное.
Разница между
соответствующими уровнями моря в этих странах составляла 27 сантиметров.
Германия и Швейцария знали об этом и учли это в своих расчётах. Тем не менее,
кто-то сделал так, что несоответствие удвоилось, в результате чего одна сторона
моста стала на 54 сантиметра выше, чем следовало.
2.2. Проблема негабаритного
поезда во Франции
В 2014 году
Societe Nationale des Chemins de Fer francai (SNCF), государственный
железнодорожный оператор Франции, обнаружил, что его новые скоростные поезда
были слишком широкими для 1300 станций по всей стране. Проблема заключалась в
том, что он заказал 1860 поездов у Alstom из Франции и Bombardier из Канады.
SNCF определил, что необходимо уменьшить ширину поездов, чтобы станции могли их
разместить. Ошибка обошлась в миллионы евро.
Этот инцидент
вызвал некоторое недовольство во Франции; Министр транспорта назвал это
«комично трагическим». Canard Enchaine, еженедельная сатирическая газета,
сделала карикатуру, в которой пассажирам на платформе было приказано «втянуть
животы», когда один из новых поездов подошёл к станции.
Ошибка произошла
потому, что французские вокзалы различаются по размеру. SNCF знал об этом и
просил Reseau ferre de France (RFF), который отвечал за пути, измерить
пространство возле путей. У SNCF и RFF возникли некоторые проблемы после того,
как выяснилось, что RFF пропустил 1300 старых станций в своих первоначальных
расчётах. Эти станции были уже, чем другие. Было слишком поздно, так как
некоторые поезда уже доставили, а другие находились в стадии строительства.
2.1.Ошибка муниципального
совета Амстердама на 188 миллионов евро
В декабре 2013
года финансовое управление городского совета Амстердама отправило 188 миллионов
евро более чем 10000 бедных семей, проживающих в городе. Позже город обнаружил,
что совершил ошибку в платежах. Изначально планировалось направить 1,8 миллиона
евро, а не 188 миллионов евро.
Платёжное
программное обеспечение было запрограммировано в центах, а не в евро. Люди
получили 15500 евро вместо 155 евро и в одном случае 34000 евро вместо 340
евро.
К счастью, город
смог вернуть все деньги, за исключением 2,4 миллиона евро, когда в новостях
ошибка была обнародована. Ожидалось, что городу будет сложно вернуть 1,2
миллиона евро. Это значительная сумма вместе с 300000 евро, которые город уже
потратил на ликвидацию последствий бедствия.
Человеческий
фактор – самая главная причина различных катастроф. И обидно бывает, когда
огромный труд многих людей губится из-за «незначительных» ошибок в расчетах, а
то и вовсе из-за глупости тех, кто эти расчеты делал.
3.Математические ошибки,
которые привели к значительным катастрофам
Приведу еще
несколько примеров.
3.1..Самолет с квадратными
иллюминаторами
Реактивное
авиастроение в 1950-х годах только начиналось. Первым лайнером стала «Комета» –
детище de Havilland. Это был ультрасовременный реактивный пассажирский самолёт
с уникальными для того времени техническими характеристиками и герметичной
кабиной. К сожалению, в 1954-м две «Кометы» развалились прямо в полёте. Погибло
56 человек. Причина проста: квадратные иллюминаторы.
Это была одна из
тех досадных мелочей, которые легко упустить при проектировании. Как оказалось,
круглые иллюминаторы позволяют давлению распределяться по всему фюзеляжу, и не
дают разорвать самолет на куски.
Возьмем плитку
шоколада. Как вы думаете, в каком месте она переломится, если на неё
надавить? Правильно, вдоль этих выемок.
Так вот,
квадратное окно состоит из четырех 90-градусных выемок, а стало быть, у него
есть четыре слабых места. Если бы на ваш дом надавили, то трещина непременно
прошла бы через угол какого-нибудь окна. Вы замечали, что иллюминаторы во всех
самолётах круглые? Это делается не для красоты – круглая форма не позволяет
разорвать самолёт на куски. Давление распределяется по всей кривой, вместо
того, чтобы идти трещинами по углам (как выяснилось) и разрывать самолёт в
клочья.
Выяснить это было
нелегко. Эксперты понятия не имели, почему конструкция самолёта разваливается,
пока не протестировали структуру путём многократной симуляции давления на
кабину. Конечно же, фюзеляж, в конце концов, лопнул, и разрыв начинался как раз
с этих пресловутых углов.
С тех пор
иллюминаторы у всех самолётов только круглые.
3.2 Прямые взлетно-посадочные
полосы на авианосцах
Не надо быть
пилотом, чтобы понять – посадить самолёт на авианосец чрезвычайно сложно. Эта
взлетно-посадочная полоса в миниатюре, напичканная другими самолётами, вдобавок
ещё и качается на волнах.
Но была и ещё
одна проблема.
Первые авианосцы
имели прямые полосы для взлета и посадки и были очень опасны как для самолетов,
заходящих на посадку, так и для тех, которые ожидают взлета.
Дело в том, что
истребители, которые не поймали тормозной трос, «сваливались» с
полосы, и часто врезались в другие самолеты. Чтобы хоть как-то обезопасить
авианосцы, было решено использовать перехватывающие сети, но и они не помогали.
Позже было решено
отвернуть посадочную полосу на 9 градусов влево, и количество аварий сократилось
в разы: пилоты, которые не успевали поймать тормозной трос, могли быстро дать
«полный газ» и зайти на второй круг без угрозы для остальных
самолетов.
3.3 Цельный мост в США
Мост
Такома-Нэрроуз в американском штате Вашингтон — один из крупнейших в США
висячих мостов. Его открыли 1 июля 1940 года и считали настоящим чудом: общая
длина моста составляла 1,8 км, и при этом он был цельным.
Но 7 ноября 1940
года из-за сильных порывов ветра (скорость ветра достигала 65 км/час) рухнул
центральный пролет моста. В это время на мосту была одна машина, водителю
которой удалось вовремя выбраться из салона и убежать.
Так что, железные
«кружева», которых так много на современных мостах, сделаны не для
красоты или экономии металла, а, чтобы пропускать воздух. В 1943 году мост
открыли заново и добавили в него открытые фермы, стойки жесткости,
деформационные швы и системы гашения вибраций.
3.4 Петли на дверях ночного
клуба
Клуб Cocoanut
Grove был самым модным местом Бостона в 30-х годах прошлого века. По
документам, заведение вмещало 460 человек, но во время праздников туда
набивалось куда больше народу.
В 1942 году
помощник официанта не мог найти розетку и решил подсветить себе дорогу спичкой.
Он оглянуться не успел, как за считанные секунды вспыхнули декорации, и пламя
перебросилось в зал. За несколько минут 492 человека погибли в огне.
Расследование, которое провели пожарные, показало, что такого количества жертв
можно было бы избежать, если бы двери клуба открывались наружу, а не вовнутрь
заведения.
3.5 Центральный винт, который
не может менять направление движения
Многие эксперты
сходятся во мнение, что причина крушения «Титаника» является
механической. Дело в том, что на теплоходе было установлено три винта: два
наружных, которые приводились в движение турбинами и большой центральный,
управляемый паровой турбиной. Но пар не может менять направление движения, и
поэтому мощный центральный винт вращался только в одну сторону. Вероятно
поэтому, когда помощник капитана Мэрдок отдал приказ «полный назад»,
внешние винты завертелись в обратную сторону, а центральный (самый мощный)
просто остановился. Это существенно уменьшило маневренность судна. У паровых
турбин по сравнению с их поршневыми аналогами есть существенное преимущество –
сочетание меньшего размера и большей эффективности. Но есть и недостаток – они
могут вращаться только в одну сторону. Если бы центральный винт, в случае
необходимости, мог дать задний ход, и не мешал управлять движением судна (или
если бы они вообще не давали задний ход), то вполне возможно, что Титаник
вообще не задел бы айсберг, и жизни 1514 человек и восьми собак оказались бы
вне опасности.
3.6 Несущественное изменение
дизайна
Владельцы Hyatt
Regency – нового отеля в Канзас Сити, мечтали, чтобы отель был необычный.
Архитектурная фирма, ответственная за дизайн здания, выступила с предложением сделать
несколько галерей, которые крепились бы к потолку. Недостаток проекта был в
том, что один длинный стержень был заменен на два коротких. Первоначальный
план заключался в том, чтобы расположить две галереи одна над другой, причём
обе должны были поддерживаться одним длинным стержнем, прикреплённым к потолку.
Вся конструкция висит на одном длинном стержне, что делает её настолько же
прочной, насколько и сложной для сборки – стержень должен проходить сквозь обе
галереи.
Но с большими
деталями сложно управляться – затащить в дом стол гораздо легче в разобранном
виде. Кроме того, у стержня должна быть резьба по всей длине – чтобы можно было
закрутить гайку до верхней галереи. Сталелитейная компания, ответственная за
изготовление стержня, внесла в конструкцию одно небольшое изменение – заменила
один длинный стержень двумя короткими.
Это небольшое
изменение убило 114 человек, покалечило 216 и обошлось компании в 140 миллионов
долларов по судебным искам.
Один стержень,
две гайки. Каждая гайка должна была нести вес только своей собственной
платформы. После изменения дизайна получилось, что верхняя гайка должна была
нести вес двух галерей. И вот, однажды ночью во время конкурса танцев несущая
гайка не выдержала, и обе галереи рухнули.
В ходе
последующих судебных разбирательств выяснилось, что ни сталелитейная компания,
ни инженерные фирмы, отвечающие за строительство, не потрудились даже сделать
расчёт, который показал бы этот изъян.
Заключение
Мною был собран и
оформлен материал о последствиях математической ошибки. Продемонстрирована
значимость математической ошибки.
Нашла своё
подтверждение гипотеза: математическая ошибка может привести не только к
курьёзным ситуациям, но и к серьёзным проблемам (авариям, катастрофам,
разрушениям). В ходе работы над темой я научилась разбирать математические
ошибки и поняла, что их поиск – очень полезное занятие.
Поиск ошибок
приучает внимательно и настороженно продвигаться вперед, тщательно следить за
точностью формулировок, правильностью записи чертежей, за законностью математических
операций. Если нашел ошибку, значит, ты ее осознал, а осознание ошибки
предупреждает от ее повторения в дальнейших математических рассуждениях.
Главный вывод
исследования: последствия даже маленьких математических ошибок могут быть
непредсказуемыми. Необходимо помнить об этом каждому и учиться находить и
своевременно исправлять свои ошибки. Взять себе за правило: не позволять себе
допускать даже самых незначительных математических ошибок.
Поэтому, хочется
сказать: «Ребята, уделяйте достаточно внимания изучению математики за школьной
партой!» Дело в том, что когда мы станем взрослыми, то даже одна очень
маленькая ошибка может стоить жизни многим людям.
Список использованных источников и литературы
1. Савин, А.П. Энциклопедический словарь юного математика / А.П.Савин.
— М.: Педагогика, 1989.-352 с.
2. Перельман, Я. И. Занимательная алгебра / Я.И.Перельман — Москва:
Государственное издательство физико-математической литературы, 1959.- 184 с.
3. Игнатьев, Е.И. В царстве смекалки / Е.И.Игнатьев — Москва:
Наука, 1984.- 192 с.
4.Гарднер, М. Математические чудеса и тайны / М.Гарднер —
Москва: Наука, 1982.- 128 с
5.РИА Новости (RIA.RU).
6.http://mixednews.ru/archives/15234
7.http://hijos.ru/2011/11/06/matematicheskie-kinolyapy
8.https://www.liveinternet.ru/community/for_men_only/post265675202/
9.https://pikabu.ru/story/10_prostyikh_no_dorogostoyashchikh_matematicheskikh_oshibok_v_istorii_6912640
Чтобы успешно сдать экзамен, подготовку нужно начинать заранее. И если вы не можете самостоятельно определить свои слабые места и проблемы, рекомендуем начать с разбора типичных ошибок ЕГЭ и ОГЭ по математике.
Здесь мы приведем анализ типичных ошибок 2023 и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.
Базовый уровень математики
Ошибки в задачах на проценты
Чаще всего их допускают, так как не разбираются в сути процента.
Возьмем пример задачи, когда нужно сначала снизить цену на 25%, а потом повысить ее на 25%. Самая частая ошибка – полагать, что эти проценты будут равны одной и той же сумме. На самом же деле база их зачисления будет совершенно разной.

В этом примере 6% участников допустили вариант, что новую цену нужно понизить на 25%. На самом же деле новая цена – это 125% от старой. И вопрос в этой задаче – узнать, сколько будет 100% от старой цены.
Совет: повторить основы расчета процентов, повторить взаимосвязи величин, подумать над способом решения таких задач.
Невнимательное прочтение условия задания
Волнение и психологическое напряжение приводят к тому, что участники часто неправильно понимают условие задания. В итоге – снижение итогового балла по невнимательности, а не по незнанию.
Например:
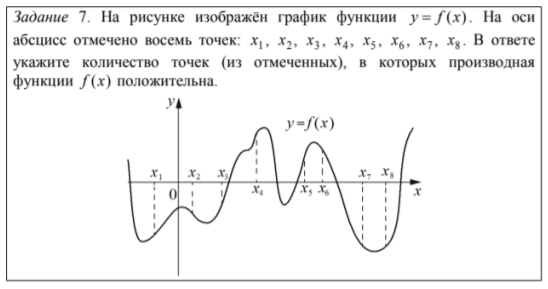
В 24% участников упомянули те точки, где значение функции (а не производной) положительное. Еще 2% указали номера точек, где производная принимает положительное значение.
Совет: вдумчиво, медленно и несколько раз читайте задание.
Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)
Учащиеся могут не только неправильно понять, но и вовсе не понять условия. Иногда это происходит из-за незнания величин, единиц их измерения или плохой работы с формулами. Многие просто пропускают эту часть тестирования.
Вот пример задачи:

Её выполнило только 57% участников тестирования. 8% вообще не дали ответа, 6% дали ответ «чем ближе, тем лучше», 4% – «лампочку необходимо поместить в середину разрешенного интервала», еще 4,5% приняли фокус за основной параметр.
Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.
Ошибки в вычислениях
Школьная привычка использовать даже в самых легких примерах калькулятор приводит к плачевному результату на экзамене. Если учащийся не научиться быстро считать в уме или хотя бы на бумаге, во время тестирования он может ошибиться даже в самых простых заданиях.
Особенно сложно участникам тестирования даются дроби, отрицательные числа, элементарные преобразования выражений и другие проблемы, копившиеся еще с 5 класса.
Совет: если в чем-то не разбираетесь, обязательно отработайте эту тему до автоматизма перед экзаменом, потому что она обязательно попадется.
Ошибки теоретического характера
Это касается фактов по геометрии и алгебре, незнание которых приводит к снижению процента выполнения заданий и базового, и профильного уровней.
Например:

В этой задаче около 8% участников вообще не ответили на поставленное условие, 38% дали ответ с ошибками относительно боковой поверхности конуса, а 12% совершили ошибки в расчёте объёма.
Статистика показывает, что в таких заданиях ошибок гораздо больше, чем в гораздо более сложных профильных заданиях.
Совет: потренируйтесь перед тестированием. Если ответы не сходятся с ключами, обратитесь за помощью к стороннему специалисту (репетитору или сервису студенческой помощи), чтобы они указали, где вы ошибаетесь.
Ошибки в алгоритмах и методах решения
Этот тип ошибок встречается во всех заданиях.
Например:
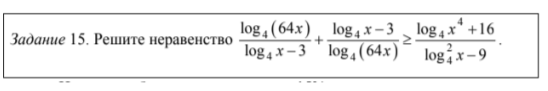
Около 15% участников получили нулевые баллы из-за проблем с невнимательным чтением неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств.
Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.
Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.
Ошибки в чтении и построении чертежа
Такое случается, когда ученик не понимает взаимосвязь элементов геометрических конструкций, а также не обладает основными пространственными представлениями.
Например:

Около 10% участников экзамена сделали ошибки в вычислении углов по их записи, просто перепутав буквы или не понимая, где расположены вершины всех углов. Еще 5% решили, что угол ACD прямой. А 3% увидели в угле ABD равносторонний треугольник.
Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.
Неумение обосновывать и доказывать
14 и 16 задания по стереометрии и планиметрии отличаются повышенным уровнем сложности и требуют развернутого ответа. В каждом по 2 пункта: в первом нужно доказать, во втором – произвести вычисления.
Самые распространенные ошибки касаются первого пункта, так как у участников выявились проблемы с умением доказывать.
Есть проблемы и в оформлении доказательств. Например:

Основная трудность в отсутствии понимания логики построения доказательства.
Совет: тренируйтесь в доказательной базе, повышайте математическую культуру, учитесь обосновывать выбранные методы и способы их решения.
Ошибки в заданиях по тригонометрии
Из-за невнимательности и неаккуратности, а также отсутствия знаний по большому количеству теоретических фактов и способности их применять на практике, участники совершают частые ошибки в решении тригонометрических заданий.
Например:

Только 34% участников выполнили его. Самые частые ошибки (около 12%) связаны в первую очередь с нахождением тригонометрического знака – чаще всего потеря знака «минус». Еще 22% ждут «красивого» ответа, равного 1 или 2.
Ошибки математического моделирования
В 11 и 17 заданиях проверяют способность учащихся к построению и исследованию простейших математических моделей.
В текстовых задачах основную роль играет сюжетная часть – она имеет практическую ориентацию. И часто из-за непонимания взаимосвязи величин в этих заданиях допускают ошибки.
Например, в задачах на движение примерно 10% не понимают принципы движения по реке – они умножают собственную скорость на время движения.
Совет: тренируйте текстовые задачи, внимательно читайте условие задачи.
Профильный уровень
Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:
- Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей.
- Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры).
- Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже.
- Задание 8 – ошибаются в наглядном решении.
- Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики.
- Задание 12 – ошибаются в задачах с нулями производной.
Как правильно читать задание, чтобы не совершать ошибок по невнимательности
Есть несколько рекомендаций, чтобы избежать ошибок из-за невнимательного прочтения задания. Это и будет алгоритмом решения задачи:
- прочтите условие;
- выпишите данные величины, сделайте рисунок в геометрическом задании;
- установите и запишите отношения и взаимосвязи между известными данными;
- выпишите что найти, ответ на какой вопрос нужно дать;
- определите тип задания;
- сформулируйте содержание и последовательность действий.
Это будет ваш своеобразный чек-лист, который обязательно нужно соблюдать при решении любой задачи, чтобы не допустить обидных ошибок.
Данные условия важно именно выписывать, а не иметь в виду. Фиксация их в уме чаще всего приводит к записи неправильного ответа.
И еще момент: не приступайте к решению задачи сразу же после ее прочтения. Психологи утверждают, что важно выдержать паузу между стимулом и реакцией – именно при этом условии удастся добиться оптимальных результатов:
- сориентироваться в условии,
- обдумать и спланировать ее решение,
- понять уровень ее сложности и решить, откладывать ли ее решение напоследок.
Кроме сложности задачи оцените, сколько баллов она принесет и насколько она утомительна. Важно оставить энергию для решения других заданий при сдаче единого государственного экзамена.
Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.
Знание типичных ошибок ЕГЭ и ОГЭ по математике даст вам полную картину того, к каким заданиями нужно готовиться с большим усилием. А чтобы не отвлекаться на другие учебные дела, не забывайте: рядом есть сервис студенческой помощи, который подставит плечо в трудную минуту.
«Недействительное доказательство» перенаправляется сюда. По поводу любого типа недействительных доказательств, кроме математических, см. Заблуждение.
В математика, некоторые виды ошибочных доказательств часто выставляются, а иногда и собираются в качестве иллюстраций концепции, называемой математическая ошибка. Есть различие между простым ошибка и математическая ошибка в доказательстве, когда ошибка в доказательстве приводит к недействительному доказательству, в то время как в наиболее известных примерах математических ошибок присутствует некоторый элемент утаивания или обмана в представлении доказательства.[1]
Например, причину, по которой не действует достоверность, можно отнести к деление на ноль что скрыто алгебраической записью. Есть определенное качество математической ошибки: в том виде, в котором ее обычно представляют, она приводит не только к абсурдному результату, но и делает это хитрым или хитрым способом.[2] Поэтому эти заблуждения по педагогическим причинам обычно принимают форму ложных доказательства очевидного противоречия. Хотя доказательства ошибочны, ошибки, как правило, преднамеренные, являются сравнительно малозаметными или предназначены для демонстрации того, что определенные шаги являются условными и неприменимы в случаях, которые являются исключениями из правил.
Традиционный способ представления математической ошибки состоит в том, чтобы дать неверный шаг вывода, смешанный с действительными шагами, так что значение заблуждение здесь немного отличается от логическая ошибка. Последнее обычно применяется к форме аргументации, которая не соответствует действующим правилам логического вывода, тогда как проблемный математический шаг обычно является правильным правилом, применяемым с неявным неправильным предположением. Помимо педагогики, разрешение ошибки может привести к более глубокому пониманию предмета (например, введение Аксиома Паша из Евклидова геометрия[3], то теорема пяти цветов из теория графов ). Псевдария, древняя утерянная книга ложных доказательств, приписывается Евклид.[4]
Математические ошибки существуют во многих областях математики. В элементарная алгебра, типичные примеры могут включать этап, на котором деление на ноль выполняется, где корень неправильно извлекается или, в более общем смысле, где разные значения многозначная функция приравниваются. Известные заблуждения существуют также в элементарной евклидовой геометрии и исчисление.[5][6]
Ревуны
Аномальный
отмена
в исчислении
Существуют примеры математически правильных результатов, полученных в результате неправильных рассуждений. Такой аргумент, каким бы верным он ни казался, математически неверен. инвалид и широко известен как ревун.[1] Ниже приводится пример ревуна, включающего аномальная отмена:
Здесь хотя вывод 16/64 = 1/4 правильно, на среднем этапе происходит ошибочная, недействительная отмена.[примечание 1] Другой классический пример ревуна — доказательство теоремы Кэли – Гамильтона простой заменой скалярных переменных характеристического полинома матрицей.
Поддельные доказательства, вычисления или выводы, построенные для получения правильного результата, несмотря на неправильную логику или операции, Максвелл назвал «воплями».[7] За пределами области математики термин ревун имеет различные значения, как правило, менее конкретные.
Деление на ноль
В ошибка деления на ноль есть много вариантов. В следующем примере используется замаскированное деление на ноль, чтобы «доказать», что 2 = 1, но его можно изменить, чтобы доказать, что любое число равно любому другому числу.
- Позволять а и б равны, ненулевые величины
- Умножить на а
- Вычесть б2
- Фактор обе стороны: левые факторы как разница квадратов, право факторизуется путем извлечения б с обоих условий
- Разделить (а − б)
- Наблюдая за этим а = б
- Объедините похожие термины слева
- Разделить на ненулевое б
- Q.E.D.[8]
Ошибка в строке 5: переход от строки 4 к строке 5 включает деление на а − б, который равен нулю, поскольку а = б. С деление на ноль не определено, аргумент недопустим.
Анализ
Математический анализ как математическое исследование изменений и пределы может привести к математическим ошибкам — если свойства интегралы и дифференциалы игнорируются. Например, наивное использование интеграция по частям может использоваться для ложного доказательства того, что 0 = 1.[9] Сдача ты = 1/бревно Икс и dv = dx/Икс, мы можем написать:
после чего первообразные могут быть отменены, давая 0 = 1. Проблема в том, что первообразные определены только вплоть до а постоянный и смещение их на 1 или любое другое число разрешено. Ошибка действительно обнаруживается, когда мы вводим произвольные пределы интегрирования а и б.
Поскольку разница между двумя значениями постоянной функции равна нулю, по обе стороны уравнения появляется один и тот же определенный интеграл.
Многозначные функции
Многие функции не имеют уникального обратный. Например, возведение числа в квадрат дает уникальное значение, но есть два возможных квадратные корни положительного числа. Квадратный корень многозначный. По соглашению можно выбрать одно значение в качестве основная стоимость; в случае квадратного корня неотрицательное значение является главным значением, но нет гарантии, что квадратный корень, заданный как главное значение квадрата числа, будет равен исходному числу (например, главный квадратный корень квадрата −2 равно 2). Это остается верным для энные корни.
Положительные и отрицательные корни
Следует соблюдать осторожность при приеме квадратный корень обеих сторон равенство. Невыполнение этого требования приводит к «доказательству»[10] 5 = 4.
Доказательство:
- Начать с
- Напишите это как
- Перепишите как
- Добавлять 81/4 с обеих сторон:
- Это идеальные квадраты:
- Извлеките квадратный корень из обеих частей:
- Добавлять 9/2 с обеих сторон:
- Q.E.D.
Ошибка заключается в предпоследней строке, где извлекается квадратный корень из обеих частей: а2 = б2 только подразумевает а = б если а и б имеют такой же знак, чего здесь нет. В этом случае это означает, что а = –б, поэтому уравнение должно выглядеть так:
который, добавив 9/2 с обеих сторон правильно уменьшается до 5 = 5.
Другой пример, иллюстрирующий опасность извлечения квадратного корня из обеих частей уравнения, включает следующее фундаментальное тождество[11]
которое выполняется как следствие теорема Пифагора. Затем, извлекая квадратный корень,
так что
Но оценивая это, когда Икс = π мы получаем это
или же
что неверно.
Ошибка в каждом из этих примеров в основном заключается в том, что любое уравнение вида
куда 
и важно проверить, какое из этих решений имеет отношение к рассматриваемой проблеме.[12] В указанном выше заблуждении квадратный корень, который позволил вывести второе уравнение из первого, действителен только тогда, когда cosИкс положительный. В частности, когда Икс установлен на π, второе уравнение становится недействительным.
Квадратные корни отрицательных чисел
Недействительные доказательства, использующие силы и корни, часто бывают следующего вида:
Ошибка в том, что правило 


В качестве альтернативы мнимые корни запутываются в следующем:
Ошибка здесь заключается в последнем равенстве, где мы игнорируем другие корни четвертой степени из 1,[заметка 2] которые равны −1, я и —я (куда я это мнимая единица ). Поскольку мы возводили нашу фигуру в квадрат, а затем пустили корни, мы не всегда можем предположить, что все корни будут правильными. Итак, правильные корни четвертой степени я и —я, которые представляют собой мнимые числа, которые возводятся в квадрат до -1.
Комплексные показатели
Когда число возводится в комплексную степень, результат не определяется однозначно (см. Несостоятельность тождеств силы и логарифма ). Если это свойство не распознается, могут возникнуть следующие ошибки:
Ошибка здесь в том, что правило умножения показателей степени, как при переходе к третьей строке, не применяется без изменений со сложными показателями, даже если при установке обеих сторон в степень я выбирается только главное значение. Когда рассматривается как многозначные функции, обе стороны производят одинаковый набор значений, будучи {е2πп | п ∈ ℤ}.
Геометрия
Многие математические ошибки в геометрия возникают из-за использования аддитивного равенства, включающего ориентированные величины (например, добавление векторов вдоль заданной линии или добавление ориентированных углов в плоскости) к действительной идентичности, но которое фиксирует только абсолютное значение (одной из) этих величин. Затем эта величина включается в уравнение с неправильной ориентацией, чтобы сделать абсурдный вывод. Эта неправильная ориентация обычно подразумевается путем предоставления неточной схемы ситуации, в которой относительное положение точек или линий выбирается таким образом, который фактически невозможен в соответствии с гипотезами аргумента, но неочевидно.
В общем, такое заблуждение легко выявить, нарисовав точную картину ситуации, в которой некоторые относительные положения будут отличаться от тех, что указаны на представленной диаграмме. Чтобы избежать таких заблуждений, правильный геометрический аргумент с использованием сложения или вычитания расстояний или углов должен всегда доказывать, что величины включаются с их правильной ориентацией.
Ошибка равнобедренного треугольника

Ошибочность равнобедренного треугольника из (Максвелл 1959, Глава II, § 1), имеет целью показать, что каждый треугольник является равнобедренный, что означает, что две стороны треугольника равны конгруэнтный. Это заблуждение было приписано Льюис Кэрролл.[14]
Для треугольника △ ABC докажите, что AB = AC:
- Нарисуйте линию деление пополам ∠А.
- Нарисуйте серединный перпендикуляр к отрезку BC, который делит BC пополам в точке D.
- Пусть эти две прямые пересекаются в точке O.
- Проведите линию OR перпендикулярно AB, линию OQ перпендикулярно AC.
- Нарисуйте линии OB и OC.
- К ААС, △ RAO ≅ △ QAO (∠ORA = ∠OQA = 90 °; ∠RAO = ∠QAO; AO = AO (общая сторона)).
- К RHS,[заметка 3] △ ROB ≅ △ QOC (∠BRO = ∠CQO = 90 °; BO = OC (гипотенуза); RO = OQ (нога)).
- Таким образом, AR = AQ, RB = QC и AB = AR + RB = AQ + QC = AC.
Q.E.D.
Как следствие, можно показать, что все треугольники равносторонние, показав, что AB = BC и AC = BC таким же образом.
Ошибка доказательства состоит в предположении на диаграмме, что точка O внутри треугольник. Фактически, O всегда лежит в описанной окружности треугольника ABC (за исключением равнобедренных и равносторонних треугольников, в которых AO и OD совпадают). Кроме того, можно показать, что если AB длиннее, чем AC, то R будет лежать в AB, а Q будет лежать за пределами переменного тока, и наоборот (фактически, любая диаграмма, нарисованная с помощью достаточно точных инструментов, подтвердит два вышеуказанных факта). Из-за этого AB по-прежнему AR + RB, но AC на самом деле AQ — QC; и, следовательно, длины не обязательно одинаковы.
Доказательство по индукции.
Существует несколько ошибочных доказательства по индукции в котором один из компонентов, базисный случай или индуктивный шаг, неверен. Интуитивно, индукционные доказательства работают, утверждая, что если утверждение истинно в одном случае, оно истинно в следующем, и, следовательно, многократно применяя это утверждение, можно показать, что оно истинно для всех случаев. Следующее «доказательство» показывает, что все лошади одного цвета.[15][примечание 4]
- Скажем, что любая группа N лошади все одного цвета.
- Если мы удалим лошадь из группы, у нас будет группа N — 1 лошадь такого же цвета. Если мы добавим еще одну лошадь, у нас будет еще одна группа N лошади. По нашему предыдущему предположению, все лошади в этой новой группе одного цвета, поскольку это группа N лошади.
- Таким образом, мы построили две группы N лошади все одного цвета, с N — 1 общая лошадь. Поскольку у этих двух групп есть несколько общих лошадей, они должны быть одного цвета.
- Следовательно, объединив всех используемых лошадей, мы получим группу N + 1 лошадь одного цвета.
- Таким образом, если N лошади все одного цвета, любые N + 1 лошади одного цвета.
- Это явно верно для N = 1 (т.е. одна лошадь — это группа, в которой все лошади одного цвета). Таким образом, по индукции N лошади одного цвета для любого положительного целого числа N. т.е. все лошади одного цвета.
Ошибка в этом доказательстве возникает в строке 3. Ибо N = 1, две группы лошадей имеют N — 1 = 0 общих лошадей и, следовательно, не обязательно одного цвета, поэтому группа N + 1 = 2 лошади не обязательно одного цвета. Значение «каждый N лошади одного цвета, то N + 1 лошадь одного цвета «работает на любые N > 1, но это не так, когда N = 1. Базовый случай правильный, но индукционный шаг имеет фундаментальный недостаток. Если бы нам дополнительно дали тот факт, что любые две лошади одного цвета, то мы могли бы правильно произвести индукцию из базового случая N = 2.
Смотрите также
- Аномальная отмена — арифметическая ошибка
- Деление на ноль — Результат, полученный как действительное число при делении на ноль
- Список неполных доказательств — Статья со списком Википедии
- Математическое совпадение — совпадение по математике
- Парадокс — Заявление, которое явно противоречит самому себе
- Доказательство запугиванием — Метод убедить кого-то, используя жаргон или заявляя, что он понятен
Примечания
Рекомендации
- ^ а б «Окончательный глоссарий высшего математического жаргона — математическая ошибка». Математическое хранилище. 2019-08-01. Получено 2019-10-24.
- ^ Максвелл 1959, п. 9
- ^ Максвелл 1959
- ^ Хит и Хелберг 1908, Глава II, §I
- ^ Барбо, Эд (1991). «Заблуждения, недостатки и вздор» (PDF). Математический журнал колледжа. 22 (5). ISSN 0746-8342.
- ^ «Мягкий вопрос — Лучшие фальшивые доказательства? (Коллекция, посвященная Дню дураков от M.SE)». Обмен стеками математики. Получено 2019-10-24.
- ^ Максвелл 1959
- ^ Хойзер, Харро (1989), Lehrbuch der Analysis — часть 1 (6-е изд.), Teubner, p. 51, ISBN 978-3-8351-0131-9
- ^ Барбо, Эд (1990), «Заблуждения, недостатки и вздор № 19: Теорема Долта», Математический журнал колледжа, 21 (3): 216–218
- ^ Frohlichstein, Джек (1967). Математические развлечения, игры и головоломки (иллюстрированный ред.). Курьерская корпорация. п. 207. ISBN 0-486-20789-7. Отрывок страницы 207
- ^ Максвелл 1959, Глава VI, §I.1
- ^ Максвелл 1959, Глава VI, §II
- ^ Нахин, Пол Дж. (2010). Воображаемая сказка: История «я«. Издательство Принстонского университета. п. 12. ISBN 978-1-4008-3029-9. Выдержка страницы 12
- ^ Робин Уилсон (2008), Льюис Кэрролл в Numberland, Penguin Books, стр. 169–170, ISBN 978-0-14-101610-8
- ^ Полиа, Джордж (1954). Индукция и аналогия в математике. Математика и правдоподобные рассуждения. 1. Принстон. п. 120.
- Барбо, Эдвард Дж. (2000), Математические заблуждения, недостатки и вздор, МАА Спектр, Математическая ассоциация Америки, ISBN 978-0-88385-529-4, МИСТЕР 1725831.
- Связка, Брайан (1997), Математические заблуждения и парадоксы, Нью-Йорк: Dover Publications, ISBN 978-0-486-29664-7, МИСТЕР 1461270.
- Хит, сэр Томас Литтл; Хейберг, Йохан Людвиг (1908), Тринадцать книг Евклида Элементов, Том 1, Университетское издательство.
- Максвелл, Э. (1959), Заблуждения в математике, Издательство Кембриджского университета, ISBN 0-521-05700-0, МИСТЕР 0099907.
внешняя ссылка
- Недействительные доказательства в Разрезать узел (включая литературные ссылки)
- Классические заблуждения с некоторым обсуждением
- Больше недействительных доказательств с AhaJokes.com
- Математические анекдоты с недействительным доказательством
Ошибки учащихся при изучении математики,
их предупреждение и объяснение
Автор работы:
Дука Наталья Ивановна
учитель математики МОУ «СОШ №4 г. Ртищево Саратовской обл.» ____________________________
Аннотация
В данной работе рассматриваются типичные ошибки, которые допускают учащиеся при выполнении математических заданий. Здесь разобраны причины, способы исправления и предупреждения ошибок, разобраны конкретные ошибки из курса алгебры и начал анализа и способы их объяснения и устранения, указаны ошибки в работах государственной итоговой аттестации учащихся 9 и 11 классов. Рассмотрены ошибки по математике в учебниках и методической литературе. Материал, представленный в работе, может заинтересовать учителей математики.
Тезисы
В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная.
Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.
Объект исследования: процесс обучения математике в основной общеобразовательной школе.
Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.
Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =
. Это очень грубая ошибка. Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.
Иногда ученики используют неверную формулу, не задумываясь над ней.
Например, определяя, является ли число рациональным, ученик пишет:
=
и получает неверный ответ,
При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Должна появиться верная запись
.
При выполнении преобразований со степенями учащиеся не только допускают ошибки, но просто забывают формулы, например формулу
an am = an+m.
Пример ошибки на свойство степени: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Необходимо в результате записать формулу
.
Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х
2.
Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x».
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний.
В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена некорректно составленная задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С». Треугольник, описанный в условии задачи, не существует.
Объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких) дается с ошибкой.
В газете «Математика» предлагается уравнение и к нему ответ:1. Приведенное решение неверное, так как приводит к потере корней.
Вступление
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.
Причины ошибок, допускаемых учащимися при изучении математики
Проблема исследования состоит в теоретическом обосновании и разработке такой методики обучения математике, которая создавала бы условия для развития рефлексивной деятельности учащихся, способствующей предупреждению типичных ошибок.
Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.
Объект исследования: процесс обучения математике в основной общеобразовательной школе.
Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.
Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления. Снижает, но не исключает. Можно ли избавиться от таких ошибок? Ученик знает, что нужно решать внимательно, но ничего не может с собой поделать.
Известно, что осознание правила или определяет действия, или, по крайней мере, их контролирует. Знание правила необходимо и для того, чтобы осуществить проверку решения и дать его обоснование. Но большинство учащихся воспринимают курс алгебры как набор несвязанных между собой правил, которые заучиваются (иногда формально) для применения их к решению задач. Поэтому необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.
Выполняя математические задания, учащиеся допускают типичные ошибки:
- Незнание правил, определений, формул.
- Непонимание правил, определений, формул.
- Неумение применять правила, определения, формулы.
- Неверное применение формул.
- Невнимательное чтение условия и вопроса задания.
- Вычислительные ошибки.
- Не использование свойств фигур при решении геометрических задач.
- Логические ошибки при решении текстовых задач.
- Раскрытие скобок и применение формул сокращенного умножения.
Какие причины ошибок по математике?
- Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
- Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
- Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
- Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся не всегда сами понимают, что именно они написали.
- Усталость. Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
- Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
- Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
- Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Работа над ошибками
В приемах работы над ошибками отсутствует диагностика причин ошибок. Не уделяется должного внимания работе по формированию рефлексивной деятельности учащихся и ее использованию в работе по предупреждению и исправлению математических ошибок. При отсутствии должной доли самостоятельности при работе над ошибками, совершаемые учеником действия никак не контролируются, допущенные ошибки не замечаются, причины их появления остаются невыясненными, что приводит к их повторению. Напротив, самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления. При этом у школьников постепенно развиваются стремление и умение разобраться в задаче, планировать ее решение, продумывать возможные варианты действий и прогнозировать их результаты. Например, ученик многократно применяет к преобразованию алгебраических выражений формулы квадрата суммы и разности двух чисел, но получив задание представить в виде многочлена
(–х–5)2, теряется. Следует предложить учащемуся ответить на вопрос что вызывает затруднение? И как преобразовать выражение, чтобы можно было применить одну из формул в том виде, в каком они предложены в учебнике. Другой пример неосознанного применения алгоритма: получив уравнение
sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x. Полезно предложить ученику представить наглядное решение на тригонометрическом круге.
Самоконтроль
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; б) умения её объяснить и исправить. В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
- проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
- проверка правильности решения задач путём составления и решения задач, обратных к данной;
- оценка результата решения задачи с точки зрения здравого смысла;
- проверка аналитического решения графическим способом.
Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.
Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.
Ученик написал = 52, ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130” .
Объяснение и предупреждение ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры.
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
Например, перед изучением темы «Теоремы сложения» следует повторить следующие теоретические вопросы:
1. Четные и нечетные функции.
2. Изменение тригонометрических функций при возрастании и убывании аргумента.
3. Знаки тригонометрических функций.
4. Таблицы значений тригонометрических функций.
А также выполнить задания:
1. Определите четность и нечетность тригонометрической функции:
а) y = – cos x + x2; б) y = sin2 x; в) y = .
2. Найдите область определения функции y = x2 – 6x + 10.
3. При каких значениях x функции y = sin x и y = cos x принимают одинаковые значения?
Перед прохождением темы «Первообразная и интеграл» повторяем все формулы дифференцирования. Затем предлагается самостоятельная работа (на 10–15 мин), на которой ученики получают карточки-задания, в которых «опущены» один–два компонента из формулы дифференцирования и приведены две функции, производные которых необходимо найти. После проверки самостоятельной работы анализируем допущенные ошибки, определяем пробелы в знаниях и проводим работу по их устранению.
Рассмотрим ошибки, допускаемые в курсе алгебры и начал анализа. Задание. Найти точное значение arcsin (sin).
Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =
. Это очень грубая ошибка. По определению
. Следовательно, число arcsin(sin
) должно принадлежать промежутку
, число
этому промежутку не принадлежит. Имеем: arcsin (sin
) = arcsin (sin
)) = arcsin (sin
) = arcsin
=
Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о. Можно исправить ошибку следующим образом: учитывая, что 90о
90о для любого
и arctg (tgх) = х при
х arctg (tg130о) = arctg (tg180о
50о) = arctg (tg(
50о)) =
50о. Существует второй способ решения. Пусть arctg (tg130о) = х, получаем tg х = tg (arctg (tg130о)), откуда tg х = tg 130о. По условию равенства тангенсов имеем х = 130о +
k, где k
Z. Учитывая область определения функции у = arctg х, где х
(
90О; 90О), при k =
1 х = 130о
180о =
50о.
Рассмотрим еще один пример правильного решения аналогичного задания вычислить arcsin(sin2) при неверном ответе учащихся «2». Решение: arcsin (sink) = k, если , arcsin (sin2) = arcsin (sin(
) =
2, т. к.
2
.
Иногда ученики используют неверную формулу, не задумываясь над ней. Например, определяя, является ли число рациональным, ученик пишет:
=
и получает неверный ответ, выполняя преобразование иррационального выражения, учащийся получил
= х+2. Во-первых, учащиеся забывают, что
, во-вторых, опять ошибочная аналогия с формулой
=
, где
Применение «формулы
=
» в классе обязательно происходит независимо от того, повторяются свойства радикалов на уроках или нет. Ученик проводит аналогию с формулой
=
, где
и не понимает, почему он неправ. Если заставить ученика написать правильно по свойству, то долговременного эффекта не получится. Необходимо, чтобы ученик понял и осознал свою ошибку. Для этой цели пригоден совет: вычислите
по тому алгоритму, который только что применили, имеем
=
и по действиям
2 = 1 и определите, какое решение верное. Ученик задумывается и находит ошибку.
Можно предложить учащимся проверить себя, взяв, например, значение х = 2 но
;
при х = –2 но
.
Делаем вывод: преобразование выполнено неверно, формула «=
» не существует и
При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Нужно посоветовать ученику проверить написанное при конкретных значениях переменных. Так, при a = b = 1, c = 2, получим
, с другой стороны
, тогда 2=
В результате ученик должен сделать вывод, что при работе с «трехэтажными дробями» лучше ставить скобки, чем сравнивать длины дробных «черточек»:
. И, разумеется, должна появиться верная запись
.
При выполнении преобразований со степенями учащиеся не только допускают ошибки, но просто забывают формулы, например формулу
an am = an+m. Полезно учащимся показать, как они могут вспомнить формулу, пользуясь определением степени, например a3a4=aaa
=a 7=a 3+4. Применяя определение степени в подобных ситуациях, учащиеся могут вывести любую формулу действий со степенями. Аналогично можно показать ошибки в действиях со степенями.
Ещё пример ошибки: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Следует привести конкретный пример с удобным вычислением
=
. Здесь же можно предложить другой способ
Необходимо в результате записать формулу .
Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х
2. Полезно в этом случае предложить учащимся проверить число, например. -3, при этом учащиеся убеждаются в неверности ответа. Можно показать три способа решения этого неравенства. 1 способ тот, которым и пользовались учащиеся «
», но допустили следующую ошибку «
=х». Верное решение
Этот способ решения содержит опасный момент – необходимо обратить внимание на возрастание функции у =
при х
0, иначе в дальнейшем будут еще ошибки при решении неравенств. Второй способ основан на методе интервалов х2
4, х2
,
(х-2)(х+2)0,
. Третий способ графический.
х24 при
.
Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x». В этом случае можно поступить двумя способами: подставить х =/6 и получить неверное равенство sin
2sin
,
/2 = 2
1/2 или вспомнить определение sin х на тригонометрическом круге. Наглядно хорошо видно, что sin 2х
2sinх. Обращение к тригонометрическому кругу всегда полезно повторением определения тригонометрических функций и наглядностью определений.
у
Не нужно специально исправлять каждое ошибочное утверждение ученика и предупреждать его об ошибках. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Практика показывает, что систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении»:
Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.
Анализ работ ГИА и ЕГЭ
Анализ работ государственной итоговой аттестации учащихся 11-х классов показал, что типичные ошибки допущены при:
- преобразовании дробно-рациональных выражений, содержащих корень
n-ой степени
- исследовании функций на наибольшее и наименьшее значения;
- решении показательных и логарифмических неравенств (отсутствует ссылка на соответствующие свойства функций);
- вычислении площади криволинейной трапеции;
- построении графика функции с модулем;
- изображении тел вращения в геометрической задаче;
- теоретическом обосновании используемых формул и фактов при решении задачи по стереометрии;
- построении множества точек плоскости, удовлетворяющего заданному условию;
- решении задач с параметром.
Для повышения уровня учебных достижений учащихся на ГИА за курс старшей школы рекомендуется обратить внимание на следующие темы и разделы курса алгебры и начал анализа и геометрии:
- комбинация тел;
- углы в пространстве;
- производная и её применение к исследованию функции на отрезке;
- построение ГМТ, удовлетворяющего заданным условиям;
- логарифмические и показательные неравенства;
- тригонометрические функции и их свойства;
- тождественные преобразования дробно-рациональных выражений, содержащих корень n-ой степени.
Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний, построение и развитие межпредметных связей и осознание взаимосвязи с ранее выученными темами, на подготовку к итоговому оцениванию знаний, установлению формально-логических подходов к построению курса школьной математики, закрепление необходимости обосновывать и доказывать математические факты.
Ошибки в учебниках и методической литературе
В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С».
Решение.
ВD – биссектриса АВС
=
∠ВDС = ∠С ВDС равнобедренный
ВD = DС
=
Отсюда СD =
Ответ:
Решим задачу вторым способом.
ВЕ – высота АВС. Пусть DЕ = х. Из прямоугольных треугольников АВЕ и DВЕ получаем:
АВ2 – АЕ2 = ВD2 – DЕ2,
302 – (20 + х)2 = 162 – х2,
900 – 400 – 40х – х2 = 256 – х2,
40х = 244,
х = 6,1.
ВЕ высота и медиана
DЕ = СЕ
СD = 2х = 12,2. Получили несоответствие с ответом первого способа решения.
Проверим, существует ли треугольник, у которого выполнены условия: ∠ВDС = ∠С и ∠АВD = ∠DВС. Найдем величины ∠DВС, ∠ВDС, ∠С.
АD2 = АВ2 + ВD2 – 2
cos ∠AВD
cos ∠AВD =
Тогда ∠АВD 38,5о. ∠DВС = ∠АВD
38,5о.
Аналогично cos ∠ADВ =
Тогда ∠АDВ = 180о – 67,59о ∠ВDС
67,59о. Из
ВDС
∠С = 180о – 38,05о – 67,59о = 74,36о,
Отсюда следует, что ∠ВDС ∠С и треугольник DВС неравнобедренный.
Значит, задача составлена некорректно: треугольник, описанный в условии задачи, не существует.
Возможны два корректных варианта задачи:
- Дан треугольник АВС, точка D лежит на стороне ВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С.
В этом случае ВD не является медианой. По второму способу получаем СD = 12,2.
- Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30. АD = 20, ВD = 16.
∠ВDС ∠С, в этом случае из треугольника DВС по теореме синусов получаем
В действующем учебнике задача № 536 имеет вид:
Отрезок BD является биссектрисой треугольника АВС. а) Найдите АВ, если ВС = 9 см, АD = 7,5 см, DС = 4,5 см. б) Найдите DС, если АВ = 30. АD = 20, ВD = 16.
Посмотрим объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких).
Цитируем: «Прочитай, объясни и проверь записи.
190 : 20 = 190 : 10 : 2 = 9 ( 1 остаток)
190 : 20 = 19 д. : 2 д. = 9 ( 1 остаток)
4700 : 500 = 4700 : 100 : 5 = 9 ( 2 остаток)
4700 : 500 = 47 с. : 5 с. = 9 ( 2 остаток)»
Проверяем 20 ∙ 9 + 1 = 190 – равенство неверное, делаем вывод: ошибка при выполнении деления с остатком. В чем ошибка? Анализируем 1-ое равенство 190 : 20 = 190 : 10 : 2 = 19 : 2, получаем деление числа 19 на число 2 и соответственно остаток от деления 19 на 2, но не от деления 190 на 20, действительно 19 : 2 = 9 ( 1 остаток). В этом случае 19 показывает, сколько десятков содержится в числе 190, поэтому остаток так же получаем в десятках, но не в единицах.
Анализируем 2-ое равенство 190 : 20 = 19 д. : 2 д. здесь мы делим десятки, поэтому остаток также будет в десятках 9 о чем сказано ранее), т, е. получаем 19 д. : 2 д. = 9 (1 д. остаток), проверкой убеждаемся в истинности деления 9 ∙ 2 д. + 1 д. = 19 д. = 190.
Предлагаем верные записи:
190 : 20 = 190 : 10 : 2 = 9 ( 1 д. остаток)
190 : 20 = 19 д. : 2 д. = 9 ( 1 д. остаток)
4700 : 500 = 4700 : 100 : 5 = 9 ( 2 с. остаток)
4700 : 500 = 47 с. : 5 с. = 9 ( 2 с. остаток).
В газете «Математика» предлагается уравнение и к нему ответ:1. Предложено решение уравнения по следующей схеме:
af(x)bg(x) = ap
bp
Приведенное решение неверное, так как приводит к потере корней. данное уравнение следует решать по схеме:
a f(x) b g(x) = a p
b p
a f(x)– р
b
q – g(x)
Вернемся к данном уравнению.
= 40
2 3
Заключение
Хотя проблемы формирования и развития рефлексивной деятельности в процессе обучения и поиск новых форм работы над математическими ошибками школьников и не являются абсолютно новыми, изучение такого аспекта, как использование рефлексивной деятельности учащихся при работе над типичными ошибками всегда актуальны. В данной работе рассмотрены некоторые типичные ошибки, допускаемые учащимися при изучении математики, их объяснение, меры их предупреждения. Хорошо организованная учителем работа учащихся над типичными ошибками посредством исследовательского приема приводит к улучшению результата обучению математики и развитию рядя показателей логического мышления. К тому же предмет «математика» настолько сложен, что даже методисты допускают ошибки.
Литература
- Далингер В. А. «Анализ типичных ошибок, допускаемых в курсе алгебры и начала анализа» «Математика в школе» 6-98
- 2-98 Ярский А. С, «Что делать с ошибками»
- Хэкало С. П. «Корни терять нельзя» 5-98
- Игнатенко В. З. «Сюрпризы биссектрисы» 5-98
Интернет-ресурсы
- http://mat.1september.ru/view_article.php?ID=200900304
- http://www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/1998/no38.htm
- http://www.ankolpakov.ru/2011/10/03/repetitor-po-matematike-o-durackix-oshibkax/
- http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r#ixzz2PJHLl9cJ
- http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r
Математическая ошибка
В математике определенные виды ошибочного доказательства часто показываются, и иногда собираются как иллюстрации понятия математической ошибки. Есть различие между простой ошибкой и математической ошибкой в доказательстве: ошибка в доказательстве приводит к недействительному доказательству просто таким же образом, но в самых известных примерах математических ошибок, есть некоторое укрывательство в представлении доказательства. Например, причиной, которую подводит законность, может быть деление на нуль, которое скрыто алгебраическим примечанием. Есть поразительное качество математической ошибки: как, как правило, представлено, это приводит не только к абсурдному результату, но и делает так лукавым или умным способом. Поэтому эти ошибки, по педагогическим причинам, обычно принимают форму поддельных доказательств очевидных противоречий. Хотя доказательства испорчены, ошибки, обычно дизайном, сравнительно тонкие, или разработанные, чтобы показать, что определенные шаги условны, и не должны быть применены в случаях, которые являются исключениями к правилам.
Традиционный способ представить математическую ошибку состоит в том, чтобы дать недействительный шаг вычитания, смешанного в с действительными шагами, так, чтобы значение ошибки здесь немного отличалось от логической ошибки. Последний обычно обращается к форме аргумента, который не является подлинным правилом логики, где проблематичный математический шаг, как правило — правильное правило, примененное с молчаливым неправильным предположением. Вне педагогики разрешение ошибки может привести к более глубокому пониманию предмета (такому как введение аксиомы Паша Евклидовой геометрии и пяти цветных теорем теории графов). Pseudaria, древняя потерянная книга ложных доказательств, приписан Евклиду.
Математические ошибки существуют во многих отраслях математики. В элементарной алгебре типичные примеры могут включить шаг, где деление на нуль выполнено, где корень неправильно извлечен или, более широко, где различные ценности многократной ценной функции равняются. Известные ошибки также существуют в элементарной Евклидовой геометрии и исчислении.
Howlers
Примеры существуют математически ‘правильных результатов, полученных неправильными цепями рассуждений. Такой аргумент, однако верный заключение, математически недействителен и обычно известен как ‘howler. Рассмотрите, например, вычисление (аномальная отмена):
:
Хотя заключение правильно, в среднем шаге есть ошибочная, недействительная отмена. Поддельные доказательства, вычисления или происхождения, построенные, чтобы привести к правильному результату несмотря на неправильную логику или операции, назвал howlers Максвелл. Вне области математики у термина «howler» есть различные значения, обычно менее определенные.
Деление на нуль
У
ошибки деления на нуль есть много вариантов.
Все числа равняются всем другим числам
Следующий пример использует деление на нуль, чтобы «доказать», что, но может быть изменен, чтобы доказать, что любое число равняется любому другому числу.
- Позвольте и будьте равными количествами отличными от нуля
- :
- Умножьтесь
- :
- Вычтите
- :
- Фактор обе стороны; левые факторы как различие квадратов, право — factored через свой самый большой общий делитель)
,
- :
- Отделите
- :
- Наблюдение этого
- :
- Объединитесь как условия слева
- :
- Разделитесь на отличный от нуля
- :
Q.E.D.
Ошибка в гармонии 5: прогрессия от линии 4, чтобы выровнять 5 вовлекает подразделение − b, который является нолем начиная с равняния b. Так как деление на нуль не определено, аргумент недействителен.
Многозначные функции
У
многих функций нет уникальной инверсии. Например, возведение в квадрат числа дает уникальную стоимость, но есть два возможных квадратных корня положительного числа. Квадратный корень многозначный. Одна стоимость может быть выбрана соглашением в качестве основной стоимости, в случае квадратного корня, неотрицательная стоимость — основная стоимость, но нет никакой гарантии, что функция квадратного корня, данная этой основной ценностью квадрата числа, будет равна оригинальному числу, например, квадратный корень квадрата −2 равняется 2.
Исчисление
Исчисление как математическое исследование бесконечно малого изменения и пределов может привести к математическим ошибкам, если свойства интегралов и дифференциалов проигнорированы. Например, наивное использование интеграции частями может использоваться, чтобы дать ложному доказательству тот 0 = 1. Позволяя и, мы можем написать:
:
после которого антипроизводные могут быть отменены, уступив 0 = 1. Проблема состоит в том, что антипроизводные только определены до константы и движущиеся их 1, или действительно любое число позволено. Ошибка действительно обнаруживается, когда мы вводим произвольные пределы интеграции a и b.
:
Так как различие между двумя ценностями постоянной функции исчезает, тот же самый определенный интеграл появляется с обеих сторон уравнения.
Власть и корень
Вовлечение ошибок, игнорируя правила элементарной арифметики через неправильную манипуляцию радикала. Для комплексных чисел неудача власти и тождеств логарифма привела ко многим ошибкам.
Положительные и отрицательные корни
Недействительные доказательства, использующие полномочия и корни часто, имеют следующий вид:
:
Ошибка — то, что правило вообще действительно, только если и x и y положительные (имея дело с действительными числами), который не имеет место здесь.
Хотя ошибка легко обнаружена здесь, иногда она скрыта эффективнее в примечании. Например, рассмотрите уравнение
:
который держится в результате теоремы Пифагора. Затем пуская квадратный корень,
:
так, чтобы
:
Но оценивая это, когда x = π подразумевает
:
или
:
который является неправильным.
Ошибка в каждом из этих примеров существенно заключается в том любое уравнение формы
:
имеет два решения, обеспечил ≠ 0,
:
и важно проверить, какое из этих решений относится к проблеме под рукой. В вышеупомянутой ошибке квадратный корень, который позволил второму уравнению быть выведенным сначала, действителен только когда, потому что x положительный. В частности когда x установлен в π, второе уравнение предоставлено инвалидом.
Другим примером этого вида ошибки, где ошибка немедленно обнаружима, является следующее недействительное доказательство это −2 = 2. Разрешение x = −2, и затем возведение в квадрат дает
:
после чего пущение квадратного корня подразумевает
:
так, чтобы x = −2 = 2, который абсурден. Ясно, когда квадратный корень был извлечен, это был отрицательный корень −2, а не положительный корень, который был важен для особого решения в проблеме.
Альтернативно, воображаемые корни запутываются в следующем:
:
Ошибка здесь находится в последнем равенстве, где мы игнорируем другие четвертые корни 1, которые являются −1, мной и −i (где я — воображаемая единица). Наблюдение, поскольку мы согласовали нашу фигуру и затем пустили корни, мы не можем всегда предполагать, что все корни будут правильны. Таким образом, правильные четвертые корни — я и −i, которые являются мнимыми числами, определенными, чтобы согласоваться к −1.
Сложные образцы
Когда число увеличено к сложной власти, результат уникально не определен (см. Неудачу власти и тождеств логарифма). Если эта собственность не признана, то ошибки, такие как следующее могут закончиться:
:
begin {выравнивают }
e^ {2 pi i} &= 1 \
(e^ {2 pi i}) ^ {я} &= 1^ {я} \
e^ {-2 pi} &= 1 \
end {выравнивают }
Ошибка здесь состоит в том, что правило умножающихся образцов, идя в третью линию не применяется неизмененный со сложными образцами, даже если, помещая обе стороны во власть только основная стоимость выбрана. Когда рассматривается как многозначные функции, обе стороны производят тот же самый набор ценностей, будучи.
Геометрия
Много математических ошибок в геометрии являются результатом использования в совокупном равенстве, включающем ориентированный на количества (такие векторы добавления вдоль данной линии или добавления ориентированных углов в самолете) действительная идентичность, но который исправления только абсолютная величина (один из) эти количества. Это количество тогда включено в уравнение с неправильной ориентацией, чтобы произвести абсурдное заключение. Эта неправильная ориентация обычно предлагается неявно, поставляя неточную диаграмму ситуации, где относительные положения пунктов или линий выбраны в пути, который фактически невозможен в соответствии с гипотезами аргумента, но неочевидно так. Такую ошибку легко выставить, рисуя точную картину ситуации, в которой некоторые относительные положения будут другой формой те в предоставленной диаграмме. Чтобы избежать таких ошибок, правильный геометрический аргумент, используя дополнение или вычитание расстояний, или углы должны всегда доказывать, что количества включаются с их правильной ориентацией.
Ошибка равнобедренного треугольника
Ошибка равнобедренного треугольника, от, подразумевает показывать, что каждый треугольник равнобедренный, означая, что две стороны треугольника подходящие. Эта ошибка была приписана Льюису Кэролу.
Учитывая треугольник △ABC, докажите что AB = AC:
- Чертите линию деля пополам ∠A
- Потяните перпендикулярную среднюю линию сегмента до н.э, который делит пополам до н.э в пункте D
- Позвольте этим двум линиям встретиться в пункте O.
- Потяните линию ИЛИ перпендикуляр к AB, перпендикуляр OQ линии к AC
- Потяните линии ОБЬ и OC
- НАУЧНЫМ РАБОТНИКОМ, △RAO ≅ △QAO (∠ORA = ∠OQA = 90; ∠RAO = ∠QAO; AO=AO (ОБЩАЯ СТОРОНА))
- RHS, △ROB ≅ △QOC
- Таким образом, AR = AQ, RB = королевский адвокат и AB = AR + RB = AQ + королевский адвокат = AC
Q.E.D.
Как заключение, можно показать, что все треугольники равносторонние, показывая что AB = до н.э и AC = до н.э таким же образом.
Ошибка в доказательстве — предположение в диаграмме, что пункт O в треугольнике. Фактически, O всегда находится в circumcircle △ABC (за исключением равнобедренных и равносторонних треугольников, где АО и ПЕРЕДОЗИРОВКА совпадают. Кроме того, можно показать, что, если AB будет более длинным, чем AC, то R ляжет в пределах AB, в то время как Q ляжет за пределами AC (и наоборот). (Любая диаграмма, оттянутая с достаточно точными инструментами, проверит вышеупомянутые два факта.) Из-за этого AB — все еще AR + RB, но AC — фактически AQ − королевский адвокат; и таким образом длины — не обязательно то же самое.
Доказательство индукцией
Там существуйте несколько ошибочных доказательств индукцией, в которой из компонентов, базисного случая или индуктивного шага, неправильный. Intuituvely, доказательства индукцией работают, утверждая, что, если заявление верно в одном случае, это верно в следующем случае, и следовательно неоднократно применяя это это, как могут показывать, верно для всех случаев. Это «доказательство» показывает, что все лошади — тот же самый цвет.
Давайте
- скажем, что любая группа лошадей N — весь тот же самый цвет.
- Если мы удаляем лошадь из группы, у нас есть группа N — 1 лошадь того же самого цвета. Если мы добавляем другую лошадь, у нас есть другая группа лошадей N. Нашим предыдущим предположением все лошади имеют то же самое, раскрашивают эту новую группу, так как это — группа лошадей N.
- Таким образом мы построили две группы лошадей N весь тот же самый цвет с N — 1 лошадь вместе. Так как у этих двух групп есть некоторые лошади вместе, эти две группы должны иметь тот же самый цвет друг как друг.
- Поэтому объединяя всех используемых лошадей, у нас есть группа N + 1 лошадь того же самого цвета.
- Таким образом, если какие-либо лошади N все одинаковые цвет, какой-либо N +, 1 лошадь — тот же самый цвет.
- Это ясно верно для N = 1 (т.е. одна лошадь — группа, где все лошади — тот же самый цвет). Таким образом, индукцией, N лошади тот же самый цвет для любого положительного целого числа, N. т.е. все лошади — тот же самый цвет.
Ошибка в этом доказательстве возникает в линии 3. Для N = 1, две группы лошадей имеют − 1 N = 0 лошадей вместе, и таким образом являются не обязательно тем же самым цветом друг как друг, таким образом, группа N + 1 = 2 лошади является не обязательно всем тем же самым цветом. Значение «Каждый лошади N имеют тот же самый цвет, тогда лошади N+1 имеют те же самые цветные» работы для любого N больше, чем один, но не верен когда N=1. Базисный случай правилен, но у шага индукции есть фундаментальный недостаток.
См. также
- Список неполных доказательств
- Парадокс
- Доказательство запугиванием
Примечания
- .
- .
- .
- .
Внешние ссылки
- Недействительные доказательства в Сокращении узла (включая литературные ссылки)
- Классические ошибки с некоторым обсуждением
- Больше недействительных доказательств от
AhaJokes.com
- Математические шутки включая недействительное доказательство

































