Какому распределению соответствует функция ошибки mae - Ремонт и установка крупной бытовой техники

From Wikipedia, the free encyclopedia

In statistics, mean absolute error (MAE) is a measure of errors between paired observations expressing the same phenomenon. Examples of Y versus X include comparisons of predicted versus observed, subsequent time versus initial time, and one technique of measurement versus an alternative technique of measurement. MAE is calculated as the sum of absolute errors divided by the sample size:^[1]

${displaystyle mathrm {MAE} ={frac {sum _{i=1}^{n}left|y_{i}-x_{i}right|}{n}}={frac {sum _{i=1}^{n}left|e_{i}right|}{n}}.}$

It is thus an arithmetic average of the absolute errors ${displaystyle |e_{i}|=|y_{i}-x_{i}|}$ , where $y_{i}$ is the prediction and $x_{i}$ the true value. Note that alternative formulations may include relative frequencies as weight factors. The mean absolute error uses the same scale as the data being measured. This is known as a scale-dependent accuracy measure and therefore cannot be used to make comparisons between series using different scales.^[2] The mean absolute error is a common measure of forecast error in time series analysis,^[3] sometimes used in confusion with the more standard definition of mean absolute deviation. The same confusion exists more generally.

Quantity disagreement and allocation disagreement[edit]

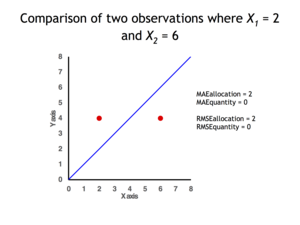
2 data points for which Quantity Disagreement is 0 and Allocation Disagreement is 2 for both MAE and RMSE

It is possible to express MAE as the sum of two components: Quantity Disagreement and Allocation Disagreement. Quantity Disagreement is the absolute value of the Mean Error given by:^[4]

${displaystyle mathrm {ME} ={frac {sum _{i=1}^{n}y_{i}-x_{i}}{n}}.}$

Allocation Disagreement is MAE minus Quantity Disagreement.

It is also possible to identify the types of difference by looking at an $(x,y)$ plot. Quantity difference exists when the average of the X values does not equal the average of the Y values. Allocation difference exists if and only if points reside on both sides of the identity line.^[4]^[5]

[edit]

The mean absolute error is one of a number of ways of comparing forecasts with their eventual outcomes. Well-established alternatives are the mean absolute scaled error (MASE) and the mean squared error. These all summarize performance in ways that disregard the direction of over- or under- prediction; a measure that does place emphasis on this is the mean signed difference.

Where a prediction model is to be fitted using a selected performance measure, in the sense that the least squares approach is related to the mean squared error, the equivalent for mean absolute error is least absolute deviations.

MAE is not identical to root-mean square error (RMSE), although some researchers report and interpret it that way. MAE is conceptually simpler and also easier to interpret than RMSE: it is simply the average absolute vertical or horizontal distance between each point in a scatter plot and the Y=X line. In other words, MAE is the average absolute difference between X and Y. Furthermore, each error contributes to MAE in proportion to the absolute value of the error. This is in contrast to RMSE which involves squaring the differences, so that a few large differences will increase the RMSE to a greater degree than the MAE.^[4] See the example above for an illustration of these differences.

Optimality property[edit]

The mean absolute error of a real variable c with respect to the random variable X is

${displaystyle E(left|X-cright|)}$

Provided that the probability distribution of X is such that the above expectation exists, then m is a median of X if and only if m is a minimizer of the mean absolute error with respect to X.^[6] In particular, m is a sample median if and only if m minimizes the arithmetic mean of the absolute deviations.^[7]

More generally, a median is defined as a minimum of

${displaystyle E(|X-c|-|X|),}$

as discussed at Multivariate median (and specifically at Spatial median).

This optimization-based definition of the median is useful in statistical data-analysis, for example, in k-medians clustering.

Proof of optimality[edit]

Statement: The classifier minimising ${displaystyle mathbb {E} |y-{hat {y}}|}$ is ${displaystyle {hat {f}}(x)={text{Median}}(y|X=x)}$ .

Proof:

The Loss functions for classification is

${displaystyle {begin{aligned}L&=mathbb {E} [|y-a||X=x]&=int _{-infty }^{infty }|y-a|f_{Y|X}(y),dy&=int _{-infty }^{a}(a-y)f_{Y|X}(y),dy+int _{a}^{infty }(y-a)f_{Y|X}(y),dyend{aligned}}}$

Differentiating with respect to a gives

${displaystyle {frac {partial }{partial a}}L=int _{-infty }^{a}f_{Y|X}(y),dy+int _{a}^{infty }-f_{Y|X}(y),dy=0}$

This means

${displaystyle int _{-infty }^{a}f(y),dy=int _{a}^{infty }f(y),dy}$

Hence

${displaystyle F_{Y|X}(a)=0.5}$

References[edit]

^ Willmott, Cort J.; Matsuura, Kenji (December 19, 2005). «Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance». Climate Research. 30: 79–82. doi:10.3354/cr030079.
^ «2.5 Evaluating forecast accuracy | OTexts». www.otexts.org. Retrieved 2016-05-18.
^ Hyndman, R. and Koehler A. (2005). «Another look at measures of forecast accuracy» [1]
^ ^a ^b ^c Pontius Jr., Robert Gilmore; Thontteh, Olufunmilayo; Chen, Hao (2008). «Components of information for multiple resolution comparison between maps that share a real variable». Environmental and Ecological Statistics. 15 (2): 111–142. doi:10.1007/s10651-007-0043-y. S2CID 21427573.
^ Willmott, C. J.; Matsuura, K. (January 2006). «On the use of dimensioned measures of error to evaluate the performance of spatial interpolators». International Journal of Geographical Information Science. 20: 89–102. doi:10.1080/13658810500286976. S2CID 15407960.
^ Stroock, Daniel (2011). Probability Theory. Cambridge University Press. pp. 43. ISBN 978-0-521-13250-3.
^ Nicolas, André (2012-02-25). «The Median Minimizes the Sum of Absolute Deviations (The $ {L}_{1} $ Norm)». StackExchange.

From Wikipedia, the free encyclopedia

${displaystyle mathrm {MAE} ={frac {sum _{i=1}^{n}left|y_{i}-x_{i}right|}{n}}={frac {sum _{i=1}^{n}left|e_{i}right|}{n}}.}$

Quantity disagreement and allocation disagreement[edit]

2 data points for which Quantity Disagreement is 0 and Allocation Disagreement is 2 for both MAE and RMSE

It is possible to express MAE as the sum of two components: Quantity Disagreement and Allocation Disagreement. Quantity Disagreement is the absolute value of the Mean Error given by:^[4]

${displaystyle mathrm {ME} ={frac {sum _{i=1}^{n}y_{i}-x_{i}}{n}}.}$

Allocation Disagreement is MAE minus Quantity Disagreement.

[edit]

Optimality property[edit]

The mean absolute error of a real variable c with respect to the random variable X is

${displaystyle E(left|X-cright|)}$

More generally, a median is defined as a minimum of

${displaystyle E(|X-c|-|X|),}$

as discussed at Multivariate median (and specifically at Spatial median).

This optimization-based definition of the median is useful in statistical data-analysis, for example, in k-medians clustering.

Proof of optimality[edit]

Statement: The classifier minimising ${displaystyle mathbb {E} |y-{hat {y}}|}$ is ${displaystyle {hat {f}}(x)={text{Median}}(y|X=x)}$ .

Proof:

The Loss functions for classification is

${displaystyle {begin{aligned}L&=mathbb {E} [|y-a||X=x]&=int _{-infty }^{infty }|y-a|f_{Y|X}(y),dy&=int _{-infty }^{a}(a-y)f_{Y|X}(y),dy+int _{a}^{infty }(y-a)f_{Y|X}(y),dyend{aligned}}}$

Differentiating with respect to a gives

${displaystyle {frac {partial }{partial a}}L=int _{-infty }^{a}f_{Y|X}(y),dy+int _{a}^{infty }-f_{Y|X}(y),dy=0}$

This means

${displaystyle int _{-infty }^{a}f(y),dy=int _{a}^{infty }f(y),dy}$

Hence

${displaystyle F_{Y|X}(a)=0.5}$

References[edit]

^ Willmott, Cort J.; Matsuura, Kenji (December 19, 2005). «Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance». Climate Research. 30: 79–82. doi:10.3354/cr030079.
^ «2.5 Evaluating forecast accuracy | OTexts». www.otexts.org. Retrieved 2016-05-18.
^ Hyndman, R. and Koehler A. (2005). «Another look at measures of forecast accuracy» [1]
^ ^a ^b ^c Pontius Jr., Robert Gilmore; Thontteh, Olufunmilayo; Chen, Hao (2008). «Components of information for multiple resolution comparison between maps that share a real variable». Environmental and Ecological Statistics. 15 (2): 111–142. doi:10.1007/s10651-007-0043-y. S2CID 21427573.
^ Willmott, C. J.; Matsuura, K. (January 2006). «On the use of dimensioned measures of error to evaluate the performance of spatial interpolators». International Journal of Geographical Information Science. 20: 89–102. doi:10.1080/13658810500286976. S2CID 15407960.
^ Stroock, Daniel (2011). Probability Theory. Cambridge University Press. pp. 43. ISBN 978-0-521-13250-3.
^ Nicolas, André (2012-02-25). «The Median Minimizes the Sum of Absolute Deviations (The $ {L}_{1} $ Norm)». StackExchange.

Перевод

Ссылка на автора

Каждая модель машинного обучения пытается решить проблему с другой целью, используя свой набор данных, и, следовательно, важно понять контекст, прежде чем выбрать метрику. Обычно ответы на следующий вопрос помогают нам выбрать подходящий показатель:

Тип задачи: регрессия? Классификация?
Бизнес цель?
Каково распределение целевой переменной?

Ну, в этом посте я буду обсуждать полезность каждой метрики ошибки в зависимости от цели и проблемы, которую мы пытаемся решить. Часть 1 фокусируется только на показателях оценки регрессии.

Остров Андрос в Греции

Метрики регрессии

Средняя квадратическая ошибка (MSE)
Среднеквадратическая ошибка (RMSE)
Средняя абсолютная ошибка (MAE)
R в квадрате (R²)
Скорректированный R квадрат (R²)
Среднеквадратичная ошибка в процентах (MSPE)
Средняя абсолютная ошибка в процентах (MAPE)
Среднеквадратичная логарифмическая ошибка (RMSLE)

Средняя квадратическая ошибка (MSE)

Это, пожалуй, самый простой и распространенный показатель для оценки регрессии, но, вероятно, наименее полезный. Определяется уравнением

гдеyᵢфактический ожидаемый результат иŷᵢэто прогноз модели.

MSE в основном измеряет среднеквадратичную ошибку наших прогнозов. Для каждой точки вычисляется квадратная разница между прогнозами и целью, а затем усредняются эти значения.

Чем выше это значение, тем хуже модель. Он никогда не бывает отрицательным, поскольку мы возводим в квадрат отдельные ошибки прогнозирования, прежде чем их суммировать, но для идеальной модели это будет ноль.

Преимущество:Полезно, если у нас есть неожиданные значения, о которых мы должны заботиться. Очень высокое или низкое значение, на которое мы должны обратить внимание.

Недостаток:Если мы сделаем один очень плохой прогноз, возведение в квадрат сделает ошибку еще хуже, и это может исказить метрику в сторону переоценки плохости модели. Это особенно проблематичное поведение, если у нас есть зашумленные данные (то есть данные, которые по какой-либо причине не совсем надежны) — даже в «идеальной» модели может быть высокий MSE в этой ситуации, поэтому становится трудно судить, насколько хорошо модель выполняет. С другой стороны, если все ошибки малы или, скорее, меньше 1, то ощущается противоположный эффект: мы можем недооценивать недостатки модели.

Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсреднее значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.

Среднеквадратическая ошибка (RMSE)

RMSE — это просто квадратный корень из MSE. Квадратный корень введен, чтобы масштаб ошибок был таким же, как масштаб целей.

Теперь очень важно понять, в каком смысле RMSE похож на MSE, и в чем разница.

Во-первых, они похожи с точки зрения их минимизаторов, каждый минимизатор MSE также является минимизатором для RMSE и наоборот, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора предсказаний, A и B, и скажем, что MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. И это также работает в противоположном направлении. ,

Что это значит для нас?

Это означает, что, если целевым показателем является RMSE, мы все равно можем сравнивать наши модели, используя MSE, поскольку MSE упорядочит модели так же, как RMSE. Таким образом, мы можем оптимизировать MSE вместо RMSE.

На самом деле, с MSE работать немного проще, поэтому все используют MSE вместо RMSE. Также есть небольшая разница между этими двумя моделями на основе градиента.

Градиент СКО относительно i-го прогноза

Это означает, что путешествие по градиенту MSE эквивалентно путешествию по градиенту RMSE, но с другой скоростью потока, и скорость потока зависит от самой оценки MSE.

Таким образом, хотя RMSE и MSE действительно схожи с точки зрения оценки моделей, они не могут быть сразу взаимозаменяемыми для методов на основе градиента. Возможно, нам нужно будет настроить некоторые параметры, такие как скорость обучения.

В MAE ошибка рассчитывается как среднее абсолютных разностей между целевыми значениями и прогнозами. MAE — это линейная оценка, которая означает, чтовсе индивидуальные различия взвешены одинаковов среднем. Например, разница между 10 и 0 будет вдвое больше разницы между 5 и 0. Однако то же самое не верно для RMSE. Математически он рассчитывается по следующей формуле:

Что важно в этой метрике, так это то, что онанаказывает огромные ошибки, которые не так плохо, как MSE.Таким образом, он не так чувствителен к выбросам, как среднеквадратическая ошибка.

MAE широко используется в финансах, где ошибка в 10 долларов обычно в два раза хуже, чем ошибка в 5 долларов. С другой стороны, метрика MSE считает, что ошибка в 10 долларов в четыре раза хуже, чем ошибка в 5 долларов. MAE легче обосновать, чем RMSE.

Еще одна важная вещь в MAE — это его градиенты относительно прогнозов. Gradiend — это пошаговая функция, которая принимает -1, когда Y_hat меньше цели, и +1, когда она больше.

Теперь градиент не определен, когда предсказание является совершенным, потому что, когда Y_hat равен Y, мы не можем оценить градиент. Это не определено.

Таким образом, формально, MAE не дифференцируемо, но на самом деле, как часто ваши прогнозы точно измеряют цель. Даже если они это сделают, мы можем написать простое условие IF и вернуть ноль, если это так, и через градиент в противном случае. Также известно, что вторая производная везде нулевая и не определена в нулевой точке.

Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсрединное значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.

R в квадрате (R²)

А что если я скажу вам, что MSE для моих моделей предсказаний составляет 32? Должен ли я улучшить свою модель или она достаточно хороша? Или что, если мой MSE был 0,4? На самом деле, трудно понять, хороша наша модель или нет, посмотрев на абсолютные значения MSE или RMSE. Мы, вероятно, захотим измерить, как Во многом наша модель лучше, чем постоянная базовая линия.

Коэффициент детерминации, или R² (иногда читаемый как R-два), является еще одним показателем, который мы можем использовать для оценки модели, и он тесно связан с MSE, но имеет преимущество в том, чтобезмасштабное— не имеет значения, являются ли выходные значения очень большими или очень маленькими,R² всегда будет между -∞ и 1.

Когда R² отрицательно, это означает, что модель хуже, чем предсказание среднего значения.

MSE модели рассчитывается, как указано выше, в то время как MSE базовой линии определяется как:

гдеYс чертой означает среднее из наблюдаемогоyᵢ.

Чтобы сделать это более ясным, этот базовый MSE можно рассматривать как MSE, чтопростейшиймодель получит. Простейшей возможной моделью было бывсегдапредсказать среднее по всем выборкам. Значение, близкое к 1, указывает на модель с ошибкой, близкой к нулю, а значение, близкое к нулю, указывает на модель, очень близкую к базовой линии.

В заключение, R² — это соотношение между тем, насколько хороша наша модель, и тем, насколько хороша модель наивного среднего.

Распространенное заблуждение:Многие статьи в Интернете утверждают, что диапазон R² лежит между 0 и 1, что на самом деле не соответствует действительности. Максимальное значение R² равно 1, но минимальное может быть минус бесконечность.

Например, рассмотрим действительно дрянную модель, предсказывающую крайне отрицательное значение для всех наблюдений, даже если y_actual положительно. В этом случае R² будет меньше 0. Это крайне маловероятный сценарий, но возможность все еще существует.

MAE против MSE

Я заявил, что MAE более устойчив (менее чувствителен к выбросам), чем MSE, но это не значит, что всегда лучше использовать MAE. Следующие вопросы помогут вам решить:

Взять домой сообщение

В этой статье мы обсудили несколько важных метрик регрессии. Сначала мы обсудили среднеквадратичную ошибку и поняли, что наилучшей константой для нее является среднее целевое значение. Среднеквадратичная ошибка и R² очень похожи на MSE с точки зрения оптимизации. Затем мы обсудили среднюю абсолютную ошибку и когда люди предпочитают использовать MAE вместо MSE.

Спасибо за чтение, и я с нетерпением жду, чтобы услышать ваши вопросы Наслаждайтесь!

P.SСледите за моей следующей статьей, которая изучает другие более продвинутые метрики регрессии. Если вы хотите больше узнать о мире машинного обучения, вы также можете подписаться на меня в Instagram, напишите мне напрямую или найди меня на linkedin, Я хотел бы услышать от вас.

Ресурсы:
[1] https://dmitryulyanov.github.io/about

17 авг. 2022 г.
читать 3 мин

Модели регрессии используются для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .

Всякий раз, когда мы подбираем регрессионную модель, мы хотим понять, насколько хорошо модель может использовать значения переменных-предикторов для прогнозирования значения переменной отклика.

Две метрики, которые мы часто используем для количественной оценки того, насколько хорошо модель соответствует набору данных, — это средняя абсолютная ошибка (MAE) и среднеквадратическая ошибка (RMSE), которые рассчитываются следующим образом:

MAE : метрика, которая сообщает нам среднюю абсолютную разницу между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже MAE, тем лучше модель соответствует набору данных.

MAE = 1/n * Σ|y i – ŷ i |

куда:

Σ — это символ, который означает «сумма»
y i — наблюдаемое значение для i -го наблюдения
ŷ i — прогнозируемое значение для i -го наблюдения
n — размер выборки

RMSE : метрика, которая сообщает нам квадратный корень из средней квадратичной разницы между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже RMSE, тем лучше модель соответствует набору данных.

Он рассчитывается как:

СКО = √ Σ(y i – ŷ i ) 2 / n

куда:

Σ — это символ, который означает «сумма»
ŷ i — прогнозируемое значение для i -го наблюдения
y i — наблюдаемое значение для i -го наблюдения
n — размер выборки

Пример: Расчет RMSE и MAE

Предположим, мы используем регрессионную модель, чтобы предсказать количество очков, которое 10 игроков наберут в баскетбольном матче.

В следующей таблице показаны прогнозируемые очки по модели и фактические очки, набранные игроками:

Используя калькулятор MAE , мы можем рассчитать MAE как 3,2.

Это говорит нам о том, что средняя абсолютная разница между прогнозируемыми значениями модели и фактическими значениями составляет 3,2.

Используя Калькулятор RMSE , мы можем рассчитать RMSE, чтобы он был равен 4 .

Это говорит нам о том, что квадратный корень из среднеквадратичной разницы между предсказанными набранными очками и фактическими набранными очками равен 4.

Обратите внимание, что каждая метрика дает нам представление о типичной разнице между прогнозируемым значением, сделанным моделью, и фактическим значением в наборе данных, но интерпретация каждой метрики немного отличается.

RMSE против MAE: какую метрику следует использовать?

Если вы хотите придать больший вес наблюдениям, которые находятся дальше от среднего (т. е. если «отклонение» на 20 более чем в два раза хуже, чем отклонение на 10 дюймов), то лучше использовать RMSE для измерения ошибки, потому что RMSE более чувствителен к наблюдениям, которые далеки от среднего.

Однако, если «выключиться» в 20 раз хуже, чем в 10, то лучше использовать MAE.

Чтобы проиллюстрировать это, предположим, что у нас есть один игрок, который явно отличается по количеству набранных очков:

Используя онлайн-калькуляторы, упомянутые ранее, мы можем рассчитать MAE и RMSE следующим образом:

МАЭ : 8
Среднеквадратичное значение : 16,4356

Обратите внимание, что RMSE увеличивается намного больше, чем MAE.

Это связано с тем, что в формуле RMSE используются квадраты разницы, а квадрат разницы между наблюдаемым значением 76 и прогнозируемым значением 22 довольно велик. Это приводит к значительному увеличению значения RMSE.

На практике мы обычно подгоняем несколько моделей регрессии к набору данных и вычисляем только одну из этих метрик для каждой модели.

Например, мы можем подобрать три разные регрессионные модели и рассчитать RMSE для каждой модели. Затем мы выберем модель с самым низким значением RMSE в качестве «лучшей» модели, потому что именно она делает прогнозы, наиболее близкие к фактическим значениям из набора данных.

В любом случае просто убедитесь, что вы вычисляете одну и ту же метрику для каждой модели. Например, не рассчитывайте MAE для одной модели и RMSE для другой модели, а затем сравнивайте эти две метрики.

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать MAE с помощью различных статистических программ:

Как рассчитать среднюю абсолютную ошибку в Excel
Как рассчитать среднюю абсолютную ошибку в R
Как рассчитать среднюю абсолютную ошибку в Python

В следующих руководствах объясняется, как рассчитать RMSE с помощью различных статистических программ:

Как рассчитать среднеквадратичную ошибку в Excel
Как рассчитать среднеквадратичную ошибку в R
Как рассчитать среднеквадратичную ошибку в Python

Вот мы проанализировали данные, вот мы сгладили временной ряд, выявили связи между переменными и решили построить некоторую математическую прогнозную модель. Давайте допустим, что мы пока решили ограничиться какой-нибудь простой моделью парной регрессии, например, такой вот:

begin{equation} label{eq:estim_linreg}
y_t = a + b x_t + e_t ,
end{equation}

где (y_t) — объём продаж мороженого, (x_t) — температура воздуха, а (e_t) — случайная ошибка модели.

Вроде бы ничего особенного и ничего сложного, но откуда же нам взять коэффициенты (a) и (b)? Надо их как-то рассчитать (или, как это говорят в статистике, «оценить»). Для этого существует множество различных методов, но все они преследуют одну и ту же цель — оптимизировать какую-нибудь функцию (минимизировать или максимизировать) путём подбора этих самых значений (a) и (b). По сути вся задача сводится к тому, чтобы провести некоторым образом линию через «облако» значений (x) и (y) так, чтобы минимизировать целевую функцию. На рисунке ниже показан пример такого облака и нескольких линий, проходящих через него.

Мороженое и палочки

Каждая из линий на рисунке соответствует одной и той же линейной функции eqref{eq:estim_linreg}, но с разными коэффициентами. Фактически любая такая линия — это последовательность некоторых расчётных значений (hat{y}_t), позволяющая оценить, какими будут продажи мороженного в среднем если температура будет принимать значения (x_t) (отложенные по оси абсцисс). Очевидно, что таких прямых на плоскости можно провести сколько угодно, и каждая из них будет минимизировать либо максимизировать какой-нибудь свой критерий. Обычно это происходит путём подбора коэффициентов с использованием различных оптимизационных методов, путём решения задач программирования (линейного, нелинейного, целочисленного) либо с использованием эвристических методов (генетические и эволюционные алгоритмы). В достаточно редких случаях для расчёта коэффициентов в нашем распоряжении могут быть формулы, гарантирующие получения оптимума (такие формулы даёт, например, Метод Наименьших Квадратов, который мы обсудим в главе про регрессии).

Очевидно, что рассмотреть все возможные целевые функции в рамках одной статьи невозможно, да и не имеет никакого смысла. Чаще всего нас интересует минимальное расстояние между точками и линиями, которое, очевидно, можно оценить по-разному.

Рассмотрим подробней самые простые и популярные в прогнозировании методы оценки коэффициентов моделей.

Но вначале R!

Прежде чем двигаться дальше, создадим в R две переменные, с которыми мы будем далее работать:

x <- rnorm(100,100,15)
y <- rep(NA,100)
y[1:95] <- 50 + 0.9 * x[1:95] + rnorm(95,0,5)
y[96:100] <- 190 + 0.2 * x[96:100] + rnorm(5,0,2)

data <- as.data.frame(matrix(NA,100,2))
colnames(data) <- c("x","y")
data[,1] <- x
data[,2] <- y

C <- rep(NA,2)

Первой строкой мы создаём нормально распределённую величину, состоящую из 100 наблюдений. Второй строкой мы создаём вторую переменную, состоящую из значений «NA» — «Np (то есть никак не заданных). Третьей и четвёртой строками мы заполняем вторую переменную так, что первые 95 наблюдений сгенерированы исходя из одной зависимости от x, а последние 5 — исходя из другой. Следующими четырьмя строками мы создаём из этих двух переменных объект с данными. Строкой за ними мы создаём вектор остатков. Пока что он пустой. Последней строкой мы создаём вектор для двух коэффициентов нашей будущей модели. Они тоже пока пустые.

MSE

MSE расшифровывается как «Mean Squared Error» и переводится как «Средняя квадратическая ошибка». Суть метода заключается по сути в том, чтобы минимизировать сумму квадратов отклонений фактических значений от расчётных (SSE — «Sum of Squared Errors»). Если полученную сумму разделить на число наблюдений, то получится та самая MSE. Формула целевой функции в этом случае выглядит следующим образом:

begin{equation} label{eq:estim_MSE}
MSE = frac{1}{T} sum_{t=1}^T e_t^2 = frac{1}{T} sum_{t=1}^T (y_t -hat{y}_t)^2 .
end{equation}

Если бы в формуле eqref{eq:estim_MSE} не было квадрата, то положительные и отрицательные отклонения друг друга погашали, из-за чего минимизировалось бы не расстояние между фактическими и расчётными значениями, а чёрт знает что. То есть наличие квадратов позволяет получить некоторую оценку расстояния от фактических значений до линии (расчётных значений).

Стоит отметить, что, как мы помним из «Статистического анализа», возведение в квадрат существенно увеличивает те значения, которые лежат далеко от всех остальных. Например, если продажи мороженого колеблются в основном в районе ста штук, но есть наблюдение в 200, то это наблюдение будет тянуть на себя одеяло — влиять существенно на оценки коэффициентов. То есть MSE является не робастной величиной и вообще позволяет получить некоторую среднюю оценку (в среднем фактическое значение (y_t) будет соответствовать (hat{y}_t) при данном значении (x_t)).

В случае с регрессиями использование MSE соответствует расчёту коэффициентов методом наименьших квадратов, к которому мы обратимся позже.

И ещё R!

Напишем в R простую функцию, которая позволит нам оценивать коэффициенты парной регрессии. Назовём её «CF» — «Cost Function»:

CF <- function(C){
  residuals <- data[,2] - (C[1] + C[2] * data[,1])
  return(mean(residuals^2))
}

Самой первой строкой мы определяем, что «CF» это объект типа «функция». Далее мы указываем, как рассчитать остатки модели: это фактические значения (второй столбец наших данных) минус расчётные, полученные по формуле eqref{eq:estim_linreg} (здесь (C[1] = a text{, } C[2] = b text{, } data[,1] = x)). Третьей строкой мы определяем нашу целевую функцию. В данном случае это средняя, взятая по остаткам, возведённым в квадрат (MSE).

Теперь проведём оптимизацию и запишем полученные коэффициенты:

result <- nlminb(c(1,1),CF)
C <- result$par

Функция «nlminb» позволяет подбирать оптимальные параметры путём минимизации некой функции. c(1,1) в данном случае задаёт функции вектор стартовых параметров для поиска. Вместо этих значений можно было бы задать и что-нибудь другое. Второй строкой мы записываем найденные параметры в наш вектор C.

Построим теперь точечную диаграмму по ряду данных и проведём на том же графике полученную линию:

plot(data)
abline(a=C[1], b=C[2], col="red")

С первой функцией мы уже сталкивались ранее, а вот со второй — пока нет. Она позволяет провести прямую линию с заданными параметрами на уже имеющемся графике. a и b соответствуют тем самым коэффициентам той самой функции eqref{eq:estim_linreg}.

MAE

MAE расшифровывается как «Mean Absolute Error», что с зарубежного на отечественный переводится как «Средняя абсолютная ошибка». Рассчитывается она так:

begin{equation} label{eq:estim_MAE}
MAE = frac{1}{T} sum_{t=1}^T |e_t| = frac{1}{T} sum_{t=1}^T |y_t -hat{y}_t| .
end{equation}

Модули в формуле eqref{eq:estim_MAE} всё так же позволяют избавиться от знаков и получить некоторую оценку расстояния от фактических до расчётных значений, которое нужно будет потом минимизировать. Несомненным преимуществом MAE является то, что модули не увеличивают в разы отклонения, считающиеся выбросами. Поэтому эта оценка является более робастной, чем MSE и фактически соответствует медиане (в 50% случаев при данном значении (x_t) зависимая величина (y_t) будет не меньше полученной (hat{y}_t)).

Разница между оценками коэффициентов, полученными при использовании MSE и MAE, наглядно показана на следующем рисунке:

Модели, оценённые с использованием MSE и MAE.

Из-за наличия аномального объёма продаж мороженного при 40 градусах по цельсию, красная линия (соответствующая регрессии, оценённой с помощью MSE) задирается и хуже описывает все остальные нормальные значения. Синяя же линия (соответствующая MAE) демонстрирует больше адекватности, так как в значительно меньшей степени реагирует на творящееся во время такой дикой жары безобразие на улицах города.

А теперь то же самое, только в R!

В R для получения оценок с помощью этого критерия нам достаточно изменить критерий в нашей функции «CF»:

CF <- function(C){
  residuals <- data[,2] - (C[1] + C[2] * data[,1])
  return(mean(abs(residuals)))
}

Теперь функция возвращает средние абсолютные ошибки (функция «abs» возвращает значения по модулю), а не квадратические.

Ещё раз проведём оптимизацию, запишем коэффициенты и построим график:

result <- nlminb(c(1,1),CF)
C <- result$par

abline(a=C[1], b=C[2], col="blue")

Если вы проделали всё это, то теперь можете сравнить полученные линии в случае с MSE и в случае с MAE. Здесь я специально опустил функцию «plot» для того, чтобы новая линия для наглядности была нанесена на тот же график.

Квантильные оценки

Прозорливые читатели уже, наверно, догадались, что помимо получения средней и медианной величин, можно так же получить и квантильные. В статистическом анализе регрессии, оценённые таким методом, называются «квантильными регрессиями».

Целевая функция, соответствующая таким квантильным оценкам, имеет вид:

begin{equation} label{eq:estim_Quantiles}
CF_alpha = (1 — alpha) sum_{y_t < hat{y}_t } |e_t| + alpha sum_{y_t geq hat{y}_t } |e_t| .
end{equation}
где (alpha) — это выбранная частота для квантиля (см. «Статистический анализ»), которая в данном случае выступает в роли веса, задаваемому тем или иным суммам. Если (alpha>0.5), то вторая сумма в правой части eqref{eq:estim_Quantiles}, соответствующая ситуации, когда фактические значения оказываются больше расчётных, будет получать больший вес. Первая же сумма (в которой все фактические значения меньше расчётных) получит меньший вес. Минимизируя такую сумму мы фактически сдвинем расчётные значения вправо — так, чтобы вторая сумма была как можно меньше. В полученных ошибках модели это будет соответствовать заданному квантилю (alpha).

Условие (y_t < hat{y}_t) может быть заменено на (e_t < 0), так как остатки модели связаны с фактическими и расчётными значениями уравнением: (e_t = y_t — hat{y}_t).

Для того, чтобы лучше понять, что происходит, когда мы используем такую функцию, рассмотрим пример с (alpha=0.5). В этом случае формула eqref{eq:estim_Quantiles} будет преобразована в:

begin{equation} label{eq:estim_Quantilesexample_1}
CF_{0.5} = 0.5 sum_{y_t < hat{y}_t } |e_t| + 0.5 sum_{y_t geq hat{y}_t } |e_t| .
end{equation}
Получается, что суммы имеют одинаковый вес, а значит данная формула может быть легко заменена на следующую:
begin{equation} label{eq:estim_Quantilesexample_2}
CF_{0.5} = sum_{t=1}^T |e_t| .
end{equation}
Минимизация функции eqref{eq:estim_Quantilesexample_2}, как легко заметить, соответствует минимизации MAE eqref{eq:estim_MAE}. Просто в MAE мы ещё и делим полученную сумму на число наблюдений, что никак на оценки во время оптимизации не влияет.

В результате использования метода квантильных оценок полученная линия регрессии пройдёт не по середине облака, а выше или ниже него, в зависимости от выбранного значения частоты квантиля (alpha). Использование этого критерия при оценке функций в прогнозировании может быть полезным, например, для построения прогнозных интервалов.

Единственная проблема метода — это сложность его использования в случае малого количества наблюдений в выборке. Действительно, нет никакой возможности однозначно определить, например, 2,5% эмпирический квантиль, если в твоём распоряжении 10 наблюдений, потому что в этой малой выборке ниже этого квантиля будет лежать только ( 10 cdot 0.025 = 0.25 ) наблюдений. Для того, чтобы методом можно было воспользоваться, в распоряжении исследователя должно быть хотя бы (frac{1}{alpha}) наблюдений, где (alpha) соответствует левому хвосту распределения (для нашего примера это ( frac{1}{0.025} = 40 )).

И опять R!

Модифицируем в R нашу многострадальную функцию «CF» следующим образом:

CF <- function(C){
  residuals <- data[,2] - (C[1] + C[2] * data[,1])
  return((1-alpha) * sum(abs(residuals[residuals<0])) +
            alpha * sum(abs(residuals[residuals>=0])))
}

В возвращении функции у нас теперь есть параметра `alpha`, который мы будем задавать в общем окружении программы чуть позже. Часть `residuals[residuals<0]` — это те остатки модели, которые оказались отрицательными.

Для примера зададим (alpha=0.05), проведём оптимизацию и построим полученную модель на том же графике, что и раньше:

alpha <- 0.05
result <- nlminb(c(1,1),CF)
C <- result$par

abline(a=C[1], b=C[2], col="darkgreen")

Теперь для полноты картины задайте (alpha=0.95) и проделайте всё то же самое с оптимизацией и построением графика:

alpha <- 0.95

В результате всего этого на ваш график должно быть добавлено две тёмно-зелёные линии, соответствующие 5% и 95% квантилям.

На следующем рисунке изображены линии, соответствующие моделям, оценённым MSE, MAE и 5% и 95% квантилям.

Модели, построенные с помощью MSE, MAE и квантильных оценок

Функция правдоподобия

Все перечисленные выше методы хороши, но сами по себе не имеют этакого статистического обоснования: мы понимаем, как себя будет вести полученная функция, как примерно она пройдёт через наши фактические значения, понимаем, чего можно ожидать в будущем, но мы не можем особо ничего сказать о том, какими будут оценки коэффициентов моделей со статистической точки зрения. Будут ли они получены случайно? Будут ли они стремиться к каким-то значениям, если мы построим модель по другой выборке из тех же данных? А как же быть, если перед нами несколько моделей, описывающих одни и те же данные по-разному? Например, несколько моделей экспоненциального сглаживания, из которых нужно выбрать одну. Или ряд регрессионных моделей… Какой же из них отдать предпочтение и как?

Для ответа на некоторые / все из этих вопросов, нужно обратиться к математической функции под названием «функция правдоподобия» (за бугром эту функцию называют «Likelihood function»). Но сначала нужно немного вспомнить теорию вероятностей. Не переживайте, много вспоминать не придётся. Нужно совсем чуть-чуть.

Итак, предположим, что мы всё ещё имеем дело с мороженным (тем более, что же может быть лучше мороженого? Разве только два мороженых!). В четверг мы замерили уровень продаж и увидели, что он составил 78.5 штук. Любой другой человек просто плюнул бы и продолжил работать дальше. Но пытливому уму статистика может стать интересно, какова вероятность получить такое значение либо значение, лежащее в некоторой области (скажем, от 70 до 80 штук) в случае, если мы предполагаем, что процесс продаж описывается некоторой математической функцией с заданными параметрами (например, простой парной регрессией eqref{eq:estim_linreg}). Такая вероятность называется условной — то есть вероятность получить определённое значение при выполнении некоторого ряда условий — и записать её математически можно так:

begin{equation} label{eq:estim_conditionalprobability}
P(y_t | theta, sigma^2)
end{equation}

где (theta) — это вектор всех наших параметров, (sigma^2) — дисперсия модели. В нашем примере с моделью eqref{eq:estim_linreg} имеем (theta = begin{pmatrix} a b end{pmatrix}).

Зачем же нам эта вероятность, когда нам нужна величина правдоподобия? Всё очень просто. Это самое правдоподобие фактически равно условной вероятности eqref{eq:estim_conditionalprobability}, но имеет другой смысл: оно показывает, насколько правдоподобны полученные значения параметров при имеющемся фактическом значении продаж. Математически это выражается следующим равенством:

begin{equation} label{eq:estim_probabilityandlikelihood}
L(theta, sigma^2 | y_t) = P(y_t | theta, sigma^2)
end{equation}

То есть это взгляд на тот же самый процесс, но с другой стороны.

Если теперь рассмотреть совместную вероятность получения параметров при всех имеющихся наблюдениях от (1 text{ до } T), то мы получим следующую функцию правдоподобия (здесь нужно иметь в виду, что при этом предполагается независимость наблюдений):

begin{equation} label{eq:estim_generallikelihood}
L(theta, sigma^2 | Y) = prod_{t=1}^T P(y_t | theta, sigma^2) ,
end{equation}

где (Y) — это вектор всех фактических значений: (Y = begin{pmatrix}y_1 y_2 vdots y_T end{pmatrix})

Теперь мы можем подставлять в eqref{eq:estim_generallikelihood} разные значения параметров модели (theta text{ и } sigma^2 ) и получать разные вероятности. Естественно, обычно мы заинтересованы в том, чтобы вероятность была максимальной, так что функцию правдоподобия eqref{eq:estim_generallikelihood} можно максимизировать, задавая разные значения параметров, и получить какие-нибудь оптимальные оценки коэффициентов.

Всё. Счастье есть! Можно откинуться на спинку стула и потягивать чай / мохито / виски / ром — в зависимости от времени года и предпочтений прогнозиста.

Однако теперь возникает другой вопрос: как же нам получить условные вероятности, использующиеся в eqref{eq:estim_generallikelihood}? А здесь как раз вступают в силу различные предположения, которые исследователь обычно накладывает относительно модели. Одно из самых популярных предположений — это то, что остатки модели распределены нормально. Оно теоретически оправдано в тех случаях, когда в нашей модели учтены все существенные переменные, а сама модель правильно специфицирована. То есть по сути мы говорим о том, что смогли угадать, что собой представляет идеальная модель. В этом случае вместо вероятности мы можем спокойно использовать функцию плотности нормального закона распределения вероятностей (который так любят все: и взрослые, и дети). Напоминаю, сама функция нормального распределения выглядит примерно так:

begin{equation} label{eq:estim_normaldensity}
P(y_t | theta, sigma^2) = frac{1}{sqrt{2 pi sigma^2}} e ^{-frac{e_t^2}{2sigma^2}},
end{equation}

где (e_t = y_t — hat{y}_t).

Подставляя eqref{eq:estim_normaldensity} в eqref{eq:estim_generallikelihood}, мы получим следующую функцию правдоподобия на основе нормального распределения:

begin{equation} label{eq:estim_likelihoodnormal}
L(theta, sigma^2 | Y) = prod_{t=1}^T frac{1}{sqrt{2 pi sigma^2}} e ^{-frac{e_t^2}{2sigma^2}} = left( 2 pi sigma^2 right)^{-frac{T}{2}} e ^ {left( -frac{1}{2} sum_{t=1}^T frac{e_t^2}{sigma^2}right)} .
end{equation}

Очевидно, что функцию eqref{eq:estim_likelihoodnormal} неудобно максимизировать в таком её виде, так как приходится сталкиваться с произведениями и экспонированием. Однако оптимальное значение коэффициентов не изменится, если мы линеаризуем эту функцию (например, прологарифмируем левую и правую части, используя натуральный логарифм). В этом случае мы получим следующую функцию (которая у них там на западе называется «log-likelihood»):

begin{equation} label{eq:estim_loglikelihoodnormal}
ell(theta, sigma^2 | Y) = ln ( L(theta, sigma^2 | Y) ) = -frac{T}{2} ln left( 2 pi sigma^2 right) -frac{1}{2} sum_{t=1}^T frac{e_t^2}{sigma^2} .
end{equation}

В правой части eqref{eq:estim_loglikelihoodnormal} дисперсию можно вынести за знак суммы, так как она представлена константой, тогда получим:

begin{equation} label{eq:estim_loglikelihoodnormal1}
ell(theta, sigma^2 | Y) = -frac{T}{2} ln left( 2 pi sigma^2 right) -frac{1}{2 sigma^2} sum_{t=1}^T e_t^2 .
end{equation}

Теперь можно попытаться математически вывести при каком значении параметров функция будет максимизироваться. Проще всего это сделать вначале с дисперсией. Для этого возьмём первую производную eqref{eq:estim_loglikelihoodnormal1} по (sigma^2) и приравняем её к нулю:

begin{equation} label{eq:estim_loglikelihoodnormaldsigma1}
frac{d ell(theta, sigma^2 | Y)}{d sigma^2} = -frac{T}{2} frac{2 pi 2 sigma}{ 2 pi sigma^2 } + 2 frac{1}{2 sigma^3} sum_{t=1}^T e_t^2 = 0.
end{equation}

Если теперь в eqref{eq:estim_loglikelihoodnormaldsigma1} сократить то, что сокращается и перенести правое слагаемое в правую часть, то получим:

begin{equation} label{eq:estim_loglikelihoodnormaldsigma2}
frac{T}{sigma} = frac{1}{sigma^3} sum_{t=1}^T e_t^2.
end{equation}

Умножим теперь левую и правую части eqref{eq:estim_loglikelihoodnormaldsigma2} на (sigma^3) и разделим на (T):

begin{equation} label{eq:estim_loglikelihoodnormalsigma}
sigma^2 = frac{1}{T} sum_{t=1}^T e_t^2.
end{equation}

Полученная формула позволяет нам оценить дисперсию ошибок по выборке с помощью статистически выверенного и корректного метода — путём максимизации функции правдоподобия на основе нормального закона распределения вероятностей. Ничего нового нам эта формула, вроде бы, не даёт, потому что мы итак знаем, как рассчитать дисперсию ошибок, но нам она полезна как раз с точки зрения статистического обоснования. Однако, чтобы не перепутать, что мы вообще-то имеем дело не с истинной дисперсией (существующей в генеральной совокупности и воображении статистиков), а с оценённой по выборке, мы будем полученную с помощью eqref{eq:estim_loglikelihoodnormalsigma} дисперсию обозначать (hat{sigma}^2). Кроме того, отметим, что мы только что показали, что дисперсия, оценённая по формуле eqref{eq:estim_loglikelihoodnormalsigma} является некой оптимальной оценкой только в случае, если мы имеем дело с нормальным распределение ошибок!

Что ж, продолжим наши пляски с бубном и подставим эту оценённую дисперсию в eqref{eq:estim_loglikelihoodnormal1}. Пойдём ещё дальше и подставим сразу значение из формулы eqref{eq:estim_loglikelihoodnormalsigma}:

begin{equation} label{eq:estim_concentratedloglikelihoodnormal}
ell(theta | Y) = -frac{T}{2} ln left( 2 pi frac{1}{T} sum_{t=1}^T e_t^2 right) -left({2 frac{1}{T} sum_{t=1}^T e_t^2}right)^{-1} sum_{t=1}^T e_t^2 .
end{equation}

Заметим, пока не поздно, что функция правдоподобия, в которой используется оценённая дисперсия, называется «концентрированной» («concentrated log-likelihood»).

В eqref{eq:estim_concentratedloglikelihoodnormal} суммы в правой части легко сокращаются, а произведение под знаком логарифма легко преобразуется в сумму логарифмов таким вот образом:

begin{equation} label{eq:estim_concentratedloglikelihoodnormal1}
ell(theta | Y) = -frac{T}{2} ln left( 2 pi right) -frac{T}{2} ln left( frac{1}{T} sum_{t=1}^T e_t^2 right) — frac{T}{2} .
end{equation}

После ряда элементарных перестановок можно получить следующую, ещё более простую, логарифмированную концетрированную функцию правдоподобия:

begin{equation} label{eq:estim_concentratedloglikelihoodnormal2}
ell(theta | Y) = -frac{T}{2} left( ln left( 2 pi e right) + ln left( frac{1}{T} sum_{t=1}^T e_t^2 right) right) .
end{equation}

Максимизировать функцию eqref{eq:estim_concentratedloglikelihoodnormal2} теперь очень просто. На самом деле ещё легче — минимизировать (-frac{2}{T} ell(theta | Y)), так как размер выборки у нас фиксирован. eqref{eq:estim_concentratedloglikelihoodnormal2} тогда преобразуется в:

begin{equation} label{eq:estim_concentratedloglikelihoodnormalnegative}
-frac{2}{T} ell(theta | Y) = ln left( 2 pi e right) + ln left( frac{1}{T} sum_{t=1}^T e_t^2 right) .
end{equation}

Ну, и в качестве финального аккорда, можно избавиться от константы (ln left( 2 pi e right)), так как она никак не влияет на получение оптимальных коэффициентов. А полученное в итоге число можно вообще проэкспонировать, для того, чтобы прийти к следующей целевой функции, минимизируя которую мы будем получать оценки максимального правдоподобия (не забываем про допущение о нормальном распределении остатков модели):

begin{equation} label{eq:estim_concentratedloglikelihoodnormal4}
CF = frac{1}{T} sum_{t=1}^T e_t^2 .
end{equation}

Удивительным образом эта целевая функция целиком и полностью соответствует MSE (формула eqref{eq:estim_MSE}).

В этом месте может возникнуть вопрос: зачем же все эти выводы и сложные процедуры, если мы в итоге получили всего лишь известный нам критерий MSE? Ответов на этот вопрос несколько:

Путём простых математических выкладок мы доказали, что MSE является эффективным критерием оценки коэффициентов моделей в том случае, если остатки модели распределены нормально. Например, для наших примеров в предыдущих параграфах (см. рисунок с MSE и MAE) эта предпосылка нарушается, поэтому MSE не является эффективным критерием.
Используя логарифмированную концентрированную функцию правдоподобия eqref{eq:estim_concentratedloglikelihoodnormal2} можно осуществлять выбор наилучшей модели из ряда имеющихся в распоряжении исследователя. Эту тему мы обсудим подробней в одном из следующих параграфов.
Кроме того, всё та же функция позволяет нам получать оценки дисперсий коэффициентов любой модели. Они нам могут понадобиться для проверки всяких статистических гипотез или построения доверительных интервалов. Для получения этих дисперсий нужно обратиться к некой вещи под названием «Информация Фишера», но здесь мы вдаваться в детали пока не будем.
Если нам не нравится предположение о нормальности распределения остатков, мы можем использовать любую другую функцию распределения в eqref{eq:estim_generallikelihood}. Конечно же, придётся произвести все последующие выводы аналогично тем, что мы произвели только что (а в некоторых случаях ничего такого сделать и не получится, функцию придётся максимизировать как есть), но зато это даст нам красивые, статистически выверенные оценки.
Используя этот подход, можно показать, что минимизация MAE является оптимальным методом оценки в случае, если остатки имеют распределение Лапласа, а квантиальные оценки дают максимум функции правдоподобия для асимметричного распределения Лапласа.

На этом простые методы оценки параметров моделей заканчиваются. В следующей статье мы перейдём к продвинутым.

Все курсы > Оптимизация > Занятие 4 (часть 2)

Во второй части занятия перейдем к практике.

Продолжим работать в том же ноутбуке⧉

Сквозной пример

Данные и постановка задачи

Обратимся к хорошо знакомому нам датасету недвижимости в Бостоне.

boston = pd.read_csv(‘/content/boston.csv’)

При этом нам нужно будет решить две основные задачи:

Задача 1. Научиться оценивать качество модели не только с точки зрения метрики, но и исходя из рассмотренных ранее допущений модели. Эту задачу мы решим в три этапа.

Этап 1. Построим базовую (baseline) модель линейной регрессии с помощью класса LinearRegression библиотеки sklearn и оценим, насколько выполняются рассмотренные выше допущения.
Этап 2. Попробуем изменить данные таким образом, чтобы модель в большей степени соответствовала этим критериям.
Этап 3. Обучим еще одну модель и посмотрим как изменится результат.

Задача 2. С нуля построить модель множественной линейной регрессии и сравнить прогноз с результатом полученным при решении первой задачи. При этом обучение модели мы реализуем двумя способами, а именно, через:

Метод наименьших квадратов
Метод градиентного спуска

Разделение выборки

Мы уже не раз говорили про важность разделения выборки на обучаущую и тестовую части. Сегодня же, с учетом того, что нам предстоит изучить много нового материала, мы опустим этот этап и будем обучать и тестировать модель на одних и тех же данных.

Исследовательский анализ данных

Теперь давайте более внимательно посмотрим на имеющиеся у нас данные. Как вы вероятно заметили, признаки в этом датасете количественные, за исключением переменной CHAS.

RangeIndex: 506 entries, 0 to 505

Data columns (total 14 columns):

# Column Non-Null Count Dtype

— —— ————— ——

0 CRIM 506 non-null float64

1 ZN 506 non-null float64

2 INDUS 506 non-null float64

3 CHAS 506 non-null float64

4 NOX 506 non-null float64

5 RM 506 non-null float64

6 AGE 506 non-null float64

7 DIS 506 non-null float64

8 RAD 506 non-null float64

9 TAX 506 non-null float64

10 PTRATIO 506 non-null float64

11 B 506 non-null float64

12 LSTAT 506 non-null float64

13 MEDV 506 non-null float64

dtypes: float64(14)

memory usage: 55.5 KB

# мы видим, что переменная CHAS категориальная

boston.CHAS.value_counts()

0.0 471

1.0 35

Name: CHAS, dtype: int64

Посмотрим на распределение признаков с помощью boxplots.

plt.figure(figsize = (10, 8))

sns.boxplot(data = boston.drop(columns = [‘CHAS’, ‘MEDV’]))

plt.show()

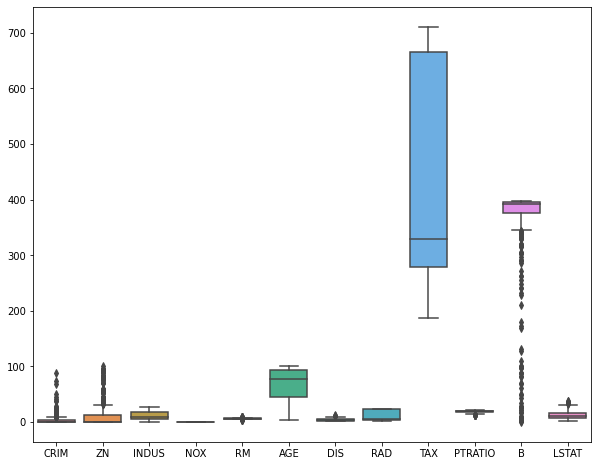
Посмотрим на распределение целевой переменной.

def box_density(x):

# создадим два подграфика

f, (ax_box, ax_kde) = plt.subplots(nrows = 2, # из двух строк

ncols = 1, # и одного столбца

sharex = True, # оставим только нижние подписи к оси x

gridspec_kw = {‘height_ratios’: (.15, .85)}, # зададим разную высоту строк

figsize = (10,8)) # зададим размер графика

# в первом подграфике построим boxplot

sns.boxplot(x = x, ax = ax_box)

ax_box.set(xlabel = None)

# во втором — график плотности распределения

sns.kdeplot(x, fill = True)

# зададим заголовок и подписи к осям

ax_box.set_title(‘Распределение переменной’, fontsize = 17)

ax_kde.set_xlabel(‘Переменная’, fontsize = 15)

ax_kde.set_ylabel(‘Плотность распределения’, fontsize = 15)

plt.show()

box_density(boston.iloc[:, —1])

Посмотрим на корреляцию количественных признаков с целевой переменной.

boston.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

Используем точечно-бисериальную корреляцию для оценки взамосвязи переменной CHAS и целевой переменной.

def pbc(continuous, binary):

# преобразуем количественную переменную в массив Numpy

continuous_values = np.array(continuous)

# классы качественной переменной превратим в нули и единицы

binary_values = np.unique(binary, return_inverse = True)[1]

# создадим две подгруппы количественных наблюдений

# в зависимости от класса дихотомической переменной

group0 = continuous_values[np.argwhere(binary_values == 0).flatten()]

group1 = continuous_values[np.argwhere(binary_values == 1).flatten()]

# найдем средние групп,

mean0, mean1 = np.mean(group0), np.mean(group1)

# а также длины групп и всего датасета

n0, n1, n = len(group0), len(group1), len(continuous_values)

# рассчитаем СКО количественной переменной

std = continuous_values.std()

# подставим значения в формулу

return (mean1 — mean0) / std * np.sqrt( (n1 * n0) / (n * (n—1)) )

pbc(boston.MEDV, boston.CHAS)

Обработка данных

Пропущенные значения

Посмотрим, есть ли пропущенные значения.

CRIM 0

ZN 0

INDUS 0

CHAS 0

NOX 0

RM 0

AGE 0

DIS 0

RAD 0

TAX 0

PTRATIO 0

B 0

LSTAT 0

MEDV 0

dtype: int64

Выбросы

Удалим выбросы.

from sklearn.ensemble import IsolationForest

clf = IsolationForest(max_samples = 100, random_state = 42)

clf.fit(boston)

boston[‘anomaly’] = clf.predict(boston)

boston = boston[boston.anomaly == 1]

boston = boston.drop(columns = ‘anomaly’)

boston.shape

При удалении выбросов важно помнить, что полное отсутствие вариантивности в данных не позволит выявить взаимосвязи

Масштабирование признаков

Приведем признаки к одному масштабу (целевую переменную трогать не будем).

boston.iloc[:, :—1] = (boston.iloc[:, :—1] — boston.iloc[:, :—1].mean()) / boston.iloc[:, :—1].std()

Замечу, что метод наименьших квадратов не требует масштабирования признаков, градиентному спуску же напротив необходимо, чтобы все значения находились в одном диапазоне (подробнее в дополнительных материалах).

Кодирование категориальных переменных

Даже после стандартизации переменная CHAS сохранила только два значения.

boston.CHAS.value_counts()

-0.182581 389

5.463391 13

Name: CHAS, dtype: int64

Ее можно не трогать.

Построение модели

Создадим первую пробную (baseline) модель с помощью библиотеки sklearn.

baseline-модель

X = boston.drop(‘MEDV’, axis = 1)

y = boston[‘MEDV’]

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества

Диагностика модели, метрики качества и функции потерь

Вероятно, вы заметили, что мы использовали MSE и для обучения модели, и для оценки ее качества. Возникает вопрос, есть ли отличие между функцией потерь и метрикой качества модели.

Функция потерь и метрика качества могут совпадать, а могут и не совпадать. Важно понимать, что у них разное назначение.

Функция потерь — это часть алгоритма, нам важно, чтобы эта функция была дифференцируема (у нее была производная)
Производная метрики качества нас не интересует. Метрика качества должна быть адекватна решаемой задаче.

MSE, RMSE, MAE, MAPE

MSE и RMSE

Для оценки качества RMSE предпочтительнее, чем MSE, потому что показывает насколько ошибается модель в тех же единицах измерения, что и целевая переменная. Например, если диапазон целевой переменной от 80 до 100, а RMSE 20, то в среднем вы ошибаетесь на 20-25 процентов.

В качестве практики напишем собственную функцию.

# параметр squared = True возвращает MSE

# параметр squared = False возвращает RMSE

def mse(y, y_pred, squared = True):

mse = ((y — y_pred) ** 2).sum() / len(y)

if squared == True:

return mse

else:

return np.sqrt(mse)

mse(y, y_pred), mse(y, y_pred, squared = False)

(9.980044349414223, 3.1591208190593507)

Сравним с sklearn.

from sklearn.metrics import mean_squared_error

# squared = False дает RMSE

mean_squared_error(y, y_pred, squared = False)

MAE

Приведем формулу.

$$ MAE = frac{sum |y-hat{y}|}{n} $$

Средняя абсолютная ошибка представляет собой среднее арифметическое абсолютной ошибки $varepsilon = |y-hat{y}| $ и использует те же единицы измерения, что и целевая переменная.

def mae(y, y_pred):

return np.abs(y — y_pred).sum() / len(y)

from sklearn.metrics import mean_absolute_error

mean_absolute_error(y, y_pred)

MAE часто используется при оценке качества моделей временных рядов.

MAPE

Средняя абсолютная ошибка в процентах (mean absolute percentage error) по сути выражает MAE в процентах, а не в абсолютных величинах, выражая отклонение как долю от истинных ответов.

$$ MAPE = frac{1}{n} sum vert frac{y-hat{y}}{y} vert $$

Это позволяет сравнивать модели с разными единицами измерения между собой.

def mape(y, y_pred):

return 1/len(y) * np.abs((y — y_pred) / y).sum()

from sklearn.metrics import mean_absolute_percentage_error

mean_absolute_percentage_error(y, y_pred)

Коэффициент детерминации

В рамках вводного курса в ответах на вопросы к занятию по регрессии мы подробно рассмотрели коэффициент детерминации ($R^2$), его связь с RMSE, а также зачем нужен скорректированный $R^2$. Как мы знаем, если использовать, например, класс LinearRegression, то эта метрика содержится в методе .score().

Также можно использовать функцию r2_score() модуля metrics.

from sklearn.metrics import r2_score

r2_score(y, y_pred)

Для скорректированного $R^2$ напишем собственную функцию.

def r_squared(x, y, y_pred):

r2 = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum()

n, k = x.shape

r2_adj = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum()

return r2, r2_adj

(0.7965234359550825, 0.7965234359550825)

Диагностика модели

Теперь проведем диагностику модели в соответствии с выдвинутыми выше допущениями.

Анализ остатков и прогнозных значений

Напишем диагностическую функцию, которая сразу выведет несколько интересующих нас графиков и метрик, касающихся остатков и прогнозных значений.

from scipy.stats import probplot

from statsmodels.graphics.tsaplots import plot_acf

from statsmodels.stats.stattools import durbin_watson

def diagnostics(y, y_pred):

residuals = y — y_pred

residuals_mean = np.round(np.mean(y — y_pred), 3)

f, ((ax_rkde, ax_prob), (ax_ry, ax_auto), (ax_yy, ax_ykde)) = plt.subplots(nrows = 3,

ncols = 2,

figsize = (12, 18))

# в первом подграфике построим график плотности

sns.kdeplot(residuals, fill = True, ax = ax_rkde)

ax_rkde.set_title(‘Residuals distribution’, fontsize = 14)

ax_rkde.set(xlabel = f‘Residuals, mean: {residuals_mean}’)

ax_rkde.set(ylabel = ‘Density’)

# во втором график нормальной вероятности остатков

probplot(residuals, dist = ‘norm’, plot = ax_prob)

ax_prob.set_title(‘Residuals probability plot’, fontsize = 14)

# в третьем график остатков относительно прогноза

ax_ry.scatter(y_pred, residuals)

ax_ry.set_title(‘Predicted vs. Residuals’, fontsize = 14)

ax_ry.set(xlabel = ‘y_pred’)

ax_ry.set(ylabel = ‘Residuals’)

# автокорреляция остатков

plot_acf(residuals, lags = 30, ax = ax_auto)

ax_auto.set_title(‘Residuals Autocorrelation’, fontsize = 14)

ax_auto.set(xlabel = f‘Lags ndurbin_watson: {durbin_watson(residuals).round(2)}’)

ax_auto.set(ylabel = ‘Autocorrelation’)

# на четвертом сравним прогнозные и фактические значения

ax_yy.scatter(y, y_pred)

ax_yy.plot([y.min(), y.max()], [y.min(), y.max()], «k—«, lw = 1)

ax_yy.set_title(‘Actual vs. Predicted’, fontsize = 14)

ax_yy.set(xlabel = ‘y_true’)

ax_yy.set(ylabel = ‘y_pred’)

sns.kdeplot(y, fill = True, ax = ax_ykde, label = ‘y_true’)

sns.kdeplot(y_pred, fill = True, ax = ax_ykde, label = ‘y_pred’)

ax_ykde.set_title(‘Actual vs. Predicted Distribution’, fontsize = 14)

ax_ykde.set(xlabel = ‘y_true and y_pred’)

ax_ykde.set(ylabel = ‘Density’)

ax_ykde.legend(loc = ‘upper right’, prop = {‘size’: 12})

plt.tight_layout()

plt.show()

Разберем полученную информацию.

В целом остатки модели распределены нормально с нулевым средним значением
Явной гетероскедастичности нет, хотя мы видим, что дисперсия не всегда равномерна
Присутствует умеренная отрицательная корреляция
График y_true vs. y_pred показывает насколько сильно прогнозные значения отклоняются от фактических. В идеальной модели (без шума, т.е. без случайных колебаний) точки должны были би стремиться находиться на диагонали, в более реалистичной модели нам бы хотелось видеть, что точки плотно сосредоточены вокруг диагонали.
Распределение прогнозных значений в целом повторяет распределение фактических.

Мультиколлинеарность

Отдельно проведем анализ на мультиколлинеарность. Напишем соответствующую функцию.

def vif(df, features):

vif, tolerance = {}, {}

# пройдемся по интересующим нас признакам

for feature in features:

# составим список остальных признаков, которые будем использовать

# для построения регрессии

X = [f for f in features if f != feature]

# поместим текущие признаки и таргет в X и y

X, y = df[X], df[feature]

# найдем коэффициент детерминации

r2 = LinearRegression().fit(X, y).score(X, y)

# посчитаем tolerance

tolerance[feature] = 1 — r2

# найдем VIF

vif[feature] = 1 / (tolerance[feature])

# выведем результат в виде датафрейма

return pd.DataFrame({‘VIF’: vif, ‘Tolerance’: tolerance})

vif(df = X.drop(‘CHAS’, axis = 1), features = X.drop(‘CHAS’, axis = 1).columns)

Дополнительная обработка данных

Попробуем дополнительно улучшить некоторые из диагностических показателей.

VIF

Уберем признак с наибольшим VIF (RAD) и посмотрим, что получится.

vif(df = X, features = [‘CRIM’,

‘ZN’,

‘INDUS’,

‘CHAS’,

‘NOX’,

‘RM’,

‘AGE’,

‘DIS’,

‘TAX’,

‘PTRATIO’,

‘B’,

‘LSTAT’])

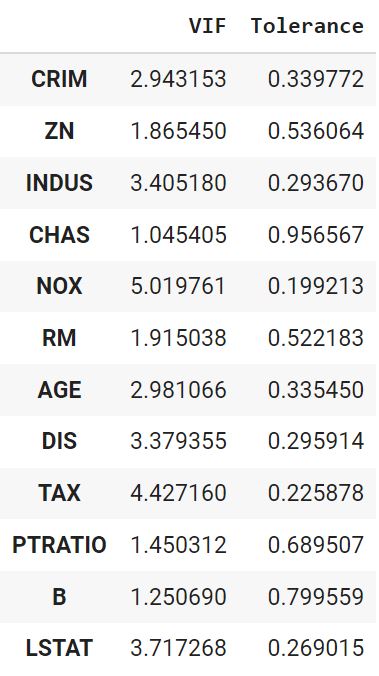
Показатели пришли в норму. Окончательно удалим RAD.

boston.drop(columns = ‘RAD’, inplace = True)

Преобразование данных

Применим преобразование Йео-Джонсона.

from sklearn.preprocessing import PowerTransformer

pt = PowerTransformer()

boston = pd.DataFrame(pt.fit_transform(boston),

columns = boston.columns)

Отбор признаков

Посмотрим на линейную корреляцию Пирсона количественных признаков и целевой переменной.

boston_t.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

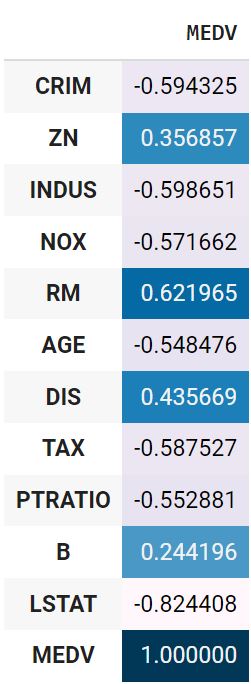
Также рассчитаем точечно-бисериальную корреляцию.

pbc(boston_t.MEDV, boston_t.CHAS)

Удалим признаки с наименьшей корреляцией, а именно ZN, CHAS, DIS и B.

boston.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’], inplace = True)

Повторное моделирование и диагностика

Повторное моделирование

Выполним повторное моделирование.

X = boston_t.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’, ‘MEDV’])

y = boston_t.MEDV

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества и диагностика

Оценим качество. Так как мы преобразовали целевую переменную, показатель RMSE не будет репрезентативен. Воспользуемся MAPE и $R^2$.

(0.7546883769637166, 0.7546883769637166)

Отклонение прогнозного значения от истинного снизилось. $R^2$ немного уменьшился, чтобы бывает, когда мы пытаемся привести модель к соответствию допущениям. Проведем диагностику.

Распределение остатков немного улучшилось, при этом незначительно усилилась их отрицательная автокорреляция. Распределение целевой переменной стало менее островершинным.

Данные можно было бы продолжить анализировать и улучшать, однако в рамках текущего занятия перейдем к механике обучения модели.

Коэффициенты

Выведем коэффициенты для того, чтобы сравнивать их с результатами построенных с нуля моделей.

model.intercept_, model.coef_

(9.574055157844797e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Обучение модели

Теперь, когда мы поближе познакомились с понятием регрессии, разобрали функции потерь и изучили допущения, при которых модель может быть удачной аппроксимацией данных, пора перейти к непосредственному созданию алгоритмов.

Векторизация уравнения

Для удобства векторизуем приведенное выше уравнение множественной линейной регрессии

$$ y = begin{bmatrix} y_1 y_2 vdots y_n end{bmatrix} X = begin{bmatrix} x_0 & x_1 & ldots & x_j x_0 & x_1 & ldots & x_j vdots & vdots & vdots & vdots x_{0} & x_{1} & ldots & x_{n,j} end{bmatrix}, theta = begin{bmatrix} theta_0 theta_1 vdots theta_n end{bmatrix}, varepsilon = begin{bmatrix} varepsilon_1 varepsilon_2 vdots varepsilon_n end{bmatrix} $$

где n — количество наблюдений, а j — количество признаков.

Обратите внимание, что мы создали еще один столбец данных $ x_0 $, который будем умножать на сдвиг $ theta_0 $. Его мы заполним единицами.

В результате такого несложного преобразования значение сдвига не изменится, но мы сможем записать записать уравнение через умножение матрицы на вектор.

$$ y = Xtheta + varepsilon $$

Кроме того, как мы увидим ниже, так нам не придется искать отдельную производную для коэффициента $ theta_0 $.

Схематично для модели с четырьмя наблюдениями (n = 4) и двумя признаками (j = 2) получаются вот такие матрицы.

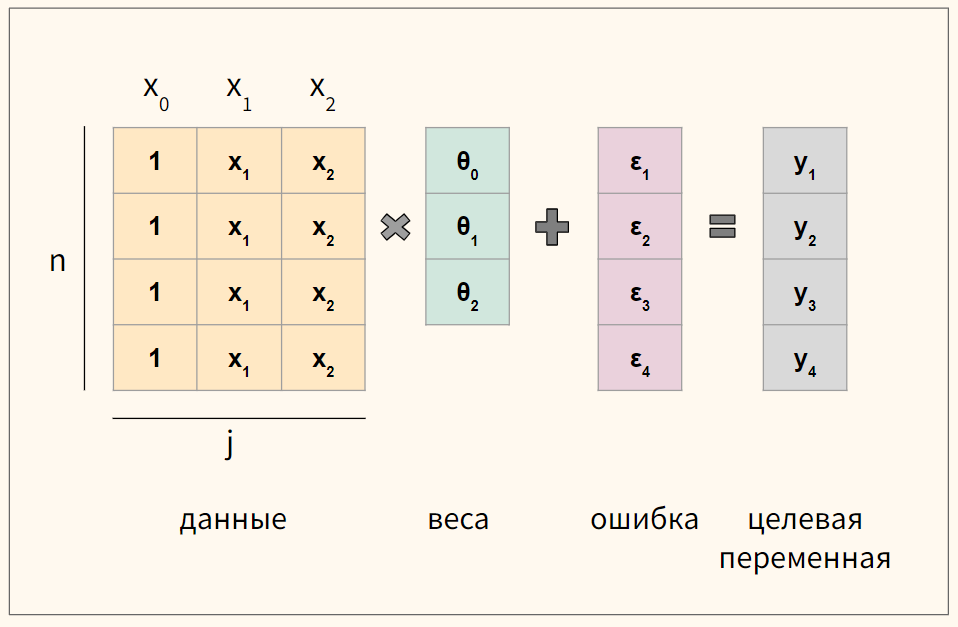
Функция потерь

Как мы уже говорили, чтобы подобрать оптимальные коэффициенты $theta$, нам нужен критерий или функция потерь. Логично измерять отклонение прогнозного значения от истинного.

$$ varepsilon = Xtheta-y $$

При этом опять же просто складывать отклонения или ошибки мы не можем. Положительные и отрицательные значения будут взаимоудалятся. Для решения этой проблемы можно, например, использовать модуль и это приводит нас к абсолютной ошибку или L1 loss.

Абсолютная ошибка, L1 loss

При усреднении на количество наблюдений мы получаем среднюю абсолютную ошибку (mean absolute error, MAE).

$$ MAE = frac{sum{|y-Xtheta|}}{n} = frac{sum{|varepsilon|}}{n} $$

Приведем пример такой функции на Питоне.

def L1(y_true, y_pred):

return np.sum(np.abs(y_true — y_pred)) / y_true.size

Помимо модуля ошибку можно возводить в квадрат.

Квадрат ошибки, L2 loss

В этом случай говорят про сумму квадратов ошибок (sum of squared errors, SSE) или сумму квадратов остатков (sum of squared residuals, SSR или residual sum of squares, RSS).

$$ SSE = sum (y-Xtheta)^2 $$

Как мы уже говорили, на практике вместо SSE часто используется MSE, или вернее half MSE для удобства нахождения производной.

$$ MSE = frac{1}{2n} sum (y-theta X)^2 $$

Ниже код на Питоне.

def L2(y_true, y_pred):

return np.sum((y_true — y_pred) ** 2) / y_true.size

На практике у обеих функций есть сильные и слабые стороны. Рассмотрим L1 loss (MAE) и L2 loss (MSE) на графике.

# для построения графиков мы используем x вместо y_true, y_pred

# в качестве входящего значения

def mse(x):

return x ** 2

def mae(x):

return np.abs(x)

plt.figure(figsize = (10, 8))

x_vals = np.arange(—3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Как мы видим, при отклонении от точки минимума из-за возведения в квадрат L2 значительно быстрее увеличивает ошибку, поэтому если в данных есть выбросы при суммированнии они очень сильно влияют на ошибку, хотя де-факто большая часть значений такого уровня потерь не дали бы.

Функция L1 не дает такой большой ошибки на выбросах, однако ее сложно дифференцировать, в точке минимума ее производная не определена.

Функция Хьюбера

Рассмотрим функцию Хьюбера (Huber loss), которая объединяет сильные стороны вышеупомянутых функций и при этом лишена их недостатков. Посмотрим на формулу.

$$ L_{delta}= left{begin{matrix} frac{1}{2}(y-hat{y})^{2} & if | y-hat{y} | < delta delta (|y-hat{y}|-frac1 2 delta) & otherwise end{matrix}right. $$

Представим ее на графике.

plt.figure(figsize = (10, 8))

def huber(x, delta = 1.):

huber_mse = 0.5 * np.square(x)

huber_mae = delta * (np.abs(x) — 0.5 * delta)

return np.where(np.abs(x) <= delta, huber_mse, huber_mae)

x_vals = np.arange(—3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.plot(x_vals, huber(x_vals, delta = 2), label = ‘Huber’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Также приведем код этой функции.

def huber(y_pred, y_true, delta = 1.0):

# пропишем обе части функции потерь

huber_mse = 0.5 * (y_true — y_pred) ** 2

huber_mae = delta * (np.abs(y_true — y_pred) — 0.5 * delta)

# выберем одну из них в зависимости от дельта

return np.where(np.abs(y_true — y_pred) <= delta, huber_mse, huber_mae)

На сегодняшнем занятии мы, как и раньше, в качестве функции потерь используем MSE.

Метод наименьших квадратов

Нормальные уравнения

Для множественной линейной регрессии коэффициенты находятся по следующей формуле

$$ theta = (X^TX)^{-1}X^Ty $$

Давайте разбираться, как мы к ней пришли. Сумма квадратов остатков (SSE) можно переписать как произведение вектора $ hat{varepsilon} $ на самого себя, то есть $ SSE = varepsilon^{T}varepsilon$. Помня, что $varepsilon = y-Xtheta $ получаем (не забывая транспонировать)

$$ (y-Xtheta)^T(y-Xtheta) $$

Раскрываем скобки

$$ y^Ty-y^T(Xtheta)-(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Заметим, что $A^TB = B^TA$, тогда

$$ y^Ty-(Xtheta)^Ty-(Xtheta)^Ty+(Xtheta)^T(Xtheta)$$

$$ y^Ty-2(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Вспомним, что $(AB)^T = A^TB^T$, тогда

$$ y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$

Теперь нужно найти частные производные этих функций

$$ nabla_{theta} J(theta) = y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$

После дифференцирования мы получаем следующую производную

$$ -2X^Ty+2X^TXtheta $$

Как мы помним, оптимум функции находится там, где производная равна нулю.

$$ -2X^Ty+2X^TXtheta = 0 $$

$$ -X^Ty+X^TXtheta = 0 $$

$$ X^TXtheta = X^Ty $$

Выражение выше называется нормальным уравнением (normal equation). Решив его для $theta$ мы найдем аналитическое решение минимизации суммы квадратов отклонений.

$$ theta = (X^TX)^{-1}X^Ty $$

Замечу только, что по теореме Гаусса-Маркова, оценка через МНК является наиболее оптимальной (обладающей наименьшей дисперсией) среди всех методов построения модели.

Код на Питоне

Перейдем к созданию класса линейной регрессии наподобие LinearRegression библиотеки sklearn. Вначале напишем функцию гипотезы (т.е. функцию самой модели), снабдив ее функцией, которая добавляет столбец из единиц к признакам.

$$ h_{theta}(x) = theta X $$

def add_ones(x):

# важно! изменяет исходный датафрейм

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def h(x, theta):

x = x.copy()

add_ones(x)

return np.dot(x, theta)

Перейдем к функции, отвечающей за обучение модели.

$$ theta = (X^TX)^{-1}X^Ty $$

# строчную `x` используем внутри функций и методов класса

# заглавную `X` вне функций и методов

def fit(x, y):

x = x.copy()

add_ones(x)

xT = x.transpose()

inversed = np.linalg.inv(np.dot(xT, x))

thetas = inversed.dot(xT).dot(y)

return thetas

Обучим модель и выведем коэффициенты.

thetas = fit(X, y)

thetas[0], thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Примечание. Замечу, что не все матрицы обратимы, в этом случае они называются вырожденными (non-invertible, degenerate). В этом случае можно найти псевдообратную матрицу (pseudoinverse). Для этого в Numpy есть функция np.linalg.pinv().

Сделаем прогноз.

y_pred = h(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим код в класс.

class ols():

def __init__(self):

self.thetas = None

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def fit(self, x, y):

x = x.copy()

self.add_ones(x)

xT = x.T

inversed = np.linalg.inv(np.dot(xT, x))

self.thetas = inversed.dot(xT).dot(y)

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса и обучим модель.

model = ols()

model.fit(X, y)

Выведем коэффициенты.

model.thetas[0], model.thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Сделаем прогноз.

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

Оценим качество через MAPE и $R^2$.

(0.7546883769637167, 0.7546883769637167)

Мы видим, что результаты аналогичны.

Метод градиентного спуска

В целом с этим методом мы уже хорошо знакомы. В качестве упражнения давайте реализуем этот алгоритм на Питоне для многомерных данных.

Нахождение градиента

Покажем расчет градиента на схеме.

В данном случае мы берем датасет из четырех наблюдений и двух признаков ($x_1$ и $x_2$) и соответственно используем три коэффициента ($theta_0, theta_1, theta_2$).

Пошаговое построение модели

Начнем с функции гипотезы.

$$ h_{theta}(x) = theta X $$

def h(x, thetas):

return np.dot(x, thetas)

Объявим функцию потерь.

$$ J({theta_j}) = frac{1}{2n} sum (y-theta X)^2 $$

def objective(x, y, thetas, n):

return np.sum((y — h(x, thetas)) ** 2) / (2 * n)

Объявим функцию для расчета градиента.

$$ frac{partial}{partial theta_j} J(theta) = -x_j(y — Xtheta) times frac{1}{n} $$

где j — индекс признака.

def gradient(x, y, thetas, n):

return np.dot(—x.T, (y — h(x, thetas))) / n

Напишем функцию для обучения модели.

$$ theta_j := theta_j-alpha frac{partial}{partial theta_j} J(theta) $$

Символ := означает, что левая часть равенства определяется правой. По сути, с каждой итерацией мы обновляем веса, умножая коэффициент скорости обучения на градиент.

def fit(x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

# функцию add_ones() мы написали раньше

add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

loss_history = []

for i in range(iter):

loss_history.append(objective(x, y, thetas, n))

grad = gradient(x, y, thetas, n)

thetas -= learning_rate * grad

return thetas, loss_history

Обучим модель, выведем коэффициенты и достигнутый (минимальный) уровень ошибки.

thetas, loss_history = fit(X, y, iter = 50000, learning_rate = 0.05)

thetas[0], thetas[1:], loss_history[—1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

Полученный результат очень близок к тому, что было найдено методом наименьших квадратов.

Прогноз

Сделаем прогноз.

def predict(x, thetas):

x = x.copy()

add_ones(x)

return np.dot(x, thetas)

y_pred = predict(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим написанные функции в класс.

class gd():

def __init__(self):

self.thetas = None

self.loss_history = []

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def objective(self, x, y, thetas, n):

return np.sum((y — self.h(x, thetas)) ** 2) / (2 * n)

def h(self, x, thetas):

return np.dot(x, thetas)

def gradient(self, x, y, thetas, n):

return np.dot(—x.T, (y — self.h(x, thetas))) / n

def fit(self, x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

self.add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

# объявляем переменную loss_history (отличается от self.loss_history (?))

loss_history = []

for i in range(iter):

loss_history.append(self.objective(x, y, thetas, n))

grad = self.gradient(x, y, thetas, n)

thetas -= learning_rate * grad

# записываем обратно во внутренние атрибуты, чтобы передать методу .predict()

self.thetas = thetas

self.loss_history = loss_history

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса, обучим модель, выведем коэффициенты и сделаем прогноз.

model = gd()

model.fit(X, y, iter = 50000, learning_rate = 0.05)

model.thetas[0], model.thetas[1:], model.loss_history[—1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

(0.7546883769637167, 0.7546883769637167)

Теперь рассмотрим несколько дополнительных соображений, касающихся построения модели линейной регрессии.

Диагностика алгоритма

Работу алгоритма можно проверить с помощью кривой обучения (learning curve).

Ошибка постоянно снижается
Алгоритм остановится, после истечения заданного количества итераций
Можно задать пороговое значение, после которого он остановится (например, $10^{-1}$)

Построим кривую обучения.

plt.plot(loss_history)

plt.show()

plt.plot(loss_history[:100])

plt.show()

Она также позволяет выбрать адекватный коэффициент скорости обучения.

Подведем итог

Сегодня мы подробно рассмотрели модель множественной линейной регрессиии. В частности, мы поговорили про построение гипотезы, основные функции потерь, допущения модели линейной регрессии, метрики качества и диагностику модели.

Кроме того, мы узнали как изнутри устроены метод наименьших квадратов и метод градиентного спуска и построили соответствующие модели на Питоне.

Отдельно замечу, что, изучив скорректированный коэффициент детерминации, мы начали постепенно погружаться в способы усовершенствования базовых алгоритмов и метрик. На последующих занятиях мы продолжим этот путь в двух направлениях: познакомимся со способами регуляризации функции потерь и начнем создавать более сложные алгоритмы оптимизации.

Но прежде предлагаю в деталях изучить уже знакомый нам алгоритм логистической регрессии.

Дополнительные материалы к занятию.

Выбор функции потерь для задач построения нейронных сетей

Время прочтения: 4 мин.

При построении нейронных сетей перед нами часто встаёт вопрос правильного выбора функции потерь, используемой для формирования соответствий между входными и выходными параметрами. Функция потерь отвечает за оценку того, насколько хорошо модель предсказывает реальное значение, и построение модели сводится к решению задачи минимизации значения этой функции на каждом этапе. И в зависимости от того, как выглядят наши данные, требуется использовать разные подходы.

В рамках данной статьи мы рассмотрим три функции потерь для нейронных сетей, решающих регрессионные задачи.

Mean Squared Error

Среднеквадратичная ошибка (MSE) — одна из основных функций расчёта отклонения. Для каждой точки вычисляется квадрат отклонения, после чего полученные значения суммируются и делятся на общее количество точек. Чем ближе полученное значение к нулю, тем точнее наша модель. Данный метод расчёта в значительной мере чувствителен к выбросам в выборке, или к выборкам где разброс значений очень большой. В основном, данная функция применяется для переменных, распределение которых близко к распределению Гаусса.

Mean Absolute Error

Средняя абсолютная ошибка (MAE) – это усреднённая сумма модулей разницы между реальным и предсказанным значениями. MAE во многом похожа на MSE, но она отличается меньшей чувствительностью к выбросам значений (так как не берётся квадрат отклонения).

Mean Squared Logarithmic Error

Среднеквадратичная логарифмическая ошибка (MSLE) – усреднённая сумма квадратов разностей между логарифмами значений. Благодаря большому гасящему эффекту логарифма она более применима к моделям, строящимся на данных, которые имеют большой разброс значений на несколько порядков.

Продемонстрируем как выбор функции потерь влияет на процесс построения нейронной сети. Для генерации данных будем использовать встроенную в scikit-learn функцию make_regression, а в качестве нейронной сети будет выступать многослойный перцептрон.

Код используемый для демонстрации:

from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# формирование датасета
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# нормализация
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# разделение
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# определение для модели
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss=вид функции потерь, optimizer=opt)
# расчёт
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Оценка качества
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot Демонстрация результата
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()

В данном коде мы будем заменять только указанный вид функции потерь.
Результат для MSE:

model.compile(loss='mean_squared_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.000, Test: 0.001

Как видно из графика, модель показывает хорошую сходимость и низкое отклонение.

Результат для MSLE:

model.compile(loss=' mean_squared_logarithmic_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.165, Test: 0.184

По графику видно, что для данного набора данных MSLE сходится медленней чем MSE. С одной стороны, это может привести к тому что модель будет строиться медленней и получится хуже, с другой – использование MSE может привести к переобучению. Результат для MAE:

model.compile(loss='mean_absolute_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.002, Test: 0.002

Здесь мы можем увидеть, что результат сходится очень эффективно, но ошибка имеет нерегулярный характер. Так как используемый нами генератор строит гауссово распределение без выбросов, использование MAE не даёт значительных преимуществ.

Очевидно, что от выбора правильной функции потерь сильно зависит точность, качество и скорость построения модели, поэтому следует внимательно подходить к выбору опираясь как на используемую модель, так и на характеристики входных данных.

@TOC
Суммируйте преимущества и недостатки функции потери MAE, функции потери MAE и плавной функции потери L1_LOSS

1. Общие функции потери MSE и MAE

1.1, средняя квадратная ошибка MSE

Средняя квадратная ошибка (средняя квадратная ошибка, MSE)Это наиболее часто используемая ошибка в функции потери регрессии. Это значение прогноза F (x) и целевое значение yСреднее разницу между разницейФормула показана ниже:

Рисунок нижеОшибка акцийРаспределение кривой значения минимальное значение — это местоположение прогнозируемого значения в качестве целевого значения. Мы видим, что потеря функции потери увеличивается быстрее по мере увеличения ошибки.

преимущество: Кривая функции MSE является гладкой и непрерывной, и может быть направлена повсюду, чтобы облегчить использование алгоритмов градиента. Более того, по мере уменьшения ошибки градиент также уменьшается, что способствует конвергенции. Даже если используется фиксированная скорость обучения, он может быстро сходиться к минимальному значению.
недостаток: Когда разница между реальным значением y и значением прогнозирования f (x) больше 1, ошибка будет увеличена; когда разница меньше 1, ошибка будет уменьшена, что определяется с помощью расчета квадратного транспорта Анкет MSE дает большее наказание за большие ошибки (> 1), а меньшие ошибки (<1) дают меньшее наказание. То есть,Это более чувствителен к группе, на которую она сильно влияет。

Если в выборке есть групповая точка, MSE придаст группе больше веса, что принесет жертву прогнозирующего эффекта других данных нормальных точек и в конечном итоге снизит общую производительность модели. Как показано ниже:

видимый,Используя функцию потери MSE, на нее сильно влияют точки группы. Хотя в выборке есть только 5 точек разделения,Линия подходящейВсе еще сравнитесьВписаться в группу。

1.2. Средняя абсолютная ошибка MAE

Средняя абсолютная ошибка (MAE)Это еще одна обычно используемая функция регрессии, которая является целевым значением и прогнозирующим значениемСреднее значение абсолютного значения разницыОн представляет среднюю амплитуду ошибки значения прогнозирования и не нужно учитывать направление ошибки (Примечание：Ошибка среднего отклонения MBEОшибка направления рассмотрения — гармония остатка), диапазон 0 до ∞, а формула, как показано ниже:

преимущество: По сравнению с MSE, MAE имеет преимущество, что он не так чувствителен к группе. Поскольку MAE вычисляет абсолютное значение ошибки (y-f (x)), наказание за разницу в любом размере является фиксированным. Независимо от того, какое входное значение у него есть стабильный градиент, который не вызовет проблемы с взрывом градиента и имеет относительно стабильное решение.
недостаток: Кривая MAE непрерывна, но она не может быть направлена на (y-f (x) = 0). И большая часть MAE равна, что означает, что даже для небольших потерь градиент большой. Это не способствует конвергенции функции и изучению модели.

Для данных с групповыми точками выше, эффект MAE лучше, чем MSE.

Очевидно, что использование функции потери MAE меньше влияет на исходящую точку, и линия FIT может лучше охарактеризовать распределение нормальных данных.

1.3, MSE и MAE CHOOCES

изРешение градиентатак же какконвергенцияначальство,MSE лучше, чем MAEСущность MSE может быть направлен повсюду, и значение градиента также динамически изменяется, что может быстро сходиться; и MAE не может быть направлен в 0 точек, и его градиент остается неизменным. Градиционная стоимость небольшой потери также очень велика. При глубоком обучении частота обучения изменений необходима для снижения уровня обучения во время потери.
ПравильноЗалоговое (ненормальное) значениеЧтобы справиться с этим,Мэй должна быть очевидной, чем MSE。

Если вам нужно обнаружить групповую точку (аномальное значение), вы можете выбрать MSE в качестве функции потери; если точка группы используется только в качестве поврежденной обработки данных, вы можете выбрать MAE в качестве функции потери.

ПричинаMAE более стабилен в качестве функции потери и не чувствителен к групповым значениям, но его производные не являются непрерывными, а эффективность решения низкая. Кроме того, в глубоком обучении конвергенция медленная. Производные MSE сильно решаются, но они чувствительны к значению Outliex, но количество руководств значения группы может быть установлено на 0 (производное значение больше, чем определенный порог), чтобы избежать этого.

При определенных обстоятельствахНи одна из вышеупомянутых потерь не может удовлетворить потребности. Например, если целевое значение 90%выборки в данных составляет 150, оставшиеся 10%составляет от 0 до 30. Затем модель, использующая MAE в качестве функции потери, может игнорировать 10%аномальной точки, а значение прогнозирования всех образцов составляет 150. Это потому, что модель будет предсказана в медиане. Модель, использующая MSE, даст много прогнозируемых значений от 0 до 30, поскольку модель компенсирует аномальную точку.

В этой ситуацииКак MSE, так и MAE нежелательны. Простой метод состоит в том, чтобы изменить целевые переменные или использовать другие убытки, такие как: Huber, Log-Cosh и потеря потери деления.

2. L1_Loss и L2_Loss

2.1, l1_loss и l2_loss

2.2, несколько ключевых понятий

Жесткость
Поскольку по сравнению с минимальным квадратом самый маленький метод абсолютного отклонения лучше, поэтому он применяется во многих случаях. Наименьшее абсолютное отклонение значения — это надежность, поскольку оно может обрабатывать аномальные значения в данных. Это может быть полезно в исследованиях, которые могут быть безопасными и эффективно игнорируемыми. Если вам нужно рассмотреть какое -либо ненормальное значение любого или всего, минимальная квадратная ошибка является лучшим выбором.
В интуитивно понятной перспективе, поскольку номера моделей L2 будут квадратными (если ошибка больше 1, ошибка будет много увеличена), а ошибка модели будет больше, чем модель L1. Поэтому модель для минимизации ошибок. Если этот образец является аномальным значением, модель должна быть скорректирована, чтобы адаптироваться к одному ненормальному значению, которое будет жертвовать многими другими нормальными образцами, поскольку ошибка этих нормальных образцов меньше, чем ошибка одностороннего аномального значения.
стабильность
Нестабильность метода минимального абсолютного отклонения значения означает, что основная цепь может прыгать много волатильности в небольшом горизонтальном направлении набора данных. В некоторых структурах данных существует множество непрерывных решений для этого метода; однако небольшое движение набора данных пропустит многие непрерывные решения структуры данных в определенной области. （Метод имеет непрерывные решения для некоторых конфигураций данных; однако, перемещая датум на небольшое количество, можно «перепрыгнуть» на конфигурацию, которая имеет несколько решений, которые охватывают область.) ， Абсолютная линия отклонения может быть больше, чем предыдущая строка. Напротив, решение минимального плоского метода является стабильным, потому что для любых небольших колебаний в точке данных обратная линия всегда немного движется немного немного; то есть параметр регрессии является непрерывной функцией набора данных.

3. Главная функция потери L1 (также известная как функция потери Huber)

Функции потерь регрессии границы в более быстрых R-CNN и SSD являются гладкими (L_1) в качестве функции потери. На самом деле, как следует из названия, гладкий L1, как говорят, является L1 после плавного. Недостаток потери L1 раньше заключается в том, что существует точка складывания, а не гладкая, как сделать его плавным?
Плавная функция потери L1за:

в,

Гладкий L1 может ограничить градиент от двух аспектов:

Когда ящик предсказания слишком отличается от наземной истины, значение градиента не слишком велика;
Когда ящик предсказания отличается от групповой истины, значение градиента достаточно мало.

Из вышеперечисленного видно, что функция на самом деле является сегментной функцией, которая на самом деле является потерей L2 между [-1,1]. Фактически, это потеря L1, которая решает проблему градиентного взрыва из группы.

Реализация Pytorch 1

torch.nn.SmoothL1Loss(reduction='mean')

Реализация Pytorch 2

def _smooth_l1_loss(input, target, reduction='none'):
    # type: (Tensor, Tensor) -> Tensor
    t = torch.abs(input - target)
    ret = torch.where(t < 1, 0.5 * t ** 2, t - 0.5)
    if reduction != 'none':
        ret = torch.mean(ret) if reduction == 'mean' else torch.sum(ret)
    return ret

Вы также можете добавить бета -версию параметра для ее управления. Какой диапазон ошибок использует MSE, а ошибка в каком диапазоне использует MAE.
Реализация Pytorch 3

def smooth_l1_loss(input, target, beta=1. / 9, reduction = 'none'):
    """
    very similar to the smooth_l1_loss from pytorch, but with
    the extra beta parameter
    """
    n = torch.abs(input - target)
    cond = n < beta
    ret = torch.where(cond, 0.5 * n ** 2 / beta, n - 0.5 * beta)
    if reduction != 'none':
        ret = torch.mean(ret) if reduction == 'mean' else torch.sum(ret)
    return ret

4. Резюме

Для большинства сетей CNN мы обычно используем L2-Loss вместо L1-Loss, потому что скорость сходимости L2-потери намного быстрее, чем L1-Loss.

Для проблемы регрессии прогноза границы вы обычно можете выбрать функцию потери квадрата (потеря L2), но недостаток модели L2 заключается в том, что когда есть выбросы, эти точки будут занимать основную часть потери. Например, реальное значение составляет 1, прогноз в 10 раз, значение прогноза составляет 1000, а остальное значение прогноза составляет примерно 1. Очевидно, что значение потери в основном определяется 1000. Следовательно, Fastrcnn использует слегка ослабленную функцию абсолютной потери (плавная потеря L1), которая линейно увеличивается с ошибками, а не в квадратном росте.

Разница между плавными функциями потери L1 и L1 заключается в том, что потеря L1 не является уникальной в 0 точках, что может повлиять на сходимость. Плавное решение L1 — использовать квадратную функцию вблизи 0 часов, чтобы сделать ее более плавной.

Преимущества плавного L1

По сравнению с функцией потери L1, он может сходиться быстрее;
По сравнению с функцией потери L2, он не чувствителен к Outliex и аномальным значениям, и изменение градиента относительно меньше, и его нелегко работать во время тренировок.

Источник

Перепечатано:https://mp.weixin.qq.com/s/Xbi5iOh3xoBIK5kVmqbKYA

https://baijiahao.baidu.com/s?id=1611951775526158371&wfr=spider&for=pc

Будь то в машинном обучении или в поле, функция потери является очень важной точкой знания. Функция потерь (функция потери) является несоответствием между прогнозирующим значением f (x), используемым для оценки модели F (x) и реальным значением y. Наша цель — минимизировать функцию потери, чтобы F (x) был как можно ближе к Y. Обычно вы можете использовать алгоритмы падения градиента, чтобы найти минимальное значение функции.

Для наиболее простого объяснения снижения градиента вы можете прочитать эту статью:

Вы действительно понимаете простой алгоритм падения градиента?

Существует много различных типов функций потерь, и никакая функция потерь не подходит для всех задач. Он должен быть выбран в соответствии с конкретной моделью и проблемой. В целом, функция потери может быть примерно разделена на две категории: регрессия и классификация. Сегодня Red Stones суммирует три функции потерь, обычно используемые в проблеме регрессии, надеясь помочь вам.

Три функции потерь в модели регрессии включают в себя: среднюю квадратную ошибку, среднюю абсолютную ошибку (MAE) и потерю Huber.

1. Средняя квадратная ошибка (MSE)

Выражаемая квадратная ошибка относится к среднему расстоянию между значением прогнозирования модели F (x) и реальным значением y выборки. Формула показана ниже:

Среди них Yi и F (xi) представляют реальные значения и значения прогнозирования образца I -i, соответственно, а M -это количество образцов.

Чтобы упростить обсуждение, игнорировать ставку I, M = 1, используйте y-f (x) в качестве горизонтальных координат, MSE в качестве вертикальных координат, нарисуйте графику функции потери:

Характеристика кривой MSE является гладкой и непрерывной, может использоваться для облегчения использования алгоритмов градиентного падения. Это обычно используемая функция потерь. Кроме того, MSE также уменьшается с уменьшением ошибок, что также способствует сходимости функции. Даже если фиксированный коэффициент обучения фиксирован, функция может быстро получить минимальное значение.

Квадратная ошибка имеет характеристику, что, когда разница между Yi и F (xi) превышает 1, она увеличит свою ошибку; когда разница между Yi и F (xi) меньше 1, она уменьшит свою ошибку. Это определяется характеристиками квадрата. Другими словами, MSE дает большее наказание ситуации больших ошибок (> 1) и меньшее наказание за ситуацию с меньшей ошибкой (<1). С точки зрения обучения, модель будет более ориентирована на наказать большие очки и придать ей больший вес.

Если в выборке есть групповая точка, MSE придаст групповой точке более высокий вес, но это за счет затрат на то, чтобы жертвовать другими нормальными точками данных, что в конечном итоге снизит общую производительность модели. Давайте посмотрим на использование MSE для решения модели регрессии, содержащей группу.

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1, 20, 40)
y = x + [np.random.choice(4) for _ in range(40)]
y[-5:] -= 8
 X = np.vstack ((np.one_like (x), x), x) # Представьте постоянный элемент 1
m = X.shape[1]
 # Инициализация параметра
W = np.zeros((1,2))

 #Тренировка 
num_iter = 20
lr = 0.01
J = []
for i in range(num_iter):
   y_pred = W.dot(X)
   loss = 1/(2*m) * np.sum((y-y_pred)**2)
   J.append(loss)
   W = W + lr * 1/m * (y-y_pred).dot(X.T)

 #    
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2])
plt.show()

Результаты подгонки показаны на рисунке ниже:

Можно видеть, что на использование функции потери MSE больше влияет точки группы. Хотя в выборке есть только 5 исходящих точек, подходящая прямая линия относительно смещена в сторону группы. Это часто то, что мы не хотим видеть.

2. Средняя абсолютная ошибка (MAE)

Средняя абсолютная ошибка относится к среднему значению прогнозирования модели F (x) и реальным значением y выборки. Формула показана ниже:

Чтобы упростить обсуждение, игнорировать ставку i, m = 1, используйте y-f (x) в качестве горизонтальных координат, и MAE в качестве вертикальных координат, чтобы нарисовать графику функции потери:

С точки зрения интуитивно понятной перспективы, кривая MAE является V-образной формой, которая непрерывна, но не управляется при Y-F (x) = 0. Трудно найти количество руководств на компьютере. И большая часть MAE равна, что означает, что даже для небольших потерь градиент большой. Это не способствует конвергенции функции и изучению модели.

Стоит отметить, что у MAE есть преимущество по сравнению с MSE, что является то, что MAE не так чувствителен и терпима к группе. Поскольку MAE вычисляет абсолютное значение ошибки y-f (x), будь то y-f (x)> 1 или y-f (x) <1, нет квадратного элемента, а сила наказания одинакова, а вес-это такой же. Для примеров в MSE давайте использовать MAE для решения его и посмотрим, что отличается от линии соответствия.

X = np.vstack ((np.one_like (x), x), x) # Представьте постоянный элемент 1
m = X.shape[1]
 # Инициализация параметра
W = np.zeros((1,2))

 #Тренировка 
num_iter = 20
lr = 0.01
J = []
for i in range(num_iter):
   y_pred = W.dot(X)
   loss = 1/m * np.sum(np.abs(y-y_pred))
   J.append(loss)
   mask = (y-y_pred).copy()
   mask[y-y_pred > 0] = 1
   mask[mask <= 0] = -1
   W = W + lr * 1/m * mask.dot(X.T)

 #    
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2],'r--')
plt.xlabel('x')
plt.ylabel('y')
plt.title('MAE')
plt.show()

Обратите внимание, что градиентная часть расчета MAE расчета MAE в вышеуказанном коде.

Результаты подгонки показаны на рисунке ниже:

Очевидно, что использование функции потери MAE меньше влияет на исходящую точку, и линия FIT может лучше охарактеризовать распределение нормальных данных. В связи с этим MAE лучше, чем MSE. Сравнительная диаграмма этих двух заключается в следующем:

Выберите MSE или MAE?

В практических приложениях мы должны выбрать MSE или MAE? С точки зрения сложности компьютера для решения градиента, MSE лучше, чем MAE, и градиент также динамически изменяется, что может быстро и точно достигать сходимости. Однако с точки зрения отправления, если группа является фактическим или важным данных, и это является аномальным значением, которое следует обнаружить, тогда мы должны использовать MSE. С другой стороны, точка группы представляет только образцы повреждения данных или ошибки, и нет необходимости уделять слишком много внимания, тогда мы должны выбрать MAE в качестве убытки.

3. Huber Loss

Поскольку у MSE и MAE есть свои собственные преимущества и недостатки, существует ли функция активации, которая может устранить недостатки двух одновременно и собирать преимущества двух? Ответ да. Huber Loss имеет это преимущество, и его формула выглядит следующим образом:

Потеря Huber является синтезом двух и содержит супер -верховный Δ. Размер значения Δ определяет фокус потери Huber для MSE и MAE. Когда | y — f (x) | ≤ Δ становится MSE; когда | y — f (x) |> Δ, он становится аналогичным схожим в Мэй, Хубер Потеря имеет преимущества MSE и MAE одновременно, уменьшает проблему чувствительности исходящих точек и реализует функцию руководства повсюду.

Вообще говоря, супер параметр δ может быть выбран путем перекрестной проверки. Ниже возьмите Δ = 0,1, Δ = 10 соответственно и нарисуйте соответствующую потерю Huber, как показано на рисунке ниже:

Когда потеря Huber находится в | y — f (x) |> Δ, градиент всегда был похож на Δ, что может гарантировать, что модель обновляет параметр с более высокой скоростью. Когда | y (f (x) | ≤ Δ, градиент постепенно уменьшается, что может гарантировать, что модель является более точной, чтобы получить глобальное оптимальное значение. Следовательно, потеря убытков имеет преимущества первых двух потерь.

Ниже мы используем потерю Huber для решения того же примера.

X = np.vstack ((np.one_like (x), x), x) # Представьте постоянный элемент 1
m = X.shape[1]
 # Инициализация параметра
W = np.zeros((1,2))

 #Тренировка 
num_iter = 20
lr = 0.01
delta = 2
J = []
for i in range(num_iter):
   y_pred = W.dot(X)
   loss = 1/m * np.sum(np.abs(y-y_pred))
   J.append(loss)
   mask = (y-y_pred).copy()
   mask[y-y_pred > delta] = delta
   mask[mask < -delta] = -delta
   W = W + lr * 1/m * mask.dot(X.T)

 #    
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2],'r--')
plt.xlabel('x')
plt.ylabel('y')
plt.title('MAE')
plt.show()

Обратите внимание на часть градиента вычислений потерь Хубер в приведенном выше коде.

Результаты подгонки показаны на рисунке ниже:

Можно видеть, что использование потери Huber в качестве функции активации все еще имеет хорошую анти -интерфейс в исходящую точку, которая сильнее MSE. Кроме того, мы нарисуем тенденцию потери, соответствующую этим трем функциям потерь как количество изменений итерации:

MSE： MAE： Huber Loss：

По сравнению с обнаружением, что потеря MSE падает по самым быстрым, потеря MAE уменьшается самая медленная, а потеря потеря Huber между MSE и MAE. Другими словами, потеря Huber компенсирует проблему медленного уменьшения снижения потерь в этом примере, что делает скорость оптимизации близко к MSE.

Наконец, мы все нарисуем все три потери в проблеме регрессии, представленной выше.

Что ж, вышеуказанное представляет собой три обычно используемые функции потерь красных камней в задаче регрессии, включают в себя: MSE, MAE, краткое введение Huber Loss и подробное сравнение. Вы уже освоили эти простые знания?

В дополнение к MSE, MAE, HUBER LOSS, в регрессионной миссии, мы также будем использовать потерю LOG-COSH, что может обеспечить существование производной второго порядка. Некоторые алгоритмы оптимизации будут использовать производные второго порядка. В XGBOOS В то же время мы будем использовать потерю сегментации, надеясь дать неопределенную меру.

В дополнение к журналу и шарниру, в классифицированных задачах у нас также есть функции потерь, такие как контрастные потери, потери сеплярного энтропии Softmax и потери центра, которые обычно используются в нейронных сетях.

4 focal loss

От:https://blog.csdn.net/zjucor/article/details/84259969

Например, партия составляет 32 образца, а 8 -й вывод метки можно рассматривать как вторую категорию из 32*8 образца. Естественно, 32*8 Образец положительных и отрицательных образцов, если 2 метки). Это фокусная потеря, которая может сыграть отличную роль

For the multi-label classification, you can try tanh+hinge with {-1, 1} values in labels like (1, -1, -1, 1). Or sigmoid + hamming loss with {0, 1} values in labels like (1, 0, 0, 1). In my case, sigmoid + focal loss with {0, 1} values in labels like (1, 0, 0, 1) worked well. You can check this paper https://arxiv.org/abs/1708.02002.

class FocalLoss(nn.Module):
    def __init__(self, gamma=2):
        super().__init__()
        self.gamma = gamma
        
    def forward(self, input, target):
        if not (target.size() == input.size()):
            raise ValueError("Target size ({}) must be the same as input size ({})"
                             .format(target.size(), input.size()))
 
        max_val = (-input).clamp(min=0)
        loss = input - input * target + max_val + 
            ((-max_val).exp() + (-input - max_val).exp()).log()
 
        invprobs = F.logsigmoid(-input * (target * 2.0 - 1.0))
        loss = (invprobs * self.gamma).exp() * loss
        
        return loss.sum(dim=1).mean()

Источник

Перевод

Ссылка на автора

Тип задачи: регрессия? Классификация?
Бизнес цель?
Каково распределение целевой переменной?

Остров Андрос в Греции

Метрики регрессии

Средняя квадратическая ошибка (MSE)
Среднеквадратическая ошибка (RMSE)
Средняя абсолютная ошибка (MAE)
R в квадрате (R²)
Скорректированный R квадрат (R²)
Среднеквадратичная ошибка в процентах (MSPE)
Средняя абсолютная ошибка в процентах (MAPE)
Среднеквадратичная логарифмическая ошибка (RMSLE)

Средняя квадратическая ошибка (MSE)

гдеyᵢфактический ожидаемый результат иŷᵢэто прогноз модели.

Среднеквадратическая ошибка (RMSE)

Теперь очень важно понять, в каком смысле RMSE похож на MSE, и в чем разница.

Что это значит для нас?

Градиент СКО относительно i-го прогноза

Средняя абсолютная ошибка (MAE)

R в квадрате (R²)

Когда R² отрицательно, это означает, что модель хуже, чем предсказание среднего значения.

MSE модели рассчитывается, как указано выше, в то время как MSE базовой линии определяется как:

гдеYс чертой означает среднее из наблюдаемогоyᵢ.

MAE против MSE

Взять домой сообщение

Спасибо за чтение, и я с нетерпением жду, чтобы услышать ваши вопросы Наслаждайтесь!

Ресурсы:
[1] https://dmitryulyanov.github.io/about

Источник

Выбор функции потерь для задач построения нейронных сетей

Время прочтения: 4 мин.

В рамках данной статьи мы рассмотрим три функции потерь для нейронных сетей, решающих регрессионные задачи.

Mean Squared Error

Mean Absolute Error

Mean Squared Logarithmic Error

Код используемый для демонстрации:

from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# формирование датасета
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# нормализация
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# разделение
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# определение для модели
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss=вид функции потерь, optimizer=opt)
# расчёт
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Оценка качества
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot Демонстрация результата
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()

В данном коде мы будем заменять только указанный вид функции потерь.
Результат для MSE:

model.compile(loss='mean_squared_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.000, Test: 0.001

Как видно из графика, модель показывает хорошую сходимость и низкое отклонение.

Результат для MSLE:

model.compile(loss=' mean_squared_logarithmic_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.165, Test: 0.184

model.compile(loss='mean_absolute_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.002, Test: 0.002

Источник

From Wikipedia, the free encyclopedia

${displaystyle mathrm {MAE} ={frac {sum _{i=1}^{n}left|y_{i}-x_{i}right|}{n}}={frac {sum _{i=1}^{n}left|e_{i}right|}{n}}.}$

It is thus an arithmetic average of the absolute errors ${displaystyle |e_{i}|=|y_{i}-x_{i}|}$ , where $y_{i}$ is the prediction and $x_{i}$ the true value. Alternative formulations may include relative frequencies as weight factors. The mean absolute error uses the same scale as the data being measured. This is known as a scale-dependent accuracy measure and therefore cannot be used to make comparisons between predicted values that use different scales.^[2] The mean absolute error is a common measure of forecast error in time series analysis,^[3] sometimes used in confusion with the more standard definition of mean absolute deviation. The same confusion exists more generally.

Quantity disagreement and allocation disagreement[edit]

2 data points for which Quantity Disagreement is 0 and Allocation Disagreement is 2 for both MAE and RMSE

It is possible to express MAE as the sum of two components: Quantity Disagreement and Allocation Disagreement. Quantity Disagreement is the absolute value of the Mean Error given by:^[4]

${displaystyle mathrm {ME} ={frac {sum _{i=1}^{n}y_{i}-x_{i}}{n}}.}$

Allocation Disagreement is MAE minus Quantity Disagreement.

[edit]

Optimality property[edit]

The mean absolute error of a real variable c with respect to the random variable X is

${displaystyle E(left|X-cright|)}$

More generally, a median is defined as a minimum of

${displaystyle E(|X-c|-|X|),}$

as discussed at Multivariate median (and specifically at Spatial median).

This optimization-based definition of the median is useful in statistical data-analysis, for example, in k-medians clustering.

Proof of optimality[edit]

Statement: The classifier minimising ${displaystyle mathbb {E} |y-{hat {y}}|}$ is ${displaystyle {hat {f}}(x)={text{Median}}(y|X=x)}$ .

Proof:

The Loss functions for classification is

${displaystyle {begin{aligned}L&=mathbb {E} [|y-a||X=x]\&=int _{-infty }^{infty }|y-a|f_{Y|X}(y),dy\&=int _{-infty }^{a}(a-y)f_{Y|X}(y),dy+int _{a}^{infty }(y-a)f_{Y|X}(y),dy\end{aligned}}}$

Differentiating with respect to a gives

${displaystyle {frac {partial }{partial a}}L=int _{-infty }^{a}f_{Y|X}(y),dy+int _{a}^{infty }-f_{Y|X}(y),dy=0}$

This means

${displaystyle int _{-infty }^{a}f(y),dy=int _{a}^{infty }f(y),dy}$

Hence

${displaystyle F_{Y|X}(a)=0.5}$

References[edit]

^ Willmott, Cort J.; Matsuura, Kenji (December 19, 2005). «Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance». Climate Research. 30: 79–82. doi:10.3354/cr030079.
^ «2.5 Evaluating forecast accuracy | OTexts». www.otexts.org. Retrieved 2016-05-18.
^ Hyndman, R. and Koehler A. (2005). «Another look at measures of forecast accuracy» [1]
^ ^a ^b ^c Pontius Jr., Robert Gilmore; Thontteh, Olufunmilayo; Chen, Hao (2008). «Components of information for multiple resolution comparison between maps that share a real variable». Environmental and Ecological Statistics. 15 (2): 111–142. doi:10.1007/s10651-007-0043-y. S2CID 21427573.
^ Willmott, C. J.; Matsuura, K. (January 2006). «On the use of dimensioned measures of error to evaluate the performance of spatial interpolators». International Journal of Geographical Information Science. 20: 89–102. doi:10.1080/13658810500286976. S2CID 15407960.
^ Stroock, Daniel (2011). Probability Theory. Cambridge University Press. pp. 43. ISBN 978-0-521-13250-3.
^ DeGroot, Morris H. (1970). Optimal Statistical Decisions. McGraw-Hill Book Co., New York-London-Sydney. p. 232. MR 0356303.

Источник

Quantity disagreement and allocation disagreement[edit]

[edit]

Optimality property[edit]

Proof of optimality[edit]

See also[edit]

References[edit]

Quantity disagreement and allocation disagreement[edit]

[edit]

Optimality property[edit]

Proof of optimality[edit]

See also[edit]

References[edit]

Метрики регрессии

Средняя квадратическая ошибка (MSE)

Среднеквадратическая ошибка (RMSE)

R в квадрате (R²)

MAE против MSE

Взять домой сообщение

Пример: Расчет RMSE и MAE

RMSE против MAE: какую метрику следует использовать?

Дополнительные ресурсы

MSE

MAE

Квантильные оценки

Функция правдоподобия

Сквозной пример

Данные и постановка задачи

Разделение выборки

Исследовательский анализ данных

Обработка данных

Пропущенные значения

Выбросы

Масштабирование признаков

Кодирование категориальных переменных

Построение модели

baseline-модель

Оценка качества

Диагностика модели, метрики качества и функции потерь

MSE, RMSE, MAE, MAPE

MSE и RMSE

MAE

MAPE

Коэффициент детерминации

Диагностика модели

Анализ остатков и прогнозных значений

Мультиколлинеарность

Дополнительная обработка данных

VIF

Преобразование данных

Отбор признаков

Повторное моделирование и диагностика

Повторное моделирование

Оценка качества и диагностика

Коэффициенты

Обучение модели

Векторизация уравнения

Функция потерь

Абсолютная ошибка, L1 loss

Квадрат ошибки, L2 loss

Функция Хьюбера

Метод наименьших квадратов

Нормальные уравнения

Код на Питоне

Создание класса

Оценка качества

Метод градиентного спуска

Нахождение градиента

Пошаговое построение модели

Прогноз

Создание класса

Оценка качества

Диагностика алгоритма

Подведем итог

Выбор функции потерь для задач построения нейронных сетей

1. Общие функции потери MSE и MAE

1.1, средняя квадратная ошибка MSE

1.2. Средняя абсолютная ошибка MAE

1.3, MSE и MAE CHOOCES

2. L1_Loss и L2_Loss

2.1, l1_loss и l2_loss