| Определение: |
| Код Грея (англ. Gray code) — такое упорядочение -ичных (обычно двоичных) векторов, что соседние вектора отличаются только в одном разряде. |
Код назван в честь Фрэнка Грея, который в 1947-ом году получил патент на «отражённый двоичный код».
Содержание
- 1 Алгоритм построения
- 1.1 Псевдокод
- 1.2 Доказательство правильности работы алгоритма
- 2 Явная формула для получения зеркального двоичного кода Грея
- 2.1 Сбалансированный код Грея
- 2.2 Однодорожечный код Грея
- 3 Применение
- 3.1 Задача о Ханойских башнях
- 4 См. Также
- 5 Примечания
- 6 Источники информации
Алгоритм построения
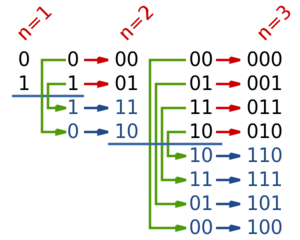
Получение зеркального двоичного кода Грея.
Существует несколько видов кода Грея, самый простой из них — так называемый зеркальный двоичный код Грея. Строится он так:
Для получения кода длины производится шагов. На первом шаге код имеет длину и состоит из двух векторов и . На каждом следующем шаге в конец списка заносятся все уже имеющиеся вектора в обратном порядке, и затем к первой половине получившихся векторов дописывается , а ко второй . С каждым шагом длина векторов увеличивается на , а их количество — вдвое.
Таким образом, количество векторов длины равно
Псевдокод
- — двумерный массив типа boolean, в котором — -ый бит в -ом коде Грея,
- — Счетчик количества уже имеющихся кодов,
- — Показывает количество кодов в -м коде Грея.
buildCode(n): GrayCode[1, n] = false GrayCode[2, n] = true // Построение кода длины 1 p = 2 for i = 2 to n t = p p = p * 2 for k = (p / 2 + 1) to p GrayCode[k] = GrayCode[t] // Отражение имеющихся кодов GrayCode[t, n + 1 - i] = false GrayCode[k, n + 1 - i] = true // Добавление 0 и 1 в начало t-- return GrayCode
Доказательство правильности работы алгоритма
По индукции:
- на первом шаге код отвечает условиям
- предположим, что код, получившийся на -ом шаге, является кодом Грея
- тогда на шаге : первая половина кода будет корректна, так как она совпадает с кодом с шага за исключением добавленного последнего бита . Вторая половина тоже соответствует условиям, так как она является зеркальным отражением первой половины, только добавлен везде бит . На стыке: первые бит совпадают в силу зеркальности, последние различны по построению.
Таким образом, этот код — код Грея. Индукционное предположение доказано, алгоритм работает верно.
Этот алгоритм можно обобщить и для -ичных векторов. Также известен алгоритм преобразования двоичного кода в код Грея.
Существует ещё несколько видов кода Грея — сбалансированный код Грея, код Баркера-Грея, одноколейный код Грея.[1] Кроме того, коды Грея используются для упорядочения перестановок.
Явная формула для получения зеркального двоичного кода Грея
| Теорема: |
|
В двоичном зеркальном коде Грея -ый код может быть получен по формуле при нумерации кодов с нуля. |
| Доказательство: |
|
Для кода длиной бит утверждение проверяется непосредственно. Пусть существует зеркальный двоичный код Грея длины , для которого выполнено, что для любого выполняется Обозначим за код длины , полученный из описанным выше алгоритмом. Тогда: Для любого выполняется и, по условию, равно раскрыв скобки, получим новое выражение : что равно (второе слагаемое равно первому, побитово сдвинутого вправо.) Для любого выполняется , где , то есть что по свойству xor () равно или (все по тому же свойству) раскрыв скобки, получим откуда получаем, зная из условия, что старший разряд равен что, аналогично первому пункту, равно Таким образом, шаг индукции доказан, следовательно, теорема верна. |

Пример однодорожечного кода грея.
Сбалансированный код Грея
Несмотря на то, что зеркальный двоичный код Грея полезен во многих случаях, он не является оптимальным в некоторых ситуациях из-за отсутствия «однородности». В сбалансированном коде Грея, количество изменений в различных координатных позициях сделаны максимально приближенными настолько, насколько это возможно.
Чтобы показать это точнее, пусть — это -ичный полный цикл Грея, имеющий последовательность перехода , , для если в коде Грея -й и биты различны и — кол-во таких различий; отсчёты переходов (спектры) являются наборами целых чисел, определенных как для .
Код Грея является однородным или равномерно сбалансированным, если все его отсчёты переходов равны, и в этом случае у нас есть для всех . Ясно, что при , такие коды существуют только при . В противном случае, если не делится на равномерно, то можно построить сбалансированные коды Грея, где каждый отсчёт перехода либо либо .
Коды Грея также могут быть экспоненциально сбалансироваными, если все их отсчеты переходов являются смежными степеням двойки, и такие коды существуют для каждой степени двойки.
Однодорожечный код Грея
Еще один вид кода Грея — это однодорожечный код Грея, разработанный Спеддингом и уточнен Хильтгеном, Патерсоном и Брандестини.
Однодорожечный код Грея является циклическим списком уникальных двоичных кодировок длины так, что два последовательных слова отличаются ровно в одной позиции, и когда список рассматривается как матрица, каждая колонка — это циклический сдвиг первого столбца. Название происходит от их использования датчиками вращения, где количество дорожек в настоящее время измеряется с помощью контактов, в результате для каждой дорожки на выход подаётся или .
Чтобы снизить уровнень шума различных контактов не переключаясь в тот же момент времени, один датчик предпочтительно устанавливает дорожки так, что выход данных от контактов находится в коде Грея. Чтобы получить высокую угловую точность, нужно много контактов; для достижения точности хотя бы в градус нужно, по крайней мере, различных позиций на оборот, который требует минимум бит данных, и тем самым такое же количество контактов.
Не путать с цепными кодами, получаемых циклическим сдвигом.
Применение
Фрэнк Грей изобрел метод для преобразования аналоговых сигналов в отраженные двоичные кодовые группы с использованием аппарата на основе вакуумной трубки. Способ и устройство были запатентованы в 1953 году, а код получил название код Грея. «PCM трубка» — аппарат, запатентованный Греем, был сделан Раймондом У. Сирсом из (англ.) Bell Labs, работая с Греем и Уильямом М. Гудоллом.
- В технике коды Грея используются для минимизации ошибок при преобразовании аналоговых сигналов в цифровые (например, в датчиках-энкодерах [2]).
В частности, коды Грея и были открыты в связи с этим применением. (Код Грея — это код преобразования бинарных символов в -арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются только одним битом. Обычная бинарная кодировка сравнивается с кодировкой Грея. При появлении ошибки в -арном символе наиболее вероятными являются ближайшие соседние символы, отличающиеся от переданного лишь одним битом, если используется кодировка Грея.
Таким образом, высока вероятность того, что при кодировании с помощью кода Грея в случае возникновения ошибки ошибочным будет только один из переданных битов.)
- Коды Грея используются для кодирования номера дорожек в жёстких дисках.
- Коды Грея широко применяются в теории генетических алгоритмов [3] для кодирования генетических признаков, представленных целыми числами.
- Коды Грея используются в Картах Карно[4] (при передаче в карту переменные сортируются в код Грея).
- Алгоритм модуляции 2B1Q (англ. 2 Binary 1 Quandary) [5]
- Код Грея можно использовать также и для решения следующей задачи[6]:
Задача о Ханойских башнях
| Задача: |
| Даны три стержня, на один из которых нанизаны восемь колец, причем кольца отличаются размером и лежат меньшее на большем. Задача состоит в том, чтобы перенести пирамиду из восьми колец за наименьшее число ходов на другой стержень. За один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее. |
Решение:
Пусть — количество дисков. Начнём с кода Грея длины , состоящего из одних нулей (т.е. ), и будем двигаться по кодам Грея (от переходить к ).
Поставим в соответствие каждому -ому биту текущего кода Грея -ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита как перемещение -го диска. То есть, будем понимать переход от последовательности к как перемещение -го диска на свободное место, а от к — как перемещение -го диска на свободное место.
Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для самого маленького диска всегда есть две свободные позиции, потому что он самый маленький, его можно положить сверху на любой диск. Если диск не самый маленький, то для него может быть не более одной свободной позиции. Допустим, что для него свободные две позиции. Это означает, что на двух других стержнях расположены диски размером больше, чем рассматриваемый. А так как рассматриваемый диск не самый маленький, то где-то расположен наименьший. Либо он расположен на рассматриваемом диске, тогда мы не можем переместить рассматриваемый, либо на каком-то другом, но тогда у нашего диска остаётся не более одной свободной позиции. Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если нечётно, то последовательность перемещений наименьшего диска имеет вид (где — стартовый стержень, — финальный стержень, — оставшийся стержень), а если чётно, то
Выбор обусловлен тем, на каком стержне окажется в конце пирамидка, решение с помощью кода Грея является следствием классического нерекурсивного решения[7].
См. Также
- Коды антигрея
Примечания
- ↑ Wikipedia — Special types of Gray codes
- ↑ Википедия — Датчик угла поворота
- ↑ Википедия — Генетический алгоритм
- ↑ Википедия — Карта Карно
- ↑ Wikipedia — 2B1Q
- ↑ Википедия — Ханойская Башня
- ↑ Wikipedia — Tower of Hanoi Non-recursive solution
Источники информации
- Wikipedia — Gray code
- Википедия — Код Грея
- Robert W. Doran The Gray Code, Journal of Universal Computer Science, vol. 13, no. 11 (2007).
| Lucal code[1][2] | |||||
|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | |
| Gray code | |||||
| 4 | 3 | 2 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 0 | 0 |
| 5 | 0 | 1 | 1 | 1 | 1 |
| 6 | 0 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 | 1 |
| 8 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 0 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 0 |
| 11 | 1 | 1 | 1 | 0 | 1 |
| 12 | 1 | 0 | 1 | 0 | 0 |
| 13 | 1 | 0 | 1 | 1 | 1 |
| 14 | 1 | 0 | 0 | 1 | 0 |
| 15 | 1 | 0 | 0 | 0 | 1 |
The reflected binary code (RBC), also known as reflected binary (RB) or Gray code after Frank Gray, is an ordering of the binary numeral system such that two successive values differ in only one bit (binary digit).
For example, the representation of the decimal value «1» in binary would normally be «001» and «2» would be «010«. In Gray code, these values are represented as «001» and «011«. That way, incrementing a value from 1 to 2 requires only one bit to change, instead of two.
Gray codes are widely used to prevent spurious output from electromechanical switches and to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.
Function[edit]
Many devices indicate position by closing and opening switches. If that device uses natural binary codes, positions 3 and 4 are next to each other but all three bits of the binary representation differ:
-
Decimal Binary … … 3 011 4 100 … …
The problem with natural binary codes is that physical switches are not ideal: it is very unlikely that physical switches will change states exactly in synchrony. In the transition between the two states shown above, all three switches change state. In the brief period while all are changing, the switches will read some spurious position. Even without keybounce, the transition might look like 011 — 001 — 101 — 100. When the switches appear to be in position 001, the observer cannot tell if that is the «real» position 1, or a transitional state between two other positions. If the output feeds into a sequential system, possibly via combinational logic, then the sequential system may store a false value.
This problem can be solved by changing only one switch at a time, so there is never any ambiguity of position, resulting in codes assigning to each of a contiguous set of integers, or to each member of a circular list, a word of symbols such that no two code words are identical and each two adjacent code words differ by exactly one symbol. These codes are also known as unit-distance,[3][4][5][6][7] single-distance, single-step, monostrophic[8][9][6][7] or syncopic codes,[8] in reference to the Hamming distance of 1 between adjacent codes.
Invention[edit]

Gray’s patent introduces the term «reflected binary code»
In principle, there can be more than one such code for a given word length, but the term Gray code was first applied to a particular binary code for non-negative integers, the binary-reflected Gray code, or BRGC. Bell Labs researcher
George R. Stibitz described such a code in a 1941 patent application, granted in 1943.[10][11][12] Frank Gray introduced the term reflected binary code in his 1947 patent application, remarking that the code had «as yet no recognized name».[13] He derived the name from the fact that it «may be built up from the conventional binary code by a sort of reflection process».
In the standard encoding the least significant bit follows a repetitive pattern of 2 on, 2 off ( … 11001100 … ); the next digit a pattern of 4 on, 4 off; the nth least significant bit a pattern of 2n on 2n off. The four-bit version of this is shown below:


Gray code along the number line
-
Decimal Binary Gray Decimal
of Gray0 0000 0000 0 1 0001 0001 1 2 0010 0011 3 3 0011 0010 2 4 0100 0110 6 5 0101 0111 7 6 0110 0101 5 7 0111 0100 4 8 1000 1100 12 9 1001 1101 13 10 1010 1111 15 11 1011 1110 14 12 1100 1010 10 13 1101 1011 11 14 1110 1001 9 15 1111 1000 8
For decimal 15 the code rolls over to decimal 0 with only one switch change. This is called the cyclic or adjacency property of the code.[14]
In modern digital communications, Gray codes play an important role in error correction. For example, in a digital modulation scheme such as QAM where data is typically transmitted in symbols of 4 bits or more, the signal’s constellation diagram is arranged so that the bit patterns conveyed by adjacent constellation points differ by only one bit. By combining this with forward error correction capable of correcting single-bit errors, it is possible for a receiver to correct any transmission errors that cause a constellation point to deviate into the area of an adjacent point. This makes the transmission system less susceptible to noise.
Despite the fact that Stibitz described this code[10][11][12] before Gray, the reflected binary code was later named after Gray by others who used it. Two different 1953 patent applications use «Gray code» as an alternative name for the «reflected binary code»;[15][16] one of those also lists «minimum error code» and «cyclic permutation code» among the names.[16] A 1954 patent application refers to «the Bell Telephone Gray code».[17] Other names include «cyclic binary code»,[11] «cyclic progression code»,[18][11] «cyclic permuting binary»[19] or «cyclic permuted binary» (CPB).[20][21]
The Gray code is sometimes misattributed to 19th century electrical device inventor Elisha Gray.[12][22][23][24]
History and practical application[edit]
Mathematical puzzles[edit]
Reflected binary codes were applied to mathematical puzzles before they became known to engineers.
The binary-reflected Gray code represents the underlying scheme of the classical Chinese rings puzzle, a sequential mechanical puzzle mechanism described by the French Louis Gros in 1872.[25][12]
It can serve as a solution guide for the Towers of Hanoi problem, based on a game by the French Édouard Lucas in 1883.[26][27][28][29] Similarly, the so-called Towers of Bucharest and Towers of Klagenfurt game configurations yield ternary and pentary Gray codes.[30]
Martin Gardner wrote a popular account of the Gray code in his August 1972 Mathematical Games column in Scientific American.[31]
The code also forms a Hamiltonian cycle on a hypercube, where each bit is seen as one dimension.
Telegraphy codes[edit]
When the French engineer Émile Baudot changed from using a 6-unit (6-bit) code to 5-unit code for his printing telegraph system, in 1875[32] or 1876,[33][34] he ordered the alphabetic characters on his print wheel using a reflected binary code, and assigned the codes using only three of the bits to vowels. With vowels and consonants sorted in their alphabetical order,[35][36][37] and other symbols appropriately placed, the 5-bit character code has been recognized as a reflected binary code.[12] This code became known as Baudot code[38] and, with minor changes, was eventually adopted as International Telegraph Alphabet No. 1 (ITA1, CCITT-1) in 1932.[39][40][37]
About the same time, the German-Austrian Otto Schäffler [de][41] demonstrated another printing telegraph in Vienna using a 5-bit reflected binary code for the same purpose, in 1874.[42][12]
Analog-to-digital signal conversion[edit]
Frank Gray, who became famous for inventing the signaling method that came to be used for compatible color television, invented a method to convert analog signals to reflected binary code groups using vacuum tube-based apparatus. Filed in 1947, the method and apparatus were granted a patent in 1953,[13] and the name of Gray stuck to the codes. The «PCM tube» apparatus that Gray patented was made by Raymond W. Sears of Bell Labs, working with Gray and William M. Goodall, who credited Gray for the idea of the reflected binary code.[43]
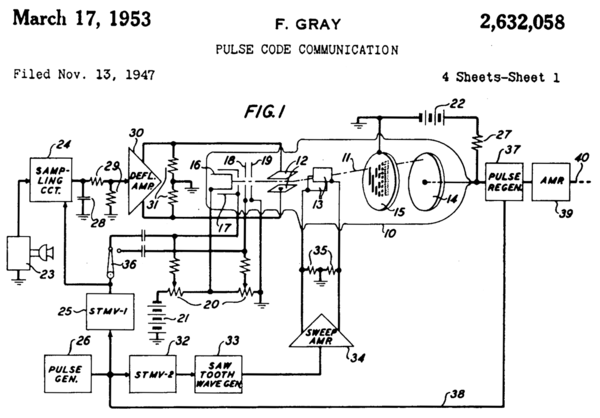
Part of front page of Gray’s patent, showing PCM tube (10) with reflected binary code in plate (15)
Gray was most interested in using the codes to minimize errors in converting analog signals to digital; his codes are still used today for this purpose.
Position encoders[edit]

Rotary encoder for angle-measuring devices marked in 3-bit binary-reflected Gray code (BRGC)

A Gray code absolute rotary encoder with 13 tracks. Housing, interrupter disk, and light source are in the top; sensing element and support components are in the bottom.
Gray codes are used in linear and rotary position encoders (absolute encoders and quadrature encoders) in preference to weighted binary encoding. This avoids the possibility that, when multiple bits change in the binary representation of a position, a misread will result from some of the bits changing before others.
For example, some rotary encoders provide a disk which has an electrically conductive Gray code pattern on concentric rings (tracks). Each track has a stationary metal spring contact that provides electrical contact to the conductive code pattern. Together, these contacts produce output signals in the form of a Gray code. Other encoders employ non-contact mechanisms based on optical or magnetic sensors to produce the Gray code output signals.
Regardless of the mechanism or precision of a moving encoder, position measurement error can occur at specific positions (at code boundaries) because the code may be changing at the exact moment it is read (sampled). A binary output code could cause significant position measurement errors because it is impossible to make all bits change at exactly the same time. If, at the moment the position is sampled, some bits have changed and others have not, the sampled position will be incorrect. In the case of absolute encoders, the indicated position may be far away from the actual position and, in the case of incremental encoders, this can corrupt position tracking.
In contrast, the Gray code used by position encoders ensures that the codes for any two consecutive positions will differ by only one bit and, consequently, only one bit can change at a time. In this case, the maximum position error will be small, indicating a position adjacent to the actual position.
Genetic algorithms[edit]
Due to the Hamming distance properties of Gray codes, they are sometimes used in genetic algorithms.[14] They are very useful in this field, since mutations in the code allow for mostly incremental changes, but occasionally a single bit-change can cause a big leap and lead to new properties.
Boolean circuit minimization[edit]
Gray codes are also used in labelling the axes of Karnaugh maps since 1953[44][45][46] as well as in Händler circle graphs since 1958,[47][48][49][50] both graphical methods for logic circuit minimization.
Error correction[edit]
In modern digital communications, Gray codes play an important role in error correction. For example, in a digital modulation scheme such as QAM where data is typically transmitted in symbols of 4 bits or more, the signal’s constellation diagram is arranged so that the bit patterns conveyed by adjacent constellation points differ by only one bit. By combining this with forward error correction capable of correcting single-bit errors, it is possible for a receiver to correct any transmission errors that cause a constellation point to deviate into the area of an adjacent point. This makes the transmission system less susceptible to noise.
Communication between clock domains[edit]
Digital logic designers use Gray codes extensively for passing multi-bit count information between synchronous logic that operates at different clock frequencies. The logic is considered operating in different «clock domains». It is fundamental to the design of large chips that operate with many different clocking frequencies.
Cycling through states with minimal effort[edit]
If a system has to cycle through all possible combinations of on-off states of some set of controls, and the changes of the controls require non-trivial expense (e.g. time, wear, human work), a Gray code minimizes the number of setting changes to just one change for each combination of states. An example would be testing a piping system for all combinations of settings of its manually operated valves.
A balanced Gray code can be constructed,[51] that flips every bit equally often. Since bit-flips are evenly distributed, this is optimal in the following way: balanced Gray codes minimize the maximal count of bit-flips for each digit.
Gray code counters and arithmetic[edit]
George R. Stibitz utilized a reflected binary code in a binary pulse counting device in 1941 already.[10][11][12]
A typical use of Gray code counters is building a FIFO (first-in, first-out) data buffer that has read and write ports that exist in different clock domains. The input and output counters inside such a dual-port FIFO are often stored using Gray code to prevent invalid transient states from being captured when the count crosses clock domains.[52]
The updated read and write pointers need to be passed between clock domains when they change, to be able to track FIFO empty and full status in each domain. Each bit of the pointers is sampled non-deterministically for this clock domain transfer. So for each bit, either the old value or the new value is propagated. Therefore, if more than one bit in the multi-bit pointer is changing at the sampling point, a «wrong» binary value (neither new nor old) can be propagated. By guaranteeing only one bit can be changing, Gray codes guarantee that the only possible sampled values are the new or old multi-bit value. Typically Gray codes of power-of-two length are used.
Sometimes digital buses in electronic systems are used to convey quantities that can only increase or decrease by one at a time, for example the output of an event counter which is being passed between clock domains or to a digital-to-analog converter. The advantage of Gray codes in these applications is that differences in the propagation delays of the many wires that represent the bits of the code cannot cause the received value to go through states that are out of the Gray code sequence. This is similar to the advantage of Gray codes in the construction of mechanical encoders, however the source of the Gray code is an electronic counter in this case. The counter itself must count in Gray code, or if the counter runs in binary then the output value from the counter must be reclocked after it has been converted to Gray code, because when a value is converted from binary to Gray code,[nb 1] it is possible that differences in the arrival times of the binary data bits into the binary-to-Gray conversion circuit will mean that the code could go briefly through states that are wildly out of sequence. Adding a clocked register after the circuit that converts the count value to Gray code may introduce a clock cycle of latency, so counting directly in Gray code may be advantageous.[53]
To produce the next count value in a Gray-code counter, it is necessary to have some combinational logic that will increment the current count value that is stored. One way to increment a Gray code number is to convert it into ordinary binary code,[54] add one to it with a standard binary adder, and then convert the result back to Gray code.[55] Other methods of counting in Gray code are discussed in a report by Robert W. Doran, including taking the output from the first latches of the master-slave flip flops in a binary ripple counter.[56]
Gray code addressing[edit]
As the execution of program code typically causes an instruction memory access pattern of locally consecutive addresses, bus encodings using Gray code addressing instead of binary addressing can reduce the number of state changes of the address bits significantly, thereby reducing the CPU power consumption in some low-power designs.[57][58]
Constructing an n-bit Gray code[edit]

The first few steps of the reflect-and-prefix method.

4-bit Gray code permutation
The binary-reflected Gray code list for n bits can be generated recursively from the list for n − 1 bits by reflecting the list (i.e. listing the entries in reverse order), prefixing the entries in the original list with a binary 0, prefixing the entries in the reflected list with a binary 1, and then concatenating the original list with the reversed list.[12] For example, generating the n = 3 list from the n = 2 list:
| 2-bit list: | 00, 01, 11, 10 | |
| Reflected: | 10, 11, 01, 00 | |
| Prefix old entries with 0: | 000, 001, 011, 010, | |
| Prefix new entries with 1: | 110, 111, 101, 100 | |
| Concatenated: | 000, 001, 011, 010, | 110, 111, 101, 100 |
The one-bit Gray code is G1 = (0,1). This can be thought of as built recursively as above from a zero-bit Gray code G0 = ( Λ ) consisting of a single entry of zero length. This iterative process of generating Gn+1 from Gn makes the following properties of the standard reflecting code clear:
- Gn is a permutation of the numbers 0, …, 2n − 1. (Each number appears exactly once in the list.)
- Gn is embedded as the first half of Gn+1.
- Therefore, the coding is stable, in the sense that once a binary number appears in Gn it appears in the same position in all longer lists; so it makes sense to talk about the reflective Gray code value of a number: G(m) = the mth reflecting Gray code, counting from 0.
- Each entry in Gn differs by only one bit from the previous entry. (The Hamming distance is 1.)
- The last entry in Gn differs by only one bit from the first entry. (The code is cyclic.)
These characteristics suggest a simple and fast method of translating a binary value into the corresponding Gray code. Each bit is inverted if the next higher bit of the input value is set to one. This can be performed in parallel by a bit-shift and exclusive-or operation if they are available: the nth Gray code is obtained by computing 


- 000,001,010,011,100,101,110,111 → 001,000,011,010,101,100,111,110 (invert bit 0)
If bit 1 is inverted, blocks of 2 codewords change order:
- 000,001,010,011,100,101,110,111 → 010,011,000,001,110,111,100,101 (invert bit 1)
If bit 2 is inverted, blocks of 4 codewords reverse order:
- 000,001,010,011,100,101,110,111 → 100,101,110,111,000,001,010,011 (invert bit 2)
Thus, performing an exclusive or on a bit 






A similar method can be used to perform the reverse translation, but the computation of each bit depends on the computed value of the next higher bit so it cannot be performed in parallel. Assuming 







To construct the binary-reflected Gray code iteratively, at step 0 start with the 




Converting to and from Gray code[edit]
The following functions in C convert between binary numbers and their associated Gray codes. While it may seem that Gray-to-binary conversion requires each bit to be handled one at a time, faster algorithms exist.[59][54][nb 1]
typedef unsigned int uint; // This function converts an unsigned binary number to reflected binary Gray code. uint BinaryToGray(uint num) { return num ^ (num >> 1); // The operator >> is shift right. The operator ^ is exclusive or. } // This function converts a reflected binary Gray code number to a binary number. uint GrayToBinary(uint num) { uint mask = num; while (mask) { // Each Gray code bit is exclusive-ored with all more significant bits. mask >>= 1; num ^= mask; } return num; } // A more efficient version for Gray codes 32 bits or fewer through the use of SWAR (SIMD within a register) techniques. // It implements a parallel prefix XOR function. The assignment statements can be in any order. // // This function can be adapted for longer Gray codes by adding steps. uint GrayToBinary32(uint num) { num ^= num >> 16; num ^= num >> 8; num ^= num >> 4; num ^= num >> 2; num ^= num >> 1; return num; } // A Four-bit-at-once variant changes a binary number (abcd)2 to (abcd)2 ^ (00ab)2, then to (abcd)2 ^ (00ab)2 ^ (0abc)2 ^ (000a)2.
On newer processors, the number of ALU instructions in the decoding step can be reduced by taking advantage of the CLMUL instruction set. If MASK is the constant binary string of ones ended with a single zero digit, then carryless multiplication of MASK with the grey encoding of x will always give either x or its bitwise negation.
Special types of Gray codes[edit]
In practice, «Gray code» almost always refers to a binary-reflected Gray code (BRGC).
However, mathematicians have discovered other kinds of Gray codes.
Like BRGCs, each consists of a list of words, where each word differs from the next in only one digit (each word has a Hamming distance of 1 from the next word).
Gray codes with n bits and of length less than 2n[edit]
It is possible to construct binary Gray codes with n bits with a length of less than 2n, if the length is even. One possibility is to start with a balanced Gray code and remove pairs of values at either the beginning and the end, or in the middle.[60] OEIS sequence A290772 [61] gives the number of possible Gray sequences of length 2 n which include zero and use the minimum number of bits.
n-ary Gray code[edit]
0 → 000
1 → 001
2 → 002
10 → 012
11 → 011
12 → 010
20 → 020
21 → 021
22 → 022
100 → 122
101 → 121
102 → 120
110 → 110
111 → 111
112 → 112
120 → 102
121 → 101
122 → 100
200 → 200
201 → 201
202 → 202
210 → 212
211 → 211
212 → 210
220 → 220
221 → 221
222 → 222
There are many specialized types of Gray codes other than the binary-reflected Gray code. One such type of Gray code is the n-ary Gray code, also known as a non-Boolean Gray code. As the name implies, this type of Gray code uses non-Boolean values in its encodings.
For example, a 3-ary (ternary) Gray code would use the values 0,1,2.[30] The (n, k)-Gray code is the n-ary Gray code with k digits.[62]
The sequence of elements in the (3, 2)-Gray code is: 00,01,02,12,11,10,20,21,22. The (n, k)-Gray code may be constructed recursively, as the BRGC, or may be constructed iteratively. An algorithm to iteratively generate the (N, k)-Gray code is presented (in C):
// inputs: base, digits, value // output: Gray // Convert a value to a Gray code with the given base and digits. // Iterating through a sequence of values would result in a sequence // of Gray codes in which only one digit changes at a time. void toGray(unsigned base, unsigned digits, unsigned value, unsigned gray[digits]) { unsigned baseN[digits]; // Stores the ordinary base-N number, one digit per entry unsigned i; // The loop variable // Put the normal baseN number into the baseN array. For base 10, 109 // would be stored as [9,0,1] for (i = 0; i < digits; i++) { baseN[i] = value % base; value = value / base; } // Convert the normal baseN number into the Gray code equivalent. Note that // the loop starts at the most significant digit and goes down. unsigned shift = 0; while (i--) { // The Gray digit gets shifted down by the sum of the higher // digits. gray[i] = (baseN[i] + shift) % base; shift = shift + base - gray[i]; // Subtract from base so shift is positive } } // EXAMPLES // input: value = 1899, base = 10, digits = 4 // output: baseN[] = [9,9,8,1], gray[] = [0,1,7,1] // input: value = 1900, base = 10, digits = 4 // output: baseN[] = [0,0,9,1], gray[] = [0,1,8,1]
There are other Gray code algorithms for (n,k)-Gray codes. The (n,k)-Gray code produced by the above algorithm is always cyclical; some algorithms, such as that by Guan,[62] lack this property when k is odd. On the other hand, while only one digit at a time changes with this method, it can change by wrapping (looping from n − 1 to 0). In Guan’s algorithm, the count alternately rises and falls, so that the numeric difference between two Gray code digits is always one.
Gray codes are not uniquely defined, because a permutation of the columns of such a code is a Gray code too. The above procedure produces a code in which the lower the significance of a digit, the more often it changes, making it similar to normal counting methods.
See also Skew binary number system, a variant ternary number system where at most two digits change on each increment, as each increment can be done with at most one digit carry operation.
Balanced Gray code[edit]
Although the binary reflected Gray code is useful in many scenarios, it is not optimal in certain cases because of a lack of «uniformity».[51] In balanced Gray codes, the number of changes in different coordinate positions are as close as possible. To make this more precise, let G be an R-ary complete Gray cycle having transition sequence 
A Gray code is uniform or uniformly balanced if its transition counts are all equal, in which case we have
for all k. Clearly, when 


For example, a balanced 4-bit Gray code has 16 transitions, which can be evenly distributed among all four positions (four transitions per position), making it uniformly balanced:[51]
- 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0
- 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0
- 0 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0
- 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1
whereas a balanced 5-bit Gray code has a total of 32 transitions, which cannot be evenly distributed among the positions. In this example, four positions have six transitions each, and one has eight:[51]
- 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
- 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 0
- 1 1 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1
- 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1
- 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 1
We will now show a construction[65] and implementation[66] for well-balanced binary Gray codes which allows us to generate an n-digit balanced Gray code for every n. The main principle is to inductively construct an (n + 2)-digit Gray code 

where 



If we define the transition multiplicities
to be the number of times the digit in position i changes between consecutive blocks in a partition, then for the (n + 2)-digit Gray code induced by this partition the transition spectrum 
The delicate part of this construction is to find an adequate partitioning of a balanced n-digit Gray code such that the code induced by it remains balanced, but for this only the transition multiplicities matter; joining two consecutive blocks over a digit 






Long run Gray codes[edit]
Long run (or maximum gap) Gray codes maximize the distance between consecutive changes of digits in the same position. That is, the minimum run-length of any bit remains unchanged for as long as possible.[67]
Monotonic Gray codes[edit]
Monotonic codes are useful in the theory of interconnection networks, especially for minimizing dilation for linear arrays of processors.[68]
If we define the weight of a binary string to be the number of 1s in the string, then although we clearly cannot have a Gray code with strictly increasing weight, we may want to approximate this by having the code run through two adjacent weights before reaching the next one.
We can formalize the concept of monotone Gray codes as follows: consider the partition of the hypercube 
for 










An elegant construction of monotonic n-digit Gray codes for any n is based on the idea of recursively building subpaths 






otherwise. Here, 




The choice of 



|
j = 0 | j = 1 | j = 2 | j = 3 |
|---|---|---|---|---|
| n = 1 | 0, 1 | |||
| n = 2 | 00, 01 | 10, 11 | ||
| n = 3 | 000, 001 | 100, 110, 010, 011 | 101, 111 | |
| n = 4 | 0000, 0001 | 1000, 1100, 0100, 0110, 0010, 0011 | 1010, 1011, 1001, 1101, 0101, 0111 | 1110, 1111 |
These monotonic Gray codes can be efficiently implemented in such a way that each subsequent element can be generated in O(n) time. The algorithm is most easily described using coroutines.
Monotonic codes have an interesting connection to the Lovász conjecture, which states that every connected vertex-transitive graph contains a Hamiltonian path. The «middle-level» subgraph 

Beckett–Gray code[edit]
Another type of Gray code, the Beckett–Gray code, is named for Irish playwright Samuel Beckett, who was interested in symmetry. His play «Quad» features four actors and is divided into sixteen time periods. Each period ends with one of the four actors entering or leaving the stage. The play begins and ends with an empty stage, and Beckett wanted each subset of actors to appear on stage exactly once.[70] Clearly the set of actors currently on stage can be represented by a 4-bit binary Gray code. Beckett, however, placed an additional restriction on the script: he wished the actors to enter and exit so that the actor who had been on stage the longest would always be the one to exit. The actors could then be represented by a first in, first out queue, so that (of the actors onstage) the actor being dequeued is always the one who was enqueued first.[70] Beckett was unable to find a Beckett–Gray code for his play, and indeed, an exhaustive listing of all possible sequences reveals that no such code exists for n = 4. It is known today that such codes do exist for n = 2, 5, 6, 7, and 8, and do not exist for n = 3 or 4. An example of an 8-bit Beckett–Gray code can be found in Donald Knuth’s Art of Computer Programming.[12] According to Sawada and Wong, the search space for n = 6 can be explored in 15 hours, and more than 9,500 solutions for the case n = 7 have been found.[71]
Snake-in-the-box codes[edit]

Maximum lengths of snakes (Ls) and coils (Lc) in the snakes-in-the-box problem for dimensions n from 1 to 4
Snake-in-the-box codes, or snakes, are the sequences of nodes of induced paths in an n-dimensional hypercube graph, and coil-in-the-box codes,[72] or coils, are the sequences of nodes of induced cycles in a hypercube. Viewed as Gray codes, these sequences have the property of being able to detect any single-bit coding error. Codes of this type were first described by William H. Kautz in the late 1950s;[4] since then, there has been much research on finding the code with the largest possible number of codewords for a given hypercube dimension.
Single-track Gray code[edit]
Yet another kind of Gray code is the single-track Gray code (STGC) developed by Norman B. Spedding[73][74] and refined by Hiltgen, Paterson and Brandestini in «Single-track Gray codes» (1996).[75][76] The STGC is a cyclical list of P unique binary encodings of length n such that two consecutive words differ in exactly one position, and when the list is examined as a P × n matrix, each column is a cyclic shift of the first column.[77]

Single-track Gray code with 5 sensors.

Animated and color-coded version of the STGC rotor.
The name comes from their use with rotary encoders, where a number of tracks are being sensed by contacts, resulting for each in an output of 0 or 1. To reduce noise due to different contacts not switching at exactly the same moment in time, one preferably sets up the tracks so that the data output by the contacts are in Gray code. To get high angular accuracy, one needs lots of contacts; in order to achieve at least 1° accuracy, one needs at least 360 distinct positions per revolution, which requires a minimum of 9 bits of data, and thus the same number of contacts.
If all contacts are placed at the same angular position, then 9 tracks are needed to get a standard BRGC with at least 1° accuracy. However, if the manufacturer moves a contact to a different angular position (but at the same distance from the center shaft), then the corresponding «ring pattern» needs to be rotated the same angle to give the same output. If the most significant bit (the inner ring in Figure 1) is rotated enough, it exactly matches the next ring out. Since both rings are then identical, the inner ring can be cut out, and the sensor for that ring moved to the remaining, identical ring (but offset at that angle from the other sensor on that ring). Those two sensors on a single ring make a quadrature encoder. That reduces the number of tracks for a «1° resolution» angular encoder to 8 tracks. Reducing the number of tracks still further cannot be done with BRGC.
For many years, Torsten Sillke[78] and other mathematicians believed that it was impossible to encode position on a single track such that consecutive positions differed at only a single sensor, except for the 2-sensor, 1-track quadrature encoder. So for applications where 8 tracks were too bulky, people used single-track incremental encoders (quadrature encoders) or 2-track «quadrature encoder + reference notch» encoders.
Norman B. Spedding, however, registered a patent in 1994 with several examples showing that it was possible.[73] Although it is not possible to distinguish 2n positions with n sensors on a single track, it is possible to distinguish close to that many. Etzion and Paterson conjecture that when n is itself a power of 2, n sensors can distinguish at most 2n − 2n positions and that for prime n the limit is 2n − 2 positions.[79] The authors went on to generate a 504-position single track code of length 9 which they believe is optimal. Since this number is larger than 28 = 256, more than 8 sensors are required by any code, although a BRGC could distinguish 512 positions with 9 sensors.
An STGC for P = 30 and n = 5 is reproduced here:
-
Single-track Gray code for 30 positions
Angle Code Angle Code Angle Code Angle Code Angle Code 0° 10000 72° 01000 144° 00100 216° 00010 288° 00001 12° 10100 84° 01010 156° 00101 228° 10010 300° 01001 24° 11100 96° 01110 168° 00111 240° 10011 312° 11001 36° 11110 108° 01111 180° 10111 252° 11011 324° 11101 48° 11010 120° 01101 192° 10110 264° 01011 336° 10101 60° 11000 132° 01100 204° 00110 276° 00011 348° 10001
Each column is a cyclic shift of the first column, and from any row to the next row only one bit changes.[80]
The single-track nature (like a code chain) is useful in the fabrication of these wheels (compared to BRGC), as only one track is needed, thus reducing their cost and size.
The Gray code nature is useful (compared to chain codes, also called De Bruijn sequences), as only one sensor will change at any one time, so the uncertainty during a transition between two discrete states will only be plus or minus one unit of angular measurement the device is capable of resolving.[81]
Two-dimensional Gray code[edit]

A Gray-coded constellation diagram for rectangular 16-QAM
Two-dimensional Gray codes are used in communication to minimize the number of bit errors in quadrature amplitude modulation (QAM) adjacent points in the constellation. In a typical encoding the horizontal and vertical adjacent constellation points differ by a single bit, and diagonal adjacent points differ by 2 bits.[82]
Two-dimensional Gray codes also have uses in location identifications schemes, where the code would be applied to area maps such as a Mercator projection of the earth’s surface and an appropriate cyclic two-dimensional distance function such as the Mannheim metric be used to calculate the distance between two encoded locations, thereby combining the characteristics of the Hamming distance with the cyclic continuation of a Mercator projection.[83]
Excess-Gray-Code[edit]
If a subsection of a specific codevalue is extracted from that value, for example the last 3 bits of a 4-bit gray-code, the resulting code will be an «excess gray code». This code shows the property of counting backwards in those extracted bits if the original value is further increased. Reason for this is that gray-encoded values do not show the behaviour of overflow, known from classic binary encoding, when increasing past the «highest» value.
Example: The highest 3-bit gray code, 7, is encoded as (0)100. Adding 1 results in number 8, encoded in gray as 1100. The last 3 bits do not overflow and count backwards if you further increase the original 4 bit code.
When working with sensors that output multiple, gray-encoded values in a serial fashion, one should therefore pay attention whether the sensor produces those multiple values encoded in 1 single gray-code or as separate ones, as otherwise the values might appear to be counting backwards when an «overflow» is expected.
Gray isometry[edit]
The bijective mapping { 0 ↔ 00, 1 ↔ 01, 2 ↔ 11, 3 ↔ 10 } establishes an isometry between the metric space over the finite field 





[edit]
There are a number of binary codes similar to Gray codes, including:
- Datex codes aka Giannini codes (1954), as described by Carl P. Spaulding,[8][86][87][88][89][7] use a variant of O’Brien code II.
- Codes used by Varec (ca. 1954),[90][91][92][93] use a variant of O’Brien code I as well as base-12 and base-16 Gray code variants.
- Lucal code (1959)[1][2][56] aka modified reflected binary code (MRB)[1][2][nb 3]
- Gillham code (1961/1962),[87][94][7][95][96] uses a variant of Datex code and O’Brien code II.
- Leslie and Russell code (1964)[97][9][98][94]
- Royal Radar Establishment code[94]
- Hoklas code (1988)[99][100][101]
The following binary-coded decimal (BCD) codes are Gray code variants as well:
- Petherick code (1953),[18][102][103][104][54][100][nb 4] also known as Royal Aircraft Establishment (RAE) code.[105]
- O’Brien codes I and II (1955)[106][107][108][88][89][100] (An O’Brien type-I code[nb 5] was already described by Frederic A. Foss of IBM[109][110] and used by Varec in 1954. Later, it was also known as Watts code or Watts reflected decimal (WRD) code and is sometimes ambiguously referred to as reflected binary modified Gray code.[111][19][20][112][113][114][115][116][117][nb 1][nb 3] An O’Brien type-II code was already used by Datex in 1954.[nb 4])
- Excess-3 Gray code (1956)[118] (aka Gray excess-3 code,[88][89][7] Gray 3-excess code, reflex excess-3 code, excess Gray code,[100] Gray excess code, 10-excess-3 Gray code or Gray–Stibitz code), described by Frank P. Turvey Jr. of ITT.[118]
- Tompkins codes I and II (1956)[3][107][108][88][89][100]
- Glixon code (1957), sometimes ambiguously also called modified Gray code[119][54][120][121][107][108][88][89][100][nb 3][nb 5]
| Name | Bit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Weights[nb 7] | Tracks | Compl. | Cyclic | 5s | Comment |
| Gray BCD | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0—3 | 4 (3[nb 8]) | No | (2, 4, 8, 16) | No | [107][108] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Paul | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1—3 | 4 (3[nb 8]) | No | 2, 10 | No | [122] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Glixon | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0—3 | 4 | No | 2, 4, 8, 10 | (shifted +1) | [119][107][108][120][121][nb 5] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |||||||
| Tompkins I | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0—4 | 2 | No | 2, 4, 10 | Yes | [3][107][108] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |||||||
| O’Brien I (Watts) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0—3 | 4 | 9[100][101][nb 9] | 2, 4, 10 | Yes | [106][107][108][nb 5] |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |||||||
| Petherick (RAE) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1—3 | 3 | 9[100][101][nb 9] | 2, 10 | Yes | [18][104][nb 4] |
| 3 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| O’Brien II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1—3 | 3 | 9[88][100][101][nb 9] | 2, 10 | Yes | [106][107][108][nb 4] |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| Susskind | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1—4 | 3 | 9[nb 9] | 2, 10 | Yes | [5] |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| Klar | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0—4 | 4 (3[nb 8]) | 9[nb 9] | 2, 10 | Yes | [123][124] |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Tompkins II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1—3 | 2 | 9[nb 10] | 2, 10 | Yes | [3][107][108] |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Excess-3 Gray | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1—4 | 4 | 9[100][101][nb 9] | 2, 10 | Yes | [7][100] |
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
See also[edit]
- Linear-feedback shift register
- De Bruijn sequence
- Steinhaus–Johnson–Trotter algorithm – an algorithm that generates Gray codes for the factorial number system
- Minimum distance code
- Prouhet–Thue–Morse sequence – related to inverse Gray code
- Ryser formula
- Hilbert curve
Notes[edit]
- ^ a b c By applying a simple inversion rule, the Gray code and the O’Brien code I can be translated into the 8421 pure binary code and the 2421 Aiken code, respectively, to ease arithmetic operations.[C]
- ^ Sequence 0, 1, 0, 2, 0, 1, 0, 3, … (sequence A007814 in the OEIS).
- ^ a b c There are several Gray code variants which are called «modified» of some sort: The Glixon code is sometimes called modified Gray code.[D] The Lucal code is also called modified reflected binary code (MRB).[E] The O’Brien code I or Watts code is sometimes referred to as reflected binary modified Gray code.[F]
- ^ a b c d By interchanging and inverting three bit rows, the O’Brien code II and the Petherick code can be transferred into each other.
- ^ a b c d By swapping two pairs of bit rows, individually shifting four bit rows and inverting one of them, the Glixon code and the O’Brien code I can be transferred into each other.
- ^ Other unit-distance BCD codes include the non-Gray code related 5-bit Libaw–Craig and the 1-2-1 code.
- ^ Depending on a code’s target application, the Hamming weights of a code can be important properties beyond coding-theoretical considerations also for physical reasons. Under some circumstances the all-cleared and/or all-set states must be omitted (f.e. to avoid non-conductive or short-circuit conditions), it may be desirable to keep the highest used weight as low as possible (f.e. to reduce power consumption of the reader circuit) or to keep the variance of used weights small (f.e. to reduce acoustic noise or current fluctuations).
- ^ a b c For Gray BCD, Paul and Klar codes, the number of necessary reading tracks can be reduced from 4 to 3 if inversion of one of the middle tracks is acceptable.
- ^ a b c d e f For O’Brien codes I and II and Petherick, Susskind, Klar as well as Excess-3 Gray codes, a 9s complement can be derived by inverting the most-significant (fourth) binary digit.
- ^ For Tompkins code II, a 9s complement can be derived by inverting the first three digits and swapping the two middle binary digits.
References[edit]
- ^ a b c Lucal, Harold M. (December 1959). «Arithmetic Operations for Digital Computers Using a Modified Reflected Binary». IRE Transactions on Electronic Computers. EC-8 (4): 449–458. doi:10.1109/TEC.1959.5222057. ISSN 0367-9950. S2CID 206673385. (10 pages)
- ^ a b c Sellers, Jr., Frederick F.; Hsiao, Mu-Yue; Bearnson, Leroy W. (November 1968). Error Detecting Logic for Digital Computers (1st ed.). New York, USA: McGraw-Hill Book Company. pp. 152–164. LCCN 68-16491. OCLC 439460.
- ^ a b c d Tompkins, Howard E. (September 1956) [1956-07-16]. «Unit-Distance Binary-Decimal Codes for Two-Track Commutation». IRE Transactions on Electronic Computers. Correspondence. Moore School of Electrical Engineering, University of Pennsylvania, Philadelphia, Pennsylvania, USA. EC-5 (3): 139. doi:10.1109/TEC.1956.5219934. ISSN 0367-9950. Retrieved 2020-05-18. (1 page)
- ^ a b Kautz, William H. (June 1958). «Unit-Distance Error-Checking Codes». IRE Transactions on Electronic Computers. EC-7 (2): 179–180. doi:10.1109/TEC.1958.5222529. ISSN 0367-9950. S2CID 26649532. (2 pages)
- ^ a b Susskind, Alfred Kriss; Ward, John Erwin (1958-03-28) [1957, 1956]. «III.F. Unit-Distance Codes / VI.E.2. Reflected Binary Codes». Written at Cambridge, Massachusetts, USA. In Susskind, Alfred Kriss (ed.). Notes on Analog-Digital Conversion Techniques. Technology Books in Science and Engineering. Vol. 1 (3 ed.). New York, USA: Technology Press of the Massachusetts Institute of Technology / John Wiley & Sons, Inc. / Chapman & Hall, Ltd. pp. 3-10–3-16 [3-13–3-16], 6-65–6-60 [6-60]. (x+416+2 pages) (NB. The contents of the book was originally prepared by staff members of the Servomechanisms Laboraratory, Department of Electrical Engineering, MIT, for Special Summer Programs held in 1956 and 1957. Susskind’s «reading-type code» is actually a minor variant of the code shown here with the two most significant bit rows swapped to better illustrate symmetries. Also, by swapping two bit rows and inverting one of them, the code can be transferred into the Petherick code, whereas by swapping and inverting two bit rows, the code can be transferred into the O’Brien code II.)
- ^ a b Chinal, Jean P. (January 1973). «3.3. Unit Distance Codes». Written at Paris, France. Design Methods for Digital Systems. Translated by Preston, Alan; Summer, Arthur (1st English ed.). Berlin, Germany: Akademie-Verlag / Springer-Verlag. p. 50. doi:10.1007/978-3-642-86187-1. ISBN 978-0-387-05871-9. S2CID 60362404. License No. 202-100/542/73. Order No. 7617470(6047) ES 19 B 1 / 20 K 3. Retrieved 2020-06-21. (xviii+506 pages) (NB. The French 1967 original book was named «Techniques Booléennes et Calculateurs Arithmétiques», published by Éditions Dunod [fr].)
- ^ a b c d e f Military Handbook: Encoders – Shaft Angle To Digital (PDF). United States Department of Defense. 1991-09-30. MIL-HDBK-231A. Archived (PDF) from the original on 2020-07-25. Retrieved 2020-07-25. (NB. Supersedes MIL-HDBK-231(AS) (1970-07-01).)
- ^ a b c Spaulding, Carl P. (1965-01-12) [1954-03-09]. «Digital coding and translating system» (PDF). Monrovia, California, USA: Datex Corporation. U.S. Patent 3165731A. Serial No. 415058. Archived (PDF) from the original on 2020-08-05. Retrieved 2018-01-21. (28 pages)
- ^ a b Russell, A. (August 1964). «Some Binary Codes and a Novel Five-Channel Code». Control (Systems, Instrumentation, Data Processing, Automation, Management, incorporating Automation Progress). Special Features. London, UK: Morgan-Grampain (Publishers) Limited. 8 (74): 399–404. Retrieved 2020-06-22. (6 pages)
- ^ a b c Stibitz, George Robert (1943-01-12) [1941-11-26]. «Binary counter». New York, USA: Bell Telephone Laboratories, Incorporated. U.S. Patent 2,307,868. Serial No. 420537. Retrieved 2020-05-24. p. 2, right column, rows 43–73:
[…] A clearer idea of the position of the balls after each pulse will be obtained if the set of balls is represented by a number having a similar number of digits, each of which may have one of two arbitrary values, for example 0 and 1. If the upper position is called 0 and the lower position […] 1, then the setting of the counter […] may be read from left to right as 0,100,000. […] Following is a translation of the number of pulses received into this form of binary notation for the first sixteen pulses as received on the first five balls […] Pulse number […] Binary notation […]
[1] (4 pages) - ^ a b c d e Winder, C. Farrell (October 1959). «Shaft Angle Encoders Afford High Accuracy» (PDF). Electronic Industries. Chilton Company. 18 (10): 76–80. Archived from the original (PDF) on 2020-09-28. Retrieved 2018-01-14. p. 78:
[…] The type of code wheel most popular in optical encoders contains a cyclic binary code pattern designed to give a cyclic sequence of «on-off» outputs. The cyclic binary code is also known as the cyclic progression code, the reflected binary code, and the Gray code. This code was originated by G. R. Stibitz, of Bell Telephone Laboratories, and was first proposed for pulse-code modulation systems by Frank Gray, also of BTL. Thus the name Gray code. The Gray or cyclic code is used mainly to eliminate the possibility of errors at code transition which could result in gross ambiguities. […]
- ^ a b c d e f g h i Knuth, Donald Ervin (2014-09-12). «Enumeration and Backtracking / Generating all n-tuples». The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1. Vol. 4A (1 ed.). Addison-Wesley Professional. pp. 442–443. ISBN 978-0-13348885-2. (912 pages)
- ^ a b Gray, Frank (1953-03-17) [1947-11-13]. Pulse Code Communication (PDF). New York, USA: Bell Telephone Laboratories, Incorporated. U.S. Patent 2,632,058. Serial No. 785697. Archived (PDF) from the original on 2020-08-05. Retrieved 2020-08-05. (13 pages)
- ^ a b Goldberg, David Edward (1989). Genetic Algorithms in Search, Optimization, and Machine Learning (1 ed.). Reading, Massachusetts, USA: Addison-Wesley. Bibcode:1989gaso.book…..G.
- ^ Breckman, Jack (1956-01-31) [1953-12-31]. Encoding Circuit (PDF). Long Branch, New Jersey, USA: US Secretary of the Army. U.S. Patent 2,733,432. Serial No. 401738. Archived (PDF) from the original on 2020-08-05. Retrieved 2020-08-05. (8 pages)
- ^ a b Ragland, Earl Albert; Schultheis, Jr., Harry B. (1958-02-11) [1953-10-16]. Direction-Sensitive Binary Code Position Control System (PDF). North Hollywood, California, USA: Bendix Aviation Corporation. U.S. Patent 2,823,345. Serial No. 386524. Archived (PDF) from the original on 2020-08-05. Retrieved 2020-08-05. (10 pages)
- ^ Domeshek, Sol; Reiner, Stewart (1958-06-24) [1954-01-08]. Automatic Rectification System (PDF). US Secretary of the Navy. U.S. Patent 2,839,974. Serial No. 403085. Archived (PDF) from the original on 2020-08-05. Retrieved 2020-08-05. (8 pages)
- ^ a b c Petherick, Edward John (October 1953). A Cyclic Progressive Binary-coded-decimal System of Representing Numbers (Technical Note MS15). Farnborough, UK: Royal Aircraft Establishment (RAE). (4 pages) (NB. Sometimes referred to as A Cyclic-Coded Binary-Coded-Decimal System of Representing Numbers.)
- ^ a b Evans, David Silvester (1960). Fundamentals of Digital Instrumentation (1 ed.). London, UK: Hilger & Watts Ltd. Retrieved 2020-05-24. (39 pages)
- ^ a b Evans, David Silvester (March 1961). «Chapter Three: Direct Reading from Coded Scales». Digital Data: Their derivation and reduction for analysis and process control (1 ed.). London, UK: Hilger & Watts Ltd / Interscience Publishers. pp. 18–23. Retrieved 2020-05-24. p. 20–23:
[…] Decoding. […] To decode C.P.B. or W.R.D. codes, a simple inversion rule can be applied. The readings of the higher tracks determine the way in which the lower tracks are translated. The inversion rule is applied line by line for the C.P.B. and for the W.R.D. it is applied decade by decade or line by line. Starting therefore with the top or slowest changing track of the C.P.B., if the result is odd (1) the next track value has to be inverted, i.e. 0 for 1 and 1 for 0. If, however, the first track is even (0), the second track is left as read, i.e. 0 for 0 and 1 for 1. Again, if the resultant reading of the second track is odd, the third track reading is inverted and so on. When an odd is changed to an even the line below is not inverted and when an even is changed to an odd the line below is inverted. The result of applying this rule to the pattern […] is the pure binary (P.B.) pattern […] where each track or digit can be given a definite numerical value (in this instance 1, 2, 4, 8, etc.). […] Using the line-by-line inversion rule on the W.R.D. code produces [a] pattern [of 1, 2, 4, 2 code] where again the digits can be given numerical values and summed decade by decade. The summing of the digits can be very useful, for example, in a high-speed scanning system; but in a parallel decoding system […], it is usual to treat each binary quartet or decade as an entity. In other words, if the first or more significant decade is odd, the second decade is rectified or complemented by inverting the D track and so on, the result being the repeating pattern of [rectified W.R.D. code]. This is an extremely easy thing to achieve since the only change required is the inversion of the meaning of the D track or complementing digit. […]
(8+82 pages) (NB. The author does not mention Gray at all and calls the standard Gray code «Cyclic Permuted Binary Code» (C.P.B.), the book index erroneously lists it as «cyclic pure binary code».) - ^ Newson, P. A. (1965). Tables for the Binary Encoding of Angles (1 ed.). United Kingdom Atomic Energy Authority, Research Group, Atomic Energy Research Establishment, Harwell, UK: H. M. Stationery Office. Retrieved 2020-05-24. (12 pages)
- ^ Heath, F. G. (September 1961). «Pioneers Of Binary Coding». Journal of the Institution of Electrical Engineers. Manchester College of Science and Technology, Faculty of Technology of the University of Manchester, Manchester, UK: Institution of Engineering and Technology (IET). 7 (81): 539–541. doi:10.1049/jiee-3.1961.0300. Retrieved 2020-06-22. (3 pages)
- ^ Cattermole, Kenneth W. (1969). Written at Harlow, Essex, UK. Principles of pulse code modulation (1 ed.). London, UK / New York, USA: Iliffe Books Ltd. / American Elsevier Publishing Company, Inc. pp. 245, 434. ISBN 978-0-444-19747-4. LCCN 78-80432. SBN 444-19747-8. p. 245:
[…] There seems to be some confusion about the attributation of this code, because two inventors named Gray have been associated with it. When I first heard the name I took it as referring to Elisha Gray, and Heath testifies to his usage of it. Many people take it as referring to Frank Gray of Bell Telephone Laboratories, who in 1947 first proposed its use in coding tubes: his patent is listed in the bibliography. […]
(2+448+2 pages) - ^ Edwards, Anthony William Fairbank (2004). Cogwheels of the Mind: The Story of Venn Diagrams. Baltimore, Maryland, USA: Johns Hopkins University Press. pp. 48, 50. ISBN 0-8018-7434-3.
- ^ Gros, Luc-Agathon-Louis (1872). Théorie du baguenodier par un clerc de notaire lyonnais (in French) (1 ed.). Lyon, France: Aimé Vingtrinier. Archived from the original on 2017-04-03. Retrieved 2020-12-17. [2](2+16+4 pages and 4 pages foldout) (NB. This booklet was published anonymously, but is known to have been authored by Louis Gros.)
- ^ Lucas, Édouard (November 1883). La tour d’Hanoï: Véritable casse tête annamite — Jeu rapporté du Tonkin par le Professeur N. Claus (de Siam) Mandarin du Collège Li Sou Stian! (in French). Imprimerie Paul Bousrez, Tours. (NB. N. Claus de Siam is an anagram of Lucas d’Amiens, pseudonym of the author Édouard Lucas.)
- ^ de Parville, Henri [in French], ed. (1883-12-27). «La tour d’Hanoï, véritable casse-tête annamite, jeu rapporté du Tonkin par le professeur N. Claus (de Siam), mandarin du collège Li-Sou-Stian. Un vrai casse-tête, en effet, mais intéressant. Nous ne saurions mieux remercier le mandarin de son aimable intention à l’égard d’un profane qu’en signalant la Tour d’Hanoï aux personnes patientes possédées par le démon du jeu». Journal des Débats Politiques et Littéraires (Review). Revue des science (in French) (Matin ed.). Paris, France: 1–2 [2]. ark:/12148/bpt6k462461g. Archived from the original on 2020-12-18. Retrieved 2020-12-18. (1 page)
- ^ Allardice, R. E.; Fraser, A. Y. (February 1883). Allardice, Robert Edgar; Fraser, Alexander Yule (eds.). «La Tour d’Hanoï». Proceedings of the Edinburgh Mathematical Society (in English and French). Edinburgh Mathematical Society. 2 (5): 50–53. doi:10.1017/S0013091500037147. eISSN 1464-3839. ISSN 0013-0915. S2CID 122159381. [3] (4 pages)
- ^ Lucas, Édouard (1979) [1892]. Récréations mathématiques (in French). Vol. 3 (Librairie Albert Blanchard reissue ed.). p. 58. (The first edition of this book was published post-humously.)
- ^ a b Herter, Felix; Rote, Günter (2018-11-14) [2018-08-09, 2017-12, 2017-08-09, 2016-04-22]. «Loopless Gray Code Enumeration and the Tower of Bucharest» (PDF). Theoretical Computer Science. Berlin, Germany. 748: 40–54. arXiv:1604.06707. doi:10.1016/j.tcs.2017.11.017. ISSN 0304-3975. S2CID 4014870. Archived (PDF) from the original on 2020-12-16. Retrieved 2020-12-16. [4] (15/18/19/24 pages)
- ^ Gardner, Martin (August 1972). «The curious properties of the Gray code and how it can be used to solve puzzles». Scientific American. Mathematical Games. Vol. 227, no. 2. p. 106. (1 page)
- ^ Zeman, Johann; Fischer, Ferdinand, eds. (1877). «Einige neuere Vorschläge zur mehrfachen Telegraphie: A. Absatzweise vielfache Telegraphie». Dingler’s Polytechnisches Journal (in German). Augsburg, Germany: J. G. Cotta’sche Buchhandlung. 226: 499–507. Archived from the original on 2020-12-21. Retrieved 2020-12-21. p. 499:
[…] Der um die Mitte des J[ahres] 1874 patenti[e]rte, ebenfalls dem Highton’schen verwandte Typendrucker des französischen Telegraphen-Verwaltungsbeamten Baudot wurde bei seiner 1875 patenti[e]rten Weiterentwicklung in einen fünffachen umgewandelt […]
- ^ Butrica, Andrew J. (1991-06-21). «Baudot, Jean Maurice Emile». In Froehlich, Fritz E.; Kent, Allen; Hall, Carolyn M. (eds.). The Froehlich/Kent Encyclopedia of Telecommunications: Volume 2 — Batteries to Codes-Telecommunications. Vol. 2. Marcel Dekker Inc. / CRC Press. pp. 31–34. ISBN 0-8247-2901-3. LCCN 90-3966. Retrieved 2020-12-20. p. 31:
[…] A Baudot prototype (4 years in the making) was built in 1876. The transmitter had 5 keys similar to those of a piano. Messages were sent in a special 5-element code devised by Baudot […]
- ^ Fischer, Eric N. (2000-06-20). «The Evolution of Character Codes, 1874–1968». ark:/13960/t07x23w8s. Retrieved 2020-12-20.
[…] In 1872, [Baudot] started research toward a telegraph system that would allow multiple operators to transmit simultaneously over a single wire and, as the transmissions were received, would print them in ordinary alphabetic characters on a strip of paper. He received a patent for such a system on June 17, 1874. […] Instead of a variable delay followed by a single-unit pulse, Baudot’s system used a uniform six time units to transmit each character. […] his early telegraph probably used the six-unit code […] that he attributes to Davy in an 1877 article. […] in 1876 Baudot redesigned his equipment to use a five-unit code. Punctuation and digits were still sometimes needed, though, so he adopted from Hughes the use of two special letter space and figure space characters that would cause the printer to shift between cases at the same time as it advanced the paper without printing. The five-unit code he began using at this time […] was structured to suit his keyboard […], which controlled two units of each character with switches operated by the left hand and the other three units with the right hand. […]
[5][6] - ^ Rothen, Timotheus (1884-12-25). «Le télégraphe imprimeur Baudot». Journal Télégraphique (in French). Berne, Switzerland: Le Bureau International des Administrations Télégraphiques. VIII / #16 (12): 241–253 [249]. eISSN 2725-738X. ISSN 2223-1420. ark:/12148/bpt6k5725454q. Retrieved 2020-12-20. [7]
- ^ Pendry, Henry Walter (1920) [October 1919]. Written at London, UK. The Baudôt Printing Telegraph System (2 ed.). London, Bath, Melbourne, New York: Sir Isaac Pitman and Sons, Ltd. pp. 43–44. LCCN 21005277. OCLC 778309351. OL 6633244M. Retrieved 2020-12-20. (vii+184 pages) (NB. A first edition was published in 1913.)
- ^ a b MacMillan, David M. (2010-04-27) [2010-04-25, 2010-04-23]. «Codes that Don’t Count — Some Printing Telegraph Codes as Products of their Technologies (With Particular Attention to the Teletypesetter)». lemur.com. Revision 3. Mineral Point, Wisconsin, USA. Archived from the original on 2020-12-18. Retrieved 2020-12-20.
- ^ Written at Lisbon, Portugual. Convention télégraphique internationale de Saint-Pétersbourg et Règlement et tarifs y annexés, Revision de Lisbonne, 1908 / Extraits de la publication: Documents de la Conférence télégraphique internationale de Lisbonne (in French). Berne, Switzerland: Bureau Internationale de L’Union Télégraphique. 1909 [1908].
- ^ «Chapter IX. Signaux de transmission, Article 35. Signaux de transmission des alphabets télegraphiques internationaux ‘nos 1 et 2, signaux d.u code Morse, de l’appareil Hughes et de l’appareil Siemens». Written at Madrid, Spain. Règlement télégraphique annexé à la convention internationale des télécommunications — protocol finale audit règlement — Madrid, 1932 (PDF) (in French). Berne, Switzerland: Bureau Internationale de L’Union Télégraphique. 1933 [1932]. pp. 31–40 [33]. Archived (PDF) from the original on 2020-12-21. Retrieved 2020-12-21. (1+188 pages) [8]
- ^ «Chapter IX. Transmission Signals. Article 35. Transmission Signals of the International Telegraph Alphabets Nos. 1 and 2, Morse Code Signals and Signals of the Hughes and Siemens Instruments.». Telegraph Regulations Annexed To The International Telecommunication Convention — Final Protocol To The Telegraph Regulations — Madrid 1932 (PDF) (in English and French). London, UK: General Post Office / His Majesty’s Stationery Office. 1933 [1932]. pp. 32–40 [34]. 43-152-2 / 18693. Archived (PDF) from the original on 2020-12-21. Retrieved 2020-12-21. (1+2*120+26 pages) [9]
- ^ Zemanek, Heinrich «Heinz» Josef (1983-12-01). Otto Schäffler (1838-1928). Pionier des Telephons, der Telegraphie und der Lochkarte sowie Erbauer der ersten Wiener Telephonzentrale. Blätter für Technikgeschichte (in German and English). Vol. 41–43 (1979–1981) (1 ed.). Vienna, Austria: Technisches Museum für Industrie und Gewerbe, Forschungsinstitut für Technikgeschichte / Springer-Verlag. pp. 81–118. ISBN 3-21181779-4. ISSN 0067-9127. OCLC 952698275.
- ^ Zemanek, Heinrich «Heinz» Josef (1976-06-07). «Computer prehistory and history in central Europe». Written at Vienna, Austria. International Workshop on Managing Requirements Knowledge. AFIPS ’76: Proceedings of the June 7–10, 1976, national computer conference and exposition June 1976. Vol. 1. New York, USA: American Federation of Information Processing Societies, Association for Computing Machinery. pp. 15–20. doi:10.1145/1499799.1499803. ISBN 978-1-4503-7917-5. S2CID 14114959. Archived from the original on 2020-12-17. Retrieved 2020-12-17. p. 17:
[…] In 1874, Schaeffler [de] invented another printing telegraph, a quadruple system like the Baudot, but mechanically more sophisticated. The Hughes telegraph had two synchronously rotating fingers, one in the sender and one in the receiver. By a piano-like keyboard the operator selected a letter and thereby made contact with the rotating finger in the corresponding direction. Since the receiving finger was in the same direction at this moment, the receiver could print the correct letter. The Baudot and the Schaeffler printing telegraphs use a five-bit binary code. … Schaeffler’s code is a reflected binary code! What F. Gray patented in 1953 for PCM, Schaeffler had applied in his telegraph in 1874, and for a similar reason: reliability. He had contact fingers sensing on five cams consecutively all combinations; the right one triggers printing. If the fingers are to make a minimal number of movements, the solution is the reflected binary code. For Schaeffler, this idea was a minor one. More exactly, the code is described in a letter by the Austrian Post employee, J[ohann] N[epomuk] Teufelhart, inserted there as a footnote and telling that Schaeffler found the code by combining wooden bars with the different combinations until he had the best solution. Another Post employee, Alexander Wilhelm Lambert of Linz, claims to have shown this code to Schaeffler as early as 1872, but this claim is not clear and cannot be checked. […]
(6 pages) - ^ Goodall, William M. (January 1951). «Television by Pulse Code Modulation». Bell System Technical Journal. 30 (1): 33–49. doi:10.1002/j.1538-7305.1951.tb01365.x. (NB. Presented orally before the I.R.E. National Convention, New York City, March 1949.)
- ^ Karnaugh, Maurice (November 1953) [1953-04-23, 1953-03-17]. «The Map Method for Synthesis of Combinational Logic Circuits» (PDF). Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics. 72 (5): 593–599. doi:10.1109/TCE.1953.6371932. S2CID 51636736. Paper 53-217. Archived from the original (PDF) on 2017-04-16. Retrieved 2017-04-16. (NB. Also contains a short review by Samuel H. Caldwell.)
- ^ Wakerly, John F. (1994). Digital Design: Principles & Practices. New Jersey, USA: Prentice Hall. pp. 48–49, 222. ISBN 0-13-211459-3. (NB. The two page sections taken together say that K-maps are labeled with Gray code. The first section says that they are labeled with a code that changes only one bit between entries and the second section says that such a code is called Gray code.)
- ^ Brown, Frank Markham (2012) [2003, 1990]. «3.9.2 Maps». Boolean Reasoning – The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York, USA: Dover Publications, Inc. p. 49. ISBN 978-0-486-42785-0. p. 49:
[…] Karnaugh’s map orders the arguments of the discriminants according to the reflected binary code, also called the Gray code. […]
(xii+291+3 pages) 1st edition - ^ Händler, Wolfgang (1958). Ein Minimisierungsverfahren zur Synthese von Schaltkreisen (Minimisierungsgraphen) (Dissertation) (in German). Potsdam, Germany: Technische Hochschule Darmstadt. D 17. (73 pages+app.) [10]
- ^ Berger, Erich R.; Händler, Wolfgang (1967) [1962]. Steinbuch, Karl W.; Wagner, Siegfried W. (eds.). Taschenbuch der Nachrichtenverarbeitung (in German) (2 ed.). Berlin, Germany: Springer-Verlag OHG. pp. 64, 1034–1035, 1036, 1038. LCCN 67-21079. Title No. 1036. p. 64:
[…] Übersichtlich ist die Darstellung nach Händler, die sämtliche Punkte, numeriert nach dem Gray-Code […], auf dem Umfeld eines Kreises anordnet. Sie erfordert allerdings sehr viel Platz. […]
[Händler’s diagram, where all points, numbered according to the Gray code, are arranged on the circumference of a circle, is easily comprehensible. It needs, however, a lot of space.] - ^ «Informatik Sammlung Erlangen (ISER)» (in German). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. Archived from the original on 2017-05-16. Retrieved 2017-04-12.
- ^ «Informatik Sammlung Erlangen (ISER) – Impressum» (in German). Erlangen, Germany: Friedrich-Alexander Universität. 2012-03-13. Archived from the original on 2012-02-26. Retrieved 2017-04-15.
- ^ a b c d e Bhat, Girish S.; Savage, Carla Diane (1996). «Balanced Gray Codes». Electronic Journal of Combinatorics. 3 (1). doi:10.37236/1249.
- ^ Donohue, Ryan (2003). «Synchronization in Digital Logic Circuits» (PDF). Archived (PDF) from the original on 2018-01-15. Retrieved 2018-01-15.
- ^ Hulst, George D. (1962-02-06) [1957-11-15]. Reflected binary code counter (PDF). Nutley, New Jersey, USA: International Telephone and Telegraph Corporation (ITT). U.S. Patent 3,020,481. Serial No. 696793. Archived (PDF) from the original on 2020-08-06. Retrieved 2020-08-06. (5 pages)
- ^ a b c d Powell, E. Alexander (June 1968). «Codes particularly useful for analogue to digital conversions». A short note on useful codes for Fluidic Control Circuits (PDF). Cranfield, UK: The College of Aeronautics, Department of Production Engineering. pp. 7, 9. S2CID 215864694. CoA Memo 156. Archived (PDF) from the original on 2020-12-15. Retrieved 2020-12-15. (18 pages) (NB. The paper names the Glixon code modified Gray code and misspells Richard W. Hamming’s name.)
- ^ Mehta, Huzefa; Owens, Robert Michael; Irwin, Mary Jane «Janie» (1996-03-22). «Some issues in Gray code addressing». Proceedings of the Sixth Great Lakes Symposium on VLSI. Proceedings of the 6th Great Lakes Symposium on VLSI (GLSVLSI 96). IEEE Computer Society. pp. 178–181. doi:10.1109/GLSV.1996.497616. ISBN 978-0-8186-7502-7. ISSN 1066-1395. S2CID 52837310.
- ^ a b Doran, Robert «Bob» William (March 2007). The Gray Code (PDF). CDMTCS Research Report Series. Centre for Discrete Mathematics and Theoretical Computer Science, University of Auckland, New Zealand. CDMTCS-304. Archived (PDF) from the original on 2020-05-22. Retrieved 2020-05-23. (25 pages)
- ^ Su, Ching-Long; Tsui, Chi-Ying; Despain, Alvin M. (1994). Low Power Architecture Design and Compilation Techniques for High-Performance Processors (PDF) (Report). Advanced Computer Architecture Laboratory. ACAL-TR-94-01. Archived (PDF) from the original on 2020-07-26. Retrieved 2020-12-17.
- ^ Guo, Hui; Parameswaran, Sri (April–June 2010). «Shifted Gray encoding to reduce instruction memory address bus switching for low-power embedded systems». Journal of Systems Architecture. 56 (4–6): 180–190. doi:10.1016/j.sysarc.2010.03.003.
- ^ Dietz, Henry Gordon «Hank» (2002). «The Aggregate Magic Algorithms: Gray Code Conversion». The Aggregate. Electrical and Computer Engineering Department, College of Engineering, University of Kentucky. Archived from the original on 2020-12-16. Retrieved 2020-12-16.
- ^ Maxfield, Max (2007-06-29). «How to generate Gray Codes for non-power-of-2 sequences». Archived from the original on 2022-01-29. Retrieved 2022-01-29.
- ^ (sequence A290772 in the OEIS)
- ^ a b Guan, Dah-Jyh (1998). «Generalized Gray Codes with Applications». Proceedings of the National Scientific Council, Republic of China, Part A. 22: 841–848. CiteSeerX 10.1.1.119.1344.
- ^ D. G. Wagner, J. West (1991). «Construction of Uniform Gray Codes». Congressus Numerantium. 80: 217–223.
- ^ a b Suparta, I. Nengah (2005). «A simple proof for the existence of exponentially balanced Gray codes». Electronic Journal of Combinatorics. 12. doi:10.37236/1986.
- ^ a b Flahive, Mary Elizabeth; Bose, Bella (2007). «Balancing cyclic R-ary Gray codes». Electronic Journal of Combinatorics. 14. doi:10.37236/949.
- ^ Strackx, Raoul; Piessens, Frank (2016). «Ariadne: A Minimal Approach to State Continuity». Usenix Security. 25.
- ^ Savage, Carla Diane (1997). «A Survey of Combinatorial Gray Codes». SIAM Review. Society for Industrial and Applied Mathematics (SIAM). 39 (4): 605–629. Bibcode:1997SIAMR..39..605S. CiteSeerX 10.1.1.39.1924. doi:10.1137/S0036144595295272. JSTOR 2132693. S2CID 6375360.
- ^ a b Savage, Carla Diane; Winkler, Peter (1995). «Monotone Gray codes and the middle levels problem». Journal of Combinatorial Theory. Series A. 70 (2): 230–248. doi:10.1016/0097-3165(95)90091-8. ISSN 0097-3165.
- ^ Savage, Carla Diane (1997-01-16). «Long cycles in the middle two levels of the Boolean lattice». Ars Combinatoria. North Carolina State University, Raleigh, North Carolina, USA. 35 (A): 97–108. CiteSeerX 10.1.1.39.2249. ISSN 0381-7032. S2CID 15975960. Archived from the original on 2020-05-13. Retrieved 2020-05-13. (15 pages)
- ^ a b Goddyn, Luis (1999). «MATH 343 Applied Discrete Math Supplementary Materials» (PDF). Department of Mathematics, Simon Fraser University. Archived from the original (PDF) on 2015-02-17.
- ^ Sawada, Joseph «Joe»; Wong, Dennis Chi-Him (2007). «A Fast Algorithm to generate Beckett–Gray codes». Electronic Notes in Discrete Mathematics. 29: 571–577. doi:10.1016/j.endm.2007.07.091.
- ^ Richards, Richard Kohler (January 1971). «Snake-in-the-Box Codes». Written at Ames, Iowa, USA. Digital Design. New York, USA: Wiley-Interscience, John Wiley & Sons, Inc. pp. 206–207. ISBN 0-471-71945-5. LCCN 73-147235. (12+577+1 pages)
- ^ a b NZ 264738, Spedding, Norman Bruce, «A position encoder», published 1994-10-28[failed verification]
- ^ Spedding, Norman Bruce (1994-10-28). «The following is a copy of the provisional patent filed on behalf of Industrial Research Limited on 1994-10-28 – NZ Patent 264738» (PDF). Industrial Research Limited. NZ Patent 264738. Archived (PDF) from the original on 2017-10-29. Retrieved 2018-01-14.
- ^ Hiltgen, Alain P.; Paterson, Kenneth G.; Brandestini, Marco (September 1996). «Single-Track Gray Codes» (PDF). IEEE Transactions on Information Theory. 42 (5): 1555–1561. doi:10.1109/18.532900. Zbl 857.94007.
- ^ Hiltgen, Alain P.; Paterson, Kenneth G. (September 2001). «Single-Track Circuit Codes» (PDF). IEEE Transactions on Information Theory. 47 (6): 2587–2595. CiteSeerX 10.1.1.10.8218. doi:10.1109/18.945274. Archived (PDF) from the original on 2018-01-15. Retrieved 2018-01-15.
- ^ Etzion, Tuvi; Schwartz, Moshe (November 1999) [1998-05-17]. «The Structure of Single-Track Gray Codes» (PDF). IEEE Transactions on Information Theory. IT-45 (7): 2383–2396. CiteSeerX 10.1.1.14.8333. doi:10.1109/18.796379. Archived (PDF) from the original on 2018-01-15. Retrieved 2018-01-15. Technical Report CS0937
- ^ Sillke, Torsten (1997) [1993-03-01]. «Gray-Codes with few tracks (a question of Marco Brandestini)». Archived from the original on 2017-10-29. Retrieved 2017-10-29.
- ^ Etzion, Tuvi; Paterson, Kenneth G. (May 1996). «Near Optimal Single-Track Gray Codes» (PDF). IEEE Transactions on Information Theory. IT-42 (3): 779–789. CiteSeerX 10.1.1.14.1527. doi:10.1109/18.490544. Archived (PDF) from the original on 2016-10-30. Retrieved 2018-04-08.
- ^ Ruskey, Frank; Weston, Mark (2005-06-18). «A Survey of Venn Diagrams: Symmetric Diagrams». Dynamic Surveys. Electronic Journal of Combinatorics. doi:10.37236/26.
- ^ Alciatore, David G.; Histand, Michael B. (1999). Mechatronics. McGraw–Hill Education – Europe. ISBN 978-0-07-131444-2.
- ^ Krishna (2008-05-11). «Gray code for QAM». Archived from the original on 2017-10-29. Retrieved 2017-10-29.
- ^ Strang, Thomas; Dammann, Armin; Röckl, Matthias; Plass, Simon (October 2009). Using Gray codes as Location Identifiers (PDF). 6. GI/ITG KuVS Fachgespräch Ortsbezogene Anwendungen und Dienste (in English and German). Oberpfaffenhofen, Germany: Institute of Communications and Navigation, German Aerospace Center (DLR). CiteSeerX 10.1.1.398.9164. Archived (PDF) from the original on 2015-05-01. Retrieved 2020-12-16. (5/8 pages) [11]
- Thomas Strang; et al. (October 2009). «Using Gray codes as Location Identifiers» (PDF). ResearchGate (Abstract) (in German and English). Archived from the original on 2020-09-03.
- ^ Greferath, Marcus (2009). «An Introduction to Ring-Linear Coding Theory». In Sala, Massimiliano; Mora, Teo; Perret, Ludovic; Sakata, Shojiro; Traverso, Carlo (eds.). Gröbner Bases, Coding, and Cryptography. Springer Science & Business Media. p. 220. ISBN 978-3-540-93806-4.
- ^ Solé, Patrick (2016-04-17). Hazewinkel, Michiel (ed.). Kerdock and Preparata codes. Encyclopedia of Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0609-8. Archived from the original on 2017-10-29. Retrieved 2017-10-29.
- ^ Spaulding, Carl P. (1965-07-12). How to Use Shaft Encoders. Monrovia, California, USA: Datex Corporation. (85 pages)
- ^ a b Wheeler, Edwin L. (1969-12-30) [1968-04-05]. Analog to digital encoder (PDF). New York, USA: Conrac Corporation. U.S. Patent 3487460A. Serial No. 719026 (397812). Archived (PDF) from the original on 2020-08-05. Retrieved 2018-01-21. p. 5, left column 9, rows 15–22:
[…] The MOA-GILLHAM code is essentially the combination of the Gray code discussed thereinabove and the well known Datex code; the Datex code is disclosed in U.S. Patent 3,165,731. The arrangement is such that the Datex code defines the bits for the units count of the encoder and the Gray code defines the bits for each of the higher order decades, the tens, hundreds, etc. […]
(11 pages) - ^ a b c d e f Dokter, Folkert; Steinhauer, Jürgen (1973-06-18). «2.4. Coding numbers in the binary system». Digital Electronics. Philips Technical Library (PTL) / Macmillan Education (Reprint of 1st English ed.). Eindhoven, Netherlands: The Macmillan Press Ltd. / N. V. Philips’ Gloeilampenfabrieken. pp. 32, 39, 50–53. doi:10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. SBN 333-13360-9. Retrieved 2020-05-11. p. 53:
[…] The Datex code […] uses the O’Brien code II within each decade, and reflected decimal numbers for the decimal transitions. For further processing, code conversion to the natural decimal notation is necessary. Since the O’Brien II code forms a 9s complement, this does not give rise to particular difficulties: whenever the code word for the tens represents an odd number, the code words for the decimal units are given as the 9s complements by inversion of the fourth binary digit. […]
(270 pages) - ^ a b c d e Dokter, Folkert; Steinhauer, Jürgen (1975) [1969]. «2.4.4.6. Einschrittige Kodes». Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher (in German). Vol. I (improved and extended 5th ed.). Hamburg, Germany: Deutsche Philips GmbH. pp. 41, 48, 51, 58, 60–61. ISBN 3-87145-272-6. (xii+327+3 pages)
- ^ «…accurate liquid level metering – at ANY DISTANCE!». Petroleum Refiner (Advertisement). Gulf Publishing Company. 33 (9): 368. September 1954. ISSN 0096-6517. p. 368:
[…] The complete dispatching operation, gauging, and remote control is integrated into one single unitized system when a «Varec» Pulse Code Telemetering System is installed. […]
- ^ Bishup, Bernard W.; Repeta, Anthony A.; Giarrizzo, Frank C. (1968-08-13) [1963-04-03]. «Telemetering and supervisory control system having normally continuous telemetering signals». Leeds and Northrup Co. US3397386A. [12]
- ^ «Encoder Pulse Format». Installation and Operations Manual for the Model 1900 Micro 4-Wire Transmitter (PDF). Cypress, California, USA: Whessoe Varec, Inc. January 1993 [1991-07-01]. pp. 04-4–04-8. 33-08461. Archived (PDF) from the original on 2020-05-16. Retrieved 2020-05-16. (38 pages) (NB. Position 5 for «Inches» on page 04-8 should read «0111» rather than «1111».)
- ^ «2.2.3.3 MSP Level Data Format». Varec Model 1900 – Micro 4-Wire Transmitter (BSAP to Mark / Space Protocol (MSP)) – Application Notes (PDF). Emerson Electric. pp. 11–14. Archived (PDF) from the original on 2020-05-16. Retrieved 2020-05-16. (vi+33 pages)
- ^ a b c Wightman, Eric Jeffrey (1972). «Chapter 6. Displacement measurement». Instrumentation in Process Control (1 ed.). London, UK: Butterworth & Co (Publishers) Ltd. pp. 122–123. ISBN 0-408-70293-1. p. 122–123:
[…] Other forms of code are also well known. Among these are the Royal Radar Establishment code; The Excess Three decimal code; Gillham code which is recommended by ICAO for automatic height transmission for air traffic control purposes; the Petherick code, and the Leslie and Russell code of the National Engineering Laboratory. Each has its particular merits and they are offered as options by various encoder manufacturers. […]
(12+367+5 pages) - ^ Phillips, Darryl (2012-07-26) [1998]. «Altitude – MODEC ASCII». AirSport Avionics. Archived from the original on 2012-07-26.
- ^ Stewart, K. (2010-12-03). «Aviation Gray Code: Gillham Code Explained». Custom Computer Services (CCS). Archived from the original on 2018-01-16. Retrieved 2018-01-14.
- ^ Leslie, William «Bill» H. P.; Russell, A. (1964). A cyclic progressive decimal code for simple translation to decimal and analogue outputs (Report). East Kilbride, Glasgow, UK: National Engineering Laboratory. NEL Report 129. (17 pages)
- ^ Leslie, William «Bill» H. P. (1974). «The work on NC at NEL». In Koenigsberger, Franz; Tobias, Stephen Albert (eds.). Proceedings of the Fourteenth International Machine Tool Design and Research Conference, 12–14 September 1973. The Macmillan Press Ltd. pp. 215–224 [215, 217]. doi:10.1007/978-1-349-01921-2_30. ISBN 978-1-34901921-2. LCCN 73-16545. SBN 333-14913-0.
- ^ Hoklas, Archibald (1989-09-06) [1988-04-29]. «Abtastvorrichtung zur digitalen Weg- oder Winkelmessung» (PDF) (in German). VEB Schiffselektronik Johannes Warnke [de]. GDR Patent DD271603A1. WP H 03 M / 315 194 8. Archived from the original (PDF) on 2018-01-18. Retrieved 2018-01-18 – via DEPATIS [de]. [13] [14]
- ^ a b c d e f g h i j k Hoklas, Archibald (2005). «Gray code – Unit distance code». Archived from the original on 2018-01-15. Retrieved 2018-01-15.
- ^ a b c d e Hoklas, Archibald (2005). «Gray-Kode – Einschrittiger Abtastkode» (in German). Archived from the original on 2018-01-15. Retrieved 2018-01-15.
- ^ Petherick, Edward John; Hopkins, A. J. (1958). Some Recently Developed Digital Devices for Encoding the Rotations of Shafts (Technical Note MS21). Farnborough, UK: Royal Aircraft Establishment (RAE).
- ^ «Digitizer als Analog-Digital-Wandler in der Steuer-, Meß- und Regeltechnik» (PDF). Technische Mitteilungen. Relais, elektronische Geräte, Steuerungen (in German). No. 13. Cologne-Niehl, Germany: Franz Baumgartner (FraBa). May 1963. pp. 1–2. Archived from the original (PDF) on 2020-05-21. Retrieved 2020-05-21. pp. 1–2:
[…] Die Firma Harrison Reproduction Equipment, Farnborough/England […] hat in jahrelanger Entwicklung in Zusammenarbeit mit der Britischen Luftwaffe und britischen Industriebetrieben den mechanischen Digitizer […] zu einer technischen Reife gebracht, die fast allen Anforderungen […] genügt. […] Um bei der dezimalen Entschlüsselung des verwendeten Binärcodes zu eindeutigen und bei der Übergabe von einer Dezimalstelle zur anderen in der Reihenfolge immer richtigen Ergebnissen zu kommen, wurde ein spezieller Code entwickelt, der jede Möglichkeit einer Fehlaussage durch sein Prinzip ausschließt und der außerdem durch seinen Aufbau eine relativ einfache Entschlüsselung erlaubt. Der Code basiert auf dem Petherick-Code. […]
(4 pages) - ^ a b Charnley, C. J.; Bidgood, R. E.; Boardman, G. E. T. (October 1965). «The Design of a Pneumatic Position Encoder» (PDF). IFAC Proceedings Volumes. The College of Aeronautics, Cranfield, Bedford, England. 2 (3): 75–88. doi:10.1016/S1474-6670(17)68955-9. Chapter 1.5. Retrieved 2018-01-14.
- ^ Hollingdale, Stuart H. (1958-09-19). «Session 14. Data Processing». Applications of Computers. Atlas – Application of Computers, University of Nottingham 15–19 September 1958 (Conference paper). Archived from the original on 2020-05-25. Retrieved 2020-05-25.
- ^ a b c O’Brien, Joseph A. (May 1956) [1955-11-15, 1955-06-23]. «Cyclic Decimal Codes for Analogue to Digital Converters». Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics. Bell Telephone Laboratories, Whippany, New Jersey, USA. 75 (2): 120–122. doi:10.1109/TCE.1956.6372498. ISSN 0097-2452. S2CID 51657314. Paper 56-21. Retrieved 2020-05-18. (3 pages) (NB. This paper was prepared for presentation at the AIEE Winter General Meeting, New York, USA, 1956-01-30 to 1956-02-03.)
- ^ a b c d e f g h i Steinbuch, Karl W., ed. (1962). Written at Karlsruhe, Germany. Taschenbuch der Nachrichtenverarbeitung (in German) (1 ed.). Berlin / Göttingen / New York: Springer-Verlag OHG. pp. 71–74, 97, 761–764, 770, 1080–1081. LCCN 62-14511.
- ^ a b c d e f g h i Steinbuch, Karl W.; Weber, Wolfgang; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik – Band II – Struktur und Programmierung von EDV-Systemen. Taschenbuch der Nachrichtenverarbeitung (in German). Vol. 2 (3 ed.). Berlin, Germany: Springer Verlag. pp. 98–100. ISBN 3-540-06241-6. LCCN 73-80607.
- ^ Foss, Frederic A. (1960-12-27) [1954-12-17]. «Control Systems» (PDF). International Business Machines Corp. Fig. 7, Fig. 8, Fig. 11. U.S. Patent 2966670A. Serial No. 475945. Archived (PDF) from the original on 2020-06-21. Retrieved 2020-08-05. (14 pages) (NB. The author called his code 2*-4-2-1 (+9-±7-±3-±1) reflected decimal code.)
- ^ Foss, Frederic A. (December 1954). «The Use of a Reflected Code in Digital Control Systems». IRE Transactions on Electronic Computers. EC-3 (4): 1–6. doi:10.1109/IREPGELC.1954.6499244. ISSN 2168-1740. (6 pages)
- ^ Evans, David Silvester (1958). «[unknown]». Transactions. Institute of Measurement and Control. 10–12: 87. (NB. The Watts code was called W.R.D. code or Watts Reflected Decimal to distinguish it from other codes used at Hilger & Watts Ltd.)
- ^ Benjamin, P. W.; Nicholls, G. S. (1963). «3.2.2 Electromechanical Digitizers». Measurement of Neutron Spectra by Semi-Automatic Scanning of Recoil Protons in Photographic Emulsions. United Kingdom Atomic Energy Authority, Atomic Weapons Research Establishment, UK: U.S. Department of Energy. pp. 8–10, 19. AWRE Report No. NR 5/63. [15] (23 pages)
- ^ Klinkowski, James J. (1967-03-14) [1964-03-23]. «Electronic Diode Matrix Decoder Circuits» (PDF). Detroit, Michigan, USA: Burroughs Corporation. U.S. Patent 3309695A. Serial No. 353845. Archived (PDF) from the original on 2020-05-23. Retrieved 2020-05-23. (5 pages) [16]
- ^ Klinkowski, James J. (1970-03-31) [1966-12-22]. «Binary-coded decimal signal converter» (PDF). Detroit, Michigan, USA: Burroughs Corporation. U.S. Patent 3504363A. Serial No. 603926. Archived (PDF) from the original on 2020-05-23. Retrieved 2020-05-23. (7 pages)
- ^ «[unknown]». Electrical Design News. Rogers Publishing Company. 12. 1967. ISSN 0012-7515. [17][18]
- ^ Tóth-Zentai, Györgyi (1979-10-05). «Some Problems Of Angular Rotational Digital Converters». Periodica Polytechnica Electrical Engineering. Department of Electronics Technology, Technical University, Budapest, Hungary. 23 (3–4): 265–270 [266]. Retrieved 2020-05-23. [19] (6 pages) (NB. Shows a 6-digit Watts code.)
- ^ Savard, John J. G. (2018) [2006]. «Decimal Representations». quadibloc. Archived from the original on 2018-07-16. Retrieved 2018-07-16.
- ^ a b Turvey, Jr., Frank P. (1958-07-29) [1956-05-17]. «Pulse-Count Coder» (PDF). Nutley, New Jersey, USA: International Telephone and Telegraph Corporation. U.S. Patent 2845617A. Serial No. 585494. Archived (PDF) from the original on 2020-05-23. Retrieved 2020-05-23. (5 pages)
- ^ a b Glixon, Harry Robert (March 1957). «Can You Take Advantage of the Cyclic Binary-Decimal Code?». Control Engineering. Technical Publishing Company, a division of Dun-Donnelley Publishing Corporation, Dun & Bradstreet Corp. 4 (3): 87–91. ISSN 0010-8049. (5 pages)
- ^ a b Borucki, Lorenz; Dittmann, Joachim (1971) [July 1970, 1966, Autumn 1965]. «2.3 Gebräuchliche Codes in der digitalen Meßtechnik». Written at Krefeld / Karlsruhe, Germany. Digitale Meßtechnik: Eine Einführung (in German) (2 ed.). Berlin / Heidelberg, Germany: Springer-Verlag. pp. 10–23 [12–14]. doi:10.1007/978-3-642-80560-8. ISBN 3-540-05058-2. LCCN 75-131547. ISBN 978-3-642-80561-5. (viii+252 pages) 1st edition (NB. Like Kämmerer, the authors describe a 6-bit 20-cyclic Glixon code.)
- ^ a b Kämmerer, Wilhelm [in German] (May 1969). «II.15. Struktur: Informationsdarstellung im Automaten». Written at Jena, Germany. In Frühauf, Hans [in German]; Kämmerer, Wilhelm; Schröder, Kurz; Winkler, Helmut (eds.). Digitale Automaten – Theorie, Struktur, Technik, Programmieren. Elektronisches Rechnen und Regeln (in German). Vol. 5 (1 ed.). Berlin, Germany: Akademie-Verlag GmbH. p. 173. License no. 202-100/416/69. Order no. 4666 ES 20 K 3. (NB. A second edition 1973 exists as well. Like Borucki and Dittmann, but without naming it Glixon code, the author creates a 20-cyclic tetradic code from Glixon code and a Glixon code variant with inverted high-order bit.)
- ^ Paul, Matthias R. (1995-08-10) [1994]. «Unterbrechungsfreier Schleifencode» [Continuous loop code]. 1.02 (in German). Retrieved 2008-02-11. (NB. The author called this code Schleifencode (English: «loop code»). It differs from Gray BCD code only in the encoding of state 0 to make it a cyclic unit-distance code for full-circle rotatory applications. Avoiding the all-zero code pattern allows for loop self-testing and to use the data lines for uninterrupted power distribution.)
- ^ Klar, Rainer (1970-02-01). Digitale Rechenautomaten – Eine Einführung [Digital Computers – An Introduction]. Sammlung Göschen (in German). Vol. 1241/1241a (1 ed.). Berlin, Germany: Walter de Gruyter & Co. / G. J. Göschen’sche Verlagsbuchhandlung [de]. p. 17. ISBN 3-11-083160-0. . Archiv-Nr. 7990709. Archived from the original on 2020-06-01. Retrieved 2020-04-13. (205 pages) (NB. A 2019 reprint of the first edition is available under ISBN 3-11002793-3, 978-3-11002793-8. A reworked and expanded 4th edition exists as well.)
- ^ Klar, Rainer (1989) [1988-10-01]. Digitale Rechenautomaten – Eine Einführung in die Struktur von Computerhardware [Digital Computers – An Introduction into the structure of computer hardware]. Sammlung Göschen (in German). Vol. 2050 (4th reworked ed.). Berlin, Germany: Walter de Gruyter & Co. p. 28. ISBN 3-11011700-2. (320 pages) (NB. The author called this code Einheitsabstandscode (English: «unit-distance code»). By swapping two bit rows and inverting one of them, it can be transferred into the O’Brien code II, whereas by swapping and inverting two bit rows, it can be transferred into the Petherick code.)
Further reading[edit]
- Richards, Richard Kohler (1955). Arithmetic Operations in Digital Computers (5 ed.). New York, USA: D. Van Nostrand Co., Inc.
- Richards, Richard Kohler (1967). Electronic Digital Components and Circuits. D. Van Nostrand Co., Inc. pp. 490, 500–504, 510–511.
- Black, Paul E. (2004-02-25). «Gray code». NIST.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007). «Section 22.3. Gray Codes». Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York, USA: Cambridge University Press. ISBN 978-0-521-88068-8.
- Savage, Carla Diane (1997). «A Survey of Combinatorial Gray Codes». SIAM Review. Society for Industrial and Applied Mathematics (SIAM). 39 (4): 605–629. Bibcode:1997SIAMR..39..605S. CiteSeerX 10.1.1.39.1924. doi:10.1137/S0036144595295272. JSTOR 2132693. S2CID 6375360.
- Wilf, Herbert Saul (1989). «Chapters 1–3». Combinatorial algorithms: An update. Society for Industrial and Applied Mathematics (SIAM). ISBN 0-89871-231-9.
- Dewar, Megan; Stevens, Brett (2012-08-29). Ordering Block Designs – Gray Codes, Universal Cycles and Configuration. CMS Books in Mathematics (1 ed.). New York, USA: Springer Science+Business Media. doi:10.1007/978-1-4614-4325-4. ISBN 978-1-46144324-7. ISSN 1613-5237.
- Maxfield, Clive «Max» (2012-10-01) [2011-05-28]. «Gray Code Fundamentals». Design How-To. EETimes. Part 1. Archived from the original on 2017-10-30. Retrieved 2017-10-30. Part 2 Part 3
- Warren, Jr., Henry S. (2013). «Chapter 13: Gray Code». Hacker’s Delight (2 ed.). Addison Wesley – Pearson Education, Inc. pp. 311–317. ISBN 978-0-321-84268-8. (7 pages)
- Zinovik, Igor; Kroening, Daniel; Chebiryak, Yury (2008-03-21). «Computing Binary Combinatorial Gray Codes Via Exhaustive Search With SAT Solvers». IEEE Transactions on Information Theory. IEEE. 54 (4): 1819–1823. doi:10.1109/TIT.2008.917695. hdl:20.500.11850/11304. S2CID 2854180. (5 pages)
- O’Brien, Joseph A. (June 1957). «Unit-Distance Binary-Decimal Code Translators». IRE Transactions on Electronic Computers. EC-6 (2): 122–123. doi:10.1109/TEC.1957.5221585. ISSN 0367-9950. Retrieved 2020-05-25. (2 pages)
- Barr, K. G. (March 1981). «A decimal Gray code – Easily converted for shaft position coding» (PDF). Wireless World. Vol. 87, no. 1542. Faculty of Natural Sciences, University of the West Indies. pp. 86–87. Archived (PDF) from the original on 2020-07-28. Retrieved 2020-07-28.
External links[edit]
- «Gray Code» demonstration by Michael Schreiber, Wolfram Demonstrations Project (with Mathematica implementation). 2007.
- NIST Dictionary of Algorithms and Data Structures: Gray code.
- Hitch Hiker’s Guide to Evolutionary Computation, Q21: What are Gray codes, and why are they used?, including C code to convert between binary and BRGC.
- Dragos A. Harabor uses Gray codes in a 3D digitizer.
- Single-track gray codes, binary chain codes (Lancaster 1994), and linear-feedback shift registers are all useful in finding one’s absolute position on a single-track rotary encoder (or other position sensor).
- AMS Column: Gray codes
- Optical Encoder Wheel Generator
- ProtoTalk.net – Understanding Quadrature Encoding – Covers quadrature encoding in more detail with a focus on robotic applications
| Lucal код | |||||
|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | |
| Код Грея | |||||
| 4 | 3 | 2 | 1 | ||
| 0 |
0 |
0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 0 | 0 |
| 5 | 0 | 1 | 1 | 1 | 1 |
| 6 | 0 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 | 1 |
| 8 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 0 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 0 |
| 11 | 1 | 1 | 1 | 0 | 1 |
| 12 | 1 | 0 | 1 | 0 | 0 |
| 13 | 1 | 0 | 1 | 1 | 1 |
| 14 | 1 | 0 | 0 | 1 | 0 |
| 15 | 1 | 0 | 0 | 0 | 1 |
Отражение двоичного кода ( RBC ), также известный как отраженный двоичный ( RB ) или код Грея после Frank Gray , является упорядочение двоичной системе счисления таким образом, что две последовательные значения различаются только в одной битовой (двоичный разряд).
Например, представление десятичного значения «1» в двоичном формате обычно будет « 001 », а «2» будет « 010 ». В коде Грея эти значения представлены как « 001 » и « 011 ». Таким образом, для увеличения значения с 1 до 2 потребуется изменить только один бит вместо двух.
Коды Грея широко используются для предотвращения паразитных выходных сигналов от электромеханических переключателей и для облегчения исправления ошибок в цифровой связи, такой как цифровое наземное телевидение и некоторые системы кабельного телевидения .
Мотивация и имя
Многие устройства указывают положение, замыкая и размыкая переключатели. Если это устройство использует естественные двоичные коды , позиции 3 и 4 находятся рядом друг с другом, но все три бита двоичного представления различаются:
-
Десятичный Двоичный … … 3 011 4 100 … …
Проблема с естественными двоичными кодами заключается в том, что физические переключатели не идеальны: очень маловероятно, что физические переключатели будут изменять состояния точно синхронно. При переходе между двумя показанными выше состояниями все три переключателя изменяют состояние. В течение короткого периода времени, когда все меняется, переключатели будут считывать какое-то ложное положение. Даже без нажатия клавиш переход может выглядеть как 011 — 001 — 101 — 100 . Когда переключатели оказываются в положении 001 , наблюдатель не может сказать, является ли это «реальным» положением 1 или переходным состоянием между двумя другими положениями. Если выходной сигнал поступает в последовательную систему, возможно, через комбинационную логику , тогда последовательная система может сохранить ложное значение.
Эта проблема может быть решена путем изменения только одного переключателя за раз, поэтому никогда не возникает двусмысленности положения, в результате чего коды присваиваются каждому из непрерывного набора целых чисел или каждому члену кругового списка, слова символов, такие как что никакие два кодовых слова не идентичны и каждые два соседних кодовых слова отличаются ровно на один символ. Эти коды также известны как коды единичного расстояния , одиночного расстояния , одношаговые , монострофические или синкопические коды в отношении расстояния Хэмминга 1 между соседними кодами.

Патент Грея вводит термин «отраженный двоичный код».
В принципе, может быть более одного такого кода для данной длины слова, но термин «код Грея» сначала был применен к конкретному двоичному коду для неотрицательных целых чисел, двоично-отраженному коду Грея или BRGC . Исследователь
Bell Labs Джордж Р. Стибиц описал такой код в заявке на патент 1941 года, выданной в 1943 году. Фрэнк Грей ввел термин « отраженный двоичный код» в своей патентной заявке 1947 года, отметив, что код «пока не имеет общепризнанного имени». Он получил название от того факта, что он «может быть построен из обычного двоичного кода посредством своего рода процесса отражения».
В стандартном кодировании младший значащий бит следует повторяющейся схеме: 2 вкл. , 2 выкл. (… 11001100 …); следующая цифра — комбинация 4 вкл., 4 выкл .; п — й наименее значимый бит картина 2 п 2 п выкл. Четырехбитная версия этого показана ниже:

-
Десятичный Двоичный серый Десятичная дробь
серого0 0000 0000 0 1 0001 0001 1 2 0010 0011 3 3 0011 0010 2 4 0100 0110 6 5 0101 0111 7 6 0110 0101 5 7 0111 0100 4 8 1000 1100 12 9 1001 1101 13 10 1010 1111 15 11 1011 1110 14 12 1100 1010 10 13 1101 1011 11 14 1110 1001 9 15 1111 1000 8
Для десятичного числа 15 код переключается на десятичный 0 с одним переключением переключателя. Это называется свойством цикличности или смежности кода.
В современной цифровой связи коды Грея играют важную роль в исправлении ошибок . Например, в схеме цифровой модуляции , такой как QAM, где данные обычно передаются в символах из 4 или более битов, диаграмма сигнального созвездия устроена так, что битовые комбинации, передаваемые соседними точками созвездия, отличаются только на один бит. Комбинируя это с прямым исправлением ошибок, способным исправлять однобитовые ошибки, приемник может исправлять любые ошибки передачи, которые вызывают отклонение точки совокупности в область соседней точки. Это делает систему передачи менее восприимчивой к шуму .
Несмотря на то, что Стибиц описал этот код до Грея, отраженный двоичный код позже был назван в честь Грея теми, кто его использовал. Две разные патентные заявки 1953 года используют «код Грея» в качестве альтернативного названия «отраженного двоичного кода»; в одном из них также указаны «минимальный код ошибки» и «код циклической перестановки» среди имен. В заявке на патент 1954 года упоминается «код Грея Белл-Телефон». Другие названия включают в себя «циклический двоичный код», «код циклической последовательности», «двоичный циклический перестановочный код» или «циклический переставляемый двоичный код» (CPB).
Код Грея иногда ошибочно приписывали Элише Грею .
История и практическое применение
Математические головоломки
Отраженные двоичные коды применялись к математическим головоломкам еще до того, как они стали известны инженерам.
Отраженный двоичным кодом код Грея представляет собой схему, лежащую в основе классической китайской головоломки с кольцами , последовательного механического механизма головоломки, описанного французом Луи Гро в 1872 году.
Он может служить руководством для решения проблемы Ханойских башен , основанной на игре французского Эдуарда Лукаса в 1883 году. Аналогичным образом, так называемые игровые конфигурации «Башни Бухареста» и «Башни Клагенфурта» дают троичные и пентарные коды Грея.
Мартин Гарднер написал популярное описание кода Грея в своей колонке «Математические игры» в журнале Scientific American за август 1972 года .
Код также формирует гамильтонов цикл на гиперкубе , где каждый бит рассматривается как одно измерение.
Коды телеграфии
Когда французский инженер Эмиль Бодо в 1875 или 1876 году перешел от использования 6-значного (6-битного) кода к 5-значному коду для своей печатной телеграфной системы, он заказал буквенные символы на своем печатном колесе, используя отраженный двоичный код, и назначил коды, используя только три из битов для гласных. Благодаря тому, что гласные и согласные звуки отсортированы в алфавитном порядке, а другие символы размещены соответствующим образом, 5-битный символьный код был распознан как отраженный двоичный код. Этот код стал известен как код Бодо и с небольшими изменениями в конечном итоге был принят как Международный телеграфный алфавит № 1 (ITA1, CCITT-1) в 1932 году.
Примерно в то же время немецко-австрийский Отто Шеффлер [ де ] продемонстрировал в Вене еще один печатный телеграф, использующий для той же цели 5-битный отраженный двоичный код, в 1874 году.
Преобразование аналого-цифрового сигнала
Фрэнк Грей , прославившийся тем, что изобрел метод передачи сигналов, который стал использоваться для совместимого цветного телевидения, изобрел метод преобразования аналоговых сигналов в группы отраженного двоичного кода с использованием устройства на основе вакуумной лампы . Поданный в 1947 году, метод и устройство получили патент в 1953 году, и имя Грэя закрепилось за кодами. Аппарат « трубка ИКМ », который запатентовал Грей, был создан Рэймондом У. Сирсом из Bell Labs в сотрудничестве с Греем и Уильямом М. Гудоллом, которые приписали Грею идею отраженного двоичного кода.

Часть первой страницы патента Грея, показывающая трубку PCM (10) с отраженным двоичным кодом на пластине (15)
Грея больше всего интересовало использование кодов для минимизации ошибок при преобразовании аналоговых сигналов в цифровые; его коды до сих пор используются для этой цели.
Датчики положения

Угловой энкодер для угловых измерительных устройств с 3-битным двоичным кодом Грея (BRGC)

Абсолютный поворотный энкодер с кодом Грея с 13 дорожками. Корпус, диск прерывателя и источник света — вверху; чувствительный элемент и компоненты поддержки находятся внизу.
Коды Грея используются в линейных и поворотных энкодерах положения ( абсолютные энкодеры и квадратурные энкодеры ) вместо взвешенного двоичного кодирования. Это исключает возможность того, что при изменении нескольких битов в двоичном представлении позиции неправильное считывание будет результатом того, что некоторые биты изменятся раньше других.
Например, некоторые поворотные энкодеры предоставляют диск, на концентрических кольцах (дорожках) которого нанесен электропроводящий код Грея. Каждая дорожка имеет неподвижный металлический пружинный контакт, который обеспечивает электрический контакт с проводящим шаблоном кода. Вместе эти контакты создают выходные сигналы в виде кода Грея. Другие кодеры используют бесконтактные механизмы на основе оптических или магнитных датчиков для создания выходных сигналов кода Грея.
Независимо от механизма или точности движущегося энкодера, ошибка измерения положения может возникать в определенных положениях (на границах кода), потому что код может изменяться в тот момент, когда он считывается (дискретизируется). Двоичный выходной код может вызвать значительные ошибки измерения положения, потому что невозможно изменить все биты в одно и то же время. Если в момент выборки позиции некоторые биты изменились, а другие нет, позиция выборки будет неправильной. В случае абсолютных энкодеров указанное положение может быть далеко от фактического положения, а в случае инкрементальных энкодеров это может нарушить отслеживание положения.
В отличие от этого, код Грея, используемый датчиками положения, гарантирует, что коды для любых двух последовательных положений будут отличаться только на один бит и, следовательно, только один бит может изменяться за раз. В этом случае максимальная ошибка положения будет небольшой, указывая на положение, смежное с фактическим положением.
Генетические алгоритмы
Из-за свойств расстояния Хэмминга кодов Грея они иногда используются в генетических алгоритмах . Они очень полезны в этой области, поскольку мутации в коде позволяют вносить в основном инкрементные изменения, но иногда изменение одного бита может вызвать большой скачок и привести к новым свойствам.
Минимизация логической схемы
Коды Грея также используются для маркировки осей карт Карно с 1953 года, а также в круговых графах Хендлера с 1958 года, оба графических метода минимизации логических схем .
Исправление ошибки
В современной цифровой связи коды Грея играют важную роль в исправлении ошибок . Например, в схеме цифровой модуляции , такой как QAM, где данные обычно передаются в символах из 4 или более битов, диаграмма сигнального созвездия устроена так, что битовые комбинации, передаваемые соседними точками созвездия, отличаются только на один бит. Комбинируя это с прямым исправлением ошибок, способным исправлять однобитовые ошибки, приемник может исправлять любые ошибки передачи, которые вызывают отклонение точки совокупности в область соседней точки. Это делает систему передачи менее восприимчивой к шуму .
Связь между доменами часов
Разработчики цифровой логики широко используют коды Грея для передачи многобитовой информации между синхронной логикой, которая работает на разных тактовых частотах. Считается, что логика работает в разных «тактовых областях». Это фундаментально для дизайна больших микросхем, которые работают с множеством разных тактовых частот.
Циклическое переключение состояний с минимальными усилиями
Если системе необходимо циклически перебрать все возможные комбинации состояний включения-выключения некоторого набора элементов управления, а изменение элементов управления требует нетривиальных затрат (например, время, износ, человеческая работа), код Грея сводит к минимуму количество настроек. изменяется только на одно изменение для каждой комбинации состояний. Примером может служить тестирование системы трубопроводов для всех комбинаций настроек клапанов с ручным управлением.
Сбалансированный Серый код может быть построен, что каждый бит переворачивается одинаково часто. Поскольку битовые перевороты распределены равномерно, это оптимально следующим образом: сбалансированные коды Грея минимизируют максимальное количество битовых переворотов для каждой цифры.
Счетчики кода Грея и арифметика
Джордж Р. Стибиц использовал отраженный двоичный код в устройстве для счета двоичных импульсов еще в 1941 году.
Типичное использование счетчиков кода Грея — это создание буфера данных FIFO (first-in, first-out), который имеет порты чтения и записи, которые существуют в разных тактовых доменах. Входные и выходные счетчики внутри такого двухпортового FIFO часто хранятся с использованием кода Грея, чтобы предотвратить захват недопустимых переходных состояний, когда счетчик пересекает тактовые области. Обновленные указатели чтения и записи должны передаваться между доменами часов при их изменении, чтобы иметь возможность отслеживать состояние пустого и полного FIFO в каждом домене. Каждый бит указателей выбирается недетерминированно для этой передачи тактовой области. Таким образом, для каждого бита распространяется либо старое значение, либо новое значение. Следовательно, если более одного бита в многобитовом указателе изменяется в точке выборки, «неправильное» двоичное значение (ни новое, ни старое) не может быть передано. Гарантируя возможность изменения только одного бита, коды Грея гарантируют, что единственными возможными значениями выборки являются новое или старое многобитовое значение. Обычно используются коды Грея с длиной степени двойки.
Иногда цифровые шины в электронных системах используются для передачи величин, которые могут увеличиваться или уменьшаться только по одному за раз, например, выход счетчика событий, который передается между доменами часов или цифро-аналоговым преобразователем. Преимущество кодов Грея в этих приложениях состоит в том, что различия в задержках распространения множества проводов, которые представляют биты кода, не могут привести к тому, что полученное значение пройдет через состояния, которые не входят в последовательность кода Грея. Это похоже на преимущество кодов Грея в конструкции механических кодировщиков, однако источником кода Грея в этом случае является электронный счетчик. Сам счетчик должен вести счет в коде Грея, или, если счетчик работает в двоичном формате, то выходное значение счетчика должно быть повторно синхронизировано после преобразования в код Грея, поскольку при преобразовании значения из двоичного кода в код Грея это возможно. что различия во времени поступления битов двоичных данных в схему преобразования двоичного кода в серый будут означать, что код может на короткое время пройти через состояния, которые сильно не соответствуют последовательности. Добавление синхронизированного регистра после схемы, которая преобразует значение счетчика в код Грея, может привести к тактовому циклу задержки, поэтому подсчет непосредственно в коде Грея может быть выгодным.
Чтобы произвести следующее значение счетчика в счетчике кода Грея, необходимо иметь некоторую комбинационную логику, которая будет увеличивать текущее сохраненное значение счетчика. Один из способов увеличения числа кода Грея — преобразовать его в обычный двоичный код, добавить к нему единицу с помощью стандартного двоичного сумматора, а затем преобразовать результат обратно в код Грея. Другие методы подсчета в коде Грея обсуждаются в отчете Роберта У. Дорана , включая получение выходных данных с первых защелок триггеров «ведущий-ведомый» в двоичном счетчике пульсаций.
Адресация кода Грея
Поскольку выполнение программного кода обычно вызывает шаблон доступа к памяти инструкций для локально последовательных адресов, кодирование шины с использованием адресации кода Грея вместо двоичной адресации может значительно уменьшить количество изменений состояния битов адреса, тем самым снижая энергопотребление ЦП в некоторой степени. -силовые конструкции.
Построение n- битного кода Грея

Первые несколько шагов метода отражения и префикса.

4-битная перестановка кода Грея
Список двоично-отраженных кодов Грея для n битов может быть сгенерирован рекурсивно из списка для n — 1 битов путем отражения списка (т. Е. Перечисления записей в обратном порядке), добавления к записям в исходном списке префикса двоичного 0 и префикса записи в отраженном списке с двоичной единицей , а затем объединение исходного списка с обратным списком. Например, создание списка n = 3 из списка n = 2:
| 2-битный список: | 00 , 01 , 11 , 10 | |
| Отражено: | 10 , 11 , 01 , 00 | |
| Префикс старых записей с 0 : | 000 , 001 , 011 , 010 , | |
| Приставьте к новым записям префикс 1 : | 110 , 111 , 101 , 100 | |
| Составные: | 000 , 001 , 011 , 010 , | 110 , 111 , 101 , 100 |
Однобитовый код Грея G 1 = ( 0,1 ). Это можно представить как построенное рекурсивно, как указано выше, из нулевого битового кода Грея G 0 = ( Λ ), состоящего из единственной записи нулевой длины. Этот итеративный процесс генерации G n +1 из G n проясняет следующие свойства стандартного отражающего кода:
- G n — это перестановка чисел 0,…, 2 n — 1. (Каждое число появляется в списке ровно один раз.)
- G n вкладывается как первая половина G n +1 .
- Следовательно, кодирование является стабильным в том смысле, что как только двоичное число появляется в G n, оно появляется в той же позиции во всех более длинных списках; так что имеет смысл говорить о с отражающим кодом Грея значение ряда: G ( м ) = в м — м , отражающий код Грея, считая от 0.
- Каждая запись в G n отличается от предыдущей только на один бит. (Расстояние Хэмминга равно 1.)
- Последняя запись в G n отличается от первой только на один бит. (Код циклический.)
Эти характеристики предлагают простой и быстрый метод преобразования двоичного значения в соответствующий код Грея. Каждый бит инвертируется, если следующий более высокий бит входного значения установлен в единицу. Это может выполняться параллельно с помощью битового сдвига и операции «исключающее ИЛИ», если они доступны: n- й код Грея получается вычислением . Добавление бита 0 оставляет порядок кодовых слов неизменным, добавление бита 1 меняет порядок кодовых слов на обратный. Если биты в позиции кодовых слов инвертируются, порядок соседних блоков кодовых слов меняется на обратный. Например, если бит 0 инвертируется в 3-битовой последовательности кодовых слов, порядок двух соседних кодовых слов меняется на противоположный.
- 000,001,010,011,100,101,110,111 → 001,000,011,010,101,100,111,110 (инвертировать бит 0)
Если бит 1 инвертирован, блоки из 2 кодовых слов изменяют порядок:
- 000,001,010,011,100,101,110,111 → 010,011,000,001,110,111,100,101 (инвертировать бит 1)
Если бит 2 инвертирован, блоки из 4 кодовых слов меняют порядок:
- 000,001,010,011,100,101,110,111 → 100,101,110,111,000,001,010,011 (инвертировать бит 2)
Таким образом, выполнение исключающего или для бита в позиции с битом в позиции оставляет порядок кодовых слов нетронутым, если , и меняет порядок блоков кодовых слов, если . Теперь это точно такая же операция, что и метод отражения и префикса для генерации кода Грея.
Аналогичный метод можно использовать для выполнения обратного преобразования, но вычисление каждого бита зависит от вычисленного значения следующего более высокого бита, поэтому его нельзя выполнять параллельно. Предполагая, что это -й бит, закодированный по Грею ( являющийся наиболее значимым битом), и является -м битом с двоичным кодированием ( являющимся наиболее значимым битом), обратное преобразование может быть выполнено рекурсивно:, и . В качестве альтернативы декодирование кода Грея в двоичное число можно описать как префиксную сумму битов в коде Грея, где каждая отдельная операция суммирования в префиксной сумме выполняется по модулю два.
Чтобы итеративно построить двоично-отраженный код Грея, на шаге 0 начните с , а на шаге найдите битовую позицию наименее значащей 1 в двоичном представлении и переверните бит в этой позиции в предыдущем коде, чтобы получить следующий код. . Позиции битов начинаются с 0, 1, 0, 2, 0, 1, 0, 3,…. См. Раздел « Найти первый набор» для получения информации об эффективных алгоритмах вычисления этих значений.
Преобразование в код Грея и обратно
Следующие функции в C преобразуют двоичные числа и связанные с ними коды Грея. Хотя может показаться, что преобразование серого в двоичное требует, чтобы каждый бит обрабатывался по отдельности, существуют более быстрые алгоритмы.
typedef unsigned int uint; // This function converts an unsigned binary number to reflected binary Gray code. uint BinaryToGray(uint num) { return num ^ (num >> 1); // The operator >> is shift right. The operator ^ is exclusive or. } // This function converts a reflected binary Gray code number to a binary number. uint GrayToBinary(uint num) { uint mask = num; while (mask) { // Each Gray code bit is exclusive-ored with all more significant bits. mask >>= 1; num ^= mask; } return num; } // A more efficient version for Gray codes 32 bits or fewer through the use of SWAR (SIMD within a register) techniques. // It implements a parallel prefix XOR function. The assignment statements can be in any order. // // This function can be adapted for longer Gray codes by adding steps. uint GrayToBinary32(uint num) { num ^= num >> 16; num ^= num >> 8; num ^= num >> 4; num ^= num >> 2; num ^= num >> 1; return num; } // A Four-bit-at-once variant changes a binary number (abcd)2 to (abcd)2 ^ (00ab)2, then to (abcd)2 ^ (00ab)2 ^ (0abc)2 ^ (000a)2.
Специальные типы кодов Грея
На практике «код Грея» почти всегда относится к двоично-отраженному коду Грея (BRGC). Однако математики открыли другие виды кодов Грея. Как и BRGC, каждое из них состоит из списка слов, где каждое слово отличается от следующего только одной цифрой (каждое слово имеет расстояние Хэмминга, равное 1, от следующего слова).
n -аричный код Грея
Тройное число → троичный код Грея
0 → 000
1 → 001
2 → 002
10 → 012
11 → 011
12 → 010
20 → 020
21 → 021
22 → 022
100 → 122
101 → 121
102 → 120
110 → 110
111 → 111
112 → 112
120 → 102
121 → 101
122 → 100
200 → 200
201 → 201
202 → 202210
→ 212
211 → 211212
→ 210
220 → 220
221 → 221
222 → 222
Помимо двоичного кода Грея, существует множество специализированных типов кодов Грея. Одним из таких типов кода Грея является n- мерный код Грея , также известный как небулев код Грея . Как следует из названия, этот тип кода Грея использует в своих кодировках не- логические значения.
Например, 3-арный ( тройной ) код Грея будет использовать значения 0,1,2. ( N , k ) — код Грея — это n- мерный код Грея с k цифрами. Последовательность элементов в (3, 2) -сером коде: 00,01,02,12,11,10,20,21,22. ( N , k ) -серый код может быть построен рекурсивно, как BRGC, или может быть построен итеративно . Алгоритм итеративно генерировать ( N , K ) -Грэй код представлено (в C ):
// inputs: base, digits, value // output: Gray // Convert a value to a Gray code with the given base and digits. // Iterating through a sequence of values would result in a sequence // of Gray codes in which only one digit changes at a time. void toGray(unsigned base, unsigned digits, unsigned value, unsigned gray[digits]) { unsigned baseN[digits]; // Stores the ordinary base-N number, one digit per entry unsigned i; // The loop variable // Put the normal baseN number into the baseN array. For base 10, 109 // would be stored as [9,0,1] for (i = 0; i < digits; i++) { baseN[i] = value % base; value = value / base; } // Convert the normal baseN number into the Gray code equivalent. Note that // the loop starts at the most significant digit and goes down. unsigned shift = 0; while (i--) { // The Gray digit gets shifted down by the sum of the higher // digits. gray[i] = (baseN[i] + shift) % base; shift = shift + base - gray[i]; // Subtract from base so shift is positive } } // EXAMPLES // input: value = 1899, base = 10, digits = 4 // output: baseN[] = [9,9,8,1], gray[] = [0,1,7,1] // input: value = 1900, base = 10, digits = 4 // output: baseN[] = [0,0,9,1], gray[] = [0,1,8,1]
Существуют и другие алгоритмы кода Грея для ( n , k ) -кодов Грея. ( N , k ) -серый код, созданный вышеуказанным алгоритмом, всегда циклический; некоторые алгоритмы, такие как алгоритм Гуана, лишены этого свойства, когда k нечетно. С другой стороны, хотя с помощью этого метода изменяется только одна цифра, она может изменяться путем переноса (цикл от n — 1 до 0). В алгоритме Гуана счетчик поочередно растет и падает, так что числовая разница между двумя цифрами кода Грея всегда равна единице.
Коды Грея не определены однозначно, потому что перестановка столбцов такого кода также является кодом Грея. Вышеупомянутая процедура создает код, в котором чем ниже значение цифры, тем чаще она изменяется, что делает его похожим на обычные методы подсчета.
См. Также Косую двоичную систему счисления , вариантную троичную систему счисления, в которой при каждом приращении изменяется не более двух цифр, поскольку каждое приращение может быть выполнено с помощью операции переноса не более одной цифры .
Сбалансированный код Грея
Хотя двоичный отраженный код Грея полезен во многих сценариях, в некоторых случаях он не оптимален из-за отсутствия «единообразия». В сбалансированных кодах Грея количество изменений в различных положениях координат максимально близко. Чтобы сделать это более точным, пусть G будет R -арным полным циклом Грея, имеющим последовательность переходов ; что отсчеты переходов ( спектр ) из G являются набором целых чисел , определенных
Код Грея является однородным или равномерно сбалансированным, если все его счетчики переходов равны, и в этом случае мы имеем
для всех k . Ясно, что когда такие коды существуют, только если n является степенью 2. В противном случае, если n не делится равномерно, можно построить хорошо сбалансированные коды, в которых каждый счетчик переходов равен или . Коды Грея также могут быть экспоненциально сбалансированы, если все их счетчики переходов являются смежными степенями двойки, и такие коды существуют для каждой степени двойки.
Например, сбалансированный 4-битный код Грея имеет 16 переходов, которые могут быть равномерно распределены между всеми четырьмя позициями (четыре перехода на позицию), что делает его равномерно сбалансированным:
- 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0
- 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0
- 0 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0
- 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1
тогда как сбалансированный 5-битный код Грея имеет всего 32 перехода, которые не могут быть равномерно распределены между позициями. В этом примере четыре позиции имеют шесть переходов каждая, а одна — восемь:
- 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
- 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 0
- 1 1 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1
- 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1
- 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 1
Теперь мы покажем конструкцию и реализацию для хорошо сбалансированных двоичных кодов Грея, которые позволяют нам генерировать n -значный сбалансированный код Грея для каждого n . Главный принцип состоит в том, чтобы индуктивно построить ( n + 2) -значный код Грея, заданный n- значным кодом Грея G, таким образом, чтобы сохранялось свойство сбалансированности. Для этого рассмотрим разбиение на четное число L непустых блоков вида
где ` ` и ). Это разбиение индуцирует -цифровой код Грея, задаваемый формулой
Если мы определим кратности переходов
— количество раз, когда цифра в позиции i изменяется между последовательными блоками в разделе, то для ( n + 2) -значного кода Грея, индуцированного этим разделом, спектр переходов равен
Сложная часть этой конструкции состоит в том, чтобы найти адекватное разбиение сбалансированного n- значного кода Грея так, чтобы индуцированный им код оставался сбалансированным, но для этого важна только кратность переходов; соединение двух последовательных блоков при переходе цифр и разделение другого блока при переходе другой цифры дает другой код Грея с точно таким же спектром переходов , поэтому можно, например, обозначить первые переходы на цифре как те, которые попадают между двумя блоками. Равномерные коды могут быть найдены, когда и , и эта конструкция может быть расширена также на R -арный случай.
Долгосрочные коды Грея
Длинные коды Грея увеличивают расстояние между последовательными сменами цифр в одной и той же позиции. То есть минимальная длина выполнения любого бита остается неизменной как можно дольше.
Монотонные коды Грея
Монотонные коды полезны в теории взаимосвязанных сетей, особенно для минимизации расширения линейных массивов процессоров. Если мы определяем вес двоичной строки как количество единиц в строке, то, хотя у нас явно не может быть кода Грея со строго возрастающим весом, мы можем аппроксимировать это, прогнав код через два смежных веса до достижения следующий.
Мы можем формализовать понятие монотонных кодов Грея следующим образом: рассмотрим разбиение гиперкуба на уровни вершин, имеющих одинаковый вес, т. Е.
для . Эти уровни удовлетворяют . Позвольте быть подграфом индуцированного , и пусть быть ребрами в . Монотонный код Грея тогда является гамильтоновым путем в таком, что всякий раз, когда он встречается раньше , тогда .
Элегантная конструкция монотонных n -значных кодов Грея для любого n основана на идее рекурсивного построения подпути длины, имеющей ребра . Мы определяем , всякий раз , когда или , и
иначе. Здесь — подходящим образом определенная перестановка, относящаяся к пути P с его координатами, переставленными на . Эти пути приводят к двум монотонным п -значных кодов Грея и задаются
Выбор того, который гарантирует, что эти коды действительно являются кодами Грея, оказывается правильным . Первые несколько значений показаны в таблице ниже.
-
Подпути в алгоритме Сэвиджа – Винклера
j = 0 j = 1 j = 2 j = 3 п = 1 0, 1 п = 2 00, 01 10, 11 п = 3 000, 001 100, 110, 010, 011 101, 111 п = 4 0000
00011000, 1100, 0100,
0110, 0010, 00111010, 1011, 1001,
1101, 0101, 01111110,
1111
Эти монотонные коды Грея могут быть эффективно реализованы таким образом, что каждый последующий элемент может быть сгенерирован за время O ( n ). Алгоритм проще всего описать с помощью сопрограмм .
Монотонные коды имеют интересную связь с гипотезой Ловаса , которая утверждает, что каждый связный вершинно-транзитивный граф содержит гамильтонов путь. Подграф «среднего уровня» является вершинно-транзитивным (то есть его группа автоморфизмов транзитивна, так что каждая вершина имеет одно и то же «локальное окружение», и ее нельзя отличить от других, так как мы можем переназначить координаты, а также двоичные цифры для получения автоморфизма ), и проблема поиска гамильтонова пути в этом подграфе называется «проблемой среднего уровня», которая может пролить свет на более общую гипотезу. На этот вопрос был дан положительный ответ , и предыдущий конструкция для монотонных кодов обеспечивает гамильтонов путь длиной не менее 0,839 N, где N — количество вершин в подграфе среднего уровня.
Код Беккета – Грея
Другой тип кода Грея, код Беккета – Грея , назван в честь ирландского драматурга Сэмюэля Беккета , интересовавшегося симметрией . Его пьеса « Квад » состоит из четырех актеров и разделена на шестнадцать временных периодов. Каждый период заканчивается тем, что один из четырех актеров выходит на сцену или покидает ее. Спектакль начинается с пустой сцены, и Беккет хотел, чтобы каждая группа актеров появлялась на сцене ровно один раз. Очевидно, что набор действующих лиц на сцене может быть представлен 4-битным двоичным кодом Грея. Беккет, однако, наложил дополнительное ограничение на сценарий: он хотел, чтобы актеры входили и выходили, чтобы актер, который находился на сцене дольше всех, всегда выходил. Затем актеры могут быть представлены очередью « первым пришел — первым вышел» , так что (из актеров на сцене) удаляемый из очереди всегда оказывается тем, кто был поставлен в очередь первым. Беккет не смог найти код Беккета – Грея для своей пьесы, и действительно, исчерпывающий список всех возможных последовательностей показывает, что такого кода не существует для n = 4. Сегодня известно, что такие коды действительно существуют для n = 2, 5. , 6, 7 и 8 и не существуют для n = 3 или 4. Пример 8-битного кода Беккета – Грея можно найти в книге Дональда Кнута « Искусство компьютерного программирования» . По словам Савады и Вонга, пространство поиска для n = 6 можно исследовать за 15 часов, и было найдено более 9500 решений для случая n = 7.
Коды змейки в коробке

Максимальные длины змей ( L s ) и витков ( L c ) в задаче змей в коробке для размерностей n от 1 до 4
Коды змеи в коробке , или змеи , представляют собой последовательности узлов индуцированных путей в n- мерном графе гиперкуба , а коды катушки в коробке, или катушки , представляют собой последовательности узлов индуцированных циклов в гиперкуб. Рассматриваемые как коды Грея, эти последовательности обладают способностью обнаруживать любую однобитовую ошибку кодирования. Коды этого типа были впервые описаны Уильямом Х. Каутцем в конце 1950-х годов; с тех пор было проведено много исследований по поиску кода с максимально возможным количеством кодовых слов для данного измерения гиперкуба.
Однодорожечный код Грея
Еще одним видом кода Грея является однопутный код Грея (STGC), разработанный Норманом Б. Спеддингом и уточненный Хильтгеном, Патерсоном и Брандестини в «Однопутных кодах Грея» (1996). STGC — это циклический список из P уникальных двоичных кодировок длины n, так что два последовательных слова отличаются ровно в одной позиции, и когда список исследуется как матрица P × n , каждый столбец представляет собой циклический сдвиг первого столбца.

Однопутный код Грея с 5 датчиками.

Анимированная версия ротора STGC с цветовой кодировкой.
Название происходит от их использования с поворотными энкодерами , где несколько дорожек распознаются контактами, в результате для каждого на выходе получается 0 или 1 . Чтобы уменьшить шум из-за того, что разные контакты не переключаются в один и тот же момент времени, желательно настроить дорожки так, чтобы данные, выводимые контактами, были в коде Грея. Чтобы получить высокую угловую точность, нужно много контактов; Чтобы достичь точности не менее 1 °, необходимо как минимум 360 различных позиций на оборот, что требует минимум 9 бит данных и, следовательно, такое же количество контактов.
Если все контакты расположены в одном угловом положении, то потребуется 9 дорожек, чтобы получить стандартный BRGC с точностью не менее 1 °. Однако, если производитель перемещает контакт в другое угловое положение (но на такое же расстояние от центрального вала), то соответствующий «кольцевой узор» необходимо повернуть на тот же угол, чтобы получить тот же выходной сигнал. Если самый старший бит (внутреннее кольцо на рисунке 1) достаточно повернуть, он точно соответствует следующему кольцу. Поскольку оба кольца в этом случае идентичны, внутреннее кольцо можно вырезать, а датчик для этого кольца переместить на оставшееся идентичное кольцо (но со смещением под этим углом от другого датчика на этом кольце). Эти два датчика на одном кольце образуют квадратурный энкодер. Это уменьшает количество дорожек для углового энкодера с разрешением 1 ° до 8 дорожек. Еще больше уменьшить количество дорожек с помощью BRGC невозможно.
В течение многих лет Торстен Силлке и другие математики считали, что невозможно закодировать положение на одной дорожке, так что последовательные положения различаются только на одном датчике, за исключением квадратурного энкодера с двумя датчиками и одной дорожкой. Поэтому для приложений, в которых 8 дорожек были слишком громоздкими, люди использовали однодорожечные инкрементальные энкодеры (квадратурные энкодеры) или двухдорожечные энкодеры «квадратурный энкодер + эталонная метка».
Однако Норман Б. Спеддинг зарегистрировал патент в 1994 году с несколькими примерами, показывающими, что это возможно. Несмотря на то, что это не возможно различить 2 н позиции с п датчиков на одной дорожке, то это можно различить близко к тому , что многие. Эцион и Патерсон предполагают, что когда n само является степенью 2, n датчиков могут различать не более 2 n — 2 n позиций, а для простого n предел составляет 2 n — 2 позиции. Авторы продолжили генерировать 504-позиционный однодорожечный код длиной 9, который, по их мнению, является оптимальным. Поскольку это число больше 2 8 = 256, для любого кода требуется более 8 датчиков, хотя BRGC может различать 512 позиций с 9 датчиками.
Здесь воспроизводится STGC для P = 30 и n = 5:
-
Однодорожечный код Грея для 30 позиций
Угол Код Угол Код Угол Код Угол Код Угол Код 0 ° 10000 72 ° 01000 144 ° 00100 216 ° 00010 288 ° 00001 12 ° 10100 84 ° 01010 156 ° 00101 228 ° 10010 300 ° 01001 24 ° 11100 96 ° 01110 168 ° 00111 240 ° 10011 312 ° 11001 36 ° 11110 108 ° 01111 180 ° 10111 252 ° 11011 324 ° 11101 48 ° 11010 120 ° 01101 192 ° 10110 264 ° 01011 336 ° 10101 60 ° 11000 132 ° 01100 204 ° 00110 276 ° 00011 348 ° 10001
Каждый столбец представляет собой циклический сдвиг первого столбца, и от любой строки к следующей строке изменяется только один бит. Одноколейный характер (например, кодовая цепь) полезен при изготовлении этих колес (по сравнению с BRGC), поскольку требуется только одна гусеница, что снижает их стоимость и размер. Природа кода Грея полезна (по сравнению с цепными кодами , также называемыми последовательностями Де Брюйна ), поскольку только один датчик будет изменяться в любой момент времени, поэтому неопределенность во время перехода между двумя дискретными состояниями будет только плюс или минус одна единица угловой измерение, которое устройство способно разрешить.
Двумерный код Грея

Созвездие в кодировке Грея для прямоугольного 16- QAM
Двумерные коды Грея используются в связи, чтобы минимизировать количество битовых ошибок в квадратурной амплитудной модуляции (QAM) в соседних точках в созвездии . При типичном кодировании горизонтальные и вертикальные соседние точки совокупности отличаются на один бит, а диагональные соседние точки отличаются на 2 бита.
Двумерные коды Грея также используются в схемах идентификации местоположения , где код будет применяться к картам местности, таким как проекция Меркатора земной поверхности, и соответствующая циклическая двумерная функция расстояния, такая как метрика Мангейма, может использоваться для расчета расстояние между двумя закодированными местоположениями, тем самым комбинируя характеристики расстояния Хэмминга с циклическим продолжением проекции Меркатора.
Серая изометрия
Биективное отображение {0 ↔ 00 , 1 ↔ 01 , 2 ↔ 11 , 3 ↔ 10 } устанавливает изометрию между метрическим пространством над конечным полем с метрикой, заданной расстоянием Хэмминга, и метрическим пространством над конечным кольцом (обычное модульная арифметика ) с метрикой, заданной расстоянием Ли . Отображение подходящим образом продолжается до изометрии пространств Хэмминга и . Его важность заключается в установлении соответствия между различными «хорошо» , но не обязательно линейные коды как Серо-карты изображений в из кольцевых линейных кодов с .


Существует ряд двоичных кодов, похожих на коды Грея, в том числе:
- Коды Datex, также известные как коды Джаннини (1954), как описано Карлом П. Сполдингом, используют вариант кода О’Брайена II .
- Коды, используемые Вареком (ок. 1954 г.), используют вариант кода О’Брайена I, а также варианты кода Грея с основанием 12 и 16.
- Lucal code (1959), также известный как модифицированный отраженный двоичный код (MRB)
- Код Гиллхэма (1961/1962), использует вариант кода Datex и кода О’Брайена II .
- Код Лесли и Рассела (1964)
- Код учреждения Royal Radar
- Кодекс Хоклас (1988 г.)
Следующие двоично-десятичные коды (BCD) также являются вариантами кода Грея:
- Код Петерика (1953 г.), также известный как код Королевского авиастроительного предприятия (RAE).
- Коды О’Брайена I и II (1955) (Код О’Брайена типа I был уже описан Фредериком А. Фоссом из IBM и использовался Вареком в 1954 году. Позже он был также известен как код Уоттса или отраженный десятичный код Уоттса ( WRD) и иногда неоднозначно называют отраженным двоичным модифицированным кодом Грея. Код О’Брайена типа II уже использовался Datex в 1954 году.)
- Код Грея с избытком-3 (1956) (также известный как код с избытком-3 по Грею, код с избытком 3 по Грею, код с избытком-3 по рефлексу, код с избытком Грея, код с избытком Грея, код с избытком 10-3 или код Грея-Стибица), описан Фрэнком П. Терви-младшим из ITT .
- Коды Томпкинса I и II (1956)
- Код Гликсона (1957 г.), иногда неоднозначно также называемый модифицированным кодом Грея.
| Имя | Немного | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Вес | Треки | Компл. | Циклический | 5 с | Комментарий |
| Серый BCD | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0–3 | 4 (3) | Нет | (2, 4, 8, 16) | Нет | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Павел | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1–3 | 4 (3) | Нет | 2, 10 | Нет | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Glixon | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0–3 | 4 | Нет | 2, 4, 8, 10 | (сдвинуто на +1) | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |||||||
| Томпкинс I | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0–4 | 2 | Нет | 2, 4, 10 | да | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |||||||
| О’Брайен I (Ватт) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0–3 | 4 | 9 | 2, 4, 10 | да | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |||||||
| Петерик (РАЭ) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1–3 | 3 | 9 | 2, 10 | да | |
| 3 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| О’Брайен II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1–3 | 3 | 9 | 2, 10 | да | |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| Сасскинд | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1–4 | 3 | 9 | 2, 10 | да | |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| Клар | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0–4 | 4 (3) | 9 | 2, 10 | да | |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Томпкинс II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1–3 | 2 | 9 | 2, 10 | да | |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Избыток-3 Серый | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1–4 | 4 | 9 | 2, 10 | да | |
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
Смотрите также
- Регистр сдвига с линейной обратной связью
- Последовательность Де Брейна — код Грея на алфавите больше 0,1.
- Алгоритм Штейнхауса – Джонсона – Троттера — алгоритм, который генерирует коды Грея для факторной системы счисления.
- Код минимального расстояния
- Последовательность Пруэ – Туэ – Морса, связанная с обратным кодом Грея
- Формула Райзера
- Кривая Гильберта
Примечания
использованная литература
дальнейшее чтение
- Ричардс, Ричард Колер (1955). Арифметические операции в цифровых компьютерах (5-е изд.). Нью-Йорк, США: D. Van Nostrand Co., Inc.
- Ричардс, Ричард Колер (1967). Электронные цифровые компоненты и схемы . Д. Ван Ностранд Ко., Инк., Стр. 490, 500–504, 510–511.
- Блэк, Пол Э. (25 февраля 2004 г.). «Код Грея» . NIST .
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007). «Раздел 22.3. Коды Грея» . Числовые рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк, США: Издательство Кембриджского университета . ISBN 978-0-521-88068-8.
- Дикарь, Карла Дайан (1997). «Обзор комбинаторных кодов Грея» . SIAM Обзор . Общество промышленной и прикладной математики (SIAM). 39 (4): 605–629. Bibcode : 1997SIAMR..39..605S . CiteSeerX 10.1.1.39.1924 . DOI : 10.1137 / S0036144595295272 . JSTOR 2132693 .
- Уилф, Герберт Сол (1989). «Главы 1–3». Комбинаторные алгоритмы: обновление . Общество промышленной и прикладной математики (SIAM). ISBN 0-89871-231-9.
- Дьюар, Меган; Стивенс, Бретт (29 августа 2012 г.). Упорядочивание конструкций блока — коды Грея, универсальные циклы и конфигурация . CMS Книги по математике (1-е изд.). Нью-Йорк, США: Springer Science + Business Media . DOI : 10.1007 / 978-1-4614-4325-4 . ISBN 978-1-46144324-7. ISSN 1613-5237 .
- Максфилд, Клайв «Макс» (01.10.2012) [28.05.2011]. «Основы кода Грея» . Практическое руководство по дизайну . EETimes . Часть 1. Архивировано 30.10.2017 . Проверено 30 октября 2017 . Часть 2 Часть 3
- Уоррен-младший, Генри С. (2013). «Глава 13: Код Грея». Восторг хакера (2-е изд.). Эддисон Уэсли — Pearson Education, Inc., стр. 311–317. ISBN 978-0-321-84268-8. (7 страниц)
- Зиновик, Игорь; Кронинг, Даниэль; Чебиряк, Юрий (21.03.2008). «Вычисление двоичных комбинаторных кодов Грея с помощью исчерпывающего поиска с помощью SAT-решателей» . IEEE Transactions по теории информации . IEEE . 54 (4): 1819–1823. DOI : 10.1109 / TIT.2008.917695 . ЛВП : 20.500.11850 / 11304 . S2CID 2854180 . (5 страниц)
- О’Брайен, Джозеф А. (июнь 1957 г.). «Преобразователи двоично-десятичного кода единица-расстояние» . Операции IRE на электронных компьютерах . ИС-6 (2): 122–123. DOI : 10.1109 / TEC.1957.5221585 . ISSN 0367-9950 . Проверено 25 мая 2020 . (2 страницы)
- Барр, К.Г. (март 1981 г.). «Десятичный код Грея — легко конвертируется для кодирования положения вала» (PDF) . Беспроводной мир . Vol. 87 нет. 1542. Факультет естественных наук Вест-Индского университета . С. 86–87. Архивировано (PDF) из оригинала 28.07.2020 . Проверено 28 июля 2020 .
внешние ссылки
- Демонстрация «Gray Code» Майкла Шрайбера, Wolfram Demonstrations Project (с реализацией Mathematica). 2007 г.
- Словарь алгоритмов и структур данных NIST: код Грея .
- Автостопщик по эволюционным вычислениям, Q21: Что такое коды Грея и почему они используются? , включая код C для преобразования между двоичным кодом и BRGC.
- Драгос А. Харабор использует коды Грея в 3D-дигитайзере .
- Однодорожечные коды Грея, двоичные цепные коды ( Lancaster, 1994 ) и регистры сдвига с линейной обратной связью — все это полезно для определения абсолютного положения на однопутном поворотном энкодере (или другом датчике положения).
- Столбец AMS: коды Грея
- Генератор колеса с оптическим кодировщиком
- ProtoTalk.net — Понимание квадратурного кодирования — более подробно описывает квадратурное кодирование с акцентом на роботизированные приложения
2-битный код Грея
00 01 11 10 |
3-битный код Грея
000 001 011 010 110 111 101 100 |
4-битный код Грея
0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 |
Код Грея — система счисления, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексивный двоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея для систем счисления с любым основанием. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея.
Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Содержание
- 1 Название
- 2 Применения
- 3 Алгоритмы преобразования
- 3.1 Преобразование двоичного кода в код Грея
- 3.2 Преобразование кода Грея в двоичный код
- 3.3 Генерация кодов Грея
- 4 См. также
- 5 Примечания
- 6 Библиография
- 7 Ссылки
Название
Название рефлексный (отражённый) двоичный код происходит от факта, что вторая половина значений в коде Грея эквивалентна первой половине, только в обратном порядке, за исключением старшего бита, который просто инвертируется. Если же разделить каждую половину ещё раз пополам, свойство будет сохраняться для каждой из половин половины и т. д.
Код получил имя исследователя лабораторий Bell Labs Фрэнка Грея. Он запатентовал и использовал этот код в своей импульсной системе связи (патент № 2632058).
Применения
Использование кодов Грея основано прежде всего на том, что он минимизирует эффект ошибок при преобразовании аналоговых сигналов в цифровые (например, во многих видах датчиков).

![]()
Фрагмент главной страницы патента Грея
![]()
Круговой энкодер с трёхбитным кодом грея
Коды Грея часто используются в датчиках-энкодерах. Их использование удобно тем, что два соседних значения шкалы сигнала отличаются только в одном разряде. Также они используются для кодирования номера дорожек в жёстких дисках.
Код Грея можно использовать также и для решения задачи о Ханойских башнях .
Широко применяются коды Грея и в теории генетических алгоритмов [1] для кодирования генетических признаков, представленных целыми числами.
Код Грея используется для генерации сочетаний методом вращающейся двери[2]
В некоторых компьютерных играх (например, Duke Nukem 3D) для успешного прохождения уровня требуется подобрать нужную комбинацию положений нескольких переключателей. Для минимизации числа переключений при переборе вариантов следует использовать код Грея.
Алгоритмы преобразования
Преобразование двоичного кода в код Грея
Коды Грея легко получаются из двоичных чисел путём побитовой операции «Исключающее ИЛИ» с тем же числом, сдвинутым вправо на один бит. Следовательно, i-й бит кода Грея Gi выражается через биты двоичного кода Bi следующим образом:

где  – операция «исключающее ИЛИ»; биты нумеруются справа налево, начиная с младшего.
– операция «исключающее ИЛИ»; биты нумеруются справа налево, начиная с младшего.
Ниже приведён алгоритм преобразования из двоичной системы счисления в код Грея, записанный на языке C:
unsigned int grayencode(unsigned int g) { return g ^ (g >> 1); }
Однако, необходимо помнить, что данный алгоритм будет работать правильно, если компилятор реализует циклический логический сдвиг (стандарт языка C не уточняет тип сдвига). Тот же самый алгоритм, записанный на языке Паскаль:
function BinToGray(b: integer): integer; begin BinToGray := b xor (b shr 1) end;
Пример: преобразовать двоичное число 10110 в код Грея.
10110 01011 ----- 11101
Преобразование кода Грея в двоичный код
Обратный алгоритм – преобразование кода Грея в двоичный код – можно выразить рекуррентной формулой

причём преобразование осуществляется побитно, начиная со старших разрядов, и значение  , используемое в формуле, вычисляется на предыдущем шаге алгоритма. Действительно, если подставить в эту формулу вышеприведённое выражение для i-го бита кода Грея, получим
, используемое в формуле, вычисляется на предыдущем шаге алгоритма. Действительно, если подставить в эту формулу вышеприведённое выражение для i-го бита кода Грея, получим

Однако приведённый алгоритм, связанный с манипуляцией отдельными битами, неудобен для программной реализации, поэтому на практике используют видоизменённый алгоритм:

где N – число битов в коде Грея (для увеличения быстродействия алгоритма в качестве N можно взять номер старшего ненулевого бита кода Грея); знак  означает суммирование при помощи операции «исключающее ИЛИ», то есть
означает суммирование при помощи операции «исключающее ИЛИ», то есть

Действительно, подставив в формулу выражение для i-го бита кода Грея, получим


Здесь предполагается, что бит, выходящий за рамки разрядной сетки ( ), равен нулю.
), равен нулю.
Ниже приведена функция на языке С, реализующая данный алгоритм. Она осуществляет последовательный сдвиг вправо и суммирование исходного двоичного числа, до тех пор, пока очередной сдвиг не обнулит слагаемое.
unsigned int graydecode(unsigned int gray) { unsigned int bin; for (bin = 0; gray; gray >>= 1) { bin ^= gray; } return bin; }
Тот же самый алгоритм, записанный на языке Паскаль:
function GrayToBin(b: integer): integer; var g: integer; begin g := 0; while b > 0 do begin g := g xor b; b := b shr 1; end; GrayToBin := g; end;
Пример: преобразовать код Грея 11101 в двоичный код.
11101 01110 00111 00011 00001 ----- 10110
Быстрое преобразование 8/16/24/32-разрядного значения кода Грея в двоичный код на языке BlitzBasic:
Function GRAY_2_BIN%(X%) Return X Xor ((X And $88888888) Shr 3) Xor ((X And $CCCCCCCC) Shr 2) Xor ((X And $EEEEEEEE) Shr 1) End Function
Простой способ преобразования двоичного числа в код Грея выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0».
Генерация кодов Грея
Код Грея для n бит может быть рекурсивно построен на основе кода для n–1 бит путём переворачивания списка бит (то есть записыванием кодов в обратном порядке), конкатенации исходного и перевёрнутого списков, дописывания нулей в начало каждого кода в исходном списке и единиц — в начало кодов в перевёрнутом списке. Так, для генерации списка для n = 3 бит на основании кодов для двух бит необходимо выполнить следующие шаги:
| Коды для n = 2 бит: | 00, 01, 11, 10 | |
| Перевёрнутый список кодов: | 10, 11, 01, 00 | |
| Объединённый список: | 00, 01, 11, 10 | 10, 11, 01, 00 |
| К начальному списку дописаны нули: | 000, 001, 011, 010 | 10, 11, 01, 00 |
| К перевёрнутому списку дописаны единицы: | 000, 001, 011, 010 | 110, 111, 101, 100 |
Ниже представлен один из алгоритмов создания последовательности кода Грея заданной глубины, записанный на языке Perl:
my $depth = 16; # generate 16 Gray codes, 4 bits wide each my @gray_codes = ( '0', '1' ); while(scalar(@gray_codes)<$depth) { my @forward_half=map{'0'.$_} @gray_codes; my @reverse_half=map{'1'.$_} reverse(@gray_codes); @gray_codes=(@forward_half,@reverse_half); }
Рекурсивная функция построение кода Грея на языке C:
//n -- требуемая длина кода, //m -- указатель на массив, способный хранить // все коды Грея, длиной до n // (должен быть выделен до вызова функции) //depth -- параметр рекурсии int gray (int n, int* m, int depth) { int i, t = (1 << (depth - 1)); if (depth == 0) m[0] = 0; else { //массив хранит десятичные записи двоичных слов for (i = 0; i < t; i++) m[t + i] = m[t - i - 1] + (1 << (depth - 1)); } if (depth != n) gray(n, m, depth + 1); return 0; }
Быстрое преобразование 8/16/24/32-разрядного бинарного кода в код Грея на языке BlitzBasic:
Function BIN_2_GRAY%(X%) Return X Xor ((X And $EEEEEEEE) Shr 1) End Function
См. также
- Код Хемминга
- Код Джонсона
Примечания
- ↑ BaseGroup.ru :: Генетические алгоритмы — математический аппарат
- ↑ Кнут, Дональд, Э. Искусство программирования, том 4, выпуск 3: генерация всех сочетаний и разбиений (раздел 7.2.1.3): Пер. с англ. — М.: ООО «И.Д. Вильямс», 2007. — 208 с. : ил.]
Библиография
- Black, Paul E. Gray code. 25 февраля 2004. NIST. [1] (англ.).
Ссылки
- NIST Dictionary of Algorithms and Data Structures: Gray code (англ.)
- Коды Грея















