Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.
In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.
Hamming Code for Single Error Correction
The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.
Encoding a message by Hamming Code
The procedure used by the sender to encode the message encompasses the following steps −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Calculating the values of each redundant bit.
Once the redundant bits are embedded within the message, this is sent to the destination.
Step 1 − Calculation of the number of redundant bits.
If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2r states, 2r must be at least equal to (m + r + 1). Thus the following equation should hold −
2r ≥ 𝑚 + 𝑟 + 1
Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (24 ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.
Step 2 − Positioning the redundant bits.
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r1 (at position 1), r2 (at position 2), r3 (at position 4), r4 (at position  and so on.
and so on.
Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −

Step 3 − Calculating the values of each redundant bit.
The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −
-
Even Parity − Here the total number of bits in the message is made even.
-
Odd Parity − Here the total number of bits in the message is made odd.
Each redundant bit, ri, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the ith position except the position of ri. Thus −
-
r1 is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
-
r2 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
-
r3 is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)
Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −

Hence, the message sent will be 11000101100.
Decoding a message in Hamming Code
Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −
-
Step 1 − Calculation of the number of redundant bits.
-
Step 2 − Positioning the redundant bits.
-
Step 3 − Parity checking.
-
Step 4 − Error detection and correction
Step 1) Calculation of the number of redundant bits
Using the same formula as in encoding, the number of redundant bits are ascertained.
2r ≥ 𝑚 + 𝑟 + 1
where m is the number of data bits and r is the number of redundant bits.
Step 2) Positioning the redundant bits
The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.
Step 3) Parity checking
Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c1, c2, c3, c4 etc. Thus
c1 = parity(1, 3, 5, 7, 9, 11 and so on)
c2 = parity(2, 3, 6, 7, 10, 11 and so on)
c3 = parity(4-7, 12-15, 20-23 and so on)
Step 4) Error detection and correction
The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c1c2c3c4 = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.
Example 4 − Suppose that an incoming message 11110101101 is received.
Step 1 − At first the number of redundant bits are calculated using the formula 2r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2r ≥ 12 is 4.
Step 2 − The redundant bits are positioned as below −

Step 3 − Even parity checking is done −
c1 = even_parity(1, 3, 5, 7, 9, 11) = 0
c2 = even_parity(2, 3, 6, 7, 10, 11) = 0
c3 = even_parity (4, 5, 6, 7) = 0
c4 = even_parity (8, 9, 10, 11) = 0
Step 4 — Since the value of the check bits c1c2c3c4 = 0000 = 0, there are no errors in this message.
Hamming Code for double error detection
The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.
Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.
At the receiver’s end, error detection is done as shown in the following table −
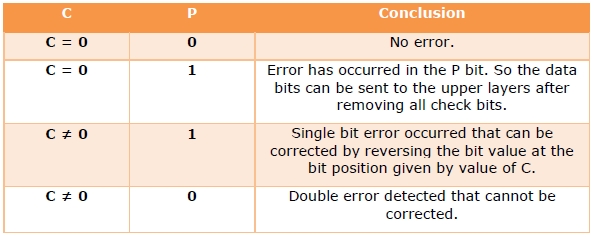
Пример
. Предположим, в канале связи под действием
помех произошло искажение и вместо
0100101 было принято 01001(1)1.
Решение:
Для обнаружения ошибки производят уже
знакомые нам проверки на четность.
Первая
проверка:
сумма П1+П3+П5+П7
= 0+0+1+1 четна.
В младший разряд номера ошибочной
позиции запишем 0.
Вторая
проверка:
сумма П2+П3+П6+П7
= 1+0+1+1 нечетна.
Во второй разряд номера ошибочной
позиции запишем 1
Третья
проверка:
сумма П4+П5+П6+П7
= 0+1+1+1 нечетна.
В третий разряд номера ошибочной позиции
запишем 1. Номер ошибочной позиции 110=
6. Следовательно,
символ шестой позиции следует изменить
на обратный, и получим правильную кодовую
комбинацию.
Код, исправляющий
одиночную и обнаруживающий двойную
ошибки
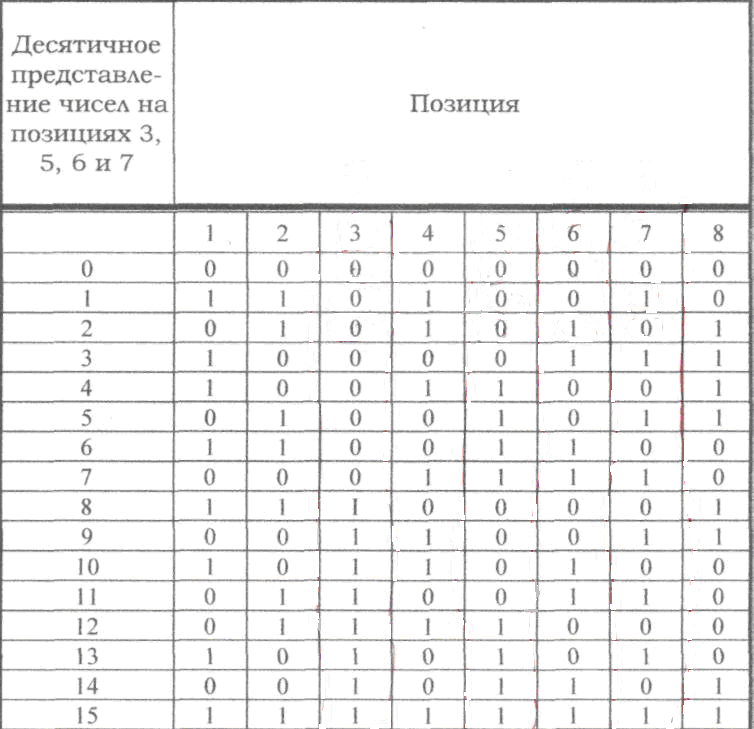
Если по изложенным
выше правилам строить корректирующий
код с обнаружением и исправлением
одиночной ошибки для равномерного
двоичного кода, то первые 16 кодовых
комбинаций будут иметь вид, показанный
в таблице. Такой код может быть использован
для построения кода с исправлением
одиночной ошибки и обнаружением двойной.
Для
этого, кроме указанных выше проверок
по контрольным позициям, следует провести
еще одну проверку на четность для всей
строки в целом. Чтобы осуществить такую
проверку, следует к каждой строке кода
добавить контрольные символы, записанные
в дополнительной колонке (таблица,
колонка 8). Тогда в случае одной ошибки
проверки по позициям укажут номер
ошибочной позиции, а проверка на четность
— на наличие ошибки. Если проверки позиций
укажут на наличие ошибки, а проверка на
четность не фиксирует ее, значит в
кодовой комбинации две ошибки.
Лекция 8
8.1 Двоичные циклические коды
Вышеприведенная
процедура построения линейного кода
матричным методом имеет ряд недостатков.
Она неоднозначна (МДР можно задать
различным образом) и неудобна
в реализации в виде технических устройств.
Этих недостатков лишены
линейные корректирующие коды, принадлежащие
к классу циклических.
Циклическими
называют
линейные (n,k)-коды,
обладающие
следующим свойством:
для любого кодового слова:
![]()
существует другое
кодовое слово:
![]()
полученное
циклическим сдвигом элементов исходного
кодового слова ||КС||
вправо
или влево, которое также принадлежит
этому коду.
Для
описания циклических кодов используют
полиномы с фиктивной переменной
X.
Например,
пусть кодовое слово ||КС||
=
||011010||.
Его
можно описать полиномом
![]()
Таким
образом, разряды кодового слова в
описывающем его полиноме используются
в качестве коэффициентов при степенях
фиктивной переменной
X.
Наибольшая
степень фиктивной переменной X
в
слагаемом с ненулевым
коэффициентом называется степенью
полинома. В вышеприведенном примере
получился полином 4-й степени.
Теперь
действия над кодовыми словами сводятся
к действиям над полиномами.
Вместо алгебры матриц здесь используется
алгебра полиномов.
Рассмотрим
алгебраические действия над полиномами,
используемые в теории
циклических кодов. Суммирование
полиномов разберем на примере
С(Х)=А(Х)+В(Х).
Пусть
||A||
= ||011010||,
||В|| =
||110111|.
Тогда
![]()
![]()
![]()
—————————————————————
![]()
Таким
образом, при суммировании коэффициентов
при X
в одинаковой степени
результат берется по модулю 2. При таком
правиле вычитание эквивалентно
суммированию.
Умножение
выполняется как обычно, но с использованием
суммирования
по модулю 2.
Рассмотрим
умножение на примере умножения полинома
(X3+X1+X0)
на
полином X1+X0
X3
+ 0*X2+X1+X0
*
X1+X0
—————————————————
X3+
0*X2+X1+Х0
X4+0*Х3+
X2+Х1
____________________________________
Х4+
X3+
X2+0*X1+X0
Операция
— обратная умножению -деление. Деление
полиномов выполняется как обычно, за
исключением того, что вычитание
выполняется по модулю 2. Вспомним, что
вычитание по модулю 2 эквивалентно
сложению по модулю 2
Пример
деления полинома X6+X4+X3
на полином
X3+X2+1
X6+0*X5+X4
+ X3+0*X2+0*X1+0
| X3+X2+1
X6+X5+0*X4+X3 результат== |X3+X2
————————————
X5
+X4
+ 0*X3+0*X2
X5
+X4
+ 0*X3+
X2
—————————————-
остаток==
X2
=
100
Циклический
сдвиг влево на одну позицию коэффициентов
полинома степени n-1
получается
путем его умножения на X
с
последующим вычитанием из
результата полинома Xn+1,
если его порядок >
п.
Проверим это на
примере.
Пусть требуется
выполнить циклический сдвиг влево на
одну позицию
коэффициентов
полинома
C(X)=X5+Х3+X2+1
→ (101101)
В результате должен
получиться полином
C1(X)=X4+Х3+X1+1
→ (011011)
Это легко
доказывается:
C1(X)=C(X)*X-(X6+1)=(X6+Х4+X3+X)+(
X6+1)=X4+Х3+X1+1
В
основе циклического кода лежит образующий
полином r-го
порядка
(напомним, что r—
число дополнительных разрядов). Будем
обозначать
его gr(X).
Образование
кодовых слов (кодирование) КС
выполняется
путем умножения
информационного полинома с коэффициентами,
являющимися информационной
последовательностью
И(Х)
порядка
i<k
на
образующий полином gr(X)
КСr+k(Х)=gr(X)+ИСk(Х).
Принятое кодовое
слово может отличаться от переданного
искаженными разрядами в результате
воздействия помех.
ПКС(Х)=КС(Х)+ВО(Х).
где
ВО(Х)
— полином
вектора ошибки, а суммирование, как
обычно, ведется
по модулю 2.
Декодирование,
как и раньше начинается с нахождения
опознавателя,
в данном случае в виде полинома ОП(Х).
Этот
полином вычисляется как
остаток от деления полинома принятого
кодового слова ПКС(Х)
на
образующий
полином g(Х):
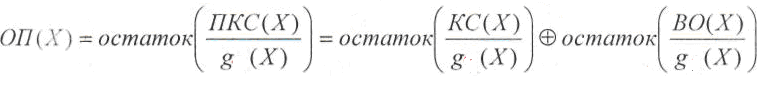
Первое
слагаемое остатка не имеет, т.к. кодовое
слово было образовано путем умножения
полинома информационной последовательности
на
образующий полином. Следовательно, и в
данном случае опознаватель
полностью зависит от вектора ошибки.
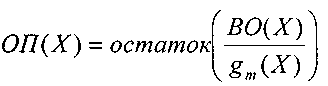
Образующий
полином выбирается таким, чтобы при
данном r
как
можно
большее число отношений ВО(Х)/g(Х)
давало
различные остатки.
Такому
требованию отвечают так называемые
неприводимые
полиномы,
которые
не делятся без остатка ни на один полином
степени r
и ниже, а
делятся только сами на себя и на 1.
Приведенная
здесь процедура образования кодового
слова неудобна тем,
что такой код получается несистематическим,
т.е. таким, в кодовых словах
которого нельзя выделить информационные
и дополнительные разряды.
Этот недостаток
был устранен следующим образом.
Способ
кодирования, приводящий к получению
систематического линейного циклического
кода, состоит в приписывании к
информационной
последовательности И
дополнительных разрядов ДР.
Эти
дополнительные разряды предлагается
находить по следующей формуле:
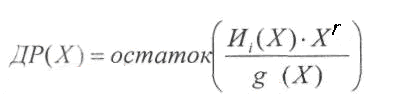
Порядок
полинома ДР(Х)
гарантировано
меньше r
(поскольку
это остаток).
Приписывание
дополнительных разрядов к информационной
последовательности,
используя алгебру полиномов, можно
описать формулой:
![]()
Одним
из свойств циклических линейных кодов
является то, что результат
деления любого разрешенного кодового
слова КС
на
образующий полином также, является
разрешенным кодовым словом.
Покажем,
что получаемые по вышеприведенному
алгоритму кодовые
слова являются кодовыми словами
циклического линейного кода. Для
этого нужно убедиться в том, что
произвольное разрешенное кодовое
слово делится на образующий полином
g(X)
без остатка:
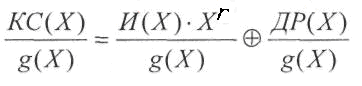
Рассмотрим первое
слагаемое:
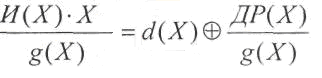
где
d(Х)
— целая
часть результата деления.
Подставим полученную
сумму на место первого слагаемого:
![]() Суммирование
Суммирование
последних двух слагаемых дает нулевой
результат (напомним,
что суммирование выполняется по модулю
2).
Значит
![]() —
—
целая часть деления. Остатка нет. Это
означает,
что описанный выше способ кодирования
соответствует циклическому
коду.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 









p2 









p4 








p8 







p16 




Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]

Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]

The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 









p2 









p4 








p8 







p16 




Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]

Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]

The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Омский государственный педагогический университет»
(ФГБОУ ВО «ОмГПУ»)
Факультет математики, информатики, физики и технологии
Кафедра прикладной информатики и математики
Курсовая работа
Код Хемминга
Направление: педагогическое образование
Профиль: Информатика и Технология
Дисциплина: Теоретические основы информатики
Выполнила: студентка
32 группы
Коробейникова
Ольга Витальевна
______________________________(подпись)
Научный руководитель:
Курганова
Наталья Александровна
к.п.н., доцент
Оценка _______________
«__» _______________ 20___г.
(подпись)
Омск, 20___
Оглавление
Введение
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
1.2. Характеристика кода Хемминга при помехоустойчивом кодировании
1.3. Алгоритмы использования кода Хемминга для нахождения ошибок
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
ЗАКЛЮЧЕНИЕ
Список литературы
Введение
На сегодняшний день в мире передается огромное количество информации, хотя системы передачи данных отвечают всем требованиям. Они не являются столь совершенными. При передаче данных могут возникать помехи. Помехоустойчивость – способность системы осуществлять прием информации в условиях наличия помех в линии связи и искажений во внутри аппаратных трактах. Помехоустойчивость обеспечивает надежность и достоверность передаваемой информации (данных).Управление правильностью передачи информации выполняется с помощью помехоустойчивого кодирования. Есть коды, обнаруживающие ошибки, и корректирующие коды, которые еще и исправляют ошибки. Помехозащищенность достигается с помощью введения избыточности, дополнительных битов. В симплексных каналах связи устраняют ошибки с помощью корректирующих кодов. В дуплексных–достаточно применения кодов, обнаруживающих ошибки. [1]
История развития помехоустойчивого кодирования началась еще с 1946г., а именно, после публикации монографии американского ученого К. Шеннона «Работы по теории информации и кибернетике».В этой работе он не показал как построить эти коды, а доказал их существование. Важно отметить, что результаты работы К. Шеннона опирались на работы советских ученых, таких как: А. Я. Хинчин, Р.Р. Варшамов и др. На сегодняшний день проблема передачи данных является особо актуальной,т.к. сбой при передаче может вызвать не только искажение сообщения в целом, но и полную потерю информации. Для этого и существуют помехоустойчивые коды, способные предотвратить потерю и искажение информации. В настоящее время существует ряд разновидностей помехоустойчивых кодов, обеспечивающих высокую достоверность при малой величине избыточности и простоте технической реализации кодирующих и декодирующих устройств. Принципиально коды могут быть использованы как для обнаружения, так и для исправления ошибок. Однако удобства построения кодирующих и декодирующих устройств определили преимущественное применение лишь некоторых из них, в частности корректирующего кода Хемминга.
Цель данной курсовой работы: Ознакомление с помехоустойчивым кодированием и изучение кода Хемминга.
Задачи:
1) Ознакомиться с видами помехоустойчивого кодирования;
2) Ознакомиться с кодом Хемминга, как с одним из видов помехоустойчивого кодирования;
3) Изучить алгоритм построения кода Хемминга.
Объект исследования: помехоустойчивое кодирование.
Предмет исследования: код Хемминга.
Данная курсовая работа состоит из титульного листа, оглавления,введения, двух глав (теоретической и практической), заключения и списка литературы.
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
В мире существует немало различных помех и искажений, это могут быть как звуковые искажения, так и на графике. Мы рассмотрим, что понимается под помехой в кодировании информации. Под помехой понимается любое воздействие, накладывающееся на полезный сигнал изатрудняющее его прием. Ниже приведена классификация помех и их источников.
Рис. 1.Помехи и их источники
Внешние источники помех вызывают в основном импульсные помехи, а внутренние –флуктуационные. Помехи, накладываясь на видеосигнал, приводят к двум типам искажений: краевыеи дробления. Краевые искажения связаны со смещением переднего или заднего фронта импульса.Дробление связано с дроблением единого видеосигнала на некоторое количество более коротких сигналов [2].
Приведем классификацию помехоустойчивых кодов.
1) Обнаруживающие ошибки:
блоковые:
А) Разделимые:
- с проверкой на четность;
- корреляционные;
- Хэмминга;
- БЧХ;
Б) Неразделимые:
- с постоянным весом;
- Грея.
2) Корректирующие коды:
Непрерывные:
А) С пороговым декодированием;
Б) По макс. правдоподобия;
В) С последовательным декодированием.
Теперь рассмотрим более подробно каждый вид кодирования.
Код с проверкой на четность.
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
В каждом пакет данных есть один бит четности, или, так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно. Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.
Пример:
Начальные данные: 1111
Данные после кодирования: 11110 (1 + 1 + 1 + 1 = 0 (mod 2))
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка [3].
Корреляционные коды (код с удвоением).
Элементы данного кода заменяются двумя символами, единица «1» преобразуется в 10, а ноль «0» в 01.
Вместо комбинации 1010011 передается 10011001011010. Ошибка обнаруживается в том случае, если в парных элементах будут одинаковые символы 00 или 11 (вместо 01 и 10) [2].
Код с постоянным весом.
Одним из простейших блочных неразделимых кодов является код с постоянным весом. Примером такого кода может служить семибитный телеграфный код МТК–3, в котором каждая разрешенная кодовая комбинация содержит три единицы и четыре нуля (рис.2). Весом кодовой комбинации называют число содержащихся в ней единиц. В рассматриваемом коде вес кодовых комбинаций равен трем.
Число разрешенных кодовых комбинаций в кодах с постоянным весом определяется как количество сочетаний изnсимволов поgи равно
(1)
Где n–длина кодовой комбинации, аg – вес разрешенной кодовой комбинации. Для кода МТК-3 число разрешенных кодовых комбинаций равно. Таким образом, из общего числа комбинаций
только 35 используются для передачи сообщений[4].
Рис.2. Примеры разрешенных и запрещенных комбинаций кода МТК-3
Инверсный код.
К исходной комбинации добавляется такая же комбинация по длине. В линию посылается удвоенное число символов. Если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную комбинацию, если нечетное, то добавляемая комбинация является инверсной по отношению к исходной.
|
k |
r |
n |
|
11011 |
11011 |
1101111011 |
|
11100 |
00011 |
1110000011 |
Прием инверсного кода осуществляется в два этапа. На первом этапе суммируются единицы в первой основной группе символов. Если число единиц четное, то контрольные символы принимаются без изменения, если нечетное, то контрольные символы инвертируются. На втором этапе контрольные символы суммируются с информационными символами по модулю два. Нулевая сумма говорит об отсутствии ошибок. При ненулевой сумме, принятая комбинация бракуется. Покажем суммирование для принятых комбинаций без ошибок (1,3) и с ошибками (2,4).
|
1) |
11011 11011 |
|
00000 |
|
|
2) |
11111 00100 |
|
11011 |
Обнаруживающие способности данного кода достаточно велики. Данный код обнаруживает практически любые ошибки, кроме редких ошибок смещения, которые одновременно происходят как среди информационных символов, так и среди соответствующих контрольных. Например, при k=5, n=10 и . Коэффициент обнаружения будет составлять
[2].
Код Грея.
По сравнению с простым кодом, код Грея позволяет уменьшить ошибки неоднозначности считывания, а также ошибки из-за помех в канале. Обычно этот код применяется для аналогово-цифрового преобразования непрерывных сообщений.
Недостатком кода Грея является его невесомость, т.е. вес единицы не определяется номером разряда. Информацию в таком виде трудно обрабатывать на ЭВМ. Декодирование кода также связано с большими затратами. Поэтому перед вводом в ЭВМ (или перед декодированием) код Грея преобразуется в простой двоичный код, который удобен для ЭВМ и легко декодируется.
Для перевода простого двоичного кода в код Грея нужно:
- под двоичным числом записать такое же число со сдвигом вправо на один разряд (при этом младший разряд сдвигаемого числа теряется);
- произвести поразрядное сложение двух чисел по модулю 2 (четности). [5].
Таким образом, мы рассмотрели виды помехоустойчивого кодирования и увидели, что их существует не так уж и мало. Каждый код по своему уникален и полезен для кодирования информации. Теперь мы ознакомимся с кодом Хемминга подробнее.
1.2.Характеристика кода Хэмминга при помехоустойчивом кодировании
В середине 40-х годов Ричард Хемминг работал в знаменитых Лабораториях Белла на счётной машине Bell Model V. Это была электромеханическая машина, использующая релейные блоки,скорость которых была очень низка: один оборот за несколько секунд. Данные вводились в машине с помощью перфокарт, и поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.
Р. Хемминг часто работал в выходные дни, и все больше и больше раздражался, потому что часто был должен перегружать свою программу из-за ненадежности перфокарт. На протяжении нескольких лет он проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 году он опубликовал способ, который на сегодняшний день мы знаем как код Хемминга.[6.].
Код Хемминга, как и любой (n,k) код, содержит k информационных и избыточных символов. Избыточная часть кода строится таким образом, чтобы при декодировании можно было бы установить не только факт наличия ошибок в принятой – комбинации, но и указать номер позиции, в которой произошла ошибка. Это достигается за счет многократной проверки принятой комбинации на четность. Каждой проверкой должны охватываться часть информационных символов и один из избыточных символов. При каждой проверке получают двоичный контрольный символ. Если результат проверки дает четное число, то контрольному символу присваивается значение 0, если нечетное число– 1. В результате всех проверок получается p-разрядное двоичное число, указывающее номер искаженного символа. Для исправления ошибки достаточно лишь изменить значение данного символа на обратное. [7]
К ним обычно относятся коды с минимальным кодовым расстояниемисправляющие все одиночные ошибки, и коды с расстоянием
исправляющие все одиночные и обнаруживающие все двойные ошибки. Длина кода Хэмминга:
(2)
(r – количество проверочных разрядов).
Характерной особенностью проверочной матрицы кода с является то, что ее столбцы представляют собой любые различные ненулевые комбинации длиной r.Например, при r=4 иn=5 для кода (15,11), проверочная матрица может иметь следующий вид (рис.3)
Рис.3. Проверочная матрица
Перестановкой столбцов, содержащих одну единицу, данную матрицу можно привести к виду(рис.4)
Рис. 4.Измененная матрица
Использование такого кода позволяет исправить любую одиночную ошибку или обнаружить произвольную ошибку кратности два.Если информационные и проверочные разряды кода нумеровать слева направо, то в соответствии с матрицей получаем систему проверочных уравнений, с помощью которых вычисляем проверочные разряды(рис.5):
Рис.5. Система проверочных уравнений
где —
-проверочные разряды;
—
-информационные разряды
Двоичный код Хэмминга с кодовым расстоянием получается путем добавления к коду Хэмминга с
одного проверочного разряда, представляющего собой результат суммирования по модулю два всех разрядов кодового слоя. Длина кода при этом
разрядов, из которых
являются проверочными.
Операция кодирования может выполняться в два этапа. На первом этапе определяется кодовая комбинация с использованием матрицы H, соответствующей коду с на втором — добавляется один проверочный разряд, в котором записывается результат суммирования по модулю два всех разрядов кодового слова, полученного на первом этапе. Операция декодирования также состоит из двух этапов. На первом вычисляется синдром, соответствующий коду на втором — проверяется последнее проверочное соотношение.[8]
Таким образом, ознакомившись с характеристикой кода Хемминга, важно сказать, что состоит код из двух частей и предполагает надежную работу нахождения ошибок и корректировки сообщений.
1.3.Алгоритмы использования кода Хэмминга для нахождения ошибок
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
1.По заданному количеству информационных символов – k, либо информационных комбинаций , используя соотношения:
,
(3)
и (4)
(5)
Вычисляют основные параметры кода m и n.
2.Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону , где i= 1,2,3,…т.е. они равны 1,2,4,8,16,…а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно . В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение – 0, в противном случае – 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n -чисел разрядностью – m (табл. 2, для m = 4) или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до
перечисленных в возрастающем порядке.
Количество разрядов m – определяет количество проверок.
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1,b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку –коэффициенты которые содержат 1 в третьем разряде и т.д.
Таблица 2
|
Десятичные числа (номера разрядов кодовой комбинации) |
Двоичные числа и их разряды |
|
|
3 |
21 |
|
|
1 |
0 |
01 |
|
2 |
0 |
10 |
|
3 |
0 |
11 |
|
4 |
1 |
00 |
|
5 |
1 |
01 |
|
6 |
1 |
10 |
|
7 |
1 |
11 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) – разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.[9]
Вывод к главе 1: Таким образом, мы узнали, что такое помехоустойчивость, помехоустойчивое кодирование, ознакомились с видами помехоустойчивого кодирования. Затем рассмотрели код Хемминга, изучили алгоритм построения кода Хемминга. При построении кода важно знать, что код Хемминга ищет и исправляет одиночную ошибку, но двойную ошибку. В итоге, изучив теоретическую часть, мы выяснили, какие существуют виды помехоустойчивого кодирования. Ознакомились подробнее с кодом Хемминга, изучили его алгоритм кодирования.
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
Существует множество различных примеров для нахождения ошибок при помощи кода Хемминга.
Пример 1. Пользуясь кодом Хэмминга найти ошибку в сообщении.
1) 1111 1011 0010 1100 1101 1100 110
РЕШЕНИЕ. Сообщение состоит из 27 символов, из них 22 информационные, а 5 – контрольные. Это разряды b1 = 1, b2 = 1, b4 = 1, b8 = 1, b16=0. Вычислим число J для обнаружения ошибки: Введем для удобства следующие множества:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27… – все числа у которых первый разрядравен 1
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27… – все числа, у которых второй разрядравен 1
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23 … – все числа, у которых третий разряд равен1
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27 … – все числа, у которых четвертый разрядравен 1,
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 … – все числа, у которых пятый разрядравен 1.
Разряды числа J определяются следующим образом:
j1 = b1 +b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1
j2=b2+b3+b6+b7+b10+b11+b14+b15+b18+b19+b22+b23+b26+b27= 0
j3 = b4+b5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23 = 0
j4 =b9+b10+b11+b12+b13+b14+b15+b24+b25+b26+b27 = 0,
j5 = b16+ b17+b18+b19+b20+b21+b22+b23+b24+b25+b26+b27 = 1
то есть число J= =
.
Таким образом, ошибка произошла в семнадцатом разряде переданного числа.[10]. В этом примере мы рассмотрели, как можно обнаружить одиночную ошибку. Далее мы проанализируем пример, как можно найти и исправить эту ошибку.
Пример 2.
Построить код Хемминга для передачи сообщений в виде последовательности десятичных цифр, представленных в виде 4 –х разрядных двоичных слов. Показать процесс кодирования, декодирования и исправления одиночной ошибки на примере информационного слова 0101.
Решение:
1. По заданной длине информационного слова (k = 4 ), определим количество контрольных разрядов m, используя соотношение:
,
при этом т. е. получили (7, 4) -код.
2. Определяем номера рабочих и контрольных позиции кодовой комбинации. Номера контрольных позиций выбираем по закону .
Для рассматриваемой задачи (при n = 7 ) номера контрольных позиций равны 1, 2, 4. При этом кодовая комбинация имеет вид:
b1 b2 b3 b4 b5 b6 b7
k1 k2 0 k2 1 0 1
3. Определяем значения контрольных разрядов (0 или 1), используя проверочную матрицу (рис.3).
Первая проверка:
k1b3 b5 b7 = k1 011 будет четной при k1 = 0.
Вторая проверка:
k2 b3 b6 b7 = k2 001 будет четной при k2 = 1.
Третья проверка:
k3 b5 b6 b7 = k3 101 будет четной при k3 = 0.
1 2 3 4 5 6 7
Передаваемая кодовая комбинация: 0100101
Допустим принято: 0110101
Для обнаружения и исправления ошибки составим аналогичные проверки на четность контрольных сумм, в соответствии с проверочной матрицей результатом которых является двоичное ( ) – разрядное число, называемое синдромом и указывающим на положение ошибки, т. е, номер ошибочной позиции.
1) k1= b3 b5 b7 = 0111 = 1.
2)k2=b3 b6 b7 = 1101 = 1.
3) k3 =b5 b6 b7 = 0101 =0.
Сравнивая синдром ошибки со столбцами проверочной матрицы, определяем номер ошибочного бита. Синдрому 011 соответствует третий столбец, т. е. ошибка в третьем разряде кодовой комбинации. Символ в третьей позиции необходимо изменить на обратный.
Рассмотрев данные задачи, мы выяснили насколько точно код Хемминга может найти и исправить одиночные ошибки.
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
Для обнаружения двойной ошибки следует только добавить еще один проверочный разряд.
Пример 1:
Принята кодовая комбинация С = 101000001001, произошло
искажение 2-го и 5-го разрядов. Обнаружить ошибки.
Решение.
Значения проверок равны:
k1= b1 b3 b5 b7 b9 b11 = 110010= 1
k2= b2 b3 b6 b7 b10 b11= 010000=1
k3=b4 b5 b6 b7 b12= 00001=1
k4= b8 b9 b10 b11 b12= 01001=0
Тогда контрольное число (синдром) ошибкиравен 0111.
Таким образом, при наличии двукратной ошибки декодирование дает
номер разряда с ошибкой в позиции 7, в то время как ошибки произошли
во 2-м и 5-м разрядах. В этом случае составляется расширенный код
Хэмминга, путем добавления одного проверочного символа.
Пример 2 :
Передана кодовая комбинация «01001011», закодированная кодом Хемминга с d = 4. Показать процесс выявления ошибки.
Решение:
Принята комбинация «01001111»:
а) проверка на общую четность указывает на наличие ошибки (число единиц четное);
б) частные проверки производятся так же, как это было в других примерах.
При составлении проверочных сумм последние единицы кодовых комбинаций (дополнительные контрольные символы) не учитываются.
2. Принята комбинация «01101111»:
а) проверка на общую четность показывает, что ошибка не фиксируется;
б) частные проверки (последний символ отбрасывается)
Первая проверка 0 1 1 1 = 1
Вторая проверка 1 1 1 1 = 0
Третья проверка 0 1 1 1 = 1
Таким образом, частные проверки фиксируют наличие ошибки. Она, якобы, имела место на пятой позиции. Но так как при этом первая проверка на общую четность ошибки не зафиксировала, то значит, имела место двойная ошибка. Исправить двойную ошибку такой код не может [14].
Вывод к главе 2: Таким образом, мы показали, как работает код Хемминга на практике. Мы видим, что при одиночной ошибке ее можно исправить, но для этого нам нужно знать, сколько потребуется контрольных разрядов, а двойную ошибку можно лишь обнаружить.
ЗАКЛЮЧЕНИЕ
Высокие требования к достоверности передачи, обработки и хранения информации диктуют необходимость такого кодированияинформации, при котором обеспечивалось бы возможность обнаружения и исправления ошибок. Широкому применению результатов теории помехоустойчивогокодирования в современных системах связи, обработки и хранения информацииследует считать отсутствие достаточно простых решений сложных теоретических достижений теории помехоустойчивого кодирования.В данной работе исследовано помехоустойчивое кодирование, в частности код Хемминга.
Список литературы
- Вернер М. Основы кодирования[Текст].– М.: Техносфера, 2004. – 288 с.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:https://clck.ru/9cWsc,свободный. Дата обращения: 27.11.2015.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:http://habrahabr.ru/post/111336/, свободный. Дата обращения: 05.12.2015.
- Файловый архив для студентов. Лекция: основные понятия кодирования в ЦСПИ [Электронный ресурс]. – Режим доступа: http://www.studfiles.ru/preview/4087325/,свободный. Дата обращения: 27.11.2015.
- Лекция «Простейшие коды» [Электронный ресурс]. – Режим доступа: http://davaiknam.ru/text/lekciya-3-kodirovanie-informacii-prostejshie-kodi, свободный. Дата обращения: 27.11.2015.
- Академик [Электронный ресурс] – Режим доступа: http://dic.academic.ru/dic.nsf/ruwiki/177544, свободный. Дата обращения: 27.11.2015
- Кузьмин И.В.Основы теории информации и кодирования [Текст]. – Киев,1986. – 237 с.
- Научная библиотека. Код Хемминга [Электронный ресурс]. – Режим доступа: http://info.sernam.ru/book_codb.php?id=28, свободный. Дата обращения: 05.12.2015
- Статья корректирующие коды [Электронный ресурс]. – Режим доступа: http://referatwork.ru/refs/source/ref-11094.html#Текст работы, свободный. Дата обращения: 05.12.2015
- МатБюро- решение задач по высшей математике [Электронный ресурс]. – Режим доступа: http://www.matburo.ru/Examples/Files/Hem2.pdf, свободный. Дата обращения: 06.12.2015.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. [Текст]. – Москва, 1986г. –576 с.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования – методы, алгоритмы, применение. [Текст]. – Москва, 2005г.–320 с.
- Р.Хемминг Теория кодирования и теория информации. / Перевод с английского С.Гальфанда. // [Текст]. – Москва, 1983г. – 176 с.
- Портал студентов «Седьмой бит» [Электронный ресурс]. – Режим доступа: http://www.itmo.ru/work/253/page4, открытый. Дата обращения: 20.12.2015.
Пример
. Предположим, в канале связи под действием
помех произошло искажение и вместо
0100101 было принято 01001(1)1.
Решение:
Для обнаружения ошибки производят уже
знакомые нам проверки на четность.
Первая
проверка:
сумма П1+П3+П5+П7
= 0+0+1+1 четна.
В младший разряд номера ошибочной
позиции запишем 0.
Вторая
проверка:
сумма П2+П3+П6+П7
= 1+0+1+1 нечетна.
Во второй разряд номера ошибочной
позиции запишем 1
Третья
проверка:
сумма П4+П5+П6+П7
= 0+1+1+1 нечетна.
В третий разряд номера ошибочной позиции
запишем 1. Номер ошибочной позиции 110=
6. Следовательно,
символ шестой позиции следует изменить
на обратный, и получим правильную кодовую
комбинацию.
Код, исправляющий
одиночную и обнаруживающий двойную
ошибки

Если по изложенным
выше правилам строить корректирующий
код с обнаружением и исправлением
одиночной ошибки для равномерного
двоичного кода, то первые 16 кодовых
комбинаций будут иметь вид, показанный
в таблице. Такой код может быть использован
для построения кода с исправлением
одиночной ошибки и обнаружением двойной.
Для
этого, кроме указанных выше проверок
по контрольным позициям, следует провести
еще одну проверку на четность для всей
строки в целом. Чтобы осуществить такую
проверку, следует к каждой строке кода
добавить контрольные символы, записанные
в дополнительной колонке (таблица,
колонка 8). Тогда в случае одной ошибки
проверки по позициям укажут номер
ошибочной позиции, а проверка на четность
— на наличие ошибки. Если проверки позиций
укажут на наличие ошибки, а проверка на
четность не фиксирует ее, значит в
кодовой комбинации две ошибки.
Лекция 8
8.1 Двоичные циклические коды
Вышеприведенная
процедура построения линейного кода
матричным методом имеет ряд недостатков.
Она неоднозначна (МДР можно задать
различным образом) и неудобна
в реализации в виде технических устройств.
Этих недостатков лишены
линейные корректирующие коды, принадлежащие
к классу циклических.
Циклическими
называют
линейные (n,k)-коды,
обладающие
следующим свойством:
для любого кодового слова:
![]()
существует другое
кодовое слово:
![]()
полученное
циклическим сдвигом элементов исходного
кодового слова ||КС||
вправо
или влево, которое также принадлежит
этому коду.
Для
описания циклических кодов используют
полиномы с фиктивной переменной
X.
Например,
пусть кодовое слово ||КС||
=
||011010||.
Его
можно описать полиномом
![]()
Таким
образом, разряды кодового слова в
описывающем его полиноме используются
в качестве коэффициентов при степенях
фиктивной переменной
X.
Наибольшая
степень фиктивной переменной X
в
слагаемом с ненулевым
коэффициентом называется степенью
полинома. В вышеприведенном примере
получился полином 4-й степени.
Теперь
действия над кодовыми словами сводятся
к действиям над полиномами.
Вместо алгебры матриц здесь используется
алгебра полиномов.
Рассмотрим
алгебраические действия над полиномами,
используемые в теории
циклических кодов. Суммирование
полиномов разберем на примере
С(Х)=А(Х)+В(Х).
Пусть
||A||
= ||011010||,
||В|| =
||110111|.
Тогда
![]()
![]()
![]()
—————————————————————
![]()
Таким
образом, при суммировании коэффициентов
при X
в одинаковой степени
результат берется по модулю 2. При таком
правиле вычитание эквивалентно
суммированию.
Умножение
выполняется как обычно, но с использованием
суммирования
по модулю 2.
Рассмотрим
умножение на примере умножения полинома
(X3+X1+X0)
на
полином X1+X0
X3
+ 0*X2+X1+X0
*
X1+X0
—————————————————
X3+
0*X2+X1+Х0
X4+0*Х3+
X2+Х1
____________________________________
Х4+
X3+
X2+0*X1+X0
Операция
— обратная умножению -деление. Деление
полиномов выполняется как обычно, за
исключением того, что вычитание
выполняется по модулю 2. Вспомним, что
вычитание по модулю 2 эквивалентно
сложению по модулю 2
Пример
деления полинома X6+X4+X3
на полином
X3+X2+1
X6+0*X5+X4
+ X3+0*X2+0*X1+0
| X3+X2+1
X6+X5+0*X4+X3 результат== |X3+X2
————————————
X5
+X4
+ 0*X3+0*X2
X5
+X4
+ 0*X3+
X2
—————————————-
остаток==
X2
=
100
Циклический
сдвиг влево на одну позицию коэффициентов
полинома степени n-1
получается
путем его умножения на X
с
последующим вычитанием из
результата полинома Xn+1,
если его порядок >
п.
Проверим это на
примере.
Пусть требуется
выполнить циклический сдвиг влево на
одну позицию
коэффициентов
полинома
C(X)=X5+Х3+X2+1
→ (101101)
В результате должен
получиться полином
C1(X)=X4+Х3+X1+1
→ (011011)
Это легко
доказывается:
C1(X)=C(X)*X-(X6+1)=(X6+Х4+X3+X)+(
X6+1)=X4+Х3+X1+1
В
основе циклического кода лежит образующий
полином r-го
порядка
(напомним, что r—
число дополнительных разрядов). Будем
обозначать
его gr(X).
Образование
кодовых слов (кодирование) КС
выполняется
путем умножения
информационного полинома с коэффициентами,
являющимися информационной
последовательностью
И(Х)
порядка
i<k
на
образующий полином gr(X)
КСr+k(Х)=gr(X)+ИСk(Х).
Принятое кодовое
слово может отличаться от переданного
искаженными разрядами в результате
воздействия помех.
ПКС(Х)=КС(Х)+ВО(Х).
где
ВО(Х)
— полином
вектора ошибки, а суммирование, как
обычно, ведется
по модулю 2.
Декодирование,
как и раньше начинается с нахождения
опознавателя,
в данном случае в виде полинома ОП(Х).
Этот
полином вычисляется как
остаток от деления полинома принятого
кодового слова ПКС(Х)
на
образующий
полином g(Х):
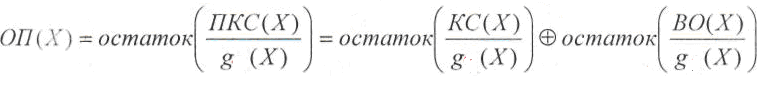
Первое
слагаемое остатка не имеет, т.к. кодовое
слово было образовано путем умножения
полинома информационной последовательности
на
образующий полином. Следовательно, и в
данном случае опознаватель
полностью зависит от вектора ошибки.
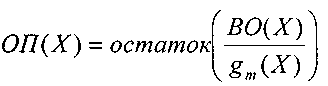
Образующий
полином выбирается таким, чтобы при
данном r
как
можно
большее число отношений ВО(Х)/g(Х)
давало
различные остатки.
Такому
требованию отвечают так называемые
неприводимые
полиномы,
которые
не делятся без остатка ни на один полином
степени r
и ниже, а
делятся только сами на себя и на 1.
Приведенная
здесь процедура образования кодового
слова неудобна тем,
что такой код получается несистематическим,
т.е. таким, в кодовых словах
которого нельзя выделить информационные
и дополнительные разряды.
Этот недостаток
был устранен следующим образом.
Способ
кодирования, приводящий к получению
систематического линейного циклического
кода, состоит в приписывании к
информационной
последовательности И
дополнительных разрядов ДР.
Эти
дополнительные разряды предлагается
находить по следующей формуле:
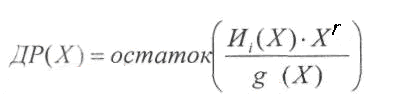
Порядок
полинома ДР(Х)
гарантировано
меньше r
(поскольку
это остаток).
Приписывание
дополнительных разрядов к информационной
последовательности,
используя алгебру полиномов, можно
описать формулой:
![]()
Одним
из свойств циклических линейных кодов
является то, что результат
деления любого разрешенного кодового
слова КС
на
образующий полином также, является
разрешенным кодовым словом.
Покажем,
что получаемые по вышеприведенному
алгоритму кодовые
слова являются кодовыми словами
циклического линейного кода. Для
этого нужно убедиться в том, что
произвольное разрешенное кодовое
слово делится на образующий полином
g(X)
без остатка:
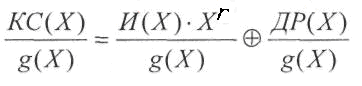
Рассмотрим первое
слагаемое:
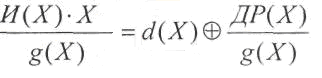
где
d(Х)
— целая
часть результата деления.
Подставим полученную
сумму на место первого слагаемого:
![]() Суммирование
Суммирование
последних двух слагаемых дает нулевой
результат (напомним,
что суммирование выполняется по модулю
2).
Значит
![]() —
—
целая часть деления. Остатка нет. Это
означает,
что описанный выше способ кодирования
соответствует циклическому
коду.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
«Цель этого курса — подготовить вас к вашему техническому будущему.»
 Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?
Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
Мы уже перевели 26 (из 30) глав. И ведем работу над изданием «в бумаге».
Глава 12. Коды с коррекцией ошибок
(За перевод спасибо Mikhail Sheblaev, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
В этой главе затронуты две темы: первая, очевидно, коды с коррекцией ошибок, а вторая — то, как иногда происходит процесс открытия. Как Вы все знаете, я официальный первооткрыватель кодов Хэмминга с коррекцией ошибок. Таким образом я, по-видимому, имею возможность описать, как они были найдены. Но вам необходимо остерегаться любых рассказов подобного типа. По правде говоря, в то время я уже очень интересовался процессом открытия, полагая во многих случаях, что метод открытия более важен, чем то, что открыто. Я знал достаточно, чтобы не думать о процессе во время исследований, так же, как спортсмены не думают о технике, когда выступают на соревнованиях, но отрабатывают её до автоматизма. Я также выработал привычку возвращаться назад после больших или малых открытий и пытаться отследить шаги, которые к ним привели. Но не обманывайтесь; в лучшем случае я могу описать сознательную часть и малую верхушку подсознательной части, но мы просто не знаем магии работы подсознания.
Я использовал релейный вычислитель Model 5 в Нью-Йорке, подготавливая его к отправке в Aberdeen Proving Grounds вместе с некоторым требуемым программным обеспечинием (главным образом математические программы). Если с помощью 2-из-5 блочных кодов обнаруживалась ошибка, машина, оставленная без присмотра, могла до трёх раз подряд повторять ошибочный цикл, прежде чем отбросить его и взять новую задачу, надеясь, что проблемное оборудование не будет задействовано в новом решении. Я был в то время, как говорится, старшим помощником младшего дворника, свободное машинное время я получал только на выходных — с 17-00 пятницы до 8-00 понедельника — это была уйма времени! Так я мог бы загрузить входную ленту с большим количеством задач и пообещать моим друзьям, вернувшись в Мюррей Хилл, Нью-Джерси, где находился исследовательский департамент, что я подготовлю ответы ко вторнику. Ну, в одни выходные, как только мы уехали вечером пятницы, машина полностью сломалась и у меня совершенно ничего не было к понедельнику. Я должен был принести извинения моим друзьям и пообещать им ответы к следующему вторнику. Увы! Та же ситуация случилась снова! Я был мягко говоря разгневан и воскликнул: «Если машина может определить, что ошибка существует, почему же она не определит где ошибка и не исправит её, просто изменив бит на противоположный?» (На самом деле, использованные выражения были чуть крепче!).
Заметим первым делом, что этот существенный сдвиг произошёл только потому, что я испытывал огромное эмоциональное напряжение в тот момент и это характерно для большинства великих открытий. Спокойная работа позволит вам улучшить и подробнее разработать идеи, но прорыв обычно приходит только после большого стресса и эмоциональной вовлечёности. Спокойный, холодный, не вовлечённый исследователь редко делает действительно большие новые шаги.
Вернёмся к рассказу. Я знал из предыдущих обсуждений, что конечно можно было бы соорудить три экземляра вычислителя, включая сравнивающие схемы, и использовать исправление ошибок методом голосования большинства. Но чего бы это стоило! Конечно, были и лучшие методы. Я также знал, как обсуждалось в предыдущей главе, о классной штуке с контролем чётности. Я разобрался в их строении очень внимательно.
С другой стороны, Пастер сказал: «Удача любит подготовленных». Как видите, я был подготовлен моей предыдущей работой. Я более чем хорошо знал кодирование «2-из-5», я понимал их фундаментально и работал и понимал общие последствия контроля чётности.

Рис. 12.I
После некоторых размышлений я понял, что если я расположу биты любого символа сообщения в виде прямоугольника и запишу чётность каждого столбца и каждой строки, то две непрошедшие проверки чётности покажут мне координаты одной ошибки и это будет включать угловой добавленный бит чётности (который мог быть установлен соответственно, если я имел нечётные значения) Рис. 12.I. Избыточность, отношение того, что Вы используете, к минимально необходимому количеству, есть
Любому, ко изучал матанализ, очевидно, что чем ближе прямоугольник к квадрату, тем меньше избыточность для сообщения того же размера. И, конечно, большие значения m и n были бы лучше, чем малые, но тогда риск двойной ошибки был бы велик с инженерной точки зрения. Заметим, что если две ошибки случаются, то Вы имеете: (1) если они не в одной строке или столбце, то просто две строки и два столбца содержат ошибки и мы не знаем, какая диагональная пара вызвала их; (2) если две ошибки случились в одной строке (или столбце), то у вас есть только один столбец (строка) и ни одной строки (столбца).
Перенесёмся сейчас на несколько недель позднее. Чтобы попасть в Нью-Йорк, я должен был добраться чуть раньше в Мюррей Хилл, Нью-Джерси, где я работал, и прокатиться на машине, доставляющей почту для компании. Ну да, поездка через северный Нью-Джерси ранним утром не очень живописна, поэтому я завёл привычку пересматривать свои достижения, так что перо вертелось в руках автоматически. В частности я крутил в голове прямоугольные коды. Внезапно, и я не знаю причин для этого, я обнаружил, что если я возьму треугольник и размещу биты контроля чётности на диагонали с тем, чтобы каждый бит проверял столбец и строку одновременно, то я получу более приемлемую избыточность, Рис 12.II.
Моя самодовольность вмиг исчезла! Получил ли я на сей раз лучший код? Спустя несколько миль размышления по этому поводу (помните, ничего не отвлекает в пейзаже северного Нью-Джерси) я понял, что куб информационных битов с контролем чётности по каждой плоскости и проверкой чётности по осям, по всем трём осям, даст мне три координаты для ошибки ценой всего 3n-2 проверок чётности для целого кодированого сообщения длины n^3. Лучше! Но было ли это самым лучшим решением? Нет! Будучи математиком, я быстро понял, что 4-х мерный куб (я не должен был размещать биты так, только обозначить внутренние связи) будет ещё лучше. Таким образом, даже более высокая размерность была бы ещё лучше. Вскоре стало ясно (скажем, миль через 5), что куб размерности 2х2х2х… х2 с n+1 проверкой чётности был бы лучше — очевидно!
Но однажды обожегши пальцы, я не собирался соглашаться с тем, что выглядело хорошо — я уже сделал эту ошибку прежде! Мог бы я доказать, что это было лучшим решением? Как это доказать? Один очевидный подход был в том, чтобы попробовать подсчитать параметры, у меня был n+1 контрольный бит, отображаемый в строку из n+1 битов, т.е. двоичное число длины n+1 разрядов, и это могло представить произвольный объект длины 2^{n+1}. Но мне был нужен только 2^n+1 разряд, 2^n точек в кубе плюс один бит, подтверждающий, что сообщение корректно. Я не учёл в рассмотрении почти что половину битов. Увы! Я прибыл к двери компании, зарегистрировался и пошёл на конференцию, дав идее вылежаться.
Когда я возвратился к идее после нескольких дней отвлекающих событий (в конце концов, предполагалось, что я способствовал командным усилиям компании), я наконец решил, что хороший подход должен будет использовать синдром ошибки как двоичное число, указывающее место ошибки, с, конечно, всеми нулевыми битами в случае корректного результата (более лёгкий тест, чем для всех единиц на большинстве компьютеров). Заметьте, знакомство с двоичной системой, которая не была тогда распространена (1947-1948) неоднократно играло заметную роль в моих построениях. Это плата за знание большего, чем нужно сиюминутно!
Как Вы сконструируете этот частный случай кода, исправляющего ошибки? Легко! Запишите позиции в двоичном коде:

Теперь очевидно, что проверка чётности в правой половине синдрома должна включать все позиции, имеющие 1 в правом столбце; вторая цифра справа должна включить числа, имеющие 1 во втором столбце и т.д. Поэтому Вы имеете:

Таким образом, если ошибка происходит в некотором разряде, соответствующие проверки чётности (и только эти) провалятся и дадут 1 в синдроме, это составит в точности двоичное представление позиции ошибки. Это просто!
Чтобы увидеть код в действии, мы ограничимся 4 битами для сообщениями и 3 контрольными позициями. Эти числа удовлетворяют условию

которое очевидно является необходимым условием, а равенство — достаточным. Выберем для положения битов проверки (так, чтобы контроль чётности был проще ) контрольные разряды 1, 2 и 4. Позиции для сообщения — 3, 5, 6 7. Пусть сообщение будет
1001
Мы (1) запишем сообщение в верхней строке, (2) закодируем следующую строку, (3) вставим ошибку в позиции 6 на следующей строке и (4) на следующих трёх строках вычислим три проверки чётности.

Применим проверки чётности к полученному сообщению:

Двоичное число 110 -> 6, следовательно измените в позиции 6, отбросьте контрольные разряды 1, 2 и 4 и Вы получите оригинальное сообщение, 1001.
Если это кажется волшебством, подумайте о сообщении из всех 0, которое будет иметь контрольные позиции в 0, а после представьте изменение одного бита и Вы увидите как позиция ошибки перемещается, а следом двоичное число синдрома соответственно изменится и будет точно соответствовать положению ошибки. Затем обратите внимание, что сумма любых двух корректных сообщений является всё ещё корректным сообщением (проверки чётности являются аддитивными по модулю 2, следовательно корректные сообщения образуют аддитивную группу по модулю 2). Корректное сообщение даст все нули, следовательно сумма корректных сообщений плюс ошибка одном разряде даст положение ошибки независимо от отправляемого сообщения. Проверки чётности концентрируются на ошибке и игнорируют сообщение.
Теперь сразу очевидно, что любой обмен любыми двумя или больше из столбцов, однажды согласованных на каждом конце канала, не будет иметь никакого существенного эффекта; код будет эквивалентен. Точно так же перестановка 0 и 1 в любом столбце не даст существенно различных кодов. В частности, (так называемый) Код Хемминга является просто красивым переупорядочиванием, и на практике Вы могли бы проверять контрольные биты в конце сообщения, вместо того, чтобы рассеивать их посреди сообщения.
Как насчёт двойной ошибки? Если мы хотим поймать (но не исправить) двойную ошибку, мы просто добавляем единственную новую проверку чётности к целому сообщению, которое мы отправляем. Давайте посмотрим то, что тогда произойдёт на Вашем конце канала.

Исправление одиночных ошибок плюс обнаружение двойных ошибок часто является хорошим балансом. Конечно, избыточность в коротком сообщении из 4 битов, теперь с 4 битами проверки, плоха, но число проверочных битов растёт (грубо ) как логарифм от длины сообщения. Слишком длинное сообщение — и Вы рискуете получить двойную неисправляемую ошибку (которую при помощи кода с исправлением одной ошибки Вы «исправите» в третью ошибку), слишком короткое сообщение — и стоимость избыточности слишком высока. Снова инженерные рассуждения в зависимости от конкретного случая…
Из аналитической геометрии Вы усвоили значимость использования дополняющих алгебраических и геометрических представлений. Естественное представление строки битов должно использовать n-мерный куб, каждая строка которого является вершиной куба. Используя эту картинку и наконец заметив, что любая одна ошибка в сообщении перемещает сообщение вдоль одного ребра, две ошибки — вдоль двух ребер и т.д., я медленно понял, что я должен был действовать в пространстве $L_1$. Расстояние между элементами есть количество разрядов, в которых они различаются. Таким образом у нас есть метрика на пространстве и она удовлетворяет трём стандартным условиям для расстояния (см Главу 10 где определяется стандартное расстояние в L_1).

Таким образом я должен был отнестись серьёзно к тому, что я знал как абстракцию Пифагоровой функции расстояния.
Имея понятие расстояние, мы можем определить сферу как все точки (вершины, поскольку всё рассматривается в множестве вершин), на фиксированном расстоянии от центра. Например, в 3-мерном кубе, который может быть легко нарисован, Рис. 12.III, точки (0,0,1), (0,1,0), и (1,0,0) находятся на единичном расстоянии от (0,0,0), в то время как точки (1,1,0), (1,0,1), и (0,1,1) находятся на расстоянии 2 далее, и наконец точка (1,1,1) находится на расстоянии 3 от начала координат.
Перейдём теперь в пространство с n измерениями и нарисуем сферу единичного радиуса вокруг каждой точки и предположим, что сферы не пересекаются. Очевидно, что центры сфер есть элементы кода и только эти точки, тогда результатом получения любой единичной ошибки в сообщении будет «не-кодовая» точка и Вы сможете понять откуда эта ошибка пришла. Она будет внутри сферы вокруг точки кода, которую я вам послал, что эквивалентно сфере радиуса 1 вокруг точки кода, которую Вы получили. Следовательно, у нас есть код с коррекцией ошибок. Минимальное расстояние между кодовыми точками равно 3. Если мы используем не пересекающиеся сферы радиуса 2, тогда двойная ошибка может быть исправлена, потому что полученная точка будет ближе к оригинальной кодовой точке, чем к любой другой точке; минимальное расстояние для двойной коррекции равно 5. Следующая таблица показывает эквивалентность расстояния между кодовыми точками и «исправимостью» ошибок:

Таким образом построение кода с коррекцией ошибок в точности то же, что построение множества кодовых точек в n-мерном пространстве
которое имеет необходимое минимальное расстояние между легальными сообщениями, так как условия, приведенные выше, необходимы и достаточны. Также должно быть понятно, что мы можем обменять исправление ошибок на их обнаружение — откажитесь от исправления одной ошибки и Вы получите обнаружение ещё двух вместо.
Ранее я показал как разработать коды, удовлетворяющие условиям в случае, когда минимальное расстояние равно 1,2, 3 или 4. Коды с большими минимальными расстояниями не так легко описываются и мы не пойдем далее в этом направлении. Легко найти верхнюю оценку того, насколько велики могут быть кодовые расстояния. Очевидно, что количество точек в сфере радиуса k есть (C(n, k) — биномиальный коэффициент)

Следовательно, если мы разделим объём всего пространства, 2^n, на объём сферы, то частное будет оценкой сверху числа не пересекающихся сфер, т.е. точек кода, в соответствующем пространстве. Чтобы получить дополнительное обнаружение ошибок, мы как и прежде добавим полную проверку чётности, таким образом увеличив минимальное расстояние, которое было 2k+1, до 2k+2 (так как любые две точки на минимальном расстоянии будут иметь одинаковую чётность, увеличим минимальное расстояние на 1).
Давайте подведём итог, где мы теперь. Мы видим, что надлежащим построением кода мы можем создать систему из ненадёжных частей и получить гораздо более надёжную машину, и мы видим сколько мы должны заплатить за это оборудование, хотя мы не исследовали стоимость скорости вычисления, если мы создаём компьютер с таким уровнем коррекции ошибок. Но я ранее упомянул другую выгоду, а именно обслуживание при эксплуатации, и я хотел бы напомнить о нём снова. Чем более изощрённое оборудование, а мы очевидно движемся в этом направлении, тем более насущным является эксплуатационное обслуживание, коды с исправлением ошибок означают, что оборудование не только будет давать (возможно) верные ответы, но и может быть успешно обслужено низкоквалифицированным персоналом.
Использование кодов с обнаружением ошибок и кодов с коррекцией ошибок постоянно растёт в нашем обществе. Отправляя сообщения с космических кораблей, посланных к дальним планетам, мы часто располагаем 20 ваттами мощности или менее (возможно даже 5 ваттами) и используем коды, которые корректируют сотни ошибок в одном блоке сообщения — коррекция производится на Земле, конечно же. Когда Вы не готовы преодолеть шум как в вышеописанной ситуации или в случае «преднамеренного затора», то такие коды — единственный известный выход в этой ситуации.
В конце лета 1961 года во время профессорского отпуска я рулил через всю страну от Стэнфорда, Калифорния к Лаборатории Белл Телефоун в Нью-Джерси. Я запланировал остановку в Моррисе, Иллинойс, где телефонная компания устанавливала первую электронную телефонную станцию, которая была уже не экспериментальной. Я знал, что станция активно использовала коды Хэмминга и, конечно, я был приглашён. Мне сказали, что никогда установка не проходила так легко, как эта. Я сказал себе: «Конечно, именно это я проповедовал в течение прошлых 10 лет». Когда во время начальной наладки все модули установлены и работают должным образом (и Вы в каком-то смысле знаете, что это из-за самопроверок и корректировки), и Вы поворачиваетесь, чтобы перейти к следующим шагам, если что-то пойдёт не так, оборудование вам просто скажет об этом! Лёгкость начальной установки, а также последующего обслуживания, просто была видна невооружённым глазом! Я могу не преувеличивать, исправление ошибок не только приводило к верным результатам во время работы, но и будучи применено правильно, значительно способствовало установке и обслуживанию на месте. И чем более изощрённо оборудование, тем более важны эти вещи!
Я хочу обратиться к другой части этой главы. Я аккуратно рассказал Вам многое из того, с чем я столкнулся на каждом этапе в обнаружении кодов с коррекцией ошибок, и что я сделал. Я сделал это по двум причинам. Во-первых, я хотел быть честным с Вами и показать Вам, как легко, следуя правилу Пастера «Удача улыбнётся подготовленным», преуспеть, просто готовя себя к успеху. Да, были элементы удачи в открытии; но в почти такой же ситуации было много других людей, и они не делали этого! Почему я? Удача, что и говорить, но также я подготовил себя к пониманию того, что происходило — больше, чем другие люди вокруг, просто реагировавшие на явления, когда они происходили, и не думающие глубоко относительно того, что было скрыто под поверхностью.
Я теперь бросаю вызов Вам. То, что я записал на нескольких страницах, было сделано в течение в общей сложности приблизительно трёх — шести месяцев, главным образом рабочих, в моменты обычного исполнения моих рабочих обязанностей в компании. (Патентование отсрочило публикацию более чем на год). Может ли кто-либо сказать, что он, на моём месте, возможно, не сделал бы это? Да, Вы так же способны, как и я, были сделать это — если бы Вы были там, и Вы подготовились также!
Конечно, проживая свою жизнь, Вы не знаете к чему готовиться — Вы хотите совершить нечто значительное и не потратить всю Вашу жизнь, являясь «швейцаром науки» или чем Вы ещё занимаетесь. Конечно, удача играет видную роль. Но насколько я вижу, жизнь дарит Вам многие, многие возможности для того, чтобы сделать нечто большое (определите это как хотите сами) и подготовленный человек обычно достигает успеха один или несколько раз, а неподготовленный человек будет проваливаться почти каждый раз.
Вышеупомянутое мнение не основано на этом опыте, или просто на моих собственных событиях, это — результат изучения жизней многих великих учёных. Я хотел быть учёным, следовательно я изучил их, и я изучил открытия, произошедшие там, где я был, я задавал вопросы тем, кто сделал это. Это мнение также основано на здравом смысле. Вы растите в себе стиль выполнения больших свершений, и затем, когда возможность находится, Вы почти автоматически реагируете с максимальной крутизной в своих действиях. Вы обучили себя думать и действовать надлежащим способам.
Существует один противный тезис, который надо упомянуть, однако, что быть великим в эпоху — это не то, что нужно в последующие годы уточнить. Таким образом Вы, готовя себя к будущим великим свершениям (а их возможность более распространена и их легче достигнуть, чем Вы думаете, так как не часто распознают большие свершения, когда это происходит под носом), необходимо думать о природе будущего, в котором Вы будете жить. Прошлое является частичным руководством, и единственное, что Вы имеете помимо истории, есть постоянное использование Вашего собственного воображения. Снова, случайный перебор случайных решений не приведёт Вас куда либо так далеко, как решения, принятые с Вашим собственным видением того, каким Ваше будущее должно быть.
Я и рассказал и показал Вам, как быть великим; теперь у Вас нет оправдания того, что Вы не делаете этого!
Продолжение следует…
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)
Содержание книги и переведенные главы
Предисловие
- Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) Перевод: Глава 1
- «Foundations of the Digital (Discrete) Revolution» (March 30, 1995) Глава 2. Основы цифровой (дискретной) революции
- «History of Computers — Hardware» (March 31, 1995) Глава 3. История компьютеров — железо
- «History of Computers — Software» (April 4, 1995) Глава 4. История компьютеров — Софт
- «History of Computers — Applications» (April 6, 1995) Глава 5. История компьютеров — практическое применение
- «Artificial Intelligence — Part I» (April 7, 1995) Глава 6. Искусственный интеллект — 1
- «Artificial Intelligence — Part II» (April 11, 1995) (готово)
- «Artificial Intelligence III» (April 13, 1995) Глава 8. Искуственный интеллект-III
- «n-Dimensional Space» (April 14, 1995) Глава 9. N-мерное пространство
- «Coding Theory — The Representation of Information, Part I» (April 18, 1995) (пропал переводчик :((( )
- «Coding Theory — The Representation of Information, Part II» (April 20, 1995) Глава 11. Теория кодирования — II
- «Error-Correcting Codes» (April 21, 1995) Глава 12. Коды с коррекцией ошибок
- «Information Theory» (April 25, 1995) (пропал переводчик :((( )
- «Digital Filters, Part I» (April 27, 1995) Глава 14. Цифровые фильтры — 1
- «Digital Filters, Part II» (April 28, 1995) Глава 15. Цифровые фильтры — 2
- «Digital Filters, Part III» (May 2, 1995) Глава 16. Цифровые фильтры — 3
- «Digital Filters, Part IV» (May 4, 1995) Глава 17. Цифровые фильтры — IV
- «Simulation, Part I» (May 5, 1995) (в работе)
- «Simulation, Part II» (May 9, 1995) Глава 19. Моделирование — II
- «Simulation, Part III» (May 11, 1995)
- «Fiber Optics» (May 12, 1995) Глава 21. Волоконная оптика
- «Computer Aided Instruction» (May 16, 1995) (пропал переводчик :((( )
- «Mathematics» (May 18, 1995) Глава 23. Математика
- «Quantum Mechanics» (May 19, 1995) Глава 24. Квантовая механика
- «Creativity» (May 23, 1995). Перевод: Глава 25. Креативность
- «Experts» (May 25, 1995) Глава 26. Эксперты
- «Unreliable Data» (May 26, 1995) Глава 27. Недостоверные данные
- «Systems Engineering» (May 30, 1995) Глава 28. Системная Инженерия
- «You Get What You Measure» (June 1, 1995) Глава 29. Вы получаете то, что вы измеряете
- «How Do We Know What We Know» (June 2, 1995) пропал переводчик :(((
- Hamming, «You and Your Research» (June 6, 1995). Перевод: Вы и ваша работа
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
|
|
|
|

правила раздела Алгоритмы
1. Помните, что название темы должно хоть как-то отражать ее содержимое (не создавайте темы с заголовком ПОМОГИТЕ, HELP и т.д.). Злоупотребление заглавными буквами в заголовках тем ЗАПРЕЩЕНО.
2. При создании темы постарайтесь, как можно более точно описать проблему, а не ограничиваться общими понятиями и определениями.
3. Приводимые фрагменты исходного кода старайтесь выделять тегами code…/code
4. Помните, чем подробнее Вы опишете свою проблему, тем быстрее получите вразумительный совет
5. Запрещено поднимать неактуальные темы (ПРИМЕР: запрещено отвечать на вопрос из серии «срочно надо», заданный в 2003 году)
6. И не забывайте о кнопочках TRANSLIT и РУССКАЯ КЛАВИАТУРА, если не можете писать в русской раскладке 

Код Хемминга
, обнаружение 2й ошибки
- Подписаться на тему
- Сообщить другу
- Скачать/распечатать тему
|
|
|
|
САБЖ. |
|
n0rd |
|
|
Если мне мой склероз не изменяет, то оно либо находит и исправляет одну ошибку, либо сигнализирует о наличии двух, но не исправляет их. |
|
Swindler |
|
|
Black Star, код Хемминга действительно исправляет одинарную ошибку при минимальном кодовом расстоянии d=3 и находит (не исправляя) двойную ошибку при d=4. Я приаттачил доку с примерами, если что-то не понятно — переведу. |
|
Black Star |
|
|
n0rd, нашел такую фразу: Цитата Коды Хемминга имеют бóльшую относительную избыточность, чем коды с проверкой на четность, и предназначены либо для исправления одиночных ошибок (при d = 3), либо для исправления одиночных и обнаружения без исправления двойных ошибок (d = 4).
Вот в ней и запутался. 1 ошибку находить знаю как. Swindler, что-то знакомое… Добавлено 24.04.06, 11:43 |
|
LuckLess |
|
|
насколько я помню это количество несовпавших символов из алфавита кодового слова. 110 Добавлено 24.04.06, 12:47 Цитата Black Star @ 24.04.06, 11:30 Расстояние между двумя любыми кодовыми комбинациями в заданном коде. значит что ты гарантируешь, что расстояние между любыми кодовыми словами, расчитанное по вышеописанному алгоритму будет такойто(3 или 4 в твоем случае)… |
|
Swindler |
|
|
Расстояние (хеминговое) — число несовпадающих одноименных позиций в комбинациях: |
|
Black Star |
|
|
Мммм… Цитата Swindler @ 25.04.06, 17:59 Расстояние (хеминговое) — число несовпадающих одноименных позиций в комбинациях И какие позиции одноименные? |
|
Swindler |
|
|
Black Star, |
|
Black Star |
|
|
Не понял Цитата Swindler @ 27.04.06, 14:42 сравниваются между собой числа, которые УЖЕ представлены в коде Хемминга. Если есть число, то оно будет одно. С чем его сравнивать? |
|
Swindler |
|
|
Black Star, в посте номер 7 есть пример: Пишу по порядку, как работают с кодом Хемминга: З.Ы. Если так непонятно, пиши формулировку задачи — будем разбираться по шагам. |
|
Black Star |
|
|
Пишу… |
|
Swindler |
|
|
Для нахождения двойной ошибки добавляеться еще 1 контрольный разряд (кроме тех, что стоят на позициях 2^(i-1))- на позиции 0, котоый означает четность всего кодового числа. Получили d=4 Пример нужен? |
|
Black Star |
|
|
Все. В итоге пришли к тому, что я и так понял давно Swindler, сп. за упорное объяснение |
0 пользователей читают эту тему (0 гостей и 0 скрытых пользователей)
0 пользователей:
- Предыдущая тема
- Алгоритмы
- Следующая тема
[ Script execution time: 0,1028 ] [ 15 queries used ] [ Generated: 23.06.23, 02:57 GMT ]







 ____________.doc (48.5 Кбайт, скачиваний: 4644)
____________.doc (48.5 Кбайт, скачиваний: 4644)
 Буду разбирать…
Буду разбирать… 


 )
)