Мо1ег, 8. 1)ахи С «Хцтег1са1 МейосЬ апс1 дойч аге'» С Ргеп1г:е-На11, 1988 С С Версия для вещественной арифметики одинарной точности. С С С С С С С С С А — КЕА1 С Нижний предел интегрирования. С В КЕА1. С Верхний предел интегрирования С Выходные параметры: С КЕБ1’1 Т вЂ” КЕА1 С Приближение к ингегралу 1. С Вычисляется с помощью 15-ТОЧЕ Ч НОГО П РАВИС ЛА КРОНРОДА 1КЕЯК), полученного оптимальным С добавлением абсцисс к 7-ТОЧЕЧНОМУ ПРАВИЛУ С ГАУССА (КЕМ). С С С С С С КЕВАВБ -КЕАЕ С Приближение к интегралу 3. С КЕ8АЯС вЂ” К ЕА1. С Приближение к интегралу для АВ8(Š— 1,/( — А)). С*»» ССЫЛКИ. Р1ЕББЕХ8 К ЕТ А1 111))АОРАСК- А 81 ВКОСЬ!Т11~Е С РАСКАС~Е РОК АЬТОМАТ1С 1ХТЕ(лКАТ1ОЧ~, С 8РК11~ОЕК, ВЕК1.1М, 1983 С ВЫЗЫВАЕМЫЕ ПОДПРОГРАММЫ: К1МАСН I’лава 5 КОНЕЦ ПРОЛОГА () К! 5 8(1ВКО()Т!ХЕ 9!Г)А(А,В,ЕРБ,К.Е,КЕ,!Н АО) НАЧАЛО ПРОЛОГА 010А Из книги: Р.
КаЬапег, С. Мо1сг, 8. Хачим «о!шпет(са! Ме!!1ойв апс! 8ойъагс» Ргспг(се-На!1, 1988 Описание параметров: А В ЕР8 (на входе) пределы интегрирования. (на входе) допустимая погрешность вычисления интеграла. чтобы получить точность до двух знаков, задайтс ЕРВ = .01, до трех знаков- ЕР8 = .001 и т.д. значение ЕР8 должно быть положительным, К (на выходе) наиболее точное из вычисленных программой 11!ПА значений вашего интеграла. Е (на выходе) оценка АВБ (интеграл — К). КЕ (на выходе) мера трудоемкости: количество вычислений вашей подынтегральной функции. КЕ всегда ке меньше ЗО.
1ЕЕА(з (на выходе) признак ошибки. Принимает значения: 0 Нормальное завершение, выполняются неравенсгва Е < ЕРВ и Е < ЕР8 е АВЯ(К). 1 Нормальное завершение, выполняются неравенства Е < ЕРБ, но Е > ЕР8~ АВБ(К). 2 Нормальное завершение, выполняются неравенства Е < ЕРБ ~ АВ8(К), но Е > ЕР8. 3 Нормальное завершение„но значение ЕР8 задано слишком малым, чтобы можно было удовлетворить требованиям абсолютной или относительной ДАТА НАПИСАНИЯ 821018 (ГГММДД) ДАТА ПЕРЕСМОТРА 870525 (ГГММДД) КАТЕГОРИЯ МО. Н2А1А1 КЛЮЧЕВЫЕ СЛОВА: адаптивная квадратура, автоматическая квадратура АВТОР: КАНА!ЧЕК О. К., 8С1ЕХТ1Г1С СОМР()Т1МСг Р1’Л81ОХ, ХВ8. НАЗНАЧЕНИЕ: 91ЭА находит приближение к одномерному интегралу для заданной пользователем подынтег ральной функции (простая в использовании программа).
ОПИСАНИЕ О10А вычисляет определенный интеграл для заданной пользователем функции одной переменной. с С с С С С С с с с с С С с с с с С с с с с С С с С С с с с С с С с с с с С С С с С С С с с Замечание. Если 1Г1.А(3 = 3, 4, 5 или 6, попробуйте вместо (~1РА воспользоваться Я11УАХ. Вы должны написать фортранную подпрограмму-функцию с именем Г, вычисляющую подынтегральную функцию. Обычно она выглядит так: ГГЧСТ1ОМ Г(Х) Е-(вычисление подынтегральной функции в точке Х) КЕТ1)КХ ЕМЭ погрешности.
4 Вычисления не завершены из-за больших ошибок округления. По-видимому, Е и К не далеки от истинных. 5 Вычисления не завершены из-за нехватки памяти. К и Е не далеки от истинных. 6 Вычисления не завершены из-за трудностей, вызванных слишком жесткими требованиями к погрешности. 7 Вычисления не завершены из-за того, что значение ЕРЯ задано с =0.0.
ИЛЛЮСТРИРУЮЩАЯ ПРОГРАММА А=00 В = 1.0 (ЗАДАНИЕ КОНЦОВ ОТРЕЗКА ИНТЕГРИРОВАНИЯ 10, Ц) ЕРЯ = 0.001 (ЗАДАНИЕ ДОПУСТИМОЙ ПОГРЕШНОСТИ) СА1.1. (~11УА (А,В,ЕРБ,К,Е,КЕ,1Г1 АС) ЕХ1:У Н1ХСТ1ОМ Г(Х) Е = 511’1(2.* Х) — Я 1КТ(Х) (НАПРИМЕР) КЕТ1)КХ Е1М1У ВЫХОДНЫЕ ДАННЫЕ ДЛЯ ЭТОГО ПРИМЕРА 0.0 1.0 .001 .041406750 .69077Š— 07 30 0 Замечание 1. Программа содержит небольшой элемент случайности. При нескольких последовательных обращениях к ней с одними и с С С с с с с С с с с с с с с с С с с С с с с с с с с С с с С С с с с с с с теми же входными параметрами результаты окажутся разными, по, как правило, близкими дру~ к другу.
Замечание 2. Программа предназначена для интегрирования по конечному отрезку. Поэтому входные параметры А и В должны быть вещественными числами из диапазона„который допустим на вашем компьютере. Если требуется произвести интегрирование по бесконечному отрезку, то задайте А или В или оба этих параметра такими, чтобы интеграл по отрезку [А, В) почти не отличался от интеграла по бесконечному отрезку. Здесь, однако, необходима осторожность. Например, чтобы проинтегрировать ЕХР( — Х*Х) по вещественной прямой, можно положить А = — 20., В = 20. или присвоить этим параметрам сходные значения, которые обеспечат хороший результат, Если вы выберете А = — 1.Е10 и В = + 1,Е10, то вы столкнетесь с двумя неприятными явлениями.
Во-первых, вы обязательно получите сообщение об ошибке из программы ЕХР, так как обращаться к ней придется при слишком малых значениях аргумента. Возможны и другие неприятности, например, произойдет исчезновение порядка. Во-вторых„даже если арифметика будет работать должным образом, О1РА, скорее всего, выдаст неверный результат, потому что по сравнению со столь большим отрезком интегрирования отрезок ( — 20., 201. который вносит основной вклад в значение интеграла.
почти «бесконечно мал», и вряд ли точки, в которых будет вычисляться подынтегральная функция, попадут в этот отрезок. Более гибкая программа О1РА представляет собой простой в использовании драйвер для другой программы (~1РАХ. (~1РАХ обладает по сравнению с О1РА дополнительными возможностями. Ссылки: нет ВЫЗЫВАЕМЫЕ ПОДПРОГРАММЫ: 01РАХ КОНЕЦ ПРОЛОГА Я1РА КЕА1 ЕСХСТ10)Х1 РСН(;1А(М.Х,Г,Р,А,В,1Е1хК) НАЧАЛО ПРОЛОГА РСНЯА ДАТА НАГ1ИСАНИЯ 870829 (ГГММДД) ДАТА ПЕРЕСМОТРА 870829 (ГГММДД) КАТЕГОРИЯ ХО. ЕЗ,Н2А2 КЛЮЧЕВЫЕ СЛОВА: простое в использовании эрмитово кубическое или сплайн-интегрирование, численное интегрирование, квадратура С*** АВТОР: КАНАХЕК 1Э К„(ХВК) С С С С С С*** НАЗНАЧЕНИЕ: РСНЯА вычисляет определенный интеграл для С кусочно-полиномиальной эрмитовой кубической С функции или сплайна по произвольному отрезку С (простая в использовании программа).
С*~* ОПИСАНИЕ 1ХТЕОЕК Х, 1ЕКК КЕА1. Х(Х), Г(Х), ЩХ), А, В С С С С С С С С С С С С С С С С С С С С С С С С С С С С С С С С С С С ЯС1ЕХТ1Г1С СОМР1)Т1ХС~ Е)171ЯОХ ХАТ10ХА1. ВБКЕАБ ОГ ЯТАХОАКОЯ КООМ А161, ТЕСНХО(.ОСУ ВШ1.ШХО ОА1ТНЕКЯВ1)КСх, МАКУ1 АМЭ, 20899 (301) 975-3808 РСНЯА: Кусочно-полиномиальное эрмитово ‘ кубическое или сплайн-интегрирование, произвольные пределы интегрирования, простота в использовании. Из книги: Р. КаЬапег, С, Мо1ег, Б.
Хаий «Хшпег)са1 МейосЬ апй Бочаге» Ргеп6се-На11, 1988 РСНЯА вычисляет по отрезку 1А, В1 определенный интеграл для кусочно-полиномиальной эрмитовой кубической функции или сплайна, заданных параметрами Х, Х, Г, В. Представляет собой простой в использовании драйвер для программы РСН1А Ф.Н. Фритча, описание которой приведено в указанной ниже работе (2). Программа обладает также другими возможностями, Обращение к подпрограмме: Ъ’А1Л.!Е = РСНЯА (Х, Х, Г, Р, А, В, 1ЕКК) Описание параметров: ЧАВ)Е-(на выходе) ЗНАЧЕНИЕ интеграла. — (на входе) число заданных точек.
(Сообщение об ошибке, если Х.1 Т.2.) -(на входе) вещественный массив значений независимой переменной. Элементы массива Х должны быть заданы в строго возрастающем порядке: Х(1 — 1) .1-Т. Х(1), 1 = 2(1) Х. (Сообщение об ошибке в противном случае.) 1ЕКК С*** ССЫЛКИ: 1. Г.Х. ГК1ТБСН, К,Е. САКЬБОХ, МОХОТОХЕ С С С С С С С С С КОНЕЦ ПРОЛОГА РСНЯА С С с С С с с с с С С С с С с С с С С С с С с с С с С с С С С С С С С с à — (на входе) вещественный массив значений функции.
Значение Г(1) соответствует Х(1). Π— (на входе) вещественный массив значений производной, Значение О(1) соответствует Х(1). А, В -(на входе) пределы интегрирования. Замечание. Здесь не требуется, чтобы отрезок (А, В) принадлежал отрезку (Х(1), Х(ХЦ. Однако если это не так, к результату нужно относиться с большой долей недоверия, — (на выходе) признак ошибки.
Нормальный выход: 1ЕКК = 0 (нет ошибок). Предупреждения: 1ЕКК = 1, если А не принадлежит отрезку (Х(1), Х(ХЦ. 1ЕКК = 2, если В не принадлежит отрезку (Х(1), Х(Х)1. 1ЕКК = 3, если выполняются оба вышеуказанных условия. (Отсюда следует, что либо отрезок [А, В | содержит отрезок (Х(1), Х(Х)3, либо эти отрезки не пересекаются.) Устранимые ошибки: 1ЕКК = — 1, если Х,ЬТ,2. 1ЕКК = — 3, если элементы массива Х заданы не в строго возрастающем порядке.
(В каждом из этих случаев интеграл не вычисляется.) Замечание, Проверка параметров осуществляется в указанном выше порядке; при обнаружении ошибки остальные параметры не проверяются. Р1ЕСЕ%1$Е С11В1С 1ХТЕКРО1.АТ1ОХ, $1АМ Я. ХБМЕК, АХА1.
17, 2 (АРК11. 1980), 238 — 24б 2. Г. Х. ГК1ТБСН, Р1ЕСЕ%1БЕ СБВ1С НЕКМ1ТЕ 1ХТЕКРОЬАТ1ОХ РАСКАБЕ, Г|ХАЬ ЯРЕС1. Г|САТ10ХБ, 1 АЮКЕХСЕ Ь|УЕКМОКЕ ХАТ1ОХА1. ЬАВОКАТОКЪ’, СОМРЬ1ТЕК РОС(3 МЕХТАТ1ОХ 13С11)-30194, А|АСЯТ 1982 ВЫЗЫВАЕМЫЕ ПОДПРОГРАММЫ: РСН1А Глава 6 Аппроксимация данных методом наименьших квадратов б.1. Введение Рассмотрим следующий эксперимент: воду прогоняют сквозь контейнер, в который добавлено некоторое количество краски. Через каждые несколько секунд измеряется концентрация ° краски в воде, вытекающей из контейнера.
Ожидается, что концентрация краски будет линейно уменьшаться со временем. Результаты измерений показаны на рис. б.!. Заметим, что точки данных не лежат на прямой линии. Это не так уж неожиданно. Измерительные приборы могут быть не совсем точными, может оказаться невозможным точно интерпретировать измерения, а смешивание может происходить не совсем так, как предсказано. Чтобы определить скорость, с которой убывает концентрация, экспериментатору следовало бы аппроксимировать данные прямой линией, которая в некотором смысле «наилучшим образом» аппроксимирует данные. На рис. б.! вычерчена одна из таких аппроксимаций. Ситуации такого типа встречаются весьма часто. Одна из причин, по которой требуется знать скорость смешивания, заключается в том, что 7.0 6.5 6.0 5.5 5.0 45 4,0 3.5 3.0 2.5 2.0 1.5 1.0 0.5 0 0 1 2 3 4 5 6 7 8 8 10 !1 12 13 Рис.
6.1. Эксперимент с изменением концентрации. мы хотим уметь предсказывать, как будут протекать другие эксперименты. При других обстоятельствах нам может потребоваться смоделировать инфляцию в экономике, распространение эпидемии или рост населения страны. Когда данные «зашумлены», т. е. полны случайных ошибок, тогда аппроксимация данных простой функцией позволяет нам изучать тренды (тенденции изменения) в данных; зто называют сглаживанием.
Возможны две качественно различные причины, по которым требуется найти линию, аппроксимируюшую данные. (1) Скорость смешивания а необходима, например, чтобы определить, не перегружено ли оборудование для инжекции краски. (2) Аппроксимирующая линия необходима, чтобы предсказать концентрацию краски в моменты времени, для которых не проводилось измерений. В этом случае нас интересуют не столько значения а и р, сколько значения приближающей функции.
 Аппроксимация зашумленной кривой с помощью модели асимметричного пика с итерационным процессом (алгоритм Гаусса – Ньютона с переменный коэффициент демпфирования α).. Вверху: необработанные данные и модель.. Внизу: эволюция нормализованной суммы квадратов ошибок.
Аппроксимация зашумленной кривой с помощью модели асимметричного пика с итерационным процессом (алгоритм Гаусса – Ньютона с переменный коэффициент демпфирования α).. Вверху: необработанные данные и модель.. Внизу: эволюция нормализованной суммы квадратов ошибок.
Аппроксимация кривой — это процесс построения кривой, или математическая функция, которая лучше всего подходит для серии точек данных, возможно, с учетом ограничений. Аппроксимация кривой может включать либо интерполяцию, где требуется точное соответствие данным, либо сглаживание, при котором строится «сглаживающая» функция, которая приблизительно соответствует данным. Связанная с этим тема — регрессионный анализ, который больше фокусируется на вопросах статистического вывода, таких как степень неопределенности в кривой, которая соответствует данным, наблюдаемым со случайными ошибками. Подгонянные кривые могут использоваться в качестве вспомогательных средств для визуализации данных, для вывода значений функции, когда данные недоступны, и для суммирования взаимосвязей между двумя или более переменными. Экстраполяция означает использование подобранной кривой за пределами диапазона наблюдаемых данных и подвержен степени неопределенности, поскольку он может отражать метод, использованный для построения кривой, в той же степени, в какой он отражает наблюдаемые данные.
Содержание
- 1 Типы
- 1.1 Подгонка функций к точкам данных
- 1.1.1 Подгонка линий и полиномиальных функций к точкам данных
- 1.1.2 Подгонка других функций к точкам данных
- 1.2 Алгебраическая подгонка Сравнение с геометрической подгонкой для кривых
- 1.3 Подгонка плоских кривых к точкам данных
- 1.3.1 Подгонка круга геометрической подгонкой
- 1.3.2 Подгонка эллипса геометрической подгонкой
- 1.4 Применение к поверхностям
- 1.1 Подгонка функций к точкам данных
- 2 Программное обеспечение
- 3 См. Также
- 4 Ссылки
- 5 Дополнительная литература
Типы
Подбор функций к точкам данных
Чаще всего подходит функция вида y = f (x).
Подгонка линий и полиномиальных функций к точкам данных
 Подгонка полиномиальных кривых к точкам, созданным с помощью синусоидальной функции. Черная пунктирная линия — это «истинные» данные, красная линия — полином первой степени, зеленая линия — вторая степень, оранжевая линия — третья степень, а синяя линия — четвертая степень.
Подгонка полиномиальных кривых к точкам, созданным с помощью синусоидальной функции. Черная пунктирная линия — это «истинные» данные, красная линия — полином первой степени, зеленая линия — вторая степень, оранжевая линия — третья степень, а синяя линия — четвертая степень.
Первая степень многочлен уравнение
- y = ax + b { displaystyle y = ax + b ;}
— это линия с наклоном a. Линия соединит любые две точки, поэтому полиномиальное уравнение первой степени точно соответствует любым двум точкам с различными координатами x.
Если порядок уравнения увеличен до полинома второй степени, будут получены следующие результаты:
- y = a x 2 + b x + c. { displaystyle y = ax ^ {2} + bx + c ;.}
Это точно соответствует простой кривой по трем точкам.
Если порядок уравнения увеличивается до полинома третьей степени, получается следующее:
- y = a x 3 + b x 2 + c x + d. { displaystyle y = ax ^ {3} + bx ^ {2} + cx + d ;.}
Это точно соответствует четырем точкам.
Более общим утверждением было бы сказать, что он точно соответствует четырем ограничениям . Каждое ограничение может быть точкой, углом или кривизной (которая является обратной величиной радиуса соприкасающейся окружности ). Ограничения угла и кривизны чаще всего добавляются к концам кривой и в таких случаях называются конечными условиями . Идентичные конечные условия часто используются для обеспечения плавного перехода между полиномиальными кривыми, содержащимися в одном сплайне . Также могут быть добавлены ограничения более высокого порядка, такие как «изменение скорости кривизны». Это, например, было бы полезно при проектировании шоссе клеверного листа, чтобы понять скорость изменения сил, приложенных к машине (см. рывок ), когда она следует за клеверным листом, и соответственно установить разумные ограничения скорости.
Полиномиальное уравнение первой степени также может точно соответствовать одной точке и углу, в то время как полиномиальное уравнение третьей степени также может точно соответствовать двум точкам, угловому ограничению и ограничению кривизны. Для них и для полиномиальных уравнений более высокого порядка возможны многие другие комбинации ограничений.
Если имеется более n + 1 ограничений (n — степень полинома), полиномиальная кривая все еще может проходить через эти ограничения. Точное соответствие всем ограничениям неизвестно (но может произойти, например, в случае полинома первой степени, точно подходящего к трем коллинеарным точкам ). В общем, однако, для оценки каждого приближения необходим некоторый метод. Метод наименьших квадратов — это один из способов сравнения отклонений.
Существует несколько причин для получения приблизительного соответствия, когда можно просто увеличить степень полиномиального уравнения и получить точное совпадение.:
- Даже если существует точное совпадение, оно не обязательно следует, что его легко обнаружить. В зависимости от используемого алгоритма могут быть разные случаи, когда невозможно вычислить точное соответствие, или на поиск решения может потребоваться слишком много компьютерного времени. Эта ситуация может потребовать приблизительного решения.
- Может быть желательным эффект усреднения сомнительных точек данных в выборке, а не искажение кривой, чтобы она точно соответствовала им.
- Феномен Рунге : высокий полиномы порядка могут быть сильно колеблющимися. Если кривая проходит через две точки A и B, можно ожидать, что кривая также будет проходить несколько ближе к середине точек A и B. Этого может не случиться с полиномиальными кривыми высокого порядка; они могут даже иметь очень большие положительные или отрицательные значения величины. С полиномами низкого порядка кривая с большей вероятностью упадет около средней точки (она даже гарантированно точно проходит через среднюю точку полинома первой степени).
- Полиномы низкого порядка имеют тенденцию быть гладкими, а полиномы высокого порядка полиномиальные кривые имеют тенденцию быть «неровными». Чтобы определить это более точно, максимальное количество точек перегиба, возможное в полиномиальной кривой, равно n-2, где n — порядок полиномиального уравнения. Точка перегиба — это место на кривой, где она переключается с положительного радиуса на отрицательный. Мы также можем сказать, что именно здесь он переходит от «удержания воды» к «проливанию воды». Обратите внимание, что полиномы высокого порядка могут быть неуклюжими только «возможно»; они также могут быть гладкими, но это не гарантирует этого, в отличие от полиномиальных кривых низкого порядка. Многочлен пятнадцатой степени может иметь не более тринадцати точек перегиба, но также может иметь двенадцать, одиннадцать или любое число вплоть до нуля.
Степень полиномиальной кривой выше, чем требуется для точной подгонки, нежелательна для всех причины, перечисленные ранее для многочленов высокого порядка, но также приводит к случаю, когда существует бесконечное количество решений. Например, полином первой степени (линия), ограниченный только одной точкой вместо обычных двух, даст бесконечное количество решений. Это поднимает проблему, как сравнить и выбрать только одно решение, что может быть проблемой как для программного обеспечения, так и для людей. По этой причине обычно лучше выбирать как можно более низкую степень для точного соответствия по всем ограничениям и, возможно, даже более низкую степень, если приблизительное соответствие приемлемо.
 Связь между урожаем пшеницы и засолением почвы
Связь между урожаем пшеницы и засолением почвы
Подгонка других функций к точкам данных
Другие типы кривых, такие как тригонометрические функции (например, синус и косинус), также могут использоваться в определенных случаях.
В спектроскопии данные могут быть подогнаны с помощью функций Гаусса, Лоренца, Фойгта и связанных с ними функций.
В сельском хозяйстве перевернутая логистическая сигмовидная функция (S-кривая) используется для описания взаимосвязи между урожайностью сельскохозяйственных культур и факторами роста. Синяя фигура получена путем сигмовидной регрессии данных, измеренных на сельскохозяйственных угодьях. Видно, что вначале, то есть при низкой засоленности почвы, урожайность сельскохозяйственных культур медленно снижается при увеличении засоления почвы, а после этого уменьшение прогрессирует быстрее.
Алгебраическая подгонка против геометрической подгонки для кривых
Для алгебраического анализа данных «подгонка» обычно означает попытку найти кривую, которая минимизирует вертикальное (ось Y) смещение точки от кривая (например, обычный метод наименьших квадратов ). Однако для графических приложений и приложений с изображениями геометрическая аппроксимация стремится обеспечить наилучшее визуальное соответствие; что обычно означает попытку минимизировать ортогональное расстояние до кривой (например, всего наименьших квадратов ) или иным образом включить обе оси смещения точки от кривой. Геометрические подгонки не популярны, потому что они обычно требуют нелинейных и / или итерационных вычислений, хотя они имеют преимущество более эстетичного и геометрически точного результата.
Подгонка плоских кривых к точкам данных
Если функция вида y = f (x) { displaystyle y = f (x)}
Другие типы кривых, такие как конические сечения (круговые, эллиптические, параболические и гиперболические дуги) или тригонометрические функции (такие как синус и косинус), также могут использоваться в определенных случаи. Например, траектории объектов под действием силы тяжести следуют параболическому пути, когда сопротивление воздуха не учитывается. Следовательно, сопоставление точек данных траектории с параболической кривой имело бы смысл. Приливы следуют синусоидальным моделям, поэтому точки данных приливов должны быть сопоставлены с синусоидальной волной или суммой двух синусоидальных волн разных периодов, если учитываются эффекты Луны и Солнца.
Для параметрической кривой эффективно подбирать каждую из ее координат как отдельную функцию от длины дуги ; предполагая, что точки данных можно упорядочить, можно использовать хордовое расстояние.
Подгонка круга геометрической подгонкой
 Подгонка круга методом Купа, точки, описывающие дугу окружности, центр (1; 1), радиус 4.
Подгонка круга методом Купа, точки, описывающие дугу окружности, центр (1; 1), радиус 4.  различные модели подгонки эллипса
различные модели подгонки эллипса  подгонка эллипса, минимизирующая алгебраическое расстояние (метод Фитцгиббона).
подгонка эллипса, минимизирующая алгебраическое расстояние (метод Фитцгиббона).
Куп подходит к проблеме поиска наилучшего визуального соответствия круга, чтобы набор 2D точек данных. Этот метод элегантно преобразует обычно нелинейную задачу в линейную, которая может быть решена без использования итерационных численных методов, и, следовательно, намного быстрее, чем предыдущие методы.
Подгонка эллипса с помощью геометрической аппроксимации
Вышеупомянутый метод расширен на общие эллипсы путем добавления нелинейного шага, что приводит к быстрому методу, но позволяет находить визуально приятные эллипсы произвольной ориентации и смещение.
Применение к поверхностям
Обратите внимание, что хотя это обсуждение касалось 2D-кривых, большая часть этой логики также распространяется на 3D-поверхности, каждый участок которых определяется сетью кривых, состоящих из двух параметрические направления, обычно называемые u и v . Поверхность может состоять из одного или нескольких участков поверхности в каждом направлении.
Программное обеспечение
Многие статистические пакеты, такие как R и числовое программное обеспечение, например gnuplot, Научная библиотека GNU, MLAB, Maple, MATLAB, Mathematica, GNU Octave и SciPy включают команды для подбора кривой в различных сценариях. Есть также программы, специально написанные для подбора кривой; их можно найти в списках программ статистического и численного анализа, а также в Категория: Программное обеспечение для регрессии и построения кривых.
См. также
Ссылки
Дополнительная литература
- Н. Чернов (2010), Круговая и линейная регрессия: аппроксимация окружностей и линий методом наименьших квадратов, Chapman Hall / CRC, Монографии по статистике и прикладной вероятности, том 117 (256 стр.). [2]
| Викискладе есть материалы, связанные с подгонкой кривой. |
Задача интерполирования состоит в том, чтобы по значениям функции f(x) в нескольких точках отрезка восстановить ее значения в остальных точках данного отрезка. Разумеется, такая постановка задачи допускает сколь угодно много решений.
Задача интерполирования возникает, например, в том случае, когда
известны результаты измерений yk = f(xk) некоторой физической величины
f(x) в точках xk, k = 0, 1,…, n и требуется определить ее значение в других точках. Интерполирование используется также при необходимости сгущения таблиц, когда вычисление значений f(x) по точным формулам трудоемко.
Иногда возникает необходимость приближенной замены (аппроксимации) данной функции (обычно заданной таблицей) другими функциями, которые легче вычислить. При обработке эмпирических (экспериментальных) зависимостей, результаты обычно представлены в табличном или графическом виде. Задача заключается в аналитическом представлении искомой функциональной зависимости, то есть в подборе формулы, корректно описывающей экспериментальные данные.
2.1 Интерполирование алгебраическими многочленами
Пусть функциональная зависимость задана таблицей
y0 = f(x0);…, y1= f(x1);…,yn = f(xn).
Обычно задача интерполирования формулируется так: найти многочлен P(x) = Pn(x) степени не выше n, значения которого в точках xi (i = 0, 1, 2,…, n) совпадают со значениями данной функции, то есть
P(xi) = yi.
Геометрически это означает, что нужно найти алгебраическую кривую вида
|
y a |
0 |
a x a |
n |
xn , |
(2.1) |
|
1 |
проходящую через заданную систему точек Мi(xi,yi), показанную на рисун-
ке 2.1. Многочлен Р(х) называется интерполяционным многочленом. Точки xi (i = 0, 1, 2,…, n) называются узлами интерполяции.
7

Y
y = P(x)
Mn
y = f(x)
M0
Рисунок 2.1 Интерполирование алгебраическим многочленом
Для любой непрерывной функции f(x) сформулированная задача имеет единственное решение. Действительно, для отыскания коэффициентов а0, а1, а2 ,…, аn получаем систему линейных уравнений
|
a |
0 |
a x |
a |
x2 |
a |
xn f (x ) |
, |
(2.2) |
||||
|
i 0, n |
||||||||||||
|
1 i |
2 i |
n i |
i |
определитель которой (определитель Вандермонда) отличен от нуля, если среди точек xi (i = 0, 1, 2,…, n) нет совпадающих.
Решение системы (2.2) можно записать различным образом. Однако наиболее употребительна запись интерполяционного многочлена в форме Лагранжа и в форме Ньютона.
Запишем без вывода интерполяционный многочлен Лагранжа:
|
n |
(x xj ) |
||||
|
j k |
|||||
|
L (x) |
f (x ). |
(2.3) |
|||
|
n |
k 0 |
(xk xj ) |
k |
||
|
j k |
Нетрудно заметить, что старшая степень аргумента х в многочлене Лагранжа равна n. Кроме этого, можно показать, что в узловых точках значения интерполяционного многочлена Лагранжа соответствуют заданным значениям f(xi).
8
2.2 Интерполяционная формула Ньютона
Интерполяционная формула Ньютона позволяет выразить интерполяционный многочлен Pn(x) через значение f(x) в одном из узлов и через разделенные разности функции f(x), построенные по узлам x0, x1,…, xn. Эта формула является разностным аналогом формулы Тейлора:
f (x) f (x0 ) (x x0 ) f (x0 ) (x x0 )2 f (x0 ) . (2.4) 2!
Прежде чем приводить формулу Ньютона, рассмотрим сведения о разделенных разностях.
Пусть в узлах xk [a,b], k 0,1,…, n известны значения функции
f(x). Предполагаем, что среди точек xk, k = 0, 1,…, n нет совпадающих. Тогда разделенными разностями первого порядка называются отношения
|
f (x , x |
j |
) |
f (x j ) f (xi ) |
, |
i, j 0,1,…, n; |
i j. |
(2.5) |
|
i |
x j xi |
||||||
Будем рассматривать разделенные разности, составленные по соседним узлам, то есть выражения
f (x0 , x1), f (x1, x2 ), , f (xn 1, xn ) .
По этим разделенным разностям первого порядка можно построить разделенные разности второго порядка:
|
f (x |
, x |
, x |
2 |
) |
f (x1, x2 ) f (x0 , x1) |
; |
||||||
|
0 |
1 |
x2 x0 |
||||||||||
|
f (x |
, x |
2 |
, x |
) |
f (x2 , x3 ) f (x1, x2 ) |
; |
||||||
|
1 |
3 |
x3 x1 |
(2.6) |
|||||||||
|
f (xn 1, xn ) f (xn 2 , xn 1) |
||||||||||||
|
f (xn 2 , xn 1, xn ) |
. |
|||||||||||
|
xn xn 2 |
Аналогично определяются разности более высокого порядка. То есть пусть известны разделенные разности k-го порядка
f (x j , x j 1, , x j k ), f (x j 1, x j 2 , , x j k 1),
тогда разделенная разность k+1-го порядка определяется как
|
f (x j , x j 1, , x j k 1) |
|||
|
f (x j 1, x j 2 , , x j k 1) f (x j , x j 1, , x j k ) |
. |
(2.7) |
|
|
x j k 1 |
x j |
||
9
Интерполяционным многочленом Ньютона называется многочлен
Pn (x) f (x0 ) (x x0 ) f (x0 , x1) (x x0 )(x x1) f (x0 , x1, x2 ) (2.8)
(x x0 )(x x1) (x xn 1) f (x0 , x1, , xn ).
Показано, что интерполяционный многочлен Лагранжа (2.3) совпадает с интерполяционным многочленом Ньютона (2.8).
2.3 Метод наименьших квадратов (МНК)
При эмпирическом (экспериментальном) изучении функциональной зависимости одной величины у от другой х производят ряд измерений величины у при различных значениях величины х. Полученные результаты можно представить в виде таблицы, графика:
|
X |
x1 |
x2 |
… |
xn |
|
Y |
y1 |
y2 |
… |
yn |
Задача заключается в аналитическом представлении искомой функциональной зависимости, то есть в подборе функции, описывающей результаты эксперимента.
Особенность задачи состоит в том, что наличие случайных ошибок измерений делает неразумным подбор такой формулы, которая точно описывала бы все опытные значения, то есть график искомой функции не должен проходить через все экспериментальные точки. Эмпирическую формулу
|
обычно выбирают из формул определенного типа: |
||
|
y ax b; |
y aebx c; |
y a h sin x . |
Таким образом, задача сводится к определению параметров a, b, c,… формулы, в то время как вид формулы известен заранее из каких-либо теоретических соображений или из соображения простоты аналитического представления эмпирического материала. Пусть выбранная эмпирическая зависимость имеет вид
yf (x, a0 , a1 ,…an )
сявным указанием всех параметров, подлежащих определению. Эти пара-
метры а0, а1, а2,…, аn нельзя определить точно по эмпирическим значениям функции y0, y1, y2,…, yk, так как последние содержат случайные ошибки.
Таким образом, речь может идти только о получении достаточно хороших оценок искомых параметров. Метод наименьших квадратов (МНК) позволяет получить несмещенные и состоятельные оценки всех парамет-
ров а0, а1, а2,…, аn.
10
Пусть все измерения значений функции y0, y1, y2,…, yn произведены с одинаковой точностью. Тогда оценка параметров а0, а1, а2,…, аn определяется из условия минимума суммы квадратов отклонений измеренных значений yk от расчетных f(xk; а0, а1, а2,…, аn):
|
k |
2 |
|||||||||
|
S yN f (xN ; a0 |
, a1, , an ) . |
(2.9) |
||||||||
|
N 1 |
||||||||||
|
Отыскание же значений параметров а0, а1, а2,…, аn, которые достав- |
||||||||||
|
ляют min значение функции |
||||||||||
|
S S(a0 ,a1, ,an ), |
(2.10) |
|||||||||
|
сводится к решению системы уравнений |
||||||||||
|
S |
0; |
S |
0; ; |
S |
0. |
(2.11) |
||||
|
a |
||||||||||
|
a |
0 |
a |
n |
|||||||
|
1 |
Наиболее распространен способ выбора функции f(xk; а0, а1, а2,…, аn) в виде линейной комбинации:
|
f a0 0 a1 1 an n . |
(2.12) |
Здесь 0 , 1, , n базисные функции (известные); n << k; а0, а1,
а2,…, аn – коэффициенты, определяемые методом наименьших квадратов. Запишем в явном виде условие (2.11), учитывая выражение (2.12):
|
k |
(xi ) a1 1(xi ) an n (xi ) yi 0 (xi ) 0; |
|
|
2 a0 0 |
||
|
i 0 |
||
|
k |
(xi ) a1 1(xi ) an n (xi ) yi 1(xi ) 0; |
|
|
2 a0 0 |
(2.13) |
|
|
i 0 |
||
|
k |
||
|
(xi ) a1 1(xi ) an n (xi ) yi n (xi ) 0. |
||
|
2 a0 0 |
||
|
i 0 |
Из системы линейных уравнений (2.13) определяются все коэффициенты ak. Система (2.13) называется системой нормальных уравнений, матрица которой имеет вид
|
( 0 , 0 ) |
( 0 , 1) |
( 0 , n ) |
|||||
|
( 0 , 1) |
( 1, 1) |
( 1, n ) |
. |
(2.14) |
|||
|
( 0 , n ) |
( 1, n ) |
( n , n ) |
11
Здесь
k
( j , k ) j (xi ) k (xi ). (2.15)
i 0
Матрица (2.14) называется матрицей Грама. Расширенную матрицу получим добавлением справа столбца свободных членов:
|
( 0 ,Y ) |
||||||||||
|
( 1,Y ) |
, |
(2.16), |
||||||||
|
( n ,Y ) |
||||||||||
|
k |
j |
(xi )Yi . |
||||||||
|
где |
( j ,Y ) |
(2.17) |
||||||||
|
i 0 |
||||||||||
|
В качестве базисных функций 0 , 1, , n можно выбрать линейно |
||||||||||
|
независимые степенные функции |
(x) xn . (2.18) |
|||||||||
|
0 |
(x) x0 1; |
(x) x1 |
x; |
; |
n |
|||||
|
1 |
Следует учесть, что n << k. Тогда для этих функций расширенная матрица Грама примет вид
|
k |
k |
… |
k |
k |
||||||||
|
x |
x2 |
xn |
y |
i |
||||||||
|
i |
i |
i |
i |
i |
i |
i |
0 |
|||||
|
0 |
0 |
0 |
||||||||||
|
k |
k |
… |
k |
k |
||||||||
|
x2 |
x3 |
xn 1 |
x y |
i |
. (2.19) |
|||||||
|
i |
i |
i |
i |
i |
i |
i |
i |
|||||
|
0 |
0 |
0 |
0 |
|||||||||
|
… |
… |
… … |
… |
|||||||||
|
k |
k |
k |
||||||||||
|
xn |
1 |
x2n |
xn y |
|||||||||
|
i |
i |
i |
i |
i |
i |
i |
||||||
|
0 |
0 |
0 |
Если выбрать n = k, то на основании единственности интерполяционного полинома получим функцию (x), совпадающую с каноническим
интерполяционным полиномом степени k. При этом аппроксимирующая кривая пройдет через все экспериментальные точки, и функция S будет равна нулю.
12

Пример Исходная функция y = f(x) задана в виде таблице 2.1.
|
Таблица 2.1 Входные данные |
20 |
||||
|
x |
10 |
15 |
17 |
||
|
y |
3 |
7 |
11 |
17 |
Аппроксимировать экспериментальные данные линейной либо квадратичной функцией. Методом наименьших квадратов необходимо уточнить коэффициенты аппроксимирующего полинома.
Решение
1 При линейной аппроксимации исходную зависимость представим в
|
виде |
f a |
0 |
a |
, где |
0 |
x0 |
1; |
x1 x . Методом |
|||
|
0 |
1 |
1 |
1 |
наименьших квадратов определим a0 и a1. Расширенная матрица Грама в нашем случае имеет вид
|
4 |
62 |
38 |
1 |
15.5 |
9.5 |
; |
а1 = 1.3774; |
а0 =-11.8491. |
||
|
1014 |
53 |
|||||||||
|
62 |
662 |
0 |
73 |
Таким образом, аппроксимирующая функция равна f 11.8491 1.3774x.
Оценим погрешность формулы, и результаты этой оценки сведем в таблицу. 2.2.
Таблица 2.2 Результаты
|
x |
y |
f |
y — f |
|y-f| / |y| |
|
10 |
3 |
1.9249 |
1.0751 |
0.3584 |
|
15 |
7 |
8.8119 |
-1.8119 |
0.2588 |
|
17 |
11 |
11.5667 |
-0.5667 |
0.0515 |
|
20 |
17 |
15.6989 |
1.3011 |
0.07654 |
Для нашей линейной функции S1 = 6.4528.
2 Решим ту же задачу, аппроксимировав эмпирические данные полиномом второй степени: f a0 a1x a2 x2 .
13
|
Матрица Грама в этом случае имеет вид |
|||||||||||||||
|
4 |
62 |
1014 |
38 |
1 |
15.5 |
253.5 |
9.5 |
||||||||
|
62 |
1014 |
17288 |
662 0 |
53 |
1571 |
73 |
|||||||||
|
17288 |
304146 |
1571 |
47097 |
||||||||||||
|
1014 |
11854 |
0 |
2221 |
||||||||||||
|
1 15.5 |
253.5 |
9.5 |
|||||||||||||
|
0 |
1 |
29.6415 |
1.3774 ; |
||||||||||||
|
0 |
530.2035 |
||||||||||||||
|
57.1046 |
|||||||||||||||
|
a2 0.1077; |
a1 |
1.8151; |
a0 |
10.3321. |
|||||||||||
|
Все результаты сведены в таблице 2.3. |
|||||||||||||||
|
Таблица 2.3 Результаты |
|||||||||||||||
|
x |
y |
f |
y – f |
|y-f| / |y| |
|||||||||||
|
10 |
3 |
2.9511 |
0.0489 |
0.0163 |
|||||||||||
|
15 |
7 |
7.3381 |
-0.3381 |
0.0483 |
|||||||||||
|
17 |
11 |
10.6007 |
0.3993 |
0.0363 |
|||||||||||
|
20 |
17 |
17.1101 |
-0.1101 |
0.0065 |
|||||||||||
В этом случае S2 = 0.2883.
Таким образом, аппроксимировав эмпирические результаты более простой функцией (линейной), мы получили погрешность в различных узловых точках, лежащую в пределах от 5 до 35 %. Более сложная формула квадратичной интерполяции обеспечивает погрешность не более 5 %. Косвенную оценку погрешности можно провести, сравнив значения S1 и S2.
14
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Постановка задачи
- 2 Описание решения
- 3 Вычислительный эксперимент: качество аппроксимации
- 4 Вычислительный эксперимент: устойчивость алгоритма
- 5 Исходный код и полный текст работы
- 6 Смотри также
- 7 Литература
В работе рассматривается метод аппроксимации функции ошибки функцией многомерного нормального распределения. Рассматриваются случаи матрицы ковариации общего вида, диагональной матрицы ковариации, а также диагональной матрицы ковариации с равными значениями дисперсии. Для нормировки получившихся функций распределения используется аппроксимация Лапласа.
Постановка задачи
Дана выборка , где
— вектора независимой переменной, а
— значения зависимой переменной.
Предполагается, что
, где
— некоторая параметрическая функция,
— вектор ее параметров.
Также предполагается, что задано апостериорное распределение параметров модели , которому соответствует функция ошибки
:
.
Пусть — наиболее вероятные параметры модели. Требуется найти аппроксимацию Лапласа для функции
в точке
. Заметим, что в данной работе в качестве функции ошибки берется сумма квадратов ошибок аппроксимации
.
Описание решения
Сначала находим оптимальные значения параметров модели :
Далее необходимо найти аппроксимацию Лапласа в точке :
,
где — матрица, обратная к ковариационной матрице нормального распределения, а
— нормирующий коэффициент. Заметим, что в силу положительной определенности матрицы
ее можно представить в соответствии с разложением Холецкого:
, где
— верхнетреугольная матрица. Параметризуем матрицу
следующим образом:
где
.
Также параметризуем нормирующий множитель .
Получаем, что .
Построим обучающую выборку , где точки
берутся равномерно из окрестности наиболее вероятных параметров
, в которой мы хотим построить аппроксимацию.
Для нахождения неизвестных параметров минимизируем квадратичный критерий для точек обучающей выборки
:
Заметим, что получаемые в результате решения данной оптимизационной задачи значения параметров могут существенно отличаться в зависимости от используемого для ее решения оптимизационного алгоритма. В данной работе рассматриваются два алгоритма оптимизации: Левенберг-Марквардт и Trust region.
После нахождения оптимальных значений параметров полученные распределения остается отнормировать в соответствии с аппроксимацией Лапласа:
.
Вычислительный эксперимент: качество аппроксимации
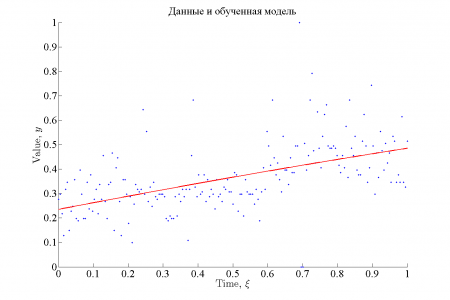
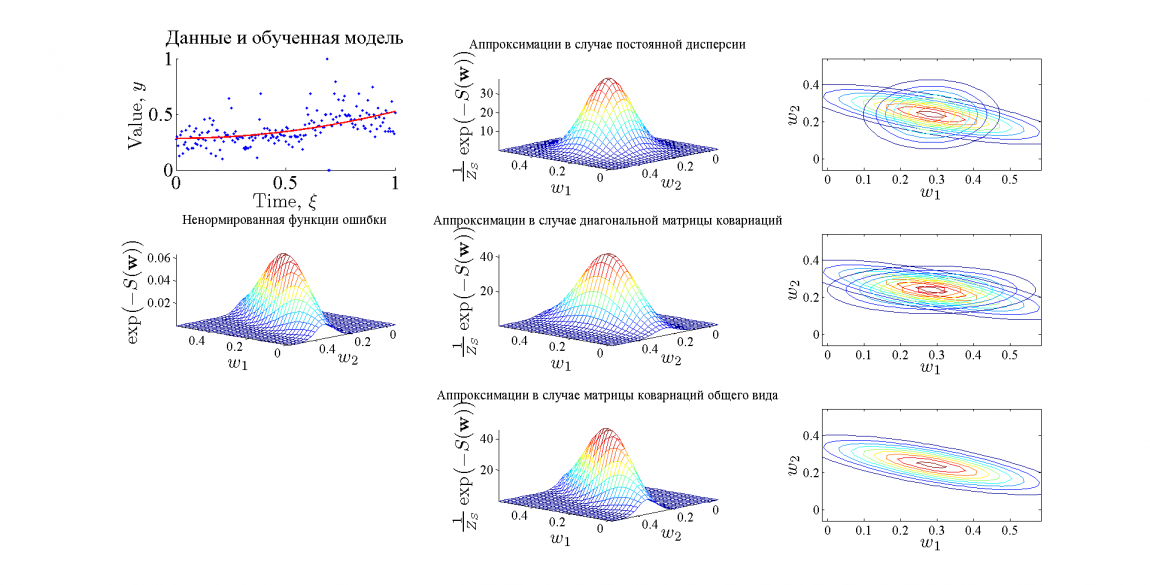
В эксперименте в качестве обучающей выборки использовался временной ряд цен на хлеб из 195 точек. Для приближения использовалась модель линейной регрессии . На картинках ниже графически представлены результаты.
![]()
Результаты эксперимента
Функция ошибки в рассмотренном случае хорошо аппроксимируется предложенным методом, причем качество аппроксимации возрастает с увеличением качества модели. Хорошее качество аппроксимации обусловлено тем, что функция ошибки в рассматриваемом примере принадлежит тому же классу, что и функция аппроксиматор.
Вычислительный эксперимент: устойчивость алгоритма
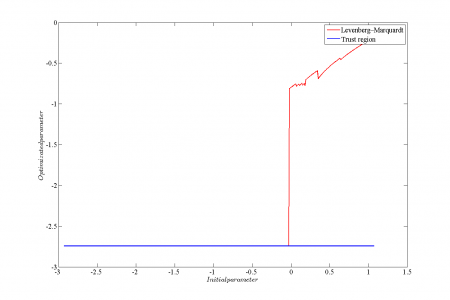
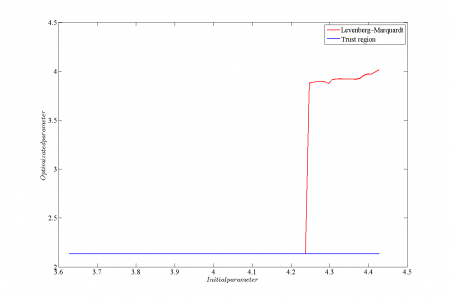
Для сравнения устойчивости алгоритмов Левенберга-Марквардта и Trust region в качестве обучающей выборки использовался временной ряд цен на хлеб из 195 точек. Для приближения использовалась регрессионная модель . При таком виде целевой функции вид функции ошибки в окрестности оптимума несколько отличается от гауссовского. Рассматривалась зависимость оптимизированного значения параметров
и
от начального значения.
|
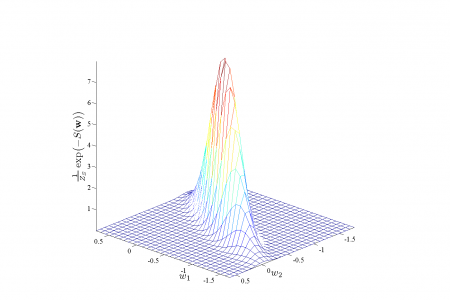
Аппроксимация данных |
Функция ошибки |
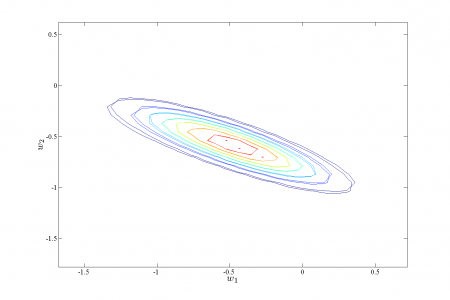
Аппроксимация функции ошибки в случае ковариационной матрицы общего вида
|
Зависимость значения параметра |
Зависимость значения параметра |
Исходный код и полный текст работы
- Panov2011ApproximateInference
Смотри также
- Аппроксимация Лапласа
- Алгоритм Левенберга-Марквардта
Литература
- Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.
| |
Данная статья была создана в рамках учебного задания.
В настоящее время задание завершено и проверено. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |
Введение
В статье Ретеншен — основная метрика F2P игры, вероятностный подход я рассматривал ретеншен как биномиально распределенную случайную величину и показал, что точность оценки его отдельных измерений невысока.
Однако, можно получить более точную оценку, если использовать данные за несколько дней наблюдений и применить их, используя известные закономерности поведения метрики. В частности, можно отметить следующие доступные средства:
-
Если рассматривать все измеренные данные как временной ряд с некоторыми известными свойствами, можно построить аппроксимирующую кривую, которая будет являться точечной оценкой матожидания метрики.
-
Часто можно показать, что мы имеем дело не с биномальной случайной величиной, а с суммой нескольких случайных величин, что сужает ее дисперсию.
-
Как правило, известны не только данные о возвратах пользователей в один конкретный день после инсталла, но другие данных об их поведении, используя которые, можно гипотетически повысить точность оценки. Например, можно использовать измеренные данные о ретеншене глубины i, для уточнения оценки ретеншена глубины k.
-
Если мы располагаем большим объемом данных о значениях метрики от большого количества проектов, это, потенциально, позволяет более точно подобрать гиперпараметры аппроксимирующей модели и также повысить точность оценки метрики.
В данной статье рассматривается первый пункт из этого списка.
Постановка задачи
Рассмотрим классический ретеншн N-го (например, 1-го дня) дня как случайный временной ряд, значения которого мы определяем экспериментально. На графике этот процесс выглядит примерно так.

Задача — оценить параметры этого случайного ряда, а именно:
-
Получить точечную оценку математического ожидания в каждой точке ряда.
-
Получить интервальную оценку математического ожидания в каждой точке.
Задача по определению является задачей анализа временных рядов. Существуют специализированные фреймворки для решения задач подобного класса, например Prophet, Neural Prophet, Nixtla/statsforecast, о которых также можно найти информацию на хабре:
Но сегодня я не буду использовать подобный фреймворк, а решаю задачу в общем виде, как задачу нелинейной аппроксимации процесса с некоторыми известными априори свойствами, подробно обосновывая принципы создания аппроксимирующей функции.
К слову, попытка использовать готовый фреймворк как черный ящик для данной задачи, не вникая в суть его работы и не вникая в суть аппроксимируемого процесса, может привести к провалу из-за некоторых особенностей задачи, в частности:
-
Процесс не стационарный. Метрика убывает со временем, на что накладывается выпуск патчей, дисперсия тоже меняется вследствие изменения количества установок приложения.
-
Исходных данных мало. Например, если проект находится в релизе целый год, у нас есть не более 365 точек наблюдения. Зачастую же надо измерить показатели патча, выпущенного только что или даже проекта только что выпущенного в релиз.
-
Данные очень сильно зашумлены. Например тут автор рассматривает вопрос анализа временного ряда метрики CCU при количестве активных пользователей ~20к-60к в час. Я же говорю о необходимости исследования метрики проекта с тысячей инсталлов в день.
-
Метрика меняется не только вследствие изменения качества игры (что мы хотим измерить), но и-за изменения трафика.
В общем, сегодня и здесь будет деконструкция метрики и последующая нелинейная аппроксимация, а Prophet и его друзья будут потом, в одной из следующих публикаций.
Рисунок 2 иллюстрирует ожидаемый результат аппроксимации.

Обозначения на графике:
-
Исходные измеренные данные изображены тонкой линией синего цвета
-
Исходная интервальная оценка каждой точки наблюдения изображена плавающим коридором темно-синего цвета
-
Аппроксимирующая кривая изображена как сплошная линия красного цвета.
-
Новая интервальная оценка, полученная при помощи аппроксимации — коридор серого цвета.
Примечание. Здесь и далее я буду показывать не настоящие данные, а смоделированные. К сожалению, у меня нет возможности публиковать данные с реальных проектов.
Анализ задачи
В задаче анализа временных радов часто используется так называемая аддитивная модель, которая представляет аппроксимируемый случайный процесс в виде суммы:
ri = g(ti) + s(ti) + a(ti) + e(ti) (1)
где
ri , ti — исходный временной ряд случайной функции
g(t) — линия общего тренда, одномерная функция
s(t) — сезонные явления, одномерная функция
a(t) — аномальные выбросы, случайная функция
e(t) — ошибка, нормально-распределенная случайная величина с нулевым матожиданием
В некоторых случаях корректнее соединять линию тренда и сезонные явления не аддитивно, а мультипликативно.
ri = g(ti) * s(ti) + a(ti) + e(ti) (2)
Обе эти математические модели являются традиционными в задаче анализа временных рядов и я буду их использовать.
Покажем, что подобные модели могут быть применены к рассматриваемой здесь метрике «ретеншен».
В конце первой статьи я привел список некоторых хорошо известных закономерностей поведения ретеншна. Большинство из них (но не все!) действительно можно разложить по четырем перечисленным выше составляющим. Рассмотрим это подробнее.
Линия тренда g(t)
Линия тренда — это и есть то, что мы хотим измерить. Это и есть среднее значение метрики, отражающее качество проекта.
Из практики известно, что ретеншен всегда плавно снижается снижается от момента релиза, но также может резко изменить значение в момент выпуска патча. Таким образом, линию тренда удобно представить в виде двух слагаемых:
g(t) = d(t) + p(t) (3)
где
d(t) — линия общего тренда, показывающая общую тенденцию поведения метрики — постоянное монотонное снижение.
p(t) — влияние патчей. Эта функция — кусочная, потому что она состоит из нескольких участков, каждый из которых соответствует одному конкретному патчу, и патчи не пересекаются.
Функции соединены аддитивно, поскольку это удобнее в работе, и, кроме того, в пределах действия одного патча значения функции d(t) существенно не меняются, следовательно мы сможем подобрать такой вид p(x), чтобы применять его аддитивно.
На рисунке 3 показана линия общего тренда (зеленая линия), линия патчей (черные линии) и их сумма — красная линия.

Ошибка e(t)
В первой статье показано, что ретеншен можно считать биномиально-распределенной случайной величиной, а также, одновременно, нормально-распределенной величиной, потому что при большом количестве установок, согласно центральной предельной теореме, биномиальное распределение становится нормальным. По правде сказать, утверждение о биномиальности взято несколько с потолка, скорее мы имеем дело с суммой нескольких распределений, вероятно, биномиальных. Но, в любом случае, количество установок большое, сотни как минимум, поэтому центральная предельная теорема работает и мы получим распределение, близкое к нормальному.
Ошибка e(t) является случайной функцией от времени, поскольку дисперсия ошибки, в общем случае, не является постоянной, а должна быть вычислена как дисперсия биномиального распределения с известными матожиданием и количеством экспериментов Бернулли (то есть установок приложения). То есть
e(t) = N(0,σ(t)) (4)
где
(5)
σ(t) — дисперсия биномиального распределения ретенешна с матожиданием M(r(t)) и количеством установок (количеством экспериментов Бернулли) I(t)
Аномальные выбросы a(t)
Помимо нормально распределенной ошибки, в формулах (1) и (2) присутствует еще одна случайная величина — a(t), аномальные выбросы.
Дело в том, что существует ряд аномальных факторов, существенно влияющих на метрику и не подчиняющихся закону биномиального распределения, основанному на количестве установок. Например, технические сбои, выпуск патчей — они приводят к существенным выбросам метрики, это уже не просто нормальный шум! И это надо как-то учитывать!
Оценка метрики в момент действия аномалии — сложная задача, выходящая за рамки настоящей статьи. Но и игнорировать факт существования аномалий нельзя, ведь они происходят действительно очень часто и сильно искажают измерения.
Буду действовать максимально просто:
-
Данные с большими аномалиями — выбрасывать из выборки.
-
Мелкие аномалии, незаметные на фоне шума, можно попробовать игнорировать — делать вид, что ничего не было.
В литературе по машинному обучению пишут, что задача обнаружения аномалий довольно сложна. К счастью, у нас не тот случай! Обнаружить аномалии можно, и не очень и сложно. Да аномалии (как правило) непредсказуемы — мы ведь не знаем (как правило), когда произойдет сбой и как количественно он повлияет на метрики. Но мы, к счастью, анализируем метрику постфактум и обладаем данными не только об этой метрике, но и огромным объемом других данных. Есть, например, метрика CCU, показывающая количество пользователей в игре в текущий момент с точностью до секунд, есть системные логи с ошибками — это отличные индикаторы аномалий. Современные средства машинного обучения отлично справятся с задачей их обнаружения. Кстати, аномальными днями зачастую следует считать и дни выпуска патчей, ведь патч тоже имеет признаки технического сбоя, о чем я писал в статье 1.
Сезонность s(t)
Функция s(t) показывает зависимость метрики от сезона. Сезонные изменения могут отражать недельные, месячные и годовые периодические процессы.
Недельная сезонность наиболее ярко выражена и хорошо объясняется поведением пользователей в разные дни недели, о чем я писал в первой статье.
Месячная сезонность как правило, очень слабо выражена, хотя иногда, в некоторых регионах, заметна. Например, в странах, где законодательно жестко зафиксирован день выплаты зарплаты, существует явная сезонность метрик, связанных с продажами, что влияет и на игровые метрики.
Годовая сезонность выражается факторами двух типов: краткосрочные события, соответствующие коротким праздникам (причем, в каждой стране — свои праздники) и долгосрочные сезонные изменения, связанные со сменой времен года. Годовая сезонность также может изменять паттерн недельной и месячной сезонности. Например, во время длинных каникул, все дни ведут себя как выходные дни.
Я не буду рассматривать здесь годовую и месячную сезонность, ограничившись недельной, как наиболее ярко выраженной.
Изменение метрики из-за изменения трафика
В формулах (1) и (2) нет очень важной составляющей — метрика меняется из-за изменения качественного состава пользователей, то есть из-за изменения траффика.
Некорректно включать это в состав функции тренда g(x), поскольку мы измеряем ретеншен как показатель качества продукта, а не влияние состава пользователей на эту метрику. Считать изменения трафика аномалией и относить их в слагаемое a(t) тоже некорректно — это не какое-то разовое событие, нельзя просто отбросить данные за 1-2 дня и успокоиться.
Хороший и простой способ исключить фактор траффика — производить все измерения на некотором эталонном трафике — из эталонного источника, эталонного региона, эталонного объема. Это позволяет, с определенной натяжкой, утверждать, что мы будем измерять качество продукта на некоторых унифицированных пользователях, следовательно состав этих пользователей уже не влияет на метрику, и, следовательно, мы измеряем именно качество продукта. Такой подход требует определенной дисциплины в маркетинге и уменьшает размер ежедневной выборки, но это едва ли не единственное, что действительно можно сделать. Именно так мы и поступим.
Если вы плохо понимаете проблемы привлечения траффика F2P игры, под катом я поместил чуть более подробную информацию об этом.
Чуть подробнее о проблеме трафика
Предположим, у вас был один источник трафика, скажем, Unity Ads, но потом почему-то вы вдруг решили, что он плохой (например, дорогой какой-то, и плохо масштабируемый), и от него избавились. Совсем. И вместо него включили Google Admob, например.
И о чудо, ретеншен изменился! Был 40%, например, а стал 35%.
Как же так? Может быть вы сломали игру? Ее качество упало? Да нет же, в игре точно ничего не меняли, вы не выпустили патч, не стартовали игровой ивент, ничего не изменилось! Это просто другой трафик, такова жизнь. Ретеншн является, строго говоря, не метрикой качества игры, а метрикой совместимости игры с некоторыми пользователями. Меняется источник трафика, значит меняются пользователи, значит меняется и метрика.
И проблема в том, что это происходит вообще постоянно. Пример выше с резким переходом с одного источника данных на другой немного утрирован (хотя и такое бывает), но мелкие изменения в маркетинге происходят вообще всегда и постепенно они могут накапливаться в очень крупные — вы действительно можете поменять полностью всю маркетинговую стратегию проекта за несколько месяцев.
И как быть? Как с этим жить?
Одна из неплохих рекомендаций — надо всегда иметь некоторый эталонный источник траффика из эталонного региона для контроля эталонного значения метрик. Вот, предположим, у вас игра ориентирована на Россию, у вас здесь много пользователей, это важный для вас регион. ОК, вот тогда пусть какая-то довольно существенная доля этих российских пользователей будет всегда из одного и того же источника с одной и той же рекламной кампанией. Всегда! А если вы хотите поменять эталонный источник, надо некоторое время, довольно продолжительное, держать включенными оба эти источника — старый и новый, чтобы подстроить метрики одного источника под другой. Проблема этого подхода (как и любой другой сегментации) — снижение статистической значимости данных. Если у вас всего 1000 пользователей в день, и из них 100 — из эталонного источника трафика, следовательно, доверительный интервал измерений (смотрим статью 1) расширяется примерно в 3.5 раза! Увы, жизнь непростая штука.
Кстати, часто эталонным трафиком считают органический трафик, что далеко не всегда корректно, ведь органика ведет себя очень непредсказуемо. Например, фичеринги попадают в органику, но это другая органика, это не ваша основная аудитория, причем состав этой органики зависит от типа фичеринга, а это полный рандом. Сегодня будет один фичеринг — трафик будет одной структуры, через неделю другой — трафик другой структуры.
Глобальные факторы несезонного характера
Некоторые факторы, очень сильно влияющие на метрику, не носят какой-то сезонный характер. Например, ковидный локдаун. Каждый такой фактор надо рассматривать индивидуально.
В настоящей статье эти факторы не рассматриваются.
Метод наименьших квадратов
Традиционно для оценки математического ожидания случайного процесса используют аппроксимацию по методу наименьших квадратов (или МНК). Я тоже буду использовать МНК, но прежде хотелось бы обосновать возможность применения этого метода, потому что он вообще-то может быть использован не всегда.
МНК используется и дает максимально точный результат в том случае, если:
-
Аппроксимируемый случайный процесс является серией нормально-распределенных испытаний.
-
Изматывания независимы.
-
Дисперсия испытаний постоянна.
-
Кроме того также делается предположение, что исследователь знает аналитически точно функцию математического ожидания этой случайной функции как обычную одномерную функцию с некоторыми коэффициентами, однако не знает значения некоторых коэффициентов, входящих в эту функцию. Задача аппроксимации (также именуемой, кстати задачей регрессии) — определить эти коэффициенты.
Рассмотрим каждое исходное требование.
Условие 1. Нормальная форма распределения
Выше мы уже договорились исключить из выборки аномальные выбросы и объяснили, что функция ошибки, присутствующая в формулах (1) и (2) — нормально распределенная величина. Условие выполнено.
Уловия 2. Независимость испытаний
В литературе по регрессии условие независимости испытаний часто называют самым натянутым и спорным. Однако, на практике все вынуждены допускать независимость испытаний, чтобы не переусложнять задачу. Что касается именно ретеншена, то требование независимости интуитивно кажется довольно правильным. Метрика складывается из поведения совершенно различных людей, слабо связанных между собой. Теоретически можно предположить, что в течении некоторого промежутка времени в игру приходят тысячи людей, которые активно общаются между собой. Первые пришедшие люди из этой группы передают свое впечатление об игре другим и таким образом влияют на их поведение. Но такая организованная группа совершенно маловероятна.
Таким образом, да, будем считать условие выполненным.
Условие 3. Дисперсия во всех точках постоянна
В общем виде требования нарушено, ведь количество инсталлов ежедневно меняется, и, следовательно, согласно формуле дисперсии биномиальной случайной величины, дисперсия тоже будет постоянно меняться. К счастью, это легко решается введением весовых коэффициентов в метод наименьших квадратов.
Итак, это условие немного нарушено, но существует простое решение.
Условие 4. Формула математического ожидания известна.
Требование звучит довольно жестко. Необходимо заранее знать формулу функции, которую мы хотим найти! Как же так? Мы хотим заранее знать то, что хотим найти.
Ну да, выбор аппроксимирующей функции — этот процесс не простой, и, отчасти искусство. Нельзя взять одну аппроксимирующую функцию, скажем линейную, и применять ее во всех случаях жизни. Здесь необходимо использовать техническую эрудицию, обобщить все априорные данные об исследуемом процессе, а также учитывать объем обучающей выборки, чтобы аппроксимируемая функция не оказалась слишком сложной.
Таким образом, необходимо выбрать хороший вид аппроксимирующей функции, которая будет качественно отражать природу рассматриваемого процесса. Конечно, нельзя гарантировать, что функция выбрана идеально точно, и это неверный выбор будет вносить некоторую погрешность в измерения.
Методика аппроксимации
Итак, подытожу все написанное выше и сформулирую методику аппроксимации.
Исходные данные задачи
-
фактические измеренные значения ретеншена — временной ряд {ri}, {ti}, i = 1…n
-
фактическое количество установок приложения — временной ряд {Ii}, {ti}, i = 1…n
Значения измерены в течении максимально доступного нам количества дней после релиза на некотором эталонном трафике, не меняющемся в течении всего периода наблюдений
Математическая модель
Будем рассматривать ri как функцию вида:
ri = d(ti) + p(ti) + s(ti) + a(ti) + N(0,σ(ti)) (6)
или
r(ti) = ( d(ti) + p(ti) ) * s(ti) + a(ti) + N(0,σ(ti)) (7)
где:
d(ti) — линия общего тренда,
p(ti) — влияние патчей,
s(ti) — недельная сезонность,
a(ti) — аномальные выбросы,
N(0,σ(ti)) — нормально-распределенная ошибка с нулевым матожиданием и дисперсией σ(t)
— дисперсия биномиального распределения ретенешна
с матожиданием M(r(ti)) и количеством установок i(ti)
Задачи
-
Определить функцию общей линии тренда d(ti), как при условии известной функции сезонности s(t), так и при неизвестной.
-
Определить линию тренда с учетом воздействия патчей, то есть d(t) + p(t), как при условии известной сезонности s(t), так и при неизвестной.
-
Определить функцию недельной сезонности s(t)
-
Определить общий вид аппроксимирующей функции, тое есть функцию:
R(t) = d(t) + p(t) + s(t) (аддитивная модель) (8)
R(t) = ( d(t) + p(t) ) * s(t) (мультипликативная модель) (9)
Методика аппроксимации
-
Выбрасываем из исходной выборки аномальные дни, для обнаружения которых используем какие-то другие, дополнительные, данные.
-
Создаем аппроксимирующую функцию, состоящую из трех составляющих
d(t) — линия общего тренда,
p(t) — влияние патчей,
s(t) — недельная сезонность,
-
Для построения аппроксимации применяем метод взвешенных наименьших квадратов с учетом меняющейся дисперсии σ(t)
-
Качество работы модели будем оценивать грубо аналитически, а также статистически на основе предыдущего опыта ее применения, поскольку наша обучающая выборка слишком мала, чтобы выделять из нее тестовую и валидационную.
Предложенная методика реализована в виде Jupyter-ноутбука retention-rate-approximator, выложенного на github в открытый доступ
Аппроксимирующая функция
Ключевой момент рассматриваемого метода аппроксимации — это, конечно, вид аппроксимирующей функции.
Аппроксимирующая функция состоит из трех функций
-
Линия общего тренда d(t)
-
Линии патчей p(t)
-
Сезонность s(t)
Как я уже писал выше, линия тренда и линия патчей объединяются аддитивно, а сезонность может быть применена аддитивно или мультипликативно. Мне кажется более корректно применять сезонность мультипликативно, но, на всякий случай, в retention-rate-approximator я реализовал оба варианта, поскольку это было не сложно.
Линия общего тренда — убывающая функция
Из практики известно, что в момент релиза игры метрика максимальна, далее снижается с убывающей скоростью, но не доходит до нуля никогда. Из этих простых соображений сформулируем требования к линии общего тренда d(t).
-
Функция определена на значениях аргумента >= 0.
-
Функция непрерывная, монотонно убывающая, первая производная всегда отрицательна.
-
На бесконечных значениях аргумента функция медленно приближается к ассимптоте.
-
Функция вогнутая, то есть вторая производная всегда положительна.
Множество функций удовлетворяет этим требованиям. Например, можно использовать варианты предложенные в главе «Как моделировать удержание» книги Василия Сабирова. «Игра в цифры» (правда, автор их применяет для аппроксимации несколько другого процесса — он рассматривает ретеншен как функцию от количества дней, прошедших с момента установки, а не как функцию времени от момента релиза проекта). Можно попробовать использовать экспоненту, гиперболический тангенс и сигмоиду — все эти функции формально удовлетворяют заявленным требованиям в диапазонах значений x > 0 и правильно выбранных коэффициентах. Также при небольшом количестве наблюдений можно использовать линейную функцию или просто константу.
Список некоторых возможных кандидатов приведен в таблице 1
|
№ |
Вид функции |
Описание |
|
1 |
d(t) = w0 |
Константа. Является единственно возможной при малом количестве наблюдений и большой дисперсии, когда совсем не видно тренда. |
|
2 |
d(t) = w0 + w1 * t |
Линейная функция. Также рекомендуется при малом количестве измерений, когда тренд прослеживается, но нелинейность — нет. |
|
3 |
d(t) = w0 + w1 / (w2 +t) |
Из книги [2]. Обратная функция |
|
4 |
d(t) = w0 + w1 * t / (w2 +t) |
Дробно-линейная функция. |
|
5 |
d(t) = w0 + w1 * t / (w2 +t^w3) |
Дробно-степенная функция |
|
6 |
d(t) = w0+ w1 / (w2 + tw3) |
Из книги [2]. Аналог функции 3, но со степенным коэффициентом в знаменателе |
|
7 |
d(t) = w0 + w1 / (w2 + ln(t)w3) |
Из книги [2]. Аналог функции 6, но с логарифмом в знаменателе |
|
8 |
d(t) = w0 + w1 / (w2 + ln(t+w4)w3) |
Из книги [2]. Аналог функции 7, но с дополнительным коэффициентом в знаменателе |
|
9 |
d(t) = w0 — w1 * exp(-w2 * t) |
Экспонента |
|
10 |
d(t) = w0 + w1 * sigma(w2 * t) |
Сигмоида |
|
11 |
d(t) = w0 + w1 * tanh(w2 * t) |
Гиперболический тангенс |
|
12 |
d(t) = w0 + w1 * arctan(w2 * t) |
Арктангенс |
Недостатком всех этих функций (за исключением первых двух) является их нелинейность как по отношению к аргументу так и весам. Следовательно, регрессия будет нелинейная, свойства ее документированы плохо, сходимость может быть плохой.
Есть способ перейти от нелинейной регрессии к линейной, если вместо одной простой функции использовать ряд из нескольких базисных функций без весов в знаменателе. Однако, в этом случае общее количество весов будет большое, и, следовательно, на нашем небольшом объеме данных мы не сможем правильно обучить модель. Целесообразнее использовать одну нелинейную функцию но с меньшим суммарным количеством весов.
В Jupyter-ноутбуке retention-rate-approximator я реализовал несколько функций из предложенного выше набора, и вы можете их попробовать на практике. Также можете реализовать свою функцию по аналогии с уже реализованными, создав класс из 3-х простых методов, это совсем нетрудно.
Ниже по тексту я напишу немного о своих собственных экспериментах с аппроксимирующей функцией и сделанных мною выводах.
Линия патча
Мы хотим проанализировать результаты внедрения патча как можно скорее, поэтому аппроксимирующая функция должна быть максимально проста.
В большинстве случаев единственно возможным вариантом аппроксимации патча будет просто константа — у каждого патча один весовой коэффициент. То есть, патч добавляет просто постоянное смещение к линии тренда. p(t) = w0
Если данных много и они слабо зашумлены, вместо константы можно использовать линейную функцию. Два весовых коэффициента на каждый патч. p(t) = w0 + w1 * t
В теории, можно использовать и функцию с 3-мя и 4-мя коэффициентами из числа рассмотренных выше. Но для применения такой функции необходимо количество инсталлов, я не буду рассматривать такой вариант.
Аппроксимация недельной сезонности
Для аппроксимации недельной сезонности часто использую для каждого дня недели свой весовой коэффициент, задающий смещение этого дня недели. Мне это подход кажется разумным, так и поступлю без дополнительных обоснований.
Нетрудно заметить, что, если каждому дню недели будет соответствовать свой вес, то есть отдельное отдельное слагаемое в аппроксимирующей функции, и мы применяем функцию недельной сезонности аддитивно (формула (6)), то один из этих 7-ми весовых коэффициентов будет являться линейной комбинации 6-ти других значений. Метод оптимизации никогда никогда не сможет найти оптимальное значение весов такой модели, ведь если увеличивать смещение w0 линии тренда, и одновременно, на такую же величину уменьшать все недельные коэффициенты, результирующая функция не меняется.
Если функция сезонности применяется мультипликативно (формула (7)), то указанная проблема тоже присутствует, но она будет применена не аддитивно, а мультипликативно.
Проблема решается двумя способами.
-
Выбрать некоторый эталонный день недели, в который вес модели будет не настраиваемым, а равен нейтральному значению (ноль при аддитивном объединении и единица — при мультипликативном). Остальные веса сезонной функции будут задавать отклонения от этого эталонного дня.
-
Потребовать, чтобы среднее значение весов недельной модели равнялось нейтральному значению (ноль при аддитивном объединении и единица — при мультипликативном).
Мне больше нравится второй вариант, поскольку мы не знаем априори, какой именно день недели следует считать эталонным.
Для того, чтобы реализовать это требование при обучении модели я использую функцию регуляризации. Возможно, это несколько нестандартный случай применения регуляризатора (обычно используются функции L1 и L2), но ведь я хочу установить динамическое ограничение на веса модели, а именно это и делают регуляризаторы.
Чуть более подробно объясняю, причем здесь регуляризаторы.
О функциях регуляризации написано немало, но, в большинстве источников рассматривается только два наиболее распространенных ее вида — регуляризаторы L1 и L2. У меня несколько другая ситуация, поэтому позволю себе небольшое лирическое отступление.
Для построения регрессии необходимо две вещи — аппроксимирующая функция, и обучающие данные. Вид аппроксимирующей функции задает априорные теоретические данные об исследуемом процессе. Например, мы знаем, что процесс периодической, поэтому и аппроксимирующая сезонная функция будет периодическая. Обучающие данные — это практические данные. В процессе обучения модели теория соединяется с практикой.
Но иногда у исследователя еще некоторая дополнительная теоретическая информация, которую сложно выразить в виде аппроксимирующей функции, но зато можно выразить в виде некоторого динамического ограничения на веса этой функции. Например в, нашем случае, мы должны потребовать, чтобы в среднем все веса сезонной периодической модели равнялись нулю.
Для этого к обычной функции потерь (вычисленной, в нашем случае по методу наименьших квадратов) добавляется еще одно слагаемое, так называемая регуляризационная функция. Это слагаемое должно равняться нулю при правильных значениях весов модели и быть больше нуля при неправильных значениях весов. И, желательно, чтобы функция была дифференцируемой (хотя, например, в случае известного регуляризатора L1 это требование нарушено).
Метод градиентного спуска старается свести функцию потерь к нулю, следовательно он будет стараться свести к нулю и функцию регуляризации, являющуюся слагаемым в функции потерь, следовательно он будет стараться выполнить ограничение на веса модели, заданное этой функцией.
Функция регуляризации будет такая:
(10)
Здесь N — это требуемое нейтральное среднее значение весов, зависящее от способа объединения убывающей и периодической функций.
Если функции объединяются аддитивно, N = 0.
Если функции объединяются мультипликативно, N = 1.
Как учесть меняющуюся дисперсию
Дисперсия биномиального распределения ретеншна рассчитывается по формуле (5), повторю ее для наглядгнсти
(5)
где
Ii = I(ti) — известное нам количество установок приложения в момент времени ti
M(ri) — математическое ожидание ретеншена в момент времени ti
В качестве функции M(ri) наиболее корректно использовать вычисленное значение аппроксимирущей функции, то есть:
M(ri) ≈ R(t) = d(ti) + s(ti) + p(ti) (аддитивная модель) (11)
или
M(ri) ≈ R(t) = (d(ti) + s(ti)) * p(ti) (мультипликативная модель) (12)
На начальных итерациях градиентного спуска такая величина может быть очень далека от реального значения, она может даже не попадать в диапазон [0,1], поэтому можно попробовать использовать величину r(t).
M(ri) ≈ ri (на начальных итерациях градиентного спуска) (13)
Итак, дисперсия в каждой точке известна, поэтому можно использовать так называемый взвешенный метод наименьших квадратов. Как указано в [6] функция потерь этого метода имеет вид:
(14)
Где e(ti) — ошибка, поученная как разность аппроксимирующей и аппроксимируемой функции.
Подставив сюда формулу дисперсии, получим
(15)
Где
{ ti }, {ri } = аппроксимируемый временной ряд значений ретеншена
{ ti }, { Ii } — временной ряд соответствующего количества установок
R(t) — аппроксимирующая функция, вычисляемая по формуле (8) или (9)
M(ri) — математическое ожидание ретеншена в точке i.
Заметим, что значение, получаемое с помощью этой формулы, будет зависеть от количества установок каждый день и от количества дней наблюдений. Это плохо, поскольку мы будем суммировать эту величину с функцией регуляризации весов сезонной функции, не зависящей от количества установок и рассматриваемого промежутка времени. Поэтому разделим полученное значение на общее количество установок за рассматриваемый период и получим итоговую нормированную формулу:
(16)
Реализация. Пользовательский интерфейс
Рассмотренная выше методика реализована мною на Python + PyTorch в виде колаб ноутбука retention-rate-approximator, который я выкладываю в открытый доступ на github.
В первую очередь коротко распишу его структуру, чтобы вы могли уже его потрогать руками.
Ноутбук состоит из трех блоков:

-
«В первом блоке «Import libraries, define classes and functions» содержится описание классов и функций, которые используются ниже. Вам следует просто выполнить этот блок
, наивно надеясь, что он не сольет в сеть ваши персональные данные. -
Второй блок — пользовательский интерфейс. Этот блок надо тоже выполнить, чтобы этот интерфейс увидеть. Интерфейс состоит из двух частей. Слева — генератор временных рядов, похожих на ретеншен, справа — настройки аппроксиматора. Все параметры уже инициализированы некоторыми не абсурдными начальными значениями, поэтому при первом запуске вы можете просто нажать кнопку Genetate dataset в левой части экрана. Также можно сохранить сгенерированные данные в csv-файл, нажав кнопку Save dataset и загрузить свои собственные обучающие данные в формате csv, нажав кнопку Upload dataset

-
Третий блок «Create the regression model and train it» — собственно создание и обучение аппроксимирующей модели. Если вы заполнили все параметры параметры аппроксимирующей функции в правом блоке настройки аппроксиматора, просто запустите этот блок.
Реализация. Технические детали
Не буду подробно расписывать код ноутбука, он довольно простой и немного прокомментирован, все видно наглядно.
Конечно в процессе работы возникло, как обычно, множество нюансов, все не упомнишь, перечислю лишь несколько.
-
Использован PyTorch а не Tensorflow/Kers поскольку первый более удобен для создания кастомных регуляризаторов и для создания кастомных моделей со сложными конструкциями внутри функции forward, что мне и требовалось.
-
Хотелось добиться в результате некоего подобия продукта, легко распространяемого и удобного в использовании, поэтому был выбран формат Jupyter-ноутбука, который можно запустить на любом компьютере, в любом браузере в Google Colab. Пришлось помучаться с пользовательским интерфейсом на базе библиотеки ipywidgets, с которой работаю впервые. Результатом не вполне доволен, но, грубо, желаемый результат достигнут — получилось доступно и более-менее удобно.
-
Весь код собран в одном ноутбуке и это конечно очень громоздко и неудобно в разработке. Следовало бы отделить 1-2 py-файла, держать их на гитхабе и загружать их в первом блоке ноутбука. Но я таких больших ноутбуков еще не создавал, и не знаю, как правильнее организовать такой проект. Возможно, кто-нибудь даст дельный совет.
-
Помимо собственно аппроксиматора в ноутбуке есть генератор процессов, похожих на ретеншен, о чем я уже писал выше. Генератор довольно простой, и использует для генерации ту же самую математическую модель ретеншена, которая используется для аппроксимации.
-
Я попробовал реализовать и поэкспериментировал с несколькими вариантами функции для аппроксимации линии тренда, однако, больше всего работал только дробно-линейными функциями y(x) = w0-w1*x/(w2+x) (класс LinearFractionalFunction) и y(x) = w0-(w0-w1)*x/(1/w2+x)(класс LinearFractionalFunction_new). Именно эти классы реализованы лучше других. В частности, для качественного обучения модели имеет смысл предварительно инициализировать веса примерно подходящими подходящими значениями, используя данные обучающей выборки, этим занимается метод init_weights_from_train_data. Этот метод более-менее неплохо реализован в классах LinearFractionalFunction, LinearFractionalFunction_new и SigmoidFunction, но в остальных классах — совсем грубо.
-
Настройки стратегии обучения модели в текущий момент еще не вынесены в пользовательский интерфейс, их необходимо менять непосредственно в коде третьего блока ноутбука в переменных training_strateg, loss_function, regualizer_lambda,
number_of_sigmas_for_plotting. Что означают эти переменные написано в комментариях в коде. -
Я пробовал экспериментировать с различными типами оптимизаторов, в том числе использовал LBFGS, часто рекомендуемый для нелинейной регрессии, однако самый распространенный и популярный оптимизатор Adam, по моим наблюдениям, дает результаты как минимум не хуже большинства других. В настройках обучения, через константы, можно настроить оптимизатор Adam или LBFGS. Любой другой, разумеется тоже можно добавить, поменяв одну строчку в коде.
Эксперименты с функцией линии тренда
Выше был приведен список возможных кандидатов в функции аппроксимации тренда, он не много пугает разнообразием. Сейчас его немного отфильтруем.
Явно следует сразу исключить экспоненту — она убывает слишком быстро, совершенно не соответствует природе процесса. Гиперболический тангенс тоже выглядит не слишком удачным решением — у него есть два практически прямых участка — центральный, наклонный, и горизонтальная асимптота, соединенные перегибом — это слабо похоже на реальный процесс. Насчет других вариантов настолько однозначно сказать уже нельзя, нужно экспериментировать.
У меня нет, к сожалению, доступа к большому объему данных реальных проектов чтобы делать выводы, претендующие на объективность но по моим субъективным наблюдениям неплохо ведет себя обратная функция вида d(t) = w0 + w1 / (w2 +t) и дробно-линейная функция вида d(t) = w0 + w1 * t / (w2 +t).
В процесс экспериментов я остановился на функции вида d(t) = w0 + w1 * t / (w2 +t), но далее, в процессе многих последующих экспериментов немного ее видоизменил, выполнив небольшое преобразование ее коэффициентов и получил итоговую функцию, которую считаю наиболее удачной:
d(t) = w0 + ( w0 — w1 )* t / (1/w2 +t ) (17)
С точки зрения зависимости от входной переменной это так же формула
d(t) = w0 + w1 * t / (w2 +t), но для градиентного спуска важна зависимость не от входа, а от параметров. По поим наблюдениям, вид функции (17) благотворно сказывается на результатах градиентного спуска, и у меня есть для этого объяснение. Аргументы в пользу функции (17) такие:
-
Мало весов (3, а не 4 и не 5), что важно при небольшом объеме сильно зашумленных данных.
-
Не слишком быстро убывает, и, по моим наблюдениям, неплохо аппроксимирует ретеншн в течении довольно продолжительного количества дней после релиза.
-
Хороший физический смысл каждого параметра и они независимы друг от друга:
-
Коэффициент w0 задает начальное значение функции в нулевой момент времени.
-
Коэффициент w1 задает значений функции на бесконечном значении аргумента.
-
Коэффициент w2 задает скорость убывания функции.
-
-
Все 3 параметра имеют значения примерно одного порядка в диапазоне от 0 до 1, что, на мой взгляд, позволяет оптимизатору лучше находить минимум функции ошибки.
-
При определенных значениях параметров превращается в линейную функцию или константу.
-
Вычислительная простота.
Вовсе не утверждаю, что такая функция единственно правильная. У меня даже нет достаточного количества данных для анализа, чтобы делать такие выводы. Если исследователь располагает большой историей развития метрики за большой промежуток времени, можно попробовать функции с 4-ю или 5- коэффициентами, можно составить функцию из нескольких звеньев. Если же данных наоборот слишком мало единственным возможным вариантом является линейная функция или, даже, константа.
Также я провел эксперименты с разными видами функции аппроксимации патчей p(t).
При рассматриваемых условиях — ежедневное количество установок приложения ~1000 хороший результат можно получить только при использовании простейшего варианта функции pi(t) = w0i
Если использовать линейную функцию с двумя коэффициентами или еще более сложную функцию, получается полный провал — график ведет себя совершенно противоестественно, например, растет, а не убывает. Необходимо гораздо больше инсталлов для такой аппроксимации.
Грубая оценка доверительного интервала
А сейчас самое интересное — оценка доверительного интервала. Ради чего все и затевалось.
Непростая задача, совсем непростая. Регрессия нелинейная, теория тут сложная. Данных в обучающей выборке мало, поэтому не может быть и речи о том, чтобы ее разделить на обучающую тестовую и валидационную. У меня нет доступа к большому объему данных от множества проектов, чтобы проверить методику на большом объеме данных. Кроме того, существует огромное количеств факторов, влияющих на оценку доверительного интервала, это просто трудоемко. Например, известна или нет заранее форма сезонной функции, сколько дней прошло от момента релиза и т.д. Все эти варианты надо продумывать, прорабатывать. Большая работа, а времени у меня не так и много. И, кроме того, это не научное исследование, а практическая работа, надеюсь, полезная не только мне. Мне важнее опубликовать текущие результаты, чем тянуть время.
Ну вы поняли. Закапываться в жесткую теорию, не имея возможности проверить метод на большом объеме реальных данных совершенно глупо, не буду сейчас этого делать.
Но грубую оценку можно сделать, отталкиваясь от грубой теории и от фактических результатов измерений на моделированных данных.
Теория
Установим лучший идеальный доверительный интервал, который может быть получен при помощи такой регрессии. Доверительный интервал нашего метода не может быть лучше этого идеального.
Предположим, ретеншен не меняется в течении каждого патча, то есть линия тренда состоит из горизонтальных отрезков прямых — каждому патчу соответствует свой горизонтальный участок. Нам известна дисперсия в каждый момент времени (это биномиально-распределенная величина с известными параметрами), следовательно, полагая испытания в каждый день независимыми, мы можем посчитать дисперсию величины для каждого участка кривой (то есть для каждого патча) как взвешенное среднее значений дисперсии в каждый момент времени, а стандартное отклонение — как корень из этой дисперсии
(18)
где
k>=0 — номер патча
σk — оценка дисперсии k-го патча
nk— количество измеренных дней в патче k
σkj — дисперсия в j-й день k-го патча (посчитанная как дисперсия биномиального распределения)
Ikj — количество установок приложения в j-й день k-го патча
В эту формулу, конечно, должны входить только те точки, которые использовались для аппроксимации. Точки, отброшенные как аномальные, необходимо исключить.
Таким образом, можно построить доверительный интервал аппроксимирующей кривой в каждой точке наблюдений. На графике этот доверительный интервал изображается в виде полосы вокруг полученной аппроксимирующей кривой. Ширину полосы можно установить равной 2 сигмы (что должно соответствовать 95% точности аппроксимации) или 3 сигмы (точность аппроксимации — 99.7%)
Таким образом, лучшая точность, которую мы можем требовать от нашего метода аппроксимации, — это стопроцентное попадание в такой коридор шириной 3 сигмы. Более высокой точности требовать нельзя.
На рисунке 4 коридор такого доверительного интервала показан полосой серого цвета. Видно, что ширина коридора на различных участках различна. Чем шире участок, тем больше в ней точек наблюдений, поэтому коридор уже.

Практика
Не могу проверить адекватность предложенной модели применительно к большому объему реальных данных. Это плохо, но факт. Но можно проверить модель на аппроксимации искусственных данных, сгенерированных при помощи функции, аналогичной аппроксимирующей с добавлением биномиально-распределенного шума. Преимуществом такого метода является точное знание изначальной формы процесса, следовательно, можно точно оценить результат аппроксимации.
Я провел моделирование 1000 случайных процессов, и оценил их результаты. Во всех случаях я предполагал, что интервал между патчами — около 30 дней, и с момента релиза прошло довольно много времени, от 32 до 365 дней. Во всех экспериментах среднее количество установок в день равнялось 1000. Во всех экспериментах 30% случайных данных от выборки а также все даты старта патчей и дата релиза были отброшено из выборки как якобы аномальные. Во всех случаях сезонная функция была примерно известна заранее. Довольно много допущений, но они не очень недалеки от практики
В качестве генерирующей и аппроксимирующей функции линии тренда использовал функцию вида d(t) = w0 + ( w0 — w1 )* t / (1/w2 +t )
В качестве линии каждого патча использовал простейшую функцию вида pi(t) = w0i
В качестве критерия оценки качества модели я рассматривал простой бинарный факт — попадает ли кривая полностью в идеальный доверительный интервал 3-сигмы, полученный при помощи описанного выше метода, или нет.
Полученные результаты
-
Во всех испытаниях аппроксимируемая функция попала в идеальный доверительный интервал 3 сигмы в 100% случаях при аппроксимации всех патчей, кроме релизного.(при условии, что хотя бы одна точка наблюдений использовалась для аппроксимации патча — в редких случаях все точки патча отбрасывались как анамальные).
-
Примерно в 25% экспериментов кривая выходит из коридора доверительного интервала в первом сегменте, в начальных 2-3 точках.
Результаты грубо объясняю так:
-
В начальной стадии кривой на ее форму влияет все 3 основных веса, но, поскольку точек в этой начальной части кривой достаточно мало, такого количества недостаточно для правильного подбора всех 3-х коэффициентов. Кроме того, из рассмотрения всегда была выброшена самая первая точка наблюдений — нулевой день, как, потенциально, анормальная, но именно эта первая точка должна вносить максимальный вклад в нелинейную форму кривой. Таким образом, для моделирования кривой на ее начальном участке, до первого патча, аппроксиматор использовал только ~20 точек, чего, вероятно, мало для правильного подбора 3-х коэффициентов.
-
Что же касается аппроксимации патчей — уже через месяц после выпуска игры наиболее существенное значение на форму тренда имеет ее асимптотическое значение, а также коэффициент патча, и, следовательно, процесс приближен к рассмотренному выше идеальному случаю, и, следовательно, доверительный интервал определяется весьма точно.
Наверняка, имеют место и традиционные проблемы нелинейной регрессии — несколько локальным минимумов функции потерь, а также близость функции градиента к нулю в широком диапазоне значений параметров.
Все это , конечно, не настоящее исследование, это все сделано на глазок, но я не вижу смысла для столь грубой модели проводить исследование более полноценное без экспериментов над большими объемами реальных данных.
Критика
Самое время поговорить о недостатках методики. Они очевидны.
Необходимо весьма много данных, за большое количество дней наблюдений, чтобы аппроксимируемый процесс становился похож на реальный. Если, скажем, мы располагаем только лишь неделей наблюдений после релиза проекта, то во многих случаях о нелинейной регрессии не может идти и речи, лучше использовать обычную линейную. Или даже скалярную оценку. Попытка применить к такому процессу нелинейную регрессию приводит к неожиданным значениям коэффициентов. Ниже я привел 2 примера неверной нелинейной аппроксимации. В первом примере мы видим огромный провал в нулевой точке. Во втором примере нет такого гигантского провала, но наблюдается возрастающий процесс. Оба примера являются следствием того, что для аппроксимации были использованы только 4 из 7-ми точек — нулевая точка и еще 2 случайных были отброшены как аномальные.


Это вполне реалистичные кейсы. После выхода игры в софтланч вполне возможны сбои и действительно из 7-ми дней наблюдений у нас вполне может остаться только 4 хороших дня. Количество инсталлов также вполне может быть около 1000 в день, как в рассмотренных примерах.
Хотелось бы иметь модель, обеспечивающую более точные измерения даже в таких сложных ситуациях.
Что дальше?
Существует ли возможность повысить точность наблюдений?
Да, несомненно. Во введении я уже упоминал несколько потенциальных способов, и сейчас остановлюсь на этом вопросе чуть подробное.
-
Можно улучшить текущую методику, тщательнее проработав детали реализации, тщательнее подобрать гиперпараметры модели. Например, использовать другую, более точную, аппроксимирующую функцию, поэкспериментировать с разными оптимизаторами и видом функции потерь, более точно инициализировать начальные веса модели, добавить какие-нибудь эвристические ограничения на значения весов и т.д.
-
Более точно оценить вид исходного распределения и его дисперсию и за счет этого сузить доверительный интервал. Например, известно, что дисперсия суммы нескольких независимых биномиально-распределенных величин меньше дисперсии одного биномиального распределения (статья в википеии), этот факт можно попробовать использовать. Ретеншен действительно легко представить в виде суммы нескольких случайных величин, каждая из которых соответствует одной стране или региону, однако независимость этих величин будет под вопросом, это еще следует доказать. Кроме того, этот метод даст заметный эффект только если матожидания у разных сегментов сильно отличаются между собой, поэтому общий выигрыш будет, вероятно, небольшим. Но зато он достается практически бесплатно, без какого-либо усовершенствования метода, только теоретическим обоснованием.
Кстати, я не встречал никаких работ, посвященных исследованию функции распределения ретеншена. Ни теоретических , ни практических. Если у читателей есть информация о подобной работе, был бы очень рад получить ссылочку.
-
Следующий, потенциальный способ повысить точность — использовать для аппроксимации какие-то дополнительные данные. Например, пусть мы хотим аппроксимировать ретеншен 1 дня, располагая данными за 7 дней. Однако, в таком случае, у нас есть также данные о ретеншене 2-го дня за 6 дней измерений, данные о ретеншене 3 дня за 5 дней… , данные о ретеншене 7-го дня за 1 день. Таким образом, можно говорить о ретеншене как о двумерной функции, в координатах (время от релиза, время от инсталла) или как о некоторой поверхности в 3d пространстве. Форма этой поверхности будет довольно сложной, поскольку на нее будут накладываться и сезонные явления и выпуск патчей и аномалии, кроме того существует явная корреляция между ретеншеном N дня и ретеншеном M дня. Но, зато, такой способ позволяет увеличить количество точек наблюдения квадратично! Линия общего тренда такой поверхности должна быть непрерывной и, следовательно, может быть представлена моделью с небольшим числом коэффициентов, количество которых возрастет не квадратично.
Можно еще выше поднять размерность функции ретеншена и добавить еще больше обучающих данных, рассматривая не классический ретеншен, а роллинг ретеншен ограниченной глубины. Действительно, роллинг ретеншен — это 3d-функция в координатах (время от релиза, время от инсталла, глубина роллинга). Классический ретеншен тут является частным случаем роллинга, когда глубина роллинга равняется нулю. Такую трехмерную модель еще сложнее построить, необходимо преодолеть еще больше проблем, однако количество исходных данных увеличивается уже в кубе!
-
Следующий потенциальный способ поднять точность измерений — учесть данные, наблюдаемые в момент аномалий. Выше я отбросил все анормальные дни, однако, можно рассмотреть эти данные более детально. Тщательный анализ аномалий может позволить сохранить как минимум часть наблюдений. Например, можно заметить, что технический сбой длится не весь день, и охватывает не всех пользователей, и как минимум часть данных в аномальные дни мы сможем использовать.
-
Построить сложную модель, использующую данных с других проектов.
Вероятно, это самый мощный способ создать максимально точную аппроксимацию. Крупные паблишеры и аналитические компании располагают огромными датасетами, накопленными от проектов, ранее выпущенных в релиз. Наличие такого датасета позволяет применять сложные модели с большим количеством весов. С этой точки зрения задача аппроксимации ретеншена представляется уже как задача восстановления из помех некоторого сигнала с известными нам свойствами и подобна, например, задаче восстановления зашумленной картинки. Можно построить модель, решающую подобную задачу и обучить его на этом датасете. Такая модель будет способна спрогнозировать значение метрики проекта, возможно, уже по одной двум точкам наблюдения сразу после релиза. -
Использовать готовые фрймворки для предсказания временных рядов, например Prophet, Neural Prophet, Nixtla/statsforecast. Я только лишь поверхностно знаком с возможностями Prophet и пока не берусь судить, насколько он хорош для данной задачи. С другими фреймворками я пока совсем не сталкивался. В лоб получить заметный эффект Prophet не получилось, ведь он не знает ничего о природе нашего процесса. Однако, если можно задать ему правильный вид нашей аппроксимирующей функции, мы несомненно получим более качественное предсказание, как минимум потому, что он хорошо умеет учитывать сезонные явления — не только недельные, но и годовые, а также нацелен на нелинейную аппроксимацию и учитывает ее тонкости. Способен ли Prophet на большее, например, рассматривать процесс как двумерную функцию или трехмерную функцию, я пока не знаю, но планирую разобраться.
Заключение и выводы
Итак, подведу краткие итоги
-
Рассмотрена методика нелинейной регрессии метрики «ретеншен», учитывающий недельную сезонность и выпуск патчей.
-
Произведены эксперименты с различными видами аппроксимирующей функции и сделана субъективная рекомендация о выборе вида функции.
-
Методика реализована в виде ноутбука Jupyter-ноутбука retention-rate-approximator, выложено в открытый доступ на Githab
-
Дальнейшие планируемые направления работ — использовать для решения задачи специализированные фреймворки для анализа временных рядов, построить нейросеть с большим количеством весов, обучить ее на большом объеме данных (возможно, частично, искусственно сгенерированных), построить модель для двумерной и трехмерной аппроксимации процесса.
-
Отдельно следует рассмотреть задачу обнаружения аномалий, а также вопросы использования в аппроксимации метрики данных, полученных в аномальные дни.
-
При разработки более сложных моделей уделить больше внимания построению интервальной оценки.
Источники
-
Binomial sum variance inequality https://en.wikipedia.org/wiki/Binomial_sum_variance_inequality
-
Василий Сабиров: Игра в цифры. Как аналитика позволяет видеоиграм жить лучше
-
В.П. Лисьев ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006. – 199 с.
-
Дмитрий Балтин. Ретеншен — основная метрика F2P игры, вероятностный подход. https://habr.com/ru/articles/726396/
-
К.В. Воронцов, Машинное обучение. Нелинейная регрессия. Школа анализа данных, Яндекс. https://www.youtube.com/watch?v=—gJR8pd-jg
-
Филипп Картаев. Дружелюбная эконометрика https://books.econ.msu.ru/Introduction-to-Econometrics/
-
Биномиальное распределение https://ru.wikipedia.org/wiki/Биномиальное_распределение
-
Метрика Retention. Что означает, как ее рассчитать и как ее улучшить https://gopractice.ru/product/retention/
-
Нормальное распределение https://ru.wikipedia.org/wiki/Нормальное_распределение
Центральная предельная теорема https://ru.wikipedia.org/wiki/Центральная_предельная_теорема
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
А как вы аппроксимируете ретеншен?
33.33%
Никак, смотрим сырые значения
2
0%
Не знаю, все как-то делает наша аналитическая система, берем готовые данные
0
16.67%
Используем нелинейную регрессию, подобно предложенной в статье
1
16.67%
Используем более простую модель линейной регрессии
1
0%
Используем фрейморки для анализа временных рядов, например, Prophet
0
16.67%
Используем сложные нейросети, учим на больших данных
1
Проголосовали 6 пользователей.
Воздержались 2 пользователя.