Решение:
-
Рассчитаем
средние арифметические.
Средняя арифметическая
– это типовой размер признака,
количественно варьирующего в качественно
однородной совокупности. Для определения
такого размера признака необходимо
рассчитать объем явления, приходящийся
на 1 единицу выборки:



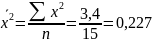

-
Определим
коэффициент регрессии.
Величина коэффициента
регрессии показывает среднее изменение
результата с изменением фактора на
одну единицу.

-
Рассчитаем
коэффициент корреляции.
Уравнение
регрессии всегда дополняется показателем
тесноты связи. При использовании
линейной регрессии в качестве такого
показателя выступает линейный коэффициент
корреляции.
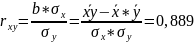
-
Рассчитаем
t-критерии
Стьюдента для коэффициентов регрессии
и корреляции.
Оценка
параметров уравнения регрессии
осуществляется с помощью t-критерия
Стьюдента. t-критерий Стьюдента —
общее название для класса
методов статистической проверки гипотез,
основанных
на распределении
Стьюдента.


-
Вычислим
стандартную ошибку для коэффициентов
регрессии и корреляции.
Величина
стандартной ошибки применяется для
проверки существенности коэффициента
регрессии и для расчета его доверительных
интервалов.


-
Определим
доверительный интервал коэффициента
регрессии.

-
Вычислим величину
исправленной дисперсии
Выборочная
дисперсия — это оценка теоретической
дисперсии распределения на основе
выборки. Несмещённая (исправленная)
дисперсия — это случайная величина.

S2=1.85
-
Вычислим
дисперсию.
Дисперсия признака
определяется как средний квадрат
отклонений от их средних значений.
Дисперсию используют для определения
показателей тесноты корреляционной
связи при анализе результатов выборочных
наблюдений.




-
Определим
доверительный интервал коэффициента
дисперсии.

-
Вычислим полосу
регрессии.
Линейная
регрессия —
это индикатор статистического анализа.
Этот инструмент используется для
предсказания будущих значений по уже
имеющимся данным.
Прежде
всего это очень эффективный индикатор
для определения тренда.

-
Вычислим
параметры уравнения линейной регрессии.

-
Определим
коридор регрессии.
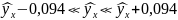
На
основании изученной информации построим
график, на котором изобразим полосу и
коридор регрессии.

Ответ
Регрессия
для представленной выборки составляет
2,89.
Данная величина показывает среднее
изменение результата с изменением
фактора на одну единицу. Одна
из характеристик связи между зависимой
у и независимой переменной х. То есть,
можно сделать вывод, что среднее
изменение факторного признака х на
одну единицу, приводит к изменению
результативного признака у на 2,89 единиц.
Доверительные
интервалы коэффициентов регрессии и
дисперсии соответственно равны:
Обратим
внимание на следующую закономерность:
при заданной доверительной вероятности
с ростом объема выборки ширина
доверительного интервала уменьшается
и стремится к нулю. При заданном объеме
выборки с ростом доверительной
вероятности ширина доверительного
интервала тоже растет. Это означает,
что, чем надежнее оценка, тем меньше
точность этой оценки. И, наоборот, чем
выше точность оценки, тем меньше ее
надежность (достоверность).
Были
построены полоса (
)
и коридор регрессии.
Доверительный
коридор не является доверительной
областью для всей линии регрессии —
он определяет только концы доверительных
интервалов для y при каждом
значении x. С помощью коридора
регрессии нельзя, например, построить
одновременно два доверительных интервала
в различных точках x0 и x1.
Такие доверительные интервалы можно
построить с помощью доверительной
полосы всей линии регрессии.
С
помощью доверительной полосы можно,
например, построить одновременно
доверительные интервалы для нескольких
различных значений переменной x.
Задание
3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение 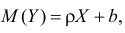
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии  неизвестны, неизвестна и величина коэффициента корреляции
неизвестны, неизвестна и величина коэффициента корреляции 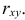 Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений:
Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений: 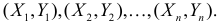 Эти результаты могут служить источником информации о неизвестных значениях
Эти результаты могут служить источником информации о неизвестных значениях 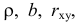 надо только уметь эту информацию извлечь оттуда.
надо только уметь эту информацию извлечь оттуда.
Неизвестная нам линия регрессии 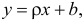 как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для
как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для  можно принять те их значения, при которых имеет минимум функция
можно принять те их значения, при которых имеет минимум функция 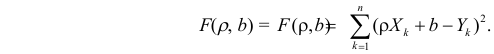
Такие значения  , согласно необходимым условиям экстремума, находятся из системы уравнений:
, согласно необходимым условиям экстремума, находятся из системы уравнений:
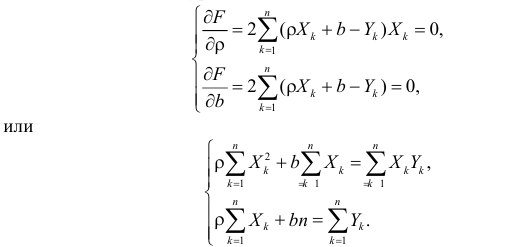
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.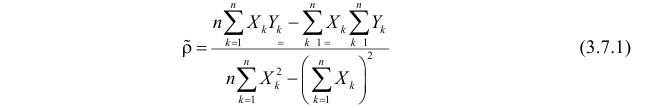
и
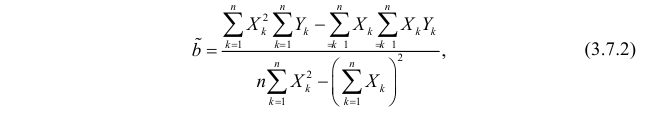
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 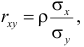 где
где 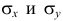 средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через
средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через 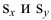 оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку
оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку 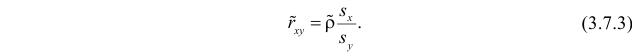
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 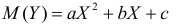 оценки параметров
оценки параметров 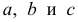 находятся из условия минимума функции
находятся из условия минимума функции
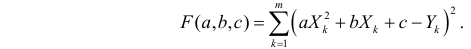
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X 
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
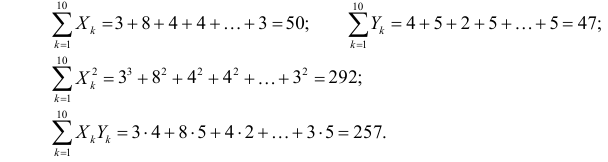
По формулам (3.7.1) и (3.7.2) получим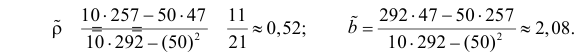
Итак, оценка линии регрессии имеет вид 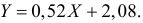 Так как
Так как 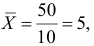 то по формуле (3.1.3)
то по формуле (3.1.3)
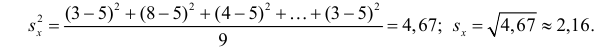
Аналогично, 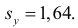 Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину
Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину 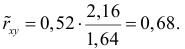
Ответ. 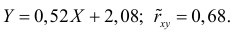
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 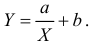 Найти оценки параметров
Найти оценки параметров 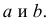
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 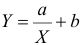 играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)
играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)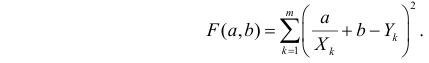
Необходимые условия экстремума приводят к системе из двух уравнений: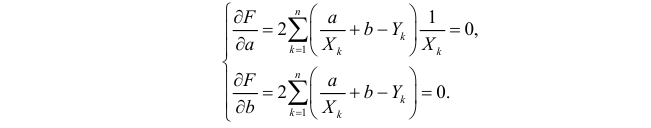
Откуда
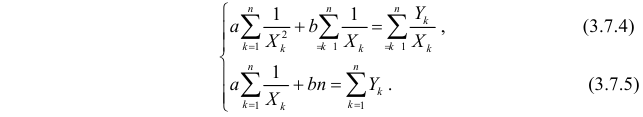
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров 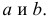
На основе опытных данных вычисляем: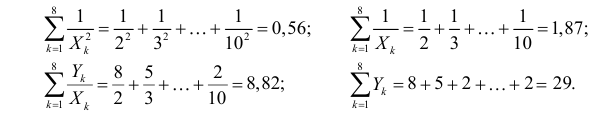
В итоге получаем систему уравнений (?????) и (?????) в виде 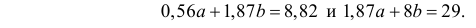
Эта система имеет решения 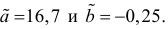
Ответ. 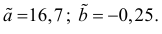
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 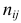 равно числу наблюдений, для которых X находится в интервале
равно числу наблюдений, для которых X находится в интервале 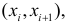 а Y – в интервале
а Y – в интервале 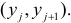 Через
Через 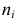 обозначено число наблюдений, при которых
обозначено число наблюдений, при которых 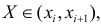 а Y произвольно. Число наблюдений, при которых
а Y произвольно. Число наблюдений, при которых 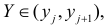 а X произвольно, обозначено через
а X произвольно, обозначено через 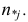
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 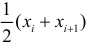 и
и 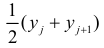 наблюдались
наблюдались 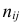 раз.
раз.
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.

Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 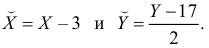 Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 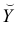 при фиксированных значениях
при фиксированных значениях 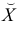 :
:
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).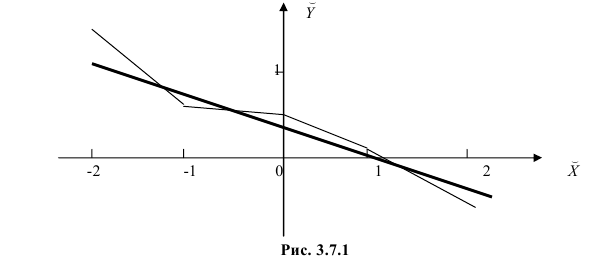
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33): 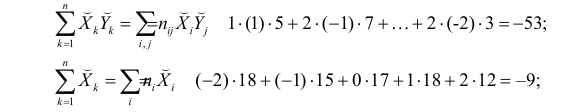
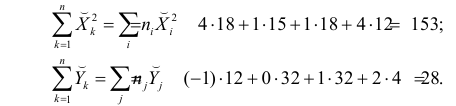
Тогда
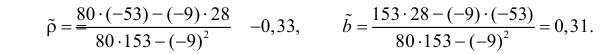
В новом масштабе оценка линии регрессии имеет вид 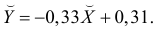 График этой прямой линии изображен на рис. 3.7.1.
График этой прямой линии изображен на рис. 3.7.1.
Для оценки 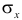 по корреляционной таблице можно воспользоваться формулой (3.1.3):
по корреляционной таблице можно воспользоваться формулой (3.1.3):
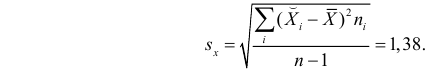
Подобным же образом можно оценить 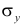 величиной
величиной 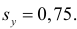 Тогда оценкой коэффициента корреляции может служить величина
Тогда оценкой коэффициента корреляции может служить величина 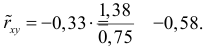
Вернемся к старому масштабу:
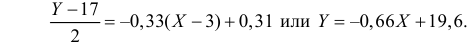
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ. 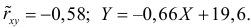
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 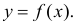 Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то
Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то 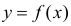 играет роль линии регрессии и все свойства линии регрессии приложимы к
играет роль линии регрессии и все свойства линии регрессии приложимы к 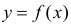 . В частности,
. В частности, 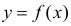 обычно находят по методу наименьших квадратов.
обычно находят по методу наименьших квадратов.
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
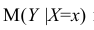 можно представить в виде
можно представить в виде 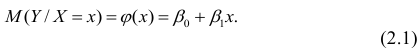
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 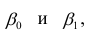 называемые коэффициентами регрессии, а также
называемые коэффициентами регрессии, а также 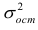 — остаточная дисперсия.
— остаточная дисперсия.
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей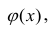 которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости
которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости 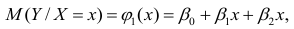
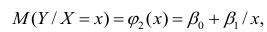
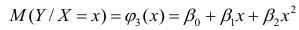 линейны относительно параметров
линейны относительно параметров 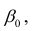
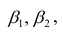 хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости
хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости 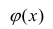 выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
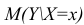 можно представить в виде (2.1).
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 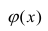 линейна и по оцениваемым параметрам, и
линейна и по оцениваемым параметрам, и
по переменным. Оценки параметров модели (2.1) 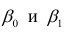 обозначил
обозначил 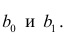 Оценку остаточной дисперсии
Оценку остаточной дисперсии 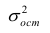 обозначим
обозначим 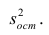 Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии
Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии 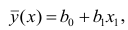 коэффициенты которого
коэффициенты которого 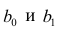 находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака
находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака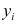 от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии 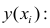
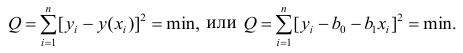
Составим систему нормальных уравнений: первое уравнение
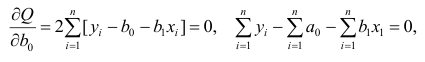
откуда 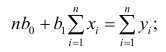
второе уравнение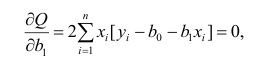
откуда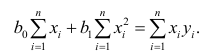
Итак,
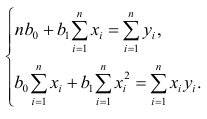
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно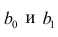 найдём оценки параметров
найдём оценки параметров 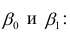
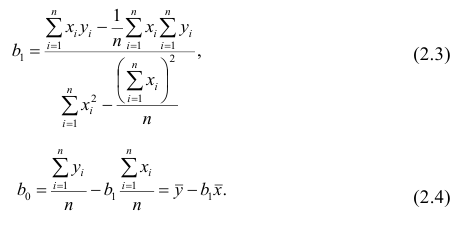
Остаётся получить оценку параметра 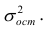 . Имеем
. Имеем
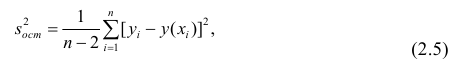
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы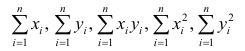 заменяют на
заменяют на
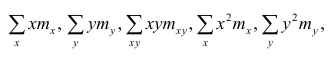
где 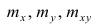 — частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
— частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
Нелинейная регрессия
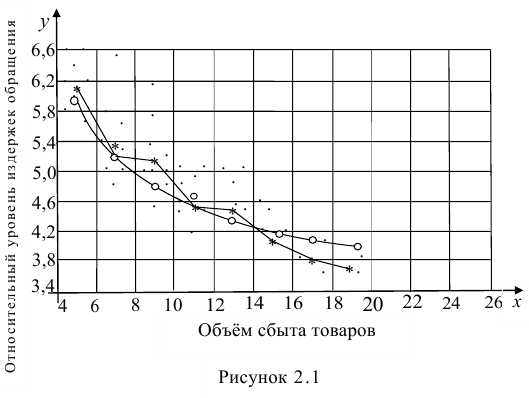
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
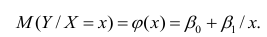
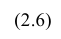
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
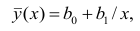
где 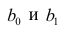 —оценки коэффициентов регрессии
—оценки коэффициентов регрессии 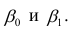
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
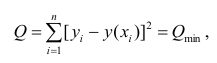
или
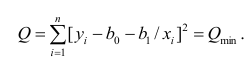
Дифференцируя последнее равенство по 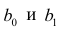 и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
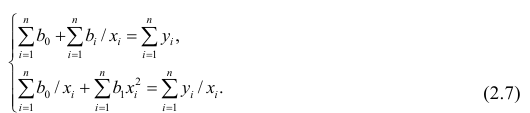
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
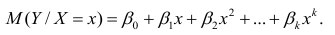
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
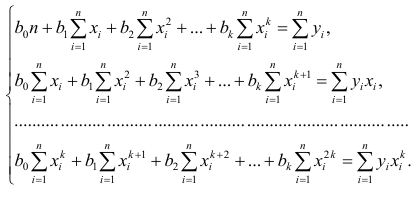
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 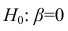 статистика
статистика

имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 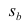 — оценка среднеквадратического отклонения
— оценка среднеквадратического отклонения
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение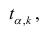 удовлетворяющее условию
удовлетворяющее условию 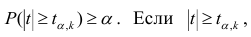 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При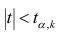 нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
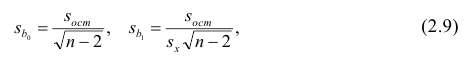
где 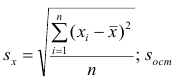 — оценка остаточной дисперсии, вычисляемая по
— оценка остаточной дисперсии, вычисляемая по
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
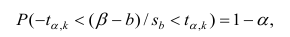
где а — уровень значимости, находим

Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 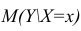 является условное среднее
является условное среднее 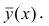 Кроме точечной оценки для
Кроме точечной оценки для 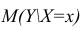 можно
можно
построить доверительный интервал в точке 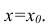
Известно, что 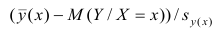 имеет распределение
имеет распределение
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания 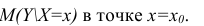
Оценку дисперсии условного среднего вычисляют по формуле
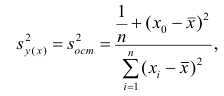
или для интервального ряда
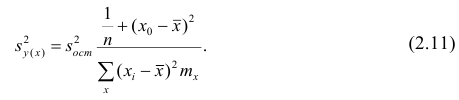
Доверительный интервал находят из условия
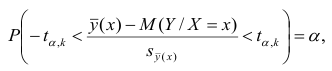
где а — уровень значимости. Отсюда
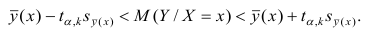
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
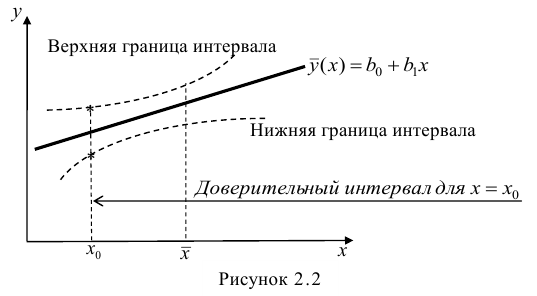
Из рис. 2.2 видно, что в точке 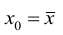 границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 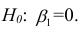 Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением
Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением 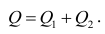 — Общая сумма квадратов отклонений результативного признака
— Общая сумма квадратов отклонений результативного признака
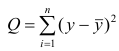 разлагается на
разлагается на 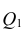 (сумму, характеризующую влияние признака
(сумму, характеризующую влияние признака
X) и 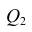 (остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
(остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
Для проверки нулевой гипотезы вычисляют статистику 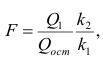 которая имеет распределение Фишера-Снедекора с А
которая имеет распределение Фишера-Снедекора с А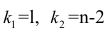 степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы
степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы 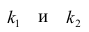 находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение
находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение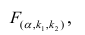 удовлетворяющее условию
удовлетворяющее условию 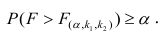 . Если
. Если 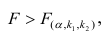 нулевую гипотезу отвергают, уравнение считают значимым. Если
нулевую гипотезу отвергают, уравнение считают значимым. Если 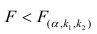 то нет оснований отвергать нулевую гипотезу.
то нет оснований отвергать нулевую гипотезу.
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 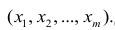 Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним
Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним 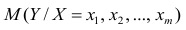 и постоянной дисперсией
и постоянной дисперсией 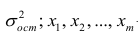 — линейно независимые векторы
— линейно независимые векторы 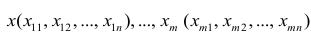 . Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
. Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
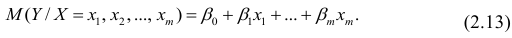
Оценке подлежат параметры 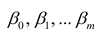 и остаточная дисперсия.
и остаточная дисперсия.
Заменив параметры их оценками, запишем уравнение регрессии
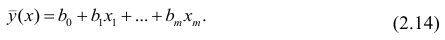
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 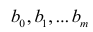 является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:
является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:

Как и в двумерном случае, составляют систему нормальных уравнений
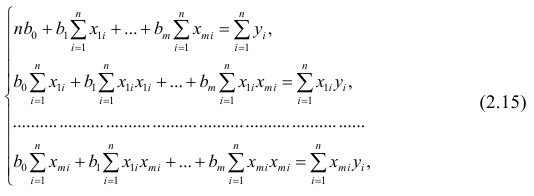
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 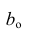 через остальные параметры:
через остальные параметры:
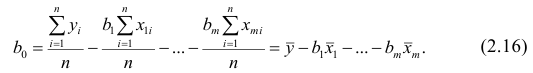
Подставим в остальные уравнения системы вместо 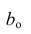 полученное выражение:
полученное выражение:
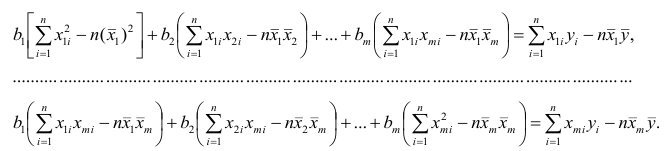
Пусть С — матрица коэффициентов при неизвестных параметрах 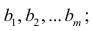
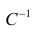 — матрица, обратная матрице С;
— матрица, обратная матрице С; 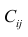 — элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы
— элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы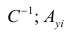 — выражение
— выражение
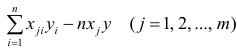 . Тогда, используя формулы линейной алгебры,
. Тогда, используя формулы линейной алгебры,
запишем окончательные выражения для параметров:
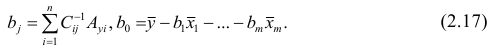
Оценкой остаточной дисперсии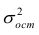 является
является
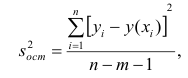
где 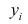 — измеренное значение результативного признака;
— измеренное значение результативного признака;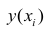 значение результативного признака, вычисленное по уравнению регрессий.
значение результативного признака, вычисленное по уравнению регрессий.
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику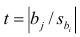 вычисляют для каждого j-го коэффициента регрессии
вычисляют для каждого j-го коэффициента регрессии
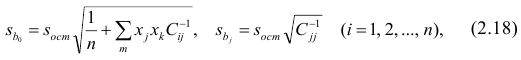
где 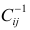 —элемент обратной матрицы, стоящий на пересечении i-й строки и j-
—элемент обратной матрицы, стоящий на пересечении i-й строки и j-
го столбца;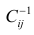 —диагональный элемент обратной матрицы.
—диагональный элемент обратной матрицы.
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 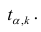 Если
Если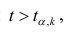 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если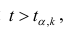 то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: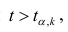
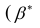 — вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики
— вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики 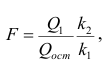 , где
, где 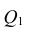 — сумма квадратов, характеризующая влияние признаков X;
— сумма квадратов, характеризующая влияние признаков X; 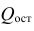 — остаточная сумма квадратов, характеризующая влияние неучтённых факторов;
— остаточная сумма квадратов, характеризующая влияние неучтённых факторов; 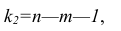
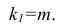 Для уровня значимости а и числа степеней свободы
Для уровня значимости а и числа степеней свободы 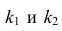 по табл. 3 приложений находят критическое значение
по табл. 3 приложений находят критическое значение 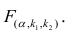 Если
Если 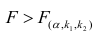 то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При
то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При 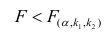 нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 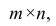 аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений
аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений 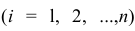 столбцы — признакам
столбцы — признакам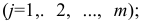 таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных
таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных 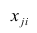 переходят к переменным
переходят к переменным 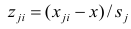 В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
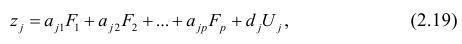
где 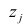 -j-й признак (величина случайная);
-j-й признак (величина случайная); 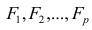 — общие факторы (величины случайные, имеющие нормальный закон распределения);
— общие факторы (величины случайные, имеющие нормальный закон распределения); 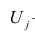 — характерный фактор;
— характерный фактор; 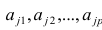 — факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);
— факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);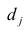 — нагрузка характерного фактора.
— нагрузка характерного фактора.
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 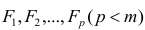 и характерного фактора
и характерного фактора 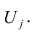
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков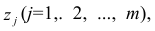 , т.е.
, т.е.
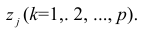
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы 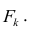
Факторные нагрузки 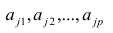 . характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
. характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
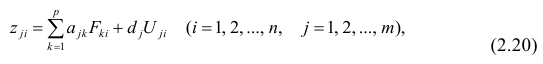
где 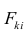 значение k-го фактора для i-го объекта.
значение k-го фактора для i-го объекта.
Дисперсию признака 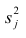 можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность
можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность 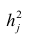 и часть, обусловленную действием j-го характера фактора, характерность
и часть, обусловленную действием j-го характера фактора, характерность 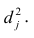 Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака
Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака 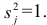 Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
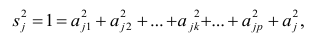
где 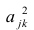 —доля дисперсии признака
—доля дисперсии признака 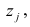 приходящаяся на k-й фактор.
приходящаяся на k-й фактор.
Полный вклад k-го фактора в суммарную дисперсию признаков
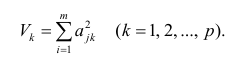
Вклад общих факторов в суммарную дисперсию 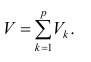
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
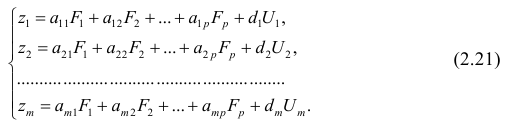
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
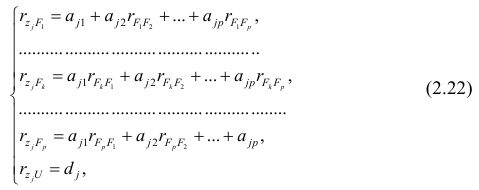
где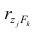 — выборочный коэффициент корреляции между j-м параметром и к-
— выборочный коэффициент корреляции между j-м параметром и к-
м фактором;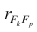 — коэффициент корреляции между к-м и р-м факторами.
— коэффициент корреляции между к-м и р-м факторами.
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
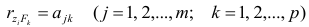 , т.е. коэффициенты отображения равны
, т.е. коэффициенты отображения равны
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам: 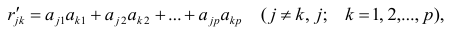
где 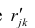 —вычисленный по отображению коэффициент корреляции между j-м
—вычисленный по отображению коэффициент корреляции между j-м
и к-м признаком. Остаточный коэффициент корреляции
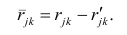
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
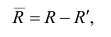
где 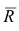 — матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
— матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
Результаты факторного анализа удобно представить в виде табл. 2.10.

Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
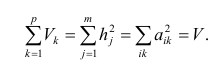
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции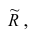 у которой на главной диагонали стоят значения общностей
у которой на главной диагонали стоят значения общностей 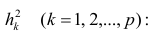 :
: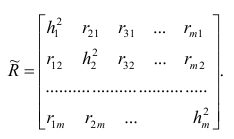
Редуцированная и полная матрицы связаны соотношением

где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 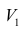 должен быть найден при условии
должен быть найден при условии
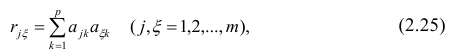
где 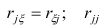 —общность
—общность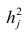 параметра
параметра
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора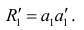 Имея эту матрицу, получают первую матрицу остатков:
Имея эту матрицу, получают первую матрицу остатков: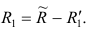
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 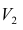 находят из условия
находят из условия
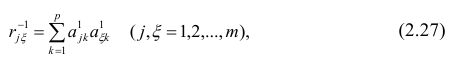
где 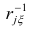 — коэффициент корреляции из первой матрицы остатков;
— коэффициент корреляции из первой матрицы остатков; 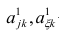 — факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков:
— факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков: 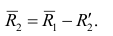
Факторный анализ учитывает суммарную общность. Исходная суммарная общность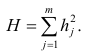 Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на
Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на 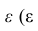 — наперёд заданное малое число).
— наперёд заданное малое число).
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных 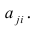
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
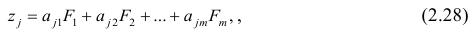
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 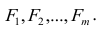 По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
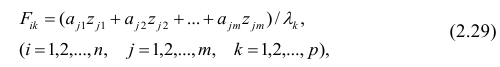
где 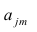 — элементы факторного решения:
— элементы факторного решения: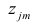 — исходные переменные;
— исходные переменные; 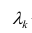 .— k-е собственное значение; р — количество оставленных главных
.— k-е собственное значение; р — количество оставленных главных
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента 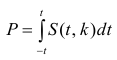
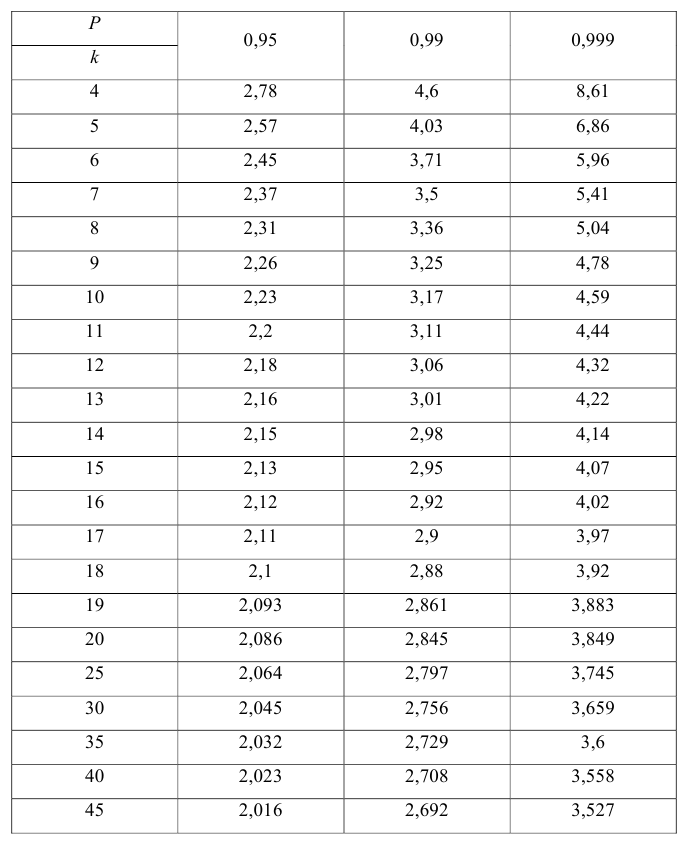
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 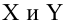 связаны линейной корреляционной зависимостью
связаны линейной корреляционной зависимостью 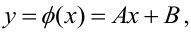 для отыскания которой проведено
для отыскания которой проведено 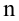 независимых измерений
независимых измерений 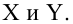
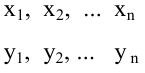
Диаграмма рассеяния (разброса, рассеивания)
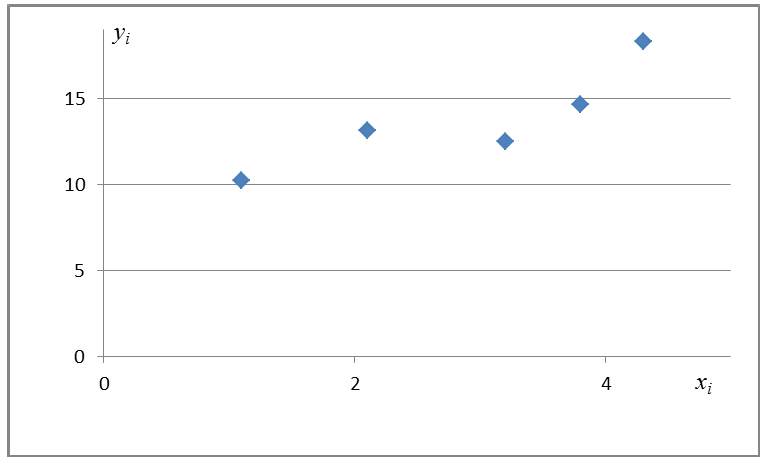
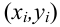 — координаты экспериментальных точек.
— координаты экспериментальных точек.
Выборочное уравнение прямой линии регрессии 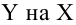 имеет вид
имеет вид
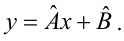
Задача: подобрать 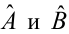 таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой
таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой 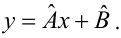
Для того, что бы провести прямую 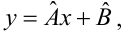 воспользуемся МНК. Потребуем,
воспользуемся МНК. Потребуем,
чтобы 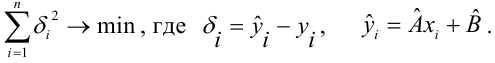
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
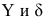 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.- Дисперсия
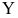 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения. - Результаты наблюдений
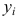 в разных точках независимы.
в разных точках независимы. - Входные переменные
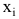 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 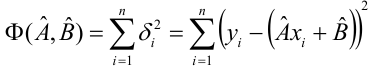 и найдём её минимальное значение
и найдём её минимальное значение
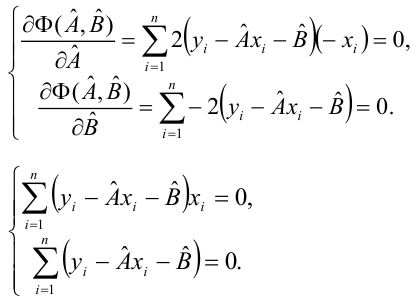
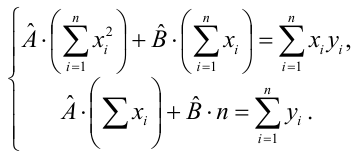
Решив систему, получим искомые значения 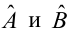
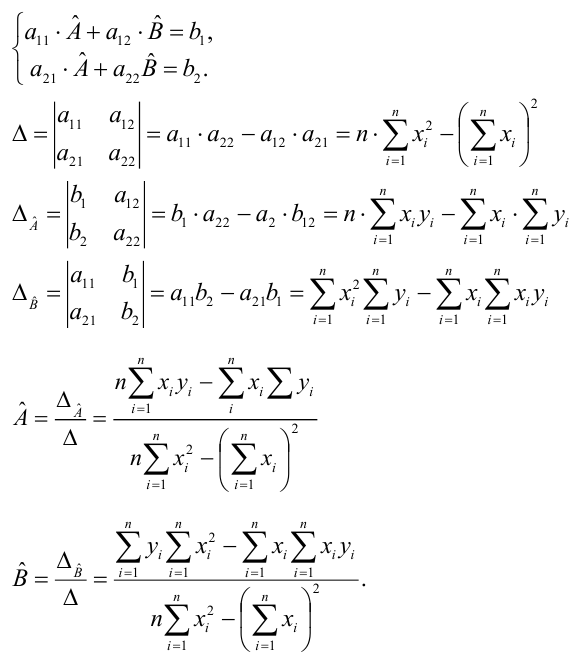
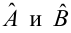 является несмещенными оценками истинных значений коэффициентов
является несмещенными оценками истинных значений коэффициентов 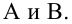
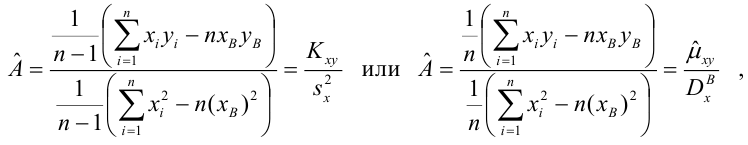 где
где
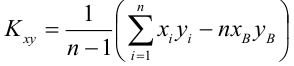 несмещенная оценка корреляционного момента (ковариации),
несмещенная оценка корреляционного момента (ковариации),
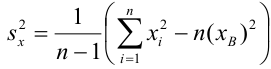 несмещенная оценка дисперсии
несмещенная оценка дисперсии 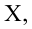
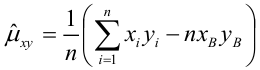 выборочная ковариация,
выборочная ковариация,
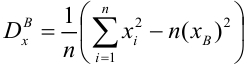 выборочная дисперсия
выборочная дисперсия 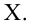
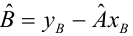
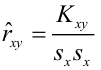 — выборочный коэффициент корреляции
— выборочный коэффициент корреляции
Коэффициент детерминации
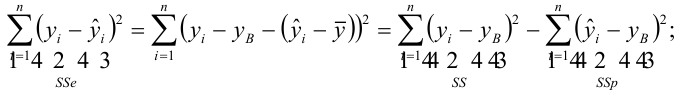
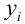 — наблюдаемое экспериментальное значение
— наблюдаемое экспериментальное значение 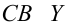 при
при 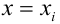
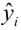 — предсказанное значение
— предсказанное значение 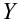 удовлетворяющее уравнению регрессии
удовлетворяющее уравнению регрессии
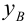 — средневыборочное значение
— средневыборочное значение 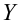
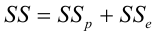
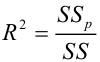 — коэффициент детерминации, доля изменчивости
— коэффициент детерминации, доля изменчивости 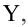 объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии
объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии 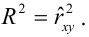
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
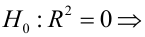 регрессия незначима
регрессия незначима
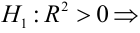 регрессия значима
регрессия значима
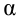 — уровень значимости
— уровень значимости
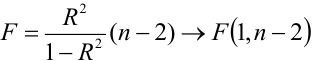 — статистический критерий
— статистический критерий
Критическая область — правосторонняя; 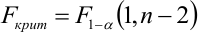
Если 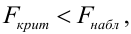 то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
Мощность статистического критерия. Функция мощности
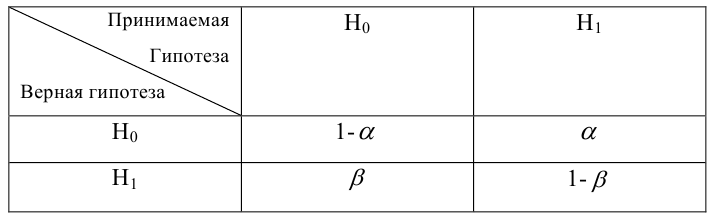
Определение. Мощностью критерия 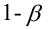 называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода 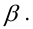
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 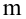 и дисперсией
и дисперсией 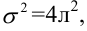 проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
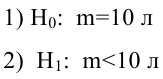
3) Уровень значимости 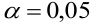
4) Статистический критерий
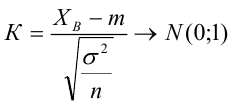
5) Критическая область — левосторонняя
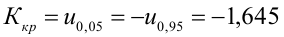
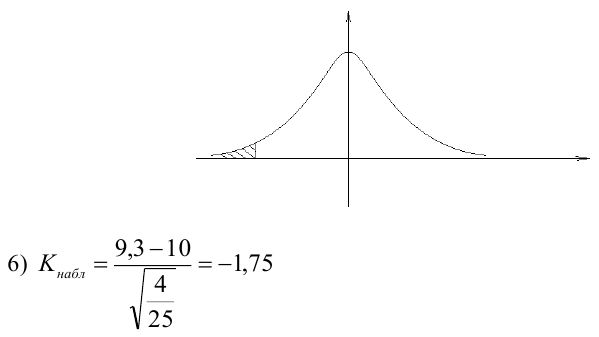
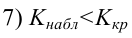 следовательно
следовательно 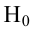 отвергается на уровне значимости
отвергается на уровне значимости 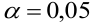
Пример:
В условиях примера 1 предположим, что наряду с 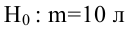 рассматривается конкурирующая гипотеза
рассматривается конкурирующая гипотеза 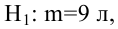 а критическая область задана неравенством
а критическая область задана неравенством 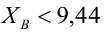 Найти вероятность ошибок I рода и II рода.
Найти вероятность ошибок I рода и II рода.
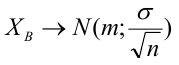
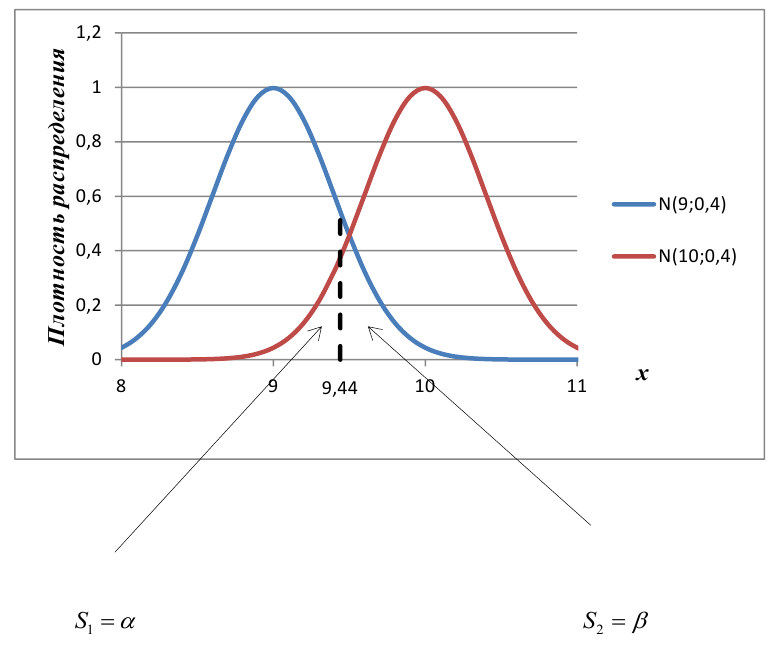
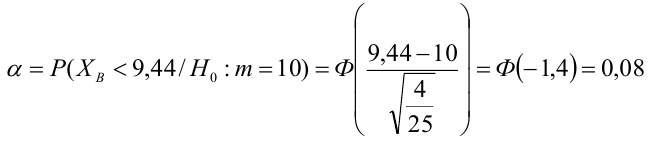
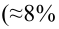 автомобилей имеют меньший расход топлива)
автомобилей имеют меньший расход топлива)
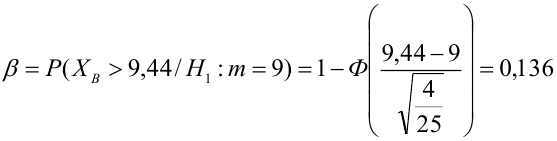
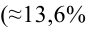 автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
Определение. Пусть проверяется 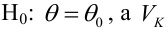 — критическая область критерия с заданным уровнем значимости
— критическая область критерия с заданным уровнем значимости 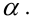 Функцией мощности критерия
Функцией мощности критерия 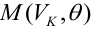 называется вероятность отклонения
называется вероятность отклонения 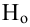 как функция параметра
как функция параметра 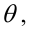 т.е.
т.е.
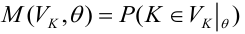
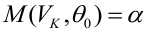 — ошибка 1-ого рода
— ошибка 1-ого рода
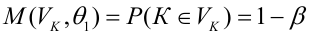 — мощность критерия
— мощность критерия
Пример:
Построить график функции мощности из примера 2 для 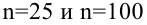
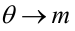
 попадает в критическую область.
попадает в критическую область.
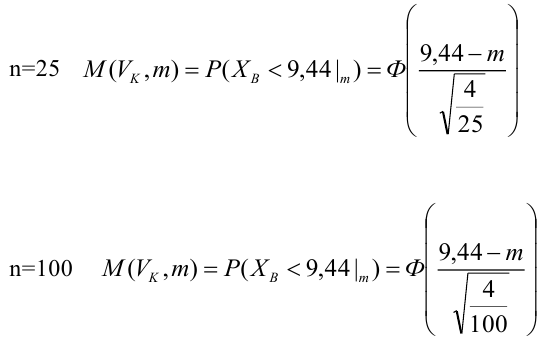
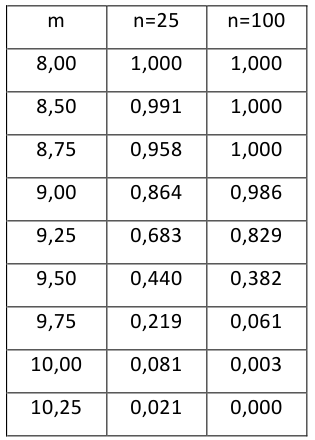
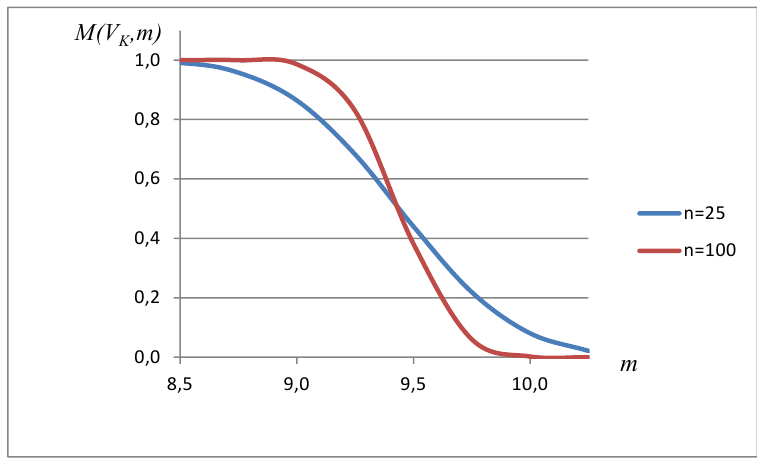
Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить 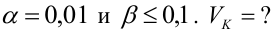
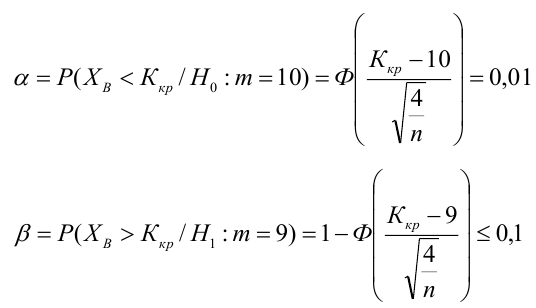
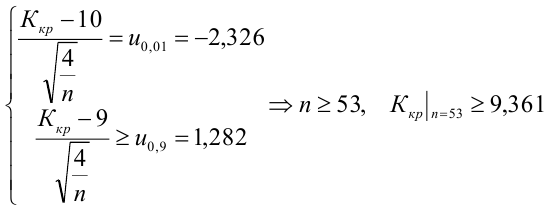
Лемма Неймана-Пирсона.
При проверке простой гипотезы 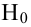 против простой альтернативной гипотезы
против простой альтернативной гипотезы 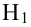 наилучшая критическая область (НКО) критерия заданного уровня значимости
наилучшая критическая область (НКО) критерия заданного уровня значимости 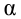 состоит из точек выборочного пространства (выборок объема
состоит из точек выборочного пространства (выборок объема 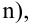 для которых справедливо неравенство:
для которых справедливо неравенство:
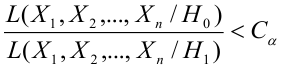
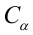 — константа, зависящая от
— константа, зависящая от 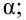
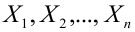 — элементы выборки;
— элементы выборки;
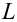 — функция правдоподобия при условии, что соответствующая гипотеза верна.
— функция правдоподобия при условии, что соответствующая гипотеза верна.
Пример:
Случайная величина 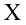 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 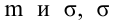 известно. Найти НКО для проверки
известно. Найти НКО для проверки 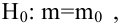 против
против 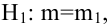 причем
причем 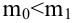
Решение:
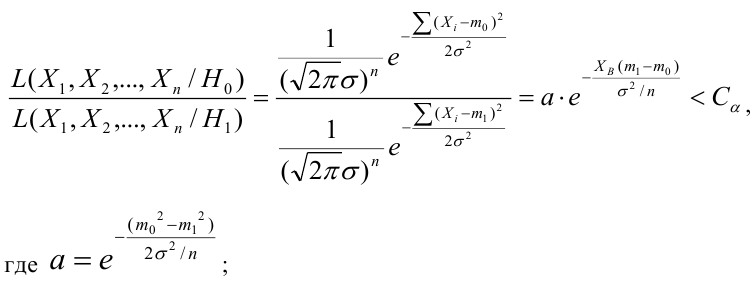
Ошибка первого рода: 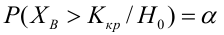
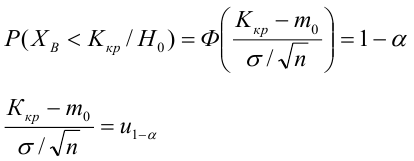
НКО: 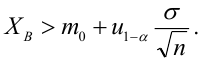
Пример:
Для зависимости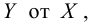 заданной корреляционной табл. 13, найти оценки параметров
заданной корреляционной табл. 13, найти оценки параметров 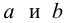 уравнения линейной регрессии
уравнения линейной регрессии 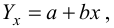 остаточную дисперсию; выяснить значимость уравнения регрессии при
остаточную дисперсию; выяснить значимость уравнения регрессии при 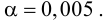
Решение. Воспользуемся предыдущими результатами
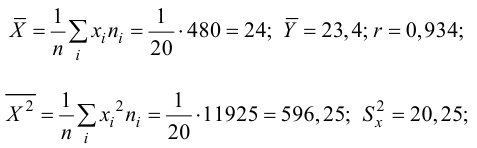
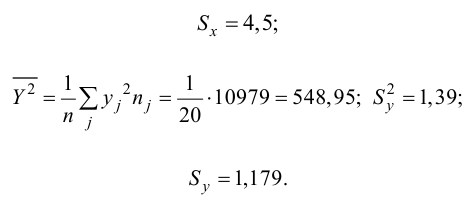
Согласно формуле (24), уравнение регрессии будет иметь вид 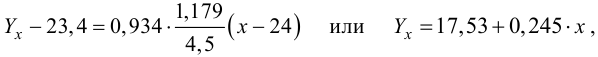 тогда
тогда 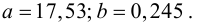
Для выяснения значимости уравнения регрессии вычислим суммы 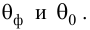 Составим расчетную таблицу:
Составим расчетную таблицу:
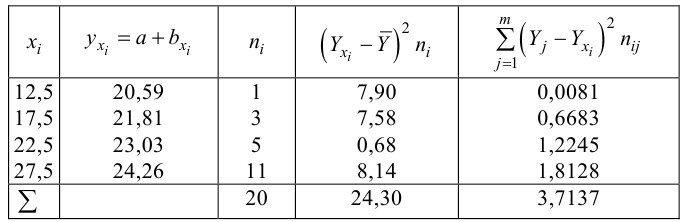
Из (27) и (28) по данным таблицы получим 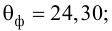
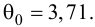
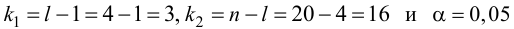 по табл. П7 находим
по табл. П7 находим 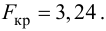
Вычислим статистику
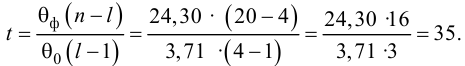
Так как 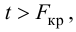 то уравнение регрессии значимо. Остаточная дисперсия равна
то уравнение регрессии значимо. Остаточная дисперсия равна 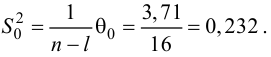
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
Основы линейной регрессии
Что такое регрессия?
Линия регрессии
Метод наименьших квадратов
Предположения линейной регрессии
Аномальные значения (выбросы) и точки влияния
Гипотеза линейной регрессии
Оценка качества линейной регрессии: коэффициент детерминации R2
Применение линии регрессии для прогноза
Простые регрессионные планы
Пример: простой регрессионный анализ
Рассмотрим две непрерывные переменные x=(x1, x2, .., xn), y=(y1, y2, …, yn).
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
Y=a+bx.
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R2 (в парной линейной регрессии это величина r2, квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P, например, 7, 4 и 9, а план включает эффект первого порядка P, то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Y = b0 + b1P
Если простой регрессионный план содержит эффект высшего порядка для P, например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b0 + b1P2
Сигма-ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X. При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X, а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 (Pt_Poor) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 (Pop_Chng) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374. Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p<.05. Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor.

Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию (-.65) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor, p<.001.
Итог
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
Связанные определения:
Линейная регрессия
Матрица плана
Общая линейная модель
Регрессия
В начало
Содержание портала
Все курсы > Оптимизация > Занятие 5
Как мы уже знаем, несмотря на название, логистическая регрессия решает задачу классификации. Сегодня мы подробно разберем принцип работы и составные части алгоритма логистической регрессии, а также построим модели с одной и несколькими независимыми переменными.
Бинарная логистическая регрессия
Задача бинарной классификации
Вернемся к задаче кредитного скоринга, про которую мы говорили, когда обсуждали принцип машинного обучения. Предположим, что мы собрали данные и выявили зависимость возвращения кредита (ось y) от возраста заемщика (ось x).
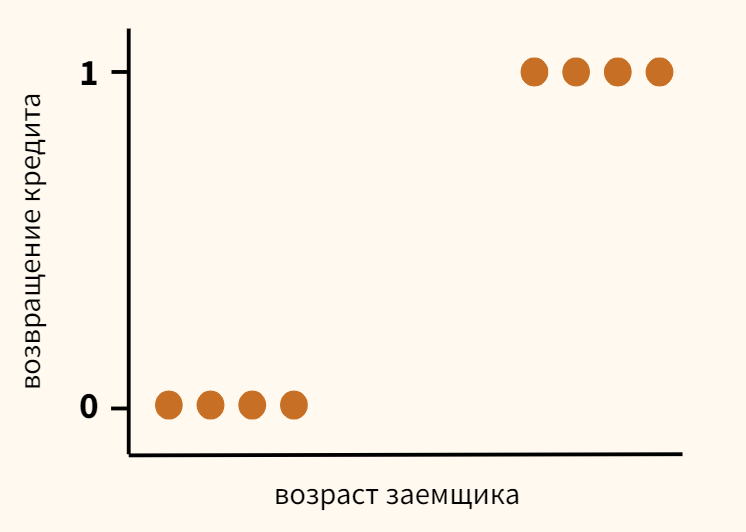
Как мы видим, в среднем более молодые заемщики реже возвращают кредит. Возникает вопрос, с помощью какой модели можно описать эту зависимость? Казалось бы, можно построить линейную регрессию таким образом, чтобы она выдавала некоторое значение и, если это значение окажется ниже 0,5 — отнести наблюдение к классу 0, если выше — к классу 1.

- Если $ f_w(x) < 0,5 rightarrow hat{y} = 0 $
- Если $ f_w(x) geq 0,5 rightarrow hat{y} = 1 $
Однако, даже если предположить, что мы удачно провели линию регрессии (а на графике выше мы действительно провели ее вполне удачно), и наша модель может делать качественный прогноз, появление новых данных сместит эту границу, и, как следствие, ничего не добавит, а только ухудшит точность модели.
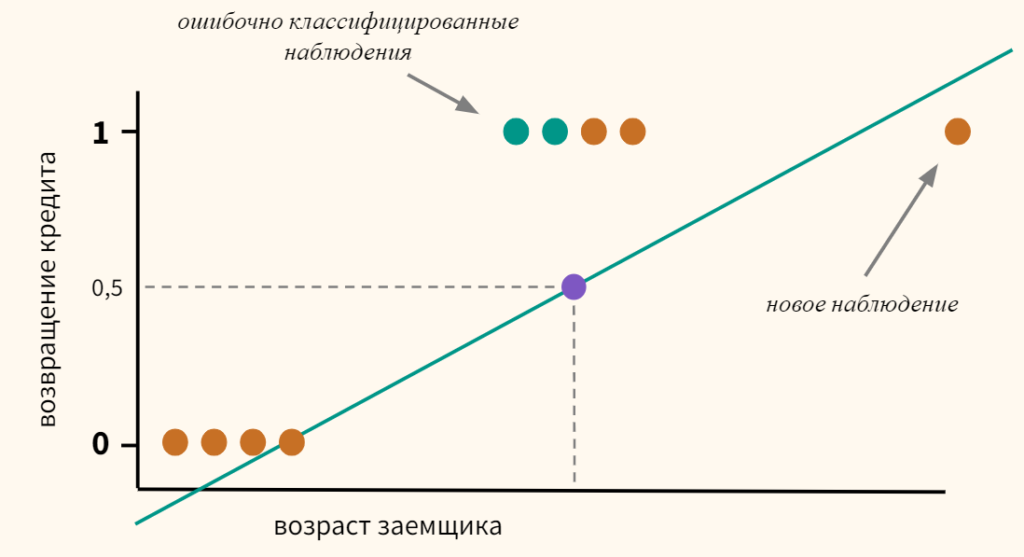
Теперь часть наблюдений, принадлежащих к классу 1, будет ошибочно отнесено моделью к классу 0.
Кроме этого, линейная регрессия по оси y выдает значения, сильно выходящие за пределы интересующего нас интервала от нуля до единицы.
Откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# помимо стандартных библиотек мы также импортируем библиотеку warnings # она позволит скрыть предупреждения об ошибках import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings # кроме того, импортируем датасеты библиотеки sklearn from sklearn import datasets # а также функции для расчета метрики accuracy и построения матрицы ошибок from sklearn.metrics import accuracy_score, confusion_matrix # построенные нами модели мы будем сравнивать с результатом # класса LogisticRegression библиотеки sklearn from sklearn.linear_model import LogisticRegression # среди прочего, мы построим модели полиномиальной логистической регрессии from sklearn.preprocessing import PolynomialFeatures |
Функция логистической регрессии
Сигмоида
Возможно решение упомянутых выше сложностей — пропустить значение линейной регрессии через сигмоиду (sigmoid function), которая при любом значении X не выйдет из необходимого нам диапазона $0 leq h(x) leq 1 $. Напомню формулу и график сигмоиды.
$$ g(z) = frac{1}{1+e^{-z}} $$

Примечание: обратие внимание, когда z представляет собой большое отрицательное число, знаменатель становится очень большим $ 1 + e^{-(-5)} approx 148, 413 $ и значение сигмоиды стремится к нулю; когда z является большим положительным числом, знаменатель, а вместе с ним и все выражение стремятся к единице $ 1 + e^{-(5)} approx 0,0067 $.
Тогда мы можем построить линейную модель, значение которой будет подаваться в сигмоиду.
$$ z = Xtheta rightarrow h_{theta}(x) = frac{1}{1+e^{-(Xtheta)}} $$
В этом смысле никакой ошибки в названии «логистическая регрессия». Этот алгоритм решает задачу классификации через модель линейной регрессии.
Если вы не помните, почему мы записали множественную линейную функцию как $theta x$, посмотрите предыдущую лекцию.
Приведем код на Питоне.
|
def h(x, thetas): z = np.dot(x, thetas) return 1.0 / (1 + np.exp(—z)) |
Теперь посмотрим, как интерпретировать коэффициенты.
Интерпретация коэффициентов
Для любого значения x через $ h_{theta}(x) $ мы будем получать вероятность от 0 до 1, что объект принадлежит к классу y = 1. Например, если класс 1 означает, что заемщик вернул кредит, то $ h_{theta}(x) = 0,8 $ говорит о том, что согласно нашей модели (с параметрами $theta$), для данного заемщика (x) вероятность возвращения кредита состаляет 80 процентов.
В общем случае мы можем записать вероятность вот так.
$$ h_{theta}(x) = P(y = 1 | x; theta) $$
Это выражение можно прочитать как вероятность принадлежности к классу 1 при условии x с параметрами $theta$ (probability of y = 1 given x, parameterized by $theta$).
Поскольку, как мы помним, сумма вероятностей событий, образующих полную группу, всегда равна единице, вероятность принадлежности к классу 0 будет равна
$$ P(y = 0 | x; theta) = 1-P(y = 1 | x; theta) $$
Решающая граница
Решающая граница (decision boundary) — это порог, который определяет к какому классу отнести то или иное наблюдение. Если выбрать порог на уровне 0,5, то все что выше или равно этому порогу мы отнесем к классу 1, все что ниже — к классу 0.
$$ y = 1, h_{theta}(x) geq 0,5 $$
$$ y = 0, h_{theta}(x) < 0,5 $$
Теперь обратите внимание на сигмоиду. Сигмоида $ g(z) $ принимает значения больше 0,5, если $ z geq 0 $, а так как $ z = Xtheta $, то можно сказать, что
- $h_{theta}(x) geq 0,5$ и $ y = 1$, когда $ Xtheta geq 0 $, и соответственно
- $h_{theta}(x) < 0,5 $ и $ y = 0$, когда $ Xtheta < 0 $.
Уравнение решающей границы
Предположим, что у нас есть два признака $x_1$ и $x_2$. Вместе они образуют так называемое пространство ввода (input space), то есть все имеющиеся у нас наблюдения. Мы можем представить его на координатной плоскости, дополнительно выделив цветом наблюдения, относящиеся к разным классам.
Кроме того, представим, что мы уже построили модель логистической регрессии, и она провела для нас соответствующую границу между двумя классами.

Возникает вопрос. Как, зная коэффициенты $theta_0$, $theta_1$ и $theta_2$ модели, найти уравнение линии решающей границы? Для начала договоримся, что уравнение решающией границы будет иметь вид $x_2 = mx_1 + c$, где m — наклон прямой, а c — сдвиг.
Теперь вспомним, что модель с двумя признаками (до подачи в сигмоиду) имеет вид
$$ z = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Также не забудем, что граница проходит там, где $ h_{theta}(x) = 0,5 $, а значит z = 0. Значит,
$$ 0 = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Чтобы найти с (то есть сдвиг линии решающей границы вдоль оси $x_2$) приравняем $x_1$ к нулю и решим для $x_2$ (именно эта точка и будет сдвигом c).
$$ 0 = theta_0 + 0 + theta_2 x_2 rightarrow x_2 = -frac{theta_0}{theta_2} rightarrow c = -frac{theta_0}{theta_2} $$
Теперь займемся наклоном m. Возьмем некоторую точку на линии решающей границы с координатами $(x_1^a, x_2^a)$, $(x_1^b, x_2^b)$. Тогда наклон m будет равен
$$ m = frac{x_2^b-x_2^a}{x_1^b-x_1^a} $$
Так как эти точки расположены на решающей границе, то справедливо, что
$$ 0 = theta_1x_1^b + theta_2x_2^b + theta_0-(theta_1x_1^a + theta_2x_2^a + theta_0) $$
$$ -theta_2(x_2^b-x_2^a) = theta_1(x_1^b-x_1^a) $$
А значит,
$$ frac{x_2^b-x_2^a}{x_1^b-x_1^a} = -frac{theta_1}{theta_2} rightarrow m = -frac{theta_1}{theta_2} $$
Вычислительная устойчивость сигмоиды
При очень больших отрицательных или положительных значениях z может возникнуть переполнение памяти (overflow).
|
# возьмем большое отрицательное значение z = —999 1 / (1 + np.exp(—z)) |
|
RuntimeWarning: overflow encountered in exp 0.0 |
Преодолеть это ограничение и добиться вычислительной устойчивости (numerical stability) алгоритма можно с помощью следующего тождества.
$$ g(z) = frac{1}{1+e^{-z}} = frac{1}{1+e^{-z}} times frac{e^z}{e^z} = frac{e^z}{e^z(1+e^{-z})} = frac {e^z}{e^z + 1} $$
Что интересно, первая часть тождества устойчива при очень больших положительных значениях z.
|
z = 999 1 / (1 + np.exp(—z)) |
При этом вторая стабильна при очень больших отрицательных значениях.
|
z = —999 np.exp(z) / (np.exp(z) + 1) |
Объединим обе части с помощью условия с if.
|
def stable_sigmoid(z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Примечание. Мы не использовали более лаконичный код, например, функцию np.where(), потому что эта функция прежде чем применить условие рассчитывает оба сценария (в данном случае обе части тождества), а это ровно то, чего мы хотим избежать, чтобы не возникло ошибки. Простое условие с if препятствует выполнению той части кода, которая нам не нужна.
Остается написать линейную функцию и подать ее результат в сигмоиду.
|
def h(x, thetas): z = np.dot(x, thetas) return np.array([stable_sigmoid(value) for value in z]) |
Протестируем код. Предположим, что в нашем датасете четыре наблюдения и три коэффициента. Схематично расчеты будут выглядеть следующим образом.
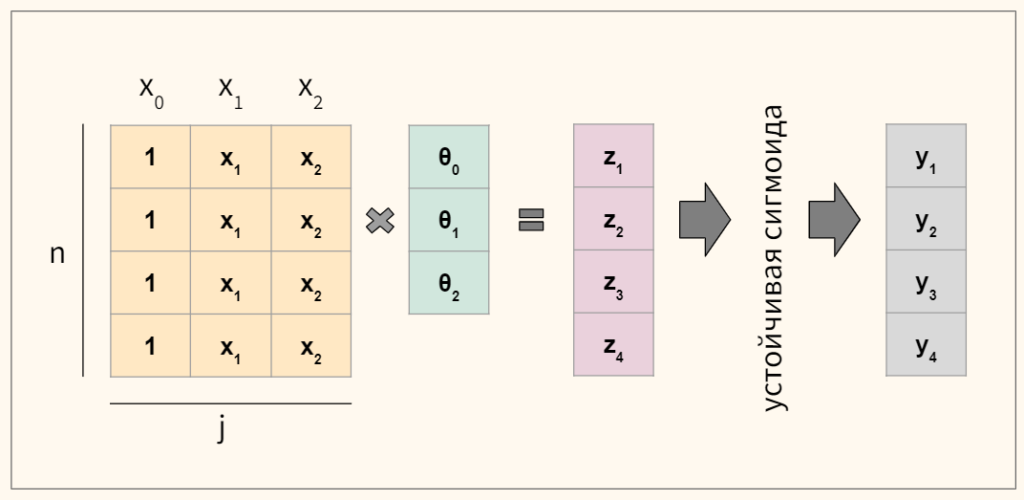
Пропишем это на Питоне.
|
# возьмем массив наблюдений 4 х 3 с числами от 1 до 12 x = np.arange(1, 13).reshape(4, 3) # и трехмерный вектор коэффициентов thetas = np.array([—3, 1, 1]) # подадим их в модель h(x, thetas) |
|
array([0.88079708, 0.26894142, 0.01798621, 0.00091105]) |
Модель работает корректно. Теперь обсудим, как ее обучать, то есть какую функцию потерь использовать для оптимизации параметров $theta$.
Logistic loss или функция кросс-энтропии
В модели логистической регрессии мы не можем использовать MSE. Дело в том, что если мы поместим результат сигмоиды (представляющей собою нелинейную функцию) в MSE, то на выходе получим невыпуклую функцию (non-convex), глобальный минимум которой довольно сложно найти.

Вместо MSE мы будем использовать функцию логистической ошибки, которую еще называют функцией бинарной кросс-энтропии (log loss, binary cross-entropy loss).
График и формула логистической ошибки
Вначале посмотрим на нее на графике.

Разберемся, как она работает. Наша модель $h_{theta}(x)$ может выдавать вероятность от 0 до 1, фактические значения $y$ только 0 и 1.
Сценарий 1. Предположим, что для конкретного заемщика в обучающем датасете истинное значение/ целевой класс записан как 1 (то есть заемщик вернул кредит). Тогда «срабатывает» синяя ветвь графика и ошибка измеряется по ней. Соответственно, чем ближе выдаваемая моделью вероятность к единице, тем меньше ошибка.
$$ -log(P(y = 1 | x; theta)) = -log(h_{theta}(x)), y = 1 $$
Сценарий 2. Заемщик не вернул кредит и его целевая переменная записана как 0. Тогда срабатывает оранжевая ветвь. Ошибка модели будет минимальна при значениях близких к нулю.
$$ -log(1-P(y = 1 | x; theta)) = -log(1-h_{theta}(x)), y = 0 $$
Добавлю, что минус логарифм в данном случае очень удачно отвечает нашему желанию иметь нулевую ошибку при правильном прогнозе и наказать алгоритм высокой ошибкой (асимптотически стремящейся к бесконечности) в случае неправильного прогноза.
В итоге нам нужно будет найти сумму вероятностей принадлежности к классу 1 для сценария 1 и сценария 2.
$$ J(theta) = begin{cases} -log(h_{theta}(x)) | y=1 -log(1-h_{theta}(x)) | y=0 end{cases} $$
Однако, для каждого наблюдения нам нужно учитывать только одну из вероятностей (либо $y=1$, либо $y=0$). Как нам переключаться между ними? На самом деле очень просто.
В качестве переключателя можно использовать целевую переменную. В частности, умножим левую часть функции на y, а правую на 1-y. Тогда если речь идет о классе 1 первая часть умножится на единицу, вторая на ноль и исчезнет. Если речь идет о классе 0, произойдет обратное, исчезнет левая часть, а правая останется. Получается
$$ J(theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Рассмотрим ее работу на учебном примере.
Расчет логистической ошибки
Предположим, мы построили модель и для каждого наблюдения получили некоторый прогноз (вероятность).
|
# выведем результат работы модели (вероятности) y_pred и целевую переменную y output = pd.DataFrame({ ‘y’ :[1, 1, 1, 0, 0, 1, 1, 0], ‘y_pred’ :[0.93, 0.81, 0.78, 0.43, 0.54, 0.49, 0.22, 0.1] }) output |

Найдем вероятность принадлежности к классу 1.
|
# оставим вероятность, если y = 1, и вычтем вероятность из единицы, если y = 0 output[‘y=1 prob’] = np.where(output[‘y’] == 0, 1 — output[‘y_pred’], output[‘y_pred’]) output |

Возьмем отрицательный логарифм из каждой вероятности.
|
output[‘-log’] = —np.log(output[‘y=1 prob’]) output |

Выведем каждое из получившихся значений на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
plt.figure(figsize = (10, 8)) # создадим точки по оси x в промежутке от 0 до 1 x_vals = np.linspace(0, 1) # выведем кривую функции логистической ошибки plt.plot(x_vals, —np.log(x_vals), label = ‘-log(h(x)) | y = 1’) # выведем каждое из значений отрицательного логарифма plt.scatter(output[‘y=1 prob’], output[‘-log’], color = ‘r’) # зададим заголовок, подписи к осям, легенду и сетку plt.xlabel(‘h(x)’, fontsize = 16) plt.ylabel(‘loss’, fontsize = 16) plt.title(‘Функция логистической ошибки’, fontsize = 18) plt.legend(loc = ‘upper right’, prop = {‘size’: 15}) plt.grid() plt.show() |
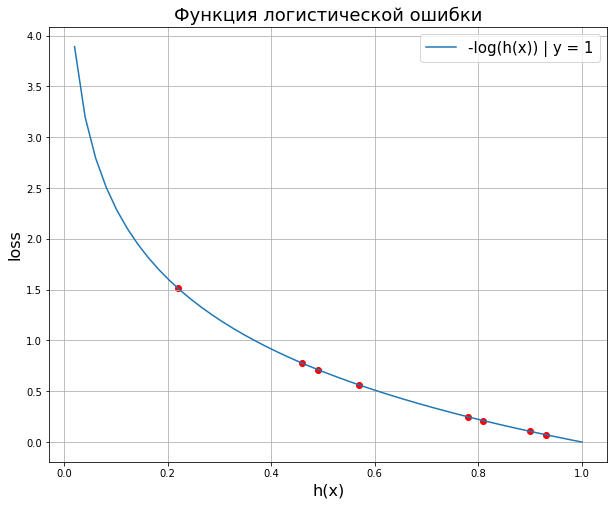
Как мы видим, так как мы всегда выражаем вероятность принадлежности к классу 1, графически нам будет достаточно одной ветви. Остается сложить результаты и разделить на количество наблюдений.
Окончательный вариант
Напишем функцию логистической ошибки, которую будем использовать в нашем алгоритме.
|
def objective(y, y_pred): # рассчитаем функцию потерь для y = 1, добавив 1e-9, чтобы избежать ошибки при log(0) y_one_loss = y * np.log(y_pred + 1e—9) # также рассчитаем функцию потерь для y = 0 y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) # сложим и разделим на количество наблюдений return —np.mean(y_zero_loss + y_one_loss) |
Проверим ее работу на учебных данных.
|
# проверим ее работу на учебных данных objective(output[‘y’], output[‘y_pred’]) |
Теперь займемся поиском производной.
Производная функции логистической ошибки
Предположим, что $G(theta)$ — одна из частных производных описанной выше функции логистической ошибки $J(theta)$,
$$ G = y cdot log(h) + (1-y) cdot log(1-h) $$
где h — это сигмоида $1/1+e^{-z}$, а $z(theta)$ — линейная функция $xtheta$. Тогда по chain rule нам нужно найти производные следующих функций
$$ frac{partial G}{partial theta} = frac{partial G}{partial h} cdot frac{partial h}{partial z} cdot frac{partial z}{partial theta} $$
Производная логарифмической функции
Начнем с производной логарифмической функции.
$$ frac{partial}{partial x} ln f(x) = frac{1}{f(x)} $$
Теперь, помня, что x и y — это константы, найдем первую производную.
$$ frac{partial G}{partial h} left[ y cdot log(h) + (1-y) cdot log(1-h) right] $$
$$ = y cdot frac{partial G}{partial h} [log(h)] + (1-y) cdot frac{partial G}{partial h} [log(1-h)] $$
$$ = frac{1}{h}y + frac{1}{1-h} cdot frac{partial G}{partial h} [1-h] cdot (1-y) $$
Упростим выражение (не забыв про производную разности).
$$ = frac{h}{y} + frac{frac{partial G}{partial h} (1-h) (1-y)}{1-h} = frac{h}{y}+frac{(0-1)(1-y)}{1-h} $$
$$ = frac{y}{h}-frac{1-y}{1-h} = frac{y-h}{h(1-h)} $$
Теперь займемся производной сигмоиды.
Производная сигмоиды
Вначале упростим выражение.
$$ frac{partial h}{partial z} left[ frac{1}{1+e^{-z}} right] = frac{partial h}{partial z} left[ (1+e^{-z})^{-1}) right] $$
Теперь перейдем к нахождению производной
$$ = -(1+e^{-z})^{-2}) cdot (-e^{-z}) = frac{e^{-z}}{(1+e^{-z})^2} $$
$$ = frac{1}{1+e^{-z}} cdot frac{e^{-z}}{1+e^{-z}} = frac{1}{1+e^{-z}} cdot frac{(1+e^{-z})-1}{1+e^{-z}} $$
$$ = frac{1}{1+e^{-z}} cdot left( frac{1+e^{-z}}{1+e^{-z}}-frac{1}{1+e^{-z}} right) $$
$$ = frac{1}{1+e^{-z}} cdot left( 1-frac{1}{1+e^{-z}} right) $$
В терминах предложенной выше нотации получается
$$ h(1-h) $$
Производная линейной функции
Наконец найдем производную линейной функции.
$$ frac{partial z}{partial theta} = x $$
Перемножим производные и найдем градиент по каждому из признаков j для n наблюдений.
$$ frac{partial J}{partial theta} = frac{y-h}{h(1-h)} cdot h(1-h) cdot x_j cdot frac{1}{n} = x_j cdot (y-h) cdot frac{1}{n} $$
Замечу, что хотя производная похожа на градиент функции линейной регрессии, на самом деле это разные функции, $h$ в данном случае это сигмоида.
Для нахождения градиента (всех частных производных одновременно) перепишем формулу в векторной нотации.
$$ nabla_{theta} J = X^T(h(Xtheta)-y) times frac{1}{n} $$
Схематично для четырех наблюдений и трех коэффициентов нахождение градиента будет выглядеть следующим образом.

Объявим соответствующую функцию.
|
def gradient(x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n |
На всякий случай напомню, что прогнозные значения (y_pred) мы получаем с помощью объявленной ранее функции $h(x, thetas)$.
Подготовка данных
В качестве примера возьмем встроенный в sklearn датасет, в котором нам предлагается определить класс вина по его характеристикам.
|
# импортируем датасет о вине из модуля datasets data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную df[‘target’] = data.target # посмотрим на первые три строки df.head(3) |

Целевая переменная
Посмотрим на количество наблюдений и признаков (размерность матрицы), а также уникальные значения (классы) в целевой переменной.
|
df.shape, np.unique(df.target) |
|
((178, 14), array([0, 1, 2])) |
Как мы видим, у нас три класса, а должно быть два, потому что пока что мы создаем алгоритм бинарной классификации. Отфильтруем значения так, чтобы осталось только два класса.
|
# применим маску датафрейма и удалим класс 2 df = df[df.target != 2] # посмотрим на результат df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Отбор признаков
Наша целевая переменная выражена бинарной категорией или, как еще говорят, находится на дихотомической шкале (dichotomous variable). В этом случае применять коэффициент корреляции Пирсона не стоит и можно использовать точечно-бисериальную корреляцию (point-biserial correlation). Рассчитаем корреляцию признаков и целевой переменной нашего датасета.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# импортируем модуль stats из библиотеки scipy from scipy import stats # создадим два списка, один для названий признаков, второй для корреляций columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем корреляцию этого признака с целевой переменной # и поместим результат в список корреляций correlations.append(stats.pointbiserialr(df[col], df[‘target’])[0]) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |

Наиболее коррелирующим с целевой переменной признаком является пролин (proline). Визуально оценим насколько сильно отличается этот показатель для классов вина 0 и 1.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме выведем пролин по оси x, а класс вина по оси y sns.scatterplot(x = df.proline, y = df.target, s = 80); |

Теперь посмотрим на зависимость двух признаков (спирт и пролин) от целевой переменной.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме по осям x и y выведем признаки, # с помощью параметра hue разделим соответствующие классы целевой переменной sns.scatterplot(x = df.alcohol, y = df.proline, hue = df.target, s = 80) # добавим легенду, зададим ее расположение и размер plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # выведем результат plt.show() |
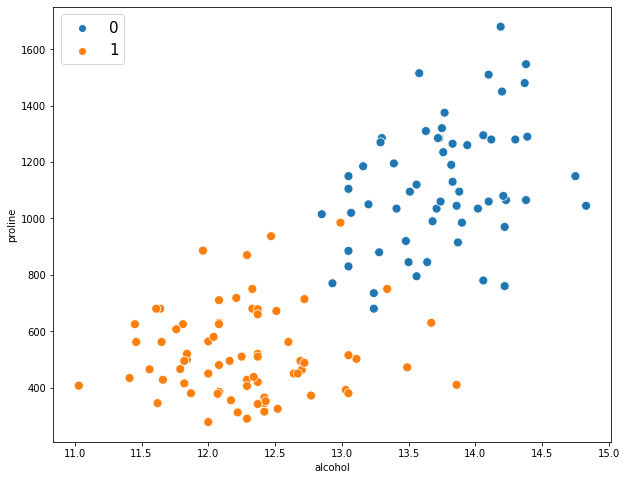
В целом можно сказать, что классы линейно разделимы (другими словами, мы можем провести прямую между ними). Поместим признаки в переменную X, а целевую переменную — в y.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] |
Масштабирование признаков
Как и в случае с линейной регрессией, для алгоритма логистической регрессии важно, чтобы признаки были приведены к одному масштабу. Для этого используем стандартизацию.
|
# т.е. приведем данные к нулевому среднему и единичному СКО X = (X — X.mean()) / X.std() X.head() |

Проверим результат.
|
X.alcohol.mean(), X.alcohol.std(), X.proline.mean(), X.proline.std() |
|
(6.8321416900009635e-15, 1.0, -5.465713352000771e-17, 1.0) |
Теперь мы готовы к созданию и обучению модели.
Обучение модели
Вначале объявим уже знакомую нам функцию, которая добавит в датафрейм столбец под названием x0, заполненный единицами.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
Применим ее к нашему датафрейму с признаками.
|
# добавим столбец с единицами add_ones(X) # и посмотрим на результат X.head() |

Создадим вектор начальных весов (он будет состоять из нулей), а также переменную n, в которой будет храниться количество наблюдений.
|
thetas, n = np.zeros(X.shape[1]), X.shape[0] thetas, n |
|
(array([0., 0., 0.]), 130) |
Кроме того, создадим список, в который будем записывать размер ошибки функции потерь.
Теперь выполним основную работу по минимизации функции потерь и поиску оптимальных весов (выполнение кода ниже у меня заняло около 30 секунд).
|
# в цикле из 20000 итераций for i in range(20000): # рассчитаем прогнозное значение с текущими весами y_pred = h(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(objective(y, y_pred)) # рассчитаем градиент grad = gradient(X, y, y_pred, n) # используем градиент для улучшения весов модели # коэффициент скорости обучения будет равен 0,001 thetas = thetas — 0.001 * grad |
Посмотрим на получившиеся веса и финальный уровень ошибки.
|
# чтобы посмотреть финальный уровень ошибки, # достаточно взять последний элемент списка loss_history thetas, loss_history[—1] |
|
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Модель обучена. Теперь мы можем сделать прогноз и оценить результат.
Прогноз и оценка качества
Прогноз модели
Объявим функцию predict(), которая будет предсказывать к какому классу относится то или иное наблюдение. От функции $h(x, thetas)$ эта функция будет отличаться тем, что выдаст не только вероятность принадлежности к тому или иному классу, но и непосредственно сам предполагаемый класс (0 или 1).
|
def predict(x, thetas): # найдем значение линейной функции z = np.dot(x, thetas) # проведем его через устойчивую сигмоиду probs = np.array([stable_sigmoid(value) for value in z]) # если вероятность больше или равна 0,5 — отнесем наблюдение к классу 1, # в противном случае к классу 0 # дополнительно выведем значение вероятности return np.where(probs >= 0.5, 1, 0), probs |
Вызовем функцию predict() и запишем прогноз класса и вероятность принадлежности к этому классу в переменные y_pred и probs соответственно.
|
# запишем прогноз класса и вероятность этого прогноза в переменные y_pred и probs y_pred, probs = predict(X, thetas) # посмотрим на прогноз и вероятность для первого наблюдения y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
Здесь важно напомнить, что вероятность близкая к нулю говорит о пренадлжености к классу 0. В качестве упражнения выведите класс последнего наблюдения и соответствующую вероятность.
Метрика accuracy и матрица ошибок
Оценим результат с помощью метрики accuracy и матрицы ошибок.
|
# функцию accuracy_score() мы импортировали в начале ноутбука accuracy_score(y, y_pred) |
|
# функцию confusion_matrix() мы импортировали в начале ноутбука # столбцами будут прогнозные значения (Forecast), # строками — фактические (Actual) pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |

Как мы видим, алгоритм ошибся пять раз. Дважды он посчитал, что наблюдение относится к классу 1, хотя на самом деле это был класс 0, и трижды, наоборот, неверно отнес класс 1 к классу 0.
Решающая граница
Выше мы уже вывели уравнение решающей границы. Воспользуемся им, чтобы визуально оценить насколько удачно классификатор справился с поставленной задачей.
|
# рассчитаем сдвиг (c) и наклон (m) линии границы c, m = —thetas[0]/thetas[2], —thetas[1]/thetas[2] c, m |
|
(0.1227046263531282, -0.915731474695505) |
|
# найдем минимальное и максимальное значения для спирта (ось x) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) # найдем минимальное и максимальное значения для пролина (ось y) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) # запишем значения оси x в переменную xd xd = np.array([xmin, xmax]) xd |
|
array([-2.15362589, 2.12194856]) |
|
# подставим эти значения, а также значения сдвига и наклона в уравнение линии yd = m * xd + c # в результате мы получим координаты двух точек, через которые проходит линия границы (xd[0], yd[0]), (xd[1], yd[1]) |
|
((-2.1536258890738247, 2.0948476376971197), (2.1219485561396647, -1.8204304541886445)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# зададим размер графика plt.figure(figsize = (11, 9)) # построим пунктирную линию по двум точкам, найденным выше plt.plot(xd, yd, ‘k’, lw = 1, ls = ‘—‘) # дополнительно отобразим наши данные sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) # которые снова снабдим легендой plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # минимальные и максимальные значения по обеим осям будут границами графика plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) # по желанию, разделенные границей половинки можно закрасить # tab: означает, что цвета берутся из палитры Tableau # plt.fill_between(xd, yd, ymin, color=’tab:blue’, alpha = 0.2) # plt.fill_between(xd, yd, ymax, color=’tab:orange’, alpha = 0.2) # а также добавить обозначения переменных в качестве подписей к осям # plt.xlabel(‘x_1’) # plt.ylabel(‘x_2’) plt.show() |

На графике хорошо видны те пять значений, в которых ошибся наш классификатор.
Написание класса
Остается написать класс бинарной логистической регрессии.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class LogReg(): # в методе .__init__() объявим переменные для весов и уровня ошибки def __init__(self): self.thetas = None self.loss_history = [] # метод .fit() необходим для обучения модели # этому методу мы передадим признаки и целевую переменную # кроме того, мы зададим значения по умолчанию # для количества итераций и скорости обучения def fit(self, x, y, iter = 20000, learning_rate = 0.001): # метод создаст «правильные» копии датафрейма x, y = x.copy(), y.copy() # добавит столбец из единиц self.add_ones(x) # инициализирует веса и запишет в переменную n количество наблюдений thetas, n = np.zeros(x.shape[1]), x.shape[0] # создадим список для записи уровня ошибки loss_history = [] # в цикле равном количеству итераций for i in range(iter): # метод сделает прогноз с текущими весами y_pred = self.h(x, thetas) # найдет и запишет уровень ошибки loss_history.append(self.objective(y, y_pred)) # рассчитает градиент grad = self.gradient(x, y, y_pred, n) # и обновит веса thetas -= learning_rate * grad # метод выдаст веса и список с историей ошибок self.thetas = thetas self.loss_history = loss_history # метод .predict() делает прогноз с помощью обученной модели def predict(self, x): # метод создаст «правильную» копию модели x = x.copy() # добавит столбец из единиц self.add_ones(x) # рассчитает значения линейной функции z = np.dot(x, self.thetas) # передаст эти значения в сигмоиду probs = np.array([self.stable_sigmoid(value) for value in z]) # выдаст принадлежность к определенному классу и соответствующую вероятность return np.where(probs >= 0.5, 1, 0), probs # ниже приводятся служебные методы, смысл которых был разобран ранее на занятии def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим работу написанного нами класса. Вначале подготовим данные и обучим модель.
|
# проверим работу написанного нами класса # поместим признаки и целевую переменную в X и y X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # приведем признаки к одному масштабу X = (X — X.mean())/X.std() # создадим объект класса LogReg model = LogReg() # и обучим модель model.fit(X, y) # посмотрим на атрибуты весов и финального уровня ошибки model.thetas, model.loss_history[—1] |
|
(array([ 0.23234188, —1.73394252, —1.89350543]), 0.12282503517421262) |
Затем сделаем прогноз и оценим качество модели.
|
# сделаем прогноз y_pred, probs = model.predict(X) # и посмотрим на класс первого наблюдения и вероятность y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
|
# рассчитаем accuracy accuracy_score(y, y_pred) |
|
# создадим матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |

Модель показала точно такой же результат. Методы класса LogReg работают. Теперь давайте сравним работу нашего класса с классом LogisticRegression библиотеки sklearn.
Сравнение с sklearn
Обучение модели
Вначале обучим модель.
|
# подготовим данные X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression() # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([0.30838852]), array([[-2.09622008, -2.45991159]])) |
Прогноз
Теперь необходимо сделать прогноз и найти соответствющие вероятности. В классе LogisticRegression библиотеки sklearn метод .predict() отвечает за предсказание принадлежности к определенному классу, а метод .predict_proba() отвечает за вероятность такого прогноза.
|
# выполним предсказание класса y_pred = model.predict(X) # и найдем вероятности probs = model.predict_proba(X) # посмотрим на класс и вероятность первого наблюдения y_pred[0], probs[0] |
|
(0, array([0.9904622, 0.0095378])) |
Модель предсказала для первого наблюдения класс 0. При этом, обратите внимание, что метод .predict_proba() для каждого наблюдения выдает две вероятности, первая — это вероятность принадлежности к классу 0, вторая — к классу 1.
Оценка качества
Рассчитаем метрику accuracy.
|
accuracy_score(y, y_pred) |
И построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |

Как мы видим, хотя веса модели и предсказанные вероятности немного, ее точность осталась неизменной.
Решающая граница
Построим решающую границу.
|
# найдем сдвиг и наклон для уравнения решающей границы c, m = —model.intercept_ / model.coef_[0][1], —model.coef_[0][0] / model.coef_[0][1] c, m |
|
(array([0.12536569]), -0.8521526076691505) |
|
# посмотрим на линию решающей границы plt.figure(figsize = (11, 9)) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) xd = np.array([xmin, xmax]) yd = m*xd + c plt.plot(xd, yd, ‘k’, lw=1, ls=‘—‘) sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) plt.show() |

Бинарная полиномиальная регрессия
Идея бинарной полиномиальной логистической регрессии (binary polynomial logistic regression) заключается в том, чтобы использовать полином внутри сигмоиды и соответственно создать нелинейную границу между двумя классами.

Полиномиальные признаки
Уравнение полинома на основе двух признаков будет выглядеть следующим образом.
$$ y = theta_{0}x_0 + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
Реализуем этот алгоритм на практике и посмотрим улучшатся ли результаты. Вначале, подготовим и масштабируем данные.
|
# подготовим и X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # масштабируем данные X = (X — X.mean())/X.std() |
Теперь преобразуем наши данные так, как если бы мы использовали полином второй степени.
Смысл создания полиномиальных признаков мы детально разобрали на занятии по множественной линейной регрессии.
|
# создадим объект класса PolynomialFeatures # укажем, что мы хотим создать полином второй степени polynomial_features = PolynomialFeatures(degree = 2) # преобразуем данные с помощью метода .fit_transform() X_poly = polynomial_features.fit_transform(X) |
Сравним исходные признаки с полиномиальными.
|
# посмотрим на первое наблюдение X.head(1) |

|
# должно получиться шесть признаков X_poly[:1] |
|
array([[1. , 1.44685785, 0.77985116, 2.09339765, 1.12833378, 0.60816783]]) |
Моделирование и оценка качества
Обучим модель, сделаем прогноз и оценим результат.
|
# создадим объект класса LogisticRegression poly_model = LogisticRegression() # обучим модель на полиномиальных признаках poly_model = poly_model.fit(X_poly, y) # сделаем прогноз y_pred = poly_model.predict(X_poly) # рассчитаем accuracy accuracy_score(y_pred, y) |
Построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |

Для того чтобы визуально оценить качество модели, построим два графика: фактических классов и прогнозных. Вначале создадим датасет, в котором будут исходные признаки (alcohol, proline) и прогнозные значения (y_pred).
|
# сделаем копию исходного датафрейма с нужными признаками predictions = df[[‘alcohol’, ‘proline’]].copy() # и добавим новый столбец с прогнозными значениями predictions[‘y_pred’] = y_pred # посмотрим на результат predictions.head(3) |
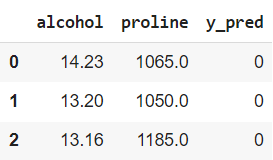
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим два подграфика с помощью функции plt.subplots() # расположим подграфики на одной строке fig, (ax1, ax2) = plt.subplots(1, 2, # пропишем размер, figsize = (14, 6), # а также расстояние между подграфиками по горизонтали gridspec_kw = {‘wspace’ : 0.2}) # на левом подграфики выведем фактические классы sns.scatterplot(data = df, x = ‘alcohol’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) # на правом — прогнозные sns.scatterplot(data = predictions, x = ‘alcohol’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз’, fontsize = 14) # зададим общий заголовок fig.suptitle(‘Бинарная полиномиальная регрессия’, fontsize = 16) plt.show() |
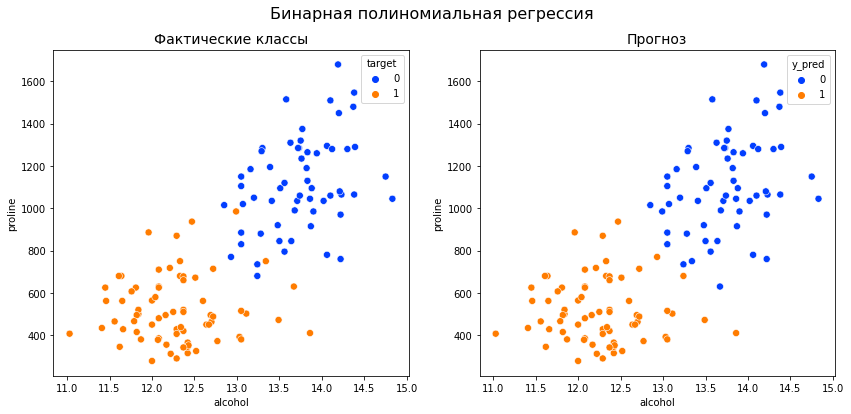
Как вы видите, нам не удалось добиться улучшения по сравнению с обычной полиномиальной регрессией.
Напомню, что создание подграфиков мы подробно разобрали на занятии по исследовательскому анализу данных.
В качестве упражнения предлагаю вам выяснить, какая степень полинома позволит улучшить результат прогноза на этих данных и насколько, таким образом, улучшится качество предсказаний.
Перейдем ко второй части нашего занятия.
Мультиклассовая логистическая регрессия
Как поступить, если нужно предсказать не два класса, а больше? Сегодня мы рассмотрим два подхода: one-vs-rest и кросс-энтропию. Начнем с того, что подготовим данные.
Подготовка данных
Вернем исходный датасет с тремя классами.
|
# вновь импортируем датасет о вине data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # приведем признаки к одному масштабу df = (df — df.mean())/df.std() # добавим целевую переменную df[‘target’] = data.target # убедимся, что у нас присутствуют все три класса df.target.value_counts() |
|
1 71 0 59 2 48 Name: target, dtype: int64 |
В целевой переменной большое двух классов, а значит точечно-бисериальный коэффициент корреляции мы использовать не можем. Воспользуемся корреляционным отношением (correlation ratio).
|
# код ниже был подробно разобран на предыдущем занятии def correlation_ratio(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# создадим два списка, один для названий признаков, второй для значений корреляционного отношения columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем взаимосвязь этого признака с целевой переменной # и поместим результат в список значений корреляционного отношения correlations.append(correlation_ratio(df[col], df[‘target’])) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |

Теперь наибольшую корреляцию с целевой переменной показывают флавоноиды (flavanoids) и пролин (proline). Их и оставим.
|
df = df[[‘flavanoids’, ‘proline’, ‘target’]].copy() df.head(3) |
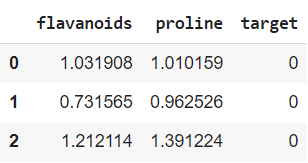
Посмотрим насколько легко можно разделить эти классы.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # построим точечную диаграмму с двумя признаками, разделяющей категориальной переменной будет класс вина sns.scatterplot(x = df.flavanoids, y = df.proline, hue = df.target, palette = ‘bright’, s = 100) # добавим легенду plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.show() |

Перейдем непосредственно к алгоритмам мультиклассовой логистической регрессии. Начнем с подхода one-vs-rest.
Подход one-vs-rest
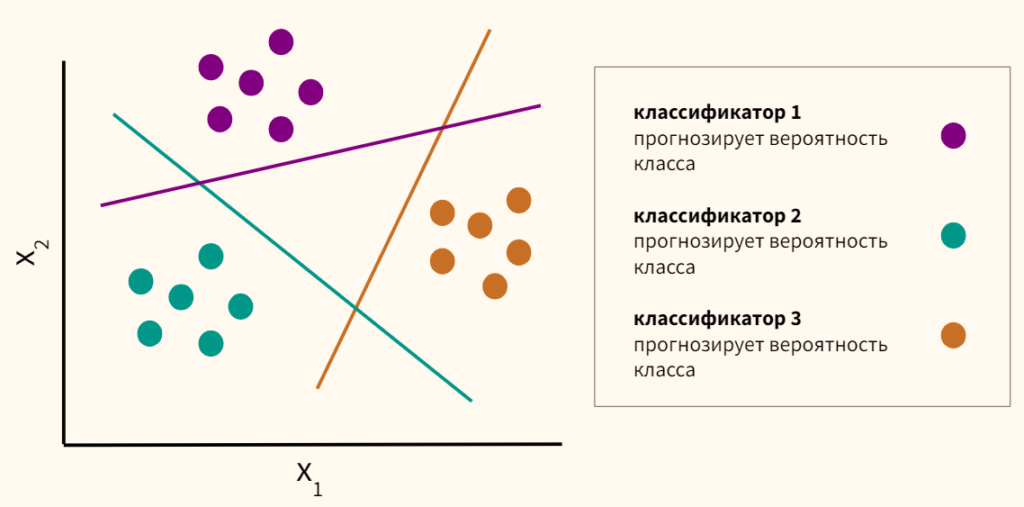
Подход one-vs-rest или one-vs-all предполагает, что мы отделяем один класс, а остальные наоборот объединяем. Так мы поступаем с каждым классом и строим по одной модели логистической регрессии относительно каждого из класса. Например, если у нас три класса, то у нас будет три модели логистической регрессии. Далее мы смотрим на получившиеся вероятности и выбираем наибольшую.
$$ h_theta^{(i)}(x) = P(y = i | x; theta), i in {0, 1, 2} $$
При таком подходе сам по себе алгоритм логистической регрессии претерпевает лишь несущественные изменения, главное правильно подготовить данные для обучения модели.
Подготовка датасетов
|
# поместим признаки и данные в соответствующие переменные x1, x2 = df.columns[0], df.columns[1] target = df.target.unique() target |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# сделаем копии датафреймов ovr_0, ovr_1, ovr_2 = df.copy(), df.copy(), df.copy() # в каждом из них сделаем целевым классом 0-й, 1-й или 2-й классы # например, в ovr_0 нулевым будет класс 0, а классы 1 и 2 первым ovr_0[‘target’] = np.where(df[‘target’] == target[0], 1, 0) ovr_1[‘target’] = np.where(df[‘target’] == target[1], 1, 0) ovr_2[‘target’] = np.where(df[‘target’] == target[2], 1, 0) # выведем разделение на классы на графике fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (16, 4), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = ovr_0, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax1) ax1.set_title(‘Прогнозирование класса 0’, fontsize = 14) sns.scatterplot(data = ovr_1, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax2) ax2.set_title(‘Прогнозирование класса 1’, fontsize = 14) sns.scatterplot(data = ovr_2, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax3) ax3.set_title(‘Прогнозирование класса 2’, fontsize = 14) plt.show() |

Обучение моделей
|
models = [] # поочередно обучим каждую из моделей for ova_n in [ovr_0, ovr_1, ovr_2]: X = ova_n[[‘flavanoids’, ‘proline’]] y = ova_n[‘target’] model = LogReg() model.fit(X, y) # каждую обученную модель поместим в список models.append(model) |
|
# убедимся, что все работает # например, выведем коэффициенты модели 1 models[0].thetas |
|
array([-0.99971466, 1.280398 , 2.04834457]) |
Прогноз и оценка качества
|
# вновь перенесем данные из исходного датафрейма X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # в список probs будем записывать результат каждой модели # для каждого наблюдения probs = [] for model in models: _, prob = model.predict(X) probs.append(prob) |
|
# очевидно, для каждого наблюдения у нас будет три вероятности # принадлежности к целевому классу probs[0][0], probs[1][0], probs[2][0] |
|
(0.9161148288779738, 0.1540913395345091, 0.026621132600103174) |
|
# склеим и изменим размерность массива таким образом, чтобы # строки были наблюдениями, а столбцы вероятностями all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T all_probs.shape |
|
# каждая из 178 строк — это вероятность одного наблюдения # принадлежать к классу 0, 1, 2 all_probs[0] |
|
array([0.91611483, 0.15409134, 0.02662113]) |
Обратите внимание, при использовании подхода one-vs-rest вероятности в сумме не дают единицу!
|
# например, первое наблюдение вероятнее всего принадлежит к классу 0 np.argmax(all_probs[0]) |
|
# найдем максимальную вероятность в каждой строке, # индекс вероятности [0, 1, 2] и будет прогнозом y_pred = np.argmax(all_probs, axis = 1) # рассчитаем accuracy accuracy_score(y, y_pred) |
|
# выведем матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |

Сравним фактическое и прогнозное распределение классов на точечной диаграмме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз one-vs-rest’, fontsize = 14) plt.show() |
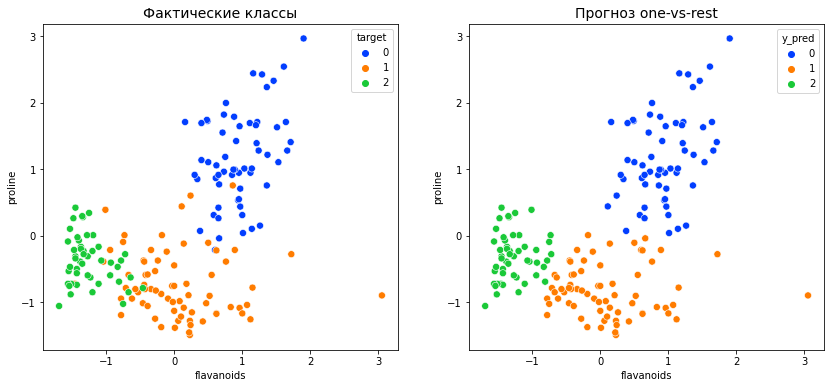
Написание класса
Поместим достигнутый выше результат в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
class OVR_LogReg(): def __init__(self): self.models_thetas = [] self.models_loss = [] def fit(self, x, y, iter = 20000, learning_rate = 0.001): dfs = self.preprocess(x, y) models_thetas, models_loss = [], [] for ovr_df in dfs: x = ovr_df.drop(‘target’, axis = 1).copy() y = ovr_df.target.copy() self.add_ones(x) loss_history = [] thetas, n = np.zeros(x.shape[1]), x.shape[0] for i in range(iter): y_pred = self.h(x, thetas) loss_history.append(self.objective(y, y_pred)) grad = self.gradient(x, y, y_pred, n) thetas -= learning_rate * grad models_thetas.append(thetas) models_loss.append(loss_history) self.models_thetas = models_thetas self.models_loss = models_loss def predict(self, x): x = x.copy() probs = [] self.add_ones(x) for t in self.models_thetas: z = np.dot(x, t) prob = np.array([self.stable_sigmoid(value) for value in z]) probs.append(prob) all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T y_pred = np.argmax(all_probs, axis = 1) return y_pred, all_probs def preprocess(self, x, y): x, y = x.copy(), y.copy() x[‘target’] = y classes = x.target.unique() dfs = [] ovr_df = None for c in classes: ovr_df = x.drop(‘target’, axis = 1).copy() ovr_df[‘target’] = np.where(x[‘target’] == classes[c], 1, 0) dfs.append(ovr_df) return dfs def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим класс в работе.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = OVR_LogReg() model.fit(X, y) y_pred, probs = model.predict(X) accuracy_score(y_pred, y) |
Сравнение с sklearn
Сравним с sklearn. Для того чтобы применить подход one-vs-rest в классе LogisticRegression, необходимо использовать значение параметра multi_class = ‘ovr’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] ovr_model = LogisticRegression(multi_class = ‘ovr’) ovr_model = ovr_model.fit(X, y) y_pred = ovr_model.predict(X) accuracy_score(y_pred, y) |
Мультиклассовая полиномиальная регрессия
Как мы увидели в предыдущем разделе, линейная решающая граница допустила некоторое количество ошибок. Попробуем улучшить результат, применив мультиклассовую полиномиальную логистическую регрессию.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] polynomial_features = PolynomialFeatures(degree = 7) X_poly = polynomial_features.fit_transform(X) poly_ovr_model = LogisticRegression(multi_class = ‘ovr’) poly_ovr_model = poly_ovr_model.fit(X_poly, y) y_pred = poly_ovr_model.predict(X_poly) accuracy_score(y_pred, y) |
Как мы видим результат, по сравнению с моделью sklearn без полиномиальных признаков, стал чуть лучше. Однако это было достигнуто за счет полинома достаточно высокой степени (degree = 7), что неэффективно с точки зрения временной сложности алгоритма.
Посмотрим, какие нелинейные решающие границы удалось построить алгоритму.
|
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Полиномиальная регрессия’, fontsize = 14) plt.show() |

Softmax Regression
Еще один подход при создании мультиклассовой логистической регрессии заключается в том, чтобы не разбивать многоклассовые данные таким образом, чтобы использовать бинарный классификатор, а сразу применять функции, которые подходят для работы с множеством классов.
Такую регрессию часто называют Softmax Regression из-за того, что в ней используется уже знакомая нам по занятию об основах нейросетей функция softmax. Вначале подготовим данные.
Подготовка признаков
Возьмем признаки flavanoids и proline и добавим столбец из единиц.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
X = df[[‘flavanoids’, ‘proline’]] add_ones(X) X.head(3) |

Кодирование целевой переменной
Напишем собственную функцию для one-hot encoding.
|
def ohe(y): # количество примеров и количество классов examples, features = y.shape[0], len(np.unique(y)) # нулевая матрица: количество наблюдений x количество признаков zeros_matrix = np.zeros((examples, features)) # построчно проходимся по нулевой матрице и с помощью индекса заполняем соответствующее значение единицей for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
y = df[‘target’] y_enc = ohe(df[‘target’]) y_enc[:3] |
|
array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]]) |
Такой же результат можно получить с помощью класса LabelBinarizer.
|
lb = LabelBinarizer() lb.fit(y) lb.classes_ |
|
y_lb = lb.transform(y) y_lb[:5] |
|
array([[1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0]]) |
Инициализация весов
Создадим нулевую матрицу весов. Она будет иметь размерность: количество признаков (строки) х количество классов (столбцы). Приведем схематичный пример для четырех наблюдений, трех признаков (включая сдвиг $theta_0$) и трех классов.

Инициализируем веса.
|
thetas = np.zeros((3, 3)) thetas |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Функция softmax
Подробнее изучим функцию softmax. Приведем формулу.
$$ text{softmax}(z)_{i} = frac{e^{z_i}}{sum_{k=1}^N e^{z_k}} $$
Рассмотрим ее реализацию на Питоне.
Напомню, что $ z = (-Xtheta) $. Соответственно в нашем случае мы будем умножать матрицу 178 x 3 на 3 x 3.
В результате получим матрицу 178 x 3, где каждая строка — это прогнозные значения принадлежности одного наблюдения к каждому из трех классов.
|
z = np.dot(—X, thetas) z.shape |
Так как мы умножаем на ноль, при первой итерации эти значения будут равны нулю.
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Для того чтобы обеспечить вычислительную устойчивость softmax мы можем вычесть из z максимальное значение в каждой из 178 строк (пока что, опять же на первой итерации, оно равно нулю).
$$ text{softmax}(z)_{i} = frac{e^{z_i-max(z)}}{sum_{k=1}^N e^{z_k-max(z)}} $$
|
# axis = -1 — это последняя ось # keepdims = True сохраняет размерность (в данном случае двумерный массив) np.max(z, axis = —1, keepdims = True)[:5] |
|
array([[0.], [0.], [0.], [0.], [0.]]) |
|
z = z — np.max(z, axis = —1, keepdims = True) z[:5] |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Смысл такого преобразования⧉ в том, что оно делает значения z нулевыми или отрицательными.
|
arr = np.array([—2, 3, 0, —7, 6]) arr — max(arr) |
|
array([ -8, -3, -6, -13, 0]) |
Далее, число возводимое в увеличивающуюся отрицательную степень стремится к нулю, а не к бесконечности и, таким образом, не вызывает переполнения памяти. Найдем числитель и знаменатель из формулы softmax.
|
numerator = np.exp(z) numerator[:5] |
|
array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.]]) |
|
denominator = np.sum(numerator, axis = —1, keepdims = True) denominator[:5] |
|
array([[3.], [3.], [3.], [3.], [3.]]) |
Разделим числитель и знаменатель и, таким образом, вычислим вероятность принадлежности каждого из наблюдений (строки результата) к одному из трех классов (столбцы).
|
softmax = numerator / denominator softmax[:5] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
На первой итерации при одинаковых $theta$ мы получаем, что логично, одинаковые вероятности принадлежности к каждому из классов. Напишем функцию.
|
def stable_softmax(x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax |
|
probs = stable_softmax(X, thetas) probs[:3] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
Примечание. Обратите внимание, что сигмоида — это частный случай функции softmax для двух классов $[z_1, 0]$. Вероятность класса $z_1$ будет равна
$$ softmax(z_1) = frac{e^{z_1}}{e^{z_1}+e^0} = frac{e^{z_1}}{e^{z_1}+1} $$
Если разделить и числитель, и знаменатель на $e^{z_1}$, то получим
$$ sigmoid(z_1) = frac{e^{z_1}}{1 + e^{-z_1}} $$
Вычислять вероятность принадлежности ко второму классу нет необходимости, достаточно вычесть результат сигмроиды из единицы.
Теперь нужно понять, насколько сильно при таких весах ошибается наш алгоритм.
Функция потерь
Вспомним функцию бинарной кросс-энтропии. То есть функции ошибки для двух классов.
$$ L(y, theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Напомню, что y выступает в роли своего рода переключателя, сохраняющего одну из частей выражения, и обнуляющего другую. Теперь посмотрите на функцию категориальной (многоклассовой) кросс-энтропии (categorical cross-entropy).
$$ L(y_{ohe}, softmax) = -sum y_{ohe} log(softmax) $$
Разберемся, что здесь происходит. $y_{ohe}$ содержит закодированную целевую переменную, например, для наблюдения класса 0 [1, 0, 0], softmax содержит вектор вероятностей принадлежности набюдения к каждому из классов, например, [0,3 0,4 0,3] (мы видим, что алгоритм ошибается).
В данном случае закодированная целевая переменная также выступает в виде перерключателя. Здесь при умножении «срабатывает» только первая вероятность $1 times 0,3 + 0 times 0,4 + 0 times 0,4 $. Если подставить в формулу, то получаем (np.sum() добавлена для сохранения единообразия с формулой выше, в данном случае у нас одно наблюдение и сумма не нужна)
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.3, 0.4, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Если бы модель в своих вероятностях ошибалась бы меньше, то и общая ошибка была бы меньше.
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.4, 0.3, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Функция $-log$ позволяет снижать ошибку при увеличении вероятности верного (сохраненного переключателем) класса.
|
x_arr = np.linspace(0.001,1, 100) sns.lineplot(x=x_arr,y=—np.log(x_arr)) plt.title(‘Plot of -log(x)’) plt.xlabel(‘x’) plt.ylabel(‘-log(x)’); |

Напишем функцию.
|
# добавим константу в логарифм для вычислительной устойчивости def cross_entropy(probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Рассчитаем ошибку для нулевых весов.
|
ce = cross_entropy(probs, y_enc) ce |
Для снижения ошибки нужно найти градиент.
Градиент
Приведем формулу градиента без дифференцирования.
$$ nabla_{theta}J = frac{1}{n} times X^T cdot (y_{ohe}-softmax) $$
По сути, мы умножаем транспонированную матрицу признаков (3 x 178) на разницу между закодированной целевой переменной и вероятностями функции softmax (178 x 3).
|
def gradient_softmax(X, probs, y_enc): # если не добавить функцию np.array(), будет выводиться датафрейм return np.array(1 / probs.shape[0] * np.dot(X.T, (y_enc — probs))) |
|
gradient_softmax(X, probs, y_enc) |
|
array([[-0.00187266, 0.06554307, -0.06367041], [ 0.31627721, 0.02059572, -0.33687293], [ 0.38820566, -0.28801792, -0.10018774]]) |
Обучение модели, прогноз и оценка качества
Выполним обучение модели.
|
loss_history = [] # в цикле for i in range(30000): # рассчитаем прогнозное значение с текущими весами probs = stable_softmax(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(cross_entropy(probs, y_enc, epsilon = 1e—9)) # рассчитаем градиент grad = gradient_softmax(X, probs, y_enc) # используем градиент для улучшения весов модели thetas = thetas — 0.002 * grad |
Посмотрим на получившиеся коэффициенты (напомню, что первая строка матрицы это сдвиг (intercept, $theta_0$)) и достигнутый уровень ошибки.
|
array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]) |
|
loss_history[0], loss_history[—1] |
|
(1.0986122856681098, 0.2569641080523888) |
Сделаем прогноз и оценим качество.
|
y_pred = np.argmax(stable_softmax(X, thetas), axis = 1) |
|
accuracy_score(y, y_pred) |
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |

Написание класса
Объединим созданные выше компоненты в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
class SoftmaxLogReg(): def __init__(self): self.loss_ = None self.thetas_ = None def fit(self, x, y, iter = 30000, learning_rate = 0.002): loss_history = [] self.add_ones(x) y_enc = self.ohe(y) thetas = np.zeros((x.shape[1], y_enc.shape[1])) for i in range(iter): probs = self.stable_softmax(x, thetas) loss_history.append(self.cross_entropy(probs, y_enc, epsilon = 1e—9)) grad = self.gradient_softmax(x, probs, y_enc) thetas = thetas — 0.002 * grad self.thetas_ = thetas self.loss_ = loss_history def predict(self, x, y): return np.argmax(self.stable_softmax(x, thetas), axis = 1) def stable_softmax(self, x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax def cross_entropy(self, probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce def gradient_softmax(self, x, probs, y_enc): return np.array(1 / probs.shape[0] * np.dot(x.T, (y_enc — probs))) def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def ohe(self, y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
Обучим модель, сделаем прогноз и оценим качество.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = SoftmaxLogReg() model.fit(X, y) model.thetas_, model.loss_[—1] |
|
(array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]), 0.2569641080523888) |
|
y_pred = model.predict(X, y) accuracy_score(y, y_pred) |
Сравнение с sklearn
Для того чтобы использовать softmax логистическую регрессию в sklearn, соответствующему классу нужно передать параметр multi_class = ‘multinomial’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression(multi_class = ‘multinomial’) # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([ 0.09046097, 1.12593099, -1.21639196]), array([[ 1.86357908, 1.89698292], [ 0.86696131, -1.43973164], [-2.73054039, -0.45725129]])) |
|
y_pred = model.predict(X) accuracy_score(y, y_pred) |
Подведем итог
Сегодня мы разобрали множество разновидностей и подходов к использованию линейной регрессии. Давайте систематизируем изученный материал с помощью следующей схемы.

Рассмотрим обучение нейронных сетей.
|
|
Макеты страниц
а) Оценки. Наиболее распространенные формы представления данных в задаче оценивания коэффициентов линейной регрессии показаны в табл. 6.5.1 и 6.5.2. Причем мы предполагаем, что

В целях удобства формулу для  в (6.5.1) перепишем в несколько ином виде:
в (6.5.1) перепишем в несколько ином виде:

где

Необходимо оценить три параметра  и а (заметим, что здесь а отлична от а в формуле (6.5.1)). Обозначая а из (6.5.1) через а, мы получаем
и а (заметим, что здесь а отлична от а в формуле (6.5.1)). Обозначая а из (6.5.1) через а, мы получаем

В дальнейшем будем использовать запись (6.5.4). Функция правдоподобия, нетрудно видеть, пропорциональна

где, следуя обозначениям табл. 6.5.1,

где  Логарифм функции правдоподобия равен:
Логарифм функции правдоподобия равен:

 — общий объем выборки. Дифференцируем:
— общий объем выборки. Дифференцируем:

что приводит к

поскольку  по определению х. Аналогично
по определению х. Аналогично

Приравнивая обе производные к нулю, приходим к оценкам максимального правдоподобия:

общее среднее,

где x определяется по формуле (6.5.5).
Если бы  задавались по формуле (6.5.1), а не по формуле (6.5.4), то мы бы имели недиагональную систему уравнений относительно
задавались по формуле (6.5.1), а не по формуле (6.5.4), то мы бы имели недиагональную систему уравнений относительно  решить которую было бы сложнее; по этой причине более простой вид имеют и решения этой системы — (6.5.6) и (6.5.7). Еще одно положительное свойство записи (6.5.4) заключается в том, что оценки
решить которую было бы сложнее; по этой причине более простой вид имеют и решения этой системы — (6.5.6) и (6.5.7). Еще одно положительное свойство записи (6.5.4) заключается в том, что оценки  распределены независимо друг от друга.
распределены независимо друг от друга.
б) Выборочные свойства оценок. Чтобы получить представление о точности этих оценок, нет необходимости пользоваться приближенными формулами из раздела 6.2.5. Поскольку  — линейные функции
— линейные функции  которые по условию нормально распределены, они также имеют нормальное распределение. Выборочные математические ожидания, дисперсия и ковариации будут следующими:
которые по условию нормально распределены, они также имеют нормальное распределение. Выборочные математические ожидания, дисперсия и ковариации будут следующими:

т. е. оценки не смещены:

Таким образом,  независимо распределены [см. II, раздел 13.4.2].
независимо распределены [см. II, раздел 13.4.2].
Теперь найдем оценку для  . Уравнение
. Уравнение  приводит к следующей оценке:
приводит к следующей оценке:

где  обозначает сумму квадратов (Sum of Squared) отклонений:
обозначает сумму квадратов (Sum of Squared) отклонений:

С вычислительной точки зрения формула  лучше, чем
лучше, чем 
На практике пользуются не оценкой максимального правдоподобия для  а некоторой ее модификацией:
а некоторой ее модификацией:

Можно показать, что в отличие от первой оценки она является несмещенной. Однако не свойство несмещенности делает эту оценку предпочтительней. Более важно то, что оценка (6.5.11) согласована с существующими статистическими таблицами. (Несколько замечаний сделаем относительно последней формулы. Читателю может показаться странным, что в (6.5.11) делителем является значение  , а не более привычное
, а не более привычное  Использование
Использование  вместо
вместо  повлекло бы за собой лишь дополнительное видоизменение статистических таблиц, к тому же статистика (6.5.11) является несмещенной оценкой
повлекло бы за собой лишь дополнительное видоизменение статистических таблиц, к тому же статистика (6.5.11) является несмещенной оценкой 
в) Доверительные интервалы для  Как уже было отмечено,
Как уже было отмечено,  являются линейными комбинациями нормально распределенных случайных величин и имеют математические ожидания, равные
являются линейными комбинациями нормально распределенных случайных величин и имеют математические ожидания, равные  соответственно. Их дисперсии можно оценить как
соответственно. Их дисперсии можно оценить как

где  задается формулой (6.5.11), т. е.
задается формулой (6.5.11), т. е.

где  определяется в (6.5.10). Можно показать (например, с помощью методов из раздела 2.5.8), что случайная величина
определяется в (6.5.10). Можно показать (например, с помощью методов из раздела 2.5.8), что случайная величина

имеет распределение  степенями свободы [см. раздел 2.5.4, а)] и стохастически независима от
степенями свободы [см. раздел 2.5.4, а)] и стохастически независима от  . Отсюда следует, что
. Отсюда следует, что

имеет распределение Стьюдента с  степенями свободы [см. раздел 2.5.5]. Таким образом, центральным 95%-ным доверительным интервалом для а будет
степенями свободы [см. раздел 2.5.5]. Таким образом, центральным 95%-ным доверительным интервалом для а будет

[ср. с примером 4.5.2], где  является 97,5%-ной точкой распределения Стьюдента с
является 97,5%-ной точкой распределения Стьюдента с  степенями свободы.
степенями свободы.
Аналогично находят 95%-ный доверительный интервал для  :
:

г) Критерий значимости для  Как следует из предыдущих рассуждений (односторонний) уровень значимости для разности
Как следует из предыдущих рассуждений (односторонний) уровень значимости для разности  , где
, где  — гипотетическое значение неизвестного коэффициента регрессии, может быть найден благодаря тому, что случайная величина t имеет распределение Стьюдента с
— гипотетическое значение неизвестного коэффициента регрессии, может быть найден благодаря тому, что случайная величина t имеет распределение Стьюдента с  степенями свободы, где
степенями свободы, где

Аналогичное утверждение справедливо и для  в этом случае
в этом случае

При двухстороннем критерии уровень значимости удваивается.
Критерий, основанный на (6.5.16), — один из наиболее распространенных статистических критериев. Наиболее часто он применяется при условии  в этом случае на основе его проверяется, есть ли значимая (линейная) зависимость у от х.
в этом случае на основе его проверяется, есть ли значимая (линейная) зависимость у от х.
д) Доверительный интервал для  Линейная модель
Линейная модель

эквивалентна

или

где  обозначает оценку ожидаемого отклика при условии, что независимая переменная х примет значение
обозначает оценку ожидаемого отклика при условии, что независимая переменная х примет значение  вычислено по формуле (6.5.5). Поскольку
вычислено по формуле (6.5.5). Поскольку  нормально распределены с параметрами, задаваемыми выражениями (6.5.8) и (6.5.9), случайная величина
нормально распределены с параметрами, задаваемыми выражениями (6.5.8) и (6.5.9), случайная величина  также будет иметь нормальное распределение с математическим
также будет иметь нормальное распределение с математическим

Рис. 6.5.1. Линия регрессии и 95%-ный доверительный интервал (коридор) для 
ожиданием, равным а  и дисперсией, оценку которой можно найти по формуле
и дисперсией, оценку которой можно найти по формуле

Легко видеть, что минимальное значение этой величины достигается при  (т. е. наименьшая дисперсия будет наблюдаться вблизи «середины» данных по х). Наоборот, при возрастании расстояния
(т. е. наименьшая дисперсия будет наблюдаться вблизи «середины» данных по х). Наоборот, при возрастании расстояния  от х дисперсия также будет возрастать. Этот эффект иллюстрируется на рис. 6.5.1, где показаны также линия регрессии
от х дисперсия также будет возрастать. Этот эффект иллюстрируется на рис. 6.5.1, где показаны также линия регрессии  и кривые
и кривые  которые для каждого х задают приближенно 95%-ный доверительный интервал (коридор) для а
которые для каждого х задают приближенно 95%-ный доверительный интервал (коридор) для а  Расчет данных показателей позволяет оценить качество экстраполяции у по х в зависимости от величины
Расчет данных показателей позволяет оценить качество экстраполяции у по х в зависимости от величины  Множитель 2 получен в результате округления, более точно интервальной оценкой значения а
Множитель 2 получен в результате округления, более точно интервальной оценкой значения а  на основе а
на основе а  служит 95%-ный доверительный интервал
служит 95%-ный доверительный интервал

где  -ная точка распределения Стьюдента с
-ная точка распределения Стьюдента с  степенями свободы
степенями свободы 
Пример 6.5.1. Линейная регрессия. Методы, изложенные в разделе 6.5.3, проиллюстрируем на данных из табл. 6.5.3, где измерения зависимой переменной являются логарифмом числа фацет глаза насекомых семейства Drosophela Melanogaster при различных уровнях

Рис. 6.5.2. Зависимость средних значений от температуры, данные см. в табл. 6.5.3 (наблюдения отмечены кружками). Оцененная линия регрессий  )
)
температуры. Данные имеют вид таблицы частот типа табл. 5.8.4 (значения зависимой переменной обозначают  тогда как в табл. 5.8.4 они обозначены как
тогда как в табл. 5.8.4 они обозначены как  значения независимой переменной обозначены
значения независимой переменной обозначены  и соответствуют выбранным экспериментатором уровням температуры).
и соответствуют выбранным экспериментатором уровням температуры).
Данные из табл. 6.5.3 анализировались в примере 5.8.5, где было обнаружено влияние температуры. Даже визуальный анализ убеждает в том, что температура оказывает отрицательное воздействие на зависимую переменную; это и было подтверждено в примере 5.8.5. Цель данного примера — провести анализ данных в предположении, что исследуемая зависимость от температуры представляет собой линейную регрессию. Прежде чем приступать к соответствующим расчетам, необходимо убедиться в том, что гипотеза линейности в действительности справедлива. Для этого нанесем данные на график (рис. 6.5.2), по оси ординат отложим средние значения зависимой переменной, а по оси абсцисс — соответствующую температуру. Как следует из этого графика, за исключением скачка между 23° и 25°, который вполне мог произойти за счет случайных колебаний, средние действительно достаточно хорошо ложатся на прямую линию. Наклон этой прямой, оцененный на глаз, приблизительно равен —0,79.
Итак, будем считать, что линейная регрессия в данной задаче адекватна; для оценивания параметров  модели
модели

воспользуемся методами из раздела 6.5.3. Оценкой отклика тогда будет служить выражение

Для нашей выборки статистики принимают следующие значения:

Как следует из (6.5.6) и (6.5.7),

В табл. 6.5.4 приведены значения  с наблюдаемыми значениями у.
с наблюдаемыми значениями у.
Таблица 6.5.3. (см. скан) Зависимость числа фацет глаза от температуры
Продолжение табл. 6.5.3 (см. скан)
Таблица 6.5.4. (см. скан) Оцененные значения  и их сравнения с наблюдаемыми величинами
и их сравнения с наблюдаемыми величинами 
При оценивании стандартных ошибок для  и необходимо вычислить сумму квадратов отклонений (т. е. сумму квадратов разности между наблюдаемыми значениями и значениями, полученными по модели) по формуле (6.5.10). В наших обозначениях эта величина равна:
и необходимо вычислить сумму квадратов отклонений (т. е. сумму квадратов разности между наблюдаемыми значениями и значениями, полученными по модели) по формуле (6.5.10). В наших обозначениях эта величина равна:

Поскольку  первые два члена равны
первые два члена равны  что представляет собой общую сумму квадратов см. (5.8.18), ее численное значение можно найти в табл. 5.8.5, оно равно 16,202. Таким образом,
что представляет собой общую сумму квадратов см. (5.8.18), ее численное значение можно найти в табл. 5.8.5, оно равно 16,202. Таким образом,

Отсюда следует, что оценка дисперсии, определяемая по формуле (6.5.11), равна:

а соответствующие оценки выборочных дисперсий для  вычисляемые по формуле (6.5.12), равны:
вычисляемые по формуле (6.5.12), равны:

95%-ные доверительные интервалы для  определяются в (6.5.13) и (6.5.14). Для параметра а:
определяются в (6.5.13) и (6.5.14). Для параметра а:

для параметра (3:

Для проверки гипотезы  (зависимость от температуры отсутствует), как следует из (6.5.15) и (6.5.16), необходимо найти значение
(зависимость от температуры отсутствует), как следует из (6.5.15) и (6.5.16), необходимо найти значение  -статистики
-статистики

Высокое значение этой статистики не вызывает сомнения в ошибочности гипотезы 
95%-ный доверительный коридор для значений регрессии, задаваемый формулой (6.5.18), требует знания величины  которая вычисляется по формуле (6.5.17); в нашем случае она равна:
которая вычисляется по формуле (6.5.17); в нашем случае она равна:

Подставляя это выражение в (6.5.18) и полагая  находим доверительный коридор для Я. Для некоторых х он показан в табл. 6.5.5.
находим доверительный коридор для Я. Для некоторых х он показан в табл. 6.5.5.
1
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- Глава I. ВВЕДЕНИЕ В СТАТИСТИКУ
- 1.1. СМЫСЛ ПОНЯТИЯ «СТАТИСТИКА»
- 1.2. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ, СТАТИСТИКА, ОЦЕНКА
- 1.3. ТЕМА ЭТОЙ КНИГИ
- 1.4. СОГЛАШЕНИЯ И ОБОЗНАЧЕНИЯ
- Глава 2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
- 2.1. МОМЕНТЫ И ДРУГИЕ СТАТИСТИКИ
- 2.1.2. МОМЕНТЫ
- 2.2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ: ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
- 2.3. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАТИСТИК
- 2.3.1. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ СРЕДНЕГО ЗНАЧЕНИЯ ВЫБОРКИ
- 2.3.2. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ ДИСПЕРСИИ ВЫБОРКИ
- 2.3.3. ВЫБОРОЧНАЯ КОВАРИАЦИЯ МЕЖДУ СРЕДНИМ ЗНАЧЕНИЕМ ВЫБОРКИ x И ДИСПЕРСИЕЙ ВЫБОРКИ v
- 2.3.4. ВЫБОРОЧНЫЕ МОМЕНТЫ ДЛЯ МОМЕНТОВ ВЫБОРКИ БОЛЕЕ ВЫСОКИХ ПОРЯДКОВ
- 2.3.5. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАНДАРТНОГО ОТКЛОНЕНИЙ ВЫБОРКИ
- 2.3.6. ВЫБОРОЧНЫЕ МОМЕНТЫ КОЭФФИЦИЕНТА АСИММЕТРИИ ВЫБОРКИ
- 2.4. РАСПРЕДЕЛЕНИЯ СУММ НЕЗАВИСИМЫХ ОДИНАКОВО РАСПРЕДЕЛЕННЫХ ПЕРЕМЕННЫХ
- 2.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
- 2.5.2. РЕЗУЛЬТАТ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СТАНДАРТИЗАЦИЯ
- 2.5.3. ЛИНЕЙНЫЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
- 2.5.4. КВАДРАТИЧЕСКИЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
- 2.5.5. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА (t-распределение)
- 2.5.6. РАСПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ДИСПЕРСИЙ (F-распределение)
- 2.5.7. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ВЫБОРКИ
- 2.5.8. НЕЗАВИСИМОСТЬ КВАДРАТИЧНЫХ ФОРМ. ТЕОРЕМА ФИШЕРА—КОКРЕНА. ТЕОРЕМА КРЕЙГА
- 2.5.9. РАЗМАХ И СТЬЮДЕНТИЗИРОВАННЫЙ РАЗМАХ
- 2.6. АССИМПТОТИЧЕСКОЕ ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ х И НЕЛИНЕЙНЫХ ФУНКЦИЙ ОТ х
- 2.7. ПРИБЛИЖЕНИЕ ВЫБОРОЧНЫХ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ НЕЛИНЕЙНЫХ СТАТИСТИК. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
- 2.7.1. АППРОКСИМАЦИЯ
- 2.7.2. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ
- 2.7.3. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
- 2.7.4. ПРЕОБРАЗОВАНИЯ, ВЫПРЯМЛЯЮЩИЕ ЗАВИСИМОСТЬ
- 2.7.5. ПРЕОБРАЗОВАНИЕ ВЫБОРОЧНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ПРИ r=0 В СТЬЮДЕНТОВУ ВЕЛИЧИНУ
- 2.7.6. ПРЕОБРАЗОВАНИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПЕРЕМЕННОЙ В «хи-квадрат»-ПЕРЕМЕННУЮ
- 2.8. НЕЦЕНТРАЛЬНЫЕ ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
- 2.8.1. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ХИ-КВАДРАТ
- 2.8.2. НЕЦЕНТРАЛЬНОЕ F-РАСПРЕДЕЛЕНИЕ
- 2.8.3. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
- 2.9. ПОЛИНОМИАЛЬНОЕ (МУЛЬТИНОМИАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ В ТЕОРИИ ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ
- 2.9.1. БИНОМИАЛЬНОЕ, ТРИНОМИАЛЬНОЕ И МУЛЬТИНОМИАЛЬНОЕ (ПОРЯДКА m) РАСПРЕДЕЛЕНИЯ
- 2.9.2. СВОЙСТВА ПОЛИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 2.9.3. ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК УСЛОВНОЕ ОТ СОВМЕСТНОГО РАСПРЕДЕЛЕНИЯ НЕЗАВИСИМЫХ ПУАССОНОВСКИХ ПЕРЕМЕННЫХ
- 2.9.4. ТАБЛИЦЫ ЧАСТОТ
- 2.10. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
- Глава 3. ОЦЕНИВАНИЕ. ВВОДНОЕ ОБОЗРЕНИЕ
- 3.1. ЗАДАЧА ОЦЕНИВАНИЯ
- 3.2. ИНТУИТИВНЫЕ ПРЕДСТАВЛЕНИЯ И ГРАФИЧЕСКИЙ МЕТОД
- 3.2.2. ЧАСТОТНЫЕ ТАБЛИЦЫ, ГИСТОГРАММЫ И ЭМПИРИЧЕСКАЯ ф.р.
- 3.3. НЕКОТОРЫЕ ОБЩИЕ КОНЦЕПЦИИ И КРИТЕРИИ ОЦЕНОК
- 3.3.1. ВВЕДЕНИЕ. РАЗМЕРНОСТЬ, ЗАМЕНЯЕМОСТЬ, СОСТОЯТЕЛЬНОСТЬ, КОНЦЕНТРАЦИЯ
- 3.3.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ И НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ
- 3.3.3. ЭФФЕКТИВНОСТЬ. ГРАНИЦА КРАМЕРА—РАО
- 3.4. ДОСТАТОЧНОСТЬ
- 3.4.2. КРИТЕРИЙ ФАКТОРИЗАЦИИ И ЭКСПОНЕНЦИАЛЬНОЕ СЕМЕЙСТВО
- 3.4.3. ДОСТАТОЧНОСТЬ И НЕСМЕЩЕННАЯ МИНИМАЛЬНО ДИСПЕРСНАЯ ОЦЕНКА
- 3.4.4. ДОСТАТОЧНОСТЬ В СЛУЧАЕ МНОГИХ ПАРАМЕТРОВ
- 3.5. ПРАКТИЧЕСКИЕ МЕТОДЫ ПОСТРОЕНИЯ ОЦЕНОК. ВВЕДЕНИЕ
- 3.5.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 3.5.3. МЕТОД МОМЕНТОВ
- 3.5.4. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 3.5.5. НОРМАЛЬНЫЕ ЛИНЕЙНЫЕ МОДЕЛИ, В КОТОРЫХ ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ И НАИМЕНЬШИХ КВАДРАТОВ СОВПАДАЮТ
- Глава 4. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
- 4.1.2. СТАНДАРТНОЕ ОТКЛОНЕНИЕ
- 4.1.3. ИНТЕРВАЛЫ ВЕРОЯТНОСТИ
- 4.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ
- 4.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА С ПОМОЩЬЮ ОПОРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
- 4.4. ИСТОЛКОВАНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА КАК МЕРЫ ТОЧНОСТИ ОЦЕНКИ НЕИЗВЕСТНОГО ПАРАМЕТРА
- 4.5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ПРИ НЕСКОЛЬКИХ ПАРАМЕТРАХ
- 4.5.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ФУНКЦИЙ ДВУХ ПАРАМЕТРОВ, ВКЛЮЧАЮЩИХ ОТНОШЕНИЕ ПАРАМЕТРОВ И ИХ РАЗНОСТЬ (ТЕОРЕМА ФЕЛЛЕРА)
- 4.6. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ БЕЗ ИСПОЛЬЗОВАНИЯ ОПОРНОЙ ПЕРЕМЕННОЙ
- 4.7. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ ДЛЯ ПАРАМЕТРОВ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ
- 4.8. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ КВАНТИЛЕЙ, НЕ ЗАВИСЯЩИЕ ОТ ИСХОДНОГО РАСПРЕДЕЛЕНИЯ (РАСПРЕДЕЛЕННЫЕ СВОБОДНО)
- 4.9. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ МНОГОМЕРНОГО ПАРАМЕТРА
- 4.9.2. ЭЛЛИПТИЧЕСКИЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ВЕКТОРА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ДВУМЕРНОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ. ПРИБЛИЖЕННЫЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ОЦЕНОК НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ
- 4.10. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ НА ОСНОВЕ БОЛЬШИХ ВЫБОРОК С ИСПОЛЬЗОВАНИЕМ ФУНКЦИИ ПРАВДОПОДОБИЯ
- 4.10.2. ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ ПРОИЗВОДНОЙ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ ПРАВДОПОДОБИЯ
- 4.10.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ (ПРИБЛИЖЕННО) НОРМАЛИЗУЮЩЕГО ПРЕОБРАЗОВАНИЯ
- 4.11. ДОВЕРИТЕЛЬНАЯ ПОЛОСА ДЛЯ НЕИЗВЕСТНОЙ НЕПРЕРЫВНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- 4.11.2. РАССТОЯНИЕ КОЛМОГОРОВА—СМИРНОВА МЕЖДУ ИСТИННОЙ (ТЕОРЕТИЧЕСКОЙ) И ЭМПИРИЧЕСКОЙ ФУНКЦИЯМИ РАСПРЕДЕЛЕНИЯ
- 4.11.3. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ СТАТИСТИКИ КОЛМОГОРОВА—СМИРНОВА. ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ ДЛЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- 4.12. ТОЛЕРАНТНЫЕ ИНТЕРВАЛЫ
- 4.13. ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
- 4.13.2. ПРАВДОПОДОБНЫЕ ЗНАЧЕНИЯ И ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
- 4.13.3. СИТУАЦИЯ С ДВУМЯ ПАРАМЕТРАМИ
- 4.14. БАЙЕСОВСКИЕ ИНТЕРВАЛЫ
- Глава 5. СТАТИСТИЧЕСКИЕ КРИТЕРИИ
- 5.2.1. ДВУХСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ. СОСТАВНЫЕ ЧАСТИ, ПРОЦЕДУРА И ИНТЕРПРЕТАЦИЯ
- 5.2.2. ТРАДИЦИОННАЯ ИНТЕРПРЕТАЦИЯ УРОВНЕЙ ЗНАЧИМОСТИ; ИСПОЛЬЗУЕМЫЕ НА ПРАКТИКЕ УРОВНИ ЗНАЧИМОСТИ; КРИТИЧЕСКАЯ ОБЛАСТЬ
- 5.2.3. ОДНОСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ
- 5.2.4. КРИТЕРИИ О РАСПРЕДЕЛЕНИИ ПУАССОНА
- 5.2.5. КРИТЕРИИ ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
- 5.2.6. ВЫБОР СТАТИСТИКИ КРИТЕРИЯ
- 5.3. КРИТЕРИИ ДЛЯ ПРОВЕРКИ ГИПОТЕЗ
- 5.3.2. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ОДНОСТОРОННЕГО КРИТЕРИЯ ДЛЯ ВЫБОРКИ ИЗ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ, КОГДА ЗНАЧЕНИЕ «сигма» НЕИЗВЕСТНО
- 5.3.3. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ДВУХСТОРОННЕГО КРИТЕРИЯ
- 5.4. КРИТЕРИИ ДЛЯ СЛОЖНЫХ НУЛЕВЫХ ГИПОТЕЗ
- 5.4.2. КРИТЕРИИ НЕЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ 2×2. ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА
- 5.5. КРИТЕРИИ, СОДЕРЖАЩИЕ БОЛЕЕ ОДНОГО ПАРАМЕТРА. ОБОБЩЕННЫЕ КРИТЕРИИ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
- 5.6. АППРОКСИМАЦИЯ УРОВНЯ ЗНАЧИМОСТИ КРИТЕРИЯ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ ДЛЯ БОЛЬШИХ ВЫБОРОК
- 5.7. КРИТЕРИИ РАНДОМИЗАЦИИ
- 5.8. СТАНДАРТНЫЕ КРИТЕРИИ ДЛЯ МОДЕЛИ С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
- 5.8.2. ЗНАЧИМОСТЬ СРЕДНЕГО, КОГДА ДИСПЕРСИЯ НЕИЗВЕСТНА. t-КРИТЕРИЙ СТЬЮДЕНТА
- 5.8.3. КРИТЕРИЙ ФИШЕРА-БЕРЕНСА ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ
- 5.8.4. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ (КОГДА ДИСПЕРСИИ РАВНЫ)
- 5.8.5. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА РЕГРЕССИИ В ПРОСТОЙ ЛИНЕЙНОЙ МОДЕЛИ
- 5.8.6. КРИТЕРИЙ РАВЕНСТВА ДВУХ ДИСПЕРСИЙ
- 5.8.7 ПРОВЕРКА РАВЕНСТВА НЕКОТОРЫХ СРЕДНИХ. ВВЕДЕНИЕ В ДИСПЕРСИОННЫЙ АНАЛИЗ
- 5.9. ПРОВЕРКА НОРМАЛЬНОСТИ
- 5.10. ПРОВЕРКА РАВЕНСТВА к ДИСПЕРСИЙ (КРИТЕРИЙ БАРТЛЕТТА)
- 5.11. СОЧЕТАНИЕ РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ КРИТЕРИЕВ
- 5.12. ТЕОРИЯ НЕЙМАНА—ПИРСОНА
- 5.12.2. ТЕОРИЯ НЕЙМАНА-ПИРСОНА ПРОВЕРКИ ГИПОТЕЗ
- Глава 6. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.2. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.2.2. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.2.3. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ИНТУИТИВНАЯ АРГУМЕНТАЦИЯ
- 6.2.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ТИПЫ МАКСИМУМОВ
- 6.2.5. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ. СВОЙСТВА ФУНКЦИИ ПРАВДОПОДОБИЯ
- 6.2.6. ОЦЕНИВАНИЕ ФУНКЦИИ ПАРАМЕТРА «тетта». СВОЙСТВО ИНВАРИАНТНОСТИ
- 6.3. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ В ОДНОПАРАМЕТРИЧЕСКОЙ СИТУАЦИИ
- 6.4. ПРИМЕРЫ О.М.П. В МНОГОПАРАМЕТРИЧЕСКИХ СЛУЧАЯХ
- 6.5. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ РЕГРЕССИИ
- 6.5.2. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ ЛИНЕЙНОЙ РЕГРЕССИИ С ВЕСАМИ
- 6.5.3. ЛИНЕЙНАЯ РЕГРЕССИЯ С ОДИНАКОВЫМИ ВЕСАМИ
- 6.6. ОЦЕНИВАНИЕ ЗАВИСИМОСТИ ТОКСИЧНОСТИ ИНСЕКТИЦИДА ОТ УРОВНЯ ДОЗИРОВКИ
- 6.6.2. ВЕРОЯТНОСТНАЯ МОДЕЛЬ
- 6.6.3. ИССЛЕДОВАНИЕ ПОВЕРХНОСТИ ФУНКЦИИ ПРАВДОПОДОБИЯ
- 6.6.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
- 6.6.5. ТОЧНОСТЬ ОЦЕНОК
- 6.6.6. ДОЗА, НЕОБХОДИМАЯ ДЛЯ ЗАДАННОГО ЗНАЧЕНИЯ ОТКЛИКА
- 6.7. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ПО ГРУППИРОВАННЫМ, ЦЕНЗУРИРОВАННЫМ И УСЕЧЕННЫМ ДАННЫМ
- 6.7.2. НЕПРЕРЫВНЫЕ ДАННЫЕ И ГРУППИРОВКА. ПОПРАВКА ШЕППАРДА
- ГЛАВА 7. СТАТИСТИКА ХИ-КВАДРАТ. КРИТЕРИИ СОГЛАСИЯ, НЕЗАВИСИМОСТИ И ОДНОРОДНОСТИ
- 7.1.2. АДЕКВАТНОСТЬ ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ
- 7.2. РАССТОЯНИЕ К. ПИРСОНА: КРИТЕРИЙ «хи-квадрат»
- 7.3. ОБЪЕДИНЕНИЕ ЯЧЕЕК С НИЗКИМИ ЧАСТОТАМИ. КРИТЕРИЙ У. КОКРЕНА
- 7.4. КРИТЕРИЙ «хи-квадрат» ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
- 7.5. ТАБЛИЦЫ ЧАСТОТ ПЕРЕКРЕСТНОЙ КЛАССИФИКАЦИИ (ТАБЛИЦЫ СОПРЯЖЕННОСТИ). КРИТЕРИИ НЕЗАВИСИМОСТИ
- 7.5.2. ТАБЛИЦЫ k x m
- 7.6. ИНДЕКС РАССЕЯНИЯ
- 7.6.1. ИНДЕКС РАССЕЯНИЯ ДЛЯ ВЫБОРКИ ИЗ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 7.6.2. ИНДЕКС РАССЕЯНИЯ ДЛЯ ПУАССОНОВСКИХ ВЫБОРОК
- Глава 8. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ И ДИСПЕРСИОННЫЙ АНАЛИЗ
- 8.1. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ МОДЕЛЕЙ ОБЩЕГО ВИДА
- 8.2. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ЛИНЕЙНЫХ МОДЕЛЕЙ ПОЛНОГО РАНГА. НОРМАЛЬНЫЕ УРАВНЕНИЯ. ТЕОРЕМА ГАУССА—МАРКОВА
- 8.2.1. ПРИМЕРЫ ОЦЕНИВАНИЯ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
- 8.2.2. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ МОДЕЛЕЙ
- 8.2.3. СВОЙСТВА ОЦЕНОК МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 8.2.4. ОСТАТКИ
- 8.2.5. ОРТОГОНАЛЬНЫЕ ПЛАНЫ И ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 8.2.6. МОДИФИКАЦИИ ДЛЯ НЕРАВНОТОЧНЫХ НАБЛЮДЕНИЙ; ВЗВЕШЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 8.2.7. МОДИФИКАЦИИ ДЛЯ НЕ НЕЗАВИСИМЫХ НАБЛЮДЕНИЙ
- 8.3. ДИСПЕРСИОННЫЙ АНАЛИЗ И ПРОВЕРКА ГИПОТЕЗ ДЛЯ ПЛАНОВ ПОЛНОГО РАНГА
- 8.3.2. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ
- 8.2 3. ПРОВЕРКА ГИПОТЕЗ
- 8.3.4. ОСНОВНЫЕ ТОЖДЕСТВА
- 8.3.5. ПРОВЕРКИ ГИПОТЕЗ В ОРТОГОНАЛЬНЫХ ПЛАНАХ
- 8.3.6. ПРОВЕРКА ГИПОТЕЗ ДЛЯ НЕ ОРТОГОНАЛЬНЫХ ПЛАНОВ
- 8.3.7 ГРУППОВАЯ ОРТОГОНАЛЬНОСТЬ
- 8.3.8. ОБЩИЕ ЛИНЕЙНЫЕ ГИПОТЕЗЫ
- Глава 9. ПЛАНИРОВАНИЕ СРАВНИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
- 9.3. БОЛЕЕ СЛОЖНЫЙ ПРИМЕР: ЭКСПЕРИМЕНТ ДАРВИНА
- 9.4. ПОЛНОСТЬЮ РАНДОМИЗИРОВАННЫЕ БЛОЧНЫЕ ПЛАНЫ
- 9.5. ОБРАБОТКИ НА ОДНОМ И НА НЕСКОЛЬКИХ УРОВНЯХ
- 9.6. ПОТРЕБНОСТЬ В РАЗРАБОТКАХ ПО УМЕНЬШЕНИЮ РАЗМЕРОВ БЛОКОВ
- 9.7. СБАЛАНСИРОВАННЫЕ НЕПОЛНЫЕ БЛОКИ ДЛЯ СРАВНЕНИЯ ОДНОУРОВНЕВЫХ ОБРАБОТОК
- 9.8. ПОЛНЫЙ ФАКТОРНЫЙ ПЛАН
- 9.8.2. ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЯ: ТРИ ФАКТОРА НА ДВУХ УРОВНЯХ
- 9.8.3. ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЯ В ПЛАНЕ 2^j
- 9.9. НЕПОЛНЫЕ БЛОКИ: СМЕШИВАНИЕ
- 9.10. ЧАСТИЧНОЕ СМЕШИВАНИЕ
- 9.11. ФАКТОРЫ НА ТРЕХ И БОЛЕЕ УРОВНЯХ
- 9.11.2. ГРЕКО-ЛАТИНСКИЙ КВАДРАТ
- Глава 10. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И АНАЛИЗ СТАТИСТИЧЕСКИХ ЭКСПЕРИМЕНТОВ: ВЫРОЖДЕННЫЕ МОДЕЛИ, МНОЖЕСТВЕННЫЕ КРИТЕРИИ
- 10.1.2. ОЦЕНИВАНИЕ. ФУНКЦИИ, ДОПУСКАЮЩИЕ ОЦЕНКУ
- 10.1.3. ПРОВЕРКА ГИПОТЕЗ
- 10.1.4. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ИЕРАРХИЧЕСКАЯ КЛАССИФИКАЦИЯ
- 10.1.5. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ПЕРЕКРЕСТНАЯ КЛАССИФИКАЦИЯ
- 10.1.6. КЛАССИФИКАЦИИ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
- 10.1.7. КОВАРИАЦИОННЫЙ АНАЛИЗ
- 10.2. МНОЖЕСТВЕННЫЕ КРИТЕРИИ И СРАВНЕНИЯ
- 10.2.2. КОМБИНАЦИИ ПРОВЕРОК И ОБЩИЙ РАЗМЕР КРИТЕРИЯ
- 10.2.3. МНОЖЕСТВЕННЫЕ СРАВНЕНИЯ
- 10.3. ПРЕДПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ОШИБОК
- 10.3.2. АНАЛИЗ ОСТАТКОВ
Решение:
-
Рассчитаем
средние арифметические.
Средняя арифметическая
– это типовой размер признака,
количественно варьирующего в качественно
однородной совокупности. Для определения
такого размера признака необходимо
рассчитать объем явления, приходящийся
на 1 единицу выборки:



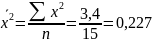

-
Определим
коэффициент регрессии.
Величина коэффициента
регрессии показывает среднее изменение
результата с изменением фактора на
одну единицу.

-
Рассчитаем
коэффициент корреляции.
Уравнение
регрессии всегда дополняется показателем
тесноты связи. При использовании
линейной регрессии в качестве такого
показателя выступает линейный коэффициент
корреляции.
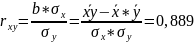
-
Рассчитаем
t-критерии
Стьюдента для коэффициентов регрессии
и корреляции.
Оценка
параметров уравнения регрессии
осуществляется с помощью t-критерия
Стьюдента. t-критерий Стьюдента —
общее название для класса
методов статистической проверки гипотез,
основанных
на распределении
Стьюдента.


-
Вычислим
стандартную ошибку для коэффициентов
регрессии и корреляции.
Величина
стандартной ошибки применяется для
проверки существенности коэффициента
регрессии и для расчета его доверительных
интервалов.


-
Определим
доверительный интервал коэффициента
регрессии.

-
Вычислим величину
исправленной дисперсии
Выборочная
дисперсия — это оценка теоретической
дисперсии распределения на основе
выборки. Несмещённая (исправленная)
дисперсия — это случайная величина.

S2=1.85
-
Вычислим
дисперсию.
Дисперсия признака
определяется как средний квадрат
отклонений от их средних значений.
Дисперсию используют для определения
показателей тесноты корреляционной
связи при анализе результатов выборочных
наблюдений.




-
Определим
доверительный интервал коэффициента
дисперсии.

-
Вычислим полосу
регрессии.
Линейная
регрессия —
это индикатор статистического анализа.
Этот инструмент используется для
предсказания будущих значений по уже
имеющимся данным.
Прежде
всего это очень эффективный индикатор
для определения тренда.

-
Вычислим
параметры уравнения линейной регрессии.

-
Определим
коридор регрессии.
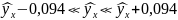
На
основании изученной информации построим
график, на котором изобразим полосу и
коридор регрессии.

Ответ
Регрессия
для представленной выборки составляет
2,89.
Данная величина показывает среднее
изменение результата с изменением
фактора на одну единицу. Одна
из характеристик связи между зависимой
у и независимой переменной х. То есть,
можно сделать вывод, что среднее
изменение факторного признака х на
одну единицу, приводит к изменению
результативного признака у на 2,89 единиц.
Доверительные
интервалы коэффициентов регрессии и
дисперсии соответственно равны:
Обратим
внимание на следующую закономерность:
при заданной доверительной вероятности
с ростом объема выборки ширина
доверительного интервала уменьшается
и стремится к нулю. При заданном объеме
выборки с ростом доверительной
вероятности ширина доверительного
интервала тоже растет. Это означает,
что, чем надежнее оценка, тем меньше
точность этой оценки. И, наоборот, чем
выше точность оценки, тем меньше ее
надежность (достоверность).
Были
построены полоса (
)
и коридор регрессии.
Доверительный
коридор не является доверительной
областью для всей линии регрессии —
он определяет только концы доверительных
интервалов для y при каждом
значении x. С помощью коридора
регрессии нельзя, например, построить
одновременно два доверительных интервала
в различных точках x0 и x1.
Такие доверительные интервалы можно
построить с помощью доверительной
полосы всей линии регрессии.
С
помощью доверительной полосы можно,
например, построить одновременно
доверительные интервалы для нескольких
различных значений переменной x.
Задание
3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В некотором эксперименте измерены значения пары случайных величин y и x
(x1, y1), (x2, y2), …(xn, yn).
Без ограничения общности можно считать, что величина x измерена точно, в то время как измерение величины y содержит случайные погрешности. Это означает, что погрешность измерения величины x пренебрежимо мала по сравнению с погрешностью измерения величины y. Таким образом, результаты эксперимента можно рассматривать как выборочные значения случайной величины h(x), зависящей от x как от параметра.
Пусть требуется построить зависимость y(x).
Регрессией называют зависимость условного математического ожидания величины h(x) от x: ![]() .
.
Задача регрессионного анализа состоит в восстановлении функциональной зависимости y(x) по результатам измерений {(xi,yi)}, i = 1, 2, …, n.
В случае простейшей линейной регрессии выдвигается гипотеза о том, что функция f(x; a0, a1, …, ak) имеет вид
f(x; a, b)= ax + b.
Доверительный коридор линии регрессии
Пусть линейная регрессия построена: ![]() .
.
Возьмем в области изменения аргумента некоторую точку x0 и вычислим
![]() .
.
Эта величина случайная и меняется от выборки к выборке.
Ее математическое ожидание равно истинному значению функции f(x) в точке x0, величине y0 = a x0+ b.
Доверительный коридор линии регрессии — интервал
 ,
,
накрывающий истинное значение величины y0 с вероятностью 1– a.
Величина tn— 2, a — корень уравнения ![]() , где F(tn— 2, a) — функция распределения Стьюдента с (n – 2) степенями свободы.
, где F(tn— 2, a) — функция распределения Стьюдента с (n – 2) степенями свободы.
Внимание! Функция Excel СТЬЮДРАСПОБР(p, k) возвращает значение t, при котором P(|x| > t) = p, x — значение случайной величины, имеющей распределение Стьюдента с k степенями свободы. Поэтому решение уравнения ![]() в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
Важно понимать, что доверительный коридор не является доверительной областью для всей линии регрессии — он определяет только концы доверительных интервалов для y при каждом значении x. С помощью коридора регрессии нельзя, например, построить одновременно два доверительных интервала в различных точкахx0 и x1. Такие доверительные интервалы можно построить с помощью доверительной полосы всей линии регрессии.
Пример 1
Пример 1. В таблице приведены некоторые экспериментальные данные:
|
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
|
y |
1.156 |
1.382 |
1.553 |
1.705 |
1.831 |
2.204 |
2.388 |
2.656 |
|
x |
0.9 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
|
|
y |
3.019 |
3.081 |
3.299 |
3.486 |
3.692 |
3.867 |
3.896 |
Построим доверительный коридор линии регрессии y (x)= ax + b.
В Excel все эти вычисления можно выполнить, используя процедуру «Регрессия» пакета «Анализ данных» и «Описательные статистики».
Прежде чем приступать к вычислениям в Excel, перепишем формулы для границ доверительного коридора в удобном для работы виде.
Легко убедиться, что границы коридора можно записать в виде
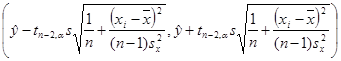 ,
,
где s – стандартное отклонение остатков, ![]() – выборочная дисперсия переменной x. Значения s и sx вычисляются в Excel процедурой «Описательные статистики».
– выборочная дисперсия переменной x. Значения s и sx вычисляются в Excel процедурой «Описательные статистики».
Важно также помнить, что решение уравнения ![]() в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
в Excel возвращает функция СТЬЮДРАСПОБР(a/2, n – 2).
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.

Пример 2
Пример 2. Управляющий сетью магазинов планирует открыть несколько новых магазинов. Он полагает, что объёмы продаж напрямую зависит от величин торговых площадей. Ваша задача разработать статистическую модель, позволяющую прогнозировать объёмы продаж в зависимости от величины торговых площадей новых магазинов.
Вы располагаете данными о размере годовых продаж четырнадцати магазинов и знаете величины торговых площадей этих магазинов.
Данные приведены в таблице.
|
Номер магазина |
Площадь (в сотнях м2) |
Объём продаж (выручка в десятках тыс. рублей) |
|
1 |
1.7 |
3.7 |
|
2 |
1.6 |
3.9 |
|
3 |
2.8 |
6.7 |
|
4 |
5.6 |
9.5 |
|
5 |
1.3 |
3.4 |
|
6 |
2.2 |
5.6 |
|
7 |
1.3 |
3.7 |
|
8 |
1.1 |
2.7 |
|
9 |
3.2 |
5.5 |
|
10 |
1.5 |
2.9 |
|
11 |
5.2 |
10.7 |
|
12 |
4.6 |
7.6 |
|
13 |
5.8 |
11.8 |
|
14 |
3.0 |
4.1 |
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.

Доверительная полоса линии регрессии
Пусть линейная регрессия построена: ![]() .
.
Доверительная полоса для всей линии регрессии определяется неравенством 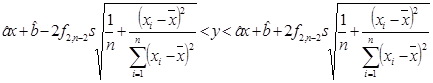 .
.![]()
Здесь f2,n-2— корень уравнения ![]() , Fn-2(x) — функция распределения Фишера с 2 и (n – 2) степенями свободы.
, Fn-2(x) — функция распределения Фишера с 2 и (n – 2) степенями свободы.
Внимание! В Excel функция распределения случайной величины определена нестандартно: Fx(x) = P(x >x). Поэтому решение уравнения ![]() возвращает функция FРАСПРОБР(a, n – 2).
возвращает функция FРАСПРОБР(a, n – 2).
С помощью доверительной полосы можно, например, построить одновременно доверительные интервалы для нескольких различных значений переменной x.
Пример 3
В таблице приведены некоторые экспериментальные данные:
|
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
|
y |
1.156 |
1.382 |
1.553 |
1.705 |
1.831 |
2.204 |
2.388 |
2.656 |
|
x |
0.9 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
|
|
y |
3.019 |
3.081 |
3.299 |
3.486 |
3.692 |
3.867 |
3.896 |
Легко убедиться, что границы полосы можно записать в виде
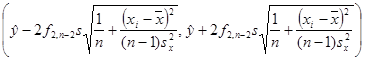 ,
,
где s – стандартное отклонение остатков, ![]() – выборочная дисперсия переменной x. Значения s и sx вычисляются в Excel процедурой «Описательные статистики».
– выборочная дисперсия переменной x. Значения s и sx вычисляются в Excel процедурой «Описательные статистики».
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.

Пример 4
Управляющий сетью магазинов планирует открыть несколько новых магазинов. Он полагает, что объёмы продаж напрямую зависит от величин торговых площадей. Ваша задача разработать статистическую модель, позволяющую прогнозировать объёмы продаж в зависимости от величины торговых площадей новых магазинов.
Вы располагаете данными о размере годовых продаж четырнадцати магазинов и знаете величины торговых площадей этих магазинов.
Данные приведены в таблице.
|
Номер магазина |
Площадь (в сотнях м2) |
Объём продаж (выручка в десятках тыс. рублей) |
|
1 |
1.7 |
3.7 |
|
2 |
1.6 |
3.9 |
|
3 |
2.8 |
6.7 |
|
4 |
5.6 |
9.5 |
|
5 |
1.3 |
3.4 |
|
6 |
2.2 |
5.6 |
|
7 |
1.3 |
3.7 |
|
8 |
1.1 |
2.7 |
|
9 |
3.2 |
5.5 |
|
10 |
1.5 |
2.9 |
|
11 |
5.2 |
10.7 |
|
12 |
4.6 |
7.6 |
|
13 |
5.8 |
11.8 |
|
14 |
3.0 |
4.1 |
На приведенном ниже рисунке изображён фрагмент листа Excel , содержащий все вычисления.
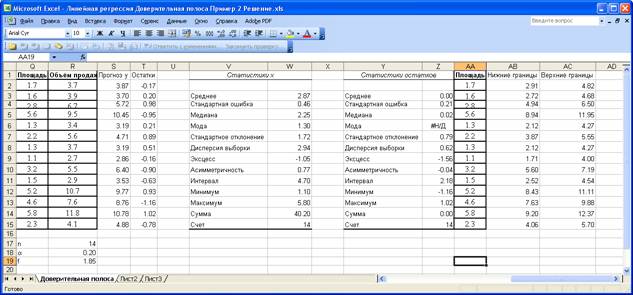
В статистике регрессия — это метод, который можно использовать для анализа взаимосвязи между переменными-предикторами и переменной-откликом.
Когда вы используете программное обеспечение (например, R, SAS, SPSS и т. д.) для выполнения регрессионного анализа, вы получите в качестве выходных данных таблицу регрессии, в которой суммируются результаты регрессии. Важно уметь читать эту таблицу, чтобы понимать результаты регрессионного анализа.
В этом руководстве рассматривается пример регрессионного анализа и дается подробное объяснение того, как читать и интерпретировать выходные данные таблицы регрессии.
Пример регрессии
Предположим, у нас есть следующий набор данных, который показывает общее количество часов обучения, общее количество сданных подготовительных экзаменов и итоговый балл за экзамен, полученный для 12 разных студентов:

Чтобы проанализировать взаимосвязь между учебными часами и сданными подготовительными экзаменами и окончательным экзаменационным баллом, который получает студент, мы запускаем множественную линейную регрессию, используя отработанные часы и подготовительные экзамены, взятые в качестве переменных-предикторов, и итоговый экзаменационный балл в качестве переменной ответа.
Мы получаем следующий вывод:

Проверка соответствия модели
В первом разделе показано несколько различных чисел, которые измеряют соответствие регрессионной модели, т. е. насколько хорошо регрессионная модель способна «соответствовать» набору данных.

Вот как интерпретировать каждое из чисел в этом разделе:
Несколько R
Это коэффициент корреляции.Он измеряет силу линейной зависимости между переменными-предикторами и переменной отклика. R, кратный 1, указывает на идеальную линейную зависимость, тогда как R, кратный 0, указывает на отсутствие какой-либо линейной зависимости. Кратный R — это квадратный корень из R-квадрата (см. ниже).
В этом примере множитель R равен 0,72855 , что указывает на довольно сильную линейную зависимость между предикторами часов обучения и подготовительных экзаменов и итоговой оценкой экзаменационной переменной ответа.
R-квадрат
Его часто записывают как r 2 , а также называют коэффициентом детерминации.Это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.
Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
В этом примере R-квадрат равен 0,5307 , что указывает на то, что 53,07% дисперсии итоговых экзаменационных баллов можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Связанный: Что такое хорошее значение R-квадрата?
Скорректированный R-квадрат
Это модифицированная версия R-квадрата, которая была скорректирована с учетом количества предикторов в модели. Он всегда ниже R-квадрата. Скорректированный R-квадрат может быть полезен для сравнения соответствия различных моделей регрессии друг другу.
В этом примере скорректированный R-квадрат равен 0,4265.
Стандартная ошибка регрессии
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 7,3267 единиц.
Связанный: Понимание стандартной ошибки регрессии
Наблюдения
Это просто количество наблюдений в нашем наборе данных. В этом примере общее количество наблюдений равно 12 .
Тестирование общей значимости регрессионной модели
В следующем разделе показаны степени свободы, сумма квадратов, средние квадраты, F-статистика и общая значимость регрессионной модели.

Вот как интерпретировать каждое из чисел в этом разделе:
Степени свободы регрессии
Это число равно: количеству коэффициентов регрессии — 1. В этом примере у нас есть член пересечения и две переменные-предикторы, поэтому у нас всего три коэффициента регрессии, что означает, что степени свободы регрессии равны 3 — 1 = 2 .
Всего степеней свободы
Это число равно: количество наблюдений – 1. В данном примере у нас 12 наблюдений, поэтому общее количество степеней свободы 12 – 1 = 11 .
Остаточные степени свободы
Это число равно: общая df – регрессионная df.В этом примере остаточные степени свободы 11 – 2 = 9 .
Средние квадраты
Средние квадраты регрессии рассчитываются как регрессия SS / регрессия df.В этом примере регрессия MS = 546,53308/2 = 273,2665 .
Остаточные средние квадраты вычисляются как остаточный SS / остаточный df.В этом примере остаточная MS = 483,1335/9 = 53,68151 .
F Статистика
Статистика f рассчитывается как регрессия MS/остаточная MS. Эта статистика показывает, обеспечивает ли регрессионная модель лучшее соответствие данным, чем модель, которая не содержит независимых переменных.
По сути, он проверяет, полезна ли регрессионная модель в целом. Как правило, если ни одна из переменных-предикторов в модели не является статистически значимой, общая F-статистика также не является статистически значимой.
В этом примере статистика F равна 273,2665/53,68151 = 5,09 .
Значение F (P-значение)
Последнее значение в таблице — это p-значение, связанное со статистикой F. Чтобы увидеть, значима ли общая модель регрессии, вы можете сравнить p-значение с уровнем значимости; распространенные варианты: 0,01, 0,05 и 0,10.
Если p-значение меньше уровня значимости, имеется достаточно доказательств, чтобы сделать вывод о том, что регрессионная модель лучше соответствует данным, чем модель без переменных-предикторов. Этот вывод хорош, потому что он означает, что переменные-предикторы в модели действительно улучшают соответствие модели.
В этом примере p-значение равно 0,033 , что меньше обычного уровня значимости 0,05. Это указывает на то, что регрессионная модель в целом статистически значима, т. е. модель лучше соответствует данным, чем модель без переменных-предикторов.
Тестирование общей значимости регрессионной модели
В последнем разделе показаны оценки коэффициентов, стандартная ошибка оценок, t-stat, p-значения и доверительные интервалы для каждого термина в регрессионной модели.

Вот как интерпретировать каждое из чисел в этом разделе:
Коэффициенты
Коэффициенты дают нам числа, необходимые для записи оценочного уравнения регрессии:
у шляпа знак равно б 0 + б 1 Икс 1 + б 2 Икс 2 .
В этом примере расчетное уравнение регрессии имеет вид:
итоговый балл за экзамен = 66,99 + 1,299 (часы обучения) + 1,117 (подготовительные экзамены)
Каждый отдельный коэффициент интерпретируется как среднее увеличение переменной отклика на каждую единицу увеличения данной переменной-предиктора при условии, что все остальные переменные-предикторы остаются постоянными. Например, для каждого дополнительного часа обучения среднее ожидаемое увеличение итогового экзаменационного балла составляет 1,299 балла при условии, что количество сданных подготовительных экзаменов остается постоянным.
Перехват интерпретируется как ожидаемый средний итоговый балл за экзамен для студента, который учится ноль часов и не сдает подготовительных экзаменов. В этом примере ожидается, что учащийся наберет 66,99 балла, если он будет заниматься ноль часов и не сдавать подготовительных экзаменов. Однако будьте осторожны при интерпретации перехвата выходных данных регрессии, потому что это не всегда имеет смысл.
Например, в некоторых случаях точка пересечения может оказаться отрицательным числом, что часто не имеет очевидной интерпретации. Это не означает, что модель неверна, это просто означает, что перехват сам по себе не должен интерпретироваться как означающий что-либо.
Стандартная ошибка, t-статистика и p-значения
Стандартная ошибка — это мера неопределенности оценки коэффициента для каждой переменной.
t-stat — это просто коэффициент, деленный на стандартную ошибку. Например, t-stat для часов обучения составляет 1,299 / 0,417 = 3,117.
В следующем столбце показано значение p, связанное с t-stat. Это число говорит нам, является ли данная переменная отклика значимой в модели. В этом примере мы видим, что значение p для часов обучения равно 0,012, а значение p для подготовительных экзаменов равно 0,304. Это указывает на то, что количество учебных часов является важным предиктором итогового экзаменационного балла, а количество подготовительных экзаменов — нет.
Доверительный интервал для оценок коэффициентов
В последних двух столбцах таблицы представлены нижняя и верхняя границы 95% доверительного интервала для оценок коэффициентов.
Например, оценка коэффициента для часов обучения составляет 1,299, но вокруг этой оценки есть некоторая неопределенность. Мы никогда не можем знать наверняка, является ли это точным коэффициентом. Таким образом, 95-процентный доверительный интервал дает нам диапазон вероятных значений истинного коэффициента.
В этом случае 95% доверительный интервал для часов обучения составляет (0,356, 2,24). Обратите внимание, что этот доверительный интервал не содержит числа «0», что означает, что мы вполне уверены, что истинное значение коэффициента часов обучения не равно нулю, т. е. является положительным числом.
Напротив, 95% доверительный интервал для Prep Exams составляет (-1,201, 3,436). Обратите внимание, что этот доверительный интервал действительно содержит число «0», что означает, что истинное значение коэффициента подготовительных экзаменов может быть равно нулю, т. е. несущественно для прогнозирования результатов итоговых экзаменов.
Дополнительные ресурсы
Понимание нулевой гипотезы для линейной регрессии
Понимание F-теста общей значимости в регрессии
Как сообщить о результатах регрессии
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение 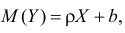
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии  неизвестны, неизвестна и величина коэффициента корреляции
неизвестны, неизвестна и величина коэффициента корреляции 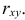 Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений:
Над случайными величинами X и Y проделано n независимых наблюдений, в результате которых получены n пар значений: 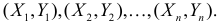 Эти результаты могут служить источником информации о неизвестных значениях
Эти результаты могут служить источником информации о неизвестных значениях 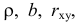 надо только уметь эту информацию извлечь оттуда.
надо только уметь эту информацию извлечь оттуда.
Неизвестная нам линия регрессии 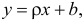 как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для
как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений Y от нее минимален. Поэтому в качестве оценок для  можно принять те их значения, при которых имеет минимум функция
можно принять те их значения, при которых имеет минимум функция 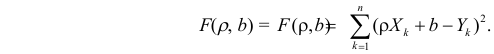
Такие значения  , согласно необходимым условиям экстремума, находятся из системы уравнений:
, согласно необходимым условиям экстремума, находятся из системы уравнений:
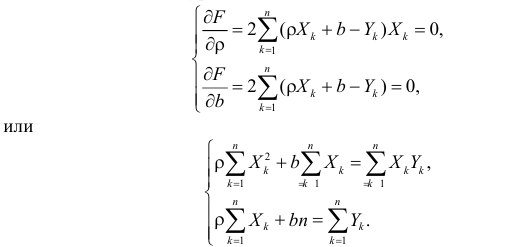
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.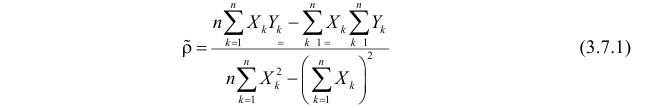
и
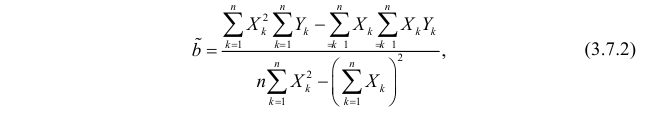
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 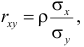 где
где 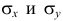 средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через
средние квадратические отклонения случайных величин X и Y соответственно. Обозначим через 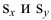 оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку
оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (3.1.3). Тогда для коэффициента корреляции имеем оценку 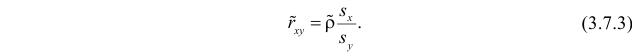
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 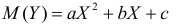 оценки параметров
оценки параметров 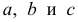 находятся из условия минимума функции
находятся из условия минимума функции
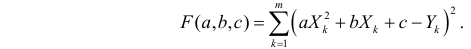
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X 
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
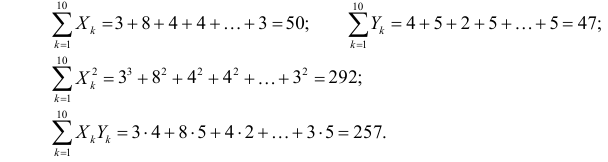
По формулам (3.7.1) и (3.7.2) получим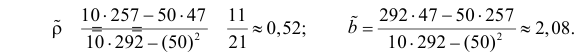
Итак, оценка линии регрессии имеет вид 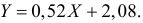 Так как
Так как 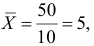 то по формуле (3.1.3)
то по формуле (3.1.3)
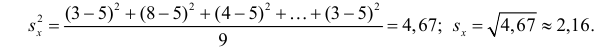
Аналогично, 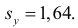 Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину
Поэтому в качестве оценки коэффициента корреляции имеем по формуле (3.7.3) величину 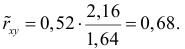
Ответ. 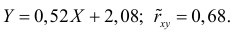
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 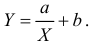 Найти оценки параметров
Найти оценки параметров 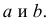
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 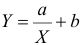 играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)
играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений Y от линии должна быть минимальной по свойству линии регрессии)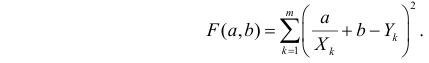
Необходимые условия экстремума приводят к системе из двух уравнений: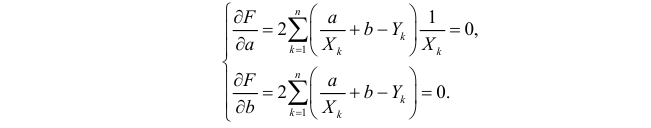
Откуда
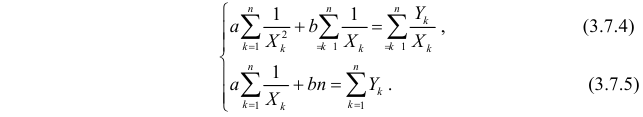
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров 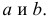
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде 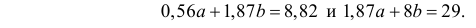
Эта система имеет решения 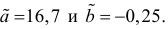
Ответ. 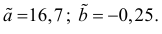
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 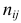 равно числу наблюдений, для которых X находится в интервале
равно числу наблюдений, для которых X находится в интервале 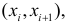 а Y – в интервале
а Y – в интервале 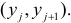 Через
Через 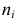 обозначено число наблюдений, при которых
обозначено число наблюдений, при которых 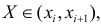 а Y произвольно. Число наблюдений, при которых
а Y произвольно. Число наблюдений, при которых 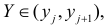 а X произвольно, обозначено через
а X произвольно, обозначено через 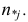
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 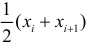 и
и 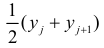 наблюдались
наблюдались 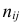 раз.
раз.
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.

Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 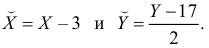 Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце таблицы.
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 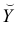 при фиксированных значениях
при фиксированных значениях 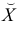 :
:
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33): 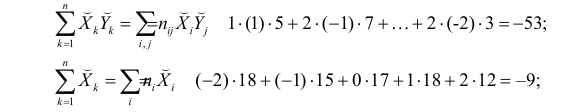
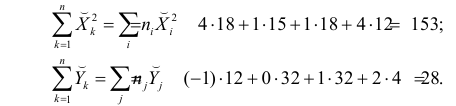
Тогда
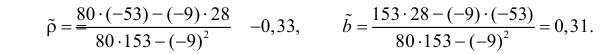
В новом масштабе оценка линии регрессии имеет вид 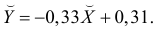 График этой прямой линии изображен на рис. 3.7.1.
График этой прямой линии изображен на рис. 3.7.1.
Для оценки 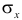 по корреляционной таблице можно воспользоваться формулой (3.1.3):
по корреляционной таблице можно воспользоваться формулой (3.1.3):
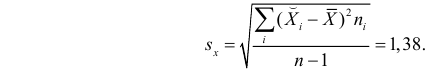
Подобным же образом можно оценить 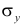 величиной
величиной 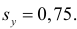 Тогда оценкой коэффициента корреляции может служить величина
Тогда оценкой коэффициента корреляции может служить величина 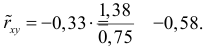
Вернемся к старому масштабу:
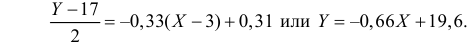
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ. 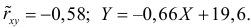
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 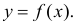 Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то
Для изучения этой зависимости производят измерения Y при разных значениях X. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то 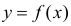 играет роль линии регрессии и все свойства линии регрессии приложимы к
играет роль линии регрессии и все свойства линии регрессии приложимы к 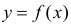 . В частности,
. В частности, 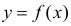 обычно находят по методу наименьших квадратов.
обычно находят по методу наименьших квадратов.
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
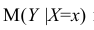 можно представить в виде
можно представить в виде 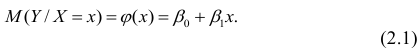
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 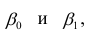 называемые коэффициентами регрессии, а также
называемые коэффициентами регрессии, а также 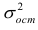 — остаточная дисперсия.
— остаточная дисперсия.
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей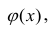 которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости
которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменным X. Например, зависимости 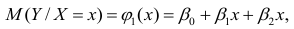
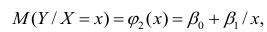
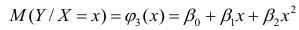 линейны относительно параметров
линейны относительно параметров 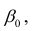
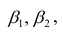 хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости
хотя вторая и третья зависимости нелинейны относительно переменных х. Вид зависимости 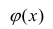 выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
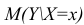 можно представить в виде (2.1).
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 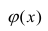 линейна и по оцениваемым параметрам, и
линейна и по оцениваемым параметрам, и
по переменным. Оценки параметров модели (2.1) 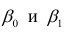 обозначил
обозначил 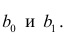 Оценку остаточной дисперсии
Оценку остаточной дисперсии 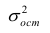 обозначим
обозначим 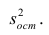 Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии
Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии 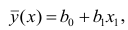 коэффициенты которого
коэффициенты которого 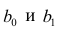 находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака
находят из условия минимума суммы квадратов отклонений измеренных значений результативного признака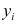 от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии 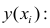
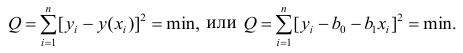
Составим систему нормальных уравнений: первое уравнение
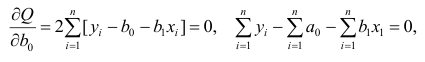
откуда 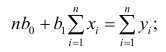
второе уравнение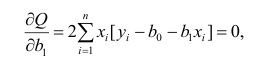
откуда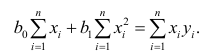
Итак,
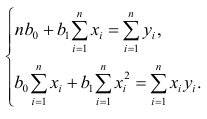
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно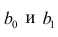 найдём оценки параметров
найдём оценки параметров 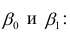
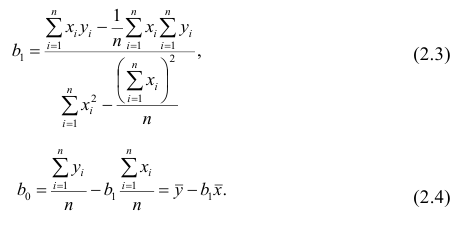
Остаётся получить оценку параметра 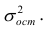 . Имеем
. Имеем
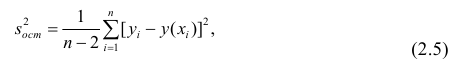
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы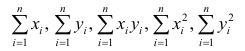 заменяют на
заменяют на
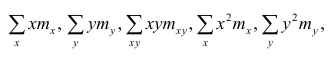
где 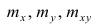 — частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
— частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
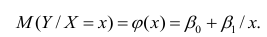
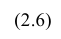
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
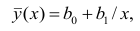
где 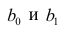 —оценки коэффициентов регрессии
—оценки коэффициентов регрессии 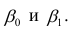

Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
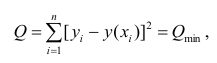
или
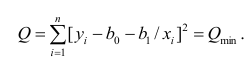
Дифференцируя последнее равенство по 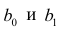 и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
и приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:
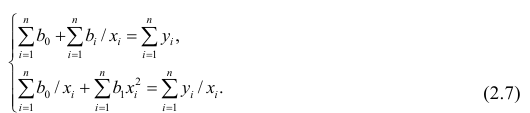
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
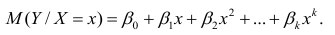
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
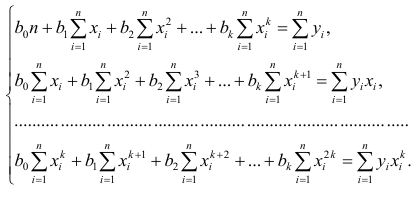
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 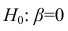 статистика
статистика

имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 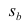 — оценка среднеквадратического отклонения
— оценка среднеквадратического отклонения
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение удовлетворяющее условию
удовлетворяющее условию 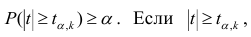 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. При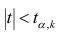 нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
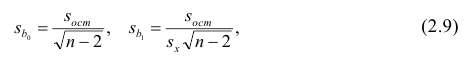
где 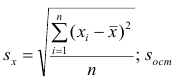 — оценка остаточной дисперсии, вычисляемая по
— оценка остаточной дисперсии, вычисляемая по
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
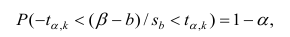
где а — уровень значимости, находим

Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 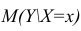 является условное среднее
является условное среднее 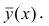 Кроме точечной оценки для
Кроме точечной оценки для 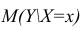 можно
можно
построить доверительный интервал в точке 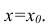
Известно, что 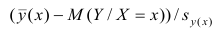 имеет распределение
имеет распределение
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания 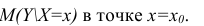
Оценку дисперсии условного среднего вычисляют по формуле
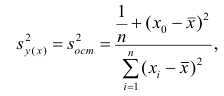
или для интервального ряда
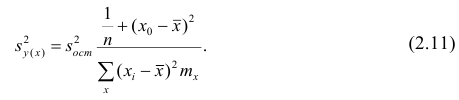
Доверительный интервал находят из условия
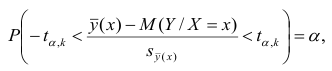
где а — уровень значимости. Отсюда
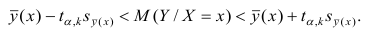
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).

Из рис. 2.2 видно, что в точке 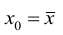 границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значение х не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 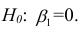 Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением
Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением 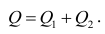 — Общая сумма квадратов отклонений результативного признака
— Общая сумма квадратов отклонений результативного признака
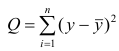 разлагается на
разлагается на 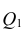 (сумму, характеризующую влияние признака
(сумму, характеризующую влияние признака
X) и 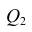 (остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
(остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.
Для проверки нулевой гипотезы вычисляют статистику 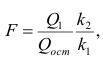 которая имеет распределение Фишера-Снедекора с А
которая имеет распределение Фишера-Снедекора с А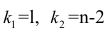 степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы
степенями свободы (в п — число наблюдений). По уровню значимости а и числу степеней свободы 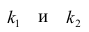 находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение
находят по таблицам F-распределение для уровня значимости а=0,05 (см. табл. 3 приложений) критическое значение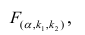 удовлетворяющее условию
удовлетворяющее условию 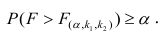 . Если
. Если 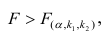 нулевую гипотезу отвергают, уравнение считают значимым. Если
нулевую гипотезу отвергают, уравнение считают значимым. Если 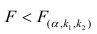 то нет оснований отвергать нулевую гипотезу.
то нет оснований отвергать нулевую гипотезу.
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 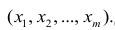 Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним
Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: У -независимые случайные величины со средним 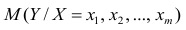 и постоянной дисперсией
и постоянной дисперсией 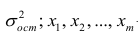 — линейно независимые векторы
— линейно независимые векторы 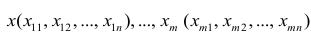 . Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
. Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида
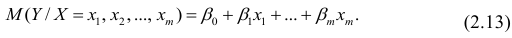
Оценке подлежат параметры 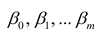 и остаточная дисперсия.
и остаточная дисперсия.
Заменив параметры их оценками, запишем уравнение регрессии
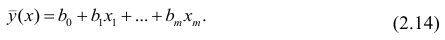
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 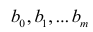 является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:
является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:

Как и в двумерном случае, составляют систему нормальных уравнений
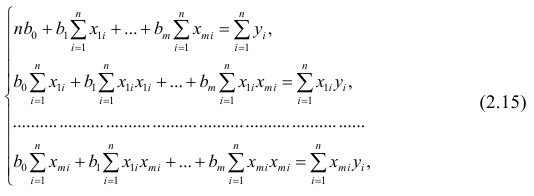
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 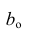 через остальные параметры:
через остальные параметры:
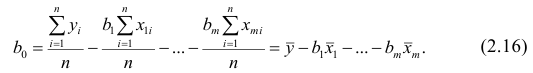
Подставим в остальные уравнения системы вместо 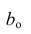 полученное выражение:
полученное выражение:
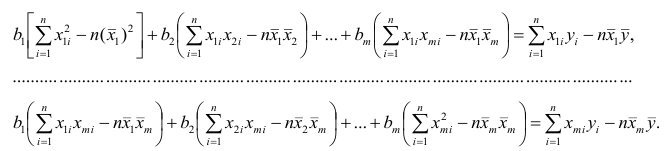
Пусть С — матрица коэффициентов при неизвестных параметрах 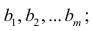
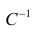 — матрица, обратная матрице С;
— матрица, обратная матрице С; 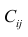 — элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы
— элемент, стоящий на пересечении i-Й строки и i-го столбца матрицы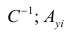 — выражение
— выражение
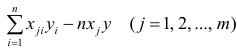 . Тогда, используя формулы линейной алгебры,
. Тогда, используя формулы линейной алгебры,
запишем окончательные выражения для параметров:
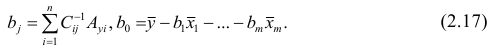
Оценкой остаточной дисперсии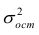 является
является
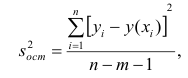
где 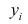 — измеренное значение результативного признака;
— измеренное значение результативного признака;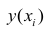 значение результативного признака, вычисленное по уравнению регрессий.
значение результативного признака, вычисленное по уравнению регрессий.
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику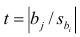 вычисляют для каждого j-го коэффициента регрессии
вычисляют для каждого j-го коэффициента регрессии
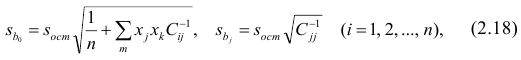
где 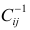 —элемент обратной матрицы, стоящий на пересечении i-й строки и j-
—элемент обратной матрицы, стоящий на пересечении i-й строки и j-
го столбца;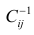 —диагональный элемент обратной матрицы.
—диагональный элемент обратной матрицы.
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 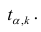 Если
Если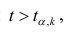 то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если
то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если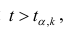 то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: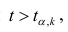
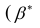 — вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики
— вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики 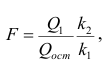 , где
, где 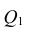 — сумма квадратов, характеризующая влияние признаков X;
— сумма квадратов, характеризующая влияние признаков X; 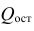 — остаточная сумма квадратов, характеризующая влияние неучтённых факторов;
— остаточная сумма квадратов, характеризующая влияние неучтённых факторов; 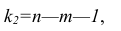
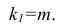 Для уровня значимости а и числа степеней свободы
Для уровня значимости а и числа степеней свободы 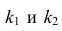 по табл. 3 приложений находят критическое значение
по табл. 3 приложений находят критическое значение 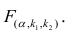 Если
Если 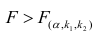 то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При
то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При 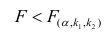 нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 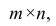 аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений
аналогичной приведенной в п. 2.7 (матрица исходных данных). Строки этой матрицы должны соответствовать объектам наблюдений 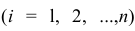 столбцы — признакам
столбцы — признакам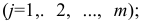 таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных
таким образом, каждый признак является как бы статистическим рядом, в котором наблюдения варьируют от объекта к объекту. Признаки, характеризующие объект наблюдения, как правило, имеют различную размерность. Чтобы устранить влияние размерности и обеспечить сопоставимость признаков, матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным видом нормировки является стандартизация. От переменных 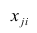 переходят к переменным
переходят к переменным 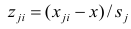 В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
В дальнейшем, говоря о матрице исходных переменных, всегда будем иметь в виду стандартизованную матрицу.
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
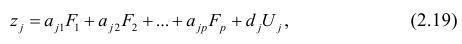
где 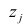 -j-й признак (величина случайная);
-j-й признак (величина случайная); 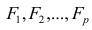 — общие факторы (величины случайные, имеющие нормальный закон распределения);
— общие факторы (величины случайные, имеющие нормальный закон распределения); 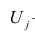 — характерный фактор;
— характерный фактор; 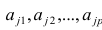 — факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);
— факторные нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);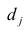 — нагрузка характерного фактора.
— нагрузка характерного фактора.
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 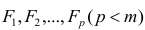 и характерного фактора
и характерного фактора 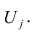
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков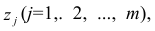 , т.е.
, т.е.
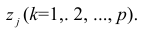
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы 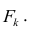
Факторные нагрузки 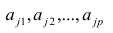 . характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
. характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа — определение факторных нагрузок. Факторная модель относится к классу аппроксимационных. Параметры модели должны быть выбраны так, чтобы наилучшим образом аппроксимировать корреляции между наблюдаемыми признаками.
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
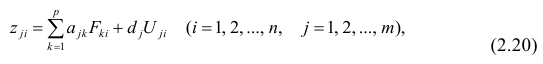
где 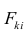 значение k-го фактора для i-го объекта.
значение k-го фактора для i-го объекта.
Дисперсию признака 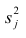 можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность
можно разложить на составляющие: часть, обусловленную действием общих факторов, — общность 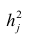 и часть, обусловленную действием j-го характера фактора, характерность
и часть, обусловленную действием j-го характера фактора, характерность 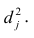 Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака
Все переменные представлены в стандартизированном виде, поэтому дисперсий у-го признака 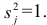 Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Дисперсия признака может быть выражена через факторы и в конечном счёте через факторные нагрузки.
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
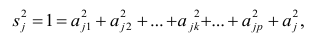
где 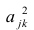 —доля дисперсии признака
—доля дисперсии признака 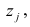 приходящаяся на k-й фактор.
приходящаяся на k-й фактор.
Полный вклад k-го фактора в суммарную дисперсию признаков
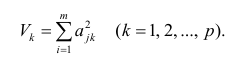
Вклад общих факторов в суммарную дисперсию 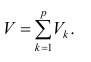
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
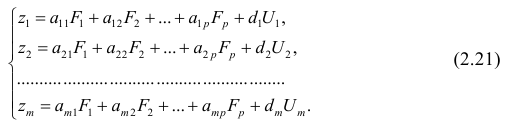
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
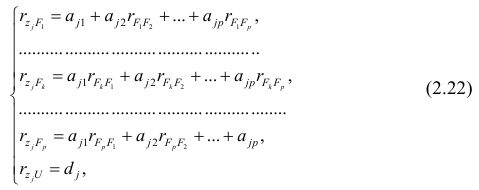
где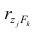 — выборочный коэффициент корреляции между j-м параметром и к-
— выборочный коэффициент корреляции между j-м параметром и к-
м фактором;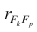 — коэффициент корреляции между к-м и р-м факторами.
— коэффициент корреляции между к-м и р-м факторами.
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
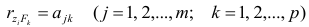 , т.е. коэффициенты отображения равны
, т.е. коэффициенты отображения равны
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам: 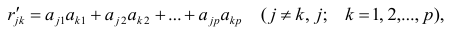
где 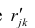 —вычисленный по отображению коэффициент корреляции между j-м
—вычисленный по отображению коэффициент корреляции между j-м
и к-м признаком. Остаточный коэффициент корреляции
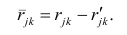
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
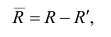
где 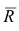 — матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
— матрица остатков; R — матрица выборочных парных коэффициентов корреляции, или полная матрица; R’— матрица вычисленных по отображению коэффициентов корреляции.
Результаты факторного анализа удобно представить в виде табл. 2.10.

Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
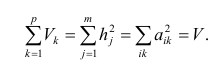
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции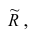 у которой на главной диагонали стоят значения общностей
у которой на главной диагонали стоят значения общностей 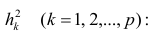 :
: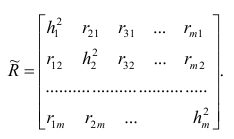
Редуцированная и полная матрицы связаны соотношением

где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 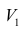 должен быть найден при условии
должен быть найден при условии
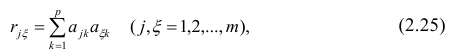
где 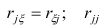 —общность
—общность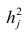 параметра
параметра
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора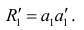 Имея эту матрицу, получают первую матрицу остатков:
Имея эту матрицу, получают первую матрицу остатков: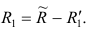
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 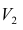 находят из условия
находят из условия
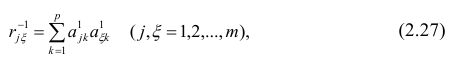
где 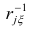 — коэффициент корреляции из первой матрицы остатков;
— коэффициент корреляции из первой матрицы остатков; 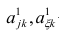 — факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков:
— факторные нагрузки с учётом второго фактора. Затем рассчитыва коэффициентов корреляций с учётом второго фактора и вычисляют вторую матрицу остатков: 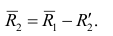
Факторный анализ учитывает суммарную общность. Исходная суммарная общность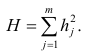 Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на
Итерационный процесс выделения факторов заканчивают, когда учтённая выделенными факторами суммарная общность отличается от исходной суммарной общности меньше чем на 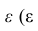 — наперёд заданное малое число).
— наперёд заданное малое число).
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных 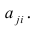
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
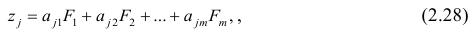
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 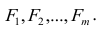 По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
По сравнению с моделью факторного анализа (2.19) в модели (2.28) отсутствует характерный фактор, т.е. считается, что вся вариация параметра может быть объяснена только действием общих или главных факторов. В случае компонентного анализа исходной является матрица коэффициентов корреляции, где на главной диагонали стоят единицы. Результатом компонентного анализа, так же как и факторного, является матрица факторных нагрузок. Поиск факторного решения — это ортогональное преобразование матрицы исходных переменных, в результате которого каждый параметр может быть представлен линейной комбинацией найденных m факторов, которые называют главными компонентами. Главные компоненты легко выражаются через наблюдённые параметры.
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
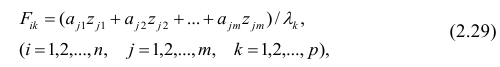
где 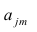 — элементы факторного решения:
— элементы факторного решения: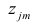 — исходные переменные;
— исходные переменные; 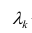 .— k-е собственное значение; р — количество оставленных главных
.— k-е собственное значение; р — количество оставленных главных
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента 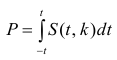

Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 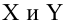 связаны линейной корреляционной зависимостью
связаны линейной корреляционной зависимостью 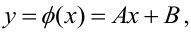 для отыскания которой проведено
для отыскания которой проведено 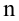 независимых измерений
независимых измерений 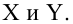
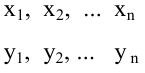
Диаграмма рассеяния (разброса, рассеивания)

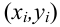 — координаты экспериментальных точек.
— координаты экспериментальных точек.
Выборочное уравнение прямой линии регрессии 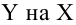 имеет вид
имеет вид
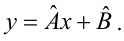
Задача: подобрать 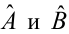 таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой
таким образом, чтобы экспериментальные точки как можно ближе лежали к прямой 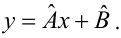
Для того, что бы провести прямую 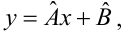 воспользуемся МНК. Потребуем,
воспользуемся МНК. Потребуем,
чтобы 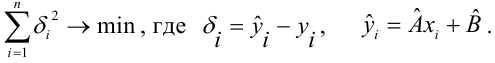
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
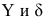 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.- Дисперсия
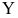 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения. - Результаты наблюдений
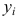 в разных точках независимы.
в разных точках независимы. - Входные переменные
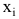 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 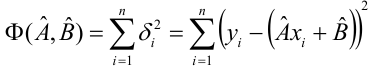 и найдём её минимальное значение
и найдём её минимальное значение
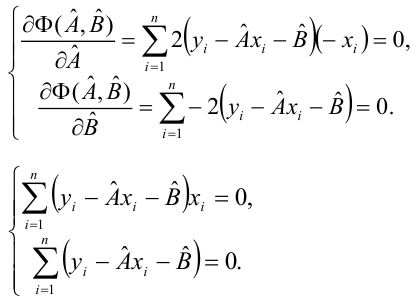
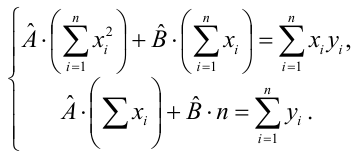
Решив систему, получим искомые значения 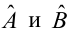
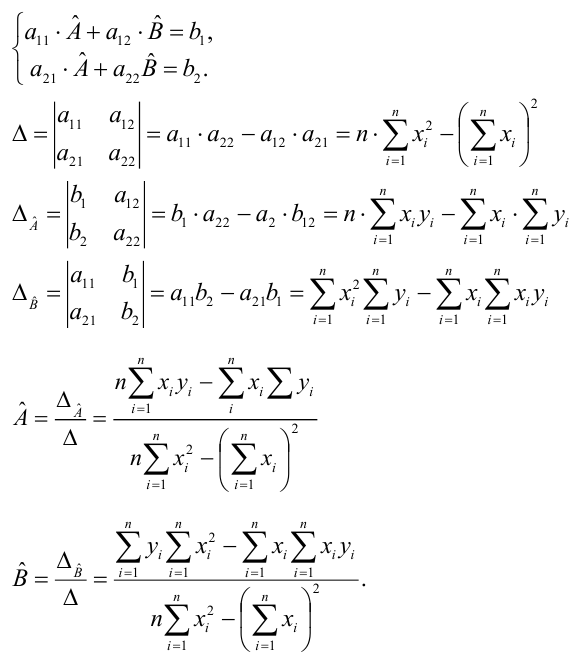
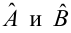 является несмещенными оценками истинных значений коэффициентов
является несмещенными оценками истинных значений коэффициентов 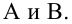
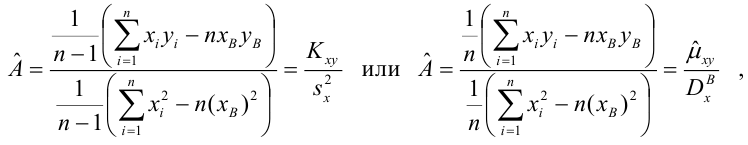 где
где
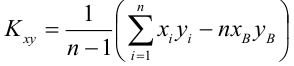 несмещенная оценка корреляционного момента (ковариации),
несмещенная оценка корреляционного момента (ковариации),
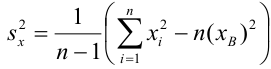 несмещенная оценка дисперсии
несмещенная оценка дисперсии 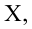
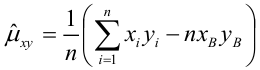 выборочная ковариация,
выборочная ковариация,
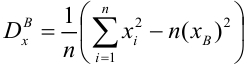 выборочная дисперсия
выборочная дисперсия 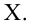
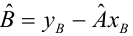
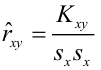 — выборочный коэффициент корреляции
— выборочный коэффициент корреляции
Коэффициент детерминации
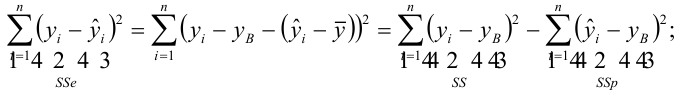
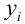 — наблюдаемое экспериментальное значение
— наблюдаемое экспериментальное значение 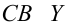 при
при 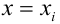
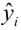 — предсказанное значение
— предсказанное значение 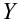 удовлетворяющее уравнению регрессии
удовлетворяющее уравнению регрессии
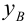 — средневыборочное значение
— средневыборочное значение 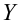
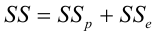
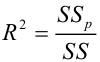 — коэффициент детерминации, доля изменчивости
— коэффициент детерминации, доля изменчивости 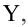 объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии
объясняемая рассматриваемой регрессионной моделью. Для парной линейной регрессии 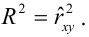
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
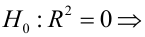 регрессия незначима
регрессия незначима
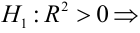 регрессия значима
регрессия значима
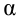 — уровень значимости
— уровень значимости
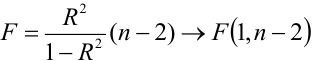 — статистический критерий
— статистический критерий
Критическая область — правосторонняя; 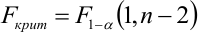
Если 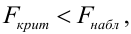 то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
то нулевая гипотеза отвергается на заданном уровне значимости, следовательно, коэффициент детерминации значим, следовательно, регрессия адекватна.
Мощность статистического критерия. Функция мощности

Определение. Мощностью критерия 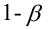 называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода 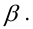
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 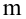 и дисперсией
и дисперсией 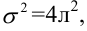 проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
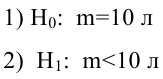
3) Уровень значимости 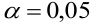
4) Статистический критерий
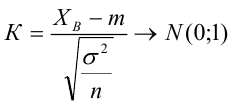
5) Критическая область — левосторонняя
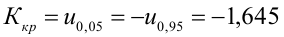

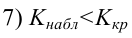 следовательно
следовательно 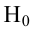 отвергается на уровне значимости
отвергается на уровне значимости 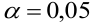
Пример:
В условиях примера 1 предположим, что наряду с 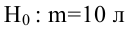 рассматривается конкурирующая гипотеза
рассматривается конкурирующая гипотеза 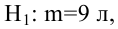 а критическая область задана неравенством
а критическая область задана неравенством 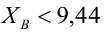 Найти вероятность ошибок I рода и II рода.
Найти вероятность ошибок I рода и II рода.
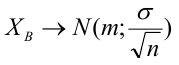

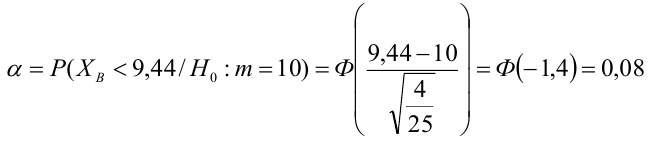
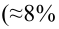 автомобилей имеют меньший расход топлива)
автомобилей имеют меньший расход топлива)
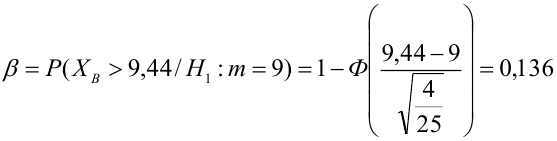
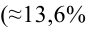 автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
автомобилей, имеющих расход топлива 9л на 100 км, классифицируются как автомобили, имеющие расход 10 литров).
Определение. Пусть проверяется 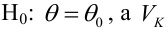 — критическая область критерия с заданным уровнем значимости
— критическая область критерия с заданным уровнем значимости 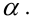 Функцией мощности критерия
Функцией мощности критерия 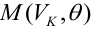 называется вероятность отклонения
называется вероятность отклонения 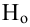 как функция параметра
как функция параметра 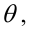 т.е.
т.е.
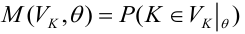
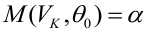 — ошибка 1-ого рода
— ошибка 1-ого рода
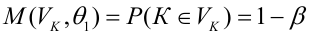 — мощность критерия
— мощность критерия
Пример:
Построить график функции мощности из примера 2 для 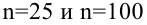
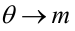
 попадает в критическую область.
попадает в критическую область.
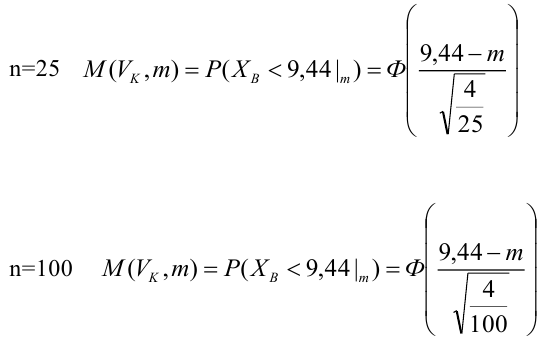


Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить 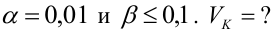
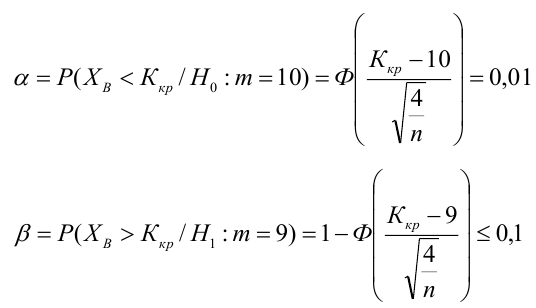
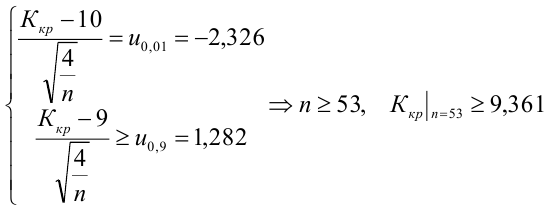
Лемма Неймана-Пирсона.
При проверке простой гипотезы 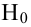 против простой альтернативной гипотезы
против простой альтернативной гипотезы 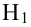 наилучшая критическая область (НКО) критерия заданного уровня значимости
наилучшая критическая область (НКО) критерия заданного уровня значимости 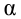 состоит из точек выборочного пространства (выборок объема
состоит из точек выборочного пространства (выборок объема 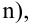 для которых справедливо неравенство:
для которых справедливо неравенство:
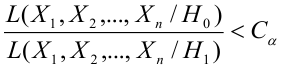
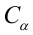 — константа, зависящая от
— константа, зависящая от 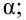
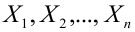 — элементы выборки;
— элементы выборки;
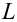 — функция правдоподобия при условии, что соответствующая гипотеза верна.
— функция правдоподобия при условии, что соответствующая гипотеза верна.
Пример:
Случайная величина 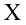 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 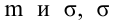 известно. Найти НКО для проверки
известно. Найти НКО для проверки 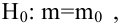 против
против 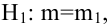 причем
причем 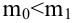
Решение:
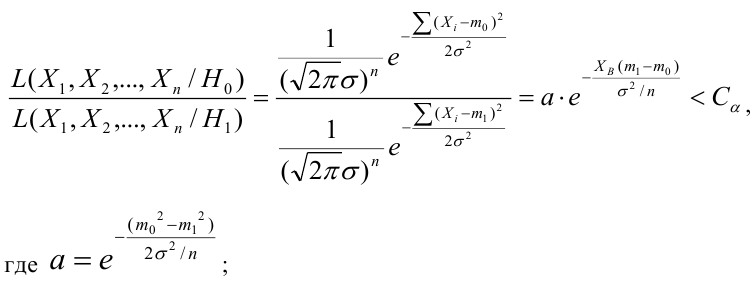
Ошибка первого рода: 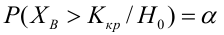
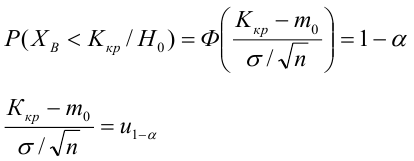
НКО: 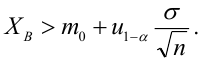
Пример:
Для зависимости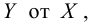 заданной корреляционной табл. 13, найти оценки параметров
заданной корреляционной табл. 13, найти оценки параметров 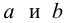 уравнения линейной регрессии
уравнения линейной регрессии 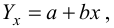 остаточную дисперсию; выяснить значимость уравнения регрессии при
остаточную дисперсию; выяснить значимость уравнения регрессии при 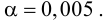
Решение. Воспользуемся предыдущими результатами
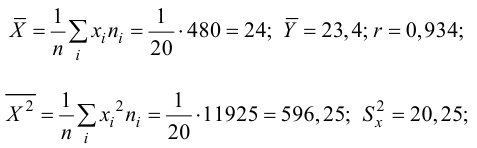
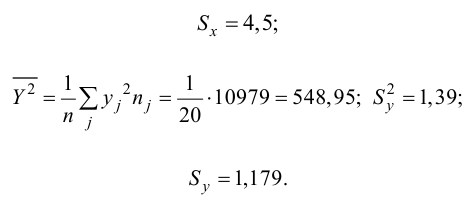
Согласно формуле (24), уравнение регрессии будет иметь вид 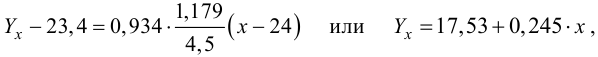 тогда
тогда 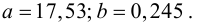
Для выяснения значимости уравнения регрессии вычислим суммы 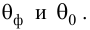 Составим расчетную таблицу:
Составим расчетную таблицу:

Из (27) и (28) по данным таблицы получим 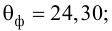
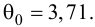
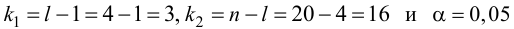 по табл. П7 находим
по табл. П7 находим 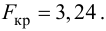
Вычислим статистику
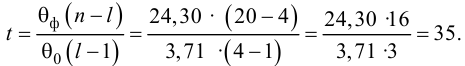
Так как 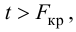 то уравнение регрессии значимо. Остаточная дисперсия равна
то уравнение регрессии значимо. Остаточная дисперсия равна 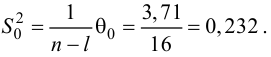
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез

