18
Ч
а с т ь I
ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ
1.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
Абсолютная
и относительная ошибки
Никакую
физическую величину невозможно измерить
абсолютно точно: как бы тщательно ни
был поставлен опыт, измеренное значение
величины х
будет
отличаться от ее истинного значения Х.
Разница между этими значениями
представляет собой абсолютную
ошибку (или
абсолютную
погрешность*)
измерения х :
х
= х – Х.
(1)
Абсолютная погрешность
является размерной величиной: она
выражается в тех же единицах, что и сама
измеряемая величина (например, абсолютная
погрешность измерения длины выражается
в метрах, силы тока – в амперах и т.д.).
Как следует из выражения (1), х
может быть как положительной, так и
отрицательной величиной.
Хотя
величина х
показывает, насколько измеренное
значение отличается от истинного, одной
лишь абсолютной ошибкой нельзя полностью
характеризовать точность проделанного
измерения. Пусть, например, известно,
что абсолютная погрешность измерения
расстояния равна 1 м.
Если измерялось расстояние между
географическими пунктами (порядка
нескольких километров), то точность
такого измерения следует признать
весьма высокой; если же измерялись
размеры помещения (не превышающие
десятка метров), то измерение является
грубым. Для характеристики точности
существует понятие относительной
ошибки
(или относительной
погрешности)
Е,
представляющей собой отношение модуля
абсолютной ошибки к измеряемой величине:
![]() .
.
(2)
Очевидно, что
относительная погрешность – величина
безразмерная, чаще всего ее выражают в
процентах.
При
определении ошибок измерений важно
иметь в виду следующее. Выражения (1) и
(2) содержат истинное значение измеряемой
величины Х,
которое точно знать невозможно: поэтому
значения х
и Е
в принципе не могут быть рассчитаны
точно. Можно лишь оценить
эти значения, т.е. найти их приближенно
с той или иной степенью достоверности.
Поэтому все расчеты, связанные с
определением погрешностей, должны
носить приближенный (оценочный) характер.
Случайная
и приборная погрешности
Разнообразные ошибки,
возникающие при измерениях, можно
классифицировать как по их происхождению,
так и по характеру их проявления.
По происхождению
ошибки делятся на инструментальные и
методические.
Инструментальные
погрешности обусловлены несовершенством
применяемых измерительных приборов и
приспособлений. Эти погрешности могут
быть уменьшены за счет применения более
точных приборов. Так, размер детали
можно измерить линейкой или штанген-циркулем.
Очевидно, что во втором случае ошибка
измерения меньше, чем в первом.
Методические
погрешности возникают из-за того, что
реальные физические процессы всегда в
той или иной степени отличаются от их
теоретических моделей. Например, формула
для периода колебаний математического
маятника в точности верна лишь при
бесконечно малой амплитуде колебаний;
формула Стокса, определяющая силу трения
при движении шарика в вязкой жидкости,
справедлива только в случае идеально
сферической формы и т.д. Обнаружить и
учесть методическую погрешность можно
путем измерения той же величины совершенно
иным независимым методом.
По характеру проявления
ошибки бывают систематические и
случайные.
Систематическая
погрешность может быть обусловлена как
приборами, так и методикой измерения.
Она имеет две характерные особенности.
Во-первых, систематическая погрешность
всегда либо положительна, либо отрицательна
и не меняет своего знака от опыта к
опыту. Во-вторых, систематическую
погрешность нельзя уменьшить за счет
увеличения числа измерений. Например,
если при отсутствии внешних воздействий
стрелка измерительного прибора показывает
величину х0 , отличную от
нуля, то во всех дальнейших измерениях
будет присутствовать систематическая
ошибка, равная х0 .
Случайная
ошибка также может быть как инструментальной,
так и методической. Причину ее появления
установить трудно, а чаще всего –
невозможно (это могут быть различные
помехи, случайные толчки, вибрации,
неверно взятый отсчет по прибору и
т.д.). Случайная погрешность бывает и
положительной и отрицательной, причем
непредсказуемо изменяет свой знак от
опыта к опыту. Значение ее можно уменьшить
путем увеличения числа измерений.
Детальный
анализ погрешностей измерения представляет
собой сложную задачу, для решения которой
не существует единого рецепта. Поэтому
в каждом конкретном случае этот анализ
проводят по-разному. Однако, в первом
приближении, если исключена систематическая
ошибка, то остальные можно условно
свести к следующим двум видам: приборная
и случайная.
Приборной
погрешностью в дальнейшем будем
называть случайную ошибку, обусловленную
измерительными приборами и приспособлениями,
а случайной – ошибку, причина
появления которой неизвестна. Приборную
погрешность измерения величины х
будем обозначать как х,
случайную – как s x.
Оценка
случайной погрешности. Доверительный
интервал
Методика оценки
случайной погрешности основана на
положениях теории вероятностей и
математической статистики. Оценить
случайную ошибку можно только в том
случае, когда проведено неоднократное
измерение одной и той же величины.
Пусть
в результате проделанных измерений
получено п
значений величины х:
х1 ,
х2 ,
…, хп .
Обозначим через
![]()
среднеарифметическое значение
![]() .
.
(3)
В
теории вероятностей доказано, что при
увеличении числа измерений п
среднеарифметическое значение измеряемой
величины приближается к истинному:
![]()
При
небольшом числе измерений (п 10)
среднее значение может существенно
отличаться от истинного. Для того, чтобы
знать, насколько точно значение
![]()
характеризует измеряемую величину,
необходимо определить так называемый
доверительный интервал полученного
результата.
Поскольку
абсолютно точное измерение невозможно,
то вероятность правильности утверждения
«величина х
имеет значение, в точности равное
![]() »
»
равна нулю. Вероятность же утверждения
«величина х
имеет какое-либо значение»
равна единице (100%). Таким образом,
вероятность правильности любого
промежуточного утверждения лежит в
пределах от 0 до 1. Цель измерения – найти
такой интервал, в котором с наперед
заданной вероятностью
(0 < < 1)
находится истинное значение измеряемой
величины. Этот интервал называется
доверительным
интервалом,
а неразрывно связанная с ним величина
–
доверительной вероятностью
(или коэффициентом
надежности).
За середину интервала принимается
среднее значение, рассчитанное по
формуле (3). Половина ширины доверительного
интервала представляет собой случайную
погрешность s x
(рис. 1).

Рис.1
Очевидно,
что
ширина доверительного интервала (а
следовательно, и ошибка s x)
зависит от того, насколько сильно
отличаются отдельные измерения величины
хi
от среднего
значения
![]() .
.
«Разброс» результатов измерений
относительно среднего характеризуется
среднеквадратичной
ошибкой ,
которую находят по формуле
![]() ,
,
(4)
где
![]() .
.
Ширина
искомого доверительного интервала
прямо пропорциональна среднеквадратичной
ошибке:
![]() .
.
(5)
Коэффициент
пропорциональности tn,
называется
коэффициентом
Стьюдента;
он зависит от числа опытов п
и доверительной вероятности .
На
рис. 1, а, б
наглядно
показано, что при прочих равных условиях
для увеличения вероятности попадания
истинного значения в доверительный
интервал необходимо увеличить ширину
последнего (вероятность «накрывания»
значения Х
более широким интервалом выше).
Следовательно, величина tn,
должна быть тем больше, чем выше
доверительная вероятность
.
С
увеличением количества опытов среднее
значение приближается к истинному;
поэтому при той же вероятности
доверительный интервал можно взять
более узким (см. рис. 1, а,в).
Таким образом, с ростом п
коэффициент Сьюдента должен
уменьшаться. Таблица значений коэффи-циента
Стьюдента в зависимости от п
и
дана в приложениях к настоящему пособию.
Следует
отметить, что доверительная вероятность
никак не связана с точностью результата
измерений. Величиной
задаются
заранее, исходя из требований к их
надежности. В большинстве технических
экспериментов и в лабораторном практикуме
значение
принимается
равным 0,95.
Расчет
случайной погрешности измерения величины
х проводится
в следующем порядке:
1) вычисляется
сумма измеренных значений, а затем –
среднее значение величины
![]()
по формуле (3);
2) для
каждого i-го
опыта рассчитываются разность между
измеренным и средним значениями
![]() ,
,
а также квадрат этой разности (отклонения)
( хi)2 ;
3) находится
сумма квадратов отклонений, а затем –
средне-квадратичная ошибка
по формуле (4);
4) по
заданной доверительной вероятности
и числу
проведенных опытов п
из таблицы на с. 149 приложений выбирается
соответствующее значение коэффициента
Стьюдента tn,
и определяется случайная погрешность
s x
по формуле (5).
Для
удобства расчетов и проверки промежуточных
результатов данные заносятся в таблицу,
три последних столбца которой заполняются
по образцу табл.1.
Таблица
1
|
Номер опыта |
… |
х |
х |
( х)2 |
|
1 |
… |
|||
|
2 |
… |
|||
|
… |
… |
|||
|
п |
… |
|||
|
= |
= |
В
каждом конкретном случае величина х
имеет определенный физический смысл и
соответствующие единицы измерения. Это
может быть, например, ускорение свободного
падения g
(м/с2),
коэффициент вязкости жидкости
(Пас)
и т.д. Пропущенные столбцы табл. 1
могут содержать промежуточные измеряемые
величины, необходимые для расчета
соответствующих значений х.
Пример
1. Для
определения ускорения а
движения тела измерялось время t
прохождения им пути S
без начальной
скорости. Используя известное соотношение
![]() ,
,
получим расчетную формулу
![]() .
.
(6)
Результаты
измерений пути S
и времени t
приведены во втором и третьем столбцах
табл. 2. Проведя вычисления по формуле
(6), заполним
четвертый
столбец значениями ускорения ai
и найдем их сумму, которую запишем под
этим столбцом в ячейку «
= ». Затем рассчитаем среднее значение
![]()
по формуле (3)
![]() .
.
Таблица
2
|
Номер |
S, м |
t, c |
а, м/с2 |
а, м/с2 |
(а)2, (м/с2)2 |
|
1 |
5 |
2,20 |
2,07 |
0,04 |
0,0016 |
|
2 |
7 |
2,68 |
1,95 |
-0,08 |
0,0064 |
|
3 |
9 |
2,91 |
2,13 |
0,10 |
0,0100 |
|
4 |
11 |
3,35 |
1,96 |
-0,07 |
0,0049 |
|
= |
8,11 |
= |
0,0229 |
Вычитая
из каждого значения ai
среднее, найдем разности ai
и занесем их в пятый столбец таблицы.
Возводя эти разности в квадрат, заполним
последний столбец. Затем рассчитаем
сумму квадратов отклонений и запишем
ее во вторую ячейку «
= ». По формуле (4) определим
среднеквадратичную погрешность:
![]() .
.
Задавшись
величиной доверительной вероятности
= 0,95,
для числа опытов п = 4
из таблицы в приложениях (с. 149) выбираем
значение коэффициента Стьюдента tn,
= 3,18; с помощью формулы (5) оценим
случайную погрешность измерения
ускорения
s а
= 3,180,0437 0,139 (м/с2) .
Способы
определения приборных ошибок
Основными характеристиками
измерительных приборов являются предел
измерения и цена деления, а также –
главным образом для электро-измерительных
приборов – класс точности.
Предел
измерения П
– это максимальное значение величины,
которое может быть измерено с помощью
данной шкалы прибора. Если
предел измерения не указан отдельно,
то его определяют по оцифровке шкалы.
Так, если рис. 2
изображает шкалу миллиамперметра, то
его предел измерения равен 100 мА.
Р
ис.2
Цена
деления Ц –
значение измеряемой величины,
соответствующее самому малому делению
шкалы. Если шкала начинается с нуля, то
![]() ,
,
где
N
– общее количество делений (например,
на рис. 2
N = 50).
Если эта шкала принадлежит амперметру
с пределом измерения 5 А,
то цена деления равна 5/50 = 0,1 (А).
Если шкала принадлежит термометру и
проградуирована в С,
то цена деления Ц = 100/50 = 2 (С).
Многие электроизмерительные приборы
имеют несколько пределов измерения.
При переключении их с одного предела
на другой изменяется и цена деления
шкалы.
Класс
точности К
представляет собой отношение абсолютной
приборной погрешности к пределу измерения
шкалы, выраженное в процентах:
![]() .
.
(7)
Значение класса
точности (без символа «%») указывается,
как правило, на электроизмерительных
приборах.
В зависимости от вида
измерительного устройства абсолютная
приборная погрешность определяется
одним из нижеперечисленных способов.
1. Погрешность
указана непосредственно на приборе.
Так, на микрометре есть надпись «0,01 мм».
Если с помощью этого прибора измеряется,
например, диаметр шарика D
(лабораторная работа 1.2), то погрешность
его измерения D = 0,01 мм.
Абсолютная ошибка указывается обычно
на жидкостных (ртутных, спиртовых)
термометрах, штангенциркулях и др.
2. На приборе указан
класс точности. Согласно определению
этой величины, из формулы (7) имеем
![]() .
.
(8)
Например, для вольтметра
с классом точности 2,5 и пределом измерения
600 В абсолютная приборная ошибка
измерения напряжения
![]() .
.
3. Если на приборе
не указаны ни абсолютная погрешность,
ни класс точности, то в зависимости от
характера работы прибора возможны два
способа определения величины х:
а) указатель
значения измеряемой величины может
занимать только определенные (дискретные)
положения, соответствующие делениям
шкалы (например, электронные часы,
секундомеры, счетчики импульсов и т.п.).
Такие приборы являются приборами
дискретного действия, и их абсолютная
погрешность равна цене деления шкалы:
х = Ц.
Так, при измерении промежутка времени
t секундомером с ценой
деления 0,2 с погрешность t = 0,2 с;
б) указатель
значения измеряемой величины может
занимать любое положение на шкале
(линейки, рулетки, стрелочные весы,
термометры и т.п.). В этом случае абсолютная
приборная погрешность равна половине
цены деления: х = Ц/2.
Точность снимаемых показаний прибора
не должна превышать его возможностей.
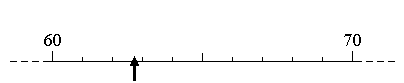
Например, при показанном на рис. 3
положении стрелки прибора следует
записать либо 62,5 либо 63,0 – в обоих
случаях ошибка не превысит половины
цены деления. Записи же типа 62,7 или 62,8
не имеют смысла.
Рис.3
4. Если какая-либо
величина не измеряется в данном оыте,
а была измерена независимо и известно
лишь ее значение, то она является заданным
параметром. Так, в работе 2.1 по
определению коэффициента вязкости
воздуха такими параметрами являются
размеры капилляра, в опыте Юнга по
интерференции света (работа 5.1) –
расстояние между щелями и т.д. Погрешность
заданного параметра принимается равной
половине единицы последнего разряда
числа, которым задано значение этого
параметра. Например, если радиус капилляра
r задан с точностью
до сотых долей миллиметра, то его
погрешность r = 0,005 мм.
Погрешности
косвенных измерений
В большинстве физических
экспериментов искомая величина и
не измеряется непосредственно каким-либо
одним прибором, а рассчитывается на
основе измерения ряда промежуточных
величин x, y, z,…
Расчет проводится по определенной
формуле, которую в общем виде можно
записать как
и = и ( x, y, z,…).
(9)
В этом случае говорят,
что величина и представляет собой
результат косвенного измерения в
отличие от x, y, z,…,
являющихся результатами прямых
измерений. Например, в
работе 1.2 коэффициент вязкости жидкости
рассчитывается по формуле
![]() ,
,
(10)
где ш
– плотность материала шарика; ж
– плотность жидкости; g
– ускорение свободного падения; D
– диаметр шарика; t –
время его падения в жидкости; l
– расстояние между метками на сосуде.
В данном случае результатами прямых
измерений являются величины l,
D и t,
а коэффициент вязкости
– результат косвенного
измерения. Величины ш,
ж
и g представляют
собой заданные параметры.
Абсолютная
погрешность косвенного измерения и
зависит от погрешностей прямых измерений
x,
y,
z…и
от вида функции (9). Как правило, величину
и
можно оценить по формуле
вида
![]() ,
,
(11)
где
коэффициенты kx ,
ky ,
kz ,…
определяются видом зависимостей величины
и от x,
y, z,…
Приведенная ниже табл. 3 позволяет
найти эти коэффициенты для наиболее
распространенных элементарных функций
(a, b, c, n
– заданные константы).
Таблица
3
|
и(х) |
kx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На
практике зависимость (9) чаще всего имеет
вид степенной функции
![]() ,
,
показатели степеней
которой k,
m, n,…
– вещественные (положительные или
отрицательные, целые или дробные) числа;
С – постоянный коэффициент. В этом
случае абсолютная приборная погрешность
и
оценивается по формуле
![]() ,
,
(12)
где
![]()
– среднее значение величины и;
![]()
– относительные приборные погрешности
прямых измерений величин x,
y, z,…
Для подстановки в формулу (12) выбираются
наиболее представительные, т.е.
близкие к средним значения x,
y, z,…
При расчетах по
формулам типа (12) необходимо помнить
следующее.
1. Измеряемые
величины и их абсолютные погрешности
(например, х и х)
должны быть выражены в одних и тех же
единицах.
2. Расчеты не требуют
высокой точности вычислений и должны
иметь оценочный характер. Так, входящие
в подкоренное выражение и возводимые
в квадрат величины ( kEx ,
mEy ,
nEz ,…)
обычно округляются с точностью до
двух значащих цифр (напомним, что ноль
является значащей цифрой только тогда,
когда перед ним слева есть хотя бы одна
цифра, отличная от нуля). Далее, если
одна из этих величин (например, | kEx | ) по
модулю превышает наибольшую из остальных
( | mEy | ,
| nEz | ,…)
более чем в три раза, то можно, не прибегая
к вычислениям по формуле (12), принять
абсолютную ошибку равной
![]() .
.
Если же одна из них более чем в три раза
меньше наименьшей из остальных, то при
расчете по формуле (12) ею можно пренебречь.
Пример 2.
Пусть при определении ускорения тела
(см. пример 1) путь S
измерялся рулеткой с ценой деления
1 мм, а время t
– электронным секундомером. Тогда, в
соответствии с изложенными в п.3, а, б
(с. 13) правилами, погрешности прямых
измерений будут равны
S = 0,5 мм = 0,0005 м;
t = 0,01 с.
Расчетную формулу
(6) можно записать в виде степенной
функции
a( S, t ) = 2S 1t – 2 ;
тогда на основании
(12) погрешность косвенного измерения
ускорения а
определится выражением
![]() .
.
В
качестве наиболее представительных
значений измеренных величин возьмем
(см. табл. 2) S 8 м;
t 3 с
и оценим по модулю относительные
приборные ошибки прямых измерений с
учетом их весовых коэффициентов:
![]() ;
;
![]() .
.
Очевидно,
что в данном случае величиной ES
можно пренебречь и принять погрешность
а
равной
![]()
Пример 3.
Вернемся к определению коэффициента
вязкости жидкости (работа 1.2). Расчетную
формулу (10) можно представить в виде

Московский государственный технический
УНИВЕРСИТЕТ «МАМИ»
Кафедра
физики
ЛАБОРАТОРНАЯ
РАБОТА 1.01
ОПРЕДЕЛЕНИЕ
ПЛОТНОСТИ ТВЕРДЫХ ТЕЛ
Москва
2005 г.
Лабораторная
работа 101
Теория
ошибок, определение плотности твердых
тел.
В лабораторном
практикуме студенты при выполнении
работ должны производить измерения, но
при использовании даже очень точных и
чувствительных приборов и наилучших
условий проведения эксперимента во
всяком измерении содержится ошибка
(погрешность) характер и причины которой
могут быть различными. Существуют методы
анализа и учета влияния различных
погрешностей на результаты измерений.
Все погрешности (ошибки) измерений
принято подразделять на систематические
и случайные.
Систематические
ошибки
обусловлены постоянными, но односторонними
внешними воздействиями. Например,
измерение температуры термометром, у
которого нулевая точка смешена, будет
систематически неправильным, пока в
результаты измерений не будет внесена
соответствующая поправка.
Так как
систематическая ошибка имеет одно и
тоже значение, ее нельзя устранить
увеличением числа повторных измерений.
Но можно уменьшить систематическую
ошибку, критически анализируя факторы,
которые могут повлиять на результаты,
проверяя используемые приборы по
соответствующим эталонам, внося поправки
в показания приборов, используя более
точные приборы и инструменты.
Случайные
ошибки
при измерениях обусловлены влиянием
большого числа факторов, случайным
образом изменяющихся в процессе
эксперимента. Например, источником
случайных ошибок при взвешивании на
аналитических весах может явиться
неоднородность в распределении
температуры в различных частях весов,
влияние колебаний стола из-за проезжающего
мимо здания грузовика и т.п.
При повторных
измерениях случайные ошибки с одинаковой
вероятностью приводят к отклонениям
значений измеряемых величин от истинного
значения как в сторону увеличения, так
и в сторону уменьшения, т.е. случайные
ошибки имеют разные численные значения
и знаки.
Полностью
исключить случайные ошибки нельзя, но
их можно уменьшить за счет увеличения
числа измерений при одних и тех же
условиях эксперимента.
Итак, при измерениях
неизбежно возникают погрешности. Теория
погрешностей указывает на то, как следует
вести измерения и их обработку, чтобы
допущенные ошибки были минимальными.
Кроме того, устанавливаются пределы,
внутри которых заключается точное
значение определяемой величины.
Теория погрешностей
I. Погрешности при прямых измерениях
Прямыми измерениями
называются такие, при которых измерение
величины производится непосредственно
по шкале прибора. Например,
2
измерение длины
штангенциркулем, измерение веса тела
на весах, определение промежутков
времени с помощью секундомера. Если
отклонение результатов измерений от
истинного значения измеряемой величины
происходит как в сторону увеличения,
так и в сторону уменьшения результатов
измерений, то наиболее вероятным
значением измеряемой величины будет
среднее арифметическое всех сделанных
измерений:
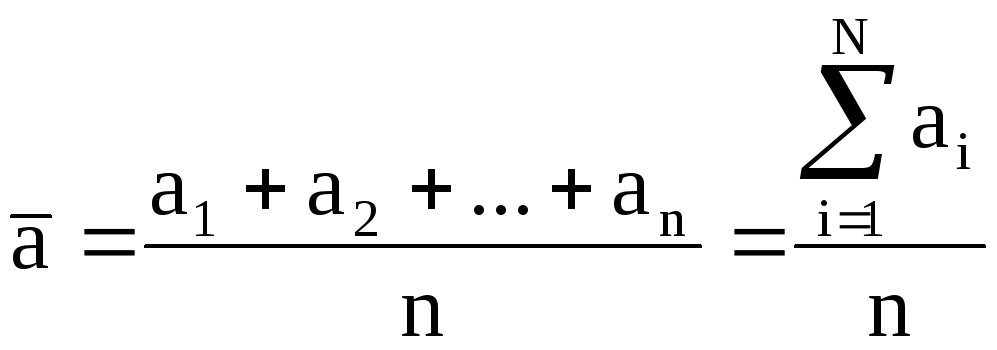 ,
,
(1)
где
![]()
результаты отдельных измерений, n
число измерений.
Для
характеристики степени приближения к
истинному значению измеряемой
величины вводится понятие абсолютной
погрешности
величины, показывающей насколько
найденное (среднее арифметическое)
значение может отличаться от истинного
значения измеряемой величины.
Для
определения абсолютной погрешности
сначала нужно найти отклонения каждого
отдельного измерения от среднего
арифметического:
![]() ,
,
где![]()
отклонение данного измерения, равное
разности между средним значением
измеряемой величины
![]() и результатом этого измерения
и результатом этого измерения![]() .
.
Случайная погрешность
вычисляется по формуле:
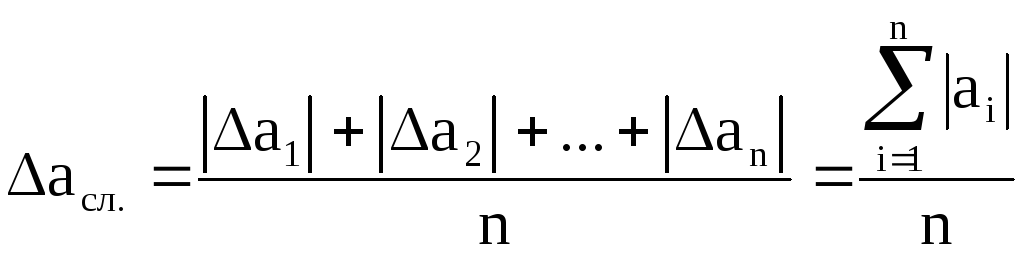 ,
,
(2)
где
![]()
модули отклонений каждого отдельного
измерения от среднего арифметического
значения.
Из
формулы (2) и теории вероятностей следует,
что с увеличением числа измерений n
случайная погрешность будет уменьшаться.
В
качестве систематической погрешности
берется приборная погрешность, равная
половине цены деления шкалы прибора.
Ценой деления прибора называется
минимальная величина, измеряемая
прибором.
В
общем случае необходимо принимать во
внимание как случайные, так и систематические
погрешности прямых измерений. Поэтому
абсолютная погрешность
![]() при прямых измерениях рассчитывается
при прямых измерениях рассчитывается
по формуле:
![]() (3)
(3)
где
![]()
случайная погрешностей, определяемых
по формуле (2),
3
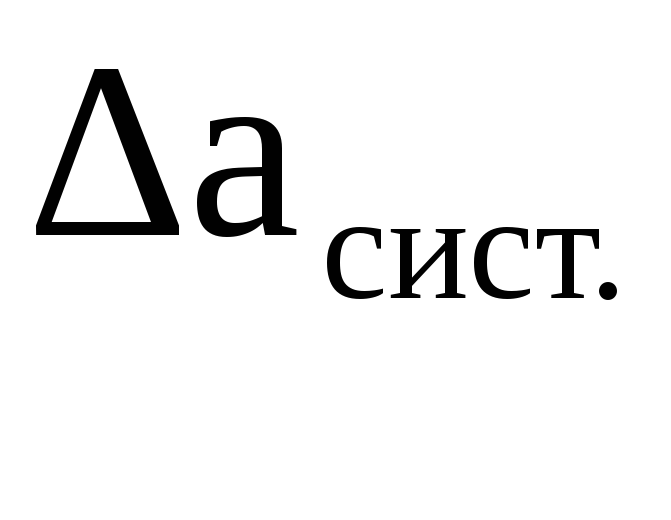 систематическая
систематическая
погрешность прибора, инструмента.
Примечание:
Если случайная погрешность много меньше
систематической, то для повышения
точности результата измерений нет
смысла увеличивать число измерений, а
нужно принять меры к уменьшению
систематической погрешности (например,
использовать более точные приборы).
Пример.
Пусть
измеряется диаметр цилиндрического
стержня с помощью штангенциркуля и
делается 5 измерений: 34.50
мм,
34.65
мм,
34.30
мм,
34.70
мм,
34.55
мм.
Среднее арифметическое
всех сделанных измерений:
![]()
Полученное
значение
![]() даёт наиболее вероятное значение
даёт наиболее вероятное значение
измеряемой величиныD.
Для
нахождения случайной погрешности
![]() нужно найти абсолютное значение
нужно найти абсолютное значение
отклонения каждого из 5-ти измерений от
среднего арифметического![]() и затем определить среднее значение
и затем определить среднее значение
этих отклонений:
![]()
Цена
деления штангенциркуля равна 0.05 мм,
следовательно, систематическая
погрешность равна
![]() .
.
Абсолютная
погрешность при измерении диаметра
стержня:
![]()
Результат
измерений принято записывать следующим
образом:
![]() .
.
(Результат измерений
34,54 мм и абсолютная погрешность 0,12 мм
должны заканчиваться в одинаковом
разряде)
Для характеристики
точности измерения вводится понятие
относительной погрешности:
![]()
Относительная
погрешность ε представляет собой
отношение абсолютной погрешности
![]() к среднему значению измеряемой величины.
к среднему значению измеряемой величины.
В нашем примере относительная погрешность
при измерении диаметра:
4
![]()
Относительная
погрешность является безразмерной
величиной. Она показывает, какую часть
измеряемой величины составляет абсолютная
погрешность.
Соседние файлы в папке 001_MEHANIKA
- #
- #
- #
- #
- #
- #
Содержание
- Лабораторная работа n102 методы обработки физических измерений Измерение физических величин
- Классификация ошибок измерений
- Лабораторные работы / Основные понятия теории ошибок
Лабораторная работа n102 методы обработки физических измерений Измерение физических величин
Физическими величинами называются характеристики свойств тел или процессов, которые могут быть определены количественно при помощи измерений. Измерение представляет собой познавательный процесс. заключающийся в сравнении данной величины опытным путем с некоторым ее значением, условно принятым за единицу измерения.
Измерения разделяют на прямые и косвенные. При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно или же при помощи приборов, отградуированных в требуемых единицах. При косвенных измерениях искомая величина вычисляется из результатов прямых измерений других величин, которые связаны с ней функциональной зависимостью.
Измерение любой физической величины обычно связано с выполнением трех последовательных операций:
а) проверкой и установкой приборов,
б) наблюдением и отсчетом их показаний,
в) вычислением искомой величины из результатов измерений и оценки точности окончательного результата.
Измеряя какую-нибудь физическую величину, мы принципиально не можем получить ее истинное значение. Поэтому в задачу измерений входит определение наиболее достоверного значениия искомой величины и обоснованная оценка допущенных при этом ошибок. Без оценки ошибок измерений нельзя делать определенные выводы из эксперимента.
Классификация ошибок измерений
Ошибкой или погрешностью называется отклонение результата измерения от истинного значения измеряемой величины. По характеру и происхождению, а также по способам оценка и уменьшений их влияния на результат различают три вида ошибок; промахи, случайные и систематические ошибки.
Промахи — это грубые ошибки, обусловленные неверными отсчетами, неверными записями показаний прибора или резко изменившимися внешними условиями эксперимента. Обычно результаты, содержащие грубые ошибки, сильно отличаются от других данных и хорошо заметны на их фоне. Имеются правила, позволяющие исключать их из таблицы измерений.
Случайными ошибками называются ошибки природа и величина которых неизвестна. Их присутствие обнаруживается в том, что при повторных измерениях одной и той же величины с одинаковой тщательностью получаются числовые результаты, несколько отличающиеся по последним значащим цифрам.
Случайные погрешности отдельных измерений не могут быть исключены опытным путей. Теория ошибок, как увидим далее, дает два способа уменьшения их влияния на окончательный результат в серии измерений:
1) тщательное проведение отдельных измерений о возможно малым разбросом результатов;
2) выполнение большого числа измерений в серии.
Систематическими ошибками называются ошибка, которые при повторных измерениях одной и той же величины сохраняются постоянными или изменяются по определенному закону. Они вызывают смещение, сдвиг ΔХ результатов в каком-то направлении от истинного значения. Систематические ошибки часто возникают из-за того, что условия эксперимента отличаются от предполагаемых теорией, а поправку на это несоответствие не делают. Другим обычным источником этих ошибок являются инструментальные погрешности, обусловленные несовершенством изготовления средств измерения, например, неточностью градуировки шкалы прибора, неравноплечностью весов и т.п.
Систематическую ошибку модно выявить либо путем использования более точных средств измерения, либо изменив сам метод измерения.
Оценки точности измерений
По форме числового выражения различают абсолютные и относительные ошибки.
Абсолютная ошибка измерения — это ошибка, выраженная в единицах измеряемой величины. Количественно она определяется разностью между подученным при измерении значением величины Xi и ее истинным значением X:
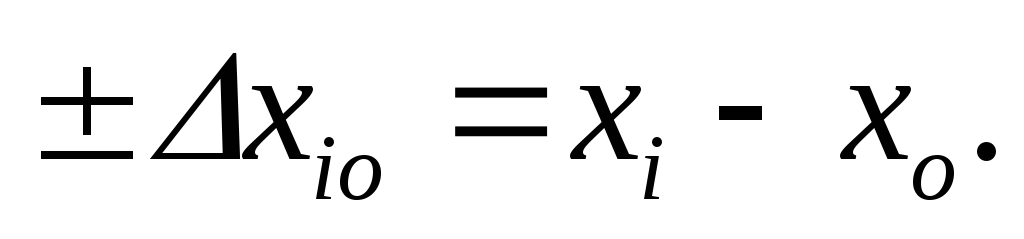 . (1)
. (1)
Чем меньше погрешность измерения, тем оно точнее.
Отношение ошибки измерения к истинному значению измеряемой величины (если последняя не равна нулю) называется относительной ошибкой измерения:
 или
или 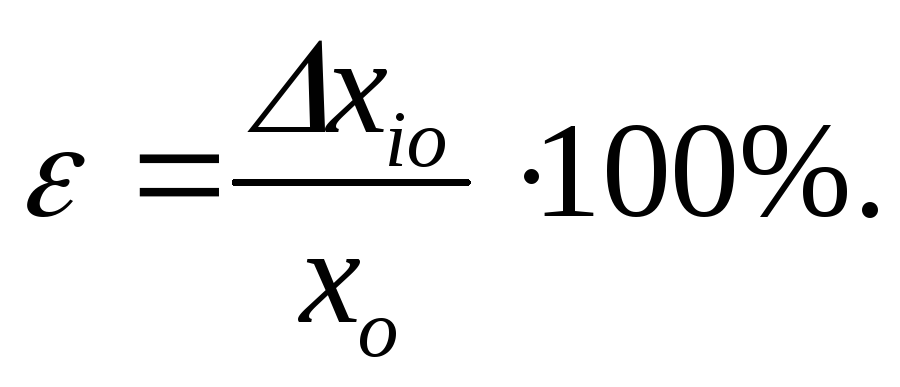 (2)
(2)
Она является величиной безразмерной, показывает, какую долю измеряемой величины составляет ошибка и обычно выражается в процентах.
Указание относительных ошибок приобретает особое значе-ние оттого, что позволяет сравнивать качество измерений величин разных наименований и порядков. Например, по относительным погрешностям можно сопоставлять точность измерения массы и длины, размеров микро- и макрообъектов.
Под точностью измерения понимают качество измерения, отражающее близость результата к истинному значению измеряемой величины. Точность измерения количественно характеризуется числом, равным обратному значению относительной погрешности, выраженной в долях измеряемой величины. Например, если погрешность измерения составляет ε=2·10 -5 , то точность этого измерения будет 5·10 4 .
Результат измерения модно было бы записать в виде

однако истинная ошибка 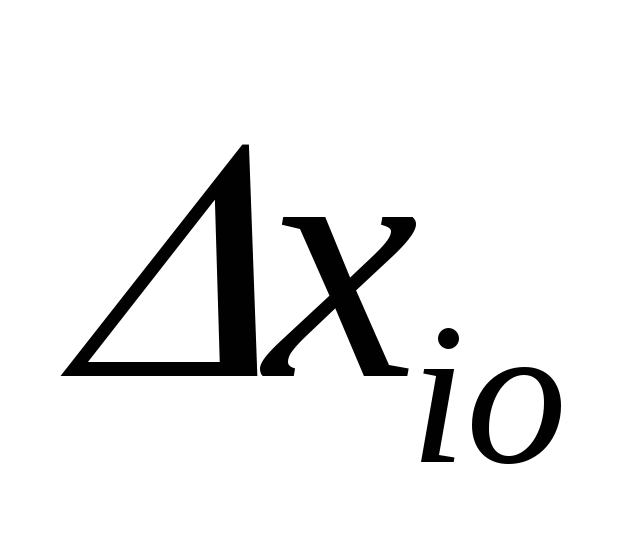 нам неизвестна, так как неиз -вестно истинное значение измеряемой величины Хо.
нам неизвестна, так как неиз -вестно истинное значение измеряемой величины Хо.
Поэтому обычно производят несколько (n раз) измерений искомой величины, и в качестве результата наиболее близкого к хо принимают их среднее арифметическое
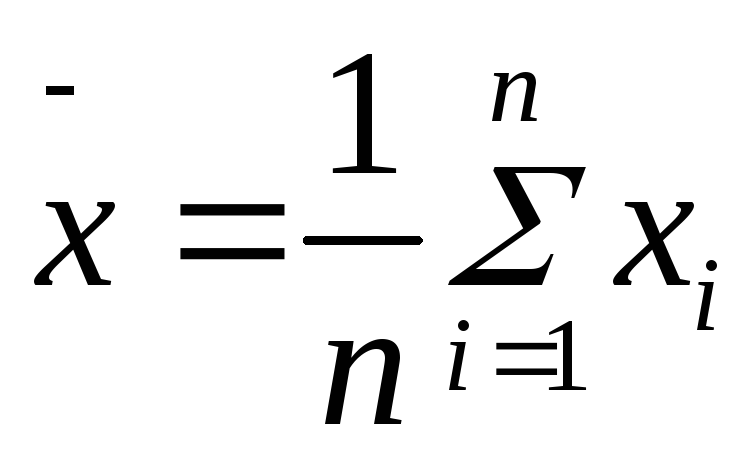 . (3)
. (3)
Под истинным значением измеряемой величины подразумевают
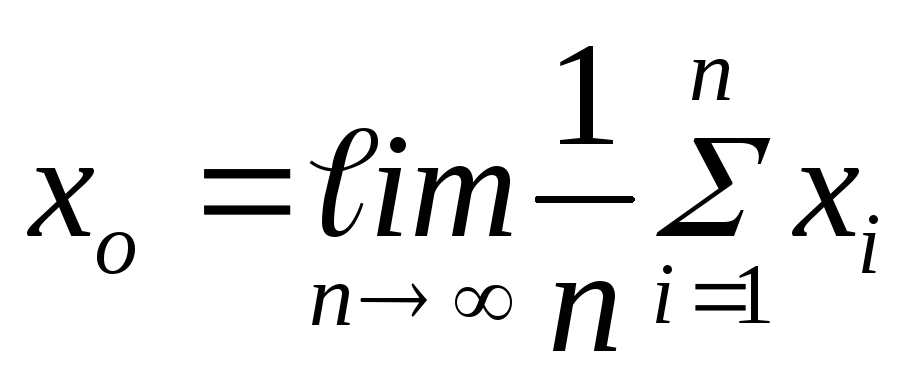 (4)
(4)
Теория ошибок по результатам отдельных измерений позволяет вычислить пределы ±  вблизи
вблизи , внутри которых может находиться
, внутри которых может находиться — с любой заданной вероятностьюδ. Результат измерения представляют в форме
— с любой заданной вероятностьюδ. Результат измерения представляют в форме

 при
при  . (5)
. (5)
Эта запись означает, что истинное значение  с вероятностью
с вероятностью находится внутри доверительного интервала
находится внутри доверительного интервала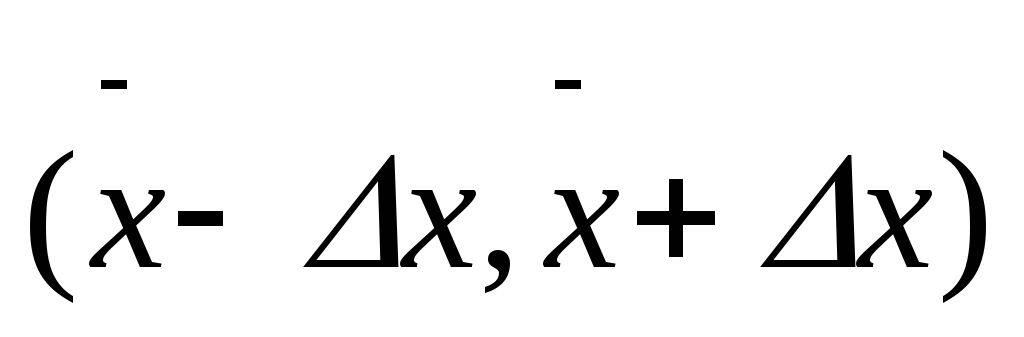
Источник
Лабораторные работы / Основные понятия теории ошибок
Основные понятия теории ошибок. Оценка точности наблюдений.
Для последующей ясности, в этой статье, под наблюдениями будем подразумевать совокупность одиночных измерений определенной величины: разница в блеске, показание шкалы микрометра и прочее. Это величина называется измеряемой или наблюдаемой. По особенности проведения, все наблюдения можно разделить на две группы: равноточные и неравноточные. К первой категории относятся такие наблюдения, которые были выполнены одним человеком, на одном приборе (инструменте) в сравнительно короткий промежуток времени (то есть одинаковое воздействие внешних факторов). Во вторую категорию, естественно, попадают те наблюдения, которые не соответствуют одному, нескольким или всем условиям принадлежности к равноточным наблюдениям. В этой статье не будут описаны точностные расчеты для наблюдений второй категории, они более сложны и громоздки, и применяются чаще в обработке геодезических измерений и при комплексных астронаблюдениях. Планируется подробно остановится на неравноточных измерениях в следующей статье из этого цикла, которая будет содержать основные принципы совместного уравнивания результатов наблюдений по способу наименьших квадратов.
Типы погрешностей наблюдений и особенности их учета
Любое измерение в реальных условиях производится с погрешностью, которую можно разделить на две составляющие — систематическую и случайную. Систематическая погрешность возникает в основном из-за ограниченной точности измерительных приборов, отчетных механизмов, а так же в связи с отсутствием учета второстепенных факторов, влияющих на измерения, или, если этот учет ведется не корректно. Систематические погрешности ведут к одностороннему искажению результатов наблюдений (постоянное завышение или занижение значения измеряемой величины). Их главная особенность — в ходе поверок инструментов и тестовых измерений вполне реально выявить такие погрешности (найти их численные значения и знаки), и тем самым свести их влияние на результаты наблюдений к минимуму. Случайные погрешности появляются из-за непредсказуемых, хаотичных причин, искажающих результаты наблюдений. Их особенность в том, что они приводят к получению разных значений измерений при их многократных повторах, проведенных в одинаковых условиях. Выявить случайные погрешности из отдельных замеров практически невозможно, но зато при достаточном количестве однородных измерений вполне реально «свести на нет» их совокупное влияние на результаты наблюдений. Такое минимизирование случайных искажений данных основано на ряде процедур, которые в свою очередь базируются на выводах и следствиях теории ошибок. Теория ошибок — математическая дисциплина, изучающая законы и особенности «поведения» погрешностей (ошибок) измерений. Например, нормальное распределение, эффект взаимной компенсации по знакам и так далее. Возникла эта дисциплина, как одно из многочисленных «ответвлений» от Теории Вероятностей. Математическая обработка различна для обоих видов погрешностей. Учет систематической составляющей есть процесс почти уникальный для каждого типа приборов и инструментов, для различных природных и прочих факторов, в том числе для каждого отдельного наблюдателя (так называемая личная ошибка, которую обычно классифицируют как подтип систематической составляющей). Случайные ошибки подчиняются универсальным законам, которые можно применять не только при наблюдениях разных объектов и измерениях разных величин, но и в разных науках — будь то астрономия, физика или геодезия. Основные принципы обработки везде одни и те же. Впрочем существует еще один класс погрешностей — грубая ошибка, или ложное измерение.
Точностной расчет для серии равноточных наблюдений
Рассмотрим алгоритм первичной обработки серии равноточных наблюдений. Пусть мы получили массив замеров измеряемой величины «Х», который имеет вид: X1, X2, . Xn, где n — количество замеров на сеансе.
Находим среднее арифметическое значение «Х» на сеансе:
Xs = ( X1 + X2 + . + Xn ) / n
Рассчитываем отклонения среднего значения от измеренных:
d1 = X1 — Xs, d2 = X2 — Xs, . dn = Xn — Xs
Определяем среднюю квадратическую погрешность одного измерения, это параметр, который характеризует среднюю точность проведения одного замера:
MX = SQR ( ( d1 ^ 2 + d2 ^ 2 + . + dn ^ 2 ) / ( n — 1 ) )
Находим среднюю квадратическую ошибку среднего арифметического, которая определяет надежность полученного результата:
MXs = MX / SQR ( n )
Рассчитываем относительную погрешность результата наблюдений:
U ( в процентах ) = ( MXs * 100% ) / Xs
Таким образом, получаем, что наиболее вероятное значение измеряемой величины на сеансе имеет значение:
Особенности точностного расчета для прямых и косвенных измерений
По признаку анализирования получаемой при наблюдении информации, измерения делятся на прямые и косвенные. При прямых измерениях значение исследуемой величины измеряют непосредственно, например момент или промежуток времени. При косвенных измерениях, искомую величину рассчитывают по определенной формуле, в которую входят величины, измеряемые непосредственно, а так же заданные значения вспомогательных величин и констант, то есть можем записать: Y = F ( X1, X2, . Xn ), где Y — искомая величина, а X1, X2, . Xn — ее аргументы, измеряемые непосредственно. Пример косвенного измерения: исходя из снятых отчетов по окулярному микрометру, впоследствии переходим к координатам объекта. Важной задачей при обработке косвенных наблюдений является определение погрешности искомой величины по известным погрешностям величин ее составляющих. Формула, которая связывает эти параметры, имеет следующий вид:
MY = SQR ( ( ( dY / dX1 ) ^ 2 ) * MX1 ^ 2 + ( dY / dX2 ) ^ 2 ) * MX2 ^ 2 + . . + ( dY / dXn ) ^ 2 ) * MXn ^ 2 ),
где ( Di / dXi ) — частная производная функции Y = F ( X1, X2, . Xn ) по аргументу Xi, вычисленная в точке Xi.
Пример: А теперь еще раз «пробежимся» по описанной выше методики оценки точности проведенных наблюдений, но уже на базе конкретного случая. При наблюдениях деталей на диске Юпитера, на протяжении ночи были сделаны несколько зарисовок/фотографий.  На всех рисунках/фотографиях отмечено точечное образование, находящееся в южном полушарии и медленно передвигающееся параллельно экватору за счет суточного вращения планеты. Задача: определить широту наблюдаемого образования — по всей видимости ядра нового мощного антициклона, на которые богата бурная юпитерианская атмосфера. С изображения Юпитера снимем два линейных значения: расстояние от экватора (его легко прочертить учитывая значительное сжатие планеты) до полюса — Y и расстояние от экватора до зафиксированного образования. (см. рис 1). Так как масштаб зарисовок/фотографий может быть разным, вычислим для всех изображений относительные значения величины Х ( Y приравняем к единице). Далее приводится таблица с примером вычисления средних квадратических погрешностей одного наблюдения и всего результата.
На всех рисунках/фотографиях отмечено точечное образование, находящееся в южном полушарии и медленно передвигающееся параллельно экватору за счет суточного вращения планеты. Задача: определить широту наблюдаемого образования — по всей видимости ядра нового мощного антициклона, на которые богата бурная юпитерианская атмосфера. С изображения Юпитера снимем два линейных значения: расстояние от экватора (его легко прочертить учитывая значительное сжатие планеты) до полюса — Y и расстояние от экватора до зафиксированного образования. (см. рис 1). Так как масштаб зарисовок/фотографий может быть разным, вычислим для всех изображений относительные значения величины Х ( Y приравняем к единице). Далее приводится таблица с примером вычисления средних квадратических погрешностей одного наблюдения и всего результата. 
Xs = 2.88 / 8 = 0.360 MX = SQR ( 0.0114 / 8 — 1 ) = 0.040 MXs = 0.040 / SQR ( 8 ) = 0.014 U = ( 0.014 * 100% ) / 0.360 = 3.889% Xsv = 0.360 + 0.014, или: 0.346 Соседние файлы в папке Лабораторные работы
- #
Источник
Работа добавлена на сайт samzan.net: 2016-06-20
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.

Предоплата всего
от 25%

Подписываем
договор
Лабораторная работа 1
Основы измерений и обработки результатов
Цель работы: знакомство с элементами теории погрешностей, методами измерения основных физических величин и правилами обработки результатов измерений.
Основные теоретические положения
(элементарные представления теории погрешностей)
Измерением называется процедура определения действительного значения физической величины с помощью специальных технических средств. Указанная процедура состоит из нескольких этапов: выбора измеряемой величины, метода измерения, приборов для наблюдения, метода обработки результатов наблюдения. Поэтому результаты наблюдения, как правило, не дают истинного значения измеряемой величины, то есть они содержат погрешности измерений.
По способу получения результата все измерения делятся на прямые и косвенные. Измерение, при котором значение физической величины находится непосредственно из опытных данных, называется прямым измерением – это, например, измерение температуры термометром, длины – линейкой.
Измерение, при котором искомое значение физической величины вычисляют по формуле на основании известной зависимости между ней и величинами, получаемыми при прямых измерениях, называется косвенным измерением, − например, измерение плотности тела по его массе и геометрическим параметрам, сопротивление проводника по напряжению и току.
Погрешность измерения – это отклонение результата измерения от истинного значения, которое может быть получено с помощью более совершенных методов и средств измерений. Различают абсолютную и относительную погрешности.
Абсолютная погрешность ΔX равна разности между результатом измерения X и истинным или точным значением измеряемой величины:
. (1.1)
Относительная погрешность измерения представляет собой отношение абсолютной погрешности к истинному или точному значению измеряемой величины:
(1.2)
Погрешности измерения имеют случайную и систематическую составляющие.
Составляющая погрешности измерения, которая случайным образом изменяется при повторных измерениях одной и той же величины, называется случайной погрешностью. Случайная погрешность определяется факторами, проявляющимися нерегулярно с изменяющейся интенсивностью. Значение случайной составляющей невозможно предвидеть, следовательно, исключить.
Случайная погрешность прямых измерений вычисляется следующим образом:
. (1.3)
Здесь − коэффициент Стьюдента, − среднее квадратичное отклонение, вычисляемое по формуле
, (1.4)
а − среднее значение измеряемой величины
. (1.5)
Результат измерения представляется в виде
.
Для нахождения предельной случайной абсолютной погрешности косвенных измерений в том случае, когда интересующая экспериментатора величина связана с несколькими измеряемыми величинами функциональной зависимостью
(1.6)
используется формула
. (1.7)
Предельная относительная погрешность рассчитывается по формуле:
. (1.8)
Результат измерения представляется в виде
, (1.9)
где
Отдельные результаты измерений могут сильно отличаться от среднего значения, что вызывается кратковременным и сильным воздействием какого-либо внешнего фактора. Возникающая при этом погрешность называется промахом. Ошибочный результат наблюдения в этом случае должен быть исключен при обработке результатов измерения.
Погрешности, которые при повторных измерениях остаются постоянными или закономерно изменяются, называются систематическими. Их можно оценить или исключить из результатов измерений путем введения поправок.
Систематические погрешности классифицируются следующим образом:
1. Систематические погрешности, о существовании которых ничего не известно, но которые могут иметь значительную величину.
Такие погрешности проявляются при сложных измерениях и их почти никогда не удается устранить. Измерение с такой ошибкой является неверным.
2. Погрешности известного происхождения, но неизвестной величины, которые не могут быть исключены, но могут учитываться в конечном результате. Наиболее распространенной погрешностью такого типа является погрешность измерительных приборов, определяемая классом его точности.
3. Систематические погрешности, природа которых известна, а их величина может быть установлена более или менее точно. Для устранения таких погрешностей в измерения вводятся поправки.
Различают систематические погрешности прямых и косвенных измерений. Систематическая погрешность прямого измерения – это, как правило, величина погрешности при нормальных условиях эксплуатации средства измерения.
В случае применения нескольких средств измерений, образующих комбинированное устройство, возникает систематическая погрешность косвенных измерений, предельная величина которой рассчитывается по формуле, аналогичной (1.7):
, (1.10)
где функция , − систематическая погрешность каждого отдельно взятого измерительного средства, входящего в устройство.
В большинстве случаев результаты эксперимента содержат и систематические, и случайные погрешности. Поэтому целесообразно организовать эксперимент таким образом, чтобы исключить одну из них. Для этого можно использовать следующие правила:
1. Если систематическая погрешность значительно больше случайной, то нет смысла уменьшать случайную погрешность, увеличивая число экспериментов, и достаточно осуществить наблюдение один раз.
2. Если случайная погрешность является определяющей, то для уменьшения число наблюдений следует выбирать таким, чтобы случайная погрешность среднего арифметического была меньше систематической погрешности. В этом случае результирующая погрешность определяется, в основном, систематической погрешностью.
3. Если в эксперименте присутствуют систематические погрешности неизвестного типа и большой величины, то их можно устранить, организовав измерение таким образом, чтобы постоянный фактор, вызывающий систематическую погрешность, в каждом из наблюдений действовал различным образом. В результате такой организации эксперимента постоянно действующий фактор становиться случайным, а систематическая погрешность превращается в случайную. Этот прием называется рандомизацией и позволяет практически исключить многие неизвестные погрешности.
Если все же не удается обеспечить исключение погрешности, какого–либо типа, то при обработке результатов эксперимента возникает необходимость суммирования погрешностей.
В простейшем случае величина предельной суммарной погрешности прямых измерений вычисляется по формуле
, (1.11)
где − значение коэффициента Стьюдента при .
Величина предельной суммарной погрешности косвенных измерений рассчитывается по формуле
. (1.12)
Все измерения осуществляются с помощью средств измерений – технических устройств, имеющих нормированные метрологические характеристики. Применяемые на практике средства измерений подразделяют на измерительные приборы, измерительные преобразователи, измерительные установки и измерительные системы.
Важнейшей характеристикой средств измерений является их точность, которая характеризуется соответствующими составляющими погрешности результата измерений.
Погрешность средств измерений – это метрологическая характеристика, количественно выражающая отклонение номинального значения физической величины, воспроизводимой или измеряемой данным средством измерений, от истинного или точного значения.
Различают абсолютную, относительную и приведенную погрешности измерительных приборов.
Абсолютная погрешность прибора есть разность между показанием прибора А и истинным значением измеряемой величины , то есть
(1.13)
Относительная погрешность представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины:
. (1.14)
Приведенная погрешность есть отношение абсолютной погрешности к нормирующему значению , то есть условно принятому значению физической величины, постоянному во всем диапазоне измерений или некоторой его части:
. (1.15)
Важной эксплуатационной характеристикой прибора является чувствительность S, то есть отношение изменения сигнала на выходе измерительного прибора к вызывающему его изменению измеряемой величины:
. (1.16)
Величина, обратная чувствительности , называется ценой деления прибора.
Более подробно указанные характеристики описаны для электроизмерительных приборов в лабораторной работе 11 настоящего руководства.
Описание лабораторной установки и последовательность проведения измерений
Установка представляет собой специальный ящик, в котором представлен набор измерительных инструментов: линейка, штангенциркуль, микрометр, транспортир, секундомер, термометр, а также исследуемые объекты: параллелепипед, неравноугольный треугольники сосуд с нагревателем.
Задание 1. Измерение линейных размеров с помощью линейки, штангенциркуля и микрометра.
1. Однократные измерения размера линейкой.
Линейка является простейшим измерительным устройством. Цена деления линейки может быть различной. Для измерения с помощью линейки необходимо нулевую отметку шкалы совместить с краем измеряемого отрезка.
Результат измерения считывается по шкале линейки по другому краю измеряемого отрезка.
Погрешность измерения с помощью линейки составляет не более ½ цены ее наименьшего деления. Доли наименьшего деления считываются на глаз с точностью, не превышающей погрешность измерения, то есть 0,5 цены деления.
Пример 1. По линейке с ценой деления 1 мм произведен отсчет . Результат измерения записывается так:
Пример 2. Той же линейкой измерен размер . Результат измерения записывается следующим образом: При выполнении этого задания проводятся однократные измерения размера любого предмета линейкой, например, размер грани параллелепипеда или стороны треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде: , (см. примеры 1 и 2).
2. Однократные измерения штангенциркулем.
Штангенциркуль представляет собой металлическую линейку 1, на конце которой имеется поперечный выступ 2. Другой такой же выступ имеется на обойме 3. Они движутся по линейке. Обойма имеет окно 4, позволяющее видеть основную шкалу линейки. Внутренние поверхности выступов строго перпендикулярны линейке. Когда они прилегают друг к другу, указатель «нуль» на обойме находится против нулевого деления шкалы линейки. Измеряемый предмет зажимается между выступами.
Для измерения внутренних размеров отверстий наружные стороны концов выступов обычно делаются строго перпендикулярными линейке и слегка закругляются. Расстояние между ними при установке обоймы на нуль шкалы (обычно 8 или 10 мм) указывается на штангенциркуле 6. Иногда для измерения внутренних размеров делаются специальные ножи на тыльной стороне выступов, концы выступов заостряются. Такое устройство позволяет измерять отверстия малых размеров, но точность измерения при этом меньше.
Достаточно высокая точность измерения штангенциркулем достигается с помощью нониуса. Нониус – это дополнительная линейка со шкалой 5, нанесенной по краю подвижной 3.
Нулевой штрих шкалы нониуса служит одновременно указателем для считывания числа целых делений по основной шкале и началом отсчета долей миллиметра по шкале нониуса. Обычно число делений нониуса n = 10 или n=20.При 10 делениях нониуса всей длине его шкалы соответствует 19мм основной шкалы, то есть 10 делений нониуса имеют длину, на 1 мм меньшую, чем 20 делений основной шкалы. Цену деления нониуса штангенциркуля можно найти по формуле . При 10 делениях нониуса и . При 20 делениях нониуса . Погрешность градуировки штангенциркуля при n = 10 равна 0,1 мм, а при n = 20 равна 0,05 мм.
Пример 3. Нониус штангенциркуля имеет цену деления 0,1 мм. Число целых делений шкалы до нуля нониуса – 12. Штрих основной шкалы совпадает со штрихом шкалы нониуса, которому предшествует 4 деления его шкалы. Результат отсчета Результат измерения записывается в виде:
При выполнении этого задания проводятся однократные измерения размера любого предмета штангенциркулем, оцениваются погрешности измерения и результат представляется в виде (см. пример 3).
3. Однократные измерения размера микрометром.
Для измерения внешних размеров предметов с большой точностью, чем штангенциркулем, служит микрометр. Он состоит из скобы 1, жестко соединенной с измерительным упором 2, цилиндра 3, барабана 4, который соединен с микрометрическим винтом и подвижным измерительным упором 5. На цилиндре 3 нанесено 2 миллиметровых шкалы: нижняя – основная, верхняя – дополнительная, смещенные относительно друг друга на 0,5 мм. Левый конусный конец барабана имеет круговую шкалу 6, состоящую из 50 делений. Шаг микрометрического винта равен 0,5 мм, поэтому один оборот барабана соответствует изменению линейного размера 0,5 мм.
Измеряемый предмет помещают между винтом 5 и противоположным ему упором 2 так, как показано на рисунке 1.3. Винт вращают и доводят до соприкосновения с предметом. При измерении микрометром существенно постоянство вращательного момента, приложенного к барабану при соприкосновении упоров с измеряемым предметом. Поэтому барабан 4 следует вращать, прикладывая усилие не к нему самому, а к головке 7. Она соединяется с винтом с помощью «трещотки», которая передает усилие только до тех пор, пока она не достигнет определенной величины. Когда же эта величина достигнута, дальнейшее вращение головки происходит в «холостую» и не изменяет показания микрометра.
Результат измерения получают в следующем порядке. Сначала производят отсчет размера по основной и дополнительным шкалам с точностью до 0,5 мм, после этого осуществляется отсчет сотых долей миллиметра по шкале барабана и результаты суммируются.
Погрешность градуировки микрометров составляет 0,004 мм.
Пример 4. На основной шкале видно 5 целых миллиметровых делений. Следующая справа за меткой 5 основной шкалы отметка дополнительной шкалы не видна. Отсчет по шкале барабана – 24.
Результат отсчета . Результат измерения:.
При выполнении этого задания проводятся однократные измерения размера любого предмета микрометром, оценивается погрешность и результат представляется в виде: (см. пример 4).
4. Повторное измерение размеров
Повторные измерения предметов являются прямыми наблюдениями. Процедура их осуществляется очень просто: одним и тем же измерительным инструментом – линейкой, штангенциркулем или микрометром измеряют один и тот же размер несколько раз через определенный интервал времени, и результаты заносятся в таблицу.
Обработка результатов эксперимента.
- Погрешность величины l в каждом измерении отдельным измерительным инструментом находится по методике расчета погрешностей прямых измерений, задавая доверительную вероятность и коэффициент Стьюдента .
, (1.17)
где
, (1.18)
. (1.19)
2. Погрешность смешанных измерений вычисляется аналогично:
(1.20)
Сравниваются погрешности и объясняются расхождения.
Задание 2. Измерение объема параллелепипеда.
Такие измерения являются косвенными и их можно осуществить двумя способами.
Способ 1. Однократные измерения
Одним из измерительных инструментов один раз определяется длина одной грани параллелепипеда и результат записывается в виде:
(1.21)
Обработка результатов эксперимента.
1. Погрешность однократных косвенных измерений различными инструментами рассчитывается по формуле (1.10). Так как объем , то
, , ,
и, следовательно,
,
то есть:
,
. (1.22)
Результат измерения представляется в виде
2. В том случае, если длина всех граней измерена одним и тем же инструментом с одинаковой погрешностью ,то
Способ 2. Повторные измерения
Осуществляются повторные измерения любым измерительным инструментом одной грани несколько раз, и результаты заносятся в таблицу.
Обработка результатов эксперимента.
Вычисляется среднее значение объема и погрешность
его определения по формуле (1.22):
, (1.23)
где , , вычисляют по методике расчета погрешностей прямых измерений.
Любопытно провести эти измерения, используя для получения результата различные измерительные инструменты, вычислить погрешность и сравнить значения объема и погрешности, полученные при измерении линейкой, штангенциркулем и микрометром, а также при смешанных измерениях.
Задание 3. Измерение плоских углов транспортиром.
Для простейших измерений углов применяется транспортир, который представляет собой полукруг, дуга которого разделена на через . Чтобы измерить угол у, накладывают транспортир (рис. 1.4) так, чтобы вершина угла совпала с центром полукруга, а стороны – с радиусами ОА и ОВ. Тогда число градусов, содержащихся в дуге, заключенной между сторонами угла АОВ, дает числовое значение его величины. Погрешность измерения углов по транспортиру составляет половину деления шкалы – 0,5.
Пример 5. Результат отсчета по шкале транспортира . Результат измерения
Более сложные и более точные приборы для измерения углов мы не рассматриваем.
1. Однократное измерение углов.
При выполнении этого задания проводятся однократные измерения углов треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде: , причем очевидно, что .
2. Многократные измерения углов.
Погрешности величин у, b, а находятся по формуле расчета погрешностей прямых измерений:
. (1.26)
И в первом, и во втором случае можно проверить результат, используя формулу . При этом погрешность суммы углов отличается от погрешности измерения отдельного угла и вычисляется по формуле
(1.27)
Задание 4. Измерение времени секундомером.
Для измерения времени применяются секундомеры. Механические секундомеры имеют цену деления 0,1 и 0,2 с.
Основная погрешность этих секундомеров равна цене деления, а погрешность отсчета зависит от быстроты реакции на включение и остановку секундомера. Установлено, что неточности пуска и остановки дают погрешность порядка 0,3 с. Таким образом, при работе с секундомером с ценой деления 0,2 с погрешность может достигать 0,5 с.
Применяются электронные секундомеры с ценой деления 0,01 и 0,001 с. Их целесообразно использовать вместе с устройствами, обеспечивающими совпадение пуска и остановки с началом и концом процесса, длительность которого определяется.
Пример 6. По индикатору электронного секундомера с ценой деления 0,01 с зарегистрировано некоторое время . Результат измерения Методика измерения интервалов времени и обработки результатов при однократных и повторных измерениях та же, что и в предыдущих заданиях по измерению линейных размеров и углов.
Задание 5. Измерение температуры термометром.
Термометр представляет собой капиллярную трубку из стекла, которая заполнена жидкостью, обычно ртутью или подкрашенным спиртом. Капиллярная трубка помещена в корпус из стекла, в котором также закреплена измерительная шкала. Погрешность измерения температуры термометрами различных типов регламентируется ГОСТ 400-80 и имеет, в большинстве случаев, величину, равную цене деления.
Методика измерения температуры и обработки результатов при однократных и многократных измерениях та же, что и в предыдущих заданиях.
Лабораторная работа 2
Ускорение свободного падения
Цель работы: изучение закона всемирного тяготения, кинематики материальной точки, экспериментальное определение ускорения свободного падения из кинематического уравнения.
Основные теоретические положения
Гравитационное взаимодействие лежит в основе многих механических явлений. Оно возникает между любыми видами материи и является одним из фундаментальных взаимодействий. Гравитационное взаимодействие осуществляется посредством гравитационного поля. Всякое тело изменяет свойства окружающего его пространства, создавая в нем гравитационное поле. Это поле проявляет себя в том, что на помещенное в него другое тело действует сила.
Сила гравитационного притяжения, действующая между двумя материальными точками, в соответствии с законом всемирного тяготения (Ньютон, 1678 г.) пропорциональна произведению масс материальных точек и , обратно пропорциональна квадрату расстояния между ними (рис.2.1).Силы направлены по прямой, соединяющей материальные точки, и в векторном виде записываются в следующем виде:
(2.1)
где и – силы, действующие на соответствующие материальные точки, – радиус-вектор, направленный от первой точки ко второй, – гравитационная постоянная .
Формулы (2.1) справедливы для материальных точек, то есть тел, размерами которых можно пренебречь по сравнению с расстоянием между ними, а так же в случае тел сферической формы (однородные шары, шаровые оболочки), размерами которых пренебречь нельзя, при этом под следует понимать расстояние между центрами тел. Во всех остальных случаях формулы (2.1) неприменимы.
Согласно формуле (2.1) на всякое тело, находящееся вблизи поверхности Земли действует сила , где – единичный вектор, направленный от центра Земли к телу. При , гравитационное поле Земли можно считать однородным и силу можно представить в виде , где – вектор ускорения свободного падения, направленный к центру Земли. Для среднего значения радиуса Земли его величина равна .
Получим кинематические уравнения для материальной точки, движущейся с постоянным вектором ускорения , то есть в поле однородной силы тяжести.
По определению вектор ускорения материальной точки есть первая производная по времени от вектора скорости , отсюда
. (2.2)
Проинтегрируем последнее уравнение с учётом, что :
,
отсюда
, (2.3)
где , – скорости материальной точки в начальный момент времени и в некоторый последующий момент времени . Положив , получаем кинематическое уравнение для вектора скорости
(2.4)
Используя определение вектора скорости материальной точки , преобразуем уравнение (2.4) к виду
. (2.5)
Проинтегрируем уравнение (2.5)
, (2.6)
где и – радиус-векторы точки в моменты времени и , соответственно. Из (2.6) получим
. (2.7)
В проекциях на ось OX декартовой системы координат кинематические уравнения (2.4) и (2.7) имеют вид
и , (2.8)
где , – проекции соответствующих векторов на ось OX. Уравнения (2.4) и (2.7) в проекциях на оси OY и OZ имеют аналогичный вид.
Получим из (2.8) кинематические уравнения для тела, падающего с некоторой высоты с нулевой начальной скоростью. Начало отсчёта оси OY свяжем с уровнем, относительно которого отсчитывается высота , ось направим вертикально вверх. Представим вектора , в координатной записи , , . Так как проекции векторов на оси OX, OZ равны нулю, то получаем уравнения только в проекциях на ось OY:
и . (2.9)
Из (2.9) следует формула связи высоты со временем, за которое совершается падение тела. Так как тело упало, то , отсюда
. (2.10)
Экспериментальная установка и методика измерений.
Экспериментально измерив время падения тела с высоты , можно, используя соотношение (2.10), рассчитать ускорение свободного падения.
Основным конструктивным элементом установки (рис. 2.2) является штатив (1), по длине которого может перемещаться электромагнит (2), к которому притягивается шарик (3). Электромагнит снабжён указателем высоты шарика (4) по линейке (5). Время падения шарика определяется по секундомеру (6). В момент перевода ключа К – «Пуск» из положения (а) в положение (б) электромагнит отключается, шарик начинает падать и включается секундомер. Когда падающий шарик размыкает контакты (7) секундомер отключается.
Сначала на установке проверяется зависимость (2.10). Для этого шарик устанавливается на высоту и измеряется время его падения с этой высоты. Затем высота меняется и измеряется время падения. Измерение повторяется несколько раз при разных значениях .
В следующем опыте определяется ускорение свободного падения. Для этого шарик поднимается на максимально возможную высоту и многократно измеряется время его падения с этой высоты.
Обработка результатов эксперимента
1. Выбрать различные пары измерений , и рассчитать отношения и .
2. Рассчитать погрешности измерений величин и как погрешности косвенных измерений по формуле
, , (2.11)
где – систематическая погрешность измерения расстояния по линейке, – систематическая погрешность измерения времени по секундомеру.
3. Провести сравнение величин и по формуле
(2.12)
с учётом рассчитанных в п. 2 погрешностей.
4. Ускорение свободного падения рассчитать по формуле
, (2.13)
где – среднее арифметическое значение времени падения , – количество измерений.
5. Рассчитать погрешность измерения величины как погрешность косвенных измерений по формуле
, (2.14)
где − случайная погрешность прямых измерений времени,
,
где − коэффициент Стьюдента.
Лабораторная работа 3
Баллистический маятник
Цель работы: изучение закона сохранения импульса при неупругом ударе, определение скорости полета пули методом баллистического маятника.
Основные теоретические положения
Баллистический маятник представляет собой тяжелое тело, подвешенное на двойных нитях. В маятник стреляют по горизонтали пулей, которая застревает в нем. Пуля сообщает маятнику некоторую скорость, в результате чего маятник отклоняется. Измеряют величину отклонения маятника и по ней определяют скорость пули. Таким образом, методом баллистического маятника можно косвенно измерить скорость пули.
Если время соударения пули с маятником мало по сравнению с периодом колебаний маятника, то маятник не успевает заметно отклониться от исходного положения за время соударения. Это значит, что во время удара не возникнут силы, стремящиеся вернуть маятник в исходное положение, и систему пуля – маятник можно рассматривать как замкнутую. Удар пули, при котором она застревает в маятнике, является неупругим. При неупругом ударе выполняется закон сохранения импульса, который для системы из двух тел имеет вид
, (3.1)
где и − массы пули и баллистического маятника, и скорости пули и маятника до удара, − скорость маятника с пулей после удара. Поскольку до удара скорость маятника была равна нулю, в левой части формулы (3.1) останется только первое слагаемое. Направим ось вдоль скорости движения пули и спроектируем формулу (3.1) на ось :
. (3.2)
После удара маятник с пулей будет двигаться по дуге радиуса , где − длина нитей подвеса, и поднимется на некоторую высоту . Вследствие действия силы тяжести скорость системы «маятник-пуля»и ее кинетическая энергия будут убывать до нуля. Потенциальная энергия системы наоборот будет возрастать. За нуль отсчета потенциальной энергии примем вертикальную координату центра масс маятника перед выстрелом пули.
Кинетическая энергия системы сразу после удара пули равна , потенциальная энергия системы при ее отклонении до высоты равна . Для системы маятник-пуля после удара применим закон сохранения механической энергии, на основании которого можно записать
(3.3)
Из уравнений (3.2) и (3.3) выразим скорость пули
(3.4)
Поскольку масса пули во много раз меньше массы маятника, величиной в числителе формулы (3.4) по сравнению с величиной , можно пренебречь и получить формулу для расчета скорости пули в следующем виде:
. (3.5)
Производить непосредственное измерение высоты не всегда удобно, но ее можно определить либо по горизонтальному отклонению, либо по углу поворота маятника после попадания пули. Пусть маятник с застрявшей пулей отклонился на угол от вертикали.
Из рис. 3.1 видно, что высота отклонения выражается через угол отклонения следующим образом:
, (3.6)
при условии, что угол мал, примем, что
С учетом этого скорость пули из формулы (3.4) выражается следующим образом:
(3.7)
Выразим высоту подъема центра масс маятника через величину его отклонения по горизонтали. Используем для прямоугольного треугольника, изображенного на рис.3.1.,теорему Пифагора и запишем . Раскроем скобки в левой части; примем, что величина мала по сравнению с другими слагаемыми и тогда получим , откуда . Таким образом скорость пули может быть выражена через горизонтальное отклонение маятника по формуле
. (3.8)
Методика эксперимента
Установка состоит из штатива 6, на котором на двойном подвесе 2 закреплен баллистический маятник 1 в виде трубки, заполненной ватой (рис.3.2). Напротив открытого конца трубки на той же высоте располагается пистолет 3. Для измерения угла отклонения маятника после попадания в него пули служат стрелка 4 и транспортир 5. К корпусу маятника прикреплен указатель, позволяющий контролировать отклонение маятника по горизонтали. Измерение горизонтального отклонения производится по линейке 7, которая крепится к подставке.
Последовательность выполнения работы.
1 способ. Определение скорости по измерению угла отклонения маятника.
Отмечают положение стрелки 4 на шкале транспортира 5 – начальный угол . Из пистолета 3 делают выстрел, замечают положение стрелки 4 при отклонении маятника – записывают значение .
Определяют угол отклонения маятника .
Опыты проводятся с двумя пулями массами и . Для каждой пули производится 5−6 выстрелов.
2 способ. Определение скорости по измерению горизонтального отклонения маятника. По линейке 7 отмечают начальное положение указателя. Производят выстрел, маятник отклоняется. Отмечают его положение при отклонении .
Определяют перемещение маятника по горизонтали .
Опыты проделывают 5−7 раз с двумя пулями разной массы. Масса баллистического маятника и массы пуль указаны на лабораторной установке.
Обработка результатов эксперимента
- Вычислить последовательно средние значения величин , .
- Величину вычислить по формуле (3.8), в которой или .
Для второй пули производятся такие же расчеты.
Расчет погрешностей.
- Погрешность косвенных измерений скорости пули, выполняемых первым способом, рассчитывается по формуле
. (3.9)
В (3.9) входит погрешность прямых измерений угла
, (3.10)
где − коэффициент Стьюдента, − среднее квадратичное отклонение.
- Погрешность косвенных измерений скорости пули, выполняемых вторым способом, рассчитывается по формуле
. (3.11)
В этом случае погрешность прямых измерений отклонения маятника по горизонтали находят по формуле
. (3.12)
- Результат для каждого способа представить в виде:
Дополнительное задание: Определение скорости пули по дальности полета при горизонтальной стрельбе.
Движение тела, брошенного горизонтально с некоторой высоты, представляет собой два одновременных движения: равномерное по горизонтали и равноускоренное по вертикали с ускорением, равным ускорению свободного падения (рис. 3.3).
Дальность полета, то есть перемещение по горизонтали определяется по формуле. . Время движения тела зависит от высоты точки бросания и связано с ней формулой . Отсюда выражаем время полета и затем дальность полета .
Таким образом скорость полета пули может быть рассчитать по формуле
. (3.13)
Методика эксперимента
В этом задании используется только пистолет 3, который разворачивают к краю стола, чтобы пуля не попадала в маятник.
Измеряют высоту пистолета над столом . После выстрела определяют дальность полета пули − расстояние, которое она пролетела по горизонтали. Для измерений используют линейку 8. Опыт проводят 3−5 раз.
Проводят измерения дальности полета для двух других значений высоты пистолета , .
Обработка результатов эксперимента
- Для каждого значения высоты пистолета над столом находят среднее значение дальности полета , , и рассчитывают среднее значение скорости пули по формуле
. (3.14)
- Определяют погрешность прямых измерений дальности полета по формуле
. (3.15)
- Находят случайную составляющую погрешности косвенных измерений скорости пули:
. (3.16)
- Приборную погрешность величины скорости , связанную с измерением величины , рассчитать по формуле
. (3.17)
- Суммарную погрешность косвенных измерений величины определить по формуле:
. (3.18)
- Результат представить в виде: .
Лабораторная работа 4
Математический маятник
Цель работы: изучение гармонических колебаний, экспериментальная проверка зависимости периода колебаний маятника от его длины; определение ускорения свободного падения.
Основные теоретические положения
Колебательным движением или колебанием называется такое движение, при котором тело остается вблизи некоторого положения равновесия. В качестве примеров колебаний на рис. 4.1 приведены математический, пружинный и физический маятники.
Если положение системы в любой момент времени может быть описано единственным параметром, то говорят, что система имеет одну степень свободы. Для всех систем с одной степенью свободы, вне зависимости от их физической природы, закон движения имеет одну и ту же математическую форму. Получим ее на примере пружинного маятника (рис. 4.1). На первом этапе рассмотрения силу сопротивления не учитываем.
Определим положение точки массой m ее смещением x из положения равновесия, в котором x = 0. Сила упругости , действующая на массу, будет стремиться вернуть ее в положение равновесия. Она называется возвращающей силой. По закону Гука , k>0 . Знак «минус» означает, что сила направлена в сторону, противоположную смещению. По второму закону Ньютона
имеем: , где − ускорение точки. Так как , то , . Так как k>0, m>0, то можно положить . Тогда
(4.1)
Из уравнения (4.1), описывающего колебания в среде без сопротивления − свободные колебания, следует, что движение точки под действием возвращающей силы происходит таким образом, что ее ускорение пропорционально смещению из положения равновесия.
Для того чтобы определить закон колебательного движения, необходимо решить дифференциальное уравнение (4.1), то есть найти зависимость . Предположим, что
, (4.2)
где и − произвольные постоянные величины. Подставив функцию (4.2) в уравнение (4.1), вычислив предварительно производные, можно убедиться, что она является решением уравнения и описывает гармоническое колебательное движение (рис. 4.2). Исследуем эту функцию в различные моменты времени, считая (рис. 4.3): . В момент времени точка находится в положении максимального правого отклонения, в момент − в положении равновесия, в момент − в положении максимального левого отклонения, и, наконец, в момент точка возвращается в положение равновесия. Таким образом колеблющаяся точка проходит каждую точку своего пути, в данном примере – положение равновесия, два раза за время . Это время T называется периодом колебаний. Величина , показывающая, сколько колебаний точка совершает за единиц времени, называется круговой или циклической частотой колебаний. Величина А является наибольшим отклонением колеблющейся точки от положения равновесия амплитудой колебаний.
Начальная фаза определяет положение колеблющейся точки в начальный момент времени . Величина называется фазой колебаний и определяет отклонение точки из положения равновесия в произвольный момент времени.
Наряду с циклической частотой можно ввести частоту , показывающую, сколько колебаний точка совершила за единицу времени. При этом .
Вычислим период колебаний математического маятника (см. рис. 4.1). Из треугольника сил видно, что . Если угол отклонения мал, то , . Знак «минус» означает, что возвращающая сила направлена в сторону, противоположную направлению отсчёта угла против часовой стрелки. Так как − это касательное к траектории ускорение, то по второму закону Ньютона имеем . Тогда: , или , , , или
. (4.3)
Из формулы (4.3) следует, что период колебаний математического маятника не зависит от массы груза. Поэтому для данного положения на Земле и для определенного значения g период зависит только от длины подвеса l. В частности, в той степени, в какой справедливо приближение , период колебаний не зависит от амплитуды.
Определим теперь период колебаний математического маятника в зависимости от амплитуды. На основании закона сохранения энергии и рис. 4.1 имеем
(4.4)
Из равенства (4.4) легко найти круговую частоту и период колебаний:
, (4.5)
где К(k)= − полный эллиптический интеграл первого рода.
При малых колебаниях, когда выполнено , разложение функции K(k) в ряд даёт
. (4.6)
Нетрудно увидеть, что при из (4.6) следует выражение для периода малых колебаний (4.3).
Лабораторная установка и проведение эксперимента.
Математический маятник представляет собой груз 1, подвешенный на длинной тонкой нити 2 (рис. 4.4). За длину маятника принимается расстояние от подвижной точки подвеса до центра масс груза. Свободный конец нити зажат в подвесе 2, закреплённом на зажиме 3 штатива 4. Время качаний определяется секундомером с помощью оптических датчиков, а угол отклонения – по специальной линейке 5.
Задание 1. Изучение зависимости периода малых колебаний от амплитуды.
Маятник откланяется от положения равновесия на небольшой угол и без толчка отпускается. Определяется время, в течение которого маятник сделает n полных колебаний, за одно полное колебание шарик проходит путь, равный четырём амплитудам. Изменяется начальное отклонение шарика и определяется время колебаний.
Обработка результатов и расчёт погрешностей
1. Погрешности периода колебаний определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность и коэффициент Стьюдента.
2. При проверке независимости периода колебаний от амплитуды сравниваются периоды для различных амплитуд и находится такая величина , при которой . Это означает, что при амплитуде колебаний , большей , период зависит от амплитуды.
Задание 2. Изучение зависимости периода малых колебаний от длины маятника.
Изменяется длина маятника l и определяется период колебания. При этом масса маятника не изменяется, а амплитуда выбирается такой, при которой период не зависит от амплитуды. Для каждого значения длины маятника определяется время отклонений.
Обработка результатов и расчёт погрешностей
При обработке данных проверяется соотношение:
(4.7)
Точность выполнения этого соотношения можно определить следующим образом:
- Вычислить систематическую погрешность величины по формуле
, (4.8)
где − систематическая погрешность определения длины по линейке.
- Погрешность косвенных повторных измерений величины вычислить по формуле
. (4.9)
- Случайные погрешности величин и рассчитать по методике расчёта погрешностей прямых измерений, задавая доверительную вероятность и коэффициент Стьюдента.
- Результаты расчётов проверить сравнением пар экспериментальных данных с учётом рассчитанных погрешностей.
Задание 3. Изучение зависимости периода малых колебаний от массы маятника.
Исследуется зависимость периода колебаний от массы маятника. Для этого изменяется масса маятника и остается неизменной его длина. Определяется период колебаний, и результаты опытов заносятся в таблицу.
Обработка результатов и расчёт погрешностей
- Обработку результатов таблицы провести по п. 1 задания 1.
- Сравнить периоды колебаний для различных масс груза и показать независимость периода от массы. При этом должно выполняться равенство
. (4.10)
Задание 4. Измерение ускорения свободного падения. Используются результаты, полученные в задании 1, 2 или 3.
Обработка результатов и расчёт погрешностей.
- Ускорение свободного падения рассчитать по зависимости, следующей из (4.3):
, (4.11)
где время выбирают из таблиц.
- Погрешность случайных косвенных измерений величины g рассчитать по формуле
, (4.12)
где величины , взяты по данным таблиц.
- Погрешность приборных косвенных измерений величины g рассчитать по формуле
. (4.13)
- Полученную погрешность вычислить по формуле
. (4.14)
- Результаты представить в виде: .
Задание 5. Изучение больших колебаний математического маятника.
При фиксированной массе груза и длине маятника измерить зависимость периода колебаний от угла отклонения маятника в пределах до 30− 35 градусов через пять градусов. Для каждого отклонения маятника измерения провести несколько раз и заполнить таблицу.
Обработка результатов и расчёт погрешностей.
1. Погрешности периода колебаний определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность р0 и коэффициент Стьюдента.
2. Построить зависимость нормированного теоретическим значением (4.3) периода колебаний маятника от угла отклонения , указав на графике нормированные доверительные интервалы по вертикальной оси координат. При этом в качестве по горизонтальной оси выбирается систематическая погрешность, равная половине деления шкалы, по которой измеряется первоначальное отклонение маятника.
3. На том же графике для данной длины маятника по формуле (4.5) построить нормированную теоретическую зависимость периода колебаний от угла первоначального отклонения маятника.
4. На том же графике для данной длины маятника по формуле (4.6) построить приближённую нормированную теоретическую зависимость периода колебаний от угла первоначального отклонения маятника.
5. Сравнить графики и найти величину отклонения, при которой выполняется приближение малых колебаний. Сравнить её с величиной , определённой в задании 1.
Лабораторная работа 5
УПРУГИЙ УДАР
Цель работы: исследование удара, изучение законов сохранения импульса и механической энергии при ударе.
Основные теоретические положения
Удар – совокупность явлений, возникающих при кратковременном приложении к телу внешних сил, например, при взаимодействии с другим движущимся относительно него телом, связанных со значительным изменением его скорости за очень короткий промежуток времени.
Абсолютно неупругим называют такой удар, после которого скорости обоих соударяющихся тел оказываются одинаковыми.
Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает – кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса и имеет место закон сохранения суммарной энергии различных видов – механической и внутренней.
Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. Потенциальная энергия упругой деформации вновь переходит в кинетическую энергию, и тела разлетаются со скоростями, величина которых определяется двумя условиями – сохранением полной энергии и сохранением полного импульса системы тел. Рассмотрим центральный абсолютно упругий удар двух шаров.
Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры.
Пусть шары массами и движутся до соударения со скоростями и , а после соударения со скоростями и (рис. 5.1). Согласно закону сохранения импульса
.
Выберем ось x в направлении движения шаров, тогда в проекции на эту ось закон сохранения импульса принимает вид
. (5.1)
На основании закона сохранения энергии имеем
. (5.2)
Сгруппировав слагаемые с одинаковыми индексами, перепишем эти равенства в виде
, (5.3)
. (5.4)
Поделив (5.4) на (5.3), получим
(5.5)
или
. (5.6)
Таким образом, при абсолютно упругом ударе относительная скорость шаров остается неизменной величиной.
Решая совместно уравнения (5.5) и (5.3), получим
, (5.7)
. (5.8)
Рассмотрим два частных случая.
1. Сумма импульсов обоих шаров до ударов равна нулю, то есть
, (5.9)
тогда , ,
отсюда, применяя (5.9), находим: , , то есть скорости обоих шаров при ударе только изменяют свой знак.
2. Один шар до удара покоится . Тогда
, .
После удара второй шар двинется в ту же сторону, куда двигался первый до удара. Скорость и поведение первого шара зависит от соотношения масс шаров.
а) Если , то первый шар продолжает двигаться в том же направлении, что и до удара, но с меньшей скоростью. Скорость второго шара после удара больше, чем скорость первого до удара.
б) Если , то направление движения первого шара при ударе изменяется – шар отскакивает обратно. Второй шар движется в ту сторону, в которую двигался первый до удара, но с меньшей скоростью.
в) Массы шаров одинаковы , тогда , , то есть шары при ударе обмениваются скоростями. В случае абсолютно неупругого удара:
, (5.10)
где – одинаковая для обоих шаров скорость после удара.
Из (5.10) следует, что . (5.11)
В частном случае, когда массы шаров равны, .
В случае нецентрального удара можно разложить скорости шаров на составляющие и в направлении линии центров и и в перпендикулярном направлении, а затем написать два уравнения, выражающие закон сохранения импульса для соответствующих составляющих:
, (5.12)
. (5.13)
Так как , то закон сохранения энергии после сокращения на множитель ½ можно написать в виде
. (5.14)
Для четырех неизвестных компонент скорости , , и получили только три уравнения. Но, поскольку мы сделали предположение, что энергия при ударе сохраняется, мы должны считать, что силы трения отсутствуют, то есть шары абсолютно гладкие. Из этого следует, что при ударе не могут измениться тангенциальные составляющие скоростей, так как для этого нужны тангенциальные силы, которые между абсолютно гладкими шарами возникнуть не могут. Поэтому вместо (5.13) можно записать
.
Соответствующие слагаемые в (5.14) сократятся, и для нормальных составляющих мы получим два уравнения:
. (5.15)
Эти уравнения совершенно аналогичны тем, которые были получены для центрального удара. Таким образом, при нецентральном абсолютно упругом ударе гладких шаров нормальные составляющие скоростей ведут себя так же, как при центральном ударе; тангенциальные же составляющие не изменяются.
В случае не абсолютно упругого удара часть кинетической энергии шаров при соударении переходит в энергию остаточной деформации. Тогда . Отсюда можно получить, что , то есть при неупругом ударе относительная скорость их меняет свое направление на противоположное, уменьшаясь в то же время по абсолютной величине .
Неупругий удар сопровождается остаточной деформацией. Если пренебречь всякого рода сопротивлениями, закон сохранения энергии для удара двух одинаковых шаров запишется так
, (5.16)
где – энергия остаточной деформации одного шара, относящаяся к одному соударению.
Экспериментальная установка и методика измерений
Схема лабораторной установки показана на рис. 5.3. К штативу 3 на бифилярных подвесах 4 и 5 прикреплены два шара 1 и 2. Бифилярный подвес используется для исключения вращения шаров. Шарики подвешены так, что их центры находятся на одном уровне, а сами шарики соприкасаются.
На столе под шариками в плоскости их колебания размещена линейка 6 (рис. 5.3).
Отведем один из шаров (например, большой) на некоторый угол θ (рис. 5,4) и отпустим без начальной скорости. Отклоненный шар будет двигаться вниз, разгоняясь, при этом его потенциальная энергия будет переходить в кинетическую. Пусть столкновение со вторым шаром происходит в тот момент, когда подвес первого шара становится вертикально. Если удар происходит достаточно быстро, так, что нити во время удара не успевают отклониться на заметный угол, то в направлении горизонтальной оси x не возникает внешних сил и выполняется закон сохранения импульса в проекции на эту ось
. (5.17)
По закону сохранения механической энергии (рис. 5.3)
, (5.18)
где – масса шара, – ускорение свободного падения, – высота шара в отведенном положении относительно нижней точки траектории, – скорость первого шара в нижней точке перед соударением со вторым. Из рис. 5.4. видно, что , где – расстояние от точки подвеса до центра тяжести шара.
При достаточно малых отклонениях (≤ 5°)
.
Тогда с учетом приближенного равенства , где x1 – горизонтальное смещение шара, можно записать
. (5.19)
Из соотношений (5.18) и (5.19) получаем
. (5.20)
После удара оба шарика отклонятся от положения равновесия на расстояния и и приобретут скорости u1 и u2:
, . (5.21)
Подставляя эти соотношения в закон сохранения импульса (5.17), после несложных преобразований получаем
(5.22)
Задание 1. Проверка соотношения (5.22).
Экспериментально проводится в следующей последовательности: большой шарик отклоняется из положения равновесия на фиксированную величину x1, и после соударения по шкалам визуально определяются отклонения шаров и . Опыт повторяют 5–7 раз.
Если в эксперименте отклоняется шарик меньшей массы, то при ударе о шар большей массы он отскакивает в противоположную сторону.
В этом случае , , .
После подстановки в закон сохранения импульса получим
. (5.23)
Задание 2. Проверка соотношения (5.23).
Эксперимент проводят точно так же, как и в предыдущем случае.
Задание 3. Реальные тела являются промежуточными между телами абсолютно упругими и абсолютно неупругими, поэтому при соударении реальных тел всегда имеют место и упругие, и остаточные деформации. Коэффициент восстановления скорости определяется как отношение относительной скорости шаров после удара к относительной скорости шаров до удара:
. (5.24)
В случае первоначального отклонения большего шара формула (5.24) с учетом (5.20) и (5.21) преобразуется к виду
. (5.25)
Для абсолютно упругого удара =1. При столкновении реальных шаров <1. При ударе стальных шаров = 0,56, для шаров из слоновой кости = 0,89, для свинцовых шаров близко к нулю.
В случае первоначального отклонения меньшего шара формула (5.25) с учетом (5.21) и (5.22) преобразуется к виду
. (5.26)
Кроме коэффициента восстановления скорости соударение тел характеризуется коэффициентом восстановления энергии, равным отношению кинетической энергии тел после удара к их кинетической энергии до удара:
. (5.27)
Учитывая, что скорость второго шара до удара = 0 и подставляя для скоростей выражения (5.20) и (5.21), находим рабочую формулу для коэффициента восстановления энергии:
. (5.28)
Обработка результатов эксперимента
- Найдите средние значения величины отскока шаров после удара и по формулам (5.22) и (5.23), соответственно.
- Используя средние значения и по формулам (5.25),(5.26) и (5.28) определите коэффициенты восстановления скорости и энергии .
- По методике расчета случайных погрешностей прямых измерений найдите погрешности измерения отклонений и .
- Найдите погрешность определения по методике вычисления погрешностей косвенных измерений:
а) для случая отклонения большего шара
; (5.29)
б) для случая отклонения меньшего шара
. (5.30)
5. Сравните полученное из эксперимента значение x1 с учетом его приборной погрешности, то есть со значением x1, рассчитанным по формуле (5.22) или (5.23). Приборную погрешность определите по цене деления линейки.
6. Погрешность определения коэффициента восстановления скорости определяется по формуле
. (5.31)
7. Погрешность определения коэффициента восстановления энергии определяется по формуле
. (5.32)
Лабораторная работа 6
Коэффициент поверхностного натяжения
Цель работы: изучение основных свойств жидкости, знакомство с некоторыми экспериментальными методами измерения коэффициента поверхностного натяжения жидкости.
Основные теоретические положения
По своим свойствам жидкости похожи и на газы и на твёрдые тела. Этот двойственный характер связан с особенностью движения молекул жидкости. В твердом теле молекулы составляют кристаллическую решетку и колеблются около своего положения равновесия (тепловое их движение). В жидкостях среднее расстояние между молекулами больше, чем у кристаллов, и поэтому молекулы жидкости могут отходить от своих правильных положений. Молекулы жидкости совершают колебания около временных положений равновесия.
Побыв в таком положении некоторое время, молекула «перескакивает» в другое место и снова какое-то время живет в этом месте (совершая колебания) «оседлой жизнью». В «оседлом» состоянии молекулу удерживают упругие силы. Эти упругие силы обусловлены действием соседних молекул расположенных на близком расстоянии. Молекулярные силы очень быстро убывают с увеличением расстояния. Если по отношению к какой — то молекуле М (рис. 6.1), находящейся внутри жидкости, соседние молекулы расположены симметрично, то равнодействующая R всех сил, приложенных к молекуле М, равна нулю R = 0. Однако вследствие теплового движения равновесие нарушается, и молекула приходит в движение под влиянием равнодействующей силы R ≠ 0 . Силы притяжения между молекулами жидкости быстро убывают с увеличением расстояния. Они практически обращаются в нуль уже на расстоянии порядка 109 м. Поэтому результат воздействия на каждую молекулу определяется только ближайшими ее соседями. Он существенно зависит от того, где находится рассматриваемая молекула. Если последняя расположена внутри жидкости (на расстоянии, большем чем 109 м от границы жидкости), то силы взаимодействия со всеми окружающими ее молекулами в среднем уравновешиваются. В отличие от этого, среднее значение силы, действующей на молекулу поверхностного слоя жидкости толщиной порядка 109 м, не равно нулю; это обусловливается тем, что молекула, расположенная на поверхности, частично граничит с молекулами той же жидкости, а частично − с молекулами другой среды, например воздуха и пара или стенки. Вследствие разных плотностей и природы молекул сила, действующая на выделенную молекулу жидкости со стороны другой среды, отличается от силы ее взаимодействия с молекулами жидкости. В итоге результирующая сила, действующая на каждую молекулу поверхностного слоя, направлена либо внутрь жидкости, либо в сторону граничащей с ней среды. Поэтому при перемещении молекул из поверхностного слоя в глубь жидкости или наоборот из глубины жидкости на поверхность совершается работа. Эта работа тем больше, чем больше различие между силами взаимодействия молекул поверхностного слоя с молекулами жидкости и молекулами граничащей среды.
Молекулы жидкости, расположенные на поверхности, находятся в особом состоянии, например молекулы М1 и М2. Действие на эти молекулы со стороны молекул жидкости больше, чем со стороны молекул пара или воздуха, и поэтому равнодействующая всех действующих на молекулу М1 и М2 молекулярных сил направлена внутрь жидкости нормально к ее поверхности. Отсюда следует, что на все молекулы, расположенные в тонком поверхностном слое, действуют силы, стремящиеся втянуть их внутрь жидкости. Благодаря этому поверхностный слой давит с большой силой на жидкость, создавая в ней так называемое внутреннее или молекулярное давление. Это давление очень велико (для воды, например, около 11∙108 н/м2).
Молекулы поверхностного слоя жидкости обладают избытком энергии сравнительно с молекулами, находящимися внутри жидкости. Эта избыточная энергия называется свободной поверхностной энергией или поверхностной энергией. Указанными свойствами поверхностного слоя обусловлено особое его состояние, которое подобно состоянию натянутой упругой пленки, стремящейся сократить свою поверхность до малых размеров.
Это стремление жидкости сократить свою свободную поверхность называется поверхностным натяжением.
Силы поверхностного натяжения F направлены по касательной к поверхности жидкости и действуют нормально к любой линии, проведенной на этой поверхности.
Для количественной характеристики силы поверхностного натяжения жидкости вводят коэффициент поверхностного натяжения α, который численно равен силе F, действующей на единицу длины произвольной линии L, мысленно проведенной на поверхности жидкости:
. (6.1)
В этом случае коэффициент поверхностного натяжения измеряется в ньютонах на метр (н/м).
Из рассмотрения свойств поверхностного слоя можно показать, что коэффициент поверхностного натяжения численно равен свободной поверхности энергии W, рассчитанной на квадратный метр поверхности жидкости S: .
Благодаря поверхностному натяжению любой объём жидкости стремится уменьшить площадь поверхности, уменьшая таким образом и потенциальную энергию. Крошечные капли воды имеют в воздухе почти сферическую форму, поскольку для сферы характерно меньшее отношение площади поверхности к объёму, чем для любой другой геометрической формы.
Коэффициент поверхностного натяжения различен для разных жидкостей. Он зависит от рода жидкости, температуры (уменьшается с повышением температуры) и от степени чистоты поверхности (изменяется от малейшего загрязнения).
Существование поверхностного натяжения приводит к тому, что свободная поверхность жидкости ведёт себя так, как будто она сделана из упругой оболочки. Однако существует большое отличие между эластичностью этой оболочки, определяемой поверхностным натяжением, и эластичностью вещества типа резины. В случае плоской поверхности жидкости сила натяжения не зависит от того, насколько поверхность растянута. Для того чтобы увеличить площадь поверхности, вытягивая в поверхностный слой всё новые и новые молекулы, необходимо прикладывать постоянную силу. С другой стороны, чтобы растянуть резину, приходится прикладывать силу, пропорциональную растяжению.
До сих пор мы рассуждали о поверхности между жидкостью и газом. У края сосуда жидкость находится в контакте и с твёрдым телом, и с газом. На рис. 6.3 показаны три различных случая.
В первом случае (рис. 6.3 а) взаимодействие молекул жидкости с твердым телом достаточно сильно, чтобы изогнуть жидкость кверху на границе с твердым телом. В этом случае обычно говорят, что жидкость смачивает поверхность твердого тела.
Такая ситуация характерна для воды, соприкасающейся со стеклом. Во втором случае (рис.6.3 б) результирующая сила, действующая на жидкость на границе с твердым телом, направлена внутрь жидкости. Это не смачивающаяся жидкость. Такая ситуация характерна для ртути в стеклянном сосуде. В третьем случае (рис. 6.3 в) поверхность жидкости перпендикулярна стенке. Так ведет себя вода в сосудах из серебра и некоторых видов пластмасс.
Изогнутая поверхность жидкости в сосуде называется мениском. При взаимодействии со стенкой сосуда силы поверхностного натяжения стремятся либо поднять уровень жидкости, либо опустить его. Это называется капиллярным эффектом.
Капиллярные явления.
В узких стеклянных трубках, капиллярах, опущенных в жидкость, хорошо заметно поднятие или опускание жидкости. Поверхностная пленка жидкости в трубке под действием молекулярных сил жидкости и стекла принимает вогнутую форму (вогнутый мениск). На такой искривленной поверхности силы поверхностного натяжения вызывают добавочное давление ∆p, обусловленное кривизной поверхности, направленное всегда в сторону вогнутой поверхности.
Название связано с тем, что высота подъема жидкости велика в достаточно узких трубках, называемых капиллярами.
У верхнего края, где жидкость касается стекла, форма её поверхности очень похожа на полусферу мыльного пузыря, которую мы рассматривали(рис. 6.4). Сила поверхностного натяжения направлена вдоль поверхности жидкости. Вертикальная составляющая этой силы равна
.
Она уравновешивается силой тяжести столба жидкости с плотностью : . Таким образом, имеем . Следовательно
. (6.2)
Если жидкость в капилляре не смачивающая, уровень её в капилляре оказывается ниже уровня в жидкости в широком сосуде. Это в точности такой же эффект, и описывается он той же формулой (6.2).
Описание экспериментальной установки и последовательность
проведения измерений
Исследуемая жидкость находится в сосуде А. Кольцо В, изготовленное из материала, хорошо смачиваемого этой жидкостью, подвешено на пружине С.
1. Определить коэффициент упругости пружины k, для чего на чашечку 2 положить груз m и отметить растяжение пружины x. Вычислить k по формуле
(6.3)
Измерения провести 3−4 раза с разными грузами и затем определить среднее значение .
2. Измерить длину пружины , затем кольцо опустить в сосуд с водой. Сосуд опускать вниз до отрыва кольца от воды. Измерить длину пружины в момент отрыва кольца от воды. Эксперимент провести 5−6 раз.
- Измерить штангенциркулем наружный и внутренний диаметры кольца D и d, а затем определить сумму наружной и внутренней длин окружностей кольца L
, (6.4)
а затем найти коэффициент поверхностного натяжения
. (6.5)
Обработка результатов эксперимента
- Величина полной погрешности определения определяется по формуле
, (6.6)
где
, (6.7)
, (6.8)
где − приборная погрешность линейки.
Погрешности и определяются по методике расчета погрешностей прямых измерений.
2. Результат представить в виде .
Определение коэффициента поверхностного натяжения методом поднятия жидкости в капилляре
Капилляр вставляется в широкий сосуд с исследуемой жидкостью. С помощью масштабной линейки определяется высота подъёма жидкости h. Этот опыт проводится не менее 5 раз.
Если известен радиус r капилляра, то сила поверхностного натяжения:
(6.9)
Сила тяжести столба жидкости равна , а так как F=P, то получаем , то есть
. (6.10)
Обработка результатов и расчёт погрешностей
- Погрешность величины h определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность и коэффициент Стьюдента.
- Погрешность косвенных измерений величины a рассчитать по формуле
. (6.11)
- Результат записать в виде: .
Представляет интерес сравнение величин коэффициентов поверхностного натяжения одной и той же жидкости, полученных различными методами, и погрешностей их определения.
Лабораторная работа 7
ИЗМЕРЕНИЕ ГАЗОВОЙ ПОСТОЯННОЙ
Цель работы: изучение газовых законов, экспериментальная проверка уравнения состояния идеального газа, ознакомление с работой газового термометра.
Основные теоретические положения
В молекулярно-кинетической теории объектом исследования является идеализированная модель реального газа − идеальный газ. Идеальным газом называется газ, между молекулами которого отсутствуют силы взаимодействия. При этом принимается, что при соударениях между собой и со стенками сосуда молекулы такого газа ведут себя как абсолютно упругие шарики конечных, но весьма малых размеров. Эти соударения молекул происходят по законам абсолютно упругого удара.
Величинами, определяющими состояние газа, являются: давление р, под которым он находится, его температура Т , объем V, занимаемый определенной массой газа М. Величины p, V, T, M называются параметрами состояния. Давлением Р называется физическая величина, равная пределу отношения численного значения нормальной силы , действующей на единицу поверхности , к величине этой поверхности:
Единицей давления в системе СИ является паскаль ([P]=[F]/[S]= H/=Па)
Температурой называется физическая величина, характеризующая степень нагретости тела.
Параметры состояния связаны между собой различными газовыми законами.
Если газ находится при постоянной температуре T=const, то объем газа и давление связаны законом Бойля-Мариотта pV=const.
При постоянном объеме − это закон Шарля, в котором − термический коэффициент давления, и − давление газа при начальной и конечной температуре.
При постоянном давлении объем газа пропорционален температуре и определяется законом Гей–Люссака: , где термический коэффициент объемного расширения, − объемы газа при начальной и конечной температуре.
Теперь возвращаемся к уравнению состояния идеального газа, то есть найдём связь между P, V и T. Рассмотрим определённую массу газа m, которая заполняет объём , имеет давление и находится при температуре . Пусть в другом состоянии та же масса газа характеризуется объёмом, давлением и температурой: , , . Установим на основании законов Бойля-Мариотта, Гей-Люссака и Шарля связь между , , и , , . Для этого сначала газ из состояния , и при постоянном давлении нагреем до температуры . По закону Гей-Люссака . Так как , то . Из этого состояния в окончательное состояние, характеризующееся параметрами , , , его можно перевести изотермическим изменением объёма, для которого по закону Бойля-Мариотта имеем: . Подставляя , получим , то есть , откуда следует, что при изменении состояния данной массы газа величина PV/T остаётся постоянной, то есть PV/T=B.
Если это соотношение относить к одному молю, то постоянная В будет иметь одно и то же значение для всех газов. Эта общая для всех газов постоянная обозначается R и носит название универсальной газовой постоянной. Вводя в предыдущую формулу вместо объема V молярный объем Vо, то есть объем одного моля газа, получим
. (7.1)
Эта формула представляет собой уравнение состояния идеального газа и носит название уравнения Менделеева-Клапейрона.
Уравнение Менделеева-Клапейрона, справедливое для одного моля газа, можно обобщить и на любую массу. Если — молярная масса и при некотором данном давлении и температуре 1 моль газа занимает объем , то при том же давлении и температуре т граммов газа займут объем . Тогда и, подставляя в уравнение Менделеева-Клапейрона (7.1), получим
. (7.2)
В работе предлагается на опыте убедиться в справедливости формулы (7.2), а также определить универсальную газовую постоянную.
Описание лабораторной установки и последовательность проведения измерений
Прибор состоит из стеклянной трубки 1, запаянной с одного конца и газового термометра Жоли, частями которого являются: соединительная резиновая трубка 2, смотровая стеклянная трубка 3, резиновый шланг 4, стеклянная трубка 5; трубка 7, соединенная с резервуаром 8. Все стеклянные трубки имеют одинаковое сечение. Прибор крепится на штативе 6 и заполняется водой так, чтобы ее уровень располагался посредине трубок 3 и 5. Уровень воды в трубке 3 отмечается резиновым колечком.
Задание 1. Проверка уравнения состояния идеального газа (7.2).
При равенстве уровней воды в трубках 3 и 5 измеряется длина воздушного столба от уровня воды в трубке 1. Объём воздуха пропорционален длине столба плюс объём колбы , то есть . Давление воздуха равно атмосферному . Температура воздуха равна температуре воздуха в лаборатории и определяется по термометру. Параметры указанного состояния , , , а величина .
Включается нагреватель, и температура воды в стакане увеличивается до . При этом уровень воды в трубке 5 поднимается, то есть газ в колбе 1 расширяется и его часть выходит из объёма колбы. Если перемещать трубку 5 вверх − вниз на величину , то можно добиться равенства уровня воды в трубках 3 и 5. Тогда давление воздуха в колбе 1 будет равно атмосферному давлению , а длина воздушного столба или объём , где , − поперечное сечение трубки. Получаются вторые данные , , . Далее вода в стакане нагревается до температуры и проделывается то же, что и с холодной водой. Получается третий набор данных: , , . Все полученные данные измерений заносятся в таблицу.
Величина (j=1,2) рассчитывается следующим образом. В каждом эксперименте при нагревании колбы до температуры объём газа в ней увеличивается на , и при этом высота жидкости в манометре изменяется на . Поэтому на основании уравнения (7.2)
,
откуда изменение объёма равно , то есть , а .
Обработка результатов и расчёт погрешностей
- Приборную погрешность величины определить по формуле
. (7.3)
- Результат представить в виде .
- Погрешность величины (j=1,2) рассчитать по формуле
. (7.4)
- Результат представить в виде: , .
- Сравнить величины , , и сделать вывод о формуле (7.2).
Задание 2. Определение универсальной газовой постоянной
Обработка результатов и расчёт погрешностей.
- Величину газовой постоянной для двух случаев j 1,2 рассчитать по формуле
, (7.5)
считая, что величины и являются приборными константами.
- Погрешность вычислить с учётом зависимости (7.4) по формуле
. (7.6)
- Результат представить в виде , j=1,2.
- Сравнить величины и с табличным значением R.
Задание 3. Определение газовой постоянной методом измерения объема и давления паров жидкости.
Если в сосуд известного объема ввести определенную массу легко испаряющейся жидкости, а после того, как она полностью испарится, измерить, насколько увеличится давление внутри сосуда, то, зная молекулярную массу жидкости и температуру, можно вычислить R по формуле
(7.7)
Установка (рис. 7.3) состоит из стеклянного сосуда 1, закрытого резиновой пробкой 3 с двумя отверстиями: в одно вставлена стеклянная трубка 2, в другое − 4 микробюретка с ацетоном. На верхний конец микробюретки 5 надета резиновая трубка с винтовым зажимом 6. Конец трубки закрыт пробкой 7. Сосуд 1 соединен с левым коленом водяного манометра 10 с помощью резиновой трубки 8 и стеклянного тройника с краном 9. Правое колено манометра подвижно. Его положение фиксируется зажимом 11.
В сосуд вводится ацетон из микробюретки: ац= 0,058 кг/моль, 790 кг/м3,
, (7.8)
где Vац – объем ацетона, введенного в сосуд.
Так как парциальное давление паров ацетона измеряется водяным манометром по разности уровней воды в его коленах, то
(7.9)
где разность уровней воды в коленах манометра.
Учитывая (7.8) и (7.9), можно записать
(7.10)
Первый сомножитель в (7.8) является величиной постоянной, второй − постоянен для конкретных условий проведения опыта при постоянной температуре и объеме сосуда. Таким образом определение R сводится к измерению объема жидкого ацетона, введенного в сосуд, и разности уровней воды в коленах манометра, обусловленной давлением паров ацетона. Точный объем сосуда с учетом объема резинового шланга, соединяющего сосуд с манометром и объема трубки манометра до уровня нулевой отметки написан на стенке сосуда. Работа выполняется в такой последовательности:
1. Измеряется объем ацетона микробюретке.
2. Открывается кран у тройника 9 и перемещением правого колена манометра уровень воды устанавливается на нулевую отметку шкалы. После этого закрывается кран 9.
3. Весь ацетон из микробюретки выливается в сосуд, в результате чего изменяются показания манометра. После того, как весь ацетон испарится, показания манометра перестанут изменяться.
4. Передвижением правого колена манометра устанавливается уровень воды в левом колене на нулевую отметку. Это необходимо сделать для сохранения объема воздуха в сосуде и трубках таким же, как в начале опыта. Тогда манометр покажет только парциальное давление паров ацетона, так как температура не изменилась.
5. По шкале манометра отсчитывается разность уровней воды и в его коленах и данные записываются в таблицу.
Обработка результатов
1. Газовая постоянная вычисляется по формуле (7.11).
2. Так как измеряется только одна переменная один раз, то предельная погрешность косвенных измерений величины R определяется по формуле
, (7.11)
где , и − систематические погрешности определения разности уровней в манометре после испарения ацетона, температуры и объёма ацетона.
3. Сравниваются величины газовой постоянной, полученные разными методами, и погрешности этих методов.
4. Если измерения проводятся несколько раз, то процедура расчёта погрешностей несколько отличается. В этом случае при измерениях изменяются две величины: , . Поэтому
, (7.12)
где погрешность величины / необходимо определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность и коэффициент Стьюдента.
Лабораторная работа 8
ТЕПЛОЕМКОСТЬ ЖИДКОСТИ
Цель работы: изучение классической теории теплоемкости, экспериментальное определение теплоемкости жидкости калориметрическим методом.
Основные теоретические положения
Количество независимых координат, характеризующих положение материального объекта в пространстве, называется числом его степеней свободы. Молекулу одноатомного идеального газа можно рассматривать как материальную точку, так как ее масса сосредоточена в ядре малого размера. Такая молекула (атом) имеет три степени свободы, то есть для описания ее поступательного движения требуется три независимых координаты. Для того чтобы охарактеризовать положение в пространстве двухатомной молекулы, состоящей из жестко связанных атомов, необходимо задать пять независимых координат. Из них три служат для описания ее поступательного движения, а две характеризуют вращательное движение вокруг осей и (рис. 8.1). Трехатомная молекула имеет три вращательные степени свобода. Реальные молекулы не являются системами жестко связанных атомов. Так как атомы могут колебаться друг относительно друга, появляются дополнительные колебательные степени свободы.
Одним из основных положений классической молекулярно-кинетической теории является закон равномерного распределения энергии по степеням свободы: на каждую поступательную, а также вращательную степень свободы газовой молекулы приходится одинаковая энергия, равная . При колебательном движении молекулы имеют и кинетическую и потенциальную энергию. При этом если колебания гармонические, то и на основании закона равнораспределения энергии по степеням свободы полная энергия, приходящаяся на одну колебательную степень свободы, равна . Она вдвое превышает среднюю энергию на одну степень свободы поступательного или вращательного движения.
Если считать, что в газах, жидкостях и твердых телах молекулы колеблются независимо друг от друга, то на три колебательные степени свободы каждой молекулы приходится энергия
. (8.1)
Полная внутренняя энергия одного моля такой системы молекул равна:
(8.2)
где − число Авогадро, − универсальная газовая постоянная.
Молярной теплоемкостью называется количество энергии, поглощаемой одним молем вещества при нагревании на 1 К, то есть
(8.3)
Это закон Дюлонга и Пти: молярные теплоемкости химически простых веществ одинаковы и не зависят от температуры.
Закон Дюлонга и Пти хорошо выполняется при комнатной температур. Для более низкой температуры наблюдаются отклонения, связанные с тем, что энергию колебательного движения молекул нельзя вычислять на основании закона о равнораспределении энергии по степеням свободы. Теплоемкость в этой области уменьшается, стремясь к нулю при .
Качественное согласие с результатами эксперимента было достигнуто в теории Эйнштейна, в которой предполагалось, что молекула представляет собой не классический, а квантово-механический гармонический осциллятор, средняя энергия которого определяется соотношением:
, (8.4)
где − приведенная постоянная Планка, − частота гармонического осциллятора. Используя для внутренней энергии кристалла формулу (8.2) и дифференцируя по температуре, находим молярную теплоемкость:
. (8.5)
При высоких температурах из (8.5) имеем , что совпадает с законом Дюлонга и Пти (8.2). При низких температурах
(8.6)
Выражение (8.6) при приближается к нулю по экспоненциальному закону (рис. 8.2, левая часть графика).
Теория Эйнштейна лишь качественно совпадает с результатами эксперимента в области низких температур. Строгая теория, описывающая довольно сложная и ее трудно реализовать для структур со сложными молекулами, например, для органических жидкостей. Поэтому на практике применяются экспериментальные методы определения теплоемкости, в частности, калориметрический метод.
Описание экспериментальной установки
Калориметр представляет собой сосуд 1, стенки которого теплоизолированы между собой с помощью прокладки из теплоизолирующего материала 2, а также от окружающей среды крышкой 3. В сосуд помещается исследуемое вещество 4 (в нашем случае жидкость), температура которой определяется термометром 5. Нагревание жидкости осуществляется нагревателем 6, мощность которого определяется по току, регистрируемому стрелочным прибором (рис. 8.3). Для изменения тока применяется реостат R. Для улучшения условий теплообмена жидкость в эксперименте перемешивается специальной мешалкой 7, которая вращается электродвигателем.
Теплота нагревателя расходуется на нагревание жидкости , калориметра со всеми его деталями, термометром, мешалкой и прочим , также тепловые потери на излучение, неидеальность теплоизоляции и другое.
Уравнение теплового баланса записывается так
(8.7)
Теплоемкость исследуемой жидкости в интервале температур от до определим как количество тепла , необходимое для нагревания единицы ее массы на 1 градус Кельвина, то есть
(8.8)
Поэтому
(8.9)
С учетом этого уравнение теплового баланса записывается в виде
(8.10)
Если бы тепловые потери отсутствовали, , то нагревание жидкости произошло бы до более высокой температуры , и тогда уравнение теплового баланса (8.10) перепишется в виде
(8.11)
Пусть , где — постоянная калориметра, которую в дальнейшем надо определить.
Тогда из формулы (8.11) получим
(8.12)
Отсюда теплоемкость жидкости в калориметре
(8.13)
Таким образом, для определения теплоемкости исследуемой жидкости необходимо знать температуру и постоянную калориметра . Найти их можно следующим образом.
Рассмотрим процесс нагревания жидкости в калориметре. До включения нагревателя температура всех узлов установки равна температуре окружающей среды (линия а-b, рис. 8.4). При включении в момент нагревателя температура возрастает до значения по кривой b—d. После выключения нагревателя происходит процесс охлаждения, характеризуемый дифференциальным уравнением:
(8.14)
где − постоянная охлаждения.
Согласно (8.14) скорость убывания температуры пропорциональна разности температур установки и окружающей среды.
Из (8.14) находим
(8.15)
Выполняя интегрирование, получим
(8.16)
где А − константа интегрирования, которая должна быть определена из начального условия :
(8.17)
Из (8.16) и (8.17) находим
(8.18)
что соответствует экспоненциальному участку кривой d—e.
Если бы потери отсутствовали, то процесс нагревания происходил бы по кривой a—b—c до температуры , а охлаждение – по кривой c—d—e в соответствии с экспоненциальной зависимостью (8.18). Таким образом величину температуры можно найти из (8.18) при по формуле
(8.19)
Величина постоянной находится по экспериментальному значению температуры на участке охлаждения d—e, например, в момент времени :
(8.20)
Чтобы найти постоянную калориметра, необходимо провести дополнительный эксперимент с жидкостью, теплоемкость которой хорошо известна, например с водой. Тогда из уравнения теплового баланса (8.12) можно найти постоянную калориметра :
(8.21)
где − температура точки с (рис. 8.4) при нагревании воды, − средняя теплоемкость воды в интервале , масса воды в калориметре.
Методика эксперимента
1. В калориметр заливается вода при комнатной температуре
2. Одновременно включается нагреватель, мешалка и секундомер, регистрируется ток через нагреватель, через некоторое время (порядка минуты) фиксируется значение температуры. Данные заносятся в таблицу.
3. Когда вода нагреется на 10 градусов, нагреватель выключается. Вследствие инерции нагревателя после выключения тока температура некоторое время возрастает, затем начинает спадать, что также фиксируется, а данные записываются в таблицу.
4. После полного охлаждения воды она выливается из калориметра, который заполняется исследуемой жидкостью и опыт повторяется. Данные заносятся в таблицу.
Обработка результатов
1. По данным полученным в п.1. строится график зависимости температуры от времени нагревания для калориметра с водой.
2. По формуле (8.20) определяется величина .
3. По формуле (8.19) вычисляется температура .
4. По формуле (8.21) рассчитывается постоянная калориметра.
При этом величина определяется по формуле
(8.22)
где − момент времени отключения нагревателя, − полное сопротивление цепи нагревателя, указанное на стенде.
5. По данным получившимся в п. 2 строится график зависимости температуры от времени нагревания для калориметра с исследуемой жидкостью.
6. По формуле (8.20) находится величина .
7. По формуле (8.19) вычисляется температура .
8. По формуле (8.13) и найденному ранее значению постоянной калориметра вычисляется теплоемкость исследуемой жидкости. При этом рассчитывается по формуле (8.22).
9. По методике расчета погрешностей косвенных измерений осуществить расчет погрешности постоянной охлаждения для воды по формуле:
(8.23)
где и − систематические погрешности измерения времени и температуры.
10. Найти погрешность определения температуры для воды:
(8.24)
11. Для воды определить погрешность :
, (8.25)
где — погрешность тока, определяемая классом точности амперметра.
12. Определить погрешность постоянной калориметра :
. (8.26)
13. Найти погрешность определения постоянной охлаждения , температуры и теплоты нагревателя для исследуемой жидкости по формулам (8.23), (8.24) и (8.25).
14. Вычислить погрешность определения теплоемкости исследуемой жидкости по формуле
. (8.27)
15.Представить окончательный результат в виде
, (8.28)
где − значение теплоемкости исследуемой жидкости полученное по формуле (8.13).
Лабораторная работа 9
КОЛЕБАНИЯ СТРУНЫ
Цель работы: изучение волновых явлений, условия существования стоячих волн, исследование упругих свойств струны.
Основные теоретические положения
Пусть точка, совершающая колебания, находится в среде, все частицы которой связаны между собой. Тогда энергия колебаний точки может передаваться окружающим точкам, вызывая их колебания. Явление распространения колебаний в среде называется волной. При этом колеблющиеся частицы не перемещаются с распространяющимся колебательным процессом, а колеблются около своих положений равновесия.
Если в неограниченной среде беспрепятственно распространяется единственная волна, то она называется бегущей. Составим уравнение бегущей волны, позволяющее определять смещение любой точки волны в любой момент времени.
Рассмотрим непрерывную однородную среду − струну, которая на конце x=0 присоединена к источнику гармонических колебаний в момент времени t’:D(t’)=Asint’. Найдём смещение элементов струны, как функцию координаты x и времени t, то есть функцию . Очевидно, что для точки x=0, =D(t’)=Asint’ (рис. 9.1). Предположим, что бегущее по струне возмущение распространяется с некоторой скоростью . Смещение элемента струны x в момент t равно смещению элемента x=0 в момент t’ =, если расстояние между ними равно расстоянию, которое возмущение проходит за время t—t’ со скоростью . Тогда точки x=0 и x=x колеблются в одной фазе: x=(t—t’), , . Поэтому уравнение бегущей синусоидальной волны == Asint’, то есть
. (9.1)
Преобразуем функцию (9.1): . Обозначим =k и назовём его волновым числом, тогда =. Следовательно, скорость , . Величину , равную расстоянию, которое возмущение преодолевает за период колебаний, назовём длиной волны, то есть , тогда , .
Уравнение (9.1) и есть уравнение бегущей одномерной (или плоской) волны. При заданном x оно позволяет определить положение точки (с координатой равновесного положения x) в любой момент времени t. При заданном t оно позволяет определить мгновенные положения всех колеблющихся точек.
Таким образом, видим, что в волновом движении имеет место двоякая периодичность. С одной стороны, каждая частица среды совершает периодическое движение во времени, с другой стороны, в каждый момент времени все частицы располагаются на линии, форма которой периодически повторяется в пространстве.
Определим скорость распространения продольных колебаний вдоль бесконечно длинного стержня с постоянным поперечным сечением.
При действии на левое сечение силой (рис. 9.2) вблизи этого сечения происходит уплотнение материала стержня, и возникает деформация сжатия. Появляются упругие силы, стремящиеся восстановить первоначальную плотность, в результате чего возникает сжатие соседних областей и таким образом локальное возмущение плотности вблизи левого края стержня распространяется вправо со скоростью . Импульс силы упругости равен . Если Е − модуль сжатия, иначе называемый модулем Юнга, то. За время деформация распространяется на расстояние . Масса участка стержня, охваченная деформацией, увеличится на вследствие увеличения плотности материала на . Так как , то . В соответствии со вторым зaконом Ньютона импульс силы упругости равен изменению импульса, то есть . Подставляя все величины, получим
или , (9.2)
где — погодная плотность материала стержня.
Уравнение (9.1) описывает волну, распространяющуюся в положительном направлении оси ох. При изменении направления распространения волны на противоположное второе слагаемое в аргументе косинуса изменяет знак, так как заменяется на
. (9.3)
Рассмотрим теперь распространение волны в струне, закрепленной с обеих сторон. При этом волна, движущаяся в одном направлении, достигнув второго закрепленного конца струны, отразится и станет распространяться в противоположном направлении. Таким образом вдоль длины струны возникнет явление наложения волн, распространяющихся в противоположных направлениях. Если свойства среды не изменяются под воздействием распространяющейся волны, то будет выполняться принцип суперпозиции, согласно которому каждая волна распространяется в среде независимо от других. В этом случае результирующее смещение z частиц среды будет определяться как сумма смещений z1 и z2, обусловленных прохождением отдельных волн. В результате будет наблюдаться в различных точках среды усиление или ослабление колебаний в зависимости от фаз приходящих возмущений.
Сложение волн, при котором в разных точках среды образуются усиления и ослабления амплитуды колебаний, называется интерференцией волн. Такая интерференционная картина сохраняется во времени.
Рассмотрим интерференцию двух волн с одинаковой амплитудой, распространяющихся в противоположных направлениях, как в случае струны, закрепленной с обеих сторон. При этом необходимо учитывать следующее явление. После отражения от закрепленного конца отраженная деформация имеет противоположный знак. Это становится понятным, если учесть, что так, как смещение закрепленного конца все время отсутствует, у точки крепления развиваются силы, препятствующие приходящему изгибу струны. Эти силы порождают изгиб противоположного знака, начинающий распространяться в обратную сторону. Поэтому и в отраженной деформации знак смещения изменяется на обратный. Если отражается гармоническая волна, то такое изменение равносильно «потере» полуволны при отражении.
Таким образом, наложение двух волн даст следующее:
.
Используя формулу разности синусов, получим
. (9.4)
Это выражение называется уравнением стоячей волны, при этом предполагается режим установившихся колебаний, то есть режим, возникающий после многократного пробега волн между креплениями струны. Из (9.4) видно, что в стоячей волне все точки среды (любое значение x) колеблются по гармоническому закону с круговой частотой .
Амплитуда колебаний различна для разных точек и определяется из (9.4) следующим образом:
. (9.5)
Из последнего выражения вытекает, что есть точки среды, называемые узлами, в которых колебания отсутствуют Zm = 0, следовательно, z = 0. Координаты этих точек определятся из условия равенства нулю синуса в выражении (9.5), то есть
. (9.6)
Отсюда, так как , получаем
.
Следовательно, расстояние между соседними узлами равно половине длины волны. Так как узлы все время остаются в покое, то в стоячей волне нет направленного переноса энергии, энергия не может перейти через узел. Передача энергии по струне производится только бегущей волной.
Те точки, в которых значение амплитуды достигает максимума , называются пучностями. Как следует из выражения (9.5), координаты этих точек определяются из условия , то есть отвечают уравнению . Видим, что расстояние между соседними пучностями также равно половине длины волны.
Множитель при переходе через узел меняет знак, вследствие чего фаза колебаний по разные стороны от узла отличается на . Все точки, находящиеся между двумя соседними узлами, колеблются в одинаковой фазе (их отклонения имеют одинаковый знак). Условие неподвижности обоих концов закрепленной струны приводит к тому, что на длине струны должно укладываться целое число полуволн:
. (9.7)
Таким образом, стоячая волна образуется только при надлежащем соотношении размеров струны и длины волны (частоты колебаний). Для разных значений n = 1, 2,… получим различные типы, или моды, колебаний, при этом n определяет число пучностей, а не узлов. Из (9.6) с учетом (9.7) получим формулу для частот, при которых в струне устанавливаются стоячие волны
, (9.8)
Частоты называют собственными частотами струны. Частоту называют основной частотой, остальные – обертонами. Видим, что определяемые формулой (9.8) собственные частоты не зависят от модуля Юнга материала. Этот результат является следствием того, что мы пренебрегли изменением натяжения струны при колебаниях.
В общем случае в струне могут одновременно существовать колебания с различными собственными частотами. Так, наряду с основным тоном n = 1, могут возбуждаться обертоны n = 2, 3, 4,….
Полученные выше уравнения описывают движение идеально гибкой струны в вакууме. При колебаниях реальной струны всегда происходят потери энергии.
Часть энергии теряется вследствие трения о воздух, другая часть уходит через концы струны и т.д. Для поддержания незатухающих колебаний служит вибратор. Если энергия потерь в точности компенсируется энергией, поступающей от вибратора, то в струне можно наблюдать стоячие волны. Но теперь по струне должна происходить передача энергии. Поэтому наряду со стоячими будут существовать бегущие волны, в результате чего узлы окажутся несколько размытыми. Если потери энергии за период малы по сравнению с запасом колебательной энергии в струне, то искажение стоячих волн бегущей волной будет незначительным.
Другим приближением в изложенной выше теории является пренебрежение неоднородностью струны. В реальной струне и плотность, и натяжение могут являться непрерывными функциями координаты Х. Например, если струна подвешена вертикально, то учет массы струны приведет к тому, что натяжение в верхних частях будет больше, чем внизу. Любая неоднородность приведет к искажению формы колебаний, так как синусоидальные колебания в пространстве характерны только для нормальных мод однородных систем.
Экспериментальная установка и методика измерений
Схема экспериментальной установки приведена на рис. 9.4 к штативу 4 крепится кронштейн с электромагнитным вибратором 3, с помощью которого в струне 1 возбуждаются синусоидальные колебания от звукового генератора. Если нагрузить струну и включить звуковой генератор, от вибратора по струне побегут поперечные волны, которые, отражаясь от концов, образуют сложную картину колебаний. Медленно изменяя частоту звукового генератора, можно заметить, что колебания струны при некоторых частотах стабилизируются – появляются стоячие волны. При этом струна делится неподвижными узлами на несколько равных отрезков. Амплитуда колебаний отдельных точек струны не зависит от времени и определяется только их положением на струне. При изменении нагрузки картина немедленно размывается. Меняя частоту генератора, можно вновь получить стоячую волну с тем же числом узлов.
Последовательность выполнения работы
1. Влючите звуковой генератор и дайте ему прогреться в течение 5 минут. Установите частоту генератора на 0.
2. Нагрузите струну и изменением частоты генератора получите стоячие волны для нескольких значений числа пучностей n = 1, 2, 3,… при фиксированном значении нагрузки. Все измерения повторите 3–4 раза.
3. Повторите измерения по п. 2 с другими значениями нагрузки. Число различных значений нагрузки должно быть не менее пяти.
4. Изменяя частоту звукового генератора при некотором постоянном натяжении струны, получите стоячие волны, соответствующие различным n. Повторите процесс измерения не менее трех раз.
5. Проделайте измерения по п. 4 для различных значений натяжения струны (не менее пяти значений).
Обработка результатов эксперимента
- По измерениям п. 2 постройте график зависимости от при различных натяжениях струны F. Методом наименьших квадратов найдите тангенсы угла наклона прямых к оси абсцисс и погрешность определения тангенсов.
- Найдите линейную плотность струны по формуле
.
- Найдите погрешность косвенного измерения линейной плотности струны по формуле
.
- Систематическую погрешность, связанную с измерением длины струны, рассчитайте по формуле
.
- Суммарную погрешность измерения линейной плотности рассчитайте по формуле
.
- По измерениям п. 2 построить графики зависимости от n при различных натяжениях струны F. Методом наименьших квадратов найти тангенсы угла наклона прямых к оси абсцисс и погрешность определения тангенсов.
- Найдите скорость распространения волны при данном натяжении по формуле
.
- Найдите погрешность определения скорости по формуле:
.
- Систематическую погрешность, связанную с измерением длины струны рассчитайте по формуле
.
- Суммарную погрешность измерения скорости рассчитайте по формуле
.
- По измерениям п. 4 проверьте выполнение соотношения
.
Лабораторная работа 10
Вязкость жидкости
Цель работы: определение коэффициента вязкости по методу Стокса.
Основные теоретические положения
Явление внутреннего трения (вязкости) наблюдается в телах во всех агрегатных состояниях, но большое практическое значение это имеет для жидкостей и газов.
При движении жидкости или газа возникают силы внутреннего трения. Эти силы возникают вследствие того, что движение жидкости или газа слоистое, и скорости перемещающихся слоев разные.
Представим себе две пластинки, разделенные плоскопараллельным слоем жидкости. Рассмотрим, что произойдет, если сначала перемещать верхнюю пластинку относительно нижней в направлении, указанном стрелкой. Мысленно разобьем жидкость на тончайшие слои. Молекулы жидкости, ближайшие к верхней пластинке, прилипают к ней и в силу этого начинают перемещаться вместе с пластинкой с той же скоростью. Эти молекулы в свою очередь увлекают молекулы следующего слоя и так далее Слой молекул, непосредственно прилегающих к нижней неподвижной пластине, остается в покое, а остальные слои перемещаются, скользя друг по другу со скоростями тем большими, чем больше их расстояние от нижнего слоя.
Силы внутреннего трения направлены к уравниванию скорости движения всех слоев. Уравнивание скорости слоев осуществляется путем передачи молекулами более быстрого слоя количества движения mυ молекулам слоя, движущегося медленнее. Это приводит к увеличению скорости движения движущийся быстрее слой, начинает двигаться медленнее, так как молекулы из медленного слоя, попадая в более быстрый слой, получают в быстром слое некоторое количество движения, что приводит к его торможению.
Таким образом, внутреннее трение обусловлено переносом количества движения веществ mυ молекулами вещества, которые переходят из слоя в слой и создают возникновение сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными скоростями.
Опыт показал, что сила внутреннего трения F пропорциональна величине площади соприкосновения движущихся слоев S, градиенту скорости движения слоев, коэффициенту пропорциональности η, который называется коэффициентом вязкости (закон Ньютона):
. (10.1)
Градиентом скорости называется изменение скорости dυ на единицу длины dx в направлении, перпендикулярном движению слоев (рис.10.1). Коэффициент вязкости
. (10.2)
Коэффициент вязкости, или коэффициент внутреннего трения, есть физическая величина, численно равная силе внутреннего трения, между двумя слоями с площадью, равной единице при градиенте скорости, равном единице. В СИ [η] кг/(м∙сек).
Знак минус в формуле Ньютона показывает, что сила F направлена противоположно изменению скорости.
В некоторых случаях вместо определенной выше динамичской вязкости удобнее пользоваться кинематической вязкостью — отношением динамической вязкости η к плотности ρ жидкости или газа: . Иногда вязкость растворов характеризуют относительной вязкостью — отношением вязкости раствора к вязкости растворителя. Приборы, служащие для измерения вязкости, называют вискозиметрами. Вязкость жидкостей зависит от температуры: она резко уменьшается с повышением температуры; особенно сильно зависит от температуры вязкость масел. Так, например, вязкость касторового масла при изменении температуры от 18 до 40оС падает почти в четыре раза.
Теперь установим выражение для коэффициента вязкости через молекулярные характеристики. Для этого выведем общее уравнение переноса. Рассмотрим молекулы, которые проходят через поперечное сечение S в точке x, двигаясь слева и справа, − средняя длина свободного пробега молекул (рис. 10.2). В поперечном сечении и молекулы испытывают последнее столкновение перед пролетом сквозь сечение S. Поэтому концентрации молекул n и их скорости диффузии в обоих объемах слева и справа от x неизменны и такие же, как в сечениях и . За промежуток dt слева через сечение S проходит количество молекул , а справа . Множитель появляется за счет того, что у каждой молекулы шесть степеней свободы, то есть шесть возможных направлений, и по направлению к стенке S летит только их шестая часть.
Результирующий поток молекул в направлении оси ох определяется как разность: .
В предельном случае при , стремящемся к нулю, получим и, следовательно, общее уравнение переноса запишется следующим образом:
. (10.3)
При внутреннем трении перпендикулярно к направлению диффузии молекулы получают добавочную скорость и, следовательно, приобретают добавочный импульс . Для суммарного потока импульса имеем . Так как по второму закону Ньютона , то получим , откуда находим выражение для вязкости .
Определение коэффициента внутреннего трения маловязких жидкостей (глицерин, касторовое масло) методом Стокса.
Коэффициент вязкости может быть определен методом падающего шарика в вязкой среде — методом Стокса.
Стокс установил, что сила внутреннего трения, действующая на шарик радиусом r, движущийся со скоростью υ в жидкости, определяется по формуле
F=6πηrυ.
На шарик, свободно падающий в жидкости, действуют силы тяжести (Р), выталкивающая (Q), и вязкого сопротивления (F) (рис. 10.3):
P=mшg=4/3πr3ρшg,
Q=mжg=4/3πr3ρжg,
F=6πηrυ,
где mш и mж — массы шарика и жидкости, ρш и ρж их плотности; r — радиус; υ — скорость падения шарика; g — ускорение свободного падения; η — коэффициент вязкости.
Движение шарика, падающего в жидкости, лишь первое время будет ускоренным. С возрастанием скорости будет возрастать сила вязкого сопротивления и с некоторого момента движение можно считать равномерным, то есть справедливо равенство
;.
Или
6πηrυ=4/3πr3g(ρш—ρж),
откуда
. (10.4)
Для средней части сосуда, ограниченной рисками А и В, где движение равномерное, скорость равна
υ= l / t,
где l — расстояние, t — время падения шарика между рисками А и В.
Подставляя значение скорости в уравнение (10.2), получим
, (10.5)
Строго говоря, соотношение (10.5), , справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиусом R, в (10.4) необходимо ввести поправку, учитывающую наличие стенок трубки. У стенок исследуемая жидкость покоится, а пограничный слой жидкости около шарика движется вместе с ним. Это приводит к увеличению градиента скорости, и, следовательно, скорость равномерного падения шарика в трубке будет меньше, чем в безграничной среде. Учет этого обстоятельства приводит к следующему выражению:
. (10.6)
Описание экспериментальной установки
Вискозиметр для определения вязкости по методу Стокса представляет собой стеклянный цилиндрический сосуд (рис. 10.3), наполненный исследуемой жидкостью, и с двух сторон закрытый крышками. На цилиндре нанесены две горизонтальные метки А и В, расположенные на расстоянии l. Диаметр шариков измеряется микрометром. Измерив диаметр шарика, его опускают в жидкость как можно ближе к оси трубки. В момент прохождения шариком верхней метки пускают в ход секундомер, а в момент прохождения шариком нижней метки секундомер останавливают. Опыт проводят 5−7 раз.
Обработка результатов
- Скорость равномерного движения шарика , поэтому коэффициент вязкости можно рассчитать по формуле
, (10.7)
где . (10.8)
- Погрешность величины t определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность и коэффициент Стьюдента.
- Погрешность косвенных измерений величины вычислить по формуле
. (10.9)
- Результат представить в виде .
- Если измерение проводится один раз, и при этом измеряются все три величины l, r и t, входящие в формулу , то приборную погрешность необходимо рассчитать по формуле
. (10.10)
- Результат представить в виде: .
Возможны различные другие варианты, при которых предварительно оцениваются погрешности измеряемых величин и не учитываются в конечном результате, если они малы. Но все эти варианты являются частными случаями рассмотренных.
ЛИТЕРАТУРА
1. Курс физики: в 3 т. Т. 1. Механика. Молекулярная физика./ И.В.Савельев.М : Наука, 1989, c. 432.
2. Методические указания по обработке результатов измерений в физическом практикуме / сост.: Е.И. Дмитриева, Л.А. Захарова, Н.Е. Попова, А.Н. Сальников. – Саратов: СГТУ, 1998, c.31.
3. Физический практикум 1 / А.Н.Сальников. – Саратов: СГТУ, 2003,c.137.
PAGE * MERGEFORMAT 68
Рис. 1.1. Линейка
Рис. 1.2. Штангенциркуль
Рис. 1.3. Микрометр
Рис. 1.4. Транспортир
Рис. 2.1. Иллюстрация закона всемирного тяготения
Рис. 2.2. Экспериментальная установка
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
Рис. 3.1. Баллистический маятник
Рис. 3.2. Схема экспериментальной установки
Рис. 3.3 Принцип независимости движений.
Рис. 4.1. Различные механические колебательные системы-маятники: математический, пружинный, физический
x
EMBED Equation.DSMT4
C
O
EMBED Equation.DSMT4
EMBED Equation.DSMT4
O`
φ
Рис 1.2 Штангенциркуль
0
l cosφ
l cosφ0
φ0
φ
m
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
A
A
x
0
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
Рис. 4.2. Зависимость смещения x при гармонических колебаниях от времени при EMBED Equation.3 :
EMBED Equation.3 − положения равновесия,
×− положения крайнего отклонения.
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
0
x
x
x
0
0
0
x
Рис. 4.3. Положение колеблющейся точки в различные моменты времени
2
4
3
1
2
1
5
Рис. 4.4. Общий вид установки
5
Рис. 5.1. Упругое соударение шаров
m1
m2
m1
m2
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
x
EMBED CorelDRAW.Graphic.12
Рис. 5.2. Соударение шаров
EMBED CorelDRAW.Graphic.12
Рис. 5.3. Схема установки
EMBED CorelDRAW.Graphic.12
Рис. 5.4. Соударение шаров
Х
Рис. 6.1. Молекулы внутри жидкости и вблизи поверхности
R
R
M 1
F
M2
M
F
EMBED Equation.DSMT4
Рис. 6.2. Силы на полусфере мыльного пузыря
а б в
ис. 6.3. Три различных случая контакта жидкости с твёрдым телом ( — результирующая сила, действующая на молекулу)
Рис. 6.4. Силы в капилляре
h
R=r
Вода
Ртуть
h
Стекло
EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
С
N
M
li
B
L
Рис.6.5. Общий вид установки
EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3
EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3
EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3
EMBED Equation.3
EMBED Equation.3
Рис. 7.1. К выводу уравнения состояния идеального газа
EMBED Word.Picture.8
Рис. 7.2.Экспериментальная установка
EMBED Word.Picture.8
Рис. 7.3 Схема экспериментальной
установки
Рис. 8.1. Двух (а) и трехатомная (б) молекула
EMBED Word.Picture.8
EMBED Word.Picture.8
Рис. 8.2. Зависимость теплоемкости от температуры
EMBED Word.Picture.8
Рис. 8.3. Экспериментальная установка
EMBED Word.Picture.8
Рис. 8.4. Диаграмма нагревания жидкости в калориметре
Рис. 9.1. К выводу уравнения бегущей волны
EMBED Equation.DSMT4
x = 0
z
(t’)
EMBED Equation.DSMT4
x
(t)
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
Рис. 9.2. Распространение упругой деформации вдоль стержня
Рис. 9.3. Различные моды колебаний струны
EMBED CorelDRAW.Graphic.12
Рис. 9.4. Схема экспериментальной установки
EMBED CorelDRAW.Graphic.12
V
х
V2
V1
dx
X
EMBED Equation.3
Рис. 10.1. Схема внутреннего трения
z
S
dN1
dN2
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
EMBED Equation.DSMT4
Рис. 10.2 Общая картина движения молекул в жидкости
EMBED Equation.3
А
В
l
Рис. 10.3. Схема установки
EMBED Equation.3 EMBED Equation.3

Лабораторная работа № 1 Тема: Теория погрешностей

1. Источники и классификация погрешности Под погрешностью понимается некоторая величина, характеризующая точность результата. Выделяют три вида погрешностей: 1. Неустранимая погрешность – эта погрешность связана с ошибками в исходной информации. Причинами этих ошибок могут быть, например, неточность измерений, невозможность представления некоторой величины конечной дробью. 2. Погрешность метода связана с тем, что точные операторы и исходные данные заменяются приближенными. Например, заменяют интеграл суммой, производную – разностью, функцию – многочленом или строят бесконечный итерационный процесс, который обрывают после конечного числа итераций. 3. Погрешность вычислений возникает при округлении промежуточных и конечных результатов. 2

2. Абсолютная и относительная погрешности Пусть – точное значение величины, а – ее приближенное значение. Абсолютной погрешностью числа называется наименьшая величина , удовлетворяющая условию , (1) т. е. точное значение величины лежит в интервале. (2) Относительной погрешностью называется величина удовлетворяющая условию , (3) или (4) Относительную погрешность часто выражают в процентах. Для этого необходимо величину умножить на 100%. 3

3. Верные значащие цифры Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева, например: 1) — все цифры значащие; 2) – значащие только ; первые три нуля незначащие, т. к. они служат вспомогательной цели – определению положения цифр , поэтому может быть принята запись ; 3) и. В первой записи все семь цифр (и последние четыре нуля) значащие, во второй – значащие только . 4

Верные значащие цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре. Пример 1. Пусть и известно, что. Определить число верных значащих цифр у числа. Имеем: Значит, у числа ; и верные знаки . а и – сомнительные. Пример 2. Определить число верных значащих цифр у числа Пусть и. Так как верные. , то у числа . три знака после запятой 5

Правила округления При записи чисел руководствуются следующим правилом: все значащие цифры должны быть верными. Поэтому округление чисел, записанных в десятичной системе, производится по правилу первой отбрасываемой цифры: если первая из отбрасываемых цифр меньше 5, то оставляемые десятичные знаки сохраняются без изменения; если первая из отбрасываемых цифр больше 5, то последняя оставляемая цифра увеличивается на единицу; если первая из отбрасываемых цифр равна 5, а за ней идут не нули, то последняя оставляемая цифра увеличивается на единицу; если первая из отбрасываемых цифр равна 5 и все значащие цифры, идущие за ней, – нули, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остается без изменения, если – четная. Примеры. Округлить числа: 1) 1, 2537≈1, 25, m=3 – количество верных значащих цифр; 2) 1, 2563≈1, 26, m=3; 3) 2, 36566≈2, 37, m=3; 4) 2, 665≈2, 66, m=3, 6 -четная; 2, 635≈2, 64, m=3, 3 -нечетная. 6

4. Прямая задача теории погрешностей: Оценить погрешность вычисления значений функции по заданной погрешности аргументов. Пусть — непрерывно дифференцируемая функция, где ; — приближенные значения аргументов, ; — абсолютные погрешности аргументов. Тогда абсолютная погрешность вычисления значения функции в точке равна (5) Относительная погрешность значения в точке равна (6) 7

Погрешность результатов арифметических операций Погрешность суммы. Абсолютная погрешность алгебраической суммы приближенных чисел равна сумме абсолютных погрешностей этих чисел. Пусть , тогда (7) Погрешность разности. Абсолютная погрешность разности приближенных чисел равна сумме абсолютных погрешностей уменьшаемого и вычитаемого. Пусть , тогда (8) Погрешность произведения. Пусть , известны и , , тогда абсолютная погрешность произведения вычисляется по формуле (9) 8

Погрешность частного. Пусть . Тогда, (10) Из формул (1. 3) – (1. 6) выводятся формулы для соответствующих относительных погрешностей: (11) (12) (13) 9

Пример (прямая задача) а) Записать порядок выполняемых операций, оценить погрешности их результатов, вычислить и оценить погрешность искомого значения. б) Определить число верных знаков в результате. Решение. а) приближенные значения исходных данных: , , . Абсолютные погрешности исходных данных: , . Относительные погрешности исходных данных: 10

Порядок выполняемых операций: 11

б) Для определения числа верных знаков воспользуемся определением и оценкой (5) для абсолютной погрешности функции. Таким образом, По определению числа верных знаков, Ответ: число верных знаков и 12

5. Обратная задача теории погрешностей Необходимо определить допустимую погрешность аргументов по допустимой погрешности функции. Для функции одной переменной абсолютную погрешность можно приближенно вычислить по формуле (14) Для функции нескольких переменных : применяют принцип равных влияний, т. е. считают, что все слагаемые , равны между собой. Тогда абсолютные погрешности всех аргументов определяются формулой (15) 13

Пример (обратная задача) Выяснить погрешность задания исходных данных, необходимую для получения результата с верными значащими цифрами. Решение. Находим (полагаем первые Согласно определению цифр верными). -верного знака, абсолютная погрешность 14

Исходим из того, что Для использования принципа равных влияний считаем, что все слагаемые , равны между собой. Тогда абсолютные погрешности всех аргументов определяются формулой: Находим 15

Задание № 1 Тема: Погрешность 1. Определить, какое равенство точнее. 2. Округлить сомнительные цифры числа, оставив верные знаки. 3. Найти абсолютные и относительные погрешности чисел, если они имеют только верные цифры. 4. а) Записать порядок выполняемых операций, оценить погрешности их результатов, вычислить и оценить погрешность искомого значения (прямая задача). б) Определить число верных знаков в результате. 5. Выяснить погрешность задания исходных данных, необходимую для получения результата с верными значащими цифрами (обратная задача). 16
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
