-
Обнаружение и исправление ошибок
-
Общие понятия
-
Для
защиты полезной информации от помех
необходимо в том или ином виде вводить
избыточность: увеличивать число символов
и время их передачи, повторять целые
сообщения, повышать мощность сигнала
— все это ведет к усложнению и удорожанию
аппаратуры. В качестве исследуемой
модели достаточно рассмотреть канал
связи с помехами, потому что к этому
случаю легко сводятся остальные.
Например, запись на диск можно рассматривать
как передачу данных в канал, а чтение с
диска – как прием данных из канала.
Коды
без избыточности обнаружить, а тем более
исправлять
ошибки не могут.
Количество символов, в которых любые
две комбинации кода отличаются друг от
друга, называется кодовым
расстоянием.
Минимальное
количество символов, в которых все
комбинации кода отличаются друг от
друга, называется минимальным
кодовым расстоянием.
Минимальное кодовое расстояние —
параметр, определяющий помехоустойчивость
кода и заложенную в коде избыточность,
т.е. корректирующие свойства кода.
В
общем случае для обнаружения t
ошибок минимальное кодовое расстояние
d0
= t
+ 1.
Минимальное
кодовое расстояние, необходимое для
одновременного обнаружения t
и исправления
ошибок,
d0
= t
+
+ 1.,
Для
кодов, только исправляющих
ошибок,
d0
= 2
+ 1.
Для
того чтобы определить кодовое расстояние
между двумя комбинациями двоичного
кода, достаточно просуммировать эти
комбинации по модулю 2 и подсчитать
число единиц полученной комбинации.
Для
обнаружения и исправления одиночной
ошибки соотношение между числом
информационных разрядив k
и числом корректирующих разрядов
должно удовлетворять следующим условиям:
![]() ,
,
![]() ,
,
при
этом подразумевается, что общая длина
кодовой комбинации
n
= k + ρ
Для
практических расчетов при определении
числа контрольных разрядов кодов с
минимальным кодовым расстоянием d0
= 3 удобно
пользоваться выражениями
ρ1(2)
= [ log2
( n + 1
) ],
если
известна длина полной кодовой комбинации
n,
и
ρ
1(2) =
[log2 {
( k
+ 1 ) + [ log2
(
k + 1) ] } ],
если
при расчетах удобнее исходить из
заданного числа информационных символов
k
.
Для
кодов, обнаруживающих все трехкратные
ошибки (d0
= 4),
ρ
1(3)
1
+ log2
(
n + 1
),
или
ρ
1(3)
1 + log2
[ (
k + 1
) + log2
(
k + 1
) ].
Для
кодов длиной в n
символов, исправляющих одну или две
ошибки (d0
= 5),
ρ
2
log2
(Cn2
+ Cn1
+ 1).
Для практических
расчетов можно пользоваться выражением:
![]() .
.
Для
кодов, исправляющих 3 ошибки (d0
= 7),
![]() .
.
-
Линейные групповые коды
Линейными
называются коды, в которых проверочные
символы представляют собой линейные
комбинации информационных символов.
Для
двоичных кодов в качестве линейной
операции используется сложение по
модулю 2.
Последовательность
нулей и единиц, принадлежащих данному
коду, будем называть кодовым
вектором.
Свойство
линейных кодов:
сумма
(разность) кодовых векторов линейного
кода дает вектор, принадлежащий данному
коду.
Линейные
коды образуют алгебраическую группу
по отношению к операции сложения по
модулю 2. В этом смысле они являются
групповыми
кодами.
Свойство
группового кода:
минимальное кодовое
расстояние между кодовыми векторами
группового кода равно минимальному
весу ненулевых кодовых векторов.
Вес
кодового вектора
(кодовой комбинации) равен числу его
ненулевых компонент.
Расстояние
между двумя кодовыми векторами
равно весу вектора, полученного в
результате сложения исходных векторов
по модулю 2. Таким образом, для данного
группового кода
Wmin
=d0.
Групповые
коды удобно задавать матрицами,
размерность которых определяется
параметрами кода k
и .
Число строк матрицы равно k,
число столбцов равно
n
= k +
:
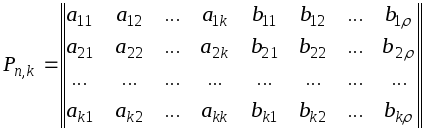
Коды,
порождаемые этими матрицами, известны
как (n,k)-коды,
соответствующие им матрицы называют
порождающими
(производящими, образующими).
Порождающая
матрица P
может быть представлена двумя матрицами
Uk
и H
(информационной и проверочной). Число
столбцов матрицы H
равно ,
число столбцов матрицы Uk
равно k
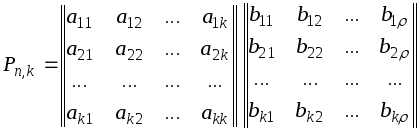
Теорией
и практикой установлено, что в качестве
матрицы Uk
удобно брать единичную матрицу в
канонической форме
![]()
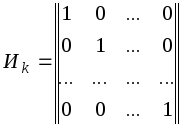
Для
кодов с d0
= 2
производящая матрица P
имеет вид
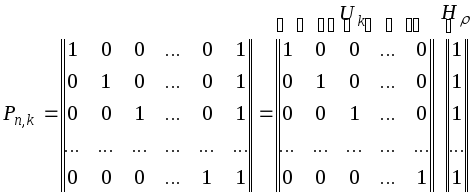
Во всех комбинациях
кода построенного при помощи такой
матрицы, четное число единиц.
Для
кодов с d0
3 порождающая
матрица не может быть представлена в
форме, общей для всех кодов с данным
d0.
Вид матрицы
зависит от конкретных требований к
порождающему коду. Этими требованиями
могут быть либо минимум корректирующих
разрядов, либо максимальная простота
аппаратуры.
Корректирующие
коды с минимальным количеством избыточных
разрядов называют плотно
упакованными
или
совершенными
кодами.
Для
кодов d0
= 3
соотношения n
и k
следующие: (3; 1), (7; 4),
(15; 11), (31; 26), (63; 57)
и так далее.
Строчки
образующей матрицы P
представляют собой k
комбинаций искомого кода. Остальные
комбинации кода строятся при помощи
образующей матрицы по следующему
правилу: корректирующие символы,
предназначенные для обнаружения и
исправления ошибки в информационной
части кода, находятся путем суммирования
по модулю 2 тех строк матрицы H,
номера которых совпадают с номерами
разрядов, содержащих единицы в кодовом
векторе, представляющем информационную
часть кода. Полученную комбинацию
приписывают справа к информационной
части кода и получают полный вектор
корректирующего кода. Аналогичную
процедуру проделывают со второй, третьей
и последующими информационными кодовыми
комбинациями, пока не будет построен
корректирующий код для передачи всех
символов первичного алфавита.
Алгоритм
образования проверочных символов по
известной информационной части кода
может быть записан следующим образом

или
![]() .
.
В процессе
декодирования осуществляются проверки,
идея которых в общем виде может быть
представлена следующим образом
![]()
Для
каждой конкретной матрицы существует
своя, одна-единственная система проверок.
Проверки производятся по следующему
правилу : в первую проверку вместе с
проверочным рядом b1
входят информационные разряды, которые
соответствуют единицам первого столбца
проверочной матрицы H;
во вторую проверку входит второй
проверочный разряд b2
и информационные
разряды, и т. д. Число проверок равно
числу проверочных разрядов корректирующего
кода .
В
результате осуществления проверок
образуется проверочный
вектор
S1,
S2,
…, S,
который называется синдромом.
Если вес синдрома равен нулю, то принятая
комбинация считается безошибочной.
Если хотя бы один разряд проверочного
вектора содержит единицу, то принятая
комбинация содержит ошибку. Исправление
ошибки производится по виду синдрома,
так как каждому ошибочному разряду
соответствует один единственный
проверочный вектор.
Вид
синдрома для каждой конкретной матрицы
может быть определен при помощи
проверочной матрицы Н’,
которая представляет собой транспонированную
матрицу H,
дополненной единичной матрицей I,
число столбцов которой равно число
проверочных разрядов кода
Н’
= HТI.
Столбцы
такой матрицы представляют собой
значение синдрома для разряда,
соответствующего номеру столбца матрицы
Н’.
Процедура исправления
ошибок в процессе декодирования групповых
кодов сводится к следующему.
Строится
кодовая таблица. В первой строке таблицы
располагаются все кодовые векторы Ai.
В первом столбце второй строки размещается
вектор a1,
вес которого равен 1.
Остальные
позиции второй строки заполняются
векторами, полученными в результате
суммирования по модулю 2 вектора a1
с Аi,
расположенным в соответствующем столбце
первой строки. В первом столбце третьей
строки записывается вектор a2,
вес которого также равен 1, однако , если
вектор a1
содержит единицу в первом разряде, то
a2
— во втором. В остальные позиции третьей
строки записывают суммы Аi
и a2
.
Аналогично
поступают до тех пор, пока не будут
просуммированы с векторами Аi
все векторы
aj
весом 1, с единицей в каждом из n
разрядов. Затем суммируются по модулю
2 векторы aj,
весом 2, с последовательным перекрытием
всех возможных разрядов. Вес вектора
aj
определяет число исправляемых ошибок.
Число векторов aj
определяется возможным числом
неповторяющихся синдромов и равно 2-1
(нулевая комбинация говорит об отсутствии
ошибки). Условие неповторяемости синдрома
позволяет по его виду определять
один-единственный соответствующий ему
вектор aj.
Векторы aj
есть векторы
ошибок, которые могут быть исправлены
данным групповым кодом.
По
виду синдрома принятая комбинация может
быть отнесена к тому или иному смежному
классу, образованному сложением по
модулю 2 кодовой комбинации Аi
с вектором ошибки aj,
т. е. к определенной строке кодовой
таблицы 3.2.1.
Таблица 3.2.1-
Кодовая таблица групповых кодов
|
a |
A1 |
A2 |
… |
A(2k-1) |
|
a1 |
a1A1 |
a2A2 |
… |
a1A(2k-1) |
|
a2 |
a2A1 |
a2A2 |
… |
a2A(2k-1) |
|
… |
… |
… |
… |
… |
|
a(2-1) |
a(2 |
a(2-1)A2 |
… |
a(2-1)A(2k-1) |
Принятая
кодовая комбинация Axn
сравнивается
с векторами, записанными в строке,
соответствующей полученному в результате
проверок синдрому. Истинный код будет
расположен в строке той же колонки
таблицы. Процесс исправления ошибки
заключается в замене на обратное значение
разрядов.
Векторы
a1,
a2,
…,a(2-1)
не должны
быть равными ни одному из векторов А1,
А2,
…, А(2-1),
в противном случае в таблице появились
бы нулевые векторы.
Пример.
Построить
кодовую таблицу, при помощи которой
обнаруживаются и исправляются все
одиночные ошибки и некоторые ошибки
кратностью r
+ 1,
в информационной
части кода (11,7), построенного по матрице

Решение.
Используя
таблицу 3.2.1, строим кодовую таблицу
3.2.2 для кодов, построенных по данной
матрице P,
кодовые комбинации строятся путем
добавления к четырехразрядным комбинациям
натурального двоичного кода корректирующих
разрядов по правилу, описанному выше.
Определяем
систему проверок исходя из матрицы H
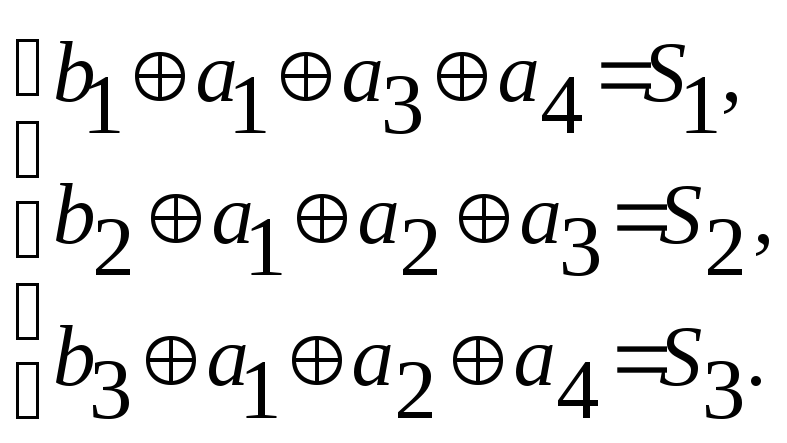
Находим
вид синдрома для каждой строки таблицы.
Для этого достаточно произвести проверки
для кодовых комбинаций любого столбца
кодовой таблицы.
Для
нашего примера возьмем столбец A3
.
Таблица 3.2.1 – Пример таблицы
для столбца А3
|
№ |
e |
A1 1000111 |
A2 0100011 |
A3 1100100 |
A4 0010110 |
A5 1010001 |
A6 0110101 |
A7 1110010 |
|
1 2 3 4 5 6 7 |
1000000 0100000 0010000 0001000 1100000 1001000 1010000 |
0000111 1100111 1010111 1001111 0100111 0001111 0010111 |
1100011 0000011 0110011 0101011 1000011 1101011 1110011 |
0100100 1000100 1110100 1101100 0000100 0101100 0110100 |
1010110 0110110 0000110 0011110 1110110 1011110 1000110 |
0010001 1110001 1000001 1011001 0110001 0011001 0000001 |
1110101 0010101 0100101 0111101 1010101 1111101 1100101 |
0110010 1010010 1100010 1111010 0010010 0111010 0100010 |
|
№ |
A8 0001101 |
A9 1001010 |
A10 0101110 |
A11 1101001 |
A12 0011011 |
A13 1011100 |
A14 0111000 |
A15 1111111 |
|
1 2 3 4 5 6 7 |
1001101 0101101 0011101 0000101 1101101 1000101 1011101 |
0001010 1101010 1011010 1000010 0101010 0000010 0011010 |
1101110 0001110 0111110 0100110 1001110 1100110 1111110 |
0101001 1001001 1111001 1100001 0001001 0100001 0111001 |
1011011 0111011 0001011 0010011 1111011 1010011 1001011 |
0011100 1111100 1001100 1010100 0111100 0010100 0001100 |
1111000 0011000 0101000 0110000 1011000 1110000 1101000 |
0111111 1011111 1101111 1110111 0011111 0110111 0101111 |
-
0
1 0 0 1 0 0 -
1
0 0 0 1 0 0 -
1
1 1 0 1 0 0 -
1
1 0 1 1 0 0 -
0
0 0 0 1 0 0 -
0
1 0 1 1 0 0 -
0
1 1 0 1 0 0







Таким
образом вектору ошибки a1
соответствует синдром 1 1 1
“ a2 “ 0
1 1
“ a3 “ 1
1 0
“ a4 “ 1
0 1
“ a5 “ 1
0 0
“ a6 “ 0
1 0
“ a7 “ 0
0 1
Предположим,
приняты комбинации 1011001, 1000101, 0001100,
0000001 и 1010001. Производим проверки





Синдром
первой принятой комбинации — 101, значит
вектор ошибки а4
= 0001000, исправление ошибки производится
заменой символа в четвертом разряде
принятой комбинации на обратный. Истинная
комбинация — А5,
так как принятая комбинация находится
в шестом столбце таблицы в строке,
соответствующей синдрому 101.
Синдром
второй принятой комбинации — 010, находим
ее в шестой строке (010 соответствует а6)
и в девятом столбце. Истинная комбинация
А8
= 0001101, т.е. исправлена двойная ошибка.
Синдром
третьей принятой комбинации — 001
соответствует а7,
истинная комбинация А13.
Синдром
четвертой из принятых комбинаций — 001
также соответствует а7,
но принятую комбинацию мы находим в
шестом столбце таблицы , следовательно,
истинная комбинация — А5.
Синдром шестой
принятой комбинации — 000. Ошибки нет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types.[1] Linear codes allow for more efficient encoding and decoding algorithms than other codes (cf. syndrome decoding).[citation needed]
Linear codes are used in forward error correction and are applied in methods for transmitting symbols (e.g., bits) on a communications channel so that, if errors occur in the communication, some errors can be corrected or detected by the recipient of a message block. The codewords in a linear block code are blocks of symbols that are encoded using more symbols than the original value to be sent.[2] A linear code of length n transmits blocks containing n symbols. For example, the [7,4,3] Hamming code is a linear binary code which represents 4-bit messages using 7-bit codewords. Two distinct codewords differ in at least three bits. As a consequence, up to two errors per codeword can be detected while a single error can be corrected.[3] This code contains 24=16 codewords.
Definition and parameters[edit]
A linear code of length n and dimension k is a linear subspace C with dimension k of the vector space 

The weight of a codeword is the number of its elements that are nonzero and the distance between two codewords is the Hamming distance between them, that is, the number of elements in which they differ. The distance d of the linear code is the minimum weight of its nonzero codewords, or equivalently, the minimum distance between distinct codewords. A linear code of length n, dimension k, and distance d is called an [n,k,d] code (or, more precisely, ![[n,k,d]_{q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eef76e1d6b74cc535236a6249e75afeea540ee3)
We want to give 
Generator and check matrices[edit]
As a linear subspace of 

![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)



A matrix H representing a linear function 
![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)
![{displaystyle {boldsymbol {H}}=[-P^{T}|I_{n-k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf073820dfea39e704650fee6958cf29c59f03c7)


Linearity guarantees that the minimum Hamming distance d between a codeword c0 and any of the other codewords c ≠ c0 is independent of c0. This follows from the property that the difference c − c0 of two codewords in C is also a codeword (i.e., an element of the subspace C), and the property that d(c, c0) = d(c − c0, 0). These properties imply that
In other words, in order to find out the minimum distance between the codewords of a linear code, one would only need to look at the non-zero codewords. The non-zero codeword with the smallest weight has then the minimum distance to the zero codeword, and hence determines the minimum distance of the code.
The distance d of a linear code C also equals the minimum number of linearly dependent columns of the check matrix H.
Proof: Because 


















Example: Hamming codes[edit]
As the first class of linear codes developed for error correction purpose, Hamming codes have been widely used in digital communication systems. For any positive integer 
![[2^{r}-1,2^{r}-r-1,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4b7099796302beb1cea00796f3d9a67b448e08c)

Example : The linear block code with the following generator matrix and parity check matrix is a ![[7,4,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499457f6464e18a49d7e72d66681299c4862829a)
Example: Hadamard codes[edit]
Hadamard code is a ![[2^{r},r,2^{r-1}]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e698d84a6a5cfe250e1e1831a36917bc5f6dbc60)




Example: The linear block code with the following generator matrix is a ![[8,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e2abe070a736c1d85fc3d68f41ad9d65cc9a85)

Hadamard code is a special case of Reed–Muller code. If we take the first column (the all-zero column) out from 
![[7,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61062d9e8384323c74a528929abb584e5c30caba)
Nearest neighbor algorithm[edit]
The parameter d is closely related to the error correcting ability of the code. The following construction/algorithm illustrates this (called the nearest neighbor decoding algorithm):
Input: A received vector v in 
Output: A codeword 


We say that a linear 




Popular notation[edit]
Codes in general are often denoted by the letter C, and a code of length n and of rank k (i.e., having k code words in its basis and k rows in its generating matrix) is generally referred to as an (n, k) code. Linear block codes are frequently denoted as [n, k, d] codes, where d refers to the code’s minimum Hamming distance between any two code words.
(The [n, k, d] notation should not be confused with the (n, M, d) notation used to denote a non-linear code of length n, size M (i.e., having M code words), and minimum Hamming distance d.)
Singleton bound[edit]
Lemma (Singleton bound): Every linear [n,k,d] code C satisfies 
A code C whose parameters satisfy k+d=n+1 is called maximum distance separable or MDS. Such codes, when they exist, are in some sense best possible.
If C1 and C2 are two codes of length n and if there is a permutation p in the symmetric group Sn for which (c1,…,cn) in C1 if and only if (cp(1),…,cp(n)) in C2, then we say C1 and C2 are permutation equivalent. In more generality, if there is an 

Lemma: Any linear code is permutation equivalent to a code which is in standard form.
Bonisoli’s theorem[edit]
A code is defined to be equidistant if and only if there exists some constant d such that the distance between any two of the code’s distinct codewords is equal to d.[4] In 1984 Arrigo Bonisoli determined the structure of linear one-weight codes over finite fields and proved that every equidistant linear code is a sequence of dual Hamming codes.[5]
Examples[edit]
Some examples of linear codes include:
- Repetition codes
- Parity codes
- Cyclic codes
- Hamming codes
- Golay code, both the binary and ternary versions
- Polynomial codes, of which BCH codes are an example
- Reed–Solomon codes
- Reed–Muller codes
- Goppa codes
- Low-density parity-check codes
- Expander codes
- Multidimensional parity-check codes
- Toric codes
- Turbo codes
Generalization[edit]
Hamming spaces over non-field alphabets have also been considered, especially over finite rings, most notably Galois rings over Z4. This gives rise to modules instead of vector spaces and ring-linear codes (identified with submodules) instead of linear codes. The typical metric used in this case the Lee distance. There exist a Gray isometry between 



More recently,[when?] some authors have referred to such codes over rings simply as linear codes as well.[9]
See also[edit]
- Decoding methods
References[edit]
- ^ William E. Ryan and Shu Lin (2009). Channel Codes: Classical and Modern. Cambridge University Press. p. 4. ISBN 978-0-521-84868-8.
- ^ MacKay, David, J.C. (2003). Information Theory, Inference, and Learning Algorithms (PDF). Cambridge University Press. p. 9. Bibcode:2003itil.book…..M. ISBN 9780521642989.
In a linear block code, the extra
bits are linear functions of the original
bits; these extra bits are called parity-check bits
- ^ Thomas M. Cover and Joy A. Thomas (1991). Elements of Information Theory. John Wiley & Sons, Inc. pp. 210–211. ISBN 978-0-471-06259-2.
- ^ Etzion, Tuvi; Raviv, Netanel (2013). «Equidistant codes in the Grassmannian». arXiv:1308.6231 [math.CO].
- ^ Bonisoli, A. (1984). «Every equidistant linear code is a sequence of dual Hamming codes». Ars Combinatoria. 18: 181–186.
- ^ Marcus Greferath (2009). «An Introduction to Ring-Linear Coding Theory». In Massimiliano Sala; Teo Mora; Ludovic Perret; Shojiro Sakata; Carlo Traverso (eds.). Gröbner Bases, Coding, and Cryptography. Springer Science & Business Media. ISBN 978-3-540-93806-4.
- ^ «Encyclopedia of Mathematics». www.encyclopediaofmath.org.
- ^ J.H. van Lint (1999). Introduction to Coding Theory (3rd ed.). Springer. Chapter 8: Codes over ℤ4. ISBN 978-3-540-64133-9.
- ^ S.T. Dougherty; J.-L. Kim; P. Sole (2015). «Open Problems in Coding Theory». In Steven Dougherty; Alberto Facchini; Andre Gerard Leroy; Edmund Puczylowski; Patrick Sole (eds.). Noncommutative Rings and Their Applications. American Mathematical Soc. p. 80. ISBN 978-1-4704-1032-2.
Bibliography[edit]
- J. F. Humphreys; M. Y. Prest (2004). Numbers, Groups and Codes (2nd ed.). Cambridge University Press. ISBN 978-0-511-19420-7. Chapter 5 contains a more gentle introduction (than this article) to the subject of linear codes.
External links[edit]
- q-ary code generator program
- Code Tables: Bounds on the parameters of various types of codes, IAKS, Fakultät für Informatik, Universität Karlsruhe (TH)]. Online, up to date table of the optimal binary codes, includes non-binary codes.
- The database of Z4 codes Online, up to date database of optimal Z4 codes.
From Wikipedia, the free encyclopedia
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types.[1] Linear codes allow for more efficient encoding and decoding algorithms than other codes (cf. syndrome decoding).[citation needed]
Linear codes are used in forward error correction and are applied in methods for transmitting symbols (e.g., bits) on a communications channel so that, if errors occur in the communication, some errors can be corrected or detected by the recipient of a message block. The codewords in a linear block code are blocks of symbols that are encoded using more symbols than the original value to be sent.[2] A linear code of length n transmits blocks containing n symbols. For example, the [7,4,3] Hamming code is a linear binary code which represents 4-bit messages using 7-bit codewords. Two distinct codewords differ in at least three bits. As a consequence, up to two errors per codeword can be detected while a single error can be corrected.[3] This code contains 24=16 codewords.
Definition and parameters[edit]
A linear code of length n and dimension k is a linear subspace C with dimension k of the vector space 

The weight of a codeword is the number of its elements that are nonzero and the distance between two codewords is the Hamming distance between them, that is, the number of elements in which they differ. The distance d of the linear code is the minimum weight of its nonzero codewords, or equivalently, the minimum distance between distinct codewords. A linear code of length n, dimension k, and distance d is called an [n,k,d] code (or, more precisely, ![[n,k,d]_{q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eef76e1d6b74cc535236a6249e75afeea540ee3)
We want to give 
Generator and check matrices[edit]
As a linear subspace of 

![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)



A matrix H representing a linear function 
![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)
![{displaystyle {boldsymbol {H}}=[-P^{T}|I_{n-k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf073820dfea39e704650fee6958cf29c59f03c7)


Linearity guarantees that the minimum Hamming distance d between a codeword c0 and any of the other codewords c ≠ c0 is independent of c0. This follows from the property that the difference c − c0 of two codewords in C is also a codeword (i.e., an element of the subspace C), and the property that d(c, c0) = d(c − c0, 0). These properties imply that
In other words, in order to find out the minimum distance between the codewords of a linear code, one would only need to look at the non-zero codewords. The non-zero codeword with the smallest weight has then the minimum distance to the zero codeword, and hence determines the minimum distance of the code.
The distance d of a linear code C also equals the minimum number of linearly dependent columns of the check matrix H.
Proof: Because 


















Example: Hamming codes[edit]
As the first class of linear codes developed for error correction purpose, Hamming codes have been widely used in digital communication systems. For any positive integer 
![[2^{r}-1,2^{r}-r-1,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4b7099796302beb1cea00796f3d9a67b448e08c)

Example : The linear block code with the following generator matrix and parity check matrix is a ![[7,4,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499457f6464e18a49d7e72d66681299c4862829a)
Example: Hadamard codes[edit]
Hadamard code is a ![[2^{r},r,2^{r-1}]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e698d84a6a5cfe250e1e1831a36917bc5f6dbc60)




Example: The linear block code with the following generator matrix is a ![[8,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e2abe070a736c1d85fc3d68f41ad9d65cc9a85)

Hadamard code is a special case of Reed–Muller code. If we take the first column (the all-zero column) out from 
![[7,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61062d9e8384323c74a528929abb584e5c30caba)
Nearest neighbor algorithm[edit]
The parameter d is closely related to the error correcting ability of the code. The following construction/algorithm illustrates this (called the nearest neighbor decoding algorithm):
Input: A received vector v in 
Output: A codeword 


We say that a linear 




Popular notation[edit]
Codes in general are often denoted by the letter C, and a code of length n and of rank k (i.e., having k code words in its basis and k rows in its generating matrix) is generally referred to as an (n, k) code. Linear block codes are frequently denoted as [n, k, d] codes, where d refers to the code’s minimum Hamming distance between any two code words.
(The [n, k, d] notation should not be confused with the (n, M, d) notation used to denote a non-linear code of length n, size M (i.e., having M code words), and minimum Hamming distance d.)
Singleton bound[edit]
Lemma (Singleton bound): Every linear [n,k,d] code C satisfies 
A code C whose parameters satisfy k+d=n+1 is called maximum distance separable or MDS. Such codes, when they exist, are in some sense best possible.
If C1 and C2 are two codes of length n and if there is a permutation p in the symmetric group Sn for which (c1,…,cn) in C1 if and only if (cp(1),…,cp(n)) in C2, then we say C1 and C2 are permutation equivalent. In more generality, if there is an 

Lemma: Any linear code is permutation equivalent to a code which is in standard form.
Bonisoli’s theorem[edit]
A code is defined to be equidistant if and only if there exists some constant d such that the distance between any two of the code’s distinct codewords is equal to d.[4] In 1984 Arrigo Bonisoli determined the structure of linear one-weight codes over finite fields and proved that every equidistant linear code is a sequence of dual Hamming codes.[5]
Examples[edit]
Some examples of linear codes include:
- Repetition codes
- Parity codes
- Cyclic codes
- Hamming codes
- Golay code, both the binary and ternary versions
- Polynomial codes, of which BCH codes are an example
- Reed–Solomon codes
- Reed–Muller codes
- Goppa codes
- Low-density parity-check codes
- Expander codes
- Multidimensional parity-check codes
- Toric codes
- Turbo codes
Generalization[edit]
Hamming spaces over non-field alphabets have also been considered, especially over finite rings, most notably Galois rings over Z4. This gives rise to modules instead of vector spaces and ring-linear codes (identified with submodules) instead of linear codes. The typical metric used in this case the Lee distance. There exist a Gray isometry between 



More recently,[when?] some authors have referred to such codes over rings simply as linear codes as well.[9]
See also[edit]
- Decoding methods
References[edit]
- ^ William E. Ryan and Shu Lin (2009). Channel Codes: Classical and Modern. Cambridge University Press. p. 4. ISBN 978-0-521-84868-8.
- ^ MacKay, David, J.C. (2003). Information Theory, Inference, and Learning Algorithms (PDF). Cambridge University Press. p. 9. Bibcode:2003itil.book…..M. ISBN 9780521642989.
In a linear block code, the extra
bits are linear functions of the original
bits; these extra bits are called parity-check bits
- ^ Thomas M. Cover and Joy A. Thomas (1991). Elements of Information Theory. John Wiley & Sons, Inc. pp. 210–211. ISBN 978-0-471-06259-2.
- ^ Etzion, Tuvi; Raviv, Netanel (2013). «Equidistant codes in the Grassmannian». arXiv:1308.6231 [math.CO].
- ^ Bonisoli, A. (1984). «Every equidistant linear code is a sequence of dual Hamming codes». Ars Combinatoria. 18: 181–186.
- ^ Marcus Greferath (2009). «An Introduction to Ring-Linear Coding Theory». In Massimiliano Sala; Teo Mora; Ludovic Perret; Shojiro Sakata; Carlo Traverso (eds.). Gröbner Bases, Coding, and Cryptography. Springer Science & Business Media. ISBN 978-3-540-93806-4.
- ^ «Encyclopedia of Mathematics». www.encyclopediaofmath.org.
- ^ J.H. van Lint (1999). Introduction to Coding Theory (3rd ed.). Springer. Chapter 8: Codes over ℤ4. ISBN 978-3-540-64133-9.
- ^ S.T. Dougherty; J.-L. Kim; P. Sole (2015). «Open Problems in Coding Theory». In Steven Dougherty; Alberto Facchini; Andre Gerard Leroy; Edmund Puczylowski; Patrick Sole (eds.). Noncommutative Rings and Their Applications. American Mathematical Soc. p. 80. ISBN 978-1-4704-1032-2.
Bibliography[edit]
- J. F. Humphreys; M. Y. Prest (2004). Numbers, Groups and Codes (2nd ed.). Cambridge University Press. ISBN 978-0-511-19420-7. Chapter 5 contains a more gentle introduction (than this article) to the subject of linear codes.
External links[edit]
- q-ary code generator program
- Code Tables: Bounds on the parameters of various types of codes, IAKS, Fakultät für Informatik, Universität Karlsruhe (TH)]. Online, up to date table of the optimal binary codes, includes non-binary codes.
- The database of Z4 codes Online, up to date database of optimal Z4 codes.
В области математики и теории информации линейный код — это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации.
Основы
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи поврежденных блоков — этот подход применяется в основном на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание поврежденных блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (англ. forward error correction) применяется на физическом уровне.
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию, а при чтении (приеме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и сверточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной 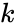

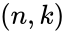
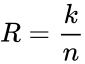
Если исходные 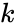
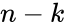
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из 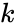

- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведенные требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую легкость кодирования и декодирования.
Линейные пространства
Порождающая матрица
Пусть векторы 

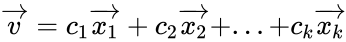
либо в матричной форме, как:

где
называется порождающей матрицей линейного пространства.
Это соотношение устанавливает связь между векторами коэффициентов
и векторами 
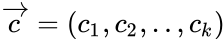

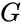
Проверочная матрица
Другим способом задания линейных пространств является описание через проверочную матрицу.
Пусть 
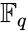
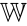

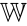

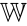
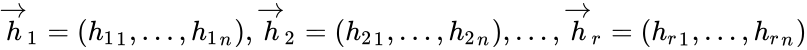
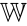
Тогда любой вектор 

Или в матричной форме:

где
— проверочная матрица.
Приведенную систему линейных уравнений следует рассматривать, как систему проверок для всех векторов линейного пространства, поэтому матрица 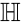
Формальное определение
Линейный код длины n и ранга k является линейным подпространством C размерности k векторного пространства 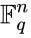
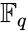
Линейный (блоковый) код — такой код, что множество его кодовых слов образует 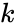
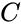

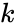
Это значит, что операция кодирования соответствует умножению исходного 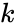
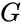
Пусть 
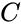
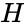

.
Свойства и важные теоремы
Минимальное расстояние и корректирующая способность
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 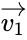
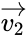

Минимальное расстояние 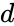
Вес вектора — 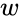
Теорема 1:
Минимальное расстояние 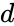
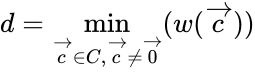
Доказательство:
Расстояние между двумя векторами 
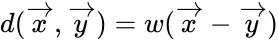

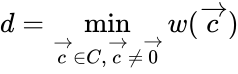
Минимальное расстояние Хемминга 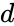
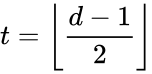
Корректирующая способность определяет, какое максимальное число ошибок в одном кодовом слове код может гарантированно исправить.
Поясним на примере. Предположим, что есть два кодовых слова A и B, расстояние Хемминга между ними равно 3. Если было передано слово A, и канал внес ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову A, чем B. Но если каналом были внесены ошибки в двух битах, декодер может посчитать, что было передано слово B.
Число обнаруживаемых ошибок — число ошибок, при котором код может судить об ошибочной ситуации. Это число равно
.
Теорема 2 (без доказательства):
Если любые 
Теорема 3 (без доказательства):
Если минимальное расстояние линейного (n, k)-кода равно d, то любые 
Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор,
будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Код Рида-Малера
Код Рида-Малера [en:Reed-Muller code] — линейный код.
Общий метод кодирования линейных кодов
Линейный код длины n с k информационными символами является k-мерным линейным подпространством, поэтому каждое кодовое слово является линейной комбинацией базисных векторов 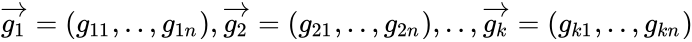
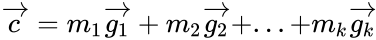
Либо с помощью порождающей матрицы:

где 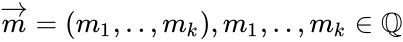
Это соотношение есть правило кодирование, по которому информационное слово 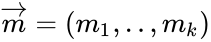
Общий метод обнаружения ошибок в линейном коде
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 


Линейные циклические коды
Несмотря на то, что исправление ошибок в линейных кодах уже значительно проще исправления в большинстве нелинейных, для большинства кодов этот процесс все ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 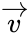
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 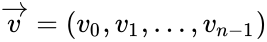
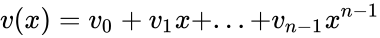

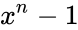
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 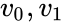
Порождающий полином
Можно показать, что все кодовые слова конкретного циклического кода кратны определенному порождающему полиному 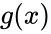
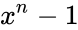
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC
Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления 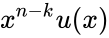
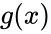
Таким образом, вид полинома g(x) задает конкретный код CRC. Примеры наиболее популярных полиномов:
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | 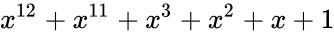 |
| CRC-16 | 16 | 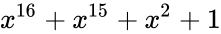 |
| CRC-CCITT | 16 | 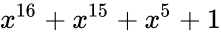 |
| CRC-32 | 32 |  |
Коды БЧХ
Коды Боуза-Чоудхури-Хоквингема (БЧХ) являются подклассом двоичных циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически построение кодов БЧХ и их декодирование используют разложение порождающего полинома 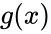
Коды Рида-Соломона
Коды Рида-Соломона (РС-коды) фактически являются недвоичными кодами БЧХ, то есть элементы кодового вектора являются не битами, а группами битов. Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Преимущества и недостатки линейных кодов
Хотя линейные коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических приложений.
Оценка эффективности
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
Пусть имеется двоичный блоковый 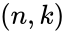
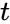
.
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида-Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определенных системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение
Линейные коды применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Линейные коды применяются в сетевых протоколах различных уровней.
См. также
- Циклический код
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Линейный код. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
From Wikipedia, the free encyclopedia
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types.[1] Linear codes allow for more efficient encoding and decoding algorithms than other codes (cf. syndrome decoding).[citation needed]
Linear codes are used in forward error correction and are applied in methods for transmitting symbols (e.g., bits) on a communications channel so that, if errors occur in the communication, some errors can be corrected or detected by the recipient of a message block. The codewords in a linear block code are blocks of symbols that are encoded using more symbols than the original value to be sent.[2] A linear code of length n transmits blocks containing n symbols. For example, the [7,4,3] Hamming code is a linear binary code which represents 4-bit messages using 7-bit codewords. Two distinct codewords differ in at least three bits. As a consequence, up to two errors per codeword can be detected while a single error can be corrected.[3] This code contains 24=16 codewords.
Definition and parameters[edit]
A linear code of length n and dimension k is a linear subspace C with dimension k of the vector space 

The weight of a codeword is the number of its elements that are nonzero and the distance between two codewords is the Hamming distance between them, that is, the number of elements in which they differ. The distance d of the linear code is the minimum weight of its nonzero codewords, or equivalently, the minimum distance between distinct codewords. A linear code of length n, dimension k, and distance d is called an [n,k,d] code (or, more precisely, ![[n,k,d]_{q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eef76e1d6b74cc535236a6249e75afeea540ee3)
We want to give 
Generator and check matrices[edit]
As a linear subspace of 

![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)



A matrix H representing a linear function 
![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)
![{displaystyle {boldsymbol {H}}=[-P^{T}|I_{n-k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf073820dfea39e704650fee6958cf29c59f03c7)


Linearity guarantees that the minimum Hamming distance d between a codeword c0 and any of the other codewords c ≠ c0 is independent of c0. This follows from the property that the difference c − c0 of two codewords in C is also a codeword (i.e., an element of the subspace C), and the property that d(c, c0) = d(c − c0, 0). These properties imply that
In other words, in order to find out the minimum distance between the codewords of a linear code, one would only need to look at the non-zero codewords. The non-zero codeword with the smallest weight has then the minimum distance to the zero codeword, and hence determines the minimum distance of the code.
The distance d of a linear code C also equals the minimum number of linearly dependent columns of the check matrix H.
Proof: Because 


















Example: Hamming codes[edit]
As the first class of linear codes developed for error correction purpose, Hamming codes have been widely used in digital communication systems. For any positive integer 
![[2^{r}-1,2^{r}-r-1,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4b7099796302beb1cea00796f3d9a67b448e08c)

Example : The linear block code with the following generator matrix and parity check matrix is a ![[7,4,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499457f6464e18a49d7e72d66681299c4862829a)
Example: Hadamard codes[edit]
Hadamard code is a ![[2^{r},r,2^{r-1}]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e698d84a6a5cfe250e1e1831a36917bc5f6dbc60)




Example: The linear block code with the following generator matrix is a ![[8,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e2abe070a736c1d85fc3d68f41ad9d65cc9a85)

Hadamard code is a special case of Reed–Muller code. If we take the first column (the all-zero column) out from 
![[7,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61062d9e8384323c74a528929abb584e5c30caba)
Nearest neighbor algorithm[edit]
The parameter d is closely related to the error correcting ability of the code. The following construction/algorithm illustrates this (called the nearest neighbor decoding algorithm):
Input: A received vector v in 
Output: A codeword 


We say that a linear 




Popular notation[edit]
Codes in general are often denoted by the letter C, and a code of length n and of rank k (i.e., having k code words in its basis and k rows in its generating matrix) is generally referred to as an (n, k) code. Linear block codes are frequently denoted as [n, k, d] codes, where d refers to the code’s minimum Hamming distance between any two code words.
(The [n, k, d] notation should not be confused with the (n, M, d) notation used to denote a non-linear code of length n, size M (i.e., having M code words), and minimum Hamming distance d.)
Singleton bound[edit]
Lemma (Singleton bound): Every linear [n,k,d] code C satisfies 
A code C whose parameters satisfy k+d=n+1 is called maximum distance separable or MDS. Such codes, when they exist, are in some sense best possible.
If C1 and C2 are two codes of length n and if there is a permutation p in the symmetric group Sn for which (c1,…,cn) in C1 if and only if (cp(1),…,cp(n)) in C2, then we say C1 and C2 are permutation equivalent. In more generality, if there is an 

Lemma: Any linear code is permutation equivalent to a code which is in standard form.
Bonisoli’s theorem[edit]
A code is defined to be equidistant if and only if there exists some constant d such that the distance between any two of the code’s distinct codewords is equal to d.[4] In 1984 Arrigo Bonisoli determined the structure of linear one-weight codes over finite fields and proved that every equidistant linear code is a sequence of dual Hamming codes.[5]
Examples[edit]
Some examples of linear codes include:
- Repetition codes
- Parity codes
- Cyclic codes
- Hamming codes
- Golay code, both the binary and ternary versions
- Polynomial codes, of which BCH codes are an example
- Reed–Solomon codes
- Reed–Muller codes
- Algebraic geometry codes
- Binary Goppa codes
- Low-density parity-check codes
- Expander codes
- Multidimensional parity-check codes
- Toric codes
- Turbo codes
Generalization[edit]
Hamming spaces over non-field alphabets have also been considered, especially over finite rings, most notably Galois rings over Z4. This gives rise to modules instead of vector spaces and ring-linear codes (identified with submodules) instead of linear codes. The typical metric used in this case the Lee distance. There exist a Gray isometry between 



More recently,[when?] some authors have referred to such codes over rings simply as linear codes as well.[9]
See also[edit]
- Decoding methods
References[edit]
- ^ William E. Ryan and Shu Lin (2009). Channel Codes: Classical and Modern. Cambridge University Press. p. 4. ISBN 978-0-521-84868-8.
- ^ MacKay, David, J.C. (2003). Information Theory, Inference, and Learning Algorithms (PDF). Cambridge University Press. p. 9. Bibcode:2003itil.book…..M. ISBN 9780521642989.
In a linear block code, the extra
bits are linear functions of the original
bits; these extra bits are called parity-check bits
- ^ Thomas M. Cover and Joy A. Thomas (1991). Elements of Information Theory. John Wiley & Sons, Inc. pp. 210–211. ISBN 978-0-471-06259-2.
- ^ Etzion, Tuvi; Raviv, Netanel (2013). «Equidistant codes in the Grassmannian». arXiv:1308.6231 [math.CO].
- ^ Bonisoli, A. (1984). «Every equidistant linear code is a sequence of dual Hamming codes». Ars Combinatoria. 18: 181–186.
- ^ Marcus Greferath (2009). «An Introduction to Ring-Linear Coding Theory». In Massimiliano Sala; Teo Mora; Ludovic Perret; Shojiro Sakata; Carlo Traverso (eds.). Gröbner Bases, Coding, and Cryptography. Springer Science & Business Media. ISBN 978-3-540-93806-4.
- ^ «Encyclopedia of Mathematics». www.encyclopediaofmath.org.
- ^ J.H. van Lint (1999). Introduction to Coding Theory (3rd ed.). Springer. Chapter 8: Codes over ℤ4. ISBN 978-3-540-64133-9.
- ^ S.T. Dougherty; J.-L. Kim; P. Sole (2015). «Open Problems in Coding Theory». In Steven Dougherty; Alberto Facchini; Andre Gerard Leroy; Edmund Puczylowski; Patrick Sole (eds.). Noncommutative Rings and Their Applications. American Mathematical Soc. p. 80. ISBN 978-1-4704-1032-2.
Bibliography[edit]
- J. F. Humphreys; M. Y. Prest (2004). Numbers, Groups and Codes (2nd ed.). Cambridge University Press. ISBN 978-0-511-19420-7. Chapter 5 contains a more gentle introduction (than this article) to the subject of linear codes.
External links[edit]
- q-ary code generator program
- Code Tables: Bounds on the parameters of various types of codes, IAKS, Fakultät für Informatik, Universität Karlsruhe (TH)]. Online, up to date table of the optimal binary codes, includes non-binary codes.
- The database of Z4 codes Online, up to date database of optimal Z4 codes.
Корректирующие коды «на пальцах»
Время на прочтение
11 мин
Количество просмотров 63K
 Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.
Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.
Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
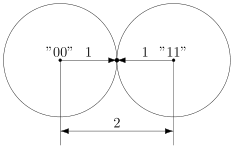
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
Лекция №
.
Линейные коды.
Самый
большой класс разделимых блочных кодов
составляют систематические
или линейные коды.
k
r
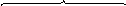

-
a1
a2
a3
ai
…
ak
b1
b2
bi
br
n
Линейными
называются коды, в которых проверочные
символы представляют собой линейные
комбинации информационных символов.
Для
двоичных кодов в качестве линейной
операции используются сложение по mod
2.
bj
=
ai
(основаны
на применении мат. аппарата алгебры
Жегалкина (
Основное
свойство линейного кода:
сумма(разность) кодовых комбинаций
является также разрешённой кодовой
комбинацией.
Пример:
[
] — разрешённая
[ ] — разрешённая
=
[ ] — разрешённая
Отсюда
– сумма(разность) произвольного числа
разрешённых кодовых комбинаций является
разрешённой
кодовой комбинацией.
Линейные
коды образуют алгебраическую группу
по отношению к операции сложения
по mod 2.
В этом
смысле они являются групповыми
кодами.
Свойство
группового кода:
(dmin)
Минимальное
кодовое расстояние
между векторами линейного кода равно
линейному
весу ненулевых кодовых векторов.
Для
построения групповых кодов (т.е. перехода
от информационных разрядов к полному
кодовому слову, включающему также и
проверочные разряды, целесообразно
использовать специальные матрицы: n
*
k
= (k + r) *
k/
Порождающая
матрица может быть представлена в виде
2х
матриц И(информационной) и П(проверочной)
||G|| = |[И]|
|[П]|





a11
a12
… a1k p11
p12
… p1r
Gn,k
= a21
a22
… a2k p21
p22
… p2r
k
k
……………… ………………..

ak1
ak2
… akk pk1
pk2
… pkr

k
r
n
Получение
кодовой комбинации осуществляется
путём суммирования элементов
||И||
и
параллельного суммирования строк ||П||.
1).
На практике
установлено, что в качестве информационной
матрицы ||И||
удобно
брать единичную матрицу в канонической
форме:


100…0
Iи
= 010…0
………
000…1
2).
Строчки образуют матрицы ||C||
= ||И||
||П|| представляют собой “К”
комбинаций(разрешённых) искомого кода.
Остальные комбинации кода строятся при
помощи образующей матрицы.
Пример


 a1
a1
1
1000 111 011 Необходимо
закодировать
a2
0
0100 110 101
информационную комбинацию:
a3
1 0010 101 110
1011
a4
1 0001 011 111

Полученное
значение проверочных

1011
001
разрядов.
В
общем случае: a1,
a2,
a3,
a4
– информационная
кодовая комбинация в общем виде:
a 1
1
a2
a3
a4
b1
b2
b3
b1
=
a1
a2
a3
Для
заданной образующей матрицы
b2
= a1
a2
a4
b3
=
a1
a3
a4
В
самом общем случае алгоритм образования
проверочных символов b1…b2
по известной
информационной части a1,
a2,
… ak
может быть
записан следующем образом :
k
b1
=
p11a1
p21a2
…
pk1ak
=
pi1ai
i=1
k
b2
=
p12a1
p22a2
…
pk2ak
=
pi2ai
i=1
———————————————-
k
bj
= p1ja1
p2ja2
…
pkjak
=
pijai
i=1
———————————————-
k
br
= p1ra1
p2ra2
…
pkrak
=
pirai
i
Рассмотрим теперь
метод построения образующей матрицы
Из свойств группового
следует, что
W
dmin
С другой
стороны Wi
= Wнi
+ Wпi
dmin
Wп
dmin
– Wн
Т.к.
вес всех сторон ||Н||
: W11=1,
то имеем
Wп
dmin
– 1, dmin
t+1
dmin
–1
t
Wп
dmin
–
1
t
Wп
t
Необходимые
и
Отсюда:
для кодов, обнаруживающих t
– кратные ошибки:
достаточные
требования Wп
(строки)
t
для
построения проверочной для
кодов, исправляющих t – кратные
ошибки :
матрицы
Wп
(строки)
2t
Рассмотрим
частные случаи:
1.)
Коды, обнаруживающие одиночную ошибку.
dmin
= 2 ( N=15, t=1 )
Wп
1
Единая
матрица для dmin
2




100…0
1 k
k
010…0
1 b1
=
aip1i
=
ai
Не что иное, как
001…0
1
i=1 i=1
проверка на четность.

000…1
1


И П
Во
всех комбинациях построенного кода –
четное.
Для
dmin
3 проверочная
матрица не может быть представлена в
общей (единой) форме, т.к. для dmin
3
r зависит
от k.
Построение
кодовой комбинации E
в матричной форме имеет вид:
образующая
матрица
E
= IGn,k
, где I
– вектор длины k,
компонентами
которой являются


информационные
разряды.
кодовый вектор
информационный
вектор
Пример
Построить образующую
матрицу и кодовую комбинацию для
линейного кода, исправляющие одиночные
ошибки при передаче собщений.
1.
t =
1; N = 16;
2.
dmin
= 3; Wп
= 2; k = [ log15] = 4; 2r
> k + r
r = 3;
3. Gп,к
= G7,4
=



a1 ..a4
b1.b3
1000 011 b1
= a2
a3
a4
0100 101
b2 =
a1
a3
a4
0010 110
b3 =
a1
a2
a4
-
111
4.
E = IGп,к = 0 100.101
Рассмотрим этап
депозирования S1,
S2 …
Sr;
а.) В
процессе депозирования осуществляются
проверки, идея которых в общем случае
может быть представлена следующем
образом :
k
Sj
= bj
pijai
Sj
= bj
bj’;
j1r;
i=1
новый
старый из канала до передачи
проверочные
символы
б.)
Sj
– называется
проверочным синдромом или синдромом
ошибок и имеет число разрядов равное:
r
( S1,
S2
…Sr
)
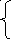
Если
w(Sj’)
= 0, но нет
ошибок;
w(Sj)
0, есть
ошибки.
в.)
Рассмотрим процедуру исправления ошибки
по виду Sj
(из
предыдущего примера
E =
0101.101)
Групповой
код построен по матрице


1000.011
0100.101
= G7,4
0010.110
0001.111
Покажем
процесс исправления ошибки в произвольном
разряде корректирующего кода.
-
Согласно
правилу построения проверочного
синдрома
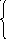
S1’
= (b1,a2,a3,a4)
S2
= (b2,a1,a3,a4)
S3
= (b3,a1,a2,a4)
Определим
соответствие между ошибкой в определенном
разряде принятой комбинации и видом
проверочного синдрома. (Напоминаю, что
для удобства полученную кодовую
комбинацию будем рассматривать как
суперпозицию (данном случае, как сумму
по mod2)
правильной
(разрешенной, передаваемой) кодовой
комбинации A
и вектора
одиночной ошибки e).
2.
Пусть информация принята верно, т.е. ни
один из разрядов ai,
bj
не исказился.
В этом случае b1=
a2
a3
a4
сохранится
равенство для всех трех строчек, а
следовательно Si
= 0.
Это
подтверждает необходимый и достаточный
признак принятия правильной информации.
3.
Строем проверочную
матрицу H,
для которой строки – возможные вектора
ошибок, а столбцы – проверочные синдромы
соответствующие данной ошибке.
e1 S1
e2 S2
. .
. .
. .
en Sn
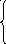


 1
1
0
0
0
0
0
0 0 1 1
Корректирующая матрица H:
ошибка 0
1
0
0
0
0
0 1 0 1
iая
строка корректирующей
в информационном 0
0
1
0
0
0
0 1 1 0
матрицы H
содержит
синдром,
разряде 0
0
0
1
0
0
0 1 1 1
= H
который
соответствует ошибке


в i-ом
разряде кодовой
ошибка 0
0
0
0
1
0
0 1 0 0
комбинации.
в проверочном 0
0
0
0
0
1
0 0 1 0
разряде 0
0
0
0
0
0
1 0 0 1

a1a2a3a4
b1b2b3
S1S2S3
Для
e1
из выражений для Si
находим
S1,
S2,
S3.
Подчеркнуть,
что Si=0,
если ошибочная комбинация не попадает
в систему проверки для Si.
Мы
видим, что проверочная матрица H
состоит из двух частиц матрицы П и
единичной матрицы.
Данная методика
построения проверочной матрицы является
обобщающей (одинаковой для всех образующих
матриц).
Т.о.
процесс декодирования кодовых комбинаций
(для линейного группового кода) состоит
в следующем:
-
Определение
проверочного синдрома Si
в соответствии с видом проверочной
матрицы П. -
Если
Si
=
0 – комбинация
принята верно,
если Si0,
произошла
ошибка. -
Построение
проверочной матрицы, которая устанавливает
соответствие между значением Si
и позиций, в которой произошла ошибка. -
Исправление
(коррекция [инверсия])
ошибочной позиции.
Мы
рассмотрели групповые линейные коды и
процедуры кодирования и декодирования,
в основе которых лежит построение
порождающей (S)
и проверочных матриц (H).
Наряду
с решением вопроса построения линейного
кода с заданной корректирующей
способностью, существенным является
вопрос об избыточности
и простоте
структурной реализации.
С этой точки зрения линейные коды
разделяются на совершенные
(плотно упакованные)
и несовершенные
линейные
коды.
1.
Совершенные коды – коды с min
количеством избыточных разрядов. [2r
= k+r+1]
Пример
для кодов, исправляющих одиночные
разряды.
(l
= 1)
2r
> k+r,
k(количество
информац.) r(количество
проверочн.)
-
3
-
3


-
4
(7,4) -
4

-
4
«совершенные» min
избыточность:
r/(k+2) -
4

-
4
-
4

(15,11) -
4
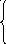
-
5

-
5
-
5
-
5
несовершенные
коды
2. С точки зрения
простой структурной реализации:
экономические
коды
коды с
повышенной
с
min количеством
проверок на четность корректирующей
способностью
При
построении проверочной матрицы
П ,
условие Wп
2l.
Wп
= min: 2l, 2l +1, 2l +2, … Wп
= max: r, r-1, r-2 … Min количество
проверок на четность, Наиболее высокие
корректирующие
min
количество аппаратурных затрат способности.
Представление
операции декодирования в матричной
форме.
а)
ẼH
= S
– из
условия построения проверочного
синдрома.
б)
ẼH
= (E
e)H
= EH
eH
= S;
П ри
ри
отсутствие ошибок: Ẽ=E;
S=0; отсюда
EH=0;
eH=S;
т.к. E=Gn,k,
то Gn,kH=0,
и имеем
Gn,kH=0,
условие
построение H
по известной
Gn,k.
Пример:


 1.
1.
1000 011 011
Gn,k=
G7,4
= 0100 101 ; H = 101 ,
0010 110 111
0001 111 100
010
001
 2.
2.
I = 1010 E=IG7,4=1010.101;
e =0010.000;
Ẽ
= 1000.101





 3.
3.
S=ẼH
= 110 011
1000011 101 000
GH
= 0100101
110 = 000 = 0.
0010110 111
000
0001111 100
000
010
001
Важным
вопросом на практике является структурная
реализация кодирующих и декодирующих
устройств.
Поэтому (для
сравнения) рассмотрим коды, Хэмминга,
обладающие аналогичной корректирующей
способностью, но с точки зрения структурной
реализации дающие несколько другие
результаты.
Матричное
представление кода Хэмминга.
а)
а4
а3
а2
а1
b3
b2
b1
a4
a3
a2
b3
a1
b2
b1

1 0 0 0 1 1 1
1 0 0 1 0 1 1

0
1 0 0 1 1 0 G7,4x
= 0 1 0 1 0 1 0
0 0 1 0 1 0 1 0
0 1 1 0 0 1
0 0 0 1 0 1 1
0 0 0 0 1 1 1
a1
a2
a3
b1
a4
b2
b3
E
= IG7,4
= (0101)
G7,4x
= 0 1 0 1 1 0 1
a1
a2
a3
b1
a4
b2
b3
S1
S2
S3

 1
1
0 0 0 0 0 0 1 1 1
0
1 0 0 0 0 0 1 1 0
0
0 1 0 0 0 0 1 0 1
0
0 0 1 0 0 0 1 0 0
0
0 0 0 1 0 0 0 1 1
0
0 0 0 0 1 0 0 1 0
0
0 0 0 0 0 1 0 0 1
б)
Этап
декодирования.


111
Из
определения H,
в которой каждая строка равна
100
синдрому ошибки.
101
S
= ẼH
=
Ẽ
100
010
010
001
S
= 0111.101H
= 101.
Структурная
реализация линейных кодов и Хэмминга.
а) Кодирование
б) Декодирование
Модифицированный
код Хэмминга.
Для исправления
одиночной и обнаружения двойной ошибки,
кроме проверок по контрольным позициям,
следует проводить еще одну проверку на
четность.
3
4
Тогда
: b4=
bi
ai
; Код
(8, 4)
i=1
i=1 a4a3a2b3a1b2b1b4
S=EH;
4
4
S1=
bi
ai
i=1
i=1
|
S |
S1 |
|
|
0 |
0 |
Нет |
|
0 |
1 |
Одиночная |
|
0 |
0 |
Двойная |
|
? |
1 |
Тройная |
Заключение:
а) Рассмотрены
групповые линейные коды
Дстоинства
б) Достаточно
эффективны при малой кратности ошибок
(как правило, t=1).
Недостатки
в) При ошибках большей кратности –
резкое усложнение кодирующих и (особенно)
декодирующих устройств.
г) Более совершенными являются
циклические коды.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
7.1. Классификация корректирующих кодов
7.2. Принципы помехоустойчивого кодирования
7.3. Систематические коды
7.4. Код с четным числом единиц. Инверсионный код
7.5. Коды Хэмминга
7.6. Циклические коды
7.7. Коды с постоянным весом
7.8. Непрерывные коды
7.1. Классификация корректирующих кодов
В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать или обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим, кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны также коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.
Для того чтобы «од обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.
Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.
В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов [12]. На рис. 7.1 показана схема, поясняющая классификацию, проведенную по способам построения корректирующих кодов.
Все известные в настоящее время коды могут быть разделены
на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.
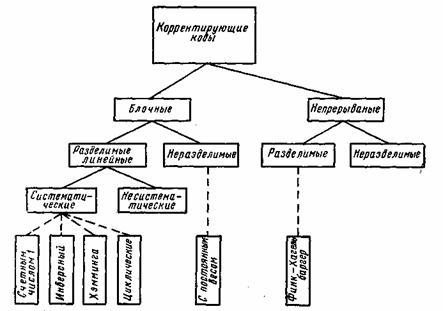
Рис. 7.1. Классификация корректирующих кодов
Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат ‘исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.
Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.
В свою очередь, линейные коды могут быть |разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими. Вертикальными прямоугольниками на схеме рис. 7.1 представлены некоторые конкретные коды, описанные в последующих параграфах.
7.2. Принципы помехоустойчивого кодирования
В теории помехоустойчивого кодирования важным является вопрос об использовании избыточности для корректирования возникающих при передаче ошибок. Здесь удобно рассмотреть блочные моды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Напомним, что для равномерных кодов, которые в дальнейшем только и будут изучаться, число возможных комбинаций равно M=2n, где п — значность кода. В обычном некорректирующем коде без избыточности, например в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М0и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число сообщений источника М0. Однако в.этом случае лишь М0комбинаций из общего числа используется для передачи информации. Эти комбинации называются разрешенными, а остальные М—М0комбинаций носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.
Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние d![]() между двумя комбинациями
между двумя комбинациями ![]() и
и ![]() определяется количеством единиц в сумме этих комбинаций по модулю два. Например,
определяется количеством единиц в сумме этих комбинаций по модулю два. Например,
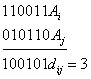
Для любого кода d![]()
![]() . Минимальное расстояние между разрешенными комбинациями ,в данном коде называется кодовым расстоянием d.
. Минимальное расстояние между разрешенными комбинациями ,в данном коде называется кодовым расстоянием d.
Расстояние между комбинациями ![]() и
и ![]() условно обозначено на рис. 7.2а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. B общем случае некоторая пара разрешенных комбинаций
условно обозначено на рис. 7.2а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. B общем случае некоторая пара разрешенных комбинаций ![]() и
и ![]() , разделенных кодовым расстоянием d, изображается на прямой рис. 7.2б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация
, разделенных кодовым расстоянием d, изображается на прямой рис. 7.2б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация ![]() преобразовалась в другую разрешенную комбинацию
преобразовалась в другую разрешенную комбинацию ![]() , должно исказиться d символов.
, должно исказиться d символов.
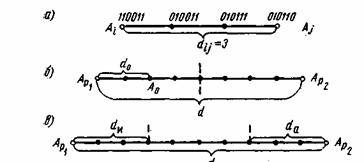
Рис. 7.2. Геометрическое представление разрешенных и запрещенных кодовых комбинаций
При искажении меньшего числа символов комбинация ![]() перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации,
перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации,
![]() (7.1)
(7.1)
Если g>d, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация ib этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d=2.
Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g символов в n-значной комбинации будет равна:
![]() (7.2)
(7.2)
где ![]() — вероятность искажения одного символа. Так как обычно
— вероятность искажения одного символа. Так как обычно ![]() <<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация
<<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация ![]() (см.рис.7.2б), тогда принимается решение, что была передана комбинация
(см.рис.7.2б), тогда принимается решение, что была передана комбинация ![]() . Это .правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального числа ошибок. Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который ib наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности
. Это .правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального числа ошибок. Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который ib наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности
![]() (7.3)
(7.3)
Минимальное значение d, при котором еще возможно исправление любых одиночных ошибок, равно 3.
Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 7.2в ошибки кратности ![]() исправляются, а ошибки, кратность которых лежит в пределах
исправляются, а ошибки, кратность которых лежит в пределах ![]() только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах
только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах ![]() , то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А
, то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А![]() вместо A
вместо A![]() или наоборот.
или наоборот.
Существуют двоичные системы связи, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще так называемый символ стирания ![]() . Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов
. Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов ![]() оказалось равным gc, причем
оказалось равным gc, причем
![]() (7.4)
(7.4)
а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов ![]() необходимо перебрать всевозможные сочетания из gc символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок
необходимо перебрать всевозможные сочетания из gc символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок ![]() , то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из gc символов совместно с правильно принятыми символами образуют запрещенные комбинации и только одно- сочетание стертых символов даст разрешенную комбинацию, которую и следует считать как правильно восстановленную.
, то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из gc символов совместно с правильно принятыми символами образуют запрещенные комбинации и только одно- сочетание стертых символов даст разрешенную комбинацию, которую и следует считать как правильно восстановленную.
Если ![]() , то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.
, то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.
Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или .восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие «оды обычно используются для корректирования ошибок малой кратности.
Корректирующая способность кода возрастает с увеличением d. При фиксированном числе разрешенных комбинаций М![]() увеличение d возможно лишь за счет роста количества запрещенных комбинаций:
увеличение d возможно лишь за счет роста количества запрещенных комбинаций:
![]() (7.5)
(7.5)
что, в свою очередь, требует избыточного числа символов r=n—k, где k — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить ее по аналогии с (6.12) как
![]() (7.6)
(7.6)
При независимых ошибках вероятность определенного сочетания g ошибочных символов в n-значной кодовой комбинации выражается ф-лой ((7.2), а количество всевозможных сочетаний g ошибочных символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний
![]()
Отсюда полная вероятность ошибки кратности g, учитывающая все сочетания ошибочных символов, равняется:
![]() (7.7)
(7.7)
Используя (7.7), можно записать формулы, определяющие вероятность отсутствия ошибок в кодовой комбинации, т. е. вероятность правильного приема
![]()
и вероятность правильного корректирования ошибок
![]()
Здесь суммирование ‘Производится по всем значениям кратности ошибок g, которые обнаруживаются и исправляются. Таким образом, вероятность некорректируемых ошибок равна:
![]() (7.8)
(7.8)
Анализ ф-лы (7.8) показывает, что при малой величине Р0и сравнительно небольших значениях п наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.
Вероятность Р![]() , избыточность
, избыточность ![]() и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.
и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.
Общая задача, которая ставится при создании кода, заключается, в достижении наименьших значений Р![]() и
и ![]() . Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.
. Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.
В соответствии с общим принципом корректирования ошибок, основанным на использовании разрешенных и запрещенных комбинаций, необходимо сравнивать принятую комбинацию со всеми комбинациями данного кода. В результате М сопоставлений и принимается решение о переданной комбинации. Этот способ декодирования логически является наиболее простым, однако он требует сложных устройств, так как в них должны запоминаться все М комбинаций кода. Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодовых символов извлечь из них всю информацию о корректируемых ошибках. Изучению таких кодов и посвящены последующие разделы.
7.3. Систематические коды
Изучение конкретных способов помехоустойчивого кодирования начнем с систематических кодов, которые в соответствии с классификацией (рис. 7.1) относятся к блочным разделимым кодам, т. е. к кодам, где операции кодирования осуществляются независимо в пределах каждой комбинации, состоящей из информационных и контрольных символов.
Остановимся кратко на общих принципах построения систематических кодов. Если обозначить информационные символы буквами с, а контрольные — буквами е, то любую кодовую комбинацию, содержащую k информационных и r контрольных символов, можно представить последовательностью:![]() , где с и е в двоичном коде принимают значения 0 или 1.
, где с и е в двоичном коде принимают значения 0 или 1.
Процесс кодирования на передающем конце сводится к образованию контрольных символов, которые выражаются в виде линейной функции информационных символов:
![]()
![]() (7.9)
(7.9)
Здесь ![]() — коэффициенты, равные 0 или 1, а
— коэффициенты, равные 0 или 1, а ![]() и
и ![]() — знаки суммирования по модулю два. Значения
— знаки суммирования по модулю два. Значения ![]()
![]() выбираются по определенным правилам, установленным для данного вида кода. Иными словами, символы е представляют собой суммы по модулю два информационных символов в различных сочетаниях. Процедура декодирования принятых комбинаций может осуществляться различными» методами. Один из них, так называемый метод контрольных чисел, состоит в следующем. Из информационных символов принятой кодовой комбинации
выбираются по определенным правилам, установленным для данного вида кода. Иными словами, символы е представляют собой суммы по модулю два информационных символов в различных сочетаниях. Процедура декодирования принятых комбинаций может осуществляться различными» методами. Один из них, так называемый метод контрольных чисел, состоит в следующем. Из информационных символов принятой кодовой комбинации ![]()
![]()
![]() образуется по правилу (7.9) вторая группа контрольных символов
образуется по правилу (7.9) вторая группа контрольных символов ![]()
![]()
Затем производится сравнение обеих групп контрольных символов путем их суммирования по модулю два:
![]()
 (7.10)
(7.10)
Полученное число X называется контрольным числом или синдромом. С его помощью можно обнаружить или исправить часть ошибок. Если ошибки в принятой комбинации отсутствуют, то все суммы![]()
![]() , а следовательно, и контрольное число X будут равны .нулю. При появлении ошибок некоторые значения х могут оказаться равным 1. В этом случае
, а следовательно, и контрольное число X будут равны .нулю. При появлении ошибок некоторые значения х могут оказаться равным 1. В этом случае ![]() , что и позволяет обнаружить ошибки. Таким образом, контрольное число Х определяется путем r проверок на четность.
, что и позволяет обнаружить ошибки. Таким образом, контрольное число Х определяется путем r проверок на четность.
Для исправления ошибок знание одного факта их возникновения является недостаточным. Необходимо указать номер ошибочно принятых символов. С этой целью каждому сочетанию исправляемых ошибок в комбинации присваивается одно из контрольных чисел, что позволяет по известному контрольному числу определить место положения ошибок и исправить их.
Контрольное число X записывается в двоичной системе, поэтому общее количество различных контрольных чисел, отличающихся от нуля, равно![]()
![]() . Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно
. Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно ![]() . В этом случае должно выполняться условие
. В этом случае должно выполняться условие
![]() (7.11)
(7.11)
Формула (7.11) позволяет при заданном количестве информационных символов k определить необходимое число контрольных символов r, с помощью которых исправляются все одиночные ошибки.
7.4. Код с чётным числом единиц. Инверсионный код
Рассмотрим некоторые простейшие систематические коды, применяемые только для обнаружения ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит, помимо информационных символов, один контрольный символ, выбираемый равным 0 или 1 так, чтобы сумма единиц в комбинации всегда была четной. Примером могут служить пятизначные комбинации кода Бодо, к которым добавляется шестой контрольный символ: 10101,1 и 01100,0. Правило вычисления контрольного символа можно выразить на
основании (7.9) в следующей форме: ![]() . Отсюда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю (
. Отсюда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю (![]() — суммирование по модулю):
— суммирование по модулю):
![]() (7.12)
(7.12)
Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем, случае ошибок нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы (7.12), поэтому такие ошибки не обнаруживаются. На основании ,(7.8) вероятность необнаруженной ошибки равна:
![]()
![]()
К достоинствам кода следует отнести простоту кодирующих и декодирующих устройств, а также малую .избыточность ![]() , однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.
, однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.
Значительно лучшими корректирующими способностями обладает инверсный код, который также применяется только для обнаружения ошибок. С принципом построения такого кода удобно ознакомиться на примере двух комбинаций: 11000, 11000 и 01101, 10010. В каждой комбинации символы до запятой являются информационными, а последующие — контрольными. Если количество единиц в информационных символах четное, т. е. сумма этих
символов
![]() (7.13)
(7.13)
равна нулю, то контрольные символы представляют собой простое повторение информационных. В противном случае, когда число единиц нечетное и сумма (7.13) равна 1, контрольные символы получаются из информационных посредством инвертирования, т. е. путем замены всех 0 на 1, а 1 на 0. Математическая форма записи образования контрольных символов имеет вид ![]() . При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е.
. При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е. ![]() , то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда c‘
, то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда c‘![]() =1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность:
=1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность: ![]() . Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.
. Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.
Анализ показывает, что при ![]() наименьшая кратность необнаруживаемой ошибки g=4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100, 10100, а принята 10111, 10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения
наименьшая кратность необнаруживаемой ошибки g=4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100, 10100, а принята 10111, 10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения ![]() равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением
равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением
![]()
Для g>4 вероятность необнаруженных ошибок еще меньше. Поэтому при достаточно малых вероятностях ошибочных символов ро можно полагать, что полная вероятность необнаруженных ошибок ![]()
Инверсный код обладает высокой обнаруживающей способностью, однако она достигается ценой сравнительно большой избыточности, которая, как нетрудно определить, составляет величину ![]() =0,5.
=0,5.
7.5. Коды Хэмминга
К этому типу кодов обычно относят систематические коды с расстоянием d=3, которые позволяют исправить все одиночные ошибки (7.3).
Рассмотрим построение семизначного кода Хэмминга, каждая комбинация которого содержит четыре информационных и триконтрольных символа. Такой код, условно обозначаемый (7.4), удовлетворяет неравенству (7.11) и имеет избыточность ![]()
Если информационные символы с занимают в комбинация первые четыре места, то последующие три контрольных символа образуются по общему правилу (7.9) как суммы:
![]() (7.14)
(7.14)
Декодирование осуществляется путем трех проверок на четность (7.10):
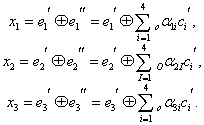 (7.15)
(7.15)
Так как х равно 0 или 1, то всего может быть восемь контрольных чисел Х=х1х2х3: 000, 100, 010, 001, 011, 101, 110 и 111. Первое из них имеет место в случае правильного приема, а остальные семь появляются при наличии искажений и должны использоваться для определения местоположения одиночной ошибки в семизначной комбинации. Выясним, каким образом устанавливается взаимосвязь между контрольными числами я искаженными символами. Если искажен один из контрольных символов: ![]() или
или ![]() , то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах.
, то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах.
Таблица 7.1

Порядок присвоения контрольных чисел ошибочным информационным символам может устанавливаться любой, например, как показано в табл. 7.1. Нетрудно показать, что этому распределению контрольных чисел соответствуют коэффициенты ![]() , приведенные в табл. 7.2.
, приведенные в табл. 7.2.
Таблица 7.2
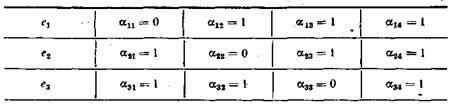
Если подставить коэффициенты ![]() в выражение (7.15), то получим:
в выражение (7.15), то получим:
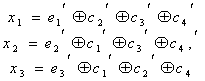 (7.16)
(7.16)
При искажении одного из информационных символов становятся равными единице те суммы х, в которые входит этот символ. Легко проверить, что получающееся в этом случае контрольное число![]() согласуется с табл. 7.1.Нетрудно заметить, что первые четыре контрольные числа табл. 7.1 совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов
согласуется с табл. 7.1.Нетрудно заметить, что первые четыре контрольные числа табл. 7.1 совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов ![]() . Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1 определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 1 на 0. B качестве примера рассмотрим передачу комбинации, в которой информационными символами являются
. Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1 определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 1 на 0. B качестве примера рассмотрим передачу комбинации, в которой информационными символами являются ![]() , Используя ф-лу (7.14) и табл. 7.2, вычислим контрольные символы:
, Используя ф-лу (7.14) и табл. 7.2, вычислим контрольные символы:
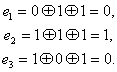
Передаваемая комбинация при этом будет ![]() . Предположим, что принята комбинация — 1001, 010 (искажен символ
. Предположим, что принята комбинация — 1001, 010 (искажен символ ![]() ). Подставляя соответствующие значения в (7.16), получим:
). Подставляя соответствующие значения в (7.16), получим:
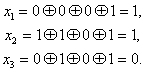
Вычисленное таким образом контрольное число ![]() 110 позволяет согласно табл. 7.1 исправить ошибку в символе.
110 позволяет согласно табл. 7.1 исправить ошибку в символе.
Здесь был рассмотрен простейший способ построения и декодирования кодовых комбинаций, в которых первые места отводились информационным символам, а соответствие между контрольными числами и ошибками определялось таблице. Вместе с тем существует более изящный метод отыскания одиночных ошибок, предложенный впервые самим Хэммингом. При этом методе код строится так, что контрольное число в двоичной системе счисления сразу указывает номер искаженного символа. Правда, в этом случае контрольные символы необходимо располагать среди информационных, что усложняет процесс кодирования. Для кода (7.4) символы в комбинации должны размещаться в следующем порядке: ![]() , а контрольное число вычисляться по формулам:
, а контрольное число вычисляться по формулам:
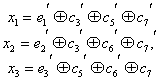 (7.17)
(7.17)
Так, если произошла ошибка в информационном символе с’5 то контрольное число ![]() , что соответствует числу 5 в двоичной системе.
, что соответствует числу 5 в двоичной системе.
В заключение отметим, что в коде (7.4) при появлении многократных ошибок контрольное число также может отличаться от нуля. Однако декодирование в этом случае будет проведено неправильно, так как оно рассчитано на исправление лишь одиночных ошибок.
7.6. Циклические коды
Важное место среди систематических кодов занимают циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации ![]() дает другую комбинацию
дает другую комбинацию ![]() также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например,
также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например, ![]()
![]()
![]()
![]() .
.
Комбинации циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты которых равны 0 или 1. Примером этому может служить следующая запись:
![]()
Помимо цикличности, кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени ![]() , где k—значность первичного кода без избыточности, а п-значность циклического кода
, где k—значность первичного кода без избыточности, а п-значность циклического кода
Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода A*(z) ,на порождающий полином G(z):
A(z)=A*(z)G(z).
Умножение производится по модулю zn и в данном случае сводится к умножению по обычным правилам с приведением подобных членов по модулю два.
В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: деления A(z) на G(z).
Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа г нулей, что эквивалентно повышению полинома A*(z) на ,г разрядов, т. е. умножению его на гг. Затем произведение zrA*(z) делится на порождающий полином. B общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда
![]()
Вычисленный остаток К(г) я используется для образования комбинации циклического кода в виде суммы
A(z)=zrA*(z)@R(z).
Так как сложение и вычитание по модулю два дают один и тот же результат, то нетрудно заметить, что A(z) = Q(z)G(z), т. е. полученная комбинация удовлетворяет требованию делимости на порождающий полином. Степень полинома R{z) не превышает r—1, поэтому он замещает нули в комбинации z![]() A*(z).
A*(z).
Для примера рассмотрим циклический код c n = 7, k=4, r=3 и G(z)=z3-z+1=1011. Необходимо закодировать комбинацию A*(z)=z*+1 = 1001. Тогда z![]() A*(z)=z
A*(z)=z![]() +z
+z![]() = 1001000. Для определения остатка делим z3A*(z) на G(z):
= 1001000. Для определения остатка делим z3A*(z) на G(z):
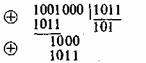
Окончательно получаем
В А(z) высшие четыре разряда занимают информационные символы, а остальные при — контрольные.
Контрольные символы в циклическом коде могут быть вычислены по общим ф-лам (7.9), однако здесь определение коэффициентов ![]() затрудняется необходимостью выполнять требования делимости А(z) на порождающий полином G(z).
затрудняется необходимостью выполнять требования делимости А(z) на порождающий полином G(z).
Процедура декодирования принятых комбинаций также основана на использовании полиномов G(z). Если ошибок в процессе передачи не было, то деление принятой комбинации A(z) на G(z) дает целое число. При наличии корректируемых ошибок в результате деления образуется остаток, который и позволяет обнаружить или исправить ошибки.
Кодирующие и декодирующие устройства циклических кодов в большинстве случаев обладают сравнительной простотой, что следует считать одним из основных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где действуют импульсные и сосредоточенные помехи или наблюдаются замирания сигнала.
В теории кодирования весом кодовых комбинаций принято называть .количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.
Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код обнаруживает все ошибки нечетной краткости и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей. Можно показать, что вероятность необнаруженной ошибки для кода 3/4 равна:
![]() при
при ![]() (7.18)
(7.18)
В этом коде из общего числа комбинаций М = 27=128 разрешенными являются лишь ![]() , поэтому в соответствии с (7.6) коэффициент избыточности
, поэтому в соответствии с (7.6) коэффициент избыточности
![]()
Код 3/4 находит применение при частотной манипуляции в каналах с селективными замираниями, где вероятность ошибок смещения невелика.
7.8. Непрерывные коды
Из непрерывных кодов, исправляющих ошибки, наиболее известны коды Финка—Хагельбаргера, в которых контрольные символы образуются путем линейной операции над двумя или более информационными символами. Принцип построения этих кодов рассмотрим на примере простейшего цепного кода. Контрольные символы в цепном коде формируются путем суммирования двух информационных символов, расположенных один относительно другого на определенном расстоянии:
![]() ;
;![]() (7.19)
(7.19)
Расстояние между информационными символами l=k—i определяет основные свойства кода и называется шагом сложения. Число контрольных символов при таком способе кодирования равно числу информационных символов, поэтому избыточность кода ![]() =0,5. Процесс образования последовательности контрольных символов показан на рис.7. символы разметаются между информационными символами с задержкой на два шага сложения.
=0,5. Процесс образования последовательности контрольных символов показан на рис.7. символы разметаются между информационными символами с задержкой на два шага сложения.
Рис. 7.3. Образование и размещение контрольных символов в цепном коде Финка—Хагельбаргера
При декодировании из принятых информационных символов по тому же правилу (7.19) формируется вспомогательная последовательность контрольных символов е», которая сравнивается с принятой последовательностью контрольных символов е’ (рис. 7.36). Если произошла ошибка в информационном символе, например, c‘k, то это вызовет искажения сразу двух символов e«k и e«km, что и обнаружится в результате их сравнения с ![]() и e‘km. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с’
и e‘km. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с’![]() Ошибка в принятом контрольном символе, например, e‘k приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление такой ошибки не требуется.
Ошибка в принятом контрольном символе, например, e‘k приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление такой ошибки не требуется.
Важное преимущество непрерывных кодов состоит в их способности исправлять не только одиночные ошибки, но я группы (пакеты) ошибок. Если задержка контрольных символов выбрана равной 2l, то можно показать, что максимальная длина исправляемого пакета ошибок также равна 2l при интервале между пакетами не менее 6l+1. Таким образом, возможность исправления длинных пакетов связана с увеличением шага сложения, а следовательно, и с усложнением кодирующих и декодирующих устройств.
Вопросы для повторения
1. Как могут быть классифицированы корректирующие коды?
2. Каким образом исправляются ошибки в кодах, которые только их обнаруживают?
3. В чем состоят основные принципы корректирования ошибок?
4. Дайте определение кодового расстояния.
5. При каких условиях код может обнаруживать или исправлять ошибки?
6. Как используется корректирующий код в системах со стиранием?
7. Какие характеристики определяют корректирующие способности кода?
8. Как осуществляется построение кодовых комбинаций в систематических кодах?
9. На чем основан принцип корректирования ошибок с использованием контрольного числа?
10. Объясните метод построения кода с четным числом единиц.
11. Как осуществляется процедура кодирования в семизначном коде Хэмминга?
12. Почему семизначный код 3/4 не обнаруживает ошибки смещения?
13. Каким образом производится непрерывное кодирование?
14. От чего зависит длина пакета исправляемых ошибок в коде Финка—Хагельбаргера?





