Локальная ошибка это что

Локальная и глобальная ошибки дискретизации при численном интегрировании дифференциальных уравнений

последовательностью точек x₀,x₁. в соответствующие моменты времени t₀,t₁. Значения точек должны удоволетворять приближенному равенству

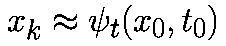
Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть

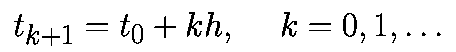
Аппроксимируем производную в момент времени t_k соотношением

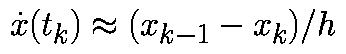
При такой аппроксимации уравнение (1) примет вид:

Формула (2) известна как прямой метод Эйлера.

На рис.1(a) показана графическая интерпретация прямого метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k,t_k).

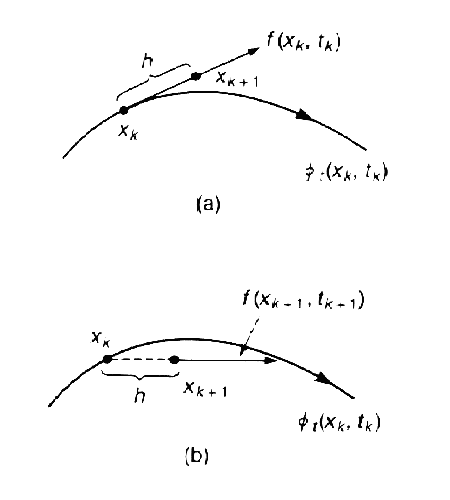
Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера

Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0.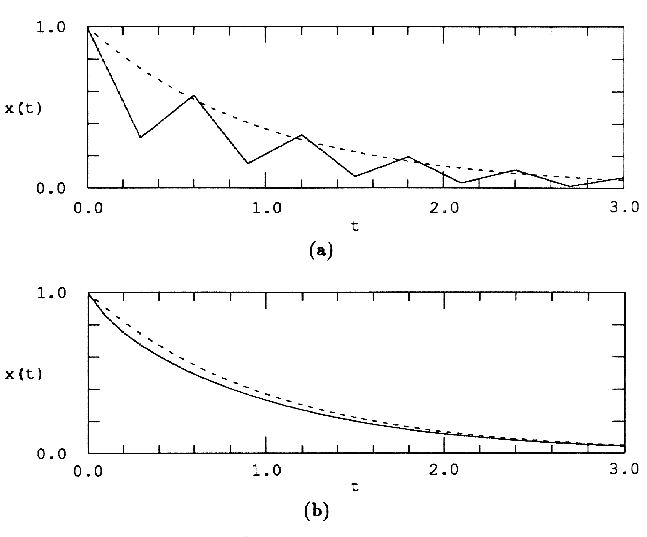

Рис.2 Влияние величины шага. Уравнение dx/dt=-6x+5t -t интегрируется от x=1 прямым методом Эйлера при h=0.3 (а) и при h=0.1 (b). Точное решение показано штриховой линией.

Обратный метод Эйлера подобен прямому, но есть одно отличие в аппроксимации для производной

Такая аппроксимация дает формулу обратного метода Эйлера:

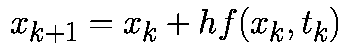
На рис.1(b) показана геометрическая интерпретация обратного метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k+1,t_k+1).

Обратный метод Эйлера — это пример неявного алгоритма интегрирования , где x_k+1 является функцией от самой себя. И напротив, прямой метод Эйлера представляет собой явный алгоритм. В неявных алгоритмах для определения x_k+1 требуются дополнительные вычисления, но они по сравнению с аналогичными прямыми алгоритмами более устойчивы и дают более высокую точность вычислений (см. рис.3). Возможно это обусловлено наличием члена x_k+1 в правой части формулы, что может рассматриваться как вид обратной связи.

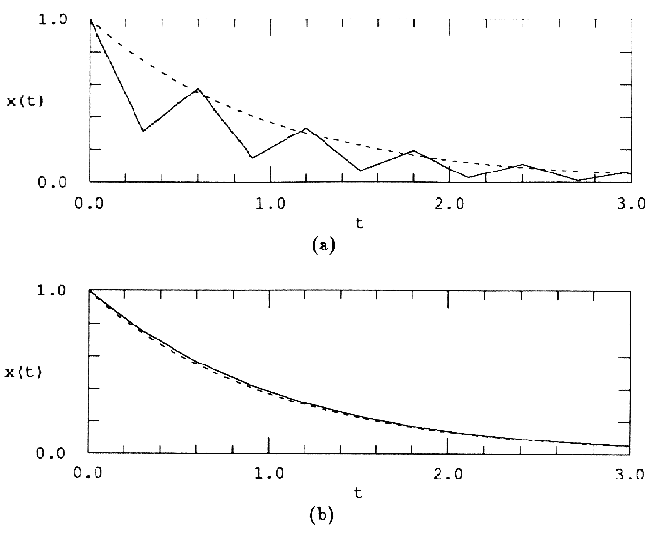
Рис.3 Та же система, что и на рис.2 проинтегрирована от x₀=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией.

Трапецеидальный алгоритм имеет вид:

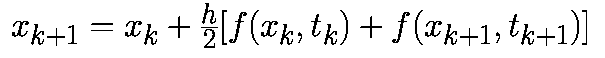
Имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением:

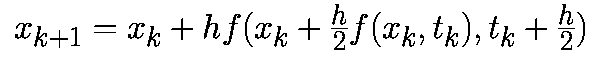
Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (t_k+h/2):

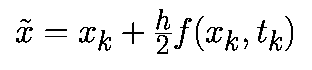
На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа:

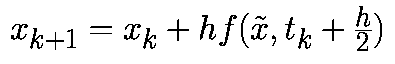
Как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени t_k+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка:

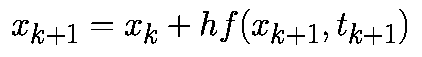
Для определенных выше алгоритмов на каждом шаге требуется только одна начальная точка x_k. Такие алгоритмы называются одношаговыми. Одношаговые алгоритмы высокого порядка имеют высокую точность, но они не эффективны, если велики затраты на вычисление f. Например, алгоритм Рунге-Кутта четвертого порядка требует на шаге четыре значения f. Кроме того, на текущем шаге не выполняются оценки функций с целью их использования на последующих шагах.
В отличие от одношаговых алгоритмов, многошаговые алгоритмы повторно используют предыдущую информацию о траектории. В m-шаговом алгоритме для определения x_k+1 используют m предыдущих точек x_k, x_k-1. x_k-m+1 и значения f в этих точках. Общая формула m-шагового алгоритма имеет вид

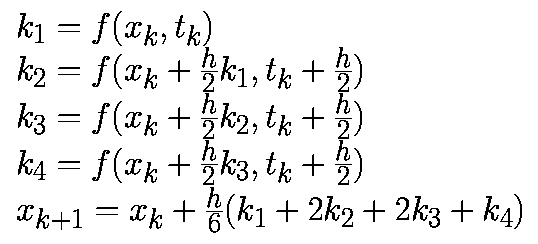
Локальная ошибка определяется как ошибка на шаге алгоритма:

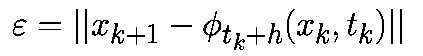
Для m-шаговых алгоритмов предполагается, что предыдущие m точек x_k-i при i=0. m-1 являются точно заданными, т.е.

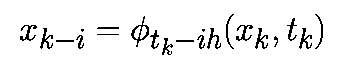
Ошибка усечения — это локальная ошибка, которая получилась бы в результате выполнения алгоритма на компьютере с бесконечной точностью.
Другими словами, подразумевается, что эта локальная ошибка возникает помимо ошибки округления. Также важно помнить, что для m-шаговых алгоритмов предыдущие m точек x_k. x_k-m+1 предполагаются точно заданными.
Ошибка усечения берет свое название от алгоритмов, основанных на рядах Тейлора (например, Рунге-Кутта). Эти алгоритмы были бы точными, если бы использовались полные (бесконечные) ряды. Ошибка возникает при усечении ряда до конечного числа членов.
Ошибка усечения зависит только от алгоритма. Она не зависит от используемого компьютера и, следовательно, может быть проанализирована. Для алгоритмов Рунге-Кутта K-го порядка, при подходящих условиях, локальная ошибка усечения представляет собой

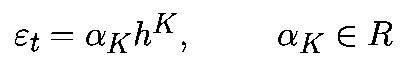
где «альфа» зависит от K, f и x_k, но не зависит от h. Для многошагового алгоритма K-го порядка локальная ошибка усечения имеет вид

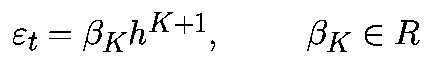
Глобальнае ошибка округления — это простое накопление локальных ошибок округления. Если локальная ошибка составляет «эпсилон», то ошибка округления на единичном интервале будет

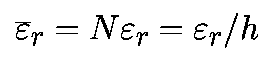
Подобно ошибке округления, локальная ошибка усечения также накапливается с каждым шагом. Для одношаговых алгоритмов K-го порядка локальная ошибка усечения составляет

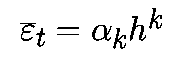
Если пренебречь зависимостью a_k от x_k, то на единичном интервале времени ошибка усечения будет:

Порядок метода интегрирования.

Дата добавления: 2015-06-12 ; просмотров: 3180 ; Нарушение авторских прав

Главный вопрос при использовании любого численного метода состоит в оценке точности приближенных вычислений 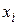. В разд. 3.2.1 уже отмечалось, что существуют два источника погрешности при выполнении шага интегрирования:

· ошибка дискретизации, возникающая в результате замены дифференциального уравнения (3.1) разностной аппроксимацией (3.2);

· ошибка округления, накопившаяся при выполнении арифметических операций.

При этом доминирующей является, как правило, ошибка дискретизации.

Будем считать, что все вычисления проводятся точно. Интуитивно ясно, что при 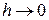ошибка дискретизации также должна стремиться к нулю и это действительно имеет место для любого метода. Однако взаимосвязь скорости уменьшения ошибки от скорости уменьшения для разных методов интегрирования различна.

Введем величину 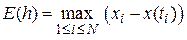, называемую глобальной ошибкой дискретизации. Отметим, что 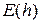зависит от величины шага, поскольку предполагается, что значения 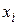вычисляются при определенном . Воспользуемся также стандартным обозначением 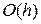для величины, стремящейся к нулю при 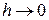с той же скоростью, что и . В общем случае будем говорить, что функция 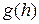равна 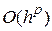, если при 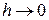величина 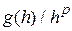ограничена. Проведя анализ можно показать [23], что для метода Эйлера 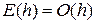. Это, обычно, выражают утверждением, что метод Эйлера имеет первый порядок. Практическим следствием этого факта является то, что при уменьшении приближенное решение будет все более точным, и при 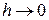будет сходиться к точному решению с линейной скоростью по , т.е. при уменьшении шага вдвое ошибка дискретизации уменьшится примерно в 2 раза. Столь медленная сходимость служит препятствием использования простых методов первого порядка.

Очевидно, что повышение порядка метода позволяет повысить точность интегрирования при той же величине шага интегрирования . Способы повышения порядка могут быть различными.

Рассмотрим, например, явный одношаговый метод Хьюна (или метод Рунге – Кутты второго порядка). Он определяется формулой

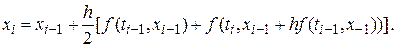
Сравнивая его с методом Эйлера легко заметить, что значение 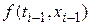заменено на среднее значений функции 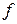, вычисленных в двух различных точках. Данный метод имеет ошибку дискретизации .

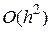Наиболее знаменитым из методов Рунге – Кутты, а возможно и из всех методов численного интегрирования, является классический метод четвертого порядка, задаваемый формулой

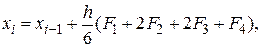
где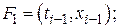

;

;

.

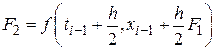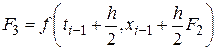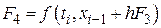Суть метода в том, что вектор-функция правых частей системы ОДУ определяется не только в узлах сетки, но и в промежуточных точках интервала 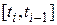, а величина 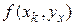в методе Эйлера заменена на взвешенное среднее значений 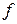, вычисленных в четырех различных точках.

Как видно, повышение порядка метода связано с повышением затрат на вычисление значений функции 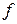. При нелинейной связи между ростом точности метода и объемом вычислений можно ожидать, что для каждой схемы интегрирования существует некоторый оптимальный порядок метода.

Для многошаговых методов порядок напрямую связан с объемом информации, используемой на каждом шаге. В частности, двух и трехшаговые методы Адамса – Бишфорта, задаваемые формулами (3.10) и (3.11) имеют второй и третий порядок, соответственно.

3.2.6. Процедуры численного моделирования
с автоматическим выбором шага

Данный раздел касается не выбора того или иного метода интегрирования, а реализации самой процедуры интегрирования на ЭВМ.

Выше уже отмечалось, что выбор шага интегрирования связан с динамическими свойствами моделируемого объекта. Для явных методов он должен быть меньше минимальной постоянной времени объекта, с тем, чтобы обеспечить устойчивость и позволить моделировать самые высокочастотные составляющие процесса. Неявные методы позволяют использовать больший шаг, но общий характер зависимости остается тем же самым. В то же время, на интервале моделирования характер моделируемых процессов может меняться. Например, в большинстве реальных систем высокочастотные составляющие переходного процесса затухают быстрее, чем низкочастотные, и процесс со временем приобретает более плавный характер. Это наводит на мысль организовать процедуру моделирования таким образом, чтобы шаг интегрирования менялся в процессе работы алгоритма. Там, где решение меняется плавно, можно вести интегрирование с относительно большим шагом. В областях же, где решение изменяется резко, необходимо считать с маленьким шагом. Проблема заключается в том, как определить величину шага, с которым следует начать следующий шаг интегрирования.

На выбор шага, как обычно влияют два фактора – точность и устойчивость. Шаг целесообразно поддерживать таким, чтобы погрешность интегрирования не превышала допустимого значения и величина шага при этом была максимально возможной.

Обычный подход состоит в оценке локальной ошибки дискретизации и, в зависимости от ее величины, уменьшении или увеличении текущего значения шага.

Два простых способа состоят либо в прохождении последнего шага интегрирования с половинным шагом и сравнении двух полученных результатов, либо в использовании двух методов интегрирования, имеющих разный порядок. Оба эти способа требуют дополнительных вычислений значений .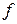

Первый способ реализует правило Рунге [29, 23], при котором ошибка дискретизации определяется по формуле

,

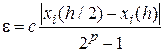где 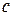– некоторая константа;

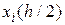– значение фазовой переменной 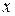, полученной в точке 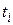тем же методом, что и 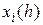, но только за два шага интегрирования от точки 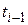, каждый из которых в два раза меньше обычного шага ;

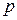– порядок метода интегрирования.

Для метода Эйлера формула Рунге дает

,

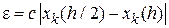для метода Рунге – Кутты 4-го порядка

.

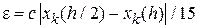Величина погрешности аппроксимации на каждом шаге 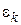не должна превышать допускаемой погрешности 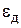. Обычно полагают, что она составляет от 0,01 до 0,001 от текущего значения определяемой фазовой координаты .

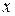При автоматическом выборе шага наиболее популярным является алгоритм «трех зон» [29]:

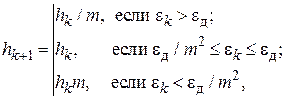
где 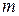– коэффициент изменения шага, обычно равный 2, позволяет дискретно менять шаг в процессе интегрирования. Другим вариантом является алгоритм плавного изменения шага интегрирования

,

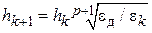где 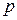– порядок метода интегрирования.

3.2.7. Особенности численного интегрирования
технических систем

Обширный набор методов численного интегрирования, которым обладают современные пакеты моделирования, позволяет эффективно решать самые различные задачи исследования технических систем, но при этом возникает проблема выбора наиболее подходящего метода
и правильного задания его параметров. Очень часто пользователь задает только интервал интегрирования и не обращает внимания на другие опции решателя. При решении простых задач с умеренной точностью такой подход вполне допустим, однако при решении сложных задач неудачный выбор метода либо неправильное задание его параметров может привести к неоправданно большим затратам машинного времени либо, вообще, к невозможности получить правильное решение.

Таким образом, для профессиональной работы с любым моделирующим программным обеспечением пользователь должен обладать некоторыми знаниями о реализованных в нем численных методах
и применимости их к требуемому кругу задач.

Практика показала, что наличие в технических системах объектов различной физической природы приводит к тому, что процессы в них характеризуются разнотемповостью, т.е. наличием быстрых и медленных составляющих движения. Кроме того, возможно одновременное присутствие как монотонных, так и медленно затухающих гармонических составляющих. Свойство системы содержать в своем переходном процессе существенно различные по своим спектральным характеристикам составляющие принято называть жесткостью[27].

Примером жесткой системы может служить робототехническая система, в которой быстрые составляющие связаны с включением тормозных устройств и демпферов, взятием или освобождением груза.

Жесткость часто является следствием избыточности модели, связанной с введением в нее малозначащих составляющих. Однако на этапе предварительных исследований такой избыточности трудно избежать. С другой стороны, часто жесткость имеет принципиальный характер и неучет быстрых движений может привести к неадекватности модели.

Жесткие системы требуют особого подхода к процедуре численного интегрирования, так как наличие быстрых и медленных составляющих в спектре движений предъявляет совершенно разные требования к методам интегрирования. Необходимо уметь оценивать характеристики жесткости и использовать эти оценки для выбора или настройки процедуры интегрирования.

Пусть исследуемая система 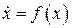является линейной и может быть описана матричными уравнениями состояния

.

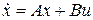Матрица 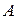называется матрицей состояния или матрицей Якоби. Собственные значения 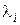матрицы 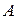определяют устойчивость и характер переходных процессов в исследуемой системе.

Составляющие движения (обычно называемые модами), связанные с собственными значениями 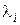, лежащими в левой полуплоскости далеко от мнимой оси, соответствуют быстро протекающим и, обычно, быстро затухающим процессам в системе. Собственные значения малые по модулю, лежащие близко к мнимой оси, определяют основное движение системы.

Исходя из распределения собственных значений матрицы Якоби на комплексной плоскости, можно назвать жесткой системой ОДУ такую систему, у которой матрица Якоби имеет различающиеся на несколько порядков максимальное и минимальное по модулю собственные значения.

Оценкой жесткости системы ОДУ обычно считается число обусловленности матрицы Якоби

,

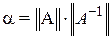где 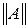– норма матрицы .

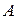Для целей управления процессом моделирования под числом обусловленности чаще понимают отношение модулей максимального и минимального собственных значений матрицы

.

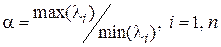К жестким относят системы ОДУ, у которых 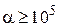. Их также называют плохо обусловленными, хотя, чаще, этот термин относится к системам алгебраических уравнений.

Для нелинейной системы матрицу Якоби можно определить после ее линеаризации в рабочей точке, как это описано в разд. 3.2.2.

Элементами матрицы Якоби являются частные производные от
нелинейной вектор функции 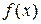по переменным состояния системы 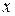. Для нелинейных систем жесткость, в общем случае, не является постоянной величиной и меняется в процессе интегрирования.

При умеренных значениях числа обусловленности 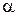(нежесткие задачи) интегрирование обычно выполняется традиционными явными методами и требует небольших вычислительных затрат. Трудности возникают при больших значениях 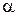, когда для получения правильного решения бывает необходимо выбирать очень малый шаг интегрирования.

При моделировании такой системы в начальный момент времени инициируются все, или большинство мод, как быстрых так и медленных. Однако через некоторое время быстрые моды затухают и решение сходится к медленному движению.

Исследователя могут интересовать и быстрые и медленные составляющие движения. В этом случае, целесообразно использование явных методов в сочетании с эффективной процедурой изменения величины шага интегрирования в зависимости от состояния моделируемой системы. Это позволит достаточно точно смоделировать быстрые движения и избежать чрезмерных затрат машинного времени, так как явные методы требуют минимальных временных затрат на каждый шаг интегрирования.

Если исследователя мало интересуют быстро затухающие движения, но отбросить их на этапе формирования модели у него нет достаточных оснований, предпочтительными являются неявные методы, которые в сумме способны дать меньшее время интегрирования при удовлетворительном качестве. Такие методы подавляют все составляющие решения, соответствующие большим по модулю собственным значениям (если только шаг не выбран очень малым).

Изложенные рекомендации по выбору методов интегрирования жестких систем предполагают, что исследователь хорошо знаком с особенностями объекта. Например, если речь идет о проектировании или оптимизации системы управления некоторого хорошо изученного объекта, то выбор метода интегрирования может быть проведен путем сравнения нескольких вариантов. Если же объект недостаточно исследован, то эффективными могут оказаться процедуры, обладающие элементами адаптации к особенностям объекта.

Некоторые современные моделирующие программные комплексы содержат наборы методов, расчетные формулы которых настраиваются на решаемую задачу, используя для этого оценки некоторых параметров, обычно, собственных значений якобиана. Особенно перспективными считаются явные адаптивные методы, не требующие при своей реализации вычисления матрицы Якоби и решения алгебраических уравнений [27]. Такие методы есть, в частности, среди решателей ОДУ программного комплекса «МВТУ».

3.3. Моделирование гибридных (событийно-управляемых)
технических систем

Технические системы, по определению, относятся к сложным техническим системам. Одной из особенностей этих систем является то, что поведение многих из них определяется событиями, происходящими как внутри этих систем, так и в окружающей среде. Соответственно, они обладают как непрерывной, так и дискретной динамикой, находящимися в сложном взаимодействии. Подобные системы часто называют гибридными системами [20, 21]. В отечественной литературе также используются синонимы – непрерывно-дискретные, системы с переменной структурой, реактивные, событийно-управляемые.

Примерами гибридных технических систем могут служить системы управления, используемые в промышленности (автоматизированные технологические процессы), в быту (сложные бытовые приборы), в военной области (высокотехнологичные виды вооружений), в сфере космонавтики, транспорта и связи.

Гибридное поведение может быть связано со следующими факторами:

· совместное функционирование непрерывных и дискретных объектов. Подобное поведение является типовым для непрерывных объектов (механических, гидравлических и т.д.) управляемых цифровыми регуляторами, например, для ИСЗ. Управление может формироваться как в фиксированные моменты времени, так и асинхронно, в зависимости от изменения фазовых координат объекта;

· гибридное поведение, связанное с особенностями физических процессов в непрерывных объектах. Например, учет в моделях механических систем таких эффектов как сухое трение или люфт может быть реализован в виде некоторых логических условий, меняющих модель системы;

· гибридное поведение, обусловленное изменением состава системы.

Все перечисленные факторы являются типичными для технических систем.

Учет дискретной динамики приводит к тому, что фазовое пространство гибридных систем разбивается на области с различным поведением, при этом фазовая траектория в зависимости от происходящих событий оказывается то в одной области фазового пространства, то в другой. Достижение фазовой траекторией границы областей является событием, приводящим к смене поведения.

События могут быть как внутренними, так и внешними. Например, при моделировании робота-манипулятора внутренние события могут быть связаны с типовыми нелинейностями механической части, а внешние – являться следствием взаимодействия со средой.

Очевидной и удобной моделью систем, управляемых событиями, является конечно-автоматная модель. Например, можно использовать конечный автомат, чтобы описать автоматическую передачу автомобиля. Передача имеет ряд состояний: парковка, нейтраль, движение, реверс и т.д. Система переходит из одного состояния в другое, когда водитель перемещает рычаг из одной позиции в другую, например, из позиции парковка в нейтральное положение.

При всей ее простоте и наглядности конечно-автоматная модель достаточно строга и формальна. Однако классическое графическое представление конечных автоматов обладает рядом недостатков. Главным недостатком является отсутствие понятия времени, что предполагает статичность состояний. Другие недостатки – отсутствие иерархии состояний, обобщения переходов, средств выражения прерываний
и продолжения нормальной работы после их обработки [11].

Для полноценного компьютерного моделирования физики процессов необходимо обеспечить сопряжение непрерывной составляющей поведения системы и логики работы управляющих ей устройств (дискретная компонента). Математический аппарат описания в данном случае – это система уравнений, но не дифференциальных, а дифференциально-алгебраическо-логических, для которых отсутствует стройная теория и единый подход.

В настоящее время для моделирования систем, управляемых событиями, широко используется предложенный Д. Харелом [7] визуальный формализм – Statechart (карты состояний и переходов). Карты состояния были разработаны применительно к моделированию дискретных систем, однако они могут служить хорошей основой и для моделирования гибридных систем, т.е. с их помощью можно описать поведение системы как в дискретном, так и в непрерывном времени [8]. Основные
неграфические компоненты таких диаграмм – это событие и действие, основные графические компоненты – состояние и переход.

Событие – нечто, происходящее вне рассматриваемой системы, возможно требующее некоторых ответных действий. События могут быть вызваны поступлением некоторых данных или некоторых задающих сигналов со стороны человека или некоторой другой части системы. События считаются мгновенными.

Действия –это реакции моделируемой системы на события. Подобно событиям, действия принято считать мгновенными.

Состояние –условия, в которых моделируемая система пребывает некоторое время, в течение которого она ведет себя одинаковым образом. В диаграмме переходов состояния представлены прямоугольными полями со скругленными углами.

Переход – изменение состояния, обычно вызываемое некоторым событием. Как правило, состояние соответствует промежутку времени между двумя такими событиями. Переходы показываются в диаграммах переходов линиями со стрелками, указывающими направление перехода. Каждому переходу могут быть сопоставлены условия, при выполнении которых переход осуществляется.

С каждым переходом и каждым состоянием могут быть соотнесены некоторые действия. Действия могут дополнительно обозначаться как действия, выполняемые однократно при входе в состояние; действия, выполняемые многократно внутри некоторого состояния; действия, выполняемые однократно при выходе из состояния.

В [25] качестве примера простой дискретной системы (частного случая гибридной системы) рассмотрена диаграмма (карта) состояний и переходов цифровых часов, представленная на рис. 3.4.

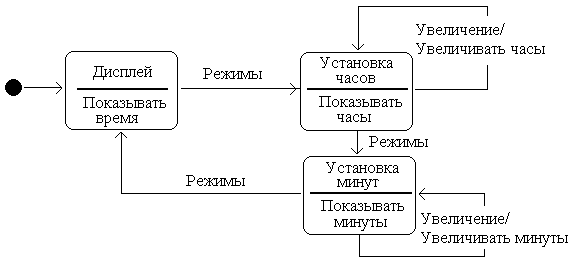
Рис. 3.4. Диаграмма состояний и переходов цифровых часов

На часах имеется две кнопки: Кнопка Режима и Кнопка Увеличения. Нажатие любой из них генерирует событие, которое может вызывать переход из одного состояния в другое. Имеются три состояния: Дисплей, Установка Часов и Установка Минут. Состояние Дисплей – начальное состояние (что обозначается стрелкой, направленной от блока перехода по умолчанию в виде черного круга). Нажатие кнопки Режимы в состоянии Дисплей вызывает появление события Режимы и переход в состояние Установка часов. В состоянии Установка Часов, событие Режимы вызывает переход к состоянию Установка Минут, тогда как событие Увеличение увеличивает текущее время (число часов), которое отображается на экране, причем это происходит без изменения состояния. Каждому состоянию часов соответствует действие, записанное ниже горизонтальной линии. Оно начинает выполняться после того, как переход в это состояние произошел.

В [21] в качестве примера рассмотрена модель, которая описывает поведение маятника в виде шарика на нити, у которого в некоторый момент времени (событие «Обрыв») рвется нить. У этой модели два состояния – «Колебания» и «Полет». Оба описываются системами дифференциальных уравнений, каждая из которых является динамической системой. Карта поведений представляет собой совокупность состояний и переходов. В любой момент времени только одно состояние является текущим.

На рис. 3.5, а показана карта состояний обрывающегося маятника, на которой кроме двух обычных состояний помещены два особых состояния – начальное и конечное.

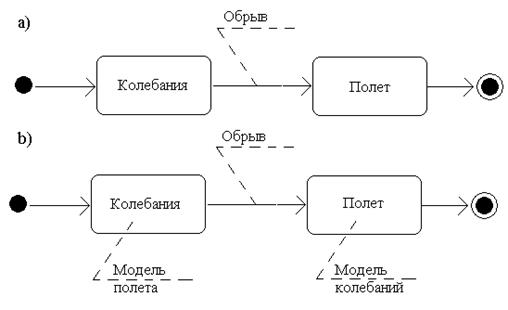
Рис. 3.5. Карта состояний и карта поведений обрывающегося маятника

В общем случае для состояния могут быть определены входные воздействия, выходные воздействия, а также локальная деятельность. Последовательность входных воздействий выполняется при каждом входе в состояние, последовательность выходных действий – при каждом выходе. Локальные действия выполняются все время, пока состояние является текущим.

Рис. 3.5, а отражает качественное поведение маятника. Для получения количественной картины необходимо связать с каждым состоянием локальное действие, в частности, интегрирование систем уравнений «Модель колебаний» и «Модель полета», как это сделано на рис. 3.5, b. Карта состояний, дополненная моделями состояний, названа в [20] картой поведения гибридной системы.

Одна из доступных реализаций концепции гибридного моделирования реализована в пакете StateFlow среды MATLAB, который кратко описан в главе 5. Также следует выделить отечественный пакет Model Vision Studium, ориентированный на моделирование сложных поведений [19].

Глава 4
Автоматизированное моделирование
технических объектов

Исторический экскурс. Необходимость автоматизации процессов моделирования технических объектов возникла практически одновременно с появлением вычислительных машин. Однако, исторически, разные этапы моделирования автоматизировались в разное время. Первым этапом следует считать создание библиотек численных методов исследования систем. Сами численные методы были разработаны задолго до появления ЭВМ и предназначались, прежде всего, для решения задач небесной механики. Так как первоначально расчеты велись вручную, алгоритмы методов были хорошо отлажены и оптимизированы. К концу 70-х годов прошлого столетия были созданы специализированные коллекции численных методов практически для всех областей численного анализа.

Дальнейшие шаги на пути автоматизации моделирования были связаны с разработкой систем автоматизированного проектирования (САПР) и систем автоматизации вычислительного эксперимента – пакетов прикладных программ. Автоматизации подлежали стандартные расчеты и оформление результатов экспериментов. Как правило, эти системы создавались под определенную предметную область, прежде всего, в наукоемких отраслях (космическая, авиация и т.д.). Для создания большинства пакетов прикладных программ для численных расчетов использовался язык Фортран, хорошо приспособленный именно для этих целей. Подобные пакеты создавались годами, их модификация и развитие требовали специальных знаний в предметной области, численных методах и программировании.

Наиболее трудно автоматизируемым этапом явился процесс построения модели. Ручная подготовка модели сложного технического объекта связана с большим объемом преобразований, в которых легко допустить ошибку. Использование систем автоматизации моделирования (САМ) позволило существенно повысить производительность труда, снизить число ошибок и, во многих случаях, исключить необходимость привлечение программистов к решению конкретных предметных задач. Опираясь на САМ, специалист в предметной (прикладной) области может самостоятельно создавать достаточно сложные модели.

При использовании системы автоматизированного моделирования исследователь формулирует математическую модель исследуемой системы на формальном входном языке моделирования. На ранних этапах развития САМ, когда отсутствовали возможности прямого изображения структуры модели на экране монитора, использовались методы кодирования структурной информации [1, 6]. Программа модели представляла собой последовательность вызовов процедур, каждая из которых являлась моделью структурного компонента. После связывания с модулями исполняющей системы пакета моделирования список компонентов преобразовывался в независимую исполняемую программу.

В современных системах автоматизированного моделирования, исходя из соображений удобства восприятия человеком, используются, как правило, графические средства задания исходной информации о модели. Переход к изображению структуры системы на экране монитора позволил исключить этап ручного кодирования схемы, однако потребовал разработки нового принципа организации самого процесса численных расчетов – принципа Data Flow, или принципа потока данных.

Можно отметить следующие факторы, способствующие внедрению систем автоматизированного моделирования:

· трудоемкость получения математической модели сложных технических объектов, связанная с опасностью совершить ошибку в многочисленных преобразованиях модельных выражений;

· необходимость многовариантного моделирования, при котором необходимо иметь для одного объекта несколько моделей, отличающихся по сложности;

· желание иметь дружественный интерфейс с программой и возможность оперативно вносить изменения в модель, что проще всего на основе использования графических языков задания исходной информации.

4.1. Особенности современных систем
автоматизированного моделирования

Современные профессиональные САМ имеют следующие отличительные черты [31]:

· поддержка иерархического проектирования как сверху – вниз, так и снизу – вверх, за счет реализации многоуровневого моделирования и метода локальной детализации модели;

· компонентное моделирование на основе использования библиотек, содержащих большое число графических и функциональных описаний компонентов, причем эти библиотеки открыты для добавления в них новых описаний, которые может сделать сам пользователь;

· графический пользовательский интерфейс, сочетающий графические средства формирования визуального образа исследуемого технического устройства с автоматической генерацией модели всей схемы по ее структурному описанию;

· наличие интерактивной рабочей среды проектирования (управляющей оболочки, монитора), т.е. специальной программы, из которой можно запускать все или большинство других программ пакета, не обращаясь к услугам штатной операционной системы;

· наличие в современных САПР и САМ постпроцессоров моделирования, что позволяет не только просматривать в удобной для пользователя форме результаты моделирования, но и обрабатывать эти результаты;

· наличие встроенных средств численного моделирования рабочего процесса в режиме реального времени или в режиме масштабирования модельного времени;

· реализация механизмов продвижения модельного времени, основанных как на принципе 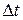, так и на принципе ;

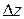· интегрируемость с другими пакетами аналогичного назначения, которая обеспечивается соответствующими программами – конверторами, позволяющими импортировать и экспортировать данные из одной системы в другую;

· наличие средств, обеспечивающие формирование виртуальных аналогов измерительно-управляющей аппаратуры.

Если САМ предназначена для решения исследовательских задач, то к перечисленным качествам добавляются возможности активного вычислительного эксперимента [21]. В частности:

· визуализация результатов во время эксперимента;

· возможность интерактивного вмешательства в ход моделирования;

· возможность использования 2D и 3D анимации.

4.2. Иерархическое проектирование
и многоуровневое моделирование технических систем

С точки зрения инженера, основное назначение моделирования – поддержка процедур проектирования технических объектов и систем. Процедуры проектирования работают с моделями объектов реального мира и должны быть подстроены под их свойства.

Сложные системы имеют, как правило, иерархическую структуру. Естественные возможности человека позволяют оперативно обрабатывать не более 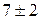единиц информации одновременно. В процессе проектирования исследователю удобно сосредотачиваться сначала на поведении отдельных компонентов системы, а затем на их взаимодействии [21]. При необходимости модели компонентов могут детализироваться или, наоборот, укрупняться.

Такой подход, известный как иерархическое проектирование [21, 31], является типовым при разработке сложных технических объектов и заключается в разбиении исходной задачи на подзадачи.

В процессе проектирования сложной системы формируются определенные представления о системе, отражающие ее существенные свойства с той или иной степенью подробности. В этих представлениях можно выделить составные части – уровни проектирования. В один уровень, как правило, включаются представления, имеющие общую физическую основу и допускающие для своего описания использование одного и того же математического аппарата. Уровни проектирования можно выделять по степени подробности, с какой отражаются свойства проектируемого объекта. Тогда их называют горизонтальными (иерархическими) уровнями проектирования.

В результате такого подхода объект проектирования декомпозируется на фрагменты (подсхемы) и проектирование каждого из них ведется в определенном смысле самостоятельно. На каждом уровне иерархии этот принцип применяется вновь, что позволяет заменить решение одной сложной задачи многократным решением задач меньшей размерности.

При иерархическом проектировании разработчику достаточно держать в поле зрения лишь один фрагмент объекта. Остальные части лишь имитируют внешнюю среду, т.е. взаимодействие проектируемого фрагмента с другими частями объекта.

Использование принципа иерархического проектирования позволяет ограничить текущую сложность проекта на приемлемом уровне, за счет того, что в каждый момент времени разработчик имеет дело только с двумя смежными уровнями декомпозиции объекта – структурным описанием проектируемого в данный момент фрагмента и функциональным описанием внешней среды.

Инструментальной поддержкой иерархического проектирования является многоуровневое моделирование.При многоуровневом моделировании различные фрагменты представляются на различных уровнях иерархии, т.е. с разной степенью детальности. Например, проектируемая в настоящий момент времени часть объекта раскрыта до уровня элементарных динамических компонентов и имитируется структурной моделью, а остальные фрагменты представлены на соседнем более высоком уровне в виде функциональных моделей.

Завершив проектирование одного фрагмента, разработчик может свернуть его в функциональный блок и перейти к детальной модели следующего фрагмента, с которым он собирается работать. Эта процедура повторяется многократно, на разных уровнях иерархии проектируемого объекта. Достоинством такого подхода является то, что в поле зрения разработчика находится в каждый момент времени минимум
необходимой информации, не перегруженной лишними деталями. Описанный метод проектирования называется методом локальной детализации объекта.

Программной поддержкой многоуровневого моделирования, реализованной в большинстве языков графического программирования, является процедура инкапсуляции, которая позволяет «свернуть» любой смысловой фрагмент графического представления в единичный блок. Кроме того, что инкапсуляция служит основой получения иерархически структурированных моделей, она так же позволяет расширить библиотеку базовых блоков блоками пользователя, которые, впоследствии, можно многократно использовать (например, типовые динамические звенья).

Такой возможностью обладает, в частности, пакет LabVIEW, пакет Simulink и основанные на нем пакеты SimMechanics и SimPower. Пакеты IDEF-моделирования (ERWIN, BPWIN) принципиально основаны на многоуровневом изображении объектов.

4.4. Архитектура программ
автоматизированного моделирования

Существующие инструментальные средства автоматизированного моделирования могут относиться к разным предметным областям и существенно различаться по своим возможностям, но их модульные структуры мало отличаются друг от друга. На рис. 4.1 представлена типовая структура современного пакета визуального компонентного моделирования. Рассмотрим более детально назначение и особенности основных элементов этой структуры.

4.4.1. Графический интерфейс программ математического
моделирования динамических систем

Графический интерфейс является в настоящее время стандартным компонентом современной САМ. Он создает дружественный интерфейс между пользователем и программой, дает возможность оперировать с графическими образами вместо аналитических выражений. Это значительно облегчает работу в САМ и снижает вероятность ошибок при вводе информации о системе.

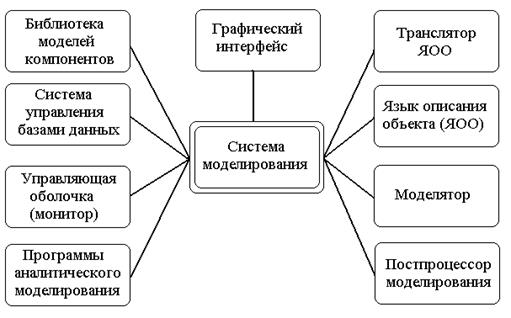
Рис. 4.1. Модульная структура
системы автоматизированного моделирования

Графический пользовательский интерфейс позволяет вводить информацию об исследуемой системе путем «рисования» на экране монитора проектируемой схемы в виде, понятном широкому кругу специалистов. Формой графического представления информации о моделируемой системе могут быть [16]:

· операторно-структурные схемы, принятые в ТАУ;

· функциональные и принципиальные схемы различных физических устройств;

· кинематические схемы механизмов;

· блок-схемы алгоритмов и другие графические модели.

Однако простым «рисованием» роль графического интерфейса не ограничивается. Задачами графического интерфейса, кроме того, могут быть [16]:

· контроль за соблюдением некоторых правил в процессе создания графического изображения на экране монитора (обычно накладываются ограничения на способы соединения компонентов и т.п.);

· преобразование информации о схеме в команды для моделирующей программы (моделятора);

· контроль за процессом моделирования, визуализация результатов моделирования.

П.5. Локальные и глобальные погрешности одношаговых методов решения ДУ

(метода Эйлера и методов Рунге-Кутта 2го, 4го порядка).

Теорема 6.1:

Если локальная погрешность метода , то глобальная .

как и при численном интегрировании, при переходе от локальной погрешности к глобальной, точность метода уменьшается на порядок. (6.8):

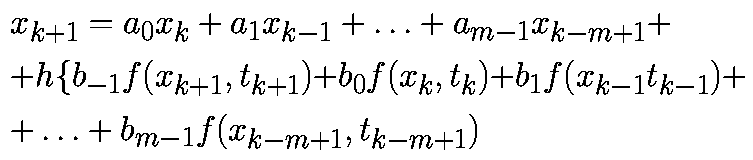
Методы	Локальная	Глобальная
Эйлер	const*h 2	const*h
Р.–К. 2го порядка по времени	const*h 3	const*h 2
Р.–К. 2го порядка по производной	const*h 3	const*h 2
Р.–К. 4го порядка	const*h 5	const*h 4

Как и при численном интегрировании, порядок метода – степень h в глобальной погрешности.

П.6. Многошаговые методы решения ДУ и СДУ.

Все рассмотренные ранее методы – одношаговые, т.к. для нахождения мы использовали только лишь значения с предыдущего шага. В многошаговых методах для нахождения используется не только лишь одно , но и предыдущие значения.

В k-шаговом методе используются значения с k предыдущих шагов.

Многошаговые методы, как правило, дают лучший результат, чем одношаговые, в силу того, что более устойчивы к вычислительным погрешностям. Многошаговых методов много, самый распространенный среди них – метод Милна.

Формулы метода Милна:

(6.9)

Метод Милна – 4х шаговый (т.к. использует 4 предыдущих значения) и имеет 4-ый порядок точности. Перед применением метода Милна нам надо знать 4y, следовательно, необходимо сделать хотя бы 3 шага каким-нибудь одношаговым методом.

П.7. Оценка погрешности решения ДУ и СДУ методом двойного пересчета. Коррекция решения.

Используя такую же идею, как и в численном интегрировании, находим решение ДУ на [a,b] дважды с шагом h и с шагом h/2. Получим следующую картину:

Сравниваем попарно, если расхождение между для метода 2го порядка, для метода 4го порядка, то в качестве точного решения берём . Если же точность не достигнута, то шаг h уменьшаем вдвое и т.д., пока она не будет достигнута.

Метод двойного пересчёта при решении ДУ и СДУ практически единственный имеет возможность для оценки погрешностей, так как иные формулы очень сложны и требуют оценок различных производных.

Как и при ЧИ, при решении ДУ и СДУ после 2го пересчёта в качестве точного решения выгодно брать не , а .

— для второго порядка

Метод двойного пересчёта применим не только лишь при ЧИ, при решении ДУ и СДУ, но и при решении других численных методов.

П.7. Краевые задачи для дифференциальных уравнений.

Выше рассматривалось решение ДУ и СДУ с начальными условиями, заданными в одной точке, так называемую задачу Коши, но для ДУ высших порядков часто бывает необходимо решить не з. Коши, а так называемую краевую задачу, т.е. начальные условия, которые заданы в разных точках.

Рассмотрим простейшую краевую задачу для ДУ 2го порядка:

(6.10)

А мы умеем решать:

(6.11),

В (6.11) нам известно , поэтому для решения задачи (6.10) мы будем подбирать в (6.11), с тем, чтобы у(b) = у₁

Метод стрельб

После пристрелки и определения интервала [a,b],

где идёт смена знака, запускаем МПД или МХ.

На практике это выглядит так, как будто мы

решаем уравнение , где 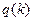возвращает

решение задачи Коши (6.11) в точке b при

П.9. Что делать, если ДУ не может быть разрешено относительно старшей производной?

Так как ДУ не может быть решено относительно старшей производной, то тогда на каждом шаге решаем нелинейное уравнение относительно y ( n) (все остальные неизвестные y,y’,y”,…, y ( n-1) -к этому моменту уже известны).

Решать уравнение относительно старшей производной любым методом(Хорд, МПД, Ньютона).

Замечание:

Таким образом, если ДУ не разрешается относительно старшей производной, то у нас возникает дополнительный цикл (самый внутренний) при написании программы.

Типы и классификация ошибок численного интегрирования

Современный численный метод одновременно с решением задачи Коши должен вычислять значение или оценку ошибки. Первый такой метод был предложен Мсрсоном в 1959 году (метод Рунгс-Кутта-Мсрсона). Теоретически таких методов описано достаточно много. Однако хороших практических реализаций в виде алгоритмов или прикладных программ мало. Рассмотрим причины возникновения ошибки при решении задачи Коши. Эта ошибка складывается из следующих компонент.

• 1. Неустранимая погрешность исходных данных. На нее повлиять нельзя, но учесть необходимо.
• 2. Локальная ошибка метода. Ее величина определяется порядком р используемого метода и зависит от шага: е,

()(h p *’). Эта ошибка связана с отбрасыванием остатка ряда при разложении точного решения в ряд по шагу при условии, что вес исходные данные заданы точно и вычисления проводятся без ошибок округления.

3. Ошибка переноса, которая возникает из-за того, что ошибка, сделанная на предыдущем шаге, переносится на следующий шаг с каким- то коэффициентом.

4. Ошибка округления, сопровождающая любые расчеты. Она возникает как при выполнении арифметических операций, так и при использовании алгоритмов вычисления значений многих элементарных функций (тригонометрических, показательных и других).

Если производить расчет на малом отрезке интегрирования, то ошибкой округления можно пренебречь, и преобладающей становится ошибка метода. Но когда количество шагов велико, ошибки округления накапливаются и становятся преобладающими. Экспериментально устаО а

количестве шагов взаимодействуют, в результате возникает общая ошибка, накопленная на веем отрезке интегрирования при применении данного метода. Эта общая ошибка ?_г называется глобальной ошибкой. Известно, что при интегрировании на отрезке |0; Т|

Здесь множитель Т)(Т) зависит только от вида функции f(x) и нс зависит от шага интегрирования. Соотношение (7.9) называют правилом Рунге.

Общая ошибка ?у, порожденная всеми составляющими, сеть их сумма (рис. 7.1). Существует оптимальное значение шага /Г, обеспечивающее наименьшую суммарную ошибку. В случае, изображенном на рис. 7.1, отклонение от этого оптимального значения нс вызывает силь-

„ _ , „ , ного изменения ошибки. Возможно, однако, си-

Рнс.7.1. Суммарная ошибка

численного интегрирования туация, когда график суммарной ошибки столь крут, что даже малое изменение шага вызывает резкий рост суммарной ошибки. Такая ситуация характеризует вычислительную неустойчивость процесса интегрирования.

Полученную в результате интегрирования ошибку нужно уметь оценивать. Кроме того, полезно иметь возможность сознательно так выбирать шаг интегрирования, чтобы влиять на величину ошибки.

Наиболее популярный метод вычисления локальной ошибки основан на разложении решения в ряд по шагу. Если используется метод порядка р. то остаток ряда начинается с члена, содержащего

Очевидно, именно этот член и характеризует величину ошибки. Значит, следует оценить значение величины R. Будем считать, что при малом /| на протяжении шага R = const. Пусть на некотором шаге с номером г выбрана точка t е [t_r‘,t_nl]. Тогда x(t’) — точное, а х*/, — вычисленное при интегрировании с шагом /; значение искомой функции. Можно считать, что на шаге

Теперь разобьем шаг на два, длины —. и вычислим то же значение,

выполнив два шага интегрирования. Будем считать, что величина R при этом нс изменилась. Получим:

Вычитая уравнения, можно получить

И можно считать, что при интегрировании с постоянным шагом И верно соотношение

Таким образом, схема выбора величины /г на шаге для достижения заданной точности Очакова:

1. при известном х, с шагом /г вычислить т_г+/;

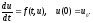(0)

При рассмотрении метода Эйлера было
показано, что глобальная погрешность
приближенного решения совпадает с
локальной погрешностью метода –
погрешностью аппроксимации дифференциальной
задачи.

При оценке локальной погрешности
стандартной процедурой является
следующая. Точное решение дифференциальной
задачи подставляется в вычислительную
схему, при этом учитывается, что его
значение в некоторых узлах (узле) сетки
уже известно (из начальных условий либо
предыдущих вычислений), а значение
решения в других узлах (узле) может быть
выражено отрезком степенного ряда,
используя исходное дифференциальное
уравнение для нахождения соответствующих
производных функции.

Зная
смысл погрешности аппроксимации задачи
несложно понять, как взаимосвязана
погрешность приближенного решения с
погрешностью аппроксимации задачи
(локальной ошибкой метода).

Общая схема рассуждений такова.

Мы
имеем некоторый одношаговый численный
метод, в котором приближенное решение
в каждом новом узле сетки вычисляется
с использованием некоторой функции F
дискретных аргументов и параметра
:

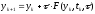
(1)

Если
подстановка точного решения дифференциальной
задачи в уравнение (1) приводит к тождеству

,

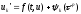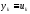
(2) или

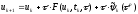
(3)

то
говорят, что схема (1) аппроксимирует
исходное уравнение (0) с порядном
.

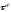Таким образом, происхождение погрешности
численного метода можно интерпретировать
либо как возмущение исходной
дифференциальной задачи, обусловленное
появлением в правой части уравнения
(2) дополнительного малого слагаемого
,
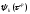либо как отбрасывание такого рода
слагаемых при переходе от точного
выражения для решения (3) к приближенной
схеме (1).

Анализ
погрешности численной схемы ведется
на основе уравнения для погрешности
,
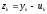которое получается при вычитании (3) из
(1):

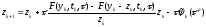(4)

Из ограниченности величины

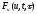
в окрестности точного решения следует,
что, согласно (4), ошибка приближенного
решения на каждом шаге метода может
возрастать на величину порядка
.
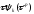Учитывая, что количество шагов сетки
на конечном отрезке по t
есть величина порядка
,
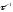то в худшем случае суммирования
погрешностей на каждом шаге, максимальная
ошибка на всем интервале будет величиной
порядка
,
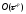т.е. иметь тот же порядок, что и погрешность
аппроксимации метода.

Заметим, что совпадение локальной и
глобальной ошибки одношаговых численных
методов следует понимать только в
смысле совпадения порядка малости
данных величин. В силу этого, если
некоторая стандартная программа,
реализующая метод Рунге-Кутты, содержит
среди входных параметров значение
локальной погрешности для оценки
требуемых шагов сетки при численном
интегрировании задачи, не следует
думать, что приближенное решение будет
получено именно с такой точностью на
произвольном отрезке численного
интегрирования. При моделировании
длительной динамики решения истинная
(глобальная) погрешность приближенного
решения может испытывать экспоненциальный
рост и существенно отличаться от
локальной погрешности. Чтобы убедиться
в удовлетворительной точности решения
в большинстве случаем достаточно
сравнить приближенные решения, полученные
на сетках с шагами

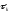
и
.

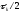При оценке погрешности метода Эйлера
и методов Рунге-Кутты мы неявно полагали,
что сами вычисления производятся точно.
На практике, вообще говоря, это не так,
поскольку реализация арифметических
операций с действительными числами,
имеющими компьютерное представление
на конечной разрядной сетке, неизбежно
ведет к округлению как самих действительных
чисел, так результатов арифметических
операций с ними. В силу этого, наряду с
погрешностью аппроксимации дифференциальной
задачи, приближенное решение будет
содержать также ошибку, связанную с
погрешностями представления и операций
с действительными числами. Таким
образом, погрешность приближенного
решения дифференциальной задачи будет
состоять из погрешности дискретизации
задачи и вычислительной ошибки.
Идентифицировать вычислительную
погрешность численной схемы и оценить
ее величину, для методов, обладающих
сходимостью при
,
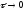можно следующим образом. Выполнить
расчеты на последовательности сеток с
шагами
.
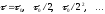Далее, следует оценить погрешность
приближенного решения на каждой сетке,
используя точное решение задачи (заметим,
что понятие точного решения при
оценках вычислительной погрешности
весьма условно, поскольку вычисленное
«точное» решение также будет
содержать некоторую вычислительную
погрешность). При уменьшении шага
оказывается, что, начиная с некоторой
достаточно малой величины
,
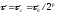его дальнейшее уменьшение не приводит
к уменьшению погрешности решения, или
даже напротив – ведет к возрастанию
ошибки. Это является следствием того,
что ошибка, обусловленная погрешностью
метода, при

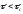
уменьшилась настолько, что стала ниже
вычислительной погрешности. С
уменьшением шага сетки на конечном
интервале численного интегрирования
задачи растет число шагов, требуемое
для покрытия данного интервала. Как
следствие, растет общий объем вычислений
с округлениями, дающими вклад в
вычислительную погрешность. Накопление
вычислительной погрешности, хотя это
и не обязательно, может приводить к
некоторому росту общей ошибки решения
при
.

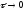При численном решении задачи Коши обычно
предпочтение отдают одношаговым методам,
которые обладают устойчивостью
вычислений, возможностью легко менять
шаг сетки и отсутствием предварительного
построения начала таблицы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

The truncation error does not satisfy that equation, it’s just its definition.

Consider two following problems:

• The first is an ODE.
  $$
  y'(t) = f(t, y(t))\
  y(0) = a.
  $$
  Its solution is some smooth function $y(t)$.
• The second is a difference equation
  $$
  frac{z_{i+1} — z_i}{h} = f(t_i, z_i)\
  z_0 = a.
  $$
  Its solution is some discrete function $z_i$.

I’ve intentionally used different letters to denote those two solutions. They are quite different, the former is a smooth function while the latter is a discrete one. One needs to be careful even to compare those two. Usually the third function is introduced. It is defined as a restriction of the smooth $y(t)$ to the grid $t_i$, where the discrete function $z_i$ is defined. Let’s denote the restriction as $w_i$:
$$
w_i equiv y(t_i).
$$

The function $w_i$ is discrete just like $z_i$ and $w_i$ coincide with $y(t)$ at grid points. Since now $w_i$ and $z_i$ are functions of the same class we can easily compare them:
$$
e_i = w_i — z_i equiv y(t_i) — z_i.
$$
So, roughly speaking, the global error shows how close are $y(t)$ and $z_i$ (by restricting the former to the grid). When someone is solving some problem numerically the global error is what he is interesting in. Anyway, direct computation of global error is almost impossible, since we often simply do not have the exact values of $w_i = y(t_i)$ (
in contradistinction to $z_i$, which we can compute easily).

And the local truncation error concept comes to the rescue. Note that previously we’ve compared the solutions. Now we’re going to compare problems. Take $z_i$. It is the solution to the second problem. Plugging $z_i$ into it makes it a valid identity
$$
frac{z_{i+1} — z_i}{h} = f(t_i, z_i)\
z_0 = a.
$$
But if we now take $w_i$ and try to plug it into the difference scheme we wont get an identity. Instead we’ll get a residual:
$$
frac{w_{i+1} — w_i}{h} = f(t_i, w_i) color{red}{{}+ d_i}\
w_0 = a color{red}{{} + d_0}.
$$
If we are very lucky, some residuals may vanish, like $d_0$, but often it is not the case.

So why is $d_i$ interesting while it also is defined in terms of $w_i$ (the unknown solution to the original problem)? It turns out that we can estimate the $d_i$ without knowing the exact values of $w_i$ by just knowing the original problem.
$$
d_i = frac{w_{i+1} — w_i}{h} — f(t_i, w_i) equiv
frac{y(t_{i+1}) — y(t_i)}{h} — f(t_i, y(t_i)) = \ =
y'(t_i) + h frac{y»(t_i)}{2} + O(h^2) — f(t_i, y(t_i)) = \ =
color{blue}{left[y'(t_i) — f(t_i, y(t_i))right]} + color{red}{h frac{y»(t_i)}{2} + O(h^2)}
$$
The blue term in braces is exactly the original ODE, and $y(t)$ is exactly its solution. So the term is equal to zero.
$$
d_i = h frac{y»(t_i)}{2} + O(h^2).
$$
Similar result may be obtained if using different form of Taylor’s formula:
$$
d_i = h frac{y»(xi_i)}{2}, qquad xi_i in [t_{i}, t_{i+1}].
$$

So now we can estimate the local truncation error, but we’re interested in the global error.

To relate them we need to introduce another concept of stability. Consider the two discrete problems
$$
begin{aligned}
&frac{z_{i+1} — z_i}{h} = f(t_i, z_i)\
&z_0 = a
end{aligned}
qquadtext{and}qquad
begin{aligned}
&frac{w_{i+1} — w_i}{h} = f(t_i, w_i) color{green}{{} + d_i}\
&w_0 = a color{green}{{} + d_0}
end{aligned}.
$$
Pretend that we know $d_i$. Let’s view the second problem as a perturbation of the first one. That’s reasonable, since $d_i$ is a small value of $O(h)$ magnitude. A difference problem is called stable if such small perturbations result in small changes of the solution. For this case this means that the difference $z_i — w_i$ will also be small. Precisely
$$
max_i |z_i — w_i| leq C max_i |d_i|
$$
where $C$ is called the stability constant of the method. For the explicit Euler method it can be shown that for Lipschitz-continuous $f$
$$
C leq e^{LT}
$$
with $L$ being the Lipschitz constant of $f$ and $T$ is the total integration time $T = max_i t_i$.

Finally we can relate the global error and the local truncation error by
$$
|e_i| leq C max_i |d_i|
$$

If the local truncation error tends to zero when the discrete mesh is refined the numerical method is called consistent. The Lax theorem states that a stable consistent method converges, in sense that $e_i to 0$ when the mesh is refined.

Локальная ошибка: определение, значение, предложения

Как исправить ошибку сети

Опубликовано 06.04.2022

Ошибка сети — как исправить

Без подключения к интернету любой гаджет сегодня теряет больше половины своих полезных качеств. Поэтому ошибка сети является одной из самых неприятных ситуаций для пользователя. Немало проблем возникает и у организаций — вплоть до полной остановки работы. В нашей статье мы подскажем, как поступить, если невозможно выйти в интернет или открыть сайты, подключить Wi-Fi или опознать сеть. Прежде чем переходить к серьезным вмешательствам в операционную систему, попробуйте следующие действия:

• Обычная перезагрузка компьютера и роутера.
• Проверка плотности прилегания LAN-кабеля.
• Отключение антивируса, межсетевого экрана, VPN-клиентов и другого софта, влияющего на подключение к Internet. Возможно, антивирус даже придется полностью удалить с устройства.
• Обращение в техподдержку провайдера для уточнения ситуации. Возможно, поставщик интернет-услуг проводит ремонтно-профилактические работы либо меняет параметры сетевого соединения.

Если эти действия не дали результата, используйте инструкции, данные нами в этой статье.

Самая простая, но частая ошибка сети

Часто ошибка сети появляется при неправильном вводе пароля от Wi-Fi-роутера. Компьютер сообщает о невозможности подключения или о применении недопустимого ключа. Даже если вы считаете себя достаточно уверенным пользователем, проверьте следующие моменты:

• Клавиатура работает в обычной раскладке. Если это не так, переключите язык.
• Учитывается верхний и нижний регистр.
• Пароль маршрутизатора состоит только из латинских букв и цифр. Не применяйте кириллицу и специальные символы.
• Пароль от Wi-Fi-роутера самовольно никем не был изменен.

Также обратите внимание: если ваше устройство нашло несколько сетей, то подключиться вы сможете только к открытой либо той, от которой знаете пароль.

Ошибка подключения к сети из-за сбоя драйверов

Причиной сетевых неполадок часто выступают сбои в работе драйверов. Кроме этого, Центр обновления или сторонний софт могут инсталлировать в систему неподходящее для подключения к интернету ПО. Как наладить стабильную работу, читайте ниже.

Обновление или откат сетевого драйвера

1. Открываем диспетчер устройств.
2. В ветке «Сетевые адаптеры» находим конфликтное устройство.
3. Кликаем по его наименованию ПКМ и заходим в «Свойства».
4. Переходим в категорию «Драйвер».
5. Нажимаем «Откатить» (если эта кнопка активна).
6. Перезагружаем компьютер.
7. Если кнопка неактивна либо действие не дало желаемый результат, совершаем шаги 1—4 и кликаем «Обновить».

Выбираем сначала автопоиск драйверов. Если он не справляется, ищем нужный софт на компьютере или в интернете и устанавливаем вручную.

Запрет на отключение сетевой карты

Windows может отключать сетевой адаптер в целях экономии электроэнергии, т. к. это устройство относится к некритическим компонентам ПК. В таком случае снова выполняем шаги 1—3, как в предыдущем блоке, и переходим в категорию «Управление электропитанием». Если в строке «Разрешить отключение этого устройства…» стоит галочка, снимаем ее.

Проверка параметров подключения к Internet

Если корректировка работы драйверов не принесла желаемого результата, необходимо проверить параметры интернет-подключения.

Контроль процессов деятельности сетевых протоколов

Для нормального обслуживания интернет-соединения необходимо включить основной протокол IPv4. В некоторых случаях можно попробовать активировать и отключить протокол IPv6 (иногда его работа вызывает сбой соединения).

1. Заходим в «Сетевые подключения» (набрать win+r и вбить в строку ncpa.cpl).
2. Кликаем ПКМ по соответствующему сетевому подключению и переходим в «Свойства».
3. Ставим галочку в строке «IP версии 4 (TCP/IPv4)» и перезагружаем ПК.
4. В отсутствие результата повторяем этапы 1 и 2, снимаем или ставим галочку в строке «IP версии 6 (TCP/IPv6)» (с учетом того, есть она там или нет) и снова отправляем ПК на перезагрузку.

Контроль настроек IP и DNS

Если вышеописанные действия не принесли желаемого результата, проверяем параметры IP и DNS. Повторяем этапы 1 и 2, как в предыдущем разделе, выделяем «IP версии 4 (TCP/IPv4)» и нажимаем «Свойства». Активируем автоматическое получение IP и DNS путем проставления галочек в соответствующих строках и повторяем этот алгоритм с IP версии 6 (TCP/IPv6).

Часто решить проблему помогает установка тех значений DNS, что предоставляет Google.

1. Ставим отметку «Использовать следующие DNS-адреса».
2. В строке «Предпочитаемый…» вводим 4 цифры «8».
3. В «Альтернативный…» — меняем третью и четвертую «восьмерки» на «четверки».

Кликаем OK и перезагружаем устройство.

Активация/деактивация FIPS

Этот стандарт действует для американских госучреждений, но его могут применить пользователи любого региона. Снова открываем «Сетевые подключения», кликаем по действующему адаптеру ПКМ и заходим в «Состояние». Выбираем «Свойства беспроводной сети» и во вкладке «Безопасность» — «Доппараметры». Если галочка стоит, убираем ее, если нет, то ставим и перезагружаем ПК.

Произошла ошибка сети — как исправить с помощью командной консоли

Если вышеописанные манипуляции не помогли, попробуем поработать с системными файлами и настройками. Внимание — сброс интернет-подключения обнуляет все значения. В случае, когда настройки устанавливаются не автоматически, а вручную, то по завершении манипуляций нужно будет заново ввести параметры. Поэтому перед началом работы выписываем IP и DNS (либо потом узнаем у провайдера) и запускаем командную строку с админскими правами. Потом поочередно набираем 6 команд (каждую из них вводим в действие с помощью Enter):

• netsh winsock reset;
• netsh int ip reset;
• netsh int tcp reset;
• ipconfig /release;
• ipconfig /renew;
• ipconfig /flushdns.

Набираем команды без точки с запятой, соблюдая пробелы. В конце перезагружаем компьютер.

Исполняя 2-ую команду, система может выдать ошибку доступа к сети. Справляемся с этим с помощью редактора реестра. Раскрываем ветку HKEY_LOCAL_MACHINE, переходим в SYSTEM, а далее по пути CurrentControlSet→Control→Nsi→{eb004a00-9b1a-11d4-9123-0050047759bc}→26.

1. Кликаем ПКМ по директории «26» и переходим в «Разрешения».
2. Разрешаем полный доступ, потом «Применить»→OK.
3. Заново вводим вышеуказанный блок из 6 команд.
4. Перезагружаем ПК.

Теперь снова необходимо зайти в редактор реестра и вернуть первоначальные настройки. Выполняем пункт 1, запрещаем полный доступ, потом «Применить»→OK.

Как исправить ошибку сети в стандартном приложении

Встроенный инструмент Windows может оказать действенную помощь в поиске и решении ошибки сети. Кликаем ПКМ по значку интернет-соединения на панели задач и выбираем «Диагностика…». Далее делаем следующее:

1. Выбираем «Другая проблема».
2. Теперь «Использование конкретного сетевого адаптера».
3. Указываем проблемное или «Все устройства».
4. Ожидаем завершения работы приложения.
5. В завершение диагностики утилита предложит ознакомиться с дополнительной информацией по проблеме или закрыть инструмент.

Если у вас наблюдаются неполадки только при посещении определенных интернет-ресурсов, то на первом этапе укажите «Я пытаюсь получить доступ…» и действуйте по подсказкам системы.

Сброс сети для исключения ошибки

В качестве радикального средства возможно применить сброс сети, подразумевающий удаление всех настроек.

• Открываем«Параметры» (win+I), потом «Сеть и интернет».
• Прокручиваем вниз и щелкаем «Сброс сети».
• Действуем согласно подсказкам системы и перезагружаем компьютер.

Если эта манипуляция не дала результат, загружаемся в безопасном режиме с поддержкой сетевых драйверов и проверяем, наблюдается ли там ошибка. При ее наличии, скорее всего, придется переустановить Windows.

Ошибку сети могут вызвать настройки роутера

Ошибка сети может быть вызвана определенными настройками маршрутизатора. Например, если активна опция, блокирующая подключение устройств по их MAC-адресу, то необходимо ее отключить. Заодно нужно попробовать деактивировать особую функцию Windows 10, которая подбирает случайные аппаратные адреса. Она расположена (при наличии в конкретной версии ОС) по адресу «Параметры»→«Сеть и интернет»→Wi-Fi. Проходим по этому пути и отключаем опцию.

Современные маршрутизаторы функционируют в двухканальном режиме, настроенном на частоты 2.4 ГГц и 5 ГГц. Меняя параметры подключения к сети (как было описано выше), проверяйте их работу в обоих диапазонах, чтобы сразу проверить, исчезла ли ошибка интернет-подключения.

Заключение

Мы познакомили вас с основными способами исправления ошибки сети. Это то, что вам по силам сделать самостоятельно. Но, даже если эти шаги вызывают у вас определенные трудности, лучше обратитесь за профессиональной помощью к специалистам компании «АйТи Спектр». Мы корректно настроим подключение к сети и, если нужно, отремонтируем компьютер и другие устройства, а также проведем техобслуживание.