Максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления - Ремонт и установка крупной бытовой техники

Верны ли определения?
А) Бесповторная выборка — выборка, при которой объекты извлекают по одному из всей генеральной совокупности.
В) Выборочная совокупность или выборка представляет собой результаты наблюдений над ограниченным числом объектов из этой совокупности.
Подберите правильный ответ
Верны ли определения?
А) Варианта — это среднее арифметическое значение признака выборочной совокупности.
В) Предельная ошибка выборки — это максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.
Подберите правильный ответ
Верны ли определения?
А) Внутригрупповая дисперсия определяется как средняя арифметическая дисперсий, взвешенная по объемам групп.
В) Распределение случайной величины — совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины.
Подберите правильный ответ
Верны ли определения?
А) Выборочная дисперсия определяется как среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
В) Генеральная дисперсия определяется как среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
Подберите правильный ответ
Верны ли определения?
А) Выборочная средняя есть среднее арифметическое значение признака выборочной совокупности.
В) Простой случайный отбор — выборка, при которой отобранный объект в генеральную совокупность не возвращается.
Подберите правильный ответ
Верны ли определения?
А) Выборочная средняя определяется как среднее арифметическое значение признака выборочной совокупности.
В) Генеральная средняя — среднее арифметическое значение признака выборочной совокупности.
Подберите правильный ответ
Верны ли определения?
А) Повторная выборка — выборка, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
В) Выборочное распределение — это вероятностное пространство, элементами которого являются наблюдения (х1), (х2), (xn) и все элементы которого равновероятны: (Р(хi) = 1/n).
Подберите правильный ответ
Верны ли определения?
А) Статистическое распределение выборки — это функция распределения F (х) генеральной совокупности.
В) Частота — это число наблюдений значения случайной величины.
Подберите правильный ответ
Верны ли определения?
А) Эффективная статистическая оценка — статистическая оценка, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
В) Выборочное пространство — вероятностное пространство, элементами которого являются наблюдения (х1), (х2), (xn) и все элементы которого равновероятны: (Р(хi) = 1/n).
Подберите правильный ответ
Верны ли определения?
А) Генеральная совокупность — это совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины, или совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов.
В) Выборочное среднее квадратическое отклонение можно рассчитать как квадратный корень из выборочной дисперсии.
Подберите правильный ответ
Верны ли определения?
А) Дисперсия дискретной случайной величины равна математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания.
В) Групповая дисперсия есть среднее арифметическое значений признака, принадлежащих группе.
Подберите правильный ответ
Верны ли определения?
А) Коэффициент вариации определяется как выраженное в процентах отношение выборочной средней к выборочному среднему квадратическому отклонению:
В) Доверительный интервал покрывает неизвестный параметр с заданной надежностью.
Подберите правильный ответ
Верны ли определения?
А) Мода — элемент выборки, встречающийся с наибольшей частотой.
В) Медиана — элемент выборки, встречающийся с наибольшей частотой.
Подберите правильный ответ
Верны ли определения?
А) Отклонение определяется как разность между наибольшей и наименьшей вариантами.
В) Размах варьирования — определяется как разность между наибольшей и наименьшей вариантами.
Подберите правильный ответ
Верны ли утверждения?
А) Состоятельная статистическая оценка — это свойство выборки отражать характеристики изучаемой генеральной совокупности.
В) Статистическая оценка есть приближенное значение неизвестного параметра, полученное по выборке.
Подберите правильный ответ
Выборочная совокупность задана таблицей распределения

Выборочная средняя равна 2, n = 50. Выборочная дисперсия равна __________
Выборочная совокупность задана таблицей распределения

Найти выборочную среднюю.
Дана таблица частот выборочного распределения:

Общая средняя равна __________
Пусть дана таблица частот для некоторых двух групп:

Межгрупповая средняя равна
_________ называют математическое ожидание величины Xk: μ = M (Xk)
__________ определяется как число наблюдений значения случайной величины
Вероятность заданной ошибки выборки составляет __________
Дисперсия групповых средних относительно общей средней —
Дисперсия значений признака всей совокупности относительно общей средней
Дисперсия значений признака, принадлежащих группе, относительно групповой средней —
К отбору, не требующему расчленения генеральной совокупности на части, относятся: 1) простой случайный бесповторный отбор; 2) простой случайный повторный отбор; 3) типический отбор; 4) серийный отбор
К отбору, требующему расчленения генеральной совокупности на части, относятся: 1) механический; 2) простой случайный повторный отбор; 3) типический отбор; 4) серийный отбор
Максимально возможное расхождение средних или максимум ошибки при заданной вероятности ее появления называют __________
Математическое ожидание величины (Х-М(Х))k — это
Отношение суммы частот вариант, попавших в i-й интервал, к длине интервала — это _________
Отношение частоты случайной величины к объему выборки — это
Последовательность вариант, записанных в возрастающем порядке, — это
Приближенное значение неизвестного параметра, полученное по выборке, — это
Разность между значением признака и общей средней — это _________
Разность между наибольшей и наименьшей вариантами составляет __________
Совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов, — это
Соответствие между наблюдаемыми вариантами и их частотами или относительными частотами — это
Среднее арифметическое значение признака выборочной совокупности называют __________
Среднее арифметическое значений признака генеральной совокупности называют __________
Среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения — это _________
Среднее значение k-x степеней разностей хi — С: Mk* = (Σni (xi — С)k)/n называют _________
Среднее значение отклонения равно
Статистическая оценка, которая имеет наименьшую возможную дисперсию, — это
Статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, — это _________
Сумма произведений отклонений на соответствующие частоты равна __________

Источник

Предельная ошибка выборки

Предельная ошибка — максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.

1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:

Предельная ошибка выборки для средней при повторном отборе

где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;

мю х — средняя ошибка выборки.

2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:

Предельная ошибка выборки для доли при повторном отборе

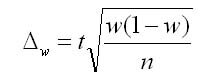
3. Предельная ошибка выборки для средней при бесповторном отборе:

Предельная ошибка выборки при бесповторном отборе

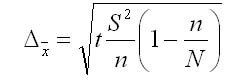
4. Предельная ошибка выборки для доли при бесповторном отборе:

Предельная ошибка выборки для доли при бесповторном отборе

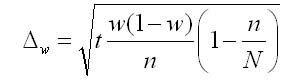
Предельная относительная ошибка выборки

Предельную относительную ошибку выборки определяют как процентное соотношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности. Она определяется таким образом:

Предельная относительная ошибка выборки

Малая выборка

Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц.

Межсерийная дисперсия

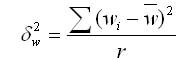
Средняя и предельная ошибки для малой выборки

В малой выборке средняя ошибка рассчитывается по формуле:

средняя ошибка малой выборки

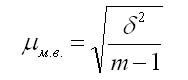
Предельная ошибка малой выборки рассчитывается по формуле:

Предельная ошибка малой выборки

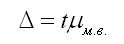
где t — отношение Стьюдента

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

Материалы сайта

Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.

Источник

Ошибки выборочного наблюдения

Информация, получаемая в результате
любого статистического наблюдения,
имеет расхождение с реальной
действительностью. Такое расхождение
получило название ошибок статистического
наблюдения. При массовом наблюдении
ошибки неизбежны, но возникают они
в результате действия различных причин
(см. гл. 4).

В данной главе рассматривается только
ошибка репрезентативности и причины
ее возникновения. Под ошибкой
репрезентативности (представительства)
понимают расхождение между выборочной
характеристикой и предполагаемой
характеристикой генеральной
совокупности. Причиной образования
этой ошибки является то обстоятельство,
что обследуются не все единицы генеральной
совокупности, а лишь их некоторая часть,
и различия между единицами, попавшими
в выборку, не соответствуют различиям
единиц, не попавших в выборку. Вследствие
этого выборочная совокупность становится
непредставительной по отношению к
генеральной совокупности. Ошибка
репрезентативности может возникнуть
по двум причинам: из-за нарушения научных
принципов отбора —систематическая
ошибка — и в результате случайности
отбора —случайная ошибка. В результате
первой причины выборка легко может
оказаться смещенной, так как при отборе
каждой единицы допускается ошибка,
всегда направленная в одну и ту же
сторону. Эта ошибка получила названиеошибки смещения. Ее размер может
превышать величину случайной ошибки.
Особенность ошибки смещения состоит
в том, что, представляя собой постоянную
часть ошибки репрезентативности, она
увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить (см. ниже), тогда как размер
ошибки смещения непосредственно
практически определить очень сложно,
а иногда — невозможно. Поэтому необходимо
знать причины, вызывающие ошибку смещения
и меры, способствующие её устранению.

Ошибки смещения бывают преднамеренные
и непреднамеренные. Причиной
возникновения преднамеренной ошибки
является тенденциозный подход к
выбору единиц из генеральной совокупности.
Мерой устранения этой ошибки может быть
только исключение тенденциозности.
Выявить эту ошибку можно только путем
проведения повторного отбора с
обязательным соблюдением принципа
случайности.

Непреднамеренные ошибки могут
возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чаще всего создаются условия
для возникновения ошибок смещения на
стадии подготовки выборочного наблюдения.
Недостаточно хорошо продуманные и четко
сформулированные взаимоувязанные
вопросы плана организации и проведения
выборочного обследования могут дать
информацию, не соответствующую цели
исследования или, что еще хуже, вводящую
в заблуждение. Если при сплошном
наблюдении это возможно только при
преднамеренном искажении фактов, то
при выборочном это связано с
непреднамеренными ошибками смещения.
При разработке плана организации и
проведения выборочного наблюдения
особое внимание следует уделятьединице
отбора, т. е. такой единице изучаемой
совокупности, которая является
основанием самого процесса отбора.
Единицей отбора могут служить естественные
единицы изучаемого явления, например
предприятие, рабочий, покупатель, семья
и т. д. В некоторых случаях необходимо
создать искусственные единицы, не
соответствующие естественному делению
изучаемой совокупности. Удачное
установление единицы отбора уменьшает
вероятность получить смещенную выборку.

Сокращению опасности возникновения
ошибок смещения во многом способствует
хорошая основа выборки, т. е. та
генеральная совокупность, из которой
предполагается производить отбор,
например список единиц отбора. Поэтому
при подготовке выборочного наблюдения
необходимо особенно тщательно
ознакомиться с тем, какова основа
выборки, пригодна ли она для производства
отбора, позволит ли она образовать
несмещенную выборку. Если готовой основы
выборки нет, то ее необходимо построить.

Основа выборки должна быть достоверной,
полной и соответствовать цели
исследования, а единицы отбора и их
характеристики должны соответствовать
действительному их состоянию на
момент подготовки выборочного наблюдения.
Если основа выборки не отвечает
перечисленным требованиям, ее
необходимо либо существенно улучшить,
внеся соответствующие изменения,
уточнения, дополнения, либо создать
заново.

На стадиях формирования выборочной
совокупности и производства наблюдения
ошибки смещения особенно опасны, так
как их трудно заметить и исправить. При
формировании выборочной совокупности
ошибку смещения чаще всего дает неточное
соблюдение установленного порядка
отбора, предусматривающего отбор
вполне определенных единиц. Иногда
может показаться, что выборочная
совокупность «не пострадает», если,
например, вместо предусмотренной десятой
единицы по списку взять одиннадцатую
или двенадцатую; в действительности же
такое нарушение установленного порядка
отбора нередко приводит к смещенной
выборке. Ошибки смещения при анализе
данных могут возникнуть из-за неправильных
приемов распространения выборочных
характеристик на генеральную
совокупность (см. 11.4).

Случайная ошибка выборки возникает
в результате случайных различий
между единицами, попавшими в выборку,
и единицами генеральной совокупности,
т. е. она связана со случайным отбором.
Теоретическим обоснованием появления
случайных ошибок выборки является
теория вероятностей и ее предельные
теоремы.

Сущность предельных теорем состоит в
том, что в массовых явлениях совокупное
влияние различных случайных причин на
формирование закономерностей и обобщающих
характеристик будет сколь угодно малой
величиной или практически не зависит
от случая. Так как случайная ошибка
выборки возникает в результате случайных
различий между единицами выборочной
и генеральной совокупностей, то при
достаточно большом объеме выборки она
будет сколь угодно мала. Этот вывод,
опирающийся на доказательства предельных
теорем, позволяет предполагать, что
характеристики выборочного наблюдения
могут достаточно хорошо представлять
характеристики генеральной
совокупности.

Предельные теоремы исходят из закона
нормального распределения, согласно
которому большая часть выборочных
средних сосредоточивается около
генеральной средней
.
Следовательно, закон нормального
распределения теоретически позволяет
установить, в какой мере изменяется
размер случайной ошибки выборки с
изменением вероятности ее появления.
Так как многие массовые явления
подчиняются закону нормального
распределения, то он служит основой при
оценке вероятности тех или иных
результатов выборочного наблюдения.

Предельные теоремы теории вероятностей
позволяют определять размер случайных
ошибок выборки. Различают среднюю
(стандартную) и предельную ошибку
выборки. Под средней (стандартной)
ошибкой выборки понимают расхождение
между средней выборочной и генеральной
совокупностей,не
превышающее.
Предельной ошибкой выборки принято
считать максимально возможное расхождение,
т. е. максимум ошибки при заданной
вероятности ее появления. На основании
теоремы, доказанной П. Л. Чебышевым,
величину стандартной ошибки так
называемого собственно-случайного
отбора при достаточно большом объёме
выборки можно определить по формуле:

где
— стандартная ошибка.

Величина стандартной ошибки прямо
пропорциональна колеблемости признака
в генеральной совокупности и обратно
пропорциональна квадратному корню
объёма выборки. Величина
зависит также от способа и вида отбора.

Академик А.М.Ляпунов, продолжив разработки
П.Л.Чебышева, доказал, что вероятность
появления случайной ошибки выборки при
её достаточно большом объёме подчиняется
закону нормального распределения. Эта
вероятность определяется по формуле:

Значения функции
табулированы
при различных значенияхt.

Предельная ошибка выборки определяется
по формуле

где
-предельная
ошибка,t– заданный
коэффициент доверия.

Так, при t=1 величина
предельной ошибки составит,
гарантированную с вероятностью 0,683. Это
означает, что в 683 выборках из тысячи
подобных максимальная ошибка выборки
(предельная) не превысит.
Приt=2 с вероятностью
0,954 она не выйдет за пределыи
т.д. В практике выборочных наблюдений
массовых общественных явлений максимальный
предел ошибок, как правило, вполне
достаточен в пределах.

Однако приведённые формулы нахождения
ошибок выборки практически непригодны,
т.к. в них σ – это показатель колеблемости
признака в генеральной совокупности,
который неизвестен, как неизвестна и
генеральная средняя. Но в теории
вероятностей доказывается, что

Так как
при
достаточно большомn– величина, близкая к единице, то условно
принимается, что.
На основании этого утверждения в
вышеприведённых формулах вместо
генеральной дисперсии принимают значение
выборочной дисперсии.

Предельная ошибка выборки позволяет
определять предельные значения
характеристик генеральной совокупности
при заданной вероятности и их доверительные
интервалы:

Это означает следующее: с заданной
вероятностью можно утверждать, что
значение генеральной средней ожидается
в пределах от
до.

Наряду с абсолютной величиной предельной
ошибки выборки рассчитывают и относительную
ошибку, определяемую как процентное
отношение предельной ошибки выборки к
соответствующей характеристике
выборочной совокупности:

Если при выборочном наблюдении изучению
подлежит альтернативный признак, то
случайная ошибка выборки для доли
определяется в соответствии с теоремой
Я.Бернулли. так
как вероятность расхождения между
частостью и долей тоже подчиняется
закону нормального распределения, то
стандартная ошибка выборки альтернативного
признака определяется по формуле:

где pq– дисперсия
доли альтернативного признака в
генеральной совокупности.

Так как pqнеизвестно,
то на практике её заменяют дисперсией
выборочной совокупностиw(1-w)
и формула принимает вид:

Соседние файлы в папке 14-05-2013_10-41-11

Источник

Вопрос посетителя

Ответ эксперта

Источник