Исправление кратных ошибок при кодировании сообщений

В информационных системах обмен сообщениями в сетях связи или вычислительных сопровождается возмущающими воздействиями среды или нарушителя, что приводит к появлению искажений сигналов и к ошибкам в символах при цифровой передаче. Борьбу с этим явлением ведут, используя корректирующие коды. Ранее я описывал код Хемминга, и показал как исправляется одиночная ошибка в кодовом слове. Естественно возник вопрос и о ситуациях с большим количеством ошибок. Сегодня рассмотрим случай двух ошибок в кодовом слове (кратную ошибку). С одной стороны, все в теории более менее просто и понятно, но с другой — совершенно не очевидно. Изложение материала выполнено на основе работ Э. Берлекемпа.
Теоретические положения
Идея использования организованной избыточности в сообщениях привела Р. Хемминга к построению корректирующего кода описанного здесь. Линейный корректирующий (n, k)-код характеризуется проверочной (m×n) матрицей H. Требования к матрице просты: число строк совпадает с числом проверочных символов, ее столбцы должны быть отличны от нулевого и все различны. Более того, значения столбцов описывают номера позиций, занимаемых в кодовом слове символами слова, являющимися элементами конечного поля.
Часто для установления ошибочности переданного слова декодер использует вычисление синдрома, вычисляемого для этого слова. Синдром равен сумме столбцов этой матрицы, умноженных на компоненты вектора ошибки. Если в H имеется m строк и код позволяет исправлять одиночные ошибки, то длина блока (кодового слова) не превышает . Важна также выполнимость требуемой удаленности кодовых слов друг от друга.
Коды Хемминга достигают этой границы. Каждая позиция кодового слова кода Хемминга может быть занумерована двоичным вектором, совпадающим с соответствующим столбцом матрицы H. При этом синдром будет совпадать непосредственно с номером позиции, в которой произошла ошибка (если она только одна) или с двоичной суммой номеров (если ошибок несколько).
Идея векторной нумерации весьма плодотворна. Далее будем полагать и, что i-я позиция слова занумерована числом i.
Нумерацию в двоичном виде,(т.е. такое представление) называют локатором позиции. Допустим, что требуется исправлять все двойные и одиночные ошибки. Видимо, для этого потребуется большая избыточность кода, т.е. матрица H должна иметь больше строк (вдвое большое число). Поэтому будем формировать матрицу H с 2m строками и с столбцами, и эти столбцы разумно выбирать различными. В качестве первых m строк будем брать прежнюю матрицу кода Хемминга. Это базисные векторы-слова пространства слов.
Пример 1
Пусть m = 5 и n = 31. Желательно было бы получить (n, k)-код, исправляющий двойные ошибки, с проверочной матрицей Н в виде:

Для обозначенных в матрице функций fj(ξ) желательно иметь функцию, которая отображала бы множество 5-мерных векторов в себя. Последние 5 строк матрицы будут задавать код Хемминга тогда и только тогда, когда функция f является биекцией (перестановкой).
Если первые 5 строк и последние 5 строк в отдельности позволят исправлять одиночные ошибки, то возможно совместно они позволят исправлять две ошибки.
Мы должны научиться складывать, вычитать, умножать и делить двоичные 5-ти мерные векторы, представлять их многочленами степени не выше 4-ой, чтобы находить требуемую функцию fj(ξ).
Пример 2
00000 ←→ 0
00010 ←→ 1
00011 ←→ х
…
Сумма и разность таких многочленов соответствует сумме и разности векторов:
0 ± 0 = 0, 0 ± 1 = 1, 1 ± 0 = 1, 1 ± 1 = 0, знаки ± имеют в двоичном случае совпадающий смысл. Не так с умножением, показатель степени результата умножения может превысить 4.
Пример 3
.
Необходим метод понижения степеней больше 4.
Он называется (редукцией) построением вычетов по модулю неприводимого многочлена M(x) степени 5; метод состоит в переходе от многочленов произведений к их остаткам от деления на

Так что
или
Символ ≡ читается «сравнимо с».
В общем виде A(x) ≡a(x)mod M(x)
Тогда и только тогда, когда существует такой многочлен C(x), что
A(x)= M(x)C(x) +a(x) коэффициенты многочленов приводятся по модулю два:
A(x) ≡ a(x)mod(2,M(x)).
Важные свойства сравнений
Если а(x) ≡А(x)mod M(x) и b(x) ≡ B(x)mod M(x), то
а(x) ± b(x) ≡ А(x) ± B(x)mod M(x) и
а(x)·b(x) ≡ А(x)·B(x)mod M(x).
Более того, если степени многочленов а(х) и А(х) меньше степени М(х), то из формулы
а(x) ≡ А(x)mod(2,M(x)) следует, что а(x) = А(x).
Различных классов вычетов существует 2 в степени degM(x) – т.е. столько, сколько существует различных многочленов степени, меньшей m, т.е. сколько может быть различных остатков при делении. С делением еще больше сложностей.
Алгоритм деления
Для чисел.
Для данных a и M существуют однозначно определенные числа q и A, такие, что а =qM + A, 0 ≤ A ≤ M,
Для многочленов с коэффициентами из данного поля.
Для данных a(x) и M(x) существуют однозначно определенные многочлены q(x) и A(x), такие, что a(x) = q(x)M(x) + A(x), degA(x) <deg M(x).
Возможность деления многочленов обеспечивается алгоритмом Евклида.
Для чисел пример расширенного НОД описан здесь.
Для заданных a и b существуют такие числа A и B, что aA +bB = (a,b), где (a,b) – НОД чисел a и b.
Для многочленов с коэффициентами из данного поля.
Для заданных a(x) и b(x) существуют такие многочлены A(x) и B(x), что
a(x)A(x) + b(x)B(x) = (a(x), b(x)),
где (a(x), b(x)) — нормированный общий делитель a(x) и b(x) наибольшей степени.
Если а(х) и М(х) имеют общий делитель d(x) ≠ 1, то деление на a(x) по mod M(x) не всегда возможно.
Очевидно, что деление на a(x) эквивалентно умножению на A(x).
Так как если (a(x), b(x))= 1 =НОД, то согласно алгоритму Евклида, существуют такие A(x) и B(x), что a(x)A(x) + b(x)B(x) = 1, так, что a(x)A(x) ≡ 1mod b(x). Проверка того, что двоичный многочлен является неприводимым над полем GF (), выполняется непосредственным делением на всевозможные делители со степенями, меньшими, чем deg M(x).
Пример 4. делим на х и на (х + 1)
на линейные делители. Результат деления не нуль. Делим на квадратные делители . Они выдают остатки, не равные нулю. Делителей степени ≥ 3 не существует, так как их произведение дает степень ≥ 6.
Таким образом, многочлены можно складывать, вычитать, умножать и делить по модулю .
Переходим к поиску функции для проверочной матрицы H, задающей код с исправлением двойных ошибок с блоковой длиной 31 и скоростью 21/31; 31-21=10 =2t – проверочных символов = 10. Такая функция должна иметь своими корнями номера ошибочных позиций в кодовом слове, т.е. при подстановке в эту функцию номеров позиций, обращает ее в нуль.
Поиск функции
Предположим, что β1 и β2 — номера искаженных символов (позиций) слова. Используя двоичную запись чисел β1 и β2 можно представить эти номера в виде классов вычетов по модулю M(x) т.е. установить соответствие βi → β(i)(x) — двоичные многочлены степени < 5.
Первые 5 проверочных условий определяют β1 + β2; второе множество проверочных уравнений должны определять f(β1) + f(β2).
Декодер должен определить β1 и β2 по заданной системе:

Какой же должна быть функция f(x)?
Простейшая функция – это умножение на константу f(β)≡ αβ(х)modM(x).
Но тогда ξ2 = αξ1, т.е. уравнения системы зависимы. Новая пятерка проверочных условий декодеру не даст ничего нового.
Аналогично и функция f(β) = β + α не изменяет ситуацию, так как ξ2 = ξ1.
Пробуем степенные функции: сначала возьмем . При этом

Эти уравнения также зависимы, так как
Таким образом, второе уравнение является квадратом первого.
Пробуем . Уравнения декодера меняют вид:
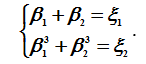
Откуда
Так что при ξ1≠0 имеем
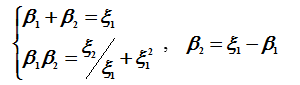
Значит, β1 и β2 удовлетворяют уравнению

Таким образом, если произошло точно две ошибки, то их локаторы удовлетворяют этому уравнению.
Так как в поле двоичных многочленов по модулю M(x) данное уравнение имеет точно 2 корня, то декодер всегда сможет найти два нужных локатора.
Если произошла только одна ошибка, то β1=ξ1 и . Следовательно, в этом случае единственная ошибка удовлетворяет уравнению β + ξ1 = 0 или 1+ ξ1β-1= 0.
Наконец, декодер всегда производит декодирование, если ошибок не произошло, то в этом случае ξ1 + ξ2 = 0 .
Более удобно (на практике) оперировать не непосредственно с многочленом, корнями которого являются локаторы ошибок, а с многочленом, корни которого взаимны к локаторам; т.е. являются к ним мультипликативным обратными величинами.
Ясно, что при не более чем двух ошибках декодер может определить номера ошибок. Если же искажаются три или более символов, то произойдет ошибка декодирования или отказ от декодирования.
Таким образом, функция подходит для построения нижних пяти строк проверочной матрицы Н двоичного кода с длиной кодовых слов 31 и 10-ю проверочными символами, исправляющего все двойные ошибки.
Первые пять проверок задают сумму номеров ошибок (S1); вторые пять проверок задают сумму кубов номеров ошибок (S3).
Процедура декодирования состоит из трех основных шагов:
- каждое полученное кодовое слово проверяется и вычисляются S1 и S3;
- находится многочлен локаторов ошибок от σ(z);
- вычисляются взаимные величины для корней σ(z) и изменяются символы в соответствующих позициях полученного слова.
Для того чтобы в принятом сообщении можно было обнаружить ошибку, это сообщение должно обладать некоторой избыточной информацией, позволяющей отличать ошибочный код от правильного. Например, если переданное сообщение состоит из трёх абсолютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следующим примером:
10110 – переданная кодовая комбинация;
10010 – 1-я принятая комбинация;
10100 – 2-я принятая комбинация;
00110 – 3-я принятая комбинация;
10110 — накопленная комбинация . Как видим, несмотря на то, что во всех трёх принятых комбинациях были ошибки накопленная не содержит ошибок1.
Принятое сообщение может также состоять из кода и его инверсии. Код инверсии посылается в канал связи как одно целое. Ошибка на приёмном конце выделяется при сопоставлении кода и его инверсии (подробнее см. тема 7).
Для того чтобы искажение любого из символов сообщения привело к запрещенной комбинации. Необходимо в коде выделить комбинации, отличающиеся друг от друга в ряде символов, часть из этих комбинаций запретить и тем самым ввести в код избыточность. Например, в равномерном блочном коде считать разрешенными кодовые комбинации с постоянным соотношением нулей и единиц в каждой кодовой комбинации. Такие коды получили название кодов с постоянным весом. Для двоичных кодов число кодовых комбинаций с постоянным весом длиной в n символов равно
![]() , (55)
, (55)
где l – число единиц в кодовом слове. Если бы не существовало условие постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно 2n. Примером кода с постоянным весом может служить стандартный телеграфный код №3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течении которых должна быть принята одна комбинация, всегда приходятся три токовые и четыре без токовые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибок.
Еще одним примером ведения избыточности в код является метод суть которого состоит в том, что к исходным кодам добавляются нули либо единицы таким образом, чтобы сумма их была всегда четной или нечетной. Сбой любого одного символа всегда нарушит условия четности(нечетности), и ошибка будет обнаружена. В этом случае комбинации друг от друга должны отличаться минимум в двух символах (см. задачу 6.9), то есть ровно половина комбинаций кода является запрещенной (запрещенными являются все нечетные комбинации при проверке на четность или наоборот).
Во всех упомянутых выше случаях сообщения обладают избыточной информацией. Избыточность сообщения говорит о том, что оно могло бы содержать большее количество информации, если бы не многократное повторение одного и того же кода не добавления коду его инверсии, не несущей никакой информации, если бы не искусственное запрещение части комбинаций кода и т. д. Но все перечисленные виды избыточности приходиться вводить для того, что бы можно было отличить ошибочную комбинацию от правильной.
Коды без избыточности обнаруживать, а тем более исправлять ошибки не могут1. минимальное количество символов, в которых любые две комбинации кода отличаются друг от друга называются кодовым расстоянием. Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называются минимальным кодовым расстоянием. Минимальное кодовое расстояние – параметр, определяющий помехоустойчивость кода и заложенную в коде избыточности. Минимальным кодовым расстоянием определяются корректирующие свойства кода.
В общем случае для обнаружения r ошибок минимальное кодовое расстояние
![]() . (56)
. (56)
Минимальное кодовое расстояние, необходимое для одновременного обнаружения и исправления ошибок,
![]() , (57)
, (57)
где s – число исправляемых ошибок.
Для кодов, только исправляющих ошибки, ![]() . (58)
. (58)
Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и посчитать число единиц в полученной комбинации (см. задачу 6.21).
Понятие кодового расстояния хорошо усваиваются на примере построения геометрических моделей кодов. На геометрических моделях вершинах n – угольников, где n – значность кода, расположены кодовые комбинации, а количества рёбер n угольника, отделяющих одну комбинацию от другой равно кодовому расстоянию (см. задачу 6.19).
Если кодовая комбинация двоичного кода A отстоит от кодовой комбинации B на расстоянии d, то это значит, что в коде A нужно d символов заменить на обратные, чтобы получить код B, но это не означает, что нужно d добавочных символов, чтобы код
обладал данными корректирующими свойствами. В двоичных кодах для обнаружения одиночной ошибки достаточно иметь 1 дополнительный символ независимо от числа информационных разрядов кода, а минимально кодовое расстояние d0=2.
Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов ![]() и числом корректирующих разрядов
и числом корректирующих разрядов ![]() должно удовлетворять следующим условиям:
должно удовлетворять следующим условиям:
![]() , (59)
, (59)
![]() , (60)
, (60)
при этом подразумевается, что общая длина кодовой комбинации
![]() . (61)
. (61)
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d0 = 3 удобно пользоваться выражениями
![]() , (62)
, (62)
если известна длина полной кодовой комбинации n, и
![]() , (63)
, (63)
если при расчетах удобней исходить из заданного числа информационных символов ![]() 1.
1.
Для кодов, обнаруживающих трёхкратные ошибки (d0=4),
![]() (64)
(64)
или
![]() . (65)
. (65)
Для кодов длиной в n символов, исправляющих одну или две ошибки (d0=5),
![]() . (66)
. (66)
Для практических расчетов можно пользоваться выражением
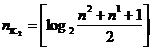 . (67)
. (67)
Для кодов, исправляющих 3 ошибки (d0=7),
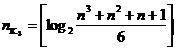 . (68)
. (68)
Для кодов, исправляющих s ошибок (d0=2s+1),
![]() . (69)
. (69)
Выражение слева известно как нижняя граница Хэмминга [16], а выражение справа – как верхняя граница Варшамова – Гильбета [3]1.
Для приближенных расчетов можно пользоваться выражением
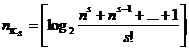 . (70)
. (70)
Можно предположить, что значение ![]() будет приближаться к верхней или нижней границе в зависимости от того, на сколько выражены выражения под знаком логарифма (см. страницу 7) приближается к целой степени двух.
будет приближаться к верхней или нижней границе в зависимости от того, на сколько выражены выражения под знаком логарифма (см. страницу 7) приближается к целой степени двух.
Линейные групповые коды
Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.
Для двоичных кодов в качестве линейной операции используют сложение по модулю 2.
Правила сложения по модулю 2 определяются следующими равенствами:
![]()
![]()
![]()
![]()
Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.
Свойства линейных кодов: сумма (разность) кодовых векторов линейного кода даёт вектор, принадлежащий данному коду.
Линейные коды образуют алгебраическую группу по отношению к операции сложению по модулю 2. в этом смысле они являются групповыми кодами.
Свойства группового кода: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.
Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов (см. задачу 6.42).
Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2 (см. задачу 6.44). Таким образом, для данного группового кода![]() .
.
Групповые коды удобно задавать матрицам, размерность которых определяется параметрами кода ![]() и
и ![]() . Число строк в матрице равно
. Число строк в матрице равно ![]() , число столбцов матрицы равно
, число столбцов матрицы равно ![]() :
:
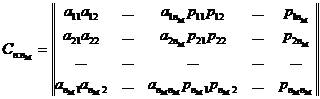 . (71)
. (71)
Коды, порождаемые этими матрицами, известны как (n;k) – коды, где k = ![]() , а соответствующие им матрицы называются порождающими, производящими, образующими.
, а соответствующие им матрицы называются порождающими, производящими, образующими.
Порождающая матрица С может быть представлена двумя матрицами И и П (информационная и проверочная). Число столбцов матрицы П равно nK, число столбцов матрицы И равно nM:
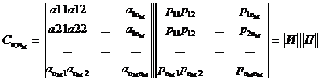 . (72)
. (72)
Теорией и практикой установлено [8,9,13], что в качестве матрицы удобно брать единичную матрицу в канонической формуле:
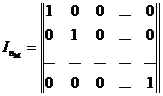 .
.
При выборе матрицы П исходят из следующих соображений: чем больше единиц в разрядах проверочной матрицы П, тем ближе соответствующий порождаемый код к оптимальному код к оптимальному1, с другой стороны, число единиц матрицы П определяет число сумматоров по модулю 2 в шифраторе и дешифратор, т. е. Чем больше единиц в матрице П, тем сложнее аппаратура. Вес каждой строки матрицы П должен быть не менее ![]() , гдеWИ – вес соответствующей строки матрицы И. Если матрица И – единичная, то WИ = 1 (удобство выбора в количестве матрицы И единичной матрицы очевидно: при WИ > 1 усложнилась бы как построение кодов, так и их технологическая реализация).
, гдеWИ – вес соответствующей строки матрицы И. Если матрица И – единичная, то WИ = 1 (удобство выбора в количестве матрицы И единичной матрицы очевидно: при WИ > 1 усложнилась бы как построение кодов, так и их технологическая реализация).
При соблюдении перечисленных условий любую порождающую матрицу группового кода можно привести к следующему виду:
![]() …
… ![]() …
… ![]()
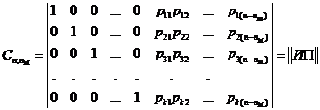 ,
,
называемому левой канонической формой порождающей матрицы.
Для кодов с ![]() производящая матрица С имеет вид:
производящая матрица С имеет вид:

![]() .
.
Во всех комбинациях кода, построенного при помощи такой матрицы, четное число единиц.
Для кодов с ![]() порождающая матрица не может быть представлена в форме, общей для всех видов с данными
порождающая матрица не может быть представлена в форме, общей для всех видов с данными ![]() . Вид матрицы зависит от конкретных требований к порождаемому коду (в качестве примера построения некоторого абстрактного группового кода с
. Вид матрицы зависит от конкретных требований к порождаемому коду (в качестве примера построения некоторого абстрактного группового кода с ![]() может быть предложена задача 6.48). Этим требованиям могут быть либо минимум корректирующих разрядов, либо максимальная простата аппаратуры.
может быть предложена задача 6.48). Этим требованиям могут быть либо минимум корректирующих разрядов, либо максимальная простата аппаратуры.
Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными или совершенными кодами.
Для кодов с ![]() соотношения n и n0 следующее: (3;1), (7;4), (15;11), (31;26), (63;57) и т. д. (см., например, задачу 6.52).
соотношения n и n0 следующее: (3;1), (7;4), (15;11), (31;26), (63;57) и т. д. (см., например, задачу 6.52).
Плотно упакованные коды, оптимальные с точки зрения минимума избыточных символов, обнаруживающие максимально возможное количество вариантов ошибок кратностью ![]() ,
, ![]() и имеющие
и имеющие ![]() и
и ![]() , были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь
, были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь
комбинации с максимальным весом. Для этого при построении кодов с ![]() последовательно используются векторы длиной
последовательно используются векторы длиной ![]() , весом
, весом ![]() ,
, ![]() , …,
, …, ![]() (см. задачи 6.50; 6.65). Тем же Слепяном в работе[11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом
(см. задачи 6.50; 6.65). Тем же Слепяном в работе[11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом ![]() (см. задачи 6.55; 6.65). если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяют условию
(см. задачи 6.55; 6.65). если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяют условию ![]() , больше
, больше ![]() , то в первом случае не используют наборы с наименьшим весом, а во втором – с наибольшим.
, то в первом случае не используют наборы с наименьшим весом, а во втором – с наибольшим.
Строчки образующей матрицы С представляют собой ![]() комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй , третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита (см. задачу 6.57).
комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй , третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита (см. задачу 6.57).
Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом:
![]()
![]()
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
![]()
или ![]() (73)
(73)
В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом:
![]() , j = 1, 2, …,
, j = 1, 2, …, ![]() . (74) Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом p1 входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд p2 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода
. (74) Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом p1 входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд p2 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода ![]() (см. задачу 6.60).
(см. задачу 6.60).
В результате осуществления проверок образуется проверочный вектор![]() ,
,![]() , …,
, …, ![]() , который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор (см. задачи 6.60; 6.62).
, который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор (см. задачи 6.60; 6.62).
Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н, которая представляет собой транспонированную матрицу П, дополненную единичной матрицей ![]() , число столбцов которой равно числу проверочных разрядов кода:
, число столбцов которой равно числу проверочных разрядов кода:![]() .
.
Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н (см. задачи 6.60; 6.62).
Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему.
Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы ![]() . В первом столбце второй строки размещается вектор
. В первом столбце второй строки размещается вектор ![]() , вес которого равен 1.
, вес которого равен 1.
Остальные позиции второй строки заполняются векторами, по лученными в результате суммирования по модулю 2 вектора ![]() с вектором
с вектором ![]() расположенными в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор
расположенными в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор ![]() , вес которого также равен 1, однако, если вектор
, вес которого также равен 1, однако, если вектор ![]() содержит единицу в первом разряде, то
содержит единицу в первом разряде, то ![]() — во втором. В остальные позиции третьей строки записывают суммы
— во втором. В остальные позиции третьей строки записывают суммы ![]() и
и ![]() .
.
Аналогично поступают до тех пор, пока не будут просуммированы с векторами ![]() все векторы
все векторы ![]() , весом 1, с единицами в каждом из n разрядов. Затем суммируются по модулю 2 векторы
, весом 1, с единицами в каждом из n разрядов. Затем суммируются по модулю 2 векторы ![]() , с весом 2, с последовательным перекрытием всех возможных разрядов. Все вектора
, с весом 2, с последовательным перекрытием всех возможных разрядов. Все вектора ![]() определяет число исправляемых ошибок. Число векторов
определяет число исправляемых ошибок. Число векторов ![]() определяется возможным числом неповторяющихся синдромов и равно
определяется возможным числом неповторяющихся синдромов и равно ![]() (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определить один-единственный соответствующий ему вектор
(нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определить один-единственный соответствующий ему вектор ![]() . Векторы
. Векторы ![]() есть векторы ошибок, которые могут быть исправлены данным групповым кодом.
есть векторы ошибок, которые могут быть исправлены данным групповым кодом.
По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинацией ![]() с вектором ошибки
с вектором ошибки ![]() , т. е. к определенной строке кодовой табл. 6.1.
, т. е. к определенной строке кодовой табл. 6.1.
Таблица 6.1.
Ar |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
Принятая кодовая комбинация ![]() сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы (см. задачу 6.68). процесс исправления ошибки заключается в замене на обратное значение разрядов., соответствующих единицам в векторе ошибок
сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы (см. задачу 6.68). процесс исправления ошибки заключается в замене на обратное значение разрядов., соответствующих единицам в векторе ошибок ![]() .
.
Векторы ![]() ,
, ![]() , …,
, …, ![]() не должны быть равны ни одному из векторов
не должны быть равны ни одному из векторов ![]() ,
, ![]() , …,
, …, ![]() в противном случае в таблице появились бы нулевые векторы.
в противном случае в таблице появились бы нулевые векторы.
Тривиальные систематические коды. Код Хэмминга.
Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.
Тривиальные систематические коды могут строиться, как и групповые, на основе производящей матрицы. Обычно производящая матрица строится при помощи матриц единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее ![]() единиц, а сумма по модулю для любых строк не менее
единиц, а сумма по модулю для любых строк не менее ![]() единиц (где
единиц (где ![]() минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю для строк производящей матрицы во всех возможных сочетаниях (см. например, задачу 6.74).
минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю для строк производящей матрицы во всех возможных сочетаниях (см. например, задачу 6.74).
Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных символов, либо количество информационных комбинаций ![]() . При помощи (59) и (60) вычисляются
. При помощи (59) и (60) вычисляются ![]() и
и ![]() . Соотношения между n,
. Соотношения между n, ![]() , и
, и ![]() для Хэмминга предоставлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону
для Хэмминга предоставлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону ![]() , где
, где ![]() 0, 1, 2 и т. д. — натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.
0, 1, 2 и т. д. — натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.
Затем определяется значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на контрольных позициях должна быть четной. Если эта сумма четна, то значение контрольного коэффициента — 0, в противно случае — 1.
Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы:
![]() .
.
Первой строке соответствует проверочный коэффициент ![]() , второй
, второй ![]() и т. д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т. е.
и т. д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т. е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д.; во вторую — коэффициенты, содержащие 1 во втором разряде, т. е.
и т. д.; во вторую — коэффициенты, содержащие 1 во втором разряде, т. е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д.; в третью проверку — коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствует номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также и порядок следования разрядов в получения разрядов в полученном двоичном коде.
и т. д.; в третью проверку — коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствует номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также и порядок следования разрядов в получения разрядов в полученном двоичном коде.
Если в принятом коде есть ошибка, то результат проверок по контрольным позициям образует двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции а обратный (см. задачу 6.78).
Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации всегда была четной. Тогда в случае одиночной ошибки проверки по позициям укажут на наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки (см. задачу 6.82).
Циклические коды.
Циклические коды [4, 6, 7, 9, 12, 13] названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путем циклического сдвига одной или нескольких комбинацикода. Циклический сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Циклические коды, практически1, все относятся к систематическим кодам, в них контрольные и информационные разряды расположены на строго определенных местах. Кроме того, циклические коды относятся к числу блочных кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно.
Идея построения циклических кодов базируется на использовании неприводимых в поле[1] двоичных чисел многочленов. Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней с коэффициентами из того же поля, так же, как простые числа не могут быть представлены произведением других чисел. Иными словами, неприводимые многочлены делятся без остатка только на себя или на единицу.
Неприводимые многочлены в теории циклических кодов играют роль образующих (генераторных, производящих) многочленов. Если заданную кодовую комбинацию умножить на выбранный неприводимый многочлен, то получим циклический код, корректирующие способности которого определяются неприводимым многочленом.
Предположим, требуется закодировать одну из комбинаций четырехзначного двоичного кода. Предположим также, что эта комбинация ![]() . Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен
. Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен ![]() . Затем умножим
. Затем умножим ![]() на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени n степень каждого члена многочлена повысится на n, что эквивалентно приписыванию n нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:
на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени n степень каждого члена многочлена повысится на n, что эквивалентно приписыванию n нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:
![]()
Это делается для того, чтобы впоследствии на мест этих нулей можно было бы записать корректирующие разряды.
Значение корректирующих разрядов находят по результату от деления ![]() на
на ![]() :
:
|
|
|
||||||
|
|
|
||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
или
|
1101000 |
1011 |
|||||||
|
1011 |
1111+ |
|||||||
|
1100 |
||||||||
|
1011 |
||||||||
|
1110 |
||||||||
|
1011 |
||||||||
|
1010 |
||||||||
|
1011 |
||||||||
|
001 |
||||||||
Таким образом,
![]() ,
,
или в общем виде
![]() , (75)
, (75)
где ![]() частное, а
частное, а ![]() остаток от деления
остаток от деления ![]() на
на ![]() .
.
Так как в двоичной арифметике ![]() , а значит,
, а значит, ![]() , то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида
, то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида ![]() можно записать и как
можно записать и как ![]() , и как
, и как ![]() . Все три равенства данном случае означают, что либо a и b равны 0, либо a и b равны 1, т. е. имеют одинаковую четность.
. Все три равенства данном случае означают, что либо a и b равны 0, либо a и b равны 1, т. е. имеют одинаковую четность.
Таким образом, выражение (75) можно записать как
![]() , (76)
, (76)
что в случае нашего примера даст
![]()
или
![]() 1 1 1 1
1 1 1 1 ![]() 1 0 1 1 = 1 1 0 1 0 0 0 + 0 0 1 =
1 0 1 1 = 1 1 0 1 0 0 0 + 0 0 1 =
=1 1 0 1 0 0 1
Многочлен 1101001 и есть искомая комбинация, где 1101 – информационная часть, а 001 – контрольные символы. Заметим, что искомую комбинацию мы получили бы и как в результате умножения одной из комбинаций полного четырехзначного двоичного кода (в двоичном случае 1111) на образующий многочлен, так и умножением заданной комбинации на одночлен, имеющий ту же степень, что и выбранный образующий многочлен (в нашем случае таким образом была получена комбинация 1101000) с последующим добавлением к полученному произведению остатка от деления этого произведения на образующий многочлен (в нашем примере остаток имел вид 001).
Таким образом, мы уже знаем два способа образования комбинаций линейных систематических кодов, к которым относятся и интересующие нас циклические коды. Эти способы явились теоретическим основанием для построения кодирующих и декодирующих устройств.
Шифраторы циклических кодов, в том или ином виде, построены по принципу умножения двоичных многочленов. Кодовые комбинации получаются в результате сложения соседних комбинаций по модулю два, что, как мы увидим ниже, эквивалентно умножению первой комбинации на двучлен ![]() .
.
Итак, комбинации циклических кодов можно представить в виде многочлена, у которых показатели степени x соответствуют номером разрядов, коэффициенты при x равны 0 или 1 в зависимости от того, стоит 0 или 1 в разряде кодовой комбинации , которую представляет данный многочлен. Например,
000101![]() ;
;
001010![]() ;
;
010100![]() ;
;
101000![]() .
.
Циклический сдвиг кодовой комбинации аналогичен умножению соответствующего многочлена на x:
![]() ;
;
![]() ;
;
![]() .Если степень многочлена достигает разрядности кода, то происходит «перенос» в нулевую степень при x. В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда.
.Если степень многочлена достигает разрядности кода, то происходит «перенос» в нулевую степень при x. В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда.
Сложение по модулю 2 любых двух соседних комбинаций циклического кода эквивалентного операции умножения многочлена соответствующего комбинации первого слагаемого на многочлен ![]() , если приведение подобных членов осуществляется по модулю 2:
, если приведение подобных членов осуществляется по модулю 2:
|
0 0 0 1 0 1 |
|
|
|||
|
|
|
||||
|
0 0 1 0 1 0 |
|
||||
|
0 0 1 1 1 1 |
|
||||
|
|
|
||||
|
|
|
||||
т. е. существует принципиальная возможность получения любой кодовой комбинации циклического кода путем умножения соответствующим образом подобного образующего многочлена на некоторый другой многочлен.
Однако мало построить циклический код. Надо уметь выделить из него возможные ошибочные разряды, т. е. ввести некоторые опознаватели ошибок, которые выделяли бы ошибочный блок из всех других. Так, как циклические коды – блочные, то каждый блок должен иметь свой опознаватель. И тут решающую роль играют свойства образующего многочлена ![]() . Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклического кодов.
. Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклического кодов.
С другой стороны, остатки от деления единицы с нулями на образующий многочлен используются для построения циклических кодов (возможность этого видна из выражения (76)).
При делении единицы с нулями образующих многочлен следует помнить, что длина остатка должна быть не меньше числа контрольных разрядов, поэтому в случае нехватки разрядов в остатке к остатку приписывают справа необходимое число нулейНапример,
|
1 0 0 0 0 0 0 0 0 0 0 |
1 0 1 1 |
||||||||||
|
1 0 1 1 |
1 1 1 1 1 + |
||||||||||
|
0 1 1 0 0 |
|||||||||||
|
1 0 1 1 |
Остатки |
||||||||||
|
1 1 1 0 |
0 1 1 |
||||||||||
|
1 0 1 1 |
1 1 0 |
||||||||||
|
1 0 1 0 |
1 1 1 |
||||||||||
|
1 0 1 1 |
1 0 1 |
||||||||||
|
1 0 0 0 |
0 0 1 |
||||||||||
|
1 0 1 1 |
0 1 0 |
||||||||||
|
1 1 |
1 0 0 |
||||||||||
|
0 1 1 |
|||||||||||
|
1 1 0 |
|||||||||||
|
и т. д., |
|||||||||||
начиная с восьмого, остатки будут повторятся.
Остатки от деления используют для построения образующих матриц, которые, благодоря вой наглядности и удобству получения производных комбинаций, получили широкое распространение для построения циклических кодов. Построение образующей матицы сводится к составлению единичной транспонированной и дополнительной матрицы, элементы которой представляют собой остатки от деления единицы с нулями на образующий многочлен ![]() 1. Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой – нули, кроме элементов, расположенных по диагонали справа на лево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева на права сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы.
1. Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой – нули, кроме элементов, расположенных по диагонали справа на лево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева на права сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы.
Однако не все остатки от деления единицы с нулями на образующий многочлен могут быть использованы в качестве элементов дополнительной матрицы. Использоваться могут лишь те остатки вес которых ![]() , где
, где ![]() минимальное кодовое расстояние длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.
минимальное кодовое расстояние длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.
Строки образующие матрицы представляют собой первые комбинации искомого кода. Остальные комбинации кода получаются в результате суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы (см. задачу 6.108)1.
Описанный выше метод построения образующих матриц не является единственным. Образующая матрица может быть построена в результате непосредственного умножения элементов единичной матрицы на образующий многочлен. Это часто бывает удобнее чем нахождение остатков от деления. Полученные коды ничем не отличаются от кодов, построенных по образующим матрицам, а которых дополнительная матрица состоит из остатков от деления единицы с нулями на образующий многочлен ( см. задачи 6.103; 6.108; 6.110).
Образующая матрица может быть построена таким путем циклического сдвига комбинации, полученной в результате умножения строки единичной матрицы ранга ![]() на образующий многочлен (см. задачу 6.126).
на образующий многочлен (см. задачу 6.126).
В заключение предлагаем еще один метод построения циклических кодов. Достоинством этого метода является исключительная простота схемных реализаций кодирующих и декодирующих устройств.
Для получения комбинаций циклического кода в этом случае достаточно произвести циклический сдвиг строки образующей матрицы и комбинации, являющейся ее зеркальным отображением (см. задача 6.112). При построении кодов с ![]() число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации (см. задачи 6.103; 6.112). Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при
число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации (см. задачи 6.103; 6.112). Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при ![]() число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы (см., например, задачи 6.123 и 6.128).
число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы (см., например, задачи 6.123 и 6.128).
Число ненулевых комбинаций, получаемых в результате суммирования по модулю 2 всевозможных два строк образующей матрицы,
![]() , (77)
, (77)
где ![]() число информационных разрядов кода2.
число информационных разрядов кода2.
Число ненулевых комбинаций, получаемых в результате циклического сдвига любой строки образующей матрицы и зеркальной ей комбинации,
![]() , (78)
, (78)
где n – длина кодовой комбинации.
При числе информационных разрядов ![]() число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий.
число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий.
Ошибки в циклических кодах обнаруживаются и исправляются при помощи остатков от деления полученной комбинации на образующий многочлен. Остатки от деления являются опознавателями ошибок, но не указывают непосредственно на место ошибки в циклическом коде.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется»под остаток таким образом, что в сумме с остатком она дает исправленную комбинацию. Остаток при этом представляет собой не что иное, как разницу между искаженными и правильными символами, единицы в остатке стоят как раз на местах искаженных разрядов в подогнанной циклическими сдвигами комбинации. Подгоняют искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть либо равно числу ошибок s; исправляемых данным кодом (код исправляют 3 ошибки и в искаженной комбинации 3 ошибки), либо меньше s (код исправляет 3 ошибки, а в принятой комбинации – 1 ошибка).
Место ошибки в кодовой комбинации не имеет значения. Если ![]() , то после определенного количества сдвигов все ошибки окажутся в зоне «разового» действия образующего многочлена, т. е. достаточно получить один остаток, вес которого
, то после определенного количества сдвигов все ошибки окажутся в зоне «разового» действия образующего многочлена, т. е. достаточно получить один остаток, вес которого ![]() , и этого уже будет достаточно для исправления искажаемой комбинации. В смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s.
, и этого уже будет достаточно для исправления искажаемой комбинации. В смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s.
Подробно процесс исправления ошибок рассматривается ниже на примере построения конкретных кодов.
Построение и декодирование конкретных циклических кодов.
I. Коды исправляющие одиночную ошибку, ![]() .
.
1. Расчет соотношения между контрольными и информационными символами кода производятся на основании выражений (59) — (69).
Если задано число информационных разрядов ![]() , то число контрольных разрядов
, то число контрольных разрядов ![]() находим из выражения
находим из выражения
![]() .
.
Общее число символов кода
![]() .
.
Если задана длина кода n, то число контрольных разрядов
![]() .
.
Соотношение числа контрольных и информационных символов для кодов с ![]() приведены в табл. 3 приложения 9.
приведены в табл. 3 приложения 9.
2. Выбор образующего многочлена производится по таблицам неприводимых двоичных многочленов.
Образующий многочлен ![]() следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов
следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов ![]() , а число ненулевых членов – не меньше минимального кодового расстояния
, а число ненулевых членов – не меньше минимального кодового расстояния ![]() .
.
Выбор параметров единичной транспонированной матрицы происходит из условия, что число столбцов (строк) матрицы определяется числом информационных разрядов, т. е. ранг единичной матрицы равен ![]() .
.
3. Определение элементов дополнительной матрицы производится по остаткам от деления последней строки транспонированной матрицы (единицы с нулями) на образующий многочлен. Полученные остатки должны удовлетворять следующим требованиям:
а) число разрядов каждого остатка должно быть равно числу контрольных символов ![]() , следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена;
, следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена;
б) число остатков должно быть не меньше числа строк единичной транспонированной матрицы, т. е. должно быть равно числу информационных разрядов ![]() ;
;
в) число единиц каждого остатка, т. е . его вес должно быть не менее величены ![]() , где
, где ![]() минимальное кодовое расстояние, не меньше числа обнаруженных ошибок;
минимальное кодовое расстояние, не меньше числа обнаруженных ошибок;
г) количество нулей, приписанных к единице с нулями в делении ее на выбранный неприводимый многочлен, должно быть таким, чтобы соблюдались условия а), б), в).
4. Образующая матрица составляется дописыванием элементов дополнительной матрицы справа от единичной транспонированной матрицы либо умножением элементов единичной матрицы на образующий многочлен.
5. Комбинациями искомого кода являются строки образующий матрицы и все возможные суммы по модулю 2 различных сочетаний строк образующей матрицы (см. задачу 6.108).
Как видно из решения задач 6.103 и 6.108, коды, получены при использовании неприводимых многочленов ![]() и
и ![]() , подобны друг другу и обладают равноценными корректирующими способностями. Сами же многочлены 1101 и 1011 называют обратными, или двойственными, многочленам. Если данный многочлен неприводимый, то неприводимый будет и двойственный ему многочлен.
, подобны друг другу и обладают равноценными корректирующими способностями. Сами же многочлены 1101 и 1011 называют обратными, или двойственными, многочленам. Если данный многочлен неприводимый, то неприводимый будет и двойственный ему многочлен.
6. Обнаружение и исправление ошибок производится по остатку от деления принятой комбинации ![]() на образующий многочлен
на образующий многочлен ![]() . Если принятая комбинация делится на образующий многочлен без остатка, то код принят без ошибочно. Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции:
. Если принятая комбинация делится на образующий многочлен без остатка, то код принят без ошибочно. Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции:
а) принятую комбинацию делят на образующий многочлен;
б) подсчитывают количество единиц в остатке (вес остатка). Если ![]() , где s – допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если
, где s – допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если ![]() , то
, то
в) производят циклический сдвиг принятой комбинация ![]() влево на один разряд. Комбинацию, полученную в результате этого повторного деления
влево на один разряд. Комбинацию, полученную в результате этого повторного деления ![]() , то делимое суммируют с остатком, затем
, то делимое суммируют с остатком, затем
г) производят циклический сдвиг вправо на один разряд комбинации, полученной в результате суммирования последнего делим, с последним остатком. Полученная в результате комбинация уже не содержит ошибок. Если после первого циклического сдвига последующего деления остаток получается таким, что его вес ![]() ,
,
д) повторяют операцию пункта в) до тех пор, пока не будет ![]() . В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатка от деления этой комбинации на образующий многочлен, а затем
. В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатка от деления этой комбинации на образующий многочлен, а затем
е) производят циклический сдвиг вправо ровно на столько разрядов, на сколько была сдвинута суммируемая с последним остатком
комбинации относительно принятой комбинации. В результате получим исправленную комбинацию (см. задачи 6.113 – 6.116)1.
II. Коды обнаруживающие трехкратные ошибки. ![]() .
.
1. Выбор числа корректирующих разрядов производится из соотношения
![]() ,
,
или
![]() .
.
2. Выбор образующего многочлена производят, исходя из следующих соображений: для обнаружения трехкратной ошибки
![]() ,
,
Поэтому степень образующего многочлена не может быть меньше четырех; многочлен третьей степени, имеющий число ненулевых членов больше или равное трем, позволяет обнаруживать все двойные ошибки (см. задачи 6.121; 6.122), многочлен первой степени (х+1) обнаруживает любое количество нечетных ошибок (см. задачи 6.119; 6.120), следовательно, многочлен четвертой степени, получаемый в результате умножения этих многочленов, обладает их корректирующими свойствами: может обнаруживать две ошибки а также одну и три, т. е. все трехкратные ошибки (см. задачу 6.117).
3. Построение образующей матрицы производят либо нахождением остатков от деления единицы с нулями на образующий многочлен, либо умножением строк единичной матрицы на образующий многочлен (си. задачу 6.121).
4. Остальные комбинации корректирующего кода находят суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы.
5. Обнаружение ошибок производится по остаткам от деления принятой комбинации ![]() на образующий многочлен
на образующий многочлен ![]() . Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3.П р и м е р. Исходная кодовая комбинация – 0101111000, принятая – 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибки если известно, что комбинации кода были образованы при помощи многочлена 101111.
. Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3.П р и м е р. Исходная кодовая комбинация – 0101111000, принятая – 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибки если известно, что комбинации кода были образованы при помощи многочлена 101111.
|
Р е ш е н и е. |
0 0 0 1 0 1 1 0 0 1 |
1 0 1 1 1 1 |
|
|
1 0 1 1 1 1 |
|||
|
0 0 0 0 1 1 1 |
|||
Остаток ненулевой, комбинация бракуется. Указать ошибочные разряды при трехкратных искажениях такие коды не могут.
III. Циклические коды, исправляющие две и большее количество ошибок, ![]() .
.
Методика построения циклических кодов с ![]() отличается от методики построения циклических кодов
отличается от методики построения циклических кодов ![]() только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем – авторов методики построения циклических кодов с
только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем – авторов методики построения циклических кодов с ![]() ).
).
Построение образующего многочлена зависит в основном, от двух параметров: от длины кодового слова n и от числа исправляемых ошибок s. Остальные параметры, участвующие в построении образующего многочлена в зависимости от заданных n и s могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже.
Для исправления числа ошибок ![]() еще недостаточно условие, что бы между комбинациями кода минимальное кодовое расстояние
еще недостаточно условие, что бы между комбинациями кода минимальное кодовое расстояние ![]() , необходимо также чтобы длина кода n удовлетворяла условию
, необходимо также чтобы длина кода n удовлетворяла условию
![]() , (79)
, (79)
при этом n всегда будет нечетным числом. Величина h определяет выбор числа контрольных символов ![]() и связанна с
и связанна с ![]() и s следующим соотношением:
и s следующим соотношением:
![]() . (80)
. (80)
C другой стороны, число контрольных символов определяется образующим много членом и равно его степени (к этому вопросу мы еще вернемся). При больших значениях h длина кода n становиться очень большой, что вызывает вполне определенные трудности при технической реализации кодирующих и декодирующих устройств. При этом часть информационных разрядов порой остается неиспользованной. В таких случаях для определения h удобно пользоваться выражением
![]() , (81)
, (81)
где С является одним из сомножителей на которое разлагается число n.
Соотношение между n, С и h могут быть сведены в следующую таблицу:
|
№ п/п |
h |
|
C |
|
1 |
3 |
7 |
1 |
|
2 |
4 |
15 |
5; 3 |
|
3 |
5 |
31 |
1 |
|
4 |
6 |
63 |
7; 3; 3 |
|
5 |
7 |
127 |
1 |
|
6 |
8 |
255 |
17; 5; 3 |
|
7 |
9 |
511 |
7; 3; 7 |
|
8 |
10 |
1023 |
31; 11; 3 |
|
9 |
11 |
2047 |
89; 23 |
|
10 |
12 |
4095 |
3; 3; 5; 7; 13 |
Например, при h=10 длина кодовой комбинации может быть равна и 1023 (C=1) и 341 (С=3), и 33 (С=31), и 31 (С=33), понятно, что n не может быть меньше![]() . Величина С влияет выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются С. сказанное выше хорошо усваивается на конкретном примере (см. задачу 6.132).
. Величина С влияет выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются С. сказанное выше хорошо усваивается на конкретном примере (см. задачу 6.132).
Построение образующего многочлена ![]() производится при помощи так называемых минимальных многочленов
производится при помощи так называемых минимальных многочленов ![]() , которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок
, которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок ![]() определяет номер последнего из выбираемых табличных минимальных многочленов
определяет номер последнего из выбираемых табличных минимальных многочленов
![]() , (82)
, (82)
Порядок многочлена используется при определении числа сомножителей ![]() . Например, если s=6, то
. Например, если s=6, то ![]() . Так как для построения
. Так как для построения ![]() используются только нечетные многочлены, то ими будут:
используются только нечетные многочлены, то ими будут: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() , старший из них имеет порядок
, старший из них имеет порядок ![]() . Как видим число сомножителей
. Как видим число сомножителей ![]() равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,
равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,
![]() , (83)
, (83)
а старшая степень
![]() (84)
(84)
(l указывает колонку в таблице минимальных многочленов, из которой обычно выбирается многочлен для построения ![]() ).
).
Степень образующего многочлена полученного в результате перемножения выбранных минимальных многочленов,
![]() . (85)
. (85)
В общем виде
![]() , (86)
, (86)
Декодирование кодов БЧХ производится по той же методике, что и декодирование циклических кодов с ![]() . Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с n
. Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с n![]() 15, могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию полученную после k-кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на n – k циклических сдвигов. Это целесообразно делать только при
15, могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию полученную после k-кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на n – k циклических сдвигов. Это целесообразно делать только при ![]() (см. задачу 6.134).
(см. задачу 6.134).
Предлагаю ознакомиться с аналогичными статьями:
Исправление кратных ошибок при кодировании сообщений
Время на прочтение
6 мин
Количество просмотров 2.7K

В информационных системах обмен сообщениями в сетях связи или вычислительных сопровождается возмущающими воздействиями среды или нарушителя, что приводит к появлению искажений сигналов и к ошибкам в символах при цифровой передаче. Борьбу с этим явлением ведут, используя корректирующие коды. Ранее я описывал код Хемминга, и показал как исправляется одиночная ошибка в кодовом слове. Естественно возник вопрос и о ситуациях с большим количеством ошибок. Сегодня рассмотрим случай двух ошибок в кодовом слове (кратную ошибку). С одной стороны, все в теории более менее просто и понятно, но с другой — совершенно не очевидно. Изложение материала выполнено на основе работ Э. Берлекемпа.
Теоретические положения
Идея использования организованной избыточности в сообщениях привела Р. Хемминга к построению корректирующего кода описанного здесь. Линейный корректирующий (n, k)-код характеризуется проверочной (m×n) матрицей H. Требования к матрице просты: число строк совпадает с числом проверочных символов, ее столбцы должны быть отличны от нулевого и все различны. Более того, значения столбцов описывают номера позиций, занимаемых в кодовом слове символами слова, являющимися элементами конечного поля.
Часто для установления ошибочности переданного слова декодер использует вычисление синдрома, вычисляемого для этого слова. Синдром равен сумме столбцов этой матрицы, умноженных на компоненты вектора ошибки. Если в H имеется m строк и код позволяет исправлять одиночные ошибки, то длина блока (кодового слова) не превышает . Важна также выполнимость требуемой удаленности кодовых слов друг от друга.
Коды Хемминга достигают этой границы. Каждая позиция кодового слова кода Хемминга может быть занумерована двоичным вектором, совпадающим с соответствующим столбцом матрицы H. При этом синдром будет совпадать непосредственно с номером позиции, в которой произошла ошибка (если она только одна) или с двоичной суммой номеров (если ошибок несколько).
Идея векторной нумерации весьма плодотворна. Далее будем полагать и, что i-я позиция слова занумерована числом i.
Нумерацию в двоичном виде,(т.е. такое представление) называют локатором позиции. Допустим, что требуется исправлять все двойные и одиночные ошибки. Видимо, для этого потребуется большая избыточность кода, т.е. матрица H должна иметь больше строк (вдвое большое число). Поэтому будем формировать матрицу H с 2m строками и с столбцами, и эти столбцы разумно выбирать различными. В качестве первых m строк будем брать прежнюю матрицу кода Хемминга. Это базисные векторы-слова пространства слов.
Пример 1
Пусть m = 5 и n = 31. Желательно было бы получить (n, k)-код, исправляющий двойные ошибки, с проверочной матрицей Н в виде:

Для обозначенных в матрице функций fj(ξ) желательно иметь функцию, которая отображала бы множество 5-мерных векторов в себя. Последние 5 строк матрицы будут задавать код Хемминга тогда и только тогда, когда функция f является биекцией (перестановкой).
Если первые 5 строк и последние 5 строк в отдельности позволят исправлять одиночные ошибки, то возможно совместно они позволят исправлять две ошибки.
Мы должны научиться складывать, вычитать, умножать и делить двоичные 5-ти мерные векторы, представлять их многочленами степени не выше 4-ой, чтобы находить требуемую функцию fj(ξ).
Пример 2
00000 ←→ 0
00010 ←→ 1
00011 ←→ х
…
Сумма и разность таких многочленов соответствует сумме и разности векторов:
0 ± 0 = 0, 0 ± 1 = 1, 1 ± 0 = 1, 1 ± 1 = 0, знаки ± имеют в двоичном случае совпадающий смысл. Не так с умножением, показатель степени результата умножения может превысить 4.
Пример 3
.
Необходим метод понижения степеней больше 4.
Он называется (редукцией) построением вычетов по модулю неприводимого многочлена M(x) степени 5; метод состоит в переходе от многочленов произведений к их остаткам от деления на

Так что
или
Символ ≡ читается «сравнимо с».
В общем виде A(x) ≡a(x)mod M(x)
Тогда и только тогда, когда существует такой многочлен C(x), что
A(x)= M(x)C(x) +a(x) коэффициенты многочленов приводятся по модулю два:
A(x) ≡ a(x)mod(2,M(x)).
Важные свойства сравнений
Если а(x) ≡А(x)mod M(x) и b(x) ≡ B(x)mod M(x), то
а(x) ± b(x) ≡ А(x) ± B(x)mod M(x) и
а(x)·b(x) ≡ А(x)·B(x)mod M(x).
Более того, если степени многочленов а(х) и А(х) меньше степени М(х), то из формулы
а(x) ≡ А(x)mod(2,M(x)) следует, что а(x) = А(x).
Различных классов вычетов существует 2 в степени degM(x) – т.е. столько, сколько существует различных многочленов степени, меньшей m, т.е. сколько может быть различных остатков при делении. С делением еще больше сложностей.
Алгоритм деления
Для чисел.
Для данных a и M существуют однозначно определенные числа q и A, такие, что а =qM + A, 0 ≤ A ≤ M,
Для многочленов с коэффициентами из данного поля.
Для данных a(x) и M(x) существуют однозначно определенные многочлены q(x) и A(x), такие, что a(x) = q(x)M(x) + A(x), degA(x) <deg M(x).
Возможность деления многочленов обеспечивается алгоритмом Евклида.
Для чисел пример расширенного НОД описан здесь.
Для заданных a и b существуют такие числа A и B, что aA +bB = (a,b), где (a,b) – НОД чисел a и b.
Для многочленов с коэффициентами из данного поля.
Для заданных a(x) и b(x) существуют такие многочлены A(x) и B(x), что
a(x)A(x) + b(x)B(x) = (a(x), b(x)),
где (a(x), b(x)) — нормированный общий делитель a(x) и b(x) наибольшей степени.
Если а(х) и М(х) имеют общий делитель d(x) ≠ 1, то деление на a(x) по mod M(x) не всегда возможно.
Очевидно, что деление на a(x) эквивалентно умножению на A(x).
Так как если (a(x), b(x))= 1 =НОД, то согласно алгоритму Евклида, существуют такие A(x) и B(x), что a(x)A(x) + b(x)B(x) = 1, так, что a(x)A(x) ≡ 1mod b(x). Проверка того, что двоичный многочлен является неприводимым над полем GF (), выполняется непосредственным делением на всевозможные делители со степенями, меньшими, чем deg M(x).
Пример 4. делим на х и на (х + 1)
на линейные делители. Результат деления не нуль. Делим на квадратные делители . Они выдают остатки, не равные нулю. Делителей степени ≥ 3 не существует, так как их произведение дает степень ≥ 6.
Таким образом, многочлены можно складывать, вычитать, умножать и делить по модулю .
Переходим к поиску функции для проверочной матрицы H, задающей код с исправлением двойных ошибок с блоковой длиной 31 и скоростью 21/31; 31-21=10 =2t – проверочных символов = 10. Такая функция должна иметь своими корнями номера ошибочных позиций в кодовом слове, т.е. при подстановке в эту функцию номеров позиций, обращает ее в нуль.
Поиск функции
Предположим, что β1 и β2 — номера искаженных символов (позиций) слова. Используя двоичную запись чисел β1 и β2 можно представить эти номера в виде классов вычетов по модулю M(x) т.е. установить соответствие βi → β(i)(x) — двоичные многочлены степени < 5.
Первые 5 проверочных условий определяют β1 + β2; второе множество проверочных уравнений должны определять f(β1) + f(β2).
Декодер должен определить β1 и β2 по заданной системе:

Какой же должна быть функция f(x)?
Простейшая функция – это умножение на константу f(β)≡ αβ(х)modM(x).
Но тогда ξ2 = αξ1, т.е. уравнения системы зависимы. Новая пятерка проверочных условий декодеру не даст ничего нового.
Аналогично и функция f(β) = β + α не изменяет ситуацию, так как ξ2 = ξ1.
Пробуем степенные функции: сначала возьмем . При этом

Эти уравнения также зависимы, так как
Таким образом, второе уравнение является квадратом первого.
Пробуем . Уравнения декодера меняют вид:
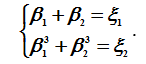
Откуда
Так что при ξ1≠0 имеем
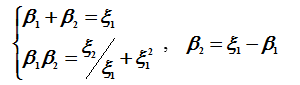
Значит, β1 и β2 удовлетворяют уравнению

Таким образом, если произошло точно две ошибки, то их локаторы удовлетворяют этому уравнению.
Так как в поле двоичных многочленов по модулю M(x) данное уравнение имеет точно 2 корня, то декодер всегда сможет найти два нужных локатора.
Если произошла только одна ошибка, то β1=ξ1 и . Следовательно, в этом случае единственная ошибка удовлетворяет уравнению β + ξ1 = 0 или 1+ ξ1β-1= 0.
Наконец, декодер всегда производит декодирование, если ошибок не произошло, то в этом случае ξ1 + ξ2 = 0 .
Более удобно (на практике) оперировать не непосредственно с многочленом, корнями которого являются локаторы ошибок, а с многочленом, корни которого взаимны к локаторам; т.е. являются к ним мультипликативным обратными величинами.
Ясно, что при не более чем двух ошибках декодер может определить номера ошибок. Если же искажаются три или более символов, то произойдет ошибка декодирования или отказ от декодирования.
Таким образом, функция подходит для построения нижних пяти строк проверочной матрицы Н двоичного кода с длиной кодовых слов 31 и 10-ю проверочными символами, исправляющего все двойные ошибки.
Первые пять проверок задают сумму номеров ошибок (S1); вторые пять проверок задают сумму кубов номеров ошибок (S3).
Процедура декодирования состоит из трех основных шагов:
- каждое полученное кодовое слово проверяется и вычисляются S1 и S3;
- находится многочлен локаторов ошибок от σ(z);
- вычисляются взаимные величины для корней σ(z) и изменяются символы в соответствующих позициях полученного слова.
|
Таблица 2.7 |
|||||
|
Код Бергера |
|||||
|
Инфор- |
Контрольные символы |
Полная |
|||
|
мацион- |
Количество единиц |
Количество нулей в |
кодовая |
||
|
ные |
в двоичном коде |
двоичном коде |
комбинация |
||
|
символы |
прямом |
инверсном |
прямом |
инверсном |
n=k+r |
|
101011 |
100 |
101011100 |
|||
|
101011 |
011 |
101011011 |
|||
|
101011 |
010 |
101011010 |
|||
|
101011 |
101 |
101011101 |
|||
Данный код обнаруживает все одиночные и большую часть многократных ошибок.
2.3. Коды с обнаружением и исправлением ошибок
Если кодовые комбинации составлены так, что отличаются друг от друга на кодовое расстояние d ≥ 3, то они образуют корректирующий код, который позволяет по имеющейся в кодовой комбинации избыточности не только обнаруживать, но и исправлять ошибки. Большую группу кодов, исправляющих ошибки, составляют систематические коды. Рассмотрим общие принципы построения этих кодов.
2.3.1. Систематические коды. Систематическими кодами называются блочные (n, k) коды, у которых k (обычно первые) разрядов представляют собой двоичный неизбыточный код, а последующие r-контрольные разряды сформированные путем линейных комбинаций над информационными.
Основное свойство систематических кодов: сумма по модулю 2 двух и более разрешенных кодовых комбинаций также дает разрешенную кодовую комбинацию.
Правило формирования кода обычно выбирают так, чтобы при декодировании имелась возможность выполнить ряд проверок на четность для некоторых определенным образом выбранных подмножеств информационных и контрольных символов каждой кодовой комбинации. Анализируя результаты проверок, можно обнаружить или исправить ошибку ожидаемого вида.
Информацию о способе построения такого кода содержит проверочная матрица, которая составляется на базе образующей матрицы.
Образующая матрица M состоит из единичной матрицы размерностью k k и приписанной к ней справа матрицы дополнений размерностью k r :
34
|
1 |
0 |
0…0 |
b11 |
b12 |
…b1r |
||||||
|
0 |
1 |
0…0 |
b21 |
b22 |
…b2r |
||||||
|
M = |
0 |
0 |
1…0 |
b31 |
b32 |
…b3r |
. |
||||
|
. . . … . |
. |
. … . |
|||||||||
|
0 |
0 |
0…1 |
bk1 |
bk 2 |
…bkr |
(2.10) |
|||||
Разрядность матрицы дополнений выбирается из выражения (2.4) или (2.5). Причем вес w (число ненулевых элементов) каждой строки матрицы дополнений должен быть не меньше чем dmin −1.
Проверочная матрица N строится из образующей матрицы следующим образом. Строками проверочной матрицы являются столбцы матрицы дополнений образующей матрицы. К полученной матрице дописывается справа единичная матрица размерностью r × r . Таким образом, проверочная матрица размерностью r × k имеет вид
|
b11 |
b21 |
b31 |
… bk1 |
1 |
0 |
0 |
…0 |
|||||
|
N = |
b12 |
b22 |
b32 |
…bk 2 |
0 |
1 |
0 |
…0 |
. |
(2.11) |
||
|
. |
. |
. … . . . . … . |
||||||||||
|
b1r |
b2r |
b3r |
… bkr |
0 |
0 |
0 |
…1 |
Единицы, стоящие в каждой строке, однозначно определяют, какие символы должны участвовать в определении значения контрольного разряда. Причем единицы в единичной матрице определяют номера контрольных разрядов.
Пример 2.1. Получить алгоритм кодирования в систематическом коде всех четырехразрядных кодовых комбинаций, позволяющего исправлять единичную ошибку. Таким образом, задано число информационных символов k=4 и кратность исправления S= 1. По выражению (2.5) определим число контрольных символов:
r ≥ E log((4 + 1) + E log(4 + 1)) = 3.
Минимальное кодовое расстояние определим из выражения (2.2)
dmin ≥ 2 1 + 1 = 3 .
Строим образующую матрицу
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|||||
|
M = |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
||||
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|||||
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
. |
||||
35
Проверочная матрица будет иметь вид
а1 а2 а3 а4 а5 а6 а7
|
N = |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|||||||
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
. |
|||||||
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
Обозначим символы, стоящие в каждой строке, через ai (a1a2a3a4a5a6a7 ) . Символы a5 , a6 и a7 примем за контрольные, так как они будут входить толь-
ко в одну из проверок.
Составим проверки для каждого контрольного символа. Из первой строки имеем
Из второй строки получим алгоритм для формирования контрольного символа a6 :
Аналогично из третьей строки получим алгоритм для формирования контрольного символа а7:
Нетрудно убедиться, что все результаты проверок на четность по выражениям (2.12)–(2.14) дают нуль, что свидетельствует о правильности составления образующей и проверочной матриц.
Пример 2.2. На основании алгоритма, полученного в примере 2.1, закодировать кодовую комбинацию G(x) = 1101 = a1a2a3a4 в систематическом ко-
де, позволяющем исправлять одиночную ошибку.
По выражениям (2.12), (2.13) и (2.14) найдем значения для контрольных символов a5 , a6 и a7 .
|
a5 |
= 1 0 1 = 0, |
|
|
a6 |
= 1 1 1 = 1, |
(2.15) |
|
a5 |
= 1 0 1 = 0. |
Таким образом, кодовая комбинация F(x) в систематическом коде будет иметь вид:
36
На приемной стороне производятся проверки Si принятой кодовой комбинации, которые составляются на основании выражений (2.12)–(2.14):
|
S1 |
= a2 |
a3 |
a4 |
a5 , |
|
|
S2 |
= a1 |
a2 |
a4 |
a6 , |
(2.17) |
|
S3 |
= a1 |
a3 |
a4 |
a7 . |
Если синдром (результат проверок на четность) S1S2S3 будет нулевого порядка, то искажений в принятой кодовой комбинации F ‘ (x) нет. При наличии искажений синдром S1S2S3 указывает, какой был искажен символ. Рассмотрим всевозможные состояния S1S2S3 :
S1 S2 S3
00 0 – искажений нет,
10 0 – искажен символ a5 ,
|
0 |
1 |
0 – искажен символ a6 , |
|
|
0 |
0 |
1 – искажен символ a7 , |
|
|
1 |
1 |
0 – искажен символ a2 , |
(2.18) |
01 1 – искажен символ a1,
11 1 – искажен символ a4 ,
10 1 – искажен символ a3 .
Пример 2.3. Кодовая комбинация F(x) = 1101010 (пример 2.2) при передаче была искажена и приняла вид F ‘ (x) = 1111010 = a1a2a3a4a5a6a7 . Декоди-
ровать принятую кодовую комбинацию.
Произведем проверки согласно выражениям (2.17)
S1 =1 1 1 0 =1,
S2 =1 1 1 1 = 0,
S3 =1 1 1 0 =1.
Полученный синдром S1S2S3 = 101 согласно (2.18) свидетельствует об искажении символа a3 . Заменяем этот символ на противоположный и получаем исправленную кодовую комбинацию F(x) = 1101010 , а исходная кодовая комбинация имеет G(x) = 1101, что совпадает с кодовой комбинацией, подлежащей кодированию в примере 2.2.
2.3.2. Код Хемминга. Данный код относится к числу систематических кодов. По существу, это целая группа кодов, при dmin = 3 исправляющая все
37
одиночные или обнаруживающая двойные ошибки, а при dmin = 4 исправ-
ляющая одиночные и обнаруживающая двойные ошибки.
В качестве исходных берут двоичный код на все сочетания с числом информационных символов k , к которому добавляют контрольные символы r. Таким образом, общая длина закодированной комбинации n = k + r .
Рассмотрим последовательность кодирования и декодирования кода Хемминга.
Кодирование. Определение числа контрольных символов. При передаче по каналу с шумами может быть или искажен любой из n символов кода, или слово передано без искажений. Таким образом, может быть n + 1 вариантов принятых сообщений. Используя контрольные символы, необходимо различить все n + 1 вариантов. С помощью контрольных символов r можно описать
2n событий. Значит, должно быть выполнено условие
|
2r ≥ n +1 = k + r +1. |
(2.19) |
В табл. 2.8 представлена зависимость между k и r, полученная из этого неравенства.
Таблица 2.8
Число контрольных символов r в коде Хэмминга в зависимости от числа информационных символов
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
r |
2 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
5 |
5 |
Чаще всего заданными является число информационных символов, тогда число контрольных символов можно определить из выражения (2.5).
Размещение контрольных символов. К построению кодов Хемминга обыч-
но привлекают производящие матрицы, а процедура проверок при обнаружении и исправлении ошибок проводится с помощью проверочных матриц.
Ниже приводится более простой алгоритм, получивший широкое распространение.
В принципе, место расположения контрольных символов не имеет значения: их можно приписывать и перед информационными символами, и после них, и чередуя информационные символы с контрольными. Для удобства обнаружения искаженного символа целесообразно размещать их на местах, кратных степени 2, т.е. на позициях 1, 2, 4, 8 и т.д. Информационные символы располагаются на оставшихся местах. Поэтому, например, для девятиэлементной закодированной комбинации можно записать
|
r1, r2 , k5 , r3, k4 , k3 , k2 , r4 , k1, |
(2.20) |
38
где k5 – старший (пятый) разряд исходной кодовой комбинации двоичного
кода, подлежащий кодированию; k1 – младший (первый) разряд.
Определение состава контрольных символов. Какой из символов должен стоять на контрольной позиции (1 или 0), выявляют с помощью проверки на четность. Для этого составляют колонку ряда натуральных чисел в двоичном коде, число строк в которой равно n, а рядом справа, сверху вниз проставляют символы комбинации кода Хемминга, записанные в такой последовательности
(2.20):
|
0001 |
– r1 |
0110 |
– k3 |
|
|
0010 |
– r2 |
0111 |
– k2 |
|
|
0011 – k5 |
1000 – r4 |
(2.21) |
||
|
0100 |
– r3 |
1001 |
– k1 . |
|
|
0101 |
– k4 |
Затем составляются проверки по следующему принципу: первая проверка – коэффициенты с единицей в младшем разряде ( r1, k5 , k4 , k2 , k1 ); вто-
рая – коэффициенты во втором разряде ( r2 , k5 , k3, k2 ); третья – коэффициенты с единицей в третьем разряде ( r3, k4 , k3, k2 ); четвертая – коэффициенты в четвертом разряде ( r4 , k1). Рассматривая проверки, видим, что каждый контроль-
ный символ входит только в одну из проверок, а поэтому для определения состава контрольных символов суммируют информационные символы, входящие в каждую строку. Если сумма единиц в данной строке четная, то значение символа r, входящего в эту строку, равно нулю, если нечетная, то единице. Таким образом,
|
r1 |
= k5 |
k4 |
k2 k1, |
|
|
r2 |
= k5 |
k3 |
k2 , |
(2.22) |
|
r3 |
= k4 |
k3 |
k2 , |
|
|
r4 |
= k1. |
В случае кодирования более длинных кодовых комбинаций нужно лишь увеличить число разрядов двоичного кода в колонках (2.21).
Декодирование. Для проверки правильности принятой комбинации производят Si проверок на четность:
|
S1 |
= r1 |
k5 |
k4 |
k2 k1, |
|
|
S2 |
= r2 |
k5 |
k3 |
k2 , |
(2.23) |
|
S3 |
= r3 |
k4 |
k3 |
k2 , |
|
|
S4 |
= r4 |
k1. |
39
Если комбинация принята без искажений, то сумма единиц по модулю 2 дает нуль. При искажении какого-либо символа суммирование при проверке дает единицу. По результату суммирования каждой из проверок (2.23) составляют двоичное число S4 , S3, S2 , S1 (синдром), указывающее на место искаже-
ния. Например, первая и вторая проверки показали наличие искажения, а суммирования при третьей и четвертой проверках (2.23) дали нули. Записываем число S4 , S3 , S2 , S1 = 0011, которое означает, что в третьем символе кодовой
комбинации (2.20), включающей и контрольные символы (счет производится слева направо), возникло искажение, значит, этот символ нужно исправить на обратный ему. После этого контрольные символы, стоящие на заранее известных местах, отбрасываются.
Код Хемминга с dmin = 4 строится на базе кода Хемминга с dmin = 3 путем добавления дополнительного контрольного символа к закодированной комбинации, который позволяет производить проверку на четность всей комбинации. Поэтому контрольный символ должен быть равен единице, если число единиц в закодированной комбинации нечетное, и нулю, если число единиц четное, т.е. закодированная комбинация будет иметь вид
|
r1, r2 , k5 , r3, k4 , k3, k2 , r4 , k1, r5 , |
(2.24) |
где
|
r5 = r1 r2 k5 r3 k4 k3 k2 r4 k1. |
(2.25) |
При декодировании дополнительно к проверкам (2.23) производится проверка
|
S∑ |
= r1 r2 k5 r3 k4 k3 k2 r4 k1 r5 . (2.26) |
||
|
При этом возможны следующие варианты: |
|||
|
1) |
частные проверки (2.23) Si = 0 и общая (2.25) S∑ = 0 — ошибок нет; |
||
|
2) |
Si ≠ 0 |
и S∑ |
= 0 — двойная ошибка, принятая кодовая комбинация |
|
бракуется; |
и S∑ |
||
|
3) |
Si ≠ 0 |
≠ 0 — одиночная ошибка, синдром указывает номер в |
|
|
двоичном коде искаженного разряда, который корректируется; |
|||
|
4) |
Si = 0 |
и S∑ |
≠ 0 — искажен последний разряд общей проверки на |
четность, информационные символы поступают потребителю.
Пример 2.4. Закодировать в коде Хемминга с d = 4 кодовую комбинацию
G(X ) = 10011 т.е. k = 5 .
Решение. Согласно табл. 2.8, число контрольных символов rd =3 = 4 , размещаются они на позициях 1, 2, 4 и 8, и информационные — на позициях 3,
40
5, 6, 7, 9. Учитывая, что G(X ) необходимо закодировать в коде Хемминга с
d = 4 , добавляют пятый контрольный разряд общей проверки на четность (2.25). Тогда последовательность в общем виде можно записать так:
r1, r2 , k5 , r3 , k4 , k3, k2 , r4 , k1, r5
? ? 1 ? 0 0 1 ? 1 ? . (2.27)
Для определения контрольных символов r1 − r4 подставим значения k1 ÷ k5 в (2.22) и получим
r1 = 1 0 1 1 = 1, r2 = 1 0 1 = 0,
r3 = 0 0 1 = 1, r4 = 1.
Контрольный символ r5 определим из выражения (2.25):
r5 = 1 0 1 1 0 0 1 1 1 = 0.
Таким образом, в линию связи будет послан код
F(X ) = 1011001110.
Пример 2.5. В приемник поступила кодовая комбинация
F‘ (X ) = 1010001110 в коде Хемминга с d = 4 . Декодировать ее; если имеются
искажения, то обнаружить и при возможности исправить.
Решение. Произведем Si проверки согласно (2.23) и S∑ согласно (2.26), в результате получим:
|
S1 |
= 1 1 0 1 1 = 0, |
|
S2 |
= 0 1 0 1 = 0, |
|
S3 |
= 0 0 0 1 = 1, |
|
S4 |
= 1 1 = 0. |
|
S∑ |
= 1 0 1 0 0 0 1 1 1 0 = 1. |
Таким образом, получим синдром S4S3S2S1 = 0100 и S∑ = 1, что указывает на то, что искажен четвертый разряд кодовой комбинации F‘ (X ) . После исправления получим F(X ) = 1011001110 , а следовательно, информационная последовательность будет иметь вид G(X ) = 10011, что соответствует исходной кодовой комбинации примера 2.4.
41
2.3.3. Циклические коды. Общие понятия и определения. Циклические коды относятся к числу блоковых систематических кодов, в которых каждая комбинация кодируется самостоятельно (в виде блока) таким образом, что информационные k и контрольные r символы всегда находятся на определенных местах.
Любой групповой код (n, k) может быть записан в виде матрицы, вклю-
чающей k линейно независимых строк по n символов, и, наоборот, любая совокупность k линейно независимых n -разрядных кодовых комбинаций может рассматриваться как образующая матрица некоторого группового кода. Среди всего многообразия таких кодов можно выделить коды, у которых строки образующих матриц связаны дополнительным условием цикличности.
Все строки образующей матрицы такого кода могут быть получены циклическим сдвигом одной комбинации, называемой образующей для данного кода. Коды, удовлетворяющие этому условию, получили название циклических кодов. Сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Запишем, например, совокупность кодовых комбинаций, получающихся циклическим сдвигом комбинации
001011:
|
0 |
0 |
1 |
0 |
1 |
1 |
|||
|
0 |
1 |
0 |
1 |
1 |
0 |
|||
|
G = |
1 |
0 |
1 |
1 |
0 |
0 |
. |
|
|
0 |
1 |
1 |
0 |
0 |
1 |
|||
|
1 |
1 |
0 |
0 |
1 |
0 |
|||
|
1 |
0 |
0 |
1 |
0 |
1 |
При описании циклических кодов n -разрядные кодовые комбинации представляются в виде многочленов фиктивной переменной x (см.подразд.1.2.1). Тогда циклический сдвиг строки матрицы с единицей в старшем ( n -м) разряде (слева) равносилен умножению соответствующего строке многочлена на x с одновременным вычитанием из результата много-
члена X n + 1 = X n − 1, т.е. с приведением по модулю X n +1. Умножив, например, первую строку матрицы (001011) , соответствующую многочлену
G0 (X ) = x3 + x + 1, на x , получим вторую строку матрицы (010110) , соответствующую многочлену X G0 (X ). Нетрудно убедиться, что кодовая комбинация, получающаяся при сложении этих двух комбинаций, также будет соответ-
ствовать результату умножения многочлена x3 + x + 1 на многочлен x + 1. Действительно,
001011 010110 = 011101 = x4 + x3 + x2 + 1, (x3 + x + 1)(x + 1) = = x4 + x3 + x2 + 1 = 011101.
42
Отсюда ясно, что любая разрешенная кодовая комбинация циклического кода может быть получена в результате умножения образующего многочлена
на некоторый другой многочлен с приведением результата по модулю xn + 1. Иными словами, при соответствующем выборе образующего многочлена, любой многочлен циклического кода будет делиться на него без остатка.
Ни один многочлен, соответствующий запрещенной кодовой комбинации, на образующий многочлен без остатка не делится. Это свойство позволяет обнаружить ошибку. По виду остатка можно определить и вектор ошибки.
Умножение и деление многочленов весьма просто осуществляется на регистрах сдвига с обратными связями и сумматорах по модулю 2.
В основу циклического кодирования положено использование неприводимого многочлена P(X ) , который применительно к циклическим кодам называ-
ется образующим, генераторным или производящим многочленом (полиномом).
Многочлен в поле двоичных чисел называется неприводимым, если он делится без остатка только на себя или на единицу. Неприводимые полиномы приведены в прил. 1.
Методы построения циклического кода. Существует несколько различных способов кодирования. Принципиально наиболее просто комбинации циклического кода можно получить, умножая многочлены G(X ) , соответствующие
комбинациям безызбыточного кода (информационным символам), на образующий многочлен кода P(X ) . Такой способ легко реализуется, однако он
имеет тот существенный недостаток, что получающиеся в результате умножения комбинации кода не содержат информационных символов в явном виде. После исправления ошибок такие комбинации для выделения информационных символов приходится делить на образующий многочлен кода. Ситуацию можно значительно упростить, если контрольные символы переписать в конце кода, т.е. после информационных символов. Для этой цели прибегают к следующему искусственному приему.
Умножаем кодовую комбинацию G(X ) , которую мы хотим закодировать, на одночлен X r , имеющий ту же степень, что и образующий многочлен P(X ) . Делим произведение G(X )X r на образующий полином P(X ) :
|
G(X ) X r |
R(X ) |
|||
|
= Q(X ) + |
, |
(2.28) |
||
|
P(X ) |
||||
|
P(X ) |
где Q(X) – частное от деления; R(X ) – остаток.
Умножая выражение (2.28) на P(X ) и перенося R(X ) в другую часть ра-
венства, согласно правилам алгебры двоичного поля, т.е. без перемены знака на обратный, получаем
43
|
F(X ) = Q(X ) P(X ) = G(X ) X r + R(X ). |
(2.29) |
Таким образом, согласно равенству (2.29), циклический код можно образовать двумя способами:
1)умножением одной из комбинаций двоичного кода на все сочетания (комбинация Q(X) принадлежит к той же группе того же кода, что и заданная комбинация G(X ) ) на образующий многочлен P(X ) ;
2)умножением заданной комбинации G(X ) на одночлен X r , имеющий ту же степень, что и образующий многочлен P(X ) , с добавлением к этому произ-
ведению остатка R(X ) , полученного после деления произведения G(X ) X r на генераторный полином P(X ) .
Пример 2.6. Закодировать кодовую комбинацию G(X) = 1111= x3+x2+x+1 циклическим кодом.
Решение. Не останавливаясь на выборе генераторного полинома P(X ) , о чем будет сказано подробно далее, возьмем из прил. 1 многочлен P(X) = x3+x+1 = 1011. Умножая G(X ) X r , получаем
G(X ) X n = (x3 + x2 + x + 1)x3 = x6 + x5 + x4 + x3 → 1111000.
От умножения степень каждого члена повысилась, что равносильно приписыванию трех нулей к многочлену, выраженному в двоичной форме.
|
Разделив на G(X ) X r |
на P(X ), согласно (2.28) получим |
|||
|
x6 + x5 + x4 + x3 |
+ x2 |
+1) + |
x2 + x +1 |
, |
|
x3 |
= (x3 |
x3 + x +1 |
||
|
+ x +1 |
или в двоичном эквиваленте
1111000 1011 =1101 +111
1011 =1101 +111 1011.
1011.
Таким образом, в результате деления получаем частное Q(X) = 1101 той же степени, что и G(X ) = 1111, и остаток R(X ) = 111. В итоге комбинация
двоичного кода, закодированная циклическим кодом, согласно (2.29) примет вид
F (X ) =1101 1011 =1111000 111 =1111111.
Действительно, умножение 1101 1011 (первый способ) дает тот же результат, что и сложение 1111000 111 (второй способ).
Циклические коды, обнаруживающие одиночную ошибку (d = 2). Код,
образованный генераторным полиномом P(X ) = x + 1, обнаруживает любое нечетное число ошибок.
44

Закодируем сообщение G(X ) = 1101 с помощью многочлена P(X ) = 11. Поступая по методике, рассмотренной выше, получим
F(X ) = G(X ) X r + R(X ) =11010 +1 =11011,
т.е. на первых четырех позициях находятся разряды исходной комбинации G(X ) , а на пятой – контрольный символ.
Сообщение 1101 является одной из 16 комбинаций четырехразрядного кода. Если требуется передать все эти сообщения в закодированном виде, то каждое из них следует кодировать так же, как и комбинацию G(X ) = 1101. Од-
нако проделывать дополнительно 15 расчетов (в общем случае 2r расчетов) нет необходимости. Это можно сделать проще, путем составления образующей матрицы. Образующая матрица составляется из единичной транспонированной и матрицы дополнений, составленной из остатков от деления единицы с нулями на образующий многочлен P(X ) , выраженный в двоичном эквиваленте (см.
подразд. 1.2.4.). Образующая матрица в данном случае имеет вид:
|
0 |
0 |
0 |
1 |
1 |
a1 |
||||
|
M = |
0 |
0 |
1 |
0 |
1 |
a2 |
|||
|
0 |
1 |
0 |
0 |
1 |
a |
||||
|
3 |
|||||||||
|
1 |
0 |
0 |
0 |
1 |
a4 |
Четыре кодовые комбинации, из которых состоит образующая матрица, являются первыми кодовыми комбинациями циклического кода. Пятая комбинация нулевая, а так как в четырехразрядном непомехозащищенном коде всего
N = 24 = 16 комбинаций, то остальные 11 ненулевых комбинаций находят суммированием по модулю 2 всевозможных комбинаций строк матрицы M:
|
5. |
0000, |
9. a2 a3 = 01100, |
13. a2 |
a3 |
a4 |
= 11101, |
||||
|
6. |
a1 |
a2 |
= 00110, |
10. a2 |
a4 |
= 10100, |
14. a1 |
a3 |
a4 |
= 11011, |
|
7. |
a1 |
a3 |
= 01010, |
11. a3 |
a4 |
= 11000, |
15. a1 |
a2 |
a4 |
= 10111, |
|
8. |
a1 |
a4 |
= 10010, |
12. a1 |
a2 |
a3 = 01111, |
16. a1 |
a2 |
a3 |
a4 = 11110. |
Рассмотрение полученных комбинаций показывает, что все они имеют четное число единиц. Таким образом, циклический код с обнаружением одиночной ошибки d = 2 является кодом с проверкой на четность.
Циклический код с d = 3 . Эти коды могут обнаруживать одиночные и двойные ошибки или обнаруживать и исправлять одиночные ошибки. Можно предложить следующий порядок кодирования кодовых комбинаций в циклическом коде с d = 3.
45
1)выбор числа контрольных символов. Выбор r производят, как и для ко-
да Хемминга, с исправлением одиночной ошибки, по выражению (2.4) или
(2.5);
2)выбор образующего многочлена P(X ) . Степень образующего много-
члена не может быть меньше числа контрольных символов r . Если в прил. 1 имеется ряд многочленов с данной степенью, то из них следует выбирать самый короткий. Однако число ненулевых членов многочлена P(X ) не должно
быть меньше кодового расстояния d ;
3) нахождение элементов дополнительной матрицы. Дополнительную матрицу составляют из остатков, полученных от деления единицы с нулями на образующий полином P(X ) . Порядок получения остатков показан в под-
разд. 1.2.4. При этом должны соблюдаться следующие условия:
а) число остатков должно быть равно числу информационных символов
k ;
б) для дополнительной матрицы пригодны лишь остатки с весом w, не меньшим числа обнаруживаемых ошибок m , т.е. в данном случае не меньшим
2(w ≥ 2) ;
в) количество нулей, приписываемых к единице при делении ее на многочлен P(X ) , определяется из условий а и б;
г) число разрядов дополнительной матрицы равно числу контрольных символов r ;
4) составление образующей матрицы. Берут транспонированную единич-
ную матрицу размерностью k ×k и справа приписывают к ней дополнительную матрицу размерностью k ×r ;
5)нахождение всех комбинаций циклического кода данного сомножества.
Это достигается суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, как было показано при рассмотрении циклического кода
сd = 2;
6)при индивидуальном кодировании любой из кодовых комбинаций, принадлежащей к сомножеству k разрядных комбинаций, поступают по общей методике в соответствии с (2.29).
Пример 2.7. Образовать циклический код, позволяющий обнаруживать двукратные ошибки или исправлять одиночные ошибки из всех комбинаций двоичного кода на все сочетания с числом информационных символов k = 5.
Решение. По уравнению (2.5) находим число контрольных символов
r = E log((k +1) + E log(k +1)) = E log((5 +1) + E log(5 +1)) = 4 .
Из прил. 1 выбираем образующий многочлен P(X ) = x4 + x +1. Находим остатки от деления единицы с нулями на P(X ) , которые соответственно равны
0011, 0110, 1100, 1011, 0101.
46

Строим образующую матрицу
00001 0011 a1
00010 0110 a2 M = 00100 1100 a3 .
01000 1011 a4
10000 0101 a5
Так как все члены единичной матрицы являются комбинациями заданного пятиразрядного двоичного кода, то пять комбинаций образующей матрицы представляют собой пять комбинаций требуемого циклического кода. Остальные 26 комбинаций циклического кода (начиная с шестой) могут быть получены путем суммирования по модулю 2 строк образующей матрицы в различном сочетании.
Пример 2.8. Закодировать комбинацию G(X ) =111011 циклическим ко-
дом с d = 3 .
Решение. Находим число контрольных символов по (2.5)
r = E log((6 +1) + E log(6 +1)) = 4 .
Из прил. 1 выбираем образующий многочлен P(X ) = x4 + x3 +1.
|
Умножая G(X ) на xr , получим G(X ) xr |
= 1110110000 . |
|
Разделив полученный результат, на |
P(X ) =11001, найдем остаток |
R(X ) =1110. И тогда окончательно в соответствии с (2.29) получаем кодовую комбинацию в циклическом коде с d = 3 :
F(X ) =1110111110.
Циклические коды с d=4. Эти коды могут обнаруживать одиночные, двойные и тройные ошибки или обнаруживать двойные и исправлять одиночные. При построении данного кода придерживаются следующего порядка:
1) выбор числа контрольных символов. Число контрольных символов в этом коде должно быть на единицу больше, чем для кода с d = 3 :
|
rd =4 = rd =3 +1; |
(2.30) |
|
2) выбор образующего многочлена. Образующий многочлен P(X )d =4 ра- |
|
|
вен произведению двучлена (x +1) на многочлен P(X )d =3 : |
|
|
P(X )d =4 = P(X )d =3 (x +1). |
(2.31) |
47
Это объясняется тем, что двучлен (x +1) позволяет обнаруживать все одиночные и тройные ошибки, а многочлен P(X )d =3 – двойные ошибки.
В общем случае степень генераторного полинома P(X )d =4 равно числу r .
Дальнейшая процедура кодирования остается такой же, как и при образовании кода с d = 3 .
Пример 2.9. Требуется закодировать сообщение C(X) = 10101010101010 циклическим кодом с d = 4 .
Решение. Определяем число контрольных символов по уравнению (2.5):
rd =3 = E log((14 +1) + E log(14 +1)) = E log(15 + 4) = 5 .
Из уравнения (2.30) следует, что rd =4 = 5 +1 = 6 .
Выбираем из прил. 1 образующий полином для d = 3 . Пусть P(X )d =3 = x5 + x2 +1. Тогда
P(X )d =4 = (x +1)(x5 + x2 +1) = x6 + x5 + x3 + x2 + x +1 =1101111.
Так как необходимо закодировать только одно сообщение G(X ) , а не весь
ансамбль двоичных кодов с k =14 , то в дальнейшем будем придерживаться процедуры кодирования, выполняемой по уравнению (2.29). Выбираем одночлен xr = x6 . Тогда
xr G(X ) = x19 + x17 + x15 + x13 + x11 + x9 + x7 →10101010101010000000.
Разделив полученное выражение на P(X )d =4 , находим остаток:
R(X ) = x4 + x3 + x2 + x + 1 → 011111.
Следовательно, передаваемая закодированная комбинация будет иметь
вид
F(X ) =10101010101010 011111 .
1442443 123
информационные контрольные символы символы
Циклические коды с d ≥ 5. Эти коды, разработанные Боузом, Чоудхури и Хоквинхемом (сокращенно код БЧХ), позволяют обнаруживать и исправлять любое число ошибок. Заданными при кодировании является число исправляемых ошибок s и длина слова n . Число информационных символов k и контрольных символов r , а также состав контрольных символов подлежат определению.
48

Методика кодирования такова:
1) выбор длины слова. При кодировании по методу БЧХ нельзя выбирать произвольную длину слова n . Первым ограничением является то, что слово может иметь только нечетное число символов. Во-вторых, при заданном n должно соблюдаться одно из равенств:
|
2h −1 = n; |
(2.32) |
|
(2h −1) q = n, |
(2.33) |
где h>0 – целое число, q – нечетное положительное число, при делении на которое n получается целым нечетным числом.
Так, при h=6 длина слова может быть равна не только 63 (2.32), но и 21
при q = 3 (2.33).
2)определение кодового расстояния. Кодовое расстояние определяют со-
гласно (2.2), т.е. d = 2s +1;
3)определение образующего многочлена P(X ) . Образующий многочлен
есть наименьшее общее кратное (НОК) так называемых минимальных многочленов M (X ) до порядка 2s −1 включительно, причем берутся все нечетные:
|
P(X ) = НОК[M1(X ) M 3 (X ) …M 2s−1 (X ) ]. |
(2.34) |
Таким образом, число минимальных многочленов равно L = s , т.е. равно числу исправленных ошибок. Минимальные многочлены являются простыми неприводимыми многочленами (прил. 2);
4) определение старшей степени t минимального многочлена. Степень t
есть такое наименьшее целое число, при котором 2t −1 нацело делится на n или nc , т. е. n = 2t −1 или 2t −1 = cn. Отсюда следует, что
5)выбор минимальных многочленов. После того как определено число минимальных многочленов L и степень старшего многочлена t , многочлены выписывают из прил. 2. При этом НОК может быть составлено не только из многочленов старшей степени t. Это, в частности, касается многочленов четвертой и шестой степеней;
6)определение степени β образующего многочлена P(X ) . Степень обра-
зующего многочлена зависит от НОК и не превышает произведения t s ;
7) определение числа контрольных символов. Так как число контрольных
|
символов r равно степени образующего полинома, то в коде длины n |
|
|
β = r ≤ t s ; |
(2.36) |
49

 определение числа информационных символов. Его производят обычным порядком из равенства
определение числа информационных символов. Его производят обычным порядком из равенства
Дальнейшие этапы кодирования аналогичны рассмотренным для циклических кодов с d < 4.
Пример 2.10. Закодировать все комбинации двоичного кода, чтобы
|
n =15 , а s = 2 . |
|||||
|
Решение. |
Определяем |
кодовое |
расстояние |
по |
(2.2): |
|
d = 2s +1 = 2 2 +1 = 5 (код БЧХ). Число минимальных многочленов |
L = s = 2. |
||
|
Старшая степень минимального |
многочлена |
по (2.35) t = h = 4 |
, так как |
|
15 = 24 −1. Выписываем из |
прил. 2 |
минимальные многочлены: |
M1(X ) = x4 + x +1 и M 3 (X ) = x4 + x3 + x2 + x +1. Образующий многочлен определяем по (2.34):
P(X ) = (x4 + x +1)(x4 + x3 + x2 + x +1) = x8 + x7 + x6 + x4 +1.
Число контрольных символов r равно по (2.36) степени β образующего многочлена, т.е. r = β = 8, а значит, число информационных символов k по (2.37) равно: k = n − r =15 −8 = 7 . Таким образом, получаем код БЧХ (15, 7) с
s = 2 .
После нахождения остатков получаем образующую матрицу (2.38)
(2.38)
Пример 2.11. Найти образующий полином для циклического кода, исправляющего двукратные ошибки, s = 2 , если общая длина кодовых комбинаций n = 21.
Решение. Определяем, что d = 2 2 +1 = 5, L = 2 . Наименьшее значение t,
при котором 2t −1 нацело делится на 21, есть число 6. Из таблицы прил. 2 выписываем два минимальных многочлена, номера которых определяют сле-
50

дующим образом: берут многочлены M1(X ) и M 3 (X ) и их индексы умножают на q = c = 3 . В результате получаем M 3 (X ) и M 9 (X ) . Таким образом,
P(X ) = НОК[M3 (X )M9 (X )]= (x6 + x4 + x2 + x + 1)(x3 + x2 + 1) = = x9 + x8 + x7 + +x5 + +x4 + x + 1,
откуда r = 9 , а k =12 . Получаем код БЧХ (21, 12) . Кроме того, доказано, что
этот код, имеющий d = 7, может также обнаруживать и исправлять ошибки кратностью s = 3.
Построение кодов БЧХ возможно и с помощью таблицы [1], которая приведена в прил. 3 в сокращенном виде. В соответствии с изложенной ранее методикой в таблице по заданным длине кодовой комбинации n и числу исправляемых ошибок s рассчитаны число информационных символов k и образующий многочлен P(X ) . Число контрольных символов r определяется из
уравнения r = n − k , и запись образующего многочлена в виде десятичных цифр преобразуется путем перевода каждой десятичной цифры в трехразрядное двоичное число. Например, во второй строке таблицы P(X ) = 23. Цифре 2
соответствует двоичное число 010, а цифре 3 – число 011. В результате получаем двоичное число 010011, которое записывается в виде многочлена
x4 + x +1. Таким образом, в двоичный эквивалент переводится каждая из десятичных цифр, а не все десятичное число. Действительно, числу 23 соответству-
ет уже многочлен P(X ) = x4 + x +1. Из прил. 3 следует, что при n = 31, k = 21 и s = 2 образующий многочлен
P(X ) = x10 + x9 + x8 + x6 + x5 + x + 1 = 011101101001 .
Коды БЧХ для обнаружения ошибок. Их строят следующим образом.
Если необходимо образовать код с обнаружением четного числа ошибок, то по заданному числу обнаруживаемых ошибок m согласно (2.1) и (2.2) находят значения d и s . Дальнейшее кодирование выполняют, как и раньше. Если требуется обнаружить нечетное число ошибок, то находят ближайшее меньшее целое число s и кодирование производят так же, как и в предыдущем случае, с той лишь разницей, что найденный согласно (2.34) образующий многочлен дополнительно умножают на двучлен x +1.
Пример 2.12. Построить код БЧХ, обнаруживающий пять ошибок при длине кодовых комбинаций n =15 .
Решение. Находим, что d = m +1 = 5 +1 = 6 , а ближайшее меньшее значение s определим из выражения d = 2s +1, откуда s = (d −1) 2 = 5 2 = 2. Да-
лее определяем многочлен P(X ) , как указано в примере 2.10, и умножаем его на двучлен (x +1) , т. е. получаем
51
P(X ) = (x4 + x + 1)(x4 + x3 + x2 + x + 1)(x + 1) = (x8 + x7 + x6 + x4 + 1)(x + 1) = = x9 + x8 + x7 + x5 + x + x8 + x7 + x6 + x4 + 1 = x9 + x6 + x5 + x4 + x + 1.
Таким образом, получаем код БЧХ (15, 6) .
Коды Файра. Это циклические коды, обнаруживающие и исправляющие пакеты ошибок. Определение пакета (пачки) ошибки дано в подразд. 2.1. Непременным условием пакета данной длины b является поражение крайних символов и нахождение между ними b − 2 разрядов.
Коды Файра могут исправлять пакет ошибок длиной bs и обнаруживать пакеты ошибок длиной bm . Заметим, что в кодах Файра понятие кодового рас-
стояния d , а следовательно, и уравнение (2.3) не используются. Образующий многочлен кода Файра P(X )Ф определяется из выражения
|
P(X )Ф = P(X )(X C +1), |
(2.39) |
|
где P(X ) – неприводимый многочлен степени |
|
|
t ≥ bs , |
(2.40) |
|
принадлежащий показателю степени |
|
|
E = 2t −1; |
(2.41) |
|
C ≥ bs + bm −1. |
(2.42) |
|
Неприводимый многочлен P(X ) выбирают из прил. |
1 согласно уравне- |
нию (2.40).
Длина слова n равна наименьшему общему кратному чисел E и C , так
|
как только в этом случае многочлен xn +1 делится на |
P(X )Ф без остатка. При |
|
n* < n никакой многочлен xn* +1 не делится на P(X )Ф . Таким образом, |
|
|
n = НОК(E, C) . |
(2.43) |
|
Число контрольных символов |
|
|
r = t + C . |
(2.44) |
Дальнейшая процедура кодирования такая же, как и для циклического кода с d = 3 .
Пример 2.13. Найти образующий полином и определить общую длину кодовых комбинаций n , а также число контрольных и информационных символов для кода, позволяющего исправлять пакеты ошибок длиной bs = 4 и обна-
руживать пакеты ошибок длиной bm = 5.
52
Исправить пакет bs = 4 – значит исправить одну из следующих комбина-
ций ошибок, пораженных помехами: 1111, 1101, 1011 и 1001. В то же время этот код может обнаруживать одну из комбинаций в пять символов: 11111, 10111, 10011, 10001 и т.д.
На основании (2.40) и (2.42) t ≥ 4, C ≥ 8. Из прил. 1 находим неприводи-
мый многочлен четвертой степени: P(X ) = x4 + x +1. Согласно (2.39) образующий многочлен P(X)Ф = (x4+x+1)(x8+1) = x12 + x9 + x8 + x4 + x + 1. По выра-
жению (2.41) находим E = 24 −1 =15 . Поэтому длина кода из (2.43) n =15 8 =120. Из (2.44) число контрольных символов r = 4 +8 =12 . В итоге получаем циклический код (120, 108). Избыточность такого кода, если учитывать его исправляющую способность, невелика: R = 12 120 = 0,1.
120 = 0,1.
Сравнение кодов БЧХ и Файра. Представляет интерес сравнение по избыточности кода при исправлении того же числа ошибок, но не сгруппированных в пакет, т.е. рассеянных по всей длине слова. Если воспользоваться для этой цели кодами БЧХ и близким значением n =127 , то при s = 4 можно по изложенной методике подсчитать, что число контрольных символов r = 28, т.е. получен код (127, 99). Избыточность такого кода R = 28 127 = 0,22, т.е. значи-
127 = 0,22, т.е. значи-
тельно выше, чем у кода Файра. Это очевидно: исправить четыре ошибки, находящиеся в одном месте, проще, чем ошибки, рассредоточенные по всей длине комбинации.
Заметим, что существует следующее правило: если циклический код рассчитан на обнаружение независимых ошибок, он может обнаруживать также пакет ошибок длиной bm .
Укороченные циклические коды. Предположим, что требуется получить 15 комбинаций, закодированных так, чтобы в любой из них могло исправляться по две ошибки, т.е. s = 2 , d = 5 . Для этого следует взять код с числом информационных символов k = 4. Код (7, 4) не подходит, так как он исправляет только одну ошибку. Как указывалось, число n, промежуточное между 7 и 15, в коде БЧХ брать нельзя. Поэтому необходимо взять код (15, 7), рассмотренный
в примере 2.10. Однако разрешенных комбинаций в таком коде (27 ) значи-
тельно больше 15, поэтому код (15, 7) укорачивают путем вычеркивания трех столбцов слева и трех строк снизу, как это показано пунктирной линией в образующей матрице (2.38). В результате образующая матрица укороченного кода (12, 4) принимает вид
|
k4 |
k3 |
k2 |
k1 |
r8 |
r7 |
r6 |
r5 |
r4 |
r3 |
r2 |
r1 |
a1 |
|||
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
||||
|
M = |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
a2 . |
(2.45) |
|
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
a3 |
|||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
a4 |
53
В матрице (2.45) dmin = 5 . И она представляет четыре кодовые комбина-
ции в коде БЧХ, остальные 11 комбинаций укороченного циклического кода (12, 4) могут быть получены суммированием комбинаций образующей матрицы.
Корректирующая способность укороченного циклического кода, по крайней мере, не ниже корректирующей способности исходного полного циклического кода. Техника кодирования и декодирования в обоих случаях одна и та же. Однако циклический сдвиг кодовой комбинации укороченного циклического кода не всегда приводит к образованию разрешенной комбинации, поэтому укороченные коды относят к числу псевдоциклических.
Декодирование циклических кодов. Обнаружение ошибок. Идея обна-
ружения ошибок в принятом циклическом коде заключается в том, что при отсутствии ошибок закодированная комбинация F(X ) делится на образующий
многочлен P(X ) без остатка. При этом контрольные символы r отбрасывают-
ся, а информационные символы k используются по назначению. Если произошло искажение принятой комбинации, то эта комбинация F(X ) преобразу-
ется в комбинацию
|
F * (X ) = F(X ) + E(X ) , |
(2.46) |
где E(X ) – многочлен ошибок, содержащий столько единиц, сколько элемен-
тов в принятой комбинации не совпадает с элементами переданной комбинации.
Пусть, например, была передана комбинация кода (7, 4) F(X ) =1101001, закодированная с помощью P(X ) =1011. Если она принята правильно, то деление на P(X ) дает остаток, равный нулю. Если же комбинация принята как F * (X ) =1101011, то при делении на P(X ) образуется остаток R(X ) = 010 ,
что свидетельствует об ошибке, и принятая комбинация бракуется.
Обнаружение и исправление ошибок. Существует несколько вариантов декодирования циклических кодов [2]. Один из них заключается в следующем:
1)вычисление остатка. Принятую кодовую комбинацию делят на P(X ) ,
иесли остаток R(X ) = 0 , то комбинация принята без искажений. Наличие ос-
татка свидетельствует о том, что комбинация принята искаженной. Дальнейшая процедура исправления рассматривается ниже;
2)подсчет веса остатка w . Если вес остатка равен или меньше числа исправляемых ошибок, т.е. w ≤ s , то принятую комбинацию складывают по модулю 2 с остатком и получают исправленную комбинацию;
3)циклический сдвиг на один символ влево. Если w > s , то производят циклический сдвиг на один символ влево и полученную комбинацию снова делят на P(X ) . Если вес полученного остатка w ≤ s , то циклически сдвинутую
комбинацию складывают с остатком и затем циклически сдвигают ее в обратную сторону вправо на один символ. В результате получают исправленную комбинацию;
54
4) дополнительные циклические сдвиги влево. Если после циклического сдвига на один символ по-прежнему w > s , производят дополнительные циклические сдвиги влево. При этом после каждого сдвига сдвинутую комбинацию делят на P(X ) и проверяют вес остатка. При w ≤ s выполняют действия,
указанные в подразд. 3, с той лишь разницей, что обратных циклических сдвигов вправо делают столько, сколько их было сделано влево.
Пример 2.14. Пусть исходная комбинация G(X ) =1001, закодированная с помощью P(X ) =1011 и s =1, имела вид F(X ) =1001110. При передаче по каналу связи была искажена и в приемник поступила в виде F * (X ) =1101110 .
Проверить наличие ошибки и в случае обнаружения исправлять ее.
Делим комбинацию 1101110 на 1011 и находим, что остаток R(X ) =111.
Так как w = 3 > s =1, то сдвигаем комбинацию 1101110 циклически на один символ влево. Получаем 1011101. В результате деления этой комбинации на P(X ) находим остаток R(X ) =101. Вес этого остатка w = 2 > s = 1.
Осуществляем новый циклический сдвиг влево. Получаем 0111011. Деление на P(X ) дает остаток R(X ) = 001, вес которого равен s . Складываем:
0111011 001 = 0111010 . Теперь осуществляем два циклических сдвига последней комбинации вправо: после первого она принимает вид 0011101, после второго 1001110, т.е. получается уже исправленная комбинация. Проверка показывает, что эта комбинация делится на P(X ) без остатка.
Пример 2.15. При передаче комбинации, представленной в седьмой строке матрицы (2.38), исказились два символа и комбинация была принята в виде
111000011101000 (искаженные символы помечены точками). Непосредственное деление этой комбинации на P(X ) = x8 + x7 + x6 + x4 +1 дает остаток ве-
сом w = 4 . После первого циклического сдвига комбинация принимает вид
110000111010001. Деление этой комбинации на P(X ) снова дает остаток с ве-
сом w = 4 . После второго сдвига и повторного деления ничего не меняется. Вес остатка w = 4 . Делаем третий сдвиг, комбинация принимает вид
000011101000111. И вновь делим на P(X ) . На этот раз остаток R(X)=00000011
имеет вес w = 2 = s = 2 . Складываем 000011101000111 00000011, получаем
000011101000100. Произведя три циклические сдвига комбинации вправо, получаем исходную комбинацию 100000011101000 .
Второй метод определения номеров элементов, в которых произошла ошибка, основан на свойстве, которое заключается в том, что остаток R(X ) ,
полученный при делении принятой кодовой комбинации F * (X ) на P(X ) , равен остатку R *(X ) , полученному в результате деления соответствующего многочлена ошибок E(X ) на P(X ) .
55

|
Многочлен ошибок |
может |
быть представлен в следующем виде |
|
E(X ) = F(X ) + F * (X ) , где |
F(X ) |
— исходный многочлен циклического кода. |
Так, если ошибка произошла в первом символе, то E1(X ) =100…0 , если во втором — E2 (X ) = 010…0 и т.д. Остатки от деления каждого многочлена Ei (X ) на P(X ) будут различны и однозначно связаны с искаженными символами,
причем не зависят от вида передаваемой комбинации, а определяются лишь видом P(X ) и длиной кодовых комбинаций n . Указанное однозначное соот-
ветствие можно использовать для определения места ошибки.
На основании приведенного свойства существует следующий метод определения места ошибки. Сначала определяется остаток R(X ) , соответствующий
наличию ошибки в старшем разряде. Если ошибка произошла в следующем разряде, то такой же остаток получится в произведении принятого многочлена
на X , т.е. F * (X ) X . Это служит основанием для следующего приема. Вычисляем R* (X ) как остаток от деления E1(X ) на P(X ) . Далее делим
принятую комбинацию F* (X ) на P(X ) и получаем R(X ) . Если R(X ) = R* (X ) , то ошибка в старшем разряде. Если нет, то дописываем нуль,
что равносильно умножению на X , и продолжаем деление. Номер искаженного разряда (отсчет слева направо) на единицу больше числа приписанных ну-
лей, после которых остаток окажется равным R* (X ) .
Пример 2.16. Задан циклический код (11, 7) в виде кодовой комбинации F(X ) =10110111100, полученной с помощью полинома P(X ) = 10011. В ре-
зультате воздействия помех получена кодовая комбинация F*(X)=10111111100. Определить искаженный разряд.
|
Решение. |
Вычисляем |
R*(X ) |
как |
остаток |
от |
деления |
|
|
E |
(X ) = 10000000000 на P(X ) = 10011, получаем R* (X ) = 0111. Далее делим |
||||||
|
1 |
F * (X ) на P(X ) , отмечая полученные остатки Ri (X ) :
дописываемые нули
}
101111111000000 10011
10011 1010000101
10011
10011 R1(x)=11000(1)
10011
R2(x)=10110(2) 10011
R3(x)=01010(3) 10100(4) 10011
R4(x)=0111=R*(x)
56
Для достижения равенства R(X ) = R* (X ) пришлось дописать четыре ну-
ля. Это означает, что ошибка произошла в пятом разряде, т.е. исправленная кодовая комбинация будет иметь вид:
F(X ) =10111111100 00001000000 =10110111100.
Мажоритарное декодирование циклических кодов. Мажоритарный способ исправления ошибок основан на принятии решения о значении того или иного разряда декодируемой кодовой комбинации по большинству результатов проверок на четность.
Проверки на четность для каждого разряда составляются на основании некоторой матрицы L , которая составляется из проверочной матрицы N путем μ – линейных операций над строками.
Матрица L характеризуется двумя свойствами:
1)один из столбцов содержит только единичные элементы;
2)все остальные столбцы содержат не более чем по одному единичному элементу.
Проверочная матрица может быть построена путем вычисления так называемого проверочного полинома
|
h(X ) = |
X n +1 |
, |
(2.46) |
|
|
P−1 |
(X ) |
|||
где P−1(X ) – полином, сопряженный с P(X ) .
В сопряженных P−1(X ) – полиномах члены расположены в обратном по-
рядке. Так, например, P(X ) =100011, а P−1 (X ) =110001.
Первая строка проверочной матрицы циклического кода есть проверочный полином h(X ) , умноженный на X r−1 (т.е. дополненный справа r −1 нулями).
Последующие строки проверочной матрицы есть циклический сдвиг вправо первой. Число сдвигов равно числу дописанных справа нулей. Матрица L определяет μ проверок на четность для разряда, соответствующего единичному
|
столбцу. |
Добавив |
к этой совокупности проверок тривиальную проверку |
|
ai = ai , |
получим |
μ + 1 независимых проверочных соотношений для одного |
разряда ai , причем свойства матрицы L таковы, что каждый разряд кодовой
комбинации входит только в одну проверку. Такая совокупность проверок называется системой разделенных (ортогональных) проверок относительно разряда ai . Системы разделенных проверок для остальных разрядов получаются
циклическим сдвигом строк матрицы L , что равносильно добавлению единицы к индексу разряда предыдущей проверки, причем при добавлении единицы к номеру старшего разряда номер последнего заменяется на нуль.
57
Мажоритарное декодирование осуществляется следующим образом. Если в принятой кодовой комбинации ошибки отсутствуют, то при определении значения разряда ai все μ + 1 проверки укажут одно и то же значение (либо 1,
либо 0). Одиночная ошибка в кодовой комбинации может вызвать искажение лишь одной проверки, двойная ошибка – двух и т. д. Решения о значении разряда ai принимаются по большинству (т.е. мажоритарно) одноименных ре-
зультатов проверок. При этом декодирование безошибочно, если число ошибок в кодовой комбинации не превышает μ 2 , т.е. искажено не более μ
2 , т.е. искажено не более μ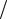 2 прове-
2 прове-
рок. Если все системы разделенных проверок для каждого разряда кодовой комбинации содержат не менее μ + 1 разделенных проверок, то реализуемое минимальное кодовое расстояние
Поясним принцип мажоритарного декодирования на конкретных примерах. Пример 2.17. Построить матрицы N и L и найти систему проверок для
циклического кода (7, 3), образованного с помощью полинома P(X ) = (x3 + + x +1)(x +1) = x4 + x3 + x2 +1 и позволяющего обнаруживать двойные и ис-
правлять одиночные ошибки.
Решение. Находим проверочный полином
|
h(X ) = |
X n +1 |
= |
x7 +1 |
= x3 |
+ x +1 →1011. |
|||||
|
P−1 |
(X ) |
x4 |
+ x2 |
+ x +1 |
||||||
Строим проверочную матрицу
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|||
|
N = |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
. |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|||
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
Для построения матрицы L преобразуем матрицу следующим образом. Сложим 2–, 3– и 4–ю строки матрицы:
0101100 0010110 0001011 = 0110001.
Аналогично сложим 1–, 3– и 4–ю строки:
1011000 0010110 0001011 =1000101.
58
Составим матрицу L , использовав для ее построения две полученные суммы и 4–ю строку проверочной матрицы N :
|
a6 |
a5 |
a4 |
a3 a2 |
a1 a0 |
||||
|
L = |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
. |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
||
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
Легко видеть, что в этой матрице один из столбцов состоит только из единиц, а все остальные столбцы содержат не более одной единицы. Матрица L дает три независимых проверочных соотношений с разделенными относительно члена a0 проверками. Добавив к этим соотношениям тривиальную провер-
ку a0 = a0 , получим систему разделенных относительно a0 проверок:
|
a0 |
= a4 |
a5 |
|
|
a |
= a |
a |
|
|
a0 |
= a2 |
a 6 |
. |
|
0 |
1 |
3 |
|
|
a0 |
= a0 |
||
Систему проверок для a1 получим из (2.48) в виде
|
a1 |
= a5 |
a6 |
|||
|
a1 |
= a3 |
a0 |
|||
|
a |
= a |
2 |
a |
4 |
. |
|
1 |
|||||
|
a1 |
= a1 |
||||
Для остальных разрядов a2 Ka6 можно получить аналогичные системы проверок.
Пример 2.18. Исходная комбинация G(X ) =101, закодированная генераторным полиномом P(X ) = x4 + x3 + x2 +1, поступила в канал связи в виде F(X ) =1010011. В результате действия помех была искажена (одиночная
•
ошибка) и в приемник поступила в виде F * (X ) =1010010. Воспользовавшись
системой проверок примера 2.17, определить номер искаженного разряда и исправить его.
Решение. Пронумеруем разряды принятой кодовой комбинации следующим образом:
a6 a5 a4 a3 a2 a1 a0
F* (X ) = 1 0 1 0 0 1 0 .
59
Произведем проверку правильности приема символа a0 по выражениям
(2.48):
|
a0 =1 0 =1, |
a0 =1 0 =1, |
|
a0 = 0 1 =1, |
0 = 0. |
Большинство проверок указывают, что разряду a0 должен быть присвоен символ 1. Таким образом, исправленная комбинация будет F(X ) =1010011,
что соответствует переданной в канал связи.
Для остальных разрядов проверки не проводились, так как в условии задачи указано, что имела место одиночная ошибка.
Пример 2.19. Найти систему проверок для символа a0 кода БЧХ (15, 7),
образованного генераторным полиномом P(X) = x8 + x7 + x6 + x4 + 1=111010001 и позволяющего исправлять двойные ошибки.
Решение. Вычислим проверочный полином:
|
h(X ) = |
X n +1 |
= x7 |
+ x3 |
+ x +1 |
→10001011. |
|||||||||||||||
|
P−1(X ) |
||||||||||||||||||||
|
Построим проверочную матрицу, в качестве первой строки которой ис- |
||||||||||||||||||||
|
пользуем проверочный полином, умноженный на |
X r−1 , |
а остальные строки |
||||||||||||||||||
|
получим циклическим сдвигом первой: |
||||||||||||||||||||
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
||||||
|
N = |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
. |
||||
|
0 0 0 0 1 |
0 0 0 1 0 1 1 |
0 0 0 |
||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
Преобразуем проверочную матрицу следующим образом. Сложим по мо-
дулю два 1–, 5–, 7– и 8–ю; 2–, 3–, 6–, 7– и 8–ю; 4–, 6–, 7– и 8–ю строки матри-
цы и в результате получим кодовые комбинации соответственно:
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1, |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1, |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1. |
60
Составим матрицу L , использовав для ее построения три полученные суммы и 8-ю строку проверочной матрицы N :
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
||
|
L = |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
. |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
||
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
a14 a13 a12 a11 a10 a9 a8 a7 a6 a5 a4 a3 a2 a1 a0
Полученная матрица удовлетворяет требованиям, предъявляемым к матрице L .
Данная матрица L дает четыре независимых проверочных соотношения с разделенными относительно члена a0 проверками; добавив к ним тривиальную
проверку a0 = a0 , получим следующую систему для проверки a0 :
a0 = a1 a3 a7 ,
a0 = a2 a6 a14 , a0 = a4 a12 a13 , a0 = a8 a9 a11,
a0 = a0.
Пусть при передаче был искажен разряд a6 . Этот разряд входит только во
вторую проверку, поэтому четыре проверки дадут правильный результат, а вторая проверка – неправильный. Решение о значении разряда a0 принимается
по критерию большинства и поэтому будет правильным. Ошибочная регистрация разряда произойдет при действии трех и более ошибок, приводящих к неправильным результатам трех и более проверок.
Системы раздельных проверок для остальных разрядов получаются циклическим сдвигом строк матрицы L .
2.3.4. Итеративные коды. Данные коды характеризуются наличием двух или более систем проверок внутри каждой кодовой комбинации. Принцип построения итеративного кода проще всего представлять на конкретном примере. Запишем все информационные разряды блока, подлежащего передаче, в виде таблицы (рис. 2.3).
Каждая строка этой таблицы кодируется каким-либо кодом, а затем кодируется каждый столбец, причем не обязательно тем же кодом. Символы, расположенные в правом нижнем углу таблицы, получаются в результате проверки проверочных символов. Они могут быть построены на основе проверки по строкам и тогда будут удовлетворять проверке по столбцам, и наоборот.
В качестве примера рассмотрим итерированные коды (рис. 2.4) с одной проверкой на четность для каждого столбца и строки. Такой код имеет
61
большую корректирующую способность по сравнению с кодом с одной проверкой на четность, который позволяет только обнаруживать нечетно-кратные ошибки.
Итерированный код позволяет исправить все одиночные ошибки, так как пересечение строки и столбца, содержащих ошибку, однозначно указывает ее место. Передача комбинации итеративного кода обычно происходит по строкам последовательно, от первой строки к последней.
Свойства итеративного кода полностью определяются параметрами итерируемых кодов, в зависимости от которых итеративный код может быть как систематическим, так и несистематическим, как разделимым, так и неразделимым. Длина кодовой комбинации, число информационных разрядов и минимальное кодовое расстояние итеративного кода очень просто выражаются через соответствующие параметры этих кодов:
|
S |
S |
S |
|
|
n = ∏ni , |
k = ∏ki , |
dmin = ∏di , |
(2.50) |
|
i =1 |
i =1 |
i =1 |
где ni , ki , di – параметры итерируемых кодов; S – кратность итерирования.
|
Информационные |
Проверочные символыпо строкам |
|
символы |
|
|
Проверочные символы по |
Проверка |
|
столбцам |
проверок |
Рис. 2.3. Расположение символов итеративного кода
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
9 |
9 |
9 |
9 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
Рис. 2.4. Итеративный код
Таким образом, простейший итеративный код, образованный путем проверок на четность (нечетность) строк и столбцов, обладает минимальным кодовым расстоянием dmin = 4 и поэтому позволяет обнаруживать все ошибки
кратности до 3. Не обнаруживаются четырехкратные ошибки, располагающиеся в вершинах правильного четырехугольника, а также некоторые шестикратные, восьмикратные и т.д. ошибки (рис. 2.5).
Простейший итеративный код обладает довольно высокими обнаруживающими способностями при действии пакетных ошибок – обнаруживается любой пакет ошибок длиной l +1 и менее, где l – длина строки.
62

Рис. 2.5. Ошибки, не обнаруживаемые простейшим итеративным кодом
Могут быть образованы также многомерные итеративные коды, в которых каждый информационный разряд входит в комбинации трех, четырех и т.д. итерируемых кодов.
На рис. 2.6 показан пример применения третьей проверки по диагонали. Порядок формирования контрольных символов Pi показан сплошными
линиями.
Р2
Р3
Р4
Р5
Р1
Рис. 2.6. Итеративный код с тремя проверками
На практике наибольшее распространение получили двумерные итеративные коды. Длина строки обычно выбирается равной длине одного знака первичного кода. В качестве итерируемых кодов чаще всего используются коды с одной и двумя проверками на четность и коды Хемминга.
2.3.5. Рекуррентные коды. Эти коды относятся к числу непрерывных кодов, в которых операции кодирования и декодирования производятся непрерывно над последовательностью информационных символов без деления на блоки. Рекуррентные коды применяются для обнаружения и исправления пакетов ошибок. В данном коде
после каждого информационного элемента следует проверочный элемент. Проверочные элементы формируются путем сложения по модулю два двух информационных элементов, отстоящих друг от друга на шаг сложения, равный b .
Рассмотрим процесс кодирования на примере кодовой комбинации, приведенной на рис. 2.7 (верхняя строка), если шаг сложения b = 2 . Процесс образования контрольных символов показан на этом же рисунке (нижняя строка).
63

Кодирование и декодирование производится с помощью регистров сдвига и сумматоров по модулю два.
|
b=2 |
||||||||||||||
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 …. |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
||
|
Рис. 2.7. Схема построения рекуррентного кода |
На выходе кодирующего устройства (рис. 2.8) получим последовательность символов
1000111000111110010011. (2.51)
Эта последовательность поступает в дискретный канал связи.
|
Вход |
Устройство |
Устройство |
Сумматор по |
|
|
задержки на b |
задержки на b |
|||
|
10110111001 |
модулю 2 |
|||
|
тактов |
тактов |
|||
|
Ключ |
Выход |
|||
|
1 3 |
||||
|
2 |
1000111000111110010011 |
Рис. 2.8. Структурная схема кодера рекуррентного кода
Структурная схема декодера приведена на рис. 2.9. Процесс декодирования заключается в выработке контрольных символов из информационных, поступивших на декодер, и их сравнении с контрольными символами, пришедшими из канала связи. В результате сравнения вырабатывается корректирующая последовательность, которая и производит исправление информационной последовательности. Рассмотрим этот процесс более подробно. Пусть из дискретного канала связи на вход подается искаженная помехами последовательность (искаженные символы обозначены сверху чертой)
64

1000101110111110010011. (2.52)
Устройство разделения (рис. 2.9) разделяет последовательность (2.52) на информационные
и контрольные символы
00010110101. (2.54)
Последовательности символов (2.53) и (2.54) содержат ошибочные символы, которые подчеркнуты сверху. Формирователь контрольных символов из (2.53) выдает последовательность символов
которая в сумме по модулю два с последовательностью (2.54) дает исправляющую последовательность
00110010100. (2.56)
Исправляющая последовательность (2.56) подается на инвертор, который выдает последовательность (2.57) и одновременно поступает на устройства задержки на b и 2b тактов. На выходе устройств задержки появляются последовательности (2.58) и (2.59) соответственно. На выходе схемы совпадения получаем последовательность (2.60)
|
11001101011… |
(2.57) |
|
|
. .001100101… |
(2.58) |
|
|
. . . .0011001… |
(2.59) |
|
|
00000000001… |
(2.60) |
Точки в последовательности слева обозначают задержку символов на соответствующее число тактов. Единица на выходе схемы совпадения возникает только в тех случаях, когда на все ее три входа подаются единицы. Она представляет собой команду исправить ошибку.
65

66
Устройство
разделения
Вход на информа-  ционные и
ционные и
контрольные символы
|
Устройство |
Устройство |
||||||||||
|
задержки на |
|||||||||||
|
коррекции |
Исправлен- |
||||||||||
|
Информационная последовательность, |
b тактов |
||||||||||
|
ная инфор- |
|||||||||||
|
задержанная на 2b тактов |
|||||||||||
|
мационная |
|||||||||||
|
Формирователь контрольных |
последова- |
||||||||||
|
тельность |
|||||||||||
|
символов |
|||||||||||
|
Информа- |
|||||||||||
|
Устройство |
Устройство |
||||||||||
|
ционные |
|||||||||||
|
символы |
задержки на |
задержки на |
|||||||||
|
b тактов |
b тактов |
||||||||||
|
Контроль- |
Сумматор |
Схема |
|||
|
ные |
Инвертор |
||||
|
по модулю 2 |
совпадения |
||||
|
символы |
|||||
|
Сумматор |
Устройство |
Устройство |
|
|
задержки на |
задержки на |
||
|
по модулю 2 |
|||
|
b тактов |
b тактов |
||
Синдром
Рис. 2.9. Структурная схема декодера рекуррентного кода
Для того чтобы в принятом сообщении можно было обнаружить ошибку, это сообщение должно обладать некоторой избыточной информацией, позволяющей отличать ошибочный код от правильного. Например, если переданное сообщение состоит из трёх абсолютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следующим примером:
10110 – переданная кодовая комбинация;
10010 – 1-я принятая комбинация;
10100 – 2-я принятая комбинация;
00110 – 3-я принятая комбинация;
10110 — накопленная комбинация . Как видим, несмотря на то, что во всех трёх принятых комбинациях были ошибки накопленная не содержит ошибок1.
Принятое сообщение может также состоять из кода и его инверсии. Код инверсии посылается в канал связи как одно целое. Ошибка на приёмном конце выделяется при сопоставлении кода и его инверсии (подробнее см. тема 7).
Для того чтобы искажение любого из символов сообщения привело к запрещенной комбинации. Необходимо в коде выделить комбинации, отличающиеся друг от друга в ряде символов, часть из этих комбинаций запретить и тем самым ввести в код избыточность. Например, в равномерном блочном коде считать разрешенными кодовые комбинации с постоянным соотношением нулей и единиц в каждой кодовой комбинации. Такие коды получили название кодов с постоянным весом. Для двоичных кодов число кодовых комбинаций с постоянным весом длиной в n символов равно
![]() , (55)
, (55)
где l – число единиц в кодовом слове. Если бы не существовало условие постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно 2n. Примером кода с постоянным весом может служить стандартный телеграфный код №3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течении которых должна быть принята одна комбинация, всегда приходятся три токовые и четыре без токовые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибок.
Еще одним примером ведения избыточности в код является метод суть которого состоит в том, что к исходным кодам добавляются нули либо единицы таким образом, чтобы сумма их была всегда четной или нечетной. Сбой любого одного символа всегда нарушит условия четности(нечетности), и ошибка будет обнаружена. В этом случае комбинации друг от друга должны отличаться минимум в двух символах (см. задачу 6.9), то есть ровно половина комбинаций кода является запрещенной (запрещенными являются все нечетные комбинации при проверке на четность или наоборот).
Во всех упомянутых выше случаях сообщения обладают избыточной информацией. Избыточность сообщения говорит о том, что оно могло бы содержать большее количество информации, если бы не многократное повторение одного и того же кода не добавления коду его инверсии, не несущей никакой информации, если бы не искусственное запрещение части комбинаций кода и т. д. Но все перечисленные виды избыточности приходиться вводить для того, что бы можно было отличить ошибочную комбинацию от правильной.
Коды без избыточности обнаруживать, а тем более исправлять ошибки не могут1. минимальное количество символов, в которых любые две комбинации кода отличаются друг от друга называются кодовым расстоянием. Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называются минимальным кодовым расстоянием. Минимальное кодовое расстояние – параметр, определяющий помехоустойчивость кода и заложенную в коде избыточности. Минимальным кодовым расстоянием определяются корректирующие свойства кода.
В общем случае для обнаружения r ошибок минимальное кодовое расстояние
![]() . (56)
. (56)
Минимальное кодовое расстояние, необходимое для одновременного обнаружения и исправления ошибок,
![]() , (57)
, (57)
где s – число исправляемых ошибок.
Для кодов, только исправляющих ошибки, ![]() . (58)
. (58)
Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и посчитать число единиц в полученной комбинации (см. задачу 6.21).
Понятие кодового расстояния хорошо усваиваются на примере построения геометрических моделей кодов. На геометрических моделях вершинах n – угольников, где n – значность кода, расположены кодовые комбинации, а количества рёбер n угольника, отделяющих одну комбинацию от другой равно кодовому расстоянию (см. задачу 6.19).
Если кодовая комбинация двоичного кода A отстоит от кодовой комбинации B на расстоянии d, то это значит, что в коде A нужно d символов заменить на обратные, чтобы получить код B, но это не означает, что нужно d добавочных символов, чтобы код
обладал данными корректирующими свойствами. В двоичных кодах для обнаружения одиночной ошибки достаточно иметь 1 дополнительный символ независимо от числа информационных разрядов кода, а минимально кодовое расстояние d0=2.
Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов ![]() и числом корректирующих разрядов
и числом корректирующих разрядов ![]() должно удовлетворять следующим условиям:
должно удовлетворять следующим условиям:
![]() , (59)
, (59)
![]() , (60)
, (60)
при этом подразумевается, что общая длина кодовой комбинации
![]() . (61)
. (61)
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d0 = 3 удобно пользоваться выражениями
![]() , (62)
, (62)
если известна длина полной кодовой комбинации n, и
![]() , (63)
, (63)
если при расчетах удобней исходить из заданного числа информационных символов ![]() 1.
1.
Для кодов, обнаруживающих трёхкратные ошибки (d0=4),
![]() (64)
(64)
или
![]() . (65)
. (65)
Для кодов длиной в n символов, исправляющих одну или две ошибки (d0=5),
![]() . (66)
. (66)
Для практических расчетов можно пользоваться выражением
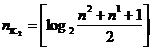 . (67)
. (67)
Для кодов, исправляющих 3 ошибки (d0=7),
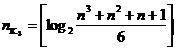 . (68)
. (68)
Для кодов, исправляющих s ошибок (d0=2s+1),
![]() . (69)
. (69)
Выражение слева известно как нижняя граница Хэмминга [16], а выражение справа – как верхняя граница Варшамова – Гильбета [3]1.
Для приближенных расчетов можно пользоваться выражением
 . (70)
. (70)
Можно предположить, что значение ![]() будет приближаться к верхней или нижней границе в зависимости от того, на сколько выражены выражения под знаком логарифма (см. страницу 7) приближается к целой степени двух.
будет приближаться к верхней или нижней границе в зависимости от того, на сколько выражены выражения под знаком логарифма (см. страницу 7) приближается к целой степени двух.
Линейные групповые коды
Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.
Для двоичных кодов в качестве линейной операции используют сложение по модулю 2.
Правила сложения по модулю 2 определяются следующими равенствами:
![]()
![]()
![]()
![]()
Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.
Свойства линейных кодов: сумма (разность) кодовых векторов линейного кода даёт вектор, принадлежащий данному коду.
Линейные коды образуют алгебраическую группу по отношению к операции сложению по модулю 2. в этом смысле они являются групповыми кодами.
Свойства группового кода: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.
Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов (см. задачу 6.42).
Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2 (см. задачу 6.44). Таким образом, для данного группового кода![]() .
.
Групповые коды удобно задавать матрицам, размерность которых определяется параметрами кода ![]() и
и ![]() . Число строк в матрице равно
. Число строк в матрице равно ![]() , число столбцов матрицы равно
, число столбцов матрицы равно ![]() :
:
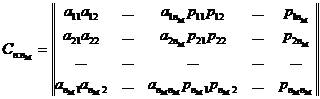 . (71)
. (71)
Коды, порождаемые этими матрицами, известны как (n;k) – коды, где k = ![]() , а соответствующие им матрицы называются порождающими, производящими, образующими.
, а соответствующие им матрицы называются порождающими, производящими, образующими.
Порождающая матрица С может быть представлена двумя матрицами И и П (информационная и проверочная). Число столбцов матрицы П равно nK, число столбцов матрицы И равно nM:
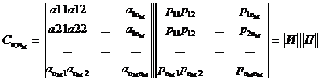 . (72)
. (72)
Теорией и практикой установлено [8,9,13], что в качестве матрицы удобно брать единичную матрицу в канонической формуле:
 .
.
При выборе матрицы П исходят из следующих соображений: чем больше единиц в разрядах проверочной матрицы П, тем ближе соответствующий порождаемый код к оптимальному код к оптимальному1, с другой стороны, число единиц матрицы П определяет число сумматоров по модулю 2 в шифраторе и дешифратор, т. е. Чем больше единиц в матрице П, тем сложнее аппаратура. Вес каждой строки матрицы П должен быть не менее ![]() , гдеWИ – вес соответствующей строки матрицы И. Если матрица И – единичная, то WИ = 1 (удобство выбора в количестве матрицы И единичной матрицы очевидно: при WИ > 1 усложнилась бы как построение кодов, так и их технологическая реализация).
, гдеWИ – вес соответствующей строки матрицы И. Если матрица И – единичная, то WИ = 1 (удобство выбора в количестве матрицы И единичной матрицы очевидно: при WИ > 1 усложнилась бы как построение кодов, так и их технологическая реализация).
При соблюдении перечисленных условий любую порождающую матрицу группового кода можно привести к следующему виду:
![]() …
… ![]() …
… ![]()
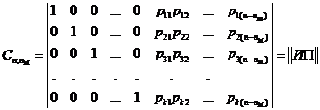 ,
,
называемому левой канонической формой порождающей матрицы.
Для кодов с ![]() производящая матрица С имеет вид:
производящая матрица С имеет вид:

![]() .
.
Во всех комбинациях кода, построенного при помощи такой матрицы, четное число единиц.
Для кодов с ![]() порождающая матрица не может быть представлена в форме, общей для всех видов с данными
порождающая матрица не может быть представлена в форме, общей для всех видов с данными ![]() . Вид матрицы зависит от конкретных требований к порождаемому коду (в качестве примера построения некоторого абстрактного группового кода с
. Вид матрицы зависит от конкретных требований к порождаемому коду (в качестве примера построения некоторого абстрактного группового кода с ![]() может быть предложена задача 6.48). Этим требованиям могут быть либо минимум корректирующих разрядов, либо максимальная простата аппаратуры.
может быть предложена задача 6.48). Этим требованиям могут быть либо минимум корректирующих разрядов, либо максимальная простата аппаратуры.
Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными или совершенными кодами.
Для кодов с ![]() соотношения n и n0 следующее: (3;1), (7;4), (15;11), (31;26), (63;57) и т. д. (см., например, задачу 6.52).
соотношения n и n0 следующее: (3;1), (7;4), (15;11), (31;26), (63;57) и т. д. (см., например, задачу 6.52).
Плотно упакованные коды, оптимальные с точки зрения минимума избыточных символов, обнаруживающие максимально возможное количество вариантов ошибок кратностью ![]() ,
, ![]() и имеющие
и имеющие ![]() и
и ![]() , были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь
, были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь
комбинации с максимальным весом. Для этого при построении кодов с ![]() последовательно используются векторы длиной
последовательно используются векторы длиной ![]() , весом
, весом ![]() ,
, ![]() , …,
, …, ![]() (см. задачи 6.50; 6.65). Тем же Слепяном в работе[11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом
(см. задачи 6.50; 6.65). Тем же Слепяном в работе[11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом ![]() (см. задачи 6.55; 6.65). если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяют условию
(см. задачи 6.55; 6.65). если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяют условию ![]() , больше
, больше ![]() , то в первом случае не используют наборы с наименьшим весом, а во втором – с наибольшим.
, то в первом случае не используют наборы с наименьшим весом, а во втором – с наибольшим.
Строчки образующей матрицы С представляют собой ![]() комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй , третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита (см. задачу 6.57).
комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй , третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита (см. задачу 6.57).
Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом:
![]()
![]()
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
![]()
или ![]() (73)
(73)
В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом:
![]() , j = 1, 2, …,
, j = 1, 2, …, ![]() . (74) Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом p1 входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд p2 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода
. (74) Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом p1 входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд p2 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода ![]() (см. задачу 6.60).
(см. задачу 6.60).
В результате осуществления проверок образуется проверочный вектор![]() ,
,![]() , …,
, …, ![]() , который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор (см. задачи 6.60; 6.62).
, который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор (см. задачи 6.60; 6.62).
Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н, которая представляет собой транспонированную матрицу П, дополненную единичной матрицей ![]() , число столбцов которой равно числу проверочных разрядов кода:
, число столбцов которой равно числу проверочных разрядов кода:![]() .
.
Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н (см. задачи 6.60; 6.62).
Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему.
Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы ![]() . В первом столбце второй строки размещается вектор
. В первом столбце второй строки размещается вектор ![]() , вес которого равен 1.
, вес которого равен 1.
Остальные позиции второй строки заполняются векторами, по лученными в результате суммирования по модулю 2 вектора ![]() с вектором
с вектором ![]() расположенными в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор
расположенными в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор ![]() , вес которого также равен 1, однако, если вектор
, вес которого также равен 1, однако, если вектор ![]() содержит единицу в первом разряде, то
содержит единицу в первом разряде, то ![]() — во втором. В остальные позиции третьей строки записывают суммы
— во втором. В остальные позиции третьей строки записывают суммы ![]() и
и ![]() .
.
Аналогично поступают до тех пор, пока не будут просуммированы с векторами ![]() все векторы
все векторы ![]() , весом 1, с единицами в каждом из n разрядов. Затем суммируются по модулю 2 векторы
, весом 1, с единицами в каждом из n разрядов. Затем суммируются по модулю 2 векторы ![]() , с весом 2, с последовательным перекрытием всех возможных разрядов. Все вектора
, с весом 2, с последовательным перекрытием всех возможных разрядов. Все вектора ![]() определяет число исправляемых ошибок. Число векторов
определяет число исправляемых ошибок. Число векторов ![]() определяется возможным числом неповторяющихся синдромов и равно
определяется возможным числом неповторяющихся синдромов и равно ![]() (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определить один-единственный соответствующий ему вектор
(нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определить один-единственный соответствующий ему вектор ![]() . Векторы
. Векторы ![]() есть векторы ошибок, которые могут быть исправлены данным групповым кодом.
есть векторы ошибок, которые могут быть исправлены данным групповым кодом.
По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинацией ![]() с вектором ошибки
с вектором ошибки ![]() , т. е. к определенной строке кодовой табл. 6.1.
, т. е. к определенной строке кодовой табл. 6.1.
Таблица 6.1.
Ar |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
Принятая кодовая комбинация ![]() сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы (см. задачу 6.68). процесс исправления ошибки заключается в замене на обратное значение разрядов., соответствующих единицам в векторе ошибок
сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы (см. задачу 6.68). процесс исправления ошибки заключается в замене на обратное значение разрядов., соответствующих единицам в векторе ошибок ![]() .
.
Векторы ![]() ,
, ![]() , …,
, …, ![]() не должны быть равны ни одному из векторов
не должны быть равны ни одному из векторов ![]() ,
, ![]() , …,
, …, ![]() в противном случае в таблице появились бы нулевые векторы.
в противном случае в таблице появились бы нулевые векторы.
Тривиальные систематические коды. Код Хэмминга.
Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.
Тривиальные систематические коды могут строиться, как и групповые, на основе производящей матрицы. Обычно производящая матрица строится при помощи матриц единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее ![]() единиц, а сумма по модулю для любых строк не менее
единиц, а сумма по модулю для любых строк не менее ![]() единиц (где
единиц (где ![]() минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю для строк производящей матрицы во всех возможных сочетаниях (см. например, задачу 6.74).
минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю для строк производящей матрицы во всех возможных сочетаниях (см. например, задачу 6.74).
Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных символов, либо количество информационных комбинаций ![]() . При помощи (59) и (60) вычисляются
. При помощи (59) и (60) вычисляются ![]() и
и ![]() . Соотношения между n,
. Соотношения между n, ![]() , и
, и ![]() для Хэмминга предоставлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону
для Хэмминга предоставлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону ![]() , где
, где ![]() 0, 1, 2 и т. д. — натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.
0, 1, 2 и т. д. — натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.
Затем определяется значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на контрольных позициях должна быть четной. Если эта сумма четна, то значение контрольного коэффициента — 0, в противно случае — 1.
Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы:
![]() .
.
Первой строке соответствует проверочный коэффициент ![]() , второй
, второй ![]() и т. д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т. е.
и т. д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т. е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д.; во вторую — коэффициенты, содержащие 1 во втором разряде, т. е.
и т. д.; во вторую — коэффициенты, содержащие 1 во втором разряде, т. е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д.; в третью проверку — коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствует номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также и порядок следования разрядов в получения разрядов в полученном двоичном коде.
и т. д.; в третью проверку — коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствует номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также и порядок следования разрядов в получения разрядов в полученном двоичном коде.
Если в принятом коде есть ошибка, то результат проверок по контрольным позициям образует двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции а обратный (см. задачу 6.78).
Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации всегда была четной. Тогда в случае одиночной ошибки проверки по позициям укажут на наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки (см. задачу 6.82).
Циклические коды.
Циклические коды [4, 6, 7, 9, 12, 13] названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путем циклического сдвига одной или нескольких комбинацикода. Циклический сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Циклические коды, практически1, все относятся к систематическим кодам, в них контрольные и информационные разряды расположены на строго определенных местах. Кроме того, циклические коды относятся к числу блочных кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно.
Идея построения циклических кодов базируется на использовании неприводимых в поле[1] двоичных чисел многочленов. Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней с коэффициентами из того же поля, так же, как простые числа не могут быть представлены произведением других чисел. Иными словами, неприводимые многочлены делятся без остатка только на себя или на единицу.
Неприводимые многочлены в теории циклических кодов играют роль образующих (генераторных, производящих) многочленов. Если заданную кодовую комбинацию умножить на выбранный неприводимый многочлен, то получим циклический код, корректирующие способности которого определяются неприводимым многочленом.
Предположим, требуется закодировать одну из комбинаций четырехзначного двоичного кода. Предположим также, что эта комбинация ![]() . Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен
. Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен ![]() . Затем умножим
. Затем умножим ![]() на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени n степень каждого члена многочлена повысится на n, что эквивалентно приписыванию n нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:
на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени n степень каждого члена многочлена повысится на n, что эквивалентно приписыванию n нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:
![]()
Это делается для того, чтобы впоследствии на мест этих нулей можно было бы записать корректирующие разряды.
Значение корректирующих разрядов находят по результату от деления ![]() на
на ![]() :
:
|
|
|
||||||
|
|
|
||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
или
|
1101000 |
1011 |
|||||||
|
1011 |
1111+ |
|||||||
|
1100 |
||||||||
|
1011 |
||||||||
|
1110 |
||||||||
|
1011 |
||||||||
|
1010 |
||||||||
|
1011 |
||||||||
|
001 |
||||||||
Таким образом,
![]() ,
,
или в общем виде
![]() , (75)
, (75)
где ![]() частное, а
частное, а ![]() остаток от деления
остаток от деления ![]() на
на ![]() .
.
Так как в двоичной арифметике ![]() , а значит,
, а значит, ![]() , то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида
, то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида ![]() можно записать и как
можно записать и как ![]() , и как
, и как ![]() . Все три равенства данном случае означают, что либо a и b равны 0, либо a и b равны 1, т. е. имеют одинаковую четность.
. Все три равенства данном случае означают, что либо a и b равны 0, либо a и b равны 1, т. е. имеют одинаковую четность.
Таким образом, выражение (75) можно записать как
![]() , (76)
, (76)
что в случае нашего примера даст
![]()
или
![]() 1 1 1 1
1 1 1 1 ![]() 1 0 1 1 = 1 1 0 1 0 0 0 + 0 0 1 =
1 0 1 1 = 1 1 0 1 0 0 0 + 0 0 1 =
=1 1 0 1 0 0 1
Многочлен 1101001 и есть искомая комбинация, где 1101 – информационная часть, а 001 – контрольные символы. Заметим, что искомую комбинацию мы получили бы и как в результате умножения одной из комбинаций полного четырехзначного двоичного кода (в двоичном случае 1111) на образующий многочлен, так и умножением заданной комбинации на одночлен, имеющий ту же степень, что и выбранный образующий многочлен (в нашем случае таким образом была получена комбинация 1101000) с последующим добавлением к полученному произведению остатка от деления этого произведения на образующий многочлен (в нашем примере остаток имел вид 001).
Таким образом, мы уже знаем два способа образования комбинаций линейных систематических кодов, к которым относятся и интересующие нас циклические коды. Эти способы явились теоретическим основанием для построения кодирующих и декодирующих устройств.
Шифраторы циклических кодов, в том или ином виде, построены по принципу умножения двоичных многочленов. Кодовые комбинации получаются в результате сложения соседних комбинаций по модулю два, что, как мы увидим ниже, эквивалентно умножению первой комбинации на двучлен ![]() .
.
Итак, комбинации циклических кодов можно представить в виде многочлена, у которых показатели степени x соответствуют номером разрядов, коэффициенты при x равны 0 или 1 в зависимости от того, стоит 0 или 1 в разряде кодовой комбинации , которую представляет данный многочлен. Например,
000101![]() ;
;
001010![]() ;
;
010100![]() ;
;
101000![]() .
.
Циклический сдвиг кодовой комбинации аналогичен умножению соответствующего многочлена на x:
![]() ;
;
![]() ;
;
![]() .Если степень многочлена достигает разрядности кода, то происходит «перенос» в нулевую степень при x. В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда.
.Если степень многочлена достигает разрядности кода, то происходит «перенос» в нулевую степень при x. В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда.
Сложение по модулю 2 любых двух соседних комбинаций циклического кода эквивалентного операции умножения многочлена соответствующего комбинации первого слагаемого на многочлен ![]() , если приведение подобных членов осуществляется по модулю 2:
, если приведение подобных членов осуществляется по модулю 2:
|
0 0 0 1 0 1 |
|
|
|||
|
|
|
||||
|
0 0 1 0 1 0 |
|
||||
|
0 0 1 1 1 1 |
|
||||
|
|
|
||||
|
|
|
||||
т. е. существует принципиальная возможность получения любой кодовой комбинации циклического кода путем умножения соответствующим образом подобного образующего многочлена на некоторый другой многочлен.
Однако мало построить циклический код. Надо уметь выделить из него возможные ошибочные разряды, т. е. ввести некоторые опознаватели ошибок, которые выделяли бы ошибочный блок из всех других. Так, как циклические коды – блочные, то каждый блок должен иметь свой опознаватель. И тут решающую роль играют свойства образующего многочлена ![]() . Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклического кодов.
. Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклического кодов.
С другой стороны, остатки от деления единицы с нулями на образующий многочлен используются для построения циклических кодов (возможность этого видна из выражения (76)).
При делении единицы с нулями образующих многочлен следует помнить, что длина остатка должна быть не меньше числа контрольных разрядов, поэтому в случае нехватки разрядов в остатке к остатку приписывают справа необходимое число нулейНапример,
|
1 0 0 0 0 0 0 0 0 0 0 |
1 0 1 1 |
||||||||||
|
1 0 1 1 |
1 1 1 1 1 + |
||||||||||
|
0 1 1 0 0 |
|||||||||||
|
1 0 1 1 |
Остатки |
||||||||||
|
1 1 1 0 |
0 1 1 |
||||||||||
|
1 0 1 1 |
1 1 0 |
||||||||||
|
1 0 1 0 |
1 1 1 |
||||||||||
|
1 0 1 1 |
1 0 1 |
||||||||||
|
1 0 0 0 |
0 0 1 |
||||||||||
|
1 0 1 1 |
0 1 0 |
||||||||||
|
1 1 |
1 0 0 |
||||||||||
|
0 1 1 |
|||||||||||
|
1 1 0 |
|||||||||||
|
и т. д., |
|||||||||||
начиная с восьмого, остатки будут повторятся.
Остатки от деления используют для построения образующих матриц, которые, благодоря вой наглядности и удобству получения производных комбинаций, получили широкое распространение для построения циклических кодов. Построение образующей матицы сводится к составлению единичной транспонированной и дополнительной матрицы, элементы которой представляют собой остатки от деления единицы с нулями на образующий многочлен ![]() 1. Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой – нули, кроме элементов, расположенных по диагонали справа на лево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева на права сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы.
1. Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой – нули, кроме элементов, расположенных по диагонали справа на лево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева на права сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы.
Однако не все остатки от деления единицы с нулями на образующий многочлен могут быть использованы в качестве элементов дополнительной матрицы. Использоваться могут лишь те остатки вес которых ![]() , где
, где ![]() минимальное кодовое расстояние длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.
минимальное кодовое расстояние длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.
Строки образующие матрицы представляют собой первые комбинации искомого кода. Остальные комбинации кода получаются в результате суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы (см. задачу 6.108)1.
Описанный выше метод построения образующих матриц не является единственным. Образующая матрица может быть построена в результате непосредственного умножения элементов единичной матрицы на образующий многочлен. Это часто бывает удобнее чем нахождение остатков от деления. Полученные коды ничем не отличаются от кодов, построенных по образующим матрицам, а которых дополнительная матрица состоит из остатков от деления единицы с нулями на образующий многочлен ( см. задачи 6.103; 6.108; 6.110).
Образующая матрица может быть построена таким путем циклического сдвига комбинации, полученной в результате умножения строки единичной матрицы ранга ![]() на образующий многочлен (см. задачу 6.126).
на образующий многочлен (см. задачу 6.126).
В заключение предлагаем еще один метод построения циклических кодов. Достоинством этого метода является исключительная простота схемных реализаций кодирующих и декодирующих устройств.
Для получения комбинаций циклического кода в этом случае достаточно произвести циклический сдвиг строки образующей матрицы и комбинации, являющейся ее зеркальным отображением (см. задача 6.112). При построении кодов с ![]() число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации (см. задачи 6.103; 6.112). Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при
число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации (см. задачи 6.103; 6.112). Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при ![]() число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы (см., например, задачи 6.123 и 6.128).
число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы (см., например, задачи 6.123 и 6.128).
Число ненулевых комбинаций, получаемых в результате суммирования по модулю 2 всевозможных два строк образующей матрицы,
![]() , (77)
, (77)
где ![]() число информационных разрядов кода2.
число информационных разрядов кода2.
Число ненулевых комбинаций, получаемых в результате циклического сдвига любой строки образующей матрицы и зеркальной ей комбинации,
![]() , (78)
, (78)
где n – длина кодовой комбинации.
При числе информационных разрядов ![]() число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий.
число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий.
Ошибки в циклических кодах обнаруживаются и исправляются при помощи остатков от деления полученной комбинации на образующий многочлен. Остатки от деления являются опознавателями ошибок, но не указывают непосредственно на место ошибки в циклическом коде.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется»под остаток таким образом, что в сумме с остатком она дает исправленную комбинацию. Остаток при этом представляет собой не что иное, как разницу между искаженными и правильными символами, единицы в остатке стоят как раз на местах искаженных разрядов в подогнанной циклическими сдвигами комбинации. Подгоняют искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть либо равно числу ошибок s; исправляемых данным кодом (код исправляют 3 ошибки и в искаженной комбинации 3 ошибки), либо меньше s (код исправляет 3 ошибки, а в принятой комбинации – 1 ошибка).
Место ошибки в кодовой комбинации не имеет значения. Если ![]() , то после определенного количества сдвигов все ошибки окажутся в зоне «разового» действия образующего многочлена, т. е. достаточно получить один остаток, вес которого
, то после определенного количества сдвигов все ошибки окажутся в зоне «разового» действия образующего многочлена, т. е. достаточно получить один остаток, вес которого ![]() , и этого уже будет достаточно для исправления искажаемой комбинации. В смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s.
, и этого уже будет достаточно для исправления искажаемой комбинации. В смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s.
Подробно процесс исправления ошибок рассматривается ниже на примере построения конкретных кодов.
Построение и декодирование конкретных циклических кодов.
I. Коды исправляющие одиночную ошибку, ![]() .
.
1. Расчет соотношения между контрольными и информационными символами кода производятся на основании выражений (59) — (69).
Если задано число информационных разрядов ![]() , то число контрольных разрядов
, то число контрольных разрядов ![]() находим из выражения
находим из выражения
![]() .
.
Общее число символов кода
![]() .
.
Если задана длина кода n, то число контрольных разрядов
![]() .
.
Соотношение числа контрольных и информационных символов для кодов с ![]() приведены в табл. 3 приложения 9.
приведены в табл. 3 приложения 9.
2. Выбор образующего многочлена производится по таблицам неприводимых двоичных многочленов.
Образующий многочлен ![]() следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов
следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов ![]() , а число ненулевых членов – не меньше минимального кодового расстояния
, а число ненулевых членов – не меньше минимального кодового расстояния ![]() .
.
Выбор параметров единичной транспонированной матрицы происходит из условия, что число столбцов (строк) матрицы определяется числом информационных разрядов, т. е. ранг единичной матрицы равен ![]() .
.
3. Определение элементов дополнительной матрицы производится по остаткам от деления последней строки транспонированной матрицы (единицы с нулями) на образующий многочлен. Полученные остатки должны удовлетворять следующим требованиям:
а) число разрядов каждого остатка должно быть равно числу контрольных символов ![]() , следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена;
, следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена;
б) число остатков должно быть не меньше числа строк единичной транспонированной матрицы, т. е. должно быть равно числу информационных разрядов ![]() ;
;
в) число единиц каждого остатка, т. е . его вес должно быть не менее величены ![]() , где
, где ![]() минимальное кодовое расстояние, не меньше числа обнаруженных ошибок;
минимальное кодовое расстояние, не меньше числа обнаруженных ошибок;
г) количество нулей, приписанных к единице с нулями в делении ее на выбранный неприводимый многочлен, должно быть таким, чтобы соблюдались условия а), б), в).
4. Образующая матрица составляется дописыванием элементов дополнительной матрицы справа от единичной транспонированной матрицы либо умножением элементов единичной матрицы на образующий многочлен.
5. Комбинациями искомого кода являются строки образующий матрицы и все возможные суммы по модулю 2 различных сочетаний строк образующей матрицы (см. задачу 6.108).
Как видно из решения задач 6.103 и 6.108, коды, получены при использовании неприводимых многочленов ![]() и
и ![]() , подобны друг другу и обладают равноценными корректирующими способностями. Сами же многочлены 1101 и 1011 называют обратными, или двойственными, многочленам. Если данный многочлен неприводимый, то неприводимый будет и двойственный ему многочлен.
, подобны друг другу и обладают равноценными корректирующими способностями. Сами же многочлены 1101 и 1011 называют обратными, или двойственными, многочленам. Если данный многочлен неприводимый, то неприводимый будет и двойственный ему многочлен.
6. Обнаружение и исправление ошибок производится по остатку от деления принятой комбинации ![]() на образующий многочлен
на образующий многочлен ![]() . Если принятая комбинация делится на образующий многочлен без остатка, то код принят без ошибочно. Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции:
. Если принятая комбинация делится на образующий многочлен без остатка, то код принят без ошибочно. Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции:
а) принятую комбинацию делят на образующий многочлен;
б) подсчитывают количество единиц в остатке (вес остатка). Если ![]() , где s – допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если
, где s – допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если ![]() , то
, то
в) производят циклический сдвиг принятой комбинация ![]() влево на один разряд. Комбинацию, полученную в результате этого повторного деления
влево на один разряд. Комбинацию, полученную в результате этого повторного деления ![]() , то делимое суммируют с остатком, затем
, то делимое суммируют с остатком, затем
г) производят циклический сдвиг вправо на один разряд комбинации, полученной в результате суммирования последнего делим, с последним остатком. Полученная в результате комбинация уже не содержит ошибок. Если после первого циклического сдвига последующего деления остаток получается таким, что его вес ![]() ,
,
д) повторяют операцию пункта в) до тех пор, пока не будет ![]() . В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатка от деления этой комбинации на образующий многочлен, а затем
. В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатка от деления этой комбинации на образующий многочлен, а затем
е) производят циклический сдвиг вправо ровно на столько разрядов, на сколько была сдвинута суммируемая с последним остатком
комбинации относительно принятой комбинации. В результате получим исправленную комбинацию (см. задачи 6.113 – 6.116)1.
II. Коды обнаруживающие трехкратные ошибки. ![]() .
.
1. Выбор числа корректирующих разрядов производится из соотношения
![]() ,
,
или
![]() .
.
2. Выбор образующего многочлена производят, исходя из следующих соображений: для обнаружения трехкратной ошибки
![]() ,
,
Поэтому степень образующего многочлена не может быть меньше четырех; многочлен третьей степени, имеющий число ненулевых членов больше или равное трем, позволяет обнаруживать все двойные ошибки (см. задачи 6.121; 6.122), многочлен первой степени (х+1) обнаруживает любое количество нечетных ошибок (см. задачи 6.119; 6.120), следовательно, многочлен четвертой степени, получаемый в результате умножения этих многочленов, обладает их корректирующими свойствами: может обнаруживать две ошибки а также одну и три, т. е. все трехкратные ошибки (см. задачу 6.117).
3. Построение образующей матрицы производят либо нахождением остатков от деления единицы с нулями на образующий многочлен, либо умножением строк единичной матрицы на образующий многочлен (си. задачу 6.121).
4. Остальные комбинации корректирующего кода находят суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы.
5. Обнаружение ошибок производится по остаткам от деления принятой комбинации ![]() на образующий многочлен
на образующий многочлен ![]() . Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3.П р и м е р. Исходная кодовая комбинация – 0101111000, принятая – 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибки если известно, что комбинации кода были образованы при помощи многочлена 101111.
. Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3.П р и м е р. Исходная кодовая комбинация – 0101111000, принятая – 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибки если известно, что комбинации кода были образованы при помощи многочлена 101111.
|
Р е ш е н и е. |
0 0 0 1 0 1 1 0 0 1 |
1 0 1 1 1 1 |
|
|
1 0 1 1 1 1 |
|||
|
0 0 0 0 1 1 1 |
|||
Остаток ненулевой, комбинация бракуется. Указать ошибочные разряды при трехкратных искажениях такие коды не могут.
III. Циклические коды, исправляющие две и большее количество ошибок, ![]() .
.
Методика построения циклических кодов с ![]() отличается от методики построения циклических кодов
отличается от методики построения циклических кодов ![]() только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем – авторов методики построения циклических кодов с
только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем – авторов методики построения циклических кодов с ![]() ).
).
Построение образующего многочлена зависит в основном, от двух параметров: от длины кодового слова n и от числа исправляемых ошибок s. Остальные параметры, участвующие в построении образующего многочлена в зависимости от заданных n и s могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже.
Для исправления числа ошибок ![]() еще недостаточно условие, что бы между комбинациями кода минимальное кодовое расстояние
еще недостаточно условие, что бы между комбинациями кода минимальное кодовое расстояние ![]() , необходимо также чтобы длина кода n удовлетворяла условию
, необходимо также чтобы длина кода n удовлетворяла условию
![]() , (79)
, (79)
при этом n всегда будет нечетным числом. Величина h определяет выбор числа контрольных символов ![]() и связанна с
и связанна с ![]() и s следующим соотношением:
и s следующим соотношением:
![]() . (80)
. (80)
C другой стороны, число контрольных символов определяется образующим много членом и равно его степени (к этому вопросу мы еще вернемся). При больших значениях h длина кода n становиться очень большой, что вызывает вполне определенные трудности при технической реализации кодирующих и декодирующих устройств. При этом часть информационных разрядов порой остается неиспользованной. В таких случаях для определения h удобно пользоваться выражением
![]() , (81)
, (81)
где С является одним из сомножителей на которое разлагается число n.
Соотношение между n, С и h могут быть сведены в следующую таблицу:
|
№ п/п |
h |
|
C |
|
1 |
3 |
7 |
1 |
|
2 |
4 |
15 |
5; 3 |
|
3 |
5 |
31 |
1 |
|
4 |
6 |
63 |
7; 3; 3 |
|
5 |
7 |
127 |
1 |
|
6 |
8 |
255 |
17; 5; 3 |
|
7 |
9 |
511 |
7; 3; 7 |
|
8 |
10 |
1023 |
31; 11; 3 |
|
9 |
11 |
2047 |
89; 23 |
|
10 |
12 |
4095 |
3; 3; 5; 7; 13 |
Например, при h=10 длина кодовой комбинации может быть равна и 1023 (C=1) и 341 (С=3), и 33 (С=31), и 31 (С=33), понятно, что n не может быть меньше![]() . Величина С влияет выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются С. сказанное выше хорошо усваивается на конкретном примере (см. задачу 6.132).
. Величина С влияет выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются С. сказанное выше хорошо усваивается на конкретном примере (см. задачу 6.132).
Построение образующего многочлена ![]() производится при помощи так называемых минимальных многочленов
производится при помощи так называемых минимальных многочленов ![]() , которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок
, которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок ![]() определяет номер последнего из выбираемых табличных минимальных многочленов
определяет номер последнего из выбираемых табличных минимальных многочленов
![]() , (82)
, (82)
Порядок многочлена используется при определении числа сомножителей ![]() . Например, если s=6, то
. Например, если s=6, то ![]() . Так как для построения
. Так как для построения ![]() используются только нечетные многочлены, то ими будут:
используются только нечетные многочлены, то ими будут: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() , старший из них имеет порядок
, старший из них имеет порядок ![]() . Как видим число сомножителей
. Как видим число сомножителей ![]() равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,
равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,
![]() , (83)
, (83)
а старшая степень
![]() (84)
(84)
(l указывает колонку в таблице минимальных многочленов, из которой обычно выбирается многочлен для построения ![]() ).
).
Степень образующего многочлена полученного в результате перемножения выбранных минимальных многочленов,
![]() . (85)
. (85)
В общем виде
![]() , (86)
, (86)
Декодирование кодов БЧХ производится по той же методике, что и декодирование циклических кодов с ![]() . Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с n
. Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с n![]() 15, могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию полученную после k-кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на n – k циклических сдвигов. Это целесообразно делать только при
15, могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию полученную после k-кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на n – k циклических сдвигов. Это целесообразно делать только при ![]() (см. задачу 6.134).
(см. задачу 6.134).
