На сколько изменилось среднее значение после исключения ошибки

Для
исключения грубых ошибок наблюдений,
искажающих статистические характеристики
распределения, необходимо провести
оценку резко выделяющихся членов
выборки. Для этого используются различные
методы. Конечно, прежде всего следует
быть уверенным, что резко выделяющиеся
члены выборки не являются результатом
ошибки, нарушения условий эксперимента.
Если такой уверенности нет, то грубые
ошибки сразу следует исключить из
дальнейшего анализа.

Разработанные
методы для оценки резко выделяющихся
членов выборки применимы, если известно
распределение, которому подчиняются
наблюдаемые случайные величины. Их
применение при других распределениях
может привести к серьезным ошибкам [3].
Это часто не указывается в литературе,
где приводятся такие методы. Большинство
методов разработано для случаев, когда
исследуемые величины подчиняются
нормальному распределению. Эти методы
(часто они носят название критериев),
как правило, требуют предварительного
вычисления среднего значения и среднего
квадратического отклонения исследуемой
величины. Во всех методах рассчитываемая
величина сравнивается с критическим
значением этой величины, найденным из
соответствующих таблиц при выбранном
проценте риска. После чего принимается
решение о том, является ли резко
выделяющееся значение случайной величины
грубой ошибкой и его следует отбросить
или оно не подлежит исключению из
выборки.

Рассмотрим
методы (критерии), которые применяются
при нормальном распределении исследуемой
случайной величины. В литературе
приводятся следующие методы (критерии):
критерий, основанный на теореме
Р.Фишера[4], критерий типа r [4], упрощенные
критерии [4], метод Грэббса [5], метод
Романовского [5], метод исключения при
известной [6], оценка
анормальности результатов измерений
при известной генеральной дисперсии
[3], метод исключения при неизвестной[6], оценка анормальности
результатов измерений при неизвестной
генеральной дисперсии [3]. Следует
отметить, что в [5] и [6] не указано, что
перечисленные методы применимы только
при нормальном распределении.

Критерий,
основанный на теореме Фишера [4], приведен
в одной из работ В.Н.Романовского. В нем
рассматривается неравенство

,

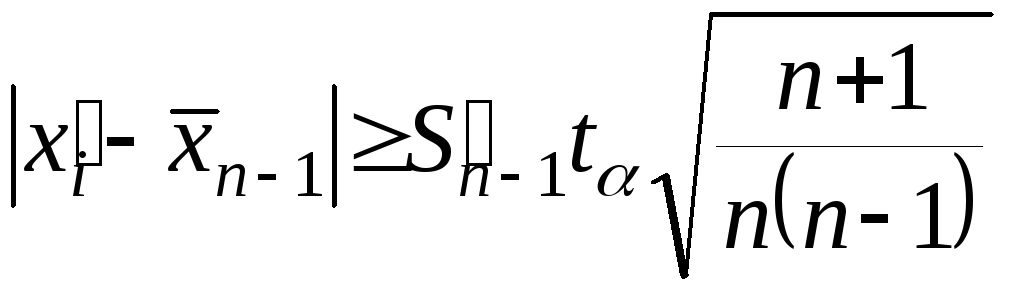где
n

— число членов выборки;

—
резко выделяющийся член выборки;

—
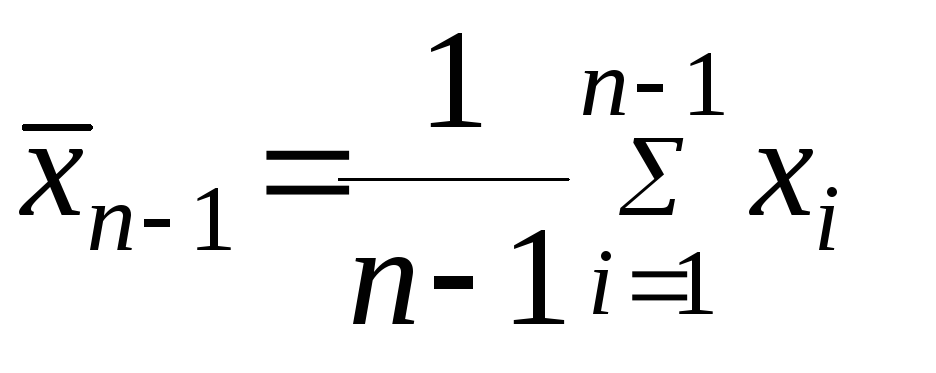среднее значение исследуемой величины,
подсчитанное при исключенном резко
выделяющемся члене выборки;

Если преобразовать неравенство к виду

то
оно напоминает метод Романовского [5],
при котором оценивается

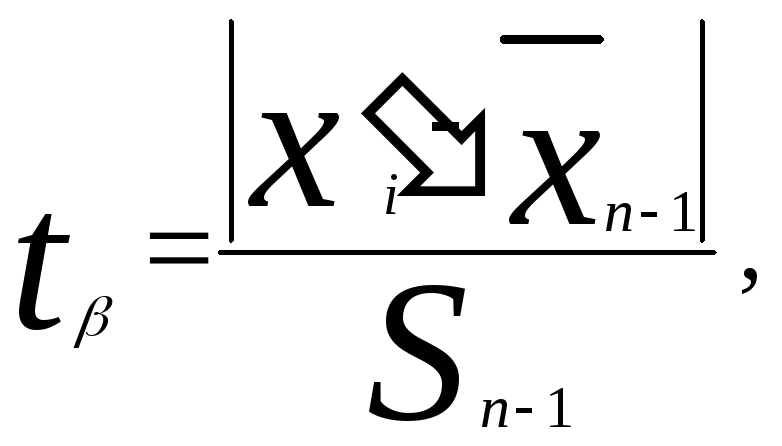
где
— среднее квадратическое отклонение,
подсчитанное при исключенном резко
выделяющемся члене выборки.

В
рассмотренных двух методах не приходится
пересчитывать среднее значение
и среднее квадратическое отклонениеисследуемой случайной величины после
исключения резко выделяющегося члена
выборки. Но если его исключить не удается,
то следует при дальнейшей обработке
пересчитатьис учетом значения.

Во всех
остальных методах (кроме упрощенных
критериев) приходится после исключения
грубой ошибки снова определять значения
и.

Критерий
типа r
[4] определяет величину

,

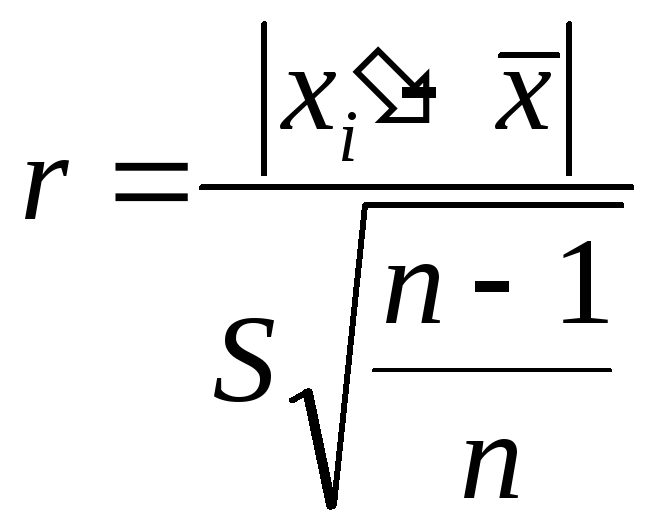где
и.

Если преобразовать знаменатель этого критерия, то мы получим

,

где

.

Полученное выражение совпадает с методом Грэббса [5]

.

В методе исключения
грубой ошибки при известной 
[6] определяется величина

,

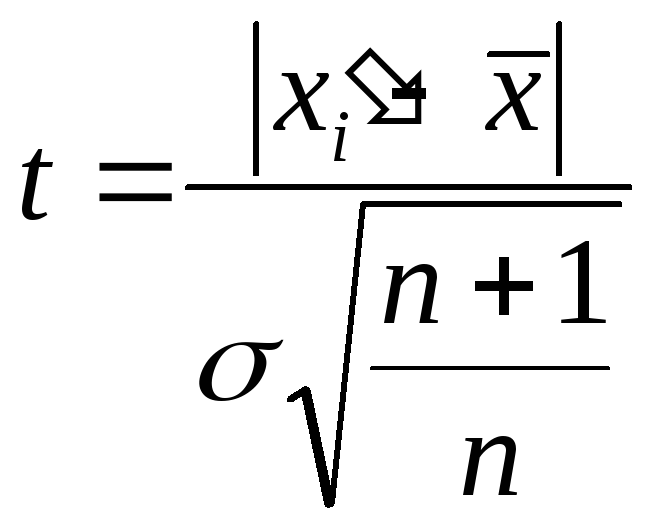а в методе оценки
анормальности результатов измерений
при известной генеральной дисперсии
[3] определяется величина

.

В методе исключения
грубых ошибок при неизвестной [6] определяется величина

,

то есть та же, что и в
методе оценки анормальности результатов
измерений при неизвестной генеральной
дисперсии [3].

Таким
образом, последний метод отличается от
критерия типа r
и метода Грэббса только способом
определения среднего квадратического
отклонения (несмещенная оценка).

Метод
упрощенных критериев [4] предполагает
определение отношения отклонения
экстремального члена выборки к ее
размаху. Определяются величины

и

,

поскольку экстремальные
члены могут лежать слева и (или) справа
от основной части выборки. Как указано
выше, в этом методе не приходится
определять
и,
что значительно уменьшает объем
вычислительной работы.

Для
случая оценки резко выделяющегося члена
выборки при справедливости показательного
распределения используется критерий
Р. Фишера [4].

Таблицы
для сравнения полученных критериев с
их критическими значениями приведены
в указанной в тексте литературе. А для
метода Грэббса можно использовать [8].

Существует
также критерий Ирвина [4,5], о котором не
указывается, что он применим при
определенном распределении. Метод или
критерий Ирвина основан на оценке
разности двух наибольших или наименьших
членов выборки. Определяется величина
,
равная

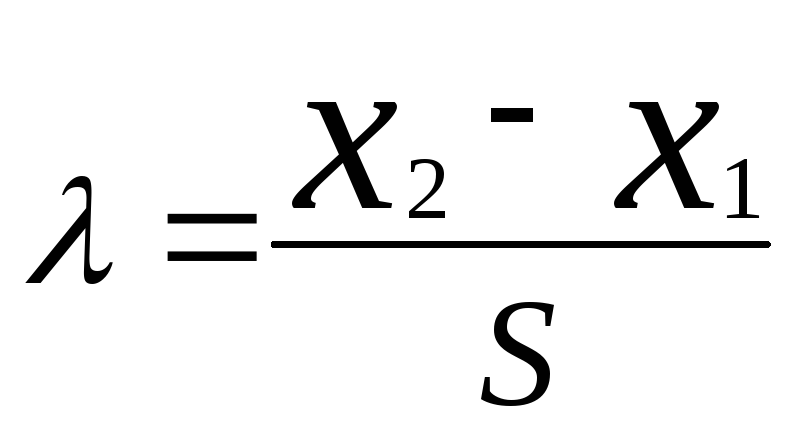или

,

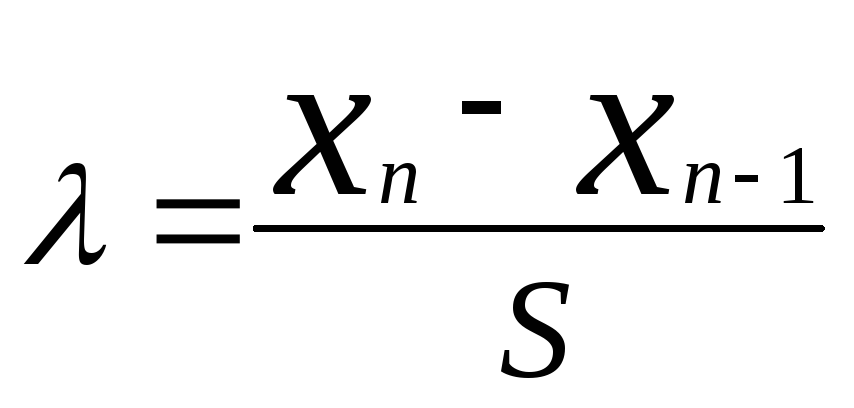в
зависимости от того, с какой стороны
выборки расположен резко выделяющийся
член выборки. По приведенной таблице
(или таблице [7]) в зависимости от объема
выборки n при уровне значимости =0,95
находят критическое значение
.

n	20	30	50	100	400	1000
0,95	1,3	1,2	1,1	1,0	0,9	0,8

Если
оказывается, что рассчитанная
,то
оцениваемый результат является случайным
и не подлежит исключению из выборки.
Если
,то
следует исключить из выборки оцениваемое
резко выделяющееся наименьшее или
наибольшее значение случайной величины
(или оба вместе), так как оно представляет
собой грубую ошибку. После исключения
ошибки необходимо снова вычислить
значения
и
.

Соседние файлы в папке ТОПИН.Лекции, задания

• #

  11.05.201512.39 Mб591.rtf

• #
• #
• #
• #
• #

Когда вы применяете функцию СРЕДНЕЕ для вычисления среднего значения диапазона ячеек, включающего некоторые значения ошибок, вы получите результат ошибки. В следующей статье будет рассказано о том, как усреднить ячейки, игнорируя ошибки в Excel.

Средние ячейки, игнорирующие значения ошибок с помощью формул массива

---

Средние ячейки, игнорирующие значения ошибок с помощью формул массива

Следующие удобные формулы массива могут помочь вам вычислить среднее значение ячеек без учета ошибок. Пожалуйста, сделайте так:

1. Введите эту формулу массива: = СРЕДНИЙ (ЕСЛИ (ЕСТЬ ОШИБКА (A1: C6); «»; A1: C6)), см. снимок экрана:

2, Затем нажмите Shift + Ctrl + Enter одновременно, и вы получите средний результат, как показано на скриншоте ниже:

Ноты:

1. Кроме приведенной выше формулы, вам может помочь еще одна формула: = СРЕДНИЙ (ЕСЛИ (ЕЧИСЛО (A1: C6); A1: C6)), пожалуйста, не забудьте нажать Shift + Ctrl + Enter ключи.

2. В приведенных выше формулах A1: C6 — это диапазон данных, который вы хотите вычислить, вы можете изменить его по своему усмотрению.

---

Статьи по теме:

Как усреднить абсолютные значения в Excel?

Как усреднить только положительные или отрицательные числа в Excel?

Как усреднить диапазон данных, игнорируя ноль в Excel?

Как рассчитать среднее значение без максимальных и минимальных значений в Excel?

---

Лучшие инструменты для работы в офисе

Kutools for Excel Решит большинство ваших проблем и повысит вашу производительность на 80%

• Снова использовать: Быстро вставить сложные формулы, диаграммы и все, что вы использовали раньше; Зашифровать ячейки с паролем; Создать список рассылки и отправлять электронные письма …
• Бар Супер Формулы (легко редактировать несколько строк текста и формул); Макет для чтения (легко читать и редактировать большое количество ячеек); Вставить в отфильтрованный диапазон…
• Объединить ячейки / строки / столбцы без потери данных; Разделить содержимое ячеек; Объединить повторяющиеся строки / столбцы… Предотвращение дублирования ячеек; Сравнить диапазоны…
• Выберите Дубликат или Уникальный Ряды; Выбрать пустые строки (все ячейки пустые); Супер находка и нечеткая находка во многих рабочих тетрадях; Случайный выбор …
• Точная копия Несколько ячеек без изменения ссылки на формулу; Автоматическое создание ссылок на несколько листов; Вставить пули, Флажки и многое другое …
• Извлечь текст, Добавить текст, Удалить по позиции, Удалить пробел; Создание и печать промежуточных итогов по страницам; Преобразование содержимого ячеек в комментарии…
• Суперфильтр (сохранять и применять схемы фильтров к другим листам); Расширенная сортировка по месяцам / неделям / дням, периодичности и др .; Специальный фильтр жирным, курсивом …
• Комбинируйте книги и рабочие листы; Объединить таблицы на основе ключевых столбцов; Разделить данные на несколько листов; Пакетное преобразование xls, xlsx и PDF…
• Более 300 мощных функций. Поддерживает Office/Excel 2007-2021 и 365. Поддерживает все языки. Простое развертывание на вашем предприятии или в организации. Полнофункциональная 30-дневная бесплатная пробная версия. 60-дневная гарантия возврата денег.

---

Office Tab Добавляет в Office интерфейс с вкладками и значительно упрощает вашу работу

• Включение редактирования и чтения с вкладками в Word, Excel, PowerPoint, Издатель, доступ, Visio и проект.
• Открывайте и создавайте несколько документов на новых вкладках одного окна, а не в новых окнах.
• Повышает вашу продуктивность на 50% и сокращает количество щелчков мышью на сотни каждый день!

Комментарии (13)

Оценок пока нет. Оцените первым!

Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.

Расчет ошибки средней арифметической

Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.

В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.

Способ 1: расчет с помощью комбинации функций

Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.

Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.

1. Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».

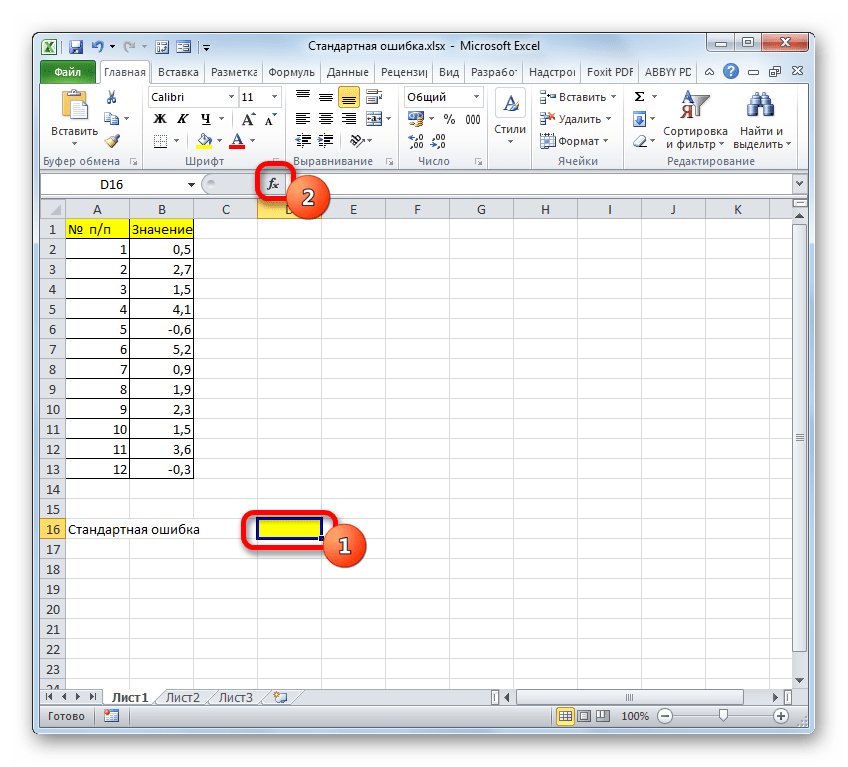
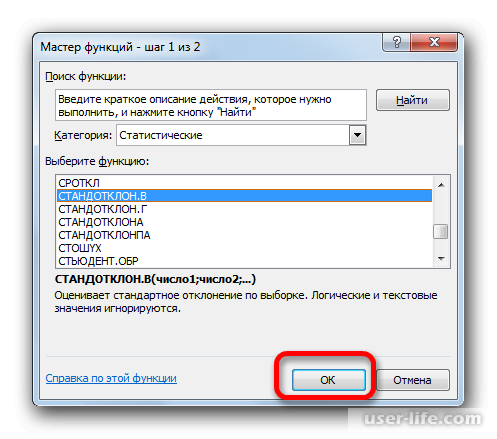
Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».

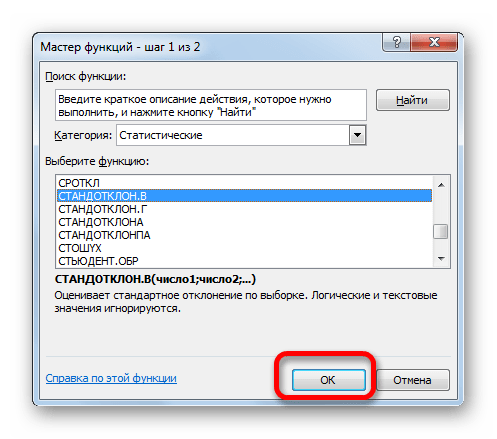
Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:

«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.

Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».

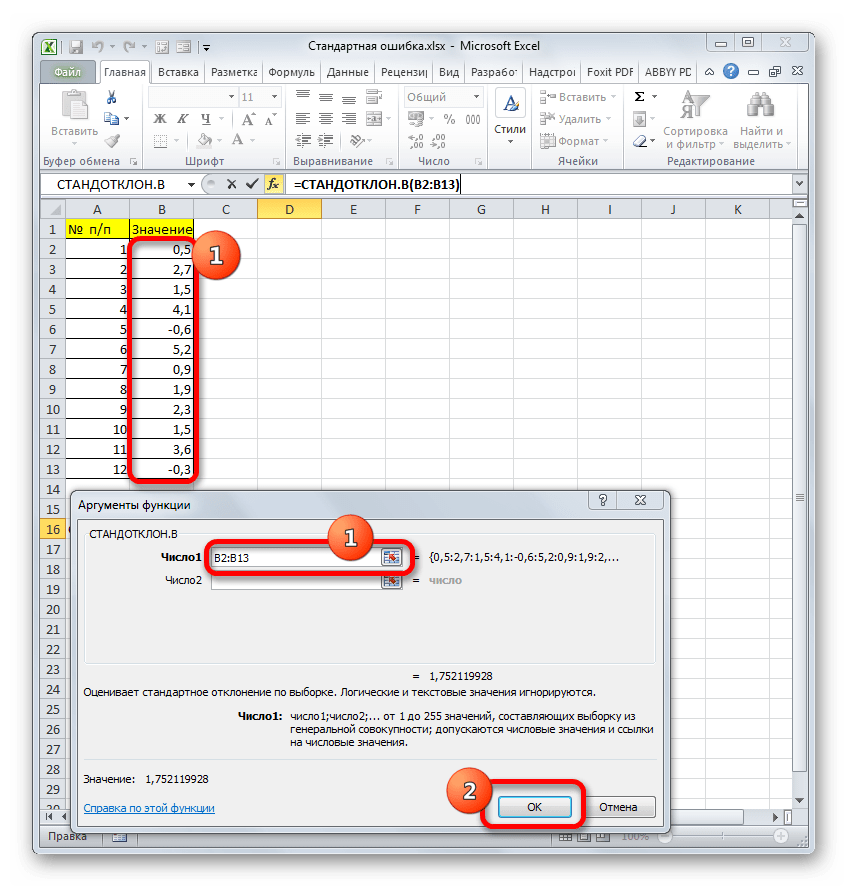
В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».

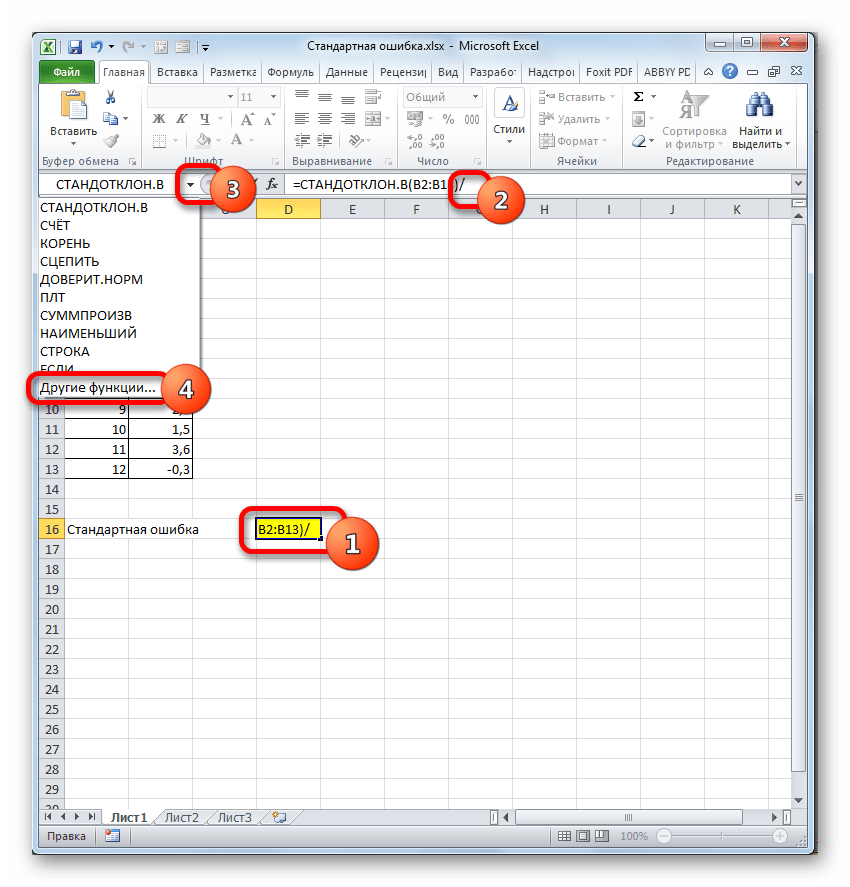
Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».

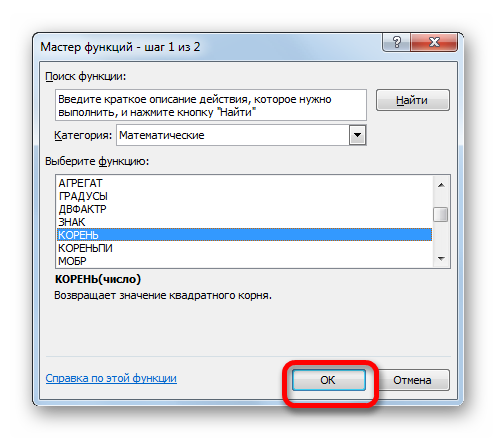
Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:

Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.

Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».

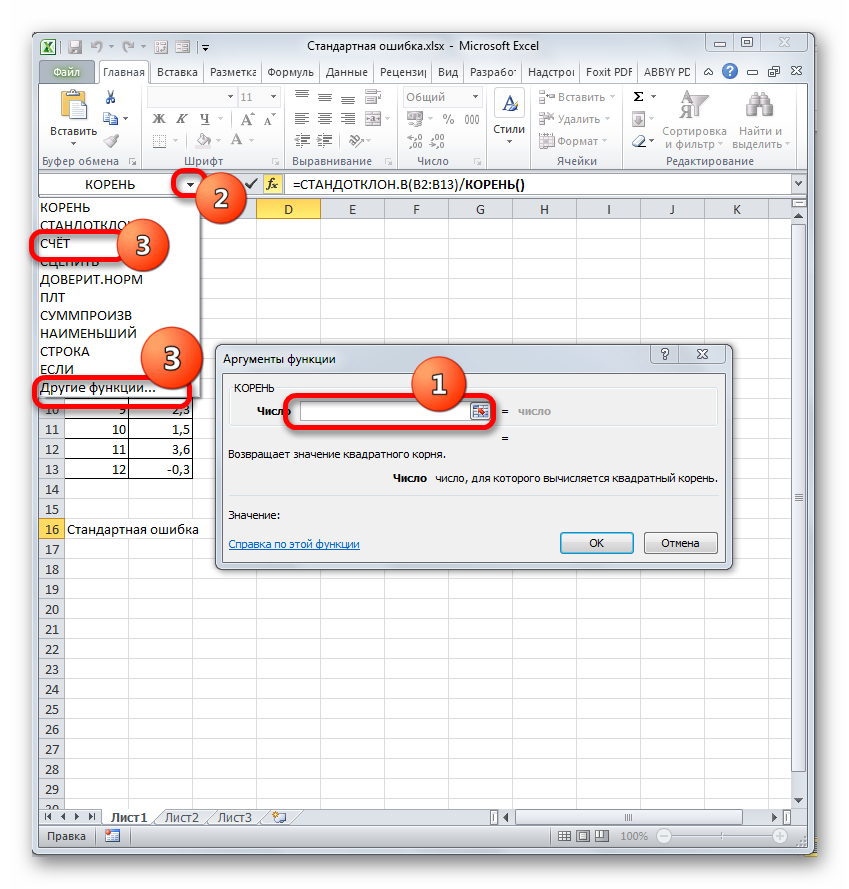
В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».

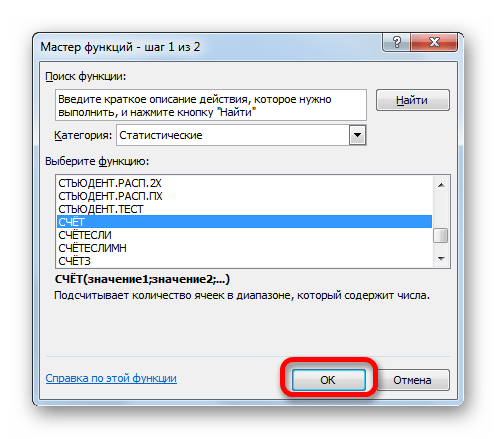
Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:

В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».

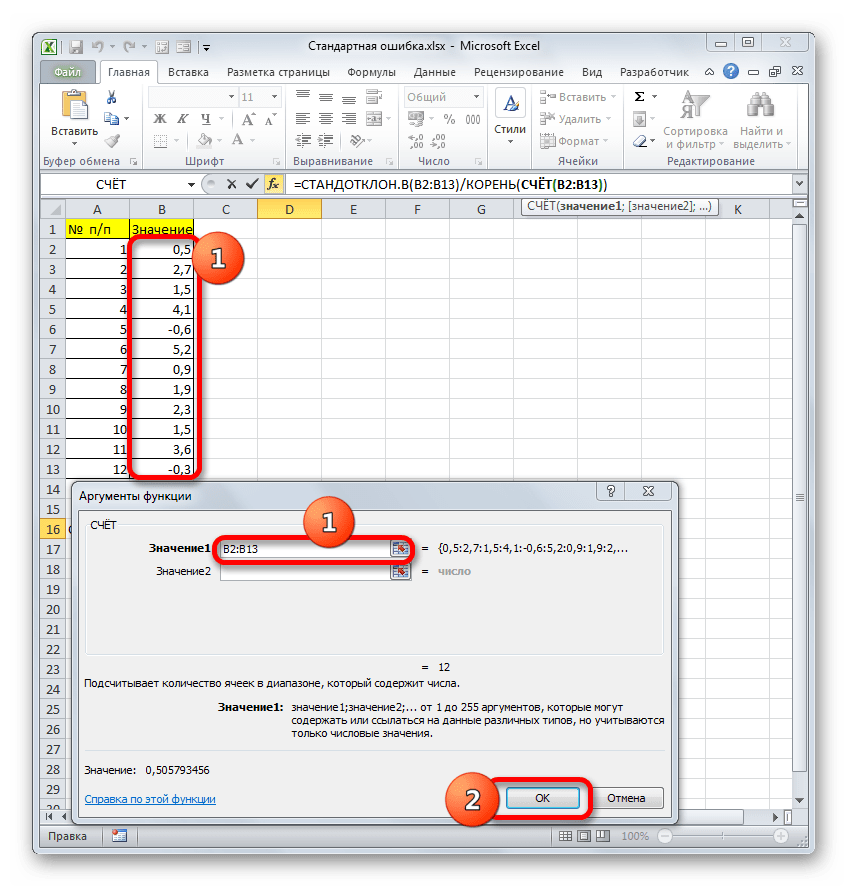
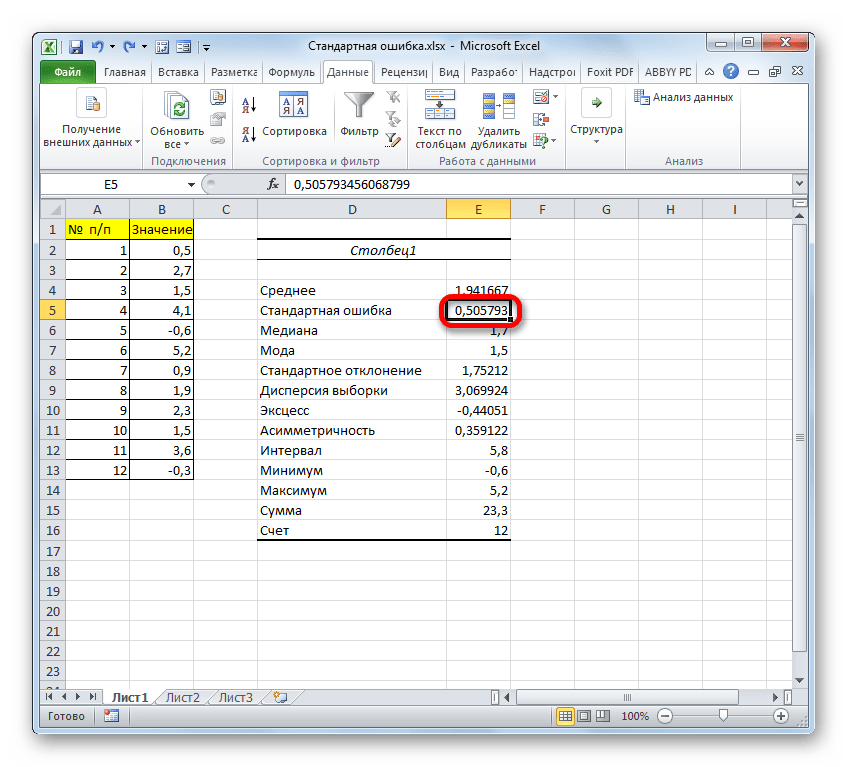
После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:

Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.

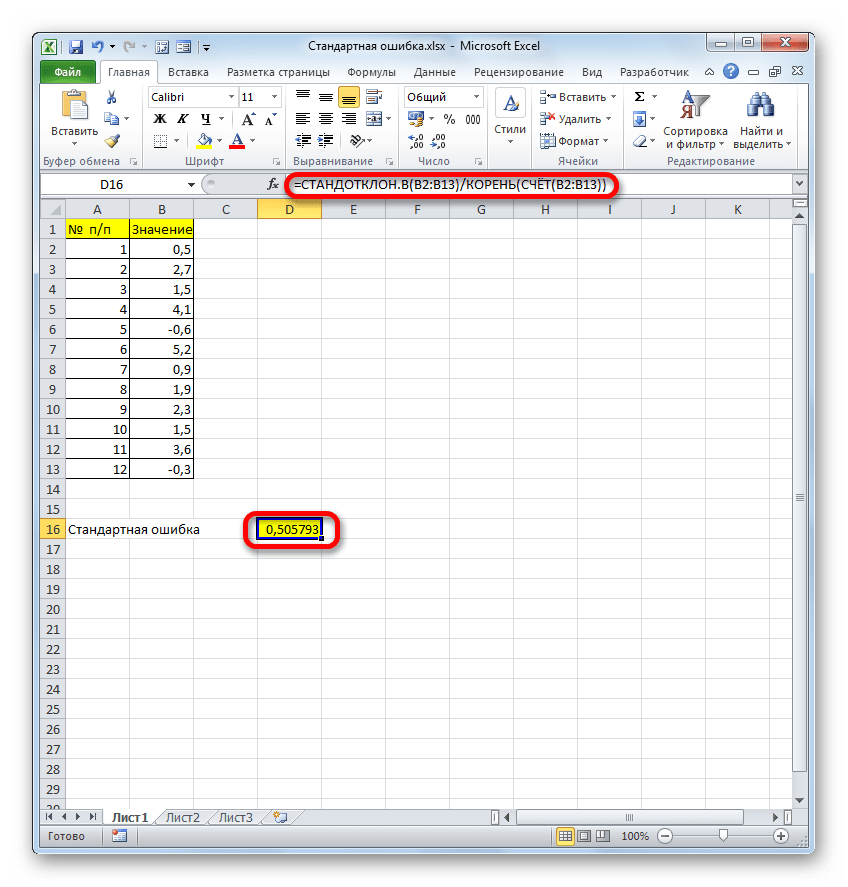
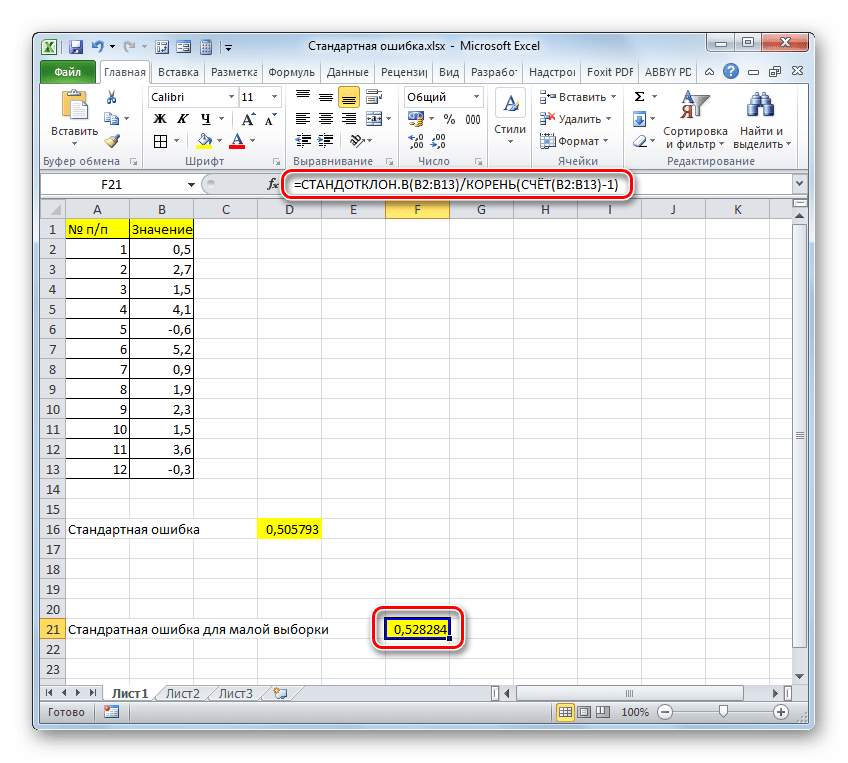
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:

Способ 2: применение инструмента «Описательная статистика»

Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.

Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.

После того, как открыт документ с выборкой, переходим во вкладку «Файл».

Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».

Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».

В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.

Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.

После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».

После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.

Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.

Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».

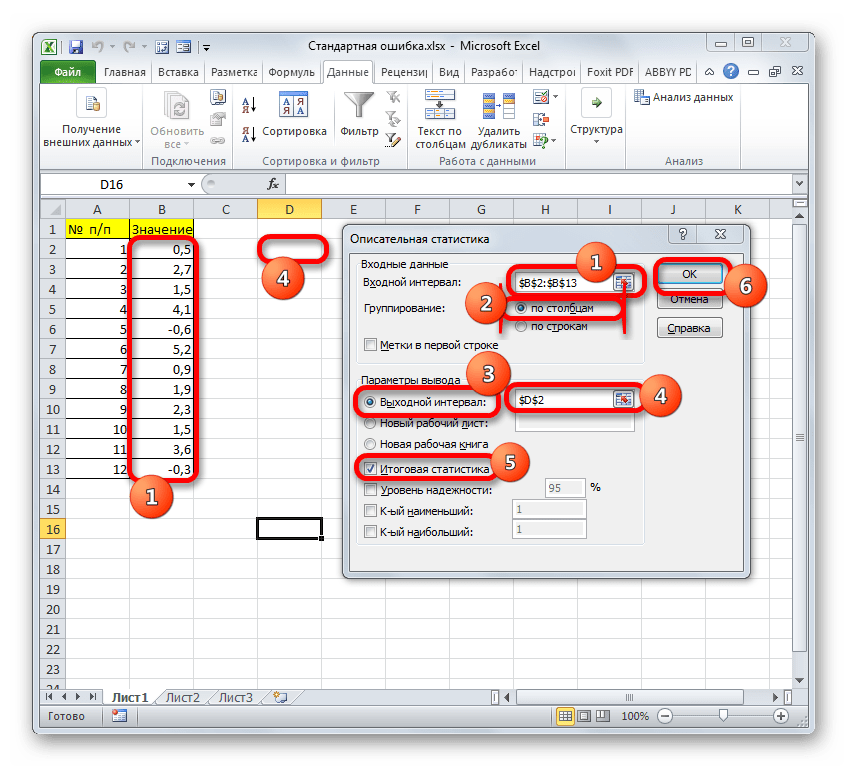
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.

В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.

Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.

Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:

• На новый лист;
• В новую книгу (другой файл);
• В указанный диапазон текущего листа.

Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.

Далее следует блок настроек определяющий, какие именно данные нужно вводить:

• Итоговая статистика;
• К-ый наибольший;
• К-ый наименьший;
• Уровень надежности.

Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.

После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.

После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.

Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Расчет с помощью комбинаций функций

На примере рассмотрим составленный алгоритм действий по расчету ошибки средней арифметической с использованием комбинаций функций. Для того чтобы выполнить задачу, нужно использовать операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ. Выборка будет использоваться из 12 чисел, которые представлены в таблице.

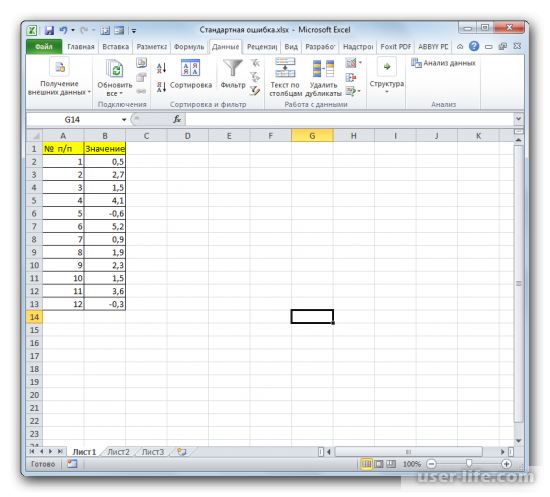
Выделите ячейку, в которой отобразится итоговое значение стандартной ошибки. Кликаете на иконку «Вставить функцию».

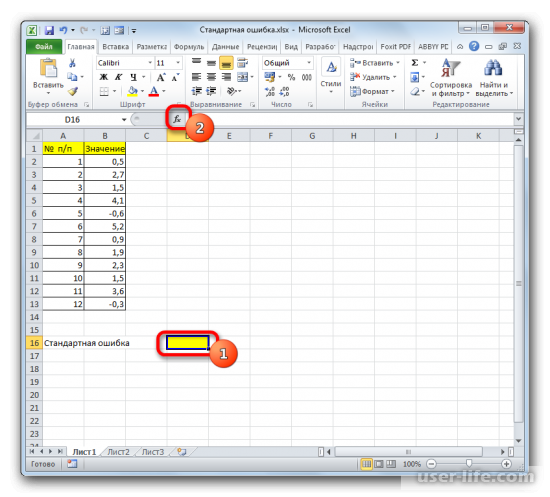
Появится Мастер функций, в котором нужно произвести перемещение в блок «Статистические». Появится список наименований, выбираете «СТАНДОТКЛОН.В».

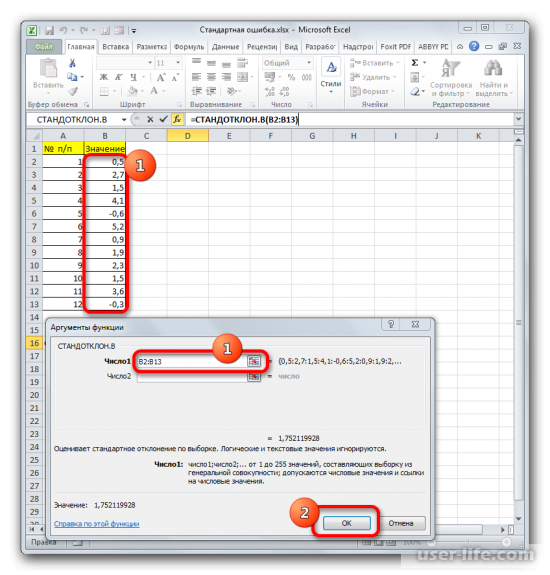
Запустится окно аргументов выбранного оператора, предназначенного для оценивания стандартного отклонения при выборке. У него такой синтаксис — =СТАНДОТКЛОН.В(число1;число2;…). Устанавливаете курсор в полу «Число1». Далее, зажав левую кнопку мыши, выделяете курсором весь диапазон выборки, чтобы координаты этого массива отобразились там же в поле окна. Кликаете на ОК.

В ячейке появится проделанный результат, но это еще не то, что мы хотим получить в итоге. Теперь нужно стандартное отклонение разделить на квадратный корень от числа элементов выборки. Выделяете ячейку с нужной функцией и устанавливаете курсор мышки в строку формул. Дописываете выражение, которое там уже существует, знаком деления (/). Далее нажимаете на пиктограмму перевернутого вниз углом треугольника (находится слева от строки формул). Должен открыться список недавно использованных функций. Находите оператора «КОРЕНЬ» и нажимаете на него. Если его нет в списке, то кликайте на «Другие функции…».

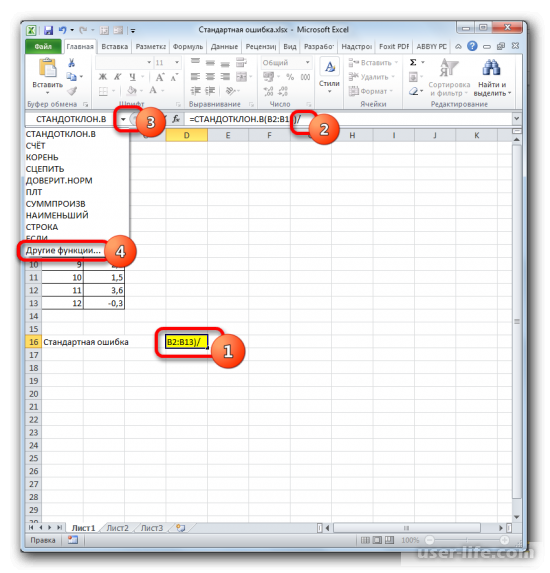
Должен снова запуститься Мастер функций, в котором нужно перейти в категорию «Математические». Выделяете там «КОРЕНЬ» и кликаете ОК.

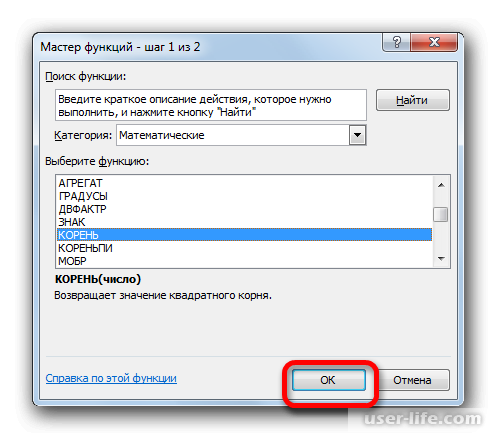
Далее должно открыться окно аргументов функции КОРЕНЬ. Его синтаксис простой — =КОРЕНЬ(число). Устанавливаете курсор в поле «Число» и нажимаете на уже знакомый треугольник, чтобы показался список последних использованных функций. Находите «СЧЕТ» и нажимаете на него. Если в списке его нет, тогда нажимаете на «Другие функции…».

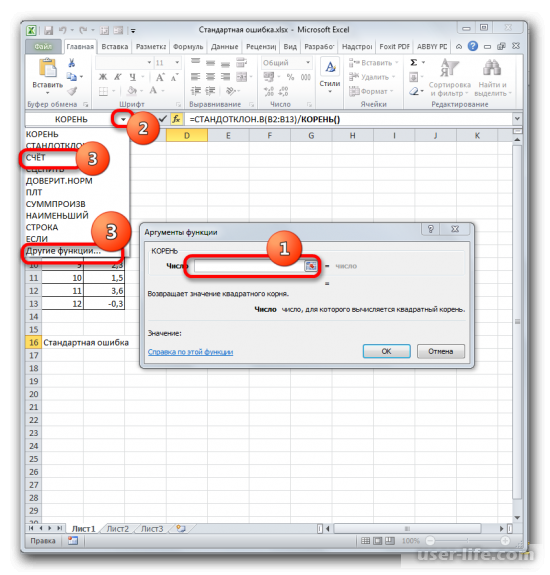
Появится раскрывшееся окно Мастера функций, в котором нужно переместиться в группу «Статистические». В ней выделяете «СЧЕТ» и кликаете ОК.

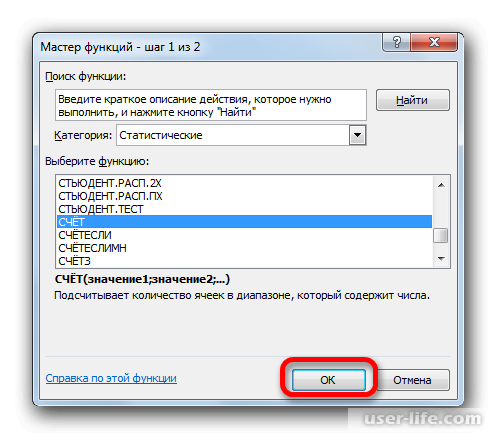
Должно запуститься окно аргументов функции СЧЕТ. Синтаксис функции будет таким — =СЧЁТ(значение1;значение2;…). Ставите курсор в строку «Значение1» и зажимаете левую кнопку мыши, чтобы выделить весь диапазон выборки. Когда координаты отобразятся, жмите ОК.

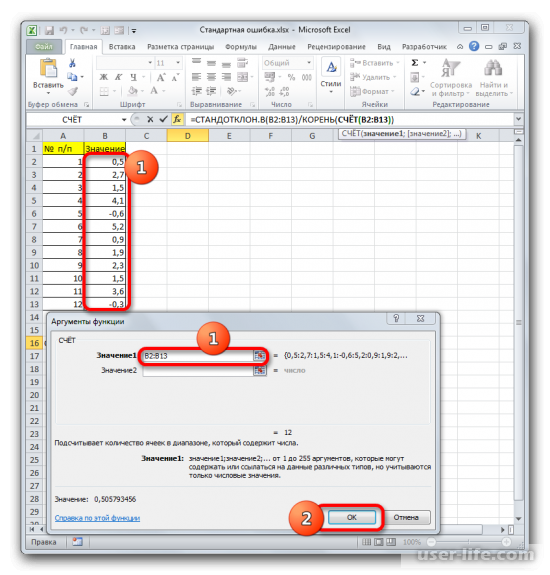
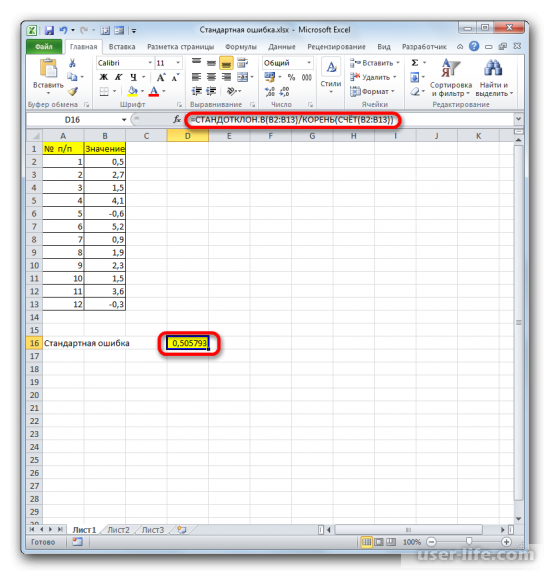
Когда будет выполнено последнее действие, то не только произведется расчет количества ячеек, которые заполнены числами, но и вычисляется ошибка средней арифметической. Величина будет выведена в ячейку с размещенной сложной формулой, вид которой таков — =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)).

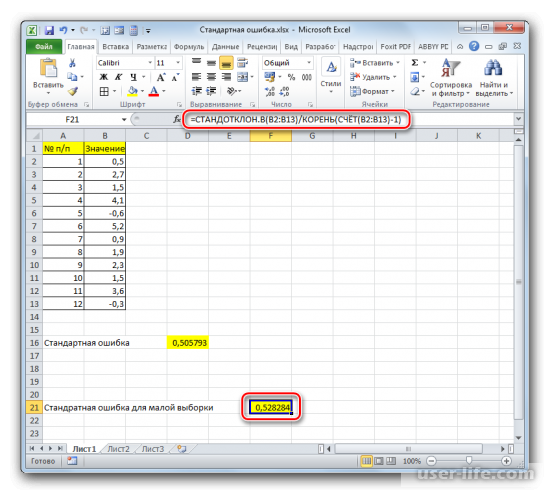
Если выборка до 30 единиц, тогда лучше применять немного другую формулу — =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1).

Применение инструмента «Описательная статистика»

Когда будет открыт документ с выборкой, нужно перейти во вкладку «Файл».

В левом вертикальном меню заходите в раздел «Параметры».

Должно запуститься окно параметров Excel, в левой части которого нужно перейти в «Надстройки».

В самом низу окна находите «Управление» в выставляете в нем параметр «Надстройки Excel». Кликаете на «Перейти…» справа от него.

В окне надстроек появится список скриптов, которые доступны и нужно отметить галочкой «Пакет анализа», а затем нажать ОК.

Теперь на странице должна появиться новая группа инструментов «Анализ». Для перехода к ней кликаете на вкладку «Данные».

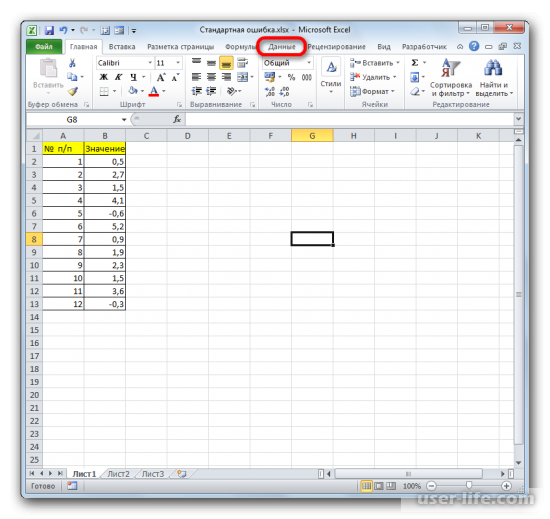
Кликаете на «Анализ данных» в блоке инструментов «Анализ» в самом конце.

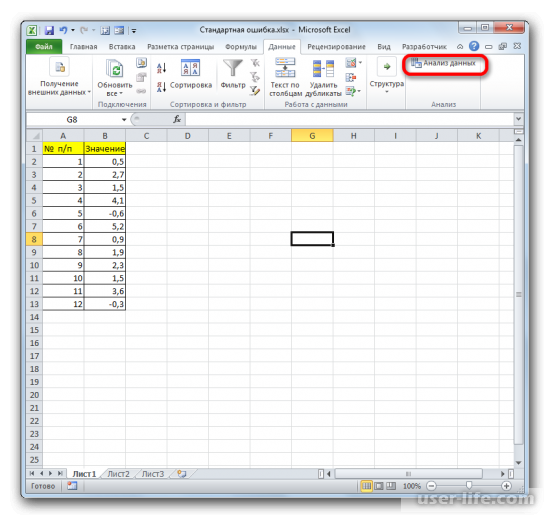
Запустится окно выбора инструмента анализа, в котором необходимо выделить «Описательная статистика» и нажать справа на ОК.

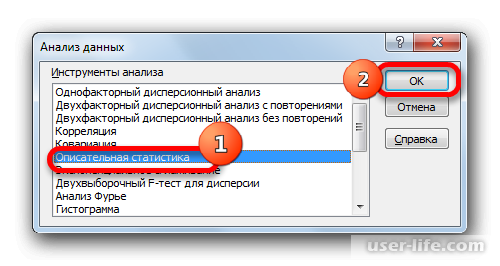
Далее запустится окно настроек инструмента комплексного статистического анализа «Описательная статистика». Здесь нужно установить все так, в зависимости от того, что именно вы хотите получить в итоге.

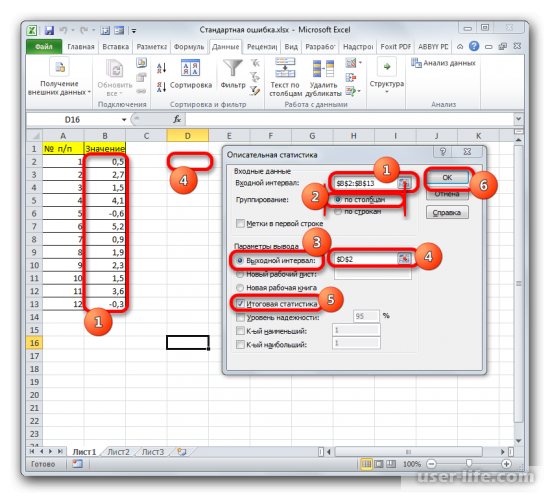
После всех совершенных манипуляций, инструмент «Описательная статистика» должен отобразить результаты обработки выборки на текущем листе. Разноплановых статистических показателей будет немало, но среди них находится и тот, который нам нужен – «Стандартная ошибка».

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

где x_i – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение x_i обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Используя более привычные обозначения, формулу записывают как:

где σ 2 – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.