Несмещенная оценка выборочной дисперсии
Краткая теория
Пусть из генеральной совокупности в результате
независимых наблюдений над количественным
признаком
извлечена повторная выборка объема
:
При этом
Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию
.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой
,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:
Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить
на дробь
.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через
:
Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:
Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:
Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:
При достаточно больших значениях
объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно
.
Пример решения задачи
Задача
Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.
Сумма
частот:
Вычислим
среднюю:
Средняя квадратов:
Несмещенная
выборочная дисперсия:
Ответ:
Кроме этой задачи на другой странице сайта есть
пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда
При проведении регрессионного анализа
основная трудность заключается в том,
что генеральная дисперсия случайной
ошибки является неизвестной величиной,
что вызывает необходимость в расчёте
её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии(или
исправленной дисперсией) случайной
ошибки линейной модели парной регрессии
называется величина, рассчитываемая
по формуле:
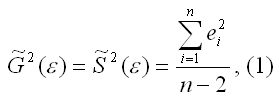
где n
– это объём выборочной совокупности;
еi– остатки регрессионной модели:
![]()
Для линейной модели множественной
регрессии несмещённая оценка дисперсии
случайной ошибки рассчитывается по
формуле:

где k
– число оцениваемых параметров модели
регрессии.
Оценка матрицы ковариаций случайных
ошибок Cov(ε) будет являться оценочная
матрица ковариаций:
![]()
где In
– единичная матрица.
Оценка дисперсии случайной
ошибки модели регрессии распределена
по ε2(хи-квадрат)
закону распределения с (n-k-1)
степенями свободы.
Для доказательства несмещённости оценки
дисперсии случайной ошибки модели
регрессии необходимо доказать
справедливость равенства
![]()
Доказательство. Примем без
доказательства справедливость следующих
равенств:

где G2(ε)
– генеральная дисперсия случайной
ошибки;
S2(ε)– выборочная дисперсия случайной
ошибки;
![]()
– выборочная оценка дисперсии
случайной ошибки.
Тогда:

т. е.
![]()
что и требовалось доказать.
Следовательно, выборочная оценка
дисперсии случайной ошибки
![]()
является несмещённой оценкой
генеральной дисперсии случайной ошибки
модели регрессии G2(ε).
При условии извлечения из
генеральной совокупности нескольких
выборок одинакового объёма n
и при одинаковых значениях объясняющих
переменных х,
наблюдаемые значения зависимой переменной
у будут случайным образом колебаться
за счёт случайного характера случайной
компоненты β.
Отсюда можно сделать вывод, что будут
варьироваться и зависеть от значений
переменной у значения оценок коэффициентов
регрессии и оценка дисперсии случайной
ошибки модели регрессии.
Для иллюстрации данного утверждения
докажем зависимость значения МНК-оценки
![]()
от величины случайной ошибки
ε.
МНК-оценка коэффициента β1 модели
регрессии определяется по формуле:

В связи с тем, что переменная
у зависит от случайной компоненты ε
(yi=β0+β1xi+εi), то ковариация
между зависимой переменной у
и независимой переменной х
может быть представлена следующим
образом:
![]()
Для дальнейших преобразования используются
свойства ковариации:
1) ковариация между переменной
х и
константой С
равна нулю: Cov(x,C)=0,
C=const;
2) ковариация
переменной х
с самой собой равна дисперсии этой
переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации,
справедливы следующие равенства:
Cov(x,β0)=0
(β0=const);
Cov(x, β1x)=
β1*Cov(x,x)=
β1*G2(x).
Следовательно, ковариация
между зависимой и независимой переменными
Cov(x,y)
может быть записана как:
Cov(x,y)=
β1G2(x)+Cov(x,ε).
В результате МНК-оценка коэффициента
β1 модели регрессии примет вид:
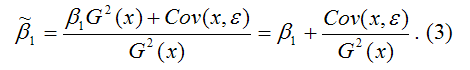
Таким образом, МНК-оценка
![]()
может быть представлена как сумма двух
компонент:
1) константы β1,
т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,ε),
вызывающей вариацию коэффициента модели
регрессии.
Однако на практике подобное разложение
МНК-оценки невозможно, потому что
истинные значения коэффициентов модели
регрессии и значения случайной ошибки
являются неизвестными. Теоретически
данное разложение можно использовать
при изучении статистических свойств
МНК-оценок.
Аналогично доказывается, что МНК-оценка
![]()
коэффициента модели регрессии и
несмещённая оценка дисперсии случайной
ошибки
![]()
могут быть представлены как сумма
постоянной составляющей (константы) и
случайной компоненты, зависящей от
ошибки модели регрессии ε.
Задача 55. Из генеральной совокупности извлечена выборка объема N, заданная вариантами ХI и соответствующими им частотами. Найти несмещенную оценку генеральной средней.
|
Варианта ХI |
2 |
5 |
7 |
10 |
|
Частота Ni |
16 |
12 |
8 |
14 |
Решение. Множество всех объектов, подлежащих изучению, называется Генеральной совокупностью. Множество случайно отобранных объектов называется выборочной совокупностью или Выборкой.
Для оценки неизвестных параметров теоретического распределения служат статистические оценки. Статистическая оценка, определяемая одним числом, называется Точечной оценкой.
Точечная статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, называется Несмещенной оценкой. Статистическая оценка, математическое ожидание которой не равно оцениваемому параметру является Смещенной.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя
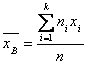 (1),
(1),
Где ХI – варианта выборки (элемент выборки); Ni – частота варианты ХI (число наблюдений варианты ХI); ![]() – объем выборки (число элементов совокупности).
– объем выборки (число элементов совокупности).
Объем данной выборки равен ![]() .
.
Далее по формуле (1) вычисляем несмещенную оценку генеральной средней:
![]()
Задача 56. По выборке объема N=41 найдена смещенная оценка генеральной дисперсии ![]() . Найти несмещенную оценку дисперсии генеральной совокупности.
. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
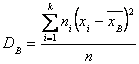
Несмещенной оценкой генеральной дисперсии является «исправленная дисперсия»
![]() или
или 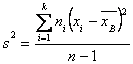
Таким образом, мы получаем искомую несмещенную оценку дисперсии генеральной совокупности:
![]()
Задача 57. Найти доверительный интервал для оценки с надежностью P=0,95 неизвестного математического ожидания A нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение S=5, выборочная средняя ![]() , а объем выборки N=25.
, а объем выборки N=25.
Решение. Интервальной оценкой называется интервал, покрывающий оцениваемый параметр. Доверительным интервалом является интервал, который с данной надежностью покрывает оцениваемый параметр.
Для оценки математического ожидания A нормально распределенного количественного признака Х по выборочной средней ![]() при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал
при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал
![]() ,
,
Где ![]() – точность оценки, T – значение аргумента функции Лапласа
– точность оценки, T – значение аргумента функции Лапласа ![]() (приложение, таблица 2).
(приложение, таблица 2).
В данной задаче T находим из условия ![]() . По таблице 2 определяем
. По таблице 2 определяем ![]() . Таким образом, T=1,96.
. Таким образом, T=1,96.
Далее получаем
![]()
Или ![]()
Задача 58. По данным N=9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений ![]() и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью
и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью ![]() =0,99.
=0,99.
Решение. Оценкой математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения является доверительный интервал
![]() .
.
По таблице 3 приложения, по заданным N и ![]() находим
находим ![]() =3,36.
=3,36.
Таким образом
![]()
Окончательно получаем
![]()
Задача 59. Из генеральной совокупности извлечена выборка объема N. Оценить с надежностью ![]() =0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.
=0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.
|
Значение признака ХI |
-2 |
1 |
1 |
3 |
4 |
5 |
|
Частота Ni |
2 |
1 |
2 |
2 |
2 |
1 |
Решение. Объем данной выборки равен ![]()
![]()
По данным задачи находим выборочную среднюю:
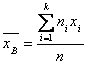
![]()
Далее находим исправленное среднее квадратическое отклонение S:
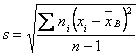
![]()
Для оценки математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения служит доверительный интервал
![]() .
.
По таблице 3 приложения по заданным N и ![]() находим
находим ![]() =2,26.
=2,26.
Таким образом
![]()
Окончательно получаем
![]()
Задача 60. Построить полигон частот и эмпирическую функцию по данному распределению выборки:
|
Варианты ХI |
-3 |
0 |
1 |
4 |
6 |
7 |
|
Частоты Ni |
3 |
6 |
1 |
2 |
5 |
1 |
Решение. Полигоном частот называют ломаную, отрезки которой соединяют точки ![]() ;
; ![]() ;…;
;…;![]() , где ХI – варианты выборки, Ni – соответствующие им частоты.
, где ХI – варианты выборки, Ni – соответствующие им частоты.
Полигон частот для данного распределения изображен на рисунке 15.

Рис. 15
Эмпирической функцией распределения (функцией распределения выборки) называют функцию ![]() , определяющую для каждого значения X относительную частоту события
, определяющую для каждого значения X относительную частоту события ![]() :
:
![]() ,
,
Где ![]() – число вариант, меньших Х; N – объем выборки.
– число вариант, меньших Х; N – объем выборки.
Из определения следует, что ![]() .
.
Найдем эмпирическую функцию распределения.
Объем данной выборки равен ![]() =18.
=18.
Если ![]() , то
, то ![]() =0 (так как -3 – наименьшая варианта). Если
=0 (так как -3 – наименьшая варианта). Если ![]() , то значение
, то значение ![]() , а именно
, а именно ![]() наблюдалось 3 раза, следовательно,
наблюдалось 3 раза, следовательно, ![]() . При
. При ![]() значения
значения ![]() , а именно
, а именно ![]() и
и ![]() наблюдались 3+6=9 раз, следовательно,
наблюдались 3+6=9 раз, следовательно, ![]() .
.
Аналогично получаем, что при ![]() функция распределения
функция распределения ![]() ; при
; при ![]() функция распределения
функция распределения ![]() ; при
; при ![]() функция распределения
функция распределения ![]() . Далее, если
. Далее, если ![]() , то
, то ![]() (так как 7 – наибольшая варианта).
(так как 7 – наибольшая варианта).
Таким образом, эмпирическая функция распределения равна:

График полученной эмпирической функции распределения изображен на рисунке 16.
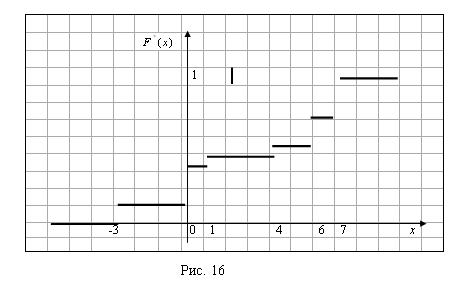
Задача 61. Найти методом сумм асимметрию и эксцесс по заданному распределению выборки объема N=100:
|
Варианта ХI |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
80 |
84 |
|
Частота Ni |
2 |
4 |
6 |
8 |
12 |
30 |
18 |
8 |
7 |
5 |
Решение. Асимметрия ![]() эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством:
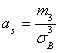 ,
,
Где ![]() — центральный эмпирический момент третьего порядка, вычисляемый по формуле:
— центральный эмпирический момент третьего порядка, вычисляемый по формуле: 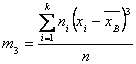
Эксцесс ![]() эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством:
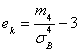 ,
,
Где ![]() — центральный эмпирический момент четвертого порядка, вычисляемый по формуле:
— центральный эмпирический момент четвертого порядка, вычисляемый по формуле: 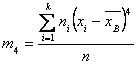
Асимметрия и эксцесс служат для оценки отклонения эмпирического распределения от нормального. Для нормального распределения эти характеристики равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Кроме того, если эксцесс положительный, то распределение будет островершинным; если отрицательный, то распределение будет плосковершинным по сравнению с нормальным распределением.
Для практического расчета асимметрии и эксцесса непосредственно пользоваться вышеуказанными формулами довольно затруднительно, поэтому воспользуемся методом сумм. Составим расчетную таблицу 1, для этого:
1) Запишем варианты в первый столбец.
2) Запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца.
3) В качестве ложного нуля С выберем варианту (68), которая имеет наибольшую частоту (в качестве С можно взять любую варианту, расположенную примерно в середине столбца); в клетках строки, содержащей ложный нуль, запишем нули; в четвертом столбце над и под уже помещенным нулем запишем еще по одному нулю.
4) В оставшихся незаполненными над нулем клетках третьего столбца (исключая самую верхнюю) запишем последовательно накопленные частоты:
2; 2+4=6; 6+6=12; 12+8=20; 20+12=32.
Сложив все накопленные частоты, получим число B1=72, которое поместим в верхнюю клетку третьего столбца. В оставшихся незаполненными под нулем клетках третьего столбца (исключая самую нижнюю) запишем последовательно накопленные частоты:
5; 5+7=12; 12+8=20; 20+18=38.
Сложив все накопленные частоты, получим число A1=75, которое поместим в нижнюю клетку третьего столбца.
5) Аналогично заполняется четвертый столбец, причем суммируют частоты третьего столбца. Сложив все накопленные частоты, расположенные над нулем, получим число B2=70, которое поместим в верхнюю клетку четвертого столбца. Сумма накопленных частот, расположенных под нулем, равна числу A2=59, которое поместим в нижнюю клетку четвертого столбца.
6) Для заполнения столбца 5 запишем нуль в клетке строки, содержащей ложный нуль (68); над этим нулем и под ним поставим еще по два нуля. В клетках над нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 сверху вниз; в итоге будем иметь следующие накопленные частоты:
2; 2+8=10; 10+20=30.
Сложив накопленные частоты, получим число B3=42, которое поместим в верхнюю клетку пятого столбца. В клетках под нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 снизу вниз; в итоге будем иметь следующие накопленные частоты:
5; 5+17=22.
Сложив накопленные частоты, получим число A3=27, которое поместим в нижнюю клетку пятого столбца.
7) Аналогично заполняется столбец 6, причем суммируют частоты столбца 5.
В итоге получим расчетную таблицу 1:
Расчетная таблица 1
|
1 |
2 |
3 |
4 |
5 |
6 |
|
ХI |
Ni |
B1=72 |
B2=70 |
B3=42 |
B4=14 |
|
48 |
2 |
2 |
2 |
2 |
2 |
|
52 |
4 |
6 |
8 |
10 |
12 |
|
56 |
6 |
12 |
20 |
30 |
0 |
|
60 |
8 |
20 |
40 |
0 |
0 |
|
64 |
12 |
32 |
0 |
0 |
0 |
|
68 |
30 |
0 |
0 |
0 |
0 |
|
72 |
18 |
38 |
0 |
0 |
0 |
|
76 |
8 |
20 |
37 |
0 |
0 |
|
80 |
7 |
12 |
17 |
22 |
0 |
|
84 |
5 |
5 |
5 |
5 |
5 |
|
N=100 |
A1=75 |
A2=59 |
A3=27 |
A4=5 |
Теперь найдем Di (I=1, 2, 3) и si (I=1, 2, 3, 4):
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Найдем условные моменты первого, второго, третьего и четвертого порядков:
![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.
Найдем далее центральные эмпирические моменты третьего и четвертого порядков, учитывая, что шаг ![]() (разность между двумя соседними вариантами):
(разность между двумя соседними вариантами):
![]() ;
;

Так как дисперсия ![]() , то выборочное среднее квадратическое отклонение
, то выборочное среднее квадратическое отклонение ![]() .
.
Учитывая определения асимметрии и эксцесса, окончательно получаем:
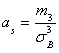
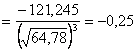 ;
; 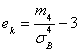
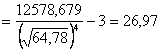 .
.
| < Предыдущая | Следующая > |
|---|
Пусть
![]()
![]()
Поскольку
заменяются две величины (![]()
и
![]()
),
то это вызывает смещение оценки
![]()
:
![]()
. (1.22)
Покажем
это .
![]()
Известно
что
![]()
![]()
.
Пусть
Х1,
Х2,…,
Хi
,…,Xn
— независимые случайные величины, каждая
из которых имеет один и тот же закон
распределения с числовыми характеристиками:
![]()
и D(Xi)=D0.
Пусть
![]()
подставим в (*), тогда:
![]()
Найдем
E[Dв]:
![]()
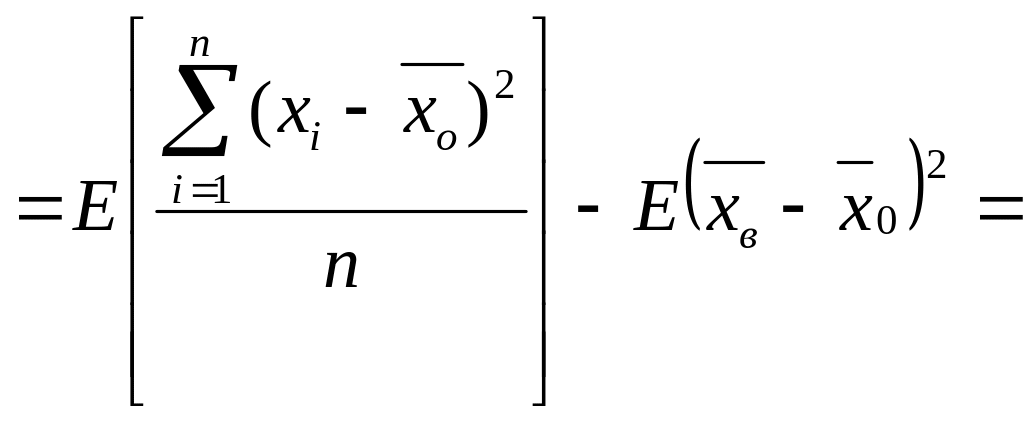
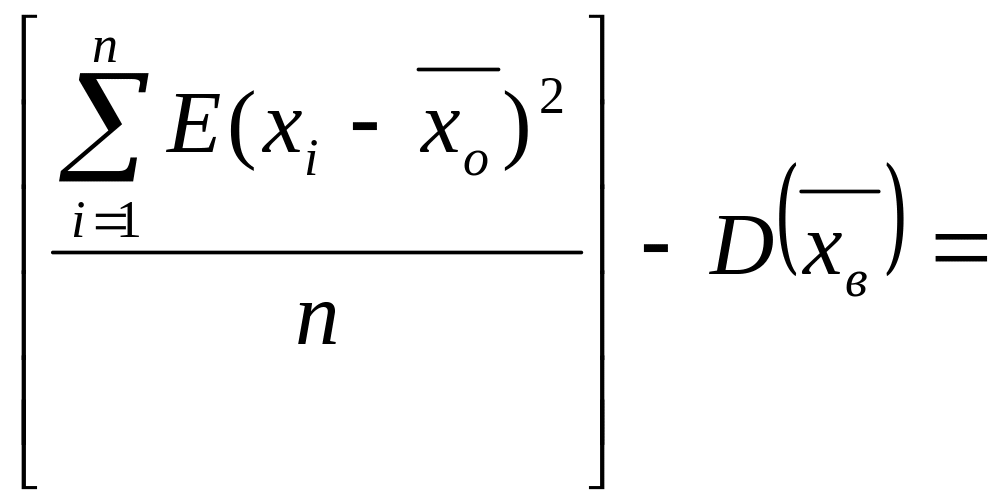
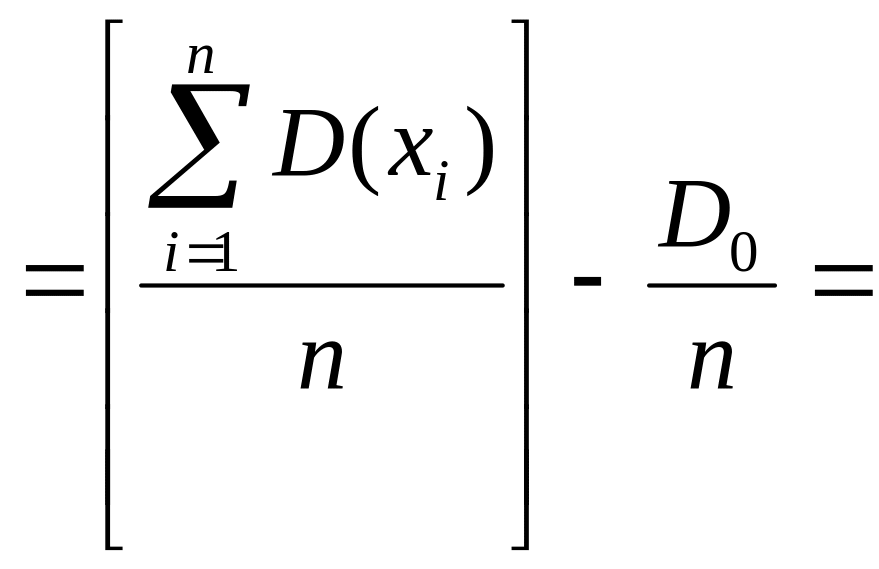
![]()
![]()
Итак
![]()
Что и требовалось доказать.
При
больших п
смещение невелико, им можно пренебречь,
но при малых выборках оно существенно.
Таким
образм,
![]()
есть несмещенная оценка дисперсии или
![]()
.
(1.23)
Тогда
исправленное среднее квадратическое
отклонение имеет вид:
![]()
.
(1.24)
Для
интервальной оценки используется
выражение
![]()
,
где
![]()
находится по формуле (1.24).
Замечание.
Однако для больших выборок можно считать,
что
![]()
.
В случае малых выборок (п
< 30) пользуются исправленной дисперсией
по формуле (1.24).
По
закону больших чисел
![]()
является состоятельной оценкой для
![]()
генеральной дисперсии. А так как множитель
![]()
при
![]()
,
то
![]()
также является состоятельной оценкой
для
.
Оценка
![]()
,
строго говоря, не является эффективной
оценкой для
,
однако при наличии нормального
распределения ее можно считать приближенно
эффективной.
Замечание.
Если известно точное значение
математического ожидания «![]()
»
для n
измерений, то E(Xi)
=
где хi
– отдельные измерения. Исправленная
(несмещённая) дисперсия находится по
формуле
![]()
(1.25)
Действительно.
![]()
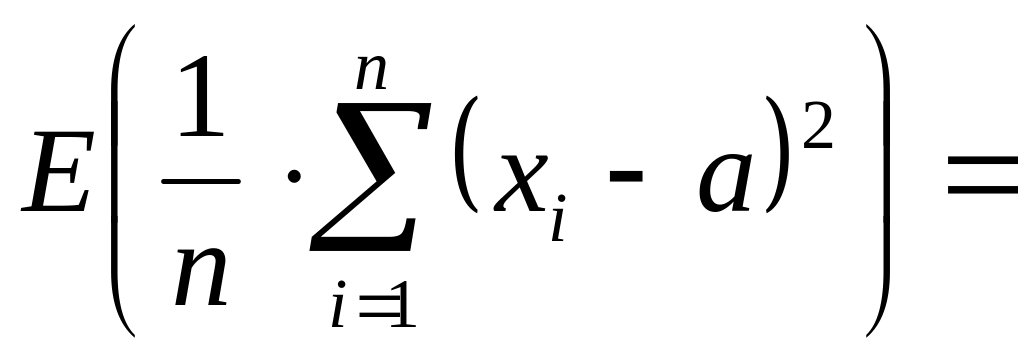
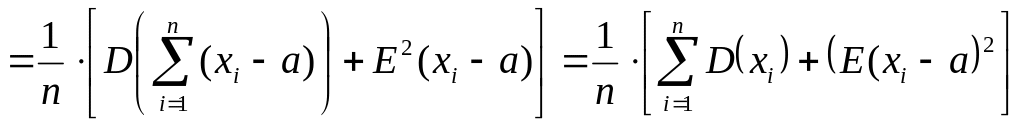
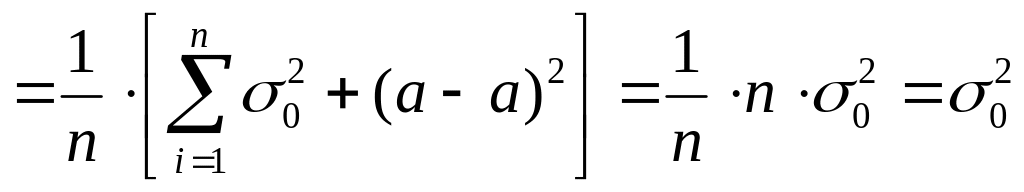
,
т.е. E(D*в)
= D0
.
Пример
1.19. В ящике содержатся стержни трех
размеров (N
= 3): 12 см, 14 см и 16 см с соответствующими
долями 0,1; 0,3; 0,6. Производится повторная
выборка двух стержней (n
= 2). Найти
все возможные выборочные распределения
и построить законы распределения для
![]()
![]()
и
![]()
.
Проверить на данном примере справедливость
равенств
![]()
.
Решение.
Определим
количество возможных выборок:
![]()
.
Закон
распределения генеральной совокупности
представлен в следующей в таблице
|
X |
12 |
14 |
16 |
|
P |
0,1 |
0,3 |
0,6 |
Вычислим
генеральные характеристики :
![]()
Все
выборочные законы представлены в
следующей таблице.
|
№ выборки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
12 12 |
12 14 |
12 16 |
14 12 |
14 14 |
14 16 |
16 12 |
16 14 |
16 16 |
|
|
2 |
1 1 |
1 1 |
1 1 |
2 |
1 1 |
1 1 |
1 1 |
2 |
|
|
12 |
13 |
14 |
13 |
14 |
15 |
14 |
15 |
16 |
|
|
0 |
1 |
4 |
1 |
0 |
1 |
4 |
1 |
0 |
|
|
0,01 |
0,03 |
0,06 |
0,03 |
0,09 |
0,18 |
0,06 |
0,18 |
0,36 |
Проверим,
что
![]()
.
По
данным последней таблицы получим строим
законы распределения для
![]()
и Dв
и находим соответствующие характеристики.
|
|
12 |
13 |
14 |
15 |
16 |
|
|
P |
0,01 |
0,06 |
0,21 |
0,36 |
0,36 |
1 |
![]()
,![]()
|
|
0 |
1 |
4 |
|
|
|
0,46 |
0,42 |
0,12 |
1 |
E[Dв]=0,42+0,48=0.9/
Итак,
![]()
![]()
![]()
,
Откуда
следует:
![]()
и
![]()
при n
= 2.
Пример
1.20. Даны результаты 6 независимых
измерений одной и той же величины
прибором, не имеющим систематических
ошибок: 36; 37; 32; 43; 39; 41. Найдите несмещенную
оценку дисперсии ошибок измерений,
если истинная длина неизвестна.
Решение.
Представим исходные данные в виде
таблицы:
|
xi |
32 |
36 |
37 |
39 |
41 |
43 |
|
р |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Вычислим
последовательно
![]()
;
![]()
![]()
![]()
![]()
Отсюда
![]()
![]()
Пример
1.21.
В условиях предыдущей задачи найдите
несмещённую оценку дисперсии ошибок
измерений, если истинная величина
известна и равна 37,8.
Решение
В этом случае в формулу подставляется
не выборочное среднее, а истинная
величина:
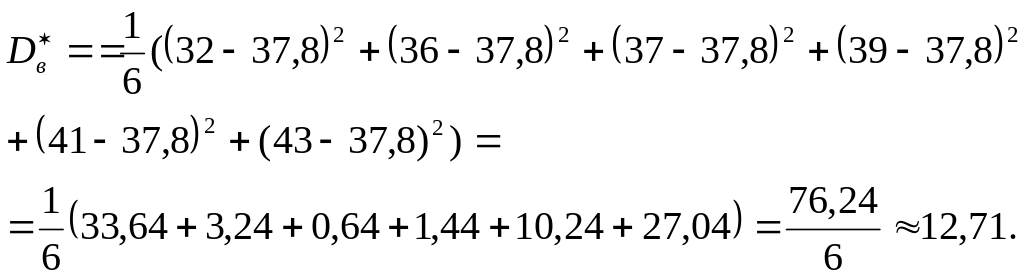
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В предыдущем параграфе мы выяснили, что дисперсия оценки (widehat {beta _2}) равна:
begin{equation*} mathit{var}left(widehat {beta _2}right)=frac{sigma ^2}{Sigma left(x_i-overline xright)^2}. end{equation*}
Это полезная информация, так как дисперсия (widehat {beta _2}) характеризует точность результатов оценивания соответствующего параметра (чем меньше дисперсия, тем точнее наша оценка). Проблема в том, что непосредственно величину (mathit{var}left(widehat {beta _2}right)) мы вычислить не можем: хотя мы наблюдаем значения (x_i,) (i=1,2,{dots},n), но мы не наблюдаем величину (sigma ^2). Этот параметр является неизвестным параметром классической линейной модели подобно величинам (beta _1) и (beta _2). Впрочем, как и в случае с (beta _1) и (beta _2), мы можем получить оценку неизвестного параметра (sigma ^2). Несмещенная оценка дисперсии случайной ошибки (sigma ^2) имеет вид:
begin{equation*} S^2=frac 1{n-2}{ast}sum _{i=1}^ne_i^2 end{equation*}
Чтобы доказать её несмещенность, достаточно осуществить выкладки, аналогичные преобразованиям из предыдущего параграфа, и убедиться, что (Eleft(S^2right)=sigma ^2).
Если в формуле для (mathit{var}left(widehat {beta _2}right)) вместо дисперсии случайной ошибки (sigma ^2) подставить её оценку (S^2), мы получим несмещенную оценку дисперсии МНК-оценки (widehat {beta _2}), которая будет иметь вид:
begin{equation*} widehat {mathit{var}}left(widehat {beta _2}right)=frac{S^2}{Sigma left(x_i-overline xright)^2} end{equation*}
Корень из этой величины называется стандартной ошибкой оценки коэффициента (widehat {beta _2}):
begin{equation*} mathit{se}left(widehat {beta _2}right)=sqrt{widehat {mathit{var}}left(widehat {beta _2}right)}=sqrt{frac{S^2}{Sigma left(x_i-overline xright)^2}} end{equation*}
Аналогичным образом вычисляется стандартная ошибка оценки коэффициента (widehat {beta _1}) (здесь мы опираемся на равенство 2.4, заменяя в нем дисперсию случайной ошибки её оценкой).
begin{equation*} mathit{se}left(widehat {beta _1}right)=sqrt{widehat {mathit{var}}left(widehat {beta _1}right)}=sqrt{frac{frac{S^2} n{ast}sum x_i^2}{sum left(x_i-overline xright)^2}} end{equation*}
Стандартные ошибки оценок коэффициентов пригодятся нам для тестирования гипотез.
Представим, что мы хотим выяснить, влияет ли уровень образования (переменная x) на заработную плату работника в некоторой отрасли (переменная y)? Ответы на такого сорта вопросы, как мы обсудили в первой главе, и есть одна из главных задач эконометрики.
Представим также, что все предпосылки классической линейной модели парной регрессии выполнены. Тогда в терминах нашей модели вопрос «Верно ли, что образование не влияет на заработную плату?» эквивалентен вопросу «Верно ли, что в регрессии (y_i=beta _1+beta _2x_i+varepsilon _i) коэффициент (beta _2) равен нулю?».
Как мы могли бы ответить на этот вопрос?
Естественная идея состоит в том, чтобы посмотреть оценки коэффициентов (widehat {beta _1}) и (widehat {beta _2}) и увидеть, равен ли коэффициент (widehat {beta _2}) нулю. Однако при этом возникает следующая проблема: (widehat {beta _1}) и (widehat {beta _2}) — оценки, полученные при помощи МНК на основе случайной выборки. Следовательно, они сами являются случайными величинами, которые могут принимать значения лишь «приблизительно» равные истинным. Поэтому, даже если истинное значение коэффициента (beta _2) равно нулю, его оценка (widehat {beta _2}), скорее всего, будет отклоняться от нуля.
Следовательно, нужно уметь определять, достаточно ли сильно (widehat {beta _2}) отличается от нуля для того, чтобы можно было с уверенностью утверждать, что и истинное значение коэффициента (beta _2) также не равно нулю. Опишем процедуру, которая позволяет это сделать.
Процедура тестирования незначимости коэффициента:
Формулируем тестируемую гипотезу (H_0:beta _2=0) («переменная x не влияет на переменную y») и альтернативную гипотезу (H_1:beta _2{neq}0) («переменная x влияет на переменную y»)
Находим расчетное значение тестовой статистки по формуле
(frac{widehat {beta _2}}{mathit{se}left(widehat {beta }_2right)}.)
Выбираем уровень значимости (alpha ). Уровнем значимости в математической статистике называется вероятность ошибки первого рода, то есть вероятность отклонить тестируемую гипотезу при условии, что в действительности эта гипотеза верна. Разумеется, нам хотелось бы ошибаться не слишком часто, поэтому данную вероятность обычно выбирают маленькой. Чаще всего в эконометрике используются уровни значимости 1% и 5%.
Из таблиц распределения Стьюдента находим критическое значение тестовой статистки (t_{n-2}^{alpha }) для выбранного уровня значимости и так называемого числа степеней свободы, которое в нашем случае равно (left(n-2right)).
Если (left|frac{widehat {beta _2}}{mathit{se}left(widehat {beta }_2right)}right|>t_{n-2}^{alpha }), то есть (widehat {beta _2}) достаточно велик по абсолютной величине, следует отвергнуть гипотезу (H_0:beta _2=0) и сделать вывод в пользу альтернативной гипотезы, то есть заключить, что переменная x влияет на переменную y. В этом случае переменную x называют статистически значимой при уровне значимости (alpha ). В противном случае, соответственно, гипотеза (H_0) не может быть отвергнута, и переменную x называют статистически незначимой при уровне значимости (alpha ).
Здесь и далее во всех тестах, если явно не указано иное, мы подразумеваем альтернативную гипотезу «(beta _2) не равно c» , а не (beta _2<c) или (beta _2>c). Поэтому под критическими значениями из таблиц распределения Стьюдента по умолчанию подразумеваются критические значения для двусторонних (а не односторонних) тестов. Все стандартные эконометрические пакеты используют такой же подход.}
Замечание 1. В этой процедуре мы опираемся на тот факт, что тестовая статистика имеет t-распределение Стьюдента. Чтобы это было верно, как раз и нужна предпосылка №6 КЛМПР, которую мы до этого никак не использовали.
В соответствии с этой предпосылкой случайные ошибки имеют нормальное распределение. Мы показали (см. равенство (2.2)), что (widehat {beta _2}) — это линейная комбинация случайных ошибок, то есть независимых, одинаково и нормально распределенных случайных величин.
Из математической статистики известно, что отсюда следуют два утверждения:
Во-первых, (widehat {beta _2}) имеет нормальное распределение (так как линейная комбинация нормальных случайных величин является нормальной случайной величиной), дисперсию и математическое ожидание которого мы вычислили в предыдущем параграфе. Иными словами (widehat {beta _2}) имеет вот такое распределение:
begin{equation*} Nleft(beta _2,frac{sigma ^2}{Sigma left(x_i-overline xright)^2}right) end{equation*}
Во-вторых, случайная величина (frac{widehat {beta _2}-beta _2}{mathit{se}left(widehat {beta _2}right)}) имеет t-распределение Стьюдента. В нашем случае это будет распределение с (n-2) степенями свободы: (frac{widehat {beta _2}-beta _2}{mathit{se}left(widehat {beta _2}right)})~(t_{n-2})
В частности, если верна сформулированная нами гипотеза (beta _2=0), то распределение Стьюдента имеет дробь (frac{widehat {beta }_2}{mathit{se}left(widehat {beta }_2right)}), которую мы используем в нашей процедуре. В этом случае критическое значение определяется из вот такого условия (его геометрическая интерпретация представлена в примере 2.3):
begin{equation*} Pleft(left|frac{widehat {beta }_2}{mathit{se}left(widehat {beta }_2right)}right|<t_{n-2}^{alpha }right)=1-alpha . end{equation*}
Замечание 2. Аналогичным образом можно тестировать гипотезу (H_0:beta _2=c) (против альтернативной гипотезы (H_0:beta _2{neq}c)), где c — это некоторая константа. В этом случае процедура тестирования остается такой же с одним исключением: расчетное значение тестовой статистики будет иметь вид (frac{widehat {beta }_2-c}{mathit{se}left(widehat {beta }_2right)}).
Замечание 3. Раньше для определения величины критического значения (t_{n-2}^{alpha }) было необходимо использовать таблицы распределения Стьюдента. Сейчас этот способ тоже доступен (например, соответствующая таблица представлена в Приложении 3.А в конце третьей главы), однако теперь это значение можно рассчитать непосредственно в эконометрическом пакете или, например, в MS Excel (см. пример ниже).
Альтернативным способом является использование для тестирования гипотезы так называемого p-значения. P-значением называют такой уровень значимости, при котором тестируемая гипотеза находится на грани между отвержением и принятием.
Поэтому использовать p-значение при принятии решения очень просто: если оно меньше заранее выбранного уровня значимости (alpha ), то тестируемая гипотеза отвергается при уровне значимости (alpha ). Например, если при тестировании незначимости коэффициента вы используете пятипроцентный уровень значимости ( (alpha =0,05)), а p-значение оказалось равно 0,0002, следует заключить, что соответствующий коэффициент является значимым. Удобство использования p-значения состоит в том, что эта величина автоматически рассчитывается всеми стандартными эконометрическими пакетами, поэтому для принятия решения о значимости или незначимости того или иного коэффициента (а также для проведения любых других тестов, которые мы обсудим далее) вам не требуется никаких таблиц распределения и никаких дополнительных расчетов.
Рассмотрим для большей наглядности еще один пример.
Пример 2.3. Тестирование незначимости коэффициента и графическая иллюстрация
Представим, что у нас 10 наблюдений ( (n=10)), оценка коэффициента оказалась равна (widehat {beta _2})= 8,0, а ее стандартная ошибка (mathit{se}left(widehat {beta }_2right))= 4,0. Если использовать подход, связанный с критическими значениями, нужно открыть таблицу распределения Стьюдента (см. Приложение 3.А), и найти критическое значение для пятипроцентного уровня значимости и (left(n-2right)=8) степеней свободы2. Это критическое значение (t_{mathit{text{к}text{р}}}=t_8^{0,05}{approx}2,3). Расчетное значение t-статистики здесь тоже посчитать несложно
begin{equation*} t_{mathit{text{р}text{а}text{с}text{ч}}}=frac{widehat {beta }_2}{mathit{se}left(widehat {beta }_2right)}=frac 8 4=2 end{equation*}
Если мы нанесем все указанные значения на картинку, у нас получится рисунок 2.4а. Критическое значение отсекает по 2,5% слева и справа (всего 5%). Следовательно, вероятность попасть между (-t_{mathit{text{к}text{р}}}) и (t_{mathit{text{к}text{р}}}) будет 95%. Нанесем также (-t_{mathit{text{р}text{а}text{с}text{ч}}}) и (t_{mathit{text{р}text{а}text{с}text{ч}}}). Эти значения отсекают по 3% справа и слева, как это показано на рисунке 2.4б.
Обозначим (xi ) — случайную величину, имеющую распредление стьюдента с (left(n-2right)=8) степенями свободы. Тогда формально P-значение в нашем случае — это вот такая вероятность:
p-значение (Pleft(left|xi right|>2right)).
То есть в нашем примере p-значение — это вероятность такого события, что случайная величина, имеющая t-распределение Стьюдента с 8 степенями свободы, по модулю превысит (t_{mathit{text{р}text{а}text{с}text{ч}}}=2). Как видно из рисунка, в нашем случае эта вероятность равна 0,03+0,03=0,06.
Рисунок 2.4а. Расчетное и критическое значения тестовой статистики для примера 2.3.
Рисунок 2.4б. P-значение для примера 2.3.
Как видно из нашего примера, P-значение больше заранее выбранного уровня значимости только тогда, когда (left|t_{mathit{text{р}text{а}text{с}text{ч}}}right|<t_{mathit{text{к}text{р}}}), что подтверждает сформулированное нами правило принятия решения при помощи P-значения: если P-значение больше уровня значимости, то нулевая гипотеза не отвергается. Если P-значение меньше уровня значимости, то нулевая гипотеза отвергается.
***
Решив неравенство (left|frac{widehat {beta }_2-beta _2}{mathit{se}left(widehat {beta }_2right)}right|<t_{n-2}^{alpha }) относительно (beta _2), получим:
begin{equation*} widehat {beta }_2-mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha }<beta _2<widehat {beta }_2+mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha } end{equation*}
Иными словами, с вероятностью (1-alpha ) интервал (left(widehat {beta }_2-mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha },widehat {beta }_2+mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha }right)) содержит истинное значение оцениваемого параметра. Например, если (alpha =0,05) и, следовательно, (1-alpha =0,95), этот интервал и называют 95-процентным доверительным интервалом для параметра (beta _2).
Возможность построения доверительных интервалов важна с практической точки зрения. Дело в том, что, так как (widehat {beta }_2) является лишь приблизительной оценкой параметра (beta _2), эта точечная оценка сама по себе несет гораздо меньше информации, чем интервал. Ведь без доверительного интервала невозможно понять, насколько она эта оценка на самом деле (не)точная. Например, утверждение « (widehat {beta }_2) равно 23,4» куда менее информативно, чем утверждение «истинное значение оцениваемого параметра с вероятностью 95 процентов содержится в пределах от 23,1 до 23,7».
Завершим раздел еще двумя примерами. В первом из них все расчеты проделаны вручную, чтобы, проследив их, можно было еще раз разобраться во взаимосвязях между введенными нами понятиями. Во втором примере используется эконометрический пакет, что позволяет продемонстрировать, как подобные вычисления осуществляются в реальных прикладных исследованиях.
Пример 2.4. Доходы индивидов и потребление риса
Исследователь анализирует зависимость потребления риса от уровня дохода (кривую Энгеля) для однородной группы из 20 потребителей. Все потребители из этой группы сталкиваются с одинаковыми ценами на рис и другие товары, и только уровни дохода у них различны, поэтому исследователь использует модель парной регрессии.
Обозначим:
(x_i) — ежемесячный располагаемый доход i-го потребителя (в тысячах денежных единиц),
(y_i) — ежемесячное потребление риса i-м потребителем (в килограммах).
Имеются следующие данные о переменных x и y:
begin{equation*} sum _{i=1}^{20}x_i=20,sum _{i=1}^{20}x_i^2=40,sum _{i=1}^{20}y_i=42,sum _{i=1}^{20}y_i^2=108, end{equation*}
begin{equation*} sum _{i=1}^{20}x_i{ast}y_i=60 end{equation*}
(а) Вычислите МНК-оценки коэффициентов в регрессии
begin{equation*} y_i=beta _1+beta _2{ast}x_i+varepsilon _i. end{equation*}
Выпишите полученное уравнение регрессии и коэффициент (R^2).
(б) При уровне значимости 5% проверьте значимость переменной x.
(в) Дайте содержательную интерпретацию коэффициента при переменной x.
(г) Вспомнив соответствующие определения из курса микроэкономики и вычислив необходимую эластичность, определите: является ли рис для этой группы потребителей низкокачественным товаром, товаром первой необходимости или предметом роскоши?
(д) При уровне значимости 5% проверьте гипотезу о том, что коэффициент (beta _2) равен единице.
(е) Постройте 95-процентный доверительный интервал для коэффициента (beta _2).
Решение:
(а) Вычислим средние значения:
begin{equation*} overline x=1,overline{x^2}=2,overline y=2,1,overline{y^2}=5,4,overline{mathit{xy}}=3 end{equation*}
Найдем оценки коэффициентов:
begin{equation*} widehat {beta _2}=frac{overline{mathit{xy}}-overline x{ast}overline y}{overline{x^2}-overline x^2}=frac{3-1{ast}2,1}{2-1}=0,9 end{equation*}
begin{equation*} widehat {beta _1}=overline y-widehat {beta _2}{ast}overline x=2,1-1{ast}0,9=1,2 end{equation*}
Таким образом, (widehat y_i=1,2+0,9{ast}x_i).
Теперь вычислим (R^2). Для этого воспользуемся тем, что по определению он равен отношению объясненной суммы квадратов к общей сумме квадратов:
begin{equation*} R^2=frac{sum _{i=1}^{20}left(widehat y_i-overline yright)^2}{sum _{i=1}^{20}left(y_i-overline yright)^2}. end{equation*}
Вычислим каждую из этих сумм по отдельности. Сначала найдем общую сумму квадратов:
begin{equation*} mathit{TSS}=sum _{i=1}^{20}left(y_i-overline yright)^2=sum _{i=1}^{20}y_i^2-2{ast}sum _{i=1}^{20}y_i{ast}overline y+sum _{i=1}^{20}overline y^2= end{equation*}
begin{equation*} sum _{i=1}^{20}y_i^2-2{ast}overline y{ast}sum _{i=1}^{20}y_i+20{ast}overline y^2=108-2{ast}2,1{ast}42+20{ast}2,1^2=19,8 end{equation*}
Теперь найдем объясненную сумму квадратов:
begin{equation*} sum _{i=1}^{20}left(widehat y_i-overline yright)^2=sum _{i=1}^{20}left(1,2+0,9{ast}x_i-2,1right)^2=sum _{i=1}^{20}left(0,9{ast}x_i-0,9right)^2= end{equation*}
begin{equation*} 0,9^2sum _{i=1}^{20}left(x_i-1right)^2=0,81{ast}left(sum _{i=1}^{20}x_i^2-2{ast}sum _{i=1}^{20}x_i+20right)=16,2 end{equation*}
Теперь можно вычислить коэффициент детерминации:
begin{equation*} R^2=frac{sum _{i=1}^{20}left(widehat y_i-overline yright)^2}{sum _{i=1}^{20}left(y_i-overline yright)^2}=frac{16,2}{19,8}=0,82 end{equation*}
Ответ на пункт (а): (widehat y_i=1,2+0,9{ast}x_i,R^2=0,82)
(б) Тестируемая гипотеза (H_0:beta _2=0). Альтернативная гипотеза (H_1:beta _2{neq}0).
Чтобы проверить значимость, нам понадобится стандартная ошибка оценки коэффициента. Для этого нам придется оценить сумму квадратов остатков. Воспользуемся тем фактом, что для регрессии с константой верно равенство:
begin{equation*} sum _{i=1}^{20}left(y_i-overline yright)^2=sum _{i=1}^{20}left(widehat y_i-overline yright)^2+sum _{i=1}^{20}e_i^2 end{equation*}
В этой формуле мы вычислили все элементы, кроме суммы квадратов остатков:
begin{equation*} 19,8=16,2+sum _{i=1}^{20}e_i^2 end{equation*}
Следовательно, (sum _{i=1}^{20}e_i^2=19,8-16,2=3,6).
Вычислим оценку дисперсии случайной ошибки:
begin{equation*} S^2=frac{sum _{i=1}^{20}e_i^2}{n-2}=frac{3,6}{20-2}=0,2 end{equation*}
Теперь вычислим стандартную ошибку оценки коэффициента:
begin{equation*} mathit{se}left(widehat {beta _2}right)=sqrt{frac{S^2}{sum _{i=1}^{20}left(x_i-overline xright)^2}}=end{equation*}
begin{equation*} =sqrt{frac{0,2}{sum _{i=1}^{20}x_i^2-n{ast}left(overline xright)^2}}=sqrt{frac{0,2}{40-20}}=0,1 end{equation*}
Расчетное значение t-статистики равно (frac{widehat {beta _2}}{mathit{se}left(widehat {beta _2}right)}=frac{0,9}{0,1}=9).
Критическое значение t-статистки из таблицы распределения Стьюдента при уровне значимости 5% и (20–2)=18 степенях свободы составляет 2,101. Расчетное значение больше критического, следовательно, мы отклоняем нулевую гипотезу и делаем вывод о том, что уровень дохода индивида значимо влияет на его спрос на рис.
Ответ на пункт (б): Переменная значима.
Ответ на пункт (в): При увеличении располагаемого дохода потребителя на одну тысячу денежных единиц его спрос на рис увеличивается в среднем на 0,9 кг.
(г) Вычислим эластичность спроса на рис по доходу. По определению эластичность равна:
begin{equation*} frac{frac{dwidehat y}{mathit{dx}}{ast}x}{widehat y}=frac{0,9{ast}x}{1,2+0,9{ast}x} end{equation*}
Легко видеть, что при любых положительных значениях (x) эластичность спроса по доходу лежит между нулем и единицей, следовательно, для рассматриваемой группы потребителей рис является товаром первой необходимости. Что, в общем-то, неудивительно.
Ответ на пункт (г): Товар первой необходимости.
(д) Тестируемая гипотеза (H_0:beta _2=1). Альтернативная гипотеза (H_1:beta _2{neq}1).
Для проверки значимости нам понадобится стандартная ошибка оценки коэффициента.
Расчетное значение t-статистики равно (frac{widehat {beta _2}-1}{mathit{se}left(widehat {beta _2}right)}=frac{0,9-1}{0,1}=-1).
Критическое значение t-статистки из таблицы распределения Стьюдента при уровне значимости 5% и (20–2)=18 степенях свободы составляет 2,101. Расчетное значение по модулю меньше критического, следовательно, мы принимаем (не отклоняем) нулевую гипотезу.
Ответ на пункт (д): Гипотеза не отклоняется.
(е) В рамках предпосылок классической линейной модели парной регрессии доверительный интервал может быть посчитан следующим образом:
begin{equation*} left(widehat {beta _2}-mathit{se}left(widehat {beta _2}right){ast}t_{n-2},widehat {beta _2}+mathit{se}left(widehat {beta _2}right){ast}t_{n-2}right) end{equation*}
begin{equation*} left(0,9-0,1{ast}2,101,0,9+0,1{ast}2,101right) end{equation*}
Таким образом, c вероятностью 95% интервал (left(0,69,1,11right)) содержит истинное значение коэффициента (beta _2).
Ответ на пункт (е): (left(0,69,1,11right)).
***
Пример 2.5. Площадь однокомнатной квартиры и её цена
В этом задании вам предлагается проанализировать взаимосвязь между площадью квартиры и ее ценой. Вам доступны следующие данные о московском рынке недвижимости в 2012 году (файл Price2012):
Price — рыночная цена однокомнатной квартиры в Москве (в тысячах руб.), выкуп которой был осуществлен с 10.01.2012 по 28.09.2012
TotalArea — общая площадь квартиры (кв. м)
(а) Оцените регрессию переменной Price на переменную TotalArea. Запишите оцененное уравнение регрессии, указав коэффициент детерминации и (в скобках под соответствующими коэффициентами) стандартные ошибки. Постройте диаграмму рассеяния с линией регрессии.
(б) Является ли коэффициент при переменной TotalArea статистически значимым при уровне значимости 1%? Дайте содержательную интерпретацию для этого коэффициента.
Решение:
(а) Ниже представлена распечатка результатов оценивания уравнения в эконометрическом пакете Gretl3. (Любой стандартный эконометрический пакет, например R, Stata или Econometric Views, выдаст аналогичную табличку. Пользуйтесь тем из них, который вам больше нравится. Ну или тем, который есть под рукой.)
Модель 1: МНК, использованы наблюдения 1-121
Зависимая переменная: Price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | 786,456 | 583,051 | 1,349 | 0,1799 | |
| TotalArea | 135,317 | 16,5144 | 8,194 | 0,0001 | *** |
| Среднее зав. перемен | 5540,335 | Ст. откл. зав. перемен | 792,7127 | |
| Сумма кв. остатков | 48208118 | Ст. ошибка модели | 636,4827 | |
| R-квадрат | 0,360696 | Испр. R-квадрат | 0,355324 | |
| F(1, 119) | 67,14000 | Р-значение (F) | 3,30e-13 | |
| Лог. правдоподобие | $-$951,8540 | Крит. Акаике | 1907,708 | |
| Крит. Шварца | 1913,300 | Крит. Хеннана-Куинна | 1909,979 |
В столбце «Коэффициент» указаны оценки коэффициентов, а в столбце «Ст. ошибка» — их стандартные ошибки. В нижней части таблицы среди прочих показателей можно найти и коэффициент R-квадрат.
Общепринятый формат записи полученных результатов имеет следующий вид (в скобках под оценками коэффициентов указаны соответствующие стандартные ошибки):
begin{equation*} widehat {mathit{Price}}_i=underset{left(583,051right)}{786,456}+underset{left(16,514right)}{135,317}mathit{TotalArea}_i,R^2=0,36 end{equation*}
Обратите внимание, что в скобках под оценками коэффициентов мы указали их стандартные ошибки. Такой формат является хорошим тоном при записи результатов эконометрического моделирования, так как позволяет читателю оценить точность ваших результатов и прикинуть доверительные интервалы для коэффициентов.
(б) В столбце «P-значение» указано, что P-значение для оценки коэффициента при переменной TotalArea меньше, чем 0,0001 (и тем более меньше, чем 0,01). Следовательно, этот коэффициент является статистически значимым при уровне значимости 1%.
Содержательная интерпретация: при увеличении общей площади квартиры на один квадратный метр ее цена в среднем при прочих равных условиях увеличивается на 135 тысяч рублей.
Отметим, что свободное слагаемое в данном случае отличается от нуля статистически незначимо, так как соответствующее P-значение равно 0,18, что больше любого разумного уровня значимости. Да и если бы даже эта константа была значима, все равно отдельно интерпретировать её смысла не было бы, ведь константа показывает значение зависимой переменной при условии, что регрессор TotalArea равен нулю (то есть при условии, что анализируемая квартира имеет нулевую площадь). Вряд ли кто-то всерьез интересуется ценой квартиры площадью 0 квадратных метров.
- Вместо использования готовых таблиц распределения можно, например, ввести в MS Excel формулу =СТЬЮДЕНТ.ОБР( 1 — 0,05 / 2; 10 — 2) ↵
- Для получения этого результата достаточно запустить Gretl; используя пункт меню «Импорт», импортировать данные из файла MS Excel (или просто мышкой «перетащить» нужный файл в рабочую область эконометрического пакета); выбрать в меню «Модель» пункт «Метод наименьших квадратов» и указать в качестве зависимой переменной переменную Price, а в качестве объясняющей — переменную TotalArea. ↵
Найти несмещенную оценку дисперсии ошибок измерений
03.08.2016, 18:54. Показов 8421. Ответов 1
Метки нет (Все метки)

Даны результаты 5 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 10, 9, 11, 8, 12. Найти несмещенную оценку дисперсии ошибок измерений, если истинная длина неизвестна.
Правильно ли я нашел нужное значение?
Несмещенная оценка дисперсии ошибок измерений вычисляется как:
Найдем выборочное среднее:
Используем формулу для :
Ответ 2 правильный?
0
