Лабораторная
работа №2
Линейная искусственная
нейронная сеть.
Правило обучения
Видроу-Хоффа.
Цель работы: Изучить обучение и
функционирование линейной ИНС при
решении задач прогнозирования.
1.Правило обучения
Видроу-Хоффа
Используется для обучения нейронной
сети, состоящей из распределительных
нейронов и одного выходного нейрона,
который имеет линейную функцию активации
(рис.1):
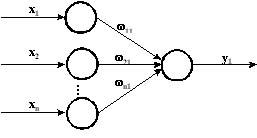
Рис. 1.Линейная сеть.
Такая сеть называется адаптивным
нейронным элементом или «ADALINE»
(Adaptive Linear Element). Его предложили в 1960 г.
Видроу (Widrow) и Хофф (Hoff). Выходное значение
такой сети определяется, как
 .
.
(1.2)
Правило обучения Видроу Хоффа известно
под названием дельта правила
(delta rule). Оно предполагает минимизацию
среднеквадратичной ошибки нейронной
сети, которая для L входных образов
определяется следующим образом:
 (1.3)
(1.3)
где
![]() —
—
среднеквадратичная ошибка сети для
k-го образа;
![]() и
и
![]() —
—
соответственно выходное и эталонное
значение нейронной сети для k-го
образа.
Критерий (1.3) характеризуется тем, что
при малых ошибках ущерб является также
малой величиной, т. к.
![]() меньше
меньше
чем величина отклонения
![]() .
.
При больших ошибках ущерб возрастает,
так как
![]() возрастает
возрастает
с ростом величины ошибки.
Среднеквадратичная ошибка нейронной
сети для одного входного образа
определяется, как
 (1.4)
(1.4)
Правило обучения Видроу-Хоффа базируется
на методе градиентного спуска в
пространстве весовых коэффициентов и
порогов нейронной сети. Согласно этому
правилу, весовые коэффициенты и пороги
нейронной сети необходимо изменять с
течением времени по следующим выражениям:
 (1.5)
(1.5)
 (1.6)
(1.6)
где
![]() ;
;
![]() —
—
скорость или шаг обучения. Найдем
производные
среднеквадратичной ошибки
![]() по
по
настраиваемым параметрам сети
![]() и
и
![]() .
.
Тогда


где xjk — j-ая
компонента k-го образа.
Отсюда получаем следующие выражения
для обучения нейронной сети по дельта
правилу:
 (1.7)
(1.7)
 (1.8)
(1.8)
где
![]() .
.
Видроу и Хофф доказали [18], что данный
закон обучения всегда позволяет находить
весовые коэффициенты нейронного элемента
таким образом, чтобы минимизировать
среднеквадратичную ошибку сети независимо
от начальных значений весовых
коэффициентов.
Алгоритм обучения, в основе которого
лежит дельта правило состоит из следующих
шагов:
1. Задается скорость обучения
![]() и
и
минимальная среднеквадратичная ошибка
сети
![]() ,
,
которой необходимо достичь в процессе
обучения.
2. Случайным образом инициализируются
весовые коэффициенты и порог нейронной
сети.
3. Подаются входные образы на нейронную
сеть и вычисляются векторы выходной
активности сети.
4. Производится изменение весовых
коэффициентов и порога нейронной сети
согласно выражениям (1.7) и (1.8).
5. Алгоритм продолжается до тех пор, пока
суммарная среднеквадратичная ошибка
сети не станет меньше заданной, т. е.
![]() .
.
В алгоритме Видроу-Хоффа существует
проблема выбора значения шага обучения
![]() .
.
Если коэффициент
![]() слишком
слишком
мал, то процесс обучения является очень
длительным. В случае, когда шаг обучения
большой, процесс обучения может оказаться
расходящимся, то есть не привести к
решению задачи. Таким образом сходимость
алгоритма обучения не избавляет от
разумного выбора значения шага обучения.
1.13. Использование
линейной нейронной сети для прогнозирования
Способность нейронных сетей после
обучения к обобщению и пролонгации
результатов создает потенциальные
предпосылки для построения на базе их
различного рода прогнозирующих систем.
В данном разделе рассмотрим прогнозирование
временных рядов при помощи линейных
нейронных сетей. Пусть дан временной
ряд
![]() на
на
промежутке
![]() .
.
Тогда задача прогнозирования состоит
в том, чтобы найти продолжение временного
ряда на неизвестном промежутке, т. е.
необходимо определить
![]() ,
,
![]() и
и
так далее (рис. 1.2):
Совокупность известных значений
временного ряда образуют обучающую
выборку, размерность которой равняется
m. Для прогнозирования временных
рядов используется метод «скользящего
окна». Он характеризуется длиной окна
n, которая равняется
количеству элементов ряда, одновременно
подаваемых на нейронную сеть. Это
определяет структуру нейронной сети,
которая состоит из n
распределительных нейронов и одного
выходного нейрона.
Такая модель соответствует линейной
авторегрессии и описывается следующим
выражением:
где
![]() —
—
весовые коэффициенты нейронной сети;
![]() —
—
оценка значения ряда
![]() в
в
момент времени
![]() .
.

Рис. 1.2. Прогнозирование временного
ряда.
Ошибка прогнозирования определяется,
как
 .
.
Модель линейной авторегрессии формирует
значение ряда
![]() ,
,
как взвешенную сумму предыдущих значений
ряда. Обучающую выборку нейронной сети
можно представить в виде матрицы, строки
которой характеризуют векторы, подаваемые
на вход сети:
 .
.
Это эквивалентно перемещению окна по
ряду
![]() с
с
единичным шагом.
Таким образом для обучения нейронной
сети прогнозированию используется
выборка известных членов ряда. После
обучения сеть должна прогнозировать
временной ряд на упреждающий промежуток
времени.
Задание.
1. Написать на любом ЯВУ программу
моделирования прогнозирующей линейной
ИНС. Для тестирования использовать
функцию
![]()
.
Варианты заданий приведены в следующей
таблице:
|
№ варианта |
a |
b |
d |
Кол-во входов |
|
1 |
1 |
5 |
0.1 |
3 |
|
2 |
2 |
6 |
0.2 |
4 |
|
3 |
3 |
7 |
0.3 |
5 |
|
4 |
4 |
8 |
0.4 |
3 |
|
5 |
1 |
9 |
0.5 |
4 |
|
6 |
2 |
5 |
0.6 |
5 |
|
7 |
3 |
6 |
0.1 |
3 |
|
8 |
4 |
7 |
0.2 |
4 |
|
9 |
1 |
8 |
0.3 |
5 |
|
10 |
2 |
9 |
0.4 |
3 |
|
11 |
3 |
5 |
0.5 |
4 |
Обучение и прогнозирование производить
на 30 и 15 значениях соответственно
табулируя функцию с шагом 0.1. Скорость
обучения выбирается студентом
самостоятельно, для чего моделирование
проводится несколько раз для разных .
Результаты оцениваются по двум критериям
— скорости обучения и минимальной
достигнутой ошибке. Необходимо заметить,
что эти критерии в общем случае являются
взаимоисключающими, и оптимальные
значения для каждого критерия достигаются
при разных .
2. Результаты представить в виде отчета
содержащего:
-
Титульный лист,
-
Цель работы,
-
Задание,
-
Результаты обучения: таблицу со
столбцами: эталонное значение, полученное
значение, отклонение; график изменения
ошибки в зависимости от итерации. -
Результаты прогнозирования: таблицу
со столбцами: эталонное значение,
полученное значение, отклонение. -
Выводы по лабораторной работе.
Результаты для пунктов 3 и 4 приводятся
для значения , при
котором достигается минимальная ошибка.
В выводах анализируются все полученные
результаты.
Контрольные вопросы.
-
ИНС какой архитектуры Вы использовали
в данной работе? Опишите принцип
построения этой ИНС. -
Как функционирует используема Вами
ИНС? -
Опишите (в общих чертах) алгоритм
обучения Вашей ИНС. -
Как формируется обучающая выборка для
решения задачи прогнозирования? -
Как выполняется многошаговое
прогнозирование временного ряда? -
Предложите критерий оценки качества
результатов прогноза.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Перевод
Ссылка на автора
Каждая модель машинного обучения пытается решить проблему с другой целью, используя свой набор данных, и, следовательно, важно понять контекст, прежде чем выбрать метрику. Обычно ответы на следующий вопрос помогают нам выбрать подходящий показатель:
- Тип задачи: регрессия? Классификация?
- Бизнес цель?
- Каково распределение целевой переменной?
Ну, в этом посте я буду обсуждать полезность каждой метрики ошибки в зависимости от цели и проблемы, которую мы пытаемся решить. Часть 1 фокусируется только на показателях оценки регрессии.

Метрики регрессии
- Средняя квадратическая ошибка (MSE)
- Среднеквадратическая ошибка (RMSE)
- Средняя абсолютная ошибка (MAE)
- R в квадрате (R²)
- Скорректированный R квадрат (R²)
- Среднеквадратичная ошибка в процентах (MSPE)
- Средняя абсолютная ошибка в процентах (MAPE)
- Среднеквадратичная логарифмическая ошибка (RMSLE)
Средняя квадратическая ошибка (MSE)
Это, пожалуй, самый простой и распространенный показатель для оценки регрессии, но, вероятно, наименее полезный. Определяется уравнением

гдеyᵢфактический ожидаемый результат иŷᵢэто прогноз модели.
MSE в основном измеряет среднеквадратичную ошибку наших прогнозов. Для каждой точки вычисляется квадратная разница между прогнозами и целью, а затем усредняются эти значения.
Чем выше это значение, тем хуже модель. Он никогда не бывает отрицательным, поскольку мы возводим в квадрат отдельные ошибки прогнозирования, прежде чем их суммировать, но для идеальной модели это будет ноль.
Преимущество:Полезно, если у нас есть неожиданные значения, о которых мы должны заботиться. Очень высокое или низкое значение, на которое мы должны обратить внимание.
Недостаток:Если мы сделаем один очень плохой прогноз, возведение в квадрат сделает ошибку еще хуже, и это может исказить метрику в сторону переоценки плохости модели. Это особенно проблематичное поведение, если у нас есть зашумленные данные (то есть данные, которые по какой-либо причине не совсем надежны) — даже в «идеальной» модели может быть высокий MSE в этой ситуации, поэтому становится трудно судить, насколько хорошо модель выполняет. С другой стороны, если все ошибки малы или, скорее, меньше 1, то ощущается противоположный эффект: мы можем недооценивать недостатки модели.
Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсреднее значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.
Среднеквадратическая ошибка (RMSE)
RMSE — это просто квадратный корень из MSE. Квадратный корень введен, чтобы масштаб ошибок был таким же, как масштаб целей.

Теперь очень важно понять, в каком смысле RMSE похож на MSE, и в чем разница.
Во-первых, они похожи с точки зрения их минимизаторов, каждый минимизатор MSE также является минимизатором для RMSE и наоборот, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора предсказаний, A и B, и скажем, что MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. И это также работает в противоположном направлении. ,

Что это значит для нас?
Это означает, что, если целевым показателем является RMSE, мы все равно можем сравнивать наши модели, используя MSE, поскольку MSE упорядочит модели так же, как RMSE. Таким образом, мы можем оптимизировать MSE вместо RMSE.
На самом деле, с MSE работать немного проще, поэтому все используют MSE вместо RMSE. Также есть небольшая разница между этими двумя моделями на основе градиента.

Это означает, что путешествие по градиенту MSE эквивалентно путешествию по градиенту RMSE, но с другой скоростью потока, и скорость потока зависит от самой оценки MSE.
Таким образом, хотя RMSE и MSE действительно схожи с точки зрения оценки моделей, они не могут быть сразу взаимозаменяемыми для методов на основе градиента. Возможно, нам нужно будет настроить некоторые параметры, такие как скорость обучения.
Средняя абсолютная ошибка (MAE)
В MAE ошибка рассчитывается как среднее абсолютных разностей между целевыми значениями и прогнозами. MAE — это линейная оценка, которая означает, чтовсе индивидуальные различия взвешены одинаковов среднем. Например, разница между 10 и 0 будет вдвое больше разницы между 5 и 0. Однако то же самое не верно для RMSE. Математически он рассчитывается по следующей формуле:

Что важно в этой метрике, так это то, что онанаказывает огромные ошибки, которые не так плохо, как MSE.Таким образом, он не так чувствителен к выбросам, как среднеквадратическая ошибка.
MAE широко используется в финансах, где ошибка в 10 долларов обычно в два раза хуже, чем ошибка в 5 долларов. С другой стороны, метрика MSE считает, что ошибка в 10 долларов в четыре раза хуже, чем ошибка в 5 долларов. MAE легче обосновать, чем RMSE.
Еще одна важная вещь в MAE — это его градиенты относительно прогнозов. Gradiend — это пошаговая функция, которая принимает -1, когда Y_hat меньше цели, и +1, когда она больше.
Теперь градиент не определен, когда предсказание является совершенным, потому что, когда Y_hat равен Y, мы не можем оценить градиент. Это не определено.

Таким образом, формально, MAE не дифференцируемо, но на самом деле, как часто ваши прогнозы точно измеряют цель. Даже если они это сделают, мы можем написать простое условие IF и вернуть ноль, если это так, и через градиент в противном случае. Также известно, что вторая производная везде нулевая и не определена в нулевой точке.
Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсрединное значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.
R в квадрате (R²)
А что если я скажу вам, что MSE для моих моделей предсказаний составляет 32? Должен ли я улучшить свою модель или она достаточно хороша? Или что, если мой MSE был 0,4? На самом деле, трудно понять, хороша наша модель или нет, посмотрев на абсолютные значения MSE или RMSE. Мы, вероятно, захотим измерить, как Во многом наша модель лучше, чем постоянная базовая линия.
Коэффициент детерминации, или R² (иногда читаемый как R-два), является еще одним показателем, который мы можем использовать для оценки модели, и он тесно связан с MSE, но имеет преимущество в том, чтобезмасштабное— не имеет значения, являются ли выходные значения очень большими или очень маленькими,R² всегда будет между -∞ и 1.
Когда R² отрицательно, это означает, что модель хуже, чем предсказание среднего значения.

MSE модели рассчитывается, как указано выше, в то время как MSE базовой линии определяется как:

гдеYс чертой означает среднее из наблюдаемогоyᵢ.
Чтобы сделать это более ясным, этот базовый MSE можно рассматривать как MSE, чтопростейшиймодель получит. Простейшей возможной моделью было бывсегдапредсказать среднее по всем выборкам. Значение, близкое к 1, указывает на модель с ошибкой, близкой к нулю, а значение, близкое к нулю, указывает на модель, очень близкую к базовой линии.
В заключение, R² — это соотношение между тем, насколько хороша наша модель, и тем, насколько хороша модель наивного среднего.
Распространенное заблуждение:Многие статьи в Интернете утверждают, что диапазон R² лежит между 0 и 1, что на самом деле не соответствует действительности. Максимальное значение R² равно 1, но минимальное может быть минус бесконечность.
Например, рассмотрим действительно дрянную модель, предсказывающую крайне отрицательное значение для всех наблюдений, даже если y_actual положительно. В этом случае R² будет меньше 0. Это крайне маловероятный сценарий, но возможность все еще существует.
MAE против MSE
Я заявил, что MAE более устойчив (менее чувствителен к выбросам), чем MSE, но это не значит, что всегда лучше использовать MAE. Следующие вопросы помогут вам решить:

Взять домой сообщение
В этой статье мы обсудили несколько важных метрик регрессии. Сначала мы обсудили среднеквадратичную ошибку и поняли, что наилучшей константой для нее является среднее целевое значение. Среднеквадратичная ошибка и R² очень похожи на MSE с точки зрения оптимизации. Затем мы обсудили среднюю абсолютную ошибку и когда люди предпочитают использовать MAE вместо MSE.

Спасибо за чтение, и я с нетерпением жду, чтобы услышать ваши вопросы Наслаждайтесь!
P.SСледите за моей следующей статьей, которая изучает другие более продвинутые метрики регрессии. Если вы хотите больше узнать о мире машинного обучения, вы также можете подписаться на меня в Instagram, напишите мне напрямую или найди меня на linkedin, Я хотел бы услышать от вас.
Ресурсы:
[1] https://dmitryulyanov.github.io/about
В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.
Обучение сверточной нейронной сети
На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.
Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.
Алгоритм обратного распространения ошибки
Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.
Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.
Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:

Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:

Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:

Выход каждого нейрона j является значением активационной функции
 , которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:
, которая переводит нейрон в активированное состояние. В качестве функции активации может использоваться любая непрерывно дифференцируемая монотонная функция. Активированное состояние нейрона вычисляется по формуле 2.10:

В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.

Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:
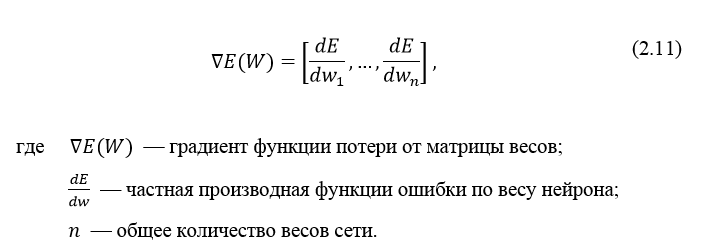
Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:

Ошибка нейрона  обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.
обычно записывается в виде символа δ (дельта). Для выходного слоя ошибка определена в явном виде, если взять производную от формулы 2.8, то получим t минус y, то есть разницу между желаемым и полученным выходом. Но как рассчитать ошибку для скрытых слоев? Для решения этой задачи, как раз и был придуман алгоритм обратного распространения ошибки. Суть его заключается в последовательном вычислении ошибок скрытых слоев с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.
Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:

Алгоритм распространения ошибки сводится к следующим этапам:
- прямое распространение сигнала по сети, вычисления состояния нейронов;
- вычисление значения ошибки δ для выходного слоя;
- обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
- обновление весов сети на вычисленную ранее δ ошибки.
Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:
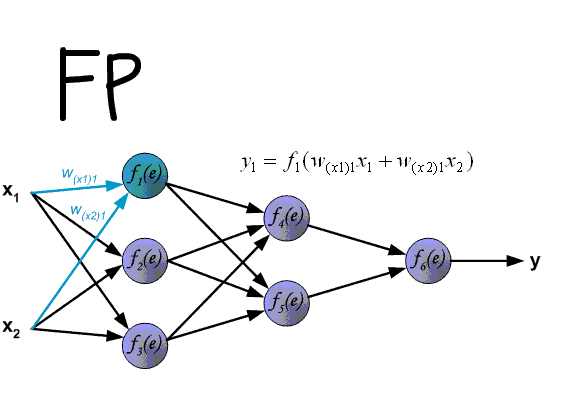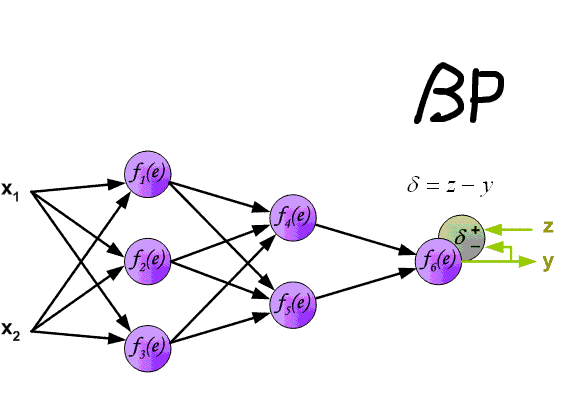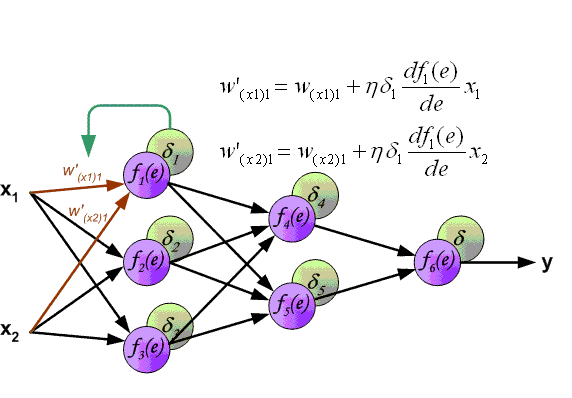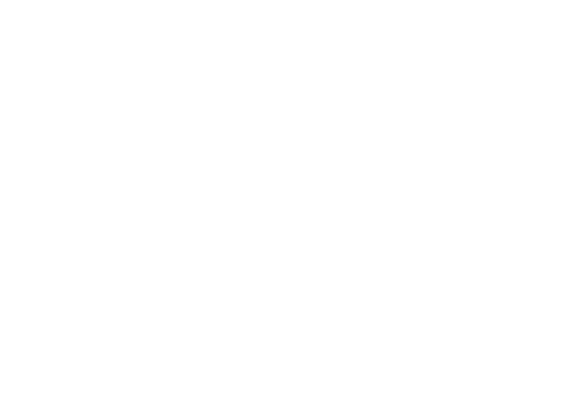
До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.
Расчет ошибки на подвыборочном слое
Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.
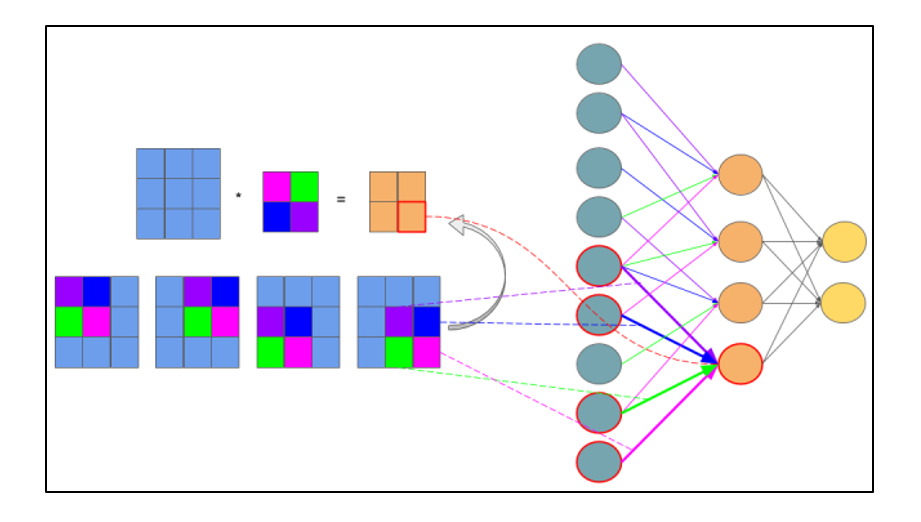
Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.
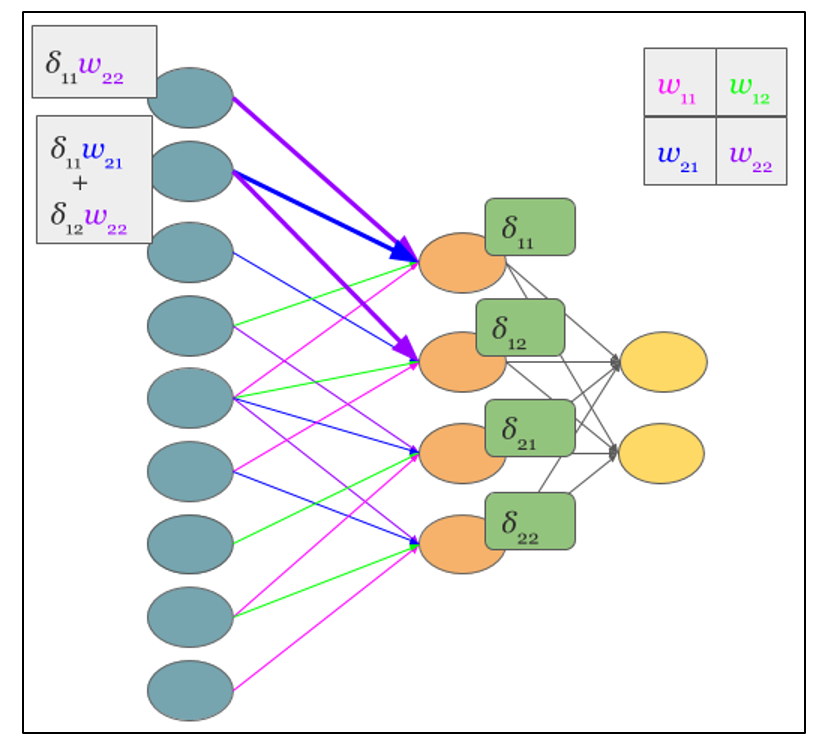
Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.

Рисунок 2.10 — Результат операции обратной свертки
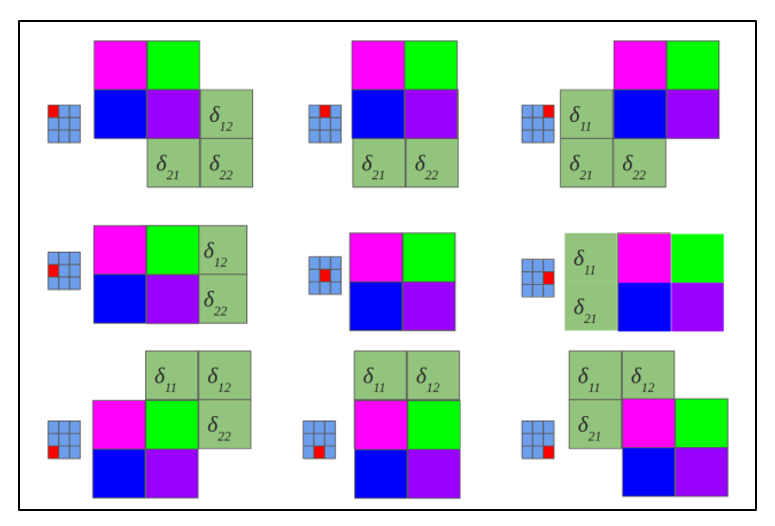
Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту
Расчет ошибки на сверточном слое
Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.
Заключение
Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.
Источники
Алгоритм обратного распространения ошибки для сверточной нейронной сети
Обратное распространение ошибки в сверточных слоях
раз и два
Обратное распространение ошибки в персептроне
Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ
оглавление
1 связанные термины
2 функция потерь
2.1 Определение
2.2 Среднеквадратичная ошибка
2.3 Ошибка перекрестной энтропии
2.4 данные партии
2.5 Зачем нужна функция потерь
3 Численное дифференцирование
3.1 Производная
3.2 частные производные
4 градиента
5 реализация корпуса
5.1dataset
5.2common
5.2.1functions.py:
5.2.2gradient.py:
5.3ch04
5.3.1two_layer_net.py
5.3.2train_neuralnet.py
Эта статья представляет собой краткое изложение «Введение в теорию глубокого обучения и реализацию на основе Python», автор — [ ] Сайто Ясуи.
1 связанные термины
В нейронных сетях данные очень важны, также очень важно извлечение функций данных.
«Количество функций»Это преобразователь, который может точно извлекать важные данные (важные данные) из входных данных (входное изображение).
Сравнение нейронной сети и машинного обучения выглядит следующим образом:

В машинном обучении данные обычно делятся наДанные обученияс участиемДанные испытанийДве части для обучения и экспериментов
ОбобщениеОтносится к способности обрабатывать ненаблюдаемые данные (данные не включаются в данные обучения). Получение способности обобщения — конечная цель машинного обучения.
Состояние переобучения только на определенный набор данных называетсяПереоснащение(over fitting)
2 функция потерь
2.1 Определение
Функция потерьЭто показатель «плохой степени» производительности нейронной сети, то есть степени, в которой текущая нейронная сеть не соответствует данным наблюдения, и насколько она непоследовательна. Использование «плохой производительности» в качестве индикатора может заставить людей чувствовать себя неестественно, но если вы умножите функцию потерь на отрицательное значение, это можно интерпретировать как «насколько плохая производительность», то есть «насколько хороша производительность».
2.2 Среднеквадратичная ошибка
Формат среднеквадратичной ошибки следующий:

[Примечание]: y k — это выходной сигнал нейронной сети, t k — это данные наблюдения, а k — размер данных.
Код реализован следующим образом:
import numpy as np
def mean_squared_error(y, t):
return 0.5*np.sum((y-t)**2)
if __name__ == "__main__":
# Используйте распознавание чисел, чтобы понять, что y - это прогнозируемые данные (с точки зрения вероятности), а t - реальные данные
# Установите 2 как правильное решение
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 2 имеет самую высокую вероятность и составляет 0,6
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# 7 имеет самую высокую вероятность 0,6
y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
# Среднеквадратичная ошибка
# r1 = mean_squared_error(np.array(y), np.array(t))
# r2 = mean_squared_error(np.array(y1), np.array(t))
# print(r1) # 0.09750000000000003
# print(r2) # 0.5975
# Мы обнаружили, что значение функции потерь в первом примере меньше, и разница между
# Ошибка небольшая. Другими словами, среднеквадратичная ошибка показывает, что результат первого примера более согласуется с данными наблюдения.
2.3 Ошибка перекрестной энтропии
Формат функции потерь кросс-энтропийной ошибки следующий:
[Примечание]: log представляет собой натуральный логарифм с основанием e (log e). y k — выход нейронной сети, а t k — метка правильного решения.
Код реализован следующим образом:
import numpy as np
# Добавлена крошечная дельта значения. Это потому, что когда появляется np.log (0), np.log (0) становится отрицательным бесконечным -inf
# Это приведет к сбою последующих вычислений. В качестве защитной меры добавление небольшого значения может предотвратить возникновение отрицательной бесконечности.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
if __name__ == "__main__":
# Установите 2 как правильное решение
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 2 имеет самую высокую вероятность и составляет 0,6
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# 7 имеет самую высокую вероятность 0,6
y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
# Ошибка перекрестной энтропии
r1 = cross_entropy_error(np.array(y), np.array(t))
r2 = cross_entropy_error(np.array(y1), np.array(t))
print(r1) # 0.510825457099338
print(r2) # 2.302584092994546
2.4 данные партии
В приведенных выше примерах функций потерь рассматриваются все функции потерь для отдельных данных. Если требуется сумма функций потерь всех обучающих данных, взяв в качестве примера кросс-энтропийную ошибку, ее можно записать в виде следующей формулы:

[Примечание]: Предполагая, что имеется N данных, t nk представляет значение k-го элемента n-х данных (y nk — это выходной сигнал нейронной сети, t nk — это данные наблюдения).
Данные пакетной обработки, тогда как читать несколько частей данных случайным образом за раз? Вы можете использовать np.random.choice () NumPy, например, np.random.choice (60000, 10) случайным образом выберет 10 чисел от 0 до 59999.
Например:
import sys,os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# print(x_train.shape) # (60000, 784)
# print(t_train.shape) # (60000, 10)
# Произвольно рисуем 10 данных
train_size = x_train.shape[0] # 60000
batch_size = 10
# Случайно выбрать 10 чисел от 0 до 59999
batch_mask = np.random.choice (train_size, batch_size) # случайным образом выбираем желаемое число из указанных чисел
# print(batch_mask) # [40011 45133 49757 27590 11182 32214 23597 45193 56422 33356]
x_batch = x_train[batch_mask] # (10, 784)
t_batch = t_train[batch_mask] # (10, 10)
Можно добиться следующегоОдновременная обработка отдельных данных и пакетных данных(Данные вводятся централизованно) Функция двух наблюдений.
В коде реализована ошибка кросс-энтропии mini_batch:
def batch_cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7))/batch_size[Примечание]: y — выход нейронной сети, t — данные наблюдения. Когда размерность y равна 1, то есть, когда вычисляется ошибка кросс-энтропии отдельных данных, форму данных необходимо изменить. И, когда вводится мини-пакетом, нормализуйте с количеством пакетов, чтобы вычислить среднюю ошибку кросс-энтропии отдельных данных.
Когда данные мониторингаФорма этикетки(Не одна горячая, а метки типа «2» и «7»), ошибка перекрестной энтропии может быть достигнута с помощью следующего кода.
def batch_cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7))/batch_size[Примечание]: для np.log (y [np.arange (batch_size), t]). np.arange (batch_size) сгенерирует массив от 0 до batch_size-1. Например, когда batch_size равно 5, np.arange (batch_size) сгенерирует массив NumPy [0, 1, 2, 3, 4]. Поскольку метка в t хранится в форме [2, 7, 0, 9, 4], y [np.arange (batch_size), t] может извлекать выходные данные нейронной сети, соответствующие правильной маркировке каждого данных (в В этом примере y [np.arange (batch_size), t] сгенерирует массив NumPy [y [0,2], y [1,7], y [2,0], y [3,9], y [ 4,4]]).
2.5 Зачем нужна функция потерь
1. При поиске оптимальных параметров (весов и смещений) при обучении нейронных сетей,Найдите параметр, чтобы сделать значение функции потерь как можно меньше. Чтобы найти место, где значение функции потерь является как можно меньшим, необходимо вычислить производную параметра (а точнее, градиент), а затем использовать эту производную в качестве руководства для постепенного обновления значения параметра.
2. Если значение производной отрицательное, значение функции потерь может быть уменьшено путем изменения весового параметра в положительном направлении; наоборот, если значение производной положительно, весовой параметр может быть изменен в отрицательном направлении для уменьшения Значение функции малых потерь. Однако, когда значение производной равно 0, независимо от того, в каком направлении изменяется весовой параметр, значение функции потерь не изменится, и обновление весового параметра здесь остановится.
3 Численное дифференцирование
3.1 Производная
Производная означает количество изменений в определенный момент (предел коэффициента приращения) и имеет следующий формат:

[Примечание]: левая часть знака равенства представляет собой производную от значения функции, а правая часть представляет степень изменения значения функции f (x) относительно независимой переменной x (представленной пределами)
Ошибка округления: Относится к ошибке в окончательном результате вычисления, вызванной пропуском значения точной части десятичной дроби (например, значения после восьмой десятичной точки).
Например:
print(np.float32(1e-50)) # 10^-50 = 0.0[Примечание]: указанное выше значение h необходимо установить разумно, иначе это приведет к большой ошибке, вы можете изменить 1e-50 на 1e-4.
Помимо изменения значения h, вторая область, которая нуждается в улучшении, связана с различием функции f. Хотя разность между x + h и x функции f вычисляется в приведенной выше реализации, необходимо отметить, что это вычисление имеет ошибки с самого начала. «Истинная производная» соответствует наклону функции в точке x (называемой касательной), но производная, вычисленная в приведенной выше реализации, соответствует наклону между (x + h) и x.
Чтобы уменьшить эту ошибку, мы можем вычислить разницу функции f между (x + h) и (x — h). Поскольку этот метод расчета принимает x в качестве центра и вычисляет разницу между его левой и правой сторонами, его также называютЦентральная разница(Разница между (x + h) и x называется прямой разницей).
Производный код реализован следующим образом:
import numpy as np
# Плохая реализация, примерная разница
def forward_numerical_diff(f, x):
h = 10e-50
# h = 1e-4 # 0.0001
return (f(x+h) - f(x))/h
# Центральное отличие
def center_numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h))/(2*h)
def fun(x):
return 0.01*x**2 + 0.1*x
def fun2(x):
# return x[0]**2 + x[1]**2
return np.sum(x**2)
if __name__ == "__main__":
# Аппроксимация производной при x = 5
z = center_numerical_diff(fun, 5) # 0.1999999999990898
# Аппроксимация производной при x = 10
z1 = center_numerical_diff(fun, 10) # 0.2999999999986347
3.2 частные производные
Когда в функции несколько параметров, ищется частная производная функции.
Например:

Когда требуется частная производная от x0, рассматривайте x1 как константу. При поиске x1 также рассматривайте x0 как константу.
Остальные такие же, как и в предыдущем методе поиска производной.
4 градиента
Основная задача машинного обучения — найти оптимальные параметры во время обучения.Точно так же нейронная сеть должна также найти оптимальные параметры (веса и смещения) во время обучения. Упомянутый здесь оптимальный параметр относится к параметру, когда функция потерь принимает минимальное значение. Градиент представляет направление, в котором значение функции в каждой точке уменьшается в наибольшей степени.
Формат градиентного метода следующий:
Скорость обучения необходимо определить заранее до определенного значения, например 0,01 или 0,001. Приведенная выше формула обновляется один раз, и этот шаг будет повторяться. Другими словами, каждый шаг обновляет значение переменной в соответствии с приведенной выше формулой и постепенно уменьшает значение функции, повторяя этот шаг.
[Примечание]: η представляет собой количество обновлений, которое называется скоростью обучения при обучении нейронных сетей.
Код для поиска градиента реализован следующим образом:
import numpy as np
# Определить функцию
def fun2(x):
return x[0]**2 + x[1]**2
# Найдите частную производную
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like (x) # Сгенерировать тот же массив, что и x
for idx in range(x.size):
tmp_val = x[idx]
# f (x + h) вычисление
x[idx] = tmp_val + h
fxh1 = f (x) # При вычислении x! = [3, 4], но [3 + h, 4]
# f (x-h) вычисление
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2)/(2*h)
x [idx] = tmp_val # значение восстановления
return grad
# Реализация метода градиентного спуска
# f: функция для оптимизации, init_x: начальное значение, lr: скорость обучения, step_num: время повторения градиентного метода
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numeric_gradient (f, x) # Найти градиент функции
x -= lr * grad
return x
if __name__ == "__main__":
x, y = numerical_gradient(fun2, np.array([3.0, 4.0]))
# print(x) # 6.00000000000378
# print(y) # 7.999999999999119
# Установить начальное значение
init_x = np.array([-3.0, 4.0])
# m, n = gradient_descent(fun2, init_x=init_x, lr=0.1, step_num=100)
# print(m) # -6.111107928998789e-10
# print(n) # 8.148143905314271e-10
# Скорость обучения слишком велика
# m, n = gradient_descent(fun2, init_x=init_x, lr=10, step_num=100)
# print(m) # -25898374737328.363
# print(n) # -1295248616896.5398
# Скорость обучения слишком мала
m, n = gradient_descent(fun2, init_x=init_x, lr=1e-4, step_num=100)
print(m) # -2.9405901379497053
print(n) # 3.920786850599603
'''
Если скорость обучения слишком велика, она превратится в большое значение; и наоборот, если скорость обучения слишком мала, она в основном закончится без значительного обновления.
'''
5 реализация корпуса
Документы, необходимые для реализации дела:

5.1dataset
Можно найти в предыдущей главе
5.2common
5.2.1functions.py:
Этот файл играет роль функции активации и функции потери.
# coding: utf-8
import numpy as np
def identity_function(x):
return x
def step_function(x):
return np.array(x > 0, dtype=np.int)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def relu(x):
return np.maximum(0, x)
def relu_grad(x):
grad = np.zeros(x)
grad[x>=0] = 1
return grad
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) #
return np.exp(x) / np.sum(np.exp(x))
def sum_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def softmax_loss(X, t):
y = softmax(X)
return cross_entropy_error(y, t)
5.2.2gradient.py:
Файл воспроизводит производную, градиент
# coding: utf-8
import numpy as np
# Найти одномерную частную производную
def _numerical_gradient_1d(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x [idx] = tmp_val # восстановление
return grad
# Найдите двумерную частную производную
def numerical_gradient_2d(f, X):
if X.ndim == 1:
return _numerical_gradient_1d(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_1d(f, x)
return grad
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
# flags: использовать внешние циклы, мультииндекс: каждая итерация может отслеживать один тип индекса
# У объекта nditer есть еще один необязательный параметр op_flags. По умолчанию nditer будет рассматривать массив, который будет повторяться, как объект только для чтения.
# Чтобы понять, что элементы массива стоит изменять при обходе массива, вы должны указать режим чтения-записи или только для записи.
it = np.nditer (x, flags = ['multi_index'], op_flags = ['readwrite']) # итерация
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x [idx] = tmp_val # восстановление
it.iternext()
return grad
5.3ch04
5.3.1two_layer_net.py
Этот документ создает двухуровневую сеть
# coding: utf-8
import sys, os
sys.path.append (os.pardir) # путь загрузки
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# Инициализация сети
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x: прогнозируемое значение, t: истинное значение
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
dz1 = np.dot(dy, W2.T)
da1 = sigmoid_grad(a1) * dz1
grads['W1'] = np.dot(x.T, da1)
grads['b1'] = np.sum(da1, axis=0)
return grads
5.3.2train_neuralnet.py
Используйте нейронные сети для обучения
# coding: utf-8
import sys, os
sys.path.append (os.pardir) # путь загрузки
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from ch04.two_layer_net import TwoLayerNet
# Прочитать набор данных
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000 # количество итераций 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# Расчет градиента
# grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# Обновление параметров
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# Рисование
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
Получите окончательный результат

Среднеквадратичная ошибка в PyTorch рассчитывается почти так же, как и общее уравнение потерь, приведенное ранее. Мы также рассмотрим значение смещения, поскольку это также параметр, который необходимо обновлять в процессе обучения.
(y-Ax+b)2
Среднеквадратичная ошибка лучше всего поясняется иллюстрацией.
Предположим, у нас есть набор значений, и мы начинаем с рисования некоторого параметра линии регрессии, размер которого определяется случайным набором веса и значения смещения, как и раньше.

Ошибка соответствует тому, как далеко фактическое значение от прогнозируемого значения – фактическое расстояние между ними.

Для каждой точки ошибка рассчитывается путем сравнения прогнозируемых значений, сделанных нашей линейной моделью, с фактическим значением по следующей формуле.

Каждая точка связана с ошибкой, что означает, что мы должны выполнить суммирование ошибки для каждой точки. Мы знаем, что прогноз можно переписать как:

Поскольку мы вычисляем среднеквадратичную ошибку, мы должны взять среднее значение, разделив его на количество точек данных. Упомянутый ранее градиент функции ошибки должен вести нас в направлении наибольшего увеличения ошибки.
Двигаясь к отрицательному градиенту нашей функции стоимости, мы движемся в направлении наименьшей ошибки. Мы будем использовать этот градиент как компас, который всегда ведет нас вниз. В градиентном спуске мы игнорируем наличие смещения, но для ошибки требуется определить оба параметра A и b.
Теперь мы вычисляем частные производные для каждого, и, как и раньше, мы начинаем с любой пары значений A и b.

Мы используем алгоритм градиентного спуска для обновления A и b в направлении наименьшей ошибки на основе двух частных производных, упомянутых выше. Для каждой отдельной итерации новый вес равен:
A1=A0-∝ f'(A).
И новое значение смещения равно
b1=b0-∝ f'(b).
Основная идея написания кода в том, что мы начинаем с некоторой случайной модели со случайным набором параметров веса и значения смещения. Эта случайная модель будет иметь большую функцию ошибки, большую функцию стоимости, и затем мы используем градиентный спуск, чтобы обновить вес нашей модели в направлении наименьшей ошибки. Минимизация этой ошибки возвращает оптимизированный результат.


Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
y question is about Neural Network Training. I already searched about this but, there is no good explanation about it.
There are dozens of good explanations on the web, and in the literature, one such example may be the book by Haykin: Neural Networks and Learning machines
So for the first one, how to calculate mean square error? (I know this is silly, but I really don’t get it)
In the most simple terms, mean squared error is defined as
sum_i 1/n (desired_output(i) - model_output(i))^2
So you simply calculate the mean of the squares of the errors (differences between your output, and the desired one).
Now when should we calculate the mean square error? does it when we already take all pairs? or does we calculate it for each pair?
Both methods are used, one is called batch learning, and one is online learning. So all next questions have the answer «both are correct, depending whether you are using batch or online learning». Which one to choose? Obviously — it depends, but for a sake of simplicity I would suggest starting with batch learning (so you compute the error over all training samples and then update).
оглавление
1 связанные термины
2 функция потерь
2.1 Определение
2.2 Среднеквадратичная ошибка
2.3 Ошибка перекрестной энтропии
2.4 данные партии
2.5 Зачем нужна функция потерь
3 Численное дифференцирование
3.1 Производная
3.2 частные производные
4 градиента
5 реализация корпуса
5.1dataset
5.2common
5.2.1functions.py:
5.2.2gradient.py:
5.3ch04
5.3.1two_layer_net.py
5.3.2train_neuralnet.py
Эта статья представляет собой краткое изложение «Введение в теорию глубокого обучения и реализацию на основе Python», автор — [ ] Сайто Ясуи.
1 связанные термины
В нейронных сетях данные очень важны, также очень важно извлечение функций данных.
«Количество функций»Это преобразователь, который может точно извлекать важные данные (важные данные) из входных данных (входное изображение).
Сравнение нейронной сети и машинного обучения выглядит следующим образом:

В машинном обучении данные обычно делятся наДанные обученияс участиемДанные испытанийДве части для обучения и экспериментов
ОбобщениеОтносится к способности обрабатывать ненаблюдаемые данные (данные не включаются в данные обучения). Получение способности обобщения — конечная цель машинного обучения.
Состояние переобучения только на определенный набор данных называетсяПереоснащение(over fitting)
2 функция потерь
2.1 Определение
Функция потерьЭто показатель «плохой степени» производительности нейронной сети, то есть степени, в которой текущая нейронная сеть не соответствует данным наблюдения, и насколько она непоследовательна. Использование «плохой производительности» в качестве индикатора может заставить людей чувствовать себя неестественно, но если вы умножите функцию потерь на отрицательное значение, это можно интерпретировать как «насколько плохая производительность», то есть «насколько хороша производительность».
2.2 Среднеквадратичная ошибка
Формат среднеквадратичной ошибки следующий:

[Примечание]: y k — это выходной сигнал нейронной сети, t k — это данные наблюдения, а k — размер данных.
Код реализован следующим образом:
import numpy as np
def mean_squared_error(y, t):
return 0.5*np.sum((y-t)**2)
if __name__ == "__main__":
# Используйте распознавание чисел, чтобы понять, что y - это прогнозируемые данные (с точки зрения вероятности), а t - реальные данные
# Установите 2 как правильное решение
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 2 имеет самую высокую вероятность и составляет 0,6
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# 7 имеет самую высокую вероятность 0,6
y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
# Среднеквадратичная ошибка
# r1 = mean_squared_error(np.array(y), np.array(t))
# r2 = mean_squared_error(np.array(y1), np.array(t))
# print(r1) # 0.09750000000000003
# print(r2) # 0.5975
# Мы обнаружили, что значение функции потерь в первом примере меньше, и разница между
# Ошибка небольшая. Другими словами, среднеквадратичная ошибка показывает, что результат первого примера более согласуется с данными наблюдения.
2.3 Ошибка перекрестной энтропии
Формат функции потерь кросс-энтропийной ошибки следующий:
[Примечание]: log представляет собой натуральный логарифм с основанием e (log e). y k — выход нейронной сети, а t k — метка правильного решения.
Код реализован следующим образом:
import numpy as np
# Добавлена крошечная дельта значения. Это потому, что когда появляется np.log (0), np.log (0) становится отрицательным бесконечным -inf
# Это приведет к сбою последующих вычислений. В качестве защитной меры добавление небольшого значения может предотвратить возникновение отрицательной бесконечности.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
if __name__ == "__main__":
# Установите 2 как правильное решение
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 2 имеет самую высокую вероятность и составляет 0,6
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# 7 имеет самую высокую вероятность 0,6
y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
# Ошибка перекрестной энтропии
r1 = cross_entropy_error(np.array(y), np.array(t))
r2 = cross_entropy_error(np.array(y1), np.array(t))
print(r1) # 0.510825457099338
print(r2) # 2.302584092994546
2.4 данные партии
В приведенных выше примерах функций потерь рассматриваются все функции потерь для отдельных данных. Если требуется сумма функций потерь всех обучающих данных, взяв в качестве примера кросс-энтропийную ошибку, ее можно записать в виде следующей формулы:

[Примечание]: Предполагая, что имеется N данных, t nk представляет значение k-го элемента n-х данных (y nk — это выходной сигнал нейронной сети, t nk — это данные наблюдения).
Данные пакетной обработки, тогда как читать несколько частей данных случайным образом за раз? Вы можете использовать np.random.choice () NumPy, например, np.random.choice (60000, 10) случайным образом выберет 10 чисел от 0 до 59999.
Например:
import sys,os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# print(x_train.shape) # (60000, 784)
# print(t_train.shape) # (60000, 10)
# Произвольно рисуем 10 данных
train_size = x_train.shape[0] # 60000
batch_size = 10
# Случайно выбрать 10 чисел от 0 до 59999
batch_mask = np.random.choice (train_size, batch_size) # случайным образом выбираем желаемое число из указанных чисел
# print(batch_mask) # [40011 45133 49757 27590 11182 32214 23597 45193 56422 33356]
x_batch = x_train[batch_mask] # (10, 784)
t_batch = t_train[batch_mask] # (10, 10)
Можно добиться следующегоОдновременная обработка отдельных данных и пакетных данных(Данные вводятся централизованно) Функция двух наблюдений.
В коде реализована ошибка кросс-энтропии mini_batch:
def batch_cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7))/batch_size[Примечание]: y — выход нейронной сети, t — данные наблюдения. Когда размерность y равна 1, то есть, когда вычисляется ошибка кросс-энтропии отдельных данных, форму данных необходимо изменить. И, когда вводится мини-пакетом, нормализуйте с количеством пакетов, чтобы вычислить среднюю ошибку кросс-энтропии отдельных данных.
Когда данные мониторингаФорма этикетки(Не одна горячая, а метки типа «2» и «7»), ошибка перекрестной энтропии может быть достигнута с помощью следующего кода.
def batch_cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7))/batch_size[Примечание]: для np.log (y [np.arange (batch_size), t]). np.arange (batch_size) сгенерирует массив от 0 до batch_size-1. Например, когда batch_size равно 5, np.arange (batch_size) сгенерирует массив NumPy [0, 1, 2, 3, 4]. Поскольку метка в t хранится в форме [2, 7, 0, 9, 4], y [np.arange (batch_size), t] может извлекать выходные данные нейронной сети, соответствующие правильной маркировке каждого данных (в В этом примере y [np.arange (batch_size), t] сгенерирует массив NumPy [y [0,2], y [1,7], y [2,0], y [3,9], y [ 4,4]]).
2.5 Зачем нужна функция потерь
1. При поиске оптимальных параметров (весов и смещений) при обучении нейронных сетей,Найдите параметр, чтобы сделать значение функции потерь как можно меньше. Чтобы найти место, где значение функции потерь является как можно меньшим, необходимо вычислить производную параметра (а точнее, градиент), а затем использовать эту производную в качестве руководства для постепенного обновления значения параметра.
2. Если значение производной отрицательное, значение функции потерь может быть уменьшено путем изменения весового параметра в положительном направлении; наоборот, если значение производной положительно, весовой параметр может быть изменен в отрицательном направлении для уменьшения Значение функции малых потерь. Однако, когда значение производной равно 0, независимо от того, в каком направлении изменяется весовой параметр, значение функции потерь не изменится, и обновление весового параметра здесь остановится.
3 Численное дифференцирование
3.1 Производная
Производная означает количество изменений в определенный момент (предел коэффициента приращения) и имеет следующий формат:

[Примечание]: левая часть знака равенства представляет собой производную от значения функции, а правая часть представляет степень изменения значения функции f (x) относительно независимой переменной x (представленной пределами)
Ошибка округления: Относится к ошибке в окончательном результате вычисления, вызванной пропуском значения точной части десятичной дроби (например, значения после восьмой десятичной точки).
Например:
print(np.float32(1e-50)) # 10^-50 = 0.0[Примечание]: указанное выше значение h необходимо установить разумно, иначе это приведет к большой ошибке, вы можете изменить 1e-50 на 1e-4.
Помимо изменения значения h, вторая область, которая нуждается в улучшении, связана с различием функции f. Хотя разность между x + h и x функции f вычисляется в приведенной выше реализации, необходимо отметить, что это вычисление имеет ошибки с самого начала. «Истинная производная» соответствует наклону функции в точке x (называемой касательной), но производная, вычисленная в приведенной выше реализации, соответствует наклону между (x + h) и x.
Чтобы уменьшить эту ошибку, мы можем вычислить разницу функции f между (x + h) и (x — h). Поскольку этот метод расчета принимает x в качестве центра и вычисляет разницу между его левой и правой сторонами, его также называютЦентральная разница(Разница между (x + h) и x называется прямой разницей).
Производный код реализован следующим образом:
import numpy as np
# Плохая реализация, примерная разница
def forward_numerical_diff(f, x):
h = 10e-50
# h = 1e-4 # 0.0001
return (f(x+h) - f(x))/h
# Центральное отличие
def center_numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h))/(2*h)
def fun(x):
return 0.01*x**2 + 0.1*x
def fun2(x):
# return x[0]**2 + x[1]**2
return np.sum(x**2)
if __name__ == "__main__":
# Аппроксимация производной при x = 5
z = center_numerical_diff(fun, 5) # 0.1999999999990898
# Аппроксимация производной при x = 10
z1 = center_numerical_diff(fun, 10) # 0.2999999999986347
3.2 частные производные
Когда в функции несколько параметров, ищется частная производная функции.
Например:

Когда требуется частная производная от x0, рассматривайте x1 как константу. При поиске x1 также рассматривайте x0 как константу.
Остальные такие же, как и в предыдущем методе поиска производной.
4 градиента
Основная задача машинного обучения — найти оптимальные параметры во время обучения.Точно так же нейронная сеть должна также найти оптимальные параметры (веса и смещения) во время обучения. Упомянутый здесь оптимальный параметр относится к параметру, когда функция потерь принимает минимальное значение. Градиент представляет направление, в котором значение функции в каждой точке уменьшается в наибольшей степени.
Формат градиентного метода следующий:
Скорость обучения необходимо определить заранее до определенного значения, например 0,01 или 0,001. Приведенная выше формула обновляется один раз, и этот шаг будет повторяться. Другими словами, каждый шаг обновляет значение переменной в соответствии с приведенной выше формулой и постепенно уменьшает значение функции, повторяя этот шаг.
[Примечание]: η представляет собой количество обновлений, которое называется скоростью обучения при обучении нейронных сетей.
Код для поиска градиента реализован следующим образом:
import numpy as np
# Определить функцию
def fun2(x):
return x[0]**2 + x[1]**2
# Найдите частную производную
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like (x) # Сгенерировать тот же массив, что и x
for idx in range(x.size):
tmp_val = x[idx]
# f (x + h) вычисление
x[idx] = tmp_val + h
fxh1 = f (x) # При вычислении x! = [3, 4], но [3 + h, 4]
# f (x-h) вычисление
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2)/(2*h)
x [idx] = tmp_val # значение восстановления
return grad
# Реализация метода градиентного спуска
# f: функция для оптимизации, init_x: начальное значение, lr: скорость обучения, step_num: время повторения градиентного метода
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numeric_gradient (f, x) # Найти градиент функции
x -= lr * grad
return x
if __name__ == "__main__":
x, y = numerical_gradient(fun2, np.array([3.0, 4.0]))
# print(x) # 6.00000000000378
# print(y) # 7.999999999999119
# Установить начальное значение
init_x = np.array([-3.0, 4.0])
# m, n = gradient_descent(fun2, init_x=init_x, lr=0.1, step_num=100)
# print(m) # -6.111107928998789e-10
# print(n) # 8.148143905314271e-10
# Скорость обучения слишком велика
# m, n = gradient_descent(fun2, init_x=init_x, lr=10, step_num=100)
# print(m) # -25898374737328.363
# print(n) # -1295248616896.5398
# Скорость обучения слишком мала
m, n = gradient_descent(fun2, init_x=init_x, lr=1e-4, step_num=100)
print(m) # -2.9405901379497053
print(n) # 3.920786850599603
'''
Если скорость обучения слишком велика, она превратится в большое значение; и наоборот, если скорость обучения слишком мала, она в основном закончится без значительного обновления.
'''
5 реализация корпуса
Документы, необходимые для реализации дела:

5.1dataset
Можно найти в предыдущей главе
5.2common
5.2.1functions.py:
Этот файл играет роль функции активации и функции потери.
# coding: utf-8
import numpy as np
def identity_function(x):
return x
def step_function(x):
return np.array(x > 0, dtype=np.int)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def relu(x):
return np.maximum(0, x)
def relu_grad(x):
grad = np.zeros(x)
grad[x>=0] = 1
return grad
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) #
return np.exp(x) / np.sum(np.exp(x))
def sum_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def softmax_loss(X, t):
y = softmax(X)
return cross_entropy_error(y, t)
5.2.2gradient.py:
Файл воспроизводит производную, градиент
# coding: utf-8
import numpy as np
# Найти одномерную частную производную
def _numerical_gradient_1d(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x [idx] = tmp_val # восстановление
return grad
# Найдите двумерную частную производную
def numerical_gradient_2d(f, X):
if X.ndim == 1:
return _numerical_gradient_1d(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_1d(f, x)
return grad
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
# flags: использовать внешние циклы, мультииндекс: каждая итерация может отслеживать один тип индекса
# У объекта nditer есть еще один необязательный параметр op_flags. По умолчанию nditer будет рассматривать массив, который будет повторяться, как объект только для чтения.
# Чтобы понять, что элементы массива стоит изменять при обходе массива, вы должны указать режим чтения-записи или только для записи.
it = np.nditer (x, flags = ['multi_index'], op_flags = ['readwrite']) # итерация
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x [idx] = tmp_val # восстановление
it.iternext()
return grad
5.3ch04
5.3.1two_layer_net.py
Этот документ создает двухуровневую сеть
# coding: utf-8
import sys, os
sys.path.append (os.pardir) # путь загрузки
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# Инициализация сети
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x: прогнозируемое значение, t: истинное значение
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
dz1 = np.dot(dy, W2.T)
da1 = sigmoid_grad(a1) * dz1
grads['W1'] = np.dot(x.T, da1)
grads['b1'] = np.sum(da1, axis=0)
return grads
5.3.2train_neuralnet.py
Используйте нейронные сети для обучения
# coding: utf-8
import sys, os
sys.path.append (os.pardir) # путь загрузки
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from ch04.two_layer_net import TwoLayerNet
# Прочитать набор данных
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000 # количество итераций 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# Расчет градиента
# grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# Обновление параметров
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# Рисование
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
Получите окончательный результат

