Для линейных кодов,
рассчитанных на исправление многократных
ошибок, часто более простыми оказываются
декодирующие устройства, построенные
по мажоритарному принципу. Это метод
декодирования называют также принципом
голосования или способом декодирования
по большинству проверок. В настоящее
время известно значительное число
кодов, допускающих мажоритарную схему
декодирования, а также сформулированы
некоторые подходы при конструировании
таких кодов.
Мажоритарное
декодирование тоже базируется на системе
проверочных равенств. Система
последовательно может быть разрешена
относительно каждой из независимых
переменных, причем в силу избыточности
это можно сделать не единственным
способом.
Любой символ аi
выражается d (минимальное кодовое
расстояние) различными независимыми
способами в виде линейных комбинаций
других символов. При этом может
использоваться тривиальная проверка
аi
= аi.
Результаты вычислений подаются на
соответствующий этому символу мажоритарный
элемент. Последний представляет собой
схему, имеющую d входов и один выход, на
котором появляется единица, когда
возбуждается больше половины его входов,
и нуль, когда возбуждается число таких
входов меньше половины. Если ошибки
отсутствуют, то проверочные равенства
не нарушаются и на выходе мажоритарного
элемента получаем истинное значение
символа. Если число проверок d![]() 2s+
2s+
1 и появление ошибки кратности s и менее
не приводит к нарушению более s проверок,
то правильное решение может быть принято
по большинству неискаженных проверок.
Чтобы указанное условие выполнялось,
любой другой символ aj(j![]() i)
i)
не должен входить более чем в одно
проверочное равенство. В этом случае
мы имеем дело с системойразделенных
проверок.
Пример 7.12.
Построим
систему разделенных проверок для
декодирования информационных символов
рассмотренного ранее группового кода
(8,2).
Решение.
Поскольку
код рассчитан на исправление любых
единичных и двойных ошибок, число
проверочных равенств для определения
каждого символа должно быть не менее
5. Подставив в равенства (7.2 а) и (7.2 б)
значения а8,
полученные из равенств (7.2 д) и (7.2 е) и
записав их относительно a5
совместно с равенствами (7.2 в) и (7.2 г) и
тривиальным равенством a5
= a5,
получим следующую систему разделенных
проверок для символа a5:
a5
= a6![]() a1,
a1,
a5
= a7![]() a2,
a2,
а5
= а3,
а5
= a4,
а5
= а5.
Для символа a8
систему разделенных проверок строим
аналогично:
a8
= a3![]() a1,
a1,
a8
= a4![]() a2,
a2,
a8
= а6,
a8
= a7,
a8
= а8.
7.13. Матричное представление линейных кодов
Матрицей
размерности
l![]() n
n
называют упорядоченное множество l![]() n
n
элементов, расположенных в виде
прямоугольной таблицы с l
строками и n
столбцами:

Транспонированной
матрицей к
матрице А
называют матрицу, строками которой
являются столбцы, а столбцами строки
матрицы А:

Матрицу размерности
n![]() n
n
называют квадратной
матрицей порядка n.
Квадратную матрицу, у которой по одной
из диагоналей расположены только
единицы, а все остальные элементы равны
нулю, называют единичной
матрицей I.
Суммой двух матриц А
![]() |аij|
|аij|
и В![]() |bij|
|bij|
размерности l![]() n
n
называют матрицу размерности l![]() n:
n:
А+В![]() |аij|
|аij|
+ |bij|![]() |аij+bij|.
|аij+bij|.
Умножение матрицы
А
![]() |аij|
|аij|
размерности l![]() n
n
на скаляр с
дает матрицу размерности l![]() n:
n:
сА
![]() c
c
|аij|![]() |c
|c
аij|.
Матрицы А
![]() |аij|
|аij|
размерности l![]() n
n
и В![]() |bjk|
|bjk|
размерности n![]() m
m
могут быть перемножены, причем элементами
cik
матрицы — произведения размерности
l![]() m
m
являются суммы произведений элементов
l-й
строки матрицы А
на соответствующие элементы k-го
столбца матрицы В:
cik=
![]()
В теории кодирования
элементами матрицы являются элементы
некоторого поля GF(P), а строки и столбцы
матрицы рассматриваются как векторы.
Сложение и умножение элементов матриц
осуществляется по правилам поля GF(P).
Пример 7.13.
Вычислим
произведение матриц с элементами из
поля GF (2):


Элементы cik
матрицы произведения М
= M1M2
будут равны:
c11
= (011) (101) = 0 + 0 + 1 = 1
c12
= (011) (110) = 0 + 1 + 0 = 1
c13
= (011) (100) = 0 + 0 + 0 = 0
c21
= (100) (101) = 1 + 0 + 0 = 1
c22
= (100) (110) = 1 + 0 + 0 = 1
c23
= (100) (100) = 1 + 0 + 0 = 1
c31
= (001) (101) = 0 + 0 + 1 = 1
c32
= (001) (110) = 0 + 0 + 0 = 0
c33
= (001) (100) = 0 + 0 + 0 = 0
Следовательно,

Зная закон построения
кода, определим все множество разрешенных
кодовых комбинаций. Расположив их друг
под другом, получим матрицу, совокупность
строк которой является подпространством
векторного пространства n-разрядных
кодовых комбинаций (векторов) из элементов
поля GF(P). В случае двоичного (n,
k)-кода
матрица насчитывает n
столбцов и 2k—1
строк (исключая нулевую). Например, для
рассмотренного ранее кода (8,2), исправляющего
все одиночные и двойные ошибки, матрица
имеет вид
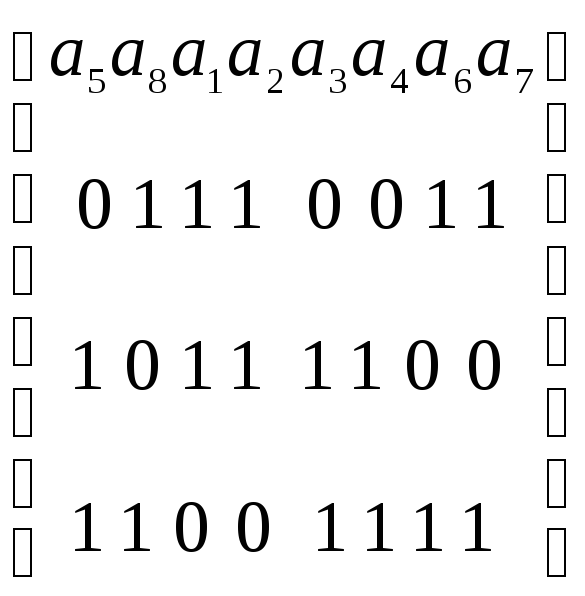
При больших n
и k матрица, включающая все векторы кода,
слишком громоздка. Однако совокупность
векторов, составляющих линейное
пространство разрешенных кодовых
комбинаций, является линейно зависимей,
так как часть векторов может быть
представлена в виде линейной комбинации
некоторой ограниченной совокупности
векторов, называемой базисом
пространства.
Совокупность
векторов V1,
V2,
V3,
…, Vn
называют линейно
зависимой,
когда существуют скаляры с1,..сn
(не все
равные нулю), при которых
c1V1
+ c2V2+…+
cnVn=
0
В приведенной
матрице, например, третья строка
представляет собой суммы по модулю два
первых двух строк. Для полного определения
пространства разрешенных кодовых
комбинаций линейного кода достаточно
записать в виде матрицы только совокупность
линейно независимых векторов. Их число
называют размерностью
векторного пространства.
Среди 2k
– 1 ненулевых
двоичных кодовых комбинаций — векторов
их только k. Например, для кода (8,2)

Матрицу, составленную
из любой совокупности векторов линейного
кода, образующей базис пространства,
называют порождающей
(образующей)
матрицей кода.
Если порождающая
матрица содержит k строк по n
элементов поля GF(q), то код называют (n,
k)-кодом.
В каждой комбинации (n,
k)-кода
k информационных символов и n
– k проверочных. Общее число разрешенных
кодовых комбинаций (исключая нулевую)
Q = qk-1.
Зная порождающую
матрицу кода, легко найти разрешенную
кодовую комбинацию, соответствующую
любой последовательности Аki
из k информационных символов.
Она получается в
результате умножения вектора Аki
на порождающую матрицу Мn,k:
Аni=Аki•Мn,k.
Найдем, например,
разрешенную комбинацию кода (8,2),
соответствующую информационным символам
a5=l,
a8
= 1:
 .
.
Пространство строк
матрицы остается неизменным при
выполнении следующих элементарных
операций над строками: 1) перестановка
любых двух строк; 2) умножение любой
строки на ненулевой элемент поля; 3)
сложение какой-либо строки с произведением
другой строки на ненулевой элемент
поля, а также при перестановке столбцов.
Если образующая
матрица кода M2
получена из образующей матрицы кода M1
с помощью элементарных операций над
строками, то обе матрицы порождают один
и тот же код. Перестановка столбцов
образующей матрицы кода приводит к
образующей матрице эквивалентного
кода. Эквивалентные коды весьма близки
по своим свойствам. Корректирующая
способность таких кодов одинакова.
Для анализа
возможностей линейного (n,
k)-кода,
а также для упрощения процесса кодирования
удобно, чтобы порождающая матрица (Мn,k)
состояла из двух матриц: единичной
матрицы размерности k
![]() k и дописываемой справаматрицы-дополнения
k и дописываемой справаматрицы-дополнения
(контрольной подматрицы) размерности
k • (n
– k), которая соответствует n
– k проверочным разрядам:
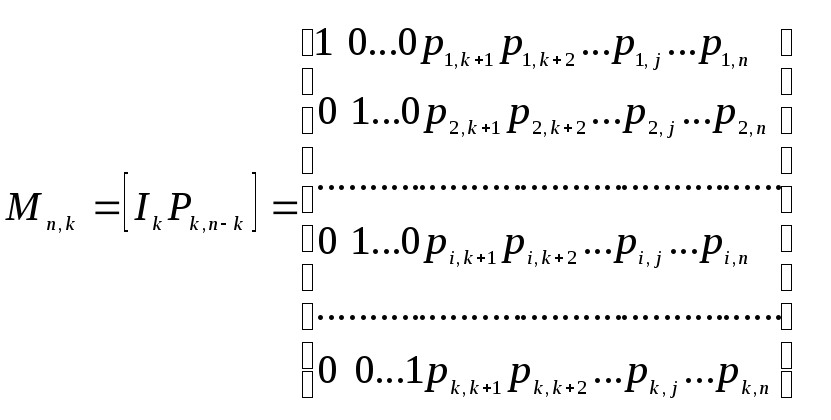 (7.3)
(7.3)
Разрешенные кодовые
комбинации кода с такой порождающей
матрицей отличаются тем, что первые k
символов в них совпадают с исходными
информационными, а проверочными
оказываются (n — k) последних символов.
Действительно, если умножим вектор-строку
Ak,i
= = (a1
a2…ai…ak)
на матрицу Мn,k=
[IkPk,n—k],
получим вектор
An,i
= (a1a2…ai…ak…ak+1…aj…an),
где проверочные
символы аj(k
+1![]() j
j![]() n)
n)
являются линейными комбинациями
информационных:
![]() (7.4)
(7.4)
Коды, удовлетворяющие
этому условию, называют систематическими.
Для каждого линейного кода существует
эквивалентный систематический код. Как
следует из (7.3), (7.4), информацию о способе
построения такого кода содержит
матрица-дополнение. Если правила
построения кода (уравнения кодирования)
известны, то значения символов любой
строки матрицы-дополнения получим,
применяя эти правила к символам
соответствующей строки единичной
матрицы.
Пример 7.14.
Запишем матрицы Ik,
Рk,n—k_и
Mn,k
для двоичного кода (7,4).
Единичная матрица
на четыре разряда имеет вид

Один из вариантов
матрицы дополнения можно записать,
используя соотношения (4.1)

Тогда для двоичного
кода Хэммннга имеем:
![]()

Запишем также
матрицу для систематического кода
(7,4):
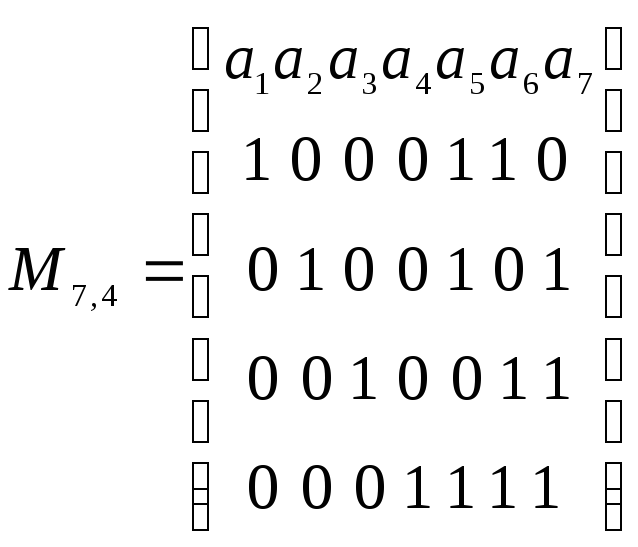
В свою очередь, по
заданной матрице-дополнению Pk,n-k
можно
определить равенства, задающие правила
построения кода. Единица в первой строке
каждого столбца указывает на то, что в
образовании соответствующего столбцу
проверочного разряда участвовал первый
информационный разряд. Единица в
следующей строке любого столбца говорит
об участии в образовании проверочного
разряда второго информационного разряда
и т, д.
Так как
матрица-дополнение содержит всю
информацию о правилах построения кода,
то систематический код с заданными
свойствами можно синтезировать путем
построения соответствующей
матрицы-дополнения.
Так как минимальное
кодовое расстояние d для линейного кода
равно минимальному весу его ненулевых
векторов, то в матрицу-дополнение должны
быть включены такие k строк, которые
удовлетворяли бы следующему общему
условию: вектор-строка образующей
матрицы, получающаяся при суммировании
любых l
(1![]() l
l![]() k)
k)
строк, должна содержать не менее d – l
отличных от нуля символов.
Действительно,
при выполнении указанного условия любая
разрешенная кодовая комбинация,
полученная суммированием l
строк образующей матрицы, имеет не менее
d ненулевых символов, так как l
ненулевых символов она всегда содержит
в результате суммирования строк единичной
матрицы. Синтезируем таким путем
образующую матрицу двоичного
систематического кода (7,4) с минимальным
кодовым расстоянием d = 3. В каждой
вектор-строке матрицы-дополнения
согласно сформулированному условию
(при l=1)
должно быть не менее двух единиц. Среди
трехразрядных векторов таких имеется
четыре: 011, 110, 101, 111.
Эти
векторы могут быть сопоставлены со
строками единичной матрицы в любом
порядке. В результате получим матрицы
систематических кодов, эквивалентных
коду Хэмминга, например:
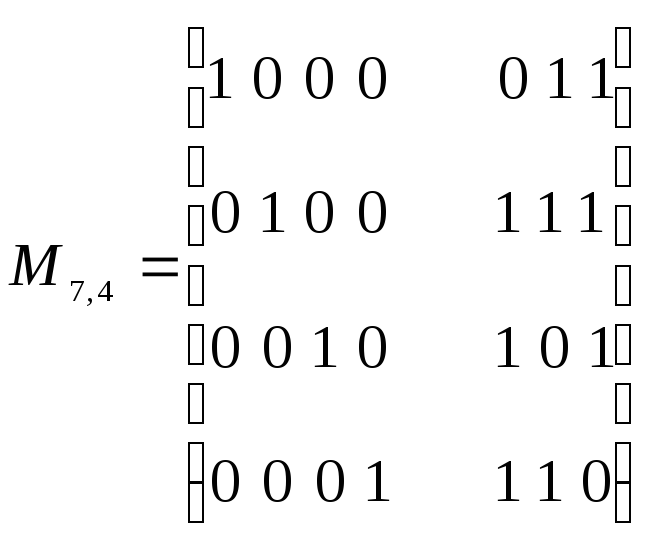
Нетрудно убедиться,
что при суммировании нескольких строк
такой матрицы (l>1)
получим вектор-строку, содержащую не
менее d=3 ненулевых символов.
Имея образующую
матрицу систематического кода
Мn,k=
[IkPk,n—k],
можно построить так называемую проверочную
(контрольную) матрицу Н
размерности (n
– k)![]() n:
n:

При умножении
неискаженного кодового вектора Аni
на матрицу, транспонированную к матрице
Н,
получим вектор, все компоненты которого
равны нулю:

Каждая компонента
Sj
является результатом проверки
справедливости соответствующего
уравнения декодирования:
![]()
В общем случае,
когда кодовый вектор Аni
=(a1,
a2,…,
ai,…,ak,ak+1,…,aj,…,an)
искажен вектором ошибки
ξni
=(ξ1,
ξ2,…,
ξi,…,ξk,aξk+1,…,ξj,…,ξn),
умножение вектора (Аni
+ ξni)
на матрицу Нт
дает ненулевые компоненты:
![]()
Отсюда видно, что
Sj(k
+1![]() j
j![]() n)
n)
представляют собой символы, зависящие
только от вектора ошибки, а вектор S
= (Sk
+ 1, Sk
+ 2, …,, Sj,
…, Sn)
является не чем иным, как опознавателем
ошибки (синдромом).
Для двоичных кодов
(операция сложения тождественна операции
вычитания) проверочная матрица имеет
вид

Пример 7.15.
Найдем
проверочную матрицу Н
для кода (7,4) с образующей матрицей М:

Определим синдромы
в случаях отсутствия и наличия ошибки
в кодовом векторе 1100011.
Выполним
транспонирование матрицы P4,3
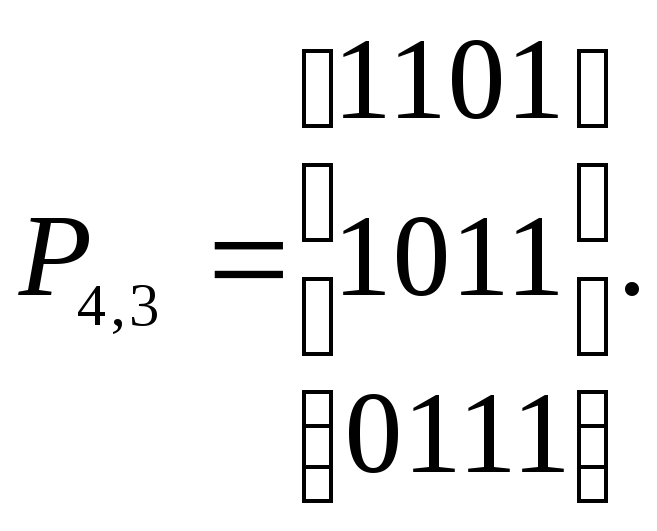
Запишем проверочную
матрицу:

Умножение на Нт
неискаженного кодового вектора 1100011
дает нулевой синдром:

При наличии в
кодовом векторе ошибки, например, в 4-м
разряде (1101011) получим:

Следовательно,
вектор-строка 111 в данном коде является
опознавателем (синдромом) ошибки в
четвертом разряде. Аналогично можно
найти и синдромы других ошибок. Множество
всех опознавателей идентично множеству
опознавателей кода Хэмминга (7,4), но
сопоставлены они конкретным векторам
ошибок по-иному, в соответствии с
образующей матрицей данного (эквивалентного)
кода.
Задание
1
Построить
линейный групповой код, способный исправлять одиночную ошибку.
Код
предусматривает возможность посылки N = 64 сообщений,
тогда:
![]() ;
; ![]()
nu=6
nk=4
n=nu+nk=10
Построим
производящую матрицу G, она представляется слиянием
матриц И и П.
В качестве И
выбирают единичную матрицу размером nu:
|
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
Определим вес
строк матрицыП:
WП > = d0 —
1
d0 = 3
Следовательно:
WП ≥ 2, исходя из этого, составим матрицу
П:
|
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
Тогда
производящая матрица будет иметь вид:
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
Задание
2
Привести
пример 10 кодовых комбинаций.
Кодирование сообщений:
1) 19 в
двоичной системе: 010011
Для
определения значения кодовых разрядов сложим по правилам двоичного поля строки
с номерами, соответствующими номерам ненулевых разрядов сообщения:
2 – 1110
5 – 0111
6 – 1100
0101
Следовательно,
линейный групповой код имеет вид: 0100110101
2) 20 в
двоичной системе: 010100
2 – 1110
4 – 1011
0101
Линейный
групповой код: 0101000101
3) 35 в
двоичной системе имеет вид: 100011
1 – 1111
5 – 0111
6 – 1100
0100
Линейный
групповой код: 1000110100
4) 38 в
двоичной системе: 100110
1 – 1111
4 – 1011
5 – 0111
0011
Линейный
групповой код: 1001100011
5) 44 в
двоичной системе: 101100
1 – 1111
3 – 1101
4 – 1011
1001
Линейный
групповой код: 1011001001
6) 47 в
двоичной системе: 101111
1 – 1111
3 – 1101
4 – 1011
5 – 0111
6 – 1100
0010
Линейный
групповой код: 1011110010
7) 49 в
двоичной системе: 110001
1 – 1111
2 – 1110
6 – 1100
1101
Линейный
групповой код: 1100011101
55 в
двоичной системе: 110111
1 – 1111
2 – 1110
4 – 1011
5 – 0111
6 – 1100
0001
Линейный
групповой код: 1101110001
9) 56 в
двоичной системе: 111000
1 – 1111
2 – 1110
3 – 1101
1100
Линейный
групповой код: 1110001100
10) 63
в двоичной системе: 111111
1 – 1111
2 – 1110
3 – 1101
4 – 1011
5 – 0111
6 – 1100
1100
Линейный
групповой код: 1111111100
Задание
3
Показать процесс исправления ошибки в заданном разряде k .
Для
исправления одинарной ошибки построим матрицу Н, которая получается путем
транспонирования матрицы П и присоединения к ней единичной матрицы размерностью
nk:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Покажем процедуру
исправления одиночной ошибки на примере сообщения 60:
Отправленное
сообщение: 1111000111
Принятое сообщение:
1111001111
т.е. имеется
ошибка в седьмом разряде.
Проведем
проверки:
1) Для
первой проверки берем P1 и те разряды из
информационной части кода, которые совпадают с ненулевыми разрядами первого
столбца матрицы П:
S1=P1+а1+а2+а3+а4+а6=1+1+1+1+1+0=1
По аналогии
проводим остальные проверки.
2) S2=P2+а1+а2+а3+а5+а6=1+1+1+1+0+0=0
3) S3=P3+а1+а2+а4+а5=1+1+1+1+0=0
4) S4=P4+а1+а3+а4+а5=1+1+1+1+0=0
В результате
получаем вектор S= 1000
Он
соответствует седьмому столбцу матрицы Н, следовательно, ошибка в седьмом
разряде полученного кода.
Индивидуальное задание по Теории информации
Подготовил В.С. Прохоров
Построить групповой корректирующий код объёмом 9 слов. Код должен обеспечивать исправление одиночных и обнаружение двойных ошибок.
Разработать функциональные, а затем построить принципиальные электрические схемы кодирующего и декодирующего устройств для технической реализации сформированного кода.
Определим число информационных разрядов кода из соотношения
,
где Q – требуемый объём кода. В нашем случае Q=9, поэтому
Отсюда получаем .
Далее находим число n из неравенства
Подставляем и подбором находим минимальное n, удовлетворяющее неравенству. В нашем случае
.
Далее мы должны составить таблицу опознавателей. Для этого необходимо ввести понятие вектора ошибок и опознавателя. Вектор ошибок это n-разрядная двоичная последовательность, имеющая единицы во всех разрядах, подвергшихся искажению, и нули в остальных разрядах. (Пример: искажению подверглись два младших разряда 6-разрядного сообщения — тогда вектор ошибки будет выглядеть как 000011), а опознаватель – некоторая сопоставленная этому вектору контрольная последовательность символов. В нашем случае векторы ошибок имеют разрядность 7 бит, так как , опознаватели имеют разрядность 3 бит, так как . Опознаватели рекомендуется записывать в порядке возрастания (нулевую комбинацию не используем).
|
Векторы ошибок |
Опознаватели |
|
|
1 |
0000001 |
001 |
|
2 |
0000010 |
010 |
|
3 |
0000100 |
011 |
|
4 |
0001000 |
100 |
|
5 |
0010000 |
101 |
|
6 |
0100000 |
110 |
|
7 |
1000000 |
111 |
Теперь необходимо определить проверочные равенства и сформулировать правила построения кода, способного исправлять все одиночные ошибки.
Выбираем из таблицы строки, где опознаватели имеют в первом (младшем) разряде единицу. Это строки 1, 3, 5 и 7. Тогда первое проверочное равенство будет выглядеть так:
Теперь выбираем строки, где опознаватели имеют во втором разряде единицу.
Это строки 2, 3, 6, 7.
Тогда второе проверочное правило выглядит так:
И, наконец выбираем строки, где опознаватели имеют единицу в третьем разряде. Это строки 4, 5, 6, 7. Следовательно третье проверочное равенство выглядит так:
Далее нужно отобрать строки, где опознаватели имеют всего одну единицу. В нашем случае это строки 1, 2 и 4. Возвращаемся к полученным ранее уравнениям. В левой части оставляем члены с выбранными нами только что индексами, а остальные переносим в правую часть:
Эти три уравнения и называются правилами построения кода. Код, построенный по этим правилам, может исправить все одиночные ошибки. Но нам необходимо, чтобы код также мог обнаруживать двойные ошибки. Для этого добавим к трём уравнениям, полученным ранее, ещё одно:
Мы получили окончательные правила построения кода, способного исправлять все одиночные и обнаруживать двойные ошибки:
Используя правила построения корректирующего кода (*), построим таблицу разрешённых комбинаций группового кода объёмом 9 слов, способного исправлять все одиночные и обнаруживать двойные ошибки. В колонку «безызбыточный код» записываем девять (по заданию Q=9) комбинаций по возрастанию (нулевую комбинацию не используем).
Все колонки, кроме , , и , содержимое которых определяется формулами (*), заполняем цифрами из безызбыточного кода:
|
слово |
безызбыточный код |
код |
|||||||
|
0001 |
0 |
0 |
0 |
1 |
|||||
|
0010 |
0 |
0 |
1 |
0 |
|||||
|
0011 |
0 |
0 |
1 |
1 |
|||||
|
0100 |
0 |
1 |
0 |
0 |
|||||
|
0101 |
0 |
1 |
0 |
1 |
|||||
|
0110 |
0 |
1 |
1 |
0 |
|||||
|
0111 |
0 |
1 |
1 |
1 |
|||||
|
1000 |
1 |
0 |
0 |
0 |
|||||
|
1001 |
1 |
0 |
0 |
1 |
Чтобы заполнить колонки , , и , подставляем значения необходимых переменных в соответствующие уравнения из (*). Например, для строки 9 (слово ) получаем следующее:
|
слово |
безызбыточный код |
избыточный код |
|||||||
|
0001 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
0010 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
|
0011 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
|
0100 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
|
0101 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
|
0110 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
0111 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
1000 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
1001 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
Перейдём к построению функциональной схемы кодирующего устройства (см. соответствующий рисунок ниже). Назначение кодирующего устройства – внесение избыточности в код по заданным нами правилам. Схему строим на основании равенств (*). На схеме используется логический элемент «сумматор по модулю два», обозначенный М2. На схеме имеются два регистра, построенные на D-триггерах. Один из них содержит безызбыточный код и имеет разрядность 4 бит, так как , а другой содержит избыточный код и имеет разрядность 8 бит, так как . Принцип работы схемы таков: по сигналу синхронизации на k-разрядный регистр поступает кодовая комбинация, подлежащая кодированию. Затем с помощью сумматоров эта комбинация кодируется (вносится избыточность). Сумматор С1 реализует первое равенство из (*), сумматор С2 – второе, С3 – третье, а С4 – четвёртое. И, наконец, по сигналу синхронизации полученный избыточный код записывается в 8-разрядный регистр. Далее начинается кодирование следующей комбинации.
Нарисуем общую
схему декодирующего устройства с двумя
схемами деления.

Рис. 6.10. Схема
декодирующего устройства с двумя схемами
деления
Пусть имеет место
ошибка в старшем разряде К.К., принятой
из линии связи. Пока она доберется до
выхода из приемного регистра, все n
тактов она делится в схеме деления 1. На
n-ном
такте остаток переписывается в схему
деления 2. На (n
+ 1) такте ошибка выходит из регистра и
поступает на сумматор. Одновременно из
схемы деления 2 кодовая комбинация,
соответствующая ошибке в старшем
разряде, поступает на схему опознавателя
остатка ошибки в старшем разряде.
Последняя вырабатывает сигнал на
исправление ошибки и обнуление схемы
деления 2, если других ошибок нет. Если
же ошибка имеет место не в старшем
разряде, то остаток, переписанный из
схемы деления 1 в схему деления 2,
продолжает делиться до тех пор, пока
ошибка не доберется до выхода из регистра,
то есть в обеих схемах деления 1 и 2 ошибка
будет всегда делиться n
раз.
Разберем конкретный
пример.
Имеем: ai(x)
= x3
Е 1 = 1001; g(x)
= x3
Е x2
Е 1 = 1101.
Циклический код
(7; 4), исправляющий одиночные ошибки.

ƒi(x)
— послали в линию связи. Из линии связи
получили ƒi*(x):
1101011. Необходимо построить схему Д.У.,
исправляющего одиночные ошибки.
Решение.
1. Выберем схему
деления. Пусть это будет схема деления
с первого такта.

Рис. 6.11
2. Определим
остаток, который получается в схеме
деления на n-ном
такте ( в нашем случае n
= 7), если имеет место ошибка в старшем
разряде, то есть
![]() .
.
Для этого поделим![]() наg(x):
наg(x):

Остаток на седьмом
такте деления r7(x)
= 100.
3. Спроектируем
схему распознавания остатка. Минимальные
затраты оборудования (считаются по
числу входов-выходов) будут иметь место
при инверсии «1» в «0» и установки схемы
«исключающего или», когда при входе
трех нулей на выходе берется инверсный
выход, дающий «1», т.е.
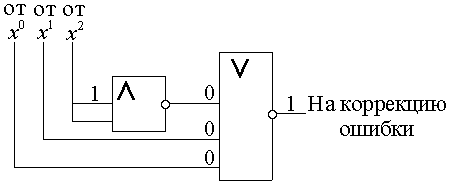
Рис. 6.12
Для построения
логических схем можно использовать
схемы «И» с прямым и инверсным выходами
и схемы «ИЛИ» с прямым и инверсным
выходами.
4. Нарисуем схему
декодирующего устройства с заведением
обратной связи от сигнала коррекции
ошибки на обнуление схемы деления 2.

Рис. 6.13
5. Приведем таблицу
потактовой работы декодирующего
устройства.
Таблица 6.6
|
№/№ |
Вход |
Ячейки |
Выход |
Примечание |
Примечание |
||
|
x0 |
x1 |
x2 |
|||||
|
1 |
1 |
1 |
0 |
1 |
– |
Идет |
|
|
2 |
1 |
0 |
1 |
0 |
– |
||
|
3 |
0 |
0 |
0 |
1 |
– |
||
|
4 |
1 |
0 |
0 |
0 |
– |
||
|
5 |
0 |
0 |
0 |
0 |
– |
||
|
6 |
1 |
1 |
0 |
1 |
– |
||
|
7 |
1 |
0 |
1 |
0 |
– |
Переписывается |
|
|
8 |
1 |
0 |
0 |
1 |
1 |
Соответствует |
Входной |
|
9 |
– |
0 |
0 |
0 |
1 |
Идет |
|
|
10 |
– |
0 |
0 |
0 |
0 |
Исправление |
|
|
11 |
– |
0 |
0 |
0 |
1 |
||
|
12 |
– |
0 |
0 |
0 |
0 |
||
|
13 |
– |
0 |
0 |
0 |
1 |
||
|
14 |
– |
0 |
0 |
0 |
1 |
На 9-том такте на
первый сумматор в схеме деления 2 приходят
две единицы: одна от обратной связи с
x2
и вторая со схемы коррекции. Они дают
«0» и все содержание схемы деления 2
превращается в «0». Однако, это не всегда
так получается. Особенно, когда n
≠ 2m
– 1 и обращение схемы деления 2 в «0»
следует проектировать особо.
Задание
1
Построить
линейный групповой код, способный исправлять одиночную ошибку.
Код
предусматривает возможность посылки N = 64 сообщений,
тогда:
![]() ;
; ![]()
nu=6
nk=4
n=nu+nk=10
Построим
производящую матрицу G, она представляется слиянием
матриц И и П.
В качестве И
выбирают единичную матрицу размером nu:
|
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
Определим вес
строк матрицыП:
WП > = d0 —
1
d0 = 3
Следовательно:
WП ≥ 2, исходя из этого, составим матрицу
П:
|
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
Тогда
производящая матрица будет иметь вид:
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
Задание
2
Привести
пример 10 кодовых комбинаций.
Кодирование сообщений:
1) 19 в
двоичной системе: 010011
Для
определения значения кодовых разрядов сложим по правилам двоичного поля строки
с номерами, соответствующими номерам ненулевых разрядов сообщения:
2 – 1110
5 – 0111
6 – 1100
0101
Следовательно,
линейный групповой код имеет вид: 0100110101
2) 20 в
двоичной системе: 010100
2 – 1110
4 – 1011
0101
Линейный
групповой код: 0101000101
3) 35 в
двоичной системе имеет вид: 100011
1 – 1111
5 – 0111
6 – 1100
0100
Линейный
групповой код: 1000110100
4) 38 в
двоичной системе: 100110
1 – 1111
4 – 1011
5 – 0111
0011
Линейный
групповой код: 1001100011
5) 44 в
двоичной системе: 101100
1 – 1111
3 – 1101
4 – 1011
1001
Линейный
групповой код: 1011001001
6) 47 в
двоичной системе: 101111
1 – 1111
3 – 1101
4 – 1011
5 – 0111
6 – 1100
0010
Линейный
групповой код: 1011110010
7) 49 в
двоичной системе: 110001
1 – 1111
2 – 1110
6 – 1100
1101
Линейный
групповой код: 1100011101
 55 в
55 в
двоичной системе: 110111
1 – 1111
2 – 1110
4 – 1011
5 – 0111
6 – 1100
0001
Линейный
групповой код: 1101110001
9) 56 в
двоичной системе: 111000
1 – 1111
2 – 1110
3 – 1101
1100
Линейный
групповой код: 1110001100
10) 63
в двоичной системе: 111111
1 – 1111
2 – 1110
3 – 1101
4 – 1011
5 – 0111
6 – 1100
1100
Линейный
групповой код: 1111111100
Задание
3
Показать процесс исправления ошибки в заданном разряде k .
Для
исправления одинарной ошибки построим матрицу Н, которая получается путем
транспонирования матрицы П и присоединения к ней единичной матрицы размерностью
nk:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Покажем процедуру
исправления одиночной ошибки на примере сообщения 60:
Отправленное
сообщение: 1111000111
Принятое сообщение:
1111001111
т.е. имеется
ошибка в седьмом разряде.
Проведем
проверки:
1) Для
первой проверки берем P1 и те разряды из
информационной части кода, которые совпадают с ненулевыми разрядами первого
столбца матрицы П:
S1=P1+а1+а2+а3+а4+а6=1+1+1+1+1+0=1
По аналогии
проводим остальные проверки.
2) S2=P2+а1+а2+а3+а5+а6=1+1+1+1+0+0=0
3) S3=P3+а1+а2+а4+а5=1+1+1+1+0=0
4) S4=P4+а1+а3+а4+а5=1+1+1+1+0=0
В результате
получаем вектор S= 1000
Он
соответствует седьмому столбцу матрицы Н, следовательно, ошибка в седьмом
разряде полученного кода.
