Определите вектор однократной ошибки для принятой кодовой комбинации 0100111 кода хэмминга 7 4 - Ремонт и установка крупной бытовой техники

Проблемы информационной безопасности требуют изучения и решения ряда теоретических и практических задач при информационном взаимодействии абонентов систем. В нашей доктрине информационной безопасности формулируется триединая задача обеспечения целостности, конфиденциальности и доступности информации. Представляемые здесь статьи посвящаются рассмотрению конкретных вопросов ее решения в рамках разных государственных систем и подсистем. Ранее автором были рассмотрены в 5 статьях вопросы обеспечения конфиденциальности сообщений средствами государственных стандартов. Общая концепция системы кодирования также приводилась мной ранее.

Введение

По основному своему образованию я не математик, но в связи с читаемыми мной дисциплинами в ВУЗе пришлось в ней дотошно разбираться. Долго и упорно читал классические учебники ведущих наших Университетов, пятитомную математическую энциклопедию, множество тонких популярных брошюр по отдельным вопросам, но удовлетворения не возникало. Не возникало и глубокое понимание прочитанного.

Вся математическая классика ориентирована, как правило, на бесконечный теоретический случай, а специальные дисциплины опираются на случай конечных конструкций и математических структур. Отличие подходов колоссальное, отсутствие или недостаток хороших полных примеров — пожалуй главный минус и недостаток вузовских учебников. Очень редко существует задачник с решениями для начинающих (для первокурсников), а те, что имеются, грешат пропусками в объяснениях. В общем я полюбил букинистические магазины технической книги, благодаря чему пополнилась библиотека и в определенной мере багаж знаний. Читать довелось много, очень много, но «не заходило».

Этот путь привел меня к вопросу, а что я уже могу самостоятельно делать без книжных «костылей», имея перед собой только чистый лист бумаги и карандаш с ластиком? Оказалось совсем немного и не совсем то, что было нужно. Пройден был сложный путь бессистемного самообразования. Вопрос был такой. Могу ли я построить и объяснить, прежде всего себе, работу кода, обнаруживающего и исправляющего ошибки, например, код Хемминга, (7, 4)-код?

Известно, что код Хемминга широко используется во многих прикладных программах в области хранения и обмена данными, особенно в RAID; кроме того, в памяти типа ECC и позволяет «на лету» исправлять однократные и обнаруживать двукратные ошибки.

Информационная безопасность. Коды, шифры, стегосообщения

Информационное взаимодействие путем обмена сообщениями его участников должно обеспечиваться защитой на разных уровнях и разнообразными средствами как аппаратными так и программными. Эти средства разрабатываются, проектируются и создаются в рамках определенных теорий (см. рис.А) и технологий, принятых международными договоренностями об OSI/ISO моделях.

Защита информации в информационных телекоммуникационных системах (ИТКС) становится практически основной проблемой при решении задач управления, как в масштабе отдельной личности – пользователя, так и для фирм, объединений, ведомств и государства в целом. Из всех аспектов защиты ИТКС в этой статье будем рассматривать защиту информации при ее добывании, обработке, хранении и передаче в системах связи.

Уточняя далее предметную область, остановимся на двух возможных направлениях, в которых рассматриваются два различных подхода к защите, представлению и использованию информации: синтаксическом и семантическом. На рисунке используются сокращения: кодек–кодер-декодер; шидеш – шифратор-дешифратор; скриз – скрыватель – извлекатель.

Рисунок А – Схема основных направлений и взаимосвязи теорий, направленных на решение задач защиты информационного взаимодействия

Синтаксические особенности представления сообщений позволяют контролировать и обеспечивать правильность и точность (безошибочность, целостность) представления при хранении, обработке и особенно при передаче информации по каналам связи. Здесь главные задачи защиты решаются методами кодологии, ее большой части — теории корректирующих кодов.

Семантическая (смысловая) безопасность сообщений обеспечивается методами криптологии, которая средствами криптографии позволяет защитить от овладения содержанием информации потенциальным нарушителем. Нарушитель при этом может скопировать, похитить, изменить или подменить, или даже уничтожить сообщение и его носитель, но он не сможет получить сведений о содержании и смысле передаваемого сообщения. Содержание информации в сообщении останется для нарушителя недоступным. Таким образом, предметом дальнейшего рассмотрения будет синтаксическая и семантическая защита информации в ИТКС. В этой статье ограничимся рассмотрением только синтаксического подхода в простой, но весьма важной его реализации корректирующим кодом.

Сразу проведу разграничительную линию в решении задач информационной безопасности:
теория кодологии призвана защищать информацию (сообщения) от ошибок (защита и анализ синтаксиса сообщений) канала и среды, обнаруживать и исправлять ошибки;
теория криптологии призвана защищать информацию от несанкционированного доступа к ее семантике нарушителя (защита семантики, смысла сообщений);
теория стеганологии призвана защищать факт информационного обмена сообщениями, а также обеспечивать защиту авторского права, персональных данных (защита врачебной тайны).

В общем «поехали». По определению, а их довольно много, понять что есть код очень даже не просто. Авторы пишут, что код — это алгоритм, отображение и ещё что-то. О классификации кодов я не буду здесь писать, скажу только, что (7, 4)-код блоковый.

В какой-то момент до меня дошло, что код — это кодовые специальные слова, конечное их множество, которыми заменяют специальными алгоритмами исходный текст сообщения на передающей стороне канала связи и которые отправляются по каналу получателю. Замену осуществляет устройство-кодер, а на приемной стороне эти слова распознает устройство-декодер.

Поскольку роль сторон переменчива оба этих устройства объединяют в одно и называют сокращенно кодек (кодер/декодер), и устанавливают на обоих концах канала. Дальше, раз есть слова, есть и алфавит. Алфавит — это два символа {0, 1}, в технике массово используются блоковые двоичные коды. Алфавит естественного языка (ЕЯ) — множество символов — букв, заменяющих при письме звуки устной речи. Здесь не будем углубляться в иероглифическую письменность в слоговое или узелковое письмо.

Алфавит и слова — это уже язык, известно, что естественные человеческие языки избыточны, но что это означает, где обитает избыточность языка трудно сказать, избыточность не очень хорошо организована, хаотична. При кодировании, хранении информации избыточность стремятся уменьшить, пример, архиваторы, код Морзе и др.

Ричард Хемминг, наверное, раньше других понял, что если избыточность не устранять, а разумно организовать, то ее можно использовать в системах связи для обнаружения ошибок и автоматического их исправления в кодовых словах передаваемого текста. Он понял, что все 128 семиразрядных двоичных слов могут использоваться для обнаружения ошибок в кодовых словах, которые образуют код — подмножество из 16 семиразрядных двоичных слов. Это была гениальная догадка.

До изобретения Хемминга ошибки приемной стороной тоже обнаруживались, когда декодированный текст не читался или получалось не совсем то, что нужно. При этом посылался запрос отправителю сообщения повторить блоки определенных слов, что, конечно, было весьма неудобно и тормозило сеансы связи. Это было большой не решаемой десятилетиями проблемой.

Построение (7, 4)-кода Хемминга

Вернемся к Хеммингу. Слова (7, 4)-кода образованы из 7 разрядов С j = $(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$ , j = 0(1)15, 4-информационные и 3-проверочные символа, т.е. по существу избыточные, так как они не несут информации сообщения. Эти три проверочных разряда удалось представить линейными функциями 4-х информационных символов в каждом слове, что и обеспечило обнаружение факта ошибки и ее места в словах, чтобы внести исправление. А (7, 4)-код получил новое прилагательное и стал линейным блоковым двоичным.

Линейные функциональные зависимости (правила (*)) вычислений значений символов
$p_i$ имеют следующий вид:

$ p_1 + i_2 +i_3 + i_4 = 0, → p_1 = i_2 + i_3 + i_4,$
$ p_2 + i_1 + i_3 + i_4 = 0, → p_2 = i_1+ i_3 + i_4, (*)$
$ p_3 + i_1 + i_2 + i_4 = 0, → p_3 = i_1+i_2 + i_4. $

Исправление ошибки стало очень простой операцией — в ошибочном разряде определялся символ (ноль или единица) и заменялся другим противоположным 0 на 1 или 1 на 0.
Сколько же различных слов образуют код? Ответ на этот вопрос для (7, 4)-кода получается очень просто. Раз имеется лишь 4 информационных разряда, а их разнообразие при заполнении символами имеет $2^4$ = 16 вариантов, то других возможностей просто нет, т. е. код состоящий всего из 16 слов, обеспечивает представление этими 16-ю словами всю письменность всего языка.

Информационные части этих 16 слов получают нумерованный вид №
( $i_1,i_2,i_3,i_4$ ):

0=0000; 4= 0100; 8=1000; 12=1100;
1=0001; 5= 0101; 9=1001; 13=1101;
2=0010; 6= 0110; 10=1010; 14=1110;
3=0011; 7= 0111; 11=1011; 15=1111.

Каждому из этих 4-разрядных слов необходимо вычислить и добавить справа по 3 проверочных разряда, которые вычисляются по правилам (*). Например, для информационного слова №6 равного 0110 имеем $i_1=0, i_2=1, i_3=1,i_4=0$ и вычисления проверочных символов дают для этого слова такой результат:

$(р_1 = 0, р_2 = 1, р_3 = 1)$
$р_1=i_2 +i_3 +i_4 =1 + 1 + 0(mod2)=2(mod2)=0,$
$р_2=i_1 +i_3 +i_4 =0 + 1 + 0(mod2)=1(mod2)=1,$
$р_3=i_1 +i_2 +i_4 =0 + 1 + 0(mod2)=1(mod2)=1.$

Шестое кодовое слово при этом приобретает вид: $С_6=(i_1,i_2,i_3,i_4,p_1,p_2,p_3)=(0110011).$ Таким же образом необходимо вычислить проверочные символы для всех 16-и кодовых слов. Подготовим для слов кода 16-строчную таблицу К и последовательно будем заполнять ее клетки (читателю рекомендую проделать это с карандашом в руках).

Таблица К – кодовые слова Сj, j = 0(1)15, (7, 4) – кода Хемминга

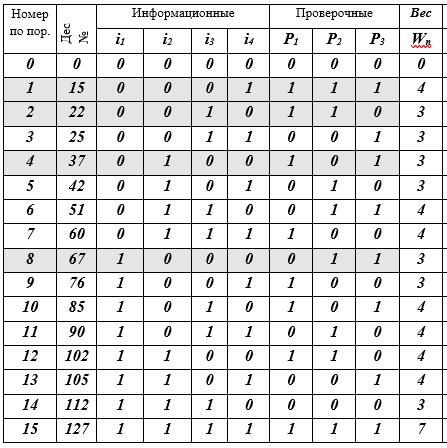
Описание таблицы: 16 строк — кодовые слова; 10 колонок: порядковый номер, десятичное представление кодового слова, 4 информационных символа, 3 проверочных символа, W-вес кодового слова равен числу ненулевых разрядов (≠ 0). Заливкой выделены 4 кодовых слова-строки — это базис векторного подпространства. Собственно, на этом все — код построен.

Таким образом, в таблице получены все слова (7, 4) — кода Хемминга. Как видите это было не очень сложно. Далее речь пойдет о том, какие идеи привели Хемминга к такому построению кода. Мы все знакомы с кодом Морзе, с флотским семафорным алфавитом и др. системами построенными на разных эвристических принципах, но здесь в (7, 4)-коде используются впервые строгие математические принципы и методы. Рассказ будет как раз о них.

Математические основы кода. Высшая алгебра

Подошло время рассказать какая Р.Хеммингу пришла идея открытия такого кода. Он не питал особых иллюзий о своем таланте и скромно формулировал перед собой задачу: создать код, который бы обнаруживал и исправлял в каждом слове одну ошибку (на деле обнаруживать удалось даже две ошибки, но исправлялась лишь одна из них). При качественных каналах даже одна ошибка — редкое событие. Поэтому замысел Хемминга все-таки в масштабах системы связи был грандиозным. В теории кодирования после его публикации произошла революция.

Это был 1950 год. Я привожу здесь свое простое (надеюсь доступное для понимания) описание, которого не встречал у других авторов, но как оказалось, все не так просто. Потребовались знания из многочисленных областей математики и время, чтобы все глубоко осознать и самому понять, почему это так сделано. Только после этого я смог оценить ту красивую и достаточно простую идею, которая реализована в этом корректирующем коде. Время я в основном, потратил на разбирательство с техникой вычислений и теоретическим обоснованием всех действий, о которых здесь пишу.

Создатели кодов, долго не могли додуматься до кода, обнаруживающего и исправляющего две ошибки. Идеи, использованные Хеммингом, там не срабатывали. Пришлось искать, и нашлись новые идеи. Очень интересно! Захватывает. Для поиска новых идей потребовалось около 10 лет и только после этого произошел прорыв. Коды, обнаруживающие произвольное число ошибок, были получены сравнительно быстро.

Векторные пространства, поля и группы. Полученный (7, 4)-код (Таблица К) представляет множество кодовых слов, являющихся элементами векторного подпространства (порядка 16, с размерностью 4), т.е. частью векторного пространства размерности 7 с порядком $2^7=128.$ Из 128 слов в код включены лишь 16, но они попали в состав кода не просто так.

Во-первых, они являются подпространством со всеми вытекающими отсюда свойствами и особенностями, во-вторых, кодовые слова являются подгруппой большой группы порядка 128, даже более того, аддитивной подгруппой конечного расширенного поля Галуа GF( $2^7$ ) степени расширения n = 7 и характеристики 2. Эта большая подгруппа раскладывается в смежные классы по меньшей подгруппе, что хорошо иллюстрируется следующей таблицей Г. Таблица разделена на две части: верхняя и нижняя, но читать следует как одну длинную. Каждый смежный класс (строка таблицы) — элемент факторгруппы по эквивалентности составляющих.

Таблица Г – Разложение аддитивной группы поля Галуа GF () в смежные классы (строки таблицы Г) по подгруппе 16 порядка.

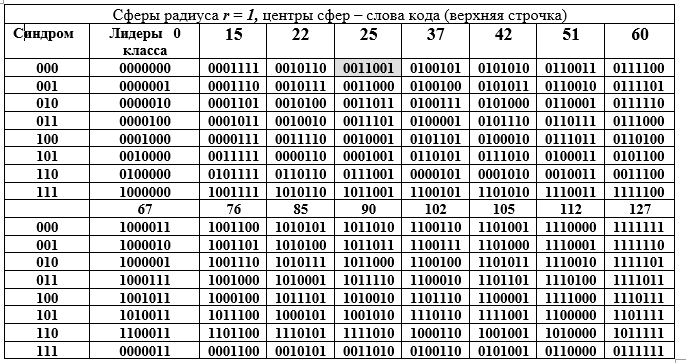
Столбцы таблицы – это сферы радиуса 1. Левый столбец (повторяется) – синдром слова (7, 4)-кода Хемминга, следующий столбец — лидеры смежного класса. Раскроем двоичное представление одного из элементов (25-го выделен заливкой) факторгруппы и его десятичное представление:

$0·x^6+0·x^5+1·x^4+1·x^3+0x^2+0x+1=1·2^4+1·2^3+1·2^0=16+8+1=25$

Техника получение строк таблицы Г. Элемент из столбца лидеров класса суммируется с каждым элементом из заголовка столбца таблицы Г (суммирование выполняется для строки лидера в двоичном виде по mod2). Поскольку все лидеры классов имеют вес W=1, то все суммы отличаются от слова в заголовке столбца только в одной позиции (одной и той же для всей строки, но разных для столбца). Таблица Г имеет замечательную геометрическую интерпретацию. Все 16 кодовых слов представляются центрами сфер в 7-мерном векторном пространстве. Все слова в столбце от верхнего слова отличаются в одной позиции, т. е. лежат на поверхности сферы с радиусом r =1.

В этой интерпретации скрывается идея обнаружения одной ошибки в любом кодовом слове. Работа идет со сферами. Первое условие обнаружения ошибки — сферы радиуса 1 не должны касаться или пересекаться. Это означает, что центры сфер удалены друг от друга на расстояние 3 или более. При этом сферы не только не пересекаются, но и не касаются одна другой. Это требование для однозначности решения: какой сфере отнести полученное на приемной стороне декодером ошибочное (не кодовое одно из 128 -16 = 112) слово.

Второе — все множество 7-разрядных двоичных слов из 128 слов равномерно распределено по 16 сферам. Декодер может получить слово лишь из этого множества 128-ми известных слов с ошибкой или без нее. Третье — приемная сторона может получить слово без ошибки или с искажением, но всегда принадлежащее одной из 16-и сфер, которая легко определяется декодером. В последней ситуации принимается решение о том, что послано было кодовое слово — центр определенной декодером сферы, который нашел позицию (пересечение строки и столбца) слова в таблице Г, т. е номера столбца и строки.

Здесь возникает требование к словам кода и к коду в целом: расстояние между любыми двумя кодовыми словами должно быть не менее трех, т. е. разность для пары кодовых слов, например, Сi = 85= $(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$ =1010101; Сj = 25== 0011001 должна быть не менее 3; 85 — 25 = 1010101 — 0011001 =1001100 = 76, вес слова-разности W(76) = 3. (табл. Д заменяет вычисления разностей и сумм). Здесь под расстоянием между двоичными словами-векторами понимается количество не совпадающих позиций в двух словах. Это расстояние Хемминга, которое стало повсеместно использоваться в теории, и на практике, так как удовлетворяет всем аксиомам расстояния.

Замечание. (7, 4)-код не только линейный блоковый двоичный, но он еще и групповой, т. е. слова кода образуют алгебраическую группу по сложению. Это означает, что любые два кодовых слова при суммировании снова дают одно из кодовых слов. Только это не обычная операция суммирования, выполняется сложение по модулю два.

Таблица Д — Сумма элементов группы (кодовых слов), используемой для построения кода Хемминга

Сама операция суммирования слов ассоциативна, и для каждого элемента в множестве кодовых слов имеется противоположный ему, т. е. суммирование исходного слова с противоположным дает нулевое значение. Это нулевое кодовое слово является нейтральным элементом в группе. В таблице Д- это главная диагональ из нулей. Остальные клетки (пересечения строка/столбец) — это номера-десятичные представления кодовых слов, полученные суммированием элементов из строки и столбца.При перестановке слов местами (при суммировании) результат остается прежним, более того, вычитание и сложение слов имеют одинаковый результат. Дальше рассматривается система кодирования/декодирования, реализующая синдромный принцип.

Применение кода. Кодер

Кодер размещается на передающей стороне канала и им пользуется отправитель сообщения. Отправитель сообщения (автор) формирует сообщение в алфавите естественного языка и представляет его в цифровом виде. (Имя символа в ASCII-соде и в двоичном виде).
Тексты удобно формировать в файлах для ПК с использованием стандартной клавиатуры (ASCII — кодов). Каждому символу (букве алфавита) соответствует в этой кодировке октет бит (восемь разрядов). Для (7, 4)- кода Хемминга, в словах которого только 4 информационных символа, при кодировании символа клавиатуры на букву требуется два кодовых слова, т.е. октет буквы разбивается на два информационных слова естественного языка (ЕЯ) вида
$i<4> = <i_1, i_2, i_3, i_4>$ .

Пример 1. Необходимо передать слово «цифра» в ЕЯ. Входим в таблицу ASCII-кодов, буквам соответствуют: ц –11110110, и –11101000, ф – 11110100, р – 11110000, а – 11100000 октеты. Или иначе в ASCII — кодах слово «цифра» = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000

с разбивкой на тетрады (по 4 разряда). Таким образом, кодирование слова «цифра» ЕЯ требует 10 кодовых слов (7, 4)-кода Хемминга. Тетрады представляют информационные разряды слов сообщения. Эти информационные слова (тетрады) преобразуются в слова кода (по 7 разрядов) перед отправкой в канал сети связи. Выполняется это путем векторно-матричного умножения: информационного слова на порождающую матрицу. Плата за удобства получается весьма дорого и длинно, но все работает автоматически и главное — сообщение защищается от ошибок.
Порождающая матрица (7, 4)-кода Хемминга или генератор слов кода получается выписыванием базисных векторов кода и объединением их в матрицу. Это следует из теоремы линейной алгебры: любой вектор пространства (подпространства) является линейной комбинацией базисных векторов, т.е. линейно независимых в этом пространстве. Это как раз и требуется — порождать любые векторы (7-разрядные кодовые слова) из информационных 4-разрядных.

Порождающая матрица (7, 4, 3)-кода Хемминга или генератор слов кода имеет вид:

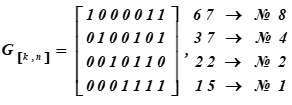
Справа указаны десятичные представления кодовых слов Базиса подпространства и их порядковые номера в таблице К
№ i строки матрицы — это слова кода, являющиеся базисом векторного подпространства.

Пример кодирования слов информационных сообщений (порождающая матрица кода выстраивается из базисных векторов и соответствует части таблицы К). В таблице ASCII-кода берем букву ц = <1111 0110>.

Информационные слова сообщения имеют вид:

$i_{k1} = <1111>, i_{k2} = <0110>$ .

Это половины символа (ц). Для (7, 4)-кода, определенного ранее, требуется найти кодовые слова, соответствующее информационному слову-сообщению (ц) из 8-и символов в виде:

$i_{k1} = <1111>, i_{k2} = <0110>$ .

Чтобы превратить эту букву–сообщение (ц) в кодовые слова u, каждую половинку буквы-сообщения i умножают на порождающую матрицу G[k, n] кода (матрица для таблицы К):

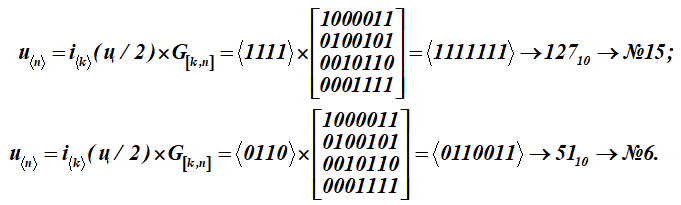
Получили два кодовых слова с порядковыми номерами 15 и 6.

Покажем детальное формирование нижнего результата №6 – кодового слова (умножение строки информационного слова на столбцы порождающей матрицы); суммирование по (mod2)

<0110> ∙ <1000> = 0∙1 +1∙0 + 1∙0 + 0∙0 = 0(mod2);
<0110> ∙ <0100> = 0∙0 +1∙1 + 1∙0 + 0∙0 = 1(mod2);
<0110> ∙ <0010> = 0∙0 +1∙0 + 1∙1 + 0∙0 = 1(mod2);
<0110> ∙ <0001> = 0∙0 +1∙0 + 1∙0 + 0∙1 = 0(mod2);
<0110> ∙ <0111> = 0∙0 +1∙1 + 1∙1 + 0∙1 = 0(mod2);
<0110> ∙ <1011> = 0∙1 +1∙0 + 1∙1 + 0∙1 = 1(mod2);
<0110> ∙ <1101> = 0∙1 +1∙1 + 1∙0 + 0∙1 = 1(mod2).

Получили в результате перемножения пятнадцатое и шестое слова из таблицы К. Первые четыре разряда в этих кодовых словах (результатах умножения) представляют информационные слова. Они имеют вид: $i_{k1} = <1111>, i_{k2}= <0110>$ , (в таблице ASCII это только половины буквы ц). Для кодирующей матрицы выбраны в качестве базисных векторов в таблице К совокупности слов с номерами: 1, 2, 4, 8. В таблице они выделены заливкой. Тогда для этой таблицы К кодирующая матрица получит вид G[k,n].

В результате перемножения получили 15 и 6 слова таблицы К кода.

Применение кода. Декодер

Декодер размещается на приемной стороне канала там, где находится получатель сообщения. Назначение декодера состоит в предоставлении получателю переданного сообщения в том виде, в котором оно существовало у отправителя в момент отправления, т.е. получатель может воспользоваться текстом и использовать сведения из него для своей дальнейшей работы.

Основной задачей декодера является проверка того, является ли полученное слово (7 разрядов) тем, которое было отправлено на передающей стороне, не содержит ли слово ошибок. Для решения этой задачи для каждого полученного слова декодером путем умножения его на проверочную матрицу Н[n-k, n] вычисляется короткий вектор-синдром S (3 разряда).

Для слов, которые являются кодовыми, т. е. не содержат ошибок, синдром всегда принимает нулевое значение S =<000>. Для слова с ошибкой синдром не нулевой S ≠ 0. Значение синдрома позволяет обнаружить и локализовать положение ошибки с точностью до разряда в принятом на приемной стороне слове, и декодер может изменить значение этого разряда. В проверочной матрице кода декодер находит столбец, совпадающий со значением синдрома, и порядковый номер этого столбца принимает равным искаженному ошибкой разряду. После этого для двоичных кодов декодером выполняется изменение этого разряда – просто замена на противоположное значение, т. е. единицу заменяют нулем, а нуль – единицей.

Рассматриваемый код является систематическим, т. е. символы информационного слова размещаются подряд в старших разрядах кодового слова. Восстановление информационных слов выполняется простым отбрасыванием младших (проверочных) разрядов, число которых известно. Далее используется таблица ASCII-кодов в обратном порядке: входом являются информационные двоичные последовательности, а выходом – буквы алфавита естественного языка. Итак, (7, 4)-код систематический, групповой, линейный, блочный, двоичный.

Основу декодера образует проверочная матрица Н[n-k, n], которая содержит число строк, равное числу проверочных символов, а столбцами все возможные, кроме нулевого, столбцы из трех символов $2^3 – 1 = 7$ . Проверочная матрица строится из слов таблицы К, они выбираются так, чтобы быть ортогональными к кодирующей матрице, т.е. их произведение — нулевая матрица. Проверочная матрица получает следующий вид в операциях умножения она транспонируется. Для конкретного примера проверочная матрица Н[n-k, n] приведена ниже:

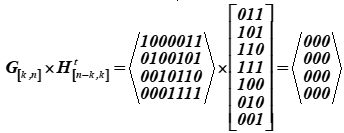
Видим, что произведение порождающей матрицы на проверочную в результате дает нулевую матрицу.

Пример 2. Декодирование слова кода Хемминга без ошибки (е<7> =<0000000>).
Пусть на приемном конце канала приняты слова №7→60 и №13→105 из таблицы К,
u<7> + е<7> = <0 1 1 1 1 0 0 > + <0 0 0 0 0 0 0>,
где ошибка отсутствует, т. е. имеет вид е<7> = <0 0 0 0 0 0 0>.

В результате вычисленный синдром имеет нулевое значение, что подтверждает отсутствие ошибки в словах кода.

Пример 3. Обнаружение одной ошибки в слове, полученном на приемном конце канала (таблица К).

А) Пусть требуется передать 7 – е кодовое слово, т.е.

u<7> = <0 1 1 1 1 0 0> и в одном третьем слева разряде слова, допущена ошибка. Тогда она суммируется по mod2 с 7-м передаваемым по каналу связи кодовым словом
u<7> + е<7> = <0 1 1 1 1 0 0 > + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0>,
где ошибка имеет вид е<7> = <0 0 1 0 0 0 0>.

Установление факта искажения кодового слова выполняется умножением полученного искаженного слова на проверочную матрицу кода. Результатом такого умножения будет вектор, называемый синдромом кодового слова.

Выполним такое умножение для наших исходных (7-го вектора с ошибкой) данных.

В результате такого умножения на приемном конце канала получили вектор-синдром S<n-k>, размерность которого (n–k). Если синдром S<3>= <0,0,0> нулевой, то делается вывод о том, что принятое на приемной стороне слово принадлежит коду С и передано без искажений. Если синдром не равен нулю S<3> ≠ <0,0,0>, то его значение указывает на наличие ошибки и ее место в слове. Искаженный разряд соответствует номеру позиции столбца матрицы Н[n-k, n], совпадающего с синдромом. После этого искаженный разряд исправляется, и полученное слово обрабатывается декодером далее. На практике для каждого принятого слова сразу вычисляется синдром и при наличии ошибки, она автоматически устраняется.

Итак, при вычислениях получен синдром S=<110> для обоих слов одинаковый. Смотрим на проверочную матрицу и отыскиваем в ней столбец, совпадающий с синдромом. Это третий слева столбец. Следовательно, ошибка допущена в третьем слева разряде, что совпадает с условиями примера. Этот третий разряд изменяется на противоположное значение и мы вернули принятые декодером слова к виду кодовых. Ошибка обнаружена и исправлена.

Вот собственно и все, именно так устроен и работает классический (7, 4)-код Хемминга.

Здесь не рассматриваются многочисленные модификации и модернизации этого кода, так как важны не они, а те идеи и их реализации, которые в корне изменили теорию кодирования, и как следствие, системы связи, обмена информацией, автоматизированные системы управления.

Заключение

В работе рассмотрены основные положения и задачи информационной безопасности, названы теории, призванные решать эти задачи.

Задача защиты информационного взаимодействия субъектов и объектов от ошибок среды и от воздействий нарушителя относится к кодологии.

Рассмотрен в деталях (7, 4)-код Хемминга, положивший начало нового направлению в теории кодирования — синтеза корректирующих кодов.

Показано применение строгих математических методов, используемых при синтезе кода.
Приведены примеры иллюстрирующие работоспособность кода.

Литература

Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. М.: Мир, 1976, 594 c.
Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер.с англ. М.: Мир, 1986, 576 с.

Источник

Пример
. Предположим, в канале связи под действием
помех произошло искажение и вместо
0100101 было принято 01001(1)1.

Решение:
Для обнаружения ошибки производят уже
знакомые нам проверки на четность.

Первая
проверка:
сумма П1+П3+П5+П7
= 0+0+1+1 четна.
В младший разряд номера ошибочной
позиции запишем 0.

Вторая
проверка:
сумма П2+П3+П6+П7
= 1+0+1+1 нечетна.
Во второй разряд номера ошибочной
позиции запишем 1

Третья
проверка:
сумма П4+П5+П6+П7
= 0+1+1+1 нечетна.
В третий разряд номера ошибочной позиции
запишем 1. Номер ошибочной позиции 110=
6. Следовательно,
символ шестой позиции следует изменить
на обратный, и получим правильную кодовую
комбинацию.

Код, исправляющий
одиночную и обнаруживающий двойную
ошибки

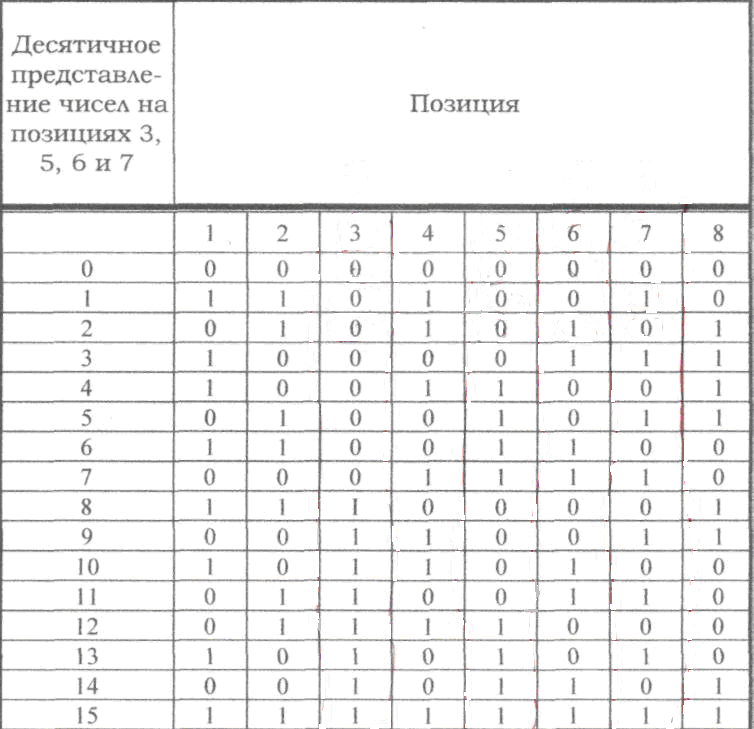
Если по изложенным
выше правилам строить корректирующий
код с обнаружением и исправлением
одиночной ошибки для равномерного
двоичного кода, то первые 16 кодовых
комбинаций будут иметь вид, показанный
в таблице. Такой код может быть использован
для построения кода с исправлением
одиночной ошибки и обнаружением двойной.

Для
этого, кроме указанных выше проверок
по контрольным позициям, следует провести
еще одну проверку на четность для всей
строки в целом. Чтобы осуществить такую
проверку, следует к каждой строке кода
добавить контрольные символы, записанные
в дополнительной колонке (таблица,
колонка 8). Тогда в случае одной ошибки
проверки по позициям укажут номер
ошибочной позиции, а проверка на четность
— на наличие ошибки. Если проверки позиций
укажут на наличие ошибки, а проверка на
четность не фиксирует ее, значит в
кодовой комбинации две ошибки.

Лекция 8

8.1 Двоичные циклические коды

Вышеприведенная
процедура построения линейного кода
матричным методом имеет ряд недостатков.
Она неоднозначна (МДР можно задать
различным образом) и неудобна
в реализации в виде технических устройств.
Этих недостатков лишены
линейные корректирующие коды, принадлежащие
к классу циклических.

Циклическими
называют
линейные (n,k)-коды,
обладающие
следующим свойством:
для любого кодового слова:

существует другое
кодовое слово:

полученное
циклическим сдвигом элементов исходного
кодового слова ||КС||
вправо
или влево, которое также принадлежит
этому коду.

Для
описания циклических кодов используют
полиномы с фиктивной переменной
X.

Например,
пусть кодовое слово ||КС||
=
||011010||.

Его
можно описать полиномом

Таким
образом, разряды кодового слова в
описывающем его полиноме используются
в качестве коэффициентов при степенях
фиктивной переменной
X.

Наибольшая
степень фиктивной переменной X
в
слагаемом с ненулевым
коэффициентом называется степенью
полинома. В вышеприведенном примере
получился полином 4-й степени.

Теперь
действия над кодовыми словами сводятся
к действиям над полиномами.
Вместо алгебры матриц здесь используется
алгебра полиномов.

Рассмотрим
алгебраические действия над полиномами,
используемые в теории
циклических кодов. Суммирование
полиномов разберем на примере
С(Х)=А(Х)+В(Х).

Пусть

||A||
= ||011010||,
||В|| =
||110111|.

Тогда

—————————————————————

Таким
образом, при суммировании коэффициентов
при X
в одинаковой степени
результат берется по модулю 2. При таком
правиле вычитание эквивалентно
суммированию.

Умножение
выполняется как обычно, но с использованием
суммирования
по модулю 2.

Рассмотрим
умножение на примере умножения полинома
(X³+X¹+X⁰)

на
полином X¹+X⁰

X³
+ 0*X²+X¹+X⁰

X¹+X⁰

^{—————————————————}

X³+
0*X²+X¹+Х⁰

X⁴+0*Х³+
X²+Х¹

^{____________________________________}

Х⁴+
X³+
X²+0*X¹+X⁰

Операция
— обратная умножению -деление. Деление
полиномов выполняется как обычно, за
исключением того, что вычитание
выполняется по модулю 2. Вспомним, что
вычитание по модулю 2 эквивалентно
сложению по модулю 2

Пример
деления полинома X⁶+X⁴+X³
на полином
X³+X²+1

X⁶+0*X⁵+X⁴
+ X³+0*X²+0*X¹+0
| X³+X²+1

X⁶+X⁵+0*X⁴+X³результат== |X³+X²

————————————

X⁵
+X⁴
+ 0*X³+0*X²

X⁵
+X⁴
+ 0*X³+
X²

—————————————-

остаток==
X²=
100

Циклический
сдвиг влево на одну позицию коэффициентов
полинома степени n-1
получается
путем его умножения на X
с
последующим вычитанием из
результата полинома Xⁿ+1,
если его порядок >
п.

Проверим это на
примере.

Пусть требуется
выполнить циклический сдвиг влево на
одну позицию

коэффициентов
полинома

C(X)=X⁵+Х³+X²+1
→ (101101)

В результате должен
получиться полином

C₁(X)=X⁴+Х³+X¹+1
→ (011011)

Это легко
доказывается:

C₁(X)=C(X)*X-(X⁶+1)=(X⁶+Х⁴+X³+X)+(
X⁶+1)=X⁴+Х³+X¹+1

В
основе циклического кода лежит образующий
полином r-го
порядка
(напомним, что r—
число дополнительных разрядов). Будем
обозначать
его g_r(X).

Образование
кодовых слов (кодирование) КС
выполняется
путем умножения
информационного полинома с коэффициентами,
являющимися информационной
последовательностью
И(Х)
порядка
i<k
на
образующий полином g_r(X)

КС_r₊_k(Х)=g_r(X)+ИС_k(Х).

Принятое кодовое
слово может отличаться от переданного
искаженными разрядами в результате
воздействия помех.

ПКС(Х)=КС(Х)+ВО(Х).

где
ВО(Х)
— полином
вектора ошибки, а суммирование, как
обычно, ведется
по модулю 2.

Декодирование,
как и раньше начинается с нахождения
опознавателя,
в данном случае в виде полинома ОП(Х).
Этот
полином вычисляется как
остаток от деления полинома принятого
кодового слова ПКС(Х)
на
образующий
полином g(Х):

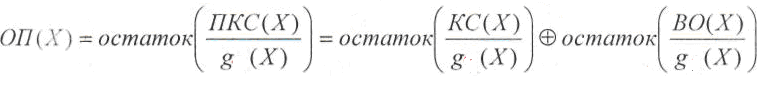
Первое
слагаемое остатка не имеет, т.к. кодовое
слово было образовано путем умножения
полинома информационной последовательности
на
образующий полином. Следовательно, и в
данном случае опознаватель
полностью зависит от вектора ошибки.

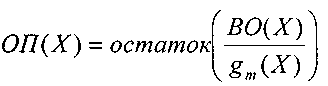
Образующий
полином выбирается таким, чтобы при
данном r
как
можно
большее число отношений ВО(Х)/g(Х)
давало
различные остатки.

Такому
требованию отвечают так называемые
неприводимые
полиномы,
которые
не делятся без остатка ни на один полином
степени r
и ниже, а
делятся только сами на себя и на 1.

Приведенная
здесь процедура образования кодового
слова неудобна тем,
что такой код получается несистематическим,
т.е. таким, в кодовых словах
которого нельзя выделить информационные
и дополнительные разряды.

Этот недостаток
был устранен следующим образом.

Способ
кодирования, приводящий к получению
систематического линейного циклического
кода, состоит в приписывании к
информационной
последовательности И
дополнительных разрядов ДР.

Эти
дополнительные разряды предлагается
находить по следующей формуле:

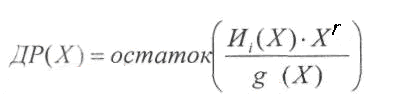
Порядок
полинома ДР(Х)
гарантировано
меньше r
(поскольку
это остаток).

Приписывание
дополнительных разрядов к информационной
последовательности,
используя алгебру полиномов, можно
описать формулой:

Одним
из свойств циклических линейных кодов
является то, что результат
деления любого разрешенного кодового
слова КС
на
образующий полином также, является
разрешенным кодовым словом.

Покажем,
что получаемые по вышеприведенному
алгоритму кодовые
слова являются кодовыми словами
циклического линейного кода. Для
этого нужно убедиться в том, что
произвольное разрешенное кодовое
слово делится на образующий полином
g(X)
без остатка:

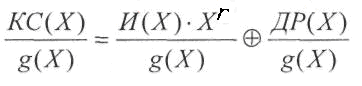
Рассмотрим первое
слагаемое:

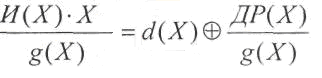
где
d(Х)
— целая
часть результата деления.

Подставим полученную
сумму на место первого слагаемого:

Суммирование
последних двух слагаемых дает нулевой
результат (напомним,
что суммирование выполняется по модулю
2).

Значит

—
целая часть деления. Остатка нет. Это
означает,
что описанный выше способ кодирования
соответствует циклическому
коду.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.

In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.

Hamming Code for Single Error Correction

The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.

Encoding a message by Hamming Code

The procedure used by the sender to encode the message encompasses the following steps −

Step 1 − Calculation of the number of redundant bits.
Step 2 − Positioning the redundant bits.
Step 3 − Calculating the values of each redundant bit.

Once the redundant bits are embedded within the message, this is sent to the destination.

Step 1 − Calculation of the number of redundant bits.

If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2^r states, 2^r must be at least equal to (m + r + 1). Thus the following equation should hold −

2^r ≥ 𝑚 + 𝑟 + 1

Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (2⁴ ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.

Step 2 − Positioning the redundant bits.

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r₁ (at position 1), r₂ (at position 2), r₃ (at position 4), r₄ (at position and so on.

Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −

Step 3 − Calculating the values of each redundant bit.

The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −

Even Parity − Here the total number of bits in the message is made even.
Odd Parity − Here the total number of bits in the message is made odd.

Each redundant bit, r_i, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the i^th position except the position of r_i. Thus −

r₁is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
r₂ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
r₃ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)

Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −

Hence, the message sent will be 11000101100.

Decoding a message in Hamming Code

Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −

Step 1 − Calculation of the number of redundant bits.
Step 2 − Positioning the redundant bits.
Step 3 − Parity checking.
Step 4 − Error detection and correction

Step 1) Calculation of the number of redundant bits

Using the same formula as in encoding, the number of redundant bits are ascertained.

2^r ≥ 𝑚 + 𝑟 + 1

where m is the number of data bits and r is the number of redundant bits.

Step 2) Positioning the redundant bits

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.

Step 3) Parity checking

Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c₁, c₂, c₃, c₄ etc. Thus

c₁ = parity(1, 3, 5, 7, 9, 11 and so on)

c₂ = parity(2, 3, 6, 7, 10, 11 and so on)

c₃ = parity(4-7, 12-15, 20-23 and so on)

Step 4) Error detection and correction

The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c₁c₂c₃c₄ = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.

Example 4 − Suppose that an incoming message 11110101101 is received.

Step 1 − At first the number of redundant bits are calculated using the formula 2^r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2^r ≥ 12 is 4.

Step 2 − The redundant bits are positioned as below −

Step 3 − Even parity checking is done −

c₁ = even_parity(1, 3, 5, 7, 9, 11) = 0

c₂ = even_parity(2, 3, 6, 7, 10, 11) = 0

c₃ = even_parity (4, 5, 6, 7) = 0

c₄ = even_parity (8, 9, 10, 11) = 0

Step 4 — Since the value of the check bits c₁c₂c₃c₄ = 0000 = 0, there are no errors in this message.

Hamming Code for double error detection

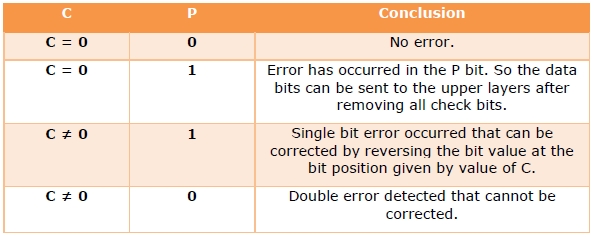
The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.

Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.

At the receiver’s end, error detection is done as shown in the following table −

Источник

Хэмминг (7,4) -Код

Назван в честь	Ричарда В. Хэмминга
Классификация
Тип	Линейный код блока
Длина блока	7
Длина сообщения	4
Скорость	4/7 ~ 0,571
Расстояние	3
Размер алфавита	2
Обозначение	[ 7,4,3] 2 -код
Свойства
совершенный код
v t

Графическое изображение 4 битов данных от d 1 до d 4 и 3 бита четности p 1 до p 3 и какие биты четности применяются к каким битам данных

В теории кодирования, Хэмминга (7, 4) — это код линейного исправления ошибок, который кодирует четыре бита данных в семь битов путем добавления трех битов четности. Это член более крупного семейства кодов Хэмминга, но термин код Хэмминга часто относится к этому конкретному коду, который Ричард У. Хэмминг ввел в 1950 году. В то время Хэмминг работал в Bell Telephone Laboratories и был разочарован подверженным ошибкам считывателем перфокарт , поэтому он начал работать над кодами исправления ошибок.

Код Хэмминга добавляет три дополнительных контрольных бита на каждые четыре бита данных сообщения. Алгоритм Хэмминга (7,4) может исправить любую однобитовую ошибку или обнаружить все однобитовые и двухбитовые ошибки. Другими словами, минимальное расстояние Хэмминга между любыми двумя правильными кодовыми словами равно 3, и принятые слова могут быть правильно декодированы, если они находятся на расстоянии не более одного от кодового слова, которое было передано отправителем. Это означает, что для ситуаций среды передачи, в которых пакетных ошибок не возникает, эффективен код Хэмминга (7,4) (поскольку среда должна быть чрезвычайно шумной для переключения двух из семи битов).

В квантовой информации код Хэмминга (7,4) используется в качестве основы для кода Стейна, типа кода CSS используется для квантовой коррекции ошибок.

Содержание

1 Цель
2 Матрицы Хэмминга
3 Канальное кодирование
4 Проверка четности
5 Исправление ошибок
6 Декодирование
7 Множественные битовые ошибки
8 Все кодовые слова
9 E 7 решетка
10 Ссылки
11 Внешние ссылки

Цель

Целью кодов Хэмминга является для создания набора битов четности, которые перекрываются, так что однобитовая ошибка в бите данных или бите четности может быть обнаружена и исправлена. Хотя может быть создано несколько перекрытий, общий метод представлен в кодах Хэмминга.

Бит №	1	2	3	4	5	6	7
Переданный бит	p 1 { displaystyle p_ {1}} $p_ {1}$	p 2 { displaystyle p_ {2}} $p_{2}$	d 1 { displaystyle d_ {1}} $d_ {1}$	p 3 { displaystyle p_ {3}} $p_ {3}$	d 2 { displaystyle d_ {2}} $d_ {2}$	d 3 { displaystyle d_ {3}} $d_ {3}$	d 4 { displaystyle d_ {4}} $d_ {4 }$
p 1 { displaystyle p_ {1}} $p_ {1}$	Да	Нет	Да	Нет	Да	Нет	Да
p 2 { displaystyle p_ {2}} $p_{2}$	Нет	Да	Да	Нет	Нет	Да	Да
p 3 { displaystyle p_ {3}} $p_ {3}$	Нет	Нет	Нет	Да	Да	Да	Да

Это Таблица описывает, какие биты четности покрывают переданные биты в закодированном слове. Например, p 2 обеспечивает четность для битов 2, 3, 6 и 7. Он также детализирует, какой переданный бит покрывается каким битом четности при чтении столбца. Например, d 1 покрывается p 1 и p 2, но не p 3. Эта таблица будет иметь поразительное сходство с таблицей. матрица проверки на четность (H ) в следующем разделе.

Кроме того, если столбцы четности в приведенной выше таблице были удалены

	d 1 { displaystyle d_ {1}} $d_ {1}$	d 2 { displaystyle d_ {2}} $d_ {2}$	d 3 { displaystyle d_ {3}} $d_ {3}$	d 4 { displaystyle d_ {4}} $d_ {4 }$
p 1 { displaystyle p_ {1}} $p_ {1}$	Да	Да	Нет	Да
p 2 { displaystyle p_ {2}} $p_{2}$	Да	Нет	Да	Да
p 3 { displaystyle p_ {3}} $p_ {3}$	Нет	Да	Да	Да

, тогда сходство со строками 1, 2 и 4 кода образующая матрица (G ) ниже также будет очевидна.

Таким образом, при правильном выборе покрытия битов четности все ошибки с расстоянием Хэмминга, равным 1, могут быть обнаружены и исправлены, что и является целью использования кода Хэмминга.

Матрицы Хэмминга

Коды Хэмминга могут быть вычислены в терминах линейной алгебры через матрицы, потому что коды Хэмминга являются линейными кодами. Для кодов Хэмминга могут быть определены две матрицы Хэмминга : порождающая матрица кода Gи матрица проверки на четность H:

GT: = (1 1 0 1 1 0 1 1 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 0 0 1), H: = (1 0 1 0 1 0 1 0 1 1 0 0 1 1 0 0 0 1 1 1 1). { displaystyle mathbf {G ^ {T}}: = { begin {pmatrix} 1 1 0 1 \ 1 0 1 1 \ 1 0 0 0 \ 0 1 1 1 \ 0 1 0 0 \ 0 0 1 0 \ 0 0 0 1 \} end {pqumatrix} mathbf {H}: = { begin {pmatrix} 1 0 1 0 1 0 1 \ 0 1 1 0 0 1 1 1 \ 0 0 0 1 1 1 1 \ end {pmatrix}}.} ${ displaystyle mathbf {G ^ {T}}: = { begin {pmatrix} 1 1 0 1 \ 1 0 1 1 \ 1 0 0 0 \ 0 1 1 1 \ 0 1 0 0 \ 0 0 1 0 0 \ 1 0 0 0 end {pmatrix}}, qquad mathbf {H}: = { begin {pmatrix} 1 0 1 0 1 0 1 \ 0 1 1 0 0 1 1 \ 0 0 0 0 1 1 1 1 1 1 \ end {pmatrix}}.}$

Разрядность строк и биты четности

Как упоминалось выше,, 2 и 4 из G должны выглядеть знакомо, поскольку они отображают биты данных в свои биты четности:

p1охватывает d 1, d 2, d 4
p2охватывает d 1, d 3, d 4
p3охватывает d 2, d 3, d 4

оставшиеся строки (3, 5, 6, 7) отображают данные в их позицию в закодированной форме, и в этой строке только 1, поэтому это идентичная копия. Фактически, эти четыре строки являются линейно независимыми и образуют единичную матрицу (по замыслу, а не совпадение).

Также, как упоминалось выше, три строки H должны быть знакомы. Эти строки используются для вычисления вектора синдрома на принимающей стороне, и если вектор синдрома является нулевым вектором (все нули), то полученное слово не содержит ошибок; если не ноль, то значение указывает, какой бит был перевернут.

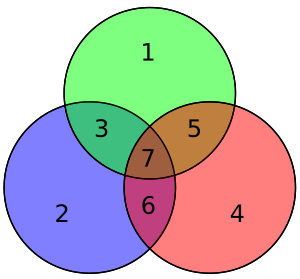
Четыре бита данных, собранные как вектор p, предварительно умножаются на G (т. Е. Gp ) и берутся по модулю 2, чтобы получить передаваемое закодированное значение. Исходные 4 бита данных преобразуются в семь битов (отсюда и название «Хэмминга (7,4)») с добавлением трех битов четности для обеспечения четности с использованием вышеуказанных покрытий битов данных. В первой таблице выше показано отображение между каждым битом данных и битом четности в его конечную битовую позицию (с 1 по 7), но это также может быть представлено на диаграмме Венна. На первой диаграмме в этой статье показаны три круга (по одному для каждого бита четности), в которые включены биты данных, которые покрывает каждый бит четности. Вторая диаграмма (показанная справа) идентична, но вместо этого отмечены позиции битов.

В оставшейся части этого раздела следующие 4 бита (показаны как вектор-столбец) будут использоваться в качестве рабочего примера:

p = (d 1 d 2 d 3 d 4) = (1 0 1 1) { displaystyle mathbf {p} = { begin {pmatrix} d_ {1} \ d_ {2} \ d_ {3} \ d_ {4} \ end {pmatrix}} = { begin {pmatrix} 1 \ 0 \ 1 \ 1 end {pmatrix}}} ${ mathbf {p}} = { begin {pmatrix} d_ {1} \ d_ {2} \ d_ {3} \ d_ {4} \ end {pmatrix}} = { begin {pmatrix} 1 \ 0 \ 1 \ 1 end {pmatrix}}$

Кодирование канала

Отображение в примере x . Четность красных, зеленых и синих кругов четная.

Предположим, мы хотим передать эти данные (1011) по шумному каналу связи. В частности, двоичный симметричный канал означает, что искажение ошибок не способствует ни нулю, ни единице (он симметричен по возникновению ошибок). Кроме того, предполагается, что все исходные векторы равновероятны. Возьмем произведение G и p с элементами по модулю 2, чтобы определить переданное кодовое слово x:

x = G p = (1 1 0 1 1 0 1 1 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 0 0 1) (1 0 1 1) = (2 3 1 2 0 1 1) = (0 1 1 0 0 1 1) { Displaystyle mathbf {x} = mathbf {G} mathbf {p} = { begin {pmatrix} 1 1 0 1 \ 1 0 1 1 \ 1 0 0 0 \ 0 1 1 1 \ 0 1 0 0 \ 0 0 1 1 0 \ 0 0 0 1 \ }} end {p begin {pmatrix} 1 \ 0 \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 2 \ 3 \ 1 \ 2 \ 0 \ 1 \ 1 end {pmatrix }} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix}}} ${ mathbf {x}} = { mathbf {G}} { mathbf {p}} = { begin {pmatrix } 1 1 0 1 \ 1 0 1 1 \ 1 0 0 0 \ 0 1 1 1 \ 0 1 0 0 \ 0 0 1 0 \ 0 0 0 1 \ end {pmatrix}} { begin {pmatrix} 1 \ 0 \ 1 \ 1} end {pmatrix = { begin {pmatrix} 2 \ 3 \ 1 \ 2 \ 0 \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 0 \ 1 \ 1 end {pmatrix}}$

Это означает, что 0110011будет передается вместо передачи 1011.

Программисты, озабоченные умножением, должны заметить, что каждая строка результата является младшим значащим битом Счетчика популяции установленных битов, полученных в результате того, что строка и столбец Побитовое И, а не умножение.

На соседней диаграмме семь бит кодированного слова вставлены в свои соответствующие места; при осмотре видно, что четность красного, зеленого и синего кругов четная:

красный круг имеет две единицы
зеленый круг имеет две единицы
синий круг имеет четыре единицы

Вскоре будет показано, что если во время передачи бит перевернут, то четность двух или всех трех кругов будет неправильной, и ошибочный бит может быть определен (даже если один из битов четности), зная, что четность всех трех этих кругов должна быть четной.

Проверка четности

Если во время передачи ошибок не возникает, то полученное кодовое слово r идентично переданному кодовому слову x:

r = x { displaystyle mathbf { r} = mathbf {x}} ${ mathbf {r}} = { mathbf {x}}$

Получатель умножает H и r, чтобы получить вектор синдрома z, который указывает, произошла ли ошибка, и если да, то для какого бита кодового слова. Выполнение этого умножения (опять же, записи по модулю 2):

z = H r = (1 0 1 0 1 0 1 0 1 1 0 0 1 1 0 0 0 1 1 1 1) (0 1 1 0 0 1 1) = (2 4 2) = (0 0 0) { Displaystyle mathbf {z} = mathbf {H} mathbf {r} = { begin {pmatrix} 1 0 1 0 1 0 1 \ 0 1 1 0 0 1 1 \ 0 0 1 1 end 1 1 {pmatrix}} { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 2 \ 4 \ 2 end {pmatrix}} = { begin {pmatrix} 0 \ 0 \ 0 end {pmatrix}}} ${ mathbf {z}} = { mathbf {H}} { mathbf {r}} = { begin {pmatrix} 1 0 1 0 1 0 1 \ 0 1 1 0 0 1 1 \ 0 0 0 1 1 1 1 \ end {pmatrix}} { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix}} = { begin { pmatrix} 2 \ 4 \ 2 end {pmatrix}} = { begin {pmatrix} 0 \ 0 \ 0 end {pmatrix}}$

Поскольку синдром z является нулевым вектором, приемник может сделать вывод, что ошибки не произошло. Этот вывод основан на наблюдении, что когда вектор данных умножается на G, смена базиса происходит в векторном подпространстве, которое является ядром H . Пока во время передачи ничего не происходит, r будет оставаться в ядре H, и умножение даст нулевой вектор.

Исправление ошибок

В противном случае предположим, что произошла ошибка одного бита. Математически мы можем написать

r = x + ei { displaystyle mathbf {r} = mathbf {x} + mathbf {e} _ {i}} ${ mathbf {r}} = { mathbf {x}} + { mathbf {e}} _ {i}$

по модулю 2, где ei- это ith { displaystyle i_ {th}} $i _ {{th}}$ единичный вектор, то есть нулевой вектор с 1 в i { displaystyle i ^ {th}} $i ^ {th}$ , считая от 1.

e 2 = (0 1 0 0 0 0 0) { displaystyle mathbf {e} _ {2} = { begin {pmatrix} 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 end {pmatrix}}} ${ mathbf {e}} _ {2} = { begin {pmatrix} 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 end {pmatrix}}$

Таким образом, приведенное выше выражение означает одну битовую ошибку в i { displaystyle i ^ {th}} $i ^ {th}$ месте.

Теперь, если мы умножим этот вектор на H:

H r = H (x + ei) = H x + H ei { displaystyle mathbf {Hr} = mathbf {H} left ( mathbf {x} + mathbf {e} _ {i} right) = mathbf {Hx} + mathbf {He} _ {i}} ${ mathbf {Hr}} = { mathbf {H}} left ({ mathbf {x}} + { mathbf {e}} _ {i} right) = { mathbf {Hx}} + { mathbf {He}} _ {i}$

Поскольку x — переданные данные, это безошибочно, и в результате произведение H и x равно нулю. Таким образом,

H x + H ei = 0 + H ei = H ei { displaystyle mathbf {Hx} + mathbf {He} _ {i} = mathbf {0} + mathbf {He} _ {i } = mathbf {He} _ {i}} ${ mathbf {Hx}} + { mathbf {He}} _ {i} = { mathbf {0 }} + { mathbf {He}} _ {i} = { mathbf {He}} _ {i}$

Теперь произведение H со стандартным базисом i { displaystyle i ^ {th}} $i ^ {th}$ vector выбирает этот столбец H, мы знаем, что ошибка возникает в том месте, где встречается этот столбец H .

Например, предположим, что мы ввели битовую ошибку в бит №5

r = x + e 5 = (0 1 1 0 0 1 1) + (0 0 0 0 1 0 0) = (0 1 1 0 1 1 1) { Displaystyle mathbf {r} = mathbf {x} + mathbf {e} _ {5} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix}} + { begin {pmatrix} 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 end {pmatrix}} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 1 \ 1 \ 1 end {pmatrix}}} ${ mathbf {r}} = { mathbf {x}} + { mathbf {e}} _ {5} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix }} + { begin {pmatrix} 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 end {pmatrix}} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 1 \ 1 \ 1 end {pmatrix}}$

Битовая ошибка в бите 5 приводит к плохой четности в красных и зеленых кругах

На диаграмме справа показаны битовая ошибка (показана синим текстом) и созданная плохая четность (показана красным текстом) в красном и зеленом кругах. Битовую ошибку можно обнаружить, вычислив четность красного, зеленого и синего кружков. Если обнаружена плохая четность, то бит данных, который перекрывает только круги плохой четности, является битом с ошибкой. В приведенном выше примере красный и зеленый кружки имеют плохую четность, поэтому бит, соответствующий пересечению красного и зеленого, но не синего, указывает на бит с ошибкой.

Теперь

z = H r = (1 0 1 0 1 0 1 0 1 1 0 0 1 1 0 0 0 1 1 1 1) (0 1 1 0 1 1 1) = ( 3 4 3) = (1 0 1) { displaystyle mathbf {z} = mathbf {Hr} = { begin {pmatrix} 1 0 1 0 1 0 1 \ 0 1 1 0 0 1 1 \ 0 0 0 0 1 1 1 1 \ end {begin {pmatrix}} { pmatrix} 0 \ 1 \ 1 \ 0 \ 1 \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 3 \ 4 \ 3 end {pmatrix}} = { begin {pmatrix} 1 \ 0 \ 1 end {pmatrix}}} ${ mathbf {z}} = { mathbf {Hr}} = { begin {pmatrix} 1 0 1 0 1 0 1 \ 0 1 1 0 0 1 1 \ 0 0 0 1 1 1 1 \ end {pmatrix}} { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 1 \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 3 \ 4 \ 3 end {pmatrix}} = { begin {pmatrix} 1 \ 0 \ 1 end {pmatrix}}$

, что соответствует пятому столбцу H . Кроме того, использованный общий алгоритм (см. код Хэмминга # Общий алгоритм ) был преднамеренным в своей конструкции, так что синдром 101 соответствует двоичному значению 5, которое указывает, что пятый бит был поврежден. Таким образом, в бите 5 обнаружена ошибка, и ее можно исправить (просто переверните или отмените ее значение):

r исправлено = (0 1 1 0 1 ¯ 1 1) = (0 1 1 0 0 1 1) { Displaystyle mathbf {r} _ { text {исправлено}} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ { overline {1}} \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix}}} ${ mathbf {r}} _ {{{ text {corrected}}}} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ overline {1} \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 1 \ 1 end {pmatrix}}$

Это исправленное полученное значение действительно теперь соответствует переданное значение x сверху.

Декодирование

После того, как полученный вектор был определен как свободный от ошибок или исправлен, если произошла ошибка (при условии, что возможны только нулевые или однобитовые ошибки), тогда полученные данные необходимо декодировать обратно в исходные четыре бита.

Сначала определите матрицу R:

R = (0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1) { displaystyle mathbf {R} = { begin {pmatrix} 0 0 1 0 0 0 0 \ 0 0 0 0 1 0 0 \ 0 0 0 0 0 1 0 \ 0 0 0 0 0 0 1 \ end {pmatrix}}} ${mathbf {R}}={begin{pmatrix}0010000\0000100\0000010\0000001\end{pmatrix}}$

<40867>, полученное значение равно <40867>212>. Используя приведенный выше пример выполнения

pr = (0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1) (0 1 1 0 0 1 1) = (1 0 1 1) { displaystyle mathbf {p_ {r}} = { begin {pmatrix} 0 0 1 0 0 0 0 \ 0 0 0 0 1 0 0 \ 0 0 0 0 0 1 0 \ 0 0 0 0 0 0 0 1 \} end \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 1 \ 0 \ 1 \ 1 end {pmatrix}}} ${ mathbf {p_ {r}}} = { begin {pmatrix } 0 0 1 0 0 0 0 \ 0 0 0 0 1 0 0 \ 0 0 0 0 0 0 1 0 \ 0 0 0 0 0 0 1 \ end {pmatrix}} { begini n {pmatrix} 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 end {pmatrix}} = { begin {pmatrix} 1 \ 0 \ 1 \ 1 end {pmatrix }}$

Множественные битовые ошибки

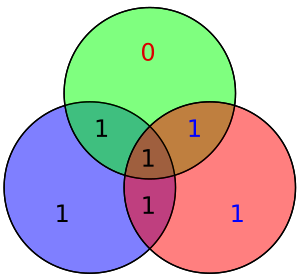В битах 4 и 5 появляются битовые ошибки (показаны синим текстом) с плохой четностью только в зеленом кружке (показанном красным текстом)

Нетрудно показать, что только одиночные битовые ошибки могут быть исправлены с помощью этой схемы. В качестве альтернативы, коды Хэмминга могут использоваться для обнаружения одиночных и двойных битовых ошибок, просто отмечая, что произведение H не равно нулю всякий раз, когда возникают ошибки. На соседней диаграмме биты 4 и 5 были перевернуты. Это дает только один кружок (зеленый) с недопустимой четностью, но ошибки не подлежат исправлению.

Однако код Хэмминга (7,4) и аналогичные коды Хэмминга не могут различать однобитовые ошибки и двухбитовые ошибки. То есть двухбитовые ошибки появляются так же, как однобитовые ошибки. Если исправление ошибок выполняется для двухбитовой ошибки, результат будет неверным.

Точно так же коды Хэмминга не могут обнаружить или исправить произвольную трехбитовую ошибку; Рассмотрим диаграмму: если бы бит в зеленом кружке (окрашенный в красный цвет) был равен 1, проверка четности вернула бы нулевой вектор, указывая, что в кодовом слове нет ошибки.

Все кодовые слова

Поскольку у источника всего 4 бита, то есть только 16 возможных передаваемых слов. Включено восьмибитовое значение, если используется дополнительный бит четности (см. код Хэмминга (7,4) с дополнительным битом четности ). (Биты данных показаны синим цветом; биты четности показаны красным; бит дополнительной четности показан желтым.)

Данные. (d 1, d 2, d 3, d 4) { displaystyle ({ color {blue} d_ {1}}, { color {blue} d_ {2}}, { color {blue} d_ {3}}, { color {blue} d_ {4}) })} $({ color {blue} d_ {1}}, { color {blue} d_ {2}}, { color {blue} d_ {3}}, { color {blue} d_ {4}})$	Хэмминга (7,4)	Хэмминга (7,4) с дополнительным битом четности (Хэмминг (8,4))
Передано. (p 1, п 2, d 1, п 3, d 2, d 3, d 4) { displaystyle ({ color {red} p_ {1}}, { color {red} p_ {2}}, { color { синий} d_ {1}}, { color {красный} p_ {3}}, { color {синий} d_ {2}}, { color {синий} d_ {3}}, { color {синий} d_ {4}})} $({ color {red} p_ {1}}, { color {red} p_ {2}}, { color {blue } d_ {1}}, { color {red} p_ {3}}, { color {blue} d_ {2}}, { color {blue} d_ {3}}, { color {blue} d_ {4}})$	Диаграмма	Передано. (p 1, p 2, d 1, p 3, d 2, d 3, d 4, p 4) { displaystyle ({ color {красный} p_ {1}}, { color {red} p_ {2}}, { color {blue} d_ {1}}, { color {red} p_ {3}}), { color {blue} d_ {2}}, { color {blue} d_ {3}}, { color {blue} d_ {4}}, { color {green} p_ {4}})} $({ color {red} p_ {1}}, { color {red} p_ {2}) }, { color {blue} d_ {1}}, { color {red} p_ {3}}, { color {blue} d_ {2}}, { color {blue} d_ {3}}, { color {blue} d_ {4}}, { color {green} p_ {4}})$	Диаграмма
0000	0000000		00000000
1000	1110000		11100001
0100	1001100		10011001
1100	0111100		01111000
0010	0101010		01010101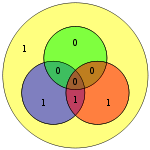
1010	1011010		10110100
0110	1100110		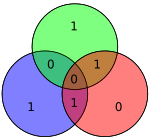11001100
1110	0010110		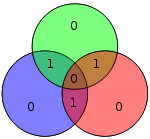00101101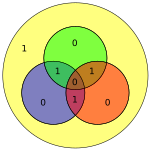
0001	1101001		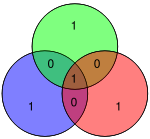11010010
1001	0011001		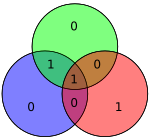00110011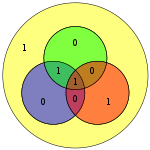
0101	0100101		01001011
1101	1010101		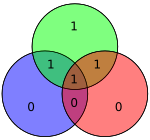10101010
0011	1000011		10000111
1011	0110011		01100110
0111	0001111		00011110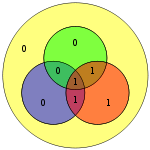
1111	1111111		11111111

E7решетка

Хэмминга ( 7,4) код тесно связан с E7решеткой и, фактически, может быть использован для ее построения, точнее, ее двойственной решетки E 7 (аналогичная конструкция для E 7 использует двойной код [7,3,4] 2). В частности, если взять набор всех векторов x в Z с x, конгруэнтным (по модулю 2) кодовому слову Хэмминга (7,4), и изменить масштаб на 1 / √2, получится решетка E 7

E 7 ∗ = 1 2 {x ∈ Z 7: x mod 2 ∈ [7, 4, 3] 2}. { displaystyle E_ {7} ^ {*} = { tfrac {1} { sqrt {2}}} left {x in mathbb {Z} ^ {7}: x , { bmod { ,}} 2 in [7,4,3] _ {2} right }.} ${ displaystyle E_ {7} ^ {*} = { tfrac {1} { sqrt {2}}} left {x in mathbb {Z} ^ {7}: x , { bmod {,}} 2 in [7,4,3] _ {2} right }.}$

Это частный пример более общего отношения между решетками и кодами. Например, расширенный (8,4) -код Хэмминга, который возникает в результате добавления бита четности, также связан с решеткой E8.

Ссылки

Внешние ссылки

Источник