Остаточная стандартная ошибка оценки - Ремонт и установка крупной бытовой техники

Как интерпретировать остаточную стандартную ошибку

17 авг. 2022 г.
читать 2 мин

Остаточная стандартная ошибка используется для измерения того, насколько хорошо модель регрессии соответствует набору данных.

Проще говоря, он измеряет стандартное отклонение остатков в регрессионной модели.

Он рассчитывается как:

Остаточная стандартная ошибка = √ Σ(y – ŷ) 2 /df

куда:

y: наблюдаемое значение
ŷ: Прогнозируемое значение
df: Степени свободы, рассчитанные как общее количество наблюдений – общее количество параметров модели.

Чем меньше остаточная стандартная ошибка, тем лучше регрессионная модель соответствует набору данных. И наоборот, чем выше остаточная стандартная ошибка, тем хуже регрессионная модель соответствует набору данных.

Модель регрессии с небольшой остаточной стандартной ошибкой будет иметь точки данных, которые плотно упакованы вокруг подобранной линии регрессии:

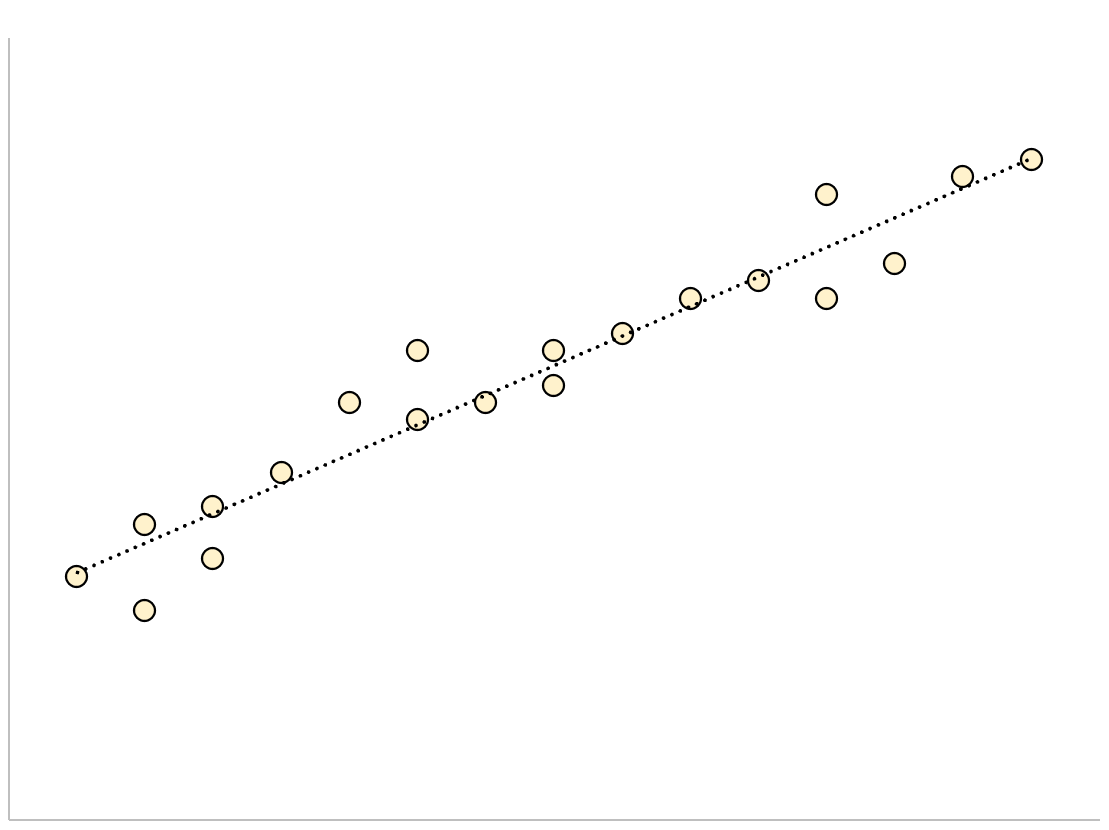
Остатки этой модели (разница между наблюдаемыми значениями и прогнозируемыми значениями) будут малы, что означает, что остаточная стандартная ошибка также будет небольшой.

И наоборот, регрессионная модель с большой остаточной стандартной ошибкой будет иметь точки данных, которые более свободно разбросаны по подобранной линии регрессии:

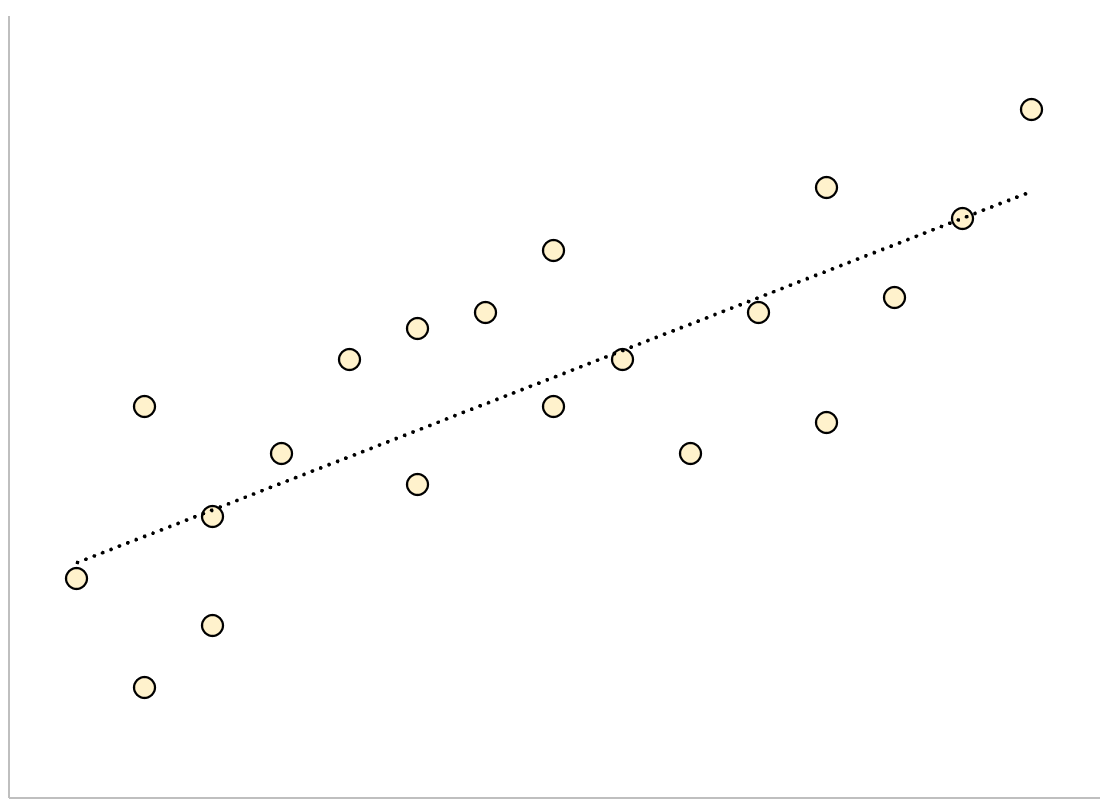
Остатки этой модели будут больше, что означает, что стандартная ошибка невязки также будет больше.

В следующем примере показано, как рассчитать и интерпретировать остаточную стандартную ошибку регрессионной модели в R.

Пример: интерпретация остаточной стандартной ошибки

Предположим, мы хотели бы подогнать следующую модель множественной линейной регрессии:

миль на галлон = β 0 + β 1 (смещение) + β 2 (лошадиные силы)

Эта модель использует переменные-предикторы «объем двигателя» и «лошадиная сила» для прогнозирования количества миль на галлон, которое получает данный автомобиль.

В следующем коде показано, как подогнать эту модель регрессии в R:

#load built-in *mtcars* dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
 Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
 Estimate Std. Error t value Pr(>|t|) 
(Intercept) 30.735904 1.331566 23.083 < 2e-16 ***
disp -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679.
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

В нижней части вывода мы видим, что остаточная стандартная ошибка этой модели составляет 3,127 .

Это говорит нам о том, что регрессионная модель предсказывает расход автомобилей на галлон со средней ошибкой около 3,127.

Использование остаточной стандартной ошибки для сравнения моделей

Остаточная стандартная ошибка особенно полезна для сравнения соответствия различных моделей регрессии.

Например, предположим, что мы подогнали две разные регрессионные модели для прогнозирования расхода автомобилей на галлон. Остаточная стандартная ошибка каждой модели выглядит следующим образом:

Остаточная стандартная ошибка модели 1: 3,127
Остаточная стандартная ошибка модели 2: 5,657

Поскольку модель 1 имеет меньшую остаточную стандартную ошибку, она лучше соответствует данным, чем модель 2. Таким образом, мы предпочли бы использовать модель 1 для прогнозирования расхода автомобилей на галлон, потому что прогнозы, которые она делает, ближе к наблюдаемым значениям расхода автомобилей на галлон.

Дополнительные ресурсы

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как создать остаточный график в R

$begingroup$

A standard error is the estimated standard deviation $hat sigma(hattheta)$ of an estimator $hattheta$ for a parameter $theta$.

Why is the estimated standard deviation of the residuals called «residual standard error» (e.g., in the output of R’s summary.lm function) and not «residual standard deviation»? What parameter estimate do we equip with a standard error here?

Do we consider each residual as an estimator for «its» error term and estimate the «pooled» standard error of all these estimators?

asked Apr 1, 2015 at 19:39

$endgroup$

$begingroup$

I think that phrasing is specific to R’s summary.lm() output. Notice that the underlying value is actually called «sigma» (summary.lm()$sigma). I don’t think other software necessarily uses that name for the standard deviation of the residuals. In addition, the phrasing ‘residual standard deviation’ is common in textbooks, for instance. I don’t know how that came to be the phrasing used in R’s summary.lm() output, but I always thought it was weird.

answered Apr 1, 2015 at 20:12

$endgroup$

$begingroup$

From my econometrics training, it is called «residual standard error» because it is an estimate of the actual «residual standard deviation». See this related question that corroborates this terminology.

A Google search for the term residual standard error also shows up a lot of hits, so it is by no means an R oddity. I tried both terms with quotes, and both show up roughly 60,000 times.

answered Apr 1, 2015 at 23:47

HeisenbergHeisenberg

4,3694 gold badges25 silver badges56 bronze badges

$endgroup$

$begingroup$

Put simply, the standard error of the sample is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.

Standard error — Wikipedia, the free encyclopedia

answered Apr 1, 2015 at 19:47

$endgroup$

$begingroup$

A fitted regression model uses the parameters to generate point estimate predictions which are the means of observed responses if you were to replicate the study with the same XX values an infinite number of times (when the linear model is true).

The difference between these predicted values and the ones used to fit the model are called «Residuals» which, when replicating the data collection process, have properties of random variables with 0 means. The observed residuals are then used to subsequently estimate the variability in these values and to estimate the sampling distribution of the parameters.

Note:

When the residual standard error is exactly 0 then the model fits the data perfectly (likely due to overfitting).

If the residual standard error can not be shown to be significantly different from the variability in the unconditional response, then there is little evidence to suggest the linear model has any predictive ability.

answered Nov 29, 2016 at 15:54

$endgroup$

$begingroup$

A standard error is the estimated standard deviation $hat sigma(hattheta)$ of an estimator $hattheta$ for a parameter $theta$.

Do we consider each residual as an estimator for «its» error term and estimate the «pooled» standard error of all these estimators?

asked Apr 1, 2015 at 19:39

$endgroup$

$begingroup$

answered Apr 1, 2015 at 20:12

$endgroup$

$begingroup$

A Google search for the term residual standard error also shows up a lot of hits, so it is by no means an R oddity. I tried both terms with quotes, and both show up roughly 60,000 times.

answered Apr 1, 2015 at 23:47

HeisenbergHeisenberg

4,3694 gold badges25 silver badges56 bronze badges

$endgroup$

$begingroup$

Put simply, the standard error of the sample is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.

Standard error — Wikipedia, the free encyclopedia

answered Apr 1, 2015 at 19:47

$endgroup$

$begingroup$

Note:

When the residual standard error is exactly 0 then the model fits the data perfectly (likely due to overfitting).

answered Nov 29, 2016 at 15:54

$endgroup$

Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.

Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать

и около 95% модулей разностей будет не
больше 2.

Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически

оценивает стандартное отклонение

слагаемого ошибки

в статистической модели простой линейной
регрессии. Другими словами,

оценивает общее стандартное отклонение

нормального распределения значений Y,
имеющих математические ожидания

для каждого X.

Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.

2.3 Прогнозирование величины y

Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.

Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.

Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.

Неопределенность,
обусловленная отклонением точек данных
от выборочной прямой регрессии.
Неопределенность,
обусловленная отклонением выборочной
прямой регрессии от регрессионной
прямой генеральной совокупности.

Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.

Стандартная
ошибка прогноза

дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:

Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.

минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.

Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:

где

— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:

Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.

Для
заданного значения X генеральная
совокупность значений Y имеет нормальное
распределение относительно регрессионной
прямой совокупности. На практике
приемлемые результаты получаются
и
тогда, когда значения Y имеют
нормальное распределение лишь
приблизительно.
Разброс
генеральной совокупности точек данных
относительно регрессионной прямой
совокупности остается постоянным всюду
вдоль этой прямой. Иными словами, при
возрастании значений X в точках данных
дисперсия генеральной совокупности
не увеличивается и не уменьшается.
Нарушение этого предположения называется
гетероскедастичностью.
Слагаемые
ошибок

независимы между собой. Это предположение
определяет случайность выборки точек
Х-Y.
Если точки данных X-Y
записывались в течение некоторого
времени, данное предположение часто
нарушается. Вместо независимых данных,
такие последовательные наблюдения
будут давать серийно коррелированные
значения.
В
генеральной совокупности существует
линейная зависимость между X и Y.
По аналогии с простой линейной регрессией
может рассматриваться и нелинейная
зависимость между X и У. Некоторые такие
случаи будут обсуждаться ниже.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Почему мы говорим «Остаточная стандартная ошибка»?

Стандартной ошибкой является оценочное стандартное отклонение оценки для параметра . & thetas ; & thetasσ^(θ^)θ^θ

Почему расчетное стандартное отклонение от остатков называется «остаточной стандартной ошибкой» (например, при выводе функции R summary.lm), а не «остаточное стандартное отклонение»? Какую оценку параметров мы снабжаем здесь стандартной ошибкой?

Рассматриваем ли мы каждый остаток как оценщик для «своего» члена ошибки и оцениваем «объединенную» стандартную ошибку всех этих оценок?

Ответы:

Я думаю, что формулировка специфична для summary.lm()вывода Р. Обратите внимание, что базовое значение на самом деле называется «сигма» ( summary.lm()$sigma). Я не думаю, что другое программное обеспечение обязательно использует это имя для стандартного отклонения остатков. Кроме того, выражение «остаточное стандартное отклонение» встречается, например, в учебниках. Я не знаю, как это стало выражением, использованным в summary.lm()выводе R , но я всегда думал, что это странно.

Из моего обучения эконометрике это называется «остаточная стандартная ошибка», потому что это оценка фактического «остаточного стандартного отклонения». Посмотрите на этот связанный вопрос, который подтверждает эту терминологию.

Поиск в Google по термину «остаточная стандартная ошибка» также показывает много совпадений, так что это ни в коем случае не является странностью. Я попробовал оба условия с кавычками, и оба появляются примерно 60000 раз.

Проще говоря, стандартная ошибка выборки — это оценка того, как далеко среднее значение выборки, вероятно, от среднего значения по совокупности, тогда как стандартное отклонение выборки — это степень, в которой отдельные лица в выборке отличаются от среднего значения по выборке.

Стандартная ошибка — Википедия, свободная энциклопедия

Подходящая регрессионная модель использует параметры для генерации точечных прогнозов, которые являются средством наблюдаемых ответов, если вы должны были повторить исследование с одинаковыми значениями XX бесконечное число раз ( когда линейная модель верна ).

Разница между этими прогнозируемыми значениями и значениями, используемыми для подгонки модели, называется « Остатки », которые при репликации процесса сбора данных имеют свойства случайных величин со значением 0. Наблюдаемые остатки затем используются для последующей оценки изменчивости этих значений и для оценки выборочного распределения параметров.

Замечания:

Когда остаточная стандартная ошибка точно равна 0, тогда модель идеально соответствует данным (вероятно, из-за переобучения).

Если нельзя доказать, что остаточная стандартная ошибка значительно отличается от изменчивости безусловного отклика, то имеется мало свидетельств того, что линейная модель обладает какой-либо прогнозирующей способностью.

Что такое Остаточное стандартное отклонение?

Остаточное стандартное отклонение – это статистический термин, используемый для описания разницы в стандартных отклонениях наблюдаемых значений по сравнению с прогнозируемыми значениями, как показано точками в регрессионном анализе .

Регрессионный анализ – это метод, используемый в статистике, чтобы показать взаимосвязь между двумя разными переменными и описать, насколько хорошо вы можете предсказать поведение одной переменной на основе поведения другой.

Остаточное стандартное отклонение также называется стандартным отклонением точек вокруг подобранной линии или стандартной ошибкой оценки.

Ключевые моменты

Остаточное стандартное отклонение – это стандартное отклонение остаточных значений или разница между набором наблюдаемых и прогнозируемых значений.
Стандартное отклонение остатков вычисляет, насколько точки данных разбросаны по линии регрессии.
Результат используется для измерения ошибки предсказуемости линии регрессии.
Чем меньше остаточное стандартное отклонение по сравнению со стандартным отклонением выборки, тем более предсказуемой или полезной является модель.

Понимание остаточного стандартного отклонения

Остаточное стандартное отклонение является благость-из-приступа меры , которая может быть использована для анализа того, насколько хорошо набор точек данных согласуются с реальной моделью. В бизнес-среде, например, после выполнения регрессионного анализа по нескольким точкам данных затрат с течением времени, остаточное стандартное отклонение может предоставить владельцу бизнеса информацию о разнице между фактическими затратами и прогнозируемыми затратами, а также представление о том, сколько из них прогнозируется. затраты могут отличаться от среднего значения исторической стоимости.

Формула для остаточного стандартного отклонения

Residualзнак равно(Y-Yеsт)Sреsзнак равно∑(Y-Yеsт)2п-2жчере:Sреsзнак равноРезидуал стиндард девиатинонYзнак равноOBсекхгVед облуйYеsтзнак равноEсектямтедотргоJестедоблуе пзнак равноДата поинтс ин популатион begin {align} & text {Residual} = left (Y-Y_ {est} right) & S_ {res} = sqrt { frac { sum left (Y-Y_ {est} right ) ^ 2} {n-2}} & textbf {где:} & S_ {res} = text {Остаточное стандартное отклонение} & Y = text {Наблюдаемое значение} & Y_ {est} = text {Расчетное или прогнозируемое значение} & n = text {Точки данных в совокупности} end {выровнены}Взаимодействие с другими людьмиОстаточныйзнак равно(Y-YестВзаимодействие с другими людьми)SresВзаимодействие с другими людьмизнак равноп-2

c3.3,-7.3,9.3,-11,18,-11H400000v40H1017.7s-90.5,478,-276.2,1466c-185.7,988,
-279.5,1483,-281.5,1485c-2,6,-10,9,-24,9c-8,0,-12,-0.7,-12,-2c0,-1.3,-5.3,-32,
-16,-92c-50.7,-293.3,-119.7,-693.3,-207,-1200c0,-1.3,-5.3,8.7,-16,30c-10.7,
21.3,-21.3,42.7,-32,64s-16,33,-16,33s-26,-26,-26,-26s76,-153,76,-153s77,-151,
77,-151c0.7,0.7,35.7,202,105,604c67.3,400.7,102,602.7,104,606z
M1001 80H400000v40H1017z”>

Как рассчитать остаточное стандартное отклонение

Чтобы рассчитать остаточное стандартное отклонение, сначала необходимо рассчитать разницу между прогнозируемыми значениями и фактическими значениями, сформированными вокруг подобранной линии. Эта разница известна как остаточное значение или просто остатки или расстояние между известными точками данных и теми точками данных, которые предсказаны моделью.

Чтобы вычислить остаточное стандартное отклонение, подставьте остатки в уравнение остаточного стандартного отклонения, чтобы решить формулу.

Пример остаточного стандартного отклонения

Начните с расчета остаточной стоимости. Например, если у вас есть набор из четырех наблюдаемых значений для безымянного эксперимента, в таблице ниже показаны значения y, наблюдаемые и записанные для заданных значений x:

Если линейное уравнение или наклон линии, предсказанный данными в модели, задан как y est = 1x + 2, где y est = предсказанное значение y, можно найти остаток для каждого наблюдения.

Остаточная величина равна (y – y est ), поэтому для первого набора фактическое значение y равно 1, а прогнозируемое значение y est, заданное уравнением, равно y est = 1 (1) + 2 = 3. Остаточное значение Таким образом, 1 – 3 = -2, отрицательная остаточная стоимость.

Для второго набора точек данных x и y прогнозируемое значение y, когда x равно 2, а y равно 4, можно рассчитать как 1 (2) + 2 = 4.

В этом случае фактическое и прогнозируемое значения совпадают, поэтому остаточное значение будет равно нулю. Вы можете использовать тот же процесс для получения прогнозируемых значений y в оставшихся двух наборах данных.

После того, как вы рассчитали остатки для всех точек с помощью таблицы или графика, используйте формулу стандартного отклонения остатка.

Расширяя приведенную выше таблицу, вы вычисляете остаточное стандартное отклонение:

Обратите внимание, что сумма квадратов остатков = 6, что представляет собой числитель уравнения стандартного отклонения остатка.

Для нижней части или знаменателя уравнения остаточного стандартного отклонения n = количество точек данных, которое в данном случае равно 4. Вычислите знаменатель уравнения как:

(Количество остатков – 2) = (4 – 2) = 2

Загрузить PDF

Стандартная ошибка оценки служит для того, чтобы выяснить, как линия регрессии соответствует набору данных. Если у вас есть набор данных, полученных в результате измерения, эксперимента, опроса или из другого источника, создайте линию регрессии, чтобы оценить дополнительные данные. Стандартная ошибка оценки характеризует, насколько верна линия регрессии.

1

Создайте таблицу с данными. Таблица должна состоять из пяти столбцов, и призвана облегчить вашу работу с данными. Чтобы вычислить стандартную ошибку оценки, понадобятся пять величин. Поэтому разделите таблицу на пять столбцов. Обозначьте эти столбцы так:^[1]
2
Введите данные в таблицу. Когда вы проведете эксперимент или опрос, вы получите пары данных — независимую переменную обозначим как $x$ , а зависимую или конечную переменную как $y$ . Введите эти значения в первые два столбца таблицы.
- Не перепутайте данные. Помните, что определенному значению независимой переменной должно соответствовать конкретное значение зависимой переменной.
- Например, рассмотрим следующий набор пар данных:
  - (1,2)
  - (2,4)
  - (3,5)
  - (4,4)
  - (5,5)
3
Вычислите линию регрессии. Сделайте это на основе представленных данных. Эта линия также называется линией наилучшего соответствия или линией наименьших квадратов. Расчет можно сделать вручную, но это довольно утомительно. Поэтому рекомендуем воспользоваться графическим калькулятором или онлайн-сервисом, которые быстро вычислят линию регрессии по вашим данным.^[2]
- В этой статье предполагается, что уравнение линии регрессии дано (известно).
- В нашем примере линия регрессии описывается уравнением $y^{{prime }}=0,6x+2,2$ .
4

Вычислите прогнозируемые значения по линии регрессии. С помощью уравнения линии регрессии можно вычислить прогнозируемые значения «y» для значений «x», которые есть и которых нет в наборе данных.

Реклама

1
Вычислите ошибку каждого прогнозируемого значения. В четвертом столбце таблицы запишите ошибку каждого прогнозируемого значения. В частности, вычтите прогнозируемое значение ( $y^{{prime }}$ ) из фактического (наблюдаемого) значения ( $y$ ).^[3]
- В нашем примере вычисления будут выглядеть так:
2
Вычислите квадраты ошибок. Возведите в квадрат каждое значение четвертого столбца, а результаты запишите в последнем (пятом) столбце таблицы.
- В нашем примере вычисления будут выглядеть так:
3
Найдите сумму квадратов ошибок. Она пригодится для вычисления стандартного отклонения, дисперсии и других величин. Чтобы найти сумму квадратов ошибок, сложите все значения пятого столбца. ^[4]
- В нашем примере вычисления будут выглядеть так:
  - $0,64+0,36+1,0+0,36+0,04=2,4$
4
Завершите расчеты. Стандартная ошибка оценки — это квадратный корень из среднего значения суммы квадратов ошибок. Обычно ошибка оценки обозначается греческой буквой $sigma$ . Поэтому сначала разделите сумму квадратов ошибок на число пар данных. А потом из полученного значения извлеките квадратный корень.^[5]
- Если рассматриваемые данные представляют всю совокупность, среднее значение находится так: сумму нужно разделить на N (количество пар данных). Если же рассматриваемые данные представляют некоторую выборку, вместо N подставьте N-2.
- В нашем примере, скорее всего, имеет место выборка, потому что мы рассматриваем всего 5 пар данных. Поэтому стандартную ошибку оценки вычислите следующим образом:
5
Интерпретируйте полученный результат. Стандартная ошибка оценки — это статистический показатель, которые оценивает, насколько близко измеренные данные лежат к линии регрессии. Ошибка оценка «0» означает, что каждая точка лежит непосредственно на линии. Чем выше ошибка оценки, тем дальше от линии регрессии лежат точки.^[6]
- В нашем примере выборка достаточно маленькая, поэтому стандартная оценка ошибки 0,894 является довольно низкой и характеризует близко расположенные данные.
Реклама

Об этой статье

Эту страницу просматривали 4133 раза.

Была ли эта статья полезной?

Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач — файл n1.doc

приобрести
Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач
скачать (17128 kb.)
Доступные файлы (1):

Рушайло М.Ф. Элементы теории вероятностей и математической статистики (Документ)
Рушайло М.Ф. Элементы теории вероятностей и математической статистики (Документ)
Кремер Н.Ш. Теория вероятностей и математическая статистика (Документ)
Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных: Дополнительные параграфы к курсу алгебры 7-9 кл. общеобразовательных учреждений (Документ)
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
Кремер Н.Ш. Теория вероятностей и математическая статистика (Документ)
Коваленко И.Н., Гнеденко Б.В. Теория вероятностей (Документ)
Кафедра «Электроснабжение» В. Б. Козловская, В. В. Сталович математические задачи энергетики (Документ)

n1.doc

Хотя метод наименьших квадратов дает нам линию регрессии, которая обеспечивает минимум вариации, регрессионное уравнение не является идеальным в смысле предсказания, поскольку не все значения зависимого признака Y удовлетворяют уравнению регрессии. Нам необходима статистическая мера вариации фактических значений Y от предсказанных значений Y. Эта мера в то же время является средней вариацией каждого значения относительно среднего значения Y. Мера вариации относительно линии регрессии называется стандартной ошибкой оценки.

Колеблемость фактических значений признака Y относительно линии регрессии показана на рис. 9.3.

Из диаграммы видно, что хотя теоретическая линия регрессии проходит относительно близко от фактических значений Y, часть этих точек лежит выше или ниже линии регрессии. При этом

Стандартная ошибка оценки определяется как

где у_i — фактические значения Y;

y_x — предсказанные значения Y для заданного х.

Для вычисления более удобна следующая формула:

Нам уже известны

Тогда

Итак, для нашего примера: S_yx = 0,497. Эта стандартная ошибка характеризует меру вариации фактических данных относительно линии регрессии. Интерпретация этой меры аналогична интерпретации среднего квадратического отклонения. Если среднее квадратическое отклонение — это мера вариации относительно средней, то стандартная ошибка — это оценка меры вариации относительно линии регрессии. Однако стандартная ошибка оценки может быть использована для выводов о значении y_x и выяснения, является ли статистически значимой взаимосвязь между двумя переменными.

9.11. Измерение вариации по уравнению регрессии

Для проверки того, насколько хорошо независимая переменная предсказывает зависимую переменную в нашей модели, необходим расчет ряда мер вариации. Первая из них — общая (полная) сумма квадратов отклонений результативного признака от средней — есть мера вариации значений Y относительно их среднего Y . В регрессионном анализе общая сумма квадратов может быть разложена на объясняемую вариацию или сумму квадратов отклонений за счет регрессии и необъясняемую вариацию или остаточную сумму квадратов отклонений (рис. 9.4).

Сумма квадратов отклонений вследствие регрессии это — сумма квадратов разностей между y

(средним значением Y) и y_x (значением Y, предсказанным по уравнению регрессии). Сумма квадратов отклонений, не объясняемая регрессией (остаточная сумма квадратов), — это сумма квадратов разностей y и y_x . Эти меры вариации могут быть представлены следующим образом (табл. 9.8):

Таблица 9.8

Общая сумма квадратов

(S_T)

Сумма квадратов за счет регрессии

(S_R)

Остаточная сумма квадратов

(S_E)

Легко увидеть, что остаточная сумма квадратов (y-y_x)² — это выражение, стоящее под знаком корня в формуле (9.25) (стандартной ошибки оценки). Тем не менее в процессе вычислений стандартной ошибки мы всегда вначале вычисляем сумму квадратов ошибки.

Остаточная сумма квадратов может быть представлена следующим образом:

Объясняемая сумма квадратов выразится так:

В самом деле

51,3605 = 46,9145 + 4,4460.

Из этого соотношения определяется коэффициент детерминации:

Отсюда коэффициент детерминации — доля вариации Y, которая объясняется независимыми переменными в регрессионной модели. Для нашего примера r^г= 46,9145/51,3605 = 0,913.

Следовательно, 91,3% вариации еженедельной выручки магазинов могут быть объяснены числом покупателей, варьирующим от магазина к магазину. Только 8,7% вариации можно объяснить иными факторами, не включенными в уравнение регрессии.

В случае парной регрессии коэффициент детерминации равен квадратному корню из квадрата коэффициента линейной корреляции Пирсона

В простой линейной регрессии г имеет тот же знак, что и b₁, Если b₁ > 0, то r > 0; если b₁ < 0, то r < 0, если b₁ = 0, то r = 0.

В нашем примере r² = 0,913 и b₁ > 0, коэффициент корреляции r = 0,956. Близость коэффициента корреляции к 1 свидетельствует о тесной положительной связи между выручкой магазина от продажи пива и числом посетителей.

Мы интерпретировали коэффициент корреляции в терминах регрессии, однако корреляция и регрессия — две различные техники. Корреляция устанавливает силу связи между признаками, а регрессия — форму этой связи. В ряде случаев для анализа достаточно найти меру связи между признаками, без использования одного из них в качестве факторного признака для другого.

9.12. Доверительные интервалы для оценки неизвестного генерального значения y_ген(_yх) и индивидуального значения y_i

Поскольку в основном для построения регрессионных моделей используются данные выборок, то зачастую интерпретация взаимоотношений между переменными в генеральной совокупности базируется на выборочных результатах.

Как было сказано выше, регрессионное уравнение используется для прогноза значений Y по заданному значению X. В нашем примере показано, что при 600 посетителях магазина сумма выручки могла бы быть 7,661 у. е. Однако это значение — только точечная оценка истинного среднего значения. Мы знаем, что для оценки истинного значения генерального параметра возможна интервальная оценка.

Доверительный интервал для оценки неизвестного генерального значения y_ген(_yх) имеет вид

где

Здесь y_x — предсказанное значение Y

(y_x₌=b₀+b₁y_i);

S_yx — стандартная ошибка оценки;

п — объем выборки;

х_i — заданное значение X.

Легко видеть, что длина доверительного интервала зависит от нескольких факторов. Для заданного уровня значимости  увеличение вариации вокруг линии регрессии, измеряемой стандартной ошибкой оценки, увеличивает длину интервала. Увеличение объема выборки уменьшит длину интервала. Более того, ширина интервала также варьирует с различными значениями X. Когда оценивается y_x по значениям X, близким к x, то интервал тем уже, чем меньше абсолютное отклонение х_i от x (рис. 9.5).

Когда оценка осуществляется по значениям X, удаленным от среднего x, то длина интервала возрастает.

Рассчитаем 95%-й доверительный интервал для среднего значения выручки во всех магазинах с числом посетителей, равным 600. По данным нашего примера уравнение регрессии имеет вид

y_x = 2,423 + 0,00873x:

и для x_i = 600 получим y_i; =7,661, а также

По таблице Стьюдента (приложение 5)

t₁₈ = 2,10.

Отсюда, используя формулы (9.31) и (9.32), рассчитаем границы искомого доверительного интервала для _yx

Итак, 7,369  _yx 7,953.

Следовательно, наша оценка состоит в том, что средняя дневная выручка находится между 7,369 и 7,953 у. е. для всех магазинов с 600 посетителями.

Для построения доверительного интервала для индивидуальных значений Y_x, лежащих на линии регрессии, используется доверительный интервал регрессии вида

где h_i y_i_,, S_yx ,п и х_i — определяются, как и в формулах (9.31) и (9.32).

Определим 95% -и доверительный интервал для оценки дневных продаж отдельного магазина с 600 посетителями

В результате вычислений получим

Итак, 6,577 y_i  8,745.

Следовательно, с 95%-й уверенностью можно утверждать, что ежедневная выручка отдельного магазина, который посетили 600 покупателей, находится в пределах от 6,577 до 8,745 у. е. Длина этого интервала больше чем длина интервала, полученного ранее для оценки среднего значения Y.

9.10. Стандартная ошибка оценки уравнения регрессии

Источник

Как интерпретировать остаточную стандартную ошибку

17 авг. 2022 г.
читать 2 мин

Проще говоря, он измеряет стандартное отклонение остатков в регрессионной модели.

Он рассчитывается как:

Остаточная стандартная ошибка = √ Σ(y – ŷ) 2 /df

куда:

y: наблюдаемое значение
ŷ: Прогнозируемое значение
df: Степени свободы, рассчитанные как общее количество наблюдений – общее количество параметров модели.

Остатки этой модели будут больше, что означает, что стандартная ошибка невязки также будет больше.

Пример: интерпретация остаточной стандартной ошибки

Предположим, мы хотели бы подогнать следующую модель множественной линейной регрессии:

миль на галлон = β 0 + β 1 (смещение) + β 2 (лошадиные силы)

В следующем коде показано, как подогнать эту модель регрессии в R:

#load built-in *mtcars* dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
 Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
 Estimate Std. Error t value Pr(>|t|) 
(Intercept) 30.735904 1.331566 23.083 < 2e-16 ***
disp -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679.
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

В нижней части вывода мы видим, что остаточная стандартная ошибка этой модели составляет 3,127 .

Использование остаточной стандартной ошибки для сравнения моделей

Остаточная стандартная ошибка особенно полезна для сравнения соответствия различных моделей регрессии.

Остаточная стандартная ошибка модели 1: 3,127
Остаточная стандартная ошибка модели 2: 5,657

Дополнительные ресурсы

Источник

Остаточная стандартная ошибка данных с заданными степенями свободы Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Остаточная сумма квадратов: 15 —> Конверсия не требуется
Степени свободы: 9 —> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

1.29099444873581 —> Конверсия не требуется

7 Ошибки Калькуляторы

Остаточная стандартная ошибка данных с заданными степенями свободы формула

Остаточная стандартная ошибка данных = sqrt(Остаточная сумма квадратов/Степени свободы)

RSE = sqrt(RSS/df)

Что такое стандартная ошибка и ее важность?

В статистике и анализе данных большое значение имеет стандартная ошибка. Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных выборочных статистических данных, таких как среднее значение или медиана. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности. Соотношение между стандартной ошибкой и стандартным отклонением таково, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; чем больше размер выборки, тем меньше стандартная ошибка, потому что статистика будет приближаться к фактическому значению.

Источник

Стандартная
ошибка оценки по регрессии.
Как было отмечено, несмещённая оценка
дисперсии остатков уравнения регрессии
называется остаточной дисперсией

=
=.

Корень
квадратный из остаточной дисперсии
называется стандартной ошибкой оценки
по регрессии. Обозначается она обычно
S_y_,_x
и вычисляется по формуле

S_y_,_x
=
.

Стандартная
ошибка оценки по регрессии показывает,
насколько в среднем мы ошибаемся,
оценивая значение зависимой переменной
по найденному уравнению регрессии при
фиксированном значении независимой
переменной.

Оценка
значимости уравнения регрессии
(дисперсионный анализ регрессии).
Для
оценки значимости уравнения регрессии
устанавливают, соответствует ли выбранная
модель анализируемым данным. Для этого
используется дисперсионный анализ
регрессии. Основная его посылка – это
разложение общей суммы квадратов
отклонений
на
составляющие. Известно, что такое
разложение имеет вид

=+,

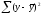если
в уравнении регрессии присутствует
свободный член. В противном случае в
правую часть надо добавить слагаемое
2.
Но как было показано, второй член этого
слагаемого (равен нулю, если в уравнении регрессии
присутствует свободный член.

Второе
слагаемое в правой части этого разложения
уже встречалось и обсуждалось – это
часть общей суммы квадратов отклонений,
объясняемая действием случайных и
неучтенных факторов. Первое слагаемое
этого разложения –
это часть общей суммы квадратов
отклонений, объясняемая регрессионной
зависимостью. Следовательно, если
регрессионная зависимость между у
и х
отсутствует, то общая сумма квадратов
отклонений объясняется действием только
случайных факторов или ошибок, т.е.
=.
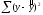В случае функциональной зависимости
между
у
и х
действие случайных факторов и ошибок
отсутствует и тогда
=.

Будучи
отнесёнными к соответствующему числу
степеней свободы эти суммы называются
средними квадратами отклонений и служат
оценками дисперсии
в разных предположениях. Одна из них
рассчитывается в предположении отсутствия
регрессионной зависимости, а другая –
без такого предположения. Следовательно,
если регрессионная зависимость
отсутствует, то эти оценки должны быть
близкими. Сравниваются они на основеF-отношения:

F
= MSR/
MSE.
Таким образом, F-статистика
проверяет гипотезу о незначимости
уравнения регрессии (H₀:
=
0), т. е. о том, что зависимости между
анализируемыми переменными нет. Если
верна нулевая гипотеза, тоF-статистика
следует распределению Фишера и, зная
уровень значимости и число степеней
свободы числителя и знаменателя, можно
определить критические значения этого
распределения.

Расчётное
значение F-статистики
сравнивается с критическим значением
(в нашем случае число степеней свободы
числителя равно 1 (число регрессоров),
а число степеней свободы знаменателя
равно (n
– 2)) с уровнем значимости
.
ЕслиF<
F,
то гипотеза о незначимости уравнения
регрессии не отклоняется, т. е. не
отклоняется гипотеза о том, что
=
0, и уравнение регрессии признаётся
незначимым. В этом случае надо либо
изменить вид зависимости, либо пересмотреть
набор исходных данных.

При
компьютерных расчётах в некоторых
статистических пакетах программ оценка
значимости уравнения регрессии
осуществляется на основе дисперсионного
анализа в таблицах вида:

Таблица
1.1 – Дисперсионный анализ регрессии

Источник вариации	Суммы квадратов	Степени свободы	Средние квадраты	F- отношение	p-value
Модель	SSR	1	MSR	MSR/ MSE	Уровень
Ошибки	SSE	n – 2	MSE		знач-ти
Общая	SST	n – 1

Здесь
p-value
– это вероятность выполнения неравенства
F<
F
или расчётный уровень значимости. Если
эта вероятность мала (меньше
),
то нулевая гипотеза отклоняется.

В
некоторых статистических пакетах
программ значение F-статистики
и вероятность для неё приводятся без
показа процедуры их вычисления.

Если
в уравнении регрессии нет константы,
то в некоторых статистических пакетах
F-статистика
просто не вычисляется.

Интервальные
оценки параметров уравнения регрессии.
При использовании параметров уравнения
регрессии в анализе и прогнозировании
для них необходимо уметь строить
интервальные оценки.

Доверительный
интервал для коэффициента регрессии
определяется из соотношения (btS_b),
где S_b
– стандартная ошибка оценки коэффициента
регрессии. Известно, что

S_b=.

Доверительный
интервал для свободного члена уравнения
регрессии определяется из соотношения
(аtS_а),
где S_а
– стандартная ошибка оценки свободного
члена уравнения регрессии. Известно,
что

S_а=.

Интервальная
оценка расчетных значений
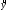определяется доверительным интервалом
(),
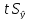где
стандартная
ошибка оценки,
определяемая из соотношения

=
.

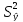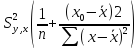Интервальная
оценка прогнозных значений определяется
из подобного же соотношения, только в
стандартную ошибку добавляется ещё
стандартное отклонение,
характеризующее рассеяние прогнозных
значений зависимой переменной вокруг
линии регрессии.

Проверка
значимости параметров уравнения
регрессии.

Кроме проверки значимости уравнения
регрессии в целом необходимо уметь
проверять значимость каждого параметра
уравнения регрессии в отдельности.
Осуществляется это на основе t-статистик.
Значения этих статистик рассчитываются
из соотношений: t_a=
a/S_a,
t_b=
b/S_b.
Для этих статистик определяются
критические значения или расчётные
уровни значимости, на основе которых и
принимаются решения о значимости или
незначимости соответствующих параметров.

В
случае парной линейной регрессии
проверка значимости уравнения регрессии
в целом и проверка значимости коэффициента
уравнения регрессии по сути дела одно
и то же, т. к. в том и другом случае
проверяется одна и та же гипотеза о том,
что коэффициент уравнения регрессии
равен нулю. Кроме того, можно показать,
что для парной линейной регрессии F
=
.

Уравнение
простой регрессии в компьютерных
расчётах обычно выдаётся в виде следующей
таблицы.

Таблица
1.2 – Уравнение простой регрессии

Параметр	Оценка	Ст. ошибка	t-статистика	р-value
Пересечение	а	S_a	t_a=a/S_a
Наклон	b	S_b	t_b=b/S_b

Пересечение
и наклон
– это другое название свободного члена
уравнения регрессии и его коэффициента,
основанное на геометрическом смысле
этих величин, если рассматривать
уравнение регрессии как уравнение
прямой линии или линии регрессии. Смысл
остальных столбцов понятен из их
названия.

Кроме
уже рассмотренных показателей точности
уравнения регрессии обычно ещё используют
коэффициент
детерминации.

Коэффициент
детерминации
(R—квадрат)
является удобной оценкой качества
подгонки данных моделью. Выясним его
смысл. В общем случае коэффициент
детерминации определяется из соотношения

R²
=
,

т.
е. это доля выборочной дисперсии
переменной y,
которая объясняется моделью. Следует
иметь в виду, что
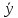также соответствует выборочному среднему(см. соотношение (1.2)). Следовательно,
коэффициент детерминации характеризует
долю вариации зависимой переменной,
обусловленную вариацией независимой
переменной. Обычно он выражается в
процентах, поэтому, например, еслиR²=
75%, то это значит, что 75% вариации зависимой
переменной у
объясняется вариацией независимой
переменной х,
а остальные 25% изменения у
объясняются либо ошибками наблюдений,
либо действием неучтенных факторов,
либо тем и другим.

Известно,
что если модель содержит свободный
член, то справедливо соотношение (следует
из
)()
=()
+(),
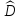откуда следует, что

=
1 –
= 1 –.

Отсюда
следует, что
действительно
определяет, какую долю выборочной
вариацииможно объяснить моделью.

Если
уравнение регрессии содержит свободный
член, то оба выражения для
эквивалентны. Кроме того, в этом случае
можно показать, что 0всеравны 0 и равен 1, если в уравнении
регрессии содержится только константа).

Можно
показать, что в случае парной линейной
регрессии коэффициент детерминации
равен квадрату коэффициента корреляции,
т.е. R²=.

Следует
иметь в виду, что
измеряет только качество линейной
аппроксимации, но не меру качества
статистической модели. Кроме того,чувствителен к определению зависимой
переменной и в случае её изменения
разные модели посравнивать нельзя.

Спецификация
уравнения регрессии

Под
спецификацией уравнения регрессии
понимают выбор объясняющих переменных
и установление вида связи между изучаемыми
явлениями. В случае парной регрессии
эта задача сводится к выбору независимой
переменной и вида связи. Решение этих
вопросов должна давать теория, описывающая
взаимосвязи изучаемых процессов.

К
ошибкам спецификации в случае парной
регрессии можно отнести неправильный
выбор доминирующего фактора, влияющего
на изменение изучаемого показателя,
или неправильный выбор вида зависимости
между изучаемыми показателями. И в том
и в другом случае будут нарушены
предпосылки МНК, особенно 3-я и 4-я, т.е.
остатки регрессии будут гетероскедастичными
и автокоррелироваными.

Гетероскедастичность
и автокорреляция остатков уравнения
регрессии могут сказаться на эффективности
оценок, полученных на основе МНК и на
смещённости оценки их дисперсии. Поэтому
интервальные оценки и статистические
выводы о значимости оценок в этом случае
могут быть ненадёжными.

Разработаны
специальные статистические методы
проверки остатков на гомоскедастичность
и автокорреляцию. Рассмотрим сначала
наиболее простые из них.

1.3.1.
Проверка остатков регрессии на
гетероскедастичность
(тест Голдфелда –
Квандта)

Этот
тест применяется в предположении
нормально распределённых остатков и в
предположении их пропорциональности
величинам объясняющей переменной х.
Для применения рассматриваемого теста
пары наблюдений упорядочиваются в
порядке роста значений независимой
переменной х.
Затем выбираются первые и последние
наблюдения в количестве не менее n/3.
По выбранным наблюдениям строятся
уравнения регрессии (отдельно по каждому
набору) и сравниваются их остаточные
суммы квадратов. Гипотеза о гомоскедастичности
в этом случае будет равносильна гипотезе
о том, что остатки в этих уравнениях
представляют собой выборочные наблюдения
нормально распределённых случайных
величин с одинаковыми дисперсиями.
Сравнивая эти дисперсии по критерию
Фишера (число степеней свободы числителя
и знаменателя здесь совпадают, т. к.
слева и справа берётся одинаковое число
наблюдений) принимаем или отклоняем
гипотезу о гомоскедастичности остатков.

Несмотря
на ограниченность применения этого
критерия (пропорциональность величин
остатков значениям независимой
переменной), данный тест работает с
элементами выборки и не требует больших
объёмов выборки как асимптотические
тесты.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

(Оценочная) стандартная ошибка регрессии ( английская (оценочная) стандартная ошибка регрессии, кратко: SER ) и стандартная ошибка , стандартная ошибка оценки ( английская стандартная ошибка оценки ) или квадратный корень из среднеквадратичной ошибки. ( английский корень среднеквадратичной ошибка , RMSE для короткого замыкания ) является мерой точности регрессии в статистике, особенно в регрессионном анализе . Он определяется как квадратный корень из несмещенной оценки для неизвестной дисперсии возмущающих переменных ( остаточная дисперсия ) и может интерпретироваться как квадратный корень из « среднего квадрата невязки » ( среднеквадратичная ошибка английского корня , сокращенно RMSE ), который используется при использовании рассчитанной линии регрессии для прогнозирования возникновения целевых переменных. Он измеряет среднее расстояние между точками данных и линией регрессии. Стандартная ошибка регрессии может использоваться для оценки дисперсии параметров регрессии, поскольку они зависят от неизвестного стандартного отклонения . Стандартная ошибка регрессии и коэффициент детерминации являются наиболее часто используемыми показателями в регрессионном анализе . Однако стандартная ошибка регрессии следует иной философии, чем коэффициент детерминации. В отличие от коэффициента детерминации, который количественно оценивает объясняющую силу модели, стандартная ошибка регрессии дает оценку стандартного отклонения ненаблюдаемых эффектов, которые влияют на результат (или, что то же самое, оценку стандартного отклонения ненаблюдаемые эффекты, которые влияют на результат после того, как эффекты объясняющих переменных были удалены). Стандартная ошибка регрессии обычно отмечается значком или . Иногда это также отмечается. $сигма$ ${ displaystyle { hat { sigma}}}$ ${ displaystyle { text {SER}}}$ $s$

Введение в проблему

«Качество» регрессии может использовать оцененную стандартную ошибку остатков (англ. Residual standard error ) быть оцененным, это один из стандартных выходных данных большинства пакетов статистического программного обеспечения. Расчетная стандартная ошибка остатков указывает на уверенность, с которой остатки приближаются к истинным смешивающим переменным . Таким образом, остатки являются приближением переменных возмущения . Расчетная стандартная ошибка остатков сопоставима с коэффициентом детерминации и скорректированным коэффициентом детерминации и должна интерпретироваться аналогичным образом. Расчетная стандартная остаточная ошибка определяется как
${ Displaystyle { шляпа { varepsilon}} _ {я}}$ $varepsilon_i$ ${ Displaystyle varepsilon _ {я} приблизительно { шляпа { varepsilon}} _ {я}}$

${ displaystyle { tilde {s}} = { sqrt {{ tfrac {1} {n}} sum nolimits _ {i = 1} ^ {n} { hat { varepsilon}} _ {я } ^ {2}}}}$ .

Следует отметить, однако, что это смещенная оценка от истинной дисперсии искажающих факторов , так как оценки дисперсии используется не несмещенные . Если учесть , что при оценке двух параметров регрессии и теряет две степени свободы, и это компенсируется за счет удерживается образца размером от числа степеней свободы , разделенной, чтобы получить «среднюю Residuenquadrat» ( М edium Q uadratsumme the R esiduen , сокращенно: MQR ) и, следовательно, неискаженное представление. Это объективное представление известно как стандартная ошибка регрессии.
${ Displaystyle { тильда {s}} ^ {2}}$ ${ Displaystyle sigma _ { varepsilon} ^ {2} = sigma ^ {2}}$ $beta _ {0}$ $beta _ {1}$ $п$ $(п-2)$ ${ Displaystyle MQR = SQR / (n-2)}$

определение

Стандартная ошибка регрессии определяется как квадратный корень из несмещенной оценки дисперсии смешивающих переменных , так называемой остаточной дисперсии.

${ displaystyle { hat { sigma}} = + { sqrt {{ hat { sigma}} ^ {2}}}}$ .

Стандартная ошибка регрессии имеет ту же единицу, что и целевая переменная . Стандартная ошибка регрессии обычно меньше стандартной ошибки значений. Следует отметить, что стандартная ошибка регрессии может либо уменьшаться, либо увеличиваться, если (для данной выборки) к модели регрессии добавляется другая независимая переменная. Это связано с тем, что остаточная сумма квадратов всегда уменьшается, когда в регрессионную модель добавляется другая независимая переменная, но степени свободы также уменьшаются на единицу или p. Поскольку остаточная сумма квадратов находится в числителе, а количество степеней свободы — в знаменателе, невозможно предсказать, какой эффект будет преобладающим. Для вывода стандартной ошибки регрессии обычно предполагается, что остатки некоррелированы , имеют нулевое математическое ожидание и однородную дисперсию ( предположения Гаусса-Маркова ). Если хотя бы одно из этих предположений нарушается, стандартная ошибка регрессии, рассчитанная по приведенной выше формуле, не будет оценивать истинное значение в среднем , т.е. ЧАС. быть предвзятой оценкой неизвестного стандартного отклонения.
$у$

Простая линейная регрессия

В простой линейной регрессии стандартная ошибка регрессии определяется как

${ displaystyle { hat { sigma}} = + { sqrt {SQR / (n-2)}} = + { sqrt {{ frac {1} {n-2}} sum limits _ { i = 1} ^ {n} { hat { varepsilon}} _ {i} ^ {2}}} = + { sqrt {{{ frac {1} {n-2}} sum limits _ {i = 1} ^ {n} left (y_ {i} -b_ {0} -b_ {1} x_ {i} right) ^ {2}}}}$ , с оценкой наименьших квадратов и для наклона и точки пересечения . ${ displaystyle b_ {1} = { frac { sum nolimits _ {i = 1} ^ {n} (x_ {i} - { overline {x}}) (y_ {i} - { overline { y}})} { sum nolimits _ {i = 1} ^ {n} (x_ {i} - { overline {x}}) ^ {2}}} ;}$ ${ displaystyle ; b_ {0} = { overline {y}} - b_ {1} { overline {x}}}$ $beta _ {1}$ $beta _ {0}$

Представление не искажено, потому что, включая степени свободы оценок дисперсии, оно соответствует ожиданиям при предположениях Гаусса-Маркова (см. Также оценки дисперсии переменных возмущения ). Стандартная ошибка регрессии рассчитывается как квадратный корень из среднего квадрата остатка и является отдельной мерой качества модели. Он показывает, насколько велико среднее отклонение измеренных значений от линии регрессии. Чем больше стандартная ошибка регрессии, тем хуже линия регрессии описывает распределение измеренных значений. Стандартная ошибка регрессии обычно меньше стандартной ошибки целевой переменной . Коэффициент детерминации указывается чаще, чем стандартная ошибка остатков, хотя стандартная ошибка остатков может быть более полезной при оценке качества соответствия. Если стандартная ошибка регрессии в простой линейной регрессии вставить в формулы дисперсии для и , то можно получить несмещенные оценки для и ${ Displaystyle mathbb {E} ({ шляпа { sigma}} ^ {2}) = sigma ^ {2}}$ ${ displaystyle { hat { sigma}} _ {y}}$ $beta _ {0}$ $beta _ {1}$ ${ displaystyle sigma _ {{ hat { beta}} _ {0}} ^ {2}}$ ${ displaystyle sigma _ {{ hat { beta}} _ {1}} ^ {2}}$

${ displaystyle { hat { sigma}} _ {{ hat { beta}} _ {0}} ^ {2} = { hat { sigma}} ^ {2} { frac { sum nolimits _ {i = 1} ^ {n} x_ {i} ^ {2}} {n sum nolimits _ {i = 1} ^ {n} (x_ {i} - { overline {x}}) ^ {2}}} ;}$ и . ${ displaystyle ; { hat { sigma}} _ {{ hat { beta}} _ {1}} ^ {2} = { hat { sigma}} ^ {2} { frac {1 } { sum nolimits _ {i = 1} ^ {n} (x_ {i} - { overline {x}}) ^ {2}}}}$

Кроме того, доверительные интервалы могут быть построены с использованием стандартной ошибки остатков .

Множественная линейная регрессия

В множественной линейной регрессии , то стандартная ошибка регрессии определяются

${ displaystyle { hat { sigma}} = + { sqrt {MQR}} = + { sqrt {SQR / (nk-1)}} = + { sqrt { frac {{ hat { varvec) { varepsilon}}} ^ { top} { hat { boldsymbol { varepsilon}}}} {nk-1}}} = + { sqrt { frac { left ( mathbf {y} - mathbf {X} mathbf {b} right) ^ { top} left ( mathbf {y} - mathbf {X} mathbf {b} right)} {nk-1}}}}$ с помощью оценщика наименьших квадратов . ${ Displaystyle mathbf {b} = ( mathbf {X} ^ { top} mathbf {X}) ^ {- 1} mathbf {X} ^ { top} mathbf {y}}$

Альтернативное представление стандартной ошибки регрессии является следствием того факта, что остаточная сумма квадратов также может быть представлена с использованием порождающей невязки матрицы как . Это дает стандартную ошибку регрессии
${ displaystyle SQR = { hat { varepsilon}}} ^ { top} { hat { varepsilon}}} = { varepsilon}} ^ { top} mathbf {Q} { boldsymbol { varepsilon }}}$

${ displaystyle { hat { sigma}} = { sqrt { frac { mathbf {y} ^ { top} mathbf {y} - mathbf {b} ^ { top} mathbf {X} ^ { top} mathbf {y}} {np}}} = { sqrt { frac { mathbf {y} ^ { top} { varvec {Q}} mathbf {y}} {np} }} = { sqrt { frac {{ varepsilon { varepsilon}} ^ { top} { varvec {Q}} { varepsilon}}} {np}}}}$

Если заменить неизвестное на известное в стандартном отклонении соответствующего средства оценки параметра , стандартная ошибка коэффициента регрессии возникает из ${ displaystyle { sqrt { operatorname {Var} (b_ {j})}}}$ $сигма$ $hat { sigma}$ $б_ {j}$

${ displaystyle operatorname {SE} (b_ {j}) = { sqrt { frac {{ tfrac {1} {np}} sum nolimits _ {i = 1} ^ {n} { has { varepsilon}} _ {i} ^ {2}} {(1 - { mathit {R}} _ {j} ^ {2}) sum nolimits _ {i = 1} ^ {n} (x_ { ij} - { overline {x}} _ {j}) ^ {2}}}}}$ .

Таким образом, размер стандартных ошибок оцененных параметров регрессии зависит от остаточной дисперсии, взаимозависимости объясняющих переменных и разброса соответствующих объясняющих переменных.

Индивидуальные доказательства

↑ Питер Хакл : Введение в эконометрику. 2-е обновленное издание, Pearson Deutschland GmbH, 2008 г., ISBN 978-3-86894-156-2 , стр. 72.
↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 4-е издание. Nelson Education, 2015, стр.102.
↑ Вернер Тимишль : Прикладная статистика. Введение для биологов и медицинских работников. 2013, издание 3-е, с. 313.
↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 4-е издание. Nelson Education, 2015, стр.110.
^ А. Колин Камерон, Правин К. Триведи: Микроэконометрика. Методы и приложения. Издательство Кембриджского университета, 2005, ISBN 0-521-84805-9 , стр.287.
↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 4-е издание. Nelson Education, 2015, стр. 58.
↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 5-е издание. Nelson Education, 2015, стр.101.

Источник

Как интерпретировать остаточную стандартную ошибку

Пример: интерпретация остаточной стандартной ошибки

Использование остаточной стандартной ошибки для сравнения моделей

Дополнительные ресурсы

Note:

Note:

2.3 Прогнозирование величины y

Почему мы говорим «Остаточная стандартная ошибка»?

Замечания:

Что такое Остаточное стандартное отклонение?

Ключевые моменты

Понимание остаточного стандартного отклонения

Формула для остаточного стандартного отклонения

Как рассчитать остаточное стандартное отклонение

Пример остаточного стандартного отклонения

Об этой статье

Была ли эта статья полезной?

Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач — файл n1.doc

n1.doc

9.11. Измерение вариации по уравнению регрессии

9.12. Доверительные интервалы для оценки неизвестного генерального значения yген(yх) и индивидуального значения yi

Как интерпретировать остаточную стандартную ошибку

Пример: интерпретация остаточной стандартной ошибки

Использование остаточной стандартной ошибки для сравнения моделей

Дополнительные ресурсы

Остаточная стандартная ошибка данных с заданными степенями свободы Решение

7 Ошибки Калькуляторы

Остаточная стандартная ошибка данных с заданными степенями свободы формула

Что такое стандартная ошибка и ее важность?

Введение в проблему

определение

Простая линейная регрессия

Множественная линейная регрессия

Индивидуальные доказательства

9.12. Доверительные интервалы для оценки неизвестного генерального значения y_ген(_yх) и индивидуального значения y_i