Остаточную сумму квадратов ошибки можно исследовать - Ремонт и установка крупной бытовой техники

Пусть на количественный
нормально распределенный признак X
воздействует фактор F,
который имеет p
постоянных уровней. Будем предполагать,
что число
наблюдений
(испытаний) на каждом уровне одинаково
и равно q.

Таблица 1

Номер испытания	Уровни фактора
		…
1 2 … q	…	…	… … … …	…
Групповая средняя			…

Пусть наблюдалось
значений

признака X,
где i
– номер испытания (j
– номер уровня фактора (
Результаты наблюдений приведены в
таблице 1.

Введем,
по определению,

(общая
сумма
квадратов отклонений наблюдаемых
значений от общей средней ),

(факторная
сумма квадратов
отклонений групповых средних от общей
средней, которая характеризует рассеяние
«между группами»),

(остаточная
сумма
квадратов отклонений наблюдаемых
значений группы от своей групповой
средней, которая характеризует рассеяние
«внутри групп»).

Практически
остаточную сумму находят по равенству:

Элементарными
преобразованиями можно получить формулы,
более удобные для расчетов:

где
– сумма квадратов значений
признака на уровне

сумма
значений признака на уровне .

Замечание.
Для упрощения
вычислений вычитают из каждого
наблюдаемого значения одно и то же число
C,
примерно равное общей средней. Если
уменьшенные значения ,
то

где
– сумма квадратов
уменьшенных значений признака на

уровне

– сумма уменьшенных значений
признака на уровне

Для вывода формул

и
достаточно подставить

в
соотношение
и
в

соотношение

Пояснения.
1. Убедимся,
что
характеризует воздействие фактора F.
Допустим, что фактор оказывает
существенное влияние на X.
Тогда группа наблюдаемых значений при
одном определенном уровне, вообще
говоря, отличается от групп наблюдений
на других уровнях. Следовательно,
различаются и групповые средние, причем
они тем больше рассеяны вокруг общей
средней, чем большим окажется воздействие
фактора. Отсюда следует, что для оценки
воздействия фактора целесообразно
составить сумму квадратов отклонений
групповых средних об общей средней
(отклонение возводят в квадрат, чтобы
исключить погашение положительных и
отрицательных отклонений). Умножив эту
сумму на q,
получим .
Итак,
характеризует воздействие фактора.

2. Убедимся, что

отражает влияние случайных причин.
Казалось бы, наблюдения одной группы
не должны различаться. Однако, поскольку
на X,
кроме фактора F,
воздействуют и случайные причины
наблюдения одной и той же группы, вообще
говоря, различны и, значит, рассеяны
вокруг своей групповой средней. Отсюда
следует, что для оценки влияния случайных
причин целесообразно составить сумму
квадратов отклонений наблюдаемых
значений каждой группы от своей групповой
средней, т.е. .
Итак,
характеризует воздействие случайных
причин.

3. Убедимся, что

отражает влияние и фактора и случайных
причин. Будем рассматривать все наблюдения
как единую совокупность. Наблюдаемые
значения признака различны вследствие
воздействия фактора и случайных причин.
Для оценки этого воздействия целесообразно
составить сумму квадратов отклонений
наблюдаемых значений от общей средней,
т.е. .

Итак,
характеризует влияние фактора и случайных
причин.

Приведем пример,
который наглядно показывает, что
факторная сумма отражает влияние
фактора, а остаточная – влияние случайных
причин.

Пример.
Двумя приборами произведены по два
измерения физической величины, истинный
размер которой равен x.
Рассматривая в качестве фактора
систематическую ошибку C,
а в качестве его уровней – систематические
ошибки
и
соответственно первого и второго
прибора, показать, что
определяется систематическими, а
– случайными ошибками измерений.

Решение.
Введем обозначения:
– случайные ошибки первого и второго
измерений первым прибором;
– случайные ошибки первого и второго
измерений вторым прибором.

Тогда наблюдения
значения результатов измерений
соответственно равны (первый индекс
при x
указывает номер измерения, а второй –
номер прибора):

Средние значения
измерений первым и вторым приборами
соответственно равны:

Общая
средняя

факторная
сумма

Подставив величины,
заключенные в скобках, после элементарных
преобразований получим

Мы видим, что
определяется главным образом, первым
слагаемым (поскольку случайные ошибки
измерений малы) и, следовательно,
действительно отражает влияние фактора
C.

Остаточная сумма

Подставив
величины, заключенные в скобках, получим

Мы видим, что
определяются случайными ошибками
измерений и, следовательно, действительно
отражает влияние случайных причин.

Замечание.
То, что
порождается случайными причинами,
следует также из равенства:

Действительно,

является результатом воздействия
фактора и случайных причин; вычитая
мы исключаем влияние фактора. Следовательно,
«оставшаяся часть» отражает влияние
случайных причин.

В статистике и оптимизации ошибки и остатки тесно связаны и легко запутанные меры отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». ошибка (или возмущение ) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинного значения интересующей величины (например, среднего генерального значения), и остаток наблюдаемого значения представляет собой разность между наблюдаемым значением и оценочным значением представляющей интерес величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибками регрессии и остатками регрессии, и где они приводят к концепции студентизированных остатков.

Содержание

1 Введение
2 В одномерных распределениях
- 2.1 Замечание
3 Регрессии
4 Другие варианты использования слова «ошибка» в статистике
5 См. Также
6 Ссылки
7 Внешние ссылки

Введение

Предположим, есть серия наблюдений из одномерного распределения, и мы хотим оценить среднее этого распределения. (так называемая локационная модель ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.

A статистическая ошибка (или нарушение ) — это величина, на которую наблюдение отличается от его ожидаемого значения, последнее основано на всей генеральной совокупности из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся средним для всей генеральной совокупности, обычно ненаблюдаемо, и, следовательно, статистическая ошибка также не может быть обнаружена.

A невязка (или аппроксимирующее отклонение), с другой стороны, представляет собой наблюдаемую оценку ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка из n человек. среднее значение выборки может служить хорошей оценкой среднего значения генеральной совокупности. Тогда у нас есть:

Разница между ростом каждого человека в выборке и ненаблюдаемым средним по совокупности является статистической ошибкой, тогда как
разница между ростом каждого человека в выборке и наблюдаемой выборкой среднее — это остаток.

Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, таким образом, остатки не обязательно независимы. Статистические ошибки, с другой стороны, независимы, и их сумма в случайной выборке почти наверняка не равна нулю.

Можно стандартизировать статистические ошибки (особенно нормального распределения ) в z-балле (или «стандартном балле») и стандартизировать остатки в t-статистика или, в более общем смысле, стьюдентизированные остатки.

в одномерном распределении

Если мы предположим нормально распределенную совокупность со средним μ и стандартным отклонением σ и независимо выбираем людей, тогда мы имеем

X 1,…, X n ∼ N (μ, σ 2) { displaystyle X_ {1}, dots, X_ {n} sim N ( mu, sigma ^ {2}) ,} $X_1, dots, X_n sim N ( mu, sigma ^ 2) ,$

и выборочное среднее

X ¯ = X 1 + ⋯ + X nn { displaystyle { overline {X}} = {X_ { 1} + cdots + X_ {n} over n}} $overline {X} = {X_1 + cdots + X_n over n}$

— случайная величина, распределенная так, что:

X ¯ ∼ N (μ, σ 2 n). { displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).} ${ displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).}$

Тогда статистические ошибки

ei = X i — μ, { displaystyle e_ {i} = X_ {i} — mu, ,} $e_ {i} = X_ {i} - mu, ,$

с ожидаемыми значениями нуля, тогда как остатки равны

ri = X i — X ¯. { displaystyle r_ {i} = X_ {i} — { overline {X}}.} $r_ {i} = X_ {i} - overline {X}.$

Сумма квадратов статистических ошибок, деленная на σ, имеет хи -квадратное распределение с n степенями свободы :

1 σ 2 ∑ i = 1 nei 2 ∼ χ n 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.} ${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.$

Однако это количество не наблюдается, так как среднее значение для генеральной совокупности неизвестно. Сумма квадратов остатков, с другой стороны, является наблюдаемой. Частное этой суммы по σ имеет распределение хи-квадрат только с n — 1 степенями свободы:

1 σ 2 ∑ i = 1 n r i 2 ∼ χ n — 1 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} r_ {i} ^ {2} sim chi _ {n-1} ^ { 2}.} ${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} r_ {i} ^ {2} sim chi _ {{n-1}} ^ {2}.$

Эта разница между n и n — 1 степенями свободы приводит к поправке Бесселя для оценки выборочной дисперсии генеральной совокупности с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.

Замечание

Примечательно, что сумма квадратов остатков и выборочного среднего могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу вычислений с использованием t-статистики :

T = X ¯ n — μ 0 S n / n, { displaystyle T = { frac {{ overline {X}} _ {n} — mu _ {0}} {S_ {n} / { sqrt {n}}}},} ${ displaystyle T = { frac {{ overline {X}} _ {n} - mu _ {0}} {S_ {n} / { sqrt {n}}}},}$

где X ¯ n — μ 0 { displaystyle { overline {X}} _ {n} — mu _ {0}} ${ displaystyle { overline {X}} _ {n} - mu _ {0}}$ представляет ошибки, S n { displaystyle S_ {n}} $S_ {n}$ представляет стандартное отклонение для выборки размера n и неизвестного σ, а член знаменателя S n / n { displaystyle S_ {n} / { sqrt {n}}} $S_n / sqrt n$ учитывает стандартное отклонение ошибок в соответствии с:

Var ⁡ (X ¯ n) = σ 2 n { displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}} ${ displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}}$

Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения генеральной совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяет. Это удачно, потому что это означает, что, хотя мы не знаем σ, мы знаем распределение вероятностей этого частного: оно имеет t-распределение Стьюдента с n — 1 степенями свободы. Таким образом, мы можем использовать это частное, чтобы найти доверительный интервал для μ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».

Регрессии

В регрессионном анализе различие между ошибками и остатками является тонким и важным, и приводит к концепции стьюдентизированных остатков. Для ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от подобранной функции являются остатками. Если линейная модель применима, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам. Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичностью. Если все остатки равны или не разветвляются, они проявляют гомоскедастичность.

Однако терминологическое различие возникает в выражении среднеквадратическая ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатков, а не ненаблюдаемых ошибок. Если эту сумму квадратов разделить на n, количество наблюдений, результатом будет среднее квадратов остатков. Поскольку это смещенная оценка дисперсии ненаблюдаемых ошибок, смещение устраняется путем деления суммы квадратов остатков на df = n — p — 1 вместо n, где df — число степеней свободы (n минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует объективную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.

Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они одинаковы, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равно n — p — 1, где p — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать путем деления среднего квадрата модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с.).

Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) могут различаться, даже если сами ошибки распределены одинаково. Конкретно, в линейной регрессии , где ошибки одинаково распределены, изменчивость остатков входных данных в середине области будет выше, чем изменчивость остатков на концах области: линейные регрессии соответствуют конечным точкам лучше среднего. Это также отражено в функциях влияния различных точек данных на коэффициенты регрессии : конечные точки имеют большее влияние.

Таким образом, чтобы сравнить остатки на разных входах, нужно скорректировать остатки на ожидаемую изменчивость остатков, что называется стьюдентизацией. Это особенно важно в случае обнаружения выбросов, когда рассматриваемый случай каким-то образом отличается от другого в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.

Другое использование слова «ошибка» в статистике

Использование термина «ошибка», как обсуждалось в разделах выше, означает отклонение значения от гипотетического ненаблюдаемого значение. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:

Среднеквадратичная ошибка или Среднеквадратичная ошибка (MSE) и Среднеквадратичная ошибка (RMSE) относятся к величине, на которую значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).

Сумма квадратов ошибок (SSE или SSe), обычно сокращенно SSE или SS e, относится к остаточной сумме квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой методом наименьших квадратов, где коэффициенты регрессии выбираются так, чтобы сумма квадратов минимально (т.е. его производная равна нулю).

Аналогично, сумма абсолютных ошибок (SAE) является суммой абсолютных значений остатков, которая минимизирована в наименьшие абсолютные отклонения подход к регрессии.

См. также

Портал математики

Абсолютное отклонение
Консенсус-прогнозы
Обнаружение и исправление ошибок
Объясненная сумма квадраты
Инновация (обработка сигналов)
Неподходящая сумма квадратов
Погрешность
Средняя абсолютная погрешность
Погрешность наблюдения
Распространение ошибки
Вероятная ошибка
Случайные и систематические ошибки
Разбавление регрессии
Среднеквадратичное отклонение
Ошибка выборки
Стандартная ошибка
Стьюдентизированная невязка
Ошибки типа I и типа II

Ссылки

Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Отредактированный ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X. Проверено 23 февраля 2013 г.
Кокс, Дэвид Р. ; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30(2): 248–275. JSTOR 2984505.
Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Проверено 23 февраля 2013 г.
, Энциклопедия математики, EMS Press, 2001 [1994]

Внешние ссылки

СМИ, связанные с ошибками и остатками на Викимедиа Commons

Регрессивный анализ
Часть серии по

Модели
Линейная регрессия Простая регрессия Полиномиальная регрессия Общая линейная модель
Обобщенная линейная модель Дискретный выбор Биномиальная регрессия Бинарная регрессия Логистическая регрессия Полиномиальный логит Смешанный логит Пробит Полиномиальный пробит Заказал логит Заказал пробит Пуассон
Многоуровневая модель Фиксированные эффекты Случайные эффекты Линейная модель смешанных эффектов Нелинейная модель смешанных эффектов
Нелинейная регрессия Непараметрический Полупараметрический Крепкий Квантиль Изотонический Основные компоненты Наименьший угол Местный Сегментированный
Ошибки в переменных
Оценка
Наименьших квадратов Линейный Нелинейный
Обычный Взвешенный Обобщенный
Частичное Общий Неотрицательный Регрессия хребта Регулярный
Наименьшие абсолютные отклонения Итеративно переназначенный Байесовский Байесовский многомерный
Фон
Проверка регрессии Средний и прогнозируемый ответ Ошибки и остатки Доброту соответствия Студентизованный остаток Теорема Гаусса – Маркова
Математический портал

В статистике и оптимизации ошибки и остатки являются двумя тесно связанными и легко путаемыми мерами отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». В ошибка (или же беспокойство) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинный значение интересующей величины (например, среднее значение генеральной совокупности), и остаточный наблюдаемого значения — это разница между наблюдаемым значением и по оценкам значение интересующей величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибки регрессии и остатки регрессии и где они приводят к концепции стьюдентизированных остатков.

Вступление

Предположим, что есть серия наблюдений из одномерное распределение и мы хотим оценить иметь в виду этого распределения (так называемый модель местоположения ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.

А статистическая ошибка (или же беспокойство) — это величина, на которую наблюдение отличается от ожидаемое значение, последнее основано на численность населения из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся иметь в виду всего населения, обычно не наблюдается, и, следовательно, статистическая ошибка также не может быть обнаружена.

А остаточный (или подходящее отклонение), с другой стороны, является наблюдаемым оценивать ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка п люди. В выборочное среднее может служить хорошей оценкой численность населения иметь в виду. Тогда у нас есть:

Разница между ростом каждого человека в выборке и ненаблюдаемой численность населения означает это статистическая ошибка, в то время как
Разница между ростом каждого человека в выборке и наблюдаемым образец означает это остаточный.

Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, следовательно, остатки обязательно нет независимый. Статистические ошибки, с другой стороны, независимы, и их сумма в пределах случайной выборки равна почти наверняка не ноль.

Можно стандартизировать статистические ошибки (особенно нормальное распределение ) в z-оценка (или «стандартная оценка») и стандартизируйте остатки в т-статистический, или в более общем смысле стьюдентизированные остатки.

В одномерных распределениях

Если предположить нормально распределенный совокупность со средними μ и стандартное отклонение σ, и выбираем индивидуумов независимо, то имеем

$X_1, точки, X_n sim N ( mu, sigma ^ 2) ,$

и выборочное среднее

$overline {X} = {X_1 + cdots + X_n over n}$

случайная величина, распределенная таким образом, что:

${ displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).}$

В статистические ошибки тогда

$e_ {i} = X_ {i} - mu, ,$

с ожидал значения нуля,^[1] тогда как остатки находятся

$r_ {i} = X_ {i} - overline {X}.$

Сумма квадратов статистические ошибки, деленное на σ², имеет распределение хи-квадрат с п степени свободы:

${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.$

Однако это количество не наблюдается, так как среднее значение для населения неизвестно. Сумма квадратов остатки, с другой стороны, наблюдается. Частное этой суммы по σ² имеет распределение хи-квадрат только с п — 1 степень свободы:

${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} r_ {i} ^ {2} sim chi _ {{n-1}} ^ {2 }.$

Эта разница между п и п — 1 степень свободы дает Поправка Бесселя для оценки выборочная дисперсия популяции с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.

Примечательно, что сумма квадратов остатков и средние выборочные значения могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу расчетов, включающих t-статистика:

${ displaystyle T = { frac {{ overline {X}} _ {n} - mu _ {0}} {S_ {n} / { sqrt {n}}}},}$

куда ${ displaystyle { overline {X}} _ {n} - mu _ {0}}$ представляет ошибки, $S_ {n}$ представляет собой стандартное отклонение выборки для выборки размера п, и неизвестно σ, а член знаменателя $S_n / sqrt n$ учитывает стандартное отклонение ошибок согласно:^[2]

${ displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}}$

Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяется. Это удачно, потому что это означает, что даже если мы не знаемσ, мы знаем распределение вероятностей этого частного: оно имеет Распределение Стьюдента с п — 1 степень свободы. Поэтому мы можем использовать это частное, чтобы найти доверительный интервал заμ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».^[3]

Регрессии

В регрессивный анализ, различие между ошибки и остатки тонкий и важный, и ведет к концепции стьюдентизированные остатки. При наличии ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от приспособленный функции — остатки. Если применима линейная модель, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам.^[2] Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичность. Если все остатки равны или не разветвляются, они демонстрируют гомоскедастичность.

Однако возникает терминологическая разница в выражении среднеквадратичная ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатки, а не ненаблюдаемые ошибки. Если эту сумму квадратов разделить на п, количество наблюдений, результат — это среднее квадратов остатков. Поскольку это пристрастный Для оценки дисперсии ненаблюдаемых ошибок смещение устраняется путем деления суммы квадратов остатков на df = п − п — 1 вместо п, куда df это количество степени свободы (п минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует несмещенную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.^[4]

Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они такие же, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равны п − п — 1, где п — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать, разделив средний квадрат модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с).^[5]

Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) может отличаться даже если сами ошибки одинаково распределены. Конкретно в линейная регрессия где ошибки одинаково распределены, вариативность остатков входных данных в середине области будет выше чем изменчивость остатков на концах области:^[6] линейные регрессии лучше подходят для конечных точек, чем средние. Это также отражено в функции влияния различных точек данных на коэффициенты регрессии: конечные точки имеют большее влияние.

Таким образом, чтобы сравнить остатки на разных входах, необходимо скорректировать остатки на ожидаемую изменчивость остатки, который называется студенчество. Это особенно важно в случае обнаружения выбросы, где рассматриваемый случай чем-то отличается от другого случая в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.

Другое использование слова «ошибка» в статистике

Термин «ошибка», как обсуждалось в предыдущих разделах, используется в смысле отклонения значения от гипотетического ненаблюдаемого значения. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:

Средняя квадратичная ошибка или же среднеквадратичная ошибка (MSE) и Средняя квадратическая ошибка (RMSE) относятся к количеству, на которое значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).

Сумма квадратов ошибок (SSE или же SS_е), обычно сокращенно SSE или SS_е, относится к остаточная сумма квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой наименьших квадратов, когда коэффициенты регрессии выбираются таким образом, чтобы сумма квадратов была минимальной (т. Е. Ее производная равна нулю).

Точно так же сумма абсолютных ошибок (SAE) — сумма абсолютных значений остатков, которая минимизируется в наименьшие абсолютные отклонения подход к регрессу.

Смотрите также

Абсолютное отклонение
Консенсус-прогнозы
Обнаружение и исправление ошибок
Объясненная сумма квадратов
Инновации (обработка сигналов)
Неподходящая сумма квадратов
Допустимая погрешность
Средняя абсолютная ошибка
Ошибка наблюдения
Распространение ошибки
Вероятная ошибка
Случайные и систематические ошибки
Разбавление регрессии
Среднеквадратичное отклонение
Ошибка выборки
Стандартная ошибка
Студентизованный остаток
Ошибки типа I и типа II

внешняя ссылка

СМИ, связанные с Ошибки и остатки в Wikimedia Commons

From Wikipedia, the free encyclopedia

In statistics, the residual sum of squares (RSS), also known as the sum of squared estimate of errors (SSE), is the sum of the squares of residuals (deviations predicted from actual empirical values of data). It is a measure of the discrepancy between the data and an estimation model, such as a linear regression. A small RSS indicates a tight fit of the model to the data. It is used as an optimality criterion in parameter selection and model selection.

In general, total sum of squares = explained sum of squares + residual sum of squares. For a proof of this in the multivariate ordinary least squares (OLS) case, see partitioning in the general OLS model.

One explanatory variable[edit]

In a model with a single explanatory variable, RSS is given by:^[1]

${displaystyle operatorname {RSS} =sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}}$

where y_i is the i^th value of the variable to be predicted, x_i is the i^th value of the explanatory variable, and $f(x_{i})$ is the predicted value of y_i (also termed ${hat {y_{i}}}$ ).
In a standard linear simple regression model, ${displaystyle y_{i}=alpha +beta x_{i}+varepsilon _{i},}$ , where $alpha$ and $beta$ are coefficients, y and x are the regressand and the regressor, respectively, and ε is the error term. The sum of squares of residuals is the sum of squares of ${displaystyle {widehat {varepsilon ,}}_{i}}$ ; that is

${displaystyle operatorname {RSS} =sum _{i=1}^{n}({widehat {varepsilon ,}}_{i})^{2}=sum _{i=1}^{n}(y_{i}-({widehat {alpha ,}}+{widehat {beta ,}}x_{i}))^{2}}$

where ${displaystyle {widehat {alpha ,}}}$ is the estimated value of the constant term $alpha$ and ${displaystyle {widehat {beta ,}}}$ is the estimated value of the slope coefficient $beta$ .

Matrix expression for the OLS residual sum of squares[edit]

The general regression model with n observations and k explanators, the first of which is a constant unit vector whose coefficient is the regression intercept, is

$y=Xbeta +e$

where y is an n × 1 vector of dependent variable observations, each column of the n × k matrix X is a vector of observations on one of the k explanators, $beta$ is a k × 1 vector of true coefficients, and e is an n× 1 vector of the true underlying errors. The ordinary least squares estimator for $beta$ is

${displaystyle X{hat {beta }}=yiff }$

${displaystyle X^{operatorname {T} }X{hat {beta }}=X^{operatorname {T} }yiff }$

${displaystyle {hat {beta }}=(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y.}$

The residual vector ${displaystyle {hat {e}}=y-X{hat {beta }}=y-X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y}$ ; so the residual sum of squares is:

${displaystyle operatorname {RSS} ={hat {e}}^{operatorname {T} }{hat {e}}=|{hat {e}}|^{2}}$ ,

(equivalent to the square of the norm of residuals). In full:

${displaystyle operatorname {RSS} =y^{operatorname {T} }y-y^{operatorname {T} }X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y=y^{operatorname {T} }[I-X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }]y=y^{operatorname {T} }[I-H]y}$ ,

where H is the hat matrix, or the projection matrix in linear regression.

Relation with Pearson’s product-moment correlation[edit]

The least-squares regression line is given by

$y=ax+b$ ,

where ${displaystyle b={bar {y}}-a{bar {x}}}$ and ${displaystyle a={frac {S_{xy}}{S_{xx}}}}$ , where ${displaystyle S_{xy}=sum _{i=1}^{n}({bar {x}}-x_{i})({bar {y}}-y_{i})}$ and ${displaystyle S_{xx}=sum _{i=1}^{n}({bar {x}}-x_{i})^{2}.}$

Therefore,

${displaystyle {begin{aligned}operatorname {RSS} &=sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}=sum _{i=1}^{n}(y_{i}-(ax_{i}+b))^{2}=sum _{i=1}^{n}(y_{i}-ax_{i}-{bar {y}}+a{bar {x}})^{2}[5pt]&=sum _{i=1}^{n}(a({bar {x}}-x_{i})-({bar {y}}-y_{i}))^{2}=a^{2}S_{xx}-2aS_{xy}+S_{yy}=S_{yy}-aS_{xy}=S_{yy}left(1-{frac {S_{xy}^{2}}{S_{xx}S_{yy}}}right)end{aligned}}}$

where ${displaystyle S_{yy}=sum _{i=1}^{n}({bar {y}}-y_{i})^{2}.}$

The Pearson product-moment correlation is given by ${displaystyle r={frac {S_{xy}}{sqrt {S_{xx}S_{yy}}}};}$ therefore, ${displaystyle operatorname {RSS} =S_{yy}(1-r^{2}).}$

References[edit]

^ Archdeacon, Thomas J. (1994). Correlation and regression analysis : a historian’s guide. University of Wisconsin Press. pp. 161–162. ISBN 0-299-13650-7. OCLC 27266095.

Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley. ISBN 0-471-17082-8.

From Wikipedia, the free encyclopedia

One explanatory variable[edit]

In a model with a single explanatory variable, RSS is given by:^[1]

${displaystyle operatorname {RSS} =sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}}$

${displaystyle operatorname {RSS} =sum _{i=1}^{n}({widehat {varepsilon ,}}_{i})^{2}=sum _{i=1}^{n}(y_{i}-({widehat {alpha ,}}+{widehat {beta ,}}x_{i}))^{2}}$

where ${displaystyle {widehat {alpha ,}}}$ is the estimated value of the constant term $alpha$ and ${displaystyle {widehat {beta ,}}}$ is the estimated value of the slope coefficient $beta$ .

Matrix expression for the OLS residual sum of squares[edit]

The general regression model with n observations and k explanators, the first of which is a constant unit vector whose coefficient is the regression intercept, is

$y=Xbeta +e$

${displaystyle X{hat {beta }}=yiff }$

${displaystyle X^{operatorname {T} }X{hat {beta }}=X^{operatorname {T} }yiff }$

${displaystyle {hat {beta }}=(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y.}$

The residual vector ${displaystyle {hat {e}}=y-X{hat {beta }}=y-X(X^{operatorname {T} }X)^{-1}X^{operatorname {T} }y}$ ; so the residual sum of squares is:

${displaystyle operatorname {RSS} ={hat {e}}^{operatorname {T} }{hat {e}}=|{hat {e}}|^{2}}$ ,

(equivalent to the square of the norm of residuals). In full:

where H is the hat matrix, or the projection matrix in linear regression.

Relation with Pearson’s product-moment correlation[edit]

The least-squares regression line is given by

$y=ax+b$ ,

Therefore,

where ${displaystyle S_{yy}=sum _{i=1}^{n}({bar {y}}-y_{i})^{2}.}$

The Pearson product-moment correlation is given by ${displaystyle r={frac {S_{xy}}{sqrt {S_{xx}S_{yy}}}};}$ therefore, ${displaystyle operatorname {RSS} =S_{yy}(1-r^{2}).}$

References[edit]

^ Archdeacon, Thomas J. (1994). Correlation and regression analysis : a historian’s guide. University of Wisconsin Press. pp. 161–162. ISBN 0-299-13650-7. OCLC 27266095.

Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley. ISBN 0-471-17082-8.

Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.

Мы часто используем три разных значения суммы квадратов , чтобы измерить, насколько хорошо линия регрессии действительно соответствует данным:

1. Общая сумма квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).

SST = Σ(y i – y ) 2

2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).

SSR = Σ(ŷ i – y ) 2

3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между предсказанными точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).

SSE = Σ(ŷ i – y i ) 2

Между этими тремя показателями существует следующая зависимость:

SST = SSR + SSE

Таким образом, если мы знаем две из этих мер, мы можем использовать простую алгебру для вычисления третьей.

SSR, SST и R-квадрат

R-квадрат , иногда называемый коэффициентом детерминации, является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных. Он представляет собой долю дисперсии переменной отклика , которая может быть объяснена предикторной переменной.

Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.

Используя SSR и SST, мы можем рассчитать R-квадрат как:

R-квадрат = SSR / SST

Например, если SSR для данной модели регрессии составляет 137,5, а SST — 156, тогда мы рассчитываем R-квадрат как:

R-квадрат = 137,5/156 = 0,8814

Это говорит нам о том, что 88,14% вариации переменной отклика можно объяснить переменной-предиктором.

Расчет SST, SSR, SSE: пошаговый пример

Предположим, у нас есть следующий набор данных, который показывает количество часов, отработанных шестью разными студентами, а также их итоговые оценки за экзамены:

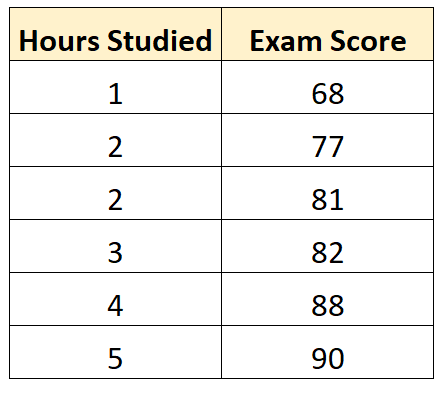
Используя некоторое статистическое программное обеспечение (например, R , Excel , Python ) или даже вручную , мы можем найти, что линия наилучшего соответствия:

Оценка = 66,615 + 5,0769 * (часы)

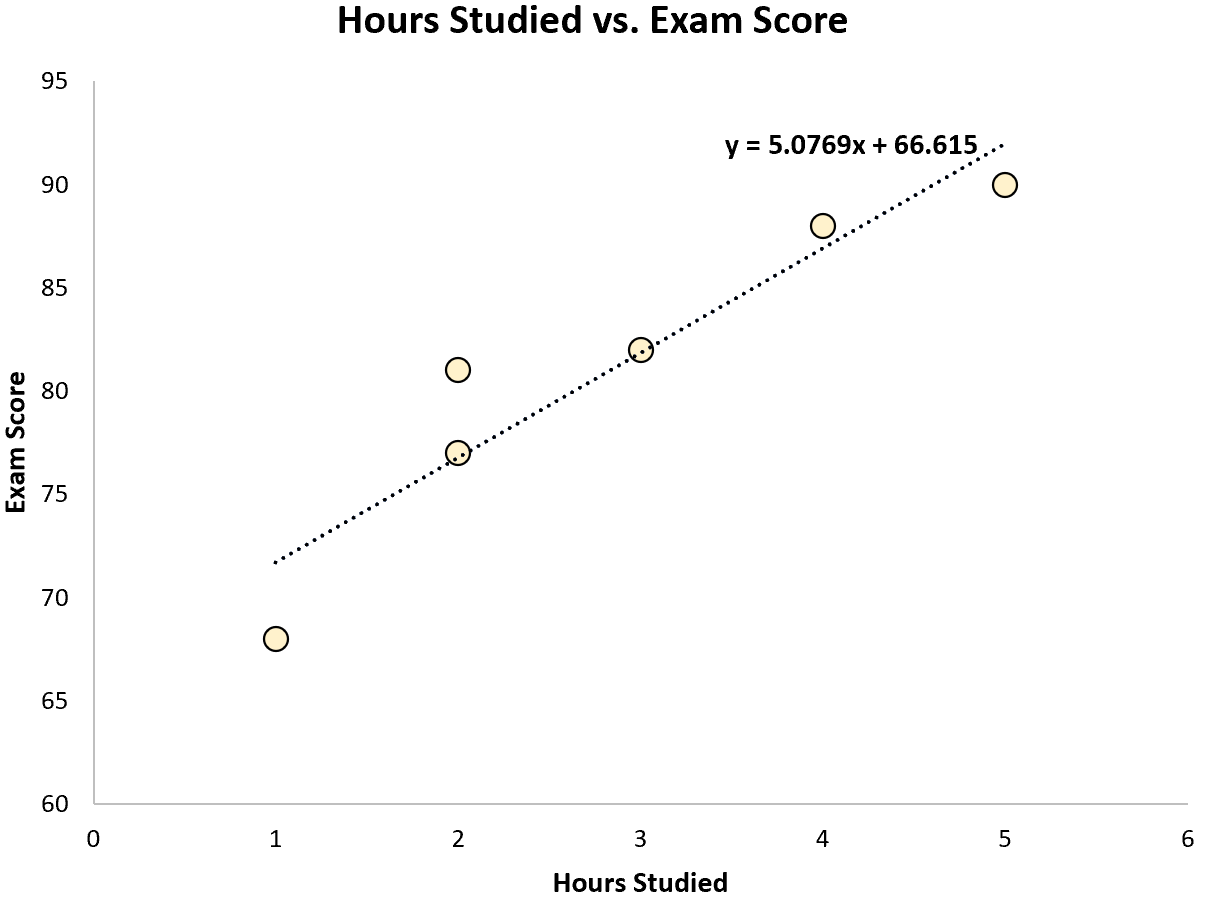
Как только мы узнаем строку уравнения наилучшего соответствия, мы можем использовать следующие шаги для расчета SST, SSR и SSE:

Шаг 1: Рассчитайте среднее значение переменной ответа.

Среднее значение переменной отклика ( y ) оказывается равным 81 .

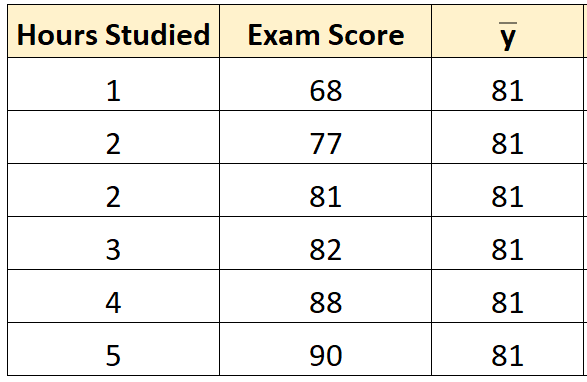
Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.

Затем мы можем использовать уравнение наилучшего соответствия для расчета прогнозируемого экзаменационного балла () для каждого учащегося.

Например, предполагаемая оценка экзамена для студента, который учился один час, такова:

Оценка = 66,615 + 5,0769*(1) = 71,69 .

Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого ученика:

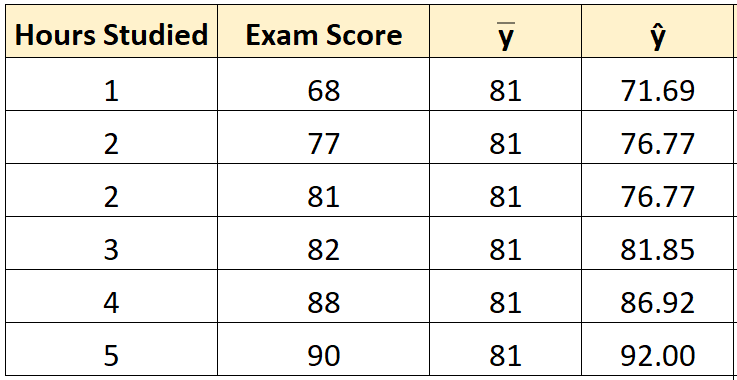
Шаг 3: Рассчитайте общую сумму квадратов (SST).

Далее мы можем вычислить общую сумму квадратов.

Например, сумма квадратов для первого ученика равна:

(y i – y ) 2 = (68 – 81) 2 = 169 .

Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:

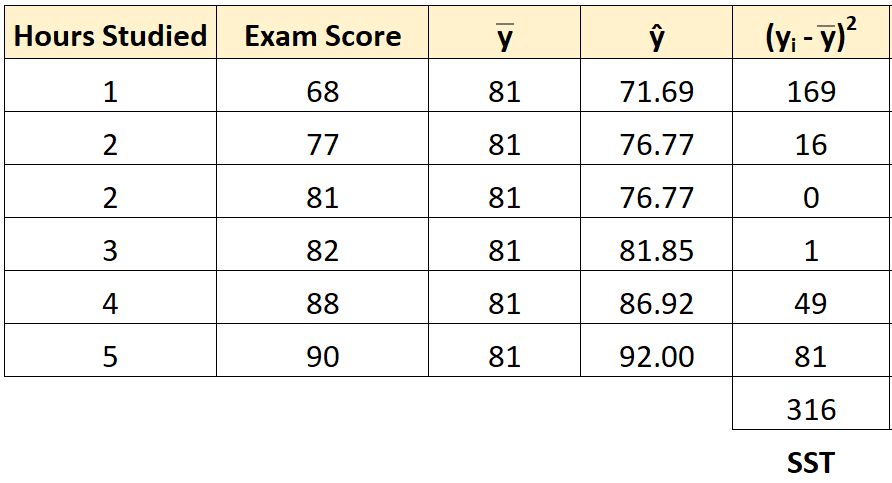
Сумма квадратов получается 316 .

Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).

Далее мы можем вычислить сумму квадратов регрессии.

Например, сумма квадратов регрессии для первого ученика равна:

(ŷ i – y ) 2 = (71,69 – 81) 2 = 86,64 .

Мы можем использовать тот же подход, чтобы найти сумму квадратов регрессии для каждого ученика:

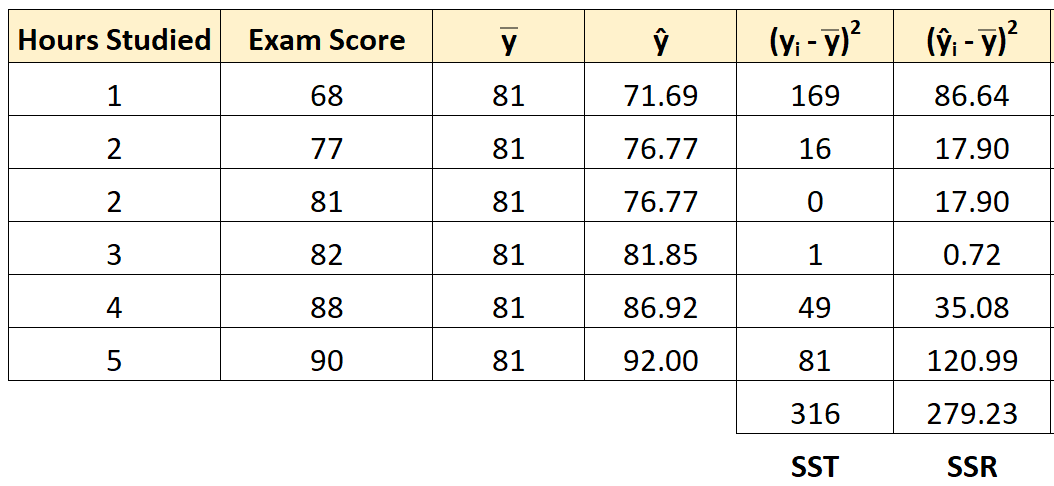
Сумма квадратов регрессии оказывается равной 279,23 .

Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).

Далее мы можем вычислить сумму квадратов ошибок.

Например, ошибка суммы квадратов для первого ученика:

(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .

Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:

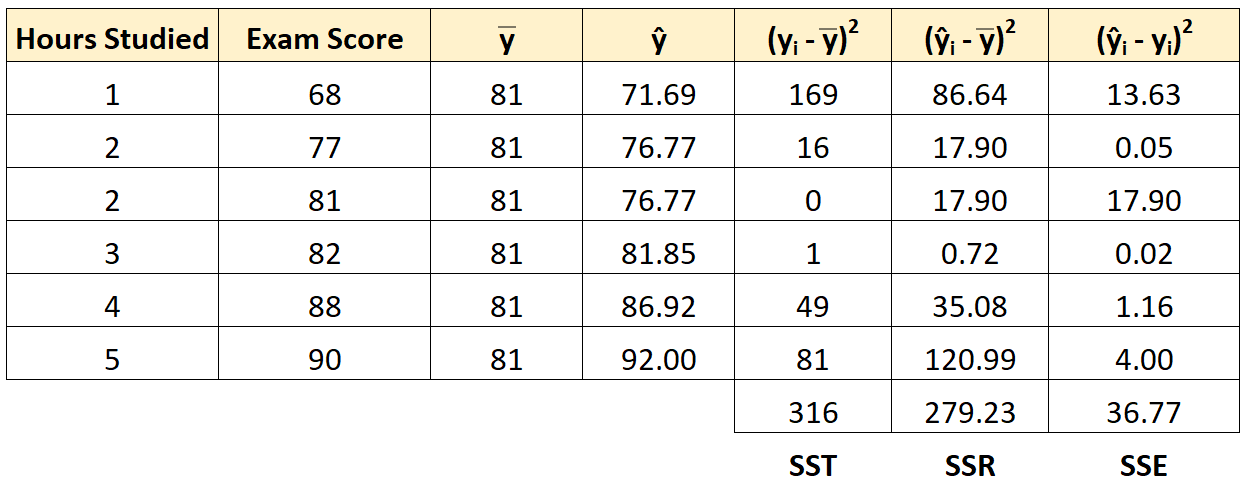
Пример расчета SST, SSR и SSE для линейной регрессии

Мы можем проверить, что SST = SSR + SSE

SST = SSR + SSE
316 = 279,23 + 36,77

Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:

R-квадрат = SSR / SST
R-квадрат = 279,23/316
R-квадрат = 0,8836

Это говорит нам о том, что 88,36% вариаций в экзаменационных баллах можно объяснить количеством часов обучения.

Дополнительные ресурсы

Вы можете использовать следующие калькуляторы для автоматического расчета SST, SSR и SSE для любой простой линии линейной регрессии:

Калькулятор ТПН
Калькулятор ССР
Калькулятор SSE

Макеты страниц

информацию относительно того, почему построенная модель недостаточна правильно объясняет наблюдаемый разброс значений зависимой переменной исследовании остатков см. гл. 3.) Пусть обозначает величину среднего для «истинной» модели при Тогда мы можем записать:

где

Величина это ошибка смещения при Если модель верна, то Если же модель не верна, то и его значение зависит от «истинной» модели и значения Переменная это случайная величина, имеющая нулевое среднее, так как

и это верно независимо от того, будет ли модель правильна будет ли равно

Можно показать, что коррелированны и величина имеет математическое ожидание, или среднее значение где дисперсия ошибки. Исходя из этого можно далее показать, что остаточный средний квадрат, т. е. величина

имеет математическое ожидание, или среднее значение если постулированная модель корректна, и если модель не корректна. Если модель корректна, т. е. то остатки будут (коррелированными) случайными отклонениями и остаточный средний квадрат можно использовать как оценку дисперсии ошибки

Однако если модель не корректна, т. е. то остатки содержат оба компонента: случайный и систематический Мы можем рассматривать их соответственно как случайную ошибку разброса и систематическую ошибку смещения. Таким образом, остаточная сумма квадратов будет иметь тенденцию к разбуханию и перестанет служить удовлетворительной мерой случайных вариаций, имеющихся в наблюдениях. Однако так как средний квадрат есть случайная величина, то может оказаться, что он не будет иметь большого значения, даже если смещение существует. С некоторыми аналогичными задачами в общей проблеме регрессии можно познакомиться в параграфе 2.12.

В простом случае подбора прямой обычно можно определить ошибку смещения, непосредственно исследуя график с данными (см.,

например, рис. 1.10). Если модель более сложна и (или) включает больше переменных, то это невозможно. Если существует априорная оценка (под «априорной оценкой» мы понимаем оценку, полученную на основе ранее выполненных опытов, в которых варьировались изучаемые условия), то можно увидеть (или проверить по F-критерию), значимо ли остаточная сумма квадратов превышает нашу априорную оценку. Если она значимо больше, то мы говорим, что имеет место неадекватность и следует пересмотреть модель, поскольку в данной форме она непригодна. Если априорной оценки нет, но измерения повторялись (два раза или более) при одинаковых значениях X, то мы можем использовать эти повторения для получения оценки Про такую оценку говорят, что она представляет «чистую» ошибку, потому что если сделать X одинаковыми для двух наблюдений, то только случайные вариации могут влиять на результаты и создавать разброс между ними. Такие различия обычно будут обеспечивать получение оценки которая более надежна, чем оценки, получаемые из любых других источников. По этой причине имеет смысл при планировании экспериментов ставить опыты с повторениями.

(Примечание. Важно понимать, что повторение опытов может быть в некотором смысле верным и неверным. Пусть, например, мы будем пытаться применять регрессионный метод к зависимости (тест на коэффициент интеллекта от X (рост человека). Можно получить верные повторные точки, если измерять отдельно у двух людей абсолютно одинакового роста. Если, однако, мы измеряем дважды одного человека, то сможем получить вовсе не правильные повторные точки в нашем смысле, а только «переподтвержденную» единственную точку. Она будет содержать информацию о разбросе метода испытаний, являющемся составной частью разброса но не сможет обеспечить информацию относительно разброса в между людьми с одинаковым ростом, определяющим в нашей задаче. В химических экспериментах последовательные наблюдения, выполненные при установившемся состоянии, тоже не дают верных повторных точек. Если же, однако, некоторое множество условий проведения опыта устанавливать заново после промежуточных опытов при других уровнях X и в отсутствии дрейфа уровня отклика, то удается получить верные повторные опыты. Имея это в виду, к повторяющимся опытам, обнаруживающим вопреки ожиданиям заметное согласие, следует всегда относиться с осторожностью и подвергать их дополнительному исследованию.)

Когда в данных содержатся повторные опыты, нам нужны дополнительные обозначения для множества наблюдений при одном и том же значении Пусть мы имеем различных значений X и

к из этих значений где относятся наблюдений. Тогда мы говорим, что

Всего получается

наблюдений. Вклад суммы квадратов, связанной с «чистой» ошибкой для наблюдений при будет равен внутренней сумме квадратов относительно их среднего

Объединяя внутренние суммы квадратов для всех серий повторных опытов, мы получим общую сумму квадратов «чистых» ошибок в виде

со степенями свободы

Отсюда средний квадрат «чистых» ошибок равен:

и он служит оценкой безотносительно к тому, корректна ли подобранная модель. Словом, эта величина — полная сумма квадратов «между повторениями (параллельными опытами)», деленная на общее число степеней свободы.

(Примечание. Если имеются только два наблюдения в точке то

Это удобная форма для вычислений. Такая имеет одну степень свободы.)

Таким образом, сумма квадратов «чистых» ошибок фактически оказывается частью остаточной суммы квадратов, что мы теперь и покажем. Остаток для наблюдения при можно записать в виде

воспользовавшись тем обстоятельством, что все повторные точки при любом имеют одно и то же предсказанное значение Если мы возведем в квадрат обе части этого выражения, а затем просуммируем их по и по то получим причем парные произведения исчезают при суммировании по и для каждого

Рис. 1.9. Разложение остаточной суммы квадратов на суммы квадратов, обусловленные неадекватностью и «чистой» ошибкой

Слева в уравнении (1.5.8) стоит остаточная сумма квадратов. Первый член в правой части — это сумма квадратов чистых ошибок. Последний член мы называем суммой квадратов неадекватности. Отсюда следует, что сумму квадратов, обусловленную «чистой» ошибкой, можно ввести в таблицу дисперсионного анализа, как показано на рис. 1.9. Обычный прием — это сравнение отношений со -ной точкой -распределения при и степенях свободы. Если это отношение является:

1) значимым, то это показывает, что модель, по-видимому, неадекватна. Можно попытаться изучить, когда и как встречается неадекватность. (См. комментарии к различным графикам остатков в гл. 3. Заметим, однако, что графики остатков — стандартная процедура, которая должна применяться в любом регрессионном анализе, а не только в тех случаях, когда неадекватность может быть продемонстрирована с помощью этого критерия.);

2) незначимым, то это показывает, что, по-видимому, нет оснований сомневаться в адекватности модели и что как средний квадрат, связанный с «чистой» ошибкой, так и средний квадрат, обусловленный

неадекватностью, могут использоваться как оценки Объединенная оценка может быть получена из суммы квадратов, связанной с «чистой» ошибкой, и суммы квадратов, связанной с неадекватностью, путем объединения их в остаточную сумму квадратов и деления ее на остаточное число степеней свободы что дает внимание, что остатки все же должны исследоваться — см. замечания после нижеследующего примера, с. 61.)

Мы уже отмечали выше, что повторные опыты должны быть действительно повторными. Если же это не так, то будет проявлять склонность к переоценке а -критерий для проверки неадекватности в свою очередь будет иметь тенденцию к ошибочному «определению» отсутствия неадекватности.

Пример. Так как предыдущий пример, который включал данные из приложения А, не содержал параллельных опытов, мы рассмотрим специально построенный пример (табл. 1.6), иллюстрирующий материал этого параграфа о неадекватности и «чистой» ошибке. По следующим данным была оценена линия регрессии Таблица дисперсионного анализа представлена табл. 1.7. Заметим, что на этом этапе значение F для регрессии не проверяется, поскольку мы еще не знаем, адекватна ли модель.

Таблица 1.6. Двадцать четыре наблюдения с частичными повторами

Таблица 1.7. Таблица дисперсионного анализа для данных из табл. 1.6

1. связанная с «чистой» ошибкой, из повторений при есть с 1 степенью свободы.

2. связанная с «чистой» ошибкой, из повторений при есть с 2 степенями свободы. Аналогичные вычисления дают следующие величины:

Теперь можно переписать данные дисперсионного анализа, как показано в табл. 1.8. Отношение не значимо, так как оно меньше единицы Поэтому на основе такого критерия по крайней мере нет оснований сомневаться в адекватности нашей модели и можно использовать как оценку для чтобы иметь возможность воспользоваться -критерием для проверки значимости всей регрессии.

Таблица 1.8. Дисперсионный анализ (демонстрация неадекватности)

Этот последний -критерий состоятелен, только если нет неадекватности представления результатов нашей моделью. Чтобы подчеркнуть этот момент, мы подытожим все необходимые действия, когда наши данные содержат повторные наблюдения:

1. Подобрать модель, составить простую таблицу дисперсионного анализа с двумя входами: регрессией и остатком. Но для общей регрессии пока не использовать -критерий.

2. Вычислить сумму квадратов, связанную с «чистой» ошибкой и разложить остаточную сумму квадратов, как на рис. 1.9. (Ну а если «чистой» ошибки нет, то остается проверять неадекватность посредством анализа графиков остатков (см. гл. 3).)

3. Применить -критерий для неадекватности. Если критерий неадекватности не значим, т. е. нет смысла сомневаться в адекватности модели, то перейти к пункту 46.

4а. Значимая неадекватность. Прекратить анализ подобранной модели и искать пути улучшения модели методами анализа остатков (см. гл. 3). Не применять -критерий для общей регрессии (см. с. 157) и не пытаться строить доверительные интервалы. Если нет адекватности подобранной модели, то не верны предпосылки, которые лежат в основе этих операций.

46. Неадекватность не значима. Снова объединить суммы квадратов для «чистых» ошибок и неадекватности в остаточную сумму квадратов. Использовать остаточный средний квадрат в качестве оценки для применить -критерий для общей регрессии, получить доверительные пределы для «истинного» среднего значения вычислить и т. д. А графики для остатков все-таки надо строить и надо исследовать их особенности (см. гл. 3).

Заметим, что если модель «проходит через все барьеры», это еще не означает, что она правильна; просто нет оснований считать ее неадекватной имеющимся данным. Если неадекватность обнаружена, то может понадобиться другая модель, возможно, квадратичная вида На рис. 1.10 показаны некоторые ситуации, которые могут возникнуть, когда прямая строится по данным шаг за шагом

Влияние повторных опытов на R2

Как мы отмечали в параграфе 1.4, невозможно, чтобы величина достигла 1, если есть повторные опыты, сколько бы членов ни использовалось в модели. (Тривиальное исключение появляется, когда что случается крайне редко при повторении опытов.) Никакая модель не может изменить вариацию, обусловленную «чистой» ошибкой (см. решение упражнения 13 из гл. 1).

Для демонстрации этого в нашем последнем примере напомним, что сумма квадратов, обусловленная «чистой» ошибкой, равна 12,470 при 11 степенях свободы. То, что модель подогнана к этим данным, не имеет значения, все равно величина 12,470 остается неизменяемой и необъясняемой. Следовательно, максимум достижимый при этих данных, есть

(кликните для просмотра скана)

или 54,68 %. Однако то значение что фактически достигнуто для подобранной модели, равно:

Иными словами, мы можем объяснить или около того, что вообще может быть объяснено. Этот результат, хоть он и не слишком впечатляющ, выглядит привлекательнее. Такие расчеты часто позволяют глубже понять, чего модель действительно стоит по сравнению с тем, что она могла бы стоить в лучшем случае.

«Чистая» ошибка в многофакторном случае

Приведенные выше для случая одной переменной формулы применимы и в общем, сколько бы предикторов ни оказалось в данных. Единственный момент, который надо иметь в виду, состоит в том, что у повторных опытов должны совпадать все координаты, т. е. они должны иметь одни и те же значения для совпадающие значения для и т. д. Например, следующие 4 отклика для 4 точек

дают повторные опыты. Однако 4 точки

уже не дают повторных опытов, поскольку координаты во всех этих случаях различны.

Приблизительные повторы

Некоторые наборы данных не имеют или имеют очень мало повторных опытов, зато в них есть приблизительные повторы, т. е. множества опытов, которые очень близки друг к другу в пространстве X по сравнению с общим разбросом точек в этом пространстве. В таких случаях мы можем воспользоваться этими псевдоповторами так, как будто они обычные повторы и вычислить по ним приближенную сумму квадратов, связанную с «чистой» ошибкой. Тогда ее можно использовать в анализе стандартным способом. Пример такого использования приведен в упражнении 12 из гл. 1.

Оглавление

ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Глава 1. ПОДБОР ПРЯМОЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
1.1. ПРЯМОЛИНЕЙНАЯ ЗАВИСИМОСТЬ МЕЖДУ ДВУМЯ ПЕРЕМЕННЫМИ
1.2. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПОДБОР ПРЯМОЙ
1.3. ТОЧНОСТЬ ОЦЕНКИ РЕГРЕССИИ
1.4. ИССЛЕДОВАНИЕ УРАВНЕНИЯ РЕГРЕССИИ
Стандартное отклонение углового коэффициента … доверительный интервал для …
Стандартное отклонение свободного члена; доверительный интервал для …
Стандартное отклонение
F-критерий значимости регрессии
1.5. НЕАДЕКВАТНОСТЬ И «ЧИСТАЯ» ОШИБКА
1.6. КОРРЕЛЯЦИЯ МЕЖДУ X И Y
Корреляция и регрессия
Проверка значимости коэффициента парной корреляции
1.7. ОБРАТНАЯ РЕГРЕССИЯ (СЛУЧАЙ ПРЯМОЙ ЛИНИИ)
1.8. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ГЛ. 1, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ЗНАЧЕНИЕ
Глава 2. МАТРИЧНЫЙ ПОДХОД К ЛИНЕЙНОЙ РЕГРЕССИИ
Правила операций с матрицами
Транспонирование и обращение
Решение нормальных уравнений
2.2. ДИСПЕРСИОННЫЙ АНАЛИЗ В МАТРИЧНЫХ ОБОЗНАЧЕНИЯХ
2.3. ДИСПЕРСИЯ И КОВАРИАЦИЯ КОЭФФИЦИЕНТОВ НА ОСНОВЕ МАТРИЧНЫХ ВЫЧИСЛЕНИЙ
2.4. ДИСПЕРСИЯ ВЕЛИЧИНЫ Y В МАТРИЧНЫХ ОБОЗНАЧЕНИЯХ
2.5. РЕЗЮМЕ К МАТРИЧНОМУ ПОДХОДУ ПРИ ПОДБОРЕ ПРЯМОЙ
2.6. СЛУЧАЙ ОБЩЕЙ РЕГРЕССИИ
Предположения, независимые от распределения
Приведенная R2-статистика
Предположения, связанные с распределением
2.7. ПРИНЦИП «ДОПОЛНИТЕЛЬНОЙ СУММЫ КВАДРАТОВ»
2.8. ОРТОГОНАЛЬНЫЕ СТОЛБЦЫ В МАТРИЦЕ X
2.9. ЧАСТНЫЕ И ПОСЛЕДОВАТЕЛЬНЫЕ F-КРИТЕРИИ
2.10. ПРОВЕРКА ОБЩЕЙ ЛИНЕЙНОЙ ГИПОТЕЗЫ В РЕГРЕССИОННЫХ ЗАДАЧАХ
Проверка общей линейной гипотезы Cb = 0
2.11. ВЗВЕШЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Остатки во взвешенном методе наименьших квадратов
Численный пример использования взвешенного метода наименьших квадратов
2.12. СМЕЩЕНИЕ РЕГРЕССИОННЫХ ОЦЕНОК
Влияние смещения на анализ с помощью метода наименьших квадратов
Определение математического ожидания средних квадратов
2.13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
2.14. НЕКОТОРЫЕ ЗАМЕЧАНИЯ ОТНОСИТЕЛЬНО ОШИБОК В ПРЕДИКТОРАХ (ОДНОВРЕМЕННО С ОШИБКАМИ В ОТКЛИКАХ)
2.15. ОБРАТНАЯ РЕГРЕССИЯ (В СЛУЧАЕ МНОГОМЕРНОГО ПРЕДИКТОРА)
Приложение 2А. НЕКОТОРЫЕ ПОЛЕЗНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ
Приложение 2Б. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДОПОЛНИТЕЛЬНОЙ СУММЫ КВАДРАТОВ
Приложение 2В. НАСКОЛЬКО ЗНАЧИМОЙ ДОЛЖНА БЫТЬ РЕГРЕССИЯ?
Приложение 2Г. НЕОПРЕДЕЛЕННЫЕ МНОЖИТЕЛИ ЛАГРАНЖА
Глава 3. ИССЛЕДОВАНИЕ ОСТАТКОВ
3.2. ГРАФИК ВРЕМЕННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
3.3. ГРАФИК ЗАВИСИМОСТИ ОСТАТКОВ ОТ Yi
3.4. ГРАФИК ЗАВИСИМОСТИ ОСТАТКОВ ОТ ПРЕДИКТОРНЫХ ПЕРЕМЕННЫХ
3.5. ДРУГИЕ ГРАФИКИ ОСТАТКОВ
3.6. СТАТИСТИКИ ДЛЯ ИССЛЕДОВАНИЯ ОСТАТКОВ
3.7. КОРРЕЛЯЦИЯ МЕЖДУ ОСТАТКАМИ
3.8. ВЫБРОСЫ
3.9. СЕРИАЛЬНАЯ КОРРЕЛЯЦИЯ ОСТАТКОВ
3.10. ИССЛЕДОВАНИЕ СЕРИЙ НА ГРАФИКАХ ВРЕМЕННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ОСТАТКОВ
3.11. КРИТЕРИЙ ДАРВИНА—УОТСОНА ДЛЯ НЕКОТОРЫХ ВИДОВ СЕРИАЛЬНОЙ КОРРЕЛЯЦИИ
3.12. ОПРЕДЕЛЕНИЕ ВЛИЯЮЩИХ НАБЛЮДЕНИЙ
Приложение 3А. НОРМАЛЬНЫЕ И ПОЛУНОРМАЛЬНЫЕ ГРАФИКИ
Глава 4. ДВЕ ПРЕДИКТОРНЫЕ ПЕРЕМЕННЫЕ
4.1. СВЕДЕНИЕ МНОЖЕСТВЕННОЙ РЕГРЕССИИ С ДВУМЯ ПРЕДИКТОРНЫМИ ПЕРЕМЕННЫМИ К ПОСЛЕДОВАТЕЛЬНОСТИ ПРОСТЫХ ЛИНЕЙНЫХ РЕГРЕССИЙ
4.2. ИССЛЕДОВАНИЕ УРАВНЕНИЯ РЕГРЕССИИ
Глава 5. БОЛЕЕ СЛОЖНЫЕ МОДЕЛИ
5.1. ПОЛИНОМИАЛЬНЫЕ МОДЕЛИ РАЗЛИЧНЫХ ПОРЯДКОВ
5.2. МОДЕЛИ, ВКЛЮЧАЮЩИЕ ПРЕОБРАЗОВАНИЯ, ОТЛИЧНЫЕ ОТ ЦЕЛЫХ СТЕПЕНЕЙ
5.3. СЕМЕЙСТВА ПРЕОБРАЗОВАНИЙ
5.4. ИСПОЛЬЗОВАНИЕ «ФИКТИВНЫХ» ПЕРЕМЕННЫХ В МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Временные тренды в данных
5.5. ЦЕНТРИРОВАНИЕ И МАСШТАБИРОВАНИЕ. ПРЕДСТАВЛЕНИЕ РЕГРЕССИИ В КОРРЕЛЯЦИОННОЙ ФОРМЕ
Корреляционная матрица
Частные корреляции
5.6. ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
5.7. ПРЕОБРАЗОВАНИЕ МАТРИЦЫ X ДЛЯ ПОЛУЧЕНИЯ ОРТОГОНАЛЬНЫХ СТОЛБЦОВ
5.8. РЕГРЕССИОННЫЙ АНАЛИЗ УСРЕДНЕННЫХ ДАННЫХ

Источник

Что такое остаточная сумма квадратов?

Остаточная сумма квадратов (RSS) — это статистический метод, который помогает определить уровень несоответствия в наборе данных, не предсказанный регрессионной моделью. Таким образом, он измеряет дисперсию значения наблюдаемых данных по сравнению с его прогнозируемым значением в соответствии с моделью регрессии. Следовательно, RSS указывает, хорошо ли модель регрессии соответствует фактическому набору данных или нет.

Остаточная сумма квадратов

Также называемая суммой квадратов ошибок (SSE), RSS получается путем сложения квадрата остатков. Остатки представляют собой предполагаемые отклонения от фактических значений данных и представляют ошибки в регрессии Регрессия Регрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать дальшеоценка модели. Более низкий RSS указывает на то, что модель регрессии хорошо соответствует данным и имеет минимальную вариацию данных. В финансах Финансы — это широкий термин, который по существу относится к управлению капиталом или направлению денег для различных целей. Более того, инвесторы используют RSS для отслеживания изменений цен на акции, чтобы предсказать их будущие движения цен.

Оглавление

Что такое остаточная сумма квадратов?
- Объяснение остаточной суммы квадратов
- Остаточная сумма квадратов в финансах
- Формула
- Пример расчета
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Остаточная сумма квадратов (RSS) — это статистический метод, используемый для измерения отклонения в наборе данных, не объясненного регрессионной моделью.
Остаток или ошибка — это разница между фактическим и прогнозируемым значением наблюдения.
Если значение RSS низкое, это означает, что данные хорошо соответствуют модели оценки, что указывает на наименьшую дисперсию. Если он равен нулю, модель идеально соответствует данным, не имея вообще никакой дисперсии.
Это помогает игрокам фондового рынка оценивать будущие движения цен на акции, отслеживая колебания цен на акции.

Объяснение остаточной суммы квадратов

RSS — это один из типов суммы квадратов (SS), остальные два — это общая сумма квадратов (TSS) и сумма квадратов из-за регрессии (SSR) или объясненная сумма квадратов (ESS). Сумма квадратов — это статистическая мера, посредством которой дисперсия данных. Дисперсия В статистике дисперсия (или разброс) — это средство описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных. Читать далее оценивается, чтобы определить, насколько хорошо данные будут соответствовать модели в регрессионном анализе.

В то время как TSS измеряет изменение значений наблюдаемой переменной по отношению к ее выборочному среднему, SSR или ESS вычисляют отклонение между оценочным значением и средним значением наблюдаемой переменной. Если TSS равен SSR, это означает, что модель регрессии идеально подходит для данных, поскольку она отражает всю изменчивость фактических данных.

С другой стороны, RSS измеряет степень изменчивости наблюдаемых данных, не отображаемых регрессионной моделью. Чтобы вычислить RSS, сначала найдите уровень ошибки или остатка модели, вычитая фактические наблюдаемые значения из оценочных значений. Затем возведите в квадрат и сложите все значения ошибок, чтобы получить RSS.

Чем ниже ошибка модели, тем лучше прогноз регрессии. Другими словами, более низкий RSS означает, что регрессионная модель лучше объясняет данные, указывая на наименьшую дисперсию. Это означает, что модель хорошо соответствует данным. Аналогичным образом, если значение достигает нуля, оно считается наиболее подходящим без отклонений.

Обратите внимание, что RSS не похож на R-SquaredR-SquaredR-squared (R2 или коэффициент детерминации) — это статистическая мера, которая показывает степень вариации зависимой переменной из-за независимой переменной. Подробнее. В то время как первый определяет точную величину вариации, R-квадрат — это величина вариации, определяемая относительно доли общей вариации.

Остаточная сумма квадратов в финансах

Несоответствие, обнаруженное в наборе данных через RSS, указывает, соответствуют ли данные регрессионной модели или нет. Таким образом, это помогает фондовому рынкуФондовый рынокФондовый рынок работает по основному принципу согласования спроса и предложения посредством аукционного процесса, когда инвесторы готовы заплатить определенную сумму за актив и они готовы продать то, что у них есть, по определенной цене. узнайте больше игроков, чтобы понять колебания цен на активы, что позволит им оценить свои будущие движения цен.

Функции регрессии формируются для прогнозирования движения цен акций. Но польза от этих регрессионных моделей зависит от того, хорошо ли они объясняют колебания цен на акции. Однако если в модели есть ошибки или остатки, не объясняемые регрессией, то модель может оказаться бесполезной для прогнозирования движения запасов в будущем.

В результате инвесторы и инвестиционные менеджеры получают возможность принимать оптимальные и наиболее взвешенные решения с помощью RSS. Кроме того, RSS также позволяет политикам анализировать различные переменные, влияющие на экономическую стабильность страны, и соответствующим образом формировать экономические модели.

Формула

Вот формула для вычисления остаточной суммы квадратов:

формула расчета остаточной суммы квадратов

Где,

вычислить остаточную сумму квадратов

Пример расчета

Рассмотрим следующее остаточная сумма квадратов пример на основе набора данных ниже:

пример 1 пример 1-1

Абсолютную дисперсию можно легко узнать, применив приведенную выше формулу RSS:

формула остаточной суммы квадратов

= {1 – [1+(2*0)]}2 + {2 – [1+(2*1)]}2 + {6 – [1+(2*2)]}2 + {8 – [1+(2*3)]}2

= 0+1+1+1 = 3

регрессионная модель, представленная

Часто задаваемые вопросы (FAQ)

Что такое остаточная сумма квадратов (RSS)?

RSS — это статистический метод, используемый для определения уровня несоответствия в наборе данных, не выявленного с помощью регрессии. Если остаточная сумма квадратов приводит к меньшему значению, это означает, что модель регрессии объясняет данные лучше, чем когда результат выше. На самом деле, если его значение равно нулю, оно считается наилучшим соответствием без каких-либо ошибок.

В чем разница между ESS и RSS?

ESS расшифровывается как «Объясненная сумма квадратов», что означает изменение данных, объясненное регрессионной моделью. С другой стороны, остаточная сумма квадратов (RSS) определяет вариации, отмеченные несоответствиями в наборе данных, не объясняемыми моделью оценки.

Чем отличаются TSS и RSS?

Общая сумма квадратов (TSS) определяет отклонения наблюдаемых значений или наборов данных от среднего значения. Напротив, остаточная сумма квадратов (RSS) оценивает ошибки или расхождения в наблюдаемых данных и смоделированных данных.

What Is the Residual Sum of Squares (RSS)?

The residual sum of squares (RSS) is a statistical technique used to measure the amount of variance in a data set that is not explained by a regression model itself. Instead, it estimates the variance in the residuals, or error term.

Linear regression is a measurement that helps determine the strength of the relationship between a dependent variable and one or more other factors, known as independent or explanatory variables.

Key Takeaways

The residual sum of squares (RSS) measures the level of variance in the error term, or residuals, of a regression model.
The smaller the residual sum of squares, the better your model fits your data; the greater the residual sum of squares, the poorer your model fits your data.
A value of zero means your model is a perfect fit.
Statistical models are used by investors and portfolio managers to track an investment’s price and use that data to predict future movements.
The RSS is used by financial analysts in order to estimate the validity of their econometric models.

Understanding the Residual Sum of Squares

In general terms, the sum of squares is a statistical technique used in regression analysis to determine the dispersion of data points. In a regression analysis, the goal is to determine how well a data series can be fitted to a function that might help to explain how the data series was generated. The sum of squares is used as a mathematical way to find the function that best fits (varies least) from the data.

The RSS measures the amount of error remaining between the regression function and the data set after the model has been run. A smaller RSS figure represents a regression function that is well-fit to the data.

The RSS, also known as the sum of squared residuals, essentially determines how well a regression model explains or represents the data in the model.

How to Calculate the Residual Sum of Squares

RSS = ∑ⁿ_i=1(yⁱ — f(x_i))²

Where:

y_i = the i^th value of the variable to be predicted

f(x_i) = predicted value of y_i

n = upper limit of summation

Residual Sum of Squares (RSS) vs. Residual Standard Error (RSE)

The residual standard error (RSE) is another statistical term used to describe the difference in standard deviations of observed values versus predicted values as shown by points in a regression analysis. It is a goodness-of-fit measure that can be used to analyze how well a set of data points fit with the actual model.

RSE is computed by dividing the RSS by the number of observations in the sample less 2, and then taking the square root: RSE = [RSS/(n-2)]^1/2

Special Considerations

Financial markets have increasingly become more quantitatively driven; as such, in search of an edge, many investors are using advanced statistical techniques to aid in their decisions. Big data, machine learning, and artificial intelligence applications further necessitate the use of statistical properties to guide contemporary investment strategies. The residual sum of squares—or RSS statistics—is one of many statistical properties enjoying a renaissance.

Statistical models are used by investors and portfolio managers to track an investment’s price and use that data to predict future movements. The study—called regression analysis—might involve analyzing the relationship in price movements between a commodity and the stocks of companies engaged in producing the commodity.

Finding the residual sum of squares (RSS) by hand can be difficult and time-consuming. Because it involves a lot of subtracting, squaring, and summing, the calculations can be prone to errors. For this reason, you may decide to use software, such as Excel, to do the calculations.

Any model might have variances between the predicted values and actual results. Although the variances might be explained by the regression analysis, the RSS represents the variances or errors that are not explained.

Since a sufficiently complex regression function can be made to closely fit virtually any data set, further study is necessary to determine whether the regression function is, in fact, useful in explaining the variance of the dataset.

Typically, however, a smaller or lower value for the RSS is ideal in any model since it means there’s less variation in the data set. In other words, the lower the sum of squared residuals, the better the regression model is at explaining the data.

Example of the Residual Sum of Squares

For a simple (but lengthy) demonstration of the RSS calculation, consider the well-known correlation between a country’s consumer spending and its GDP. The following chart reflects the published values of consumer spending and Gross Domestic Product for the 27 states of the European Union, as of 2020.

Consumer Spending vs. GDP for EU Member States
Country	Consumer Spending (Millions)	GDP (Millions)
Austria	309,018.88	433,258.47
Belgium	388,436.00	521,861.29
Bulgaria	54,647.31	69,889.35
Croatia	47,392.86	57,203.78
Cyprus	20,592.74	24,612.65
Czech Republic	164,933.47	245,349.49
Denmark	251,478.47	356,084.87
Estonia	21,776.00	30,650.29
Finland	203,731.24	269,751.31
France	2,057,126.03	2,630,317.73
Germany	2,812,718.45	3,846,413.93
Greece	174,893.21	188,835.20
Hungary	110,323.35	155,808.44
Ireland	160,561.07	425,888.95
Italy	1,486,910.44	1,888,709.44
Latvia	25,776.74	33,707.32
Lithuania	43,679.20	56,546.96
Luxembourg	35,953.29	73,353.13
Malta	9,808.76	14,647.38
Netherlands	620,050.30	913,865.40
Poland	453,186.14	596,624.36
Portugal	190,509.98	228,539.25
Romania	198,867.77	248,715.55
Slovak Republic	83,845.27	105,172.56
Slovenia	37,929.24	53,589.61
Spain	997,452.45	1,281,484.64
Sweden	382,240.92	541,220.06

World Bank, 2020.

Consumer spending and GDP have a strong positive correlation, and it is possible to predict a country’s GDP based on consumer spending (CS). Using the formula for a best fit line, this relationship can be approximated as:

GDP = 1.3232 x CS + 10447

The units for both GDP and Consumer Spending are in millions of U.S. dollars.

This formula is highly accurate for most purposes, but it is not perfect, due to the individual variations in each country’s economy. The following chart compares the projected GDP of each country, based on the formula above, and the actual GDP as recorded by the World Bank.

Projected and Actual GDP Figures for EU Member States, and Residual Squares
Country	Consumer Spending Most Recent Value (Millions)	GDP Most Recent Value (Millions)	Projected GDP (Based on Trendline)	Residual Square (Projected — Real)^2
Austria	309,018.88	433,258.47	419,340.782016	193,702,038.819978
Belgium	388,436.00	521,861.29	524,425.52	6,575,250.87631504
Bulgaria	54,647.31	69,889.35	82,756.320592	165,558,932.215393
Croatia	47,392.86	57,203.78	73,157.232352	254,512,641.947534
Cyprus	20,592.74	24,612.65	37,695.313568	171,156,086.033474
Czech Republic	164,933.47	245,349.49	228,686.967504	277,639,655.929706
Denmark	251,478.47	356,084.87	343,203.311504	165,934,549.28587
Estonia	21,776.00	30,650.29	39,261.00	74,144,381.8126542
Finland	203,731.24	269,751.31	280,024.176768	105,531,791.633079
France	2,057,126.03	2,630,317.73	2,732,436.162896	10,428,174,337.1349
Germany	2,812,718.45	3,846,413.93	3,732,236.05304	13,036,587,587.0929
Greece	174,893.21	188,835.20	241,865.695472	2,812,233,450.00581
Hungary	110,323.35	155,808.44	156,426.85672	382,439.239575558
Ireland	160,561.07	425,888.95	222,901.407824	41,203,942,278.6534
Italy	1,486,910.44	1,888,709.44	1,977,926.894208	7,959,754,135.35658
Latvia	25,776.74	33,707.32	44,554.782368	117,667,439.825176
Lithuania	43,679.20	56,546.96	68,243.32	136,804,777.364243
Luxembourg	35,953.29	73,353.13	58,020.393328	235,092,813.852894
Malta	9,808.76	14,647.38	23,425.951232	77,063,312.875298
Netherlands	620,050.30	913,865.40	830,897.56	6,883,662,978.71
Poland	453,186.14	596,624.36	610,102.900448	181,671,052.608372
Portugal	190,509.98	228,539.25	262,529.805536	1,155,357,865.6459
Romania	198,867.77	248,715.55	273,588.833264	618,680,220.331183
Slovak Republic	83,845.27	105,172.56	121,391.061264	263,039,783.25037
Slovenia	37,929.24	53,589.61	60,634.970368	49,637,102.7149851
Spain	997,452.45	1,281,484.64	1,330,276.08184	2,380,604,796.8261
Sweden	382,240.92	541,220.06	516,228.185344	624,593,798.821215

World Bank, 2020.

The column on the right indicates the residual squares–the squared difference between each projected value and its actual value. The numbers appear large, but their sum is actually lower than the RSS for any other possible trendline. If a different line had a lower RSS for these data points, that line would be the best fit line.

Is the Residual Sum of Squares the Same as R-Squared?

The residual sum of squares (RSS) is the absolute amount of explained variation, whereas R-squared is the absolute amount of variation as a proportion of total variation.

Is RSS the Same as the Sum of Squared Estimate of Errors (SSE)?

The residual sum of squares (RSS) is also known as the sum of squared estimate of errors (SSE).

What Is the Difference Between the Residual Sum of Squares and Total Sum of Squares?

The total sum of squares (TSS) measures how much variation there is in the observed data, while the residual sum of squares measures the variation in the error between the observed data and modeled values. In statistics, the values for the residual sum of squares and the total sum of squares (TSS) are oftentimes compared to each other.

Can a Residual Sum of Squares Be Zero?

The residual sum of squares can be zero. The smaller the residual sum of squares, the better your model fits your data; the greater the residual sum of squares, the poorer your model fits your data. A value of zero means your model is a perfect fit.

Источник

В статистике, то остаточная сумма квадратов ( RSS), также известные как сумма квадратов остатков ( SSR) или сумму квадратов оценки ошибок ( SSE), является суммой из квадратов из остатков (отклонения предсказывали от реальных эмпирических значений данных). Это мера расхождения между данными и моделью оценки, такой как линейная регрессия. Небольшой RSS указывает на точное соответствие модели данным. Он используется как критерий оптимальности при выборе параметров и выбора модели.

В общем, общая сумма квадратов = объясненная сумма квадратов + остаточная сумма квадратов. Для доказательства этого в многомерном обычном случае наименьших квадратов (OLS) см. Разделение в общей модели OLS.

СОДЕРЖАНИЕ

1 Одна объясняющая переменная
2 Матричное выражение для остаточной суммы квадратов OLS
3 Связь с корреляцией продукта и момента Пирсона
4 См. Также
5 ссылки

Одна объясняющая переменная

В модели с единственной независимой переменной RSS задается следующим образом:

RSS знак равно ∑ я знак равно 1 п ( у я — ж ( Икс я ) ) 2 { displaystyle operatorname {RSS} = sum _ {i = 1} ^ {n} (y_ {i} -f (x_ {i})) ^ {2}} ${ displaystyle operatorname {RSS} = sum _ {i = 1} ^ {n} (y_ {i} -f (x_ {i})) ^ {2}}$

где y i — это i- ^е значение переменной, которую нужно спрогнозировать, x i — это i- ^е значение объясняющей переменной, и — это предсказанное значение y i (также называемое). В стандартной линейной простой модели регрессии, где и являются коэффициентами, у и х являются regressand и регрессор, соответственно, а ε является вектор ошибок. Сумма квадратов остатков — это сумма квадратов ; это ж ( Икс я ) { displaystyle f (x_ {i})} $f (x_ {i})$ у я ^ { displaystyle { hat {y_ {i}}}} ${ hat {y_ {i}}}$ у я знак равно α + β Икс я + ε я { displaystyle y_ {i} = alpha + beta x_ {i} + varepsilon _ {i} ,} ${ displaystyle y_ {i} = alpha + beta x_ {i} + varepsilon _ {i} ,}$ α { displaystyle alpha} $альфа$ β { displaystyle beta} $бета$ ε ^ я { Displaystyle { widehat { varepsilon ,}} _ {я}} ${ Displaystyle { widehat { varepsilon ,}} _ {я}}$

RSS знак равно ∑ я знак равно 1 п ( ε ^ я ) 2 знак равно ∑ я знак равно 1 п ( у я — ( α ^ + β ^ Икс я ) ) 2 { displaystyle operatorname {RSS} = sum _ {i = 1} ^ {n} ({ widehat { varepsilon ,}} _ {i}) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} — ({ widehat { alpha ,}} + { widehat { beta ,}} x_ {i})) ^ {2}} ${ displaystyle operatorname {RSS} = sum _ {i = 1} ^ {n} ({ widehat { varepsilon ,}} _ {i}) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} - ({ widehat { alpha ,}} + { widehat { beta ,}} x_ {i})) ^ {2}}$

где — оценочное значение постоянного члена, а — оценочное значение коэффициента наклона. α ^ { displaystyle { widehat { alpha ,}}} ${ displaystyle { widehat { alpha ,}}}$ α { displaystyle alpha} $альфа$ β ^ { displaystyle { widehat { beta ,}}} ${ displaystyle { widehat { beta ,}}}$ β { displaystyle beta} $бета$

Матричное выражение для остаточной суммы квадратов OLS

Общая регрессионная модель с n наблюдениями и k объяснителями, первый из которых представляет собой постоянный единичный вектор, коэффициент которого является пересечением регрессии, имеет вид

у знак равно Икс β + е { Displaystyle у = Х бета + е} $у = Х бета + е$

где y — вектор наблюдений зависимой переменной размера n × 1, каждый столбец матрицы X размера n × k — вектор наблюдений на одном из k объяснителей, — вектор истинных коэффициентов k × 1, а e — размер n × 1 вектор истинных основных ошибок. В обычный метод наименьших квадратов Оценщик IS β { displaystyle beta} $бета$ β { displaystyle beta} $бета$

Икс β ^ знак равно у ⟺ { Displaystyle Х { шляпа { бета}} = у iff} ${ Displaystyle Х { шляпа { бета}} = у iff}$

Икс Т Икс β ^ знак равно Икс Т у ⟺ { displaystyle X ^ { operatorname {T}} X { hat { beta}} = X ^ { operatorname {T}} y iff} ${ displaystyle X ^ { operatorname {T}} X { hat { beta}} = X ^ { operatorname {T}} y iff}$

β ^ знак равно ( Икс Т Икс ) — 1 Икс Т у . { displaystyle { hat { beta}} = (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y.} ${ displaystyle { hat { beta}} = (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y.}$

Остаточный вектор = ; поэтому остаточная сумма квадратов равна: е ^ { displaystyle { hat {e}}} ${ненавидеть}}$ у — Икс β ^ знак равно у — Икс ( Икс Т Икс ) — 1 Икс Т у { displaystyle yX { hat { beta}} = yX (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y} ${ displaystyle yX { hat { beta}} = yX (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y}$

RSS знак равно е ^ Т е ^ знак равно ‖ е ^ ‖ 2 { displaystyle operatorname {RSS} = { hat {e}} ^ { operatorname {T}} { hat {e}} = | { hat {e}} | ^ {2}} ${ displaystyle operatorname {RSS} = { hat {e}} ^ { operatorname {T}} { hat {e}} = | { hat {e}} | ^ {2}}$ ,

(эквивалентно квадрату нормы остатков). В полном объеме:

RSS знак равно у Т у — у Т Икс ( Икс Т Икс ) — 1 Икс Т у знак равно у Т [ я — Икс ( Икс Т Икс ) — 1 Икс Т ] у знак равно у Т [ я — ЧАС ] у { displaystyle operatorname {RSS} = y ^ { operatorname {T}} yy ^ { operatorname {T}} X (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y = y ^ { operatorname {T}} [IX (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}}] y = y ^ { имя оператора {T}} [IH] y} ${ displaystyle operatorname {RSS} = y ^ { operatorname {T}} yy ^ { operatorname {T}} X (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}} y = y ^ { operatorname {T}} [IX (X ^ { operatorname {T}} X) ^ {- 1} X ^ { operatorname {T}}] y = y ^ { имя оператора {T}} [IH] y}$ ,

где H — матрица шляпы или матрица проекции в линейной регрессии.

Связь с корреляцией продукта и момента Пирсона

Линия регрессии методом наименьших квадратов определяется выражением

у знак равно а Икс + б { displaystyle y = ax + b} $у = ах + Ь$ ,

где и, где и б знак равно у ¯ — а Икс ¯ { displaystyle b = { bar {y}} — а { bar {x}}} ${ displaystyle b = { bar {y}} - а { bar {x}}}$ а знак равно S Икс у S Икс Икс { displaystyle a = { frac {S_ {xy}} {S_ {xx}}}} ${ displaystyle a = { frac {S_ {xy}} {S_ {xx}}}}$ S Икс у знак равно ∑ я знак равно 1 п ( Икс ¯ — Икс я ) ( у ¯ — у я ) { displaystyle S_ {xy} = sum _ {i = 1} ^ {n} ({ bar {x}} — x_ {i}) ({ bar {y}} — y_ {i})} ${ displaystyle S_ {xy} = sum _ {i = 1} ^ {n} ({ bar {x}} - x_ {i}) ({ bar {y}} - y_ {i})}$ S Икс Икс знак равно ∑ я знак равно 1 п ( Икс ¯ — Икс я ) 2 . { displaystyle S_ {xx} = sum _ {i = 1} ^ {n} ({ bar {x}} — x_ {i}) ^ {2}.} ${ displaystyle S_ {xx} = sum _ {i = 1} ^ {n} ({ bar {x}} - x_ {i}) ^ {2}.}$

Следовательно,

RSS знак равно ∑ я знак равно 1 п ( у я — ж ( Икс я ) ) 2 знак равно ∑ я знак равно 1 п ( у я — ( а Икс я + б ) ) 2 знак равно ∑ я знак равно 1 п ( у я — а Икс я — у ¯ + а Икс ¯ ) 2 знак равно ∑ я знак равно 1 п ( а ( Икс ¯ — Икс я ) — ( у ¯ — у я ) ) 2 знак равно а 2 S Икс Икс — 2 а S Икс у + S у у знак равно S у у — а S Икс у знак равно S у у ( 1 — S Икс у 2 S Икс Икс S у у ) { displaystyle { begin {align} operatorname {RSS} amp; = sum _ {i = 1} ^ {n} (y_ {i} -f (x_ {i})) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} — (ax_ {i} + b)) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} -ax_ {i } — { bar {y}} + a { bar {x}}) ^ {2} \ [5pt] amp; = sum _ {i = 1} ^ {n} (a ({ bar {x }} — x_ {i}) — ({ bar {y}} — y_ {i})) ^ {2} = a ^ {2} S_ {xx} -2aS_ {xy} + S_ {yy} = S_ {yy} -aS_ {xy} = S_ {yy} left (1 — { frac {S_ {xy} ^ {2}} {S_ {xx} S_ {yy}}} right) end {выровнено} }} ${ displaystyle { begin {align} operatorname {RSS} amp; = sum _ {i = 1} ^ {n} (y_ {i} -f (x_ {i})) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} - (ax_ {i} + b)) ^ {2} = sum _ {i = 1} ^ {n} (y_ {i} -ax_ {i } - { bar {y}} + a { bar {x}}) ^ {2} \ [5pt] amp; = sum _ {i = 1} ^ {n} (a ({ bar {x }} - x_ {i}) - ({ bar {y}} - y_ {i})) ^ {2} = a ^ {2} S_ {xx} -2aS_ {xy} + S_ {yy} = S_ {yy} -aS_ {xy} = S_ {yy} left (1 - { frac {S_ {xy} ^ {2}} {S_ {xx} S_ {yy}}} right) end {выровнено} }}$

где S у у знак равно ∑ я знак равно 1 п ( у ¯ — у я ) 2 . { displaystyle S_ {yy} = sum _ {i = 1} ^ {n} ({ bar {y}} — y_ {i}) ^ {2}.} ${ displaystyle S_ {yy} = sum _ {i = 1} ^ {n} ({ bar {y}} - y_ {i}) ^ {2}.}$

Соотношение произведение-момент Пирсона определяется следующим образом: р знак равно S Икс у S Икс Икс S у у ; { displaystyle r = { frac {S_ {xy}} { sqrt {S_ {xx} S_ {yy}}}};} ${ displaystyle r = { frac {S_ {xy}} { sqrt {S_ {xx} S_ {yy}}}};}$ RSS знак равно S у у ( 1 — р 2 ) . { displaystyle operatorname {RSS} = S_ {yy} (1-r ^ {2}).} ${ displaystyle operatorname {RSS} = S_ {yy} (1-r ^ {2}).}$

Смотрите также

Информационный критерий Акаике # Сравнение методом наименьших квадратов
Распределение хи-квадрат # Приложения
Степени свободы (статистика) # Сумма квадратов и степеней свободы
Ошибки и неточности в статистике
Неподходящая сумма квадратов
Среднеквадратичная ошибка
Сниженная статистика хи-квадрат, RSS на степень свободы
Квадратные отклонения
Сумма квадратов (статистика)

Что такое Остаточная сумма квадратов (RSS)?

Остаточная сумма квадратов (RSS) — это статистический метод, используемый для измерения количества дисперсии в наборе данных, который не объясняется регрессионной моделью. Регрессия — это измерение, которое помогает определить силу взаимосвязи между зависимой переменной и рядом других изменяющихся переменных или независимых переменных.

Остаточная сумма квадратов измеряет количество ошибок, остающихся между функцией регрессии и набором данных. Меньшая сумма квадратов остатков представляет собой функцию регрессии. Остаточная сумма квадратов, также известная как сумма квадратов остатков, по существу определяет, насколько хорошо регрессионная модель объясняет или представляет данные в модели.

Ключевые моменты

Остаточная сумма квадратов (RSS) — это статистический метод, используемый для измерения количества дисперсии в наборе данных, который не объясняется регрессионной моделью.
Остаточная сумма квадратов — одно из многих статистических свойств, переживающих ренессанс на финансовых рынках.
В идеале сумма квадратов остатков должна быть меньшим или меньшим значением в любой регрессионной модели.

Понимание остаточной суммы квадратов (RSS)

Финансовые рынки становятся все более управляемыми в количественном отношении; Таким образом, в поисках преимущества многие инвесторы используют передовые статистические методы для принятия решений. Приложения для больших данных, машинного обучения и искусственного интеллекта дополнительно требуют использования статистических свойств для определения современных инвестиционных стратегий. Остаточная сумма квадратов — или статистика RSS — одна из многих статистических характеристик, переживающих ренессанс.

Статистические модели используются инвесторами и управляющими портфелями для отслеживания цены инвестиций и использования этих данных для прогнозирования будущих движений. Исследование, называемое регрессионным анализом, может включать анализ взаимосвязи в динамике цен между товаром и акциями компаний, занимающихся его производством.

Любая модель может иметь расхождения между прогнозируемыми значениями и фактическими результатами. Хотя отклонения можно объяснить с помощью регрессионного анализа, остаточная сумма квадратов представляет собой отклонения или ошибки, которые не объяснены.

Поскольку можно сделать достаточно сложную функцию регрессии, которая точно соответствует практически любому набору данных, необходимы дальнейшие исследования, чтобы определить, действительно ли функция регрессии полезна для объяснения дисперсии набора данных. Однако, как правило, меньшее или меньшее значение остаточной суммы квадратов является идеальным для любой модели, поскольку это означает меньшую вариативность в наборе данных. Другими словами, чем меньше сумма квадратов остатков, тем лучше регрессионная модель объясняет данные.

Источник

Содержание

Введение

в одномерном распределении

Замечание

Регрессии

Другое использование слова «ошибка» в статистике

См. также

Ссылки

Внешние ссылки

Вступление

В одномерных распределениях

Регрессии

Другое использование слова «ошибка» в статистике

Смотрите также

Рекомендации

внешняя ссылка

One explanatory variable[edit]

Matrix expression for the OLS residual sum of squares[edit]

Relation with Pearson’s product-moment correlation[edit]

See also[edit]

References[edit]

One explanatory variable[edit]

Matrix expression for the OLS residual sum of squares[edit]

Relation with Pearson’s product-moment correlation[edit]

See also[edit]

References[edit]

SSR, SST и R-квадрат

Расчет SST, SSR, SSE: пошаговый пример

Дополнительные ресурсы

Влияние повторных опытов на R2

«Чистая» ошибка в многофакторном случае

Приблизительные повторы

Что такое остаточная сумма квадратов?

Объяснение остаточной суммы квадратов

Остаточная сумма квадратов в финансах

Формула

Пример расчета

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи

What Is the Residual Sum of Squares (RSS)?

Key Takeaways

Understanding the Residual Sum of Squares

How to Calculate the Residual Sum of Squares

Residual Sum of Squares (RSS) vs. Residual Standard Error (RSE)

Special Considerations

Example of the Residual Sum of Squares

Is the Residual Sum of Squares the Same as R-Squared?

Is RSS the Same as the Sum of Squared Estimate of Errors (SSE)?

What Is the Difference Between the Residual Sum of Squares and Total Sum of Squares?

Can a Residual Sum of Squares Be Zero?

СОДЕРЖАНИЕ

Одна объясняющая переменная

Матричное выражение для остаточной суммы квадратов OLS

Связь с корреляцией продукта и момента Пирсона

Смотрите также

Рекомендации

Что такое Остаточная сумма квадратов (RSS)?

Ключевые моменты

Понимание остаточной суммы квадратов (RSS)