Относительная ошибка определения химия

Лекция
1.

Аналитическая
химия – не
просто дисциплина, накапливающая и
систематизирующая знания; эта наука
имеет огромное практическое значение
в жизни общества, она создает средства
для химического анализа и обеспечивает
его осуществление – в этом ее главное
предназначение. Без эффективного
химического анализа невозможно
функционирование ведущих отраслей
народного хозяйства, систем охраны
природы и здоровья населения, оборонного
комплекса, невозможно развитие многих
смежных областей знания.

Ошибки при количественном анализе.

По своему характеру
ошибки анализа подразделяются на
систематические, случайные и промахи.

1. Систематические
   – погрешности, одинаковые по знаку и
   влияющие на результат в сторону его
   увеличения, либо в сторону уменьшения.

а)
Методические – это ошибки, которые
зависят от особенности применяемого
метода (неполное протекание реакции,
частичное растворение осадка, свойство
индикатора).

б)
Оперативные – недостаточное промывание
осадка на фильтре, ошибки

приборные
или реактивов, неравноплечность весов.

в)
Индивидуальные – ошибки лаборантов
(способность точно определять

окраску
при титровании, психологические ошибки).

г)
Приборные
или реактивные (эти ошибки связаны с
недостаточной точностью используемых
приборов, ошибки лаборанта).

1. Случайные
   — они неизбежны при любом определении.
   Они могут быть значительно уменьшены
   при увеличении числа параллельных
   определений.

2. Промахи
   — грубые ошибки, которые обусловлены
   от неправильного подсчета разновесок,
   поливания части раствора, просыпания
   осадка.

Чувствительность, правильность и точность анализа.

Чувствительность
– минимальная определяемая концентрация
вещества.

Правильность
– близость полученного результата к
истинному.

Точность
— характеристика
воспроизводимости определения от опыта
к опыту. Анализ считается выполненным
более точным, чем меньше различаются
результаты параллельных определений
между собой.

Абсолютная
ошибка –
разность между полученным результатом
и истинным или наиболее достоверным
значением.

Относительная
ошибка – отношение абсолютной ошибки
к истинному значению.

Группы методов анализа.

Принято
делить методы анализа на три большие
группы:

1. химические
   методы анализа
   — когда данные получаются в результате
   выделения осадка, выделения газа,
   изменения цвета окраски;

2. физико-химические
   методы анализа
   — может быть зафиксировано какое-нибудь
   физическое или химическое изменение
   величин;

3. физические
   методы анализа

К
химическим методам относят:

• гравиметрический
  (весовой) анализ

• титриметрический
  (объемный) анализ

• газоволюмометрический
  анализ

К
физико–химическим методам относят все
способы инструментального анализа:

• фотоколориметрический

• спектрофотометрический

• нефелометрический

• потенциометрический

• кондуктометрический

• полярографический

К
физическим относятся:

• спектральный
  эмиссионный

• радиометрический
  (метод меченых атомов)

• рентгеноспектральный

• люминесцентный

• нейтронно-активизационный

• эмиссионный
  (пламенная фотометрия)

• атомно-абсорбционный

• ядерно-магнитный
  резонанс

Лекция
2. Гравиметрический
метод анализа.

Гравиметрический
анализ основан на точном измерении
массы определяемого вещества в виде
соединения или простого вещества
определенного состава. Основным
инструментом являются весы.

Гравиметрические
методы подразделяются на две подгруппы:

I.
методы осаждения

II.
методы отгонки.

В
методах осаждения
навеску анализируемого вещества
переводят в раствор, после этого
определяемый элемент осаждают в виде
малорастворимого соединения. Выпавший
осадок отделяют фильтрованием, тщательно
промывают или высушивают, и точно
взвешивают. По массе осадка и его формуле
рассчитывают содержание определенного
элемента в % по массе.

В
методах отгонки
определяемый компонент удаляют в виде
летучих продуктов, и по убыли в весе
судят о содержании элемента.

Требования
к осадкам:

Осаждаемой
формой – называют то соединение, которое
образуется при взаимодействии с реагентом
– осадителем,
а весовой формой – соединение, которое
взвешивают для получения окончательного
результата анализа.

Например,
при определении кремния в чугунах формой
осаждения является кремниевая кислота
H₂SiO₃·nH₂O,
а весовой формой является безводная
двуокись кремния, получающаяся в
результате прокаливания при температуре
около 1000^оС.
иногда осаждаемая и весовая форма могут
представлять собой одно и тоже соединение.
Например, при определении серы весовым
методом ее осаждают из раствора, и
взвешивают в виде сульфата бария, который
при прокаливании химически не изменяется.

Требования
к осаждаемой форме:

1)
Малая растворимость осаждаемой формы
соединения, содержащего определенное
вещество и как более низкое содержание
в ней определяющего вещества.

осаждаемая
форма весовая форма

Требование
к осаждению – малая растворимость.

Произведение
растворимости

К
ним относятся: AgCl,
BaSO₄,
Fe(OH)₃,
Sb₂S₃

2)
Структура осадка должна отвечать
условиям фильтрования и позволять
отмывку осадков с достаточной скоростью.

Мелкокристаллические
осадки, могут пройти через поры фильтра.
Наиболее удобны крупнокристаллические
осадки, т.к. они не забивают поры фильтра,
имеют слабо развитую поверхность, мало
адсорбируют посторонние ионы и легко
отмываются от них. Фильтруются через
фильтр средней плотности, маркируемый
Белой лентой. Аморфные осадки, например,
многие гидроксиды имеют сильно развитую
поверхность, адсорбируют посторонние
вещества из раствора и трудно от них
отмываются. Фильтрование таких осадков
проводят через неплотный фильтр,
маркируемый Красной лентой. Самые
мелкокристаллические осадки (например,
BaSO₄),
фильтруются через фильтр с Синей лентой.

Окклюзия
– внедрение посторонних ионов в структуру
кристаллической решетки.

BaSO₄

°	xBa+2	°	x
x	°	K+	°

K⁺
— 1, 37 A

Na⁺
— 0, 95 A

Ba⁺²
-1,35 A

3)
Важно, чтобы осаждаемая форма легко
переходила в весовую.

Осаждаемая
и весовая формы должны быть химически
инертными, чтобы не приводить к
количественным ошибкам.

Пример:

1)

2)

CaO
— высокореакционное вещество, это
означает, что оно может «захватить»
пары воды или углекислый газ

белая
лента

красная
лента фильтры

синяя
лента

Требования
к весовой форме:

1. Точное
   соответствие ее состава химической
   формуле. Если такого соответствия нет,
   вычисление результатов невозможно.

1. Химическая
   устойчивость весовой формы.

1. Содержание
   определяемого в весовой форме должно
   быть как можно меньшим, тогда погрешности
   определения меньше скажутся на
   окончательном результате анализа.

Искомое
процентное содержание ( Р ) рассчитывают
по формуле:

,

где
b
– количество весовой формы

a
– навеска исследуемого вещества

F
– фактор пересчета

Фактор
пересчета показывает, скольким граммам
определяемого элемента соответствует
1 г весовой формы.

Из
двух возможных гравиметрических методов
определения элемента при прочих равных
условиях будет более точным тот, для
которого фактор пересчета будет меньше.

;

;

Анализ
может быть:

а)
частным – определяется один или несколько
веществ, а другие не интересуют

б)
полным – на содержание всех входящих
составных частей (Σ = 100%).

Полный
анализ проводится для того, чтобы узнать
все составные части данного вещества.

Цемент
– CaO, MgO, Fe₂O₃,
Al₂O₃,
SiO₂,
CaSO₄,
SO₃.

FeCl₃
+ NH₄OH
→ Fe₂(OH)₃.

При проведении
химического анализа необходимо очень
внимательно выполнять вычисления.
Математическая ошибка, допущенная в
числовых значениях, равносильна ошибке
в анализе.

Числовые значения
можно разделить на точные и приближенные.
К точным можно отнести, например, число
выполненных определений, порядковый
номер элемента в периодической системе,
а к приближенным числам – массу вещества
или объем раствора в количественном
анализе. Точность приближенного числа
и воспроизводимость анализа определяется
количеством значащих цифр. Значащими
цифрами приближенного числа являются
все достоверно известные цифры плюс
первая из недостоверных. Нуль в числах
может быть значимым и незначимым. Нули,
стоящие в начале числа, всегда незначимы
и служат лишь для указания места запятой
в десятичной дроби. Например, число 0,01
содержит одну значащую цифру. Нули,
стоящие между цифрами, всегда значимы.
Например, в числе 0,508 три значащие цифры.
Нули в конце числа могут быть значимыми
и незначимыми. Нули, стоящие после
запятой в десятичной дроби, считаются
значимыми. Например, в числе 200,0 четыре
значащие цифры.

В числовом значении
результата анализа оставляют определённое
количество значащих цифр так, чтобы
только последняя цифра была сомнительной,
а предпоследняя достоверной. Сохранение большого числа
значащих цифр характеризует не высокую
точность, а только недостаточное
представление исполнителя анализа о
воспроизводимости и правильности
измерений. Если числа для выполнения
расчета известны с большей степенью
точности, а результат расчета требуется
получить с меньшей степенью точности,
тогда все данные округляют так, чтобы
в них осталось на одну значащую цифру
больше, чем их требуется получить в
результате расчета.

Приближенные
числа округляются
по правилу:
если последняя цифра меньше 5, то ее
отбрасывают, если же она равна или больше
5, то предпоследнюю цифру увеличивают
на единицу. Рекомендуется округлять
конечный результат после выполнения
всех арифметических действий.

При
различных вычислениях необходимо иметь
в виду, что если в цепи вычислений имеется
какое-либо не очень надежное число, то
точность
конечного результата не может быть
большей, чем точность наименее надежного
звена в цепи вычислений.
Теория ошибок приводит к следующим
выводам, важным для расчетов в
количественном анализе:

1.
При сложении и вычитании следует
сохранять в окончательном результате
(как и в слагаемых) не больше знаков
после запятой, чем их имеется в наименее
достоверном числе.

2. При умножении
и делении следует сохранять в конечном
результате не более значащих цифр, чем
их имеется в наименее достоверном числе.

Пример.
Вычислить молярную массу М(AuCl₃).

Находим
в таблице значения атомных весов:
А(Au) = 197,0 г/моль и А(Cl) = 35,457
г/моль. Для трех атомов хлора получаем:
35,457  36 = 106,371.
Молярная масса AuCl₃
равна

правильная
запись 197,0
+ 106,4 = 303,4 г/моль

неправильная
запись 197,0
+ 106,371 = 303,371 г/моль

Наименее
достоверное число 197,0. Следовательно,
М(AuCl₃)
должна быть записана с точностью не
более 0,1.

Точность определения
и записи измеряемых и рассчитываемых
величин приведена в табл. 7, 8.

Таблица 7

Точность определения
и записи измеряемых величин

Измеряемая величина	Средство измерения	Пример записи	Точность измерения
V, мл, л	Точная мерная посуда (пипетка, бюретка, мерная колба)	25,00 мл 12,47 мл	 0,01-0,03 мл (0,1 %)
m, г	аналитические весы	0,1200 г (весы ВЛР или АДВ); 0,12000 г (весы ВЛА)	 0,0001  0,00005
	технические весы	0,10 г	 0,01 г

Таблица 8

Точность расчета
величин

Рассчитываемые величины	Точность расчета	Пример записи
, %	 0,01 %	8,65 %
, [доли]	0,0865
Атомная масса, молярная масса, г/моль	с точностью, указанной в табл. Д. И. Менделеева или приводимой в справочнике [7]
С, моль/л	4 значащие цифры	0,1025
*, г/л	0,09168
Т, Т(А/В), г/мл	0,005286
рН	2 знака после запятой	6,50

При
проведении химического анализа как бы
тщательно ни выполнялись определенные
операции, почти всегда получается
некоторая ошибка, сказывающаяся на
результате анализа. По характеру ошибки
подразделяются на:

1. Случайные
   (зависят от недоброкачественного
   выполнения отдельных операций в
   анализе, могут быть выявлены по
   различным результатам параллельных
   определений. При аккуратной работе
   случайные ошибки можно исключить или
   свести до минимума.);

2. Систематические
   (вызваны несовершенством прибора или
   неправильным выбором метода анализа,
   их можно выявить, устранить или учесть
   при расчетах с внесением соответствующих
   поправок; служат оценкой правильности
   измерения или метода измерения.);

3. Абсолютная
   ошибка –
   это разница в абсолютных цифрах между
   полученным результатом и истинным
   (или наиболее достоверным) или средним
   значением:

D
= x_i
– ,

где
D
– абсолютная погрешность (в тех же
единицах, что и измеряемая величина);
x_i
– единичное измерение; 
– истинное значение;

4.
Относительная
ошибка –
это отношение (обычно в %) абсолютной
ошибки к истинному (или среднему)
значению:

D
= (x_i
–  / )

100,

где
D
– относительная погрешность (в процентах).

Если
истинное содержание компонента в
анализируемом образце не известно, то
из 3–4 близких параллельных результатов
анализа вычисляют среднее арифметическое
и его принимают за точное (истинное).

Математическая
обработка результатов анализа проводится
с применением микрокалькуляторов и/или
ЭВМ. В пособии [42] приведены основные
формулы и примеры расчёта.

Число, которым
выражают результат количественного
анализа, должно характеризовать не
только содержание данного компонента,
но и воспроизводимость анализа. Для
характеристики воспроизводимости, с
которой определена данная величина,
необходимо писать определенное число
значащих цифр: в полученном результате
(и в числовых данных вообще) пишут столько
значащих цифр, чтобы только последняя
цифра была сомнительной, а предпоследняя
достоверной.

3.
ОПРЕДЕЛЕНИЕ КАЧЕСТВЕННОГО СОСТАВА
неизвестного
вещества

Зачётная работа
по качественному анализу выполняется
в соответствии с планом, представленным
в разделе 1.3. Начальные этапы работы
(см. рис. 1) выполняются так же, как
описано выше в разделах 2.1 и 2.2.

Анализируемый
объект может
быть твердым веществом (металл, сплав,
горная порода, минерал, соль или смесь
солей и т.д.) или водным раствором. В
зависимости от конкретного объекта
анализа поиск литературы и подготовка
к выполнению работы будут различаться:

1. Если
   качественный состав объекта анализа
   точно не
   известен,
   то надо сделать попытку найти
   литературные данные о его возможном
   составе. Например,
   составы многих минералов приведены
   в энциклопедиях и справочниках.
   Получив такую информацию, надо
   составить химико-аналитическую
   характеристику объекта анализа (в
   чем растворяется, какие катионы и
   анионы может содержать, классифицировать
   ионы по аналитическим группам);

2. Если
   же это окажется невозможным, то в
   п. 3
   плана
   надо отметить, что Вы будете проводить
   качественный анализ неизвестного
   вещества.
   Следовательно, в образце не исключено
   содержание любого катиона и аниона.

В
обоих случаях обязательно составляется
схема анализа (п. № 4 плана), исходя
из химико-аналитической характеристики
объекта. Она оформляется заранее в виде
блок–схемы (см. пример в лабораторной
работе № 4 [116]). Если у Вас имеется
возможность провести дробное обнаружение
компонентов, то надо обязательно
обосновать её. При этом необходимо
учитывать следующее:

• дробный
  анализ,
  проводимый с помощью специфических
  реакций, применяется при анализе
  простых
  образцов (< 5 ионов)
  и если состав ориентировочно известен;

• систематический
  анализ
  (система последовательных операций
  по разделению ионов на группы, отделению
  мешающих ионов внутри групп и обнаружению
  каждого иона с помощью характерной
  реакции) применяется при полном
  качественном анализе
  объектов, включающих большое
  количество ионов.

Подготовка
исследуемого вещества к анализу – это
очень важная операция. Способы подготовки
зависят от характера вещества и целей
исследования, поэтому Вам надо продумать
этот вопрос, исходя из химико-аналитической
характеристики объекта анализа и схемы
анализа. Самое главное – надо так
отобрать пробу для анализа, чтобы её
состав отвечал среднему составу всей
массы вещества (см. раздел 2.6).

Качественный
анализ неизвестного вещества всегда
начинают с предварительных испытаний.
Если Вы
правильно их проведёте и сделаете верные
выводы, то это значительно облегчит
дальнейший анализ. Не
забывайте фиксировать в рабочем журнале
все наблюдаемые аналитические эффекты!

3.1. Предварительные
испытания

В
зависимости от физического состояния
вещества проводят разные предварительные
испытания. Пробу
сухого твёрдого вещества
сначала следует рассмотреть невооруженным
глазом, отмечая однородность, характер
и цвет кристаллов. Если проба дана в
виде крупных
кристаллов,
её измельчают в фарфоровой ступке.
Отбрасывать труднорастираемые кристаллы
совершенно недопустимо.
Для равномерного измельчения образец
просеивают через сито, а остаток
продолжают растирать.

1.
Микрокристаллоскопические исследования
и определение цвета.
Пробу распределяют на предметном стекле
тонким слоем и исследуют под микроскопом.
Эти исследования позволяют установить
неоднородность образца, при этом получают
информацию о вероятном числе компонентов,
входящих в его состав. Необходимо
обратить внимание на цвет: соли Сr (III)
окрашены в зелёный цвет, соли Со (II)
и Мn (II)

в розовый, многие соли Сu (II)

в синий или сине-зелёный цвет, соли
Fe (III) 
в бурый или жёлтый, соли Fe (II) и Ni (II)

в зелёный, хроматы 
в жёлтый, дихроматы 
в оранжевый. Бесцветные
или белые кристаллы свидетельствуют
об отсутствии солей окрашенных катионов
и анионов.

2.
Запах 
важный признак некоторых солей слабых
оснований или слабых кислот. Например,
твёрдый (NH₄)₂CО₃
пахнет аммиаком, NaHSО₃

сернистым газом и т.д.

3.
Определение растворимости вещества
проводят в отдельных пробах с малыми
количествами исследуемого вещества (~
0,01 г).

Последовательность
испытаний на растворимость:

• проверить
  растворимость образца в воде при
  обычной температуре;

• если
  предыдущая проба отрицательна –
  проверить то же при нагревании;

• проверить
  растворимость в кислотах и щелочах,
  постепенно переходя от разбавленных
  растворов к более концентрированным
  и от обычных кислот к кислотам-окислителям
  (HNO₃ и
  концентрированная H₂SO₄);

• если
  предыдущая проба отрицательна – можно
  попытаться растворить образец в смеси
  кислот или смеси кислота+окислитель;

• если
  проба не растворяется, то её сплавляют,
  а затем растворяют.

3.1.Растворимость веществав воде. Если
проба не растворяется на холоду, следует
нагреть содержимое пробирки на водяной
бане.

Если
дана смесь солей, то может случиться,
что каждая соль в отдельности в воде
растворяется, а когда эти соли будут
растворяться, произойдет их взаимодействие,
в результате которой образуется осадок.
Например,
ВаС1₂
и Na₂SО₄
в отдельности растворяются в воде, а
когда их будут растирать и затем
растворять, произойдет реакция:

ВаС1₂
+ Na₂SО₄
= BaSО₄
+ 2NaCl

Осадок
BaSО₄
в воде не растворяется.

Если заметного
растворения вещества в воде не наблюдается,
необходимо выяснить возможность
частичного растворения. Для этого не
растворившийся в воде остаток отделяют
центрифугированием и несколько капель
прозрачного центрифугата выпаривают
на предметном стекле. Появление налёта
на стекле подтверждает частичную
растворимость вещества в воде. Об этом
же свидетельствует возможное изменение
окраски водной вытяжки и изменение
среды (рН) раствора.

3.2.
Если проба
не растворяется в воде даже при нагревании,
её пробуют растворить
в кислотах и щелочах,
причем в следующем порядке:

1. в
   СН₃СООН
   (2 н.);

2. в
   НСl
   (2 н.) на холоду и при нагревании;

3. в
   НСl
   (конц.);

4. в
   HNО₃
   (2 н.) без нагревания и при нагревании;

5. в
   HNО₃
   (конц.);

6. в
   H₂SО₄
   (2 н.) без нагревания и при нагревании;

7. в
   H₂SО₄
   (конц.) (оcmopожно!
   разбрызгивание!);

8. в
   царской водке (смеси трех объемов конц.
   НСl
   и одного объема конц. HNО₃);

9. NH₄OH
   (2 н.);

10. NH₄OH
    (конц.);

11. NaOH
    (2 н.);

12. NaOH (конц.).

По
исследованию растворимости вещества
в разных кислотах и щелочах также можно
сделать некоторые предварительные
выводы о составе анализируемого объекта.
Так, если вещество растворилось в НСl,
то в растворе не могут присутствовать
катионы II группы; сернокислый раствор
не будет содержать катионы III группы и
Рb²⁺.

Если
при добавлении кислот к анализируемой
пробе выделяются газы, то по характеру
газа можно определить анион, входящий
в состав вещества (табл. 9)

Таблица
9

Характеристика
газов, выделяющихся из пробы

при добавлении
кислот

Наблюдаемый эффект	Газ	Предполагаемые анионы
Газ без запаха, вызывающий помутнение известковой воды	СО2	Карбонаты (СО32, НСО3), оксалаты
1. Запах горящей серы; 2. Запах горящей серы с выделением осадка свободной серы	SO2	1. Сульфиты (SO32) 2. Тиосульфаты (S2O32)
Запах уксуса	СН3СООН	Ацетаты (СН3СОО)
Запах тухлых яиц	H2S	Сульфиды (S2), тиосульфаты (S2O32), сульфиты (SO32)
Красно-бурые или бурые пары	NO2	Нитриты (NO2)
Зеленоватый газ с характерным резким запахом (удушливый газ), помутнение раствора AgNО3	Сl2 и НСl	Хлориды (Сl—), гипохлориты (СlO)
Жёлто-бурый газ или красно-бурые пары (при действии окислителя)	Вr2 и НВr	Бромиды (Вr)
Фиолетовые пары (при действии окислителя)	I2	Иодиды (I)
Газ без запаха, поддерживающий горение (вспыхивание тлеющей лучины)	O2	Пероксиды, оксиды и анионы-окислители кислородсодержащих кислот (МnO4, СlO4, Сг2О7, СгО42, H2O2)
Запах горького миндаля (осторожно! ядовиты!)	HCN	Цианиды (CN)
Газ желтого цвета	ClO2	Хлораты

3.3. Органические
растворители большей частью применяются
для растворения органических соединений,
не растворимых в воде, кислотах и
основаниях.

3.4. Если анализируемое
вещество не растворимо в воде, кислотах
и щелочах, то для переведения его в
растворимое состояние проводят сплавление
с Na₂CО₃, KHSО₄или другими
подходящими плавнями.

При анализе смеси
веществ может оказаться, что часть пробы
растворима в воде, часть в кислоте, частьв
растворе аммиака и т.д. В этом случае
целесообразно провести дробное
растворение пробы и получить ряд фракций
(«вытяжек»растворов,
содержащих различные катионы и анионы
смеси). Следует при этом добиваться,
чтобы та часть пробы, которая растворяется
в данном растворителе, была полностью
извлечена из смеси и переведена в
соответствующую фракцию. Каждую фракцию
анализируют отдельно, т.к. при этом
достигается дополнительное разделение
сложной смеси и устраняется мешающее
действие некоторых ионов. Растворимость
веществ в воде приведена в [7]. Если соль
может быть растворена в нескольких
кислотах, то предпочтение отдают
уксусной, т.к. излишняя кислотность
усложняет последующий анализ, далееазотной и серной, поскольку сульфаты и
нитраты не так летучи, как хлориды.

При использовании
кислот в качестве растворителя необходимо
избегать их избытка. Для удаления избытка
кислоты полученный раствор кипятят в
фарфоровой чашке или тигле, выпаривая
почти досуха (но избегая прокаливания!).
Затем прибавляют 2530
капель воды при перемешивании и переносят
раствор в пробирку.

При анализе пробы
на содержание анионов использование
кислот в качестве растворителя
нежелательно, т.к. при этом могут быть
потеряны анионы летучих или неустойчивых
кислот.

В
процессе растворения необходимо делать
запись визуальных наблюдений о том, как
растворяется анализируемое вещество,
отмечать цвет получаемого раствора и
изменения, которые могут происходить
с ним (например, выпадение осадка или
помутнение раствора вследствие
гидролиза). В случае гидролиза необходимо
его предотвратить. Предварительное
заключение о возможном присутствии тех
или иных катионов можно сделать также
по окраске их растворов.
Сведения о возможной окраске катионов
металлов полезно предварительно свести
в таблицу.

Желательно
подобрать такой растворитель в котором
анализируемое вещество растворяется
без остатка.

4.
Определение рН (если
вещество растворимо в воде или
анализируемый объект 
жидкость).
Стеклянной полочкой берут одну каплю
полученного раствора и помещают её на
полоску лакмусовой бумажки. Отмечают,
какую реакцию имеет раствор. Делают
заключение, какого характера соль или
смесь солей была растворена.

Возможный состав
исследуемого вещества при различных
значениях рН приведен в табл. 10.

Таблица 10

Возможный состав
исследуемого вещества

рН	Внешний вид	Могут присутствовать	Отсутствуют
7	Раствор с осадком	Катионы и анионы всех групп	Кислоты, основания, соли, подвергающиеся гидролизу
	Раствор без осадка	Катионы и анионы, не образующие осадков при их совместном присутствии	Катионы и анионы, образующие осадки при их совместном присутствии
<7	Раствор с осадком	Соединения, не раство-римые в кислотах	Соли, в состав которых входят анионы легко разлагаемых кислот
	Раствор без осадка	Соединения, растворимые в кислотах	Не растворимые в кислотах соединения
	Осадок обра-зуется при раз-бавлении раствора водой	Все катионы и анионы, не образующие осадков при совместном присутствии. Соли, легко гидролизующиеся при разбавлении	Не растворимые в кислотах соединения
>7	Раствор с осадком; нет запаха аммиака	Катионы всех групп и соединения, не растворимые в избытке щелочей	Zn2+, Аl3+, Сr3+, Sn2+, SnIV, SbIII, SbV
	Раствор без осадка; нет запаха аммиака	K+, Na+, Са2+, Ва2+, Sr2+ и катионы, образующие растворимые в избытке щелочи соединения	Все соединения, не растворимые в избытке щелочи
	Раствор с осадком; пахнет аммиаком	Соединения, не растворимые в избытке водного раствора аммиака	
	Раствор без осадка; пахнет аммиаком	Соединения, растворимые в избытке водного раствора аммиака	Все соединения, не растворимые в избытке водного раствора аммиака

Если
реакция раствора кислая (рН<7), это
значит, что вещество может являться
кислой солью (например, KHSO₄)
или солью сильной кислоты и слабого
основания (например, FеС1₃).
В кислом растворе при низких значениях
рН не могут содержаться соли летучих
кислот (угольной, тиосернистой,
сероводородной кислот), не могут совместно
присутствовать окислители и восстановители,
а также соли щелочных и щелочноземельных
металлов слабых кислот: уксусной,
фосфорной и др.

Если
реакция раствора щелочная (рН>7), то
растворена соль сильного основания и
слабой кислоты (К₂СO₃)
и не могут присутствовать соли слабых
оснований и сильных кислот.

Нейтральную
реакцию имеют растворы солей сильных
оснований и сильных кислот (NaCl)
или же солей слабых оснований и слабых
кислот (CH₃COONH₄).

4.
Обнаружение окислителей и восстановителей.
Так как в процессе анализа окислители
и восстановители могут претерпевать
изменения, то необходимо предварительно
провести их определение: окислители
определяют с помощью H₂SO₄
+ KI,
восстановители 
с помощью H₂SO₄
+ KMnO₄,
H₂SO₄
+ I₂,
Fe³⁺
+ K₃[Fe(CN)₆].

Статистическая обработка результатов химического эксперимента (ОФС.1.1.0013.15)

Государственная фармакопея 13 издание (ГФ XIII)

ОБЩАЯ ФАРМАКОПЕЙНАЯ СТАТЬЯ

Взамен ст. ГФ XI, вып.1

Требования данной общей фармакопейной статьи распространяются на методы, используемые при статистической обработке результатов химического эксперимента.

Обозначения:

А — измеряемая величина;

a — свободный член линейной зависимости;

b — угловой коэффициент линейной зависимости;

F — критерий Фишера;

f — число степеней свободы;

i — порядковый номер варианты;

L — фактор, используемый при оценке сходимости результатов параллельных определений;

т, п — объемы выборки;

P, P̅ — доверительная вероятность соответственно при дву- и односторонней постановке задачи;

Q 1, Qn — контрольные критерии идентификации грубых ошибок;

R — размах варьирования;

r — коэффициент корреляции;

s — стандартное отклонение;

s² — дисперсия;

s _o̅ — стандартное отклонение среднего результата;

s _o̅ ,% — относительное стандартное отклонение среднего результата (коэффициент вариации);

s lg — логарифмическое стандартное отклонение;

s 2lg — логарифмическая дисперсия;

S_lgo̅g — логарифмическое стандартное отклонение среднего геометрического результата;

S²₀ , S²_b , S²_a — общая дисперсия и дисперсия коэффициентов линейной зависимости;

t — критерий Стьюдента;

U — коэффициент для расчета границ среднего результата гарантии качества анализируемого продукта;

х, у — текущие координаты в уравнении линейной зависимости;

Хi, Yi — вычисленные, исходя из уравнения линейной зависимости, значения переменных х и у;

x, у — средние выборки (координаты центра линейной зависимости);

Xi, yi — i-тая варианта (i-тая пара экспериментальных значений х и у);

x ± Δx — граничные значения доверительного интервала среднего результата;

Xi ± Δх — граничные значения доверительного интервала результата отдельного определения;

d, А — разность некоторых величин;

α — уровень значимости, степень надежности;

Δх- полуширина доверительного интервала величины;

δ — относительная величина систематической ошибки;

ε, ε̅ — относительные ошибки соответственно результата отдельного

определения и среднего результата;

μ — истинное значение измеряемой величины;

Σ — знак суммирования (сумма);

X² — критерий хи-квадрат.

Примечание. Термины доверительная вероятность P и уровень значимости (степень надежности) α взаимозаменяемы, поскольку их сумма равна либо 1, либо 100 %.

Метрологические характеристики методов и результатов, получаемых при статистической обработке данных эксперимента, позволяют проводить оценку и сравнение, как методик аналитического эксперимента, так и исследуемых при таком эксперименте объектов, и на этой основе решать ряд прикладных задач.

1. Основные статистические характеристики однородной выборки и их вычисление

Проверка однородности выборки. Исключение выпадающих значений вариант. Термином «выборка» обозначают совокупность статистически эквивалентных найденных в эксперименте величин (вариант). В качестве такой совокупности можно, например, рассматривать ряд результатов, полученных при параллельных определениях содержания какого-либо вещества в однородной по составу пробе.

Допустим, что отдельные значения вариант выборки объема п обозначены через x_i (1 ≤ i ≤ n) и расположены в порядке возрастания:

Х₁; х₂; … x_i; …х_n-1; х_n. (1.1)

Результаты, полученные при статистической обработке выборки, будут достоверны лишь в том случае, если эта выборка однородна, т. е. если варианты, входящие в нее, не отягощены грубыми ошибками, допущенными при измерении или расчете. Такие варианты должны быть исключены из выборки перед окончательным вычислением ее статистических характеристик. Для выборки небольшого объема (n < 10) идентификация вариант, отягощенных грубыми ошибками, может быть выполнена, исходя из величины размаха варьирования R, см. уравнения (1.12), (1.13). Для идентификации таких вариант в выборке большого объема (n ≥ 10) целесообразно проводить предварительную статистическую обработку всей выборки, полагая ее однородной, и уже затем на основании найденных статистических характеристик решать вопрос о справедливости сделанного предположения об однородности, см. выражение (1.14).

В большинстве случаев среднее выборки х̅ является наилучшей оценкой истинного значения измеряемой величины μ, если его вычисляют как среднее арифметическое всех вариант:

  (1.2)

При этом разброс вариант х_i вокруг среднего х̅ характеризуется величиной стандартного отклонения s. В количественном химическом анализе величина s часто рассматривается как оценка случайной ошибки, свойственной данному методу анализа. Квадрат этой величины s² называют дисперсией. Величина дисперсии может рассматриваться как мера воспроизводимости результатов, представленных в данной выборке. Вычисление величин (оценок) s и s² проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений d_i и число степеней свободы (число независимых вариант) f:

Стандартное отклонение среднего результата S_0̅  рассчитывают по уравнению:

Отношение S_0̅  к x , выраженное в процентах, называют относительным стандартным отклонением среднего результата или коэффициентом вариации S_0̅ %.

Примечание 1.1. При наличии ряда из g выборок с порядковыми номерами k (1 ≤ k ≤ g) расчет дисперсии s целесообразно проводить по формуле:

При этом число степеней свободы равно:

где x_k — среднее k-той выборки;

n_k — число вариант в k-той выборке;

x_ik — i-тая варианта к-той выборки;

s²_k — дисперсия к-той выборки;

d_ik — отклонение i-той варианты к-той выборки.

Необходимым условием применения уравнений (1.8) и (1.9) является отсутствие статистически достоверной разницы между отдельными значениями S²_k. В простейшем случае сравнение крайних значений S²_k проводят, исходя из величины критерия F, которую вычисляют по уравнению (3.4) и интерпретируют, как указано в разделе 3.

Примечание 1.2. Если при измерениях получают логарифмы искомых вариант, среднее выборки вычисляют как среднее геометрическое, используя логарифм вариант:

Откуда

Значения s², s и S^—_x в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через S²_lg , S_lg и S_lgo̅

Пример 1.1. При определении содержания стрептоцида в образце линимента были получены следующие данные:

Как было указано выше, значения x̅, s², s и s_x̅ могут быть признаны достоверными, если ни одна из вариант выборки не отягощена грубой ошибкой, т. е. если выборка однородна.

Проверка однородности выборок малого объема (n < 10) осуществляется без предварительного вычисления статистических характеристик, с этой целью после представления выборки в виде (1.1) для крайних вариант x₁ и x_n рассчитывают значения контрольного критерия Q, исходя из величины размаха варьирования R:

Выборка признается неоднородной, если хотя бы одно из вычисленных значений Q превышает табличное значение Q (P, n), найденное для доверительной вероятности P̅ (см. табл. I приложения). Варианты х1 или xn, для которых соответствующее значение Q > Q (P, n), отбрасываются и для полученной выборки уменьшенного объема выполняют новый цикл вычислений по уравнениям (1.12) и (1.13) с целью проверки ее однородности. Полученная в конечном счете однородная выборка используется для вычисления x̅, s², s и s_x̅.

Примечание 1.3.

При |x₁ – x₂| < |x₂ – x₃| и x_n – x_n-1 < |x_n-1 – x_n-2| уравнения (1.13 а) и (1.13 б) принимают соответственно вид:

Пример 1.2. При проведении девяти (n = 9) определений содержания общего азота в плазме крови крыс были получены следующие данные (в порядке возрастания):

По уравнениям (1.12) и (1.13 а) находим:

По табл. I приложения находим:

Q(9; 95%) = 0,46 < Q₁ = 0,51;

Q(9; 99%) = 0,55 < Q₁ = 0,51;

Следовательно, гипотеза о том, что значение x₁ = 0,62 должно быть исключено из рассматриваемой совокупности результатов измерений как отягощенное грубой ошибкой, может быть принята с доверительной вероятностью 95 %, но должна быть отвергнута, если выбранное значение доверительной вероятности равно 99 %.

Для выборок большого объема (n ≥ 10) проверку однородности проводят после предварительного вычисления статистических характеристик x̅, s², s и s_x̅. При этом выборка признается однородной, если для всех вариант выполняется условие:

| d_i | ≤ 3s. (1.14)

Если выборка признана неоднородной, то варианты, для которых | di | > 3s, отбрасываются как отягощенные грубыми ошибками с доверительной вероятностью Р > 99,0 %. В этом случае для полученной выборки сокращенного объема повторяют цикл вычислений статистических характеристик по уравнениям (1.2), (1.5), (1.6), (1.9) и снова проводят проверку однородности. Вычисление статистических характеристик считают законченным, когда выборка сокращенного объема оказывается однородной.

Примечание 1.4. При решении вопроса об однородности конкретной выборки небольшого объема также можно воспользоваться выражением (1.14), если известна оценка величины s, ранее найденная для данного метода измерения (расчета) вариант.

2. Доверительные интервалы и оценка их величины

Если случайная однородная выборка конечного объема n получена в результате последовательных измерений некоторой величины А, имеющей истинное значение μ, то среднее этой выборки x следует рассматривать лишь как приближенную оценку величины А. Достоверность этой оценки характеризуется величиной доверительного интервала x̅ ± ∆x̅, для которой с заданной доверительной вероятностью Р выполняется условие:

(x̅ — ∆x̅) ≤ μ ≤ (x̅ — ∆x̅) (2.1)

Следует отметить, что данный доверительный интервал не характеризует погрешность определения величины μ, поскольку найденная величина x̅ может быть в действительности очень близка к истинному значению μ. Полученный доверительный интервал характеризует степень неопределенности истинного значения μ величины А по результатам последовательных измерений выборки конечного объема п. Поэтому правильно говорить о «неопределенности результатов анализа» (которая характеризуется доверительным интервалом) вместо выражения «погрешность результатов анализа», которое нередко не совсем корректно используется.

Расчет граничных значений доверительного интервала проводят по критерию Стьюдента, предполагая, что варианты, входящие в выборку, распределены нормально:

Здесь t (P, f) — табличное значение критерия Стьюдента (см. табл. II приложения).

Если при измерении одним и тем же методом двух близких значений А были получены две случайные однородные выборки с объемами п и m, то при m < п для выборки объема m справедливо выражение:

где индекс указывает принадлежность величин к выборке объема m или n.

Выражение (2.3) позволяет оценить величину доверительного интервала среднего x̅_(m), найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего x̅_(m) для выборки относительно малого объема m может быть сужен благодаря использованию известных величин, S_(n) и t (P, f_(n)) найденных ранее для выборки большего объема n (в дальнейшем индекс n будет опущен).

Примечание 2.1. Если n ≤ 15, а ((m + n) / n) > 1,5 , величины s и f целесообразно вычислять, как указано в примечании 1.1.

Подставляя n = 1 в выражение (2.2), или m = 1 в выражение (2.3), получаем:

x_i ± ∆x = x_i ± t (P, f) _* s (2.4)

Этот интервал является доверительным интервалом результата единичного определения. Для него с доверительной вероятностью Р выполняются взаимосвязанные условия:

x_i — ∆x ≤ μ ≤ x_i + ∆x (2.5)

μ — ∆x ≤ x_i ≤ μ + ∆x (2.6)

Значения ∆x̅ и ∆x из выражений (2.2) и (2.4) используют при вычислении относительных погрешностей отдельной варианты (ε) и среднего результата ( ε̅ ), выражая эти величины в %:

Пример 2.1. В результате определения содержания хинона в стандартном образце хингидрона были получены следующие данные (n = 10):

Расчеты по формулам (1.2), (1.4), (1.5), (1.6), (1.9) дали следующие результаты:

Доверительные интервалы результата отдельного определения и среднего результата при Р = 90 % получаем согласно (2.4) и (2.2):

Тогда относительные погрешности ε и ε‾ согласно (2.7) и (2.8), равны:

Обозначая истинное содержание хинона в хингидроне через μ, можно считать, что с 90 % доверительной вероятностью справедливы неравенства:

Примечание 2.2. Вычисление доверительных интервалов для случая, описанного в примечании 1.2, проводят, исходя из логарифмов вариант. Тогда выражения (2.2) и (2.4) принимают вид:

Потенцирование выражений (2.9) и (2.10) приводит к несимметричным доверительным интервалам для значений х и x_i.

При этом для нижних и верхних границ доверительных интервалов и x имеем:

3. Метрологическая характеристика метода анализа. Сравнение двух методов анализа по воспроизводимости.

С целью получения метрологической характеристики метода проводят совместную статистическую обработку одной или нескольких выборок, полученных при анализе образцов с известным содержанием определяемого компонента μ. Результаты статистической обработки представляют в виде табл. 1.

*- Графа 10 заполняется в том случае, если реализуется неравенство (3.2).

Примечание 3.1. При проведении совместной статистической обработки нескольких выборок, полученных при анализе образцов с разным содержанием определяемого компонента μ, данные в графах 1, 2, 3, 4, 9 и 10 табл. 1 приводят отдельно для каждой выборки. При этом в графах 2, 4, 5, 7, 8 в последней строке под чертой приводят обобщенные значения f, s², s, t, ∆x, вычисленные с учетом примечания 1.1.

Если для выборки объема m величина |μ – x̅| > 0, следует решить вопрос о наличии или отсутствии систематической ошибки. Для этого вычисляют критерий Стьюдента t:

Если, например, при Р = 95 % и f = m — 1, реализуется неравенство

t > t (P, f) (3.2)

то полученные данным методом результаты отягощены систематической ошибкой, относительная величина которой δ вычисляется по формуле:

Следует помнить, что если величина А определена как среднее x̅ некоей выборки, полученной эталонным методом, критерий Стьюдента t может рассчитываться по уравнению (4.5).

При сравнении воспроизводимости двух методов анализа с оценками дисперсий s²₁ и s²₂ (s²₁ > s²₂) вычисляют критерий Фишера F:

F = s²₁ / s²₂ (3.4)

Критерий F характеризует при s²₁ > s²₂ достоверность различия между s²₁ и s²₂. Вычисленное значение F сравнивают с табличным значением F (P, f₁, f₂) найденным при P = 99 % (см. табл. III приложения).

Если для вычисленного значения F выполняется неравенство:

F > F (P, f₁, f₂) (3.5)

различие дисперсий s²₁ и s²₂ признается статистически значимым с вероятностью Р, что позволяет сделать заключение о более высокой воспроизводимости второго метода. Если выполняется неравенство:

F ≤ F (P, f₁, f₂) (3.5a)

различие значений s²₁ и s²₂ не может быть признано значимым и заключение о различии воспроизводимости методов сделать нельзя ввиду недостаточного объема информации.

Примечание 3.2. Для случая, описанного в примечании 1.2, в табл. 1 вместо величин μ, x̅, s² и s приводят величины lgμ, lg x̅ _g, s²_lg и s_lg. При этом в графу 8, согласно примечанию 2.2, вносят величину ∆lg x, а в графу 9 — максимальное по абсолютной величине значение ε. Аналогичные замены проводят при вычислении t по уравнению (3.1) и F — по уравнению (3.4).

Для сравнения двух методов анализа результаты статистической обработки сводят в табл.2.

Таблица 2 — Данные для сравнительной метрологической оценки двух методов анализа

Метрологическое сравнение методов анализа желательно проводить при μ₁ = μ₂, f₁ > 10 и f₂ > 10. Если точные значения μ1 и μ2 неизвестны, величины δ и tвыч не определяют.

Пример 3.1. Пусть для двух выборок аналитических данных (1 и 2), характеризующих, например, различные методы анализа, получены метрологические характеристики, приведенные в графах 1 — 10 табл. 3

Для заполнения графы 11 вычислим значения tвыч(1) и tвыч(2):

Поскольку t_выч(1) = 1,28 < t₁ (95 %, 20) = 2,09, гипотеза |μ₁ – x̅₂| ≠ 0 может быть отвергнута, что позволяет считать результаты выборки 1 свободными от систематической ошибки. Напротив, поскольку t_выч(2) = 72,36 » t2 (95 %, 15) = 2,13, гипотезу |μ₂ – x̅₂| ≠ 0 приходится признать статистически достоверной, что свидетельствует о наличии систематической ошибки в результатах выборки 2.

В графу 14 вносим вычисленное значение δ2:

Заполним графы 12 и 13:

Следовательно, при Р = 99 % гипотезу о различии дисперсий s²₁ и s²₂ следует признать статистически достоверной.

Выводы:

1. результаты, полученные первым методом, являются правильными, т. е. они не отягощены систематической ошибкой;
2. результаты, полученные вторым методом, отягощены систематической ошибкой;
3. по воспроизводимости второй метод существенно превосходит первый метод.

4. Метрологическая характеристика среднего результата. Сравнение средних результатов двух выборок.

Если с помощью данного метода анализа (измерения) следует определить значение некоторой величины А, то для полученной экспериментально однородной выборки объема m рассчитывают значения величин, необходимые для заполнения табл. 4. Так поступают в том случае, если применяемый метод анализа (измерения) не был ранее аттестован метрологически. Если же этот метод уже имеет метрологическую аттестацию, графы 2, 4, 5, 7, 8 и 9 табл. 4 заполняются на основании данных табл. 1, полученных при его аттестации. При заполнении табл. 4 следует при необходимости учитывать примечания 2.1 и 3.1.

Таблица 4 — Метрологические характеристики среднего результата

Таким образом, на основании выражения (2.1) для измеряемой величины А в предположении отсутствия систематической ошибки с вероятностью Р выполняется условие:

x — ∆x ≤ A ≤ x + ∆x , (4.1)

то есть величина А при отсутствии систематической ошибки лежит в пределах:

A = x ± ∆x . (4.2)

Примечание 4.1. В случае, предусмотренном в примечании 1.2, в графе 9 табл. 4 приводят величину ∆lg x̅, а каждую из граф 3, 10 и 11 разбивают на две (а, б). В графе 3а приводят значение x̅_g, в графе 3б – значение lg x̅ _g, в графах 10а и 10б — соответственно значения нижней и верхней границ доверительного интервала для xg (см. уравнения (2.11), (2.12)). Наконец, в графе 11 приводят максимальное по абсолютной величине значение ε̅ (см. уравнение (2.12 а)).

Если в результате измерений одной и той же величины А получены две выборки объема n 1 и n2, причем x1 ≠ x2, может возникнуть необходимость проверки статистической достоверности гипотезы:

x̅1 = x̅2, (4.3)

то есть значимости величины разности ( x̅1 — x̅2)

Такая проверка необходима, если величина А определялась двумя разными методами с целью их сравнения или если величина А определялась одним и тем же методом для двух разных объектов, идентичность которых требуется доказать. Для проверки гипотезы (4.3) следует установить, существует ли статистически значимое различие между дисперсиями s²₁ и s²₂ . Эта проверка проводится так, как указано в разделе 3 (см. выражения (3.4), (3.5), (3.5 а)).

Рассмотрим три случая.

1. Различие дисперсий s²₁ и s²₂ статистически недостоверно (справедливо неравенство (3.5 а)). В этом случае средневзвешенное значение s₂ вычисляют по уравнению (1.7), а дисперсию s²_p разности |x̅₁ – x̅₂| — по уравнению:

Далее вычисляют критерий Стьюдента:

Если при выбранном значении Р (например, при Р = 95 %):

t > t (P, f), (4.6)

то результат проверки положителен — значение (xi — x2) является значимым и
гипотезу xi = x2 отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.

2. Различие значений s²₁ и s²₂ статистически достоверно (справедливо неравенство (3.5)). Если s²₁ > s²₂, дисперсию s²₁ разности (x̅₁ – x̅₂) находят по уравнению (4.7), а число степеней свободы по f ’ по уравнению (4.8):

Следовательно, в данном случае:

Вычисленное по уравнению (4.9) значение t сравнивают с табличным значением t (Р, f ‘ ), как это описано выше для случая 1.

Рассмотрение проблемы упрощается, когда n₁ ≈ n₂ и s²₁ >> s²₂. Тогда в отсутствие систематической ошибки среднее x̅₂ выборки объема n₂ принимают за достаточно точную оценку величины А, т. е. принимают x2 = μ. Справедливость гипотезы x₁ = μ, эквивалентной гипотезе (4.3), проверяют с помощью выражений (3.1), (3.2), принимая f1 = n 1 — 1. Гипотеза (4.3) отклоняется как статистически недостоверная, если выполнятся неравенство (3.2).

3. Известно точное значение величины А. Если A = μ, проверяют две гипотезы:

x̅₁ = μ (4.3 a) и x̅₂ = μ (4.3 б).

Проверку выполняют так, как описано в разделе 3 с помощью выражений (3.1) и (3.2) отдельно для каждой из гипотез. Если гипотезы (4.3 а) и (4.3 б) статистически достоверны, то следует признать достоверной и гипотезу (4.3). В противном случае гипотеза (4.3) должна быть отброшена.

Примечание 4.2. В случае, предусмотренном примечанием 1.2, при сравнении средних используют величины lgx̅_g , s²_lg и s_lg.

Когда разность (x 1 — x 2) оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних :

Пример 4.1. При определении содержания основного вещества в двух образцах препарата, изготовленных по разной технологии, получены метрологические характеристики средних результатов, приведенные в табл. 5.

Таблица 5 -Полученные данные метрологических характеристик средних результатов

Требуется решить, является ли первый образец по данному показателю лучшим в сравнении со вторым образцом. Поскольку

то согласно неравенству (3.5 а) статистически достоверное различие величин s²₁ и s²₂ отсутствует. Следовательно, гипотеза x̅₁ = x̅₂ (4.3) проверяется с помощью уравнений (1.7), (1.8), (4.4) и (4.5).

Следовательно, с доверительной вероятностью Р = 95 % гипотеза x̅₁ ≠ x̅₂ может быть принята. Однако с доверительной вероятностью Р = 99 % принять эту гипотезу нельзя из-за недостатка информации.

Если гипотеза x̅₁ ≠ x̅₂ принята, то определяют доверительный интервал разности генеральных средних (уравнение (4.10)):

5. Интерпретация результатов анализа

Оценка сходимости результатов параллельных определений. При рядовых исследованиях аналитик обычно проводит 2 — 3, реже 4 параллельных определения. Варианты полученной при этом упорядоченной выборки объема m, как правило, довольно значительно отличаются друг от друга. Если метод анализа метрологически аттестован, то максимальная разность результатов двух параллельных определений должна удовлетворять неравенству:

|x₁ — x_n| < L(P, m)_*s, (5.1)

где L (P, m) — фактор, вычисленный по Пирсону при Р = 95 %.

Если неравенство (5.1) не выполняется, необходимо провести дополнительное определение и снова проверить, удовлетворяет ли величина |x₁ — x_n| неравенству (5.1).

Если для результатов 4 параллельных определений неравенство (5.1) не выполняется, одна из вариант (х₁ или xn) должна быть отброшена и заменена новой. При невозможности добиться выполнения неравенства (5.1) следует считать, что конкретные условия анализа привели к снижению воспроизводимости метода и принятая оценка величины s применительно к данному случаю является заниженной. В этом случае поступают, как указано в разделе 1.

Определение необходимого числа параллельных определений. Если необходимо получить средний результат x̅ с относительной погрешностью ε̅ ≤ φ, причем метод анализа метрологически аттестован, необходимое число параллельных определений m находят учетом с уравнений (2.3) и (2.4):

Гарантия качества продукции. Предположим, что качество продукции регламентируется предельными значениями amin и amax величины А, которую определяют на основании результатов анализа. Примем, что вероятность соответствия качества продукта условию:

a_min < A < a_max, (5.3)

должна составлять P̅ %.

Пусть величину А находят экспериментально, как среднее выборки объема т, а метод ее определения метрологически аттестован. Тогда условие (5.3) будет выполняться с вероятностью P̅, если значение x̅ = A будет лежать в пределах:

Значения коэффициента U для вероятности P̅ = 95 % и P̅ = 99 % соответственно равны 1,65 и 2,33. Иными словами, для гарантии качества наблюдаемые пределы изменения величины А на практике следует ограничить значениями:

Наоборот, если заданы значения A_min и A_max, значения a_min и a_max, входящие в неравенство (5.3), могут быть найдены путем решения уравнений (5.6) и (5.7). Наконец, если заданы пары значений A min, amin и A max, amax, то уравнения (5.6) и (5.7) могут быть решены относительно т. Это может быть использовано для оценки необходимого числа параллельных определений величины А.

Примечание 5.1. В уравнениях (5.5), (5.6) и (5.7) величина коэффициента U(P) должна быть заменена величиной t (P, f), если значение f, определенное по уравнениям (1.4) или (1.8), меньше 15.

Примечание 5.2. Для случая, предусмотренного примечанием 1.2, описанные в разделе 5 вычисления проводят с использованием величин и т. п.

Пример 5.1. Рассмотрим данные табл. 3, относящиеся к выборке 1, как метрологическую характеристику используемого метода анализа.

a) Пусть amin = 98 %, amax = 100,50 %. Тогда для испытуемого образца продукта средний результат анализа A̅ при проведении трех параллельных определений (m = 3) должен находиться в пределах:

б) Реальный средний результат анализа образца испытуемого продукта А = 99 % (при т = 3). Тогда определение пределов amin и amax, гарантированно характеризующих качество данного образца с заданной доверительной вероятностью P, проводим, исходя из уравнения (5.6) или (5.7), полагая

Полученные оценки amin и amax близки к границам доверительного интервала
что соответствует примечанию 5.1.

6. Расчет и статистическая оценка параметров линейной зависимости (линейной регрессии)

При использовании ряда химических и физико-химических методов количественного анализа непосредственному измерению подвергается некоторая величина у, которая рассматривается как линейная функция искомой концентрации (количества) х определяемого вещества или элемента. Иными словами, в основе таких методов анализа лежит экспериментально подтвержденная линейная зависимость:

y = bx + a, (6.1)

где у — измеряемая величина;

х — концентрация (количество) определяемого вещества или элемента;

b — угловой коэффициент линейной зависимости;

а — свободный член линейной зависимости.

(Здесь b и а рассматриваются как коэффициенты (параметры) линейной регрессии y на x).

Для использования зависимости (6.1) в аналитических целях, т. е. для определения конкретной величины х по измеренному значению у, необходимо заранее найти числовые значения констант b и а, иными словами провести калибровку. Если константы зависимости (6.1) рассматриваются с учетом их физического смысла, то, при необходимости, их значения могут оцениваться с учетом доверительных интервалов.

Если калибровка проведена и значения констант а и b определены, величину X_i находят по измеренному значению y_i:

При калибровке величину х рассматривают как аргумент, а величину у — как функцию.

Наличие линейной зависимости между х и у целесообразно подтверждать расчетным путем. Для этого по экспериментальным данным, полученным при калибровке, оценивают достоверность линейной связи между х и у с использованием корреляционного анализа и лишь затем рассчитывают значения констант а и b зависимости (6.1) и их доверительные интервалы. В первом приближении судить о достоверности линейной связи между переменными х и у можно по эмпирической величине коэффициента корреляции r, который вычисляют по уравнению:

исходя из экспериментальных данных, представленных в табл. 6. Чем ближе значение |r| к единице, тем менее наблюдаемая линейная зависимость между переменными х и у может рассматриваться как случайная. В аналитической химии в большинстве случаев используют линейные зависимости, отвечающие условию |r| > 0,98, и только при анализе следовых количеств рассматривают линейные зависимости, для которых |r| > 0,90. При столь близких к 1 значениях величины |r| формальное подтверждение наличия линейной связи между переменными x и у проводить не следует.

Коэффициенты а и b и метрологические характеристики зависимости (6.1) рассчитывают с использованием регрессионного анализа, т. е. методом наименьших квадратов по экспериментально измеренным значениям переменной у для заданных значений аргумента х. Пусть в результате эксперимента найдены представленные в табл. 6 пары значений аргумента х и функции у.

Таблица 6. Значения аргумента х и функции у.

Если полученные значения коэффициентов а и b использовать для вычисления значений у по заданным в табл. 6 значениям аргумента х согласно зависимости (6.1), то вычисленные значения у обозначают через Y 1, Y2, … , Yi, … Yn. Разброс значений Yi относительно значений yi характеризуется величиной дисперсии s²₀, которую вычисляют по уравнению:

В свою очередь, дисперсии констант b и а находят по уравнениям:

Стандартные отклонения s_b и s_a и величины ∆b и ∆a, необходимые для оценки доверительных интервалов констант уравнения регрессии, рассчитывают по уравнениям:

Уравнению (6.1) с константами а и b обязательно удовлетворяет точка с координатами x и у, называемая центром калибровочного графика:

Наименьшие отклонения значений y_i от значений Y_i наблюдаются в окрестностях центра графика. Стандартные отклонения sy и sx величин Y и X, рассчитанных соответственно по уравнениям (6.1) и (6.2), исходя соответственно из известных значений х и у, определяются с учетом удаления последних от центра графика:

где y̅_j — среднее значение для n_j— вариант y, по которым вычислено искомое значение X.

При x = x̅ и y̅_j = y̅ выражения (6.16) и (6.17) принимают вид:

С учетом значений sy и sx могут быть найдены значения величин ∆Y и ∆X:

∆Y = s_y*t(P, f); (6.18)

∆X = s_x*t(P, f). (6.19)

Значения sx и ∆X, найденные при n_j = 1, являются характеристиками воспроизводимости аналитического метода, если х — концентрация (количество), а у есть функция х.

Обычно результаты статистической обработки по методу наименьших квадратов сводят в таблицу (табл. 7).

Таблица 7. Результаты статистической обработки экспериментальных данных, полученных при изучении линейной зависимости у = bx + a

Примечание 6.1. Если целью экспериментальной работы являлось определение констант b и a, графы 11, 12 и 13 табл. 7 не заполняются.

Примечание 6.2. Если y = b lg x + a, вычисления, описанные в разделе 6, выполняют с учетом примечаний 1.2 и 2.2.

Примечание 6.3. Сравнение дисперсий s²₀, полученных в разных условиях для двух линейных зависимостей, может быть проведено, как указано в разделе 3 (см. выражения (3.4), (3.5) и (3.5 а)).

7. Расчет неопределенности функции нескольких случайных переменных

Описанные в разделах 1 — 6 настоящей общей фармакопейной статьи расчеты доверительных интервалов результатов методик анализа применимы лишь в том случае, если измеряемая величина (концентрация, содержание и т.д.) является функцией только одной случайной переменной. Такая ситуация обычно возникает при использовании прямых методов анализа (титрование, определение сульфатной золы, тяжелых металлов и т.д.). Однако большинство методик количественного определения в фармакопейном анализе являются косвенными, то есть используют стандартные образцы. Следовательно, измеряемая величина является функцией, как минимум, двух случайных переменных — аналитических сигналов (оптическая плотность, высота или площадь пика и т.д.) испытуемого и стандартного образцов. Кроме того, нередко возникает проблема прогнозирования неопределенности аналитической методики, состоящей из нескольких стадий (взвешивание, разбавление, конечная аналитическая операция), каждая из которых является по отношению к другой случайной величиной.

Таким образом, возникает общая проблема оценки неопределенности косвенно измеряемой величины, зависящей от нескольких измеряемых величин, в частности, как рассчитывать неопределенность всей аналитической методики, если известны неопределенности отдельных ее составляющих (стадий)?

Если измеряемая на опыте величина у является функцией п независимых случайных величин x_i, то есть:

y = f(x₁, x₂, … x_n), (7.1)

и число степеней свободы величин xi одинаково или достаточно велико (> 30, чтобы можно было применять статистику Гаусса, а не Стьюдента), то диспер­сия величины у связана с дисперсиями величин xi соотношением (правило рас­пространения неопределенностей):

Однако на практике степени свободы величин xt обычно невелики и не равны друг другу. Кроме того, обычно интерес представляют не сами дисперсии (стандартные отклонения), а доверительные интервалы, рассчитать которые, используя уравнение (7.2), при небольших и неодинаковых степенях свободы невозможно. Поэтому для расчета неопределенности величины у (∆у) предложены различные подходы, среди которых можно выделить два основных: линейная модель и подход Уэлча-Сатертуэйта.

7.1. Линейная модель

Если случайные переменные xi статистически независимы, то доверительный интервал функции ∆у связан с доверительными интервалами переменных ∆xi соотношением (доверительные интервалы берутся для одной и той же вероятности):

Данное выражение является обобщением соотношения (7.2).

В фармакопейном анализе измеряемая величина у представляет собой обычно произведение или частное случайных и постоянных величин (масс навесок, разбавлений, оптических плотностей или площадей пиков и т.д.), т.е. (К — некая константа):

В этом случае соотношение (7.2) принимает вид:

где использованы относительные доверительные интервалы.

Соотношение (7.4) применимо при любых (разных) степенях свободы (в том числе и бесконечных) для величин x_i. Его преимуществом является простота и наглядность. Использование абсолютных доверительных интервалов приводит к гораздо более громоздким выражениям, поэтому рекомендуется использовать относительные величины.

При проведении фармакопейного анализа в суммарной неопределенности (∆_As,r) анализа обычно всегда можно выделить такие типы неопределенностей: неопределенность пробоподготовки (∆_SP,r), неопределенность конечной аналитической операции (∆_FAO,r) и неопределенность аттестации стандартного образца (∆_RS,r). Величина (∆_RS,r) обычно столь мала, что ею можно пренебречь. Учитывая это, а также то, что анализ проводится и для испытуемого раствора (индекс «smp»), и для раствора сравнения (индекс «st»), выражение (7.5) можно представить в виде:

При этом каждое из слагаемых рассчитывается из входящих в него ком­понентов по формуле (7.5).

Если число степеней свободы величин xi одинаково или достаточно велико (> 30), выражение (7.5) дает:

Это же соотношение получается при тех же условиях и из выражения (7.2).

7.2. Подход Уэлча-Сатертуэйта

В этом подходе дисперсию величины у (s²_y) рассчитывают по соотношению (7.2), не обращая внимания на различие в степенях свободы (v_i) величин x_i. Для полученной дисперсии s²_y рассчитывают некое «эффективное» число степеней свободы veff (которое обычно является дробным), на основе которого затем по таблицам для заданной вероятности находят интерполяцией значения критерия Стьюдента. На основе его далее рассчитывают обычным путем доверительный интервал величины y (∆_у):

В фармакопейном анализе для определяемой величины у обычно выполняется уравнение (7.4). В этом случае в подходе Уэлча-Сатертуэйта соотношение (7.2) переходит в выражение (7.7), и соотношение (7.8) принимает более простой вид:

Здесь величина s_y,r⁴ рассчитывается из соотношения (7.7).

Подход Уэлча-Сатертуэйта обычно дает более узкие доверительные ин­тервалы, чем линейная модель. Однако он гораздо сложнее в применении и не позволяет выделить так просто неопределенности разных этапов (с последующими рекомендациями по их минимизации), как линейная модель в форме выражения (7.6).

При прогнозе неопределенности анализа используются генеральные величины (с бесконечным числом степеней свободы). В этом случае подход Уэлча-Сатертуэйта совпадает с линейной моделью.

ПРИЛОЖЕНИЯ

Таблица I. Критические значения контрольного критерия Q (Р, n)

Таблица II. Критические значения критерия Стьюдента

t = 1,958788 + 2,429953/f + 2,189891/f ² + 4,630189/f ³ + 1,398179/f ⁹ при P = 95%;

t = 2,5638 + 5,49059/f + 2,72654/f ² + 31,2446/f ³ + 21,6745/f ⁹ при P = 99%.

Таблица III. Критические значения критерия Фишера

F для P = 95 % напечатаны жирным шрифтом, а F для P = 99 % — обычным.

Как рассчитать экспериментальную ошибку в химии

На чтение 1 мин Просмотров 392 Опубликовано 05.06.2021

Ошибка – это мера точности значений в вашем эксперименте. Важно уметь вычислить экспериментальную ошибку, но есть несколько способов ее вычислить и выразить. Вот наиболее распространенные способы вычисления экспериментальной ошибки:

Содержание

1. Формула ошибки
2. Формула относительной ошибки
3. Формула процента ошибки
4. Пример расчета ошибки

Формула ошибки

В общем, ошибка – это разница между принятым или теоретическое значение и экспериментальное значение.

Ошибка = экспериментальное значение – известное значение

Формула относительной ошибки

Относительная ошибка = ошибка/известное значение

Формула процента ошибки

% Error = относительная ошибка x 100%

Пример расчета ошибки

Допустим, исследователь измеряет массу образца, который должен быть 5,51 грамм. Известно, что фактическая масса образца составляет 5,80 грамма. Рассчитайте погрешность измерения.

Экспериментальное значение = 5,51 грамма
Известное значение = 5,80 грамма

Ошибка = экспериментальное значение – известное значение
Ошибка = 5,51 г – 5,80 грамма
Ошибка = – 0,29 грамма

Относительная ошибка = ошибка/известное значение
Относительная ошибка = – 0,29 г/5,80 г
Относительная ошибка = – 0,050

% Error = относительная ошибка x 100%
% Error = – 0,050 x 100%
% Error = – 5,0%

Классификация и оценка погрешностей количественного анализа

По способу вычисления различают абсолютную 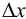и относительную (ранее 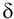) погрешности.

Если среднее арифметическое значение 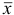для 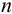полученных результатов анализа составляет:

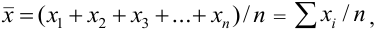
то абсолютную погрешность выражают как

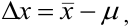
где 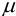— истинное содержание определяемого компонента (например, известное для стандартного образца или контрольной пробы). Очевидно, что абсолютная погрешность может быть положительной или отрицательной, в зависимости от того, каким получился результат: завышенным или заниженным по сравнению с истинным (рис. 9.1).

Относительная погрешность может быть выражена в долях или процентах и обычно не имеет знака:

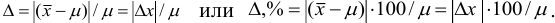
По происхождению погрешности делят на систематические, случайные и промахи (грубые ошибки).

Погрешность определения, обусловленная постоянно действующей причиной, неизменная во всех измерениях, сохраняющая знак от опыта к опыту или закономерно изменяющаяся, называется систематической погрешностью. Погрешность, случайным образом изменяющаяся от опыта к опыту, называется случайной погрешностью. Грубые погрешности или промахи резко искажают результат анализа, вызываются небрежностью и обычно легко обнаруживаются.

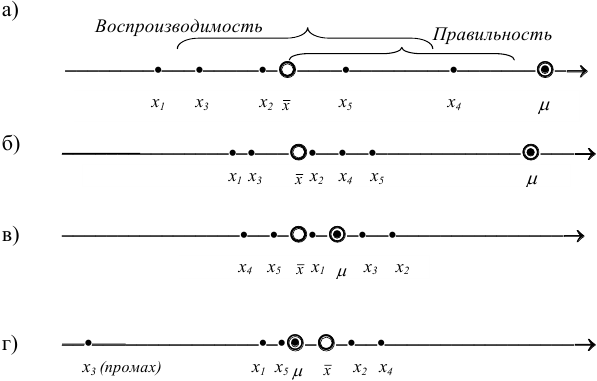
Рис. 9.1. Воспроизводимость и правильность химического анализа. Результаты: а) невоспроизводимы и неправильны; б) воспроизводимы, но неправильны; в) воспроизводимы и правильны; г) воспроизводимы и правильны, но есть промах.

С систематическими погрешностями связана правильность анализа, со случайными погрешностями — воспроизводимость. Правильность и воспроизводимость являются метрологическими характеристиками анализа и входят в понятие «точность анализа».

Воспроизводимость результатов анализа характеризует рассеяние единичных результатов относительно среднего.

Правильность характеризует отклонение полученного результата от истинного и показывает, насколько близка к нулю систематическая погрешность. Систематические погрешности выявляют и устраняют. Если же устранение невозможно, то при постоянном значении систематической погрешности ее учитывают, вводя поправку. Для выявления используют различные приемы и методы, например “введено — найдено”, анализ стандартного образца, “двойной или тройной добавки”.

Оценка случайных погрешностей проводится методами математической статистики. В обычной практике выполняют ограниченное число параллельных измерений п (обычно 3-5), называемое выборочной совокупностью данных или просто выборкой (в отличие от генеральной совокупности — при 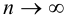). При 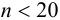математическую обработку результатов проводят с использованием распределения Стьюдепта, связывающего вероятность попадания величины в данный доверительный интервал и объем выборки 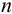. Среднее для ряда параллельных определений, 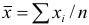, является наиболее вероятным значением измеряемой величины.

Характеристики случайной погрешности (воспроизводимости) для выборки: выборочная дисперсия 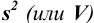, стандартное отклонение 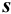и относительное стандартное отклонение :

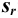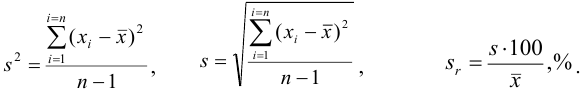
С ними связаны дисперсия среднего 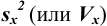и стандартное отклонение среднего :

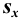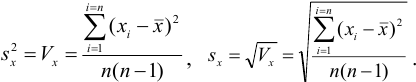
При обработке данных химического анализа определяют границы доверительного интервала 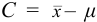, вводя число степеней свободы .

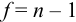Доверительный интервал (С) — это интервал значений, в котором для данного вида распределения случайных величин (при отсутствии систематических погрешностей), при заданной доверительной вероятности Р и числе степеней свободы 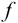лежит истинное значение определяемой величины:

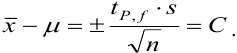
Доверительная вероятность попадания величины внутрь доверительного интервала в химическом анализе принята равной 0,95 или 95 %. Это означает, что в рассчитанный интервал попадут 95 из 100 значений. Коэффициенты 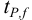— коэффициенты нормированных отклонений Стьюдента приведены в табл. 8 приложения. Зависимость 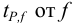показывает, что с возрастанием числа степеней свободы, т. е. числа параллельных результатов, увеличивается и точность анализа, поскольку доверительный интервал характеризует воспроизводимость и, в какой-то мере, правильность результатов химического анализа. С учетом доверительного интервала истинное значение представляют выражением:

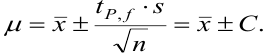
Оценка промахов (выбраковка результатов). Перед обработкой данных методами математической статистики необходимо выявить промахи и исключить их из числа обрабатываемых результатов. Для выявления промахов используют различные критерии, в частности, -критерий. Проверку соответствия -критерию про водят следующим образом. Все параллельные результаты располагают в последовательности их убывания или возрастания. При этом 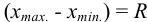— размах варьирования. Затем рассчитывают :

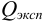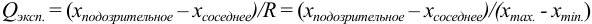
и сравнивают с критическим значением 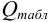при доверительной вероятности 0,90 (табл. 9 приложения).
Если 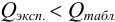, то промах отсутствует и подозрительный результат оставляют в составе выборки. Если же 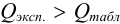, то подозрительное значение является промахом, грубой погрешностью; его отбрасывают.

— критерий рекомендуется применять к выборкам с 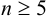. При малой выборке 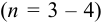заметно отличающийся от других результат просто отбрасывают, а определение повторяют и после этого оценивают случайную погрешность. Если 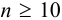, промахи можно установить с помощью 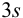— критерия, проверяя для каждого отклонения 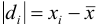выполнение условия 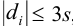, позволяющего оставить результат в составе выборки.

Пример 9.1.

Контрольный раствор соли кальция имеет концентрацию 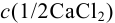, равную 0,1056 моль/л. Студентом было получено методом перманганатометрии среднее значение 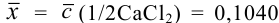. Вычислите абсолютную и относительную погрешности.

Решение:

Абсолютная погрешность результата:

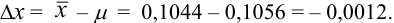
Относительная погрешность:

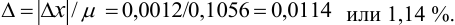
Пример 9.2.

При определении содержания аскорбиновой кислоты в пробе картофеля по новой методике пробоподготовки получены следующие результаты (мг/100 г): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,25; 14,49. Оцените:

а) наличие грубых погрешностей (промахов);

б) воспроизводимость результатов анализа.

Решение:

а) наличие промахов оценим по -критерию. Представим экспериментальные данные в порядке возрастания: 14,25; 14,40; 14,43; 14,44; 14,45; 14,49; 14,50; 14,52; 14,54; 14,58. Проверим подозрительные значения 14,25 и 14,58. Вычислим — критерий для этих величин:

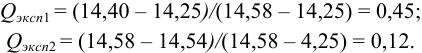
Из табл. 9 приложения при 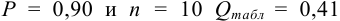; 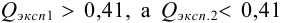, следовательно, значение 14,25 недостоверно и его исключаем, сокращая объем выборки до .

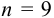б) после исключения промаха найдем среднее и характеристики воспроизводимости: дисперсию 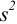, стандартное отклонение 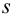и относительное стандартное отклонение :

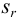Пример 9.3.

Используя условия примера 9.2 и считая, что содержание аскорбиновой кислоты для той же пробы картофеля, определенное по стандартной методике составляет 14,58 мг/100 г, рассчитайте доверительный интервал и установите, свидетельствуют ли полученные результаты о наличии систематической погрешности при работе по новой методике?

Решение:

Для расчета доверительного интервала при числе степеней свободы 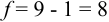и доверительной вероятности Р = 0,95 из табл. 8 приложения находим коэффициент Стьюдента .

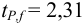Находим полуширину доверительного интервала, оставляя значащие цифры:

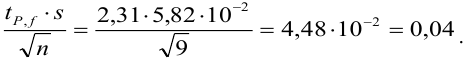
Таким образом, среднее содержание аскорбиновой кислоты лежит в границах

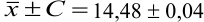или 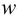(кислоты), мг/100 г = 14,48 ± 0,04. Истинное значение содержания аскорбиновой кислоты14,58 не попадает в доверительный интервал, следовательно, такой метод пробоподготовки картофеля к анализу имеет систематическую погрешность, причину которой надо выяснять.

Пример 9.4.

При анализе стандартного образца, содержащего 1,44 % , были получены результаты (%): 1,31; 1,45; 1,42; 1,32; 1,30. Определить стандартное отклонение, доверительный интервал и сделать выводы о наличии систематической погрешности в использованном методе определения серебра.

Решение:

Проверим наличие грубых погрешностей по -критерию. Располагаем экспериментальные данные в порядке возрастания численных значений: 1,30; 1,31; 1,32; 1,42; 1,45. Предполагаем, что значение 1,45 является результатом грубой погрешности. Рассчитываем для него -критерий:

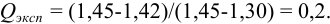
Для 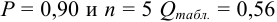(табл. 9 приложения). Вычисленное значение -критерия 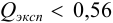, следовательно, грубая погрешность отсутствует.

Находим среднее значение из пяти определений:

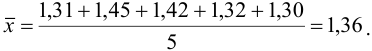
Вычисляем стандартное отклонение:

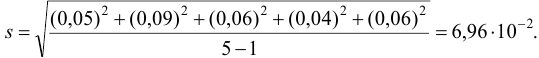
По табл. 8 приложения для 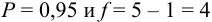находим 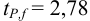и рассчитываем полуширину доверительного интервала для :

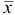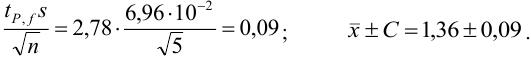
Результат представляем в виде: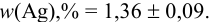

Наличие систематической погрешности можно выявить, как в предыдущем примере, проверяя попадает ли истинное значение содержания серебра в доверительный интервал. В данном случае для 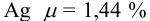попадает в границы доверительного интервала, следовательно, систематическая погрешность в этом методе определения серебра отсутствует.

Ответить на вопрос задачи о присутствии систематической погрешности можно, используя критерий Стьюдента и сравнивая вычисленное значение 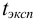с табличным значением 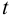— критерия при 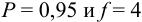, равным 2,78:

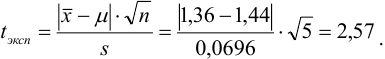
Поскольку 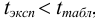делаем вывод о вероятном отсутствии систематической погрешности.

Пример 9.5.

При определении ванадия были получены результаты: 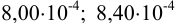г. Чему равен доверительный интервал? Сколько параллельных определений необходимо провести для достижения доверительного интервала с полушириной?

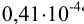Решение:

Находим среднее значение:

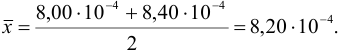
Вычислим стандартное отклонение:

По табл. 8 приложения находим 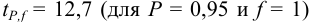и вычисляем полуширину доверительного интервала:

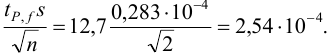
Требуется же получить доверительный интервал с полушириной 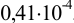Найдем необходимое для этого соотношение :

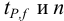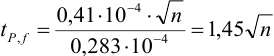или 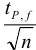должно быть .

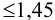При 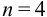значение критерия 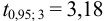, а отношение 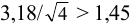; при 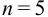значение критерия 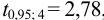, а отношение .

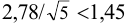Таким образом, для сужения границ доверительного интервала до 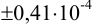необходимо провести 5 параллельных определений.

Эти примеры взяты со страницы примеров решения задач по аналитической химии:

Решение задач по аналитической химии

Возможны вам будут полезны эти страницы: