Относительная ошибка
Ошибки средняя квадратичная т, истинная А называются абсолютными ошибками.
В некоторых случаях абсолютная ошибка недостаточно показательна, в частности, при линейных измерениях. Например, линия измерена с ошибкой ±5 см. Для длины линии в 1 метр эта точность, очевидно, низкая, а для длины линии в 1 километр точность безусловно более высокая. Поэтому нагляднее точность измерения будет характеризоваться отношением абсолютной ошибки к полученному значению измеренной величины. Такое отношение называется относительной ошибкой. Относительная ошибка выражается дробью, причем дробь преобразуется так, чтобы числитель ее был равен единице.
Относительную ошибку определяют по соответствующей абсолютной
ошибке. Пусть X — полученное значение некоторой величины, тогда  — средняя квадратичная относительная ошибка этой величины;
— средняя квадратичная относительная ошибка этой величины;  — истинная относительная ошибка.
— истинная относительная ошибка.
Знаменатель относительной ошибки целесообразно округлять до двух значащих цифр с нулями.
Пример. В приведенном случае средняя квадратичная относительная ошибка измерения линии будет равна 
Предельная ошибка
Предельной ошибкой называется наибольшее значение случайной ошибки, которое может появиться при данных условиях равноточных измерений.
Теорией вероятности доказано, что случайные ошибки только в трех случаях из 1000 могут превзойти величину Зт; 5 ошибок из 100 могут превзойти 2т и 32 ошибки из 100 могут превзойти т.
Исходя из этого, в геодезической практике результаты измерений, содержащие ошибки 0>3т, относят к измерениям, содержащим грубые ошибки, и в обработку не принимают.
Значения ошибок 0 = 2т используют как предельные при составлении технических требований для данного вида работ, т. е. все случайные ошибки измерений, превышающие по своей величине эти значения, считают недопустимыми. При получении расхождений, превышающих величину 2т, принимают меры по улучшению условий измерений, а сами измерения повторяют.
math4school.ru








Ошибки в уравнениях

При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.
Потеря корней
При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней , либо появление посторонних корней .
При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного , а значит, корни могут оказаться потерянными.
K Упражнение. Решить уравнение lg (x – 10) 2 + lg x 2 = 2lg 24 .
L Неправильное решение.
2lg (x – 10) + 2lg x = 2lg 24,
Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.
Комментарий . Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.
J Правильное решение.
Ответ: –2; 4; 6 и 12.

При делении обеих частей уравнения на выражение, содержащее неизвестное , могут быть потеряны корни, которые обращают эти выражения в ноль.
K Упражнение 1. Решить уравнение 3 х ( х 2 – 2 х – 3) = 9 ( х 2 – 2 х – 3) .
L Неправильное решение.
Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:
J Правильное решение.
Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:
K Упражнение 2. Решить уравнение lg 2 x – lg x = 0 .
L Неправильное решение.
Разделим обе части уравнения на lg x и получим:
J Правильное решение.
Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.
Посторонние корни
При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.
Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного. Рассмотрим далее некоторые случаи появления посторонних корней.
Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину .
K Упражнение. Решить уравнение
| 5 – x | – | 5 + 3х | = 0 . |
| x – 1 | x 2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х 2 – 1 и получим:
Комментарий . Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки .
J Правильный ответ: х = 0.

Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину .
K Упражнение. Решить уравнение
L Неправильное решение.
Заметим, что х 2 – 81 = (x – 9) (x + 9) и произведем сокращение дроби на x – 9 . Имеем:
Комментарий . Был приобретен посторонний корень х = 9 .
J Правильный ответ: решений нет.

Приведение подобных слагаемых с неизвестным в знаменателе, в том случае, если они взаимно уничтожаются, также может привести к приобретению постороннего корня.
K Упражнение. Решить уравнение
| 2 | + х 2 – | 2 | – 4х = 0 . |
| 3х 2 | 3х 2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
Комментарий . Был приобретен посторонний корень х = 0 .
J Правильный ответ: 4 .
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.

Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения . Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √ х + 3 + √ 7 – х = 2 .
L Неправильное решение.
И число –2 , и число 6 содержатся в области допустимых значений переменной х , значит, являются решениями исходного уравнения.
Комментарий . Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1 . Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1 , которое стало верным именно в результате возведения в квадрат, ведь 1 2 = (–1) 2 . Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
которое уже имеет один корень –2 , к уравнению
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4 , которые соответствуют этим уравнениям для случая х = 6 . Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.

Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю , прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение ( x – 5) (х + 2) √ х – 3 = 0 .
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
Комментарий . Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3 .

Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения . Таких равенств много, вот некоторые из них:
| tg ( x + y ) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2 x = | 2 tg x |
| 1 + tg 2 x |
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней .
L Неправильное решение.
так как х ≥ 3 , то |х – 1| = х – 1 и
Комментарий . Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1 . И вот почему. Исходное уравнение имеет область допустимых значений <1>∪[3; +∞) , а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt=x-1) – только [3; +∞) , что и привело к потере 1 .
Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.
J Правильное решение.
(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)
(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)
(left(x-1 right)^2cdot left(x-4 right)=0;)
Проверкой убеждаемся, что оба корня действительные.
Ошибки, связанные с заменой переменной
При решении некоторых уравнений достаточно удачным является метод замены переменной . Но применение этого метода учащиеся осуществляют не всегда правильно.
Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший .
K Упражнение. Решить уравнение (5 left(x-3 right)^<1/4>-6=left(x-3 right)^<1/2>.)
L Неправильное решение.
Сделав замену ( left(x-3 right)^<1/2>=t), считают, что ( left(x-3 right)^<1/4>=t^2) и уравнение переписывают в виде 5t 2 – t – 6 = 0 , после чего, конечно, верный результат уже не получить.
J Правильное решение.
Верный результат можно получить, сделав замену ( left(x-3 right)^<1/4>=t), тогда ( left(x-3 right)^<1/2>=t^2) с продолжением:

Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась .
K Упражнение. Решить уравнение х + 4 √ x – 5 = 0 .
L Неправильное решение.
Комментарий . После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √ x = t , а не x = t 2 .
J Правильное решение.

При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца .
K Упражнение. Решить уравнение (x^2-4x-sqrt<2x^2-8x+12>=6.)
L Неправильное (нерациональное) решение.
Чаще всего данное уравнение начинают решать так:
Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.
Комментарий . В качестве альтернативы можно предложить способ введения новой переменной.
J Правильное решение.
и исходное уравнение принимает вид:
А дальше все просто:
Комментарий . Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.
Ошибки, связанные с использованием модуля
При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня , допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.
K Упражнение 1. Решить уравнение (sqrt=9.)
L Неправильное решение.
J Правильное решение.
K Упражнение 2. Решить уравнение (sqrt<(x+3)^2>=x+3.)
L Неправильное решение.
Ответ: корнем данного уравнения является любое действительное число.
J Правильное решение.

Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1 .
J Правильное решение.
Находим нули модулей, для |х – 3| это 3 , для |x – 4| это 4 , и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
На каждом из этих промежутков исходное уравнение принимает свой вид.
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
так как 3 ∉ (–∞; 3 ) , то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
так как 4 ∈ [4; +∞) , то 4 – корень уравнения.
Так как [3; 4)∪ <4>= [3; 4] , то корнями исходного уравнения являются все числа числового промежутка [3; 4] .
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности .
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24 .
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Комментарий . Был подобран корень х = 1 , но не обнаружен еще один корень х = –4 , который соответствует разложению 24 = –4 · (–3) · (–2) · (–1) . Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
введем новую переменную x 2 + 3х + 1 = t , тогда
1) x 2 + 3х + 1 = –5, x 2 + 3х + 6 = 0, решений нет;

Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций . Часто при этом используется производная.
K Упражнение. Решить уравнение x 11 + 5х – 6 = 0 .
L Неправильное решение.
Методом подбора находим корень уравнения х = 1 .
Комментарий . Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x 10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x 11 + 5х – 6 , что и доказывает единственность подобранного корня.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями , не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7 x) 1 /3 = 1 .
L Неправильное решение.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
K Упражнение 2. Решить уравнение (х + 5) х 2 + х – 2 = 1 .
L Неправильное решение.
Комментарий . Потерян корень х = –4 . Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5 , тогда
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.

При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями . При применении этих свойств учащиеся часто допускают ошибки.
L Неправильное решение.
Комментарий . В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х 2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
K Упражнение 2. Решить уравнение lg x 2 = 4 .
L Неправильное решение.
J Правильное решение 1.
2lg |x| = 4; lg | x| = 2; |x| = 100; x = ±100.
J Правильное решение 2.
lg x 2 = lg 10000; x 2 = 10000; x = ±100.

Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями , так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.
Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней .
K Упражнение 1. Решить уравнение (left(log_5 +2 right)<log _<5>>^2 ;x=0.)
L Неправильное решение.
(left(1 +2 log _<5>xright)log _<5>x=0;)
Комментарий . Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.
J Правильное решение.
Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞) . И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞) , а, значит, не является корнем.
K Упражнение 2. Решить уравнение (20log_<4x>sqrt+ 7log_<16x>x^3-3log _x^2=0.)
L Неправильное решение.
Комментарий . В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х . Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1 . Поэтому число 1 , как возможный корень исходного уравнения, следует рассмотреть отдельно.
J Правильное решение.
Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение .
Разница между абсолютной ошибкой и относительной ошибкой
Видео: Разница между абсолютной ошибкой и относительной ошибкой | Сравните разницу между похожими терминами
Содержание:
Ключевое различие — абсолютная ошибка против относительной ошибки
Абсолютная ошибка и относительная ошибка — это два способа указания ошибок в экспериментальных измерениях, хотя существует разница между абсолютной ошибкой и относительной ошибкой на основе их расчета. Большинство измерений в научных экспериментах содержат ошибки из-за инструментальных ошибок и ошибок человека. В некоторых случаях для конкретного измерительного прибора существует заранее определенное постоянное значение абсолютной погрешности. (Наименьшее показание. Например: — линейка = +/- 1 мм.) Это разница между истинным значением и экспериментальным значением. Однако относительная ошибка варьируется в зависимости от экспериментального значения и абсолютной ошибки. Он определяется отношением абсолютной ошибки к экспериментальному значению. Таким образом ключевое отличие между абсолютной ошибкой и относительной ошибкой, абсолютная ошибкаэтовеличина разницы между точным значением и приближением в то время как Относительная погрешность рассчитывается путем деления абсолютной погрешности на величину точного значения.
Что такое абсолютная ошибка?
Абсолютная ошибка — это показатель неопределенности измерения. Другими словами, он измеряет, в какой степени истинное значение может отличаться от экспериментального. Абсолютная погрешность выражается в тех же единицах, что и измерения.
Пример: Допустим, мы хотим измерить длину карандаша с помощью линейки с миллиметровыми отметками. Мы можем измерить его длину с точностью до миллиметра. Если вы получите значение 125 мм, оно будет выражено как 125 +/- 1 мм. Абсолютная погрешность составляет +/- 1 мм.
Что такое относительная ошибка?
Относительная ошибка зависит от двух переменных; абсолютная погрешность и экспериментальное значение измерения. Следовательно, эти два параметра должны быть известны для расчета относительной ошибки. Относительная ошибка вычисляется как отношение абсолютной ошибки к экспериментальному значению. Выражается в процентах или дробях; так что в нем нет единиц.
Относительная ошибка интегрирования Монте-Карло для вычисления числа пи
В чем разница между абсолютной ошибкой и относительной ошибкой?
Определение абсолютной ошибки и относительной ошибки
Абсолютная ошибка:
Абсолютная ошибка — это значение Δx (+ или — значение), где x — переменная; это физическая погрешность измерения. Он также известен как фактическая ошибка измерения.
Другими словами, это разница между истинным значением и экспериментальным значением.
Абсолютная ошибка = фактическое значение — измеренное значение
Относительная ошибка:
Относительная ошибка — это отношение абсолютной ошибки (Δx) к измеренному значению (x). Он выражается либо в процентах (процентная погрешность), либо в виде дроби (дробная погрешность).
Единицы и расчет абсолютной погрешности и относительной погрешности
Единицы
Абсолютная ошибка:
Он имеет те же единицы измерения, что и измеренное значение. Например, если вы измеряете длину книги в сантиметрах (см), абсолютная ошибка также будет иметь те же единицы.
Относительная ошибка:
Относительная погрешность может быть выражена в виде дроби или процента. Однако у обоих нет единицы в стоимости.
Расчет ошибок
Пример 1:Фактическая длина земли составляет 500 футов. Измерительный прибор показывает, что длина составляет 508 футов.
Абсолютная ошибка:
Абсолютная ошибка = [Фактическое значение — измеренное значение] = 508 футов = 8 футов
Относительная ошибка:
Студент хотел измерить высоту стены в комнате. Он измерил значение с помощью метровой линейки (с точностью до миллиметра), оно составило 3,215 м.
Абсолютная ошибка:
Абсолютная погрешность = +/- 1 мм = +/- 0,001 м (Наименьшее значение, которое можно прочитать с помощью линейки)
Относительная ошибка:
Относительная погрешность = Абсолютная погрешность ÷ Экспериментальное значение = 0,001 м ÷ 3,215 м * 100 = 0,0003%
источники:
http://math4school.ru/oshibki_v_uravnenijah.html
http://ru.strephonsays.com/absolute-error-and-vs-relative-error-7294
Разница между абсолютной ошибкой и относительной ошибкой
Разница между абсолютной ошибкой и относительной ошибкой — Наука
Содержание:
Ключевое различие — абсолютная ошибка против относительной ошибки
Абсолютная ошибка и относительная ошибка — это два способа указания ошибок в экспериментальных измерениях, хотя существует разница между абсолютной ошибкой и относительной ошибкой на основе их расчета. Большинство измерений в научных экспериментах содержат ошибки из-за инструментальных ошибок и ошибок человека. В некоторых случаях для конкретного измерительного прибора существует заранее определенное постоянное значение абсолютной погрешности. (Наименьшее показание. Например: — линейка = +/- 1 мм.) Это разница между истинным значением и экспериментальным значением. Однако относительная ошибка варьируется в зависимости от экспериментального значения и абсолютной ошибки. Он определяется отношением абсолютной ошибки к экспериментальному значению. Таким образом ключевое отличие между абсолютной ошибкой и относительной ошибкой, абсолютная ошибкаэтовеличина разницы между точным значением и приближением в то время как Относительная погрешность рассчитывается путем деления абсолютной погрешности на величину точного значения.
Что такое абсолютная ошибка?
Абсолютная ошибка — это показатель неопределенности измерения. Другими словами, он измеряет, в какой степени истинное значение может отличаться от экспериментального. Абсолютная погрешность выражается в тех же единицах, что и измерения.
Пример: Допустим, мы хотим измерить длину карандаша с помощью линейки с миллиметровыми отметками. Мы можем измерить его длину с точностью до миллиметра. Если вы получите значение 125 мм, оно будет выражено как 125 +/- 1 мм. Абсолютная погрешность составляет +/- 1 мм.
Что такое относительная ошибка?
Относительная ошибка зависит от двух переменных; абсолютная погрешность и экспериментальное значение измерения. Следовательно, эти два параметра должны быть известны для расчета относительной ошибки. Относительная ошибка вычисляется как отношение абсолютной ошибки к экспериментальному значению. Выражается в процентах или дробях; так что в нем нет единиц.
Относительная ошибка интегрирования Монте-Карло для вычисления числа пи
В чем разница между абсолютной ошибкой и относительной ошибкой?
Определение абсолютной ошибки и относительной ошибки
Абсолютная ошибка:
Абсолютная ошибка — это значение Δx (+ или — значение), где x — переменная; это физическая погрешность измерения. Он также известен как фактическая ошибка измерения.
Другими словами, это разница между истинным значением и экспериментальным значением.
Абсолютная ошибка = фактическое значение — измеренное значение
Относительная ошибка:
Относительная ошибка — это отношение абсолютной ошибки (Δx) к измеренному значению (x). Он выражается либо в процентах (процентная погрешность), либо в виде дроби (дробная погрешность).
Единицы и расчет абсолютной погрешности и относительной погрешности
Единицы
Абсолютная ошибка:
Он имеет те же единицы измерения, что и измеренное значение. Например, если вы измеряете длину книги в сантиметрах (см), абсолютная ошибка также будет иметь те же единицы.
Относительная ошибка:
Относительная погрешность может быть выражена в виде дроби или процента. Однако у обоих нет единицы в стоимости.
Расчет ошибок
Пример 1:Фактическая длина земли составляет 500 футов. Измерительный прибор показывает, что длина составляет 508 футов.
Абсолютная ошибка:
Абсолютная ошибка = [Фактическое значение — измеренное значение] = 508 футов = 8 футов
Относительная ошибка:
Студент хотел измерить высоту стены в комнате. Он измерил значение с помощью метровой линейки (с точностью до миллиметра), оно составило 3,215 м.
Абсолютная ошибка:
Абсолютная погрешность = +/- 1 мм = +/- 0,001 м (Наименьшее значение, которое можно прочитать с помощью линейки)
Относительная ошибка:
Относительная погрешность = Абсолютная погрешность ÷ Экспериментальное значение = 0,001 м ÷ 3,215 м * 100 = 0,0003%
Измерения. Классификация ошибок измерений
В физике и в других науках весьма часто приходится производить измерения различных величин (например, длины, массы, времени, температуры, электрического сопротивления и т. д.).
Измерение – процесс нахождения значения физической величины с помощью специальных технических средств – измерительных приборов.
Измерительным прибором называют устройство, с помощью которого осуществляется сравнение измеряемой величины с физической величиной того же рода, принятой за единицу измерения.
Различают прямые и косвенные методы измерений.
Прямые методы измерений – методы, при которых значения определяемых величин находятся непосредственным сравнением измеряемого объекта с единицей измерения (эталоном). Например, измеряемая линейкой длина какого-либо тела сравнивается с единицей длины – метром, измеряемая весами масса тела сравнивается с единицей массы – килограммом и т. д. Таким образом, в результате прямого измерения определяемая величина получается сразу, непосредственно.
Косвенные методы измерений – методы, при которых значения определяемых величин вычисляются по результатам прямых измерений других величин, с которыми они связаны известной функциональной зависимостью. Например, определение длины окружности по результатам измерения диаметра или определение объема тела по результатам измерения его линейных размеров.
Ввиду несовершенства измерительных приборов, наших органов чувств, влияния внешних воздействий на измерительную аппаратуру и объект измерения, а также прочих факторов все измерения можно производить только с известной степенью точности; поэтому результаты измерений дают не истинное значение измеряемой величины, а лишь приближенное. Если, например, вес тела определен с точностью до 0,1 мг, то это значит, что найденный вес отличается от истинного веса тела менее чем на 0,1 мг.
Точность измерений – характеристика качества измерений, отражающая близость результатов измерений к истинному значению измеряемой величины.
Чем меньше погрешности измерений, тем больше точность измерений. Точность измерений зависит от используемых при измерениях прибо- ров и от общих методов измерений. Совершенно бесполезно стремиться при измерениях в данных условиях перейти за этот предел точности. Можно свести к минимуму воздействие причин, уменьшающих точность измерений, но полностью избавиться от них невозможно, то есть при измерениях всегда совершаются более или менее значительные ошибки (погрешности). Для увеличения точности окончательного результата всякое физическое измерение необходимо делать не один, а несколько раз при одинаковых условиях опыта.
Абсолютная и относительная погрешность — методы и алгоритмы вычислений

Чтобы оценить степень отклонения, используется показатель абсолютной и относительной погрешности.
В математике, физике и метрологии этот коэффициент может быть использован для округления полученных результатов.
Показатель бывает нескольких видов. Для его определения применяют разные методы.
Понятие и классификация
Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.
Существует несколько разновидностей погрешности:

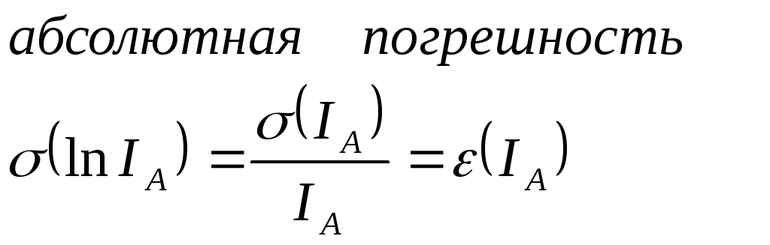
- Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
- Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
- Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
- Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
- Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
- Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
- Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
- Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
- Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
- Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.
Выделяют также отклонения прямых или косвенных измерений. Вторая разновидность учитывается в тех случаях, когда измерить величину напрямую невозможно и ее можно посчитать по формулам исходя из других данных.
Абсолютная и относительная погрешности
Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.
Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г

Для вычислений разработана специальная формула: Δа=А-а,
где А — это точная величина,
а — приближенная, это число, которое немного отличается от точного.
Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.
Чтобы получить измерения высокой точности, рассчитать абсолютную погрешность недостаточно. Если измерять предмет длиной 30 см и допустить неточность в 1 см, ее величина будет значительной. При измерении 30-метрового участка дороги то же самое отклонение в 1 см допускается, такое измерение будет наиболее точным. При вычислении ускорения свободного падения с помощью маятника неточность не превышает 10 -5 м/с. 2
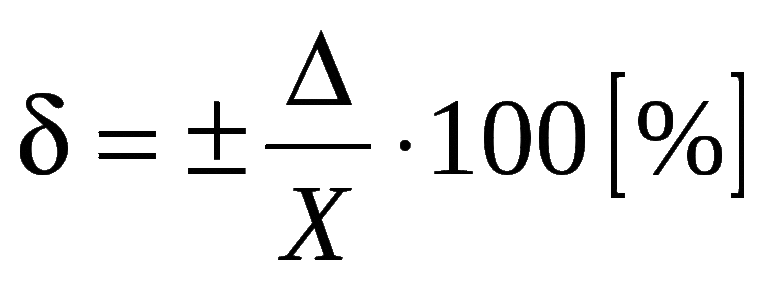
Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.
Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.
Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.
Методики расчета
Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

- Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
- Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
- Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение. Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
- Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение. Полученное число умножают на 100%.
Для определения предельного отклонения выбирают наибольшее значение из всех полученных.
Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:
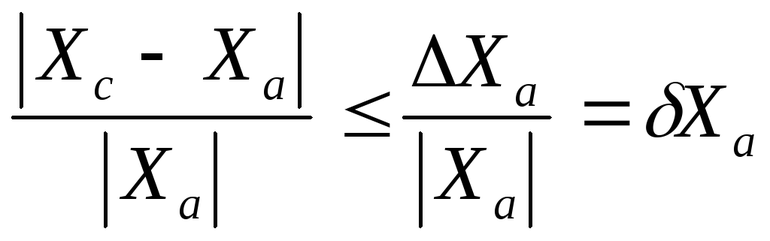
- Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
- Полученные результаты складывают между собой.
- Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
- Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.
Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.
Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение. При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.
При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.
Произвести необходимые расчеты можно с помощью онлайн-калькулятора. В окошки вносятся необходимые данные, после чего программа выдает результат.
Методы Корнфельда и Стьюдента
Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.
Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

- Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
- Из этих величин выбирают минимальную и максимальную.
- Вычисляют среднее значение Х.
- В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
- Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.
Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.
Эти показатели вычисляются на основе доверительной вероятности и большого количества измерений.
источники:
http://fevt.ru/load/klassifikacija_oshibok/75-1-0-299
http://nauka.club/matematika/absolyutn%D0%B0y%D0%B0-i-otnositeln%D0%B0y%D0%B0-pogreshnost.html
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
![]() ;
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
![]() .
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
![]() ,
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
![]() принимают отношение исправленных
принимают отношение исправленных
выборочных дисперсий: .
.
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
![]() называют значение критерия, вычисленное
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсии![]() и
и![]() ,
,
то наблюдаемое значение критерия .
.
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
![]() — одномерная случайная величина, все её
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
![]() называют точки, отделяющие критическую
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
![]() >
>![]() ,
,
где![]() — положительное число.
— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
![]() <
<![]() ,
,
где![]() — отрицательное число.
— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
![]() где
где![]() .
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
![]() >0):
>0):
![]() ,
,
или равносильным неравенством
![]() .
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
![]() >
>![]() ,
,
где![]() >0.
>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
![]() .
.
Затем ищут критическую точку![]() ,
,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерий![]() примет значение, большее
примет значение, большее![]() ,
,
была равна принятому уровню значимости:
Р(![]() >
>![]() )=
)=![]() .
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
![]() >
>![]() ,
,
то нулевую гипотезу отвергают; если же![]() <
<![]() ,
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(![]() >
>![]() )=
)=![]() ?
?
(*)
Поскольку вероятность
события
![]() >
>![]() мала (
мала (![]() — малая вероятность), такое событие при
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше![]() ,
,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
![]() не потому, что нулевая гипотеза ложна,
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости![]() .
.
Итак, пользуясь требованием (*), мы с
вероятностью![]() рискуем совершить ошибку первого рода.
рискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
![]() <
<![]() (
(![]() <0).
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее![]() ,
,
была равна принятому уровню значимости:
Р(![]() <
<![]() )=
)=![]() .
.
Двусторонняя
критическая область определяется
неравенствами
![]() Критические
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшее![]() или большее
или большее![]() ,
,
была равна принятому уровню значимости:
![]() .
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
![]() )и
)и![]() (
(![]() >0),
>0),
то
![]() Учитывая (*), получим
Учитывая (*), получим
![]() .
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
![]() при условии, что нулевая гипотеза
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
![]() ,
,
то мощность равна 1-![]() .
.
Действительно, если![]() — вероятность ошибки второго рода, т.е.
— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —![]() .
.
Пусть мощность 1
—
![]() возрастает; следовательно, уменьшается
возрастает; следовательно, уменьшается
вероятность![]() совершить ошибку второго рода. Таким
совершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
![]() ,
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —![]() ,
,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
![]() и
и![]() невозможно; если уменьшить
невозможно; если уменьшить![]() ,
,
то![]() будет возрастать. Например, если принять
будет возрастать. Например, если принять![]() =0,
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятность![]() ошибки второго рода.
ошибки второго рода.
Как же выбрать
![]() наиболее целесообразно? Ответ на этот
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее![]() .
.
Если
![]() уже выбрано, то, пользуясь теоремой Ю.
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которой![]() будет минимальным и, следовательно,
будет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Содержание:
Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной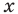
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
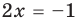 — линейное уравнение;
— линейное уравнение;
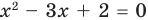 — квадратное уравнение;
— квадратное уравнение;
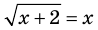 — иррациональное уравнение (содержит переменную под знаком корня)
— иррациональное уравнение (содержит переменную под знаком корня)
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
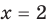 — корень уравнения
— корень уравнения 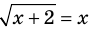 , так как при
, так как при 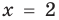 получаем верное равенство:
получаем верное равенство: 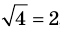 , то есть
, то есть 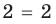
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 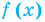 и
и 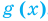 , стоящих в левой и правой частях уравнения
, стоящих в левой и правой частях уравнения
Для уравнения 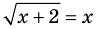 ОДЗ:
ОДЗ: 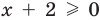 , то есть
, то есть 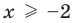 , так как область определения функции
, так как область определения функции 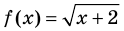 определяется условием:
определяется условием:  , а область определения функции
, а область определения функции 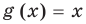 — множество всех действительных чисел
— множество всех действительных чисел
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
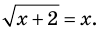
Решение:
► Возведем обе части уравнения в квадрат:
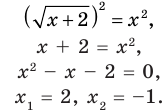
Проверка, 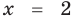 — корень (см. выше);
— корень (см. выше); 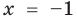 — посторонний корень (при
— посторонний корень (при 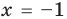 получаем неверное равенство
получаем неверное равенство 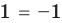 ).
).
Ответ: 2.
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
5. Схема поиска плана решения уравнений
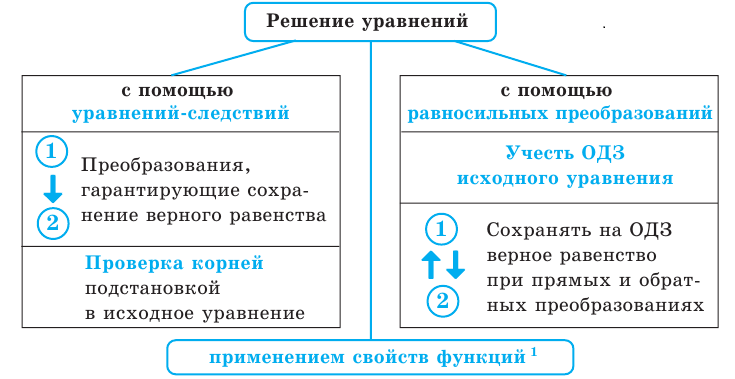
 — исходное уравнение;
— исходное уравнение;
 — уравнение, полученное в результате преобразования исходного;
— уравнение, полученное в результате преобразования исходного;
 — символические изображения направления выполненных преобразований
— символические изображения направления выполненных преобразований
 Применение свойств функций к решению уравнений рассмотрено в пункте 3.2.
Применение свойств функций к решению уравнений рассмотрено в пункте 3.2.
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 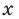 записывают так:
записывают так:
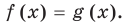
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 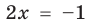 имеет единственный корень
имеет единственный корень 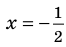 ,
,
а уравнение 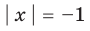 не имеет корней, поскольку значение
не имеет корней, поскольку значение 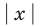 не может быть отрицательным числом.
не может быть отрицательным числом.
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 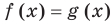 , то общая область определения для функций
, то общая область определения для функций 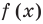 и
и 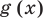 называется областью допустимых значений этого уравнения. (Иногда используются также термины «область определения уравнения» или «множество допустимых значений уравнения».) Например, для уравнения
называется областью допустимых значений этого уравнения. (Иногда используются также термины «область определения уравнения» или «множество допустимых значений уравнения».) Например, для уравнения 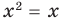 областью допустимых значений являются все действительные числа. Это можно записать, например, так:
областью допустимых значений являются все действительные числа. Это можно записать, например, так: 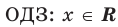 , поскольку функции
, поскольку функции 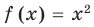 и
и 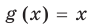 имеют области определения
имеют области определения 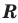 .
.
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 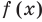 , так и области определения функции
, так и области определения функции 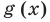 (иначе мы не сможем получить верное числовое равенство). Поэтому каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях применить анализ ОДЗ уравнения при его решении.
(иначе мы не сможем получить верное числовое равенство). Поэтому каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях применить анализ ОДЗ уравнения при его решении.
Например, в уравнении 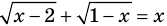 функция
функция 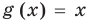 определена при всех действительных значениях
определена при всех действительных значениях 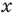 , а функция
, а функция 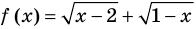 только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Следовательно, ОДЗ этого уравнения задается системой
только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Следовательно, ОДЗ этого уравнения задается системой 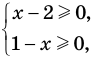 из которой получаем систему
из которой получаем систему 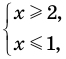 не имеющую решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
не имеющую решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 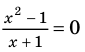 (пока что не используя известное условие равенства дроби нулю).
(пока что не используя известное условие равенства дроби нулю).
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 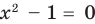 . Но тогда верно, что
. Но тогда верно, что 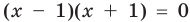 . Последнее уравнение имеет два корня:
. Последнее уравнение имеет два корня: 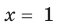 и
и 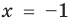 . Подставляя их в заданное уравнение, видим, что только корень
. Подставляя их в заданное уравнение, видим, что только корень 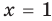 удовлетворяет исходному уравнению. Почему это случилось?
удовлетворяет исходному уравнению. Почему это случилось?
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
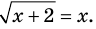 (1)
(1)
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
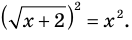 (2)
(2)
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 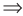 , но его использование для записи решения не является обязательным. Вместе с тем, если этот значок записан, то это свидетельствует о том, что мы воспользовались уравнениями-следствиями, и поэтому обязательно в запись решения необходимо включить проверку полученных корней.
, но его использование для записи решения не является обязательным. Вместе с тем, если этот значок записан, то это свидетельствует о том, что мы воспользовались уравнениями-следствиями, и поэтому обязательно в запись решения необходимо включить проверку полученных корней.
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 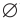 ).
).
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 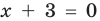 и
и 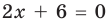 — равносильные, поскольку оба имеют одинаковый корень
— равносильные, поскольку оба имеют одинаковый корень 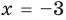 и других корней не имеют. Таким образом, каждое из них имеет те же решения, что и второе. При рассмотрении равносильности уравнений на множестве, которое отличается от множества всех действительных чисел, ответ на вопрос «Равносильны ли данные уравнения?» может существенно зависеть от того, на каком множестве мы рассматриваем эти уравнения. Например, если рассмотреть уравнения:
и других корней не имеют. Таким образом, каждое из них имеет те же решения, что и второе. При рассмотрении равносильности уравнений на множестве, которое отличается от множества всех действительных чисел, ответ на вопрос «Равносильны ли данные уравнения?» может существенно зависеть от того, на каком множестве мы рассматриваем эти уравнения. Например, если рассмотреть уравнения:
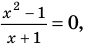 (3)
(3)
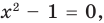 (4)
(4)
то, как было показано выше, уравнение (3) имеет единственный корень 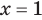 , а уравнение (4) — два корня:
, а уравнение (4) — два корня: 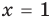 и
и 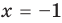 . Таким образом, на множестве
. Таким образом, на множестве
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 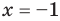 , которого нет у уравнения (3). Но на множестве положительных действительных чисел эти уравнения равносильны, поскольку на этом множестве уравнение (3) имеет единственный положительный корень
, которого нет у уравнения (3). Но на множестве положительных действительных чисел эти уравнения равносильны, поскольку на этом множестве уравнение (3) имеет единственный положительный корень 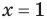 и уравнение (4) также имеет единственный положительный корень
и уравнение (4) также имеет единственный положительный корень 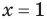 . Следовательно, на множестве положительных чисел каждое из этих уравнений имеет те же решения, что и второе.
. Следовательно, на множестве положительных чисел каждое из этих уравнений имеет те же решения, что и второе.
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 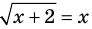 задается неравенством
задается неравенством 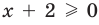 . Когда мы переходим к уравнению
. Когда мы переходим к уравнению  , то для всех его корней это уравнение является верным равенством. Тогда выражение
, то для всех его корней это уравнение является верным равенством. Тогда выражение 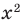 , стоящее в правой части этого равенства, всегда неотрицательно (
, стоящее в правой части этого равенства, всегда неотрицательно (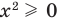 ), таким образом, и равное ему выражение
), таким образом, и равное ему выражение 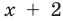 также будет неотрицательным:
также будет неотрицательным:  . Но это и означает, что ОДЗ данного уравнения (
. Но это и означает, что ОДЗ данного уравнения ( ) учтено автоматически для всех корней второго уравнения и поэтому при переходе от уравнения
) учтено автоматически для всех корней второго уравнения и поэтому при переходе от уравнения 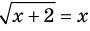 к уравнению
к уравнению 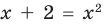 ОДЗ заданного уравнения можно не записывать в решение.
ОДЗ заданного уравнения можно не записывать в решение.
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 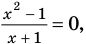 достаточно учесть его ОДЗ:
достаточно учесть его ОДЗ: 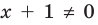 и условие равенства дроби нулю (дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю). Также следует обратить внимание на то, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлениях с сохранением правильности равенства.
и условие равенства дроби нулю (дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю). Также следует обратить внимание на то, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлениях с сохранением правильности равенства.
Запись решения в этом случае может быть такой:
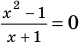 . ОДЗ:
. ОДЗ: 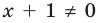 . Тогда
. Тогда 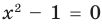 . Отсюда
. Отсюда 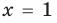 (удовлетворяет условию ОДЗ) или
(удовлетворяет условию ОДЗ) или 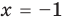 (не удовлетворяет условию ОДЗ).
(не удовлетворяет условию ОДЗ).
Ответ: 1.
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок  , но его использование при записи решений не является обязательным. Например, запись решения последнего из рассмотренных уравнений может быть такой.
, но его использование при записи решений не является обязательным. Например, запись решения последнего из рассмотренных уравнений может быть такой.
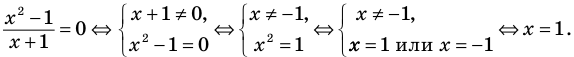
Ответ: 1.
Пример №423
Решите уравнение 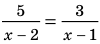 .
.
Решение:
► ОДЗ:  и
и 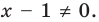
На этой ОДЗ данное уравнение равносильно уравнениям:
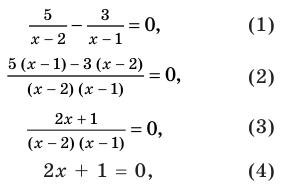
то есть 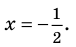
Учтем ОДЗ. При 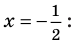
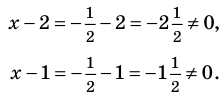
Таким образом, 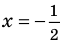 — корень.
— корень.
Ответ: 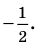
Комментарий:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.




- Заказать решение задач по высшей математике
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Ориентир
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
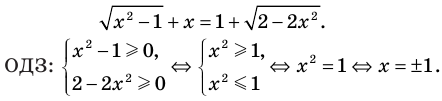
Проверка.
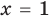 — корень (
— корень (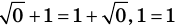 ),
),
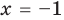 — не корень (
— не корень (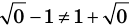 ).
).
Ответ: 1.
2. Оценка левой и правой частей уравнения

Если надо решить уравнение вида 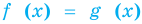 и выяснилось, что
и выяснилось, что  то равенство между левой и правой частями возможно тогда и только тогда, когда
то равенство между левой и правой частями возможно тогда и только тогда, когда  и
и 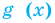 одновременно равны
одновременно равны 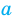
Пример:
►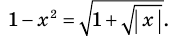
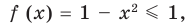
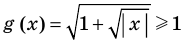 (так как
(так как 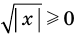 ).
).
Итак, заданное уравнение равносильно системе
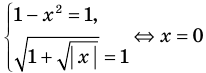
Ответ: 0.
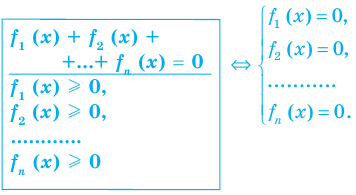
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►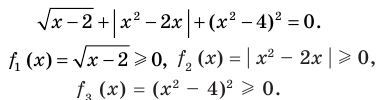
Итак, заданное уравнение равносильно системе
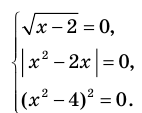
Из первого уравнения получаем 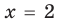 , что удовлетворяет всей системе
, что удовлетворяет всей системе
Ответ: 2.
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
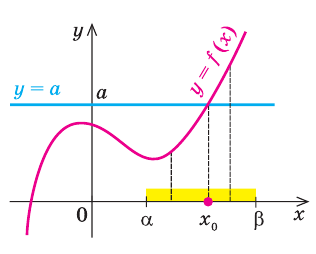
Теоремы о корнях уравнения
Если в уравнении 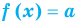 функция
функция 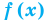 возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
Пример:
Уравнение 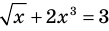 имеет единственный корень
имеет единственный корень 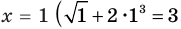 , то есть
, то есть 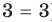 ), поскольку функция
), поскольку функция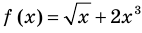 возрастает на всей области определения
возрастает на всей области определения 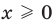
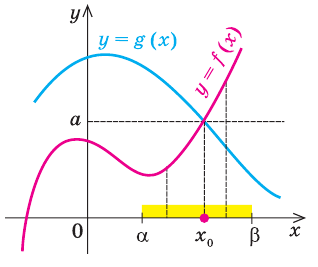
Если в уравнении 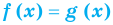 функция
функция 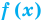 возрастает на некотором промежутке, а функция
возрастает на некотором промежутке, а функция 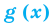 убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
Пример:
Уравнение 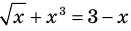 имеет единственный корень
имеет единственный корень 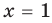 (
(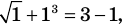 то есть
то есть 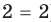 ), поскольку
), поскольку 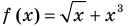 возрастает на всей области определения
возрастает на всей области определения  , a
, a 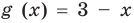 убывает (на множестве
убывает (на множестве 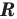 , а следовательно, и при
, а следовательно, и при 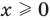 )
)
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 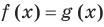 , общая область определения для функций
, общая область определения для функций 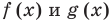 называется областью допустимых значений этого уравнения. Понятно, что каждый корень заданного уравнения принадлежит как области определения функции
называется областью допустимых значений этого уравнения. Понятно, что каждый корень заданного уравнения принадлежит как области определения функции 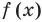 , так и области определения функции
, так и области определения функции 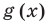 . Таким образом, каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях за счет анализа ОДЗ получить решение уравнения. Например, если дано уравнение
. Таким образом, каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях за счет анализа ОДЗ получить решение уравнения. Например, если дано уравнение 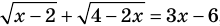 , то его ОДЗ можно записать с помощью системы
, то его ОДЗ можно записать с помощью системы 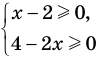 . Решая эту систему, получаем
. Решая эту систему, получаем 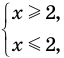 то есть
то есть  . Таким образом, ОДЗ данного уравнения состоит только из одного значения
. Таким образом, ОДЗ данного уравнения состоит только из одного значения  . Но если только для одного числа необходимо выяснить, является ли оно корнем данного уравнения, то для этого достаточно подставить это значение в уравнение. В результате получаем верное числовое равенство (
. Но если только для одного числа необходимо выяснить, является ли оно корнем данного уравнения, то для этого достаточно подставить это значение в уравнение. В результате получаем верное числовое равенство ( ). Следовательно,
). Следовательно,  — корень данного уравнения. Других корней у этого уравнения быть не может, поскольку все корни уравнения находятся в его ОДЗ, а там нет других значений, кроме
— корень данного уравнения. Других корней у этого уравнения быть не может, поскольку все корни уравнения находятся в его ОДЗ, а там нет других значений, кроме  .
.
Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 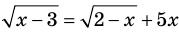 , то его ОДЗ задается системой
, то его ОДЗ задается системой 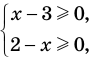 то есть системой
то есть системой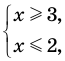 которая не имеет решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
которая не имеет решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 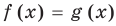 , и нам удалось выяснить, что для всех допустимых значений
, и нам удалось выяснить, что для всех допустимых значений 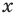 значение
значение  , а значение
, а значение 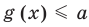 .
.
Рассмотрим два случая: 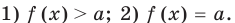
Если 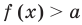 , то равенство
, то равенство 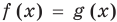 не может выполняться, потому что
не может выполняться, потому что 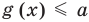 , то есть при
, то есть при 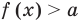 данное уравнение корней не имеет. Остается только случай
данное уравнение корней не имеет. Остается только случай 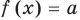 , но, учитывая необходимость выполнения равенства
, но, учитывая необходимость выполнения равенства 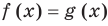 , имеем, что тогда и
, имеем, что тогда и 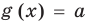 . Таким образом, мы обосновали, что выполнение равенства
. Таким образом, мы обосновали, что выполнение равенства 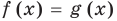 (при условии
(при условии 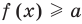 и
и 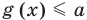 ) гарантирует одновременное выполнение равенств
) гарантирует одновременное выполнение равенств 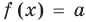 и
и 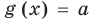 (и наоборот, если одновременно выполняются равенства
(и наоборот, если одновременно выполняются равенства 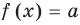 и
и 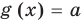 , то выполняется и равенство
, то выполняется и равенство 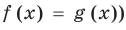 . Как было показано в п. 3.1, это и означает, что уравнение
. Как было показано в п. 3.1, это и означает, что уравнение 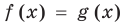 равносильно системе
равносильно системе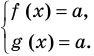
Коротко это можно записать так:
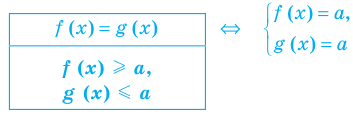
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 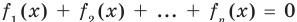 , в котором все функции-слагаемые неотрицательны
, в котором все функции-слагаемые неотрицательны 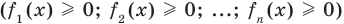 .
.
Если предположить, что 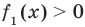 , то сумма всех функций, стоящих в левой части этого уравнения, может равняться нулю только тогда, когда сумма
, то сумма всех функций, стоящих в левой части этого уравнения, может равняться нулю только тогда, когда сумма  будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при
будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при 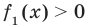 данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство
данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство 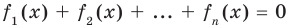 обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
Например, чтобы решить уравнение 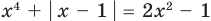 , достаточно перенести все члены в одну сторону, записать уравнение в виде
, достаточно перенести все члены в одну сторону, записать уравнение в виде 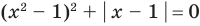 и учесть, что функции
и учесть, что функции 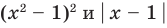 неотрицательные. Таким образом, данное уравнение равносильно системе
неотрицательные. Таким образом, данное уравнение равносильно системе 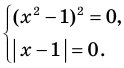
Из второго уравнения получаем 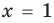 , что удовлетворяет и всей системе. Следовательно, данное уравнение имеет единственный корень
, что удовлетворяет и всей системе. Следовательно, данное уравнение имеет единственный корень 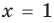 .
.
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
Теорема 1. Если в уравнении 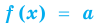 функция
функция 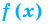 возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 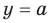 пересекает график возрастающей на промежутке
пересекает график возрастающей на промежутке 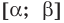 функции
функции 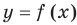 только в одной точке. Это и означает, что уравнение
только в одной точке. Это и означает, что уравнение 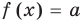 не может иметь больше одного корня на промежутке
не может иметь больше одного корня на промежутке 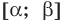 . Докажем это утверждение аналитически.
. Докажем это утверждение аналитически.
• Если на промежутке 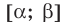 уравнение имеет корень
уравнение имеет корень 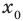 , то
, то 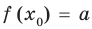 . Других корней быть не может, поскольку для возрастающей функции
. Других корней быть не может, поскольку для возрастающей функции 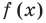 при
при 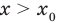 получаем неравенство
получаем неравенство 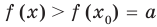 , а при
, а при 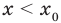 — неравенство
— неравенство 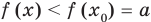 . Таким образом, при
. Таким образом, при 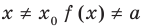 . Аналогично и для убывающей функции при
. Аналогично и для убывающей функции при 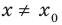 получаем
получаем 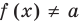 .
.
Теорема 2. Если в уравнении 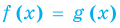 функция
функция 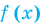 возрастает на некотором промежутке, а функция
возрастает на некотором промежутке, а функция 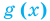 убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
Графически утверждение теоремы проиллюстрировано на рисунке 53.
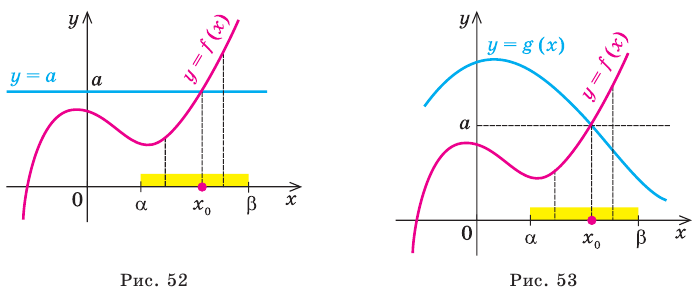
• Если на промежутке 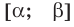 уравнение имеет корень
уравнение имеет корень 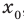 , то
, то 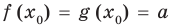 . Других корней быть не может, поскольку, например, для возрастающей функции
. Других корней быть не может, поскольку, например, для возрастающей функции 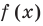 и убывающей функции
и убывающей функции 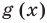 при
при 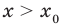 имеем
имеем 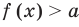 , a
, a 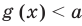 , таким образом,
, таким образом, 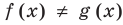 . Аналогично и при
. Аналогично и при 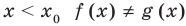 .
.
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 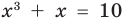 , достаточно заметить, что функция
, достаточно заметить, что функция 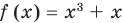 является возрастающей на всей числовой прямой (как сумма двух возрастающих функций) и что
является возрастающей на всей числовой прямой (как сумма двух возрастающих функций) и что  — корень
— корень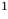 этого уравнения (
этого уравнения (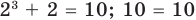 ). Таким образом, данное уравнение
). Таким образом, данное уравнение 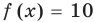 имеет единственный корень
имеет единственный корень 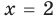 .
.
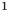 Корень
Корень  получен подбором. Как правило, подбор начинают с целых значений:
получен подбором. Как правило, подбор начинают с целых значений: 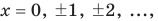 которые подставляются в данное уравнение.
которые подставляются в данное уравнение.
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение  .
.
► Сначала следует учесть его ОДЗ: 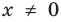 и вспомнить, что функция
и вспомнить, что функция 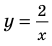 на всей области определения не является ни убывающей, ни возрастающей (п. 2.2), но она убывает на каждом из промежутков
на всей области определения не является ни убывающей, ни возрастающей (п. 2.2), но она убывает на каждом из промежутков 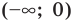 и
и 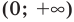 . Поэтому рассмотрим каждый из этих промежутков отдельно.
. Поэтому рассмотрим каждый из этих промежутков отдельно.
1) При 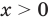 данное уравнение имеет корень
данное уравнение имеет корень 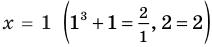 . Функция
. Функция 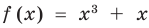 возрастает при
возрастает при  (как было показано выше, она возрастает на множестве
(как было показано выше, она возрастает на множестве 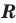 ), а функция
), а функция 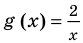 убывает на промежутке
убывает на промежутке  . Таким образом, данное уравнение
. Таким образом, данное уравнение 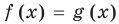 при
при 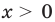 имеет единственный корень
имеет единственный корень 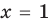 .
.
2) При 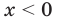 данное уравнение имеет корень
данное уравнение имеет корень 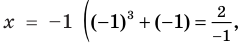
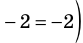 . Функция
. Функция 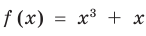 возрастает при
возрастает при 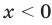 , а функция
, а функция 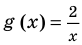 убывает на этом промежутке. Поэтому данное уравнение
убывает на этом промежутке. Поэтому данное уравнение 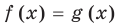 при
при 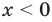 имеет единственный корень
имеет единственный корень 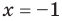 . В ответ следует записать все найденные корни (хотя на каждом из промежутков корень единственный, но всего корней — два). Итак, данное уравнение имеет только два корня: 1 и -1.
. В ответ следует записать все найденные корни (хотя на каждом из промежутков корень единственный, но всего корней — два). Итак, данное уравнение имеет только два корня: 1 и -1.
Примеры решения задач:
Пример №424
Решите уравнение 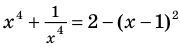 .
.
Решение:
► ОДЗ: 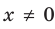 . На ОДЗ
. На ОДЗ 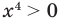 . Тогда функция
. Тогда функция 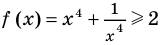 (как сумма двух взаимно обратных положительных чисел), а функция
(как сумма двух взаимно обратных положительных чисел), а функция 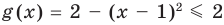 .
.
Таким образом, данное уравнение равносильно системе 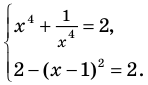 . Из второго уравнения системы получаем
. Из второго уравнения системы получаем  , что удовлетворяет и первому уравнению. Таким образом, система (а значит, и данное уравнение) имеет единственное решение
, что удовлетворяет и первому уравнению. Таким образом, система (а значит, и данное уравнение) имеет единственное решение  .
.
Ответ: 1.
Комментарий:
Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 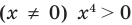 , то в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. В правой части из 2 вычитается неотрицательное число
, то в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. В правой части из 2 вычитается неотрицательное число 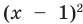 . Таким образом, при всех значениях
. Таким образом, при всех значениях 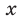 получаем значение, меньшее или равное 2. Равенство между левой и правой частями возможно тогда и только тогда, когда обе части равны 2.
получаем значение, меньшее или равное 2. Равенство между левой и правой частями возможно тогда и только тогда, когда обе части равны 2.
Пример №425
Решите систему уравнений 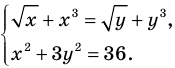
Решение:
► ОДЗ: 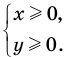 Рассмотрим функцию
Рассмотрим функцию 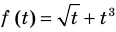 . На своей области определения
. На своей области определения 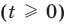 эта функция является возрастающей (как сумма двух возрастающих функций). Тогда первое уравнение заданной системы, которое имеет вид
эта функция является возрастающей (как сумма двух возрастающих функций). Тогда первое уравнение заданной системы, которое имеет вид 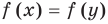 , равносильно уравнению
, равносильно уравнению 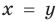 . Таким образом, на ОДЗ заданная система равносильна системе
. Таким образом, на ОДЗ заданная система равносильна системе 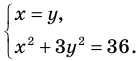
Подставляя 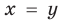 во второе уравнение системы, имеем
во второе уравнение системы, имеем 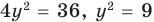 ,
, 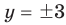 . Учитывая, что на ОДЗ
. Учитывая, что на ОДЗ  , получаем
, получаем 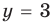 . Тогда
. Тогда 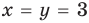 .
.
Ответ: (3; 3).
Комментарий:
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 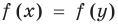 для возрастающей функции возможно тогда и только тогда, когда
для возрастающей функции возможно тогда и только тогда, когда 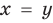 , поскольку возрастающая функция может принимать одинаковые значения только при одном значении аргумента. (Заметим, что такое же свойство будет иметь место и для убывающей функции.)
, поскольку возрастающая функция может принимать одинаковые значения только при одном значении аргумента. (Заметим, что такое же свойство будет иметь место и для убывающей функции.)
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 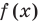 является возрастающей (или убывающей) на определенном множестве, то на этом множестве
является возрастающей (или убывающей) на определенном множестве, то на этом множестве 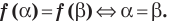
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ![]() ).
).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки, встроенные в систему: их роль в статистике
В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.
Ошибка и некорректное применение: в чем разница?
В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.
И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.
То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.
Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.
Ошибки первого и второго рода
Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.
Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:

До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.
Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.
Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.
Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?
ROC-анализ
ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.
Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):

Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:
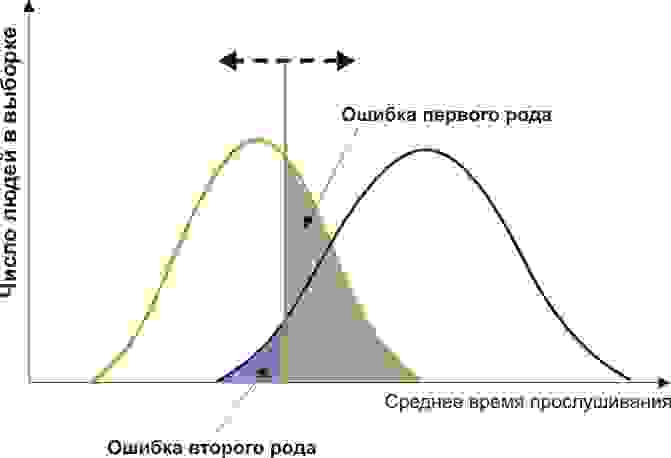
Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):
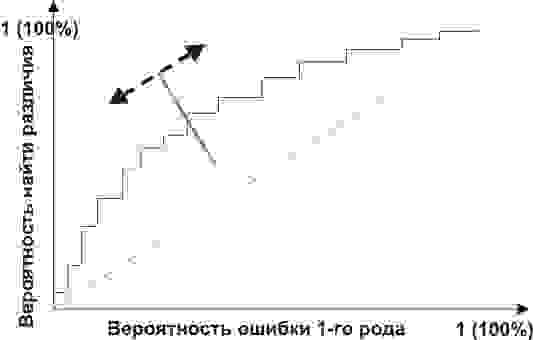
А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.
С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.
Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.
С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.
Разница между абсолютной ошибкой и относительной ошибкой
Разница между абсолютной ошибкой и относительной ошибкой — Наука
Содержание:
Ключевое различие — абсолютная ошибка против относительной ошибки
Абсолютная ошибка и относительная ошибка — это два способа указания ошибок в экспериментальных измерениях, хотя существует разница между абсолютной ошибкой и относительной ошибкой на основе их расчета. Большинство измерений в научных экспериментах содержат ошибки из-за инструментальных ошибок и ошибок человека. В некоторых случаях для конкретного измерительного прибора существует заранее определенное постоянное значение абсолютной погрешности. (Наименьшее показание. Например: — линейка = +/- 1 мм.) Это разница между истинным значением и экспериментальным значением. Однако относительная ошибка варьируется в зависимости от экспериментального значения и абсолютной ошибки. Он определяется отношением абсолютной ошибки к экспериментальному значению. Таким образом ключевое отличие между абсолютной ошибкой и относительной ошибкой, абсолютная ошибкаэтовеличина разницы между точным значением и приближением в то время как Относительная погрешность рассчитывается путем деления абсолютной погрешности на величину точного значения.
Что такое абсолютная ошибка?
Абсолютная ошибка — это показатель неопределенности измерения. Другими словами, он измеряет, в какой степени истинное значение может отличаться от экспериментального. Абсолютная погрешность выражается в тех же единицах, что и измерения.
Пример: Допустим, мы хотим измерить длину карандаша с помощью линейки с миллиметровыми отметками. Мы можем измерить его длину с точностью до миллиметра. Если вы получите значение 125 мм, оно будет выражено как 125 +/- 1 мм. Абсолютная погрешность составляет +/- 1 мм.
Что такое относительная ошибка?
Относительная ошибка зависит от двух переменных; абсолютная погрешность и экспериментальное значение измерения. Следовательно, эти два параметра должны быть известны для расчета относительной ошибки. Относительная ошибка вычисляется как отношение абсолютной ошибки к экспериментальному значению. Выражается в процентах или дробях; так что в нем нет единиц.
Относительная ошибка интегрирования Монте-Карло для вычисления числа пи
В чем разница между абсолютной ошибкой и относительной ошибкой?
Определение абсолютной ошибки и относительной ошибки
Абсолютная ошибка:
Абсолютная ошибка — это значение Δx (+ или — значение), где x — переменная; это физическая погрешность измерения. Он также известен как фактическая ошибка измерения.
Другими словами, это разница между истинным значением и экспериментальным значением.
Абсолютная ошибка = фактическое значение — измеренное значение
Относительная ошибка:
Относительная ошибка — это отношение абсолютной ошибки (Δx) к измеренному значению (x). Он выражается либо в процентах (процентная погрешность), либо в виде дроби (дробная погрешность).
Единицы и расчет абсолютной погрешности и относительной погрешности
Единицы
Абсолютная ошибка:
Он имеет те же единицы измерения, что и измеренное значение. Например, если вы измеряете длину книги в сантиметрах (см), абсолютная ошибка также будет иметь те же единицы.
Относительная ошибка:
Относительная погрешность может быть выражена в виде дроби или процента. Однако у обоих нет единицы в стоимости.
Расчет ошибок
Пример 1:Фактическая длина земли составляет 500 футов. Измерительный прибор показывает, что длина составляет 508 футов.
Абсолютная ошибка:
Абсолютная ошибка = [Фактическое значение — измеренное значение] = 508 футов = 8 футов
Относительная ошибка:
Студент хотел измерить высоту стены в комнате. Он измерил значение с помощью метровой линейки (с точностью до миллиметра), оно составило 3,215 м.
Абсолютная ошибка:
Абсолютная погрешность = +/- 1 мм = +/- 0,001 м (Наименьшее значение, которое можно прочитать с помощью линейки)
Относительная ошибка:
Относительная погрешность = Абсолютная погрешность ÷ Экспериментальное значение = 0,001 м ÷ 3,215 м * 100 = 0,0003%
Измерения. Классификация ошибок измерений
В физике и в других науках весьма часто приходится производить измерения различных величин (например, длины, массы, времени, температуры, электрического сопротивления и т. д.).
Измерение – процесс нахождения значения физической величины с помощью специальных технических средств – измерительных приборов.
Измерительным прибором называют устройство, с помощью которого осуществляется сравнение измеряемой величины с физической величиной того же рода, принятой за единицу измерения.
Различают прямые и косвенные методы измерений.
Прямые методы измерений – методы, при которых значения определяемых величин находятся непосредственным сравнением измеряемого объекта с единицей измерения (эталоном). Например, измеряемая линейкой длина какого-либо тела сравнивается с единицей длины – метром, измеряемая весами масса тела сравнивается с единицей массы – килограммом и т. д. Таким образом, в результате прямого измерения определяемая величина получается сразу, непосредственно.
Косвенные методы измерений – методы, при которых значения определяемых величин вычисляются по результатам прямых измерений других величин, с которыми они связаны известной функциональной зависимостью. Например, определение длины окружности по результатам измерения диаметра или определение объема тела по результатам измерения его линейных размеров.
Ввиду несовершенства измерительных приборов, наших органов чувств, влияния внешних воздействий на измерительную аппаратуру и объект измерения, а также прочих факторов все измерения можно производить только с известной степенью точности; поэтому результаты измерений дают не истинное значение измеряемой величины, а лишь приближенное. Если, например, вес тела определен с точностью до 0,1 мг, то это значит, что найденный вес отличается от истинного веса тела менее чем на 0,1 мг.
Точность измерений – характеристика качества измерений, отражающая близость результатов измерений к истинному значению измеряемой величины.
Чем меньше погрешности измерений, тем больше точность измерений. Точность измерений зависит от используемых при измерениях прибо- ров и от общих методов измерений. Совершенно бесполезно стремиться при измерениях в данных условиях перейти за этот предел точности. Можно свести к минимуму воздействие причин, уменьшающих точность измерений, но полностью избавиться от них невозможно, то есть при измерениях всегда совершаются более или менее значительные ошибки (погрешности). Для увеличения точности окончательного результата всякое физическое измерение необходимо делать не один, а несколько раз при одинаковых условиях опыта.
Абсолютная и относительная погрешность — методы и алгоритмы вычислений

Чтобы оценить степень отклонения, используется показатель абсолютной и относительной погрешности.
В математике, физике и метрологии этот коэффициент может быть использован для округления полученных результатов.
Показатель бывает нескольких видов. Для его определения применяют разные методы.
Понятие и классификация
Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.
Существует несколько разновидностей погрешности:

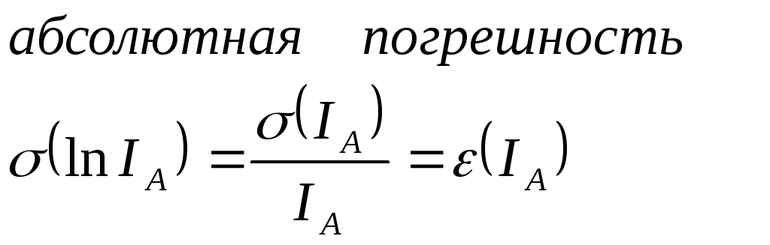
- Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
- Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
- Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
- Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
- Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
- Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
- Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
- Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
- Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
- Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.
Выделяют также отклонения прямых или косвенных измерений. Вторая разновидность учитывается в тех случаях, когда измерить величину напрямую невозможно и ее можно посчитать по формулам исходя из других данных.
Абсолютная и относительная погрешности
Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.
Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г

Для вычислений разработана специальная формула: Δа=А-а,
где А — это точная величина,
а — приближенная, это число, которое немного отличается от точного.
Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.
Чтобы получить измерения высокой точности, рассчитать абсолютную погрешность недостаточно. Если измерять предмет длиной 30 см и допустить неточность в 1 см, ее величина будет значительной. При измерении 30-метрового участка дороги то же самое отклонение в 1 см допускается, такое измерение будет наиболее точным. При вычислении ускорения свободного падения с помощью маятника неточность не превышает 10 -5 м/с. 2
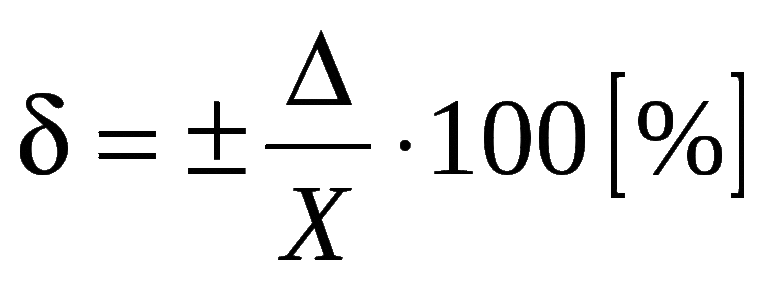
Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.
Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.
Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.
Методики расчета
Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

- Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
- Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
- Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение. Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
- Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение. Полученное число умножают на 100%.
Для определения предельного отклонения выбирают наибольшее значение из всех полученных.
Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:
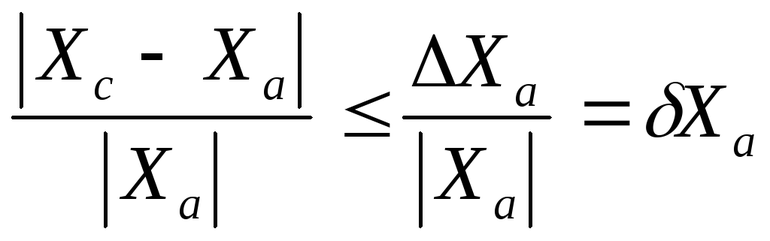
- Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
- Полученные результаты складывают между собой.
- Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
- Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.
Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.
Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение. При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.
При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.
Произвести необходимые расчеты можно с помощью онлайн-калькулятора. В окошки вносятся необходимые данные, после чего программа выдает результат.
Методы Корнфельда и Стьюдента
Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.
Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

- Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
- Из этих величин выбирают минимальную и максимальную.
- Вычисляют среднее значение Х.
- В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
- Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.
Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.
Эти показатели вычисляются на основе доверительной вероятности и большого количества измерений.
источники:
http://fevt.ru/load/klassifikacija_oshibok/75-1-0-299
http://nauka.club/matematika/absolyutn%D0%B0y%D0%B0-i-otnositeln%D0%B0y%D0%B0-pogreshnost.html

При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.
Потеря корней
При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней, либо появление посторонних корней.
При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного, а значит, корни могут оказаться потерянными.
K Упражнение. Решить уравнение lg (x – 10)2 + lg x2 = 2lg 24.
L Неправильное решение.
2lg (x – 10) + 2lg x = 2lg 24,
lg (x – 10) + lg x = lg 24,
lg x(x – 10) = lg 24,
x2 – 10x = 24,
x2 – 10x – 24 = 0,
x1 = –2, x2 = 12.
Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.
Ответ: –2 и 12.
Комментарий. Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.
J Правильное решение.
ОДЗ: х ≠ 0, х ≠ 10,
2lg |x – 10| + 2lg|x| = 2lg 24,
lg |x – 10| + lg|x| = lg 24,
lg |x(x – 10)| = lg 24,
|x2 – 10x| = 24,
x2 – 10x = ± 24,
1) x2 – 10x – 24 = 0, x1 = –2, x2 = 12;
2) x2 – 10x + 24 = 0, x3 = 4, x4 = 6.
Ответ: –2; 4; 6 и 12.
![]()
При делении обеих частей уравнения на выражение, содержащее неизвестное, могут быть потеряны корни, которые обращают эти выражения в ноль.
K Упражнение 1. Решить уравнение 3х (х2 – 2х – 3) = 9 (х2 – 2х – 3).
L Неправильное решение.
Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:
3х = 9;
3х = 32;
х = 2.
Ответ: 2.
J Правильное решение.
Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:
3х (х2 – 2х – 3) – 9 (х2 – 2х – 3) = 0;
(3х – 9) (х2 – 2х – 3) = 0;
1) 3х – 9 = 0; 3х = 32; х = 2;
2) х2 – 2х – 3 = 0; х = –1 и х = 3.
Ответ: –1; 2 и 3.
K Упражнение 2. Решить уравнение lg2 x – lg x = 0.
L Неправильное решение.
ОДЗ: х > 0.
Разделим обе части уравнения на lg x и получим:
lg x – 1 = 0;
lg x = 1;
x = 10.
Ответ: 10.
J Правильное решение.
lg2 x – lg x = 0;
ОДЗ: х > 0;
lg x (lg x – 1) = 0;
1) lg x = 0; x = 1;
2) lg x – 1 = 0; lg x = 1; x = 10.
Ответ: 1 и 10.
Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.
Посторонние корни
При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.
Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного. Рассмотрим далее некоторые случаи появления посторонних корней.
Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину.
K Упражнение. Решить уравнение
| 5 – x | – | 5 + 3х | = 0. |
| x – 1 | x2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х2 – 1 и получим:
(5 – x) (x + 1) – (5 + 3x) = 0;
–х2 + x =0;
х2 – x =0;
х (х – 1) =0.
Ответ: 0 и 1.
Комментарий. Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки.
J Правильный ответ: х = 0.
![]()
Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину.
K Упражнение. Решить уравнение
L Неправильное решение.
Заметим, что х2 – 81 = (x – 9) (x + 9) и произведем сокращение дроби на x – 9. Имеем:
(x + 9) – 2х = 0;
– х + 9 = 0;
х = 9.
Ответ: 9.
Комментарий. Был приобретен посторонний корень х = 9.
J Правильный ответ: решений нет.
![]()
Приведение подобных слагаемых с неизвестным в знаменателе, в том случае, если они взаимно уничтожаются, также может привести к приобретению постороннего корня.
K Упражнение. Решить уравнение
| 2 | + х2 – | 2 | – 4х = 0. |
| 3х2 | 3х2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
х2 – 4х = 0;
х (х – 4) =0;
х = 0, х = 4.
Ответ: 0 и 4.
Комментарий. Был приобретен посторонний корень х = 0.
J Правильный ответ: 4.
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.
![]()
Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения. Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √х + 3 + √7 – х = 2.
L Неправильное решение.
ОДЗ: –3 ≤ х ≤ 7;
√х + 3 = 2 – √7 – х;
x + 3 = 4 – 4 · √7 – х + 7 – x;
2x – 8 = –4 · √7 – х;
2 · √7 – х = 4 – x;
4 (7 – x) = 16 – 8x + х2;
х2 – 4x – 12 = 0;
x1 = –2, x2 = 6.
И число –2, и число 6 содержатся в области допустимых значений переменной х, значит, являются решениями исходного уравнения.
Ответ: –2 и 6.
Комментарий. Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
√х + 3 = 2 – √7 – х
к уравнению
x + 3 = 4 – 4 · √7 – х + 7 – x.
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1. Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1, которое стало верным именно в результате возведения в квадрат, ведь 12 = (–1)2. Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
2 · √7 – х = 4 – x,
которое уже имеет один корень –2, к уравнению
4 (7 – x) = 16 – 8x + х2.
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4, которые соответствуют этим уравнениям для случая х = 6. Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
х2 – 4x – 12 = 0,
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.
![]()
Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю, прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение (x – 5) (х + 2) √х – 3 = 0.
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
х – 5 = 0, х + 2 = 0, х – 3 = 0;
х = 5, х = –2, х = 3.
Ответ: 5; –2; 3.
Комментарий. Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3.
![]()
Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения. Таких равенств много, вот некоторые из них:
x = (√ х)2
√ х · y = √ х · √ y
| tg (x + y) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2x = | 2 tg x |
| 1 + tg2 x |
loga х2 = 2 loga x
loga х · y = loga x + loga y
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней.
K Упражнение. Решить уравнение (sqrt{left(x-1 right)^2left(x-3 right)}=x-1.)
L Неправильное решение.
(sqrt{left(x-1 right)^2}cdot sqrt{x-3}=x-1;)
(left| x-1right|cdot sqrt{x-3}=x-1;)
(sqrt{x-3}=frac{x-1}{left|x-1 right|};)
так как х ≥ 3, то |х – 1| = х – 1 и
(sqrt{x-3}=1;)
(x=4.)
Ответ: 4.
Комментарий. Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1. И вот почему. Исходное уравнение имеет область допустимых значений {1}∪[3; +∞), а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt{x-3}=x-1) – только [3; +∞), что и привело к потере 1.
Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.
J Правильное решение.
(sqrt{left(x-1 right)^2left(x-3 right)}=x-1;)
(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)
(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)
(left(x-1 right)^2cdot left(x-4 right)=0;)
(left(x-1 right)^2=0,;; x-4 =0;)
(x=1,;;x=4.)
Проверкой убеждаемся, что оба корня действительные.
Ответ: 1 и 4.
Ошибки, связанные с заменой переменной
При решении некоторых уравнений достаточно удачным является метод замены переменной. Но применение этого метода учащиеся осуществляют не всегда правильно.
Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший.
K Упражнение. Решить уравнение (5 left(x-3 right)^{1/4}-6=left(x-3 right)^{1/2}.)
L Неправильное решение.
Сделав замену ( left(x-3 right)^{1/2}=t), считают, что ( left(x-3 right)^{1/4}=t^2) и уравнение переписывают в виде 5t2 – t – 6 = 0, после чего, конечно, верный результат уже не получить.
J Правильное решение.
Верный результат можно получить, сделав замену ( left(x-3 right)^{1/4}=t), тогда ( left(x-3 right)^{1/2}=t^2) с продолжением:
(5t-6=t^2;)
(t^2-5t+6=0;)
(t_{1}=2,;;t_{2}=3;)
1)(; left(x-3 right)^{1/4}=2,;;;) (x-3 =16,;;;) (x=19;)
2)(; left(x-3 right)^{1/4}=3,;;;) (x-3=81,;;;) (x=84.;;;)
Ответ: 19 и 84.
![]()
Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась.
K Упражнение. Решить уравнение х + 4√x – 5 = 0.
L Неправильное решение.
√x = t, x = t2;
t2 + 4t – 5 = 0;
t1 = 1, t2 = –5;
1) x = (t1)2 = 12 = 1;
2) x = (t2)2 = (–5)2 = 25.
Ответ: 1 и 25.
Комментарий. После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √x = t, а не x = t2.
J Правильное решение.
√x = t, x = t2;
t2 + 4t – 5 = 0;
t1 = 1, t2 = –5;
1) √x = t1 = 1; x = 1;
2) √x = t2 = –5; решений нет.
Ответ: 1.
![]()
При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца.
K Упражнение. Решить уравнение (x^2-4x-sqrt{2x^2-8x+12}=6.)
L Неправильное (нерациональное) решение.
Чаще всего данное уравнение начинают решать так:
(x^2-4x-6=sqrt{2x^2-8x+12};)
(left( x^2-4x-6right)^2=2x^2-8x+12;)
(x^4-8x^3+2x^2+56x+24=0.)
Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.
Комментарий. В качестве альтернативы можно предложить способ введения новой переменной.
J Правильное решение.
(x^2-4x-sqrt{2x^2-8x+12}=6;)
пусть (sqrt{2x^2-8x+12}=m,) тогда (x^2-4x=0,5(m^2-12),)
и исходное уравнение принимает вид:
(0,5(m^2-12)-m=6.)
А дальше все просто:
(m^2-2m-24=0;)
(m_{1}=-4;;;m_{2}=6;)
1) (sqrt{2x^2-8x+12}=-4,) решений нет;
2) (sqrt{2x^2-8x+12}=6,;;2x^2-8x+12=36,;;x^2-4x-12=0,;;x_{1}=-2,;x_{2}=6.)
Ответ: –2 и 6.
Комментарий. Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.
Ошибки, связанные с использованием модуля
При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня, допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.
K Упражнение 1. Решить уравнение (sqrt{x^2}=9.)
L Неправильное решение.
(sqrt{x^2}=9;;;x=9.)
Ответ: 9.
J Правильное решение.
(sqrt{x^2}=9;;;left|x right|=9;;;x=pm 9.)
Ответ: ±9.
K Упражнение 2. Решить уравнение (sqrt{(x+3)^2}=x+3.)
L Неправильное решение.
(sqrt{(x+3)^2}=x+3;)
(x+3=x+3.)
Ответ: корнем данного уравнения является любое действительное число.
J Правильное решение.
(sqrt{(x+3)^2}=x+3;;;left|x+3 right|=x+3geq 0;;;xgeq -3.)
Ответ: х ≥ –3.
![]()
Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1.
J Правильное решение.
Находим нули модулей, для |х – 3| это 3, для |x – 4| это 4, и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
(–∞; 3), [3; 4) и [4; +∞).
На каждом из этих промежутков исходное уравнение принимает свой вид.
Так как
[left|x-3 right|=begin{cases} ;;;;x-3, ;;;xgeq 3; \ -(x-3), ;;x< 3; end{cases};;;;; left|x-4 right|=begin{cases} ;;;;x-4, ;;xgeq 4; \ -(x-4), ;x< 4; end{cases}]
то
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
– (х – 3) – (х – 4) = 1,
– х + 3 – х + 4 = 1,
2х = 6,
х = 3;
так как 3 ∉ (–∞; 3), то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
(х – 3) – (х – 4) = 1,
х – 3 – х + 4 = 1,
1 = 1;
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
(х – 3) + (х – 4) = 1,
х – 3 + х – 4 = 1,
2х = 8,
х = 4;
так как 4 ∈ [4; +∞), то 4 – корень уравнения.
Так как [3; 4)∪{4} = [3; 4], то корнями исходного уравнения являются все числа числового промежутка [3; 4].
Ответ: [3; 4].
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности.
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24.
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Ответ: 1.
Комментарий. Был подобран корень х = 1, но не обнаружен еще один корень х = –4, который соответствует разложению 24 = –4 · (–3) · (–2) · (–1). Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
х (х + 1) (х + 2) (х + 3) = 24,
(х (х + 3)) ((х + 1) (х + 2)) = 24,
(x2 + 3х) (x2 + 3х + 2) = 24,
введем новую переменную x2 + 3х + 1 = t, тогда
(t – 1) (t + 1) = 24,
t2 – 1 = 24,
t2 = 25,
t1 = –5, t2 = 5,
1) x2 + 3х + 1 = –5, x2 + 3х + 6 = 0, решений нет;
2) x2 + 3х + 1 = 5, x2 + 3х – 4 = 0, х1 = –4, х2 = 1.
Ответ: –4 и 1.
![]()
Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций. Часто при этом используется производная.
K Упражнение. Решить уравнение x11 + 5х – 6 = 0.
L Неправильное решение.
Методом подбора находим корень уравнения х = 1.
Ответ: 1.
Комментарий. Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x11 + 5х – 6, что и доказывает единственность подобранного корня.
Ответ: 1.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями, не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7 x)1/3 = 1.
L Неправильное решение.
(log7 x)1/3 = (log7 x)0.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
log7 x = 1,
x = 7.
Ответ: 7.
K Упражнение 2. Решить уравнение (х + 5) х2 + х – 2 = 1.
L Неправильное решение.
(х + 5) х2 + х – 2 = (х + 5) 0,
х2 + х – 2 = 0,
х1 = –2, х2 = 1.
Ответ: –2 и 1.
Комментарий. Потерян корень х = –4. Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
х + 5 = 1,
х = –4.
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5, тогда
(х2 + х – 2) · lg (x + 5) = 0;
1) х2 + х – 2 = 0; х1 = –2, х2 = 1;
2) lg (x + 5) = 0; x + 5 = 1; x = –4.
Ответ: –4, –2 и 1.
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.
![]()
При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями. При применении этих свойств учащиеся часто допускают ошибки.
K Упражнение 1. Решить уравнение log3 x · log3 (3x) =log3 (81x).
L Неправильное решение.
log3 (3х2) =log3 (81x),
3х2 = 81x,
3х = 81,
х = 27.
Ответ: 27.
Комментарий. В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
ОДЗ: х > 0;
log3 x · (log3 3 + log3 x) = log3 81 + log3 x;
log3 x · (1 + log3 x) = 4 + log3 x;
log3 x + log32 x = 4 + log3 x;
log32 x = 4;
log3 x = ±2;
x = 9, x = 1/9.
Ответ: 9 и 1/9.
K Упражнение 2. Решить уравнение lg x2 = 4.
L Неправильное решение.
2lg x = 4; lg x = 2; x = 100.
Ответ: 100.
J Правильное решение 1.
2lg |x| = 4; lg |x| = 2; |x| = 100; x = ±100.
Ответ: ±100.
J Правильное решение 2.
lg x2 = lg 10000; x2 = 10000; x = ±100.
Ответ: ±100.
![]()
Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями, так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.
Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней.
K Упражнение 1. Решить уравнение (left(log_{x}5 +2 right){log _{5}}^2 ;x=0.)
L Неправильное решение.
(left(log_{x}5 +2 right){log _{5}}^2 ;x=0;)
(left(frac{1}{log_{5}x} +2 right){log _{5}}^2 ;x=0;)
(left(1 +2 log _{5}xright)log _{5}x=0;)
1) (1 +2 log _{5}x=0;;;;log _{5}x=-^1/_2;;;;x=;^1/_{sqrt{5}};)
2) (log _{5}x=0;;;; x=1.)
Ответ: (;^1/_{sqrt{5}};;;;;1.)
Комментарий. Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.
J Правильное решение.
Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞). И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞), а, значит, не является корнем.
Ответ: (;^1/_{sqrt{5}};.)
K Упражнение 2. Решить уравнение (20log_{4x}sqrt{x}+ 7log_{16x}x^3-3log _{x/2}x^2=0.)
L Неправильное решение.
(10log_{4x}x+ 21log_{16x}x-6log _{x/2}x=0;)
(large frac{10}{log_{x}4x}+ frac{21}{log_{x}16x}-frac{6}{log _{x}x/2}=0;)
(large frac{10}{log_{x}4+log_{x}x}+ frac{21}{log_{x}16+log_{x}x}-frac{6}{log _{x}x-log _{x}2}=0;)
(large frac{10}{2log_{x}2+1}+ frac{21}{4log_{x}2+1}-frac{6}{1-log _{x}2}=0.)
Пусть logx 2 = t, тогда
(large frac{10}{2t+1}+ frac{21}{4t+1}-frac{6}{1-t}=0;)
(large frac{10(4t+1)(1-t)+21(2t+1)(1-t)-6(2t+1)(4t+1)}{(2t+1)(4t+1)(1-t)}=0;)
(26t^2-3t-5=0,;;;;tneq 1,;tneq -^1/_2,;tneq -^1/_4;)
(1);t=;^1/_2,;;;log _x{2}=;^1/_2,;;;x^{1/2}=2,;;;x=4;)
(2);t=-;^5/_{13},;;;log _x{2}=-;^5/_{13},;;;x^{-5/13}=2,;;;x=;^1/_{4sqrt[5]{8}};.)
Ответ: (4;;;^1/_{4sqrt[5]{8}};.)
Комментарий. В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х. Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1. Поэтому число 1, как возможный корень исходного уравнения, следует рассмотреть отдельно.
J Правильное решение.
Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.
Ответ: (1;;;4;;;^1/_{4sqrt[5]{8}};.)
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение.
|
K Решить уравнение |
L Неправильный ответ |
J Правильный ответ |
|
sin x – cos x = 0 |
x = π/4 |
x = π/4 + πk, k ∈ Z |
|
tg x = 1/√3 |
x = π/6 + 2πk, k ∈ Z |
x = π/6 + πk, k ∈ Z |
|
sin x = 1/2 |
x = (–1)k arcsin π/6 + πk, k ∈ Z |
x = (–1)k · π/6 + πk, k ∈ Z |
|
cos x = 1/2 |
x = π/3 + 2πk, k ∈ Z |
x = ± π/3 + 2πk, k ∈ Z |
![]()
В тригонометрических уравнениях, как и в уравнениях других видов, причиной многих ошибок становится невнимательное отношение к области допустимых значений неизвестного.
K Упражнение. Решить уравнение tg 3x – tg x = 4sin x.
L Неправильное решение.
| sin (3x – x) | = 4sin x; |
| cos 3x cos x |
| sin 2x | = 4sin x; |
| cos 3x cos x |
sin 2x = 4sin x cos 3x cos x;
sin 2x = 2sin 2x cos 3x;
sin 2x – 2sin 2x cos 3x = 0;
sin 2x (1 – 2cos 3x) = 0;
1) sin 2x = 0; 2x = πn, n ∈ Z; x = πn/2, n ∈ Z;
2) 1 – 2cos 3x = 0; cos 3x = 1/2; 3x = ± π/3 + 2πk, k ∈ Z; x = ± π/9 + 2πk/3, k ∈ Z.
Ответ: πn/2 , n ∈ Z; ± π/9 + 2πk/3, k ∈ Z.
Комментарий. Была допущена серьезная ошибка. При x = πn/2 и нечетных n исходное уравнение не имеет смысла. Ошибка осталась незамеченной в результате того, что не была установлена область допустимых значений переменной.
J Правильный ответ: πn, n ∈ Z; ± π/9 + 2πk/3, k ∈ Z.
![]()
Не редкость – появление ошибок по причине невнимательного отношения ко всем заданным в уравнении условиям.
K Упражнение. Решить уравнение cos x – cos 2x = 1, если 0 < x < π/2 .
L Неправильное решение.
cos x – (2cos2 x – 1) = 1;
cos x – 2cos2 x = 0;
cos x (1 – 2cos x) = 0;
1) cos x = 0; x = π/2 + πk, k ∈ Z;
2) 1 – 2cos x = 0; cos x = 1/2; x = ± π/3 + 2πn, n ∈ Z.
Ответ: π/2 + πk, k ∈ Z; ± π/3 + 2πn, n ∈ Z.
Комментарий. Ответ не верен, так как условию 0 < x < π/2 удовлетворяют только один корень.
J Правильный ответ: π/3.
![]()
Следует не забывать, что сокращение всех членов уравнения на функцию, содержащее неизвестное не редко приводит к потере корней уравнения.
K Упражнение. Решить уравнение cos x (2sin 2x – 1) = cos x sin 2x.
L Неправильное решение.
2sin 2x – 1 = sin 2x;
sin 2x = 1;
2x = π/2 + 2πk, k ∈ Z;
x = π/4 + πk, k ∈ Z.
Ответ: π/4 + πk, k ∈ Z.
J Правильное решение.
cos x (2sin 2x – 1) – cos x sin 2x = 0;
cos x (2sin 2x – 1 – sin 2x) = 0;
cos x (sin 2x – 1) = 0;
1) cos x = 0; x = π/2 + πn, n ∈ Z;
2) sin 2x – 1 = 0; sin 2x = 1; 2x = π/2 + 2πk, k ∈ Z; x = π/4 + πk, k ∈ Z.
Ответ: π/2 + πn, n ∈ Z; π/4 + πk, k ∈ Z.
![]()
Еще одна причина появления ошибок – недостаточное внимание к проверке. Следует не забывать, что при проверке посторонних корней тригонометрических уравнений часто удобно использовать единичную окружность.
K Упражнение. Решить уравнение sin x + cos x = 1.
L Неправильное решение.
(sin x + cos x)2 = 12;
sin2 x + 2sin x cos x + cos2 x = 1;
1 + 2sin x cos x = 1;
sin 2x = 0;
2x = πn, n ∈ Z;
x = πn/2, n ∈ Z.
Ответ: πn/2, n ∈ Z.
Комментарий. Так как при решении обе части исходного уравнения возводили в квадрат, а его левая часть может быть как положительной, так и отрицательной величиной, могли появиться посторонние корни, следовательно, проверка обязательна.
J Правильное решение.

Дополним приведенное выше решение следующими рассуждениями.
Значениям x = πn/2, n ∈ Z соответствуют четыре точки, отмеченные на единичной окружности. Причем зеленые точки соответствуют корням уравнения, а красные – посторонним корням.
Так как зеленой точке на Ох соответствуют значения n = 4k, где k ∈ Z, а на оси Оу – значения n = 4m + 1, где m ∈ Z, то
1) x = 4πk/2 = 2πk, k ∈ Z;
2) x = 4πm+π/2 = π/2 + 2πm, m ∈ Z.
Ответ: 2πk, k ∈ Z и π/2 + 2πm, m ∈ Z.
![]()
Как и в любых других уравнениях, при решении тригонометрических уравнений не редкость – применение вспомогательной переменной. Но не следует забывать, что при этом может быть сужена область определения, что может привести к потере корней.
K Упражнение. Решить уравнение sin 2x + 3cos 2x + 3 = 0.
L Неправильное решение.
Так как
| sin 2x = | 2tg x | ; |
| 1 + tg2 x | ||
| cos 2x = | 1 – tg2 x | , |
| 1 + tg2 x |
то для исходного уравнения имеем:
| 2tg x | + 3 · | 1 – tg2 x | + 3 = 0; |
| 1 + tg2 x | 1 + tg2 x |
2tg x + 3 – 3tg2 x + 3 + 3tg2 x = 0;
2tg x + 6 = 0;
tg x = –3;
x = arctg (–3) + πk, k ∈ Z.
Ответ: arctg (–3) + πk, k ∈ Z.
Комментарий. Область допустимых значений неизвестного в исходном уравнении – все действительные числа. Но при x = π/2 + πn переход от sin 2x и cos 2x к tg x невозможен. Таким образом область допустимых значений неизвестного сузилась, а значит, случай x = π/2 + πn необходимо проверить отдельно.
J Правильное решение.
Продолжим решение уравнения. Подставим π/2 + πn в исходное уравнение:
sin 2(π/2 + πn) + 3cos 2(π/2 + πn) + 3 = 0;
sin (π + 2πn) + 3cos (π + 2πn) + 3 = 0;
sin π + 3cos π + 3 = 0;
0 – 3 + 3 = 0;
0 = 0 – верно и, значит, π/2 + πn, n ∈ Z – корни уравнения.
Ответ: π/2 + πn, n ∈ Z; arctg (–3) + πk, k ∈ Z.
Смотрите так же:
Ошибки в тождественных преобразованиях
Ошибки в системах уравнений
Ошибки в неравенствах
Ошибки в упражнениях с параметрами
Ошибки в упражнениях о функциях
Ошибки в упражнениях из начал анализа
Ошибки в геометрических задачах
![]()
Относительная ошибка аппроксимации
Оценивает отклонение
теоретических оценок от реальных. Ошибка
аппроксимации ε. Формула 17.
Значение этой ошибки,
не превышающее 8-10% говорит о хорошем
качестве уравнения регрессии.
Εср=2,62/30*100%=8,7%.
В регрессионном
анализе общая колеблемость результата
представляется следующим образом:
∑=
*100%
∑(y—
)2=∑(yi—
)2+∑(
—yi)2
∑(y-
)2-общая
колеблемость результата, ∑(y-
)2
–от фактических данных отнимаем
теоретические = остаточная колеблемость,
∑(
-yi)2
– колеблемость результата, объясненная
уравнением регрессии
Это разложение вариации
зависимой переменной лежит в основе
качества полученного уравнения регрессии,
т.е. чем бОльшая часть вариации у
объясняется уравнением регрессии, тем
лучше качество уравнения, т.е. правильно
выбран тип функции для описания
зависимости результата и фактора y=f(x)
и правильно выбрана сама объясняющая
переменная х. отношение объясненной
вариации к общей позволяет найти индекс
детерминации η2.
η2=
Он определяет степень
детерминации регрессией вариации у.
Корень квадратный из индекса детерминации
называется теоретическим корреляционным
отношением, оно показывает тесноту
связи между результатом и фактором, как
при линейной, так и при нелинейной связи.
Измеряется η [0,1].
В нашем примере
∑(
—
)2=∑(yi—
))2+∑(
)2
= 7,5-1,094=6,064,
η2=6,406/7,5=0,85
(85%)
Оценка значимости
производится на основе F-критерия
Фишера, которому предшествует дисперсионный
анализ, применяемый как вспомогательное
средство для изучения качества
регрессионной модели. Схему дисперсионного
анализа представим в таблице, где
n-число наблюдений, а
m-число параметров при х.
Таблица
дисперсионного анализа
|
Компоненты ди сперсии |
Сумма квадратов (SS) |
Число степеней свободы (df) |
Дисперсия на одну степень свободы |
|
Общая дисперсия |
|
n-1 |
|
|
Факторная |
|
m |
|
|
Остаточная |
|
n-m-1 |
|
Дисперсия на одну
степень свободы приводит дисперсии к
сопоставимому виду. Поэтому, сопоставляя
факторную и остаточную дисперсии,
получают фактическое значение F-критерия
Фишера.
F=MSФАКТ/MSОСТ
Фактическое значение
F-критерия Фишера
сравнивается с табличным значением
F-критерия Фишера Fтабл(α,
k1, k2),
которое зависит от уровня значимости
α и степеней свободы k1
(факторная), k2
(остаточная).
Если фактическое
значение F-критерия Фишера
больше табличного, то уравнение регрессии
является статистически значимым в целом
Для парной линейной
регрессии этот пример может быть записан
следующим образом:
Fфакт=
,
Fфакт=
F-критерий
Фишера говорит о статистической
значимости уравнения. В парной линейной
регрессии оценивается значимость
отдельных параметров уравнения регрессии
a и b. С этой
целью определяется его стандартная
ошибка:
mb=MSост/σx
t-критерий
Стьюдента. Для оценки существенности
коэф-та регрессии определяется фактическое
значение t-критерия
Стьюдента: фактическое значение
t-критерия Стьюдента для
параметра b:
tb=b/mb
Далее это фактическое
значение сравнивается с табличным
значением t-критерия
Стьюдента, которое зависит от уровня
значимости α и числа степеней свободы
df (n-2).
Если фактическое
значение больше табличного, то параметр
регрессии статистически значим. Кроме
того, можно определить границы
доверительного интервала коэф-та
регрессии b.

=a+bx
b ±∆
(предельная ошибка)
b-∆b≤b≤b+∆b
∆b=tтабл*m*b,
где ∆b –предельная
ошибка коэф-та регрессии b.
Если -2≤b≤3,
значит, b-статистически
незначим.
Стандартной ошибкой
для параметра а ma
= MSост

.
Значимость параметра
а определяется аналогично параметру
b.
ta=a/∆ma
ta=a/ma
>ta(α,
df)
Если фактическое
больше табличного – параметр статистически
значим.
Аналогичным образом
проверяется статистическая значимость
линейного коэф-та кореляции.
mσyx=
И это значение
сравнивается с табличным значением
t-критерия Стьюдента.
При прогнозировании
по уравнению регрессии вычисляется
прогнозное значение результата
(
подстановкой
в уравнение регрессии прогнозного или
желаемого значения фактора.

=a+bxnp
Полученное по этому
уравнению значение результат называется
точечным прогнозом.
Здесь также считаются
доверительные интервалы прогноза. Они
считаются следующим образом:
yp-∆y≤
≤yp+∆p,
где ∆p –
предельная ошибка прогноза.
∆y=tтабл*my,
где my—
стандартная ошибка прогноза
mУp=MSост
*

,
где
—
фактическое значение исходных данных.
Выполнить
корреляционно-регрессионный анализ
можно, воспользовавшись пакетами
прикладных программ. Самый простой –
Excel.
Нужно в закладке
«Данные» — «Анализ данных» — «Регрессия»
— «Входной интервал у»
|
х |
у |
|
1 |
5 |
|
2 |
7 |
|
3 |
8 |
Поставить флажок
«Метки», «Const 0» – флажка
не должно быть, иначе параметр а = 0.
Дальше «Выходной интервал» номер
свободной ячейки на рабочем листе –
Ок.
Вывод итогов представляет
собой 3 таблички:
-
Регрессионная
статистика
-
Множественный R (парный
линейный коэф-т корреляции)R-квадрат (коэф-т
детерминации)Нормированный R-квадрат
(скорректированный коэф-т корреляции)Стандартная ошибка коэф-та корреляции
Наблюдение
-
Дисперсионный
анализ
-
df
SS
MS
F
F значимое
Регрессия (факторная)
Остаток
Итого:
-
Коэф-ты
Стандартная ошибка параметров
t-статистика (факт.
значения t-критерия для
параметров а и b)Нижняя 95%
Верхняя 95% (границы доверительного
интервала)У — пересечение
Параметр а
Число
х
b
Число
95% -означает,
что уровень значимости α = 5% (вероятность
– 95%).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
УДК 517
Николаева И.В. студент магистратуры 1 курс, институт «Экономики и управления» Самарский национальный исследовательский университет имени академика С.П.Королева
Россия, г. Самара ОСОБЕННОСТИ ПРИМЕНЕНИЯ АБСОЛЮТНОЙ И ОТНОСИТЕЛЬНОЙ ОШИБКИ АППРОКСИМАЦИИ В РЕГРЕССИОННОМ АНАЛИЗЕ Аннотация: Статья посвящена абсолютной, и относительной ошибкам аппроксимации для линейных регрессионных моделей, как наиболее часто встречающихся на практике.
Ключевые слова: регрессионный анализ, аппроксимация, относительная ошибка, абсолютная ошибка.
Nikolaeva I. V. student magistracy 1 course, Institute «Economy and management» Samara national research University named after academician S. P.
Korolev Russia, Samara APPLICATION FEATURES ABSOLUTE AND RELATIVE APPROXIMATION ERRORS IN REGRESSION ANALYSIS Abstract: the Article deals with both absolute and relative approximation errors for linear regression models, as the most common in practice.
Key words: regression analysis, approximation, relative error, absolute
error.
Разработка эконометрических моделей является целью эконометрического анализа, позволяющая спрогнозировать тенденции развития экономических процессов для принятия обоснованных решений. Эконометрические модели позволяют выявить особенности функционирования объекта и благодаря этому предсказать будущее его поведение при изменении какого-либо параметра. Для любого субъекта возможность прогнозирования ситуации значит получение наилучших результатов, избежание потерь, минимизация рисков. Построение эконометрических моделей с целью анализа и прогнозирования экономических процессов является важной задачей при проведении исследования любого уровня. Однако проблема оценки качества полученной модели является ключевой в моделировании.
Оценка значимости как уравнения в целом, так и отдельных его параметров проводится после того как уравнение регрессии найдено. Значимость уравнения регрессии — это установление соответствия математической модели, выражающей зависимость между переменными, эмпирическим данным и определение достаточного количества включенных
в уравнение объясняющих переменных для описания зависимой переменной. При подборе уравнения тренда, значение ошибки аппроксимации может служить для выбора наиболее подходящего уравнения. Аппроксимация результатов наблюдений может идти по разным моделям, но наилучшей аппроксимацией является та, в которой минимально отклонение между моделью и реальными данными в относительных значениях.
Фактические значения результативного признака отличаются от теоретических значений, рассчитанных по уравнению регрессии, т. е. у и ух. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у — ух) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у — ух) несравнимы между собой, исключая величину, равную нулю. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.
Отклонения (у — ух) можно рассматривать как абсолютную ошибку аппроксимации. Поскольку (у — ух) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю. Относительная ошибка аппроксимации рассчитывается по формуле:
У-Ух
* 100 (1)
У
Чем ближе измеренное значение к истинному значению, тем точнее измерение. Если экспериментальное значение меньше реального, то абсолютная ошибка отрицательна, а если экспериментальное значение больше реального, то абсолютная ошибка положительна.
Таким образом, величина отклонения теоретического значения результативного признака от фактического значения, взятая по модулю, представляет собой абсолютную ошибку аппроксимации. А величина, равная отношению абсолютной ошибки к фактическим значениям результативного признака, выраженная в процентах, является относительной ошибкой аппроксимации.
Для иллюстрации приведены данные опроса шести семей (в которой два работающих взрослых и один ребенок) г.Самара по связи расходов на продукты питания с уровнем доходов этих семей.
_Таблица 1 — Данные опроса
Расходы семьи на продукты питания, y, руб/месяц Доходы семьи, x, руб/месяц
8000 21000
18000 50000
10000 23000
15000 40000
11000 27000
12000 30000
На основе поля корреляции можно сделать предположение, что связь между доходами и расходами на продукты питания — линейная.
б
у
я р
К
и ь м 64 и К т
е Н
с и
ы С
д о ы
х
с гг1 у
Рн до
р
с
20000 15000 10000 5000 0
10000 20000 30000 40000 Доходы семьи, руб.
50000
60000
Рисунок 2 — Поле корреляции по данным опроса
Предположительно зависимость является линейной, поэтому получены следующие параметры линейного уравнения парной регрессии.
Ь = 0,322112
а = 2079,451
А уравнение парной регрессии для представленных данных будет следующее:
% = 2079,451 + 0,322112 * х
Рисунок 3 — Поле корреляции и линия тренда
Из уравнения можно сделать вывод, что с увеличением доходов семьи на 1000 рублей, расходы на питание увеличиваются на 322,112 рублей.
0
Таблица 2 — Расчет абсолютной, относительной, средней ошибки _аппроксимации
х у х*у X2 У2 ух у-ух |у-ух 1 /у*100
1 21000 8000 168000000 441000000 64000000 8843,8 843,8 10,5
2 50000 18000 900000000 2500000000 324000000 18185,0 185,0 1,0
3 23000 10000 230000000 529000000 100000000 9488,0 512,0 5,1
4 40000 15000 600000000 1600000000 225000000 14963,9 36,1 0,2
5 27000 11000 297000000 729000000 121000000 10776,5 223,5 2,0
6 30000 12000 360000000 900000000 144000000 11742,8 257,2 2,1
Итого 191000 74000 2555000000 6699000000 978000000 74000,0 — 21,1
Ср. знач 31833,3 12333,3 425833333,3 1116500000 163000000 12333,3 — 3,5
Таким образом, средняя ошибка аппроксимации А = 3,5%, что говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным и показывает, что линия регрессии хорошо приближает исходные данные.
На основе проведенного расчета можно сделать следующие выводы. Чем ближе измеренное значение к реальному значению, тем точнее измерение. Абсолютная ошибка является недостаточно показательной. Поэтому нагляднее точность измерения будет характеризоваться отношением абсолютной ошибки к полученному значению измеренной величины, а именно относительная ошибка. Если в ряде данных имеются значения у, близкие к нулю, то значение абсолютной ошибки аппроксимации также становится чрезмерно завышенным вне зависимости от адекватности построенной модели. Кроме того, если значение ух имеет значение равное нулю или близко к нулю, то, относительная ошибка аппроксимации перестает учитывать разницу между фактическим и расчетным значениями — под знаком суммы получается единица. А также, если фактические данные ряда имеют очень большие значения, то есть измеряются в тысячах единиц, то знаменатель становится очень большим, в результате чего средняя ошибка аппроксимации существенно занижается, вне зависимости от качества построенной модели.
Таким образом, можно сделать вывод, что объективно оценить качество модели только по абсолютной, относительной ошибкам аппроксимации не представляется возможным, так как абсолютная ошибка зависит от выбора масштаба измерения, а относительная ошибка завышает вклад ошибки вблизи нулевого значения.
Использованные источники: 1.Эконометрика : учебник для бакалавриата и магистратуры /И. И. Елисеева [и др.] ; под ред. И. И. Елисеевой. — М. : Издательство Юрайт, 2015. — 449 с. — Серия : Бакалавр и магистр. Академический курс.
2.О.В. Любимцев, О.Л. Любимцева, Линейные регрессионные модели в эконометрике. Методическое пособие. Нижний Новгород, ННГАСУ, 2016. З.Федеральная служба государственной статистики http://www.gks.ru
УДК 378.1(063)
Овакимян М.А., кандидат экономических наук, доцент кафедра «Государственное и муниципальное управление» Южно-Российский институт управления-филиал РАНХиГС
Россия, г. Ростов-на-Дону Андриасова К.Г. студент магистратуры 2 курс, факультет управления Южно-Российский институт управления-филиал РАНХиГС
Россия, г. Ростов-на-Дону ОЦЕНКА КАДРОВОГО ПОТЕНЦИАЛА ОБРАЗОВАТЕЛЬНОЙ ОРГАНИЗАЦИИ Аннотация: проблема кадрового потенциала в системе высшего образования представляется ключевой. Именно от уровня кадрового потенциала ВУЗа в конечном итоге будет зависеть уровень квалификации, полученный выпускником. Образовательная система является фундаментом развития общества в целом, что актуализирует необходимость определения критериев оценки кадров и формирование системы аттестационных мероприятий в соответствии с требованиями времени.
Основой для повышения эффективности кадрового потенциала ВУЗа является разработка профессиональных стандартов, определяющая уровень компетенций сотрудников. Важно понимать, что оценочная система должна учитывать различные формы оценивания, с учетом специфики ВУЗа.
Ключевые слова: оценка, компетенция, инновация, аттестация, квалификация, подготовка и т.д.
Оvakimyan M.A., Candidate of Economic Sciences, Associate Professor
Public Administration South-Russia Institute of Management RANEPA
Russia, Rostov-on-Don Andriasova K. G. master’s student 2nd year, Faculty Public Administration, South-Russia Institute of Management RANEPA
Russia, Rostov-on-Don ASSESSMENT OF PERSONNEL POTENTIAL OF THE EDUCATIONAL ORGANIZATION Abstract: the problem of human resources in the higher education system seem to be key. It is the level of personnel potential of the University will






