Ошибка Даламбера
Другой великий француз – Даламбер – вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов.
Задача: Какова вероятность, что подброшенные вверх две правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером: Опыт имеет три равновозможных исхода:
1. обе монеты упали на «орла»;
2. обе монеты упали на «решку»;
3. одна из монет упала на «орла», другая на «решку».
Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна 2/3.
Правильное решение: Опыт имеет четыре равновозможных исхода:
1. первая монета упала на «орла», вторая тоже на «орла»;
2. первая монета упала на «решку», вторая тоже на «решку»;
3. первая монета упала на «орла», а вторая на — «решку»;
4. первая монета упала на «решку», а вторая на — «орла».
Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна = .
Даламбер совершил одну из самых распространенных ошибок, допускаемую при вычислении вероятности: он объединил два принципиально разных исхода в один. Чтобы не повторить эту ошибку, помните, что природа различает все предметы, даже если внешне они для нас неотличимы.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ ИСТОРИЧЕСКИЙ ОЧЕРК
Оппозиция со стороны Даламбера
Среди богатого научного наследства Ж. Даламбера (1717—1783 гг.) имеется ряд работ, посвященных теории вероятностей [50}. Вопросов теории вероятностей он касается и во многих письмах [145}.
Имя Ж- Даламбера в литературе по теории вероятностей встречается только с целью иллюстрации того, что даже очень крупные математики ошибались иногда при решении самых элементарных вероятностных задач.
Приведем пример: «Монета бросается два раза. Какова вероятность того, что хотя бы раз появится герб? Да- ламбер по поводу этой задачи рассуждал следующим образом: герб появится либо при первом бросании, либо при втором, либо совсем не появится. Всех случаев три, из них благоприятствуют ожидаемому событию два, следовательно, искомая вероятность равна 2/3» [6, стр. 35— 36]. Даламбер здесь не различает равновозможные и неравновозможные случаи.
Э. Кольман объясняет происхождение этой ошибки тем, что основные идеи теории вероятностей не свойственны математике, и поэтому математики, в частности Даламбер, допускали самые элементарные ошибки [19, стр. 230}. Другие авторы вообще не касаются причин такой ошибки.
Даламбер вместе с Д. Дидро издавал и редактировал знаменй*гуЮ «Энциклопедию». Первое ее издание выходило с 1751 г. по 1780 г. и состояло из 35 томов. После выхода 7-го тома в 1757 г. Даламбер отошел от «Энциклопедии». Но в семи томах он поместил много статей, в том числе и по теории вероятностей. Первой по времени была статья «Герб и решетка» помещенная в четвертом томе «Энциклопедии» [168]. В этой статье Даламбер решает вопрос о шансах получить два раза герб при двух бросаниях монеты. Эту задачу он решает неправильно, т. к. полагает, что имеется всего три случая, которые следует учитывать, а не четыре. Если в первом броске выпадает решетка, то делать второй бросок не имеет смысла, так как два раза герб выпасть уже не может— это, по Даламберу, первый случай. Второй случай состоит в получении герба в обоих бросках ( + , +). Третий — в получении герба в первом броске и решетки во втором ( + , —). Поэтому, по Даламберу, искомый шанс равен ‘/з- Даламбер не замечает, что указанные им три случая не являются равновозможными. Как легко видеть, в действительности здесь имеется четыре равновозможных случая ( + , +), ( + , —), (—, +), (—, —) и искомая вероятность равна ‘Д.
Далее в этой же статье Даламбер ищет вероятность того, что при трех бросаниях монеты герб выпадет, по крайней мере, один раз. Вместо 8 равновозможных случаев, из которых нашему событию будут благоприятны 7, и, следовательно, искомая вероятность равна 7/8. Даламбер составляет следующую табличку:
- герб;
- решетка, герб;
- решетка, решетка, герб;
- решетка, решетка, решетка.
Он считает, что после того, как при первом или втором броске появился герб, остальные броски делать не следует. Не замечая, что эти четыре случая не равновозможны, Даламбер ошибочно считает, что искомая вероятность равна 3/4, а не 7/8.
В этой же статье Даламбер касается Петербургской задачи и приводит следующее замечание по поводу решения этой задачи Д. Бернулли: «Но мы не знаем, можно ли быть им удовлетворенным; здесь имеется какой-то скандал, который заслуживает внимания математиков» [168, стр. 512]. Сам он склоняется к возможности бесконечного ожидания.
В 7-м томе «Энциклопедии» [169] Даламбер приводит возражения Неккера (профессор математики из Женевы) против его статьи «Герб и решетка». Неккер сообщил эти возражения Даламберу в письме. Неккер указывает, что три случая, которые рассматривает Даламбер, не являются равновозможными. Далее он приводит правильное решение задачи и в конце говорит, что взгляды Даламбера по этому вопросу неприемлемы, так как они ведут к очевидной ошибке.
В статье «Отсутствующий» Даламбер касается работы Н. Бернулли. Ссылаясь на таблицы смертности А. Депарсье (1703—1768 гг.), он приходит к выводу, что безвестно отсутствующий должен считаться умершим в возрасте 75 лет. Далее он говорит, что, учитывая замечания Бюффона о моральной вероятности событий, следует считать, что вероятность меньше 0,0001 является несуществующей.
Другие статьи, такие как «Выгода», «Бассет», (азартная игра), «Плитка» (азартная игра), «Кость», «Лотерея», «Пари», «Карты», хотя и содержат материал, связанный с теорией вероятностей, но они еще менее значительны, чем рассмотренные нами.
Во II томе «Математических произведений» Даламбера помещена его работа «Размышления о теории вероятностей» [50]. В начале работы он приводит обычное определение математического ожидания и замечает, что хотя это определение принято всеми математиками, но имеются случаи, когда оно оказывается несостоятельным. Наглядным примером вопроса, к которому неприменимо математическое ожидание, Даламбер считает Петербургскую задачу, по поводу которой пишет: «Неограниченная сумма является химерой; не существует человека, который захотел бы заплатить за право играть в эту игру, не говорю неограниченную, но даже и весьма скромную сумму» [50, стр. 2].
Далее приводятся рассуждения о необходимости делать различие между метафизически возможным и физически возможным. Чтобы разъяснить эти понятия, Даламбер приводит следующий пример. Метафизически возможно получить сто раз подряд по 6 очков на каждой кости при бросании двух костей, но физически это невозможно*,,дртому что это никогда не происходило и не произойдет. Это является для Даламбера подтверждением того, что очень малая вероятность должна рассматриваться равной нулю.
Даламбер предлагает устанавливать вероятность событий на основании опыта. При этом он считает, что если при бросании монеты появился три раза подряд герб, то вероятнее, что при следующем броске выпадет решетка. Это соображение он приводит как аргумент против основных установленных положений теории вероятностей.
Работа заканчивается следующим образом: «Из этих всех размышлений заключаем: 1. Что если правило, которое я дал в «Энциклопедии» (не зная лучшего), для определения отношения вероятностей при игре в герб и решетку не является строго точным, то общепринятое правило для определения этого отношения является еще менее точным. 2. Что для того, чтобы прийти к удовлетворительной теории вычисления вероятностей, нужно решить несколько задач, которые являются, может быть, неразрешимыми, а именно, установить истинное отношение вероятностей в случаях, не являющихся равновозможными или могущих не рассматриваться как таковые; определить, когда вероятность должна рассматриваться как несуществующая, наконец, установить, как нужно оценивать ожидание или ставку в зависимости от того, является ли вероятность большей или меньшей» [50, стр. 24}.
Несмотря на свое в общем негативное отношение к теории вероятностей, Даламбер поставил такие принципиально важные вопросы: 1) Как определять вероятность, когда нет налицо равновозможных случаев? 2) Какой вероятностью можно пренебрегать и что это означает? и др.
В работе об оспопрививании Д. Бернулли пришел к выводу, что прививка оспы увеличивает среднюю продолжительность жизни на 3—4 года. Даламбер выступает с критикой этой работы [170]. Он не отрицает пользы оспопрививания, но считает, что его положительные и отрицательные стороны неправильно сравниваются и оцениваются Д. Бернулли. По мнению Даламбера, Д. Бернулли рассматривает оспопрививание с точки зрения интересов государства и доказывает, что оно является желательным, так как увеличивает среднюю продолжительность жизни. Даламбер же подходит к вопросу с точки зрения отдельного индивидуума, который может рассматривать выгоду выиграть три или четыре года в вероятной продолжительности жизни как не окупающую непосредственной опасности от прививки. Связь между этими двумя оценками, по Даламберу, настолько неопределенна, что она не может служить предметом точного подсчета. По этому вопросу Даламбер выступил в Академии наук с докладом 12.ХІ 1760 г., где опровергал идеи Д. Бернулли. Даламбер писал: «Я полагаю, что в среднем 30-летнему человеку предстоит прожить еще 30 лет и что он вполне может надеяться прожить еще 30 лет, полагаясь на природу и не делая себе прививки. Затем я предполагаю, что после операции средняя продолжительность жизни будет 34 года. Не кажется ли, что для оценки преимуществ прививки следует сравнить не только среднюю продолжительность жизни в 30 лет и среднюю продолжительность жизни в 34 года, но и риск, равный 1 против 200, умереть через месяц от прививки с отдаленным преимуществом жить на 4 года больше после 60?» [170].
Даламбер обращает внимание на существование двух различных способов оценки продолжительности жизни для лиц данного возраста. Первая оценка — это средняя продолжительность жизни; вторая — вероятная продолжительность жизни — это такая продолжительность жизни, которая имеет равные шансы как быть недостигнутой, так и быть превзойденной. Даламбер не предлагает разграничивать эти понятия. Его мысль состоит в том, что каждое из них может служить для определения ожидаемой продолжительности жизни. Именно это соображение он выдвигает против теории вероятностей, указывая, что она дает два ответа на один и тот же вопрос.
В I томе собраний сочинений Даламбера, изданном в 1820 г., напечатаны его «Сомнения и вопросы относительно теории вероятностей» и «Размышления об оспопрививании» [171]. Эти работы являются изложением уже упоминавшихся выше работ и предназначены для более широкого круга читателей.
Касаясь теории вероятностей в целом, он пишет: «Я первый осмелился высказать сомнения относительно некоторых^иринципов, которые служат основанием для этой теории. Одни великие математ лки сочли эти сомнения достойными внимания, другие великие математики нашли их абсурдными (зачем я буду смягчать выражения, которыми они пользовались). Задача состоит в том, чтобы узнать, не были ли они неправы, применяя их, и в этом случае они оказались бы вдвое неправыми. Их решение, которое они не сочли нужным мотивировать, придало храбрость средним математикам, которые поторопились написать по этому вопросу и напасть на меня, не выслушав меня. Я попытаюсь объясниться настолько ясно, чтобы все мои читатели были в состоянии судить меня».
Следует отметить, что доводы, приводимые против теории вероятностей, повторяют доводы предыдущих работ и нового материала, по существу, не содержат.
В 4-м томе «Математических произведений» [145] помещены выдержки из писем Даламбера, касающиеся теории вероятностей. В них рассматривается «Петербургская задача», анализ отдельных игр, вопросы продолжительности жизни, оспопрививание и другие вопросы. В одном из писем он возражает против общепринятого уже в то время понятия математического ожидания: «Пусть будет предложено выбрать из 100 сочетаний одно. Из этих ста 99 дают выигрыш по 1000 экю и сотое дает выигрыш в 99 тысяч экю. Кто будет настолько бессмысленным, чтобы предпочесть сочетание, которое дает 99 тысяч экю. Ожидание в обоих случаях в действительности не является одним и тем же, хогя оно является одним и тем же согласно правилам теории вероятностей».
Даламбер в своих письмах неоднократно повторяет знакомые нам возражения против теории вероятностей: «Уже около тридцати лет тому назад у меня сформировались эти сомнения при чтении превосходной книги г. Бернулли».
Возвращаясь к решению задачи о получении двух гербов при двух бросаниях монеты, Даламбер пишет: «Если три случая, единственные, которые могут произойти в этой игре, не являются одинаково возможными, то это вовсе, как мне кажется, не на том основании, которое этому придают, что вероятность первого есть 1/2, а вероятности двух других 1/2 • 1/2 или 1/4. Чем больше об этом я думаю, тем больше мне представляется, что, говоря математически, эти три бросания являются одинаково возможными».
Он считает, что для подсчетов вероятностей не будет одинаково, бросают ли п раз последовательно одну монету или одновременно бросают п монет.
В одном из писем Даламбер рассматривает вопрос: при скольких последовательных бросаниях кости можно заключать пари на появление заданного числа очков? Даламбер указывает, что, согласно общепринятым правилам, это пари с выгодой можно заключать при четырех бросаниях. Действительно: (5/6) 4< 1/2; 1—(5/6) 4> 1/2, но (5/4) 3> 1/2 и 1—(5/6) 3< 1/2. Но, ссылаясь на одного игрока, он заявляет, что в данном случае теория не соответствует практике.
Далее Даламбер ссылается на письма к нему трех математиков, одного из которых характеризует как очень образованного писателя, который разрабатывал с успехом математику и который известен превосходной работой по филологии. Этот его корреспондент писал: «Все, что вы высказываете о вероятности, превосходно и весьма очевидно; старое исчисление вероятностей разрушено». Даламбер делает примечание к этому месту: «Я вовсе не претендую на это, я не претендую вовсе разрушить исчисление вероятностей, я желаю, чтобы оно было изменено и улучшено».
В 7-м томе, опубликованном в 1780 г., помещен его мемуар «Об исчислении вероятностей» [172]. Этот мемуар посвящен главным образом «Петербургской задаче». Даламбер начинает этот мемуар словами: «Я прошу прощения у математиков за то, что снова возвращаюсь к этому вопросу. Но я признаюсь, что чем больше я о нем думаю, тем более я убеждаюсь в своих сомнениях относительно принципов общепринятой теории. Я желаю, чтобы эти сомнения были разъяснены и чтобы эта теория, будут ли в ней изменены некоторые принципы, или она будет сохранена такой, какая она есть, по меньшей мере излагалась бы впредь так, чтобы не было места туману».
Даламбер предлагает следующее совершенно произвольное и необоснованное решение. Он считает, что если герб выпадет при первом бросании, то шансы на его вы-
14-а
падение при втором бросании будут —— , а не 1/2. Если
герб выпал при первом и втором бросании, то шансы на его появление:
Причем а, р,~.— положительные числа, а их сумма меньше единицы. В заключение этого решения он пишет. «Этого достаточно, чтобы показать, что члены ставки, начиная с третьего бросания, уменьшаются. Мы доказали, что вся ставка, являющаяся суммой этих членов, конечна даже при предположении бесконечного числа требований. Таким образом, даваемый нами здесь результат решения петербургской задачи не подвержен неразрушимой трудности обычных решений».
Любопытно, что к статье Даламбера «Отсутствующий» написал дополнение Дидро.
Конечно, против основных принципов теории вероятностей выступал не только Даламбер. Вся история этой науки наполнена борьбой с ее извращениями, борьбой с неоправданными применениями ее к законам развития общества, борьбой за признание ее равноправной математической дисциплиной, борьбой с различными идеалистическими извращениями (см. [65]).
Пусть имеются наблюдения или испытания, которые хотя бы теоретически допускают возможность неограниченного повторения, Каждое отдельное испытание может иметь тот или иной исход в зависимости от случая. Совокупность всех этих возможных …
В основе любой аксиоматической системы теории вероятностей лежит определение понятия вероятности. На недостатки классического определения вероятности указывали давно. Были видны и недостатки субъективной трактовки вероятности, идущей от Лапласа. Критику этих …
Пересмотр логических основ теории вероятностей явился началом нового, наиболее плодотворного этапа ее развития. Первые работы в этом направлении принадлежат С. Н. Бернштейну. В 1917 г. в «Записках харьковского математического товарищества» …
Пример 1. Правильная монета подбрасывается 2 раза.
Событие A: Выпадение хотя бы одного “орла”.
Решение. Число возможных исходов в серии из двух испытаний равно 4:
ОО, ОР, РО, РР.
Число исходов, благоприятствующих событию A, равно 3:
ОО, ОР, РО.
Следовательно,
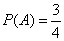 .
.
Пример 2. В семье имеется 2 ребенка.
Событие A: Хотя бы один из детей – мальчик.
Решение. Задача по своей сути не отличается от предыдущей. Только под испытанием теперь следует понимать рождение ребенка. Если рождение мальчика или девочки в одном испытании представляют собой случайные события, то число равновероятных исходов равно 4:
ММ, МД, ДМ, ДД.
Только первые 3 исхода благоприятствуют событию A. Поэтому
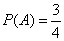 .
.
Ошибочное решение. Число возможных вариантов в серии из двух испытаний равно 3:
ММ, МД, ДД.
Первые два исхода благоприятствуют событию A. Поэтому
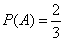 .
.
Анализ. Три события:
“2 мальчика”,
“1 мальчик и одна девочка” и
“2 девочки”
не являются равновозможными, поскольку ММ и ДД представляют собой элементарные события, тогда как событие “1 мальчик и одна девочка” – составное событие, которое разлагается на 2 исхода: МД и ДМ.
Любопытно, что подобную ошибку в рассуждениях допустил в свое время великий математик Даламбер, рассматривая задачу о подбрасывании монеты (см. Пример 1).
Задачи Даламбера.
а) Монета бросается два раза. Какова вероятность того, что хотя бы один раз выпадет герб?
б) Монета бросается три раза. Какова вероятность того, что герб выпадет по крайней мере один раз?

reshalka.com
Математика 6 класс Никольский. Номер №163
Решение
Решение:
а) число всех равновозможных случаев, одно из которых обязательно произойдет при бросании монеты равно 2, так как монета имеет две стороны;
количество случаев, благоприятствующих выпадению герба равно 1, так как герб расположен только на одной стороне монеты;
вероятность выпадения герба при однократном бросании монеты равна
1
2
.
Для того чтобы найти какова вероятность того, чтобы хотя бы один раз выпадет герб при двух бросках монеты необходимо из 1 вычесть вероятность не выпадения герба при двух бросках монеты.
Вероятность не выпадения герба при однократном бросании монеты равна
1
2
и
вероятность не выпадения герба при втором броске монеты так же равна
1
2
;
вероятность не выпадения герба при двух бросках монеты равна
1
2
*
1
2
=
1
4
, тогда 1 −
1
4
=
3
4
вероятность того, чтобы хотя бы один раз выпадет герб при двух бросках монеты.
б)по аналогии с подпунктом а) Для того чтобы найти какова вероятность того, чтобы хотя бы один раз выпадет герб при трёх бросках монеты необходимо из 1 вычесть вероятность не выпадения герба при трёх бросках монеты.
Вероятность не выпадения герба при трёх бросках монеты равна
1
2
*
1
2
*
1
2
=
1
8
, тогда 1 −
1
8
=
7
8
вероятность того, чтобы хотя бы один раз выпадет герб при трёх бросках монеты.
Ответ:
а)
3
4
;
б)
7
8
.
Каждый год учителя жалуются на то, что падает
интерес у учеников к учебе, и каждый год
усложняются задания ГИА и ЕГЭ. Вот уже и элементы
теории вероятностей стали полноправными
заданиями в тестах. Этой теме в школьном курсе не
уделялось должного внимания и казалось, что
сложно будет побороть страх учеников перед этими
задачами. Но мы, учителя, поняли, что т.к. изменить
ситуацию невозможно, под нее надо
подстраиваться.
Проанализировав демонстрационные варианты,
убедилась, что для успешного решения указанных
задач необходимо повторить (а может быть выучить)
основные положения теории вероятностей.
Прежде всего, напомним учащимся, что же изучает
этот раздел математики?
Наблюдая со стороны за различными явлениями
или участвуя в проведении опытов, мы замечаем,
что некоторое явление может произойти, а может и
нет. Те события, исход которых предсказать
нельзя, назовем случайным.
Например, нельзя заранее предсказать будет ли
цифра «6» в номере машины, проезжающей сейчас
мимо вас, будет ли вынут именно красный шар из
коробки, в которой 4 шара разного цвета?
Предсказать исход одного испытания мы не можем, а
вот подсчитать вероятность его наступления при
большом количестве произведенных однородных
испытаний – это под силу теории вероятностей.
Основная формула классической вероятности
всего одна: ![]() , где n
, где n
– число благоприятных исходов, m – общее число
исходов.
При этом надо подчеркивать, что общее число
исходов конечно и все исходы равнозначны (в
противном случае применение этой формулы
невозможно, т.к. получим неверный результат).
Ученики школы среднего и старшего звена
знакомятся только со случайными событиями.
Причем, это знакомство в основном опирается на их
жизненный опыт, интуицию.
В своей повседневной жизни мы часто повторяем:
«с достаточной долей вероятности…», «мне
кажется невероятно, что это произойдет», «почти
со 100% вероятностью можно утверждать…». Этими
фразами мы, опираясь на знания предыдущих лет (а
иногда и на интуицию) прогнозируем исход
какого-то события. Однако, не смотря на наш
прогноз, указанное событие может произойти, а
может и нет. Так, купив лотерейный билет, мы
рассчитываем, конечно, на выигрыш. Подбрасывая
монету, скажем, 4 раза, предполагаем, что «орел» и
«решка» выпадут по 2 раза. Но проделав этот
нехитрый опыт, убеждаемся, что это совсем не так в
реальности. Вот тогда и возникает вопрос: а
сколько раз надо бросить монету, что б
вероятность выпадения нужной стороны её была
почти 50%?
На все эти вопросы и отвечает теория
вероятностей. Она дает возможность численно
характеризовать возможность наступления того
или иного события.
Еще очень важным моментом в подсчете
вероятности наступления события, является то,
что все испытания и их исход договорились
считать равновозможными (равновероятными).
Что это значит?
Рассмотрим, например, опыт, с однократным
подбрасыванием монеты. В реальной жизни может
быть несколько исходов: выпадет «орел», выпадет
«решка», монета встанет на ребро, укатится
куда-нибудь. Кроме того, при многократном
подбрасывании, может оказаться, что выпадение,
скажем, «орла» намного чаще, чем «решки».При
детальном исследовании монеты оказалось, что на
сторону «герба»ушло больше металла(при отливке
монеты) и эта сторона тяжелее. Может сказаться и
неоднородность металла при плавке, порыв ветра
при бросании монеты, неровность поверхности, на
которую падает монета и т.д. Чтоб исход испытания
не зависел от этих частностей, договорились
считать монету «правильной» или «симметричной»,
т.е. одинаковой по весу с обеих сторон, падающей
на одну и ту же плоскость в безветренную погоду.
Аналогично надо считать симметричными игральный
кубик и игральные кости при бросании их во время
эксперимента.
Следует предостеречь учеников от неверного
способа решения задач рассуждением, без учета
всех возможностей исходов. Приведу пример.
Задача. Бросают два игральных кубика.
Найти вероятность того, что сумма выпавших очков
будет равна пяти.
Ошибочное решение. В данной ситуации
возможны два исхода: либо сумма будет равна пяти,
либо не будет. Значит, общее число исходов – два,
а из них благоприятных – один (т.е. сумма равна
пяти). Значит, по формуле вероятности: ![]()
В чем ошибка ученика? Как мы знаем, каждый кубик
имеет 6 граней, на которых расположены точки от
одной до шести. Бросая оба кубика одновременно,
число очков, выпавших на первом кубике, не
зависит от того, какое число очков в это время
выпадет на втором. Т.е. шесть исходов первого
кубика сочетаются с шестью исходами второго. И
общее число равновозможных исходов: 6 • 6 = 36.
Тогда, благоприятных исходов, т.е. сумма равна
пяти будет 4 : 3+2; 2+3; 1+4; 4+1. Следовательно, ответ на
вопрос задачи: ![]()
Очень уместно здесь познакомить учеников со
знаменитой ошибкой Даламбера.
Пример. Ошибка Даламбера. Какова
вероятность, что подброшенные, вверх две
правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером. Опыт
имеет три равновозможных исхода:
1) обе монеты упали на «орла»;
2) обе монеты упали на «решку»;
3) одна из монет упала на «орла», другая на
«решку».
Из них благоприятными для нашего событиями
будут два исхода, поэтому искомая вероятность
равна ![]() .
.
Правильное решение. Опыт имеет четыре
равновозможных исхода:
1) первая монета упала на «орла», вторая тоже на
«орла»;
2) первая монета упала на «решку», вторая тоже на
«решку»;
3) первая монета упала на «орла», вторая – на
«решку»;
5) первая монета упала на «решку», вторая – на
«орла».
Из них благоприятными для нашего события будут
два исхода, поэтому искомая вероятность равна ![]()
Даламбер совершил одну из самых
распространенных ошибок, допускаемую при
вычислении вероятности: он объединил два
принципиально разных исхода в один. Чтобы не
повторить эту ошибку, помните, что природа
различает все предметы, даже если внешне
они для нас неотличимы.
Надо напоминать учащимся, что нужно
анализировать полученный результат: найденная
вероятность не может быть больше 1, как не может,
например, упасть на землю яблок больше, чем их
находится на дереве. Что при бросании монеты,
вероятность выпадения «орла» или «решки» почти
одинакова, а вот вероятность, скажем, отказа
тормозов у автомобиля добросовестного водителя,
крайне мала. Поэтому учащиеся должны помнить, что
p є [0;1].
Крайне редко, но бывают задания, где
вероятность оказывается равной нулю (нулевая
вероятность). События, вероятность которых равна
нулю называются невозможными. Например,
сумма выпавших очков на двух костях равна 13 (мы
знаем, что максимальное число очков одной грани
– 6, значит для двух граней – 12).
Если же вероятность равна 1 (иногда говорят
«стопроцентная вероятность»), то событие
называем достоверным. Примером может служить
опыт с игральным кубиком и утверждение, что при
подбрасывании выпало не более 6 очков.
Все остальные события, вероятность которых
находится в интервале (0;1), будем называть случайными.
Они и составляют основную часть задач в теории
вероятностей. Их-то и решают по уже упомянутой
формуле.
Хочется еще раз напомнить, что половина успеха
в решении той или иной задачи (совсем
необязательно по теории вероятностей) заложена
во внимательном чтении условия. Очень много
ошибок допускают ученики торопясь сделать
задание, которое, как кажется, им знакомо и, не
вникнув в исходные данные, допускают
непростительные ошибки.
Приведу пример двух похожих, но абсолютно
разных по смыслу (и, естественно, по способу
решения) задач.
Задача №1. Фабрика выпускает сумки. В
среднем, на 100 сумок, приходится 8 сумок со
скрытыми дефектами. Найдите вероятность того,
что купленная сумка окажется качественной. (Если
необходимо, результат округлите до сотых).
Решение. Вероятность найдем по
формуле: ![]() .
.
Здесь из 100 сумок 8 некачественных, следовательно,
остальные качественные, т.е. 100 – 8 = 92 сумки.
m = 100,
n = 92
![]()
Ответ: 0,92
Задача №2. Фабрика выпускает сумки. В
среднем, на каждые 100 качественных сумок
приходится 8 сумок со скрытыми дефектами. Найдите
вероятность того, что купленная сумка окажется
качественной. (Если необходимо, результат
округлите до сотых).
Решение. Вероятность найдем по формуле: ![]() . В этой задаче, в
. В этой задаче, в
отличие от предыдущей общее количество сумок
складывается из качественных ( 100 штук) и
некачественных (8 штук), т.е. m = 100 + 8 = 108 .
Среди этих 108 сумок, качественных было 100 штук, n
= 100
![]()
Ответ: 0,93
Литература.
- Бунимович Е.А., Булычев В.А. «Вероятность и
статистика» .М «Дрофа». 2002г. - Колмогоров А.Н.и др. Введение в теорию
вероятностей.. М. «Наука» 1982г. - Скопец З.А. «Дополнительные главы по курсу
математики». М. «Просвещение» .1974г. - Чистяков В.П. «Курс теории вероятностей». М.
«Наука» 1982г.
