Ошибка измерения некоторого параметра технической системы является случайной величиной
.pdf
Подпишись на нашего бота Кампус Хаб и получи неограниченный доступ к материалам, а также много полезностей от Кампус и Автор24
Условие
Ошибка измерения некоторого параметра технической системы является случайной величиной, распределенной по нормальному закону со стандартным отклонением σ=1. Какую точность измерения параметра технической системы можно гарантировать с вероятностью 0,9?
Решение
Случайная величина X – ошибка измерения некоторого параметра технической системы.
a – математическое ожидание; σ=1 – стандартное отклонение.
Для нормально распределенной случайной величины X, вероятность
PX-a<δ=2Фδσ
Фx – функция Лапласа (находим по таблице).
Тогда
PX-a<δ=2Фδ1=2Фδ=0,9
2Фδ=0,9
Фδ=0,45
δ=1,65
С вероятностью 0,9 можно гарантировать ошибку измерения в пределах ±1,65.
Ответ: 1,65.
50% задачи недоступно для прочтения
Полное решение в телеграм. Перейди по ссылке и получи решение бесплатно, в формате PDF
23.Учебник издан тиражом 50000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0002. Найти вероятность того, что тираж содержит: а) четыре бракованные книги; б) менее двух бракованных книг.
24.Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0,002. Найти вероятность того, что среди 1000 отобранных деталей окажется: а) 5 бракованных; б) хотя бы одна бракованная.
25.Автоматическая телефонная станция получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно два вызова?
26.Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10?
27.Аппаратура содержит 2000 одинаково надежных элементов, вероятность отказа для каждого из которых равна p = 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов?
28.Сообщение содержит 1000 символов. Вероятность искажения одного символа равна 0,004. Найти среднее число искаженных символов; вероятность того, что будет искажено не более 3–х символов.
29.Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов равно 5000.
30.Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность, что в течение часа позвонят 5 абонентов?
31.Имеется общество из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна 1/365.
ЗАДАНИЕ 17
1.Поезда метро идут равномерно с интервалом 3 минуты. Какова вероятность, что подошедший пассажир будет ожидать ближайший поезд менее полминуты. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
2.Случайная величина равномерно распределена на интервале (1;5). Найти еѐ плотность и функцию распределения. Построить их графики.
3.Автобусы некоторого маршрута следуют строго по расписанию с интервалом 5 минут. Найти вероятность, что подошедший к остановке пассажир
будет ожидать не менее 1 минуты. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
4. Для случайной величины Х , равномерно распределенной на интервале (2;6), найти Р( 2< Х <3) , плотность и функцию распределения.
93
5.Интервал движения трамваев равен 4 мин. Какова вероятность, что подошедший к остановке пассажир будет ожидать вагон не более 2 минут Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
6.Радиус окружности измерен приближенно на интервале (а;b). Полагая, что радиус является случайной величиной Х, равномерно распределенной на этом интервале, найти математическое ожидание и дисперсию длины окружности.
7.Паром для перевозки машин через реку подходит к причалу через каждые
40минут. X – время прибытия машины к причалу. Найти вероятность, что подъехавшая случайным образом автомашина будет ожидать прибытия парома не более 10 мин. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
8.Для случайной величины Х, равномерно распределенной на промежутке (–1;5), математическое ожидание и Р(0 < X < 3).
9.Кабинки фуникулѐра подъезжают к подножию горы через каждые полчаса. Какова вероятность, что подошедшим лыжникам ждать придется менее 5 минут. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
10.Математическое ожидание равномерно распределенной случайной величины Х на интервале (1; b) равно 2. Найти параметр b и D(X).
11.Время ожидания троллейбуса на остановке имеет равномерное распределение на промежутке (0;10) минут. Какова вероятность, что ожидать ближайший троллейбус придется более 8 мин. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
12.Станок – автомат выдает обработанную деталь через каждые 7 минут. Найти вероятность, что подошедший контролѐр будет ожидать готовую деталь менее 30 секунд. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
13.Х – равномерно распределенная случайная величина на интервале (а;5). Дисперсия еѐ равна 1/3 . Найти параметр а и математическое ожидание.
14.Паром для перевозки пассажиров и машин через залив приплывает к причалу через каждые 3 часа. Какова вероятность, что подъехавшая машина попадет на паром менее, чем через полчаса? Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
15.Ребро куба приближенно измерено в интервале (а;b). Найти математическое ожидание и среднее квадратическое отклонение площади повер х- ности куба, если его ребро рассматривать как случайную величину, равномерно распределѐнную на этом интервале.
16.Время ожидания автобуса на остановке имеет равномерное распределение в промежутке (0;20) мин. Найти вероятность ожидания автобуса бо-
94
лее 15 минут. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания.
17.Вычислить математическое ожидание и дисперсию для площади равностороннего треугольника, сторона которого приближенно измерена в интервале (а;b) и равномерно распределена на данном интервале.
18.Цена деления шкалы амперметра 0,1А. Показания округляются до ближайшего целого деления. Найти вероятность, что при измерении будет допущена ошибка, не превышающая 0,03А.
19.Вычислить среднее время ожидания троллейбуса и среднее квадратическое отклонение при условии строгого соблюдения графика движения с интервалом 6 минут.
20.Случайная величина Х равномерно распределена на интервале (3;7). Найти Р(4<X<6 ), плотность и функцию распределения.
21.Цена деления шкалы измерительного прибора равна 0,5. Показания прибора округляются до ближайшего целого деления. Найти вероятность, что при измерении будет допущена ошибка, не превышающая 0,02.
22.Минутная стрелка электронных часов перемещается скачком в конце каждой минуты. Найти вероятность, что в данный момент часы покажут время, которое отличается от истинного не более чем на 10 секунд.
23.Диагональ квадрата приближенно измерена на промежутке (а;b). Найти математическое ожидание и среднее квадратическое отклонение площади квадрата, если считать диагональ случайной величиной, равномерно распределенной на данном промежутке.
24.Найти математическое ожидание и дисперсию случайной величины Х, равномерно распределенной на интервале (8;11).
25.Цена деления штангенциркуля равна 0,1 мм. Показания при измерении округляются до ближайшего целого деления. Найти вероятность, что при измерении детали будет допущена ошибка, превышающая 0,03 мм.
26.Случайная величина Х равномерно распределена на интервале (1;b). Вероятность попадания в интервал (2;5) равна 0,3. Найти параметр b, математическое ожидание и дисперсию.
27.Экспресс курсирует между аэропортом и ж/д вокзалом с интервалом полтора часа. Найти вероятность, что пассажиры, не знающие его расписание, будут ждать ближайший рейс менее 20 минут.
28.Для случайной величины Х, имеющей равномерное распределение на интервале (0,6), найти Р (1 < X < 4), математическое ожидание, дисперсию и среднее квадратическое отклонение.
29.Плотность распределения равномерной случайной величины Х на промежутке (а;11) равна 0,1. Найти параметр а, математическое ожидание и дисперсию.
95
30. Время бегуна на дистанции фиксировалось секундомером с ценой деления 0,1 секунд и оказалось выше мирового рекорда на 0,02 секунды. Какова вероятность, что спортсмен, по крайней мере, повторил рекорд?
ЗАДАНИЕ 18
1. Средний срок службы коробки передач до капитального ремонта у автомобиля определенной марки составляет 56 месяцев со стандартным отклонением σ = 16 месяцев. Привлекая покупателей, производитель хочет дать гарантию на этот узел, обещая сделать ремонт коробки передач нового автомобиля в случае ее поломки до определенного срока. Пусть срок службы коробки передач подчиняется нормальному закону. На сколько месяцев в таком случае производитель должен дать гарантию для этой детали, чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей?
2. X – нормальная случайная величина с математическим ожиданием a = 4. Вероятность попадания X в интервал (3,5; 4,5) равна 0,7. Найти вероятность того, что из трех значений случайной величины X две попадут в интервал (2,5; 3,5).
3. Случайная величина X имеет плотность распределения вероятностей
|
2 |
x 1 2 |
|||||
|
f (x) |
e |
4.,5 . Найдите M(X) – математическое ожидание X, D(X) – |
||||
|
18 |
||||||
дисперсию X, вероятность того, что абсолютная величина отклонения X от математического ожидания не превысит 3.
4. Задана случайная величина X=N(3,1; 0.5) и точки х1 1 и х2 2 , разделяющие числовую ось на три интервала. Найти вероятность того, что случайная величина X принимает значения в этих интервалах
5. Плотность вероятности распределения случайной величины имеет вид
|
1 |
x |
2 2 |
|||||
|
f (x) |
e |
2 |
. Найти вероятность того, что из 4 независимых случайных |
||||
|
2 |
|||||||
величин, распределенных по данному закону, две окажутся на интервале ( ∞; 3).
6.Автоматически изготовленные детали по длине распределены нормально и расположены в интервале от 29,7 до 30,3 см. Какой длины проектировалась деталь, и с каким допуском?
7.Длина изготовляемой детали является нормально распределенной случайной величиной со средним значением a=100 мм и средним квадратическим отклонением =2 мм. Каких деталей окажется в большой партии больше – тех, у кого длина превосходит 103 мм или тех, у кого она заключается в пределах от 101 мм до 102 мм?
8.Коробки с деталями упаковываются автоматически. Их средняя масса равна 900 г. Известно, что 1% коробок имеют массу, большую 1 кг.
96
Каков % коробок, масса которых не превышает 850 г., если вес коробок – случайная величина, распределенная по нормальному закону?
9.Длина заготовок распределена по нормальному закону с математическим ожиданием 1минута и средним квадратическим отклонением 9 мм. Найти вероятность того, что в партии из 10 деталей не будет ни одной детали длиной более 105 см?
10.Диаметр болтов подчиняется нормальному распределению с параметрами M(x)=20, σ=0.1. Найти плотность распределения и количество болтов размером меньше 19,9, если всего болтов 12 штук.
11.Деталь, изготовленная автоматом, считается годной, если отклонение ее фактического размера от проектного не превосходит по абсолютной величине 8 мм. Случайные отклонения фактического размера от проектного подчинены нормальному закону со средним квадратическим отклонением σ=5 мм и математическим ожиданием a=0. Сколько процентов годных деталей изготавливает автомат?
12.Размер детали задан полем допуска 10мм – 12 мм. Оказалось, что средний размер детали равен 11,4 мм, а среднее квадратическое отклонение – 0,7 мм. Считая, что размер детали подчиняется нормальному закону распределения, определить вероятность брака по заниженному и завышенному размеру.
13.Менеджер торгово-посреднической фирмы получает жалобы от некоторых клиентов на то, что служащие фирмы затрачивают слишком много времени на выполнение их заказов. Собрав и проанализировав соответствующую информацию, он выяснил, что среднее время выполнения заказа составляет 6,6 дней, однако, для выполнения 20% заказов потребовалось 15 дней и более. Учитывая, что время выполнения заказа есть случайная величина, распределенная по нормальному закону, определите фактическое стандартное отклонение времени обслуживания клиентов.
14.Ошибка измерения некоторого параметра технической системы является случайной величиной, распределенной по нормальному закону. Если номинальное значение измеряемого параметра равно a, а стандартное отклонение от него равно 2, то какую точность измерения параметра технической системы можно гарантировать с вероятностью 0,8?
15.Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a = 120 мм. Фактическая длина изготовленных деталей не менее 116,5 мм и не более 123,5 мм. Найти вероятность того, что длина наудачу взятой детали меньше 117,2 мм.
16.По данным центрального банка России случайная величина Х – недельная потребность в купюрах достоинством 100 рублей подчиняется закону нормального распределения со средним значением а = 1160 и сред-
97
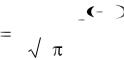
ним квадратичным отклонением σ = 240. Требуется записать функцию плотности вероятности и построить ее график.
17. Размер диаметров втулок, изготовленных цехом, можно считать нормально распределенной случайной величиной со средним 2,5 см и дисперсией 0,0001 см2. Какое следует установить поле допуска относительно номинального диаметра, чтобы брак составлял 1%?
18. Параметр X детали распределѐн нормально с m = 2, равным номиналу. Каким должно быть σ, чтобы с вероятностью 0,9 отклонение X по модулю не превышало 1% номинала?
19. Плотность вероятности нормально распределенной случайной величи-
|
1 |
x 14 2 |
||||||
|
ны Х имеет вид |
f (x) |
e |
32 |
. В каком промежутке она с большей |
|||
|
4 |
2 |
вероятностью принимает значения (6; 
или (18; 20)?
20.В результате поверки амперметра установлено, что 70% погрешностей результатов измерений, произведенных с его помощью, не превосходит ± 20 %. Считая, что погрешности распределены по нормальному закону с нулевым математическим ожиданием, определить среднеквадратическую погрешность.
21.Браковка шаров для подшипников производится следующим образом:
если шарик не проходит через отверстия d1 =5,9 мм, но проходит через отверстие d 2 =6,1 мм, то его размер считается приемлемым. Если какое–нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика есть нормально распределенная случайная величина X и M(X)=6 мм, D(X)=0.0025 мм2. Какова вероятность, что шарик забракован?
22.Изделия, выпускаемые цехом, по своим линейным размерам распределяются по нормальному закону с математическим ожиданием, равным 6 см. Известна вероятность, равная 0,9758, что наудачу взятое изделие будет иметь размеры в границах от 5,95см до 6,05 см. Найти дисперсию этой случайной величины.
23.Валик, изготовленный автоматом, считается стандартным, если отклонение его диаметра от проектного размера не превышает 2 мм. Случайные отклонения диаметров валиков подчиняются нормальному закону со средним квадратичным отклонением 1,6 мм и математическим ожиданием, равным 0. Сколько стандартных валиков (в процентах) изготавливает автомат?
24.Еженедельный выпуск продукции на заводе распределен по нормальному закону. Известно, что вероятность того, что еженедельный выпуск продукции превысит 150000 ед. равна 0,221, а вероятность того, что он окажется ниже 100000 ед. равна 0,0038. Определите, сколько в среднем единиц продукции в неделю выпускает завод.
98
25.Диаметр электродвигателя есть нормально распределенная случайная величина с параметрами а = 100 мм и σ = 1.6 мм. Найти вероятность того, что диаметр случайно взятого электродвигателя находится в интервале (98, 101).
26.Случайные ошибки измерения детали подчинены нормальному закону с параметром = 20 мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
27.Пусть X – случайная величина, подчиненная нормальному закону с математическим ожиданием а = 16 и средним квадратическим отклонением
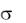1. Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2)?
28.Пусть диаметр изготовляемой в цехе детали является случайной величиной,
распределенной по нормальному закону с параметрами а = 4,5 см, = 0, 05см. Найти вероятность того, что размер диаметра взятой наудачу детали отличается от математического ожидания не более чем на 1 мм.
29.Цех изготовляет детали, длины которых представляют собой случайную величину X, распределенную по нормальному закону. Математическое ожидание и среднее квадратическое отклонение величины X соответственно равны
15см и 0,1 см. Найти вероятность того, что отклонение длины детали в ту или другую сторону от математического ожидания не превзойдет 0,25 см.
30.Автомат изготавливает шарики. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине
меньше 0,7 мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением = 0,4мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.
ЗАДАНИЕ 19
1. Найти при каких значениях А функция является функцией плотности
|
распределения. Найти M 0 , M x , Dx , As , Ex (указать их при b |
2, 1) . |
|
x Ax 2b 3e x 0, b 1 . |
|
|
2. Для геометрического распределения P m 1 p m p, m |
0,1, 2…Найти |
M x , Dx , As , Ex (указать их при p 0,5) .
3. Найти при каких значениях А функция является функцией плотности
|
распределения. Найти M 0 , M x , Dx , As , Ex (указать их при |
1) . |
|
x2 |
x
Axe 2 2 .
4. Найти при каких значениях А функция является функцией плотности
|
распределения |
случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
|
(указать их при |
0,5) . |
99
|
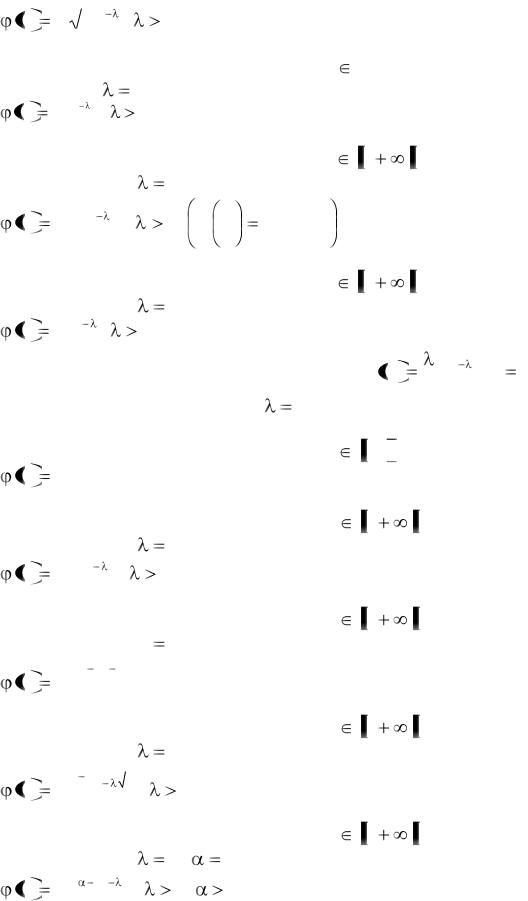
x |
A |
x e x , |
0. |
||||||||||||
|
5. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения |
случайной величины x |
R . Найти M 0 , M x , Dx , As , Ex (ука- |
|||||||||||||
|
зать их при |
1). |
||||||||||||||
|
x |
A e |
x |
, |
0 |
|||||||||||
|
6. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения |
случайной величины x |
0, |
. Найти M 0 , M x , Dx , As , Ex |
||||||||||||
|
(указать их при |
|
||||||||||||||
|
x |
Ax 2e x2 , |
0, Г |
1 |
2,68014 . |
|||||||||||
|
3 |
|||||||||||||||
|
7. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения |
случайной величины x |
0, |
. Найти M 0 , M x , Dx , As , Ex |
||||||||||||
|
(указать их при |
1). |
||||||||||||||
|
x |
A e |
х , |
0. |
||||||||||||
|
m |
|||||||||||||||
|
8. |
Для |
распределения |
Пуассона |
P m |
e , m 0,1, 2,… Найти |
||||||||||
|
m! |
|||||||||||||||
|
M x , Dx , As , Ex (указать их при |
2 ). |
||||||||||||||
|
9. |
Найти при каких значениях А функция является функцией плотности |
||||||||||||||
|
распределения случайной величины x |
1; 3 . Найти M 0 , M x , Dx , As , Ex |
xc.
10.Найти при каких значениях А функция является функцией плотности
|
распределения |
случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
||
|
(указать их при |
1). |
|||
|
3 |
x 2 |
, |
0. |
|
|
x Ax e |
11. Найти при каких значениях А функция является функцией плотности
|
распределения случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
|||
|
(указать их при n 4). |
||||
|
n |
1 |
x |
||
|
x Ax 2 |
e 2 . |
12. Найти при каких значениях А функция является функцией плотности
|
распределения случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
||||
|
(указать их при |
4). |
||||
|
1 |
|||||
|
e 3 x2 , |
|||||
|
x Ax |
3 |
0. |
13. Найти при каких значениях А функция является функцией плотности
|
распределения |
случайной величины x 0, |
. Найти M 0 , M x , Dx , As , Ex |
||
|
(указать их при |
2, |
0,5). |
||
|
1 x2 |
, |
0, |
0. |
|
|
x Ax e |
100
14. Найти при каких значениях А функция является функцией плотности
|
распределения случайной величины x |
0, |
. Найти M 0 , M x , Dx , As , Ex |
|||||||||
|
(указать их при |
2 ). |
||||||||||
|
x2 |
|||||||||||
|
x Ax2e 2 |
2 . |
||||||||||
|
15. Для биномиального закона распределения P m |
C m pmqn m , m 0,1, 2,…, n |
||||||||||
|
n |
n |
||||||||||
|
Найти M |
, D |
, A , E |
(Указать их при p |
1 |
, n |
100 ). |
|||||
|
x |
x |
||||||||||
|
x |
s |
2 |
|||||||||
ЗАДАНИЕ 20
Варианты 1 – 10
Оценить вероятность того, что частота некоторого события А отклонится от его вероятности р в каждом испытании из серии n независимых испытаний по абсолютной величине не более чем на 0,01.
|
1. |
p = |
1 |
; n = 7500. |
2. |
p |
1 |
; n 9000. |
||
|
3 |
|||||||||
|
3 |
|||||||||
|
3. |
p = |
1 |
; n = 9500. |
4. |
p = |
1 |
; n = 10000. |
||
|
3 |
3 |
||||||||
|
5. |
p = |
1 |
; n = 6000. |
6. |
p = |
1 |
; n = 8000. |
||
|
3 |
4 |
||||||||
|
7. |
p = |
1 |
; n = 2000. |
8. |
p = |
1 |
; n = 1500. |
||
|
4 |
4 |
||||||||
|
p = |
1 |
; n = 1500. |
1 |
||||||
|
9. |
10. p = |
; n = 2500. |
|||||||
|
6 |
5 |
Варианты 11 – 20
Вероятность некоторого события А в каждом испытании из серии n независимых испытаний равна р. Найти наименьшее число испытаний так, чтобы с вероятностью не меньшей 0,99 частота события А отклонялась по абсолютной величине от его вероятности р не более, чем на .
|
11. |
p = |
1 |
; |
= 0,01. |
12. |
p = |
1 |
; |
= 0,02. |
|
3 |
4 |
||||||||
|
13. |
p = |
1 |
; |
= 0,03. |
14. |
p = |
1 |
; |
= 0,04. |
|
5 |
6 |
||||||||
|
15. |
p = |
2 |
; |
= 0,01. |
16. |
p = |
2 |
; |
= 0,02. |
|
3 |
5 |
||||||||
|
17. |
p = |
1 |
; |
= 0,03. |
18. |
p = |
4 |
; |
= 0,04. |
|
2 |
7 |
101
|
19. p = |
3 |
; = 0,01. |
20. p = |
4 |
; = 0,02. |
|
8 |
9 |
Варианты 21 – 30
Вероятность некоторого события А в каждом испытании из серии n независимых испытаний равна р. Найти границу абсолютной величины отклонения частоты события А от его вероятности р, которую можно ожидать с вероятностью 0,99, произведя n испытаний.
|
21. |
p = |
1 |
; n = 12100. |
22. |
p = |
1 |
; n = 13200. |
|
3 |
3 |
||||||
|
23. |
p = |
1 |
; n = 14300. |
24. |
p = |
1 |
; n = 15100. |
|
3 |
3 |
||||||
|
25. |
p = |
1 |
; n = 16200. |
26. |
p = |
1 |
; n = 17200. |
|
3 |
3 |
||||||
|
27. |
p = |
1 |
; n = 18100. |
28. |
p = |
1 |
; n = 19200. |
|
3 |
3 |
||||||
|
29. |
p = |
1 |
; n = 20100. |
30. |
p = |
1 |
; n = 21200. |
|
3 |
3 |
ЗАДАНИЕ 21
Варианты 1 ÷ 15
За значение некоторой величины принимают среднее арифметическое достаточно большого числа еѐ измерений. Предполагая, что среднее квадратическое отклонение σ возможных результатов каждого измерения не превосходит α см, оценить вероятность того, что при n измерениях неизвестной, величина отклонений принятого значения от истинного по абсо-
|
лютной величине не превзойдет ε см. |
|||
|
1. |
α = 1 , n = 2000 , ε = 0,001. |
2. |
α = 1,2, n = 2500, ε = 0,01. |
|
3. |
α = 1,4, n = 3000, ε = 0,001. |
4. |
α = 1,6, n = 3500, ε = 0,01. |
|
5. |
α = 1,8, n = 4000, ε = 0,001. |
6. |
α = 1, n = 4500, ε = 0,01. |
|
7. |
α = 1,1, n = 5000, ε = 0,001. |
8. |
α = 1,3, n = 5500, ε = 0,01. |
|
9. |
α = 1,5, n = 6000, ε = 0,001. |
10. |
α = 1,7, n = 6500, ε = 0,01. |
|
11. |
α = 1,9, n = 7000, ε = 0,001. |
12. |
α = 1,2, n = 7500, ε = 0,01. |
|
13. |
α = 1,4, n = 8000, ε = 0,001. |
14. |
α = 1,5 , n = 8500, ε = 0,01. |
15.α = 1,6, n = 9000, ε = 0,001.
Варианты 16 ÷ 30
Дана последовательность независимых случайных величин Х1, Х2, Хn, для каждой из которых задан закон распределения, Применим ли к этой последовательности закон больших чисел?
102
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
50,00 ₽
Ссылка на скачивание будет доступна сразу после оплаты
-
Описание
Описание
Ошибка измерения некоторого параметра технической системы является случайной величиной, распределенной по нормальному закону. Если номинальное значение измеряемого параметра равно a, а стандартное отклонение от него равно 2, то какую точность измерения параметра технической системы можно гарантировать с вероятностью 0,8?
Похожие товары
-
##10072015959 Трое гостей повесили в коридоре три свои шляпы. Внезапно по
50,00 ₽
В корзину -
##10072015954 Каждый из пяти студентов, пользующихся транспортом, с равно
50,00 ₽
В корзину -
##10072015103 Из 15 конденсаторов (6 по 10 пф, 5 по 20, 4 по 30) наугад в
50,00 ₽
В корзину -
##10072015141 Из ящика, содержащего жетоны с номерами от 1 до 40, участни
50,00 ₽
В корзину
В технике приходится иметь дело со случайными событиями и связанными с ними случайными величинами. Например получение размера детали в заданных границах — случайное событие отклонения размера сделанной детали от номинала, ошибки измерения — случайные величины. [c.321]
ПРИМЕНЕНИЕ ТЕОРИИ СЛУЧАЙНЫХ ЯВЛЕНИЙ К ОШИБКАМ ИЗМЕРЕНИЯ [c.47]
Необходимость исследования в первом случае объясняется тем, что при измерении каждой отдельной детали в двух и более сечениях вся или некоторая часть погрешности может проявляться в виде систематической ошибки. Соотношение случайной и систематической составляющих суммарной погрешности измерений зависит от характера применяемых средств и методов измерений. Весьма важным представляется вопрос о зависимости погрешностей разбраковки деталей от законов распределения предельных размеров деталей. [c.157]
Ошибки измерений бывают систематические и случайные. Систематические ошибки большей частью зависят от неправильных показаний применяемых приборов и других средств измерения, от неправильных или различных методов измерений, от постоянного, но одностороннего внешнего воздействия. При производстве измерений систематические ошибки должны быть устранены. Это достигается в результате тщательного изучения и проверки применяемых измерительных средств и введения, если необходимо, соответствующих поправок в результате измерений. [c.66]
Случайные ошибки вызываются главным образом той неточностью, которая всегда имеет место при наблюдении показаний приборов и их отсчетов. Подобные ошибки не имеют какой-либо постоянной закономерности, так как при каждом измерении одинаково возможны случайные ошибки как в сторону увеличения измеряемой величины, так и в сторону ее уменьшения. Вследствие этого к случайным ошибкам следует применять законы, установленные теорией вероятностей по отношению к многократному повторению так называемых случайных явлений. Исключить при измерениях случайные ошибки, конечно, невозможно. Теория вероятностей разработала математические приемы, которые позволяют уменьшить влияние случайных ошибок на окончательное значение показателя, включаемого в стандарт. Здесь характерны два случая. [c.66]
Передаточные функции всех звеньев исследуемой системы даны на рис. I. Внешнее возмущение для системы аппроксимировано случайной стационарной функцией. Корреляционная функция как внешнего возмущения, так и ошибки измерения рассогласования регулируемого параметра принята экспоненциальной [51. [c.360]
Примеры случайных величин отклонение размера изготовленной детали от номинала число бракованных деталей в партии число вызовов в единицу времени на коммутаторе число попаданий в цель из серии выстрелов отклонение точки попадания от центра цели ошибки измерений. [c.279]
Простым следствием из теоремы Чебышева является принятие среднего арифметического значения из большого ряда наблюдений одной случайной величины за среднее значение (математическое ожидание) этой величины. Если случайной величиной являются ошибки измерений, наблюдений и т. д.. то среднее арифметическое значение многократно измеренной величины принимается за её истинное значение. [c.290]
Ошибки, являющиеся систематическими в одной задаче, могут оказаться случайными в другой. Например, инструментальная погрешность конкретного экземпляра измерительного прибора является систематической ошибкой для всех выполняемых с ним измерений. При характеристике же точности метода измерения или производственной точности изготовления партии таких приборов эта же ошибка является случайной. [c.300]
Первая задача. Определяемая величина X постоянная, не случайная. Ошибки измерения пренебрежимо малы по сравнению со значением определяемой величины. [c.301]
Вторая задача. Определяемая величина Л постоянная, не случайная. Ошибки измерений имеют существенное значение и поэтому для учёта их влияния производится многократное измерение величины. Здесь могут встретиться два случая равноточные и неравноточные измерения. [c.302]
Четвёртая задача. Определяемая величина X случайная. Ошибки измерения имеют существенное значение, т. е. не пренебрежимо малы сравнительно с рассеянием самой величины X. [c.309]
В условиях восьмой задачи ошибки измерений могут привести к случайным сочетаниям значений определяемой величины, могущим дать ошибочный или ненадёжный ответ на поставленный выше вопрос. [c.314]
Девятая задача. Из опыта получен ряд значений двух случайных величин х и у. Ошибки измерений этих значений пренебрежимо малы по сравнению с рассеиванием определяемых величая. Совокупность полученных из опыта значений называется эмпирическим распределением. [c.315]
В числителе выражения для ошибки среднего арифметического стоит стандарт распределения наблюдаемой (измеряемой) величины Ох, который включает в себя как случайную ошибку измерений, так и рассеяние объекта. При этом в подавляющем большинстве промышленных экспериментов рассеяние объекта, т. е. его нестабильность во время опыта, намного превышает случайную ошибку измерений. Отсюда следует, что мощным средством повышения точности, по своей природе совершенно равноценным числу замеров, является уменьшение рассеяния объекта, достигаемое путем стабилизации режима собственно парогенератора и защиты его от внешних возмущений. [c.73]
Остановимся на указанном вопросе несколько подробнее. Допустим, что исследуется зависимость сопротивления от расхода. Так как расход и сопротивление измеряются разными приборами, имеющими каждый свои случайные ошибки, полученные величины не будут истинными. Можно, однако, полагать, что каждое единичное значение расхода Xi является истинным, а случайно, т. е. имеет ошибку, только сопротивление. Если бы сопротивление не зависело от расхода, подобное допущение не привело бы нас к ошибке, так как безразлично, к какому значению расхода отнесено данное сопротивление. Поскольку, однако, такая зависимость есть, ошибка измерения расхода х приведет к появлению дополнительной ошибки величины сопротивления [c.89]
Примеры непрерывных случайных величин отклонение размера изготовленной детали от номинала, величина ошибки измерения (одномерные величины) отклонение центра обтачиваемой на токарном станке детали от центра базовой цилиндрической поверхности (двухмерная величина) отклонение положения инструмента относительно детали в процессе ее точения от установленного при настройке (трехмерная величина). [c.22]
Случайные ошибки измерений вызываются многочисленными факторами, малыми по своему индивидуальному влиянию на результат и не могущими быть учтенными при проведении опыта. Наличие случайных ошибок измерения проявляется при многократных повторных измерениях одной и той же неслучайной величины в том, что результаты измерения оказываются различными. Рассеяние результатов измерения обычно подчиняется закону Гаусса. [c.211]
Вторая задача. Определяемая величина X — постоянная, не случайная. Ошибки измерений имеют существенное значение, и поэтому для учета их и уменьшения влияния производится многократное измерение величины. [c.213]
Третья задача. Определяемая величина X — случайная (например, отклонение размера детали в партии от номинала). Ошибки измерения пренебрежимо малы по сравнению со значением определяемой величины и ее рассеянием. [c.215]
Следует напомнить, что абсолютная ошибка измерения температуры Ai определяется не только точностью приборов, примененных для измерения температуры, но и включает случайные ошибки измерения температуры, обусловленные, в частности, неравновесностью наблюдаемого состояния. Применительно к данной экспериментальной установке это означает, что величина М зависит от того, насколько точно температура гильзы, где расположена термопара, близка к температуре поверхности жидкости. [c.144]
Аро и Мо — абсолютные ошибки измерения параметров опорного состояния, обусловленные как систематическими погрешностями измерительных приборов, так и случайными погрешностями измерения, вызванными главным образом отсутствием равновесного состояния. [c.168]
Из уравнения (6-21) видно, что, если значение удельного объема V определяется как среднее для нескольких состояний, то точность его повышается, так как уменьшаются случайные ошибки измерения параметров. Однако погрешность определения v всегда больше, чем погрешность исходных табличных значений удельного объема. Следует заметить, что, строго говоря, значения удельного объема, соответствующие различным экспериментальным точкам, несколько отличаются друг от друга. Учет соответствующей поправки к значению удельного объема подробно описан ниже. [c.168]
Абсолютная величина случайной ошибки измерения теплоемкости может быть вычислена по формуле (4-16) [c.236]
Следует подчеркнуть, что то.в и представляют собой количества охлаждающей воды и конденсата, собранные за один и тот же промежуток времени, и поэтому для уменьшения случайной ошибки измерений начало и конец их сбора должны быть синхронизированы. 55(Сно, что ошибка, вызываемая несовпадением этих моментов, тем меньше, чем дольше длится опыт. [c.248]
Случайная ошибка измерения разности температур t»—t вызывается колебаниями этих температур во время опыта из-за непостоянства расходов охлаждающей воды и пара через установку. Эту ошибку можно уменьшить, если запись показаний термометров производить через возможно более короткие и равные промежутки времени и использовать усредненные за время опыта значения температур. [c.248]
Случайные ошибки измерения этих параметров зависят от колебания режима во время опыта для снижения ИХ следует запись показаний приборов производить [c.249]
Стандарт о распределения измеряемой величины х включает в себя как случайную ошибку измерения, так и нестабильность параметров объекта, причем эта нестабильность может намного превышать ошибку измерения. Из этого следует, что точность измерений, особенно в промышленных условиях, может быть повышена путем стабилизации параметров исследуемого объекта. [c.30]
Значительные случайные ошибки измерений легко обнаружиВЗ» ются при графическом изображении опытных данных как отклонения от гладкой кривой, например при построении графиков зависимости состав пара — состав жидкости x =f x), общее давление пара — состав жидкой или газовой фазы P=P( xi ), P=P( xi ). [c.101]
Величина ошибки измерения Д5 а является случайной и может быть существенно уменьшена многократным повторением измерений, поэтому при экспериментальном методе определения ошибки механизма величина ее в каждом положении должна определяться как среднее значение многократных измерений. В этом случае ошибка механизма будет в основном состоять из ошибок ЛЗсх и А5 . Если ошибку механизма определять для групп механизмов, вычисляя ее как среднюю средних значений ошибок каждого из механизмов в заданном положении, то найденная ошибка будет ошибкой схемы А5сх. так как среднее значение технологических ошибок А5 для группы механизмов будет близким к нулю. [c.118]
Точность определения действующих в образце напряжений зависит от величины ошибки измерения деформации пружины нагружения при тарировке и в процессе испытания, а -также от случайных отклонений диаметра образца и плеча прилагаемой нагрузки. Для повышения точности измерений статического усилия узел силонагружения выполняется так, что максимальной нагрузке соответствует деформация пружины, приблизительно равная 20 мм. В связи с тем что образцы могут быть изготовлены из материалов различной прочности, такая жесткость пружины должна обеспечиваться путем расчета или подбора, поэтому конструкцией узла предусмотрена возможность простой ее замены. [c.75]
Повышение точности измерения и увеличение быстродействия приборов, использующих радиоактивное излучение, связано, как известно, со значительным увеличением активности источников излучения [1]. Улучшение может быть достигнуто повышением эффективности регистрации радиоактивного излучения. С этой точки зрения целесообразно использовать сциитилляционные счетчики. Однако стремление применить такие счетчики в точных приборах встречает значительные трудности, связанные главным образом с сильной зависимостью коэффициента усиления фотоэлектронного умножителя от напряжения питания, а таюке с утомлением фотоумножителя и нестабильностью коэффициента усиления радиотехнических устройств. Поэтому представляет интерес разработка методов, позволяющих снизить ошибки измерения контролируемой величины, возникающие из-за случайных изменений параметров фотоэлектронного умножителя. [c.127]
Случайные ошибки измерений вызываются многочисленными факторами, малыми по своему индивидуальному влиянию на результат и не могущими быть учтёнными при проведении опыта. Наличие случайных ошибок измерения обнаруживается при многократных повторных измерениях одной и той же неслучайной величины в том, что результаты измерения оказываются различньши. Рассеяние результатов измерения обычно подчиняется закону Гаусса (см. Сведения из теории вероятностей» о теореме Ляпунова и об условиях возникновения распределений по закону Гаусса). [c.301]
В условиях эксплуатации автотолераторы работают в динамическом режиме. Поэтому наряду с проверкой метрологических характеристик в статических условиях для автотолераторов обязательна проверка их динамических характеристик. При этом главными динамическими характеристиками автотолератора следует считать амплитудно-частотную характеристику точности и время срабатывания. При проверке следует установить не только математическое ожидание погрешности, но и их случайные составляющие. Средняя арифметическая величина погрешности, ее математическое ожидание важны как для определения возможной ошибки измерения, так и для внесения динамической поправки, а случайная составляющая будет оказывать влияние па рассеи- [c.117]
Разделить случайные ошибки собственно измерений и случайные флуктуации исследуемого параметра не представляется возможным. Так как, однако, случайные погрешности приборов известны, всегда можно оценить долю их, падаюш,ую на колебания параметра. Так, например, если колебания разрежения составляют 10 Kz jM , их следует отнести за счет процесса, поскольку случайная ошибка измерений жидкостным дифмано-метром составляет всего 1—2 кгс1м . [c.50]
Ошибки измерения, наблюдения и т. д., присуш,ие проводимому опыту, разделяются на систематические и случайные. [c.211]
c.247
]
Теплотехнический справочник том 2 издание 2 (1976) — [
c.247
]