Условие
![]()
4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением сигма =1 мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм.
Отв. 0,96.
математика ВУЗ
11140
Решение
![]()
★
Пусть случайная величина Х — ошибка измерения.
Так как вероятность отклонения нормально распределенной случайной величины Х от ее математического ожидания а по абсолютной величине меньше заданного положительного числа ε вычисляется по формуле:
P(|X-a| < ε) =2Ф(ε/σ)
и
по условию
σ=1
a=0
ε=1,28
ε/σ=1,28
Ф(1,28/1)=Ф(1,28)=0,3997 ( см. приложение),
то
вероятность ошибки в одном наблюдении
2Ф(ε/σ)=2*Ф(1,28)=2*0,3997=0,7994
p=0,7994
Найдем вероятность противоположного события:, что ошибка превзойдет 1,28 мм
q=1 — p =1 — 0,7994 = 0,2006
Вероятность того, что ошибка превзойдет 1,28 в двух испытаниях
q*q=q^2=0,2006^2≈0,04
Тогда вероятность того, что из двух независимых испытаний ошибка [b] хотя бы в одном из них [/b] не превзойдет 1,28
равна
1-q^2=1-0,2006^2≈1-0,04=0,96
О т в е т. 0,96
Написать комментарий
Условие
![]()
4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением сигма =1 мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм.
Отв. 0,96.
математика ВУЗ
10140
Решение
![]()
★
Пусть случайная величина Х — ошибка измерения.
Так как вероятность отклонения нормально распределенной случайной величины Х от ее математического ожидания а по абсолютной величине меньше заданного положительного числа ε вычисляется по формуле:
P(|X-a| < ε) =2Ф(ε/σ)
и
по условию
σ=1
a=0
ε=1,28
ε/σ=1,28
Ф(1,28/1)=Ф(1,28)=0,3997 ( см. приложение),
то
вероятность ошибки в одном наблюдении
2Ф(ε/σ)=2*Ф(1,28)=2*0,3997=0,7994
p=0,7994
Найдем вероятность противоположного события:, что ошибка превзойдет 1,28 мм
q=1 — p =1 — 0,7994 = 0,2006
Вероятность того, что ошибка превзойдет 1,28 в двух испытаниях
q*q=q^2=0,2006^2≈0,04
Тогда вероятность того, что из двух независимых испытаний ошибка [b] хотя бы в одном из них [/b] не превзойдет 1,28
равна
1-q^2=1-0,2006^2≈1-0,04=0,96
О т в е т. 0,96
Написать комментарий
Нормальным
называют распределение вероятностей
непрерывной случайной величины X,
плотность которого имеет вид
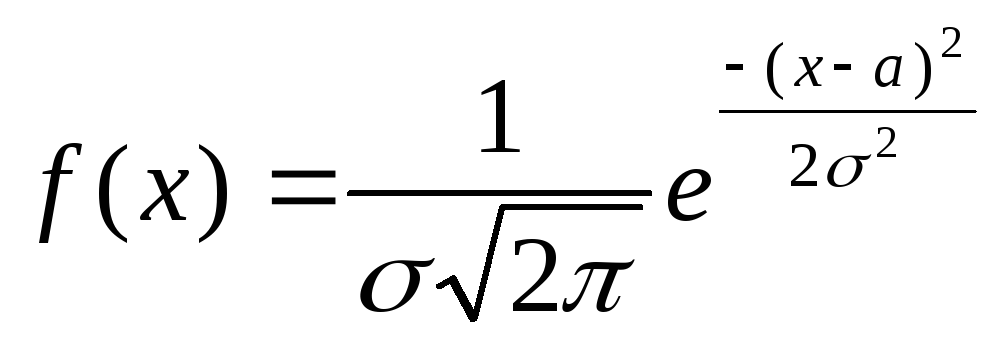 ,
,
где
a-математическое
ожидание,![]() — среднее квадратичное отклонение X.
— среднее квадратичное отклонение X.
Вероятность того, что Х примет значение,
принадлежащее интервалу (α,β):
![]() ,
,
где
![]() — функция Лапласа.
— функция Лапласа.
Пример
99.Математическое ожидание и среднее
квадратическое отклонение нормально
распределенной случайной величины Х
примет значение: а) в интервале (-1,2); б)
меньше -1; в) больше 2; г) отличающееся от
своего среднего значения по абсолютной
величине не больше, чем на 1.
Решение.По условию задачи a=0, σ=2, тогда:
а)

б)
![]()
в)
![]()
г)
![]()
Здесь
значения функции Φ(x) были найдены по
таблице и учитывалось, что Φ(-x) = -Φ(x), а
![]() .
.
100.
Плотность распределения ошибки выходного
параметра РЭА имеет вид
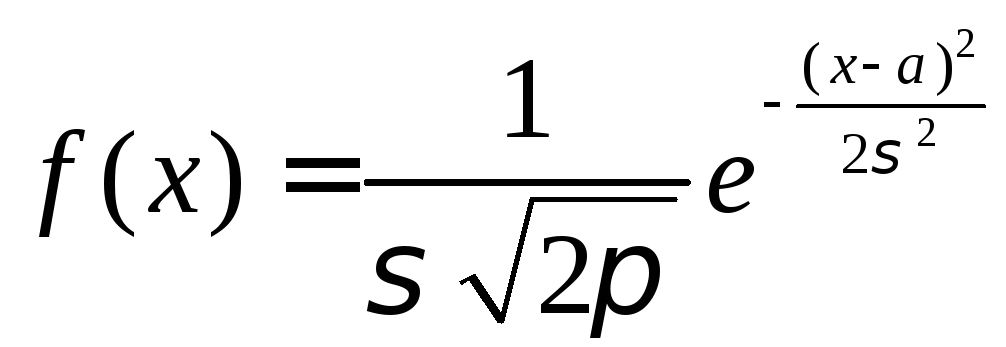 .
.
Сборочные
операции изменяют числовые характеристики
распределения, не изменяя закона. Что
больше увеличивает вероятность появления
брака: систематическое смещение значения
ошибки выходного параметра на а
единиц или увеличение
дисперсии ошибки на эти же а
единиц?
101.
Математическое ожидание и дисперсия
случайного напряжения с нормальным
распределением равны 10 В и 25 В2
соответственно. Какова вероятность
того, что измеренное значение напряжения
а) будет больше
0?
б) будет находиться
в интервале от 0 до математического
ожидания?
в) будет в два раза
больше математического ожидания?
102.
Широко распространенный метод обнаружения
сигнала в присутствии шума заключается
в установлении определенного порогового
уровня, с которым производится
сравнение результатов измерения
напряжения, включающего полезный сигнал
и шум. Если установленный порог
превышается, то считают, что полезный
сигнал присутствует. Естественно, иногда
и при отсутствии сигнала шум превосходит
этот порог, и такая ситуация называется
ложной тревогой.
Желательно, чтобы
вероятность ложной тревоги была ничтожно
мала. В то же время необходимо, чтобы
результат любого измерения, проведенного
при наличии сигнала, смешанного с шумом,
с большой вероятностью превосходил
установленный порог. Она называется
вероятностью правильного
обнаружения и должна
как можно меньше отличаться от 1.
Пусть шум характеризуется
нормальным распределением с нулевым
математическим ожиданием и дисперсией
1В2,
а установленный порог равен 5 В.
а) Определите
вероятность ложной тревоги.
б) Определите
вероятность правильного обнаружения
сигнала величиной 8 В в присутствии шума
с заданными выше параметрами.
103.
Математическое ожидание и среднее
вадратическое отклонение нормально
распределенной случайной величины X
соответственно равны 20 и 5. Найти
вероятность того, что в результате
испытания X примет значение, заключенное
в интервале (15, 25).
104.
Производится взвешивание некоторого
вещества без систематических ошибок.
Случайные ошибки взвешивания подчинены
нормальному закону со средним
квадратическим отклонением σ = 20 г. Найти
вероятность того, что взвешивание будет
произведено с ошибкой, не превосходящей
по абсолютной величине 10 г.
105. Случайные ошибки
измерения подчинены нормальному закону
со средним квадратическим отклонением
σ = 20 мм и математическим ожиданием а =
0. Найти вероятность того, что из трех
независимых измерений ошибка хотя бы
одного не превзойдет по абсолютной
величине 4 мм.
106.
Вывести «правило трех сигм»: вероятность
того, что абсолютная величина отклонения
нормально распределенной случайной
величины будет меньше утроенного
среднего квадратического отклонения,
равна 0,9973. 107. Станок-автомат изготовляет
валики, причем контролируется их диаметр
X. Считая, что X—нормально распределенная
случайная величина с математическим
ожиданием а=10мм и средним квадратическим
отклонением σ = 0,1 мм, найти интервал,
симметричный относительно математического
ожидания, в котором с вероятностью
0,9973 будут заключены диаметры изготовленных
валиков.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
 |
 |
Теория вероятностей |
 |
 |
Решение задачи |
 |
 |
18 февраля 2021 |
 |
 |
Выполнен, номер заказа №16373 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
225 руб. |
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!
Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):
Случайные ошибки измерения подчинены нормальному закону со средним квадратичным отклонением 𝜎 = 20 мм и математическим ожиданием 𝑎 = 0. Найдите вероятность того, что из трех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 4 мм.
Решение
Вероятность того, что модуль отклонения случайной величины Х от своего математического ожидания 𝑎 меньше любого положительного 𝜀, равна где Ф(𝑥) – функция Лапласа. По условию тогда, вероятность того, что при одном независимом измерений ошибка измерения не превзойдет по абсолютной величине 4 мм, равна: Воспользуемся формулой Бернулли. Если производится 𝑛 независимых испытаний, при каждом из которых вероятность осуществления события 𝐴 постоянна и равна 𝑝, а вероятность противоположного события равна , то вероятность того, что при этом событие 𝐴 осуществляется ровно 𝑚 раз, вычисляется по формуле где 𝐶𝑛 𝑚 — число сочетаний из 𝑛 элементов по 𝑚. Для данного случая Вероятность события 𝐴 – из трех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 4 мм, равна: Ответ:

Похожие готовые решения по теории вероятности:
- Пачки чая упаковываются автоматически. Масса одной пачки чая распределена по нормальному закону со средним
- Диаметр детали – случайная величина, подчиненная нормальному закону с 𝑎 = 5 см и 𝜎 = 0,9 см. Найти вероятность
- Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 20 г. Найти вероятность того
- Ошибка измерения подчинена нормальному закону с математическим ожиданием, равным 1, и дисперсией, равной 4. Определить вероятность
- Определить вероятность того, что случайная ошибка измерения ∆ не превзойдет по абсолютной величине удвоенное значение
- Диаметр выпускаемых деталей имеет нормальное распределение со стандартным значением М(Х) и средним квадратическим
- Деталь, изготовленная автоматом, считается бракованной, если отклонение ее контролируемого размера Х от номинала превышает
- Ошибка взвешивания – случайная величина, распределенная по нормальному закону с математическим ожиданием, равным нулю
- Дана выборка 1 1 3 5 4 3 2 1 1 6 3 4 4 5 0 7 5 3 0 4 Составить статистический ряд частот, статистический ряд
- Дана выборка 1 3 3 1 4 1 2 3 1 5 3 4 4 5 2 6 2 3 3 4 Составить статистический ряд частот, статистический ряд
- Дана выборка 2 3 3 5 4 2 2 1 4 6 1 4 4 5 2 7 5 5 7 2 Составить статистический ряд частот, статистический ряд
- Дана выборка -2 3 3 5 4 -1 2 -1 1 0 3 4 4 0 2 7 5 3 3 0 Составить статистический ряд частот, статистический ряд
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.
поделиться знаниями или
запомнить страничку
- Все категории
- экономические
43,607 - гуманитарные
33,643 - юридические
17,916 - школьный раздел
611,340 - разное
16,895
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
2. Пусть [math]X[/math]— ошибка измерения, [math]sigma = 10[/math] – среднеквадратичное отклонение. Тогда вероятность того, что ошибка измерения не превзойдёт 2, равна
[math]p = Pleft( {left| X right| < 2} right) = Pleft( {left| {frac{X}{sigma }} right| < frac{2}{sigma }} right) = Phi left( {0.2} right) — Phi left( { — 0.2} right) = 2 cdot Phi left( {0.2} right) — 1 = 2 cdot 0.57926 — 1 = 0.15852[/math]
Вероятность противоположного события равна [math]q = 1 — p = 0.84148[/math]
Следовательно, вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 2, равна
[math]1 — q^3 = 0.404158[/math]
Отмечу, что здесь функция Лапласа [math]Phi left( x right)[/math] отличается от функции, которую использовал Alexdemath
3. Пусть [math]T[/math] – время службы мотора. Далее есть два пути решения этой задачи.
а) Предположим, что эта случайная величина имеет показательный закон распределения (этот закон часто используют для величин такого типа). Тогда параметр этого закона равен [math]lambda = 1/8[/math] и вероятность того, что данный мотор не прослужит 15 лет, равна
[math]Pleft( {X < 15} right) = intlimits_0^{15} {lambda cdot e^{ — lambda x} dx} = 1 — e^{ — 15lambda } = 0.846645[/math]
б) Пусть закон распределения случайной величины [math]T[/math] неизвестен. Обозначим через [math]pleft( t right)[/math] – плотность распределения этого закон. Тогда, используя приём из доказательства неравенства Чебышёва, получим
[math]Pleft( {X < 15} right) = 1 — Pleft( {X > 15} right) = 1 — intlimits_{15}^infty {pleft( t right)dt} = 1 — intlimits_{15}^infty {frac{t}{t}pleft( t right)dt} geqslant 1 — frac{1}{{15}}intlimits_0^infty t pleft( t right)dt = 1 — frac{8}{{15}} = frac{7}{{15}}[/math]
Скорее всего, именно это решение ожидается проверяющими.
Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.
На рисунке ниже показан нормальный закон распределения случайной величины X в виде гистограммы.
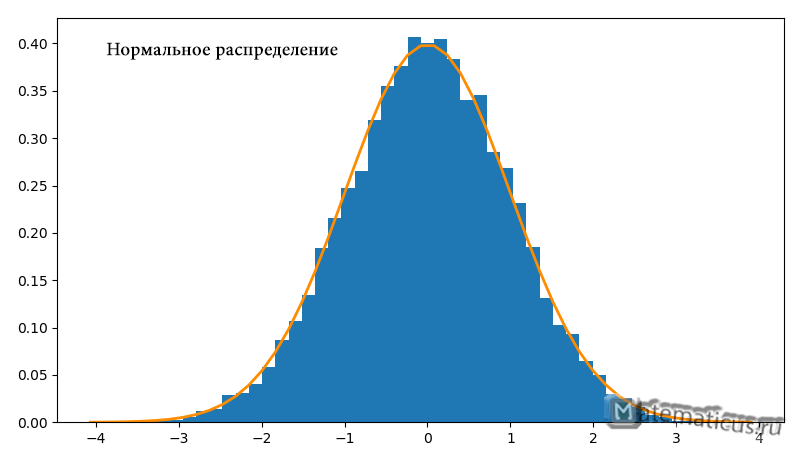
Рисунок 1 — Пример нормального закона распределения
Случайная непрерывная величина X имеет нормальный закон распределения, если ее плотность распределения вероятности имеет выражение:
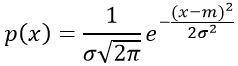
где m, σ — параметры распределения СВ;
mxили m — математическое ожидание случайной величины,
![]() — среднеквадратичное отклонение от величины a;
— среднеквадратичное отклонение от величины a;
σ2 — дисперсия.
Формула функции распределения СВ нормального закона определяется по формуле:
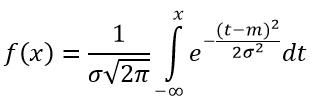
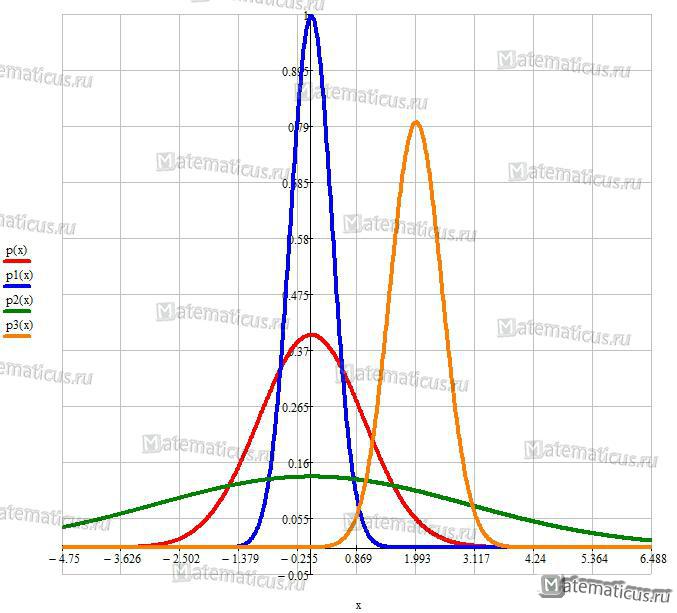
Рисунок 2 — График плотности нормального закона распределения X при m=0 и σ=1, m=0 и σ=0,4, m=0 и σ=3, m=2 и σ=0,5.
На рисунке 2 показана функция плотности нормального закона распределения при m=0 и σ=1;
при m=0 и σ=0,4 (функция плотности расширяется);
при m=0 и σ=3 (функция плотности сжимается);
при m=2 и σ=0,5 (функция плотности смещается вправо на 2 единицы относительно вершины).
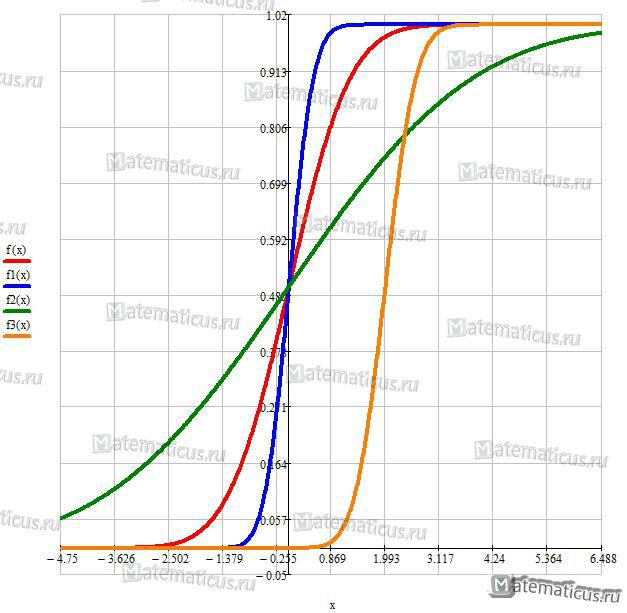
Рисунок 3 — График функции нормального закона распределения X при m=0 и σ=1, m=0 и σ=0,4, m=0 и σ=3, m=2 и σ=0,5.
При m=0 и σ=1 на рисунке 2 нормальное распределение СВ называется стандартным нормальным распределением СВ (таблица плотности вероятности нормальной случайной величины), плотность которого равна
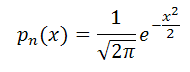
а функция распределения или функция Лапласа (таблица функции Лапласа)
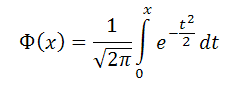
Вероятность попадания в заданный интервал (α; β) распределенной случайной величины по нормальному закону с параметрами a, σ вычисляется по формуле:
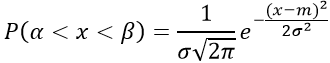
с использованием интеграла вероятности
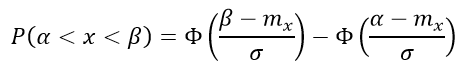
Из этих соотношений легко получить вероятность отклонения распределения случайной величины X от своего математического ожидания m:
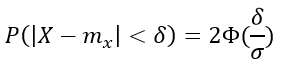
,где δ — величина отклонения.
Полагая в этой формуле δ=3σ, получаем
P(|X-mx|<δ)=2·Ф(3)=2⋅0.49865=0.9973
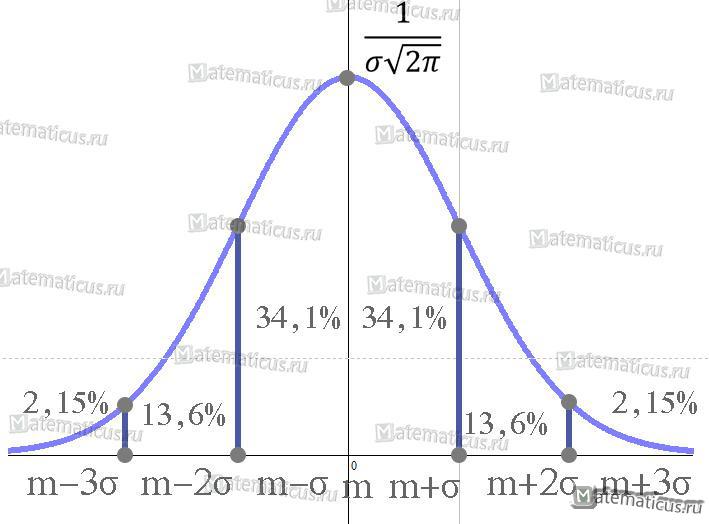
Рисунок 4
Этот правило носит название «правило трех сигм». Таким образом, см. рисунок 4 выше в 2,15+2,15+13,6+13,6+34,1+34,1=99,7% случаях все значения нормального закона распределения случайной величины сосредоточены в интервале (-3σ+m; 3σ+m). Распределение, заданное на бесконечном интервале, может быть рассмотрено на конечном интервале и погрешность при такой замене равна ,примерно, 0,3%.
Замечание
Нормальный закон распределения СВ является основным (базовым), часто встречается на практике и его также называют законом Гаусса.
Используется для построения доверительных интервалов, применяется для моделирования разброса при стрельбе, измерения ошибок и т.д.
При n→∞ биномиальное распределение быстро начинает приближаться к нормальному закону распределения СВ.
Пример 1
Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15, 25).
Решение
$Pleft( {15 < x < 25} right) =$
$={text{Φ }}left( {frac{{25 — 20}}{{5}}} right) — {text{Φ }}left( {frac{{15 — 20}}{{5}}} right) = {text{Φ }}left( 1 right) — {text{Φ}}left( { — 1} right)$
Так как функция Ф(х) нечётна:
P(15<x<25)=Ф(1)+Ф(1)=2Ф(1)
По таблице функции Лапласа находим значение Ф(1) =0,3413
Р(15<х<25)=2Ф(1) = 0,6826
Пример 2
Случайная величина X распределена нормально с дисперсией 2 и средним квадратическим отклонением 4. Найти вероятность того, что она примет значение в интервале (2, 6).
Решение
D=2 ⇒ σ=$sqrt 2 $
mx=4
$Pleft( {2 < x < 6} right) = {text{Φ }}left( {frac{{6 — 4}}{{sqrt 2 }}} right) — {text{Φ }}left( {frac{{2 — 4}}{{sqrt 2 }}} right)$
$Pleft( {2 < x < 6} right) = {text{Φ }}left( {1.41} right) — {text{Φ }}left( { — 1.41} right)$
По таблице функции Лапласа находим значение Ф(1.41) =0,3413
$Pleft( {2 < x < 6} right) = 2{text{Φ }}left( {1.41} right) = 2 cdot 0.4207 = 0.8414$
Пример 3
На станке изготавливается некоторая деталь. Ее длина представляет собой случайную величину, распределенную по нормальному закону, и имеет среднее значение 20 см и среднее квадратическое отклонение равную 0,2 см. Найти вероятность того, что длина детали будет заключена между 19,7 см и 20.3 см
Решение
$Pleft( {19.7 < x < 20.3} right) =$
$={text{Φ }}left( {frac{{20.3 — 20}}{{0.2}}} right) — {text{Φ }}left( {frac{{19.7 — 20}}{{0.2}}} right) = {text{Φ }}left( 1 right) — {text{Φ}}left( { — 1} right)$
P(19.6<x<20.4)=Ф(1)+Ф(1)=2Ф(1)
По таблице функции Лапласа находим значение Ф(1) =0,3413
Р(19,7<х<20,3)=2Ф(1) = 0,6826
Пример 4
Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением σ=10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.
Решение
P(|X-mx|<δ)=2·Ф( δ/σ )
Математическое ожидание равно нулю, δ=15, σ=10, тогда
P(|X|<15)=2·Ф(15/10)=2Ф(1.5)
По таблице функции Лапласа находим значение Ф(1.5) =0,43319
P(|X|<15)=2·Ф(1.5)=0,86638
2. Пусть [math]X[/math]— ошибка измерения, [math]sigma = 10[/math] – среднеквадратичное отклонение. Тогда вероятность того, что ошибка измерения не превзойдёт 2, равна
[math]p = Pleft( {left| X right| < 2} right) = Pleft( {left| {frac{X}{sigma }} right| < frac{2}{sigma }} right) = Phi left( {0.2} right) — Phi left( { — 0.2} right) = 2 cdot Phi left( {0.2} right) — 1 = 2 cdot 0.57926 — 1 = 0.15852[/math]
Вероятность противоположного события равна [math]q = 1 — p = 0.84148[/math]
Следовательно, вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 2, равна
[math]1 — q^3 = 0.404158[/math]
Отмечу, что здесь функция Лапласа [math]Phi left( x right)[/math] отличается от функции, которую использовал Alexdemath
3. Пусть [math]T[/math] – время службы мотора. Далее есть два пути решения этой задачи.
а) Предположим, что эта случайная величина имеет показательный закон распределения (этот закон часто используют для величин такого типа). Тогда параметр этого закона равен [math]lambda = 1/8[/math] и вероятность того, что данный мотор не прослужит 15 лет, равна
[math]Pleft( {X < 15} right) = intlimits_0^{15} {lambda cdot e^{ — lambda x} dx} = 1 — e^{ — 15lambda } = 0.846645[/math]
б) Пусть закон распределения случайной величины [math]T[/math] неизвестен. Обозначим через [math]pleft( t right)[/math] – плотность распределения этого закон. Тогда, используя приём из доказательства неравенства Чебышёва, получим
[math]Pleft( {X < 15} right) = 1 — Pleft( {X > 15} right) = 1 — intlimits_{15}^infty {pleft( t right)dt} = 1 — intlimits_{15}^infty {frac{t}{t}pleft( t right)dt} geqslant 1 — frac{1}{{15}}intlimits_0^infty t pleft( t right)dt = 1 — frac{8}{{15}} = frac{7}{{15}}[/math]
Скорее всего, именно это решение ожидается проверяющими.



