
Один из серьезных недостатков методов Рунге — Кутты состоит в отсутствии простых способов оценки ошибки интегрирования. Все же без некоторой оценки ошибки трудно правильно выбрать величину шага интегрирования h. Применим так называемый принцип Рунге.
Пусть yn(T ) есть точное решение дифференциального уравнения y/ = f (x, y) при x = x0 + nh. Тогда для метода Рунге — Кутты, описываемого формулами (7.4.13), справедлива следующая оценка погрешности:
|
h |
|||||||
|
h |
(h) |
||||||
|
2 |
|||||||
|
ε 2 |
= |
yn |
− yn |
, |
|||
|
2 p −1 |
|||||||
где yn(h ) — приближение к точному решению yn(T ), вычисленное с шагом
|
h |
h |
h |
||||
|
приближение с шагом |
, ε |
2 |
= yn(T ) − yn |
2 |
. |
|
|
2 |
||||||
(7.5.1)
h
h , yn 2 — такое же
Так как для метода, описываемого формулами (7.4.13), p = 4, то
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= |
yn |
2 |
− yn(h) . |
(7.5.2) |
|||||
|
15 |
|||||||||||
Формула (7.5.1) выведена в предположении, что на каждом шаге интегрирования допускается погрешность, приблизительно пропорциональная h p+1 , то есть yn(T ) = yn(h ) + Kh5 , что справедливо для достаточно гладких функций. Таким образом, ошибка интегрирования в предположении, что y(5)(x) практически постоянна, равна:
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= Kh5 |
= |
y |
2 |
− y(h) . |
|||||
|
15 |
|||||||||||
|
n |
n |
||||||||||
Это довольно точная оценка, однако для ее использования необходимо вычислять решение дважды.
Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности. Например, использу-
kn(2) − kn(3)
ется такое оценочное правило: если ( ) ( ) достаточно велико (обычно больше несколь- kn1 − kn2
ких сотых), то шаг интегрирования необходимо уменьшить.
Существуют более точные методы оценки погрешности интегрирования, основанные на использовании для контроля точности двух различных методов Рунге — Кутты. Один из самых эффективных — метод Рунге — Кутты — Фельберга. В этом методе для оценки погрешности метода пятого порядка используются формулы метода четвертого порядка точности, причем на одном шаге интегрирования требуется всего лишь шесть вычислений значений правой части f (x, y).
7.6. Методы прогноза и коррекции
Отличительной чертой методов Рунге — Кутты является то, что при вычислении следующей точки (xn+1 , yn+1 ) используется информация только о предыдущей (xn , yn ). Зато при-
ходится вычислять значение правой части в нескольких промежуточных точках. Это нерационально, поскольку при налаженном процессе интегрирования имеется дополнительная информация — предыдущие точки решения.
169
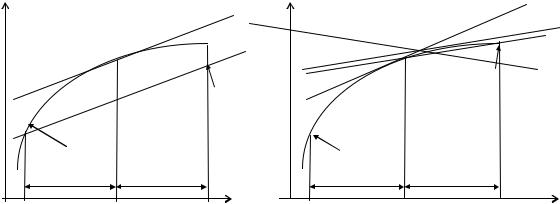
Рассмотрим общую идею группы методов, известных в литературе под названием «методов прогноза и коррекции». Как ясно из названия, вначале «предсказывается» значение yn+1 , а затем используется тот или иной метод для «корректировки» этого значения. Эту же
формулу можно использовать сколько угодно раз для повторной корректировки уже скорректированного значения yn+1 .
Для демонстрации основных идей метода можно использовать для прогноза формулу
|
любого метода численного интегрирования. Воспользуемся формулой второго порядка |
|
|
yn(0+)1 = yn−1 + 2hf (xn , yn ), |
(7.6.1) |
где индекс (0) означает исходное приближение к yn+1 . Непосредственно из написанной формулы следует, что с ее помощью нельзя вычислить, например, y1 , ибо для этого потребовалась бы точка, расположенная перед начальной точкой y0 . Чтобы начать решение по методу
прогноза и коррекции, часто используется метод Рунге — Кутты.
Геометрически предсказание сводится к тому, что находится угол наклона касательной в точке (xn , yn ) (см. левый рисунок). После этого через точку (xn−1 , yn−1 ) проводится
|
L |
L |
L |
L |
||||
|
1 |
2 |
1 |
L3 |
||||
|
(xn+1 , yn(0+)1 ) |
(xn+1 , yn(1+)1 ) |
||||||
|
L |
|||||||
|
y = f (x) |
y = f (x) |
||||||
|
h |
h |
h |
h |
||||
|
xn−1 |
xn |
xn+1 |
xn−1 |
xn |
xn+1 |
||
|
прямая L , параллельная |
L |
. Предсказанное значение y(0) |
будет расположено там, где пря- |
||||
|
1 |
n+1 |
||||||
|
мая L |
пересечется с абсциссой x = xn+1. |
Скорректируем теперь предсказанное значение. |
Вычислим наклон касательной в точке (xn+1 , yn(0+)1 ). Эта касательная изображена на правом ри-
|
сунке и обозначена L2 . Усредним тангенсы углов наклона прямых L1 и L2 |
и получим пря- |
|||||
|
мую L . Наконец, проведем через точку (x |
n |
, y |
n |
) прямую L , параллельную L , и точка пере- |
||
|
3 |
||||||
|
сечения этой прямой с абсциссой x = xn+1 даст новое приближение (xn+1 , yn(1+)1 ). |
||||||
|
Это значение вычисляется по формуле |
||||||
|
yn(1+)1 = yn + |
h |
[f (xn , yn )+ f (xn+1 , yn(0+)1 )]. |
(7.6.2) |
|||
|
2 |
В общем случае i -е приближение, очевидно, будет находиться таким образом:
|
yn(i+)1 |
= yn + h [f (xn , yn )+ f (xn+1 , yn(i+−11))]. |
(7.6.3) |
|||
|
2 |
|||||
|
Итерационный процесс можно прекратить, когда |
|||||
|
yn(i++11) − yn(i+)1 |
< ε. |
(7.6.4) |
|||
К настоящему времени разработано много методов прогноза и коррекции разных порядков, обеспечивающих очень большую точность решения. В некоторых из них по заданной точностипредусмотренавтоматическийвыбор шага и автоматический выбор порядка метода.
170

7.7. Сравнение методов
а). Методы Рунге — Кутты.
1.В этих методах используется информация только об очередной точке решения, поэтому с их помощью можно начинать решение.
2.По той же самой причине приходится многократно вычислять функцию f (x, y).
3.Методы этой группы позволяют очень легко менять величину шага h.
4.При использовании этих методов трудно получить оценку ошибки интегрирования. б). Методы прогноза и коррекции.
1. Так как в этих методах используется информация о ранее вычисленных точках решения, то с их помощью нельзя начать решение.
2. Из-за использования информации о ранее вычисленных точках методы этой группы более экономичны по затратам машинного времени.
3. При любом изменении величины шага h приходится временно возвращаться к методам Рунге — Кутты.
4. В качестве побочного продукта вычислений получается хорошая оценка ошибки интегрирования.
Как всегда, наиболее целесообразным является использование при решении практи-
|
ческих задач комбинации этих двух методов. |
|
|
Пример. Методом Рунге — Кутты с шагом h = 0.1 найти на отрезке [0, 0.3] решение |
|
|
следующего дифференциального уравнения: y/ = cos bx |
с начальным условием |
|
a + y2 |
y(0)= 0, a =1.4, b = 2.6.
|
Обозначим через yi |
приближенное значение решения в точке xi . Формулы метода: |
|||||||||||||||||||||||||||||||||||||
|
y |
i+1 |
= y |
i |
+ hk |
, |
k |
i |
= |
1 (k (1) + |
2k (2) + |
2k (3) + k (4)), |
|||||||||||||||||||||||||||
|
i |
6 |
i |
i |
i |
i |
|||||||||||||||||||||||||||||||||
|
k (1) |
), |
|||||||||||||||||||||||||||||||||||||
|
= f (x |
, |
y |
||||||||||||||||||||||||||||||||||||
|
i |
i |
i |
||||||||||||||||||||||||||||||||||||
|
k (2) |
= f |
x |
i |
+ h |
, y |
i |
+ h k (1) , |
(7.7.1) |
||||||||||||||||||||||||||||||
|
i |
2 |
2 |
i |
|||||||||||||||||||||||||||||||||||
|
h |
h |
(2) |
||||||||||||||||||||||||||||||||||||
|
(3) |
= f |
, yi |
+ |
|||||||||||||||||||||||||||||||||||
|
ki |
xi + |
2 |
2 |
ki |
, |
|||||||||||||||||||||||||||||||||
|
(4) |
(3) |
|||||||||||||||||||||||||||||||||||||
|
ki |
= f (xi + h, yi + hki |
). |
||||||||||||||||||||||||||||||||||||
|
Все вычисления удобно располагать по схеме, указанной в таблице. |
||||||||||||||||||||||||||||||||||||||
|
i |
x |
y |
k |
y |
||||||||||||||||||||||||||||||||||
|
0 |
x0 |
y0 |
k0(1) |
k0(1) |
||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(1) |
k0(2) |
2k0(2) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(2) |
k0(3) |
2k0(3) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 + h |
y0 + hk0(3) |
k0(4) |
k0(4) |
|||||||||||||||||||||||||||||||||||
Она заполняется следующим образом.
1. Записываем в первой строке x0 , y0 , вычисляем f (x0 , y0 ) и заносим в таблицу в качестве k0(1).
171
|
2. |
Для |
второй |
строки |
вычисляем |
x |
0 |
+ |
h |
и |
y |
+ |
h |
k (1) , |
затем |
находим |
|||||||||||||
|
h |
h |
2 |
0 |
2 |
0 |
|||||||||||||||||||||||
|
(1) |
(2) |
|||||||||||||||||||||||||||
|
f x0 |
+ |
, y0 + |
k0 |
и записываем в качестве k0 |
. |
|||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
3. |
Находим |
y0 |
+ h k0(2) , вычисляем |
f x0 |
+ |
h |
, y0 + |
h |
k0(2) |
и записываем в таблицу на |
||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
место k0(3) . |
2 |
|||||||||||||||||||||||||||
|
+ hk0(3) , |
||||||||||||||||||||||||||||
|
4. |
Записываем |
в четвертой строке |
x0 + h |
и |
y0 |
затем |
находим |
|||||||||||||||||||||
|
k0(4 ) = f (x0 + h, y0 + hk0(3)). |
||||||||||||||||||||||||||||
|
5. |
Суммируем числа, стоящие в столбце y , делим на шесть и заносим в таблицу в |
|||||||||||||||||||||||||||
|
качестве |
y0 . |
|||||||||||||||||||||||||||
|
6. |
Вычисляем x1 |
= x0 + h , |
y1 = y0 + |
y0 . Затем все вычисления необходимо повторить |
||||||||||||||||||||||||
|
с пункта 1, принимая за начальную точку (x1, y1 ). |
Для контроля правильности выбора ша- |
|||||||||||||||||||||||||||
|
га h рекомендуется вычислять дробь θ = |
ki(2) − ki(3) |
. Величина θ не должна превышать двух |
||||||||||||||||||||||||||
|
ki(1) − ki(2) |
||||||||||||||||||||||||||||
— трех сотых. В противном случае шаг h следует уменьшить.
|
i |
x |
y |
k |
y |
θ |
|||||||||||
|
0 |
0.00 |
0.000000 |
0.714286 |
0.14286 |
||||||||||||
|
0.05 |
0.035714 |
0.707614 |
1.415228 |
|||||||||||||
|
0.05 |
0.035381 |
0.707626 |
1.415252 |
|||||||||||||
|
0.10 |
0.070763 |
0.687818 |
0.687818 |
0.0018 |
||||||||||||
|
0.705431 |
||||||||||||||||
|
1 |
0.10 |
0.705431 |
0.509261 |
0.509262 |
||||||||||||
|
0.15 |
0.730894 |
0.478185 |
0.956370 |
|||||||||||||
|
0.15 |
0.729340 |
0.478747 |
0.957494 |
|||||||||||||
|
0.20 |
0.753306 |
0.441084 |
0.441084 |
0.0018 |
||||||||||||
|
0.477368 |
||||||||||||||||
|
2 |
0.20 |
1.182799 |
0.310045 |
0.310045 |
||||||||||||
|
0.25 |
1.198301 |
0.280714 |
0.561428 |
|||||||||||||
|
0.25 |
1.196835 |
0.281062 |
0.562124 |
|||||||||||||
|
0.30 |
1.210905 |
0.248026 |
0.248026 |
0.0012 |
||||||||||||
|
0.280270 |
||||||||||||||||
|
3 |
0.30 |
1.463069 |
7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений
Существует большое число методов приближенного решения дифференциальных уравнений, основанных на самых различных идеях. Численные методы дают приближенное решение y(x) в виде таблицы значений y1 , y2 ,…, yn в точках x1 , x2 ,…, xn .
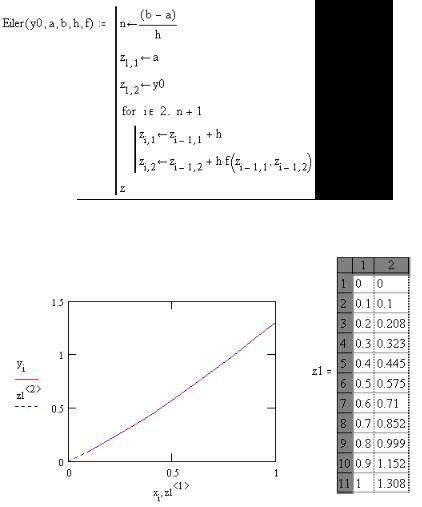
Простейшим методом численного интегрирования дифференциального уравнения первого порядка y/ = f (x, y), удовлетворяющего начальному условию y(x0 )= y0 , является метод Эйлера. В нем величины yi вычисляются по формуле
xi = x0 + ih, i = 0,1,2,…
yi+1 = yi + hf (xi , yi ).
172
Метод Эйлера относится к группе одношаговых, в которых для расчета точки (xi+1 , yi+1 ) требуется информация только о последней вычисленной точке (xi , yi ). Геометри-
ческая интерпретация метода изложена в подразд. 7.4.
В среде Mathcad имеется тринадцать встроенных функций решения дифференциальных уравнений и систем ( задача Коши, краевая задача, уравнения в частных производных). Самая употребительная из них — rkfixed, в которую заложен метод Рунге – Кутты четвертого порядка с постоянным шагом. Подпрограммы для метода Эйлера нет из-за его низкой точности. Формулы метода Эйлера настолько просты, что вычисления по ним можно организовать
|
с помощью дискретной переменной. |
|||||||||||||||||||||||||||||||||||
|
Рассмотрим пример. |
Решим |
задачу |
Коши |
для дифференциального |
уравнения |
||||||||||||||||||||||||||||||
|
y/ = cos(x − y)+ |
1.25y |
при y(0)= 0. |
|||||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
Введем начало программы |
y |
||||||||||||||||||||||||||||||||||
|
ORIGIN := 1 |
f (x, y):= cos(x − y)+1.25 |
a := 0 |
b := 1 |
h := 0.1 |
y0 := 0 |
||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
i := 1…11 |
xi := a |
+ h (i −1) |
|||||||||||||||||||||||||||||||||
|
i := 2…11 |
yi |
:= yi−1 + h f (xi−1 , yi−1 ) |
|||||||||||||||||||||||||||||||||
|
. |
|||||||||||||||||||||||||||||||||||
|
xT |
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
||||||||||||||||||||||||
|
yT |
0.000 |
0.100 |
0.208 |
0.323 |
0.445 |
0.575 |
0.710 |
0.852 |
0.999 |
1.152 |
1.308 |
||||||||||||||||||||||||
Аналогичного результата можно достигнуть, введя подпрограмму, реализующую формулы (7.4.1) метода Эйлера:
z1:= Eiler(y0,0,1,0.1, f )
173
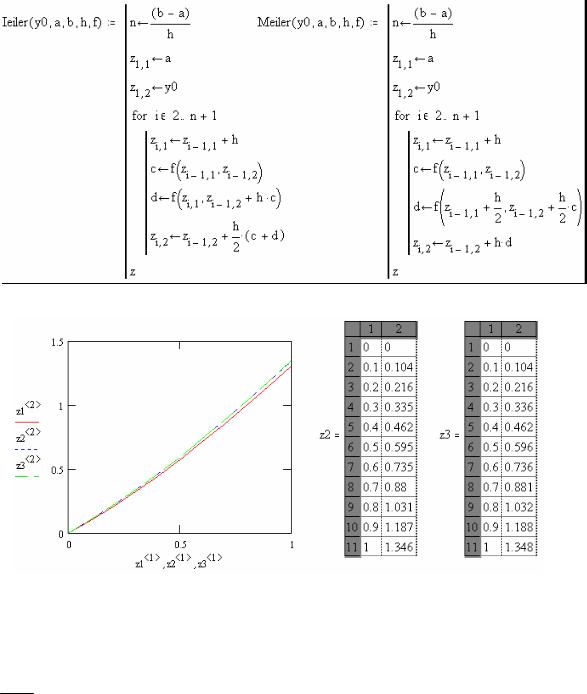
Минимальная переделка подпрограммы позволяет запрограммировать исправленный и модифицированный метод Эйлера по формулам (7.4.4) и (7.4.6).
z2 := Ieiler(y0,0,1,0.1, f ) z3 := Meiler(y0,0,1,0.1, f )
Обратимся теперь к средствам пакета Mathcad. Для решения обыкновенных «неособенных» дифференциальных уравнений здесь используются две функции rkfixed и Rkadapt,
|
реализующие метод Рунге – Кутты четвертого порядка с постоянным и переменным шагом. |
|
|
Набор параметров у этих подпрограмм одинаков: |
rkfixed(y, a,b, n, f ), где y = y(x0 ), |
|
a и b — начало и конец интервала интегрирования, n — |
число точек и, следовательно, шаг |
h = b −n a , f (x, y)— правая часть дифференциального уравнения. Несмотря на то что при ре-
шении дифференциального уравнения функция Rkadapt использует переменный шаг, она
|
тем не менее представляет ответ для n точек, находящихся на одинаковом расстоянии друг |
|||||||||||
|
от друга, равном h = |
b − a |
. |
|||||||||
|
n |
|||||||||||
|
Вводим следующую часть программы: |
yy1 |
||||||||||
|
yy1 := 0 fun(x, yy) |
:= cos(x − yy1 )+1.25 |
||||||||||
|
1.5 |
+ x |
||||||||||
|
z4 := rkfixed(yy,0,1,10,fun) |
|||||||||||
|
z5 := rkfixed(yy,0,1,20,fun) |
|||||||||||
|
z4 := Rkadapt(yy,0,1,10,fun) |
|||||||||||
|
i :=1…10 Er1 := |
(z4 2 ) −(z5 2 ) |
2 i |
|||||||||
|
i |
i |
||||||||||
|
174 |

errRGK = 5.291 10−3
|
errRKF := |
max(Er1) |
errRKF = 5.291 10−3 |
|
15 |
||
Обращение к rkfixed с h1 = 0.1 и h2 = 0.05 сделано для оценки погрешности интег-
рирования по правилу Рунге (7.5.2). errRKF — оценка погрешности.
На данном учебном примере, конечно, невозможно оценить выгоды использования функции Rkadapt вместо rkfixed. В более сложных случаях Rkadapt решает уравнение более точно и быстро. Даже в этом примере точность решения по Rkadapt выше, чем по rkfixed. Это видно из следующей таблицы:
|
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
|||||
|
z4 |
0.1040989 |
0.2161356 |
0.3357322 |
0.4625076 |
0.5960572 |
|||||
|
z5 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960578 |
|||||
|
z44 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960571 |
|||||
|
x |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|||||
|
z4 |
0.7359363 |
0.8816484 |
1.0326377 |
1.1882891 |
1.3479326 |
|||||
|
z5 |
0.7359370 |
0.8816491 |
1.0326386 |
1.1882900 |
1.3479335 |
|||||
|
z44 |
0.7359371 |
0.8816492 |
1.0326386 |
1.1882901 |
1.3479336 |
В заключение приведем подпрограмму RGK, реализующую формулы (7.4.13) метода Рунге – Кутты четвертого порядка. Далее, как и в предыдущем случае, произведена оценка погрешности по правилу Рунге и даны графики полученных решений. Программа метода Рунге – Кутты четвертого порядка (RGK) приведена после графиков проинтегрированных функций.
z6 := RGK (y0,0,1,0.1, f ) z7 := RGK (y0,0,1,0.05, f ) i := 1…10 Er2i := (z6 2 )i − (z7 2 )2 i
errRGK := max(Er2)
15

Задание № 1. Решить заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке x [0,1] с шагом h = 0.1 и оце-
|
нить погрешность интегрирования по правилу Рунге. |
|||||||||||||||||
|
1. |
y/ =1 + 0.2 y sin x − y2 , y |
(0) |
= 0.1. |
||||||||||||||
|
2. |
y/ = cos(x + y)+ 0.5(x − y), |
y(0)= 0. |
|||||||||||||||
|
3. |
y/ = |
cos x |
− 0.5y2 , |
y(0)= 0.2. |
|||||||||||||
|
x +1 |
|||||||||||||||||
|
4. |
y/ = (1 − y2 )cos x + 0.6 y, |
y(0)= 0. |
|||||||||||||||
|
5. |
y/ =1+0.4 ysin x −1.5y2 , |
y(0)=1. |
|||||||||||||||
|
6. |
y/ = |
cos y |
+ 0.3y2 , |
y(0)= 0. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
7. |
y/ = cos(1.5x + y)+ |
(x − y), |
y(0)= 0.5. |
||||||||||||||
|
8. |
y/ = 1 − sin(x + y)+ |
0.5y |
, y(0)= 0.3. |
||||||||||||||
|
x + 2 |
|||||||||||||||||
|
cos y |
|||||||||||||||||
|
9. |
y/ = |
+ 0.1y2 |
, y(0)= 0. |
||||||||||||||
|
1.5 + x |
|||||||||||||||||
|
10. |
y/ = 0.6 sin x −1.25y2 +1, y(0)=1. |
||||||||||||||||
|
11. |
y/ = cos(2x + y)+1.5(x − y), y(0)= 0.1. |
||||||||||||||||
|
12. |
y/ =1 − |
0.1y |
− sin(2x + y), |
y(0)= 0.5. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
13. |
y/ = |
cos y |
− 0.1y2 , y(0) |
= 0.2. |
|||||||||||||
|
1.25 + x |
|||||||||||||||||
|
y(0)= 0.5. |
|||||||||||||||||
|
14. |
y/ =1 + 0.8y sin x − 2 y2 , |
||||||||||||||||
|
176 |
Соседние файлы в предмете Вычислительная математика
- #
- #

Один из серьезных недостатков методов Рунге — Кутты состоит в отсутствии простых способов оценки ошибки интегрирования. Все же без некоторой оценки ошибки трудно правильно выбрать величину шага интегрирования h. Применим так называемый принцип Рунге.
Пусть yn(T ) есть точное решение дифференциального уравнения y/ = f (x, y) при x = x0 + nh. Тогда для метода Рунге — Кутты, описываемого формулами (7.4.13), справедлива следующая оценка погрешности:
|
h |
|||||||
|
h |
(h) |
||||||
|
2 |
|||||||
|
ε 2 |
= |
yn |
− yn |
, |
|||
|
2 p −1 |
|||||||
где yn(h ) — приближение к точному решению yn(T ), вычисленное с шагом
|
h |
h |
h |
||||
|
приближение с шагом |
, ε |
2 |
= yn(T ) − yn |
2 |
. |
|
|
2 |
||||||
(7.5.1)
h
h , yn 2 — такое же
Так как для метода, описываемого формулами (7.4.13), p = 4, то
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= |
yn |
2 |
− yn(h) . |
(7.5.2) |
|||||
|
15 |
|||||||||||
Формула (7.5.1) выведена в предположении, что на каждом шаге интегрирования допускается погрешность, приблизительно пропорциональная h p+1 , то есть yn(T ) = yn(h ) + Kh5 , что справедливо для достаточно гладких функций. Таким образом, ошибка интегрирования в предположении, что y(5)(x) практически постоянна, равна:
|
h |
1 |
h |
|||||||||
|
ε |
2 |
= Kh5 |
= |
y |
2 |
− y(h) . |
|||||
|
15 |
|||||||||||
|
n |
n |
||||||||||
Это довольно точная оценка, однако для ее использования необходимо вычислять решение дважды.
Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности. Например, использу-
kn(2) − kn(3)
ется такое оценочное правило: если ( ) ( ) достаточно велико (обычно больше несколь- kn1 − kn2
ких сотых), то шаг интегрирования необходимо уменьшить.
Существуют более точные методы оценки погрешности интегрирования, основанные на использовании для контроля точности двух различных методов Рунге — Кутты. Один из самых эффективных — метод Рунге — Кутты — Фельберга. В этом методе для оценки погрешности метода пятого порядка используются формулы метода четвертого порядка точности, причем на одном шаге интегрирования требуется всего лишь шесть вычислений значений правой части f (x, y).
7.6. Методы прогноза и коррекции
Отличительной чертой методов Рунге — Кутты является то, что при вычислении следующей точки (xn+1 , yn+1 ) используется информация только о предыдущей (xn , yn ). Зато при-
ходится вычислять значение правой части в нескольких промежуточных точках. Это нерационально, поскольку при налаженном процессе интегрирования имеется дополнительная информация — предыдущие точки решения.
169

Рассмотрим общую идею группы методов, известных в литературе под названием «методов прогноза и коррекции». Как ясно из названия, вначале «предсказывается» значение yn+1 , а затем используется тот или иной метод для «корректировки» этого значения. Эту же
формулу можно использовать сколько угодно раз для повторной корректировки уже скорректированного значения yn+1 .
Для демонстрации основных идей метода можно использовать для прогноза формулу
|
любого метода численного интегрирования. Воспользуемся формулой второго порядка |
|
|
yn(0+)1 = yn−1 + 2hf (xn , yn ), |
(7.6.1) |
где индекс (0) означает исходное приближение к yn+1 . Непосредственно из написанной формулы следует, что с ее помощью нельзя вычислить, например, y1 , ибо для этого потребовалась бы точка, расположенная перед начальной точкой y0 . Чтобы начать решение по методу
прогноза и коррекции, часто используется метод Рунге — Кутты.
Геометрически предсказание сводится к тому, что находится угол наклона касательной в точке (xn , yn ) (см. левый рисунок). После этого через точку (xn−1 , yn−1 ) проводится
|
L |
L |
L |
L |
||||
|
1 |
2 |
1 |
L3 |
||||
|
(xn+1 , yn(0+)1 ) |
(xn+1 , yn(1+)1 ) |
||||||
|
L |
|||||||
|
y = f (x) |
y = f (x) |
||||||
|
h |
h |
h |
h |
||||
|
xn−1 |
xn |
xn+1 |
xn−1 |
xn |
xn+1 |
||
|
прямая L , параллельная |
L |
. Предсказанное значение y(0) |
будет расположено там, где пря- |
||||
|
1 |
n+1 |
||||||
|
мая L |
пересечется с абсциссой x = xn+1. |
Скорректируем теперь предсказанное значение. |
Вычислим наклон касательной в точке (xn+1 , yn(0+)1 ). Эта касательная изображена на правом ри-
|
сунке и обозначена L2 . Усредним тангенсы углов наклона прямых L1 и L2 |
и получим пря- |
|||||
|
мую L . Наконец, проведем через точку (x |
n |
, y |
n |
) прямую L , параллельную L , и точка пере- |
||
|
3 |
||||||
|
сечения этой прямой с абсциссой x = xn+1 даст новое приближение (xn+1 , yn(1+)1 ). |
||||||
|
Это значение вычисляется по формуле |
||||||
|
yn(1+)1 = yn + |
h |
[f (xn , yn )+ f (xn+1 , yn(0+)1 )]. |
(7.6.2) |
|||
|
2 |
В общем случае i -е приближение, очевидно, будет находиться таким образом:
|
yn(i+)1 |
= yn + h [f (xn , yn )+ f (xn+1 , yn(i+−11))]. |
(7.6.3) |
|||
|
2 |
|||||
|
Итерационный процесс можно прекратить, когда |
|||||
|
yn(i++11) − yn(i+)1 |
< ε. |
(7.6.4) |
|||
К настоящему времени разработано много методов прогноза и коррекции разных порядков, обеспечивающих очень большую точность решения. В некоторых из них по заданной точностипредусмотренавтоматическийвыбор шага и автоматический выбор порядка метода.
170

7.7. Сравнение методов
а). Методы Рунге — Кутты.
1.В этих методах используется информация только об очередной точке решения, поэтому с их помощью можно начинать решение.
2.По той же самой причине приходится многократно вычислять функцию f (x, y).
3.Методы этой группы позволяют очень легко менять величину шага h.
4.При использовании этих методов трудно получить оценку ошибки интегрирования. б). Методы прогноза и коррекции.
1. Так как в этих методах используется информация о ранее вычисленных точках решения, то с их помощью нельзя начать решение.
2. Из-за использования информации о ранее вычисленных точках методы этой группы более экономичны по затратам машинного времени.
3. При любом изменении величины шага h приходится временно возвращаться к методам Рунге — Кутты.
4. В качестве побочного продукта вычислений получается хорошая оценка ошибки интегрирования.
Как всегда, наиболее целесообразным является использование при решении практи-
|
ческих задач комбинации этих двух методов. |
|
|
Пример. Методом Рунге — Кутты с шагом h = 0.1 найти на отрезке [0, 0.3] решение |
|
|
следующего дифференциального уравнения: y/ = cos bx |
с начальным условием |
|
a + y2 |
y(0)= 0, a =1.4, b = 2.6.
|
Обозначим через yi |
приближенное значение решения в точке xi . Формулы метода: |
|||||||||||||||||||||||||||||||||||||
|
y |
i+1 |
= y |
i |
+ hk |
, |
k |
i |
= |
1 (k (1) + |
2k (2) + |
2k (3) + k (4)), |
|||||||||||||||||||||||||||
|
i |
6 |
i |
i |
i |
i |
|||||||||||||||||||||||||||||||||
|
k (1) |
), |
|||||||||||||||||||||||||||||||||||||
|
= f (x |
, |
y |
||||||||||||||||||||||||||||||||||||
|
i |
i |
i |
||||||||||||||||||||||||||||||||||||
|
k (2) |
= f |
x |
i |
+ h |
, y |
i |
+ h k (1) , |
(7.7.1) |
||||||||||||||||||||||||||||||
|
i |
2 |
2 |
i |
|||||||||||||||||||||||||||||||||||
|
h |
h |
(2) |
||||||||||||||||||||||||||||||||||||
|
(3) |
= f |
, yi |
+ |
|||||||||||||||||||||||||||||||||||
|
ki |
xi + |
2 |
2 |
ki |
, |
|||||||||||||||||||||||||||||||||
|
(4) |
(3) |
|||||||||||||||||||||||||||||||||||||
|
ki |
= f (xi + h, yi + hki |
). |
||||||||||||||||||||||||||||||||||||
|
Все вычисления удобно располагать по схеме, указанной в таблице. |
||||||||||||||||||||||||||||||||||||||
|
i |
x |
y |
k |
y |
||||||||||||||||||||||||||||||||||
|
0 |
x0 |
y0 |
k0(1) |
k0(1) |
||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(1) |
k0(2) |
2k0(2) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 |
+ |
h |
y0 |
+ |
h |
k0(2) |
k0(3) |
2k0(3) |
||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
x0 + h |
y0 + hk0(3) |
k0(4) |
k0(4) |
|||||||||||||||||||||||||||||||||||
Она заполняется следующим образом.
1. Записываем в первой строке x0 , y0 , вычисляем f (x0 , y0 ) и заносим в таблицу в качестве k0(1).
171

|
2. |
Для |
второй |
строки |
вычисляем |
x |
0 |
+ |
h |
и |
y |
+ |
h |
k (1) , |
затем |
находим |
|||||||||||||
|
h |
h |
2 |
0 |
2 |
0 |
|||||||||||||||||||||||
|
(1) |
(2) |
|||||||||||||||||||||||||||
|
f x0 |
+ |
, y0 + |
k0 |
и записываем в качестве k0 |
. |
|||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
3. |
Находим |
y0 |
+ h k0(2) , вычисляем |
f x0 |
+ |
h |
, y0 + |
h |
k0(2) |
и записываем в таблицу на |
||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||
|
место k0(3) . |
2 |
|||||||||||||||||||||||||||
|
+ hk0(3) , |
||||||||||||||||||||||||||||
|
4. |
Записываем |
в четвертой строке |
x0 + h |
и |
y0 |
затем |
находим |
|||||||||||||||||||||
|
k0(4 ) = f (x0 + h, y0 + hk0(3)). |
||||||||||||||||||||||||||||
|
5. |
Суммируем числа, стоящие в столбце y , делим на шесть и заносим в таблицу в |
|||||||||||||||||||||||||||
|
качестве |
y0 . |
|||||||||||||||||||||||||||
|
6. |
Вычисляем x1 |
= x0 + h , |
y1 = y0 + |
y0 . Затем все вычисления необходимо повторить |
||||||||||||||||||||||||
|
с пункта 1, принимая за начальную точку (x1, y1 ). |
Для контроля правильности выбора ша- |
|||||||||||||||||||||||||||
|
га h рекомендуется вычислять дробь θ = |
ki(2) − ki(3) |
. Величина θ не должна превышать двух |
||||||||||||||||||||||||||
|
ki(1) − ki(2) |
||||||||||||||||||||||||||||
— трех сотых. В противном случае шаг h следует уменьшить.
|
i |
x |
y |
k |
y |
θ |
|||||||||||
|
0 |
0.00 |
0.000000 |
0.714286 |
0.14286 |
||||||||||||
|
0.05 |
0.035714 |
0.707614 |
1.415228 |
|||||||||||||
|
0.05 |
0.035381 |
0.707626 |
1.415252 |
|||||||||||||
|
0.10 |
0.070763 |
0.687818 |
0.687818 |
0.0018 |
||||||||||||
|
0.705431 |
||||||||||||||||
|
1 |
0.10 |
0.705431 |
0.509261 |
0.509262 |
||||||||||||
|
0.15 |
0.730894 |
0.478185 |
0.956370 |
|||||||||||||
|
0.15 |
0.729340 |
0.478747 |
0.957494 |
|||||||||||||
|
0.20 |
0.753306 |
0.441084 |
0.441084 |
0.0018 |
||||||||||||
|
0.477368 |
||||||||||||||||
|
2 |
0.20 |
1.182799 |
0.310045 |
0.310045 |
||||||||||||
|
0.25 |
1.198301 |
0.280714 |
0.561428 |
|||||||||||||
|
0.25 |
1.196835 |
0.281062 |
0.562124 |
|||||||||||||
|
0.30 |
1.210905 |
0.248026 |
0.248026 |
0.0012 |
||||||||||||
|
0.280270 |
||||||||||||||||
|
3 |
0.30 |
1.463069 |
7.8. Лабораторная работа № 12. Методы интегрирования обыкновенных дифференциальных уравнений
Существует большое число методов приближенного решения дифференциальных уравнений, основанных на самых различных идеях. Численные методы дают приближенное решение y(x) в виде таблицы значений y1 , y2 ,…, yn в точках x1 , x2 ,…, xn .
Простейшим методом численного интегрирования дифференциального уравнения первого порядка y/ = f (x, y), удовлетворяющего начальному условию y(x0 )= y0 , является метод Эйлера. В нем величины yi вычисляются по формуле
xi = x0 + ih, i = 0,1,2,…
yi+1 = yi + hf (xi , yi ).
172

Метод Эйлера относится к группе одношаговых, в которых для расчета точки (xi+1 , yi+1 ) требуется информация только о последней вычисленной точке (xi , yi ). Геометри-
ческая интерпретация метода изложена в подразд. 7.4.
В среде Mathcad имеется тринадцать встроенных функций решения дифференциальных уравнений и систем ( задача Коши, краевая задача, уравнения в частных производных). Самая употребительная из них — rkfixed, в которую заложен метод Рунге – Кутты четвертого порядка с постоянным шагом. Подпрограммы для метода Эйлера нет из-за его низкой точности. Формулы метода Эйлера настолько просты, что вычисления по ним можно организовать
|
с помощью дискретной переменной. |
|||||||||||||||||||||||||||||||||||
|
Рассмотрим пример. |
Решим |
задачу |
Коши |
для дифференциального |
уравнения |
||||||||||||||||||||||||||||||
|
y/ = cos(x − y)+ |
1.25y |
при y(0)= 0. |
|||||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
Введем начало программы |
y |
||||||||||||||||||||||||||||||||||
|
ORIGIN := 1 |
f (x, y):= cos(x − y)+1.25 |
a := 0 |
b := 1 |
h := 0.1 |
y0 := 0 |
||||||||||||||||||||||||||||||
|
1.5 + x |
|||||||||||||||||||||||||||||||||||
|
i := 1…11 |
xi := a |
+ h (i −1) |
|||||||||||||||||||||||||||||||||
|
i := 2…11 |
yi |
:= yi−1 + h f (xi−1 , yi−1 ) |
|||||||||||||||||||||||||||||||||
|
. |
|||||||||||||||||||||||||||||||||||
|
xT |
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
||||||||||||||||||||||||
|
yT |
0.000 |
0.100 |
0.208 |
0.323 |
0.445 |
0.575 |
0.710 |
0.852 |
0.999 |
1.152 |
1.308 |
||||||||||||||||||||||||
Аналогичного результата можно достигнуть, введя подпрограмму, реализующую формулы (7.4.1) метода Эйлера:
z1:= Eiler(y0,0,1,0.1, f )
173

Минимальная переделка подпрограммы позволяет запрограммировать исправленный и модифицированный метод Эйлера по формулам (7.4.4) и (7.4.6).
z2 := Ieiler(y0,0,1,0.1, f ) z3 := Meiler(y0,0,1,0.1, f )
Обратимся теперь к средствам пакета Mathcad. Для решения обыкновенных «неособенных» дифференциальных уравнений здесь используются две функции rkfixed и Rkadapt,
|
реализующие метод Рунге – Кутты четвертого порядка с постоянным и переменным шагом. |
|
|
Набор параметров у этих подпрограмм одинаков: |
rkfixed(y, a,b, n, f ), где y = y(x0 ), |
|
a и b — начало и конец интервала интегрирования, n — |
число точек и, следовательно, шаг |
h = b −n a , f (x, y)— правая часть дифференциального уравнения. Несмотря на то что при ре-
шении дифференциального уравнения функция Rkadapt использует переменный шаг, она
|
тем не менее представляет ответ для n точек, находящихся на одинаковом расстоянии друг |
|||||||||||
|
от друга, равном h = |
b − a |
. |
|||||||||
|
n |
|||||||||||
|
Вводим следующую часть программы: |
yy1 |
||||||||||
|
yy1 := 0 fun(x, yy) |
:= cos(x − yy1 )+1.25 |
||||||||||
|
1.5 |
+ x |
||||||||||
|
z4 := rkfixed(yy,0,1,10,fun) |
|||||||||||
|
z5 := rkfixed(yy,0,1,20,fun) |
|||||||||||
|
z4 := Rkadapt(yy,0,1,10,fun) |
|||||||||||
|
i :=1…10 Er1 := |
(z4 2 ) −(z5 2 ) |
2 i |
|||||||||
|
i |
i |
||||||||||
|
174 |

errRGK = 5.291 10−3
|
errRKF := |
max(Er1) |
errRKF = 5.291 10−3 |
|
15 |
||
Обращение к rkfixed с h1 = 0.1 и h2 = 0.05 сделано для оценки погрешности интег-
рирования по правилу Рунге (7.5.2). errRKF — оценка погрешности.
На данном учебном примере, конечно, невозможно оценить выгоды использования функции Rkadapt вместо rkfixed. В более сложных случаях Rkadapt решает уравнение более точно и быстро. Даже в этом примере точность решения по Rkadapt выше, чем по rkfixed. Это видно из следующей таблицы:
|
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
|||||
|
z4 |
0.1040989 |
0.2161356 |
0.3357322 |
0.4625076 |
0.5960572 |
|||||
|
z5 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960578 |
|||||
|
z44 |
0.1040990 |
0.2161359 |
0.3357326 |
0.4625081 |
0.5960571 |
|||||
|
x |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|||||
|
z4 |
0.7359363 |
0.8816484 |
1.0326377 |
1.1882891 |
1.3479326 |
|||||
|
z5 |
0.7359370 |
0.8816491 |
1.0326386 |
1.1882900 |
1.3479335 |
|||||
|
z44 |
0.7359371 |
0.8816492 |
1.0326386 |
1.1882901 |
1.3479336 |
В заключение приведем подпрограмму RGK, реализующую формулы (7.4.13) метода Рунге – Кутты четвертого порядка. Далее, как и в предыдущем случае, произведена оценка погрешности по правилу Рунге и даны графики полученных решений. Программа метода Рунге – Кутты четвертого порядка (RGK) приведена после графиков проинтегрированных функций.
z6 := RGK (y0,0,1,0.1, f ) z7 := RGK (y0,0,1,0.05, f ) i := 1…10 Er2i := (z6 2 )i − (z7 2 )2 i
errRGK := max(Er2)
15

Задание № 1. Решить заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке x [0,1] с шагом h = 0.1 и оце-
|
нить погрешность интегрирования по правилу Рунге. |
|||||||||||||||||
|
1. |
y/ =1 + 0.2 y sin x − y2 , y |
(0) |
= 0.1. |
||||||||||||||
|
2. |
y/ = cos(x + y)+ 0.5(x − y), |
y(0)= 0. |
|||||||||||||||
|
3. |
y/ = |
cos x |
− 0.5y2 , |
y(0)= 0.2. |
|||||||||||||
|
x +1 |
|||||||||||||||||
|
4. |
y/ = (1 − y2 )cos x + 0.6 y, |
y(0)= 0. |
|||||||||||||||
|
5. |
y/ =1+0.4 ysin x −1.5y2 , |
y(0)=1. |
|||||||||||||||
|
6. |
y/ = |
cos y |
+ 0.3y2 , |
y(0)= 0. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
7. |
y/ = cos(1.5x + y)+ |
(x − y), |
y(0)= 0.5. |
||||||||||||||
|
8. |
y/ = 1 − sin(x + y)+ |
0.5y |
, y(0)= 0.3. |
||||||||||||||
|
x + 2 |
|||||||||||||||||
|
cos y |
|||||||||||||||||
|
9. |
y/ = |
+ 0.1y2 |
, y(0)= 0. |
||||||||||||||
|
1.5 + x |
|||||||||||||||||
|
10. |
y/ = 0.6 sin x −1.25y2 +1, y(0)=1. |
||||||||||||||||
|
11. |
y/ = cos(2x + y)+1.5(x − y), y(0)= 0.1. |
||||||||||||||||
|
12. |
y/ =1 − |
0.1y |
− sin(2x + y), |
y(0)= 0.5. |
|||||||||||||
|
x + 2 |
|||||||||||||||||
|
13. |
y/ = |
cos y |
− 0.1y2 , y(0) |
= 0.2. |
|||||||||||||
|
1.25 + x |
|||||||||||||||||
|
y(0)= 0.5. |
|||||||||||||||||
|
14. |
y/ =1 + 0.8y sin x − 2 y2 , |
||||||||||||||||
|
176 |
Соседние файлы в предмете Вычислительная математика
- #
- #
Библиографическое описание:
Анализ влияния вычислительной погрешности в явных методах Рунге — Кутты / А. С. Пак, О. А. Кащеева, Н. А. Мелков [и др.]. — Текст : непосредственный // Молодой ученый. — 2020. — № 27 (317). — С. 18-23. — URL: https://moluch.ru/archive/317/72323/ (дата обращения: 30.01.2023).
Статья посвящена нахождению приемов и способов улучшения и оптимизации известных методов интегрирования систем обыкновенных дифференциальных уравнений (СОДУ). Задача уменьшения вычислительной погрешности при меньших затратах является наиболее актуальной для всех численных методов. В статье подробно рассматривается применение метода компенсированного суммирования для явного метода Рунге — Кутты четвертого порядка.
Ключевые слова:
система обыкновенных дифференциальных уравнений, компенсированное суммирование, алгоритм Гилла — Мёллера, методы Рунге — Кутты.
Двадцать первый век можно охарактеризовать как период, в течение которого классические методы решения обыкновенных дифференциальных уравнений (ОДУ), таких как методы Рунге — Кутты, разработанные для ручного счета, развивались исходя из требований и цифровых возможностей. Однако в практических вычислениях природа компьютерной арифметики может играть значительную и, возможно, подавляющую роль.
Алгоритм Гилла
— Мёллера
В книге Бутчера [1] представлен анализ влияния ошибки округления в явном методе Эйлера, а также приведен алгоритм Гилла — Мёллера (Гилл [2], Мёллер [4], [5]), который называют «компенсированным суммированием». В данном разделе будет проведен аналогичный численный эксперимент для преодоления последствий накопления ошибок округления в явном методе Рунге —Кутты 4-го порядка.
Пусть
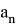
— общая погрешность, вычисленная на шаге
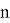
,
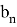
— соответствующая погрешность вычисления производной на этом же шаге, тогда
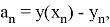
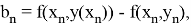
последовательности точных и приближённых значений связаны между собой следующим образом
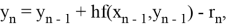
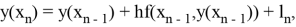
где
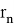
— ошибка округления, совершенная на этом шаге, а
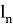
— методическая погрешность. Данная операция приводит к следующему разностному уравнению
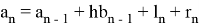
,
Так как, детальный анализ ошибки округления в расчетах данной задачи представлен в работе Хенричи [3], то вместо того, чтобы пытаться провести анализ
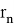
и
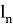
, а также, поскольку шаги вычисляются последовательно, заметим, что можно преодолеть наихудшие последствия накопления ошибок округления. Это делается путем оценки значения
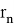
на любом конкретном шаге, а затем добавление его к значению
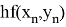
, прежде чем оно будет добавлено на следующем шаге.
Этот усовершенствованный метод, который может быть использован для многих ситуаций, связанных с суммированием большого количества малых величин, и называют алгоритмом Гилла — Мёллера или «компенсированным суммированием».
«
Компенсированное суммирование
»
в
явном методе Рунге
— Кутты 4-го порядка
Общая схема явного метода Рунге — Кутты (ЯМРК) численного интегрирования СОДУ
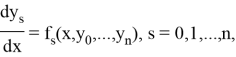
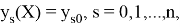
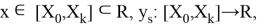
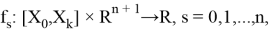
выглядит следующим образом:
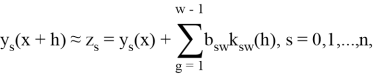
где функции
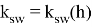
вычисляются по схеме
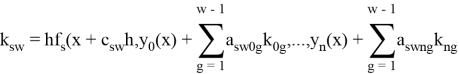
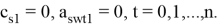
Здесь
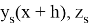
— точное и приближенное значение s-й компоненты в точке
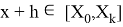
соответственно,
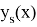
— точное значение s-й компоненты в точке
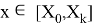
,
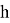
— шаг метода.
Традиционным считается символически представлять данный метод посредством таблиц Бутчера. Приведем пример таблицы Бутчера для ЯМРК 4-го порядка.
|
0 |
||||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Далее будет показано как применить «компенсированное суммирование» для уменьшения ошибки округления в ЯМРК четвертого порядка на примере системы дифференциальных уравнений
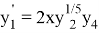
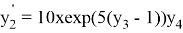
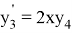
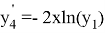
,
с начальным приближением
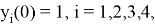
которое имеет аналитическое решение
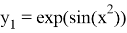
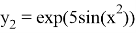
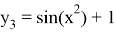
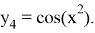
Реализация данного метода была выполнена в системе научных вычислений MATLAB.
(ЯМРК4)

ЯМРК4 с компенсированным суммированием)

В данном примере была взята последовательность шагов
Результаты
Нанесем глобальные погрешности этих двух алгоритмов на один график в логарифмическом масштабе.
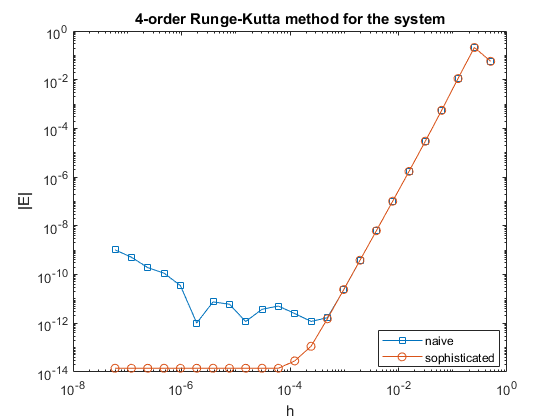
Видно, что явная форма дает результаты, которые сильнее ухудшаются при определенном шаге, в то время как компенсированная версия значительно улучшает результат.
Выводы
Как видно из проведенного исследования, метод «компенсированного суммирования» значительно улучшает ЯМРК четвертого порядка, а также его можно распространить и на другие численные методы интегрирования СОДУ.
Литература:
- Butcher J. C. «Numerical Methods for ordinary Differential Equations, Second Edition». The University of Auckland, New Zealand 2008, 463 p.
- Gill S. «A process for the step-by step integration of differential equations in an automatic computing machine». Proc. Cambridge Philos. Soc 1951.
- Henrici P. «Discrete Variable Methods in Ordinary Differential Equations». John Wiley & Sons Inc, New York 1962.
- Møller O. «Quasi double-precision in floating point addition». BIT 1965.
- Møller O. «Note on quasi double-precision». BIT 1965.
Основные термины (генерируются автоматически): явный метод, компенсированное суммирование, MATLAB, алгоритм, шаг.
The local error is typically estimated using something like an embedded pair of Runge-Kutta methods. The classic example would be the 4(5) pair (for instance, Dormand-Prince), where the error over a single step would be estimated by comparing the fourth- and fifth-order solutions. Other methods include approaches like halving the time step, or Richardson extrapolation.
The global estimate you’re referring to is one by Dahlquist, using the logarithmic norm, which is a bound on the growth of the norm of the solution to an ODE. (See reference 3 of this review paper on the logarithmic norm by Soderlind. A similar, weaker result was proven by Gronwall using Lipschitz constants; see Gronwall’s inequality.)
There are a variety of methods for bounding and estimating the global error in solutions of ODEs, and I’m sure I’ll fail to list all of them.
For estimates, the most recent paper I’m aware of is by Constantinescu, which has a large number of references worth looking at; other notable papers include the now-dated review by Skeel, the adjoint approach by Estep (he has a whole series of adjoint-based a posteriori error estimation papers), and the adjoint approach by Cao & Petzold.
Bounds could also be computed using interval arithmetic and Taylor methods. The thesis by Joseph Scott should have a number of references discussing this topic.
The local error is typically estimated using something like an embedded pair of Runge-Kutta methods. The classic example would be the 4(5) pair (for instance, Dormand-Prince), where the error over a single step would be estimated by comparing the fourth- and fifth-order solutions. Other methods include approaches like halving the time step, or Richardson extrapolation.
The global estimate you’re referring to is one by Dahlquist, using the logarithmic norm, which is a bound on the growth of the norm of the solution to an ODE. (See reference 3 of this review paper on the logarithmic norm by Soderlind. A similar, weaker result was proven by Gronwall using Lipschitz constants; see Gronwall’s inequality.)
There are a variety of methods for bounding and estimating the global error in solutions of ODEs, and I’m sure I’ll fail to list all of them.
For estimates, the most recent paper I’m aware of is by Constantinescu, which has a large number of references worth looking at; other notable papers include the now-dated review by Skeel, the adjoint approach by Estep (he has a whole series of adjoint-based a posteriori error estimation papers), and the adjoint approach by Cao & Petzold.
Bounds could also be computed using interval arithmetic and Taylor methods. The thesis by Joseph Scott should have a number of references discussing this topic.
Один из серьезных недостатков методов Рунге — Кутты состоит в отсутствии простых способов оценки ошибки интегрирования. Все же без некоторой оценки ошибки трудно правильно выбрать величину шага интегрирования ![]() Применим так называемый принцип Рунге.
Применим так называемый принцип Рунге.
Пусть ![]() есть точное решение дифференциального уравнения
есть точное решение дифференциального уравнения ![]() при
при ![]() Тогда для метода Рунге — Кутты, описываемого формулами (7.4.13), справедлива следующая оценка погрешности:
Тогда для метода Рунге — Кутты, описываемого формулами (7.4.13), справедлива следующая оценка погрешности:
 (7.5.1)
(7.5.1)
Где ![]() — приближение к точному решению
— приближение к точному решению ![]() , вычисленное с шагом
, вычисленное с шагом ![]() ,
, ![]() — такое же приближение с шагом
— такое же приближение с шагом ![]() ,
, ![]() .
.
Так как для метода, описываемого формулами (7.4.13), ![]() то
то
 (7.5.2)
(7.5.2)
Формула (7.5.1) выведена в предположении, что на каждом шаге интегрирования допускается погрешность, приблизительно пропорциональная ![]() , то есть
, то есть ![]() что справедливо для достаточно гладких функций. Таким образом, ошибка интегрирования в предположении, что
что справедливо для достаточно гладких функций. Таким образом, ошибка интегрирования в предположении, что ![]() практически постоянна, равна:
практически постоянна, равна:

Это довольно точная оценка, однако для ее использования необходимо вычислять решение дважды.
Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности. Например, используется такое оценочное правило: если  достаточно велико (обычно больше нескольких сотых), то шаг интегрирования необходимо уменьшить.
достаточно велико (обычно больше нескольких сотых), то шаг интегрирования необходимо уменьшить.
Существуют более точные методы оценки погрешности интегрирования, основанные на использовании для контроля точности двух различных методов Рунге — Кутты. Один из самых эффективных — метод Рунге — Кутты — Фельберга. В этом методе для оценки погрешности метода пятого порядка используются формулы метода четвертого порядка точности, причем на одном шаге интегрирования требуется всего лишь шесть вычислений значений правой части ![]()
| < Предыдущая |
|---|
Библиографическое описание:
Анализ влияния вычислительной погрешности в явных методах Рунге — Кутты / А. С. Пак, О. А. Кащеева, Н. А. Мелков [и др.]. — Текст : непосредственный // Молодой ученый. — 2020. — № 27 (317). — С. 18-23. — URL: https://moluch.ru/archive/317/72323/ (дата обращения: 25.06.2023).
Статья посвящена нахождению приемов и способов улучшения и оптимизации известных методов интегрирования систем обыкновенных дифференциальных уравнений (СОДУ). Задача уменьшения вычислительной погрешности при меньших затратах является наиболее актуальной для всех численных методов. В статье подробно рассматривается применение метода компенсированного суммирования для явного метода Рунге — Кутты четвертого порядка.
Ключевые слова:
система обыкновенных дифференциальных уравнений, компенсированное суммирование, алгоритм Гилла — Мёллера, методы Рунге — Кутты.
Двадцать первый век можно охарактеризовать как период, в течение которого классические методы решения обыкновенных дифференциальных уравнений (ОДУ), таких как методы Рунге — Кутты, разработанные для ручного счета, развивались исходя из требований и цифровых возможностей. Однако в практических вычислениях природа компьютерной арифметики может играть значительную и, возможно, подавляющую роль.
Алгоритм Гилла
— Мёллера
В книге Бутчера [1] представлен анализ влияния ошибки округления в явном методе Эйлера, а также приведен алгоритм Гилла — Мёллера (Гилл [2], Мёллер [4], [5]), который называют «компенсированным суммированием». В данном разделе будет проведен аналогичный численный эксперимент для преодоления последствий накопления ошибок округления в явном методе Рунге —Кутты 4-го порядка.
Пусть
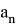
— общая погрешность, вычисленная на шаге
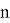
,
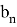
— соответствующая погрешность вычисления производной на этом же шаге, тогда
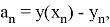
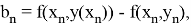
последовательности точных и приближённых значений связаны между собой следующим образом
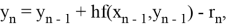
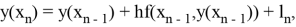
где
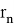
— ошибка округления, совершенная на этом шаге, а
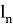
— методическая погрешность. Данная операция приводит к следующему разностному уравнению
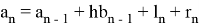
,
Так как, детальный анализ ошибки округления в расчетах данной задачи представлен в работе Хенричи [3], то вместо того, чтобы пытаться провести анализ
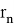
и
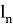
, а также, поскольку шаги вычисляются последовательно, заметим, что можно преодолеть наихудшие последствия накопления ошибок округления. Это делается путем оценки значения
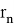
на любом конкретном шаге, а затем добавление его к значению
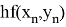
, прежде чем оно будет добавлено на следующем шаге.
Этот усовершенствованный метод, который может быть использован для многих ситуаций, связанных с суммированием большого количества малых величин, и называют алгоритмом Гилла — Мёллера или «компенсированным суммированием».
«
Компенсированное суммирование
»
в
явном методе Рунге
— Кутты 4-го порядка
Общая схема явного метода Рунге — Кутты (ЯМРК) численного интегрирования СОДУ
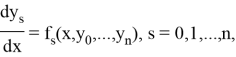
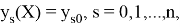
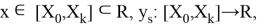
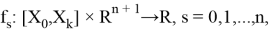
выглядит следующим образом:
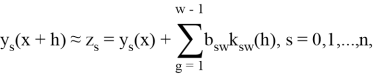
где функции
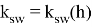
вычисляются по схеме
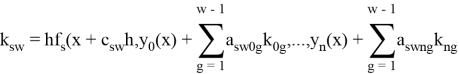
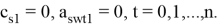
Здесь
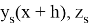
— точное и приближенное значение s-й компоненты в точке
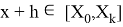
соответственно,
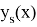
— точное значение s-й компоненты в точке
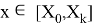
,
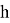
— шаг метода.
Традиционным считается символически представлять данный метод посредством таблиц Бутчера. Приведем пример таблицы Бутчера для ЯМРК 4-го порядка.
|
0 |
||||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Далее будет показано как применить «компенсированное суммирование» для уменьшения ошибки округления в ЯМРК четвертого порядка на примере системы дифференциальных уравнений
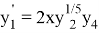
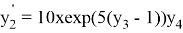
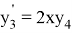
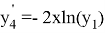
,
с начальным приближением
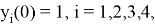
которое имеет аналитическое решение
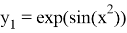
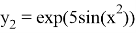
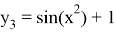
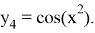
Реализация данного метода была выполнена в системе научных вычислений MATLAB.
(ЯМРК4)

ЯМРК4 с компенсированным суммированием)

В данном примере была взята последовательность шагов
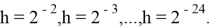
Результаты
Нанесем глобальные погрешности этих двух алгоритмов на один график в логарифмическом масштабе.

Видно, что явная форма дает результаты, которые сильнее ухудшаются при определенном шаге, в то время как компенсированная версия значительно улучшает результат.
Выводы
Как видно из проведенного исследования, метод «компенсированного суммирования» значительно улучшает ЯМРК четвертого порядка, а также его можно распространить и на другие численные методы интегрирования СОДУ.
Литература:
- Butcher J. C. «Numerical Methods for ordinary Differential Equations, Second Edition». The University of Auckland, New Zealand 2008, 463 p.
- Gill S. «A process for the step-by step integration of differential equations in an automatic computing machine». Proc. Cambridge Philos. Soc 1951.
- Henrici P. «Discrete Variable Methods in Ordinary Differential Equations». John Wiley & Sons Inc, New York 1962.
- Møller O. «Quasi double-precision in floating point addition». BIT 1965.
- Møller O. «Note on quasi double-precision». BIT 1965.
Основные термины (генерируются автоматически): явный метод, компенсированное суммирование, MATLAB, алгоритм, шаг.
|
0 / 0 / 0 Регистрация: 29.11.2021 Сообщений: 6 |
|
|
1 |
|
|
MathCAD 15 19.01.2022, 19:54. Показов 1231. Ответов 8
Выдает такую ошибку, подскажите в чем может быть проблема и как ее исправить? … Миниатюры
0 |
|
8893 / 6428 / 3468 Регистрация: 14.01.2014 Сообщений: 14,799 |
|
|
19.01.2022, 20:12 |
2 |
|
А почему индексация f в левой функции идёт не с 0? Добавлено через 10 минут
1 |
|
0 / 0 / 0 Регистрация: 29.11.2021 Сообщений: 6 |
|
|
19.01.2022, 20:28 [ТС] |
3 |
|
mathmichel, Пытался самостоятельно с примерами найденными в интернете сделать, а что нужно и как исправить?
0 |
|
8893 / 6428 / 3468 Регистрация: 14.01.2014 Сообщений: 14,799 |
|
|
19.01.2022, 21:21 |
4 |
|
РешениеВот поправки. В первой колонке идут значения переменной интегрирования t, в следующих — значения трёх интегрируемых функций. Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 29.11.2021 Сообщений: 6 |
|
|
19.01.2022, 21:54 [ТС] |
5 |
|
mathmichel, Огромное спасибо
0 |
|
8893 / 6428 / 3468 Регистрация: 14.01.2014 Сообщений: 14,799 |
|
|
19.01.2022, 22:11 |
6 |
|
РешениеСократил код (убрал ti и лишние операции транспонирования), добавил график Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 29.11.2021 Сообщений: 6 |
|
|
19.01.2022, 23:02 [ТС] |
7 |
|
mathmichel, а можно еще уточнить по данной теме пожалуйста, чтобы метод Хемминга разогнать РК4, нужно в этом же цикле записывать(как я предположил), либо цикл в цикле? Миниатюры
0 |
|
8893 / 6428 / 3468 Регистрация: 14.01.2014 Сообщений: 14,799 |
|
|
20.01.2022, 00:06 |
8 |
|
Я не очень знаком с методом Хемминга, который к тому же имеет много вариаций. Сначала надо определиться с его алгоритмом — привести его подробное описание. Судя по всему — это весьма громоздкое усложнение метода Рунге-Кутта и зачем это нужно, если Вы ещё не все ошибки исправили в самом методе Рунге-Кутта — проверьте сами, сравнив со стандартным алгоритмом!
1 |
|
0 / 0 / 0 Регистрация: 29.11.2021 Сообщений: 6 |
|
|
20.01.2022, 00:12 [ТС] |
9 |
|
mathmichel, хорошо, спасибо вам за помощь!
0 |

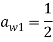
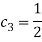
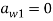
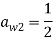
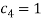
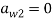
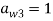

 Сообщение было отмечено VSI как решение
Сообщение было отмечено VSI как решение