61
Третье
свойство статистической совокупности
– разнообразие
признаков.
Четвертое
свойство статистической совокупности
— репрезентативность признаков
Студент
должен знать:
-
определение
второго свойства статистической
совокупности – средний уровень признака; -
виды
средних величин – статистические
критерии второго свойства статистической
совокупности; -
определение
вариационного ряда, виды вариационных
рядов; -
основные
статистические характеристики
вариационного ряда: варианты, частота,
число наблюдений; -
методика
вычисления средних величин при большом
числе наблюдений; -
методика
вычисления средних величин при малом
числе наблюдений; -
сущность
третьего свойства статистической
совокупности – разнообразие признака; -
статистические
критерии разнообразия признака
статистической совокупности (лимит,
амплитуда, среднее квадратическое
отклонение, коэффициент вариации),
особенности их использования; -
методика
вычисления среднего квадратического
отклонения при большом и малом числе
наблюдения; -
сущность
четвертого свойства
статистической совокупности –
репрезентативность (достоверность)
признаков; -
статистические
критерии, характеризующие репрезентативность
(достоверность) признака (ошибки средних
и относительных величин, доверительных
границ средних и относительных величин,
достоверности разности средних и
относительных величин); -
особенности
вычисления ошибок средних величин при
большом и малом числе наблюдений; -
особенности
вычисления ошибки относительных
величин; -
методика
определения доверительных границ
средних и относительных величин; -
методика
определения достоверности разности
средних и относительных величин; -
практическое
значение средних величин и оценки их
достоверности.
Студент
должен уметь:
-
строить
простой и сгруппированный вариационные
ряды; -
вычислять
среднюю величину (М), среднее квадратическое
отклонение (σ), ошибку средней величины
(m)
при большом и малом числе наблюдений; -
определять
доверительные границы для средней
величины при большом и малом числе
наблюдений, для относительных величин; -
определять
достоверность разности средних и
относительных величин.
План занятия
-
Сущность
второго свойства статистической
совокупности и его статистические
критерии; -
Характеристики
вариационного ряда. -
Виды
средних величин и методика их вычисления
при большом и
малом числе наблюдений.
Свойства средней величины. -
Сущность
разнообразия признака статистической
совокупности и статистические критерии.
Методика расчета среднего квадратического
отклонения при большом и малом числе
наблюдений. -
Сущность
четвертого свойства статистической
совокупности и статистические критерии
характеризующие его. -
Определение
ошибки репрезентативности средних
величин при
большом и малом числе наблюдений.
Особенности вычисления ошибки
относительных величин. -
Методика
определения доверительных границ
средних и относительных величин при
большом и малом числе наблюдений. -
Методика
определения достоверности разности
средних и относительных величин. -
Использование
средних величин в практической
деятельности врача.
Блок
информации:
Второе
свойство – средний уровень признака
используется для количественной
характеристики статистической
совокупности.
К
статистическим критериям, характеризующим
второе свойство статистической
совокупности, относят средние
величины.
Для
вычисления средних величин используются
вариационные ряды.
Вариационный
ряд, виды вариационных рядов.
Вариационный
ряд – это
ряд вариант одного и того же признака,
расположенных в определенном порядке
(по степени возрастания или убывания).
Вариационные
ряды бывают:
-
простые
и взвешенные; -
несгруппированные
и сгруппированные (интервальные); -
четные
(число вариант четное) и нечетные (число
вариант нечетное).
Простой
вариационный ряд представляет собой
ряд вариант, в котором каждая варианта
встречается с частотой, равной единице.
Взвешенный
вариационный
ряд представляет собой ряд вариант, в
котором каждая варианта встречается с
различной частотой.
Простой
и взвешенный вариационные ряды могут
быть представлены несгруппированными
и сгруппированными вариантами.
Несгруппированный
вариационный
ряд содержит отдельные варианты с
соответствующими им частотами.
Сгруппированный
(интервальный)
вариационный ряд имеет в своем составе
варианты, объединенные в пределах
определенного интервала, соответственно
с частотой их встречаемости.
Требования
к составлению сгруппированного
вариационного ряда
-
определенный
порядок расположения вариант -
непрерывность
вариационного ряда -
сгруппированный
вариационный ряд
Характеристики
вариационного ряда
Полученные
при исследовании числовые измерения
одного и того же признака называются
вариантами
(V
– vario).
Число
раз, которое встречается одна и та же
варианта в вариационном ряду называется
частотой (p
– pars).
Сумма
всех частот вариационного ряда определяет
число
наблюдений (n
= Σр).
Виды
средних величин и методика их вычисления
при большом
и малом числе наблюдений.
Свойства средней величины.
Виды
средних величин
-
мода;
-
медиана;
-
средняя
арифметическая;
Мода
(Мо) – средняя
величина, которая соответствует варианте,
встречающейся в вариационном ряду с
наибольшей частотой.
Медиана
(Ме) – средняя
величина, соответствующая варианте,
которая делит вариационный ряд пополам.
В нечетном
вариационном ряду находится в середине,
в четном
вариационном
ряду вычисляется как полусумма двух
средних вариант.
Средняя
величина
(средняя арифметическая, средняя
взвешенная) (М)
– обобщенная характеристика среднего
уровня изучаемого признака однородной
статистической совокупности в конкретных
условиях места и времени.
В
отличие от моды и медианы средняя
арифметическая учитывает все значения
вариант вариационного ряда.
Свойства
средней величины.
-
в
строго симметричном вариационном ряду
средняя величина занимает срединное
положение, поэтому средняя, мода и
медиана имеют одну и ту же величину (М
= Мо = Ме). -
средняя
величина имеет абстрактный характер
и является обобщающей величиной,
определяющей
закономерность всей совокупности. -
произведение
средней на число наблюдений всегда
равняется сумме произведений каждой
варианты на соответствующую ей частоту
встречаемости в вариационном ряду. -
алгебраическая
сумма отклонений всех вариант
вариационного ряда от средней равна
нулю. -
если
к каждой варианте вариационного ряда
прибавить или отнять одно и то же число,
то на такое же число увеличится или
уменьшится средняя арифметическая
величина. -
если
каждую варианту вариационного ряда
разделить или умножить на одно и то же
число, то во столько же раз уменьшится
или увеличится средняя арифметическая
величина.
Методика
расчета средних величин при большом и
малом числе наблюдений рассмотрена в
образцах выполнения практических
заданий.
Третье
свойство
(разнообразия
признака) характеризует
распределение
вариант количественных признаков
в однородной статистической
совокупности.
К
статистическим критериям, характеризующим
третье свойство статистической
совокупности, относят:
-
лимит
(lim)
определяется крайними значениями
вариант в вариационном ряду –
Lim
= Vmax
: Vmin; -
амплитуда
(Am)
равна разности между крайними значениями
вариант в вариационном ряду – (Am
= Vmax
–Vmin); -
среднее
квадратическое отклонение
(δ) дает наиболее полную характеристику
разнообразия признака в статистической
совокупности, так как учитывает все
значения вариант;
Методика
вычисления среднего квадратического
отклонения при большом числе наблюдений
рассмотрена в образце выполнения
практического задания.
-
коэффициент
вариации
(Cv)
является относительной мерой разнообразия
признака в статистической совокупности
–
 ,
,
где
δ
– среднее квадратическое отклонение
М
– средняя арифметическая взвешенная
Величина
коэффициента вариации больше 20%
свидетельствует о высокой степени
разнообразия признака, при величине
коэффициента вариации от 10 до 20% –
степень разнообразия средняя, величина
коэффициента вариации менее 10%
свидетельствует о низкой степени
разнообразия признака.
Среднее
квадратическое отклонение и
коэффициент вариации
являются обобщающими характеристиками
статистической совокупности.
Роль
среднего
квадратического отклонения
состоит в том, что по величине δ
можно:
-
определить
структуру вариационного ряда; -
охарактеризовать
степень однородности вариационного
ряда; -
судить
о типичности средней (арифметической
или взвешенной) величины; -
оценить
отдельные признаки у каждого индивидуума; -
оценить
достоверность (репрезентативность)
результатов исследования.
Четвертое
свойство
статистической совокупности характеризует
репрезентативность
выборки, которая может быть достигнута
специальными методами отбора выборочной
совокупности.
Репрезентативность
(достоверность) выборочной совокупности
означает представительность в ней всех
учитываемых признаков характерных для
генеральной совокупности, что гарантирует
высокую вероятность соответствия
закономерностей, полученных при
исследовании выборочной совокупности
существующим в генеральной совокупности.
Статистические
критерии,
характеризующие репрезентативность
статистической совокупности:
-
ошибки
средних и относительных величин; -
доверительные
границы средних и относительных величин; -
достоверность
различий средних и относительных
величин по критерию t.
Определение
ошибки репрезентативности.
Величина
ошибки прямо
пропорциональна степени разнообразия
признака и
обратно
пропорциональна числу наблюдений
в статистической совокупности.
Следовательно, чем менее разнообразен
признак и больше число наблюдений в
статистической совокупности, тем меньше
величина ошибки
и более
достоверен результат
исследования.
Вычисление
ошибки репрезентативности для средних
величин при большом числе (n
≥ 30) наблюдений
осуществляется по формуле:
![]() ,
,
где
mМ
– ошибка средней величины
n
– число наблюдений
δ
– среднее квадратическое отклонение
Вычисление
ошибки репрезентативности для средних
величин при малом числе наблюдений (n
< 30) осуществляется
по формуле:
![]() ,
,
где
mМ
–ошибка средней величины
n
– число наблюдений
δ
– среднее квадратическое отклонение
Вычисление
ошибки репрезентативности для
относительных величин осуществляется
по формуле:
![]() ,
,
где
m%
–ошибка относительной величины,
p
– относительный показатель, выраженный
в процентах (%),
q
– величина равная 100-p.
Методика
среднего квадратического отклонения
и ошибок при малом числе наблюдений
рассмотрена в
образцах выполнения практических
заданий.
Методика
определения доверительных границ
средней величины.
Доверительные
границы – интервал колеблемости средней
величины (или относительной величины),
выход за пределы которого имеет
незначительную вероятность.
Доверительные
границы для средних
величин
определяют по формуле:
![]() ,
,
где
М
ген
– средняя генеральной совокупности
М
выб
– средняя выборочной совокупности
m
– ошибка средней величины
t
– доверительный коэффициент
Доверительные
границы для относительных
величин
определяют по формуле:
![]() ,
,
где
Р
ген
– средняя генеральной совокупности
Р
выб
– средняя выборочной совокупности
m
– ошибка показателя (относительной
величины)
t
– доверительный коэффициент
Величина
доверительного
коэффициента
(t)
определяется величиной доверительной
вероятности,
с которой необходимо получить конечный
результат, и числом
наблюдений.
В медико-статистических
исследованиях обычно используют
доверительную вероятность, равную 95%
или-99% (или 0,95-0,99), которым соответствует
определенная величина критерия t.
При
большом числе наблюдений (n
≥ 30) и доверительной вероятности Р=95%
величина доверительного коэффициента
соответствует t
= 2, при доверительной вероятности Р=99%
величина доверительного коэффициента
соответствует t
= 3.
При
малом числе наблюдений (n
< 30) величина t
несколько больше указанных выше значений
и ее необходимо определять по таблице
Стьюдента.
Использование
средних величин и доверительных границ
в практической деятельности врача.
Средние
величины и доверительный интервал лежат
в основе определения достоверных границ
средних величин, которые широко
используются в процессе профессиональной
деятельности врача для оценки данных
физиологических и лабораторных
исследований.
И снова о погрешностях
Окончание. См. № 15/07
Д.А.ИВАШКИНА,
лицей г. Троицка, Московская обл.
aivashkin@mail.ru
И снова о погрешностях
4. Учёт случайных погрешностей при
прямых измерениях
Если, проведя одно и то же измерение
несколько раз, вы видите, что результат остаётся
одним и тем же, то случайные погрешности
эксперимента малы, их не следует учитывать. Но
если при повторении измерения получаются разные
значения, то следует взять среднее значение из
серии измерений:
![]()
где n – число измерений. Как
узнать, какова погрешность результата? Логично, и
ученики сами обычно предлагают это, определить
среднее отклонение результата от среднего
значения. Полученная величина носит название средней
арифметической ошибки: ![]() Она показывает, на сколько в
Она показывает, на сколько в
среднем каждое измеренное значение отклоняется
от среднего значения. Но эта величина слабо
зависит от количества проведённых измерений. В
чём же тогда смысл многократных измерений?
Для среднеквадратичной погрешности,
которая определяется немного сложнее:
![]()
есть простое правило: средняя
квадратичная погрешность среднего
арифметического равна средней квадратичной
погрешности отдельного результата, делённой на
корень квадратный из числа измерений: ![]() Из формулы ясно,
Из формулы ясно,
что с увеличением числа измерений случайная
погрешность среднего значения уменьшается.
Поэтому необходимо проводить столько измерений,
чтобы случайная погрешность стала меньше
значения систематической погрешности данного
измерения.
К сожалению, в лабораторных работах и
при любых других экспериментах в школе провести
достаточное количество измерений невозможно в
силу нехватки времени. Как поступать, может
решить сам учитель. На мой взгляд, для нахождения
средней арифметической погрешности среднего
значения можно использовать формулу,
аналогичную формуле для средней квадратичной
ошибки: ![]()
Хотя эта формула и неверна, она
помогает понять смысл проведения большого числа
измерений. Использоваться же она будет всего в
нескольких работах, и, следовательно, нет нужды
специально обучать нахождению погрешности
среднего значения. Зато, получив в этих работах
случайную погрешность меньше погрешности
систематической, ученик запомнит, что каждое
измерение следует производить несколько раз при
малейшем подозрении, что в данном эксперименте
имеется случайная погрешность. Как правило, уже
при пяти измерениях достигается необходимая
малость случайной погрешности по сравнению с
систематической.
5. Определение погрешности
результата косвенных измерений
К определению погрешности результата
косвенных измерений учащиеся готовы, на мой
взгляд, уже к 8-му классу. В зависимости от уровня
класса впервые метод границ [1, 12] можно
применить или в работе по сравнению количеств
теплоты при смешивании воды, или при нахождении
сопротивления проводника. Поясню на примерах.
-
Допустим, при нагревании холодной
воды в процессе смешивания мы имеем следующие
результаты измерений:
– температура холодной воды t1
= (16,0 ± 1,5) °С;
– температура смеси t = (43,0 ± 1,5) °С;
– объём холодной воды V1 = (80
± 2) мл = (80 ± 2) • 10–6 м3.
Получаем количество теплоты,
полученное холодной водой:
Q = 4190 Дж/(кг • °С) • 1000 кг/м3
• 80 • 10–6 м3 ![]() (43 – 16) °С = 9050,4 Дж.
(43 – 16) °С = 9050,4 Дж.
(1)
Возникает вопрос: а какова погрешность
полученного значения? Другими словами, на
сколько мы можем ошибиться, если точные значения
не равны измеренным, а лежат где-то в интервале,
даваемом погрешностью? Например, начальная
температура воды может быть равна 16,5 °С, 17,0 °С и
т.д. Тогда вычисленное количество теплоты будет
меньше. Логично посмотреть, на сколько мы можем
ошибиться по максимуму. Максимальное количество
теплоты получится, если взять для всех
сомножителей максимальные значения, т.е. верхние
границы интервалов значений с погрешностью, для
уменьшаемого взять верхнюю границу значения, а
для вычитаемого – нижнюю:
Qв = 4190 Дж/(кг • °С) • 1000
кг/м3 • 82 • 10–6 м3 ![]() (44,5 – 14,5)°С = 10 307,4 Дж.
(44,5 – 14,5)°С = 10 307,4 Дж.
Аналогично вычисляем нижнюю границу
значения количества теплоты:
Qн = 4190 Дж/(кг • °С) • 1000
кг/м3 • 78 • 10–6 м3 ![]() (41,5 – 17,5) °С = 7843,68
(41,5 – 17,5) °С = 7843,68
Дж.
В данных пределах и лежит искомое
значение. Чтобы сравнивать методом интервалов
это значение с количеством теплоты, отданным
горячей водой, надо округлить значения верхней и
нижней границ. Лучше это сделать, оценив
абсолютную погрешность найденного значения
количества теплоты.
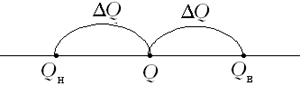
Рис. 2
Из рис. 2 видно, что
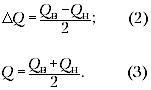
Найденное выше значение (1) близко к (3),
поэтому его не стоит находить ещё раз. А вот для
погрешности найдём с помощью (2):
![]() (две
(две
значащие цифры, т.к. первая «1»). Поэтому
количество теплоты, полученное холодной водой,
можно округлить: Qполуч = 9000 Дж ±
1200 Дж (т.е. между 7800 Дж и 10 200 Дж). Если количество
теплоты, отданное горячей водой, лежит между 8500
Дж и 11 500 Дж (Qотдан = 10 000 Дж ± 1500 Дж), то
можно видеть, что эти количества теплоты
совпадают в пределах погрешности эксперимента
(рис. 3).
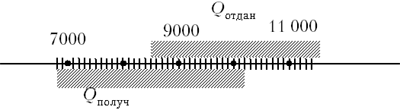
Рис.3
-
Определение сопротивления резистора.
Пусть измеренные значения напряжения и силы тока
следующие:
– U = 2,60 В ± 0,15 В (инструментальная
погрешность 0,15 В; погрешность отсчёта может быть
взята равной 0,05 В, т.е. в 3 раза меньше
инструментальной, поэтому ею можно пренебречь);
– I = 1,2 А ± 0,1 А (инструментальная
погрешность 0,05 А, погрешность отсчёта 0,05 А).
Тогда для сопротивления получаем:
![]()
Но на самом резисторе написано: «2 ± 0,1 ![]() ». Получается, что
». Получается, что
мы неверно определили сопротивление? Рассчитаем
погрешность нашего определения значения
сопротивления:
Uв = 2,75 В; Uн = 2,45 В; Iв
= 1,3 А, Iн = 1,1 А;
![]()
Полученное экспериментально значение
сопротивления R = (2,2 ± 0,3) Ом совпадает в
пределах погрешности со значением R = (2,0 ± 0,1)
Ом, указанным на резисторе.
С помощью метода границ можно вывести
и формулы для погрешности при обобщении темы
«Определение погрешности косвенных измерений»,
но уже в 9-м классе.
Определение погрешности разности. Пусть
А = В – С. Рассчитаем погрешность А в
общем виде:
Ав = Вв – Сн
= (В + ![]() В)
В)
– (С – ![]() С)
С)
= (В – С) + (![]() В
В
+ ![]() С);
С);
Ан = Вн – Св
= (В – ![]() В)
В)
– (С + ![]() С)
С)
= (В – С) – (![]() В
В
+ ![]() С);
С);
![]()
Полученное очень важно: в некоторых
работах в формулах для вычисления результата
встречается разность двух близких по значению
величин, что приводит к большой относительной
погрешности результата.
-
В cтарой работе «Определение модуля
Юнга резины» [11] удлинение резинового жгута
находилось как разность его результирующей и
начальной длин. Если условия опыта таковы, что
эта разность мала, например, составляет 1,5 см, то
относительная погрешность определения разности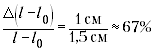 (погрешность
(погрешность
отсчёта взята гораздо меньше инструментальной
погрешности). Ясно, что такое измерение
использовать для определения модуля Юнга
нежелательно, – может получиться погрешность
больше 100%. Лучше увеличить нагрузку на жгут.
Аналогичная проблема возникает в работе
«Измерение ЭДС и внутреннего сопротивления
источника» [2] (одно сопротивление должно быть в
несколько раз больше другого) и др.
Определение погрешности частного
двух величин. Пусть ![]() Рассчитаем погрешность в общем виде:
Рассчитаем погрешность в общем виде:
![]()
Такую формулу трудно запоминать.
Поэтому найдём относительную погрешность
величины А:
![]()
Итак, относительная погрешность
частного равна сумме относительных погрешностей
величин, входящих в него. Такая же формула
получается и для относительной погрешности
произведения.
Важным я считаю не сам процесс расчёта
погрешности. Эти формулы дают мощный инструмент
для оценки обоснованности проведения
эксперимента. При их использовании легко
объяснить, при измерении какой из величин
следует увеличить точность, чтобы получить
лучший результат.
Рассмотрим формулу для нахождения
модуля Юнга: 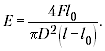
Если воспользоваться для расчёта погрешности
результата методом границ, то неясным останется,
какая из величин в формуле вносит наибольшую
погрешность.
Для нахождения относительной
погрешности результата лучше воспользоваться
формулой:
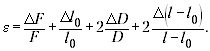
При подстановке значений оказывается,
что слагаемое 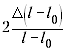
даёт максимальный вклад в сумму, а остальные
слагаемые в несколько раз меньше, так что ими
можно пренебречь. Если l – l0 будет
невелико, то значение относительной погрешности
окажется очень большим, порой выше 100%. Какой
вывод сделают в таком случае ученики?
Такая ситуация – пример того, как
применение упрощённого способа вычисления
погрешностей может привести к большим ошибкам.
Конечно же, этот эксперимент совершенно
обоснован, с помощью него можно найти модуль
Юнга. Только следует выбрать те измерения, где l
– l0 достаточно велико, и не забыть
пренебречь малыми слагаемыми при расчёте
погрешности.
6. Определение коэффициента
прямой пропорциональности
В лабораторных работах нередко
встречается ситуация, когда необходимо по
графику определить коэффициент
пропорциональности в зависимости одной величины
от другой. И здесь в учебниках встречаются две
ситуации.
В работе «Определение модуля Юнга» [13]
после нахождения модуля Юнга для измерений с
тремя различными нагрузками учащимся
предлагается найти среднее арифметическое трёх
полученных значений. Такой подход ошибочен, т.к.
каждое значение получено с различными
систематическими погрешностями, т.е. с разной
степенью точности. Нельзя суммировать эти
значения «с одинаковым весом». При подобных
вычислениях в теории ошибок находится сумма этих
значений с разными коэффициентами.
Далее, в работе «Измерение жёсткости
пружины» [7] в аналогичной ситуации совершенно
справедливо отмечено, что, поскольку жёсткость
пружины в каждом из опытов получена при разных
условиях, среднее арифметическое этих значений
находить нельзя. И предлагается найти среднее
значение коэффициента жёсткости по графику как
коэффициент пропорциональности. Однако,
поскольку учащиеся не могут найти погрешность
найденного таким образом коэффициента
пропорциональности, предлагается взять в
качестве этой погрешности погрешность
наихудшего результата. Я считаю, что такой подход
не оправдан. Зачем брать погрешность самого
ненадёжного результата, если сам способ
нахождения коэффициента жёсткости из графика
применяется для того, чтобы определить этот
коэффициент наиболее точно? Думаю, авторы просто
не хотели заострять внимание на этом вопросе.
На мой взгляд, для определения
коэффициента пропорциональности по графику
можно предложить несколько вариантов.
Вариант 1. Самый простой, а потому
пригодный для младших классов. Отмечаем на
графике экспериментальные значения с указанием
погрешности. Обращаем внимание учащихся на то,
что если бы мы не нанесли погрешности на графики,
то провести прямую было бы затруднительно. В 7-м
классе достаточно просто отметить тот факт, что
зависимость между двумя величинами прямо
пропорциональна. Но если всё-таки необходимо
найти значение коэффициента пропорциональности,
можно обойтись без расчёта погрешности, отметив
только, что этот способ (многократные измерения
при различных условиях и построение графика)
используется именно для того, чтобы уменьшить
погрешность результата.
Вариант 2. Чертим прямую, находим
экспериментальную точку, которая лежит ближе
всего к прямой, и именно эту точку и считаем самой
точной. Остаётся вычислить результат для неё по
обычным формулам, рассчитав также и погрешность.
Вариант 3. Самый логичный. Пробуем
провести через точки вместе с их погрешностями
две прямые: с наибольшим и с наименьшим наклоном.
Значения коэффициентов для них и будут верхней и
нижней границами для результата. Зная границы,
рассчитываем среднее значение коэффициента и
погрешность. Данная погрешность неявно будет
содержать в себе как систематическую
погрешность экспериментально измеренных
величин, так и случайную погрешность определения
среднего, но уже с учётом точности каждого
результата. Этот вариант годится для
использования в экспериментах, когда
коэффициент должен быть оценён достаточно точно.
Но он достаточно сложен, поэтому не стоит его
использовать во всех случаях.
Вариант 4. Использование
встроенных программ в калькуляторах или готовых
компьютерных программ для вычисления
коэффициентов по методу наименьших квадратов.
Этот способ пригоден для практикума в старших
классах и/или в классах физматпрофиля. К
сожалению, в такие программы, как правило,
встроен метод наименьших квадратов, не
учитывающий погрешностей экспериментальных
точек. Применение имеет смысл в случаях, когда
погрешности всех точек практически одинаковы
или когда доминирующей является случайная
погрешность. Она и будет учтена.
Какой из этих вариантов выбрать, может
решать сам учитель. К счастью, таких работ
довольно мало. Продемонстрируем все эти варианты
на примере.
-
Возьмём данные эксперимента по
зависимости пути от времени равномерного
движения (машинка из конструктора с
электрическим приводом):
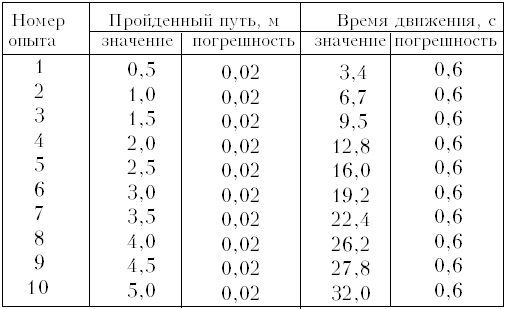
Действуя так, как описано в варианте 1,
строим график (рис. 4).
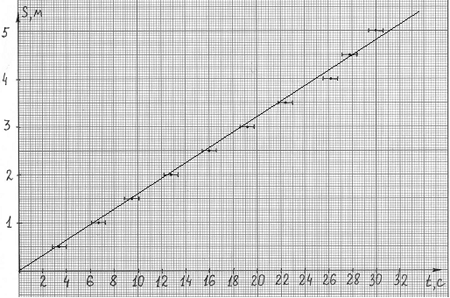
Рис. 4
Так как точек на графике много, можно с
уверенностью утверждать, что 8-я и 10-я точки
являются «выбросами», т.е. измерены небрежно.
Учитывая погрешность эксперимента, можно
провести прямую практически единственным
способом: соответствующая скорость 0,16 м/с. Если
воспользоваться методом наименьших квадратов
(например, встроенной функцией ЛИНЕЙН в
программе MicrosoftExcel), то для коэффициента мы
получим значение 0,158 ± 0,002 м/с (вариант 4).
Для варианта 2 подходит 3-я точка.
Скорость, вычисленная по данным для этой точки,
0,158 м/с. Рассчитаем погрешность: ![]() Так как относительная
Так как относительная
погрешность пути мала по сравнению с
относительной погрешностью времени,
пренебрегаем ею. Абсолютная погрешность
результата: ![]() 0,063
0,063
• 0,158 = 0,010 м/с. То есть скорость, вычисленная в
варианте 2: (0,158 ± 0,010) м/с.
Из приведённого примера видно, что
значения коэффициента пропорциональности
получаются очень близкими. В этом примере
погрешности отдельных измерений были достаточно
малы, а точек, наоборот, было много. Рассмотрим
пример, когда погрешности, напротив, велики, а
количество опытов в силу объективных причин
мало.
-
Найдём плотности пластмассы путём
измерения массы и объёмов тел.
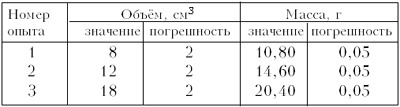
В случае варианта 1 прямую проводим
так, чтобы количество точек над и под прямой было
одинаково (рис. 5), т.е. в данном случае – одна
сверху, одна снизу (прямая 1). Плотность в
этом случае равна 1,23 г/см3.
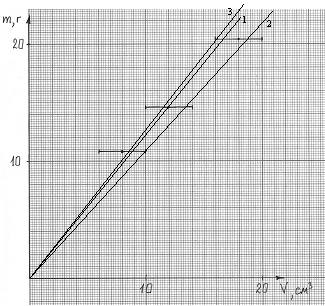
Рис. 5
В случае варианта 2 пригодна 2-я точка.
Для неё значение плотности (1,2 ± 0,2) г/см3.
Вариант 3: проведём прямые 2 и 3.
Для прямой 2 коэффициент пропорциональности
1,09 г/см3 является нижней границей
искомого значения плотности, а для прямой 3
(1,27 г/см3) – верхней. Полусумма этих
значений есть значение плотности (1,18 г/см3),
а полуразность – значение погрешности (0,09 г/см3).
Вариант 4 в данном случае менее
пригоден, т.к. не учитывает больших значений
погрешностей при измерении объёма с помощью
мерного цилиндра, но и в этом варианте плотность
(1,18 ± 0,05) г/см3.
Следует заметить, что в двух последних
примерах на графиках были обозначены только
погрешности вдоль горизонтальной оси, т.к.
погрешности значений второй переменной были
очень малы.
Послесловие
Научиться обрабатывать результаты
экспериментов учащиеся могут, лишь обрабатывая
результаты экспериментов. Это означает, что
помимо стандартного набора лабораторных работ
необходимо проводить много фронтальных и
демонстрационных экспериментов с обработкой
результатов. Это большая работа, и я хочу
пожелать успехов всем учителям, кто вступит на
этот путь или уже стоит на нём.
Литература
1. Анофрикова С.В., Стефанова Г.П.
Практическая методика преподавания физики.
Часть первая. – Астрахань: Издательство
Астраханского ГПИ, 1995.
2. Физика: Под ред. А.А.Пинского: Учебник
для 10 кл. школ и классов с угл. изучением физики. –
М.: Просвещение, 2002.
3. Попова О.Н. Обучение учащихся
выявлению устойчивых связей и отношений между
физическими величинами: Методическое пособие
для учителей физики. – Элиста: Элистинский лицей,
1998.
4. Анофрикова С.В. Азбука
учительской деятельности, иллюстрированная
примерами деятельности учителя физики. Ч. 1.
Разработка уроков. – М.: МПГУ, 2001.
5. Пёрышкин А.В. Физика-8. – М.:
Дрофа, 2004.
6. Громов С.В., Родина Н.А. Физика-8.
– М.: Просвещение, 2000.
7. Кикоин И.К., Кикоин А.К. Физика-10.
Механика. – М.: Просвещение, 2001.
8. Фронтальные лабораторные занятия по
физике в 7–11 классах общеобразовательных
учреждений. Книга для учителя: Под ред. В.А.Бурова,
Г.Г.Никифорова. – М.: Просвещение, Учебная
литература, 1996.
9. Зайдель А.Н. Элементарные оценки
ошибок измерений. – Л.: Наука, 1967.
10. Хорозов С.А. Работа над
ошибками: В кн. «Энциклопедия для детей», т. 16
«Физика», ч. 1 «Биография физики. Путешествие в
глубь материи. Механистическая картина мира». –
М.: Аванта+, 2000.
11. Мякишев Г.Я., Буховцев Б.Б., Сотский
Н.Н. Физика-10. – М.: Просвещение, 2004.
12. Кирик Л.А. Физика-9: Методические
материалы. – М.: Илекса, 2003.
13. Шахмаев Н.М., Шахмаев С.Н., Шодиев
Д.Ш. Физика-10. – М.: Просвещение, 1994.
МЕДИЦИНСКАЯ
СТАТИСТИКА
Под статистикой
понимают:
+А. Самостоятельную
общественную науку, изучающую
количественную сторону массовых
общественных явлений в неразрывной
связи с их качественной стороной;
-Б. Научную дисциплину
по сбору, обработке и хранению информации,
характеризующую количественные
закономерности общественных явлений;
-В. Научную
дисциплину, объединяющую математические
методы, применяемые при сборе, обработке
и анализе информации.
Статистический
метод в медицине и здравоохранении
применяется для:
+А. Изучения
общественного здоровья и факторов, его
определяющих;
+Б. Изучения
состояния и деятельности органов и
учреждений здравоохранения;
+В. Планирования
научных исследований, обработки и
анализа полученных результатов.
1-ый этап проведения
статистического исследования включает:
-А. Сбор материала;
+Б. Составление
плана и программы исследований;
-В. Статистическая
обработка данных;
-Д. Анализ и выводы.
План статистического
исследования включает:
+А. Определение
места проведения исследования;
-Б. Выбор единицы
наблюдения;
+В. Установление
сроков проведения исследования;
-Г. Составление
макетов статистических таблиц.
На каком этапе
статистического исследования создаются
макеты статистических таблиц:
+А. При составлении
программы исследования;
-Б. На этапе сбора
материала;
-В. На этапе
статистической обработки материалов;
-Г. При проведении
анализа результатов.
Основными методами
формирования выборочной совокупности
являются все, кроме:
-А. Типологического;
-Б. Механического;
+В. Целевого;
-Г. Случайного.
Количественная
репрезентативность выборочной
совокупности обеспечивается за счет:
-А. 10-ти процентной
выборки из генеральной совокупности;
-Б. 50-ти процентной
выборки;
+В. Выборки,
включающей достаточное число наблюдений
(рассчитывается по специальным формулам).
К какому виду
статистического наблюдения относится
регистрация рождаемости и смертности:
-А. Единовременное;
+Б. Сплошной;
+В. Текущее;
-Г. Выборочный.
Какие из ниже
перечисленных способов наблюдения при
сборе информации о состоянии здоровья
населения являются более объективными:
-А. Опрос;
-Б. Анкетирование;
+В. Выкопировка
данных из медицинской документации.
К единовременному
наблюдению относится:
-А. Регистрация
рождений;
+Б. Перепись
населения;
-В. Регистрация
браков;
-Г. Регистрация
заболеваний;
+Д. Регистрация
численности и состава больных в стационаре
на определенную дату.
Текущим наблюдением
является:
+А. Регистрация
случаев смерти;
-Б. Перепись
населения;
+В. Регистрация
случаев рождений;
+Г. Регистрация
случаев обращения в поликлинику.
Для экспертной
оценки качества и эффективности
медицинской помощи в женской консультации
отобрана каждая десятая «Индивидуальная
карта беременной и родильницы».
Выборка является:
+А. Механической;
-Б. Гнездовой
(серийный отбор).
Программа
статистического исследования включает:
+А. Составление
программы сбора материала;
+Б. Составление
программы анализа;
-В. Определение
объекта исследования;
-Г. Определение
исполнителей исследования.
Выбор единицы
наблюдения зависит от:
-А. Программы
исследования;
-Б. Плана исследования;
+В. От цели и задач
исследования.
Из перечисленных
видов статистических таблиц наиболее
информативной является:
-А. Простая таблица;
-Б. Групповая
таблица;
+В. Комбинационная
таблица.
Единица наблюдения
— это:
+А. Первичный
элемент статистической совокупности,
являющийся носителем учетных признаков,
подлежащих регистрации;
-Б. Каждый признак
явления, подлежащего регистрации.
Два участковых
врача составили возрастную группировку
обслуживаемого контингента населения.
Какой из врачей сделал это правильно:
+А. До 20 лет, 20 — 39
лет, 40 — 59 лет, 60 лет и старше;
-Б. До 20 лет, 20 — 40
лет, 40 — 60 лет, старше 60 лет.
Типологические
группировки могут включать следующие
признаки:
+А. Пол;
-Б. Рост;
-В. Массу тела;
+Г. Диагноз;
+Д. Профессию.
Заболеваемость
вирусным гепатитом А в районе N.
в текущем году составила 6,0 на 10 000
населения. Указанный показатель является:
-А. Экстенсивным;
+Б. Интенсивным;
-В. Показателем
соотношения;
-Г. Показателем
наглядности.
Какие показатели
позволяют демонстрировать изменения
явления во времени или по территории
без раскрытия истинных размеров этого
явления:
-А. Экстенсивные;
-Б. Интенсивные;
-В. Соотношения;
+Г. Наглядности.
Обеспеченность
врачами населения города N
составляет 36,0 на 10 000 населения. Этот
показатель является:
-А. Экстенсивным;
-Б. Интенсивным;
+В. Показателем
соотношения;
-Г. Показателем
наглядности.
Экстенсивные
показатели могут быть представлены
следующими видами диаграмм:
-А. Линейными;
+Б. Секторными;
-В. Столбиковыми;
+Г. Внутристолбиковыми;
-Д. Картограммами.
Интенсивные
показатели могут быть представлены
следующими видами диаграмм:
+А. Столбиковыми;
-Б. Секторными;
+В. Линейными;
+Г. Картограммами.
К экстенсивным
показателям относятся:
-А. Показатели
рождаемости;
+Б. Распределение
числа врачей по специальностям;
-В. Показатели
младенческой смертности;
+Г. Распределение
умерших по причинам смерти.
К интенсивным
показателям относятся все, кроме:
-А. Показателя
смертности;
+Б. Структуры
заболеваний по нозологическим формам;
+В. Обеспеченности
населения врачами;
-Г. Показателя
заболеваемости.
Вариационный
ряд — это:
-А. Ряд чисел,
отражающих частоту (повторяемость)
цифровых значений изучаемого признака;
-Б. Ряд цифровых
значений различных признаков;
+В. Ряд числовых
измерений признака, расположенных в
ранговом порядке и характеризующихся
определенной частотой.
Средняя
арифметическая — это:
-А. Варианта с
наибольшей частотой;
-Б. Варианта,
находящаяся в середине ряда;
+В. Обобщающая
величина, характеризующая размер
варьирующего признака в совокупности.
Что показывает
среднеквадратическое отклонение:
-А. Разность между
наибольшей и наименьшей вариантой ряда;
+Б. Степень
колеблемости вариационного ряда;
-В. Обобщающую
характеристику размера изучаемого
признака.
Для чего применяется
коэффициент вариации:
-А. Для определения
отклонения вариант от среднего результата;
+Б. Для сравнения
степени колеблемости вариационных
рядов с разноименными признаками;
-В. Для определения
ошибки репрезентативности.
При нормальном
распределении признака в пределах М±2σ
будет находиться:
-А. 68 % вариаций;
+Б. 95 % вариаций;
-В. 99 % вариаций.
Средняя ошибка
средней арифметической величины (ошибка
репрезентативности) — это:
-А. Средняя разность
между средней арифметической и вариантами
ряда;
+Б.
Величина, на которую полученная средняя
величина выборочной совокупности
отличается от среднего результата
генеральной cовокупности;
-В. Величина, на
которую в среднем отличается каждая
варианта от средней арифметической.
Средняя ошибка
средней арифметической величины прямо
пропорциональна:
-А. Числу наблюдений;
-Б. Частоте изучаемого
признака в вариационном ряду;
+В. Показателю
разнообразия изучаемого признака.
Средняя ошибка
средней арифметической величины обратно
пропорциональна:
+А. Числу наблюдений;
-Б. Показателю
разнообразия изучаемого признака;
-В. Частоте изучаемого
признака.
Размер ошибки
средней арифметической величины
зависит от:
-А. Типа вариационного
ряда;
+Б. Числа наблюдений;
-В. Способа расчета
средней;
+Г. Разнообразия
изучаемого признака.
Разность
между сравниваемыми величинами (средними,
относительными) при большом числе
наблюдений (n30)
считается существенной (достоверной),
если:
-А. t равно 1,0;
-Б. t больше 1,0 и
меньше 2,0;
+В. t больше или
равно 2,0.
С увеличением
объема выборки ошибка репрезентативности:
-А. Увеличивается;
+Б. Уменьшается;
-В. Остается
постоянной.
Малой выборкой
считается та совокупность, в которой:
-А. число наблюдений
меньше или равно 100;
+Б. число наблюдений
меньше или равно 30;
-В. число наблюдений
меньше или равно 40.
Доверительный
интервал — это:
-А. Интервал, в
пределах которого находятся не менее
68 % вариант, близких к средней величине
данного вариационного ряда;
+Б. Пределы возможных
колебаний средней величины (показателя)
в генеральной совокупности;
-В. Разница между
максимальной и минимальной вариантами
вариационного ряда.
Минимально
достаточной для медицинских статистических
исследований является вероятность
безошибочного прогноза:
-А. 68 %;
-Б. 90 %;
+В. 95 %;
-Г. 99 %.
При
оценке достоверности разности полученных
результатов исследования разность
является существенной (достоверной),
если при n
30
величина t
равна:
-А. 1,0;
-Б. 1,5;
+В. 2,0;
+Г. 3 и более.
Величина ошибки
репрезентативности средней величины
прямо пропорциональна:
-А.
Числу наблюдений (n);
+Б. Величине
среднеквадратического отклонения
(сигме).
Какой
степени вероятности соответствует
доверительный интервал M2
m (n
30):
-А. 68,3 %;
+Б. 95,5 %;
-В. 99,7 %.
Оценка достоверности
полученного значения критерия Стьюдента
(t) для малых выборок производится:
-А. По специальной
формуле;
-Б. По принципу:
если t = 2, то P = 95%;
+В. По таблице.
Чему
равно значение критерия Стьюдента (t)
при степени вероятности безошибочного
прогноза P=95,5 %, (n 30):
-А.
t
= 1,0
+Б.
t
= 2,0
-В. t = 3 и более.
При проведении
корреляционного анализа необходимо
учитывать следующие параметры:
-А. Направление
связи между признаками, её силу и ошибку
репрезентативности;
-Б. Направление
связи между признаками, её силу, ошибку
репрезентативности и величину коэффициента
вариации;
+В. Направление
связи между признаками, её силу, ошибку
репрезентативности и величину критерия
достоверности.
При следующих
условиях применяется только коэффициент
ранговой корреляции:
+А. Когда нужны
лишь ориентировочные данные о наличии
связи;
+Б. Когда ряды
распределения имеют только атрибутивные
признаки;
-В. Когда ряды
распределения взаимосвязанных признаков
имеют количественное выражение;
+Г. Когда ряды
распределения взаимосвязанных признаков
имеют открытые варианты;
+Д. Когда ряды
распределения имеют как количественное
выражение, так и атрибутивные признаки.
Коэффициент
корреляции по методу квадратов применяется
только при следующих условиях:
-А. Когда нужны
лишь ориентировочные данные о наличии
связи;
+Б. Когда ряды
распределения величины взаимосвязанных
признаков имеют только закрытые варианты;
+В. Когда ряды
распределения взаимосвязанных признаков
имеют количественное выражение;
+Г. Когда нужны
точные данные о наличии связи;
-Д. Когда ряды
распределения имеют как количественное
выражение, так и атрибутивные признаки.
Между какими из
ниже перечисленных признаков может
устанавливаться корреляционная связь:
+А. Ростом и массой
тела у детей;
+Б. Содержанием
кислорода в клетках крови и уровнем
осмотического давления;
-В. Уровнем
систолического и диастолического
давления;
+Г. Частотой случаев
хронических заболеваний и возрастом.
Коэффициент
корреляции между уровнем шума и снижением
слуха с учетом стажа у рабочих
механосборочного цеха равен
rxy + 0,91. Установленная
связь:
-А. Обратная и
слабая;
-Б. Обратная и
сильная;
-В. Прямая и слабая;
+Г. Прямая и сильная.
Для оценки
достоверности полученного значения
коэффициента корреляции используют:
+А. Таблицы
стандартных коэффициентов корреляции
для разных степеней вероятности;
+Б. Ошибку
коэффициентов корреляции;
-В. Оценку
достоверности разности результатов
статистического исследования.
Укажите первый
этап вычисления стандартизованных
показателей прямым методом:
-А. Выбор стандарта;
-Б. Расчет «ожидаемых
чисел»;
+В. Расчет общих и
погрупповых интенсивных показателей;
-Г. Сравнение общих
интенсивных и стандартизованных
показателей;
-Д. Расчет общих
стандартизованных показателей.
Какие статистические
методы позволяют оценивать достоверность
результатов, полученных при выборочных
исследованиях:
-А. Корреляция;
+Б. Определение
доверительных границ;
-В. Стандартизация;
+Г. Оценка
достоверности разности результатов.
Для установления
силы и характера связи между признаками
нужно найти:
-А. Среднеквадратическое
отклонение;
+Б. Коэффициент
корреляции;
-В. Критерий
достоверности;
-Г. Стандартизованные
показатели.
При сравнении
интенсивных показателей, полученных
на однородных по своему составу
совокупностях, необходимо применять:
-А. Метод корреляции;
-Б. Метод
стандартизации;
+В. Оценку
достоверности разности полученных
показателей.
Оценка достоверности
различий в результатах исследования
проводится с помощью:
-А. Коэффициента
корреляции (rxy);
-Б. Коэффициента
вариации (Cv);
+В. Критерия
Стьюдента (t).
Что такое
динамический ряд:
-А. Ряд числовых
измерений определенного признака,
отличающихся друг от друга по своей
величине, расположенных в ранговом
порядке;
+Б. Ряд, состоящий
из однородных сопоставимых величин,
характеризующих изменения какого-либо
явления во времени;
-В. Ряд величин,
характеризующих результаты исследований
в разных регионах.
Уровни динамического
ряда могут быть представлены:
+А. Абсолютными
величинами;
+Б. Средними
величинами;
+В. Относительными
величинами.
Способы вырвнивания
динамического ряда:
+А. Укрупнение
интервалов;
+Б. Вычисление
групповой средней;
-В. Вычисление
коэффициента вариации;
+Г. Вычисление
скользящей средней;
+Д. Использование
метода наименьших квадратов.
Основными
показателями динамического ряда являются
все, кроме:
-А. Темпа роста;
-Б. Абсолютного
прироста;
-В. Темпа прироста;
+Г. Сигмального
отклонения;
-Д. Среднего темпа
прироста.
В какую таблицу
может быть сведена информация,
представленная в виде следующих признаков
«подлежащее и взаимосвязанные между
собой сказуемые»:
-А. Групповая;
+Б. Комбинационная;
-В. Простая;
-Г. Смешанная.
Укажите признаки,
соответствующие типологическому виду
группировки:
+А. Пол: мужской,
женский;
+Б. Диагноз: ИБС,
стенокардия, инфаркт миокарда;
-В. Длительность
заболевания: 1-5 лет, 6-10 лет, более 10 лет;
-Г. Возраст: до 20
лет, 21-30 лет, 31-40 лет, старше 40 лет.
Укажите признаки
атрибутивного характера:
+А. Заболевание
+Б. Исход заболевания
-В. Длительность
заболевания
-Г. Дозы лекарства
+Д. Группа инвалидности
Динамический
ряд – это:
-А. Значения
количественного признака (варианты),
расположенные в определенном порядке
и отличающиеся друг от друга по своему
значению;
+Б. Ряд, состоящий
из однородных сопоставимых значений
признака, характеризующих изменение
какого-либо явления (процесса) во
времени;
-В. Атрибутивные
значения признака, характеризующие
качественное состояние явления в
динамике.
Динамический
ряд может быть представлен:
+А. Абсолютными
величинами;
+Б. Средними
величинами;
+В. Относительными
величинами.
Для сравнения
нескольких динамических рядов с разными
исходными уровнями необходимо рассчитывать
показатель динамического ряда:

Концепция репрезентативности часто встречается в статистических отчетах и при подготовке выступлений и отчетов. Пожалуй, без него сложно представить какое-либо представление информации для ознакомления.
Содержание
- 1 Репрезентативность — что это?
- 2 Другие определения
- 3 Репрезентативная выборка
- 4 Вероятностная выборка
- 5 Вероятностные выборки
- 6 Выборка потребителей
- 7 Размер выборки
- 8 Понятие ошибки репрезентативности
- 9 Виды ошибок
- 10 Преднамеренные и непреднамеренные ошибки репрезентативности
- 11 Валидность, надежность, репрезентативность. Расчет ошибок
- 12 Репрезентативные системы
Репрезентативность — что это?

Репрезентативность отражает степень, в которой выбранные объекты или части соответствуют содержанию и значению набора данных, из которого они были выбраны.
Другие определения
Репрезентативность можно понимать в разных контекстах. Но по своему смыслу репрезентативность — это соответствие характеристик и свойств выбранных единиц генеральной совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Кроме того, репрезентативность информации определяется как способность данных выборки представлять параметры и свойства совокупности, которые важны с точки зрения проводимых исследований.
Репрезентативная выборка
Принцип выборки заключается в выборе наиболее важных свойств, которые точно отражают общую совокупность данных. Для этого используются различные методы, позволяющие получить точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качество всех данных.
Таким образом, нет необходимости изучать весь материал, но достаточно учесть выборочную репрезентативность. Что это? Это набор отдельных данных, чтобы получить представление об общей массе информации.
В зависимости от метода они делятся на вероятностные и маловероятные. Вероятностный — это выборка, которая создается путем вычисления наиболее важных и интересных данных, которые в будущем будут репрезентативными для генеральной совокупности. Это осознанный выбор или случайная выборка, однако оправданная своим содержанием.
Маловероятно — это одна из разновидностей случайной выборки, составленной по принципу обычной лотереи. В этом случае мнение лица, взявшего такую пробу, не принимается во внимание. Используется только слепая жребий.
Вероятностная выборка
Вероятностные выборки также можно разделить на несколько типов:
- Один из самых простых и понятных принципов — нерепрезентативная выборка. Например, этот метод часто используется при проведении социальных опросов. При этом участники опроса не выбираются из общей массы по каким-либо конкретным критериям, а информация берется от первых 50 человек, принявших участие.
- Выборка вероятностей — это еще одна разновидность выборки невероятности, которая часто используется для исследования больших наборов данных. Для этого используется множество условий и правил. Выбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что будет опрошено 100 человек, но при составлении статистического отчета будет учитываться только мнение определенного количества людей, которые будут соответствовать установленным требованиям.
- Преднамеренные выборки отличаются тем, что они имеют ряд требований и условий для отбора, но все же полагаются на совпадения, не преследуя цели получения хорошей статистики.
Вероятностные выборки
Для вероятностных выборок рассчитывается ряд параметров, которым будут соответствовать объекты в выборке, и среди них различными способами могут быть выбраны именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Эти методы расчета требуемых данных могут быть:
- Простая случайная выборка. Он заключается в том, что среди выделенного сегмента методом полностью случайной лотереи выбирается необходимый объем данных, который будет репрезентативной выборкой.
- Систематическая и случайная выборка позволяет составить систему расчета необходимых данных на основе случайно выбранного сегмента. Итак, если первое случайное число, указывающее порядковый номер данных, выбранных из общей совокупности, равно 5, следующими данными для выбора могут быть, например, 15, 25, 35 и так далее. Этот пример ясно объясняет, что даже случайный выбор может быть основан на систематических вычислениях требуемых входных данных.
Выборка потребителей
Осмысленная выборка — это способ взглянуть на каждый отдельный сегмент, и на основе его оценки составляется генеральная совокупность, отражающая характеристики и свойства всей базы данных. Таким образом, собирается больше данных, отвечающих требованиям репрезентативной выборки. Легко выбрать набор параметров, которые не будут включены в общее количество, без потери качества выбранных данных, представляющих генеральную совокупность. Таким образом определяется репрезентативность результатов исследования.
Размер выборки
Не последняя проблема, которую необходимо решить, — это размер выборки для репрезентативной репрезентативности населения. Размер выборки не всегда зависит от количества источников в генеральной совокупности. Однако репрезентативность выборки напрямую зависит от того, на сколько сегментов в конечном итоге следует разделить результат. Чем больше таких сегментов, тем больше данных включается в итоговую выборку. Если результаты требуют общих обозначений и не требуют конкретики, то в результате выборка становится меньше, поскольку, не вдаваясь в детали, информация представлена более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Репрезентативная систематическая ошибка — это конкретное несоответствие между характеристиками населения и данными выборки. При проведении выборочного исследования невозможно получить абсолютно точные данные, как при полном изучении генеральных популяций и выборки, представленной только частью информации и параметров, в то время как более детальное изучение возможно только при изучении всей совокупности численность населения. Поэтому некоторые ошибки и ошибки неизбежны.
Виды ошибок
При составлении репрезентативной выборки возникают некоторые ошибки:
- Случайный.
- Стандарт.
- Не намеренно.
- Систематический.
- Предел.
- Умышленное.
Причиной появления случайных ошибок может быть прерывистый характер исследования генеральной совокупности. Обычно ошибка случайной репрезентативности незначительна по величине и характеру.
Между тем систематические ошибки возникают, когда нарушаются правила отбора данных из генеральной совокупности.
Средняя ошибка — это разница между средним значением выборки и основной совокупностью. Это не зависит от количества единиц в выборке. Он обратно пропорционален размеру выборки. Таким образом, чем больше объем, тем меньше среднее значение ошибки.
Предельная ошибка — это наибольшая возможная разница между средним значением выполненной выборки и всей генеральной совокупностью. Эта ошибка характеризуется как максимум возможных ошибок в данных условиях их возникновения.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки искажения данных могут быть преднамеренными или непреднамеренными.
Итак, причины появления преднамеренных ошибок — это подход к отбору данных с использованием метода выявления трендов. Непреднамеренные ошибки возникают и на этапе подготовки выборочного наблюдения, формирования репрезентативной выборки. Чтобы избежать таких ошибок, необходимо создать хорошую основу выборки для списков единиц выборки. Он должен полностью соответствовать целям выборки, быть надежным и охватывать все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок

Расчет ошибки репрезентативности (Mm) среднего арифметического (M).
Стандартное отклонение: размер выборки (> 30).
Репрезентативная ошибка (Мр) и относительная величина (Р): размер выборки (n> 30).
В случае, если необходимо изучить совокупность, где размер выборки невелик и менее 30 единиц, количество наблюдений уменьшится на одну единицу.
Величина ошибки прямо пропорциональна размеру выборки. Репрезентативность информации и расчет степени возможности составления точного прогноза отражает определенное значение предельной погрешности.
Репрезентативные системы
В процессе оценки представления информации используется не только репрезентативная выборка, но и лицо, получающее информацию, также использует репрезентативные системы. Таким образом, мозг обрабатывает определенный объем информации, создавая репрезентативную выборку всего потока информации, чтобы качественно и быстро оценить предоставленные данные и понять суть проблемы. Ответьте на вопрос: «Представление — что это?» — В масштабе человеческого сознания это довольно просто. Для этого мозг использует все подчиненные органы чувств, в зависимости от типа информации, которую необходимо изолировать от общего потока. Поэтому проводится различие между:
- Система визуального представления, в которой задействованы органы зрительного восприятия глаза. Людей, которые часто используют эту систему, называют визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Система кинестетической репрезентации — это обработка потока информации путем ее восприятия через обонятельные и тактильные каналы.
- Система слухового представления. Основной используемый орган — слух. Информация, предоставленная в виде аудио- или голосового файла, обрабатывается именно этой системой. Людей, которые лучше всего воспринимают информацию на слух, называют аудиалами.

- Система цифрового представления используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и понимание полученных данных.

Так что же такое репрезентативность? Простая выборка из набора или целостная процедура обработки информации? Мы можем однозначно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая выделить самые тяжелые и наиболее важные из них.
Обратная связь
Ошибка репрезентативности прямо пропорциональна колеблемости ря- да (сигме) и обратно пропорциональна числу наблюдений.
Следовательно, чем больше число наблюдений, (т.е. чем ближе по числу на- блюдений выборочная совокупность к генеральной), тем меньше ошибка репре- зентативности.
Интервал, в котором с заданным уровнем вероятности колеблется истинное значение средней величины или показателя, называется доверительным интер- валом, а его границы — доверительными границами. Они используются для оп- ределения размеров средней или показателя в генеральной совокупности.
Доверительные границы средней арифметической и показателя в генеральной совокупности равны:
М± tm
P± tm, где t — доверительный коэффициент
Доверительный коэффициент ( t )— это число, показывающее, во сколько раз надо увеличить ошибку средней величины или показателя, чтобы при данном числе наблюдений с желаемой степенью вероятности утверждать, что они не выйдут за полученные таким образом пределы.
C увеличением t степень вероятности возрастает.
Т. к. известно, что полученная средняя или показатель при повторных наблю- дениях, даже при одинаковых условиях, в силу случайных колебаний будут отли- чаться от предыдущего результата, теорией статистики установлена степень ве- роятности, с которой можно ожидать, что колебания эти не выйдут за определен- ные пределы. Так, колебания средней в интервале М ± 1m гарантируют ее точность с вероятностью 68,3% (такая степень вероятности не удовлетворяет
исследователей), в интервале М ± 2m — 95,5% (достаточная степень вероятности)
и в интервале М ± 3m — 99,7% (большая степень вероятности).
М± 1 m® 68,3 % М± 2 m® 95,5 % М± 3 m® 99,7 %
Для медико-биологических исследований принята степень вероятности
95% ( t = 2 ), что соответствует доверительному интервалу М ± 2 m.
Это означает, что практически с полной достоверностью (в 95%) можно утверждать, что полученный средний результат (М) отклоняется от ис- тинного значения не больше, чем на удвоенную (М ± 2 m) ошибку.
Конечный результат любого медико-статистического исследования выражает- ся средней арифметической и ее параметрами:
ОЦЕНКА ДОСТОВЕРНОСТИ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН (ПОКАЗАТЕЛЕЙ)
Средняя ошибка показателя также служит для определения пределов его слу- чайных колебаний, т.е. дает представление, в каких пределах может находиться показатель в различных выборках в зависимости от случайных причин. С увели- чением численности выборки ошибка уменьшается.
Мерой достоверности показателя является его средняя ошибка ( m ), ко- торая показывает, на сколько результат, полученный при выборочном исследова- нии, отличается от результата, который был бы получен при изучении всей гене- ральной совокупности.
Средняя ошибка показателя определяется по формуле:
mp =
, где mp — ошибка показателя
р — показатель
q — величина, обратная показателю (100-р, 1000-р и т.д. в зависимости от того, на какое основание рассчитан показатель)
n — число наблюдений
ПРИМЕР: Из стационара выбыло 289 больных, умерло 12.
Показатель летальности: 12 ´100
р = 289 = 4,1%
4,1 ´ (100-4,1)4,1 ´ 95,9
m p= ±Ö 289 = ±Ö 289 = ± 1.16%
Возможные пределы колебаний показателя равняются 4,1% ± 1,16% (Р±mp).
ОЦЕНКА ДОСТОВЕРНОСТИ РАЗНОСТИ СРЕДНИХ И ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН
В научных исследованиях и клинической практике с целью сравнения двух средних величин или показателей (например, для выявления преимуществ одного метода лечения перед другим, сопоставления результатов исследования в кон- трольной и экспериментальной группах, сравнения показателей здоровья двух групп населения и т.п.) возникает необходимость не только определить их раз- ность, но и оценить ее достоверность.
Разность между двумя средними или относительными величинами (показате-
лями), каждая из которых имеет свою ошибку, также имеет свою ошибку.
Средняя ошибка разности ( mразн )вычисляется по формуле:
mразн =± Ö m12 + m22 ,где m1 и m2 — средние ошибки сравниваемых
величин
Т.о., ошибка разности равняется корню квадратному из суммы квадратов ошибок сравниваемых величин.
Мерой достоверности разности двух величин является критерий досто- верности ( критерий Стьюдента — t ):
для средних величин M1 —M2
для относительных величин P1 —P2
где t — критерий достоверности
M1 и M2 — сравниваемые средние р1 и р2 — сравниваемые показатели m12 и m22 — их ошибки
Для медико-биологических исследований принято считать, что если критерий достоверности t ³ 2, то различие двух величин (средних или отно- сительных) следует считать существенным, достоверным, доказанным с ве- роятностью в 95%. Если t < 2 , то различие величин не доказано.
ПРИМЕР. Требуется определить достоверность разности показателей (средний бал успе- ваемости) студентов медицинского института. На лечебном факультете средний балл составил 3,86 ± 0,04 , на педиатрическом — 4,03 ± 0,04.
M1 — M2 4,03 — 3,86 0,17
t = ± Ö m12 + m22 = Ö 0,042 + 0,042 = Ö 0,0032 = 3,0
Таким образом, в данном случае различие между средними величинами следует считать статистически достоверным.
СПЕЦИАЛЬНЫЕ СТАТИСТИЧЕСКИЕ МЕТОДИКИ
МЕТОД СТАНДАРТИЗАЦИИ
Общие показатели интенсивности, полученные на 4 этапе статистического исследования при статистическом анализе, не всегда правильно выявляют зако- номерности изучаемых явлений, так как на их уровень может влиять различие состава сравниваемых совокупностей , в отношении которых эти показатели рас- считаны . При сравнении показателей, характеризующих то или иное явление (за- болеваемость, рождаемость, летальность и т .д) их различия могут определяться не только разным уровнем распространенности этих явлений, но и неоднородно- стью состава сравниваемых совокупностей . Эта неоднородность может быть обусловлена различным возрастным, половым, профессиональным или другим составом совокупностей.
Так, например , при изучении заболеваемости в двух изучаемых коллектива, необходимо учитывать их возрастно-половую структуру.
Статистический метод, при котором можно устранить влияние на результаты исследования различий сравниваемых совокупностей , неоднородных по своему составу, называется методом стандартизации.
Сущность этого метода заключается в том, что сравниваемые явления ис- кусственно ставятся в одинаковые условия относительно группового рас- пределения среды, т.е. совокупности, которые характеризуют анализируе- мые показатели, условно считают одинаковыми.
Результатом проведения этого метода является вычисление стандартизован- ных показателей. Эти показатели, при сопоставлении их с обычными интенсив- ными показателями, позволяют сделать вывод, связаны ли различия в интенсив- ных показателях с неоднородностью составов сравниваемых совокупностей.
Стандартизованные показатели являются условными и не отражают истинных размеров изучаемого явления. Они применяются только для сравне- ния и анализа данной ситуации вследствие того, что рассчитаны они при искусст- венно созданных условиях и не отражают действительного размера явлений.
Существует три метода расчета стандартизованных показателей: прямой, косвенный и обратный косвенному.
При проведении медицинских исследований обычно пользуются прямым методом стандартизации, который состоит из трех этапов.
1. Вычисление погрупповых показателей,т.е. ”истинных”или обычных относительных величин, характеризующих изучаемое явление в двух сравнивае- мых совокупностях. В зависимости от характера исследования это могут быть показатели заболеваемости, инфицированности, травматизма, смертности, и т.д., рассчитанные по группам (по диагнозам, тяжести заболевания, полу, возрасту, месту жительства и т.д.)
2. Вычисление стандарта, т.е. нового искусственного распределения среды в определенном масштабе. За масштаб стандарта берется основание (коэффи- циент), на который рассчитывались показатели на первом этапе: 100,1000,10000 и т.д.
©2015- 2023 pdnr.ru Все права принадлежат авторам размещенных материалов.
Подборка по базе: Исправьте ошибки в построении сложных предложений.docx, тест 1 теория и методика основы физического воспитания.docx, Найдите и исправьте ошибки в словоупотреблении.docx, тест 1 теория и методика основы физического воспитания.docx, № Правильно ли сформулированы следующие вопросы. Найдите ошибки., Памятка для родителей Как помочь ребенку победить ошибки 1.doc, Конспект урока по алгебре в 9 классе на тему _Абсолютная и относ, математика — Какие ошибки допускают младшие школьники при делени, Речевые ошибки.docx, Инструкция по устранению ошибки со входом в phpMyAdmin (1).docx
Ч а с т ь I
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК
Абсолютная и относительная ошибки
Никакую физическую величину невозможно измерить абсолютно точно: как бы тщательно ни был поставлен опыт, измеренное значение величины х будет отличаться от ее истинного значения Х. Разница между этими значениями представляет собой абсолютную ошибку (или абсолютную погрешность*) измерения х:
х = х – Х. (1)
Абсолютная погрешность является размерной величиной: она выражается в тех же единицах, что и сама измеряемая величина (например, абсолютная погрешность измерения длины выражается в метрах, силы тока – в амперах и т.д.). Как следует из выражения (1), х может быть как положительной, так и отрицательной величиной.
Хотя величина х показывает, насколько измеренное значение отличается от истинного, одной лишь абсолютной ошибкой нельзя полностью характеризовать точность проделанного измерения. Пусть, например, известно, что абсолютная погрешность измерения расстояния равна 1 м. Если измерялось расстояние между географическими пунктами (порядка нескольких километров), то точность такого измерения следует признать весьма высокой; если же измерялись размеры помещения (не превышающие десятка метров), то измерение является грубым. Для характеристики точности существует понятие относительной ошибки (или относительной погрешности) Е, представляющей собой отношение модуля абсолютной ошибки к измеряемой величине:
![]() . (2)
. (2)
Очевидно, что относительная погрешность – величина безразмерная, чаще всего ее выражают в процентах.
При определении ошибок измерений важно иметь в виду следующее. Выражения (1) и (2) содержат истинное значение измеряемой величины Х, которое точно знать невозможно: поэтому значения х и Е в принципе не могут быть рассчитаны точно. Можно лишь оценить эти значения, т.е. найти их приближенно с той или иной степенью достоверности. Поэтому все расчеты, связанные с определением погрешностей, должны носить приближенный (оценочный) характер.
Случайная и приборная погрешности
Разнообразные ошибки, возникающие при измерениях, можно классифицировать как по их происхождению, так и по характеру их проявления.
По происхождению ошибки делятся на инструментальные и методические.
Инструментальные погрешности обусловлены несовершенством применяемых измерительных приборов и приспособлений. Эти погрешности могут быть уменьшены за счет применения более точных приборов. Так, размер детали можно измерить линейкой или штанген-циркулем. Очевидно, что во втором случае ошибка измерения меньше, чем в первом.
Методические погрешности возникают из-за того, что реальные физические процессы всегда в той или иной степени отличаются от их теоретических моделей. Например, формула для периода колебаний математического маятника в точности верна лишь при бесконечно малой амплитуде колебаний; формула Стокса, определяющая силу трения при движении шарика в вязкой жидкости, справедлива только в случае идеально сферической формы и т.д. Обнаружить и учесть методическую погрешность можно путем измерения той же величины совершенно иным независимым методом.
По характеру проявления ошибки бывают систематические и случайные.
Систематическая погрешность может быть обусловлена как приборами, так и методикой измерения. Она имеет две характерные особенности. Во-первых, систематическая погрешность всегда либо положительна, либо отрицательна и не меняет своего знака от опыта к опыту. Во-вторых, систематическую погрешность нельзя уменьшить за счет увеличения числа измерений. Например, если при отсутствии внешних воздействий стрелка измерительного прибора показывает величину х0 , отличную от нуля, то во всех дальнейших измерениях будет присутствовать систематическая ошибка, равная х0 .
Случайная ошибка также может быть как инструментальной, так и методической. Причину ее появления установить трудно, а чаще всего – невозможно (это могут быть различные помехи, случайные толчки, вибрации, неверно взятый отсчет по прибору и т.д.). Случайная погрешность бывает и положительной и отрицательной, причем непредсказуемо изменяет свой знак от опыта к опыту. Значение ее можно уменьшить путем увеличения числа измерений.
Детальный анализ погрешностей измерения представляет собой сложную задачу, для решения которой не существует единого рецепта. Поэтому в каждом конкретном случае этот анализ проводят по-разному. Однако, в первом приближении, если исключена систематическая ошибка, то остальные можно условно свести к следующим двум видам: приборная и случайная.
Приборной погрешностью в дальнейшем будем называть случайную ошибку, обусловленную измерительными приборами и приспособлениями, а случайной – ошибку, причина появления которой неизвестна. Приборную погрешность измерения величины х будем обозначать как х, случайную – как s x.
Оценка случайной погрешности. Доверительный интервал
Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины.
Пусть в результате проделанных измерений получено п значений величины х: х1 , х2 , …, хп . Обозначим через ![]() среднеарифметическое значение
среднеарифметическое значение
![]() . (3)
. (3)
В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:
![]()
При небольшом числе измерений (п 10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение ![]() характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения «величина х имеет значение, в точности равное ![]() » равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).
» равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью (0 < < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3). Половина ширины доверительного интервала представляет собой случайную погрешность s x (рис. 1).

Рис.1
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка s x) зависит от того, насколько сильно отличаются отдельные измерения величины хi от среднего значения ![]() . «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
. «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой , которую находят по формуле
![]() , (4)
, (4)
где ![]() .
.
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:
![]() . (5)
. (5)
Коэффициент пропорциональности tn, называется коэффициентом Стьюдента; он зависит от числа опытов п и доверительной вероятности .
На рис. 1, а, б наглядно показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего (вероятность «накрывания» значения Х более широким интервалом выше). Следовательно, величина tn, должна быть тем больше, чем выше доверительная вероятность .
С увеличением количества опытов среднее значение приближается к истинному; поэтому при той же вероятности доверительный интервал можно взять более узким (см. рис. 1, а,в). Таким образом, с ростом п коэффициент Сьюдента должен уменьшаться. Таблица значений коэффи-циента Стьюдента в зависимости от п и дана в приложениях к настоящему пособию.
Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение принимается равным 0,95.
Расчет случайной погрешности измерения величины х проводится в следующем порядке:
1) вычисляется сумма измеренных значений, а затем – среднее значение величины ![]() по формуле (3);
по формуле (3);
2) для каждого i-го опыта рассчитываются разность между измеренным и средним значениями ![]() , а также квадрат этой разности (отклонения) ( хi)2 ;
, а также квадрат этой разности (отклонения) ( хi)2 ;
3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка по формуле (4);
4) по заданной доверительной вероятности и числу проведенных опытов п из таблицы на с. 149 приложений выбирается соответствующее значение коэффициента Стьюдента tn, и определяется случайная погрешность s x по формуле (5).
Для удобства расчетов и проверки промежуточных результатов данные заносятся в таблицу, три последних столбца которой заполняются по образцу табл.1.
Таблица 1
Номер опыта |
… | х | х | ( х)2 |
| 1 | … | |||
| 2 | … | |||
| … | … | |||
| п | … | |||
| = | = |
В каждом конкретном случае величина х имеет определенный физический смысл и соответствующие единицы измерения. Это может быть, например, ускорение свободного падения g (м/с2), коэффициент вязкости жидкости (Пас) и т.д. Пропущенные столбцы табл. 1 могут содержать промежуточные измеряемые величины, необходимые для расчета соответствующих значений х.
Пример 1. Для определения ускорения а движения тела измерялось время t прохождения им пути S без начальной скорости. Используя известное соотношение ![]() , получим расчетную формулу
, получим расчетную формулу
![]() . (6)
. (6)
Результаты измерений пути S и времени t приведены во втором и третьем столбцах табл. 2. Проведя вычисления по формуле (6), заполним
четвертый столбец значениями ускорения ai и найдем их сумму, которую запишем под этим столбцом в ячейку « = ». Затем рассчитаем среднее значение ![]() по формуле (3)
по формуле (3)
![]() .
.
Таблица 2
| Номер опыта | S,
м |
t,
c |
а,
м/с2 |
а,
м/с2 |
(а)2,
(м/с2)2 |
| 1 | 5 | 2,20 | 2,07 | 0,04 | 0,0016 |
| 2 | 7 | 2,68 | 1,95 | -0,08 | 0,0064 |
| 3 | 9 | 2,91 | 2,13 | 0,10 | 0,0100 |
| 4 | 11 | 3,35 | 1,96 | -0,07 | 0,0049 |
| = | 8,11 | = | 0,0229 |
Вычитая из каждого значения ai среднее, найдем разности ai и занесем их в пятый столбец таблицы. Возводя эти разности в квадрат, заполним последний столбец. Затем рассчитаем сумму квадратов отклонений и запишем ее во вторую ячейку « = ». По формуле (4) определим среднеквадратичную погрешность:
![]() .
.
Задавшись величиной доверительной вероятности = 0,95, для числа опытов п = 4 из таблицы в приложениях (с. 149) выбираем значение коэффициента Стьюдента tn, = 3,18; с помощью формулы (5) оценим случайную погрешность измерения ускорения
s а = 3,180,0437 0,139 (м/с2) .
Способы определения приборных ошибок
Основными характеристиками измерительных приборов являются предел измерения и цена деления, а также – главным образом для электро-измерительных приборов – класс точности.
Предел измерения П – это максимальное значение величины, которое может быть измерено с помощью данной шкалы прибора. Если предел измерения не указан отдельно, то его определяют по оцифровке шкалы. Так, если рис. 2 изображает шкалу миллиамперметра, то его предел измерения равен 100 мА.
Р
ис.2
Цена деления Ц – значение измеряемой величины, соответствующее самому малому делению шкалы. Если шкала начинается с нуля, то
![]() ,
,
где N – общее количество делений (например, на рис. 2 N = 50). Если эта шкала принадлежит амперметру с пределом измерения 5 А, то цена деления равна 5/50 = 0,1 (А). Если шкала принадлежит термометру и проградуирована в С, то цена деления Ц = 100/50 = 2 (С). Многие электроизмерительные приборы имеют несколько пределов измерения. При переключении их с одного предела на другой изменяется и цена деления шкалы.
Класс точности К представляет собой отношение абсолютной приборной погрешности к пределу измерения шкалы, выраженное в процентах:
![]() . (7)
. (7)
Значение класса точности (без символа «%») указывается, как правило, на электроизмерительных приборах.
В зависимости от вида измерительного устройства абсолютная приборная погрешность определяется одним из нижеперечисленных способов.
1. Погрешность указана непосредственно на приборе. Так, на микрометре есть надпись «0,01 мм». Если с помощью этого прибора измеряется, например, диаметр шарика D (лабораторная работа 1.2), то погрешность его измерения D = 0,01 мм. Абсолютная ошибка указывается обычно на жидкостных (ртутных, спиртовых) термометрах, штангенциркулях и др.
2. На приборе указан класс точности. Согласно определению этой величины, из формулы (7) имеем
![]() . (8)
. (8)
Например, для вольтметра с классом точности 2,5 и пределом измерения 600 В абсолютная приборная ошибка измерения напряжения
![]() .
.
3. Если на приборе не указаны ни абсолютная погрешность, ни класс точности, то в зависимости от характера работы прибора возможны два способа определения величины х:
а) указатель значения измеряемой величины может занимать только определенные (дискретные) положения, соответствующие делениям шкалы (например, электронные часы, секундомеры, счетчики импульсов и т.п.). Такие приборы являются приборами дискретного действия, и их абсолютная погрешность равна цене деления шкалы: х = Ц. Так, при измерении промежутка времени t секундомером с ценой деления 0,2 с погрешность t = 0,2 с;

б) указатель значения измеряемой величины может занимать любое положение на шкале (линейки, рулетки, стрелочные весы, термометры и т.п.). В этом случае абсолютная приборная погрешность равна половине цены деления: х = Ц/2. Точность снимаемых показаний прибора не должна превышать его возможностей. Например, при показанном на рис. 3 положении стрелки прибора следует записать либо 62,5 либо 63,0 – в обоих случаях ошибка не превысит половины цены деления. Записи же типа 62,7 или 62,8 не имеют смысла.
Рис.3
4. Если какая-либо величина не измеряется в данном оыте, а была измерена независимо и известно лишь ее значение, то она является заданным параметром. Так, в работе 2.1 по определению коэффициента вязкости воздуха такими параметрами являются размеры капилляра, в опыте Юнга по интерференции света (работа 5.1) – расстояние между щелями и т.д. Погрешность заданного параметра принимается равной половине единицы последнего разряда числа, которым задано значение этого параметра. Например, если радиус капилляра r задан с точностью до сотых долей миллиметра, то его погрешность r = 0,005 мм.
Погрешности косвенных измерений
В большинстве физических экспериментов искомая величина и не измеряется непосредственно каким-либо одним прибором, а рассчитывается на основе измерения ряда промежуточных величин x, y, z,… Расчет проводится по определенной формуле, которую в общем виде можно записать как
и = и( x, y, z,…). (9)
В этом случае говорят, что величина и представляет собой результат косвенного измерения в отличие от x, y, z,…, являющихся результатами прямых измерений. Например, в работе 1.2 коэффициент вязкости жидкости рассчитывается по формуле
![]() , (10)
, (10)
где ш – плотность материала шарика; ж – плотность жидкости; g – ускорение свободного падения; D – диаметр шарика; t – время его падения в жидкости; l – расстояние между метками на сосуде. В данном случае результатами прямых измерений являются величины l, D и t, а коэффициент вязкости – результат косвенного измерения. Величины ш, ж и g представляют собой заданные параметры.
Абсолютная погрешность косвенного измерения и зависит от погрешностей прямых измерений x, y, z…и от вида функции (9). Как правило, величину и можно оценить по формуле вида
![]() , (11)
, (11)
где коэффициенты kx , ky , kz ,… определяются видом зависимостей величины и от x, y, z,… Приведенная ниже табл. 3 позволяет найти эти коэффициенты для наиболее распространенных элементарных функций (a, b, c, n – заданные константы).
Таблица 3
| и(х) | kx |
|
|
|
|
|
|
|
|
На практике зависимость (9) чаще всего имеет вид степенной функции
![]() ,
,
показатели степеней которой k, m, n,… – вещественные (положительные или отрицательные, целые или дробные) числа; С – постоянный коэффициент. В этом случае абсолютная приборная погрешность и оценивается по формуле
![]() , (12)
, (12)
где ![]() – среднее значение величины и;
– среднее значение величины и; ![]() – относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
– относительные приборные погрешности прямых измерений величин x, y, z,… Для подстановки в формулу (12) выбираются наиболее представительные, т.е. близкие к средним значения x, y, z,…
При расчетах по формулам типа (12) необходимо помнить следующее.
1. Измеряемые величины и их абсолютные погрешности (например, х и х) должны быть выражены в одних и тех же единицах.
2. Расчеты не требуют высокой точности вычислений и должны иметь оценочный характер. Так, входящие в подкоренное выражение и возводимые в квадрат величины ( kEx , mEy , nEz ,…) обычно округляются с точностью до двух значащих цифр (напомним, что ноль является значащей цифрой только тогда, когда перед ним слева есть хотя бы одна цифра, отличная от нуля). Далее, если одна из этих величин (например, | kEx | ) по модулю превышает наибольшую из остальных ( | mEy | , | nEz | ,…) более чем в три раза, то можно, не прибегая к вычислениям по формуле (12), принять абсолютную ошибку равной ![]() . Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
. Если же одна из них более чем в три раза меньше наименьшей из остальных, то при расчете по формуле (12) ею можно пренебречь.
Пример 2. Пусть при определении ускорения тела (см. пример 1) путь S измерялся рулеткой с ценой деления 1 мм, а время t – электронным секундомером. Тогда, в соответствии с изложенными в п.3, а, б (с. 13) правилами, погрешности прямых измерений будут равны
S = 0,5 мм = 0,0005 м;
t = 0,01 с.
Расчетную формулу (6) можно записать в виде степенной функции
a( S, t) = 2S 1t – 2 ;
тогда на основании (12) погрешность косвенного измерения ускорения а определится выражением
![]() .
.
В качестве наиболее представительных значений измеренных величин возьмем (см. табл. 2) S 8 м; t 3 с и оценим по модулю относительные приборные ошибки прямых измерений с учетом их весовых коэффициентов:
![]() ;
;
![]() .
.
Очевидно, что в данном случае величиной ES можно пренебречь и принять погрешность а равной
![]()
Пример 3. Вернемся к определению коэффициента вязкости жидкости (работа 1.2). Расчетную формулу (10) можно представить в виде
![]() ,
,
где ![]() . Тогда для оценки приборной погрешности , согласно (12), получим выражение
. Тогда для оценки приборной погрешности , согласно (12), получим выражение
![]() , (13)
, (13)
где ![]() .
.
Пусть расстояние между метками l измерено сантиметровой лентой с ценой деления 0,5 см, диаметр шарика – микрометром, время его падения – электронным секундомером. Тогда l = 0,25 см; D = 0,01 мм; t = 0,01 с. Предположим, что измеренные значения равны: l 80 cм; D 4 мм; t 10 с; ![]() Пас. Оценим величины, входящие в формулу (13):
Пас. Оценим величины, входящие в формулу (13):

Пренебрегая величиной Еt , проведем расчет по формуле (13):
![]() .
.
Полная ошибка. Окончательный результат измерений
В результате оценки случайной и приборной ошибок измерения величины х получено два доверительных интервала, характеризуемые значениями s x и х. Результирующий доверительный интервал характеризуется полной абсолютной ошибкой , которая, в зависимости от соотношения между величинами s x и х, находится следующим образом.
Если одна из погрешностей более чем в три раза превышает другую (например, s x > 3х), то полная ошибка принимается равной этой большей величине (в приведенном примере s x). Если же величины s x и х близки между собой, то полная ошибка вычисляется как
![]() . (14)
. (14)
Запись окончательного результата измерений должна включать в себя следующие обязательные элементы.
1) Доверительный интервал вида
![]()
с указанием значения доверительной вероятности . Величины ![]() и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
и выражаются в одних и тех же единицах измерения, которые выносятся за скобку.
2) Значение полной относительной погрешности
![]() ,
,
выраженное в процентах и округленное до десятых долей.
Полная ошибка округляется до двух значащих цифр. Если полученное после округления число оканчивается цифрами 4, 5 или 6, то дальнейшее округление не производится; если же вторая значащая цифра 1, 2, 3, 7, 8 или 9, то значение округляется до одной значащей цифры (примеры: а) 0,2642 0,26; б) 3,177 3,2 3; в) 7,8310 – 7 810 – 7 и т.д.). После этого среднее значение ![]() округляется с той же точностью.
округляется с той же точностью.
Пример 4. В результате определения ускорения движения тела (примеры 1 и 2) получено среднее значение ускорения ![]() = 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
= 2,03 м/с2, случайная ошибка s а = 0,139 м/с2 с доверительной вероятностью = 0,95 и приборная ошибка а = 0,0136 м/с2. Так как а более чем в десять раз меньше s а, то ею можно пренебречь и принять округленную полную абсолютную погрешность равной s а 0,14 м/с2. Оценим относительную ошибку:
![]()
и запишем окончательный результат измерений:

![]()
![]()
Пример 5. Пусть при определении скорости звука и (лабораторная работа 4.2) получены следующие результаты: среднее значение ![]() = 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение
= 343,3 м/с; случайная погрешность s и = 8,27 м/с при = 0,90; абсолютная приборная погрешность и = 1,52 м/с. Очевидно, что и в данном случае величиной и можно пренебречь по сравнению с s и, и расчет по формуле (14) не требуется. Полная ошибка после округления равна s и 8 м/с; округленное среднее значение ![]() 343 м/с. Полная относительная погрешность
343 м/с. Полная относительная погрешность
![]() .
.
Окончательный результат измерений имеет вид

![]()
![]()
Пример 6. При определении длины волны лазерного излучения (работа 5.1) получено: ![]() при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
при = 0,95; = 1,8610 — 5 мм. В данном случае значения приборной и случайной погрешностей близки между собой, поэтому полную ошибку найдем по формуле (14):
![]() .
.
Округленное среднее будет равно ![]() мм. Оценим полную относительную ошибку
мм. Оценим полную относительную ошибку
![]()
и запишем окончательный результат:

![]()
Е = 4,4 %.
* Термины «ошибка» и «погрешность» применительно к измерениям имеют один и тот же смысл.
И снова о погрешностях
Окончание. См. № 15/07
Д.А.ИВАШКИНА,
лицей г. Троицка, Московская обл.
aivashkin@mail.ru
И снова о погрешностях
4. Учёт случайных погрешностей при
прямых измерениях
Если, проведя одно и то же измерение
несколько раз, вы видите, что результат остаётся
одним и тем же, то случайные погрешности
эксперимента малы, их не следует учитывать. Но
если при повторении измерения получаются разные
значения, то следует взять среднее значение из
серии измерений:
![]()
где n – число измерений. Как
узнать, какова погрешность результата? Логично, и
ученики сами обычно предлагают это, определить
среднее отклонение результата от среднего
значения. Полученная величина носит название средней
арифметической ошибки: ![]() Она показывает, на сколько в
Она показывает, на сколько в
среднем каждое измеренное значение отклоняется
от среднего значения. Но эта величина слабо
зависит от количества проведённых измерений. В
чём же тогда смысл многократных измерений?
Для среднеквадратичной погрешности,
которая определяется немного сложнее:
![]()
есть простое правило: средняя
квадратичная погрешность среднего
арифметического равна средней квадратичной
погрешности отдельного результата, делённой на
корень квадратный из числа измерений: ![]() Из формулы ясно,
Из формулы ясно,
что с увеличением числа измерений случайная
погрешность среднего значения уменьшается.
Поэтому необходимо проводить столько измерений,
чтобы случайная погрешность стала меньше
значения систематической погрешности данного
измерения.
К сожалению, в лабораторных работах и
при любых других экспериментах в школе провести
достаточное количество измерений невозможно в
силу нехватки времени. Как поступать, может
решить сам учитель. На мой взгляд, для нахождения
средней арифметической погрешности среднего
значения можно использовать формулу,
аналогичную формуле для средней квадратичной
ошибки: ![]()
Хотя эта формула и неверна, она
помогает понять смысл проведения большого числа
измерений. Использоваться же она будет всего в
нескольких работах, и, следовательно, нет нужды
специально обучать нахождению погрешности
среднего значения. Зато, получив в этих работах
случайную погрешность меньше погрешности
систематической, ученик запомнит, что каждое
измерение следует производить несколько раз при
малейшем подозрении, что в данном эксперименте
имеется случайная погрешность. Как правило, уже
при пяти измерениях достигается необходимая
малость случайной погрешности по сравнению с
систематической.
5. Определение погрешности
результата косвенных измерений
К определению погрешности результата
косвенных измерений учащиеся готовы, на мой
взгляд, уже к 8-му классу. В зависимости от уровня
класса впервые метод границ [1, 12] можно
применить или в работе по сравнению количеств
теплоты при смешивании воды, или при нахождении
сопротивления проводника. Поясню на примерах.
-
Допустим, при нагревании холодной
воды в процессе смешивания мы имеем следующие
результаты измерений:
– температура холодной воды t1
= (16,0 ± 1,5) °С;
– температура смеси t = (43,0 ± 1,5) °С;
– объём холодной воды V1 = (80
± 2) мл = (80 ± 2) • 10–6 м3.
Получаем количество теплоты,
полученное холодной водой:
Q = 4190 Дж/(кг • °С) • 1000 кг/м3
• 80 • 10–6 м3 ![]() (43 – 16) °С = 9050,4 Дж.
(43 – 16) °С = 9050,4 Дж.
(1)
Возникает вопрос: а какова погрешность
полученного значения? Другими словами, на
сколько мы можем ошибиться, если точные значения
не равны измеренным, а лежат где-то в интервале,
даваемом погрешностью? Например, начальная
температура воды может быть равна 16,5 °С, 17,0 °С и
т.д. Тогда вычисленное количество теплоты будет
меньше. Логично посмотреть, на сколько мы можем
ошибиться по максимуму. Максимальное количество
теплоты получится, если взять для всех
сомножителей максимальные значения, т.е. верхние
границы интервалов значений с погрешностью, для
уменьшаемого взять верхнюю границу значения, а
для вычитаемого – нижнюю:
Qв = 4190 Дж/(кг • °С) • 1000
кг/м3 • 82 • 10–6 м3 ![]() (44,5 – 14,5)°С = 10 307,4 Дж.
(44,5 – 14,5)°С = 10 307,4 Дж.
Аналогично вычисляем нижнюю границу
значения количества теплоты:
Qн = 4190 Дж/(кг • °С) • 1000
кг/м3 • 78 • 10–6 м3 ![]() (41,5 – 17,5) °С = 7843,68
(41,5 – 17,5) °С = 7843,68
Дж.
В данных пределах и лежит искомое
значение. Чтобы сравнивать методом интервалов
это значение с количеством теплоты, отданным
горячей водой, надо округлить значения верхней и
нижней границ. Лучше это сделать, оценив
абсолютную погрешность найденного значения
количества теплоты.

Рис. 2
Из рис. 2 видно, что
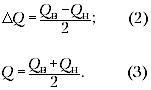
Найденное выше значение (1) близко к (3),
поэтому его не стоит находить ещё раз. А вот для
погрешности найдём с помощью (2):
![]() (две
(две
значащие цифры, т.к. первая «1»). Поэтому
количество теплоты, полученное холодной водой,
можно округлить: Qполуч = 9000 Дж ±
1200 Дж (т.е. между 7800 Дж и 10 200 Дж). Если количество
теплоты, отданное горячей водой, лежит между 8500
Дж и 11 500 Дж (Qотдан = 10 000 Дж ± 1500 Дж), то
можно видеть, что эти количества теплоты
совпадают в пределах погрешности эксперимента
(рис. 3).

Рис.3
-
Определение сопротивления резистора.
Пусть измеренные значения напряжения и силы тока
следующие:
– U = 2,60 В ± 0,15 В (инструментальная
погрешность 0,15 В; погрешность отсчёта может быть
взята равной 0,05 В, т.е. в 3 раза меньше
инструментальной, поэтому ею можно пренебречь);
– I = 1,2 А ± 0,1 А (инструментальная
погрешность 0,05 А, погрешность отсчёта 0,05 А).
Тогда для сопротивления получаем:
![]()
Но на самом резисторе написано: «2 ± 0,1 ![]() ». Получается, что
». Получается, что
мы неверно определили сопротивление? Рассчитаем
погрешность нашего определения значения
сопротивления:
Uв = 2,75 В; Uн = 2,45 В; Iв
= 1,3 А, Iн = 1,1 А;
![]()
Полученное экспериментально значение
сопротивления R = (2,2 ± 0,3) Ом совпадает в
пределах погрешности со значением R = (2,0 ± 0,1)
Ом, указанным на резисторе.
С помощью метода границ можно вывести
и формулы для погрешности при обобщении темы
«Определение погрешности косвенных измерений»,
но уже в 9-м классе.
Определение погрешности разности. Пусть
А = В – С. Рассчитаем погрешность А в
общем виде:
Ав = Вв – Сн
= (В + ![]() В)
В)
– (С – ![]() С)
С)
= (В – С) + (![]() В
В
+ ![]() С);
С);
Ан = Вн – Св
= (В – ![]() В)
В)
– (С + ![]() С)
С)
= (В – С) – (![]() В
В
+ ![]() С);
С);
![]()
Полученное очень важно: в некоторых
работах в формулах для вычисления результата
встречается разность двух близких по значению
величин, что приводит к большой относительной
погрешности результата.
-
В cтарой работе «Определение модуля
Юнга резины» [11] удлинение резинового жгута
находилось как разность его результирующей и
начальной длин. Если условия опыта таковы, что
эта разность мала, например, составляет 1,5 см, то
относительная погрешность определения разности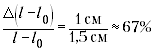 (погрешность
(погрешность
отсчёта взята гораздо меньше инструментальной
погрешности). Ясно, что такое измерение
использовать для определения модуля Юнга
нежелательно, – может получиться погрешность
больше 100%. Лучше увеличить нагрузку на жгут.
Аналогичная проблема возникает в работе
«Измерение ЭДС и внутреннего сопротивления
источника» [2] (одно сопротивление должно быть в
несколько раз больше другого) и др.
Определение погрешности частного
двух величин. Пусть ![]() Рассчитаем погрешность в общем виде:
Рассчитаем погрешность в общем виде:
![]()
Такую формулу трудно запоминать.
Поэтому найдём относительную погрешность
величины А:
![]()
Итак, относительная погрешность
частного равна сумме относительных погрешностей
величин, входящих в него. Такая же формула
получается и для относительной погрешности
произведения.
Важным я считаю не сам процесс расчёта
погрешности. Эти формулы дают мощный инструмент
для оценки обоснованности проведения
эксперимента. При их использовании легко
объяснить, при измерении какой из величин
следует увеличить точность, чтобы получить
лучший результат.
Рассмотрим формулу для нахождения
модуля Юнга: 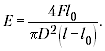
Если воспользоваться для расчёта погрешности
результата методом границ, то неясным останется,
какая из величин в формуле вносит наибольшую
погрешность.
Для нахождения относительной
погрешности результата лучше воспользоваться
формулой:
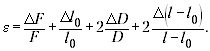
При подстановке значений оказывается,
что слагаемое 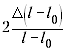
даёт максимальный вклад в сумму, а остальные
слагаемые в несколько раз меньше, так что ими
можно пренебречь. Если l – l0 будет
невелико, то значение относительной погрешности
окажется очень большим, порой выше 100%. Какой
вывод сделают в таком случае ученики?
Такая ситуация – пример того, как
применение упрощённого способа вычисления
погрешностей может привести к большим ошибкам.
Конечно же, этот эксперимент совершенно
обоснован, с помощью него можно найти модуль
Юнга. Только следует выбрать те измерения, где l
– l0 достаточно велико, и не забыть
пренебречь малыми слагаемыми при расчёте
погрешности.
6. Определение коэффициента
прямой пропорциональности
В лабораторных работах нередко
встречается ситуация, когда необходимо по
графику определить коэффициент
пропорциональности в зависимости одной величины
от другой. И здесь в учебниках встречаются две
ситуации.
В работе «Определение модуля Юнга» [13]
после нахождения модуля Юнга для измерений с
тремя различными нагрузками учащимся
предлагается найти среднее арифметическое трёх
полученных значений. Такой подход ошибочен, т.к.
каждое значение получено с различными
систематическими погрешностями, т.е. с разной
степенью точности. Нельзя суммировать эти
значения «с одинаковым весом». При подобных
вычислениях в теории ошибок находится сумма этих
значений с разными коэффициентами.
Далее, в работе «Измерение жёсткости
пружины» [7] в аналогичной ситуации совершенно
справедливо отмечено, что, поскольку жёсткость
пружины в каждом из опытов получена при разных
условиях, среднее арифметическое этих значений
находить нельзя. И предлагается найти среднее
значение коэффициента жёсткости по графику как
коэффициент пропорциональности. Однако,
поскольку учащиеся не могут найти погрешность
найденного таким образом коэффициента
пропорциональности, предлагается взять в
качестве этой погрешности погрешность
наихудшего результата. Я считаю, что такой подход
не оправдан. Зачем брать погрешность самого
ненадёжного результата, если сам способ
нахождения коэффициента жёсткости из графика
применяется для того, чтобы определить этот
коэффициент наиболее точно? Думаю, авторы просто
не хотели заострять внимание на этом вопросе.
На мой взгляд, для определения
коэффициента пропорциональности по графику
можно предложить несколько вариантов.
Вариант 1. Самый простой, а потому
пригодный для младших классов. Отмечаем на
графике экспериментальные значения с указанием
погрешности. Обращаем внимание учащихся на то,
что если бы мы не нанесли погрешности на графики,
то провести прямую было бы затруднительно. В 7-м
классе достаточно просто отметить тот факт, что
зависимость между двумя величинами прямо
пропорциональна. Но если всё-таки необходимо
найти значение коэффициента пропорциональности,
можно обойтись без расчёта погрешности, отметив
только, что этот способ (многократные измерения
при различных условиях и построение графика)
используется именно для того, чтобы уменьшить
погрешность результата.
Вариант 2. Чертим прямую, находим
экспериментальную точку, которая лежит ближе
всего к прямой, и именно эту точку и считаем самой
точной. Остаётся вычислить результат для неё по
обычным формулам, рассчитав также и погрешность.
Вариант 3. Самый логичный. Пробуем
провести через точки вместе с их погрешностями
две прямые: с наибольшим и с наименьшим наклоном.
Значения коэффициентов для них и будут верхней и
нижней границами для результата. Зная границы,
рассчитываем среднее значение коэффициента и
погрешность. Данная погрешность неявно будет
содержать в себе как систематическую
погрешность экспериментально измеренных
величин, так и случайную погрешность определения
среднего, но уже с учётом точности каждого
результата. Этот вариант годится для
использования в экспериментах, когда
коэффициент должен быть оценён достаточно точно.
Но он достаточно сложен, поэтому не стоит его
использовать во всех случаях.
Вариант 4. Использование
встроенных программ в калькуляторах или готовых
компьютерных программ для вычисления
коэффициентов по методу наименьших квадратов.
Этот способ пригоден для практикума в старших
классах и/или в классах физматпрофиля. К
сожалению, в такие программы, как правило,
встроен метод наименьших квадратов, не
учитывающий погрешностей экспериментальных
точек. Применение имеет смысл в случаях, когда
погрешности всех точек практически одинаковы
или когда доминирующей является случайная
погрешность. Она и будет учтена.
Какой из этих вариантов выбрать, может
решать сам учитель. К счастью, таких работ
довольно мало. Продемонстрируем все эти варианты
на примере.
-
Возьмём данные эксперимента по
зависимости пути от времени равномерного
движения (машинка из конструктора с
электрическим приводом):

Действуя так, как описано в варианте 1,
строим график (рис. 4).

Рис. 4
Так как точек на графике много, можно с
уверенностью утверждать, что 8-я и 10-я точки
являются «выбросами», т.е. измерены небрежно.
Учитывая погрешность эксперимента, можно
провести прямую практически единственным
способом: соответствующая скорость 0,16 м/с. Если
воспользоваться методом наименьших квадратов
(например, встроенной функцией ЛИНЕЙН в
программе MicrosoftExcel), то для коэффициента мы
получим значение 0,158 ± 0,002 м/с (вариант 4).
Для варианта 2 подходит 3-я точка.
Скорость, вычисленная по данным для этой точки,
0,158 м/с. Рассчитаем погрешность: ![]() Так как относительная
Так как относительная
погрешность пути мала по сравнению с
относительной погрешностью времени,
пренебрегаем ею. Абсолютная погрешность
результата: ![]() 0,063
0,063
• 0,158 = 0,010 м/с. То есть скорость, вычисленная в
варианте 2: (0,158 ± 0,010) м/с.
Из приведённого примера видно, что
значения коэффициента пропорциональности
получаются очень близкими. В этом примере
погрешности отдельных измерений были достаточно
малы, а точек, наоборот, было много. Рассмотрим
пример, когда погрешности, напротив, велики, а
количество опытов в силу объективных причин
мало.
-
Найдём плотности пластмассы путём
измерения массы и объёмов тел.

В случае варианта 1 прямую проводим
так, чтобы количество точек над и под прямой было
одинаково (рис. 5), т.е. в данном случае – одна
сверху, одна снизу (прямая 1). Плотность в
этом случае равна 1,23 г/см3.

Рис. 5
В случае варианта 2 пригодна 2-я точка.
Для неё значение плотности (1,2 ± 0,2) г/см3.
Вариант 3: проведём прямые 2 и 3.
Для прямой 2 коэффициент пропорциональности
1,09 г/см3 является нижней границей
искомого значения плотности, а для прямой 3
(1,27 г/см3) – верхней. Полусумма этих
значений есть значение плотности (1,18 г/см3),
а полуразность – значение погрешности (0,09 г/см3).
Вариант 4 в данном случае менее
пригоден, т.к. не учитывает больших значений
погрешностей при измерении объёма с помощью
мерного цилиндра, но и в этом варианте плотность
(1,18 ± 0,05) г/см3.
Следует заметить, что в двух последних
примерах на графиках были обозначены только
погрешности вдоль горизонтальной оси, т.к.
погрешности значений второй переменной были
очень малы.
Послесловие
Научиться обрабатывать результаты
экспериментов учащиеся могут, лишь обрабатывая
результаты экспериментов. Это означает, что
помимо стандартного набора лабораторных работ
необходимо проводить много фронтальных и
демонстрационных экспериментов с обработкой
результатов. Это большая работа, и я хочу
пожелать успехов всем учителям, кто вступит на
этот путь или уже стоит на нём.
Литература
1. Анофрикова С.В., Стефанова Г.П.
Практическая методика преподавания физики.
Часть первая. – Астрахань: Издательство
Астраханского ГПИ, 1995.
2. Физика: Под ред. А.А.Пинского: Учебник
для 10 кл. школ и классов с угл. изучением физики. –
М.: Просвещение, 2002.
3. Попова О.Н. Обучение учащихся
выявлению устойчивых связей и отношений между
физическими величинами: Методическое пособие
для учителей физики. – Элиста: Элистинский лицей,
1998.
4. Анофрикова С.В. Азбука
учительской деятельности, иллюстрированная
примерами деятельности учителя физики. Ч. 1.
Разработка уроков. – М.: МПГУ, 2001.
5. Пёрышкин А.В. Физика-8. – М.:
Дрофа, 2004.
6. Громов С.В., Родина Н.А. Физика-8.
– М.: Просвещение, 2000.
7. Кикоин И.К., Кикоин А.К. Физика-10.
Механика. – М.: Просвещение, 2001.
8. Фронтальные лабораторные занятия по
физике в 7–11 классах общеобразовательных
учреждений. Книга для учителя: Под ред. В.А.Бурова,
Г.Г.Никифорова. – М.: Просвещение, Учебная
литература, 1996.
9. Зайдель А.Н. Элементарные оценки
ошибок измерений. – Л.: Наука, 1967.
10. Хорозов С.А. Работа над
ошибками: В кн. «Энциклопедия для детей», т. 16
«Физика», ч. 1 «Биография физики. Путешествие в
глубь материи. Механистическая картина мира». –
М.: Аванта+, 2000.
11. Мякишев Г.Я., Буховцев Б.Б., Сотский
Н.Н. Физика-10. – М.: Просвещение, 2004.
12. Кирик Л.А. Физика-9: Методические
материалы. – М.: Илекса, 2003.
13. Шахмаев Н.М., Шахмаев С.Н., Шодиев
Д.Ш. Физика-10. – М.: Просвещение, 1994.
-
Значение и применение ошибки средней арифметической величины и относительного показателя.
Определение
ошибок репрезентативности: Возникает
в тех случаях, когда требуется по частям
охарактеризовать явление в целом.
Генеральная совокупность может быть
охарактеризована по выборочной только
с определенными погрешностями,
измеряемыми ошибкой репрезентативности.
По величине ошибки репрезентативности
определяют, на сколько результаты,
полученные при выборочном наблюдении,
отличаются от результатов, которые
могли бы быть получены при проведении
сплошного исследования.
-
Средняя ошибка
средней арифметической, при числе
наблюдений
п
30: тм
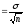 ,
,
при п
30; тм
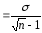
где: т
– ошибка репрезентативности средней
арифметической величины;
п – число
наблюдений;
σ- среднее
квадратическое отклонение.
Из формул видно,
что средняя ошибка средней арифметической
прямо пропорциональна степени
разнообразия признака и обратно
пропорциональна корню квадратному из
числа наблюдений, следовательно, для
уменьшения этой ошибки нужно увеличить
число наблюдений.
В) Ошибка относительных
показателей при числе наблюдений
п 30:
тр
 ,
,
при п
30 тр
 где
где
– mp –
ошибка относительных показателей
P
– показатель, выраженный в %, ‰ и.т.д.
g
– (100-Р) при Р=%; (1000-Р) при Р=‰
n
– число наблюдений.
-
Метод стандартизации, его значение и применение.
Условие для
применения метода стандартизации:
Метод стандартизации
применяется при сравнении интенсивных
показателей, рассчитанных для
совокупностей, отличающихся по своему
составу.
Сущность метода
стандартизации состоит в том, что он
позволяет устранить возможное внешнее
различие в составе совокупностей по
какому-либо признаку на величину
сравниваемых интенсивных показателей.
Это достигается путём условного
уравнивания составов этих совокупностей
по данному признаку.
Характеристика
стандартизированных показателей:
—- — это условные
величины, не дающие представление об
истинном размере явления, а указывающие
лишь на то, какова была бы величина
сравниваемых интенсивных показателей,
если бы они были бы вписаны для однородных
по своему составу совокупностей.
Назначение метода
стандартизации:
Метод стандартизации
применяется для того, чтобы установить,
повлияла ли неоднородность составов
совокупностей по какому-либо признаку
на различия сравниваемых интенсивных
показателей
Этапы расчёта
стандартизированных показателей:
I
этап. Расчёт интенсивных показателей
в отдельных группах, по признаку различия
и по совокупности в целом
II
этап. Определение стандарта, то есть
одинакового для сравниваемых совокупностей
численного состава по данному признаку.
Как правило за стандарт принимается
сумма или полу сумма численностей
соответствующих групп.
III
этап. Вычисление ожидаемых абсолютных
величин в группах стандарта на основе
групповых интенсивных показателей,
получение итоговых чисел по сравниваемым
совокупностям путём суммирования
ожидаемых величин
IV
этап. Вычисление стандартизированных
показателей для сравнивания совокупностей
V
этап. Сопоставление соотношений
стандартизированных и интенсивных
показателей. Формулировка вывода.
-
Ошибка выборки
2.1. Понятие и виды ошибок выборки
Поскольку изучаемая статистическая
совокупность состоит из единиц с
варьирующими признаками, то состав
выборочной совокупности может в той
или иной мере отличаться от состава
генеральной совокупности.
Расхождение
между характеристиками выборки и
генеральной совокупности составляет
ошибку
выборки.
Виды ошибок выборки
|
Ошибки выборки |
Систематические |
Случайные |
|
Ошибки регистрации |
Обусловлены |
Проявляются |
|
Ошибки репрезентативности |
Неправильный, |
Несмотря |
Основная
задача выборочного метода – изучение
случайных ошибок репрезентативности.
2.2. Средняя ошибка выборки
Случайная ошибка
репрезентативности зависит от следующих
фактов (при этом считается, что ошибок
регистрации нет):
-
Чем
больше численность выборки при прочих
равных условиях, тем меньше величина
ошибки выборки, т.е. ошибка выборки
обратно пропорциональна ее численности. -
Чем
меньше варьирование признака, тем
меньше ошибка выборки. Если признак
совсем не варьирует, а, следовательно,
величина дисперсии равна нулю, то ошибки
выборки не будет, т.к. любая единица
совокупности будет совершенно точно
характеризовать всю совокупность по
этому признаку. Таким образом, ошибка
выборки прямо пропорциональна величине
дисперсии.
В
математической статистике доказывается,
что величина средней ошибки случайной
повторной выборки может быть определена
по формуле
![]()
(6.1)
Однако
следует иметь в виду, что величина
дисперсии в генеральной совокупности
2
нам не известна, т.к. наблюдение выборочное.
Мы можем рассчитать лишь дисперсию в
выборочной совокупности S2.
Соотношение между дисперсиями генеральной
и выборочной совокупности выражается
формулой:
![]()
(6.2)
Если
n
велико, следовательно
![]()
Таким
образом, можно приблизительно считать,
что выборочная дисперсия равна генеральной
дисперсии.
2 =
S2
И формула средней ошибки повторной
выборки (6.1.) примет вид:
![]()
(6.3)
Но
здесь мы рассмотрели только ошибку
выборки для средней величины интересующего
признака. Существует также показатель
доли единиц с интересующим признаком.
Расчет ошибки этого показателя имеет
свои особенности.
Дисперсия
для показателя доли признака определяется
по формуле:
S2=(1-)
(6.4)
Тогда средняя ошибка повтора выборки
для показателя доли признака будет
равна:
![]()
(6.5)
Доказательство
формул (6.3) и (6.5) исходит из схемы повторной
выборки. Обычно же выборку организуют
бесповторным способом. Т.к. при бесповторном
отборе численность генеральной
совокупности N
в коде выборки сокращается, то в формулы
ошибки выборки включают дополнительный
множитель
![]() ,
,
и формулы
принимают вид:
![]()
(6.6)
![]()
(6.7)
Пример
1. Определим, на сколько отличаются
выборочные и генеральные показатели
по данным 10%-ной бесповторной выборки
успеваемости студентов.
|
Оценка, |
Число |
|
2 |
9 |
|
3 |
27 |
|
4 |
54 |
|
5 |
10 |
|
Итого |
100 |
Расчет ошибки бесповторной выборки для
средней величины:
![]()
n
= 100 N
= 1000
Найдем выборочную
дисперсию по формуле:
![]()
Здесь
не известна величина
![]() ,
,
которую можно найти как обычную среднюю
взвешенную величину:
![]()
![]()
Таким
образом,
![]()
Т.е.
можно сказать, что средний балл всех
студентов (![]() )
)
равен 3,650,07
Теперь
рассчитаем долю студентов в генеральной
совокупности, обучающихся на «4» и «5».
Найдем по выборке
долю студентов, получивших оценки «4»
и «5».
![]() (или
(или
64%)
Расчет
ошибки бесповторной выборки для доли
производится по формуле:
![]()
![]() (или
(или
4,5%)
Таким образом, доля студентов, обучающихся
на «4» и «5» по генеральной совокупности
(P) составляет
0,640,045 (или 64%4,5%).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Справочник /
Лекторий Справочник /
Лекционные и методические материалы по статистике /
Статистика: выборочное наблюдение
pptx
Конспект лекции по дисциплине «Статистика: выборочное наблюдение»,
pptx
![]()
Файл загружается
Благодарим за ожидание, осталось немного.
pptx
Конспект лекции по дисциплине «Статистика: выборочное наблюдение».
pptx
txt
Конспект лекции по дисциплине «Статистика: выборочное наблюдение», текстовый формат
СТАТИСТИКА
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
ТЕСТЫ
1. Несплошное наблюдение, при котором статистическому обследованию
подвергаются единицы изучаемой совокупности, отобранные случайным способом,
называется:
А) монографическим;
Б) основного массива;
В) выборочным.
2. Выборочная совокупность – это часть генеральной совокупности:
А) случайно попавшая в поле зрения исследователя;
Б) состоящая из единиц, отобранных в случайном порядке;
В) состоящая из единиц, номера которых отобраны в случайном порядке.
3. Укажите, при соблюдении каких условий выборка будет репрезентативной,
представительной:
А) отбор единиц совокупности, при котором каждая из единиц получает
определенную, обычно равную вероятность попасть в выборку;
Б) достаточное количество отобранных единиц совокупности;
В) отбор единиц произвольный.
4. Отбор, при котором попавшая в выборку единица не возвращается в совокупность,
из которой осуществляется дальнейший отбор, является:
А) повторным;
Б) бесповторным.
5. Укажите основные способы отбора единиц в выборочную совокупность из
генеральной:
А) собственно-случайный;
Б) механический;
В) монографический;
Г) анкетный;
Д) типический;
Е) серийный.
6. Отклонение выборочных характеристик от соответствующих характеристик
генеральной совокупности, возникающее вследствие нарушения принципа
случайности отбора, называется:
А) случайной ошибкой;
Б) систематической ошибкой репрезентативности.
7. Отклонение выборочных характеристик от соответствующих характеристик
генеральной совокупности, возникающее вследствие несплошного характера
наблюдения, называется:
А) случайной ошибкой репрезентативности;
Б) систематической ошибкой репрезентативности.
8. Преимущество выборочного наблюдения перед сплошным состоит в более точном
определении обобщающих характеристик:
А) да;
Б) нет.
9. Выборочное наблюдение в сравнении со сплошным позволяет расширить
программу исследования:
А) да;
Б) нет.
10. Вычисленные параметры по выборочной совокупности:
А) характеризует саму выборку;
Б) точно характеризуют генеральную совокупность;
В) не точно характеризуют генеральную совокупность.
11. Ошибка выборки представляет собой
характеристик
выборочной
совокупности
совокупности:
А) да;
Б) нет.
12. Величина ошибки выборки зависит от:
А) величины самого вычисляемого параметра;
Б) единиц измерения параметра;
В) объема численности выборки.
возможные пределы отклонений
от
характеристик
генеральной
13. Размер ошибки выборки прямо пропорционален:
А) дисперсии признака;
Б) среднему квадратическому отклонению.
14. Величина ошибки выборки обратно пропорциональна:
А) численности единиц выборочной совокупности;
Б) квадратному корню из этой численности.
15. Увеличение доверительной вероятности:
А) увеличивает ошибку выборки;
Б) уменьшает ошибку выборки.
16. Механический отбор всегда бывает:
А) повторным;
Б) бесповторным.
17. Типический отбор применяется в тех случаях, когда генеральная совокупность:
А) неоднородна по показателям, подлежащим изучению;
Б) однородна по показателям, подлежащим изучению.
18. Укажите, связана ли величина t с объемом выборки:
А) связана;
Б) не связана.
19. Укажите, от чего зависит величина t:
А) от вероятности, с какой необходимо гарантировать пределы ошибки выборки;
Б) от объема генеральной совокупности.
20. Укажите, что произойдет с предельной ошибкой выборки, если дисперсию
увеличить в 4 раза:
А) уменьшится в 2 раза;
Б) увеличится в 2 раза;
Г) не изменится.
21. Укажите, что произойдет с предельной ошибкой выборки, если дисперсию
уменьшить в 4 раза, численность выборки увеличить в 9 раз, а вероятность исчисления
изменится с 0,683 до 0,997 (t = 1 и t = 3):
А) уменьшится в 18 раз;
Б) увеличится в 18 раз;
В) уменьшится в 2 раза;
Г) не изменится.
22. Механический отбор точнее собственно-случайного, поскольку он:
А) более сложно организован;
Б) всегда бесповторен.
23. Расположите по возрастанию точности следующие способы отбора:
А) собственно-случайный;
Б) механический;
В) типический;
Г) серийный (гнездовой).
24. Типический отбор точнее, поскольку он:
А) наиболее сложно организован;
Б) обеспечивает попадание в выборку представителей из выделенных групп в
генеральной совокупности.
25. Величина ошибки выборки при типическом отборе меньше, поскольку в ее расчете
используется:
А) общая дисперсия признака;
Б межгрупповая дисперсия;
В) средняя из внутригрупповых дисперсий.
26. Увеличение численности выборки в 4 раза:
А) уменьшает ошибку выборки в 2 раза;
Б) увеличивает ошибку выборки в 2 раза;
В) уменьшает ошибку выборки в 4 раза;
Г) увеличивает ошибку выборки в 4 раза;
Д) не изменяет ошибку выборки.
27. Величина ошибки выборки:
А) прямо пропорциональна ;
Б) обратно пропорциональна ;
В) обратно пропорциональна n.
28. Ошибка выборки при механическом отборе уменьшится в следующем случае:
А) если уменьшить численность выборочной совокупности;
Б) если увеличить численность выборочной совокупности.
29. Укажите, при
репрезентативность:
А) серийной;
Б) типической;
В) случайной;
Г) механической.
каком
виде
выборки
обеспечивается
наибольшая
30. По данным выборочного наблюдения оценивается среднее значение некоторой
величины. Укажите, в каком направлении изменится предельная ошибка оценки, если
доверительная вероятность увеличится:
А) уменьшится;
Б) увеличится;
В) не изменится.
31. В выборах мэра примут участие около 1 млн избирателей: кандидат Р. Будет
выбран, если за него проголосуют более 50 % избирателей. Накануне выборов
проведен опрос случайно отобранных 1000 избирателей: 540 из них сказали, что будут
голосовать за Р. Укажите, можно ли при уровне доверительной вероятности 0,954
утверждать, что Р. Победит на выборах:
А) можно;
Б) нельзя.
32. Исследуемая партия состоит из 5 тыс. деталей. Предполагается, что партия деталей
содержит 8 % бракованных. Определите необходимый объем выборки, чтобы с
вероятностью 0,997 установить долю брака с погрешностью не более 2 %:
А) 1650;
Б) 1244;
В) 1300.
33. Укажите, по какой формуле определяется предельная ошибка выборки средней при
типическом отборе для бесповторной выборки:
А) ;
Б)
В)
Г)
34. Укажите, по какой формуле определяется предельная ошибка выборки для доли
при механическом отборе:
А) ;
Б)
В)
Г)
35. Из партии готовой продукции методом случайного бесповторного отбора отобрано
250 изделий, из которых пять оказались бракованными. Определите с вероятностью
0,954 возможные пределы процента брака во всей партии. Объем выборки составляет
10 % всего объема готовой продукции:
А) 2% ± 1,68%;
Б) 10% ± 2%.
36. Малой выборкой называется выборочное наблюдение, объем которого:
А) не превышает 30 единиц;
Б) не превышает 50 единиц.
37. По данным 5%-ного выборочного обследования, дисперсия среднего срока
пользования краткосрочным кредитом 1-го банка 144, а 2-го 81. Число счетов 1-го
банка в 4 раза больше, чем 2-го. Ошибка выборки больше:
А) в 1-м банке;
Б) во 2-м банке;
В) ошибки одинаковы;
Г) предсказать невозможно.
38. По выборочным данным (10%-ный отбор) удельный вес счетов со сроком
пользования кредитом, превышающим 50 дней, в 1-м банке составил 5%, во 2-м банке
10%. При одинаковой численности счетов в выборочной совокупности ошибка
выборки больше:
А) в 1-м банке;
Б) во 2-м банке;
В) ошибки равны;
Г) данные не позволяют сделать вывод.
39. Укажите, по какой формуле можно определить необходимый объем выборки при
собственно случайном повторном отборе при определении доли признака:
А) ;
Б) .
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1.
Для определения средней цены товара А в порядке случайной выборки было
обследовано 100 торговых предприятий, в результате установлено, что средняя цена в
выборке товара А составила 57 руб. при среднеквадратическом отклонении 4 руб.
Установлено, что в выборочной совокупности 20 торговых предприятий торгуют
импортным товаром.
С вероятностью 0,954 определите пределы, в которых будет находиться средняя
цена товара А во всех торговых предприятиях, и долю предприятий, торгующих
импортным товаром.
Решение.
Поскольку общая численность генеральной совокупности торговых предприятий
не указана, расчет ошибки средней можно произвести только по формуле:
Тогда пределы, в которых находится средняя цена во всей совокупности торговых
предприятий, будут:
Таким образом, с вероятностью, равной 0,954 можно утверждать, что цена товара
А, продаваемого во всех торговых предприятиях, будет не менее 56 руб. 20 коп. и не
превысит величину 57 руб. 80 коп.
Доля торговых предприятий, торгующих импортным товаром, находится в
пределах:
Выборочная доля составит:
Ошибку выборки для доли определим по формуле:
.
.
С вероятностью 0,954 можно утверждать, что доля магазинов, торгующих
импортным товаром, во всей их совокупности будет находится в пределах
р = 20% ± 8%, или 12% ≤ р ≤ 28%.
Пример 2.
Для определения среднего срока пользования краткосрочным кредитом в банке
была проведена 10%-ная механическая выборка, в которую попало 200 счетов. В
результате обследования установлено, что средний срок пользования краткосрочным
кредитом 40 дней при среднеквадратическом отклонении 8 дней. В десяти счетах срок
пользования кредитом превышал 50 дней. С вероятностью 0,954 определить пределы,
в которых будет находиться срок пользования краткосрочным кредитом в генеральной
совокупности и доля счетов со сроком пользования краткосрочным кредитом более 50
дней.
Решение.
Средний срок пользования кредитом в банке находится в пределах:
.
Т.к. выборка механическая, то ошибка выборки определяется по формуле:
С вероятностью 0,954 можно утверждать, что срок пользования краткосрочным
кредитом в банке находится в пределах:
.
Доля кредитов со сроком пользования более 50 дней находится в пределах:
Выборочная доля составит:
05
Ошибку выборки для доли определим по формуле:
.
С вероятностью 0,954 можно утверждать, что доля кредитов в банке со сроком
пользования более 50 дней будет находится в пределах р = 5% ± 2,9%, или
2,1% ≤ р ≤ 7,9%.
Пример 3.
В результате 10%-ного выборочного обследования, проведенного по методу
пропорционального типического отбора, получены исходные данные (табл.).
Показатели
Работники государственных
предприятий и учреждений
Средняя
заработ ная
плат а, руб.
Число
обследованн
ых
работников,
чел.
Среднее
квадратичес
кое
отклонение,
руб.
Удельны й
вес ж енщин
в общей
численности
работников,
%
3900
400
800
40
С вероятностью
0,954 определите
пределы,600
в которых будет
средняя
Работники
частных
5600
1200 находится 50
заработная
предприятийплата работников, и долю женщин в общей численности работников.
Решение.
1. Определим среднюю заработную плату работников:
2. Вычислим среднюю из групповых дисперсий:
.
3. Определим предельную ошибку выборки по формуле:
— средняя дисперсия выборочной совокупности.
4. Средняя заработная плата работников находится в пределах:
Т.о., с вероятностью 0,954 можно гарантировать, что средняя заработная плата
работников в генеральной совокупности будет не менее 4856 руб. 50 коп., но не более
4983 руб. 50 коп.
5. Долю женщин в общей численности работников определим по формуле:
6. Выборочную дисперсию альтернативного признака вычислим по формуле:
.
Ошибку для доли определим по формуле:
7. Доля женщин в общей численности работников находится в пределах:
Следовательно, с вероятностью 0,954 можно утверждать, что доля женщин в
генеральной совокупности находится в пределах от 43 до 49 %.
Пример 4.
В одном из учебных заведений насчитывается 50 студенческих групп. С целью
изучения успеваемости студентов произведена 10%-ная серийная выборка, в которую
попали 5 групп студентов. В результате обследования установлено, что средняя
успеваемость в группах составила: 3,2; 3,4; 3,8; 4,0; 4,1 балла. С вероятностью 0,997
определите пределы, в которых будет находиться средний балл студентов учебного
заведения.
Решение.
Средний балл всех студентов находится в пределах:
.
Определим выборочную среднюю серийной выборки:
Дисперсию серийной выборки определим по формуле:
где — выборочная средняя каждой серии;
— выборочная средняя серийной выборки.
Значение дисперсии составляет:
Рассчитаем предельную ошибку выборки для средней по формуле:
где — межсерийная дисперсия; – число отобранных серий; – число серий в
генеральной совокупности.
С вероятностью 0,997 можно утверждать, что средний балл всех студентов
учебного заведения находится в пределах , или балла.
Пример 5.
Предприятие выпустило 100 партий готовой продукции А по 50 шт. в каждой из
них. Для проверки качества готовой продукции была проведена 10%-ная серийная
выборка, в результате которой установлено, что доля бракованной продукции
составила 12%. Дисперсия серийной выборки равна 0,0036.
С вероятностью 0,997 определите пределы, в которых находится доля бракованной
продукции А.
Решение.
Доля бракованной продукции А будет находится в пределах:
Определим предельную ошибку выборки для серийного отбора:
С вероятностью 0,997 можно утверждать, что доля бракованной продукции А
находится в пределах 6,6% ≤ р ≤ 17,4%.
Пример 6.
Определите численность рабочих, которую необходимо отобрать в выборочную
совокупность с тем, чтобы при изучении их средней заработной платы предельная
ошибка выборки не превышала 30 руб. с вероятностью 0,997, если по данным
предыдущего обследования среднее квадратическое отклонение составило 70 руб.
Решение.
Поскольку способ отбора не указан, расчет следует проводить по формуле для
повторного отбора:
Пример 7.
В городе Н проживает 100 тыс. чел. С помощью механической выборки
определите долю населения со среднедушевыми денежными доходами до 1500 руб. в
месяц. Какова должна быть численность выборки, чтобы с вероятностью 0,997 ошибка
выборки не превышала 2%, если на основе предыдущих обследований известно, что
дисперсия равна 0,24?
Решение.
Определим необходимую численность выборки по формуле:
Задачи для самостоятельного решения
Задача 1.
В результате выборочного обследования незанятого населения, ищущего работу,
осуществленного на основе собственно-случайной повторной выборки, получен
следующий ряд распределения (табл.).
Возраст, лет
до 25
25 — 35
35 — 45
45 — 55
55 и
более
Численность
15
37
71
45
22
лиц данного
С вероятностью 0,954 определите границы:
возраста
а) среднего возраста незанятого населения;
б) доли (удельного веса) лиц, моложе 25 лет, в общей численности незанятого
населения.
Задачи для самостоятельного решения
Задача 2.
Определите, сколько учащихся первых классов школ района необходимо отобрать в
порядке собственно-случайной бесповторной выборки, чтобы с вероятностью 0,997
определить границы среднего роста первоклассников с предельной ошибкой 2 см.
Известно, что всего в первых классах школ района обучается 1100 учеников, а
дисперсия роста по результатам аналогичного обследования в другом районе
составила 24.
Задачи для самостоятельного решения
Задача 3.
В целях изучения доходов населения по трем районам области сформирована 2%ная выборка, пропорциональная численности населения этих районов. Полученные
результаты представлены в табл.
Район
I
Численность
населения,
чел.
Обследова
но, чел.
120 000
2400
Доход в расчете на 1
человека
средняя,
тыс. руб.
дисперсия
2,9
1,3
II
170 000
3400
2,5
1,1
Определите границы среднедушевых доходов населения по области в целом при
III
90 000
1800
2,7
1,6
уровне вероятности 0,997.
Задачи для самостоятельного решения
Задача 4.
В целях контроля качества комплектующих из партии изделий, упакованных в 50
ящиков по 20 изделий в каждом, была произведена 10%-ная серийная выборка. По
попавшим в выборку ящикам среднее отклонение параметров изделия от нормы
соответственно составило 9; 11; 12; 8 и 14 мм. С вероятностью 0,954 определите
среднее отклонение параметров по всей партии в целом.
Задача 5.
Планируется обследование населения с целью определения средних расходов на
медицинские услуги и лекарственные средства. Определите необходимый объем
собственно-случайной бесповторной выборки, чтобы получить результаты с
точностью 10 руб. при уровне вероятности 0,954. Известно, что в районе проживает 73
тыс. человек, а пробное обследование показало, что среднее квадратическое
отклонение расходов населения на эти цели составляет 38 руб.
Статистика
Статистика. Статистические данные
ПРАВИТЕЛЬСТВО САНКТ-ПЕТЕРБУРГА
КОМИТЕТ ПО НАУКЕ И ВЫСШЕЙ ШКОЛЕ
Государственное бюджетное образовательное учреждение среднего профессионального образов…

Смирнова С. О.
Авторы
Статистика
Статистика
Курс : Статистика
Статистика В.М. Гусаров Москва, Юнити , 2003г
Статистика В.С. Мхиторян , Москва, Экономист, 2005г.
Статистика И.И. Елисеева
Статисти…
Смотреть все
Поделись лекцией и получи скидку!
Заполни поля, отправь лекцию и мы вышлем тебе скидку-промокод на Автор24
Предмет
Название лекции
Авторы
Описание
Другие Экономические предметы
-
Экономика
-
Менеджмент
-
Бухгалтерский учет и аудит
-
Управление персоналом
-
Статистика
-
Маркетинг
-
Экономика предприятия
-
Государственное и муниципальное управление
-
Финансовый менеджмент
-
Эконометрика
-
Финансы
-
Менеджмент организации
-
Бизнес-планирование
-
Управление проектами
-
Экономический анализ
-
Экономическая теория
-
Микро-, макроэкономика
-
Инновационный менеджмент
-
Логистика
-
Анализ хозяйственной деятельности

Концепция репрезентативности часто встречается в статистических отчетах и при подготовке выступлений и отчетов. Пожалуй, без него сложно представить какое-либо представление информации для ознакомления.
Содержание
- 1 Репрезентативность — что это?
- 2 Другие определения
- 3 Репрезентативная выборка
- 4 Вероятностная выборка
- 5 Вероятностные выборки
- 6 Выборка потребителей
- 7 Размер выборки
- 8 Понятие ошибки репрезентативности
- 9 Виды ошибок
- 10 Преднамеренные и непреднамеренные ошибки репрезентативности
- 11 Валидность, надежность, репрезентативность. Расчет ошибок
- 12 Репрезентативные системы
Репрезентативность — что это?

Репрезентативность отражает степень, в которой выбранные объекты или части соответствуют содержанию и значению набора данных, из которого они были выбраны.
Другие определения
Репрезентативность можно понимать в разных контекстах. Но по своему смыслу репрезентативность — это соответствие характеристик и свойств выбранных единиц генеральной совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Кроме того, репрезентативность информации определяется как способность данных выборки представлять параметры и свойства совокупности, которые важны с точки зрения проводимых исследований.
Репрезентативная выборка
Принцип выборки заключается в выборе наиболее важных свойств, которые точно отражают общую совокупность данных. Для этого используются различные методы, позволяющие получить точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качество всех данных.
Таким образом, нет необходимости изучать весь материал, но достаточно учесть выборочную репрезентативность. Что это? Это набор отдельных данных, чтобы получить представление об общей массе информации.
В зависимости от метода они делятся на вероятностные и маловероятные. Вероятностный — это выборка, которая создается путем вычисления наиболее важных и интересных данных, которые в будущем будут репрезентативными для генеральной совокупности. Это осознанный выбор или случайная выборка, однако оправданная своим содержанием.
Маловероятно — это одна из разновидностей случайной выборки, составленной по принципу обычной лотереи. В этом случае мнение лица, взявшего такую пробу, не принимается во внимание. Используется только слепая жребий.
Вероятностная выборка
Вероятностные выборки также можно разделить на несколько типов:
- Один из самых простых и понятных принципов — нерепрезентативная выборка. Например, этот метод часто используется при проведении социальных опросов. При этом участники опроса не выбираются из общей массы по каким-либо конкретным критериям, а информация берется от первых 50 человек, принявших участие.
- Выборка вероятностей — это еще одна разновидность выборки невероятности, которая часто используется для исследования больших наборов данных. Для этого используется множество условий и правил. Выбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что будет опрошено 100 человек, но при составлении статистического отчета будет учитываться только мнение определенного количества людей, которые будут соответствовать установленным требованиям.
- Преднамеренные выборки отличаются тем, что они имеют ряд требований и условий для отбора, но все же полагаются на совпадения, не преследуя цели получения хорошей статистики.
Вероятностные выборки
Для вероятностных выборок рассчитывается ряд параметров, которым будут соответствовать объекты в выборке, и среди них различными способами могут быть выбраны именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Эти методы расчета требуемых данных могут быть:
- Простая случайная выборка. Он заключается в том, что среди выделенного сегмента методом полностью случайной лотереи выбирается необходимый объем данных, который будет репрезентативной выборкой.
- Систематическая и случайная выборка позволяет составить систему расчета необходимых данных на основе случайно выбранного сегмента. Итак, если первое случайное число, указывающее порядковый номер данных, выбранных из общей совокупности, равно 5, следующими данными для выбора могут быть, например, 15, 25, 35 и так далее. Этот пример ясно объясняет, что даже случайный выбор может быть основан на систематических вычислениях требуемых входных данных.
Выборка потребителей
Осмысленная выборка — это способ взглянуть на каждый отдельный сегмент, и на основе его оценки составляется генеральная совокупность, отражающая характеристики и свойства всей базы данных. Таким образом, собирается больше данных, отвечающих требованиям репрезентативной выборки. Легко выбрать набор параметров, которые не будут включены в общее количество, без потери качества выбранных данных, представляющих генеральную совокупность. Таким образом определяется репрезентативность результатов исследования.
Размер выборки
Не последняя проблема, которую необходимо решить, — это размер выборки для репрезентативной репрезентативности населения. Размер выборки не всегда зависит от количества источников в генеральной совокупности. Однако репрезентативность выборки напрямую зависит от того, на сколько сегментов в конечном итоге следует разделить результат. Чем больше таких сегментов, тем больше данных включается в итоговую выборку. Если результаты требуют общих обозначений и не требуют конкретики, то в результате выборка становится меньше, поскольку, не вдаваясь в детали, информация представлена более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Репрезентативная систематическая ошибка — это конкретное несоответствие между характеристиками населения и данными выборки. При проведении выборочного исследования невозможно получить абсолютно точные данные, как при полном изучении генеральных популяций и выборки, представленной только частью информации и параметров, в то время как более детальное изучение возможно только при изучении всей совокупности численность населения. Поэтому некоторые ошибки и ошибки неизбежны.
Виды ошибок
При составлении репрезентативной выборки возникают некоторые ошибки:
- Случайный.
- Стандарт.
- Не намеренно.
- Систематический.
- Предел.
- Умышленное.
Причиной появления случайных ошибок может быть прерывистый характер исследования генеральной совокупности. Обычно ошибка случайной репрезентативности незначительна по величине и характеру.
Между тем систематические ошибки возникают, когда нарушаются правила отбора данных из генеральной совокупности.
Средняя ошибка — это разница между средним значением выборки и основной совокупностью. Это не зависит от количества единиц в выборке. Он обратно пропорционален размеру выборки. Таким образом, чем больше объем, тем меньше среднее значение ошибки.
Предельная ошибка — это наибольшая возможная разница между средним значением выполненной выборки и всей генеральной совокупностью. Эта ошибка характеризуется как максимум возможных ошибок в данных условиях их возникновения.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки искажения данных могут быть преднамеренными или непреднамеренными.
Итак, причины появления преднамеренных ошибок — это подход к отбору данных с использованием метода выявления трендов. Непреднамеренные ошибки возникают и на этапе подготовки выборочного наблюдения, формирования репрезентативной выборки. Чтобы избежать таких ошибок, необходимо создать хорошую основу выборки для списков единиц выборки. Он должен полностью соответствовать целям выборки, быть надежным и охватывать все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок

Расчет ошибки репрезентативности (Mm) среднего арифметического (M).
Стандартное отклонение: размер выборки (> 30).
Репрезентативная ошибка (Мр) и относительная величина (Р): размер выборки (n> 30).
В случае, если необходимо изучить совокупность, где размер выборки невелик и менее 30 единиц, количество наблюдений уменьшится на одну единицу.
Величина ошибки прямо пропорциональна размеру выборки. Репрезентативность информации и расчет степени возможности составления точного прогноза отражает определенное значение предельной погрешности.
Репрезентативные системы
В процессе оценки представления информации используется не только репрезентативная выборка, но и лицо, получающее информацию, также использует репрезентативные системы. Таким образом, мозг обрабатывает определенный объем информации, создавая репрезентативную выборку всего потока информации, чтобы качественно и быстро оценить предоставленные данные и понять суть проблемы. Ответьте на вопрос: «Представление — что это?» — В масштабе человеческого сознания это довольно просто. Для этого мозг использует все подчиненные органы чувств, в зависимости от типа информации, которую необходимо изолировать от общего потока. Поэтому проводится различие между:
- Система визуального представления, в которой задействованы органы зрительного восприятия глаза. Людей, которые часто используют эту систему, называют визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Система кинестетической репрезентации — это обработка потока информации путем ее восприятия через обонятельные и тактильные каналы.
- Система слухового представления. Основной используемый орган — слух. Информация, предоставленная в виде аудио- или голосового файла, обрабатывается именно этой системой. Людей, которые лучше всего воспринимают информацию на слух, называют аудиалами.

- Система цифрового представления используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и понимание полученных данных.

Так что же такое репрезентативность? Простая выборка из набора или целостная процедура обработки информации? Мы можем однозначно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая выделить самые тяжелые и наиболее важные из них.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки ( ).
).
В теории выборочного наблюдения выведены формулы для определения  , которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
, которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.
Например, если применяется повторная собственно случайная выборка, то  определяется как:
определяется как:
 — при оценивании среднего значения признака;
— при оценивании среднего значения признака;
 — если признак альтернативный, и оценивается доля.
— если признак альтернативный, и оценивается доля.
При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):
 — для среднего значения признака;
— для среднего значения признака;
 — для доли.
— для доли.
Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки ( ) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):
 .
.
Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки ( )
)
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя

Выборочная дисперсия изучаемого признака

- Определяем среднюю ошибку повторной случайной выборки

- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна

- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности

Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле

Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:

Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:

Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности
 ;
;
- средняя ошибка выборки при использовании повторной схемы отбора составит

Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит

- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):

- установим границы для генеральной доли с вероятностью 0,997:

Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки ( ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп

Здесь  — средняя из групповых дисперсий типических групп.
— средняя из групповых дисперсий типических групп.
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия,  |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:

аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:

- Средняя из внутригрупповых дисперсий

- Средняя ошибка выборки:

С вероятностью 0,954 находим предельную ошибку выборки:

- Доверительные границы для среднего значения признака в генеральной совокупности:

Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле

Предельная ошибка малой выборки:

Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно

- Значение среднего квадратического отклонения составляет

- Средняя ошибка выборки:

- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:

- Доверительный интервал для среднего значения признака в генеральной совокупности:

То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить

При бесповторном случайном отборе потребуется проверить

Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.

Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.


