Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины.
Критерий Стьюдента определяется по формуле:
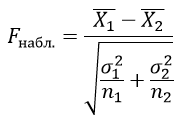
$bar{X_1}$ – выборочные средние значения первой выборки;
$bar{X_2}$ – выборочные средние значения второй выборки;
n1 – объем первой выборки;
n2 – объем второй выборки;
σ1 и σ2 – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:
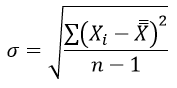
Число степеней свободы определяется по формуле:
k=n1+n2−2
Fкр(α, k) определяется по таблице
При Fнабл<Fкр нулевая гипотеза принимается.
Формула критерия Стьюдента для несвязанных независимых выборок:
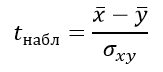
Формула для определения стандартной ошибки разности средних арифметических σxy:
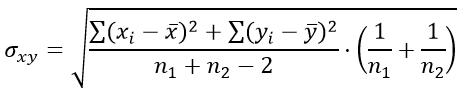
Число степеней свободы определяется выражением:
k=n1+n2–2
При n1=n2 число степеней свободы находится по формуле:
k=2n-2
а стандартная ошибка разности средних арифметических σxy задаётся выражением:
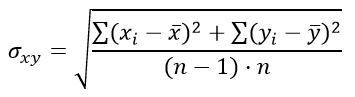
Пример
Даны две выборки.
В первой выборки продажа товара со скидкой, а во второй без скидки.
| № п/п | X | Y |
| 1 | 25 | 19 |
| 2 | 34 | 31 |
| 3 | 23 | 17 |
| 4 | 35 | 24 |
| 5 | 33 | 28 |
| 6 | 25 | 31 |
| 7 | 45 | 39 |
| 8 | 41 | 32 |
| 9 | 27 | 38 |
| 10 | 54 | 43 |
| 11 | 32 | 21 |
| 12 | 32 |
По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?
Решение
В соответствии с таблицей n1=12, n2=11
Вычислим дисперсии D(X), D(Y)
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 25 | 19 | 78,028 | 107,4 |
| 2 | 34 | 31 | 0,0278 | 2,6777 |
| 3 | 23 | 17 | 117,36 | 152,86 |
| 4 | 35 | 24 | 1,3611 | 28,769 |
| 5 | 33 | 28 | 0,6944 | 1,8595 |
| 6 | 25 | 31 | 78,028 | 2,6777 |
| 7 | 45 | 39 | 124,69 | 92,86 |
| 8 | 41 | 32 | 51,361 | 6,9504 |
| 9 | 27 | 38 | 46,694 | 74,587 |
| 10 | 54 | 43 | 406,69 | 185,95 |
| 11 | 32 | 21 | 3,3611 | 69,95 |
| 12 | 32 | 3,3611 | ||
| Сумма | 406 | 323 | 911,67 | 726,55 |
| Среднее | 33,833 | 29,364 |
Подставим значения в формулу стандартной ошибки разности средних арифметических σxy:
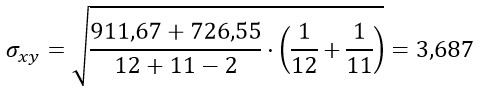
Вычисляем критерий Стьюдента:
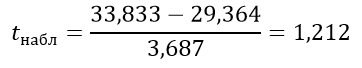
Число степеней свободы равно:
k=12+11–2=21
По таблице Стьюдента находим критическое значение:
tкрит=2,8310
Отсюда tкрит> tнабл, следовательно, зависит.
![]() 19000
19000
Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины.
Критерий Стьюдента определяется по формуле:
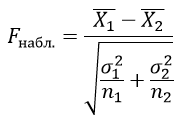
$bar{X_1}$ – выборочные средние значения первой выборки;
$bar{X_2}$ – выборочные средние значения второй выборки;
n1 – объем первой выборки;
n2 – объем второй выборки;
σ1 и σ2 – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:
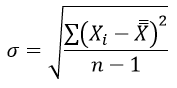
Число степеней свободы определяется по формуле:
k=n1+n2−2
Fкр(α, k) определяется по таблице
При Fнабл<Fкр нулевая гипотеза принимается.
Формула критерия Стьюдента для несвязанных независимых выборок:
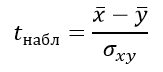
Формула для определения стандартной ошибки разности средних арифметических σxy:
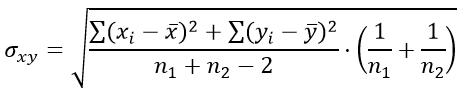
Число степеней свободы определяется выражением:
k=n1+n2–2
При n1=n2 число степеней свободы находится по формуле:
k=2n-2
а стандартная ошибка разности средних арифметических σxy задаётся выражением:
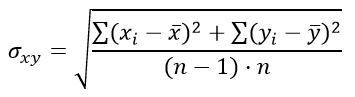
Пример
Даны две выборки.
В первой выборки продажа товара со скидкой, а во второй без скидки.
| № п/п | X | Y |
| 1 | 25 | 19 |
| 2 | 34 | 31 |
| 3 | 23 | 17 |
| 4 | 35 | 24 |
| 5 | 33 | 28 |
| 6 | 25 | 31 |
| 7 | 45 | 39 |
| 8 | 41 | 32 |
| 9 | 27 | 38 |
| 10 | 54 | 43 |
| 11 | 32 | 21 |
| 12 | 32 |
По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?
Решение
В соответствии с таблицей n1=12, n2=11
Вычислим дисперсии D(X), D(Y)
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 25 | 19 | 78,028 | 107,4 |
| 2 | 34 | 31 | 0,0278 | 2,6777 |
| 3 | 23 | 17 | 117,36 | 152,86 |
| 4 | 35 | 24 | 1,3611 | 28,769 |
| 5 | 33 | 28 | 0,6944 | 1,8595 |
| 6 | 25 | 31 | 78,028 | 2,6777 |
| 7 | 45 | 39 | 124,69 | 92,86 |
| 8 | 41 | 32 | 51,361 | 6,9504 |
| 9 | 27 | 38 | 46,694 | 74,587 |
| 10 | 54 | 43 | 406,69 | 185,95 |
| 11 | 32 | 21 | 3,3611 | 69,95 |
| 12 | 32 | 3,3611 | ||
| Сумма | 406 | 323 | 911,67 | 726,55 |
| Среднее | 33,833 | 29,364 |
Подставим значения в формулу стандартной ошибки разности средних арифметических σxy:
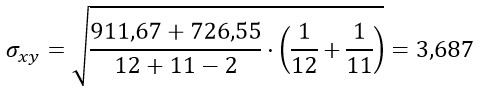
Вычисляем критерий Стьюдента:
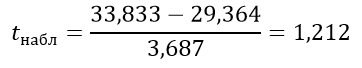
Число степеней свободы равно:
k=12+11–2=21
По таблице Стьюдента находим критическое значение:
tкрит=2,8310
Отсюда tкрит> tнабл, следовательно, зависит.
![]() 18953
18953
Условное обозначение средней ошибки среднего арифметического — т. Следует помнить, что под «ошибкой» в статистике понимается не ошибка исследования, а мера представительства данной величины, т. е. мера, которой средняя арифметическая величина, полученная на выборочной совокупности (в нашем примере — на 125 детях), отличается от истинной средней арифметической величины, которая была бы получена на генеральной совокупности (в нашем примере это были бы все дети аналогичного возраста, уровня подготовленности и т. д.). Например, в приведенном ранее примере определялась точность попадания малым мячом в цель у 125 детей и была получена средняя арифметическая величина примерно равная 5,6 см. Теперь надо установить, в какой мере эта величина будет характерна, если взять для исследования 200, 300, 500 и больше аналогичных детей. Ответ на этот вопрос и даст вычисление средней ошибки среднего арифметического, которое производится по формуле:
Для приведенного примера величина средней ошибки среднего арифметического будет равна:
Следовательно, M±m = 5,6±0,38. Это означает, что полученная средняя арифметическая величина (M = 5,6) может иметь в других аналогичных исследованиях значения от 5,22 (5,6 — 0,38 = 5,22) до 5,98 (5,6+0,38 = 5,98).
4. Вычисление средней ошибки разности
Условное обозначение средней ошибки разности — t. Таким образом, установлены основные статистические параметры, характеризующие количественную сторону эффективности одной из методик обучения метанию малых мячей в цель. Но в приведенном примере речь шла о сравнительном эксперименте, в котором сопоставлялись две методики обучения. Предположим, что вычисленные параметры характеризуют методику «А». Тогда для методики «Б» также необходимо вычислить аналогичные статистические параметры. Допустим, они будут равны:
МБ 4,7; σБ ± 3,67 mБ ± 0,33
Теперь есть числовые характеристики двух разных методик обучения. Необходимо установить, насколько эти характеристики достоверно различны, т. е. установить статистически реальную значимость разницы между ними. Условно принято считать, что если разница равна трем своим ошибкам или больше, то она является достоверной:
В приведенном примере:
0,9<1,5
Следовательно, найденные количественные характеристики двух методик обучения не имеют достоверных различий и объясняются не закономерными, а случайными факторами. Поэтому можно сделать следующий педагогический вывод: обе методики обучения равноценны по своей эффективности; новая методика расширяет существующие способы решения данной педагогической задачи.
Подобное вычисление средней ошибки разности применяется в тех случаях, когда имеются количественно значительные показатели п (т. е. при большом числе вариант). Если же в распоряжении экспериментатора имеется небольшое число наблюдений (менее 20), то целесообразно вычислять среднюю ошибку разности по формулам:
где С — число степеней свободы вариаций от 1 до ∞, которые равны числу наблюдений без единицы (С = п — 1).
В виде примера можно привести исследование, в котором оценивалась разница в величине становой динамометрии боксеров двух весовых категорий (А. Г. Жданова, 1961). Были получены следующие исходные данные: тяжелый вес — п1 = 12 человек, легкий вес — п2 = 15человек.
М1 = 139,2 кг M2 = 135,0 кг
σ1 = ± 4,2 кг σ2 = ±4,0 кг
m1 = ± 1,23 кг m2 = ± 1,69 кг
Если подставить эти значения в формулы, то получится:
Далее достоверность различия определяют по таблице вероятностей P/t/≥/t1/ по распределению Стьюдента (t — критерий Стьюдента).
В данной таблице столбец t является нормированным отклонением и содержит числа, которые показывают, во сколько раз разница больше средней ошибки. По вычисленным показателям t и С в таблице определяется число Р, которое показывает вероятность разницы между М1 и М2. Чем больше Р, тем менее существенна разница, тем меньше достоверность различий.
В приведенном примере при значении t 2,0 и С = 25 число Р будет равняться 0,0455 (в таблице оно расположено на пересечении строки, соответствующей t 2,0, и столбца, соответствующего С = ∞). Это свидетельствует о том, что реальная разница весьма вероятна.
В тех случаях, когда расчеты показывают отсутствие достоверности различия, преждевременно считать, что между изучаемыми явлениями вообще не может быть различия. Можно лишь утверждать, что нет различия при данных условиях исследования. При увеличении объема выборки достоверность в различии может появиться. Это положение является главным доказательством важности правильного определения необходимого числа исследований до начала эксперимента.
СПИСОК ЛИТЕРАТУРЫ
-
Масальгин Н.А. Математико-статистические методы в спорте. М., ФиС, 1974.
-
Методика и техника статистической обработки первичной социологической информации. Отв. ред. Г.В. Осипов. М., «Наука», 1968.
-
Начинская С.В. Основы спортивной статистики. — К.: Вища шк., 1987. — 189 с.
-
Толоконцев Н.А. Вычисление среднего квадратичного отклонения по размаху. Сравнение с общепринятым методом. Тезисы докладов третьего совещания по применению математических методов в биологии. ЛГУ, 1961, стр. 83 — 85.
-
Фаламеев А.И., Выдрин В.М. Научно-исследовательская работа в тяжелой атлетике. ГДОИФК им. П. Ф. Лесгафта, 1974.
Оценка разности двух показателей
При оценке
существенности разности двух показателей
вначале находят разность
двух показателей
α
по формуле:
![]()
После этого
вычисляют среднюю
ошибку разности Sα
и
коэффициент доверительности tα
по формулам:
![]()
,
![]()
Пример:
Из 125 студентов у 43 (pЭГ
= 34,40%) выявлен высокий уровень личностной
тревожности в экспериментальной группе
(ЭГ). В контрольной группе (КГ) из 125
студентов – высокий уровень личностной
тревожности у 59 (pКГ
= 47,20%). Необходимо определить, имеются
ли существенные различия между
показателями экспериментальной (pЭГ)
и контрольной (pКГ)
групп.
В нашем примере α
= 12,80, Sα
= 6,16, tα
= 2,08. Разность показателей α
превышает
свою ошибку Sα
более, чем в 2 раза (tα
= 2,08).
По таблице Стьюдента
находим, что эмпирическое значение tα
(2,08) превышает табличное для вероятности
ошибки P
= 0,05 (5%). Значение коэффициента Стьюдента
зависит не только от вероятности P
, но и от объема выборки. Число
степеней свободы n‘
при оценке
одного показателя равняется n
– 1, при
оценке достоверности разности двух
показателей n‘
= n1
+ n2
– 2. Так как
эмпирическое значение tα
(2,08) превышает табличное для вероятности
ошибки P
= 0,05 (5%), следовательно, имеются существенные
различия в показателях высоких уровней
личностной тревожности среди студентов
экспериментальной и контрольной групп.
Таблица 2 – Значения
критерия t
(по Стьюденту)
|
Число степеней |
Вероятность |
|||
|
0,05 = 5% |
0,02 = 2% |
0,01 = 1% |
0,001 = 0,1% |
|
|
30 |
2,042 |
2,457 |
2,750 |
3,64 |
|
∞ |
1,957 |
2,326 |
2,575 |
3,29 |
Определение средней ошибки показателей равных или близких к нулю или 100%
Величина средней
ошибки рассчитывается по формуле:
![]()
где
Sp
– величина
средней ошибки;
t
– доверительный
коэффициент;
n
– число
наблюдений (объем выборки).
Пример:
По данным минутной пробы Н.И Моисеевой
– В.М. Сысуева у всех 35 студентов
зарегистрирован средний уровень
способности к адаптации и ориентации
во времени (p
= 100%). Значит ли это, что в данной группе
отсутствуют студенты, имеющие высокие
или низкие способности к адаптации?
Принимаем
доверительный коэффициент t
= 2, что соответствует вероятности ошибки
меньше 5% (0,05), тогда средняя ошибка
показателя Sp
= 10,3%.
Следовательно,
при последующих испытаниях число лиц,
имеющих средние способности к адаптации
и ориентации во времени, может быть p
= 100% –
10,3% = 89,7%.
Если необходимо
увеличить надежность вывода, можно
принять t
= 3.
Критерий х2
Часто возникает
задача сравнения частных (например,
процентных) распределений
данных. В этом случае можно воспользоваться
статистикой, именуемой х2-критерий:
![]()
где
Pk
–
частоты
результатов наблюдений до эксперимента;
Vk
–
частоты результатов наблюдений после
эксперимента;
S
–
общее
число групп, на которые разделились
результаты наблюдений.
Полученное
расчетным путем значение х2
сопоставляется
с табличным и в случае его превышения
или равенства делается вывод о значимости
различий с определенной вероятностью
допустимой
ошибки.
Таблица 3 – Граничные
(критические)
значения х2-критерия
|
Число |
Вероятность |
||
|
0,05 |
0,01 |
0,001 |
|
|
1 |
3,84 |
6,64 |
10,83 |
|
2 |
5,99 |
9,21 |
13,82 |
|
3 |
7,81 |
11,34 |
16,27 |
|
4 |
9,49 |
13,23 |
18,46 |
|
5 |
11,07 |
15,09 |
20,52 |
|
6 |
12,59 |
16,81 |
22,46 |
|
7 |
14,07 |
18,48 |
24,32 |
|
8 |
15,51 |
20,09 |
26,12 |
|
9 |
16,92 |
21,67 |
27,88 |
|
10 |
18,31 |
23,21 |
29,59 |
Например,
из 100 испытуемых до
начала эксперимента 30 человек показали
результаты
ниже средних, 50 –
средние
и 20 –
выше средних.
После проведения формирующего эксперимента
результаты
распределились следующим образом: 20
человек
показали результаты ниже среднего, 40 –
средние и 40
–
выше среднего уровня.
Можно ли, опираясь
на эти данные, утверждать, что формирующий
эксперимент, направленный на увеличение
показателей (например, уровней самооценки)
удался?
Для
ответа на данный вопрос воспользуемся
формулой.
В данном примере переменная Pk
принимает
значение
30 %, 50 %, 20 %, a
Vk
–
20
%, 40 %, 40 %. Подставив
эти значения в формулу, получим
![]()
Воспользуемся
теперь таблицей «Граничные
(критические)
значения х2-критерия»,
где для заданного числа степеней
свободы (S–1=3–1=2)
можно определить степень
значимости различий показателей до и
после эксперимента. Полученное нами
значение 25,33 больше соответствующего
табличного значения
(13,82) при вероятности допустимой ошибки
меньше
0,1 % (0,001). Следовательно, эксперимент
удался, и мы можем
это утверждать, допуская ошибку, не
превышающую
0,1 %.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка разности средних Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Стандартное отклонение образца X: 2.8 —> Конверсия не требуется
Размер образца X: 14 —> Конверсия не требуется
Стандартное отклонение образца Y: 3.2 —> Конверсия не требуется
Размер образца Y: 16 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
1.09544511501033 —> Конверсия не требуется
7 Ошибки Калькуляторы
Стандартная ошибка разности средних формула
Стандартная ошибка разности средних = sqrt(((Стандартное отклонение образца X^2)/Размер образца X)+((Стандартное отклонение образца Y^2)/Размер образца Y))
σμ1-μ2 = sqrt(((σX^2)/NX)+((σY^2)/NY))
Что такое стандартная ошибка и ее важность?
В статистике и анализе данных большое значение имеет стандартная ошибка. Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных выборочных статистических данных, таких как среднее значение или медиана. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности. Соотношение между стандартной ошибкой и стандартным отклонением таково, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; чем больше размер выборки, тем меньше стандартная ошибка, потому что статистика будет приближаться к фактическому значению.
