1.1. Общие сведения об измерениях
Под измерением
следует понимать определение численного
значения физической величины с помощью
специальных технических средств, или
это есть процесс сравнения какой-либо
величины с другой ей однородной
величиной,
принятой за единицу.
Измеряемая величина и единица измерения
не соизмеримы друг с другом, что приводит
к возникновению ошибок.
В процессе измерения
участвуют следующие элементы: объект
измерения; наблюдатель; инструмент;
внешняя cреда. Все это образует условия
измерения,
которые и являются источниками
возникновения ошибок.
Любое измерение,
как бы оно тщательно не выполнялось,
сопровождается ошибкой, численно равной
разности между результатом измерения
и истинным значением измеряемой величины.
Это значение можно назвать истинной
ошибкой
измерения
![]() ,
,
(1.1)
гдe xi
— результаты измерения;
X-
истинное значение измеряемой величины.
Значения большинства
величин получают как в результате
непосредственных измерений, так и с
помощью вычислений, т.е. прямым
и косвенным
способами.
Объектами измерений
могут быть как однородные,
так и неоднородные
величины. Например, в триангуляции
измеряются однородные величины (углы),
а в полигонометрии — неоднородные (углы
и длины линий). Вместе с тем основные
определяемые величины — координаты
пунктов — в том и другом случае являются
однородными.
Различают необходимые
и избыточные
измеренные
величины. Необходимыми являются
измеренные величины, достаточные для
однозначного определения значений
искомых величин. Измерения, выполненные
сверх необходимых, будут избыточными.
Они играют в теории ошибок важную роль,
так как позволяют:
-
контролировать
качество выполненных работ, выявляя
результаты с грубыми ошибками; -
оценить точность
выполненных измерений; -
определять наиболее
надежные значения измеряемых величин.
По отношению к
точности результаты измерений можно
подразделить на равноточные
и неравноточные.
Равноточными являются такие измерения,
которые выполняются
а) одним и тем же
инструментом или разными инструментами,
но с одинаковой точностью;
б) одними и теми
же методами или способами;
в) в одних и тех же
условиях.
Если какое-либо
из перечисленных пунктов не соблюдается,
то измерения относятся к неравноточным.
Особым качеством
результатов измерений является их
взаимная независимость. Наиболее полная
независимость достигается в том случае,
если измерения произведены в различных
условиях. В своей же массе большинство
результатов измерений можно отнести к
зависимым. Однако практика геодезических
работ позволяет пренебречь в пределах
точности измерений возникающими в этом
случае зависимостями.
1.2. Виды ошибок измерений
Причинами
возникновения ошибок в результате
измерений являются:
1) изменение величины
или состояния объекта в процессе
измерения;
2) личные ошибки
наблюдателя;
3) инструментальные
ошибки измерений;
4) влияние внешней
cреды.
Возникшие при
этом ошибки можно подразделить на три
вида: грубые,
систематические
и случайные.
К грубым ошибкам
относятся промахи, просчеты при
измерениях, а также ошибки, превосходящие
допустимые значения. Грубые ошибки
выявляются повторными измерениями и
исключаются из результатов. Следовательно,
задача сводится к организации контроля
наблюдений.
Если среднее
арифметическое из ошибок равноточных
измерений стремится к некоторому
пределу, отличному от нуля, при увеличении
числа измерений до бесконечности, то
такие ошибки называются систематическими.
К систематическим ошибкам относятся
составляющие общей ошибки измерений,
которые постоянны или закономерно
изменяются при повторных измерениях
одной и той же величины. Систематические
ошибки по характеру действия классифицируют:
на сохраняющие знак и величину; меняющиеся
по величине, но сохраняющие знак
(одностороннее действующие); изменяющиеся
по какому-либо функциональному закону.
Анализ причин возникновения систематических
ошибок позволяет частично или полностью
исключить их из результатов измерений.
Величина систематических ошибок зависит
от методики измерений.
Если среднее
арифметическое из ошибок равноточных
измерений одной и той же величины
стремится к нулю при увеличении числа
измерений до бесконечности, то такие
ошибки называются случайными. Случайная
ошибка является той частью общей ошибки,
которая меняется при повторных измерениях
одной и той же величины. Случайные ошибки
по величине чаще всего больше
систематических, но из-за взаимных
компенсаций их влияние на окончательный
результат может быть слабее.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Перейти к содержанию

На чтение 1 мин Просмотров 4.7к.
Отклонение результата измерения от истинного значения
измеряемой величины называется погрешностью измерения. Это сумма составляющих,
каждая из которых имеет свою причину возникновения. Далее более подробно
рассмотрим основные причины возникновения погрешности измерения.
Причины возникновения погрешности измерения
1. Неправильная настройка инструментов измерения или
смещение уровня настройки во время эксплуатации является первой причиной
возникновения погрешности измерения.
2. Низкий уровень квалификации или профессионализма
оператора, который проводил измерения. Сюда также относится его плохое
настроение или ухудшения состояния здоровья. Все это влияет на возникновение
погрешности.
3. Определенные особенности или характеристики
измерительного объекта, которые влияют на процесс исследования.
4. Негативное влияние факторов внешней среды на
инструмент или измерительный объект. Это может быть резкий перепад температур
или давления, влияние магнитного или электрического поля, вибрации.
5. Возникновение ошибок при получении, переработке и
выдачи информации в измерительной цепи измерительных инструментов.
6. Неправильная установка измерительного объекта на
плоскость может привести к возникновению погрешности.
7. Несоблюдение последовательности проведения анализа исследуемого объекта.
проголосуй за пост!
![]() Загрузка…
Загрузка…
Для повышения точности измерений рекомендуется производить не одно, а несколько измерений одной и той же величины C при одних и тех же условиях. При многократных измерениях погрешность измерения от случайных ошибок уменьшается в ![]() раз, где n – число измерений.
раз, где n – число измерений.
На основе закона нормального распределения случайных величин можно многократным измерением одних и тех же величин одним и тем же измерительным средством уменьшить влияние случайных ошибок, так как они усредняются, и в итоге повышается точность результата измерения.
Это действие усреднения результатов многократных измерений подтверждается народной пословицей «семь раз отмерь – один раз отрежь». Пословица обращает внимание на то, что однократное «отмеривание» может быть неточным, а семикратное «отмеривание» предохраняет от промахов.
Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.
Оценками рассеяния результатов в ряду измерений могут быть:
· размах;
· средняя арифметическая погрешность (по модулю);
· средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение);
· доверительные границы погрешности (доверительная граница или доверительная погрешность).
Размах – это оценка Rn рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле
Rn = Хmax – Xmin,
где Хmax и Хmin – наибольшее и наименьшее значения физической величины в данном ряду измерений.
Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер.
Проведя несколько повторных измерений одной и той же величины и получив различные результаты Xi, определяют среднее арифметическое значение ряда измерений ![]() и принимают его за истинное значение измеряемой величины Cист, т.е. принимают Cист =
и принимают его за истинное значение измеряемой величины Cист, т.е. принимают Cист = ![]() :
:
![]() =
= 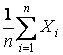 ,
,
где n – число единичных измерений в ряду.
Средняя квадратическая погрешность результатов единичных измерений в ряду измерений – это оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около их среднего значения, вычисляемая по формуле
S= 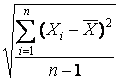 ,
,
где Хi – результат i—го единичного измерения; `Х — среднее арифметическое значение измеряемой величины из n единичных результатов.
На практике широко распространен термин среднее квадратическое отклонение – (СКО). С точки зрения упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность» (СКП). При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений.
Ценность результата многократных измерений значительно повышается, если кроме среднего арифметического значения ![]() будет определена средняя квадратическая погрешность среднего арифметического в виде S`Х, которая зависит от значения S и количества проведения измерений n:
будет определена средняя квадратическая погрешность среднего арифметического в виде S`Х, которая зависит от значения S и количества проведения измерений n:
S`Х = ![]() =
= 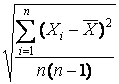 .
.
При ответственных измерениях проводят ряд повторных измерений и на основе полученных результатов всех измерений подсчитывают среднее арифметическое значение ![]() и среднюю квадратическую погрешность S, а потом и погрешность среднего арифметического S`Х.
и среднюю квадратическую погрешность S, а потом и погрешность среднего арифметического S`Х.
Доверительные границы погрешности результата измерений – это наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.
Доверительные границы распределения вычисляются как ± t S, ± t S`Х, где S, S`Х – средние квадратические погрешности соответственно единичного и среднего арифметического результатов измерений; t – коэффициент, зависящий от доверительной вероятности Р и числа измерений n.
t = 1 при Р = 35 %;
t = 2 при Р = 94,5 %;
t = 3 при Р = 99,73 %.
Для нормального закона распределения случайных величин используется t = 3.
Таким образом, результат измерения или истинное значение измеряемой величины Xист представляется так:
Xист = ![]() ± 3 S`Х или Xист =
± 3 S`Х или Xист = ![]() ±
± ![]() .
.
Полученный результат измерения не является одним конкретным числом, а представляет собой интервал, внутри которого с некоторой вероятностью Р находится истинное значение измеряемой величины.
Пример. Для определения размера отверстия опытной детали измерили его нутромером повышенной точности 10 раз (n = 10).
При подсчете получили ![]() = 60,012 мм и S = 0,00115 мм. Истинное значение размера отверстия детали представится так:
= 60,012 мм и S = 0,00115 мм. Истинное значение размера отверстия детали представится так:
Xист = 60,012 ± ![]() = 60,012 ± 0,0011 мм.
= 60,012 ± 0,0011 мм.
Результат расчета показывает, что истинное значение размера отверстия опытной детали определено с точностью ± 1,1 мкм и с вероятностью 0,9973, т.е. только в 0,27 % случаев может оказаться, что погрешность будет не 1,1 мкм.
В случае многократных повторных измерений одной и той же величины одним и тем же методом измерения и при отсутствии систематических погрешностей за предельную погрешность измерения в ряду измерений, обозначаемую Dпр, принимается значение, равное ± 3 S. Так, если бы целью десятикратных измерений являлось определение предельной погрешности данного метода измерения, то эта погрешность для любого отдельного измерения будет равна: Dпр = ± 3 S = ± 3 × 0,0011 = ± 0,003 мм.
Если при многократных измерениях появится погрешность больше 3 S, то такую погрешность считают грубой, и результат измерения с такой погрешностью отбрасывают.
Задания к разделу 8: Ответить на вопросы по своему варианту (номер варианта соответствует последней цифре номера зачетной книжки).
|
Номер варианта |
Вопрос |
|
1 |
1. Что такое погрешность результата измерения? 2. Какие погрешности называются случайными? |
|
2 |
1. Что такое погрешность средства измерения? 2. Что такое промах? Причины возникновения промахов. |
|
3 |
1. Что такое истинное значение физической величины? 2. Как отразится на результате измерений следование русской поговорке: «Семь раз отмерь – один раз отрежь»? |
|
4 |
1. Что такое действительное значение физической величины? 2. Что является оценками рассеяния результатов в ряду измерений? |
|
5 |
1. Что такое результат измерения? 2. Что такое размах и как он определяется? |
|
6 |
1. Какая погрешность называется систематической? 2. Что такое средняя квадратическая погрешность результатов единичных измерений в ряду измерений и как она определяется? |
|
7 |
1. Приведите классификацию систематических погрешностей. 2. Что такое средняя квадратическая погрешность среднего арифметического и как она определяется? |
|
8 |
1. Какая погрешность называется постоянной? 2. Что такое доверительные границы погрешности результата измерения? |
|
9 |
1. Какие погрешности называются прогрессивными? 2. Как вычисляются доверительные границы распределения? |
|
10 |
1. Какие погрешности называются периодическими? 2. Как определяется истинное значение измеряемой величины? |
Адекватным математическим аппаратом
описания случайных погрешностей является
теория вероятностей. Согласно последней
случайная величина наиболее полно
характеризуется своим законом
распределения (или  плотностью
плотностью
распределения) вероятностей. Измерителям
чаще всего приходится принимать
нормальную и равномерную плотность
распределения. Возможны и другие законы
распределения, которые обычно
аппроксимируются стандартными функциями.
Если выполняются предположения о том,
что погрешности измерений могут принимать
непрерывный ряд значений, при большом
числе измерений частота появления
погрешностей, равных по абсолютной
величине, но различного знака, одинакова
и малые погрешности встречаются чаще,
чем большие, то тогда для описания
случайных погрешностей следует применять
нормальный закон распределения
вероятностей, для которого
![]() (1.4)
(1.4)
где ![]() — плотность вероятностей случайной
— плотность вероятностей случайной
погрешности![]() ;— среднее
;— среднее
квадратическое значение случайной
погрешности.
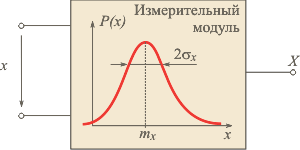
Кривые, соответствующие выражению (1.4)
для разных значений , приведены на рис. 1.1. Видно, что при
малых значениях о вероятней получить
малую погрешность измерений, нежели
при больших.
Вероятность того, что погрешность
результата измерения находится между
заданными предельными значениями ![]()
1, и![]()
2 , вычисляется по формуле
 (1.5)
(1.5)
Интеграл в формуле (1.5) можно вычислить,
используя таблицы функции Лапласа ![]() , приводимые в книгах по теории вероятностей
, приводимые в книгах по теории вероятностей
и статистической обработке экспериментальных
результатов [2,28]. Нетрудно заметить, что
![]() (1.6)
(1.6)
В табл. 1.1 приведены значения вероятностей
для некоторых интервалов ![]() , заданных в единицах.
, заданных в единицах.
Таблица 1.1
|
Интервал |
Вероятность |
1-P |
|
|
0,5 |
0,5 |
|
|
0,68 |
0,32 |
|
|
0,95 |
0,05 |
|
|
0,997 |
0,003 |
|
|
0,99993 |
0,00007 |
В первом столбце табл. 1.1 указываются
интервалы, характеризуемые своими
нижними и верхними границами ![]() и
и![]() соответственно. Второй столбец дает
соответственно. Второй столбец дает
вероятностиPтого, что случайная
погрешность результата измерения не
выходит за границы соответствующих
интервалов. В третьем столбце показано,
каковы вероятности выхода случайной
погрешности за пределы интервалов.
Согласно табл. 1.1 вероятности получения
значения случайных погрешностей в
интервале [-2/3,2/3
] и за его пределами одинаковы, в то
время как в среднем только 0,3% измерений
имеют погрешности, абсолютное значение
которых превышает 3. Значение погрешности 2/3называется вероятной погрешностью, а
значение 3часто
считают практическинаибольшей
возможной погрешностью. Однако при
большом числе измерений ( n>20 30)
максимальная погрешность нередко может
превышать 3 .
Как уже указывалось, часто распределение
погрешностей можно принять равномерным:

Такой закон распределения характерен,
например, для погрешностей отсчета по
шкале прибора, погрешностей дискретности
в цифровых измерительных приборах,
погрешностей квантования в аналого-цифровых
преобразователях (АЦП).
Рассмотрим далее оценки параметров
распределения случайных погрешностей
прямых измерений. Напомним, что случайная
абсолютная погрешность определяется
формулой ![]() , гдеx— результат измерения;x
, гдеx— результат измерения;x
и— истинное значение измеряемой
величины. Если было проведеноn прямых
измерений одной и той же величины, то в
общем случае в каждом из актов измерений
погрешность будет разной :![]() , где
, где![]()
—погрешностьi-го измерения;xi—
результатi-го измерения.
Поскольку истинное значение измеряемой
величины x инеизвестно,
непосредственно случайную абсолютную
погрешность вычислить нельзя. При
практических расчетах приходится вместоx ииспользовать его оценку.
Обычно принимают, что истинное значение
равно среднему арифметическому значению
ряда измерений:
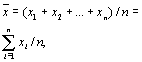 (1.7)
(1.7)
где xi— результаты отдельных
измерений;n—число измерений.
Теперь аналогично ![]() можно определить отклонение результата
можно определить отклонение результата
каждого измерения от среднего значения![]() как
как
![]() (1.8)
(1.8)
а затем по формуле
![]() (1.9)
(1.9)
вычислить оценку ![]() значения среднеквадратической погрешности
значения среднеквадратической погрешности
данного ряда измерений. Согласно теории
вероятностей при достаточно большом
числе измерений, имеющих независимые
случайные погрешности, оценка![]() сходится по вероятности к. Таким образом,
сходится по вероятности к. Таким образом,
![]() (1.10)
(1.10)
Ввиду того что среднее арифметическое
значение ![]() также является случайной величиной,
также является случайной величиной,
имеет смысл понятие среднеквадратического
отклонения среднего арифметического
значения![]() . Эту величину обозначим символом
. Эту величину обозначим символом![]() . Можно показать, что для независимых
. Можно показать, что для независимых
погрешностей
![]() (1.11)
(1.11)
Значение срхарактеризует степень разброса![]() . Как указывалось выше,
. Как указывалось выше,![]() выступает оценкой истинного значения
выступает оценкой истинного значения
измеряемой величины, т.е. является
конечным результатом выполняемых
измерений. Поэтомусрназывают также средней
квадратической погрешностью результата
измерений.
На практике значением , вычисляемым по (1.10), пользуются в том
случае, если необходимо дать характеристику
точности применяемого метода измерения:
если метод точен, то разброс результатов
отдельных измерений мал, т.е. мало
значениеЗначение
жесрвычисляемое по (1.11), используется для
характеристики точности результата
измерений некоторой величины, т.е.
результата, полученного посредством
математической обработки итогов целого
ряда отдельных прямых измерений.
Введем важные понятия доверительной
вероятности и доверительного интервала.
Как указывалось выше, среднее арифметическое
значение ![]()
, полученное в результате некоторого
ряда измерений, является оценкой
истинного значенияx ии,
конечно, как правило, не совпадает с
ним, а отличается на значение погрешности.
ПустьP Десть вероятность
того, что![]() отличается отx ине более чем
отличается отx ине более чем
на, т.е.
![]()
или
![]()
Вероятность P Дназываетсядоверительной вероятностью, а
интервал значений измеряемой величины
от![]()
до![]() — доверительным интервалом.
— доверительным интервалом.
Приведенные выше неравенства означают,
что с вероятностью P Ддоверительный интервал от![]()
до![]() заключает в себе истинное значениеx
заключает в себе истинное значениеx
иТаким образом, чтобы характеризовать
случайную погрешность достаточно полно,
надо располагать двумя числами —
доверительной вероятностью и
соответствующим ей доверительным
интервалом. Если закон распределения
вероятностей погрешностей известен,
то по заданной доверительной вероятности
можно определить доверительный интервал.
В частности, при достаточно большом
числе измерений часто бывает оправданным
использование нормального закона, в то
время как при небольшом числе измерений
( n<20) , результаты которых принадлежат
нормальному распределению, следует
пользоваться распределением Стьюдента.
Это распределение имеет плотность
вероятностей, практически совпадающую
с нормальной при большихn, но
значительно отличающуюся от нормальной
при малыхn.
В табл. 1.2 приведены так называемые
квантили распределения Стьюдента ![]() для числа измеренийn=2
для числа измеренийn=2
30 и доверительных вероятностейP
Д=0,80,99 . Более
полную таблицу можно найти, например,
в [2]. Укажем, однако, что обычно таблицы
распределения Стьюдента приводятся не
для значенийn и![]()
, а для значенийm=n-1 и=1-P Д, что следует учитывать
при пользовании ими. Чтобы определить
доверительный интервал, надо для данныхn иP Днайти квантиль![]() и вычислить величины
и вычислить величины
![]() и
и![]()
Ттаблица 1.2. Квантили распределения
Стьюдента
|
Число N |
Доверительная |
||||
|
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 17 20 30 |
3,08 1,89 1,64 1,53 1,48 1,44 1,42 1,40 1,38 1,37 1,36 1,36 1,35 1,34 1,34 1,33 1,31 |
6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,84 1,81 1,80 1,78 1,77 1,76 1,75 1,73 1,70 |
12,7 4,30 3,18 2,77 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 2,14 2,12 2,09 2,04 |
31,8 6,96 4,54 3,75 3,36 3,14 3,00 2,90 2,82 2,76 2,72 2,68 2,65 2,62 2,58 2,54 2,47 |
63,7 9,92 5,84 4,60 4,03 3,71 3,50 3,35 3,25 3,17 3,11 3,05 3,01 2,98 2,92 2,87 2,76 |
которые будут являться верхней и нижней
границами доверительного интервала.
Примеры нахождения доверительных
интервалов для заданной доверительной
вероятности приведены ниже. Там же
показана одна из наиболее употребительных
форм записи результата измерения в виде
![]()
где —
результат измерения в единицах измеряемой
величины;
— погрешность измерения;
В и
Н — верхняя и нижняя
границы погрешности измерения; P
Д— доверительная вероятность.
Пример 1. Произведено 17 отсчетов
значений измеряемой величины — напряжения
(см. ниже). Требуется произвести обработку
результатов измерений (предполагая их
нормальное распределение). Для этого
выбрать доверительную вероятностьP
Д=0.95 . Систематической погрешностью
пренебречь.
|
|
|
|
|
|
|
|
1 2 3 4 5 6 |
1681 1701 1693 1678 1686 1674 |
7 8 9 10 11 12 |
1705 1685 1697 1690 1690 1685 |
13 14 15 16 17 |
1682 1690 1687 1680 1692 |
![]() —
—
номер измерения,xi— результат
измерения.
Обработку результатов измерений будем
вести в следующей последовательности.
1. Определим среднее арифметическое
значение результатов отдельных измерений
по формуле (1.7):
![]() =
=
(1681 + 1701 + 1693 + 1678 + 1686 + 1674 + 1705 + 1685 + 1697 + +
1690 + 1690 + 1685 + 1682 + 1690 + 1687 + 1680 + 1692) /17 =
= 1688,0 мВ.
Значение ![]() будем считать оценкой истинного значения
будем считать оценкой истинного значения
измеряемого напряженияU, т.е. U=![]() 1688,0 мВ.
1688,0 мВ.
2. Вычислим отклонения результатов
отдельных измерений от среднего
значения ![]() по формуле (1.8):
по формуле (1.8):
|
|
|
|
|
|
|
|
1 2 3 4 5 6 |
-7 13 5 –10 –2 –14 |
7 8 9 10 11 12 |
17 –3 9 2 2 –3 |
13 14 15 16 17 |
–6 2 –1 –8 4 |
3. Вычислим оценку ![]() значения средней квадратической
значения средней квадратической
погрешности ряда измерений по формуле
(1.9):

Согласно (1.10)
![]() =8,1
=8,1
мВ.
Далее по (1.11) определим
ср =8,1/172,0 мВ.
Для вычисления доверительного интервала,
соответствующего доверительной
вероятности P Д =0,95 и числу
измеренийn=17, следует воспользоваться
табл. 1.2.
Находим значение квантиля:
![]()
Поскольку
ср =2мВ , то нижняя граница
доверительного интервала
![]()
а верхняя граница
![]()
Нижняя и верхняя границы погрешности
измерения
![]()
и
![]()
соответственно.
Результат измерения может быть записан
в виде
U=1688мВ;=+4мВ;РД
=0,95.
Пример 2. Произведено 10 отсчетов
значений измеряемой величины—напряжения
(см. ниже). Задание то же, что и в примере
1.
|
|
|
|
|
|
|
|
1 2 3 |
1681 1701 1693 |
4 5 6 |
1678 1686 1674 |
7 8 9 10 |
1705 1685 1697 1690 |
Следуя той же последовательности
действий что и в примере 1, получим
![]() =
=
1689,0мВ, т.е. U ![]() = 1689,0мВ;
= 1689,0мВ;
![]()
10мВ, т.е. ![]()
=10мВ;
ср=3,2мВ.
Находим из табл. 1.2 значение![]() . Следовательно, границы доверительного
. Следовательно, границы доверительного
интервала
x н =1689,0-2,263,2=1681,8=1682мВ ;
x в = 1689,0+2,263,2=1696,2=1696мВ.
Результат измерения записывается в
виде
U= 1689мВ ;=7 мВ ;P Д=0,95.
Сравнение результатов измерения в
примерах 1 и 2 показывает, что при
уменьшении числа измерений с 17 до 10
происходит увеличение доверительного
интервала, соответствующего одной и
той же доверительной вероятности P
Д =0,95.
Случайные погрешности косвенных
измерений. Если величинаАявляется
функцией величинХ, У,…, Z[А= f (Х,
У,…, Z] и определяется на основании
прямых измерений этих величин, то средняя
квадратическая погрешность измерения
величиныАможет быть вычислена по
формуле
![]() (1.12)
(1.12)
где X,Y,…,Z—средние квадратические погрешности
измерения величинХ, У,… , Z соответственно.
Производные вычисляются в точке (Х,
У,…, Z) . Формула (1.12) справедлива в том
случае, если величиныХ, У,…, Z независимы
(или некоррелированы).
Суммирование погрешностей. При
измерениях может быть несколько
источников как систематических, так и
случайных погрешностей. Поэтому
практически важным является вопрос о
правилах нахождения суммарной погрешности
измерения по известным значениям
погрешностей составляющих ее частей.
При суммировании составляющих
неисключенной систематической погрешности
их конкретные реализации можно
рассматривать как реализации случайной
величины. Если известны границы iсоставляющих неисключенной систематической
погрешности, а распределение этих
составляющих в пределах границ равномерно,
то граница неисключенной систематической
погрешности результата измерения
вычисляется по формуле
![]()
где k—коэффициент, определяемый
принятой доверительной вероятностью.
При доверительной вероятности 0,95 он
принимается равным 1,1 (ГОСТ 8.207-76) .
При суммировании случайных погрешностей
необходимо учитывать их корреляционные
связи. Суммарная средняя квадратическая
погрешность при двух составляющих может
быть вычислена по формуле
![]() (1.13)
(1.13)
где 1, и2—средние квадратические
погрешности отдельных составляющих;—коэффициент корреляции.
Поскольку на практике трудно получить
удовлетворительную оценку коэффициента
, приходится
ограничиваться крайними случаями, т.е.
считать, что либо,
либо
1. Тогда приведенная выше формула
примет вид
![]() если=0
если=0
или
![]() если1.
если1.
Таким образом, при отсутствии корреляционной
связи средние квадратические погрешности
складываются геометрически, а в случае
жесткой корреляционной
зависимости—алгебраически. Этот вывод
справедлив и для случая нескольких
источников погрешностей.
Правила нахождения границы погрешности
результата измерения при одновременном
наличии как неисключенных систематических,
так и случайных погрешностей также
регламентируются ГОСТ 8.207-76 и заключаются
в следующем. Если
< 0,8, то неисключенными систематическими
погрешностями по сравнению со случайными
пренебрегают и принимают, что граница
погрешности результата
![]()
где ![]() —коэффициент Стьюдента, определяемый
—коэффициент Стьюдента, определяемый
по табл. 1.2. Если
> 8, то, наоборот, пренебрегают
случайной погрешностью по сравнению с
систематической и считают, что граница
погрешности результата.
В случае, если эти неравенства не
выполняются, следует найти композицию
распределений случайных и неисключенных
систематических погрешностей,
рассматриваемых как случайные величины,
вычислить значение среднего квадратического
отклонения и затем границы суммарной
погрешности результата измерения.
Допускается также определение границы
погрешности результата измерения при
помощи приведенных в ГОСТ 8.207-76 эмпирических
формул.
Исключение грубых погрешностей.
Выделение грубых погрешностей
(промахов) не простая задача, она требует
достаточно глубокого понимания
особенностей поведения измеряемой
величины. Наиболее часто для обнаружения
промаха используют так называемыйкритерий Райта. Согласно этому
критерию, если случайное отклонение
какого-либо измерения от среднего
арифметического значения превышает З, то есть основание считать, что данное
измерение содержит промах. Критерий
Райта в таком виде целесообразно
применять при не очень большом числе
измеренийn20). Если же число измерений 20 <n
100, то рекомендуется вместо значения
Зиспользовать
значение 4.
Более обоснованная, хотя и более
громоздкая процедура исключения грубых
погрешностей базируется на одном из
разделов математической
статистики—статистической проверке
гипотез. В связи с тем что не предполагается
знания читателем соответствующего
материала, авторы вынуждены отослать
интересующихся к одному из курсов,
посвященных специально вопросу обработки
экспериментальных результатов [28 ].
Необходимое число измерений. Вопрос
о том, сколько измерений требуется
произвести для того, чтобы погрешность
не превышала допустимое значение, весьма
важен, так как от его решения зависит
весь последующий ход эксперимента.
Надо четко понимать, что увеличением
числа измерений можно уменьшить только
случайную составляющую погрешности
(уменьшить средние квадратические
погрешности иср, которые согласно формулам
(1.10) и (1.11) зависят от числа измеренийn) . В то же время систематическая
погрешность не уменьшается при увеличенииn. Поэтому если остаточная
систематическая погрешность является
преобладающей, то увеличение числа
измерений мало что дает. Чаще всего в
этом случае ограничиваются одним
измерением. Так, например, при измерении
напряжения сети неточным переносным
стрелочным прибором нет никакого смысла
прибегать к многократным измерениям и
статистической обработке результатов
измерения. Поскольку систематические
погрешности заведомо превышают случайные,
то достаточно провести всего одно
измерение. При более точных измерениях
на первый план могут выступить случайные
погрешности. Тогда проведение многократных
измерений является оправданным. Число
измерений нужно выбрать таким, чтобы
средняя квадратическая случайная
погрешностьсрне превышала максимального допускаемого
значенияср ,
доп. Ясно, однако, что уменьшениесрза счет многократных измерений
следует добиваться только до тех пор,
пока вклад случайных погрешностей в
общую погрешность измерения не будет
сравним со вкладом остаточных
систематических погрешностей.
Абсолютная погрешность
- Причины возникновения погрешности измерения
- Систематическая и случайная погрешности
- Определение абсолютной погрешности
- Алгоритм оценки абсолютной погрешности в серии прямых измерений
- Значащие цифры и правила округления результатов измерений
- Примеры
Причины возникновения погрешности измерения
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.
Виды погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
$$ Delta x = |x_{изм}-x_{ист} | $$
Например:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
$m_i,г$
98,4
99,2
98,1
100,3
98,5
$Delta m_i, г$
1,6
0,8
1,9
0,3
1,5
Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $
Для оценки границы абсолютной погрешности на практике используются статистические методы.
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.
Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:
$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$
Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:
$$ Delta x_i = |x_i-a| $$
Шаг 4. Находим среднее арифметическое абсолютных погрешностей:
$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$
Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.
Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:
$$ h = max {d; Delta x_{cp} } $$
Шаг 7. Округляем и записываем результаты измерений в виде:
$$ a-h le x le a+h или x = a pm h $$
Значащие цифры и правила округления результатов измерений
Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Например:
0,00501 — три значащие цифры 5,0 и 1.
5,01 — три значащие цифры.
5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.
Внимание!
Правила округления.
Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).
Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.
Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:
$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$
Примеры
Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?
По условию $11,55 le t le 11,63$. Получаем систему уравнений:
$$ {left{ begin{array}{c} a-h = 11,55 a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 h = 0,04end{array} right.} $$
$$ t = 11,59 pm 0,04 ℃ $$
Ответ: 0,04 ℃
Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.
$x_i$
15,3
16,4
15,3
15,8
15,7
16,2
15,9
Находим среднее арифметическое:
$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$
Находим абсолютные погрешности:
$$ Delta x_i = |x_i-a| $$
$ Delta x_i$
0,5
0,6
0,5
0
0,1
0,4
0,1
Находим среднее арифметическое:
$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$
Выбираем большую величину:
$$ h = max {d; Delta x_{ср} } = max {0,1; 0,31} = 0,31 $$
Округляем по правилам округления по избытку: $h approx ↑0,4$.
Получаем: x = 15, $8 pm 0,4$
Границы: $15,4 le x le 16,2$
Ответ: $15,4 le x le 16,2$
Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.
Более точное значение определяет более узкий интервал для x. По условию:
$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$
Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:
$$ 5,3 le a le 5,9 $$
Ответ: $ 5,3 le a le 5,9 $
Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
![]()
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
![]() измеряемой
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
![]()
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
![]()
(14)
Отношения
![]()
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
![]()
к среднему арифметическому значению
![]()
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
![]()
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
![]()
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
![]()
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
![]()
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
![]()
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
![]() :
:
![]() ,
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
![]() ,
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
![]()
(15)

(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
![]()
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
![]()
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:

(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
![]() —
—
среднее квадратичное отклонение;
![]() —
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).

Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
![]()
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
![]()
теоретически была определена в 1860 году
английским физиком Максвеллом

. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
![]()
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
![]() —
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:

(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.

Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n

-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
![]()
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
![]() (или
(или
высотой
![]()
– плотностью относительной частоты
![]() ).
).
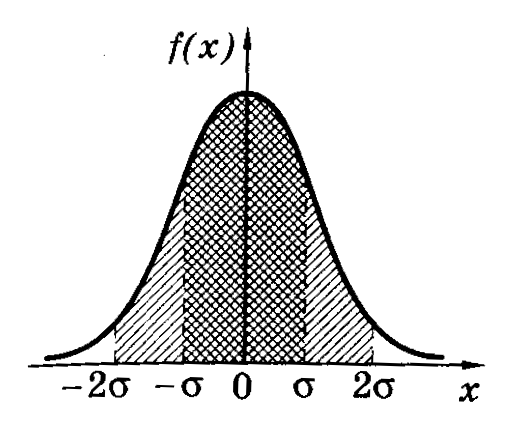
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
![]()
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:

(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
![]()
(25)
Где
![]()
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:

(26)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Абсолютная ошибка – это разность между измеренным значением и фактическим значением.[1]
Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.[2]
Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.
-

1
Запишите формулу для вычисления абсолютной ошибки. Формула:
, где
– абсолютная ошибка (разность между измеренным и фактическим значениями),
– измеренное значение,
– фактическое значение.[3]
-

2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
-

3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
-

4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[4]
Так вы вычислите абсолютную ошибку.- В нашем примере:
, то есть абсолютная ошибка измерения равна 1 м.
Реклама
- В нашем примере:
-

1
Запишите формулу для вычисления относительной ошибки. Формула:
, где
– относительная ошибка (отношение абсолютной ошибки к фактическому значению),
– измеренное значение,
– фактическое значение.[5]
-

2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
-

3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо
.
- Например, если фактическое значение равно 105 м, формула запишется так:
.
- Например, если фактическое значение равно 105 м, формула запишется так:
-

4
Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
-

5
Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете
, то есть измеренное значение.
-

6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[6]
Так вы вычислите абсолютную ошибку.- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
. Таким образом, абсолютная ошибка равна 2,1 м.
Реклама
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
-

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
-

2
-

3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.[9]
Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[10]
Так вы вычислите абсолютную ошибку.- Например, если измеренная длина поля равна
м, то есть абсолютная ошибка равна 0,5 м.
Реклама
- Например, если измеренная длина поля равна
Советы
- Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.
Реклама
Об этой статье
Эту страницу просматривали 24 549 раз.
Была ли эта статья полезной?
Статья обновлена 10.07.2022
Что такое погрешность измерения
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.

Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Приведенная погрешность: формула
Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Классификация оценочной погрешности
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
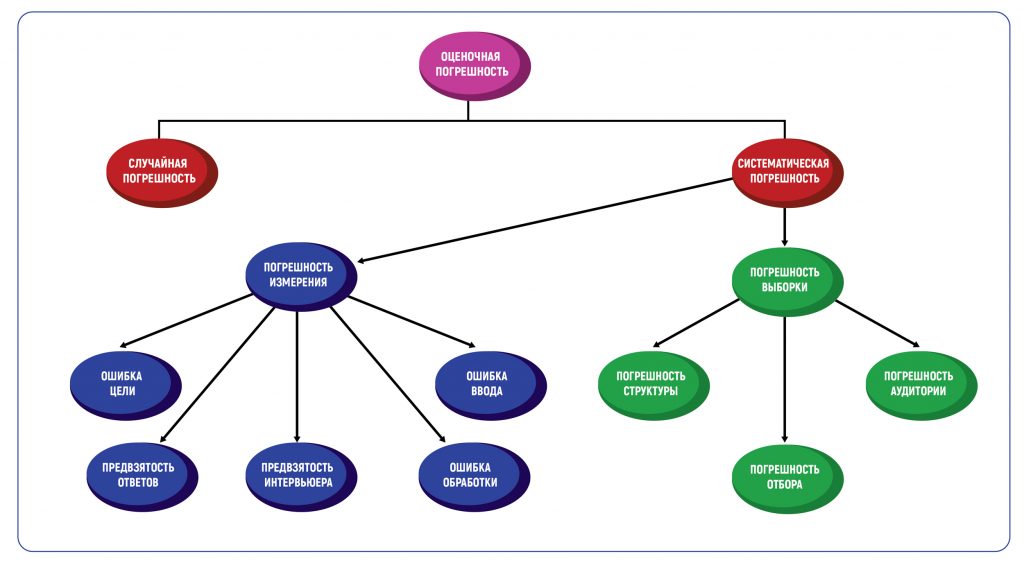
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.
Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.
Предвзятость ответов
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.
Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.
![]() (1.2), где X — результат измерения; Х0 — истинное значение этой величины.
(1.2), где X — результат измерения; Х0 — истинное значение этой величины.
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением
![]() (1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
(1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
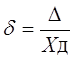 (1.4)
(1.4)
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.
Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Систематические и прогрессирующие погрешности средств измерений вызываются:
- первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
- вторые — старением элементов средства измерения.
Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Погрешности средств измерений.
Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:
![]() (1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
(1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:
![]() (1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
(1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному
(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).
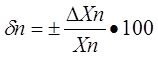 (1.7)
(1.7)
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).
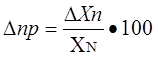 (1.8)
(1.8)
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.
Погрешности средств измерений подразделяются также на статические и динамические.
Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.
Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.
Факторы влияющие на погрешность измерений.
Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений
Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.
Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.
Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.
Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.
Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.
Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.
Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.
Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.
Шумы — любой сигнал не несущий полезной информации.
Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.
Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?
Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.
Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.
И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!
Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.
Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.
Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δx=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.
Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.
Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].
Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как
где δx — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δx;xизм+δx)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δxx⋅100%).
Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05мм (или
d=(40±5)⋅10-5м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?
Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.
С другой стороны, если погрешность δx известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δx
(и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.
В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений
Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨x⟩=x1+x2+…+xnn≡1n∑i=1nxi. | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:
| s=Δx12+Δx22+…+Δxn2n=1n∑i=1nΔxi2 | (1.2) |
или кратко
Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.
Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δxi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δxi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:
Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.
Предельную величину среднеквадратичного отклонения при n→∞
обозначим как
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.
Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):
sn-12=1n-1∑i=1nΔxi2,
(1.4)
где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:
- •
при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2). - •
выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).
Упражнение. Показать, что
s2=⟨x2⟩-⟨x⟩2.
(1.5)
то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n∑i=1nxi)2.
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.
При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.
Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.
При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить
- •
инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов; - •
методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения); - •
естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.
Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.
Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
- •
с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки); - •
с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером); - •
с несовершенством объекта измерений (неровная поверхность,
неоднородность состава); - •
со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).
Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
- 1.
Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления. - 2.
Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты. - 3.
Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов. - 4.
Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:
•
Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.
•
Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.
В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:
1.
Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.
2.
Систематическая погрешность, связанная с неправильной установкой нуля.
3.
Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).
4.2.1. Повышение точности путем усреднения результатов измерений
4.2.2. Точность и продолжительность измерений
Одной из наиболее распространенных операций, выполняемых в системах сбора данных и управления, является усреднение результатов многократных измерений. Интуитивно ясно, что этот процесс приводит к повышению точности, поскольку результаты отдельных измерений имеют как положительные, так и отрицательные отклонения от точного значения и поэтому частично взаимно компенсируются. С ростом числа измерений среднее значение отрицательных отклонений приближается по модулю к среднему значению положительных отклонений и точность их взаимной компенсации улучшается. Для практики важно получить количественную зависимость между числом измерений и погрешностью усредненного результата.
4.2.1. Повышение точности путем усреднения результатов измерений
Рассмотрим некоторое средство измерений, например, измерительный модуль аналогового ввода NL-8AI для измерения и ввода в компьютер значений напряжения ![]() (рис. 4.4). В общем случае на датчик, линию связи между датчиком и модулем и сам модуль действуют электромагнитные помехи и собственные шумы операционных усилителей, АЦП, резисторов, микропроцессорной части модуля и т. п. [Денисенко, Денисенко]. Мы не будем рассматривать помехи, действующие на объект измерений, поскольку он не входит в состав измерительного канала.
(рис. 4.4). В общем случае на датчик, линию связи между датчиком и модулем и сам модуль действуют электромагнитные помехи и собственные шумы операционных усилителей, АЦП, резисторов, микропроцессорной части модуля и т. п. [Денисенко, Денисенко]. Мы не будем рассматривать помехи, действующие на объект измерений, поскольку он не входит в состав измерительного канала.
|
|
|
Рис. 4.4. Модуль ввода измеряет физическую величину |
Указанные причины приводят к тому, что результат измерения становится случайной величиной, значение которой изменяется от измерения к измерению. Случайная величина ![]() может быть описана некоторой функцией распределения c математическим ожиданием
может быть описана некоторой функцией распределения c математическим ожиданием ![]() и среднеквадратическим отклонением
и среднеквадратическим отклонением ![]() , которое принимается за случайную составляющую погрешности измерительного прибора. Дисперсия случайной величины
, которое принимается за случайную составляющую погрешности измерительного прибора. Дисперсия случайной величины ![]() .
.
Погрешность средства измерений определяется изготовителем и указывается в эксплуатационной документации. В величину погрешности входит как систематическая, так и случайная составляющая. Если случайная составляющая превышает 10% от систематической, то она указывается отдельно (ГОСТ 8.009 [ГОСТ]). В некоторых случаях случайная составляющая указывается с помощью автокорреляционной функции или спектральной плотности мощности.
Случайная составляющая погрешности может быть снижена путем усреднения результатов многократных измерений. Если в составе погрешности преобладает систематическая компонента, то усреднение не приводит к повышению точности. О наличии случайной составляющей можно судить по рассеянию результатов однократных измерений.
Предположим, что с помощью измерительного модуля выполнено ![]() измерений, в результате которых получены значения
измерений, в результате которых получены значения ![]() . Усреднение результатов измерений выполняется по формуле среднего арифметического
. Усреднение результатов измерений выполняется по формуле среднего арифметического
|
(4.39) |
Однако ![]() также является случайной величиной, поскольку, выполняя несколько серий измерений и усредняя каждую из их, мы получим отличающиеся друг от друга средние значения
также является случайной величиной, поскольку, выполняя несколько серий измерений и усредняя каждую из их, мы получим отличающиеся друг от друга средние значения ![]() для каждой серии. Но
для каждой серии. Но ![]() будет иметь меньшую дисперсию (среднеквадратическое отклонение), чем измерительный прибор. Покажем это.
будет иметь меньшую дисперсию (среднеквадратическое отклонение), чем измерительный прибор. Покажем это.
Будем считать, что результаты измерений ![]() являются независимыми случайными величинами. Тогда дисперсия их среднего арифметического будет равна
являются независимыми случайными величинами. Тогда дисперсия их среднего арифметического будет равна
|
(4.40) |
откуда
|
(4.41) |
поскольку ![]() .
.
В (4.40) использованы два свойства оператора дисперсии: а) дисперсия произведения случайной величины и константы равна дисперсии случайной величины, умноженной на квадрат константы и б) дисперсия суммы случайных величин равна сумме дисперсий каждой из них [Гмурман]. Кроме того, считается, что все измерения выполнены одним и тем же прибором, т.е. дисперсии всех измерений одинаковы и равны ![]() , а случайные величины являются некоррелированными.
, а случайные величины являются некоррелированными.
Докажем первое из использованных свойств. По определению дисперсии ![]() и математического ожидания
и математического ожидания ![]() случайной величины
случайной величины ![]()
|
(4.42) |
Поэтому, умножая ![]() на константу
на константу ![]() , получим:
, получим: ![]() .
.
Докажем теперь, что дисперсия суммы случайных величин равна сумме их дисперсий. Для этого сначала докажем, что математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е.
|
(4.43) |
Сумма случайных величин ![]() — это такая случайная величина, которая принимает все возможные комбинации сумм случайных величин
— это такая случайная величина, которая принимает все возможные комбинации сумм случайных величин ![]() и
и ![]() , т.е.
, т.е. ![]() . Поэтому по определению математического ожидания
. Поэтому по определению математического ожидания
![]()
![]()
![]() . Аналогичное соотношение для
. Аналогичное соотношение для ![]() случайных величин можно доказать путем попарной группировки случайных величин. Формула (4.43) доказана.
случайных величин можно доказать путем попарной группировки случайных величин. Формула (4.43) доказана.
Выведем еще вспомогательное равенство, связывающее дисперсию случайной величины с математическим ожиданием. Пользуясь определением дисперсии (4.42), получим: ![]() .
.
Поскольку ![]() , получим
, получим
|
(4.44) |
Пользуясь соотношениями (4.43) и (4.44), получим дисперсию суммы двух случайных величин в виде
![]()
![]() .
.
Итак, усреднение ![]() некоррелированных измерений (см. (3.2)) позволяет уменьшить погрешность результата в
некоррелированных измерений (см. (3.2)) позволяет уменьшить погрешность результата в ![]() раз. Однако это утверждение справедливо при соблюдении нескольких условий, выполнимость которых довольно трудно проверить на практике.
раз. Однако это утверждение справедливо при соблюдении нескольких условий, выполнимость которых довольно трудно проверить на практике.
Во-первых, усреднение дает эффект только для случайной составляющей погрешности. Погрешность измерений перестает уменьшаться, когда ![]() становится настолько малой, что суммарная погрешность определяется систематической составляющей. Систематическая погрешность складывается из нелинейности АЦП и операционных усилителей, температурной зависимости напряжения смещения нуля и коэффициента передачи измерительного канала (температурно-зависимые погрешности учитываются как дополнительные), низкочастотных шумов, у которых время автокорреляции больше времени выполнения серии повторных измерений (к ним относится, в частности, «старение» элементов), динамической погрешности. Практически редко удается снизить общую погрешность измерений более чем в 2…3 раза с помощью усреднения.
становится настолько малой, что суммарная погрешность определяется систематической составляющей. Систематическая погрешность складывается из нелинейности АЦП и операционных усилителей, температурной зависимости напряжения смещения нуля и коэффициента передачи измерительного канала (температурно-зависимые погрешности учитываются как дополнительные), низкочастотных шумов, у которых время автокорреляции больше времени выполнения серии повторных измерений (к ним относится, в частности, «старение» элементов), динамической погрешности. Практически редко удается снизить общую погрешность измерений более чем в 2…3 раза с помощью усреднения.
Во-вторых, результаты измерений должны быть статистически независимы, т.е. интервал времени между соседними измерениями должен быть много больше времени автокорреляции случайной погрешности. Посмотрим на рис. 4.5: если при белом шуме средние значения за интервал времени ![]() и
и ![]() равны между собой (внизу), то при коррелированном шуме — не равны (вверху). К примеру, усреднение 100 измерений в течение 10 с не может скомпенсировать компоненты шума, спектр которых лежит ниже 0,1 Гц.
равны между собой (внизу), то при коррелированном шуме — не равны (вверху). К примеру, усреднение 100 измерений в течение 10 с не может скомпенсировать компоненты шума, спектр которых лежит ниже 0,1 Гц.
В частности, требование статистической независимости измерений не выполняется также в случае, когда действует искусственная помеха, делающая шум цветным (коррелированным), например, помеха от сотового передатчика на крыше здания, от радиотелефона, из сети 50 Гц, от сварочного аппарата, от молнии, от внутренних генераторов измерительного прибора, от электродрели и т. п. В этих случаях усреднение также ослабляет помеху, но уже не в ![]() раз, подробнее см. следующий параграф.
раз, подробнее см. следующий параграф.
Описанный эффект имеет место только для тех законов распределения случайной величины, для которых существует понятие среднего и среднеквадратического отклонения. Например, для распределения Коши интегралы, дающие названные определения, расходятся [Косарев].
Особо следует отметить, что как систематическая, так и случайная составляющая погрешности средств измерений являются случайными величинами. Однако между ними имеется принципиальное различие. Систематическая погрешность является случайной на множестве средств измерений, но детерминированной для каждого образца из множества. Поэтому систематическую погрешность невозможно уменьшить путем многократных измерений одним и тем же прибором, но можно уменьшить, усредняя результаты, полученные измерением с помощью множества средств измерений одного типа. Случайная же погрешность является случайной на множестве результатов измерений одним и тем средством измерений и поэтому ее можно уменьшить путем усреднения результатов многократных измерений.
В отличие от погрешности, разрешающая способность не зависит от величины систематической погрешности и поэтому может быть увеличена существенно. Она может стать даже меньше величины младшего значащего разряда АЦП при условии, если стабильность его уровней позволяет это сделать. На этом эффекте основан принцип действия дельта-сигма АЦП.
Если в паспорте на средство измерения не указана величина случайной составляющей погрешности, ее можно оценить по результатам измерений [Орнатский]:
|
(4.45) |
где коэффициент ![]() зависит от количества измерений
зависит от количества измерений ![]() . При
. При ![]() >60 он равен единице, при
>60 он равен единице, при ![]() <60 о выборе этого коэффициента см. в книге [Орнатский].
<60 о выборе этого коэффициента см. в книге [Орнатский].
Вопросам повышения точности путем многократных измерений посвящен ГОСТ 8.207-76 [ГОСТ].
4.2.2. Точность и продолжительность измерений
При использовании описанной выше процедуры усреднения результатов измерений никак не учитывалось, за какое время выполняется серия измерений, поскольку предполагалось, что погрешность является некоррелированным (белым) шумом. Ниже будут рассмотрены эффекты, которые возникают в реальных условиях, когда шум измерений является цветным. Попутно станет ясно, почему точные измерительные приборы работают медленно.
Измерительные каналы средств автоматизации обычно являются частью систем, компоненты которых распределены в пространстве и соединены между собой кабельными линиями. Поэтому на них воздействует весь спектр помех, имеющихся в конкретной электромагнитной обстановке. Основными компонентами случайной погрешности, вызванной помехами, являются белый шум, фликкер (1/f) шум и относительно узкополосные помехи от работающего электрооборудования, передатчиков и естественных источников электромагнитного излучения.
Пример одной реализации белого шума (некоррелированной погрешности измерения) показан на рис. 4.5, внизу. Характерной его особенностью является то, что при изменении масштаба по оси времени внешний вид графика не изменяется, уменьшается только среднеквадратическое значение шума вследствие уменьшения ширины временного окна наблюдения.
В отличие от этого, график реализации коррелированного шума изменяет свой внешний вид в зависимости от ширины окна наблюдения (рис. 4.5, вверху). Коррелированный шум с заданной автокорреляционной функцией можно получить из белого, пропустив его через фильтр с заранее рассчитанной передаточной характеристикой.
Многократные измерения с усреднением всегда выполняются на конечном интервале времени ![]() . Если случайная погрешность не коррелирована, то ее математическое ожидание равно нулю и не зависит от величины интервала
. Если случайная погрешность не коррелирована, то ее математическое ожидание равно нулю и не зависит от величины интервала ![]() (рис. 4.5) и момента начала измерения. Поэтому усреднение по формуле (3.2) может дать неограниченное уменьшение случайной составляющей погрешности измерений с ростом числа измерений.
(рис. 4.5) и момента начала измерения. Поэтому усреднение по формуле (3.2) может дать неограниченное уменьшение случайной составляющей погрешности измерений с ростом числа измерений.
Если же этот интервал усреднения ![]() меньше времени корреляции (см. рис. 4.5, вверху), то на каждом отдельно взятом интервале усреднения
меньше времени корреляции (см. рис. 4.5, вверху), то на каждом отдельно взятом интервале усреднения ![]() или
или ![]() получим разные значения погрешности. В отличие от белого шума, погрешность среднего арифметического при увеличении количества измерений будет стремиться к некоторому значению
получим разные значения погрешности. В отличие от белого шума, погрешность среднего арифметического при увеличении количества измерений будет стремиться к некоторому значению ![]() ,
, ![]() (рис. 4.5, вверху), отличному от нуля. Поэтому формула (3.2) перестает быть справедливой.
(рис. 4.5, вверху), отличному от нуля. Поэтому формула (3.2) перестает быть справедливой.
Поскольку в реальных измерениях всегда присутствует, по крайней мере, фликкер-шум (что является фундаментальным законом природы [Букингем]), который делает шум измерений отличным от белого, то усреднение измерений не может снизить случайную составляющую погрешности до нуля. Кроме того, в цифровых средствах измерений всегда присутствует помеха с частотой тактового генератора, которая придает окраску белому шуму.
Предположим, что измерения выполняются в течение конечного промежутка времени ![]() (т. е. во временном окне шириной
(т. е. во временном окне шириной ![]() ) и за это время выполняется
) и за это время выполняется ![]() измерений с равными интервалами
измерений с равными интервалами ![]() между ними, после чего находится среднее значение
между ними, после чего находится среднее значение ![]() (4.39). Предположим для простоты, что измеряемая величина равна нулю, т.е. в результате измерений мы получаем только величину случайной погрешности, которую обозначим
(4.39). Предположим для простоты, что измеряемая величина равна нулю, т.е. в результате измерений мы получаем только величину случайной погрешности, которую обозначим ![]() .
.
Найдем среднеквадратическое отклонение погрешности ![]() . Для этого выполним множество измерений сериями по
. Для этого выполним множество измерений сериями по ![]() , выполняя усреднение в пределах каждой серии. В результате получим множество значений
, выполняя усреднение в пределах каждой серии. В результате получим множество значений ![]() .
.
Измерение будем выполнять в моменты времени ![]() (рис. 4.6, слева). Обратим внимание, что измерение в моменты времени
(рис. 4.6, слева). Обратим внимание, что измерение в моменты времени ![]() эквивалентно измерению в один и тот же момент времени
эквивалентно измерению в один и тот же момент времени ![]() (рис. 4.6, справа), если использовать линии задержки, которые будут сдвигать реализацию случайного процесса на
(рис. 4.6, справа), если использовать линии задержки, которые будут сдвигать реализацию случайного процесса на ![]() . Поэтому результат усреднения измерений, выполненных за время
. Поэтому результат усреднения измерений, выполненных за время ![]() можно записать в виде
можно записать в виде
|
(4.46) |
где ![]() — момент времени выполнения измерений.
— момент времени выполнения измерений.
Функцию ![]() можно описать с помощью спектральной плотности мощности, для чего сначала найдем ее Фурье-изображение:
можно описать с помощью спектральной плотности мощности, для чего сначала найдем ее Фурье-изображение:
где сначала использована замена переменной ![]() , затем введено обозначение
, затем введено обозначение ![]() Фурье-изображения рассматриваемой случайной погрешности
Фурье-изображения рассматриваемой случайной погрешности ![]() .
.
Полученное выражение можно записать в виде
|
(4.48) |
где
|
(4.49) |
Таким образом, процесс усреднения можно рассматривать как прохождение случайного процесса через усредняющий фильтр с передаточной характеристикой (4.49). Поскольку вследствие симметрии Фурье изображений в (4.48) относительно оси ординат ![]() , то, умножая левую и правую часть этого выражения на соответствующие части в (4.48). получим:
, то, умножая левую и правую часть этого выражения на соответствующие части в (4.48). получим:
|
(4.50) |
откуда
|
(4.51) |
Пользуясь определением спектральной плотности мощности (4.15), из последнего выражения получим
|
(4.52) |
где ![]() и
и ![]() — спектральные плотности мощности случайной составляющей погрешности до процесса усреднения и после.
— спектральные плотности мощности случайной составляющей погрешности до процесса усреднения и после.
Рассмотрим передаточную функцию усредняющего фильтра (4.49). Используя формулу суммы членов геометрической прогрессии ![]() , ее можно записать в виде
, ее можно записать в виде
Пользуясь соотношением ![]() , окончательно получим
, окончательно получим
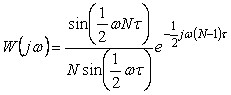 . . |
(4.54) |
Выражение (4.54) является передаточной функцией цифрового sinc-фильтра [Сергиенко], т. е. усреднение измерений, полученных в ![]() точках, отстоящих друг от друга на
точках, отстоящих друг от друга на ![]() , эквивалентно цифровой фильтрации в прямоугольном окне шириной
, эквивалентно цифровой фильтрации в прямоугольном окне шириной ![]() . В результате фильтрации ослабляются спектральные составляющие погрешности измерений, расположенные выше граничной частоты фильтра.
. В результате фильтрации ослабляются спектральные составляющие погрешности измерений, расположенные выше граничной частоты фильтра.
Дисперсию погрешности измерений можно найти, интегрируя спектральную плотность мощности погрешности по всей полосе частот, от 0 до ![]() (см. (4.18)):
(см. (4.18)):
|
(4.55) |
Это выражение справедливо для погрешности с любой спектральной плотностью. Предположим сначала, что погрешность является белым шумом, т.е. 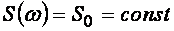 . Тогда, подставляя (4.54) в (4.55), получим
. Тогда, подставляя (4.54) в (4.55), получим
откуда
|
(4.57) |
Это выражение совпадает с ранее полученным выражением (3.2), поскольку использовано предположение о преобладании белого шума. Таким образом, усреднение ![]() однократных измерений при белом шуме уменьшает погрешность в
однократных измерений при белом шуме уменьшает погрешность в ![]() раз.
раз.
Предположим теперь, что случайная составляющая погрешности измерений обусловлена смесью белого шума со спектральной плотностью ![]() и фликкер-шума со спектральной плотностью
и фликкер-шума со спектральной плотностью ![]() , где
, где ![]() — константа, определяемая экспериментально (рис. 4.7). Тогда спектральную плотность мощности погрешности можно выразить как
— константа, определяемая экспериментально (рис. 4.7). Тогда спектральную плотность мощности погрешности можно выразить как
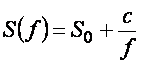 . . |
(4.58) |
Найдем частоту ![]() , на которой оба компонента шума одинаковы (рис. 4.7):
, на которой оба компонента шума одинаковы (рис. 4.7):
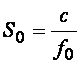 , откуда , откуда 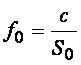 . . |
(4.59) |
|
|
|
Рис. 4.7. Спектральная плотность мощности погрешности измерений в виде смеси белого и фликкер-шума |
При ![]() спектральная плотность мощности (4.58) стремится к бесконечности, поэтому интеграл (4.55) для фликкер-шума расходится. Однако, если учесть, что измерительные каналы систем автоматизации имеют режим автокалибровки, то низкочастотные компоненты фликкер-шума будут подавлены. Это позволяет выбрать ненулевую нижнюю границу спектра фликкер-шума, равную
спектральная плотность мощности (4.58) стремится к бесконечности, поэтому интеграл (4.55) для фликкер-шума расходится. Однако, если учесть, что измерительные каналы систем автоматизации имеют режим автокалибровки, то низкочастотные компоненты фликкер-шума будут подавлены. Это позволяет выбрать ненулевую нижнюю границу спектра фликкер-шума, равную ![]() . Если калибровка в процессе эксплуатации прибора не выполняется, то величина
. Если калибровка в процессе эксплуатации прибора не выполняется, то величина ![]() будет определяться межповерочным интервалом средства измерений.
будет определяться межповерочным интервалом средства измерений.
Многократные измерения можно рассматривать как процесс дискретизации шума. Поскольку согласно теореме Котельникова для сохранения информации в дискретизированном сигнале частота отсчетов должна быть не менее удвоенной верхней частоты спектра сигнала, а шум имеет неограниченный спектр, то условие теоремы не выполняются и спектр шума после дискретизации будет сильно искажен вследствие алиасного эффекта. Однако, благодаря некоррелированности белого шума его отсчеты в любые моменты времени будут некоррелированы между собой, т.е. при дискретизации белого шума получается также белый шум. Наложение спектров вследствие алиасного эффекта также не придает окраску белому шуму, поскольку белый шум описывается функцией 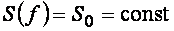 .
.
Спектр фликкер-шума после дискретизации в общем случае будет сильно искажен и будет представлять собой сумму сдвинутых друг относительно друга спектров исходного шума (см. раздел «Алиасные частоты, антиалиасные фильтры» и формулу (4.97)). Однако, чтобы упростить анализ, воспользуемся тем, что в области частот ![]() преобладает белый шум, а при
преобладает белый шум, а при ![]() — фликкер-шум. Тогда можно считать, что спектр фликкер-шума ограничен частотой
— фликкер-шум. Тогда можно считать, что спектр фликкер-шума ограничен частотой ![]() , а частота дискретизации всегда больше
, а частота дискретизации всегда больше ![]() , т. е. условия теоремы Котельникова выполнены и спектр фликкер-шума не искажается. Дисперсию погрешности измерений в условиях преобладания фликкер-шума можно найти из соотношения (4.55):
, т. е. условия теоремы Котельникова выполнены и спектр фликкер-шума не искажается. Дисперсию погрешности измерений в условиях преобладания фликкер-шума можно найти из соотношения (4.55):
где ![]() — нижняя граничная частота фликкер-шума;
— нижняя граничная частота фликкер-шума; ![]() ;
; ![]() — интегральный косинус:
— интегральный косинус: ![]() , где
, где ![]() — постоянная Эйлера.
— постоянная Эйлера.
Нормируем значение ![]() на
на ![]() . Тогда графики зависимости коэффициента уменьшения погрешности
. Тогда графики зависимости коэффициента уменьшения погрешности ![]() от количества измерений, построенные по формулам (4.60) и (3.2), будут иметь вид, приведенный на рис. 4.8. При построении графиков использованы следующие исходные данные:
от количества измерений, построенные по формулам (4.60) и (3.2), будут иметь вид, приведенный на рис. 4.8. При построении графиков использованы следующие исходные данные: ![]() , где
, где ![]() =24 час.,
=24 час., ![]() =1 с; параметр
=1 с; параметр ![]() при нормировании сокращается. Напомним, что формула (4.60) получена в предположении, что частота измерений превышает величину
при нормировании сокращается. Напомним, что формула (4.60) получена в предположении, что частота измерений превышает величину ![]() . Как видим, если при белом шуме усреднение 25 измерений дает снижение погрешности в 5 раз, то при наличии фликкер-шума — только в 1,2 раза.
. Как видим, если при белом шуме усреднение 25 измерений дает снижение погрешности в 5 раз, то при наличии фликкер-шума — только в 1,2 раза.
При белом шуме эффективность усреднения не зависит от ширины усредняющего окна, а зависит только от количества отсчетов (4.57). При наличии фликкер-шума эффективность усреднения начинает зависеть от ширины временного окна ![]() , причем увеличение его ширины менее эффективно, чем для белого шума, поскольку спектральная плотность мощности шума 1/f быстро возрастает с уменьшением частоты. Указанный эффект проявляется, в частности, в том, что различие среднего значения 100 результатов измерений, выполненных в течение 10 сек, будут сильно отличаться от среднего 100 измерений, выполненных за 10 суток. Погрешность, обусловленная фликкер-шумом, может быть существенно снижена только при условии, что ширина временного окна
, причем увеличение его ширины менее эффективно, чем для белого шума, поскольку спектральная плотность мощности шума 1/f быстро возрастает с уменьшением частоты. Указанный эффект проявляется, в частности, в том, что различие среднего значения 100 результатов измерений, выполненных в течение 10 сек, будут сильно отличаться от среднего 100 измерений, выполненных за 10 суток. Погрешность, обусловленная фликкер-шумом, может быть существенно снижена только при условии, что ширина временного окна ![]() превышает величину межкалибровочного интервала средства измерений.
превышает величину межкалибровочного интервала средства измерений.
Из вышеизложенного можно сделать следующие выводы.
- Увеличение точности путем усреднения результатов многократных измерений ограничено не только систематической составляющей погрешности, но и спектральным составом шума измерений. Фликкер-шум, спектральная плотность мощности которого растет с понижением частоты, ограничивает возможность увеличения точности путем усреднения.
- Наиболее практичным способом устранения погрешности, обусловленной фликкер-шумом, является периодическая автокалибровка средства измерений.
- Погрешность усреднения в случае некоррелированной погрешности не зависит от ширины временного окна
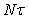 , а зависит только от количества отсчетов
, а зависит только от количества отсчетов 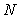 .
. - Усреднение может применяться только при постоянном значении измеряемой величины. В противном случае нужно учитывать динамическую погрешность (см. следующий параграф) или уменьшать ширину окна усреднения.
- Усреднение является разновидностью цифровой фильтрации методом «скользящего среднего», поэтому может быть использовано и при наличии шумов объекта измерений. Этой проблеме посвящена специальная литература [Сергиенко].
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookies и персональных данных в соответсвии с политикой. Окей, не возражаю
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
Страница 1 из 8
-
Форумчанин
Добрый день!
Хотелось бы увидеть обоснованное мнение форума по вопросу: можно ли прибором (к примеру 5сек тахеометром) добиться точности измерений (к примеру померить угол с точностью 1сек) выше заявленных в приборе?
Вашу точку зрения прошу подкреплять формулами.#1
-
Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.734
- Симпатии:
- 4.648
Конечно можно. Номинал точности измерений прибора показывает, какая точность гарантируется производителем прибора при соблюдении методик измерений и обработки. Но какую погрешность удалось получить Вам в конкретных условиях может определить только оценка точности.
#2
-
Форумчанин
Да. Обосновывать можно не буду? Всё же высшее техническое образование есть.
Или вы хотите устроить перепись геодезистов и кнопкодавов?#3
-
Форумчанин
- Регистрация:
- 1 янв 2009
- Сообщения:
- 5.958
- Симпатии:
- 2.151
- Адрес:
-
Москва
Нельзя. Только косвенными измерениями. Если создавать несколько фигур. Непосредственно нельзя из за таких ошибок как точность разбиения лимба и система снятия отчета.
#4
-
Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.734
- Симпатии:
- 4.648
А скп 5.1˝ получить можно?
#5
-
Форумчанин
- Регистрация:
- 1 янв 2009
- Сообщения:
- 5.958
- Симпатии:
- 2.151
- Адрес:
-
Москва
Да
— Сообщения объединены, 6 мар 2018, Оригинальное время сообщения: 6 мар 2018 —
Давным-давно читал в «Геодезии и картографии» статью о том как Т-30 смерить угол с точностью то ли 5 то ли 10 секунд.
Но Т-30 — повторительный и там насколько помню была хитрая метода совмещения штрихов на нач отчете.
И точность лимба у Т-30 с запасом. С тахеометром такое не прокатит.#6
-
Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.734
- Симпатии:
- 4.648
Но ведь, если наблюдатель выполнил все методические указания к определению величины угла, это будет нарушением требований, предъявляемых к классу этих приборов. Вы не находите?!!!
#7
-
Форумчанин
Может вы имеете ввиду случайно? Так да, нельзя.
Но.
В характеристике прибора 1″ или 5″ это средняя квадратическая ошибка измерения угла одним полным приёмом (КЛ+КП-180)/2.
А если мы увеличим количество приёмов? Применим методику круговых приёмов?#8
-
Форумчанин
- Регистрация:
- 1 янв 2009
- Сообщения:
- 5.958
- Симпатии:
- 2.151
- Адрес:
-
Москва
Можно увеличить количество приемов, но это не даст увеличение точности в 5 раз.
Я писал про ошибку разбиения лимба и т.д.
Упростим задачу. Можно ли смерить деревянным аршином с его точностью плюс минус 10 см длину 10 метровой линии с точностью 1 см?— Сообщения объединены, 6 мар 2018, Оригинальное время сообщения: 6 мар 2018 —
При увеличении числа приемов ошибка будет уменьшатся до какого то предела. Гипотенуза.
Хотя если смерить очень большое количество раз (сотни или тысячи) то я не уверен.
Но это уже из области чистой теории.— Сообщения объединены, 6 мар 2018 —
Нет. СКО дается с определенными допусками. Что бы точнее сформулировать надо залезть в инструментоведение.
#9
-
Форумчанин
Вы пытаетесь подменить понятия. Для «аршина» +/-10 см — это точность его изготовления.
Для прибора мы говорим о СКО измерения угла одним полным приёмом.
Да, увеличение количества приёмов может повысить точность измерения угла.
В разумных пределах и до определённого порога, когда ошибки наведения будут вносить сплошной «шум».
Перестановку лимба можно тоже устроить даже для прибора где она технически не предусмотрена.#10
Steinar и ЮС нравится это.
-
Форумчанин
- Регистрация:
- 1 янв 2009
- Сообщения:
- 5.958
- Симпатии:
- 2.151
- Адрес:
-
Москва
Точность изготовления лимба и системы считывающих устройств то же разные для односекундника и пятисекундника.
Не углубляясь в подробности можно сказать что для всех секундников предусмотрена двухсторонняя система считывания
а для 5 — односторонняя. Ну можете эксперементально проверить. Вроде как не менее 6 раз мериться угол полным приемом
и по формуле которую я не помню, но можно легко найти в интернете определяется СКО данного прибора.
Согласен что для отдельных приборов из партии может быть и двухкратное уменьшение СКО относительно паспортного,
но не пятикратное.— Сообщения объединены, 6 мар 2018, Оригинальное время сообщения: 6 мар 2018 —
Перестановка лимба то же в 5 раз точности не прибавит.
#11
-
Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.734
- Симпатии:
- 4.648
Вам не кажется, что Вы употребили термин «масло масляное»?
#12
-
Форумчанин
- Регистрация:
- 1 янв 2009
- Сообщения:
- 5.958
- Симпатии:
- 2.151
- Адрес:
-
Москва
Может быть. Только в точных науках каждая не абсолютная величина даётся с определённым допуском, погрешностью. Впрочем мы уходим в софистику
#13
-
Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.536
- Симпатии:
- 4.971
Да, вот в этом и есть разница.
Если измерять одним таким аршином, то вряд ли можно измерить точнее, чем +/-10 см. Но если имеются 100 аршинов с СКО длины +/-10 см, то измерив всеми ими и вычислив среднее значение, можно получить точность около +/-1 см.
Так и с измерением углов. Измеряя на одной установке лимба вряд ли можно получить точность много выше паспортной на прибор. При измерении же угла на разных установках, влияние ошибок лимба (и случайных ошибок наблюдателя) будет уменьшаться. При желании, 5″ можно получить точность угла в 1″.#14
-
Форумчанин
При многократных измерениях погрешность измерения от случайных ошибок уменьшается в корень из n раз, где n – число измерений.
На основе закона нормального распределения случайных величин можно многократным измерением одних и тех же величин одним и тем же измерительным средством уменьшить влияние случайных ошибок, так как они усредняются, и в итоге повышается точность результата измерения.
Итак. Если мы измеряем 5сек тахеометром (теодолитом) горизонтальный угол, то измерив его 25 раз полным приёмом получим 1сек точность измерения угла.
Грубые и систематические ошибки не учитываются.#15
-=13=- и BorisUK нравится это.
-
Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.734
- Симпатии:
- 4.648
Теория, в принципе, правильная, но практика не всегда соответствует теории, особенно при возрастании числа n. Там уже не столько математика, сколько другие науки, влияющие на точность геодезических работ.Абсолютно правильно, но и повышению точности тоже есть предел.Как Бог даст! Одноразово (когда-нибудь) и такое возможно…Если используются правильные методики, они исключают их.
#16
-
Форумчанин
Отнюдь… СКО в пять секунд мы и получим (либо грубее).
Паспортная точность тахеометра — это уже и есть результат его многократных измерений (намного более 25раз), выведенный в продажную характеристику..ЗЫ. Нужно ли разъяснять отличия паспортной точности от СКО наведения на цель конкретным экземпляром устройства — первый вопрос, и (второй вопрос) нужно ли приводить формулу расчета дисперсии?
#17
Последнее редактирование: 7 мар 2018
-
Форумчанин
- Регистрация:
- 29 дек 2009
- Сообщения:
- 3.743
- Симпатии:
- 4.136
Теоретически — да.
Практически — нет.#18
-
Форумчанин
- Регистрация:
- 1 янв 2009
- Сообщения:
- 5.958
- Симпатии:
- 2.151
- Адрес:
-
Москва
.
Частично согласен. При условии что ошибка центрирования не будет значительно влиять на измерение угла. То есть переставляя инструмент много раз мы уменьшим ошибку деления лимба. Про остальные различия тахеометров 5 и 1 секундной точности я имею поверхностное представление. Тут Пнг гео или Ковалев сказали бы веское слово
#19
-
Форумчанин
СКО (СКП) измерения гор. круга определяют с помощью коллиматора. 12 приёмами. После каждого приёма гор. круг переставляют на угол 15 град.
СКП вычисляют по формуле Гаусса.#20
Страница 1 из 8
Поделиться этой страницей
Причины возникновения погрешностей.
Введение.
Измерение физических величин и получение их числовых значений являются непосредственной задачей большинства физических экспериментов. При измерениях значение физической величины выражается в виде числа, которое указывает, во сколько раз измеренная величина больше (или меньше) другой величины, например, времени, пути, скорости и т. д. Физика устанавливает связь между такими величинами и выражает ее в виде формул, которые показывают, как числовые значения одних величин могут быть найдены по числовым значениям других.
Получение надежных числовых значений не является простой задачей из-за погрешностей, неизбежно возникающих при измерениях. Мы рассмотрим эти погрешности, а также методы, применяемые при обработке результатов измерений. Владение этими методами нужно для того, чтобы научиться получать из совокупности измерений наиболее близкие к истине результаты, вовремя заметить несоответствия и ошибки, разумно организовать сами измерения и правильно оценить точности полученных значений.
Измерения подразделяются на прямые и косвенные. В зависимости от вида измерений существуют различные методы оценки их точности. В свою очередь погрешности, допускаемые в процессе эксперимента, разделяются на систематические, случайные и грубые ошибки (промахи).
Прямые измерения производятся с помощью приборов, которые измеряют непосредственно саму исследуемую величину. Так, массу тела можно найти с помощью весов, длину измерить линейкой, а время – секундомером.
К косвенным относятся измерения таких физических величин, для нахождения которых необходимо использовать связь в виде формулы с другими, непосредственно измеряемыми величинами, например, нахождение объема тела по его линейным размерам, нахождение плотности тела по измеренным массе и объему, расчет сопротивления проводника по показаниям вольтметра и амперметра.
Причины возникновения погрешностей.
Из-за действия множества искажающих факторов результат каждого отдельного измерения физической величины не совпадает с ее истинным значением. Разность между результатом измерения и истинным значением измеряемой величины называется погрешностью измерений (ошибкой измерений).
Различают три типа погрешностей измерений: грубые ошибки (промахи), систематические и случайные погрешности. Грубые ошибки, или промахи, обычно бывают связаны с неисправностью измерительной аппаратуры, либо с ошибкой экспериментатора в отсчете или записи показаний приборов, либо с резким изменением условий измерений. Результаты измерений, соответствующих грубым ошибкам, нужно отбрасывать и взамен проводить новые измерения.
Методические погрешности обусловлены неадекватностью принимаемых моделей реальным объектам. Например, при измерении геометрических параметров вала или трубы их моделируют цилиндром. Диаметр цилиндра должен быть одинаков во всех сечениях и всех направлениях, образующие также должны иметь одинаковую длину. Однако в силу внутренних особенностей материала и несовершенства используемых технологий изготовления это правило обычно нарушено.
Другая причина – несовершенство методов измерений. Если расстояние между двумя точками порядка 100 м измеряется посредством многократного наложения метровой линейки, то в результате измеряется длина некоторой ломаной линии.
Погрешность может быть обусловлена также упрощением зависимостей, положенных в основу измерений. Например, ускорение свободного падения g можно определить, если измерить время t, в течение которого некоторое тело в свободном падении пройдет определенное расстояние h . При этом пользуются соотношением
 ,
,
которое справедливо, если на тело действует только сила тяжести. Реально на тело действует также сила сопротивления, которая в данном случае не учитывается.
Инструментальные (приборные) погрешности обусловлены особенностями принципов и методов измерений, используемых в приборах, а также их схемным, конструктивным и технологическим несовершенством. Одна из причин такой погрешности – погрешность калибровки, возникающая в процессе перехода от эталона к реальному средству измерения. Приборные погрешности определяются при испытании средства измерения и указываются в технической документации. Уменьшение инструментальной погрешности достигается применением более совершенных и точных приборов. Однако полностью устранить приборную погрешность невозможно.
Систематические погрешности сохраняют свою величину и знак во время эксперимента. Они могут быть связаны с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта, неравные плечи весов) и с самой постановкой опыта, например, при взвешивании тела малой плотности без учета выталкивающей архимедовой силы, которая систематически занижает вес тела. Систематические погрешности опыта могут быть изучены и учтены путем внесения поправок в результаты измерений. Если систематическая погрешность опыта слишком велика, то обычно оказывается проще использовать новые, более точные приборы, чем исследовать погрешности старых.
Оценку систематических погрешностей экспериментатор проводит, анализируя особенности методики, паспортную точность прибора и проводя контрольные опыты. В учебном практикуме учет систематических ошибок ограничивается, как правило, лишь случаем инструментальных погрешностей.
Систематические погрешности стрелочных электроизмерительных приборов (амперметров, вольтметров, потенциометров и т. п.) определяется их классом точности, который выражает абсолютную погрешность прибора в процентах от максимального значения включенной шкалы. Пусть на шкале вольтметра с диапазоном показаний от 0 до 10 В в кружке стоит цифра 1. Эта цифра показывает, что класс точности вольтметра равен 1 и предел его допустимой погрешности равен 1% от максимального значения включенной шкалы, т. е. равен  0,1 В. Общая формула для расчета максимальной абсолютной погрешности имеет вид:
0,1 В. Общая формула для расчета максимальной абсолютной погрешности имеет вид:
 ,
,
где K – класс точности прибора, Aмакс – верхний предел измерений прибора (либо данного его диапазона).
Кроме того, надо иметь в виду, что наносить деления на шкале принято с таким интервалом, чтобы величина абсолютной погрешности прибора не превышала половины цены деления шкалы.
Класс точности стрелочных электроизмерительных приборов (как и полцены деления шкалы) определяет максимальную (предельную) абсолютную погрешность, величина которой не меняется вдоль всей шкалы. Относительная же погрешность при этом резко меняется, поэтому приборы обеспечивают лучшую точность при отклонении стрелки почти на всю шкалу. Отсюда следует рекомендация: выбирать прибор так, чтобы стрелка прибора при измерениях находилась во второй половине шкалы. Относительную погрешность прибора можно рассчитать по формуле:
 .
.
В последнее время широко используются цифровые универсальные приборы, в том числе и электроизмерительные, отличающиеся высокой точностью и многоцелевым назначением. В отличие от стрелочных приборов систематические погрешности цифровых электроизмерительных приборов оцениваются по формулам, приводимым в инструкциях по эксплуатации.
Если класс точности прибора не указан и в паспорте прибора нет данных относительно его инструментальной погрешности, то обычно считают, что эта погрешность равна половине цены наименьшего деления шкалы прибора. В случае прибора, стрелка которого перемещается не равномерно, а «скачками» (например, у ручного секундомера), приборную погрешность считают равной цене деления шкалы.
Случайные погрешности измерений меняют величину и знак от опыта к опыту. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего значения.
Случайные погрешности могут быть связаны, например, с сухим трением (из-за которого стрелка прибора вместо того, чтобы останавливаться в правильном положении, «застревает» вблизи него), с люфтом в механических приспособлениях, с тряской, которую в городских условиях трудно исключить, с несовершенством объекта измерений (например, при измерении диаметра проволоки, которая из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение) или с особенностями самой измеряемой величины. Примером в последнем случае может быть число космических частиц, регистрируемых счетчиком за 1 минуту. Повторяя измерения, найдем, что в разных опытах получаются разные числа, хотя и не слишком отличающиеся друг от друга, колеблющиеся около некоторого среднего значения.
Случайные погрешности эксперимента исследуются путем сравнения результатов, полученных при нескольких измерениях, проведенных в одинаковых условиях. Если при двух-трех измерениях, проведенных в одинаковых условиях, результаты совпали, то на этом следует остановиться. Если они расходятся, нужно попытаться понять причину расхождения и устранить ее. Если устранить причину не удается, следует произвести 10-12 измерений и, записав все результаты, обработать их в соответствии с полученной закономерностью разброса величин.
Случайные погрешности устранить нельзя, но благодаря тому, что они подчиняются вероятностным закономерностям, всегда можно указать пределы, внутри которых с заданной вероятностью заключается истинное значение измеряемой величины.
Задача определения случайных погрешностей была решена созданием теории, хорошо согласующейся с экспериментом. В основе этой теории лежит закон нормального распределения, включающий следующие закономерности:
1. При большом числе измерений ошибки одинаковой величины, но разного знака, встречаются одинаково часто.
2. Частота появления ошибок уменьшается с ростом величины ошибки. Иначе говоря, большие ошибки наблюдаются реже, чем малые.
3. Ошибки измерений могут принимать непрерывный ряд значений.
Случайные погрешности изучают, опираясь на изложенные закономерности, и для понимания такого подхода требуется ввести понятие вероятности.
Статистическая вероятность события определяется отношением числа n случаев его проявления к общему числу N всех возможных равновероятных случаев:
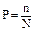
Надежностью результата измеренияфизической величины А называется вероятность Р того, что истинное значение А действительно лежит в интервале от  до
до 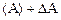
Абсолютной погрешностью измерений называют разность между найденным на опыте и истинным значением физической величины. Обозначая абсолютную погрешность измерения величины А символом  , получим
, получим
 .
.
Кроме абсолютной погрешности  часто бывает важно знать относительную погрешность
часто бывает важно знать относительную погрешность  измерений, которая равна отношению абсолютной погрешности к значению измеряемой величины:
измерений, которая равна отношению абсолютной погрешности к значению измеряемой величины:
 .
.
Качество измерений обычно определяется именно относительной, а не абсолютной погрешностью. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении стола может быть существенна, а при определении диаметра болта совершенно недопустима.
За наиболее достоверное значение непосредственно измеряемой величины А принимают среднее арифметическое <A> из всех n результатов ее измерений А1, А2, …, Аi, …, Аn:
 .
.
Окончательный результат измерения величины А представляют в форме
 .
.
При числе измерений n  5 с надежностью Р
5 с надежностью Р  2/3 можно принять, что абсолютная погрешность
2/3 можно принять, что абсолютная погрешность  равна стандартной (среднеквадратичной) погрешности
равна стандартной (среднеквадратичной) погрешности
 .
.
Если необходимо повысить надежность результата, то значение  следует соответственно увеличить, положив
следует соответственно увеличить, положив
 ,
,
где t – положительный коэффициент, задаваемый распределением Стьюдента. Значения коэффициентов Стьюдента рассчитаны и приведены в таблицах.
©2015- 2023 pdnr.ru Все права принадлежат авторам размещенных материалов.
Погрешности измерений и их
классификация .
При
измерении физических величии с помощью даже самых точных и совершенных средств
и методов их результат всегда отличается от истинного
значения измеряемой физической величины, т.е. определяется с некоторой
погрешностью. Источниками погрешностей измерения являются следующие
причины: несовершенство используемых методов и средств измерений,
нестабильность измеряемых физических величин, непостоянство климатических
условий, внешние и внутренние помехи, а также различные субъективные факторы
экспериментатора.
Определение
«погрешность» является одним из центральных в метрологии, в котором
используются понятия «погрешность результата измерения» и «погрешность
средства измерения».
Погрешностью результата измерения (погрешностью измерения) называется отклонение
результата измерения от истинного значения измеряемой физической величины. Так
как истинное значение измеряемой величины неизвестно, то при количественной
оценке погрешности пользуются действительным значением физической
величины.
Это
значение находится экспериментальным путем и настолько близко к истинному
значению, что для поставленной измерительной задачи может быть использовано
вместо него.
Погрешность средства измерения (СИ) — разность между показаниями СИ
и истинным (действительным) значением измеряемой физической величины. Она
характеризует точность результатов измерений, проводимых данным средством
Существует пять основных
признаков, по
которым классифицируются погрешности измерения.
По
способу количественного выражения погрешности измерения делятся на абсолютные,
относительные и приведенные.
![]() Абсолютной погрешностью △, выражаемой в единицах
Абсолютной погрешностью △, выражаемой в единицах
измеряемой величины, называется отклонение результата измерения х от истинного значения хн: (1.1)
и знак полученной
погрешности, но не определяет качество самого проведенного измерения.
Понятие
погрешности характеризует как бы несовершенство измерения.
Характеристикой качества измерения является используемое в метрологии понятие точности измерений, отражающее меру близости результатов измерений к истинному
значению измеряемой физической величины. Точность и погрешность связаны
обратной зависимостью. Иначе говоря, высокой точности измерений соответствует
малая погрешность. Так, например, измерение силы тока в 10 А и 100 А может быть
выполнено с идентичной абсолютной погрешностью ∆ = ±1 А. Однако качество
(точность) первого измерения ниже второго. Поэтому, чтобы иметь возможность
сравнивать качество измерений, введено понятие относительной погрешности.
Относительной погрешностью δ называется отношение
абсолютной погрешности измерения к истинному значению измеряемой величины:
 |
(1.2)
Мерой
точности измерений служит величина,
обратная модулю относительной погрешности, т.е. 1/|δ|. Погрешность δ часто выражают в
процентах:
δ
= 100△/хн (%). Поскольку обычно △⋍хн, то относительная погрешность
может быть определена как δ ⋍ △/х или δ = 100△/х (%).
Если
измерение выполнено однократно и за
абсолютную погрешность результата измерения △ принята разность между
показанием прибора и истинным значением измеряемой величины хН то из соотношения (1.2)
следует, что значение относительной погрешности δ уменьшается с ростом величины
хн (здесь предполагается
независимость △ от хн). Поэтому для измерений
целесообразно выбирать такой прибор, показания которого были бы в последней
части его шкалы (диапазона измерений), а для сравнения различных приборов
использовать понятие приведенной погрешности.
Приведенной погрешностью δпр, выражающей
потенциальную точность измерений, называется отношение абсолютной погрешности △ к некоторому нормирующему
значению XN (например, к конечному
значению шкалы прибора или сумме конечных значений шкал при двусторонней шкале).
По
характеру (закономерности) изменения погрешности измерений подразделяются на
систематические, случайные и грубые (промахи).
Систематические погрешности △с — составляющие погрешности измерений,
остающиеся постоянными или закономерно изменяющиеся , при многократных (повторных)
измерениях одной и той же величины в одних и тех же условиях. Такие погрешности
могут быть выявлены путем детального анализа возможных их источников и
уменьшены (применением более точных приборов, калибровкой приборов с помощью
рабочих мер и пр.). Однако полностью их устранить нельзя.
По
характеру изменения во времени систематические погрешности подразделяются на постоянные (сохраняющие величину и
знак), прогрессирующие (возрастающие или убывающие во времени), периодические, а также изменяющиеся во
времени по сложному непериодическому закону. Основные из этих погрешностей —
прогрессирующие.
Прогрессирующая (дрейфовая) погрешность — это непредсказуемая погрешность,
медленно меняющаяся во времени. Прогрессирующие погрешности характеризуются
следующими особенностями:
•
возможна
их коррекция поправками только в данный момент времени, а далее эти погрешности
вновь непредсказуемо изменяются;
•
изменения
прогрессирующих погрешностей во времени представляют собой нестационарный
случайный процесс (характеристики которого изменяются во времени), и поэтому в
рамках достаточно полно разработанной теории стационарных случайных процессов
они могут быть описаны лишь с некоторыми ограничениями.
Случайные погрешности
— составляющие погрешности измерений, изменяющиеся случайным образом при
повторных (многократных) измерениях одной и той же величины в одних и тех же
условиях. В появлении таких погрешностей нет каких-либо закономерностей, они
проявляются при повторных измерениях одной и той же величины в виде некоторого
разброса получаемых результатов. Практически случайные погрешности неизбежны,
неустранимы и всегда имеют место в результатах измерений. Описание случайных
погрешностей возможно только на основе теории случайных процессов и
математической статистики. В отличие от систематических случайные погрешности
нельзя исключить из результатов измерений путем введения поправки, однако их
можно существенно уменьшить путем многократного измерения этой величины и
последующей статистической обработкой полученных результатов.
Грубые погрешности (промахи) —
погрешности, существенно превышающие ожидаемые при данных условиях измерения.
Такие погрешности возникают из-за ошибок оператора или неучтенных внешних
воздействий. Их выявляют при обработке результатов измерений и исключают из рассмотрения,
пользуясь определенными правилами.
По причинам возникновения погрешности измерения подразделяются
на методические, инструментальные, внешние и субъективные.
Методические
погрешности возникают обычно из-за
несовершенства метода измерений, использования неверных теоретических
предпосылок (допущений) при измерениях, а также из-за влияния выбранного
средства измерения на измеряемые физические величины. При подключении
электроизмерительного прибора от источника сигнала потребляется некоторая
мощность. Это приводит к искажению режима работы источника сигнала и вызывает
погрешность метода измерения (методическую погрешность).
Так,
например, если вольтметр обладает недостаточно высоким входным сопротивлением,
то его подключение к исследуемой схеме способно изменить в ней распределение
токов и напряжений. При этом результат измерения может существенно отличаться
от действительного. Для расчета методической погрешности при измерении токов и
напряжений необходимо знать внутренние сопротивления амперметров RA
и вольтметров Rv. Методическую
погрешность можно уменьшить путем применения более точного метода измерения.
Инструментальные
(аппаратурные, приборные) погрешности
возникают из-за несовершенства средств измерения» т.е. из-за погрешностей
средств измерений. Источниками инструментальных погрешностей могут быть,
например, неточная градуировка прибора и смещение нуля, вариация показаний
прибора в процессе эксплуатации и т.д. Уменьшают инструментальные погрешности
применением более точного прибора.
Внешняя
погрешность — важная составляющая погрешности
измерения, связанная с отклонением одной или
нескольких влияющих величин от нормальных значений или выходом их за пределы нормальной области (например,
влияние влажности, температуры, внешних электрических и
магнитных полей, нестабильности источников питания, механических воздействий и
т.д.). В большинстве случаев внешние погрешности являются систематическими и
определяются дополнительными погрешностями применяемых средств измерений. .
Субъективные
погрешности вызываются ошибками оператора при отсчете
показаний средств измерения (погрешности от небрежности и невнимания
оператора, от параллакса, т.е. от неправильного направления взгляда при отсчете
показаний стрелочного прибора и пр.). Подобные погрешности устраняются
применением современных цифровых приборов или автоматических методов
измерения.
По характеру поведения измеряемой физической величины в процессе
измерений различают статические и динамические погрешности.
Статические
погрешности возникают при измерении
установившегося значения измеряемой величины, т.е. когда эта величина
перестает изменяться во времени.
Динамические
погрешности имеют место при динамических
измерениях, когда измеряемая величина
изменяется во времени и требуется установить закон ее изменения. Причина
появления динамических погрешностей состоит в несоответствии скоростных
(временных) характеристик прибора и скорости изменения измеряемой величины.
Средства измерений
могут применяться в нормальных и рабочих условиях.
Эти
условия для
конкретных видов СИ (средств измерения) установлены в
стандартах или технических условиях.
Нормальным
условиям применения средств измерений должен
удовлетворять ряд следующих (основных) требований:
температура
окружающего воздуха (20±5) °С;
относительная
влажность (65±15) %;
атмосферное
давление (100±4) кПа;
напряжение
питающей сети (220±4) В и (115±2,5) В;
частота
сети (50±1) Гц и (400±12) Гц.
Как
следует из перечисленных требований, нормальные условия применения СИ
характеризуются диапазоном значений влияющих на них величин типа климатических
факторов и параметров электропитания.
Рабочие
условия применения СИ определяются диапазоном
значений влияющих величин не только климатического характера и параметров
электропитания, но и типа механических воздействий. В частности, диапазон климатических
воздействий делится на ряд групп, охватывающих широкий диапазон изменения
окружающей температуры.