ОШИБКИ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
[c.169]
Поверхность тела представляется при помощи четырехугольных и треугольных элементов с квадратичным изменением формы и линейным, квадратичным или кубическим изменением перемещения и вектора напряжений относительно внутренней системы координат. Тело разбивается на подобласти производится дискретизация интегрального уравнения для каждой подобласти, и получается система уравнений ленточного типа. Для вычисления интегралов используется квадратурная формула Гаусса, число узлов в которой выбирается на основании верхней оценки для ошибки, определенной по значениям производных от подынтегральных выражений. Масштаб коэффициентов в уравнениях выбирается таким образом, чтобы получить устойчивую при счете систему, разрешимую методом исключения без итерации остатков. Поблочное решение уравнений позволяет рассматривать большие задачи. В программе используется большое число процедур, осуществляющих контроль и автоматическое формирование данных. Результаты решения задачи о фланце трубопровода и характеристики выполнения программы сравниваются с результатами, полученными методом конечных элементов, и экспериментальными результатами.
[c.111]
На рис. 77, а представлена одна из конструкций несущих платформ. Основными конструктивными элементами платформы являются пол, усиленный продольными ребрами замкнутого сечения, боковые борта, имеющие наклонный участок при переходе к полу, обвязки переднего борта, обвязки боковых бортов и задняя обвязка. Все обвязки имеют замкнутое сечение. Таким образом, платформа представляет собой пространственную тонкостенную конструкцию, которая эквивалентна открытой призматической (складчатой) системе. Расчет такой конструкции можно вести методом конечных элементов (МКЭ) с использованием балочного и оболочечного элементов. Для расчета автомобильных конструкций в настоящее время наиболее часто используют плоский треугольный симплекс-элемент. Например, таким элементом можно моделировать борта платформы. Однако функция, характеризующая перемещения в плоскости такого элемента, представляет собой полином первой степени, поэтому распределение деформаций и напряжений по стороне элемента постоянно, в то время как при закручивании открытых призматических (складчатых) систем каждая складка-пласти-на работает на изгиб в своей плоскости, что приводит к неравномерному распределению деформаций по ширине пластины. На рис. 77, б приведено характерное распределение деформаций по контуру призматической оболочки при кручении, соответствующее эпюре секториальных координат. По ширине наклонной пластины происходит резкое изменение продольных деформаций. Если этот участок моделировать треугольным элементом, то распределение деформаций будет равномерным, что приведет к большим ошибкам
[c.135]
Существует, однако, гораздо более существенный недостаток, в равной степени ограничивающий возможности обоих методов они эффективны только для закрытых систем. В разд. 3.3.2 отмечалось, что наиболее серьезные проблемы в методе конечных разностей возникают при попытке вычислить распределение поля в открытой системе. К сожалению, это справедливо и для метода конечных элементов. Если фокусирующий или отклоняющий элемент не окружен экраном, в вычислениях появляются большие ошибки. Действительно, оба метода требуют введения граничных условий всюду вокруг интересующей области. Для открытой системы приходится вводить некоторую функцию потенциала вдоль открытых границ. Если, например, положить потенциал нулевым на открытой границе, то условие, справедливое на бесконечности, перемещается ближе к самой системе. Это может внести очень серьезные ошибки. Мы уже обсуждали в разд. 3.1.2.2 ограничения, свойственные другим способам введения граничного потенциала. Всегда можно, конечно, предположить наличие эквипотенциального экрана вокруг системы, но такое дополнение неизбежно исказит поле открытой системы. Поэтому предположения такого рода ведут к существенным отличиям формулировки задачи от первоначальной.
[c.162]
Вся важная информация об элементе должна быть выведена на печать где-либо внутри указанного цикла. Вывод исходных данных на печать позволяет убедиться, что эти данные правильно от-перфорированы и введены в нужном порядке. Неверная исходная информация об элементе главный источник ошибки в программах, реализующих метод конечных элементов.
[c.118]
Для любого элемента Т обозначим через /С[г1 пространство, определяемое теми пробными функциями, которые отличны от нуля на Т. Другими словами, /С[г] есть сужение пространства пробных функций относительно элемента Т. Обозначим через /С[о] пространство таких функций u(p), для которых u(x)e/ [r]. Это пространство /С[о1 имеет особо важное значение при анализе методов конечных элементов. Порядок метода определяется максимальной степенью полинома (по р), для которого ошибка аппроксимации функцией из /С[о] равна нулю. В общем случае эта степень совпадает с таким максимальным к, для которого Я сг /С[о].
[c.122]
В добавление к, обычным ошибкам округления и аппроксимации, связанным с какой-либо вычислительной процедурой, есть и ошибки, связанные с самим методом конечных элементов [4—6]. К ним относятся .
[c.169]
Из предыдущего может показаться, что все типы элементов, для которых гарантируется сходимость, одинаково полезны, ио это далеко ие так. Нельзя игнорировать того, что на практике очень важна точность. Если. результаты при конечном размере элемента, диктуемом экономией вычислений, дают большую погрешность, то наличие элемента, который дает сходимость результата к точному решению по мере стремления размера элемента к нулю, является слабым утешением. Как можно иа практике определить точность вычисленного решения Ответ таков в общем случае никак. Одним из двух способов, однако, часто можно получить достаточный показатель точности. Первый состоит в том, что с помощью таких же элементов решается аналогичная задача с известным аналитическим решением. Определенная таким образом ошибка может быть использована для оценки ошибки в рассматриваемой задаче. Второй метод требует того, чтобы тип сходимости был предварительно определен для конкретной формулировки метода конечных элементов и для конкретной задачи. Если известно, что сходимость улучшается монотонно ) по мере уменьшения размеров сетки, то можно решить задачу несколько раз с последовательно уменьшаемыми элементами и для получения оценки сходимости решения экстраполировать результаты.
[c.175]
Следствие. Ошибка е — и — и метода конечных элементов удовлетворяет неравенствам
[c.62]
В примере, который мы рассматриваем сейчас, ошибка по перемещению действительно составляет O(h ). Одно из возможных доказательств —забыть о вариационном происхождении уравнений KQ = F метода конечных элементов и вычислить из них ошибку отсечения как из разностных уравнений (на границе х = п это уже сделано). Применяя принцип максимума, мь1 действительно получаем поточечную оценку e (x) I = О (/г ), которая оптимальна. Но этот подход не полностью удовлетворителен, так как распространение его на нерегулярные конечные элементы в задачах с двумя переменными вызывает огромные трудности. Поэтому важно найти соображения, позволяющие установить вариационно скорость сходимости ошибки по перемещению е Последующий прием приводит к успеху пусть г — решение исходной вариационной задачи на Же, в которой ошибка = z=u — u выбрана в качестве правой части. Приравняем нулю первую вариацию [c.64]
Теорема 1.6. Ошибка и — й в решении по методу конечных элементов, возникающая при замене функции f ее линейным интерполянтом fj, удовлетворяет неравенству
[c.66]
Эти результаты по аппроксимации приводят к ожидаемым скоростям сходимости метода конечных элементов при условии, что производная W обладает конечной энергией наклоны аппроксимируются с ошибкой 0(/г — ), энергия деформации с ошибкой и перемещение и — u с ошибкой О (/г ). Так
[c.79]
Г , в простейшем случае Г кусочно линейна О заменяется многоугольником О . Такой многоугольник можно разрезать на треугольники и применять далее метод конечных элементов без учета полосы Q — Q между сходной границей Г и многоугольником. Следовательно, мы как будто вдвигаем исходную дифференциальную задачу в О . В разд. 4.4 исследуется влияние этого изменения области. Кратко это влияние таково ошибка т-й производной у границы равна О (Л), но быстро убывает внутри области. Это приграничный эффект, средняя ошибка равна Так как энергия деформации зависит от
[c.131]
В этот краткий обзор теории необходимо включить также задачи на собственные значения и задачи с начальными условиями. Метод конечных элементов успешно применяется непосредственно к обеим задачам. Для самосопряженных задач на собственные значения классический прием — вычисление оценок сверху при минимизации отношения Рэлея на подпространстве он приводит к дискретной задаче на собственные значения КО = ХМЯ, где К и М — уже встречавшиеся матрицы жесткости и массы, В гл. 6 излагается эта дискретная формулировка и оцениваются ошибки в собственных векторах и функциях, зависящие от теории приближений они возникают из-за замены
[c.138]
Мы хотим предложить объяснение этого чуда, основанное на нашем наблюдении, что обычное измерение числа обусловленности для этих матриц неестественно. В вычислительных целях мы будем рассматривать эти матрицы как преобразования евклидова пространства (дискретного Ж°) в себя и потому возьмем одну и ту же норму для невязки уравнения и для результирующей ошибки в решении. Это целиком противоположно тому, что делается в дифференциальной задаче, или тому, что происходит при оценке ошибки дискретизации / измеряется в норме пространства Л1 и ее ошибка — в ш и ее ошибка — в Ж. (В вариационной задаче соответственно и Ж .) В самом деле, оператор I = с каким-либо обычным краевым условием вполне обусловлен как преобразование из Ж в Ж°. Ограниченность операторов I и была существенным моментом в разд. 1.2. Можно показать, что это верно и для разностного оператора б , а также для любого приемлемого аналога в методе конечных элементов, если только эти естественные нормы сохраняются. Следовательно, должен быть алгоритм решения уравнения КО, = Р, отражающий это свойство, и тогда чудо развеялось бы ошибки в Л1 и ш соответствовали бы их положению.
[c.147]
Обращаем внимание (и снова будем это делать), что нули функции —1/3 являются специфическими точками. Поскольку это нули полинома Лежандра, они участвуют в гауссовых квадратурах на интервале [//г, ( + 1) ] они переходят в ( + 1/2 1/л/з)/г. Для целей метода конечных элементов они специфичны еще и по другой причине в этих точках наилучшее приближение для квадратичной функции равно нулю, а, Ф абсолютно точна. (Известно, что в методе коллокации это так см.. разд. 2.3.) Будем называть их точками перемеи ения. Есть также точки напряжения, открытые Барлоу, которые еще важнее. Это точки, где производные от функции ошибки равны нулю (точка X = 0 в нашем простом примере) в разд. 3.4 мы покажем, что ошибки напряжений в этих точках меньше на добавочную степень Н.
[c.179]
Предыдущая теорема распространяется на любой конечный элемент на п-мерной равномерной сетке и даже на любой пример абстрактного метода конечных элементов. Для п переменных существует несколько производных порядка = р , возможно, связанных с разными постоянными в ошибках аппроксимации. В самом деле, если л Р оказывается в 8 , то соответствующая постоянная равна нулю. Локально можно считать функцию и разложенной в ряд Тейлора вплоть до члена степени к. Члены степени к—1 точно воспроизводятся пробным подпространством, и аппроксимация асимптотически зависит лишь от производных О и порядка к. Это обобщение теоремы 3.4 можно сформулировать, употребляя матрицы Кв вместо числовых постоянных Са.
[c.179]
Эти подсчеты подтверждаются численными экспериментами, описываемыми в технической литературе, которая отдает предпочтение конфигурации б. Для элементов более высокого порядка на ЭВМ смогли вычислить постоянные решая методом конечных элементов задачу, истинным решением которой было и = а Р. Одновременно вычисляются главные члены в ошибке усечения ряда Тейлора для конечно-разностной схемы, возникающей на равномерной сетке (см. разд. 1.3 и 3.4).
[c.181]
Предположим, наконец, что найдется М неизвестных, связанных с каждым квадратом сетки, так что уравнение метода конечных элементов (Q = Е становится объединенной системой М разностных уравнений. Неизвестными могут быть значения функции в различных узлах или значения функции и производных в кратном узле. Это не вносит сложностей, если ошибка оценивается из вариационных соображений (теорема 3.7) результат зависит только от порядка аппроксимации, достигаемого подпространством 5 , и любой дополнительный факт о подпространстве к делу не относится. Тем не менее при М > I аспект разностного уравнения становится намного тоньше.
[c.201]
Влияние на вычисляемые собственные значения других при- ближений — изменение области или коэффициентов, численные квадратуры, несогласованность элементов — сравнимо в методе конечных элементов с влиянием этих возмущений на энергию в стационарных задачах. Предупреждаем лишь, что при замене области Q многоугольником Q ошибка в энергии должна измеряться на Q. Поэтому ее порядок уже не O(li ), как было установлено в разд. 4.4 на многоугольнике если все пробные функции равны нулю на Q —то энергия по этой области полностью теряется соответствующее возмущение, пропорциональное площади этой подобласти, есть 0(h ).
[c.269]
Вычислим сначала скорость сходимости метода конечных элементов, не применяя специальные приемы — сгущение сетки и использование сингулярных функций. Оценить ошибку по энергии деформации не трудно. Как всегда, —ближайшая к и пробная функция, и, если u -Ж , эта ошибка имеет порядок Однако в общем случае и принадлежит всего лишь неко-
[c.307]
Поскольку ошибки приближения методом конечных элементов без сингулярных функций довольно быстро растут при приближении к точке Р, выбор lh = 0 h) так же хорош, как и любой другой. Эти ошибки представлены на рис. 8.6. Выводы здесь те же, что и в предыдущих экспериментах, но только теперь из-за дополнительной ошибки, возникающей в разностном отношении, метод сгущения сетки становится даже менее конкурентоспособным.
[c.316]
Естественно спросить почему конечные элементы не используются также и по временной переменной Конечно, можно было бы попытаться применить их, но это не даст особого успеха. С математической точки зрения вполне разумно изучить дискретизацию в два этапа сначала исследовать ошибку метода конечных элементов и(х, i) —u (x, t], а затем ошибку в возникающую при решении обыкновенных дифференциальных уравнений. По временной переменной геометрия области не вызывает трудностей, которые надо было бы преодолевать с помощью метода конечных элементов, и на самом деле непосредственное применение принципа Галёркина может связать все временные слои и уничтожить главное свойство распространения вперед по. времени. Мы не видим причин отказываться от этой дополнительной гибкости конечных разностей.
[c.282]
Как только что отмечалось, при анализе можно добиться доста точной математической строгости. Однако ввиду использовании метода конечных элементов для решения задач с математичесЫ сингулярным полем напряжений требуется тщательное исследова- ние точности результатов вычислений. Поскольку поставленная ав тором цель заключается в описании физического характера задачи вопрос о точности результатов считается неосновным. В остал1г ном сам метод конечных элементов и метод смыкания трещинИ для расчета скорости высвобождения энергии деформирования не влекут за собой серьезной концептуальной ошибки при использова- НИИ в задачах механики разрушения.
[c.126]
Сопоставление результатов, полученных для основной формы колебаний по методу Рэлея и методу конечных элементов, показывает достаточно хорошую точность проведенных вычислений максимальная ошибка при этом для квадратных вырезов была порядка 11%, а для прямоугольных вырезов 12 %. При использовании в вычислениях уточненного выражения для функции, аппроксимирующей перемещения плартинки, максимальная погрешность снизилась до 5%. Как уже упоминалось, результаты, полученные при помощи метода конечных элементов, показывают, что пятая и более высокие формы колебаний пластинок сложны по своей природе, особенно у пластинок с размерами вырезов более 0,4 а, Вследствие этого не делалось попыток апределять высшие формы колебаний при помощи метода Рэлея,
[c.154]
Наиболее важная часть главы — разд. 3.3. Здесь были изложены численные методы определения полей. Мы начали с обсуждения проблемы точности. Было объяснено что представляют собой ошибки округления, аппроксимации и внутренне присущие ошибки. Мы подробно рассмотрели три основных метода численных расчетов полей. Выражение (3.324) —это девятиточечная формула метода конечных разностей в случае аксиально-симметричных распределений потенциала. Метод конечных элементов основывается на вариационных уравнениях
[c.178]
Простейший метод проверки данных — записать их в в.иде описка и сравнить с исходной схемой, чтобы убедиться, что размеры элементов и номера узлов записаны правильно. Кроме этого, всегда необходимо проверять правильность расположения чисел в столбцах, потому что сдвиг в столбце. может привести к ошибочному ответу. Такая процедура проверки данных все же наименее желательна, так как человек, составляющий список, легко может ошибиться. В качестве про межуточного шага можно использовать программу, которая содержит те же операторы ввода и записи исходных данных, что и программа, реали зующая метод конечных элементов, но ко торая не выполняет никаких вычислений. Программа такого типа позволит вводить данные в ЭВМ, которая будет считывать и записывать данные. Любые неверно составленные столбцы чисел будут обнаружены при напечатании. Программа будет также обнаруживать ошибки в расположении пер-
[c.121]
В шести предыдущих главах при обсуждении различных областей применения метода конечных элементов использовались симплекс-элементы. Другой подход к прикладным задачам состоит в применении элементов высокого порядка, т. е. комплекс- или мультиплекс-элементов. Напомним, что число узлов в таких элементах превышает размерность решаемой задачи более чем на единицу. При таком подходе для достижения заданной степени точности решения требуется меньшее количество элементов, что приводит к сокращению числа перфокарт с исходными данными об элементах а это в свою очередь уменьшает вероятность ошибки при обработке данных. Применение элементов высокого порядка не всегда, однако, ведет к сокращению полного времени счета на ЭВМ. Для составления матриц элемента необходимо использовать методы численного интегрирования, которые требуют выполнения большого числа арифметических операций и, следовательно, увеличивают полное время счета, затрачиваемое на обработку одного элемента. Однако эти дополнительные затраты машинного времени компенсируются, вероятно, экономией времени в процессе обработки исходных данных.
[c.242]
Однако решения методом конечных элементов для сплошных конструкций, таких, как тонкая пластина, изображенная на рис. 2.4 (е), пространственное деформируемое тело, изгибаемая пластина и оболочка, не являются точными. Для иллюстрации этого утверждения предположим, что треугольные элементы, изображенные на рис. 2.4 (ё), построены в предположении, что для поля перемещений вдоль сторон элемента имеет место квадратичный закон распределения. На рис. 2.5(а) изображено деформированное состояние двух выбранных элементов. Если соединить элементы, как указано выше, то, вообще говоря, будет нарушена непрерывность перемещений вдоль линии, соединяющей два элемента (см. рис. 2.5 (Ь)). Соединения в вершинах элементов обеспечивают непрерывность только в этих точках. Квадратичная функция однозначно определяется по трем точкам, а так как только две концевые точки соприкасающихся сторон участвуют в определении формы смещений вдоль ребра, перемещения краев элементов будут различаться, за исключением некоторых частных случаев. Если псполь-зовать большее количество элементов, как указано на рис. 2.5(с), то различие в смещениях на сторонах соседних элементов станет меньше и вызванная указанным обстоятельством погрешность решения также уменьшится. Эта ошибка конечна для любого конечного числа элементов, поэтому решение является приближенным.
[c.43]
Основная задача состоит в исследовании точности, с которой кусочно полиномиальные функции могут аппроксимировать неизвестное решение и. Другими словами, надо определить, насколько хороши конечные элементы, построенные на основе вычислительной простоты, и дадут ли они хорошую аппроксимацию. Интуитивно ясно, что всякую достаточно хорошую функцию и можно с произвольной точностью приблизить кусочно линейными функциями. Математическая задача состоит в получении максимально точной оценки ошибки и определении скорости убывания ошибки при возрастании количества элементов )азбиения (или степени полинома внутри каждого элемента). Разумеется, метод конечных элементов можно применять, не доказывая математические теоремы так делали в течение более десяти лет. Однако мы считаем, что полезно, особенно для дальнейшего развития метода, понять и обобщить все, что уже сделано.
[c.12]
В практических задачах времт тоже должно быть дискретизировано, что предполагает применение метода конечных разностей. Например, схема- Кранка — Николсона симметрична относительно п+1/2 при вычислении uf tn+ ) через и потому имеет точность порядка At . Таким образом, окончательно вычисленное приближение содержит эту ошибку, как и ошибку метода Галёркина, вызванную дискретизацией по х. Последнюю из них мы проанализируем подробно и покажем, что при к 2т ее оптимальный порядок для 5-й производной тоже р -вен Этот результат применяется к уравнениям параболического типа, например к уравнению теплопроводности Ь — эллиптический оператор того же типа, что и в стационарных задачах. В случае гиперболических уравнений, не содержащих диссипативных членов, возможности метода конечных элементов несколько меньше трудности в сравнении с явными разностными методами- могут оказаться слишком большими. Тем не менее даже в этом случае достигнуты значительные результаты исследование границ можно проводить почти автоматически в гл. 7 включен набросок теории метода конечных элементов для гиперболического случая.
[c.139]
Множитель Лагранжа пробегает все допустимые функции, определенные на Г, а в истинной стационарной точке он связан с решением равенством % = dujdn ). Ошибку в стационарной точке ( K ) на подпространстве метода конечных элементов легко оценить [Б6].
[c.160]
В этом разделе мы применим предыдущие теоремы об аппроксимации для достижения главной цели всей нашей теории нахождение оценки ошибки и — Ф метода конечных элементов. Функция и служит решением п-мерной эллиптической краевой задачи порядка 2т, а Ф — ее приближением Ритца, вычисленным в пространстве метода конечных элементов На равномерной сетке уравненря метода конечных элементов KQ = F становятся системой разностных уравнений, и мы находим одновременно порядок точности этих разностных уравнений.
[c.195]
Короче говоря, проблема состоит в том, что не все ошибки отсечения в разностных уравнениях имеют ожидаемый порядок. Поэтому не так просто оценить эти ошибки, а затем, применяя устойчивость для обращения матрицы К, превратить их в оценки ошибки и — и . Дело в том, что задается специальной комбинацией пробных функций и, если другие комбинации почти не вносят вклад в задачу аппроксимации, их вклад в ы также оказывается малым. Напомним, что в абстрактном методе функции Фь. .., Фт порождают аппроксимацию порядка к тогда и только тогда, когда можно построить из них отдельную функцию 1 ), обладающею свойством (5), требуемым в теореме 3.2, т. е. функцию, которая сама подходит для аппроксимации. Можно считать пространство 5 порожденным этой суперфункцией ф и М—1 более или менее бесполезными функциями. Образуя соответствующую комбинацию разностных уравнений КО == Е, перепишем нашу систему метода конечных элементов в виде совокупности разностных уравнений специальной формы одно уравнение системы — точный аналог исходного дифференциального уравнения, остальные М — I уравнений (связанные с функ-
[c.201]
Приведенный список содержит также ряд численно интегрируемых элементов, но мы предпочитаем не рассматривать-численное интегрирование как производящее несогласованные элементы. Влияние такого интегрирования на самом деле состоит в замене истинного ф ункционала /(и) новым, но разность между ними не содержит граничных интегралов. Поэтому численное интегрирование и ошибку, которую оно вносит в аппроксимацию Ф метода конечных элементов, мы изучим отдельно.
[c.213]
Одновременно с приближением допустимых функций из Же кусочно полиномиальными в методе конечных элементов производятся и другие приближения, совершенно отличные от первых. Прежде всего можно менять саму область й заменяется на близкий многоугольник 2 или, в изопараметрическом методе, на область с кусочно полиномиальной границей. Любое другое приближение произвольной области вызвало бы большие труд- ности. Далее, сами краевые условия служат объектом аппроксимации. Если в задаче указано, что и — д х,у) на Г или и + а = Ь х, у), то эти функции и 6 почти неизбежно интерполируются в узлах на границе Г (или на ее приближении). Мы хотим оценить ошибку этих приближений.
[c.226]
Производные от отображения равны 0(h) около границы. Внутри они фактически равны нулю из-за множителя Заметим, что площади -обоих кругов одинаковы если бы один из них был вписан в другой, то появился бы дополнительный член гН , производные от которого не исчезают, но всюду в области 1меют меньший порядок Н . В терминах принципа Сен-Венана усреднение по локальным осцилляциям отлично от нуля и распространяется далее. Более того, если вместо волн os Q/h у круга были бы зубцы os0/i , то конформное отображение обладало бы слабыми особенностями в местах стыка. Однако при аппроксимации методом конечных элементов эти особенности смазываются и средняя ошибка в производных имеет порядок h у границы и внутри.
[c.231]
Теорема 7.1. Пусть 8 — пространство метода конечных элементов степени к—1. Тогда ошибка аппроксимации по методу Галёркина удовлетворяет неравенствам
[c.290]
На рисунках приводятся (возросшие) ошибки для пространств метода конечных элементов без сингулярных, функций. На этих графиках интересно отметить три момента. Во-первых, естественно, улучшение, достигаемое с сингулярными функциями (например, в R при h — 1/4 относительная ошибка без сингулярных функций равна примерно 40%, и она падает до 0,1% при добавлении их). Во-вторых, при отсутствии сингулярных функций поточечные ошибки максимальны вблизи Р. В частности, эти ошибки имеют порядок 0 h i ) вблизи Р и 0(h) в остальных точках ). В-третьих, обычные эрмитовы кубические элементы оказываются хуже, чем простейшие линейные элементы. Кубические элементы слишком гладки, чтобы справиться с особенностью.
[c.316]
Проверили модель, настройки программного комплекса и расчета. С виду все выглядит правильно, но в ходе выполнения расчета появляются ошибки. Знакомая ситуация? Тогда эта статья для вас. Инженеры нередко сталкиваются с одними и теми же ошибками.
Часто бывает, что нелинейный расчет не может достичь сходимости после того, как он отлично отработал в линейной области. Скорее всего, проблема в сетке конечных элементов. Создание сетки конечных элементов и ее управление — важный шаг в решении задач методом конечных элементов (МКЭ), и вычисленные результаты в КЭ имеют тенденцию быть наиболее точными, когда элементы являются компактными, без большого удлинения, перекоса и деформации, что подтверждено множество раз опытным путем.
Что вызывает искажение элементов?
Искажение элемента может произойти при описании геометрической неровности. Использование большей плотности (количества) элементов и более мелкого размера сетки в этих местах может помочь повысить точность результатов расчета и качество сетки. Однако использовать один и тот же мелкий шаг сетки по всей геометрии нецелесообразно и неэкономично, поскольку более крупный шаг сеток вполне подходит для описания геометрически более простых частей модели. Более крупный шаг сеток также применим, когда приложение нагрузки находится достаточно далеко от зоны интереса, а ожидаемый соответствующий эффект напряжений является тривиальным и вызывает незначительную деформацию. Следовательно, для моделей, которые имеют как мелкую, так и грубую сетку, искажение элементов может произойти из-за изменения размера сетки. На Рисунке 1 показаны искаженные элементы из-за перехода от крупных элементов к мелким. Они выделены зеленым цветом.
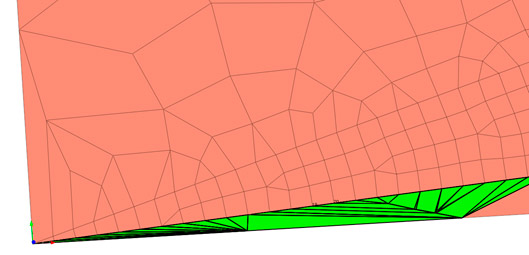
Рисунок 1. Искаженные элементы из-за перехода от крупных элементов к мелким
Искажение элементов также может происходить из-за связи между наборами сеток конечных элементов (Mesh Sets). В МКЭ связь объектов обеспечивается с помощью узловых соединений. Следовательно, самый простой способ смоделировать два соединяющихся объекта — это объединить узлы на их соединяющих границах. Однако, когда два набора сеток конечных элементов имеют разные размеры сетки, требуется переход элементов сетки (переходные элементы).
Как проверить качество элементов?
Помимо искажения элементов, относительный размер между соединенными элементами, форма и качество сетки конечных элементов оказывают большее влияние на результаты расчета, чем ее абсолютный размер: крупный или мелкий. Следовательно, после создания сеток важно проверить их качество, и в случае необходимости внести изменения.
Для того, чтобы проверить качество созданных конечных элементов в программном комплексе нужно вызвать соответствующий инструмент. Например, в расчетных комплексах midas GTS NX и midas FEA NX инструменты для такой проверки находятся по следующему пути: Mesh — Tools — Check — Check Mesh Quality.
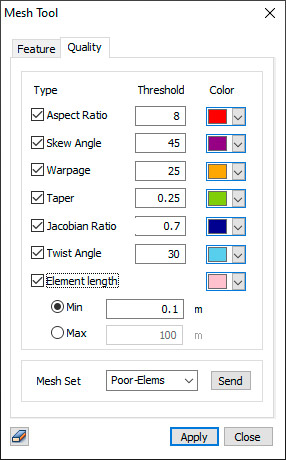
Рисунок 2. Диалоговое окно для проверки качества конечных элементов
Критерии для проверки качества конечных элементов
Соотношение сторон (Aspect Ratio)
Соотношение сторон — это отношение между шириной и длиной или отношение самой длинной стороны к самой короткой стороне 2D-элемента. Например, квадрат имеет одинаковую ширину и длину, следовательно, имеет соотношение сторон 1. По мере того, как форма отклоняется от формы квадрата, соотношение сторон становится больше. Значение близкое к 1 является идеальным — это соотношение оказывает существенное влияние на результат расчета и, если значение очень велико, может быть трудно получить нормальные результаты расчета, за счет того, что в элементах могут возникать концентрации напряжений и прочие эффекты.
Например, элемент с критерием «Aspect Ratio», равным 8, имеет самую длинную из сторон в восемь раз больше, чем самая короткая.
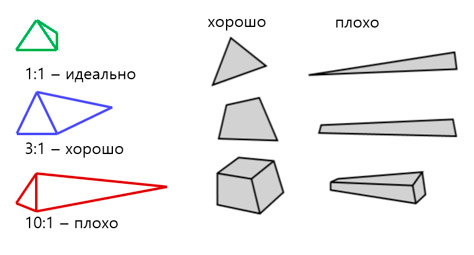
Рисунок 3. Соотношение сторон в конечных элементах
Угол наклона (Skew Angle)
Угол наклона описывает насколько форма элемента отклоняется от прямоугольной формы (90 градусов), измеренная в углах. Четырехугольник образует угол 90 градусов, угол наклона (Skew Angle) равен 0 градусов, это значение увеличивается по мере отклонения формы от четырехугольника. Для твердотельного элемента угол наклона проверяется для каждой грани, и в качестве угла наклона выбирается наименьшее значение. Значение, близкое к 0 лучше. На Рисунке 4 показан угол наклона треугольных и четырехугольных элементов.
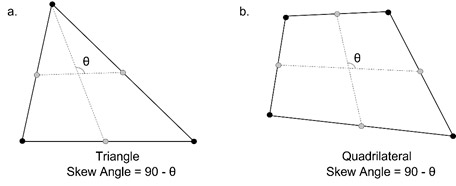
Рисунок 4. Угол наклона для треугольных и четырехугольных элементов
Коробление (Warpage)
Коробление (перекос) оценивает, насколько форма выходит за пределы плоскости. Для четырехугольного 2D-элемента, все узлы которого находятся в одной плоскости, значение равно 0. Значение увеличивается по мере отклонения формы от плоскости. Для твердотельного элемента коробление проверяется для каждой прямоугольной грани, и наименьшее значение выбирается в качестве значения коробления. Значение близкое к 0 лучше. Этот критерий влияет на результат расчета, и если значение очень велико, может быть трудно получить корректные результаты расчета. На Рисунке 5 показано, как рассчитывается величина коробления.
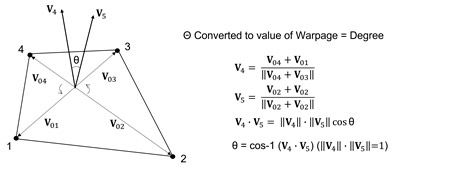
Рисунок 5. Определение значения критерия коробления
Конусность (Taper)
Данный критерий геометрически рассчитывает, насколько отклоняется четырехугольник. Не применяется к треугольным элементам. Четырехугольник имеет значение 1 и значение уменьшается по мере отклонения — это означает, что он становится ближе к треугольной форме по сравнению с его прямоугольной формой. Для твердотельного элемента значение конуса проверяется для каждой грани и наименьшее значение выбирается в качестве значения конуса. Значение близкое к 1 лучше. На Рисунке 6 показано, как рассчитывается конусность.
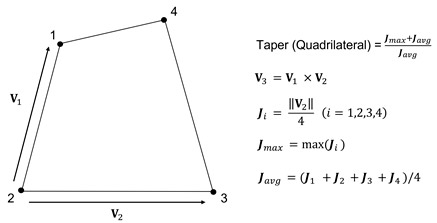
Рисунок 6. Определение значения критерия конусности
Отношение Якоби (Jacobian Ratio)
Определитель Якоби вычисляется в каждой интегральной точке Гаусса на сетке конечных элементов. Отношение Якоби — это отношение между наибольшим и наименьшим значениями детерминанта (определителя) Якоби. Для 2D-элементов определитель Якоби рассчитывается на элементе, спроецированном на плоскость. Для твердотельных элементов определитель Якоби рассчитывается напрямую. Если четырехугольный элемент не выпуклый, выводится отрицательное значение и расчет не выполняется должным образом. Определитель Якоби не должен быть отрицательным. Четырехугольные элементы должны быть выпуклыми, чем выше значение отношения Якоби, тем лучше.
В двух четырехузловых элементах, показанных ниже, элемент (а) допустим, а элемент (б) — нет.
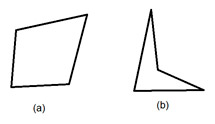
Рисунок 7. Допустимая форма элемента при оценке критерия Jacobian Ratio: а — допустимая форма, б — недопустимая форма
Скручивание (для твердотельных элементов) (Twist Angle)
Величина, которая характеризует скручивание двух противоположных граней твердотельного элемента — одной относительной другой.
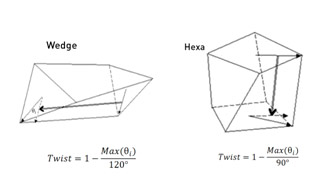
Рисунок 8. Скручивание твердотельных элементов
Для всех шести, указанных выше условий программный комплекс midas GTS NX или FEA NX выполняет автоматическую проверку и выделяет элементы, которые не удовлетворяют критериям, заданным пользователем.
Как предотвратить искажение элемента?
Для управления сеткой конечных элементов в программном обеспечении, основанном на методе конечных элементов, пользователям предоставляется большое количество инструментов, помогающих кастомизировать и сделать сетки конечных элементов качественными.
Например, в midas GTS NX или midas FEA NX есть инструменты: Mesh — Control — Size Control. Инженеры могут использовать данный инструмент управления и настройки перед генерацией сеток конечных элементов в одном из трех режимов: Point, Edge, Custom.
Режим Point
Укажите размер элементов в окрестностях выбранной точки. Опция применима только для точек, принадлежащих поверхности или являющихся внутренними объектами. Точки, расположенные на подчиненных формах (углы поверхности) автоматически игнорируются в процессе создания конечно-элементных сеток.
Например, инженеры могут указать размер элементов, окружающих выбранную точку, как показано на Рисунке 9.
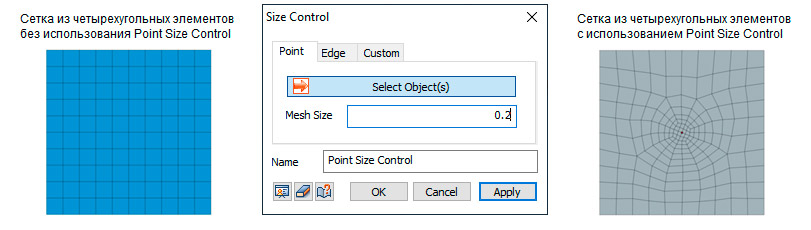
Рисунок 9. Управление сеткой конечных элементов через Size Control — Point
Режим Edge
Вы можете выбрать грани (линии) и использовать один из пяти описанных ниже методов, чтобы определить положение узлов сетки на выбранных гранях (размер сетки). Расстояние между узлами может быть задано напрямую, либо выбранная линия может быть разбита узлами на заданное число равных или переменной (по линейному закону) длины отрезков, как показано на Рисунке 10. Это особенно полезно на границе соединения нескольких объектов, где подразумевается использование сеток конечных элементов разных размеров.
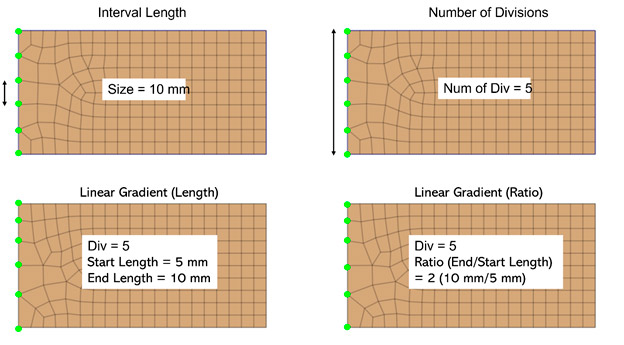
Рисунок 10. Управление сеткой конечных элементов через Size Control — Edge
-
Фиксированный типоразмер элементов (Interval Length)
Задайте регулярное расстояние между узлами в активной системе единиц измерения.
-
Фиксированное число делений грани (Number of Divisions)
Деление выбранной линии на несколько участков, в соответствии с указанным значением.
-
Линейный закон деления (Длина) (Linear Grading (Length))
Задайте расстояние между начальной и конечной точкой линии, чтобы автоматически определить расположение узлов путем линейной интерполяции.
-
Линейный закон деления (Коэффициент) (Linear Grading (Ratio))
Задайте коэффициент деления (начальный/конечный) от начальной до конечной точки линии.
-
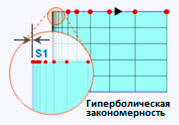
Гиперболический закон деления (Hyperbolic Tangent)
Укажите начальную длину элемента и число делений, чтобы определить расстояние между узлами с учетом полной длины линии и числа делений.
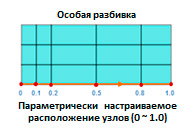
Режим Custom
Вы можете указать расположение узлов на выбранной грани путем прямого задания координат узлов в табличной форме. Задание коэффициента в пределах от 0 до 1 позволяет автоматически вычислить положение узла на выбранной линии.
Таким образом инженер может полностью контролировать, как качество создаваемых сеток конечных элементов, так и процесс их генерации, что в итоге приведет к качественной сетке конечных элементов в расчетной модели и, как следствие, к качественным результатам расчета.
В заключение
Часто встречаются случаи, когда мелкая сетка необходима вокруг конструктивных объектов или в той области, где нужно детально проанализировать результаты расчета. Например, ожидаются значительные перемещения и изменение напряжения вокруг места приложения нагрузки или значение момента может быть высоким вдоль части балочного элемента какой-либо конструкции. Для экономии ресурсов и времени имеет смысл генерировать мелкую сетку конечных элементов только вблизи указанных областей, а остальной массив модели описывать с помощью более крупной сетки. Описанное выше управление сеткой может быть реализовано для соединения мелкой и крупной сеток, которая моделирует объединенные узлы на границах набора сеток и плавный переход размера элемента для предотвращения искажения элементов.

Скачайте демо-версию midas GTS NX
Начните пользоваться уже сегодня! После скачивания демо-версии
вам будут доступны обучающие материалы по началу работы.
Марина Анатолиевна Придатко
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Метод конечных элементов используется для решения задач из области механики, гидродинамики и электродинамики.
Метод конечных элементов
Строительная механика, которая изучается студентами на 2-3 курсе, состоит из теоретического и практического курсов. Основным методов, который предстоит освоить будущим строителям является метод конечных элементов, который они будут активно использовать в дальнейших расчётах.
Суть самого метода очень проста – чтобы решить дифференциальное уравнение, ту область, в которой необходимо найти решение, разбивают на конечное, определенное (что следует из названия) количество элементов. За счет замены дифференциальных уравнений системой алгебраических, задача становится решаемой. В результате дискретизации определяется количество конечных элементов, из которых состоит система:

Подготовься к ЕГЭ и ОГЭ
Разбор ошибок в домашних заданиях с преподавателями, которые прошли через экзамен и знают все тонкости формата
Узнать подробнее
- в стержневых системах конечным элементом будут участки стержней;
- для плоских оболочек конечными элементами будут треугольные и прямоугольные элементы;
- при расчетах для трехмерных систем конечными элементами будут тетраэдры и параллелепипеды.
В дискретной модели, которая используется для решения задачи, элементы связаны друг с другом только в узлах. Искомые значения, возникающие в конечном элементе, определяются через узловые точки, а принятая произвольная нагрузка сменяется на систему эквивалентных сил. Для каждого узла может быть определено число перемещений, то есть степень его свободы. При этом число всех перемещений во всех узлах задает степень свободы конечного элемента.
Рисунок 1. Метод конечных элементов. Автор24 — интернет-биржа студенческих работ
«Метод конечных элементов» 👇
Метод получил большое распространение за рубежом, где вытеснил другие методы расчета. Его первое применение было зафиксировано в начале пятидесятых годов двадцатого века, он основывался на принципах строительной механики, что сужало сферу его применения, но, когда были сформулированы основы метода и возможности его адаптации к другим наукам, он получил широкое распространение. В России данный метод начал активно и повсеместно использоваться 20 лет назад.
Определение 1
Дискретизация – это процесс разбивки области, которая занята конструкцией, на некоторое число конечных элементов.
Виды метода
К преимуществам метода относится его гибкость при описании геометрии систем и условий в исследуемой области. Он является наглядным и универсальным и это определило его широкое применение.
Рассмотрим виды методов, которые применяются при расчетах:
- прямой метод является самым простым и наглядным, соотношения для конечных элементов выстраиваются на базе 3 групп уравнений, статики, геометрии и физики. Этот метод подходит для конечных элементов, обладающих простой геометрий и малым числом степеней свободы в узле;
- вариационный метод применяется для разных по сложности задач. Он базируется на том, что некоторая переменная может быть стационарной и зависеть от одной или ряда функций. Через постановку искомых функций в систему алгебраических уравнений могут быть найдены значения искомых узловых неизвестных;
- метод невязок подходит в том случае, когда вариационное уравнение не может быть сформировано. За счет введения отклонения решения от его точного значения, то есть невязки удается прийти к алгебраическим уравнениям;
- метод энергетического баланса использует значения баланса различных видов энергии, которые записаны в интегральной форме. Используется для динамических и нелинейных задач.
Замечание 1
Метод конечных элементов основан на физической дискретизации объекта, поэтому он отличается наглядностью.
Рисунок 2. Ошибки метода конечных элементов. Автор24 — интернет-биржа студенческих работ
Строительная механика позволяет сформировать правильное представление о работе отдельных элементов в единой системе. Метод конечных элементов является основой для дальнейших расчетов. За счет аппроксимации сплошной среды задача перестаёт быть нерешаемой и трудно описываемой. Некая, рассматривая в задаче область разбивается на конечные элементы, которые образуют сетку конечных элементов. Эти элементы соединены друг с другом в узлах, которые размещены по контуру каждого элемента Искомые значения выражаются через узловые значения, которые и являются основными неизвестными. Получившаяся дискретная система подчиняется всем принципам и методам, применяемым для любых дискретных систем.
Среди ошибок, которые могут быть допущены при применении метода можно назвать ошибки дискретизации, возникающие при замене реальной геометрии ее аппроксимацией, а также ошибки аппроксимации.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
и
пространственная изотропия
Остановимся
кратко на некоторых вопросах
математического характера.
Обычно
решение, полученное методом конечных
элементов, является приближением к
истинному, или точному решению. Как
близко это вычисленное решение к
точному, и сходится оно или нет – это
два важных вопроса, требующих ответа.
Попытаемся оценить точность и сходимость
метода конечных элементов.
Точность
– это мера близости численного решения
к точному, или истинному. Устойчивость
определяется ростом ошибок при выполнении
отдельных вычислительных операций.
Неустойчивое вычисление является
результатом аппроксимации, округления
или других ошибок, которые неограниченно
накапливаются, вследствие чего истинное
решение тонет в ошибках. Сходимость
– это постепенное приближение
последовательно вычисляемых решений
к предельному по мере того, как уточняются
некоторые вычислительные параметры,
такие, как размер элемента или ранг
базисной функции в пробном решении.
Термин “сходимость“ в этом же смысле
применяется и к итерационной процедуре,
в которой некоторые или все результаты
одного вычисления становятся входной
информацией для другого (повторного)
вычисления. В сходящейся процедуре
разница между последовательными
результатами уменьшается, стремясь в
пределе к нулю. Более подробные сведения
по этим вопросам можно найти в курсах
по численному анализу и методам
вычислений.
В
добавление к обычным ошибкам округления
и аппроксимации, связанным с какой-либо
вычислительной процедурой, есть и
ошибки,
связанные с самим методом
конечных элементов.
К ним относятся:
•
ошибки дискретизации, являющиеся
результатом геометрических различий
границы области и ее аппроксимации по
методу конечных элементов;
•
ошибки пробной, или базисной функции,
обусловленные разностью между точным
решением и его представлением пробной
функцией.
Ошибки
дискретизации могут быть уменьшены
использованием более мелких элементов
или расположением криволинейных около
границы. Ошибки пробной функции не
обязательно уменьшаются по мере
уменьшения размера элемента и могут
поэтому мешать сходимости к точному
решению или даже приводить к расходимости.
В
общем случае полиномиальная пробная
функция может только тогда дать точное
решение на элементе конечного размера,
когда полином является полным
и имеет бесконечную
степень. Последовательность линейно
независимых функций считается полной,
если можно найти такое число N
и набор постоянных аi
, при которых для произвольной допустимой
функции u
того же пространства R
справедливо неравенство
![]()
для
любой наперед заданной величины ε.
Поскольку на практике возможно
использовать конечное число членов,
представление пробной функции в виде
полинома не может быть ничем иным, как
приближением к точному решению. Это
означает, что на элементе конечного
размера пробная функция в виде полинома
конечной
степени всегда
содержит ошибку.
Элементный
вклад (5.1.5) содержит функцию
![]() и ее производные до порядкаn
и ее производные до порядкаn
включительно.
Полиномиальное представление для
![]() должно содержать, как минимум, степеньn,
должно содержать, как минимум, степеньn,
если n-я
производная отлична от нуля. Выбирая
полиномы n-ой
степени, получим в пределах элемента
следующие представления:
 (6.4.1)
(6.4.1)
Отсюда
видно, что, поскольку полином для
![]() является
является
полным, каждая из производных имеет в
своем представлении член, не зависящий
отх.
По мере того, как размер элемента
стремится к нулю, каждая из производных
стремится к своему точному значению,
и, следовательно, также ведет себя и
элементный вклад. В результате процедура
сходится.
Вышесказанное
позволяет сформулировать
критерий
1 ограниченной
сходимости:
условием сходимости является представление
переменной внутри элемента в виде
полного полинома как минимум степени
n,
где n
– наивысший порядок производной в
определяющем (ключевом) интеграле
(5.1.5).
Когда
для представления переменной
![]() используется
используется
полином более высокой степени, чем
указанный минимум, от аппроксимации
можно ожидать большей точности и меньшей
ошибки пробной функции и, как следствие,
более высокой скорости сходимости.
Наряду
с понятием полноты, вводится еще одна
характеристика пробной функции, –
согласованность.
Пробная функция рассматривается как
согласованная,
если переменная и ее производные вплоть
до порядка n-1
непрерывны
при переходе через границу между
элементами, где n
– порядок самой высокой производной
в ключевом интеграле (5.1.5) для элементного
вклада. Это позволяет сформулировать
критерий
2 ограниченной сходимости
: условие сходимости состоит в том, что
элементы
должны быть согласованными,
т.е. при переходе через границу между
элементами должны быть непрерывны
сама функция и ее производные
вплоть до порядка n-1
включительно. Отсюда следует, что
квадратичные и более высокого порядка
элементы, будучи, согласно определению,
согласованными, безусловно обеспечивают
сходимость метода конечных элементов
в версии как метода Галеркина, так и
вариационного. Для одного и того же
класса задач критерии 1 и 2 являются
достаточными
условиями сходимости метода конечных
элементов независимо от его формулировки.
Существует
еще один критерий 3 сходимости, связанный
с размером элемента, а именно, условие
сходимости состоит в том, что по мере
стремления к нулю размера элемента,
члены с производными и функцией в
уравнениях должны стремиться к функции
той гладкости, что и точное решение в
предположении непрерывности последней.
Из
изложенного выше может сложиться
впечатление, что все типы элементов,
для которых гарантируется сходимость,
одинаково полезны. Это не совсем так,
поскольку на практике очень важна
еще и точность. Как можно
практически
оценить вычисленного решения? Если
иметь в виду общий случай, то, к сожалению,
никак. Одним из двух способов, однако,
часто можно получить достаточный
показатель точности.
Первый
из них очевиден: путем сопоставления
с известным аналитическим
решением.
Второй
метод требует предварительного
определения типа сходимости для
конкретной формулировки МКЭ и для
конкретной задачи. Если окажется, что
сходимость улучшается монотонно по
мере уменьшения размеров элемента, то
можно решать задачу несколько раз с
последовательно уменьшаемыми элементами,
и для получения решения экстраполировать
результаты.
Монотонная
сходимость МКЭ к точному имеет место,
если:
•
тип элемента удовлетворяет условиям
полноты и согласованности по
критериям
1 и 2;
•
размеры сетки уменьшаются таким
образом, чтобы элементы каждого
последующего
уровня представляли собой части
соответствующих
элементов
предыдущего уровня;
•
подмножество разбиений каждого уровня
содержится в подмножествах
предыдущего
уровня.
Представление
зависимой переменной на элементе не
должно зависеть от используемой системы
координат, или, точнее, должно быть
геометрически
инвариантным
для ортогональных преобразований
системы координат. Это принято называть
пространственной, или геометрической
изотропией.
Кроме инвариантности геометрическая
изотропия также гарантирует вдоль
любой границы или ребра элемента полноту
полиномиального представления того
же порядка, что и внутри элемента.
Когда
в качестве пробной функции выбран
полный полином, то элемент обладает
геометрической изотропией. Если из
полинома исключаются некоторые члены,
то это следует сделать так, чтобы
элемент, соответствующий неполному
полиному, оставался по-прежнему
геометрически изотропным. При
определении
того, какие члены можно отбросить, ясно,
что симметричные пары (как x2,
y2
или x3,
y3,
или
x5y2,
x2y5)
не вносит несимметричность по отношению
к той или иной координате при условии,
что порядок исходного полинома не
уменьшился.
Для
иллюстрации отбрасывания симметричных
пар полного полинома, рассмотрим
содержащий десять членов полной
кубической полином от двух переменных:
![]() .
.
Элемент,
которому соответствует этот полный
полином, обладает геометрической
изотропией, но то же имеет место при
использовании следующих неполных
кубических полиномов:
![]() ,
,
или
![]() .
.
В
последних выражениях кубические члены
сохранены, чтобы порядок исходного
кубического полинома не уменьшился.
В
заключение заметим, что в практике
метода конечных элементов полные
полиномы,
как правило, не
употребляются.
Задание
6
6.1
Как изменится динамическое
уравнение для элемента, если
радиационный
компонент представить в граничных
условиях
выражением
![]() ,
,
а не в виде числа, определяемого на
предыдущем
шаге, согласно (6.5.1)? Какие трудности
программного и
математического
характера должны при этом возникнуть?
6.2
Возможны ли случаи, когда радиационный
компонент можно не
учитывать?
СПИСОК
РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
По
методу конечных элементов
-
Румянцев
А.В. Метод конечных элементов в задачах
теплопроводности: Учеб. пособ. Изд-во
Калининградского госуниверситета,
1997, 100 с. -
Сегерлинд
Л. Дж. Применение метода конечных
элементов. М.: Мир, 1979. -
Норри
Д., Ж. деФриз. Введение в метод конечных
элементов. М.: Мир, 1981. -
Зенкевич
О., Чанг И. Метод конечных элементов в
теории сооружений и в механике сплошных
сред. М.: Недра, 1974. -
Коннор
Дж., Бреббиа К. Метод конечных элементов
в механике жидкости. М.: Судостроение,
1979. -
Оден
Дж. Конечные элементы в механике
сплошных сред. М.:Мир,
1976, 464 с. -
Силвестр
П., Феррари Р. Метод конечных элементов
для радиоинженеров и инженеров-электриков.
М.: Мир, 1986. -
Кандидов
В.П., Чесноков С.С., Выслоух В.А. Метод
конечных элементов в задачах динамики.
М.: Изд-во МГУ, 1980. -
Тихонов
А.Н., Васильева А.Б., Свешников А.Г.
Дифференциальные уравнения: Учеб.
пособ, М.: Наука, 1985, 231 с. -
Кочин
Н.Е. Векторное исчисление и начала
тензорного исчисления. М.: Нау- ка,
1965, 426 с. -
Пытьев
Ю.П., Васильева А.Б., Пытьева Г.П.
Аналитическая геометрия с элементами
линейной алгебры: Учеб. пособ. М.: Изд-во
Моск. ун-та, 1986, 140 с. -
Волков
Е.А. Численные методы. М.: Наука, 1982, 254
с. -
Марчук
Г.И. Методы вычислительной математики.
М.: Наука, 1977, 536 с. -
РумянцевА.В.,
Васильев В.В. Решение нестационарной
осесимметричной задачи теплопроводности
методом конечных элементов с
использованием комплекс-элемента.
Деп. ВИНИТИ, № 123-В94.
15.Румянцев
А.В. Температура теплоносителя в длинном
неизотермическом канале. Деп.
ВИНИТИ, № 2679-В95.
16.
Румянцев А.В., Сергеенкова Р.С., Васильев
В.В. Решение нестационарной осесимметричной
задачи теплопроводности методом
конечных элементов с учетом радиационного
теплообмена. Деп. ВИНИТИ, № 125-В94.
17.
Румянцев А.В., Агапитов Д.А., Остроух
А.Н., Хоменко А.В. Система угловых
коэффициентов излучения
коническо-цилиндрической камеры с
торцами. Деп. ВИНИТИ, № 1963-В94.
18.
Румянцев А.В., Хоменко А.В., Васильев
В.В. Система угловых коэффициентов
излучения
коаксиальной камеры с кольцевыми
торцами. Деп. ВИНИТИ, №
1654-В95.
По
основам теплообмена и тепловому
проектированию
19.
Основы теплопередачи в авиационной и
ракетно-космической технике: Учебник
для авиационных специальностей вузов./
Авдуевский В.С., Галицейский Б.М., Глебов
Г.А. и др. М.: Машиностроение, 1992, 582 с.
20.
Лыков А.В. Теория теплопроводности. М.:
Высшая школа, 1967, 599 с.
21.
Арнольд П.В., Михайловский Г.А., Селиверстов
В.Н. Техническая термодинамика и
теплопередача. М.: Высшая школа, 1979, 444
с.
22.
Юдаев Б.Н. Техническая термодинамика:
Теплопередача. М.: Высшая школа, 1988, 479
с.
23.
Исаченко В.П., Осипов В.А., Сукомел А.С.
Теплопередача. М.: Энергия, 1975, 424 с.
24.
Зарубин B.C. Инженерные методы решения
задач теплопроводности. М.: Энергоатомиздат,
1983, 328 с.
25.
Темкин А.Г. Обратные методы теплопроводности.
М.: Энергия, 1973, 464 с.
26.
Лыков А.В. Тепломассообмен. Справочник.
М.: Энергия, 1978, 480 с.
27.
Дрейцер Г.А. Конвективный теплообмен
в каналах: Учеб. пособ. М.: Изд-во МАИ,
1984, 77 с.
28.
Мартыненко О.Г., Соковишин Ю.А.
Свободно-конвективный теплообмен:
Справочник. Минск: Наука и техника,
1982, 400 с.
29.
Себеси Г., Брэдшоу П. Конвективный
теплообмен. Физические основы и
вычислительные методы. М.: Мир, 1987, 592 с.
30.
Зигель Р., Хауэлл Д. Теплообмен
излучением. И.: Мир, 1975, 934 с.
31.
Зарубин B.C. Температурные поля в
конструкции летательных аппаратов.
М.: Машиностроение, 1978, 184 с.
32.
Залетаев В.М., Капинос Ю.В., Сургучев
О.В. Расчет теплообмена космического
аппарата. М.: Машиностроение, 1979, 208 с.
33.
Галицейский Б.Н. Теплопередача в
авиационных двигателях. М.: Изд-во МАИ,
1985, 82 с.
34.
Алемасов В.Е. Теория ракетных двигателей.
М.: Оборонгиз, 1965.
35.
Теплообмен в энергетических установках
космических аппаратов. Галицейский
Б.М., Данилов Ю.И., Дрейцер Г.А., Кошкин
В.К. М.: Машиностроение, 1975, 272 с.
36.
Полежаев Ю.В., Юревич Ф.Б. Тепловая
защита. М.: Энергия, 1976, 392 с.
37.Тепловой
расчет котельных агрегатов (нормативный
метод). М.: Энергия, 1973, 296 с.
38.
Вульман Ф.А., Хорьков Н.С Тепловые расчеты
на ЭВМ теплотехнических установок. М.:
Энергия, 1975, 198 с.
39.
Маргулова Т. Атомные электрические
станции. М.: Высшая школа, 1978, 311 с.
40.
Алифанов О.М. Идентификация процессов
теплообмена летательного аппарата.
М.: Машиностроение, 1979, 216 с.
41.Попырин
Л.С. Математическое моделирование и
оптимизация теплоэнергетических
установок. М: Энергия, 1978, 415 с.
42.
Вигак В.М. Оптимальное управление
нестационарными тепловыми режимами.
Киев.: Наукова думка, 1979, 359 с.
43.
Лаврентьев М.Н., Романов В.Г., Шишатский
С.П. Некорректные задачи математической
физики и анализа. М.: Наука, 1980, 288 с.
44.
Коздоба Л.А. Вычислительная теплофизика.
Киев.: Наукова думка, 1992, 276 с.
45.
Панкратов Б.М. Основы теплового
проектирования транспортных космических
систем. М.: Машиностроение, 1988, 303 с.
46.
Моделирование тепловых режимов
космического аппарата и окружающей
его среды. Под ред. акад. Петрова Г.И.
М.: Машиностроение, 1971, 380 с.
47.
Конструкция и проектирование космического
летательного аппарата. М.: Машиностроение,
1986, 344 с.
48.
Гущин В.В., Панкратов Б.Н., Родионов А.Д.
Основы устройства и конструирования
космических аппаратов. М.: Машиностроение,
1992, 278 с.
49.
Малоземов В.В. Выбор проектных параметров
подсистем терморегулирования. М.: Изд-во
МАИ, 1986, 344 с.
50.
Малоземов В.В., Логинов С.Н., Мартиросова
Е.И. Математическое моделирование
элементов, агрегатов и систем обеспечения
теплового режима летательных аппаратов.
М.: Изд-во МАИ, 1986, 91 с.
51.
Малоземов В.В., Логинов С.Н., Кутепов
С.Н. Анализ и исследование подсистем
обеспечения теплового режима летательных
аппаратов. М.: Изд-во МАИ, 1987, 103 с.
52.
Андрейчук О.Б., Малахов Н.Н. Тепловые
испытания космического аппарата. М.:
Машиностроение, 1982, 143 с.
Приложение
1
Марина Анатолиевна Придатко
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Метод конечных элементов используется для решения задач из области механики, гидродинамики и электродинамики.
Метод конечных элементов
Строительная механика, которая изучается студентами на 2-3 курсе, состоит из теоретического и практического курсов. Основным методов, который предстоит освоить будущим строителям является метод конечных элементов, который они будут активно использовать в дальнейших расчётах.
Суть самого метода очень проста – чтобы решить дифференциальное уравнение, ту область, в которой необходимо найти решение, разбивают на конечное, определенное (что следует из названия) количество элементов. За счет замены дифференциальных уравнений системой алгебраических, задача становится решаемой. В результате дискретизации определяется количество конечных элементов, из которых состоит система:

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 4 500 ₽
- в стержневых системах конечным элементом будут участки стержней;
- для плоских оболочек конечными элементами будут треугольные и прямоугольные элементы;
- при расчетах для трехмерных систем конечными элементами будут тетраэдры и параллелепипеды.
В дискретной модели, которая используется для решения задачи, элементы связаны друг с другом только в узлах. Искомые значения, возникающие в конечном элементе, определяются через узловые точки, а принятая произвольная нагрузка сменяется на систему эквивалентных сил. Для каждого узла может быть определено число перемещений, то есть степень его свободы. При этом число всех перемещений во всех узлах задает степень свободы конечного элемента.
Рисунок 1. Метод конечных элементов. Автор24 — интернет-биржа студенческих работ
«Метод конечных элементов» 👇
Метод получил большое распространение за рубежом, где вытеснил другие методы расчета. Его первое применение было зафиксировано в начале пятидесятых годов двадцатого века, он основывался на принципах строительной механики, что сужало сферу его применения, но, когда были сформулированы основы метода и возможности его адаптации к другим наукам, он получил широкое распространение. В России данный метод начал активно и повсеместно использоваться 20 лет назад.
Определение 1
Дискретизация – это процесс разбивки области, которая занята конструкцией, на некоторое число конечных элементов.
Виды метода
К преимуществам метода относится его гибкость при описании геометрии систем и условий в исследуемой области. Он является наглядным и универсальным и это определило его широкое применение.
Рассмотрим виды методов, которые применяются при расчетах:
- прямой метод является самым простым и наглядным, соотношения для конечных элементов выстраиваются на базе 3 групп уравнений, статики, геометрии и физики. Этот метод подходит для конечных элементов, обладающих простой геометрий и малым числом степеней свободы в узле;
- вариационный метод применяется для разных по сложности задач. Он базируется на том, что некоторая переменная может быть стационарной и зависеть от одной или ряда функций. Через постановку искомых функций в систему алгебраических уравнений могут быть найдены значения искомых узловых неизвестных;
- метод невязок подходит в том случае, когда вариационное уравнение не может быть сформировано. За счет введения отклонения решения от его точного значения, то есть невязки удается прийти к алгебраическим уравнениям;
- метод энергетического баланса использует значения баланса различных видов энергии, которые записаны в интегральной форме. Используется для динамических и нелинейных задач.
Замечание 1
Метод конечных элементов основан на физической дискретизации объекта, поэтому он отличается наглядностью.
Рисунок 2. Ошибки метода конечных элементов. Автор24 — интернет-биржа студенческих работ
Строительная механика позволяет сформировать правильное представление о работе отдельных элементов в единой системе. Метод конечных элементов является основой для дальнейших расчетов. За счет аппроксимации сплошной среды задача перестаёт быть нерешаемой и трудно описываемой. Некая, рассматривая в задаче область разбивается на конечные элементы, которые образуют сетку конечных элементов. Эти элементы соединены друг с другом в узлах, которые размещены по контуру каждого элемента Искомые значения выражаются через узловые значения, которые и являются основными неизвестными. Получившаяся дискретная система подчиняется всем принципам и методам, применяемым для любых дискретных систем.
Среди ошибок, которые могут быть допущены при применении метода можно назвать ошибки дискретизации, возникающие при замене реальной геометрии ее аппроксимацией, а также ошибки аппроксимации.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Слайд 2
Понятие инженерного анализа.
CAE-системы, область применения, место CAE

в процессе проектирования изделий.
Классификация методов инженерного анализа.
Математическая
основа инженерного анализа.
Метод конечных элементов.
Алгоритм анализа методом конечных
элементов: дискретизация, аппроксимация, задание граничных условий и свойств материала, формирование системы уравнений, получение и анализ результатов.
Ошибки метода конечных элементов.
Примеры реализации метода конечных элементов. Коммерческие системы инженерного анализа
Инженерный анализ методом конечных элементов
Слайд 3
6 Инженерный анализ
методом конечных элементов
Инженерный анализ — комплекс

испытаний, предназначенных для определения способности оборудования, конструкций, а также
производимой продукции выдерживать проектные нагрузки и бесперебойно функционировать при расчетных
условиях эксплуатации.
Компьютерный инженерный анализ (CAE, Computer Aided Engineering) — общее название для программ и программных пакетов, предназначенных для решения различных инженерных задач: расчётов, анализа и симуляции физических процессов.
Как правило расчётная часть пакетов основана на численных методах решения дифференциальных уравнений (метод конечных элементов, метод конечных объёмов, метод конечных разностей и др.).
CAE-системы — программные продукты, позволяющие при помощи расчётных методов оценить, как поведёт себя компьютерная модель изделия в реальных условиях эксплуатации.
Слайд 4
Прочностные расчеты
Тепловые расчеты
Акустические расчеты
Расчет частот и форм собственных
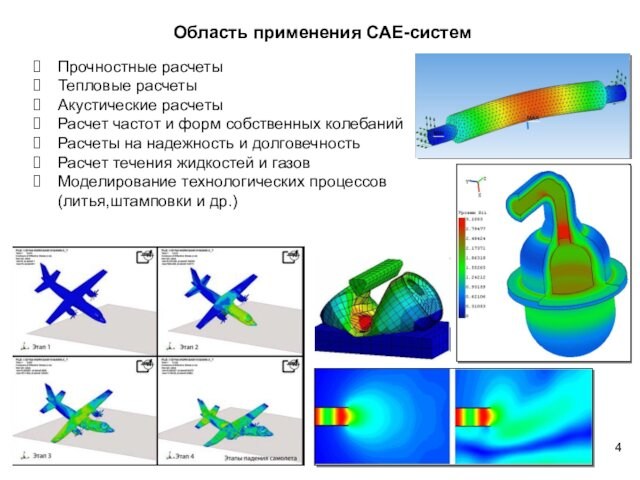
колебаний
Расчеты на надежность и долговечность
Расчет течения жидкостей и газов
Моделирование
технологических процессов (литья,штамповки и др.)
Область применения CAE-систем
Слайд 5
Место CAE-анализа в процессе проектирования изделий
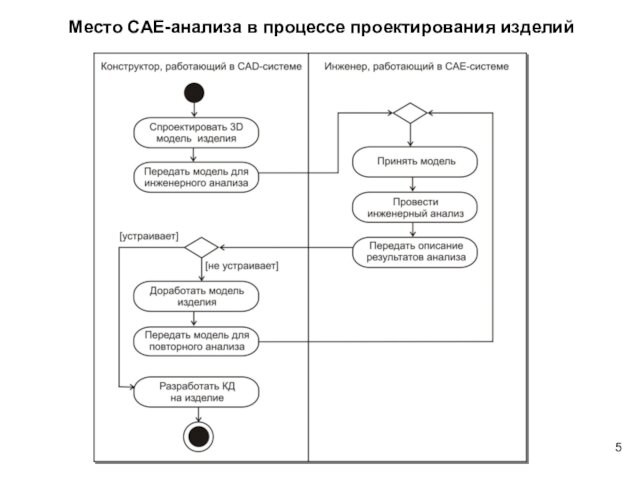
Слайд 6
Классификация методов инженерного анализа
С помощью классических методов задачи
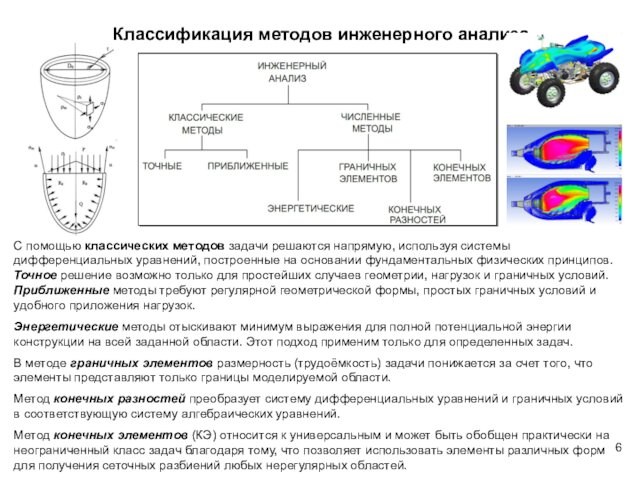
решаются напрямую, используя системы дифференциальных уравнений, построенные на основании
фундаментальных физических принципов. Точное решение возможно только для простейших случаев
геометрии, нагрузок и граничных условий.
Приближенные методы требуют регулярной геометрической формы, простых граничных условий и удобного приложения нагрузок.
Энергетические методы отыскивают минимум выражения для полной потенциальной энергии конструкции на всей заданной области. Этот подход применим только для определенных задач.
В методе граничных элементов размерность (трудоёмкость) задачи понижается за счет того, что элементы представляют только границы моделируемой области.
Метод конечных разностей преобразует систему дифференциальных уравнений и граничных условий в соответствующую систему алгебраических уравнений.
Метод конечных элементов (КЭ) относится к универсальным и может быть обобщен практически на неограниченный класс задач благодаря тому, что позволяет использовать элементы различных форм для получения сеточных разбиений любых нерегулярных областей.
Слайд 7
Коммерческие системы инженерного анализа
T-FLEX Анализ — универсальная система КЭ

анализа с встроенным пре-/постпроцессором;
APM WinMachine — отечественная универсальная система
для проектирования и расчета в области машиностроения, включающая КЭ анализ
с встроенным пре-/постпроцессором;
APM Civil Engineering — отечественная универсальная система КЭ анализа с встроенным пре-/постпроцессором для проектирования и расчета строительных конструкций;
ABAQUS — универсальная система КЭ анализа с встроенным пре-/постпроцессором;
ANSYS — универсальная система КЭ анализа с встроенным пре-/постпроцессором;
Autodesk Simulation — комплекс универсальных систем КЭ анализа со встроенными пре-/постпроцессорами (в комплекс входят Autodesk Simulation CFD — программа вычислительной гидрогазодинамики, Autodesk Simulation Mechanical — программа для механического и теплового анализа изделий и конструкций, Autodesk Simulation MoldFlow — программа моделирования процесса литья пластмассовых изделий под давлением);
ESAComp — программная система конечно-элементных расчетов тонкостенных многослойных пластин и оболочек;
MSC.Nastran — универсальная система КЭ анализа с пре-/постпроцессором MSC.Patran;
CAE Fidesys — универсальная система КЭ анализа с встроенным пре-/постпроцессором;
HyperWorks (HyperMesh, RADIOSS, OptiStruct, AcuSolve и др.) — универсальная программная платформа систем конечно-элементного анализа;
Moldex3D — программная система конечно-элементного моделирования литья армированных пластмасс под давлением;
NEiNastran — универсальная программная система конечно-элементного анализа;
NX Nastran — универсальная система МКЭ анализа;
SAMCEF — универсальная система КЭ анализа с пре-постпроцессором SAMCEF Field.
Femap — независимый от САПР пре- и постпроцессор для проведения инженерного анализа методом конечных элементов;
FEM-models — программный комплекс для моделирования и анализа методом конечных элементов. Специализация программы — геотехнические расчеты, совместные расчеты систем здание-основание.
Слайд 8
Математическая основа инженерного анализа
МКЭ работает на основе расщепления
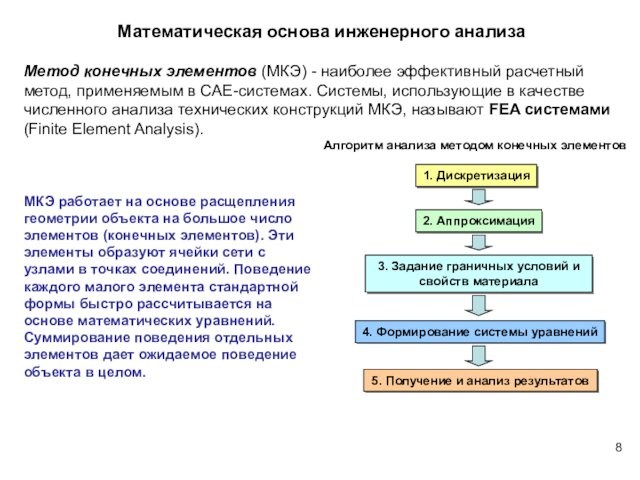
геометрии объекта на большое число элементов (конечных элементов). Эти
элементы образуют ячейки сети с узлами в точках соединений. Поведение
каждого малого элемента стандартной формы быстро рассчитывается на основе математических уравнений. Суммирование поведения отдельных элементов дает ожидаемое поведение объекта в целом.
Метод конечных элементов (МКЭ) — наиболее эффективный расчетный метод, применяемым в CAE-системах. Системы, использующие в качестве численного анализа технических конструкций МКЭ, называют FEA системами (Finite Element Analysis).
Алгоритм анализа методом конечных элементов
1. Дискретизация
2. Аппроксимация
3. Задание граничных условий и свойств материала
4. Формирование системы уравнений
5. Получение и анализ результатов
Слайд 9
1. Дискретизация
Дискретизация — деление исследуемой области на ячейки
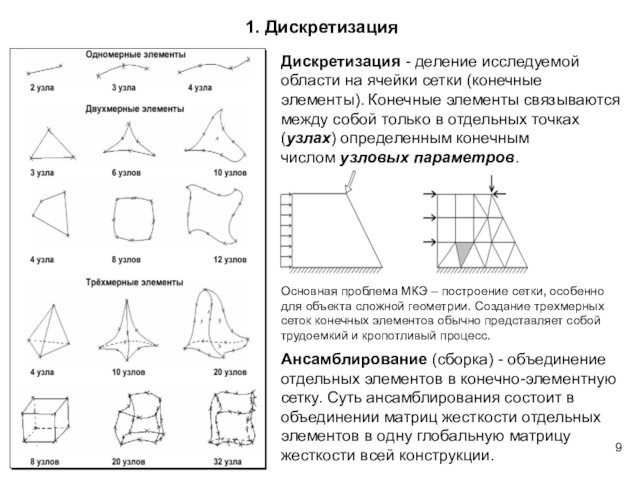
сетки (конечные элементы). Конечные элементы связываются между собой только в
отдельных точках (узлах) определенным конечным числом узловых параметров.
Основная проблема МКЭ
– построение сетки, особенно для объекта сложной геометрии. Создание трехмерных сеток конечных элементов обычно представляет собой трудоемкий и кропотливый процесс.
Ансамблирование (сборка) — объединение отдельных элементов в конечно-элементную сетку. Суть ансамблирования состоит в объединении матриц жесткости отдельных элементов в одну глобальную матрицу жесткости всей конструкции.
Слайд 10
Классификация конечных элементов, используемых в механике
Макроэлементы
Специальные КЭ
Континуальные КЭ
Простейшие
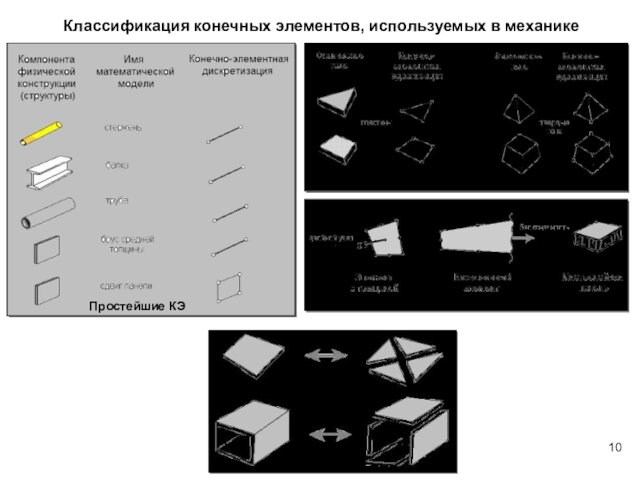
КЭ
Слайд 11
2. Аппроксимация
Реальная конструкция как сплошная среда с бесконечно

многим числом степеней свободы заменяется дискретной моделью связанных между
собой КЭ с конечным числом степеней свободы. Искомые функции в пределах
каждого КЭ (например, распределение перемещений, деформаций, напряжений и т. д.) с помощью аппроксимирующих функций выражаются через узловые значения.
Аппроксимирующие функции:
Пример для одномерного КЭ
Пример для двумерного КЭ
Аппроксимирующий полином второго порядка
Степень аппроксимирующего полинома определяет число узлов, которым должен обладать элемент
Точность решения — отклонение приближенного решения от точного или истинного решения.
Устойчивость решения определяется ростом ошибок при выполнении отдельных вычислительных операций.
Сходимость решения — постепенное приближение последовательных решений к предельному, по мере того как уточняются параметры дискретной модели.
Результат выбора аппроксимирующих функций:
Слайд 12
3. Задание граничных условий и материала
Граничные или краевые
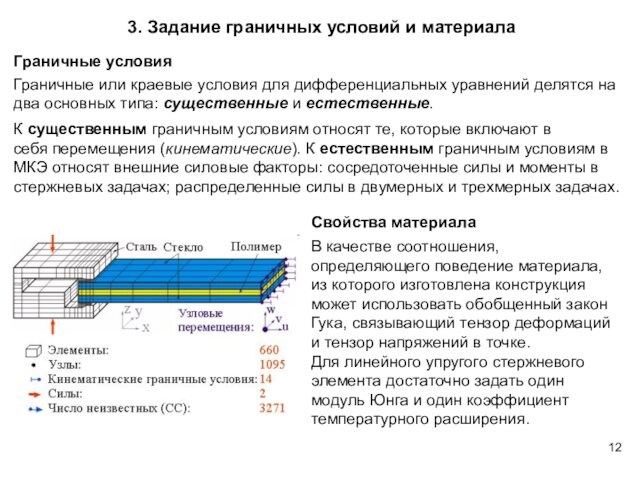
условия для дифференциальных уравнений делятся на два основных типа: существенные и естественные.
К
существенным граничным условиям относят те, которые включают в себя перемещения (кинематические).
К естественным граничным условиям в МКЭ относят внешние силовые факторы: сосредоточенные силы и моменты в стержневых задачах; распределенные силы в двумерных и трехмерных задачах.
.
В качестве соотношения, определяющего поведение материала, из которого изготовлена конструкция может использовать обобщенный закон Гука, связывающий тензор деформаций и тензор напряжений в точке. Для линейного упругого стержневого элемента достаточно задать один модуль Юнга и один коэффициент температурного расширения.
Свойства материала
Граничные условия
Слайд 13
4. Формирование системы уравнений
После задания граничных условий и

материала программа конечно-элементного анализа формирует систему уравнений, связывающую граничные
условия с неизвестными, после чего решает эту систему относительно неизвестных.
5.
Получение и анализ результатов
После нахождения значений неизвестных пользователь получает возможность рассчитать значение любого параметра в любой точке любого конечного элемента по той же искомой функции, которая использовалась при построении системы уравнений. Графические изображения обычно более информативны, поскольку дают возможность изучить поведение параметров на всей области задачи.
Слайд 14
Ошибки метода конечных элементов
Причины возникновения погрешности в методе

конечных элементов:
накапливающиеся ошибки округления;
погрешностью приближенных методов линейной
алгебры, численного дифференцирования;
ошибки дискретизации — результат различий между действительной
геометрией области и её аппроксимацией системой конечных элементов;
ошибки аппроксимации — обусловлены разностью между действительным распределением искомых функций в пределах КЭ и их представлением с помощью аппроксимирующих функций.
Ошибки дискретизации уменьшаются с увеличением числа конечных элементов и соответственно с уменьшением их размеров, причем они стремятся к нулю, когда размер элемента стремится к нулю. Для оценки погрешности аппроксимации выполняют несколько расчетов при различных разбиениях области КЭ, по результатам этих расчетов строится зависимость рассчитанных напряжений (перемещений, деформаций) от размера элемента, затем выполняется экстраполяция на случай размера элемента, стремящегося к нулю.
Слайд 15
Метод конечных элементов. Историческая справка
Метод конечных элементов впервые

был применен в инженерной практике в начале 50-х гг. XX в.
На раннем этапе формулировки МКЭ основывались на принципах строительной механики,
что ограничивало сферу его применения. И только когда были сформулированы основы метода в вариационной форме, стало возможным распространение его на многие другие задачи. Быстрое развитие МКЭ шло параллельно с прогрессом современной компьютерной техники и ее применением в различных областях науки и инженерной практики.
Значительный вклад в разработку МКЭ был сделан Иоаннисом Аргирисом. Им впервые дана общая матричная формулировка расчета стержневых систем на базе фундаментальных энергетических принципов, определена матрица податливости, а также введено понятие матрицы жесткости (как обратной матрице податливости). Аргирис — один из основателей метода конечных элементов. В 1956 г. его теоретические разработки использовались при строительстве Боинга-747. Работы Аргириса и его сотрудников, опубликованные в период 1954–1960 гг., дали отправную точку для матричной формулировки известных численных методов и применения ЭВМ в расчетах конструкций.
Первая работа, в которой была изложена современная концепция МКЭ, относится к 1956 г. Американские ученые М. Тэрнер, Р. Клафф, Г. Мартин и Л. Топп, решая плоскую задачу теории упругости, ввели элемент треугольного вида, для которого сформировали матрицу жесткости и вектор узловых сил. Название – метод конечных элементов ввел в 1960 г. Р. Клафф.
К семидесятым годам относится появление математической теории конечных элементов. Значительный вклад в разработку теоретических основ МКЭ внесли и российские ученые.
Период последних десятилетий особенно характерен для развития и применения МКЭ в таких областях механики сплошных сред, как оптимальное проектирование, учет нелинейного поведения, динамика конструкций и т. п.
Слайд 16
MSC.Nastran – расчеты прочности, устойчивости, частот и форм

колебаний, теплопередачи и др.
MSC.Dytran – анализ быстротекущих процессов, штамповки
листов, столкновения объектов и др.
MSC.Marc – нелинейный анализ конструкций, моделирование
вытяжки, сварки, экструзии и др.
MSC.Patran – интегрированная среда моделирования и анализа (импорт CAD-геометрии, построение сетки КЭ и др.)
MSC.Manufacturing (MSC.Superforge и MSC.Superform) – моделирование процессов штамповки, ковки и др.
Примеры реализации МКЭ
MSC.Software
Слайд 17
NX Nastran (MSC.Nastran)
Расчет напряженно-деформированного состояния
Расчет собственных частот
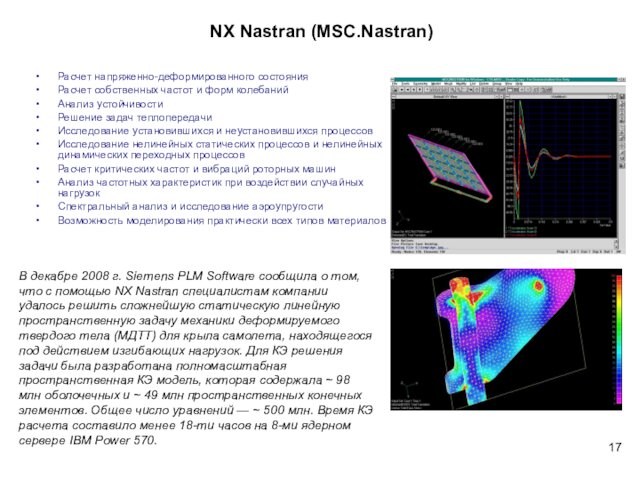
и форм колебаний
Анализ устойчивости
Решение задач теплопередачи
Исследование установившихся и
неустановившихся процессов
Исследование нелинейных статических процессов и нелинейных динамических переходных
процессов
Расчет критических частот и вибраций роторных машин
Анализ частотных характеристик при воздействии случайных нагрузок
Спектральный анализ и исследование аэроупругости
Возможность моделирования практически всех типов материалов
В декабре 2008 г. Siemens PLM Software сообщила о том, что с помощью NX Nastran специалистам компании удалось решить сложнейшую статическую линейную пространственную задачу механики деформируемого твердого тела (МДТТ) для крыла самолета, находящегося под действием изгибающих нагрузок. Для КЭ решения задачи была разработана полномасштабная пространственная КЭ модель, которая содержала ~ 98 млн оболочечных и ~ 49 млн пространственных конечных элементов. Общее число уравнений — ~ 500 млн. Время КЭ расчета составило менее 18-ти часов на 8-ми ядерном сервере IBM Power 570.
Слайд 18
Пример расчета частот и форм собственных колебаний кронштейна
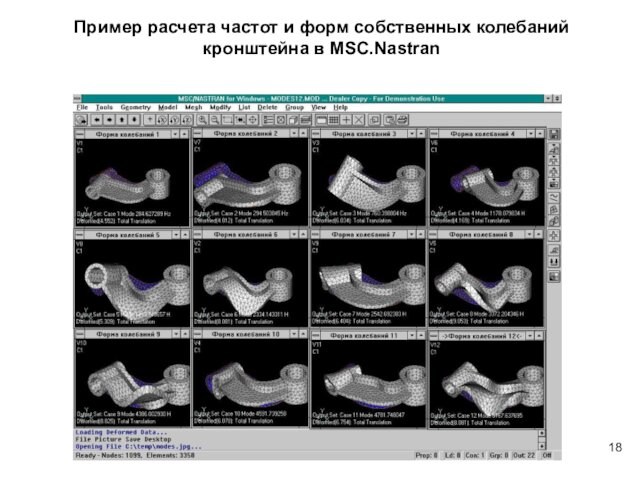
в MSC.Nastran
Слайд 19
MSC.Dytran
Области применения
взаимодействие автомобиля, препятствия, пассажира и подушки безопасности

при аварии
столкновение птиц с самолетными конструкциями
столкновение и посадка на
мель судов
взрывы в ограниченном пространстве
удар снаряда о преграду и ее
пробивание
попадание метеорита в обшивку космического аппарата
штамповка металла
поведение жидкости в неполных емкостях
Анализ высоко нелинейных быстропротекающих процессов, связанных с взаимодействием различных частей конструкции, конструкции и конструкции, а также конструкции и жидкости (газа)
Слайд 20
Распределение материала заготовки
Утонение в углах до 0.5 мм
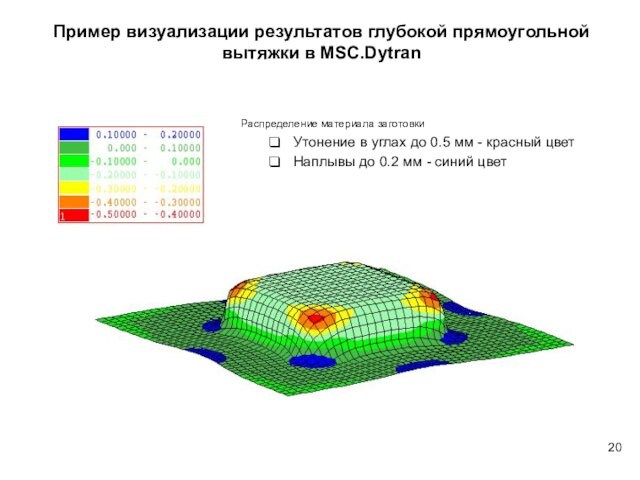
— красный цвет
Наплывы до 0.2 мм — синий цвет
Пример
визуализации результатов глубокой прямоугольной вытяжки в MSC.Dytran
Слайд 21
MSC.Manufacturing
MSC.Superforge – Анализ процессов горячей штамповки и ковки.

При анализе система учитывает подробные характеристики материала заготовки, параметры
пресса, наличие трения и температурных эффектов, фактор упругости материала, возможность
скольжения заготовки при ее укладке (ручной или автоматической) и др.
MSC.Superform – моделирование процессов объемного формования, включая экструзионное прессование, осевую и кольцевую прокатку, вырубку заготовок из листа, прокатку слитков, гибку толстых листов и резание. Система выполняет анализ процесса формования, проводит анализ поведения материала, рассчитывает нагрузки на инструмент, определяет его износ и ресурс.
Слайд 22
Постановка задачи для зуба ковша экскаватора ЭГК-8(10)
Изделие: “Зуб

ковша экскаватора типа ЭГК-8(10)”
Заказчик: ЗАО “ФЕРРО БАЛТ ПЛЮС”
Исполнитель: ОАО
“Завод турбинных лопаток” (СПб)
Характеристики предложенного технологического процесса:
штамповочный молот с
массой падающих частей 25 т.
вес заготовки 265 кг
вес штамповки 170 кг (выход 64% при норме расхода 75-80%)
вес оснастки 32 т (для предварительной и окончательной штамповки)
Задачи:
уменьшить вес заготовки
повысить стойкость оснастки
уменьшить стоимость оснастки
улучшить качество изделия
Слайд 23
Зуб ковша экскаватора типа ЭГК-8(10)

Слайд 24
Оборудование – штамповочный молот

Слайд 25
Пример визуализации результатов ковки зуба ковша экскаватора в
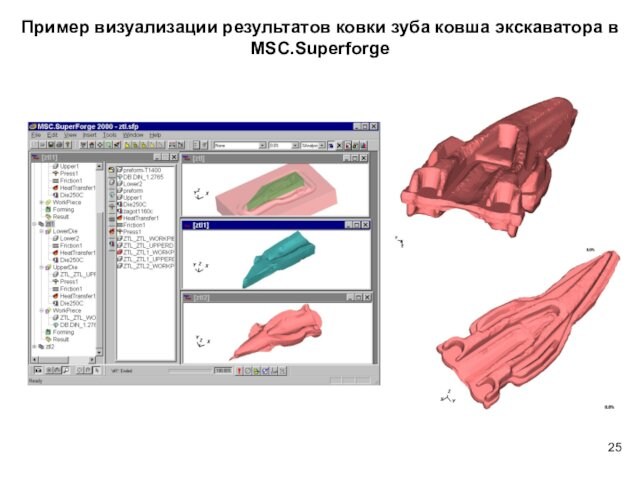
MSC.Superforge
Слайд 26
Результат после предварительной штамповки, получен в MSC.Superforge
Результат
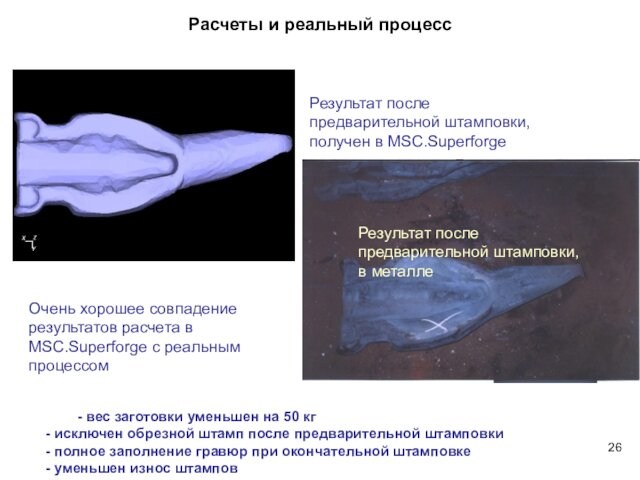
после предварительной штамповки, в металле
Очень хорошее совпадение результатов
расчета в MSC.Superforge с реальным процессом
Расчеты и реальный процесс
—
вес заготовки уменьшен на 50 кг
— исключен обрезной штамп после предварительной штамповки
— полное заполнение гравюр при окончательной штамповке
— уменьшен износ штампов
Слайд 27
Модель в MSC.Superforge и реальная деталь

Слайд 28
Моделирование процесса резания методом конечных элементов (А. Н.
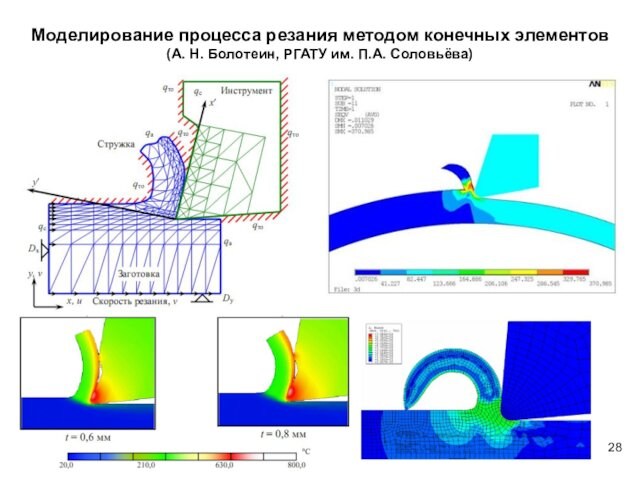
Болотеин, РГАТУ им. П.А. Соловьёва)
Как правило, реальные конструкции состоят более чем из одного элемента. В этом случае условие равновесия конечного элемента переносится на каждый элемент из ансамбля конечных элементов, образующих деформируемое тело. Таким образом, равновесие тела определяется следующим уравнением:

где — количество элементов, образующих тело;
— площадь -ого конечного элемента.
Однако, напрямую применение нецелесообразно, т.к. для каждого элемента имеем шесть уравнений, и необходимо систему дополнить связями на локальные узловые перемещения и узловые силы. Поэтому применяют переход от локальной нумерации перемещений и узловых сил к глобальной. Рассмотрим соответствующее преобразование для правой части системы:

где — количество узлов в глобальной модели; .

Под проекцией глобальной узловой силы подразумевается сумма всех локальных проекций узловых сил принадлежащих данному узлу. В качестве примера рассмотрим конечноэлементную модель, показанную на рисунках 1 и 2. Глобальный узел 2 является общим для трех элементов. Для первого элемента он совпадает с первым локальным узлом, для второго — с его первым локальным узлом, а для третьего элемента — с третьим локальным узлом. Отметим, что если глобальный узел является внутренним, то .


В силу непрерывности вектора перемещений в точке связи конечных элементов запишем правую часть соотношения через глобальные узловые перемещения:


где компоненты вектора глобальных перемещений; связаны к с глобальными узловыми перемещениями следующим образом: ,
— номер координатной оси, — глобальный номер узла;

— локальная матрица жесткости элемента в котором вершины имеют глобальную нумерацию.

Локальная матрица жесткости имеет размерность . Компоненты матрицы равны нулю за исключением тридцати шести компонент соответствующих матрице , образуемой при использовании локальной нумерации узлов.
Из представления получаем связь между матрицами жесткости элементов и глобальной матрицей жесткости:

Таким образом, приходим к следующему алгоритму сборки матрицы жесткости:
1. Триангулировать заданную область. Ввести локальную и глобальную нумерацию узлов элементов.
2. Для каждого элемента определить локальные функции формы
3. Определить коэффициенты локальной матрицы жесткости для каждого элемента.
4. Зная количество глобальных узлов , сформировать матрицу размером .


5. Преобразовать локальные матрицы жесткости в матрицы жесткости размерности .
6. Провести суммирование матриц жесткости элементов согласно формуле.
После формирования глобальной матрицы жесткости необходимо определить вектор узловых сил с компонентами размерностью . При этом нужно учесть, что для некоторых узловых точек, в силу граничных условий, компоненты узловых сил могут являться искомыми величинами.

Вектор перемещений системы является решением задачи линейной теории упругости методом конечного элемента в том случае, если граничные условия ставятся в напряжениях. При смешанных граничных условиях или при заданных граничных перемещениях необходимо преобразовать систему, по аналогии с системой, сгруппировав неизвестные задачи в векторе столбце . В этом случае матрица жесткости и столбец свободных членов модифицируются следующим образом:

1. Известная компонента вектора узлового перемещения, например стоящая в -ой строке системы, умножается на коэффициент матрицы жестокости и переносится с обратным знаком в столбец свободных членов для соответствующих уравнений. Получаемый таким способом столбец свободных членов обозначим через .
2. Неизвестная компонента вектора узловой силы в данном случае занимает -ую позицию в векторе столбце . В матрице жесткости -ый столбец обнуляется за исключением -ого элемента, где ставится (-1). Модифицированную матрицу жесткости назовем .
В итоге решение задачи сводится к решению следующей системы уравнений:

После нахождения поля узловых перемещений через функции формы определяются компоненты линейного тензора деформаций.
Ошибки метода конечных элементов
Наряду с обычными ошибками округления и погрешностью приближенных методов линейной алгебры, применяемых в МКЭ, есть и ошибки, имеющие непосредственное отношение к методу конечных элементов:
— ошибки дискретизации, являющиеся результатом различий между действительной геометрией рассчитываемой области и ее аппроксимацией системой конечных элементов;
— ошибки аппроксимации, обусловленные разностью между действительным распределением искомых функций в пределах КЭ и их представлением с помощью аппроксимирующих функций.
Ошибки дискретизации уменьшаются с увеличением числа конечных элементов и соответственно с уменьшением их размеров, причем они стремятся к нулю, когда размер элемента стремится к нулю. Эти ошибки уменьшаются и с применением криволинейных элементов на соответствующих границах области. Ошибки аппроксимации не обязательно уменьшаются по мере уменьшения размеров элементов или повышения степени аппроксимации, поэтому могут ухудшать сходимость к точному решению или даже приводить к расходимости. Однако эти ошибки можно свести к минимуму, если при построении аппроксимирующих функций обеспечить:
1) непрерывность искомой функции и ее производных в области КЭ до степени m-1 включительно (m — наибольший порядок производных искомой функции, используемых в качестве основных неизвестных в эрмитовых элементах);
2) выполнение условий полноты, т. е. при уменьшении размеров КЭ аппроксимирующие функции должны обеспечить стремление значений искомой функции, а также ее производных к постоянным значениям;
3) выполнение условий совместности искомой функции и частично ее производных на границе между смежными элементами;
4) приближенное удовлетворение условий совместности не основных переменных (например, напряжений, если основные неизвестные — перемещения) на границах КЭ, а также граничных условий в рассматриваемой области;
5) исключение концентрации напряжений в КЭ, если в рассматриваемой области такие концентрации заведомо отсутствуют;
6) при перемещениях КЭ как жесткого целого в нем не должны возникать деформации.
Требование полноты аппроксимирующих функций необходимо для учета смещения КЭ как жесткого целого и обеспечения состояния постоянных деформаций в элементе. Механический смысл совместности заключается в непрерывности основных неизвестных на смежных границах соседних КЭ.


