- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Монахова О.А.
1
Сорокина М.В.
1
1 ФГБОУ ВО «Пензенский государственный университет»
Комбинированные неравенства очень разнообразны по своему виду и предполагают применение различных методов в решении. Работа посвящена особенностям применения обобщенного метода интервалов для комбинированных неравенств, содержащих рациональные, иррациональные и трансцендентные выражения. В ходе проведенного исследования проанализированы экзаменационные работы ЕГЭ по математике профильного уровня, содержащие задание под номером 15. В результате была выделена типичная ошибка, допускаемая экзаменуемыми. Ее причиной при решении комбинированного неравенства являлось неправильное применение метода интервалов. Участники экзамена не учитывали область определения функций, входящих в неравенство, и формально расставляли знаки на промежутках. С целью предупреждения ошибок при использовании метода интервалов для решения комбинированных неравенств необходимо сформировать четкое понимание взаимосвязи этого метода с функциональной линией. Авторы предлагают серию комбинированных неравенств, содержащих функции, имеющие точечные и интервальные разрывы. Задания подобраны таким образом, чтобы показать все возможные варианты поведения знака функции при переходе через разрывы разного рода. Приводится подробное решение каждого неравенства и анализируются возможные способы его исследования. Решения сопровождаются графиками разрывных функций, содержащихся в неравенстве. Построения проводятся в среде динамической геометрии Geogebra.
комбинированные неравенства
метод интервалов
область определения функции
непрерывная функция
1. Гумеров И.С. Один из способов изучения обобщенного метода интервалов // Школьные технологии. 2017. № 6. С. 71-73.
2. Здоровенко М.Ю., Зеленина Н.А., Крутихина М.В. Решение задач темы «Неравенства» школьниками Кировской области на ЕГЭ по математике в 2014 г.: от анализа ошибок к их предупреждению // Вестник Вятского государственного университета. 2014. № 11. С. 237-246.
3. Гридчина В.Б., Осипова Л.А. Использование обобщенного метода интервалов при решении иррациональных неравенств // Информационно-коммуникационные технологии в педагогическом образовании. 2020. № 1. С. 21-23.
4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. М.: ФМЛ, 1962, 608 с.
5. Макарычев Ю.Н. Алгебра. 9 класс: учебник для общеобразовательных организаций. М.: Просвещение, 2019. 399 с.
Традиционно в школьном курсе математики одной из основных содержательно-методических линий является изучение уравнений и неравенств. Очень многие учащиеся испытывают трудности при решении неравенств, относящихся к повышенному и высокому уровню сложности. Несмотря на это, к решению неравенства, требующего развернутого ответа, на едином государственном экзамене по математике профильного уровня (задание 15) приступает достаточное количество экзаменуемых. Однако далеко не все они получают максимальный балл за выполнение этого задания. Решению задач подобного рода на ЕГЭ посвящено достаточно много методических исследований (например, [1-3]). В данном исследовании затрагиваются некоторые аспекты применения метода интервалов к решению комбинированных неравенств.
Материал и методы исследования
Для выявления типичных ошибок и составления рекомендаций по их предупреждению был проведен детальный анализ решений заданий № 15 второй части ЕГЭ по математике профильного уровня.
Результаты исследования и их обсуждение
Комбинированные неравенства очень разнообразны по своему виду и предполагают применение различных методов в решении. В ряде случаев возможно разложение на множители и рассмотрение систем условий, равносильных исходному неравенству, имеет место применение метода интервалов или метода рационализации, кроме того, возможны и нестандартные приемы. Конечно, при обучении школьников работе с неравенствами необходимо стремиться к тому, чтобы учащиеся могли в каждом конкретном случае выбирать метод, который будет минимален по временным затратам в рамках экзамена, не будет содержать громоздких вычислений и не приведет к ошибкам. Эти вопросы требуют высокого уровня математической культуры. В силу ограниченности учебного времени сформировать такие умения удается далеко не всегда. Очень часто школьники воспринимают алгоритмы решения каждого конкретного типа неравенства (рационального, показательного, логарифмического и т.д.), но испытывают трудности при работе с комбинациями в одном неравенстве. Метод интервалов является одним из тех методов, который можно применять к неравенствам любого типа. Алгоритм, лежащий в его основе, делает этот метод привлекательным для учащихся, дает возможность применения этого метода даже если он не совсем осознан ими. Многие дети просто запоминают порядок действий, не анализируя каждой конкретной ситуации. А иногда и не выполняют всех шагов решения, считая, что можно действовать по аналогии с рациональными неравенствами. Однако, для того чтобы метод интервалов стал универсальным, необходимо четко представлять его математическую основу, связь его с функциональной линией.
Напомним, что метод интервалов основан на исследовании промежутков знакопостоянства функции. Пусть нам дано неравенство вида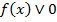 
, где Ú — это один из знаков неравенства (>, <, ³, £). Множество решений данного неравенства совпадает со множеством значений аргумента функции 
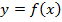, для которых значения функции имеют тот же, что и у неравенства, знак. Поэтому необходимо исследовать промежутки знакопостоянства этой функции. В основе определения знаков непрерывной на некотором интервале функции лежит теорема Больцано-Коши [4, с. 168] (которую школьникам, конечно, доказывать не представляется возможным), однако она дает нам лишь необходимое, но не достаточное условие для смены знака функции. Т.е. если непрерывная функция принимает в некоторой точке значение, равное нулю, то в этой точке возможна смена знака. Аналогичное утверждение можно сформулировать и для функций, терпящих разрыв в некоторой области: при переходе через точку (интервал) разрыва функция может (но не обязана) поменять свой знак. Из вышеприведенных очевидных умозаключений и вытекает известный большинству учащихся алгоритм метода интервалов:
1) найти область определения функции;
2) найти нули функции;
3) определить знаки на каждом из промежутков, на которые нули функции разбили область определения.
Особых трудностей с запоминанием и пониманием этого алгоритма не возникнет, если уже в 9 классе [5, с. 65] при изучении рациональных неравенств (начиная с квадратных) учащимся объяснять связь между функциональной линией и решением неравенства. Проблемы применения метода интервалов к решению комбинированных неравенств возникают по большей части тогда, когда дети привыкают при работе с дробно-рациональными неравенствами действовать бездумно по шаблону: найдите нули числителя, нули знаменателя и т.д. Сразу отметим, что из этого же следуют и ошибки с включением или исключением концов интервала в решение (закрашенные и выколотые точки). Поэтому, начиная работать с методом интервалов, прежде всего обращаем внимание на отыскание области определения: функция может быть определена не на всей числовой прямой. Поэтому в рациональных неравенствах нули знаменателя это не что иное, как область определения функции; точки, не входящие в область определения, не могут войти в решение исходного неравенства. В более сложных неравенствах, на тех промежутках, где функция не существует, просто бессмысленно говорить что-либо о ее знаке. Следующее, на что необходимо обращать внимание, это определение знаков функции на конкретных промежутках. Если говорить о рациональных неравенствах, то там очень многие учащиеся успешно пользуются правилом, позволяющим определять знаки «автоматически», опираясь на четность или нечетность степени линейных множителей, входящих в неравенство. На наш взгляд, для школьников очень опасно делать аналогичные выводы при работе с комбинированными неравенствами, особенно когда соответствующие функции имеют разрывы.
На экзамене по математике профильного уровня в 2020 году предлагалось комбинированное неравенство следующего вида:
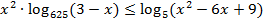. (1)
При решении этого задания многие выпускники прибегали к использованию метода интервалов. Большинство из них правильно выполняли равносильные преобразования и приходили к неравенству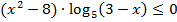 
.
Следует отметить, что уже из оформления работы можно сделать вывод о том, четко ли учащийся представляет себе математический аппарат, лежащий в основе применяемого им метода. Ненаписание «лишней» строки «рассмотрим функцию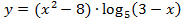
» и использование термина «ОДЗ» вместо «область определения функции» не являются ошибками, но заставляют задуматься об уровне математической культуры. Одной из самых распространенных ошибок в решении, не влияющей на ответ, являлось то, что дети, найдя нули функции, как решения соответствующего уравнения, наносили их на числовую прямую без учета области определения функции, расставляли знаки на всей числовой прямой, затем отбирая значения с учетом области допустимых значений логарифма (рис. 1).
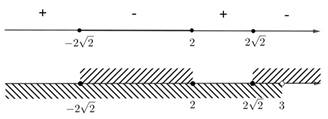
Рис. 1. Ошибка в применении метода интервалов
Это позволяет сделать выводы о том, что, во-первых, выпускник не понимает математический смысл метода интервалов, и, во-вторых, либо ему «повезло» при определении знаков на каждом промежутке, либо он их просто расставил «через один».
Чтобы избежать ошибок подобного рода при решении комбинированных неравенств, необходимо предлагать учащимся задания, содержащие разрывные функции. Тренировочные задания должны содержать функции, имеющие точечные или интервальные разрывы, с сохранением или сменой знака. Работа с такими неравенствами позволит увидеть особенности реализации метода интервалов.
Пример 1. Первое неравенство содержит функцию, не определенную на некотором интервале числовой прямой.
.
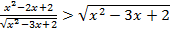Равносильным образом преобразуем неравенство: перенесем правую часть влево и приведем к общему знаменателю:
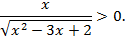
Числитель обращается в 0 при x = 0, знаменатель равен 0 при х = 2 или x = 1. Область определения функции, находящейся в левой части неравенства, является решением неравенства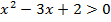 
и представляет собой объединение двух интервалов: 
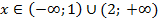. Функция 
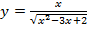имеет два бесконечных разрыва в точках 1 и 2. Бесконечные односторонние пределы в этих точках одного знака. Поведение функции легко проследить по её графику, приведённому на рисунке 2. Определяя знаки дроби на интервалах, будем иметь:
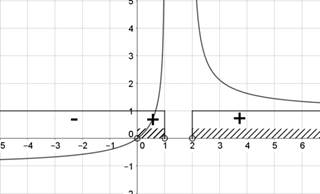
Рис. 2. График функции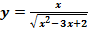 
Пример 2. Следующая серия комбинированных неравенств содержит композицию логарифмической и дробно-рациональной функции. Эта сложная функция, как и в предыдущем примере, определена на объединении двух бесконечных интервалов числовой прямой, имеет два бесконечных разрыва, но в отличие от предыдущего случая бесконечные односторонние пределы в точках разрыва имеют разные знаки:
а)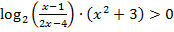 
.
Допустимыми значениями переменной в этом неравенстве является объединение двух интервалов: 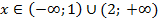. По графику функции 
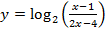на рисунке 3 проследим её поведение.
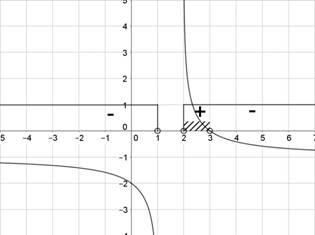
Рис. 3. График функции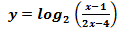
Вернемся к решению неравенства. Второй множитель произведения в левой части неравенства не влияет на знак произведения. К сожалению, не все ученики смогут «решиться» на деление обеих частей неравенства на выражение, содержащее переменную. Это «запретное» действие (ведь учитель на уроке много раз подчеркивал, что делить на переменную нельзя) могло бы свести исходное неравенство к простейшему логарифмическому неравенству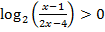 
, решение которого не составило бы труда.
Чаще срабатывает «алгоритмическое» мышление, поэтому можно ожидать, что ученик найдет нули функции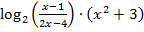 
, точку x = 3, отметит на числовой прямой эту точку и область определения функции, расставит знаки функции на интервалах. При этом ученик может ошибочно рассудить, что знак поменяется только при переходе через ноль функции. Ошибка избегается путем определения знака на каждом интервале. Но ученик «настроен» на чередование знака, тем более что кратных корней он здесь не видит, а определение знака числовых выражений, содержащих логарифмы, зачастую вызывает трудности. Такая логика приведет к ошибке. И только обращение к графику функции поможет увидеть распределение знаков (рис. 3);
б) во втором неравенстве можно предложить произведение той же логарифмической функции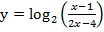 
со знакопеременным множителем. Например, такое неравенство
.
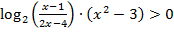Второй множитель еще более затруднит определение знаков на интервалах методом подстановки значений переменной, уж очень интервалы «малы». Какие варианты выхода из затруднительной ситуации может выбрать ученик? Обратиться к графику функции 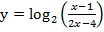, перейти от данного неравенства к совокупности двух систем, чередуя знаки множителей, все-таки оценивать знак логарифма на каждом интервале, главное, чтобы он видел это затруднение, а не «автоматически» расставлял знаки, оценивая порой и на участках, где функции не существуют. Окончательная расстановка знаков на числовой прямой для этого неравенства имеет следующий вид (рис. 4).
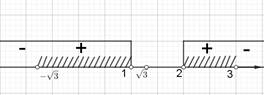
Рис. 4. Расстановка знаков для неравенства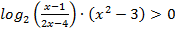 
Пример 3. Следующая серия неравенств содержит функцию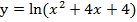 
, которая определена на всей числовой прямой за исключением одной точки -2. В ней функция имеет бесконечный разрыв, бесконечные односторонние пределы в этой точке имеют одинаковый знак.
Рассмотрим неравенство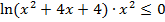 
. Левая часть неравенства обращается в 0 в точках -3, -1, 0, точка -2 не принадлежит области определения неравенства. Отметим все точки на числовой прямой, расставим знаки левой части неравенства на образовавшихся интервалах, используя график функции (рис. 5а).
С этой же функцией можно подобрать второй множитель так, чтобы при переходе через точку -2 знак неравенства менялся. Например, неравенство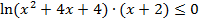 
. Расстановка знаков на числовой прямой для этого неравенства представлена на рисунке 5б.
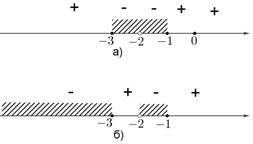
Рис. 5. Расстановка знаков для неравенств в примере 3
В каждом из рассмотренных примеров функции имели бесконечные разрывы. Школьникам довольно сложно оценить характер разрыва функции, сложным вопросом будет и определение знаков односторонних пределов, построение графиков функций. Для облегчения решения этих проблем можно воспользоваться графическими редакторами, которые строят графики функций по их аналитическим представлениям. В представленной работе графики были построены в программе Geogebra. Можно предложить ученикам самостоятельно построить графики функций. С целью углубления знаний школьников о пределах функций можно дать задание: восстановить вертикальные и горизонтальные асимптоты по построенным графикам. Такая работа очень полезна для формирования умения самостоятельно строить графики функций. Можно отметить, что, даже научившись проводить полное исследование функции, ученики затрудняются в построении графика по этому исследованию. Такая промежуточная работа с готовыми графиками даст им необходимый опыт, разовьет интуицию.
В связи с этим полезно будет познакомить школьников и с функциями, имеющими конечные разрывы, например с функцией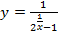 
. Функция имеет конечный разрыв в нуле, односторонние пределы в этой точке разные по знаку.
Заключение
Для успешного применения метода интервалов при решении комбинированных неравенств необходимо сформировать четкое понимание учащимися взаимосвязи этого метода с функциональной линией в школьном курсе математики. Необходимо расширять представления школьников о функциях, плавно переходя от элементарных функциональных зависимостей к более сложным, требующим достаточно глубоких исследований. В этом случае метод интервалов не будет восприниматься учащимися формально, на уровне алгоритма, что позволит избежать ошибок.
Библиографическая ссылка
Монахова О.А., Сорокина М.В. ОШИБКИ ПРИ РЕШЕНИИ КОМБИНИРОВАННЫХ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ И ПУТИ ИХ ПРЕДУПРЕЖДЕНИЯ // Современные проблемы науки и образования. – 2021. – № 2.
;
URL: https://science-education.ru/ru/article/view?id=30667 (дата обращения: 25.06.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Цель исследования данной статьи — определить основные причины, вследствие которых школьники совершают ошибки при решении неравенств; разобрать способы и методы решения некоторых видов неравенств; определить пути исправления возникающих ошибок, а в лучшем случае — вообще не допустить их появления. Рассматриваемая проблема актуальна и по сей день, более того, набирает обороты. И корни ее лежат не вовсе в специфичности конкретно неравенств или любых других видов математических задач. Значит, и пути решения проблемы также стоит искать в несколько более общих областях, о чем мы также поговорим в данной статье.
Ключевые слова:
неравенства, свойства неравенств, правила неравенств.
The purpose of this article is to determine the main reasons why students make mistakes when solving inequalities; to analyze the ways and methods of solving some types of inequalities; to determine ways to correct errors that occur, and in the best case — to prevent them from appearing at all. The problem under consideration is still relevant to this day, moreover, it is gaining momentum. And its roots do not lie in the specificity of specific inequalities or any other types of mathematical problems. This means that you should also look for ways to solve the problem in a few more General areas, which we will also discuss in this article.
Keywords:
inequalities, properties of inequalities, rules of inequalities.
Неравенства
Математика
— наука об отношениях между объектами, о которых не известно ничего, кроме описывающих их некоторых свойств, — собственно эти свойства, качестве аксиом, положены в основание той или иной математической теории. История математики ведется издревле — от простейших операций подсчёта, измерения объектов и описания их формы. Создаются математические объекты с помощью идеализации свойств объектов реальных или других математических и записи этих свойств на формальном языке. К естественным наукам математика не относится, но широко в них используется — как для точной формулировки их содержания, так и для получения новых результатов. Математика — наука фундаментальная, поскольку она предоставляет другим наукам универсальные языковые средства; с помощью этого выявляется взаимосвязь наук, а также находятся общие законы природы.
Что же касается конкретно неравенств, то с ними начинают работать еще с детского сада. Детей учат тому, что в количественном соотношении некоторые объекты больше, а некоторые — меньше других. А есть объекты, которые равны между собой. В начальных классах продолжается изучение неравенств, там сравнивают — в какой чашке больше вишен, какое число больше, а какое меньше, далее следуют более сложные примеры, например — «4+2» больше, меньше или равно «3+3»?
Конечно, чем старше класс, тем сложнее, разнообразнее и интереснее становятся неравенства и пути нахождения их решений. Однако, стоит понимать, что сама суть неравенств и умение ее понимать находятся с человеком на протяжении всей его жизни. Да, мы об этом не задумываемся, но, тем не менее, постоянно решаем эти самые неравенства в своих бытовых делах. В этой пачке больше салфеток, но она стоит дороже, а в этой — меньше, но и стоит она дешевле. Что же выгоднее приобрести? Причем, ведь роль еще играют факторы того, сколько именно нужно сейчас салфеток и пригодятся ли потом лишние… В общем, рассуждать можно долго, этот пример приведен для того, чтобы было понятно — неравенства с нами всю жизнь и, даже если мы не используем математических формул для их решения (по крайней мере, осознанно), тема эта очень важная и актуальная. Тем более острой становится необходимость ее всестороннего изучения в школьной программе. И, как следствие — выявление проблем, трудностей и пробелов, возникающих у учеников. Именно эту проблему и хотелось бы затронуть в данной статье — какие ошибки допускают ученики при решении различных неравенств и какими способами эти ошибки можно исправить или даже избежать их вовсе.
Но прежде чем перейти к проблеме и способам ее решения, стоит немного поговорить о том, что же такое неравенство, каких видов они бывают и какие существуют пути решения.
Итак, что же такое неравенство?
Неравенство
в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков.
Строгие неравенства
● — означает, что
меньше
, чем
● — означает, что
больше
, чем
Неравенства равносильны. Говорят, что знаки
противоположны
; например, выражение «знак неравенства сменился на противоположный» означает, что заменено на или наоборот.
Нестрогие неравенства
–
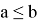
— означает, что
меньше либо равно
–
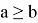
— означает, что
больше либо равно
Про знаки ⩽ и ⩾ также говорят, что они
противоположны
.
Другие типы неравенств
–
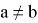
— означает, что
не равно
.
–
— означает, что величина намного больше, чем
–
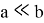
— означает, что величина намного меньше, чем
Связанные определения
Неравенства с одинаковыми знаками называются
одноимёнными
(иногда используется термин «одного смысла» или «одинакового смысла»). Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:— это краткая запись пары неравенств: и
Числовые неравенства
Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство — алгебраическое первой степени, неравенство
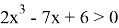
— алгебраическое третьей степени, неравенство
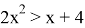
— трансцендентное.
Существуют определенные правила решения неравенства
При решении неравенств используют следующие правила:
- Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.
- Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
- Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Давайте рассмотрим несколько примеров.
1)
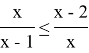
Переносим все в одну часть
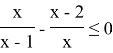
Приводим к общему знаменателю
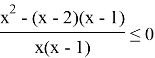
Раскрываем скобки, приводим подобные
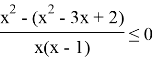
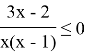
Находим точки, в которых числитель или знаменатель равны нулю.
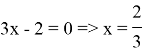
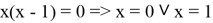
Отмечаем х на числовой прямой. Определяем знаки на каждом получившемся промежутке.
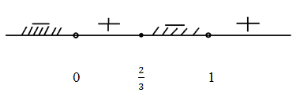
Записываем ответ
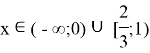
2)
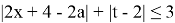
Заменим
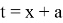
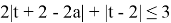
Раскрывая второй из модулей, запишем неравенство в виде системы
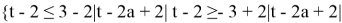
или
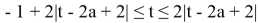
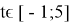
Ответ:
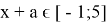
3)
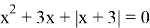
Раскрываем модуль по определению
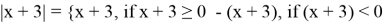
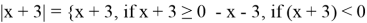
I случай
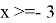
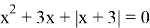
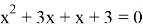
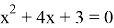
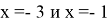
II случай
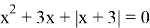
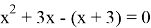
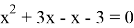
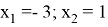
(не входит в ОДЗ)
Ответ: x=-3; x=-1.
Неравенства включены в ЕГЭ повышенной сложности. Неравенства рассматриваются в 15 пункте под C3. Эти задания рассматриваются в 2 части экзамена, задания с 13–19 с развернутым ответом (полная запись решения с обоснованием выполненных действий), проверяющих освоение математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 2 работы предназначены для проверки знаний на том уровне требований, который традиционно предъявляется ВУЗами с профильным экзаменом по математике. Поэтому для более успешной сдачи экзамена, необходимо решить вторую часть, в которую входит тема неравенства.
И вот сейчас, определив и поняв — зачем же нужно уметь решать неравенства, мы переходим к обсуждению обозначенной выше проблемы.
Ошибки, допускаемые обучающимися при решении уравнений и
неравенств.
Ошибки в этой сфере встречается самые разнообразные: от неверного оформления решения до ошибок логического характера.
- Одна из самых типичных ошибок состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
- Целая группа ошибок, а точнее будет сказать — недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
- Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами.
- Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, привычным путем, даже не задумываясь о том, что стоит посмотреть на задачу с другой стороны.
- Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода.
- При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной. Школьники же очень часто ошибочно делают обратный переход раньше. Этого делать не следует.
- Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Способы исправления и
предупреждения ошибок
Как и в случае с любой проблемой, после ее обозначения и осознания, должны искаться пути решения. Иначе говорить о проблеме становится бессмысленно. Как мы видим, многие ошибки возникают у учащихся в следствие спешки или же невнимательности. А зачастую одно приводит к другому. Поэтому для исправления и предупреждения многих ошибок важно сформировать у школьников навыки
самоконтроля
. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
– проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
– проверка правильности решения задач путём составления и решения задач, обратных к данной;
– оценка результата решения задачи с точки зрения здравого смысла;
– проверка аналитического решения графическим способом.
Сведению вероятности ошибок к минимуму также способствуют следующие профилактические меры:
– Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
– Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
– При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентирование внимания на каждом элементе формулы и выполнение разнотипных заданий позволит свести ошибочность к минимуму.
– Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
– Прочному усвоению (а, значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда возникает неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее. Тем самым новые знания будут основываться на уже сформировавшейся и закрепившейся базе, что приведет к лучшему усвоению материала. Поэтому так важен, особенно в математике, комплексный и систематический подход к обучению. С самых первых дней обучения важно заложить первые кирпичики той базы, на которую в дальнейшем будут надстраиваться новые знания. Несомненно, главную роль здесь играют способности самого ученика, но проявить и дать направление их развитию — тут уже как раз поле деятельности, которое зависит от таланта и способностей учителя, а также от влияния семьи и окружения. Не только в рассматриваемой сегодня теме, но и в процессе обучения в целом. Ведь, как мы видим, ошибки в решении неравенств возникают именно вследствие пробелов в образовательном процессе в целом, а не из-за специфичности конкретно данного раздела. Так и пути решения и исправления описанных ошибок вовсе не специфичны и уникальны, они сводятся к тому, что сначала надо устранить и/или предупредить общие пробелы в знаниях, не натаскать ребенка на конкретные шаблоны, а именно научить разбираться в рассматриваемом вопросе.
Литература:
- Математика [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeR~s
- Неравенство [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeV~s
- Анализ типичных ошибок при решении неравенств [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeW~s
- Решение неравенств: основные ошибки и полезные лайфхаки [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeY~s
- Методическое пособие. Неравенства и системы неравенств [Электронный ресурс] / Инфоурок — Режим доступа: https://goo-gl.ru/6qeZ~s
- https://infourok.ru/user/ivanova-antonina-mihaylovna/blog/problemitipichnie-oshibkidopuskaemie-uchaschimisya-pri-reshenii-uravneniy-i-neravenstv-48897.html
Основные термины (генерируются автоматически): неравенство, ошибка, знак неравенства, решение неравенств, решение уравнений, путь решения, том, часть неравенства, объяснение нового материала, процесс обучения.
14 задача ЕГЭ – это всегда неравенство. На реальных ЕГЭ бывают 3 вида неравенств: показательные, логарифмические и смешанные.
Что нужно знать?
- Метод интервалов
- Как решаются дробно-рациональные неравенства
- Как делается замена и обратная замена в неравенствах
- Как решаются показательные неравенства
- Свойства логарифмов
- Как решаются логарифмические неравенства
- Метод рационализации
Задачи, которые были на экзамене за последние 7 лет с решениями на полный балл
2022:
Решение
2021:
Решение
2020:
Решение
2019:
Решение
2018:
Решение
2017:
Решение
2016:
Решение
2015:
Решение
Процент выполнения
А вот данные сколько процентов пишущих экзамен решили задачу на неравенство в разные годы:
Сколько процентов из тех, кто решал экзамен в 2021 году*, набрал в задаче хотя бы 1 балл:
* так как в 2022 году ЕГЭ был сильно скорректирован, то некоторые задачи изменили свой номер, какие-то исчезли совсем, а другие добавились. В таблице приведены данные 2021 года, приведенные к формату экзамена 2022 (поэтому, например, в задачах 9 и 10 стоят прочерки – это новые задачи)
Типичные ошибки
1. Ошибки по невнимательности
Если вы будете готовиться к 14 задаче ЕГЭ, то практически наверняка одной из главных проблем станут ошибки по невнимательности. Из всех задач профильного ЕГЭ эта задача, пожалуй, самая опасная в плане мелких ошибок. Как научиться не допускать их написано в этой статье.
Примеры таких ошибок по невнимательности выделены желтым
2. Неправильно использовать метод интервалов
Метод интервалов – это база для 14 задачи ЕГЭ. Поэтому если вы хотите научиться решать неравенства на ЕГЭ – первым делом освойте метод интервалов, чтоб ошибок не было. Вот как «косячат» в нем школьники на реальном экзамене.
3. Умножить/делить на выражение с переменной
Почему в общем случае неравенство нельзя умножать или делить на выражение с переменной? Все дело в том, что если мы неравенство умножаем (делим) на положительное число, то должны оставить знак сравнения тем же, а если на отрицательное – перевернуть его.
(2x>4) (-2x>4)
(x>2) (x<-2)
Но чаще всего мы не знаем положительно или отрицательно выражение, на которое собрались умножать (делить), потому что при разных значениях переменной знак выражения может меняться. То есть, возникает неясность — переворачивать знак сравнения или оставить тем же? Поэтому в неравенствах так не делают. В уравнении можно, в неравенстве нет.
|
Уравнение (можно и нужно умножать на икс) |
Неравенство (нужно приводить к общему знаменателю) |
| (frac{1}{x}=1) |(·x) | (frac{1}{x}>1) |
| (1=x) | (frac{1}{x}-1>0) |
| (x=1) | (frac{1-x}{x}>0) (|·(-1)) |
| (frac{x-1}{x}<0) | |
| (x∈(0;1)) |
Хотя бывают исключения, когда знак выражения с иксом определен. Например, на (2^x) умножить или разделить неравенство можно, потому что (2^x) положительно всегда, независимо от значения (x).
(frac{2^x-1}{2^x} ≥0) (|cdot2^x)
(2^x-1≥0)
Также бывает, что выражение положительно не всегда, но мы знаем, что в данном конкретном неравенстве это так, поскольку, например, таковы требования ОДЗ.
|
(log_2x+log_2frac{1}{x^2}≥0) (log_2x frac{1}{x^2} ≥log_21) (frac{1}{x}≥ 1) (|cdot x) (1≥x) (x≤1) |
Огр. (begin{cases} x>0 \ frac{1}{x^2} >0 end{cases}) |
Несколько примеров с ошибками:
4. Неправильно привести к общему знаменателю
Чаще всего такую ошибку допускают те ученики, которые ленятся написать лишнюю строчку, делают два, а то и три действия за один ход: сразу и домножаем, и раскрываем скобки, и тут же в уме приводим подобные слагаемые. Вот, например, в примере внизу пропущен шаг домножения дробей на недостающие множители и раскрытие скобок. Подозреваю, что из-за этого и возникла ошибка.
Сравните с этим бланком, где выпускник все сделал постепенно, по шагам и закономерно получил верный ответ.
5. Не сделать обратную замену
Это вообще классика – сделать замену и забыть вернуться к исходной переменной. Вот пример.
6. Неправильно снять квадрат
Такая ошибка редко совершается на самом ЕГЭ, потому что так обычно ошибаются те, кто только начал проходить неравенства. Но зато в начале пути ее делают практически все, поэтому я внесла её в список.
Все о неравенствах: типичные ошибки, лайфхаки и приемы решения задач.
Приветствуем, друзья!
Поздравляем с началом второго семестра. В школе – четверти, а у студентов – семестры.
В нашей рассылке мы будем рассказывать о лайфхаках и приемах решения задач. Будут полезные советы о подготовке к ЕГЭ. Начнем с ЕГЭ по математике.
Цели января:
Что нужно знать и уметь в январе, чтобы сдать ЕГЭ по математике на 80+ баллов.
1. Часть 1 ЕГЭ – полностью. Надо уметь решать задачи всех типов. Включая такие темы, как производная, функции и графики, теория вероятностей.
2. Задача 12 (уравнения).
3. Стереометрия, задача 13. Все это мы прошли за сентябрь-декабрь на нашем Онлайн-курсе подготовки к ЕГЭ. Если вы уже учитесь на нашем Онлайн-курсе – эти темы вам надо пройти на онлайн-тренажере. Все проведенные занятия по ним доступны в записи.
В январе мы продолжаем штурмовать Часть 2 ЕГЭ по математике. Мы дошли до задачи 14, неравенства.
Полезные советы и лайфхаки по решению неравенств, задача 14 ЕГЭ.
Эта задача – стандартная. Ничего сложного в ней нет. Действуем по алгоритму!
1. Помним, что можно делать с неравенствами и чего с ними делать нельзя.
— Если умножить обе части неравенства на положительное число, знак неравенства останется тем же. Если на отрицательное – знак неравенства поменяется на противоположный. Умножать (или делить) неравенство на выражение, знак которого неизвестен, — нельзя.
— Возводить обе части неравенства в квадрат можно, только если они неотрицательны.
— Извлекать из неравенства квадратный корень – нельзя. Нет такого действия.
— Если в неравенстве есть модуль – раскрывать его надо по строгим правилам, а не просто «с плюсом и с минусом».
Подробно о решении неравенств здесь.
2. Оформляем решение как цепочку равносильных преобразований: переходов от неравенства – к системе условий – к следующей системе – и так далее. Все вспомогательные преобразования (например, решение квадратных уравнений) делаем на полях.
3. Помним, что квадратичные и дробно-рациональные неравенства решаются стандартно.
Не выдумываем для них сложных способов! Пользуемся свойствами квадратичной параболы и методом интервалов.
4. В показательных неравенствах помогает замена переменной. Только делаем это правильно! Смотри как сделать замену и корректно вернуться к первоначальной переменной здесь.
5. В логарифмических неравенствах – не забываем об ОДЗ. Читай о логарифмических неравенствах здесь.
6. В сложных неравенствах применяем метод рационализации, он же метод замены множителя. Необходимая теория и волшебная таблица с формулами здесь. И помним, что желательно доказывать, почему сложный множитель вы заменили на более простой.
7. Знаете, что может быть самое обидное, когда вы решаете неравенство на экзамене? Самое обидное, просто epic fail – когда вы правильно нашли все границы интервалов… а сами интервалы записали с точностью до наоборот! Аааа, ноль баллов! Как этого избежать?
— Получив ответ, подставьте 2-3 точки из найденных интервалов в исходное неравенство. Полной гарантии этот метод не дает, но хоть очевидных ошибок не сделаете.
Участникам Онлайн-курса Анны Малковой напоминаем, что первое занятие по теме «Неравенства» уже завра, 11 января. Начнем с нуля – с квадратичных неравенств, метода интервалов, простых показательных и логарифмических.
А сегодня в 17.00 по московскому времени – первое занятие Онлайн-курса по математике в этом семестре. Повторяем тему «Производная». Решаем задачи 6 и 11 ЕГЭ (Профильный уровень).
Присоединяйтесь, если еще не готовитесь к ЕГЭ с профессионалами!
Наши Онлайн-курсы:
Для тех, кому нужна выстроенная, проверенная программа подготовки от опытных преподавателей. С нуля до самых сложных тем. Есть программы для абитуриентов и преподавателей. 3 дня действует дополнительная скидка 10% по промокоду МЯТА10.
Математика
Физика
Информатика
Русский
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Неравенства: типичные ошибки и лайфхаки решения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.06.2023
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.
Анализ типичных ошибок при решении неравенств
Раздаточный материал (памятка) по решению алгебраических неравенств. Памятка содержит анализ типичных заблуждений и ошибок школьников и студентов при решении неравенств. Приводятся неверные (выделены красным) и верные (выделены зеленым) решения, а также теоретическое основание, объяснение того, почему следует решать так, а не иначе.
Описание разработки
Правило 1. Нельзя умножать или делить неравенство на выражение, не зная знака выражения.
Неправильно:
Вывод: умножать или делить обе части неравенства на x (или f(x)) можно только в том случае, если известен знак x (или f(x)).
Если x>0 (или f(x)>0), то при умножении или делении знак неравенства сохраняется.
Если x<0 (или f(x)<0), то при умножении или делении знак неравенства меняется на противоположный.
В противном случае, когда знак x (или f(x)) не известен, следует переносить правую часть неравенства влево и решать методом интервалов.
Весь материал — смотрите документ.
Содержимое разработки
Правило 1. Нельзя умножать или делить неравенство на выражение, не зная знака выражения.
Неправильно:
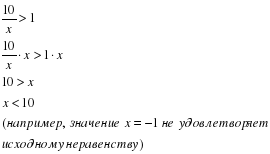
Правильно:
Вывод: умножать или делить обе части неравенства на x (или f(x)) можно только в том случае, если известен знак x (или f(x)).
Если x0 (или f(x)0), то при умножении или делении знак неравенства сохраняется.
Если xf(x)
В противном случае, когда знак x (или f(x)) не известен, следует переносить правую часть неравенства влево и решать методом интервалов.
Правило 2. Нельзя возводить неравенство в четную степень, не убедившись в том, что обе его части неотрицательны.
Неправильно:
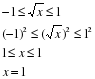
Очевидно, неравенство решено неверно.
Правильно:
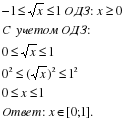
Вывод: возводить неравенство в четную степень можно только в том случае, если обе его части неотрицательны.
Правило 3. Нельзя переходить в неравенстве от функций к аргументам или от аргументов к функциям, не убедившись в монотонном возрастании (или убывании) функции.
Неправильно:
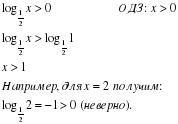
Правильно:
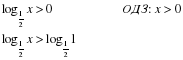
Так как a=0,5
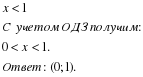
Вывод: при переходе от неравенства между функциями к неравенству между аргументами (или наоборот) следует учитывать вид монотонности функции.
Если функция монотонно возрастающая, то при переходе знак неравенства сохраняется.
Если функция монотонно убывающая, то при переходе знак неравенства меняется на противоположный.
В противном случае, когда вопрос о монотонности функции не может быть решен, переход в неравенстве от функций к аргументам и обратно невозможен.
-82%
Скачать разработку
Сохранить у себя:
Анализ типичных ошибок при решении неравенств (27.66 КB)
Похожие файлы
-
Решение задач в целых числах
-
Раздаточный материал: «Производная и первообразная»
-
Проектная работа «Обыкновенные дроби в жизни людей»
-
Программа подготовки к государственной итоговой аттестации в форме ОГЭ.
-
Преобразование обыкновенных дробей в десятичные.