Работа над уравнениями в начальной школе
методическая разработка на тему
Методическая разработка «Работа над уравнениями в начальной школе» поможет учителям начальных классов в работе над уравнениями. Здесь же прилагаются алгоритмы по решению уравнений разного вида.
Скачать:
| Вложение | Размер |
|---|---|
| rabota_nad_uravneniyami_v_nachalnoy_shkole.doc | 80.5 КБ |
Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа N135″ имени академика Б.В.Литвинова»
Работа над уравнениями в начальной школе.
Подготовила учитель начальных классов:
Самойлова Анжелика Владимировна
Работа над уравнениями в начальной школе.
Большую трудность для младшего школьного возраста представляет умение решать уравнения. Изучение уравнений в начальной школе носит пропедевтический характер. Поэтому очень важно подготовить детей в начальной школе к более глубокому изучению уравнений в старших классах. В начальной школе в процессе работы над уравнением закрепляются правила о взаимосвязи части и целого, сторон прямоугольника с его площадью, формируются вычислительные навыки и понимание связи между компонентами действий, закрепляется порядок действий и формируется умения решать текстовые задачи, идет работа над развитием правильной математической речи. На уроках закрепления уравнения позволяют разнообразить виды заданий.
Изучение уравнений начинается с подготовительного этапа уже в 1 классе, когда дети, действуя с предметами, решают такие «задачи»:
Затем учащиеся переходят к действиям над числами и выполняют задания, связанные с нахождением неизвестного числа в «окошке», например:
Дети находят число либо подбором, либо на основе знаний состава числа. На данном этапе учителю необходимо включать в устные упражнения следующие задания:
— Сколько надо вычесть из 3, чтобы получилось 2?
— Сколько надо прибавить к 2, чтобы получилось 4?
На втором этапе учащиеся знакомятся с понятиями «уравнение» и «корень уравнения». На протяжении нескольких уроков дети учатся решать уравнения с неизвестным слагаемым, уменьшаемым, вычитаемым. Названия компонентов арифметических действий были введены в речевую практику учащихся и использовались для чтения равенств и выражений, пока правило нахождения неизвестного компонента в уравнениях не заучивается. Уравнения решаются на основе взаимосвязи между частью и целым. При изучении данной темы дети должны научиться находить в уравнениях компоненты,
соответствующие целому (сумма, уменьшаемое), и компоненты, соответствующие его частям (слагаемое, уменьшаемое, разность). При решении уравнений детям нужно будет вспомнить лишь два известных правила:
— Целое равно сумме частей.
— Чтобы найти часть, надо из целого вычесть другую часть.
Эту работу облегчает графическое обозначение части ______ и целого , а также понимание того, что целое – это большее число.
Для того чтобы облегчить работу над формированием навыка решения уравнений, можно проводить в классе следующую работу.
- Составление и решение уравнений по схеме.
2. Составление и решение уравнений с помощью модели числа.
— Замените модели числами:
3. Уравнения с буквами.
— Как из волка получить вола ?
4. Составление и решение уравнений с помощью числового луча.
5. Выполни проверку и найди ошибку.
Дети решают: 24 + 8 = 16
6.Составиьуравнения с числами Х, 4, 10 и реши их.
Х + 4 = 10; 10 – Х = 4; Х – 10 = 4 и т.п.
7. Из данных уравнений реши те, где Х находится сложением.
Х +16 = 20; Х -18 = 30; 29 – Х = 19
8. Рассмотри решение уравнения и вставь соответствующий знак.
К концу изучения темы дети учатся комментировать уравнения через компоненты действий. Работа строится следующим образом:
1) читаю уравнение;
2) нахожу известные и неизвестные компоненты (части и целое);
3) применяю правило (по нахождению части или целого);
4) нахожу, чему равен Х;
5) комментирую через компоненты действий.
Следующий этап – решение уравнений вида: а ∙ Х = в; а : Х = в; Х : а = в .
Уравнения этого вида решаются на основе взаимосвязи между площадью прямоугольника и его сторонами. Поэтому изменяется и графическое обозначение компонентов уравнения:
— площадь прямоугольника, а _____ — его стороны. Здесь важно понять то, что обучение решению и комментированию уравнений ведется по определенной схеме:
1 этап: Решение с одновременным комментированием правил нахождения площади и его сторон. Например, Х : 2 = 5 ( Х – площадь прямоугольника, 2 и 5 – его стороны).
Х = 2 ∙ 5 (чтобы найти площадь прямоугольника, надо перемножить его стороны)
2 этап: Решение уравнений с комментированием(через площадь прямоугольника и его стороны).
Комментирование через компоненты действий после решения уравнения.
Для отработки навыков решения уравнений на умножение и деление можно использовать следующие упражнения.
1. Выполни проверку и найди ошибку.
Дети решают: 2 : 2 = 4
2. Проанализируй решение уравнения и найди ошибку.
Ошибки: 1) 9 – это площадь, на целое, ее надо обозначить прямоугольником;
2) Х – это сторона, надо площадь разделить на другую сторону.
3. Составь уравнения с числами 3, Х, 12 и реши их.
Дети составляют: 12 : Х = 3; 3 ∙ Х = 12 и т.п.
4. Изданных уравнений реши те, которые решаются делением.
Х ∙ 2 = 6; Х : 4 = 16; 12 : Х = 4
5. Рассмотри решение уравнений и вставь соответствующий знак в запись уравнения.
6. Составь и реши уравнение:
— Какое число надо умножить на пять, чтобы получилось 25?
Х ∙ 3 = 15; Х : 4 = 5; 16 : Х = 2
— Какое уравнение лишнее? Объясни свой выбор.
— первое уравнение – Х равен нечетному числу;
— второе уравнение – Х находим умножением;
— третье уравнение – неизвестен второй компонент и т.п.
Последний этап при работе с уравнениями в начальной школе – знакомство учащихся с составными уравнениями. Решение таких уравнений строится на качественном анализе выражения, стоящего в левой части уравнения: какие действия указаны в выражении, какое действие выполняется последним, как читается запись этого выражения, какому компоненту этого действия принадлежит неизвестное число и т.п. К этому времени учащиеся должны твердо овладеть следующими умениями:
— решение простых уравнений,
— анализ решений уравнений по компонентам действий,
— чтение записи выражений в два – три действия,
— порядок выполнения действий в выражениях со скобками и без них.
На данном этапе дети должны понимать, что в записи уравнений в качестве неизвестного числа могут использоваться различные буквы латинского алфавита, например: К + 4 = 3; Р – 3 = 8; Z : 7 = 6 и т.п.
Запись решения уравнений сопровождается словесным описанием выполняемых действий. Для выработки правильной математической речи и навыков решения первых уравнений данного вида необходимо использовать таблицы с образцами решений. Но так как дети уже с 1-го класса знакомы с записью различных алгоритмов, то можно использовать только алгоритм решения уравнений, по которому дети и анализируют уравнения.
Как решать уравнения: от простого к сложному 2-4 класс
Уравнение — равенство, содержащее букву латинского алфавита, значение которой нужно найти.
Решить уравнение — значит подобрать такое число, при котором равенство становится верным.
Любые уравнения решаются на основе зависимости между компонентами. Простые уравнения учащиеся начальной школы начинают решать уже 2 классе. По мере взросления, усложняются и уравнения, переходя от простых к сложным уравнениям в 4 классе начальной школы.
Простые уравнения во 2 классе решают на основе взаимосвязей между компонентами при сложении или вычитании. Важно соблюдать алгоритм решения уравнения.
Решение уравнения
Объяснение
чтобы найти первое слагаемое, нужно из суммы вычесть второе слагаемое.
Вычисляю: 35 — 7 = 28
Проверяю: 28 + 7 = 35
чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
Вычисляю: 20 + 13 = 33
Проверяю: 33 — 13 = 20
чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность
Вычисляю: 46 — 42 = 4
Проверяю: 46 — 4 = 42
Простые уравнения вида х • 6 = 72, х : 8 = 12, 64 : х = 16 решают на основе взаимосвязей между результатами и компонентами действий.
Решение уравнения
Объяснение
1) Читаю уравнение: произведение х и 6 равно 72.
2) Вспоминаю правило: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
3) Вычисляю: х = 72 : 6
4) Проверяю: 12 • 6 = 72
1) Читаю уравнение: частное х и 8 равно 12.
2) Вспоминаю правило: чтобы найти неизвестное делимое, надо частное умножить на делитель.
3) Вычисляю: х = 12 • 8
4) Проверяю: 96 : 8 = 12
1) Читаю уравнение: частное 64 и х равно 16.
2) Вспоминаю правило: чтобы найти неизвестный делитель, надо делимое разделить на частное.
3) Вычисляю: х = 64 : 16
4) Проверяю: 64 : 4 = 16
Сложные уравнения в начальной школе состоят из нескольких арифметических действий. Алгоритм решения заключается в превращение сложного уравнения в простое.
Уравнения на нахождение неизвестного слагаемого
1)Вычисляю значение выражения в правой части уравнения: 12 • 4 = 48.
2) В уравнении х + 13 = 48 неизвестно первое слагаемое.
3) Вспоминаю правило: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
4) Вычисляю: х = 48 — 13
5) Проверяю: 35 + 13 = 12 • 4
Уравнения на нахождение неизвестного уменьшаемого
1) Вычисляю значение выражения в правой части уравнения: 51 : 17 = 3.
2) В уравнении х — 24 = 3 неизвестно уменьшаемое.
3) Вспоминаю правило: чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
4) Вычисляю: х = 24 + 3
5) Проверяю: 27 — 24 = 51 : 17
Уравнения на нахождение неизвестного вычитаемого
640 — х = 180 + 120
640 — 340 = 180 + 120
1) Вычисляю значение выражения в правой части уравнения: 180 + 120 = 300.
2) В уравнении 640 – х = 300 неизвестно вычитаемое.
3) Вспоминаю правило: чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
4) Вычисляю: х = 649 – 300
5) Проверяю: 640 — 340 = 180+120
Уравнения на нахождение неизвестного множителя
5 • 77 = 131 + 254
1) Вычисляю значение выражения в правой части уравнения: 131 + 254 = 385.
2) В уравнении 5 • х = 385 неизвестен второй множитель.
3) Вспоминаю правило: чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
4) Вычисляю: х = 385 : 5
5) Проверяю: 5 • 77 = 131 + 254
Уравнения на нахождение неизвестного делимого
64 000 : 8 = 800 • 10
1) Вычисляю значение выражения в правой части.
2) Вспоминаю правило: чтобы найти делимое, нужно частное умножить на делитель.
Уравнения на нахождение неизвестного делителя
1) Вычисляю значение выражения вправой части.
2) Вспоминаю правило: чтобы найти неизвестный делитель, нужно делимоеразделить на частное.
Как решать сложные уравнения в 4 классе подробно рассмотрено в статье по ссылке.
Статья. Проблемы, типичные ошибки учащихся, допускаемые при решении уравнений и неравенств.

Задание «Проблемы, типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти ошибки.
Решая уравнения и неравенства учащиеся допускают типичные ошибки:
· Незнание правил, определений, формул.
· Непонимание правил, определений, формул.
· Неумение применять правила, определения, формулы.
· Неверное применение формул.
· Невнимательное чтение условия и вопроса задания.
· Раскрытие скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего характера возникают у учащихся при изучении математики ( их несомненно можно отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения и неравенства»):
· Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
· Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
· Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
· Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам . Учащиеся не всегда сами понимают, что именно они написали.
· Усталость . Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
· Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
· Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
· Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки подобного рода и определить способы их предупреждения и исправления, но прежде всего хочу обратить внимание на следующую мысль: не надо бояться приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
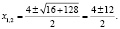
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение 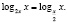
Область определения исходного уравнения задается системой
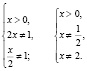
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
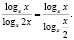
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
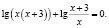
Ученик предлагает следующее ошибочное решение этого уравнения:
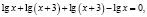
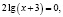
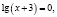
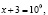
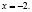
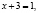 х = –2.
х = –2.
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 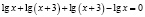 эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
Чтобы избежать потери корня, можно поступить следующим образом: перейти в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть это на следующем примере.
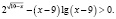
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
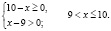
Для всех x из промежутка (9;10] выражение 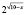 имеет положительные значения (значения показательной функции всегда положительны).
имеет положительные значения (значения показательной функции всегда положительны).
Для всех x из промежутка (9;10] выражение ( x – 9) имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение
– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x ∈ (9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
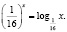
Некоторые учащиеся, решая это уравнение графически (хочу отметить, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
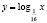 и
и 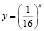 −
−
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 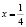 и третий корень
и третий корень 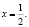 Убедиться в справедливости сказанного можно непосредственной подстановкой чисел
Убедиться в справедливости сказанного можно непосредственной подстановкой чисел 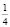 и
и 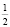 в заданное уравнение.
в заданное уравнение.
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны» (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение x х = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
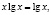
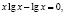
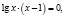
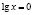 или
или 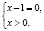
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
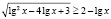 .
.
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
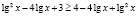 ,
,
откуда получаем неверное числовое неравенство 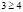 , что позволяет сделать вывод: заданное неравенство не имеет решений.
, что позволяет сделать вывод: заданное неравенство не имеет решений.
Однако полученный вывод неверен, например, при х = 1000 имеем
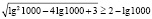 ,
, 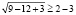 ,
, 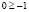 .
.
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
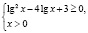 или
или 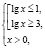
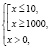 откуда
откуда 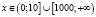 .
.
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 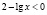 , откуда х > 100. С учетом области определения исходного неравенства имеем промежуток
, откуда х > 100. С учетом области определения исходного неравенства имеем промежуток 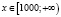 . Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что
. Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что 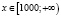 – решение заданного неравенства.
– решение заданного неравенства.
б) 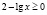 , откуда
, откуда 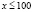 . С учетом области определения исходного неравенства имеем промежуток
. С учетом области определения исходного неравенства имеем промежуток 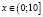 . Для всех х из промежутка
. Для всех х из промежутка 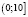 имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь:
имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь: 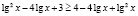 , откуда
, откуда 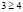 . Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка
. Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка 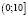 решениями исходного неравенства не являются.
решениями исходного неравенства не являются.
Ответ: 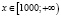 .
.
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x .
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
· проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
· проверка правильности решения задач путём составления и решения задач, обратных к данной;
· оценка результата решения задачи с точки зрения здравого смысла;
· проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
источники:
http://koncpekt.ru/nachalnye-klassy/raznoe/4057-kak-reshat-uravneniya-ot-prostogo-k-slozhnomu-2-4-klass.html
http://znanio.ru/media/statya_problemy_tipichnye_oshibki_uchaschihsya_dopuskaemye_pri_reshenii_uravnenij_i_neravenstv-173622
Работа над уравнениями в начальной школе
методическая разработка на тему
Методическая разработка «Работа над уравнениями в начальной школе» поможет учителям начальных классов в работе над уравнениями. Здесь же прилагаются алгоритмы по решению уравнений разного вида.
Скачать:
| Вложение | Размер |
|---|---|
| rabota_nad_uravneniyami_v_nachalnoy_shkole.doc | 80.5 КБ |
Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа N135″ имени академика Б.В.Литвинова»
Работа над уравнениями в начальной школе.
Подготовила учитель начальных классов:
Самойлова Анжелика Владимировна
Работа над уравнениями в начальной школе.
Большую трудность для младшего школьного возраста представляет умение решать уравнения. Изучение уравнений в начальной школе носит пропедевтический характер. Поэтому очень важно подготовить детей в начальной школе к более глубокому изучению уравнений в старших классах. В начальной школе в процессе работы над уравнением закрепляются правила о взаимосвязи части и целого, сторон прямоугольника с его площадью, формируются вычислительные навыки и понимание связи между компонентами действий, закрепляется порядок действий и формируется умения решать текстовые задачи, идет работа над развитием правильной математической речи. На уроках закрепления уравнения позволяют разнообразить виды заданий.
Изучение уравнений начинается с подготовительного этапа уже в 1 классе, когда дети, действуя с предметами, решают такие «задачи»:
Затем учащиеся переходят к действиям над числами и выполняют задания, связанные с нахождением неизвестного числа в «окошке», например:
Дети находят число либо подбором, либо на основе знаний состава числа. На данном этапе учителю необходимо включать в устные упражнения следующие задания:
— Сколько надо вычесть из 3, чтобы получилось 2?
— Сколько надо прибавить к 2, чтобы получилось 4?
На втором этапе учащиеся знакомятся с понятиями «уравнение» и «корень уравнения». На протяжении нескольких уроков дети учатся решать уравнения с неизвестным слагаемым, уменьшаемым, вычитаемым. Названия компонентов арифметических действий были введены в речевую практику учащихся и использовались для чтения равенств и выражений, пока правило нахождения неизвестного компонента в уравнениях не заучивается. Уравнения решаются на основе взаимосвязи между частью и целым. При изучении данной темы дети должны научиться находить в уравнениях компоненты,
соответствующие целому (сумма, уменьшаемое), и компоненты, соответствующие его частям (слагаемое, уменьшаемое, разность). При решении уравнений детям нужно будет вспомнить лишь два известных правила:
— Целое равно сумме частей.
— Чтобы найти часть, надо из целого вычесть другую часть.
Эту работу облегчает графическое обозначение части ______ и целого , а также понимание того, что целое – это большее число.
Для того чтобы облегчить работу над формированием навыка решения уравнений, можно проводить в классе следующую работу.
- Составление и решение уравнений по схеме.
2. Составление и решение уравнений с помощью модели числа.
— Замените модели числами:
3. Уравнения с буквами.
— Как из волка получить вола ?
4. Составление и решение уравнений с помощью числового луча.
5. Выполни проверку и найди ошибку.
Дети решают: 24 + 8 = 16
6.Составиьуравнения с числами Х, 4, 10 и реши их.
Х + 4 = 10; 10 – Х = 4; Х – 10 = 4 и т.п.
7. Из данных уравнений реши те, где Х находится сложением.
Х +16 = 20; Х -18 = 30; 29 – Х = 19
8. Рассмотри решение уравнения и вставь соответствующий знак.
К концу изучения темы дети учатся комментировать уравнения через компоненты действий. Работа строится следующим образом:
1) читаю уравнение;
2) нахожу известные и неизвестные компоненты (части и целое);
3) применяю правило (по нахождению части или целого);
4) нахожу, чему равен Х;
5) комментирую через компоненты действий.
Следующий этап – решение уравнений вида: а ∙ Х = в; а : Х = в; Х : а = в .
Уравнения этого вида решаются на основе взаимосвязи между площадью прямоугольника и его сторонами. Поэтому изменяется и графическое обозначение компонентов уравнения:
— площадь прямоугольника, а _____ — его стороны. Здесь важно понять то, что обучение решению и комментированию уравнений ведется по определенной схеме:
1 этап: Решение с одновременным комментированием правил нахождения площади и его сторон. Например, Х : 2 = 5 ( Х – площадь прямоугольника, 2 и 5 – его стороны).
Х = 2 ∙ 5 (чтобы найти площадь прямоугольника, надо перемножить его стороны)
2 этап: Решение уравнений с комментированием(через площадь прямоугольника и его стороны).
Комментирование через компоненты действий после решения уравнения.
Для отработки навыков решения уравнений на умножение и деление можно использовать следующие упражнения.
1. Выполни проверку и найди ошибку.
Дети решают: 2 : 2 = 4
2. Проанализируй решение уравнения и найди ошибку.
Ошибки: 1) 9 – это площадь, на целое, ее надо обозначить прямоугольником;
2) Х – это сторона, надо площадь разделить на другую сторону.
3. Составь уравнения с числами 3, Х, 12 и реши их.
Дети составляют: 12 : Х = 3; 3 ∙ Х = 12 и т.п.
4. Изданных уравнений реши те, которые решаются делением.
Х ∙ 2 = 6; Х : 4 = 16; 12 : Х = 4
5. Рассмотри решение уравнений и вставь соответствующий знак в запись уравнения.
6. Составь и реши уравнение:
— Какое число надо умножить на пять, чтобы получилось 25?
Х ∙ 3 = 15; Х : 4 = 5; 16 : Х = 2
— Какое уравнение лишнее? Объясни свой выбор.
— первое уравнение – Х равен нечетному числу;
— второе уравнение – Х находим умножением;
— третье уравнение – неизвестен второй компонент и т.п.
Последний этап при работе с уравнениями в начальной школе – знакомство учащихся с составными уравнениями. Решение таких уравнений строится на качественном анализе выражения, стоящего в левой части уравнения: какие действия указаны в выражении, какое действие выполняется последним, как читается запись этого выражения, какому компоненту этого действия принадлежит неизвестное число и т.п. К этому времени учащиеся должны твердо овладеть следующими умениями:
— решение простых уравнений,
— анализ решений уравнений по компонентам действий,
— чтение записи выражений в два – три действия,
— порядок выполнения действий в выражениях со скобками и без них.
На данном этапе дети должны понимать, что в записи уравнений в качестве неизвестного числа могут использоваться различные буквы латинского алфавита, например: К + 4 = 3; Р – 3 = 8; Z : 7 = 6 и т.п.
Запись решения уравнений сопровождается словесным описанием выполняемых действий. Для выработки правильной математической речи и навыков решения первых уравнений данного вида необходимо использовать таблицы с образцами решений. Но так как дети уже с 1-го класса знакомы с записью различных алгоритмов, то можно использовать только алгоритм решения уравнений, по которому дети и анализируют уравнения.
Обучение младших школьников решению уравнений посредством дифференцированного подхода
Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 1
Шелыгина Ольга Борисовна,
кандидат педагогических наук, доцент кафедры педагогики и методики дошкольного и начального образования ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Кировkaf_pmdno@vshu.kirov.ru
Каткова Александра Сергеевна,студентка ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров
Обучение младших школьников решению уравненийпосредством дифференцированного подхода
Аннотация. Статья посвящена вопросам реализации дифференцированного подхода к младшим школьникам в процессе обучения решению уравнений. Авторы предлагают различные приемы работы над уравнениями в зависимости от уровня обученности учеников, способствующие развитию мышления учащихся, их познавательного интереса. Методические приемы подкреплены примерами дифференцированных заданий по теме «Уравнения» для разных групп учащихся.Ключевые слова: обучение математике, обучение решению уравнений, младшие школьники, дифференцированный подход, разноуровневые задания.Раздел: (01) педагогика; история педагогики и образования; теория и методика обучения и воспитания (по предметным областям).
Дети приходят в школу с различным уровнем обучаемости. Часто учителю приходится вести обучение применительно к среднему уровню развития и обучаемости детей. А.Н. Конев считал, что такой подход в обучении приводит к тому, что «сильные» ученики сдерживаются в своём развитии, теряют интерес к учебе, а «слабые» обречены на отставание. Те, кто относится к «средним», тоже имеют индивидуальные особенности, и даже для них такой подход неэффективен [1].Учителю необходимо создавать условия, чтобы каждый ученик учился в соответствии со своими возможностями и способностями, развивал свои индивидуальные особенности, стал субъектом учения. Одним из способов осуществления индивидуального подхода в образовании является дифференциация обучения.Дифференцированный подход это способ организации учебного процесса, при котором для более эффективного обучения выявляются индивидуальнотипологические особенности учеников, на основе чего создаются группы учащихся. С учетом особенностей учащихся, в каждой группе применяются соответствующие формы, методы и приемы обучения. Дифференцированный подход необходимо осуществлять на разных дисциплинах. Математика, является одним из фундаментальных предметов начального школьного обучения. Важным разделом начального курса математики является алгебраический материал, в котором изучается одна из самых сложных тем для учащихся начальной школы «Уравнения». Сформированные умения решать уравнения в начальной школеоснова для дальнейшего обучения в средней и старшей школе.Уравнение математическое равенство, содержащее буквенное выражение с одной или несколькими переменными, верное только при определенных значениях этих переменных. Переменные, входящие в уравнение, называются неизвестными. Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 2
Решить уравнение значит найти все значения неизвестных, прикоторых запись обращается в верное равенство (или установить, что таких значений нет) [2].Обучение решению уравнений начинается с подготовительной работы уже в 1мклассе. Учащиеся выполняют задания, связанные с нахождением неизвестного числа в равенствес «окошечком», то есть работают с деформированными равенствами. Чаще всего дети находят число подбором. На следующем этапе младшие школьники знакомятся с понятием «уравнение», учатся выделять уравнения из других математических записей, так же вводится понятие «решение уравнения». На протяжении нескольких уроков дети учатся решать уравнения на нахождение неизвестных компонентов при сложении и вычитании. Не смотря на то, что названия компонентов и результатов арифметических действий известны учащимся, правила нахождения неизвестных чисел в уравнениях не заучиваются. Уравнения на данном этапе решаются на основе взаимосвязи между частью и целым. При изучении данной темы дети должны научиться находить в уравнениях компоненты, соответствующие целому (сумма, уменьшаемое), и компоненты, соответствующие его частям (слагаемое, вычитаемое, разность). На третьем этапе изучения темы дети учатся комментировать решение уравнений, используя правила взаимосвязи компонентов и результата соответствующего действия. Следующийэтап связан с введением новых арифметических действий умножение и деление. Соответственно, в новых видах уравнений неизвестным может быть один из множителей, делимое или делитель. Уравнения этого вида могут быть решены на основе взаимосвязи между площадью прямоугольника и его сторонами или на основе правила нахождения неизвестных компонентов (см. таблицу).
Способы комментирования решения уравнения
Решение уравнения с комментированием на основе правила нахождения площади и его сторонРешение уравнения с комментированием на основе правила нахождения неизвестных компонентовХ :2= 5
Хплощадь прямоугольника2ширина5длинаЧтобы найти площадь прямоугольника, надо длину умножить ширину Х= 5 • 2Х= 10Проверяю 10:2= 5, решено верно.Х : 2= 5Х это делимое2 делитель5 частное Чтобы найти неизвестное делимое нужночастное умножить на делитель.Х= 5 • 2Х= 10Проверяю 10:2= 5, решено верно.
Последний этап при работе с уравнениями в начальной школезнакомство учащихся с составными уравнениями (буквенные выражения в составе уравнения состоят из нескольких действий). Решение таких уравнений основано на анализе выражения, содержащего неизвестное число. Анализ осуществляется по алгоритму: определи, какиедействия в выражении; найди действие, которое выполняется последним; назови, какому компоненту этого действия принадлежит неизвестное число; вспомни, как мы находим данный неизвестный компонент; найди его, и т.п. (данный алгоритм часто является циклическим). К этому времени учащиеся должны твердо овладеть следующими умениями:решение простых уравнений в одно действие,комментирование решений уравнений на основе взаимосвязи между компонентами и результатом действия,Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 3
чтение выражений в дватри действия,знание правил порядка выполнения действий в выражениях со скобками и без них, умение ими пользоваться при нахождении значений выражений.Чтобы знания учеников были качественными и прочными, мы считаем, что целесообразно данную тему изучать в процессе реализации дифференцированного подхода в обучении, чтобы каждый ученик смог справиться с тем минимумом, который необходим при усвоении учебного материала, а также дать возможность сильным учащимся интеллектуально развиваться. Для учеников с высоким уровнем обученности необходимо:1.Разрабатывать задания, в которых нужно помимо выполнения основных заданий сделать дополнительные задания.Например:1)Реши уравнения, в таблице поставь букву под получившимся ответом и узнаешь, какое озеро называют «жемчужиной планеты».Ж:8= 3Й 6= 5В+13= 5211Б + 15= 17(А + 3): 2= 2К (6:3)= 1038 Л= 25
2)Реши уравнения. Х:6= 1212:Х= 6Х • 6= 12Раздели их на две группы (найди разные варианты).Составь аналогичные уравнения.
3)Реши уравнения.Х:8= 810:Х= 10Х • 12= 12Чем они похожи? Чем отличаются? Попробуй вывести правила для двух уравнений. Будут ли исключения из правил? Докажи.
4)Реши уравнения.У+56= 100У 33= 8458 У= 48Сейчас измени уравнения так, чтобы неизвестное число находилось противоположным действием. Какое составленное тобой уравнение отличается от остальных?
5)Реши уравнения.10• Х= 5015• Х= 7520• Х= 100Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 4
25• Х= 125Найди закономерность. Составь и реши еще два уравнения.Придумай по аналогии свою цепочку уравнений.
6)Реши уравнения.(25 Х):5= 4(49+Х):6= 9(Х+31):6= 614:(2+Х)= 2На какие две группы можно их разделить?Чем похожи уравнения?Составь свое уравнение с таким же ответом к каждой выделенной группе.
7)После решения уравнений предложить: найти сумму всех ответов, расположить ответы в порядке убывания (возрастания),разделить ответы на группы по какомулибо признаку и т.п.
2.Разрабатывать частичнопоисковые и творческие задания.Например:
1)Найди в словах числа, составь с числами уравнения и реши их: Хподвал= 34семья * Х= семьястриж + Х= сорокаХ : опять= 45
2)Догадайся, по какому принципу составлено первое уравнение. август Х= июнь8 Х= 6Х= 2Х= февраль На основе этого реши уравнения:декабрь :Х= февраль2 • (августХ)= август(Х март): март= мартПридумайте и решите аналогичные уравнения, используя дни недели.
3)Дан ряд цифр 3,5,7,9. Запиши и реши уравнения:а)если из неизвестного числа вычесть число, которое на 2 больше второго числа в ряду цифр, то получится последнее число в ряду (Х 7= 9).б)если к двузначному числу, в котором первая цифра это вторая в ряду, а вторая цифра это последняя цифра в ряду прибавить неизвестное число, то получится число, в котором первая цифра это третья цифра в ряду, а вторая первая цифра в ряду(59 + Х= 73).
4)Составь и реши уравнение: «Я загадала число. Прибавила к нему самое маленькое трехзначное число. Результат разделила на самое большое однозначное число. Получила число, которое меньше 13, больше 10, но не 11».
5)Дан ряд чисел (каждое число на 1 больше предыдущего): ¤, ∩, ↑, ᴥ,Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 5
Реши уравнения со сказочными числами.¤+Х= ↑Х= ∩
6)Рассмотри решение уравнения и запиши первоначальное уравнениеХ= 7•5Х= 43Х= 8
7)Составь и реши уравнения, в которых для нахождения корня уравнения нужно было умножить на двузначное число.8)Составьте и решите такие уравнения, чтобы можно было повторить вычитание многозначных чисел и переходом через разряд.9)Замени буквы числами (каждой букве соответствует ее порядковый номер в алфавите), составь и реши уравнения.ж + Х= мХ в= кХ : г= и
10)Запишите слово ЛЕС с помощью чиселЕ+8= 16 С4= 10 14Л= 5
3.Привлекать учеников к ведениюфрагментов уроков, назначать командирами при групповой форме работы.4. Предлагать более трудные уравнения. Высокая трудность может быть за счет:усложнения числового материала,увеличения объема выполняемых заданий,увеличения количества объектов и действий с ними,более сложных вычислительных приемов.
Учащиеся со средним уровнем обученностипо теме «Уравнения» должны упражняться в решении уравнений. Необходимо предлагать достаточное количество репродуктивных упражнений для закрепления знаний и умений. Так же можно разнообразить деятельность, предложив задания вида: 1)Раздели уравнения в два столбика по определенному признаку. Реши их. Подумай, какие ещё признаки классификации могли получиться: 25 Х= 10А + 34= 55(К5) 5= 10 Х + (17+17)= 55
2)Выбери и реши только те уравнения, в которых неизвестное находится делением: 49:Х= 7 Х • 6= 42 Р • 7= 28 45:Z= 9
3)Сделай прикидку. Выбери и реши только те уравнения, в которых неизвестное число двузначное44У= 22 19Х= 10 Х15= 15 У+12= 100 22Х= 15
4)Самолёт должен лететь на городами в определенном порядке (от большего числа к меньшему). Реши уравнения, подпиши города и составь маршрут самолёта. Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 6
42+ Х= 5848 : Х= 6А 15= 146 • M= 30Р (133)= 25(К+8) 12= 8
16Москва8 Ижевск29 НижнийНовгород5 СанктПетербург35 Рязань 12 Киров
5)Составь уравнения с числами 3, 12; 8, 32 и реши их.12 : Х= 3; 3 • Х= 12 32 : Х= 8; 8 • Х= 32
6)Рассмотри решение уравнений и вставь соответствующий знак в запись уравнения.Х ? 6= 24 Х?6= 24Х= 24 : 6 Х= 24•6
7)Составь и реши уравнение: «Какое число надо умножить на восемь, чтобы получилось 32?»
Для учащихся с низким уровнем усвоения учебного материаладолжны предлагаться репродуктивные задания на отработку материала. Если ученики не справляются и с этими заданиями, то необходимо оказать методическую направляющую помощь, предлагая задания следующего вида: 1.Реши уравнения по следующему образцу:35 Х= 8Х= 35 8 Х= 2735 27= 88= 8
2.Соедини «подсказки»с уравнениями. Пользуясь найденными подсказками, реши уравнения.Чтобынайти неизвестное вычитаемое,нужно к значению разности прибавить уменьшаемое.
С • 9= 36Чтобы найти множитель,нужно значение произведения разделить на известный множитель.
72 В= 31Чтобы найти второе слагаемое, нужно из значения суммы вычесть первое слагаемое.
64 + Х= 82Чтобы найти делимое, нужно значение частного умножить на делитель.
3.Дан необходимый теоретический материал. Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 7
Составь и реши уравнения, если известно, что сумма получается при сложении, разность при вычитании, произведение при умножении, а частное при делении.Если из неизвестного числа вычесть 20, то получится произведение чисел 9 и 6.Если к 15 прибавить неизвестное число, то получится частное 80 и 4Если неизвестное число умножить на 6, то получится сумма чисел 35 и 7
4.Пользуясь алгоритмом, реши уравнение (Х+3):8= 51)Определи по последнему действию, чем является выражение в левой части (суммой, произведением, разностью, частным)?2)Где находится Х? Как найти неизвестный компонент? Применяем правило.3)Упрощаем равенство (находим значение выражения)4)Называем компоненты.5)Решаем простое уравнение.6)Выполняем проверку.
5.Реши уравнения, пользуясь памяткой: «Чтобы найти целое надо сложить части. Чтобы найти часть надо из целого вычесть известную часть».
6.Продолжитерешение уравнений.80+Х= 100 Х 200= 220Х= …… Х= … + …
7.Даны подготовительные задания.Х38= 38 (Х+5)45= 45
8.Предварительное решение уравнений на «маленьких числах».Х7= 8 8Х= 6Х25= 54 64Х= 20Х344= 485205Х= 140
9.Приучение к самоконтролю.1)Проанализируй решения уравнений и найди ошибки. Что нужно всегда делать, что бы ошибки не допускать?Х : 2= 4 Х:5= 15 Х•8= 8 Х:10= 20Х= 4 : 2 Х= 15•5 Х= 8:8 Х= 20:10Х= 2 Х= 80 Х= 1 Х= 22)Сделай прикидку, а потом реши уравнение (из какого числа нужно вычесть двадцать, чтобы получилось сто?)Х20= 1003)Найди правильно решенное уравнение. Докажи его правильность.Х:5= 10 Х:5= 10Х:5= 10Х= 10:5 Х= 10+5 Х= 10•5Х= 2 Х= 15 Х= 50
Данные виды заданий представляют собой методическую помощь ученикам, благодаря которой учащиеся с низким уровнем обученности смогут правильно решать уравнения и со временем догнать более «сильных» учеников. Необходимо заметить, что количество методической направляющей помощи необходимо постепенно сокращать по мере продвижения учеников (дети должны понимать, что учитель не будет помогать им все время), заменяя ее на стимулирующую помощь.
Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 8
Таким образом, дифференцированный подход в обучении является эффективной формой организации учебного процесса в начальной школе на уроках математики. Для организации данного подхода необходимо подразделять класс на три группы, внутри каждой из которой будутобъединены дети с одинаковым уровнем усвоения учебного материала. Каждой группе нужно давать задания того уровня, которому соответствуют интеллектуальные возможности детей. В результате нашего исследования и внедрения в процесс обучения разработанных заданий для разных групп учащихся мы пришли к выводу, что дифференцированный подход к младшим школьникам на уроках математики в процессе обучения решению уравнений является удобной и эффективной формой организации учебного процесса. При дифференцированном подходе каждый ребёнок в классе может развивать свои знаний и умения, а тот, кто не уверен в них, может справиться с выполнением задания, используя методическую помощь.
Ссылки на источники1.Бекаревич А. Б. Уравнения в школьном курсе математики. М., 2000.
2.Конев А.Н. Индивидуальнотипологические особенности младших школьников как основа дифференцированного обучения.М., 1998.
Ph.D., Assistant Professor of pedagogy and methodology of preschool and primary education,Vyatka State University of Humanities, Kirovkaf_pmdno@vshu.kirov.ruAlexandra Katkova,Student,Vyatka State University of Humanities, KirovTraining of younger schoolboys the solution of equations through a differentiated approachAbstract. The article is devoted to the implementation of the differentiated approach to the younger students in the learning process solving equations. The authors suggest different methods work on equations, depending on the level of training of students, contributing to the development ofstudents’ thinking, their cognitive interest. Teaching methods are supported by examples of differentiated tasks on «equations» for different groups of students.Keywords: teaching mathematics, teaching solving equations, junior high school students, a differentiated approach, multilevel task.
Горевым П. М., кандидатом педагогических наук, главным редактором журнала «Концепт»
Поступила в редакциюReceived03.11.15Получена положительная рецензияReceived a positive review05.11.15ПринятакпубликацииAccepted for publication05.11.15ОпубликованаPublished11.11.15
Статья. Проблемы, типичные ошибки учащихся, допускаемые при решении уравнений и неравенств.

Задание «Проблемы, типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти ошибки.
Решая уравнения и неравенства учащиеся допускают типичные ошибки:
· Незнание правил, определений, формул.
· Непонимание правил, определений, формул.
· Неумение применять правила, определения, формулы.
· Неверное применение формул.
· Невнимательное чтение условия и вопроса задания.
· Раскрытие скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего характера возникают у учащихся при изучении математики ( их несомненно можно отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения и неравенства»):
· Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
· Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
· Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
· Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам . Учащиеся не всегда сами понимают, что именно они написали.
· Усталость . Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
· Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
· Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
· Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки подобного рода и определить способы их предупреждения и исправления, но прежде всего хочу обратить внимание на следующую мысль: не надо бояться приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
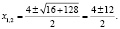
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение 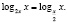
Область определения исходного уравнения задается системой
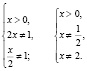
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
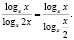
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
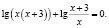
Ученик предлагает следующее ошибочное решение этого уравнения:
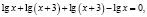
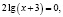
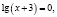
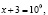
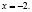
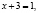 х = –2.
х = –2.
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 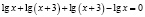 эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
Чтобы избежать потери корня, можно поступить следующим образом: перейти в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть это на следующем примере.
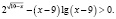
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
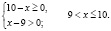
Для всех x из промежутка (9;10] выражение 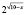 имеет положительные значения (значения показательной функции всегда положительны).
имеет положительные значения (значения показательной функции всегда положительны).
Для всех x из промежутка (9;10] выражение ( x – 9) имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение
– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x ∈ (9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
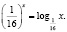
Некоторые учащиеся, решая это уравнение графически (хочу отметить, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
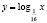 и
и 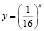 −
−
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 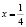 и третий корень
и третий корень 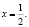 Убедиться в справедливости сказанного можно непосредственной подстановкой чисел
Убедиться в справедливости сказанного можно непосредственной подстановкой чисел 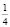 и
и 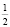 в заданное уравнение.
в заданное уравнение.
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны» (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение x х = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
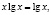
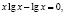
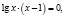
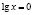 или
или 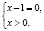
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
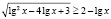 .
.
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
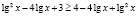 ,
,
откуда получаем неверное числовое неравенство 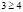 , что позволяет сделать вывод: заданное неравенство не имеет решений.
, что позволяет сделать вывод: заданное неравенство не имеет решений.
Однако полученный вывод неверен, например, при х = 1000 имеем
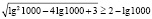 ,
, 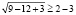 ,
, 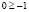 .
.
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
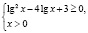 или
или 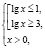
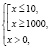 откуда
откуда 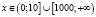 .
.
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 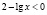 , откуда х > 100. С учетом области определения исходного неравенства имеем промежуток
, откуда х > 100. С учетом области определения исходного неравенства имеем промежуток 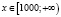 . Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что
. Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что 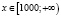 – решение заданного неравенства.
– решение заданного неравенства.
б) 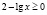 , откуда
, откуда 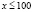 . С учетом области определения исходного неравенства имеем промежуток
. С учетом области определения исходного неравенства имеем промежуток 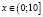 . Для всех х из промежутка
. Для всех х из промежутка 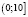 имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь:
имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь: 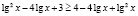 , откуда
, откуда 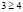 . Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка
. Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка 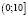 решениями исходного неравенства не являются.
решениями исходного неравенства не являются.
Ответ: 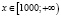 .
.
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x .
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
· проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
· проверка правильности решения задач путём составления и решения задач, обратных к данной;
· оценка результата решения задачи с точки зрения здравого смысла;
· проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
источники:
http://e-koncept.ru/2015/75367.htm
http://znanio.ru/media/statya_problemy_tipichnye_oshibki_uchaschihsya_dopuskaemye_pri_reshenii_uravnenij_i_neravenstv-173622
ВЫСТУПЛЕНИЕ
на РМО математиков
«Диагностика типичных ошибок
при решении задач»
Учитель математики
МБОУ «Ливенская СОШ №1»
Чебакова Галина Владимировна
Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.
Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.
«На ошибках учатся», — гласит народная мудрость. Но для того, чтобы извлечь урок из негативного опыта, в первую очередь, необходимо увидеть ошибку. К сожалению, школьник зачастую не способен ее обнаружить при решении той или иной задачи.
Целенаправленная работа над ошибками требует их систематизации. При этом главную роль должны сыграть группы ошибок, которые объединены общими причинами их появления, общей методикой работы над ними. Такая систематизация ошибок позволяет наметить пути их исправления и предупреждения этих ошибок в дальнейшем.
Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.
1. Ошибки и недочёты, которые обусловлены невниманием к формированию теоретико-множественных представлений учащихся:
-
ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;
-
ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.
2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:
-
ошибки, связанные с непониманием структуры теоремы;
-
ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;
-
ошибки, связанные с непониманием метода доказательства от противного.
3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.
-
Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.
-
Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.
-
Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.
-
Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.
Проанализируем некоторые типичные ошибки учащихся, допускаемых при решении тренировочных заданий для подготовки к ГИА
-
Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.
-
При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.
(Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому на путь длинной 20 км ему потребовалось на 20 мин. Меньше, чем второму. Чему равны скорости велосипедистов? Пусть х км/ч скорость первого велосипедиста.)
Типичные ошибки:
20: (х+3)-20:х=20
-
При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.
(Магазин закупил на складе футболки и стал продавать их по цене, приносящей доход в 40 % . В конце года цена была снижена на 50 %. Какая цена меньше: та, по которой магазин закупил футболки, или цена в конце года – и на сколько процентов .
Типичные ошибки: 100+40-50=90% Разница на 10 %.))
Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.
Рассмотренные ошибки свидетельствуют о том, что ученики, не справившиеся с решением задач, не смогли представить себе жизненной ситуации, отраженной в задаче, не уяснили отношений между величинами в ней, зависимости между данными и искомым, а поэтому просто механически манипулировали числами.
Почему учащиеся допустили много ошибок при повторном решении знакомых задач? Анализ результатов позволяет сделать вывод о том, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного или графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учитель нередко ограничивается правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания, т.е. не проводятся все этапы работы над задачей.
Для устранения этих недостатков необходимо прежде всего улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.
Типичные методические ошибки учителя при работе с текстовыми задачами
Ошибка 1. Пропуск этапа анализа условия задачи.
«Прочитайте условие задачи. Кто пойдет к доске?» – такое часто можно видеть на уроке. И сразу начинается оформление решения. Этап анализа отсутствует и в некоторых учебниках, и в решебниках. Может быть, проведение этого этапа обязательно не для всех учащихся. В классе найдутся такие ученики, у которых этап анализа свернут. Они его проходят очень быстро, поэтому сразу видят решение и переходят к его оформлению. Задача педагога – помогать тем, у которых не получается. Решение задачи основывается на тех связях, которые существуют между данными и искомыми величинами. На выделение этих связей и направлен анализ условия задачи. Чтобы помочь учащимся самостоятельно осуществлять анализ условия, преподаватель может предложить им специальные памятки.
Ошибка 2. Пропуск этапа поиска решения.
Пропуск этого этапа ведет к недопониманию учащимися сущности эвристической деятельности, и как результат, к возникновению трудностей при самостоятельном решении задач. В практике обучения традиционной является ситуация, когда учитель вызывает к доске учащегося, который знает, как решить задачу. Однако при личностно ориентированном обучении основная забота учителя должна быть связана с теми, кто испытывает затруднения при самостоятельном решении задач.
Тем же учащимся, которые без учителя могут решать задачи, необходимо подбирать задания, усиливающие их умения и способствующие их развитию (составить задачи на основе справочных данных; рассмотреть другие способы решения предложенной задачи; составить граф-схемы других уравнений по задаче и др.)
Ошибка 3. Пропуск этапа исследования решения.
Зачем нужен этот этап? На этапе исследования выясняем, соответствует ли полученный ответ условию задачи (правдоподобность результата); есть ли другие способы решения; что полезного можно извлечь на будущее из решенной задачи. Последний вопрос позволяет рассматривать каждую задачу как звено в общем умении решать задачи, что ведет к накоплению опыта по решению задач.
Ошибка 4. Смешение этапов анализа и поиска решения.
Чтобы этого избежать, надо точно знать, какую цель мы преследуем на каждом этапе. Цель этапа анализа условия – выявить все имеющиеся связи между данными и искомыми величинами, чему помогает составление таблицы (схемы, рисунка). Цель этапа поиска решения – выбрать метод решения (алгебраический или арифметический) и составить план решения. Цели этапов разные, значит, и смешивать эти этапы никак нельзя.
-
Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:
определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;
составляем схему уравнения, соответствующего выбранному условию;
определяем, какие величины можно обозначить за х; выбираем одну из них;
определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.
Завершается этап поиска составлением плана решения задачи.
Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.
Надо стараться зафиксировать как можно больше таких связей. Почему это важно? Упустив какую-нибудь связь, мы можем потерять:
условие для составления уравнения;
возможность одну величину выразить через другие;
предусмотреть несколько способов решения.
Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.
Обратим внимание на то, что при перечислении этапов, которые мы проходим при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике мы почти везде видим иное: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение. Вот этот момент настолько «закостенел» в нашем сознании, что от него отказаться очень трудно.
На самом деле, лучше делать «по-новому». Представьте себя на месте ученика в классе. Рассмотрим ситуацию, когда не были проведены этапы анализа и поиска решения, к доске вызван ученик, который знает, как решить задачу, и он начинает: «За х обозначим…» И что же наш ученик, который затрудняется в самостоятельном решении? Мы из решения сделали тайну непостижимую. «Как он угадал, что обозначить за х?» И когда он будет пробовать дома решать задачу, у него сразу закрадывается сомнение: «А вдруг я не угадаю?»
И насколько спокойнее и увереннее чувствует себя наш ученик, если у него есть карточка по проведению анализа и поиска решения задач; он смог составить по условию задачи таблицу; найти несколько условий для составления уравнений; записать схему уравнения для выбранного условия. Ученик знает, что за х можно обозначить любую из неизвестных величин, и, если не получится уравнение по одной схеме, то можно попробовать составить его по другой схеме.
Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.
Очень много зависит от умения ставить (задавать) вопросы учащимся. Вопросы не должны нести в себе подсказку, а подталкивать учащихся к размышлению. Вместо вопросов: «Во сколько туров проходила олимпиада?», «Как распределились посевные площади?», «Какое время находились туристы в пути?», «Какие машины находятся в автопарке?» лучше задавать общие вопросы: «Что происходит по условию задачи?», «Какие объекты участвуют в задаче?», «Какие части можно выделить в задаче?». Вместо вопроса «Можно ли найти такую-то величину?» лучше задать вопрос: «Что можно найти по данным задачи?», поскольку он может вывести на несколько вариантов решения.
Задавая вопросы, учитель не должен вести учащихся к своему решению; нужно рассмотреть все пути решения, выслушать и обсудить все варианты.
2.Для осуществления целенаправленных мер по исправлению и предупреждению ошибок учителю необходимо систематически изучать ошибки учащихся, выявлять наиболее устойчивые и типичные из них, вести учёт распространённых и индивидуальных ошибок учащихся. Знание учителем типичных ученических ошибок, а также причин их возникновения и проявления даёт ему возможность предвидеть и предупреждать их появление. Достичь этого можно путём подбора таких упражнений, которые препятствуют образованию односторонних ассоциаций и неправильных обобщений.
Ошибки учащихся, которые регистрирует и учитывает учитель, помогают ему установить, что не понимают учащиеся, что ими плохо усвоено; это даёт возможность учителю своевременно ликвидировать пробелы в знаниях учащихся и внести соответствующие коррективы в дальнейшее преподавание с целью предупреждения повторения аналогичных ошибок.
Чтобы определить сущность допускаемых учащимися ошибок, необходимо проследить ход рассуждений, который приводит к такому ошибочному решению, установить этап, на котором зарождаются такие ошибки. Как показывает опыт, часто учащемуся непонятен не весь материал, а лишь какая-то его часть. Выявив, что именно непонятно ученику, можно сосредоточить на этом материале всё внимание, не отвлекаясь на те моменты, которые уже усвоены.
Допускаемые учеником ошибки свидетельствуют не только о недостатках его знаний, но и о потенциальных возможностях. Ошибки служат также показателем проблем, которые могут быть поставлены перед учеником, а иногда они приводят к созданию проблемных ситуаций, которые необходимы в данный момент для развития действий.
Ни в коем случае нельзя снижать оценок ученикам за ошибки в процессе поиска. Очень важно приучить их не бояться допускаемых ошибок. Ошибки, допускаемые учениками, надо исправлять тактично, обоснованно, привлекая к этой работе самих учащихся.
Боязнь допустить ошибку сковывает инициативу ученика. Боясь ошибиться, он не будет сам решать поставленную проблему, а станет ждать помощи от учителя. Он будет решать только лёгкие проблемы. Но без такого самостоятельного решения задач с последовательно нарастающей сложностью не может происходить интеллектуальное развитие. Во многих случаях по этой причине учащиеся проявляют робость и интеллектуальную пассивность, что в дальнейшем приводит к неуспеваемости.
Очень оживлённо воспринимаются учащимися “Задачи на выявление ошибки”. Речь идёт не только о софизмах, но и об ошибках, которые допускают сами школьники. Не нужно специально исправлять каждое ошибочное утверждение школьника. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Если они и не допускают ошибок, то всё же нередко целесообразно проверить, насколько они “устойчивы” против типичных ошибок.
Например: Найти ошибки:
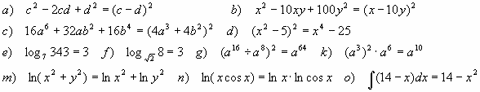
Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; в) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
-
проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
-
проверка правильности решения задач путём составления и решения задач, обратных к данной;
-
оценка результата решения задачи с точки зрения здравого смысла;
-
проверка аналитического решения графическим .
Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.
Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.
Пусть решение ученика выглядит так: ![]() . Ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130”. Такая прикидка в уме полезна при решении задач с дробными числами и процентами.
. Ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130”. Такая прикидка в уме полезна при решении задач с дробными числами и процентами.
В жизненной практике в чертежах, схемах, расчётах, с которыми ребята будут встречаться, могут быть и ошибки. Если не научить их критически относиться к данным, то могут быть и аварии, и брак, и серьёзные упущения в работе. Чтобы этого избежать, необходимо формировать у учащихся умение анализировать данные, способность обнаруживать встречающиеся ошибки и обосновывать ошибочность положения.
Польский математик Г. Штейнгауз, отмечая большое значение работы над математическими ошибками для активизации мыслительной деятельности учащихся, пишет:
“Если учащегося заверить, что в предложенном ему доказательстве есть ошибка, то можно быть уверенным даже без специальной проверки, что материал будет изучен полностью и очень тщательно”. Поэтому составление списка математических ошибок и использование его в учебных целях является одним из важных факторов повышения эффективности обучения.
Таким образом, важную роль в предупреждении ошибок играет продуманная организация изучения нового материала. Изучение нового материала надо строить так, чтобы ученик был активным участником этого процесса. Не надо бояться, если при первом изложении материала им будут допускаться ошибки, высказываться необоснованные выводы. Важно, чтобы те или иные ошибки в понимании материала исправлялись в зародыше, чтобы ученики воспринимали материал осознанно.
Такому подходу к изучению нового материала способствует создание проблемной ситуации и решение её учащимися под руководством учителя. На таких уроках ученики проходят через следующие стадии: поиск нового, возможное появление ошибок в процессе поиска нового, обоснованное опровержение этих ошибок, снова поиски, в результате которых приходят к правильной догадке, и, наконец, доказательство составленного в поисках предложения. Всё это способствует развитию математического мышления.
Текстовые задача — это способ стимулирования мыслительной активности. Считаю необходимым сформировать такой подход к задаче, при котором задача выступает как объект тщательного изучения, а ее решение — как объект конструирования и изобретения. Необходимо построить процесс обучения математике так, чтобы обеспечить успешное овладение учащимися методами и приемами решения задач и создать условия для формирования у них ряда общенаучных умений — таких, как анализ, синтез, обобщение, сравнение, аналогия.
Необходимо организовать деятельность учащихся на учебном занятии таким образом, чтобы она способствовала формированию исследовательской культуры.
Предлагаю на занятии несколько приемов организации интенсивной мыслительной деятельности, которые используются мною на различных этапах процесса обучения: при актуализации знаний, первичном усвоении материала, его осмыслении, применении и обобщении.
Это можно сделать на следующем содержании материала:
-
Правоцирующие задачи.
Это задачи, условия которых содержат упоминания, указания, намеки или другие побудители, подталкивающие учащихся к выбору ошибочного пути решения или неверного ответа. Попадая в заранее подготовленную ловушку, ученик испытывает досаду, сожаление оттого, что не придал особого значения тем нюансам условия, из-за которых он угодил в неловкое положение. Простое сообщение о том, что учащиеся, как правило, допускают в заданиях такого-то рода ошибки, несравнимо менее действенно. Ибо оно, несмотря на общность, не является для конкретно взятого ученика личностно значимым, поскольку, во-первых, события, о которых сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых, каждый из учащихся наивно полагает, что в число неудачников сам он не попадает.
Дидактическая ценность этих задач в том, что они служат предупреждением от различного рода ошибок и заблуждений.
Провоцирующие задачи обладают высоким развивающим потенциалом, они способствуют воспитанию одного из важнейших качеств мышления- критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников к занятиям математикой.
Я использую такие разновидности провоцирующих задач:
-
условия, в которых навязывают неверный ответ;
-
условия, которые подсказывают неверный путь решения;
-
условия, вводящие в заблуждение из-за неоднозначности трактовки и т.д.
В качестве примера приведу задачи, побуждающие выбор неверного способа решения.
Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?
Или, на уроке в 6 классе по теме «Простые и составные числа» предлагаю задание: «Какие из чисел 205, 206, 207, 208, 209, 210 являются простыми?»
2.Задачи стандартные с нестандартным решением.
Это задачи, при предъявлении которых учащиеся не знают заранее ни способа их решений, ни того, на какой учебный материал опирается решение. Иными словами, учащиеся в ходе решения таких задач должны провести поиск плана решения задачи, установить, какой теоретический материал дает ключ к тому или иному решению. Незначительная обработка условий той или иной задачи из учебника, изменение места и времени ее постановки существенно меняют ее дидактическую значимость, оставляя неизменным практическое содержание.
Проиллюстрирую сказанное примером. Стандартная задача для учащихся 7 класса: «В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Сколько фазанов и кроликов в клетке?». Данную задачу предлагаю решить не алгебраическим способом, приводя к стандартному уравнению, а арифметическим. Таким образом, по существу, данную задачу превращаем в нестандартную для шестиклассников и даже семиклассников.
Задачи такого плана всегда органически связаны с изучаемым материалом. Допуская нестандартное решение, приучаю школьников не довольствоваться шаблоном, а нацеливаю на вдумчивый подход, воспитываю стремление как можно лучше выполнить порученное дело. Они развивают гибкость, рациональность, целенаправленность математического мышления и ценны тем, что дается возможность каждому ученику с любой структурой мышления проявить себя.
3. Проблемные задачи.
Это задачи, алгоритм решения которых неизвестен до начала решения. Главное в том, чтобы открыть способ решения и убедиться в его пригодности. Следует иметь в виду, что определить, является данная задача проблемной или нет, можно только относительно конкретного школьника, только с учетом его знаний и умений в момент постановки задачи.
Задачи такого плана решаются исследовательским методом и этим очень интересны для учащихся. Ведь исследование предполагает творчество. Проблемы, которые ставятся перед учащимися, могут иметь разнообразный характер: введение в новую тему, решение задачи новым более эффективным способом, связь известного учебного материала с новым и т.д.
При подборе проблемных задач учитываю знания учащихся и уровень развития их логического мышления, поскольку непосильная задача порождает неуверенность в своих силах и в дальнейшем отвращение от решения любых задач, а излишне простая вводит в заблуждение относительно уровня собственных знаний и умений, не стимулирует поисковую деятельность.
Самое главное- это суметь правильно поставить вопрос, заинтриговать учащихся, создать проблему, а не дать ответ, решив ее. Учащиеся познают понятия, закономерности, теории в ходе поиска, наблюдения, анализа фактов, мыслительной деятельности, результатом чего является знание.
Приведу пример задачи из темы «Смежные углы» (геометрия 7 класс).
Найти два смежных угла, один из которых больше другого на прямой угол.
Возможны различные варианты решения, в частности, алгебраический и геометрический. Здесь проблемный характер проявляется в неявной форме, но ученики понимают непригодность геометрического способа решения.
Другой пример. В 5 классе в ходе изучения темы «Сравнение десятичных дробей» предлагаю вариант решения задания на сравнение дробей 0,31 и 0,6 ученика Петрова. Если целые части дробей равны, сравним дробные части: 31 6, значит, 0,31
6, значит, 0,31 0,6. Согласны ли вы с таким решением? Начинается обсуждение, поиск, анализ решения.
0,6. Согласны ли вы с таким решением? Начинается обсуждение, поиск, анализ решения.
-
Логические задачи.(задачи-шутки, таблицы, верные и неверные утверждения, здравый смысл)
Это задачи, ведущие к формированию важнейших характеристик творческих способностей: беглость мысли, гибкость ума, оригинальность, любознательность, умение выдвигать и разрабатывать гипотезы.
Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Логика учит, как нужно рассуждать, чтобы наше мышление было определенным, связанным, последовательным, доказательным и непротиворечивым. В математике приходится путем рассуждений выводить разнообразные формулы, числовые закономерности, правила, доказывать теоремы.
Основные методы решения логических задач:
-
метод рассуждения;
-
метод таблицы;
-
метод граф;
-
метод кругов Эйлера;
-
комбинированный метод.
Метод рассуждений сопровождаю схемами, чертежами, краткими записями, вырабатывая умения выбирать информацию, пользоваться правилом перебора.
Так, при изучении темы «Степень» в 7 классе, я даю задание: запишите степени x, x2, x3, x4, x5, x6, x7, x8, x9 в пустые клетки квадрата так, чтобы произведение их по любой горизонтали, вертикали и диагонали было равно x в 15 степени. Можно рассказать о магическом квадрате, тогда задача станет еще интереснее для учеников.
|
X5 |
||
Таблицы хорошо применять тогда, когда устанавливается соответствие между двумя множествами (можно и между тремя множествами), когда количество элементов во множествах одинаково и неодинаково. Перед составлением таблиц отрабатываю правила их заполнения.
Например, в 5 классе знакомлю детей с задачей Пуассона (на переливание). Некто имеет 12 пинт сока (пинта- 0,57л) и желает подарить половину своему другу, но у него нет сосуда в 6 пинт, а есть два сосуда в 8 и 5 пинт. Каким образом можно налить 6 пинт сока в сосуд емкостью 8 пинт?
Решение.
|
Ходы |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
12 пинт |
12 |
4 |
4 |
9 |
9 |
1 |
1 |
6 |
|
8 пинт |
— |
8 |
3 |
3 |
— |
8 |
6 |
6 |
|
5 пинт |
— |
— |
5 |
— |
3 |
3 |
5 |
— |
Логические связи, при помощи которых была выстроена общая схема решения задачи, помогут учащимся без труда решить подобного рода задачу.
Введение серии таких задач в содержание урока считаю необходимым. Это позволит стереть явную границу между занимательным и учебным материалом. Особенно целесообразно использовать задачи тогда, когда есть опасность неприятия учащимися какого-либо учебного задания; при прохождении сложных тем; при выработке умений и навыков учащихся, когда требуется выполнить значительное количество однотипных упражнений; при изучении материала, подлежащего прочному запоминанию.
Для каждой задачи, которую предполагаю использовать на уроке, прежде выясняю: будет ли она интересна классу, органично ли войдет в структуру урока, будет ли ее использование эффективным. Практика показала: учебный навык, на формирование которого направлена та или иная задача, вырабатывается быстрее, ибо он связан с продуктивной мыслительной деятельностью ученика.
При работе над провоцирующими, проблемными, логическими и стандартными с нестандартным решением задачами наиболее эффективной считаю групповую, парную, индивидуальную, фронтальную работу.
Приведу пример. Расстояние от реки до турбазы туристы рассчитывали пройти за 6 часов. Однако после 2 часов пути они уменьшили скорость на 0,5 км/ч и в результате опоздали на турбазу на 30 мин. С какой скоростью шли туристы первоначально?
Работа над задачей предполагает следующие действия учителя:
-
Предъявление задачи (читает учитель).
-
Определение вида задачи (творческая группа).
-
Выделение гипотез (индивидуальная самостоятельная работа).
-
Обмен мнениями (в творческой группе).
-
Формулировка предположительного ответа (в паре).
-
Проверка ответа на достоверность (фронтальная работа).
Или, задача. Определить площадь равнобедренной трапеции, у которой основания равны 12см и 20см, а диагонали взаимно перпендикулярны.
-
Предъявление задачи (творческие группы составляют задачи по готовому чертежу).
-
Выделение гипотез (работа в парах).
-
Обмен мнениями (фронтальная работа).
-
Формулировка предположительного ответа (индивидуальная работа).
-
Проверка ответа на достоверность (индивидуальная работа).
Обязательным этапом на уроке является устный и письменный счет. Целями устного счета являются, во-первых, совершенствование в вычислительных навыков, во-вторых, развитие творческого мышления учащихся.
На своих уроках я стараюсь разнообразить формы и методы устной работы:
— устный счет в начале, в середине, в конце урока;
-
устная форма проверки домашнего задания;
-
устная форма творческой работы;
-
устные самостоятельная и контрольная работы;
-
уроки устной работы.
Работая устно, воспитываю у учащихся навыки сознательного усвоения изучаемого материала, приучаю ценить и экономить время, развиваю желание поиска рациональных путей решения задачи. В этих целях использую такие приемы, развивающие творческие способности, как «Зашифрованные задания», «Найди ошибку», «Восстановление»,
«Выбор», «Задачи- сказки», детские презентации на устный счёт, математические листы с задачами, изготовленные самими учащимися, ребусы, кроссворды, которые учащиеся составляют самостоятельно.
Обязательно провожу подробный анализ результатов работы и коррекцию знаний. Объявляя количество набранных баллов, полученных за олимпиадное задание, называю ребят, которые представили самые «красивые» решения. При этом опираюсь на формулу «красивой» задачи по В.Г. Болтянскому: красивая задача = непредсказуемость + непредполагаемость +неожиданность + удивительная простота + простота + фантазия + революционный шаг + удивление + оптимизм + труд + …
Таким образом, решение текстовых задач не случайно всегда волновало учителей, методистов, да и самих учащихся и их родителей.
Во-первых, нельзя решить задачу, не поняв ее содержание. Следовательно, умение решать текстовые задачи свидетельствует об одной из самых важных способностей человека — способности понимать текст. Правы те учителя, которые добиваются понимания текста не только на уроках чтения, но и на уроках математики. Критерием понимания задачи является факт решения задачи.
Поэтому решение текстовых задач — это деятельность, весьма важная для общего развития. Обучая решать текстовые задачи, мы приучаем ориентироваться в ситуациях, делаем человека более компетентным. Конечно, для этого нужно резко расширить тематику задач, давать детям задачи, разнообразные по тематике, а не только «на скорость», «на работу», «на покупки».
Решение текстовых задач способствует, с одной стороны, закреплению на практике приобретённых умений и навыков, с другой стороны, развитию логического мышления учащихся.
Наблюдается активизация их мыслительной деятельности. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, развивается абстрактное мышление, умение применять теорию к решению конкретных задач.

Памятка будет полезна школьникам, родителям, учителям.
Скачать:
Предварительный просмотр:
Памятка по выполнению работы над ошибками по математике
1. Ошибки в ходе решения задачи:
- прочитай задачу;
- составь и сделай краткую запись;
- реши по действиям с пояснениями и ответом.
2. Ошибки в ходе решения уравнения:
- запиши уравнение;
- назови компоненты;
- вспомни правило нахождения неизвестного компонента; — реши уравнение верно.
3. Сложение и вычитание в пределах 10 и 20:
- повтори таблицу сложения и вычитания в пределах 10 или 20;
- запиши пример верно.
4. Сложение и вычитание многозначных чисел:
- повтори таблицу разрядов и классов;
- запиши пример правильно (разряд под разрядом);
- повтори таблицы сложения в пределах 10 и 20;
- реши пример правильно;
- проверь сложение вычитанием или вычитание сложением. Образец: + 48 Проверка: — 82
34 48
82 34
5. Таблица умножения и деления:
- повтори таблицу умножения;
- запиши пример и реши его верно;
- запиши все случаи умножения и деления с этими числами;
6. Внетабличное умножение и деление:
- запиши пример;
- разложи одно из чисел на сумму удобных или разрядных слагаемых;
- реши пример с объяснением;
- проверь умножение делением или деление умножением.
7. Деление вида 96 : 16.
- вспомни правило подбора частного.
- запиши пример и реши его верно.
- проверь умножением.
Образец: 96 : 16 = 6
Проверка: 16 * 6 = (10 + 6) * 6 = 10 * 6 + 6 * 6 = 60 + 36 = 96
8. Внетабличное умножение и деление:
- запиши пример верно;
- вспомни правило умножения или деления в столбик;
- реши пример;
- проверь умножение делением или деление умножением.
- 9. Ошибки на порядок действий в выражениях со скобками и без скобок:
- запиши выражение верно;
- вспомни порядок выполнения действий в выражениях со скобками или без скобок; — выполни действия по порядку: умножение и (или) деление, а потом сложение и (или) вычитание;
- запиши ответ.
10. Геометрический материал.
- начерти фигуру;
- напиши формулу нахождения периметра или площади;
- произведи вычисления.
|
Образец: Длина — 3 см Ширина — 2 см Р- ? Р= (a+b)*2 (3+2)*2=10 (см)- периметр прямоугольника Ответ: 10 см |
Образец: Длина — 3 см Ширина — 2 см S-? S=a*b 3*2=6 (см²) – площадь прямоугольника Ответ: 6 см² |
По теме: методические разработки, презентации и конспекты
- Мне нравится

У р о к 130.
РАБОТА НАД ОШИБКАМИ. РЕШЕНИЕ УРАВНЕНИЙ
Цели: рассмотреть типичные ошибки, допущенные в контрольной работе; закреплять умение составлять уравнения по данному условию, по схеме; развивать умение рассуждать.
Планируемые результаты образования:
Предметные: оперируют понятиями: переменная, числовое и буквенное выражение, их значение; решают составные задачи.
Личностные: проявляют познавательный интерес на основе сформированности учебных мотивов, навыки самоконтроля.
Метапредметные:
Регулятивные: самостоятельно определяют учебную задачу, планируют свое действие, контролируют выполнение учебных действий. Познавательные: общеучебные – структурируют знания; логические – осмысленно читают текст, умеют выделять существенную информацию из текста, анализируют, делают выводы и умозаключения. Коммуникативные: умеют строить взаимодействие со сверстниками, используя конструктивные способы общения, формулировать собственное мнение и позицию.
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Работа над уравнениями в начальной школе
методическая разработка на тему
Методическая разработка «Работа над уравнениями в начальной школе» поможет учителям начальных классов в работе над уравнениями. Здесь же прилагаются алгоритмы по решению уравнений разного вида.
Скачать:
| Вложение | Размер |
|---|---|
| rabota_nad_uravneniyami_v_nachalnoy_shkole.doc | 80.5 КБ |
Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа N135″ имени академика Б.В.Литвинова»
Работа над уравнениями в начальной школе.
Подготовила учитель начальных классов:
Самойлова Анжелика Владимировна
Работа над уравнениями в начальной школе.
Большую трудность для младшего школьного возраста представляет умение решать уравнения. Изучение уравнений в начальной школе носит пропедевтический характер. Поэтому очень важно подготовить детей в начальной школе к более глубокому изучению уравнений в старших классах. В начальной школе в процессе работы над уравнением закрепляются правила о взаимосвязи части и целого, сторон прямоугольника с его площадью, формируются вычислительные навыки и понимание связи между компонентами действий, закрепляется порядок действий и формируется умения решать текстовые задачи, идет работа над развитием правильной математической речи. На уроках закрепления уравнения позволяют разнообразить виды заданий.
Изучение уравнений начинается с подготовительного этапа уже в 1 классе, когда дети, действуя с предметами, решают такие «задачи»:
Затем учащиеся переходят к действиям над числами и выполняют задания, связанные с нахождением неизвестного числа в «окошке», например:
Дети находят число либо подбором, либо на основе знаний состава числа. На данном этапе учителю необходимо включать в устные упражнения следующие задания:
— Сколько надо вычесть из 3, чтобы получилось 2?
— Сколько надо прибавить к 2, чтобы получилось 4?
На втором этапе учащиеся знакомятся с понятиями «уравнение» и «корень уравнения». На протяжении нескольких уроков дети учатся решать уравнения с неизвестным слагаемым, уменьшаемым, вычитаемым. Названия компонентов арифметических действий были введены в речевую практику учащихся и использовались для чтения равенств и выражений, пока правило нахождения неизвестного компонента в уравнениях не заучивается. Уравнения решаются на основе взаимосвязи между частью и целым. При изучении данной темы дети должны научиться находить в уравнениях компоненты,
соответствующие целому (сумма, уменьшаемое), и компоненты, соответствующие его частям (слагаемое, уменьшаемое, разность). При решении уравнений детям нужно будет вспомнить лишь два известных правила:
— Целое равно сумме частей.
— Чтобы найти часть, надо из целого вычесть другую часть.
Эту работу облегчает графическое обозначение части ______ и целого , а также понимание того, что целое – это большее число.
Для того чтобы облегчить работу над формированием навыка решения уравнений, можно проводить в классе следующую работу.
- Составление и решение уравнений по схеме.
2. Составление и решение уравнений с помощью модели числа.
— Замените модели числами:
3. Уравнения с буквами.
— Как из волка получить вола ?
4. Составление и решение уравнений с помощью числового луча.
5. Выполни проверку и найди ошибку.
Дети решают: 24 + 8 = 16
6.Составиьуравнения с числами Х, 4, 10 и реши их.
Х + 4 = 10; 10 – Х = 4; Х – 10 = 4 и т.п.
7. Из данных уравнений реши те, где Х находится сложением.
Х +16 = 20; Х -18 = 30; 29 – Х = 19
8. Рассмотри решение уравнения и вставь соответствующий знак.
К концу изучения темы дети учатся комментировать уравнения через компоненты действий. Работа строится следующим образом:
1) читаю уравнение;
2) нахожу известные и неизвестные компоненты (части и целое);
3) применяю правило (по нахождению части или целого);
4) нахожу, чему равен Х;
5) комментирую через компоненты действий.
Следующий этап – решение уравнений вида: а ∙ Х = в; а : Х = в; Х : а = в .
Уравнения этого вида решаются на основе взаимосвязи между площадью прямоугольника и его сторонами. Поэтому изменяется и графическое обозначение компонентов уравнения:
— площадь прямоугольника, а _____ — его стороны. Здесь важно понять то, что обучение решению и комментированию уравнений ведется по определенной схеме:
1 этап: Решение с одновременным комментированием правил нахождения площади и его сторон. Например, Х : 2 = 5 ( Х – площадь прямоугольника, 2 и 5 – его стороны).
Х = 2 ∙ 5 (чтобы найти площадь прямоугольника, надо перемножить его стороны)
2 этап: Решение уравнений с комментированием(через площадь прямоугольника и его стороны).
Комментирование через компоненты действий после решения уравнения.
Для отработки навыков решения уравнений на умножение и деление можно использовать следующие упражнения.
1. Выполни проверку и найди ошибку.
Дети решают: 2 : 2 = 4
2. Проанализируй решение уравнения и найди ошибку.
Ошибки: 1) 9 – это площадь, на целое, ее надо обозначить прямоугольником;
2) Х – это сторона, надо площадь разделить на другую сторону.
3. Составь уравнения с числами 3, Х, 12 и реши их.
Дети составляют: 12 : Х = 3; 3 ∙ Х = 12 и т.п.
4. Изданных уравнений реши те, которые решаются делением.
Х ∙ 2 = 6; Х : 4 = 16; 12 : Х = 4
5. Рассмотри решение уравнений и вставь соответствующий знак в запись уравнения.
6. Составь и реши уравнение:
— Какое число надо умножить на пять, чтобы получилось 25?
Х ∙ 3 = 15; Х : 4 = 5; 16 : Х = 2
— Какое уравнение лишнее? Объясни свой выбор.
— первое уравнение – Х равен нечетному числу;
— второе уравнение – Х находим умножением;
— третье уравнение – неизвестен второй компонент и т.п.
Последний этап при работе с уравнениями в начальной школе – знакомство учащихся с составными уравнениями. Решение таких уравнений строится на качественном анализе выражения, стоящего в левой части уравнения: какие действия указаны в выражении, какое действие выполняется последним, как читается запись этого выражения, какому компоненту этого действия принадлежит неизвестное число и т.п. К этому времени учащиеся должны твердо овладеть следующими умениями:
— решение простых уравнений,
— анализ решений уравнений по компонентам действий,
— чтение записи выражений в два – три действия,
— порядок выполнения действий в выражениях со скобками и без них.
На данном этапе дети должны понимать, что в записи уравнений в качестве неизвестного числа могут использоваться различные буквы латинского алфавита, например: К + 4 = 3; Р – 3 = 8; Z : 7 = 6 и т.п.
Запись решения уравнений сопровождается словесным описанием выполняемых действий. Для выработки правильной математической речи и навыков решения первых уравнений данного вида необходимо использовать таблицы с образцами решений. Но так как дети уже с 1-го класса знакомы с записью различных алгоритмов, то можно использовать только алгоритм решения уравнений, по которому дети и анализируют уравнения.
Обучение младших школьников решению уравнений посредством дифференцированного подхода
Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 1
Шелыгина Ольга Борисовна,
кандидат педагогических наук, доцент кафедры педагогики и методики дошкольного и начального образования ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Кировkaf_pmdno@vshu.kirov.ru
Каткова Александра Сергеевна,студентка ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров
Обучение младших школьников решению уравненийпосредством дифференцированного подхода
Аннотация. Статья посвящена вопросам реализации дифференцированного подхода к младшим школьникам в процессе обучения решению уравнений. Авторы предлагают различные приемы работы над уравнениями в зависимости от уровня обученности учеников, способствующие развитию мышления учащихся, их познавательного интереса. Методические приемы подкреплены примерами дифференцированных заданий по теме «Уравнения» для разных групп учащихся.Ключевые слова: обучение математике, обучение решению уравнений, младшие школьники, дифференцированный подход, разноуровневые задания.Раздел: (01) педагогика; история педагогики и образования; теория и методика обучения и воспитания (по предметным областям).
Дети приходят в школу с различным уровнем обучаемости. Часто учителю приходится вести обучение применительно к среднему уровню развития и обучаемости детей. А.Н. Конев считал, что такой подход в обучении приводит к тому, что «сильные» ученики сдерживаются в своём развитии, теряют интерес к учебе, а «слабые» обречены на отставание. Те, кто относится к «средним», тоже имеют индивидуальные особенности, и даже для них такой подход неэффективен [1].Учителю необходимо создавать условия, чтобы каждый ученик учился в соответствии со своими возможностями и способностями, развивал свои индивидуальные особенности, стал субъектом учения. Одним из способов осуществления индивидуального подхода в образовании является дифференциация обучения.Дифференцированный подход это способ организации учебного процесса, при котором для более эффективного обучения выявляются индивидуальнотипологические особенности учеников, на основе чего создаются группы учащихся. С учетом особенностей учащихся, в каждой группе применяются соответствующие формы, методы и приемы обучения. Дифференцированный подход необходимо осуществлять на разных дисциплинах. Математика, является одним из фундаментальных предметов начального школьного обучения. Важным разделом начального курса математики является алгебраический материал, в котором изучается одна из самых сложных тем для учащихся начальной школы «Уравнения». Сформированные умения решать уравнения в начальной школеоснова для дальнейшего обучения в средней и старшей школе.Уравнение математическое равенство, содержащее буквенное выражение с одной или несколькими переменными, верное только при определенных значениях этих переменных. Переменные, входящие в уравнение, называются неизвестными. Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 2
Решить уравнение значит найти все значения неизвестных, прикоторых запись обращается в верное равенство (или установить, что таких значений нет) [2].Обучение решению уравнений начинается с подготовительной работы уже в 1мклассе. Учащиеся выполняют задания, связанные с нахождением неизвестного числа в равенствес «окошечком», то есть работают с деформированными равенствами. Чаще всего дети находят число подбором. На следующем этапе младшие школьники знакомятся с понятием «уравнение», учатся выделять уравнения из других математических записей, так же вводится понятие «решение уравнения». На протяжении нескольких уроков дети учатся решать уравнения на нахождение неизвестных компонентов при сложении и вычитании. Не смотря на то, что названия компонентов и результатов арифметических действий известны учащимся, правила нахождения неизвестных чисел в уравнениях не заучиваются. Уравнения на данном этапе решаются на основе взаимосвязи между частью и целым. При изучении данной темы дети должны научиться находить в уравнениях компоненты, соответствующие целому (сумма, уменьшаемое), и компоненты, соответствующие его частям (слагаемое, вычитаемое, разность). На третьем этапе изучения темы дети учатся комментировать решение уравнений, используя правила взаимосвязи компонентов и результата соответствующего действия. Следующийэтап связан с введением новых арифметических действий умножение и деление. Соответственно, в новых видах уравнений неизвестным может быть один из множителей, делимое или делитель. Уравнения этого вида могут быть решены на основе взаимосвязи между площадью прямоугольника и его сторонами или на основе правила нахождения неизвестных компонентов (см. таблицу).
Способы комментирования решения уравнения
Решение уравнения с комментированием на основе правила нахождения площади и его сторонРешение уравнения с комментированием на основе правила нахождения неизвестных компонентовХ :2= 5
Хплощадь прямоугольника2ширина5длинаЧтобы найти площадь прямоугольника, надо длину умножить ширину Х= 5 • 2Х= 10Проверяю 10:2= 5, решено верно.Х : 2= 5Х это делимое2 делитель5 частное Чтобы найти неизвестное делимое нужночастное умножить на делитель.Х= 5 • 2Х= 10Проверяю 10:2= 5, решено верно.
Последний этап при работе с уравнениями в начальной школезнакомство учащихся с составными уравнениями (буквенные выражения в составе уравнения состоят из нескольких действий). Решение таких уравнений основано на анализе выражения, содержащего неизвестное число. Анализ осуществляется по алгоритму: определи, какиедействия в выражении; найди действие, которое выполняется последним; назови, какому компоненту этого действия принадлежит неизвестное число; вспомни, как мы находим данный неизвестный компонент; найди его, и т.п. (данный алгоритм часто является циклическим). К этому времени учащиеся должны твердо овладеть следующими умениями:решение простых уравнений в одно действие,комментирование решений уравнений на основе взаимосвязи между компонентами и результатом действия,Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 3
чтение выражений в дватри действия,знание правил порядка выполнения действий в выражениях со скобками и без них, умение ими пользоваться при нахождении значений выражений.Чтобы знания учеников были качественными и прочными, мы считаем, что целесообразно данную тему изучать в процессе реализации дифференцированного подхода в обучении, чтобы каждый ученик смог справиться с тем минимумом, который необходим при усвоении учебного материала, а также дать возможность сильным учащимся интеллектуально развиваться. Для учеников с высоким уровнем обученности необходимо:1.Разрабатывать задания, в которых нужно помимо выполнения основных заданий сделать дополнительные задания.Например:1)Реши уравнения, в таблице поставь букву под получившимся ответом и узнаешь, какое озеро называют «жемчужиной планеты».Ж:8= 3Й 6= 5В+13= 5211Б + 15= 17(А + 3): 2= 2К (6:3)= 1038 Л= 25
2)Реши уравнения. Х:6= 1212:Х= 6Х • 6= 12Раздели их на две группы (найди разные варианты).Составь аналогичные уравнения.
3)Реши уравнения.Х:8= 810:Х= 10Х • 12= 12Чем они похожи? Чем отличаются? Попробуй вывести правила для двух уравнений. Будут ли исключения из правил? Докажи.
4)Реши уравнения.У+56= 100У 33= 8458 У= 48Сейчас измени уравнения так, чтобы неизвестное число находилось противоположным действием. Какое составленное тобой уравнение отличается от остальных?
5)Реши уравнения.10• Х= 5015• Х= 7520• Х= 100Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 4
25• Х= 125Найди закономерность. Составь и реши еще два уравнения.Придумай по аналогии свою цепочку уравнений.
6)Реши уравнения.(25 Х):5= 4(49+Х):6= 9(Х+31):6= 614:(2+Х)= 2На какие две группы можно их разделить?Чем похожи уравнения?Составь свое уравнение с таким же ответом к каждой выделенной группе.
7)После решения уравнений предложить: найти сумму всех ответов, расположить ответы в порядке убывания (возрастания),разделить ответы на группы по какомулибо признаку и т.п.
2.Разрабатывать частичнопоисковые и творческие задания.Например:
1)Найди в словах числа, составь с числами уравнения и реши их: Хподвал= 34семья * Х= семьястриж + Х= сорокаХ : опять= 45
2)Догадайся, по какому принципу составлено первое уравнение. август Х= июнь8 Х= 6Х= 2Х= февраль На основе этого реши уравнения:декабрь :Х= февраль2 • (августХ)= август(Х март): март= мартПридумайте и решите аналогичные уравнения, используя дни недели.
3)Дан ряд цифр 3,5,7,9. Запиши и реши уравнения:а)если из неизвестного числа вычесть число, которое на 2 больше второго числа в ряду цифр, то получится последнее число в ряду (Х 7= 9).б)если к двузначному числу, в котором первая цифра это вторая в ряду, а вторая цифра это последняя цифра в ряду прибавить неизвестное число, то получится число, в котором первая цифра это третья цифра в ряду, а вторая первая цифра в ряду(59 + Х= 73).
4)Составь и реши уравнение: «Я загадала число. Прибавила к нему самое маленькое трехзначное число. Результат разделила на самое большое однозначное число. Получила число, которое меньше 13, больше 10, но не 11».
5)Дан ряд чисел (каждое число на 1 больше предыдущего): ¤, ∩, ↑, ᴥ,Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 5
Реши уравнения со сказочными числами.¤+Х= ↑Х= ∩
6)Рассмотри решение уравнения и запиши первоначальное уравнениеХ= 7•5Х= 43Х= 8
7)Составь и реши уравнения, в которых для нахождения корня уравнения нужно было умножить на двузначное число.8)Составьте и решите такие уравнения, чтобы можно было повторить вычитание многозначных чисел и переходом через разряд.9)Замени буквы числами (каждой букве соответствует ее порядковый номер в алфавите), составь и реши уравнения.ж + Х= мХ в= кХ : г= и
10)Запишите слово ЛЕС с помощью чиселЕ+8= 16 С4= 10 14Л= 5
3.Привлекать учеников к ведениюфрагментов уроков, назначать командирами при групповой форме работы.4. Предлагать более трудные уравнения. Высокая трудность может быть за счет:усложнения числового материала,увеличения объема выполняемых заданий,увеличения количества объектов и действий с ними,более сложных вычислительных приемов.
Учащиеся со средним уровнем обученностипо теме «Уравнения» должны упражняться в решении уравнений. Необходимо предлагать достаточное количество репродуктивных упражнений для закрепления знаний и умений. Так же можно разнообразить деятельность, предложив задания вида: 1)Раздели уравнения в два столбика по определенному признаку. Реши их. Подумай, какие ещё признаки классификации могли получиться: 25 Х= 10А + 34= 55(К5) 5= 10 Х + (17+17)= 55
2)Выбери и реши только те уравнения, в которых неизвестное находится делением: 49:Х= 7 Х • 6= 42 Р • 7= 28 45:Z= 9
3)Сделай прикидку. Выбери и реши только те уравнения, в которых неизвестное число двузначное44У= 22 19Х= 10 Х15= 15 У+12= 100 22Х= 15
4)Самолёт должен лететь на городами в определенном порядке (от большего числа к меньшему). Реши уравнения, подпиши города и составь маршрут самолёта. Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 6
42+ Х= 5848 : Х= 6А 15= 146 • M= 30Р (133)= 25(К+8) 12= 8
16Москва8 Ижевск29 НижнийНовгород5 СанктПетербург35 Рязань 12 Киров
5)Составь уравнения с числами 3, 12; 8, 32 и реши их.12 : Х= 3; 3 • Х= 12 32 : Х= 8; 8 • Х= 32
6)Рассмотри решение уравнений и вставь соответствующий знак в запись уравнения.Х ? 6= 24 Х?6= 24Х= 24 : 6 Х= 24•6
7)Составь и реши уравнение: «Какое число надо умножить на восемь, чтобы получилось 32?»
Для учащихся с низким уровнем усвоения учебного материаладолжны предлагаться репродуктивные задания на отработку материала. Если ученики не справляются и с этими заданиями, то необходимо оказать методическую направляющую помощь, предлагая задания следующего вида: 1.Реши уравнения по следующему образцу:35 Х= 8Х= 35 8 Х= 2735 27= 88= 8
2.Соедини «подсказки»с уравнениями. Пользуясь найденными подсказками, реши уравнения.Чтобынайти неизвестное вычитаемое,нужно к значению разности прибавить уменьшаемое.
С • 9= 36Чтобы найти множитель,нужно значение произведения разделить на известный множитель.
72 В= 31Чтобы найти второе слагаемое, нужно из значения суммы вычесть первое слагаемое.
64 + Х= 82Чтобы найти делимое, нужно значение частного умножить на делитель.
3.Дан необходимый теоретический материал. Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 7
Составь и реши уравнения, если известно, что сумма получается при сложении, разность при вычитании, произведение при умножении, а частное при делении.Если из неизвестного числа вычесть 20, то получится произведение чисел 9 и 6.Если к 15 прибавить неизвестное число, то получится частное 80 и 4Если неизвестное число умножить на 6, то получится сумма чисел 35 и 7
4.Пользуясь алгоритмом, реши уравнение (Х+3):8= 51)Определи по последнему действию, чем является выражение в левой части (суммой, произведением, разностью, частным)?2)Где находится Х? Как найти неизвестный компонент? Применяем правило.3)Упрощаем равенство (находим значение выражения)4)Называем компоненты.5)Решаем простое уравнение.6)Выполняем проверку.
5.Реши уравнения, пользуясь памяткой: «Чтобы найти целое надо сложить части. Чтобы найти часть надо из целого вычесть известную часть».
6.Продолжитерешение уравнений.80+Х= 100 Х 200= 220Х= …… Х= … + …
7.Даны подготовительные задания.Х38= 38 (Х+5)45= 45
8.Предварительное решение уравнений на «маленьких числах».Х7= 8 8Х= 6Х25= 54 64Х= 20Х344= 485205Х= 140
9.Приучение к самоконтролю.1)Проанализируй решения уравнений и найди ошибки. Что нужно всегда делать, что бы ошибки не допускать?Х : 2= 4 Х:5= 15 Х•8= 8 Х:10= 20Х= 4 : 2 Х= 15•5 Х= 8:8 Х= 20:10Х= 2 Х= 80 Х= 1 Х= 22)Сделай прикидку, а потом реши уравнение (из какого числа нужно вычесть двадцать, чтобы получилось сто?)Х20= 1003)Найди правильно решенное уравнение. Докажи его правильность.Х:5= 10 Х:5= 10Х:5= 10Х= 10:5 Х= 10+5 Х= 10•5Х= 2 Х= 15 Х= 50
Данные виды заданий представляют собой методическую помощь ученикам, благодаря которой учащиеся с низким уровнем обученности смогут правильно решать уравнения и со временем догнать более «сильных» учеников. Необходимо заметить, что количество методической направляющей помощи необходимо постепенно сокращать по мере продвижения учеников (дети должны понимать, что учитель не будет помогать им все время), заменяя ее на стимулирующую помощь.
Шелыгина О. Б. Каткова А. С.Обучение младших школьников решению уравнений посредством дифференцированного подхода// Концепт. –2015. –Спецвыпуск №27. –ART75367. –0,4п. л. –URL: http://ekoncept.ru/2015/75367.htm. –ISSN 2304120X. 8
Таким образом, дифференцированный подход в обучении является эффективной формой организации учебного процесса в начальной школе на уроках математики. Для организации данного подхода необходимо подразделять класс на три группы, внутри каждой из которой будутобъединены дети с одинаковым уровнем усвоения учебного материала. Каждой группе нужно давать задания того уровня, которому соответствуют интеллектуальные возможности детей. В результате нашего исследования и внедрения в процесс обучения разработанных заданий для разных групп учащихся мы пришли к выводу, что дифференцированный подход к младшим школьникам на уроках математики в процессе обучения решению уравнений является удобной и эффективной формой организации учебного процесса. При дифференцированном подходе каждый ребёнок в классе может развивать свои знаний и умения, а тот, кто не уверен в них, может справиться с выполнением задания, используя методическую помощь.
Ссылки на источники1.Бекаревич А. Б. Уравнения в школьном курсе математики. М., 2000.
2.Конев А.Н. Индивидуальнотипологические особенности младших школьников как основа дифференцированного обучения.М., 1998.
Ph.D., Assistant Professor of pedagogy and methodology of preschool and primary education,Vyatka State University of Humanities, Kirovkaf_pmdno@vshu.kirov.ruAlexandra Katkova,Student,Vyatka State University of Humanities, KirovTraining of younger schoolboys the solution of equations through a differentiated approachAbstract. The article is devoted to the implementation of the differentiated approach to the younger students in the learning process solving equations. The authors suggest different methods work on equations, depending on the level of training of students, contributing to the development ofstudents’ thinking, their cognitive interest. Teaching methods are supported by examples of differentiated tasks on «equations» for different groups of students.Keywords: teaching mathematics, teaching solving equations, junior high school students, a differentiated approach, multilevel task.
Горевым П. М., кандидатом педагогических наук, главным редактором журнала «Концепт»
Поступила в редакциюReceived03.11.15Получена положительная рецензияReceived a positive review05.11.15ПринятакпубликацииAccepted for publication05.11.15ОпубликованаPublished11.11.15
Статья. Проблемы, типичные ошибки учащихся, допускаемые при решении уравнений и неравенств.

Задание «Проблемы, типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти ошибки.
Решая уравнения и неравенства учащиеся допускают типичные ошибки:
· Незнание правил, определений, формул.
· Непонимание правил, определений, формул.
· Неумение применять правила, определения, формулы.
· Неверное применение формул.
· Невнимательное чтение условия и вопроса задания.
· Раскрытие скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего характера возникают у учащихся при изучении математики ( их несомненно можно отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения и неравенства»):
· Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
· Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
· Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
· Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам . Учащиеся не всегда сами понимают, что именно они написали.
· Усталость . Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
· Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
· Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
· Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки подобного рода и определить способы их предупреждения и исправления, но прежде всего хочу обратить внимание на следующую мысль: не надо бояться приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
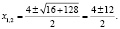
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение 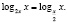
Область определения исходного уравнения задается системой
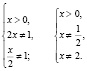
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
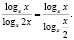
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
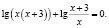
Ученик предлагает следующее ошибочное решение этого уравнения:
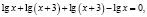
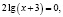
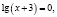
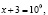
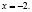
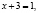 х = –2.
х = –2.
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 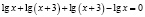 эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
Чтобы избежать потери корня, можно поступить следующим образом: перейти в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть это на следующем примере.
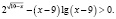
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
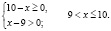
Для всех x из промежутка (9;10] выражение 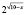 имеет положительные значения (значения показательной функции всегда положительны).
имеет положительные значения (значения показательной функции всегда положительны).
Для всех x из промежутка (9;10] выражение ( x – 9) имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение
– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x ∈ (9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
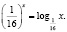
Некоторые учащиеся, решая это уравнение графически (хочу отметить, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
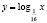 и
и 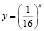 −
−
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 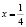 и третий корень
и третий корень 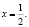 Убедиться в справедливости сказанного можно непосредственной подстановкой чисел
Убедиться в справедливости сказанного можно непосредственной подстановкой чисел 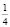 и
и 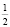 в заданное уравнение.
в заданное уравнение.
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны» (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение x х = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
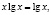
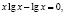
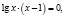
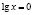 или
или 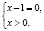
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
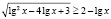 .
.
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
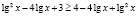 ,
,
откуда получаем неверное числовое неравенство 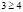 , что позволяет сделать вывод: заданное неравенство не имеет решений.
, что позволяет сделать вывод: заданное неравенство не имеет решений.
Однако полученный вывод неверен, например, при х = 1000 имеем
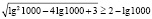 ,
, 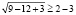 ,
, 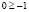 .
.
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
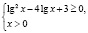 или
или 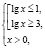
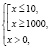 откуда
откуда 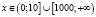 .
.
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 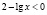 , откуда х > 100. С учетом области определения исходного неравенства имеем промежуток
, откуда х > 100. С учетом области определения исходного неравенства имеем промежуток 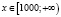 . Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что
. Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что 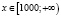 – решение заданного неравенства.
– решение заданного неравенства.
б) 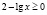 , откуда
, откуда 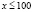 . С учетом области определения исходного неравенства имеем промежуток
. С учетом области определения исходного неравенства имеем промежуток 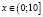 . Для всех х из промежутка
. Для всех х из промежутка 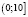 имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь:
имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь: 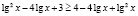 , откуда
, откуда 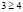 . Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка
. Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка 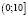 решениями исходного неравенства не являются.
решениями исходного неравенства не являются.
Ответ: 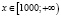 .
.
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x .
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
· проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
· проверка правильности решения задач путём составления и решения задач, обратных к данной;
· оценка результата решения задачи с точки зрения здравого смысла;
· проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
http://e-koncept.ru/2015/75367.htm
http://znanio.ru/media/statya_problemy_tipichnye_oshibki_uchaschihsya_dopuskaemye_pri_reshenii_uravnenij_i_neravenstv-173622
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем.
5. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение xх = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
или
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше. Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
Решите неравенство
.
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
,
откуда получаем неверное числовое неравенство , что позволяет сделать вывод: заданное неравенство не имеет решений.
Однако полученный вывод неверен, например, при х = 1000 имеем
, , .
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
или
откуда .
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) , откуда х > 100. С учетом области определения исходного неравенства имеем промежуток . Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что – решение заданного неравенства.
б) , откуда . С учетом области определения исходного неравенства имеем промежуток . Для всех х из промежутка имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь: , откуда . Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка решениями исходного неравенства не являются.
Ответ: .
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Самоконтроль
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
- проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
- проверка правильности решения задач путём составления и решения задач, обратных к данной;
- оценка результата решения задачи с точки зрения здравого смысла;
- проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
