Ошибки при решении задач на проценты

ВЫСТУПЛЕНИЕ

на РМО математиков

«Диагностика типичных ошибок

при решении задач»

Учитель математики

МБОУ «Ливенская СОШ №1»

Чебакова Галина Владимировна

Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.

Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.

«На ошибках учатся», — гласит народная мудрость. Но для того, чтобы извлечь урок из негативного опыта, в первую очередь, необходимо увидеть ошибку. К сожалению, школьник зачастую не способен ее обнаружить при решении той или иной задачи.

Целенаправленная работа над ошибками требует их систематизации. При этом главную роль должны сыграть группы ошибок, которые объединены общими причинами их появления, общей методикой работы над ними. Такая систематизация ошибок позволяет наметить пути их исправления и предупреждения этих ошибок в дальнейшем.

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

1. Ошибки и недочёты, которые обусловлены невниманием к формированию теоретико-множественных представлений учащихся:

• ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;

• ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.

2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:

• ошибки, связанные с непониманием структуры теоремы;

• ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;

• ошибки, связанные с непониманием метода доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.

• Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.

• Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.

• Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.

• Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Проанализируем некоторые типичные ошибки учащихся, допускаемых при решении тренировочных заданий для подготовки к ГИА

• Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.

• При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.

(Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому на путь длинной 20 км ему потребовалось на 20 мин. Меньше, чем второму. Чему равны скорости велосипедистов? Пусть х км/ч скорость первого велосипедиста.)

Типичные ошибки:

20: (х+3)-20:х=20

• При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.

(Магазин закупил на складе футболки и стал продавать их по цене, приносящей доход в 40 % . В конце года цена была снижена на 50 %. Какая цена меньше: та, по которой магазин закупил футболки, или цена в конце года – и на сколько процентов .

Типичные ошибки: 100+40-50=90% Разница на 10 %.))

Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.

Рассмотренные ошибки свидетельствуют о том, что ученики, не справившиеся с решением задач, не смогли представить себе жизненной ситуации, отраженной в задаче, не уяснили отношений между величинами в ней, зависимости между данными и искомым, а поэтому просто механически манипулировали числами.

Почему учащиеся допустили много ошибок при повторном решении знакомых задач? Анализ результатов позволяет сделать вывод о том, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного или графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учитель нередко ограничивается правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания, т.е. не проводятся все этапы работы над задачей.

Для устранения этих недостатков необходимо прежде всего улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.

Типичные методические ошибки учителя при работе с текстовыми задачами

Ошибка 1. Пропуск этапа анализа условия задачи.

«Прочитайте условие задачи. Кто пойдет к доске?» – такое часто можно видеть на уроке. И сразу начинается оформление решения. Этап анализа отсутствует и в некоторых учебниках, и в решебниках. Может быть, проведение этого этапа обязательно не для всех учащихся. В классе найдутся такие ученики, у которых этап анализа свернут. Они его проходят очень быстро, поэтому сразу видят решение и переходят к его оформлению. Задача педагога – помогать тем, у которых не получается. Решение задачи основывается на тех связях, которые существуют между данными и искомыми величинами. На выделение этих связей и направлен анализ условия задачи. Чтобы помочь учащимся самостоятельно осуществлять анализ условия, преподаватель может предложить им специальные памятки.

Ошибка 2. Пропуск этапа поиска решения.

Пропуск этого этапа ведет к недопониманию учащимися сущности эвристической деятельности, и как результат, к возникновению трудностей при самостоятельном решении задач. В практике обучения традиционной является ситуация, когда учитель вызывает к доске учащегося, который знает, как решить задачу. Однако при личностно ориентированном обучении основная забота учителя должна быть связана с теми, кто испытывает затруднения при самостоятельном решении задач.

Тем же учащимся, которые без учителя могут решать задачи, необходимо подбирать задания, усиливающие их умения и способствующие их развитию (составить задачи на основе справочных данных; рассмотреть другие способы решения предложенной задачи; составить граф-схемы других уравнений по задаче и др.)

Ошибка 3. Пропуск этапа исследования решения.

Зачем нужен этот этап? На этапе исследования выясняем, соответствует ли полученный ответ условию задачи (правдоподобность результата); есть ли другие способы решения; что полезного можно извлечь на будущее из решенной задачи. Последний вопрос позволяет рассматривать каждую задачу как звено в общем умении решать задачи, что ведет к накоплению опыта по решению задач.

Ошибка 4. Смешение этапов анализа и поиска решения.

Чтобы этого избежать, надо точно знать, какую цель мы преследуем на каждом этапе. Цель этапа анализа условия – выявить все имеющиеся связи между данными и искомыми величинами, чему помогает составление таблицы (схемы, рисунка). Цель этапа поиска решения – выбрать метод решения (алгебраический или арифметический) и составить план решения. Цели этапов разные, значит, и смешивать эти этапы никак нельзя.

• Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:

определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;

составляем схему уравнения, соответствующего выбранному условию;

определяем, какие величины можно обозначить за х; выбираем одну из них;

определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.

Завершается этап поиска составлением плана решения задачи.

Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.

Надо стараться зафиксировать как можно больше таких связей. Почему это важно? Упустив какую-нибудь связь, мы можем потерять:

условие для составления уравнения;

возможность одну величину выразить через другие;

предусмотреть несколько способов решения.

Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.

Обратим внимание на то, что при перечислении этапов, которые мы проходим при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике мы почти везде видим иное: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение. Вот этот момент настолько «закостенел» в нашем сознании, что от него отказаться очень трудно.

На самом деле, лучше делать «по-новому». Представьте себя на месте ученика в классе. Рассмотрим ситуацию, когда не были проведены этапы анализа и поиска решения, к доске вызван ученик, который знает, как решить задачу, и он начинает: «За х обозначим…» И что же наш ученик, который затрудняется в самостоятельном решении? Мы из решения сделали тайну непостижимую. «Как он угадал, что обозначить за х?» И когда он будет пробовать дома решать задачу, у него сразу закрадывается сомнение: «А вдруг я не угадаю?»

И насколько спокойнее и увереннее чувствует себя наш ученик, если у него есть карточка по проведению анализа и поиска решения задач; он смог составить по условию задачи таблицу; найти несколько условий для составления уравнений; записать схему уравнения для выбранного условия. Ученик знает, что за х можно обозначить любую из неизвестных величин, и, если не получится уравнение по одной схеме, то можно попробовать составить его по другой схеме.

Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.

Очень много зависит от умения ставить (задавать) вопросы учащимся. Вопросы не должны нести в себе подсказку, а подталкивать учащихся к размышлению. Вместо вопросов: «Во сколько туров проходила олимпиада?», «Как распределились посевные площади?», «Какое время находились туристы в пути?», «Какие машины находятся в автопарке?» лучше задавать общие вопросы: «Что происходит по условию задачи?», «Какие объекты участвуют в задаче?», «Какие части можно выделить в задаче?». Вместо вопроса «Можно ли найти такую-то величину?» лучше задать вопрос: «Что можно найти по данным задачи?», поскольку он может вывести на несколько вариантов решения.

Задавая вопросы, учитель не должен вести учащихся к своему решению; нужно рассмотреть все пути решения, выслушать и обсудить все варианты.

2.Для осуществления целенаправленных мер по исправлению и предупреждению ошибок учителю необходимо систематически изучать ошибки учащихся, выявлять наиболее устойчивые и типичные из них, вести учёт распространённых и индивидуальных ошибок учащихся. Знание учителем типичных ученических ошибок, а также причин их возникновения и проявления даёт ему возможность предвидеть и предупреждать их появление. Достичь этого можно путём подбора таких упражнений, которые препятствуют образованию односторонних ассоциаций и неправильных обобщений.

Ошибки учащихся, которые регистрирует и учитывает учитель, помогают ему установить, что не понимают учащиеся, что ими плохо усвоено; это даёт возможность учителю своевременно ликвидировать пробелы в знаниях учащихся и внести соответствующие коррективы в дальнейшее преподавание с целью предупреждения повторения аналогичных ошибок.

Чтобы определить сущность допускаемых учащимися ошибок, необходимо проследить ход рассуждений, который приводит к такому ошибочному решению, установить этап, на котором зарождаются такие ошибки. Как показывает опыт, часто учащемуся непонятен не весь материал, а лишь какая-то его часть. Выявив, что именно непонятно ученику, можно сосредоточить на этом материале всё внимание, не отвлекаясь на те моменты, которые уже усвоены.

Допускаемые учеником ошибки свидетельствуют не только о недостатках его знаний, но и о потенциальных возможностях. Ошибки служат также показателем проблем, которые могут быть поставлены перед учеником, а иногда они приводят к созданию проблемных ситуаций, которые необходимы в данный момент для развития действий.

Ни в коем случае нельзя снижать оценок ученикам за ошибки в процессе поиска. Очень важно приучить их не бояться допускаемых ошибок. Ошибки, допускаемые учениками, надо исправлять тактично, обоснованно, привлекая к этой работе самих учащихся.

Боязнь допустить ошибку сковывает инициативу ученика. Боясь ошибиться, он не будет сам решать поставленную проблему, а станет ждать помощи от учителя. Он будет решать только лёгкие проблемы. Но без такого самостоятельного решения задач с последовательно нарастающей сложностью не может происходить интеллектуальное развитие. Во многих случаях по этой причине учащиеся проявляют робость и интеллектуальную пассивность, что в дальнейшем приводит к неуспеваемости.

Очень оживлённо воспринимаются учащимися “Задачи на выявление ошибки”. Речь идёт не только о софизмах, но и об ошибках, которые допускают сами школьники. Не нужно специально исправлять каждое ошибочное утверждение школьника. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Если они и не допускают ошибок, то всё же нередко целесообразно проверить, насколько они “устойчивы” против типичных ошибок.

Например: Найти ошибки:

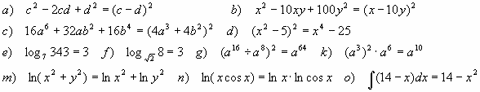
Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; в) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

• проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;

• проверка правильности решения задач путём составления и решения задач, обратных к данной;

• оценка результата решения задачи с точки зрения здравого смысла;

• проверка аналитического решения графическим .

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Пусть решение ученика выглядит так: . Ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130”. Такая прикидка в уме полезна при решении задач с дробными числами и процентами.

В жизненной практике в чертежах, схемах, расчётах, с которыми ребята будут встречаться, могут быть и ошибки. Если не научить их критически относиться к данным, то могут быть и аварии, и брак, и серьёзные упущения в работе. Чтобы этого избежать, необходимо формировать у учащихся умение анализировать данные, способность обнаруживать встречающиеся ошибки и обосновывать ошибочность положения.

Польский математик Г. Штейнгауз, отмечая большое значение работы над математическими ошибками для активизации мыслительной деятельности учащихся, пишет:

“Если учащегося заверить, что в предложенном ему доказательстве есть ошибка, то можно быть уверенным даже без специальной проверки, что материал будет изучен полностью и очень тщательно”. Поэтому составление списка математических ошибок и использование его в учебных целях является одним из важных факторов повышения эффективности обучения.

Таким образом, важную роль в предупреждении ошибок играет продуманная организация изучения нового материала. Изучение нового материала надо строить так, чтобы ученик был активным участником этого процесса. Не надо бояться, если при первом изложении материала им будут допускаться ошибки, высказываться необоснованные выводы. Важно, чтобы те или иные ошибки в понимании материала исправлялись в зародыше, чтобы ученики воспринимали материал осознанно.

Такому подходу к изучению нового материала способствует создание проблемной ситуации и решение её учащимися под руководством учителя. На таких уроках ученики проходят через следующие стадии: поиск нового, возможное появление ошибок в процессе поиска нового, обоснованное опровержение этих ошибок, снова поиски, в результате которых приходят к правильной догадке, и, наконец, доказательство составленного в поисках предложения. Всё это способствует развитию математического мышления.

Текстовые задача — это способ стимулирования мыслительной активности. Считаю необходимым сформировать такой подход к задаче, при котором задача выступает как объект тщательного изучения, а ее решение — как объект конструирования и изобретения. Необходимо построить процесс обучения математике так, чтобы обеспечить успешное овладение учащимися методами и приемами решения задач и создать условия для формирования у них ряда общенаучных умений — таких, как анализ, синтез, обобщение, сравнение, аналогия.

Необходимо организовать деятельность учащихся на учебном занятии таким образом, чтобы она способствовала формированию исследовательской культуры.

Предлагаю на занятии несколько приемов организации интенсивной мыслительной деятельности, которые используются мною на различных этапах процесса обучения: при актуализации знаний, первичном усвоении материала, его осмыслении, применении и обобщении.

Это можно сделать на следующем содержании материала:

1. Правоцирующие задачи.

Это задачи, условия которых содержат упоминания, указания, намеки или другие побудители, подталкивающие учащихся к выбору ошибочного пути решения или неверного ответа. Попадая в заранее подготовленную ловушку, ученик испытывает досаду, сожаление оттого, что не придал особого значения тем нюансам условия, из-за которых он угодил в неловкое положение. Простое сообщение о том, что учащиеся, как правило, допускают в заданиях такого-то рода ошибки, несравнимо менее действенно. Ибо оно, несмотря на общность, не является для конкретно взятого ученика личностно значимым, поскольку, во-первых, события, о которых сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых, каждый из учащихся наивно полагает, что в число неудачников сам он не попадает.

Дидактическая ценность этих задач в том, что они служат предупреждением от различного рода ошибок и заблуждений.

Провоцирующие задачи обладают высоким развивающим потенциалом, они способствуют воспитанию одного из важнейших качеств мышления- критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников к занятиям математикой.

Я использую такие разновидности провоцирующих задач:

1. условия, в которых навязывают неверный ответ;

2. условия, которые подсказывают неверный путь решения;

3. условия, вводящие в заблуждение из-за неоднозначности трактовки и т.д.

В качестве примера приведу задачи, побуждающие выбор неверного способа решения.

Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?

Или, на уроке в 6 классе по теме «Простые и составные числа» предлагаю задание: «Какие из чисел 205, 206, 207, 208, 209, 210 являются простыми?»

2.Задачи стандартные с нестандартным решением.

Это задачи, при предъявлении которых учащиеся не знают заранее ни способа их решений, ни того, на какой учебный материал опирается решение. Иными словами, учащиеся в ходе решения таких задач должны провести поиск плана решения задачи, установить, какой теоретический материал дает ключ к тому или иному решению. Незначительная обработка условий той или иной задачи из учебника, изменение места и времени ее постановки существенно меняют ее дидактическую значимость, оставляя неизменным практическое содержание.

Проиллюстрирую сказанное примером. Стандартная задача для учащихся 7 класса: «В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Сколько фазанов и кроликов в клетке?». Данную задачу предлагаю решить не алгебраическим способом, приводя к стандартному уравнению, а арифметическим. Таким образом, по существу, данную задачу превращаем в нестандартную для шестиклассников и даже семиклассников.

Задачи такого плана всегда органически связаны с изучаемым материалом. Допуская нестандартное решение, приучаю школьников не довольствоваться шаблоном, а нацеливаю на вдумчивый подход, воспитываю стремление как можно лучше выполнить порученное дело. Они развивают гибкость, рациональность, целенаправленность математического мышления и ценны тем, что дается возможность каждому ученику с любой структурой мышления проявить себя.

3. Проблемные задачи.

Это задачи, алгоритм решения которых неизвестен до начала решения. Главное в том, чтобы открыть способ решения и убедиться в его пригодности. Следует иметь в виду, что определить, является данная задача проблемной или нет, можно только относительно конкретного школьника, только с учетом его знаний и умений в момент постановки задачи.

Задачи такого плана решаются исследовательским методом и этим очень интересны для учащихся. Ведь исследование предполагает творчество. Проблемы, которые ставятся перед учащимися, могут иметь разнообразный характер: введение в новую тему, решение задачи новым более эффективным способом, связь известного учебного материала с новым и т.д.

При подборе проблемных задач учитываю знания учащихся и уровень развития их логического мышления, поскольку непосильная задача порождает неуверенность в своих силах и в дальнейшем отвращение от решения любых задач, а излишне простая вводит в заблуждение относительно уровня собственных знаний и умений, не стимулирует поисковую деятельность.

Самое главное- это суметь правильно поставить вопрос, заинтриговать учащихся, создать проблему, а не дать ответ, решив ее. Учащиеся познают понятия, закономерности, теории в ходе поиска, наблюдения, анализа фактов, мыслительной деятельности, результатом чего является знание.

Приведу пример задачи из темы «Смежные углы» (геометрия 7 класс).

Найти два смежных угла, один из которых больше другого на прямой угол.

Возможны различные варианты решения, в частности, алгебраический и геометрический. Здесь проблемный характер проявляется в неявной форме, но ученики понимают непригодность геометрического способа решения.

Другой пример. В 5 классе в ходе изучения темы «Сравнение десятичных дробей» предлагаю вариант решения задания на сравнение дробей 0,31 и 0,6 ученика Петрова. Если целые части дробей равны, сравним дробные части: 316, значит, 0,310,6. Согласны ли вы с таким решением? Начинается обсуждение, поиск, анализ решения.

1. Логические задачи.(задачи-шутки, таблицы, верные и неверные утверждения, здравый смысл)

Это задачи, ведущие к формированию важнейших характеристик творческих способностей: беглость мысли, гибкость ума, оригинальность, любознательность, умение выдвигать и разрабатывать гипотезы.

Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Логика учит, как нужно рассуждать, чтобы наше мышление было определенным, связанным, последовательным, доказательным и непротиворечивым. В математике приходится путем рассуждений выводить разнообразные формулы, числовые закономерности, правила, доказывать теоремы.

Основные методы решения логических задач:

• метод рассуждения;

• метод таблицы;

• метод граф;

• метод кругов Эйлера;

• комбинированный метод.

Метод рассуждений сопровождаю схемами, чертежами, краткими записями, вырабатывая умения выбирать информацию, пользоваться правилом перебора.

Так, при изучении темы «Степень» в 7 классе, я даю задание: запишите степени x, x², x³, x⁴, x⁵, x⁶, x⁷, x⁸, x⁹ в пустые клетки квадрата так, чтобы произведение их по любой горизонтали, вертикали и диагонали было равно x в 15 степени. Можно рассказать о магическом квадрате, тогда задача станет еще интереснее для учеников.

	X5

Таблицы хорошо применять тогда, когда устанавливается соответствие между двумя множествами (можно и между тремя множествами), когда количество элементов во множествах одинаково и неодинаково. Перед составлением таблиц отрабатываю правила их заполнения.

Например, в 5 классе знакомлю детей с задачей Пуассона (на переливание). Некто имеет 12 пинт сока (пинта- 0,57л) и желает подарить половину своему другу, но у него нет сосуда в 6 пинт, а есть два сосуда в 8 и 5 пинт. Каким образом можно налить 6 пинт сока в сосуд емкостью 8 пинт?

Решение.

Ходы	0	1	2	3	4	5	6	7
12 пинт	12	4	4	9	9	1	1	6
8 пинт	—	8	3	3	—	8	6	6
5 пинт	—	—	5	—	3	3	5	—

Логические связи, при помощи которых была выстроена общая схема решения задачи, помогут учащимся без труда решить подобного рода задачу.

Введение серии таких задач в содержание урока считаю необходимым. Это позволит стереть явную границу между занимательным и учебным материалом. Особенно целесообразно использовать задачи тогда, когда есть опасность неприятия учащимися какого-либо учебного задания; при прохождении сложных тем; при выработке умений и навыков учащихся, когда требуется выполнить значительное количество однотипных упражнений; при изучении материала, подлежащего прочному запоминанию.

Для каждой задачи, которую предполагаю использовать на уроке, прежде выясняю: будет ли она интересна классу, органично ли войдет в структуру урока, будет ли ее использование эффективным. Практика показала: учебный навык, на формирование которого направлена та или иная задача, вырабатывается быстрее, ибо он связан с продуктивной мыслительной деятельностью ученика.

При работе над провоцирующими, проблемными, логическими и стандартными с нестандартным решением задачами наиболее эффективной считаю групповую, парную, индивидуальную, фронтальную работу.

Приведу пример. Расстояние от реки до турбазы туристы рассчитывали пройти за 6 часов. Однако после 2 часов пути они уменьшили скорость на 0,5 км/ч и в результате опоздали на турбазу на 30 мин. С какой скоростью шли туристы первоначально?

Работа над задачей предполагает следующие действия учителя:

1. Предъявление задачи (читает учитель).

2. Определение вида задачи (творческая группа).

3. Выделение гипотез (индивидуальная самостоятельная работа).

4. Обмен мнениями (в творческой группе).

5. Формулировка предположительного ответа (в паре).

6. Проверка ответа на достоверность (фронтальная работа).

Или, задача. Определить площадь равнобедренной трапеции, у которой основания равны 12см и 20см, а диагонали взаимно перпендикулярны.

1. Предъявление задачи (творческие группы составляют задачи по готовому чертежу).

2. Выделение гипотез (работа в парах).

3. Обмен мнениями (фронтальная работа).

4. Формулировка предположительного ответа (индивидуальная работа).

5. Проверка ответа на достоверность (индивидуальная работа).

Обязательным этапом на уроке является устный и письменный счет. Целями устного счета являются, во-первых, совершенствование в вычислительных навыков, во-вторых, развитие творческого мышления учащихся.

На своих уроках я стараюсь разнообразить формы и методы устной работы:

— устный счет в начале, в середине, в конце урока;

• устная форма проверки домашнего задания;

• устная форма творческой работы;

• устные самостоятельная и контрольная работы;

• уроки устной работы.

Работая устно, воспитываю у учащихся навыки сознательного усвоения изучаемого материала, приучаю ценить и экономить время, развиваю желание поиска рациональных путей решения задачи. В этих целях использую такие приемы, развивающие творческие способности, как «Зашифрованные задания», «Найди ошибку», «Восстановление»,

«Выбор», «Задачи- сказки», детские презентации на устный счёт, математические листы с задачами, изготовленные самими учащимися, ребусы, кроссворды, которые учащиеся составляют самостоятельно.

Обязательно провожу подробный анализ результатов работы и коррекцию знаний. Объявляя количество набранных баллов, полученных за олимпиадное задание, называю ребят, которые представили самые «красивые» решения. При этом опираюсь на формулу «красивой» задачи по В.Г. Болтянскому: красивая задача = непредсказуемость + непредполагаемость +неожиданность + удивительная простота + простота + фантазия + революционный шаг + удивление + оптимизм + труд + …

Таким образом, решение текстовых задач не случайно всегда волновало учителей, методистов, да и самих учащихся и их родителей.

Во-первых, нельзя решить задачу, не поняв ее содержание. Следовательно, умение решать текстовые задачи свидетельствует об одной из самых важных способностей человека — способности понимать текст. Правы те учителя, которые добиваются понимания текста не только на уроках чтения, но и на уроках математики. Критерием понимания задачи является факт решения задачи.

Поэтому решение текстовых задач — это деятельность, весьма важная для общего развития. Обучая решать текстовые задачи, мы приучаем ориентироваться в ситуациях, делаем человека более компетентным. Конечно, для этого нужно резко расширить тематику задач, давать детям задачи, разнообразные по тематике, а не только «на скорость», «на работу», «на покупки».

Решение текстовых задач способствует, с одной стороны, закреплению на практике приобретённых умений и навыков, с другой стороны, развитию логического мышления учащихся.

Наблюдается активизация их мыслительной деятельности. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, развивается абстрактное мышление, умение применять теорию к решению конкретных задач.

Введение

Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».

Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.

Ныне процент — это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В школьном учебнике «Математика, 5«,авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.

Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.

Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.

В вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в младших 5-6 классах, причем непродолжительно, закрепляется в 7 классе при решении задач на повторение, а в старших классах к этой теме совсем не возвращаются.

Так, пересмотрев школьные учебники по математике, по которым обучаются ученики нашей гимназии, я выяснила, что в учебнике «Алгебра, 9», под ред. Теляковского, задач, в которых упоминается слово «процент», всего три. В учебнике «Алгебра и начала анализа, 10-11» под ред Колмогорова А.Н задач на проценты и процентную концентрацию черыре. Но, задачи на проценты уже встречались в вариантах единого государственного экзамена в 2003, 2004, 2005 годах. Предлагается такая задача и в демонстрационном варианте 2007 года. Поэтому, изучение наиболее часто встречающихся типов задач на проценты, считаю актуальным.

Объектом исследования является изучение различных типов задач по теме «Проценты».

Изучая эту тему по сборникам для поступающих в вузы[5], я пришла к мнению, что многие задачи авторы сборников предлагают решать с использованием специальных формул, которых в школьных учебниках 5-6 классов, когда и изучаются эти темы, нет.

Предмет исследования: решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.

Цель работы. Составить практическое пособие по решению задач на проценты для школьников.

Задачи исследования:

1) Изучить исторический и теоретический материал по интересующему вопросу. 
2) Систематизировать задачи на проценты по типам. 
3) Составить практические рекомендации по решению задач на проценты. 
4) Выявить практическое применение таких задач.
5) Определить план дальнейшей работы над темой.

Практическая значимость работы. Данное пособие по решению задач на проценты будет интересно не только школьникам 5-6 класса, которым интересна математика. Здесь найдут много полезного и выпускники школ, и абитуриенты при подготовке к выпускным и вступительным экзаменам.

Глава 1.Основные типы задач по теме «Проценты»

В данной главе приводятся примеры задач, которые решаются с применением определения, что такое один процент, как выразить дробь в процентах и правилам нахождения части (дроби) от числа, и числа по значению его части (дроби), т.е. это те темы и задачи, которые рассматриваются в школе. 

Обращаем внимание, что существуют и другие способы решения простейших задач на проценты, например, составляют пропорции на каждом шаге, но в этом случае решение становится на несколько шагов длиннее. Мы же видим свою задачу в нахождении более быстрых способов решения таких задач, в связи с тем, что в настоящее время редкий тест по математике для абитуриентов, обходится без задач, в которых не упоминались бы проценты.

1.1. Решение задач на применение основных понятий о процентах.

Сотая часть метра — это сантиметр, сотая часть рубля — копейка, сотая часть центнера — килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название — процент. Значит одна копейка — один процент от одного рубля, а один сантиметр — один процент от одного метра.

Один процент — это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.

Определение одного процента можно записать равенством: 1 % = 0,01 * а 

5%=0,05, 23%=0,23, 130%=1,3 и т. д

Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.

Пример. Найти: 25% от 120.

Решение:
1) 25% = 0,25;
2) 120 . 0,25 = 30.

Ответ: 30.

Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь

Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?

Решение: Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах — 25%. Получаем ответ: производительность труда токаря повысилась на 25%.

Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов. 

Пример. При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?

Решение: — такую часть составляют изготовленные автомобили от количества автомобилей по плану. Запишем в процентах =110%

Ответ: 110%

Пример. 

Ответ: 66 2/3 %, 40 %.

Пример. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?

Решение: 1) 6+ 34 =40 (кг) масса всего сплава.

2) = 85% сплава составляет медь.

Ответ. 85%.

Пример. Что произойдет с ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%?

Решение: Пусть цена товара х руб, тогда после повышения товар стоит 125% прежней цены, т.е. 1,25х;, а после понижения на 25% , его стоимость составляет 75% или 0, 75 от повышенной цены, т.е. 0,75 *1,25х= 0,9375х, тогда цена товара понизилась на 6, 25 %, т.к. х — 0,9375х = 0,0625х ; 0,0625х/х . 100% = 6,25%
Ответ: первоначальная цена товара снизилась на 6,25%.

Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%. 

Пример. Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480кг волокна.?

Решение. Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби). 480 : 0,24= 2000 кг = 2 т

Ответ: 2 т

Пример. Сколько кг белых грибов надо собрать для получения 1 кг сушеных, если при обработке свежих грибов остается 50% их массы, а при сушке остается 10% массы обработанных грибов?

Решение. 1кг сушеных грибов — это 10% или 0, 01 часть обработанных, т.е. 1 кг : 0,1=10 кг обработанных грибов, что составляет 50% или 0,5 собранных грибов, т.е. 10 кг : 0,05=20 кг

Ответ: 20 кг

Пример. Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?

Правило 4. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.

1.2. Решение задач на понятия «процентное содержание», «концентрация», «%-й раствор».

Процентное содержание. Процентный раствор.

Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.

Решение. 10 . 0,15 = 1,5 (кг) соли.

Ответ: 1,5 кг.

Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.

Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?

Решение: Процентное содержание вещества в сплаве — это часть, которую составляет вес данного вещества от веса всего сплава.

Концентрация.

Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.

Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 261 г.

Решение. 300 . 0,87 = 261 (г).

В этом примере концентрация вещества выражена в процентах.

Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.

Сумма концентраций всех компонент, составляющих смесь, равна 1.

Если известно процентное содержание вещества, то его концентрация находится по формуле: К=р/100% к — концентрация вещества; р — процентное содержание вещества (в процентах).

Пример. Имеется 2 сплава, в одном из которых, содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?

Решение: Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. Тогда получим (20 + х) кг нового сплава. В 20 кг первого сплава содержится 0,4 . 20 = 8 (кг) серебра, в х кг второго сплава содержится 0,2х кг серебра, а в (20+х) кг нового сплава содержится 0,32 . (20+х) кг серебра. Составим уравнение:

8 + 0,2х = 0,32 . (20 +х); х = 13 1/3.

Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.

Пример. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?

Решение. Пусть добавили х л 5%-ного раствора соли. Тогда нового раствора стало (15 + х) л, в котором содержаться 0,8 . (15 + х) л соли. В 15 л 10%-ного раствора содержится 15 . 0,1 = 1,5 (л) соли, в х л 5%-ного раствора содержится 0,05х (л) соли.

Составим уравнение.

1,5 + 0,05х = 0,08 . (15 + х);
х = 10.

Ответ: добавили 10 л 5%-ного раствора

1.3. Решение задач с использованием понятия коэффициента увеличения.

Чтобы увеличить положительное число а на р процентов, следует умножить число а на коэффициент увеличения к=(1+0,01р).

Чтобы уменьшить положительное число а на р процентов, следует умножить число а на коэффициент уменьшения к= (1-0,01р).

Пример. Вклад, вложенный в сбербанк два года назад, достиг суммы, равной 13125 руб. Каков был первоначальный вклад при 25% годовых?

Решение. Если а (рублей) — размер первоначального вклада, то в конце первого года вклад составит 1,25а а в конце второго года размер вклада составит 1,25 *1,25а. Решая уравнение 1,25* 1,25а=13125, находим а=8400.

Ответ: 8400 руб.

Пример. В феврале цена на нефть увеличилась на 12% по сравнению с январской. В марте цена нефти упала на 25%. На сколько процентов мартовская цена изменилась по сравнению с январской?

Решение. Если х — январская цена нефти, то февральская цена нефти равна

(1 +0,01*12)х = 1,12х. Чтобы вычислить мартовскую цену у на нефть, следует умножить февральскую цену 1,12х на (1-0,01*25)=0,75, т.е. у=0,75 1,12х=0,84х , мартовская цена отличается от январской на (0,84х)/х100 —100=84-100= −16(%), т.е. цена упала на 16 %

Ответ: цена упала на 16%.

Правило 5. Чтобы найти, на сколько % положительное число у отличается от положительного числа а , следует вычислить, сколько % у составляет от а, а затем от полученного числа отнять а.

Глава 2. Разные задачи на проценты ( с решениями)

В данной главе рассматривается выборка задач из различных источников, которые охватывают весь теоретический материал, который излагался выше, предлагаем свои решения. Отметим, что предложенный способ решения не является единственным.

2.1 Тестовые задания на проценты.

Задача 1.Товар стоил тысячу рублей. Продавец поднял цену на 10%, а через месяц снизил её на 10%.Сколько стал стоить товар?

Решение. Пусть товар стоил 1000руб., после повышения цены на 10% он стал стоить 1,1*1000 руб. После понижения этой цены на 10%, он стал стоить 0,9*1,1*1000=990 руб.

Ответ. 990 руб.

Задача 2.Собрали 100 кг грибов. Оказалось, что их влажность 99%. Когда грибы подсушили, влажность снизилась до 98%. Какой стала масса этих грибов после подсушивания?

Решение. Так как влажность грибов составляет 99%, это означает, что на так называемое «сухое вещество приходится 1% грибов, т.е 1 кг, после сушки влажность составляет 98%, т.е. на «сухое вещество» приходится 2%, т.е 1кг это 0,02 подсушенных грибов, 1 кг : 0,02=50 кг.

Ответ. 50 кг.

Задача 3. Цена входного билета на стадион была 1 рубль 80 копеек. После снижения входной платы число зрителей увеличилось на 50% , а выручка выросла на 25% .Сколько стал стоить билет после снижения?

Решение. Пусть зрителей, до понижения цены, на стадион приходило А чел. и выручка составляла 1,8А руб. После понижения цены, цена 1,8*р, зрителей стало 1,5А, выручка составляет 1,8*р*1,5*А руб. С другой стороны, выручка повысилась на 25%, т.е. составляет 1,25*1,8А. Получаем 1,8*р*1,5*А=1,25*1,8А., откуда р=12,5/15, тогда билет стоит 1,8*12,5/15=1,5 руб.

Ответ. 1руб. 50 коп

Задача 4. По дороге идут два туриста. Первый из них делает шаги на 10% короче и в то же время на 10% чаще, чем второй. Кто из туристов идет быстрее и почему?

Решение. Пусть второй турист делает а шагов, каждый из которых равен в, тогда ав это длина пройденного пути. А первый турист тогда прошел1,1*а*0,9*в=0,99*ав, что меньше ав.

Ответ. Второй турист идет быстрее.

Задача 5. Цену за товар уменьшили на 10%, а затем еще на 10%. Стоит ли он дешевле, если цену сразу снизить на 20%?

Решение. Если товар стоил А руб, после двух понижений он стал стоить 0,9*0,9*А=0,81А. А цену товара сразу понизить на 20%, то он станет стоить 0,8*А , что дешевле.

Ответ. Да.

Задача 6. Числитель дроби увеличили на 20%. На сколько процентов надо уменьшить её знаменатель, чтобы в итоге дробь возросла вдвое?

Решение. Пусть данная дробь, новая дробь. , откуда К=0,6, что означает, что знаменатель нужно уменьшить на 40%

Ответ. 40%

Задача 7. Матроскин продает молоко через магазин и хочет получать за него 25 рублей за литр. Магазин удерживает 20% стоимости проданного товара. По какой цене будет продаваться молоко в магазине?

Решение. Пусть молоко продает магазин по А руб, тогда после удержания 20% стоимости товара, Матроскину остается 0,8*А=25, откуда А=31, 25 руб.

Ответ. 31 руб. 25 коп.

Задача 8. Один покупатель купил 25% имевшегося куска полотна, второй покупатель 30% остатка, а третий — 40% нового остатка. Сколько (в процентах) полотна осталось непроданным?

Решение. Пусть полотна было р . Первый купил 0,25р,, осталось (1-0,25)р полотна, второй покупатель купил 0,3*0,75р=0,225р, осталось 0,75р —0,225р=0,525р, третий купил 0,4*0,525р=0,21р, осталось 0,525р-0,21р=0,315р, что составляет 31,5% от р.

Ответ. 31,5%

Задача 9. Бригада косарей в первый день скосила половину луга и еще 2 га, а во второй день 25% оставшейся части и последние 6 га. Найти площадь луга.

Решение. 6 га составляют 75% или0,75=3/4 от оставшейся части после 1 дня работы, т.е.6: 0,75=6 га 8+2=10 га — это половина луга, весь луг 20 га

Ответ. 20 га

Задача 10. Как изменится в процентах площадь прямоугольника, если его длина увеличится на 30%, а ширина уменьшится на 30%?

Решение. АВ- площадь исходного прямоугольника, 1,3*А*0,7*В=0,91АВ — площадь нового прямоугольника, что составляет 91% исходного.

Ответ. Уменьшится на 9%

Задача 11. В драматическом кружке число мальчиков составляет 80% от числа девочек. Сколько процентов составляет число девочек в этом кружке от числа мальчиков?

Решение. Девочек А чел, мальчиков 0,8*А, девочки составляют от мальчиков А/(0,8А)= 1,25, т.е. 125 % от числа мальчиков

Ответ. 125%

Задача 12. В бассейн проведена труба. Вследствие засорения её приток воды уменьшился на 60%. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна

Решение. Пусть Х — объем воды, который должен поступить за время Т при притоке А в ед времени., т.е. Х=АТ. Так как приток уменьшился на 60%, т.е. стал составлять 0,4А, тогда время стало ТК. Получим АТ=0,4А*КТ, откуда К = 2,5, что составляет 250% от времени, необходимого на заполнение бассейна до засорения, т.е. время увеличилось на 150%

Ответ. 150%

Задача 13. 5 литров сливок с содержанием жира 35% смешали с 4 литрами 20%-ных сливок и к смеси добавили 1 литр чистой воды. Какой жирности получилась смесь?

Решение. 0,35*5+0,2*4=р*(5+4+1), откуда р=0,255, что составляет 25,5%

Ответ. 25,5%

2.2. Избранные задачи вариантов единого государственного экзамена.

Впервые в вариантах единого государственного экзамена по математике задача на проценты появились в 2003 году в заданиях группы В, в 2004 и в 2005 годах такие задачи также были представлены в вариантах единого экзамена. В вариантах 2006 года были задачи на работу, но в демонстрационном варианте 2007 года снова появляется задача на проценты, что говорит о необходимости серьезной работы над этой темой. Следует отметить, что для решения всех задач, которые предлагались, достаточно знания тех методов, которые рассматриваются в данной работе.

2003. Тренировочный вариант. Задание В7

Банк предлагает вклад «студенческий». По этому вкладу, сумма, имеющаяся на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик положил 1 января 1000 руб. и в течение 2 лет не производил со своим вкладом никаких операций. В результате вложенная им сумма увеличилась до 1210 руб. На сколько процентов ежегодно увеличивалась сумма денег, положенная на этот вклад?

Решение. Используя формулу увеличения положительного число на p%, получим, что через год сумма вклада составит 1000*(1+0,01р), а через два года 1000*(1+0,01р)2=1210, т.е. (1+0,01р)2=1,21, 1+0,01р=1,1, 0,01р=0,1, откуда р=10%

Ответ: сумма ежегодно увеличивалась на 10%.

2003. Демонстрационный вариант. Задание В7

Владелец дискотеки имел стабильный доход. В погоне за увеличением прибыли он повысил цену на билеты на 25%. Количество посетителей резко уменьшилось, и он стал нести убытки. Тогда он вернулся к первоначальной цене билетов. На сколько процентов, владелец дискотеки снизил новую цену билетов, чтобы она стала равна первоначальной?

Решение. Пусть цена билета была А руб. После повышения на 25% цена стала 1,25А, после понижения цена билета стала р*1,25А. Т.к. цена билета вернулась к первоначальной, то получим р*1,25А=А, откуда р=1/1,25 = 0,8, что означает, что новая цена составляет 80% цены после повышения., значит владелец дискотеки снизил цену на 20%.

Ответ: 20%

2003. ЕГЭ

Предприятие уменьшило выпуск продукции на 20%. На сколько процентов, необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня?

Решение. Пусть А количество продукции, выпускаемое предприятием, 0,8А-количество продукции, которое стало выпускать предприятия после уменьшения на 20%. Из условия задачи следует уравнение р*0,8А=А, где р —коэффициент увеличения, откуда р=1/0,8=1,25, что означает, что необходимо увеличить выпуск продукции на 25%.

Ответ: 25%

2003. ЕГЭ

К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20 % той же соли. Сколько процентов соли содержится в получившемся растворе?

Решение. 1) 0,8*120=96(г)-соли в первоначальном растворе;

2) 480*0,2=96(г) соли во втором растворе;

3) ((96+96)/(120+480))*100%=32%-процентное содержание соли в получившемся растворе.

Ответ: 32%

2003. ЕГЭ

За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определить, на сколько процентов увеличилась стипендия во втором полугодии?

Решение. Пусть А- первоначальный размер стипендии, 1,1А — размер стипендии после повышения в 1 полугодии, р*1,1А- размер стипендии после увеличения во 2 полугодии, где р- коэффициент увеличения. Так как за год стипендия увеличилась на 32%, получим уравнение р*1,1А=1,32А, р=132/110=1,2, что означает , что стипендия во 2 полугодии составляет 120% стипендии 1 полугодия., т.е. стипендия во 2 полугодии увеличилась на 20%

Ответ: на 20%.

2004. ЕГЭ

Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток — 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу ( в граммах) куска, взятого от первого слитка.

Решение. Определим процентное содержание золота в обоих слитках. 1) 230+20=250(г)-масса 1 слитка, 230/250=0,92 (92%)процентное содержание золота в 1 слитке.

2) 240+60=300(г) —масса 2 слитка, 240/300=0,8 (80%)- процентное содержание золота во 2 слитке. Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение 0,92х+0,8(300-х)=0,84*300, откуда х=100

Ответ: 100г.

2004 ЕГЭ

Первый сплав серебра и меди содержит 70 г меди, а второй сплав — 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82 % серебра. Сколько граммов серебра содержалось в первом сплаве?

Решение. Пусть х г серебра содержится в 1 сплаве., тогда 70/(х+70)-какую часть 1 сплава составляет медь, 90/(210+90)-такую часть составляет медь во 2 сплаве., кусок второго сплава 300-225=75г, тогда получаем уравнение.

225*(70/(х+70))+75*(90/300)=(1-0,82)*300, откуда х=430г

Ответ: 430г

ЕГЭ 2004

В колбе было 200 г 80% -го спирта. Провизор отлил из колбы некоторое количество этого спирта и затем добавил в нее столько же воды, чтобы получить 60% — ый спирт. Сколько граммов воды добавил провизор?.

Решение. 200*0,8=160(г)-масса чистого спирта в колбе, их колбы отлили х г раствора, осталось (200-х)г раствора, в котором чистого спирта 0,8*(200-х). Когда к раствору добавили х г воды, то масса раствора снова стала 200 г, а концентрация

[(0,8*(200-х))/200]*100%=60%, откуда х=50(г).

Ответ: провизор добавил 50г воды.

ЕГЭ 2004

В колбе было 800 г 80% -ного спирта. Провизор отлил из колбы 200 г этого спирта и добавил в нее 200 г воды. Определить концентрацию ( в процентах) полученного спирта.

Решение. После того, как провизор отлил 200 г раствора, стало 600г, в котором чистого спирта 0,8*600=480г, когда добавили200г воды, то раствор снова 800г, а концентрация чистого спирта в растворе (480/800)*100%=60%

Ответ: 60%

ЕГЭ 2005

Численность населения в городе Таганроге в течение двух лет возрастала на 2 процента ежегодно. В результате число жителей возросло на 11312 человек. Сколько жителей было в Таганроге первоначально?

Решение. А- первоначальное количество жителей Таганрога. Используя формулу коэффициента увеличения, получаем

А(1+0,02)2=А+11312, откуда А=280000

Ответ: 280000 чел

ЕГЭ 2005

Из сосуда, доверху наполненного 94% -м раствором кислоты, отлили 1,5 л жидкости и долили 1,5 л 70% -го раствора этой же кислоты. После этого в сосуде получился 86% раствор кислоты. Сколько л раствора вмещает сосуд?

Решение. Пусть х л вмещает сосуд, тогда из условий задачи следует уравнение 0,94(х-1,5)+0,7*1,5=0,86х, откуда х=4,5 л.

Ответ: 4,5 л

Демонстрационный вариант 2007

Денежный вклад в банк за год увеличивается на 11 %. Вкладчик внес в банк 7000 рублей. В конце первого года он решил увеличить сумму вклада и продлить срок действия договора еще на год, чтобы в конце второго года иметь на счету не менее 10000 рублей. Какую наименьшую сумму необходимо дополнительно положить на счет по окончании первого года, чтобы при той же процентной ставке (11 %) реализовать этот план? (Ответ округлите до целых.)

Решение. 1,11* 7000=7770руб-будет на счете в конце 1 года. Пусть х руб. положили дополнительно на счет, из условия задачи получаем неравенство 1,11(7770+х)> 10000, получим х>1239, 1/111, что означает, чтобы на счету было не менее 10000 руб, нужно положить не менее12 40руб.

Ответ: 1240 руб.

Заключение

Данное практическое пособие позволит развить и закрепить навыки решения задач по теме: «Проценты» у учащихся 5-6 классов, может быть интересно учащимся, увлеченным математикой, а также полезно выпускникам школ и абитуриентам при подготовке к экзаменам. В дальнейшем на факультативных и кружковых занятиях возможны изучение вопроса применения процентов в экономике, в банковском деле. Можно провести сравнительный анализ банковских процентных ставок по потребительским кредитам и ипотечному кредитованию населения.

Литература

1. .Быков А.А. и др В помощь поступающим в ГУ — ВШЭ, Математика, М: ГУ-ВШЭ, 2004

2.Денищева Л.О., Глазков Ю.А. и др., Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика, М: Интеллект- Центр, 2003.

3. Потапов М.К., Олехник С.Н., Нестеренко Ю.В., Конкурсные задачи по математикеМ: Наука, 1992.

4. Семенко Е.А. и др., Готовимся к ЕГЭ по математике, Краснодар, Просвещение-Юг, 2005.

5. Алгебра, 9, под ред. Теляковского С.А., М: Просвещение, 2001

6. Алгебра и начала анализа, 10-11, под ред. Колмогорова А.Н., М: Просвещение, 2003.

7. Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г. М: Центр тестирования, 2004.

8. Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006, М: Центр тестирования, 2005.

[1] «Математика, 5», Виленкин Н.Я. и др., «Мнемозина», 2003, с. 337

[2] «Алгебра, 9», под ред. Теляковского С.А., М: Просвещение, 2001, с.215, 223

[3] «Алгебра и начала анализа, 10-11», под ред. Колмогорова А.Н., М: Просвещение, 2003, с.306,330.

[4] «Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика», Денищева Л.О., Гдазков Ю.А. и др., М: Интеллект- Центр, 2003.

«Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г.» М: Центр тестирования, 2004.

«Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006», М: Центр тестирования, 2005.

[5] «Конкурсные задачи по математике», Потапов М.К., Олехник С.Н., Нестеренко Ю.В., М: Наука, 1992, с330-332.

«В помощь поступающим в ГУ — ВШЭ, Математика», Быков А.А. и дрМ: ГУ-ВШЭ, 2004, с 53-64

«Готовимся к ЕГЭ по математике», Семенко Е.А. и др., Краснодар, Просвещение-Юг, 2005, с. 46-51

Автор: Валентина Молибоженко

---

---

МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ

ИЗУЧЕНИЯ ТЕМЫ «ПРОЦЕНТЫ» В 5 КЛАССЕ

(авторский подход)

Чернышев Э.Н.,

учитель математики МБОУ СОШ №3

г. Красный Сулин Ростовская область

8(86367) 5-23-37

89508548772

eduardlaw@yandex.ru

Впервые с понятием «процент» обучающиеся знакомятся в 5 классе. Так, по УМК Виленкина Н.Я. и др. «Математика 5-6» тема «Проценты» изучается в конце учебного года. С понятием процента и его использованием пятиклассники знакомятся в ознакомительном порядке. Вместе с тем, задачи на проценты присутствуют в материалах ОГЭ и ЕГЭ, обеспечивают успешность решения физических, биологических, химических задач. Не секрет, что методические «промахи» в 5 классе не позволяют ученикам успешно использовать понятие процента в последующих темах курсов математики и других дисциплин. Опыт показывает, что выпускники, будучи уверенными в простоте понятия «процент», тем не менее допускают множество ошибок при решении задач «на проценты». Эти ошибки носят технологический характер, являются следствием неэффективного первичного знакомства с этим понятием и методами использования процентов в решении задач. Именно поэтому опытные учителя очень ответственно относятся к изучению темы «Проценты» в 5 классе.

В данной статье мной описываются некоторые методические особенности авторского подхода к изучению темы «Проценты» в 5 классе.

Перед началом изучения темы необходимо восстановить с пятиклассниками навыки решения задач на доли:

найти 3/5 от числа 65 (по правилу делим число 65 на знаменатель и умножаем результат на числитель; получаем 39);

найти число, если 2/7 числа равны 42 (по правилу делим 42 на числитель и умножаем на знаменатель, получаем 147);

какую часть составляет число 4 от числа 5 (по правилу делим 4 на 5 и получаем 4/5 или 0,8).

На первом уроке по теме решаем задачи с использованием знакомого пятиклассникам из начальной школы понятия доли: «Найди сотую часть от 20 кг», «Сотая доля некоторой величины равна 2 дм. Найти указанную величину» и др.; здесь же решаем задания с использованием понятий «половина», «треть», «четверть», например – «В классе 24 ученика. Треть из них написали контрольную работу на «5», четверть оставшихся – на «3», а остальные – на «4». Сколько учеников справились с контрольной работой на «4» ?».

На следующем уроке приводится материал из СМИ, из открытого банка заданий ОГЭ, где используется понятие «процент». Это мотивирует обучающихся к освоению нового понятия. Далее вводится понятие «процент» (сотая часть (доля) величины; обращаю внимание именно на то, что процент,- это часть величины, а не числа). Решаются задачи на нахождение одного процента от различных величин и задачи на нахождение величин, если известен один процент этих величин. Обращаю внимание на то, что ста процентам в виде дроби соответствует число 1,0 или просто 1.

На этом уроке полезны сведения, открывающие историю появления процентов в математике; учащимся будет интересно узнать, что нак % произошёл благодаря опечатке. В рукописях pro centum часто заменялось словом «cento» (сто) и писали сокращённо – cto. В 1685 году в Париже была напечатана книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %. После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.

Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.

На третьем уроке определяются приемы записи части величины в трех формах: в виде обыкновенной дроби, в виде десятичной дроби (если возможен перевод обыкновенной дроби в конечную десятичную) и в виде процентов. Четко определяется алгоритм перевода процентов в десятичную дробь:

записать 56% в виде десятичной дроби:

56%:100%=0,56;

записать десятичную дробь в виде процентов:

1,07▪100%=107%;

На следующем уроке конструируются схемы решения трех «классических» задач на проценты:

На этом уроке происходит отработка навыков решения классических задач на проценты. Используются материалы открытого банка заданий ОГЭ. Проводится первичный контроль; пример самостоятельной работы: 1).В школе 300 учащихся, 80% из них занимаются в кружках. Сколько учеников занимаются в кружках ? 2).160 школьников занимаются спортом, что составляет 40% от всех учеников школы. Сколько учеников в школе ? 3).Из 400 учащихся школы 280 посещают кружки. Сколько процентов учащихся не посещают кружки ?

Пора переходить к решению более сложных задач. Решение более сложных задач предполагает умение пятиклассников пользоваться правилами упрощения выражений, иметь навыки решения сложных уравнений и действий с десятичными и обыкновенными дробями.

№1.До снижения цен холодильник стоил 25 000 руб., а после снижения стал стоить 23 000 руб. На сколько процентов снизилась стоимость холодильника ?

Решение.

1). 25000-23000=2000(руб)

2). 2000:25000=0,08.

3). 0,08▪100%=8%.

Ответ. 8%.

№2.В коробке лежали одинаковые карандаши. Сначала из коробки взяли 30% карандашей, а затем 50% остатка. После этого в коробке осталось 14 карандашей. Сколько карандашей было в коробке первоначально ?

Решение.

Пусть в коробке было первоначально х (шт) карандашей (14˂х).

1). 30%:100%=0,3.

2). 50%:100%=0,5.

3). Составляем уравнение: х-0,3х-0,5(х-0,3х)=14,

0,7х-0,5▪0,7х=14,

0,7х(1-0,5)=14,

0,7х▪0,5=14,

0,35х=14,

х=40.

Ответ 40.

№3.Когда проложили 1/3 новой дороги и еще 21 км, то осталось проложить 20% всей дороги. Найти длину всей дороги.

Решение.

С наиболее способными учениками можно разобрать задания из открытого банка ОГЭ и ЕГЭ:

№1. В таб­ли­це при­ве­де­на сто­и­мость работ по по­крас­ке по­тол­ков.

Поль­зу­ясь дан­ны­ми, пред­став­лен­ны­ми в таб­ли­це, опре­де­ли­те, ка­ко­ва будет сто­и­мость работ, если пло­щадь по­тол­ка 40 м2, по­то­лок цвет­ной и дей­ству­ет се­зон­ная скид­ка в 10%. Ответ ука­жи­те в руб­лях.

Ответ. 3240 руб.

№2.Одна таблетка весит 20 мг и содержит 14% активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 1,05 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток такого лекарства следует дать ребенку весом 8 кг в течении суток?

Решение.

20 ∙ 0,14 = 2,8 (мг) активного вещества в 1 таблетке

8 ∙ 1,05 = 8,4 (мг) – активного вещества нужно в сутки ребенку

8,4 : 2,8 = 3 (т) нужно ребенку в сутки

Ответ. 3 таблетки.

№3. Имеется 2 сплава. Первый содержит 5% никеля, второй – 25% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение.

Составим уравнение

0,05х+0,25(250-х)=0,2∙250, 0,05х – 0,25х = 50 — 62,5, х = 62,5 (кг) – 1 сплав

250 — 62,5 = 187,5 (кг) – 2 сплав.

Масса первого сплава будет меньше второго сплава на 125 кг.

Ответ. 125 кг.

Использование описанного подхода позволяет добиваться формирования прочных и осознанных знаний и навыков обучающихся по теме «Проценты».

Литература

www.fipi.ru

Буслаев А. Сложные проценты.//Математика.-2002-№30. С.29.

Виленкин Н.Я. Математика. Учебник для 5 класса.-М.:Дрофа,2016.

Захарова А.Е. Несколько задач «про цены ». //Математика в школе.-2002-№8.

Канашева Н.А. О решении задач на проценты.//Математика в школе.-1995-№5.

Усов Н.А. Повторим математику. – Киев, 1994 Дорофеев, Г. В., Седова, Е. А. Процентные вычисления. 10-11 классы: учеб.-метод. пособие. – М.: Дрофа, 2003. – 144 с.

Энциклопедический словарь юного математика/ Сост. Э-68 Савин А.П.. — М.: Педагогика, 1989. -352 с.

ПРИЛОЖЕНИЕ

Самостоятельные работы по теме «Проценты»

Самостоятельная работа №1

а) перевести в проценты:

б) перевести в десятичную дробь: 10%, 131%; 0,5%; 0,02%; 500%.

2. Дан прямоугольник:

Если его площадь принять за 100%, то площади других прямоугольников будут составлять:

а) ________% б) ________%

в) ______% г) _____%.

Самостоятельная работа №2

Задача № 1

Из овса получается 40% муки. Сколько муки получится из 26,5 т овса?

Задача № 2

Засеяли 65% поля, что составляет 325 га. Найдите площадь всего поля.

Задача № 3

В старших классах 120 учащихся. Из них 102 ученика работали летом на ферме. Сколько процентов учащихся старших классов работали летом на ферме?

Самостоятельная работа №3

Вариант I

1. В первый день вспахали 100 га, во второй 150 га. Сколько процентов всей этой площади вспахали в первый день?

2. Никелевая руда содержит 4% никеля. Сколько никеля содержится в 150 т такой руды?

3. Заасфальтировав 27,5 км дороги, ремонтники тем самым выполнили 25% плана. Сколько километров дороги надо заасфальтировать по плану?

4. В двух корзинах по 25 кг винограда. Вначале из первой корзины взяли 20% имевшегося там винограда и положили его во вторую корзину. Потом из второй корзины взяли 20% оказавшегося там винограда и положили в первую. В какой корзине винограда больше и насколько?

Вариант II

1. В первую смену засеяли 270 га, а во вторую – остальные 180 га. Сколько процентов всей площади засеяли в первую смену?

2. В железной руде содержится 54% железа. Сколько тонн железа содержится в 475 т такой руды?

3. Ученик прочитал 35 страниц. Это составляет 17,5% книги. Сколько страниц в книге?

4.В двух корзинах по 32 кг яблок. Вначале из первой корзины взяли 25% имевшихся там яблок и положили их во вторую корзину. Потом из второй корзины взяли 25% оказавшихся там яблок и положили их в первую. В какой корзине яблок стало больше и насколько?

Самостоятельная работа №4 (по материалам ОГЭ)

1.Поступивший в продажу в январе мобильный телефон стоил 4400 рублей. В апреле он стал стоить 3080 рублей. На сколько процентов снизилась цена на телефон ?

2.Магазин одежды проводит акцию. Любая футболка стоит 500рублей. При покупке двух футболок – скидка 80% на вторую футболку. Сколько рублей придется заплатить за покупку двух футболок в период действия акции ?

3.Стоимость проезда в электричке составляет 132 рубля. Ученикам предоставляется скидка 50%. Сколько рублей будет стоить проезд двух взрослых и 15 учеников ?

4.Плата за телефон составляет 420 рублей в месяц. В следующем году она увеличится на 4%. Сколько рублей придется платить за телефон ежемесячно в следующем году ?

5.Для приготовления фарша взяли говядину и свинину в отношении 22:3. Сколько процентов фарша составляет говядина ?

6.Средний вес мальчиков того же возраста, что и Сергей, равен 46кг. Вес Сергея составляет 125% среднего веса. Сколько килограммов весит Сергей ?

7.В начале года число абонентов телефонной компании составляло 40 тыс. человек, а в конце года их стало 41 тыс. чел. На сколько процентов увеличилось за год число абонентов этой компании?

8.Товар на распродаже уценили на 20%, при этом он стал стоить 1040рублей. Сколько рублей стоил до распродажи ?

9.Что больше: 5% от 7 или 7% от 5 ?

10.Свежие фрукты содержат 68% воды, а высушенные – 22%. Сколько сухих фруктов получится из 68 кг свежих фруктов ?

Самостоятельная работа №5

Время выполнения: 30 минут (с записью решения)

Критерии оценивания:

10

Проблемы при решении задач с  процентами в  школьном курсе.

(учитель математики ГБОУ школа №93 Пушкинского района города Санкт-Петербурга Макарова Наталья Геннадьевна)

        Мы привыкли к тому, что понятие процент – это математический термин. Вследствие чего у многих учащихся сложилось мнение, что изучать эту непростую тему нужно только на уроках математики. Однако, это далеко не так. На сегодняшний день проценты встречаются практически на всех предметах школьного курса. Более того, они становятся неотъемлемой частью нашей повседневной жизни.

        Уже давно математика стала общепризнанным языком науки и техники, а в последнее время с развитием информационных технологий все глубже проникает во все направления современной реальности. В процентах выражают объем работы, производительность труда, экономию материалов, топлива, электроэнергии. В физике, химии, метеорологии, технике, статистике, при всевозможных банковских расчетах широко используют это понятие. Итоги избирательной кампании подводят тоже в процентах, все показатели состояния здоровья человека фиксируют в процентном отношении от нормы. И это еще далеко не все… Сейчас процент становится универсальной единицей измерения разных величин и объектов.

        Однако, несмотря на широкий спектр применения, большинство школьников не только не справляется с решением задач на проценты, но и даже смутно представляет, какой смысл у этого понятия. Из собственного опыта могу утверждать, что многие учащиеся среднего звена при слове «процент» представляют себе какой-то термин, искусственно введенный непонятно зачем. Основная проблема изучения этой темы, на мой взгляд, заключается в том, что  в школьном курсе ей отводится место только в 5- 6 классах. В дальнейшем особое внимание задачам на проценты не уделяется, хотя при сдаче ГИА проверяется непосредственное умение их решать.  В связи с этим, главной  целью учителя при первоначальном введении этого понятия становится донести до школьников, что процент – одна сотая часть числа, т.е. просто частный вид записи десятичных дробей. А это значит, что работать с процентами можно по тем же правилам, что и с дробями. Усвоению материала значительно помогает историческое сопровождение. Рассказ о появлении процентов в Древнем Риме в качестве обозначения долга, происхождении самого слова и значка «%», о развитии этого понятия от торговли и денежных сделок до способа передачи информации в науке и технике позволяет сформировать у учащихся представление о проценте, как о сотой части числа. Немаловажное значение в этот момент отводится также обязательным тренировкам перевода процентов в десятичные дроби и обратно, четкому осознанию, что 25% — это четверть числа, а 50% — половина.

        После введения понятия процент в школьном курсе предлагаются задачи на нахождение процента от числа, числа по его проценту и процентного содержания одного числа от другого. К сожалению, несмотря на выученные алгоритмы решения, успешно справляются с поставленными проблемами далеко не все учащиеся. В первую очередь, это связано с неумением классифицировать задачи. Выбрать умножение или деление при работе с процентом от числа или числом по проценту, или правильно выбрать числа, которые нужно поделить друг на друга при вычислении процентного отношения, является для школьников сложной задачей. Хорошим подспорьем тут может стать введение пропорций. Однако при этом решении возникают свои трудности: учащиеся не всегда могут правильно выбрать число, берущееся за 100%.

        Надо отметить, что даже успешное освоение рассмотренных выше базовых задач не гарантирует, что школьник справится с заданиями на проценты, предлагаемыми при сдаче ГИА: на «концентрацию», «сплавы», «банковские расчеты». Полноценную практику для подготовки к этим задачам в 5-6 классах организовать невозможно ввиду ограниченности к данному моменту изученного математического аппарата, а сами по себе проценты не дают ни экономического представления, ни понимания химических и физических процессов. Их знание только помогает развитию практических способностей. Поэтому для учащихся 5-7 классов очень полезно предлагать  задания для представления информации в виде таблиц и диаграмм, а позднее и вероятностно-статистического материала с помощью процентов. Подобная деятельность является прекрасным способом не только усовершенствовать навыки вычислений процентов, но и в свете выполнения требований ФГОС развивать компетенции практической направленности. Такие задания на первых этапах можно рассматривать и как подготовку к проектной или исследовательской деятельности.

        В старших классах, когда уже запас алгебраических знаний довольно обширен, можно найти им прекрасное практическое применение на экономических задачах, задачах на «сплавы» и «концентрацию». Проблема только в том, что часов на проработку в школьном курсе уже нет.  Конечно, можно найти готовые формулы для тех или иных понятий, но дело в том, что на экзамене подразумевается, что учащиеся должны уметь решать задачи, опираясь не на заучивание правил, а на понимание практического смысла процента. Тут возникает вопрос о целесообразности введения некоторого спецкурса по этой теме: ведь знания, полученные на уроках в 5-6 классах, необходимо восстановить да еще и применить в новом русле. Конечно, далеко не все школы могут себе это позволить. В таком случае можно попробовать реализовать данную идею через проектную деятельность, которая становится обязательным условием получением аттестата об основном среднем образовании. Большую роль в формировании экономической математической грамотности может сыграть работа, например, по сбору предложений магазинов и банков, просчету реальных сумм, анализу результатов и выбору из них наиболее выгодных предложений.

        Подводя итог, хочется отметить, что  задачи с процентами, вопреки бытующему мнению, не так уж и страшны. Главное, начать убеждать в этом учащихся как можно раньше и проводить эту работу систематически.  

Содержание

1. Что такое процент
2. Как вычесть проценты
3. Примеры решения задач с процентами
4. Как рассчитать процентное изменение
5. Распространенные ошибки при решении задач с процентами

Эта
статья посвящена решению задач на проценты. Ниже рассмотрены некоторые из этих задач.
Большинство задач на проценты связаны с нахождением процента от числа,
нахождением числа в процентах, представлением части в процентах или
представлением отношения между несколькими объектами, числами или величинами в
процентах.

Что такое процент

Процент — это способ расчета того, сколько
чего-то есть по отношению к целому.

Проценты очень широко используются как в математике, так и в
повседневных ситуациях, и они действительно полезны для понимания относительных
величин и привнесения их значимых.

Процент может быть записан несколькими способами. Один
из способов — изобразить его как десятичную дробь. Например, 24% также могут
быть записаны как 0,24. Можно найти десятичную версию процента, разделив
процент на 100.

Вот несколько распространенных способов использования
процентов в повседневной жизни:

• расчет
  того, насколько хорошо студент сдал тест;
• выяснение
  того, сколько НДС нужно заплатить при покупке;
• расчет
  того, сколько оставить в качестве чаевых в ресторане.

Проценты обычно представлены символом %, и
есть несколько основных правил, которые нужно понять, чтобы их правильно
рассчитать.

Процентные задачи —
это общие, повседневные реальные математические задачи. Таким образом, выделяют
три типа решений, о которых следует знать:

1. Поиск
   процента от целого (отсутствующая переменная — это часть, которая
   составляет заданный процент).
2. Поиск
   целого из процента (отсутствующей переменной является целое, из которого
   была взята процентная часть).
3. Поиск
   процента от целого и части (отсутствующей переменной является процентная
   сумма, равная соотношению детали к целому).

Используя процентную формулу, легко понять, как быстро
решить процентные проблемы. Нужно помнить, что общая алгебраическая формула
процента:%?В=П.

Формула
для поиска процента

Как указано, процент — это соотношение
желаемой детали по сравнению со всем продуктом, где100%представляет собой весь процент. Формула для поиска процента может быть записана математически как: П/В =%/100

Где:

• П — это
  часть.

• В — это
  все.

• % — это
  процент.

Как вычесть проценты

Чтобы вычесть один процент из другого, просто нужно игнорировать процентные знаки и относиться к ним как к целым числам.

Например, чтобы вычесть 20% из 50%, нужно сделать следующее: 50 – 20 = 30. Ответ — 30%.

Если вычитается процент из целого числа, сначала нужно преобразовать его в десятичную дробь.

Если попросят вычесть 25% из 45 (например, при расчете скидки), то нужно начать с преобразования 25% в десятичную дробь, что составляет 0,25.

Чтобы рассчитать сумму, которую следует вычесть, нужно умножить исходное число на десятичную дробь:

45 x 0,25 = 11,25

Затем вычесть эту сумму из базовой цифры:

45 — 11,25 = 33,75

Также можно взять десятичную дробь, вычесть ее из 1, а затем умножить
исходное число на него:

25% = 0,25

1 — 0,25 = 0,75

0,75 x 45 = 33,75

Примеры решения задач с процентами

Решенные образцы
задач с процентами помогут понять, как шаг за шагом решить различные
типы таких задач.

1. На выборах кандидат О получил 75% от общего числа
действительных голосов. Если 15% от общего числа голосов были признаны
недействительными, а общее количество голосов составляет 560000, нужно найти
количество действительных голосов, опрашиваемых в пользу кандидата.

Решение выглядит следующим образом:

Общее
количество недействительных голосов = 15% из 560000

= 15/100 ?
560000

= 8400000/100

= 84000

Общее
количество действительных голосов 560000 — 84000 = 476000

Процент
голосов, проголосовавших за кандидата А = 75%

Следовательно,
количество действительных голосов, проголосовавших за кандидата А = 75% от
476000

= 75/100 ?
476000

= 35700000/100

= 357000

2. У Гриши осталось 2100 рублей после того, как он потратил
30% денег, которые он взял в магазин. Сколько денег он взял с собой?

Пример решения:

Пусть деньги,
которые он взял в магазин, будут м.

Деньги,
которые он потратил = 30% от м

= 30/100 ? м

= 3/10 м

Деньги,
оставшиеся у него = м — 3/10 м = (10 м — 3 м)/10 = 7 м/10

Но деньги
остались у него = 2100 рублей.

Поэтому 7 м/10
= 2100 рублей.

м = 2100
рублей ? 10/7;

м = $ 21000/7;

м = 3000
рублей;

Таким образом,
деньги, которые он взял на покупки, составляют 3000 рублей.

3. Владелец магазина купил 600 яблок и 400 авокадо. Он
обнаружил, что 15% яблок и 8% авокадо были гнилыми. Нужно найти процент фруктов
в хорошем состоянии.

Решение:

Общее
количество купленных фруктов в магазине = 600 + 400 = 1000

Количество
гнилых яблок = 15% от 600

= 15/100 ? 600

= 9000/100

= 90

Количество
гнилых авокадо = 8% от 400

= 8/100 ? 400

= 3200/100

= 32

Следовательно,
общее количество гнилых фруктов = 90 + 32 = 122

Поэтому
количество фруктов в хорошем состоянии = 1000 — 122 = 878

Итак, процент
фруктов в хорошем состоянии = (878/1000 ? 100)%

=
(87800/1000)%

= 87,8%

4. На экзаменах было два
студента. Один из них получил на 9 баллов больше, чем другой, и его оценки
составили 56% от суммы их баллов. Итак, чему равны полученные ими баллы.

Решение: пусть их отметки будут (x +
9) и x.

Затем x + 9 = 56 (x +
9 + x) 100 25 (x + 9) = 14 (2x
 + 9);

3x = 99;

x = 33.

Итак, их баллы 42 и 33.

5. . Население города
увеличилось с 1 75 000 до 2 62 500 человек за десятилетие. Среднепроцентный
прирост населения в год?

Решение: увеличение через 10 лет =
(262500 — 175000) = 87500.

Увеличение %= (87500/175000 * 100)=50%

Требуемое среднее = (50/10)% = 5%

Как рассчитать процентное изменение

Процентное изменение равно изменению
данного значения. Можно найти его, разделив все значение на исходное значение,
а затем умножив его на 100. Формула решения задачи на процентное изменение следующая:

Для цены или процентного увеличения:

[(Новая цена — старая цена)/Старая цена] x
100;

Для снижения цены или процента:

[(Старая цена — новая цена)/Старая цена] x
100;

Вот пример увеличения цены/процента:

Телевизор стоил 100 тысяч рублей в прошлом
году, но теперь стоит 125 тысяч рублей. Чтобы определить повышение цены, нужно
вычесть старую цену из новой цены: 125 — 100 = 25. Затем разделить это на
старую цену: 25 разделить на 100 равно 0,25. Затем умножить это число на 100:
0,25 x 100 = 25, или 25%. Таким образом, цена на телевизор выросла на 25% за
последний год.

Пример снижения цены/процента:

В прошлом году телевизор стоил 100 тысяч
рублей, но теперь стоит всего 75 тысяч рублей. Чтобы определить снижение цены, нужно
вычесть новую цену из старой цены: 100 — 75 = 25. Затем разделить это число на
старую цену: 25 разделить на 100 равно 0,25. Затем умножить на 100: 0,25 x 100
= 25 или 25%. Это означает, что телевизор стоит на 25% меньше, чем в предыдущем
году.

Распространенные ошибки при решении задач с процентами

Рассмотрим наиболее распространенные ошибки:

• При
  сравнении процентов нужно убедиться, что есть общий базовый
  уровень (в противном случае проценты не будут связаны друг с другом).
• Одной из
  задач, в которой многие часто ошибаются, является увеличение процента
  из года в год. Например, у Алины 10 рублей, и каждый год это число увеличивается
  на 5%. Сколько у нее будет через 3 года? У некоторых людей может
  возникнуть соблазн сложить 5% в течение 3 лет, т.е. 15% и умножить 10 рублей
  на 15%. Это неправильно. Правильный способ решения таких задач — помнить,
  что каждый год начальные 10 рублей увеличивались на 5%. Таким образом, в
  конце первого года у Алины будет 10 рублей x 1,05 = 10,5 рублей. В конце 2
  года у нее будет 10,5 рублей x 1,05 = 11,025 и так далее. Важно добавить в
  каждый из этих шагов, чтобы получить правильный ответ.

Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со
всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.

Чтобы успешно сдать экзамен, подготовку нужно начинать заранее. И если вы не можете самостоятельно определить свои слабые места и проблемы, рекомендуем начать с разбора типичных ошибок ЕГЭ и ОГЭ по математике.

Здесь мы приведем анализ типичных ошибок 2023 и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.

Базовый уровень математики

Ошибки в задачах на проценты

Чаще всего их допускают, так как не разбираются в сути процента.

Возьмем пример задачи, когда нужно сначала снизить цену на 25%, а потом повысить ее на 25%. Самая частая ошибка – полагать, что эти проценты будут равны одной и той же сумме. На самом же деле база их зачисления будет совершенно разной.

В этом примере 6% участников допустили вариант, что новую цену нужно понизить на 25%. На самом же деле новая цена – это 125% от старой. И вопрос в этой задаче – узнать, сколько будет 100% от старой цены.

Совет: повторить основы расчета процентов, повторить взаимосвязи величин, подумать над способом решения таких задач.

Невнимательное прочтение условия задания

Волнение и психологическое напряжение приводят к тому, что участники часто неправильно понимают условие задания. В итоге – снижение итогового балла по невнимательности, а не по незнанию.

Например:

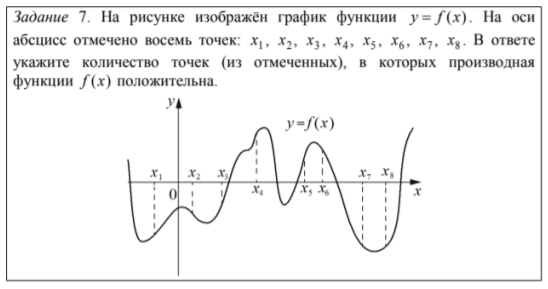
В 24% участников упомянули те точки, где значение функции (а не производной) положительное. Еще 2% указали номера точек, где производная принимает положительное значение.

Совет: вдумчиво, медленно и несколько раз читайте задание.

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Учащиеся могут не только неправильно понять, но и вовсе не понять условия. Иногда это происходит из-за незнания величин, единиц их измерения или плохой работы с формулами. Многие просто пропускают эту часть тестирования.

Вот пример задачи:

Её выполнило только 57% участников тестирования. 8% вообще не дали ответа, 6% дали ответ «чем ближе, тем лучше», 4% – «лампочку необходимо поместить в середину разрешенного интервала», еще 4,5% приняли фокус за основной параметр.

Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.

Ошибки в вычислениях

Школьная привычка использовать даже в самых легких примерах калькулятор приводит к плачевному результату на экзамене. Если учащийся не научиться быстро считать в уме или хотя бы на бумаге, во время тестирования он может ошибиться даже в самых простых заданиях. 

Особенно сложно участникам тестирования даются дроби, отрицательные числа, элементарные преобразования выражений и другие проблемы, копившиеся еще с 5 класса.

Совет: если в чем-то не разбираетесь, обязательно отработайте эту тему до автоматизма перед экзаменом, потому что она обязательно попадется.

Ошибки теоретического характера

Это касается фактов по геометрии и алгебре, незнание которых приводит к снижению процента выполнения заданий и базового, и профильного уровней.

Например:

В этой задаче около 8% участников вообще не ответили на поставленное условие, 38% дали ответ с ошибками относительно боковой поверхности конуса, а 12% совершили ошибки в расчёте объёма.

Статистика показывает, что в таких заданиях ошибок гораздо больше, чем в гораздо более сложных профильных заданиях. 

Совет: потренируйтесь перед тестированием. Если ответы не сходятся с ключами, обратитесь за помощью к стороннему специалисту (репетитору или сервису студенческой помощи), чтобы они указали, где вы ошибаетесь.

Ошибки в алгоритмах и методах решения

Этот тип ошибок встречается во всех заданиях.

Например:

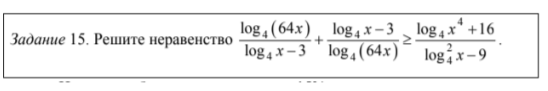
Около 15% участников получили нулевые баллы из-за проблем с невнимательным чтением неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств.

Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.

Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.

Ошибки в чтении и построении чертежа

Такое случается, когда ученик не понимает взаимосвязь элементов геометрических конструкций, а также не обладает основными пространственными представлениями. 

Например:

Около 10% участников экзамена сделали ошибки в вычислении углов по их записи, просто перепутав буквы или не понимая, где расположены вершины всех углов. Еще 5% решили, что угол ACD прямой. А 3% увидели в угле ABD равносторонний треугольник. 

Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.

Неумение обосновывать и доказывать

14 и 16 задания по стереометрии и планиметрии отличаются повышенным уровнем сложности и требуют развернутого ответа. В каждом по 2 пункта: в первом нужно доказать, во втором – произвести вычисления. 

Самые распространенные ошибки касаются первого пункта, так как у участников выявились проблемы с умением доказывать.

Есть проблемы и в оформлении доказательств. Например:

Основная трудность в отсутствии понимания логики построения доказательства.

Совет: тренируйтесь в доказательной базе, повышайте математическую культуру, учитесь обосновывать выбранные методы и способы их решения.

Ошибки в заданиях по тригонометрии

Из-за невнимательности и неаккуратности, а также отсутствия знаний по большому количеству теоретических фактов и способности их применять на практике, участники совершают частые ошибки в решении тригонометрических заданий.

Например:

Только 34% участников выполнили его. Самые частые ошибки (около 12%) связаны в первую очередь с нахождением тригонометрического знака – чаще всего потеря знака «минус». Еще 22% ждут «красивого» ответа, равного 1 или 2.

Ошибки математического моделирования

В 11 и 17 заданиях проверяют способность учащихся к построению и исследованию простейших математических моделей. 

В текстовых задачах основную роль играет сюжетная часть – она имеет практическую ориентацию. И часто из-за непонимания взаимосвязи величин в этих заданиях допускают ошибки.

Например, в задачах на движение примерно 10% не понимают принципы движения по реке – они умножают собственную скорость на время движения.

Совет: тренируйте текстовые задачи, внимательно читайте условие задачи. 

Профильный уровень

Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:

1. Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей.
2. Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры).
3. Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже.
4. Задание 8 – ошибаются в наглядном решении. 
5. Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики.
6. Задание 12 – ошибаются в задачах с нулями производной.

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

Есть несколько рекомендаций, чтобы избежать ошибок из-за невнимательного прочтения задания. Это и будет алгоритмом решения задачи:

• прочтите условие;
• выпишите данные величины, сделайте рисунок в геометрическом задании;
• установите и запишите отношения и взаимосвязи между известными данными;
• выпишите что найти, ответ на какой вопрос нужно дать;
• определите тип задания;
• сформулируйте содержание и последовательность действий.

Это будет ваш своеобразный чек-лист, который обязательно нужно соблюдать при решении любой задачи, чтобы не допустить обидных ошибок. 

Данные условия важно именно выписывать, а не иметь в виду. Фиксация их в уме чаще всего приводит к записи неправильного ответа.

И еще момент: не приступайте к решению задачи сразу же после ее прочтения. Психологи утверждают, что важно выдержать паузу между стимулом и реакцией – именно при этом условии удастся добиться оптимальных результатов:

• сориентироваться в условии,
• обдумать и спланировать ее решение,
• понять уровень ее сложности и решить, откладывать ли ее решение напоследок. 

Кроме сложности задачи оцените, сколько баллов она принесет и насколько она утомительна. Важно оставить энергию для решения других заданий при сдаче единого государственного экзамена.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Знание типичных ошибок ЕГЭ и ОГЭ по математике даст вам полную картину того, к каким заданиями нужно готовиться с большим усилием. А чтобы не отвлекаться на другие учебные дела, не забывайте: рядом есть сервис студенческой помощи, который подставит плечо в трудную минуту.