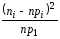В практических задачах часто требуется проверить то или иное предположение относительно
каких-нибудь свойств закона распределения наблюдаемой случайной величины X. Для проверки этого предположения
исследователь проводит эксперимент, в результате которого получает реализацию x1,…,xn
случайной выборки X1,…,Xn из генеральной совокупности X. По этим данным ему
нужно дать ответ на вопрос: согласуется ли его гипотеза с результатами эксперимента или нет? Другими словами, исследователю
нужно решить, можно ли принять выдвинутую гипотезу или её нужно отклонить как противоречащую результатам эксперимента.
Любое предположение относительно параметров или закона распределения наблюдаемой случайной
величины (или нескольких величин) называется статистической гипотезой. Проверяемую статистическую гипотезу также
называют основной, или нулевой, статистической гипотезой и, как правило, обозначают H0.
Наряду с проверяемой статистической гипотезой H0 выдвигают также
конкурирующую гипотезу, противоречащую H0. Конкурирующая гипотеза называется альтернативной и, как
правило, обозначается H1 или H’. Если в результате статистического анализа делается вывод, что
основная гипотеза H0 должна быть отвергнута, то решение принимается в пользу альтернативной
гипотезы H’. В простейшем случае альтернативная гипотеза – это отрицание основной гипотезы.
Статистическая гипотеза H0 называется простой, если она
однозначно определяет параметр или распределение наблюдаемой случайной величины X. В противном случае
гипотеза H0 называется сложной.
Если статистическая гипотеза H0 представляет собой утверждение о
некотором параметре q известного распределения случайной величины X, то гипотеза называется параметрической.
В противном случае гипотеза называется непараметрической.
![]() Пример 1
Пример 1
![]() Пример 2
Пример 2
Статистическое решение, т.е. решение о принятии или отклонении основной
гипотезы H0, проводится в соответствии с некоторым критерием.
Статистическим критерием, или решающим правилом, при проверке статистической
гипотезы H0 называется правило, в соответствии с которым гипотеза H0 принимается или
отвергается.
Статистическая гипотеза – это всегда утверждение о свойствах наблюдаемой генеральной
совокупности, а задача проверки статистической гипотезы состоит в проверке соответствия результатов
эксперимента x1,…,xn выдвинутой гипотезе. Иными словами, задача проверки
статистической гипотезы состоит в ответе на вопрос: могло ли случиться так, что выборка x1,…,
xn была получена из генеральной совокупности с указанными в гипотезе свойствами?
Как правило, статистический критерий связывают с некоторой статистикой Z,
являющейся функцией случайной выборки X1,…,Xn. Эта статистика служит мерой,
насколько наблюдаемые выборочные значения могли быть получены из генеральной совокупности с указанными в основной
гипотезе свойствами. Вопрос о том, какую статистику Z следует взять для проверки той или иной статистической
гипотезы, не имеет однозначного ответа. Это может быть любая статистика, удовлетворяющая следующим требованиям:
1)
закон распределения FZ(z | H0) при условии истинности основной
гипотезы H0 должен быть известен;
2)
закон распределения должен быть чувствителен к факту справедливости основной или альтернативной гипотезы, т.е. законы
распределения FZ(z | H0) и FZ(z | H’)
должны существенно различаться.
Для реализации x1,…,xn случайной
выборки X1,…,Xn, статистика Z примет реализацию z. Предположим, что
гипотеза H0 верна. В связи с тем, что закон распределения статистики Z при условии истинности
основной гипотезы H0 известен, то возможно рассчитать вероятность её попадания в некоторую окрестность
точки z. Если эта вероятность высока, это означает, что ничто не противоречит предположению об истинности
гипотезы H0. Если же эта вероятность мала или близка к нулю, то это может означать один из двух
вариантов:
1)
в условиях основной гипотезы H0 произошло практически невозможное событие;
2)
статистика Z на самом деле имеет некоторый другой закон распределения, отличный
от FZ(z | H0), при котором вероятность её попадания в окрестность
точки z много больше нуля. Это означает, что предположение об истинности гипотезы H0 сделано
неверно.
Статистика $ Z=Z({{X}_{1}},…,{{X}_{n}}) $, на основе реализации
которой $z=Z({{x}_{1}},…,{{x}_{n}})$ выдвигается статистическое решение, называется статистикой
критерия (test statistics). Реализация статистики критерия $z=Z({{x}_{1}},…,{{x}_{n}})$,
рассчитанная для выборки x1,…,xn, называется выборочным значением статистики
критерия.
Проверка статистических гипотез основывается на принципе, в соответствии с которым маловероятные
события относительно статистики критерия Z считаются невозможными. В соответствии с этим принципом, если
вероятность попадания статистики критерия Z в окрестность рассчитанного выборочного значения z мала, то
должен выбираться вариант 2), т.е. основная гипотеза H0 отклоняется.
Область Ω0 наиболее вероятных значений статистики критерия Z, при
попадании выборочных значений z в которую основная гипотеза H0 принимается, называется областью
допустимых значений статистики критерия Z.
Область Ω’ маловероятных значений статистики критерия Z, при попадании выборочных
значений z которую основная гипотеза H0 отклоняется, называется критической областью
значений статистики критерия Z. Множество ${{Omega }_{0}}cup Omega ‘$ должно являться множеством всех возможных
значений статистики критерия Z.
Из определений области допустимых значений и критической области следует статистический
критерий проверки гипотезы H0: если выборочное значение статистики критерия $zin {{Omega }_{0}}$,
то основная гипотеза H0 принимается, если выборочное значение статистики
критерия $zin Omega ‘$, то основная гипотеза H0 отвергается.
Пусть для выборки x1,…,xn
статистика критерия Z приняла выборочное значение z, лежащее в критической области Ω’, т.е. вероятность
попадания статистики критерия Z в окрестность которой мала. В соответствии со статистическим критерием основная
гипотеза H0 должна быть отвергнута. Однако событие $zin Omega ‘$, хоть и с малой вероятностью,
но всё же могло произойти в условиях основной гипотезы H0. Если это так, то статистическое решение об
отклонении гипотезы H0 будет ошибочным.
С другой стороны, если для выборки x1,…,xn статистика
критерия Z приняла выборочное значение z, лежащее в области допустимых значений Ω0, это могло
случиться как в условиях основной гипотезы H0 (с высокой вероятностью), так и, возможно, в условиях
альтернативной гипотезы H’ (с низкой вероятностью). В соответствии со статистическим критерием основная
гипотеза H0 принимается. Если же событие $zin {{Omega }_{0}}$ на самом деле произошло в условиях
альтернативной гипотезы H’, то статистическое решение о принятии гипотезы H0 также будет ошибочным.
В обоих случаях говорят об ошибках принятия статистического решения.
Ошибкой 1-го рода при принятии статистического решения называется событие,
состоящее в том, что основная гипотеза H0 отвергается, в то время как она верна.
Ошибкой 2-го рода при принятии статистического решения называется событие,
состоящее в том, что основная гипотеза H0 принимается, в то время как верна альтернативная
гипотеза H’.
![]() Пример 3
Пример 3
![]() Пример 4
Пример 4
Уровнем значимости α при проверке статистической гипотезы называется вероятность
ошибки первого рода:
$alpha =Pleft( Zin Omega ‘|{{H}_{0}} right)$.
Вероятность β ошибки второго рода:
$beta =Pleft( Zin {{Omega }_{0}}|H’ right)$.
Ясно, что с уменьшением вероятности ошибки первого рода возрастает вероятность ошибки
второго рода и наоборот. Это означает, что при выборе критической области и области допустимых значений статистики критерия
должен достигаться определённый компромисс.
Проиллюстрируем сказанное на примере. Пусть основная и альтернативная
гипотезы H0 и H’ являются простыми. Пусть статистики критерия Z при условии истинности
основной гипотезы H0 имеет нормальное
распределение ${{F}_{Z}}(z|{{H}_{0}})sim N({{m}_{1}},{{sigma }_{1}})$, а при условии истинности H’ –
распределение ${{F}_{Z}}(z|{{H}_{0}})sim N({{m}_{2}},{{sigma }_{2}})$.
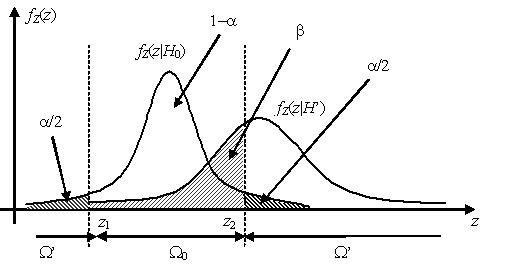
Распределения вероятностей статистики критерия Z при условии истинности основной и альтернативной гипотез
У качестве критической области Ω’ выбраны хвосты
распределения ${{f}_{Z}}(z|{{H}_{0}})$, площадь каждого из которых равна α/2. Вероятность попадания статистики
критерия Z, имеющей распределение ${{f}_{Z}}(z|{{H}_{0}})$, в критическую область, таким образом, равна вероятности
ошибки первого рода α. Вероятность ошибки второго рода β равна площади под графиком функции плотности
распределения ${{f}_{Z}}(z|H’)$ внутри области допустимых значений Ω0. Из графиков видно, что уменьшая
ширину области допустимых значений, площадь a будет увеличиваться, в то время как площадь β – уменьшаться, и наоборот.
Точки на оси значений статистики критерия z, разделяющие область допустимых
значений Ω0 и критическую область Ω’, называются критическими точками. На рисунке выше это
точки z1 и z2, являющиеся квантилями распределения ${{f}_{Z}}(z|{{H}_{0}})$ на
уровнях α/2 и 1 – α/2 соответственно.
В случае если основная и альтернативная гипотезы H0 и H’
являются простыми, величина μ = 1 – β называется мощностью критерия.
Очевидно, что при заданном значении вероятности ошибки первого рода a выбор критической
области Ω’ может быть сделан неоднозначно. Единственное требование, предъявляемое к критической области, состоит в том,
что площадь под графиком известного распределения статистики критерия ${{f}_{Z}}(z|{{H}_{0}})$ в критической области
должна быть равна α. Однако соответствующие различным критическим областям критерии будут иметь, вообще говоря, различные
вероятности β ошибок второго рода.
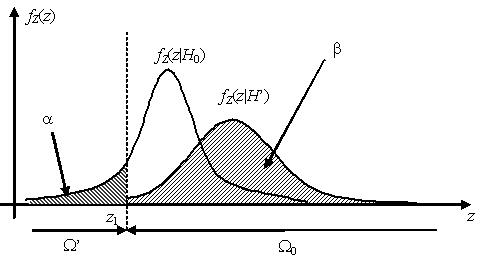
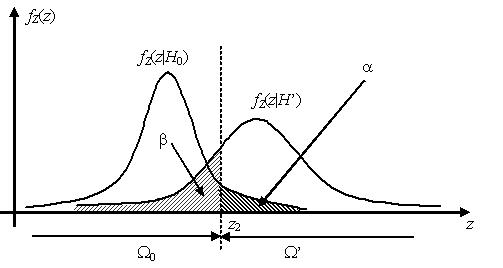
Различные варианты выбора критической области
Наилучшей критической областью (НКО) называют критическую область, которая
при заданном уровне значимости a обеспечивает минимальную вероятность β ошибки второго рода. Критерий, использующий
наилучшую критическую область, имеет максимальную мощность.
Если альтернативная гипотеза является сложной, т.е. не определяет однозначно функцию
распределения FX(x) генеральной совокупности X, а следовательно, и функцию распределения
статистики критерия ${{F}_{Z}}(z|H’)$, а определяет её с точностью до значения некоторого параметра θ, то вводят функцию
мощности критерия μ(θ) как функцию параметра θ. Значение функции мощности критерия μ(θ) в точке θ определяется как
$mu (theta )=1-beta (theta )$,
где β(θ) – вероятность ошибки второго рода при условии, что неизвестный параметр принял
значение θ, θ∈Θ, где Θ – область возможных значений параметра θ.
![]() Пример 5
Пример 5
Функция мощности имеет важное значение в задачах, связанных с оценкой необходимого объёма выборки для обеспечения
требуемой вероятности ошибки второго рода принятия статистического решения при заданной вероятности ошибки первого рода.
В практических задачах часто требуется проверить то или иное предположение относительно
каких-нибудь свойств закона распределения наблюдаемой случайной величины X. Для проверки этого предположения
исследователь проводит эксперимент, в результате которого получает реализацию x1,…,xn
случайной выборки X1,…,Xn из генеральной совокупности X. По этим данным ему
нужно дать ответ на вопрос: согласуется ли его гипотеза с результатами эксперимента или нет? Другими словами, исследователю
нужно решить, можно ли принять выдвинутую гипотезу или её нужно отклонить как противоречащую результатам эксперимента.
Любое предположение относительно параметров или закона распределения наблюдаемой случайной
величины (или нескольких величин) называется статистической гипотезой. Проверяемую статистическую гипотезу также
называют основной, или нулевой, статистической гипотезой и, как правило, обозначают H0.
Наряду с проверяемой статистической гипотезой H0 выдвигают также
конкурирующую гипотезу, противоречащую H0. Конкурирующая гипотеза называется альтернативной и, как
правило, обозначается H1 или H’. Если в результате статистического анализа делается вывод, что
основная гипотеза H0 должна быть отвергнута, то решение принимается в пользу альтернативной
гипотезы H’. В простейшем случае альтернативная гипотеза – это отрицание основной гипотезы.
Статистическая гипотеза H0 называется простой, если она
однозначно определяет параметр или распределение наблюдаемой случайной величины X. В противном случае
гипотеза H0 называется сложной.
Если статистическая гипотеза H0 представляет собой утверждение о
некотором параметре q известного распределения случайной величины X, то гипотеза называется параметрической.
В противном случае гипотеза называется непараметрической.
![]() Пример 1
Пример 1
![]() Пример 2
Пример 2
Статистическое решение, т.е. решение о принятии или отклонении основной
гипотезы H0, проводится в соответствии с некоторым критерием.
Статистическим критерием, или решающим правилом, при проверке статистической
гипотезы H0 называется правило, в соответствии с которым гипотеза H0 принимается или
отвергается.
Статистическая гипотеза – это всегда утверждение о свойствах наблюдаемой генеральной
совокупности, а задача проверки статистической гипотезы состоит в проверке соответствия результатов
эксперимента x1,…,xn выдвинутой гипотезе. Иными словами, задача проверки
статистической гипотезы состоит в ответе на вопрос: могло ли случиться так, что выборка x1,…,
xn была получена из генеральной совокупности с указанными в гипотезе свойствами?
Как правило, статистический критерий связывают с некоторой статистикой Z,
являющейся функцией случайной выборки X1,…,Xn. Эта статистика служит мерой,
насколько наблюдаемые выборочные значения могли быть получены из генеральной совокупности с указанными в основной
гипотезе свойствами. Вопрос о том, какую статистику Z следует взять для проверки той или иной статистической
гипотезы, не имеет однозначного ответа. Это может быть любая статистика, удовлетворяющая следующим требованиям:
1)
закон распределения FZ(z | H0) при условии истинности основной
гипотезы H0 должен быть известен;
2)
закон распределения должен быть чувствителен к факту справедливости основной или альтернативной гипотезы, т.е. законы
распределения FZ(z | H0) и FZ(z | H’)
должны существенно различаться.
Для реализации x1,…,xn случайной
выборки X1,…,Xn, статистика Z примет реализацию z. Предположим, что
гипотеза H0 верна. В связи с тем, что закон распределения статистики Z при условии истинности
основной гипотезы H0 известен, то возможно рассчитать вероятность её попадания в некоторую окрестность
точки z. Если эта вероятность высока, это означает, что ничто не противоречит предположению об истинности
гипотезы H0. Если же эта вероятность мала или близка к нулю, то это может означать один из двух
вариантов:
1)
в условиях основной гипотезы H0 произошло практически невозможное событие;
2)
статистика Z на самом деле имеет некоторый другой закон распределения, отличный
от FZ(z | H0), при котором вероятность её попадания в окрестность
точки z много больше нуля. Это означает, что предположение об истинности гипотезы H0 сделано
неверно.
Статистика $ Z=Z({{X}_{1}},…,{{X}_{n}}) $, на основе реализации
которой $z=Z({{x}_{1}},…,{{x}_{n}})$ выдвигается статистическое решение, называется статистикой
критерия (test statistics). Реализация статистики критерия $z=Z({{x}_{1}},…,{{x}_{n}})$,
рассчитанная для выборки x1,…,xn, называется выборочным значением статистики
критерия.
Проверка статистических гипотез основывается на принципе, в соответствии с которым маловероятные
события относительно статистики критерия Z считаются невозможными. В соответствии с этим принципом, если
вероятность попадания статистики критерия Z в окрестность рассчитанного выборочного значения z мала, то
должен выбираться вариант 2), т.е. основная гипотеза H0 отклоняется.
Область Ω0 наиболее вероятных значений статистики критерия Z, при
попадании выборочных значений z в которую основная гипотеза H0 принимается, называется областью
допустимых значений статистики критерия Z.
Область Ω’ маловероятных значений статистики критерия Z, при попадании выборочных
значений z которую основная гипотеза H0 отклоняется, называется критической областью
значений статистики критерия Z. Множество ${{Omega }_{0}}cup Omega ‘$ должно являться множеством всех возможных
значений статистики критерия Z.
Из определений области допустимых значений и критической области следует статистический
критерий проверки гипотезы H0: если выборочное значение статистики критерия $zin {{Omega }_{0}}$,
то основная гипотеза H0 принимается, если выборочное значение статистики
критерия $zin Omega ‘$, то основная гипотеза H0 отвергается.
Пусть для выборки x1,…,xn
статистика критерия Z приняла выборочное значение z, лежащее в критической области Ω’, т.е. вероятность
попадания статистики критерия Z в окрестность которой мала. В соответствии со статистическим критерием основная
гипотеза H0 должна быть отвергнута. Однако событие $zin Omega ‘$, хоть и с малой вероятностью,
но всё же могло произойти в условиях основной гипотезы H0. Если это так, то статистическое решение об
отклонении гипотезы H0 будет ошибочным.
С другой стороны, если для выборки x1,…,xn статистика
критерия Z приняла выборочное значение z, лежащее в области допустимых значений Ω0, это могло
случиться как в условиях основной гипотезы H0 (с высокой вероятностью), так и, возможно, в условиях
альтернативной гипотезы H’ (с низкой вероятностью). В соответствии со статистическим критерием основная
гипотеза H0 принимается. Если же событие $zin {{Omega }_{0}}$ на самом деле произошло в условиях
альтернативной гипотезы H’, то статистическое решение о принятии гипотезы H0 также будет ошибочным.
В обоих случаях говорят об ошибках принятия статистического решения.
Ошибкой 1-го рода при принятии статистического решения называется событие,
состоящее в том, что основная гипотеза H0 отвергается, в то время как она верна.
Ошибкой 2-го рода при принятии статистического решения называется событие,
состоящее в том, что основная гипотеза H0 принимается, в то время как верна альтернативная
гипотеза H’.
![]() Пример 3
Пример 3
![]() Пример 4
Пример 4
Уровнем значимости α при проверке статистической гипотезы называется вероятность
ошибки первого рода:
$alpha =Pleft( Zin Omega ‘|{{H}_{0}} right)$.
Вероятность β ошибки второго рода:
$beta =Pleft( Zin {{Omega }_{0}}|H’ right)$.
Ясно, что с уменьшением вероятности ошибки первого рода возрастает вероятность ошибки
второго рода и наоборот. Это означает, что при выборе критической области и области допустимых значений статистики критерия
должен достигаться определённый компромисс.
Проиллюстрируем сказанное на примере. Пусть основная и альтернативная
гипотезы H0 и H’ являются простыми. Пусть статистики критерия Z при условии истинности
основной гипотезы H0 имеет нормальное
распределение ${{F}_{Z}}(z|{{H}_{0}})sim N({{m}_{1}},{{sigma }_{1}})$, а при условии истинности H’ –
распределение ${{F}_{Z}}(z|{{H}_{0}})sim N({{m}_{2}},{{sigma }_{2}})$.

Распределения вероятностей статистики критерия Z при условии истинности основной и альтернативной гипотез
У качестве критической области Ω’ выбраны хвосты
распределения ${{f}_{Z}}(z|{{H}_{0}})$, площадь каждого из которых равна α/2. Вероятность попадания статистики
критерия Z, имеющей распределение ${{f}_{Z}}(z|{{H}_{0}})$, в критическую область, таким образом, равна вероятности
ошибки первого рода α. Вероятность ошибки второго рода β равна площади под графиком функции плотности
распределения ${{f}_{Z}}(z|H’)$ внутри области допустимых значений Ω0. Из графиков видно, что уменьшая
ширину области допустимых значений, площадь a будет увеличиваться, в то время как площадь β – уменьшаться, и наоборот.
Точки на оси значений статистики критерия z, разделяющие область допустимых
значений Ω0 и критическую область Ω’, называются критическими точками. На рисунке выше это
точки z1 и z2, являющиеся квантилями распределения ${{f}_{Z}}(z|{{H}_{0}})$ на
уровнях α/2 и 1 – α/2 соответственно.
В случае если основная и альтернативная гипотезы H0 и H’
являются простыми, величина μ = 1 – β называется мощностью критерия.
Очевидно, что при заданном значении вероятности ошибки первого рода a выбор критической
области Ω’ может быть сделан неоднозначно. Единственное требование, предъявляемое к критической области, состоит в том,
что площадь под графиком известного распределения статистики критерия ${{f}_{Z}}(z|{{H}_{0}})$ в критической области
должна быть равна α. Однако соответствующие различным критическим областям критерии будут иметь, вообще говоря, различные
вероятности β ошибок второго рода.


Различные варианты выбора критической области
Наилучшей критической областью (НКО) называют критическую область, которая
при заданном уровне значимости a обеспечивает минимальную вероятность β ошибки второго рода. Критерий, использующий
наилучшую критическую область, имеет максимальную мощность.
Если альтернативная гипотеза является сложной, т.е. не определяет однозначно функцию
распределения FX(x) генеральной совокупности X, а следовательно, и функцию распределения
статистики критерия ${{F}_{Z}}(z|H’)$, а определяет её с точностью до значения некоторого параметра θ, то вводят функцию
мощности критерия μ(θ) как функцию параметра θ. Значение функции мощности критерия μ(θ) в точке θ определяется как
$mu (theta )=1-beta (theta )$,
где β(θ) – вероятность ошибки второго рода при условии, что неизвестный параметр принял
значение θ, θ∈Θ, где Θ – область возможных значений параметра θ.
![]() Пример 5
Пример 5
Функция мощности имеет важное значение в задачах, связанных с оценкой необходимого объёма выборки для обеспечения
требуемой вероятности ошибки второго рода принятия статистического решения при заданной вероятности ошибки первого рода.
План:
1. Статистические гипотезы. Основные понятия.
2. Гипотезы о законе распределения.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
1.
Статистические гипотезы. Основные понятия.
Статистическая гипотеза— это утверждение о виде неизвестного
распределения или параметрах известного распределения. Статистические гипотезы
проверяются по результатам выборки статистическими методами в ходе эксперимента
(эмпирическим путем) с помощью статистических критериев.
В тех случаях, когда
известен закон, но неизвестны значения его параметров (дисперсия или
математическое ожидание) в конкретной ситуации, статистическую гипотезу
называют параметрической.
Например, предположение
об ожидаемом среднем доходе по акциям или разбросе дохода являются
параметрическими гипотезами.
Когда закон
распределения генеральной совокупности не известен, но есть основания
предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его
распределения называются непараметрическими.
Например, можно
выдвинуть гипотезу, что число дневных продаж в магазине или доход населения
подчинены нормальному закону распределения.
По содержанию статистические гипотезы можно классифицировать:
1.
Гипотезы о типе вероятностного закона
распределения случайной величины, характеризующего явление или процесс.
2.
Гипотезы об однородности двух или более
обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных
совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые
выборочные характеристики различаются между собой статистически значимо или
нет.
3.
Гипотезы о свойствах числовых значений
параметров исследуемой генеральной совокупности. Больше ли значения параметров
некоторого заданного номинала или меньше и т.д.
4.
Гипотезы о вероятностной зависимости двух
или более признаков, характеризующих различные свойства рассматриваемого
явления или процесса. При этом определяется характер этой зависимости.
Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).
Выдвинутую гипотезу называют основной или нулевой и обозначают H0
. Противоречащую ей гипотезу называют альтернативной или конкурирующей и обозначают
H1.
Под статистическим
критерием понимают однозначно определенное правило, устанавливающее
условие, при котором проверяемая гипотеза отвергается либо не отвергается.
Пример:
Увеличение числа заболевших некоторым
заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения
доли заболевших в обычных и экстремальных условиях используются статистические
данные, на основании которых делается вывод о том, является ли данное массовое
заболевание эпидемией. Предполагается, что существует некоторый критерий-
уровень доли заболевших, критический для этого заболевания, который
устанавливается по ранее имевшимся случаям.
Различают три вида критериев:
1.
Параметрические критерии—
критерии значимости, которые служат для проверки гипотез о параметрах
распределения генеральной совокупности при известном виде распределения.
2.
Критерии согласия—
позволяют проверить гипотезы о соответствии распределений генеральной
совокупности известной теоретической модели.
3.
Непараметрические критерии—
используются в гипотезах, когда не требуется знаний о конкретном виде
распределения.
Проверка
параметрических гипотез проводится на основе критериев значимости., а
непараметрических- критериев согласия.
Задача проверки
статистических гипотез сводится к исследованию генеральной совокупности по
выборке. Множество возможных значений элементов выборки может быть разделено на
два непересекающихся подмножества- критическую область и область принятия
гипотезы.
Областью принятия гипотезы или областью допустимых значений Iдоп
называют совокупность значений критерия,
при которых эту гипотезу принимают.
Критической областью
Iкр называют множество значений критерия, при
котором гипотезу отвергают.
Наблюдаемые значения критерия (статистика)
Kнабл
называют такое значение критерия, которое
находится по данным выборки.
Границы критической области, отделяющие ее от
области принятия гипотезы, называют критическими точками и обозначают
Kкр.
Для определения
критической области задается уровень значимости
—
некая малая вероятность попадания критерия в критическую область.
Уровень значимости— вероятность принятия
конкурирующей гипотезы, тогда как справедлива основная.
С помощью уровня
значимости определяются границы критической области.
Основной принцип проверки статистических гипотез
состоит в следующем: если наблюдаемое значение статистики критерия попадает (не
попадает) в критическую область, то гипотеза H0
отвергается (принимается), а гипотеза H1
принимается (отвергается) в качестве одного из
возможных решений с формулировкой «гипотеза
H0 противоречит (не противоречит) выборочным
данным на уровне значимости
».
В зависимости от
содержания альтернативной гипотезы осуществляется выбор критической области:
левосторонней, правосторонней, двусторонней. Если смысл исследования заключается
в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения
или увеличения), то говорят об односторонней критической области. Если смысл
исследования- выявить различия в изучаемых параметрах, но характер их
отклонения от контрольных (или теоретических) не известен, то говорят о
двусторонней критической области.
Однако, принятие той
или иной гипотезы не дает оснований утверждать, что она верна. Результат
проверки статистической гипотезы лишь устанавливают на определенном уровне
значимости ее соответствие (несоответствие) результатам эксперимента.
При проверке
статистических гипотез возможны следующие ошибки:
1.
Отвергнута правильная
H0, а принята неправильная гипотеза
H1 — ошибка
первого рода.
2. Отвергнута правильная альтернативная
гипотеза
H1 и
принята неправильная нулевая гипотеза H0
—
ошибка второго рода.
Заметим, что уровень значимости —
есть вероятность ошибки первого рода. Ошибка первого рода называется
-риском. Обычно они задаются
некоторыми конкретными значениями: 0,05; 0,01; 0,005; 0,001. Ошибки второго
рода называются -риском, а вероятность ее
допустить обозначается
(вероятность того, что принята гипотеза
H0
, когда на самом деле справедлива
альтернативная гипотеза H1
.
Можно доказать, что с
уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода
и наоборот. Поэтому, на практике пытаются подбирать значения параметров
и
опытным путем в целях минимизации суммарного
эффекта от возможных ошибок. При принятии управленческих решений для
одновременного уменьшения ошибок первого и второго рода самым действенным
средством является увеличение объема выборки, что согласуется с законом больших
чисел.
На бытовом уровне
ошибки второго рода могут иметь более трагические последствия, чем ошибки
первого рода.
2. Гипотеза о законе распределения. Критерий согласия Пирсона (
X2
-критерий).
Критериями согласия называют критерии, в
которых гипотеза определяет закон распределения либо полностью, либо с
точностью до небольшого числа параметров.
Причины расхождения
результатов эксперимента и теоретических характеристик могут быть вызваны малым
объемом выборки, неудачным способом группировки наблюдений, ошибками в
выборе гипотезы о виде распределения
генеральной совокупности и др.
Рассмотрим
универсальный критерий согласия Пирсона. Проверка гипотезы о том, что
эмпирическая частота мало отличается от соответствующей теоретической частоты,
осуществляется с помощью величины X2
—
меры расхождения между ними.
Для произвольной
выборки, когда распределение непрерывно или число различных вариант велико, все
пространство наблюдаемых вариант делят на конечное число непересекающихся
областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую
вероятность.
Для применения критерия
согласия Пирсона необходимо:
1. Вычислить значение статистики по формуле:
, где
pi –вероятность
принятия значения
xi, ni.
— эмпирическая частота для
соответствующего
xi. n— объем выборки. s— число вариант выборки.
2.
По
соответствующей таблице распределения Пирсона найти критическое значение , где k = s –
r
– 1 – число степеней свободы, s—
число различных вариант или интервалов группировки, r— число неизвестных параметров
предполагаемого теоретического распределения,
— выбранный уровень значимости. Это
значит, что строится правосторонний интервал.
3.
Если
,
то основная гипотеза отвергается, в противном случае- принимается, т.е. чем
больше отклонение, тем меньше согласованы теоретическое и эмпирическое
распределение. Поэтому принято использовать только правостороннюю критическую
область.
Расчетная таблица имеет вид:
|
Интервалы |
Середины |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
Пример:
По таблице
эмпирического распределения изменения в процентах темпа роста акций проверьте
гипотезу о нормальном распределении выборки.
|
Интервалы |
(-2; |
(-1; |
(0; |
(1; |
Итого |
|
ni |
7 |
14 |
18 |
11 |
50 |
|
pi |
0,157 |
0,341 |
0,341 |
0,157 |
1 |
Решение:
Гипотезу о нормальном
распределении проверим по критерию Пирсона.
|
Интервалы |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
|
(-2; |
7 |
0,157 |
7,85 |
0,7225 |
0,092 |
|
(-1; |
14 |
0,341 |
17,05 |
9,3025 |
0,546 |
|
(0; |
18 |
0,341 |
17,05 |
0,9025 |
0,053 |
|
(1; |
11 |
0,157 |
7,85 |
9,925 |
1,264 |
|
Итого |
|
По таблице найдем
при
=0,05
и k = s – r – 1 = 4 – 2 – 1 = 1. s = 4 – число
интервалов. r
= 2- число параметров теоретического (нормального) распределения.
Имеем . Т.к. 1,955 < 3,841, то
, т.е. гипотеза о нормальном
распределении подтверждается.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
Установление двусторонней критической
области на уровне значимости
для
проверки гипотезы соответствует отысканию соответствующего доверительного
интервала с надежностью
.
Рассмотрим условия применения некоторых
статистических гипотез.
|
Тип гипотезы H0 |
Границы критической области на уровне значимости |
Статистика наблюдений |
|
О числовом значении |
|
|
|
О числовом значении |
Распределение |
|
|
О числовом значении |
Распределение Пирсона |
|
Пример:
Результаты исследований в течение 35 лет
показали, что среднее изменение доходности векселей равно 5,5 %. Полагая, что
изменение доходности подчиняется нормальному закону распределения с
среднеквадратическим отклонением равным 2 %, на уровне значимости
, решите: можно ли принять 6 % в качестве нормативного процента
(математического ожидания) изменения доходности.
Решение:
По условию задачи
нулевая гипотеза
. Так как
, то в качестве альтернативной гипотезы
возьмем гипотезу:
, которой соответствует левосторонняя
критическая область с интервалом.
Найдем границы
критической области:
По таблице значений
функции Ф(х) найдем
, т.е. левосторонняя критическая область
лежит в интервале.
Найдем статистику
наблюдений:
.
Имеем:, нет основания отвергать нулевую
гипотезу. Значит, в качестве нормативного процента можно принять 6 %.
Пример:
Точность работы
программы проверяют по дисперсии контролируемого количества символов в коде,
которая не должна превышать 0,1. По выборке из 15 сообщений вычислена
исправленная оценка дисперсии 0,22. При
уровне значимости 0,05 проверьте, обеспечивает ли программа необходимую
точность.
Решение:
Имеем: n = 15, s2 = 0,22
, ,
.
Сформулируем гипотезу о
числовом значении дисперсии:
H0 — программа обеспечивает необходимую точность
;
H1 —
программа не обеспечивает необходимую точность
.
Определим статистику: .
Найдем границы
критической области:
.
Поскольку 30,8 >
23,7;
, принимаем гипотезу H1, т.к.
H0 противоречит опытным данным. Вывод: программа
не обеспечивает необходимую точность.
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ![]() ).
).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Статистическое
решение может быть ошибочным. При этом
различают ошибки I-го
и II-го
родов.Опр.
Ошибкой первого рода называется ошибка,
состоящая в том, что гипотеза Н0
отклоняется, когда Н0
– верна. Вероятность P{ZVkH0}=..ОпрОшибкой
второго рода называется ошибка, состоящая
в том, что принимается гипотеза Н0,
но в действительности верна альтернативная
гипотеза Н1.
Вероятность ошибки второго рода при
условии, что гипотеза Н1
– простая, P{ZVVkH1}=.Проверка
статистических гипотез и доверительных
интервалов.Проверка гипотез с
использованием критерия значимости
может быть проведена на основе
доверительных интервалов. При этом
одностороннему критерию значимости
будет соответствовать односторонний
доверительный интервал, а двустороннему
критерию значимости будет соответствовать,
двусторонний доверительный интервал.
Гипотеза Н0
– принимается, если значение 0
накрывается доверительным интервалом,
иначе отклоняется.
55. Критерий и его применение.
Критерий

применяется в частности для проверки
гипотез о виде распределения генеральной
совокупности.
Процедура
применения критерия

для проверки гипотезы H0,
утверждающей, что СВ Х
имеет закон распределения

состоит из следующих этапов.
Этапы:
-
По
выборке найти оценки неизвестных
параметров предполагаемого закона
 .
. -
Если
Х–СВДТ – определить частоты
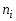 ,
,
i
= 1, 2, …, r,
с которым каждое значение встречается
в выборке.
Если
Х–СВНТ – разбить множество значений
на r
– непересекающихся интервалов

и попавших в каждый из этих интервалов
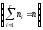 .
.
-
Х–СВДТ
вычислить
 .
.
Х–СВНТ
вычислить
 .
.

-
 .
. -
Принять
статистическое решение.

– гипотеза
Н0
– принимается.
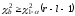
– гипотеза
Н0
– отклоняется.
e
– количество оцениваемых параметров.
Малочисленные
частоты надо будет объединять.
Проверка
гипотезы о равномерном распределении
генеральной совокупности.
n
= 200
А;
|
№ |
(xi-1, |
ni |
|
|
1 |
2 |
21 |
=0,05
|
|
2 |
4 |
16 |
|
|
3 |
6 |
15 |
|
|
4 |
8 |
26 |
|
|
5 |
10 |
22 |
|
|
6 |
12 |
14 |
|
|
7 |
14 |
21 |
|
|
8 |
16 |
22 |
|
|
9 |
18 |
18 |
|
|
10 |
20 |
25 |
1.


2.





|
|
|
|
|
21 |
17,3 |
0,79 |
|
16 |
20 |
0,8 |

k
= 10 – 2 – 1 = 7


– нет
основания отвергать гипотезу о том, что
выборка взята из генеральной совокупности
и имеет равномерное распределение.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При проверке статистических гипотез ошибка I рода — это ошибочное отклонение действительно истинной нулевой гипотезы (также известной как «ложноположительный» результат или вывод; например: «невиновный человек осужден»), а ошибка II рода — это ошибочное принятие фактически ложной нулевой гипотезы (также известное как «ложноотрицательный» вывод или вывод; пример: «виновный не осужден»). [1]Большая часть статистической теории вращается вокруг минимизации одной или обеих этих ошибок, хотя полное устранение любой из них является статистически невозможным, если результат не определяется известным, наблюдаемым причинным процессом. Выбрав низкое пороговое (отсечное) значение и изменив уровень альфа (p), можно повысить качество проверки гипотезы. [2] Информация об ошибках типа I и ошибках типа II широко используется в медицине , биометрии и информатике . [ требуется уточнение ]
Интуитивно, ошибки типа I можно рассматривать как ошибки совершения , т. е. исследователь, к несчастью, приходит к выводу, что что-то является фактом. Например, рассмотрим исследование, в котором ученые сравнивают лекарство с плацебо. Если пациенты, получающие препарат, случайно выздоравливают, чем пациенты, получающие плацебо, может показаться, что препарат эффективен, но на самом деле вывод неверен. И наоборот, ошибки II рода — это ошибки упущения .. В приведенном выше примере, если бы пациенты, получавшие лекарство, не выздоравливали быстрее, чем те, кто получал плацебо, но это была случайная случайность, это была бы ошибка II типа. Последствия ошибки типа II зависят от размера и направления пропущенного определения и обстоятельств. Дорогостоящее лекарство для одного из миллиона пациентов может быть несущественным, даже если оно действительно является лекарством.
Определение
Статистический фон
В статистической теории тестирования понятие статистической ошибки является неотъемлемой частью проверки гипотез . Тест состоит в выборе двух конкурирующих предположений, называемых нулевой гипотезой , обозначаемой H0, и альтернативной гипотезой , обозначаемой H1 . . Это концептуально похоже на приговор в судебном процессе. Нулевая гипотеза соответствует положению подсудимого: точно так же, как предполагается, что он невиновен, пока его вина не доказана, так и нулевая гипотеза считается истинной, пока данные не дают убедительных доказательств против нее. Альтернативная гипотеза соответствует позиции против подсудимого. В частности, нулевая гипотеза также предполагает отсутствие различий или отсутствие связи. Таким образом, нулевая гипотеза никогда не может состоять в том, что существует различие или ассоциация.
Если результат теста соответствует действительности, значит, принято правильное решение. Однако если результат проверки не соответствует действительности, значит, произошла ошибка. Есть две ситуации, в которых решение неверно. Нулевая гипотеза может быть верной, тогда как мы отвергаем H 0 . С другой стороны, альтернативная гипотеза H 1 может быть верной, тогда как мы не отвергаем H 0 . Различают два типа ошибок: ошибку первого рода и ошибку второго рода. [3]
Ошибка I типа
Первый вид ошибок — это ошибочное отклонение нулевой гипотезы в результате процедуры проверки. Такую ошибку называют ошибкой первого рода (ложноположительной) и иногда называют ошибкой первого рода.
С точки зрения примера с залом суда ошибка первого рода соответствует осуждению невиновного подсудимого.
Ошибка второго рода
Второй вид ошибок — ошибочное принятие нулевой гипотезы в результате процедуры проверки. Такая ошибка называется ошибкой второго рода (ложноотрицательная), а также называется ошибкой второго рода.
В примере с залом суда ошибка II рода соответствует оправданию преступника. [4]
Частота ошибок кроссовера
Коэффициент перекрестных ошибок (CER) — это точка, в которой ошибки типа I и ошибки типа II равны, и представляет собой лучший способ измерения эффективности биометрии. Система с более низким значением CER обеспечивает большую точность, чем система с более высоким значением CER.
Ложноположительный и ложноотрицательный
См. дополнительную информацию в разделе: Ложноположительные и ложноотрицательные результаты .
Что касается ложноположительных и ложноотрицательных результатов, положительный результат соответствует отклонению нулевой гипотезы, а отрицательный результат соответствует невозможности отвергнуть нулевую гипотезу; «ложный» означает, что сделанный вывод неверен. Таким образом, ошибка I рода эквивалентна ложноположительному результату, а ошибка II рода эквивалентна ложноотрицательному результату.
Таблица типов ошибок
Табличные соотношения между истинностью/ложностью нулевой гипотезы и результатами проверки: [5]
| Таблица типов ошибок |
Нулевая гипотеза ( H 0 ) |
||
|---|---|---|---|
| Истинный |
Ложь |
||
| Решение о нулевой гипотезе ( H 0 ) |
Не отвергай |
Правильный вывод (истинно отрицательный) (вероятность = 1 − α ) |
Ошибка типа II (ложноотрицательный) (вероятность = β ) |
| Отклонять |
Ошибка типа I (ложноположительный результат) (вероятность = α ) |
Правильный вывод (истинно положительный) (вероятность = 1 − β ) |
Частота ошибок
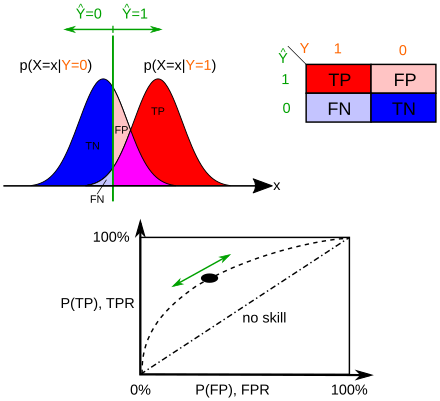
Результаты, полученные для отрицательного образца (левая кривая), перекрываются с результатами, полученными для положительных образцов (правая кривая). Перемещая пороговое значение результата (вертикальная полоса), можно уменьшить количество ложноположительных результатов (FP) за счет увеличения количества ложноотрицательных результатов (FN) или наоборот (TP = истинно положительные результаты, TPR = истинно положительные результаты). частота, FPR = частота ложных срабатываний, TN = истинные отрицательные значения).
Идеальный тест должен иметь ноль ложноположительных и ноль ложноотрицательных результатов. Однако статистические методы носят вероятностный характер, и нельзя знать наверняка, правильны ли статистические выводы. Всякий раз, когда есть неопределенность, есть вероятность совершить ошибку. Учитывая эту природу статистической науки, все проверки статистических гипотез имеют вероятность совершения ошибок первого и второго рода. [6]
- Частота ошибок первого рода или уровень значимости — это вероятность отклонения нулевой гипотезы при условии, что она верна. Он обозначается греческой буквой α (альфа) и также называется альфа-уровнем. Обычно уровень значимости устанавливается равным 0,05 (5%), подразумевая, что допустимо наличие 5% вероятности ошибочного отклонения истинной нулевой гипотезы. [7]
- Скорость ошибки II рода обозначается греческой буквой β (бета) и связана с мощностью теста , равной 1−β. [8]
Эти два типа коэффициентов ошибок компенсируются друг другом: для любого заданного набора выборок усилия по уменьшению одного типа ошибки обычно приводят к увеличению другого типа ошибки. [9]
Качество проверки гипотез
Та же идея может быть выражена в терминах доли правильных результатов и, следовательно, использована для минимизации частоты ошибок и повышения качества проверки гипотез. Чтобы уменьшить вероятность совершения ошибки типа I, достаточно просто и эффективно сделать значение альфа (p) более строгим. Чтобы уменьшить вероятность совершения ошибки типа II, которая тесно связана с мощностью анализа, либо увеличение размера выборки теста, либо ослабление альфа-уровня могут увеличить мощность анализа. [10] Тестовая статистика является надежной, если частота ошибок типа I находится под контролем.
Также можно использовать различные пороговые значения (отсечки), чтобы сделать тест более специфичным или более чувствительным, что, в свою очередь, повышает качество теста. Например, представьте себе медицинский тест, в котором экспериментатор может измерить концентрацию определенного белка в образце крови. Экспериментатор мог настроить порог (черная вертикальная линия на рисунке), и у людей диагностировали заболевание, если какое-либо число было обнаружено выше этого определенного порога. Согласно изображению, изменение порога приведет к изменению ложноположительных и ложноотрицательных результатов, соответствующих движению по кривой. [11]
Пример
Поскольку в реальном эксперименте невозможно избежать всех ошибок типа I и типа II, важно учитывать степень риска, на который человек готов пойти, чтобы ложно отвергнуть H 0 или принять H 0 . Решением этого вопроса было бы сообщить значение p или уровень значимости α статистики. Например, если p-значение статистического результата теста оценивается как 0,0596, то существует вероятность 5,96%, что мы ошибочно отвергаем H 0 . Или, если мы говорим, что статистика выполняется на уровне α, например 0,05, то мы допускаем ложное отклонение H 0 на уровне 5%. Уровень значимости α, равный 0,05, является относительно распространенным, но не существует общего правила, подходящего для всех сценариев.
Измерение скорости автомобиля
Ограничение скорости на автостраде в США составляет 120 километров в час. Установлено устройство для измерения скорости проезжающих мимо транспортных средств. Предположим, что прибор проведет три измерения скорости проезжающего автомобиля, записывая в виде случайной выборки X 1 , X 2 , X 3 . ГИБДД будет или не будет штрафовать водителей в зависимости от средней скорости. То есть тестовая статистика.
Кроме того, мы предполагаем, что измерения X 1 , X 2 , X 3 моделируются как нормальное распределение N(μ,4). Затем T должно следовать за N (μ, 4/3), а параметр μ представляет собой истинную скорость проезжающего транспортного средства. В этом эксперименте нулевая гипотеза H 0 и альтернативная гипотеза H 1 должны быть
H 0 : µ=120 против H 1 : µ 1 >120.
Если мы выполняем статистический уровень при α = 0,05, то необходимо вычислить
критическое значение c для решения
Согласно правилу замены единиц для нормального распределения. Ссылаясь на Z-таблицу , мы можем получить
Здесь критическая область. То есть, если зафиксированная скорость транспортного средства превышает критическое значение 121,9, водитель будет оштрафован. Тем не менее, еще 5% водителей оштрафованы ложно, так как зарегистрированная средняя скорость превышает 121,9, а реальная скорость не превышает 120, что мы называем ошибкой I рода.
Ошибка II рода соответствует случаю, когда истинная скорость транспортного средства превышает 120 километров в час, но водитель не оштрафован. Например, если истинная скорость автомобиля µ=125, вероятность того, что водитель не будет оштрафован, можно рассчитать как
Это означает, что если истинная скорость транспортного средства равна 125, у водителя есть вероятность 0,36% избежать штрафа, когда статистика выполняется на уровне 125, поскольку зарегистрированная средняя скорость ниже 121,9. Если истинная скорость ближе к 121,9, чем к 125, то вероятность избежать штрафа тоже будет выше.
Следует также учитывать компромиссы между ошибкой первого рода и ошибкой второго рода. То есть в этом случае, если ГАИ не хочет ложно штрафовать невиновных водителей, уровень α можно установить на меньшее значение, например 0,01. Однако, если это так, больше водителей, чья реальная скорость превышает 120 километров в час, например 125, с большей вероятностью избегут штрафа.
этимология
В 1928 году Ежи Нейман (1894–1981) и Эгон Пирсон (1895–1980), оба выдающиеся статистики, обсуждали проблемы, связанные с «решением, можно ли считать конкретную выборку вероятной случайным образом взятой из определенной совокупности». «: [12] и, как заметила Флоренс Найтингейл Дэвид , «необходимо помнить, что прилагательное «случайный» [в термине «случайная выборка»] должно относиться к методу отбора пробы, а не к самой пробе». [13]
Они выявили «два источника ошибок», а именно:
- (а) ошибка отклонения гипотезы, которую не следовало отвергать, и
- (b) ошибка, заключающаяся в том, что не удалось отвергнуть гипотезу, которую следовало отвергнуть.
В 1930 году они подробно остановились на этих двух источниках ошибок, отметив, что:
… при проверке гипотез необходимо учитывать два соображения: мы должны иметь возможность уменьшить вероятность отклонения истинной гипотезы до желаемого низкого значения; тест должен быть разработан таким образом, чтобы он отклонял проверяемую гипотезу, когда она, вероятно, окажется ложной.
В 1933 году они заметили, что эти «проблемы редко представляются в такой форме, чтобы мы могли с уверенностью отличить истинную гипотезу от ложной». Они также отметили, что, решая, не отклонить или отвергнуть конкретную гипотезу среди «набора альтернативных гипотез», H 1 , H 2 …, легко сделать ошибку:
…[и] эти ошибки будут двух видов:
- (I) мы отвергаем H 0 [т.е. гипотезу, которую нужно проверить], когда она верна, [14]
- (II) мы не можем отвергнуть H 0 , когда какая-либо альтернативная гипотеза H A или H 1 верна. (Есть различные обозначения для альтернативы).
Во всех статьях, написанных совместно Нейманом и Пирсоном, выражение H 0 всегда означает «гипотезу, подлежащую проверке».
В той же статье они называют эти два источника ошибок ошибками типа I и ошибками типа II соответственно. [15]
Нулевая гипотеза
Стандартной практикой для статистиков является проведение тестов , чтобы определить, может ли быть подтверждена « спекулятивная гипотеза » относительно наблюдаемых явлений мира (или его обитателей). Результаты такого тестирования определяют, разумно ли конкретный набор результатов согласуется (или не согласуется) с предполагаемой гипотезой.
На том основании, что согласно статистической традиции всегда предполагается, что предполагаемая гипотеза ошибочна, а так называемая « нулевая гипотеза » утверждает, что наблюдаемые явления происходят просто случайно (и что, как следствие, предполагаемый агент не имеет эффект) – тест определит, верна эта гипотеза или нет. Вот почему проверяемую гипотезу часто называют нулевой гипотезой (скорее всего, введенной Фишером (1935, стр. 19)), потому что именно эта гипотеза должна быть либо аннулирована , либо не аннулирована проверкой. Когда нулевая гипотеза аннулируется, можно заключить, что данные подтверждают « альтернативную гипотезу ».«(что является исходным предположением).
Последовательное применение статистиками соглашения Неймана и Пирсона о представлении « гипотезы, подлежащей проверке » (или « гипотезы, подлежащей аннулированию ») выражением H0 , привело к обстоятельствам, при которых многие понимают термин « нулевая гипотеза » как означающий « нулевая гипотеза » — утверждение о том, что рассматриваемые результаты возникли случайно. Это не обязательно так — ключевое ограничение, согласно Фишеру (1966), состоит в том, что « нулевая гипотеза должна быть точной, то есть свободной от неопределенности и двусмысленности, потому что она должна служить основой для «проблемы распределения». из которых критерий значимости является решением. « [16] Как следствие этого, в экспериментальной науке нулевая гипотеза обычно представляет собой утверждение о том, что конкретное лечение не имеет никакого эффекта ; в наблюдательной науке это то, что нет никакой разницы между значением конкретной измеренной переменной и значением экспериментального предсказания.
Статистическая значимость
Если вероятность получения столь же экстремального результата, как и полученный, при условии, что нулевая гипотеза верна, ниже заранее заданной пороговой вероятности (например, 5%), то результат считается статистически значимым . и нулевая гипотеза отвергается.
Британский статистик сэр Рональд Эйлмер Фишер (1890–1962) подчеркивал, что «нулевая гипотеза»:
… никогда не доказывается и не устанавливается, но, возможно, опровергается в ходе экспериментов. Можно сказать, что каждый эксперимент существует только для того, чтобы дать фактам возможность опровергнуть нулевую гипотезу.
- Фишер, 1935, стр. 19.
Домены приложений
Медицина
В медицинской практике различия между применением скрининга и тестирования значительны.
Медицинский осмотр
Скрининг включает в себя относительно дешевые тесты, которые назначаются большим группам населения, ни один из которых не проявляет каких-либо клинических признаков заболевания (например, мазок Папаниколау ).
Тестирование включает гораздо более дорогие, часто инвазивные процедуры, которые назначаются только тем, у кого проявляются некоторые клинические признаки заболевания, и чаще всего применяются для подтверждения предполагаемого диагноза.
Например, в большинстве штатов США новорожденные должны проходить скрининг на фенилкетонурию и гипотиреоз , а также на другие врожденные заболевания .
Гипотеза: «У новорожденных фенилкетонурия и гипотиреоз».
Нулевая гипотеза (H 0 ): «У новорожденных нет фенилкетонурии и гипотиреоза»,
Ошибка I рода (ложноположительный): Верно то, что у новорожденных нет фенилкетонурии и гипотиреоза, но по имеющимся данным мы считаем, что у них есть нарушения.
Ошибка II типа (ложноотрицательный): Истинный факт заключается в том, что у новорожденных есть фенилкетонурия и гипотиреоз, но мы считаем, что, согласно данным, у них нет нарушений.
Хотя они показывают высокий уровень ложноположительных результатов, скрининговые тесты считаются ценными, поскольку они значительно повышают вероятность обнаружения этих расстройств на гораздо более ранней стадии.
Простые анализы крови, используемые для скрининга возможных доноров крови на ВИЧ и гепатит , имеют значительный уровень ложноположительных результатов; однако врачи используют гораздо более дорогие и гораздо более точные тесты, чтобы определить, действительно ли человек заражен одним из этих вирусов.
Возможно, наиболее широко обсуждаемые ложноположительные результаты в медицинском скрининге связаны с процедурой маммографии для скрининга рака молочной железы.. Уровень ложноположительных маммограмм в США составляет до 15%, что является самым высоким показателем в мире. Одним из последствий высокого уровня ложноположительных результатов в США является то, что за любой 10-летний период половина американских женщин, прошедших скрининг, получают ложноположительные маммограммы. Ложноположительные маммограммы обходятся дорого: в США ежегодно тратится более 100 миллионов долларов на последующее тестирование и лечение. Они также вызывают у женщин ненужное беспокойство. В результате высокого уровня ложноположительных результатов в США до 90–95% женщин, получивших положительный результат маммографии, не имеют этого заболевания. Самый низкий показатель в мире в Нидерландах, 1%. Самые низкие показатели, как правило, в Северной Европе, где маммографические снимки считываются дважды и устанавливается высокий порог для дополнительного тестирования (высокий порог снижает мощность теста).
Идеальный скрининговый тест населения должен быть дешевым, простым в применении и по возможности не давать ложноотрицательных результатов. Такие тесты обычно дают больше ложноположительных результатов, которые впоследствии можно устранить с помощью более сложного (и дорогого) тестирования.
Медицинское тестирование
Ложноотрицательные и ложноположительные результаты являются серьезными проблемами в медицинском тестировании .
Гипотеза: «У больных специфическое заболевание».
Нулевая гипотеза (H 0 ): «У пациентов нет специфического заболевания».
Ошибка I типа (ложноположительный результат): «Истинный факт заключается в том, что у пациентов нет определенного заболевания, но врачи судят, что пациент был болен на основании отчетов об испытаниях».
Ложные срабатывания также могут привести к серьезным и нелогичным проблемам, когда искомое состояние встречается редко, как при скрининге. Если тест имеет ложноположительный результат один на десять тысяч, но только один из миллиона образцов (или людей) является истинно положительным, большинство положительных результатов, обнаруженных этим тестом, будут ложными. Вероятность того, что наблюдаемый положительный результат является ложноположительным, можно рассчитать с помощью теоремы Байеса .
Ошибка типа II (ложноотрицательный результат): «Истинный факт заключается в том, что болезнь действительно присутствует, но отчеты об испытаниях дают ложно обнадеживающее сообщение пациентам и врачам об отсутствии болезни».
Ложноотрицательные результаты приводят к серьезным и нелогичным проблемам, особенно когда искомое состояние является распространенным. Если тест с частотой ложноотрицательных результатов всего 10 % используется для проверки популяции с истинной частотой встречаемости 70 %, многие отрицательные результаты, обнаруженные тестом, будут ложными.
Иногда это приводит к неадекватному или неадекватному лечению как больного, так и его заболевания. Типичным примером является использование сердечных нагрузочных тестов для выявления коронарного атеросклероза, хотя известно, что сердечные нагрузочные тесты обнаруживают только ограничения кровотока в коронарных артериях из-за выраженного стеноза .
Биометрия
Биометрическое сопоставление, такое как распознавание отпечатков пальцев , лиц или радужной оболочки глаза , подвержено ошибкам типа I и типа II.
Гипотеза: «Ввод не идентифицирует кого-то в списке искомых людей»
Нулевая гипотеза: «Ввод действительно идентифицирует кого-то в искомом списке людей»
Ошибка I типа (коэффициент ложных отказов): «Истинный факт заключается в том, что человек находится в списке поиска, но система делает вывод, что человек не соответствует данным».
Ошибка II типа (коэффициент ложного совпадения): «Истинный факт заключается в том, что человек не является кем-то из искомого списка, но система делает вывод, что этот человек является тем, кого мы ищем, согласно данным».
Вероятность ошибок типа I называется «коэффициентом ложных отклонений» (FRR) или коэффициентом ложных несоответствий (FNMR), а вероятность ошибок типа II называется «коэффициентом ложного принятия» (FAR) или коэффициентом ложных совпадений ( ФМР).
Если система предназначена для редкого совпадения подозреваемых, то вероятность ошибок типа II можно назвать « коэффициентом ложных тревог ». С другой стороны, если система используется для валидации (а принятие является нормой), то FAR является мерой безопасности системы, а FRR измеряет уровень неудобств для пользователя.
Проверка безопасности
Основные статьи: обнаружение взрывчатых веществ и металлоискатель
Ложные срабатывания регулярно обнаруживаются каждый день при досмотре в аэропортах , которые, в конечном счете, являются системами визуального контроля . Установленная охранная сигнализация предназначена для предотвращения проноса оружия на самолет; тем не менее, они часто настроены на такую высокую чувствительность, что много раз в день реагируют на мелкие предметы, такие как ключи, пряжки ремней, мелочь, мобильные телефоны и кнопки в обуви.
Здесь гипотеза такова: «Предмет — оружие».
Нулевая гипотеза: «Предмет не является оружием».
Ошибка типа I (ложноположительный результат): «Правда в том, что предмет не является оружием, но система все равно подает сигнал тревоги».
Ошибка типа II (ложноотрицательный результат) «Правда в том, что предмет является оружием, но система в это время хранит молчание».
Таким образом, соотношение ложных срабатываний (обнаружение невиновного путешественника как террориста) и истинных срабатываний (обнаружение потенциального террориста) очень велико; и поскольку почти каждый сигнал тревоги является ложноположительным, положительная прогностическая ценность этих скрининговых тестов очень низка.
Относительная стоимость ложных результатов определяет вероятность того, что создатели тестов допустят эти события. Поскольку цена ложноотрицательного результата в этом сценарии чрезвычайно высока (необнаружение бомбы, проносимой в самолет, может привести к сотням смертей), в то время как стоимость ложноположительного результата относительно низка (достаточно простая дальнейшая проверка), наиболее подходящим тест с низкой статистической специфичностью, но высокой статистической чувствительностью (который допускает высокий уровень ложноположительных результатов в обмен на минимальные ложноотрицательные результаты).
Компьютеры
Понятия ложных срабатываний и ложных отрицаний широко распространены в сфере компьютеров и компьютерных приложений, включая компьютерную безопасность , фильтрацию спама , вредоносное ПО , оптическое распознавание символов и многие другие.
Например, в случае фильтрации спама гипотеза состоит в том, что сообщение является спамом.
Таким образом, нулевая гипотеза: «Сообщение не является спамом».
Ошибка типа I (ложное срабатывание): «Методы фильтрации или блокировки спама ошибочно классифицируют законное сообщение электронной почты как спам и, как следствие, мешают его доставке».
Хотя большинство приемов борьбы со спамом могут блокировать или фильтровать большой процент нежелательных сообщений электронной почты, делать это без значительных ложноположительных результатов — гораздо более сложная задача.
Ошибка типа II (ложноотрицательный результат): «Спам-письмо не определяется как спам, но классифицируется как не спам». Низкое количество ложных срабатываний является показателем эффективности фильтрации спама.
Смотрите также
- Бинарная классификация
- Теория обнаружения
- Эгон Пирсон
- Этика в математике
- Ложноположительный парадокс
- Частота ошибок по семейным обстоятельствам
- Показатели эффективности информационного поиска
- Лемма Неймана – Пирсона
- Нулевая гипотеза
- Вероятность гипотезы для байесовского вывода
- Точность и отзыв
- Ошибка прокурора
- Феномен прозоны
- Рабочая характеристика приемника
- Чувствительность и специфичность
- Перекрестные ссылки статистических терминов статистиков и инженеров
- Проверка гипотез, предложенных данными
- Ошибка III типа
Ссылки
- ^ «Ошибка типа I и ошибка типа II» . explorable.com . Проверено 14 декабря 2019 г. .
- ^ Чоу, Ю.В.; Пьетранико, Р .; Мукерджи, А. (27 октября 1975 г.). «Исследования энергии связи кислорода с молекулой гемоглобина». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1424–1431. doi : 10.1016/0006-291x(75)90518-5 . ISSN 0006-291X . ПМИД 6 .
- ^ Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. OCLC 262680588 .
{{cite book}}: CS1 maint: другие ( ссылка ) - ^ Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. OCLC 262680588 .
{{cite book}}: CS1 maint: другие ( ссылка ) - ^ Шескин, Дэвид (2004). Справочник по параметрическим и непараметрическим статистическим процедурам . КПР Пресс. п. 54 . ISBN 1584884401.
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование зонда с ионами галогенидов». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Линденмайер, Дэвид. (2005). Практическая природоохранная биология . Бургман, Марк А. Коллингвуд, Виктория: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357 .
- ^ Чоу, Ю.В.; Пьетранико, Р .; Мукерджи, А. (27 октября 1975 г.). «Исследования энергии связи кислорода с молекулой гемоглобина». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1424–1431. doi : 10.1016/0006-291x(75)90518-5 . ISSN 0006-291X . ПМИД 6 .
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование зонда с ионами галогенидов». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование зонда с ионами галогенидов». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Морой, К .; Сато, Т. (15 августа 1975 г.). «Сравнение метаболизма прокаина и изокарбоксазида in vitro с помощью микросомальной амидазы-эстеразы печени». Биохимическая фармакология . 24 (16): 1517–1521. doi : 10.1016/0006-2952(75)90029-5 . ISSN 1873-2968 . ПМИД 8 .
- ^ НЕЙМАН, Дж.; ПИРСОН, Э.С. (1928). «Об использовании и интерпретации некоторых критериев тестирования для целей статистического вывода, часть I». Биометрика . 20А (1–2): 175–240. doi : 10.1093/биомет/20а.1-2.175 . ISSN 0006-3444 .
- ↑ CIKF (июль 1951 г.). «Теория вероятностей для статистических методов. Ф. Н. Дэвид. [Стр. ix + 230. Издательство Кембриджского университета. 1949. Цена 155.]». Журнал актуарного общества Staple Inn . 10 (3): 243–244. doi : 10.1017/s0020269x00004564 . ISSN 0020-269X .
- ^ Обратите внимание, что нижний индекс в выражении H 0 является нулем (указывающим на ноль ) , а не «О» (указывающим на оригинал ).
- ^ Нейман, Дж.; Пирсон, ES (30 октября 1933 г.). «Проверка статистических гипотез по отношению к априорным вероятностям». Математические труды Кембриджского философского общества . 29 (4): 492–510. Бибкод : 1933PCPS…29..492N . doi : 10.1017/s030500410001152x . ISSN 0305-0041 .
- ^ Фишер, Р.А. (1966). Дизайн экспериментов . 8-е издание. Хафнер: Эдинбург.
Библиография
- Бетц, М.А. и Габриэль, К.Р. , «Ошибки типа IV и анализ простых эффектов», Журнал статистики образования , Том 3, № 2 (лето 1978 г.), стр. 121–144.
- Дэвид, Ф. Н., «Степенная функция для проверки случайности в последовательности альтернатив», Biometrika , Vol.34, Nos.3/4, (декабрь 1947 г.), стр. 335–339.
- Фишер, Р.А., План экспериментов , Оливер и Бойд (Эдинбург), 1935.
- Гэмбрилл, В., «Ложноположительные результаты тестов на заболевания новорожденных беспокоят родителей», День здоровья (5 июня 2006 г.). [1]
- Кайзер, HF, «Направленные статистические решения», Psychological Review , Vol.67, No.3, (май 1960 г.), стр. 160–167.
- Кимбалл, А.В., «Ошибки третьего рода в статистическом консультировании», Журнал Американской статистической ассоциации , том 52, № 278 (июнь 1957 г.), стр. 133–142.
- Любин, А., «Интерпретация значимого взаимодействия», Образовательные и психологические измерения , Том 21, № 4, (зима 1961 г.), стр. 807–817.
- Мараскуило, Л.А. и Левин, Дж.Р., «Подходящие апостериорные сравнения для взаимодействия и вложенных гипотез в анализе дисперсионных планов: устранение ошибок типа IV», Американский журнал исследований в области образования , том 7., № 3, (май 1970 г. ), стр. 397–421.
- Митрофф, И. И. и Фезерингем, Т. Р., «О системном решении проблем и ошибках третьего рода», Behavioral Science , том 19, № 6 (ноябрь 1974 г.), стр. 383–393.
- Мостеллер, Ф., « К -выборочный тест проскальзывания для экстремальной совокупности», Анналы математической статистики , том 19, № 1 (март 1948 г.), стр. 58–65.
- Моултон, RT, «Сетевая безопасность», Datamation , Vol.29, No.7 (июль 1983 г.), стр. 121–127.
- Райффа, Х., Анализ решений: вводные лекции о выборе в условиях неопределенности , Аддисон-Уэсли, (чтение), 1968.
Внешние ссылки
- Предвзятость и смешение – презентация Найджела Панета, Высшая школа общественного здравоохранения Питтсбургского университета
Ошибки, встроенные в систему: их роль в статистике
В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.
Ошибка и некорректное применение: в чем разница?
В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.
И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.
То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.
Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.
Ошибки первого и второго рода
Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.
Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:

До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.
Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.
Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.
Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?
ROC-анализ
ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.
Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):

Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:
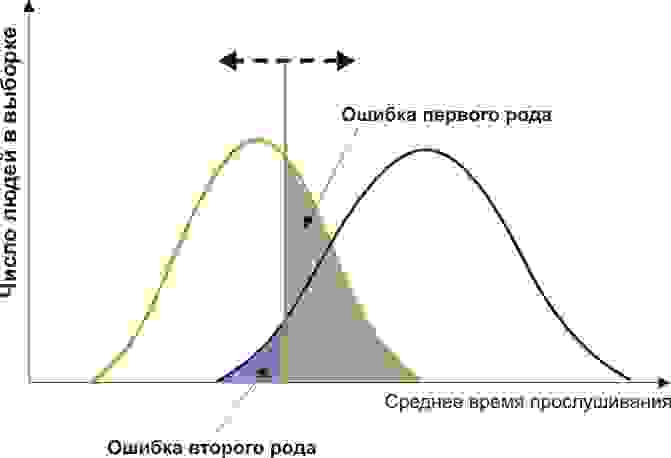
Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):
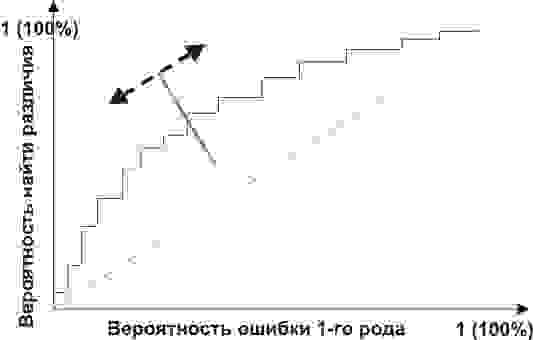
А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.
С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.
Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.
С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.
Дополнительная область V Vk называется областью допустимых значений статистики критерия. Если Z (V Vk), то гипотеза H0 при заданном уровне значимости α принимается. Обычно говорят более осторожно: H0 не противоречит имеющейся выборке, т.е. гипотеза H0 правдоподобна.
Область Vk можно выбрать неоднозначно. Однако, зная закон распределения случайной величины Z, хотя бы асимптотический, т.е. при большом объеме выборки n, и, налагая на Vk дополнительные условия, можно критическую область найти однозначно, задав величину α.
Общая схема проверки статистических гипотез
1.Выдвигаются проверяемая и альтернативная гипотезы H0, Ha.
2.Выбирается уровень значимости α (обычно 0,001; 0,01; 0,05; 0,1).
3.Выбирается статистика Z критерия значимости и соответствующая ей, уровню значимости и проверяемым гипотезам H0 и Ha критическая область Vk, являющаяся частью
области V значений статистики Z. При этом V Vk будет областью допустимых значений
Z.
4.Вычисляется выборочное значение ZB статистики Z.
5.Формулируется критерий проверки. Если ZB Vk, то гипотеза H0 отвергается, так как в результате одного лишь испытания, получения выборки произошло практически невозможное событие ZB Vk с вероятностью α. Если ZB (V Vk), то гипотеза H0 принимается.
Определение. Критерием согласия называется критерий значимости, применяемый для проверки гипотезы о генеральном законе распределения.
Заметим, что существуют и другие схемы проверки статистических гипотез.
12.3Ошибки первого и второго рода. Односторонний и двусторонний критерий
12.3.1 Ошибки первого и второго рода
Суждения о принятии или отвержении выдвинутой статистической гипотезы не являются абсолютными, а носят лишь вероятностный характер, т.е. являются правдоподобными. Принимая или отвергая гипотезу, мы можем совершить ошибку.
Определение. Ошибкой первого рода называется ошибка отвержения правильной гипотезы.
Определение. Ошибкой второго рода называется ошибка принятия основной гипотезы при условии того, что верной является альтернативная гипотеза.
Вероятность ошибки первого рода равна уровню значимости, т.е.
α = P (Z Vk/H0).
Эта формула означает, что гипотеза H0 отвергается с вероятностью α, хотя эта гипотеза верна.
Вероятность ошибки второго рода обозначается β:
β = P (Z V Vk/Ha).
Эта формула означает, что принимается гипотеза H0 с вероятностью β, хотя верна альтернативная гипотеза Ha.
8 июля 2021 г.
При проверке гипотез нулевая гипотеза — это гипотеза по умолчанию, которая утверждает, что между переменными нет статистической значимости. Исследователь проверяет нулевую гипотезу, чтобы увидеть, достаточно ли статистической значимости, чтобы опровергнуть ее, и это иногда приводит к ошибке типа 1 или типа 2. Если вы занимаетесь проверкой гипотез как частью своей работы, важно понимать, как ошибки типа 1 и типа 2 могут повлиять на ваши результаты.
В этой статье мы объясним, что такое ошибки типа 1 и типа 2, рассмотрим, как они могут возникнуть, обсудим их важность в исследованиях и приведем примеры, которые помогут вам понять эти концепции.
Ошибки типа 1 и типа 2 относятся к неправильным определениям нулевой гипотезы, но они различаются тем, что исследователь считает верным или ложным в отношении гипотезы. Ошибка 1-го типа, также называемая ложноположительной, возникает, когда исследователь отвергает нулевую гипотезу, которая является истинной, и решает, что существует статистически значимое различие, которого не существует. Ошибка типа 2 является обратной ошибкой типа 1. Также известная как ложный отрицательный результат, она возникает, когда исследователь не отвергает нулевую гипотезу, когда альтернативная гипотеза верна.
Например, в судебном деле нулевая гипотеза будет заключаться в том, что обвиняемый невиновен, пока его вина не будет доказана, а альтернативная гипотеза будет состоять в том, что он виновен. Есть четыре возможных исхода в отношении истинного характера дела:
-
Истинно отрицательный: признан невиновным в суде и невиновен на самом деле.
-
Ложное срабатывание: признан виновным в суде, но на самом деле невиновен.
-
Ложноотрицательный: признан невиновным в суде, но на самом деле виновен.
-
Истинно положительный: признан виновным в суде и фактически виновен
В приведенном выше примере второй и третий результаты являются ошибками типа 1 и типа 2 соответственно. В случае ложного срабатывания присяжные ошибочно отвергают нулевую гипотезу, утверждающую, что подсудимый невиновен. В случае ложноотрицательного результата они ошибочно не отвергают нулевую гипотезу.
Почему возникают ошибки первого рода?
Есть два фактора, которые обычно способствуют возникновению ошибок 1-го рода:
Шанс
Проверка гипотез никогда не бывает стопроцентной, поэтому всегда есть возможность сделать неверные выводы на основе имеющихся данных. Как правило, данные поступают из выборочной совокупности, относительно небольшой выборки лиц, предназначенных для обозначения более широкой демографической группы. Иногда данные, генерируемые выборочными совокупностями, искажают выводы, которые не обязательно отражают интересы всего населения. Это переменная, которую исследователи не могут контролировать, но они могут помочь смягчить ее, выбрав более крупные выборки.
Злоупотребление служебным положением
Иногда ошибки 1-го рода возникают из-за неправильной исследовательской практики. Например, исследователи могут неосознанно исказить результаты теста, завершив его слишком рано. Им может показаться, что у них достаточно данных, хотя стандартная практика рекомендует продолжить тест. В качестве альтернативы они могут сделать вывод, несмотря на то, что им не удалось достичь соответствующего уровня статистической значимости. Исследователи могут избежать выводов типа 1, связанных с злоупотреблением служебным положением, если будут следовать протоколам исследований и обеспечивать надежность своей практики.
Почему возникают ошибки второго рода?
Основным фактором, способствующим возникновению ошибок 2-го рода, является размер выборки. Чем больше размер выборки, тем больше вероятность обнаружения различий в статистическом тесте. Например, если вы хотите проверить, относятся ли студенты колледжа положительно или отрицательно к определенному продукту, группа из трех человек может выразить только два к одному разнообразию или вообще ничего не сказать. Для сравнения, выборка из 1000 человек с большей вероятностью вызовет широкий спектр мнений и, таким образом, более точно отразит большую часть населения.
Какова важность ошибок типа 1 по сравнению с ошибками типа 2?
Ошибки типа 1 и типа 2 являются значительными из-за последствий, которые они имеют в реальных приложениях. Ошибки типа 1 обычно приводят к ненужному использованию ресурсов без какой-либо выгоды. Например, если исследователь-медик совершает ошибку 1-го рода в отношении эффективности нового лечения, он может подтвердить ошибочность исследований и методов, что может привести к созданию лекарства, не приносящего облегчения.
Ошибки 2-го типа важны тем, что могут помешать выделению ресурсов и выполнению необходимых действий. Например, при скрининге пациента на наличие заболевания ложноотрицательный результат может свидетельствовать о том, что пациент здоров, хотя на самом деле он нуждается в медицинском вмешательстве.
Примеры ошибок типа 1 и типа 2
Рассмотрим эти примеры ошибок типа 1 и типа 2, чтобы помочь вам понять, что они из себя представляют:
Пример ошибки 1 рода
Медицинский исследователь проверяет эффективность домашнего средства от головной боли. Нулевая гипотеза состоит в том, что домашнее средство не влияет на головную боль, в то время как альтернативная гипотеза состоит в том, что оно лечит головную боль. Исследователь набирает выборку из 20 пациентов с хроническими головными болями и назначает лекарство половине из них в течение одного месяца. Половина, не получающая лекарство, продолжает страдать от хронических головных болей, в то время как у шести человек из оставшейся половины головные боли прекратились.
На основании вышеизложенного исследователь отвергает нулевую гипотезу. Однако, учитывая небольшое количество тех, кто испытал облегчение, могут возникнуть сомнения относительно того, было ли это лекарство или посторонний фактор, который улучшил состояние шести участников. Если эти шесть участников использовали другие средства от головной боли вместе с тестируемым средством, вполне вероятно, что исследователь совершил ошибку 1-го типа.
Пример ошибки 2 рода
Интернет-магазин хочет знать, могут ли изменения дизайна его веб-сайта помочь увеличить продажи. Нулевая гипотеза состоит в том, что изменения дизайна не влияют на продажи, а альтернативная гипотеза говорит об обратном. Продавец проводит A/B-тестирование, в ходе которого сравниваются две версии сайта, существующая версия и обновленная версия. Три дня мониторят продажи на основе существующей версии. Затем в течение следующих трех дней они представляют новую версию и смотрят, как она повлияет на продажи. По истечении шести дней они не видят значительных изменений в показателях продаж.
Однако возможно, что увеличение периодов наблюдения для каждой версии сайта привело бы к статистически значимой разнице. Если бы розничный продавец отслеживал продажи в течение одного месяца каждый и заметил увеличение продаж во втором месяце, он совершил бы ошибку второго рода, ошибочно приняв нулевую гипотезу.
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ![]() ).
).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| |
Верная гипотеза | ||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала